-
PDF
- Split View
-
Views
-
Cite
Cite
P Leto, C Trigilio, J Krtička, L Fossati, R Ignace, M E Shultz, C S Buemi, L Cerrigone, G Umana, A Ingallinera, C Bordiu, I Pillitteri, F Bufano, L M Oskinova, C Agliozzo, F Cavallaro, S Riggi, S Loru, H Todt, M Giarrusso, N M Phillips, J Robrade, F Leone, A scaling relationship for non-thermal radio emission from ordered magnetospheres: from the top of the main sequence to planets, Monthly Notices of the Royal Astronomical Society, Volume 507, Issue 2, October 2021, Pages 1979–1998, https://doi.org/10.1093/mnras/stab2168
Close - Share Icon Share
ABSTRACT
In this paper, we present the analysis of incoherent non-thermal radio emission from a sample of hot magnetic stars, ranging from early-B to early-A spectral type. Spanning a wide range of stellar parameters and wind properties, these stars display a commonality in their radio emission which presents new challenges to the wind scenario as originally conceived. It was thought that relativistic electrons, responsible for the radio emission, originate in current sheets formed, where the wind opens the magnetic field lines. However, the true mass-loss rates from the cooler stars are too small to explain the observed non-thermal broad-band radio spectra. Instead, we suggest the existence of a radiation belt located inside the inner magnetosphere, similar to that of Jupiter. Such a structure explains the overall indifference of the broad-band radio emissions on wind mass-loss rates. Further, correlating the radio luminosities from a larger sample of magnetic stars with their stellar parameters, the combined roles of rotation and magnetic properties have been empirically determined. Finally, our sample of early-type magnetic stars suggests a scaling relationship between the non-thermal radio luminosity and the electric voltage induced by the magnetosphere’s co-rotation, which appears to hold for a broader range of stellar types with dipole-dominated magnetospheres (like the cases of the planet Jupiter and the ultracool dwarf stars and brown dwarfs). We conclude that well-ordered and stable rotating magnetospheres share a common physical mechanism for supporting the generation of non-thermal electrons.
1 INTRODUCTION
The magnetic fields of magnetic MS B/A-type stars have, on average, a strength of a few kG (Shultz et al. 2019c; Sikora et al. 2019b) with stable field topologies (Shultz et al. 2018). The magnetic field topology of the majority of them can be described in terms of the oblique rotator model (ORM), predominantly involving a centred dipole field that is tilted to the stellar rotation axis (Babcock 1949; Stibbs 1950). The presence of a large-scale magnetic field induces surface chemical anisotropies on the stellar surface, making these stars variable as a consequence of stellar rotation (Krtička et al. 2007). In general, early-type magnetic stars are recognized based on their chemical peculiarities, and are classified as Ap/Bp stars (Preston 1974).
The Magnetism in Massive Stars (Wade et al. 2016) and B fields in OB stars (Morel et al. 2015) spectropolarimetric surveys concluded that magnetism characterizes about 6–8 per cent of the stars across the upper main sequence (MS; Fossati et al. 2015; Wade et al. 2016; Grunhut et al. 2017; Sikora et al. 2019a), with the incidence rate almost constant for stars ranging from the O to the Ap stars. The magnetism almost certainly has a fossil origin (Braithwaite & Spruit 2004; Duez & Mathis 2010; Neiner et al. 2015) rather than being created by a magnetic dynamo as in late-type stars; this is supported by the magnetic field decay during the stellar life (Landstreet et al. 2007, 2008; Fossati et al. 2016; Petit et al. 2019; Shultz et al. 2019c; Sikora et al. 2019b). Further, stellar mergers have been proposed as origin of the strong magnetic fields observed at the top of the MS (Bogomazov & Tutukov 2009; Schneider et al. 2016, 2019; Keszthelyi et al. 2021).
The early-type magnetic stars are sufficiently hot to radiatively drive stellar wind which, in the presence of their large-scale magnetic fields, may be strongly aspherical (Babel & Montmerle 1997; Ud-Doula & Owocki 2002). The wind plasma accumulates at low-magnetic latitudes (inner magnetosphere), whereas it freely propagates along directions aligned with the magnetic poles (Shore 1987; Shore & Brown 1990; Leone 1993).
This concept has led to the magnetically confined wind shock (MCWS) model (Babel & Montmerle 1997). In the presence of large-scale magnetic fields, the wind cannot freely propagate spherically, and the ionized wind flow is channelled by the magnetic field lines. At the magnetic equator, wind streams arising from the opposite magnetic hemispheres collide and shock, producing X-rays (Oskinova et al. 2011; Nazé et al. 2014; Robrade 2016). Detailed modelling of the magnetospheres of hot magnetic stars has progressively developed (Ud-Doula & Owocki 2002; Ud-Doula, Townsend & Owocki 2006; Ud-Doula, Owocki & Townsend 2008; ud-Doula et al. 2013, 2014; Owocki et al. 2016; Daley-Yates, Stevens & ud-Doula 2019; Munoz et al. 2020).
Rapidly rotating magnetic stars require the presence of strong magnetic fields to enable formation of centrifugal magnetospheres (Maheswaran & Cassinelli 2009; Petit et al. 2013; Shultz et al. 2019c), where the centrifugal force is strong enough to balance the gravitational infall of the circumstellar ionized material. The magnetospheric ionized matter is forced to rigidly co-rotate with the stars, producing a rigidly rotating magnetosphere, which is characterized by typical signatures recognized in the Hα line profile and photometric variability (Townsend & Owocki 2005; Townsend 2008).
Significant non-thermal radio emission is dependent on the presence of a strong magnetic field in the plasma environment of early-type magnetic stars. Indeed, about 25 per cent of the magnetic B/A type stars are non-thermal radio sources (Drake et al. 1987; Linsky, Drake & Bastian 1992; Leone, Trigilio & Umana 1994). The prevailing scenario to explain their radio emission is related to the interaction between the radiatively driven ionized stellar wind and the ambient magnetic field (André et al. 1988). The ionized stellar wind opens the magnetic field lines, and a continuous acceleration occurs in the current sheets in the equatorial plane. The distance at which the radiative wind kinetic energy density equals the magnetic energy density is the Alfvén radius (RA). Non-thermal plasma particles, propagating within the stellar magnetosphere, radiate in the radio regime through the incoherent gyro-synchrotron mechanism and produce continuum radio emission that is partially circularly polarized.
The main observational features of non-thermal radio emission from early-type magnetic stars are nearly flat spectra and rotational modulation, both for the total intensity (Stokes I) and circular polarization (Stokes V). The polarization level for incoherent non-thermal radio emission increases with frequency, reaching levels of ≈10–20 per cent (Leto et al. 2012, 2018, 2019, 2020a). Multifrequency radio light curves for Stokes I and V have been successfully reproduced using a synthetic 3D model of gyro-synchrotron emission from an oblique dipole field and co-rotating magnetosphere (Trigilio et al. 2004; Leto et al. 2006).
Superimposed on the incoherent radio emission, highly polarized (up to 100 per cent) strong pulses of coherent emission have also been detected at low frequencies in seven early-type magnetic stars (Trigilio et al. 2000; Das, Chandra & Wade 2018; Das et al. 2019a, b; Leto et al. 2019, 2020a, b). This amplified pulsed emission is stimulated via the coherent electron cyclotron maser (ECM) emission mechanism (Wu & Lee 1979; Melrose & Dulk 1982). ECM is also the process explaining highly beamed auroral radio emissions (AREs) from the magnetized planets of the Solar system (Zarka 1998). In Jupiter, auroral X-rays (Branduardi-Raymont et al. 2007, 2008) arise from the footprints of the magnetic field lines where the coherent ARE originates at a few stellar radii above the magnetic poles. ARE from some early-type magnetic stars also has corresponding X-ray emission (Pillitteri et al. 2016, 2017; Robrade et al. 2018).
Interestingly, in the lower MS, signatures of coherent AREs have also been identified in ultracool dwarf stars and brown dwarfs (UCDs; Berger 2002; Kao et al. 2018). These cold stars are fully convective, yet a well-ordered dipole-dominated magnetic field topology has been recognized in many of them (Donati et al. 2006; Morin et al. 2010). The magnetic fields of these stars are generated by a rotational-convective dynamo analogous to the Earth’s geodynamo (Christensen, Holzwarth & Reiners 2009). It is worth noting that in some cases rotationally modulated incoherent non-thermal emission has also been detected (McLean et al. 2011; Williams et al. 2015a).
The aim of this paper is to test the scenario capable of explaining the radio emission of hot magnetic stars, which works for early-B type magnetic stars through to magnetic stars at the low-temperature boundary of this group (late B/early A). For this purpose, we have identified a sample of B/A type magnetic stars that have been detected at radio wavelengths and have collected reliable information about their stellar parameters. The stellar sample is described in Section 2. Details regarding the radio measurements of the individual stars are reported in Appendix (available online). For some stars we collected enough multifrequency radio measurements to produce reliable radio spectra. Model calculations of the radio spectra of this representative sub-sample are discussed in Section 3. The results of the modelling raised a critical issue regarding the assumed wind paradigm that, up to now, has been assumed as a primary engine to support and explain all the observed radio phenomena from early-type magnetic stars (we discuss this in Section 4). We have searched for a possible dependence of the radio luminosity with stellar age in Section 5. By correlating the radio luminosities of the whole sample of stars with the parameters of their stellar magnetospheres, we obtained an empirical relation between the incoherent non-thermal radio luminosity of the B/A magnetic stars and the combined effect of rotation and magnetic properties of their large-scale dipole-dominated magnetospheres, which we describe in Section 6. In Section 7, this new result is applied in a broader context involving other classes of stars (and planets) that radiate incoherent non-thermal radio emission and have large-scale dipole dominated magnetospheres, such as Jupiter and the UCDs. In Section 8, the scaling relationship for the incoherent non-thermal radio emission has been applied to a small sample of magnetic hot Jupiters to estimate the expected flux levels and the possible detectability. In Section 9 we discuss the possible physical consequences of our results, and in Section 10 we present our conclusions.
2 THE SAMPLE
Our sample consists of stars that satisfy two conditions: each star has at least one observation in which radio emission was clearly detected, and stellar and magnetospheric parameters are available for each. The selected sources and stellar parameters with the corresponding references are listed in Table 1. Each source is identified by the number listed in column 1. Common and alternative names are given in columns 2 and 3. Column 4 lists the spectral types and chemical peculiarities of the selected stars, which together with the effective temperature (column 6), are mainly taken from Netopil et al. (2017) and Shultz et al. (2019a). Column 5 reports the distances of the sources from Gaia Collaboration (2018); in cases when Gaia measurements are not available, references for adopted distances are identified. Radii, rotation periods, and polar magnetic field strengths are given in columns 7, 8, and 9. Column 10 lists the fractional MS ages retrieved from the literature. In two cases the stellar evolutionary state had not previously analysed, so for these two stars (HD 147932 and HD 147933) we used BONNSAI1 (Schneider et al. 2014) to estimate ages using the evolutionary models given by Brott et al. (2011). Column 11 lists the average radio luminosities of each star obtained from averaging all available radio measurements.
| . | . | . | . | D . | Teff . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Frac. MS age . | Lν, rad . |
|---|---|---|---|---|---|---|---|---|---|---|
| ID . | HD . | Alt. name . | Sp. type . | (pc) . | (kK) . | (R⊙) . | (d) . | (kG) . | . | (erg s−1 Hz−1) . |
| 1 | 12447 | α Psc A | A2 SiSrCr | 50(2) | 10.2(0.5) | 2.6(0.2)(3) | 1.4907(8)(17) | 1.19 ± 0.2(33) | 0.58(0.2)(36) | 1.8(0.6) × 1015 |
| 2 | 19832 | 56 Ari | B8 Si | 124(3) | 12.5(0.5) | 2.3(0.3)(4) | 0.727 95(1)(18) | |$2.7^{+0.6}_{-0.3}\, ^{(4)}$| | 0.51(0.26)(36) | 9(2) × 1015 |
| 3 | 27309 | 56 Tau | A0 SiCr | 90(2) | 12.0(0.5) | 2.3(0.3)(10) | 1.568 82(5)(18) | |$3.6^{+1.98}_{-0.58}\, ^{(10)}$| | 0.41(0.33)(10) | 3.6(0.6) × 1015 |
| 4 | 34452 | IQ Aur | B9 Si | 145(4) | 14.1(0.5) | 3.1(0.3)(5) | 2.466 264(5)(19) | ≈4(34) | |$0.40^{+0.15}_{-0.21}\, ^{(37)}$| | 1.0(0.3) × 1016 |
| 5 | 35298 | V1156 Ori | B6 He-wk | 371(9) | 15.8(0.8) | 2.42(0.09)(6) | 1.854 58(3)(20) | 11.2 ± 1(6) | 0.06(0.02)(6) | 4(2) × 1016 |
| 6 | 35502 | BD-02 1241 | B5V He-wk | 383(9) | 18.4(0.6) | 3.0(0.1)(6) | 0.853 807(3)(7) | 7.3 ± 0.5(6) | 0.11(0.03)(6) | 4(1) × 1017 |
| 7 | 36485* | δ Ori C | B3Vp He-s | 390(10) | 20.0(2.0) | 2.97(0.08)(6) | 1.477 75(4)(21) | 8.9 ± 0.2(6) | 0.05(0.02)(6) | 1.7(0.6) × 1017 |
| 8 | 37017* | V1046 Ori | B2 He-s | 420(35)b | 21.0(2.0) | 3.6(0.2)(6) | 0.901 186(2)(20) | 6.2 ± 0.9(6) | 0.13(0.03)(6) | 4(2) × 1017 |
| 9 | 37479* | σ Ori E | B2 Vp He-s | 440(20) | 23.0(2.0) | |$3.39^{+0.06}_{-0.04}\, ^{(6)}$| | 1.190 833(3)(22) | 10.5 ± 1.5(4) | |$0.06 ^{+0.02}_{-0.03}\, ^{(6)}$| | 7(3) × 1017 |
| 10 | 40312 | θ Aur | A0 Si | 58(1) | 10.2(0.4) | 4.6(0.2)(8) | 3.618 66(1)(23) | 0.69 ± 0.01(8) | |$1.00 ^{+0.01}_{-0.06}\, ^{(10)}$| | 1.2(0.6) × 1015 |
| 11 | 79158 | 36 Lyn | B9 He-wk | 175(6) | 13.1(0.7) | 3.4(0.7)(9) | 3.834 76(4)(24) | 3.57 ± 0.36(9) | |$0.84^{+0.08}_{-0.1}\, ^{(37)}$| | 1.6(0.8) × 1016 |
| 12 | 112413 | α2 CVn | A0 EuSiCr | 35(1) | 11.5(0.5) | 2.5(0.3)(10) | 5.469 13(8)(16) | |$3.46^{+2.29}_{-0.69}\, ^{(16)}$| | |$0.53 ^{+0.28}_{-0.31}\, ^{(10)}$| | 1.1(0.7) × 1015 |
| 13 | 118022 | 78 Vir†† | A2 CrEuSr | 58.3(0.8) | 9.4(0.5) | 2.0(0.1)(10) | 3.722 084(2)(25) | |$3.65^{+0.61}_{-0.37}\, ^{(16)}$| | |$0.39 ^{+0.32}_{-0.25}\, ^{(10)}$| | 2(1) × 1015 |
| 14 | 124224* | CU Vir | B9 Si | 72(1) | 12.2(0.5) | 2.1(0.1)(11) | 0.520 714(1)(26) | 3.8 ± 0.2(11) | |$0.13 ^{+0.42}_{-0.09}\, ^{(10)}$| | 1.8(0.6) × 1016 |
| 15 | 133652 | HZ Lup | B9 Si | 121(1) | 12.8(0.5) | 2.2(0.2)(12) | 2.304 05(2)(12) | 6.1 ± 0.7(12) | 0.06(0.02)(38) | 4(2) × 1015 |
| 16 | 133880* | HR 5624 | B9 Si | 104(3) | 12.0(0.5) | 2.0(0.3)(13) | 0.877 476(9)(13) | 9.6 ± 1(13) | 0.05(0.02)(38) | 3.5(1.5) × 1016 |
| 17 | 142184* | HR 5907 | B2V He-s | 141(3) | 18.5(0.5) | 2.8(0.1)(6) | 0.508 276(15)(27) | 9 ± 2(6) | |$0.05_{-0.05}^{+0.1}\, ^{(6)}$| | 2(1) × 1018 |
| 18 | 142301* | 3 Sco | B8 He-wk Si | 148(3) | 16.2(0.7) | 2.42(0.02)(4) | 1.459 57(5)(28) | |$12.5^{+9}_{-0.3}\, ^{(4)}$| | 0.04(0.01)(38) | 9(2) × 1016 |
| 19 | 142990 | V913 Sco | B7 He-wk | 146(4) | 17.0(0.7) | 2.79(0.06)(6) | 0.978 891 793(6)(29) | 4.7 ± 0.4(6) | 0.06(0.01)(6) | 4.7(0.8) × 1016 |
| 20 | 144334 | HR 5988 | B8 He-wk | 133(2) | 15.2(0.7) | 2.27(0.04)(4) | 1.494 99(4)(4) | 3.6 ± 0.3(4) | 0.04(0.01)(38) | 7(3) × 1015 |
| 21 | 145501 | ν Sco C | B9 Si | 141(1) | 14.0(0.5) | 2.26(0.06)(4) | 1.026 48(1)(4) | 5.8 ± 0.3(4) | 0.04(0.02)(38) | 3.8(0.7) × 1015 |
| 22 | 147932* | ρ Oph C | B5Va | 134(1) | 17.0(1.0)(1) | 3.3(0.2)(14) | 0.8639(1)(30) | |$13.2_{-1.2}^{+2.6}\, ^{(14)}$| | |$0.12_{-0.03}^{+0.04}\, ^{(39)}$| | 4(1) × 1017 |
| 23 | 147933* | ρ Oph A | B2Va | 140(4) | 20.8(0.5)(2) | 4.5(0.6)(15) | 0.747 326(2)(2) | |$2.7_{-0.7}^{+0.9}\, ^{(2)}$| | 0.26(0.06)(39) | 1.7(0.5) × 1017 |
| 24 | 170000 | ϕ Dra | A0 Si | 93(3)c | 11.4(0.4) | 3.7(0.1)(10) | 1.716 65(9)(18) | |$1.75^{+0.14}_{-0.16}\, ^{(16)}$| | |$0.88 ^{+0.09}_{-0.03}\, ^{(10)}$| | 6(2) × 1015 |
| 25 | 175362 | HR 7129 | B6 He-wk | 153(4) | 16.9(0.7) | 2.7(0.2)(6) | 3.673 81(1)(20) | |$17.0^{+0.6}_{-0.4}\, ^{(6)}$| | |$0.06_{-0.06}^{+0.11}\, ^{(6)}$| | 9(3) × 1015 |
| 26 | 176582 | V545 Lyr | B5 He-wk | 301(4) | 17.2(0.7) | 3.21(0.06)(6) | 1.582 21(5)(18) | 5.4 ± 0.2(6) | 0.32(0.06)(6) | 4(1) × 1016 |
| 27 | 182180* | HR 7355 | B2Vn | 233(6) | 19.8(1.4) | 3.2(0.1)(6) | 0.521 4404(6)(31) | 9.5 ± 0.6(6) | 0.09(0.09)(6) | 9(3) × 1017 |
| 28 | 215441 | GL Lac††† | B9 Si | 490(10) | 14.7(0.5) | 3(1)(40) | 9.487 574(3)(32) | ≈62.4(35) | 0.2(0.2)(40) | 3(1) × 1017 |
| . | . | . | . | D . | Teff . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Frac. MS age . | Lν, rad . |
|---|---|---|---|---|---|---|---|---|---|---|
| ID . | HD . | Alt. name . | Sp. type . | (pc) . | (kK) . | (R⊙) . | (d) . | (kG) . | . | (erg s−1 Hz−1) . |
| 1 | 12447 | α Psc A | A2 SiSrCr | 50(2) | 10.2(0.5) | 2.6(0.2)(3) | 1.4907(8)(17) | 1.19 ± 0.2(33) | 0.58(0.2)(36) | 1.8(0.6) × 1015 |
| 2 | 19832 | 56 Ari | B8 Si | 124(3) | 12.5(0.5) | 2.3(0.3)(4) | 0.727 95(1)(18) | |$2.7^{+0.6}_{-0.3}\, ^{(4)}$| | 0.51(0.26)(36) | 9(2) × 1015 |
| 3 | 27309 | 56 Tau | A0 SiCr | 90(2) | 12.0(0.5) | 2.3(0.3)(10) | 1.568 82(5)(18) | |$3.6^{+1.98}_{-0.58}\, ^{(10)}$| | 0.41(0.33)(10) | 3.6(0.6) × 1015 |
| 4 | 34452 | IQ Aur | B9 Si | 145(4) | 14.1(0.5) | 3.1(0.3)(5) | 2.466 264(5)(19) | ≈4(34) | |$0.40^{+0.15}_{-0.21}\, ^{(37)}$| | 1.0(0.3) × 1016 |
| 5 | 35298 | V1156 Ori | B6 He-wk | 371(9) | 15.8(0.8) | 2.42(0.09)(6) | 1.854 58(3)(20) | 11.2 ± 1(6) | 0.06(0.02)(6) | 4(2) × 1016 |
| 6 | 35502 | BD-02 1241 | B5V He-wk | 383(9) | 18.4(0.6) | 3.0(0.1)(6) | 0.853 807(3)(7) | 7.3 ± 0.5(6) | 0.11(0.03)(6) | 4(1) × 1017 |
| 7 | 36485* | δ Ori C | B3Vp He-s | 390(10) | 20.0(2.0) | 2.97(0.08)(6) | 1.477 75(4)(21) | 8.9 ± 0.2(6) | 0.05(0.02)(6) | 1.7(0.6) × 1017 |
| 8 | 37017* | V1046 Ori | B2 He-s | 420(35)b | 21.0(2.0) | 3.6(0.2)(6) | 0.901 186(2)(20) | 6.2 ± 0.9(6) | 0.13(0.03)(6) | 4(2) × 1017 |
| 9 | 37479* | σ Ori E | B2 Vp He-s | 440(20) | 23.0(2.0) | |$3.39^{+0.06}_{-0.04}\, ^{(6)}$| | 1.190 833(3)(22) | 10.5 ± 1.5(4) | |$0.06 ^{+0.02}_{-0.03}\, ^{(6)}$| | 7(3) × 1017 |
| 10 | 40312 | θ Aur | A0 Si | 58(1) | 10.2(0.4) | 4.6(0.2)(8) | 3.618 66(1)(23) | 0.69 ± 0.01(8) | |$1.00 ^{+0.01}_{-0.06}\, ^{(10)}$| | 1.2(0.6) × 1015 |
| 11 | 79158 | 36 Lyn | B9 He-wk | 175(6) | 13.1(0.7) | 3.4(0.7)(9) | 3.834 76(4)(24) | 3.57 ± 0.36(9) | |$0.84^{+0.08}_{-0.1}\, ^{(37)}$| | 1.6(0.8) × 1016 |
| 12 | 112413 | α2 CVn | A0 EuSiCr | 35(1) | 11.5(0.5) | 2.5(0.3)(10) | 5.469 13(8)(16) | |$3.46^{+2.29}_{-0.69}\, ^{(16)}$| | |$0.53 ^{+0.28}_{-0.31}\, ^{(10)}$| | 1.1(0.7) × 1015 |
| 13 | 118022 | 78 Vir†† | A2 CrEuSr | 58.3(0.8) | 9.4(0.5) | 2.0(0.1)(10) | 3.722 084(2)(25) | |$3.65^{+0.61}_{-0.37}\, ^{(16)}$| | |$0.39 ^{+0.32}_{-0.25}\, ^{(10)}$| | 2(1) × 1015 |
| 14 | 124224* | CU Vir | B9 Si | 72(1) | 12.2(0.5) | 2.1(0.1)(11) | 0.520 714(1)(26) | 3.8 ± 0.2(11) | |$0.13 ^{+0.42}_{-0.09}\, ^{(10)}$| | 1.8(0.6) × 1016 |
| 15 | 133652 | HZ Lup | B9 Si | 121(1) | 12.8(0.5) | 2.2(0.2)(12) | 2.304 05(2)(12) | 6.1 ± 0.7(12) | 0.06(0.02)(38) | 4(2) × 1015 |
| 16 | 133880* | HR 5624 | B9 Si | 104(3) | 12.0(0.5) | 2.0(0.3)(13) | 0.877 476(9)(13) | 9.6 ± 1(13) | 0.05(0.02)(38) | 3.5(1.5) × 1016 |
| 17 | 142184* | HR 5907 | B2V He-s | 141(3) | 18.5(0.5) | 2.8(0.1)(6) | 0.508 276(15)(27) | 9 ± 2(6) | |$0.05_{-0.05}^{+0.1}\, ^{(6)}$| | 2(1) × 1018 |
| 18 | 142301* | 3 Sco | B8 He-wk Si | 148(3) | 16.2(0.7) | 2.42(0.02)(4) | 1.459 57(5)(28) | |$12.5^{+9}_{-0.3}\, ^{(4)}$| | 0.04(0.01)(38) | 9(2) × 1016 |
| 19 | 142990 | V913 Sco | B7 He-wk | 146(4) | 17.0(0.7) | 2.79(0.06)(6) | 0.978 891 793(6)(29) | 4.7 ± 0.4(6) | 0.06(0.01)(6) | 4.7(0.8) × 1016 |
| 20 | 144334 | HR 5988 | B8 He-wk | 133(2) | 15.2(0.7) | 2.27(0.04)(4) | 1.494 99(4)(4) | 3.6 ± 0.3(4) | 0.04(0.01)(38) | 7(3) × 1015 |
| 21 | 145501 | ν Sco C | B9 Si | 141(1) | 14.0(0.5) | 2.26(0.06)(4) | 1.026 48(1)(4) | 5.8 ± 0.3(4) | 0.04(0.02)(38) | 3.8(0.7) × 1015 |
| 22 | 147932* | ρ Oph C | B5Va | 134(1) | 17.0(1.0)(1) | 3.3(0.2)(14) | 0.8639(1)(30) | |$13.2_{-1.2}^{+2.6}\, ^{(14)}$| | |$0.12_{-0.03}^{+0.04}\, ^{(39)}$| | 4(1) × 1017 |
| 23 | 147933* | ρ Oph A | B2Va | 140(4) | 20.8(0.5)(2) | 4.5(0.6)(15) | 0.747 326(2)(2) | |$2.7_{-0.7}^{+0.9}\, ^{(2)}$| | 0.26(0.06)(39) | 1.7(0.5) × 1017 |
| 24 | 170000 | ϕ Dra | A0 Si | 93(3)c | 11.4(0.4) | 3.7(0.1)(10) | 1.716 65(9)(18) | |$1.75^{+0.14}_{-0.16}\, ^{(16)}$| | |$0.88 ^{+0.09}_{-0.03}\, ^{(10)}$| | 6(2) × 1015 |
| 25 | 175362 | HR 7129 | B6 He-wk | 153(4) | 16.9(0.7) | 2.7(0.2)(6) | 3.673 81(1)(20) | |$17.0^{+0.6}_{-0.4}\, ^{(6)}$| | |$0.06_{-0.06}^{+0.11}\, ^{(6)}$| | 9(3) × 1015 |
| 26 | 176582 | V545 Lyr | B5 He-wk | 301(4) | 17.2(0.7) | 3.21(0.06)(6) | 1.582 21(5)(18) | 5.4 ± 0.2(6) | 0.32(0.06)(6) | 4(1) × 1016 |
| 27 | 182180* | HR 7355 | B2Vn | 233(6) | 19.8(1.4) | 3.2(0.1)(6) | 0.521 4404(6)(31) | 9.5 ± 0.6(6) | 0.09(0.09)(6) | 9(3) × 1017 |
| 28 | 215441 | GL Lac††† | B9 Si | 490(10) | 14.7(0.5) | 3(1)(40) | 9.487 574(3)(32) | ≈62.4(35) | 0.2(0.2)(40) | 3(1) × 1017 |
Notes. *Radio spectrum available. †The uncertainties in the least significant digit of the rotation are given in parentheses. ††First magnetic star (Babcock 1947), except the Sun. †††Babcock’s star (mean field ≈34 kG; Babcock 1960). a Spectral type from Simbad. b HD 37017 assumed at the average distance of the stars belonging to the Ori OB1c cluster (Landstreet et al. 2007), see discussion reported in Shultz et al. (2019a). c Distance from Hipparcos (van Leeuwen 2007).
References: (1) Alecian et al. (2014); (2)Leto et al. (2020a); (3)Allende Prieto & Lambert (1999); (4)Shultz et al. (2020); (5)Pasinetti Fracassini et al. (2001); (6)Shultz et al. (2019c); (7)Sikora et al. (2016); (8)Kochukhov, Shultz & Neiner (2019); (9)Wade et al. (2006); (10)Sikora et al. (2019a); (11)Kochukhov et al. (2014); (12)Bailey & Landstreet (2015); (13)Bailey et al. (2012); (14)Leto et al. (2020b); (15)Pillitteri et al. (2018); (16)Sikora et al. (2019b); (17)Borra & Landstreet (1980); (18)Bernhard, Hümmerich & Paunzen (2020); (19)Bohlender, Landstreet & Thompson (1993); (20)Shultz et al. (2018); (21)Leone et al. (2010); (22)Townsend et al. (2010); (23)Krtička et al. (2015); (24)Oksala et al. (2018); (25)Catalano & Leone (1994); (26)Pyper, Stevens & Adelman (2013); (27)Grunhut et al. (2012); (28)Shore et al. (2004); (29)Shultz et al. (2019b); (30)Rebull et al. (2018); (31)Rivinius et al. (2013); (32)North & Adelman (1995); (33)Glagolevskij & Gerth (2010); (34)Babel & Montmerle (1997); (35)Landstreet & Mathys (2000); (36)Wraight et al. (2012); (37)Kochukhov & Bagnulo (2006); (38)Landstreet et al. (2007); (39) Schneider et al. (2014); (40) Wade (1997).
| . | . | . | . | D . | Teff . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Frac. MS age . | Lν, rad . |
|---|---|---|---|---|---|---|---|---|---|---|
| ID . | HD . | Alt. name . | Sp. type . | (pc) . | (kK) . | (R⊙) . | (d) . | (kG) . | . | (erg s−1 Hz−1) . |
| 1 | 12447 | α Psc A | A2 SiSrCr | 50(2) | 10.2(0.5) | 2.6(0.2)(3) | 1.4907(8)(17) | 1.19 ± 0.2(33) | 0.58(0.2)(36) | 1.8(0.6) × 1015 |
| 2 | 19832 | 56 Ari | B8 Si | 124(3) | 12.5(0.5) | 2.3(0.3)(4) | 0.727 95(1)(18) | |$2.7^{+0.6}_{-0.3}\, ^{(4)}$| | 0.51(0.26)(36) | 9(2) × 1015 |
| 3 | 27309 | 56 Tau | A0 SiCr | 90(2) | 12.0(0.5) | 2.3(0.3)(10) | 1.568 82(5)(18) | |$3.6^{+1.98}_{-0.58}\, ^{(10)}$| | 0.41(0.33)(10) | 3.6(0.6) × 1015 |
| 4 | 34452 | IQ Aur | B9 Si | 145(4) | 14.1(0.5) | 3.1(0.3)(5) | 2.466 264(5)(19) | ≈4(34) | |$0.40^{+0.15}_{-0.21}\, ^{(37)}$| | 1.0(0.3) × 1016 |
| 5 | 35298 | V1156 Ori | B6 He-wk | 371(9) | 15.8(0.8) | 2.42(0.09)(6) | 1.854 58(3)(20) | 11.2 ± 1(6) | 0.06(0.02)(6) | 4(2) × 1016 |
| 6 | 35502 | BD-02 1241 | B5V He-wk | 383(9) | 18.4(0.6) | 3.0(0.1)(6) | 0.853 807(3)(7) | 7.3 ± 0.5(6) | 0.11(0.03)(6) | 4(1) × 1017 |
| 7 | 36485* | δ Ori C | B3Vp He-s | 390(10) | 20.0(2.0) | 2.97(0.08)(6) | 1.477 75(4)(21) | 8.9 ± 0.2(6) | 0.05(0.02)(6) | 1.7(0.6) × 1017 |
| 8 | 37017* | V1046 Ori | B2 He-s | 420(35)b | 21.0(2.0) | 3.6(0.2)(6) | 0.901 186(2)(20) | 6.2 ± 0.9(6) | 0.13(0.03)(6) | 4(2) × 1017 |
| 9 | 37479* | σ Ori E | B2 Vp He-s | 440(20) | 23.0(2.0) | |$3.39^{+0.06}_{-0.04}\, ^{(6)}$| | 1.190 833(3)(22) | 10.5 ± 1.5(4) | |$0.06 ^{+0.02}_{-0.03}\, ^{(6)}$| | 7(3) × 1017 |
| 10 | 40312 | θ Aur | A0 Si | 58(1) | 10.2(0.4) | 4.6(0.2)(8) | 3.618 66(1)(23) | 0.69 ± 0.01(8) | |$1.00 ^{+0.01}_{-0.06}\, ^{(10)}$| | 1.2(0.6) × 1015 |
| 11 | 79158 | 36 Lyn | B9 He-wk | 175(6) | 13.1(0.7) | 3.4(0.7)(9) | 3.834 76(4)(24) | 3.57 ± 0.36(9) | |$0.84^{+0.08}_{-0.1}\, ^{(37)}$| | 1.6(0.8) × 1016 |
| 12 | 112413 | α2 CVn | A0 EuSiCr | 35(1) | 11.5(0.5) | 2.5(0.3)(10) | 5.469 13(8)(16) | |$3.46^{+2.29}_{-0.69}\, ^{(16)}$| | |$0.53 ^{+0.28}_{-0.31}\, ^{(10)}$| | 1.1(0.7) × 1015 |
| 13 | 118022 | 78 Vir†† | A2 CrEuSr | 58.3(0.8) | 9.4(0.5) | 2.0(0.1)(10) | 3.722 084(2)(25) | |$3.65^{+0.61}_{-0.37}\, ^{(16)}$| | |$0.39 ^{+0.32}_{-0.25}\, ^{(10)}$| | 2(1) × 1015 |
| 14 | 124224* | CU Vir | B9 Si | 72(1) | 12.2(0.5) | 2.1(0.1)(11) | 0.520 714(1)(26) | 3.8 ± 0.2(11) | |$0.13 ^{+0.42}_{-0.09}\, ^{(10)}$| | 1.8(0.6) × 1016 |
| 15 | 133652 | HZ Lup | B9 Si | 121(1) | 12.8(0.5) | 2.2(0.2)(12) | 2.304 05(2)(12) | 6.1 ± 0.7(12) | 0.06(0.02)(38) | 4(2) × 1015 |
| 16 | 133880* | HR 5624 | B9 Si | 104(3) | 12.0(0.5) | 2.0(0.3)(13) | 0.877 476(9)(13) | 9.6 ± 1(13) | 0.05(0.02)(38) | 3.5(1.5) × 1016 |
| 17 | 142184* | HR 5907 | B2V He-s | 141(3) | 18.5(0.5) | 2.8(0.1)(6) | 0.508 276(15)(27) | 9 ± 2(6) | |$0.05_{-0.05}^{+0.1}\, ^{(6)}$| | 2(1) × 1018 |
| 18 | 142301* | 3 Sco | B8 He-wk Si | 148(3) | 16.2(0.7) | 2.42(0.02)(4) | 1.459 57(5)(28) | |$12.5^{+9}_{-0.3}\, ^{(4)}$| | 0.04(0.01)(38) | 9(2) × 1016 |
| 19 | 142990 | V913 Sco | B7 He-wk | 146(4) | 17.0(0.7) | 2.79(0.06)(6) | 0.978 891 793(6)(29) | 4.7 ± 0.4(6) | 0.06(0.01)(6) | 4.7(0.8) × 1016 |
| 20 | 144334 | HR 5988 | B8 He-wk | 133(2) | 15.2(0.7) | 2.27(0.04)(4) | 1.494 99(4)(4) | 3.6 ± 0.3(4) | 0.04(0.01)(38) | 7(3) × 1015 |
| 21 | 145501 | ν Sco C | B9 Si | 141(1) | 14.0(0.5) | 2.26(0.06)(4) | 1.026 48(1)(4) | 5.8 ± 0.3(4) | 0.04(0.02)(38) | 3.8(0.7) × 1015 |
| 22 | 147932* | ρ Oph C | B5Va | 134(1) | 17.0(1.0)(1) | 3.3(0.2)(14) | 0.8639(1)(30) | |$13.2_{-1.2}^{+2.6}\, ^{(14)}$| | |$0.12_{-0.03}^{+0.04}\, ^{(39)}$| | 4(1) × 1017 |
| 23 | 147933* | ρ Oph A | B2Va | 140(4) | 20.8(0.5)(2) | 4.5(0.6)(15) | 0.747 326(2)(2) | |$2.7_{-0.7}^{+0.9}\, ^{(2)}$| | 0.26(0.06)(39) | 1.7(0.5) × 1017 |
| 24 | 170000 | ϕ Dra | A0 Si | 93(3)c | 11.4(0.4) | 3.7(0.1)(10) | 1.716 65(9)(18) | |$1.75^{+0.14}_{-0.16}\, ^{(16)}$| | |$0.88 ^{+0.09}_{-0.03}\, ^{(10)}$| | 6(2) × 1015 |
| 25 | 175362 | HR 7129 | B6 He-wk | 153(4) | 16.9(0.7) | 2.7(0.2)(6) | 3.673 81(1)(20) | |$17.0^{+0.6}_{-0.4}\, ^{(6)}$| | |$0.06_{-0.06}^{+0.11}\, ^{(6)}$| | 9(3) × 1015 |
| 26 | 176582 | V545 Lyr | B5 He-wk | 301(4) | 17.2(0.7) | 3.21(0.06)(6) | 1.582 21(5)(18) | 5.4 ± 0.2(6) | 0.32(0.06)(6) | 4(1) × 1016 |
| 27 | 182180* | HR 7355 | B2Vn | 233(6) | 19.8(1.4) | 3.2(0.1)(6) | 0.521 4404(6)(31) | 9.5 ± 0.6(6) | 0.09(0.09)(6) | 9(3) × 1017 |
| 28 | 215441 | GL Lac††† | B9 Si | 490(10) | 14.7(0.5) | 3(1)(40) | 9.487 574(3)(32) | ≈62.4(35) | 0.2(0.2)(40) | 3(1) × 1017 |
| . | . | . | . | D . | Teff . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Frac. MS age . | Lν, rad . |
|---|---|---|---|---|---|---|---|---|---|---|
| ID . | HD . | Alt. name . | Sp. type . | (pc) . | (kK) . | (R⊙) . | (d) . | (kG) . | . | (erg s−1 Hz−1) . |
| 1 | 12447 | α Psc A | A2 SiSrCr | 50(2) | 10.2(0.5) | 2.6(0.2)(3) | 1.4907(8)(17) | 1.19 ± 0.2(33) | 0.58(0.2)(36) | 1.8(0.6) × 1015 |
| 2 | 19832 | 56 Ari | B8 Si | 124(3) | 12.5(0.5) | 2.3(0.3)(4) | 0.727 95(1)(18) | |$2.7^{+0.6}_{-0.3}\, ^{(4)}$| | 0.51(0.26)(36) | 9(2) × 1015 |
| 3 | 27309 | 56 Tau | A0 SiCr | 90(2) | 12.0(0.5) | 2.3(0.3)(10) | 1.568 82(5)(18) | |$3.6^{+1.98}_{-0.58}\, ^{(10)}$| | 0.41(0.33)(10) | 3.6(0.6) × 1015 |
| 4 | 34452 | IQ Aur | B9 Si | 145(4) | 14.1(0.5) | 3.1(0.3)(5) | 2.466 264(5)(19) | ≈4(34) | |$0.40^{+0.15}_{-0.21}\, ^{(37)}$| | 1.0(0.3) × 1016 |
| 5 | 35298 | V1156 Ori | B6 He-wk | 371(9) | 15.8(0.8) | 2.42(0.09)(6) | 1.854 58(3)(20) | 11.2 ± 1(6) | 0.06(0.02)(6) | 4(2) × 1016 |
| 6 | 35502 | BD-02 1241 | B5V He-wk | 383(9) | 18.4(0.6) | 3.0(0.1)(6) | 0.853 807(3)(7) | 7.3 ± 0.5(6) | 0.11(0.03)(6) | 4(1) × 1017 |
| 7 | 36485* | δ Ori C | B3Vp He-s | 390(10) | 20.0(2.0) | 2.97(0.08)(6) | 1.477 75(4)(21) | 8.9 ± 0.2(6) | 0.05(0.02)(6) | 1.7(0.6) × 1017 |
| 8 | 37017* | V1046 Ori | B2 He-s | 420(35)b | 21.0(2.0) | 3.6(0.2)(6) | 0.901 186(2)(20) | 6.2 ± 0.9(6) | 0.13(0.03)(6) | 4(2) × 1017 |
| 9 | 37479* | σ Ori E | B2 Vp He-s | 440(20) | 23.0(2.0) | |$3.39^{+0.06}_{-0.04}\, ^{(6)}$| | 1.190 833(3)(22) | 10.5 ± 1.5(4) | |$0.06 ^{+0.02}_{-0.03}\, ^{(6)}$| | 7(3) × 1017 |
| 10 | 40312 | θ Aur | A0 Si | 58(1) | 10.2(0.4) | 4.6(0.2)(8) | 3.618 66(1)(23) | 0.69 ± 0.01(8) | |$1.00 ^{+0.01}_{-0.06}\, ^{(10)}$| | 1.2(0.6) × 1015 |
| 11 | 79158 | 36 Lyn | B9 He-wk | 175(6) | 13.1(0.7) | 3.4(0.7)(9) | 3.834 76(4)(24) | 3.57 ± 0.36(9) | |$0.84^{+0.08}_{-0.1}\, ^{(37)}$| | 1.6(0.8) × 1016 |
| 12 | 112413 | α2 CVn | A0 EuSiCr | 35(1) | 11.5(0.5) | 2.5(0.3)(10) | 5.469 13(8)(16) | |$3.46^{+2.29}_{-0.69}\, ^{(16)}$| | |$0.53 ^{+0.28}_{-0.31}\, ^{(10)}$| | 1.1(0.7) × 1015 |
| 13 | 118022 | 78 Vir†† | A2 CrEuSr | 58.3(0.8) | 9.4(0.5) | 2.0(0.1)(10) | 3.722 084(2)(25) | |$3.65^{+0.61}_{-0.37}\, ^{(16)}$| | |$0.39 ^{+0.32}_{-0.25}\, ^{(10)}$| | 2(1) × 1015 |
| 14 | 124224* | CU Vir | B9 Si | 72(1) | 12.2(0.5) | 2.1(0.1)(11) | 0.520 714(1)(26) | 3.8 ± 0.2(11) | |$0.13 ^{+0.42}_{-0.09}\, ^{(10)}$| | 1.8(0.6) × 1016 |
| 15 | 133652 | HZ Lup | B9 Si | 121(1) | 12.8(0.5) | 2.2(0.2)(12) | 2.304 05(2)(12) | 6.1 ± 0.7(12) | 0.06(0.02)(38) | 4(2) × 1015 |
| 16 | 133880* | HR 5624 | B9 Si | 104(3) | 12.0(0.5) | 2.0(0.3)(13) | 0.877 476(9)(13) | 9.6 ± 1(13) | 0.05(0.02)(38) | 3.5(1.5) × 1016 |
| 17 | 142184* | HR 5907 | B2V He-s | 141(3) | 18.5(0.5) | 2.8(0.1)(6) | 0.508 276(15)(27) | 9 ± 2(6) | |$0.05_{-0.05}^{+0.1}\, ^{(6)}$| | 2(1) × 1018 |
| 18 | 142301* | 3 Sco | B8 He-wk Si | 148(3) | 16.2(0.7) | 2.42(0.02)(4) | 1.459 57(5)(28) | |$12.5^{+9}_{-0.3}\, ^{(4)}$| | 0.04(0.01)(38) | 9(2) × 1016 |
| 19 | 142990 | V913 Sco | B7 He-wk | 146(4) | 17.0(0.7) | 2.79(0.06)(6) | 0.978 891 793(6)(29) | 4.7 ± 0.4(6) | 0.06(0.01)(6) | 4.7(0.8) × 1016 |
| 20 | 144334 | HR 5988 | B8 He-wk | 133(2) | 15.2(0.7) | 2.27(0.04)(4) | 1.494 99(4)(4) | 3.6 ± 0.3(4) | 0.04(0.01)(38) | 7(3) × 1015 |
| 21 | 145501 | ν Sco C | B9 Si | 141(1) | 14.0(0.5) | 2.26(0.06)(4) | 1.026 48(1)(4) | 5.8 ± 0.3(4) | 0.04(0.02)(38) | 3.8(0.7) × 1015 |
| 22 | 147932* | ρ Oph C | B5Va | 134(1) | 17.0(1.0)(1) | 3.3(0.2)(14) | 0.8639(1)(30) | |$13.2_{-1.2}^{+2.6}\, ^{(14)}$| | |$0.12_{-0.03}^{+0.04}\, ^{(39)}$| | 4(1) × 1017 |
| 23 | 147933* | ρ Oph A | B2Va | 140(4) | 20.8(0.5)(2) | 4.5(0.6)(15) | 0.747 326(2)(2) | |$2.7_{-0.7}^{+0.9}\, ^{(2)}$| | 0.26(0.06)(39) | 1.7(0.5) × 1017 |
| 24 | 170000 | ϕ Dra | A0 Si | 93(3)c | 11.4(0.4) | 3.7(0.1)(10) | 1.716 65(9)(18) | |$1.75^{+0.14}_{-0.16}\, ^{(16)}$| | |$0.88 ^{+0.09}_{-0.03}\, ^{(10)}$| | 6(2) × 1015 |
| 25 | 175362 | HR 7129 | B6 He-wk | 153(4) | 16.9(0.7) | 2.7(0.2)(6) | 3.673 81(1)(20) | |$17.0^{+0.6}_{-0.4}\, ^{(6)}$| | |$0.06_{-0.06}^{+0.11}\, ^{(6)}$| | 9(3) × 1015 |
| 26 | 176582 | V545 Lyr | B5 He-wk | 301(4) | 17.2(0.7) | 3.21(0.06)(6) | 1.582 21(5)(18) | 5.4 ± 0.2(6) | 0.32(0.06)(6) | 4(1) × 1016 |
| 27 | 182180* | HR 7355 | B2Vn | 233(6) | 19.8(1.4) | 3.2(0.1)(6) | 0.521 4404(6)(31) | 9.5 ± 0.6(6) | 0.09(0.09)(6) | 9(3) × 1017 |
| 28 | 215441 | GL Lac††† | B9 Si | 490(10) | 14.7(0.5) | 3(1)(40) | 9.487 574(3)(32) | ≈62.4(35) | 0.2(0.2)(40) | 3(1) × 1017 |
Notes. *Radio spectrum available. †The uncertainties in the least significant digit of the rotation are given in parentheses. ††First magnetic star (Babcock 1947), except the Sun. †††Babcock’s star (mean field ≈34 kG; Babcock 1960). a Spectral type from Simbad. b HD 37017 assumed at the average distance of the stars belonging to the Ori OB1c cluster (Landstreet et al. 2007), see discussion reported in Shultz et al. (2019a). c Distance from Hipparcos (van Leeuwen 2007).
References: (1) Alecian et al. (2014); (2)Leto et al. (2020a); (3)Allende Prieto & Lambert (1999); (4)Shultz et al. (2020); (5)Pasinetti Fracassini et al. (2001); (6)Shultz et al. (2019c); (7)Sikora et al. (2016); (8)Kochukhov, Shultz & Neiner (2019); (9)Wade et al. (2006); (10)Sikora et al. (2019a); (11)Kochukhov et al. (2014); (12)Bailey & Landstreet (2015); (13)Bailey et al. (2012); (14)Leto et al. (2020b); (15)Pillitteri et al. (2018); (16)Sikora et al. (2019b); (17)Borra & Landstreet (1980); (18)Bernhard, Hümmerich & Paunzen (2020); (19)Bohlender, Landstreet & Thompson (1993); (20)Shultz et al. (2018); (21)Leone et al. (2010); (22)Townsend et al. (2010); (23)Krtička et al. (2015); (24)Oksala et al. (2018); (25)Catalano & Leone (1994); (26)Pyper, Stevens & Adelman (2013); (27)Grunhut et al. (2012); (28)Shore et al. (2004); (29)Shultz et al. (2019b); (30)Rebull et al. (2018); (31)Rivinius et al. (2013); (32)North & Adelman (1995); (33)Glagolevskij & Gerth (2010); (34)Babel & Montmerle (1997); (35)Landstreet & Mathys (2000); (36)Wraight et al. (2012); (37)Kochukhov & Bagnulo (2006); (38)Landstreet et al. (2007); (39) Schneider et al. (2014); (40) Wade (1997).
Radio measurements of individual stars have been collected from both published measurements and unpublished observations, acquired by us or retrieved from the Very Large Array (VLA) data archive. The archival data have been analysed using the standard reduction steps enabled within the software package casa. We also included data from the new VLA Sky Survey (VLASS; Lacy et al. 2020). The VLASS observed the sky at δ > −40° and at ν = 3 GHz (2 GHz bandwidth). The fluxes have been corrected for systematic errors as reported by Lacy et al. (2019). For the newly obtained radio measurements, we determined fluxes using a Gaussian fit to the radio sources (using the standard procedure in casa) located at the sky position of the stars in our sample. Details regarding the radio measurements for individual stars are provided in online Appendix A, where the mean (or unique) radio frequencies of all the available flux measurements are also given. Representative frequencies where the stellar radio luminosities have been estimated lie in the range ≈3–13 GHz.
The stellar parameters of our sample (Teff, R*, Prot, Bp) and the corresponding distributions are shown in Fig. 1, where the distributions of the sub-sample analysed in detail in Section 3 are also superimposed. The effective temperatures of the selected stars ranges from ≈10 kK up to near ≈25 kK, with a broad distribution roughly peaked close to Teff ≈ 15 kK. The radii of the selected stars cover the range 2–5 R⊙. The stellar rotation periods of the sample are mainly between ≈0.5 and ≈2.5 d, with a secondary group close to Prot ≈ 3.5–4 d. Only two targets have longer rotation periods (third panel of Fig. 1). Finally, the last panel of Fig. 1 shows the polar magnetic field strength distribution. The stars analysed here have polar magnetic field strengths peaked close to Bp ≈ 3–4 kG, with a clear secondary peak centred at Bp ≈ 9–10 kG. Note that Babcock’s star (Bp = 62.4 kG) is not shown in the fourth panel of Fig. 1 to avoid enlarging the x-axis scale for just this one source.

Parameter distributions of the analysed sample. The sub-sample analysed in Section 3 is shown by the coloured areas. Note that the Babcock’s star lies outside the range of the Bp plot at 62.4 kG.
3 MODELLING OF A REPRESENTATIVE SUB-SAMPLE
Incoherent gyro-synchrotron emission from the magnetospheres of magnetic B/A stars is rotationally modulated as a consequence of the variable projected source area. To conduct a comprehensive study of radio variability ideally, multifrequency radio observations that sample the entire rotation period are needed. A detailed study of the temporal evolution of the broad-band radio spectra has been performed only for a few stars, and limited only to narrow ranges of rotational phases (Leto et al. 2012, 2017a, 2018, 2020a).
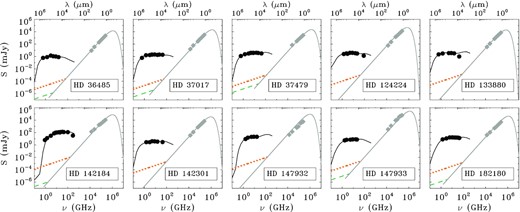
We collected all available radio measurements for the stars in our sample (Section 2). Unfortunately, there are many cases in which the data have inadequate coverage of stellar rotational phase, or only a few radio frequencies available. Even so, a representative number of stars (|$\approx 35{{\ \rm per\ cent}}$| of the total) do have a large number of multifrequency radio measurements; their parameter distributions are also highlighted by the coloured areas in Fig. 1. Such sub-sample of stars with superior frequency coverage (typically, repeated measurements of at least five radio frequencies) are listed in Table 2. 10 stars span nearly the whole range of considered stellar parameters, except for the rotation period. All the stars of this sub-sample have short periods (less than 1.5 d). This is an expected bias because only a few observing facilities are able to detect stellar radio emission, and the ability to perform radio measurements covering large portions of the stellar rotation is naturally biased toward short-period cases. For this sub-sample of 10 stars, we obtained reliable radio spectra from averaging observations repeated over more than three epochs acquired at the same frequency. The average spectra of these stars are shown in Fig. 2.
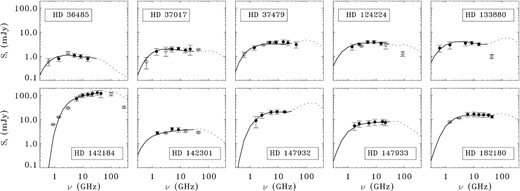
Radio spectra of the 10 stars having enough radio measurements to produce reliable average radio spectra. The data are provided in the tables reported in online Appendix A, where details on the individual stars are also described. Open symbols refer to observing frequencies having few measurements (less than three); in these cases the sampling of the stellar rotation period is poor. The modelled radio spectra are superimposed on the observed data. The dotted line show the model extrapolation to higher frequencies.
Magnetosphere parameters used to calculate the stellar radio spectra shown in Fig. 2. Fixed parameters: n0 = 3 × 109 cm−3; δ = 2.5.
| Star . | i . | β . | L . | BL . | |$\dot{M}_L$| . | nr × l . | |$\tilde{\chi }^2$| . |
|---|---|---|---|---|---|---|---|
| HD . | (deg) . | (deg) . | (R*) . | (G) . | (M⊙ yr−1) . | (1015 cm−2) . | . |
| 36485a | 19 | 4 | 16 | 1.1 | 5.1 · 10−10 | 3.5 | 0.6 |
| 37017b | 39 | 57 | 13 | 1.4 | 5.9 · 10−10 | 10 | 0.7 |
| 37479b | 77 | 38 | 15 | 1.6 | 1.4 · 10−9 | 11.2 | 0.6 |
| 124224c | 46 | 76 | 12 | 1.1 | 1.5 · 10−10 | 1.6 | 0.8 |
| 133880d | 55 | 78 | 18 | 0.8 | 2.4 · 10−10 | 3.5 | 0.3 |
| 142184b | 64 | 9 | 10 | 4.5 | 1.2 · 10−9 | 56 | 0.5 |
| 142301a | 68 | 58 | 19 | 0.9 | 4.9 · 10−10 | 2.8 | 2 |
| 147932e | 74 | 5 | 13 | 3.0 | 1.3 · 10−9 | 6.3 | 0.04 |
| 147933f | 35 | 78 | 9 | 1.8 | 7.5 · 10−10 | 2.8 | 0.1 |
| 182180a | 53 | 82 | 14 | 1.7 | 7.7 · 10−10 | 11.2 | 0.2 |
| Star . | i . | β . | L . | BL . | |$\dot{M}_L$| . | nr × l . | |$\tilde{\chi }^2$| . |
|---|---|---|---|---|---|---|---|
| HD . | (deg) . | (deg) . | (R*) . | (G) . | (M⊙ yr−1) . | (1015 cm−2) . | . |
| 36485a | 19 | 4 | 16 | 1.1 | 5.1 · 10−10 | 3.5 | 0.6 |
| 37017b | 39 | 57 | 13 | 1.4 | 5.9 · 10−10 | 10 | 0.7 |
| 37479b | 77 | 38 | 15 | 1.6 | 1.4 · 10−9 | 11.2 | 0.6 |
| 124224c | 46 | 76 | 12 | 1.1 | 1.5 · 10−10 | 1.6 | 0.8 |
| 133880d | 55 | 78 | 18 | 0.8 | 2.4 · 10−10 | 3.5 | 0.3 |
| 142184b | 64 | 9 | 10 | 4.5 | 1.2 · 10−9 | 56 | 0.5 |
| 142301a | 68 | 58 | 19 | 0.9 | 4.9 · 10−10 | 2.8 | 2 |
| 147932e | 74 | 5 | 13 | 3.0 | 1.3 · 10−9 | 6.3 | 0.04 |
| 147933f | 35 | 78 | 9 | 1.8 | 7.5 · 10−10 | 2.8 | 0.1 |
| 182180a | 53 | 82 | 14 | 1.7 | 7.7 · 10−10 | 11.2 | 0.2 |
Magnetosphere parameters used to calculate the stellar radio spectra shown in Fig. 2. Fixed parameters: n0 = 3 × 109 cm−3; δ = 2.5.
| Star . | i . | β . | L . | BL . | |$\dot{M}_L$| . | nr × l . | |$\tilde{\chi }^2$| . |
|---|---|---|---|---|---|---|---|
| HD . | (deg) . | (deg) . | (R*) . | (G) . | (M⊙ yr−1) . | (1015 cm−2) . | . |
| 36485a | 19 | 4 | 16 | 1.1 | 5.1 · 10−10 | 3.5 | 0.6 |
| 37017b | 39 | 57 | 13 | 1.4 | 5.9 · 10−10 | 10 | 0.7 |
| 37479b | 77 | 38 | 15 | 1.6 | 1.4 · 10−9 | 11.2 | 0.6 |
| 124224c | 46 | 76 | 12 | 1.1 | 1.5 · 10−10 | 1.6 | 0.8 |
| 133880d | 55 | 78 | 18 | 0.8 | 2.4 · 10−10 | 3.5 | 0.3 |
| 142184b | 64 | 9 | 10 | 4.5 | 1.2 · 10−9 | 56 | 0.5 |
| 142301a | 68 | 58 | 19 | 0.9 | 4.9 · 10−10 | 2.8 | 2 |
| 147932e | 74 | 5 | 13 | 3.0 | 1.3 · 10−9 | 6.3 | 0.04 |
| 147933f | 35 | 78 | 9 | 1.8 | 7.5 · 10−10 | 2.8 | 0.1 |
| 182180a | 53 | 82 | 14 | 1.7 | 7.7 · 10−10 | 11.2 | 0.2 |
| Star . | i . | β . | L . | BL . | |$\dot{M}_L$| . | nr × l . | |$\tilde{\chi }^2$| . |
|---|---|---|---|---|---|---|---|
| HD . | (deg) . | (deg) . | (R*) . | (G) . | (M⊙ yr−1) . | (1015 cm−2) . | . |
| 36485a | 19 | 4 | 16 | 1.1 | 5.1 · 10−10 | 3.5 | 0.6 |
| 37017b | 39 | 57 | 13 | 1.4 | 5.9 · 10−10 | 10 | 0.7 |
| 37479b | 77 | 38 | 15 | 1.6 | 1.4 · 10−9 | 11.2 | 0.6 |
| 124224c | 46 | 76 | 12 | 1.1 | 1.5 · 10−10 | 1.6 | 0.8 |
| 133880d | 55 | 78 | 18 | 0.8 | 2.4 · 10−10 | 3.5 | 0.3 |
| 142184b | 64 | 9 | 10 | 4.5 | 1.2 · 10−9 | 56 | 0.5 |
| 142301a | 68 | 58 | 19 | 0.9 | 4.9 · 10−10 | 2.8 | 2 |
| 147932e | 74 | 5 | 13 | 3.0 | 1.3 · 10−9 | 6.3 | 0.04 |
| 147933f | 35 | 78 | 9 | 1.8 | 7.5 · 10−10 | 2.8 | 0.1 |
| 182180a | 53 | 82 | 14 | 1.7 | 7.7 · 10−10 | 11.2 | 0.2 |
3.1 Model description
The 3D model of stellar radio emission from a dipole dominated magnetosphere (Trigilio et al. 2004; Leto et al. 2006) has been previously used to successfully reproduce the multiwavelength radio light curves of early-type magnetic stars, both for the total intensity (Stokes I) and for circularly polarized emission (Stokes V). The stellar geometry is described by the two characteristic angles of the ORM: the rotation axis inclination (i) from the line of sight and the tilt angle of the magnetic dipole axis (β) from rotation axis. The scenario that outlines this model is visualized in Fig. 3.
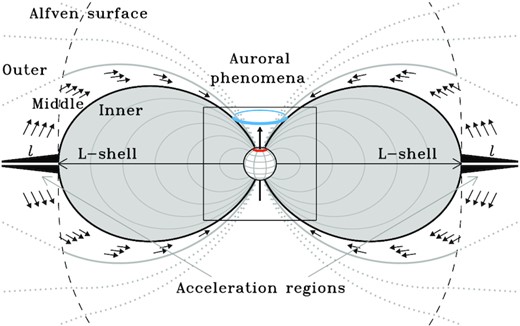
Meridional cross-section of the dipolar dominated magnetosphere of a typical hot magnetic star. Beyond the Alfvén surface, the magnetic field strength is not able to confine the ionized plasma pushed by the radiatively driven stellar wind (outer magnetosphere), with consequent formation of an equatorial magneto-disc surrounding the stellar magnetosphere, shaped like a mashed donut with a longitudinal thickness l. Closer to the star, the magnetic field is strong enough to confine the ionized gas and force it to co-rotate with the star (inner magnetosphere). The two magnetic field lines, pictured using solid lines (black: inner boundary; grey: outer boundary), locate the magnetospheric cavity (middle magnetosphere) where non-thermal electrons (evidenced by the small arrows), accelerated up to relativistic energies in the equatorial magneto-disc (black regions), produce radio emission by the incoherent gyro-synchrotron mechanism. Outside the Alfvén surface, the magnetic field topology (dotted lines) cannot easily be described by simple dipolar field lines. The box centred close to the star locates the deep magnetospheric regions where auroral phenomena can occur, including the coherent cyclotron maser (blue ring a few stellar radii above the poles) and the non-thermal X-rays from the auroral polar caps on the stellar surface (orange ring).
The calculation of observable properties involves a number of ingredients as described below. We use a 3D Cartesian grid to sample the space around the star. Physical parameters that are functions of the radial distance from the star are discretely sampled with the cubic volume elements of the grid, and in each small volume element, the physical parameters are considered constant.
In the case of a simple dipolar magnetic topology, the magnetic field vector components of each grid point have been calculated in the reference frame fixed to the magnetic dipole and then rotated to the observer reference frame. Consequently, a distant observer will perceive the vector magnetic field to change as the star rotates (see appendix of Trigilio et al. 2004).
The acceleration of relativistic electrons is assumed to coincide with the magneto-disc, where magnetic reconnection events are expected to occur. This region is described as a thin equatorial disc of length l and located beyond the last closed magnetic field line, corresponding to the distance L where the last closed magnetic field line crosses the magnetic equatorial plane. It is expected that the magnetic field topology of this ‘unstable’ magnetospheric region cannot be easily described with simple dipole magnetic field lines. However, we empirically observed that the contribution to the radio emission of the magnetospheric regions located far from the star and close to the magnetic equator is negligible, particularly at the intermediate and high-frequency ranges (Section 3.3). The non-dipolar topology of the equatorial magneto-disc has then negligible effects on the calculation for non-thermal radio emission. In fact, the bulk of the non-thermal radio emission originates from magnetospheric regions at higher magnetic latitudes, regions that are likely well-described by the simple dipole topology. Hence, the dipole like magnetic shell, where the relativistic electrons freely propagate, is delimited by the two magnetic field lines of L and L + l.
In modelling the non-thermal emission, we take the relativistic electron population to conform to an isotropic pitch-angle distribution (angle ϕ formed by the velocity direction with respect to the local magnetic field vector) and having a power-law energy distribution (∝E−δ) with spectral index δ. Up to the locations where the non-thermal emission is produced, the non-thermal electrons are assumed to freely propagate in vacuum, in accordance with the low density of the wind electrons (order of magnitude 106 cm−3 at the Alfvén radius), so the collisional energy loss mechanism is then negligible (Petrosian 1985).
In the middle magnetosphere, the number density of non-thermal electrons is approximately constant. This arises because of two effects. First, the invariance of the magnetic moment of the gyrating electron (∝ sin 2ϕ/B) causes the magnetic mirroring effect on the electrons moving towards regions of increasing magnetic field strength, which results in a decreasing number of non-thermal electrons able to reach the deep magnetospheric regions. On the other hand, the solenoidal condition of the magnetic field causes a decreasing volume of the dipole-like flux tube as the magnetic field strength increases, balancing the decreasing number of the non-thermal electron when approaching the stellar surface. The result is a nearly constant number density (nr) of the non-thermal electrons responsible for the radio emission.
All the physical parameters needed for the calculation of the emission and absorptions coefficients for the gyro-synchrotron emission mechanism (Ramaty 1969; Klein 1987) are calculated within each grid point (i.e. the local magnetic field strength and its orientation). As the final step, before the integration of the radiative transfer equation, the spatial distribution of the thermal electron density trapped within the inner magnetosphere is estimated using the MCWS model, which assumes the density is linearly decreasing outward, while the temperature is linearly increasing. The simple relationship, T ∝ r (r radial distance), was deduced by Babel & Montmerle (1997) via modelling of the post-shock region in the case of fast rotating stars. Further, following the MCWS model, the thermal plasma pressure plus the wind ram pressure is constant. Far from the boundary shock the wind pressure becomes negligible, then in the post-shock region n(r)T(r) = n0T0, following the isobaric approximation. The thermal electron density at the stellar surface (n0) is a free parameter, whereas the temperature there (T0) is set to Teff. Our model accounts for free–free absorption from thermal electrons (Dulk 1985). Then at a given radio frequency (ν), we perform a numerical integration of the radiative transfer equation along the line of sight. The solution for a grid of such rays allows us to calculate the spatial distribution of the brightness and for a given stellar distance, the predicted flux from the unresolved source.
A model realization requires the following parameters: the equatorial radius of the magnetic shell where the relativistic electrons freely propagate (L); the thickness of the magnetic shell (l); the spectral index for the energy distribution of relativistic electrons (δ); the number density of the relativistic electrons (nr); and for the thermal electrons trapped within the inner magnetosphere, the number density at the stellar surface (n0). Note that Leto et al. (2017a) showed that nr and l are degenerate parameters so that only the column density of the relativistic electrons (nr × l) can be constrained.
3.2 Radio spectra calculation over broad spectral range
For each of the 10 stars in the sub-sample, we calculated the non-thermal radio emission within the frequency range of 0.1–400 GHz. We adopted a spacing of Δlog ν = 0.2, corresponding to 19 different frequencies in the calculations, to evaluate time-averaged synthetic spectra. In particular, we analysed the orientations corresponding to the two extrema of the effective magnetic field curves and to one null (if predicted by the corresponding ORM geometry, otherwise the intermediate phase between the extrema was calculated), for a total of three different rotational phases. These particular phases were appropriately identified from each individual star using the ORM parameters as listed in Table 2 (thus each star has three tailored calculations appropriate for the three phases identified).
To make this large computational effort possible, we restricted the exploration of parameter space to L and nr × l. The other parameters of the models were assumed close to the values retrieved by analysing the individual stars already published (Trigilio et al. 2004; Leto et al. 2006, 2017a, 2018, 2020a,b), having well-sampled single-frequency radio light curves, both for Stokes I and V. In those cases, a fine-tuning of all the model parameters was performed to reproduce the observed light-curve shapes. The previously published models have thermal electron density numbers determined at the stellar surface in the range 1–5 × 109 cm−3 and spectral indices of the non-thermal electron energy distribution in the range 2–4. These values are fairly similar for all the previously analysed stars. Consequently, for this paper we adopt: n0 = 3 × 109 cm−3 and δ = 2.6. For n0 we used the average of the existing ranges of values. The adopted δ is the average of the values indirectly estimated for the few stars for which their X-ray spectra displayed a non-thermal photon component (Leto et al. 2017a, 2018; Pillitteri et al. 2018; Robrade et al. 2018).
To perform the broad-band spectral analysis, the radio spectral calculations were obtained by varying the parameter L in the range 8–20 R* (with steps of ΔL = 0.5 R*, corresponding to 24 different magnetospheric sizes) and nr × l in the range 1015–1017 cm−2 (with steps of Δlog (nr × l) = 0.05, corresponding to 40 different cases). The total number of calculations is ≈5.5 × 105. The spatial grid has different levels of resolution depending on its proximity to the star. We used narrow steps (0.1 R*) for distances below 8 R*, mid-sized steps (0.3 R*) for intermediate distances in the range 8–12 R*, and finally, coarse steps (0.5 R*) at distances beyond 12 R*.
Finally, the grid of calculated spectra was used to find the best match to observations. For goodness of the spectral fit, we calculated the reduced chi-square statistical parameter, defined as |$\tilde{\chi }^2 = \chi ^2/{\mathrm{d.\, o.\, f.}}$|, where the degrees of freedom (d. o. f.) is equal to the number n of the different observed frequencies minus the two free parameters of the model. The formulation |${\chi }^2 = \sum _{i=0}^{n} (O_i - E_i)^2/\sigma _i^2$| has been used, where Oi is the measured flux (with the related uncertainty σi) and Ei is the expected value from the calculation at the corresponding i-th frequency. For the evaluation of |$\tilde{\chi }^2$|, the calculated spectra have been interpolated to match the frequencies of the observations. To make the |$\tilde{\chi }^2$| estimation reliable, we related to the radio measurements marked by the open symbols in Fig. 2 (spectral data provided by unique or few measurements) the average fractional error gained by the other measurements, in this way the dispersion of the measurements due to the rotational modulation of the radio emission is taken into account. Further, as it will be extensively discussed later, we suspect that the theoretical high-frequency radio emission suffers from critical model limitations, then, the high-frequency measurements (ν ⪆ 30 GHz), when available, have not been taken into account when evaluating |$\tilde{\chi }^2$|. The calculated spectra superimposed with the observations are shown in Fig. 2.
Table 2 lists model parameters for the synthetic spectra that best fit the data, including the magnetic field strength (BL) at L. Values of |$\tilde{\chi }^2$| (Table 2) are always lower than 1 (or close to 1 in the case of HD 142184). Our new spectral calculations recover parameters that are fairly similar to what had been obtained for stars that had previously been modelled in terms of rotational modulations. This is encouraging since here we are modelling spectra, whereas before the emphasis was on light curves, and suggests that our approach produces consistent and reliable results. Overall, calculations for these 10 stars indicate that, on average, the relativistic electrons are injected at a distance of 〈L〉 = 14 ± 3 R*, and the local magnetic field strength is 〈BL〉 = 2 ± 1 G.
3.3 The broad-band radio spectra
The calculated radio spectra at ν⪅30 GHz for the 10 magnetic stars in our sub-sample are quite independent of their stellar parameters. The spectral shapes suggest the existence of both low- and high- frequency cutoffs, in accordance with the observations. Early-B and late-A magnetic stars have almost indistinguishable radio spectra (Fig. 2). The small differences are mainly related to the individual magnetospheric geometries. The nearly universal spectral behaviour can be summarized as follows: the radio flux increases with increasing frequency (at low-frequency), then the radio spectrum becomes almost flat (at intermediate frequency), and finally, the model spectrum has a negative slope (at high frequency), although in some cases a clear high-frequency emission peak was predicted by our calculations.
To better understand the overall spectral behaviour, we computed the spatial distribution of the radio emission from a typical dipole-dominated magnetic star. The synthetic radio maps have been obtained at low-, intermediate-, and high-frequency ranges. The three panels of Fig. 4 show the synthetic radio maps for these three radio regimes. The three calculated frequencies are respectively: low frequency (ν = 2 GHz), intermediate frequency (ν = 6 GHz), and high frequency (ν = 100 GHz). We used HD 142184 as a template, with a polar field strength of Bp = 9 kG. The radio maps clearly highlight the spatial location within the middle magnetosphere of the regions that mainly contribute to the emission at a given frequency range.
3.3.1 Low frequency behaviour
The low-frequency side of the radio spectrum tracks the radio emission arising from the furthest regions of the middle magnetosphere: see the top panel of Fig. 4. As previously explained (see Section 3.1), each grid point of the 3D model is a cube-shaped homogeneous source characterized by a typical gyro-synchrotron radio spectrum peaked at the turnover frequency, which is proportional to the local magnetic field strength (Dulk & Marsh 1982). The positive slope of the radio spectrum at the low-frequency regime, observed and calculated, is due to the grid points that should have contributed mainly to the low-frequency emission, being external to the middle magnetosphere and are not crossed by relativistic electrons. Hence, far from the star, the magnetospheric regions that should mainly radiate at low frequencies (ν⪅1–2 GHz), and where the local magnetic field strength is low (typically less than a few gauss), fall outside the middle magnetosphere. These outer regions do not contribute to the non-thermal radio emission, preventing also to further investigate for the possible effects of the non-dipolar topology of the equatorial magneto-disc on the calculation of the radio emission.
3.3.2 Intermediate frequency behaviour
The radio emission produced at this frequency range (≈2–30 GHz) has the optimal tuning for non-thermal radio emission from a dipole-dominated magnetosphere. In fact, the frequency peaks of the elementary spectra produced by each homogeneous element sampling the middle magnetosphere fall within this spectral range. The synthetic radio map reveals that the brighter source regions are located far from the middle magnetosphere boundaries, either near the stellar surface or near the Alfvén surface (see the middle panel of Fig. 4). The nearly flat spectra, which characterize the intermediate frequency behaviour, is qualitatively understood when taking into account that the brighter magnetospheric regions close to the star (where the magnetic field is stronger) have less volume than the more distant low brightness regions, where the emission at the lower radio frequencies mainly originates.
3.3.3 High frequency behaviour
Radio emission at higher frequencies (⪆30 GHz) originates from the deep magnetospheric regions close to the star (see the bottom panel of Fig. 4). In this frequency regime, the negative slope of the spectrum is the obvious consequence of the radiating regions that meet the stellar surface. The decaying of the high-frequency flux has the same qualitative explanation as the flux drop occurring when the radio frequency decreases, which is that the magnetospheric regions that should have been mainly responsible for radio emission at very high (and low) frequencies fall outside the middle magnetosphere. Further, the high-frequency side of the radio spectrum might also be strongly affected by the plasma processes responsible for auroral phenomena (i.e. possible plasma evaporation as a consequence of non-thermal auroral X-ray emission), which is plausibly always occurring for all magnetospheres in these kinds of stars. This might be a critical issue for high-frequency radio emission. In practice, the adopted model conditions may not be valid within deep magnetospheric regions where high-frequency emission originates (i.e. the spatial distribution of the non-thermal electron density might be inhomogeneous). The topic will be a matter of future study, mainly focused on the high-frequency side of the radio spectrum of such stars. At present, the limited available radio measurements prevent further investigation of the physical conditions occurring within the deep magnetospheric regions. The calculated radio light curves at the high-frequency spectral range are shown using only dotted lines in Fig. 2.
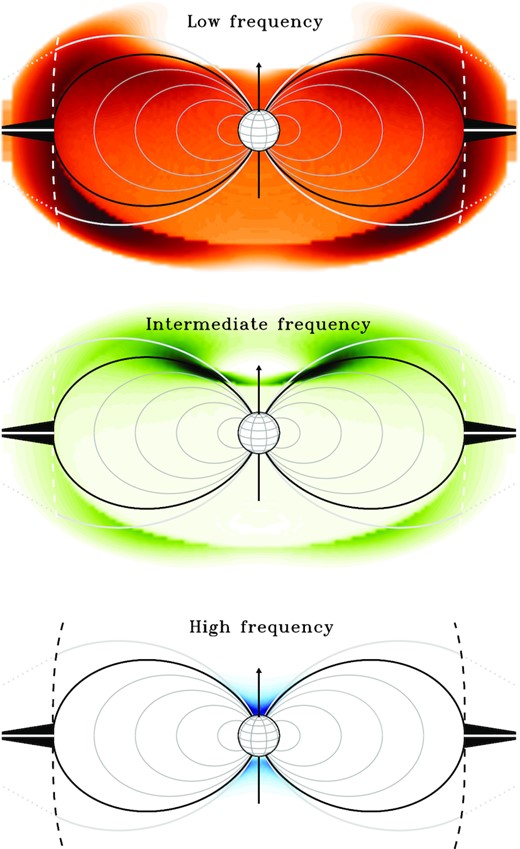
Synthetic brightness spatial distributions evaluated at three representative radio frequencies computed for the parameters of the template star HD 142184. Top panel: low frequency behaviour (red, ν = 2 GHz). Middle panel: intermediate frequency behaviour (green, ν = 6 GHz). Bottom panel: high frequency behaviour (blue, ν = 100 GHz). In all panels, the dashed line demarcates the Alfvén surface (white lines in top and middle panels, black line in the bottom panel).
The comparison between observations and calculations shows excellent accord at the low and intermediate frequency ranges (Fig. 2). At the higher frequency side of the radio spectra, the few available observations (see online Appendix A for details) are not sufficient to assert any firm conclusions regarding high-frequency spectral behaviour, nor reliable estimates of the high-frequency cutoff. The evident large discrepancies between calculations and observations require further investigation. In practice, possible plasma effects related to auroral phenomena might significantly affect the emission level and the rotational modulation of high-frequency radio emission. This possibility drives the need for a much better sampling of the entire stellar rotation period for a larger sample of stars to determine the average high-frequency spectral behaviour.
Despite some modelling limitations, particularly at high-frequency, the capability to reproduce the spectral behaviour at low and intermediate frequencies allows us to place strong constraints on the spatial location for the acceleration of the non-thermal electrons. From a qualitative point of view, once all the magnetosphere parameters have been fixed, the radio spectrum from a large magnetosphere (large L) is characterized by a turn-over, namely the narrow spectral region where the change from the rising to the flat regime of the radio spectrum occurs, situated at low frequency. Conversely, the radio spectrum from a smaller magnetosphere (small L) has its turn-over located at a higher frequency.
4 THE ROLE OF THE WIND
4.1 Indirect estimation of the wind
The MCWS paradigm successfully explains many observational features of the early-type magnetic stars, from the radio to the X-ray regime (Babel & Montmerle 1997). In particular, the thermal X-ray emission from the magnetically confined wind is produced by the strong shock occurring close to the magnetic equatorial plane (ud-Doula et al. 2014). Following the Rankine–Hugoniot condition, the temperature of the X-ray radiating plasma (TX) is related to the velocity of the colliding wind streams (vwind) arising from the stellar hemispheres with opposite magnetic polarity by the relation |$T_{\mathrm{X}} \approx 14(v_{\mathrm{wind}} / 10^3 \, {\mathrm{km\, s^{-1}}})^2$| MK. Approximating vwind with v∞, the terminal wind velocity can be indirectly constrained by the measured temperature of the thermal plasma emitting X-rays, which is TX ≈ 10 MK (Oskinova et al. 2011; Pillitteri et al. 2016, 2017; Leto et al. 2017a, 2018; Robrade et al. 2018). The corresponding value of the terminal wind velocity is v∞ ≈ 900 km s−1, which is reasonable for MS B-type stars (Prinja 1987).
In the paradigm associated with wind magnetic confinement, non-thermal acceleration is placed at the equatorial Alfvén radius. The L-shell parameter from our models (Section 3.2) can be used as an indirect estimate of RA. Thus, we can quantify the spherical wind of the stars analysed in Section 3 by equating the kinetic energy density of the wind (ram pressure plus centrifugal component) to the magnetic energy density: pram + 1/2(ρω2d2) = |$B^2/8\pi$|, where ρ is the wind density, ω is angular rotation speed, and d the distance of a generic point located on the magnetic equatorial plane from the rotation axis. As a consequence of the ORM geometry the equatorial Alfvén radius is a function of the magnetic longitude (Trigilio et al. 2004). Comparing the longitudinal average of RA with the L-shell size of the individual stars required to reproduce the measured radio spectra, we indirectly derive the mass-loss rate of the spherical wind (|$\dot{M}_{\mathrm{L}}$|) that is able to exceed the magnetic tension at the appropriate distance to originate a radio emitting magnetosphere that reproduces the spectrum. The values of |$\dot{M}_{\mathrm{L}}$|, thereby derived for the individual stars, are listed in Table 2. The mass-loss rates are in the range 10−10–10−9 M⊙ yr−1.
4.2 Comparison with the theoretical wind
The stars analysed in Section 3 have effective temperatures ranging from ≈12–23 kK. The effective temperature has a primary effect on the radiatively driven stellar wind. However, the radio spectra of our sample stars are well reproduced with similar values of the magnetic shell size L (Section 3.2), hence, no correlation seems to exist between L-shell and Teff.
Estimated values of the mass-loss rate (|$\dot{M_{\mathrm{L}}}$| listed in Table 2) for the spherical winds of non-magnetic counterparts to the individual stars of our sub-sample are shown in the top panel of Fig. 5, as a function of the corresponding effective temperature. The rather limited spread in wind mass-loss rates as estimated from the radio spectral models stands in substantial contrast with values expected from radiative wind driving, mainly owing to the rather large spread in stellar temperatures and consequently luminosities of the sub-sample. As an example, consider HD 147933 with a luminosity L* ≈ 4000 L⊙ (Pillitteri et al. 2018) as opposed to HD 133880, with L* ≈ 80 L⊙ (Netopil et al. 2017). Hence, HD 147933 is about 2 orders of magnitude brighter than HD 133880. According to Castor, Abbott & Klein (1975; hereafter CAK) framework of the radiatively driven wind acceleration, the expected mass-loss rate is related to the stellar luminosity as |$\dot{M} \propto L_{\ast }^{1/\alpha }$|, with α ≈ 0.6 (Puls, Vink & Najarro 2008; ud-Doula et al. 2014), the expected mass-loss rate from HD 147933 would be about 3 orders of magnitudes higher than for HD 133880. Further, there is a large discrepancy between the mass-loss rates empirically estimated from radio (reported in Table 2) and those predicted theoretically. Krtička (2014) theoretically derived the dependence of mass-loss rates on Teff for BA-type dwarfs, given by the relation: |$\log \dot{M}=a+b T_4+cT_4^2$| with |$T_4=T_{\mathrm{eff}}/(10^4\, {\mathrm{K}})$|, and where a = −22.7, b = 8.96, and c = −1.42. Their predictions are in good agreement with the empirically derived |$\dot{M}$| of magnetic B-type stars (Oskinova et al. 2011). Considering the top panel of Fig. 5, the |$\dot{M}$| required to reproduce the radio spectra (see Section 4.1) are significantly higher than expected with the gap widening at lower Teff. The discrepancy is especially large at the lowest Teff corresponding to Ap stars. For instance, for a template A0p star, CU Vir (HD 124224), Krtička et al. (2019) derive the upper limit |$\dot{M}=10^{-12}\,\rm M_\odot$| yr−1, which is orders of magnitude lower than that required by our radio spectra models.
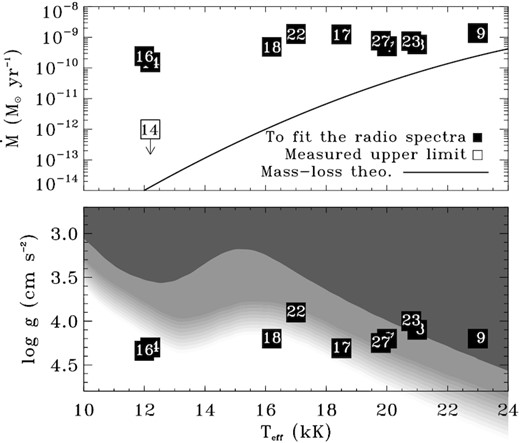
Top panel: theoretical wind prediction of Krtička (2014; solid line) compared with the mass-loss rate from modelling of the radio spectra listed in Table 2 (black squares). The numbers within squares correspond to object in Table 1. The open square represents the upper limit estimation of the wind from HD 124224. Bottom panel: location of the sub-sample stars on the log g versus Teff diagram. The shaded areas indicate different wind regimes according to Babel (1996) and Hunger & Groote (1999). The wind regions have been taken from fig. 6 of Babel (1996) and fig. 1 of Hunger & Groote (1999). Dark grey locates the homogeneous wind region; light grey locates where the expected wind is inhomogeneous; the white area corresponds to the static atmosphere.
To further investigate the physical conditions in atmosphere of our sample stars, in the bottom panel of Fig. 5 we indicate the positions of stars in our sub-sample on the log g/Teff diagram. The surface gravity (log g) was retrieved from the literature for the individual stars (Bailey et al. 2012; Grunhut et al. 2012; Rivinius et al. 2013; Alecian et al. 2014; Kochukhov et al. 2014; Pillitteri et al. 2018; Shultz et al. 2019a). The values of |$\dot{M}$| for MS B-type stars has been theoretically predicted by Babel (1996), who recognized three wind regimes, namely: a homogeneous wind, a chemically inhomogeneous wind, and static atmosphere. These three wind regimes depend on the combined effects of temperature and surface gravity. Based on results from fig. 1 of Hunger & Groote (1999), the qualitative effect of chemical anomalies is roughly to shift down the lower boundary curve taken from fig. 6 of Babel (1996). In the bottom panel of Fig. 5, the down-shifted curves are pictured using the light grey with a gradually decreasing intensity.
Black line: gyro-synchrotron spectra already shown in Fig. 2; grey line: black-body spectra obtained using the stellar parameters listed in Table 1; orange dotted line: wind spectra calculated using the relation given by Scuderi et al. (1998) and adopting the spherical mass-loss rate listed in Table 2; green dashed line: wind spectra calculated using the theoretical wind (Krtička 2014), the expected wind spectra of some stars are lower than the black-body emission. Filled bullets are the radio measurements, filled grey diamonds represent the WISE and 2MASS infrared measurements.
The location on the log g/Teff diagram of the 10 stars from our sub-sample is in accordance with the mass-loss recipe of Krtička (2014). Note that about |$85{{\ \rm per\ cent}}$| of the stars in our complete sample have Teff ⪅ 20 kK, in which case only weak metallic (|$\dot{M} \lessapprox 10^{-14}$| M⊙ yr−1) winds are expected (Babel 1996). Accounting for the corresponding magnetic field strength, we expect Alfvén radii larger than the average value retrieved by calculating the synthetic spectra (RA ≈ 14 stellar radii).
In late-B and early-A stars, the inhomogeneous (hydrogen-free) weak wind (Babel 1995, 1996) would continuously deposit a small amount of metal ions into their centrifugally supported magnetospheres. The secular accumulation of trapped ionized material eventually fills the magnetosphere. The density distribution of the magnetically confined circumstellar plasma around hot magnetic stars has been theoretically studied by Preuss et al. (2004) and Townsend & Owocki (2005). The thermal plasma accumulated by the wind at low magnetic latitudes might be the cause of significant departures from the simple dipole topologies. Far from the star, the magnetic tension might no longer be able to confine this thermal material, leading to centrifugal breakout (ud-Doula et al. 2006), with consequent local magnetic reconnection that is likely a source of plasma acceleration. Shultz et al. (2020) and Owocki et al. (2020) have demonstrated that the onset, emission strength scaling, and line profile morphologies of Hα emission from centrifugal magnetospheres can only be explained if mass balancing is achieved by continuous centrifugal breakout events occurring at small spatial scales throughout the centrifugal magnetosphere.
4.3 The wind spectra and the stellar SEDs
To further investigate the wind mass loss from early-type magnetic stars, we have taken into account possible effects due to the ionized material carried out by the radiatively driven stellar wind. We compared the wind thermal emission with the corresponding non-thermal radio emission. Both wind regimes discussed in Section 4.2 have been analysed. Further, we extended to the radio regime the expected emission from the stellar surface modelled by a simple black-body spectrum.
Radio emission from stellar winds was theoretically studied under simplified assumptions. The radio flux of a spherical wind increases as a function of the frequency like Sν ∝ ν0.6 (Wright & Barlow 1975; Panagia & Felli 1975). In online Appendix C, the equation of the wind spectrum is explicitly reported (equation C1). The wind spectra calculated using equation (C1) and adopting the indirect estimation of the spherical wind of the individual stars (|$\dot{M} _{L}$| listed in Table 2) are shown in Fig. 6, pictured by the orange dotted lines. Looking at the figure, it is clear that the expected wind radio emission from the B/A magnetic stars analysed here is faint. The wind spectra cover almost the same spectral range of the non-thermal radio emission, but are orders of magnitudes less bright.
For the 10 stars analysed in Section 3, the spectral energy distributions, from the radio to the ultraviolet (UV) domain, have been calculated combining the radio spectra (Section 3.2) and the blackbody spectra (Teff listed in Table 1) radiated from the surface scaled at the stellar distance. In the figure, the radio and infrared measurements have also been reported. To minimize for possible absorption effects, interstellar or intrinsic, we collected near- and mid-infrared measurements from the Two Micron All Sky Survey (2MASS; Cutri et al. 2003) and the Wide-field Infrared Survey Explorer (WISE; Cutri et al. 2014) catalogues; these measurements are shown in Fig. 6.
The wind spectra corresponding to the theoretical radiative wind mass-loss rates, expected on the basis of the corresponding stellar temperatures, have been calculated too. As expected by the low level of the theoretical radiative wind from B/A spectral type stars, the wind spectra are much fainter (green dashed lines shown Fig. 6). In some cases the wind mass-loss rate is so low as to radiate less than the black-body radiation of the stellar surface, at the radio spectral range analysed. In these cases the corresponding wind spectra have not been shown.
The early-type magnetic stars are surrounded by large-scale dipole-like magnetic field; in this case the spherical wind assumption is a rough schematization of the real case. In fact, the wind material can be lost from the polar caps only, where the magnetic field lines are open. At the lower magnetic latitudes, the wind is trapped and channelled by the closed field lines. The radiative wind in presence of magnetic field produces the typical observable features, from the X-ray to the radio, successfully explained by the MCWS model.
The effective wind mass-loss rate of the early-type magnetic stars is expected lower than a simple spherical wind. Therefore, it is plausible to expect that the spherical wind assumption produce overestimated effects. In any case, also adopting the simplified spherical assumption, the wind emission is never comparable to the emission level of the non-thermal radio emission produced by the MCWS model. The ionized matter released by the polar caps might produce frequency-dependent absorption effects for the non-thermal radio emission. The theory of spherical stellar winds predicts that each radio frequency of the wind spectrum arises from a well-constrained emitting region, similarly to a radio photosphere where the optical depth is τ ≈ 0.4 (Panagia & Felli 1975). The radio photosphere location is a function of the observing frequency, with the radius of this emitting region decreasing as the frequency increases, in accordance with the relation Rν ∝ ν−0.7. Adopting the spherical wind simplified assumption, the dependence of the size of the wind-emitting region on the mass-loss rate and on other stellar parameters is explicitly reported in equation (C2). The high-frequency cutoff of the wind spectrum is defined by the frequency radiated from the wind region that meets the stellar surface.
To account for possible absorption effects, we calculated the size of the wind radio photosphere at ν = 1 GHz. We chose this frequency because the bulk of the non-thermal radio emission is produced at ν > 1 GHz. The radii of the radio photosphere as a function of the size of the magnetosphere (L-shell parameter) where the non-thermal radio emission arises are shown in Fig. 7. The |$R_{\mathrm{\nu =1\, GHz}}$| values have been calculated for each star for both wind regimes: the |$\dot{M}$| theoretically expected from the stellar temperatures and the |$\dot{M}_L$| indirectly derived from the non-thermal spectra (listed in Table 2). Looking at Fig. 7 it is evident that the radio photosphere calculated using |$\dot{M}$| is contained within the non-thermal emitting region, making any possible absorption effect negligible.

Radii of the radio photosphere calculated at the representative frequency ν = 1 GHz as a function of the corresponding magnetospheric size (L-shell) required to reproduce the radio spectra of the non-thermal radio emission. The Rν values have been derived in two cases: assuming the wind mass-loss rate theoretically expected (green symbols) and assuming the |$\dot{M}_L$| required to break the stellar magnetic field lines at the distance equal to the L-shell (orange symbols). The dotted line locates the lower limit of Rν, coinciding with the stellar radius. The solid line separates the case of a wind radio photosphere that incorporates the region radiating non-thermal radio emission (upper left) from the case where the wind emitting region is located inside (bottom right).
The non-thermal radio spectra calculations have been performed under the assumption that, outside the middle magnetosphere, the absorption effects of thermal plasma can be neglected. This corresponds to assuming the electromagnetic waves propagate in vacuum. The accordance between the observed and the calculated spectra support this assumption. It follows that the negligible absorption effect predicted by the weak wind regime is in accordance with our model assumption. This is a further evidence that the mass-loss rate values indirectly derived from the non-thermal radio emission (|$\dot{M}_L$|) are unreliable.
5 IS RADIO EMISSION AGE-DEPENDENT?
As discussed in Section 4, the oversimplified assumption that the size of the radio emitting magnetosphere coincides with the Alfvén radius has something wrong. If the wind is the plasma source which continuously accumulates within the inner magnetosphere, then non-thermal radio emission from early-type magnetic stars might be potentially related to the stellar age. As suggested in Section 4.2, the wind plasma accumulation produces centrifugal breakout events (Owocki et al. 2020; Shultz et al. 2020) that might make the corresponding stellar magnetosphere radio-loud.
To search for a possible age dependence, the measured radio luminosities are shown in the top panel of Fig. 8 as a function of the corresponding fractional MS age (as listed in Table 1). The stars earlier than spectral type B8 have been marked using blue symbols, while red symbols have been used for cooler stars. Looking at the top panel of this figure, no significant relation appears evident between the stellar radio luminosity and corresponding stellar age for the hotter stars, whereas a possible decaying trend is suggested for the cooler stars. This effect resembles the results obtained by Fossati et al. (2016); moreover, this closely matches to the behaviour of the Hα emission discovered by Shultz et al. (2020). Studying a large sample of massive and hot MS magnetic stars, Fossati et al. (2016) found that large-scale magnetic fields suffered a time-dependent decaying trend, effect that was further confirmed by Shultz et al. (2019c). In particular, the magnetic flux Φ (|$=B_{\mathrm{p}} R_{\ast }^2$|) decreases more steeply than expected from the magnetic flux conservation law, as predicted by the expansion of the stellar radius along the MS evolution. Further, Sikora et al. (2019a) indicated that the chemical surface composition of early-type magnetic stars is strictly related with the stellar age, particularly for the cooler stars.
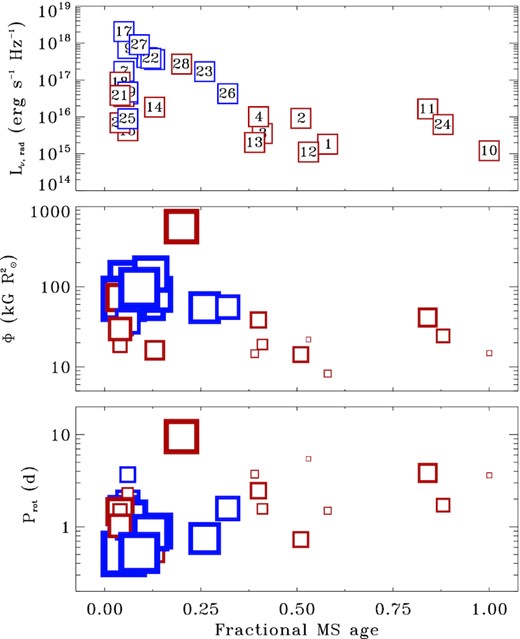
Top panel: radio luminosities as a function of the fractional MS age, where blue symbols refer to stars earlier than B8 and red symbols to the cooler stars. Middle and bottom panels show magnetic fluxes the rotation periods as a function of fractional age. The size of the symbol is proportional to the radio luminosity of the individual star.
Although the sample of early-type magnetic stars analysed here is small, we have searched for possible age-dependent effects on the magnetic flux and the stellar rotation. As already well-studied in this class of stars, the stellar rotation period is expected to increase dramatically over time (Shultz et al. 2019c; Sikora et al. 2019b). In the middle and bottom panels of Fig. 8, we show Φ and Prot as a function of the fractional MS stellar age. The corresponding stellar radio luminosity is indicated by the symbol size. For the hotter stars, the two analysed stellar parameters do not show any significant age-dependent effects, whereas the magnetic field survives on the colder stars. Among the small sample of stars here analysed, at young ages all magnetic field strengths are possible, but at old ages, there are few stars with strong fields, in particular, the older stars in our sample are also cooler stars (see Fig. 8). The same trends seem to be confirmed by the radio. In fact, there is a dearth of both old and strong radio emitters.
The large-scale magnetic fields of the early-type magnetic stars might significantly affect the stellar evolution. Shultz et al. (2019c) performed an extensive study on the dependences of the stellar magnetic flux as a function of various stellar parameters. They conclude that massive stars show a more pronounced magnetic flux decreasing with the age. Further, magnetic braking effects significantly reduce the stellar rotation period during the star’s life.
Although the small number of magnetic stars known as radio sources may introduce a selection bias, and a large fraction of stars in our sample have similar ages, their range of radio luminosities are fairly broad (see top panel of Fig. 8). This suggests that any connection between radio emission, magnetic field strength, rotation period, and age is not simple. The only relevant effect which emerged from the analysis of our small sample is the possible rough dependence of the radio luminosity with the magnetic flux and rotation period shown by the stars having similar ages. In particular, stars with a short rotation period and a high-magnetic flux produce stronger radio emission (see middle and bottom panels of Fig. 8).
6 THE EFFECT OF THE ROTATING DIPOLE
As discussed in Section 4, the wind is not the lead actor in the production of non-thermal radio emission. By contrast there may be a possible dependence on other stellar parameters that mainly characterize the rotation of the dipole-like magnetic field (Section 5).
The sample analysed in this paper has heterogeneous parameters. To well characterize the magnetic properties of the sample, a reliable parameter is the magnetic flux (|$\Phi =B_{\mathrm{p}} R_{\ast }^2$|), which combines both the effects due to the magnetic field strength and the stellar size. In the two panels of Fig. 9, the stellar radio luminosities are displayed as a function of Φ (left-hand panel) and Prot (right-hand panel). The obvious trends seen in Fig. 9, confirm the dependence of radio emission on these two parameters. In particular, Lν,rad has a positive dependence with Φ and a negative one with Prot. These trends suggest identifying a parametrization that incorporates both the parameters. The obvious way is to take their ratio.
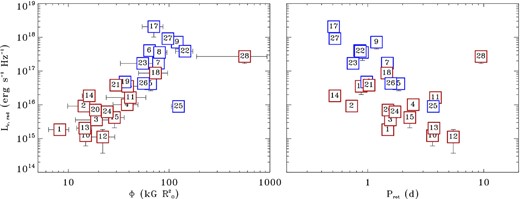
Left-hand panel: the radio luminosity as a function of the magnetic flux (Φ). Right-hand panel: radio luminosity as a function of the rotation period (Prot). The blue symbols refer to the hot stars and the red to the cooler stars (SP>B8).
In Fig. 10, the radio luminosities of the magnetic stars are reported as a function of what we are calling the ‘magnetic flux rate’, Φ/Prot (kG R|$_{\odot }^2$| d−1). Already visual inspection of Fig. 10 reveals a strong correlation. To quantify the correlation, we calculated the Pearson correlation coefficient (r) and the Spearman’s rank correlation coefficient (rs). The r statistical parameter is only sensitive to a linear relationship, whereas rs is sensitive to any possible monotonic relation between the two analysed variables. These two statistical parameters range between −1 and 1, with absolute values ≈0.7, or higher, indicating a high correlation.
It is worth noting that following the Faraday–Lenz law, the empirical parameter Φ/Prot has the physical dimension of an electromotive force (e.m.f. = −dΦ/dt). Even if in a co-rotating reference frame the stellar magnetic flux is not expected to be variable over time: a spinning dipolar magnetosphere has close similarities with Faraday disc dynamo, where the rotation of a conductive disc within a stable magnetic field, having the magnetic vector orientation aligned with the disc rotation axis, produces an e.m.f. (see experiments of Müller 2014). We analyse the rotating magnetospheres from a reverse point of view. In a reference frame anchored to a free test charge located in the equatorial plane, with distance R from the rotation axis, the magnetic field lines will be seen moving at velocity v = ωR (ω = |$2\pi/ P_{\rm rot}$| rotational angular frequency). Assuming the ideal case of aligned dipole and spin axes, the magnetic and equatorial planes are coinciding. Then in the magnetic equatorial plane the magnetic field vectors are orthogonal to the plane and also to the velocity vector. Assuming the simplified homogeneous magnetic field condition, it follows that the test charge located at the stellar equator embedded within a homogeneous field (strength Beq) will be subjected to an induced electromotive force (Jackson 1962), |${\mathrm{e.m.f.}}=-\mathrm{ d}{\Phi }/\mathrm{ d}{t}=\oint {\bf v} \times {\bf B}\, {\mathrm{ d}}{\bf l}$|, that under the above simplified conditions can be written as: |${\mathrm{e.m.f.}}=\int _0^{R_{\ast }} v\, B_{\mathrm{eq}}\, {\mathrm{ d}}r = \int _0^{R_{\ast }} \omega \, r\, B_{\mathrm{eq}}\, {\mathrm{ d}}r = 1/2 \omega B_{\mathrm{eq}} R_{\ast }^2$| (∝ Φ/Prot), (for details see Müller 2014). Note that for a real magnetized plasma, the free charged particles cannot cross the magnetic field lines. The spinning stellar dipole plunged in the magnetospheric plasma can be treated following an ideal magnetohydrodynamic approach. The above discussion is only used to illustrate that a spinning dipole may be a source of electric voltage, potentially able to originate electric currents. In fact, in astrophysical applications, the electrodynamics of spinning dipoles have been the subject of many theoretical studies (Goldreich & Julian 1969; Goldreich & Lynden-Bell 1969; Ruderman & Sutherland 1975).
The rough schematization performed above may be useful to perform order of magnitude relation between astrophysical observables (i.e. the radio luminosity) and general stellar parameters (i.e. the stellar rotation period, the radius, and the magnetic field strength). In fact, the relation |$\omega B_{\mathrm{eq}} R^2_{\ast }$| that resembles an electromotive force is a useful scaling parametrization for the realistic electrodynamics of spinning magnetospheres. The stars analysed in this paper typically have a dipolar magnetic field topology, with Beq = BP/2. Thus, the empirical parameter Φ/Prot can be easily transformed to the physical parameter |$\omega B_{\mathrm{eq}} R_{\ast }^2$|. If the rotation period is given in seconds, the equatorial magnetic field strength in Tesla, and the stellar radius in meters, the parametric electromotive force (named e.m.f.*) has the physical unit of Volts. In Fig. 11, the stellar radio luminosities are now reported as a function of the corresponding values of e.m.f.* and given in unit of 106 V. The e.m.f.* is not the true electromotive force acting within the stellar magnetosphere (its study is out of the scope of this paper), but this is rather a useful parameter with which to quantify the capability of rotating magnetospheres for producing electric currents.
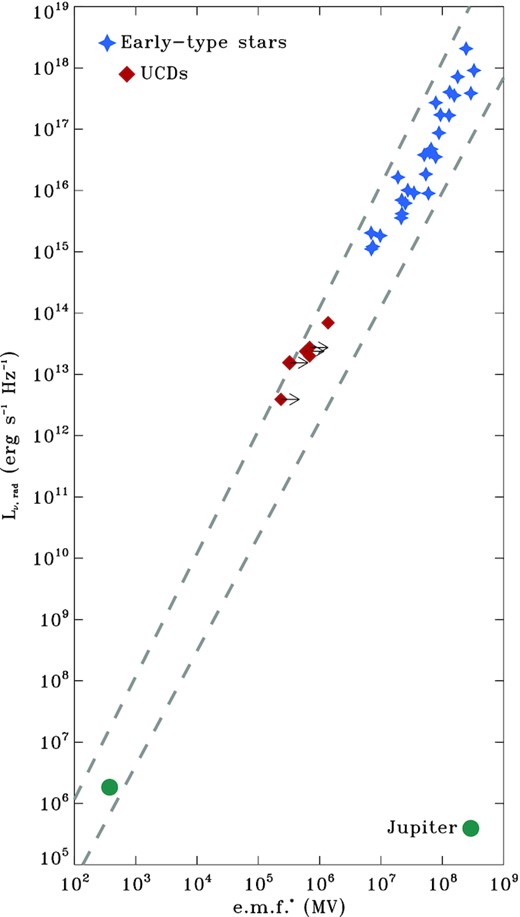
|$L_{\nu ,{\mathrm{rad}}}/{\mathrm{e.\, f.\, m.}^{\ast }}$| diagram. The dashed grey lines locate the boundary of the uncertainty range of the scaling relation derived by using the parameters of the early-type magnetic stars only.
7 OTHER ORDERED MAGNETOSPHERES
To test whether the result reported in Section 6 holds only for the early-type magnetic stars or if it is also valid in a wider context, we analysed the incoherent radio emission from other types of stars (and one planet) characterized by large-scale and well-ordered magnetospheres that are mainly described by a simple dipole magnetic field topology.
7.1 The case of Jupiter
The giant planet Jupiter is surrounded by a large-scale (almost dipolar) magnetic field, with the dipole axis nearly aligned with the planetary rotation axis (tilt angle ≈10°). Compared to the hot magnetic stars, Jupiter has a weak magnetic field, with BJ ≈ 4.17 G at the equator (Connerney et al. 2018), corresponding to BP ≈ 0.008 kG. Jupiter is surrounded by ionized matter that comes from the volcanic moon Io (Io plasma torus) or captured from the Solar wind, which is affected by the planetary magnetic field out to a large distance (10s of Jupiter radii).
The jovian magnetosphere is a site of plasma phenomena responsible for Jupiter’s radio emission, which has been well-studied using ground-based observing facilities and radiometers on-board spacecrafts. Its radio spectrum is dominated at the low-frequency side by coherent ARE (Zarka 2004), and at high frequencies (ν⪆10 GHz) by the blackbody thermal emission of Jupiter’s atmosphere. At intermediate frequencies, the incoherent synchrotron emission is another component of Jupiter’s radio spectrum. The multiwavelength VLA images of the planet Jupiter show the spatial distribution of the non-thermal radio emission component from Jupiter (de Pater 1991). This non-thermal component originates from the inner radiation belt located at L < 5 Jupiter radii inside the orbit of the moon Io.
The non-thermal radio component was disentangled from the thermal one and the wide band non-thermal jovian radio spectrum was discussed by de Pater (2004). We note that the spectral shape qualitatively resembles the overall behaviour of the radio spectra of early-type magnetic stars (see Fig. 2), but is tuned at lower frequencies. The reference frequency of the Jupiter’s incoherent non-thermal emission is in fact ≈1.6 GHz. The average luminosity of the incoherent radio emission is Lν, rad = 1.8(0.4) × 106 erg s−1 Hz−1, obtained from scaling the multifrequency fluxes measurements to the distance from Earth of 4.04 au (de Pater et al. 2003; de Pater & Dunn 2003).
Jupiter’s equatorial radius and magnetosphere rotation period are RJ = 71492 km and PJ = 9 h 55 min 29 s. In Meters Kilograms Seconds (MKS) unit, the effective electromotive force (as defined in Section 6) produced by the rotation of the Jupiter’s magnetosphere is e.m.f.* = 376 MV. This coincides with the magnetic potential energy available from the jovian magnetosphere’s corotation defined by Khurana et al. (2004) as |$\omega _{\mathrm{J}} B_{\mathrm{J}} R_{\mathrm{J}}^2$| (with ωJ = |$2\pi/ P_{\rm J}$| as Jupiter’s rotational angular frequency). Further, the rotation of the jovian magnetosphere has been recognized as a source of stationary field-aligned current systems that drive the main auroral oval centred on the magnetic poles (Cowley & Bunce 2001; Hill 2001).
The radio luminosity of Jupiter’s non-thermal incoherent radio emission is reported in Fig. 11 as a function of the corresponding e.m.f.*. Interestingly, in the Lν, rad/e.m.f.* diagram, the planet Jupiter is situated within the uncertainty range of the scaling relation retrieved by the study of the early-type magnetic stars extrapolated down to the low-radio luminosity level of Jupiter.
7.2 The case of the ultracool dwarfs
At the bottom of the MS, the fully convective UCDs show radio bursts ascribed to coherent auroral emission that closely resemble the case of Jupiter (Nichols et al. 2012). In some cases, the quiescent incoherent non-thermal radio emission component was also detected (Metodieva et al. 2017, and references therein). The UCDs largely violate (Williams, Cook & Berger 2014; Lynch et al. 2016) the Guedel–Benz relation (Guedel & Benz 1993), which couples the radio and X-ray luminosities for a large fraction of the MS stars (from the F to the early-M type stars) characterized by Solar-like magnetic activity, making the radio behaviour of these very cold objects more similar to those of the magnetic stars located at the top of the MS or to that of giant planets.
The UCDs are magnetic stars surrounded by large-scale dipole dominated magnetospheres, which, like the case of Jupiter, are strongly affected by rotation (Schrijver 2009). The measurement of an axisymmetric magnetic field was first reported for the M3.5 star V374 Peg (Donati et al. 2006). Well-ordered large-scale magnetic fields were also measured in other fully convective UCDs (Reiners & Basri 2007; Morin et al. 2010). This supports the theoretical prediction of a magnetic field generated by a process similar to the geodynamo operating in Jupiter and Earth (Christensen et al. 2009).
The UCDs are faint objects in the visual band. Further, those that are radio loud are also fast rotators (rotation periods of order an hour), allowing direct magnetic field measurements in only few cases. In some cases the magnetic fields of the UCDs can be indirectly constrained. In fact, following the basic theory of the ECM mechanism, the emission frequency (ν) of the coherent pulses occurs close to local gyro-frequency. Since the gyro-frequency is related to the local magnetic field by the relation νB = 2.8 × B/kG GHz, the polar field strength of the UCDs where the ECM is detected will be Bp⪆ν/2.8 kG. Hence, the lower limits of the polar field strengths reported in Table 3 were estimated from the maximum frequencies at which the coherent emission produced by the ECM was detected. In particular, the four listed UCDs showed coherent pulses at ν ≈ 8.4 GHz (Berger 2002; Burgasser & Putman 2005; Hallinan et al. 2007, 2008), thus Bp⪆3 kG.
| . | . | . | D . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Lν,rad . |
|---|---|---|---|---|---|---|---|
| 2MASS . | Common or alt. name . | Sp. type . | (pc) . | (R⊙) . | (h) . | (kG) . | (erg s−1 Hz−1) . |
| J00242463-0158201 | BRI 0021-02 | M9.5V | 12.50(0.03) | 0.113(0.005)(1) | ≈5(4) | ⪆3 | 1.6(0.3) × 1013 |
| J00361617 + 1821104 | LSPM J0036 + 1821 | L3.5 | 8.74(0.02) | 0.118(0.007)(1) | 3.0(7)(4) | ⪆3 | 2.4(0.2) × 1013 |
| J10481463-3956062 | DENIS J1048.0-3956 | M8.5Ve | 4.045(0.002) | 0.096(0.004)(1) | ⪅5†† | ⪆3 | 4(2) × 1012 |
| J15010818 + 2250020 | TVLM 513-46 | M8.5V | 10.70(0.02) | 0.103(0.006)(2) | 1.959 574(2)(5) | ⪆3 | 3(1) × 1013 |
| J18353790 + 3259545 | LSR J1835 + 3259 | M8.5V | 5.687(0.003) | 0.096(0.004)(1) | 2.845(3)(4) | ≈5(7) | 2.03(0.03) × 1013 |
| J22011310 + 2818248 | V374 Peg | M3.5V | 9.104(0.005) | 0.34(0.01)(3) | 10.695 70(5)(6) | ≈3(8) | 7(3) × 1013 |
| . | . | . | D . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Lν,rad . |
|---|---|---|---|---|---|---|---|
| 2MASS . | Common or alt. name . | Sp. type . | (pc) . | (R⊙) . | (h) . | (kG) . | (erg s−1 Hz−1) . |
| J00242463-0158201 | BRI 0021-02 | M9.5V | 12.50(0.03) | 0.113(0.005)(1) | ≈5(4) | ⪆3 | 1.6(0.3) × 1013 |
| J00361617 + 1821104 | LSPM J0036 + 1821 | L3.5 | 8.74(0.02) | 0.118(0.007)(1) | 3.0(7)(4) | ⪆3 | 2.4(0.2) × 1013 |
| J10481463-3956062 | DENIS J1048.0-3956 | M8.5Ve | 4.045(0.002) | 0.096(0.004)(1) | ⪅5†† | ⪆3 | 4(2) × 1012 |
| J15010818 + 2250020 | TVLM 513-46 | M8.5V | 10.70(0.02) | 0.103(0.006)(2) | 1.959 574(2)(5) | ⪆3 | 3(1) × 1013 |
| J18353790 + 3259545 | LSR J1835 + 3259 | M8.5V | 5.687(0.003) | 0.096(0.004)(1) | 2.845(3)(4) | ≈5(7) | 2.03(0.03) × 1013 |
| J22011310 + 2818248 | V374 Peg | M3.5V | 9.104(0.005) | 0.34(0.01)(3) | 10.695 70(5)(6) | ≈3(8) | 7(3) × 1013 |
Notes. †The uncertainty of the rotation periods are referred to the last digit. ††Upper limit of the rotation period estimated by the measured projected rotational velocity, vsin i = 25 ± 5 km s−1 (Stelzer et al. 2012).
| . | . | . | D . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Lν,rad . |
|---|---|---|---|---|---|---|---|
| 2MASS . | Common or alt. name . | Sp. type . | (pc) . | (R⊙) . | (h) . | (kG) . | (erg s−1 Hz−1) . |
| J00242463-0158201 | BRI 0021-02 | M9.5V | 12.50(0.03) | 0.113(0.005)(1) | ≈5(4) | ⪆3 | 1.6(0.3) × 1013 |
| J00361617 + 1821104 | LSPM J0036 + 1821 | L3.5 | 8.74(0.02) | 0.118(0.007)(1) | 3.0(7)(4) | ⪆3 | 2.4(0.2) × 1013 |
| J10481463-3956062 | DENIS J1048.0-3956 | M8.5Ve | 4.045(0.002) | 0.096(0.004)(1) | ⪅5†† | ⪆3 | 4(2) × 1012 |
| J15010818 + 2250020 | TVLM 513-46 | M8.5V | 10.70(0.02) | 0.103(0.006)(2) | 1.959 574(2)(5) | ⪆3 | 3(1) × 1013 |
| J18353790 + 3259545 | LSR J1835 + 3259 | M8.5V | 5.687(0.003) | 0.096(0.004)(1) | 2.845(3)(4) | ≈5(7) | 2.03(0.03) × 1013 |
| J22011310 + 2818248 | V374 Peg | M3.5V | 9.104(0.005) | 0.34(0.01)(3) | 10.695 70(5)(6) | ≈3(8) | 7(3) × 1013 |
| . | . | . | D . | R* . | |$P_{\mathrm{rot}}^{\dagger }$| . | Bp . | Lν,rad . |
|---|---|---|---|---|---|---|---|
| 2MASS . | Common or alt. name . | Sp. type . | (pc) . | (R⊙) . | (h) . | (kG) . | (erg s−1 Hz−1) . |
| J00242463-0158201 | BRI 0021-02 | M9.5V | 12.50(0.03) | 0.113(0.005)(1) | ≈5(4) | ⪆3 | 1.6(0.3) × 1013 |
| J00361617 + 1821104 | LSPM J0036 + 1821 | L3.5 | 8.74(0.02) | 0.118(0.007)(1) | 3.0(7)(4) | ⪆3 | 2.4(0.2) × 1013 |
| J10481463-3956062 | DENIS J1048.0-3956 | M8.5Ve | 4.045(0.002) | 0.096(0.004)(1) | ⪅5†† | ⪆3 | 4(2) × 1012 |
| J15010818 + 2250020 | TVLM 513-46 | M8.5V | 10.70(0.02) | 0.103(0.006)(2) | 1.959 574(2)(5) | ⪆3 | 3(1) × 1013 |
| J18353790 + 3259545 | LSR J1835 + 3259 | M8.5V | 5.687(0.003) | 0.096(0.004)(1) | 2.845(3)(4) | ≈5(7) | 2.03(0.03) × 1013 |
| J22011310 + 2818248 | V374 Peg | M3.5V | 9.104(0.005) | 0.34(0.01)(3) | 10.695 70(5)(6) | ≈3(8) | 7(3) × 1013 |
Notes. †The uncertainty of the rotation periods are referred to the last digit. ††Upper limit of the rotation period estimated by the measured projected rotational velocity, vsin i = 25 ± 5 km s−1 (Stelzer et al. 2012).
To determine whether the radio behaviour of UCDs matches the scaling relation given by equation (1) requires both reliable radio luminosities for the incoherent non-thermal radio emission and knowledge of stellar parameters, in particular, the magnetic field strength, rotation period, and radius. For our analysis, we excluded UCDs that are members of binary systems. The incoherent fluxes reported in online Appendix B have been used to estimate the radio luminosities of the six UCDs in Table 3. The few available radio measurements are mainly performed at a single frequency, particularly ν ≈ 5 or 8.4 GHz (see online Appendix B).
The presence of stable electric fields within the large-scale magnetospheres of the UCDs was proposed to have a possible role on the non-thermal electron production responsible for the radio emission (coherent and incoherent) from these objects (Doyle et al. 2010). In Fig. 11, the radio luminosities of the non-thermal incoherent emission of the small sample of UCDs analysed here are reported as a function of their effective electromotive forces (or lower limits). Despite the limitations explained above, the UCD parameters lie in the |$L_{\nu ,{\mathrm{rad}}}/{\mathrm{e.\, f.\, m.}^{\ast }}$| diagram either within (or very close to) the uncertainty range extrapolated from the scaling relation established by the sample of early-type magnetic stars.
8 THE SCALING RELATIONSHIP FOR THE RADIO EMISSION APPLIED TO HOT JUPITERS
Hot Jupiters are giant gaseous planets orbiting very close to their parent stars. Due to the proximity to the star, hot Jupiters have suitable conditions to develop strong star planet magnetic interactions (SPMI), extending Bode’s law that holds for the magnetized planets of the Solar system to the exo-planets (Zarka 2007). Bode’s law is an empirical scaling relation between the power of the coherent ARE from a magnetized planet and the power dissipated when interacts with the magnetized plasma released by the parent star, and vice-versa. Due to their small orbits, the extrapolated Bode’s law predicts detectable coherent ARE from magnetized hot Jupiters (Zarka 2007).
The ARE is tuned at the radio frequency typical of the ECM mechanism that, as previously discussed (see Section 7.2), depends on the magnetic field strength of the body where it originates (star or planet). The estimated magnetic field strength of the exo-planets belonging to the hot Jupiter class ranges from few G (like the case of Jupiter) up to few hundred G (Yadav & Thorngren 2017). Then, the expected ECM emission frequency lies in low-frequency spectral domain (10s to a few 100 MHz). The tentative detection by the LOFAR (Low Frequency Array) interferometer of highly polarized low-frequency radio emission from the hot Jupiter τ Bootes b has been recently reported (Turner et al. 2021). This result supports the Bode’s law extension beyond the Solar system, and further provides indirect evidence of magnetism occurring in exo-planets.
The capability to detect low-frequency radio emission from the interaction of an exo-planetary magnetosphere with its parent star has been already discussed (Zarka 2007). Similarly to the low-frequency radio emission, also the radio emission at the GHz frequency range, covered by the forthcoming Square Kilometre Array (SKA), has been already taken into account (Zarka, Lazio & Hallinan 2015). Exo-planetary ARE is a bright radio emission constrained to the low-frequency spectral domain; however, at the GHz radio frequencies the SPMI may provide detectable features too. Similarly to the ARE from Jupiter triggered by its moon Io, an exo-planet moving within the stellar magnetic field could be able to stimulate ARE on the magnetic flux tubes connected to the parent star. In this case the emission frequency of the ARE depends upon the stellar magnetic field. Magnetic field strengths at the kG level are common in case of late-type stars (Reiners & Basri 2007), then the ARE will be tuned at GHz radio frequencies. Such stellar ARE triggered by SPMI has been recently discovered from the star Proxima Cen (Pérez-Torres et al. 2021). As demonstrated by Zarka (2007), both types of SPMI produce auroral emission having radio power satisfying Bode’s law.
In accordance with the ECM elementary emission mechanism (Melrose & Dulk 1982), ARE is a highly directive phenomenon, making it difficult to detect despite its strong emission level. Similarly to the incoherent non-thermal radio emission from Jupiter, magnetized hot Jupiters might also be direct sources of such isotropic emission tuned at GHz radio frequencies. The previous Sectionss. 7.1 and 7.2 support the prediction provided by the scaling relationship obtained by analysing the behaviour at the radio regime of the early-type magnetic stars and extrapolated to lower mass objects (UCDs and the planet Jupiter), for which the detection of their incoherent non-thermal radio emissions have been already reported. These results stimulated us to adopt the scaling relationship provided in this paper (equation 1) as a predictive tool for the incoherent radio emission from astrophysical objects surrounded by large-scale magnetospheres and having known parameters. Among these, the hot Jupiter class is suitable. In fact, some of them are magnetized sub-stellar objects whose magnetic field strength, radius, and rotation period have been constrained.
The favourable condition to produce incoherent non-thermal radio emission from a large-scale rotating magnetosphere is the corresponding strength of the magnetic field. In the cases of some hot Jupiters that are particularly close to the Earth, the presence of magnetic field strengths higher than Jupiter’s have been reported (Cauley et al. 2019). The selected objects are listed in Table 4 with their corresponding parameters. The expected incoherent radio emission levels of the four magnetized hot Jupiters, derived using equation (1) with the corresponding parameter uncertainties, are reported in Fig. 12 as a function of the effective electromotive force generated by the rotation of these exo-planets. The expected fluxes are well below the |$\mu$|Jy level.
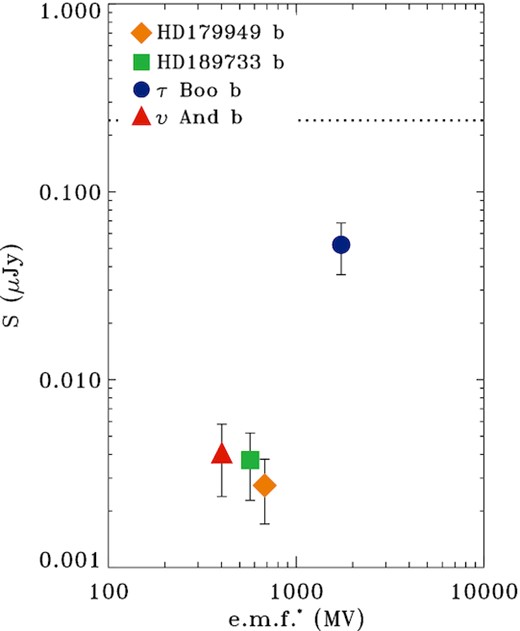
Expected fluxes at Earth of the four hot Jupiters analysed. Fluxes calculated by extending the scaling relationship of the incoherent non-thermal radio emission of the early-type magnetic stars. The error-bars follow by the parameters uncertainty of the adopted scaling relationship (equation 1). The dotted line represent the SKA detection limit.
| . | D . | Prot . | B(5) . | R(5) . |
|---|---|---|---|---|
| Name . | (pc) . | (d) . | (G) . | (RJ) . |
| HD 179949 b | 27.48(0.06)(1) | ≈7(3) | ≈90 | 1.22 ± 0.18 |
| HD 189733 b | 19.78(0.01)(1) | |$1.7^{+2.9}_{-0.4}\, ^{(4)}$| | ≈20 | 1.14 ± 0.03 |
| τ Bootes b | 15.62(0.05)(2) | ≈3.2(3) | ≈100 | 1.13 ± 0.17 |
| υ Andromedae b | 13.49(0.03)(2) | ≈12(3) | ≈80 | 1.25 ± 0.19 |
| . | D . | Prot . | B(5) . | R(5) . |
|---|---|---|---|---|
| Name . | (pc) . | (d) . | (G) . | (RJ) . |
| HD 179949 b | 27.48(0.06)(1) | ≈7(3) | ≈90 | 1.22 ± 0.18 |
| HD 189733 b | 19.78(0.01)(1) | |$1.7^{+2.9}_{-0.4}\, ^{(4)}$| | ≈20 | 1.14 ± 0.03 |
| τ Bootes b | 15.62(0.05)(2) | ≈3.2(3) | ≈100 | 1.13 ± 0.17 |
| υ Andromedae b | 13.49(0.03)(2) | ≈12(3) | ≈80 | 1.25 ± 0.19 |
| . | D . | Prot . | B(5) . | R(5) . |
|---|---|---|---|---|
| Name . | (pc) . | (d) . | (G) . | (RJ) . |
| HD 179949 b | 27.48(0.06)(1) | ≈7(3) | ≈90 | 1.22 ± 0.18 |
| HD 189733 b | 19.78(0.01)(1) | |$1.7^{+2.9}_{-0.4}\, ^{(4)}$| | ≈20 | 1.14 ± 0.03 |
| τ Bootes b | 15.62(0.05)(2) | ≈3.2(3) | ≈100 | 1.13 ± 0.17 |
| υ Andromedae b | 13.49(0.03)(2) | ≈12(3) | ≈80 | 1.25 ± 0.19 |
| . | D . | Prot . | B(5) . | R(5) . |
|---|---|---|---|---|
| Name . | (pc) . | (d) . | (G) . | (RJ) . |
| HD 179949 b | 27.48(0.06)(1) | ≈7(3) | ≈90 | 1.22 ± 0.18 |
| HD 189733 b | 19.78(0.01)(1) | |$1.7^{+2.9}_{-0.4}\, ^{(4)}$| | ≈20 | 1.14 ± 0.03 |
| τ Bootes b | 15.62(0.05)(2) | ≈3.2(3) | ≈100 | 1.13 ± 0.17 |
| υ Andromedae b | 13.49(0.03)(2) | ≈12(3) | ≈80 | 1.25 ± 0.19 |
The most sensitive ground-based radio interferometer operating at the GHz domain will be most likely the forthcoming SKA. In fact, the detection limit of the SKA in its full operational state will be |$\approx 0.24\, \mu$|Jy, for observations lasting ≈10 min of integration time (Umana et al. 2015). As seen in Fig. 12, the expected fluxes of the four hot Jupiters are below the SKA detection limit. Probably, the hot Jupiters analysed here do not rotate fast enough, or are not sufficiently magnetized to provide detectable incoherent radio emission. In any case, we suspect that in general it is unlikely to expect to detect the incoherent radio emission components of hot Jupiters. In fact, the star’s proximity that is a suitable condition for triggering the low-frequency ARE makes it difficult to spatially resolve its incoherent non-thermal radio emission from the stellar radio emission.
The most favourable condition for non-thermal radio emission detection from giant exo-planets is the planetary orbital position far from their parent stars, making it possible to spatially resolve the radio emissions from both star and exo-planet. Further, the large distance strongly reduces the star–planet interaction effects, these ice giant exo-planets might be unable to produce detectable low-frequency ARE, making the detection of the incoherent non-thermal radio emission the only way to search at the radio regime for exo-planets orbiting far from their parent stars. Non-thermal radio emission may be detectable by SKA in the case of ice giant exo-planets that, possibly, rotate faster than the tidally locked hot Jupiters and then produce higher strength magnetic fields, as expected from the rotation dependent dynamo efficiency. If the fluxes are above the detection threshold, the SKA angular resolution in its full operational state, ≈0.02 arcsec at ν ≈ 1 GHz (Umana et al. 2015), or lower (depending by the observing frequency), could be able to easily resolve from their parent stars exo-planets orbiting at the same distance of Jupiter from the Sun and within 100 pc.
9 DISCUSSION
The observed radio emission of early-type magnetic stars is compatible with gyro-synchrotron emission from a dipole-like magnetic shell co-rotating with the star. The radio spectral calculations allowed us to constrain the equatorial size (L parameter) of the radiating magnetic shells (Section 3). Following the standard scenario for the radio emission from early-B magnetic stars, the shell size was assumed to coincide with the equatorial Alfvén radius, which is the distance where the radiatively driven stellar wind opens the magnetic field lines.
The inferred wind mass-loss rates required to reproduce the radio spectra of the hottest stars are roughly close to (but always higher than) the theoretical expectations at the known effective stellar temperatures (Section 4.2). For the cooler stars, the above rough accordance totally fails (see Fig. 5). The surface chemical composition could play a role in estimation of the wind mass-loss rates (Krtička 2014), or other mass-loss recipes (Vink, de Koter & Lamers 2001) could be employed that predict higher values (see Shultz et al. 2019c, for details). Ultimately, the expected mass loss is still lower than the value required for the radio modelling. Independent evidence for a mass-loss inconsistency at these spectral types comes from HST observations of the wind sensitive UV lines of the early-A type star HD 124224 (Krtička et al. 2019). Those data allow for only an upper limit to the wind mass loss, a limit that is discrepant with that required to explain the observed radio spectrum.
Reconciling the observed common behaviour of the radio emission from the sample of early-type magnetic stars analysed in this work, with the discordance between inferred and predicted mass-loss rates, indicates that we must abandon a physical relation between the Alfvén surface size at the equator (RA) to the size of the magnetic shell (L) radiating at the radio regime. Instead, the origin of the non-thermal radio emission must relate to a physical structure which is less dependent on stellar wind properties. We suggest that the non-thermal radio emission originates from radiation belts located inside the inner magnetosphere of the early-type magnetic stars (see Fig. 13).
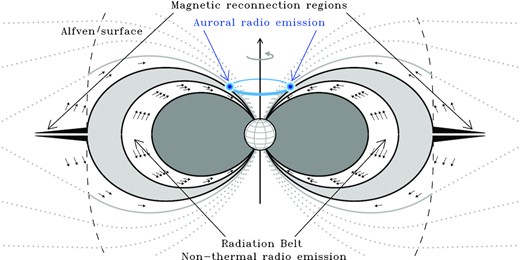
Schematic representation of the radio emission sites within a dipole-dominated magnetosphere of a typical early-type magnetic star. For this picture the field and rotation axes are assumed the same. The location of the radiation belt is highlighted by the white magnetic shell, with small arrows indicating the relativistic electrons. This region is the dominant source of the non-thermal stellar radio emission, and is located inside the inner magnetosphere. The cartoon is purely an idealization; the radiation belt and the Alvén surface are arbitrarily located. The Alfvén surface is far from the star (dashed line). Outside this surface the magnetic field lines are open (dotted lines). Magnetic reconnection events take place within the equatorial magneto-disc (dark region), with consequent production of fast-electrons, which, like the case of Jupiter, trigger the coherent and strongly beamed ARE (blue spots on the blue auroral ring).
The stellar wind still plays an important role in this new picture. The wind is likely the primary source of ionized matter that fills the stellar magnetosphere. From a qualitative point of view, hot stars have favourable conditions for the onset of all the plasma processes that trigger the stellar radio emission, simply because their powerful winds quickly deposit a large quantity of ionized matter into their magnetospheres. Cooler stars are instead characterized by weak winds and consequently the plasma accumulation is slow.
The radiation belt located inside the inner magnetosphere may be at a significant distance from the current sheet regions that form outside the equatorial Alfvén surface, and the site of magnetic reconnection events, which are the likely sources of electron acceleration. Now the question arises: What is the origin of the non-thermal electrons trapped within the radiation belt responsible for the observed radio emission? One explanation could be a relation between the origin of the relativistic electrons with the centrifugal breakout produced by the high-density magnetospheric plasma locked within the inner magnetosphere. The breakout mechanism has already been shown to explain plasma transport within the centrifugal magnetospheres of the B-type stars (Owocki et al. 2020; Shultz et al. 2020). This is also the case of Jupiter’s magnetosphere, where energetic electrons are produced in breakdown regions occurring between 15 and 30 RJ (Krupp et al. 2004). Jupiter’s radiation belt, located at L < 5RJ, has a closed magnetic topology and is the planet’s source of the non-thermal radio emission. For the radio emission from Jupiter’s belt zone, the proposed source of non-thermal electrons is the radial diffusion from the farther Jovian magnetospheric regions, where these energetic electrons are likely produced (Bolton et al. 2004).
An alternative mechanism for the production of energetic electrons within closed magnetic field regions is the resonant interaction of the local plasma with low-frequency electromagnetic waves, known as whistler modes. It is this mechanism that seems dominant in the case of Earth’s radiation belt (Boyd et al. 2018), and also observed to be active within the radiation belts of the giant planets Jupiter and Saturn (Woodfield et al. 2014, 2019). To operate efficiently, the wave-particle resonant interactions require low densities, namely νp ≤ 2.5νB (Horne, Glauert & Thorne 2003), where νB is the gyro-frequency (νB = 2.8 × B/G MHz) and νp is the plasma frequency (|$\nu _{\mathrm{p}} = 9 \times 10^{-3} \sqrt{N}_{\mathrm{e}}$| MHz). For the early-type stars of this paper, the typical strength of the magnetic field at distance L is BL ≈ 2 G (Section 3.2), corresponding to a gyro-frequency νB ≈ 6 MHz. It follows that the plasma density of the radiation belt compatible with local acceleration by wave-particle resonant interaction has to be lower than 2 × 106 cm−3.
The acceleration through this resonant interaction achieves its maximum efficiency for whistler modes at an oscillation frequency of ν ≈ 0.35 νB (Horne et al. 2003). The corresponding wave frequency of the resonant whistler mode will be ν ≈ 2 MHz, which is lower than the plasma frequency of the Earth’s ionosphere (⪅10 MHz). This puts strong technical limitations on observations below this low-frequency cutoff with ground-based radio telescopes (de Gasperin et al. 2018). But such low-frequency radiation probably cannot be detected in any case, even if we observe outside the Earth’s ionosphere.
To reproduce the observed radio emission from the early-type magnetic stars, one must account for the presence of trapped thermal plasma located within the inner magnetosphere, with a density of order 109 cm−3 close to the stellar surface. Following the MCWS model, the density of trapped plasma decreases inversely with distance from the star. The plasma surrounding the radiation belt is expected to have a density of ≈108 cm−3. At this value, low-frequency electromagnetic waves cannot escape from the stellar magnetosphere. Consequently, wave-plasma interactions as a proposed electron acceleration mechanism cannot be directly verified. Furthermore, some process is needed for forming low-density cavities within the inner magnetosphere to allow the wave–plasma interaction to accelerate local electrons efficiently.
In the case of the Earth, a correlation of whistlers mode with the electric discharges related to lightning (Green et al. 2005) was observed. The empirical correlation between the average radio luminosity of incoherent non-thermal radio emission and the magnetic flux rate (see Fig. 10) suggests that some kind of electrodynamic mechanism may act within the magnetospheres of the early-type magnetic stars. The electrodynamical processes acting within the rotating magnetosphere might be the engine to originate large-scale currents and electric discharges. Like the case of the Earth, this might be a likely condition to originate low-frequency electromagnetic waves that, similarly to the magnetized planets of the Solar system, might produce local plasma acceleration by resonant wave-particle interaction.
Following our new scenario of a radiation belt located within the inner magnetosphere, there is a possible critical issue for the low-frequency coherent ARE stimulated by the ECM emission mechanism. Is this coherent emission capable of escaping from the inner magnetosphere to be detectable? In fact, such stimulated radio emission originates from the deep magnetospheric regions close to the star. Hence, these low-frequency electromagnetic waves might be strongly suppressed by the gyro-resonant magnetic absorption of the thermal plasma surrounding the radiation belt, if the ARE arises from the same magnetic shell where the incoherent non-thermal radio emission originates.
The broad studies of Jupiter’s radio emission suggest a possible resolution to the issue raised above. Jupiter shows clear evidence of non-thermal radio emission from a radiation belt located close to the planet (L < 5 RJ), and also various components of coherent radio emission. An important source of coherent emission is associated with the moon Io, but there is also a non-Io contribution arising from the magnetic field lines anchored at the planet’s surface at high latitudes, and coinciding with the main auroral oval. It was recognized that the footprints of these field lines are related to the magnetic field lines crossing the magnetic equatorial plane at a large distance (L ⪆ 7–15 RJ) and close to the breakdown regions where magnetic reconnection events have been identified. These reconnection events provide the injection of fast electrons that trigger on Jupiter the non-Io DAM (i.e. the component of the Jovian decametric radio emission, DAM, not related to the magnetic flux tube connected with the moon Io) and the bKOM (i.e. the Jovian broad-band kilometric radiation; Zarka 1998, 2004). The Jupiter-like scenario was recently supported to be scalable also in the case of magnetic early-type stars by the frequency dependent behaviour of the wide band coherent emission from HD 124224 (CU Vir), the prototype of the class of early-type magnetic stars showing ARE, where several ARE components seem to be related to different magnetic field lines of the stellar magnetosphere (Das & Chandra 2021).
Similar to Jupiter, the ARE of early-type magnetic stars might be triggered by the non-thermal electrons accelerated within the magnetospheric regions, where the magnetic field strength is too weak to confine the magnetospheric wind plasma, or produced by continuous centrifugal breakouts events. The result is the formation of an equatorial magneto-disc site of magnetic reconnection. A cartoon that summarizes this scenario is given in Fig. 13. Even if this scenario is an oversimplified schematization of a true rotating stellar magnetosphere, this picture highlights that the injection of non-thermal electrons is not related to a unique acceleration site, where, possibly, different acceleration mechanisms are working. Beyond the magnetospheric regions where the wind plasma breaks the field lines, producing magnetic reconnection and consequent acceleration of electrons, energetic electrons can be also locally accelerated within the most internal regions where the magnetic field lines are closed, as seen in the case of Earth.
10 CONCLUSION AND OUTLOOK
In this paper, we analysed the incoherent gyro-synchrotron radio emission of a sample of early-type magnetic stars, ranging from early-B to early-A type stars, as a function of their stellar parameters. As a result of our study, we report the existence of a strict correlation between the non-thermal radio luminosity (Lν,rad) and the ratio of magnetic flux to the rotation period (Φ/Prot), given by the equation (1) and shown in Fig. 10. This relationship appears to be something analogous to the scaling relationship that describes the coherent ARE of the magnetized body of the Solar system, formalized by the radio-magnetic Bode’s law and which is extrapolated up to the exo-planets (Zarka 2007).
We also reviewed the wind scenario used to account for the non-thermal radio emission of these stars. The stellar wind has still a key role to supply ionized material within the magnetospheres of the early-type magnetic stars. But, unlike what was previously assumed, we found that the equatorial size of the magnetospheric region radiating incoherent gyro-synchrotron radio emission is not large enough to intercept the regions in which the wind pressure equals the magnetic tension. To explain the features of the non-thermal radio emission from such hot magnetized stars, we proposed the existence of a Jupiter-like radiation belt within the magnetospheres of the early-type magnetic stars. The existence of a radiation belt around the magnetized planets of the Solar system is a well-known phenomenon, already taken into account in stellar cases too. To explain the origin of the incoherent non-thermal radio emission from UCDs, a plasma radiation belt has been proposed to exist within their magnetospheres (Hallinan et al. 2006). This idea applied in the context of the early-type magnetic stars leads to convenient results. In fact, in this new picture, the magnetic shell where the non-thermal radio emission originates is formally decoupled from the wind mass-loss rate strength. Following this new wind paradigm, a more complex picture seems to come out with regard to the origin of the non-thermal electrons responsible for the incoherent gyro-synchrotron emission. In particular, the current sheets produced by the wind magnetic breakout cannot provide unique (and primary) acceleration sites.
Importantly, the scaling relationship between Lν,rad and Φ/Prot for the early-type magnetic stars also successfully predicts the non-thermal radio emission from some (six) UCDs and the planet Jupiter. The parameter Φ/Prot is related to the effective electromotive force generated by the rotation of a large-scale and well-ordered magnetic field. The rotation stimulates electrodynamic processes occurring within the stellar magnetosphere, which appear key to establishing the radio emission level of the dipole like magnetospheres surrounding objects at both the top and at the bottom of the MS (see Fig. 11). It is then possible that the mechanism for acceleration of non-thermal electrons may be related to large-scale stationary current systems.
The various plasma configurations that we have suggested as possibly existing within the magnetospheres of early-type stars certainly demands further investigation. And while we have identified a scaling relation that span magnetospheres from early-type massive stars to UCDs and planets, this needs further study. The early-type magnetic stars have a favourable condition to fill their magnetospheres with ionized material. In fact, the stellar wind, even if in some cases the mass-loss rate is at a very weak level, has a key role as a plasma source. The UCDs and Jupiter have well-ordered dipolar fields, but are cold objects lacking winds of any significance, yet they produce non-thermal radio emission. However, if some other plasma source fills their magnetospheres (i.e. exo-planetary volcanic activity analogous to that of the moon Io), suitable conditions for the radio emission generation will be realized. The radio luminosity of incoherent emission from UCDs is low, and for only a few such emission has been detected while simultaneously having reliable magnetic field strengths. None the less, the few cold objects that we have analysed display radio behaviour in remarkable accord with the empirical scaling relationship deduced from the early-type stars. This is a clear hint of a common behaviour among both stars and sub-stellar objects surrounded by large-scale and stable magnetospheres, suggesting that an underlying and unifying physical mechanism is at work. In particular, it is plausible to hypothesize the existence of a common acceleration mechanism of electrons to relativistic energies operating within the magnetospheres among these extremely different classes of objects.
Future work must enlarge the sample of early-type magnetic stars to refine the empirical relationship for the non-thermal radio emission from ordered magnetospheres. In particular, a systematic search for radio emission at the top of the MS should be useful for the indirect estimation of stellar parameters, in particular the stellar magnetic field strength. In fact, on the basis of the empirical dependence between radio luminosity and stellar parameters, the detection of non-thermal radio emission might be used to constrain the stellar magnetic field strength.
The next generation of ground-based radio interferometer (e.g. SKA) will quickly be able to reach a detection limit at the |$\mu$|Jy level such that brighter early-type magnetic stars (Lν, rad ≈ 1018 ergs s−1 Hz−1) located close to the Galactic Centre (≈9 kpc distance) will be easily detected (expected flux levels |$\approx 10\, \mu$|Jy). Ap/Bp stars are uniformly distributed in space (Renson & Manfroid 2009), and the number recognized as magnetic stars is rapidly increasing (Fossati et al. 2015; Wade et al. 2016). At the present, spectropolarimetric measurements are able to perform reliable measurements of stellar magnetic fields only for stars located within 1–2 kpc from the Sun (Shultz et al. 2019a; Bagnulo et al. 2020). We emphasize that radio emission could be used as another diagnostic tool for stellar magnetism and leveraged to investigate the incidence of magnetism at the top of the MS. The origin of magnetic fields of early-type stars, and their persistence over their MS life, and beyond (Neiner et al. 2017; Martin et al. 2018), is a crucial matter. In fact, the magnetic field of the very massive stellar progenitor might be significant to the core-collapse supernovae explosion and the potential birth of magnetars (Bucciantini et al. 2009; Kasen & Bildsten 2010).
SUPPORTING INFORMATION
stab2168_supplementary_data.pdf
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
We sincerely thank the anonymous referee for his/her very useful and constructive criticisms and suggestions. This work has extensively used the NASA’s Astrophysics Data System, and the SIMBAD data base, operated at CDS, Strasbourg, France. LMO acknowledges support from the Deutsches Zentrum fur Luft und Raumfahrt (DLR) under grant no. FKZ 50 OR 1809 and partial support by the Russian Government Program of Competitive Growth of Kazan Federal University. FL was supported by ‘Programma ricerca di ateneo Università degli Studi di Catania (UNICT) 2020-22 linea 2’. RI acknowledges funding support for this research from a grant by the National Science Foundation, AST-2009412. MG acknowledges financial contribution from the agreement Agenzia Spaziale Italiana (ASI)-Istituto Nazionale di Astrofisica (INAF) no. 2018-16-HH.0. MES acknowledges financial support from the Annie Jump Cannon Fellowship, supported by the University of Delaware and endowed by the Mount Cuba Astronomical Observatory. A special thanks to the project MOSAICo (Metodologie Open Source per l’Automazione Industriale e delle procedure di CalcOlo in astrofisica) funded by Italian MISE (Ministero Sviluppo Economico).
DATA AVAILABILITY
The data underlying this article are available in the article and in its appendices available online.
Footnotes
The BONNSAI web-service is available at www.astro.uni-bonn.de/stars/bonnsai




