-
PDF
- Split View
-
Views
-
Cite
Cite
Tim Eifler, Melanie Simet, Elisabeth Krause, Christopher Hirata, Hung-Jin Huang, Xiao Fang, Vivian Miranda, Rachel Mandelbaum, Cyrille Doux, Chen Heinrich, Eric Huff, Hironao Miyatake, Shoubaneh Hemmati, Jiachuan Xu, Paul Rogozenski, Peter Capak, Ami Choi, Olivier Doré, Bhuvnesh Jain, Mike Jarvis, Jeffrey Kruk, Niall MacCrann, Dan Masters, Eduardo Rozo, David N Spergel, Michael Troxel, Anja von der Linden, Yun Wang, David H Weinberg, Lukas Wenzl, Hao-Yi Wu, Cosmology with the Roman Space Telescope: synergies with the Rubin Observatory Legacy Survey of Space and Time, Monthly Notices of the Royal Astronomical Society, Volume 507, Issue 1, October 2021, Pages 1514–1527, https://doi.org/10.1093/mnras/stab533
Close - Share Icon Share
ABSTRACT
We explore synergies between the Nancy Grace Roman Space Telescope and the Vera Rubin Observatory’s Legacy Survey of Space and Time (LSST). Specifically, we consider scenarios where the currently envisioned survey strategy for the Roman Space Telescope’s High Latitude Survey (HLS reference), i.e. 2000 deg2 in four narrow photometric bands is altered in favour of a strategy of rapid coverage of the LSST area (to full LSST depth) in one band. We find that in only five months, a survey in the W-band can cover the full LSST survey area providing high-resolution imaging for >95 per cent of the LSST Year 10 gold galaxy sample. We explore a second, more ambitious scenario where the Roman Space Telescope spends 1.5 yr covering the LSST area. For this second scenario, we quantify the constraining power on dark energy equation-of-state parameters from a joint weak lensing and galaxy clustering analysis. Our survey simulations are based on the Roman Space Telescope exposure-time calculator and redshift distributions from the CANDELS catalogue. Our statistical uncertainties account for higher order correlations of the density field, and we include a wide range of systematic effects, such as uncertainties in shape and redshift measurements, and modelling uncertainties of astrophysical systematics, such as galaxy bias, intrinsic galaxy alignment, and baryonic physics. We find a significant increase in constraining power for the joint LSST + HLS wide survey compared to LSST Y10 (FoMHLSwide = 2.4 FoMLSST) and compared to LSST + HLS (FoMHLSwide = 5.5 FoMHLSref).
1 INTRODUCTION
Observing the large-scale structure in our Universe provides a wealth of cosmological information and allows us to constrain fundamental physics questions such as the nature of dark energy, the mass, and number of species of neutrinos, possible modifications to general relativity as a function of scale or environment, or the nature of dark matter interactions.
Early results from the Dark Energy Survey (DES,1 Krause et al. 2017; Abbott et al. 2018, 2019; Troxel et al. 2018), the Kilo-Degree Survey (KiDS,2 Hildebrandt et al. 2018; van Uitert et al. 2018; Kuijken et al. 2019), and the Hyper Suprime Cam Subaru Strategic Program (HSC,3 Hamana et al. 2019; Hikage et al. 2019) have demonstrated the feasibility of complex (multiprobe) analyses from photometric data. Within the ΛCDM model, these surveys show a ∼2σ tension/agreement with Cosmic Microwave Background (CMB) measurements from the Planck satellite (Planck Collaboration VI 2018), which sets the stage for exciting near future discoveries when the full data of DES, HSC, and KiDS are analysed.
This discovery potential will increase significantly in the coming decade when photometric data from Stage 4 surveys become available (see Weinberg et al. 2013 for a review). The Rubin Observatory Legacy Survey of Space and Time (LSST,4 Ivezić et al. 2019), Euclid5 (Laureijs et al. 2011), the Spectro-Photometer for the History of the Universe, Epoch of Reionization, and Ices Explorer (SPHEREx,6 Doré et al. 2014), and the Roman Space Telescope (Roman Space Telescope,7 Spergel et al. 2015) complement each other in terms of area, depth, wavelength, and resolution and will provide a wealth of cosmological data to be mined by the community. The concert of cosmological endeavors in the 2020s also includes several spectroscopic experiments, e.g. the Dark Energy Spectroscopic Instrument (DESI, DESI Collaboration et al. 2016), the Prime Focus Spectrograph (PFS, Takada et al. 2014), the 4-m Multiobject Spectroscopic Telescope (4MOST, de Jong 2019), and of course the spectroscopic components of Euclid and the Roman Space Telescope. Together with the next generation of CMB surveys, such as the Simons Observatory (SO, Ade et al. 2019) and CMB-S4 (Abazajian et al. 2016), these experiments form a highly synergistic ensemble of data sets to study the physics of our Universe.
In this paper, we focus on synergies between the Roman Space Telescope’s High Latitude Survey (HLS from hereon) and LSST, specifically we explore alterations to the HLS observing strategy that maximize said synergies for a joint (photometric) clustering and weak lensing (so-called 3 x 2 pt) analysis. A joint LSST + HLS data set will enable a variety of other cosmological probe combinations and we refer the reader to a companion paper (Eifler et al. in prep.) for analysis strategies that include information from galaxy clusters, spectroscopic clustering, and Type Ia supernova.
The Vera C. Rubin Observatory will start commissioning and science verification in 2021 and is scheduled to be fully operational in 2022. The LSST is best described as a wide-fast-deep-repeat survey that will collect ∼15 TB of imaging data per day. This daily delivery of high-quality data to the science community will continue for at least 10 yr, i.e. until 2032. Thanks to its 9.6 deg2 field of view, 3.2 Gigapixel camera LSST can cover 10 000 deg2 in one of its six bands (320–1050 nm) every three nights. The short exposure time of 2 × 15 s and rapid mapping of the night sky is ideal to find transients and solar objects; for cosmologists, LSST offers a wide survey of 18 000 deg2, single exposure depth of 24.7 r-band magnitude (5σ point source), and a design optimized for photometric homogeneity and astrometric accuracy. The final data set will encompass >20 billion galaxies and a coadded map down to a depth of r-band magnitude 27.5.
The Nancy Grace Roman Space Telescope (Spergel et al. 2015) is scheduled to launch mid 2020s and it is probably best described as a multipurpose space observatory, with a 100 times larger field of view than the Hubble Space Telescope. The Roman Space Telescope’s versatile capabilities address science cases ranging from exoplanets to galaxy evolution to fundamental physics. The telescope’s High Latitude Survey (HLS, Doré et al. 2018) is designed to constrain dark energy evolution and deviations from GR with excellent control of systematics via space-quality imaging, photometry across four near-infrared (NIR) bands, a 0.28 deg2 field of view with a 0.11 arcsec pixel scale, and ∼600 resolution grism spectroscopy. The Reference8 design of the HLS assumes a duration of 1.6 yr covering 2000 deg2 with the imaging and spectroscopic modes. This strategy enables deep spectroscopic galaxy redshift measurements over the same survey area as the imaging survey.
Table 1 summarizes some of the main technical specifications of the Roman Space Telescope and LSST. Most obvious is the complementarity in multiwavelength information with LSST pushing towards the blue end in the visible whereas the Roman Space Telescope extends the colour information into the NIR. We note that while the current HLS survey design plans on using the YJHF bands, there are several other filters available, in particular the W-band ranging from 0.93-2.0 micron, which was introduced for the microlensing survey (Penny et al. 2019), and also bands that overlap with LSST towards the red part of the visible spectrum >0.5 micron.
Technical specifications characterizing the photometric data sets from LSST and Roman Space Telescope. Sensitivity refers to 5σ point source depth (please see table for exact exposure times that correspond to the depth numbers). We note that the exact strategy for LSST and Roman Space Telescope exposure duration is still being discussed.
| Roman Space Telescope parameters, following Spergel et al. (2015) . | |||||||
|---|---|---|---|---|---|---|---|
| Telescope aperture . | Field of view . | Pixel scale . | Wavelength range . | ||||
| 2.4 m . | 0.28 deg2 . | 0.11 arcsec . | 0.5–2.0 |$\mu$|m . | ||||
| Filters | R062 | Z087 | Y106 | J129 | H158 | F184 | W146 |
| Wavelength (|$\mu$|m) | 0.48–0.76 | 0.76–0.98 | 0.93–1.19 | 1.13–1.45 | 1.38–1.77 | 1.68–2.00 | 0.93–2.00 |
| Sensitivity (AB mag in 1 h) | 28.5 | 28.02 | 27.95 | 27.87 | 27.81 | 27.32 | 28.33 |
| LSST parameters, following The LSST Dark Energy Science Collaboration et al. (2018) and Ivezić et al. (2019). | |||||||
| Telescope aperture | Field of view | Pixel scale | Wavelength range | ||||
| 6.67 m (effective) | 9.62 deg2 | 0.2 arcsec | 0.32–1.0 |$\mu$|m | ||||
| Filters | u | g | r | i | z | y | |
| Wavelength (|$\mu$|m) | 0.32–0.40 | 0.40–0.55 | 0.55–0.69 | 0.69–0.82 | 0.82–0.92 | 0.92–1.0 | |
| Sensitivity (AB mag, full survey) | 25.30 | 26.84 | 27.04 | 26.35 | 25.22 | 24.47 | |
| Roman Space Telescope parameters, following Spergel et al. (2015) . | |||||||
|---|---|---|---|---|---|---|---|
| Telescope aperture . | Field of view . | Pixel scale . | Wavelength range . | ||||
| 2.4 m . | 0.28 deg2 . | 0.11 arcsec . | 0.5–2.0 |$\mu$|m . | ||||
| Filters | R062 | Z087 | Y106 | J129 | H158 | F184 | W146 |
| Wavelength (|$\mu$|m) | 0.48–0.76 | 0.76–0.98 | 0.93–1.19 | 1.13–1.45 | 1.38–1.77 | 1.68–2.00 | 0.93–2.00 |
| Sensitivity (AB mag in 1 h) | 28.5 | 28.02 | 27.95 | 27.87 | 27.81 | 27.32 | 28.33 |
| LSST parameters, following The LSST Dark Energy Science Collaboration et al. (2018) and Ivezić et al. (2019). | |||||||
| Telescope aperture | Field of view | Pixel scale | Wavelength range | ||||
| 6.67 m (effective) | 9.62 deg2 | 0.2 arcsec | 0.32–1.0 |$\mu$|m | ||||
| Filters | u | g | r | i | z | y | |
| Wavelength (|$\mu$|m) | 0.32–0.40 | 0.40–0.55 | 0.55–0.69 | 0.69–0.82 | 0.82–0.92 | 0.92–1.0 | |
| Sensitivity (AB mag, full survey) | 25.30 | 26.84 | 27.04 | 26.35 | 25.22 | 24.47 | |
Technical specifications characterizing the photometric data sets from LSST and Roman Space Telescope. Sensitivity refers to 5σ point source depth (please see table for exact exposure times that correspond to the depth numbers). We note that the exact strategy for LSST and Roman Space Telescope exposure duration is still being discussed.
| Roman Space Telescope parameters, following Spergel et al. (2015) . | |||||||
|---|---|---|---|---|---|---|---|
| Telescope aperture . | Field of view . | Pixel scale . | Wavelength range . | ||||
| 2.4 m . | 0.28 deg2 . | 0.11 arcsec . | 0.5–2.0 |$\mu$|m . | ||||
| Filters | R062 | Z087 | Y106 | J129 | H158 | F184 | W146 |
| Wavelength (|$\mu$|m) | 0.48–0.76 | 0.76–0.98 | 0.93–1.19 | 1.13–1.45 | 1.38–1.77 | 1.68–2.00 | 0.93–2.00 |
| Sensitivity (AB mag in 1 h) | 28.5 | 28.02 | 27.95 | 27.87 | 27.81 | 27.32 | 28.33 |
| LSST parameters, following The LSST Dark Energy Science Collaboration et al. (2018) and Ivezić et al. (2019). | |||||||
| Telescope aperture | Field of view | Pixel scale | Wavelength range | ||||
| 6.67 m (effective) | 9.62 deg2 | 0.2 arcsec | 0.32–1.0 |$\mu$|m | ||||
| Filters | u | g | r | i | z | y | |
| Wavelength (|$\mu$|m) | 0.32–0.40 | 0.40–0.55 | 0.55–0.69 | 0.69–0.82 | 0.82–0.92 | 0.92–1.0 | |
| Sensitivity (AB mag, full survey) | 25.30 | 26.84 | 27.04 | 26.35 | 25.22 | 24.47 | |
| Roman Space Telescope parameters, following Spergel et al. (2015) . | |||||||
|---|---|---|---|---|---|---|---|
| Telescope aperture . | Field of view . | Pixel scale . | Wavelength range . | ||||
| 2.4 m . | 0.28 deg2 . | 0.11 arcsec . | 0.5–2.0 |$\mu$|m . | ||||
| Filters | R062 | Z087 | Y106 | J129 | H158 | F184 | W146 |
| Wavelength (|$\mu$|m) | 0.48–0.76 | 0.76–0.98 | 0.93–1.19 | 1.13–1.45 | 1.38–1.77 | 1.68–2.00 | 0.93–2.00 |
| Sensitivity (AB mag in 1 h) | 28.5 | 28.02 | 27.95 | 27.87 | 27.81 | 27.32 | 28.33 |
| LSST parameters, following The LSST Dark Energy Science Collaboration et al. (2018) and Ivezić et al. (2019). | |||||||
| Telescope aperture | Field of view | Pixel scale | Wavelength range | ||||
| 6.67 m (effective) | 9.62 deg2 | 0.2 arcsec | 0.32–1.0 |$\mu$|m | ||||
| Filters | u | g | r | i | z | y | |
| Wavelength (|$\mu$|m) | 0.32–0.40 | 0.40–0.55 | 0.55–0.69 | 0.69–0.82 | 0.82–0.92 | 0.92–1.0 | |
| Sensitivity (AB mag, full survey) | 25.30 | 26.84 | 27.04 | 26.35 | 25.22 | 24.47 | |
In this paper, we comment on several scenarios where a single Roman Space Telescope band is used for a rapid, deep coverage of the LSST area. The combination of colour information down to 320 nm from the ground, and high-resolution infrared coverage from space over 18 000 deg2 can potentially unlock a new level of precision for the core science cases of both experiments, if and only if, systematics control is maintained at the new level. Throughout the paper, we refer to this single-band concept as HLS wide and we will contrast it with the Reference 4 NIR-band 2000 deg2 survey design, which we refer to as HLS reference. We iterate that both concepts, HLS wide, and HLS ref, include LSST data as part of their analysis and should technically be labelled LSST + HLS.
2 MULTI-PROBE ANALYSIS BASICS – COMBINING WEAK LENSING AND GALAXY CLUSTERING
2.1 Forecasting philosophy
A large variety of cosmological probes can be extracted from wide-field imaging and spectroscopic Roman Space Telescope observations, such as various forms of weak lensing (e.g. cosmic shear using second and higher order summary statistics, magnification, galaxy–galaxy lensing, cluster weak lensing, and shear peak statistics), galaxy clustering (spectroscopic 3D and projected 2D), galaxy cluster number counts, CMB-lensing cross-correlations, Baryon Acoustic Oscillations, and redshift space distortions.
Statements about the constraining power of different survey concepts are a function of the exact ingredients for the data vector, which does not just include the combination of probes but also the exact scales and redshifts that are included, the systematics considered, the parametrization and priors of said systematics, and the priors and parameters of the cosmological model of interest.
Our forecasting philosophy is driven by the intent to model a realistic HLS and LSST 3 x 2 pt analysis (joint weak lensing and galaxy clustering). A realistic assessment of the constraining power means to compute realistic error bars, which requires accurately computing three main components of a likelihood analysis: (1) statistical uncertainties, (2) systematic uncertainties, and (3) inference aspects of the likelihood analysis.
Regarding the statistical uncertainties, we use analytic, non-Gaussian covariance matrices that include higher order moments of the density field and super-sample variance and that have been compared to numerical simulations (albeit only in less constraining cases). We also use realistic survey simulations (see Section 3) to quantify the number density and redshift distributions of source and lens sample and to compute a realistic survey area for a given scenario. Regarding systematic uncertainties, we include observational uncertainties such as shear calibration uncertainties and photo-z errors for lens and source sample. We parametrize a variety of astrophysics uncertainties: galaxy bias uncertainties are captured through a combination of scale cuts and nuisance parameters; similarly, we include uncertainties from intrinsic galaxy alignment and baryonic physics modelling again through a combination of nuisance parameters and scale cuts. The exact implementation is described in Section 4.
Regarding robust inference, we opted for simulated MCMC analyses instead of Fisher matrices in order to avoid numerical uncertainties in computing high-dimensional (56 dimensions spanning cosmological and nuisance parameters) derivatives of the observables and in order to capture posterior probabilities beyond the multivariate Gaussian.
We employ the cosmolike framework (Eifler et al. 2014; Krause & Eifler 2017) for the simulated likelihood analyses, however, we do not use its most sophisticated modules to model the density power spectrum and the subsequent projected power spectra. For example, we do not use a Boltzmann code to compute the initial power spectrum nor do we include reduced shear, non-Limber, or magnification in the calculation of the summary statistics. We reason that since the (noise-free) data vector is computed with the exact same cosmolike module, the per cent uncertainty arising from these approximations do not alter our conclusions regarding the relative merits of different survey options. Generally speaking, we argue that modelling uncertainties can be ignored for the purpose of quantifying constraining power unless they contribute to the error budget at a level comparable to our main error sources (statistical uncertainties, shear calibration, photo-z uncertainties, galaxy bias, intrinsic alignment, baryonic physics).
Adopting this strategy has the major advantage that we can use the much faster forecasting routines of cosmolike, which speeds up our simulated likelihood analysis by a factor of ∼20, from 10 s per MCMC step to ∼0.5 s . This allows us to compute long, converged chains, and it enables a future in-depth survey scenario study that varies the baseline choices and priors presented in Table 2.
Fiducial parameters, flat priors (min, max), and Gaussian priors (μ, σ) for HLS reference, LSST, and HLS wide. We include survey specific parameters with the fiducial values and priors in the upper half of the table, where Gauss(μ, σ) stands for Gaussian priors with mean μ and deviation σ. In the lower half, we list the cosmological and astrophysical parameters. Flat (min, max) stands for a flat prior between (min, max).
| . | HLS reference . | LSST . | HLS wide . | |||
|---|---|---|---|---|---|---|
| Parameter . | Fid . | Prior . | Fid . | Prior . | Fid . | Prior . |
| Survey | ||||||
| Ωs | 2000 deg2 | Fixed | 18 000 deg2 | Fixed | 18 000 deg2 | Fixed |
| nsource | 51 gal arcmin–2 | Fixed | 27 gal arcmin–2 | Fixed | 43 gal arcmin–2 | Fixed |
| σϵ | 0.26 | Fixed | 0.26 | Fixed | 0.26 | Fixed |
| nlens | 66 gal arcmin–2 | Fixed | 48 gal arcmin–2 | Fixed | 50 gal arcmin–2 | Fixed |
| Lens photo-z | ||||||
| |$\Delta _\mathrm{z,lens}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, lens | 0.01 | Gauss (0.01, 0.002) | 0.03 | Gauss (0.03, 0.003) | 0.02 | Gauss (0.02, 0.002) |
| Source photo-z | ||||||
| |$\Delta _\mathrm{z,source}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, source | 0.01 | Gauss (0.01, 0.002) | 0.05 | Gauss (0.05, 0.003) | 0.05 | Gauss (0.02, 0.002) |
| Shear calibration | ||||||
| mi | 0.0 | Gauss (0.0, 0.002) | 0.0 | Gauss (0.0, 0.003) | 0.0 | Gauss (0.0, 0.002) |
| Common assumptions across all surveys | ||||||
| Parameter | Fid | Prior | ||||
| Cosmology | ||||||
| Ωm | 0.3156 | Flat (0.1, 0.6) | ||||
| σ8 | 0.831 | Flat (0.6, 0.95) | ||||
| ns | 0.9645 | Flat (0.85, 1.06) | ||||
| w0 | –1.0 | Flat (–2.0, 0.0) | ||||
| wa | 0.0 | Flat (–2.5, 2.5) | ||||
| Ωb | 0.0492 | Flat (0.04, 0.055) | ||||
| h0 | 0.6727 | Flat (0.6, 0.76) | ||||
| Galaxy bias (tomographic bins) | ||||||
| |$b_\mathrm{g}^i$| | 1.3 + i × 0.1 | Flat (0.8, 3.0) | ||||
| Intrinsic alignment | ||||||
| AIA | 5.95 | Flat (0.0, 10) | ||||
| βIA | 1.1 | Flat (–4.0, 6.0) | ||||
| ηIA | 0.49 | Flat (–10.0, 10.0) | ||||
| |$\eta ^\mathrm{high-z}_\mathrm{IA}$| | 0.0 | Flat (–1.0, 1.0) | ||||
| Baryonic physics | ||||||
| Q1 | 0.0 | Gauss (0.0, 16.0) | ||||
| Q2 | 0.0 | Gauss (0.0, 5.0) | ||||
| Q3 | 0.0 | Gauss (0.0, 0.8) | ||||
| . | HLS reference . | LSST . | HLS wide . | |||
|---|---|---|---|---|---|---|
| Parameter . | Fid . | Prior . | Fid . | Prior . | Fid . | Prior . |
| Survey | ||||||
| Ωs | 2000 deg2 | Fixed | 18 000 deg2 | Fixed | 18 000 deg2 | Fixed |
| nsource | 51 gal arcmin–2 | Fixed | 27 gal arcmin–2 | Fixed | 43 gal arcmin–2 | Fixed |
| σϵ | 0.26 | Fixed | 0.26 | Fixed | 0.26 | Fixed |
| nlens | 66 gal arcmin–2 | Fixed | 48 gal arcmin–2 | Fixed | 50 gal arcmin–2 | Fixed |
| Lens photo-z | ||||||
| |$\Delta _\mathrm{z,lens}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, lens | 0.01 | Gauss (0.01, 0.002) | 0.03 | Gauss (0.03, 0.003) | 0.02 | Gauss (0.02, 0.002) |
| Source photo-z | ||||||
| |$\Delta _\mathrm{z,source}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, source | 0.01 | Gauss (0.01, 0.002) | 0.05 | Gauss (0.05, 0.003) | 0.05 | Gauss (0.02, 0.002) |
| Shear calibration | ||||||
| mi | 0.0 | Gauss (0.0, 0.002) | 0.0 | Gauss (0.0, 0.003) | 0.0 | Gauss (0.0, 0.002) |
| Common assumptions across all surveys | ||||||
| Parameter | Fid | Prior | ||||
| Cosmology | ||||||
| Ωm | 0.3156 | Flat (0.1, 0.6) | ||||
| σ8 | 0.831 | Flat (0.6, 0.95) | ||||
| ns | 0.9645 | Flat (0.85, 1.06) | ||||
| w0 | –1.0 | Flat (–2.0, 0.0) | ||||
| wa | 0.0 | Flat (–2.5, 2.5) | ||||
| Ωb | 0.0492 | Flat (0.04, 0.055) | ||||
| h0 | 0.6727 | Flat (0.6, 0.76) | ||||
| Galaxy bias (tomographic bins) | ||||||
| |$b_\mathrm{g}^i$| | 1.3 + i × 0.1 | Flat (0.8, 3.0) | ||||
| Intrinsic alignment | ||||||
| AIA | 5.95 | Flat (0.0, 10) | ||||
| βIA | 1.1 | Flat (–4.0, 6.0) | ||||
| ηIA | 0.49 | Flat (–10.0, 10.0) | ||||
| |$\eta ^\mathrm{high-z}_\mathrm{IA}$| | 0.0 | Flat (–1.0, 1.0) | ||||
| Baryonic physics | ||||||
| Q1 | 0.0 | Gauss (0.0, 16.0) | ||||
| Q2 | 0.0 | Gauss (0.0, 5.0) | ||||
| Q3 | 0.0 | Gauss (0.0, 0.8) | ||||
Fiducial parameters, flat priors (min, max), and Gaussian priors (μ, σ) for HLS reference, LSST, and HLS wide. We include survey specific parameters with the fiducial values and priors in the upper half of the table, where Gauss(μ, σ) stands for Gaussian priors with mean μ and deviation σ. In the lower half, we list the cosmological and astrophysical parameters. Flat (min, max) stands for a flat prior between (min, max).
| . | HLS reference . | LSST . | HLS wide . | |||
|---|---|---|---|---|---|---|
| Parameter . | Fid . | Prior . | Fid . | Prior . | Fid . | Prior . |
| Survey | ||||||
| Ωs | 2000 deg2 | Fixed | 18 000 deg2 | Fixed | 18 000 deg2 | Fixed |
| nsource | 51 gal arcmin–2 | Fixed | 27 gal arcmin–2 | Fixed | 43 gal arcmin–2 | Fixed |
| σϵ | 0.26 | Fixed | 0.26 | Fixed | 0.26 | Fixed |
| nlens | 66 gal arcmin–2 | Fixed | 48 gal arcmin–2 | Fixed | 50 gal arcmin–2 | Fixed |
| Lens photo-z | ||||||
| |$\Delta _\mathrm{z,lens}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, lens | 0.01 | Gauss (0.01, 0.002) | 0.03 | Gauss (0.03, 0.003) | 0.02 | Gauss (0.02, 0.002) |
| Source photo-z | ||||||
| |$\Delta _\mathrm{z,source}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, source | 0.01 | Gauss (0.01, 0.002) | 0.05 | Gauss (0.05, 0.003) | 0.05 | Gauss (0.02, 0.002) |
| Shear calibration | ||||||
| mi | 0.0 | Gauss (0.0, 0.002) | 0.0 | Gauss (0.0, 0.003) | 0.0 | Gauss (0.0, 0.002) |
| Common assumptions across all surveys | ||||||
| Parameter | Fid | Prior | ||||
| Cosmology | ||||||
| Ωm | 0.3156 | Flat (0.1, 0.6) | ||||
| σ8 | 0.831 | Flat (0.6, 0.95) | ||||
| ns | 0.9645 | Flat (0.85, 1.06) | ||||
| w0 | –1.0 | Flat (–2.0, 0.0) | ||||
| wa | 0.0 | Flat (–2.5, 2.5) | ||||
| Ωb | 0.0492 | Flat (0.04, 0.055) | ||||
| h0 | 0.6727 | Flat (0.6, 0.76) | ||||
| Galaxy bias (tomographic bins) | ||||||
| |$b_\mathrm{g}^i$| | 1.3 + i × 0.1 | Flat (0.8, 3.0) | ||||
| Intrinsic alignment | ||||||
| AIA | 5.95 | Flat (0.0, 10) | ||||
| βIA | 1.1 | Flat (–4.0, 6.0) | ||||
| ηIA | 0.49 | Flat (–10.0, 10.0) | ||||
| |$\eta ^\mathrm{high-z}_\mathrm{IA}$| | 0.0 | Flat (–1.0, 1.0) | ||||
| Baryonic physics | ||||||
| Q1 | 0.0 | Gauss (0.0, 16.0) | ||||
| Q2 | 0.0 | Gauss (0.0, 5.0) | ||||
| Q3 | 0.0 | Gauss (0.0, 0.8) | ||||
| . | HLS reference . | LSST . | HLS wide . | |||
|---|---|---|---|---|---|---|
| Parameter . | Fid . | Prior . | Fid . | Prior . | Fid . | Prior . |
| Survey | ||||||
| Ωs | 2000 deg2 | Fixed | 18 000 deg2 | Fixed | 18 000 deg2 | Fixed |
| nsource | 51 gal arcmin–2 | Fixed | 27 gal arcmin–2 | Fixed | 43 gal arcmin–2 | Fixed |
| σϵ | 0.26 | Fixed | 0.26 | Fixed | 0.26 | Fixed |
| nlens | 66 gal arcmin–2 | Fixed | 48 gal arcmin–2 | Fixed | 50 gal arcmin–2 | Fixed |
| Lens photo-z | ||||||
| |$\Delta _\mathrm{z,lens}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, lens | 0.01 | Gauss (0.01, 0.002) | 0.03 | Gauss (0.03, 0.003) | 0.02 | Gauss (0.02, 0.002) |
| Source photo-z | ||||||
| |$\Delta _\mathrm{z,source}^i$| | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) | 0.0 | Gauss (0.0, 0.001) |
| σz, source | 0.01 | Gauss (0.01, 0.002) | 0.05 | Gauss (0.05, 0.003) | 0.05 | Gauss (0.02, 0.002) |
| Shear calibration | ||||||
| mi | 0.0 | Gauss (0.0, 0.002) | 0.0 | Gauss (0.0, 0.003) | 0.0 | Gauss (0.0, 0.002) |
| Common assumptions across all surveys | ||||||
| Parameter | Fid | Prior | ||||
| Cosmology | ||||||
| Ωm | 0.3156 | Flat (0.1, 0.6) | ||||
| σ8 | 0.831 | Flat (0.6, 0.95) | ||||
| ns | 0.9645 | Flat (0.85, 1.06) | ||||
| w0 | –1.0 | Flat (–2.0, 0.0) | ||||
| wa | 0.0 | Flat (–2.5, 2.5) | ||||
| Ωb | 0.0492 | Flat (0.04, 0.055) | ||||
| h0 | 0.6727 | Flat (0.6, 0.76) | ||||
| Galaxy bias (tomographic bins) | ||||||
| |$b_\mathrm{g}^i$| | 1.3 + i × 0.1 | Flat (0.8, 3.0) | ||||
| Intrinsic alignment | ||||||
| AIA | 5.95 | Flat (0.0, 10) | ||||
| βIA | 1.1 | Flat (–4.0, 6.0) | ||||
| ηIA | 0.49 | Flat (–10.0, 10.0) | ||||
| |$\eta ^\mathrm{high-z}_\mathrm{IA}$| | 0.0 | Flat (–1.0, 1.0) | ||||
| Baryonic physics | ||||||
| Q1 | 0.0 | Gauss (0.0, 16.0) | ||||
| Q2 | 0.0 | Gauss (0.0, 5.0) | ||||
| Q3 | 0.0 | Gauss (0.0, 0.8) | ||||
We note that our forecasting setup differs from the recent Euclid forecasting study (Blanchard et al. 2020) in several aspects: First, the Euclid study considers a 3 x 2 pt analysis using a combination of spectroscopic and photometric data, whereas our 3 x 2 pt analysis uses photometric data only. We refer the reader to Eifler et al. (in prep.) for forecasts of the spectroscopic Roman Space Telescope component. Secondly, our focus is on exploring new survey strategies in the presence of detailed systematics modelling, whereas (Blanchard et al. 2020) focuses on code comparison and only considers very limited freedom for systematics parameters assuming most of them to be known perfectly. These aspects limit the interpretation of direct comparisons, we note however a one-to-one comparison may be of interest to the community in the future.
2.2 Modelling details
In this section, we summarize the computation of angular (cross) power spectra for the different probes closely following the notation in Krause & Eifler (2017); a more detailed derivation can be found in Hu & Jain (2004). We use capital Roman subscripts to denote observables, A, B ∈ {κ, δg}, where κ refers to the lensing of source galaxies and δg is the density contrast of the lens galaxy sample.
We note the frequent confusion originating from the terms ‘lens sample’ and ‘lensed galaxy sample’ and clarify that we only use the position information of the lens sample. Specifically, the autocorrelation of positions of lens sample galaxies will later form the galaxy clustering part of the 3 x 2 pt data vector, whereas the autocorrelation of lensed galaxy shapes, that is the cosmic shear part of the data vector, is computed using the source galaxy sample.
2.3 Covariance and inference details
The multiprobe data vector, denoted as |$\boldsymbol D$|, is computed at the fiducial cosmology and systematics parameter values (see Table 2). The same parameters are assumed in the computation of the non-Gaussian covariance matrix, |$\mathbf {C}$|. Given that this covariance matrix is calculated analytically, it is not an estimated quantity derived from either simulations or measured data. As a quantity that is free of estimator noise analytical covariance matrices can be inverted directly and do not require large amounts of realizations for the inverse to be precise (see e.g. Dodelson & Schneider 2013; Taylor, Joachimi & Kitching 2013; Friedrich & Eifler 2018, for details on the number of realizations and alternative ideas).
However, the assumption of a covariance matrix |$\mathbf {C}$| that remains constant throughout the MCMC process, with the input parameters perfectly known, is illogical given that it is exactly said parameters that we aim to constrain in a likelihood analysis. Eifler, Schneider & Hartlap (2009) explore the idea of varying the covariance as a function of parameters, similar to the way one varies the model data vector. Carron (2013) shows that using a parameter dependent covariance in combination with a Gaussian likelihood function violates the Cramér–Rao bound and recommends not to use this combination in a likelihood analysis. This recommendation has led e.g. DES likelihood analyses to adapt a second recommendation of Eifler et al. (2009): an iterative likelihood analysis approach, where the parameters of the covariance are updated in a new likelihood analysis based on the best-fitting parameters of the previous run.
We follow this approach and assume a multivariate Gaussian likelihood as described in equation (7) with a constant covariance matrix computed at the fiducial parameters for all the surveys considered.
Given the likelihood function, we compute the posterior probability in parameter space from Bayes’ theorem and we sample the parameter space using emcee9 (Foreman-Mackey et al. 2013), which is based on the affine-invariant sampler of Goodman & Weare (2010), and which can be parallelized with either MPI or shared memory multiprocessing.
3 SIMULATING THE HLS AND LSST SURVEYS
3.1 Rubin Observatory – LSST
In order to incorporate the latest analysis choices for a 3 x 2 pt LSST analysis, we closely follow the LSST DESC Science Requirements Document v1, published as The LSST Dark Energy Science Collaboration et al. (2018; D18 from hereon), which reflects a conservative consensus choice across the LSST DESC. In D18 survey, depths are based on the opsim software,10 specifically the opsim v3 minion_1016 run. The scenario described in D18 has median depth (5σ point-source detection across the survey) of 25.30, 26.84, 27.04, 26.35, 25.22, 24.47 in ugrizy after 10 yr. These numbers are determined after discarding areas with limiting i-band magnitude (AB) i-mag < 26 to homogenize the depth across the whole survey. LSST dark energy science will exclude data from regions near a Galactic latitude of zero and likely discard areas with E(B − V) > 0.2 . In D18, the resulting area after this homogenization process is 14 300 deg2; for the purpose of this paper, we however assume the more ambitious survey area of 18 000 deg2.
LSST is evaluating a variety of different survey strategies (see e.g. Lochner et al. 2018) with possible survey areas ranging from below 15 000 deg2 to more than 25 000 deg2. Our 18 000 deg2 extragalactic sky coverage scenario is well within the range of options, although, we note that the survey depth choices of this paper can only be achieved if LSST would shift observing time from the low Galactic latitudes to the extragalactic survey.
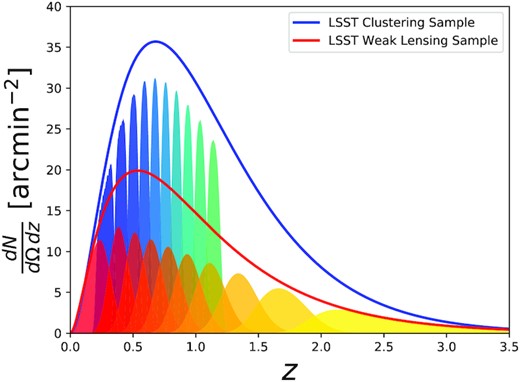
LSST redshift distribution with 10 tomographic lens bins (blue) and 10 tomographic source bins (red), based on the ingredients from D18. We note the 10 lens bins are at lower redshift (≤1.2) and are more narrow compared to the HLS bins, which leads to a larger number of galaxy–galaxy lensing bins in the data vector.
3.2 Roman Space Telescope – HLS
We use the Roman Space Telescope exposure time calculator (ETC; Hirata et al. 2012) to compute realistic survey scenarios for the HLS’ coverage of area and depth in a given band. We fix the time per exposure and vary the number of exposures to build up depth over the survey area of a given scenario. For the HLS Reference survey, this area is 2000 deg2, for the HLS wide scenario, it corresponds to the LSST area of 18 000 deg2. The total survey time for a given number of exposures includes a simple prescription for overheads and is correct to approximately 10 |${{\ \rm per\ cent}}$|.
In order to obtain accurate redshift distributions, we closely follow Hemmati et al. (2019) in applying the ETC results to the CANDELS data set (Grogin et al. 2011; Koekemoer et al. 2011), which is the only data set available that is sufficiently deep in the near-infrared to model Roman Space Telescope observations. The ETC has a built-in option to obtain a weak lensing catalogue based on an input catalogue of detected sources. The criteria for galaxies to be considered suitable for weak lensing are S/N> 18 (J + H band combined, matched filter), resolution factor R > 0.4, and ellipticity dispersion σϵ < 0.2, where we use the Bernstein & Jarvis (2002) convention (i.e. ϵ = (a2 − b2)/(a2 + b2) instead of (a − b)/(a + b)). We apply these selections to the CANDELS catalogue and obtain our source sample for the HLS reference four NIR band survey. For the lens sample, we select CANDELS galaxies with S/N > 10 in each of the four HLS reference bands. Our HLS analysis assumes LSST photometry from the ground, hence we further down-select both samples by imposing a S/N> 5 cut in each LSST band, except for the u-band. We note that nevertheless more than 50 per cent of our galaxies have S/N > 5 in u-band as well.
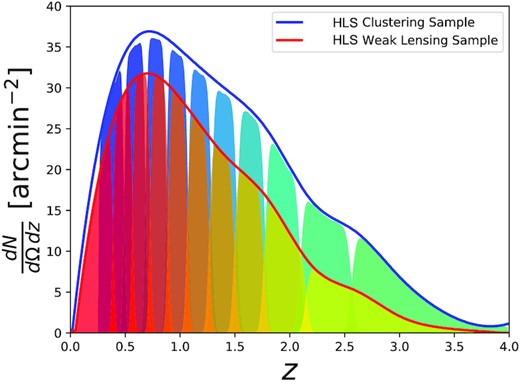
This plot shows the HLS redshift distribution with the 10 tomographic lens bins (blue) and 10 tomographic source bins (red). The Gaussian photo-z tomographic bin-width (σz = 0.01) corresponds to the optimistic scenario that we assume for the combined HLS and LSST band coverage, i.e. four NIR and six optical bands.
3.3 Roman Space Telescope survey strategy variations
After defining the LSST and the HLS reference scenario in the past sections, we now explore and motivate possible variations in the HLS survey strategy, in particular a HLS wide scenario that covers the LSST footprint in the W-band (see Table 1). We again use the CANDELS catalogue when defining galaxy samples for HLS wide and LSST below.
Fig. 3 shows the results when using the ETC to compute the depth of the W-band as a function of time under the assumption that no other bands are used. We find that a ∼5 month HLS W-band survey can obtain high-resolution space imaging for |$\sim 95{{\ \rm per\ cent}}$| of the LSST gold sample (see Fig. 3).
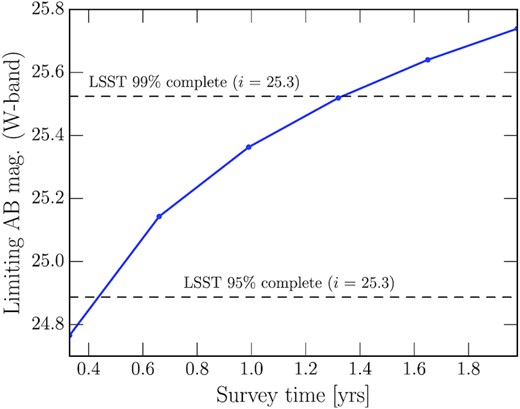
Limiting magnitude of a 18 000 deg2 HLS W-band survey as a function of survey time. We also show the 95 and 99 |${{\ \rm per\ cent}}$| completeness thresholds of the LSST gold sample (i< 25.3, as defined in LSST Science Collaboration et al. 2009, which corresponds to S/N> 20 for point sources) as dashed lines.
As a first result of this paper, we conclude that if blending poses a systematics limitation to LSST weak lensing cosmology, a dedicated 5 month HLS survey would identify almost all LSST blends and enable improved modelling of shapes and photo-z for said blends.
A 1.3 yr HLS W-band survey will provide corresponding information for |$\sim 99{{\ \rm per\ cent}}$| of the LSST gold sample and of course also substantially increase the depth of the HLS imaging. This opens up the idea to use the deeper HLS imaging for shape measurements and combine these with the ground-based LSST photometry.
To explore this idea further, we define a HLS wide scenario, perform a full simulated likelihood analysis, and compare the results to the constraining power of an LSST Year 10 survey and the HLS reference survey. We assume a 1.5-yr HLS wide survey in the W-band and follow the same procedure as for the HLS reference survey (Section 3.2) in deriving the lens and source sample.
Fig. 4 shows the number density of galaxies suitable for shape measurements from a HLS 18 000 deg2 survey as a function of survey time and Fig. 5 shows the corresponding fraction of LSST galaxies for which good photo-z information (5σ detection in the LSST bands, except for u-band) can be obtained. We also show the corresponding results for the Roman Space Telescope H-band, which is useful as an alternative to the W-band since wavelength-dependent point spread function (PSF) modelling might prohibit shape measurements from a band as broad as the W-band. Roman Space Telescope’s diffraction-limited PSF size ranges from 0.085 to 0.175 arcsec over the W-band, which is about a 50 per cent change, compared to only a 20 per cent change when using its H-band.
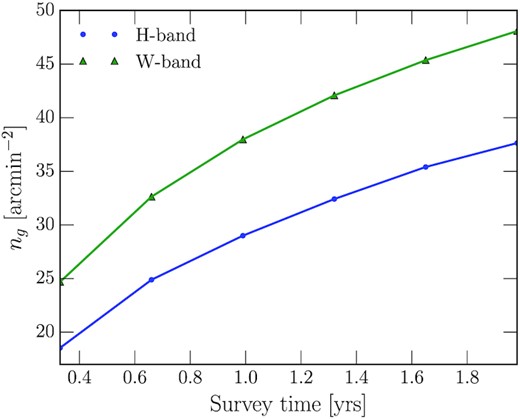
The number density of a HLS wide weak lensing galaxy sample for a 18 000 deg2 survey when conducted in W or H-band, respectively, again as a function of survey time.
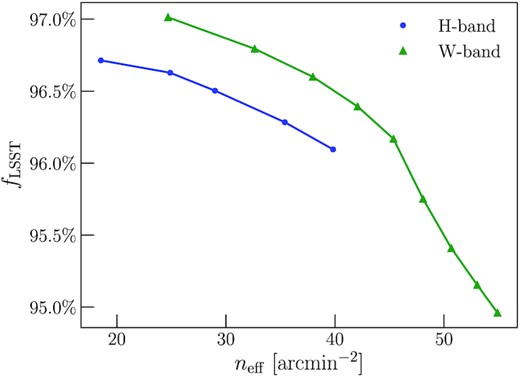
Fraction of LSST galaxies with acceptable multiband photometry as a function of number density of a HLS weak lensing sample, based on the CANDELS catalogue.
We note that the ESA/NASA Euclid satellite mission is developing mitigation techniques for a similar problem given that Euclid’s diffraction-limited PSF size ranges from 0.085 to 0.155 arcsec over the VIS band, i.e. the main band in which Euclid measures shapes. Cypriano et al. (2010), Carlsten et al. (2018), and Eriksen & Hoekstra (2018) propose a variety of methods on how to control wavelength-dependent PSF uncertainties through a combination of improved galaxy spectral energy templates or PSF measurements based on stars that span the same colour range as the galaxies. Additional photometric information from the ground is the main avenue for Euclid to gain the relevant information to mitigate this effect, albeit this is of course limited by the difference in resolution of space- and ground-based imaging (also see Meyers & Burchat 2015, for additional wavelength-dependent PSF effects from the atmosphere).
The Roman Space Telescope is in the unique position to collect narrow band, space resolution imaging over a smaller, but representative area and calibrate its HLS wide W-band survey if this effect becomes the dominant systematic.
A 1.5-yr HLS wide survey would yield 45 galaxies arcmin−2 for the source sample (cf. Fig. 4) and 68 galaxies arcmin−2 for the lens sample, which is again defined as a S/N > 10 cut based on the CANDELS catalogue. Since we require good LSST photometry for our HLS galaxy sample, these number densities are further reduced to 43 galaxies arcmin−2 (cf. Fig. 5) for the joint source and 50 galaxies arcmin−2 for the joint lens sample.
The calculation of the redshift distributions follow the same procedure as for the HLS reference survey (Section 3.2). The only difference is that we assume a slightly wider Gaussian kernel σz = 0.02 compared to the HLS reference scenario in order to account for the fact that we now only have one broad-band instead of four.
4 LIKELIHOOD ANALYSIS - WEAK LENSING AND GALAXY CLUSTERING
In Sections 2 and 3, we describe the basic setup of our analysis including covariance computation, modelling of observables, inference process, galaxy sample selection, and redshift distribution computation. In the following, we detail the analysis choices for our likelihood analysis including details on the systematics implementation.
4.1 Building a 3 x 2 pt data vector
4.1.1 Source galaxies – cosmic shear
Given the 10 tomographic bins for the source sample, we compute 55 cosmic shear auto and cross power spectra, which we divide into 15 logarithmically spaced Fourier mode bins ranging from ℓmin = 30 to ℓmax = 3000.
4.1.2 Lens galaxies – galaxy clustering
The galaxy clustering data vector is also divided into 15 ℓ-bins ranging from 30 to 3000, however, we exclude high ℓ-bins, if scales below |$R_\mathrm{\min }=2\pi /k_\mathrm{max}=21 \mathrm{\,\,Mpc}\, \rm h^{-1}$| contribute to the projected integral (see equation 1).
4.1.3 Lens × source galaxies – galaxy–galaxy lensing
The galaxy–galaxy lensing part of the data vector assumes the lens galaxy sample as foreground and the source galaxy sample as background galaxies; we only consider non-overlapping source and lens in redshift bins. We again impose a cut-off at |$R_\mathrm{\min }=21 \mathrm{\,\,Mpc}\,\rm h^{-1}$| for the baseline model. We note that the low, narrow redshift distribution of the 10 lens tomographic bins of the LSST scenario leads to a substantially higher number of galaxy–galaxy lensing power spectra (52), compared to both HLS scenarios (32).
4.2 Systematics
We parametrize uncertainties arising from systematics through nuisance parameters, which are summarized with their fiducial values and priors in Table 2. Our default likelihood analysis includes the following systematics:
Photometric redshift uncertainties. As described in detail in Section 3, we consider Gaussian photometric redshift uncertainties, which are characterized by scatter σz(z) and bias Δz(z). While these may in general be arbitrary functions, we further assume that the scatter can be described by the simple redshift scaling σz, x(1 + z), and we allow σz, x to vary around its fiducial value. Furthermore, we implement one (constant) bias parameter |$\Delta ^i_{z,x}$| per redshift bin (cf. equation 14) as a free parameter that is again allowed to vary with Gaussian priors.
Since we have 10 tomographic bins for the lens and source sample, we vary 20 photo-z bias parameters |$\Delta ^i_{z,x}$| and two photo-z scatter parameters σz, x(1 + z).
We note that the selection and characterization of lens and source galaxy samples are some of the most challenging choices in a multiprobe analysis and variations warrant future investigation. The trade space of photo-z accuracy versus number density, e.g. by using a ‘redmagic’ sample (Rozo et al. 2016) instead of the LSST Gold sample is interesting to explore further.
Linear galaxy bias is described by one nuisance parameter per lens galaxy redshift bin |$b_\mathrm{g}^i$|, which is marginalized over using conservative flat priors [0.8; 3.0].
We note that the fiducial values of the galaxy bias parameters have little impact on the results, however, a more stringent prior would be highly beneficial. For example, the interplay of galaxy bias and photo-z uncertainties limits the ability of galaxy–galaxy lensing to self-calibrate intrinsic alignment models. Prior information on linear galaxy bias parameters would also help implement higher order bias models that require additional free parameters but that would allow to push to smaller scales in clustering and galaxy–galaxy lensing (Desjacques, Jeong & Schmidt 2018; Ivanov, Simonović & Zaldarriaga 2019).
Shape measurement uncertainties are a primary concern for all weak lensing based cosmology endeavors. Substantial progress has been made in the past years to model and control shape measurement uncertainties (Huff & Mandelbaum 2017; Sheldon & Huff 2017). For LSST, the atmospheric PSF and blended objects remain major obstacles given the high level of required precision (Dawson et al. 2016; Melchior et al. 2018). For space-based missions, we already mentioned the wavelength—dependent PSF as a major uncertainty (see Section 3.3); since the Roman Space Telescope will use H4RG-10 infrared detectors, non-linear detector effects such as the brighter fatter effect and non-linear inter-pixel capacitance will need to be fully characterized before launch (Plazas et al. 2018; Choi & Hirata 2019; Hirata & Choi 2019; Freudenburg et al. 2020). Choi & Hirata (2019) measured these non-linearities for a prototype detector via a correlation analysis of flat-field data, with a statistical precision that meets Roman Space Telescope requirements. Further laboratory studies of these non-linear detector effects are underway that will bolster confidence in our ability to accurately calibrate galaxy shapes.
Intrinsic alignment (IA) of source galaxies has been studied extensively as a systematic for weak lensing through observations, simulations, and theory (e.g. Hirata & Seljak 2004; Mandelbaum et al. 2006; Joachimi & Bridle 2010;Troxel & Ishak 2014; Blazek, Vlah & Seljak 2015; Chisari et al. 2015; Singh, Mandelbaum & More 2015; Tenneti et al. 2015; Vlah, Chisari & Schmidt 2019)
The assumption that the shape and orientation of an elliptical galaxy are determined by the shape of the halo in which it resides, causes a correlation of intrinsic galaxy ellipticities with the gravitational tidal field. We employ the so-called ‘tidal alignment’ model (Catelan, Kamionkowski & Blandford 2001), specifically we use the non-linear alignment (NLA) version (Hirata & Seljak 2004; Bridle & King 2007) of the tidal alignment model to describe IA of elliptical (red) galaxies. This approach captures most to the IA signal and we do not consider quadratic alignment/tidal torquing models (see e.g. Blazek et al. 2019) or more sophisticated IA modelling as a function of galaxy colour (Samuroff et al. 2019) in this paper.
The |$C_{\delta _{\mathrm{g}}\mathrm{I}}^{ij}(l)$| effect describes a correlation of galaxy overdensity and intrinsic ellipticity (I) for galaxy pairs that are physically close and affected by the same tidal field.
We do not consider additional uncertainties in the luminosity function (cf. Krause et al. 2016, where said uncertainties are marginalized over six additional parameters), but we note that these uncertainties can be significant. This is the interface where cosmology meets galaxy formation and we acknowledge that it is critical to understand the latter to precisely constrain the former.
Baryonic physics effects on the modelling of small scales in the matter power spectrum (e.g. van Daalen et al. 2011; Chisari et al. 2018) are a pressing concern for cosmic shear (see e.g. Semboloni et al. 2011; Zentner et al. 2013; Eifler et al. 2015; Huang et al. 2019) and will become a pressing concern for galaxy–galaxy lensing and galaxy clustering if higher order bias models are included that allow the inclusion of smaller scales.
We mitigate the impact of baryonic physics in two different ways (cf. Chisari et al. 2019, for an overview on mitigation strategies): First, the scale cuts for the galaxy clustering and galaxy–galaxy lensing part of the data vector that are driven by our assumption of using linear galaxy bias, i.e. |$R_\mathrm{\min }=21 \mathrm{ Mpc}\, \rm h^{-1}$| are conservative and probably sufficient to control baryonic effects for these parts of the data vector. For cosmic shear, our ℓmax = 3000 cut also mitigates the impact of baryonic physics but as Huang et al. (2019, H19 from hereon) have shown this is insufficient as a scale cut to control baryons at the LSST Year 10 level.
We employ ‘Method C’ detailed in H19 to account for residual uncertainties in baryonic physics in our full 3 x 2 pt data vector. In short, we compute the difference of dark matter only to baryonic 3 x 2 data vectors for LSST and HLS for five different baryonic scenarios. The baryonic scenarios are extracted from hydro-simulations, in particular, we use the MassiveBlack-II simulation (Khandai et al. 2015), IllustrisTNG (Pillepich et al. 2018; Weinberger et al. 2018), Horizon-AGN (Dubois et al. 2016), Eagle simulation (Schaye et al. 2015) , and the OWLS AGN simulation (Schaye et al. 2010; van Daalen et al. 2011). This choice of simulations is motivated by the fact that we require AGN feedback to be included and that we require sufficiently high resolution to reliably model small scales (again see H19 for a summary of the simulations and motivation of this choice).
The priors for the Q are highly conservative and chosen such that the 1σ region of the Gaussian prior corresponds to twice the amplitude of Q’s needed to capture the Illustris (not TNG) simulation. The original Illustris simulation has a very strong feedback scenario which is already highly unlikely given present observations.
4.3 Simulated likelihood analysis
Using the data vectors defined in Section 4.1 and the analysis choices defined in Table 2, we simulate likelihood analyses for the LSST Year 10, HLS reference, and HLS wide scenarios. We point out that the latter two assume that LSST data exist over the corresponding area. Our likelihood analyses span 56 dimensions, 7 of which relate to cosmological parameters, and the remaining 49 describe uncertainties in modelling observational (shear calibration, lens and source photo-z uncertainties) and astrophysical systematics (galaxy bias, intrinsic alignment, baryonic physics).
We use the fast C osmoL ike forecasting modules and the emcee parallel sampling algorithm to generate chains with 1120 walkers, 8000 steps each. Altogether our chains comprise 8.96 M steps. We compare constraining power of the different scenarios through contour plots in the dark energy equation-of-state parameters (see Fig. 6) and by computing the Dark Energy Task Force Figure of Merit, |$\mathrm{FoM}=|\mathbf {C}^{-1}_{w_0,w_a}|^{1/2}$|. In other words, we obtain the FoM for a given scenario from the MCMC chains by computing the parameter covariance matrix, extracting the w0, wa submatrix, inverting it, and computing the square root of its determinant.
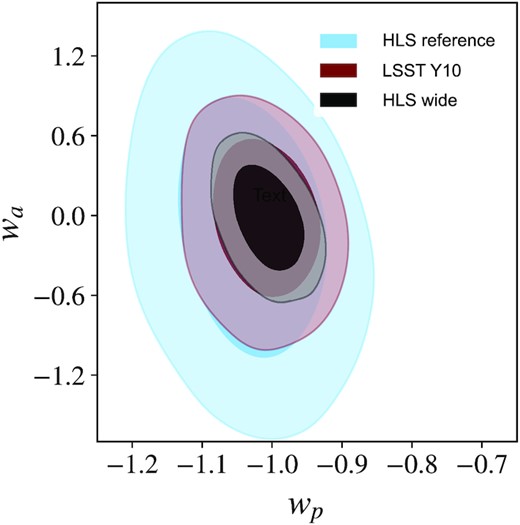
Constraining power on dark energy parameters wp (where p is a pivot redshift, chosen such that the two parameters are somewhat de-correlated) and wa, marginalized over 5 other cosmological parameters and 49 nuisance parameters describing observational and astrophysical systematics. We show results for the 18 000 deg2 LSST Year 10 data set in red, for the 2000 deg2 HLS reference survey in blue, and for the HLS wide survey (black). Both HLS scenarios assume LSST multiband photometry over the corresponding area. We show the 68 and 95 per cent contours.
To test sampling convergence, we compare sub-chains of 140 000 steps starting at step 2.1M and find that our FoMs have stabilized at 6M steps. We also vary the number of walkers and starting points (including their variance) and found our results independent of reasonable choices in these settings.
Fig. 6 shows the constraining power in the dark energy equation-of-state parameters wa and wp. The latter corresponds to w0 but computed at a different redshift, here zp = 0.4, to de-correlate the two parameters and to enable the reader to better estimate 1D projected error bars. The contours show a substantial increase in the ability to constrain time-dependent dark energy for the HLS wide scenario compared to the LSST Y10 scenario and compared to the HLS reference survey.
Regarding the HLS reference versus HLS wide comparison (blue versus black contours in Fig. 6), the gain in constraining power (FoMHLSwide = 5.5 FoMHLSref)
is mostly driven by the increased area 18 000 deg2 versus 2000 deg2. The larger number density of lens and source galaxies and the improved photo-z accuracy of the HLS cannot compensate for this effect. It is interesting to see that at the precision of HLS reference and HLS wide the results are not fully systematics dominated but that an increase in area has a substantial impact on the contours.
When comparing LSST to HLS wide (red versus black contours in Fig. 6), the increase in constraining power (FoMHLSwide = 2.4 FoMLSST) stems from a combination of increase in number density, deeper redshift distributions, and improved control of systematics, most importantly photo-z calibration. A more detailed study is required to evaluate the exact trade space, in particular, since photo-z parameters are highly correlated with our ability to model galaxy bias and intrinsic alignment. Such a study should also include more realistic photo-z errors, such as catastrophic outliers and it should investigate higher order bias models to push to smaller scales in the galaxy–galaxy lensing and galaxy clustering parts of the data vector.
It is interesting to compare the LSST and HLS reference contours (blue versus red contours in Fig. 6) given that these differ most significantly in terms of assumptions that enter the likelihood analysis. The substantial difference in area 18 000 deg2 for LSST versus 2000 deg2 for the HLS reference is countered by a significantly higher number density of galaxies (cf. Table 2), deeper redshift distribution, higher photo-z, and shape measurement accuracy for the HLS reference scenario. Despite these improvements, the increase in area is more important and favours the LSST only scenario, albeit not at a level one might have suspected. A simple 1/area scaling would suggest a factor of 9 improvement in constraining power, however, the difference between HLS and LSST Y10 is FoMHLSwide = 2.4 FoMLSST. We attribute this difference in part to the larger number density of the HLS, but also to the improved systematics control (width of the photo-z bins and priors on how well we know this width and shear calibration).
5 DISCUSSION
In terms of how to fit a wide survey into the Roman Space Telescope mission, several options arise:
The Roman Space Telescope does not have expendables that would prohibit extended observations beyond its 5-yr primary mission (it carries enough propellant for at least 10 yr of observations, and there are no active cryogens). Dedicating 1.5 yr of such an extension to a W-band survey as detailed above, which would be well-matched in terms of time-scale to LSST Y10, is a possible scenario.
A second option is to get the wide survey data earlier and to reduce the 2000 deg2 footprint of the HLS in the primary mission. As an extreme example one could even fit the 1.5 yr W-band survey outlined above into the nominal 1.6 yr HLS survey. This, however, would come at the high cost of having almost no grism spectroscopy or multiband coverage; given how important corresponding data are for systematics control, this option appears less favourable.
A third option would be to cover a subset of the 18 000 deg2 with the W-band in the Roman Space Telescope primary mission, e.g. one could survey the 10 400 deg2 of sky with E(B − V) < 0.08 that pass within 32° of zenith at LSST. This will likely be the best part of the LSST footprint for extragalactic studies, and it can be surveyed in approximately 1 yr to the same depth as the 1.5 yr survey considered in this paper.
We again refer to Fig. 3, as one of the main results of our paper, which shows that already a 5-month HLS survey with the Roman Space Telescope W-band can provide 18 000 deg2 high-resolution imaging for >95 per cent of the LSST Year 10 gold galaxy sample (S/N > 20 for point sources). For the 10 400 deg2 with E(B − V)<0.08 this type of survey would only take ∼14 week. It is important to note that the Roman Space Telescope observing time, including the survey design of the HLS, has not been allocated to date, and that corresponding decisions will depend on the science landscape in ∼5 yr. In particular, it will be important to see how strongly the first 3 yr of LSST data are affected by systematics and how much core science interests in the community (not just cosmology) would benefit from rapid W-band coverage of the Roman Space Telescope.
This analysis does not recommend replacing the entire HLS reference survey design with a wide W-band survey. The HLS reference survey ensures exquisite systematics control and it is the consensus in the community that systematics control will be more important than maximizing statistical power. We instead recommend the exploration of HLS wide survey strategies in combination with the HLS reference approach, specifically we envision that a wide survey component would use the HLS reference survey to anchor shear and photo-z calibration.
5.1 Roman Space Telescope synergies beyond weak lensing and galaxy clustering
A wide Roman Space Telescope survey in one band as described above opens numerous science applications in cosmology beyond the joint weak lensing and galaxy clustering dark energy science depicted in Fig. 6.
5.1.1 Galaxy cluster science
An 18 000 deg2W-band survey would substantially enhance the weak lensing mass calibration of clusters, a key ingredient for cluster cosmology (von der Linden et al. 2014a,b; Mantz et al. 2015; Costanzi et al. 2019; Miyatake et al. 2019; Wu et al. 2019; Salcedo et al. 2020). Both the increased spatial resolution and the broader wavelength coverage will help to decrease systematic uncertainties due to blending and photo-z misclassification, which are amplified in overdense cluster fields. An important aspect is that the W-band addition would enable precise mass calibration to higher redshift clusters than LSST alone (cf. Schrabback et al. 2018).
5.1.2 Trough cosmology
Cosmic underdensities have emerged as an interesting probe of structure formation and hence dark energy and modified gravity (Krause et al. 2013; Melchior et al. 2014; Hamaus et al. 2016; Davies, Cautun & Li 2019); potentially corresponding observables are easier to model compared to probes that rely on higher density environments. Trough cosmology (Gruen et al. 2016, 2018), and especially trough lensing, would benefit from the 18 000 deg2 wide HLS survey scenario because of the higher density of source galaxies (for trough lensing) and the higher density of detected galaxies that signify the trough boundaries.
5.1.3 Strong lensing
LSST will find a large number of strong lenses (Oguri & Marshall 2010). Colour and more importantly shape information from overlapping space observations will allow for significantly improved constraints on the value of H0 and other core cosmology questions (Birrer et al. 2019) via enhanced control of lens profile modelling uncertainties.
5.1.4 Stellar astronomy
The Roman Space Telescope’s infrared measurements will enhance the analysis of the stellar population in LSST. IR observations will be particularly valuable for tracing brown dwarfs and AGB stars and the Roman Space Telescope should be able to achieve single exposure precision of 0.01 pixels or 1.1 mas (Sanderson et al. 2017). Thus, with a 1.5 yr survey spread out over 5 yr of mission time, the mission will measure proper motions with uncertainties of |$\sim 200\, \mu {\rm as}\, {\rm yr}^{-1}$| for stars. This will help trace stellar streams in the galactic halo ∼5 magnitude fainter than Gaia.
5.2 HLS wide synergies with CMB surveys
The new generation of CMB experiments, e.g. the Simons Observatory (SO, Ade et al. 2019) and CMB-S4 (Abazajian et al. 2016), will be well underway by the mid-2020s. In particular, the survey of the Large Aperture Telescope of the Simons Observatory over the full LSST footprint will likely be completed or near completion, providing a detailed map of the integrated matter density through CMB lensing, the integrated pressure distribution through the thermal Sunyaev–Zeldovich’ (tSZ) effect, the integrated electron momentum distribution through the kinematic Sunyaev–Zeldovich (kSZ) effect, and the cosmic infrared background (CIB). The increased number density of galaxies and precision in shape measurements from space-based imaging from Roman Space Telescope over the full LSST area would therefore enable a new level of cross-correlations measurements between galaxy surveys and CMB surveys.
By cross-correlating the CMB lensing map with the large-scale structure traced by photometric redshift slices, we will be able to determine the evolution of the amplitude of density fluctuations with redshift, σ8(z). Krolewski et al. (2019) obtain a S/N of 58 measurement with unWISE x Planck. Correlating the much higher number density of the HLS + LSST sample with the much lower noise SO lensing map will boost the overall S/N significantly.
Similarly, thermal SZ observations from CMB surveys will detect a wealth of clusters (16 000 clusters forecasted for SO), all of which benefit strongly from cluster mass calibration through high-precision weak lensing from the Roman Space Telescope (see e.g. Bocquet et al. 2019; Miyatake et al. 2019, for corresponding applications to the Atacama Cosmology Telescope and the South Pole Telescope). The increased accuracy in photometric redshifts of the joint catalogue would improve the line-of-sight localization of these clusters and it would extend the redshift range of clusters for which both CMB and optical/infrared observations are matched. A joint catalogue will also enable improved measurements of cluster profiles and features such as the splashback radius observed in density and lensing profiles (Shin et al. 2019). The Roman Space Telescope lensing measurements could determine the relationship between integrated pressure (Y) and mass. This observation would determine the gas fraction in ∼1014 M⊙ groups, which could then calibrate the effect of baryon feedback on the dark matter distribution (van Daalen, McCarthy & Schaye 2019).
The combination of CMB kSZ measurements and HLS/LSST can be used to trace the distribution of electrons around galaxies either through cross-correlations with the optical shear measurements (Doré, Hennawi & Spergel 2004) or with the galaxy distribution (Ferraro et al. 2016; Hill et al. 2016). By measuring these effects as a function of redshift, this combination can trace the evolution of the circumgalactic medium (Battaglia et al. 2019).
6 CONCLUSIONS
The Rubin Observatory, SPHEREx, Euclid, and the Roman Space Telescope in combination with other spectroscopic surveys (DESI, PFS, 4MOST) and CMB surveys (Simons Observatory, CMB-S4) pose exciting opportunities for discovery in cosmological physics. The Roman Space Telescope will likely be the latest mission to join this ensemble of experiments, but given its versatile observing capabilities and its flexibility in terms of survey strategy, being last is where it can synergize best.
In this paper, we focus on synergies between the Roman Space Telescope (space-based, high resolution imaging, NIR multiband photometry, grism spectroscopy), and LSST (6-band photometry in the visible wavelengths, 10 deg2 FoV, rapid and repeated coverage of 18 000 deg2). We explore alternative scenarios to Roman Space Telescope’s HLS reference survey, which assumes both Rubin Observatory and Roman Space Telescope data over 2000 deg2. In particular, we quantify scenarios where the HLS covers the entire LSST area rapidly in one band, a concept denoted as ‘HLS wide’. Our survey simulations are based on the Roman Space Telescope exposure time calculator and redshift distributions from the CANDELS catalogue.
As a first result of our study, we find that already a 5-month HLS wide survey with the W-band can cover the full LSST survey area providing high-resolution imaging for >95 per cent of the LSST Year 10 gold galaxy sample. Given that blending is a potentially limiting issue for LSST cosmology, the concept of a 5-month HLS wide survey is an important idea to study further.
If the Roman Space Telescope were to spend 1.5 yr covering the LSST area in the W-band, it would be able to provide high-resolution imaging for >99 per cent of the LSST Year 10 gold galaxy sample. For this second scenario, we run a full 3 x 2 pt likelihood analysis that includes non-Gaussian covariances, and accounts for observational and astrophysical systematics (shear calibration, lens, and source photo-z uncertainties, galaxy bias, intrinsic alignment, baryonic physics). We run similar 3 x 2 pt likelihood analyses for the 2000 deg2 HLS reference survey and for a LSST Year 10 survey in order to compare to the HLS wide concept. We find a significant increase in constraining power for the joint LSST + HLS wide survey compared to LSST Y10 (FoMHLSwide = 2.4 FoMLSST) and compared to the HLS reference survey (FoMHLSwide = 5.5 FoMHLSref).
The assumed survey area in both the 5 month and the 1.5-yr LSST + HLS wide survey is 18 000 deg2, we however note that the best part of LSST’s footprint for extragalactic studies might be smaller and correspondingly the required time that the Roman Space Telescope would spend on a wide band survey would be shorter. Such a wide survey component could be implemented as part of the nominal HLS survey, or as part of the HLS and other survey components (depending on their interest); it could also be conducted as part of an extended mission, which would map nicely on to the LSST Y10 time-scale.
We employ a range of systematics models to realistically assess the information content encoded in the HLS and the LSST (cf. Table 2), however, we point out that future work in this area is critically important. The Gaussian photo-z errors that assume a free mean per tomographic bin and one free variance parameter with known redshift evolution across all bins might prove insufficient and will require more sophisticated models, in particular, ones that include catastropic outliers (e.g. see study by Bernstein & Huterer 2010). In addition, small-scale modelling that utilizes information on small scales in galaxy clustering, such as non-linear bias models (perturbation theory possibly in combination with Halo Occupation Distribution models) in combination will be important to fully exploit the potential of future missions. We defer corresponding studies of improved observational and astrophysical systematics modelling to future work.
By the time the Roman Space Telescope launches, the Rubin Observatory will have been in survey operation mode for several years already and will have built up substantial survey depth and area. If blending is an issue for LSST shape and photo-z measurements, the Roman Space Telescope could provide a significant contribution to a possible solution in just 5 months. It is also possible that the lack of deep training data (spectra) for photo-z, or the lack of multiband IR coverage will limit LSST photo-z accuracy. If the lack of spectroscopic information is limiting, exploring the idea of extended Roman Space Telescope grism observations across the LSST footprint might also be a good option. If narrow band IR information is useful, an HLS wide survey with the H-band is interesting to study further. An HLS H-band survey is approximately 3.5 times as slow as a W-band survey but it significantly limits wavelength-dependent PSF problems. These ideas illustrate the flexibility of the Roman Space Telescope as an observatory, which will benefit multiple science cases across the cosmological community in the next decade.
Several other missions, launching earlier than the Roman Space Telescope, will synergize with LSST. In particular, the Euclid mission will cover the LSST footprint to a large extent, creating mutually beneficial science opportunities and improved systematics control. We note, however, that Euclid will not quite achieve the depth required to fully synergize with LSST and that the combination of Euclid VIS information is highly complementary to the IR coverage from the Roman Space Telescope. Existing Euclid and LSST data over the LSST footprint will make a HLS wide mission concept as suggested here even more valuable.
Exploring optimal joint science strategies for HLS variations and LSST requires complex calculations and meaningful metrics. This paper has presented a connected infrastructure of survey simulations and sophisticated likelihood analyses that can be used to further explore joint LSST + HLS science cases. A HLS wide data set would impact multiple cosmological probes beyond 3 x 2 pt cosmology and we mention cluster cosmology, voids, and trough cosmology, strong lensing, CMB lensing, and SZ synergies as examples for future consideration.
Including these observables in a multiprobe analysis and improving the modelling of systematics are meaningful extensions of the work presented here. In particular, we plan to include catastrophic redshift outliers and higher order galaxy bias models that allow pushing to smaller scales in galaxy–galaxy lensing and galaxy clustering, in future analyses.
ACKNOWLEDGEMENTS
This work is supported by NASA ROSES ATP 16-ATP16-0084 and NASA 15-WFIRST15-0008 grants. Support for MS was provided by the Office of Research and Economic Development, University of California, Riverside through the FIELDS NASA–MIRO programme. The Flatiron Institute is supported by the Simons Foundation. Simulations in this paper use High Performance Computing (HPC) resources supported by the University of Arizona TRIF, UITS, and RDI and maintained by the UA Research Technologies department. Part of the research described in this paper was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
The Reference survey is being used to assess whether the Roman Space Telescope design meets science requirements. No decisions have been made regarding what survey will actually be executed.



