Magnetohydrodynamic stability of magnetars in the ultrastrong field regime I: the core

Rau, Peter B; Wasserman, Ira

doi:10.1093/mnras/stab1538

ABSTRACT

We study magnetohydrodynamic stability of neutron star core matter composed of neutrons, protons, and leptons threaded by a magnetar-strength magnetic field 10¹⁴–10¹⁷ G, where quantum electrodynamical effects and Landau quantization of fermions are important. Stability is determined using the Friedman–Schutz formalism for the canonical energy of fluid perturbations, which we calculate for a magnetizable fluid with H ≠ B. Using this and the Euler–Heisenberg–Fermi–Dirac Lagrangian for a strongly magnetized fluid of Landau-quantized charged fermions, we calculate the local stability criteria for a neutron star core with a spherical axisymmetric geometry threaded by a toroidal field, accounting for magnetic and composition gradient buoyancy. We find that, for sufficiently strong fields B ≳ 10¹⁵ G, the magnetized fluid is unstable to a magnetosonic-type instability with growth times of the order of 10⁻³ s. The instability is triggered by sharp changes in the second-order field derivative of the Euler–Heisenberg–Fermi–Dirac Lagrangian that occur where additional Landau levels start being populated. These sharp changes are divergent at zero temperature, but are finite for non-zero temperature, so realistic neutron star core temperatures 5 × 10⁷ K < T < 5 × 10⁸ K are used. We conjecture that this mechanism could promote the formation of magnetic domains as predicted by Blandford and Hernquist and Suh and Mathews.

instabilities, MHD, stars: magnetars, stars: magnetic field, stars: neutron

1 INTRODUCTION

The problem of magnetohydrodynamic (MHD) stability is of great importance to the study of magnetars and compact stars in general, since their magnetic field configurations must be stable over time-scales much longer than their dynamical time-scales. Determining which types of field configuration are allowed by stability considerations is of particular interest following the discovery of a multipolar field configuration in a neutron star by the NICER experiment (Bilous et al. 2019; Riley et al. 2019); the dipolar field model often assumed is clearly too simple. Understanding the field configuration of magnetars and how they could be destabilized is also of fundamental interest in helping to understand their emission mechanisms, including the theoretical explanation for soft gamma repeaters as caused by fractures in the magnetar crust (Thompson & Duncan 1995; Heyl & Hernquist 2005) or field reconnection in the magnetosphere (Lyutikov 2006). Magnetars are also a leading candidate for the source of fast radio bursts (FRBs; Popov & Postnov 2010; Lyubarsky 2014, 2020; Beloborodov 2017; Lu & Kumar 2018; Metzger, Margalit & Sironi 2019), and a recent detection by the CHIME radio telescope of an FRB originating from a magnetar in our Galaxy (CHIME/FRB Collaboration 2020) has provided evidence that this could be the case. MHD instabilities within the star could power magnetic outbursts that deposit energy into the magnetar magnetosphere, which in turn powers the different proposed FRB mechanisms.

Though the complicated nature of MHD has made aspects of MHD stability intractable to analytical study, many useful results have been proven analytically and later confirmed numerically for the stability of stellar magnetic fields. A purely toroidal stellar field is known to be unstable along the axis of symmetry to sausage (e.g. interchange) and kink instabilities (Tayler 1973), while a purely poloidal field with closed field lines within the star is also unstable to sausage and kink instabilities where the field vanishes (Markey & Tayler 1973; Wright 1973). Flowers & Ruderman (1977) showed that a star with a purely poloidal field is unstable even if no field lines are closed within it. Markey & Tayler (1973) and Wright (1973) both suggested that a mixed poloidal–toroidal field configuration could be stable, which was demonstrated numerically (Braithwaite & Spruit 2004; Braithwaite & Nordlund 2006; Yoshida, Yoshida & Eriguchi 2006; Duez, Braithwaite & Mathis 2010) for near equal-strength poloidal and toroidal fields. Simulations by Braithwaite (2009) showed that mixed toroidal–poloidal configurations can be stable with a much weaker poloidal component, which was confirmed analytically by Akgün et al. (2013). Stable stratification of a star, represented mathematically by a positive square Brunt–Väisälä frequency, has been shown analytically (Tayler 1973) and numerically (Braithwaite & Nordlund 2006) to stabilize the magnetic field, and in general it allows for a greater variety of possible field configurations since the field no longer needs to be a solution of the Grad–Shafranov equation (Reisenegger 2009). Using numerical simulations, Mitchell et al. (2015) found that different field configurations in barotropic stars always decayed away, giving further evidence to the idea that stable stratification must be included to obtain a stable field configuration. Stable stratification alone may not be sufficient to stabilize a fluid with a magnetic field that diminishes quickly enough with increasing height, which can be unstable to magnetic buoyancy (Parker 1955; Acheson 1979). Additionally, as discussed by Reisenegger (2009), the erosion of stable stratification by dissipative processes (weak decays and ambipolar diffusion in neutron stars) could lead to field rearrangement and perhaps instability.

Previous analyses of the stability of stellar magnetic fields have made the often reasonable assumption that the stellar medium through which the field is threaded is not magnetizable i.e. that B = H. This is clearly not the case for superfluid-superconducting neutron stars, nor is it true for extremely strong magnetic fields. The field strengths attained in magnetars are up to 10¹⁵ G at the surface and perhaps one to two orders of magnitude greater in the core (Mereghetti, Pons & Melatos 2015; Turolla, Zane & Watts 2015; Kaspi & Beloborodov 2017; Uryu et al. 2019). Since these fields exceed the quantum critical field |$B_{\text{crit}}=m_{\text{e}}^2/e=4.4\times 10^{13}$| G, quantum electrodynamic effects are relevant and could be important to magnetar stability. In the vacuum case, non-linear electromagnetic effects are encoded in the Euler–Heisenberg Lagrangian (Heisenberg & Euler 1936). In matter, this must be supplemented with terms accounting for the interaction of fermions with the magnetic field. These additional Lagrangian terms have been computed for a charged Fermi gas at zero temperature T (Chodos, Everding & Owen 1990) and at finite T (Elmfors, Persson & Skagerstam 1993; Persson & Zeitlin 1995). In the presence of such strong fields, the charged fermions in a neutron star will undergo Landau quantization, which modifies the equation of state (EOS; Lai & Shapiro 1991; Broderick, Prakash & Lattimer 2000; Mao, Iwamoto & Li 2003; Chamel et al. 2012; Sinha, Mukhopadhyay & Sedrakian 2013; Chamel & Stoyanov 2020), magnetization, and transport properties (Potekhin 1999; Potekhin & Yakovlev 2001; Potekhin, Pons & Page 2015) of the star. The effects of B ≲ 10¹⁸ G on the EOS are generally quite small at typical core densities, and B ≈ H to within a few per cent. However, the analysis of MHD stability requires not only examining the first-order partial derivatives of the magnetic free energy, but its second-order derivatives with respect to B and the density ρ. These derivatives have been studied in the context of magnetic domain formation in strong fields by Blandford & Hernquist (1982) and Suh & Mathews (2010), but as far as the authors are aware, the implications of strong-field quantum mechanical effects on MHD stability have not been examined in the literature.

In this paper, we study MHD stability including non-linear, non-vacuum electromagnetism appropriate for magnetar-strength magnetic fields. We employ the canonical energy approach to stability analysis (Bernstein et al. 1958) and in particular follow closely the coordinate basis version of the non-relativistic fluid perturbation theory expounded by Friedman & Schutz (1978). We extend the non-relativistic MHD perturbation theory of Glampedakis & Andersson (2007) to B ≠ H to allow us to consider the effect of the medium and vacuum magnetization on MHD stability. We also consider non-barotropic EOS, and employ a Brunt–Väisälä frequency accounting for both neutron–proton fraction buoyancy (Reisenegger & Goldreich 1992) and leptonic buoyancy (Kantor & Gusakov 2014; Passamonti, Andersson & Ho 2016; Yu & Weinberg 2017; Rau & Wasserman 2018), in contrast to e.g. Akgün et al. (2013), who only included the neutron–proton fraction buoyancy in their analysis and were considering the global instability of specific axisymmetric fields. We consider the local stability of strongly magnetized neutron star core fluid in a planar geometry, in which the effects on stability of non-linear electromagnetism and an accurate buoyant force, including magnetic buoyancy, are more easily understood than in the spheroidal star case. After reviewing the electromagnetic Lagrangian and the relevant partial derivatives of it which determine the stability, we conclude by discussing its numerical application to the stability criterion for the planar fluid case. The background magnetic field in the neutron star crust obeys a fundamentally different constraint equation compared to ideal MHD (Cumming, Arras & Zweibel 2004; Gourgouliatos et al. 2013), and the stability analysis is fundamentally different (Lyutikov 2013); we thus leave this subject to a subsequent paper.

In Section 2, we introduce the canonical energy for B ≠ H MHD, with most details of the derivation left to the supplemental Appendix A. Section 3 derives the stability criteria using the canonical energy. In Section 4, the pressure and energy density for strong fields and Landau quantized fermions are discussed in detail and the required thermodynamic derivatives are derived, and the background stellar model is described. Section 5 describes the numerical results for the stability criteria, and Section 6 discusses their observational implications. The supplemental Appendix B gives explicit expressions for thermodynamic partial derivatives used in evaluating the stability criteria. We work in Gaussian units and set c = ℏ = 1. We also employ the Einstein summation convention using Latin letters as spatial indices i = 1, 2, 3. The letter a is reserved as a subscript to denote particle species a = n, p, e, m, with sums over particle species always denoted explicitly.

2 MHD EQUATIONS AND CANONICAL ENERGY

We consider a non-rotating neutron star core composed of neutrons n, protons p, electrons e and, at sufficiently high densities, muons m. We assume the magnetic field is strong enough to destroy proton superconductivity, and ignore neutron superfluidity. We also assume that the collisional coupling time between the fluids is short and that they all comove – this would not be the case if the neutrons were a superfluid, but the charged fluids are expected to comove generally. We work in the ideal MHD approximation of zero net electric charge density ρ_e = 0 and infinite conductivity.

In non-relativistic MHD for comoving fluids and zero temperature, the appropriate independent thermodynamic variables to work with are the mass density ρ, magnetic field Bⁱ, and species fractions Y_a. The total internal energy density u for this fluid is thus

$$\begin{eqnarray*} u(B,\rho ,Y_a)=\frac{B^2}{8\pi }+u_M(B,\rho ,Y_a)=\frac{B^2}{8\pi }-\mathcal {L}_{\text{EH}}(B)+u_{\text{mat}}(B,\rho ,Y_a), \end{eqnarray*}$$

(1)

where |$B=\sqrt{g_{ij}B^iB^j}$| is the magnitude of the magnetic field and g_ij is the (Euclidean, flat space) metric tensor. u_M includes the (negative) standard vacuum Euler–Heisenberg Lagrangian |$-\mathcal {L}_{\text{EH}}$|⁠, plus the matter contribution to the energy density u_mat: combined these are responsible for the magnetization. The exact form of u_mat will be discussed in Section 4: microscopically, it will also depend on (mean) meson fields responsible for nuclear interactions. Equation (1) and standard thermodynamic relations imply that the magnetic H-field is (Landau & Lifshitz 1960)

$$\begin{eqnarray*} H_i=4\pi \left.\frac{\partial u}{\partial B^i}\right|_{\rho ,Y_a}=B_i+4\pi \left.\frac{\partial u_M}{\partial B^i}\right|_{\rho ,Y_a}=B_i-4\pi \frac{\partial \mathcal {L}_{\text{EH}}}{\partial B^i}+4\pi \left.\frac{\partial u_{\text{mat}}}{\partial B^i}\right|_{\rho ,Y_a}. \end{eqnarray*}$$

(2)

For a magnetizable medium in ideal MHD, the Euler equation takes the form

$$\begin{eqnarray*} \rho (\partial _t v_i+(v^j\nabla _j)v_i)+\nabla _iP+\rho \nabla _i\Phi =\nabla ^jT^B_{ij}, \end{eqnarray*}$$

(3)

where vⁱ is the common fluid velocity, P is the total matter pressure, including meson fields responsible for nuclear interactions (see Section 4 for further details of this) and magnetic field dependence, and Φ is the gravitational potential. |$T^B_{ij}$| is the magnetic stress tensor for a magnetizable medium (Easson & Pethick 1977):

$$\begin{eqnarray*} T^B_{ij}=\left[\frac{1}{8\pi }B^2-\mathcal {L}_{\text{EH}}-\frac{1}{4\pi }B^kH_k\right]g_{ij}+\frac{1}{4\pi }H_iB_j. \end{eqnarray*}$$

(4)

|$T^B_{ij}$| is symmetric since u_M only depends on B and hence Bⁱ and Hⁱ are aligned. We thus have

$$\begin{eqnarray*} \frac{\partial u_M}{\partial B^k}=\hat{B}_k\frac{\partial u_M}{\partial B}, \rightarrow H=4\pi \left.\frac{\partial u}{\partial B}\right|_{\rho ,Y_a}, \end{eqnarray*}$$

(5)

where |$\hat{B}^i=B^i/B$|⁠. The total mass density of the fluid is

$$\begin{eqnarray*} \rho =\sum _{a=\text{n,p,e,m}}m_an_a\approx m_{\text{N}}n_b \end{eqnarray*}$$

(6)

where m_a and n_a are the mass per particle and number density of species a, m_N = 938.92 MeV is the average nucleon mass and n_b = n_n + n_p is the total baryon number density. We could hence replace ρ with n_b as an independent variable. The species fractions Y_a can be represented using two quantities: the proton fraction (of total baryons) Y and the electron fraction (of total leptons) f, defined by

$$\begin{eqnarray*} Y=\frac{n_{\text{p}}}{n_{\text{b}}}, \quad f=\frac{n_{\text{e}}}{n_{\text{p}}}=\frac{n_{\text{e}}}{n_{\text{e}}+n_{\text{m}}}. \end{eqnarray*}$$

(7)

For simplicity, we have assumed zero temperature, and hence zero entropy, in the equations of motion. The T = 0 limit is a very good approximation for the neutron star core where the fermion chemical potentials μ_a satisfy μ_a ≫ k_BT. An exception is made for certain second-order partial derivatives of u_mat, which we discuss in Section 4. In these terms, we treat the temperature as a fixed parameter and do not concern ourselves with the dynamics of the entropy.

We now derive the canonical energy for a magnetizable fluid, which is used to study the fluid’s MHD stability. We follow the definitions of the Lagrangian perturbations of fluid quantities of Friedman & Schutz (1978), which has antecedents in Taub (1969), Carter (1973), Friedman & Schutz (1975), and Bardeen et al. (1977), and which has been applied to MHD by Glampedakis & Andersson (2007). In these definitions, we work in a coordinate basis and hence the components of (contravariant) vectors and covariant vectors are in general distinct. The perturbation theory is reviewed in Appendix A (available as an online supplement) and then applied to equation (3) and used to compute the canonical energy of the perturbations.

Using results from Appendix A, the full expression for the canonical energy E_c[ξ] for perturbation with Lagrangian displacement field ξⁱ is shown to be

$$\begin{eqnarray*} E_c[\xi ] &=& \frac{1}{2}\int \mathrm{ d}V\Bigg [\rho |\partial _t\xi ^i|^2-\rho |v^j\nabla _j\xi ^i|^2+\text{Re}[(\xi ^i)^*\xi ^j]\nabla _i\nabla _j(P+\mathcal {P}_B) +\left(\gamma P+\frac{B^2}{4\pi }+2\rho B\frac{\partial ^2 u_M}{\partial \rho \partial B}+B^2\frac{\partial ^2 u_M}{\partial B^2}\right)|\nabla _j\xi ^j|^2 \nonumber \\ &&+\frac{BH}{4\pi }\left|\hat{B}^j\nabla _j\xi ^i\right|^2 +\left(\frac{\partial ^2 u_M}{\partial B^2}-\frac{1}{B}\frac{\partial u_M}{\partial B}\right)\left| B^i\hat{B}^j\nabla _j\xi _i \right|^2 + 2\left(\frac{1}{B}\frac{\partial u_M}{\partial B}-\frac{\partial ^2 u_M}{\partial B^2}-\frac{\rho }{B}\frac{\partial ^2 u_M}{\partial \rho \partial B}\right)B^kB^j\text{Re}[\nabla _k(\xi _j)^*\nabla _i\xi ^i] \nonumber \\ &&+\frac{1}{2\pi }B^j\text{Re}\left[\nabla _i(\xi ^i)^*(\xi ^k\nabla _jH_k-H_k\nabla _j\xi ^k)\right]-2\rho \left(v^k\nabla _kv_i+\nabla _i\Phi \right)\text{Re}\left[(\xi ^i)^*\nabla _j\xi ^j\right]+\rho \text{Re}\left[(\xi ^i)^*\xi ^j\right]\nabla _i\nabla _j\Phi \nonumber \\ &&-\frac{1}{4\pi G}|\nabla ^i\delta _{\xi }\Phi |^2\Bigg ]+\frac{1}{2}\int _x\mathrm{ d}V\left(\frac{g_{ij}}{4\pi }-\frac{\partial ^2 u_M^x}{\partial B^i_x\partial B^j_x}\right)\delta _{\xi ^*}B^i_x\delta _{\xi }B^j_x \nonumber \\ &&+\frac{1}{2}\oint \mathrm{ d}S\Bigg [|\hat{n}_i\xi ^i|^2\hat{n}^j\nabla _j\left(\langle P+\mathcal {P}_B\rangle -\frac{1}{4\pi }\hat{n}_{k}B^k\hat{n}^{\ell }\langle H_{\ell }\rangle \right)-\frac{1}{4\pi }\hat{n}_iB^i\text{Re}\left[(\xi ^j)^*\xi ^k\right]\nabla _kH^x_j +\frac{1}{4\pi }\hat{n}_i\nabla _j\left(\text{Re}\left[\xi ^i(\xi ^j)^*\right]\hat{n}_{\ell }B^{\ell }\hat{n}^k\langle H_k\rangle \right) \nonumber \\ &&-\frac{1}{2\pi }\hat{n}_iB^i\langle H_j\rangle \text{Re}\left[(\xi ^k)^*\nabla _k\xi ^j\right]+\frac{1}{4\pi G}\nabla_i\left(\delta _{\xi ^*}\Phi \nabla ^i\delta _{\xi }\Phi\right) \Bigg ]. \end{eqnarray*}$$

(8)

In this expression, |$\hat{n}^i$| is the unit normal to the surface enclosing the fluid, γ is the adiabatic index defined as

$$\begin{eqnarray*} \gamma \equiv \frac{\rho }{P}\left.\frac{\partial P}{\partial \rho }\right|_{s,Y_a,B}=\frac{\rho }{P}c_s^2, \end{eqnarray*}$$

(9)

for adiabatic, constant magnetic field sound speed c_s, and δ_ξ is the Eulerian perturbation associated with the Lagrangian displacement field ξⁱ. * indicates complex conjugation, and we have defined the magnetic pressure |$\mathcal {P}_B$|⁠:

$$\begin{eqnarray*} \mathcal {P}_B\equiv -\frac{B^2}{8\pi }+\mathcal {L}_{\text{EH}}+\frac{1}{4\pi }HB=\frac{B^2}{8\pi }+\mathcal {L}_{\text{EH}}+B\frac{\partial u_M}{\partial B}, \end{eqnarray*}$$

(10)

which reduces to B²/(8π) in the vacuum, low field limit as expected. The first volume integral in equation (8) is over the fluid i.e. the star, the second is over the exterior of the fluid, denoted with a superscript or subscript x, and the final term is the surface term. In the surface term, angled brackets denote the difference between the quantity outside and inside the star. We neglect to explicitly denote that B, ρ, Y and/or f are held constant in the partial derivatives of u_M. The surface term in E_c, which is unimportant for our purposes, was calculated by making the simplifying assumption that the exterior of the star is vacuum threaded by a magnetic field, as opposed to a realistic plasma-filled magnetosphere – this was also the choice made by Glampedakis & Andersson (2007). In the exterior region, we still allow H ≠ B, but only the vacuum Euler–Heisenberg Lagrangian is included in u_M there.

In the rest of the paper, we employ the following abbreviations for partial derivatives of u_M:

$$\begin{eqnarray*} u_B\equiv \frac{\partial u_M}{\partial B}, \quad u_{\rho B}\equiv \frac{\partial ^2 u_M}{\partial \rho \partial B}, \quad u_{BB}\equiv \frac{\partial ^2 u_M}{\partial B^2}, \quad u_{BY}\equiv \frac{\partial ^2 u_M}{\partial B\partial Y}, \quad u_{Bf}\equiv \frac{\partial ^2 u_M}{\partial B\partial f}. \end{eqnarray*}$$

(11)

3 STABILITY ANALYSIS

Evaluating the integral equation (8) requires either solving for the global structure of the star and its quasi-normal modes, or guessing trial canonical data ξⁱ, though the result in the latter case could be far from correct if the initial guess is not reasonable. Instead, in the remainder of this paper we investigate the local stability. We consider the example system of an infinite slab of fluid extending in the x–y plane and stratified in the z-direction, with magnetic field varying in z and directed in the plane of the fluid. This allows us to derive the stability criterion for magnetic buoyancy. This system is used to approximate the local stability in a star where the z-direction replaces the radial direction, the magnetic field is toroidal, and where the curvature orthogonal to this direction is ignored.

The problem of magnetic buoyancy has been extensively investigated in the B = H case (Parker 1955; Newcomb 1961; Gough & Tayler 1966; Schubert 1968; Acheson 1979). We follow the canonical energy approach of Newcomb (1961) and Gough & Tayler (1966) to derive the magnetic buoyancy stability criteria for the B ≠ H case. The background magnetic field and gravitational field are

$$\begin{eqnarray*} B^i=B(z)\delta ^i_x, \quad H^i=H(z)\delta ^i_x, \quad -\nabla _i\Phi =g_i=-g\delta _i^z. \end{eqnarray*}$$

(12)

The pressure P = P(z), density ρ = ρ(z), and species fractions Y = Y(z) and f(z) are only functions of z. The only non-zero component of the background Euler equation is

$$\begin{eqnarray*} \frac{\text{d}}{\text{d}z}(P+\mathcal {P}_B)+\rho g=0. \end{eqnarray*}$$

(13)

We drop all surface and exterior vacuum terms, work in the Cowling approximation and assume zero background velocity vⁱ = 0. Define twice the canonical energy per unit mass |$\mathcal {E}_c$| via

$$\begin{eqnarray*} E_c\equiv \frac{1}{2}\int \mathrm{ d}V\rho \mathcal {E}_c. \end{eqnarray*}$$

(14)

Since there are no dissipation mechanisms included in this analysis, E_c is a conserved quantity, and hence the unstable modes must have E_c = 0 (Friedman & Schutz 1978). Since the kinetic energy term ∝ |∂_tξⁱ|² is clearly positive definite, unstable modes are possible if the remainder of E_c is negative. We henceforth drop the uninteresting kinetic energy term from |$\mathcal {E}_c$|⁠. Since we study local stability here, we look for possible instability by examining the conditions for which |$\mathcal {E}_c\lt 0$|⁠. Taking ξⁱ ∝ exp (i( k_xx + k_yy)), equations (8) and (14) give

$$\begin{eqnarray*} \mathcal {E}_c[\xi ] &=& \left(v_{\text{A}}^2k_x^2-g\frac{\text{d}\ln \rho }{\text{d}z}\right)\left|\xi ^{z}\right|^2 +\left(c_s^2+\frac{B^2}{4\pi \rho }+\frac{1}{\rho }\left[B^2u_{BB}+2B\rho u_{\rho B}\right]\right)|\partial _j\xi ^j|^2 +v_{\text{A}}^2k_x^2\left|\xi ^y\right|^2 +v^2_Bk_x^2\left|\xi ^x\right|^2 \nonumber \\ &&-2\left(Bu_{\rho B}+v^2_B\right)k_x\text{Re}[\partial _i(\xi ^i)^*{\rm i}\xi ^x] -2g\text{Re}\left[\partial _j(\xi ^j)^*\xi ^z\right], \end{eqnarray*}$$

(15)

where we used equation (13) and have defined

$$\begin{eqnarray*} v_{\text{A}}^2\equiv \frac{BH}{4\pi \rho }, \end{eqnarray*}$$

(16)

$$\begin{eqnarray*} v_{B}^2\equiv \frac{B^2}{4\pi \rho }(1+4\pi u_{BB}). \end{eqnarray*}$$

(17)

v_A is the Alfvén velocity, and in the limit H = B, v_A = v_B. We now consider the separate cases of no undulations in the direction of the magnetic field k_x = 0, and with undulations permitted in this direction k_x ≠ 0.

3.1 Case 1: k_x = 0

Setting k_x = 0 in equation (15) and expanding out the divergence ∂_jξ^j = ∂_zξ^z + ik_yξ^y gives

$$\begin{eqnarray*} \mathcal {E}_c[\xi] = V^2\left|\partial _z\xi ^z+{\rm i}k_y\xi ^y\right|^2-g\frac{\text{d}\ln \rho }{\text{d}z}\left|\xi ^{z}\right|^2 -2g\text{Re}[\partial _z\xi ^z(\xi ^z)^*]-2gk_y\text{Re}[{\rm i}\xi ^y(\xi ^z)^*], \end{eqnarray*}$$

(18)

where we define a commonly used velocity squared

$$\begin{eqnarray*} V^2\equiv c_s^2+v_B^2+2Bu_{\rho B}. \end{eqnarray*}$$

(19)

Completing the square to move all dependence on ∂_zξ^z into a single positive definite term, we obtain

$$\begin{eqnarray*} \mathcal {E}_c[\xi] = V^2\left|\partial _z\xi ^z+{\rm i}k_y\xi ^y-\frac{g\xi ^z}{V^2}\right|^2 -g\left[\frac{\text{d}\ln \rho }{\text{d}z}+\frac{g}{V^2}\right]\left|\xi ^{z}\right|^2. \end{eqnarray*}$$

(20)

For the canonical energy to be positive, it is sufficient that V² > 0 and the prefactor of |ξ^z|² is positive definite i.e.

$$\begin{eqnarray*} -\frac{\text{d}\ln \rho }{\text{d}z}-\frac{g}{V^2}\gt 0. \end{eqnarray*}$$

(21)

Using the definition of the Brunt–Väisälä frequency motivated by equation (A15)

$$\begin{eqnarray*} N^2\equiv g\left(\frac{1}{\gamma }\frac{\text{d}\ln P}{\text{d}z}-\frac{\text{d}\ln \rho }{\text{d}z}-\frac{\zeta B}{\gamma P}\frac{\text{d}\ln B}{\text{d}z}\right)=\frac{g}{\rho c_s^2}\left(\frac{\partial P}{\partial Y}\frac{\text{d}Y}{\text{d}z}+\frac{\partial P}{\partial f}\frac{\text{d}f}{\text{d}z}\right), \end{eqnarray*}$$

(22)

and equations (13), (17), and (21) can be rewritten as

$$\begin{eqnarray*} \text{SC1}\equiv \frac{c_s^2N^2}{g}+\frac{B^2}{4\pi \rho }\left(1+4\pi u_{BB}\right)\frac{\text{d}}{\text{d}z}\ln \left(\frac{B}{\rho }\right)-Bu_{\rho B}\frac{\text{d}\ln \rho }{\text{d}z}+\frac{B}{\rho }u_{BY}\frac{\text{d}Y}{\text{d}z}+\frac{B}{\rho }u_{Bf}\frac{\text{d}f}{\text{d}z}\gt 0. \end{eqnarray*}$$

(23)

This is analogous to the criterion for stability against magnetic buoyancy derived in Schubert (1968) but generalized to include B ≠ H. The second term on the right is the B ≠ H analogue of the d/dzln (B/ρ) term in the usual k_x = 0 magnetic buoyancy stability criterion (e.g. equation 1.2 in Acheson 1979). The species fraction dependence of H also contributes new terms proportional to dY/dz and df/dz – this is analogous to the usual composition gradient Brunt–Väisälä frequencies, whose effects are included in N². This motivates a redefinition of the Brunt–Väisälä frequency to absorb these magnetic contributions:

$$\begin{eqnarray*} \tilde{N}^2\equiv \frac{g}{\rho c_s^2}\left[\left(\frac{\partial P}{\partial Y}+Bu_{BY}\right)\frac{\text{d}Y}{\text{d}z}+\left(\frac{\partial P}{\partial f}+Bu_{Bf}\right)\frac{\text{d}f}{\text{d}z}\right]. \end{eqnarray*}$$

(24)

The two stability criterion, V² > 0 and SC1 > 0, are both sufficiency conditions; a fluid configuration may still be stable globally if either one of them is violated locally.

3.2 Case 2: k_x ≠ 0

Allowing k_x ≠ 0 in equation (15) and expanding out ∂_jξ^j gives

$$\begin{eqnarray*} \mathcal {E}_c[\xi ] &=& V^2|\partial _z\xi ^z|^2+\left(v_{\text{A}}^2k_x^2-g\frac{\mathrm{ d}\ln \rho }{\mathrm{ d}z}\right)|\xi ^{z}|^2 +\left(V^2k_y^2+v_{\text{A}}^2k_x^2\right)|\xi ^y|^2 +c^2_sk_x^2|\xi ^x|^2+2k_y\left(c_s^2+v_B^2\right)\text{Re}[\partial _z(\xi ^z)^*{\rm i}\xi ^y] \nonumber \\ &&+2k_xk_y\left(c_s^2+Bu_{\rho B}\right)\text{Re}[\xi ^x(\xi ^y)^*]+2k_x\left(c_s^2+Bu_{\rho B}\right)\text{Re}[\partial _z(\xi ^z)^*i\xi ^x] -2gk_x\text{Re}[{\rm i}\xi ^x(\xi ^z)^*] -2gk_y\text{Re}[{\rm i}\xi ^y(\xi ^z)^*] \nonumber \\ &&-2g\text{Re}[\partial _z\xi ^z(\xi ^z)^*], \end{eqnarray*}$$

(25)

To simplify this somewhat, we can complete the square in an analogous manner to the k_x = 0 case. Combining all terms depending on ξ^x into a single positive definite contribution to |$\mathcal {E}_c[\xi ]$|⁠, we obtain

$$\begin{eqnarray*} \mathcal {E}_c[\xi ] &=& c^2_s\left|{\rm i}k_x\xi ^x+\frac{\big(c_s^2+Bu_{\rho B}\big)(\partial _z\xi ^z+{\rm i}k_y\xi ^y)-g\xi ^z}{c^2_s}\right|^2 +K_1|\partial _z\xi ^z|^2 +\big(K_1k_y^2+v^2_{\text{A}}k_x^2\big)\left|\xi ^y\right|^2 +\big(K_2+v_{\text{A}}^2k_x^2\big)\left|\xi ^{z}\right|^2 \nonumber \\ &&+2L_1k_y\text{Re}[\partial _z(\xi ^z)^*i\xi ^y] +2L_2\text{Re}[\partial _z\xi ^z(\xi ^z)^*] +2L_2k_y\text{Re}[{\rm i}\xi ^y(\xi ^z)^*]. \end{eqnarray*}$$

(26)

where we define

$$\begin{eqnarray*} K_1\equiv V^2-\frac{\left(c_s^2+Bu_{\rho B}\right)^2}{c^2_s}, \end{eqnarray*}$$

(27)

$$\begin{eqnarray*} K_2\equiv -g\frac{\mathrm{ d}\ln \rho }{\mathrm{ d}z}-\frac{g^2}{c_s^2}, \end{eqnarray*}$$

(28)

$$\begin{eqnarray*} L_1\equiv c_s^2+v_B^2-\frac{\left(c_s^2+Bu_{\rho B}\right)^2}{c_s^2}=K_1-2Bu_{\rho B}, \end{eqnarray*}$$

(29)

$$\begin{eqnarray*} L_2\equiv g\frac{Bu_{\rho B}}{c_s^2}. \end{eqnarray*}$$

(30)

Completing the square once again to combine the ∂_zξ^z terms outside the first term of equation (26) into a single term, we obtain

$$\begin{eqnarray*} \mathcal {E}_c[\xi ] &=&c^2_s\left|{\rm i}k_x\xi ^x+\frac{(c_s^2+Bu_{\rho B})(\partial _z\xi ^z+{\rm i}k_y\xi ^y)-g\xi ^z}{c^2_s}\right|^2 +K_1\left|\partial _z\xi ^z+\frac{L_1{\rm i}k_y\xi ^y+L_2\xi ^z}{K_1}\right|^2 +\left[\left(K_1-\frac{L_1^2}{K_1}\right)k_y^2+v^2_{\text{A}}k_x^2\right]\left|\xi ^y\right|^2 \nonumber \\ &&+\left[K_2-\frac{L_2^2}{K_1}+v_{\text{A}}^2k_x^2\right]\left|\xi ^{z}\right|^2 +2k_yL_2\left(1-\frac{L_1}{K_1}\right)\text{Re}[{\rm i}\xi ^y(\xi ^z)^*]. \end{eqnarray*}$$

(31)

We see that one stability criterion is |$c_s^2\gt 0$|⁠. This could only possibly be violated by magnetic terms, and we show that this is not the case, at least in a neutron star core: |$c_s^2$| is always positive there. We can now take the k_x → 0 limit since the |$v^2_{\text{A}}k_x^2$| contributions to the prefactors of |ξ^y|² and |ξ^z|² will only help to stabilize the system, and the k_x contribution to the first term will always be positive as long as |$c_s^2\gt 0$|⁠. After taking this limit, if both |$c_s^2\gt 0$| and K₁ > 0, equation (31) consists of positive definite terms plus a quadratic form in ik_yξ^y and ξ^z. This quadratic form is positive definite as long as the following three criteria are satisfied:

$$\begin{eqnarray*} \text{SC2}\equiv K_1-\frac{L_1^2}{K_1}=4Bu_{\rho B}\left(1-\frac{Bu_{\rho B}}{K_1}\right)\gt 0, \end{eqnarray*}$$

(32a)

$$\begin{eqnarray*} \text{SC3}\equiv K_2-\frac{L_2^2}{K_1}\gt 0, \end{eqnarray*}$$

(32b)

$$\begin{eqnarray*} \text{SC4}\equiv K_1\left(1-\frac{L_1^2}{K_1^2}\right)\left(K_2-\frac{L_2^2}{K_1}\right)-L_2^2\left(1-\frac{L_1}{K_1}\right)^2\gt 0. \end{eqnarray*}$$

(32c)

SC2 is a purely MHD stability criterion since it is independent of the gravitational acceleration, while SC3 and SC4, like SC1, are associated with gravity and hence buoyancy.

The K₁ > 0 stability condition can be rewritten as

$$\begin{eqnarray*} K_1=\frac{B^2}{4\pi \rho }\left(1+4\pi u_{BB}\right)-\frac{B^2u^2_{\rho B}}{c_s^2}\gt 0. \end{eqnarray*}$$

(33)

This is identical to equation (122) of Akgün & Wasserman (2008), though note that we define the magnetic free energy in a different way here. The instability associated with this criterion not being met is the Muzikar–Pethick–Roberts (MPR) instability (Muzikar & Pethick 1981; Roberts 1981), a magnetosonic-type instability first derived in the context of type-II superconducting fluids. In such systems the instability acts to attract flux tubes together – this suggests that, in the normal fluid case, it will concentrate magnetic field lines and create regions of higher and lower magnetic flux. Strictly speaking, the original MPR instability criterion is associated with the second term in equation (33) being larger in magnitude than the first term, while in this paper it will turn out that the first term is of greater interest as a potential source of instability. The connection of SC3 and SC4 to buoyancy can be made clear by rewriting K₂ similarly to equation (23) using

$$\begin{eqnarray*} -c_s^2\frac{\mathrm{ d}\ln \rho }{\mathrm{ d}z}-g=\frac{c_s^2\tilde{N}^2}{g}+\left(\frac{B^2}{4\pi \rho }+\frac{B^2}{\rho }u_{BB}+Bu_{\rho B}\right)\frac{\mathrm{ d}\ln B}{\mathrm{ d}z}-Bu_{\rho B}\frac{\mathrm{ d}}{\mathrm{ d}z}\ln \left(\frac{B}{\rho }\right), \end{eqnarray*}$$

(34)

which can be used where K₂ appears in equations (32b)–(32c). This is the analogue to the k_x ≠ 0 magnetic buoyancy in equation (1.4) of Acheson (1979).

4 THERMODYNAMICS

The quantum mechanical effects of strong magnetic fields on the MHD are incorporated within an electromagnetic Lagrangian density computed in quantum electrodynamics (QED). In the vacuum case, this is the Euler–Heisenberg Lagrangian (Heisenberg & Euler 1936) computed by integrating out the charged fermion species from the QED action. In a neutron star core at densities of the order of the nuclear saturation density n₀ = 0.16 fm⁻³ populated by degenerate charged fermion species, a vacuum background cannot be assumed. The non-vacuum thermal background of fermions is incorporated by computing the effective action in an analogous manner to the usual Euler–Heisenberg Lagrangian but including a fermion chemical potential (and finite temperature if desired): we refer to this background as a Fermi–Dirac vacuum. The resulting Euler–Heisenberg–Fermi–Dirac Lagrangian was computed by Elmfors, Persson & Skagerstam (1993). The finite density corrections to the vacuum Euler–Heisenberg Lagrangian can be written as separate terms in the Lagrangian, and combined (Persson & Zeitlin 1995) with the zero-field fermion Lagrangian to give the usual Lagrangian (or pressure) of Landau-quantized fermions. It will be the Landau quantization that has the most important effect on the MHD stability as we later show. We ignore anomalous magnetic moments; the effect of the nucleon anomalous magnetic moments on stellar structure is not significant until B ≳ 10¹⁸ G (Broderick, Prakash & Lattimer 2000), and we will only examine fields an order of magnitude below this.

To be consistent with a realistic stellar core and the specified particle content of our hydrodynamics, we employ an EOS including neutrons, protons, electrons, and muons in beta equilibrium and with interactions between the neutrons and protons. The proton-neutron interactions are important for obtaining realistic values for the n_a and hence Y and f at a given chemical potential (e.g. muons appearing when the total number density is ≈0.8 times nuclear saturation density). We mostly work in the temperature T = 0 limit, which is a very good approximation for a neutron star core for most of the star’s life. An exception is made only for certain second-order partial derivatives of the pressure, which we discuss briefly in this section.

There is a straightforward way to generalize the pressure of Landau-quantized fermions to include proton–neutron interactions. This is to use the σωρ nuclear mean-field theory EOS (e.g. Walecka 1995; Glendenning 1997), which has been generalized to the case of strong magnetic fields (Broderick et al. 2000; Mao, Iwamoto & Li 2003; Sinha, Mukhopadhyay & Sedrakian 2013). In effect, this is accomplished by replacing the mass and chemical potentials of the protons and neutrons in the non-interacting theory with their effective values |$m_a^*$| and |$\mu _a^*$| computed in the σωρ model and simultaneously solving the self-consistency equation for the mean-field value of the scalar meson field σ. The mass terms for the meson fields must also be added to the pressure, and we include cubic and quartic interactions for the σ meson.

Following e.g. Broderick et al. (2000), the total matter pressure in the strong-field, σωρ mean-field model at zero temperature is

$$\begin{eqnarray*} P\big(B,\mu _a,\sigma ,\omega _0,\rho _0^3\big)=\sum _a P_{\text{f},a}(B,\mu _a,\sigma ,\omega _0,\rho _0)-\frac{1}{2}m_{\sigma }^2\sigma ^2-\frac{1}{3}b_{\sigma }m_{\text{N}}(g_{\sigma }\sigma)^3-\frac{1}{4}c_{\sigma }(g_{\sigma }\sigma)^4+\frac{1}{2}m_{\omega }^2\omega _0^2+\frac{1}{2}m_{\rho }^2\big(\rho ^3_0\big)^2, \end{eqnarray*}$$

(35)

where P_{f, a}(B, μ_a, σ, ω₀, ρ₀) is the fermion pressure for each species, μ_a are the (bare) chemical potentials, σ, ω₀, and |$\rho ^3_0$| are the mean-field values of the mesons,¹g_σ, g_ω, and g_ρ are the coupling constants between the baryons and the mesons, m_ω, m_ρ, and m_σ are the meson masses, and b_σ and c_σ are the self-coupling constants for the σ meson. While in the full σωρ model the ρ meson is an isovector of meson fields with charges 0, ±1 and thus the interaction of this meson with the electromagnetic field would be included, in the mean-field model only the neutral meson ρ³ has a non-zero expectation value.

The baryon fermion pressure depends on the meson fields through the baryon effective mass m* and effective chemical potentials |$\mu _a^*$|⁠:

$$\begin{eqnarray*} m_* = m_{\text{N}}-g_{\sigma }\sigma , \quad \mu _{\text{p}}^* = \mu _{\text{p}} - g_{\omega }\omega _0 - \frac{1}{2}g_{\rho }\rho _0^3, \quad \mu _{\text{n}}^* = \mu _{\text{n}} - g_{\omega }\omega _0 + \frac{1}{2}g_{\rho }\rho _0^3. \end{eqnarray*}$$

(36)

The mean-field values for ω₀ and |$\rho ^3_0$| in terms of the neutron and proton number densities are

$$\begin{eqnarray*} \omega _0=\frac{g_{\omega }n_{\text{b}}}{m^2_{\omega }}, \quad \rho ^3_0=\frac{g_{\rho }(n_{\text{p}}-n_{\text{n}})}{2m^2_{\rho}}. \end{eqnarray*}$$

(37)

Note that these are equations of motion that hold in equilibrium and must only be imposed after taking the desired partial derivatives of the thermodynamic potential of interest.

Since we ignore anomalous magnetic moments, the neutron pressure has no B-dependence and is

$$\begin{eqnarray*} P_{\text{f},\text{n}}\big(\mu _n,\sigma ,\omega _0,\rho _0^3\big)=\frac{\mu _n^*\big(2\mu _n^{*2}-m_*^2\big)\sqrt{\mu _n^{*2}-m_*^2}}{24\pi ^2}+\frac{m_*^4}{8\pi ^2}\ln \left[\frac{\mu _n^*+\sqrt{\mu _n^{*2}-m_*^2}}{m_*}\right]. \end{eqnarray*}$$

(38)

For the Landau-quantized charged fermions a = p, e, m, the pressure is given as a sum over occupied Landau levels:

$$\begin{eqnarray*} P_{\text{f},p}\big(\mu _p,B,\sigma ,\omega _0,\rho _0^3\big)=\frac{eB}{4\pi ^2}\sum _{n=0}^{n_{\text{max}}}\gamma _n\left[\mu _p^*\sqrt{\mu _p^{*2}-m_*^2-2eBn}-\big(m_*^2+2eBn\big)\ln \left(\frac{\mu _p^*+\sqrt{\mu _p^{*2}-m_*^2-2eBn}}{\sqrt{m_*^2+2eBn}}\right)\right], \end{eqnarray*}$$

(39)

$$\begin{eqnarray*} P_{\text{f},a}(\mu _a,B)=\frac{eB}{4\pi ^2}\sum _{n=0}^{n_{\text{max}}}\gamma _n\left[\mu _a\sqrt{\mu _a^2-m_a^2-2eBn}-\big(m_a^2+2eBn\big)\ln \left(\frac{\mu _a+\sqrt{\mu _a^2-m_a^2-2eBn}}{\sqrt{m_a^2+2eBn}}\right)\right], \quad a\in \lbrace \text{e,m}\rbrace , \end{eqnarray*}$$

(40)

where γ_n = 2 − δ_{n, 0} is the degeneracy factor of Landau level n and |$n_{\text{max}}=\lfloor (\mu _a^{2}-m_a^2)/(2eB)\rfloor$|⁠.

The appearance of n_p and n_n in the expressions for |$\mu _{\text{p}}^*$| and |$\mu _{\text{n}}^*$| means that the equations for n_p and n_n must be solved simultaneously with the self-consistency equation for σ, which is

$$\begin{eqnarray*} 0 &=& -m_{\sigma }^2\sigma -b_{\sigma }m_{\text{N}}g_{\sigma }^3\sigma ^2-c_{\sigma }g_{\sigma }^4\sigma ^3+\frac{g_{\sigma }m_*}{2\pi ^2}\left[\mu ^*_n\sqrt{\mu _n^{*2}-m_*^2}-m_*^2\ln \left(\frac{\mu _n^*+\sqrt{\mu _n^{*2}-m_*^2}}{m_*}\right)\right.\nonumber\\ &&\left.+\,eB\sum _{n=0}^{n_{\text{max}}}\gamma _n\ln \left(\frac{\mu _p^*+\sqrt{\mu _p^{*2}-m_*^2-2neB}}{\sqrt{m_*^2+2neB}}\right)\right] \nonumber \\ &=& -m_{\sigma }^2\sigma -b_{\sigma }m_{\text{N}}g_{\sigma }^3\sigma ^2-c_{\sigma }g_{\sigma }^4\sigma ^3-g_{\sigma }\left.\frac{\partial P}{\partial m_*}\right|_{\mu _a,B,\phi }. \end{eqnarray*}$$

(41)

For the charged fermions, the second-order partial derivatives that we require are divergent at zero temperature – this can be seen from equations (B2c)–(B2e). Instead, we must use the finite temperature versions of P_{f, a} to compute these partial derivatives: it is given by (e.g. Persson & Zeitlin 1995)

$$\begin{eqnarray*} P_{\text{f},a}\big(\mu _a,B,T,\sigma ,\omega _0,\rho _0^3\big)=\frac{eB}{2\pi ^2}\sum _{n=0}^{\infty }\int _{m_a^2+2eBn}^{\infty }\mathrm{ d}E\sqrt{E^2-m_a^2-2eBn}f_a(E), \end{eqnarray*}$$

(42)

where m_a → m_* for protons. f_a(E) is the Fermi–Dirac distribution

$$\begin{eqnarray*} f_{a}(E)=\frac{\theta (E)}{\exp (\beta (E-\mu _a))+1}, \end{eqnarray*}$$

(43)

where β = (k_BT)⁻¹, θ(x) is the Heaviside step function, and |$\mu _a\rightarrow \mu _p^*$| for a = p. We have dropped the antifermion contribution from f_a(E) since these species will not be present in neutron stars. Even including the finite temperature, the second-order partial derivatives of P_{f, a} for the charged fermions will still exhibit strongly peaked behaviour where new Landau levels start being populated i.e. where |$(\mu _a^2-m_a^2)/(2eB)$| takes integer values, and thus will play a dominant role in the local stability criteria discussed later. Since we are not interested in the dynamics of heat flow inside the star, T is treated as a fixed parameter in equation (42), and we assume it is held constant in all thermodynamic partial derivatives.

The regulating effect of finite temperature on eliminating the divergences when a new Landau level begins to be populated |$(\mu _a^2-m_a^2)/(2eB)=$| an integer is illustrated in Fig. 1. The temperature dependence of these functions will have an important role in the MHD instabilities we show later in the paper, and sufficiently high temperatures can stabilize the magnetized fluid in regions of parameter space that would otherwise be unstable.

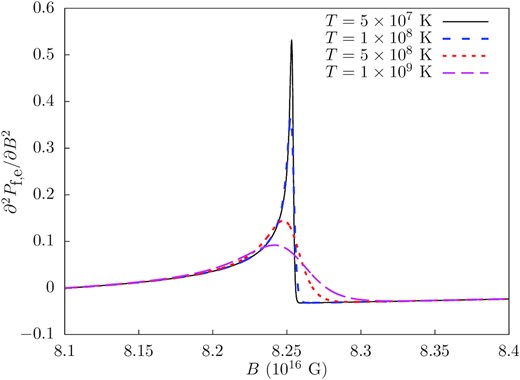
∂2Pf, e/∂B2 in units of c2 near where a new Landau level begins being filled for μe = 125 MeV, computed using the finite temperature-including form of Pf, a, equation (42). The explicit expression for ∂2Pf, e/∂B2 at finite T is given by equation (B3c). The damping effect of increasing temperature is clearly demonstrated.

Figure 1.

∂²P_{f, e}/∂B² in units of c² near where a new Landau level begins being filled for μ_e = 125 MeV, computed using the finite temperature-including form of P_{f, a}, equation (42). The explicit expression for ∂²P_{f, e}/∂B² at finite T is given by equation (B3c). The damping effect of increasing temperature is clearly demonstrated.

Open in new tab Download slide

For g_σ/m_σ, g_ω/m_ω, g_ρ/m_ρ, b_σ, c_σ, we use the tabulated parameters for the nuclear compressibility K = 300 MeV, m_*/m_N = 0.78 at saturation density σωρ model from table 5.5 of Glendenning (1997); these are g_σ/m_σ = 3.024 fm, g_ω/m_ω = 2.195 fm, g_ρ/m_ρ = 2.189 fm, b_σ = 3.478 × 10⁻³, c_σ = 1.328 × 10⁻². Unlike the reference, we do not include hyperons as our stellar model does not reach the densities at which they appear. The maximum Tolman–Oppenheimer–Volkoff (TOV) mass possible with this EOS is only ≈1.7 M_⊙, so it does not cover the entire range of observed neutron star masses, but it does allow us to discuss MHD stability inside a reasonable model of a neutron star core.

The matter pressure must be supplemented by the vacuum magnetic field contributions, giving the grand potential density Ω_G

$$\begin{eqnarray*} \Omega _G\big(B,\mu _a,\sigma ,\omega _0,\rho _0^3\big)=-P\big(B,\mu _a,\sigma ,\omega _0,\rho _0^3\big)+\frac{B^2}{8\pi }-\mathcal {L}_{\text{EH}}(B), \end{eqnarray*}$$

(44)

where |$\mathcal {L}_{\text{EH}}$| is the vacuum Euler–Heisenberg Lagrangian for only a magnetic field

$$\begin{eqnarray*} \mathcal {L}_{\text{EH}}=-\sum _{a=\text{e,p,m}}\frac{m_a^4}{8\pi ^2}\int ^{\infty }_0\frac{\mathrm{ d}x}{x^3}e^{-x}\left[x\frac{eB}{m_a^2}\text{coth}\left(x\frac{eB}{m_a^2}\right)-1-\frac{1}{3}\left(x\frac{eB}{m_a^2}\right)^2\right]. \end{eqnarray*}$$

(45)

|$\mathcal {L}_{\text{EH}}$| is significant (e.g. has magnitude greater than 5 per cent of the linear term −B²/8π) for species a when |$B\gtrsim 1.26\times 10^{17}m^2_{a,\text{MeV}}$| G. This corresponds to B ≳ 3.3 × 10¹⁶ G for electrons and magnetic fields far stronger than any field expected to exist even within magnetars for the protons and muons, so we can safely drop |$\mathcal {L}_{\text{EH}}$| for the latter two species.

The first law of thermodynamics for Ω_G is

$$\begin{eqnarray*} \text{d}\Omega _G &=& \sum _a\left.\frac{\partial \Omega _G}{\partial \mu _a}\right|_{\mu _b\ne \mu _a,B,\phi }\text{d}\mu _a+\left.\frac{\partial \Omega _G}{\partial B}\right|_{\mu _a,\phi }\text{d}B+\left.\frac{\partial \Omega _G}{\partial \sigma }\right|_{\mu _a,B,\omega _0,\rho _0^3}\text{d}\sigma +\left.\frac{\partial \Omega _G}{\partial \omega _0}\right|_{\mu _a,B,\sigma ,\rho _0^3}\text{d}\omega _0+\left.\frac{\partial \Omega _G}{\partial \rho _0^3}\right|_{\mu _a,B,\sigma ,\omega _0}\text{d}\rho _0^3 \nonumber \\ &=& -\sum _a\left.\frac{\partial P_{\text{f},a}}{\partial \mu _a}\right|_{B,\phi }\text{d}\mu _a +\left.\frac{\partial \Omega _G}{\partial B}\right|_{\mu _a,\phi }\text{d}B+\left.\frac{\partial P}{\partial \sigma }\right|_{\mu _a,B,\omega _0,\rho _0^3}\text{d}\sigma +\left.\frac{\partial P}{\partial \omega _0}\right|_{\mu _a,B,\sigma ,\rho _0^3}\text{d}\omega _0+\left.\frac{\partial P}{\partial \rho _0^3}\right|_{\mu _a,B,\sigma ,\omega _0}\text{d}\rho _0^3, \end{eqnarray*}$$

(46)

where ϕ is used to denote all the meson fields being held constant during differentiation. Using equations (37)–(41) and standard thermodynamic definitions (Landau & Lifshitz 1960), we have

$$\begin{eqnarray*} n_a=\left.\frac{\partial P_{\text{f},a}}{\partial \mu _a}\right|_{B,\phi }, \end{eqnarray*}$$

(47)

$$\begin{eqnarray*} H=4\pi \left.\frac{\partial \Omega _G}{\partial B}\right|_{\mu _a,\phi }=B-4\pi \frac{\partial \mathcal {L}_{\text{EH}}}{\partial B}-4\pi \left.\frac{\partial P}{\partial B}\right|_{\mu _a,\phi }, \end{eqnarray*}$$

(48)

$$\begin{eqnarray*} 0=\left.\frac{\partial P}{\partial \sigma }\right|_{\mu _a,B,\omega _0,\rho _0^3}=\left.\frac{\partial P}{\partial \omega _0}\right|_{\mu _a,B,\sigma ,\rho _0^3}=\left.\frac{\partial P}{\partial \rho _0^3}\right|_{\mu _a,B,\sigma ,\omega _0}, \end{eqnarray*}$$

(49)

where H is the magnetic H-field and is identical to equation (2) as we show in the next subsection. Hence when computing the first-order partial derivatives of Ω_G or P with respect to their natural (independent) variables μ_a and B, we can hold the meson fields constant.

4.1 Changes of variable and connection to magnetohydrodynamics

Because it is derived in the framework of quantum statistical mechanics using the grand canonical ensemble, the expression for P is in terms of chemical potentials of the fermions as opposed to their number densities. This is inconvenient for hydrodynamics where we work with conserved currents and fixed (number) densities and not at fixed chemical potentials. To compute the thermodynamic partial derivatives u_B, u_BB, u_ρB, u_BY, and u_Bf which appear in the stability criteria and which are computed at fixed ρ, Y, f and/or B, we must first relate the pressure P, or more generally Ω_G of equation (44), to the internal energy density defined in equation (1).

We start by computing the internal energy density corresponding to equation (44) using the Legendre transformation

$$\begin{eqnarray*} u\big(n_a,B,\sigma ,\omega _0,\rho _0^3\big)&=& \sum _an_a\mu _a+\Omega _G\big(\mu _a,B,\sigma ,\omega _0,\rho _0^3\big)=-\sum _a\mu _a\left.\frac{\partial P_{\text{f},a}}{\partial \mu _a}\right|_{B,\phi }+\Omega _G\big(\mu _a,B,\sigma ,\omega _0,\rho _0^3\big) \nonumber \\ &=& \frac{B^2}{8\pi }-\mathcal {L}_{\text{EH}}(B)+u_{\text{mat}}\big(n_a,B,\sigma ,\omega _0,\rho _0^3\big). \end{eqnarray*}$$

(50)

The internal energy density of the matter |$u_{\text{mat}}\big(n_a,B,\sigma ,\omega _0,\rho _0^3\big)$| including meson fields is

$$\begin{eqnarray*} u_{\text{mat}}\big(n_a,B,\sigma ,\omega _0,\rho _0^3\big) &=& \sum _au_{\text{f},a}\big(n_a,B,\sigma ,\omega _0,\rho _0^3\big)+\frac{1}{2}m_{\sigma }^2\sigma ^2+\frac{1}{3}b_{\sigma }m_{\text{N}}(g_{\sigma }\sigma)^3+\frac{1}{4}c_{\sigma }(g_{\sigma }\sigma)^4-\frac{1}{2}m_{\omega }^2\omega _0^2-\frac{1}{2}m_{\rho }^2\big(\rho ^3_0\big)^2 \nonumber \\ &&+g_{\omega }\omega _0n_{\text{b}}+\frac{1}{2}g_{\rho }\rho ^3_0(n_{\text{p}}-n_{\text{n}}), \end{eqnarray*}$$

(51)

where u_{f, a} is the internal energy for the fermions of species a and is expressed in terms of P_{f, a} as

$$\begin{eqnarray*} u_{\text{f},a}=\mu _a\left.\frac{\partial P_{\text{f},a}}{\partial \mu _a}\right|_{B,\phi }-P_{\text{f},a}. \end{eqnarray*}$$

(52)

Equation (51) can be simplified at equilibrium using equation (37). Since we can easily switch between ρ, Y, f, →n_n, n_p, n_e, n_m, equations (1) and (50) are identical except for the dependence on the meson fields in u_mat. Since the meson fields are in a sense ‘microscopic’ variables that should not affect the macroscopic fluid flow except through their influence on the baryons with which they interact, we do not hold them constant when calculating u_B, u_BB, etc. Hence u_B, u_BB, etc. may depend on partial derivatives of the meson fields, as we now show.

Taking the differential of n_a = n_a(μ_a, B, σ, ω₀, ρ₀) (the meson field dependence can be neglected for the leptons), we can write the following matrix equation

$$\begin{eqnarray*} \begin{pmatrix}\text{d}n_a \\ \text{d}B \\ \text{d}\sigma \\ \text{d}\omega _0 \\ \text{d}\rho _0^3 \end{pmatrix}=\begin{pmatrix}\partial n_a/\partial \mu _a &\quad \partial n_a/\partial B &\quad \partial n_a/\partial \sigma &\quad \partial n_a/\partial \omega _0 &\quad \partial n_a/\partial \rho _0^3\\ 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1\end{pmatrix}\begin{pmatrix}\text{d}\mu _a \\ \text{d}B \\ \text{d}\sigma \\ \text{d}\omega _0 \\ \text{d}\rho _0^3\end{pmatrix}, \end{eqnarray*}$$

(53)

where all variables except that being differentiated with respect to are implicitly held constant. This can be inverted to give

$$\begin{eqnarray*} \text{d}\mu _a=\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\left[\text{d}n_a-\left.\frac{\partial n_a}{\partial B}\right|_{\mu _a,\phi }\text{d}B-\left.\frac{\partial n_a}{\partial \sigma }\right|_{\mu _a,B,\omega _0,\rho _0^3}\text{d}\sigma -\left.\frac{\partial n_a}{\partial \omega _0}\right|_{\mu _a,B,\sigma ,\rho _0^3}\text{d}\omega _0-\left.\frac{\partial n_a}{\partial \rho _0^3}\right|_{\mu _a,B,\sigma ,\omega _0}\text{d}\rho _0^3\right] \end{eqnarray*}$$

(54)

where the meson field-dependent terms only contribute to dμ_n and dμ_p. Using equations (35) and (36),

$$\begin{eqnarray*} \left.\frac{\partial n_a}{\partial \sigma }\right|_{\mu _a,B,\omega _0,\rho _0^3}=\frac{\partial m_*}{\partial \sigma }\left.\frac{\partial n_a}{\partial m_*}\right|_{\mu _a,B,\phi }=g_{\sigma }\frac{m_*}{\mu _a^*}\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }, \end{eqnarray*}$$

(55a)

$$\begin{eqnarray*} \left.\frac{\partial n_a}{\partial \omega _0}\right|_{\mu _a,B,\sigma ,\rho _0^3}=\left.\frac{\partial n_a}{\partial \mu _a^*}\right|_{\mu _a,B,\phi }\left.\frac{\partial \mu _a^*}{\partial \omega _0}\right|_{\mu _a,B,\phi }=-g_{\omega }\left.\frac{\partial n_a}{\partial \mu _a}\right|_{\mu _a,B,\phi }, \end{eqnarray*}$$

(55b)

$$\begin{eqnarray*} \left.\frac{\partial n_a}{\partial \rho _0^3}\right|_{\mu _a,B,\sigma ,\omega _0}=\left.\frac{\partial n_a}{\partial \mu _a^*}\right|_{\mu _a,B,\phi }\left.\frac{\partial \mu _a^*}{\partial \rho _0^3}\right|_{\mu _a,B,\phi }=-g_{\rho }I_3\left.\frac{\partial n_a}{\partial \mu _a}\right|_{\mu _a,B,\phi }, \end{eqnarray*}$$

(55c)

where I₃ = ±1/2 is the third component of isospin for protons/neutrons. Inserting these into equation (54) gives

$$\begin{eqnarray*} \text{d}\mu _a=\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\text{d}n_a-\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial n_a}{\partial B}\right|_{\mu _a,\phi }\text{d}B-g_{\sigma }\frac{m_*}{\mu _a^*}\text{d}\sigma +g_{\omega }\text{d}\omega _0+g_{\rho }I_3\text{d}\rho _0^3. \end{eqnarray*}$$

(56)

Inserting this into equation (46) and using equation (44) to isolate dP, we obtain

$$\begin{eqnarray*} \text{d}P &=&\sum _an_a\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\text{d}n_a+\sum _a\left[\left.\frac{\partial P_{\text{f},a}}{\partial B}\right|_{\mu _a,\phi }-n_a\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial n_a}{\partial B}\right|_{\mu _a,\phi }\right]\text{d}B+g_{\omega }n_{\text{b}}\text{d}\omega _0+\frac{1}{2}g_{\rho }(n_{\text{p}}-n_{\text{n}})\text{d}\rho _0^3 \nonumber \\ &&-g_{\sigma }m_*\left(\frac{n_{\text{n}}}{\mu _{\text{n}}^*}+\frac{n_{\text{p}}}{\mu _{\text{p}}^*}\right)\text{d}\sigma . \end{eqnarray*}$$

(57)

This expression is necessary to compute the partial derivatives of the pressure with respect to ρ = m_Nn_b, B, Y and/or f with the other variables held constant as needed in the hydrodynamics.

The first law of thermodynamics for |$u(n_a,B,\sigma ,\omega _0,\rho _0^3)$| is most conveniently found by taking the differential of equation (50). Doing so and using equations (56) and (57) gives

$$\begin{eqnarray*} \text{d}u=\sum _a\left.\frac{\partial u}{\partial n_a}\right|_{n_c\ne n_a,B,\phi }\text{d}n_a+\left.\frac{\partial u}{\partial B}\right|_{n_a,\phi }\text{d}B+\left.\frac{\partial u}{\partial \sigma }\right|_{n_a,B,\phi }\text{d}\sigma +\left.\frac{\partial u}{\partial \omega _0}\right|_{n_a,B,\phi }\text{d}\omega _0+\left.\frac{\partial u}{\partial \rho _0^3}\right|_{n_a,B,\phi }\text{d}\rho _0^3=\sum _a\mu _a \text{d} n_a+\left.\frac{\partial u}{\partial B}\right|_{n_a,\phi }\text{d}B, \end{eqnarray*}$$

(58)

We see that, like for Ω_G and P, when computing the first-order partial derivatives of u with respect to its natural variables n_a and B the meson fields can be held constant. Taking the differential of the first equality in equation (50) and using equation (46) gives u_B:

$$\begin{eqnarray*} \left.\frac{\partial \Omega _G}{\partial B}\right|_{\mu _a,\phi }=\left.\frac{\partial u}{\partial B}\right|_{n_a,\phi }=\frac{H}{4\pi }\rightarrow u_B=\left.\frac{\partial u_M}{\partial B}\right|_{\rho ,Y_a}=-\left.\frac{\partial (P+\mathcal {L}_{\text{EH}})}{\partial B}\right|_{\mu _a,\phi }=\left.\frac{\partial (u_{\text{mat}}-\mathcal {L}_{\text{EH}})}{\partial B}\right|_{n_a,\phi }. \end{eqnarray*}$$

(59)

The required second-order partial derivatives can all be computed starting from u_B. Since it is most convenient to compute thermodynamic derivatives starting from P or Ω_G, we take the differential

$$\begin{eqnarray*} \text{d}u_B=\text{d}\left(\left.\frac{\partial P}{\partial B}\right|_{\mu _a,\phi }\right) &=&-\left.\frac{\partial ^2(P+\mathcal {L}_{\text{EH}})}{\partial B^2}\right|_{\mu _a,\phi }\text{d}B-\sum _a\left.\frac{\partial ^2P}{\partial B\partial \mu _a}\right|_{\mu _b\ne \mu _a,\phi }\text{d}\mu _a-\left.\frac{\partial ^2P}{\partial B\partial \sigma }\right|_{\mu _a,\omega _0,\rho _0^3}\text{d}\sigma -\left.\frac{\partial ^2P}{\partial B\partial \omega _0}\right|_{\mu _a,\sigma ,\omega _0}\text{d}\omega _0 \nonumber \\ &&-\left.\frac{\partial ^2P}{\partial B\partial \rho _0^3}\right|_{\mu _a,\sigma ,\omega _0}\text{d}\rho _0^3. \end{eqnarray*}$$

(60)

Using equation (56) and

$$\begin{eqnarray*} \left.\frac{\partial ^2P}{\partial B\partial \sigma }\right|_{\mu _a,\omega _0,\rho _0^3}=-g_{\sigma }\left.\frac{\partial ^2P}{\partial B\partial m_*}\right|_{\mu _a,\phi }, \end{eqnarray*}$$

(61a)

$$\begin{eqnarray*} \left.\frac{\partial ^2P}{\partial B\partial \omega _0}\right|_{\mu _a,\sigma ,\omega _0}=\left.\frac{\partial ^2P}{\partial B\partial \mu _a^*}\right|_{\mu _a,\phi }\left.\frac{\partial \mu _a^*}{\partial \omega _0}\right|_{\mu _a,B,\sigma ,\rho _0^3}=-g_{\omega }\left.\frac{\partial ^2P}{\partial B\partial \mu _a}\right|_{\mu _b\ne \mu _c,\phi }=-g_{\omega }\left.\frac{\partial n_a}{\partial B}\right|_{\mu _a,\phi }, \end{eqnarray*}$$

(61b)

$$\begin{eqnarray*} \left.\frac{\partial ^2P}{\partial B\partial \rho _0^3}\right|_{\mu _a,\sigma ,\omega _0}=\left.\frac{\partial ^2P}{\partial B\partial \mu _a^*}\right|_{\mu _a,\phi }\left.\frac{\partial \mu _a^*}{\partial \rho _0^3}\right|_{\mu _a,B,\sigma ,\omega _0}=-g_{\rho }I_3\left.\frac{\partial ^2P}{\partial B\partial \mu _a}\right|_{\mu _b\ne \mu _c,\phi }=-g_{\rho }I_3\left.\frac{\partial n_a}{\partial B}\right|_{\mu _a,\phi }, \end{eqnarray*}$$

(61c)

we find (using equation 47 to replace n_a)

$$\begin{eqnarray*} \text{d}u_B &=&\left[-\left.\frac{\partial ^2(P+\mathcal {L}_{\text{EH}})}{\partial B^2}\right|_{\mu _a,\phi }+\sum _a\left(\left.\frac{\partial ^2 P_{\text{f},a}}{\partial \mu _a^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2 P_{\text{f},a}}{\partial B\partial \mu _a}\right|_{\phi }\right]\text{d}B -\sum _a\left(\left.\frac{\partial ^2 P_{\text{f},a}}{\partial \mu _a^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},a}}{\partial B\partial \mu _a}\right|_{\phi }\text{d}n_a \nonumber\\ &&+\,g_{\sigma }\left[\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial m_*}\right|_{\mu _{\text{p}},\phi }+\frac{m_*}{\mu _{\text{p}}^*}\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }\right]\text{d}\sigma . \end{eqnarray*}$$

(62)

This expression is required to compute u_BB, u_ρB, u_BY, and u_Bf as found in the hydrodynamics. Since we know P and |$\mathcal {L}_{\text{EH}}$|⁠, we can compute all of the coefficients appearing in this expression.

In the non-relativistic, non-magnetic limit, equation (56) gives the differential mass density dρ

$$\begin{eqnarray*} \text{d}u &=& \sum _a\mu _a\text{d}n_a=[\mu _{\text{n}}(1-Y)+\mu _{\text{p}}Y+\mu _{\text{e}}Yf+\mu _{\text{m}}Y(1-f)]\text{d}n_{\text{b}}+[\mu _{\text{p}}-\mu _{\text{n}}+\mu _{\text{e}}f+\mu _{\text{m}}(1-f)]n_{\text{b}}\text{d}Y+(\mu _{\text{e}}-\mu _{\text{m}})n_{\text{b}}Ydf=\mu _{\text{n}}\text{d}n_{\text{b}} \nonumber \\ \rightarrow \text{d}\rho &=& m_{\text{N}}\text{d}n_{\text{b}}, \end{eqnarray*}$$

(63)

where we used beta equilibrium μ_n = μ_p + μ_e and μ_e = μ_m. So the differential dn_b can be replaced with dρ/m_N. The non-relativistic, non-magnetic limit of equation (51) is

$$\begin{eqnarray*} u_{\text{mat}}(B=0)=m_*n_{\text{b}}+m_{\text{e}}n_{\text{e}}+m_{\text{m}}n_{\text{m}}+\frac{1}{2}m_{\sigma }^2\sigma ^2+\frac{1}{3}b_{\sigma }m_{\text{N}}(g_{\sigma }\sigma)^3+\frac{1}{4}c_{\sigma }(g_{\sigma }\sigma)^4+\frac{1}{2}m_{\omega }^2\omega _0^2+\frac{1}{2}m_{\rho }^2\big(\rho ^3_0\big)^2, \end{eqnarray*}$$

(64)

which is within a few per cent of ρ = m_Nn_b. We hence use the latter expression throughout the rest of the paper as we discussed in Section 2. The similarity of ρ = m_Nn_b and u_mat(B = 0) is shown in Fig. 2.

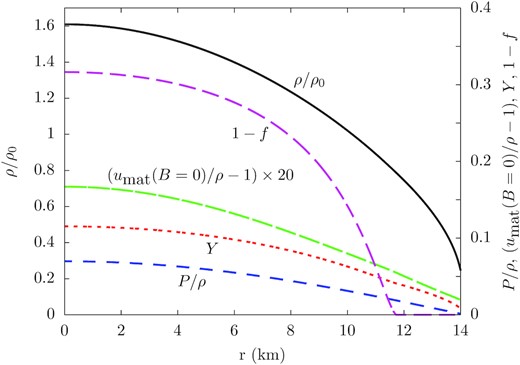
$Properties of the neutron star model used to analyse the MHD stability: the mass density ρ divided by nuclear saturation density ρ0 = 2.7 × 1014 g cm−3, pressure P divided by ρ, the fractional difference between the internal energy density of the matter umat at B = 0 and ρ (scaled by a factor of 20), the proton fraction Y and one minus the electron fraction f. Only the properties within 14 km (ρ > 0.25ρ0) are shown, as the crust-core transition is expected to occur before these densities and a different EOS would be needed in this region.$

Figure 2.

Properties of the neutron star model used to analyse the MHD stability: the mass density ρ divided by nuclear saturation density ρ₀ = 2.7 × 10¹⁴ g cm⁻³, pressure P divided by ρ, the fractional difference between the internal energy density of the matter u_mat at B = 0 and ρ (scaled by a factor of 20), the proton fraction Y and one minus the electron fraction f. Only the properties within 14 km (ρ > 0.25ρ₀) are shown, as the crust-core transition is expected to occur before these densities and a different EOS would be needed in this region.

Open in new tab Download slide

Returning to equation (62) and using equation (63), we compute the required second-order partial derivatives for computing the stability criteria

$$\begin{eqnarray*} u_{BB}=\left.\frac{\partial ^2 u_M}{\partial B^2}\right|_{\rho ,Y,f}=-\left.\frac{\partial ^2(P+\mathcal {L}_{\text{EH}})}{\partial B^2}\right|_{\mu _a,\phi }+\sum _a\left(\left.\frac{\partial ^2 P_{\text{f},a}}{\partial \mu _a^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2 P_{\text{f},a}}{\partial B\partial \mu _a}\right|_{\phi }+g_{\sigma }\left[\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial m_*}\right|_{\mu _p,\phi }+\frac{m_*}{\mu _{\text{p}}^*}\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }\right]\left.\frac{\partial \sigma }{\partial B}\right|_{\rho ,Y,f}, \end{eqnarray*}$$

(65a)

$$\begin{eqnarray*} u_{\rho B}=\left.\frac{\partial ^2 u_M}{\partial B\partial \rho }\right|_{Y,f}=-\frac{1}{m_{\text{N}}}\sum _a\left(\left.\frac{\partial ^2 P_{\text{f},a}}{\partial \mu _a^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},a}}{\partial B\partial \mu _a}\right|_{\mu _b\ne \mu _a,\phi }+\frac{g_{\sigma }}{m_{\text{N}}}\left[\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial m_*}\right|_{\mu _p,\phi }+\frac{m_*}{\mu _{\text{p}}^*}\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }\right]\left.\frac{\partial \sigma }{\partial n_{\text{b}}}\right|_{Y,f,B}, \end{eqnarray*}$$

(65b)

$$\begin{eqnarray*} u_{BY} &=&\left.\frac{\partial ^2 u_M}{\partial B\partial Y}\right|_{\rho ,f}=-n_{\text{b}}\left[\left(\left.\frac{\partial ^2 P_{\text{f},\text{p}}}{\partial \mu _{\text{p}}^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }+f\left(\left.\frac{\partial ^2 P_{\text{f},\text{e}}}{\partial \mu _{\text{e}}^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},\text{e}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }+(1-f)\left(\left.\frac{\partial ^2 P_{\text{f},\text{m}}}{\partial \mu _{\text{m}}^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},\text{m}}}{\partial B\partial \mu _{\text{m}}}\right|_{\phi }\right] \nonumber \\ && -g_{\sigma }m_*n_{\text{b}}\left(\frac{1}{\mu _{\text{n}}^*}-\frac{1}{\mu _{\text{p}}^*}\right)\left.\frac{\partial \sigma }{\partial Y}\right|_{\rho ,f,B} \end{eqnarray*}$$

(65c)

$$\begin{eqnarray*} u_{Bf} &=& \left.\frac{\partial ^2 u_M}{\partial B\partial f}\right|_{\rho ,Y}=-n_{\text{b}}Y\left[\left(\left.\frac{\partial ^2 P_{\text{f},\text{e}}}{\partial \mu _{\text{e}}^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},\text{e}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }-\left(\left.\frac{\partial ^2 P_{\text{f},\text{m}}}{\partial \mu _{\text{m}}^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial ^2P_{\text{f},\text{m}}}{\partial B\partial \mu _{\text{m}}}\right|_{\phi }\right] \end{eqnarray*}$$

(65d)

where we have used that ∂σ/∂f|_{ρ, Y, B} = 0. The partial derivatives of σ must be computed implicitly using the σ meson self-consistency condition equation (41). Starting with ∂σ/∂n_b|_{Y, f, B}

$$\begin{eqnarray*} 0=\left.\frac{\partial \sigma }{\partial n_{\text{b}}}\right|_{Y,f,B}\left[-m_{\sigma }^2-2b_{\sigma }m_{\text{N}}g_{\sigma }^3\sigma -3c_{\sigma }g_{\sigma }^4\sigma ^2+g_{\sigma }^2\left.\frac{\partial ^2 P}{\partial m_*^2}\right|_{\mu _a,B,\phi }\right]-g_{\sigma }\left.\frac{\partial ^2 P_{\text{f},\text{n}}}{\partial m_*\partial \mu _{\text{n}}^*}\right|_{B,\phi }\left.\frac{\partial \mu _{\text{n}}^*}{\partial n_{\text{b}}}\right|_{Y,f,B}-g_{\sigma }\left.\frac{\partial ^2 P_{\text{f},\text{p}}}{\partial m_*\partial \mu _{\text{p}}^*}\right|_{B,\phi }\left.\frac{\partial \mu _{\text{p}}^*}{\partial n_{\text{b}}}\right|_{Y,f,B}. \end{eqnarray*}$$

(66)

Using equations (36) and (56), we have

$$\begin{eqnarray*} \text{d}\mu _a^*=\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\text{d}n_a+\left(\left.\frac{\partial n_a}{\partial \mu _a}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial n_a}{\partial B}\right|_{\mu _a,\phi }\text{d}B-g_{\sigma }\frac{m_*}{\mu _a^*}\text{d}\sigma , \end{eqnarray*}$$

(67)

and hence it can be shown that

$$\begin{eqnarray*} \left.\frac{\partial \sigma }{\partial n_{\text{b}}}\right|_{Y,f,B}=\frac{g_{\sigma }m_*}{W}\left(\frac{n_{\text{n}}}{\mu _{\text{n}}^*}+\frac{n_{\text{p}}}{\mu _{\text{p}}^*}\right), \end{eqnarray*}$$

(68)

where W is

$$\begin{eqnarray*} W &\equiv & m_{\sigma }^2+2b_{\sigma }m_{\text{N}}g_{\sigma }^3\sigma +3c_{\sigma }g_{\sigma }^4\sigma ^2+\frac{g_{\sigma }^2}{2\pi ^2}\left[\frac{(2m_*^2+\mu _{\text{n}}^*)\sqrt{\mu _{\text{n}}^{*2}-m_*^2}}{\mu _{\text{n}}^*}-3m_*^2\ln \left(\frac{\mu _{\text{n}}^*+\sqrt{\mu _{\text{n}}^{*2}-m_*^2}}{m_*}\right)\right] \nonumber \\ &&+\frac{g_{\sigma }^2eB}{2\pi ^2}\sum _{n=0}^{n_{\text{max}}}\gamma _n\left[\ln \left(\frac{\mu _{\text{p}}^*+\sqrt{\mu _{\text{p}}^{*2}-m_*^2-2eBn}}{\sqrt{m_*^2+2eBn}}\right)-\frac{m_*^2\sqrt{\mu _{\text{p}}^{*2}-m_*^2-2eBn}}{\mu _{\text{p}}^*(m_*^2+2eBn)}\right]. \end{eqnarray*}$$

(69)

Analogous calculations for ∂σ/∂B|_{ρ, Y, f} and ∂σ/∂Y|_{ρ, f, B} give

$$\begin{eqnarray*} \left.\frac{\partial \sigma }{\partial B}\right|_{\rho ,Y,f} = \frac{g_{\sigma }}{W}\left(\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial m_*}\right|_{\mu _p,\phi }+\frac{m_*}{\mu _{\text{p}}^*}\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial B\partial \mu _{\text{p}}}\right|_{\phi }\right), \end{eqnarray*}$$

(70)

$$\begin{eqnarray*} \left.\frac{\partial \sigma }{\partial Y}\right|_{\rho ,Y,B} = \frac{g_{\sigma }m_*n_{\text{b}}}{W}\left(\frac{1}{\mu _{\text{p}}^*}-\frac{1}{\mu _{\text{n}}^*}\right). \end{eqnarray*}$$

(71)

Expressions for the partial derivatives of P with respect to μ_a, B, and m_* are relegated to Appendix B (online supplement).

4.2 Background stellar model

The evaluation of the stability criteria in Section 3 requires a background equilibrium fluid configuration which is perturbed according to the Lagrangian displacement field ξⁱ. For this background model, we use a canonical neutron star with mass M_* = 1.4 M_⊙ and structure determined by the σωρ EOS discussed earlier. The presence of the magnetic field changes the stellar equilibrium, since the equation of hydrostatic balance for the background star is equation (3) with vⁱ = 0. If the magnetic forces are small compared to the mechanical pressure, which is true for P ≫ BH/(8π), the magnetic forces will have a negligible effect on the stellar structure. For even the strongest fields B = 10¹⁷ G that we employ in this paper, this will be approximately true, with (10¹⁷G)²/(8π) at most a few per cent of the central pressure of the stellar model. Hence, when computing the background stellar model we use to find the gravitational acceleration g and the species gradients that appear in the Brunt–Väisälä frequency, we ignore the effect of the magnetic field.

Under the assumptions described above, the background star will be spherically symmetric and its structure determined by solving the non-relativistic hydrostatic balance equations

$$\begin{eqnarray*} \frac{\mathrm{ d}P}{\mathrm{ d}r}=-\frac{G\rho M(r)}{r^2}, \quad \frac{\mathrm{ d}M(r)}{\mathrm{ d}r}=4\pi \rho r^2, \end{eqnarray*}$$

(72)

where the mass enclosed in radius r is M(r). P in the stellar core is given by equation (35) but using the non-magnetic fermion pressure (equation 38) for all fermion species and using the mean-field values of ω₀ and |$\rho _0^3$| given by equation (37) and the self-consistently calculated value of σ found using equation (41). The mass density is ρ = m_Nn_b. The muon threshold density for this EOS is ρ = 0.79ρ₀. To extend the star out to the exterior vacuum, we use the BPS EOS as tabulated in Glendenning (1997). This provides only a small contribution to the overall mass and radius of the star, and does not affect the properties of the outer core like the local gravitational acceleration or gradients of the species fractions.

For a canonical neutron star with M_⋆ = M(R_⋆) = 1.4 M_⊙, the required central pressure and density for our choice of EOS are P_c = 2.71 × 10³⁴ dyn cm⁻² and ρ_c = 4.35 × 10¹⁴ g cm⁻³, and the stellar radius is R_⋆ = 15.56 km. This radius is unrealistically large because we used the non-relativistic equation for hydrostatic balance – if we had used the TOV equation, the M_* = 1.4 M_⊙ star would have R_⋆ = 13.35 km. Solving equation (72) determines the gravitational acceleration g and radial derivatives of Y_a and ρ as functions of distance from the centre of the star, or equivalently, as functions of ρ. In beta equilibrium, we have

$$\begin{eqnarray*} \mu _{\text{n}}=\mu _{\text{p}}+\mu _{\text{e}},\quad \mu _{\text{e}}=\mu _{\text{m}}, \end{eqnarray*}$$

(73)

which along with the requirement of local charge neutrality

$$\begin{eqnarray*} n_{\text{p}}=n_{\text{e}}+n_{\text{m}}, \end{eqnarray*}$$

(74)

constrains all four chemical potentials. Using this and equation (47), for a particular value of μ_e and B, we can solve for all of the number densities n_a and hence the total mass density ρ, so we can find the corresponding value of g, dY/dr, etc. by interpolation of the stellar model. ρ, P, Y, and 1 − f for the stellar model used to study the MHD stability are given as a function of stellar radius in Fig. 2.

The other required stellar properties are the sound speed c_s and the Brunt–Väisälä frequency |$\tilde{N}^2$|⁠. The former is computed using equation (57) and by differentiating (37):

$$\begin{eqnarray*} c_s^2=\left.\frac{\partial P}{\partial \rho }\right|_{B,Y,f}=\frac{1}{m_{\text{N}}}\left[\sum _an_a\left(\left.\frac{\partial ^2P_{\text{f},a}}{\partial \mu _a^2}\right|_{B,\phi }\right)^{-1}\left.\frac{\partial n_a}{\partial n_{\text{b}}}\right|_{Y,f,B}+\left(\frac{g_{\omega }}{m_{\omega }}\right)^2n_b+\frac{1}{4}\left(\frac{g_{\rho }}{m_{\rho }}\right)^2(2Y-1)^2n_b-g_{\sigma }m_*\left(\frac{n_p}{\mu ^*_{\text{p}}}+\frac{n_n}{\mu ^*_{\text{n}}}\right)\frac{\partial \sigma }{\partial n_b}\right]. \end{eqnarray*}$$

(75)

This expression is given exclusively in terms of partial derivatives computed in Section 4.1 or listed in Appendix B. Similarly, |$\tilde{N}^2$| as defined in equation (24) requires

$$\begin{eqnarray*} \left.\frac{\partial P}{\partial Y}\right|_{\rho ,f,B} &=& n_{\text{b}}^2\left[Y\left(\left.\frac{\partial ^2P_{\text{f},\text{p}}}{\partial \mu _{\text{p}}^2}\right|_{B,\phi }\right)^{-1}-(1-Y)\left(\left.\frac{\partial ^2P_{\text{f},\text{n}}}{\partial \mu _{\text{n}}^2}\right|_{B,\phi }\right)^{-1}+Yf\left(\left.\frac{\partial ^2P_{\text{f},\text{e}}}{\partial \mu _{\text{e}}^2}\right|_{B,\phi }\right)^{-1}+Y(1-f)\left(\left.\frac{\partial ^2P_{\text{f},\text{m}}}{\partial \mu _{\text{m}}^2}\right|_{B,\phi }\right)^{-1} \right] \nonumber \\ &&+\frac{1}{2}\left(\frac{g_{\rho }}{m_{\rho }}\right)^2n_b^2(2Y-1)-g_{\sigma }m_*\left(\frac{n_{\text{n}}}{\mu ^*_{\text{n}}}+\frac{n_{\text{p}}}{\mu ^*_{\text{p}}}\right)\frac{\partial \sigma }{\partial Y}, \end{eqnarray*}$$

(76)

$$\begin{eqnarray*} \left.\frac{\partial P}{\partial f}\right|_{\rho ,Y,B}=Y^2n_{\text{b}}^2\left[f\left(\left.\frac{\partial ^2P_{\text{f},\text{e}}}{\partial \mu _{\text{e}}^2}\right|_{B,\phi }\right)^{-1}-(1-f)\left(\left.\frac{\partial ^2P_{\text{f},\text{m}}}{\partial \mu _{\text{m}}^2}\right|_{B,\phi }\right)^{-1}\right], \end{eqnarray*}$$

(77)

which are also computed using equations (57) and (37). u_BY and u_Bf, also required in |$\tilde{N}^2$|⁠, are given by equations (65c)–(65d). |$\tilde{N}$| is plotted in Fig. 3 for three different magnetic field strengths, showing how the magnetic field-dependent terms modify the usual neutron–proton and leptonic buoyancy.

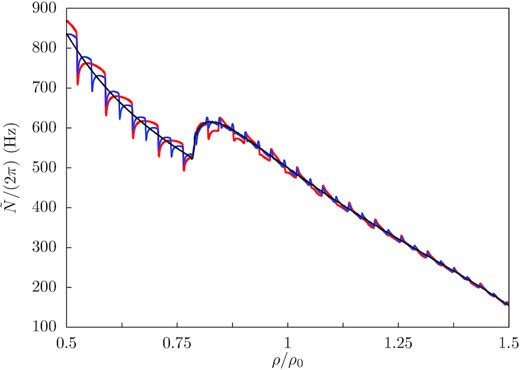
$Brunt–Väisälä frequency with magnetic contributions $\tilde{N}$ as a function of density for three different magnetic field strengths: B = 1015 G (black), B = 5 × 1016 G (blue), B = 1017 G (red). ρ0 = 2.7 × 1014 g cm−3. The bump starting at ρ = 0.79ρ0 is the leptonic buoyancy contribution that occurs where muons are present in the star.$

Figure 3.

Brunt–Väisälä frequency with magnetic contributions |$\tilde{N}$| as a function of density for three different magnetic field strengths: B = 10¹⁵ G (black), B = 5 × 10¹⁶ G (blue), B = 10¹⁷ G (red). ρ₀ = 2.7 × 10¹⁴ g cm⁻³. The bump starting at ρ = 0.79ρ₀ is the leptonic buoyancy contribution that occurs where muons are present in the star.

Open in new tab Download slide

The functional form of the background magnetic field, as opposed to solely the field strength, is required to compute the magnetic buoyancy stability criteria. We assume a completely toroidal field: though this is not stable globally, we are only interested in the local stability here. The toroidal field in a stable, combined poloidal–toroidal field configuration inside a neutron star can also be two orders of magnitude stronger than the poloidal field (Akgün et al. 2013), providing justification for us to ignore the latter as a first approximation. Being perpendicular to the gravitational field, a toroidal field is the analogue to the field in the x-direction used in deriving the magnetic buoyancy stability criterion in Section 3. Following e.g. Lander & Jones (2009), we use

$$\begin{eqnarray*} B^i=B_0\frac{\rho }{\rho _cR_{\star }}\delta ^i_{\phi }\rightarrow B=\sqrt{B^iB_i}=B_0\frac{\rho }{\rho _c}\frac{\varpi }{R_{\star }}, \end{eqnarray*}$$

(78)

where B₀ is a constant and ϖ = rsin θ the cylindrical radius (θ = polar angle). This field vanishes at the surface of the star due to its ρ dependence. This is unstable to the sausage and kink instability along the z-axis, but could be stabilized by a weaker poloidal field which we ignore. When looking at the stability properties of the star, the z-axis is excised since the field vanishes here and the strong-field MHD in which we are interested is not relevant.

We convert this field to Cartesian coordinates in line with our local analysis: the ϕ-direction is changed to the x-direction and the (spherical) radial direction is changed to the z-direction. Equation (78) hence implies d/dzln (B/ρ) = 1/z and d/dzln B = dln ρ/dz + 1/z. Since we are free to choose B₀, we will pick values of B independent of the radial position and density with the understanding that B₀ can be chosen appropriately to satisfy equation (78). Based on the density profile in Fig. 2, the maximum value of B within the core is ≈0.42B₀.

5 NUMERICAL CALCULATION OF STABILITY CRITERIA

The properties of the stellar model discussed in Section 4.2 and the thermodynamic derivatives of u_M discussed in Section 4 are the only inputs required to compute the local stability criteria from Section 3. Before doing so, we compute the first and second-order partial derivatives of u_M with respect to B and ρ. In Fig. 4, we plot H, |$c_s^2$|⁠, Bρu_ρB, and B²u_BB/ρ as a function of B or ρ, for a representative core temperature for a magnetar over a few hundred years old (Potekhin & Chabrier 2018) of 10⁸ K. Panel (a) shows that B ≈ H as mentioned in the introduction, and prominently shows the de Haas–van Alphen oscillations of H, resulting from the population of successive Landau levels as B is decreased, where a new Landau level starts being populated significantly at |$B=(\mu _a^2-m_a^2)/(2en)$| for integer n. At T = 0, the slope of H(B) is discontinuous at |$B=(\mu _a^2-m_a^2)/(2en)$| for integer n; non-zero T restores continuity. However, the derivatives of H(B) fluctuate rapidly with large positive and negative values near |$B=(\mu _a^2-m_a^2)/(2en)$|⁠. As the inset in (b) shows, the Landau quantization of the fermions also has a small effect on the sound speed, causing fluctuations of a few per cent around its zero field value. Landau quantization also results in the spikes that are observed in Bu_ρB and B²u_BB/ρ for B ≳ 10¹⁵. Bu_ρB and B²u_BB/ρ can clearly be negative, which will lead to potential instabilities. Since their sign change is associated with Landau quantization, we conclude that this will be the dominant mechanism in any potential instability that will occur as opposed to the vacuum Euler–Heisenberg Lagrangian. However, Bu_ρB and B²u_BB/ρ are much smaller than |$c_s^2$|⁠, so it is clear that V² defined in equation (19) will be positive, and so for the k_x = 0 perturbations to be unstable will require the k_x = 0 magnetic buoyancy criterion SC1 (equation 23) to be negative.

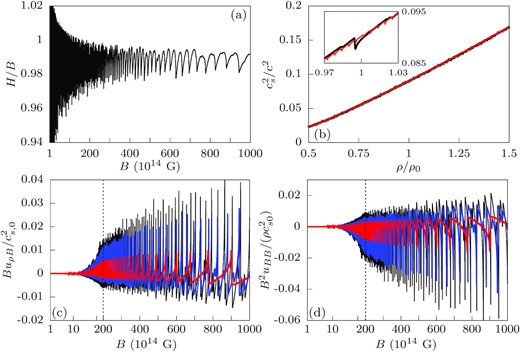
$(a) H/B as a function of B- this is comparable to Broderick et al. (2000), Fig. 2. The fine details visible at B ≳ 7 × 1016 G are due to including multiple fermion species; the overall curve is dominated by the Landau quantization of the electrons. (b) $c_s^2/c^2$ as a function of mass density for B = 1016 G (red) and B = 1017 G (black). The inset shows the small fluctuations in $c_s^2$ due to Landau quantization. (c) $Bu_{\rho B}/c_{s,0}^2$ as a function of B, where $c_{s,0}^2\equiv 0.09c^2$ is the approximate sound speed squared at nuclear saturation density ρ0. The three curves are computed for fixed μe = 80 MeV (red), 125 MeV (blue) and 150 MeV (black), corresponding to ρ ≈ 0.56ρ0, ρ0 and 1.34ρ0, respectively. (d) $B^2u_{BB}/(\rho c_{s,0}^2)$ as a function of B. The three curves are computed for the same values of μe as panel (d). Note the change from logarithmic to linear scaling of the horizontal axis at B = 2 × 1016 G, separated by a dotted line, in (c) and (d). All curves shown were computed using T = 108 K.$

Figure 4.

(a) H/B as a function of B- this is comparable to Broderick et al. (2000), Fig. 2. The fine details visible at B ≳ 7 × 10¹⁶ G are due to including multiple fermion species; the overall curve is dominated by the Landau quantization of the electrons. (b) |$c_s^2/c^2$| as a function of mass density for B = 10¹⁶ G (red) and B = 10¹⁷ G (black). The inset shows the small fluctuations in |$c_s^2$| due to Landau quantization. (c) |$Bu_{\rho B}/c_{s,0}^2$| as a function of B, where |$c_{s,0}^2\equiv 0.09c^2$| is the approximate sound speed squared at nuclear saturation density ρ₀. The three curves are computed for fixed μ_e = 80 MeV (red), 125 MeV (blue) and 150 MeV (black), corresponding to ρ ≈ 0.56ρ₀, ρ₀ and 1.34ρ₀, respectively. (d) |$B^2u_{BB}/(\rho c_{s,0}^2)$| as a function of B. The three curves are computed for the same values of μ_e as panel (d). Note the change from logarithmic to linear scaling of the horizontal axis at B = 2 × 10¹⁶ G, separated by a dotted line, in (c) and (d). All curves shown were computed using T = 10⁸ K.

Open in new tab Download slide

The quantity K₁ defined in equation (27) and rewritten in equation (33) is plotted in Fig. 5 for a range of reasonable neutron star core temperatures T = 5 × 10⁷, 10⁸, 5 × 10⁸ K. The damping effect of increasing temperature is clearly demonstrated, but is important only where new Landau levels become populated i.e. where the second-order partial derivatives of P would be divergent at zero temperature. Increasing the temperature stabilizes the fluid; as the temperature is increased, fewer ‘spikes’ in K₁ become negative. The unstable regions are very narrow in B-space for constant ρ and in ρ-space for constant B.

$The MPR stability criterion K1 defined in equation (19) divided by $c_{s,0}^2$ as a function of B (a,b) and ρ (c,d) for T = 5 × 107 (black), 108 K (blue), and 5 × 108 K (red). Values below the thin grey line (i.e. negative values) are unstable. μe = 80 MeV (ρ ≈ 0.56ρ0) and μe = 125 MeV (ρ ≈ ρ0) are used in (a) and (b), respectively; note the change from logarithmic to linear scaling of the horizontal axis at B = 2 × 1016 G, separated by a dotted line. B = 5 × 1016 and 1017 G are used in (c) and (d). The Alfvén velocity squared BH/(4πρ) ≈ B2/(4πρ), also divided by $c_{s,0}^2$, is shown as a dot–dashed line in each panel. The irregular-looking behaviour that occurs in (c) and (d) for ρ > 0.79ρ0 is due to the presence of the muons, which misaligns the Fermi momenta of the protons and electrons. Additional evidence of this effect can be seen by comparing (a) and (b), since (a) is at a density below the muon threshold and (b) is above it.$

Figure 5.

The MPR stability criterion K₁ defined in equation (19) divided by |$c_{s,0}^2$| as a function of B (a,b) and ρ (c,d) for T = 5 × 10⁷ (black), 10⁸ K (blue), and 5 × 10⁸ K (red). Values below the thin grey line (i.e. negative values) are unstable. μ_e = 80 MeV (ρ ≈ 0.56ρ₀) and μ_e = 125 MeV (ρ ≈ ρ₀) are used in (a) and (b), respectively; note the change from logarithmic to linear scaling of the horizontal axis at B = 2 × 10¹⁶ G, separated by a dotted line. B = 5 × 10¹⁶ and 10¹⁷ G are used in (c) and (d). The Alfvén velocity squared BH/(4πρ) ≈ B²/(4πρ), also divided by |$c_{s,0}^2$|⁠, is shown as a dot–dashed line in each panel. The irregular-looking behaviour that occurs in (c) and (d) for ρ > 0.79ρ₀ is due to the presence of the muons, which misaligns the Fermi momenta of the protons and electrons. Additional evidence of this effect can be seen by comparing (a) and (b), since (a) is at a density below the muon threshold and (b) is above it.

Open in new tab Download slide

Because |$c_s^2$| can be so large, the behaviour of K₁ is dominated by the first term in equation (33). This term is approximately the Alfvén velocity squared, multiplied by a factor which can change sign because u_BB can be negative (Fig. 4d). The fluctuations of u_BB are responsible for K₁ < 0 in parts of B–ρ parameters space, indicating a possible MPR instability. Increasing B at fixed density makes K₁ more stable, while increasing density at fixed B leads to further unstable regions in parameter space. Recall that Alfvén waves have magnetic tension as their restoring force, and that likewise there is a magnetic pressure contribution to the restoring force for standard magnetosonic waves. Intuitively, the instability occurs because the (1 + 4πu_BB) factor multiplying |$B^2/\rho \propto v_{\text{A}}^2$| becoming negative corresponds to an effective negative magnetic tension/pressure. Thus, changes in the field strength or direction in these unstable regions are energetically favourable, if the (always positive) sound speed (i.e. the matter pressure) is unable to stabilize the fluid. We discuss ways around stabilization by the sound speed at the conclusion of this section.

In Fig. 6, K₁ is plotted in the neutron star core for the field in equation (78) with specific values of B₀. The maximum field inside the star is ≈0.42B₀. For fixed B, the higher density regions are more unstable (have more negative K₁), and as B is increased, higher densities are required for the fluid to become unstable at all (cf. Fig. 5c and d). For fixed ρ, instability can occur at intermediate fields – as B → 0, the fluid is stable, and for sufficiently high fields it can also become stable (cf. Fig. 5a and b), with the field required to stabilize the fluid increasing with increasing density.

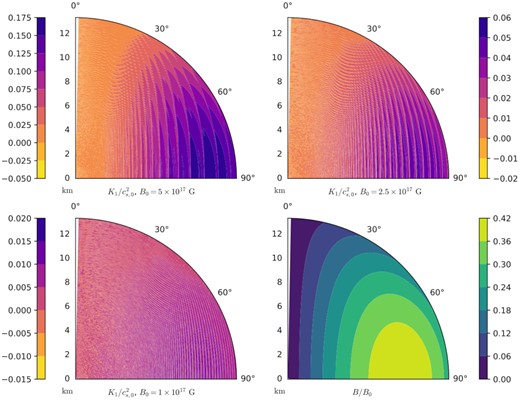
$$K_1/c_{s,0}^2$ for different values of B0, and B/B0 (lower right), for a cross-section of the model stellar core at T = 5 × 107 K. Negative values correspond to unstable regions. Instability is associated with negative values that occur near lines of $(\mu _{\text{e}}^2-m_{\text{e}}^2)/(2eB)=$ an integer. Note that some of the small-scale structure at high densities is spurious and due to interpolation based on a limited sampling in B–ρ parameter space, and that the region along the symmetry axis θ < 1° was excluded as B vanishes here.$

Figure 6.

|$K_1/c_{s,0}^2$| for different values of B₀, and B/B₀ (lower right), for a cross-section of the model stellar core at T = 5 × 10⁷ K. Negative values correspond to unstable regions. Instability is associated with negative values that occur near lines of |$(\mu _{\text{e}}^2-m_{\text{e}}^2)/(2eB)=$| an integer. Note that some of the small-scale structure at high densities is spurious and due to interpolation based on a limited sampling in B–ρ parameter space, and that the region along the symmetry axis θ < 1° was excluded as B vanishes here.

Open in new tab Download slide

The unstable regions are localized in spheroidal shells where |$B=(\mu _a^2-m_a^2)/(2en)$| for a fixed integer n is satisfied – as n increases (e.g. with increasing density) these shells become more closely spaced, leading to the appearance of nearly continuously unstable regions deep in the core. This is observed in Fig. 6 as the field is decreased from the B₀ = 5 × 10¹⁷ G to the B₀ = 2.5 × 10¹⁷ G to the B₀ = 1 × 10¹⁷ G subfigures: the spacing between the unstable regions decreases, to the point that it is difficult to distinguish these regions in the B₀ = 1 × 10¹⁷ G subfigure. However, these locations are not required to be unstable, since for sufficiently strong B/sufficiently high temperature, they will be stable (cf. Fig. 5a and b). This leads to the highest field regions in the B₀ = 5 × 10¹⁷ subfigure of Fig. 6 being stable. Fig. 7 shows a magnified section of the B₀ = 5 × 10¹⁷ G, T = 5 × 10⁷ K stellar model; the alternating pattern of stable and narrow unstable regions is more apparent here.

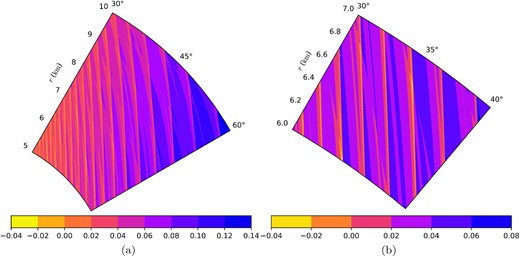
$(a) $K_1/c_{s,0}^2$ for a slice of a stellar core model seen in Fig. (6) (B0 = 5 × 1017 G, T = 5 × 107 K); a further magnified section is shown in (b). This shows the fine details of the narrow unstable regions.$

Figure 7.

(a) |$K_1/c_{s,0}^2$| for a slice of a stellar core model seen in Fig. (6) (B₀ = 5 × 10¹⁷ G, T = 5 × 10⁷ K); a further magnified section is shown in (b). This shows the fine details of the narrow unstable regions.

Open in new tab Download slide

Figs 6 and 7 show many unstable regions in the star of thickness ≲a few metres. The spacing between these regions can be estimated as follows: since the unstable regions occur where new electron Landau levels start being populated, for neighbouring unstable regions we can write

$$\begin{eqnarray*} \Delta n = 1 \approx \frac{(\mu _{\text{e}}+\Delta \mu _{\text{e}})^2-m_{\text{e}}^2}{2eB(1+\Delta B/B)}-\frac{\mu _{\text{e}}^2-m_{\text{e}}^2}{2eB}\approx \frac{(\mu _{\text{e}}+\Delta \mu _{\text{e}})^2}{2eB(1+\Delta B/B)}-n, \end{eqnarray*}$$

(79)

where we can approximate the electrons as ultrarelativistic since μ_e ≫ m_e. Δμ_e and ΔB are the changes in μ_e and B between the two unstable regions. Taking ΔB = (dB/dϖ)Δϖ and Δμ_e = (dμ_e/dϖ)Δϖ, equation (79) gives

$$\begin{eqnarray*} \Delta \varpi =\left(2n\frac{\text{d}\mu _{\text{e}}}{\text{d}\varpi }-(n+1)\frac{\text{d}B}{\text{d}\varpi }\right)^{-1}. \end{eqnarray*}$$

(80)

Working on the equator so ϖ = r, estimating from Fig. 2 that |$\rho \approx \rho _c(1-\varpi ^2/R_{\star }^2)$|⁠, and also using the standard (and large number of occupied Landau levels result) that |$\mu _{\text{e}}\approx (3\pi ^2n_{\text{e}})^{1/3}\approx (3\pi ^2Yf\rho /\overline{m})^{1/3}$| where we approximate Y and f as constant, we find

$$\begin{eqnarray*} \Delta \varpi =-\frac{\rho }{\rho _c}\left(\frac{n+1}{\varpi }-\frac{\varpi }{R_{\star }^2}\left(\frac{5n}{3}+3\right)\right)^{-1}, \end{eqnarray*}$$

(81)

where the negative sign arises because the consecutive unstable regions for larger integers n are located interior to each other. Thus, Δϖ ∼ −ϖ/n, which matches what we observe: in the low-density regions far from the centre of the star, where B can be larger and hence n smaller, the spacing between potentially unstable regions Δϖ is larger (up to ∼km between them), whereas at shorter distances from the centre where B is weaker/n larger, the separation between neighbouring unstable regions can be of the order of metres to tens of metres. Thus, the patterns of alternating stable-unstable regions extend into the higher density regions of the star, though resolving these becomes more difficult at high densities.

Following the argument of equation (168) of Akgün & Wasserman (2008), the growth time τ for the MPR instability can be estimated using the approximate dispersion relation

$$\begin{eqnarray*} \omega ^2=K_1k_x^2\rightarrow \tau =\frac{1}{|\text{Im}(\sqrt{K_1})k_x|}, \end{eqnarray*}$$

(82)

which applies for k_z ≫ k_x. From Fig. 5, in the unstable regions of parameter space K₁ ≳ −10⁻³c², so we obtain an approximate instability growth time-scale

$$\begin{eqnarray*} \tau \sim 1.6\times 10^{-3}\left(\frac{c}{\sqrt{1000|K_1|}}\right)\left(\frac{R^{-1}_{\star }}{k_x}\right)\text{ s}. \end{eqnarray*}$$

(83)

In the most unstable regions of the B–ρ–T parameter space, the instability is so fast that it is unlikely to be mitigated by viscous dissipation. The required kinematic viscosity for the unstable modes to be dissipated is of the order

$$\begin{eqnarray*} \nu \sim \frac{1}{k^2\tau }\approx 1.5\times 10^{15}\left(\frac{\sqrt{1000|K_1|}}{c}\right)\left(\frac{R^{-1}_{\star }}{k}\right)\left(\frac{k_x}{k}\right)\text{ cm}^2\text{ s}^{-1}. \end{eqnarray*}$$

(84)

Even for k_z ≪ k ≈ k_x, this can be many orders of magnitude beyond the typical kinematic viscosities ν ∼ 10⁶–10⁷ cm²s⁻¹ expected in a normal fluid neutron star core, and also above the ν ∼ 10⁷–10⁸ cm² s⁻¹ viscosities expected in a superfluid-superconducting neutron star core (Schmitt & Shternin 2018).

Now that the behaviour V² and K₁ is understood, we examine the other stability criteria. In Fig. 8, we show the k_x = 0 stability criterion equation (23) (SC1) and the first k_x ≠ 0 criterion equation (32a) (SC2). In Fig. 8, we show the two k_x ≠ 0 criteria equations (32b)–(32c) (SC3,SC4). We note again that SC1, SC3, and SC4 are associated with magnetic buoyancy, while SC2 is a purely MHD stability criterion. SC2, SC3, and SC4 have all been multiplied by a factor K₁ to eliminate the divergent behaviour for K₁ → 0: since K₁ < 0 is already potentially unstable, such regions have been excised from the plots of SC2, SC3, and SC4.

Figure 8.

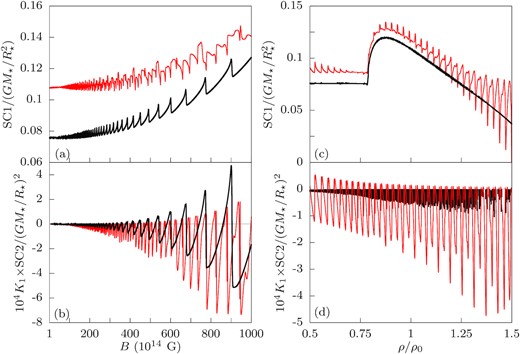
The magnetic buoyancy stability criterion for k_x = 0 defined in equation (23) (SC1), and the stability criterion SC2 defined in (32a), as functions of B (a,b) and ρ (c,d). Each quantity is scaled by appropriate factors of G, M_⋆, and R_⋆ to make them dimensionless, while SC2 is multiplied by K₁ to eliminate divergent behaviour and an additional factor of 10⁴. In (a) and (b), the black and red curves correspond to μ_e = 80 MeV (ρ ≈ 0.56ρ₀) and μ_e = 125 MeV (ρ ≈ ρ₀), respectively. In (c) and (d), the black and red curves correspond to B = 10¹⁵ and 5 × 10¹⁶ G, respectively. All curves are computed at T = 5 × 10⁸ K. The B = 10¹⁵ G curve in (d) is multiplied by an additional factor of 2000 (on top of the other factors) for display purposes.

Open in new tab Download slide

SC1 is always positive in the stellar model we have considered, and hence the fluid and field configuration we examine is magnetic buoyancy-stable for k_x = 0 perturbations (i.e. purely radial perturbations). The stable stratification is large enough to suppress the instability i.e. |$\tilde{N}$| is large enough to overwhelm the second term in equation (23), which is proportional to the same term which results in negative values of K₁ and which could destabilize the system for sufficiently small |$\tilde{N}$|⁠. This demonstrates the importance of stable stratification to MHD stability even in the strong-field case. SC2, SC3, and SC4 all involve K₁, which we have seen undergoes large fluctuations and can change sign for fields ≳10¹⁵ G. Also note the similarities between Fig. 3 and Figs 8 and 9 panel (c), as the latter depend on scaled versions of |$\tilde{N}^2$|⁠.

Figure 9.

The magnetic buoyancy stability criteria defined in equation (32b) (SC3) and (32c) (SC4), as functions of B (a,b) and ρ (c,d). Each quantity is scaled by appropriate factors of G, M_⋆, and R_⋆ to make them dimensionless, and both are multiplied by K₁ to eliminate divergent behaviour. SC4 is scaled by an additional factor of 10⁴. In (a) and (b), the black and red curves correspond to μ_e = 80 MeV (ρ ≈ 0.56ρ₀) and μ_e = 125 MeV (ρ ≈ ρ₀), respectively. In (c) and (d), the black, red, and blue curves correspond to B = 10¹⁵, 5 × 10¹⁶ and 10¹⁷ G, respectively. All curves are computed at T = 5 × 10⁸ K. The B = 10¹⁵ G curves in (c) and (d) are multiplied by an additional factor of 100 and 10 000, respectively (on top of the other factors) for display purposes.

Open in new tab Download slide

SC2, SC3, and SC4 can all be negative in large parts of the B–ρ parameter space, contrasting with the limited regions of the parameter space in which K₁ can be negative which are localized at where additional Landau levels start filling. The region of parameter space where SC2 is negative increases as B and ρ are increased, as is demonstrated in Fig. 10, where K₁ ×SC2 is plotted in a cross-section of the stellar model. SC3 is negative in limited regions where additional Landau levels start being populated, and also for regions where B ≳ 6 × 10¹⁶ G and ρ ≲ 0.8ρ₀. The latter SC3 < 0 regions are due to the second term in equation (34), since the |$\text{d}\ln B/\text{d}z=\text{d}\ln \rho /\text{d}z+\frac{1}{z}$| is the most negative at low densities (see Fig. 2) and the coefficient of this derivative becomes large for large B. SC4 is generally positive or marginally negative at B ≲ 2 × 10¹⁶ G, and can be unstable for all densities examined.

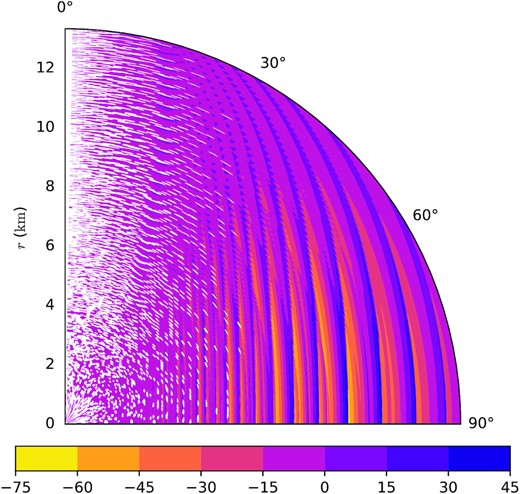
104K1 ×SC2/(GM⋆/R⋆)2 for the stellar core model with B0 = 5 × 1017 G and T = 5 × 108 K. Negative values correspond to potentially unstable regions. The empty regions correspond to where K1 < 0 and the fluid is already unstable to the MPR instability – such regions correspond to the unstable regions in the upper left plot of Fig. 6, though not every K1 < 0 region is resolved in each figure.

Figure 10.

10⁴K₁ ×SC2/(GM_⋆/R_⋆)² for the stellar core model with B₀ = 5 × 10¹⁷ G and T = 5 × 10⁸ K. Negative values correspond to potentially unstable regions. The empty regions correspond to where K₁ < 0 and the fluid is already unstable to the MPR instability – such regions correspond to the unstable regions in the upper left plot of Fig. 6, though not every K₁ < 0 region is resolved in each figure.

Open in new tab Download slide

The stability implications of these results can be further examined using the definition of the canonical energy per unit mass in the k_x ≠ 0 case. Upon taking k_x → 0 as before and using |$c_s^2\gg Bu_{\rho B}$| and |$|g\xi ^z/c_s^2|\ll 1$|⁠, equation (31) becomes

$$\begin{eqnarray*} \mathcal {E}_c[\xi ] &\approx & c^2_s\left|\partial _z\xi ^z+{\rm i}k_y\xi ^y\right|^2 +K_1\left|\partial _z\xi ^z+{\rm i}k_y\xi ^y\left(1-\frac{2Bu_{\rho B}}{K_1}\right)+\frac{L_2}{K_1}\xi ^z\right|^2 +(\text{SC2})k_y^2\left|\xi ^y\right|^2+(\text{SC3})\left|\xi ^{z}\right|^2 \nonumber \\ &&\pm 2k_y\sqrt{(\text{SC2})(\text{SC3})-(\text{SC4})}\text{Re}[{\rm i}\xi ^y(\xi ^z)^*]. \end{eqnarray*}$$

(85)

First, we note that in the absence of gravity, only the first three terms will be present. In the zero gravity, vacuum MHD case, K₁ would be positive definite and SC2 would be zero, and hence instability impossible. In the non-vacuum, strong field case examined in this paper, neither K₁ nor SC2 can be sufficiently negative such that they are larger in magnitude than |$c_s^2$|⁠, but it is still possible for certain types of modes to have zero canonical energy and hence be unstable despite the strong stabilizing effect provided by the first term. For example, for incompressible modes the first term is zero, and hence such modes could be made unstable by K₁ and SC2 being negative. These instabilities would likely result in transfer of magnetic flux within the star to stabilize the fluid by decreasing or increasing the field strength in the unstable regions. They are analogous to the MPR instability in superconducting fluids in which flux tubes are clumped together to create regions of greater/lesser magnetic flux. Since the k_x = 0 modes are stable, the unstable perturbations that transfer flux to try to stabilize the fluid must have a non-zero component along the magnetic field.

In the case where the buoyancy terms SC3 and SC4 are relevant, these can further destabilize the fluid, but like K₁ and SC2 will require a particular class of perturbation (e.g. incompressible) to overcome the stabilizing effect of the sound speed squared term in equation (85). However, the pure MHD terms are much more significant for the stability than those associated with buoyancy except for the longest wavelength perturbations. The minimum relevant wavenumber for a perturbation is k_min ≈ 2π/R_⋆ ∼ 4 × 10⁻⁶ cm⁻¹, at which point |$K_1k_{\text{min}}^2\sim$|SC2|$k_{\text{min}}^2\sim$|SC3. For shorter wavelength perturbations, the wavenumber dependence of the pure MHD terms mean that they will be much larger in magnitude than the magnetic buoyancy terms.

6 DISCUSSION AND CONCLUSION

In this paper, we have extended the MHD stability analysis of Friedman & Schutz (1978) and Glampedakis & Andersson (2007) to magnetizable fluids with B ≠ H, and applied this to the study of MHD stability in the presence of extremely strong fields where QED effects and Landau quantization of fermions are relevant. This regime is important to magnetars, which have surface fields ∼10¹⁵ G and likely stronger fields in their interiors. Using the canonical energy approach to studying stability, we determined sufficient local stability criteria for magnetic buoyancy, magnetosonic stability, and the MPR instability for magnetizable media with an electromagnetic Lagrangian depending on the magnetic field B, mass density ρ and species fractions Y_a. The fluid perturbation theory and canonical energy results derived here are general and can be used for other applications where H ≠ B e.g. superfluid-superconducting neutron stars.

We find that the inclusion of strong-field effects to the MHD of a neutron star core leads to a possible MPR instability associated with the Landau quantization of fermions for fields B ≳ 10¹⁵ G and at typical core densities. These instabilities can have growth times of the order of 10⁻³ s, and are not stabilized by viscous dissipation under expected neutron star viscosities. The magnetic buoyancy instability associated with the strong-field, B ≠ H MHD studied here can also be active in the neutron star core, and the stability criteria associated with it are violated in broader regions of the B–ρ parameter space than the narrow regions in which the MPR instability criterion is violated. However, these terms are only comparable in magnitude to the purely MHD terms associated with the MPR instability for long wavelength perturbations, and are unimportant for stability at shorter wavelengths. The vacuum Euler–Heisenberg Lagrangian was found to be unimportant to MHD stability overall at the magnetic fields B ≲ 10¹⁷ G we considered.

Perhaps the most important question regarding the MPR instability discussed in this paper is what implications it has on the evolution of magnetar fields. The alternating stable-unstable regions in B–ρ space, demonstrated in a stellar model in Figs 6 and 7, suggest that the instability could lead to the formation of magnetic domains. This instability will likely be triggered throughout the star’s life for two reasons: (1) previously stable regions become unstable as the star cools and the ‘spikes’ in u_BB become sharper (cf. Fig. 5); (2) field evolution that changes the field strength within the star such that certain regions now lie in the unstable parts of B–ρ parameter space. One response to this destabilization is the transfer of magnetic flux from unstable regions until the local field is in the stable region of the B–ρ parameter space. Since the unstable regions themselves generally span very narrow length scales of the order of ≲metres, the magnetic field only needs to change by a small fraction of its strength to be stabilized, so unstable modes could transfer flux to stabilize the fluid. This suggests that the observational implications for these domains and the instability that could form them are limited, at least within the stellar core.

The formation of magnetic domains in strongly magnetized neutron star matter has previously been discussed in Blandford & Hernquist (1982) and Suh & Mathews (2010). In these calculations, it is the differential magnetic susceptibility χ, corresponding here to −u_BB,² which encourages magnetic domain formation, and when χ > 4π the system is thermodynamically unstable to domain formation. The MPR instability discussed in our paper also originates from u_BB < −1/(4π), in contrast to the original MPR instability in superconducting fluids that depends on the |$u_{\rho B}^2$| term in K₁. Magnetic domain formation encouraged by the instability discussed here suggests that smoothly varying fields are not solutions to the background magnetohydrostatic equilibrium for sufficiently strong magnetic fields ≳10¹⁵ G and at low temperatures.

Though we have made some simplifying assumptions for the background stellar model, our conclusions about the MPR instability arising from the Euler–Heisenberg–Fermi–Dirac Lagrangian should be robust. This is because the instability depends on u_BB, which is simply a function of B and the n_a (or the μ_a), and is independent of the exact structure of the star (including the EOS) or the magnetic field direction. We thus do not expect our main argument about the generic instability of ultrastrong fields to change significantly when using a relativistic stellar model, different EOS and/or including the effect of the magnetic field on the background equilibrium model. Our restriction to toroidal fields does not affect our main results about the instability to MPR modes, since the same requirements on K₁ will appear independent of the direction of Bⁱ: if Bⁱ was a poloidal field, only the magnetic buoyancy conditions, and the exact location of the unstable regions within the star, would be changed.

The next logical step is to apply this formalism to the crust (Rau & Wasserman, in preparation), which due to lower densities and sound speeds may support similar instabilities as in the core even with lower field strengths. However, the stability analysis in the crust is fundamentally different due to the lack of a canonical energy procedure (Lyutikov 2013), so this is left to a follow-up paper. The canonical energy procedure can also be applied to a complete model of a neutron star core to study its global stability. An additional interesting area of future study would be to include a physically correct stellar exterior, which would modify the treatment of the surface terms examined in Appendix A2, in which exterior vacuum was assumed. Such a study could examine the effect on the stability of different pulsar magnetosphere models and could potentially help judge their feasibility.

SUPPORTING INFORMATION

APPENDIX A. Fluid Perturbation Theory.

APPENDIX B. Thermodynamic Derivatives Of Euler–Heisenberg–Fermi–Dirac Lagrangian.

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

ACKNOWLEDGEMENTS

We would like to thank the referee for useful comments. PBR would also like to acknowledge the support of Cornell’s Boochever Fellowship for spring 2020.

DATA AVAILABILITY

The data underlying this article will be shared on reasonable request to the corresponding author.

Footnotes

1

The zeroth space–time component of the ω meson and the zeroth space–time component of the I₃ isospin component of the ρ meson – the ‘3’ superscript on |$\rho ^3_0$| denotes the isospin component and not exponentiation.

2

Though noting the other references perform the calculation of the differential susceptibility at fixed chemical potentials and not fixed density as used here.

REFERENCES

Acheson

D. J.

,

1979

,

Sol. Phys.

,

62

,

23

10.1007/BF00150129

Crossref

Akgün

T.

,

Wasserman

I.

,

2008

,

MNRAS

,

383

,

1551

10.1111/j.1365-2966.2007.12660.x

Crossref

Akgün

T.

,

Reisenegger

A.

,

Mastrano

A.

,

Marchant

P.

,

2013

,

MNRAS

,

433

,

2445

10.1093/mnras/stt913

Crossref

Bardeen

J. M.

,

Friedman

J. L.

,

Schutz

B. F.

,

Sorkin

R.

,

1977

,

ApJ

,

217

,

L49

10.1017/CBO9781107415324.004

Crossref

Beloborodov

A. M.

,

2017

,

ApJ

,

843

,

L26

10.3847/2041-8213/aa78f3

Crossref

Bernstein

I. B.

,

Frieman

E. A.

,

Kruskal

M. D.

,

Kulsrud

R. M.

,

1958

,

Proc. R. Soc. A

,

244

,

17

10.1098/rspa.1958.0023

Crossref

Bilous

A. V.

et al. ,

2019

,

ApJ

,

887

,

L23

10.3847/2041-8213/ab53e7

Crossref

Blandford

R. D.

,

Hernquist

L.

,

1982

,

J. Phys. C: Solid State Phys.

,

15

,

6233

10.1088/0022-3719/15/30/017

Crossref

Braithwaite

J.

,

2009

,

MNRAS

,

397

,

763

10.1111/j.1365-2966.2008.14034.x

Crossref

Braithwaite

J.

,

Nordlund

Å.

,

2006

,

A&A

,

450

,

1077

10.1051/0004-6361:20041980

Crossref

Braithwaite

J.

,

Spruit

H. C.

,

2004

,

Nature

,

431

,

819

10.1038/nature02934

Crossref

Broderick

A.

,

Prakash

M.

,

Lattimer

J. M.

,

2000

,

ApJ

,

537

,

351

10.1086/309010

Crossref

Carter

B.

,

1973

,

Commun. Math. Phys.

,

30

,

261

10.1007/BF01645505

Crossref

Chamel

N.

,

Stoyanov

Z. K.

,

2020

,

Phys. Rev. C

,

101

,

65802

10.1103/PhysRevC.101.065802

Crossref

Chamel

N.

et al. ,

2012

,

Phys. Rev. C

,

86

,

055804

10.1103/PhysRevC.86.055804

Crossref

CHIME/FRB Collaboration

,

2020

,

Nature

,

587

,

54

10.1038/s41586-020-2863-y

Crossref

Chodos

A.

,

Everding

K.

,

Owen

D. A.

,

1990

,

Phys. Rev. D

,

42

,

2881

10.1103/PhysRevD.42.2881

Crossref

Cumming

A.

,

Arras

P.

,

Zweibel

E.

,

2004

,

ApJ

,

609

,

999

10.1086/421324

Crossref

Duez

V.

,

Braithwaite

J.

,

Mathis

S.

,

2010

,

ApJ

,

724

,

34

10.1088/2041-8205/724/1/L34

Crossref

Easson

I.

,

Pethick

C. J.

,

1977

,

Phys. Rev. D

,

16

,

275

10.1103/PhysRevD.16.275

Crossref

Elmfors

P.

,

Persson

D.

,

Skagerstam

B. S.

,

1993

,

Phys. Rev. Lett.

,

71

,

480

10.1017/CBO9781107415324.004

Crossref

Flowers

E.

,

Ruderman

M. A.

,

1977

,

ApJ

,

215

,

302

10.1086/155359

Crossref

Friedman

J. L.

,

Schutz

B. F.

,

1975

,

ApJ

,

200

,

204

10.1017/CBO9781107415324.004

Crossref

Friedman

J. L.

,

Schutz

B. F.

,

1978

,

ApJ

,

221

,

937

10.1086/156098

Crossref

Glampedakis

K.

,

Andersson

N.

,

2007

,

MNRAS

,

377

,

630

10.1111/j.1365-2966.2007.11625.x

Crossref

Glendenning

N. K.

,

1997

,

Compact Stars

.

Springer

,

New York

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Gough

D. O.

,

Tayler

R. J.

,

1966

,

MNRAS

,

133

,

85

10.1093/mnras/133.1.85

Crossref

Gourgouliatos

K. N.

,

Cumming

A.

,

Reisenegger

A.

,

Armaza

C.

,

Lyutikov

M.

,

Valdivia

J. A.

,

2013

,

MNRAS

,

434

,

2480

10.1093/mnras/stt1195

Crossref

Heisenberg

W.

,

Euler

H.

,

1936

,

Z. Phys.

,

98

,

714

10.1007/BF01343663

Crossref

Heyl

J. S.

,

Hernquist

L.

,

2005

,

ApJ

,

618

,

463

10.1086/425974

Crossref

Kantor

E. M.

,

Gusakov

M. E.

,

2014

,

MNRAS

,

442

,

90

10.1093/mnrasl/slu061

Crossref

Kaspi

V. M.

,

Beloborodov

A. M.

,

2017

,

ARA&A

,

55

,

261

10.1146/annurev-astro-081915-023329

Crossref

Lai

D.

,

Shapiro

S. L.

,

1991

,

ApJ

,

383

,

745

10.1086/170831

Crossref

Landau

L. D.

,

Lifshitz

E. M.

,

1960

,

Electrodynamics of Continuous Media, 2nd edn

.

Pergamon Press

,

Oxford

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lander

S. K.

,

Jones

D. I.

,

2009

,

MNRAS

,

395

,

2162

10.1111/j.1365-2966.2009.14667.x

Crossref

Lu

W.

,

Kumar

P.

,

2018

,

MNRAS

,

477

,

2470

10.1093/mnras/sty716

Crossref

Lyubarsky

Y.

,

2014

,

MNRAS

,

442

,

L9

10.1093/mnrasl/slu046

Crossref

Lyubarsky

Y.

,

2020

,

ApJ

,

897

,

1

10.3847/1538-4357/ab97b5

Crossref

Lyutikov

M.

,

2006

,

MNRAS

,

367

,

1594

10.1111/j.1365-2966.2006.10069.x

Crossref

Lyutikov

M.

,

2013

,

Phys. Rev. E

,

88

,

1

10.1103/PhysRevE.88.053103

Crossref

Mao

G.-J.

,

Iwamoto

A.

,

Li

Z.-X.

,

2003

,

Chinese J. Astron. Astrophys.

,

3

,

359

10.1088/1009-9271/3/4/359

Crossref

Markey

P.

,

Tayler

R. J.

,

1973

,

MNRAS

,

163

,

77

10.1093/mnras/163.1.77

Crossref

Mereghetti

S.

,

Pons

J. A.

,

Melatos

A.

,

2015

,

Space Sci. Rev.

,

191

,

315

10.1007/s11214-015-0146-y

Crossref

Metzger

B. D.

,

Margalit

B.

,

Sironi

L.

,

2019

,

MNRAS

,

485

,

4091

10.1093/mnras/stz700

Crossref

Mitchell

J. P.

,

Braithwaite

J.

,

Reisenegger

A.

,

Spruit

H.

,

Valdivia

J. A.

,

Langer

N.

,

2015

,

MNRAS

,

447

,

1213

10.1093/mnras/stu2514

Crossref

Muzikar

P.

,

Pethick

C. J.

,

1981

,

Phys. Rev. B

,

24

,

2533

10.1103/PhysRevB.24.2533

Crossref

Newcomb

W. A.

,

1961

,

Phys. Fluids

,

4

,

391

10.1063/1.1706342

Crossref

Parker

E. N.

,

1955

,

ApJ

,

121

,

491

10.1017/CBO9781107415324.004

Crossref

Passamonti

A.

,

Andersson

N.

,

Ho

W. C. G.

,

2016

,

MNRAS

,

455

,

1489

10.1093/mnras/stv2149

Crossref

Persson

D.

,

Zeitlin

V.

,

1995

,

Phys. Rev. D

,

51

,

2026

10.1103/PhysRevD.51.2026

Crossref

Popov

S. B.

,

Postnov

K. A.

,

2010

, in

Harutyunian

H. A.

,

Mickaelian

A. M.

,

Terzian

Y.

, eds,

Evolution of Cosmic Objects through their Physical Activity

.

National Academy of Sciences of the Republic of Armenia

,

Yerevan

, p.

129

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Potekhin

A. Y.

,

1999

,

A&A

,

351

,

787

Potekhin

A. Y.

,

Chabrier

G.

,

2018

,

A&A

,

609

,

1

10.1051/0004-6361/201731866

Crossref

Potekhin

A. Y.

,

Pons

J. A.

,

Page

D.

,

2015

,

Space Sci. Rev.

,

191

,

239

10.1007/s11214-015-0180-9

Crossref

Potekhin

A. Y.

,

Yakovlev

D. G.

,

2001

,

A&A

,

374

,

213

10.1051/0004-6361:20010698

Crossref

Rau

P. B.

,

Wasserman

I.

,

2018

,

MNRAS

,

481

,

4427

10.1093/mnras/sty2458

Crossref

Reisenegger

A.

,

2009

,

A&A

,

499

,

557

10.1051/0004-6361/200810895

Crossref

Reisenegger

A.

,

Goldreich

P.

,

1992

,

ApJ

,

395

,

240

10.1086/171645

Crossref

Riley

T. E.

et al. ,

2019

,

ApJ

,

887

,

L21

10.3847/2041-8213/ab481c

Crossref

Roberts

P. H.

,

1981

,

Q. J. Mech. Appl. Math.

,

34

,

327

10.1093/qjmam/34.3.327

Crossref

Schmitt

A.

,

Shternin

P.

,

2018

, in

Rezzolla

L.

,

Pizzochero

P.

,

Jones

D. I.

,

Rea

N.

,

Vidaña

I.

, eds,

The Physics and Astrophysics of Neutron Stars

.

Springer

,

Heidelberg

, p.

455

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Schubert

G.

,

1968

,

ApJ

,

151

,

1099

10.1086/149508

Crossref

Sinha

M.

,

Mukhopadhyay

B.

,

Sedrakian

A.

,

2013

,

Nucl. Phys. A

,

898

,

43

10.1016/j.nuclphysa.2012.12.076

Crossref

Suh

I. S.

,

Mathews

G. J.

,

2010

,

ApJ

,

717

,

843

10.1088/0004-637X/717/2/843

Crossref

Taub

A. H.

,

1969

,

Commun. Math. Phys.

,

15

,

235

10.1007/BF01073578

Crossref

Tayler

R. J.

,

1973

,

MNRAS

,

161

,

365

10.1093/mnras/161.4.365

Crossref

Thompson

C.

,

Duncan

R. C.

,

1995

,

MNRAS

,

275

,

255

10.1093/mnras/275.2.255

Crossref

Turolla

R.

,

Zane

S.

,

Watts

A. L.

,

2015

,

Rep. Prog. Phys.

,

78

,

116901

10.1088/0034-4885/78/11/116901

Crossref

Uryu

K.

,

Yoshida

S.

,

Gourgoulhon

E.

,

Markakis

C.

,

Fujisawa

K.

,

Tsokaros

A.

,

Taniguchi

K.

,

Eriguchi

Y.

,

2019

,

Phys. Rev. D

,

100

,

123019

10.1103/PhysRevD.100.123019

Crossref

Walecka

J. D.

,

1995

,

Theoretical Nuclear and Subnuclear Physics

.

Oxford Univ. Press

,

New York

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Wright

G. A. E.

,

1973

,

MNRAS

,

162

,

339

10.1093/mnras/162.4.339

Crossref

Yoshida

S.

,

Yoshida

S.

,

Eriguchi

Y.

,

2006

,

ApJ

,

651

,

462

10.1086/507513

Crossref

Yu

H.

,

Weinberg

N. N.

,

2017

,

MNRAS

,

464

,

2622

10.1093/mnras/stw2552

Crossref

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
June 2021	4
July 2021	7
August 2021	17
September 2021	4
October 2021	14
November 2021	3
December 2021	2
January 2022	2
February 2022	1
March 2022	1
April 2022	2
May 2022	2
June 2022	2
July 2022	1
October 2022	3
January 2023	3
February 2023	4
March 2023	2
April 2023	2
July 2023	3
September 2023	1
November 2023	3
December 2023	2
January 2024	5
February 2024	5
March 2024	7
April 2024	3
May 2024	14
June 2024	11
July 2024	27
August 2024	7
September 2024	10
October 2024	9
November 2024	8
December 2024	1
January 2025	5
February 2025	11
March 2025	13
April 2025	6
May 2025	4

Article Contents

Magnetohydrodynamic stability of magnetars in the ultrastrong field regime I: the core

ABSTRACT

1 INTRODUCTION

2 MHD EQUATIONS AND CANONICAL ENERGY

3 STABILITY ANALYSIS

3.1 Case 1: k_x = 0

3.2 Case 2: k_x ≠ 0

4 THERMODYNAMICS

4.1 Changes of variable and connection to magnetohydrodynamics

4.2 Background stellar model

5 NUMERICAL CALCULATION OF STABILITY CRITERIA

6 DISCUSSION AND CONCLUSION

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Magnetohydrodynamic stability of magnetars in the ultrastrong field regime I: the core Purchased

ABSTRACT

1 INTRODUCTION

2 MHD EQUATIONS AND CANONICAL ENERGY

3 STABILITY ANALYSIS

3.1 Case 1: kx = 0

3.2 Case 2: kx ≠ 0

4 THERMODYNAMICS

4.1 Changes of variable and connection to magnetohydrodynamics

4.2 Background stellar model

5 NUMERICAL CALCULATION OF STABILITY CRITERIA

6 DISCUSSION AND CONCLUSION

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Magnetohydrodynamic stability of magnetars in the ultrastrong field regime I: the core

3.1 Case 1: k_x = 0

3.2 Case 2: k_x ≠ 0