-
PDF
- Split View
-
Views
-
Cite
Cite
Tsun Hin Navin Tsung, S Peng Oh, Yan-Fei Jiang(姜燕飞), Fluid simulations of cosmic ray-modified shocks, Monthly Notices of the Royal Astronomical Society, Volume 506, Issue 3, September 2021, Pages 3282–3300, https://doi.org/10.1093/mnras/stab1926
Close - Share Icon Share
ABSTRACT
Cosmic ray (CR)-modified shocks are a demanding test of numerical codes. We use them to test and validate the two-moment method for CR hydrodynamics, as well as characterize the realism of CR shock acceleration in two-fluid simulations which inevitably arises. Previously, numerical codes were unable to incorporate streaming in this demanding regime, and have never been compared against analytic solutions. First, we find a new analytic solution highly discrepant in acceleration efficiency from the standard solution. It arises from bi-directional streaming of CRs away from the subshock, similar to a Zeldovich spike in radiative shocks. Since fewer CRs diffuse back upstream, this favours a much lower acceleration efficiency, typically |${\lesssim}10{{\ \rm per\ cent}}$| (even for Mach number > 10) as opposed to |${\gtrsim}50{{\ \rm per\ cent}}$| found in previous analytic work. At Mach number ≳10, the new solution bifurcates into three branches, with efficient, intermediate, and inefficient CR acceleration. Our two-moment code accurately recovers these solutions across the entire parameter space probed, with no ad hoc closure relations. For generic initial conditions, the inefficient branch is robustly chosen by the code; the intermediate branch is unstable. The preferred branch is very weakly modified by CRs. At high Mach numbers (≳10), the gas jump conditions approach that of a purely hydrodynamic shock, and a sub-grid prescription for thermal injection is required for reasonable acceleration efficiencies |${\sim}10{{\ \rm per\ cent}}$|. CR-modified shocks have very long equilibration times (∼1000 diffusion time) required to develop the precursor, which must be resolved by ≳10 cells for convergence. Non-equilibrium effects, poor resolution, and obliquity of the magnetic field all reduce CR acceleration efficiency. Shocks in galaxy-scale simulations will generally contribute little to CR acceleration without sub-grid modification.
1 INTRODUCTION
Cosmic rays (CRs) are close to energy equipartition with thermal gas in the local interstellar medium (ISM), and have been observed in many astrophysical scenarios. They are now thought to be dynamically important to galaxy evolution, both in providing non-thermal support to the Circumgalactic Medium (CGM) gas and in driving a wind that initiates a feedback cycle (e.g. see Zweibel 2017 for a recent review), which has become the focus of intense study by numerous groups in recent years. It has even been suggested that the CGM is CR dominated (Ji et al. 2020). CRs are believed to be accelerated at shocks to high energies through diffusive shock acceleration (DSA). Test particle theories developed in the 1970s (Axford, Leer & Skadron 1977; Krymskii 1977; Bell 1978; Blandford & Ostriker 1978) were instrumental in explaining the observed power law in CR energy. It was later realized that CR coupling to the background thermal gas through plasma instabilities can affect the acceleration efficiency by generating a shock precursor where upstream thermal particles can be decelerated, compressed, and scattered, thus facilitating further acceleration (Drury & Voelk 1981). The two-fluid model and Monte Carlo simulation were two common methods utilized to study this non-linear behaviour. These variant models all point to the same conclusion, that the non-linear modification of the shock by CRs is substantial.
Magnetic field amplification due to compression, baroclinic vorticity, and plasma instabilities can be dynamically important too, and has been seen in X-ray observations (Ballet 2006; Morlino et al. 2010). With the growth of computational power it became possible to perform Particle-In-Cell (PIC)/hybrid simulations that capture the most important microphysics of CR shock acceleration, including various kinetic instabilities and their non-linear evolution into turbulence (e.g. Caprioli & Spitkovsky 2014a). These simulations continue to show that shock acceleration is very efficient.
This collective streaming causes energy transfer from CR to the gas at the volumetric rate of vs · ∇Pc. In steady state, wave growth is balanced by various damping mechanisms (e.g. see Wiener, Oh & Guo 2013). The finite scattering rate of CRs means that they are not perfectly locked to the Alfven frame; slippage with respect to the Alfven frame is expressed in terms of an anisotropic diffusive flux |$\bar{\kappa } \nabla P_c$|, where |$\bar{\kappa }$| is dependent on the CR energy spectrum, the various plasma parameters, and the damping mechanisms at play. We forgo these complications and assume the diffusion coefficient is constant in time and space though our work can be extended to account for a more detailed treatment of diffusion.
The two-fluid treatment was historically the first method used to study CR-modified shocks. However, it has several shortcomings. Since momentum information is integrated out, CR pressure and energy (which are moments of the full distribution function) have to be related by an equation of state, with adiabatic index γc = 1 + Pc/Ec that is usually assumed to be constant, γc = 4/3. In reality, γc depends on the detailed shape of the distribution function and evolves continuously from 5/3 to 4/3 as particles are accelerated. Shock structure, compressibility, and acceleration efficiency are all sensitive to assumptions about the adiabatic index (Achterberg, Blandford & Periwal 1984; Duffy, Drury & Voelk 1994). Similarly, the diffusion coefficient |$\bar{\kappa }$| is averaged over the CR spectrum. Furthermore, it is not self-consistently calculated.1 In general it should evolve with the time-dependent distribution function. In particular, since generically κ(p) rises with energy, this can lead to a CR flux dominated by the highest-energy particles; in this case a steady-state shock structure no longer exists. In this paper, we simply assume a constant, time-steady |$\bar{\kappa }$| (and hereafter drop the overbar). Finally, the standard CR hydrodynamic equations ignore microscopic physics such as thermal injection and magnetohydrodynamic (MHD) wave growth which PIC and hybrid simulations take into account.2
Given these serious shortcomings, it may seem a step backwards to simulate CR-modified shocks using the two-fluid approach. Certainly, if our main interest is understanding CR acceleration at shocks, then PIC and hybrid simulations are unquestionably the tools of choice. However, there are still compelling reasons for two-fluid CR shock simulations:
Code testing. In recent years, as interest in the role of CRs in galaxy formation has rapidly grown, many new codes for simulating CR transport in the two-fluid approximation have been developed [CR streaming with regularization (Sharma, Colella & Martin 2009); enzo (Salem & Bryan 2014); arepo (Pfrommer et al. 2017); GIZMO (Chan et al. 2019); gadget-2 (Pfrommer et al. 2006); ramses (Dubois & Commerçon 2016; Booth et al. 2013); flash (Yang et al. 2012) among others]. These must be subjected to a battery of tests to ensure they are correctly solving the CR transport equations. Perhaps the most demanding test for such codes are CR shocks; this is also one of the few regimes where analytic solutions exists. However, to date codes have only been compared against analytic solutions in the purely advective regime, with both CR streaming and diffusion turned off. Even in this restricted regime, numerical methods do not appear to be robust. When the post-shock CR pressure is a small fraction of the gas pressure, simulations appear to agree with existing analytic solutions (Pfrommer et al. 2006). However, once this is no longer true, outcomes are non-unique and dependent on numerical method such as discretization, time-steppping, spatial reconstruction, and CFL number (Kudoh & Hanawa 2016; Gupta, Sharma & Mignone 2019). This was attributed to the fact that the equations can no longer be written in conservative form, due to the presence of a source term involving spatial derivatives. It was therefore suggested that additional assumptions are required at CR shocks to achieve closure, such as constant CR entropy across the shock (Kudoh & Hanawa 2016), or a priori prescription of the post-shock CR pressure (Gupta et al. 2019). We shall clarify this situation by showing that such potentially unphysical assumptions are unnecessary in the full problem where CR transport (diffusion and streaming) is considered.
Even more pressing is the need to compare codes with CR streaming to analytic solutions. In the past, simulations with CR streaming have been afflicted by severe grid-scale instabilities due to the requirement that CRs can only stream down their gradient (Sharma et al. 2009). The only known cure, adding artificial diffusion, led to severe time-step requirements (Δt ∝ (Δx)2 as well as dependence on the adopted smoothing parameter).3 Thus, simulations with CR streaming (and particularly CR shocks with streaming) were infeasible. These problems were resolved with a new two-moment method for CR transport (Jiang & Oh 2018), which has no arbitrary smoothing and only linear time-step scaling with resolution (Δt ∝ Δx); since then similar formulations (albeit with some important differences) have been proposed (Chan et al. 2019; Thomas & Pfrommer 2019) and employed in galaxy formation simulations. For instance, Thomas & Pfrommer (2019) claim that expansion to |$\mathcal {O}(v_{\rm A}^2/c^2)$| is necessary, but did not present a specific scenario demonstrating this claim. No codes to date have been compared against existing analytic solutions with streaming (Voelk, Drury & McKenzie 1984). We shall show that these old analytic solutions are in fact incomplete, and develop a new set of solutions. The Jiang & Oh (2018) method matches the new analytic solutions we develop.
CR shocks in galaxy formation simulations. Another compelling motivation to understand CR shocks in the two-fluid approximation is that at present it is the only one used in galaxy formation simulations; no other method has been shown to be feasible. Shocks are also omni-present in such simulations, and it is important to understand the mutual interaction and impact of CRs on shocks and vice versa, particularly in the presence of CR streaming. For instance, it is usually prescribed in cosmological simulations that |$f_{\rm CR} \sim 10{{\ \rm per\ cent}}$| of supernova energy is injected into CR (via a sub-grid recipe) and that most of the CRs in the simulation comes from this source. However, in a two-fluid code, shocks will enhance CR energy density. Thus, shocks generated by e.g. SNe blast waves, galactic wind termination shocks (e.g. Bustard, Zweibel & Cotter 2017), and structure formation shocks may produce CRs in excess of that from sub-grid injection recipes, and also alter the spatial distribution of CRs. It is important to understand this effect and its dependence on numerical resolution. The simulation results must also be checked to ensure they make physical sense (for instance, that CR acceleration efficiencies are not wildly discrepant with PIC simulations), given the approximations inherent in the two-fluid method. It is also important to understand how CRs affect shock jump conditions (e.g. compression ratios, which is increased in the presence of CRs), and whether the simulations are handling this correctly. Only by doing so can we assess whether the astrophysical impact of shocks is correctly handled, and the robustness of observational predictions that depend on conditions at the shock (e.g. radio relics; Botteon et al. 2020).
The outline of this paper is as follows. In Section 2, we develop analytic solutions for CR-modified shocks, and in particular a new solution that takes bi-directional streaming into account. In Section 3, we show simulation results and compare them to the analytic solution. This is followed by a study on the equilibration time, resolution dependence, effect of oblique magnetic fields, and injection. We conclude in Section 4.
2 ANALYTICS
2.1 Governing equations
Our analytic study follows the treatment by Voelk et al. (1984), hereafter VDM84, of CR shocks with streaming, but with some important modifications. We consider 1D adiabatic non-relativistic steady-state shocks in the two-fluid approximation. As noted in the Introduction, we do not assume any injection of CRs from the thermal pool; we simply assume a non-zero upstream CR pressure. With a shock finding algorithm, it is possible to include prescriptions for thermal injection (e.g. Pfrommer et al. 2017), but we eschew this for the sake of simplicity. At high Mach numbers (|$\mathcal {M} \gt 5$|), it has been suggested that the acceleration efficiency is independent of injection, maintaining at or above |$50{{\ \rm per\ cent}}$| (Eichler 1979; Achterberg et al. 1984; Ellison & Eichler 1984; Falle & Giddings 1987; Kang & Jones 1990). We also ignore magnetic field amplification and subsequent back-reaction on the shock, which can alter compressibility and hence CR acceleration efficiency (Caprioli et al. 2008, 2009). This is standard in the two-fluid formalism.
Equation (7) captures energy transferred from CRs to the gas, either by mechanical work done (v · ∇Pc), or heating (vs · ∇Pc). Transport by streaming and diffusion are captured, respectively, by the first and second terms on the RHS of equation (8). VDM84 assumed that CRs only stream towards the upstream. However, this assumption is unclear downstream given equation (1); CRs can only stream down their gradient. We therefore restrain from presupposing a CR streaming direction. The direction will become clear as we go along. In the following, we take γg = 5/3, γc = 4/3 to be the adiabatic indices of the gas and CR. ‘Upstream’ means the fluid state at x = −∞, ‘downstream’ means the post-subshock fluid state if there is a subshock or x = +∞ if there is not.
The non-conservative form of the CR subsystem leads to the presence of derivatives in equations (7) and (8). This implies that we cannot simply use conservation laws to determine jump conditions, but must solve for the detailed structure of the front. In particular, we must solve ODEs. For this to be possible, the CR variables Pc, Fc (unlike the gas variables) must be continuous across the front. Physically, the smoothness of Pc, Fc across the shock is guaranteed by the large mean free path of CRs, λ ∼ rc/(δB/B)2 ≫ λi, where rg is the CR gyroradius and λi is the ion mean free path; the (much smaller) thermal ion mean free path sets the characteristic thickness of any gas shock discontinuity. Mathematically, the smooth solutions are guaranteed by the diffusion term in the above equations; we just need to resolve the diffusion length lD ∼ κ/cs. Note that if Pc were discontinuous, similar to Pg, then equation (8) would imply an infinite CR flux Fc.
2.2 Shock structure and solution method
2.2.1 Previous solution: uni-directional streaming
Before solving the above equations, we describe the overall features of the shock. CR acceleration implies that Pc is higher in downstream gas. However, downstream CRs can diffuse upstream and affect the flow. The CR precursor significantly affects fluid flow and decelerates incoming gas, from being supersonic with respect to the overall acoustic speed of the plasma (which includes both gas and CR contributions to gas pressure; |$c_{\rm s,tot}^{2} \approx \mathrm{d}{(p_g + p_c)}/\mathrm{d}{\rho }$|) to subsonic with respect to cs, tot. There are two possibilities: (i) in a CR-dominated shock, the post-shock CR pressure absorbs a significant fraction of the incoming ram pressure. In this case, the ‘shock’ simply consists of a smooth deceleration and compression; all fluid variables are continuous. After the compression, the flow is still supersonic with respect to the gas sound speed. (ii) The gas must absorb a significant fraction of incoming ram pressure, an amount that is inconsistent with just adiabatic compression. This implies a discontinuous gas subshock in the gas variables only, and a jump in gas entropy. The subshock renders the flow subsonic with respect to the gas sound speed. The effect of CR streaming is transfer energy from CRs to the gas in the precursor, preheating the gas, and thus increase in the importance of gas decelerating the flow, thus increasing the strength of the subshock.
2.2.1.1 The smooth precursor.
2.2.1.2 The subshock.
2.2.1.3 Solution method.
In the standard treatment by VDM84, for a given upstream, the downstream can be found by a modification of the procedure described in Drury & Voelk (1981; hereafter DV81). The solution procedure can be expressed graphically, as in the top panel of Fig. 1, which shows a Pg against v diagram. Each curve on the diagram describes a constraint characteristic to the shock structure:
Pc = 0 (blue curve). Pressure must be positive. The plot shows Pg > 0 only; another obvious constraint is Pc > 0. Thus, all valid solutions must lie below the blue line, which shows Pc = 0 (obtained from equation 5). Lines parallel to this line correspond to Pc = const, which we will use shortly.
Hugoniot (black curve). The black curve references equation 10, showing where N(y) = 0, or equivalently where the gradients of the fluid variables are zero. This corresponds to far upstream and downstream. It is called the Hugoniot. For a given upstream, the Hugoniot encompasses possible downstream states.
Wave adiabat (green curve). The wave adiabat, given by equation (9), is set by upstream conditions and conserved throughout the precursor. The initial intersection of the wave adiabat and the Hugoniot at the far right gives the upstream state; the subsequent intersection at the left gives the downstream state if there is no subshock. The ordering of these states is unambiguous, since the shock decelerates the flow.
Sonic boundary (orange line). The orange line shows the sonic condition given by equation (18). If the wave adiabat does not cross this boundary before reaching the Hugoniot, then it never undergoes a sonic transition and there is no subshock. The structure of the shock can then be read off graphically by following the wave adiabat from the upstream to the downstream state. On the other hand, if it crosses this line, then the gas will shock.
Reflected Hugoniot (purple line). If the gas undergoes a subshock, how do we proceed? Since Pc is continuous, [Pc] = [ρv2 + Pg] = 0 across the subshock, the jump in fluid variables must be parallel to the Pc = 0 (blue) line. In addition, from equation (17), the sonic boundary (orange line) must bisect this line, since the sonic boundary gives the relationship between the mean of the pre-shock and post-shock pressure and velocities. From these facts, we can construct a ‘reflected Hugoniot’ (purple curve), which is the locus of points traced out by lines parallel to the blue Pc = 0 line, which start at the Hugoniot (black) and are bisected by the sonic boundary. The reflected Hugoniot shows all the possible pre-subshock states connected to the downstream by the subshock jump conditions (equation 13–16). The intersection of the wave adiabat (green) and reflected Hugoniot (purple) therefore gives the pre-subshock state.
Subshock jump (red line). Now that we have identified the pre-subshock state, we insert the subshock jump (red line), which as discussed must be parallel to the Pc = 0 (red) line. The intersection of the subshock jump (red line) with the Hugoniot (black line) gives the post subshock (and final downstream) state.
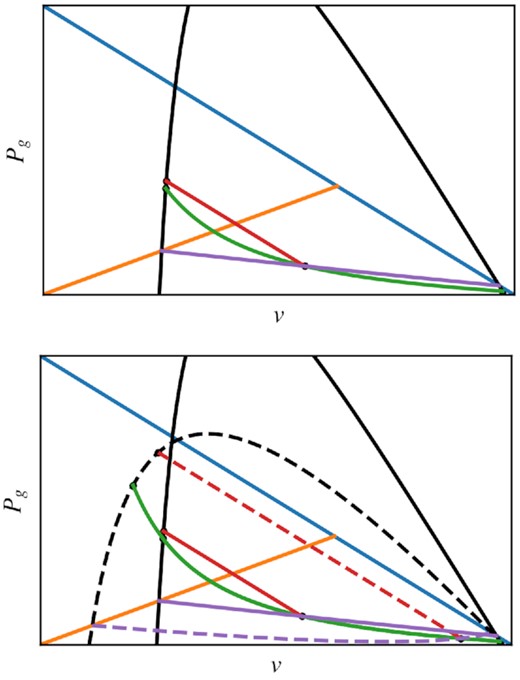
Top: Typical Pg against v diagram without bi-directional streaming. Each colored curve represents a Pg − v relation given a condition, as described in Drury & Voelk (1981). Blue – Pc = 0; orange – γgPg = Jv; black – the Hugoniot, N(y) = 0; red – jump in (Pg, v) satisfying the subshock jump conditions (equations 13–16); green – the wave adiabat, equation 9; purple – the reflected Hugoniot. Bottom: Same as the top but with bi-directional streaming, which leads to the dotted lines. The dotted black line expresses the Pg − v relation for |$\tilde{N}(y) = 0$|. Construction of the dotted red and purple line follows that of the solid red and purple line. For reference, |$\mathcal {M} = 5, Q = 0.5, \beta =1$| for these two plots.
In summary, the solution procedure is: follow the wave adiabat (green) in the direction of decreasing v until it intersects with the reflected Hugoniot (purple), then follow the subshock jump (red) directly to the downstream. In the absence of a subshock, possible if the wave adiabat does not cross the sonic boundary (orange), the downstream is simply given by the intersection of the Hugoniot and the wave adiabat. Such smooth transitions can occur if the shock is CR dominated.
2.2.2 New solution: bi-directional streaming
The aforementioned solution method assumes the direction of CR streaming is the same throughout the shock profile, i.e. towards the upstream. However, post-subshock CR can stream towards the downstream too. At the early stages of shock formation, strong compression at the subshock can cause the CR pressure to overshoot, forming a small spike from which CR stream away in opposite directions (Fig. 2). This is entirely analogous to the ‘Zeldovich spike’ (Zel’dovich & Raizer 1967) which occurs in radiative shocks. The spike is a non-equilibrium state which slowly flattens as CRs stream out. However, it sets up a shock structure where downstream CRs stream away from the shock, rather than towards it, as VDM84 assumed. Note that the downstream CR profile is almost flat (|$P_c\rightarrow \rm const$|), so the direction of streaming is set by small changes in the CR profile at the shock.
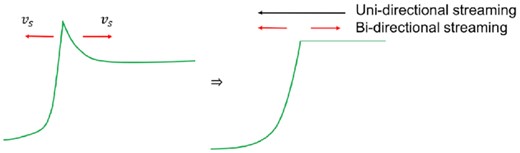
Conceptual plot of Pc leading to bi-directional streaming. The direction of streaming assumed in VDM84 is added for comparison.
The standard Hugoniot (solid black line in Fig. 1) shows possible downstream solutions for which vs = −vA, where post-shock CR streams toward the shock. With the sign flip, the new Hugoniot (dotted black line) shows possible downstream solutions for which vs = vA, and the post-shock CR stream away from the shock. The switch in direction of downstream CRs changes not just the magnitude of the subshock, but also where it occurs. One can see it is not possible to jump, from the standard location where the subshock occurs (intersection between the solid green and purple lines), to the new Hugoniot while satisfying the subshock jump conditions. The sonic boundary (orange) would no longer bisect the line connecting pre-shock and post-shock states. To determine when the subshock occurs, a new reflected Hugoniot (dotted purple line) has to be calculated, in a similar manner as in the standard treatment.
Fluid flow in the precursor conserves the same wave adiabat as before since CR still streams towards the upstream. Therefore, precursor fluid states continue to trace the same green curve. The subshock occurs at intersections between the new reflected Hugoniot and the wave adiabat, which brings the fluid directly to the downstream.
2.2.2.1 Existence of the new solution.
In the case of uni-directional streaming, the shock profile can be smooth (i.e. no subshock) if the wave adiabat does not cross the sonic boundary. This happens when the upstream Pc is sufficiently high. However, the new solution always requires a subshock. Bi-directional streaming can only occur if there is a maximum in Pc, at which ∇Pc = 0. As previously discussed (see equation 20), unless dρ/dx = 0, a maximum in Pc is equivalent to a sonic point in the gas, and thus a subshock must occur, which brings the fluid to its downstream state without further relaxation. Otherwise, the profile will be non-monotonic. This means that in CR-dominated regimes, the new solution may cease to exist because the subshock has been smoothed out.
Fig. 3 shows an example where a new solution is not allowed for the above reasons. The wave adiabat (green) does not cross the sonic boundary before intersecting with the standard Hugoniot (black). Thus, the standard solution involves a smooth transition, with no subshock. The wave adiabat (green) does also intersect with the new reflected Hugoniot (dotted purple), but only after crossing the standard Hugoniot (solid black), where dPc/dx = 0. Continuing after this would imply a change in sign for dPc/dx and other fluid derivatives, i.e. a non-monotonic profile. This solution therefore has to be rejected.
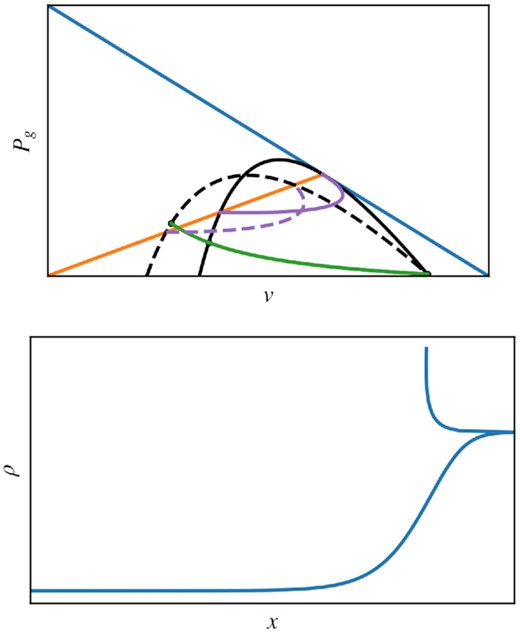
Top: Pg − v diagram for |$\mathcal {M} = 2, Q = 0.95, \beta = 1$|. The colour of the curves mean the same as in Fig. 1. Bottom: Density plot of the new solution shows that it is non-monotonic.
2.3 Solution structure
Fig. 4 shows the acceleration efficiency, measured by the ratio of the change in CR pressure to the upstream ram pressure (|$(P_{c2} - P_{c1})/\rho _1 v_1^2 \equiv \Delta P_c/\rho _1 v_1^2$|), against Mach number for upstream non-thermal fraction Q = 0.1, 0.5 and β = 1. Fig. 5 shows the acceleration efficiency against Q for a sample of Mach number and plasma beta. In these two figures, two different solutions emerge, corresponding to uni-directional (black curves) or bi-directional streaming (blue curves). At high β, the two solutions converge since the contribution of streaming is small in that limit, so it does not matter which way the CRs stream. In magnetically significant regimes (β ∼ 1), the new branch introduces two main differences: first, the acceleration efficiency is in general lower. For bi-directional streaming, downstream CRs stream away from the subshock, and fewer CRs diffuse to the upstream precursor. In the two-fluid formalism, all CR ‘acceleration’ is essentially compressional (adiabatic) heating. With a smaller precursor, the shock is more hydrodynamic and less compressible (since the γg = 5/3 gas is less compressible than the γc = 4/3 CRs). Lower compression implies less overall less adiabatic heating of the CRs. The difference is small at low Mach numbers (|$\mathcal {M}\sim 1-2$|) but becomes more apparent as |$\mathcal {M}$| increases. At |$\mathcal {M}\sim 10$| the acceleration efficiency can drop from |${\sim}40-50{{\ \rm per\ cent}}$| for the standard branch to less than |$10{{\ \rm per\ cent}}$|. However, at moderate Mach numbers, a transition occurs, and that brings us to the second point: the new solution bifurcates into multiple branches. A similar bifurcation occurs for CR shocks without streaming, which is equivalent to our high β limit (DV81; Jones & Ellison 1991; Donohue & Zank 1993; Mond & O’C. Drury 1998; Becker & Kazanas 2001; Saito, Hoshino & Amano 2013). This does not happen for uni-directional solutions with streaming. Even so, bifurcation in the no streaming case happens only at very small Q, and within an intermediate range of Mach numbers. In contrast, the new bifurcation can occur at high Q (for β ∼ 1, it can occur for equipartition CR energy densities or even in CR-dominated regimes) and persists even as |$\mathcal {M}$| continue to increase. Fig. 6 shows a summary of the solution multiplicity for |$(\mathcal {M}, Q)$| and β = 1, 20, 1000. Multiple solutions for the new branch are common, particularly for high Mach numbers and when magnetic fields are significant (lower β). The new branch usually bifurcates into three solutions, and in order of increasing acceleration efficiency we shall call them the inefficient, intermediate, and efficient branch.
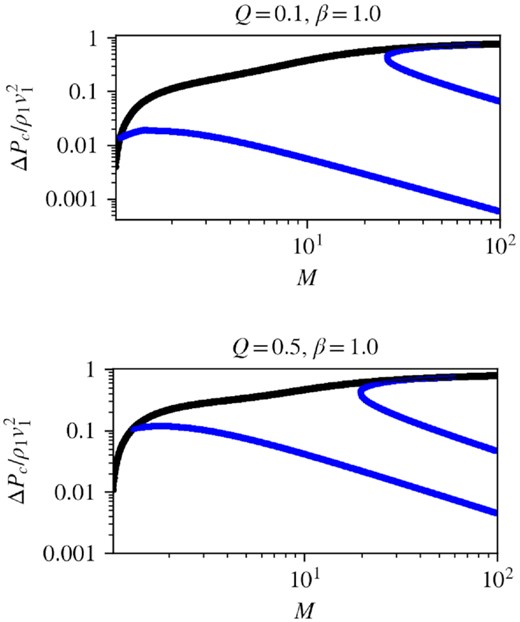
Acceleration efficiency against mach number |$\mathcal {M}$| for Q = 0.1 (top) and = 0.5 (bottom) and β = 1. The black curve denotes the standard branch while the blue curve denotes the new solution branches (efficient, intermediate, and inefficient).
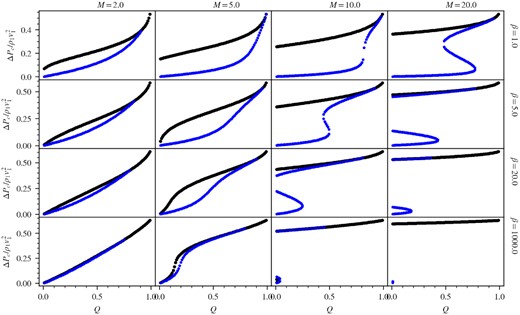
Acceleration efficiency against upstream non-thermal fraction (Q) for Mach number |$\mathcal {M}=2,5,10,15$| and plasma beta β = 1, 5, 20, 1000. The black curve denotes the standard branch while the blue curve denotes the new solution branches (efficient, intermediate, and inefficient). In each panel, the efficient branch gradually merges with the standard branch as Q increases. At sufficiently CR-dominated regimes (high Q), the efficient branch cease to exist by the monotony argument in Secrion 2.2.
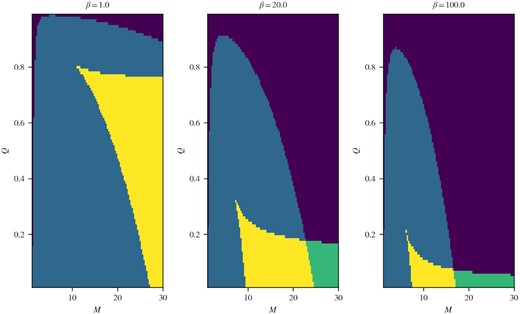
Color plots showing the multiplicity of the new + standard solution for a given |$(\mathcal {M}, Q, \beta)$|. Purple = 1, blue = 2, green = 3, yellow = 4.
The uni-directional solution poses a difficulty at low β: a significant downstream non-thermal fraction exists even as Q → 0. This solution has been argued to be physically unrealistic (Malkov 1997). It is unclear physically how, without injection, one can accelerate particles without an existing CR population. By contrast, the bi-directional solution has at least one branch where ΔPc → 0 as Q → 0.
The behaviour of different branches of solution are markedly different. The ‘inefficient’ branch corresponds to the test particle limit where CRs have nearly no effect on the shock structure. The downstream fluid is gas dominated and the shock appears hydrodynamic, giving a compression ratio ∼4 at high Mach number. At equipartition (Q ∼ 0.5, β ∼ 1), the typical acceleration efficiency |${\sim}10{{\ \rm per\ cent}}$| for Mach numbers below 10 and decreases with increasing Mach number (see Fig. 4). At low Mach numbers, the acceleration efficiency of this branch appears consistent with PIC/hybrid simulations (Caprioli & Spitkovsky 2014a), which found an efficiency of |${\lesssim}10{{\ \rm per\ cent}}$| for |$\mathcal {M} \lt 10$|. It is, however, at odds with the behaviour at very high Mach numbers |$\mathcal {M} \gt 10$|, for which PIC/hybrid simulations show an increase in efficiency. We shall see that if we include thermal injection into DSA (Section 3.5.4), this decline in efficiency at high Mach number goes away. With less ambient CR (Q = 0.1), the acceleration efficiency of the inefficient branch drops to |${\sim}1{{\ \rm per\ cent}}$|. This reflects, in the two-fluid model, a substantial ambient CR population is required for efficient acceleration.
The efficient branch is strongly CR-modified. Having a smaller adiabatic index γc = 4/3, the fluid is more compressible, so the compression ratio ∼7 at high Mach number. This leads to much higher adiabatic heating of the CRs. At equipartition, this branch emerge at Mach numbers higher than ∼12 and has a typical efficiency of |${\gtrsim}60{{\ \rm per\ cent}}$|. The acceleration efficiency continues to increase with Mach number such that at Mach number of a few tens and above the subshock is smoothed out by the dominating CR population and the efficient branch merges with the standard branch. In the following, we shall often refer to the efficient branch and standard solution collectively as the efficient/standard branch due to their similarity in acceleration efficiency. An acceleration efficiency of this order has been found in previous works, both analytically (Caprioli et al. 2008, in a two-fluid model; Caprioli et al. 2009, in a kinetic description; both works include magnetic field amplification) and in simulations (Ellison & Eichler 1984, in a Monte Carlo approach).
While some previous analytics have assumed CR entropy (|$P_c/\rho ^{\gamma _c}$|) to be constant (Pfrommer et al. 2006; Gupta et al. 2019) across the shock, we find this to be untrue; CR entropy increases across the shock for all branches of solution (in ascending order of increase: inefficient, intermediate, and efficient branch).
The downstream Pc can be different by decades across branches of solution, so knowing which one will be selected is important. We seek to answer this with simulation. In the following sections, we will demonstrate numerically that the standard and new solutions are all valid steady-state shock profiles, but the intermediate branch of the new solution is unstable. We also illustrate, with different initial setups, how various branches can be captured. They turn out to be sensitive to local upstream conditions, but generically, the inefficient branch of the new solution is the one most likely to be realized in realistic settings.
3 SIMULATION
3.1 Code
The following simulations were performed with athena+ + (Stone et al. 2020), an Eulerian grid based MHD code using a directionally unsplit, high order Godunov scheme with the constrained transport technique. CR streaming was implemented with the two moment method introduced by Jiang & Oh (2018). This code solves equation (9) in Jiang & Oh (2018), which reduces to our equation (2) in 1D (where the B-field is constant and parallel to the shock normal). Unless otherwise specified, a 1D Cartesian grid is used and the magnetic field points in the +x direction.
3.2 Setup 1: imposed shock profile
We begin by verifying the analytic standard and new solutions, by imposing the steady-state analytic profiles as initial conditions, and verifying that they are time-steady in the code. For a given upstream state, the downstream state can be determined by the method described in Section 2.2. The shock profiles can be calculated from equation (10) supplemented by a subshock that brings the fluid to the downstream state. This profile is input into the simulation domain and evolved in time. Since the shock structure depends only on |$\mathcal {M}, Q, \beta$|, we fix the upstream ρ = 100, Pg = 1 in code units, implying an unstream gas sound speed of cs = 0.13. We set the reduced speed of light |$\tilde{c} = 100$|.6 Some simulations were rerun with |$\tilde{c}=1000$| with no apparent difference. The diffusion coefficient (which we set to κ = 0.1) has no effect on downstream values, it only sets the shock width. The number of grid cells is 4096; at this resolution the diffusive length is typically resolved with nshock ≡ κ/v1Δx ≳ 40 cells. Previously, nshock ∼ 10–20 was found to be sufficient for convergence (Frank, Jones & Ryu 1994). Outflow boundary conditions were used on both sides. The result is independent of the boundary conditions as increasing the domain size and imposing the ghost zones yield no difference. Unless specified, the following simulations assume β = 1. CR transport at high β is purely diffusive, a limit that has been extensively studied, which we will not investigate in this work.
Fig. 7 shows, respectively, the shock profiles of the standard, efficient, intermediate, and inefficient branch at t = 0, 1502tdiff, 3003tdiff for |$\mathcal {M}=20, Q=0.6, \beta =1$|, where |$t_{\text{diff}}=\kappa /v_1^2$| is the diffusion time-scale. The solutions at t = 1502tdiff are relatively well maintained, with a little numerical shift. Such numerical shifts are expected to equilibrate after ∼1000tdiff (Kang & Jones 1990). Behavior of the solutions vary drastically after ∼2000tdiff, with the intermediate branch diverging exponentially from its original profile. The standard and efficient branch show small spatial shifts, but overall the profile is maintained, with the same acceleration efficiency. The inefficient branch appears the most robust. In general, solution branches with significant downstream CR fraction tend to be the most susceptible to this numerical shift. Such shift originate at the subshock (we do not observe this for smooth shocks). The problem lies with how the direction of the streaming velocity vs is determined. The direction is determined by sgn(∇Pc), which is estimated by a finite difference scheme: sgn(∇Pc, i) = sgn((Pc, i + 1 − Pc, i − 1)/Δx). The cells at the subshock therefore would still have positive ∇Pc whereas it should, for bi-directional streaming, be negative. This causes vs to be positive at the subshock and Fc (equation 8) to overshoot slightly, hence causing the shift in Pc profile. Since Fc scales linearly with Pc, the overshoot is larger for more CR-dominated downstream. The inefficient branch, which has the lowest downstream CR fraction, is therefore the least affected. Another possible source of shift comes from the finite coupling time for Fc to attain its steady-state value (equation 8), given roughly by |$t_\mathrm{coup} = 1/\sigma _c \tilde{c}^2$|. Across the subshock, σc drops abruptly, leading to a rise in the coupling time. Deviations of Fc from the steady-state expression (equation 8) causes the tiny discrepancy seen.
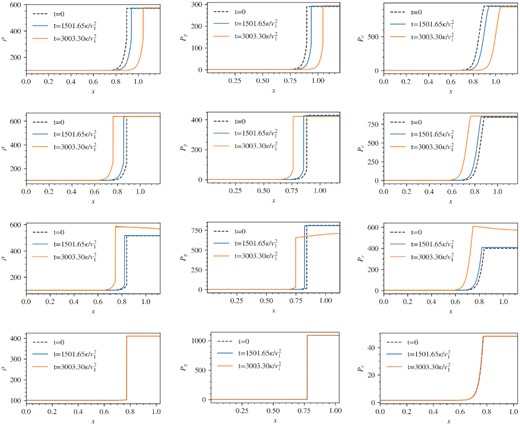
Simulation results for Setup 1. Top row: From left to right: density, gas pressure, and CR pressure profiles for the standard branch. Second row: Profiles for efficient branch. Third row: Profiles for the intermediate branch. Bottom row: Profiles for the inefficient branch.
The intermediate branch has a profile that does not just translate spatially; it also clearly evolves. Furthermore, in the example above, the acceleration efficiency of the intermediate branch diverges with time and evolves to the standard/efficient branch efficiencies, while the other branches remain close to their initial values. Thus, the intermediate branch is unstable. The same multiplicity (3) of solutions appears in standard solutions with diffusion only, and the intermediate branch is also unstable in this case. Mond & O’C. Drury (1998) suggested that this divergent behaviour is a consequence of a corrugational instability. Nevertheless, along with Donohue & Zank (1993) and Saito et al. (2013), we have found that the intermediate branch is unstable without invoking a corrugation mode (since our simulations are 1D). It is also unlikely to be due to the acoustic instability (Drury 1984; Dorfi & Drury 1985; Zank & McKenzie 1985; Drury & Falle 1986; Kang, Jones & Ryu 1992; Wagner et al. 2006), triggered at the shock precursor by phase shifts between the acoustic disturbances in the gas and CR components due to CR diffusivity: the typical growth time (i.e. e-folding time) of the acoustic instability is |$t_\mathrm{grow}\sim \kappa /c_{c1}^2$|. whereas the advection time across the shock precursor is tadv ∼ κ/v1cs1. The ratio of these two time-scales is |$t_\mathrm{grow}/t_\mathrm{adv}\sim \mathcal {M} \gg 1$|, i.e. there is insufficient time for the instability to grow.
We proceed to test the analytic shock profiles for other values of Q. The result is shown in Fig. 8. The acceleration efficiencies of the standard, efficient, and inefficient branches are stable and remain close to their initial setups while that of the intermediate branch is unstable, and asymptotes to the standard and efficient branch. These results show that our two-moment code handles this demanding test well, and in agreement with analytic expectations.
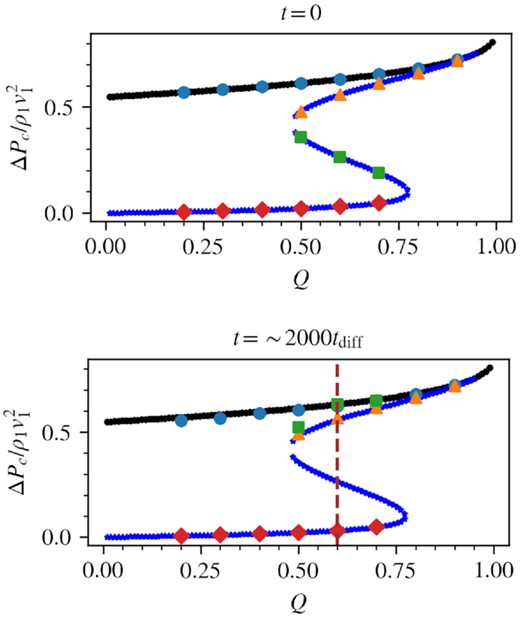
Acceleration efficiency against Q for |$\mathcal {M}=20, \beta =1$| at two time instances, at t = 0 (top) and t ∼ 2000tdiff (bottom). The markers denote the simulation data, the different marker shapes represents the solution branch the simulation was set up with (red diamond: inefficient, green squares: intermediate, yellow triangle: efficient, blue circles: standard). The markers are threaded by black and blue lines, denoting the analytic acceleration efficiency (black corresponds to standard branch, blue corresponds to the new solution branches, i.e. efficient, intermediate, inefficient). The vertical brown dashed line indicates the value of Q used in the test cases displayed in Fig. 7.
3.3 Setup 2: free flow
Next, we show how initial conditions influence which solution branch is realized. We simulate a fluid moving supersonically towards a reflecting boundary on the right at high speed, as in a converging flow. This causes the fluid to shock. The initial flow is either uniform or has background gradients. The left boundary is set to outflow if the flow is uniform initially, or with linear extrapolation in the ghost zones otherwise. The initial flow speeds are listed in Table 1 (top table) and Pc is set by Q. The CR flux Fc is determined by equation 8.
Top table: Summary of test cases with uniform initial flow (Section 3.3). The first column catalogues the corresponding figure. The second column lists the initial flow speed. The third column lists the upstream shock parameters. The forth column enumerates the number of analytical solution branches for each case. The fifth column records the branch selected by simulation. The last column measures the acceleration efficiency by |$(P_{c2} - P_{c1})/\rho _1 v_1^2$|. Lower table: Summary of the oblique shock parameters (Section 3.5.3). Column 1: Angle between upstream magnetic field and shock normal. Column 2: Time of measurement in code unit and in unit of the diffusion time in parenthesis. Column 3: Upstream Mach number (defined relative to the fast magnetosonic speed), non-thermal fraction and plasma beta. Column 4: Compression ratio. Column 5: Acceleration efficiency. Column 6: Angle between downstream magnetic field and shock normal.
| Case . | v . | (M, Q, β) . | # of . | Selected . | Acc. eff. . |
|---|---|---|---|---|---|
| . | . | . | sol. branch . | branch . | . |
| Fig. 9(a) | 0.5 | (14.8, 0.2, 1) | 2 | Inefficient | 0.93 per cent |
| Fig. 9(b) | 1.23 | (26.6, 0.6, 1) | 4 | Inefficient | 2.1 per cent |
| Fig. 9(c) | 3.31 | (22.4, 0.95, 1) | 1 | Standard | 77.0 per cent |
| θ (deg) | t (t/tdiff) | |$(\mathcal {M}_f,Q,\beta)$| | r | Acc. eff. | θout (deg) |
| 5 | 60 (1299) | (7.6, 0.5, 1) | 4.0 | 1.1 per cent | 19.5 |
| 45 | 60 (1304) | (7.6, 0.5, 1) | 4.0 | 0.9 per cent | 76 |
| 5 | 200 (3435) | (7.7, 0.5, 100) | 6.8 | 81.1 per cent | 30.8 |
| 45 | 200 (4344) | (8.65, 0.5, 100) | 4.0 | 1.2 per cent | 76 |
| Case . | v . | (M, Q, β) . | # of . | Selected . | Acc. eff. . |
|---|---|---|---|---|---|
| . | . | . | sol. branch . | branch . | . |
| Fig. 9(a) | 0.5 | (14.8, 0.2, 1) | 2 | Inefficient | 0.93 per cent |
| Fig. 9(b) | 1.23 | (26.6, 0.6, 1) | 4 | Inefficient | 2.1 per cent |
| Fig. 9(c) | 3.31 | (22.4, 0.95, 1) | 1 | Standard | 77.0 per cent |
| θ (deg) | t (t/tdiff) | |$(\mathcal {M}_f,Q,\beta)$| | r | Acc. eff. | θout (deg) |
| 5 | 60 (1299) | (7.6, 0.5, 1) | 4.0 | 1.1 per cent | 19.5 |
| 45 | 60 (1304) | (7.6, 0.5, 1) | 4.0 | 0.9 per cent | 76 |
| 5 | 200 (3435) | (7.7, 0.5, 100) | 6.8 | 81.1 per cent | 30.8 |
| 45 | 200 (4344) | (8.65, 0.5, 100) | 4.0 | 1.2 per cent | 76 |
Top table: Summary of test cases with uniform initial flow (Section 3.3). The first column catalogues the corresponding figure. The second column lists the initial flow speed. The third column lists the upstream shock parameters. The forth column enumerates the number of analytical solution branches for each case. The fifth column records the branch selected by simulation. The last column measures the acceleration efficiency by |$(P_{c2} - P_{c1})/\rho _1 v_1^2$|. Lower table: Summary of the oblique shock parameters (Section 3.5.3). Column 1: Angle between upstream magnetic field and shock normal. Column 2: Time of measurement in code unit and in unit of the diffusion time in parenthesis. Column 3: Upstream Mach number (defined relative to the fast magnetosonic speed), non-thermal fraction and plasma beta. Column 4: Compression ratio. Column 5: Acceleration efficiency. Column 6: Angle between downstream magnetic field and shock normal.
| Case . | v . | (M, Q, β) . | # of . | Selected . | Acc. eff. . |
|---|---|---|---|---|---|
| . | . | . | sol. branch . | branch . | . |
| Fig. 9(a) | 0.5 | (14.8, 0.2, 1) | 2 | Inefficient | 0.93 per cent |
| Fig. 9(b) | 1.23 | (26.6, 0.6, 1) | 4 | Inefficient | 2.1 per cent |
| Fig. 9(c) | 3.31 | (22.4, 0.95, 1) | 1 | Standard | 77.0 per cent |
| θ (deg) | t (t/tdiff) | |$(\mathcal {M}_f,Q,\beta)$| | r | Acc. eff. | θout (deg) |
| 5 | 60 (1299) | (7.6, 0.5, 1) | 4.0 | 1.1 per cent | 19.5 |
| 45 | 60 (1304) | (7.6, 0.5, 1) | 4.0 | 0.9 per cent | 76 |
| 5 | 200 (3435) | (7.7, 0.5, 100) | 6.8 | 81.1 per cent | 30.8 |
| 45 | 200 (4344) | (8.65, 0.5, 100) | 4.0 | 1.2 per cent | 76 |
| Case . | v . | (M, Q, β) . | # of . | Selected . | Acc. eff. . |
|---|---|---|---|---|---|
| . | . | . | sol. branch . | branch . | . |
| Fig. 9(a) | 0.5 | (14.8, 0.2, 1) | 2 | Inefficient | 0.93 per cent |
| Fig. 9(b) | 1.23 | (26.6, 0.6, 1) | 4 | Inefficient | 2.1 per cent |
| Fig. 9(c) | 3.31 | (22.4, 0.95, 1) | 1 | Standard | 77.0 per cent |
| θ (deg) | t (t/tdiff) | |$(\mathcal {M}_f,Q,\beta)$| | r | Acc. eff. | θout (deg) |
| 5 | 60 (1299) | (7.6, 0.5, 1) | 4.0 | 1.1 per cent | 19.5 |
| 45 | 60 (1304) | (7.6, 0.5, 1) | 4.0 | 0.9 per cent | 76 |
| 5 | 200 (3435) | (7.7, 0.5, 100) | 6.8 | 81.1 per cent | 30.8 |
| 45 | 200 (4344) | (8.65, 0.5, 100) | 4.0 | 1.2 per cent | 76 |
3.3.1 Uniform background
For initially uniform flow, we show three different cases, which are tabulated in Table 1 and have profiles in Figs 9(a), (b), and (c). The Mach number is measured in the shock frame with the shock velocity calculated by imposing continuity: vsh = [ρv]/[ρ]. In each case, it took ∼1000tdiff for the shock to equilibrate. We comment further on these long equilibration times in Section 3.5. Equilibration generally takes longer for CR-dominated flows. In Fig. 9(c), where there is a transition from low to high CR dominance, the equilibration time is extended by a factor of two. We compare the simulated shock profile against the analytic prediction well after equilibration, and find good agreement. We show an example in Fig. 9(d). This shows that bi-directional streaming is indeed necessary to understand the shock profiles. The slight discrepancy in the Pc profile is due to fluctuations at the subshock associated with sgn(∇Pc), as discussed in Section 3.2. In Table 1, it appears the inefficient branch is favoured whenever it is a possible solution of the shock equations. We have found in all other shock simulations with uniform flow that the simulation indeed selects the inefficient branch whenever possible. It is unclear physically why this is the case, but could be related to the fact that the inefficient branch maximizes the wave entropy (the quantity on the LHS of equation 9), and in particular has strongest subshock and hence the largest jump for the gas entropy. Consistent with the results of the previous section, the intermediate branch is never selected.
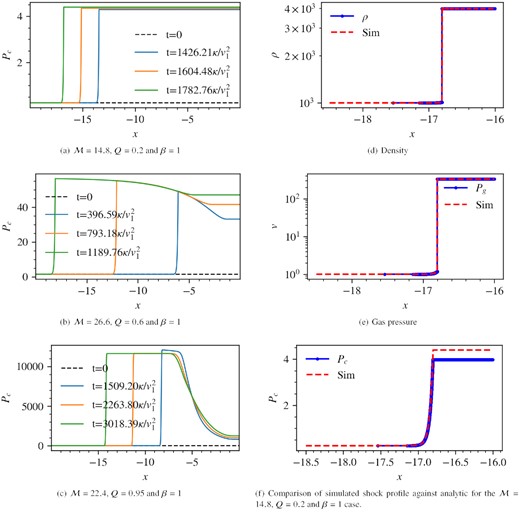
Simulation results for Setup 2 without background gradients, as in Table 1.
3.3.2 Gradient background
Fig. 10(a) shows the evolution of a shock in a background Pc gradient, where Q0, the initial non-thermal fraction at the left boundary, was 0.2, while Q1, that at the right boundary, was 0.95. This was meant to simulate a shock propagating from a CR-dominated region (Q1 = 0.95), where only the efficient/standard branch is permissible, to a progressively gas-dominated area, where the inefficient branch also exists. It is clear that the efficient/standard branch is picked throughout. As a comparison, a similar test where Q1 = 0.8 was performed (not shown). The inefficient branch is selected throughout for this case. The reason for this discrepant solution pick is as follows: as shown in Fig. 11, at Q1 = 0.95, only the efficient/standard branch is possible, so the shock will pick this solution. Under continuously varying background conditions (in this case the gradually decreasing Pc), the shock will shift to a proximate point on the same branch. The shock remains on the same branch even if subsequent upstream conditions permit the inefficient branch. The same logic applies to the case Q1 = 0.8. At Q1 = 0.8, there are four possible branches. As in our uniform background tests, the inefficient branch is picked. Subsequent evolution of the shock down the Pc gradient follows the same branch. These two test cases have been repeated without the balancing source terms, causing the shock and the background to co-evolve with time. Nevertheless, the same result applies: the inefficient branch is selected for Q1 = 0.8 while the efficient/standard branch is selected for Q1 = 0.95. Branch selection is unaffected by source terms.
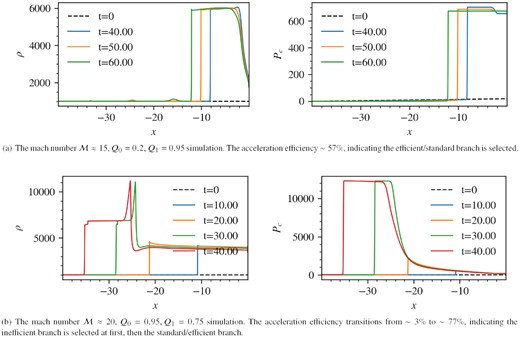
Simulation of Setup 2 with background gradient. Time is given in code units because there is not a well-defined |$\kappa /v_1^2$| due to varying background.
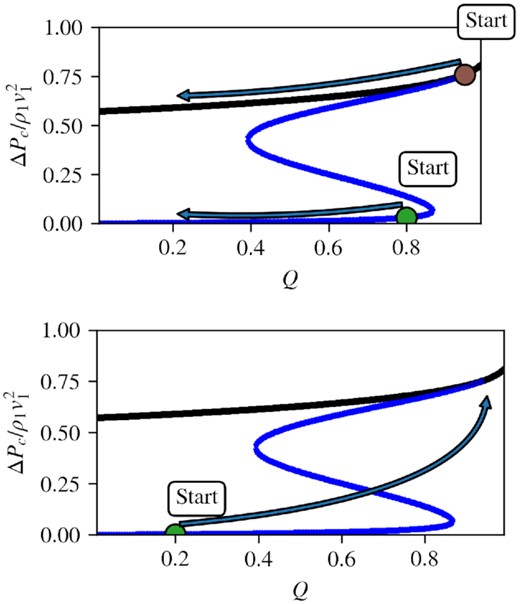
Acceleration efficiency against Q plot showing how various solution branches are captured. Top: A shock beginning at the efficient/standard branch (brown dot) would, under continuously varying background conditions, shift to another point on the same branch. The same holds for the green dot on the inefficient branch. Bottom: A shock beginning at the inefficient branch (green dot) can transition to the efficient/standard branch if the background transitions into one for which only the efficient/standard branch is permissible. As before, the black solid line denotes the standard branch while the blue line denotes the new solution branches (efficient, intermediate, and inefficient).
The reverse is also true. A shock beginning at the inefficient branch can, as in Fig. 10(b), transition to the efficient/standard branch provided the upstream has shifted to conditions where only the efficient/standard branches are permissible. This could happen if the upstream is more CR dominated, or has higher plasma β.
The findings of these simulations are summarized in Fig. 11. The branch selected by the shock is dependent on the local upstream conditions where the shock is formed. Where possible, the inefficient branch is picked. The shock will remain on the same branch unless the upstream transitions into conditions where only the efficient/standard branches are permissible. It will then switch to these branches and remain there. Thus, a shock passing through a CR-dominated region (e.g. a cold cloud) will change its properties and continue to efficiently accelerate CRs, even after leaving the cloud. Two-fluid shock simulations appear to have hysteresis, likely because downstream conditions set boundary conditions for CR streaming that impact the shock itself. We will not consider the physics of this hysteresis, or the preference for the inefficient branch, further in this paper. The full realism of these properties is unclear, given the limitations of the standard two-fluid approach. For now, it is important to be aware of them, given that two-fluid CR hydrodynamics is essentially the only approach used in galaxy formation simulations.
3.4 Setup 3: 1D blast wave
Thus far, we have focused on the properties of steady-state shocks, and not examined properties of the time-dependent stage. We have already seen that the equilibration time of shocks can be long, ∼1000tdiffuse. Thus, the acceleration efficiency of shocks will be time-dependent in a realistic setting. Here, as the simplest possible example, we consider a plane-parallel analog to a blast wave.
In cosmological simulations, an SN (Supernova) event is typically prescribed to deposit mass, metals, momentum, and energy to nearby cells of gas, generating an expanding shock wave. The energy deposited to CR (i.e. acceleration efficiency) is often taken to be |$10{{\ \rm per\ cent}}$| of the total energy ∼1051erg. If CR is treated as a fluid coupled to the thermal gas, additional CR will be generated at the expanding shock. As we have seen, this can be handled self-consistently by a fluid code without a sub-grid prescription, though whether the acceleration efficiency is correct as compared to PIC/hybrid simulations is another matter.
In our setup, a total energy of Eej = 1051 erg was deposited uniformly over a volume of radius R = 10 pc. |$70{{\ \rm per\ cent}}$| of this was deposited into thermal energy, |$10{{\ \rm per\ cent}}$| into CR energy and the remaining |$20{{\ \rm per\ cent}}$| into kinetic energy. For a swept-up mass to be 50 M⊙, the average density was |$\rho = 8.12\times 10^{-25}\ \mathrm{g}\, \mathrm{cm}^{-3}$|. The average outflow velocity was therefore |$v = 632\ \mathrm{km}\, \mathrm{s}^{-1}$|, yielding a temperature of T = 5.64 × 107 K from the ideal gas law for a gas of molecular weight μ = 1. The surrounding ISM was assumed to have density |$\rho _\mathrm{ISM} = 10^{-25}\ \mathrm{g}\, \mathrm{cm}^{-3}$| and |$P_{g,\mathrm{ISM}} = P_{c,\mathrm{ISM}} = 10^3\, k_B\ \mathrm{K}\, \mathrm{cm}^{-3}$|. The Mach number of the expanding remnant is ≈40. We consider both βISM = 2, 100 cases. Following the analytic solution method described in Section 2, there are four solution branches for the βISM = 2 case, of which we expect the inefficient branch to be picked. For the βISM = 100 case, only the efficient/standard branch is permissible. The whole domain spanned −2000 pc < x < 2000 pc, with outflow boundary conditions and |$\kappa = 3\times 10^{25}\ \mathrm{cm}^2\, \mathrm{s}^{-1}$|. The acceleration efficiency is independent of the diffusion coefficient; the specific value chosen allowed the precursor to be resolved without an equilibration time which is too long (and requires a large box). It is also consistent, but on the low side, with the value used in (Gupta et al. 2018) and observations of SN shocks cited therein. A smaller diffusion coefficient is reasonable given the shorter mean free path of CRs at strong shocks, due to the amplification of magnetic perturbations. The domain was resolved with N = 65536 cells (i.e. 0.06pc per grid cell). For simplicity and to avoid computational cost, the calculation is done in planar 1D geometry, and only meant to be illustrative.
The top and bottom rows of Fig. 12 shows the time evolution of an expansion shock from a top-hat SNR setup for βISM = 2 and βISM = 100, respectively. After an initial transient of ∼1000 kyr, the SNR settles on to a relatively stable structure. For βISM = 2, the forward shock at t = 5871 kyr has a compression ratio ∼4 and an acceleration efficiency of |${\sim}4.6{{\ \rm per\ cent}}$|, indicating the inefficient branch is selected as expected. For βISM = 100, the compression ratio rises to ∼6 and the acceleration efficiency to |$67.3{{\ \rm per\ cent}}$|, indicating the efficient/standard branch is selected. As in Fig. 9(c) in Section 3.3, the shock profile for the βISM = 100 case underwent an extended transient of ∼1500 kyr at low post-shock CR dominance before transitioning to the expected efficient/standard branch. Thus, the acceleration efficiency ramps up while the blast wave expands. Comparing the CR energy contained within the SNR of the two test cases (Fig. 13), the high βISM case is clearly much more CR populated (∼3.5 times in this case).
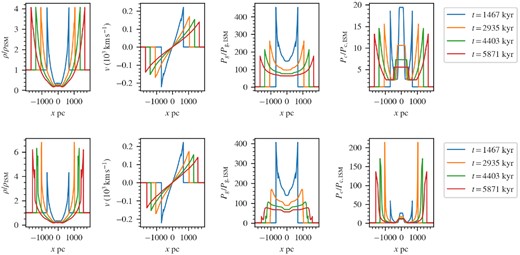
Evolution of 1D blast wave. Top row: βISM = 2 Bottom row: βISM = 100. The compression ratio and acceleration efficiency taken at 5871 kyr are ∼4 and |$4.6{{\ \rm per\ cent}}$| for β = 2 and ∼6 and |$67.3{{\ \rm per\ cent}}$| for β = 100.
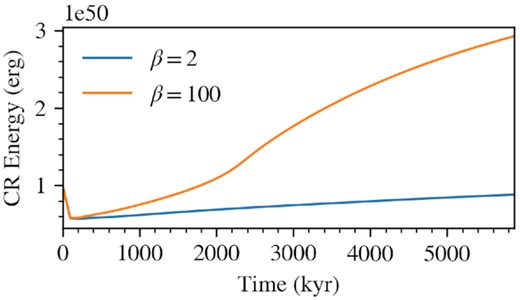
CR energy enclosed by the blast wave as a function of time for βISM = 2 (blue) and βISM = 100 (orange). The initial CR energy is 1050 erg, i.e. |$10{{\ \rm per\ cent}}$| of the total energy ejected. After an initial transient phase, CR energy begins to rise due to particle acceleration.
Our test case is clearly idealized and we expect the simulated profiles to change in realistic 3D spherical geometry, as well as the inclusion of additional physics such as radiative cooling and collisional losses. In particular, the forward shock should decelerate faster from stronger adiabatic cooling, reducing the acceleration efficiency and the net CR produced. Nevertheless, it shows how shocks can potentially add CRs over and above the initial values input by a sub-grid recipe, as well as the influence of CR streaming losses (which differ in the low and high β regimes) in reducing acceleration efficiency.
3.5 Further considerations
Through most of this paper, we have considered time-steady numerically resolved parallel shocks only involving acceleration of pre-existing CRs (no injection from the thermal pool). Here, we briefly discuss the impact of relaxing these assumptions.
3.5.1 Long equilibration times
We have already seen that shocks require |${\sim}1000 t_\mathrm{diff}\sim 1000\kappa /v_1^2$| to equilibrate, where tdiff is the diffusion time and v1 is the upstream velocity in the shock frame. The non-linear build up of the CR precursor, which significantly affects shock structure and CR acceleration, takes many CR diffusion cycles across the shock. The long equilibration time reflects the time required for the upstream flow to respond to the acceleration and diffusion of CR. This has been seen in previous work with diffusion only: for instance, Jones & Kang (1990) found it took ∼200–1000tdiff for their solutions to equilibrate, which is very similar to our findings. Fig. 14 plots the acceleration efficiency and the instantaneous diffusion time of the forward shock in the setup described in Section 3.4. Clearly, the equilibration time for the efficient/standard branch (the βISM = 100 case) is longer, ∼2500 kyr. This time-scale is indeed of order ∼1000tdiff.
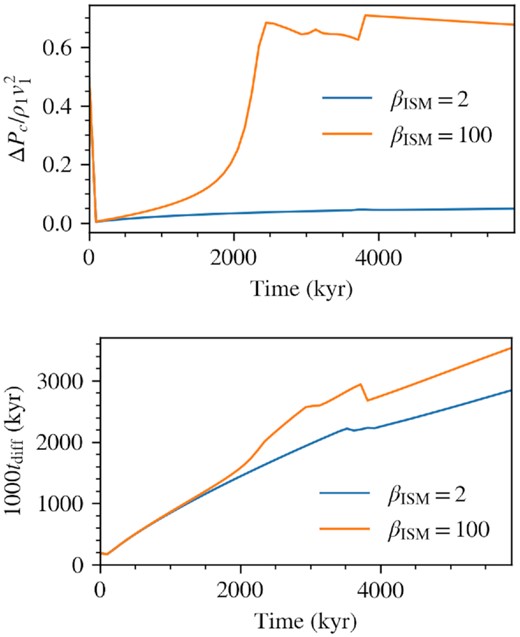
Top: Acceleration efficiency as a function of time for the 1D blast wave example. Bottom: Instantaneous diffusion time of the forward shock.
The equilibration time is longer for the efficient/standard branch because the post-shock CR pressure is higher, leading to a stronger precursor which takes a longer time to build up. By the same token, the more pre-existing CRs there are in the upstream, the more rapidly the precursor equilibrates. As mentioned in Sections 3.3 and 3.4, when only the efficient/standard branch is permissible, there is usually an extended transient in which the shock transitions from low to high post-shock CR dominance (i.e. low to high CR acceleration efficiency), which coincides with the build-up of the precursor. This behaviour was also seen by Dorfi & Drury (1985) and Jones & Kang (1990) in simulations without CR streaming. Jones & Kang (1990) derived an approximate analytic formula for the equilibration time and found that the number of diffusion time required is dependent on γc as well. The equilibration time is the longest for γc = 4/3 and decreases for a stiffer CR equation of state, when the plasma is less compressible and the precursor plays a smaller role. For instance, in oblique shock simulations assuming γc = 4/3, we find an equilibration time of ∼2500tdiff for |$\theta =5\ \rm deg, \beta =100$| case, whereas Jun & Jones (1997) find teq ∼ 36tdiff for γc = 5/3. Thus, in more realistic scenarios where γc is self-consistently calculated (and varies continuously from γc = 5/3 to γc = 4/3), equilibration times will be smaller.
None the less, the long equilibration times are important to keep in mind. Before reaching steady state, shocks will have lower acceleration inefficiencies. One should be careful before grafting the result of steady-state shock calculations in many astrophysical settings (for instance, when using a shock-finding algorithm to inject CRs by hand). For example, in SNR presented in Section 3.4, the equilibration time is of order of 1 Myr, comparable to the expansion time, and the acceleration efficiency was clearly time-dependent. Other factors not present in our current simulations will affect whether the standard/high efficiency branch will appear in two-fluid galaxy formation simulations: by 1 Myr, radiative cooling will put the SNR in the snowplough phase, and various instabilities (e.g. Rayleigh–Taylor, CR acoustic instability, corrugational instability), if resolved, can disrupt the shock profile and truncate build-up of a precursor. It is important to bear in mind the use of a galaxy-scale CR diffusion coefficient in cosmological simulations, of order |$10^{28}\ \mathrm{cm}^2\, \mathrm{s}^{-1}$| or above, would have an equilibration time significantly longer than 1 Myr.
3.5.2 Numerical resolution
It is clear that our high resolution simulations are converged, since they match analytic predictions. However, it is interesting to understand the minimal resolution needed to obtain accurate acceleration efficiencies. To study numerical convergence, we repeated the setup described in 3.4 at different resolutions, and compared solutions at t = 5871 kyr. The number of grids used were: 512, 2048, 8192, 16384, 32768, 65536, 131072. Equivalently, taking the shock width at this time instance to be |${\sim}\kappa /v_1 = 3\times 10^{25}\ \mathrm{cm}^2\, \mathrm{s}^{-1}/150 \ \mathrm{km}\, \mathrm{s}^{-1} = 0.67\ \mathrm{pc}$| and a domain size of 4000 pc gives, in ascending order of resolution, the approximate number of grids nshock the shock was resolved with: 0.085 (res = 512), 0.34 (res = 2048), 1.37 (res = 8192), 2.73 (res = 16384), 5.46 (res = 32768), 10.9 (res = 65536), 21.9 (res = 131072). For nshock < 1, the shock is unresolved. One can see in Fig. 15 that the solutions converges steadily for the βISM = 2 case, whereas for the βISM = 100 case, there is an abrupt transition from the inefficient branch to the efficient branch once nshock > 5.5. We quantified this by looking at the acceleration efficiency across the forward shock at different resolutions (Fig. 16). The acceleration efficiency converges smoothly for the βISM = 2 case, while in the βISM = 100 case, there is slow change at low resolution followed by an abrupt rise at nshock ∼ 5.
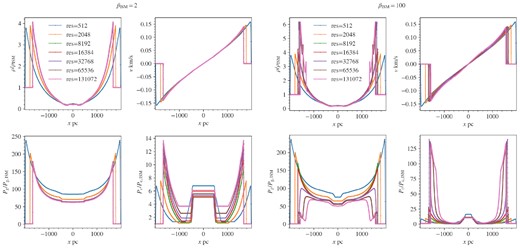
Plot of density, velocity, gas, and CR pressure at t = 5871 kyr at different resolutions for βISM = 2 (left four panels) and βISM = 100 (right four). The legend indicates the number of grids used to resolve the simulation domain. Equivalently, the approximate number of grids the shock is resolved with is: 0.085 (res = 512), 0.34 (res = 2048), 1.37 (res = 8192), 2.73 (res = 16384), 5.46 (res = 32768), 10.9 (res = 65536), 21.9 (res = 131072).
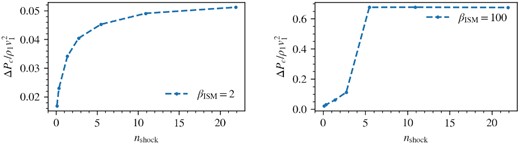
Acceleration efficiency across the forward shock as a function of nshock for βISM = 2 (left) and βISM = 100 (right) case.
Thus, the diffusion length must be resolved by ∼10 grid cells for convergence in acceleration efficiency. At a lower Mach number, and if the upstream is highly CR dominated, the precursor is smaller and somewhat lower resolution may suffice. At insufficient resolution, the acceleration efficiency at shocks is underestimated. Except perhaps for very high resolution zoom simulations, most shocks in galaxy-scale simulations will not resolve such length-scales and will thus have very low acceleration efficiencies. For this reason alone, it is likely safe to presume that the only source of CRs in such simulations are those injected by a sub-grid recipe.
3.5.3 Oblique magnetic fields
An oblique shock, where the magnetic field is no longer parallel to the shock normal, suppresses CR acceleration. This is because CR transport across the shock is suppressed. In the post-shock fluid, compression preferentially amplifies the perpendicular B-field component, so the B-fields are aligned parallel to the shock front, suppressing diffusion upstream.
Here we describe four 2D test cases involving oblique magnetic fields. The setups were as follow: We initialized a uniform 2D flow of density ρ = 1000, velocity v = 1.108, gas pressure Pg = 1, and CR pressure Pc = 1 (i.e. Q = 0.5) crashing towards the right boundary. The magnetic field was oriented at angle |$\theta =5,45\ \rm deg$| to the shock normal for plasma beta β = 1, 100. The reduced speed of light was set to c = 50 and CR diffusivity to κ∥ = 0.1 along the magnetic field and κ⊥ = 1.67 × 10−9 perpendicular to it. The domain spanned −30 < x < 0, −5 < y < 5 for the β = 1 case and −90 < x < 0, −5 < y < 5 for the β = 100 case. The whole domain was resolved with 2048 × 512 grids for β = 1 and 8192 × 512 grids for β = 100, corresponding to a precursor resolved by nshock ≈ 6, 8 grid cells, respectively. Reflecting boundary was set at the right and outflow at the left.
A summary of the oblique shock results is given in Table 1 (lower table). The magnetic field for an example is also shown in Fig. 17. Shock compression deflects the magnetic field away from the shock normal and increases its strength. Compressive amplification of magnetic field is stronger for higher obliquity as only the perpendicular component is boosted. The acceleration efficiencies of the β = 1 case are very low (|${\sim}1.1{{\ \rm per\ cent}}$| for |$\theta =5\ \rm deg$| and |${\sim}0.9{{\ \rm per\ cent}}$| for |$\theta =45\ \rm deg$|). This is inconsistent with the analytic prediction by Webb, Drury & Volk (1986; that included oblique magnetic fields and CR diffusion but no streaming), which predicted an efficiency of |${\gtrsim}50{{\ \rm per\ cent}}$|. The reduction in acceleration efficiency seen in our simulations is caused by bi-directional streaming, with the inefficient branch being picked. For simplicity we eschew repeating the analytic calculation in Section 2 including oblique magnetic fields.
The shock profile for θ = 45 deg, β = 1 at t = 60 showing the magnetic field. The arrows indicate the orientation of the field.
The difference is more marked at different obliquity for β = 100. At |$\theta =5\ \rm deg$|, the efficient/standard branch is recovered, achieving an efficiency |${\sim}81{{\ \rm per\ cent}}$|. The acceleration efficiency decreases drastically at |$\theta =45\ \rm deg$| to |${\sim}1.2{{\ \rm per\ cent}}$|. This suggests that the inefficient branch may be more extensive at high obliquity in parameter space (|$\mathcal {M},Q,\beta$|) than in the 1D case. Given that oblique shocks are the most common case, we expect the inefficient branch to appear more commonly in cosmological simulations than expected from 1D analytics and simulations.
3.5.4 Injection of thermal particles
Thus far, we only consider acceleration of pre-existing CRs, which can easily take part in diffusive shock acceleration. However, suprathermal particles in the Maxwellian tail of the plasma can also be injected into the DSA process, and contribute to the CR population. This is particularly important when the pre-existing CR population is sparse (small Q). Here, we consider a simple prescription for injection which illustrates some potential effects.
Graphically, equation (31) modifies the sonic boundary by a factor of (1 + δinj). However, δinj is not known a priori, so one must guess a value for δinj first, then iteratively, using the updated pre- and post-subshock quantities, find an improved solution until the downstream state stays the same within some tolerance (taken to be 10−4 here). A good initial guess would be δ0 = ϵλ2/2.
We inject a fixed fraction ϵ ∼ 10−3of the thermal particles into the CR population at the subshock, which is roughly the fraction of particles in a Maxwellian with λ ∼ 3 times the sound speed. This fraction is consistent with the injection parameters in (Caprioli & Spitkovsky 2014a). Fig. 18 shows a case where most of the CRs come from injection (Q = 0.01). The acceleration efficiency including thermal injection as a function of Mach number is displayed by the blue curve. The uni-directional and bi-directional solutions without injection are shown by the translucent black and red curve, respectively, for comparison. Two points are worth noting: (i) The acceleration efficiency of the bi-directional solution increases with Mach number instead of the other way around. (ii) At high Mach number the inefficient branch vanishes. For small Mach number (|$\mathcal {M} \lt 14$|) acceleration efficiency of the bi-directional solution with injection (|${\sim}1{-}2{{\ \rm per\ cent}}$|) appear roughly consistent but a few per cent lower than that found in hybrid simulations (Caprioli & Spitkovsky 2014a). Our current simulation code not yet include injection; it is left for future work. However, it will improve the realism of two-fluid shocks. We believe that most of the properties we have found (in particular, the fact that the inefficient bi-directional branch is favoured) will continue to be found in simulations with injection.
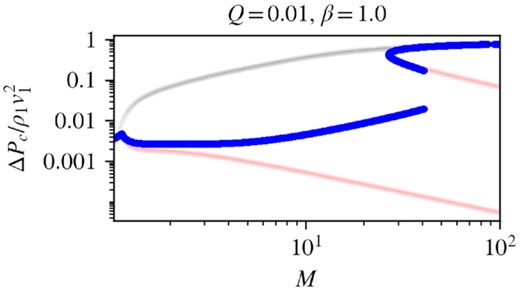
Acceleration efficiency against Mach number with injection. A fraction of 10−3 of the thermal particles is injected at the subshock. Injection is included only for the bi-directional solutions (blue curve). The acceleration efficiency without injection (for the same Q and β) is displayed here for comparison (black and red translucent curves for the uni-directional and bi-directional solutions. respectively).
4 DISCUSSION AND CONCLUSION
In this work, we studied steady-state CR-modified shocks in the two-fluid approximation, with the inclusion of both CR diffusion and streaming in the CR transport. This is a demanding test of new two-moment CR codes (Jiang & Oh 2018) that are the first to be able to handle such shocks with CR streaming; they have never been compared against analytic solutions. It also allows us to understand and quantify the effects of CR-modified shocks in galaxy formation simulations. In a two-fluid code, shocks can accelerate CRs, over and above CRs injected via a sub-grid prescription; it is important to understand their contribution quantitatively. We only consider acceleration of pre-existing CRs, although one can modify the code to include thermal injection. Our findings are as follows:
New analytic solutions: bi-directional streaming. Previous analytic solutions (Voelk et al. 1984) assumed uni-direction streaming of CRs toward the upstream. In fact, overcompression at the subshock can lead to a transient spike (similar to the Zeldovich spike in radiative shocks) that seeds bi-directional streaming. The upstream and downstream CRs stream in opposite directions, away from the subshock. We obtain analytic profiles for this new solution. Streaming leads to lower acceleration efficiency with increasing magnetic field (due to increased gas heating and reduced compression). Furthermore, the new solution has a lower acceleration efficiency compared to the standard streaming, since downstream CRs propagate away rather than diffusing back to the shock. The CR precursor is smaller and less compressible. At Mach number |$\mathcal {M} \gtrsim 15$|, the new solution bifurcates into inefficient, intermediate, and efficient acceleration efficiency solution branches (Figs 4 and 5). The inefficient branch is a hydrodynamic shock only weakly modified by CRs, with acceleration efficiencies that typically do not exceed |$10{{\ \rm per\ cent}}$|. The efficient branch is CR dominated, with typical acceleration efficiency |${\gtrsim}60{{\ \rm per\ cent}}$|, similar to the standard branch. The intermediate branch lies somewhere in between. For weaker magnetic fields (higher β), the standard and new solutions merge closer together. At β ≳ 100 essentially only the efficient branch is left.
Simulations match analytic solutions. The simulations reproduces the standard analytic solution as well as all three branches of the new solution. The predicted acceleration efficiency also agrees extremely well with analytic predictions (Fig. 9d). It is excellent news that the two-moment method can pass this demanding test, which should lay to rest concerns about solution degeneracy and numerical robustness at CR shocks (Kudoh & Hanawa 2016; Gupta et al. 2019). As long as explicit diffusion is included (and for Fermi acceleration to operate, diffusion must be present), the analytic solution does not require ad hoc closure relations. As long as the diffusion length is resolved, numerical simulations closely match analytic solutions across a wide range of parameters.
Inefficient branch favoured. Which of the various solution branches is actually realized in nature? The intermediate branch is unstable (perturbations cause the acceleration efficiency to diverge to either the inefficient or efficient branch), so it is not realized. Of the remaining two possibilities, the branch selected is dependent upon the local upstream conditions where the shock is formed. In CR-dominated shocks, only the efficient/standard branch is possible, since the compression ratio is high. However, if both branches are possible, the inefficient branch is selected, though transition to the efficient branch is possible if the upstream condition shifts to one for which only the efficient/standard branch is permissible. Once the shock selects the efficient/standard branch, it will remain there. See Fig. 11. The reason for this preference for the inefficient branch is unclear, though it is worth noting that it maximizes entropy generation at the shock (see discussion for diffusion only case in Becker & Kazanas 2001).
Assumptions of time-steady, resolved, and parallel shocks often not satisfied. These calculations focus on well-resolved, steady-state, parallel shocks. These conditions are unlikely to be true in galaxy-scale simulations, and changes to these assumptions all point in the direction of reduced CR modification of the shock and lower acceleration efficiency: (i) The equilibration time for a shock to reach its steady-state structure is tequil ∼ 1000tdiff (where tdiff is the diffusion time); higher for CR-dominated shocks with high acceleration efficiency, and somewhat smaller for shocks with lower acceleration efficiency. This is because the build-up of the CR precursor is a non-linear process which requires many diffusion times. This is often longer than shock crossing times (e.g. supernova remnants). Thus, shocks in realistic settings are not time-steady and cannot be compared directly to our results. (ii) As shown in Section 3.5.2, the precursor needs to be resolved by at least 10 grid cells for convergence. Lower resolution will lead to lower acceleration efficiency (Fig. 16). (iii) High obliquity magnetic fields will suppress formation of the CR precursor and hence acceleration efficiency, since the shock will more closely resemble a hydrodynamic shock with lower compression ratio (Table 1, lower table). (iv) If thermal injection is taken into account, the efficiency of the ‘inefficient’ branch of the bi-directional solution (|${\sim}5{-}10{{\ \rm per\ cent}}$|) is in good agreement with hybrid/PIC simulations.
In summary, in a two-fluid code, the CR acceleration efficiency of shocks in a galaxy-scale simulation is likely small (|${\ll}10{{\ \rm per\ cent}}$|) and thus the prevailing tendency to assume that they do not contribute significantly is likely reasonable. However, one must be careful to test this assumption, particularly in high resolution simulations, because the high efficiency branch converts such a large fraction (|${\sim}60{{\ \rm per\ cent}}$|) of the shock kinetic energy to CRs (e.g. see Fig 13 where the CR energy rises far above the initial value), far above that obtained by kinetic simulations. In the end, we find that in most settings a two-fluid code ‘does no harm’ at shocks and gives roughly physical reasonable solutions, despite the significant shortcomings of the fluid approach in handling a fundamentally kinetic problem, as discussed in the Introduction. The fluid approach can probably be modified (e.g. introducing thermal injection, as in Section 3.5.4, and potentially introduce a time-dependent κ and γc as the shock evolves) which further improves agreement with kinetic results. In the end, however, the most pragmatic approach for galaxy-scale simulations is to simply leave the code as is, effectively ignoring CR injection at shocks. If the CR acceleration at shocks is a critical application, then one can simply apply a shock-finding algorithm and inject CRs by hand (e.g. Pinzke, Oh & Pfrommer 2013; Pfrommer et al. 2017), but carefully taking the time-dependence of shock equilibration into account.
ACKNOWLEDGEMENTS
We thank Omer Blaes and Eliot Quataert for helpful conversations. We acknowledge National Science Foundation (NSF) grant AST-1911198 and Extreme Science and Engineering Discovery Environment (XSEDE) grant TG-AST180036 for support. The Center for Computational Astrophysics at the Flatiron Institute is supported by the Simons Foundation.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
The calculation of the diffusion coefficient itself requires calculating wave growth by the resonant streaming instability (Kulsrud & Pearce 1969), the current-driven non-resonant Bell instability (Bell 2004), as well as associated damping mechanisms. Our current study essentially assumes that waves are strongly damped, although kinetic simulations show that waves can be amplified to the non-linear regime (Caprioli & Spitkovsky 2014b), which facilitates CR scattering.
It is possible to include streaming by modeling it as diffusion coefficient using a time-implicit scheme (Dubois et al. 2019).
Note that this differs from simply summing the gas and CR pressure to get the total pressure in an adiabatic medium, because energy is transferred between the gas and CRs.
The reduced speed of light |$\tilde{c}$| is a free simulation parameter governing the CR free stream speed in the decoupled limit. It should be much greater than other characteristic speeds. See Jiang & Oh (2018) for a detailed discussion.



