HL Dra: an active Algol-like binary system with a pulsating component star and a cool third body

ABSTRACT

HL Draconis (HL Dra) is an oscillating eclipsing binary with an orbital period of 0.944276 d. By analysing the light curves observed with the Transiting Exoplanet Survey Satellite (TESS), it has been detected that HL Dra is an Algol-like binary system with a mass ratio of 0.361, where the radius filling factor (=r/R_L) of the primary and secondary component is |$87\, {{\ \rm per\ cent}}$| and |$98\, {{\ \rm per\ cent}}$|⁠, respectively. The secondary component is almost filling its critical Roche lobe, but not entirely. The absolute parameters of the component are estimated in this paper. Both the variable O’Connell effect and the existence of superflares indicate that the secondary should have strong magnetic activities. It is discovered that the O − C curve shows a sinusoidal variation with a period of 129.88 yr. This cyclic change might be caused by the effects of the light travel time as a result of the presence of a cool red dwarf third body. The correlations between the changes of the O − C diagrams and the variable O’Connell effect during TESS observations might be caused by the magnetic activity of the secondary (i.e. the Applegate mechanism). After removal of the binary model, a total of 252 pulsation frequencies are detected from the high-precision photometric data of TESS, including 28 multiplets of tidally split frequencies. We identify two radial modes, 21 non-radial p-modes and three non-radial f-modes from the possible independent frequencies. All of these features reveal that HL Dra is a very interesting system for further investigations of binary formation and evolution, and for tidal interactions on stellar pulsations and on magnetic activities.

stars: activity, stars: binaries: close, stars: binaries: eclipsing, stars: individual: HL Draconis, stars: variables: Scuti

1 INTRODUCTION

Binary systems are the most reliable objects to derive absolute stellar parameters and to create stellar evolutionary models. If a pulsator is a component of a binary system, we can use the analysis method of binary systems (of stars) to study it. Oscillating eclipsing binaries of Algol type (oEAs; Mkrtichian et al. 2002) are Algol-type binary systems in which the primary component shows δ Scuti-like oscillations. Its primary component is generally an A-F type main-sequence star, and its secondary component is an F-G-K type giant or subgiant star in the state of filling, or almost filling, its Roche lobe. Mass transfer plays an important role in the evolution of Algol-type systems because they have experienced rapid and large mass exchange, which leads to the inversion of the mass ratio (i.e. the former primary component has become the present secondary component; Pustylnik 1998). The pulsating stars in binary stars formed after mass transfer might carry a lot of evidence of binary interaction, which would allow us to further improve the theory of stellar structure and evolution (Chen et al. 2020). The late-type secondary component is likely to be accompanied by strong magnetic activity. Therefore, it is very interesting and necessary to make a detailed analysis of this kind of target in combination with these phenomena. The continuous and unbroken high-precision time series photometric data of Kepler and the Transiting Exoplanet Survey Satellite (TESS) provide a good opportunity to study this kind of object.

δ Sct-type pulsating stars are located inside the bottom of the classical Cepheid instability strip intersecting with the main sequence. The transition zone from convective envelopes to radiative envelopes for intermediate-mass A-F type stars is also in this strip. δ Sct-type pulsating stars generally have a surface effective temperature range from 6700 to 8900 K, and a mass range from 1.5 to 2.5 |$\, \mathrm{M}_{\odot }$|⁠. Typically, they pulsate in radial and non-radial p-modes (with pressure as the restoring force) and g-modes (with buoyancy as the restoring force) with a period range of 0.02–0.3 d (e.g. Aerts, Christensen-Dalsgaard & Kurtz 2010; Bowman & Kurtz 2018). Because of the complex pulsating feature and the key evolution stages of δ Sct stars, they have become important objects in the study of stellar structure.

HL Draconis (HL Dra) was discovered as a β Lyrae (EB-type) eclipsing binary star with an A5-type primary component by the Hipparcos survey (ESA 1997), and its linear ephemeris was derived as

$$\begin{eqnarray*} {\rm HJD}_{\rm Min.I}=244\,8500.189+0{^{\rm d}_{.}}944276\, E. \end{eqnarray*}$$

(1)

From 2004 to 2005, Pribulla et al. (2006) obtained the radial velocities of the primary component and determined its spectral type as A6 V. Liakos et al. (2012) observed the multicolour light curves of HL Dra. Their analysis shows that it is an oscillating eclipsing binary of an Algol-type system (Mkrtichian et al. 2002) with a prominent pulsation frequency 26.91 d⁻¹. We check the changes of the orbital period of HL Dra using the times of minima at the O − C gateway¹ and we find a downward parabolic variation, which usually means that the orbital period is decreasing. However, the orbital period of such an Algol-type binary system should normally be increasing or constant, because the secondary component might be in the state of overflowing its Roche lobe and transferring mass to the primary component, or just filling and stopping mass transfer (Kopal 1955). To investigate the reason for this periodic change and other physical properties, we collected available survey data to analyse HL Dra.

2 CHANGES OF THE ORBITAL PERIOD AND THE PHOTOMETRIC LIGHT CURVE OF HL DRA

The TESS space mission (Ricker et al. 2015) observed the HL Dra light curves of 13 quarters, about 352 d (above 200 000 data points), from TJD 1683 to 2035 (hereafter TJD = BJD 245 7000.0) with an interval of 120 s. We downloaded the simple aperture photometry data from the Mikulski Archive for Space Telescopes (MAST) data base. We used the following two steps to process the original light curve: (i) calculate the flux to magnitude, and (ii) subtract the average value of each quarter to make them at the same level. The detrended TESS light curve for HL Dra is displayed in Fig. 1, where the light curve is almost at the same level. The light curve converted to phase is shown in Fig. 2. As can be seen in this figure, the light curve is asymmetric, where the light maximum near phase 0.25 (hereafter Max I) is brighter than near phase 0.75 (hereafter Max II), and an optical flare can be seen near phase 0.2. The O’Connell effect refers to the phenomenon that Max I is not equal to Max II (Milone 1969), which is very common and complex in the light curves of eclipsing binaries. This phenomenon can be caused by many mechanisms, including any mode that can cause local brightness change of the surface of the binary components, such as flares, spots, mass transfer, etc.

Figure 1.

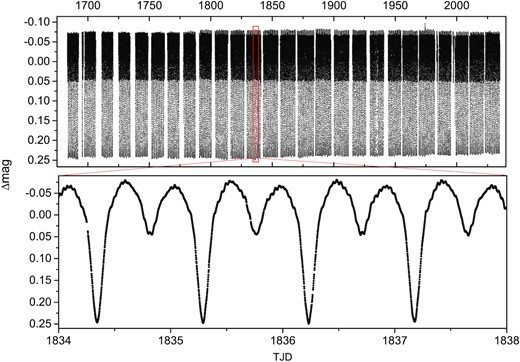
The detrended TESS light curve for HL Dra (TJD = BJD 245 7000.0).

Open in new tab Download slide

Figure 2.

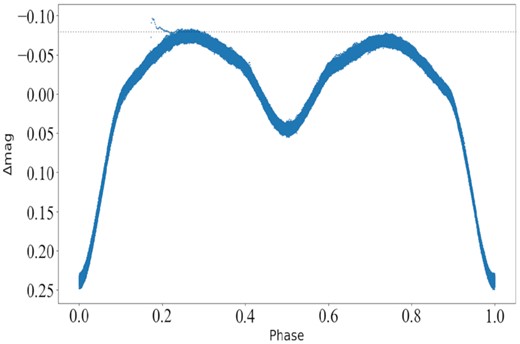
Light curve of HL Dra. The phase was calculated by using the period 0.944276 d and the time of light minimum 245 8686.09270.

Open in new tab Download slide

To obtain long-time data to analyse the changes of the orbital period, we also collected the digitized photographic data from Digital Access to a Sky Century @ Harvard (DASCH; Grindlay et al. 2012; Grindlay & Griffin 2012). There are two ways to obtain the minimum time of the light curve: the first is to use parabola fitting (Method 1); the second is to construct a phase diagram over more than one period (such as 5 d) and to use parabola fitting (Method 2). As there are few data points, only Method 2 can be used to obtain the minimum of DASCH data. For TESS data, we use both methods to calculate the minimum time. As shown in Fig. 3, there is not much difference between the results of the two methods, but Method 2 shows less scattered data, which might be because the average light curve weakens the effect of pulsation. We use Method 2 to obtain 13 primary eclipsing times and 12 secondary eclipsing times from DASCH data, and 61 primary eclipsing times and 48 secondary eclipsing times from TESS data. Together with 12 light minima at the O − C gateway obtained by Perryman et al. (1997), Pribulla et al. (2006), Liakos & Niarchos (2010), Arena et al. (2011), Banfi et al. (2012) and Bahar et al. (2017), a total of 147 light minima are given as Supporting Information with the electronic version of the paper and a sample of these light minima are given in Table 1.

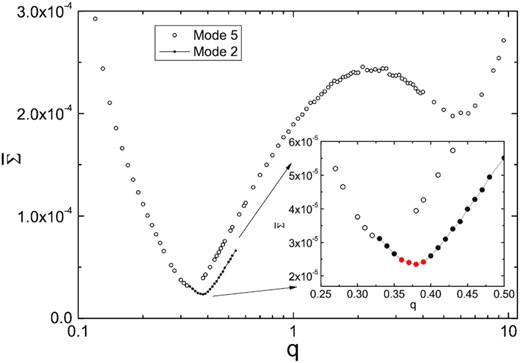
$The relations between q and the mean weighted residuals $\overline{\Sigma }$ for different modes. Mode 2 is for detached binaries, and mode 5 is for semidetached binaries with star 2 accurately filling its limiting lobe.$

Figure 6.

The relations between q and the mean weighted residuals |$\overline{\Sigma }$| for different modes. Mode 2 is for detached binaries, and mode 5 is for semidetached binaries with star 2 accurately filling its limiting lobe.

Open in new tab Download slide

Figure 7.

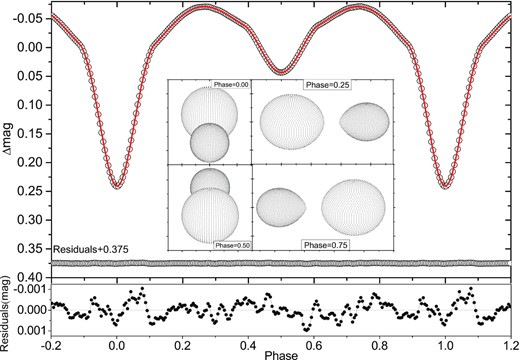
The diagram of basic solutions for HL Dra. Top panel: the average light curve (black open circles) and the theoretical fitting light curves (red solid line), and the theoretical geometrical structure. Bottom panel: the enlarged view of residuals for the average light curve.

Open in new tab Download slide

Figure 14.

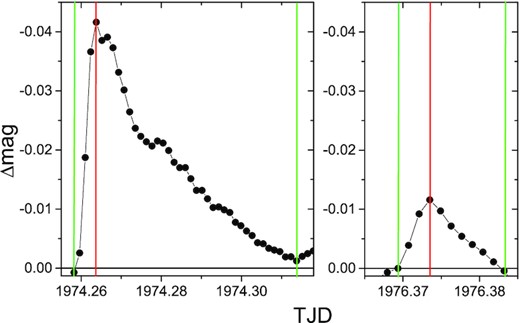
The optical flares of HL Dra after subtracting the binary brightness changes. The solid green lines indicate the start and end of the flares, the solid red line indicates the maximum brightness and the solid black line indicates the quiescent brightness.

Open in new tab Download slide

Table 1.

Open in new tab

Eclipse times for HL Dra. This is a sample of the full table, which is available at MNRAS online.

Eclipse-times(HJD)	Error(days)	E	O-C(days)	Eclipse	Observer	References
2416391.01759	0.01011	-34004	-0.01031	P	DASCH	This papar
2418396.65506	0.00951	-31880	-0.01506	P	DASCH	This papar
2420119.00531	0.00801	-30056	-0.02424	P	DASCH	This papar
2421337.12500	0.00982	-28766	-0.02058	P	DASCH	This papar

Eclipse-times(HJD)	Error(days)	E	O-C(days)	Eclipse	Observer	References
2416391.01759	0.01011	-34004	-0.01031	P	DASCH	This papar
2418396.65506	0.00951	-31880	-0.01506	P	DASCH	This papar
2420119.00531	0.00801	-30056	-0.02424	P	DASCH	This papar
2421337.12500	0.00982	-28766	-0.02058	P	DASCH	This papar

Table 1.

Open in new tab

Eclipse times for HL Dra. This is a sample of the full table, which is available at MNRAS online.

Eclipse-times(HJD)	Error(days)	E	O-C(days)	Eclipse	Observer	References
2416391.01759	0.01011	-34004	-0.01031	P	DASCH	This papar
2418396.65506	0.00951	-31880	-0.01506	P	DASCH	This papar
2420119.00531	0.00801	-30056	-0.02424	P	DASCH	This papar
2421337.12500	0.00982	-28766	-0.02058	P	DASCH	This papar

Eclipse-times(HJD)	Error(days)	E	O-C(days)	Eclipse	Observer	References
2416391.01759	0.01011	-34004	-0.01031	P	DASCH	This papar
2418396.65506	0.00951	-31880	-0.01506	P	DASCH	This papar
2420119.00531	0.00801	-30056	-0.02424	P	DASCH	This papar
2421337.12500	0.00982	-28766	-0.02058	P	DASCH	This papar

Using equation (1), the O − C values of the eclipsing times are calculated; these are shown in the upper panel of Fig. 4. Considering the large error and scatter, the secondary eclipsing times are not used in the analysis process. In this figure, the O − C curve shows a cyclic change instead of the downward parabolic change when only the O − C gateway data from E = 0–9541 (about 9000 d) is used. Using the least-squares method, the fitting equation is derived as

$$\begin{eqnarray*} {\rm O} - {\rm C}\, ({\rm d}) &=&-0.01509(1)+0.0196(1)\times \sin[0.000125(1)\nonumber \\ &&\times E +290.08(1)]. \end{eqnarray*}$$

(2)

The sine term of equation (2) is a cyclic variation with an amplitude of 0.0196 d and a period of 129.88 yr. The residual fitted by equation (2) is displayed in the lower panel of Fig. 4.

Figure 3.

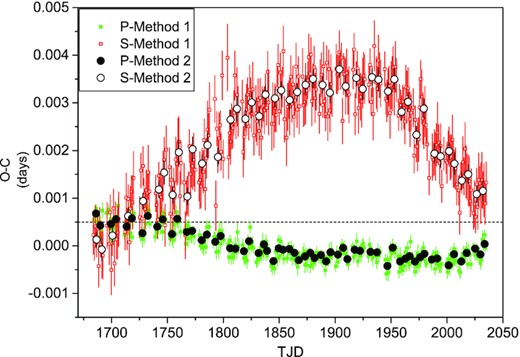
The O − C curves during TESS observations. The O − C curves have removed the sinusoidal variation with a period of 129.88 yr by using equation (2). Methods 1 and 2 are described in the text.

Open in new tab Download slide

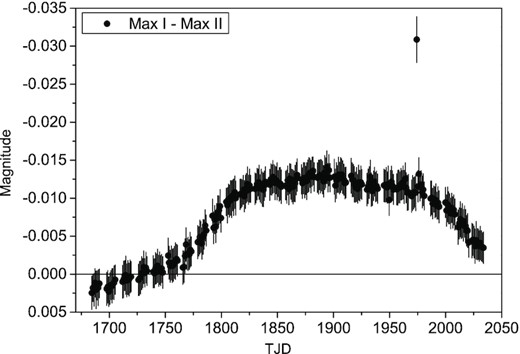
The O − C curves during TESS observations are shown in Fig. 3, and we find that the curves of primary and secondary eclipsing minima exhibit opposite trends. To study whether the variation of the O − C curves during TESS observations is related to the O’Connell effect, we fitted the light curve of each period using the tenth-order Fourier series of the orbital frequency and we calculated the magnitude of Max I and Max II using the scipy.optimize package of Python 3.6. The variation of Max I minus Max II is displayed in Fig. 5. There are many parallels between Figs 3 and 5. For example, the period change in Figs 3 and 5 may be almost the same; at about TJD 1725, both the O − C curves of the primary and secondary eclipsing minima are crossing each other, and Max I is equal to Max II. Therefore, we suggest that there is a correlation between the O − C curve and the O’Connell effect, such as in KIC 06852488 (Shi et al. 2021) and KIC 6048106 (Samadi Ghadim, Lampens & Jassur 2018b).

Figure 4.

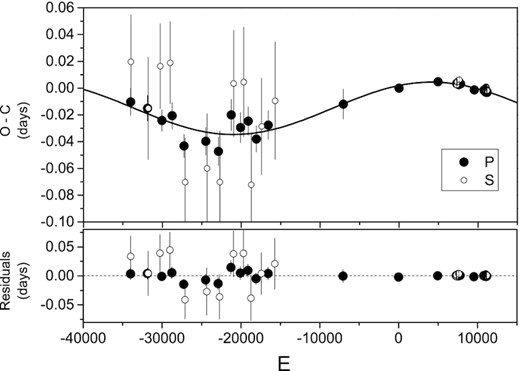
The O − C diagrams for HL Dra. The solid lines refer to the fitting curve of sine.

Open in new tab Download slide

Figure 5.

The variation of Max I minus Max II during TESS observations.

Open in new tab Download slide

3 PHOTOMETRIC SOLUTIONS AND ABSOLUTE PARAMETERS FOR HL DRA

As can be seen from Fig. 5, the value of Max I equals Max II near TJD 1725, which means that the light curves observed by TESS near TJD 1725 are almost symmetrical and with a minimum of the O’Connell effect. So, we select the data of the Sector 15, which is near TJD 1725 about 26 d from TJD 1711 to 1737, to analyse the basic solution without a spot. To eliminate the brightness change caused by a pulsation, we create an average light curve, including the calculation of a phase diagram such as Fig. 2 and the reduction of the data points from more than 18 000 points to 200 points by averaging (i.e. these points in the 0.005 phase are averaged as one point). Then, the Wilson–Devinney (W–D) program (Wilson & Devinney 1971; Wilson 1979, 1990, 2012; Van Hamme & Wilson 2007) is used for light-curve analysis.

The spectral type of the primary component of HL Dra was determined as A5 by ESA (1997), and then determined as A6 V by Pribulla et al. (2006). We assume that the surface effective temperature of the primary star is 7961 K, which is obtained by Data Release 2 (DR2) of Gaia (Prusti et al. 2016; Brown et al. 2018) and is consistent with the spectral type A6 V using the relations of Cox (2000). Considering that the primary component is an early-type star, its bolometric albedo A₁ is assumed to be 1.00 (Ruciński 1969), and its gravity-darkening coefficient g₁ is assumed to be 1.00 (Lucy 1967). According to the iterative temperature below 5000 K, the secondary component is a late-type star and its gravity-darkening coefficient g₂ is set to 0.32 (Lucy 1967). The limb darkening is set according to the law of logarithm to obtain the bolometric and bandpass limb-darkening coefficients. If there is no special description, the grid fineness for micro-integration on each surface element NF is set to be more precise 90 × 90 by default. Finally, the convergence solution is obtained after continuous iteration and adjusting the free parameters that include the mass ratio q (M₂/M₁), the orbital inclination i, the luminosity L₁ of star 1, the dimensionless potential Ω₁ of star 1, the bolometric albedo A₂ of star 2, the temperature T₂ of star 2, and the dimensionless potential Ω₂ of star 2 for mode 2 (Ω₂ is not a free parameter for mode 5).

According to experience, mode 5 (semidetached binaries with star 2 filling its limiting lobe) or mode 2 (detached binaries, because star 2 might just be close to filling its limiting lobe) should be suitable for HL Dra. For the critical parameter q, we use mode 5 to search for a series of parameters from 0.1 to 10 and we find that the minimum residual value should be between 0.3 and 0.4, as shown in Fig. 6. Near the minimum residua, several data points of q are not convergent, but when we set the grid fineness NF to be more crude 30 × 30 and q is a free parameter, we obtain a convergent result at q = 0.366. This means that mode 5 may not be suitable, but the actual results are very close. We also use mode 2 to search for the q value and we find that mode 2 can have a smaller residual than mode 5. Then, by setting q as a free parameter, the convergence result is obtained at q = 0.361. The final solutions of mode 2 and mode 5 are listed in Table 2. On the whole, the solution of mode 2 is more reliable. The related graph of the result is shown in the top panel of Fig. 7, which includes the average and the residual light curve (the black open circles), the fitting curves (the red solid line) and the geometrical structure. After enlarging the residual curve (in the bottom panel of Fig. 7), we find some changes, which seem to be due to the pulsating component that has not been completely eliminated. The volume filling factor (= V_star/V_L) of the primary and secondary components is |$65.4{{\ \rm per\ cent}}$| and |$94.2{{\ \rm per\ cent}}$|⁠, which corresponds to a radius filling factor (= r/R_L) of about |$87\, {{\ \rm per\ cent}}$| and |$98\, {{\ \rm per\ cent}}$|⁠, respectively. The secondary component is almost filling its critical Roche lobe, indicating that it is an Algol-like system. The radius filling factors of both components are more than 80 per cent and the orbital period is less than 1 d, so its components should be in a tidally locked and synchronous rotation state. We try to search for the orbital ecccentricity e and the dimensionless rotation parameters F₁ and F₂ of stars 1 and 2 using the W–D code, and the results support our hypothesis that they rotate synchronously in circular orbits.

Table 2.

Open in new tab

Photometric solutions of HL Dra using the W–D code. The numbers in parentheses are the errors on the last two bits of the data. The units of most parameters are dimensionless, except those already mentioned.

Parameters	Mode 5	Mode 2
NF^a	30 × 30 (assumed)	90 × 90 (assumed)
\|$g_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
\|$g_{2}\, ^a$\|	0.32 (assumed)	0.32 (assumed)
\|$A_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
A₂	0.596 (6)	0.587 (7)
\|$T_{1}\, ^a$\| (K)	7961 (assumed)	7961 (assumed)
i (°)	66.663 (29)	66.901 (43)
q(M₂/M₁)	0.3664 (19)	0.3610 (21)
T₂/T₁	0.58799 (68)	0.58410 (63)
L₁/(L₁ + L₂)_TESS	0.918628 (54)	0.926522 (77)
Ω₁	2.9424 (49)	2.8983 (62)
\|$\Omega _{2}\, ^b$\|	2.60882	2.6166 (46)
\|$r_{1}\,{\rm (pole)}\,^c$\|	0.38466 (48)	0.39049 (67)
\|$r_{2}\,{\rm (pole)}\,^c$\|	0.27583 (38)	0.2709 (19)
\|$r_{1}\,{\rm (point)}\,^c$\|	0.42886 (62)	0.43814 (95)
\|$r_{2}\,{\rm (point)}\,^c$\|	0.39835 (38)	0.355 (12)
\|$r_{1}\,{\rm (side)}\,^c$\|	0.40135 (55)	0.40824 (78)
\|$r_{2}\,{\rm (side)}\,^c$\|	0.28742 (41)	0.2817 (23)
\|$r_{1}\,{\rm (back)}\,^c$\|	0.41432 (56)	0.42196 (82)
\|$r_{2}\,{\rm (back)}\,^c$\|	0.32014 (41)	0.3119 (38)
\|$f_{1}\, ^d$\|	62.72 (23)%	65.37 (30)%
\|$f_{2}\, ^d$\|	100.00 (23)%	94.2 (2.2)%

Parameters	Mode 5	Mode 2
NF^a	30 × 30 (assumed)	90 × 90 (assumed)
\|$g_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
\|$g_{2}\, ^a$\|	0.32 (assumed)	0.32 (assumed)
\|$A_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
A₂	0.596 (6)	0.587 (7)
\|$T_{1}\, ^a$\| (K)	7961 (assumed)	7961 (assumed)
i (°)	66.663 (29)	66.901 (43)
q(M₂/M₁)	0.3664 (19)	0.3610 (21)
T₂/T₁	0.58799 (68)	0.58410 (63)
L₁/(L₁ + L₂)_TESS	0.918628 (54)	0.926522 (77)
Ω₁	2.9424 (49)	2.8983 (62)
\|$\Omega _{2}\, ^b$\|	2.60882	2.6166 (46)
\|$r_{1}\,{\rm (pole)}\,^c$\|	0.38466 (48)	0.39049 (67)
\|$r_{2}\,{\rm (pole)}\,^c$\|	0.27583 (38)	0.2709 (19)
\|$r_{1}\,{\rm (point)}\,^c$\|	0.42886 (62)	0.43814 (95)
\|$r_{2}\,{\rm (point)}\,^c$\|	0.39835 (38)	0.355 (12)
\|$r_{1}\,{\rm (side)}\,^c$\|	0.40135 (55)	0.40824 (78)
\|$r_{2}\,{\rm (side)}\,^c$\|	0.28742 (41)	0.2817 (23)
\|$r_{1}\,{\rm (back)}\,^c$\|	0.41432 (56)	0.42196 (82)
\|$r_{2}\,{\rm (back)}\,^c$\|	0.32014 (41)	0.3119 (38)
\|$f_{1}\, ^d$\|	62.72 (23)%	65.37 (30)%
\|$f_{2}\, ^d$\|	100.00 (23)%	94.2 (2.2)%

^aThese are obtained by the method described in Section 3.

^bΩ₂ is a free parameter for mode 2, not for mode 5.

^cIn units of semimajor axis.

^dThe ratio of star volume to Roche lobe volume (= V_star/V_L) .

Table 2.

Open in new tab

Parameters	Mode 5	Mode 2
NF^a	30 × 30 (assumed)	90 × 90 (assumed)
\|$g_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
\|$g_{2}\, ^a$\|	0.32 (assumed)	0.32 (assumed)
\|$A_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
A₂	0.596 (6)	0.587 (7)
\|$T_{1}\, ^a$\| (K)	7961 (assumed)	7961 (assumed)
i (°)	66.663 (29)	66.901 (43)
q(M₂/M₁)	0.3664 (19)	0.3610 (21)
T₂/T₁	0.58799 (68)	0.58410 (63)
L₁/(L₁ + L₂)_TESS	0.918628 (54)	0.926522 (77)
Ω₁	2.9424 (49)	2.8983 (62)
\|$\Omega _{2}\, ^b$\|	2.60882	2.6166 (46)
\|$r_{1}\,{\rm (pole)}\,^c$\|	0.38466 (48)	0.39049 (67)
\|$r_{2}\,{\rm (pole)}\,^c$\|	0.27583 (38)	0.2709 (19)
\|$r_{1}\,{\rm (point)}\,^c$\|	0.42886 (62)	0.43814 (95)
\|$r_{2}\,{\rm (point)}\,^c$\|	0.39835 (38)	0.355 (12)
\|$r_{1}\,{\rm (side)}\,^c$\|	0.40135 (55)	0.40824 (78)
\|$r_{2}\,{\rm (side)}\,^c$\|	0.28742 (41)	0.2817 (23)
\|$r_{1}\,{\rm (back)}\,^c$\|	0.41432 (56)	0.42196 (82)
\|$r_{2}\,{\rm (back)}\,^c$\|	0.32014 (41)	0.3119 (38)
\|$f_{1}\, ^d$\|	62.72 (23)%	65.37 (30)%
\|$f_{2}\, ^d$\|	100.00 (23)%	94.2 (2.2)%

Parameters	Mode 5	Mode 2
NF^a	30 × 30 (assumed)	90 × 90 (assumed)
\|$g_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
\|$g_{2}\, ^a$\|	0.32 (assumed)	0.32 (assumed)
\|$A_{1}\, ^a$\|	1.00 (assumed)	1.00 (assumed)
A₂	0.596 (6)	0.587 (7)
\|$T_{1}\, ^a$\| (K)	7961 (assumed)	7961 (assumed)
i (°)	66.663 (29)	66.901 (43)
q(M₂/M₁)	0.3664 (19)	0.3610 (21)
T₂/T₁	0.58799 (68)	0.58410 (63)
L₁/(L₁ + L₂)_TESS	0.918628 (54)	0.926522 (77)
Ω₁	2.9424 (49)	2.8983 (62)
\|$\Omega _{2}\, ^b$\|	2.60882	2.6166 (46)
\|$r_{1}\,{\rm (pole)}\,^c$\|	0.38466 (48)	0.39049 (67)
\|$r_{2}\,{\rm (pole)}\,^c$\|	0.27583 (38)	0.2709 (19)
\|$r_{1}\,{\rm (point)}\,^c$\|	0.42886 (62)	0.43814 (95)
\|$r_{2}\,{\rm (point)}\,^c$\|	0.39835 (38)	0.355 (12)
\|$r_{1}\,{\rm (side)}\,^c$\|	0.40135 (55)	0.40824 (78)
\|$r_{2}\,{\rm (side)}\,^c$\|	0.28742 (41)	0.2817 (23)
\|$r_{1}\,{\rm (back)}\,^c$\|	0.41432 (56)	0.42196 (82)
\|$r_{2}\,{\rm (back)}\,^c$\|	0.32014 (41)	0.3119 (38)
\|$f_{1}\, ^d$\|	62.72 (23)%	65.37 (30)%
\|$f_{2}\, ^d$\|	100.00 (23)%	94.2 (2.2)%

^aThese are obtained by the method described in Section 3.

^bΩ₂ is a free parameter for mode 2, not for mode 5.

^cIn units of semimajor axis.

^dThe ratio of star volume to Roche lobe volume (= V_star/V_L) .

According to our photometric solution and the parameters of single-lined binaries obtained by Pribulla et al. (2006), the mass of the primary component is calculated using (e.g. Hilditch 2001)

$$\begin{eqnarray*} f(m)&=&M_2^{3}\sin^{3}i/(M_1+M_2)^{2}\nonumber \\ &=&(1.0361\times {}10^{-7})(1-e^{2})^{3/2}K_1^{3}P \, \mathrm{M}_{\odot }, \end{eqnarray*}$$

(3)

where the mass of the secondary component M₂ = q × M₁ = 0.3610(± 0.0021) × M₁, the orbital inclination i = 66|${_{.}^{\circ}}$|901 (±0|${_{.}^{\circ}}$|043), the eccentricity e = 0, the semi-amplitude K₁ = 81.04 (±0.60) (Pribulla et al. 2006) and P = 0.944276 d (the upper limit of the error is 0.00001 d). The masses of the primary and secondary components are calculated as |$M_1 = 2.63(\pm 0.06)\, \mathrm{M}_{\odot }$| and |$M_2 = 0.95(\pm 0.02)\, \mathrm{M}_{\odot }$|⁠. According to Kepler’s third law and previous results, the semimajor axis a is estimated as |$6.20(\pm 0.05)\, \mathrm{R}_{\odot }$| (⁠|$a_{1} = 1.65\,(\pm 0.01)\, \mathrm{R}_{\odot }, a_{2} = 4.55\,(\pm 0.04)\, \mathrm{R}_{\odot }$|⁠). Setting the value of semimajor axis in the W–D program, we can obtain the absolute bolometric magnitude |$M_{\rm bol_{1}} = 1.34\,(\pm 0.02)$| mag and |$M_{\rm bol_{2}} = 4.46\,(\pm 0.02)$| mag, and the mean radius |$R_{1} = 2.52\,(\pm 0.02)\, \mathrm{R}_{\odot }$| and |$R_{2} = 1.79\,(\pm 0.02)\, \mathrm{R}_{\odot }$|⁠. The visual magnitude in the V band m_V can be estimated with (e.g. Chen et al. 2018)

$$\begin{eqnarray*} \log (L/{\rm L}_{\odot })=0.4\times {(4.74-M_{\rm bol})} , \end{eqnarray*}$$

(4)

$$\begin{eqnarray*} M_{V}=M_{\rm bol}-BC \end{eqnarray*}$$

(5)

and

$$\begin{eqnarray*} m_{V}=M_{V}+5\times {\log (1000/\pi)}-5+A_{V}, \end{eqnarray*}$$

(6)

where the parallax π = 6.4408 (±0.0305) mas (Prusti et al. 2016; Brown et al. 2018), the interstellar extinction A_V ≈ 0, and BC = −0.01 (Bessell, Castelli & Plez 1998). The total luminosity is estimated as |$L = L_{1}+L_{2} = 22.91\,(\pm 0.42) \, \mathrm{L}_{\odot } + 1.29\,(\pm 0.03) \, \mathrm{L}_{\odot }$| using equation (4). We check the photometric data in the V band from the Kamogata/Kiso/Kyoto Wide-field Survey (KWS)² using maehara/VSdata.py, and we find that the light maximum of HL Dra is near 7.23 mag. Considering the influence of pulsation and observation error, it is very close to our calculation of m_V = 7.25 (±0.02) mag, which means that the photometric solution and the subsequent calculation are reliable and reasonable.

4 PULSATION ANALYSIS

To analyse the pulsational characteristics of HL Dra, we subtract the tenth-order Fourier series fitting of the orbital frequency (i.e. the multifrequency harmonic model of the orbital frequency; see, e.g. Southworth, Bowman & Pavlovski 2021), from the light curve of each quarter. An example light curve is shown in Fig. 8. We analyse the frequency of the residual light curve (hereafter, the pulsation light curve) using the period04 software (Lenz & Breger 2005), which is based on classical Fourier analysis. The amplitude spectra for the original light curve and the pulsation light curve are displayed in the top and middle panels of Fig. 9, which show that the multifrequency harmonic model of the orbital frequency just removes the orbital harmonics less than or equal to ten times the orbital frequency.

Figure 8.

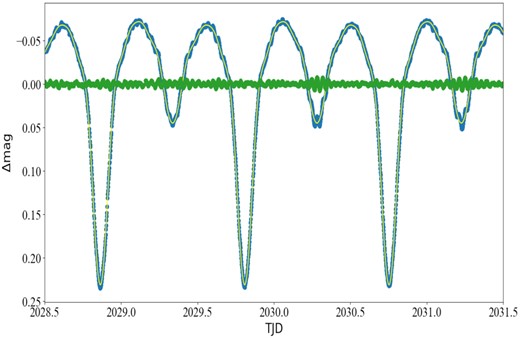
Example light curves of the tenth-order Fourier series fitting of the orbital frequency. The solid blue circles refer to the observation light curve. The yellow solid line represents the fitting light curve. The solid green circles refer to the fitting residuals.

Open in new tab Download slide

Figure 9.

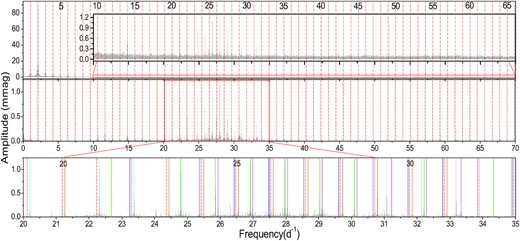
The amplitude spectra of the light curve for HL Dra. Top panel: the original light curve. Middle panel: the light curve minus the tenth-order Fourier series fitting. Bottom panel: same as the middle panel, but for a different view. The red dotted lines represent the harmonics of the orbital frequency. The coloured solid lines represent the six highest amplitude multiplets.

Open in new tab Download slide

Using the period04 software, the signal-to-noise ratio (S/N) calculations are based on the residuals at the original and a box size of 1 d⁻¹. According to Loumos & Deeming (1978) and Lee, Hong & Kristiansen (2019), the Nyquist frequency and the frequency resolutions are Nyq = 359.1 d⁻¹ and δf = 1.5/ΔT ≈ 0.0043 d⁻¹, respectively, where ΔT is the time range of observations. We extract and prewhiten the frequency in the range of 0−70 d⁻¹ because no more than 70 d⁻¹ frequencies are detected.

The overall and detailed amplitude spectra of the pulsation light curve are shown in the middle and bottom panels of Fig. 9. We extracted 255 significant frequencies that have already reached the maximum number allowed by the software period04. Excluding three frequencies with S/N lower than 4 (Breger et al. 1993), these prominent frequencies are listed in Table 3, where the errors of frequency, amplitude and phase are calculated following Montgomery & O’Donoghue (1999) and are listed in parentheses. A frequency is considered to be a combination frequency if the amplitudes of the two parent frequencies are greater than that of the presumed combination frequency, and if the difference between the detected and predicted frequency is smaller than δf. We find that many pulsating frequencies are spaced as the multiplets by the orbital frequency (f0 = 1.0590124 d⁻¹). This phenomenon has also been reported in other recent studies, such as studies of KIC 9851944 (Guo et al. 2016) and RS Cha (Steindl, Zwintz & Bowman 2021).

Table 3.

Open in new tab

The pulsating frequency for HL Dra. The numbers in parentheses are the errors on the last bit of the data. The capital letters from A to Z and A1, B1in parentheses represent 28 multiplets. An asterisk indicates that the AMP-PH diagram trend of this frequency is different from the same multiplet. Here, f0 is the orbital frequency.

	Frequency	Amplitude	Phase	Combination	S/N		Frequency	Amplitude	Phase	Combination	S/N
	(d⁻¹)	(mmag)	(rad/2π)				(d⁻¹)	(mmag)	(rad/2π)
f1	27.974241(3)	1.203(2)	0.1837(3)	(A)	235.3	f117	13.76714(5)	0.063(2)	0.580(6)	13f0	17.5
f4	22.316723(4)	0.906(2)	0.6843(4)	(B)	224.8	f77	26.16552(4)	0.081(2)	0.162(4)	(B1)	17.0
f7	14.826233(6)	0.551(2)	0.8360(6)	14f0	161.2	f56	32.64831(3)	0.109(2)	0.149(3)	(P)	16.3
f5	29.107404(4)	0.868(2)	0.4022(4)	(C)	138.0	f70	30.05512(4)	0.097(2)	0.363(4)	(S)	16.2
f13	16.944260(9)	0.381(2)	0.6427(9)	16f0	110.5	f64	33.28395(3)	0.100(2)	0.544(3)	(R)	14.9
f20	67.78847(1)	0.263(2)	0.417(1)	(H)	107.2	f76	29.65243(4)	0.086(2)	0.028(4)	28f0	14.2
f10	27.484214(7)	0.490(2)	0.6844(7)	(E)	95.4	f193	40.24269(8)	0.041(2)	0.809(8)	38f0	13.1
f8	30.794131(6)	0.530(2)	0.0346(7)	(D)	85.9	f127	24.75387(6)	0.059(2)	0.803(6)	(U)	12.9
f16	12.70816(1)	0.323(2)	0.610(1)	12f0	84.6	f234	64.0604(1)	0.033(2)	0.97(1)		11.7
f11	31.073961(7)	0.466(2)	0.7479(7)	(F)	75.5	f162	22.23896(7)	0.047(2)	0.885(7)	21f0	11.7
f22	21.18030(1)	0.229(2)	0.779(2)	20f0	67.4	f216	44.4788(1)	0.036(2)	0.89(1)	42f0	10.1
f18	26.30896(1)	0.301(2)	0.895(1)	(G)	62.8	f123	33.88855(6)	0.060(2)	0.964(6)	32f0	9.5
f24	15.88524(2)	0.210(2)	0.256(2)	15f0	57.3	f134	30.06331(6)	0.055(2)	0.331(6)		9.3
f35	19.06228(2)	0.152(2)	0.969(2)	18f0	45.5	f157	36.00652(7)	0.048(2)	0.892(7)	34f0	8.8
f26	24.03637(2)	0.192(2)	0.937(2)	(I)	43.3	f202	24.35725(9)	0.039(2)	0.677(9)	23f0	8.6
f29	11.56305(2)	0.172(2)	0.622(2)	(K)	43.2	f37	0.04048(2)	0.141(2)	0.509(2)		8.5
f30	25.41650(2)	0.171(2)	0.594(2)	24f0	39.2	f238	23.2980(1)	0.033(2)	0.65(1)	22f0	8.4
f34	11.64914(2)	0.154(2)	0.217(2)	11f0	39.0	f42	0.06555(3)	0.133(2)	0.378(3)		8.1
f36	11.75876(2)	0.150(2)	0.554(2)	(M)	38.8	f147	33.47664(7)	0.051(2)	0.001(7)	(Z)	7.6
f32	26.10287(2)	0.157(2)	0.334(2)	(L)	32.9	f169	34.43309(8)	0.045(2)	0.973(8)	(A1)	7.4
f58	21.60050(3)	0.109(2)	0.963(3)	(Q)	31.0	f172	28.64426(8)	0.044(2)	0.722(8)	(X)	7.3
f51	11.57592(3)	0.120(2)	0.287(3)	(N)	30.0	f170	30.40788(8)	0.044(2)	0.040(8)	(Y)	7.3
f27	28.87629(2)	0.178(2)	0.869(2)	(J)	27.2	f213	26.47531(9)	0.037(2)	0.44(1)	25f0	7.2
f45	27.53504(3)	0.127(2)	0.768(3)	26f0	24.7	f167	31.80752(8)	0.045(2)	0.433(8)	(W)	6.6
f112	55.45850(5)	0.064(2)	0.241(5)	(T)	22.9	f103	0.98864(5)	0.067(2)	0.526(5)		6.4
f82	20.12128(4)	0.080(2)	0.402(4)	19f0	21.4	f190	31.77065(8)	0.041(2)	0.442(8)	30f0	6.1
f131	56.59172(6)	0.056(2)	0.841(6)	(V)	19.8	f214	31.29566(9)	0.037(2)	0.94(1)		5.8
f54	29.71071(3)	0.111(2)	0.305(3)	(O)	18.8	f233	30.7117(1)	0.034(2)	0.97(1)	29f0	5.7
f122	18.00321(6)	0.060(2)	0.176(6)	17f0	17.6	...	...	...	...	...	...
f229	15.2659(1)	0.035(2)	0.61(1)	f1 − 12f0(A)	10.6	f2	26.915225(3)	1.091(2)	0.2303(3)	f1 − f0(A)	215.1
f204	16.32499(9)	0.038(2)	0.925(9)	f1 − 11f0(A)	10.5	f14	29.033258(9)	0.366(2)	0.586(1)	f1 + f0(A)	56.1
f165	17.38415(7)	0.046(2)	0.080(8)	f1 − 10f0(A)	13.7	f25	30.09224(2)	0.195(2)	0.063(2)	f1 + 2f0(A)	32.7
f116	18.44321(5)	0.063(2)	0.407(6)	f1 − 9f0(A)	18.8	f59	32.21026(3)	0.108(2)	0.875(3)	f1 + 4f0(A)	15.6
f200	19.50197(9)	0.039(2)	0.320(9)	f1 − 8f0(A)	10.9	f232	33.2726(1)	0.034(2)	0.48(1)	f1 + 5f0(*A)	5.1
f230	22.6789(1)	0.034(2)	0.82(1)	f1 − 5f0(A)	9.1	f135	34.32855(6)	0.055(2)	0.141(6)	f1 + 6f0(A)	8.9
f3	24.797185(4)	0.941(2)	0.4841(4)	f1 − 3f0(A)	207.6	f227	35.3871(1)	0.035(2)	0.45(1)	f1 + 7f0(A)	6.0
f6	25.856212(5)	0.645(2)	0.3891(5)	f1 − 2f0(A)	138.0	...	...	...	...		...
f49	0.07436(3)	0.123(2)	0.933(3)	f4 − 21f0(*B)	7.4	f79	24.43500(4)	0.081(2)	0.506(4)	f4 + 2f0(B)	17.7
f72	0.07844(4)	0.096(2)	0.514(4)	f4 − 21f0(*B)	5.8	f205	25.49371(9)	0.038(2)	0.857(9)	f4 + 3f0(B)	8.8
f105	1.13806(5)	0.066(2)	0.728(5)	f4 − 20f0(B)	6.9	f38	26.55263(2)	0.140(2)	0.100(2)	f4 + 4f0(B)	27.7
f225	18.0804(1)	0.035(2)	0.52(1)	f4 − 4f0(B)	10.0	f154	27.61169(7)	0.049(2)	0.356(7)	f4 + 5f0(B)	9.6
f130	19.13988(6)	0.057(2)	0.711(6)	f4 − 3f0(B)	16.5	f144	28.67044(7)	0.051(2)	0.245(7)	f4 + 6f0(B)	8.4
f43	20.19862(3)	0.132(2)	0.034(3)	f4 − 2f0(B)	34.3	f114	29.72935(5)	0.064(2)	0.890(5)	f4 + 7f0(B)	10.7
f108	21.25741(5)	0.066(2)	0.972(5)	f4 − f0(B)	19.5	f171	30.78928(8)	0.044(2)	0.595(8)	f4 + 8f0(B)	7.1
f9	23.375774(7)	0.526(2)	0.4676(7)	f4 + f0(B)	130.3	...	...	...	...	...	...
f21	25.93035(1)	0.232(2)	0.783(2)	f5 − 3f0(C)	48.5	f121	31.22547(6)	0.061(2)	0.753(6)	f5 + 2f0(C)	9.8
f48	26.98936(3)	0.123(2)	0.210(3)	f5 − 2f0(C)	24.5	f239	32.2846(1)	0.033(2)	0.39(1)	f5 + 3f0(C)	4.7
f83	28.04861(4)	0.078(2)	0.178(4)	f5 − f0(C)	15.1	f106	33.34330(5)	0.066(2)	0.335(5)	f5 + 4f0(C)	10.0
f96	30.16661(5)	0.069(2)	0.186(5)	f5 + f0(C)	11.6	...	...	...	...	...	...
f97	0.08636(5)	0.069(2)	0.970(5)	f8 − 29f0(*D)	4.2	f137	31.85310(6)	0.053(2)	0.540(7)	f8 + f0(D)	7.6
f140	1.14352(7)	0.052(2)	0.848(7)	f8 − 28f0(*D)	5.5	f163	32.91206(7)	0.047(2)	0.608(7)	f8 + 2f0(D)	6.8
f236	19.1449(1)	0.033(2)	0.85(1)	f8 − 11f0(D)	9.7	f217	35.0303(1)	0.036(2)	0.55(1)	f8 + 4f0(D)	6.5
f203	21.26321(9)	0.039(2)	0.073(9)	f8 − 9f0(D)	11.4	f201	36.08921(9)	0.039(2)	0.612(9)	f8 + 5f0(D)	7.3
f101	24.44004(5)	0.068(2)	0.683(5)	f8 − 6f0(D)	15.0	f118	37.14834(5)	0.063(2)	0.802(6)	f8 + 6f0(D)	13.8
f102	25.49931(5)	0.067(2)	0.612(5)	f8 − 5f0(D)	15.4	f187	39.26644(8)	0.042(2)	0.452(8)	f8 + 8f0(D)	12.3
f235	26.5583(1)	0.033(2)	0.66(1)	f8 − 4f0(D)	6.7	f133	40.32528(6)	0.056(2)	0.194(6)	f8 + 9f0(D)	18.3
f153	27.61754(7)	0.050(2)	0.567(7)	f8 − 3f0(D)	9.8	f185	41.38441(8)	0.042(2)	0.381(8)	f8 + 10f0(D)	12.4
f113	28.67575(5)	0.064(2)	0.969(5)	f8 − 2f0(D)	10.4	f179	42.44345(8)	0.043(2)	0.725(8)	f8 + 11f0(D)	12.3
f196	29.73510(9)	0.040(2)	0.195(9)	f8 − f0(D)	6.8	f211	43.50254(9)	0.037(2)	0.989(9)	f8 + 12f0(D)	11.1
f191	23.24792(8)	0.041(2)	0.633(8)	f10 − 4f0(E)	10.4	f66	30.66126(3)	0.099(2)	0.369(4)	f10 + 3f0(E)	16.6
f150	25.36603(7)	0.050(2)	0.625(7)	f10 − 2f0(E)	11.3	f212	31.72054(9)	0.037(2)	0.805(9)	f10 + 4f0(E)	5.4
f19	26.42520(1)	0.279(2)	0.307(1)	f10 − f0(E)	56.6	f47	32.77935(3)	0.124(2)	0.578(3)	f10 + 5f0(E)	18.8
f12	28.543232(8)	0.427(2)	0.0837(8)	f10 + f0(E)	74.2	f104	33.83834(5)	0.067(2)	0.017(5)	f10 + 6f0(E)	10.2
f17	29.60227(1)	0.310(2)	0.848(1)	f10 + 2f0(E)	50.4	f132	34.89736(6)	0.056(2)	0.384(6)	f10 + 7f0(E)	10.2
f75	32.13288(4)	0.087(2)	0.936(4)	f11 + f0(F)	12.7	f15	33.191998(9)	0.361(2)	0.050(1)	f11 + 2f0(F)	53.5
f146	24.19078(7)	0.051(2)	0.364(7)	f18 − 2f0(G)	11.3	f111	28.42697(5)	0.065(2)	0.218(5)	f18 + 2f0(G)	11.5
f46	27.36798(3)	0.124(2)	0.694(3)	f18 + f0(G)	24.7	f151	30.54497(7)	0.050(2)	0.119(7)	f18 + 4f0(G)	8.5
f81	68.84752(4)	0.080(2)	0.285(4)	f20 + f0(H)	34.1	f164	65.67053(7)	0.046(2)	0.943(8)	f20 − 2f0(H)	17.7
f145	66.72936(7)	0.051(2)	0.701(7)	f20 − f0(H)	20.1	...	...	...	...	...	...
f249	18.7414(1)	0.032(2)	0.32(1)	f26 − 5f0(I)	9.8	f99	22.97738(5)	0.068(2)	0.889(5)	f26 − f0(I)	18.8
f39	20.85932(2)	0.138(2)	0.240(3)	f26 − 3f0(I)	36.9	f250	27.2132(1)	0.032(2)	0.06(1)	f26 + 3f0(I)	6.3
f53	21.91832(3)	0.115(2)	0.188(3)	f26 − 2f0(I)	29.4	...	...	...	...	...	...
f28	30.99440(2)	0.173(2)	0.054(2)	f27 + 2f0(J)	27.9	f143	32.05339(7)	0.052(2)	0.077(7)	f27 + 3f0(J)	7.6
f243	9.4450(1)	0.033(2)	0.03(1)	f29 − 2f0(K)	10.5	f74	12.62198(4)	0.089(2)	0.196(4)	f29 + f0(K)	23.5
f84	10.50387(4)	0.077(2)	0.517(5)	f29 − f0(K)	18.3	f199	13.68112(9)	0.039(2)	0.427(9)	f29 + 2f0(K)	11.0
f237	25.0438(1)	0.033(2)	0.40(1)	f32 − f0(L)	7.6	f128	30.33728(6)	0.058(2)	0.514(6)	f32 + 4f0(*L)	9.6
f100	28.22100(5)	0.068(2)	0.963(5)	f32 + 2f0(L)	12.1	...	...	...	...	...	...
f93	0.10969(5)	0.070(2)	0.235(5)	f41 − 10f0(M)	4.3	f155	13.87674(7)	0.049(2)	0.017(7)	f41 + 3f0(M)	13.7
f228	7.5228(1)	0.035(2)	0.27(1)	f41 − 3f0(M)	9.9	f221	20.2310(1)	0.035(2)	0.17(1)	f41 + 9f0(M)	9.1
f92	9.64067(5)	0.072(2)	0.950(5)	f41 − f0(M)	22.7	f138	31.87963(6)	0.053(2)	0.256(7)	f41 + 20f0(M)	7.6
f41	10.69986(3)	0.134(2)	0.981(3)	f36 − f0(M)	31.4	f124	33.99701(6)	0.060(2)	0.724(6)	f41 + 22f0(M)	9.6
f152	10.51686(7)	0.050(2)	0.971(7)	f50 − f0(N)	11.9	f126	12.63496(6)	0.059(2)	0.662(6)	f50 + f0(N)	15.5
f65	26.53372(3)	0.100(2)	0.036(3)	f54 − 3f0(O)	19.7	f251	31.8291(1)	0.032(2)	0.55(1)	f54 + 2f0(O)	4.6
f173	28.65174(8)	0.044(2)	0.848(8)	f54 − f0(O)	7.2	f85	32.88784(4)	0.077(2)	0.410(5)	f54 + 3f0(O)	11.2
f180	30.76958(8)	0.043(2)	0.024(8)	f54 + f0(O)	7.1	f186	33.94669(8)	0.042(2)	0.146(8)	f54 + 4f0(O)	6.7
f73	30.53026(4)	0.092(2)	0.393(4)	f54 − 2f0(P)	15.5	f125	31.58920(6)	0.059(2)	0.949(6)	f54 − f0(P)	8.9
f206	23.71868(9)	0.038(2)	0.066(9)	f58 + 2f0(Q)	8.8	f176	26.89501(8)	0.044(2)	0.564(8)	f58 + 5f0(Q)	8.6
f129	24.77760(6)	0.057(2)	0.933(6)	f58 + 3f0(Q)	12.7	f40	27.95460(3)	0.136(2)	0.868(3)	f58 + 6f0(Q)	27.2
f141	25.83667(7)	0.052(2)	0.889(7)	f58 + 4f0(Q)	11.4	...	...	...	...	...	...
f71	31.16577(4)	0.096(2)	0.519(4)	f64 − 2f0(R)	15.3	...	...	...	...	...	...
f207	27.93747(9)	0.038(2)	0.858(9)	f70 − 2f0(S)	7.6	f182	35.35117(8)	0.043(2)	0.924(8)	f70 + 5f0(S)	7.4
f220	32.1737(1)	0.035(2)	0.21(1)	f70 + 2f0(S)	5.0	...	...	...	...	...	...
f248	54.3994(1)	0.032(2)	0.06(1)	f112 − f0(T)	11.8	f183	56.51752(8)	0.042(2)	0.640(8)	f112 + f0(T)	14.4
f160	23.69492(7)	0.048(2)	0.243(7)	f127 − f0(U)	11.0	f177	26.87212(8)	0.043(2)	0.170(8)	f127 + 2f0(U)	8.5
f136	25.81283(6)	0.054(2)	0.720(7)	f127 + f0(U)	11.7	...	...	...	...	...	...
f158	58.70967(7)	0.048(2)	0.844(7)	f131 + 2f0(V)	13.9	f219	59.7687(1)	0.035(2)	0.28(1)	f131 + 3f0(V)	10.9
f197	30.74829(9)	0.040(2)	0.403(9)	f169 − f0(W)	6.7	f208	32.86651(9)	0.038(2)	0.881(9)	f169 + f0(W)	5.6
f246	29.7030(1)	0.033(2)	0.67(1)	f172 + f0(X)	5.5	f189	30.76239(8)	0.042(2)	0.322(8)	f172 + 2f0(X)	6.9
f244	28.2900(1)	0.033(2)	0.01(1)	f172 − 2f0(Y)	5.8	...	...	...	...	...	...
f226	35.5944(1)	0.035(2)	0.71(1)	f147 + 2f0(Z)	6.0	...	...	...	...	...	...
f181	33.37397(8)	0.043(2)	0.290(8)	f169 − f0(A1)	6.5	...	...	...	...	...	...
f119	24.04733(6)	0.062(2)	0.657(6)	f77 + 2f0(B1)	14.2	...	...	...	...	...	...
f55	0.11576(3)	0.110(2)	0.704(3)	2f54 − 56f0	6.7	f142	29.23290(7)	0.052(2)	0.936(7)	6f103 + 22f0	8.4
f23	61.58830(2)	0.214(2)	0.007(2)	2f8	67.9	f148	31.54531(7)	0.050(2)	0.789(7)	4f26 − 61f0	7.6
f31	59.33744(2)	0.160(2)	0.451(2)	3f11 − 32f0	46.7	f149	2.25075(7)	0.050(2)	0.753(7)	2f42 + 2f0	7.8
f33	31.07265(2)	0.155(2)	0.515(2)	≈f11(*F)	25.1	f156	27.48266(7)	0.049(2)	0.308(7)	≈f10	9.5
f50	0.06995(3)	0.120(2)	0.159(3)	5f37 − 2f42	7.2	f159	1.12725(7)	0.048(2)	0.918(7)	f42 + f0	4.9
f44	31.01335(3)	0.127(2)	0.489(3)	4f10 − 3f18	20.8	f161	1.10827(7)	0.047(2)	0.662(7)	27f0 − f10	4.9
f52	0.09073(3)	0.117(2)	0.853(3)	2f42 − f37	7.1	f166	22.31479(8)	0.046(2)	0.042(8)	≈f4	11.3
f57	0.05093(3)	0.109(2)	0.161(3)	26f0 − f10	6.6	f168	26.03155(8)	0.045(2)	0.975(8)	51f0 − f1	9.3
f60	0.03298(3)	0.104(2)	0.430(3)	55f0 − 2f5	6.3	f174	67.78675(8)	0.044(2)	0.893(8)	≈f20	17.8
f61	33.19053(3)	0.103(2)	0.111(3)	≈f15(*F)	15.3	f175	28.87392(8)	0.044(2)	0.549(8)	≈f27	6.7
f62	0.10357(3)	0.102(2)	0.766(3)	52f0 − 2f10	6.2	f178	28.85307(8)	0.043(2)	0.814(8)	3f1 − 52f0	6.6
f63	0.02784(3)	0.100(2)	0.349(3)	55f0 − 2f5	6.1	f184	29.14661(8)	0.042(2)	0.495(8)	f37 + f5	6.8
f67	0.13980(3)	0.099(2)	0.651(4)	4f42 − 3f37	6.1	f188	57.78346(8)	0.042(2)	0.790(8)	55f0 − 7f42	13.5
f68	0.15413(4)	0.098(2)	0.174(4)	2f4 − 42f0	6.1	f192	11.23338(8)	0.041(2)	0.448(8)	56f0 − 2f26	9.9
f69	0.22816(4)	0.097(2)	0.646(4)	3f4 − 63f0	6.3	f194	11.61045(8)	0.041(2)	0.785(9)	11f0 − f37	10.3
f78	33.32775(4)	0.081(2)	0.666(4)	7f54 − 6f5	12.1	f195	2.04757(8)	0.041(2)	0.914(9)	f103 + f0	6.1
f80	0.04427(4)	0.080(2)	0.090(4)	≈f37	4.8	f198	27.66546(9)	0.040(2)	0.509(9)	2f42 + 26f0	8.0
f86	0.12696(4)	0.077(2)	0.795(5)	2f42	4.7	f209	31.27830(9)	0.038(2)	0.117(9)	2f27 − 25f0	6.0
f87	57.08645(4)	0.076(2)	0.052(5)	2f10 + 2f0	25.0	f210	6.95971(9)	0.037(2)	0.673(9)	38f0 − f64	10.5
f88	0.06252(5)	0.075(2)	0.257(5)	≈f42	4.5	f215	33.33240(9)	0.036(2)	0.71(1)	7f54 − 6f5	5.5
f89	0.98433(5)	0.075(2)	0.320(5)	22f0 − f4	7.1	f218	29.4626(1)	0.035(2)	0.98(1)	2f103 + f10	5.8
f90	0.05287(5)	0.073(2)	0.197(5)	26f0 − f10	4.4	f222	58.2147(1)	0.035(2)	0.58(1)	2f5	11.2
f91	0.16382(5)	0.072(2)	0.153(5)	2f8 − 58f0	4.5	f223	61.7353(1)	0.035(2)	0.60(1)	4f4 − 26f0	10.8
f94	0.14492(5)	0.070(2)	0.120(5)	f42 + 2f37	4.4	f224	32.7563(1)	0.035(2)	0.43(1)	9f41 − 60f0	5.3
f95	0.21085(5)	0.070(2)	0.495(5)	2f42 + 2f37	4.5	f231	32.2188(1)	0.034(2)	0.62(1)	2f172 − 27f0	5.0
f98	0.14686(5)	0.069(2)	0.163(5)	63f0 − 2f64	4.3	f240	30.9908(1)	0.033(2)	0.02(1)	≈f28	5.4
f107	12.15524(5)	0.066(2)	0.315(5)	62f0 − 5f41	17.4	f241	35.3021(1)	0.033(2)	0.23(1)	10f103 + 24f0	5.8
f109	1.13352(5)	0.066(2)	0.824(5)	≈f105	6.8	f242	30.9376(1)	0.033(2)	0.40(1)	3f103 + f1	5.3
f110	0.13506(5)	0.065(2)	0.379(5)	2f42	4.0	f245	33.2555(1)	0.033(2)	0.67(1)	9f103 + 23f0	4.8
f115	29.00851(5)	0.063(2)	0.115(6)	2f26 − 18f0	9.7	f247	27.9768(1)	0.033(2)	0.23(1)	≈f1	6.4
f120	53.83040(6)	0.062(2)	0.072(6)	2f1 − 2f0	21.6	f252	59.4461(1)	0.032(2)	0.40(1)	58f0 − 2f103	9.5
f139	66.02716(7)	0.053(2)	0.559(7)	9f37 + 62f0	19.7	...	...	...	...	...	...

	Frequency	Amplitude	Phase	Combination	S/N		Frequency	Amplitude	Phase	Combination	S/N
	(d⁻¹)	(mmag)	(rad/2π)				(d⁻¹)	(mmag)	(rad/2π)
f1	27.974241(3)	1.203(2)	0.1837(3)	(A)	235.3	f117	13.76714(5)	0.063(2)	0.580(6)	13f0	17.5
f4	22.316723(4)	0.906(2)	0.6843(4)	(B)	224.8	f77	26.16552(4)	0.081(2)	0.162(4)	(B1)	17.0
f7	14.826233(6)	0.551(2)	0.8360(6)	14f0	161.2	f56	32.64831(3)	0.109(2)	0.149(3)	(P)	16.3
f5	29.107404(4)	0.868(2)	0.4022(4)	(C)	138.0	f70	30.05512(4)	0.097(2)	0.363(4)	(S)	16.2
f13	16.944260(9)	0.381(2)	0.6427(9)	16f0	110.5	f64	33.28395(3)	0.100(2)	0.544(3)	(R)	14.9
f20	67.78847(1)	0.263(2)	0.417(1)	(H)	107.2	f76	29.65243(4)	0.086(2)	0.028(4)	28f0	14.2
f10	27.484214(7)	0.490(2)	0.6844(7)	(E)	95.4	f193	40.24269(8)	0.041(2)	0.809(8)	38f0	13.1
f8	30.794131(6)	0.530(2)	0.0346(7)	(D)	85.9	f127	24.75387(6)	0.059(2)	0.803(6)	(U)	12.9
f16	12.70816(1)	0.323(2)	0.610(1)	12f0	84.6	f234	64.0604(1)	0.033(2)	0.97(1)		11.7
f11	31.073961(7)	0.466(2)	0.7479(7)	(F)	75.5	f162	22.23896(7)	0.047(2)	0.885(7)	21f0	11.7
f22	21.18030(1)	0.229(2)	0.779(2)	20f0	67.4	f216	44.4788(1)	0.036(2)	0.89(1)	42f0	10.1
f18	26.30896(1)	0.301(2)	0.895(1)	(G)	62.8	f123	33.88855(6)	0.060(2)	0.964(6)	32f0	9.5
f24	15.88524(2)	0.210(2)	0.256(2)	15f0	57.3	f134	30.06331(6)	0.055(2)	0.331(6)		9.3
f35	19.06228(2)	0.152(2)	0.969(2)	18f0	45.5	f157	36.00652(7)	0.048(2)	0.892(7)	34f0	8.8
f26	24.03637(2)	0.192(2)	0.937(2)	(I)	43.3	f202	24.35725(9)	0.039(2)	0.677(9)	23f0	8.6
f29	11.56305(2)	0.172(2)	0.622(2)	(K)	43.2	f37	0.04048(2)	0.141(2)	0.509(2)		8.5
f30	25.41650(2)	0.171(2)	0.594(2)	24f0	39.2	f238	23.2980(1)	0.033(2)	0.65(1)	22f0	8.4
f34	11.64914(2)	0.154(2)	0.217(2)	11f0	39.0	f42	0.06555(3)	0.133(2)	0.378(3)		8.1
f36	11.75876(2)	0.150(2)	0.554(2)	(M)	38.8	f147	33.47664(7)	0.051(2)	0.001(7)	(Z)	7.6
f32	26.10287(2)	0.157(2)	0.334(2)	(L)	32.9	f169	34.43309(8)	0.045(2)	0.973(8)	(A1)	7.4
f58	21.60050(3)	0.109(2)	0.963(3)	(Q)	31.0	f172	28.64426(8)	0.044(2)	0.722(8)	(X)	7.3
f51	11.57592(3)	0.120(2)	0.287(3)	(N)	30.0	f170	30.40788(8)	0.044(2)	0.040(8)	(Y)	7.3
f27	28.87629(2)	0.178(2)	0.869(2)	(J)	27.2	f213	26.47531(9)	0.037(2)	0.44(1)	25f0	7.2
f45	27.53504(3)	0.127(2)	0.768(3)	26f0	24.7	f167	31.80752(8)	0.045(2)	0.433(8)	(W)	6.6
f112	55.45850(5)	0.064(2)	0.241(5)	(T)	22.9	f103	0.98864(5)	0.067(2)	0.526(5)		6.4
f82	20.12128(4)	0.080(2)	0.402(4)	19f0	21.4	f190	31.77065(8)	0.041(2)	0.442(8)	30f0	6.1
f131	56.59172(6)	0.056(2)	0.841(6)	(V)	19.8	f214	31.29566(9)	0.037(2)	0.94(1)		5.8
f54	29.71071(3)	0.111(2)	0.305(3)	(O)	18.8	f233	30.7117(1)	0.034(2)	0.97(1)	29f0	5.7
f122	18.00321(6)	0.060(2)	0.176(6)	17f0	17.6	...	...	...	...	...	...
f229	15.2659(1)	0.035(2)	0.61(1)	f1 − 12f0(A)	10.6	f2	26.915225(3)	1.091(2)	0.2303(3)	f1 − f0(A)	215.1
f204	16.32499(9)	0.038(2)	0.925(9)	f1 − 11f0(A)	10.5	f14	29.033258(9)	0.366(2)	0.586(1)	f1 + f0(A)	56.1
f165	17.38415(7)	0.046(2)	0.080(8)	f1 − 10f0(A)	13.7	f25	30.09224(2)	0.195(2)	0.063(2)	f1 + 2f0(A)	32.7
f116	18.44321(5)	0.063(2)	0.407(6)	f1 − 9f0(A)	18.8	f59	32.21026(3)	0.108(2)	0.875(3)	f1 + 4f0(A)	15.6
f200	19.50197(9)	0.039(2)	0.320(9)	f1 − 8f0(A)	10.9	f232	33.2726(1)	0.034(2)	0.48(1)	f1 + 5f0(*A)	5.1
f230	22.6789(1)	0.034(2)	0.82(1)	f1 − 5f0(A)	9.1	f135	34.32855(6)	0.055(2)	0.141(6)	f1 + 6f0(A)	8.9
f3	24.797185(4)	0.941(2)	0.4841(4)	f1 − 3f0(A)	207.6	f227	35.3871(1)	0.035(2)	0.45(1)	f1 + 7f0(A)	6.0
f6	25.856212(5)	0.645(2)	0.3891(5)	f1 − 2f0(A)	138.0	...	...	...	...		...
f49	0.07436(3)	0.123(2)	0.933(3)	f4 − 21f0(*B)	7.4	f79	24.43500(4)	0.081(2)	0.506(4)	f4 + 2f0(B)	17.7
f72	0.07844(4)	0.096(2)	0.514(4)	f4 − 21f0(*B)	5.8	f205	25.49371(9)	0.038(2)	0.857(9)	f4 + 3f0(B)	8.8
f105	1.13806(5)	0.066(2)	0.728(5)	f4 − 20f0(B)	6.9	f38	26.55263(2)	0.140(2)	0.100(2)	f4 + 4f0(B)	27.7
f225	18.0804(1)	0.035(2)	0.52(1)	f4 − 4f0(B)	10.0	f154	27.61169(7)	0.049(2)	0.356(7)	f4 + 5f0(B)	9.6
f130	19.13988(6)	0.057(2)	0.711(6)	f4 − 3f0(B)	16.5	f144	28.67044(7)	0.051(2)	0.245(7)	f4 + 6f0(B)	8.4
f43	20.19862(3)	0.132(2)	0.034(3)	f4 − 2f0(B)	34.3	f114	29.72935(5)	0.064(2)	0.890(5)	f4 + 7f0(B)	10.7
f108	21.25741(5)	0.066(2)	0.972(5)	f4 − f0(B)	19.5	f171	30.78928(8)	0.044(2)	0.595(8)	f4 + 8f0(B)	7.1
f9	23.375774(7)	0.526(2)	0.4676(7)	f4 + f0(B)	130.3	...	...	...	...	...	...
f21	25.93035(1)	0.232(2)	0.783(2)	f5 − 3f0(C)	48.5	f121	31.22547(6)	0.061(2)	0.753(6)	f5 + 2f0(C)	9.8
f48	26.98936(3)	0.123(2)	0.210(3)	f5 − 2f0(C)	24.5	f239	32.2846(1)	0.033(2)	0.39(1)	f5 + 3f0(C)	4.7
f83	28.04861(4)	0.078(2)	0.178(4)	f5 − f0(C)	15.1	f106	33.34330(5)	0.066(2)	0.335(5)	f5 + 4f0(C)	10.0
f96	30.16661(5)	0.069(2)	0.186(5)	f5 + f0(C)	11.6	...	...	...	...	...	...
f97	0.08636(5)	0.069(2)	0.970(5)	f8 − 29f0(*D)	4.2	f137	31.85310(6)	0.053(2)	0.540(7)	f8 + f0(D)	7.6
f140	1.14352(7)	0.052(2)	0.848(7)	f8 − 28f0(*D)	5.5	f163	32.91206(7)	0.047(2)	0.608(7)	f8 + 2f0(D)	6.8
f236	19.1449(1)	0.033(2)	0.85(1)	f8 − 11f0(D)	9.7	f217	35.0303(1)	0.036(2)	0.55(1)	f8 + 4f0(D)	6.5
f203	21.26321(9)	0.039(2)	0.073(9)	f8 − 9f0(D)	11.4	f201	36.08921(9)	0.039(2)	0.612(9)	f8 + 5f0(D)	7.3
f101	24.44004(5)	0.068(2)	0.683(5)	f8 − 6f0(D)	15.0	f118	37.14834(5)	0.063(2)	0.802(6)	f8 + 6f0(D)	13.8
f102	25.49931(5)	0.067(2)	0.612(5)	f8 − 5f0(D)	15.4	f187	39.26644(8)	0.042(2)	0.452(8)	f8 + 8f0(D)	12.3
f235	26.5583(1)	0.033(2)	0.66(1)	f8 − 4f0(D)	6.7	f133	40.32528(6)	0.056(2)	0.194(6)	f8 + 9f0(D)	18.3
f153	27.61754(7)	0.050(2)	0.567(7)	f8 − 3f0(D)	9.8	f185	41.38441(8)	0.042(2)	0.381(8)	f8 + 10f0(D)	12.4
f113	28.67575(5)	0.064(2)	0.969(5)	f8 − 2f0(D)	10.4	f179	42.44345(8)	0.043(2)	0.725(8)	f8 + 11f0(D)	12.3
f196	29.73510(9)	0.040(2)	0.195(9)	f8 − f0(D)	6.8	f211	43.50254(9)	0.037(2)	0.989(9)	f8 + 12f0(D)	11.1
f191	23.24792(8)	0.041(2)	0.633(8)	f10 − 4f0(E)	10.4	f66	30.66126(3)	0.099(2)	0.369(4)	f10 + 3f0(E)	16.6
f150	25.36603(7)	0.050(2)	0.625(7)	f10 − 2f0(E)	11.3	f212	31.72054(9)	0.037(2)	0.805(9)	f10 + 4f0(E)	5.4
f19	26.42520(1)	0.279(2)	0.307(1)	f10 − f0(E)	56.6	f47	32.77935(3)	0.124(2)	0.578(3)	f10 + 5f0(E)	18.8
f12	28.543232(8)	0.427(2)	0.0837(8)	f10 + f0(E)	74.2	f104	33.83834(5)	0.067(2)	0.017(5)	f10 + 6f0(E)	10.2
f17	29.60227(1)	0.310(2)	0.848(1)	f10 + 2f0(E)	50.4	f132	34.89736(6)	0.056(2)	0.384(6)	f10 + 7f0(E)	10.2
f75	32.13288(4)	0.087(2)	0.936(4)	f11 + f0(F)	12.7	f15	33.191998(9)	0.361(2)	0.050(1)	f11 + 2f0(F)	53.5
f146	24.19078(7)	0.051(2)	0.364(7)	f18 − 2f0(G)	11.3	f111	28.42697(5)	0.065(2)	0.218(5)	f18 + 2f0(G)	11.5
f46	27.36798(3)	0.124(2)	0.694(3)	f18 + f0(G)	24.7	f151	30.54497(7)	0.050(2)	0.119(7)	f18 + 4f0(G)	8.5
f81	68.84752(4)	0.080(2)	0.285(4)	f20 + f0(H)	34.1	f164	65.67053(7)	0.046(2)	0.943(8)	f20 − 2f0(H)	17.7
f145	66.72936(7)	0.051(2)	0.701(7)	f20 − f0(H)	20.1	...	...	...	...	...	...
f249	18.7414(1)	0.032(2)	0.32(1)	f26 − 5f0(I)	9.8	f99	22.97738(5)	0.068(2)	0.889(5)	f26 − f0(I)	18.8
f39	20.85932(2)	0.138(2)	0.240(3)	f26 − 3f0(I)	36.9	f250	27.2132(1)	0.032(2)	0.06(1)	f26 + 3f0(I)	6.3
f53	21.91832(3)	0.115(2)	0.188(3)	f26 − 2f0(I)	29.4	...	...	...	...	...	...
f28	30.99440(2)	0.173(2)	0.054(2)	f27 + 2f0(J)	27.9	f143	32.05339(7)	0.052(2)	0.077(7)	f27 + 3f0(J)	7.6
f243	9.4450(1)	0.033(2)	0.03(1)	f29 − 2f0(K)	10.5	f74	12.62198(4)	0.089(2)	0.196(4)	f29 + f0(K)	23.5
f84	10.50387(4)	0.077(2)	0.517(5)	f29 − f0(K)	18.3	f199	13.68112(9)	0.039(2)	0.427(9)	f29 + 2f0(K)	11.0
f237	25.0438(1)	0.033(2)	0.40(1)	f32 − f0(L)	7.6	f128	30.33728(6)	0.058(2)	0.514(6)	f32 + 4f0(*L)	9.6
f100	28.22100(5)	0.068(2)	0.963(5)	f32 + 2f0(L)	12.1	...	...	...	...	...	...
f93	0.10969(5)	0.070(2)	0.235(5)	f41 − 10f0(M)	4.3	f155	13.87674(7)	0.049(2)	0.017(7)	f41 + 3f0(M)	13.7
f228	7.5228(1)	0.035(2)	0.27(1)	f41 − 3f0(M)	9.9	f221	20.2310(1)	0.035(2)	0.17(1)	f41 + 9f0(M)	9.1
f92	9.64067(5)	0.072(2)	0.950(5)	f41 − f0(M)	22.7	f138	31.87963(6)	0.053(2)	0.256(7)	f41 + 20f0(M)	7.6
f41	10.69986(3)	0.134(2)	0.981(3)	f36 − f0(M)	31.4	f124	33.99701(6)	0.060(2)	0.724(6)	f41 + 22f0(M)	9.6
f152	10.51686(7)	0.050(2)	0.971(7)	f50 − f0(N)	11.9	f126	12.63496(6)	0.059(2)	0.662(6)	f50 + f0(N)	15.5
f65	26.53372(3)	0.100(2)	0.036(3)	f54 − 3f0(O)	19.7	f251	31.8291(1)	0.032(2)	0.55(1)	f54 + 2f0(O)	4.6
f173	28.65174(8)	0.044(2)	0.848(8)	f54 − f0(O)	7.2	f85	32.88784(4)	0.077(2)	0.410(5)	f54 + 3f0(O)	11.2
f180	30.76958(8)	0.043(2)	0.024(8)	f54 + f0(O)	7.1	f186	33.94669(8)	0.042(2)	0.146(8)	f54 + 4f0(O)	6.7
f73	30.53026(4)	0.092(2)	0.393(4)	f54 − 2f0(P)	15.5	f125	31.58920(6)	0.059(2)	0.949(6)	f54 − f0(P)	8.9
f206	23.71868(9)	0.038(2)	0.066(9)	f58 + 2f0(Q)	8.8	f176	26.89501(8)	0.044(2)	0.564(8)	f58 + 5f0(Q)	8.6
f129	24.77760(6)	0.057(2)	0.933(6)	f58 + 3f0(Q)	12.7	f40	27.95460(3)	0.136(2)	0.868(3)	f58 + 6f0(Q)	27.2
f141	25.83667(7)	0.052(2)	0.889(7)	f58 + 4f0(Q)	11.4	...	...	...	...	...	...
f71	31.16577(4)	0.096(2)	0.519(4)	f64 − 2f0(R)	15.3	...	...	...	...	...	...
f207	27.93747(9)	0.038(2)	0.858(9)	f70 − 2f0(S)	7.6	f182	35.35117(8)	0.043(2)	0.924(8)	f70 + 5f0(S)	7.4
f220	32.1737(1)	0.035(2)	0.21(1)	f70 + 2f0(S)	5.0	...	...	...	...	...	...
f248	54.3994(1)	0.032(2)	0.06(1)	f112 − f0(T)	11.8	f183	56.51752(8)	0.042(2)	0.640(8)	f112 + f0(T)	14.4
f160	23.69492(7)	0.048(2)	0.243(7)	f127 − f0(U)	11.0	f177	26.87212(8)	0.043(2)	0.170(8)	f127 + 2f0(U)	8.5
f136	25.81283(6)	0.054(2)	0.720(7)	f127 + f0(U)	11.7	...	...	...	...	...	...
f158	58.70967(7)	0.048(2)	0.844(7)	f131 + 2f0(V)	13.9	f219	59.7687(1)	0.035(2)	0.28(1)	f131 + 3f0(V)	10.9
f197	30.74829(9)	0.040(2)	0.403(9)	f169 − f0(W)	6.7	f208	32.86651(9)	0.038(2)	0.881(9)	f169 + f0(W)	5.6
f246	29.7030(1)	0.033(2)	0.67(1)	f172 + f0(X)	5.5	f189	30.76239(8)	0.042(2)	0.322(8)	f172 + 2f0(X)	6.9
f244	28.2900(1)	0.033(2)	0.01(1)	f172 − 2f0(Y)	5.8	...	...	...	...	...	...
f226	35.5944(1)	0.035(2)	0.71(1)	f147 + 2f0(Z)	6.0	...	...	...	...	...	...
f181	33.37397(8)	0.043(2)	0.290(8)	f169 − f0(A1)	6.5	...	...	...	...	...	...
f119	24.04733(6)	0.062(2)	0.657(6)	f77 + 2f0(B1)	14.2	...	...	...	...	...	...
f55	0.11576(3)	0.110(2)	0.704(3)	2f54 − 56f0	6.7	f142	29.23290(7)	0.052(2)	0.936(7)	6f103 + 22f0	8.4
f23	61.58830(2)	0.214(2)	0.007(2)	2f8	67.9	f148	31.54531(7)	0.050(2)	0.789(7)	4f26 − 61f0	7.6
f31	59.33744(2)	0.160(2)	0.451(2)	3f11 − 32f0	46.7	f149	2.25075(7)	0.050(2)	0.753(7)	2f42 + 2f0	7.8
f33	31.07265(2)	0.155(2)	0.515(2)	≈f11(*F)	25.1	f156	27.48266(7)	0.049(2)	0.308(7)	≈f10	9.5
f50	0.06995(3)	0.120(2)	0.159(3)	5f37 − 2f42	7.2	f159	1.12725(7)	0.048(2)	0.918(7)	f42 + f0	4.9
f44	31.01335(3)	0.127(2)	0.489(3)	4f10 − 3f18	20.8	f161	1.10827(7)	0.047(2)	0.662(7)	27f0 − f10	4.9
f52	0.09073(3)	0.117(2)	0.853(3)	2f42 − f37	7.1	f166	22.31479(8)	0.046(2)	0.042(8)	≈f4	11.3
f57	0.05093(3)	0.109(2)	0.161(3)	26f0 − f10	6.6	f168	26.03155(8)	0.045(2)	0.975(8)	51f0 − f1	9.3
f60	0.03298(3)	0.104(2)	0.430(3)	55f0 − 2f5	6.3	f174	67.78675(8)	0.044(2)	0.893(8)	≈f20	17.8
f61	33.19053(3)	0.103(2)	0.111(3)	≈f15(*F)	15.3	f175	28.87392(8)	0.044(2)	0.549(8)	≈f27	6.7
f62	0.10357(3)	0.102(2)	0.766(3)	52f0 − 2f10	6.2	f178	28.85307(8)	0.043(2)	0.814(8)	3f1 − 52f0	6.6
f63	0.02784(3)	0.100(2)	0.349(3)	55f0 − 2f5	6.1	f184	29.14661(8)	0.042(2)	0.495(8)	f37 + f5	6.8
f67	0.13980(3)	0.099(2)	0.651(4)	4f42 − 3f37	6.1	f188	57.78346(8)	0.042(2)	0.790(8)	55f0 − 7f42	13.5
f68	0.15413(4)	0.098(2)	0.174(4)	2f4 − 42f0	6.1	f192	11.23338(8)	0.041(2)	0.448(8)	56f0 − 2f26	9.9
f69	0.22816(4)	0.097(2)	0.646(4)	3f4 − 63f0	6.3	f194	11.61045(8)	0.041(2)	0.785(9)	11f0 − f37	10.3
f78	33.32775(4)	0.081(2)	0.666(4)	7f54 − 6f5	12.1	f195	2.04757(8)	0.041(2)	0.914(9)	f103 + f0	6.1
f80	0.04427(4)	0.080(2)	0.090(4)	≈f37	4.8	f198	27.66546(9)	0.040(2)	0.509(9)	2f42 + 26f0	8.0
f86	0.12696(4)	0.077(2)	0.795(5)	2f42	4.7	f209	31.27830(9)	0.038(2)	0.117(9)	2f27 − 25f0	6.0
f87	57.08645(4)	0.076(2)	0.052(5)	2f10 + 2f0	25.0	f210	6.95971(9)	0.037(2)	0.673(9)	38f0 − f64	10.5
f88	0.06252(5)	0.075(2)	0.257(5)	≈f42	4.5	f215	33.33240(9)	0.036(2)	0.71(1)	7f54 − 6f5	5.5
f89	0.98433(5)	0.075(2)	0.320(5)	22f0 − f4	7.1	f218	29.4626(1)	0.035(2)	0.98(1)	2f103 + f10	5.8
f90	0.05287(5)	0.073(2)	0.197(5)	26f0 − f10	4.4	f222	58.2147(1)	0.035(2)	0.58(1)	2f5	11.2
f91	0.16382(5)	0.072(2)	0.153(5)	2f8 − 58f0	4.5	f223	61.7353(1)	0.035(2)	0.60(1)	4f4 − 26f0	10.8
f94	0.14492(5)	0.070(2)	0.120(5)	f42 + 2f37	4.4	f224	32.7563(1)	0.035(2)	0.43(1)	9f41 − 60f0	5.3
f95	0.21085(5)	0.070(2)	0.495(5)	2f42 + 2f37	4.5	f231	32.2188(1)	0.034(2)	0.62(1)	2f172 − 27f0	5.0
f98	0.14686(5)	0.069(2)	0.163(5)	63f0 − 2f64	4.3	f240	30.9908(1)	0.033(2)	0.02(1)	≈f28	5.4
f107	12.15524(5)	0.066(2)	0.315(5)	62f0 − 5f41	17.4	f241	35.3021(1)	0.033(2)	0.23(1)	10f103 + 24f0	5.8
f109	1.13352(5)	0.066(2)	0.824(5)	≈f105	6.8	f242	30.9376(1)	0.033(2)	0.40(1)	3f103 + f1	5.3
f110	0.13506(5)	0.065(2)	0.379(5)	2f42	4.0	f245	33.2555(1)	0.033(2)	0.67(1)	9f103 + 23f0	4.8
f115	29.00851(5)	0.063(2)	0.115(6)	2f26 − 18f0	9.7	f247	27.9768(1)	0.033(2)	0.23(1)	≈f1	6.4
f120	53.83040(6)	0.062(2)	0.072(6)	2f1 − 2f0	21.6	f252	59.4461(1)	0.032(2)	0.40(1)	58f0 − 2f103	9.5
f139	66.02716(7)	0.053(2)	0.559(7)	9f37 + 62f0	19.7	...	...	...	...	...	...

Table 3.

Open in new tab

	Frequency	Amplitude	Phase	Combination	S/N		Frequency	Amplitude	Phase	Combination	S/N
	(d⁻¹)	(mmag)	(rad/2π)				(d⁻¹)	(mmag)	(rad/2π)
f1	27.974241(3)	1.203(2)	0.1837(3)	(A)	235.3	f117	13.76714(5)	0.063(2)	0.580(6)	13f0	17.5
f4	22.316723(4)	0.906(2)	0.6843(4)	(B)	224.8	f77	26.16552(4)	0.081(2)	0.162(4)	(B1)	17.0
f7	14.826233(6)	0.551(2)	0.8360(6)	14f0	161.2	f56	32.64831(3)	0.109(2)	0.149(3)	(P)	16.3
f5	29.107404(4)	0.868(2)	0.4022(4)	(C)	138.0	f70	30.05512(4)	0.097(2)	0.363(4)	(S)	16.2
f13	16.944260(9)	0.381(2)	0.6427(9)	16f0	110.5	f64	33.28395(3)	0.100(2)	0.544(3)	(R)	14.9
f20	67.78847(1)	0.263(2)	0.417(1)	(H)	107.2	f76	29.65243(4)	0.086(2)	0.028(4)	28f0	14.2
f10	27.484214(7)	0.490(2)	0.6844(7)	(E)	95.4	f193	40.24269(8)	0.041(2)	0.809(8)	38f0	13.1
f8	30.794131(6)	0.530(2)	0.0346(7)	(D)	85.9	f127	24.75387(6)	0.059(2)	0.803(6)	(U)	12.9
f16	12.70816(1)	0.323(2)	0.610(1)	12f0	84.6	f234	64.0604(1)	0.033(2)	0.97(1)		11.7
f11	31.073961(7)	0.466(2)	0.7479(7)	(F)	75.5	f162	22.23896(7)	0.047(2)	0.885(7)	21f0	11.7
f22	21.18030(1)	0.229(2)	0.779(2)	20f0	67.4	f216	44.4788(1)	0.036(2)	0.89(1)	42f0	10.1
f18	26.30896(1)	0.301(2)	0.895(1)	(G)	62.8	f123	33.88855(6)	0.060(2)	0.964(6)	32f0	9.5
f24	15.88524(2)	0.210(2)	0.256(2)	15f0	57.3	f134	30.06331(6)	0.055(2)	0.331(6)		9.3
f35	19.06228(2)	0.152(2)	0.969(2)	18f0	45.5	f157	36.00652(7)	0.048(2)	0.892(7)	34f0	8.8
f26	24.03637(2)	0.192(2)	0.937(2)	(I)	43.3	f202	24.35725(9)	0.039(2)	0.677(9)	23f0	8.6
f29	11.56305(2)	0.172(2)	0.622(2)	(K)	43.2	f37	0.04048(2)	0.141(2)	0.509(2)		8.5
f30	25.41650(2)	0.171(2)	0.594(2)	24f0	39.2	f238	23.2980(1)	0.033(2)	0.65(1)	22f0	8.4
f34	11.64914(2)	0.154(2)	0.217(2)	11f0	39.0	f42	0.06555(3)	0.133(2)	0.378(3)		8.1
f36	11.75876(2)	0.150(2)	0.554(2)	(M)	38.8	f147	33.47664(7)	0.051(2)	0.001(7)	(Z)	7.6
f32	26.10287(2)	0.157(2)	0.334(2)	(L)	32.9	f169	34.43309(8)	0.045(2)	0.973(8)	(A1)	7.4
f58	21.60050(3)	0.109(2)	0.963(3)	(Q)	31.0	f172	28.64426(8)	0.044(2)	0.722(8)	(X)	7.3
f51	11.57592(3)	0.120(2)	0.287(3)	(N)	30.0	f170	30.40788(8)	0.044(2)	0.040(8)	(Y)	7.3
f27	28.87629(2)	0.178(2)	0.869(2)	(J)	27.2	f213	26.47531(9)	0.037(2)	0.44(1)	25f0	7.2
f45	27.53504(3)	0.127(2)	0.768(3)	26f0	24.7	f167	31.80752(8)	0.045(2)	0.433(8)	(W)	6.6
f112	55.45850(5)	0.064(2)	0.241(5)	(T)	22.9	f103	0.98864(5)	0.067(2)	0.526(5)		6.4
f82	20.12128(4)	0.080(2)	0.402(4)	19f0	21.4	f190	31.77065(8)	0.041(2)	0.442(8)	30f0	6.1
f131	56.59172(6)	0.056(2)	0.841(6)	(V)	19.8	f214	31.29566(9)	0.037(2)	0.94(1)		5.8
f54	29.71071(3)	0.111(2)	0.305(3)	(O)	18.8	f233	30.7117(1)	0.034(2)	0.97(1)	29f0	5.7
f122	18.00321(6)	0.060(2)	0.176(6)	17f0	17.6	...	...	...	...	...	...
f229	15.2659(1)	0.035(2)	0.61(1)	f1 − 12f0(A)	10.6	f2	26.915225(3)	1.091(2)	0.2303(3)	f1 − f0(A)	215.1
f204	16.32499(9)	0.038(2)	0.925(9)	f1 − 11f0(A)	10.5	f14	29.033258(9)	0.366(2)	0.586(1)	f1 + f0(A)	56.1
f165	17.38415(7)	0.046(2)	0.080(8)	f1 − 10f0(A)	13.7	f25	30.09224(2)	0.195(2)	0.063(2)	f1 + 2f0(A)	32.7
f116	18.44321(5)	0.063(2)	0.407(6)	f1 − 9f0(A)	18.8	f59	32.21026(3)	0.108(2)	0.875(3)	f1 + 4f0(A)	15.6
f200	19.50197(9)	0.039(2)	0.320(9)	f1 − 8f0(A)	10.9	f232	33.2726(1)	0.034(2)	0.48(1)	f1 + 5f0(*A)	5.1
f230	22.6789(1)	0.034(2)	0.82(1)	f1 − 5f0(A)	9.1	f135	34.32855(6)	0.055(2)	0.141(6)	f1 + 6f0(A)	8.9
f3	24.797185(4)	0.941(2)	0.4841(4)	f1 − 3f0(A)	207.6	f227	35.3871(1)	0.035(2)	0.45(1)	f1 + 7f0(A)	6.0
f6	25.856212(5)	0.645(2)	0.3891(5)	f1 − 2f0(A)	138.0	...	...	...	...		...
f49	0.07436(3)	0.123(2)	0.933(3)	f4 − 21f0(*B)	7.4	f79	24.43500(4)	0.081(2)	0.506(4)	f4 + 2f0(B)	17.7
f72	0.07844(4)	0.096(2)	0.514(4)	f4 − 21f0(*B)	5.8	f205	25.49371(9)	0.038(2)	0.857(9)	f4 + 3f0(B)	8.8
f105	1.13806(5)	0.066(2)	0.728(5)	f4 − 20f0(B)	6.9	f38	26.55263(2)	0.140(2)	0.100(2)	f4 + 4f0(B)	27.7
f225	18.0804(1)	0.035(2)	0.52(1)	f4 − 4f0(B)	10.0	f154	27.61169(7)	0.049(2)	0.356(7)	f4 + 5f0(B)	9.6
f130	19.13988(6)	0.057(2)	0.711(6)	f4 − 3f0(B)	16.5	f144	28.67044(7)	0.051(2)	0.245(7)	f4 + 6f0(B)	8.4
f43	20.19862(3)	0.132(2)	0.034(3)	f4 − 2f0(B)	34.3	f114	29.72935(5)	0.064(2)	0.890(5)	f4 + 7f0(B)	10.7
f108	21.25741(5)	0.066(2)	0.972(5)	f4 − f0(B)	19.5	f171	30.78928(8)	0.044(2)	0.595(8)	f4 + 8f0(B)	7.1
f9	23.375774(7)	0.526(2)	0.4676(7)	f4 + f0(B)	130.3	...	...	...	...	...	...
f21	25.93035(1)	0.232(2)	0.783(2)	f5 − 3f0(C)	48.5	f121	31.22547(6)	0.061(2)	0.753(6)	f5 + 2f0(C)	9.8
f48	26.98936(3)	0.123(2)	0.210(3)	f5 − 2f0(C)	24.5	f239	32.2846(1)	0.033(2)	0.39(1)	f5 + 3f0(C)	4.7
f83	28.04861(4)	0.078(2)	0.178(4)	f5 − f0(C)	15.1	f106	33.34330(5)	0.066(2)	0.335(5)	f5 + 4f0(C)	10.0
f96	30.16661(5)	0.069(2)	0.186(5)	f5 + f0(C)	11.6	...	...	...	...	...	...
f97	0.08636(5)	0.069(2)	0.970(5)	f8 − 29f0(*D)	4.2	f137	31.85310(6)	0.053(2)	0.540(7)	f8 + f0(D)	7.6
f140	1.14352(7)	0.052(2)	0.848(7)	f8 − 28f0(*D)	5.5	f163	32.91206(7)	0.047(2)	0.608(7)	f8 + 2f0(D)	6.8
f236	19.1449(1)	0.033(2)	0.85(1)	f8 − 11f0(D)	9.7	f217	35.0303(1)	0.036(2)	0.55(1)	f8 + 4f0(D)	6.5
f203	21.26321(9)	0.039(2)	0.073(9)	f8 − 9f0(D)	11.4	f201	36.08921(9)	0.039(2)	0.612(9)	f8 + 5f0(D)	7.3
f101	24.44004(5)	0.068(2)	0.683(5)	f8 − 6f0(D)	15.0	f118	37.14834(5)	0.063(2)	0.802(6)	f8 + 6f0(D)	13.8
f102	25.49931(5)	0.067(2)	0.612(5)	f8 − 5f0(D)	15.4	f187	39.26644(8)	0.042(2)	0.452(8)	f8 + 8f0(D)	12.3
f235	26.5583(1)	0.033(2)	0.66(1)	f8 − 4f0(D)	6.7	f133	40.32528(6)	0.056(2)	0.194(6)	f8 + 9f0(D)	18.3
f153	27.61754(7)	0.050(2)	0.567(7)	f8 − 3f0(D)	9.8	f185	41.38441(8)	0.042(2)	0.381(8)	f8 + 10f0(D)	12.4
f113	28.67575(5)	0.064(2)	0.969(5)	f8 − 2f0(D)	10.4	f179	42.44345(8)	0.043(2)	0.725(8)	f8 + 11f0(D)	12.3
f196	29.73510(9)	0.040(2)	0.195(9)	f8 − f0(D)	6.8	f211	43.50254(9)	0.037(2)	0.989(9)	f8 + 12f0(D)	11.1
f191	23.24792(8)	0.041(2)	0.633(8)	f10 − 4f0(E)	10.4	f66	30.66126(3)	0.099(2)	0.369(4)	f10 + 3f0(E)	16.6
f150	25.36603(7)	0.050(2)	0.625(7)	f10 − 2f0(E)	11.3	f212	31.72054(9)	0.037(2)	0.805(9)	f10 + 4f0(E)	5.4
f19	26.42520(1)	0.279(2)	0.307(1)	f10 − f0(E)	56.6	f47	32.77935(3)	0.124(2)	0.578(3)	f10 + 5f0(E)	18.8
f12	28.543232(8)	0.427(2)	0.0837(8)	f10 + f0(E)	74.2	f104	33.83834(5)	0.067(2)	0.017(5)	f10 + 6f0(E)	10.2
f17	29.60227(1)	0.310(2)	0.848(1)	f10 + 2f0(E)	50.4	f132	34.89736(6)	0.056(2)	0.384(6)	f10 + 7f0(E)	10.2
f75	32.13288(4)	0.087(2)	0.936(4)	f11 + f0(F)	12.7	f15	33.191998(9)	0.361(2)	0.050(1)	f11 + 2f0(F)	53.5
f146	24.19078(7)	0.051(2)	0.364(7)	f18 − 2f0(G)	11.3	f111	28.42697(5)	0.065(2)	0.218(5)	f18 + 2f0(G)	11.5
f46	27.36798(3)	0.124(2)	0.694(3)	f18 + f0(G)	24.7	f151	30.54497(7)	0.050(2)	0.119(7)	f18 + 4f0(G)	8.5
f81	68.84752(4)	0.080(2)	0.285(4)	f20 + f0(H)	34.1	f164	65.67053(7)	0.046(2)	0.943(8)	f20 − 2f0(H)	17.7
f145	66.72936(7)	0.051(2)	0.701(7)	f20 − f0(H)	20.1	...	...	...	...	...	...
f249	18.7414(1)	0.032(2)	0.32(1)	f26 − 5f0(I)	9.8	f99	22.97738(5)	0.068(2)	0.889(5)	f26 − f0(I)	18.8
f39	20.85932(2)	0.138(2)	0.240(3)	f26 − 3f0(I)	36.9	f250	27.2132(1)	0.032(2)	0.06(1)	f26 + 3f0(I)	6.3
f53	21.91832(3)	0.115(2)	0.188(3)	f26 − 2f0(I)	29.4	...	...	...	...	...	...
f28	30.99440(2)	0.173(2)	0.054(2)	f27 + 2f0(J)	27.9	f143	32.05339(7)	0.052(2)	0.077(7)	f27 + 3f0(J)	7.6
f243	9.4450(1)	0.033(2)	0.03(1)	f29 − 2f0(K)	10.5	f74	12.62198(4)	0.089(2)	0.196(4)	f29 + f0(K)	23.5
f84	10.50387(4)	0.077(2)	0.517(5)	f29 − f0(K)	18.3	f199	13.68112(9)	0.039(2)	0.427(9)	f29 + 2f0(K)	11.0
f237	25.0438(1)	0.033(2)	0.40(1)	f32 − f0(L)	7.6	f128	30.33728(6)	0.058(2)	0.514(6)	f32 + 4f0(*L)	9.6
f100	28.22100(5)	0.068(2)	0.963(5)	f32 + 2f0(L)	12.1	...	...	...	...	...	...
f93	0.10969(5)	0.070(2)	0.235(5)	f41 − 10f0(M)	4.3	f155	13.87674(7)	0.049(2)	0.017(7)	f41 + 3f0(M)	13.7
f228	7.5228(1)	0.035(2)	0.27(1)	f41 − 3f0(M)	9.9	f221	20.2310(1)	0.035(2)	0.17(1)	f41 + 9f0(M)	9.1
f92	9.64067(5)	0.072(2)	0.950(5)	f41 − f0(M)	22.7	f138	31.87963(6)	0.053(2)	0.256(7)	f41 + 20f0(M)	7.6
f41	10.69986(3)	0.134(2)	0.981(3)	f36 − f0(M)	31.4	f124	33.99701(6)	0.060(2)	0.724(6)	f41 + 22f0(M)	9.6
f152	10.51686(7)	0.050(2)	0.971(7)	f50 − f0(N)	11.9	f126	12.63496(6)	0.059(2)	0.662(6)	f50 + f0(N)	15.5
f65	26.53372(3)	0.100(2)	0.036(3)	f54 − 3f0(O)	19.7	f251	31.8291(1)	0.032(2)	0.55(1)	f54 + 2f0(O)	4.6
f173	28.65174(8)	0.044(2)	0.848(8)	f54 − f0(O)	7.2	f85	32.88784(4)	0.077(2)	0.410(5)	f54 + 3f0(O)	11.2
f180	30.76958(8)	0.043(2)	0.024(8)	f54 + f0(O)	7.1	f186	33.94669(8)	0.042(2)	0.146(8)	f54 + 4f0(O)	6.7
f73	30.53026(4)	0.092(2)	0.393(4)	f54 − 2f0(P)	15.5	f125	31.58920(6)	0.059(2)	0.949(6)	f54 − f0(P)	8.9
f206	23.71868(9)	0.038(2)	0.066(9)	f58 + 2f0(Q)	8.8	f176	26.89501(8)	0.044(2)	0.564(8)	f58 + 5f0(Q)	8.6
f129	24.77760(6)	0.057(2)	0.933(6)	f58 + 3f0(Q)	12.7	f40	27.95460(3)	0.136(2)	0.868(3)	f58 + 6f0(Q)	27.2
f141	25.83667(7)	0.052(2)	0.889(7)	f58 + 4f0(Q)	11.4	...	...	...	...	...	...
f71	31.16577(4)	0.096(2)	0.519(4)	f64 − 2f0(R)	15.3	...	...	...	...	...	...
f207	27.93747(9)	0.038(2)	0.858(9)	f70 − 2f0(S)	7.6	f182	35.35117(8)	0.043(2)	0.924(8)	f70 + 5f0(S)	7.4
f220	32.1737(1)	0.035(2)	0.21(1)	f70 + 2f0(S)	5.0	...	...	...	...	...	...
f248	54.3994(1)	0.032(2)	0.06(1)	f112 − f0(T)	11.8	f183	56.51752(8)	0.042(2)	0.640(8)	f112 + f0(T)	14.4
f160	23.69492(7)	0.048(2)	0.243(7)	f127 − f0(U)	11.0	f177	26.87212(8)	0.043(2)	0.170(8)	f127 + 2f0(U)	8.5
f136	25.81283(6)	0.054(2)	0.720(7)	f127 + f0(U)	11.7	...	...	...	...	...	...
f158	58.70967(7)	0.048(2)	0.844(7)	f131 + 2f0(V)	13.9	f219	59.7687(1)	0.035(2)	0.28(1)	f131 + 3f0(V)	10.9
f197	30.74829(9)	0.040(2)	0.403(9)	f169 − f0(W)	6.7	f208	32.86651(9)	0.038(2)	0.881(9)	f169 + f0(W)	5.6
f246	29.7030(1)	0.033(2)	0.67(1)	f172 + f0(X)	5.5	f189	30.76239(8)	0.042(2)	0.322(8)	f172 + 2f0(X)	6.9
f244	28.2900(1)	0.033(2)	0.01(1)	f172 − 2f0(Y)	5.8	...	...	...	...	...	...
f226	35.5944(1)	0.035(2)	0.71(1)	f147 + 2f0(Z)	6.0	...	...	...	...	...	...
f181	33.37397(8)	0.043(2)	0.290(8)	f169 − f0(A1)	6.5	...	...	...	...	...	...
f119	24.04733(6)	0.062(2)	0.657(6)	f77 + 2f0(B1)	14.2	...	...	...	...	...	...
f55	0.11576(3)	0.110(2)	0.704(3)	2f54 − 56f0	6.7	f142	29.23290(7)	0.052(2)	0.936(7)	6f103 + 22f0	8.4
f23	61.58830(2)	0.214(2)	0.007(2)	2f8	67.9	f148	31.54531(7)	0.050(2)	0.789(7)	4f26 − 61f0	7.6
f31	59.33744(2)	0.160(2)	0.451(2)	3f11 − 32f0	46.7	f149	2.25075(7)	0.050(2)	0.753(7)	2f42 + 2f0	7.8
f33	31.07265(2)	0.155(2)	0.515(2)	≈f11(*F)	25.1	f156	27.48266(7)	0.049(2)	0.308(7)	≈f10	9.5
f50	0.06995(3)	0.120(2)	0.159(3)	5f37 − 2f42	7.2	f159	1.12725(7)	0.048(2)	0.918(7)	f42 + f0	4.9
f44	31.01335(3)	0.127(2)	0.489(3)	4f10 − 3f18	20.8	f161	1.10827(7)	0.047(2)	0.662(7)	27f0 − f10	4.9
f52	0.09073(3)	0.117(2)	0.853(3)	2f42 − f37	7.1	f166	22.31479(8)	0.046(2)	0.042(8)	≈f4	11.3
f57	0.05093(3)	0.109(2)	0.161(3)	26f0 − f10	6.6	f168	26.03155(8)	0.045(2)	0.975(8)	51f0 − f1	9.3
f60	0.03298(3)	0.104(2)	0.430(3)	55f0 − 2f5	6.3	f174	67.78675(8)	0.044(2)	0.893(8)	≈f20	17.8
f61	33.19053(3)	0.103(2)	0.111(3)	≈f15(*F)	15.3	f175	28.87392(8)	0.044(2)	0.549(8)	≈f27	6.7
f62	0.10357(3)	0.102(2)	0.766(3)	52f0 − 2f10	6.2	f178	28.85307(8)	0.043(2)	0.814(8)	3f1 − 52f0	6.6
f63	0.02784(3)	0.100(2)	0.349(3)	55f0 − 2f5	6.1	f184	29.14661(8)	0.042(2)	0.495(8)	f37 + f5	6.8
f67	0.13980(3)	0.099(2)	0.651(4)	4f42 − 3f37	6.1	f188	57.78346(8)	0.042(2)	0.790(8)	55f0 − 7f42	13.5
f68	0.15413(4)	0.098(2)	0.174(4)	2f4 − 42f0	6.1	f192	11.23338(8)	0.041(2)	0.448(8)	56f0 − 2f26	9.9
f69	0.22816(4)	0.097(2)	0.646(4)	3f4 − 63f0	6.3	f194	11.61045(8)	0.041(2)	0.785(9)	11f0 − f37	10.3
f78	33.32775(4)	0.081(2)	0.666(4)	7f54 − 6f5	12.1	f195	2.04757(8)	0.041(2)	0.914(9)	f103 + f0	6.1
f80	0.04427(4)	0.080(2)	0.090(4)	≈f37	4.8	f198	27.66546(9)	0.040(2)	0.509(9)	2f42 + 26f0	8.0
f86	0.12696(4)	0.077(2)	0.795(5)	2f42	4.7	f209	31.27830(9)	0.038(2)	0.117(9)	2f27 − 25f0	6.0
f87	57.08645(4)	0.076(2)	0.052(5)	2f10 + 2f0	25.0	f210	6.95971(9)	0.037(2)	0.673(9)	38f0 − f64	10.5
f88	0.06252(5)	0.075(2)	0.257(5)	≈f42	4.5	f215	33.33240(9)	0.036(2)	0.71(1)	7f54 − 6f5	5.5
f89	0.98433(5)	0.075(2)	0.320(5)	22f0 − f4	7.1	f218	29.4626(1)	0.035(2)	0.98(1)	2f103 + f10	5.8
f90	0.05287(5)	0.073(2)	0.197(5)	26f0 − f10	4.4	f222	58.2147(1)	0.035(2)	0.58(1)	2f5	11.2
f91	0.16382(5)	0.072(2)	0.153(5)	2f8 − 58f0	4.5	f223	61.7353(1)	0.035(2)	0.60(1)	4f4 − 26f0	10.8
f94	0.14492(5)	0.070(2)	0.120(5)	f42 + 2f37	4.4	f224	32.7563(1)	0.035(2)	0.43(1)	9f41 − 60f0	5.3
f95	0.21085(5)	0.070(2)	0.495(5)	2f42 + 2f37	4.5	f231	32.2188(1)	0.034(2)	0.62(1)	2f172 − 27f0	5.0
f98	0.14686(5)	0.069(2)	0.163(5)	63f0 − 2f64	4.3	f240	30.9908(1)	0.033(2)	0.02(1)	≈f28	5.4
f107	12.15524(5)	0.066(2)	0.315(5)	62f0 − 5f41	17.4	f241	35.3021(1)	0.033(2)	0.23(1)	10f103 + 24f0	5.8
f109	1.13352(5)	0.066(2)	0.824(5)	≈f105	6.8	f242	30.9376(1)	0.033(2)	0.40(1)	3f103 + f1	5.3
f110	0.13506(5)	0.065(2)	0.379(5)	2f42	4.0	f245	33.2555(1)	0.033(2)	0.67(1)	9f103 + 23f0	4.8
f115	29.00851(5)	0.063(2)	0.115(6)	2f26 − 18f0	9.7	f247	27.9768(1)	0.033(2)	0.23(1)	≈f1	6.4
f120	53.83040(6)	0.062(2)	0.072(6)	2f1 − 2f0	21.6	f252	59.4461(1)	0.032(2)	0.40(1)	58f0 − 2f103	9.5
f139	66.02716(7)	0.053(2)	0.559(7)	9f37 + 62f0	19.7	...	...	...	...	...	...

	Frequency	Amplitude	Phase	Combination	S/N		Frequency	Amplitude	Phase	Combination	S/N
	(d⁻¹)	(mmag)	(rad/2π)				(d⁻¹)	(mmag)	(rad/2π)
f1	27.974241(3)	1.203(2)	0.1837(3)	(A)	235.3	f117	13.76714(5)	0.063(2)	0.580(6)	13f0	17.5
f4	22.316723(4)	0.906(2)	0.6843(4)	(B)	224.8	f77	26.16552(4)	0.081(2)	0.162(4)	(B1)	17.0
f7	14.826233(6)	0.551(2)	0.8360(6)	14f0	161.2	f56	32.64831(3)	0.109(2)	0.149(3)	(P)	16.3
f5	29.107404(4)	0.868(2)	0.4022(4)	(C)	138.0	f70	30.05512(4)	0.097(2)	0.363(4)	(S)	16.2
f13	16.944260(9)	0.381(2)	0.6427(9)	16f0	110.5	f64	33.28395(3)	0.100(2)	0.544(3)	(R)	14.9
f20	67.78847(1)	0.263(2)	0.417(1)	(H)	107.2	f76	29.65243(4)	0.086(2)	0.028(4)	28f0	14.2
f10	27.484214(7)	0.490(2)	0.6844(7)	(E)	95.4	f193	40.24269(8)	0.041(2)	0.809(8)	38f0	13.1
f8	30.794131(6)	0.530(2)	0.0346(7)	(D)	85.9	f127	24.75387(6)	0.059(2)	0.803(6)	(U)	12.9
f16	12.70816(1)	0.323(2)	0.610(1)	12f0	84.6	f234	64.0604(1)	0.033(2)	0.97(1)		11.7
f11	31.073961(7)	0.466(2)	0.7479(7)	(F)	75.5	f162	22.23896(7)	0.047(2)	0.885(7)	21f0	11.7
f22	21.18030(1)	0.229(2)	0.779(2)	20f0	67.4	f216	44.4788(1)	0.036(2)	0.89(1)	42f0	10.1
f18	26.30896(1)	0.301(2)	0.895(1)	(G)	62.8	f123	33.88855(6)	0.060(2)	0.964(6)	32f0	9.5
f24	15.88524(2)	0.210(2)	0.256(2)	15f0	57.3	f134	30.06331(6)	0.055(2)	0.331(6)		9.3
f35	19.06228(2)	0.152(2)	0.969(2)	18f0	45.5	f157	36.00652(7)	0.048(2)	0.892(7)	34f0	8.8
f26	24.03637(2)	0.192(2)	0.937(2)	(I)	43.3	f202	24.35725(9)	0.039(2)	0.677(9)	23f0	8.6
f29	11.56305(2)	0.172(2)	0.622(2)	(K)	43.2	f37	0.04048(2)	0.141(2)	0.509(2)		8.5
f30	25.41650(2)	0.171(2)	0.594(2)	24f0	39.2	f238	23.2980(1)	0.033(2)	0.65(1)	22f0	8.4
f34	11.64914(2)	0.154(2)	0.217(2)	11f0	39.0	f42	0.06555(3)	0.133(2)	0.378(3)		8.1
f36	11.75876(2)	0.150(2)	0.554(2)	(M)	38.8	f147	33.47664(7)	0.051(2)	0.001(7)	(Z)	7.6
f32	26.10287(2)	0.157(2)	0.334(2)	(L)	32.9	f169	34.43309(8)	0.045(2)	0.973(8)	(A1)	7.4
f58	21.60050(3)	0.109(2)	0.963(3)	(Q)	31.0	f172	28.64426(8)	0.044(2)	0.722(8)	(X)	7.3
f51	11.57592(3)	0.120(2)	0.287(3)	(N)	30.0	f170	30.40788(8)	0.044(2)	0.040(8)	(Y)	7.3
f27	28.87629(2)	0.178(2)	0.869(2)	(J)	27.2	f213	26.47531(9)	0.037(2)	0.44(1)	25f0	7.2
f45	27.53504(3)	0.127(2)	0.768(3)	26f0	24.7	f167	31.80752(8)	0.045(2)	0.433(8)	(W)	6.6
f112	55.45850(5)	0.064(2)	0.241(5)	(T)	22.9	f103	0.98864(5)	0.067(2)	0.526(5)		6.4
f82	20.12128(4)	0.080(2)	0.402(4)	19f0	21.4	f190	31.77065(8)	0.041(2)	0.442(8)	30f0	6.1
f131	56.59172(6)	0.056(2)	0.841(6)	(V)	19.8	f214	31.29566(9)	0.037(2)	0.94(1)		5.8
f54	29.71071(3)	0.111(2)	0.305(3)	(O)	18.8	f233	30.7117(1)	0.034(2)	0.97(1)	29f0	5.7
f122	18.00321(6)	0.060(2)	0.176(6)	17f0	17.6	...	...	...	...	...	...
f229	15.2659(1)	0.035(2)	0.61(1)	f1 − 12f0(A)	10.6	f2	26.915225(3)	1.091(2)	0.2303(3)	f1 − f0(A)	215.1
f204	16.32499(9)	0.038(2)	0.925(9)	f1 − 11f0(A)	10.5	f14	29.033258(9)	0.366(2)	0.586(1)	f1 + f0(A)	56.1
f165	17.38415(7)	0.046(2)	0.080(8)	f1 − 10f0(A)	13.7	f25	30.09224(2)	0.195(2)	0.063(2)	f1 + 2f0(A)	32.7
f116	18.44321(5)	0.063(2)	0.407(6)	f1 − 9f0(A)	18.8	f59	32.21026(3)	0.108(2)	0.875(3)	f1 + 4f0(A)	15.6
f200	19.50197(9)	0.039(2)	0.320(9)	f1 − 8f0(A)	10.9	f232	33.2726(1)	0.034(2)	0.48(1)	f1 + 5f0(*A)	5.1
f230	22.6789(1)	0.034(2)	0.82(1)	f1 − 5f0(A)	9.1	f135	34.32855(6)	0.055(2)	0.141(6)	f1 + 6f0(A)	8.9
f3	24.797185(4)	0.941(2)	0.4841(4)	f1 − 3f0(A)	207.6	f227	35.3871(1)	0.035(2)	0.45(1)	f1 + 7f0(A)	6.0
f6	25.856212(5)	0.645(2)	0.3891(5)	f1 − 2f0(A)	138.0	...	...	...	...		...
f49	0.07436(3)	0.123(2)	0.933(3)	f4 − 21f0(*B)	7.4	f79	24.43500(4)	0.081(2)	0.506(4)	f4 + 2f0(B)	17.7
f72	0.07844(4)	0.096(2)	0.514(4)	f4 − 21f0(*B)	5.8	f205	25.49371(9)	0.038(2)	0.857(9)	f4 + 3f0(B)	8.8
f105	1.13806(5)	0.066(2)	0.728(5)	f4 − 20f0(B)	6.9	f38	26.55263(2)	0.140(2)	0.100(2)	f4 + 4f0(B)	27.7
f225	18.0804(1)	0.035(2)	0.52(1)	f4 − 4f0(B)	10.0	f154	27.61169(7)	0.049(2)	0.356(7)	f4 + 5f0(B)	9.6
f130	19.13988(6)	0.057(2)	0.711(6)	f4 − 3f0(B)	16.5	f144	28.67044(7)	0.051(2)	0.245(7)	f4 + 6f0(B)	8.4
f43	20.19862(3)	0.132(2)	0.034(3)	f4 − 2f0(B)	34.3	f114	29.72935(5)	0.064(2)	0.890(5)	f4 + 7f0(B)	10.7
f108	21.25741(5)	0.066(2)	0.972(5)	f4 − f0(B)	19.5	f171	30.78928(8)	0.044(2)	0.595(8)	f4 + 8f0(B)	7.1
f9	23.375774(7)	0.526(2)	0.4676(7)	f4 + f0(B)	130.3	...	...	...	...	...	...
f21	25.93035(1)	0.232(2)	0.783(2)	f5 − 3f0(C)	48.5	f121	31.22547(6)	0.061(2)	0.753(6)	f5 + 2f0(C)	9.8
f48	26.98936(3)	0.123(2)	0.210(3)	f5 − 2f0(C)	24.5	f239	32.2846(1)	0.033(2)	0.39(1)	f5 + 3f0(C)	4.7
f83	28.04861(4)	0.078(2)	0.178(4)	f5 − f0(C)	15.1	f106	33.34330(5)	0.066(2)	0.335(5)	f5 + 4f0(C)	10.0
f96	30.16661(5)	0.069(2)	0.186(5)	f5 + f0(C)	11.6	...	...	...	...	...	...
f97	0.08636(5)	0.069(2)	0.970(5)	f8 − 29f0(*D)	4.2	f137	31.85310(6)	0.053(2)	0.540(7)	f8 + f0(D)	7.6
f140	1.14352(7)	0.052(2)	0.848(7)	f8 − 28f0(*D)	5.5	f163	32.91206(7)	0.047(2)	0.608(7)	f8 + 2f0(D)	6.8
f236	19.1449(1)	0.033(2)	0.85(1)	f8 − 11f0(D)	9.7	f217	35.0303(1)	0.036(2)	0.55(1)	f8 + 4f0(D)	6.5
f203	21.26321(9)	0.039(2)	0.073(9)	f8 − 9f0(D)	11.4	f201	36.08921(9)	0.039(2)	0.612(9)	f8 + 5f0(D)	7.3
f101	24.44004(5)	0.068(2)	0.683(5)	f8 − 6f0(D)	15.0	f118	37.14834(5)	0.063(2)	0.802(6)	f8 + 6f0(D)	13.8
f102	25.49931(5)	0.067(2)	0.612(5)	f8 − 5f0(D)	15.4	f187	39.26644(8)	0.042(2)	0.452(8)	f8 + 8f0(D)	12.3
f235	26.5583(1)	0.033(2)	0.66(1)	f8 − 4f0(D)	6.7	f133	40.32528(6)	0.056(2)	0.194(6)	f8 + 9f0(D)	18.3
f153	27.61754(7)	0.050(2)	0.567(7)	f8 − 3f0(D)	9.8	f185	41.38441(8)	0.042(2)	0.381(8)	f8 + 10f0(D)	12.4
f113	28.67575(5)	0.064(2)	0.969(5)	f8 − 2f0(D)	10.4	f179	42.44345(8)	0.043(2)	0.725(8)	f8 + 11f0(D)	12.3
f196	29.73510(9)	0.040(2)	0.195(9)	f8 − f0(D)	6.8	f211	43.50254(9)	0.037(2)	0.989(9)	f8 + 12f0(D)	11.1
f191	23.24792(8)	0.041(2)	0.633(8)	f10 − 4f0(E)	10.4	f66	30.66126(3)	0.099(2)	0.369(4)	f10 + 3f0(E)	16.6
f150	25.36603(7)	0.050(2)	0.625(7)	f10 − 2f0(E)	11.3	f212	31.72054(9)	0.037(2)	0.805(9)	f10 + 4f0(E)	5.4
f19	26.42520(1)	0.279(2)	0.307(1)	f10 − f0(E)	56.6	f47	32.77935(3)	0.124(2)	0.578(3)	f10 + 5f0(E)	18.8
f12	28.543232(8)	0.427(2)	0.0837(8)	f10 + f0(E)	74.2	f104	33.83834(5)	0.067(2)	0.017(5)	f10 + 6f0(E)	10.2
f17	29.60227(1)	0.310(2)	0.848(1)	f10 + 2f0(E)	50.4	f132	34.89736(6)	0.056(2)	0.384(6)	f10 + 7f0(E)	10.2
f75	32.13288(4)	0.087(2)	0.936(4)	f11 + f0(F)	12.7	f15	33.191998(9)	0.361(2)	0.050(1)	f11 + 2f0(F)	53.5
f146	24.19078(7)	0.051(2)	0.364(7)	f18 − 2f0(G)	11.3	f111	28.42697(5)	0.065(2)	0.218(5)	f18 + 2f0(G)	11.5
f46	27.36798(3)	0.124(2)	0.694(3)	f18 + f0(G)	24.7	f151	30.54497(7)	0.050(2)	0.119(7)	f18 + 4f0(G)	8.5
f81	68.84752(4)	0.080(2)	0.285(4)	f20 + f0(H)	34.1	f164	65.67053(7)	0.046(2)	0.943(8)	f20 − 2f0(H)	17.7
f145	66.72936(7)	0.051(2)	0.701(7)	f20 − f0(H)	20.1	...	...	...	...	...	...
f249	18.7414(1)	0.032(2)	0.32(1)	f26 − 5f0(I)	9.8	f99	22.97738(5)	0.068(2)	0.889(5)	f26 − f0(I)	18.8
f39	20.85932(2)	0.138(2)	0.240(3)	f26 − 3f0(I)	36.9	f250	27.2132(1)	0.032(2)	0.06(1)	f26 + 3f0(I)	6.3
f53	21.91832(3)	0.115(2)	0.188(3)	f26 − 2f0(I)	29.4	...	...	...	...	...	...
f28	30.99440(2)	0.173(2)	0.054(2)	f27 + 2f0(J)	27.9	f143	32.05339(7)	0.052(2)	0.077(7)	f27 + 3f0(J)	7.6
f243	9.4450(1)	0.033(2)	0.03(1)	f29 − 2f0(K)	10.5	f74	12.62198(4)	0.089(2)	0.196(4)	f29 + f0(K)	23.5
f84	10.50387(4)	0.077(2)	0.517(5)	f29 − f0(K)	18.3	f199	13.68112(9)	0.039(2)	0.427(9)	f29 + 2f0(K)	11.0
f237	25.0438(1)	0.033(2)	0.40(1)	f32 − f0(L)	7.6	f128	30.33728(6)	0.058(2)	0.514(6)	f32 + 4f0(*L)	9.6
f100	28.22100(5)	0.068(2)	0.963(5)	f32 + 2f0(L)	12.1	...	...	...	...	...	...
f93	0.10969(5)	0.070(2)	0.235(5)	f41 − 10f0(M)	4.3	f155	13.87674(7)	0.049(2)	0.017(7)	f41 + 3f0(M)	13.7
f228	7.5228(1)	0.035(2)	0.27(1)	f41 − 3f0(M)	9.9	f221	20.2310(1)	0.035(2)	0.17(1)	f41 + 9f0(M)	9.1
f92	9.64067(5)	0.072(2)	0.950(5)	f41 − f0(M)	22.7	f138	31.87963(6)	0.053(2)	0.256(7)	f41 + 20f0(M)	7.6
f41	10.69986(3)	0.134(2)	0.981(3)	f36 − f0(M)	31.4	f124	33.99701(6)	0.060(2)	0.724(6)	f41 + 22f0(M)	9.6
f152	10.51686(7)	0.050(2)	0.971(7)	f50 − f0(N)	11.9	f126	12.63496(6)	0.059(2)	0.662(6)	f50 + f0(N)	15.5
f65	26.53372(3)	0.100(2)	0.036(3)	f54 − 3f0(O)	19.7	f251	31.8291(1)	0.032(2)	0.55(1)	f54 + 2f0(O)	4.6
f173	28.65174(8)	0.044(2)	0.848(8)	f54 − f0(O)	7.2	f85	32.88784(4)	0.077(2)	0.410(5)	f54 + 3f0(O)	11.2
f180	30.76958(8)	0.043(2)	0.024(8)	f54 + f0(O)	7.1	f186	33.94669(8)	0.042(2)	0.146(8)	f54 + 4f0(O)	6.7
f73	30.53026(4)	0.092(2)	0.393(4)	f54 − 2f0(P)	15.5	f125	31.58920(6)	0.059(2)	0.949(6)	f54 − f0(P)	8.9
f206	23.71868(9)	0.038(2)	0.066(9)	f58 + 2f0(Q)	8.8	f176	26.89501(8)	0.044(2)	0.564(8)	f58 + 5f0(Q)	8.6
f129	24.77760(6)	0.057(2)	0.933(6)	f58 + 3f0(Q)	12.7	f40	27.95460(3)	0.136(2)	0.868(3)	f58 + 6f0(Q)	27.2
f141	25.83667(7)	0.052(2)	0.889(7)	f58 + 4f0(Q)	11.4	...	...	...	...	...	...
f71	31.16577(4)	0.096(2)	0.519(4)	f64 − 2f0(R)	15.3	...	...	...	...	...	...
f207	27.93747(9)	0.038(2)	0.858(9)	f70 − 2f0(S)	7.6	f182	35.35117(8)	0.043(2)	0.924(8)	f70 + 5f0(S)	7.4
f220	32.1737(1)	0.035(2)	0.21(1)	f70 + 2f0(S)	5.0	...	...	...	...	...	...
f248	54.3994(1)	0.032(2)	0.06(1)	f112 − f0(T)	11.8	f183	56.51752(8)	0.042(2)	0.640(8)	f112 + f0(T)	14.4
f160	23.69492(7)	0.048(2)	0.243(7)	f127 − f0(U)	11.0	f177	26.87212(8)	0.043(2)	0.170(8)	f127 + 2f0(U)	8.5
f136	25.81283(6)	0.054(2)	0.720(7)	f127 + f0(U)	11.7	...	...	...	...	...	...
f158	58.70967(7)	0.048(2)	0.844(7)	f131 + 2f0(V)	13.9	f219	59.7687(1)	0.035(2)	0.28(1)	f131 + 3f0(V)	10.9
f197	30.74829(9)	0.040(2)	0.403(9)	f169 − f0(W)	6.7	f208	32.86651(9)	0.038(2)	0.881(9)	f169 + f0(W)	5.6
f246	29.7030(1)	0.033(2)	0.67(1)	f172 + f0(X)	5.5	f189	30.76239(8)	0.042(2)	0.322(8)	f172 + 2f0(X)	6.9
f244	28.2900(1)	0.033(2)	0.01(1)	f172 − 2f0(Y)	5.8	...	...	...	...	...	...
f226	35.5944(1)	0.035(2)	0.71(1)	f147 + 2f0(Z)	6.0	...	...	...	...	...	...
f181	33.37397(8)	0.043(2)	0.290(8)	f169 − f0(A1)	6.5	...	...	...	...	...	...
f119	24.04733(6)	0.062(2)	0.657(6)	f77 + 2f0(B1)	14.2	...	...	...	...	...	...
f55	0.11576(3)	0.110(2)	0.704(3)	2f54 − 56f0	6.7	f142	29.23290(7)	0.052(2)	0.936(7)	6f103 + 22f0	8.4
f23	61.58830(2)	0.214(2)	0.007(2)	2f8	67.9	f148	31.54531(7)	0.050(2)	0.789(7)	4f26 − 61f0	7.6
f31	59.33744(2)	0.160(2)	0.451(2)	3f11 − 32f0	46.7	f149	2.25075(7)	0.050(2)	0.753(7)	2f42 + 2f0	7.8
f33	31.07265(2)	0.155(2)	0.515(2)	≈f11(*F)	25.1	f156	27.48266(7)	0.049(2)	0.308(7)	≈f10	9.5
f50	0.06995(3)	0.120(2)	0.159(3)	5f37 − 2f42	7.2	f159	1.12725(7)	0.048(2)	0.918(7)	f42 + f0	4.9
f44	31.01335(3)	0.127(2)	0.489(3)	4f10 − 3f18	20.8	f161	1.10827(7)	0.047(2)	0.662(7)	27f0 − f10	4.9
f52	0.09073(3)	0.117(2)	0.853(3)	2f42 − f37	7.1	f166	22.31479(8)	0.046(2)	0.042(8)	≈f4	11.3
f57	0.05093(3)	0.109(2)	0.161(3)	26f0 − f10	6.6	f168	26.03155(8)	0.045(2)	0.975(8)	51f0 − f1	9.3
f60	0.03298(3)	0.104(2)	0.430(3)	55f0 − 2f5	6.3	f174	67.78675(8)	0.044(2)	0.893(8)	≈f20	17.8
f61	33.19053(3)	0.103(2)	0.111(3)	≈f15(*F)	15.3	f175	28.87392(8)	0.044(2)	0.549(8)	≈f27	6.7
f62	0.10357(3)	0.102(2)	0.766(3)	52f0 − 2f10	6.2	f178	28.85307(8)	0.043(2)	0.814(8)	3f1 − 52f0	6.6
f63	0.02784(3)	0.100(2)	0.349(3)	55f0 − 2f5	6.1	f184	29.14661(8)	0.042(2)	0.495(8)	f37 + f5	6.8
f67	0.13980(3)	0.099(2)	0.651(4)	4f42 − 3f37	6.1	f188	57.78346(8)	0.042(2)	0.790(8)	55f0 − 7f42	13.5
f68	0.15413(4)	0.098(2)	0.174(4)	2f4 − 42f0	6.1	f192	11.23338(8)	0.041(2)	0.448(8)	56f0 − 2f26	9.9
f69	0.22816(4)	0.097(2)	0.646(4)	3f4 − 63f0	6.3	f194	11.61045(8)	0.041(2)	0.785(9)	11f0 − f37	10.3
f78	33.32775(4)	0.081(2)	0.666(4)	7f54 − 6f5	12.1	f195	2.04757(8)	0.041(2)	0.914(9)	f103 + f0	6.1
f80	0.04427(4)	0.080(2)	0.090(4)	≈f37	4.8	f198	27.66546(9)	0.040(2)	0.509(9)	2f42 + 26f0	8.0
f86	0.12696(4)	0.077(2)	0.795(5)	2f42	4.7	f209	31.27830(9)	0.038(2)	0.117(9)	2f27 − 25f0	6.0
f87	57.08645(4)	0.076(2)	0.052(5)	2f10 + 2f0	25.0	f210	6.95971(9)	0.037(2)	0.673(9)	38f0 − f64	10.5
f88	0.06252(5)	0.075(2)	0.257(5)	≈f42	4.5	f215	33.33240(9)	0.036(2)	0.71(1)	7f54 − 6f5	5.5
f89	0.98433(5)	0.075(2)	0.320(5)	22f0 − f4	7.1	f218	29.4626(1)	0.035(2)	0.98(1)	2f103 + f10	5.8
f90	0.05287(5)	0.073(2)	0.197(5)	26f0 − f10	4.4	f222	58.2147(1)	0.035(2)	0.58(1)	2f5	11.2
f91	0.16382(5)	0.072(2)	0.153(5)	2f8 − 58f0	4.5	f223	61.7353(1)	0.035(2)	0.60(1)	4f4 − 26f0	10.8
f94	0.14492(5)	0.070(2)	0.120(5)	f42 + 2f37	4.4	f224	32.7563(1)	0.035(2)	0.43(1)	9f41 − 60f0	5.3
f95	0.21085(5)	0.070(2)	0.495(5)	2f42 + 2f37	4.5	f231	32.2188(1)	0.034(2)	0.62(1)	2f172 − 27f0	5.0
f98	0.14686(5)	0.069(2)	0.163(5)	63f0 − 2f64	4.3	f240	30.9908(1)	0.033(2)	0.02(1)	≈f28	5.4
f107	12.15524(5)	0.066(2)	0.315(5)	62f0 − 5f41	17.4	f241	35.3021(1)	0.033(2)	0.23(1)	10f103 + 24f0	5.8
f109	1.13352(5)	0.066(2)	0.824(5)	≈f105	6.8	f242	30.9376(1)	0.033(2)	0.40(1)	3f103 + f1	5.3
f110	0.13506(5)	0.065(2)	0.379(5)	2f42	4.0	f245	33.2555(1)	0.033(2)	0.67(1)	9f103 + 23f0	4.8
f115	29.00851(5)	0.063(2)	0.115(6)	2f26 − 18f0	9.7	f247	27.9768(1)	0.033(2)	0.23(1)	≈f1	6.4
f120	53.83040(6)	0.062(2)	0.072(6)	2f1 − 2f0	21.6	f252	59.4461(1)	0.032(2)	0.40(1)	58f0 − 2f103	9.5
f139	66.02716(7)	0.053(2)	0.559(7)	9f37 + 62f0	19.7	...	...	...	...	...	...

To further study the variation of pulsation amplitude with orbital motion, we fit the amplitude of each pulsating frequency to a subset of the pulsation light curve, where the orbital phase is divided into 100 subsets, with about 2000 data points each. The relationships between the amplitude variations of pulsating frequency and the orbital phases (AMP-PH) are displayed in Fig. 10. After checking every frequency, we find that the AMP-PH diagram of subfrequency in each multiplet has almost the same trend. For the multiplet A (f1, f2, f3, f6, ...), the AMP-PH diagram of three frequencies shows a similar variation in the top-left panel of Fig. 10, and the other panels are the same but for other multiplets. Combining the AMP-PH diagram and the calculation of the combination frequency, we have identified a total of 28 multiplets and we mark these with the capital letters from A to Z in Table 1 and A1 and B1 in Table 3.

Figure 10.

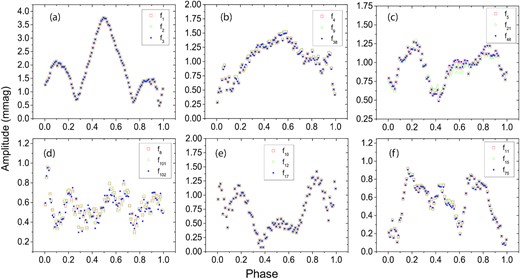
The diagram of the amplitude variations of pulsating frequency and the orbital phases (the AMP-PH diagram). Each panel shows three frequencies of a multiplet.

Open in new tab Download slide

In Fig. 11, we show the echelle diagram of all frequencies above 3 d⁻¹ versus they modulo the orbital frequency f0 = 1.0590124 d⁻¹. We can clearly see that there are 28 sets of multiple frequencies split by orbital frequency. These are the multiplets of tidally split frequencies, similar to KIC 9851944 (Guo et al. 2016), KIC 6048106 (Samadi Ghadim, Lampens & Jassur 2018a) and U Gru (Bowman et al. 2019).

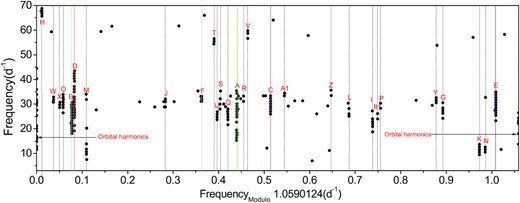
Echelle diagram of all frequencies above 3 d−1 versus they modulo the orbital frequency. The coloured solid lines are the same as those in the bottom panel of Fig. 9.

Figure 11.

Echelle diagram of all frequencies above 3 d⁻¹ versus they modulo the orbital frequency. The coloured solid lines are the same as those in the bottom panel of Fig. 9.

Open in new tab Download slide

In Table 3, f37, f42, f103 and f214, with a frequency lower than f0 = 1.0590124 d⁻¹, may be caused by the residual O’Connell effect or detrend. We surmise that f134 and f234 may also be in a multiplet, but others with lower amplitudes are not identified. So, we calculate the pulsation constant Q for the most prominent frequency of each multiplet, f134 and f234, using the basic relation for pulsating stars:

$$\begin{eqnarray*} Q=P_{\rm osc} \sqrt{\bar{\rho }/\bar{\rho }_{\odot }}. \end{eqnarray*}$$

(7)

Here, P_osc is the oscillation period and the mean density is |$\bar{\rho }= 0.1643\,(\pm 0.0025)\rho _{\odot }$|⁠. We compare the Q value of each frequency with the theoretical models (Fitch 1981) for |$M = 2.5 \, \mathrm{M}_{\odot }$|⁠. Table 4 lists the probable l-degrees and the type of each frequency, except for f20, f112, f131 and f234. We tentatively identify two radial modes f1 and f26, 21 non-radial p-modes and three non-radial f-modes. The value of Q for f20, f112, f131 and f234 is less than 0.01, which is beyond the range given by Fitch (1981).

Table 4.

Open in new tab

Independent oscillation frequencies for the pulsating component. The errors are given in parentheses alongside values and correspond to the last digit(s). R denotes radial pulsation and NR denotes non-radial pulsation.

	Frequency	Label	Q	l-degree	Mode
	(d⁻¹)		(d)
f1	27.974241(3)	(A)	0.01449(37)	0	R 4H
f4	22.316723(4)	(B)	0.01817(42)	1	NR p3
f5	29.107404(4)	(C)	0.01393(36)	3	NR p4
f8	30.794131(6)	(D)	0.01316(35)	1	NR p5
f10	27.484214(7)	(E)	0.01475(37)	2	NR p4
f11	31.073961(7)	(F)	0.01305(35)	2	NR p5
f18	26.30896(1)	(G)	0.01541(38)	1	NR p4
f20	67.78847(1)	(H)	0.00598(24)
f26	24.03637(2)	(I)	0.01687(40)	0	R 3H
f27	28.87629(2)	(J)	0.01404(37)	3	NR p4
f29	11.56305(2)	(K)	0.03506(58)	2	NR f
f32	26.10287(2)	(L)	0.01553(38)	1	NR p4
f36	11.75876(2)	(M)	0.03448(57)	3	NR f
f51	11.57592(3)	(N)	0.03502(58)	2	NR f
f54	29.71071(3)	(O)	0.01364(36)	1	NR p5
f56	32.64831(3)	(P)	0.01242(34)	3	NR p5
f58	21.60050(3)	(Q)	0.01877(42)	1	NR p3
f64	33.28395(3)	(R)	0.01218(34)	3	NR p5
f70	30.05512(4)	(S)	0.01349(36)	1	NR p5
f112	55.45850(5)	(T)	0.00731(26)
f127	24.75387(6)	(U)	0.01638(39)	3	NR p3
f131	56.59172(6)	(V)	0.00716(26)
f167	31.80752(8)	(W)	0.01275(35)	2	NR p5
f172	28.64426(8)	(X)	0.01415(37)	3	NR p4
f170	30.40788(8)	(Y)	0.01333(36)	1	NR p5
f147	33.47664(7)	(Z)	0.01211(34)	3	NR p5
f169	34.43309(8)	(A1)	0.01177(33)	1	NR p6
f77	26.16552(4)	(B1)	0.01549(38)	1	NR p4
f234	64.0604(1)		0.00633(25)
f134	30.06331(6)		0.01348(36)	1	NR p5

	Frequency	Label	Q	l-degree	Mode
	(d⁻¹)		(d)
f1	27.974241(3)	(A)	0.01449(37)	0	R 4H
f4	22.316723(4)	(B)	0.01817(42)	1	NR p3
f5	29.107404(4)	(C)	0.01393(36)	3	NR p4
f8	30.794131(6)	(D)	0.01316(35)	1	NR p5
f10	27.484214(7)	(E)	0.01475(37)	2	NR p4
f11	31.073961(7)	(F)	0.01305(35)	2	NR p5
f18	26.30896(1)	(G)	0.01541(38)	1	NR p4
f20	67.78847(1)	(H)	0.00598(24)
f26	24.03637(2)	(I)	0.01687(40)	0	R 3H
f27	28.87629(2)	(J)	0.01404(37)	3	NR p4
f29	11.56305(2)	(K)	0.03506(58)	2	NR f
f32	26.10287(2)	(L)	0.01553(38)	1	NR p4
f36	11.75876(2)	(M)	0.03448(57)	3	NR f
f51	11.57592(3)	(N)	0.03502(58)	2	NR f
f54	29.71071(3)	(O)	0.01364(36)	1	NR p5
f56	32.64831(3)	(P)	0.01242(34)	3	NR p5
f58	21.60050(3)	(Q)	0.01877(42)	1	NR p3
f64	33.28395(3)	(R)	0.01218(34)	3	NR p5
f70	30.05512(4)	(S)	0.01349(36)	1	NR p5
f112	55.45850(5)	(T)	0.00731(26)
f127	24.75387(6)	(U)	0.01638(39)	3	NR p3
f131	56.59172(6)	(V)	0.00716(26)
f167	31.80752(8)	(W)	0.01275(35)	2	NR p5
f172	28.64426(8)	(X)	0.01415(37)	3	NR p4
f170	30.40788(8)	(Y)	0.01333(36)	1	NR p5
f147	33.47664(7)	(Z)	0.01211(34)	3	NR p5
f169	34.43309(8)	(A1)	0.01177(33)	1	NR p6
f77	26.16552(4)	(B1)	0.01549(38)	1	NR p4
f234	64.0604(1)		0.00633(25)
f134	30.06331(6)		0.01348(36)	1	NR p5

Table 4.

Open in new tab

	Frequency	Label	Q	l-degree	Mode
	(d⁻¹)		(d)
f1	27.974241(3)	(A)	0.01449(37)	0	R 4H
f4	22.316723(4)	(B)	0.01817(42)	1	NR p3
f5	29.107404(4)	(C)	0.01393(36)	3	NR p4
f8	30.794131(6)	(D)	0.01316(35)	1	NR p5
f10	27.484214(7)	(E)	0.01475(37)	2	NR p4
f11	31.073961(7)	(F)	0.01305(35)	2	NR p5
f18	26.30896(1)	(G)	0.01541(38)	1	NR p4
f20	67.78847(1)	(H)	0.00598(24)
f26	24.03637(2)	(I)	0.01687(40)	0	R 3H
f27	28.87629(2)	(J)	0.01404(37)	3	NR p4
f29	11.56305(2)	(K)	0.03506(58)	2	NR f
f32	26.10287(2)	(L)	0.01553(38)	1	NR p4
f36	11.75876(2)	(M)	0.03448(57)	3	NR f
f51	11.57592(3)	(N)	0.03502(58)	2	NR f
f54	29.71071(3)	(O)	0.01364(36)	1	NR p5
f56	32.64831(3)	(P)	0.01242(34)	3	NR p5
f58	21.60050(3)	(Q)	0.01877(42)	1	NR p3
f64	33.28395(3)	(R)	0.01218(34)	3	NR p5
f70	30.05512(4)	(S)	0.01349(36)	1	NR p5
f112	55.45850(5)	(T)	0.00731(26)
f127	24.75387(6)	(U)	0.01638(39)	3	NR p3
f131	56.59172(6)	(V)	0.00716(26)
f167	31.80752(8)	(W)	0.01275(35)	2	NR p5
f172	28.64426(8)	(X)	0.01415(37)	3	NR p4
f170	30.40788(8)	(Y)	0.01333(36)	1	NR p5
f147	33.47664(7)	(Z)	0.01211(34)	3	NR p5
f169	34.43309(8)	(A1)	0.01177(33)	1	NR p6
f77	26.16552(4)	(B1)	0.01549(38)	1	NR p4
f234	64.0604(1)		0.00633(25)
f134	30.06331(6)		0.01348(36)	1	NR p5

	Frequency	Label	Q	l-degree	Mode
	(d⁻¹)		(d)
f1	27.974241(3)	(A)	0.01449(37)	0	R 4H
f4	22.316723(4)	(B)	0.01817(42)	1	NR p3
f5	29.107404(4)	(C)	0.01393(36)	3	NR p4
f8	30.794131(6)	(D)	0.01316(35)	1	NR p5
f10	27.484214(7)	(E)	0.01475(37)	2	NR p4
f11	31.073961(7)	(F)	0.01305(35)	2	NR p5
f18	26.30896(1)	(G)	0.01541(38)	1	NR p4
f20	67.78847(1)	(H)	0.00598(24)
f26	24.03637(2)	(I)	0.01687(40)	0	R 3H
f27	28.87629(2)	(J)	0.01404(37)	3	NR p4
f29	11.56305(2)	(K)	0.03506(58)	2	NR f
f32	26.10287(2)	(L)	0.01553(38)	1	NR p4
f36	11.75876(2)	(M)	0.03448(57)	3	NR f
f51	11.57592(3)	(N)	0.03502(58)	2	NR f
f54	29.71071(3)	(O)	0.01364(36)	1	NR p5
f56	32.64831(3)	(P)	0.01242(34)	3	NR p5
f58	21.60050(3)	(Q)	0.01877(42)	1	NR p3
f64	33.28395(3)	(R)	0.01218(34)	3	NR p5
f70	30.05512(4)	(S)	0.01349(36)	1	NR p5
f112	55.45850(5)	(T)	0.00731(26)
f127	24.75387(6)	(U)	0.01638(39)	3	NR p3
f131	56.59172(6)	(V)	0.00716(26)
f167	31.80752(8)	(W)	0.01275(35)	2	NR p5
f172	28.64426(8)	(X)	0.01415(37)	3	NR p4
f170	30.40788(8)	(Y)	0.01333(36)	1	NR p5
f147	33.47664(7)	(Z)	0.01211(34)	3	NR p5
f169	34.43309(8)	(A1)	0.01177(33)	1	NR p6
f77	26.16552(4)	(B1)	0.01549(38)	1	NR p4
f234	64.0604(1)		0.00633(25)
f134	30.06331(6)		0.01348(36)	1	NR p5

The AMP-PH diagrams of the radial modes f1 and f26 are shown in Fig. 12, where they display similar trends with the orbital phase. The peaks of the pulsation amplitude are at the orbital phases 0.5, 0.1 and 0.9, which correspond to the maxima of light ratio for the primary component (i.e. the secondary component is eclipsed at phase 0.5, and the primary component’s beginning and ending are eclipsed at phases 0.9 and 0.1). However, similar trends are not found in non-radial modes. This variation caused by the changing light ratio during the orbital motion should be the main feature of the radial mode in the AMP-PH diagram.

Figure 12.

The AMP-PH diagram for the radial modes f1 and f26.

Open in new tab Download slide

The frequency difference between adjacent radial modes of HL Dra is Δν = f₁ − f₂₆ = 3.93787 (± 0.00003) d⁻¹ (⁠|$45.5772 \, \mu$|Hz). Its position in the large separation–mean density relation diagram is shown in Fig. 13, where the eclipsing binaries with a δ Sct component are collected by García Hernández et al. (2015). As can be seen in this figure, HL Dra can be seen to be very consistent with the relation constructed by García Hernández et al. (2015). However, we try to plot a new echelle diagram using the large frequency separation Δν = |$45.5772 \, \mu$|Hz, and we are not successful in finding the spherical wavenumbers of the pulsation modes. The determination of the large frequency separation is possibly hampered by the presence of the regularly (tidally) split multiplets.

$The position of HL Dra in the large separation–mean density relation diagram for the eclipsing binaries with a δ Sct component ($\Delta \nu _{\odot } = 134.8 \, \mu$Hz).$

Figure 13.

The position of HL Dra in the large separation–mean density relation diagram for the eclipsing binaries with a δ Sct component (⁠|$\Delta \nu _{\odot } = 134.8 \, \mu$|Hz).

Open in new tab Download slide

5 DISCUSSION AND CONCLUSION

After subtracting the brightness changes of the binary, two flares are found in TJD 1974 and TJD 1976. The properties of these two flares in the TESS band are displayed in Fig. 14 and listed in Table 5, where the energy of flares is calculated using the method described by Shi et al. (2021). They are both superflares because their energy is more than 10³³ erg (Shibayama et al. 2013). The O’Connell effect of HL Dra should be due to the existence of dark spots on the late-type secondary component, such as for CN And (Van Hamme et al. 2001), GR Tau (Qian 2002) and V1007 Cas (Li et al. 2018), etc. As suggested in Section 3, the secondary component is probably in the synchronous rotation state with a rotation period of 0.944276 d, which is about 30 times faster than the Sun’s rotation. Because of the state of fast rotation and deep convective envelope, and the existence of dark spots and superflares, the late-type secondary component should have strong magnetic activity (e.g. Qian et al. 2014).

Table 5.

Open in new tab

Properties of the two flares found in the TESS light curve of HL Dra. The columns show the following: (1) time of flare peak in TJD; (2) amplitude of the flare; (3) duration of rise time of the flare; (4) duration of decay time of the flare; (5) energy of the flare in the TESS band.

T_peak (d)	ΔM (mmag)	t_rise (min)	t_decay (min)	E_flare (erg)
(1)	(2)	(3)	(4)	(5)
1974.26376	42	8	72	6.61 × 10³⁶
1976.37351	12	6	14	5.56 × 10³⁵

T_peak (d)	ΔM (mmag)	t_rise (min)	t_decay (min)	E_flare (erg)
(1)	(2)	(3)	(4)	(5)
1974.26376	42	8	72	6.61 × 10³⁶
1976.37351	12	6	14	5.56 × 10³⁵

Table 5.

Open in new tab

T_peak (d)	ΔM (mmag)	t_rise (min)	t_decay (min)	E_flare (erg)
(1)	(2)	(3)	(4)	(5)
1974.26376	42	8	72	6.61 × 10³⁶
1976.37351	12	6	14	5.56 × 10³⁵

T_peak (d)	ΔM (mmag)	t_rise (min)	t_decay (min)	E_flare (erg)
(1)	(2)	(3)	(4)	(5)
1974.26376	42	8	72	6.61 × 10³⁶
1976.37351	12	6	14	5.56 × 10³⁵

The analysis of period change shows that the orbital period of HL Dra does not decrease or increase for a long time, which is consistent with the photometric solution that HL Dra is a detached binary system. The previously downward parabolic change of the O − C curve is part of the periodic variation. A sinusoidal curve with a period of 129.88 yr and an amplitude of 0.0196 d can fit the periodic variation well. Considering the secondary component with strong magnetic activity, the Applegate mechanism (Applegate 1992) is a potential explanation for periodic modulation, so we calculate the quadrupole moment variation ΔQ using the InPeVEBsoftware (Liakos 2015). The result of ΔQ ≈ 2 × 10⁵⁰ g cm² is less than the criterion 10⁵¹ g cm² (Lanza & Rodonò 2002). Therefore, the periodic variation with a period of 129.88 yr of the O − C curve should not be caused by magnetic activity, which should be caused by the appearance of the third body. This idea is also supported by the variation of the proper motions observed by the Hipparcos and Gaia satellites (Kervella et al. 2019), where HL Dra, with a proper motion anomaly (PMa) between the long-term proper motion vector and the GDR2 or Hipparcos measurements of 2.32 mas yr⁻¹, is a candidate with a third body. The parameters of the third body are calculated using

$$\begin{eqnarray*} f(m)=\frac{4\pi ^{2}}{{\it G}P_{3}^{2}}\times (a_{12}^{\prime }\sin {i}^{\prime })^{3} \end{eqnarray*}$$

(8)

$$\begin{eqnarray*} f(m)=\frac{(M_{3}\sin {i^{\prime }})^{3}}{(M_{1}+M_{2}+M_{3})^{2}}, \end{eqnarray*}$$

(9)

where |$a_{12}^{\prime }\sin {i}^{\prime }=A\times {c}$| (see Table 6). The photometric analysis results of both Liakos et al. (2012) and this paper do not find the appearance of a third light. This means that the third body with a very low luminosity contribution could not be observed. So, its orbital inclination should not be very low, and it should be a cool red dwarf star.

Table 6.

Open in new tab

The orbital parameters of the third body in HL Dra.

Parameters	Value	Units
A	0.0196 (±0.0001)	d
P₃	129.88 (assumed)	yr
\|$a_{12}^\prime \sin i^\prime$\|	3.40 (±0.02)	au
f(m)	2.32 (±0.04) × 10⁻³	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 90°)	0.329 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 70°)	0.351 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 50°)	0.437 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 30°)	0.698 (±0.004)	\|$\, \mathrm{M}_{\odot }$\|
a₃ (i ′ = 90°)	37.00 (±0.28)	au
a₃ (i ′ = 70°)	36.86 (±0.27)	au
a₃ (i ′ = 50°)	36.33 (±0.27)	au
a₃ (i ′ = 30°)	34.84 (±0.27)	au

Parameters	Value	Units
A	0.0196 (±0.0001)	d
P₃	129.88 (assumed)	yr
\|$a_{12}^\prime \sin i^\prime$\|	3.40 (±0.02)	au
f(m)	2.32 (±0.04) × 10⁻³	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 90°)	0.329 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 70°)	0.351 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 50°)	0.437 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 30°)	0.698 (±0.004)	\|$\, \mathrm{M}_{\odot }$\|
a₃ (i ′ = 90°)	37.00 (±0.28)	au
a₃ (i ′ = 70°)	36.86 (±0.27)	au
a₃ (i ′ = 50°)	36.33 (±0.27)	au
a₃ (i ′ = 30°)	34.84 (±0.27)	au

Table 6.

Open in new tab

The orbital parameters of the third body in HL Dra.

Parameters	Value	Units
A	0.0196 (±0.0001)	d
P₃	129.88 (assumed)	yr
\|$a_{12}^\prime \sin i^\prime$\|	3.40 (±0.02)	au
f(m)	2.32 (±0.04) × 10⁻³	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 90°)	0.329 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 70°)	0.351 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 50°)	0.437 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 30°)	0.698 (±0.004)	\|$\, \mathrm{M}_{\odot }$\|
a₃ (i ′ = 90°)	37.00 (±0.28)	au
a₃ (i ′ = 70°)	36.86 (±0.27)	au
a₃ (i ′ = 50°)	36.33 (±0.27)	au
a₃ (i ′ = 30°)	34.84 (±0.27)	au

Parameters	Value	Units
A	0.0196 (±0.0001)	d
P₃	129.88 (assumed)	yr
\|$a_{12}^\prime \sin i^\prime$\|	3.40 (±0.02)	au
f(m)	2.32 (±0.04) × 10⁻³	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 90°)	0.329 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 70°)	0.351 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 50°)	0.437 (±0.002)	\|$\, \mathrm{M}_{\odot }$\|
m₃(i ′ = 30°)	0.698 (±0.004)	\|$\, \mathrm{M}_{\odot }$\|
a₃ (i ′ = 90°)	37.00 (±0.28)	au
a₃ (i ′ = 70°)	36.86 (±0.27)	au
a₃ (i ′ = 50°)	36.33 (±0.27)	au
a₃ (i ′ = 30°)	34.84 (±0.27)	au

As shown in Figs 3 and 5, the correlations between the changes of the O − C diagrams and the variable O’Connell effect during TESS observations should be caused by the magnetic activity of the secondary component. We further use the InPeVEB software to estimate the variation of the O − C curves during TESS observations, where we roughly assume the period of variation as 2 yr and the amplitude as 0.003 d (i.e. this estimated period comes from the modulation observed in Fig. 3 as a half-cycle). The result of ΔQ is more than the criterion 10⁵¹ g cm², which further proves our conclusion that the variation of the O − C curves during TESS observations is caused by the Applegate mechanism.

We analysed the frequency components of the pulsation light curve and identified a total of 28 multiplets that are spaced by the orbital frequency. According to the theoretical prediction (Reyniers & Smeyers 2003a, 2003b; Smeyers 2005), these multiplets are the tidally split mode caused by the equilibrium tide of the close binary system with a circular orbit. We identify two probable radial modes, 21 probable non-radial p-modes and three probable non-radial f-modes from the possible independent frequencies. Compared with other studies, it seems unusual that so many pulsating modes, even f-modes, have been identified, which is probably attributed to two aspects. One is the high-resolution frequency brought by the continuous high-precision observations of TESS over 352 d. The other is the strong tidal effect caused by the high filling factor of the primary and secondary components (87 per cent and 98 per cent). As shown in Fig. 12, the variation of radial mode in the AMP-PH diagram is mainly caused by the changing light ratio during the orbital motion, which is helpful for the identification of pulsation modes. However, more research is needed.

The special configuration (a detached system but both the primary and secondary components with a high filling factor), the pulsations of the primary component, the magnetic activity of the secondary and the presence of the third body all reveal that HL Dra is a very interesting system for further investigations of binary formation and evolution, and for tidal interactions on stellar pulsations and on magnetic activities.

SUPPORTING INFORMATION

Table 1. Eclipse times for HL Dra.

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

ACKNOWLEDGEMENTS

This work is supported by the Chinese Natural Science Foundation (Nos 11933008, 11873017 and 11803084). The photometric data obtained with DASCH were used to calculate the times of light minima. The visual magnitude in the V band was obtained from the KWS using maehara/VSdata.py. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC; https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The TESS data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST) at the Space Telescope Science Institute (STScI). STScI is operated by the Association of Universities for Research in Astronomy, Inc. Support to MAST for these data is provided by the NASA Office of Space Science. Funding for the TESS mission is provided by the NASA Explorer Program. We thank the anonymous referee for valuable comments and suggestions, which have improved the manuscript greatly.

DATA AVAILABILITY

The data underlying this article will be shared on reasonable request to the corresponding author.

Footnotes

See http://var.astro.cz/ocgate/.

See http://kws.cetus-net.org/.

REFERENCES

Aerts

Christensen-Dalsgaard

Kurtz

D. W.

2010

Asteroseismology

Springer

Berlin

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Applegate

J. H.

1992

ApJ

385

621

10.1086/170967

Crossref

Arena

et al. ,

2011

IBVS

5997

Bahar

et al. ,

2017

IBVS

6209

10.22444/IBVS.6209

Crossref

Banfi

et al. ,

2012

IBVS

6033

Bessell

M. S.

Castelli

Plez

1998

A&A

333

231

Bowman

D. M.

Kurtz

D. W.

2018

MNRAS

476

3169

10.1093/mnras/sty449

Crossref

Bowman

D. M.

Johnston

Tkachenko

Mkrtichian

D. E.

Gunsriwiwat

Aerts

2019

ApJ

883

L26

10.3847/2041-8213/ab3fb2

Crossref

Breger

et al. ,

1993

A&A

271

482

Brown

A. G. A.

(Gaia Collaboration) et al.

(Gaia Collaboration)

2018

A&A

616

10.1051/0004-6361/201833051

Crossref

Chen

Deng

de Grijs

Wang

Feng

2018

ApJ

859

140

10.3847/1538-4357/aabe83

Crossref

Chen

et al. ,

2020

ApJ

895

136

10.3847/1538-4357/ab8bd2

Crossref

Cox

A. N.

2000

Allen's Astrophysical Quantities

AIP Press

New York

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

ESA

1997

ESA-SP 1200, The Hipparcos and Tycho Catalogues

ESA Publications

Noordwijk

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Fitch

W. S.

1981

ApJ

249

218

10.1086/159278

Crossref

García Hernández

Martín-Ruiz

Monteiro

M. J. P. F. G.

Suárez

J. C.

Reese

D. R.

Pascual-Granado

Garrido

2015

ApJ

811

L29

10.1088/2041-8205/811/2/L29

Crossref

Grindlay

J. E.

Griffin

R. E.

2012

Proc. IAU Symp. Vol. 295, New Horizons in Time Domain Astronomy

Cambridge Univ. Press

Cambridge

, p.

243

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Grindlay

Tang

Los

Servillat

2012

, in

Griffin

Hanisch

R. J.

Seaman

R. L.

, eds,

Proc. IAU Symp. Vol. 285, New Horizons in Time-Domain Astronomy

Cambridge Univ. Press

Cambridge

, p.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Guo

Gies

D. R.

Matson

R. A.

García Hernández

2016

ApJ

826

10.3847/0004-637X/826/1/69

Crossref

Hilditch

R. W.

2001

An Introduction to Close Binary Stars

Cambridge University Press

Cambridge

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kervella

Arenou

Mignard

Thévenin

2019

A&A

623

A72

10.1051/0004-6361/201834371

Crossref

Kopal

1955

Ann. Astroph.

379

Lanza

A. F.

Rodonò

2002

323

424

10.1002/1521-3994(200208)323:3/43.0.CO;2-1

Crossref

Lee

J. W.

Hong

Kristiansen

M. H.

2019

157

10.3847/1538-3881/aaf0fb

Crossref

Lenz

Breger

2005

CoAst

146

10.1553/cia146s53

Crossref

Liakos

2015

, in

Rucinski

S. N.

Torres

Zejda

, eds,

ASP Conf. Ser. Vol. 496, Living Together: Planets, Host Stars and Binaries

Astron. Soc. Pac

San Francisco, CA

, p.

286

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Liakos

Niarchos

2010

IBVS

5958

Liakos

Niarchos

Soydugan

Zasche

2012

MNRAS

422

1250

10.1111/j.1365-2966.2012.20704.x

Crossref

Xia

Q.-Q.

S.-M.

Guo

D.-F.

Chen

2018

PASP

130

074201

10.1088/1538-3873/aac067

Crossref

Loumos

G. L.

Deeming

T. J.

1978

Ap&SS

285

10.1007/BF01879560

Crossref

Lucy

L. B.

1967

Z. Astroph.

Milone

E. F.

1969

Communications of the Konkoly Observatory

457

Mkrtichian

D. E.

Kusakin

A. V.

Gamarova

A. Y.

Nazarenko

2002

, in

Aerts

Bedding

T. R.

Christensen-Dalsgaard

, eds,

ASP Conf. Ser. Vol. 259, Radial and Nonradial Pulsations as Probes of Stellar Physics

Astron. Soc. Pac

San Francisco, CA

, p.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Montgomery

M. H.

O’Donoghue

1999

Delta Scuti Star Newsletter

Perryman

M. A. C.

et al. ,

1998

A&A

331

Pribulla

et al. ,

2006

132

769

10.1086/505536

Crossref

Prusti

(Gaia Collaboration) et al.

(Gaia Collaboration)

2016

A&A

595

10.1051/0004-6361/201629272

Crossref

Pustylnik

1998

Astron. Astrophys. Trans.

357

Qian

2002

MNRAS

336

1247

10.1046/j.1365-8711.2002.05862.x

Crossref

Qian

S-B.

et al. ,

2014

ApJS

212

10.1088/0067-0049/212/1/4

Crossref

Reyniers

Smeyers

2003a

A&A

404

1051

10.1051/0004-6361:20030501

Crossref

Reyniers

Smeyers

2003b

A&A

409

677

10.1051/0004-6361:20031098

Crossref

Ricker

G. R.

et al.

2015

J. Astron. Telescopes, Instruments, and Systems

014003

Ruciński

S. M.

1969

AcA

245

Samadi Ghadim

Lampens

Jassur

D. M.

2018a

AcA

425

10.32023/0001-5237/68.4.6

Crossref

Samadi Ghadim

Lampens

Jassur

2018b

MNRAS

474

5549

10.1093/mnras/stx3072

Crossref

Shibayama

et al. ,

2013

ApJS

209

10.1088/0067-0049/209/1/5

Crossref

Shi

X-d.

Qian

S-b.

L-j.

Liu

N-p.

2021

161

10.3847/1538-3881/abccd7

Crossref

Smeyers

2005

, in

Claret

Giménez

Zahn

J. P.

, eds,

ASP Conf. Ser. Vol. 333, Tidal Evolution and Oscillations in Binary Stars: Third Granada Workshop on Stellar Structure

Astron. Soc. Pac

San Francisco, CA

, p.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Southworth

Bowman

D. M.

Pavlovski

2021

MNRAS

501

L65

10.1093/mnrasl/slaa197

Crossref

Steindl

Zwintz

Bowman

D. M.

2021

A&A

645

A119

10.1051/0004-6361/202039093

Crossref

Van Hamme

Wilson

R. E.

2007

ApJ

661

1129

10.1086/517870

Crossref

Van Hamme

Samec

R. G.

Gothard

N. W.

Wilson

R. E.

Faulkner

D. R.

Branly

R. M.

2001

122

3436

10.1086/324110

Crossref

Wilson

R. E.

1979

ApJ

234

1054

10.1086/157588

Crossref

Wilson

R. E.

1990

ApJ

356

613

10.1086/168867

Crossref

Wilson

R. E.

2012

144

10.1088/0004-6256/144/3/73

Crossref

Wilson

R. E.

Devinney

E. J.

1971

ApJ

166

605

10.1086/150986

Crossref

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.

Download all slides

Month:	Total Views:
July 2021	146
August 2021	56
September 2021	49
October 2021	69
November 2021	32
December 2021	40
January 2022	41
February 2022	24
March 2022	32
April 2022	29
May 2022	17
June 2022	10
July 2022	34
August 2022	40
September 2022	28
October 2022	30
November 2022	25
December 2022	20
January 2023	19
February 2023	16
March 2023	11
April 2023	31
May 2023	9
June 2023	23
July 2023	35
August 2023	22
September 2023	31
October 2023	23
November 2023	40
December 2023	28
January 2024	40
February 2024	16
March 2024	30
April 2024	20
May 2024	32
June 2024	27
July 2024	25
August 2024	27
September 2024	22
October 2024	17
November 2024	23
December 2024	15
January 2025	13
February 2025	17
March 2025	40
April 2025	11
May 2025	8

Article Contents

HL Dra: an active Algol-like binary system with a pulsating component star and a cool third body

ABSTRACT

1 INTRODUCTION

2 CHANGES OF THE ORBITAL PERIOD AND THE PHOTOMETRIC LIGHT CURVE OF HL DRA

3 PHOTOMETRIC SOLUTIONS AND ABSOLUTE PARAMETERS FOR HL DRA

4 PULSATION ANALYSIS

5 DISCUSSION AND CONCLUSION

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

HL Dra: an active Algol-like binary system with a pulsating component star and a cool third body

ABSTRACT

1 INTRODUCTION

2 CHANGES OF THE ORBITAL PERIOD AND THE PHOTOMETRIC LIGHT CURVE OF HL DRA

3 PHOTOMETRIC SOLUTIONS AND ABSOLUTE PARAMETERS FOR HL DRA

4 PULSATION ANALYSIS

5 DISCUSSION AND CONCLUSION

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only