Intrinsic and extrinsic correlations of galaxy shapes and sizes in weak lensing data

Ghosh, Basundhara; Durrer, Ruth; Schäfer, Björn Malte

doi:10.1093/mnras/stab1435

ABSTRACT

The subject of this paper is to build a physical model describing shape and size correlations of galaxies due to weak gravitational lensing and due to direct tidal interaction of elliptical galaxies with gravitational fields sourced by the cosmic large-scale structure. Setting up a linear intrinsic alignment model for elliptical galaxies that parametrizes the reaction of the galaxy to an external tidal shear field is controlled by the velocity dispersion; we predict intrinsic correlations and cross-correlations with weak lensing for both shapes and sizes, juxtaposing both types of spectra with lensing. We quantify the observability of the intrinsic shape and size correlations and estimate with the Fisher formalism how well the alignment parameter can be determined from the Euclid weak lensing survey. Specifically, we find a contamination of the weak lensing convergence spectra with an intrinsic size correlation amounting to up to 10 per cent over a wide multipole range (ℓ = 100…300), with a corresponding cross-correlation exhibiting a sign change, similar to the cross-correlation between weak lensing shear and intrinsic shapes. A determination of the alignment parameter yields a precision of a few per cent forecasted for Euclid, and we show that all shape and many size correlations should be measurable with Euclid.

gravitational lensing: weak, dark energy, large-scale structure of Universe

1 INTRODUCTION

Weak lensing has emerged as a powerful probe for investigating the cosmic large-scale structure (Mellier 1999; Bartelmann & Schneider 2001; Amara & Refregier 2007; Bartelmann 2010; Kilbinger 2015), for testing gravitational theories and for constraining cosmological parameters. As gravitational lensing probes fluctuations in the gravitational potential directly (Kaiser 1992; Hu & Tegmark 1999; Hu 2001, 2002; Heavens 2003; Bernstein & Jain 2004; Heavens, Kitching & Taylor 2006; Munshi et al. 2008; Grassi & Schäfer 2014), it depends on minimal assumptions and is fixed for a given gravitational theory. Correlations in the shapes of galaxies induced by weak lensing (Bernstein & Jarvis 2002; Bernstein 2009) have been detected almost two decades ago, and by now lensing is recognized as a tool for investigating cosmological theories alongside the cosmic microwave background (CMB) and galaxy clustering (van Waerbeke, Bernardeau & Mellier 1999; Huterer 2002, 2010; Mortonson, Weinberg & White 2013). The last generation of surveys, most notably KiDS and DES (Abbott et al. 2018; Joudaki et al. 2018, 2020), has provided independent confirmation for the Lambda cold dark matter (ΛCDM) model and supports parameter determinations from the CMB, even though tensions between the two probes, most notably in the matter density Ω_m and σ₈, remain (MacCrann et al. 2014; Douspis, Salvati & Aghanim 2018). The next generation of surveys, in particular Euclid (Amendola et al. 2018) and LSST (LSST Dark Energy Science Collaboration 2012), will probe cosmological models to almost fundamental limits of cosmic variance, but with decreasing statistical errors the control of systematical errors will become one of the central questions for data analysis, along with higher order effects in the lensing signal related to evaluating the tidal shear fields along a geodesic (Thomas, Bruni & Wands 2015), effects of lensing on galaxy number counts (Ghosh, Durrer & Sellentin 2018) in galaxy–galaxy lensing correlation, and non-Gaussian statistics of the lensing signal due to non-linear structure formation and non-Gaussian contributions to the covariance (Jain & Seljak 1997; Kayo & Takada 2013; Kayo, Takada & Jain 2013; Munshi, Coles & Kilbinger 2014).

Among astrophysical contaminants of the weak lensing signal, intrinsic alignments (Jing 2002; Mackey, White & Kamionkowski 2002; Heymans et al. 2004; Altay, Colberg & Croft 2006; Kirk, Bridle & Schneider 2010; Massey et al. 2013; Kitching et al. 2017) are perhaps the most dramatic, leading to significant biases in the estimation of cosmological parameters, surpassing most likely baryonic corrections (White 2004; Semboloni et al. 2011), below multipoles of ℓ ≤ 10³. There are two primary models for the two dominant galaxy types for linking the apparent shapes to tidal gravitational fields in the large-scale structure (Dubinski 1992), which acts, due to long-ranged correlations, as the medium to reduce randomness and to correlate the measured ellipticities. The shapes of spiral galaxies are thought to be determined by the orientation of the angular momentum of the stellar disc (Catelan, Kamionkowski & Blandford 2001; Crittenden et al. 2001; Bailin & Steinmetz 2005), and ultimately of the dark matter halo harbouring the stellar component. With this idea in mind, shape correlations are traced back to angular momentum correlations, which in turn would depend on the tidal shear fields through tidal torquing as the angular momentum generating mechanism. Tidal torquing models commonly predict ellipticity correlations on small scales at a level of at most 10 per cent of the weak lensing signal on multipoles above ℓ ≃ 300 for a survey like Euclid. Many physical assumptions have been challenged, most notably the orientation of the disc relative to the host halo angular momentum, as well as an over-prediction of the correlation inherent to the torquing mechanism.

Elliptical galaxies, on the other hand, are thought to acquire shape correlations through direct interaction with the tidal shear field (Schneider & Bridle 2010; Blazek et al. 2012; Merkel & Schaefer 2013; Tugendhat & Schaefer 2018; Blazek et al. 2019): Second derivatives of the gravitational potential would give rise to an anisotropic deformation of the galaxy, in the principal directions of the tidal shear tensor. Interestingly, the reaction of a galaxy to the tidal shear field is determined by the inverse velocity dispersion 1/σ² similar to lensing, where the relevant quantity is the gravitational potential in units of c². Tidal alignments of elliptical galaxies are thought to be present at intermediate angular scales of a few hundreds in multipole ℓ for a survey like Euclid, with amplitudes being typically an order of magnitude smaller than that of the weak lensing effect. In parallel, alignment models using ideas from effective field theories provide parametrized relationships between tensors constructed from the cosmic density and velocity fields and can capture a wider range of alignment mechanisms and track them into the non-linear regime (Vlah, Chisari & Schmidt 2020), but perhaps with a less clear physical picture. There are indications that this in fact takes place in Nature, for instance in measurements of shape correlations in the local universe (Brown et al. 2002), in shallow surveys (Lee & Erdogdu 2007; Chisari & Dvorkin 2013; Pahwa et al. 2016), using stacking techniques or correlation techniques in deeper surveys (Hirata et al. 2004b; Mandelbaum et al. 2011; Chisari et al. 2014a) and correlation techniques in weak lensing surveys (Heavens, Refregier & Heymans 2000; Heymans & Heavens 2003; Kilbinger et al. 2009; Joachimi et al. 2011; de Jong et al. 2013; Heymans et al. 2013; Jee et al. 2013; Kilbinger et al. 2013; Schneider et al. 2013; Kirk et al. 2015b; Joudaki et al. 2017; Johnston et al. 2018). Likewise, intrinsic alignment effects have been investigated in fluid-mechanical simulations of galaxy formation (see for instance Tenneti et al. 2014, 2015; Chisari et al. 2014b, 2016; Debattista et al. 2015; Hilbert et al. 2017a; Bate et al. 2019).

While intrinsic alignments refer to a physical change of the appearance of the galaxies (for reviews, see Joachimi et al. 2015; Kiessling et al. 2015; Kirk et al. 2015a; Troxel & Ishak 2015), there is an analogous deformation effect on the shape of the light bundle emanating from a galaxy by gravitational lensing. To lowest order, both effects depend on tidal gravitational field, which suggests that the effects must be correlated. The main difference is that while lensing shear comes from the gravitational tidal field integrated along the line of sight, intrinsic alignment is due to the local gravitational tidal field. Nevertheless, cross-correlations between the physical change in shape and the apparent change in shape are predicted to be non-zero for elliptical galaxies, and more precisely, should in fact be negative as galaxies align themselves radially with a large structure while lensing generates a tangential alignment. As a result, ellipticity correlations of galaxies are a sum of the conventional weak lensing (often referred to as GG), the intrinsic alignment (or II), and the cross-correlation between the two (called GI). Parameter estimation from weak lensing (Casarini et al. 2011; Capranico, Merkel & Schäfer 2013; Blazek et al. 2019) as well as weak lensing mass reconstructions (Fan 2007; Chang et al. 2018) would be affected by these intrinsic contributions, and can be taken care of by direct modelling or by self-calibration (Troxel & Ishak 2012; Yao et al. 2017, 2019a; Yao, Ishak & Troxel 2019b; Pedersen et al. 2020). In addition, intrinsic alignments can show up in cross-correlation with the reconstructed CMB-lensing deflection field (Hirata et al. 2004a; Hall & Taylor 2014; Chisari et al. 2015; Larsen & Challinor 2016; Merkel & Schaefer 2017), and they might be usable as cosmological probes in their own right (Pandya et al. 2019; Taruya & Okumura 2020).

There should be analogous effects of the size of an elliptical galaxy due to tidal gravitational fields: In gravitational lensing the light bundle can be isotropically enlarged, i.e. changed in size while the shape is conserved: This non-zero convergence is caused by the trace of the tidal field, and determines to lowest order magnification as well, adding cosmological information (Huff & Graves 2014; Takahashi et al. 2011). Similarly, the size of an elliptical galaxy would physically change for a fixed velocity dispersion if the trace of the tidal field is non-zero,¹ or equivalently, if it resides in an overdense or underdense region. An underdense region with a density contrast δ < 0 would source a gravitational potential Φ through the Poisson equation |$\Delta \Phi /c^2 = 3\Omega _\mathrm{ m}/(2\chi _\mathrm{ H}^2)\delta$|⁠, with the Hubble distance χ_H = c/H₀, such that the eigenvalues of ∂_i∂_jΦ would be negative, stretching the galaxy to a physically larger size. Alternatively, one can argue that the change of volume (or area) is given by the Jacobian of the differential acceleration, i.e. of the tidal field, such that the perturbed volume is V/V₀ = det(δ_ab + ∂_a∂_bΦ), implying that |$\ln V-\ln V_0 = \ln \det (\delta _{ab} + \partial _a\partial _b\Phi) = \mathrm{tr}\ln (\delta _{ab} + \partial _a\partial _b\Phi) \simeq \mathrm{tr}(\partial _a\partial _b\Phi) = \Delta \Phi$| and consequently V/V₀ = exp (ΔΦ) and (V − V₀)/V ≃ ΔΦ. To what extent extrinsic and intrinsic size correlations can add to our understanding of cosmology has been investigated by Heavens, Alsing & Jaffe (2013).

The motivation of our paper is the study of these correlations between the sizes of elliptical galaxies as they would be predicted by a linear alignment model as a consequence of the trace ΔΦ of the tidal tensor ∂_a∂_bΦ being non-zero, as proposed by Hirata et al. (2004b) and Hirata & Seljak (2010). These intrinsic size correlations would be generated in complete analogy to intrinsic shape correlations caused by the traceless part of the tidal, and would contaminate measurements of weak lensing convergence correlations (Alsing et al. 2015) in the same way as intrinsic shape correlations are a nuisance to the weak lensing shear. Alternatively, one can imagine these as a manifestation of ellipticity–density correlations (Hui & Zhang 2002), only that density is mapped out by the galaxy size. After introducing tidal interactions of elliptical galaxies with their surrounding large-scale structure in Section 2, we compute shape correlations from direct tidal interaction and through gravitational lensing in Section 3. We quantify the information content of each of the correlations and the amount of covariance in Section 4, before discussing our results in Section 5. In general, we work in the context of a wCDM cosmology with a constant equation-of-state value of w close to −1, and standard values for the cosmological parameters, i.e. Ω_m = 0.3, σ₈ = 0.8, h = 0.7, and n_s = 0.96, and a parametrized spectrum for non-linearly evolving scales. We compute numerical results on the information content of size correlations for the case of a tomographic weak lensing survey like Euclid (Amendola et al. 2018). Throughout the paper, summation convention is implied.

2 TIDAL INTERACTIONS OF GALAXIES AND GRAVITATIONAL LENSING

In a simplified way, one can imagine elliptical galaxies as a stellar component in virial equilibrium with a velocity dispersion of σ², filling the gravitational potential. Piras et al. (2018) then argue that if the velocity dispersion is isotropic, one can invoke the Jeans equation for stationary and static systems in order to relate density ρ(r) and potential Φ(r):

$$\begin{eqnarray*} \sigma ^2\partial _r\ln \rho (r) = -\partial _r\Phi \quad \rightarrow \quad \rho (r) \propto \exp \left(-\frac{\Phi (r)}{\sigma ^2}\right), \end{eqnarray*}$$

(1)

reminiscent of the barometric formula. Here, r = 0 is the centre of our galaxy where the density ρ is highest and Φ has a minimum. If the gravitational potential is distorted by external fields as the galaxy is not an isolated object, the equipotential contours get distorted correspondingly and the stellar component reacts and galaxy assumes a different shape. We still assume that Φ has a minimum at the centre of the galaxy, r = 0. To lowest order, the change in shape takes place along the principal axes of the tidal tensor ∂_a∂_bΦ, which is defined as the tensor of second derivatives of the gravitational potential Φ,

$$\begin{eqnarray*} \Phi (r) \rightarrow \Phi (r) + \frac{1}{2}r_a r_b\partial _a\partial _b\Phi \:, \end{eqnarray*}$$

(2)

leading to a distortion of the density of the stellar component. For weak tidal fields, the exponential can be Taylor expanded to yield

$$\begin{eqnarray*} \rho \propto \exp \left(-\frac{\Phi (r)}{\sigma ^2}\right)\left[1-\frac{\partial _a\partial _b\Phi }{2\sigma ^2}r_a r_b\right]. \end{eqnarray*}$$

(3)

For this perturbed stellar component, one can compute the change of the second moments of the brightness distribution, where we ignore projection effects for a moment and use ρ(r) for projected quantities,

$$\begin{eqnarray*} \Delta q_{cd} = \int \mathrm{d}^2r\:\rho (r)\: r_c r_d\: r_a r_b\times \frac{\partial _a\partial _b\Phi }{2\sigma ^2} = S_{abcd}\:\Phi _{ab}, \qquad \Phi _{ab} \equiv \partial _a\partial _b\Phi \, , \end{eqnarray*}$$

(4)

which bears a resemblance to the generalized Hooke law Δq_cd = S_abcd Φ_ab, relating the stresses Φ_ab to the observable strains Δq_cd, which suggests to think of S_abcd as the susceptibility of a galaxy to change its shape or size under the influence of tidal gravitational fields. In the theory of elastic media, one would then in fact use index symmetries to derive that there must be two material constants; similarly, in the theory of viscous fluids, one defines two Lamé viscosity coefficients (bulk and shear viscosity), so naturally the question arises whether the same constant of proportionality determines the size and the shape deformation as in the case of lensing. As consequence of the Jeans equation (1), the relevant quantity for shape and size distortions is the tidal field normalized by the galaxy’s velocity dispersion (Camelio & Lombardi 2015; Piras et al. 2018). With an extension of the virial law, one can show that R²/σ² is constant for a galaxy of size R and velocity dispersion σ², as one would evaluate the Taylor expansion (2) up to distances corresponding to R. Computing the second moment Δq_cd for the ellipticity perturbation in equation (4), one obtains a scaling proportional to R², and using virial arguments again, with M^2/3, reproducing the observed behaviour of stronger alignments with increasing galaxy mass M.

In our model, we assume that the reaction of the galaxy to the tidal is instantaneous, which is an assumption that can be challenged: Adjustment to a new tidal field should take place on the free-fall time-scale |$t_\mathrm{ff} = 1/\sqrt{G\rho }$| with the total matter density ρ, which is typically a factor of Δ = 200 higher than the background density Ω_mρ_crit with |$\rho _\mathrm{crit} = 3H_0^2/(8\pi G)$|⁠. Substitution shows that the free-fall time-scale is only |$\sqrt{8\pi /(3\Omega _\mathrm{ m}\Delta)}\simeq 0.37$| times shorter than the age of the Universe 1/H₀, but because at least in linear structure formation tidal gravitational fields are close to constant in dark energy cosmologies, the approximation might not be too bad. Of course, in non-linear structure formation, the time-scale of evolution would be much shorter and could give rise to an interesting time evolution of intrinsic alignments even for elliptical galaxies (Lee & Pen 2008; Schäfer & Merkel 2012; Schmitz et al. 2018). Separated from the question of the time dependence of the tidal interaction is whether the interaction can be the cause of shape distortions at all: Camelio & Lombardi (2015) have investigated this by considering the stellar distribution function in a perturbed potential and raise doubts whether alignments of the magnitude observed in ellipticity density correlations can be explained by a tidal alignment model: We would argue while acknowledging the difficulties of a self-consistent modelling that many details, for instance the tightly binding potential and the inconsistency introduced by working with a constant velocity dispersion and a cored potential, can affect the results, as well as ignoring a dynamical change of the galaxy’s own potential due to tidal interaction.

After introducing polar coordinates, assuming spherical symmetry for the unperturbed galaxy and writing r₀ = rcos ϕ and r₁ = rsin ϕ for the vector components, the elasticity tensor is in our case given by

$$\begin{eqnarray*} S_{abcd} = \frac{1}{2\sigma ^2}\int \mathrm{d}r\:r^5\rho (r)\int \mathrm{d}\phi \:\cos ^{4-(a+b+c+d)}\phi \sin ^{a+b+c+d}\phi , \end{eqnarray*}$$

(5)

has 16 entries, and is fully symmetric under index exchange. Up to a numerical pre-factor depending on the radial light distribution and on the velocity dispersion, S_abcd can only assume three different values, namely S₀₀₀₀ = ∫dϕ cos ⁴ϕ = S₁₁₁₁ = ∫dϕ sin ⁴ϕ = 3|$\pi$|/4, S₀₀₀₁ = ∫dϕ cos ³ϕsin ϕ = S₁₁₁₀ = ∫dϕ cos ϕsin ³ϕ = 0, and S₀₀₁₁ = ∫dϕ cos ²ϕsin ²ϕ =|$\pi$|/4.

Let us introduce the four Pauli matrices |$\sigma ^{(n)}_{ab}$| as the basis for the tidal ∂_a∂_bΦ:

$$\begin{eqnarray*} \sigma ^{(0)} = \begin{pmatrix}+1 & 0 \\ 0 & +1 \end{pmatrix},~ \sigma ^{(1)} = \begin{pmatrix}+1 & 0 \\ 0 & -1 \end{pmatrix},~ \sigma ^{(2)} = \begin{pmatrix}0 & +1 \\ -1 & 0 \end{pmatrix}, \mathrm{~and~} \sigma ^{(3)} = \begin{pmatrix}0 & +1 \\ +1 & 0 \end{pmatrix}. \end{eqnarray*}$$

(6)

Since σ⁽²⁾ is antisymmetric while the tidal tensor is symmetric as partial differentiations interchange, the component of Φ_ab in direction σ⁽²⁾ vanishes. We now determine the change in size s that is introduced by a tidal field |$\Phi _{ab}\propto \sigma _{ab}^{(0)}$|⁠:

$$\begin{eqnarray*} s = \frac{1}{2}\Delta q_{cd}\sigma ^{(0)}_{cd} = \frac{1}{2}S_{abcd}\sigma ^{(0)}_{cd}\sigma ^{(0)}_{ab} = \frac{1}{2}\left(S_{0000} + S_{0011} + S_{1100} + S_{1111}\right) = \pi . \end{eqnarray*}$$

(7)

The change in shape ϵ₊ introduced by a tidal field |$\Phi _{ab}\propto \sigma ^{(1)}_{ab}$| is

$$\begin{eqnarray*} \epsilon _+ = \frac{1}{2}\Delta q_{cd}\sigma ^{(1)}_{cd} = \frac{1}{2}S_{abcd}\sigma ^{(1)}_{cd}\sigma ^{(1)}_{ab} = \frac{1}{2}\left(S_{0000} - S_{0011} - S_{1100} + S_{1111}\right) = \frac{\pi }{2}, \end{eqnarray*}$$

(8)

while the change in shape ϵ_× generated by the tidal field |$\Phi _{ab}\propto \sigma ^{(3)}_{ab}$| is given by The changes in shape, ϵ_+,×, are only half as large as the change in size, s, analogously to the weak lensing convergence with Δψ = 2κ. With an assumption on the shape of the projected stellar density ρ(r), for instance a Sérsic profile (Sérsic 1963; Graham & Driver 2005),

$$\begin{eqnarray*} \rho (r) \propto \exp \left(-b(n)\left[\left(\frac{r}{r_0}\right)^{1/n}+1\right]\right), \end{eqnarray*}$$

(10)

it is possible to derive the scaling of ellipticity induced by the influence of a tidal gravitational field, dominantly with the size of the galaxy but also with the Sérsic index n. In equation (10), r₀ is the scale radius of the stellar component, and b(n) ≃ 2n − 1/3, approximately (de Vaucouleurs 1948). Computing the relevant integral ∫dr r⁵ρ(r) for a properly normalized density distribution ∫d²r ρ(r) = 2|$\pi$|∫dr rρ(r) = 1 and using the definition of ellipticity ϵ as it would result from the second moments q_ab of the normalized brightness distribution I(r) that we equate to the stellar density ρ(r),

$$\begin{eqnarray*} \epsilon = \frac{q_{xx}-q_{yy}}{q_{xx}+q_{yy}} + 2\mathrm{i}\frac{q_{xy}}{q_{xx}+q_{yy}}, \quad \mathrm{with}\quad q_{ab} = \int \mathrm{d}^2 r\:\rho (r)\:r_a r_b, \end{eqnarray*}$$

(11)

where one recognizes the size of the image in the denominator, q_xx + q_yy = ∫d²r ρ(r)(x² + y²) = 2|$\pi$|∫dr r³ρ(r), it is possible to show the scaling of the ellipticity to be

$$\begin{eqnarray*} \epsilon \propto \left(\int _0^\infty \mathrm{d}r\:r^5\rho (r)\right) \Bigg / \left(\int _0^\infty \mathrm{d}r\:r^3\rho (r)\right) = r_0^2 \times \int _{-b}^\infty \mathrm{d}x\:\left(\frac{x}{b}+1\right)^{6n-1}\exp (-x) \Bigg / \int _{-b}^\infty \mathrm{d}x\:\left(\frac{x}{b}+1\right)^{4n-1}\exp (-x). \end{eqnarray*}$$

(12)

Technically, we obtained this result after substitution x = b[(r/r₀)^1/n − 1], where the ratio of integrals has in general only a numerical solution and shows the dependence of the susceptibility to shape change due to tidal forces caused by the distribution of the stars inside the galaxy. The dominant scaling of ellipticity with the size |$r_0^2$| of the galaxy is dimensionally consistent with the linear tidal model q_ab = S_abcd Φ_cd. The results are shown in Fig. 1, which indicates a strong scaling of the alignment parameter with increasing Sérsic index n, where we should note that we consider the Sérsic profile as a reasonably simple model for the stellar distribution, which is not consistent with a constant velocity dispersion σ², and neither a gravitating self-consistent solution. Rather, it is supposed to illustrate that the internal dynamics of an elliptical galaxy can impact the magnitude of tidal alignment and that not all elliptical galaxies should have the same alignment parameter if their Sérsic index varies. We would like to mention here that effects like isophotal twisting are neglected in our model, and are discussed in literature such as Singh, Mandelbaum & More (2015). Effectively, isophotal twisting would correspond to different measurements of ellipticity at different radii of an elliptical galaxy and is possibly induced by a complex velocity structure of the elliptical galaxy: How these features could be related to tidal interaction and anisotropic accretion is not well understood and subject of debate.

Figure 1.

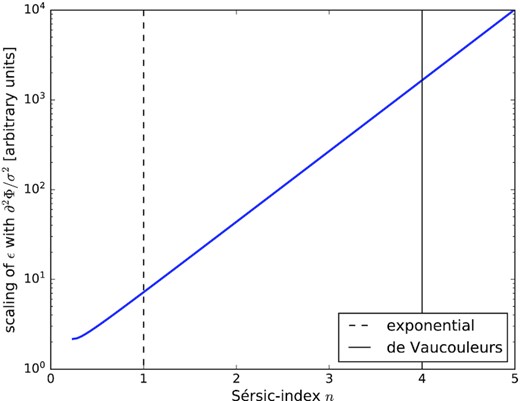
Scaling of the relation between ellipticity ϵ and Sérsic index n, for a given tidal gravitational field and a given velocity dispersion σ². As particular cases, the exponential profile for n = 1 and the de Vaucouleurs profile for n = 4 are indicated by vertical lines.

Open in new tab Download slide

It is straightforward to show that the distortion modes are all independent for the linear model; i.e. tidal fields |$\propto \sigma ^{(m)}_{ab}$| will never source distortion modes |$\propto \sigma ^{(n)}_{cd}$| with m ≠ n. For making the influence of the tidal field on the galaxy size more specific, we compute the change in size s explicitly as the second moment of the brightness distribution for the isotropic case,

$$\begin{eqnarray*} s = \frac{1}{2\sigma ^2}\int \mathrm{d}^2r\:r^2\rho (r)\left[\frac{1}{2}\partial _a\partial _b\Phi \: r_ar_b\right] = \frac{1}{2\sigma ^2}\int \mathrm{d}^2r\:r^2\rho (r)\left[\frac{1}{4}\Delta \Phi \:r^2\right] = \frac{\pi }{\sigma ^2}\int r^5\mathrm{d}r\:\rho (r)\frac{\Delta \Phi }{4} \propto \frac{\pi }{2}\Delta \Phi \end{eqnarray*}$$

(13)

such that the change in size comes out proportional to the trace ΔΦ of the tidal field.

Defining the alignment parameter D_IA as the constant of proportionality between ellipticity tensor ϵ_ab = q_ab/(q_xx + q_yy) and the tidal gravitational field ∂_a∂_bΦ,

$$\begin{eqnarray*} \epsilon _{ab} \simeq \frac{1}{2}\left(\frac{c}{\sigma }\right)^2\frac{\int \mathrm{d}^2r\:\rho \:r^4}{\int \mathrm{d}^2r\:\rho \:r^2}\times \partial _a\partial _b\:\frac{\Phi }{c^2} ~\equiv D_{IA}\times \partial _a\partial _b\:\frac{\Phi }{c^2}, \end{eqnarray*}$$

(14)

determines the unit to be comoving (Mpc/h)² (we compute the derivatives with respect to comoving coordinates, and relate it to the CDM spectrum P(k) as a function of comoving wavenumber k. We also carry out the Limber projection with a line-of-sight integration in comoving coordinates for consistency). The same argument is valid for the relationship between size s and the trace ΔΦ. In order to complete the analogy with lensing, we work with the dimensionless potential Φ/c² as the quantity that appears as the metric perturbation.

The mass scaling of the alignment parameter D_IA requires the combination of a number of arguments evolving around the virial law and galaxy scaling relations: Assuming the weighted volume element d²r ρ to be scalar and assuming a scaling of the size r of the galaxy proportional to M^1/3, as well as the virial relation σ² = GM/r, in order to relate the specific kinetic and potential energies with the size r and mass M of the galaxy implies a scaling of the ratio of the two integrals in (14) ∝ M^2/3, which is exactly cancelled by the inverse velocity dispersion, σ² ∝ r² ∝ M^2/3, such that the entire alignment parameter D_IA should be independent of the mass, as long as the virial argument and the scaling of galaxy size with mass are valid.

Concerning the actual numerical value of D_IA, one can set up an interesting argument by means of the comoving Poisson equation |$\Delta \Phi /c^2 = 3\Omega _\mathrm{ m}/(2\chi _\mathrm{ H}^2)\:\delta$|⁠: In fact, replacing the derivatives ∂_i∂_jΦ with ΔΦ, which is sufficient for scaling arguments, then yields the expression

$$\begin{eqnarray*} \epsilon \sim \frac{1}{2}\left(\frac{c}{\sigma }\right)^2\frac{\int \mathrm{d}^2\rho \:r^4}{\int \mathrm{d}^2r\rho \:r^2}\times \frac{3\Omega _\mathrm{ m}}{2\chi _\mathrm{ H}^2}\delta . \end{eqnarray*}$$

(15)

For a typical density perturbation of order δ ≃ 1, one obtains an intrinsic size or ellipticity perturbation of ϵ ≃ 10⁻⁵ if the velocity dispersion has a value of σ = 10⁵ m s⁻¹, yielding c/σ ≃ 10⁷ and if the ratio of the integrals in equation (14) is set to a value of 10⁻⁵ (Mpc h⁻¹)², which we call the alignment parameter in the remainder of the paper. The factor |$3\Omega _\mathrm{ m}/(2\chi _\mathrm{ H}^2)$| is typically of the order of ≃10⁻⁷ (Mpc h⁻¹)⁻². The alignment parameter physically depends on the area of the galaxy. Assuming an exponential Sérsic profile with n = 1 then implies that the scale length of a galaxy of mass 10¹² M_⊙ h⁻¹ is a few kpc h⁻¹, which coincides roughly with the numerical value of 10⁻⁵ (Mpc h⁻¹)² chosen in our study. A comparison with other values of D_IA will follow in Section 3.

From our derivation, it becomes apparent that the reaction of the galaxy to a tidal gravitational field in terms of shape and size distortions is governed by the same parameter. Shape and size distortions are merely different and mutually orthogonal modes of the second moments of the brightness distribution, which our linear model relates directly to the tidal gravitational field. This situation is completely analogous with gravitational lensing.

Deviations from this simple scaling of D_IA with mass at lowest order can be due to a number of effects: There can be systematic trends of the virial relationship with mass, deviating from a pure power law. The smoothing of the tidal field on the mass scale will certainly have an influence on the measured alignment parameter as it impacts the spectra on small scales, as well as the Abel integration that relates the three-dimensional light distribution to the two-dimensional one, and finally the scale radius r₀ in the Sérsic profile family might deviate from the scaling ∝ M^1/3, similar to the concentration parameter in the NFW-profile family. It has also been argued that more massive galaxies tend to have larger Sérsic index (Lange et al. 2015), leading to a mass dependence of the alignment parameter. We point out that residual scaling properties of the alignment parameter with mass can be significant, if galaxies over a wide range of masses are observed, since the steepness of the Press–Schechter function biases averages towards the value of D_IA at low masses.

It is interesting to note that shape and size distortions caused by a single perturbation are comparable for intrinsic alignments and for gravitational lensing, but lensing, as an integrated effect, dominates ultimately. Repeating the above argument would lead to expressing the weak lensing shear given by

$$\begin{eqnarray*} \gamma = \frac{3\Omega _\mathrm{ m}}{2\chi _\mathrm{ H}^2}\int _0^{\chi _\mathrm{ H}}\mathrm{d}\chi \:\frac{\chi _\mathrm{ H}-\chi }{\chi _\mathrm{ H}}\chi \:\delta \end{eqnarray*}$$

(16)

in the simplest case, with a single source distance at χ_H. Placing a single lens with the longitudinal extension of Δχ = 1 Mpc h⁻¹ and density δ at χ = χ_H/2 yields κ ≃ 10⁻⁴. Combining all shape and size distortions in an uncorrelated random walk with χ_H/Δχ steps amplifies the signal by a factor of |$\sqrt{\chi _\mathrm{ H}/\Delta \chi }$|⁠, which brings the lensing signal to values between 10⁻³ and 10⁻², which one typically cites as a weak shear distortion.

With many galaxies in a tomographic bin A with a suitable, normalized redshift distribution p_A(z)dz, one can define the line-of-sight-averaged ellipticity from second angular derivatives of the weighted projection of the potential Φ:

$$\begin{eqnarray*} \varphi _{A,ab} = \partial _a\partial _b\varphi _A \quad \mathrm{with}\quad \varphi _A = D_{IA}\int \mathrm{d}\chi \:p_A(z(\chi))\frac{\mathrm{d}z}{\mathrm{d}\chi }\frac{1}{\chi ^2}\frac{D_+(a)}{a}\:\frac{\Phi }{c^2} = \int \mathrm{d}\chi \:W_{\varphi ,A}(\chi)\:\frac{\Phi }{c^2}, \end{eqnarray*}$$

(17)

with the Hubble function H(χ)/c = dz/dχ that originates from the transformation of the redshift distribution, and the growth rate D₊(a)/a of gravitational potentials, and the alignment parameter D_IA, which encapsulates the proportionality between tidal field and physical shape and size change. The line-of-sight-weighting function W_φ,A of bin A is defined by the last equals sign. The parameter D_IA reflects the brightness distribution of a galaxy through its second moments and scales inversely with the velocity dispersion σ². Because linear intrinsic alignments have opposite signs compared to gravitational lensing in the same gravitational potential, we choose a negative value for the alignment parameter D_IA in order to not having to carry through minus signs explicitly. This is due to the fact that an overdense region enlarges the image of a galaxy in lensing but compresses a galaxy physically.

Modelling the statistics of the intrinsic alignment effects from a Gaussian random field as we do in equation (17) subsequently ignores that the galaxy shapes and sizes provide a measurement of the tidal field restricted to peak regions of the large-scale structure, which influences the statistics of tidal fields (Peacock & Heavens 1985; Schäfer & Merkel 2012). On the other hand, correlations between tidal fields and characterizations of the environment, for instance in terms of the eigenvalues of the tidal shear tensor (Forero-Romero, Contreras & Padilla 2014; Reischke & Schäfer 2019), should apply directly to correlations of shear or size as observables. A related point would be the introduction of a density weighting of the tidal gravitational fields that give rise to the intrinsic shape and size correlations: Those weightings are straightforward to construct as they involve a convolution between the tidal field and density spectra, if one restricts oneself to a reasonably simple multiplicative weighting. This density weighting would associate terms analogous to source–source and source–lens clustering known from gravitational lensing with those arising in alignment models, but would necessitate new parameters and would introduce non-Gaussian statistical properties. In a certain sense, effective field theory models of intrinsic alignments pursue exactly this route (Blazek et al. 2019). Phenomenologically, enhancing the ellipticity correlation function with a linear and deterministic biasing term would be possible, too, but with an ambiguous physical interpretation: While it is clear that the observed ellipticity correlations arise from tidal field correlation with a modulation mediated by the galaxy density, only the relation between galaxy size and galaxy density is given by the ambient matter density, as a consequence of the Poisson relation s ∼ ΔΦ ∼ δ.

The angular derivatives ∂_a are related to the spatial derivatives ∂_x through ∂_a = χ∂_x, with x = θχ in the small-angle approximation. From that, one can recover the ellipticity components ϵ_+,A and ϵ_×,A as well as the size s_A from a decomposition of the tensor φ_A,ab with the Pauli matrices |$\sigma _{ab}^{(n)}$|⁠,

$$\begin{eqnarray*} \varphi _{A,ab} = s_A\sigma ^{(0)}_{ab} + \epsilon _{+,A}\sigma ^{(1)}_{ab} + \epsilon _{\times ,A}\sigma ^{(3)}_{ab}, \end{eqnarray*}$$

(18)

where these three components are sufficient because of the symmetry φ_A,ab = φ_A,ba. Using two properties of the Pauli matrices |$\sigma _{ab}^{(n)}$|⁠, namely |$\sigma _{ab}^{(l)}\sigma _{bc}^{(m)} = \delta _{lm}\sigma ^{(0)}_{ac} + \epsilon _{lmn}\sigma ^{(n)}_{ac}$|⁠, and their tracelessness |$\sigma ^{(m)}_{aa} = 0$|⁠, it is possible to invert the last relation and to obtain the expansion coefficients:

$$\begin{eqnarray*} s_A = \frac{1}{2}\varphi _{A,ab}\sigma ^{(0)}_{ab}, \quad \epsilon _{+,A} = \frac{1}{2}\varphi _{A,ab}\sigma ^{(1)}_{ab}, \mathrm{~and}\quad \epsilon _{\times ,A} = \frac{1}{2}\varphi _{A,ab}\sigma ^{(3)}_{ab}. \end{eqnarray*}$$

(19)

The approach above is motivated by the weak lensing shear γ in some bin B, which results from the tensor ψ_B,ab containing the second derivatives of the weak lensing potential ψ_B,

$$\begin{eqnarray*} \psi _{B,ab} = \partial _a\partial _b\psi _B \quad \mathrm{with}\quad \psi _B = 2\int \mathrm{d}\chi \:\frac{G_B(\chi)}{\chi }\frac{D_+(a)}{a}\frac{\Phi }{c^2} = \int \mathrm{d}\chi \:W_{\psi ,B}(\chi)\frac{\Phi }{c^2}, \end{eqnarray*}$$

(20)

with the lensing efficiency

$$\begin{eqnarray*} G_B(\chi) = \int _{\mathrm{max}(\chi ,\chi _B)}^{\chi _{B+1}}\mathrm{d}\chi ^\prime \:p_B(\chi ^\prime)\frac{\mathrm{d}z}{\mathrm{d}\chi ^\prime }\left(1-\frac{\chi }{\chi ^\prime }\right). \end{eqnarray*}$$

(21)

It is interesting to note that the effects of convergence and shear are fully analogous to the changes in size and shape due to direct tidal interaction, up to some interesting details: A light bundle, consisting of photons as relativistic test particles for the gravitational potential, is deflected twice as strongly compared to non-relativistic test particles such as the stars inside an elliptical galaxy, and the constant of proportionality that makes the gravitational potential dimensionless is c² in lensing instead of σ² for the intrinsic alignments. Finally, the lensing kernel G_B/χ is non-zero not only inside the bin B under consideration but also the integral extends from χ = 0 to the outer rim of bin B, χ_{B + 1}. We compute both lensing and intrinsic alignments from the dimensionless potential Φ given in units of c² and we use a numerical value for the alignment parameter scaled by c²/σ². Again, there is an analogous decomposition

$$\begin{eqnarray*} \psi _{B,ab} = \kappa _B\sigma ^{(0)}_{ab} + \gamma _{+,B}\sigma ^{(1)}_{ab} +\gamma _{\times ,B}\sigma ^{(3)}_{ab} \end{eqnarray*}$$

(22)

with the analogous inversion,

$$\begin{eqnarray*} \kappa _B = \frac{1}{2}\psi _{B,ab}\sigma ^{(0)}_{ab}, \quad \gamma _{+,B} = \frac{1}{2}\psi _{B,ab}\sigma ^{(1)}_{ab}, \mathrm{~and}\quad \gamma _{\times ,B} = \frac{1}{2}\psi _{B,ab}\sigma ^{(3)}_{ab}. \end{eqnarray*}$$

(23)

The intrinsic size field provides a measure of the projected density in the same way as the weak lensing convergence κ, but with a different weighting function:

$$\begin{eqnarray*} s = \frac{1}{2}\varphi _{ab}\sigma ^{(0)}_{ab} = \frac{D_{IA}}{2}\sigma ^{(0)}_{ab}\partial _a\partial _b\int \mathrm{d}\chi \: p(\chi)\frac{1}{\chi ^2}\frac{D_+(a)}{a}\frac{\Phi }{c^2} = \frac{D_{IA}}{2}\int \mathrm{d}\chi \:p(\chi)\frac{D_+(a)}{a}\frac{\Delta \Phi }{c^2} = \frac{3\Omega _m}{4\chi _H^2}D_{IA}\int \mathrm{d}\chi \:p(\chi)\frac{D_+(a)}{a}\delta \, . \end{eqnarray*}$$

(24)

We have substituted the Poisson equation |$\Delta \Phi /c^2 = 3\Omega _\mathrm{ m}/(2\chi _\mathrm{ H}^2)\delta$|⁠, using ∂_a = χ∂_x for the derivatives, and approximated the full Laplacian by the one containing the derivatives perpendicular to the line of sight, as well as the Hubble distance χ_H = c/H₀. Again, one recognizes a factor of 2 between the gravitational acceleration of photons in gravitational lensing and non-relativistic particles as in our case of stars inside an elliptical galaxy. As discussed before, an actual measurement of the mean size s of the galaxies into a certain direction would in addition be weighted with a biasing factor because the tidal field is only measurable at positions where galaxies exist: While the inclusion of a reasonably simple linear and deterministic biasing model is certainly possible and straightforward, we ignore this here for simplicity.

This implies that the statistics of all modes of the shape and size field can be described by spectra of the source fields, which in turn are given by a Limber projection. Specifically, the spectrum of φ_A,ab reads

$$\begin{eqnarray*} \langle \varphi _{A,ab}(\boldsymbol \ell)\varphi _{B,cd}^*(\boldsymbol \ell ^\prime)\rangle = (2\pi)^2\delta _D(\boldsymbol \ell -\boldsymbol \ell ^\prime)\:C^{\varphi _A\varphi _B}_{abcd}(\ell) \quad \mathrm{with}\quad C^{\varphi _A\varphi _B}_{abcd}(\ell) = \ell _a\ell _b\ell _c\ell _d\:\int \frac{\mathrm{d}\chi }{\chi ^2}\:W_{\varphi ,A}(\chi)W_{\varphi ,B}(\chi)\:P_{\Phi \Phi }(k = \ell /\chi), \end{eqnarray*}$$

(25)

similarly, one obtains for the field ψ_B,ab,

$$\begin{eqnarray*} \langle \psi _{A,ab}(\boldsymbol \ell)\psi _{B,cd}^*(\boldsymbol \ell ^\prime)\rangle = (2\pi)^2\delta _D(\boldsymbol \ell -\boldsymbol \ell ^\prime)\:C^{\psi _A\psi _B}_{abcd}(\ell) \quad \mathrm{with}\quad C^{\psi _A\psi _B}_{abcd}(\ell) = \ell _a\ell _b\ell _c\ell _d\:\int \frac{\mathrm{d}\chi }{\chi ^2}\:W_{\psi ,A}(\chi)W_{\psi ,B}(\chi)\:P_{\Phi \Phi }(k = \ell /\chi), \end{eqnarray*}$$

(26)

and finally for their cross-correlation,

$$\begin{eqnarray*} \langle \varphi _{A,ab}(\boldsymbol \ell)\psi _{B,cd}^*(\boldsymbol \ell ^\prime)\rangle = (2\pi)^2\delta _D(\boldsymbol \ell -\boldsymbol \ell ^\prime)\:C^{\varphi _A\psi _B}_{abcd}(\ell) \quad \mathrm{with}\quad C^{\varphi _A\psi _B}_{abcd}(\ell) = \ell _a\ell _b\ell _c\ell _d\:\int \frac{\mathrm{d}\chi }{\chi ^2}\:W_{\varphi ,A}(\chi)W_{\psi ,B}(\chi)\:P_{\Phi \Phi }(k = \ell /\chi), \end{eqnarray*}$$

(27)

where the four powers of ℓ arise through the double differentiation of the potentials ϕ and ψ to link them to tidal fields, which are subsequently squared in computing the spectrum. In general, all lensing effects originating from a tidal gravitational field will have the opposite sign than the intrinsic tidal alignment, which causes the cross-correlation between lensing and intrinsic alignments to have a negative sign. This is taken care of numerically by choosing a negative value for the alignment parameter D_IA, which does not affect the autocorrelations: Those are proportional to |$D_{IA}^2$| and therefore positive. In analogy, we define the angular spectra |$C^{\varphi _A\varphi _B}(\ell)$|⁠, |$C^{\psi _A\psi _B}(\ell)$|⁠, and |$C^{\varphi _A\psi _B}(\ell)$| of the potentials φ_A and ψ_B. For the spectrum of the gravitational potential, we use a linear spectrum of the form |$P_{\Phi \Phi }(k)\propto k^{n_s-4}T^2(k)$| with a transfer function T(k) and a non-linear extension on small scales (Cooray & Hu 2001; Huterer & Takada 2005), normalized to σ₈, but assume Gaussian statistics throughout. We apply a smoothing on a scale defined through M = 4 |$\pi$|/3 Ω _mρ_critR³, |$\rho _\mathrm{crit} = 3H_0^2/(8\pi G)$|⁠,

$$\begin{eqnarray*} \Phi (k) \rightarrow \Phi (k)\exp \left(-\frac{(kR)^2}{2}\right), \end{eqnarray*}$$

(28)

to the potential used for intrinsic alignments, where we set the mass scale to be that of a small elliptical galaxy, M = 10¹² M_⊙ h⁻¹: In doing this, we can control how closely size and shape correlations trace the tidal shear field, and select the relevant long-wavelength modes. We set value of the velocity dispersion σ² to be consistent with the mass scale according to the assumed virial equilibrium.

3 ANGULAR SPECTRA OF GALAXY SHAPES AND SIZES

The pre-factors ℓ_aℓ_b appearing in the expressions for the spectra of the projected tidal shears can be compactly written by introducing polar coordinates, ℓ₀ = ℓcos ϕ and ℓ₁ = ℓsin ϕ. Then,

$$\begin{eqnarray*} \ell _a\ell _b = \frac{\ell ^2}{2}\left(\sigma ^{(0)}_{ab} + (\cos ^2\phi -\sin ^2\phi)\sigma ^{(1)}_{ab} + 2\sin \phi \cos \phi \sigma ^{(3)}_{ab}\right) = \frac{\ell ^2}{2}\left(\sigma ^{(0)}_{ab} + \cos (2\phi)\sigma ^{(1)}_{ab} + \sin (2\phi)\sigma ^{(3)}_{ab}\right), \end{eqnarray*}$$

(29)

recovering the fact that the phase angle rotates twice as fast as the coordinate system. We are going to make the choice ϕ = 0 by a suitable rotation of the coordinate frame, such that there are no contractions with |$\sigma ^{(3)}_{ab}$|⁠, and correspondingly vanishing γ_× or ϵ_×. This corresponds effectively to the computation of E- and B-modes of the shear field and of the ellipticity field, with

$$\begin{eqnarray*} e(\boldsymbol {\ell }) = &\hphantom{-}\cos (2\phi)\gamma _+(\boldsymbol {\ell }) + \sin (2\phi)\gamma _\times (\boldsymbol {\ell }), \end{eqnarray*}$$

(30)

$$\begin{eqnarray*} b(\boldsymbol {\ell }) = &-\sin (2\phi)\gamma _+(\boldsymbol {\ell }) + \cos (2\phi)\gamma _\times (\boldsymbol {\ell }), \end{eqnarray*}$$

(31)

where in our model there are no B-modes due to the index exchange symmetry. This is in contrast to the predictions of tidal torquing models for spiral galaxies, where an ellipticity B-mode comparable to the ellipticity E-mode appears very naturally. For Gaussian tidal gravitational fields, one would not expect cross-correlations between the shapes of spirals and ellipticals, if in fact the alignment of spirals is given by the quadratic tidal torquing model, but that can be different if one takes non-Gaussian statistics of the tidal fields at late times and on small scales into account. Comparing intrinsic spectra for elliptical galaxies to higher order effects in gravitational lensing, it is certainly the case that intrinsic alignments are the dominating contributions to shape and size correlations on all scales, whereas other effects such as Born corrections, lens–lens coupling, or reduced shear corrections are present only at predominantly small scales (Krause & Hirata 2010). In our model, we use a non-linear fit to the CDM spectrum P(k) to include non-linear scales, which is directly applicable to non-linear tidal gravitational fields because of the linearity of the Poisson equation, i.e. the alignment mechanism is still linear; nevertheless, the ambient density field generating the tidal gravitational field is in a stage of non-linear structure formation.

Now, the decomposition with Pauli matrices makes it possible to write down all ellipticity spectra as contractions of the possible spectra of the source terms, for lensing,

$$\begin{eqnarray*} C^{\gamma \gamma }_{AB}(\ell) = \frac{1}{4}\sigma ^{(1)}_{ab}\sigma ^{(1)}_{cd}C^{\psi _A\psi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\psi _A\psi _B}(\ell), \end{eqnarray*}$$

(32)

for intrinsic alignments,

$$\begin{eqnarray*} C^{\epsilon \epsilon }_{AB}(\ell) = \frac{1}{4}\sigma ^{(1)}_{ab}\sigma ^{(1)}_{cd}C^{\varphi _A\varphi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\varphi _A\varphi _B}(\ell), \end{eqnarray*}$$

(33)

and for the cross-correlation between the two,

$$\begin{eqnarray*} C^{\epsilon \gamma }_{AB}(\ell) = \frac{1}{4}\sigma ^{(1)}_{ab}\sigma ^{(1)}_{cd}C^{\varphi _A\psi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\varphi _A\psi _B}(\ell). \end{eqnarray*}$$

(34)

A measurement of the shape correlations is limited by a Poissonian shape noise contribution,

$$\begin{eqnarray*} N_{AB}^\mathrm{shape}(\ell) = \sigma ^2_\mathrm{shape}\frac{n_\mathrm{tomo}}{\bar{n}}\delta _{AB}, \end{eqnarray*}$$

(35)

with a value of σ_shape = 0.4 and the number density |$\bar{n} = 4.727\times 10^8$| galaxies per steradian typical for Euclid studies. It is straightforward to show that of the 20 possible spectra 10 are in fact non-zero, and that certain consistency relations hold, for instance |$\langle \kappa \kappa ^\prime \rangle = \langle \gamma _+\gamma _+^\prime \rangle + \langle \gamma _\times \gamma _\times ^\prime \rangle$| as well as |$\langle ss^\prime \rangle = \langle \epsilon _+\epsilon _+^\prime \rangle + \langle \epsilon _\times \epsilon _\times ^\prime \rangle$|⁠, in any coordinate frame.

The resulting extrinsic and intrinsic shape spectra are shown for a tomographic survey in Fig. 2: Intrinsic shape correlations are relevant at intermediate multipoles, but are surpassed by one to two orders of magnitude by weak lensing-induced shape correlations, for realistic values of the alignment parameter D_IA. Intrinsic and extrinsic shapes are anticorrelated, and the cross-correlation is modulating the spectra over much wider multipole ranges. In fulfilment of the Cauchy–Schwarz inequality, the cross-correlation has values between the pure lensing and intrinsic alignment effect. The alignment parameter D_IA was chosen to be 10⁻⁵ (Mpc h⁻¹)², and scales proportional to σ², where σ = 10⁵ m s⁻¹ would be a typical value for a Milky Way-sized object with 10¹² M_⊙ h⁻¹: Increasing the velocity dispersion (where σ ∝ M^1/3 due to the viral law) requires a larger alignment parameter D_IA. This value of the alignment parameter is chosen lower than the value measured by Tugendhat & Schaefer (2018) in the CFHTLenS data, with a value of 10⁻⁴ (Mpc h⁻¹)² for D_IA, but with an uncertainty to which mass scale this parameter actually corresponds, making direct comparisons difficult: There are, in fact, many relevant issues to consider: First of all, the choice of a mass scale determines the smoothing scale on which the CDM spectrum P(k) for computing tidal fields is cut off, because tidal shear field fluctuations on scales smaller than the galaxy itself cannot be relevant to the alignment process. Secondly, the mass scale enters the alignment parameter through the arguments discussed in the introduction, and because mass functions are commonly strongly decreasing with mass, the choice of the lower mass limit matters tremendously when considering averaged values of virial quantities and consequently, of the alignment parameter. Lastly, there is an implicit mass dependence generated by the strong dependence of the induced ellipticity change with the Sérsic index, as more massive galaxies tend to have higher Sérsic indices, i.e. n ≃ 4 for ordinary ellipticals versus n ≃ 1 for dwarf ellipticals.

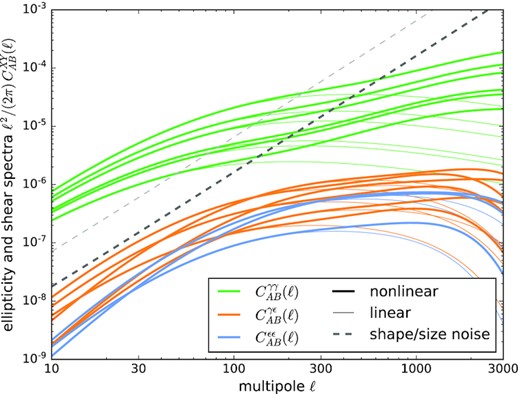
$Shape–shape correlations as a function of multipole order ℓ, separated by gravitational lensing $C_{AB}^{\gamma \gamma }(\ell)$, intrinsic size correlations $C_{AB}^{\epsilon \epsilon }(\ell)$, and the cross-correlation $C_{AB}^{\gamma \epsilon }(\ell)$ (of which we show the absolute value), with the Poissonian noise contributions $N_{AB}^\mathrm{shape}(\ell)$ (dark grey) and $N_{AB}^\mathrm{size}(\ell)$ (light grey, a factor of 4 higher) in comparison, for Euclid’s redshift distribution and tomography with three bins, for a ΛCDM cosmology with an alignment parameter DIA = −10−5 (Mpc h−1)2 on a mass scale M = 1012 M⊙ h−1, corresponding to a virial velocity of σ ≃ 105 m s−1. Thick and thin lines indicate a non-linear spectrum and a linear spectrum, respectively.$

Figure 2.

Shape–shape correlations as a function of multipole order ℓ, separated by gravitational lensing |$C_{AB}^{\gamma \gamma }(\ell)$|⁠, intrinsic size correlations |$C_{AB}^{\epsilon \epsilon }(\ell)$|⁠, and the cross-correlation |$C_{AB}^{\gamma \epsilon }(\ell)$| (of which we show the absolute value), with the Poissonian noise contributions |$N_{AB}^\mathrm{shape}(\ell)$| (dark grey) and |$N_{AB}^\mathrm{size}(\ell)$| (light grey, a factor of 4 higher) in comparison, for Euclid’s redshift distribution and tomography with three bins, for a ΛCDM cosmology with an alignment parameter D_IA = −10⁻⁵ (Mpc h⁻¹)² on a mass scale M = 10¹² M_⊙ h⁻¹, corresponding to a virial velocity of σ ≃ 10⁵ m s⁻¹. Thick and thin lines indicate a non-linear spectrum and a linear spectrum, respectively.

Open in new tab Download slide

Compared to the IllustrisTNG simulation (Zjupa, Schaefer & Hahn 2020), where the alignment parameter as a constant of proportionality is measured directly in the relation between ellipticity and tidal shear, our value for D_IA is higher by a factor of 4, because the measurement of the ambient tidal shear field contains a contribution from the local matter density and disregards biasing effects. Currently, there are still large uncertainties concerning the value and its dependence on galaxy mass as well as a possible evolution in redshift and galaxy biasing, such that we decided to use an intermediate value. A direct measurement of shape alignments in the IllustrisTNG simulation without a differentiation between galaxy types carried out by Hilbert et al. (2017a) yields a higher value of D_IA ≃ 1.5 × 10⁻⁴ (Mpc h⁻¹)², but a direct comparison is difficult as galaxy biasing plays certainly a role in correlations as a function of physical separation but less so in line-of-sight-averaged quantities. Given these arguments, we settle for a conservative choice of 10⁻⁵ (Mpc h⁻¹)² for D_IA and discuss the implications of different parameter values in Section 4. On the other side, modelling of intrinsic alignments with effective field theories of Blazek et al. (2019) and Fang et al. (2017) would be, in contrast to our analytical approach, able to simulate the combined effect of alignment and biasing, at the expense of a potentially larger number of alignment parameters.

The shape correlations on very small scales would be dominated by spiral galaxies, for Euclid’s redshift distribution and with the assumption of the tidal torquing model this would be the case on multipoles above ℓ ≃ 300. As in this model the ellipticities are proportional to the quadratic tidal shear field, one would not expect for Gaussian fields a cross-correlation with the shapes of elliptical galaxies nor with lensing, making the shapes of spiral galaxies statistically uncorrelated.

In a similar manner as in the previous section, one obtains the size spectra from contracting the possible spectra of the source terms, for lensing,

$$\begin{eqnarray*} C^{\kappa \kappa }_{AB}(\ell) = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(0)}_{cd}C^{\psi _A\psi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\psi _A\psi _B}(\ell), \end{eqnarray*}$$

(36)

for intrinsic alignments,

$$\begin{eqnarray*} C^{ss}_{AB}(\ell) = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(0)}_{cd}C^{\varphi _A\varphi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\varphi _A\varphi _B}(\ell), \end{eqnarray*}$$

(37)

and again, for the cross-correlation between the two,

$$\begin{eqnarray*} C^{s\kappa }_{AB}(\ell) = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(0)}_{cd}C^{\varphi _A\psi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\varphi _A\psi _B}(\ell), \end{eqnarray*}$$

(38)

i.e. all size-spectra are equal to their shape counterparts. In the estimation process, there is a constant, diagonal noise contribution

$$\begin{eqnarray*} N_{AB}^\mathrm{size}(\ell) = \sigma ^2_\mathrm{size} \frac{n_\mathrm{tomo}}{\bar{n}}\delta _{AB}, \end{eqnarray*}$$

(39)

with the size noise σ_size = 0.8.

Fig. 2 shows at the same time the intrinsic and extrinsic spectra of galaxy shapes, as they would result from a tomographic survey similar to the Euclid lensing survey. In fact, as a consequence of the linear alignment model and the linearity of weak lensing the size correlations are identical to the shape correlations, including the anticorrelation between intrinsic and extrinsic size: The GI term arising when correlating lensing convergence with intrinsic size is negative due to exactly the same reasons as lensing shear is anticorrelated with intrinsic ellipticity.

Given the fact that there is a slightly higher uncertainty in the measurement of angular size in comparison to shape, one can already now expect that the corresponding signal-to-noise ratios for size correlations are slightly inferior to shapes. These statements rely on the fact that the same alignment parameter D_IA is relevant for both shapes and sizes, as the linear alignment model would suggest. Similarly, we show in Fig. 3 the Pearson correlation coefficient r_γϵ(ℓ) as a function of multipole ℓ,

$$\begin{eqnarray*} r_{\gamma \epsilon }(\ell) = \frac{C^{\gamma \epsilon }_{AA}(\ell)}{\sqrt{C^{\gamma \gamma }_{AA}(\ell)\: C^{\epsilon \epsilon }_{AA}(\ell)}}, \end{eqnarray*}$$

(40)

where we would like to emphasize that the Pearson coefficients for shapes and sizes are identical, r_γϵ(ℓ) = r_κsℓ. The Pearson coefficient shows how statistically independent cross-correlations are from autocorrelations. In equation (40), this coefficient r_γϵ(ℓ) is zero if there is no correlation, 1 if the correlation is perfect, and −1 if there is perfect anticorrelation. The boundedness of the values of r_γϵ(ℓ) is a consequence of the Cauchy–Schwarz inequality, which states that |$\left|C^{\gamma \epsilon }_{AA}(\ell)\right|\le \sqrt{C^{\gamma \gamma }_{AA}C^{\epsilon \epsilon }_{AA}(\ell)}$|⁠. Again, the negative values of r_γϵ(ℓ) indicate the negative sign of the GI terms, for shape and size correlations alike. We set the bin indices equal, A = B, because only in this case |$C^{\epsilon \epsilon }_{AB}(\ell)$| and |$C^{ss}_{AB}(\ell)$| are unequal to zero. The values for r_γϵ(ℓ) suggest that there is in fact redundancy in the spectra.

Figure 3.

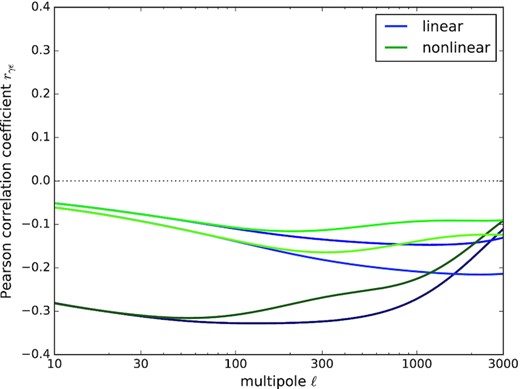
Pearson correlation coefficients r_γϵ(ℓ) as a function of multipole order ℓ. The curves correspond to low redshift (bottom pair), intermediate redshift (top pair), and high redshift (centre pair), and contrast linear (blue lines) and non-linear (green lines) spectra.

Open in new tab Download slide

Finally, we compute the cross-correlations between galaxy shapes and sizes, for lensing,

$$\begin{eqnarray*} C_{AB}^{\kappa \gamma }(\ell) = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(1)}_{cd}C^{\psi _A\psi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\psi _A\psi _B}(\ell) , \end{eqnarray*}$$

(41)

for intrinsic alignments,

$$\begin{eqnarray*} C_{AB}^{s\epsilon }(\ell) = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(1)}_{cd}C^{\varphi _A\varphi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\varphi _A\varphi _B}(\ell) , \end{eqnarray*}$$

(42)

and for the cross-correlation between lensing and alignments,

$$\begin{eqnarray*} C_{AB}^{\kappa \epsilon }(\ell) & = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(1)}_{cd}C^{\psi _A\varphi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\psi _A\varphi _B}(\ell) \end{eqnarray*}$$

(43)

$$\begin{eqnarray*} C_{AB}^{s\gamma }(\ell) & = \frac{1}{4}\sigma ^{(0)}_{ab}\sigma ^{(1)}_{cd}C^{\psi _A\varphi _B}_{abcd}(\ell) = \frac{\ell ^4}{4}C^{\varphi _A\psi _B}(\ell), \end{eqnarray*}$$

(44)

where due to the independence of the errors in the shape and size correlations one does not have to deal with a noise contribution when estimating spectra. Effectively, the cross-correlations between shape and size look identical to the autocorrelations, but in their estimation process there is no noise term, if statistical independence of the two measurement processes for shape and size is given. This can be seen in Heavens et al. (2013) and Alsing et al. (2015), who as well estimate the amount of shape and size noise.

4 INFORMATION CONTENT OF SHAPE AND SIZE CORRELATIONS

For quantifying the information content of intrinsic size and shape correlations in comparison to weak lensing convergence and shear, we use the Fisher-matrix formalism. Arranging the measurements of galaxy shapes and sizes into a data vector yields the data covariance matrix:

$$\begin{eqnarray*} C = \begin{pmatrix}C^{\epsilon \epsilon }_{AB}(\ell) + 2C^{\epsilon \gamma }_{AB}(\ell) + C^{\gamma \gamma }_{AB}(\ell) + N^\mathrm{shape}_{AB} & C^{s\epsilon }_{AB^\prime }(\ell) + C^{s\gamma }_{AB^\prime }(\ell) + C^{\kappa \epsilon }_{AB^\prime }(\ell) + C^{\kappa \gamma }_{AB^\prime }(\ell) \\ C^{s\epsilon }_{A^\prime B}(\ell) + C^{s\gamma }_{A^\prime B}(\ell) + C^{\kappa \epsilon }_{A^\prime B}(\ell) + C^{\kappa \gamma }_{A^\prime B}(\ell) & C^{ss}_{A^\prime B^\prime }(\ell) + 2C^{s\kappa }_{A^\prime B^\prime }(\ell) + C^{\kappa \kappa }_{A^\prime B^\prime }(\ell) + N^\mathrm{size}_{A^\prime B^\prime } \end{pmatrix} . \end{eqnarray*}$$

(45)

Given the similarities between the shape and size correlations, it allows us to rewrite the covariance matrix as

$$\begin{eqnarray*} C = \begin{pmatrix}\frac{\ell ^4}{4}\left(C^{\varphi _A\varphi _B}(\ell)+2C^{\varphi _A\psi _B}(\ell)+C^{\psi _A\psi _B}(\ell)\right) + N^\mathrm{shape}_{AB} & \frac{\ell ^4}{4}\left(C^{\varphi _A\varphi _{B^\prime }}(\ell)+2C^{\varphi _A\psi _{B^\prime }}(\ell)+C^{\psi _A\psi _{B^\prime }}(\ell)\right)\\ \frac{\ell ^4}{4}\left(C^{\varphi _{A^\prime }\varphi _B}(\ell)+2C^{\varphi _{A^\prime }\psi _B}(\ell)+C^{\psi _{A^\prime }\psi _B}(\ell)\right) & \frac{\ell ^4}{4}\left(C^{\varphi _{A^\prime }\varphi _{B^\prime }}(\ell)+2C^{\varphi _{A^\prime }\psi _{B^\prime }}(\ell)+C^{\psi _{A^\prime }\psi _{B^\prime }}(\ell)\right) + N^\mathrm{size}_{A^\prime B^\prime } \end{pmatrix}, \end{eqnarray*}$$

(46)

which is dangerously close to being singular, underlining the degeneracy between the shape and size measurements: In fact, without the noise contributions |$N^\mathrm{shape}_{AB}(\ell)$| and |$N^\mathrm{size}_{AB}(\ell)$| the covariance matrix would have a vanishing determinant, detC, and would be singular: This would exactly correspond to the cosmic variance limit, in which the two measurements cannot be combined in a sensible way. Already at this stage, one should expect that a combined measurement of shear and size does not yield strong improvements of the signal-to-noise ratio alone, and given the fact that the same potentials are involved with identical physical dependences on cosmology, resulting Fisher matrices will be very similar. We use the Fisher-matrix formalism as a quick way to quantify the fundamental sensitivities and degeneracies, while noting that the non-Gaussian shape of the likelihood matters in most cases and that tools for dealing with non-Gaussian likelihoods analytically exist (Takada & Jain 2009; Sellentin & Schäfer 2015).

The Fisher matrix F_μν for a tomographic survey assumes the generic form

$$\begin{eqnarray*} F_{\mu \nu } = f_\mathrm{sky}\sum _\ell \frac{2\ell +1}{2}\mathrm{tr}\left(C^{-1}\partial _\mu S\:C^{-1}\partial _\nu S\right) , \end{eqnarray*}$$

(47)

where we implicitly assume a full sky coverage by having independent Fourier modes. At this point, it is worth emphasizing that we choose to work with the Fisher matrix that quantifies the compatibility of an ensemble of modes ϵ_ℓm and γ_ℓm of the ellipticity and shear field, all with vanishing mean, with the variance predicted by the spectra, and for the modes s_ℓm and κ_ℓm in complete analogy. Similarly, we define the signal-to-noise ratio Σ as

$$\begin{eqnarray*} \Sigma ^2 = f_\mathrm{sky}\sum _\ell \frac{2\ell +1}{2}\mathrm{tr}\left(C^{-1}S\:C^{-1}S\right), \end{eqnarray*}$$

(48)

with the noiseless spectrum S(ℓ) of which the signal strength is sought. For the case of Euclid, we extend the summation over the multipoles from ℓ = 10 to 3000, and we are assuming for simplicity a full-sky coverage with no correlations between different multipoles, which would typically arise in the case of incomplete sky coverage. Instead, we scale down the signal with a sky coverage of |$\sqrt{f_\mathrm{sky}}$| in a Poissonian manner, and argue that ignoring the correlations between different multipoles is a small error because most of the signal originates on small angular scales, where these correlations are weak. We set the number of tomographic bins to n_tomo = 5 to demonstrate the behaviour and scaling of the alignment signal relative to the lensing signal.

Clearly, not all galaxies are ellipticals for which the tidal alignment model would apply, but only a fraction of q ≃ 1/3 of them. Therefore, we compute two values for the signal-to-noise ratio Σ: First, we weight the GI-type spectra by a factor q, and the II-type spectra by a factor q² relative to the GG term, as lensing operates on all galaxies identically irrespective of their type. These numbers for Σ would correspond to estimates of the spectra from the full data set and indicate the level of significance by which the shape or size correlations are incompatible with a pure gravitational lensing model. Fig. 4 quantifies the signal-to-noise ratio Σ for measuring intrinsic shape and intrinsic size correlations: We compute the signal-to-noise ratio for a measurement of the II and GI terms in both shape and size correlations in the presence of the full cosmic variance, which is dominated by gravitational lensing, i.e. by the GG terms. As expected, lensing-induced shape correlations are measurable at a higher signal-to-noise ratio compared to size correlations, but both are easily within the reach of Euclid. The signal-to-noise ratio suggests that GI-type terms are detectable in shape correlations and perhaps marginally in size correlations, and II terms are marginally detectable, with intrinsic shape correlations being the least disappointing. Because the covariance in equation (48) is by far dominated by weak lensing and by the shape noise and size noise contributions, it will be the case that Σ is proportional to |$\sqrt{D_{IA}}$| for the GI terms and to D_IA for the II terms, and other values than D_IA ≃ −10⁻⁵ (Mpc h⁻¹)² than the one adopted here will be directly reflected by the signal-to-noise prediction.

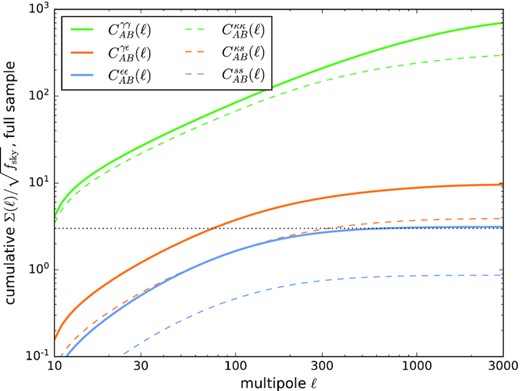
$Cumulative signal-to-noise ratio $\Sigma (\ell)/\sqrt{f_\mathrm{sky}}$ for Euclid five-bin tomography for measuring shape correlations and intrinsic size correlations, for the full galaxy sample.$

Figure 4.

Cumulative signal-to-noise ratio |$\Sigma (\ell)/\sqrt{f_\mathrm{sky}}$| for Euclid five-bin tomography for measuring shape correlations and intrinsic size correlations, for the full galaxy sample.

Open in new tab Download slide

As the II terms are proportional to |$D_{IA}^2$| and the GI terms are proportional to D_IA, the inverse Σ⁻¹ of the signal-to-noise ratio is at the same time the relative error |$D_{IA}/\sigma _{D_{IA}}$| on the alignment parameter D_IA for the GI terms, and the absolute error σ = 1/(2Σ) on D_IA for the II terms. This suggests that measurements of the alignment parameter can be carried out at the level of a few 10 per cent, so the investigation of trends with galaxy mass, type, or redshift seems feasible. We have chosen a rather conservative value for D_IA, nothing precludes the usage of a strategy to boost intrinsic alignments relative to lensing. As for the morphological mix of spiral and elliptical galaxies, we conclude that the signal-to-noise ratios are likewise proportional to q for the GI terms and to q² for the II terms, such that effectively the combined parameter q × D_IA is determined through a measurement. In the same way as adopting higher values for the alignment parameter D_IA, a higher fraction of elliptical galaxies q would be reflected in the signal-to-noise ratio Σ.

On the other hand, one could pursue the strategy to pre-select elliptical galaxies on the basis of their colours or morphologies and to measure the shape and size correlations on the resulting, reduced data set. In this case, effectively, the total number of galaxies |$\bar{n}$| is reduced by q and the number of galaxy pairs by q², leading to an increased Poissonian noise term, which becomes larger by a factor of q. Consequently, the signal strength for weak lensing is much weaker, as it is estimated from a much smaller number of galaxies, but the ratio of the amplitudes between intrinsic alignment and lensing is smaller compared to the previous case: In short, one has a cleaner data set because all galaxy pairs carry the intrinsic alignment signal, but this comes at the expense of having lower galaxy numbers and a higher Poisson noise in the estimates for all spectra. For the case of a misidentification of galaxies, we refer the reader to Tugendhat, Reischke & Schaefer (2020), where a formalism is presented based on probabilities of misidentification of the first and second kinds. The resulting numbers are shown in Fig. 5, where the overall higher shape and size noise terms decrease the significance, but vice versa, the amplitude of the intrinsic correlations relative to those of lensing are higher, such that a feasible strategy for measuring intrinsic shape correlations could be to measure the GI terms and the II terms with a selected sample of elliptical galaxies. The intrinsic size correlations, however, seem to be out of reach with Euclid, no matter the strategy. The attainable signal-to-noise ratio depends not only on the alignment parameter D_IA but also on the mass scale on which the spectra are smoothed: The two are not independent and should be related through a virial relationship linking velocity dispersion σ² and mass M, σ² ∝ M^2/3, but choosing a smaller mass scale has the consequence that higher multipoles contribute an increase Σ(ℓ) to the signal. The morphological ratio between spiral and elliptical galaxies impacts in this case only the total number of galaxies and therefore the shape and size noise amplitude, as in this case too the cosmic variance is lensing dominated.

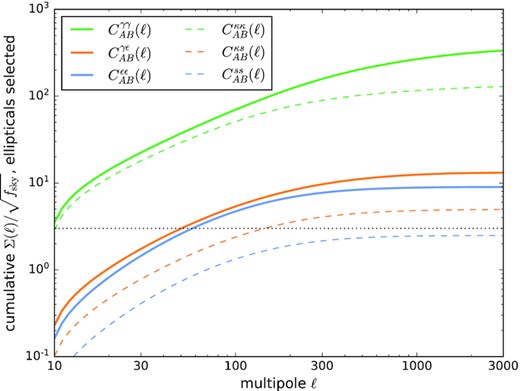
$Cumulative signal-to-noise ratio $\Sigma (\ell)/\sqrt{f_\mathrm{sky}}$ for Euclid five-bin tomography for measuring shape correlations and size correlations, for a case when elliptical galaxies are selected for the estimation of correlations.$

Figure 5.

Cumulative signal-to-noise ratio |$\Sigma (\ell)/\sqrt{f_\mathrm{sky}}$| for Euclid five-bin tomography for measuring shape correlations and size correlations, for a case when elliptical galaxies are selected for the estimation of correlations.

Open in new tab Download slide

While the second strategy delivers directly the significances of the GI and II terms for a sample of elliptical galaxies, we should be careful in pointing out that the first strategy quantifies the significance of a contribution of elliptical galaxies to the total intrinsic shape correlations, to which spiral galaxies contribute as well, albeit only on higher multipoles (Tugendhat & Schaefer 2018). If alignments of spiral galaxies follow from the quadratic model (Crittenden et al. 2001), their shapes would be statistically uncorrelated with the shapes of elliptical galaxies and they would not generate a cross-correlation with lensing (Tugendhat et al. 2020), such that both signal-to-noise ratios would add in quadrature.

Fig. 6 shows constraints on a wCDM cosmology from galaxy shapes and galaxy sizes: It is always the case that using the entire galaxy sample leads to tighter constraints than pre-selecting elliptical galaxies; i.e. the lower Poisson error dominates over the weaker correlations. As both observables are probing tidal gravitational fields with identical physical dependences, there cannot be any fundamental difference in the degeneracies, with the only exception that the noise in the size measurement is typically larger than the one of the shape measurement, which effectively cuts off high multipoles from contributing to the signal. We emphasize that the two measurements are highly correlated such that one does not gain an advantage from combining the two. We would argue, however, that there is potential to use shape and size correlations to investigate deviations from the Newtonian form of the Poisson equation, e.g. by modified theories of gravity. The relative amplitudes of the GG, GI, and II terms are sensitive to gravitational slip, because one compares the effect of gravitational potential on relativistic (lensing) to non-relativistic (stars inside a galaxy) test particles, with the potential advantage over the combination of lensing with peculiar velocities that the measurement combines two probes on the same scale. For this, one needs a very good understanding of the detailed mechanisms of alignment with possibly non-linear corrections to the tidal alignment model, as well as the scaling behaviour of the alignment parameter with redshift and galaxy mass (Hirata et al. 2007), and possibly different alignment parameters for subpopulations of elliptical galaxies, as the strong dependence on the Sérsic index suggests. Ultimately, one would need to resort to the concept that on galactic scales Newtonian gravity is prevalent, such that the amount of shape (or size) distortion of an elliptical galaxy can be predicted from simulations of galaxy formation and evolution. Then, relative to the Newtonian prediction, modified gravity effects on larger scales can be parametrized and determined by gravitational lensing. Without detailed input from numerical simulations or a much deeper understanding of galaxy scaling relations, the degeneracy between gravitational slip and the alignment parameter D_IA cannot be broken.

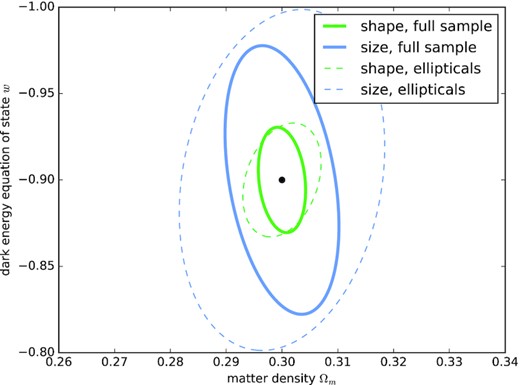
Marginalized 1σ contours from the Fisher-matrix analysis on a standard wCDM cosmology (with w = −0.9) for a fixed value DIA = −10−5 (Mpc h−1)2 for the alignment parameter and a smoothing scale of 1012 M⊙ h−1: We give contours separated by shape and size correlations, and for the full galaxy sample versus a sample containing only elliptical galaxies.

Figure 6.

Marginalized 1σ contours from the Fisher-matrix analysis on a standard wCDM cosmology (with w = −0.9) for a fixed value D_IA = −10⁻⁵ (Mpc h⁻¹)² for the alignment parameter and a smoothing scale of 10¹² M_⊙ h⁻¹: We give contours separated by shape and size correlations, and for the full galaxy sample versus a sample containing only elliptical galaxies.

Open in new tab Download slide

Fundamental degeneracies in the spectra are present between the alignment parameter D_IA and σ₈, which are perfectly degenerate in the linear regime, but the degeneracy is broken by combining the GG, GI, and II terms in the measurement, as they are proportional to |$\sigma _8^2$|⁠, |$\sigma _8^2D_{IA}$|⁠, and |$\sigma _8^2D_{IA}^2$|⁠, respectively. In a similar way, the proportionality of the lensing spectrum to |$\Omega _\mathrm{ m}^2$| to first order translates to the GI term, which is proportional to Ω_m. The influence of the particular dark energy model by mapping the redshift distribution of the galaxies on to a distribution in comoving distance is identical for all correlations. Pursuing the two strategies of either keeping the full galaxy sample and down-weighting GI spectra by q = 1/3 and II terms by q² yields smaller errors than pre-selecting elliptical galaxies first, because of the smaller Poisson noise, but the second strategy has a higher relative contribution from intrinsic alignments, which start to matter when deriving constraints, as they provide cosmological information. In both cases, we obtain the result that the dominating constraint on the alignment parameter D_IA is derived from the GI term due to its higher amplitude compared to the II term, if all other parameters are fixed.

5 SUMMARY

The subjects of our investigation were extrinsic and intrinsic shape and size correlations of elliptical galaxies due to weak gravitational lensing and intrinsic alignments, using an analytical model, without any simulation. Our starting point was the description of the stellar density of a virialized system through the Jeans equation, in which we perturb the gravitational potential with an external tidal field. Under the condition that this field is reasonably weak and the galaxy compact enough, one can compute the response in shape and size of a galaxy in linear approximation in the tidal field, controlled by the galaxy’s velocity dispersion σ². The susceptibility of a galaxy to tidal distortions is highly dependent on the stellar profile: A toy model using the Sérsic profile family shows a strong increase in the response from exponential profiles to de Vaucouleurs profiles.

These are our main findings:

Assuming a weakly perturbed Jeans equilibrium for elliptical galaxies naturally reproduces a linear response of the shape and the size of a galaxy to external tidal gravitational fields, and suggests that the same alignment parameter is responsible for the change in shape and in size. Nominally, the velocity dispersion σ of the galaxy sets the scale for the gravitational field, which is remarkably similar to the quantity 2Φ/c² in gravitational lensing. With virial equilibrium, one can continue to argue that σ² is proportional to M/R with the mass M and the size R, such that the ratio (R/σ)², which controls the strength of the tidal interaction, is in fact constant (compare Piras et al. 2018). A mass dependence of the intrinsic alignment effect would be introduced by the convolution of the tidal shear spectrum with a filter function corresponding to the galaxy mass M, and the strong scaling of the expected alignment effect with Sérsic index n, which commonly tends to increase with galaxy mass. Galaxy biasing would introduce an additional modulation of the intrinsic alignment effect and should be included in particular when comparing intrinsic alignment spectra with straightforward galaxy clustering; in this sense, the intrinsic shapes and sizes become weighted clustering spectra. Again, one finds typically higher biases for more massive galaxies, adding another scaling of the results with mass.
Using the standard Poisson equation, the galaxy sizes provide a direct mapping of the ambient matter density, and the intrinsic and extrinsic shapes and sizes are consistent with each other, including the factor of 2 that appears in the relationship between the angular Laplacian of the lensing potential ψ and the weak lensing convergence κ for gravitational lensing and the relation between the angular Laplacian of the alignment potential Φ (which is simply the projected Newtonian gravitational potential) and the intrinsic size s of a galaxy. To which extent this can be used to probe deviations from Newtonian gravity is largely unclear and depends on a detailed understanding of the astrophysics of the objects, and ultimately, the constant of proportionality between intrinsic alignment and tidal field has to be determined from simulations because it does not, unlike gravitational lensing, follow from fundamental physics. When using shape and size correlations as cosmological probes, the Poisson equation causes them to contain only degenerate information, and there is a direct mapping between GG-, GI-, and II-type terms. In addition, the shape and size correlations are highly degenerate to the point where size correlations become redundant in comparison to the stronger and more sensitive shape correlations. We note, however, that size correlations can provide an alternative method for mapping out the matter distribution.
Similar to the case of shape correlations, one obtains a completely diagonal autocorrelation for the intrinsic sizes, |$C^{ss}_{AB}(\ell)\propto \delta _{AB}$| and a non-diagonal cross-correlation between size and convergence, |$C^{s\kappa }_{AB}(\ell)$|⁠. The non-diagonal part of the lensing signal only contains GG and GI, but never II terms (Jain & Taylor 2003; Takada & White 2004; Huterer & White 2005), and in principle nulling and boosting techniques (Joachimi & Schneider 2009; Joachimi & Schneider 2010a; Joachimi & Schneider 2010b) are applicable to size correlations as well.
Computing a forecast for Euclid, we find that intrinsic shape and size correlations as well as their cross-correlations with lensing are measurable. Typical signal-to-noise ratios obtained for five-bin tomography are around 10 with the range of Euclid for |$C^{\gamma \epsilon }_{AB}(\ell)$| and |$C^{\epsilon \epsilon }_{AB}(\ell)$| correlations, while size correlations are more difficult to detect. Simulating two strategies, measuring correlations in the full galaxy sample or pre-selecting elliptical galaxies first, showed that the latter could be able to make |$C^{\epsilon \epsilon }_{AB}(\ell)$| correlations detectable. Our forecasts use a conservative value for the alignment parameter, D_IA ≃ −10⁻⁵ (Mpc h⁻¹)², which should strongly depend on the mass scale (Piras et al. 2018) and potentially on the profile shape as well. With this particular value of D_IA, among the size correlations, only |$C^{\kappa s}_{AB}(\ell)$| could yield a marginal detection. However, since the intrinsic signal is directly proportional to D_IA, increasing D_IA by a factor of 3–4 would change this result and would shift all intrinsic spectra within the reach of Euclid.
Investigating the dependence of the spectra on the fundamental parameters of the cosmological model with a standard Fisher-matrix analysis shows that intrinsic shape and size correlations have essentially identical parameter dependences, irrespective of whether the mechanism is gravitational lensing or intrinsic alignments, similar to the results presented by Alsing et al. (2015). Typically, the shape measurement yields smaller Poissonian errors compared to the size estimation, such that the value of the errors is smaller in a size measurement. A combination of the two does not yield significant improvements due to the large covariance between the two measurements. Nevertheless, since they are complementary, the two measurements can provide a consistency test for General Relativity on cosmological scales. We pursued two strategies, which consist in pre-selecting the elliptical galaxies, which increases the noise due to reducing the data, or keeping the full galaxy sample and down-weighting the GI and II terms with the fraction of elliptical galaxies. The first strategy yields tighter errors, but the second strategy picks up stronger contributions from the GI and II terms to the Fisher matrix, which in turn are very similar to galaxy clustering correlations. Estimation biases, as they would arise in fitting lensing models to data that include both lensing and intrinsic alignments, should arise in complete analogy in the size sector as they have been demonstrated to matter for shape correlations (Joachimi & Bridle 2010; Joachimi et al. 2015; Kirk et al. 2015a; Krause, Eifler & Blazek 2016).

In the future, we plan to investigate the usability of both types of shape and size spectra for designing specific tests of gravity, for instance for Vainshtein-type screening mechanisms (Kirk et al. 2011; Tessore et al. 2015), which would manifest themselves in differences between the intrinsic and extrinsic shape and size spectra. Likewise, there is the question whether measurements of the velocity dispersion can help us to disentangle intrinsic size from lensing shear, as the size effect causes galaxies with the same velocity dispersion to appear systematically larger in underdense regions, and through velocity dispersion a common baseline could be established. Again, we point out that these studies would need to be informed with a prior on D_IA obtained from simulations. In addition, we point out that the susceptibility ∫dr r⁵ρ(r) of a stellar system with density ρ could differ for subclasses of elliptical galaxies, giving rise to different effective alignment parameters D_IA. Let us briefly comment on possible intrinsic size and shape effects arising at second order: Similar to lens–lens coupling, one can expect a B-mode generation if lensing shear acts on a correlated intrinsic ellipticity field (similar to Cooray & Hu 2002) and if lensing deflection shifts the galaxies to new positions (Giahi-Saravani & Schäfer 2013, 2014). To what extent spiral galaxies exhibit similar intrinsic size correlations is unclear, and possibly much more dependent on the astrophysics of galaxy formation, beyond models of tidal torquing (Schaefer 2009). Finally, we point out that intrinsic size correlations are straightforward to be implemented in effective field theories of structure formation (Fang et al. 2017; Vlah et al. 2020), as they only require the computation of ΔΦ on a smoothed field.

ACKNOWLEDGEMENTS

BG thanks the University of Heidelberg for hospitality. BMS likes to thank the Universidad del Valle in Cali, Colombia, for their kind hospitality. We thank Eileen Sophie Giesel and Jolanta Zjupa for spotting mistakes in an early version of the draft. We are also grateful to the anonymous referee for their valuable insights and comments for our paper. BG and RD acknowledge support from the Swiss National Science Foundation.

DATA AVAILABILITY

There are no new data associated with this article.

Footnotes

1

While in certain definitions the trace is subtracted in the tidal field, here the tidal field is simply ∂_a∂_bΦ including the trace that is important as it is responsible for size changes.

REFERENCES

Abbott

T. M. C.

et al. ,

2018

,

Phys. Rev. D

,

98

,

043526

10.1103/PhysRevD.98.043526

Crossref

Alsing

J.

,

Kirk

D.

,

Heavens

A.

,

Jaffe

A.

,

2015

,

MNRAS

,

452

,

1202

Altay

G.

,

Colberg

J. M.

,

Croft

R. A. C.

,

2006

,

MNRAS

,

370

,

1422

10.1111/j.1365-2966.2006.10555.x

Crossref

Amara

A.

,

Refregier

A.

,

2007

,

MNRAS

,

381

,

1018

10.1111/j.1365-2966.2007.12271.x

Crossref

Amendola

L.

et al. ,

2018

,

Living Rev. Relativ.

,

21

,

345

Bailin

J.

,

Steinmetz

M.

,

2005

,

ApJ

,

627

,

647

10.1086/430397

Crossref

Bartelmann

M.

,

2010

,

Class. Quantum Gravity

,

27

,

233001

Bartelmann

M.

,

Schneider

P.

,

2001

,

Phys. Rep.

,

340

,

291

Bate

J.

,

Chisari

N. E.

,

Codis

S.

,

Martin

G.

,

Dubois

Y.

,

Devriendt

J.

,

Pichon

C.

,

Slyz

A.

,

2019

,

MNRAS

,

491

,

4057

10.1093/mnras/stz3166

Crossref

Bernstein

G. M.

,

2009

,

ApJ

,

695

,

652

10.1088/0004-637X/695/1/652

Crossref

Bernstein

G.

,

Jain

B.

,

2004

,

ApJ

,

600

,

17

10.1086/379768

Crossref

Bernstein

G. M.

,

Jarvis

M.

,

2002

,

AJ

,

123

,

583

10.1086/338085

Crossref

Blazek

J.

,

Mandelbaum

R.

,

Seljak

U.

,

Nakajima

R.

,

2012

,

JCAP

,

2012

,

041

Blazek

J. A.

,

MacCrann

N.

,

Troxel

M. A.

,

Fang

X.

,

2019

,

Phys. Rev. D

,

100

,

103506

10.1103/PhysRevD.100.103506

Crossref

Brown

M. L.

,

Taylor

A. N.

,

Hambly

N. C.

,

Dye

S.

,

2002

,

MNRAS

,

333

,

501

10.1046/j.1365-8711.2002.05354.x

Crossref

Camelio

G.

,

Lombardi

M.

,

2015

,

A&A

,

575

,

A113

Capranico

F.

,

Merkel

P. M.

,

Schäfer

B. M.

,

2013

,

MNRAS

,

435

,

194

10.1093/mnras/stt1269

Crossref

Casarini

L.

,

La Vacca

G.

,

Amendola

L.

,

Bonometto

S. A.

,

Macciò

A. V.

,

2011

,

JCAP

,

3

,

26

10.1088/1475-7516/2011/03/026

Crossref

Catelan

P.

,

Kamionkowski

M.

,

Blandford

R. D.

,

2001

,

MNRAS

,

320

,

L7

Chang

C.

et al. ,

2018

,

MNRAS

,

475

,

3165

Chisari

N. E.

,

Dvorkin

C.

,

2013

,

JCAP

,

12

,

29

10.1088/1475-7516/2013/12/029

Crossref

Chisari

N. E.

,

Mandelbaum

R.

,

Strauss

M. A.

,

Huff

E. M.

,

Bahcall

N. A.

,

2014a

,

MNRAS

,

445

,

726

10.1093/mnras/stu1786

Crossref

Chisari

N. E.

et al. ,

2014b

,

MNRAS

,

454

,

2736

Chisari

N. E.

,

Dunkley

J.

,

Miller

L.

,

Allison

R.

,

2015

,

MNRAS

,

453

,

682

10.1093/mnras/stv1655

Crossref

Chisari

N. E.

et al. ,

2016

,

MNRAS

,

461

,

2702

10.1093/mnras/stw1409

Crossref

Cooray

A.

,

Hu

W.

,

2001

,

ApJ

,

554

,

56

10.1086/321376

Crossref

Cooray

A.

,

Hu

W.

,

2002

,

ApJ

,

574

,

19

10.1086/340892

Crossref

Crittenden

R. G.

,

Natarajan

P.

,

Pen

U.-L.

,

Theuns

T.

,

2001

,

ApJ

,

559

,

552

10.1086/322370

Crossref

Debattista

V. P.

,

van den Bosch

F. C.

,

Roskar

R.

,

Quinn

T.

,

Moore

B.

,

Cole

D. R.

,

2015

,

MNRAS

,

452

,

4094

de Jong

J. T. A.

,

Verdoes Kleijn

G. A.

,

Kuijken

K. H.

,

Valentijn

E. A.

,

2013

,

Exp. Astron.

,

35

,

25

10.1007/s10686-012-9306-1

Crossref

de Vaucouleurs

G.

,

1948

,

Ann. Astrophys.

,

11

,

247

Douspis

M.

,

Salvati

L.

,

Aghanim

N.

,

2018

,

Proc. Sci., On the Tension between Large Scale Structures and Cosmic Microwave Background (Vol. 335, EDSU2018)

.

SISSA

,

Trieste

,

PoS#

037

10.22323/1.335.0037

Crossref

Dubinski

J.

,

1992

,

ApJ

,

401

,

441

10.1086/172076

Crossref

Fan

Z.-H.

,

2007

,

ApJ

,

669

,

10

10.1086/521182

Crossref

Fang

X.

,

Blazek

J. A.

,

McEwen

J. E.

,

Hirata

C. M.

,

2017

,

JCAP

,

02

,

030

10.1088/1475-7516/2017/02/030

Crossref

Forero-Romero

J. E.

,

Contreras

S.

,

Padilla

N.

,

2014

,

MNRAS

,

443

,

1090

10.1093/mnras/stu1150

Crossref

Ghosh

B.

,

Durrer

R.

,

Sellentin

E.

,

2018

,

JCAP

,

1806

,

008

10.1088/1475-7516/2018/06/008

Crossref

Giahi-Saravani

A.

,

Schäfer

B. M.

,

2013

,

MNRAS

,

428

,

1312

10.1093/mnras/sts110

Crossref

Giahi-Saravani

A.

,

Schäfer

B. M.

,

2014

,

MNRAS

,

437

,

1847

10.1093/mnras/stt2016

Crossref

Graham

A. W.

,

Driver

S. P.

,

2005

,

Publ. Astron. Soc. Aust.

,

22

,

118

10.1071/AS05001

Crossref

Grassi

A.

,

Schäfer

B. M.

,

2014

,

MNRAS

,

437

,

2632

10.1093/mnras/stt2075

Crossref

Hall

A.

,

Taylor

A.

,

2014

,

MNRAS

,

443

,

L119

10.1093/mnrasl/slu094

Crossref

Heavens

A.

,

2003

,

MNRAS

,

343

,

1327

10.1046/j.1365-8711.2003.06780.x

Crossref

Heavens

A.

,

Refregier

A.

,

Heymans

C.

,

2000

,

MNRAS

,

319

,

649

Heavens

A. F.

,

Kitching

T. D.

,

Taylor

A. N.

,

2006

,

MNRAS

,

373

,

105

Heavens

A.

,

Alsing

J.

,

Jaffe

A.

,

2013

,

MNRAS

,

433

,

L6

10.1093/mnrasl/slt045

Crossref

Heymans

C.

,

Heavens

A.

,

2003

,

MNRAS

,

339

,

711

10.1046/j.1365-8711.2003.06213.x

Crossref

Heymans

C.

,

Brown

M.

,

Heavens

A.

,

Meisenheimer

K.

,

Taylor

A.

,

Wolf

C.

,

2004

,

MNRAS

,

347

,

895

10.1111/j.1365-2966.2004.07264.x

Crossref

Heymans

C.

et al. ,

2013

,

MNRAS

,

432

,

2433

10.1093/mnras/stt601

Crossref

Hilbert

S.

,

Xu

D.

,

Schneider

P.

,

Springel

V.

,

Vogelsberger

M.

,

Hernquist

L.

,

2017a

,

MNRAS

,

468

,

790

Hirata

C. M.

,

Seljak

U.

,

2010

,

Phys. Rev. D

,

82

,

049901

10.1103/PhysRevD.82.049901

Crossref

Hirata

C. M.

,

Padmanabhan

N.

,

Seljak

U.

,

Schlegel

D.

,

Brinkmann

J.

,

2004a

,

Phys. Rev. D

,

70

,

103501

10.1103/PhysRevD.70.103501

Crossref

Hirata

C. M.

et al. ,

2004b

,

MNRAS

,

353

,

529

10.1111/j.1365-2966.2004.08090.x

Crossref

Hirata

C. M.

,

Mandelbaum

R.

,

Ishak

M.

,

Seljak

U.

,

Nichol

R.

,

Pimbblet

K. A.

,

Ross

N. P.

,

Wake

D.

,

2007

,

MNRAS

,

381

,

1197

10.1111/j.1365-2966.2007.12312.x

Crossref

Huff

E. M.

,

Graves

G. J.

,

2014

,

ApJ

,

780

,

L16

10.1088/2041-8205/780/2/L16

Crossref

Hui

L.

,

Zhang

J.

,

2002

,

preprint (astro-ph/0205512)

Huterer

D.

,

2002

,

Phys. Rev. D

,

65

,

063001

10.1103/PhysRevD.65.063001

Crossref

Huterer

D.

,

2010

,

Gen. Relativ. Gravit.

,

42

,

2177

10.1007/s10714-010-1051-z

Crossref

Huterer

D.

,

Takada

M.

,

2005

,

Astropart. Phys.

,

23

,

369

10.1016/j.astropartphys.2005.02.006

Crossref

Huterer

D.

,

White

M.

,

2005

,

Phys. Rev. D

,

72

,

043002

10.1103/PhysRevD.72.043002

Crossref

Hu

W.

,

2001

,

Phys. Rev. D

,

65

,

023003

10.1103/PhysRevD.65.023003

Crossref

Hu

W.

,

2002

,

Phys. Rev. D

,

66

,

083515

10.1103/PhysRevD.66.083515

Crossref

Hu

W.

,

Tegmark

M.

,

1999

,

ApJ

,

514

,

L65

10.1086/311947

Crossref

Jain

B.

,

Seljak

U.

,

1997

,

ApJ

,

484

,

560

Jain

B.

,

Taylor

A.

,

2003

,

Phys. Rev. Lett.

,

91

,

141302

10.1103/PhysRevLett.91.141302

Crossref

Jee

M. J.

,

Tyson

J. A.

,

Schneider

M. D.

,

Wittman

D.

,

Schmidt

S.

,

Hilbert

S.

,

2013

,

ApJ

,

765

,

74

10.1088/0004-637X/765/1/74

Crossref

Jing

Y. P.

,

2002

,

MNRAS

,

335

,

L89

10.1046/j.1365-8711.2002.05899.x

Crossref

Joachimi

B.

,

Bridle

S. L.

,

2010

,

A&A

,

523

,

A1

10.1051/0004-6361/200913657

Crossref

Joachimi

B.

,

Schneider

P.

,

2009

,

A&A

,

507

,

105

10.1051/0004-6361/200912420

Crossref

Joachimi

B.

,

Schneider

P.

,

2010a

,

preprint (arXiv:1009.2024)

Joachimi

B.

,

Schneider

P.

,

2010b

,

A&A

,

517

,

A4

10.1051/0004-6361/201014482

Crossref

Joachimi

B.

,

Mandelbaum

R.

,

Abdalla

F. B.

,

Bridle

S. L.

,

2011

,

A&A

,

527

,

A26

10.1051/0004-6361/201015621

Crossref

Joachimi

B.

et al. ,

2015

,

Space Sci. Rev.

,

193

,

1

10.1007/s11214-015-0177-4

Crossref

Johnston

H.

et al. ,

2018

,

A&A

,

624

,

A30

Joudaki

S.

et al. ,

2017

,

MNRAS

,

465

,

2033

10.1093/mnras/stw2665

Crossref

Joudaki

S.

et al. ,

2018

,

MNRAS

,

474

,

4894

10.1093/mnras/stx2820

Crossref

Joudaki

S.

et al. ,

2020

,

A&A

,

638

,

L1

10.1051/0004-6361/201936154

Crossref

Kaiser

N.

,

1992

,

ApJ

,

388

,

272

10.1086/171151

Crossref

Kayo

I.

,

Takada

M.

,

2013

,

preprint (arXiv:1306.4684)

Kayo

I.

,

Takada

M.

,

Jain

B.

,

2013

,

MNRAS

,

429

,

344

10.1093/mnras/sts340

Crossref

Kiessling

A.

et al. ,

2015

,

Space Sci. Rev.

,

193

,

67

10.1007/s11214-015-0203-6

Crossref

Kilbinger

M.

,

2015

,

Rep. Prog. Phys.

,

78

,

086901

10.1088/0034-4885/78/8/086901

Crossref

Kilbinger

M.

et al. ,

2009

,

A&A

,

497

,

677

10.1051/0004-6361/200811247

Crossref

Kilbinger

M.

et al. ,

2013

,

MNRAS

,

430

,

2200

10.1093/mnras/stt041

Crossref

Kirk

D.

,

Bridle

S.

,

Schneider

M.

,

2010

,

MNRAS

,

408

,

1502

10.1111/j.1365-2966.2010.17213.x

Crossref

Kirk

D.

,

Laszlo

I.

,

Bridle

S.

,

Bean

R.

,

2011

,

MNRAS

,

430

,

197

Kirk

D.

et al. ,

2015a

,

Space Sci. Rev.

,

193

,

139

10.1007/s11214-015-0213-4

Crossref

Kirk

D.

et al. ,

2015b

,

MNRAS

,

459

,

21

Kitching

T. D.

,

Alsing

J.

,

Heavens

A. F.

,

Jimenez

R.

,

McEwen

J. D.

,

Verde

L.

,

2017

,

MNRAS

,

469

,

2737

Krause

E.

,

Hirata

C. M.

,

2010

,

A&A

,

523

,

A28

10.1051/0004-6361/200913524

Crossref

Krause

E.

,

Eifler

T.

,

Blazek

J.

,

2016

,

MNRAS

,

456

,

207

10.1093/mnras/stv2615

Crossref

Lange

R.

et al. ,

2015

,

MNRAS

,

447

,

2603

10.1093/mnras/stu2467

Crossref

Larsen

P.

,

Challinor

A.

,

2016

,

MNRAS

,

461

,

4343

10.1093/mnras/stw1645

Crossref

Lee

J.

,

Erdogdu

P.

,

2007

,

ApJ

,

671

,

1248

Lee

J.

,

Pen

U.-L.

,

2008

,

ApJ

,

681

,

798

LSST Dark Energy Science Collaboration

,

2012

,

preprint (arXiv:1211.0310)

MacCrann

N.

,

Zuntz

J.

,

Bridle

S.

,

Jain

B.

,

Becker

M. R.

,

2014

,

MNRAS

,

451

,

2877

Mackey

J.

,

White

M.

,

Kamionkowski

M.

,

2002

,

MNRAS

,

332

,

788

10.1046/j.1365-8711.2002.05337.x

Crossref

Mandelbaum

R.

et al. ,

2011

,

MNRAS

,

410

,

844

10.1111/j.1365-2966.2010.17485.x

Crossref

Massey

R.

et al. ,

2013

,

MNRAS

,

429

,

661

10.1093/mnras/sts371

Crossref

Mellier

Y.

,

1999

,

ARA&A

,

37

,

127

10.1146/annurev.astro.37.1.127

Crossref

Merkel

P. M.

,

Schaefer

B. M.

,

2013

,

MNRAS

,

434

,

1808

10.1093/mnras/stt1151

Crossref

Merkel

P. M.

,

Schaefer

B. M.

,

2017

,

MNRAS

,

471

,

2431

10.1093/mnras/stx1664

Crossref

Mortonson

M. J.

,

Weinberg

D. H.

,

White

M.

,

2013

,

preprint (arXiv:1401.0046)

Munshi

D.

,

Coles

P.

,

Kilbinger

M.

,

2014

,

JCAP

,

04

,

004

10.1088/1475-7516/2014/04/004

Crossref

Munshi

D.

,

Valageas

P.

,

van Waerbeke

L.

,

Heavens

A.

,

2008

,

Phys. Rep.

,

462

,

67

10.1016/j.physrep.2008.02.003

Crossref

Pahwa

I.

et al. ,

2016

,

MNRAS

,

457

,

695

10.1093/mnras/stv2930

Crossref

Pandya

V.

et al. ,

2019

,

MNRAS

,

488

,

5580

10.1093/mnras/stz2129

Crossref

Peacock

J. A.

,

Heavens

A. F.

,

1985

,

MNRAS

,

217

,

805

Pedersen

E. M.

,

Yao

J.

,

Ishak

M.

,

Zhang

P.

,

2020

,

ApJ

,

899

,

L5

10.3847/2041-8213/aba51b

Crossref

Piras

D.

,

Joachimi

B.

,

Schäfer

B. M.

,

Bonamigo

M.

,

Hilbert

S.

,

van Uitert

E.

,

2018

,

MNRAS

,

474

,

1165

10.1093/mnras/stx2846

Crossref

Reischke

R.

,

Schäfer

B. M.

,

2019

,

JCAP

,

04

,

031

Schäfer

B. M.

,

2009

,

Int. J. Mod. Phys. D

,

18

,

173

10.1142/S0218271809014388

Crossref

Schäfer

B. M.

,

Merkel

P. M.

,

2012

,

MNRAS

,

421

,

2751

10.1111/j.1365-2966.2011.20224.x

Crossref

Schmitz

D. M.

,

Hirata

C. M.

,

Blazek

J.

,

Krause

E.

,

2018

,

JCAP

,

07

,

030

Schneider

M. D.

,

Bridle

S.

,

2010

,

MNRAS

,

402

,

2127

10.1111/j.1365-2966.2009.15956.x

Crossref

Schneider

M. D.

et al. ,

2013

,

MNRAS

,

433

,

2727

10.1093/mnras/stt855

Crossref

Sellentin

E.

,

Schäfer

B. M.

,

2015

,

MNRAS

,

456

,

1645

Semboloni

E.

,

Hoekstra

H.

,

Schaye

J.

,

van Daalen

M. P.

,

McCarthy

I. G.

,

2011

,

MNRAS

,

417

,

2020

10.1111/j.1365-2966.2011.19385.x

Crossref

Sérsic

J. L.

,

1963

,

Bol. Asociacion Argentina Astron. La Plata Argentina

,

6

,

41

Singh

S.

,

Mandelbaum

R.

,

More

S.

,

2015

,

MNRAS

,

450

,

2195

10.1093/mnras/stv778

Crossref

Takada

M.

,

Jain

B.

,

2009

,

MNRAS

,

395

,

2065

10.1111/j.1365-2966.2009.14504.x

Crossref

Takada

M.

,

White

M.

,

2004

,

ApJ

,

601

,

L1

10.1086/381870

Crossref

Takahashi

R.

,

Oguri

M.

,

Sato

M.

,

Hamana

T.

,

2011

,

ApJ

,

742

,

15

10.1088/0004-637X/742/1/15

Crossref

Taruya

A.

,

Okumura

T.

,

2020

,

ApJ

,

891

,

L42

10.3847/2041-8213/ab7934

Crossref

Tenneti

A.

,

Mandelbaum

R.

,

Di Matteo

T.

,

Feng

Y.

,

Khandai

N.

,

2014

,

MNRAS

,

441

,

470

10.1093/mnras/stu586

Crossref

Tenneti

A.

,

Singh

S.

,

Mandelbaum

R.

,

Matteo

T. D.

,

Feng

Y.

,

Khandai

N.

,

2015

,

MNRAS

,

448

,

3522

10.1093/mnras/stv272

Crossref

Tessore

N.

,

Winther

H. A.

,

Metcalf

R. B.

,

Ferreira

P. G.

,

Giocoli

C.

,

2015

,

JCAP

,

10

,

036

10.1088/1475-7516/2015/10/036

Crossref

Thomas

D. B.

,

Bruni

M.

,

Wands

D.

,

2015

,

JCAP

,

09

,

021

Troxel

M. A.

,

Ishak

M.

,

2012

,

MNRAS

,

423

,

1663

10.1111/j.1365-2966.2012.20987.x

Crossref

Troxel

M. A.

,

Ishak

M.

,

2015

,

Phys. Rep.

,

558

,

1

10.1016/j.physrep.2014.11.001

Crossref

Tugendhat

T. M.

,

Schaefer

B. M.

,

2018

,

MNRAS

,

476

,

3460

10.1093/mnras/sty323

Crossref

Tugendhat

T. M.

,

Reischke

R.

,

Schaefer

B. M.

,

2020

,

MNRAS

,

494

,

2969

10.1093/mnras/staa641

Crossref

van Waerbeke

L.

,

Bernardeau

F.

,

Mellier

Y.

,

1999

,

A&A

,

342

,

15

Vlah

Z.

,

Chisari

N. E.

,

Schmidt

F.

,

2020

,

JCAP

,

01

,

025

White

M.

,

2004

,

Astropart. Phys.

,

22

,

211

10.1016/j.astropartphys.2004.06.001

Crossref

Yao

J.

,

Ishak

M.

,

Lin

W.

,

Troxel

M. A.

,

2017

,

JCAP

,

10

,

056

Yao

J.

,

Pedersen

E. M.

,

Ishak

M.

,

Zhang

P.

,

Agashe

A.

,

Xu

H.

,

Shan

H.

,

2019a

,

MNRAS

,

495

,

3900

Yao

J.

,

Ishak

M.

,

Troxel

M. A.

,

2019b

,

MNRAS

,

483

,

276

Zjupa

J.

,

Schaefer

B. M.

,

Hahn

O.

,

2020

,

MNRAS

,

submitted (arXiv: 2010.07951)

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
May 2021	1
June 2021	7
July 2021	17
August 2021	7
September 2021	6
October 2021	7
November 2021	3
December 2021	3
January 2022	7
February 2022	9
March 2022	8
April 2022	1
June 2022	2
July 2022	1
August 2022	1
October 2022	6
December 2022	3
January 2023	2
April 2023	2
August 2023	1
September 2023	1
November 2023	3
December 2023	3
January 2024	10
February 2024	11
March 2024	10
April 2024	6
May 2024	14
June 2024	5
July 2024	8
August 2024	3
September 2024	16
October 2024	11
November 2024	2
December 2024	1
January 2025	6
February 2025	2
March 2025	5
May 2025	5

Article Contents

Intrinsic and extrinsic correlations of galaxy shapes and sizes in weak lensing data

ABSTRACT

1 INTRODUCTION

2 TIDAL INTERACTIONS OF GALAXIES AND GRAVITATIONAL LENSING

3 ANGULAR SPECTRA OF GALAXY SHAPES AND SIZES

4 INFORMATION CONTENT OF SHAPE AND SIZE CORRELATIONS

5 SUMMARY

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Intrinsic and extrinsic correlations of galaxy shapes and sizes in weak lensing data Free

ABSTRACT

1 INTRODUCTION

2 TIDAL INTERACTIONS OF GALAXIES AND GRAVITATIONAL LENSING

3 ANGULAR SPECTRA OF GALAXY SHAPES AND SIZES

4 INFORMATION CONTENT OF SHAPE AND SIZE CORRELATIONS

5 SUMMARY

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Intrinsic and extrinsic correlations of galaxy shapes and sizes in weak lensing data