-
PDF
- Split View
-
Views
-
Cite
Cite
S F Zhu, John D Timlin, W N Brandt, The X-ray spectral and variability properties of typical radio-loud quasars, Monthly Notices of the Royal Astronomical Society, Volume 505, Issue 2, August 2021, Pages 1954–1971, https://doi.org/10.1093/mnras/stab1406
Close - Share Icon Share
ABSTRACT
We present X-ray spectral and long-term variability analyses of an unbiased sample of 361 optically selected radio-loud quasars (RLQs) utilizing sensitive serendipitous X-ray data from the Chandra and XMM-Newton archives. The spectral and temporal properties of RLQs are compared with those of radio-quiet quasars (RQQs) matched in L2500Å and z. The median power-law photon index (Γ) of RLQs is |$1.84_{-0.01}^{+0.01}$|, which is close to that of matched RQQs (|$1.90_{-0.01}^{+0.02}$|). No significant correlations between Γ and radio-loudness, Lx/Lx, rqq (the X-ray luminosity over that expected from the Lx–Luv relation for RQQs), redshift, or Eddington ratio are found for our RLQs. The stacked X-ray spectra of our RLQs show strong iron-line emission and a possible Compton-reflection hump. The intrinsic X-ray variability amplitude is ≈40 per cent for RLQs on time-scales of months-to-years in the rest frame, which is somewhat smaller than for the matched RQQs (≈60 per cent) on similar time-scales, perhaps due to the larger black hole masses and lower Eddington ratios in our RLQ sample. The X-ray spectral and variability results for our RLQs generally support the idea that the X-ray emission of typical RLQs is dominated by the disc/corona, as is also indicated by a recent luminosity correlation study.
1 INTRODUCTION
Radio-loud quasars (RLQs) have powerful relativistic jets that are absent in radio-quiet quasars (RQQs; e.g. Padovani et al. 2017). These two types of quasars are observationally distinguished by the radio-loudness parameter, R ≡ L5GHz/L4400Å, where L5GHz and L4400Å are monochromatic luminosities at rest-frame 5 GHz and 4400 Å, respectively (Kellermann et al. 1989). Only 10–20 per cent of quasars are RLQs with R ≥ 10, while the rest are RQQs (e.g. Ivezić et al. 2002). Typical RLQs have similar near-infrared-to-UV spectral energy distributions (SEDs) to those of RQQs, showing the so-called big blue bump with strong emission lines superimposed (e.g. Elvis et al. 1994; Shang et al. 2011). However, RLQs are generally brighter X-ray emitters than RQQs and thus have a flatter optical/ultraviolet (UV)-to-X-ray spectral slope, αox (e.g. Worrall et al. 1987; Miller et al. 2011), where αox ≡ log (L2 keV/L2500 Å)/log (ν2 keV/ν2500 Å) assuming a power-law spectral shape between rest-frame 2 keV and 2500 Å (Tananbaum et al. 1979). Furthermore, the excess X-ray emission of RLQs above that of RQQs correlates with both R and L5GHz, which has been taken as an evidence that the nuclear X-ray emission of RLQs contains both a standard accretion-disc corona component as well as a distinct X-ray component associated with the base of the powerful radio jets (e.g. Worrall et al. 1987; Miller et al. 2011). This explanation seems consistent with some previous studies that have found that RLQs have systematically flatter X-ray (<10 keV) spectra than those of RQQs (e.g. Wilkes & Elvis 1987; Reeves et al. 1997; Page et al. 2005), which could arise due to the mixture of the coronal X-ray emission and a generally harder X-ray spectrum from the jet-linked emission (e.g. Grandi & Palumbo 2004).
This original two-component model of the nuclear X-ray emission from typical RLQs has recently been challenged by Zhu et al. (2020), who studied the correlations of the continuum emission from the corona, disc, and jets of RLQs. Zhu et al. (2020) investigated the correlations between X-ray, optical/UV, and radio luminosities1 using a large and well-characterized sample consisting of more than 700 optically selected RLQs. The steep-spectrum radio quasars (SSRQs), which have a radio spectral slope αr ≤ −0.5, showed a Lx–Luv relation that is quantitatively similar to that of RQQs (i.e. |$L_\mathrm{x}\propto L_\mathrm{uv}^\gamma$|, γ ≈ 0.6; e.g. Just et al. 2007; Risaliti & Lusso 2019), despite the fact that these SSRQs are typically a factor of ≈2–3 times more X-ray luminous than RQQs at a given Luv. The quantitatively similar Lx–Luv correlation for SSRQs supports the idea that the nuclear X-ray emission of these SSRQs is still dominated by the corona that is coupled with the accretion disc (e.g. Arcodia et al. 2019), and no jet component is required. Zhu et al. (2020) also showed that the jet-linked component is only important for a small fraction (|$\lt 10{{\ \rm per\ cent}}$|) of flat-spectrum radio quasars (FSRQs; αr > −0.5); thus, the corona-linked component also dominates the X-ray emission of most typical FSRQs. The relation between αox and the equivalent width (EW) of He ii in RLQs is consistent with the result of Zhu et al. (2020) that RLQ X-ray emission is mainly related to the disc/corona instead of the jets (Timlin et al. 2021).
In light of these new results, it is important to investigate further the X-ray spectral properties of typical RLQs to assess whether they are indeed consistent with being mainly corona-linked. The primary X-ray continuum radiated from the hot corona is approximately described by a power law with a typical photon index of Γ = 1.7–2.3 and an exponential cutoff at ∼100 keV (e.g. Mushotzky, Done & Pounds 1993; Kamraj et al. 2018; Molina et al. 2019), while the spectrum from the jets in the same band is a flatter power law (Γ ∼ 1.5; e.g. Paliya et al. 2020) that might extend to γ-rays (e.g. Hartman et al. 1992). Kang, Wang & Kang (2020) recently analysed the NuSTAR spectra of 28 radio galaxies and detected the hard X-ray cutoff for 13 objects with sufficient net counts, which thus supports the idea that the hard X-rays of these radio galaxies are dominated by their coronae. Reprocessed X-ray emission can also be used to constrain the origin of the primary X-ray continuum. The iron emission lines between rest-frame 6.4–7.0 keV are of particular interest for this work, given their ubiquity in radio-quiet Seyfert galaxies (e.g. Nandra et al. 2007). If a beamed jet-linked continuum dominates the X-ray emission of RLQs, the iron-line emission is expected to be weak to undetectable owing to flux dilution (e.g. Reeves et al. 1997); otherwise, the corona-dominated interpretation for the X-ray emission of RLQs is favoured. The Compton-reflection hump that broadly peaks at rest-frame 20–30 keV is also consistently expected if strong iron lines are detected (e.g. George & Fabian 1991).
Previous X-ray spectral studies of RLQs have often used small, heterogeneously-selected samples that might be biased. For example, previous RLQs selected in the radio band usually contain a significant portion of extreme FSRQs2 that have prominent jet-linked X-ray emission (see Section 2 for further discussion). In this paper, we focus on the X-ray spectral properties of a large and optically selected RLQ sample (e.g. Zhu et al. 2020). Furthermore, we use only serendipitously obtained X-ray data to reduce potential selection effects caused by targeted X-ray observations (see Section 2.1).
Further insights into the nature of the X-ray emission of RLQs can also be obtained by studying their X-ray variability properties, in comparison with those of RQQs. Generally, the X-ray variability properties of RLQs have only been investigated for either individual objects (e.g. Leighly et al. 1997; Hayashida et al. 2015) or small samples (e.g. Zamorani et al. 1984; Sambruna 1997; Gibson & Brandt 2012) rather than for large, homogeneous, statistically meaningful samples. In this work, we thus also investigate the X-ray variability properties of the typical RLQs selected by Zhu et al. (2020). See Section 2.1 for the improvements of our sample relative to past work.
The sample construction and X-ray data analysis are discussed in Section 2. The method used to fit the X-ray spectra and the fitting results are reported in Section 3, and the long-term X-ray variability of RLQs is discussed in Section 4. We adopt a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1 and |$(\Omega _\Lambda , \Omega _\mathrm{M})=(0.7, 0.3)$|.
2 QUASAR SAMPLES AND X-RAY DATA ANALYSIS
2.1 RLQ sample
Zhu et al. (2020) constructed a sample of 729 RLQs, utilizing the Sloan Digital Sky Survey (SDSS; York et al. 2000), the Faint Images of the Radio Sky at Twenty-Centimeters (FIRST; Becker, White & Helfand 1995), and the NRAO VLA Sky Survey (NVSS; Condon et al. 1998). These 729 quasars were initially selected using SDSS colours and are therefore not biased by their X-ray or radio properties. Archival Chandra, XMM-Newton, and ROSAT observations are used to calculate the X-ray luminosities of these optically selected quasars. Only a small fraction (|$\lesssim 15{{\ \rm per\ cent}}$|) of the RLQ sample is targeted by these X-ray observations; therefore this sample is not significantly biased by the target selection of these X-ray observations (e.g. Gibson & Brandt 2012). This RLQ sample also has large fractions of X-ray detections and spectroscopic confirmations by SDSS (see Table 1 of Zhu et al. 2020). Furthermore, almost all of the RLQs are classified as either FSRQs or SSRQs, utilizing radio surveys at frequencies other than 1.4 GHz, in particular, the Very Large Array Sky Survey (Lacy et al. 2020) at ≈3 GHz. Broad absorption line quasars, quasars that suffer from strong dust extinction, and quasars with prominent jet emission in the infrared-through-UV bands were excluded from this sample.
The RLQ sample used in this paper. The quasar properties are taken from Zhu et al. (2020).
| Name . | z . | mi . | log L2500Å . | log L5GHz . | log L2keV . | log R . | αr . | |$\log (L_\mathrm{x}/L_\mathrm{x,rqq})\, ^a$| . |
|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 1.008 | 18.91 | 30.22 | 32.08 | 26.91 | 1.74 | - | 0.56 |
| 000622.60 − 000424.4 | 1.038 | 19.51 | 30.04 | 34.94 | 27.31 | 4.76 | −0.54 | 1.08 |
| 001646.54 − 005151.7 | 2.243 | 20.94 | 30.20 | 32.66 | 26.35 | 2.33 | 0.03 | 0.02 |
| 001910.95 + 034844.6 | 2.022 | 20.26 | 30.35 | 32.91 | 26.53 | 2.43 | −0.75 | 0.10 |
| 003054.63 + 045908.4 | 2.201 | 20.92 | 30.18 | 33.81 | 26.59 | 3.49 | −0.57 | 0.26 |
| Name . | z . | mi . | log L2500Å . | log L5GHz . | log L2keV . | log R . | αr . | |$\log (L_\mathrm{x}/L_\mathrm{x,rqq})\, ^a$| . |
|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 1.008 | 18.91 | 30.22 | 32.08 | 26.91 | 1.74 | - | 0.56 |
| 000622.60 − 000424.4 | 1.038 | 19.51 | 30.04 | 34.94 | 27.31 | 4.76 | −0.54 | 1.08 |
| 001646.54 − 005151.7 | 2.243 | 20.94 | 30.20 | 32.66 | 26.35 | 2.33 | 0.03 | 0.02 |
| 001910.95 + 034844.6 | 2.022 | 20.26 | 30.35 | 32.91 | 26.53 | 2.43 | −0.75 | 0.10 |
| 003054.63 + 045908.4 | 2.201 | 20.92 | 30.18 | 33.81 | 26.59 | 3.49 | −0.57 | 0.26 |
The X-ray luminosity divided by that predicted by the Lx−Luv relation for RQQs (Zhu et al. 2020).
The RLQ sample used in this paper. The quasar properties are taken from Zhu et al. (2020).
| Name . | z . | mi . | log L2500Å . | log L5GHz . | log L2keV . | log R . | αr . | |$\log (L_\mathrm{x}/L_\mathrm{x,rqq})\, ^a$| . |
|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 1.008 | 18.91 | 30.22 | 32.08 | 26.91 | 1.74 | - | 0.56 |
| 000622.60 − 000424.4 | 1.038 | 19.51 | 30.04 | 34.94 | 27.31 | 4.76 | −0.54 | 1.08 |
| 001646.54 − 005151.7 | 2.243 | 20.94 | 30.20 | 32.66 | 26.35 | 2.33 | 0.03 | 0.02 |
| 001910.95 + 034844.6 | 2.022 | 20.26 | 30.35 | 32.91 | 26.53 | 2.43 | −0.75 | 0.10 |
| 003054.63 + 045908.4 | 2.201 | 20.92 | 30.18 | 33.81 | 26.59 | 3.49 | −0.57 | 0.26 |
| Name . | z . | mi . | log L2500Å . | log L5GHz . | log L2keV . | log R . | αr . | |$\log (L_\mathrm{x}/L_\mathrm{x,rqq})\, ^a$| . |
|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 1.008 | 18.91 | 30.22 | 32.08 | 26.91 | 1.74 | - | 0.56 |
| 000622.60 − 000424.4 | 1.038 | 19.51 | 30.04 | 34.94 | 27.31 | 4.76 | −0.54 | 1.08 |
| 001646.54 − 005151.7 | 2.243 | 20.94 | 30.20 | 32.66 | 26.35 | 2.33 | 0.03 | 0.02 |
| 001910.95 + 034844.6 | 2.022 | 20.26 | 30.35 | 32.91 | 26.53 | 2.43 | −0.75 | 0.10 |
| 003054.63 + 045908.4 | 2.201 | 20.92 | 30.18 | 33.81 | 26.59 | 3.49 | −0.57 | 0.26 |
The X-ray luminosity divided by that predicted by the Lx−Luv relation for RQQs (Zhu et al. 2020).
In order to investigate the X-ray temporal properties of RLQs using multiple-epoch observations, we match the RLQ list of Zhu et al. (2020) with the observation catalogues of Chandra and XMM-Newton. We only retain serendipitous observations (i.e. where the quasar position is >1 arcmin off-axis), which further minimizes the impacts of a small portion of RLQs in Zhu et al. (2020) that might be exceptional objects. The matching results in 326 Chandra/ACIS observations of 202 quasars and 474 XMM-Newton/EPIC observations of 293 quasars. The X-ray data reduction and quality cuts are described in the following subsections. Together, 333 RLQs will be used for X-ray spectral studies and 105 RLQs with more than one Chandra/XMM-Newton observation will be used to investigate the X-ray variability properties of RLQs. We list our final RLQ sample in Table 1 and X-ray observation sample in Table 2, respectively. The resulting RLQ sample in the luminosity-redshift plane is shown in Fig. 1.
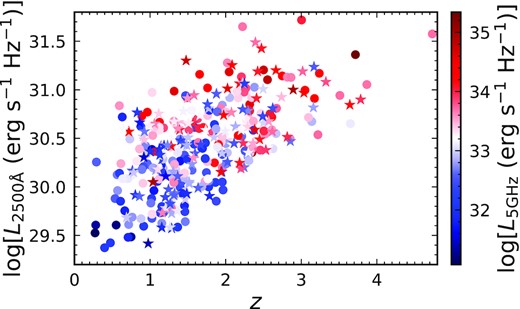
The distribution of RLQs from Zhu et al. (2020) with serendipitous Chandra/XMM-Newton observations in the L2500 Å − z plane. The stars and circles represent quasars having multiple X-ray observations or a single observation, respectively. The colours of the data points represent the radio luminosities as per the scale bar. Since the X-ray observations are serendipitous, these quasars span wide ranges in L2500 Å, L5 GHz, and z.
| Name . | ObsID . | MJDa . | Inst.b . | |$\log f_\mathrm{det}\, ^c$| . | netd . | SNRe . | |$\log f_\mathrm{x}\, ^f$| . | xdetg . | |$\Gamma \, ^h$| . | Goodness-of-fiti . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 0305751001 | 53714.8 | MOS2 | −13.92 | 263.1 | 15.5 | −12.59 | 1 | 2.00|$_{-0.19}^{+0.19}$| | 132.8/152.7/14.7 |
| 000622.60 − 000424.4 | 4096 | 52853.3 | ACIS | −13.74 | 220.8 | 14.4 | −12.35 | 1 | 1.76|$_{-0.21}^{+0.22}$| | 214.3/188.3/16.1 |
| 000622.60 − 000424.4 | 5617 | 53579.5 | ACIS | −14.35 | 806.8 | 28.3 | −12.21 | 1 | 1.69|$_{-0.10}^{+0.11}$| | 241.9/235.4/19.8 |
| 001646.54 − 005151.7 | 0403760101 | 54076.0 | pn | −13.98 | 12.9 | 2.6 | −13.82 | 1 | 1.23|$_{-1.11}^{+1.48}$| | 80.1/83.8/10.1 |
| 001646.54 − 005151.7 | 0403760701 | 54295.3 | pn | −14.38 | 24.3 | 4.0 | −13.91 | 1 | 2.37|$_{-0.75}^{+0.93}$| | 78.3/88.7/10.7 |
| Name . | ObsID . | MJDa . | Inst.b . | |$\log f_\mathrm{det}\, ^c$| . | netd . | SNRe . | |$\log f_\mathrm{x}\, ^f$| . | xdetg . | |$\Gamma \, ^h$| . | Goodness-of-fiti . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 0305751001 | 53714.8 | MOS2 | −13.92 | 263.1 | 15.5 | −12.59 | 1 | 2.00|$_{-0.19}^{+0.19}$| | 132.8/152.7/14.7 |
| 000622.60 − 000424.4 | 4096 | 52853.3 | ACIS | −13.74 | 220.8 | 14.4 | −12.35 | 1 | 1.76|$_{-0.21}^{+0.22}$| | 214.3/188.3/16.1 |
| 000622.60 − 000424.4 | 5617 | 53579.5 | ACIS | −14.35 | 806.8 | 28.3 | −12.21 | 1 | 1.69|$_{-0.10}^{+0.11}$| | 241.9/235.4/19.8 |
| 001646.54 − 005151.7 | 0403760101 | 54076.0 | pn | −13.98 | 12.9 | 2.6 | −13.82 | 1 | 1.23|$_{-1.11}^{+1.48}$| | 80.1/83.8/10.1 |
| 001646.54 − 005151.7 | 0403760701 | 54295.3 | pn | −14.38 | 24.3 | 4.0 | −13.91 | 1 | 2.37|$_{-0.75}^{+0.93}$| | 78.3/88.7/10.7 |
Observation start time.
The instrument used for the observation: ACIS for Chandra observations and pn/MOS1/MOS2 for XMM-Newton observations.
The detection flux limit in the 0.5–7 keV band at the position of the quasar on the detector. See Section 2.3.
The net source counts after subtracting expected background counts, net = s − b/k, where k is the background-to-source area ratio.
The signal-to-noise ratio, |$\mathrm{SNR}=\mathrm{net}/\sqrt{s+b/k^2}$|.
The energy flux in the 0.5–7 keV band if the the quasar is detected. Otherwise, the upper bound of the 90 per cent confidence interval is given.
If the quasar is detected in the X-ray observation, xdet = 1. Otherwise, xdet = 0.
The power-law photon index derived from our spectral fitting. Γ = −99 is used for cases of non-detection.
The goodness-of-fit of the spectral fitting, cstat/Ecstat/Scstat, where cstat is the statistic of the fit, and Ecstat and Scstat are the expectation and standard deviation of cstat, respectively (Kaastra 2017). For example, if (cstat − Ecstat)/Scstat > 4, the fitting result is disfavoured at a 4σ significance level.
| Name . | ObsID . | MJDa . | Inst.b . | |$\log f_\mathrm{det}\, ^c$| . | netd . | SNRe . | |$\log f_\mathrm{x}\, ^f$| . | xdetg . | |$\Gamma \, ^h$| . | Goodness-of-fiti . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 0305751001 | 53714.8 | MOS2 | −13.92 | 263.1 | 15.5 | −12.59 | 1 | 2.00|$_{-0.19}^{+0.19}$| | 132.8/152.7/14.7 |
| 000622.60 − 000424.4 | 4096 | 52853.3 | ACIS | −13.74 | 220.8 | 14.4 | −12.35 | 1 | 1.76|$_{-0.21}^{+0.22}$| | 214.3/188.3/16.1 |
| 000622.60 − 000424.4 | 5617 | 53579.5 | ACIS | −14.35 | 806.8 | 28.3 | −12.21 | 1 | 1.69|$_{-0.10}^{+0.11}$| | 241.9/235.4/19.8 |
| 001646.54 − 005151.7 | 0403760101 | 54076.0 | pn | −13.98 | 12.9 | 2.6 | −13.82 | 1 | 1.23|$_{-1.11}^{+1.48}$| | 80.1/83.8/10.1 |
| 001646.54 − 005151.7 | 0403760701 | 54295.3 | pn | −14.38 | 24.3 | 4.0 | −13.91 | 1 | 2.37|$_{-0.75}^{+0.93}$| | 78.3/88.7/10.7 |
| Name . | ObsID . | MJDa . | Inst.b . | |$\log f_\mathrm{det}\, ^c$| . | netd . | SNRe . | |$\log f_\mathrm{x}\, ^f$| . | xdetg . | |$\Gamma \, ^h$| . | Goodness-of-fiti . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000442.18 + 000023.3 | 0305751001 | 53714.8 | MOS2 | −13.92 | 263.1 | 15.5 | −12.59 | 1 | 2.00|$_{-0.19}^{+0.19}$| | 132.8/152.7/14.7 |
| 000622.60 − 000424.4 | 4096 | 52853.3 | ACIS | −13.74 | 220.8 | 14.4 | −12.35 | 1 | 1.76|$_{-0.21}^{+0.22}$| | 214.3/188.3/16.1 |
| 000622.60 − 000424.4 | 5617 | 53579.5 | ACIS | −14.35 | 806.8 | 28.3 | −12.21 | 1 | 1.69|$_{-0.10}^{+0.11}$| | 241.9/235.4/19.8 |
| 001646.54 − 005151.7 | 0403760101 | 54076.0 | pn | −13.98 | 12.9 | 2.6 | −13.82 | 1 | 1.23|$_{-1.11}^{+1.48}$| | 80.1/83.8/10.1 |
| 001646.54 − 005151.7 | 0403760701 | 54295.3 | pn | −14.38 | 24.3 | 4.0 | −13.91 | 1 | 2.37|$_{-0.75}^{+0.93}$| | 78.3/88.7/10.7 |
Observation start time.
The instrument used for the observation: ACIS for Chandra observations and pn/MOS1/MOS2 for XMM-Newton observations.
The detection flux limit in the 0.5–7 keV band at the position of the quasar on the detector. See Section 2.3.
The net source counts after subtracting expected background counts, net = s − b/k, where k is the background-to-source area ratio.
The signal-to-noise ratio, |$\mathrm{SNR}=\mathrm{net}/\sqrt{s+b/k^2}$|.
The energy flux in the 0.5–7 keV band if the the quasar is detected. Otherwise, the upper bound of the 90 per cent confidence interval is given.
If the quasar is detected in the X-ray observation, xdet = 1. Otherwise, xdet = 0.
The power-law photon index derived from our spectral fitting. Γ = −99 is used for cases of non-detection.
The goodness-of-fit of the spectral fitting, cstat/Ecstat/Scstat, where cstat is the statistic of the fit, and Ecstat and Scstat are the expectation and standard deviation of cstat, respectively (Kaastra 2017). For example, if (cstat − Ecstat)/Scstat > 4, the fitting result is disfavoured at a 4σ significance level.
We compare our spectral RLQ sample with those from previous investigations in Table 3, where the size of our RLQ sample is larger than those of previous samples by about one order of magnitude. Importantly, our RLQs are all optically selected quasars, while those previous samples are generally heterogeneous with a large portion that are radio selected, and the rest being optically or X-ray selected. Furthermore, all of our utilized X-ray observations were serendipitously observed, rendering our RLQ sample an unbiased subset of the optically selected SDSS quasars. In contrast, the previous samples usually utilized targeted X-ray observations, where the selection effects are hard to assess. Similarly, for our X-ray variability investigations, the sizes of the RLQ sample and X-ray observation sample are also significantly larger (by factors of ≈3–100) than those in the literature, as reported in Table 4.
Previous sample-based investigations of the X-ray spectral properties of RLQs.
| Sample . | Telescope . | No. of RLQsa . | Radio/Optb . | FSRQ/SSRQc . |
|---|---|---|---|---|
| This paper (SNR > 3) | XMM-Newton/Chandra | 333 | 0/333 | 184/134d |
| Zhou & Gu (2020) | Chandra | 43 | 43/0 | 14/29 |
| Grandi, Malaguti & Fiocchi (2006) | BeppoSAX | 22 | 17/5 | 16/6 |
| Page et al. (2005) | XMM-Newton | 16 | 10/4e | - |
| Reeves & Turner (2000) | ASCA | 35 | 33/2 | - |
| Sambruna, Eracleous & Mushotzky (1999) | ASCA | 5 | 5/0 | - |
| Lawson & Turner (1997) | Ginga | 18 | 17/1 | 10/5f |
| Reeves et al. (1997) | ASCA | 15 | 13/2 | 8/0g |
| Lawson et al. (1992) | EXOSAT | 18 | 12/6 | 12/6 |
| Wilkes & Elvis (1987) | Einstein | 17 | 14/3 | - |
| Sample . | Telescope . | No. of RLQsa . | Radio/Optb . | FSRQ/SSRQc . |
|---|---|---|---|---|
| This paper (SNR > 3) | XMM-Newton/Chandra | 333 | 0/333 | 184/134d |
| Zhou & Gu (2020) | Chandra | 43 | 43/0 | 14/29 |
| Grandi, Malaguti & Fiocchi (2006) | BeppoSAX | 22 | 17/5 | 16/6 |
| Page et al. (2005) | XMM-Newton | 16 | 10/4e | - |
| Reeves & Turner (2000) | ASCA | 35 | 33/2 | - |
| Sambruna, Eracleous & Mushotzky (1999) | ASCA | 5 | 5/0 | - |
| Lawson & Turner (1997) | Ginga | 18 | 17/1 | 10/5f |
| Reeves et al. (1997) | ASCA | 15 | 13/2 | 8/0g |
| Lawson et al. (1992) | EXOSAT | 18 | 12/6 | 12/6 |
| Wilkes & Elvis (1987) | Einstein | 17 | 14/3 | - |
We use only serendipitous X-ray observations to ensure that our RLQs form a representative subset of the parent sample (i.e. optically selected SDSS RLQs). In contrast, all previous investigations listed here used targeted X-ray observations, which may be subject to complex selection effects (except for Zhou & Gu 2020).
We provide the number of luminous quasars in this column, and other types of radio-loud AGNs (i.e. broad- and narrow-line radio galaxies) are excluded.
The number of quasars that are selected in the radio/optical band.
We list the number of FSRQs/SSRQs if the relevant paper provides radio-spectral information. Zhou & Gu (2020) divide their RLQs into core-dominated and lobe-dominated classes, which we associate with FSRQs and SSRQs, respectively.
The remaining 15 RLQs do not have radio slope measurements.
There are two X-ray selected objects in Page et al. (2005).
Lawson & Turner (1997) separate the three optically violent variables (OVVs) from other FSRQs.
The remaining seven RLQs of Reeves et al. (1997) are either OVVs or Gigahertz-peaked spectrum (GPS) radio sources.
Previous sample-based investigations of the X-ray spectral properties of RLQs.
| Sample . | Telescope . | No. of RLQsa . | Radio/Optb . | FSRQ/SSRQc . |
|---|---|---|---|---|
| This paper (SNR > 3) | XMM-Newton/Chandra | 333 | 0/333 | 184/134d |
| Zhou & Gu (2020) | Chandra | 43 | 43/0 | 14/29 |
| Grandi, Malaguti & Fiocchi (2006) | BeppoSAX | 22 | 17/5 | 16/6 |
| Page et al. (2005) | XMM-Newton | 16 | 10/4e | - |
| Reeves & Turner (2000) | ASCA | 35 | 33/2 | - |
| Sambruna, Eracleous & Mushotzky (1999) | ASCA | 5 | 5/0 | - |
| Lawson & Turner (1997) | Ginga | 18 | 17/1 | 10/5f |
| Reeves et al. (1997) | ASCA | 15 | 13/2 | 8/0g |
| Lawson et al. (1992) | EXOSAT | 18 | 12/6 | 12/6 |
| Wilkes & Elvis (1987) | Einstein | 17 | 14/3 | - |
| Sample . | Telescope . | No. of RLQsa . | Radio/Optb . | FSRQ/SSRQc . |
|---|---|---|---|---|
| This paper (SNR > 3) | XMM-Newton/Chandra | 333 | 0/333 | 184/134d |
| Zhou & Gu (2020) | Chandra | 43 | 43/0 | 14/29 |
| Grandi, Malaguti & Fiocchi (2006) | BeppoSAX | 22 | 17/5 | 16/6 |
| Page et al. (2005) | XMM-Newton | 16 | 10/4e | - |
| Reeves & Turner (2000) | ASCA | 35 | 33/2 | - |
| Sambruna, Eracleous & Mushotzky (1999) | ASCA | 5 | 5/0 | - |
| Lawson & Turner (1997) | Ginga | 18 | 17/1 | 10/5f |
| Reeves et al. (1997) | ASCA | 15 | 13/2 | 8/0g |
| Lawson et al. (1992) | EXOSAT | 18 | 12/6 | 12/6 |
| Wilkes & Elvis (1987) | Einstein | 17 | 14/3 | - |
We use only serendipitous X-ray observations to ensure that our RLQs form a representative subset of the parent sample (i.e. optically selected SDSS RLQs). In contrast, all previous investigations listed here used targeted X-ray observations, which may be subject to complex selection effects (except for Zhou & Gu 2020).
We provide the number of luminous quasars in this column, and other types of radio-loud AGNs (i.e. broad- and narrow-line radio galaxies) are excluded.
The number of quasars that are selected in the radio/optical band.
We list the number of FSRQs/SSRQs if the relevant paper provides radio-spectral information. Zhou & Gu (2020) divide their RLQs into core-dominated and lobe-dominated classes, which we associate with FSRQs and SSRQs, respectively.
The remaining 15 RLQs do not have radio slope measurements.
There are two X-ray selected objects in Page et al. (2005).
Lawson & Turner (1997) separate the three optically violent variables (OVVs) from other FSRQs.
The remaining seven RLQs of Reeves et al. (1997) are either OVVs or Gigahertz-peaked spectrum (GPS) radio sources.
| Sample . | No. of RLQs/object name . | No. of observations . | No. of pairs . | Time-scalea . |
|---|---|---|---|---|
| Studies of ensemble X-ray variability | ||||
| This paper (Down-sampled) | 105 | 297 | 314 | 1.7 yr |
| Gibson & Brandt (2012; High-quality sample) | 8 | 20 | 15 | 1 yr |
| Zamorani et al. (1984) | 7 | 14 | 7 | 1 yr |
| Studies of individual objects | ||||
| Marscher et al. (2018) | 3C 120 | ≈110 | - | 8.3 months |
| Chatterjee et al. (2011) | 3C 111 | 822 | - | 5.9 yr |
| Soldi et al. (2008)b | 3C 273 | 1036 | - | 31 yr |
| Marscher (2006) | 3C 120 | ≈550 | - | 3 yr |
| Marscher et al. (2002) | 3C 120 | ≈190 | - | 3 yr |
| McHardy et al. (1999) | 3C 273 | 84 | - | 1.4 months |
| Leighly et al. (1997) | 3C 390.3 | 90 | - | 4.6 months |
| Sambruna (1997)c | 0923 + 392 | 7 | - | 2 yr |
| 3C 345 | 6 | - | 3 yr | |
| Sample . | No. of RLQs/object name . | No. of observations . | No. of pairs . | Time-scalea . |
|---|---|---|---|---|
| Studies of ensemble X-ray variability | ||||
| This paper (Down-sampled) | 105 | 297 | 314 | 1.7 yr |
| Gibson & Brandt (2012; High-quality sample) | 8 | 20 | 15 | 1 yr |
| Zamorani et al. (1984) | 7 | 14 | 7 | 1 yr |
| Studies of individual objects | ||||
| Marscher et al. (2018) | 3C 120 | ≈110 | - | 8.3 months |
| Chatterjee et al. (2011) | 3C 111 | 822 | - | 5.9 yr |
| Soldi et al. (2008)b | 3C 273 | 1036 | - | 31 yr |
| Marscher (2006) | 3C 120 | ≈550 | - | 3 yr |
| Marscher et al. (2002) | 3C 120 | ≈190 | - | 3 yr |
| McHardy et al. (1999) | 3C 273 | 84 | - | 1.4 months |
| Leighly et al. (1997) | 3C 390.3 | 90 | - | 4.6 months |
| Sambruna (1997)c | 0923 + 392 | 7 | - | 2 yr |
| 3C 345 | 6 | - | 3 yr | |
In this table, we do not include the X-ray monitoring studies of blazars and related highly jet-dominated objects (e.g. Chatterjee et al. 2008).
The median rest-frame time-scale is reported for the ensemble studies, while the maximum rest-frame time-scale is reported for individual studies.
We consider the 5 keV light curve of 3C 273 in Soldi et al. (2008).
We do not include 3C 279 and 0208−512 in Sambruna (1997), of which the former is a blazar and the data of the latter span only 12 d.
| Sample . | No. of RLQs/object name . | No. of observations . | No. of pairs . | Time-scalea . |
|---|---|---|---|---|
| Studies of ensemble X-ray variability | ||||
| This paper (Down-sampled) | 105 | 297 | 314 | 1.7 yr |
| Gibson & Brandt (2012; High-quality sample) | 8 | 20 | 15 | 1 yr |
| Zamorani et al. (1984) | 7 | 14 | 7 | 1 yr |
| Studies of individual objects | ||||
| Marscher et al. (2018) | 3C 120 | ≈110 | - | 8.3 months |
| Chatterjee et al. (2011) | 3C 111 | 822 | - | 5.9 yr |
| Soldi et al. (2008)b | 3C 273 | 1036 | - | 31 yr |
| Marscher (2006) | 3C 120 | ≈550 | - | 3 yr |
| Marscher et al. (2002) | 3C 120 | ≈190 | - | 3 yr |
| McHardy et al. (1999) | 3C 273 | 84 | - | 1.4 months |
| Leighly et al. (1997) | 3C 390.3 | 90 | - | 4.6 months |
| Sambruna (1997)c | 0923 + 392 | 7 | - | 2 yr |
| 3C 345 | 6 | - | 3 yr | |
| Sample . | No. of RLQs/object name . | No. of observations . | No. of pairs . | Time-scalea . |
|---|---|---|---|---|
| Studies of ensemble X-ray variability | ||||
| This paper (Down-sampled) | 105 | 297 | 314 | 1.7 yr |
| Gibson & Brandt (2012; High-quality sample) | 8 | 20 | 15 | 1 yr |
| Zamorani et al. (1984) | 7 | 14 | 7 | 1 yr |
| Studies of individual objects | ||||
| Marscher et al. (2018) | 3C 120 | ≈110 | - | 8.3 months |
| Chatterjee et al. (2011) | 3C 111 | 822 | - | 5.9 yr |
| Soldi et al. (2008)b | 3C 273 | 1036 | - | 31 yr |
| Marscher (2006) | 3C 120 | ≈550 | - | 3 yr |
| Marscher et al. (2002) | 3C 120 | ≈190 | - | 3 yr |
| McHardy et al. (1999) | 3C 273 | 84 | - | 1.4 months |
| Leighly et al. (1997) | 3C 390.3 | 90 | - | 4.6 months |
| Sambruna (1997)c | 0923 + 392 | 7 | - | 2 yr |
| 3C 345 | 6 | - | 3 yr | |
In this table, we do not include the X-ray monitoring studies of blazars and related highly jet-dominated objects (e.g. Chatterjee et al. 2008).
The median rest-frame time-scale is reported for the ensemble studies, while the maximum rest-frame time-scale is reported for individual studies.
We consider the 5 keV light curve of 3C 273 in Soldi et al. (2008).
We do not include 3C 279 and 0208−512 in Sambruna (1997), of which the former is a blazar and the data of the latter span only 12 d.
2.2 Data reduction
The Chandra and XMM-Newton observations were reduced using the ciao (v4.12) and sas (v18.0.0) packages, respectively. The Chandra data were reprocessed using chandra_repro and the most recent caldb (v4.9.3). Background flares were then removed using deflare. From the reprocessed, flare-filtered event files, we create clean images in the 0.5–7 keV band. Source detection is then performed using wavedetect with a threshold of 10−6 to obtain a list of X-ray sources in the field of view. If a RLQ is detected (i.e. an X-ray source is found within 2 arcsec of the quasar position), the X-ray position will be used for the following analysis; otherwise, the optically determined quasar position is used. Note that cases where the quasar position is near the detector edge (i.e. the quasar lies within 40 pixels from the edge), falls in a detector gap, or is near an X-ray luminous cluster are excluded from further analysis. An elliptical region that encloses 90 per cent of the counts at the position of the quasar is created using the marx (v5.5.0) package (see Section 3.1 of Timlin et al. 2020). The background region is defined as an annulus that is centred at the quasar position, with inner and outer radii of 15 and 50 arcsec, respectively. X-ray sources detected in the background region are excluded from the background region or, in a few cases where the RLQ is in a crowded field, a nearby circular background region is used. The source spectrum and associated response files and background spectrum are extracted using the specextract tool.
The EPIC-pn and EPIC-MOS data from XMM-Newton observations were reprocessed and cleaned using epproc and emproc, respectively. We filtered background-flaring periods using espflit. Clean images are produced using evselect, and source detection is then performed using edetect_chain. Similar to the Chandra observations, cases where the quasar position is near the detector edge (i.e. the source region defined below overlaps with the detector boundary), falls in a detector gap, or is near an X-ray luminous cluster are excluded. Furthermore, if the background flaring is consistently strong throughout the exposure, we exclude the observation entirely. The source region is defined by a circle centred at the quasar position (or the X-ray position if an X-ray source is found within 5 arcsec of the quasar position). The radius of the circle is determined by eregionanalyse to optimize the signal-to-noise ratio. The background region is chosen to be a source-free circular region on the same chip, with a radius of ≳ 40 arcsec. The source and background spectra are then extracted using evselect. The corresponding RMFs and ARFs are created using rmfgen and arfgen, respectively.
In total, we obtain 300 useful Chandra/ACIS spectra of 195 RLQs and 401 useful XMM-Newton/EPIC spectra3 of 258 RLQs All of the following analyses are uniformly performed utilizing the spectral and associated response files, regardless of the observatories and instruments. Note that the RLQs being analysed here are generally consistent with being X-ray point sources. The extended X-ray jet emission from RLQs, if it is spatially resolved, typically contributes only 1–3 per cent to the total X-ray flux being analysed (e.g. Marshall et al. 2018; Schwartz et al. 2020), and thus we do not expect such emission to affect our X-ray spectral and variability analyses below materially. Pileup is generally not a concern for serendipitous X-ray data with large off-axis angles (>1 arcmin).4
2.3 Calculating energy flux and detection flux limit
Using the instrumental response files of each observation, an energy conversion factor (ECF) that converts the number of net counts to 0.5–7 keV energy flux is derived using sherpa (v4.13, Burke et al. 2020). The spectral shape of the photons that enter the X-ray telescopes is assumed to be a Galactic absorption-modified power law with Γ = 1.8.5 This method is similar to that adopted in the XMM-Newton serendipitous source catalogue (e.g. Rosen et al. 2016) and the Chandra source catalogue (e.g. Evans et al. 2019).
In total, 641 X-ray observations of 361 RLQs passed the flux-limit cut, of which 12 RLQs (3.3 per cent) are not detected in any epoch and thus are not considered in the following analysis. Our X-ray spectral (Section 3) and variability (Section 4) investigations each utilize a subset of the remaining 349 RLQs, which are detected at least once in 628 X-ray observations. The vast majority of these observations (98.7 per cent) result in significant X-ray detections, and thus our results are not substantively affected by X-ray upper limits.
2.4 Comparison RQQ sample
As part of this investigation, we will analyse the X-ray variability properties of our RLQ sample and require a suitable matched sample of RQQs with which we can compare our results. We select RQQs mainly from the sample of Timlin et al. (2020), who analysed ≈1600 serendipitous Chandra X-ray observations of 462 typical, non-BAL RQQs. These spectroscopically confirmed RQQs span a similar redshift range (z = 0.1–4) to that of our RLQs (Fig. 1); however, Timlin et al. (2020) selected quasars with mi ≤ 20.2, which is about one magnitude brighter than the RLQs in our sample (mi ≲ 21). We therefore extended the analysis of Timlin et al. (2020) to fainter magnitude (mi = 20.2–20.8) quasars in the SDSS DR14Q (Pâris et al. 2018) following the selection method outlined in Section 2 of Timlin et al. (2020). Note that all observations (including those from Timlin et al. 2020 and newly selected) are consistently analysed in the same way as described above in Section 2.2 and 2.3. In total, we obtain 2341 serendipitous Chandra observations of 606 RQQs. We list the RQQ sample and corresponding X-ray observations in the tables presented in Appendix A.
Furthermore, to compare appropriately the long-term X-ray variability properties of RLQs with those of RQQs, we generated a sub-sample of RQQs that is matched in redshift, optical/UV luminosity, and time-scale space to the RLQ sample. We describe the selection method in more detail in Section 4.3. The redshift, optical/UV luminosity, and time-scale distributions of the matched RQQs are compared with those of RLQs in Fig. 2. Note that two-sample Anderson-Darling (AD; Anderson & Darling 1952) tests are performed for all three panels of Fig. 2, and the distributions of RLQs and RQQs are always statistically consistent. We also selected a RQQ sample that matches with the RLQs used in Section 3 as a reference for RQQ coronal X-ray spectral properties. To generate this sample, we selected the nearest RQQ in the L 2500 Å- z space (without replacement) to each RLQ. An AD test indicates that the L2500 Å and z distributions of this RQQ sample are statistically consistent with those of the RLQs used in Section 3.
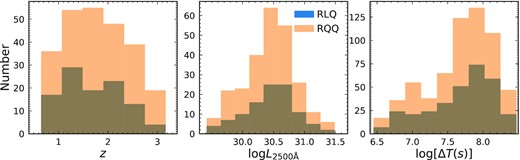
Comparisons of the matched RQQ and RLQ distributions of redshift, UV luminosity, and time-scale (left-hand, centre, and right-hand panels). The X-ray light curves of the quasars in both samples have been down-sampled using the method in Section 4.1. The RLQ and RQQ distributions in each parameter space are statistically consistent, according to AD tests of similarity for the three panels that all result in p-values >0.16.
3 X-RAY SPECTRAL PROPERTIES
We investigate the shape of the primary X-ray continuum in Section 3.1 by fitting the X-ray spectra of individual quasars. The properties of X-ray reflection features, namely, the fluorescent iron line and the Compton hump, are analysed in Section 3.2, utilizing X-ray spectral stacking and joint spectral fitting.
3.1 Fitting the X-ray continuum using a power-law model
3.1.1 Fitting methods
We perform X-ray spectral fitting using sherpa, focusing on the observed-frame 0.5–7 keV band (rest-frame 0.55–7.7 keV for quasars at z ∼ 0.1 and 2.8–40 keV for quasars at z ∼ 4.5). We use a simple power-law model to describe the shape of the quasar X-ray spectra, which is then multiplied by a z = 0 absorption component with a fixed NH value estimated using the COLDEN tool (Dickey & Lockman 1990). The median number of counts between 0.5 and 7 keV of our X-ray spectra is 111, and the interquartile (25th to 75th percentile) range is (42, 289). Many X-ray spectra therefore do not have a sufficient number of counts to allow for further grouping, The c-stat statistic (denoted as cstat) is thus utilized, which provides maximum-likelihood estimates of model parameters without requiring a minimum number of counts in each bin/channel (Cash 1979; Baker & Cousins 1984; Humphrey, Liu & Buote 2009).
When employing the c-stat statistic, the background contribution cannot be directly subtracted from the source spectrum; therefore, we fit the background spectra explicitly using empirical models.8 The background models are derived from principal component analysis using a larger number of background spectra of each instrument (i.e. ACIS, EPIC-pn, and EPIC-MOS; see Appendix A of Simmonds et al. 2018). After fitting the background spectra, the shape and amplitude of the background model is fixed, and a background component is added to the source model with a scaling factor (i.e. 1/k; see Section 2.3). The source spectra are then fitted with the full model that includes a Galactic absorption-modified power-law component (with two free parameters) and a fixed background component.
We assess the fit quality using the expectation and variance of the c-stat statistic of the best-fitting model (Kaastra 2017). We denote the expectation and standard deviation of c-stat with Ecstat and Scstat, respectively. Ideally, the distribution of (cstat − Ecstat)/Scstat is close to a standard normal distribution; in cases where (cstat − Ecstat)/Scstat ≫ 1, the model is strongly disfavoured. The X-ray spectra of RQQs are analysed using the same methodology.
3.1.2 The X-ray power-law photon indices of RLQs
In this section, we present fitting results for the X-ray spectra of 333 RLQs with SNR (i.e. signal-to-noise ratio) ≥3 (16/349 RLQs fail this cut), where SNR = 3 is approximately equivalent to a minimum number of 9 net counts between 0.5 and 7 keV.9 If a quasar has multiple observations, we utilize the X-ray spectrum from the observation with the smallest fdet and ignore the rest. The distribution of net counts for our RLQs is presented in the top panel of Fig. 3. In the middle panel of Fig. 3, we show the distribution of (cstat − Ecstat)/Scstat. There are seven objects with (cstat − Ecstat)/Scstat ≥ 2, which is consistent with the number expected from a standard normal distribution at ≥2σ, i.e. |$2.28{{\ \rm per\ cent}}\times 333\approx 7.6$|. Therefore, our spectral-fitting results are generally acceptable, and the power-law model is a good phenomenological description of the rest-frame ≈0.5–40 keV spectra of our RLQs. We show the distributions of Γ of RLQs in Fig. 3 (bottom). The median Γ for Chandra/ACIS and XMM-Newton/EPIC spectra are |$1.82_{-0.01}^{+0.03}$| and |$1.85_{-0.01}^{+0.02}$|, respectively, where the uncertainties are estimated using bootstrapping. Therefore, any cross-calibration uncertainties between the instruments do not affect our results below.
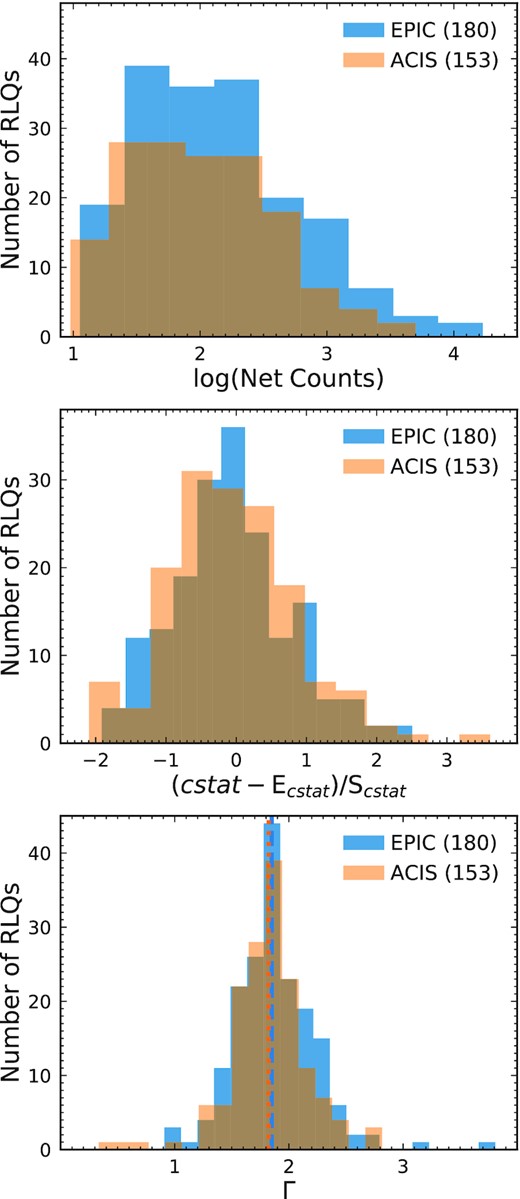
Top: the distribution of net counts (0.5–7 keV) for the 333 RLQ X-ray spectra with SNR ≥3, where (and in panels below), we distinguish the 153 Chandra/ACIS spectra from the remaining 180 XMM-Newton/EPIC spectra. Middle: The distribution of the quality of the spectral fits, (cstat − Ecstat)/Scstat. See the main text in Section 3. Bottom: the distribution of Γ, where the median values are |$1.82_{-0.01}^{+0.03}$| (dotted line) and |$1.85_{-0.01}^{+0.02}$| (dashed line) for the ACIS and EPIC spectra, respectively.
We show the dependence of the resulting photon index Γ on the SNR in Fig. 4 (top), where the orange dashed line represents the median Γ. The data points are also grouped into five equally sized SNR bins, each of which contains ≈66 spectra. The median Γ values (as well as uncertainties derived using bootstrapping) of each bin are represented by red open squares with error bars in Fig. 4 (top). Since the error bars of each median Γ are small compared to the symbol size, we also depict the median Γ uncertainty for individual RLQs in each bin as the red error bars above the red squares. Fig. 4 shows no clear correlation between Γ and SNR; thus, our methodology of X-ray spectral fitting is not sensitive to the data quality of the spectra. We repeat the procedure above for RQQs and show the results in Fig. 4 (bottom).
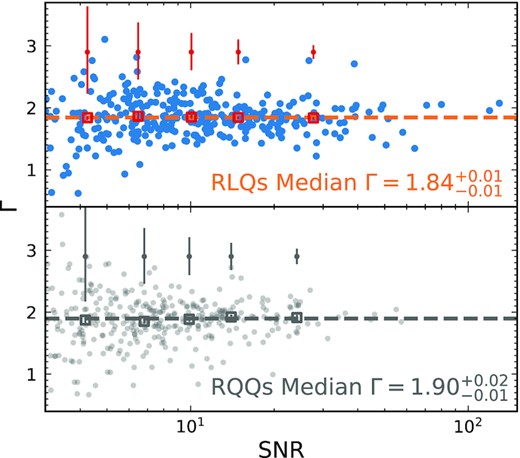
The best-fitting power-law photon index (Γ) as a function of the SNR (see Table 2) of the spectrum for RLQs (top) and comparison RQQs (bottom). Both samples contain 333 quasars, and they are matched in L2500Å and z. This figure demonstrates that the photon index does not depend on the quality of the data. The median photon index of all quasars in each panel is provided at the lower right corner. The RLQs are grouped into five SNR bins of nearly equal size (65–67 quasars per bin), and the median Γ in each bin is calculated and shown as open squares. The uncertainties of the median Γ of each bin are estimated using the bootstrapping method, and these uncertainties are relatively small compared with the size of the square symbols. Therefore, we additionally show the median uncertainties for individual sources in each bin above the squares. The binning scheme for RQQs follows that for RLQs. The X-ray spectra of RLQs are only flatter than those of RQQs by a small amount according to our serendipitous data.
The median photon indexes of RLQs and matched RQQs10 are |$1.84_{-0.01}^{+0.01}$| and |$1.90_{-0.01}^{+0.02}$|, respectively, the difference between which is small compared with the intrinsic spread of their Γ distributions (0.19 and 0.25).11 The flat-spectrum and steep-spectrum RLQ subsets have median photon indexes of |$1.84_{-0.02}^{+0.02}$| and |$1.85_{-0.02}^{+0.04}$|, respectively, the difference between which is small as well. However, in past work, the photon indexes of RLQs (Γ ≈ 1.5–1.7) were often found to be significantly flatter than those of RQQs (Γ ≈ 1.7–2.3; Wilkes & Elvis 1987; Reeves et al. 1997; Page et al. 2005), though this notable spectral difference was not always confirmed (e.g. Lawson et al. 1992; Sambruna et al. 1999; Grandi et al. 2006). Sambruna et al. (1999) found that the evidence is weak that broad-line radio galaxies have flatter X-ray spectra than those of radio-quiet Seyfert 1 galaxies. Furthermore, previous studies that utilized RLQ samples containing SSRQs and treated them separately as a group (i.e. Lawson et al. 1992; Lawson & Turner 1997; Grandi et al. 2006) generally noticed a similarity between the photon indexes of SSRQs and those of RQQs. However, these studies had only a small number of SSRQs in their samples, which prevented solid conclusions from being drawn.
Zhu et al. (2020) found that the nuclear X-ray emission of RLQs is generally dominated by the corona, and the coronal X-ray luminosity depends on optical/UV luminosity and radio-loudness parameter, which indicate a disc-corona interplay and corona-jet connection, respectively. In Fig. 5, we investigate the correlations of the photon index of RLQs with other quasar properties. In particular, we are interested in testing if the corona-jet connection could affect, in addition to the X-ray brightness of the corona, the shape of the coronal X-ray spectrum. Specifically, correlations of the Γ of coronal X-rays with R and Lx/Lx, rqq would provide insights into more details of the corona-jet connection. Even though Zhu et al. (2020) did not find a distinct jet X-ray component in SSRQs, the X-ray emission of a small portion (≲ 10 per cent) of FSRQs likely contains a significant (>30 per cent) jet X-ray component. We therefore treat FSRQs and SSRQs separately in Fig. 5, which is enabled by our large sample size. Furthermore, since statistical correlation analyses generally do not consider the effects of measurement errors, we apply a cut of SNR >5 to the spectra to reduce the scatter caused by measurement errors, which results in 150 and 114 spectra of FSRQs and SSRQs, respectively, which are shown in Fig. 5.
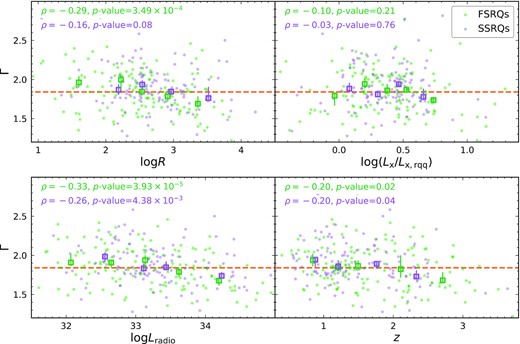
The correlations of photon index (Γ) with log R, Lx/Lx, rqq, Lradio, and z for FSRQs (green symbols, 150 quasars) and SSRQs (purple symbols, 114 quasars), separately. Spectra with SNR ≤ 5 are omitted. The Spearman rank correlation statistic ρ and the corresponding p-value are given at the upper-left corner of each panel. The median Γ = 1.84 of the RLQ sample is shown in all four panels using orange dashed lines. In each panel, FSRQs and SSRQs are grouped into 5 and 4 bins of comparable size, respectively, according to their x-axis values. The median Γ of each bin is calculated (open squares), the error bar of which is estimated using bootstrapping. There are no strong correlations (p-value <10−3) between Γ and R, Lx/Lx, rqq, Lradio, and z for FSRQs and SSRQs, except for the anticorrelation between Γ and Lradio for FSRQs (lower left). A less significant anticorrelation between Γ and R for FSRQs (upper left) is probably driven by the Γ-Lradio anticorrelation for these FSRQs. However, if the 14 FSRQs with log Lradio > 34.3 are removed, both anticorrelations disappear (p-value > 0.05), suggesting that these FSRQs are the rare population of RLQs with a strong jet X-ray component and a flat photon index Γ ∼ 1.5–1.6. The lack of a correlation between Γ and log (Lx/Lx, rqq) argues against an important role of jet X-ray emission for general RLQs (e.g. Zhu et al. 2020). The photon index of the coronal X-ray component does not depend on the quasar properties under consideration here.
We show the correlations of Γ with R, Lx/Lx, rqq, Lradio, and z for FSRQs and SSRQs in Fig. 5. We perform Spearman rank-correlation tests and show the results in the upper-left corner of each panel. In addition, we group FSRQs and SSRQs into five and four bins of comparable size, respectively; the median Γ is calculated for each bin and shown as large open squares in Fig. 5, the errors of which are estimated using bootstrapping. Neither the p-values resulting from correlation tests nor the median photon indexes support correlations (more significant than p-value = 10−3) between Γ and R, Lx/Lx, rqq, Lradio, and z for SSRQs. No strong correlation is found for FSRQs either, except for the anticorrelation between Γ and Lradio and a less-significant anticorrelation between Γ and R; the latter correlation is probably driven by the former. There are 14 log Lradio > 34.3 FSRQs in the lower-left panel of Fig. 5, almost all of which have Γ that is smaller than the median photon index (1.84) of all RLQs. Instead, the photon indices of these most radio-luminous FSRQs are around 1.5–1.6. If these 14 FSRQs are removed in the correlation tests, the tentative Γ–Lradio and Γ–R correlations disappear among the remaining 136 FSRQs. Therefore, these FSRQs likely represent the rare population that has a strong jet X-ray component (Zhu et al. 2020).
Finally, we matched the utilized RLQs and RQQs with the quasar-property catalogue of Shen et al. (2011). There are 138 and 136 black hole mass measurements (based on Mg ii or H β) for RLQs and RQQs, respectively. The median Eddington ratio of the RLQs (|$-0.93_{-0.06}^{+0.04}$|) is about 0.2 dex smaller than that of the RQQs (|$-0.73_{-0.06}^{+0.03}$|), which might explain the mild difference between the median Γ values of RLQs and RQQs if both groups follow the previously known correlation between Γ and Eddington ratio (e.g. Shemmer et al. 2008; Brightman et al. 2013). However, a correlation between Eddington ratio and Γ is not found for RLQs (see the top panel of Fig. 6), and a correlation test using Spearman’s ρ results in p-value = 0.76. A similar correlation test for the RQQ sample results in a negative result as well (see the bottom panel of Fig. 6), suggesting that our data quality might play an important role in the negative result for RLQs. Future RLQ samples with high-quality X-ray and infrared spectroscopy can address better the correlations between Γ and Eddington ratio and FWHM of H β (e.g. Brandt, Mathur & Elvis 1997; Laor et al. 1997).
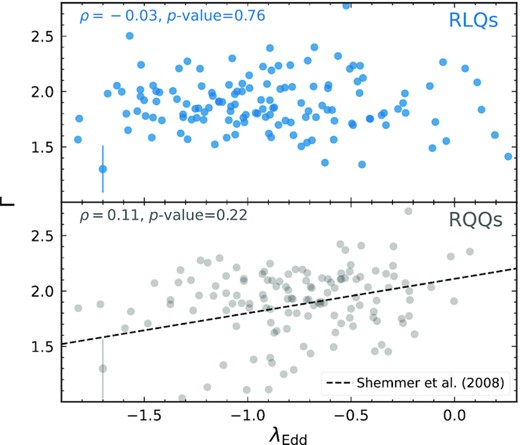
Top: the correlation between X-ray power-law photon index and Eddington ratio of RLQs. The median error bar of Γ is shown in the lower-left corner. The Spearman rank correlation coefficient and associated p-value are shown in the upper-left corner. Bottom: same as the top panel for comparison RQQs. The Γ–λEdd relation from Shemmer et al. (2008) is also shown for comparison. No strong correlation between Γ and λEdd is found for either RLQs or RQQs.
3.2 Iron-line emission and the Compton-reflection hump
The distribution of the fitting statistic in Section 3.1.2 (i.e. the middle panel of Fig. 3) indicates that the power-law function is, globally, an acceptable description of the X-ray spectra of our individual RLQs; other features that arise in a narrow rest-frame X-ray band (e.g. fluorescent iron line emission) cannot be detected in individual spectra, given their limited numbers of counts. We therefore utilize a stacking technique to constrain the average properties of the fluorescent iron line and Compton reflection for our RLQs. We only consider RLQs with a spectroscopic redshift (83 per cent of our sample) and an X-ray spectrum with SNR > 5. We exclude 14 FSRQs with log Lradio > 34.3 as these are potentially beamed objects (see Section 3.1.2 and Fig. 5) and 2 other RLQs with >104 net counts since we do not want individual objects to dominate the spectral stacking,12 which results in 216 RLQ spectra for the analyses below. We first fit the individual X-ray spectra of RLQs using a power-law model with fixed Γ = 1.84 (cf. Section 3.1.2) excluding channels that correspond to the rest-frame <2, 5–8, and >10 keV bands, where additional emission features might exist.13 The single free parameter of the model, i.e. the normalization factor of the power-law function, is also fixed after fitting. For each X-ray spectrum, the data-to-model ratio is calculated over a grid of pre-defined rest-frame energy bins. Note that the background is subtracted from the total counts in each bin, and the model here refers to the Galactic absorbed power-law function. Finally, the data-to-model ratios of different RLQs are averaged in each energy bin.
We show the stacked data-to-model ratio over the rest-frame 3–20 keV band of 58 RLQs at z > 2 (with a total of 7.4 × 103 net counts) in the top panel of Fig. 7, where bins with a size of 1 keV are utilized. The error bars of each bin are estimated using bootstrapping. The data points that deviate from unity (the grey dashed line in the top panel of Fig. 7) show the locations where excess spectral features are present in the stacked residual spectrum. The vertical dotted line indicates the position (6.4 keV) of the fluorescent iron line expected from X-rays illuminating neutral material. The data between 6 and 7 keV signify that strong iron-line emission is present in the stacked spectrum. At ≥14 keV, another strong feature is also apparent that might be associated with the Compton-reflection hump. We thus utilize the pexrav model (Magdziarz & Zdziarski 1995) of xspec to assess if the blue data points in Fig. 7 (top) are consistent with the prediction of Compton reflection for an X-ray source over a slab of neutral material. We choose a set of typical parameters, Γ = 1.84, Ecut = 300 keV, and cos i = 0.5, with other parameters being set at their defaults. The resulting prediction is shown as the orange curve in Fig. 7 (top). The blue data points at E > 14 keV generally follow the Compton-reflection model.
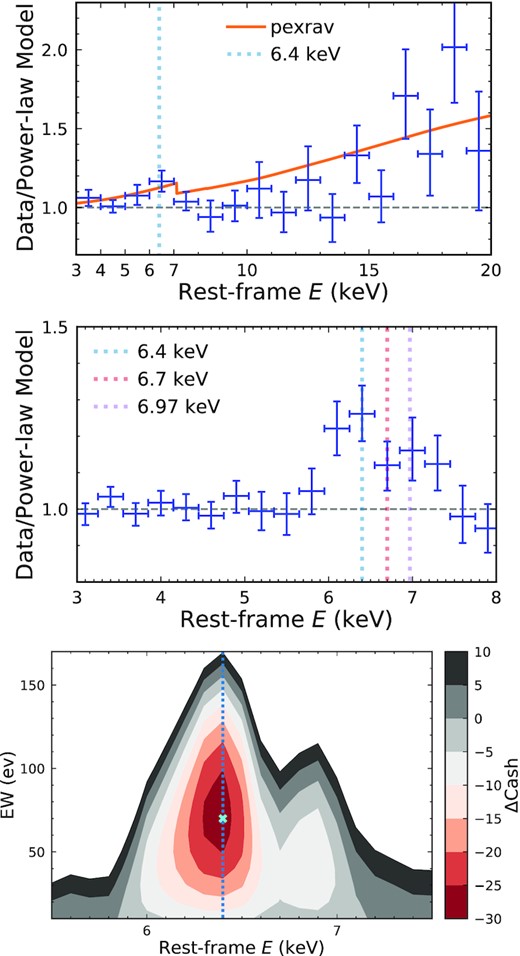
Top: the stacked ratio of the background-subtracted X-ray spectrum to the best-fitting power-law model (with fixed Γ = 1.84). We stacked the rest-frame 3–20 keV band using a bin size of 1 keV for the 58 RLQs with z > 2 in our sample. The orange curve represents the prediction of Compton reflection from neutral material (i.e. pexrav, Magdziarz & Zdziarski 1995). Middle: the stacked data-to-model ratio in the rest-frame 3–8 keV band for 216 RLQs (0.27 < z < 3.9). Iron-line emission is clearly present in this residual spectrum. Bottom: the contour of the improvement of the fitting statistic (ΔCash) when a narrow emission line (a Gaussian profile with rest-frame FWHM =20 eV) is added to the power-law model (that is used in the top and middle panels). The cyan cross marks the minimum of the fitting statistic, where ΔCash=−27.9 indicates a 5.3σ detection for a narrow iron line at 6.4 keV. The EW of the narrow iron line is |$70_{-20}^{+30}$| eV.
The middle panel of Fig. 7 shows the stacking results using all 216 RLQs over the rest-frame 2.95–8.05 keV band (with a total of 2.9 × 104 net counts) with a bin size of 0.3 keV. We show the positions of rest-frame 6.4, 6.7, and 6.97 keV using vertical dotted lines. From this plot, it is apparent that the iron-line emission is not localized in a single bin but is distributed from <6 up to >7 keV, which cannot be explained by instrumental dispersion of a single narrow emission line. Possibly, both neutral and ionized material contributes to the iron-line production (e.g. Nandra et al. 1997), and Fig. 7 (middle) shows the blending of several narrow lines. Furthermore, since the excess emission also arises in the bin at <6.4 keV, a broad relativistic component is also likely present (e.g. Brenneman & Reynolds 2009).
To constrain the contribution from the narrow component of the neutral iron line at 6.4 keV, we utilize a method that is able to obtain the optimal energy resolution. We add a Gaussian function to the fixed power-law function to represent a narrow-line component for each quasar. The FWHM of the Gaussian function is fixed to be 20 eV in the rest frame, which is much smaller than the instrumental dispersion. The strength of the narrow emission line is parametrized using rest-frame EW. We sequentially increase the location of the narrow emission line from rest-frame 5.5 to 7.5 keV, with a step size of 0.1 keV. At each position, we iterate the EW of the line from 10 up to 200 eV, with a step size of 10 eV. The corresponding Cash statistic is calculated over the 21 × 20 grid of line properties (i.e. location and strength). The Cash statistic of the simple power-law model without the narrow emission line is then subtracted, resulting in a 2D ΔCash map for each quasar. We then summed the ΔCash maps of all quasars and show a contour plot of the results in Fig. 7 (bottom).
The minimum value in the contour plot, which corresponds to the largest improvement to the power-law model, occurs when the contour is at E = 6.4 keV and EW =70 eV. The ΔCash value given these parameters is ΔCash =−27.9 and indicates that the neutral iron line is detected at a 5.3σ significance level. The 90 per cent confidence uncertainty of the EW is (−20, +30) eV, which corresponds to a change in ΔCash of 2.71. Hu et al. (2019) measured a strength of EW ≈50 eV for a narrow emission line at 6.4 keV using the composite X-ray spectrum of 97 RL active galactic nuclei (AGNs), which is consistent with our measurement within uncertainties. This method indicates that the strongest narrow component of the iron emission is located at E = 6.4 keV; however, substantial emission remains in the stacked spectrum at rest-frame 6–7 keV. Integrating the data-to-model ratio over 6–7 keV reveals a total iron-line emission EW of |$189_{-44}^{+49}$| eV, leaving EW ≈120 eV to other iron species and the possible broad-line component. We discuss the implications of the strong iron-line emission in Section 5. Similar analyses for the matched RQQs result in EW |$=100_{-30}^{+20}$| eV for the narrow emission component at 6.4 keV. Thus, the EWs for RLQs and RQQs appear statistically consistent.
4 ENSEMBLE X-RAY VARIABILITY OF RLQS
4.1 Energy flux ratio and down-sampling method
There are 117 RLQs in our sample that have more than one X-ray observation, and thus we are able to investigate, with a large set of data, how the X-ray brightness of these RLQs varies over time (in the quasar rest frame).14 For every pair of time-ordered data points in the X-ray light curve of a quasar in our sample, we calculate the ratio of the flux of the later-epoch data over that of the earlier epoch. For each of these energy flux ratios, there is a corresponding time-scale (denoted ΔT), which represents the time interval of the two observations corrected to the rest-frame of quasar. The dependence of energy flux ratio on the time-scale is shown in the top panel of Fig. 8.
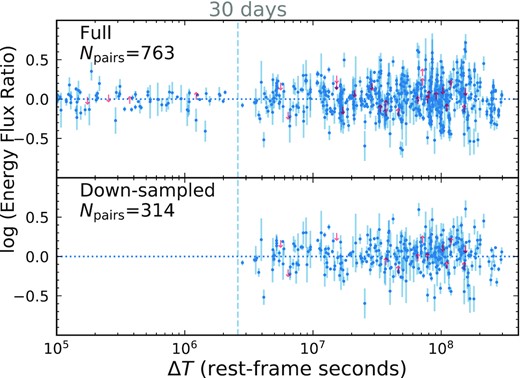
Energy flux ratio as a function of the rest-frame time-scale, where the red downward and upward arrows represent upper and lower limits, respectively. The top panel shows all permutations of the full sample, while the bottom panel shows the permutations after removing repeated observations within 30 rest-frame days and down-sampling the X-ray data so that the number of observations of any RLQ is less than or equal to seven.
These 117 RLQs have 386 X-ray observations in total, where the number of observations of each quasar ranges from 2 to 20. The distribution of the number of observations of each quasar is shown as the blue bar plot in Fig. 9. For a quasar with n X-ray observations, n(n − 1)/2 energy flux ratios can be computed using the method outlined above. In Fig. 9, more than half of the quasars (65/117) have only two X-ray observations, resulting in 65 energy flux ratios; however, a single quasar with 20 X-ray observations produces 190 energy flux ratios. Therefore, to prevent the distribution of energy flux ratio from being dominated by a small number of quasars with a relatively large number of observations, we elect to down-sample the X-ray light curves. We first grouped any consecutive observations that are separated by <30 rest-frame days,15 and assigned each group an ID number. Among the observations with the same group ID, we keep only the most-sensitive observation (smallest fdet), which removes 84 of the 386 observations. If the number of observations is still >7 after the grouping-and-selecting procedure above, we randomly remove observations (excluding the first and last ones to keep the maximum light-curve baseline) until only seven observations remain,16 which removes five more observations. Note that if we down-sample the data to a maximum number of observations of three, the main results of Section 4 are not affected. The resulting distribution of the number of observations of each quasar is shown as the orange bars in Fig. 9, and the down-sampled energy flux ratio versus rest-frame time-scale is shown in the bottom panel of Fig. 8. The down-sampled data are used in the following analyses. After down-sampling the light-curves and restricting the time-scale to ΔT ≥ 30 rest-frame days, 297 observations of 105 RLQs remained, producing 314 energy flux ratios (see Table 4).
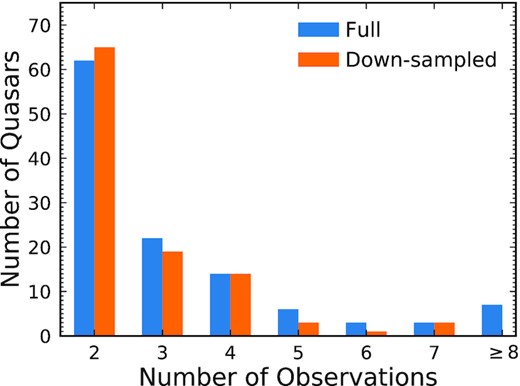
The number of X-ray observations for each RLQ in our variability study. The blue bars depict the 117 RLQs that have multiple Chandra/XMM-Newton observations with sensitivity better than f = 3 × 10−14 erg cm−2 s−1. The orange bars show the 105 RLQs remaining after removing repeated observations of the same RLQ within 30 d (in the rest frame) and down-sampling the X-ray data to reduce the maximum number of observations to seven per RLQ (see Section 4.1).
4.2 X-ray variability of typical RLQs
We depict the distribution of the energy flux ratio in the top panel of Fig. 10 and the result of an AD normality test performed on the distribution of the energy fluxes in the first row of Table 5; the distribution does not depart significantly from a normal distribution. We calculated the kurtosis17 and estimated its uncertainties using bootstrapping. The kurtosis of the energy flux distribution for the RLQs is consistent with that of a normal distribution as well.
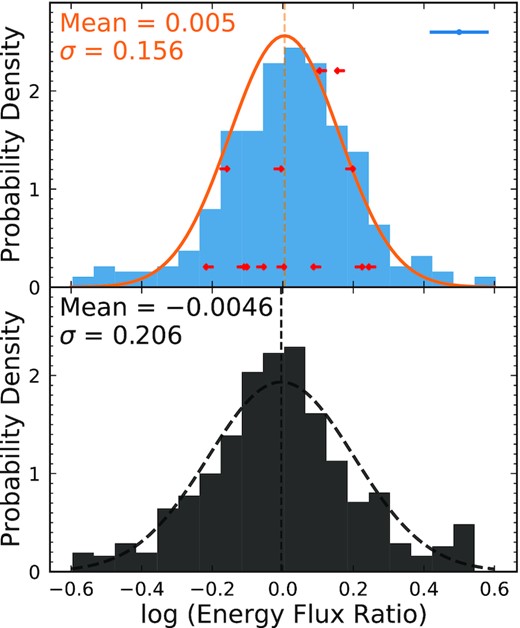
The distribution of log (energy flux ratio) after down-sampling for RLQs is shown in the top panel, where red arrows represent upper/lower limits. The magnitude of the median measurement uncertainty is shown in the upper-right corner. The orange curve depicts the deconvolved normal function that represents the intrinsic variability. Note that the standard deviations of the distribution before and after deconvolution are 0.190 and 0.156, respectively. Therefore, the intrinsic variability dominates the spread of log (energy flux ratio). The mean and standard deviation of the intrinsic distribution are presented in the upper-left corner (orange). In the bottom panel, the distribution in black represents the matched RQQ sample with its respective deconvolved variability distribution (black dashed curve).
| Sample . | Npairs . | Normality (p-value)a . | Kurtosisb . |
|---|---|---|---|
| Down-sampled | 314 | 0.02 | |$0.73_{-0.45}^{+0.38}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | 184 | 0.08 | |$0.66_{-0.43}^{+0.35}$| |
| Low-luminosity (log L2500 Å < 30.45) | 130 | 0.45 | |$0.11_{-0.41}^{+0.31}$| |
| Long-time-scale (log ΔT ≥ 7.79) | 157 | 0.46 | |$0.35_{-0.37}^{+0.29}$| |
| Short-time-scale (log ΔT < 7.79) | 157 | 0.41 | |$0.27_{-0.47}^{+0.35}$| |
| Sample . | Npairs . | Normality (p-value)a . | Kurtosisb . |
|---|---|---|---|
| Down-sampled | 314 | 0.02 | |$0.73_{-0.45}^{+0.38}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | 184 | 0.08 | |$0.66_{-0.43}^{+0.35}$| |
| Low-luminosity (log L2500 Å < 30.45) | 130 | 0.45 | |$0.11_{-0.41}^{+0.31}$| |
| Long-time-scale (log ΔT ≥ 7.79) | 157 | 0.46 | |$0.35_{-0.37}^{+0.29}$| |
| Short-time-scale (log ΔT < 7.79) | 157 | 0.41 | |$0.27_{-0.47}^{+0.35}$| |
The p-value resulting from the AD normality test.
The kurtosis values do not strongly deviate from that of a normal distribution (kurtosis = 0). The uncertainties of the kurtosis values are estimated using bootstrapping.
| Sample . | Npairs . | Normality (p-value)a . | Kurtosisb . |
|---|---|---|---|
| Down-sampled | 314 | 0.02 | |$0.73_{-0.45}^{+0.38}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | 184 | 0.08 | |$0.66_{-0.43}^{+0.35}$| |
| Low-luminosity (log L2500 Å < 30.45) | 130 | 0.45 | |$0.11_{-0.41}^{+0.31}$| |
| Long-time-scale (log ΔT ≥ 7.79) | 157 | 0.46 | |$0.35_{-0.37}^{+0.29}$| |
| Short-time-scale (log ΔT < 7.79) | 157 | 0.41 | |$0.27_{-0.47}^{+0.35}$| |
| Sample . | Npairs . | Normality (p-value)a . | Kurtosisb . |
|---|---|---|---|
| Down-sampled | 314 | 0.02 | |$0.73_{-0.45}^{+0.38}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | 184 | 0.08 | |$0.66_{-0.43}^{+0.35}$| |
| Low-luminosity (log L2500 Å < 30.45) | 130 | 0.45 | |$0.11_{-0.41}^{+0.31}$| |
| Long-time-scale (log ΔT ≥ 7.79) | 157 | 0.46 | |$0.35_{-0.37}^{+0.29}$| |
| Short-time-scale (log ΔT < 7.79) | 157 | 0.41 | |$0.27_{-0.47}^{+0.35}$| |
The p-value resulting from the AD normality test.
The kurtosis values do not strongly deviate from that of a normal distribution (kurtosis = 0). The uncertainties of the kurtosis values are estimated using bootstrapping.
To remove the broadening of the distribution of energy flux ratio that is caused by measurement errors, and obtain the amplitude of the instrinsic X-ray variability, we fit a normal function to the distribution in Fig. 10 (top) using a maximum-likelihood method that distinguishes the measurement errors and intrinsic scatter (e.g. Maccacaro et al. 1988). The likelihood function includes terms that account for the few upper and lower limits in the data (e.g. see Appendix B of Zhu et al. 2019). The best-fitting normal function that represents the intrinsic distribution of the energy flux ratio is shown as the orange curve in Fig. 10 (top), where the model parameters are presented in the upper-left corner.
To assess the dependence of X-ray variability amplitude on quasar luminosity and time-scale, we divide the data at the median UV luminosity (log L2500 Å = 30.45) and median time-scale (log ΔT = 7.79). We perform statistical tests on these sub-samples and report the results in Table 5. The distributions of energy flux ratio are consistent with a normal distribution in both luminosity and time-scale bins. We also performed model fitting, as we did with the full sample, to the energy flux distributions of the luminosity and time-scale bins and list the results in Table 6. There is strong evidence that the variability amplitude (i.e. σ) increases with rest-frame time-scale (e.g. Timlin et al. 2020); however, the dependence of variability amplitude on quasar luminosity is only marginal.
Intrinsic variability distribution of RLQs compared with those of matched RQQs.
| Sample . | |$m\, ^a$| . | |$\sigma \, ^b$| . | ||
|---|---|---|---|---|
| . | RLQs . | RQQs . | RLQs . | RQQs . |
| Down-sampled | |$0.005_{-0.010}^{+0.010}$| | |$-0.004_{-0.009}^{+0.009}$| | |$0.156_{-0.007}^{+0.010}$| | |$0.212_{-0.007}^{+0.009}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | |$0.016_{-0.014}^{+0.015}$| | |$-0.020_{-0.016}^{+0.016}$| | |$0.160_{-0.009}^{+0.015}$| | |$0.190_{-0.011}^{+0.015}$| |
| Low-luminosity (log L2500 Å < 30.45) | |$-0.007_{-0.014}^{+0.014}$| | |$0.004_{-0.012}^{+0.012}$| | |$0.150_{-0.010}^{+0.016}$| | |$0.208_{-0.009}^{+0.011}$| |
| Long-time-scale (log ΔT ≥ 7.79) | |$-0.003_{-0.015}^{+0.016}$| | |$0.002_{-0.015}^{+0.015}$| | |$0.178_{-0.010}^{+0.016}$| | |$0.211_{-0.010}^{+0.014}$| |
| Short-time-scale (log ΔT < 7.79) | |$0.014_{-0.013}^{+0.014}$| | |$-0.010_{-0.012}^{+0.013}$| | |$0.131_{-0.008}^{+0.014}$| | |$0.195_{-0.009}^{+0.012}$| |
| Sample . | |$m\, ^a$| . | |$\sigma \, ^b$| . | ||
|---|---|---|---|---|
| . | RLQs . | RQQs . | RLQs . | RQQs . |
| Down-sampled | |$0.005_{-0.010}^{+0.010}$| | |$-0.004_{-0.009}^{+0.009}$| | |$0.156_{-0.007}^{+0.010}$| | |$0.212_{-0.007}^{+0.009}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | |$0.016_{-0.014}^{+0.015}$| | |$-0.020_{-0.016}^{+0.016}$| | |$0.160_{-0.009}^{+0.015}$| | |$0.190_{-0.011}^{+0.015}$| |
| Low-luminosity (log L2500 Å < 30.45) | |$-0.007_{-0.014}^{+0.014}$| | |$0.004_{-0.012}^{+0.012}$| | |$0.150_{-0.010}^{+0.016}$| | |$0.208_{-0.009}^{+0.011}$| |
| Long-time-scale (log ΔT ≥ 7.79) | |$-0.003_{-0.015}^{+0.016}$| | |$0.002_{-0.015}^{+0.015}$| | |$0.178_{-0.010}^{+0.016}$| | |$0.211_{-0.010}^{+0.014}$| |
| Short-time-scale (log ΔT < 7.79) | |$0.014_{-0.013}^{+0.014}$| | |$-0.010_{-0.012}^{+0.013}$| | |$0.131_{-0.008}^{+0.014}$| | |$0.195_{-0.009}^{+0.012}$| |
The mean of the deconvolved energy flux ratio distribution.
The intrinsic variability amplitude after removing the contribution of the measurement errors.
Intrinsic variability distribution of RLQs compared with those of matched RQQs.
| Sample . | |$m\, ^a$| . | |$\sigma \, ^b$| . | ||
|---|---|---|---|---|
| . | RLQs . | RQQs . | RLQs . | RQQs . |
| Down-sampled | |$0.005_{-0.010}^{+0.010}$| | |$-0.004_{-0.009}^{+0.009}$| | |$0.156_{-0.007}^{+0.010}$| | |$0.212_{-0.007}^{+0.009}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | |$0.016_{-0.014}^{+0.015}$| | |$-0.020_{-0.016}^{+0.016}$| | |$0.160_{-0.009}^{+0.015}$| | |$0.190_{-0.011}^{+0.015}$| |
| Low-luminosity (log L2500 Å < 30.45) | |$-0.007_{-0.014}^{+0.014}$| | |$0.004_{-0.012}^{+0.012}$| | |$0.150_{-0.010}^{+0.016}$| | |$0.208_{-0.009}^{+0.011}$| |
| Long-time-scale (log ΔT ≥ 7.79) | |$-0.003_{-0.015}^{+0.016}$| | |$0.002_{-0.015}^{+0.015}$| | |$0.178_{-0.010}^{+0.016}$| | |$0.211_{-0.010}^{+0.014}$| |
| Short-time-scale (log ΔT < 7.79) | |$0.014_{-0.013}^{+0.014}$| | |$-0.010_{-0.012}^{+0.013}$| | |$0.131_{-0.008}^{+0.014}$| | |$0.195_{-0.009}^{+0.012}$| |
| Sample . | |$m\, ^a$| . | |$\sigma \, ^b$| . | ||
|---|---|---|---|---|
| . | RLQs . | RQQs . | RLQs . | RQQs . |
| Down-sampled | |$0.005_{-0.010}^{+0.010}$| | |$-0.004_{-0.009}^{+0.009}$| | |$0.156_{-0.007}^{+0.010}$| | |$0.212_{-0.007}^{+0.009}$| |
| High-luminosity (log L2500 Å ≥ 30.45) | |$0.016_{-0.014}^{+0.015}$| | |$-0.020_{-0.016}^{+0.016}$| | |$0.160_{-0.009}^{+0.015}$| | |$0.190_{-0.011}^{+0.015}$| |
| Low-luminosity (log L2500 Å < 30.45) | |$-0.007_{-0.014}^{+0.014}$| | |$0.004_{-0.012}^{+0.012}$| | |$0.150_{-0.010}^{+0.016}$| | |$0.208_{-0.009}^{+0.011}$| |
| Long-time-scale (log ΔT ≥ 7.79) | |$-0.003_{-0.015}^{+0.016}$| | |$0.002_{-0.015}^{+0.015}$| | |$0.178_{-0.010}^{+0.016}$| | |$0.211_{-0.010}^{+0.014}$| |
| Short-time-scale (log ΔT < 7.79) | |$0.014_{-0.013}^{+0.014}$| | |$-0.010_{-0.012}^{+0.013}$| | |$0.131_{-0.008}^{+0.014}$| | |$0.195_{-0.009}^{+0.012}$| |
The mean of the deconvolved energy flux ratio distribution.
The intrinsic variability amplitude after removing the contribution of the measurement errors.
4.3 Comparing RLQs with matched RQQs
The energy flux ratios of RQQs are calculated and down-sampled following the method described in Section 4.1. We then selected a matched sample of RQQs in the z, log L2500 Å, and log ΔT parameter spaces. For each RLQs in the z-log L2500Å-log ΔT space, we select the two nearest RQQs, without replacement. We compare the distributions (z, L2500 Å, and ΔT) of matched RQQs in Fig. 2. AD tests are performed for the distributions in the three panels of Fig. 2, which support that the RQQs and RLQs are suitably matched.
We depict the energy flux ratio distribution of matched RQQs in the bottom panel of Fig. 10, where the black-dashed curve represents the normal function resulting from model fitting. Model fitting is also performed for sub-samples of RQQs divided by luminosity and time-scale, and the results are summarized in Table 6. We find that, in our sample, the intrinsic X-ray variability amplitude of our RLQ sample is always smaller than that of the matched RQQ sample.
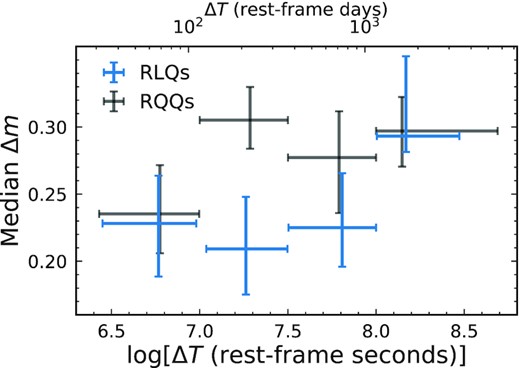
The ensemble SF for the X-ray variability of RLQs (blue) compared with that of matched RQQs (black). The x-axis values are in units of both rest-frame seconds (bottom ticks) and days (top ticks). The X-ray variability amplitude of RQQs seems to be insensitive to time-scale above ≈200 rest-frame days. However, the SF of RLQs apparently increases with ΔT out to the last bin, where RLQs become as variable as RQQs.
The SF of RQQs increases with ΔT in the first two bins; however, no significant increase is found at time-scales above ≈200 d. This result is consistent with Shemmer et al. (2017), who utilized a similar method and created an ensemble SF that increases at relatively short time-scales and shows no substantial changes at relatively long time-scales (see their Fig. 4). On the other hand, although the SF of RLQs is generally smaller than that of matched RQQs, it is consistent with increasing with ΔT out to the largest time-scale bin, where the two types of quasars have similar variability amplitudes. The SF of RLQs is unconstrained at longer time-scales and requires X-ray data with an extended baseline to test if a flattening occurs at >3000 d in the rest frame. (see Section 6.2).
5 DISCUSSION
5.1 Comparison with previous sample-based X-ray spectral studies
X-ray observations of RLQs starting in the Einstein era have repeatedly found in sample-based studies (see Section 2 and Table 1) that their X-ray continua below a few tens of keV (rest-frame) are significantly flatter than those of RQQs. The spectral-fitting results of our investigation, however, show that the median photon index of the X-ray spectra of our RLQ sample is |$1.84_{-0.01}^{+0.01}$|, which is significantly steeper than that obtained in previous studies (Γ ∼ 1.6) and is found to be closer to that of the similarly selected RQQ sample (|$1.90_{-0.01}^{+0.02}$|). The median photon indexes of FSRQs and SSRQs are also consistent with each other. One of the main differences between our current work and previous investigations is that our work utilizes RLQs selected in SDSS colour space whereas previous investigations mainly utilize radio-selected quasars. A bias was likely introduced when generalizing the high-energy properties of a small number of radio-selected RLQs to the full RLQ population in previous investigations. Radio surveys tend to select the most radio-luminous quasars in the Universe, which may exhibit more extreme properties than their lower-luminosity counterparts that are included in optically selected RLQ samples (e.g. Kellermann et al. 1994; Gürkan et al. 2019). For example, the radio-selected FSRQs are generally considered to be beamed objects (e.g. Orr & Browne 1982), whereas most optically selected FSRQs seem to be an intermediate population between SSRQs and RQQs (e.g. Boroson & Green 1992; Falcke, Patnaik & Sherwood 1996; Laor 2000), rather than highly beamed RLQs. Indeed, we find in the most radio-luminous regime (log Lradio > 34.3) that FSRQs with flatter power-law slopes (Γ ∼ 1.55) dominate the population (see Section 3.1.2). Additionally, it is risky to draw conclusions from sample-based studies that largely use targeted observations from archival X-ray data, since targeted objects have a poorly defined selection function and tend to have unique properties that are atypical of those of their parent population.18
Siemiginowska et al. (2008) report the X-ray properties of a sample of RLQs that are also GPS and compact steep spectrum (CSS) radio sources. They measured a median photon index of Γ = 1.84, which is consistent with our results and indicates that the X-ray spectral properties of GPS and CSS quasars are not necessarily different from those of typical RLQs.
5.2 The X-ray reflection features of RLQs
We detected strong iron K α emission in the rest-frame 6–7 keV band and a feature at rest-frame >14 keV that is likely the Compton-reflection hump in Section 3.2. Such features are expected if the X-ray emission of RLQs is dominated by their coronae as for radio-quiet AGNs, where the evidence for iron-line emission is ubiquitous (e.g. Nandra et al. 2007). Iron-line emission can be detected from many radio-loud AGNs (e.g. Eracleous, Halpern & Livio 1996; Lohfink et al. 2017; Rani & Stalin 2018) but is not ubiquitously observed (e.g. Eracleous & Halpern 1998). The general consensus is that the X-ray reflection features of radio-loud AGNs generally seem to be weaker than those of radio-quiet AGNs (e.g. Wozniak et al. 1998; Eracleous, Sambruna & Mushotzky 2000), possibly due to dilution by a beamed X-ray continuum from jets (e.g. Ghisellini et al. 2019), an ionized accretion disc (e.g. Ballantyne et al. 2014), or an outflowing corona (e.g. King, Lohfink & Kara 2017).
The iron-line emission from AGNs shows an X-ray Baldwin effect such that the EW of the narrow component of the neutral iron line decreases with increasing 2–10 keV luminosity (Iwasawa & Taniguchi 1993). This anticorrelation is significant for radio-quiet AGN samples (e.g. Bianchi et al. 2007; Shu et al. 2012), but it remains unclear if radio-loud AGNs follow the same relation. Typically, radio-loud AGNs are removed from such correlation studies since their supposed jet-linked X-ray emission can increase continuum X-ray luminosity, reduce the EW of iron line emission, and cause an artificial X-ray Baldwin effect (e.g. Jiménez-Bailón et al. 2005; Jiang, Wang & Wang 2006). If the iron-line emission from our RLQs is produced by the primary X-ray continuum radiated from a RQQ-like corona and is then diluted by a jet-linked continuum (with an intensity comparable to that of the coronal component), we would expect a typical strength of EW ≈20 eV (e.g. equation 1 in Bianchi et al. 2007), which is considerably weaker than the EW |$=70_{-20}^{+30}$| eV that we found for our RLQ sample in Section 3.2. If we instead consider the X-ray emission to be dominated by the corona, the EW we measure is still somewhat stronger than that predicted by the X-ray Baldwin effect (EW ≈ 40 eV). Possibly, a broad component contributes some amount of the emission at 6.4 keV due to limited energy resolution (especially at high redshift). Future X-ray missions with improved energy resolution and throughput can probe the details of the profile of the iron lines (see Section 6.2). It is also possible that RLQs follow a different X-ray Baldwin relation from that of RQQs if the decrease of iron-line EW is related to but not directly caused by the increase of Lx. For example, if the X-ray Baldwin effect is caused by a receding torus (e.g. Lawrence 1991; Simpson 2005) and the inner radius (and thereby the covering factor) of the torus is mainly determined by the UV luminosity, RLQs of similar radio-loudness will have a distinct EW–Lx relation. All in all, our investigation indicates that the iron-line emission of RLQs is not considerably diluted by a strong jet X-ray component.
The spectral shape and prominence of the iron line found in this work, along with our other measurements of X-ray spectral properties, put constraints on the model of the AGN corona. For example, a dynamic corona (e.g. Beloborodov 1999; Malzac, Beloborodov & Poutanen 2001) is used to explain the X-ray properties of AGNs in some studies (e.g. King et al. 2017). This model invokes a hot corona that moves away from the supermassive black hole (SMBH) at a mildly relativistic velocity and is accelerated into the large-scale jet in radio-loud AGNs; the hot corona in radio-quiet AGNs is static or moves at a lower velocity. According to this model, the flatter X-ray continuum, lower level of X-ray reflection, and higher jet power of radio-loud AGNs are attributed to the higher outflow velocities of their coronae than those of radio-quiet AGNs. However, our spectral-fitting and X-ray spectral-stacking results do not support a substantial difference between the shapes of the X-ray continua of RLQs and RQQs or significantly weaker reflection in RLQs, and therefore rule out the idea that the outflow velocity of the corona is the key parameter controlling the X-ray and jet properties (e.g. Gupta, Sikora & Rusinek 2020).
5.3 The X-ray variability of RLQs
The typical X-ray variability amplitude of our optically selected RLQs on time-scales of months-to-years in the rest frame is |$\approx 40{{\ \rm per\ cent}}$|, and extreme variations are rare in our data (see Fig. 8), which is not consistent with jet-dominated objects that show frequent large-amplitude flares in their X-ray light curves (e.g. Ulrich, Maraschi & Urry 1997; Chatterjee et al. 2008; Castignani et al. 2017; Weaver et al. 2020). This qualitative similarity to the variability of RQQs (e.g. Timlin et al. 2020) may indicate that the X-ray emission of our RLQs is coronal-dominated. The overall variability amplitude is somewhat smaller than that of matched RQQs (≈ 60 per cent), and the X-ray variability amplitude increases with time-scale, consistent with a red-noise-type power spectrum (e.g. Uttley & McHardy 2005).19 The fact that RLQs vary less than RQQs in the X-ray band at fixed time-scale might suggest that RLQs require a relatively longer time-scale to vary as much as RQQs, which is supported by the SFs depicted in Fig. 11.
Assuming that the fluctuations of the accretion flow propagate at similar speeds in both RQQs and RLQs, the time-scale of flux variability then reflects the physical scale of the X-ray emitting region; the coronae of RLQs would be larger than those of matched RQQs. It is possible that the size of the corona is larger in RLQs than in RQQs at fixed black hole mass (e.g. Dogruel et al. 2020). An anticorrelation between the X-ray variability amplitude and black hole mass among radio-quiet AGNs is observed (e.g. O’Neill et al. 2005; Ponti et al. 2012). It is therefore also possible to consider a simpler scenario where the corona size scales with the black hole mass similarly for both RLQs and RQQs, provided that the SMBHs of our RLQs are generally more massive than those of matched RQQs (e.g. Laor 2000). Indeed, there are 47 and 94 black hole mass measurements (based on either Mg ii or H β) in the catalogue of Shen et al. (2011) for the utilized RLQs and RQQs in our X-ray variability investigation, and the median black hole mass of the RLQs is ≈0.2 dex larger than that of the RQQs. Furthermore, the median Eddington ratio of the former group is ≈0.3 dex smaller than that of the later, which might play an independent role as well (e.g. O’Neill et al. 2005). There is a characteristic time-scale (TB) in the X-ray power spectrum of AGNs, above which the increase of the variability power per decade time-scale is not as significant as below TB. This time-scale depends on both the black hole mass (e.g. Markowitz et al. 2003; Papadakis 2004) and Eddington ratio such that TB ∝ MBH/λEdd (e.g. McHardy et al. 2006). Assuming that the X-ray power spectra of RLQs have a similar shape to those of radio-quiet AGNs and the characteristic time-scale follows the same scaling relation above, the most significant increase of the X-ray variability amplitude of RLQs will occur at time-scales ≈0.5 dex larger than those of RQQs, which is roughly consistent with Fig. 11. To further assess the relation between black hole mass/Eddington ratio and X-ray variability, we divide the 47 RLQs with measured black hole masses into high-MBH/low-λEdd and low-MBH/high-λEdd groups at the median MBH20 and found that the variability amplitude of the former group (|$\sigma =0.15_{-0.01}^{+0.02}$|) is significantly smaller than that of the later (|$\sigma =0.22_{-0.02}^{+0.03}$|), consistent with the assumption above.
Another possible explanation for the smaller variability amplitudes of RLQs is that the fluctuations of the inner accretion flow are relatively weak in RLQs compared to RQQs at fixed time-scale. MacLeod et al. (2010) compared the optical/UV variability properties of quasars of different radio-loudness using SDSS Stripe 82 data. Except for the most radio-loud group that might be contaminated by jet emission in the optical/UV band, the variability amplitudes of moderately radio-loud quasars are slightly (but significantly) smaller than those of radio-nondetected quasars (with controlled black hole mass, luminosity, and Eddington ratio). Cai et al. (2019) also suggest that the UV-emitting inner accretion flows of RLQs are stabilized (relative to those of RQQs) by the jet-launching magnetic field.
5.4 The Lx–Luv–Lradio relation of RLQs
The X-ray spectral and variability properties obtained in this paper generally support the result of Zhu et al. (2020) that the X-ray emission of general RLQs is mainly radiated from their coronae. In particular, the lack of a strong correlation of Γ with Lx/Lx, rqq further disputes an important role of a jet X-ray component. Zhu et al. (2020) suggested that only in a small portion of FSRQs is the jet-linked X-ray component apparent. The parametrized model fitting in the correlation analyses in Section 3.2 of Zhu et al. (2020) supports that both the coronal and jet X-ray components of FSRQs increase with radio luminosity such that |$L_\mathrm{x,corona}\propto L_\mathrm{radio}^{0.2}$| (following the corona-jet connection, Lx, corona ∝ R0.2) and Lx, jet ∝ Lradio, predicting that the jet-linked X-ray component most clearly emerges in the most radio-luminous objects. Our spectral fitting results in Section 3.1.2 (and the discussion above) of this paper are consistent with such a picture; in the most radio-luminous (likely beamed) FSRQs the jet core dominates the X-ray emission, resulting in significantly flattened X-ray spectra.
5.5 Connections with the hard X-ray emission of stellar-mass black holes
Several lines of evidence support a unification of the properties of the disc-corona/jet system surrounding accreting black holes spanning a wide range of mass (e.g. Merloni, Heinz & di Matteo 2003; Körding, Jester & Fender 2006; McHardy et al. 2006; Zhu et al. 2020). Black-hole X-ray binaries (BHXRBs) usually show a high-energy cutoff and Compton reflection in their hard X-ray spectra (e.g. Gierlinski et al. 1997), similar to that of AGNs. Poutanen & Zdziarski (2003) pointed out that since the cut-off energy is always around several hundred keV, this feature is consistent with thermal Comptonization as well as a thermostat due to pair production but is not consistent with non-thermal synchrotron emission, the cut-off energy of which varies by large factors.21 Moreover, the reflection features are not consistent with the idea that the X-ray source is beamed away from the disc (Poutanen & Zdziarski 2003). The lack of abrupt changes during state transitions of BHXRBs is not expected if a radiatively inefficient jet dominates the X-ray emission (Maccarone 2005). Furthermore, the optical depth and temperature required by the jet-dominated model (e.g. Markoff, Nowak & Wilms 2005) are often physically unrealistic (Malzac, Belmont & Fabian 2009). There is sometimes a non-thermal tail that emerges in the MeV γ-ray spectra of BHXRBs (e.g. McConnell et al. 2002), which might come from a jet. However, this component is never energetically dominant in the X-ray band. Therefore, a jet-dominated model for the hard X-ray emission is disfavoured for both accreting stellar-mass black holes and SMBHs, supporting unification ideas.
6 SUMMARY AND FUTURE PROSPECTS
6.1 Summary of main results
We present X-ray spectral and long-term variability analyses of a large sample of optically selected RLQs from Zhu et al. (2020). We utilize serendipitous X-ray data from the Chandra and XMM-Newton archives that are more sensitive than 3 × 10−14 er g cm−2 s−1 in the 0.5–7 keV energy band. The spectral and temporal properties of these RLQs are compared with those of matched RQQs (Timlin et al. 2020) using similarly selected X-ray data (see Section 2 for details). The main results are summarized as follows:
The X-ray spectra of RLQs can be well described using a simple power-law model. From our model fits, we find the median photon index of RLQs is |$1.84_{-0.01}^{+0.01}$|, which is close to that of matched RQQs (|$1.90_{-0.01}^{+0.02}$|). The median photon indices are similar between FSRQs and SSRQs. We also investigated whether the Γ values for FSRQs and SSRQs correlate with R, Lx/Lx, rqq, Lradio, and z. No strong correlations are found. A small number of the most radio-luminous FSRQs (log Lradio > 34.3), however, have flatter (Γ ∼ 1.55) X-ray spectra than those of other RLQs. The stacked X-ray spectra of our RLQs show strong iron-line emission and a possible Compton-reflection hump. The narrow iron line at 6.4 keV is detected at a 5.3σ significance level with EW = |$70_{-20}^{+30}$| eV. See Section 3.
We quantify the X-ray variability amplitude of the RLQs with multiple serendipitous observations. We required the interval between X-ray measurements to be larger than 30 d in the quasar rest frame; the median time-scale is 1.7 yr, and the longest time-scale probed by our data is ≈10 yr. Extreme large-amplitude variations are rare for our RLQs. The intrinsic variability amplitude after removing the scatter caused by measurement errors is |$0.156_{-0.007}^{+0.010}$| (43.2 per cent) for RLQs, which is significantly smaller than for the matched RQQs (|$0.212_{-0.007}^{+0.009}$| or 62.9 per cent) on similar time-scales. The X-ray variability amplitude of RLQs increases with time-scale, and the most significant increase occurs at longer time-scales than for RQQs. See Section 4.
The X-ray spectral (including the power-law photon index of the primary continuum and the strength of superimposed reflection features) and variability analyses of our RLQs support the results of Zhu et al. (2020) indicating that the X-ray emission of typical RLQs is dominated by the disc/corona. The previous claims that RLQs have substantially flatter X-ray spectra than those of RQQs are likely affected by various selection effects. Given the smaller variability amplitude of RLQs relative to RQQs matched in Luv, z, and time-scale, the physical scale of the X-ray emitting region of the disc/corona system may be larger in RLQs, caused by their more massive SMBHs and/or lower Eddington ratio. A predominantly coronal origin for the X-ray emission of RLQs is also consistent with the results for the hard X-ray emission from stellar-mass black holes. See Section 5.
6.2 Future work
Despite the notable connection between the X-ray brightness of the disc/corona and the jet efficiency of RLQs (Zhu et al. 2020), the basic spectral shape of the X-rays (i.e. Γ) radiated from the hot corona does not seem to be strongly affected by such a connection, demonstrated by the similarity between the median Γ values of RLQs and RQQs and also by the fact that the Γ values of individual RLQs do not seem to correlate with either R or Lx/Lx, rqq. It therefore would be valuable to investigate how the physical properties of the corona (i.e. temperature, optical depth, and geometry) change with R and Lx/Lx, rqq, which probably would require a powerful X-ray observatory with broadband response and excellent hard X-ray sensitivity (e.g. HEX-P; Harrison & HEX-P Collaboration 2017).
The next-generation X-ray observatories (e.g. Athena; Nandra et al. 2013) with orders of magnitude increases in effective area and energy resolution relative to current instruments will probe the iron emission lines and the Compton-reflection humps of individual RLQs, which can constrain the geometry and physical conditions of the material spiraling on to the black hole. Furthermore, it will be important to study if RLQs follow a similar Γ–λEdd relation as for RQQs.
The advent of eROSITA (Merloni et al. 2012) will produce copious well-sampled time-domain X-ray data that, when combined with existing archival data, will allow for better constraints upon the correlation between the variability amplitude of RLQs and time-scale. X-ray variability is one of the most-promising methods that can constrain the physical scale of the quasar corona, and eROSITA measurements may allow testing of the variability scenarios described in Section 5.3.
SUPPORTING INFORMATION
suppl_data
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
We thank the referee for a constructive review. We have benifitted from discussions with Thomas Maccarone about the hard X-ray emission of black-hole X-ray binaries. We thank Ari Laor for helpful comments that improved the manuscript. SFZ, JDT, and WNB acknowledge support from CXC grant AR1-22008X, NASA ADAP grant 80NSSC18K0878, and the Penn State ACIS Instrument Team Contract SV4-74018 (issued by the Chandra X-ray Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of NASA under contract NAS8-03060). The Chandra ACIS team Guaranteed Time Observations (GTO) utilized were selected by the ACIS Instrument Principal Investigator, Gordon P. Garmire, currently of the Huntingdon Institute for X-ray Astronomy, LLC, which is under contract to the Smithsonian Astrophysical Observatory via Contract SV2-82024. This research has made use of data obtained from the Chandra Data Archive and the Chandra Source Catalogue. Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
DATA AVAILABILITY
The data used in this investigation are available in the article and in its online supplementary material.
Footnotes
We use L2 keV, L2500 Å, and L5 GHz interchangeably with Lx, Luv, and Lradio to denote the X-ray, optical/UV, and radio luminosities in this paper.
The radio slopes of these most radio luminous objects are flat because their core emission is beamed towards the Earth, which is generally not true for FSRQs in optically selected samples.
The number of epochs here reflects the number of unique XMM-Newton ObsIDs rather than the number of spectra (i.e. from pn, MOS1, and MOS2). See the last paragraph of Section 2.3 for details regarding how we select the most sensitive spectrum.
We checked the brightest X-ray sources with the highest count rates and found no strong pileup effects.
The adopted photon index is consistent with the typical value from our spectral fitting results in Section 3.
Visual inspection of the images of the sources with PB ≤ 0.002 confirms the existence of a X-ray source.
If we utilize data from all working cameras and perform simultaneous source detection, the number of XMM-Newton detections increases only by one, which is probably caused by the fact that the XMM-Newton observations are generally background-limited (i.e. sensitivity improves with the square root of the exposure time) as opposed to photon-limited observations (i.e. sensitivity improves linearly with exposure time) for Chandra. We thereby elect not to analyse jointly the data from different cameras onboard XMM-Newton in this paper, which also maximizes the uniformity between the flows of the data analyses for XMM-Newton and Chandra.
The w-stat (a variant of c-stat; Wachter, Leach & Kellogg 1979) does not require the background to be explicitly modelled; however, to use w-stat, the background spectrum needs to be grouped such that each bin contains at least about five counts to avoid bias caused by zero/low-counts channels (e.g. see Appendix A of Willis et al. 2005). Our method is not subject to this binning restriction.
Zhou & Gu (2021) selected 664 RLQs that are in the 3XMM footprint. However, only the 160 RLQs with >200 X-ray counts were utilized to create their composite X-ray spectrum, which results in an X-ray completeness of only 24 per cent.
The (16, 50, and 84)th percentiles of redshift are (1.01, 1.51, and 2.35) and (1.02, 1.62, and 2.39) for RLQs and RQQs, respectively. Therefore, the spectra of both samples mainly probe the rest-frame ≈1–24 keV band.
The method of Maccacaro et al. (1988) was used to remove the amount of scatter caused by measurement uncertainties of the Γ values.
The ΔCash map utilized below is weighted by the number of counts in each spectrum. After removing these two objects, the RLQ with the largest number of net counts contributes ≈5 per cent to the total net counts. The data-to-model ratio is not weighted by the number of counts of single objects in stacking.
If Γ is allowed to be freely varying, we obtain a median |$\Gamma =1.87_{-0.04}^{+0.03}$|, which is consistent with 1.84. Therefore, the results in Section 3.1.2 are not strongly biased given the strength of the iron-line emission and Compton reflection we found in this section.
The FSRQs with log Lradio > 34.3 are excluded from consideration.
The number of data points is too small to constrain well variability at ΔT < 30 d in the top panel of Fig. 8.
In this way, no single quasar can produce more than 10 per cent of the energy flux ratios.
Soldi et al. (2014) compared the hard X-ray variability of radio galaxies to that of radio-quiet Seyfert galaxies selected from the BAT 58-month survey. The variability amplitude of these radio-loud AGNs is consistent with that of radio-quiet AGNs in the 14–24 keV band, while in the 35–100 keV band the former group varies more than the latter. Considering the fact that these are hard X-ray-selected, low-luminosity objects, a direct compairson of their results with ours is probably unjustified.
The two groups have nearly identical median Luv. Therefore, MBH and λEdd are related to each other, the role of which cannot be separated.
Fine tuning is probably also required to produce a nearly constant cut-off energy for the case of emission from non-thermal Comptonization.
REFERENCES
APPENDIX A: RQQ SAMPLE
The properties of the comparison RQQ sample (see the end of Section 2.4) in this work are presented in Table A1. The serendipitous Chandra observations utilized for these RQQs, along with resulting derived X-ray properties, are listed in Table A2.
| Name . | z . | mi . | log L2500 Å . |
|---|---|---|---|
| 000 635.69 − 000 721.04 | 0.891 | 20.65 | 29.47 |
| 002 312.05 + 002 545.99 | 2.657 | 20.64 | 30.48 |
| 002 402.12 − 020 101.13 | 2.614 | 19.90 | 30.77 |
| 002 707.56 + 170 617.88 | 0.947 | 20.25 | 29.69 |
| 002 751.16 + 262 437.66 | 1.173 | 20.40 | 29.77 |
| Name . | z . | mi . | log L2500 Å . |
|---|---|---|---|
| 000 635.69 − 000 721.04 | 0.891 | 20.65 | 29.47 |
| 002 312.05 + 002 545.99 | 2.657 | 20.64 | 30.48 |
| 002 402.12 − 020 101.13 | 2.614 | 19.90 | 30.77 |
| 002 707.56 + 170 617.88 | 0.947 | 20.25 | 29.69 |
| 002 751.16 + 262 437.66 | 1.173 | 20.40 | 29.77 |
| Name . | z . | mi . | log L2500 Å . |
|---|---|---|---|
| 000 635.69 − 000 721.04 | 0.891 | 20.65 | 29.47 |
| 002 312.05 + 002 545.99 | 2.657 | 20.64 | 30.48 |
| 002 402.12 − 020 101.13 | 2.614 | 19.90 | 30.77 |
| 002 707.56 + 170 617.88 | 0.947 | 20.25 | 29.69 |
| 002 751.16 + 262 437.66 | 1.173 | 20.40 | 29.77 |
| Name . | z . | mi . | log L2500 Å . |
|---|---|---|---|
| 000 635.69 − 000 721.04 | 0.891 | 20.65 | 29.47 |
| 002 312.05 + 002 545.99 | 2.657 | 20.64 | 30.48 |
| 002 402.12 − 020 101.13 | 2.614 | 19.90 | 30.77 |
| 002 707.56 + 170 617.88 | 0.947 | 20.25 | 29.69 |
| 002 751.16 + 262 437.66 | 1.173 | 20.40 | 29.77 |
| Name . | ObsID . | MJD . | Inst. . | log fdet . | net . | SNR . | log fx . | xdet . | Γ . | Goodness-of-fit . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000 635.69 − 000 721.04 | 4096 | 52853.3 | ACIS | −14.02 | 3.1 | 1.5 | −14.02 | 0 | −99 | 17.5/25.2/9.2 |
| 000 635.69 − 000 721.04 | 5617 | 53579.5 | ACIS | −14.13 | 32.4 | 4.8 | −13.55 | 1 | |$2.06_{-0.58}^{+0.69}$| | 116.5/128.7/13.6 |
| 002 312.05 + 002 545.99 | 2252 | 51915.4 | ACIS | −14.45 | 105.2 | 8.8 | −13.11 | 1 | |$1.14_{-0.29}^{+0.31}$| | 121.4/117.4/12.1 |
| 002 402.12 − 020 101.13 | 2099 | 52141.1 | ACIS | −14.53 | 9.6 | 3.0 | −13.96 | 1 | |$2.04_{-0.90}^{+1.0}$| | 40.6/47.4/11.2 |
| 002 402.12 − 020 101.13 | 8918 | 54768.1 | ACIS | −14.71 | 7.7 | 2.5 | −14.39 | 1 | |$2.05_{-1.09}^{+1.48}$| | 44.9/50.7/12.2 |
| Name . | ObsID . | MJD . | Inst. . | log fdet . | net . | SNR . | log fx . | xdet . | Γ . | Goodness-of-fit . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000 635.69 − 000 721.04 | 4096 | 52853.3 | ACIS | −14.02 | 3.1 | 1.5 | −14.02 | 0 | −99 | 17.5/25.2/9.2 |
| 000 635.69 − 000 721.04 | 5617 | 53579.5 | ACIS | −14.13 | 32.4 | 4.8 | −13.55 | 1 | |$2.06_{-0.58}^{+0.69}$| | 116.5/128.7/13.6 |
| 002 312.05 + 002 545.99 | 2252 | 51915.4 | ACIS | −14.45 | 105.2 | 8.8 | −13.11 | 1 | |$1.14_{-0.29}^{+0.31}$| | 121.4/117.4/12.1 |
| 002 402.12 − 020 101.13 | 2099 | 52141.1 | ACIS | −14.53 | 9.6 | 3.0 | −13.96 | 1 | |$2.04_{-0.90}^{+1.0}$| | 40.6/47.4/11.2 |
| 002 402.12 − 020 101.13 | 8918 | 54768.1 | ACIS | −14.71 | 7.7 | 2.5 | −14.39 | 1 | |$2.05_{-1.09}^{+1.48}$| | 44.9/50.7/12.2 |
The columns of this table are similar to those of Table 2, where further explanations are provided.
| Name . | ObsID . | MJD . | Inst. . | log fdet . | net . | SNR . | log fx . | xdet . | Γ . | Goodness-of-fit . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000 635.69 − 000 721.04 | 4096 | 52853.3 | ACIS | −14.02 | 3.1 | 1.5 | −14.02 | 0 | −99 | 17.5/25.2/9.2 |
| 000 635.69 − 000 721.04 | 5617 | 53579.5 | ACIS | −14.13 | 32.4 | 4.8 | −13.55 | 1 | |$2.06_{-0.58}^{+0.69}$| | 116.5/128.7/13.6 |
| 002 312.05 + 002 545.99 | 2252 | 51915.4 | ACIS | −14.45 | 105.2 | 8.8 | −13.11 | 1 | |$1.14_{-0.29}^{+0.31}$| | 121.4/117.4/12.1 |
| 002 402.12 − 020 101.13 | 2099 | 52141.1 | ACIS | −14.53 | 9.6 | 3.0 | −13.96 | 1 | |$2.04_{-0.90}^{+1.0}$| | 40.6/47.4/11.2 |
| 002 402.12 − 020 101.13 | 8918 | 54768.1 | ACIS | −14.71 | 7.7 | 2.5 | −14.39 | 1 | |$2.05_{-1.09}^{+1.48}$| | 44.9/50.7/12.2 |
| Name . | ObsID . | MJD . | Inst. . | log fdet . | net . | SNR . | log fx . | xdet . | Γ . | Goodness-of-fit . |
|---|---|---|---|---|---|---|---|---|---|---|
| 000 635.69 − 000 721.04 | 4096 | 52853.3 | ACIS | −14.02 | 3.1 | 1.5 | −14.02 | 0 | −99 | 17.5/25.2/9.2 |
| 000 635.69 − 000 721.04 | 5617 | 53579.5 | ACIS | −14.13 | 32.4 | 4.8 | −13.55 | 1 | |$2.06_{-0.58}^{+0.69}$| | 116.5/128.7/13.6 |
| 002 312.05 + 002 545.99 | 2252 | 51915.4 | ACIS | −14.45 | 105.2 | 8.8 | −13.11 | 1 | |$1.14_{-0.29}^{+0.31}$| | 121.4/117.4/12.1 |
| 002 402.12 − 020 101.13 | 2099 | 52141.1 | ACIS | −14.53 | 9.6 | 3.0 | −13.96 | 1 | |$2.04_{-0.90}^{+1.0}$| | 40.6/47.4/11.2 |
| 002 402.12 − 020 101.13 | 8918 | 54768.1 | ACIS | −14.71 | 7.7 | 2.5 | −14.39 | 1 | |$2.05_{-1.09}^{+1.48}$| | 44.9/50.7/12.2 |
The columns of this table are similar to those of Table 2, where further explanations are provided.



