The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: N-body mock challenge for galaxy clustering measurements

HOD parameters adopted for the Zheng et al. (2007) model, corresponding to different ‘luminosity threshold’ values.

ZHENG MODEL
Threshold	log M_min	\|$\sigma _{ \log \rm M}$\|	α	M₀	M₁
Th1 (M_r = −19)	11.60	0.26	1.02	11.49	12.83
Std (M_r = −20)	12.02	0.26	1.06	11.38	13.31
Th2 (M_r = −21)	12.79	0.39	1.15	11.92	13.94

ZHENG MODEL
Threshold	log M_min	\|$\sigma _{ \log \rm M}$\|	α	M₀	M₁
Th1 (M_r = −19)	11.60	0.26	1.02	11.49	12.83
Std (M_r = −20)	12.02	0.26	1.06	11.38	13.31
Th2 (M_r = −21)	12.79	0.39	1.15	11.92	13.94

Table 1.

HOD parameters adopted for the Zheng et al. (2007) model, corresponding to different ‘luminosity threshold’ values.

ZHENG MODEL
Threshold	log M_min	\|$\sigma _{ \log \rm M}$\|	α	M₀	M₁
Th1 (M_r = −19)	11.60	0.26	1.02	11.49	12.83
Std (M_r = −20)	12.02	0.26	1.06	11.38	13.31
Th2 (M_r = −21)	12.79	0.39	1.15	11.92	13.94

ZHENG MODEL
Threshold	log M_min	\|$\sigma _{ \log \rm M}$\|	α	M₀	M₁
Th1 (M_r = −19)	11.60	0.26	1.02	11.49	12.83
Std (M_r = −20)	12.02	0.26	1.06	11.38	13.31
Th2 (M_r = −21)	12.79	0.39	1.15	11.92	13.94

The shapes of the Zheng HODs used in this work are shown in Fig. 1, for the three conventional choices of HOD parameters corresponding to the previously mentioned threshold values (see Table 1). Note also that in our HOD modelling we do not modulate the satellite distribution by the central one, unless specified otherwise.

Figure 1.

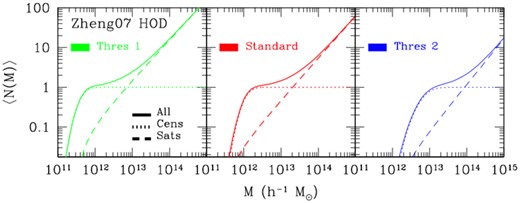
HOD shapes in the Zheng, Coil & Zehavi (2007) model, used for the production of galaxy mocks. In the various panels, dotted lines describe the central occupation statistics (equation 2), dashed lines are used for the satellite occupation statistics (equation 3), and solid lines represent the composite HODs. Three luminosity thresholds are considered, corresponding to different HOD parameter choices, as reported in Table 1. See the main text for more details.

3.3 Adding the SHMR complexity: Leauthaud model

The second model we consider is the Leauthaud prescription (Leauthaud et al. 2011, 2012), a composite HOD framework that extends the standard Zheng formalism by including a parametrization of an underlying stellar-to-halo mass relation (SHMR), which specifies the mean mass of a galaxy as a function of halo mass. The main assumption in this picture is that the SHMR is valid only for central galaxies, as satellites and centrals experience distinct stellar growth rates and so it is necessary to model them separately. To this end, the conditional stellar mass function (CSMF) – denoted as Φ(M_*|M_h), with M_* the mass in stars and M_h the mass of the parent halo – is divided into centrals and satellites, namely Φ(M_*|M_h) = Φ_cen(M_*|M_h) + Φ_sat(M_*|M_h). Moreover, Φ_cen(M_*|M_h) is modelled stochastically as a lognormal PDF with a lognormal scatter |$\sigma _{\log \rm M_{*}}$|⁠, and normalized to unity. The exact form is (Leauthaud et al. 2012):

$$\begin{eqnarray*} \Phi _{\rm cen} (M_{*}|M_{\rm h}) &=& {1 \over \ln (10) \sigma _{\log \rm M_{*}} \sqrt{2 \pi }} \cdot \nonumber \\ && \exp \bigg[ {-}{ \lbrace \log {M_{*} - \log [f_{\rm SHMR} (M_{\rm h}) ]} \rbrace ^2 \over 2 \sigma ^2_{\log \rm M_{*}} } \bigg] , \end{eqnarray*}$$

(4)

where f_SHMR is the logarithmic mean of the stellar mass given the halo mass for the Φ_cen distribution function. Equation (4) incorporates the scatter associated with the determination of stellar masses, as well as the intrinsic scatter in stellar mass at fixed halo mass due to astrophysical processes. The functional form for f_SHMR is described by five shape parameters (M₀, M₁, β, δ, γ), and defined via its inverse function as (Behroozi et al. 2010):

$$\begin{eqnarray*} \log [f^{-1}_{\rm SHMR} (M_{*}) ] &=& \log (M_1) + f_{\rm low}(M_{*}/M_{0}) + f_{\rm high}(M_{*}/M_{0}) \nonumber \\ &=& \log (M_1) + \beta \log \Big ({M_{*} \over M_{0} } \Big) + \nonumber \\ && { (M_{*} /M_{0})^{\delta } \over 1 + (M_{*} /M_{0})^{- \gamma } }- {1\over 2}, \end{eqnarray*}$$

(5)

with f_low and f_high the low and high mass parts of the SHMF, respectively. In the previous expression, M₀ and M₁ are characteristic stellar and halo masses – respectively – in the 〈M_*〉(M_h) map, β is a low-mass slope of the 〈M_*〉(M_h) map, δ is the high-mass slope of the same map, and γ represents the transition between the low- and high-mass behaviour of the 〈M_*〉(M_h) mapping. The redshift evolution of the SHMR is modelled by allowing the parameters that define f_SHMR in equation (5) to vary linearly with the scale factor a as:

$$\begin{eqnarray*} \log [M_1(a)] &=& \log (M_{1,0}) + \log (M_{1a}) (a-1) \end{eqnarray*}$$

(6)

$$\begin{eqnarray*} \log [M_{0}(a)] &=& \log (M_{0,0}) + \log (M_{0a}) (a-1) \end{eqnarray*}$$

(7)

$$\begin{eqnarray*} \beta (a) &=& \beta _{0} + \beta _{a} (a-1) \end{eqnarray*}$$

(8)

$$\begin{eqnarray*} \delta (a) &=& \delta _{0} + \delta _{a} (a-1) \end{eqnarray*}$$

(9)

$$\begin{eqnarray*} \gamma (a) &=& \gamma _{0} + \gamma _{a} (a-1). \end{eqnarray*}$$

(10)

Therefore, the model for the SHMR effectively requires 10 parameters. For our modelling, we adopt the same literature values as in the second column of Table 2 in Behroozi et al. (2010) at z = 0, and also reported in the upper part of Table 2 for convenience. Furthermore, equation (4) requires a functional form for the lognormal scatter |$\sigma _{\log \rm M_{*}}$| in the SHMR: motivated by Leauthaud et al. (2012), who found that a halo mass-varying scatter produced no better fit than a model with constant scatter, we assume a constant scatter in this work – which can be thought as the sum in quadrature of an intrinsic component plus a measurement error component. Specifically, we set |$\sigma _{\log \rm M_{*}}=0.20$| in our modelling for all the redshifts considered.

Table 2.

HOD parameters for central and satellite galaxies assumed for the calibration of the Leauthaud et al. (2011) model.

Leauthaud model
Centrals
log [M_{1, 0}]	12.35
\|$\log [M_{1 \rm a}]$\|	0.30
log [M_{0, 0}]	10.72
\|$\log [M_{0 \rm a}]$\|	0.59
β₀	0.43
β_a	0.18
δ₀	0.56
δ_a	0.18
γ₀	1.54
γ_a	2.52
\|$\sigma _{\log M_{*}}$\|	0.20
Satellites
α_sat	1.0
β_sat	0.859
B_sat	10.62
β_cut	−0.13
B_cut	1.47

Leauthaud model
Centrals
log [M_{1, 0}]	12.35
\|$\log [M_{1 \rm a}]$\|	0.30
log [M_{0, 0}]	10.72
\|$\log [M_{0 \rm a}]$\|	0.59
β₀	0.43
β_a	0.18
δ₀	0.56
δ_a	0.18
γ₀	1.54
γ_a	2.52
\|$\sigma _{\log M_{*}}$\|	0.20
Satellites
α_sat	1.0
β_sat	0.859
B_sat	10.62
β_cut	−0.13
B_cut	1.47

Table 2.

HOD parameters for central and satellite galaxies assumed for the calibration of the Leauthaud et al. (2011) model.

Leauthaud model
Centrals
log [M_{1, 0}]	12.35
\|$\log [M_{1 \rm a}]$\|	0.30
log [M_{0, 0}]	10.72
\|$\log [M_{0 \rm a}]$\|	0.59
β₀	0.43
β_a	0.18
δ₀	0.56
δ_a	0.18
γ₀	1.54
γ_a	2.52
\|$\sigma _{\log M_{*}}$\|	0.20
Satellites
α_sat	1.0
β_sat	0.859
B_sat	10.62
β_cut	−0.13
B_cut	1.47

Leauthaud model
Centrals
log [M_{1, 0}]	12.35
\|$\log [M_{1 \rm a}]$\|	0.30
log [M_{0, 0}]	10.72
\|$\log [M_{0 \rm a}]$\|	0.59
β₀	0.43
β_a	0.18
δ₀	0.56
δ_a	0.18
γ₀	1.54
γ_a	2.52
\|$\sigma _{\log M_{*}}$\|	0.20
Satellites
α_sat	1.0
β_sat	0.859
B_sat	10.62
β_cut	−0.13
B_cut	1.47

The top panel of Fig. 2 provides an example of the effects of varying in turn the five main parameters that control the SHMF (equation 5) at z = 0 by 10 per cent and up to 50 per cent – as specified in the plot with different line styles and colours, when the lognormal scatter is kept constant. The baseline parameters are fixed as in Behroozi et al. (2010) at z = 0 (solid black line, and upper part in Table 2). The bottom panel of the same figure displays the SHMF underlying the Leauthaud model at z = 0, along with its redshift evolution for the two main redshift snapshots considered in our mock-making procedure (z = 0.695 and z = 0.865, respectively – see Section 4): we use these SHMRs in our modelling.

$[Top] Effects of varying the main parameters controlling the SHMF for central galaxies (equation 5), modelled as a mean–log relation in the Leauthaud model and heavily based on Behroozi, Conroy & Wechsler (2010). The key shape parameters are altered in turn by $10{{\ \rm per\ cent}}$ (M0, M1), $20{{\ \rm per\ cent}}$ (β, δ), and $50{{\ \rm per\ cent}}$ (γ), respectively, from the baseline Behroozi et al. (2010) model at z = 0 (solid black line and upper part in Table 2), when $\sigma _{\log \rm M_{*}}=0.20$. Different line styles and colors refer to such variations, as clearly indicated in the panel. [Bottom] SHMF underlying the Leauthaud model at z = 0, and its redshift evolution at z = 0.695 and z = 0.865: we use these SHMRs in our mock-making procedure.$

Figure 2.

[Top] Effects of varying the main parameters controlling the SHMF for central galaxies (equation 5), modelled as a mean–log relation in the Leauthaud model and heavily based on Behroozi, Conroy & Wechsler (2010). The key shape parameters are altered in turn by |$10{{\ \rm per\ cent}}$| (M₀, M₁), |$20{{\ \rm per\ cent}}$| (β, δ), and |$50{{\ \rm per\ cent}}$| (γ), respectively, from the baseline Behroozi et al. (2010) model at z = 0 (solid black line and upper part in Table 2), when |$\sigma _{\log \rm M_{*}}=0.20$|⁠. Different line styles and colors refer to such variations, as clearly indicated in the panel. [Bottom] SHMF underlying the Leauthaud model at z = 0, and its redshift evolution at z = 0.695 and z = 0.865: we use these SHMRs in our mock-making procedure.

The key difference with respect to the Zheng model relies in the assumption that the stellar mass, rather than the galaxy luminosity, is used to implement the HOD as a more reliable tracer of the halo mass – see e.g. Leauthaud et al. (2011, 2012), Tinker et al. (2013). To this end, for a volume-limited sample of galaxies such that |$M_{*} \gt M^{\rm thr}_{*}$|⁠, with |$M^{\rm thr}_{*}$| a galaxy threshold mass, the central occupation function |$\langle N_{\rm cen} (M_{\rm h} | M_{*}^{\rm thr}) \rangle$| is fully specified given Φ_cen(M_*|M_h) according to (Leauthaud et al. 2011):

$$\begin{eqnarray*} \langle N_{\rm cen} (M_{\rm h} | M_{*}^{\rm thr}) \rangle = \int _{M^{\rm thr}_{*}}^{\infty } \Phi _{\rm cen} (M_{*} | M_{\rm h}) {\rm d}M_{*}. \end{eqnarray*}$$

(11)

Assuming that |$\sigma _{\log \rm M_{*}}$| is constant, the previous expression can be readily integrated and becomes:

$$\begin{eqnarray*} \langle N_{\rm cen} (M_{\rm h} | M_{*}^{\rm thr}) \rangle = {1 \over 2} \Big [ 1 - {\rm erf} \Big \lbrace { \log (M^{\rm thr}_{*}) - \log [ f_{\rm SHMR}(M_{\rm h}) ] \over \sqrt{2} \sigma _{\log \rm M_{*}} } \Big \rbrace \Big ]. \nonumber \\ \end{eqnarray*}$$

(12)

Equation (12) represents a generalization of the Zheng HOD formula (equation 2), and it is controlled by five parameters that enter in the SHMR – plus 1, if we allow for a varying scatter in the SHMR, and plus additional five parameters if we also consider redshift evolution in the SHMR. Interestingly, equation (2) – i.e. the Zheng model – can be readily recovered from (11) as a limiting case by assuming a constant scatter in the SHMR and by setting f_SHMR to be a power law; however, this latter assumption is not realistic.

Regarding the satellite occupation function, in the Leauthaud model it is parametrized as a power law of host mass with an exponential cutoff, and can be optionally scaled by 〈N_cen〉 (this is not done in our case). Specifically:

$$\begin{eqnarray*} \langle N_{\rm sat} (M_{\rm h} | M_{*}^{\rm thr}) \rangle = \Big ({ M_{\rm h} \over M_{\rm sat}} \Big)^{\alpha _{\rm sat}} \exp \Big (- {M_{\rm cut} \over M_{\rm h}} \Big) , \end{eqnarray*}$$

(13)

where M_sat defines the amplitude of the power law and M_cut sets the scale of the exponential cutoff; haloes with masses M_h < M_cut are extremely unlikely to host a satellite galaxy. Instead of simply modelling M_sat and M_cut as constant factors of |$f^{-1}_{\rm SHMR} (M^{\rm thr}_{*})$|⁠, flexibility is added by enabling M_sat and M_cut to vary as power-law functions of |$f^{-1}_{\rm SHMR} (M^{\rm thr}_{*})$|⁠:

$$\begin{eqnarray*} {M_{\rm sat} \over \bar{M}_{12} } = B_{\rm sat} \Big [ {f^{-1}_{\rm SHMR} (M^{\rm thr}_{*}) \over \bar{M}_{12} } \Big ]^{\beta _{\rm sat}} \end{eqnarray*}$$

(14)

$$\begin{eqnarray*} {M_{\rm cut} \over \bar{M}_{12} } = B_{\rm cut} \Big [ {f^{-1}_{\rm SHMR} (M^{\rm thr}_{*}) \over \bar{M}_{12} } \Big ]^{\beta _{\rm cut}} , \end{eqnarray*}$$

(15)

where |$\bar{M}_{12} = 10^{12} \, \mathrm{M}_{\odot }$|⁠. Hence, satellite occupation statistics, independent of binning schemes and parametrized with threshold samples, are modelled by five parameters: α_sat, β_sat, B_sat, β_cut, B_cut. In detail, α_sat is the power-law slope of the relation between halo mass and the satellite mean occupation function 〈N_sat〉, β_sat and B_sat control the amplitude of the power-law slope of 〈N_sat〉, and β_cut and B_cut control the low-mass cut off in 〈N_sat〉. These satellites parameters are fixed as in table 5 of Leauthaud et al. (2011) for the first redshift bin, and also reported in the bottom part of Table 2 for convenience.

In summary, the Leauthaud framework is completely determined by 11 HOD parameters: six controlling the central galaxies and five for satellite galaxies, plus additional five if we also take into account the redshift evolution of the SHMR. In this framework, ‘threshold’ should be intended as the minimal stellar mass of the galaxy sample, rather than galaxy luminosity.

The shapes of the HODs in the Leauthaud model adopted in this work are shown in the top panels of Fig. 4 for three thresholds in mass, indicated as ‘Threshold 1’ (Th1; |$M^{\rm thr}_{*}=10^{10} \, h^{-1} \, \mathrm{M}_{\odot }$|⁠), ‘Standard’ (Std; |$M^{\rm thr}_{*}=10^{10.5} \, h^{-1} \, \mathrm{M}_{\odot }$|⁠), and ‘Threshold 2’ (Th2; |$M^{\rm thr}_{*}=10^{11} \, h^{-1} \, \mathrm{M}_{\odot }$|⁠), when z = 0.695. In particular, Th2 is the one closer to the eBOSS LRG sample, and we mainly focus on this mass interval in our analysis. Note finally that in the Leauthaud framework |$\langle N_{\rm sat} (M_{\rm h} | M_{*}^{\rm thr}) \rangle$| depends on |$\langle N_{\rm cen} (M_{\rm h} | M_{*}^{\rm thr}) \rangle$|⁠, indicating that in this particular model the occupation statistics of centrals and satellites are correlated: this constitutes an important difference with respect to the traditional five-parameter HOD. In fact, as pointed out by Contreras et al. (2017) and Duan & Eisenstein (2019), if the goal is not to constrain HOD parameters and this fitting difficulty is not of concern (as in our specific case), there is no advantage or motivation for insisting on no correlations between centrals and satellites.

3.4 HOD with colour/SFR: Tinker model

The next HOD framework we consider has been introduced by Tinker et al. (2013): it is an extension of the Leauthaud formalism previously described, to samples defined by both stellar mass and star formation (SF) activity. In this context, galaxies can be roughly categorized into the star-forming sequence of blue, discy, gas-rich galaxies, and the quiescent, ellipsoidal galaxies with old stellar populations and red colours: the bimodality is firmly in place at z = 1 (Tinker et al. 2013, 2019). Therefore, in this model galaxies are divided into quiescent, to indicate galaxies that have little to no star formation and are intrinsically located on the red sequence, and the set of star-forming galaxies. Hence, the Tinker model represents a minimal modification of the Leauthaud prescription to adapt it to passive and SF subsamples of galaxies. The HOD behaviour is in fact governed by an assumed underlying SHMR as first introduced in Behroozi et al. (2010), but that is now distinct for star-forming and quiescent populations: each subsample will then have a separate f_SHMR, with two different sets of HOD parameters related to their specific SHMRs. A constant scatter |$\sigma _{\log \rm M_{*}}$| in the SHMR is adopted here, but the scatter is different and independent for passive and SF central galaxies. The main difference with respect to the Leauthaud formalism is the following requirement:

$$\begin{eqnarray*} \int \Big \lbrace f_{\rm q}(M_{\rm h}) \times \Phi _{\rm cen}^{\rm q} (M_{*}|M_{\rm h}) + [1-f_{\rm q} (M_{\rm h})] \times \Phi _{\rm cen}^{\rm SF} (M_{*}| M_{\rm h}) \Big \rbrace {\rm d}M_{*}=1 ,\end{eqnarray*}$$

(16)

where f_q(M_h) is a function specifying the fraction of times that a halo of mass M_h contains a quenched central galaxy (independent of galaxy mass), and |$\Phi _{\rm cen}^{\rm x}$| is the conditional stellar mass function for central quiescent or star-forming galaxies, each normalized to unity. The function f_q(M_h) does not have a parametric form, but five halo mass points are chosen at which to specify f_q(M_h) and smoothly interpolate between them, where the five masses are evenly spaced in log M_h. Moreover, to avoid explicit dependencies of HOD parameters on bin sizes, all HODs are defined as threshold quantities, which provides maximal flexibility.

Fig. 3 shows the SHMFs adopted in the Tinker model, as well as in our mock-making procedure, along with their redshift evolution: solid lines refer to z = 0, dotted and dashed lines are at z = 0.695 and z = 0.865, respectively. Active galaxies are represented in blue, while quiescent galaxies are displayed in brown.

Figure 3.

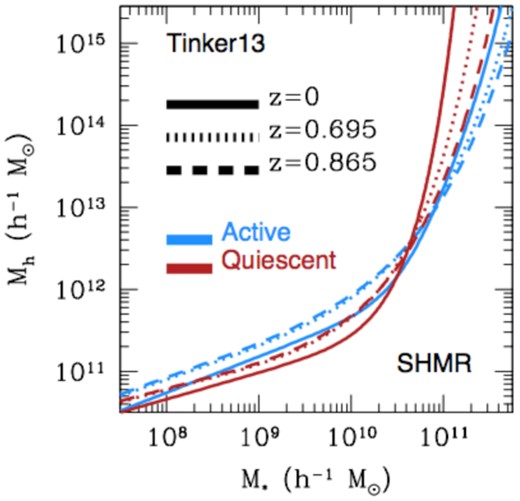
SHMFs for central galaxies adopted in the Tinker model and in our mock-making procedure at z = 0 (solid lines), z = 0.695 (dotted lines), and z = 0.865 (dashed lines). Active galaxies are displayed in blue, while quiescent galaxies are represented in brown.

As the Tinker model inherits almost all the features and methods of the Leauthaud framework, the HOD for centrals is the same as in equation (12), but the parameters of the f_SHMR are independent for each subsample: this is indeed an important aspect that clearly differentiates the two models. Moreover, for red central galaxies, the HOD is multiplied by f_q(M_h), and by 1 − f_q(M_h) for SF central galaxies.

The occupation statistics of satellite galaxies as a function of halo mass are similar to those of Leauthaud et al. (2011), although the satellite occupation of passive and star-forming galaxies subsamples are treated independently. Hence, a modification is introduced in order to produce a proper cutoff scale by including |$f_{\rm SHMR}^{-1}$| to the numerator in the exponential cutoff, so that:

$$\begin{eqnarray*} \langle N_{\rm sat} (M_{\rm h} | M_{*}^{\rm thr}) \rangle = \Big ({ M_{\rm h} \over M_{\rm sat}} \Big)^{\alpha _{\rm sat}} \exp \Big ({-} {[M_{\rm cut} + f_{\rm SHMR}^{-1} (M_{*})]\over M_{\rm h}} \Big). \end{eqnarray*}$$

(17)

This guarantees that satellite occupation fully cuts off at the same halo mass scale as central galaxies of the same mass. In addition, while in Leauthaud et al. (2011) α_sat = 1, here the fraction of satellites that are star forming depends on halo mass, so α_sat = 1 is allowed to be free for both passive and star-forming subsamples.

In summary, the Tinker model is characterized by 27 free parameters: 11 are needed for the composite HOD of a given subsample (5 for the central SHMR, one additional for the SHMR scatter, plus 5 for the satellite occupation statistics), and 5 pivot points are necessary to specify f_q(M_h). Each set of 27 parameters describes the galaxy–halo relation at a given redshift, and clearly additional quantities are required to characterize the redshift evolution. In this work, we adopt literature values from the lowest redshift bin in table 2 of Tinker et al. (2013), as reported in Table 3; we note that adopting these parameters makes the model differing from that of Leauthaud, even when the full HOD shape is considered.

Table 3.

HOD parameters for central and satellite galaxies assumed for the calibration of the Tinker et al. (2013) model.

TINKER MODEL
Centrals
\|$\log [M_{1,0, \rm active}]$\|	12.56
\|$\log [M_{1,0, \rm quiescent}]$\|	12.08
\|$\log [M_{0,0, \rm active}]$\|	10.96
\|$\log [M_{0, 0, \rm quiescent}]$\|	10.70
\|$\beta _{0, \rm active}$\|	0.44
\|$\beta _{0, \rm quiescent}$\|	0.32
\|$\delta _{0, \rm active}$\|	0.52
\|$\delta _{0, \rm quiescent}$\|	0.93
\|$\gamma _{0, \rm active}$\|	1.48
\|$\gamma _{0, \rm quiescent}$\|	0.81
\|$\sigma _{\log \rm M_{*}, active}$\|	0.21
\|$\sigma _{\log \rm M_{*}, quiescent}$\|	0.28
Satellites
α_{sat, active}	0.99
α_{sat, quiescent}	1.08
β_{sat, active}	1.05
β_{sat, quiescent}	0.62
B_{sat, active}	33.96
B_{sat, quiescent}	17.90
β_{cut, active}	0.77
β_{cut, quiescent}	−0.12
B_{cut, active}	0.28
B_{cut, quiescent}	21.42

TINKER MODEL
Centrals
\|$\log [M_{1,0, \rm active}]$\|	12.56
\|$\log [M_{1,0, \rm quiescent}]$\|	12.08
\|$\log [M_{0,0, \rm active}]$\|	10.96
\|$\log [M_{0, 0, \rm quiescent}]$\|	10.70
\|$\beta _{0, \rm active}$\|	0.44
\|$\beta _{0, \rm quiescent}$\|	0.32
\|$\delta _{0, \rm active}$\|	0.52
\|$\delta _{0, \rm quiescent}$\|	0.93
\|$\gamma _{0, \rm active}$\|	1.48
\|$\gamma _{0, \rm quiescent}$\|	0.81
\|$\sigma _{\log \rm M_{*}, active}$\|	0.21
\|$\sigma _{\log \rm M_{*}, quiescent}$\|	0.28
Satellites
α_{sat, active}	0.99
α_{sat, quiescent}	1.08
β_{sat, active}	1.05
β_{sat, quiescent}	0.62
B_{sat, active}	33.96
B_{sat, quiescent}	17.90
β_{cut, active}	0.77
β_{cut, quiescent}	−0.12
B_{cut, active}	0.28
B_{cut, quiescent}	21.42

Table 3.

HOD parameters for central and satellite galaxies assumed for the calibration of the Tinker et al. (2013) model.

TINKER MODEL
Centrals
\|$\log [M_{1,0, \rm active}]$\|	12.56
\|$\log [M_{1,0, \rm quiescent}]$\|	12.08
\|$\log [M_{0,0, \rm active}]$\|	10.96
\|$\log [M_{0, 0, \rm quiescent}]$\|	10.70
\|$\beta _{0, \rm active}$\|	0.44
\|$\beta _{0, \rm quiescent}$\|	0.32
\|$\delta _{0, \rm active}$\|	0.52
\|$\delta _{0, \rm quiescent}$\|	0.93
\|$\gamma _{0, \rm active}$\|	1.48
\|$\gamma _{0, \rm quiescent}$\|	0.81
\|$\sigma _{\log \rm M_{*}, active}$\|	0.21
\|$\sigma _{\log \rm M_{*}, quiescent}$\|	0.28
Satellites
α_{sat, active}	0.99
α_{sat, quiescent}	1.08
β_{sat, active}	1.05
β_{sat, quiescent}	0.62
B_{sat, active}	33.96
B_{sat, quiescent}	17.90
β_{cut, active}	0.77
β_{cut, quiescent}	−0.12
B_{cut, active}	0.28
B_{cut, quiescent}	21.42

TINKER MODEL
Centrals
\|$\log [M_{1,0, \rm active}]$\|	12.56
\|$\log [M_{1,0, \rm quiescent}]$\|	12.08
\|$\log [M_{0,0, \rm active}]$\|	10.96
\|$\log [M_{0, 0, \rm quiescent}]$\|	10.70
\|$\beta _{0, \rm active}$\|	0.44
\|$\beta _{0, \rm quiescent}$\|	0.32
\|$\delta _{0, \rm active}$\|	0.52
\|$\delta _{0, \rm quiescent}$\|	0.93
\|$\gamma _{0, \rm active}$\|	1.48
\|$\gamma _{0, \rm quiescent}$\|	0.81
\|$\sigma _{\log \rm M_{*}, active}$\|	0.21
\|$\sigma _{\log \rm M_{*}, quiescent}$\|	0.28
Satellites
α_{sat, active}	0.99
α_{sat, quiescent}	1.08
β_{sat, active}	1.05
β_{sat, quiescent}	0.62
B_{sat, active}	33.96
B_{sat, quiescent}	17.90
β_{cut, active}	0.77
β_{cut, quiescent}	−0.12
B_{cut, active}	0.28
B_{cut, quiescent}	21.42

The central panels of Fig. 4 show the shapes of the HODs in the Tinker model adopted in this work at z = 0.695, for the same three thresholds in mass described before in relation to the Leauthaud framework, and also distinguishing between centrals and satellites. Active and quiescent galaxy HODs are represented by different colours, as indicated in the panels, and the global HODs are also displayed. As noted by Tinker et al. (2013) and also evident from our figures, the number of quiescent satellites exhibits minimal redshift evolution; all evolution in the red sequence is due to low-mass central galaxies being quenched of their star formation. Moreover, the efficiency of quenching star formation for centrals increases with cosmic time, while the mechanisms that quench the star formation of satellite galaxies in groups and clusters is losing efficiency.

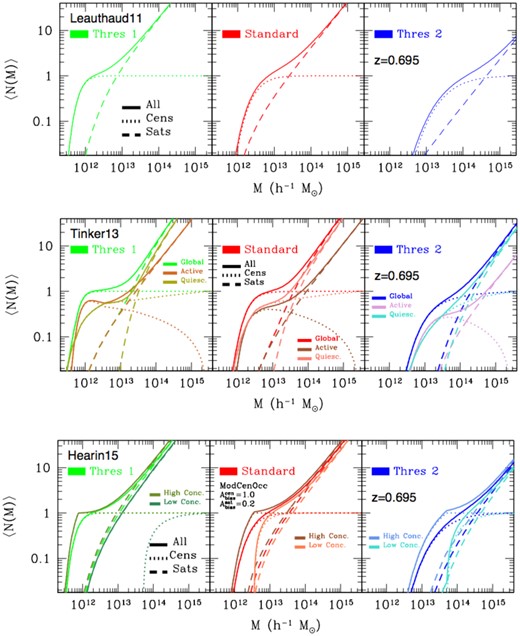
$HOD shapes adopted in our mock-making procedure, at z = 0.695, for three thresholds in mass, denoted as ‘Thres 1’ ($M^{\rm thr}_{*}=10^{10} \, h^{-1} \, \mathrm{M}_{\odot }$), ‘Standard’ ($M^{\rm thr}_{*}=10^{10.5} \, h^{-1} \, \mathrm{M}_{\odot }$), and ‘Thres 2’ ($M^{\rm thr}_{*}=10^{11} \, h^{-1} \, \mathrm{M}_{\odot }$). Top panels display the various HODs in the Leauthaud model. Central panels show the Tinker model, where active and quiescent galaxy HODs are represented by different colours, as indicated in the figure. Bottom panels are for the Hearin HODs, where galaxies are split into upper- and lower-percentiles in terms of halo concentration, respectively, with different assembly bias strength for centrals and satellites ($A_{\rm bias}^{\rm cen} =1.0$ and $A_{\rm bias}^{\rm sat}=0.2$). In all the plots, the central occupation statistics is displayed with dotted lines, the satellite occupation statistics with dashed lines, and the global HOD shapes with solid lines.$

Figure 4.

HOD shapes adopted in our mock-making procedure, at z = 0.695, for three thresholds in mass, denoted as ‘Thres 1’ (⁠|$M^{\rm thr}_{*}=10^{10} \, h^{-1} \, \mathrm{M}_{\odot }$|⁠), ‘Standard’ (⁠|$M^{\rm thr}_{*}=10^{10.5} \, h^{-1} \, \mathrm{M}_{\odot }$|⁠), and ‘Thres 2’ (⁠|$M^{\rm thr}_{*}=10^{11} \, h^{-1} \, \mathrm{M}_{\odot }$|⁠). Top panels display the various HODs in the Leauthaud model. Central panels show the Tinker model, where active and quiescent galaxy HODs are represented by different colours, as indicated in the figure. Bottom panels are for the Hearin HODs, where galaxies are split into upper- and lower-percentiles in terms of halo concentration, respectively, with different assembly bias strength for centrals and satellites (⁠|$A_{\rm bias}^{\rm cen} =1.0$| and |$A_{\rm bias}^{\rm sat}=0.2$|⁠). In all the plots, the central occupation statistics is displayed with dotted lines, the satellite occupation statistics with dashed lines, and the global HOD shapes with solid lines.

3.5 Decorated HOD: Hearin model

The fourth galaxy–halo prescription we consider is the Hearin model (Hearin et al. 2016), a decorated HOD framework designed to account for galaxy assembly bias, that naturally extends the standard HOD approach, minimally expands the parameter space, and maximizes the independence between traditional and novel HOD parameters. Galaxy assembly bias, namely the correlation between galaxy properties and halo properties at fixed halo mass, is a challenging and yet important ingredient in the galaxy–halo connection framework. The model builds on early work by Wechsler et al. (2006). The halo occupation statistics are described in terms of two halo properties rather than just one, and the extra degree of freedom has relevant impact on galaxy clustering. The formalism of the model is general and flexible, with parametric freedom, and it can be applied to any halo property in addition to halo mass; it is also readily extendable to describe HODs that depend upon numerous additional halo properties. Interestingly, the decorated HOD formalism allows one to characterize and quantify the degree of central–satellite correlation at fixed halo mass, which is an indication of compelling astrophysics – such as galactic cannibalism or conformity. We refer the reader to Hearin et al. (2016) for extensive modelling details, and report here only a few key aspects relevant to our work – see also, e.g. Xu, Zehavi & Contreras (2020) and Xu & Zheng (2020) for recent studies.

In particular, the core idea is based on the principle of ‘HOD conservation’, which preserves the moments of the standard HOD formalism: namely, it is required that the marginalized moments of a new decorated framework are equal to those of the standard HOD model, in order to minimize the modifications needed for assembly bias. In this regard, any model P_dec(N_g|M_h, x) with marginalized moments that satisfy the HOD conservation preserves the moments of P_std(N_g|M_h), where P_std is the occupation statistics of a standard HOD, P_dec is the occupation statistics of a decorated HOD model, and x represents a secondary halo property such that the HOD depends both on x and M_h, and the clustering of haloes depends upon x. Within this formalism, a standard HOD is recovered in the limiting condition that the strength of the assembly bias is zero.

For central galaxies, in order to construct decorated HOD models that preserve the full P_std(N_cen|M_h) one just needs to ensure that the first-order decoration function |$\delta N_{\rm cen}^{1}$| satisfies the integral relation (Hearin et al. 2016):

$$\begin{eqnarray*} \int \delta N_{\rm cen}^{\rm 1} (M_{\rm h}, x) P(x|M_{\rm h}) {\rm d} x = 0 . \end{eqnarray*}$$

(18)

For satellites the situation is more complex, as it is not possible to conserve the HOD under the assumption that both P(N_sat|M_h) and P(N_sat|M_h, x) obey Poisson statistics – as typically done: intuitively, this is because there is an additional source of variance associated with the allocation of satellites into sub-populations at a given halo mass. Moreover, under HOD conservation, the average number of central–satellite pairs in massive haloes for a decorated model is identical to that of its standard baseline model, except for the narrow range in halo masses for which 0 ≤ 〈N_cen|M_h〉 ≤ 1.

For our purposes, we consider the Hearin model in its simplest formulation, by assuming two discrete halo subpopulations with different occupation statistics at fixed mass; this is essentially a perturbation of the Leauthaud et al. (2011) formalism, with the addition of assembly bias both in centrals and satellites. We choose the halo NFW concentration as the secondary halo property (x) used to modulate the assembly bias. Specifically, the first halo subpopulation (indicated as ‘type 1’ haloes) contains a fraction P₁ of all haloes at fixed mass, for which |$x \gt \bar{x} (M_{\rm h})$|⁠; the second subpopulation (‘type 2’ haloes) contains P₂ = 1 − P₁ of all haloes at fixed mass, for which |$x \lt \bar{x} (M_{\rm h})$|⁠. The halo population is split into the P₁ percentile of highest concentration haloes, and assigned a satellite galaxy occupation enhancement, while the remaining P₂ = 1 − P₁ percentile of lowest concentration haloes receive a satellite galaxy occupation decrement. Essentially, we require haloes at fixed mass above- or below-average concentration to have above- or below-average mean occupation. For simplicity, we assume a 50/50 split at each halo mass based on the conditional secondary percentiles: haloes within the top 50 per cent of concentration at fixed M_h are assigned to the first subpopulation, and the remaining to the second population (so P₁ = P₂ = 0.5). The strength of assembly bias in the occupation statistics of centrals and satellite galaxies is modulated with two free parameters |$A_{\rm bias}^{\rm cen}$| and |$A_{\rm bias}^{\rm sat}$|⁠, respectively, where |$-1 \le A_{\rm bias}^{\rm cen} \le 1$| and |$-1 \le A_{\rm bias}^{\rm sat} \le 1$|⁠. With this choice, a positive value for A_bias implies that haloes with above-average concentration have boosted galaxy occupations; note also that more positive values of A_bias correspond to models in which more concentrated haloes host more galaxies relative to less concentrated haloes of the same mass. When both of these parameters are set to zero, the model is formally equivalent to the baseline ‘no assembly bias model’ of Leauthaud et al. (2011). We consider a constant assembly bias strength at all masses for simplicity, and the sign convention is to choose type-1 haloes in the upper percentile of the secondary property. Moreover, we assume that both P_std(N_sat|M_h) and P_dec(N_sat|M_h, x) are Poisson distributions, so that the decorated HOD is entirely specified by |$A_{\rm bias}^{\rm cen}$| and |$A_{\rm bias}^{\rm sat}$|⁠.

In our mock-making procedure, we consider two cases for the strength of assembly bias related to centrals and satellites: in the first case (more conservative), we simply set |$A_{\rm bias}^{\rm cen} = A_{\rm bias}^{\rm sat}=0.5$|⁠, namely the strength of assembly bias is equal for both centrals and satellites, with the boost to their mean occupation equal to 50 per cent of the maximum allowable strength at each mass; in the second case (less conservative), we set different assembly bias strengths for centrals and satellites, namely |$A_{\rm bias}^{\rm cen} =1.0$| and |$A_{\rm bias}^{\rm sat}=0.2$|⁠. This latter choice is shown in the lower panels of Fig. 4, where we display the shapes of the Hearin HODs for the upper- and lower-percentile split in halo concentration, respectively, as indicated in the plot. In this case, the satellite HODs are also modulated by their corresponding central distributions. The same three thresholds in mass described before for the Leauthaud framework are adopted, at z = 0.695, and as usual we display the central occupation statistics (dotted lines), satellite occupation statistics (dashed lines), as well as the global HOD shapes (solid lines).

As noted by Hearin et al. (2016, 2017) and Tinker et al. (2019), assembly bias can enhance or diminish the clustering on large scales, but in general it increases the clustering on scales below Mpc – being qualitatively different at large and small scales. Also, assembly bias in satellites versus centrals imprints a distinct signature on galaxy clustering as well as lensing, and the degree to which assembly bias alters galaxy clustering statistics can be quite sensitive to the underlying baseline mass-only HOD of the galaxy population under consideration. In particular, the impact of assembly bias on galaxy clustering is quite sensitive to the steepness of the transition from 〈N_cen|M_h〉_std = 0 at low host masses to 〈N_cen|M_h〉_std = 1 at high host masses. This steepness is controlled by the level of stochasticity in the central galaxy stellar mass at fixed halo mass, parametrized in our baseline model by |$\sigma _{\log \rm M_{*}}$|⁠. Note that changing the values of A_bias does not change 〈N_g|M_h〉, the mean number of galaxies averaged over all haloes of fixed mass: this is the defining feature of the decorated HOD, and the meaning of the principle of HOD conservation.

4 MODELLING THE GALAXY–HALO CONNECTION: TOOLS AND METHODOLOGY

In this section, we briefly describe the tools and methodologies behind our mock-making procedure, the main N-body simulation used, and the pipeline to produce novel heterogeneous sets of Outer Rim-based galaxy catalogues.

4.1 Outer Rim mocks

The baseline simulation used for all our mock-making procedure is the Outer Rim (OR) run, extensively described in Heitmann et al. (2019). The simulation has been developed along the glorious tradition of the Millennium simulation (Springel 2005), with similar mass resolution but a volume coverage increase by more than a factor of 200. Currently, the Outer Rim is among the largest high-resolution gravity-only N-body simulations ever performed, spanning a (⁠|$3 \, h^{-1}\, {\rm Gpc})^3$| volume, and characterized by an unprecedented combination of volume and mass resolution (down to |$1.85 \times 10^9 \, h^{-1} \, \mathrm{M}_{\odot }$|⁠) evolving 1.07 trillion particles – i.e. 10240³. The actual size of the simulation was chosen to cover a volume large enough to enable synthetic sky catalogues for eBOSS, DESI, and LSST, while maintaining adequate mass resolution to capture haloes reliably down to small masses. The entire run was carried out at the Argonne Leadership Computing Facility on Mira, a Blue-Gene/Q many-core supercomputer. The simulation code adopted is an optimized version of the Hardware/Hybrid Accelerated Cosmology Code (hacc), designed to overcome numerical challenges; see Habib et al. (2016) for all the details. The cosmology of the simulation is close to the best-fittingWMAP-7 fiducial model (Komatsu et al. 2011), namely ω_c = 0.1109, ω_b = 0.02258, n_s = 0.963, h = 0.71, σ₈ = 0.8, w = −1, with no massive neutrinos (Ω_ν = 0) and assuming flatness. The dynamical range of the simulation is remarkable, spanning 10⁶ orders of magnitudes, with a force resolution of |$6h^{-1}\, {\rm kpc}$|⁠. Initial conditions are fixed at z_in = 200 with the Zel’dovich approximation (Zel’dovich 1970). Transfer functions are generated via camb (Lewis, Challinor & Lasenby 2000).

A total of 101 redshifts in output were originally saved, from z = 10 to z = 0, evenly spaced in log a, with a the scale factor. In our study, we mainly focus on 2 redshift intervals, namely z = 0.695 and z = 0.865, although we also consider a variety of other redshifts from some of the realizations to assess redshift evolution. Each snapshot encompasses globally about 40TB of data, and the entire data volume of the simulation is more than 5PB; all particle information for haloes with more than 100 000 particles is stored for substructures and shape studies, as well as a random selection of 1 per cent of particles in each halo (with a minimum of five particles per halo).

For our mock-making purposes, we had access to the friends-of-friends (FOF) halo catalogue at various redshifts, generated using a linking length b = 0.168.⁵ Haloes are defined by more than 20 particles, and found with a customized FOF finder (Woodring et al. 2011; Heitmann et al. 2019) that follows the standard implementation, having the linking length defined with respect to the mean interparticle spacing. All the centres of the haloes are determined by the location of the FOF halo’s minimum gravitational potential, and the centre-of-mass and the halo velocities are obtained by summing over all positions and velocities and dividing by the number of particles. The FOF halo mass is simply determined by the number count of particles in each halo.

For a given redshift, our halo catalogue (split into 110 subfiles, stored in a way such that they are not contiguous volumes) contains the number of particles in halo (Halo Count), the halo ID (Halo Tag), the halo FOF mass in |$h^{-1}\, {\rm M}_{\odot }$| units, the comoving halo centre positions from the potential minimum (in |$h^{-1}\, {\rm Mpc}$|⁠), and the comoving peculiar velocities of halo centres (in km s⁻¹). Note that the halo centre is defined by its potential minimum most bound particle, since accurate centre-finding is important for measuring the halo concentration, for halo stacking, and for placing central galaxies from HOD modelling.

Fig. 5 visualizes a small portion of the Outer Rim halo catalogue at z = 0.865. Specifically, the left-hand panel shows a |$100 \times 100 ~[h^{-1} \, {\rm Mpc}]^2$| projection along x and y and across z, having thickness |$\Delta z=50~h^{-1} \, {\rm Mpc}$|⁠; points in the figure are FOF haloes, colour coded by their mass. The middle panel is a progressive zoom into a |$50 \times 50 ~[h^{-1} \, {\rm Mpc}]^2$| block having the same depth as the left one, while the right-hand panel shows an individual halo of mass |$4.938 \times 10^{13}~h^{-1}\, {\rm M_{\odot }}$| rendered with 1 per cent of random particles, located inside the smaller |$7 \times 7~[h^{-1} \, {\rm Mpc}]^2$| white inset: it is possible to appreciate the neat ellipsoidal halo shape. Length units displayed in the left-hand panel are in |$h^{-1} \, {\rm Mpc}$|⁠. The high resolution of the simulation, down to |$1.85 \times 10^9 \, h^{-1} \, \mathrm{M}_{\odot }$|⁠, allows one to resolve accurately also relatively low-mass haloes.

$Small portion of the Outer Rim halo catalogue at z = 0.865. The left-hand panel is a $100 \times 100 ~[h^{-1} \, {\rm Mpc}]^2$ projection along x and y and across z, with thickness $\Delta z=50~h^{-1} \, {\rm Mpc}$, while the middle panel is a progressive zoom into a $50 \times 50 ~[h^{-1} \, {\rm Mpc}]^2$ block. Points the figure are FOF haloes, colour coded by their mass. Zooming into a smaller $7 \times 7~[h^{-1} \, {\rm Mpc}]^2$ inset of the halo catalogue, the right-hand panel displays the ellipsoidal shape of a halo of mass $4.938 \times 10^{13}~h^{-1}\, {\rm M_{\odot }}$ contained inside that area, rendered with a 1 per cent random particle subsample. Length units displayed in the left-hand panel are in $h^{-1} \, {\rm Mpc}$. The high resolution of the simulation, down to $1.85 \times 10^9 \, h^{-1} \, {\rm M_{\odot }}$, allows one to resolve accurately also relatively low-mass haloes.$

Figure 5.

Small portion of the Outer Rim halo catalogue at z = 0.865. The left-hand panel is a |$100 \times 100 ~[h^{-1} \, {\rm Mpc}]^2$| projection along x and y and across z, with thickness |$\Delta z=50~h^{-1} \, {\rm Mpc}$|⁠, while the middle panel is a progressive zoom into a |$50 \times 50 ~[h^{-1} \, {\rm Mpc}]^2$| block. Points the figure are FOF haloes, colour coded by their mass. Zooming into a smaller |$7 \times 7~[h^{-1} \, {\rm Mpc}]^2$| inset of the halo catalogue, the right-hand panel displays the ellipsoidal shape of a halo of mass |$4.938 \times 10^{13}~h^{-1}\, {\rm M_{\odot }}$| contained inside that area, rendered with a 1 per cent random particle subsample. Length units displayed in the left-hand panel are in |$h^{-1} \, {\rm Mpc}$|⁠. The high resolution of the simulation, down to |$1.85 \times 10^9 \, h^{-1} \, {\rm M_{\odot }}$|⁠, allows one to resolve accurately also relatively low-mass haloes.

4.2 nseries mocks

In addition to the heterogeneous sets of high-fidelity Outer Rim mocks developed in this work, we also exploit a small homogeneous set indicated as the nseries, which has been previously used in the SDSS DR12 galaxy clustering analysis (Alam et al. 2017). The homogeneous set, comprised of 84 mocks in total, is particularly suitable to address cosmic variance and modelling systematics at the sub-per cent level, since all mocks have the same underlying galaxy bias model built upon the same cosmology, but each mock is a quasi-independent realization – thus not sharing the same LSS. Moreover, these mocks are cut sky: they have the same angular and radial selection function as the NGC DR12 CMASS sample within the redshift range 0.43 < z < 0.70, and therefore they include observational artefacts closer to the eBOSS DR16 sample. The N-body simulations from which these cut-sky mocks were created have been produced with gadget2 (Springel 2005), with input parameters to ensure sufficient mass and spatial resolution to resolve the haloes that BOSS galaxies occupy. Specifically, the nseries cosmology is characterized by Ω_m = 0.286, h = 0.7, Ω_b = 0.047, σ₈ = 0.820, and n_s = 0.96. The main difference with respect to the Outer Rim mocks – apart from being cut sky and not built on periodic cubes – is that the nseries derive from multiple realizations of the dark matter field on a larger volume with different random seeds (i.e. a series of N-body simulations identical in all but in the initial random seed), which allows one to address the impact of cosmic variance: this is not achievable with only a halo catalogue nor a single N-body simulation at hands.

4.3 EZMOCKS

For determining the rescaled covariance matrices functional to the subsequent analyses, we also make use of a new series of DR16 ezmocks, thoroughly described in Zhao et al. (2020). These large number of galaxy catalogues (1000 per tracer), having accurate clustering properties, are generated with a complex methodology built around the Zel’dovich approximation (Zel’dovich 1970), and effectively including stochastic scale-dependent, non-local, and non-linear biasing contributions; extensive details on the methodology can be found in the first release paper by Chuang et al. (2015). Non-local effects, such as tidal fields not included in linear Lagrangian Perturbation Theory (LPT) or other biasing contributions, are effectively included in both the scatter relation and the tilting of the initial power spectrum. The missing power towards small scales of perturbative approaches is included in the modulation of the initial power spectrum, when fitting for the resulting halo populations. These mocks have accurate clustering properties – nearly indistinguishable from full N-body solutions – in terms of the one-point, two-point, and three-point statistics. The underlying cosmology is based on a flat ΛCDM model, with Ω_m = 0.307115, Ω_b = 0.048206, h = 0.6777, σ₈ = 0.8225, and n_s = 0.9611. Specifically for LRGs, they contain the complexity of blending the CMASS plus eBOSS LRG samples, as well as all the realistic effects of mask, cut sky, and observational systematics (i.e. fibre completeness, spectroscopic success rate, redshift failures, photometric systematics). For our analysis, we adopt dedicated cubic ezmocks rather than the cut sky set for covariance estimations, to comply with the characteristics of the high-fidelity Outer Rim-based realizations. The ezmocks are extensively used in all the supporting eBOSS DR16 papers and in the final eBOSS consensus analysis. For additional technical details, we refer the reader to the companion paper by Zhao et al. (2020).

4.4 Galaxy mock-making procedure: methods

Our synthetic high-fidelity galaxy mocks are primarily produced exploiting the standard halotools⁶ framework (Hearin et al. 2017), and by introducing a number of customizations depending on the desired challenge and model explored (see Section 6, as well as the previous theoretical part). In particular, we interface halotools capabilities with the Outer Rim halo catalogue at different redshifts. halotools is an open-source, community-driven Python powerful package for studying the galaxy–halo connection, which provides a highly modular, object-oriented platform for building HOD models, so that individual modelling features can easily be swapped in and out. This modularity facilitates rigorous study of all the components that makes up a halo occupation model, and has been designed from the ground-up with assembly bias applications in mind. In this view, although our main products are based on the Outer Rim simulation, following the halotools philosophy the pipelines developed here are written in a general and flexible manner, so that any type of customization is readily achievable with minimal efforts and modifications; hence, our modular approach procedure is quite general, and readily applicable to any halo catalogue and survey design in mind. The concept of generality and reusability of the code is in fact what has driven this design from the start. In this view, although we limit here our modelling approach to HOD-based techniques (mainly due to limitations in our available halo catalogue products), we plan to pursue subhalo and abundance matching methods in follow-up studies, using the same code and modular structure.

Adopting halotools conventions, three main primary keyword arguments are used to customize all the instances retrieved by the mock factory, common to all the different HOD models developed here (besides specific HOD parameters), namely: redshift, threshold, and modulate_with_cenocc – the latter being the modulation of the satellite distribution with the central one. In our mock-making procedure, except for the Hearin framework, all other satellite HODs are not modulated by their corresponding central distributions. Also, as previously mentioned, we treat the conventional Zheng model separately since its HOD is effectively redshift-independent and the meaning of ‘threshold’ in the model is based on luminosity rather than stellar mass, unlike for the other three frameworks considered (i.e. Leauthaud, Tinker, Hearin). Specifically, halotools is used to populate dark matter haloes in the Outer Rim simulation with galaxies having a stellar mass |$M_{*} \gt 10^{10.0}~h^{-1} \, \mathrm{M}_{\odot }$| (‘Threshold 1’), |$M_{*} \gt 10^{10.5}~h^{-1} \, \mathrm{M}_{\odot }$| (‘Standard’), and |$M_{*} \gt 10^{11.0}~h^{-1} \, \mathrm{M}_{\odot }$| (‘Threshold 2’). This roughly correspond to ‘Threshold 1’ (M_r = −19), ‘Standard’ (M_r = −20), and ‘Threshold 2’ (M_r = −21), respectively, in the Zheng formalism.

A composite HOD model is fully defined once one specifies the occupation statistics and phase space prescription for centrals and satellites. The theoretical formalism related to each individual model has been presented in Section 3. The corresponding numerical implementation is briefly explained in what follows – noting that dealing with the Outer Rim simulation poses several non-trivial challenges in handling massive data sets. Specifically, at the highest level, we select the redshift, threshold, and number of desired mocks to produce. Then, to populate haloes with central galaxies we first calculate the value of 〈N_cen〉 for every halo in the simulation according to the HOD formulas in our different prescriptions (Section 3). For every halo in the simulation, we draw a random number r from |${\cal {U}}[0,1]$|⁠, a uniform distribution between zero and unity. For all haloes with r ≤ 〈N_cen〉, we place a central galaxy at the halo centre, leaving all other haloes devoid of centrals. Populating satellites is more complicated, because the spatial distributions are non-trivial. The first step is similar to that of the centrals, namely compute 〈N_sat〉 for every halo using our specified formulas for a given HOD model (see again Section 3). For each halo, the number of satellites that will be assigned to the halo is then determined by drawing an integer from the assumed satellite occupation distribution p(N_sat|M_h) or p(N_sat|M_h, x). Satellites are modelled as being isotropically distributed within their haloes according to an NFW profile with concentration equal to the parent halo, using the Dutton-Macciò model (Dutton & Macciò 2014). Monte Carlo realizations of both radial and angular positions are generated via the method of inverse transformation sampling. Briefly, first one generates realizations of points uniformly distributed on the unit sphere. These halocentric (x,y,z) coordinates are then multiplied by the corresponding realization of the radial position r, which is determined as follows: first, calculate |$P_{\rm NFW}(\lt \tilde{r}|c)$| where c is the concentration, |$\tilde{r} =r/R_{\rm vir}$| is the scale radius, R_vir the virial radius of the halo, and |$P_{\rm NFW}(\lt \tilde{r}|c)$| is the cumulative probability distribution function of the mass profile of an NFW halo:

$$\begin{eqnarray*} P_{\rm NFW} (\lt \tilde{r} | c) = {M_{\rm NFW} (\lt \tilde{r} | c) \over M_{\rm tot} } = {g(c \tilde{r}) \over g(c)} , \end{eqnarray*}$$

(19)

where

$$\begin{eqnarray*} g(x) = \ln (1+x) - {x \over 1 + x}. \end{eqnarray*}$$

(20)

Then, for a halo with concentration c populated by N_sat, draw N_sat random numbers p from |${\cal {U}}[0,1]$|⁠. Each value of p is interpreted as a probability where the corresponding value for the scaled radius |$\tilde{r}$| comes from numerically inverting |$p=P_{\rm NFW} (\lt \tilde{r} | c)$|⁠. Scaling the (x,y,z) points on the unit sphere by the value r gives the halocentric position of the satellites.

All these high-fidelity mocks have been produced at the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy, under Contract No. DE-AC02-05CH11231 using the Cori supercomputer, a Cray XC40 with a peak performance of about 30 petaflops. Cori is comprised of 2388 Intel Xeon ‘Haswell’ processor nodes, and 9688 Intel Xeon Phi ‘Knight’s Landing’ (KNL) nodes. The system also has a large Lustre scratch file system and a first-of-its kind NVRAM ‘burst buffer’ storage device. We devised new customized scripts and pipelines to produce such mocks on Cori, exploiting especially the multithread architecture. Our mock-making code/pipeline is memory efficient and optimized to the machine. Some additional supporting numerical work has also been carried out using the Korea Institute of Science and Technology Information (KISTI) supercomputing infrastructure.

In closing this part, we note that our main goal in the cubic N-body-based mock-making production and in the related mock challenge is to test the validity and robustness of different BAO and RSD fitting techniques on a common ground against a series of different HOD prescriptions, and validate the clustering analysis pipelines and the various RSD models. Hence, we are not concerned with reproducing exactly all the features of the eBOSS DR16 LRG sample, and this is why the various HOD parameters that enter in the models outlined in Section 3 have been maintained to their corresponding literature values. Nevertheless, in Section 6 we show an instructive comparison between eBOSS measurements and those obtained from Outer Rim TH2 mocks. Note also that the HOD parameters adopted from the literature were chosen under cosmologies different from that of the Outer Rim, and therefore we do not expect to find the same results as in the corresponding original publications: this is clearly not affecting the conclusions of our work. Realistic observational artefacts related to the LRG sample, such as cut sky, matching number density, observational systematics, etc., are instead part of the ezmocks release (Zhao et al. 2020).

5 ANALYSIS: METHODOLOGY

In this section, we briefly describe the three configuration and Fourier space techniques used in the analysis of the challenge mocks, based on three different RSD analytical models – exploiting the FS information in the correlation function or power spectrum. The detailed BAO modelling is instead described in our LRG companion papers. All these methods are adopted in the main analysis of the final eBOSS DR16 LRG sample.

5.1 CLPT-GS

The CLPT-GS-based method is a combination of the Convolutional Lagrangian Perturbation Theory (CLPT) and the RSD Gaussian Streaming (GS) formalism, originally developed by Reid & White (2011), Carlson, Reid & White (2013), and Wang, Reid & White (2014). CLPT provides a non-perturbative resummation of Lagrangian perturbation to the two-point statistic in real space for biased tracers. In particular, the two-point correlation function is expanded in its Lagrangian coordinates considering the LRG tracer to be locally biased with respect to the initial CDM overdensity, and the expansion is performed over different orders of the Lagrangian bias function. The key equation for the two-point correlation |$\xi _{\rm LRG}({\bf r}) = \left\langle \delta _{\rm LRG} (\bf x) \delta _{\rm LRG} (\bf x + \bf r)\right\rangle $|⁠, with q and x the Lagrangian and Eulerian coordinates, respectively, δ the overdensity, and r the LRG separation, is

$$\begin{eqnarray*} 1+\xi _{\rm LRG}({\bf r})=\int M({\bf r, \bf q}) {\rm d}{\bf q}, \end{eqnarray*}$$

(21)

where |$M({\bf r, \bf q})$| is the convolution kernel taking into account the displacements and bias expansion up to its second derivative term. The bias derivative terms are computed using a linear power spectrum, obtained with camb (Lewis et al. 2000) for a fixed cosmology – namely, the fiducial cosmology of the analysis. The peculiar velocity effect on clustering statistic is also modelled, and the pairwise velocity distribution v₁₂ and velocity dispersion σ₁₂ are given by (Wang et al. 2014):

$$\begin{eqnarray*} {\bf v}_{12}(r)=[1+\xi _{\rm LRG}({\bf r})]^{-1}\int {M_1}({\bf r}, {\bf q}) {\rm d} {\bf q} \end{eqnarray*}$$

(22)

and

$$\begin{eqnarray*} \sigma _{12}(r)=[1+\xi _{\rm LRG}({\bf r})]^{-1}\int M_2({\bf r}, {\bf q}){\rm d}{\bf q} , \end{eqnarray*}$$

(23)

where the kernels M₁(r, q) and M₂(r, q) also depend on the first two derivatives of the Lagrangian bias, which are free parameters in the model, in addition to the growth factor. CLPT generates more accurate multipoles than linear theory and even the Lagrangian Resummation Theory (LRT; Matsubara 2008), but a better performance is needed in order to study the smaller scales of quadrupoles. To achieve such precision, the real space CLPT models of the two-point statistics are mapped into redshift space following the Gaussian Streaming Model (GSM) formalism proposed by Reid & White (2011). In particular, the pairwise velocity distribution is assumed to have a Gaussian shape dependent on both the angle μ between the separation vector and the line-of-sight (LOS), and the LRG separation r in its parallel (r_||) and perpendicular (r_⊥) components with respect to the LOS. The main equation for the correlation function is given by

$$\begin{eqnarray*} 1+\xi _{\rm LRG}(r_\perp ,r_\parallel)& = & \int \frac{1}{\sqrt{2\pi (\sigma _{12}^2(r,\mu)+\sigma ^2_{\rm FoG})}}[1+\xi _{\rm LRG}(r)]\nonumber \\ && \times \exp \Big [{-\frac{[r_\parallel -y-\mu v_{12}(r,\mu)]^2}{2(\sigma _{12}^2(r,\mu)+\sigma ^2_{\rm FoG})}} \Big ]{\rm d}y, \end{eqnarray*}$$

(24)

where ξ_LRG(r), v₁₂(r), and σ₁₂(r) are computed from CLPT as previously indicated, and σ_FOG is the Fingers of God (FoG) parameter to account for an additional contribution to the velocity dispersion given by satellite galaxies. For the RSD model, the Alcock & Paczynski (1979) effect implementation follows that of Xu et al. (2013). The AP distortions are modelled through the α and ϵ parameters, which characterize respectively the isotropic and anisotropic distortion components.

With this technique, the FS RSD analysis in configuration space is performed, and for a given cosmology the model has four free parameters, namely (fσ₈, F^′, F^″, σ_FOG), with f the linear growth factor and F^′ and F^″ the first and second derivatives of the Lagrangian bias function F. For extensive details on this method see Bautista et al. (2020) and Icaza-Lizaola et al. (2020).

5.2 TNS in configuration space

The modified TNS-based method (also indicated in this paper as ‘CF-TNS’, where ‘CF’ stands for ‘correlation function’) is a combination of the Taruya, Nishimichi & Saito (TNS; Taruya, Nishimichi & Saito 2010) technique and a galaxy non-linear bias prescription (Beutler et al. 2017a; de la Torre et al. 2017). This model is based on the conservation of the number density in real- and z-space (Kaiser 1987). In this framework, the anisotropic power spectrum for unbiased matter tracers (P^s) follows the general form of Scoccimarro, Zaldarriaga & Hui (1999), which in the approximation proposed by Taruya et al. (2010) reads:

$$\begin{eqnarray*} P^{\rm s}(k,\mu)&=& D(k\mu \sigma _{\rm v})\big [ P_{\delta \delta }(k) +2\mu ^2f P_{\delta \theta }(k) + \mu ^4f^2P_{\theta \theta }(k)+ \nonumber \\ && C_{\rm A}(k,\mu ,f)+C_{\rm B}(k,\mu ,f) \big ]\, . \end{eqnarray*}$$

(25)

In the previous expression, f is the linear growth factor; θ is the divergence of the velocity field defined as θ = −∇· μ/(aHf); μ = k_∥/k, with k_∥ the line-of-sight component of the wave vector k; H is the Hubble constant at the considered redshift; a is the scale factor; δ is the matter density field; P_δδ, P_θθ, and P_δθ are the non-linear matter density, velocity divergence, and density-velocity divergence power-spectra, respectively; C_A(k, μ, f) and C_B(k, μ, f) are two correction terms expressed as integrals of the matter power spectrum – see Taruya et al. (2010) for their detailed expressions; and D(kμσ_v) is a phenomenological damping function modelled as a Lorentzian so that D(k, μ, σ_v) = [1 + (kμσ_v)²]⁻¹, with σ_v an effective pairwise velocity dispersion that is later treated as a nuisance parameter in the cosmological inference.

This model can be generalized for biased tracers via the inclusion of a galaxy biasing model, so that the anisotropic galaxy power spectrum becomes (Beutler et al. 2014; Gil-Marín et al. 2017):

$$\begin{eqnarray*} P^{\rm s}_{\rm g}(k,\mu) &=& D(k\mu \sigma _{\rm v}) \big [ P_{\rm gg}(k) + 2\mu ^2fP_{\rm {g} \theta } + \mu ^4f^2 P_{\theta \theta }(k) + \nonumber \\ && C_{\rm A}(k,\mu ,f,b) + C_{\rm B}(k,\mu ,f,b) \big ] \end{eqnarray*}$$

(26)

with b the galaxy linear bias. Specifically, here we assume a non-linear, non-local, galaxy biasing prescription that follows the work of McDonald & Roy (2009) and Assassi, Simonovic & Zaldarriaga (2017). Explicit expressions for C_A(k, μ, f, b) and C_B(k, μ, f, b) that enter in equation (26) can be found in de la Torre & Guzzo (2012), while detailed expressions for the galaxy–galaxy and galaxy–velocity divergence power spectra – P_gg(k) and P_gθ(k), respectively – for a 1-loop perturbative expansion of the biasing function are given in Bautista et al. (2020).

The linear and non-linear matter power spectra entering in the model are computed with camb and the halofit semi-analytical prescription, respectively. To obtain P_θθ and P_δθ, we use the universal fitting functions provided by Bel et al. (2019). In particular, the overall degree of non-linear evolution is encoded via the amplitude of the matter fluctuation at the effective redshift considered. Finally, the multipole moments of the anisotropic correlation function are obtained by performing the Hankel transform of the model, and regarding the RSD part, the implementation of the AP effect follows the formalism of Xu et al. (2013): the AP distortions are modelled through the α and ϵ parameters, which characterize the isotropic and anisotropic distortion components, respectively.

With this technique, the FS RSD analysis in configuration space is performed, and for a given cosmology the model has five free parameters, namely (f, σ₈, b₁, b₂, σ_v) – although since f and σ₈ are degenerate they are thus combined at the level of the likelihood into the single parameter fσ₈. For extensive details on this method see de la Torre et al. (2017), Mohammad et al. (2018), and Bautista et al. (2020).

5.3 TNS in Fourier space

While the previous techniques are used to carry out the analysis of the LRG sample in configuration space, the method described here – also based on the TNS model and indicated as ‘P_k-TNS’ – is performed in Fourier space. To this end, the modelling of the BAO signal within this framework – along with the BAO fitting procedure in Fourier space – are described in Gil-Marín et al. (2020). Here, we briefly illustrate only the strategy adopted for the RSD and AP analysis, exploiting the FS information in the power spectrum.

Specifically, the FS formalism employed to describe power spectrum multipoles is the same as the one previously used in BOSS and eBOSS studies for galaxies (Gil-Marín et al. 2016) and quasars (Gil-Marín et al. 2018). We adopt the Eulerian non-linear bias model of McDonald & Roy (2009), consisting of four bias parameters: namely, the linear galaxy bias b₁, the non-linear galaxy bias b₂, and two non-local galaxy bias parameters, |$b_{\rm s^2} =-4/7\, (b_1-1)$| (Baldauf et al. 2012) and |$b_{3{\rm nl}}=32/315\, (b_1-1)$| (Saito et al. 2014) – with b₁ and b₂ considered as free nuisance parameters in the fitting. The density–density (δδ), density–velocity (δθ), and velocity–velocity (θθ) real space DM auto- and cross-power spectra are obtained via 2-loop resummation perturbation theory, as in Gil-Marín et al. (2012): these moments accurately describe the DM clustering up to k ≃ 0.15 at z = 0.5, k ≃ 0.20 at z = 1.0, and k ≃ 0.30 at z = 1.5, respectively. Expressions for those galaxy power spectra – with no velocity bias – are given by (Beutler et al. 2014):

$$\begin{eqnarray*} P_{\rm g,\, \delta \delta }(k)&=&b_1^2P_{\delta \delta }(k)+2b_2b_1P_{\rm b2,\, \delta }(k)+2b_{\rm s2}b_1P_{\rm bs2,\, \delta }(k)+\nonumber \\ &\quad &b_2^2P_{\rm b22}+2b_2b_{\rm s2}P_{\rm b2s2}(k)+b^2_{\rm s2}P_{\rm bs22}(k)+\nonumber \\ &\quad & 2b_1b_{3\rm nl}\sigma _3^2(k)P_{\rm lin}(k) \end{eqnarray*}$$

(27)

$$\begin{eqnarray*} P_{\rm g,\, \delta \theta }(k)&=&b_1P_{\delta \theta }(k)+b_2P_{\rm b2,\, \theta }(k)+b_{\rm s2}P_{\rm bs2,\, \theta }(k)+\nonumber \\ &\quad &b_{3\rm nl}\sigma _3^2(k)P_{\rm lin}(k) \end{eqnarray*}$$

(28)

$$\begin{eqnarray*} P_{\rm g,\, \theta \theta }(k)&=&P_{\theta \theta }(k). \end{eqnarray*}$$

(29)

RSD effects are incorporated following Taruya et al. (2010), who extended the original methodology of Scoccimarro (2004), so that the redshift space galaxy power spectrum reads:

$$\begin{eqnarray*} \nonumber P^{(\rm s)}_{\rm g}(k,\, \mu)&=&D_{\rm FoG}(k,\, \mu)\left[P_{\rm g\, \delta \delta }(k)+2f\mu ^2P_{\rm g,\, \delta \theta }(k) +\right. \\ \nonumber &\quad &f^2\mu ^4P_{\theta \theta }(k)+b_1^3A^{\rm TNS}(k,\mu ,f/b_1)+\\ &\quad &\left. b_1^4B^{\rm TNS}(k,\, \mu ,f/b_1) \right]. \end{eqnarray*}$$

(30)

In particular, galaxy real space quantities are computed as previously described, assuming a fixed linear power spectrum template (obtained with camb) at the fiducial cosmology. The various power spectrum multipoles encode the coherent velocity field through the redshift space displacement and the logarithmic growth of structure parameter, which boosts the amplitude of the isotropic power spectrum and generates an anisotropic component. In equation (30), the term D_FoG accounts for FoG effects along the LOS direction, and it is modelled as a Lorentzian, while A^TNS and B^TNS are second-order corrections. Finally, the AP effect is added when computing the multipoles as

$$\begin{eqnarray*} P_{\rm g}^{(\ell)}(k)=\frac{2\ell +1}{2\alpha _\parallel \alpha _\perp ^2}\int _{-1}^{1}d\mu \mathcal {L}_{\ell }(\mu)P_{\rm g}^{(s)}[k^{\prime }(k,\mu),\mu ^{\prime }(\mu)], \end{eqnarray*}$$

(31)

where explicit expressions for k^′(k, μ) and μ^′(μ) are given in Gil-Marín et al. (2020). We also consider that the shot noise contribution in the power spectrum monopole may differ from a Poisson sampling prediction, and parametrize this potential deviation with a free parameter (A_noise), which modifies the shot noise amplitude without introducing any scale dependence. By default, our measured power spectrum monopole has a fixed Poissonian shot noise contribution subtracted, whereas this is not the case for higher other multipoles.

With this technique, the FS RSD analysis in Fourier space is performed, and for a given cosmology the model has seven free parameters, namely (α_∥, α_⊥, fσ₈) and (b₁, b₂, A_noise, σ_FoG). Note that while the BAO analysis consists of using a fixed and arbitrary template to compare the relative BAO-peak positions in the power spectrum multipoles, the FS analysis allows for a full modelling of the shape and amplitude of the power spectrum multipoles, taking into account DM non-linear effects, galaxy bias, and RSDs. For extensive details on this method see Gil-Marín et al. (2020).

6 THE GALAXY MOCK CHALLENGE

In this section, we present the main outcomes of the galaxy mock challenge. After a brief description of the mock products directly useful in the actual fits considered in the HOD systematic error budget, we show selected results in configuration and Fourier space. We eventually compare the complementary BAO/RSD models adopted for the analysis of the complete DR16 eBOSS LRG sample, assessing the theoretical systematic budget. Our findings demonstrate that all the methods are mutually consistent, with comparable systematic errors on the AP parameters and the growth of structures, and robust to different HOD prescriptions – thus validating the clustering analysis pipelines.

6.1 Mock products used in the analysis

For the galaxy mock challenge, we devised three sets of heterogeneous Outer Rim-based galaxy mocks (indicated as ‘Challenge Set 1’, ‘Challenge Set 2’, ‘Challenge Set 3’, respectively).⁷ These are cubic mocks, in the Outer Rim cosmology, obtained by populating Outer Rim halo catalogues with galaxies using the Zheng, Leauthaud, Tinker, and Hearin HOD prescriptions – as explained in Section 4.1. Extensive details regarding each set are provided in Appendix A. For the main analysis presented here, focused on testing the BAO templates and the RSD models adopted for the characterization of LRG clustering systematics, we only use a subset of those mocks drawn from ‘Challenge Set 1’ at z = 0.695 assuming the ‘Threshold 2’ (Th2) flavour. As explained in Sections 3 and 4.4, the meaning of ‘flavour’ is related to the halotools key parameter ‘threshold’, which globally sets all the individual HOD parameters as best-fitting realizations from the corresponding literature dictionary of each HOD model (unless customizations are introduced). Specifically, we select Th2 mocks with the Leauthaud, Tinker, and Hearin prescriptions, respectively, since their number density is closer to the eBOSS LRG sample (see Table A2). Moreover, since we require fully independent mocks (i.e. not sharing the same DM field), we only consider 27 realizations per HOD per flavour: such realizations are obtained by populating once the full |$3 \, h^{-1} \, {\rm Gpc}$| Outer Rim periodic halo catalogue box with galaxies, and then by cutting the full box into 27 non-overlapping subcubes of |$1h^{-1}\, {\rm Gpc}$| side and rescaling the various spatial positions accordingly. In fact, by construction, at a fixed z and for a fixed set of HOD parameters, the central galaxies will always reside at the centre of their hosted haloes, inheriting the same halo velocity; hence, additional subcubes would be fully or highly correlated in the central galaxy population, depending on how the box is cut. We then add RSDs to each individual mock in two different ways: radially, or with the usual plane-parallel approximation.

In Fig. 6, we show an example on how satellite galaxies are distributed within the same Outer Rim halo, according to the different HOD prescriptions presented in Section 3, to convey some intuition on the galaxy–halo connection modelling and the spatial location of satellites. The plot displays the x–y spatial projection at z = 0.695 of a randomly chosen halo, with its spherical shape determined by its virial radius. The standard Zheng model is shown in the upper left-hand panel, and clockwise the Leauthaud, Hearin, and Tinker models are displayed, respectively. While in all the HOD schemes the satellite phase space statistics follow an unbiased NFW profile with a phase space distribution in isotropic Jeans equilibrium and galaxy concentration identical to that of the parent halo, more sophisticated frameworks such as the Tinker model (lower left corner) are able to distinguish between active and quiescent populations (indicated with different colours in the panel), thus providing additional useful physical insights.

Figure 6.

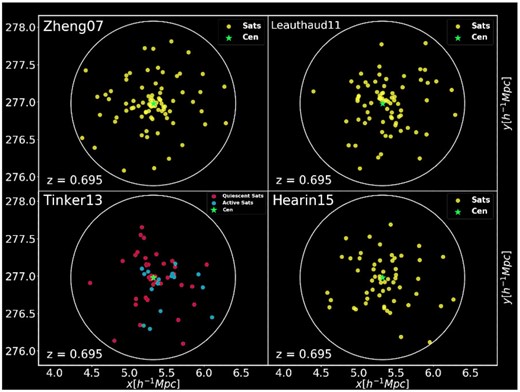
Example of the distribution of satellite galaxies within the same and randomly chosen Outer Rim halo, at z = 0.695, according to the different HOD prescriptions presented in Section 3. The plot represents a spatial projection (x − y) of the halo, and its spherical shape as determined by its virial radius is also indicated in the various panels. Clockwise, starting from the upper left corner, the Zheng, Leauthaud, Hearin, and Tinker models are shown, respectively.

Moreover, in addition to the heterogeneous Outer Rim mocks, as detailed in Section 4.2 we also exploit 84 homogeneous cut-sky nseries mocks, which have been previously used in the SDSS DR12 galaxy clustering analysis (Alam et al. 2017), to address cosmic variance in the various methods – since the nseries derive from multiple realizations of the dark matter field with different random seeds. Here we show only one global nseries application, while in Gil-Marín et al. (2020) and Bautista et al. (2020) those mocks are extensively used to assess systematics related to each individual fitting method in configuration or Fourier space, respectively.

6.2 Galaxy mock challenge: BAO analysis and HOD systematics

Approximate catalogues such as the ezmocks (Zhao et al. 2020) are in principle sufficient for covariance estimates and for quantifying systematic biases in BAO studies, while the analysis of the FS of the correlation function and power spectrum requires high-fidelity (N-body-based) mocks to precisely test the modelling. Nevertheless, using high-resolution mocks, we are able to characterize the impact of systematics in HOD modelling both on BAO and RSD constraints with high-accuracy. Specifically, the main goals are to quantify possible effects induced by different galaxy HOD schemes on the cosmic growth rate and obtain useful information on parameter inference based on HOD variations, to assess the impact of an arbitrary choice of the BAO reference template on the inferred cosmological parameters, and more generally to determine the theoretical systematic budget and validate the clustering analysis pipelines.

The standard procedure common to all BAO fitting methods is to assume a fixed and arbitrary template, and compare the relative BAO peak positions in the correlation function or power spectrum multipoles. Reconstruction techniques such as those presented in Burden et al. (2014), Burden, Percival & Howlett (2015) are then applied to the density field, in order to remove a fraction of the RSDs and the non-linear motions of galaxies. The BAO feature in the 2-point statistics (both in configuration and Fourier space) is sharpened, increasing the precision of the measurement of the acoustic scale.

The BAO scale measurement in configuration space adopted here is the same as the one described in previous SDSS publications (i.e. Alam et al. 2017; Ata et al. 2018; Bautista et al. 2018), and thoroughly illustrated in our companion paper Bautista et al. (2020), while the modelling of the BAO signal along with the BAO fitting procedure in Fourier space are explained in detail in Gil-Marín et al. (2020). In particular, for the latter case, the power spectrum anisotropic signal is modelled in order to measure the BAO peak position and marginalize over the broad-band information – taking into account the BAO signal both in the radial and transverse LOS directions. Generally, BAO results are obtained from pre- and post-reconstructed data, while RSD results use only the non-reconstructed sample. In the following analyses, we assume standard dependence of the growth rate f, and adopt a smoothing scale of 15 h⁻¹Mpc. Whenever required, galaxy redshifts are converted into radial comoving distances for clustering measurements, using the cosmological parameters of the OR simulation. As shown in Bautista et al. (2020), the analysis methodology is insensitive to the choice of a fiducial cosmology.

Fig. 7 is an example of the redshift-space galaxy clustering (monopole and quadrupole), along with corresponding BAO fits, as inferred from the average of 27 Th2 OR-based mocks at z = 0.695 having different HOD schemes. From left to right, the Leauthaud, Tinker, and Hearin models are displayed, respectively. Top panels are for the pre-reconstructed fields, while bottom panels refer to post-reconstructed fields. Specifically, for cosmological analyses the information contained in the anisotropic 2-point correlation function ξ(s, μ) – decomposed into polar coordinates (s, μ) aligned with the LOS direction, with μ the cosine of the angle between the LOS and separation vector directions, and s the norm of the galaxy separation vector s – is compressed into the correlation function multipole moments ξ_ℓ, obtained by decomposing ξ(s, μ) on the basis of Legendre polynomials P_ℓ as:

$$\begin{eqnarray*} {\xi }_{\ell } (s) = {(2 \ell + 1)} \sum _{\rm i} \xi (s, \mu _{\rm i}) P_{\ell } (\mu _{\rm i}) {\rm \Delta }\mu . \end{eqnarray*}$$

(32)

In the previous expression, only even multipoles do not vanish, and the correlation function is binned according to the absolute value of μ. In our analyses, we only consider the ℓ = 0, 2, 4 moments, namely monopole, quadrupole, and hexadecapole (whenever specified), and ξ(s, μ) is quantified with the classical Landy & Szalay (1993) estimator. The pair counts are binned into |$5h^{-1}\, {\rm Mpc}$| bins in separation and 0.01 in μ. In the panels of Fig. 7, the BAO feature is clearly seen at |$s \simeq 100 \, h^{-1} \, {\rm Mpc}$|⁠, as well as the impact of the reconstruction procedure: the BAO feature appears in fact much sharper in the bottom panels. The various fits shown in the figure are obtained with the BAO technique adopted in Bautista et al. (2020) for the analysis of the correlation function in configuration space, and correlation function multipoles ξ_ℓ(s) are rendered as a function of separations s relevant for BAO (⁠|$30 \le s \le 180 \, h^{-1}\, {\rm Mpc}$|⁠), starting from the modelling of the redshift-space anisotropic power spectrum. In particular, as explained in Bautista et al. (2020), the non-linear broadening of the BAO peak is modelled by multiplying the ‘peak-only’ power spectrum P_peak by a Gaussian term with |$\Sigma _{\rm nl}^2(\mu) = \Sigma _\parallel ^2 \mu ^2 + \Sigma ^2_\perp (1-\mu ^2)$|⁠, with Σ_∥ and Σ_⊥ the BAO damping terms, and the non-linear random motions on small scales are rendered with a Lorentzian term parametrized by Σ_s. When performing fits to the multipoles of a single realization of the survey, the values of (Σ_∥, Σ_⊥, Σ_s) are maintained fixed to improve convergence. Moreover, the BAO peak position is parametrized via two dilation parameters that scale separations into transverse (α_⊥) and radial (α_∥) directions. These quantities are related to the comoving angular diameter distance D_M(z) = (1 + z)D_A(z) and to the Hubble distance D_H(z) = c/H(z) as

$$\begin{eqnarray*} \alpha _{\perp } = {D_{\rm M}(z_{\rm eff})/r_{\rm drag} \over D_{\rm M}^{\rm fid}(z_{\rm eff})/r_{\rm drag}^{\rm fid} }, \end{eqnarray*}$$

(33)

$$\begin{eqnarray*} \alpha _{\parallel } = {D_{\rm H}(z_{\rm eff})/r_{\rm drag} \over D_{\rm H}^{\rm fid}(z_{\rm eff})/r_{\rm drag}^{\rm fid} }, \end{eqnarray*}$$

(34)

with r_drag the comoving horizon scale at the drag epoch. Fits on mock multipoles are performed – including hexadecapole, which however does not add extra information. In the procedure, BAO broad-band parameters are let free while both dilation parameters are allowed to vary between 0.5 and 1.5. A total of nine parameters are fitted simultaneously. Table 4 contains the results of such BAO fits in configuration space, where in particular b is the linear bias and β = f/b is the RSD parameter. The covariance matrix used for the fit is obtained from 1000 ezmocks, properly rescaled by the difference in particle number to match the characteristics of the OR-based mocks. Note that expected statistical errors in the eBOSS LRG data sample are of the order of |$\sim 1.9{{\ \rm per\ cent}}$| for α_⊥ and |$\sim 2.6{{\ \rm per\ cent}}$| for α_∥, and that reconstruction improves constraints on α_⊥ and α_∥, as expected.

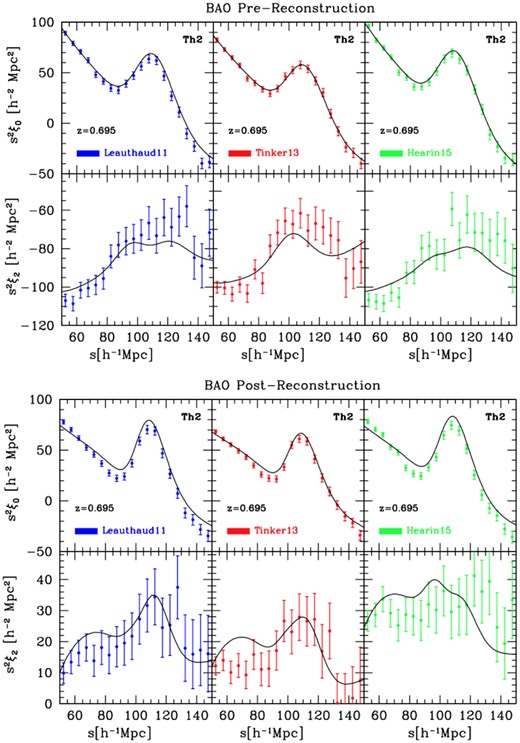
$Monopole and quadrupole of the average 2PCFs as computed from a subset of 27 OR-based mocks per HOD type, and fits of the BAO feature as seen in the correlation function multipoles. Top panels show results for the pre-reconstruction case, bottom panels refer to the reconstructed density field. The HOD models of Leauthaud, Tinker, and Hearin are shown – from left to right, respectively – for the ‘Th2’ flavour at z = 0.695. Note that the BAO feature (around $100 \, h^{-1}\, {\rm Mpc}$) appears much sharper after application of the reconstruction procedure, as expected. Results of these fits are reported in Table 4.$

Figure 7.

Monopole and quadrupole of the average 2PCFs as computed from a subset of 27 OR-based mocks per HOD type, and fits of the BAO feature as seen in the correlation function multipoles. Top panels show results for the pre-reconstruction case, bottom panels refer to the reconstructed density field. The HOD models of Leauthaud, Tinker, and Hearin are shown – from left to right, respectively – for the ‘Th2’ flavour at z = 0.695. Note that the BAO feature (around |$100 \, h^{-1}\, {\rm Mpc}$|⁠) appears much sharper after application of the reconstruction procedure, as expected. Results of these fits are reported in Table 4.

Table 4.

BAO fits to the average pre- and post-reconstructed 2PCFs for different HOD prescriptions over 27 corresponding Outer Rim mock realizations, at z = 0.695, with the ‘Th2’ flavour – as displayed in Fig. 7.

CF [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	0.9990 ± 0.0080	0.9922 ± 0.0073	1.0074 ± 0.0083
α_∥	1.0084 ± 0.0164	1.0234 ± 0.0147	1.0040 ± 0.0157
Σ_⊥	6.7663 ± 1.1320	7.6741 ± 1.2932	7.4335 ± 1.0760
Σ_∥	10.5333 ± 1.5795	8.4652 ± 1.5436	9.5687 ± 1.6354
β	0.2685 ± 0.0965	0.2404 ± 0.1017	0.2137 ± 0.0910
b	2.6748 ± 0.1315	2.4769 ± 0.1393	2.7525 ± 0.1339
χ²	129.4	115.4	126.0
	BAO	Post-Rec
α_⊥	1.0045 ± 0.0056	1.0014 ± 0.0060	1.0066 ± 0.0057
α_∥	0.9937 ± 0.0084	0.9976 ± 0.0090	1.0115 ± 0.0094
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	2.0002 ± 11.9307	2.0000 ± 0.9844	2.9483 ± 1.3018
Σ_∥	4.0169 ± 1.6667	4.9272 ± 1.3161	6.8683 ± 1.1810
β	0.4018 ± 0.0911	0.5127 ± 0.0863	0.4157 ± 0.0849
b	2.3873 ± 0.0744	2.1669 ± 0.0710	2.5137 ± 0.0879
χ²	131.3	130.0	164.5

CF [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	0.9990 ± 0.0080	0.9922 ± 0.0073	1.0074 ± 0.0083
α_∥	1.0084 ± 0.0164	1.0234 ± 0.0147	1.0040 ± 0.0157
Σ_⊥	6.7663 ± 1.1320	7.6741 ± 1.2932	7.4335 ± 1.0760
Σ_∥	10.5333 ± 1.5795	8.4652 ± 1.5436	9.5687 ± 1.6354
β	0.2685 ± 0.0965	0.2404 ± 0.1017	0.2137 ± 0.0910
b	2.6748 ± 0.1315	2.4769 ± 0.1393	2.7525 ± 0.1339
χ²	129.4	115.4	126.0
	BAO	Post-Rec
α_⊥	1.0045 ± 0.0056	1.0014 ± 0.0060	1.0066 ± 0.0057
α_∥	0.9937 ± 0.0084	0.9976 ± 0.0090	1.0115 ± 0.0094
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	2.0002 ± 11.9307	2.0000 ± 0.9844	2.9483 ± 1.3018
Σ_∥	4.0169 ± 1.6667	4.9272 ± 1.3161	6.8683 ± 1.1810
β	0.4018 ± 0.0911	0.5127 ± 0.0863	0.4157 ± 0.0849
b	2.3873 ± 0.0744	2.1669 ± 0.0710	2.5137 ± 0.0879
χ²	131.3	130.0	164.5

Table 4.

BAO fits to the average pre- and post-reconstructed 2PCFs for different HOD prescriptions over 27 corresponding Outer Rim mock realizations, at z = 0.695, with the ‘Th2’ flavour – as displayed in Fig. 7.

CF [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	0.9990 ± 0.0080	0.9922 ± 0.0073	1.0074 ± 0.0083
α_∥	1.0084 ± 0.0164	1.0234 ± 0.0147	1.0040 ± 0.0157
Σ_⊥	6.7663 ± 1.1320	7.6741 ± 1.2932	7.4335 ± 1.0760
Σ_∥	10.5333 ± 1.5795	8.4652 ± 1.5436	9.5687 ± 1.6354
β	0.2685 ± 0.0965	0.2404 ± 0.1017	0.2137 ± 0.0910
b	2.6748 ± 0.1315	2.4769 ± 0.1393	2.7525 ± 0.1339
χ²	129.4	115.4	126.0
	BAO	Post-Rec
α_⊥	1.0045 ± 0.0056	1.0014 ± 0.0060	1.0066 ± 0.0057
α_∥	0.9937 ± 0.0084	0.9976 ± 0.0090	1.0115 ± 0.0094
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	2.0002 ± 11.9307	2.0000 ± 0.9844	2.9483 ± 1.3018
Σ_∥	4.0169 ± 1.6667	4.9272 ± 1.3161	6.8683 ± 1.1810
β	0.4018 ± 0.0911	0.5127 ± 0.0863	0.4157 ± 0.0849
b	2.3873 ± 0.0744	2.1669 ± 0.0710	2.5137 ± 0.0879
χ²	131.3	130.0	164.5

CF [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	0.9990 ± 0.0080	0.9922 ± 0.0073	1.0074 ± 0.0083
α_∥	1.0084 ± 0.0164	1.0234 ± 0.0147	1.0040 ± 0.0157
Σ_⊥	6.7663 ± 1.1320	7.6741 ± 1.2932	7.4335 ± 1.0760
Σ_∥	10.5333 ± 1.5795	8.4652 ± 1.5436	9.5687 ± 1.6354
β	0.2685 ± 0.0965	0.2404 ± 0.1017	0.2137 ± 0.0910
b	2.6748 ± 0.1315	2.4769 ± 0.1393	2.7525 ± 0.1339
χ²	129.4	115.4	126.0
	BAO	Post-Rec
α_⊥	1.0045 ± 0.0056	1.0014 ± 0.0060	1.0066 ± 0.0057
α_∥	0.9937 ± 0.0084	0.9976 ± 0.0090	1.0115 ± 0.0094
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	2.0002 ± 11.9307	2.0000 ± 0.9844	2.9483 ± 1.3018
Σ_∥	4.0169 ± 1.6667	4.9272 ± 1.3161	6.8683 ± 1.1810
β	0.4018 ± 0.0911	0.5127 ± 0.0863	0.4157 ± 0.0849
b	2.3873 ± 0.0744	2.1669 ± 0.0710	2.5137 ± 0.0879
χ²	131.3	130.0	164.5

As mentioned in Section 4.4, the OR-based mocks have not been designed to reproduce all of the features of the eBOSS DR16 LRG sample, since that level of complexity is not necessary for our subsequent analysis. Hence, we clearly do not expect to exactly match the clustering properties of the eBOSS LRG sample. Nevertheless, as an instructive example, we show in Fig. 8 a comparison between eBOSS measurements and those made from Th2 OR mocks at z = 0.695. Specifically, green triangles in the figure display eBOSS plus CMASS measurements for the NGC, pink squares are used for eBOSS plus CMASS SGC measurements, and yellow circles show results obtained from the combined samples. Open symbols refer to pre-reconstruction calculations (top panel), while filled symbols indicate post-reconstruction results (bottom panel). Errorbars are estimated from analogous measurements performed on 1000 ezmocks, and via averaging. The solid black line in both panels represents the redshift-space 2PCF monopole expectation assuming the Tinker HOD recipe, derived from 27 Th2 OR mocks. Note that, besides not tuning the various HOD parameters to reproduce the exact clustering properties of the eBOSS DR16 LRG sample, our OR-based realizations are cubic mocks, and do not contain the complications of masks, cut sky, and observational artefacts (as opposed to the ezmocks and nseries) – which would be instead more appropriate for a fair data-mock comparison.

Figure 8.

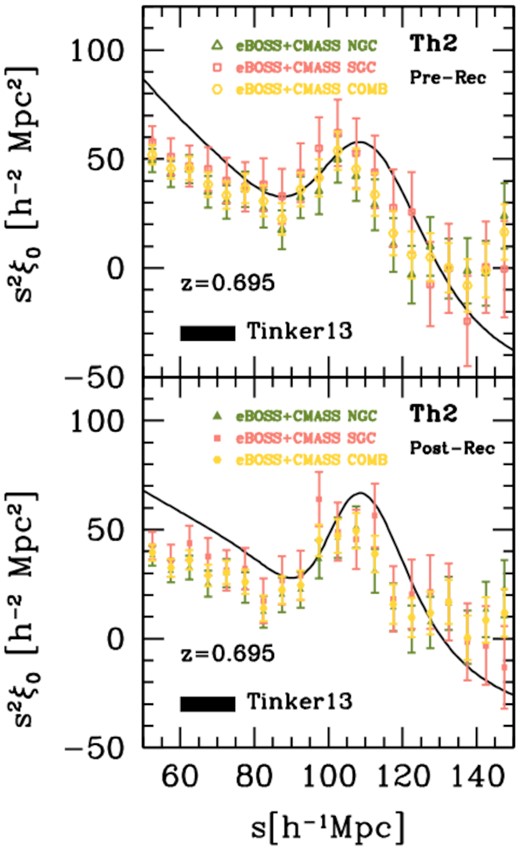
Illustrative example showing the comparison between eBOSS measurements and those made from Th2 OR mocks at z = 0.695. The top panel displays pre-reconstruction calculations (reported with open symbols), while the bottom panel refers to post-reconstruction results (indicated with filled symbols). The green triangles in the figure show eBOSS+CMASS measurements for the NGC, pink squares are used for eBOSS + CMASS SGC measurements, and yellow circles represent the combined samples. Errorbars are estimated from 1000 ezmocks. The solid black line in both panels is the redshift-space 2PCF monopole expectation assuming the Tinker HOD recipe, derived from 27 Th2 OR mocks, without including the complications of masks, cut sky, and observational artefacts.

Fig. 9 shows examples of redshift-space galaxy power spectra as computed from the average of 27 OR-based mocks, each set being characterized by a different HOD scheme, at z = 0.695 for the ‘Th2’ flavour. The plot represents the analogous, in Fourier space, of the previous correlation function estimates in configuration space. The pre- (top panels) and post-reconstructed (bottom panels) monopoles and quadrupoles of the power spectra are shown, for the Leauthaud, Tinker, and Hearin models – from left to right, respectively. Fits are obtained with the BAO theoretical model of Gil-Marín et al. (2020), considering wave numbers between 0.02 ≤ k[hMpc⁻¹] ≤ 0.30, and the corresponding results are reported in Table 5. Unlike correlation function calculations, Discrete Fourier Transform (DFT) methods used to compute the power spectrum multipoles are quite sensitive to the assumption of periodic boundary conditions, and therefore a procedure denoted as ‘padding’ is applied in this process, to mitigate non-periodicity effects. The detailed effects of non-periodicity on BAO measurements are discussed in Gil-Marín et al. (2020). In particular, results of such analyses show that no significant changes are observed in terms of α_⊥, while shifts at the level of |$2\!-\!3{{\,\rm per\,cent}}$| can be systematically seen in α_∥ if padding is not applied. Hence, non-periodic effects are relevant in determining α_∥, but they do not impact significantly α_⊥. Moreover, no relative shifts in any of the α parameters are seen when the HOD model or flavour is varied – as we show next.

Figure 9.

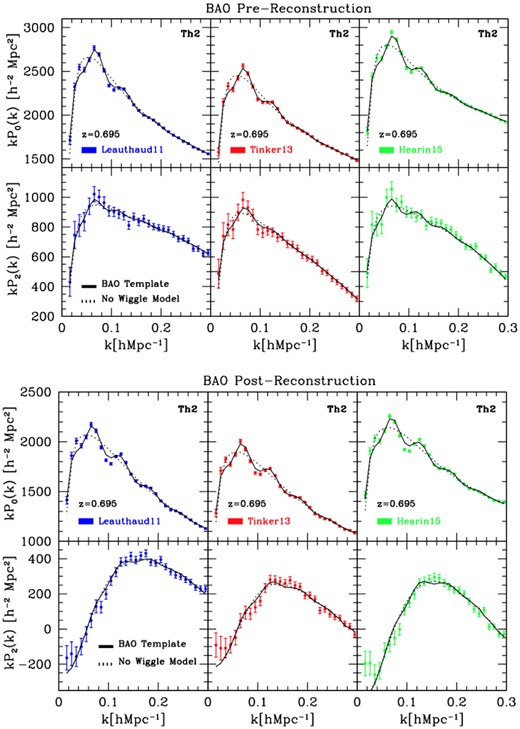
Monopole and quadrupole of the average power spectra as computed from a subset of 27 OR-based mocks per HOD type, and fits of the BAO feature as seen in the power spectrum multipoles (solid lines). The corresponding no-wiggle model is also reported in the figure, with dotted lines. Top panels show results for the pre-reconstruction case, bottom panels refer to the reconstructed density field. The HOD models of Leauthaud, Tinker, and Hearin are shown – from left to right, respectively – for the ‘Th2’ flavour at z = 0.695. Results of these fits are reported in Table 5.

Table 5.

BAO fits to the average pre- and post-reconstructed power spectra for different HOD prescriptions over 27 corresponding Outer Rim mock realizations, at z = 0.695, with the ‘Th2’ flavour – as displayed in Fig. 9.

PS [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	1.0028 ± 0.0107	0.9953 ± 0.0124	1.0108 ± 0.0099
α_∥	0.9885 ± 0.0178	1.0023 ± 0.0177	0.9779 ± 0.0143
Σ_⊥	4.2992 ± 1.8875	5.9568 ± 2.0364	4.1865 ± 1.8043
Σ_∥	9.6867 ± 1.8250	7.5044 ± 2.2301	7.0045 ± 2.0438
χ²	44.3	34.5	57.8
	BAO	Post-Rec
α_⊥	0.9976 ± 0.0075	0.9975 ± 0.0088	1.0122 ± 0.0075
α_∥	0.9938 ± 0.0104	0.9976 ± 0.0121	1.0002 ± 0.0113
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	1.0585 ± 0.7909	1.3377 ± 0.9904	1.1071 ± 0.8221
Σ_∥	1.5451 ± 1.1110	1.9511 ± 1.3408	2.5084 ± 1.5258
χ²	94.4	69.0	120.1

PS [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	1.0028 ± 0.0107	0.9953 ± 0.0124	1.0108 ± 0.0099
α_∥	0.9885 ± 0.0178	1.0023 ± 0.0177	0.9779 ± 0.0143
Σ_⊥	4.2992 ± 1.8875	5.9568 ± 2.0364	4.1865 ± 1.8043
Σ_∥	9.6867 ± 1.8250	7.5044 ± 2.2301	7.0045 ± 2.0438
χ²	44.3	34.5	57.8
	BAO	Post-Rec
α_⊥	0.9976 ± 0.0075	0.9975 ± 0.0088	1.0122 ± 0.0075
α_∥	0.9938 ± 0.0104	0.9976 ± 0.0121	1.0002 ± 0.0113
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	1.0585 ± 0.7909	1.3377 ± 0.9904	1.1071 ± 0.8221
Σ_∥	1.5451 ± 1.1110	1.9511 ± 1.3408	2.5084 ± 1.5258
χ²	94.4	69.0	120.1

Table 5.

BAO fits to the average pre- and post-reconstructed power spectra for different HOD prescriptions over 27 corresponding Outer Rim mock realizations, at z = 0.695, with the ‘Th2’ flavour – as displayed in Fig. 9.

PS [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	1.0028 ± 0.0107	0.9953 ± 0.0124	1.0108 ± 0.0099
α_∥	0.9885 ± 0.0178	1.0023 ± 0.0177	0.9779 ± 0.0143
Σ_⊥	4.2992 ± 1.8875	5.9568 ± 2.0364	4.1865 ± 1.8043
Σ_∥	9.6867 ± 1.8250	7.5044 ± 2.2301	7.0045 ± 2.0438
χ²	44.3	34.5	57.8
	BAO	Post-Rec
α_⊥	0.9976 ± 0.0075	0.9975 ± 0.0088	1.0122 ± 0.0075
α_∥	0.9938 ± 0.0104	0.9976 ± 0.0121	1.0002 ± 0.0113
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	1.0585 ± 0.7909	1.3377 ± 0.9904	1.1071 ± 0.8221
Σ_∥	1.5451 ± 1.1110	1.9511 ± 1.3408	2.5084 ± 1.5258
χ²	94.4	69.0	120.1

PS [Th2]	Leauthaud	Tinker	Hearin
	BAO	Pre-Rec
α_⊥	1.0028 ± 0.0107	0.9953 ± 0.0124	1.0108 ± 0.0099
α_∥	0.9885 ± 0.0178	1.0023 ± 0.0177	0.9779 ± 0.0143
Σ_⊥	4.2992 ± 1.8875	5.9568 ± 2.0364	4.1865 ± 1.8043
Σ_∥	9.6867 ± 1.8250	7.5044 ± 2.2301	7.0045 ± 2.0438
χ²	44.3	34.5	57.8
	BAO	Post-Rec
α_⊥	0.9976 ± 0.0075	0.9975 ± 0.0088	1.0122 ± 0.0075
α_∥	0.9938 ± 0.0104	0.9976 ± 0.0121	1.0002 ± 0.0113
Σ_rec	15.0 ± 1.5	15.0 ± 1.5	15.0 ± 1.5
Σ_⊥	1.0585 ± 0.7909	1.3377 ± 0.9904	1.1071 ± 0.8221
Σ_∥	1.5451 ± 1.1110	1.9511 ± 1.3408	2.5084 ± 1.5258
χ²	94.4	69.0	120.1

Fig. 10 summarizes and confronts the performance of the BAO fitting technique adopted in the analysis of the final eBOSS LRG sample, in configuration and Fourier space, with respect of variations in the underlying HOD model. For each mock realization, at a fixed HOD scheme and threshold flavour, the correlation function and power spectrum are computed along with their multipoles, respectively. Subsequently, fits for the BAO peak position are performed – both to the pre- and post-reconstructed synthetic catalogues – to determine the dilation parameters α_∥ and α_⊥ and their corresponding errors. The expected values for the dilation parameters are computed in the OR cosmology, at the effective redshift |$\bar{z} =0.695$|⁠. In addition, fits to the average multipoles of a given set of mocks (27 mocks per set) are also carried out, to probe biases in a very high precision configuration. In particular, the BAO pipeline on the power spectrum monopole and quadrupole is run in the interval 0.02 ≤ k[hMpc⁻¹] ≤ 0.30. The various BAO fittings are performed by fixing the BAO damping parameters (Σ_∥, Σ_⊥) at their best-fitting values on the mean of the pre- and post-reconstructed mocks, and the analysis is done in terms of the scaling parameters α_⊥ and α_∥. The various covariances used in the analysis of the OR-based mocks are derived from the ezmocks, properly rescaled to account for differences in number density (see Table A2). As explained in detail in Bautista et al. (2020), the final BAO model is a combination of the cosmological multipoles ξ_ℓ and a smooth function of separation, which accounts for unknown systematic effects in the survey that can potentially contaminate the results.

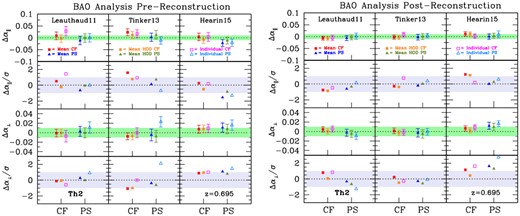
$Performance of the BAO fitting methods in configuration and Fourier space, with respect of variations in the underlying HOD model. Fits to individual mock realizations as well as to the mean of a set of 27 independent realizations of the OR mocks (from the ‘Challenge Set 1’) are carried out (see Table B2). The difference between the measured α∥ and α⊥ from pre- (left-hand panels) and post-reconstructed (right-hand panels) catalogues are displayed with different symbols and colours, as indicated in the figure. This BAO fitting methodology is adopted in the analysis of the final eBOSS LRG sample. The shaded dark-green areas in the figure highlight the $1{{\ \rm per\ cent}}$ error level, while horizontal grey bands display 1σ error levels. Overall, we do not detect any significant systematics due to different HOD prescriptions: after application of the BAO reconstruction procedure, all of the mean measurements are within $0.5\!-\!1.2{{\ \rm per\ cent}}$ of their expected values, thus below the statistical precision of the eBOSS LRG sample. See the main text for more details.$

Figure 10.

Performance of the BAO fitting methods in configuration and Fourier space, with respect of variations in the underlying HOD model. Fits to individual mock realizations as well as to the mean of a set of 27 independent realizations of the OR mocks (from the ‘Challenge Set 1’) are carried out (see Table B2). The difference between the measured α_∥ and α_⊥ from pre- (left-hand panels) and post-reconstructed (right-hand panels) catalogues are displayed with different symbols and colours, as indicated in the figure. This BAO fitting methodology is adopted in the analysis of the final eBOSS LRG sample. The shaded dark-green areas in the figure highlight the |$1{{\ \rm per\ cent}}$| error level, while horizontal grey bands display 1σ error levels. Overall, we do not detect any significant systematics due to different HOD prescriptions: after application of the BAO reconstruction procedure, all of the mean measurements are within |$0.5\!-\!1.2{{\ \rm per\ cent}}$| of their expected values, thus below the statistical precision of the eBOSS LRG sample. See the main text for more details.

Table B2 contains the results when fitting the mean correlation functions and power spectra (rows labelled ‘Mean’) of the 27 independent realizations of the OR-based mocks with different HOD prescriptions, as well as the mean of the fits of individual realizations (rows labelled ‘Individual’). Those data are shown in Fig. 10, where each subpanel displays the difference between the measured α_∥ and α_⊥: their expected value are inferred for the pre- (left-hand panels) and post-reconstructed (right-hand panels) catalogues. Mean estimates are displayed in red with filled rectangles as derived from configuration space techniques, and in blue with filled triangles as determined with Fourier space techniques; in the figure, these points are indicated as ‘MEAN CF’ or ‘MEAN PS’, respectively. The associated errors are consistently the errors of the mean, obtained by rescaling the related ezmocks covariance by the number of realizations, N_OR = 27. Therefore, these errors are a factor of |$\sqrt{N_{\rm OR}}$| smaller than the error one would obtain for a single realization of these mocks. In the figure, the dark-orange filled rectangles (related to configuration space measurements, and denoted ‘MEAN HOD CF’) and light-green filled triangles (related to Fourier space measurements, and termed ‘MEAN HOD PS’) show the same mean estimates but now normalized by the corresponding mean expectation value averaged over all the three HODs: hence, by construction, the sum of those points for a given method (CF or PS) will be zero. In this way, one can better disentangle the systematics introduced by the HOD modelling versus the theoretical systematics related to BAO fitting methodologies. Analogous empty symbols are used to display the corresponding individual measurements for pre-and post-reconstruction catalogues, respectively. In this case the error associated is the root mean square (rms) of all the individual fits, scaled by the square root of the number of realizations (⁠|$\sqrt{N_{\rm OR}}$|⁠). The shaded dark-green areas represent the |$1{{\ \rm per\ cent}}$| error level on the α parameters. The second and fourth subpanels in Fig. 10 show the difference between the measured and the expected values of α_∥ and α_⊥ in terms of number of statistical σ of the error of the mean, and the |${ \rm rms}/\sqrt{N_{\rm OR}}$|⁠. The horizontal grey bands highlight the 1σ error level. In general, considering fits to the mean over 27 realizations, the reported dilation parameters for all the different HODs are consistent with their expected values within |$0.8{{\ \rm per\ cent}}$| for α_⊥ and |$1.2{{\ \rm per\ cent}}$| for α_∥. Recall that the expected statistical errors in the eBOSS LRG data sample are of the order of |$\sim 1.9{{\ \rm per\ cent}}$| for α_⊥ and |$\sim 2.6{{\ \rm per\ cent}}$| for α_∥. From the N-body mocks we do not observe any significant BAO peak position shift with respect to their corresponding expected value in any of the post-reconstructed catalogues analysed. The BAO pipeline performs well with different HOD models; some fluctuations are present, but their values lie always below the ±2σ limit, hence the shifts are not significant. Overall, we do not detect any relative systematics due to different HOD modelling, although the statistical precision of the Outer Rim-based mocks is comparable to the statistical precision of the LRG sample (see Section 7). Interestingly, from Fig. 10 it is evident that the reconstruction procedure (right-hand panels) generally ameliorates the agreements of the α-parameters with their expected values. Moreover, it is also worth noticing that for the average values most of the detected discrepancy (after reconstruction) arises from the Hearin HOD model; this is not unexpected, since we have considered a quite extreme case of assembly bias both in the central and satellite galaxy population – as explained in Section 3. Finally, after application of the BAO reconstruction procedure, we find all of the mean measurements to be within |$0.5\!-\!1.2{{\ \rm per\ cent}}$| of their expected values, thus below the statistical precision of the eBOSS LRG sample. Hence, for BAO-only fitting methods, both modelling and HOD systematics are subdominant to the global systematic error budget and the BAO analysis is unbiased. However, sub-per cent level corrections may become relevant for future surveys like DESI, that are expected to achieve sub-per cent statistical precision on the galaxy sample.

6.3 Galaxy mock challenge: RSD analysis and HOD systematics

In Section 5, we have briefly described the three RSD theoretical models adopted for the analysis of the final eBOSS DR16 LRG sample. Here, we confront those models and show that they are mutually consistent, with comparable systematic errors on the AP parameters and the growth of structure – as well as robust to different HOD prescriptions. While for the previous BAO-only analysis simply the BAO peak position has been taken into account, here we consider a full modelling of the shape and amplitude of the correlation function and power spectrum multipoles, including non-linear DM effects, galaxy bias, and RSDs. We generically refer to this methodology as the ‘full shape’ (FS) analysis. Quantitative investigations involving the correlation function or power spectrum FS require high fidelity N-body-based mocks to test and validate the underlying RSD models, and typically such analyses are only performed over pre-reconstructed synthetic catalogues. The overall aim is to quantify the impact of the different HOD prescriptions used to populate simulated haloes with galaxies on RSD constraints. Our primary focus here is thus on modelling and HOD systematics, while Bautista et al. (2020), Gil-Marín et al. (2020), and Icaza-Lizaola et al. (2020) also examined the impact of the choice of scales in the fits and the choice of a fiducial cosmology. In particular, their conclusions (directly relevant for this work) suggest that the most robust results and optimal configuration for the FS analysis of the correlation function are obtained with monopole and quadrupole in the range |$20 \le s {\rm [} \, h^{-1}\, {\rm Mpc} \, {\rm ]} \le 130$|⁠, and hexadecapole in the interval |$25 \le s {\rm [} \, h^{-1}\, {\rm Mpc} \, {\rm ]} \le 130$| for the TNS model in configuration space, while using the interval |$25 \le s {\rm [} \, h^{-1}\, {\rm Mpc} \, {\rm ]} \le 130$| for all the moments when considering CLPT-GS. Regarding power spectrum computations, the optimal range of scales are 0.02 ≤ k[h/Mpc] ≤ 0.15, and results include the hexadecapole. In what follows, the analysis is carried out in the Outer Rim fiducial cosmology, and the monopole, quadrupole, and hexadecapole ranges are those previously specified – always set for optimal performance. Moreover, for the analysis of the challenge mocks in Fourier space, a procedure called padding is applied, in order to prevent the impact of non-periodicity to affect results when applying the discrete Fourier transform. Also, the mock covariances adopted in these investigations are derived from a set of 1000 ezmocks, and properly rescaled by the difference in particle number.

Fig. 11 summarizes the main results of the RSD FS analysis, confronting the three different modelling techniques: two in configuration space (CLPT-GS and CF-TNS), and one in Fourier space (P_k-TNS). Specifically, we analysed the Leauthaud, Tinker, and Hearin HODs (from left to right in the plots) corresponding to ‘Th2’, both in configuration and Fourier space – closer to the characteristics of the eBOSS LRG sample. Individual fits on each of the 27 realizations per model are performed (i.e. open symbols in the panels, denoted with the letter ‘I’ following the specific model), as well as fits on the mean of the mocks (i.e. filled symbols indicated with the letter ‘M’ in the panels, adopting similar conventions). Results are also reported in Table B3. In detail, circles refer to CLPT-GS measurements, squares are used for the CF-TNS model, and triangles indicate results from the P_k-TNS technique. Moreover, open symbols are related to individual fits, while filled symbols display fits on the mean. In the latter case, similarly to what has been done in Fig. 10, we also show fits on the mean normalized by the corresponding mean expectation value averaged over all the three HODs: such points are denoted as ‘MH’ (or ‘Mean HOD’), and are useful to separate the systematics introduced by the HOD modelling versus the theoretical systematics related to individual RSD FS fitting methodologies. In the figure, shaded orange areas represent the |$1{{\ \rm per\ cent}}$| error levels on the α parameters and the |$3{{\ \rm per\ cent}}$| error on fσ₈, while shaded grey areas highlight the 1σ error level.

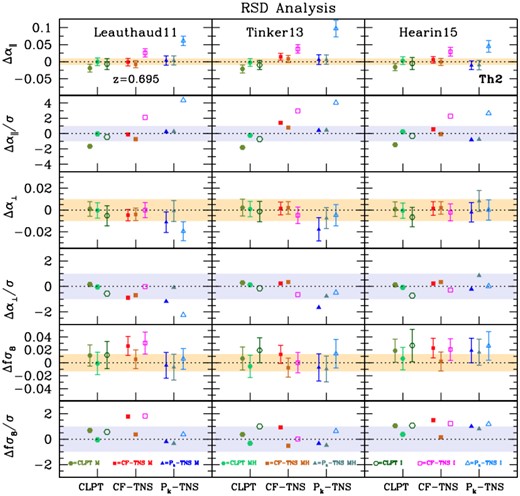
$Full shape RSD analysis: main results on the AP parameters and the growth of structure. The three techniques adopted for the analysis of the final eBOSS LRG sample, two in configuration space (CLPT-GS and CF-TNS) and one in Fourier space (Pk-TNS), are confronted on a series of Outer Rim mocks having different HOD prescriptions. From left to right, the Leauthaud, Tinker, and Hearin models corresponding to ‘Th2’ are analysed, as they are closer to the characteristics of the eBOSS LRG sample. Individual fits on each of the 27 realizations per model are performed (open points), as well as fits on the mean of the mocks (filled points), allowing one to obtain accurate estimates of α∥, α⊥, and fσ8. Scatter plots in terms of σ-deviations are also shown. The shaded orange areas represent the $1{{\ \rm per\ cent}}$ error levels on the α parameters and the $3{{\ \rm per\ cent}}$ error on fσ8, while shaded grey areas highlight the 1σ error level. The corresponding numerical results are reported in Table B3. Errorbars follow the same conventions as in Fig. 10. See the main text for more details.$

Figure 11.

Full shape RSD analysis: main results on the AP parameters and the growth of structure. The three techniques adopted for the analysis of the final eBOSS LRG sample, two in configuration space (CLPT-GS and CF-TNS) and one in Fourier space (P_k-TNS), are confronted on a series of Outer Rim mocks having different HOD prescriptions. From left to right, the Leauthaud, Tinker, and Hearin models corresponding to ‘Th2’ are analysed, as they are closer to the characteristics of the eBOSS LRG sample. Individual fits on each of the 27 realizations per model are performed (open points), as well as fits on the mean of the mocks (filled points), allowing one to obtain accurate estimates of α_∥, α_⊥, and fσ₈. Scatter plots in terms of σ-deviations are also shown. The shaded orange areas represent the |$1{{\ \rm per\ cent}}$| error levels on the α parameters and the |$3{{\ \rm per\ cent}}$| error on fσ₈, while shaded grey areas highlight the 1σ error level. The corresponding numerical results are reported in Table B3. Errorbars follow the same conventions as in Fig. 10. See the main text for more details.

Overall, from the fit of the mean, biases observed for CLPT-GS and CF-TNS are mostly within 1.5σ away from the expected values for all the parameters across all models (and always less than 2σ away), and errors estimated from the different RSD models are mutually compatible. In general, CF-TNS seems to imply slightly larger errors than CLPT-GS. Comparing fits on the mean with the mean of individual fits, for α_⊥ and fσ₈ there is good agreement in values and errors. Also, for α_∥, the fit of the mean is a more robust estimate of potential biases. The most significant differences are found for the best fits of α_∥, but this comes with no surprise: it is in fact expected that fits on individual mocks are dominated by the low signal to noise, as the effective volume of a single OR mock is 1.10 Gpc³ – thus relatively small. Namely, given the low volume spanned by OR mocks, the fit to the mean and the mean of the fits differ, primarily because individual subcubes are dominated by noise and there are not enough subcubes for this effect to effectively cancel out. A good proof of this fact is provided by Fig. 10: when reconstruction is applied to the mocks (i.e. signal-to-noise increased), the differences between fits to the mean and mean of the fits shrink – as can be inferred by comparing the left-hand and right-hand panels of Fig. 10. Moreover, the ∼4σ discrepancy shown in Fig. 11 from individual fits to the Tinker model happens only for P(k) measurements, and affects primarily α_∥ – the variable with the lowest signal (hence providing noisy spectra), as it depends only on the radial direction. In such case, very likely the fitting procedure tends to (incorrectly) identify the BAO signal in those noisier regions of the spectra; however, this does not happen for configuration space analyses, since the BAO signal is localized. In other terms, this is a clear example of inadequate BAO detections in individual fits. Finally, another source of discrepancy could be due to the rescaling for the ezmock covariance adopted in the analysis, that may not provide a full accurate description and causes a much larger variation on individual mocks.

In summary, from the results of fitting the mean, since we do not observe biases larger than 2σ, we conclude that different HODs do not have a significant impact in the fits even from an FS RSD analysis. This type of systematics is always below the statistical error of the LRG sample. It is also quite interesting to notice the remarkable consistency and (non-trivial) agreement between RSD FS techniques in configuration and Fourier space. In general, as demonstrated by Fig. 11, the HOD systematics derived from fits on the mean are within the |$\sim 1{{\ \rm per\ cent}}$| level, even smaller than the modelling systematics, and always below the statistical precision of the eBOSS LRG sample. The modelling systematics instead could reach the percentage level particularly in α_∥ and fσ₈, and could represent a dominant source of systematics. From a more extensive FS analysis, we thus conclude that while HOD systematics are subdominant to the global systematic error budget, the modelling systematics should be taken into account – although both are below the statistical precision of the eBOSS LRG sample. Moreover, from the FS study, we conclude that the different methodologies adopted for the analysis of the final eBOSS LRG sample are mutually consistent and robust, thus validating the clustering analysis pipelines.

6.4 Galaxy mock challenge: modelling systematics

The heterogeneous set of Outer Rim mocks previously adopted for assessing possible systematic effects in the galaxy–halo connection and imprecisions related to the galaxy clustering modelling (i.e. impact of HODs on BAO and RSD methods, and RSD modelling systematics) is suboptimal in accuracy at the sub-per cent level, although this type of accuracy is well-below the statistical sensitivity of the eBOSS LRG sample. This is mainly because of the relatively small effective volume spanned by each individual independent mock, due to the limitations posed by having only a single Outer Rim halo catalogue at z = 0.695 combined with the constraints intrinsic to the LRG modelling (see Section 3). For this reason, only 27 mocks were used in the previous analyses, as fully independent realizations (i.e. not sharing the same DM field) are required to properly assess cosmic variance. In terms of errorbars, the resolution limit of the OR mocks is in fact around the |$\sim\!1\!-\!2{{\ \rm per\ cent}}$| level. In order to evaluate the performance of the BAO and RSD modelling at a sub-per cent level, a more suitable choice is to abandon a single simulation – although of exquisite mass-resolution such as the Outer Rim – and opt instead for multiple realizations of the same box (i.e. identical initial conditions in all but the random seeds) at a lower mass-resolution and with a larger effective volume.⁸ This is the logic beyond the nseries, a small homogeneous set of 84 pseudo-independent mocks constructed from seven independent periodic boxes of |$2.6h^{-1}\, {\rm Gpc}$| side, projected through 12 different orientations and cuts per box; the mass resolution of these periodic boxes is much lower than that of the Outer Rim run, but it is still sufficient for resolving LRG-type haloes (⁠|$1.5 \times 10^{11} \, h^{-1}\, \mathrm{M}_{\odot }$|⁠, with 2048³ particles per box). The global effective volume spanned is 84 × 3.67 [Gpc]³. The nseries are characterized by the same underlying galaxy bias model built upon the same cosmology, but each mock is a quasi-independent realization – thus not sharing exactly the same LSS – and including observational artefacts closer to the eBOSS DR16 sample, with similar angular and radial selection function of the observed sample. The HOD used is targeted to BOSS CMASS galaxies, at an effective redshift of |$\bar{z}=0.56$|⁠. Although this set was originally devised for BOSS galaxies, it is still useful for evaluating modelling systematics at the sub-percentage level also for eBOSS tracers. This is why the nseries is extensively used in Bautista et al. (2020) and in Gil-Marín et al. (2020) for addressing the modelling systematics related to each complementary analysis in configuration and Fourier space, respectively. Here, we show only an interesting combined example, confronting the fitting methodologies in configuration and Fourier space and the performance of the RSD models previously introduced in Section 5.

Fig. 12 provides a summary result obtained by running the various BAO and RSD FS analysis pipelines on the average of 84 nseries mocks. Specifically, the left-hand panels display the AP parameters derived from a BAO-only fit in configuration and Fourier space, respectively. Filled symbols are used for pre-reconstructed catalogues, while open symbols refer to post-reconstructed catalogues. The left-hand panels show analogous quantities, as well as the growth of structure in terms of fσ₈, derived from RSD FS fits. In this case the analysis is performed only over pre-reconstructed catalogues, and carried out in the nseries cosmology (see Section 4.2). Results from the three different RSD models – two in configuration space (CLPT-GS and CF-TNS) and one in Fourier space (P_k-TNS), all set for optimal performance as explained before, including the hexadecapole – are displayed with filled symbols. The corresponding numerical values are reported in Table B4. The grey areas in the figure highlight the |$0.5{{\ \rm per\ cent}}$| error level for the AP parameters, and the |$1.0{{\ \rm per\ cent}}$| error level for fσ₈. As clearly seen, all the different methods are mutually consistent, showing a remarkable accuracy in recovering the expected cosmological parameters (α_∥, α_⊥, fσ₈) at an exquisite level of precision, within at worst |$0.9{{\ \rm per\ cent}}$| of their expected values for the α’s and within |$1.5{{\ \rm per\ cent}}$| for fσ₈ – as a conservative estimate. These results can be compared with analogous measurements performed on the Outer Rim mocks displayed in Figs 10 and 11. Although here at a sub-percentage level precision, results from the two different sets of mocks are consistent: we observe a similar trend at a fixed HOD recipe, indicating an impressive level of consistency between techniques in configuration and Fourier space. Clearly, the modelling systematics is addressed here with higher accuracy, showing deviations at the sub-per cent level for the AP parameters and fσ₈. While this type of systematics may be a dominant source of error in the global systematic budget (despite sub-per cent deviations), the LRG sample is primarily dominated by the statistical error of the data.

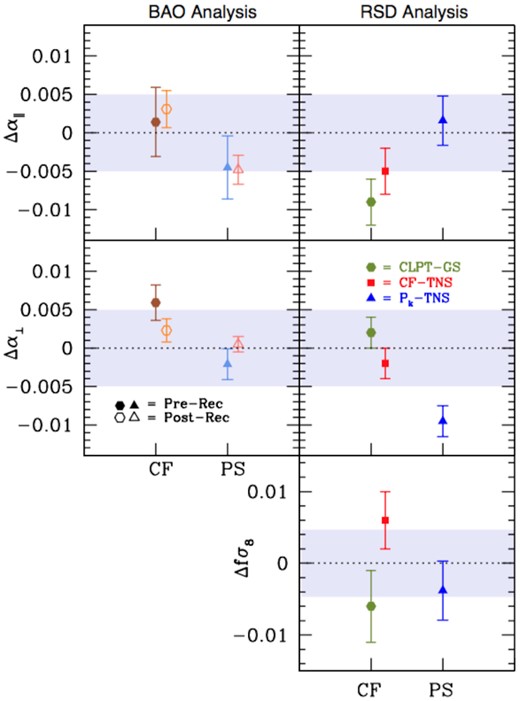
$Comparing modelling systematics in BAO and RSD methods, estimated from 84 nseries mocks. Left-hand panels show the AP parameters derived from BAO-only fits in configuration and Fourier space, respectively. Right-hand panels refer to RSD full shape analyses. The filled symbols are used for pre-reconstructed catalogues, while open symbols refer to post-reconstructed catalogues. The gray areas in the figure highlight the $0.5{{\ \rm per\ cent}}$ error level on α∥ and α⊥, and the $1.0{{\ \rm per\ cent}}$ error on fσ8. These numerical results are reported in Table B4. All the different methods adopted for the clustering analysis of the eBOSS LRG sample are mutually consistent, showing a remarkable accuracy in recovering the expected cosmological parameters at an exquisite level of precision.$

Figure 12.

Comparing modelling systematics in BAO and RSD methods, estimated from 84 nseries mocks. Left-hand panels show the AP parameters derived from BAO-only fits in configuration and Fourier space, respectively. Right-hand panels refer to RSD full shape analyses. The filled symbols are used for pre-reconstructed catalogues, while open symbols refer to post-reconstructed catalogues. The gray areas in the figure highlight the |$0.5{{\ \rm per\ cent}}$| error level on α_∥ and α_⊥, and the |$1.0{{\ \rm per\ cent}}$| error on fσ₈. These numerical results are reported in Table B4. All the different methods adopted for the clustering analysis of the eBOSS LRG sample are mutually consistent, showing a remarkable accuracy in recovering the expected cosmological parameters at an exquisite level of precision.

7 SYSTEMATIC ERROR BUDGET

Finally, we address here the LRG global error budget with a major focus on theoretical systematics, and also summarize the previous mock challenge results in term of biases in the estimation of α_∥, α_⊥, and fσ₈.

7.1 Global error budget

In our companion papers Bautista et al. (2020) and Gil-Marín et al. (2020), besides modelling and HOD imperfections, detailed investigations regarding the impact of a fiducial cosmology, the optimal fitting range of scales, effects on non-periodicity, and observational artefacts such as redshift failures, completeness, close-pair collisions, and radial integral constraint (de Mattia et al. 2021) are carried out in configuration and Fourier space, respectively, and the associated errors are carefully quantified using all the available types of mocks. In the following, we indicate the contribution of all these additional systematics as |$\sigma _{\rm syst}^{\rm other}$|⁠, while we use |$\sigma _{\rm syst}^{\rm model}$| for denoting the theoretical systematics ascribed to imperfections in the RSD modelling. Adopting similar conventions as in the companion papers, for a given cosmological parameter x_p measured with error σ_p whose reference value is |$x_{\rm p}^{\rm ref}$|⁠, the systematic error assigned is

$$\begin{eqnarray*} \sigma _{\rm p, syst} = 2 \sigma _{\rm p} ~~ {\rm if} ~ |x_{\rm p} - x_{\rm p}^{\rm ref}| \lt 2 \sigma _{\rm p}; \end{eqnarray*}$$

(35)

$$\begin{eqnarray*} \sigma _{\rm p, syst} = |x_{\rm p} - x_{\rm p}^{\rm ref}| ~~ {\rm if} ~ |x_{\rm p} - x_{\rm p}^{\rm ref}| \ge 2 \sigma _{\rm p}. \end{eqnarray*}$$

(36)

In essence, anything above the 2σ level is considered as a detected systematics (corresponding to a |$95{{\ \rm per\ cent}}$| confidence level on the mean of the mocks), and the maximal value is always used as a conservative choice. The statistical properties of the LRG sample are also characterized in Bautista et al. (2020) and in Gil-Marín et al. (2020), and the consensus statistical error related to each individual method is denoted here as σ_stat. Recall again that from a joint BAO and RSD FS analysis, both in configuration and Fourier space, the statistical consensus errors are |$1.9{{\ \rm per\ cent}}$| on α_⊥ and |$2.6{{\ \rm per\ cent}}$| on α_∥, respectively. In the subsequent analysis, we always consider fits to the mean, as they are less sensitive to noise effects compared to individual fits, and only focus on RSD FS results.

Table 6 summarizes the global error budget for the eBOSS DR16 LRG sample. Here, the modelling systematics is inferred from the nseries (see Table B4) and indicated as |$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$|⁠: we explain later on the reason behind this choice, and why the Outer Rim contribution is not included here. The comprehensive systematic error budget intrinsic to each RSD method (σ_syst) is simply obtained by summing in quadrature the modelling and additional systematics, and the total error budget σ_tot is also derived in quadrature from the contributions of σ_syst and σ_stat. In the table, we provide some useful ratios as well, that allow one to directly compare the contribution of systematics or statistics to the total error estimate. While the BAO-only pipeline is essentially unbiased, from the RSD FS analyses we conclude that systematic errors account for a significant fraction of the total error budget, contributing up to |$50{{\ \rm per\ cent}}$| (or more) to the uncertainties associated with the AP parameters and the growth of structures (see the various ratios). The impact in the determination of α_∥ and α_⊥ is at the |$\sim 1.0{{\ \rm per\ cent}}$| level, and it can reach even |$\sim\!1.5\!-\!2.0{{\ \rm per\ cent}}$| for fσ₈. From configuration space analyses, the most relevant contribution to systematics is caused by observational artefacts. In Fourier space, the most dominant systematic is arising from the assumption of a reference cosmology, that can bias in particular the estimation of fσ₈ up to |$2.0{{\ \rm per\ cent}}$|⁠. All of the other effects, including modelling systematics, are within the |$1.0{{\ \rm per\ cent}}$| range or below. Eventually, systematic errors are added only to the diagonal of the covariance of each measurement, assuming that all the contributions to systematics are independent.

Table 6.

Global error budget for the final eBOSS DR16 LRG sample, as derived from configuration and Fourier space analyses.

RSD-FS analysis	Global Syst.
Error type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0090	0.0040	0.0100
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small NS}}]$\|	CF-TNS	0.0060	0.0040	0.0080
	P_k-TNS	0.0064	0.0095	0.0082
RSD additional	CLPT-GS	0.0156	0.0127	0.0220
\|$[\sigma _{\rm syst}^{\rm other}]$\|	CF-TNS	0.0153	0.0112	0.0216
	P_k-TNS	0.0117	0.0068	0.0155
RSD systematics	CLPT-GS	0.0180	0.0133	0.0242
[σ_syst]	CF-TNS	0.0164	0.0119	0.0230
	P_k-TNS	0.0133	0.0117	0.0175
RSD statistical	CLPT-GS	0.0280	0.0200	0.0450
[σ_stat]	CF-TNS	0.0310	0.0180	0.0400
	P_k-TNS	0.0360	0.0270	0.0420
RSD total	CLPT-GS	0.0333	0.0240	0.0511
[σ_tot]	CF-TNS	0.0351	0.0216	0.0462
	P_k-TNS	0.0384	0.0294	0.0455
	CLPT-GS	0.3214	0.2000	0.2222
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_stat	CF-TNS	0.1935	0.2222	0.2000
	P_k-TNS	0.1778	0.3518	0.1952
	CLPT-GS	0.5571	0.6350	0.4889
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_stat	CF-TNS	0.4935	0.6222	0.5400
	P_k-TNS	0.3250	0.2518	0.3690
	CLPT-GS	0.6432	0.6658	0.5370
σ_syst/σ_stat	CF-TNS	0.5301	0.6607	0.5758
	P_k-TNS	0.3704	0.4327	0.4175
	CLPT-GS	0.2703	0.1665	0.1958
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_tot	CF-TNS	0.1710	0.1854	0.1733
	P_k-TNS	0.1667	0.3229	0.1802
	CLPT-GS	0.4686	0.5286	0.4307
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_tot	CF-TNS	0.4361	0.5191	0.4679
	P_k-TNS	0.3048	0.2311	0.3406
	CLPT-GS	0.5410	0.5542	0.4731
σ_syst/σ_tot	CF-TNS	0.4684	0.5513	0.4990
	P_k-TNS	0.3474	0.3971	0.3853
	CLPT-GS	0.8410	0.8324	0.8810
σ_stat/σ_tot	CF-TNS	0.8835	0.8343	0.8666
	P_k-TNS	0.9378	0.9178	0.9228

RSD-FS analysis	Global Syst.
Error type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0090	0.0040	0.0100
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small NS}}]$\|	CF-TNS	0.0060	0.0040	0.0080
	P_k-TNS	0.0064	0.0095	0.0082
RSD additional	CLPT-GS	0.0156	0.0127	0.0220
\|$[\sigma _{\rm syst}^{\rm other}]$\|	CF-TNS	0.0153	0.0112	0.0216
	P_k-TNS	0.0117	0.0068	0.0155
RSD systematics	CLPT-GS	0.0180	0.0133	0.0242
[σ_syst]	CF-TNS	0.0164	0.0119	0.0230
	P_k-TNS	0.0133	0.0117	0.0175
RSD statistical	CLPT-GS	0.0280	0.0200	0.0450
[σ_stat]	CF-TNS	0.0310	0.0180	0.0400
	P_k-TNS	0.0360	0.0270	0.0420
RSD total	CLPT-GS	0.0333	0.0240	0.0511
[σ_tot]	CF-TNS	0.0351	0.0216	0.0462
	P_k-TNS	0.0384	0.0294	0.0455
	CLPT-GS	0.3214	0.2000	0.2222
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_stat	CF-TNS	0.1935	0.2222	0.2000
	P_k-TNS	0.1778	0.3518	0.1952
	CLPT-GS	0.5571	0.6350	0.4889
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_stat	CF-TNS	0.4935	0.6222	0.5400
	P_k-TNS	0.3250	0.2518	0.3690
	CLPT-GS	0.6432	0.6658	0.5370
σ_syst/σ_stat	CF-TNS	0.5301	0.6607	0.5758
	P_k-TNS	0.3704	0.4327	0.4175
	CLPT-GS	0.2703	0.1665	0.1958
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_tot	CF-TNS	0.1710	0.1854	0.1733
	P_k-TNS	0.1667	0.3229	0.1802
	CLPT-GS	0.4686	0.5286	0.4307
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_tot	CF-TNS	0.4361	0.5191	0.4679
	P_k-TNS	0.3048	0.2311	0.3406
	CLPT-GS	0.5410	0.5542	0.4731
σ_syst/σ_tot	CF-TNS	0.4684	0.5513	0.4990
	P_k-TNS	0.3474	0.3971	0.3853
	CLPT-GS	0.8410	0.8324	0.8810
σ_stat/σ_tot	CF-TNS	0.8835	0.8343	0.8666
	P_k-TNS	0.9378	0.9178	0.9228

Table 6.

Global error budget for the final eBOSS DR16 LRG sample, as derived from configuration and Fourier space analyses.

RSD-FS analysis	Global Syst.
Error type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0090	0.0040	0.0100
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small NS}}]$\|	CF-TNS	0.0060	0.0040	0.0080
	P_k-TNS	0.0064	0.0095	0.0082
RSD additional	CLPT-GS	0.0156	0.0127	0.0220
\|$[\sigma _{\rm syst}^{\rm other}]$\|	CF-TNS	0.0153	0.0112	0.0216
	P_k-TNS	0.0117	0.0068	0.0155
RSD systematics	CLPT-GS	0.0180	0.0133	0.0242
[σ_syst]	CF-TNS	0.0164	0.0119	0.0230
	P_k-TNS	0.0133	0.0117	0.0175
RSD statistical	CLPT-GS	0.0280	0.0200	0.0450
[σ_stat]	CF-TNS	0.0310	0.0180	0.0400
	P_k-TNS	0.0360	0.0270	0.0420
RSD total	CLPT-GS	0.0333	0.0240	0.0511
[σ_tot]	CF-TNS	0.0351	0.0216	0.0462
	P_k-TNS	0.0384	0.0294	0.0455
	CLPT-GS	0.3214	0.2000	0.2222
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_stat	CF-TNS	0.1935	0.2222	0.2000
	P_k-TNS	0.1778	0.3518	0.1952
	CLPT-GS	0.5571	0.6350	0.4889
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_stat	CF-TNS	0.4935	0.6222	0.5400
	P_k-TNS	0.3250	0.2518	0.3690
	CLPT-GS	0.6432	0.6658	0.5370
σ_syst/σ_stat	CF-TNS	0.5301	0.6607	0.5758
	P_k-TNS	0.3704	0.4327	0.4175
	CLPT-GS	0.2703	0.1665	0.1958
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_tot	CF-TNS	0.1710	0.1854	0.1733
	P_k-TNS	0.1667	0.3229	0.1802
	CLPT-GS	0.4686	0.5286	0.4307
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_tot	CF-TNS	0.4361	0.5191	0.4679
	P_k-TNS	0.3048	0.2311	0.3406
	CLPT-GS	0.5410	0.5542	0.4731
σ_syst/σ_tot	CF-TNS	0.4684	0.5513	0.4990
	P_k-TNS	0.3474	0.3971	0.3853
	CLPT-GS	0.8410	0.8324	0.8810
σ_stat/σ_tot	CF-TNS	0.8835	0.8343	0.8666
	P_k-TNS	0.9378	0.9178	0.9228

RSD-FS analysis	Global Syst.
Error type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0090	0.0040	0.0100
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small NS}}]$\|	CF-TNS	0.0060	0.0040	0.0080
	P_k-TNS	0.0064	0.0095	0.0082
RSD additional	CLPT-GS	0.0156	0.0127	0.0220
\|$[\sigma _{\rm syst}^{\rm other}]$\|	CF-TNS	0.0153	0.0112	0.0216
	P_k-TNS	0.0117	0.0068	0.0155
RSD systematics	CLPT-GS	0.0180	0.0133	0.0242
[σ_syst]	CF-TNS	0.0164	0.0119	0.0230
	P_k-TNS	0.0133	0.0117	0.0175
RSD statistical	CLPT-GS	0.0280	0.0200	0.0450
[σ_stat]	CF-TNS	0.0310	0.0180	0.0400
	P_k-TNS	0.0360	0.0270	0.0420
RSD total	CLPT-GS	0.0333	0.0240	0.0511
[σ_tot]	CF-TNS	0.0351	0.0216	0.0462
	P_k-TNS	0.0384	0.0294	0.0455
	CLPT-GS	0.3214	0.2000	0.2222
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_stat	CF-TNS	0.1935	0.2222	0.2000
	P_k-TNS	0.1778	0.3518	0.1952
	CLPT-GS	0.5571	0.6350	0.4889
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_stat	CF-TNS	0.4935	0.6222	0.5400
	P_k-TNS	0.3250	0.2518	0.3690
	CLPT-GS	0.6432	0.6658	0.5370
σ_syst/σ_stat	CF-TNS	0.5301	0.6607	0.5758
	P_k-TNS	0.3704	0.4327	0.4175
	CLPT-GS	0.2703	0.1665	0.1958
\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|/σ_tot	CF-TNS	0.1710	0.1854	0.1733
	P_k-TNS	0.1667	0.3229	0.1802
	CLPT-GS	0.4686	0.5286	0.4307
\|$\sigma _{\rm syst}^{\rm other}$\|/σ_tot	CF-TNS	0.4361	0.5191	0.4679
	P_k-TNS	0.3048	0.2311	0.3406
	CLPT-GS	0.5410	0.5542	0.4731
σ_syst/σ_tot	CF-TNS	0.4684	0.5513	0.4990
	P_k-TNS	0.3474	0.3971	0.3853
	CLPT-GS	0.8410	0.8324	0.8810
σ_stat/σ_tot	CF-TNS	0.8835	0.8343	0.8666
	P_k-TNS	0.9378	0.9178	0.9228

7.2 Impact of modelling systematics

The modelling systematics estimated from ‘Th2’ Outer Rim mocks analysed in Section 6 are detailed in Table 7, where we list all the contributions inferred from the individual HODs of Leauthaud (LH), Tinker (TK), and Hearin (HE), respectively, as well as the combined theoretical systematics derived by simply averaging those contributions (⁠|$\sigma _{\rm syst}^{\rm model, OR}$|⁠). We also report some useful ratios, for the ease of comparison. Not surprisingly, the modelling systematics obtained from Outer Rim mocks are much larger than those derived from the nseries. The reason is related to the difference in effective volume, combined with the limited number of fully independent realizations available (27 synthetic catalogues per flavour). In fact, the global effective volume of ‘Th2’ Outer Rim mocks is 29.7 Gpc³, about 11 times bigger than the combined CMASS plus eBOSS LRG sample, but ∼10.27 times smaller than the global effective volume spanned by the nseries – which is 308.28 Gpc³, and thus 113 times larger than the combined DR16 LRG sample. In this respect, the statistical threshold of the nseries is at the |$0.1\!-\!0.5{{\ \rm per\ cent}}$| level, while the resolution of Outer Rim mocks is around |$1.0\!-\!1.5{{\ \rm per\ cent}}$|⁠. As evident from Table 7, the modelling systematics inferred from Outer Rim mocks is closer to the statistical error of the LRG sample (see the various ratios |$\sigma _{\rm syst, LH}^{\rm model, OR}/\sigma _{\rm stat}$|⁠, |$\sigma _{\rm syst, TK}^{\rm model, OR}/\sigma _{\rm stat}$|⁠, |$\sigma _{\rm syst, HE}^{\rm model, OR}/\sigma _{\rm stat}$|⁠), and a factor ∼2–5 times bigger than uncertainties derived from the nseries. The size of the errorbars simply scales with the global effective volume and the number of available realizations, as clearly highlighted by the various ratios |$\sigma _{\rm syst, LH}^{\rm model,OR}/\sigma _{\rm syst}^{\rm model,NS}$|⁠, |$\sigma _{\rm syst, TK}^{\rm model,OR}/\sigma _{\rm syst}^{\rm model,NS}$|⁠, and |$\sigma _{\rm syst, HE}^{\rm model,OR}/\sigma _{\rm syst}^{\rm model,NS}$|⁠. This is the main reason why we omit to include these theoretical systematics in the previous global error budget, as the larger errorbars are primarily due to limited volume and statistics. Note, however, that the Outer Rim mocks are fully independent, and not pseudo-independent realizations, hence the errorbars are completely uncorrelated. After all, although closer to the statistical limit of the sample, the Outer Rim mocks allowed us to test and validate the robustness of the LRG analysis pipelines, the sensitivity to a number of HOD prescriptions, and to confirm the remarkable consistency across different methods in configuration and Fourier space.

Table 7.

Modelling systematics derived from RSD FS analyses of the ‘Th2’ Outer Rim challenge mocks (see Tables A1 and A2).

RSD-FS analysis	Model. Syst.
Systematic type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0228	0.0134	0.0330
\|$[\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0220	0.0104	0.0292
	P_k-TNS	0.0276	0.0188	0.0400
RSD modelling	CLPT-GS	0.0234	0.0154	0.0356
\|$[\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0204	0.0118	0.0280
	P_k-TNS	0.0288	0.0214	0.0420
RSD modelling	CLPT-GS	0.0218	0.0134	0.0356
\|$[\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0196	0.0124	0.0304
	P_k-TNS	0.0258	0.0178	0.0380
RSD modelling	CLPT-GS	0.0227	0.0141	0.0347
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0207	0.0115	0.0292
	P_k-TNS	0.0274	0.0193	0.0400
	CLPT-GS	0.8143	0.6700	0.7334
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.7097	0.5778	0.7300
	P_k-TNS	0.7667	0.6963	0.9524
	CLPT-GS	0.8357	0.7700	0.7911
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6581	0.6556	0.7000
	P_k-TNS	0.8000	0.7926	1.0000
	CLPT-GS	0.7786	0.6700	0.7911
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6323	0.6889	0.7600
	P_k-TNS	0.7167	0.6593	0.9048
	CLPT-GS	0.8095	0.7033	0.7718
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6667	0.6407	0.7300
	P_k-TNS	0.7611	0.7160	0.9524
	CLPT-GS	2.5334	3.3500	3.3000
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.6667	2.6000	3.6500
	P_k-TNS	4.3125	1.9789	4.8781
	CLPT-GS	2.6000	3.8000	3.5600
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4000	2.9500	3.5000
	P_k-TNS	4.5000	2.2526	5.1219
	CLPT-GS	2.4222	3.3500	3.5600
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.2667	3.1000	3.8000
	P_k-TNS	4.0312	1.8737	4.6341
	CLPT-GS	2.5185	3.5167	3.4733
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4445	2.8834	3.6500
	P_k-TNS	4.2812	2.0351	4.8780

RSD-FS analysis	Model. Syst.
Systematic type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0228	0.0134	0.0330
\|$[\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0220	0.0104	0.0292
	P_k-TNS	0.0276	0.0188	0.0400
RSD modelling	CLPT-GS	0.0234	0.0154	0.0356
\|$[\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0204	0.0118	0.0280
	P_k-TNS	0.0288	0.0214	0.0420
RSD modelling	CLPT-GS	0.0218	0.0134	0.0356
\|$[\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0196	0.0124	0.0304
	P_k-TNS	0.0258	0.0178	0.0380
RSD modelling	CLPT-GS	0.0227	0.0141	0.0347
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0207	0.0115	0.0292
	P_k-TNS	0.0274	0.0193	0.0400
	CLPT-GS	0.8143	0.6700	0.7334
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.7097	0.5778	0.7300
	P_k-TNS	0.7667	0.6963	0.9524
	CLPT-GS	0.8357	0.7700	0.7911
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6581	0.6556	0.7000
	P_k-TNS	0.8000	0.7926	1.0000
	CLPT-GS	0.7786	0.6700	0.7911
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6323	0.6889	0.7600
	P_k-TNS	0.7167	0.6593	0.9048
	CLPT-GS	0.8095	0.7033	0.7718
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6667	0.6407	0.7300
	P_k-TNS	0.7611	0.7160	0.9524
	CLPT-GS	2.5334	3.3500	3.3000
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.6667	2.6000	3.6500
	P_k-TNS	4.3125	1.9789	4.8781
	CLPT-GS	2.6000	3.8000	3.5600
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4000	2.9500	3.5000
	P_k-TNS	4.5000	2.2526	5.1219
	CLPT-GS	2.4222	3.3500	3.5600
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.2667	3.1000	3.8000
	P_k-TNS	4.0312	1.8737	4.6341
	CLPT-GS	2.5185	3.5167	3.4733
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4445	2.8834	3.6500
	P_k-TNS	4.2812	2.0351	4.8780

Table 7.

See https://github.com/astropy/halotools

Modelling systematics derived from RSD FS analyses of the ‘Th2’ Outer Rim challenge mocks (see Tables A1 and A2).

RSD-FS analysis	Model. Syst.
Systematic type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0228	0.0134	0.0330
\|$[\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0220	0.0104	0.0292
	P_k-TNS	0.0276	0.0188	0.0400
RSD modelling	CLPT-GS	0.0234	0.0154	0.0356
\|$[\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0204	0.0118	0.0280
	P_k-TNS	0.0288	0.0214	0.0420
RSD modelling	CLPT-GS	0.0218	0.0134	0.0356
\|$[\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0196	0.0124	0.0304
	P_k-TNS	0.0258	0.0178	0.0380
RSD modelling	CLPT-GS	0.0227	0.0141	0.0347
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0207	0.0115	0.0292
	P_k-TNS	0.0274	0.0193	0.0400
	CLPT-GS	0.8143	0.6700	0.7334
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.7097	0.5778	0.7300
	P_k-TNS	0.7667	0.6963	0.9524
	CLPT-GS	0.8357	0.7700	0.7911
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6581	0.6556	0.7000
	P_k-TNS	0.8000	0.7926	1.0000
	CLPT-GS	0.7786	0.6700	0.7911
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6323	0.6889	0.7600
	P_k-TNS	0.7167	0.6593	0.9048
	CLPT-GS	0.8095	0.7033	0.7718
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6667	0.6407	0.7300
	P_k-TNS	0.7611	0.7160	0.9524
	CLPT-GS	2.5334	3.3500	3.3000
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.6667	2.6000	3.6500
	P_k-TNS	4.3125	1.9789	4.8781
	CLPT-GS	2.6000	3.8000	3.5600
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4000	2.9500	3.5000
	P_k-TNS	4.5000	2.2526	5.1219
	CLPT-GS	2.4222	3.3500	3.5600
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.2667	3.1000	3.8000
	P_k-TNS	4.0312	1.8737	4.6341
	CLPT-GS	2.5185	3.5167	3.4733
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4445	2.8834	3.6500
	P_k-TNS	4.2812	2.0351	4.8780

RSD-FS analysis	Model. Syst.
Systematic type	Model	\|$\sigma _{\alpha _\parallel }$\|	\|$\sigma _{\alpha _\perp }$\|	\|$\sigma _{\rm f \sigma _8}$\|
RSD modelling	CLPT-GS	0.0228	0.0134	0.0330
\|$[\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0220	0.0104	0.0292
	P_k-TNS	0.0276	0.0188	0.0400
RSD modelling	CLPT-GS	0.0234	0.0154	0.0356
\|$[\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0204	0.0118	0.0280
	P_k-TNS	0.0288	0.0214	0.0420
RSD modelling	CLPT-GS	0.0218	0.0134	0.0356
\|$[\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0196	0.0124	0.0304
	P_k-TNS	0.0258	0.0178	0.0380
RSD modelling	CLPT-GS	0.0227	0.0141	0.0347
\|$[\sigma _{\rm syst}^{\rm model, \rm {\small OR}}]$\|	CF-TNS	0.0207	0.0115	0.0292
	P_k-TNS	0.0274	0.0193	0.0400
	CLPT-GS	0.8143	0.6700	0.7334
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.7097	0.5778	0.7300
	P_k-TNS	0.7667	0.6963	0.9524
	CLPT-GS	0.8357	0.7700	0.7911
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6581	0.6556	0.7000
	P_k-TNS	0.8000	0.7926	1.0000
	CLPT-GS	0.7786	0.6700	0.7911
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6323	0.6889	0.7600
	P_k-TNS	0.7167	0.6593	0.9048
	CLPT-GS	0.8095	0.7033	0.7718
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/σ_stat	CF-TNS	0.6667	0.6407	0.7300
	P_k-TNS	0.7611	0.7160	0.9524
	CLPT-GS	2.5334	3.3500	3.3000
\|$\sigma _{\rm syst, LH}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.6667	2.6000	3.6500
	P_k-TNS	4.3125	1.9789	4.8781
	CLPT-GS	2.6000	3.8000	3.5600
\|$\sigma _{\rm syst, TK}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4000	2.9500	3.5000
	P_k-TNS	4.5000	2.2526	5.1219
	CLPT-GS	2.4222	3.3500	3.5600
\|$\sigma _{\rm syst, HE}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.2667	3.1000	3.8000
	P_k-TNS	4.0312	1.8737	4.6341
	CLPT-GS	2.5185	3.5167	3.4733
\|$\sigma _{\rm syst}^{\rm model, \rm {\small OR}}$\|/\|$\sigma _{\rm syst}^{\rm model, \rm {\small NS}}$\|	CF-TNS	3.4445	2.8834	3.6500
	P_k-TNS	4.2812	2.0351	4.8780

8 CONCLUSIONS AND OUTLOOK

In support of the final analysis of the eBOSS DR16 galaxy sample, we have carried out an extensive N-body data challenge with the aim of testing and validating the robustness of the LRG clustering pipelines of Bautista et al. (2020) in configuration space, and of Gil-Marín et al. (2020) in Fourier space. We have also quantified the theoretical systematics related to BAO and RSD fitting methodologies, and the bias intrinsic to the modelling of the galaxy–halo connection.

To this end, we have constructed new heterogeneous galaxy mocks from the Outer Rim simulation spanning different redshift intervals, using a variety of HOD schemes of increasing complexity and characterized by analogous clustering properties. The theoretical foundation for modelling the galaxy–halo connection is laid out in Section 3, and the mock-making procedure is explained in detail in Section 4. Moving from the most conventional HOD approach, we have considered more sophisticated scenarios able to distinguish between quiescent or star-forming galaxies, and with the inclusion of assembly bias that generalize further the standard HOD framework. Our Outer Rim-based mocks cover a range of number densities and effective volumes, and are well-suited for a variety of studies. In this work, we have mainly focused on a subset at z = 0.695, with characteristics closer to the eBOSS LRG sample (i.e. ‘Th2’ flavour with the Leauthaud, Tinker, and Hearin prescriptions). We have also briefly exploited a small homogeneous synthetic set (the nseries), which has been previously used in the SDSS DR12 galaxy clustering analysis and is more suitable to assess theoretical systematics at the sub-per cent level, thanks to a larger effective volume.

In our challenge, detailed in Section 6, we have tested the performance of BAO and RSD fitting techniques against different galaxy population schemes and bias models having analogous clustering properties, with the main objective of validation and calibration of such methods and the quantification of theoretical systematics. The mock products have allowed us to confront on a common ground and assess the performance of the BAO fitting methodologies for the LRG sample, and of three complementary RSD models in configuration and Fourier space – denoted as CLPT-GS, CF-TNS, and P_k-TNS, respectively. Overall, we have found a remarkable agreement at the sub-per cent level between different techniques in configuration and Fourier space (see in particular Figs 10, 11, and 12), along with an impressive level of consistency among BAO fitting and reconstruction procedures and from all the RSD models used in FS analyses. All of the methods performed equally well, with comparable errors on the AP parameters and the growth of structure. Moreover, reconstruction significantly improved the constraints on both α_∥ and α_⊥. We have thus validated the robustness of the LRG clustering analysis pipelines.

Including in our analysis the complexity of more sophisticated HODs schemes that go beyond the traditional mass-only ansatz, such as models with central and satellite velocity bias (Tinker 2007; Guo et al. 2015), generalizations of the standard five parameter HOD model with various halo-scale physics (Yuan et al. 2018; Duan & Eisenstein 2019; Xu et al. 2020; Xu & Zheng 2020), and forward-modelling approaches using satellite kinematics (Lange et al. 2019a, b; van den Bosch, Lange & Zentner 2019) is left to future studies. However, as pointed out by Duan & Eisenstein (2019), only a rather unrealistic extreme level of velocity bias of the central galaxies would produce a shift of 0.7 per cent in the LOS acoustic scale, and basically other bias models including satellite velocity bias are consistent with zero shift at the 0.2 per cent level after reconstruction. Since current surveys such as eBOSS measure the acoustic scale to |$\sim 1{{\ \rm per\ cent}}$| precision, they are insensitive to the galaxy bias effect – and we expect that similar conclusions will hold for the related AP parameters.

Regarding systematics and the global error budget (Section 7), we have found that the impact of different HOD prescriptions is always sub-dominant to the total systematics, and that modelling systematics in the estimation of α_∥ and fσ₈, although at worst around |$\sim 1.5{{\ \rm per\ cent}}$|⁠, may be a dominant source of error in the comprehensive quantification of systematics. In particular, from the analysis in configuration space of pre-reconstructed mocks (considering only fits to the mean), biases in the recovered α values reach up to |$0.5{{\ \rm per\ cent}}$| in α_⊥ and |$1.0{{\ \rm per\ cent}}$| in α_∥. After reconstruction, there is a reduction of the biases to less than |$0.2{{\ \rm per\ cent}}$|⁠, hence the BAO analysis is unbiased. For RSD analyses in configuration space, the most significant contribution to systematic errors arises from observational effects. From the Fourier space methodology, for the post-reconstruction BAO analysis we detected a |$0.5{{\ \rm per\ cent}}$| systematic shift induced by modelling systematic on α_∥, and none for α_⊥, with a resolution limit of |$0.2{{\ \rm per\ cent}}$| for the nseries mocks. The systematic shift is of order |$1.5{{\ \rm per\ cent}}$| for the FS analysis from Outer Rim mocks instead. Moreover, we did not detect any significant relative shift on the cosmological parameters when either the HOD model or the flavour is varied. Such results put constrains in the upper limit of systematic errors in the modelling, as a result of different HODs, with upper limits of order |$0.5\!-\!1.1{{\ \rm per\ cent}}$| systematic shifts. In any case, both HOD and modelling systematics are below the statistical error of the eBOSS LRG data. The expected statistical errors in the eBOSS LRG data sample are in fact of the order of |$\sim 1.9{{\ \rm per\ cent}}$| for α_⊥, and |$\sim 2.6{{\ \rm per\ cent}}$| for α_∥. Eventually, these systematic corrections in the AP parameters and the growth of structure are combined with additional sources of systematics (Table 6), and such errors are accounted for in the final consensus results (eBOSS Collaboration 2020) from the analysis of the LRG DR16 galaxy sample. Finally, our analysis provides a global and complementary perspective of the systematic studies carried out in Bautista et al. (2020) in configuration space, and in Gil-Marín et al. (2020) in Fourier space: their overall agreement at such level of precision is remarkable.

Quantifying the modelling systematics in BAO clustering estimators and in RSD methods for all the eBOSS tracers, as well as characterizing the robustness of the analysis pipelines, are essential tasks in order to obtain unbiased cosmological parameters, accurate fσ₈ constraints, and reliable consensus likelihoods. In this respect, besides being relevant for the final eBOSS DR16 ‘consensus cosmology’ – as the systematic error budget is informed by testing the results of analyses against these high-resolution mocks – our study represents also a testbed for future large-volume surveys. In particular, similar mock-making techniques and systematic corrections can be readily extended to model for instance the DESI galaxy sample, and we expect that more extensive mock challenges along these lines will be necessary and progressively relevant in the next few years. In fact, mock challenges designed to validate data analysis pipelines and assess the impact of systematics in massive data sets are becoming increasingly important for large-volume surveys – see for example the recent works by MacCrann et al. (2018) for the Dark Energy Survey (DES; The Dark Energy Survey Collaboration 2005), and by Sánchez et al. (2020) for LSST (Ivezić et al. 2019). In this view, while the sub-per cent level theoretical systematic corrections quantified in this study may not be relevant for the current state of the art (as they are always inferior to the statistical precision of the data), soon they will become relevant for DESI and LSST, that are expected to achieve sub-per cent statistical precision on the galaxy sample; for such surveys, it will be crucial to control the systematics at an extremely low level. To this end, our flexible and highly modular pipeline for building complex HODs offers several directions of extension, as well as applications that go beyond the modelling of LRGs – toward more elaborated galaxy–halo connection physics, particularly in relation to ELGs.

ACKNOWLEDGEMENTS

GR, PDC, and JM acknowledge support from the National Research Foundation of Korea (NRF) through Grants No. 2017R1E1A1A01077508 and No. 2020R1A2C1005655 funded by the Korean Ministry of Education, Science and Technology (MoEST), and from the faculty research fund of Sejong University. GR was on sabbatical leave in 2020, when this research was completed. Some numerical work performed in this paper was carried out using the Korea Institute of Science and Technology Information (KISTI) supercomputing infrastructure under allocations KSC-2018-G3-0008 and KSC-2018-T1-0061, and with computing resources at Sejong University (Xeon Silver 4114 master node and Xeon Gold 6126 computing node architecture).

HGM acknowledges support from la Caixa Foundation (ID 100010434) which code LCF/BQ/PI18/11630024.

RP, SdlT, and SE acknowledge support from the eBOSS ANR grant (under contract ANR-16-CE31-0021) and the OCEVU LABEX (Grant No. ANR-11-LABX-0060) of the French National Research Agency.

Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.

SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.

In addition, this research relied on resources provided to the eBOSS Collaboration by the National Energy Research Scientific Computing Center (NERSC). NERSC is a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.

DATA AVAILABILITY

All of the SDSS mock products developed in this study, listed in Table A1, are stored at the National Energy Research Scientific Computing Center (NERSC) and are available upon request. The Outer Rim halo catalogues used to produce the Outer Rim-based mocks are publicly available at https://cosmology.alcf.anl.gov.

Footnotes

1

A description of eBOSS and a link to its associated publications can be found at this URL: https://www.sdss.org/surveys/eboss/.

2

See github.com/desihub/redrock

3

Throughout the paper, we implicitly assume base 10 for all the logarithmic notations indicated with log, namely log ≡ log₁₀, and drop the understood subscript for clarity of notation.

4

As pointed out by Zheng et al. (2007), M_min can also be interpreted as the mass of such haloes for which half of them host galaxies above the given luminosity threshold, i.e. 〈N_cen(M_min)〉 = 0.5.

5

The Outer Rim halo catalogues used here are publicly available at https://cosmology.alcf.anl.gov

6

7

We have also devised an additional set which includes a variety of customizations, beyond the scope of the current analysis, exploring extreme variations in HOD parameters for all of the models, quenching, assembly bias, and modulations with the central distribution.

8

Another alternative would be to pursue instead a subhalo-type modelling approach, rather than the more traditional HOD framework, but we do not have access to full merger trees from the Outer Rim simulation.

REFERENCES

Alam

S.

et al. ,

2017

,

MNRAS

,

470

,

2617

10.1093/mnras/stx721

Alam

S.

et al. ,

2020

,

preprint (arXiv:2007.09004)

Alcock

C.

,

Paczynski

B.

,

1979

,

Nature

,

281

,

358

10.1038/281358a0

Alpaslan

M.

,

Tinker

J. L.

,

2020

,

MNRAS

,

496

,

5463

10.1093/mnras/staa1844

10.1088/1475-7516/2017/11/054

Assassi

V.

,

Simonovic

M.

,

Zaldarriaga

M.

,

2017

,

J. Cosmol. Astropart. Phys.

,

11

,

054

Ata

M.

et al. ,

2018

,

MNRAS

,

473

,

4773

10.1093/mnras/stx2630

10.1103/PhysRevD.92.123516

Aubourg

É.

et al. ,

2015

,

Phys. Rev. D

,

92

,

123516

Avila

S.

et al. ,

2020

,

MNRAS

,

499

,

5486

10.1093/mnras/staa2951

10.1103/PhysRevD.86.083540

Baldauf

T.

,

Seljak

U.

,

Desjacques

V.

,

McDonald

P.

,

2012

,

Phys. Rev. D

,

86

,

083540

Bautista

J. E.

et al. ,

2018

,

ApJ

,

863

,

110

10.3847/1538-4357/aacea5

Bautista

J. E.

et al. ,

2020

,

MNRAS

,

500

,

736

10.1093/mnras/staa2800

10.1088/0004-637X/717/1/379

Behroozi

P. S.

,

Conroy

C.

,

Wechsler

R. H.

,

2010

,

ApJ

,

717

,

379

10.1051/0004-6361/201834513

Bel

J.

,

Pezzotta

A.

,

Carbone

C.

,

Sefusatti

E.

,

Guzzo

L.

,

2019

,

A&A

,

622

,

A109

Berlind

A. A.

,

Weinberg

D. H.

,

2002

,

ApJ

,

575

,

587

10.1086/341469

Beutler

F.

et al. ,

2014

,

MNRAS

,

443

,

1065

10.1093/mnras/stu1051

Beutler

F.

et al. ,

2017a

,

MNRAS

,

464

,

3409

10.1093/mnras/stw2373

Beutler

F.

et al. ,

2017b

,

MNRAS

,

466

,

2242

10.1093/mnras/stw3298

Blanton

M. R.

,

Berlind

A. A.

,

2007

,

ApJ

,

664

,

791

10.1086/512478

Blanton

M. R.

et al. ,

2017

,

AJ

,

154

,

28

10.3847/1538-3881/aa7567

10.1051/0004-6361/201935641

Blomqvist

M.

et al. ,

2019

,

A&A

,

629

,

A86

Burden

A.

,

Percival

W. J.

,

Manera

M.

,

Cuesta

A. J.

,

Vargas Magana

M.

,

Ho

S.

,

2014

,

MNRAS

,

445

,

3152

10.1093/mnras/stu1965

Burden

A.

,

Percival

W. J.

,

Howlett

C.

,

2015

,

MNRAS

,

453

,

456

10.1093/mnras/stv1581

Carlson

J.

,

Reid

B.

,

White

M.

,

2013

,

MNRAS

,

429

,

1674

10.1093/mnras/sts457

Chuang

C.-H.

,

Kitaura

F.-S.

,

Prada

F.

,

Zhao

C.

,

Yepes

G.

,

2015

,

MNRAS

,

446

,

2621

10.1093/mnras/stu2301

10.1111/j.1365-2966.2005.09318.x

Cole

S.

et al. ,

2005

,

MNRAS

,

362

,

505

10.1051/0004-6361/201527377

Colless

M.

et al. ,

2003

,

preprint (arXiv:astro-ph/0306581)

Comparat

J.

et al. ,

2016

,

A&A

,

592

,

A121

Contreras

S.

,

Zehavi

I.

,

Baugh

C. M.

,

Padilla

N.

,

Norberg

P.

,

2017

,

MNRAS

,

465

,

2833

10.1093/mnras/stw2826

10.3847/0004-6256/151/2/44

Dawson

K. S.

et al. ,

2016

,

AJ

,

151

,

44

de Mattia

A.

et al. ,

2021

,

MNRAS

,

in press

10.1093/mnras/staa3891

10.1111/j.1365-2966.2012.21824.x

DESI Collaboration

,

2016

,

preprint (arXiv:1611.00036)

de la Torre

S.

,

Guzzo

L.

,

2012

,

MNRAS

,

427

,

327

10.1051/0004-6361/201630276

de la Torre

S.

et al. ,

2017

,

A&A

,

608

,

A44

10.1051/0004-6361/201935638

de Sainte Agathe

V.

et al. ,

2019

,

A&A

,

629

,

A85

du Mas des Bourboux

H.

et al. ,

2020

,

ApJ

,

901

,

153

10.3847/1538-4357/abb085

Duan

Y.

,

Eisenstein

D.

,

2019

,

MNRAS

,

490

,

2718

10.1093/mnras/stz2578

Dutton

A. A.

,

Macciò

A. V.

,

2014

,

MNRAS

,

441

,

3359

10.1093/mnras/stu742

10.1088/0004-6256/142/3/72

eBOSS Collaboration

,

2020

,

preprint (arXiv: 2007.08991)

Eisenstein

D. J.

et al. ,

2011

,

AJ

,

142

,

72

Eisenstein

D. J.

et al. ,

2005

,

ApJ

,

633

,

560

10.1086/466512

10.1088/1475-7516/2014/12/029

Gil-Marín

H.

,

Wagner

C.

,

Verde

L.

,

Porciani

C.

,

Jimenez

R.

,

2012

,

J. Cosmol. Astropart. Phys.

,

2012

,

029

Gil-Marín

H.

et al. ,

2016

,

MNRAS

,

460

,

4188

10.1093/mnras/stw1096

Gil-Marín

H.

,

Percival

W. J.

,

Verde

L.

,

Brownstein

J. R.

,

Chuang

C.-H.

,

Kitaura

F.-S.

,

Rodríguez-Torres

S. A.

,

Olmstead

M. D.

,

2017

,

MNRAS

,

465

,

1757

10.1093/mnras/stw2679

Gil-Marín

H.

et al. ,

2018

,

MNRAS

,

477

,

1604

10.1093/mnras/sty453

Gil-Marín

H.

et al. ,

2020

,

MNRAS

,

498

,

2492

10.1093/mnras/staa2455

Gunn

J. E.

et al. ,

2006

,

AJ

,

131

,

2332

10.1086/500975

Guo

H.

et al. ,

2015

,

MNRAS

,

453

,

4368

10.1093/mnras/stv1966

10.3847/0004-637X/831/1/3

Guo

H.

et al. ,

2016

,

ApJ

,

831

,

3

Guo

H.

et al. ,

2019

,

ApJ

,

871

,

147

10.3847/1538-4357/aaf9ad

10.1016/j.newast.2015.06.003

Habib

S.

et al. ,

2016

,

New A

,

42

,

49

Hadzhiyska

B.

,

Bose

S.

,

Eisenstein

D.

,

Hernquist

L.

,

Spergel

D. N.

,

2020

,

MNRAS

,

493

,

5506

10.1093/mnras/staa623

Hearin

A. P.

,

Zentner

A. R.

,

van den Bosch

F. C.

,

Campbell

D.

,

Tollerud

E.

,

2016

,

MNRAS

,

460

,

2552

10.1093/mnras/stw840

Hearin

A. P.

et al. ,

2017

,

AJ

,

154

,

190

10.3847/1538-3881/aa859f

Heitmann

K.

et al. ,

2019

,

ApJS

,

245

,

16

10.3847/1538-4365/ab4da1

Hou

J.

et al. ,

2018

,

MNRAS

,

480

,

2521

10.1093/mnras/sty1984

Hou

J.

et al. ,

2021

,

MNRAS

,

500

,

1201

10.1093/mnras/staa3234

Icaza-Lizaola

M.

et al. ,

2020

,

MNRAS

,

492

,

4189

10.1093/mnras/stz3602

Ivezić

Ž.

et al. ,

2019

,

ApJ

,

873

,

111

10.3847/1538-4357/ab042c

Kaiser

N.

,

1987

,

MNRAS

,

227

,

1

10.1093/mnras/227.1.1

10.1088/0067-0049/192/2/18

Komatsu

E.

et al. ,

2011

,

ApJS

,

192

,

18

Kravtsov

A. V.

,

Berlind

A. A.

,

Wechsler

R. H.

,

Klypin

A. A.

,

Gottlöber

S.

,

Allgood

B. o.

,

Primack

J. R.

,

2004

,

ApJ

,

609

,

35

10.1086/420959

Kravtsov

A. V.

,

Nagai

D.

,

Vikhlinin

A. A.

,

2005

,

ApJ

,

625

,

588

10.1086/429796

Landy

S. D.

,

Szalay

A. S.

,

1993

,

ApJ

,

412

,

64

10.1086/172900

Lange

J. U.

,

van den Bosch

F. C.

,

Zentner

A. R.

,

Wang

K.

,

Villarreal

A. S.

,

2019a

,

MNRAS

,

482

,

4824

10.1093/mnras/sty2950

Lange

J. U.

,

van den Bosch

F. C.

,

Zentner

A. R.

,

Wang

K.

,

Villarreal

A. S.

,

2019b

,

MNRAS

,

487

,

3112

10.1093/mnras/stz1466

10.1088/0004-637X/738/1/45

Leauthaud

A.

,

Tinker

J.

,

Behroozi

P. S.

,

Busha

M. T.

,

Wechsler

R. H.

,

2011

,

ApJ

,

738

,

45

10.1088/0004-637X/744/2/159

Leauthaud

A.

et al. ,

2012

,

ApJ

,

744

,

159

Lewis

A.

,

Challinor

A.

,

Lasenby

A.

,

2000

,

ApJ

,

538

,

473

10.1086/309179

Lin

S.

et al. ,

2020

,

MNRAS

,

498

,

5251

10.1093/mnras/staa2571

Lyke

B. W.

et al. ,

2020

,

ApJS

,

250

,

8

10.3847/1538-4365/aba623

MacCrann

N.

et al. ,

2018

,

MNRAS

,

480

,

4614

10.1093/mnras/sty1899

10.1103/PhysRevD.77.063530

Matsubara

T.

,

2008

,

Phys. Rev. D

,

77

,

063530

10.1088/1475-7516/2009/08/020

McDonald

P.

,

Roy

A.

,

2009

,

J. Cosmol. Astropart. Phys.

,

08

,

020

10.1103/PhysRevLett.116.041301

Miyatake

H.

,

More

S.

,

Takada

M.

,

Spergel

D. N.

,

Mandelbaum

R.

,

Rykoff

E. S.

,

Rozo

E.

,

2016

,

Phys. Rev. Lett.

,

116

,

041301

10.1051/0004-6361/201731685

Mohammad

F. G.

et al. ,

2018

,

A&A

,

610

,

A59

Mueller

E.-M.

,

Percival

W.

,

Linder

E.

,

Alam

S.

,

Zhao

G.-B.

,

Sánchez

A. G.

,

Beutler

F.

,

Brinkmann

J.

,

2018

,

MNRAS

,

475

,

2122

10.1093/mnras/stx3232

Navarro

J. F.

,

Frenk

C. S.

,

White

S. D. M.

,

1997

,

ApJ

,

490

,

493

10.1086/304888

Neveux

R.

et al. ,

2020

,

MNRAS

,

499

,

210

10.1093/mnras/staa2780

10.1088/1475-7516/2020/10/058

Obuljen

A.

,

Percival

W. J.

,

Dalal

N.

,

2020

,

J. Cosmol. Astropart. Phys.

,

2020

,

058

10.1046/j.1365-8711.2000.03779.x

Peacock

J. A.

,

Smith

R. E.

,

2000

,

MNRAS

,

318

,

1144

10.3847/0067-0049/224/2/34

Prakash

A.

et al. ,

2016

,

ApJS

,

224

,

34

Raichoor

A.

et al. ,

2017

,

MNRAS

,

471

,

3955

10.1093/mnras/stx1790

Raichoor

A.

et al. ,

2020

,

MNRAS

,

498

,

2354

10.1093/mnras/staa2416

10.1111/j.1365-2966.2011.19379.x

Reid

B. A.

,

White

M.

,

2011

,

MNRAS

,

417

,

1913

Ross

A. J.

et al. ,

2020

,

MNRAS

,

498

,

2354

10.1093/mnras/staa2416

Ruggeri

R.

et al. ,

2019

,

MNRAS

,

483

,

3878

10.1093/mnras/sty3395

10.1103/PhysRevD.90.123522

Saito

S.

,

Baldauf

T.

,

Vlah

Z.

,

Seljak

U.

,

Okumura

T.

,

McDonald

P.

,

2014

,

Phys. Rev. D

,

90

,

123522

Sánchez

F. J.

et al. ,

2020

,

MNRAS

,

497

,

210

10.1093/mnras/staa1957

10.1103/PhysRevD.70.083007

Scoccimarro

R.

,

2004

,

Phys. Rev. D

,

70

,

083007

Scoccimarro

R.

,

Zaldarriaga

M.

,

Hui

L.

,

1999

,

ApJ

,

527

,

1

10.1086/308059

Scoccimarro

R.

,

Sheth

R. K.

,

Hui

L.

,

Jain

B.

,

2001

,

ApJ

,

546

,

20

10.1086/318261

10.1046/j.1365-8711.2000.03715.x

Seljak

U.

,

2000

,

MNRAS

,

318

,

203

Smith

A.

et al. ,

2020

,

MNRAS

,

499

,

269

10.1093/mnras/staa2825

10.1111/j.1365-2966.2005.09655.x

Springel

V.

,

2005

,

MNRAS

,

364

,

1105

Tamone

A.

et al. ,

2020

,

MNRAS

,

499

,

5527

10.1093/mnras/staa3050

10.1103/PhysRevD.82.063522

Taruya

A.

,

Nishimichi

T.

,

Saito

S.

,

2010

,

Phys. Rev. D

,

82

,

063522

10.1111/j.1365-2966.2006.11157.x

The Dark Energy Survey Collaboration

,

2005

,

preprint (arXiv:astro-ph/0510346)

Tinker

J. L.

,

2007

,

MNRAS

,

374

,

477

10.1088/0004-637X/778/2/93

Tinker

J. L.

,

Leauthaud

A.

,

Bundy

K.

,

George

M. R.

,

Behroozi

P.

,

Massey

R.

,

Rhodes

J.

,

Wechsler

R. H.

,

2013

,

ApJ

,

778

,

93

Tinker

J. L.

,

Cao

J.

,

Alpaslan

M.

,

DeRose

J.

,

Mao

Y.-Y.

,

Wechsler

R. H.

,

2019

,

preprint (arXiv:1911.04507)

van den Bosch

F. C.

,

Lange

J. U.

,

Zentner

A. R.

,

2019

,

MNRAS

,

488

,

4984

10.1093/mnras/stz2017

Vargas-Magaña

M.

et al. ,

2018

,

MNRAS

,

477

,

1153

10.1093/mnras/sty571

Wang

L.

,

Reid

B.

,

White

M.

,

2014

,

MNRAS

,

437

,

588

10.1093/mnras/stt1916

Wang

D.

et al. ,

2018a

,

MNRAS

,

477

,

1528

10.1093/mnras/sty654

Wang

Y.

,

Zhao

G.-B.

,

Chuang

C.-H.

,

Pellejero-Ibanez

M.

,

Zhao

C.

,

Kitaura

F.-S.

,

Rodriguez-Torres

S.

,

2018b

,

MNRAS

,

481

,

3160

10.1093/mnras/sty2449

Wechsler

R. H.

,

Zentner

A. R.

,

Bullock

J. S.

,

Kravtsov

A. V.

,

Allgood

B.

,

2006

,

ApJ

,

652

,

71

10.1086/507120

10.1088/0067-0049/195/1/11

Woodring

J.

,

Heitmann

K.

,

Ahrens

J.

,

Fasel

P.

,

Hsu

C.-H.

,

Habib

S.

,

Pope

A.

,

2011

,

ApJS

,

195

,

11

Xu

X.

,

Zheng

Z.

,

2020

,

MNRAS

,

492

,

2739

10.1093/mnras/staa009

Xu

X.

,

Cuesta

A. J.

,

Padmanabhan

N.

,

Eisenstein

D. J.

,

McBride

C. K.

,

2013

,

MNRAS

,

431

,

2834

10.1093/mnras/stt379

10.1111/j.1365-2966.2006.11091.x

Xu

X.

,

Zehavi

I.

,

Contreras

S.

,

2020

,

preprint (arXiv:2007.05545)

Yang

X.

,

Mo

H. J.

,

van den Bosch

F. C.

,

Jing

Y. P.

,

Weinmann

S. M.

,

Meneghetti

M.

,

2006

,

MNRAS

,

373

,

1159

York

D. G.

et al. ,

2000

,

AJ

,

120

,

1579

10.1086/301513

Yuan

S.

,

Eisenstein

D. J.

,

Garrison

L. H.

,

2018

,

MNRAS

,

478

,

2019

10.1093/mnras/sty1089

Yuan

S.

,

Hadzhiyska

B.

,

Bose

S.

,

Eisenstein

D. J.

,

Guo

H.

,

2020

,

preprint (arXiv:2010.04182)

Zarrouk

P.

et al. ,

2018

,

MNRAS

,

477

,

1639

10.1093/mnras/sty506

Zel’dovich

Y. B.

,

1970

,

Astrofizika

,

6

,

319

Zentner

A. R.

,

Hearin

A. P.

,

van den Bosch

F. C.

,

2014

,

MNRAS

,

443

,

3044

10.1093/mnras/stu1383

Zentner

A. R.

,

Hearin

A.

,

van den Bosch

F. C.

,

Lange

J. U.

,

Villarreal

A.

,

2019

,

MNRAS

,

485

,

1196

10.1093/mnras/stz470

Zhao

C.

et al. ,

2020

,

preprint (arXiv:2007.08997)

Zhao

G.-B.

et al. ,

2019

,

MNRAS

,

482

,

3497

10.1093/mnras/sty2845

Zheng

Z.

,

Coil

A. L.

,

Zehavi

I.

,

2007

,

ApJ

,

667

,

760

10.1086/521074

Zheng

Z.

et al. ,

2005

,

ApJ

,

633

,

791

10.1086/466510

Zheng

J.

,

Zhao

G.-B.

,

Li

J.

,

Wang

Y.

,

Chuang

C.-H.

,

Kitaura

F.-S.

,

Rodriguez-Torres

S.

,

2019

,

MNRAS

,

484

,

442

10.1093/mnras/stz026

Zhu

F.

et al. ,

2018

,

MNRAS

,

480

,

1096

10.1093/mnras/sty1955

Zu

Y.

,

Mandelbaum

R.

,

Simet

M.

,

Rozo

E.

,

Rykoff

E. S.

,

2017

,

MNRAS

,

470

,

551

10.1093/mnras/stx1264

APPENDIX A: MOCK PRODUCTS

We have devised three sets of heterogeneous Outer Rim-based galaxy mocks (indicated as ‘Challenge Set 1’, ‘Challenge Set 2’, ‘Challenge Set 3’, respectively) for the galaxy mock challenge. These are cubic mocks, in the Outer Rim cosmology, obtained by populating Outer Rim halo catalogues with galaxies as explained in Section 4.1. Details regarding each set are provided next.

Specifically, ‘Challenge Set 1’ (HOD VARIATIONS) contains a total of 3240 mocks (1620 at z = 0.695, and 1620 at z = 0.865), grouped into four model categories according to the underlying HOD scheme (i.e. Zheng, Leauthaud, Tinker, Hearin); each model category consists of three ‘flavours’, denoted as ‘Standard’ (Std), ‘Threshold 1’ (Th1), and ‘Threshold 2’ (Th2). As explained in Sections 3 and 4.4, the meaning of ‘flavour’ is related to the key parameter ‘threshold’, which globally sets all the individual HOD parameters as best-fitting realizations from the corresponding literature dictionary of each HOD model (unless specific customizations are introduced). At a given redshift, we produced 135 mocks per model flavour, by populating the full |$3 \, h^{-1} \, {\rm Gpc}$| Outer Rim periodic halo catalogue box five times, and then cutting each full box into 27 subcubes of |$1h^{-1}\, {\rm Gpc}$| side and rescaling the various spatial positions accordingly. This means that effectively we have 27 fully independent (i.e. not sharing the same DM field) mocks per realization, and each of these 27 mocks will have five different replicas. According to the modelling explained in Section 3, central galaxies are always located at the centre of their parent haloes with identical velocities, while the satellite population is statistically different in all the realizations – assuming a NFW profile. We then add RSDs to each individual mock in two different ways: radially, or with the usual plane-parallel approximation. This is the primary set considered in our main analysis presented in Section 6.

‘Challenge Set 2’ (REDSHIFT EVOLUTION) is similar to the previous one, but now the redshift evolution is taken into account for one threshold flavour and three different HOD prescriptions. In detail, we consider seven redshift intervals, namely z = 0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006, and produced a set of 2835 mocks (135 × 7 × 3) with three HOD schemes (Leauthaud, Tinker, Hearin), for the ‘Th1’ flavour. Even in this case, we consider subcubes of |$1h^{-1}\, {\rm Gpc}$| side.

Finally, ‘Challenge Set 3’ (HOD VARIATIONS / LARGE BOX) is similar to the first one, but in this case we exploit the full Outer Rim box (⁠|$3h^{-1}\, {\rm Gpc}$|⁠) with periodic boundary conditions rather than subcubes, and produced 100 realizations per flavour for all the HODs and thresholds considered in the first set – for a total of 2400 mocks. If desirable, these large-box realizations can be casted into smaller pseudo-independent mocks by performing cuts along different directions of the boxes, and also via the inclusion of partial overlaps in order to maximize the effective volume.

Regardless of the specific set, each mock contains the following information: galaxy spatial positions (in |$h^{-1}\, {\rm Mpc}$|⁠), galaxy velocities (in comoving km s⁻¹), the galaxy type (central, satellite), the number of centrals that a halo hosts (either 0 or 1), the number of satellites per halo, the global ID of the halo a galaxy belongs to, the halo mass and virial radius, the central star formation designation for some models (active, quiescent), the number of active or quiescent satellites, and the percentile spit in concentration for models with assembly bias.

A summary of all the synthetic products available, categorized by HOD and redshift, is provided in Table A1. While only a subset of these mocks is used for testing the BAO templates and the RSD models adopted for the characterization of LRG clustering systematics, with this work we release the entire suite of products – that are suitable to several interesting applications.

Table A1.

List of Outer Rim synthetic products developed for the galaxy mock challenge.

Set	HOD Style	HOD Flavour	Redshift	Box [\|$h^{-1}\, {\rm Gpc}$\|]	Total mocks
	Zheng07	Th1, Std, Th2	0.695, 0.865	1.0	810
Challenge Set 1	Leauthaud11	Th1, Std, Th2	0.695, 0.865	1.0	810
	Tinker13	Th1, Std, Th2	0.695, 0.865	1.0	810
	Hearin15	Th1, Std, Th2	0.695, 0.865	1.0	810
					3240
	Leauthaud11	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
Challenge Set 2	Tinker13	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
	Hearin15	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
					2835
	Zheng07	Th1, Std, Th2	0.695, 0.865	3.0	600
Challenge Set 3	Leauthaud11	Th1, Std, Th2	0.695, 0.865	3.0	600
	Tinker13	Th1, Std, Th2	0.695, 0.865	3.0	600
	Hearin15	Th1, Std, Th2	0.695, 0.865	3.0	600
					2400

Set	HOD Style	HOD Flavour	Redshift	Box [\|$h^{-1}\, {\rm Gpc}$\|]	Total mocks
	Zheng07	Th1, Std, Th2	0.695, 0.865	1.0	810
Challenge Set 1	Leauthaud11	Th1, Std, Th2	0.695, 0.865	1.0	810
	Tinker13	Th1, Std, Th2	0.695, 0.865	1.0	810
	Hearin15	Th1, Std, Th2	0.695, 0.865	1.0	810
					3240
	Leauthaud11	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
Challenge Set 2	Tinker13	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
	Hearin15	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
					2835
	Zheng07	Th1, Std, Th2	0.695, 0.865	3.0	600
Challenge Set 3	Leauthaud11	Th1, Std, Th2	0.695, 0.865	3.0	600
	Tinker13	Th1, Std, Th2	0.695, 0.865	3.0	600
	Hearin15	Th1, Std, Th2	0.695, 0.865	3.0	600
					2400

Table A1.

List of Outer Rim synthetic products developed for the galaxy mock challenge.

Set	HOD Style	HOD Flavour	Redshift	Box [\|$h^{-1}\, {\rm Gpc}$\|]	Total mocks
	Zheng07	Th1, Std, Th2	0.695, 0.865	1.0	810
Challenge Set 1	Leauthaud11	Th1, Std, Th2	0.695, 0.865	1.0	810
	Tinker13	Th1, Std, Th2	0.695, 0.865	1.0	810
	Hearin15	Th1, Std, Th2	0.695, 0.865	1.0	810
					3240
	Leauthaud11	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
Challenge Set 2	Tinker13	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
	Hearin15	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
					2835
	Zheng07	Th1, Std, Th2	0.695, 0.865	3.0	600
Challenge Set 3	Leauthaud11	Th1, Std, Th2	0.695, 0.865	3.0	600
	Tinker13	Th1, Std, Th2	0.695, 0.865	3.0	600
	Hearin15	Th1, Std, Th2	0.695, 0.865	3.0	600
					2400

Set	HOD Style	HOD Flavour	Redshift	Box [\|$h^{-1}\, {\rm Gpc}$\|]	Total mocks
	Zheng07	Th1, Std, Th2	0.695, 0.865	1.0	810
Challenge Set 1	Leauthaud11	Th1, Std, Th2	0.695, 0.865	1.0	810
	Tinker13	Th1, Std, Th2	0.695, 0.865	1.0	810
	Hearin15	Th1, Std, Th2	0.695, 0.865	1.0	810
					3240
	Leauthaud11	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
Challenge Set 2	Tinker13	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
	Hearin15	Th1	0.402, 0.502, 0.618, 0.695, 0.779, 0.865, 1.006	1.0	945
					2835
	Zheng07	Th1, Std, Th2	0.695, 0.865	3.0	600
Challenge Set 3	Leauthaud11	Th1, Std, Th2	0.695, 0.865	3.0	600
	Tinker13	Th1, Std, Th2	0.695, 0.865	3.0	600
	Hearin15	Th1, Std, Th2	0.695, 0.865	3.0	600
					2400

Table A2 reports the number densities of the challenge mocks, expressed in units of 10⁻⁴[h³Mpc⁻³], and ordered by HOD type and flavour. The ‘Th2’ models of Leauthaud, Tinker, and Hearin are those characterized by a number density closer to the eBOSS LRG sample (see e.g. fig. 1 in Gil-Marín et al. 2020 and fig. 1 in Bautista et al. 2020 for details), and are extensively used in Section 6 to test the LRG BAO and RSD analysis pipelines. The other threshold levels are more suitable for example for assessing the details of the satellite distributions and for studying the galaxy–halo connection, particularly in relation to ELGs; they are only marginally explored in this work, although of high interest, and left to future applications.

Table A2.

Number densities of the challenge mocks listed in Table A1, ordered per HOD type and flavour.

Number density [\|$10^{-4} \, (h^3\, {\rm Mpc}^{-3})$\|]
HOD model	Th1	Std	Th2
Zheng07	67.05	34.26	5.64
Leauthaud11	50.55	11.85	0.69
Tinker13	26.37	8.12	0.79
Hearin15	44.93	10.82	0.69

Number density [\|$10^{-4} \, (h^3\, {\rm Mpc}^{-3})$\|]
HOD model	Th1	Std	Th2
Zheng07	67.05	34.26	5.64
Leauthaud11	50.55	11.85	0.69
Tinker13	26.37	8.12	0.79
Hearin15	44.93	10.82	0.69

Table A2.

Number densities of the challenge mocks listed in Table A1, ordered per HOD type and flavour.

Number density [\|$10^{-4} \, (h^3\, {\rm Mpc}^{-3})$\|]
HOD model	Th1	Std	Th2
Zheng07	67.05	34.26	5.64
Leauthaud11	50.55	11.85	0.69
Tinker13	26.37	8.12	0.79
Hearin15	44.93	10.82	0.69

Number density [\|$10^{-4} \, (h^3\, {\rm Mpc}^{-3})$\|]
HOD model	Th1	Std	Th2
Zheng07	67.05	34.26	5.64
Leauthaud11	50.55	11.85	0.69
Tinker13	26.37	8.12	0.79
Hearin15	44.93	10.82	0.69

Fig. A1 shows examples of the 3D galaxy clustering quantified by the 2-point spatial correlation ξ(r), as a function of separation r. The various measurements are performed at z = 0.695 (top panels) and at z = 0.865 (bottom panels), for the mocks belonging to ‘Challenge Set 1’. From left to right, the ‘Th1’, ‘Std’, and ‘Th2’ flavours are displayed, respectively. The HOD models of Leauthaud (blue), Tinker (red), and Hearin (green) are displayed with different colours: they are characterized by approximately similar clustering properties, at a fixed threshold level. Each measurement represents an average over 135 mocks, according to the specific HOD style and flavour, and errorbars are 1σ variations. The effect of a decreasing number density (from left to right) is of an overall increase in the clustering and BAO peak amplitude, with a relatively small redshift dependence.

Figure A1.

Clustering properties of the ‘Challenge Set 1’. Examples of 2-point spatial correlation functions computed at z = 0.695 (top panels) and at z = 0.865 (bottom panels), for the three threshold levels denoted as ‘Th1’, ‘Std’, and ‘Th2’ – in decreasing number density order, from left to right. The Leauthaud (blue), Tinker (red), and Hearin (green) HOD models are displayed with different colours. They are characterized by approximately similar clustering properties, at a fixed threshold level.

Finally, Fig. A2 displays an example of the 2-point spatial clustering of satellites, split by active/star-forming (blue) and quiescent (red) galaxies, at z = 0.865 for the ‘Std’ threshold level (see Table A2). The Tinker HOD formalism used in this work – primarily for LRG studies – could also potentially provide interesting applications to ELGs that go beyond the scope of this paper, and that highlight the flexibility of our mock-making procedure and mock products in exploring the physics of the galaxy–halo connection.

Figure A2.

Spatial clustering of satellite galaxies at z = 0.865, split by active/star-forming (blue) and quiescent (red) – as described by the Tinker model for the ‘Std’ threshold level. This more complex HOD framework provides interesting insights on the galaxy–halo connection physics.

APPENDIX B: USEFUL TABLES

We provide here some useful tables with numerical results that appear in the various plots displayed in the manuscript, for the ease of direct comparisons, or that include additional information not reported in the main text.

Specifically, Table B1 contains results from the BAO and RSD analyses in Fourier space related to the Zheng model – see also our companion paper Gil-Marín et al. (2020) for additional extensive details.

Table B1.

Impact of the Zheng HOD model, presented in three different flavours (see Table 1), on pre-reconstructed BAO and FS fits on OR cubic boxes (1|$h^{-1}\, {\rm Gpc}$|⁠; ‘Challenge Set 1’), from a Fourier space analysis. For simplicity, only the fit to the mean is provided – see Gil-Marín et al. (2020) for extensive details.

Analysis type	HOD type	HOD flavour	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|
BAO Fourier space	Zheng	Th1	0.0270 ± 0.0110	−0.0006 ± 0.0062	–
[Pre-Rec]	Zheng	Std	0.0240 ± 0.0100	−0.0005 ± 0.0060	–
	Zheng	Th2	0.0310 ± 0.0130	−0.0014 ± 0.0075	–
RSD Fourier space	Zheng	Th1	0.0107 ± 0.0069	−0.0035 ± 0.0052	−0.0085 ± 0.0073
[Pre-Rec]	Zheng	Std	0.0108 ± 0.0067	−0.0025 ± 0.0051	−0.0083 ± 0.0065
	Zheng	Th2	0.0138 ± 0.0095	−0.0049 ± 0.0072	0.0080 ± 0.0130

Analysis type	HOD type	HOD flavour	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|
BAO Fourier space	Zheng	Th1	0.0270 ± 0.0110	−0.0006 ± 0.0062	–
[Pre-Rec]	Zheng	Std	0.0240 ± 0.0100	−0.0005 ± 0.0060	–
	Zheng	Th2	0.0310 ± 0.0130	−0.0014 ± 0.0075	–
RSD Fourier space	Zheng	Th1	0.0107 ± 0.0069	−0.0035 ± 0.0052	−0.0085 ± 0.0073
[Pre-Rec]	Zheng	Std	0.0108 ± 0.0067	−0.0025 ± 0.0051	−0.0083 ± 0.0065
	Zheng	Th2	0.0138 ± 0.0095	−0.0049 ± 0.0072	0.0080 ± 0.0130

Table B1.

Impact of the Zheng HOD model, presented in three different flavours (see Table 1), on pre-reconstructed BAO and FS fits on OR cubic boxes (1|$h^{-1}\, {\rm Gpc}$|⁠; ‘Challenge Set 1’), from a Fourier space analysis. For simplicity, only the fit to the mean is provided – see Gil-Marín et al. (2020) for extensive details.

Analysis type	HOD type	HOD flavour	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|
BAO Fourier space	Zheng	Th1	0.0270 ± 0.0110	−0.0006 ± 0.0062	–
[Pre-Rec]	Zheng	Std	0.0240 ± 0.0100	−0.0005 ± 0.0060	–
	Zheng	Th2	0.0310 ± 0.0130	−0.0014 ± 0.0075	–
RSD Fourier space	Zheng	Th1	0.0107 ± 0.0069	−0.0035 ± 0.0052	−0.0085 ± 0.0073
[Pre-Rec]	Zheng	Std	0.0108 ± 0.0067	−0.0025 ± 0.0051	−0.0083 ± 0.0065
	Zheng	Th2	0.0138 ± 0.0095	−0.0049 ± 0.0072	0.0080 ± 0.0130

Analysis type	HOD type	HOD flavour	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|
BAO Fourier space	Zheng	Th1	0.0270 ± 0.0110	−0.0006 ± 0.0062	–
[Pre-Rec]	Zheng	Std	0.0240 ± 0.0100	−0.0005 ± 0.0060	–
	Zheng	Th2	0.0310 ± 0.0130	−0.0014 ± 0.0075	–
RSD Fourier space	Zheng	Th1	0.0107 ± 0.0069	−0.0035 ± 0.0052	−0.0085 ± 0.0073
[Pre-Rec]	Zheng	Std	0.0108 ± 0.0067	−0.0025 ± 0.0051	−0.0083 ± 0.0065
	Zheng	Th2	0.0138 ± 0.0095	−0.0049 ± 0.0072	0.0080 ± 0.0130

Table B2 reports the results when fitting the mean correlation functions and power spectra (rows labelled ‘Mean’) of a set of 27 independent realizations of the OR-based mocks with different HOD prescriptions (‘Challenge Set 1’), as well as the mean of the fits of individual realizations (rows labelled ‘Individual’), in relation to the BAO analyses presented in Section 6.2.

Table B2.

Performance of the BAO templates on OR-based mocks, for the ‘Th2’ flavour and different HOD models. Mocks are analysed in their own Outer Rim cosmology, so the expected values for both α_∥ and α_⊥ are 1. For each set of mocks, the results from pre- and post-reconstruction catalogues are presented. We report both the results of fitting the mean of all the mocks, indicated with ‘Mean’, and the mean of individual fits on the mocks, indicated as ‘Individual’. For the fit to the mean, the error quoted is the 1σ of the error on this fit, where the covariances are scaled by the 27 Outer Rim realizations per HOD used to compute the mean. For the mean of individual best-fits, the error quoted is the rms divided by |$\sqrt{N_{\rm OR}}$|⁠, where N_OR = 27. The average of the best-fits is then performed over N_OR. Consequently, the errors of ‘Mean’ and ‘Individual’ are comparable. Results of these fits are displayed in Fig. 10.

BAO analysis type	HOD Type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	0.0084 ± 0.0164	−0.0010 ± 0.0080	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0283 ± 0.0197	−0.0072 ± 0.0123	27/27
	Tinker	Th2	Mean	0.0234 ± 0.0147	−0.0078 ± 0.0073	1/1
	Tinker	Th2	Individual	0.0166 ± 0.0172	0.0000 ± 0.0104	27/27
	Hearin	Th2	Mean	0.0040 ± 0.0157	0.0074 ± 0.0083	1/1
	Hearin	Th2	Individual	0.0035 ± 0.0185	0.0090 ± 0.0089	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0063 ± 0.0084	0.0045 ± 0.0056	1/1
[Post-Rec]	Leauthaud	Th2	Individual	−0.0050 ± 0.0108	0.0053 ± 0.0063	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0090	0.0014 ± 0.0060	1/1
	Tinker	Th2	Individual	0.0078 ± 0.0103	−0.0017 ± 0.0065	27/27
	Hearin	Th2	Mean	0.0115 ± 0.0094	0.0066 ± 0.0057	1/1
	Hearin	Th2	Individual	0.0019 ± 0.0097	0.0087 ± 0.0054	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0114 ± 0.0178	0.0028 ± 0.0107	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0000 ± 0.0180	0.0110 ± 0.0120	27/27
	Tinker	Th2	Mean	0.0023 ± 0.0177	−0.0047 ± 0.0124	1/1
	Tinker	Th2	Individual	−0.0110 ± 0.0160	0.0230 ± 0.0110	27/27
	Hearin	Th2	Mean	−0.0221 ± 0.0143	0.0108 ± 0.0099	1/1
	Hearin	Th2	Individual	−0.0210 ± 0.0160	0.0160 ± 0.0110	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0062 ± 0.0104	−0.0024 ± 0.0075	1/1
[Post-Rec]	Leauthaud	Th2	Individual	0.0020 ± 0.0130	−0.0093 ± 0.0074	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0121	−0.0025 ± 0.0088	1/1
	Tinker	Th2	Individual	0.0038 ± 0.0097	−0.0006 ± 0.0072	27/27
	Hearin	Th2	Mean	0.0002 ± 0.0113	0.0122 ± 0.0075	1/1
	Hearin	Th2	Individual	0.0090 ± 0.0150	0.0167 ± 0.0061	27/27

BAO analysis type	HOD Type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	0.0084 ± 0.0164	−0.0010 ± 0.0080	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0283 ± 0.0197	−0.0072 ± 0.0123	27/27
	Tinker	Th2	Mean	0.0234 ± 0.0147	−0.0078 ± 0.0073	1/1
	Tinker	Th2	Individual	0.0166 ± 0.0172	0.0000 ± 0.0104	27/27
	Hearin	Th2	Mean	0.0040 ± 0.0157	0.0074 ± 0.0083	1/1
	Hearin	Th2	Individual	0.0035 ± 0.0185	0.0090 ± 0.0089	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0063 ± 0.0084	0.0045 ± 0.0056	1/1
[Post-Rec]	Leauthaud	Th2	Individual	−0.0050 ± 0.0108	0.0053 ± 0.0063	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0090	0.0014 ± 0.0060	1/1
	Tinker	Th2	Individual	0.0078 ± 0.0103	−0.0017 ± 0.0065	27/27
	Hearin	Th2	Mean	0.0115 ± 0.0094	0.0066 ± 0.0057	1/1
	Hearin	Th2	Individual	0.0019 ± 0.0097	0.0087 ± 0.0054	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0114 ± 0.0178	0.0028 ± 0.0107	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0000 ± 0.0180	0.0110 ± 0.0120	27/27
	Tinker	Th2	Mean	0.0023 ± 0.0177	−0.0047 ± 0.0124	1/1
	Tinker	Th2	Individual	−0.0110 ± 0.0160	0.0230 ± 0.0110	27/27
	Hearin	Th2	Mean	−0.0221 ± 0.0143	0.0108 ± 0.0099	1/1
	Hearin	Th2	Individual	−0.0210 ± 0.0160	0.0160 ± 0.0110	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0062 ± 0.0104	−0.0024 ± 0.0075	1/1
[Post-Rec]	Leauthaud	Th2	Individual	0.0020 ± 0.0130	−0.0093 ± 0.0074	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0121	−0.0025 ± 0.0088	1/1
	Tinker	Th2	Individual	0.0038 ± 0.0097	−0.0006 ± 0.0072	27/27
	Hearin	Th2	Mean	0.0002 ± 0.0113	0.0122 ± 0.0075	1/1
	Hearin	Th2	Individual	0.0090 ± 0.0150	0.0167 ± 0.0061	27/27

Table B2.

Performance of the BAO templates on OR-based mocks, for the ‘Th2’ flavour and different HOD models. Mocks are analysed in their own Outer Rim cosmology, so the expected values for both α_∥ and α_⊥ are 1. For each set of mocks, the results from pre- and post-reconstruction catalogues are presented. We report both the results of fitting the mean of all the mocks, indicated with ‘Mean’, and the mean of individual fits on the mocks, indicated as ‘Individual’. For the fit to the mean, the error quoted is the 1σ of the error on this fit, where the covariances are scaled by the 27 Outer Rim realizations per HOD used to compute the mean. For the mean of individual best-fits, the error quoted is the rms divided by |$\sqrt{N_{\rm OR}}$|⁠, where N_OR = 27. The average of the best-fits is then performed over N_OR. Consequently, the errors of ‘Mean’ and ‘Individual’ are comparable. Results of these fits are displayed in Fig. 10.

BAO analysis type	HOD Type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	0.0084 ± 0.0164	−0.0010 ± 0.0080	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0283 ± 0.0197	−0.0072 ± 0.0123	27/27
	Tinker	Th2	Mean	0.0234 ± 0.0147	−0.0078 ± 0.0073	1/1
	Tinker	Th2	Individual	0.0166 ± 0.0172	0.0000 ± 0.0104	27/27
	Hearin	Th2	Mean	0.0040 ± 0.0157	0.0074 ± 0.0083	1/1
	Hearin	Th2	Individual	0.0035 ± 0.0185	0.0090 ± 0.0089	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0063 ± 0.0084	0.0045 ± 0.0056	1/1
[Post-Rec]	Leauthaud	Th2	Individual	−0.0050 ± 0.0108	0.0053 ± 0.0063	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0090	0.0014 ± 0.0060	1/1
	Tinker	Th2	Individual	0.0078 ± 0.0103	−0.0017 ± 0.0065	27/27
	Hearin	Th2	Mean	0.0115 ± 0.0094	0.0066 ± 0.0057	1/1
	Hearin	Th2	Individual	0.0019 ± 0.0097	0.0087 ± 0.0054	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0114 ± 0.0178	0.0028 ± 0.0107	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0000 ± 0.0180	0.0110 ± 0.0120	27/27
	Tinker	Th2	Mean	0.0023 ± 0.0177	−0.0047 ± 0.0124	1/1
	Tinker	Th2	Individual	−0.0110 ± 0.0160	0.0230 ± 0.0110	27/27
	Hearin	Th2	Mean	−0.0221 ± 0.0143	0.0108 ± 0.0099	1/1
	Hearin	Th2	Individual	−0.0210 ± 0.0160	0.0160 ± 0.0110	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0062 ± 0.0104	−0.0024 ± 0.0075	1/1
[Post-Rec]	Leauthaud	Th2	Individual	0.0020 ± 0.0130	−0.0093 ± 0.0074	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0121	−0.0025 ± 0.0088	1/1
	Tinker	Th2	Individual	0.0038 ± 0.0097	−0.0006 ± 0.0072	27/27
	Hearin	Th2	Mean	0.0002 ± 0.0113	0.0122 ± 0.0075	1/1
	Hearin	Th2	Individual	0.0090 ± 0.0150	0.0167 ± 0.0061	27/27

BAO analysis type	HOD Type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	0.0084 ± 0.0164	−0.0010 ± 0.0080	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0283 ± 0.0197	−0.0072 ± 0.0123	27/27
	Tinker	Th2	Mean	0.0234 ± 0.0147	−0.0078 ± 0.0073	1/1
	Tinker	Th2	Individual	0.0166 ± 0.0172	0.0000 ± 0.0104	27/27
	Hearin	Th2	Mean	0.0040 ± 0.0157	0.0074 ± 0.0083	1/1
	Hearin	Th2	Individual	0.0035 ± 0.0185	0.0090 ± 0.0089	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0063 ± 0.0084	0.0045 ± 0.0056	1/1
[Post-Rec]	Leauthaud	Th2	Individual	−0.0050 ± 0.0108	0.0053 ± 0.0063	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0090	0.0014 ± 0.0060	1/1
	Tinker	Th2	Individual	0.0078 ± 0.0103	−0.0017 ± 0.0065	27/27
	Hearin	Th2	Mean	0.0115 ± 0.0094	0.0066 ± 0.0057	1/1
	Hearin	Th2	Individual	0.0019 ± 0.0097	0.0087 ± 0.0054	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0114 ± 0.0178	0.0028 ± 0.0107	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0000 ± 0.0180	0.0110 ± 0.0120	27/27
	Tinker	Th2	Mean	0.0023 ± 0.0177	−0.0047 ± 0.0124	1/1
	Tinker	Th2	Individual	−0.0110 ± 0.0160	0.0230 ± 0.0110	27/27
	Hearin	Th2	Mean	−0.0221 ± 0.0143	0.0108 ± 0.0099	1/1
	Hearin	Th2	Individual	−0.0210 ± 0.0160	0.0160 ± 0.0110	27/27
Fourier space	Leauthaud	Th2	Mean	−0.0062 ± 0.0104	−0.0024 ± 0.0075	1/1
[Post-Rec]	Leauthaud	Th2	Individual	0.0020 ± 0.0130	−0.0093 ± 0.0074	27/27
	Tinker	Th2	Mean	−0.0024 ± 0.0121	−0.0025 ± 0.0088	1/1
	Tinker	Th2	Individual	0.0038 ± 0.0097	−0.0006 ± 0.0072	27/27
	Hearin	Th2	Mean	0.0002 ± 0.0113	0.0122 ± 0.0075	1/1
	Hearin	Th2	Individual	0.0090 ± 0.0150	0.0167 ± 0.0061	27/27

Table B3 reports the main results of the RSD FS analyses presented in Section 6.3, confronting the three different modelling techniques: two in configuration space (CLPT-GS and CF-TNS), and one in Fourier space (P_k-TNS). Individual fits on each of the 27 realizations per model are performed, as well as fits on the mean of the mocks.

Table B3.

Performance of the RSD FS methods evaluated on the OR-based mocks, for the ‘Th2’ flavour with different HOD models. Mocks are analysed in their own Outer Rim cosmology, so the expected values are 1 for the α parameters and |$f\sigma _8^{\rm exp} = 0.447$|⁠. For each set of mocks, the results from pre-reconstructed catalogues are presented. We report both the results of fitting the mean of all the 27 realization per HOD, indicated with ‘Mean’, and the mean of individual fits on the mocks, indicated as ‘Individual’. For the fit to the mean, the error quoted is the 1σ of the error on the fit, where the covariances are scaled by the 27 realizations. For the mean of individual best-fits, the error quoted is the rms divided by the number of realizations. These results are visualized in Fig. 11.

RSD analysis type	HOD type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	−0.0189 ± 0.0114	0.0010 ± 0.0067	0.0113 ± 0.0165	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	−0.0069 ± 0.0159	−0.0052 ± 0.0092	0.0119 ± 0.0209	27/27
CLPT-GS	Tinker	Th2	Mean	−0.0211 ± 0.0117	0.0022 ± 0.0077	0.0066 ± 0.0178	1/1
	Tinker	Th2	Individual	−0.0096 ± 0.0135	−0.0014 ± 0.0093	0.0193 ± 0.0193	27/27
	Hearin	Th2	Mean	−0.0158 ± 0.0109	0.0008 ± 0.0067	0.0187 ± 0.0178	1/1
	Hearin	Th2	Individual	−0.0053 ± 0.0176	−0.0065 ± 0.0089	0.0267 ± 0.0250	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0012 ± 0.0110	−0.0046 ± 0.0052	0.0260 ± 0.0146	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0259 ± 0.0122	−0.0001 ± 0.0069	0.0305 ± 0.0168	27/27
CF-TNS	Tinker	Th2	Mean	0.0144 ± 0.0102	0.0014 ± 0.0059	0.0130 ± 0.0140	1/1
	Tinker	Th2	Individual	0.0375 ± 0.0126	−0.0049 ± 0.0076	0.0002 ± 0.0157	27/27
	Hearin	Th2	Mean	0.0056 ± 0.0098	0.0014 ± 0.0062	0.0227 ± 0.0152	1/1
	Hearin	Th2	Individual	0.0291 ± 0.0127	−0.0022 ± 0.0077	0.0205 ± 0.0168	27/27
Fourier space	Leauthaud	Th2	Mean	0.0034 ± 0.0138	−0.0111 ± 0.0094	−0.0040 ± 0.0200	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0610 ± 0.0140	−0.0195 ± 0.0087	0.0060 ± 0.0160	27/27
P_k-TNS	Tinker	Th2	Mean	0.0060 ± 0.0144	−0.0177 ± 0.0107	−0.0070 ± 0.0210	1/1
	Tinker	Th2	Individual	0.0970 ± 0.0240	−0.0047 ± 0.0097	0.0140 ± 0.0220	27/27
	Hearin	Th2	Mean	−0.0104 ± 0.0129	−0.0020 ± 0.0089	0.0190 ± 0.0190	1/1
	Hearin	Th2	Individual	0.0450 ± 0.0170	0.0001 ± 0.0093	0.0260 ± 0.0220	27/27

RSD analysis type	HOD type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	−0.0189 ± 0.0114	0.0010 ± 0.0067	0.0113 ± 0.0165	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	−0.0069 ± 0.0159	−0.0052 ± 0.0092	0.0119 ± 0.0209	27/27
CLPT-GS	Tinker	Th2	Mean	−0.0211 ± 0.0117	0.0022 ± 0.0077	0.0066 ± 0.0178	1/1
	Tinker	Th2	Individual	−0.0096 ± 0.0135	−0.0014 ± 0.0093	0.0193 ± 0.0193	27/27
	Hearin	Th2	Mean	−0.0158 ± 0.0109	0.0008 ± 0.0067	0.0187 ± 0.0178	1/1
	Hearin	Th2	Individual	−0.0053 ± 0.0176	−0.0065 ± 0.0089	0.0267 ± 0.0250	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0012 ± 0.0110	−0.0046 ± 0.0052	0.0260 ± 0.0146	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0259 ± 0.0122	−0.0001 ± 0.0069	0.0305 ± 0.0168	27/27
CF-TNS	Tinker	Th2	Mean	0.0144 ± 0.0102	0.0014 ± 0.0059	0.0130 ± 0.0140	1/1
	Tinker	Th2	Individual	0.0375 ± 0.0126	−0.0049 ± 0.0076	0.0002 ± 0.0157	27/27
	Hearin	Th2	Mean	0.0056 ± 0.0098	0.0014 ± 0.0062	0.0227 ± 0.0152	1/1
	Hearin	Th2	Individual	0.0291 ± 0.0127	−0.0022 ± 0.0077	0.0205 ± 0.0168	27/27
Fourier space	Leauthaud	Th2	Mean	0.0034 ± 0.0138	−0.0111 ± 0.0094	−0.0040 ± 0.0200	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0610 ± 0.0140	−0.0195 ± 0.0087	0.0060 ± 0.0160	27/27
P_k-TNS	Tinker	Th2	Mean	0.0060 ± 0.0144	−0.0177 ± 0.0107	−0.0070 ± 0.0210	1/1
	Tinker	Th2	Individual	0.0970 ± 0.0240	−0.0047 ± 0.0097	0.0140 ± 0.0220	27/27
	Hearin	Th2	Mean	−0.0104 ± 0.0129	−0.0020 ± 0.0089	0.0190 ± 0.0190	1/1
	Hearin	Th2	Individual	0.0450 ± 0.0170	0.0001 ± 0.0093	0.0260 ± 0.0220	27/27

Table B3.

Performance of the RSD FS methods evaluated on the OR-based mocks, for the ‘Th2’ flavour with different HOD models. Mocks are analysed in their own Outer Rim cosmology, so the expected values are 1 for the α parameters and |$f\sigma _8^{\rm exp} = 0.447$|⁠. For each set of mocks, the results from pre-reconstructed catalogues are presented. We report both the results of fitting the mean of all the 27 realization per HOD, indicated with ‘Mean’, and the mean of individual fits on the mocks, indicated as ‘Individual’. For the fit to the mean, the error quoted is the 1σ of the error on the fit, where the covariances are scaled by the 27 realizations. For the mean of individual best-fits, the error quoted is the rms divided by the number of realizations. These results are visualized in Fig. 11.

RSD analysis type	HOD type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	−0.0189 ± 0.0114	0.0010 ± 0.0067	0.0113 ± 0.0165	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	−0.0069 ± 0.0159	−0.0052 ± 0.0092	0.0119 ± 0.0209	27/27
CLPT-GS	Tinker	Th2	Mean	−0.0211 ± 0.0117	0.0022 ± 0.0077	0.0066 ± 0.0178	1/1
	Tinker	Th2	Individual	−0.0096 ± 0.0135	−0.0014 ± 0.0093	0.0193 ± 0.0193	27/27
	Hearin	Th2	Mean	−0.0158 ± 0.0109	0.0008 ± 0.0067	0.0187 ± 0.0178	1/1
	Hearin	Th2	Individual	−0.0053 ± 0.0176	−0.0065 ± 0.0089	0.0267 ± 0.0250	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0012 ± 0.0110	−0.0046 ± 0.0052	0.0260 ± 0.0146	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0259 ± 0.0122	−0.0001 ± 0.0069	0.0305 ± 0.0168	27/27
CF-TNS	Tinker	Th2	Mean	0.0144 ± 0.0102	0.0014 ± 0.0059	0.0130 ± 0.0140	1/1
	Tinker	Th2	Individual	0.0375 ± 0.0126	−0.0049 ± 0.0076	0.0002 ± 0.0157	27/27
	Hearin	Th2	Mean	0.0056 ± 0.0098	0.0014 ± 0.0062	0.0227 ± 0.0152	1/1
	Hearin	Th2	Individual	0.0291 ± 0.0127	−0.0022 ± 0.0077	0.0205 ± 0.0168	27/27
Fourier space	Leauthaud	Th2	Mean	0.0034 ± 0.0138	−0.0111 ± 0.0094	−0.0040 ± 0.0200	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0610 ± 0.0140	−0.0195 ± 0.0087	0.0060 ± 0.0160	27/27
P_k-TNS	Tinker	Th2	Mean	0.0060 ± 0.0144	−0.0177 ± 0.0107	−0.0070 ± 0.0210	1/1
	Tinker	Th2	Individual	0.0970 ± 0.0240	−0.0047 ± 0.0097	0.0140 ± 0.0220	27/27
	Hearin	Th2	Mean	−0.0104 ± 0.0129	−0.0020 ± 0.0089	0.0190 ± 0.0190	1/1
	Hearin	Th2	Individual	0.0450 ± 0.0170	0.0001 ± 0.0093	0.0260 ± 0.0220	27/27

RSD analysis type	HOD type	HOD flavour	Analysis details	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|	N_det/N_tot
Configuration space	Leauthaud	Th2	Mean	−0.0189 ± 0.0114	0.0010 ± 0.0067	0.0113 ± 0.0165	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	−0.0069 ± 0.0159	−0.0052 ± 0.0092	0.0119 ± 0.0209	27/27
CLPT-GS	Tinker	Th2	Mean	−0.0211 ± 0.0117	0.0022 ± 0.0077	0.0066 ± 0.0178	1/1
	Tinker	Th2	Individual	−0.0096 ± 0.0135	−0.0014 ± 0.0093	0.0193 ± 0.0193	27/27
	Hearin	Th2	Mean	−0.0158 ± 0.0109	0.0008 ± 0.0067	0.0187 ± 0.0178	1/1
	Hearin	Th2	Individual	−0.0053 ± 0.0176	−0.0065 ± 0.0089	0.0267 ± 0.0250	27/27
Configuration space	Leauthaud	Th2	Mean	−0.0012 ± 0.0110	−0.0046 ± 0.0052	0.0260 ± 0.0146	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0259 ± 0.0122	−0.0001 ± 0.0069	0.0305 ± 0.0168	27/27
CF-TNS	Tinker	Th2	Mean	0.0144 ± 0.0102	0.0014 ± 0.0059	0.0130 ± 0.0140	1/1
	Tinker	Th2	Individual	0.0375 ± 0.0126	−0.0049 ± 0.0076	0.0002 ± 0.0157	27/27
	Hearin	Th2	Mean	0.0056 ± 0.0098	0.0014 ± 0.0062	0.0227 ± 0.0152	1/1
	Hearin	Th2	Individual	0.0291 ± 0.0127	−0.0022 ± 0.0077	0.0205 ± 0.0168	27/27
Fourier space	Leauthaud	Th2	Mean	0.0034 ± 0.0138	−0.0111 ± 0.0094	−0.0040 ± 0.0200	1/1
[Pre-Rec]	Leauthaud	Th2	Individual	0.0610 ± 0.0140	−0.0195 ± 0.0087	0.0060 ± 0.0160	27/27
P_k-TNS	Tinker	Th2	Mean	0.0060 ± 0.0144	−0.0177 ± 0.0107	−0.0070 ± 0.0210	1/1
	Tinker	Th2	Individual	0.0970 ± 0.0240	−0.0047 ± 0.0097	0.0140 ± 0.0220	27/27
	Hearin	Th2	Mean	−0.0104 ± 0.0129	−0.0020 ± 0.0089	0.0190 ± 0.0190	1/1
	Hearin	Th2	Individual	0.0450 ± 0.0170	0.0001 ± 0.0093	0.0260 ± 0.0220	27/27

Finally, Table B4 provides the numerical results obtained by running the various BAO and RSD FS analysis pipelines on the average of 84 nseries mocks, as detailed in Section 6.4. The analysis is performed only over pre-reconstructed catalogues, and carried out in the nseries cosmology (Section 4.2).

Table B4.

Modelling systematics related to BAO and RSD methodologies, addressed with the nseries. These numerical results are shown in Fig. 12.

Analysis Type	Analysis space	Analysis method	Fitting model	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|
BAO [Pre-Rec]	Configuration space	CF – BAO Peak	BAO Template	0.0014 ± 0.0045	0.0059 ± 0.0023	–
BAO [Pre-Rec]	Fourier space	PS – BAO Peaks	BAO Template	−0.0045 ± 0.0041	−0.0021 ± 0.0020	–
BAO [Post-Rec]	Configuration space	CF – BAO Peak	BAO Template	0.0031 ± 0.0024	0.0023 ± 0.0015	–
BAO [Post-Rec]	Fourier space	PS – BAO Peaks	BAO Template	−0.0048 ± 0.0019	0.0005 ± 0.0010	–
RSD [Pre-Rec]	Configuration space	CF – Full Shape	CLPT-GS	−0.0090 ± 0.0030	0.0020 ± 0.0020	−0.0060 ± 0.0050
RSD [Pre-Rec]	Configuration space	CF – Full Shape	CF-TNS	−0.0050 ± 0.0030	−0.0020 ± 0.0020	0.0060 ± 0.0040
RSD [Pre-Rec]	Fourier space	PS – Full Shape	P_k-TNS	0.0016 ± 0.0032	−0.0095 ± 0.0020	−0.0038 ± 0.0041

Analysis Type	Analysis space	Analysis method	Fitting model	\|$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$\|	\|$\alpha _\perp -\alpha _\perp ^{\rm exp}$\|	\|$f\sigma _8 - f\sigma _8^{\rm exp}$\|
BAO [Pre-Rec]	Configuration space	CF – BAO Peak	BAO Template	0.0014 ± 0.0045	0.0059 ± 0.0023	–
BAO [Pre-Rec]	Fourier space	PS – BAO Peaks	BAO Template	−0.0045 ± 0.0041	−0.0021 ± 0.0020	–
BAO [Post-Rec]	Configuration space	CF – BAO Peak	BAO Template	0.0031 ± 0.0024	0.0023 ± 0.0015	–
BAO [Post-Rec]	Fourier space	PS – BAO Peaks	BAO Template	−0.0048 ± 0.0019	0.0005 ± 0.0010	–
RSD [Pre-Rec]	Configuration space	CF – Full Shape	CLPT-GS	−0.0090 ± 0.0030	0.0020 ± 0.0020	−0.0060 ± 0.0050
RSD [Pre-Rec]	Configuration space	CF – Full Shape	CF-TNS	−0.0050 ± 0.0030	−0.0020 ± 0.0020	0.0060 ± 0.0040
RSD [Pre-Rec]	Fourier space	PS – Full Shape	P_k-TNS	0.0016 ± 0.0032	−0.0095 ± 0.0020	−0.0038 ± 0.0041

Table B4.