-
PDF
- Split View
-
Views
-
Cite
Cite
K Misra, L Resmi, D A Kann, M Marongiu, A Moin, S Klose, G Bernardi, A de Ugarte Postigo, V K Jaiswal, S Schulze, D A Perley, A Ghosh, Dimple , H Kumar, R Gupta, M J Michałowski, S Martín, A Cockeram, S V Cherukuri, V Bhalerao, G E Anderson, S B Pandey, G C Anupama, C C Thöne, S Barway, M H Wieringa, J P U Fynbo, N Habeeb, Low frequency view of GRB 190114C reveals time varying shock micro-physics, Monthly Notices of the Royal Astronomical Society, Volume 504, Issue 4, July 2021, Pages 5685–5701, https://doi.org/10.1093/mnras/stab1050
Close - Share Icon Share
ABSTRACT
We present radio and optical afterglow observations of the TeV-bright long gamma-ray burst 190114C at a redshift of z = 0.425, which was detected by the Major Atmospheric Gamma Imaging Cherenkov telescope. Our observations with Atacama Large Millimeter/submillitmeter Array, Australia Telescope Compact Array, and upgraded Giant Metre-wave Radio Telescope were obtained by our low frequency observing campaign and range from ∼1 to ∼140 d after the burst and the optical observations were done with three optical telescopes spanning up to ∼25 d after the burst. Long-term radio/mm observations reveal the complex nature of the afterglow, which does not follow the spectral and temporal closure relations expected from the standard afterglow model. We find that the microphysical parameters of the external forward shock, representing the share of shock-created energy in the non-thermal electron population and magnetic field, are evolving with time. The inferred kinetic energy in the blast-wave depends strongly on the assumed ambient medium density profile, with a constant density medium demanding almost an order of magnitude higher energy than in the prompt emission, while a stellar wind-driven medium requires approximately the same amount energy as in prompt emission.
1 INTRODUCTION
Gamma-ray bursts (GRBs) dissipate between 1051 and 1054 erg (assuming isotropy) of energy in electromagnetic radiation (e.g. Amati et al. 2008) during an ephemeral flash of γ-ray photons that can last up to thousands of s (e.g. Kouveliotou et al. 1993; Levan et al. 2014). As the blastwave from the explosion sweeps up the external medium, local random magnetic fields accelerate electrons to ultra-relativistic velocities, these eventually generate a long lasting afterglow from radio to X-ray frequencies, predominantly via synchrotron radiation (for a review see Piran 2004; Kumar & Zhang 2015). Afterglow studies are an invaluable tool to answer fundamental questions on radiation processes in extreme environments. Various physical parameters such as the jet collimation angle, the state of the plasma via microphysical parameters describing magnetic field generation and electron acceleration, and the environment properties such as the density profile of the circumburst medium and dust extinction, can be constrained by modelling the multiband evolution of the afterglow.
The simplest afterglow model considers a power-law shape in the electron energy distribution p, a break between the optical and X-rays due to the passage of the cooling frequency and a jet with half opening angle θj traversing in a constant density (Schulze et al. 2011) or wind medium (Chevalier & Li 1999).
However, well-sampled GRB afterglows (in the time and frequency domain) have not been found to be fully consistent with the simple afterglow model. Swift observations of the X-ray afterglows revealed plateaus, in the light curves, which can last upto 104 s and whose origin continues to be poorly understood (Nousek et al. 2006; Liang, Zhang & Zhang 2007). A small number of afterglows showed a rapid decline in the early optical and radio light curves due to the reverse shock (RS; e.g. Sari & Piran 1999; Kobayashi & Zhang 2003; Laskar et al. 2013; Martin-Carrillo et al. 2014; Gao & Mészáros 2015; Alexander et al. 2017). Others exhibited rebrightenings from X-rays to radio frequencies due to refreshed shocks (Björnsson, Gudmundsson & Jóhannesson 2004; Zhang et al. 2006) and flares (Chincarini et al. 2010; Margutti et al. 2010) due to on-going central-engine activity on all time-scales. But the jet geometry can also show deviations from the simplest model, a uniform top-hat jet (Oates et al. 2007; Racusin et al. 2008; Filgas et al. 2011a) for example a two component jet (Resmi et al. 2005) and a structured jet (Granot et al. 2018; Margutti et al. 2018; Resmi et al. 2018; Lamb et al. 2019).
While most of these findings require only adjustments or additions to the standard model, a growing number of GRB afterglows start to challenge the well-established paradigm. The Fermi satellite recorded delayed, extended GeV emission for a number of GRBs, which may be connected to the afterglow (Abdo et al. 2009; Kumar & Barniol Duran 2010). In the time domain, high-cadence observations of the optical and Near InfraRed (NIR) afterglow of GRB 091127 pointed to a time-dependent fraction of energy stored in the magnetic field of the blastwave (Filgas et al. 2011b). But very loDng monitoring campaigns also revealed new challenges. De Pasquale et al. (2016) monitored the X-ray afterglow of the highly energetic GRB 130427A for 80 × 106 s which follows a single power-law decay. This suggested a low collimation and/or extreme properties of the circumburst medium. Hancock, Gaensler & Murphy (2013) have indicated two physically distinct population of GRBs – the radio bright and radio faint and suggested that this difference is due to the gamma-ray efficiency of the prompt emission between the two populations.
To understand how these examples fit into the established afterglow framework, afterglows are needed with well-sampled light curves from radio to X-ray frequencies. Among the >1200 Swift GRBs, only ∼20–30 were bright enough to perform precision tests of afterglow models (e.g. Panaitescu & Kumar 2002; Yost et al. 2003; Björnsson et al. 2004; Resmi et al. 2005; Chandra et al. 2008; Laskar et al. 2013; Alexander et al. 2017; Sánchez-Ramírez et al. 2017). With the dawn of the Atacama Large Millimeter/submillitmeter Array (ALMA; Wootten & Thompson 2009), upgraded Giant Metre-wave Radio Telescope (uGMRT; Swarup et al. 1991), the Karl G. Jansky Very Large Array (VLA), and the NOrthern Extended Millimeter Array, it is finally feasible to not only monitor bright GRBs over a substantially longer period of time, but also less luminous and more distant GRBs. In addition, analytical and sophisticated numerical models, e.g. Jóhannesson, Björnsson & Gudmundsson (2006), van der Horst (2007), van Eerten, van der Horst & MacFadyen (2012), and Laskar et al. (2013), Laskar et al. (2015), were also revised to account for the observed afterglow diversity.
On 2019 January 14, the Major Atmospheric Gamma Imaging Cherenkov (MAGIC) air Cherenkov telescope recorded for the first time very high-energy (VHE) photons from a GRB, GRB 190114C. This provides an opportunity to study not only leptonic but also hadronic processes in GRBs and their afterglows. In this paper, we present the results of our observing campaign of the afterglow of GRB 190114C with Australia Telescope Compact Array (ATCA), ALMA, and GMRT at radio frequencies and with the 0.7 m GROWTH-India telescope (GIT), the 1.3 m Devasthal Fast Optical Telescope (DFOT), and the 2.0 m Himalayan Chandra Telescope (HCT) in the optical bands. A brief description of the burst properties is given in Section 2. The data acquisition and analysis procedures are described in Section 3. The multiband afterglow light curves and the description of the afterglow in the context of other GRB afterglows are discussed in Section 4. We discuss the interstellar scintillation (ISS) in the radio bands in Section 5. A detailed multiband modelling of the afterglow light curves reveals the evolution of microphysical parameters with time, as presented in Section 6. The conclusions of this work are given in Section 7. The time since burst (T-T0) is taken to be the Swift trigger time. We adopt the convention of Fν(t)∝tανβ throughout the description given in this work.
Throughout the paper, we report all uncertainties at 1σ confidence and the brightness in the ultraviolet (UV)/optical/NIR in the AB magnitude system. We use a ΛCDM cosmology with |$H_0=67.3~{\rm km\, s}^{-1}\, {\rm Mpc}^{-1}$|, |$\Omega _\Lambda =0.685$|, and Ωm = 0.315 (Planck Collaboration 2014).
2 THE MAGIC BURST GRB 190114C
GRB 190114C was first detected by the Burst Alert Telescope (BAT; Barthelmy et al. 2005) onboard the Neil Gehrels Swift Observatory satellite (hereafter Swift, Gehrels et al. 2004) on 2019 January 14 at 20:57:03.19 UT with a T90 duration of 25 s (Gropp et al. 2019; Hamburg et al. 2019). The GRB was also detected by other high-energy missions such as the SPI-ACS detector onboard INTEGRAL which recorded prolonged emission up to ∼5000 s (Minaev & Pozanenko 2019), Insight-HXMT (Xiao et al. 2019), Konus-Wind, which recorded emission in the 30 keV to 20 MeV energy band (Frederiks et al. 2019), as well as the GBM and LAT instruments onboard the Fermi satellite, with the highest energy photon detected at 22.9 GeV 15 s after the GBM trigger.
A historically rapid follow-up observation, ∼50 s after the BAT trigger, of GRB 190114C was performed by the twin MAGIC telescopes (Gropp et al. 2019; Mirzoyan et al. 2019). The MAGIC real-time analysis detected very high-energy emission >300 GeV with a significance of more than 20σ in the first 20 min of observations. The higher detection threshold comes due to the large zenith angle of the observation (>60 deg) and the presence of a partial Moon. However, after an initial flash of very high energy gamma-ray photons, the VHE emission quickly faded, as expected for a GRB and corroborating the connection between the VHE flash with the GRB.
Furthermore, the Swift X-ray Telescope (XRT; Burrows et al. 2005) started observing the field 64 s after the BAT trigger and located an uncatalogued X-ray source (Gropp et al. 2019). The UV/optical afterglow was also detected by the Swift UV/Optical Telescope (UVOT; Roming et al. 2005) 73 s after the BAT trigger.
A series of optical observations were obtained with several telescopes, such as the Master-SAAO robotic telescope (Tyurina et al. 2019), the 2.5 m NOT (Selsing et al. 2019), the 0.5 m OASDG (Izzo et al. 2019), as well as the 2.0 m MPG/ESO telescope with GROND (Greiner et al. 2008) which detected the afterglow in multiple filters (Bolmer & Schady 2019). A redshift of z = 0.425 (Selsing et al. 2019) was measured from the strong absorption lines seen in the spectrum taken with the ALFOSC instrument on the 2.5 m NOT. This was further refined (z = 0.4245 ± 0.0005) and confirmed by GTC (Castro-Tirado et al. 2019) and VLT X-shooter (Kann et al. 2019) spectroscopic observations. The measured fluence by the Fermi GBM is 3.99 × 10−4 ± 8 × 10−7 erg/cm2 in the 10–1000 keV energy range, hence the total isotropic energy and isotropic luminosity of the burst are Eiso ∼ 3 × 1053 erg and Liso ∼ 1 × 1053 erg/s, respectively (Hamburg et al. 2019). The values for this burst are in agreement with the Epeak − Eiso (Amati et al. 2002) and Epeak − Liso (Yonetoku et al. 2004) correlations.
3 DATA ACQUISITION AND ANALYSIS
3.1 Optical observations
We undertook photometric observations of GRB 190114C with the 0.7 m GIT and the 2.0 m HCT, located at the Indian Astronomical Observatory, Hanle, India, as well as the 1.3 m DFOT, located in Devasthal, ARIES, Nainital, India. The first observations with GIT were performed about 16.36 h after the initial alert. A faint afterglow was detected in g′, r′, and i′ filters (Kumar et al. 2019a). We monitored the afterglow upto 25.71 d after the trigger. The GIT is equipped with a wide-field camera with large (∼0|${_{.}^{\prime\prime}}$|7) pixels, and typical stars in our images in this data set had a full width at half-maximum (FWHM) of 4 arcsec. Image processing including bias subtraction, flat-fielding, and cosmic ray removal was done using standard tasks in iraf (Tody 1993). Source Extractor (Bertin 2011) was used to extract the sources in GIT images. The zero-points were calculated using PanSTARRS reference stars in the GRB field. In DFOT and HCT images, psf photometry was performed to estimate the instrumental magnitudes of the afterglow which were calibrated against the same set of stars as used in GIT using USNO catalogue. The final photometry is listed in Table 1.
Optical photometry of the afterglow of GRB 190114C using GIT, DFOT, and HCT. The magnitudes are not corrected for Galactic extinction. The GIT magnitudes are in the AB and the DFOT and HCT magnitudes are in the Vega system.
| T-T0 . | Filter . | Magnitude . | Telescope . | Image FWHM . |
|---|---|---|---|---|
| (d) . | . | . | . | (arcsec) . |
| 0.677 | g′ | 20.61 ± 0.32 | GIT | 3.63 |
| 0.697 | r′ | 19.46 ± 0.07 | GIT | 3.23 |
| 0.707 | i′ | 19.48 ± 0.16 | GIT | 3.77 |
| 0.724 | R | 19.39 ± 0.06 | DFOT | 3.18 |
| 0.729 | R | 19.46 ± 0.07 | DFOT | 3.25 |
| 0.748 | R | 19.70 ± 0.10 | HCT | 2.18 |
| 0.803 | R | 19.81 ± 0.09 | HCT | 2.10 |
| 1.827 | r′ | 19.96 ± 0.20 | GIT | 3.27 |
| 1.839 | r′ | 20.04 ± 0.26 | GIT | 3.44 |
| 2.715 | r′ | 20.71 ± 0.27 | GIT | 3.57 |
| 2.782 | i′ | 19.78 ± 0.24 | GIT | 3.21 |
| 3.819 | i′ | 19.53 ± 0.45 | GIT | 4.18 |
| 4.813 | r′ | 20.23 ± 0.37 | GIT | 4.51 |
| 9.753 | R | 21.38 ± 0.16 | HCT | 2.73 |
| 9.757 | r′ | 21.53 ± 0.32 | GIT | 3.98 |
| 9.791 | i′ | 20.35 ± 0.39 | GIT | 4.04 |
| 10.788 | g′ | 21.96 ± 0.40 | GIT | 4.08 |
| 10.801 | r′ | 21.35 ± 0.41 | GIT | 4.01 |
| 10.813 | i′ | 20.05 ± 0.37 | GIT | 4.05 |
| 11.770 | r′ | 21.44 ± 0.45 | GIT | 4.35 |
| 11.782 | i′ | 20.32 ± 0.36 | GIT | 4.07 |
| 12.757 | r′ | 21.65 ± 0.35 | GIT | 4.85 |
| 12.768 | r′ | 21.74 ± 0.41 | GIT | 4.95 |
| 12.800 | i′ | 20.11 ± 0.22 | GIT | 3.81 |
| 13.703 | g′ | 21.70 ± 0.40 | GIT | 4.04 |
| 13.726 | r′ | 21.56 ± 0.36 | GIT | 4.03 |
| 13.736 | r′ | 21.44 ± 0.28 | GIT | 4.03 |
| 13.747 | i′ | 20.29 ± 0.24 | GIT | 3.97 |
| 15.692 | r′ | 21.35 ± 0.31 | GIT | 4.12 |
| 15.728 | i′ | 20.59 ± 0.35 | GIT | 4.01 |
| 18.736 | i′ | 20.76 ± 0.33 | GIT | 3.97 |
| 19.772 | i′ | 20.57 ± 0.24 | GIT | 3.72 |
| 24.709 | r′ | 21.26 ± 0.30 | GIT | 4.09 |
| 24.724 | i′ | 20.42 ± 0.30 | GIT | 4.09 |
| 25.697 | r′ | 21.25 ± 0.31 | GIT | 4.17 |
| 25.714 | i′ | 20.70 ± 0.40 | GIT | 4.18 |
| T-T0 . | Filter . | Magnitude . | Telescope . | Image FWHM . |
|---|---|---|---|---|
| (d) . | . | . | . | (arcsec) . |
| 0.677 | g′ | 20.61 ± 0.32 | GIT | 3.63 |
| 0.697 | r′ | 19.46 ± 0.07 | GIT | 3.23 |
| 0.707 | i′ | 19.48 ± 0.16 | GIT | 3.77 |
| 0.724 | R | 19.39 ± 0.06 | DFOT | 3.18 |
| 0.729 | R | 19.46 ± 0.07 | DFOT | 3.25 |
| 0.748 | R | 19.70 ± 0.10 | HCT | 2.18 |
| 0.803 | R | 19.81 ± 0.09 | HCT | 2.10 |
| 1.827 | r′ | 19.96 ± 0.20 | GIT | 3.27 |
| 1.839 | r′ | 20.04 ± 0.26 | GIT | 3.44 |
| 2.715 | r′ | 20.71 ± 0.27 | GIT | 3.57 |
| 2.782 | i′ | 19.78 ± 0.24 | GIT | 3.21 |
| 3.819 | i′ | 19.53 ± 0.45 | GIT | 4.18 |
| 4.813 | r′ | 20.23 ± 0.37 | GIT | 4.51 |
| 9.753 | R | 21.38 ± 0.16 | HCT | 2.73 |
| 9.757 | r′ | 21.53 ± 0.32 | GIT | 3.98 |
| 9.791 | i′ | 20.35 ± 0.39 | GIT | 4.04 |
| 10.788 | g′ | 21.96 ± 0.40 | GIT | 4.08 |
| 10.801 | r′ | 21.35 ± 0.41 | GIT | 4.01 |
| 10.813 | i′ | 20.05 ± 0.37 | GIT | 4.05 |
| 11.770 | r′ | 21.44 ± 0.45 | GIT | 4.35 |
| 11.782 | i′ | 20.32 ± 0.36 | GIT | 4.07 |
| 12.757 | r′ | 21.65 ± 0.35 | GIT | 4.85 |
| 12.768 | r′ | 21.74 ± 0.41 | GIT | 4.95 |
| 12.800 | i′ | 20.11 ± 0.22 | GIT | 3.81 |
| 13.703 | g′ | 21.70 ± 0.40 | GIT | 4.04 |
| 13.726 | r′ | 21.56 ± 0.36 | GIT | 4.03 |
| 13.736 | r′ | 21.44 ± 0.28 | GIT | 4.03 |
| 13.747 | i′ | 20.29 ± 0.24 | GIT | 3.97 |
| 15.692 | r′ | 21.35 ± 0.31 | GIT | 4.12 |
| 15.728 | i′ | 20.59 ± 0.35 | GIT | 4.01 |
| 18.736 | i′ | 20.76 ± 0.33 | GIT | 3.97 |
| 19.772 | i′ | 20.57 ± 0.24 | GIT | 3.72 |
| 24.709 | r′ | 21.26 ± 0.30 | GIT | 4.09 |
| 24.724 | i′ | 20.42 ± 0.30 | GIT | 4.09 |
| 25.697 | r′ | 21.25 ± 0.31 | GIT | 4.17 |
| 25.714 | i′ | 20.70 ± 0.40 | GIT | 4.18 |
Optical photometry of the afterglow of GRB 190114C using GIT, DFOT, and HCT. The magnitudes are not corrected for Galactic extinction. The GIT magnitudes are in the AB and the DFOT and HCT magnitudes are in the Vega system.
| T-T0 . | Filter . | Magnitude . | Telescope . | Image FWHM . |
|---|---|---|---|---|
| (d) . | . | . | . | (arcsec) . |
| 0.677 | g′ | 20.61 ± 0.32 | GIT | 3.63 |
| 0.697 | r′ | 19.46 ± 0.07 | GIT | 3.23 |
| 0.707 | i′ | 19.48 ± 0.16 | GIT | 3.77 |
| 0.724 | R | 19.39 ± 0.06 | DFOT | 3.18 |
| 0.729 | R | 19.46 ± 0.07 | DFOT | 3.25 |
| 0.748 | R | 19.70 ± 0.10 | HCT | 2.18 |
| 0.803 | R | 19.81 ± 0.09 | HCT | 2.10 |
| 1.827 | r′ | 19.96 ± 0.20 | GIT | 3.27 |
| 1.839 | r′ | 20.04 ± 0.26 | GIT | 3.44 |
| 2.715 | r′ | 20.71 ± 0.27 | GIT | 3.57 |
| 2.782 | i′ | 19.78 ± 0.24 | GIT | 3.21 |
| 3.819 | i′ | 19.53 ± 0.45 | GIT | 4.18 |
| 4.813 | r′ | 20.23 ± 0.37 | GIT | 4.51 |
| 9.753 | R | 21.38 ± 0.16 | HCT | 2.73 |
| 9.757 | r′ | 21.53 ± 0.32 | GIT | 3.98 |
| 9.791 | i′ | 20.35 ± 0.39 | GIT | 4.04 |
| 10.788 | g′ | 21.96 ± 0.40 | GIT | 4.08 |
| 10.801 | r′ | 21.35 ± 0.41 | GIT | 4.01 |
| 10.813 | i′ | 20.05 ± 0.37 | GIT | 4.05 |
| 11.770 | r′ | 21.44 ± 0.45 | GIT | 4.35 |
| 11.782 | i′ | 20.32 ± 0.36 | GIT | 4.07 |
| 12.757 | r′ | 21.65 ± 0.35 | GIT | 4.85 |
| 12.768 | r′ | 21.74 ± 0.41 | GIT | 4.95 |
| 12.800 | i′ | 20.11 ± 0.22 | GIT | 3.81 |
| 13.703 | g′ | 21.70 ± 0.40 | GIT | 4.04 |
| 13.726 | r′ | 21.56 ± 0.36 | GIT | 4.03 |
| 13.736 | r′ | 21.44 ± 0.28 | GIT | 4.03 |
| 13.747 | i′ | 20.29 ± 0.24 | GIT | 3.97 |
| 15.692 | r′ | 21.35 ± 0.31 | GIT | 4.12 |
| 15.728 | i′ | 20.59 ± 0.35 | GIT | 4.01 |
| 18.736 | i′ | 20.76 ± 0.33 | GIT | 3.97 |
| 19.772 | i′ | 20.57 ± 0.24 | GIT | 3.72 |
| 24.709 | r′ | 21.26 ± 0.30 | GIT | 4.09 |
| 24.724 | i′ | 20.42 ± 0.30 | GIT | 4.09 |
| 25.697 | r′ | 21.25 ± 0.31 | GIT | 4.17 |
| 25.714 | i′ | 20.70 ± 0.40 | GIT | 4.18 |
| T-T0 . | Filter . | Magnitude . | Telescope . | Image FWHM . |
|---|---|---|---|---|
| (d) . | . | . | . | (arcsec) . |
| 0.677 | g′ | 20.61 ± 0.32 | GIT | 3.63 |
| 0.697 | r′ | 19.46 ± 0.07 | GIT | 3.23 |
| 0.707 | i′ | 19.48 ± 0.16 | GIT | 3.77 |
| 0.724 | R | 19.39 ± 0.06 | DFOT | 3.18 |
| 0.729 | R | 19.46 ± 0.07 | DFOT | 3.25 |
| 0.748 | R | 19.70 ± 0.10 | HCT | 2.18 |
| 0.803 | R | 19.81 ± 0.09 | HCT | 2.10 |
| 1.827 | r′ | 19.96 ± 0.20 | GIT | 3.27 |
| 1.839 | r′ | 20.04 ± 0.26 | GIT | 3.44 |
| 2.715 | r′ | 20.71 ± 0.27 | GIT | 3.57 |
| 2.782 | i′ | 19.78 ± 0.24 | GIT | 3.21 |
| 3.819 | i′ | 19.53 ± 0.45 | GIT | 4.18 |
| 4.813 | r′ | 20.23 ± 0.37 | GIT | 4.51 |
| 9.753 | R | 21.38 ± 0.16 | HCT | 2.73 |
| 9.757 | r′ | 21.53 ± 0.32 | GIT | 3.98 |
| 9.791 | i′ | 20.35 ± 0.39 | GIT | 4.04 |
| 10.788 | g′ | 21.96 ± 0.40 | GIT | 4.08 |
| 10.801 | r′ | 21.35 ± 0.41 | GIT | 4.01 |
| 10.813 | i′ | 20.05 ± 0.37 | GIT | 4.05 |
| 11.770 | r′ | 21.44 ± 0.45 | GIT | 4.35 |
| 11.782 | i′ | 20.32 ± 0.36 | GIT | 4.07 |
| 12.757 | r′ | 21.65 ± 0.35 | GIT | 4.85 |
| 12.768 | r′ | 21.74 ± 0.41 | GIT | 4.95 |
| 12.800 | i′ | 20.11 ± 0.22 | GIT | 3.81 |
| 13.703 | g′ | 21.70 ± 0.40 | GIT | 4.04 |
| 13.726 | r′ | 21.56 ± 0.36 | GIT | 4.03 |
| 13.736 | r′ | 21.44 ± 0.28 | GIT | 4.03 |
| 13.747 | i′ | 20.29 ± 0.24 | GIT | 3.97 |
| 15.692 | r′ | 21.35 ± 0.31 | GIT | 4.12 |
| 15.728 | i′ | 20.59 ± 0.35 | GIT | 4.01 |
| 18.736 | i′ | 20.76 ± 0.33 | GIT | 3.97 |
| 19.772 | i′ | 20.57 ± 0.24 | GIT | 3.72 |
| 24.709 | r′ | 21.26 ± 0.30 | GIT | 4.09 |
| 24.724 | i′ | 20.42 ± 0.30 | GIT | 4.09 |
| 25.697 | r′ | 21.25 ± 0.31 | GIT | 4.17 |
| 25.714 | i′ | 20.70 ± 0.40 | GIT | 4.18 |
3.2 ATCA
Radio observations of the GRB 190114C Swift XRT position (Osborne et al. 2019) were carried out with the ATCA, operated by CSIRO Astronomy and Space Science under a joint collaboration team project (project code CX424; Schulze et al. 2019). Data were obtained using the CABB continuum mode (Wilson et al. 2011) with the 4 cm (band centres: 5.5 and 9 GHz), 15 mm (band centres: 17 and 19 GHz), and 7 mm receivers (band centres 43 and 45 GHz), which provided two simultaneous bands, each with 2 GHz bandwidth. Data reduction was done using the Miriad (Sault, Teuben & Wright 1995) and Common Astronomy Software Applications (casa; McMullin et al. 2007) software packages and standard interferometry techniques were applied. Time-dependent gain calibration of the visibility data was performed using the ATCA calibrator sources 0237-233 (RA = 2h40m8s.17, Dec. = −23°09′15″.7) or 0402-362 (RA = 4h3m53s.750, Dec. = −36°05′01″.91), and absolute flux-density calibration was carried out on primary ATCA flux calibrator PKS B1934-638 (Partridge et al. 2016). Visibilities were inverted using standard tasks to produce GRB 190114C field images. The final flux-density values were estimated by employing model-fitting in both image and visibility planes to check for consistency. Table 2 shows the epochs of ATCA observations, frequency bands, the observed flux densities along with the errors, and the telescope configuration during the observations. The quoted errors are 1σ, which include the RMS and Gaussian 1σ errors.
| T-T0 . | Frequency . | Flux density . | Configuration . |
|---|---|---|---|
| (d) . | (GHz) . | (mJy) . | . |
| 3.291 | 45 | 1.311 ± 0.101 | H75 |
| 9.334 | 45 | 0.547 ± 0.127 | H75 |
| 10.331 | 45 | 0.516 ± 0.143 | H75 |
| 12.321 | 45 | <0.113 | H75 |
| 20.377 | 45 | <0.094 | H75 |
| 3.291 | 43 | 1.491 ± 0.085 | H75 |
| 9.334 | 43 | 0.583 ± 0.084 | H75 |
| 10.331 | 43 | 0.534 ± 0.110 | H75 |
| 12.321 | 43 | 0.403 ± 0.104 | H75 |
| 20.377 | 43 | 0.362 ± 0.088 | H75 |
| 3.322 | 19 | 2.810 ± 0.059 | H75 |
| 5.332 | 19 | 2.440 ± 0.200 | H75 |
| 9.366 | 19 | 2.730 ± 0.054 | H75 |
| 10.362 | 19 | 2.000 ± 0.070 | H75 |
| 16.328 | 19 | 1.180 ± 0.031 | H75 |
| 35.430 | 19 | 0.732 ± 0.028 | H75 |
| 1.455 | 18 | 2.000 ± 0.800 | 1.5D |
| 3.322 | 18 | 2.530 ± 0.280 | H75 |
| 5.332 | 18 | 2.060 ± 0.260 | H75 |
| 9.366 | 18 | 1.820 ± 0.078 | H75 |
| 10.362 | 18 | 1.820 ± 0.120 | H75 |
| 16.328 | 18 | 0.770 ± 0.050 | H75 |
| 35.430 | 18 | 0.520 ± 0.090 | H75 |
| 52.338 | 18 | <0.48 | |
| 3.322 | 17 | 3.180 ± 0.037 | H75 |
| 5.332 | 17 | 2.995 ± 0.068 | H75 |
| 9.366 | 17 | 2.081 ± 0.033 | H75 |
| 10.362 | 17 | 2.130 ± 0.030 | H75 |
| 12.352 | 17 | 1.050 ± 0.150 | H75 |
| 16.328 | 17 | 1.142 ± 0.010 | H75 |
| 24.422 | 17 | 0.560 ± 0.080 | H75 |
| 35.430 | 17 | 0.614 ± 0.032 | H75 |
| 1.424 | 9.0 | 1.820 ± 0.040 | 1.5D |
| 3.489 | 9.0 | 2.080 ± 0.040 | H75 |
| 5.301 | 9.0 | 2.230 ± 0.045 | H75 |
| 9.334 | 9.0 | 1.580 ± 0.017 | H75 |
| 10.331 | 9.0 | 1.500 ± 0.021 | H75 |
| 16.297 | 9.0 | 0.927 ± 0.019 | H75 |
| 20.377 | 9.0 | 0.802 ± 0.016 | H75 |
| 24.262 | 9.0 | 0.560 ± 0.050 | H75 |
| 35.315 | 9.0 | 0.420 ± 0.020 | H75 |
| 52.307 | 9.0 | 0.240 ± 0.020 | H214 |
| 72.515 | 9.0 | 0.150 ± 0.010 | 6A |
| 119.282 | 9.0 | 0.108 ± 0.015 | 1.5B |
| 138.217 | 9.0 | 0.094 ± 0.014 | 6A |
| 1.424 | 5.5 | 1.930 ± 0.030 | 1.5D |
| 3.489 | 5.5 | 1.140 ± 0.030 | H75 |
| 5.301 | 5.5 | 1.770 ± 0.037 | H75 |
| 9.334 | 5.5 | 2.210 ± 0.032 | H75 |
| 10.331 | 5.5 | 1.200 ± 0.031 | H75 |
| 16.297 | 5.5 | 0.735 ± 0.023 | H75 |
| 20.377 | 5.5 | 0.720 ± 0.018 | H75 |
| 24.262 | 5.5 | 0.670 ± 0.040 | H75 |
| 35.315 | 5.5 | 0.480 ± 0.030 | H75 |
| 52.307 | 5.5 | 0.340 ± 0.020 | H214 |
| 72.515 | 5.5 | 0.240 ± 0.020 | 6A |
| 119.282 | 5.5 | 0.140 ± 0.015 | 1.5B |
| 138.217 | 5.5 | 0.126 ± 0.013 | 6A |
| T-T0 . | Frequency . | Flux density . | Configuration . |
|---|---|---|---|
| (d) . | (GHz) . | (mJy) . | . |
| 3.291 | 45 | 1.311 ± 0.101 | H75 |
| 9.334 | 45 | 0.547 ± 0.127 | H75 |
| 10.331 | 45 | 0.516 ± 0.143 | H75 |
| 12.321 | 45 | <0.113 | H75 |
| 20.377 | 45 | <0.094 | H75 |
| 3.291 | 43 | 1.491 ± 0.085 | H75 |
| 9.334 | 43 | 0.583 ± 0.084 | H75 |
| 10.331 | 43 | 0.534 ± 0.110 | H75 |
| 12.321 | 43 | 0.403 ± 0.104 | H75 |
| 20.377 | 43 | 0.362 ± 0.088 | H75 |
| 3.322 | 19 | 2.810 ± 0.059 | H75 |
| 5.332 | 19 | 2.440 ± 0.200 | H75 |
| 9.366 | 19 | 2.730 ± 0.054 | H75 |
| 10.362 | 19 | 2.000 ± 0.070 | H75 |
| 16.328 | 19 | 1.180 ± 0.031 | H75 |
| 35.430 | 19 | 0.732 ± 0.028 | H75 |
| 1.455 | 18 | 2.000 ± 0.800 | 1.5D |
| 3.322 | 18 | 2.530 ± 0.280 | H75 |
| 5.332 | 18 | 2.060 ± 0.260 | H75 |
| 9.366 | 18 | 1.820 ± 0.078 | H75 |
| 10.362 | 18 | 1.820 ± 0.120 | H75 |
| 16.328 | 18 | 0.770 ± 0.050 | H75 |
| 35.430 | 18 | 0.520 ± 0.090 | H75 |
| 52.338 | 18 | <0.48 | |
| 3.322 | 17 | 3.180 ± 0.037 | H75 |
| 5.332 | 17 | 2.995 ± 0.068 | H75 |
| 9.366 | 17 | 2.081 ± 0.033 | H75 |
| 10.362 | 17 | 2.130 ± 0.030 | H75 |
| 12.352 | 17 | 1.050 ± 0.150 | H75 |
| 16.328 | 17 | 1.142 ± 0.010 | H75 |
| 24.422 | 17 | 0.560 ± 0.080 | H75 |
| 35.430 | 17 | 0.614 ± 0.032 | H75 |
| 1.424 | 9.0 | 1.820 ± 0.040 | 1.5D |
| 3.489 | 9.0 | 2.080 ± 0.040 | H75 |
| 5.301 | 9.0 | 2.230 ± 0.045 | H75 |
| 9.334 | 9.0 | 1.580 ± 0.017 | H75 |
| 10.331 | 9.0 | 1.500 ± 0.021 | H75 |
| 16.297 | 9.0 | 0.927 ± 0.019 | H75 |
| 20.377 | 9.0 | 0.802 ± 0.016 | H75 |
| 24.262 | 9.0 | 0.560 ± 0.050 | H75 |
| 35.315 | 9.0 | 0.420 ± 0.020 | H75 |
| 52.307 | 9.0 | 0.240 ± 0.020 | H214 |
| 72.515 | 9.0 | 0.150 ± 0.010 | 6A |
| 119.282 | 9.0 | 0.108 ± 0.015 | 1.5B |
| 138.217 | 9.0 | 0.094 ± 0.014 | 6A |
| 1.424 | 5.5 | 1.930 ± 0.030 | 1.5D |
| 3.489 | 5.5 | 1.140 ± 0.030 | H75 |
| 5.301 | 5.5 | 1.770 ± 0.037 | H75 |
| 9.334 | 5.5 | 2.210 ± 0.032 | H75 |
| 10.331 | 5.5 | 1.200 ± 0.031 | H75 |
| 16.297 | 5.5 | 0.735 ± 0.023 | H75 |
| 20.377 | 5.5 | 0.720 ± 0.018 | H75 |
| 24.262 | 5.5 | 0.670 ± 0.040 | H75 |
| 35.315 | 5.5 | 0.480 ± 0.030 | H75 |
| 52.307 | 5.5 | 0.340 ± 0.020 | H214 |
| 72.515 | 5.5 | 0.240 ± 0.020 | 6A |
| 119.282 | 5.5 | 0.140 ± 0.015 | 1.5B |
| 138.217 | 5.5 | 0.126 ± 0.013 | 6A |
| T-T0 . | Frequency . | Flux density . | Configuration . |
|---|---|---|---|
| (d) . | (GHz) . | (mJy) . | . |
| 3.291 | 45 | 1.311 ± 0.101 | H75 |
| 9.334 | 45 | 0.547 ± 0.127 | H75 |
| 10.331 | 45 | 0.516 ± 0.143 | H75 |
| 12.321 | 45 | <0.113 | H75 |
| 20.377 | 45 | <0.094 | H75 |
| 3.291 | 43 | 1.491 ± 0.085 | H75 |
| 9.334 | 43 | 0.583 ± 0.084 | H75 |
| 10.331 | 43 | 0.534 ± 0.110 | H75 |
| 12.321 | 43 | 0.403 ± 0.104 | H75 |
| 20.377 | 43 | 0.362 ± 0.088 | H75 |
| 3.322 | 19 | 2.810 ± 0.059 | H75 |
| 5.332 | 19 | 2.440 ± 0.200 | H75 |
| 9.366 | 19 | 2.730 ± 0.054 | H75 |
| 10.362 | 19 | 2.000 ± 0.070 | H75 |
| 16.328 | 19 | 1.180 ± 0.031 | H75 |
| 35.430 | 19 | 0.732 ± 0.028 | H75 |
| 1.455 | 18 | 2.000 ± 0.800 | 1.5D |
| 3.322 | 18 | 2.530 ± 0.280 | H75 |
| 5.332 | 18 | 2.060 ± 0.260 | H75 |
| 9.366 | 18 | 1.820 ± 0.078 | H75 |
| 10.362 | 18 | 1.820 ± 0.120 | H75 |
| 16.328 | 18 | 0.770 ± 0.050 | H75 |
| 35.430 | 18 | 0.520 ± 0.090 | H75 |
| 52.338 | 18 | <0.48 | |
| 3.322 | 17 | 3.180 ± 0.037 | H75 |
| 5.332 | 17 | 2.995 ± 0.068 | H75 |
| 9.366 | 17 | 2.081 ± 0.033 | H75 |
| 10.362 | 17 | 2.130 ± 0.030 | H75 |
| 12.352 | 17 | 1.050 ± 0.150 | H75 |
| 16.328 | 17 | 1.142 ± 0.010 | H75 |
| 24.422 | 17 | 0.560 ± 0.080 | H75 |
| 35.430 | 17 | 0.614 ± 0.032 | H75 |
| 1.424 | 9.0 | 1.820 ± 0.040 | 1.5D |
| 3.489 | 9.0 | 2.080 ± 0.040 | H75 |
| 5.301 | 9.0 | 2.230 ± 0.045 | H75 |
| 9.334 | 9.0 | 1.580 ± 0.017 | H75 |
| 10.331 | 9.0 | 1.500 ± 0.021 | H75 |
| 16.297 | 9.0 | 0.927 ± 0.019 | H75 |
| 20.377 | 9.0 | 0.802 ± 0.016 | H75 |
| 24.262 | 9.0 | 0.560 ± 0.050 | H75 |
| 35.315 | 9.0 | 0.420 ± 0.020 | H75 |
| 52.307 | 9.0 | 0.240 ± 0.020 | H214 |
| 72.515 | 9.0 | 0.150 ± 0.010 | 6A |
| 119.282 | 9.0 | 0.108 ± 0.015 | 1.5B |
| 138.217 | 9.0 | 0.094 ± 0.014 | 6A |
| 1.424 | 5.5 | 1.930 ± 0.030 | 1.5D |
| 3.489 | 5.5 | 1.140 ± 0.030 | H75 |
| 5.301 | 5.5 | 1.770 ± 0.037 | H75 |
| 9.334 | 5.5 | 2.210 ± 0.032 | H75 |
| 10.331 | 5.5 | 1.200 ± 0.031 | H75 |
| 16.297 | 5.5 | 0.735 ± 0.023 | H75 |
| 20.377 | 5.5 | 0.720 ± 0.018 | H75 |
| 24.262 | 5.5 | 0.670 ± 0.040 | H75 |
| 35.315 | 5.5 | 0.480 ± 0.030 | H75 |
| 52.307 | 5.5 | 0.340 ± 0.020 | H214 |
| 72.515 | 5.5 | 0.240 ± 0.020 | 6A |
| 119.282 | 5.5 | 0.140 ± 0.015 | 1.5B |
| 138.217 | 5.5 | 0.126 ± 0.013 | 6A |
| T-T0 . | Frequency . | Flux density . | Configuration . |
|---|---|---|---|
| (d) . | (GHz) . | (mJy) . | . |
| 3.291 | 45 | 1.311 ± 0.101 | H75 |
| 9.334 | 45 | 0.547 ± 0.127 | H75 |
| 10.331 | 45 | 0.516 ± 0.143 | H75 |
| 12.321 | 45 | <0.113 | H75 |
| 20.377 | 45 | <0.094 | H75 |
| 3.291 | 43 | 1.491 ± 0.085 | H75 |
| 9.334 | 43 | 0.583 ± 0.084 | H75 |
| 10.331 | 43 | 0.534 ± 0.110 | H75 |
| 12.321 | 43 | 0.403 ± 0.104 | H75 |
| 20.377 | 43 | 0.362 ± 0.088 | H75 |
| 3.322 | 19 | 2.810 ± 0.059 | H75 |
| 5.332 | 19 | 2.440 ± 0.200 | H75 |
| 9.366 | 19 | 2.730 ± 0.054 | H75 |
| 10.362 | 19 | 2.000 ± 0.070 | H75 |
| 16.328 | 19 | 1.180 ± 0.031 | H75 |
| 35.430 | 19 | 0.732 ± 0.028 | H75 |
| 1.455 | 18 | 2.000 ± 0.800 | 1.5D |
| 3.322 | 18 | 2.530 ± 0.280 | H75 |
| 5.332 | 18 | 2.060 ± 0.260 | H75 |
| 9.366 | 18 | 1.820 ± 0.078 | H75 |
| 10.362 | 18 | 1.820 ± 0.120 | H75 |
| 16.328 | 18 | 0.770 ± 0.050 | H75 |
| 35.430 | 18 | 0.520 ± 0.090 | H75 |
| 52.338 | 18 | <0.48 | |
| 3.322 | 17 | 3.180 ± 0.037 | H75 |
| 5.332 | 17 | 2.995 ± 0.068 | H75 |
| 9.366 | 17 | 2.081 ± 0.033 | H75 |
| 10.362 | 17 | 2.130 ± 0.030 | H75 |
| 12.352 | 17 | 1.050 ± 0.150 | H75 |
| 16.328 | 17 | 1.142 ± 0.010 | H75 |
| 24.422 | 17 | 0.560 ± 0.080 | H75 |
| 35.430 | 17 | 0.614 ± 0.032 | H75 |
| 1.424 | 9.0 | 1.820 ± 0.040 | 1.5D |
| 3.489 | 9.0 | 2.080 ± 0.040 | H75 |
| 5.301 | 9.0 | 2.230 ± 0.045 | H75 |
| 9.334 | 9.0 | 1.580 ± 0.017 | H75 |
| 10.331 | 9.0 | 1.500 ± 0.021 | H75 |
| 16.297 | 9.0 | 0.927 ± 0.019 | H75 |
| 20.377 | 9.0 | 0.802 ± 0.016 | H75 |
| 24.262 | 9.0 | 0.560 ± 0.050 | H75 |
| 35.315 | 9.0 | 0.420 ± 0.020 | H75 |
| 52.307 | 9.0 | 0.240 ± 0.020 | H214 |
| 72.515 | 9.0 | 0.150 ± 0.010 | 6A |
| 119.282 | 9.0 | 0.108 ± 0.015 | 1.5B |
| 138.217 | 9.0 | 0.094 ± 0.014 | 6A |
| 1.424 | 5.5 | 1.930 ± 0.030 | 1.5D |
| 3.489 | 5.5 | 1.140 ± 0.030 | H75 |
| 5.301 | 5.5 | 1.770 ± 0.037 | H75 |
| 9.334 | 5.5 | 2.210 ± 0.032 | H75 |
| 10.331 | 5.5 | 1.200 ± 0.031 | H75 |
| 16.297 | 5.5 | 0.735 ± 0.023 | H75 |
| 20.377 | 5.5 | 0.720 ± 0.018 | H75 |
| 24.262 | 5.5 | 0.670 ± 0.040 | H75 |
| 35.315 | 5.5 | 0.480 ± 0.030 | H75 |
| 52.307 | 5.5 | 0.340 ± 0.020 | H214 |
| 72.515 | 5.5 | 0.240 ± 0.020 | 6A |
| 119.282 | 5.5 | 0.140 ± 0.015 | 1.5B |
| 138.217 | 5.5 | 0.126 ± 0.013 | 6A |
3.3 ALMA
The afterglow of GRB 190114C was observed with the Atacama Large Millimetre/Submillimetre Array (ALMA) in Bands 3 and 6. These observations were performed between 2019 January 15 and March 1 (1.1 and 45.5 d after the burst). The angular resolution of the observations ranged between 2|${_{.}^{\prime\prime}}$|58 and 3|${_{.}^{\prime\prime}}$|67 in Band 3 and was 1|${_{.}^{\prime\prime}}$|25 in Band 6.
Band 6 observations were performed within the context of DDT programme ADS/JAO.ALMA#2018.A.00020.T (P.I.: de Ugarte Postigo). Five individual executions were performed in three independent epochs ranging between 2019 January 17 and 18. The configuration used 47–48 antennas with baselines ranging from 15 to 313 m (12–253 kλ at the observed frequency). Each observation consisted of 43 min integration time on source with average weather conditions of precipitable water vapour (pwv) ∼3–4 mm. The receivers were tuned to a central frequency of 235.0487 GHz, so that the upper side band spectral windows would cover the CO(3-2) transition at the redshift of the GRB. The spectroscopic analysis of these data was presented by de Ugarte Postigo et al. (2020), whereas in this paper, we make use of the continuum measurements. The spatial resolution of the spectral data cube obtained by the pipeline products that combined all five executions was 1|${_{.}^{\prime\prime}}$|16 × 0|${_{.}^{\prime\prime}}$|867 (Position Angle −87.9°).
The ALMA Band 3 observations were performed within the ToO programme ADS/JAO.ALMA#2018.1.01410.T (P.I.: Perley) on January 15, 19, and 25, and on March 1 following the annual February shutdown. Integration times were 8.6 min on-source per visit. Weather conditions were relatively poor, with pwv 3–4 mm (accompanying Band 7 observations were requested, but could not be executed under the available conditions).
All data were calibrated within casa version 5.4.0 using the pipeline calibration. Photometric measurements were also performed within casa. The flux calibration was performed using J0423-0120 (for the first Band 3 epoch and the last Band 6 epoch) and J0522-3627 (for the remaining epochs). The log of ALMA observations and flux density measurements along with the errors are given in Table 3.
ALMA observing log of the afterglow of GRB 190114C. For each epoch, we provide photometric measurements performed in the four side bands, as well as the combined photometry of all the bands, indicated with a *.
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.240 | 227.399 | 1.459 ± 0.043 |
| 2.240 | 229.505 | 1.443 ± 0.045 |
| 2.240 | 240.581 | 1.559 ± 0.048 |
| 2.240 | 242.698 | 1.480 ± 0.057 |
| 2.240* | 235.048 | 1.480 ± 0.026 |
| 2.301 | 227.399 | 1.180 ± 0.056 |
| 2.301 | 229.505 | 1.261 ± 0.061 |
| 2.301 | 240.581 | 1.132 ± 0.061 |
| 2.301 | 242.697 | 1.475 ± 0.071 |
| 2.301* | 235.048 | 1.267 ± 0.034 |
| 3.209 | 227.399 | 1.468 ± 0.092 |
| 3.209 | 229.505 | 1.459 ± 0.099 |
| 3.209 | 240.581 | 1.382 ± 0.044 |
| 3.209 | 242.698 | 1.510 ± 0.048 |
| 3.209* | 235.048 | 1.462 ± 0.020 |
| 3.254 | 227.399 | 1.340 ± 0.045 |
| 3.254 | 229.505 | 1.338 ± 0.043 |
| 3.254 | 240.581 | 1.321 ± 0.093 |
| 3.254 | 242.698 | 1.360 ± 0.048 |
| 3.254* | 235.048 | 1.322 ± 0.025 |
| 4.093 | 227.399 | 1.300 ± 0.041 |
| 4.093 | 229.505 | 1.442 ± 0.041 |
| 4.093 | 240.581 | 1.386 ± 0.057 |
| 4.093 | 242.698 | 1.495 ± 0.059 |
| 4.093* | 235.048 | 1.393 ± 0.026 |
| 1.080 | 90.5 | 2.668 ± 0.051 |
| 1.080 | 92.5 | 2.758 ± 0.053 |
| 1.080 | 102.5 | 2.533 ± 0.052 |
| 1.080 | 104.5 | 2.524 ± 0.056 |
| 1.080* | 97.5 | 2.618 ± 0.027 |
| 4.130 | 90.5 | 1.711 ± 0.052 |
| 4.130 | 92.5 | 1.764 ± 0.049 |
| 4.130 | 102.5 | 1.618 ± 0.050 |
| 4.130 | 104.5 | 1.557 ± 0.052 |
| 4.130* | 97.5 | 1.682 ± 0.029 |
| 10.240 | 90.5 | 1.189 ± 0.054 |
| 10.240 | 92.5 | 0.948 ± 0.062 |
| 10.240 | 102.5 | 0.984 ± 0.055 |
| 10.240 | 104.5 | 0.911 ± 0.060 |
| 10.240* | 97.5 | 1.005 ± 0.032 |
| 45.5* | 97.5 | <0.14 |
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.240 | 227.399 | 1.459 ± 0.043 |
| 2.240 | 229.505 | 1.443 ± 0.045 |
| 2.240 | 240.581 | 1.559 ± 0.048 |
| 2.240 | 242.698 | 1.480 ± 0.057 |
| 2.240* | 235.048 | 1.480 ± 0.026 |
| 2.301 | 227.399 | 1.180 ± 0.056 |
| 2.301 | 229.505 | 1.261 ± 0.061 |
| 2.301 | 240.581 | 1.132 ± 0.061 |
| 2.301 | 242.697 | 1.475 ± 0.071 |
| 2.301* | 235.048 | 1.267 ± 0.034 |
| 3.209 | 227.399 | 1.468 ± 0.092 |
| 3.209 | 229.505 | 1.459 ± 0.099 |
| 3.209 | 240.581 | 1.382 ± 0.044 |
| 3.209 | 242.698 | 1.510 ± 0.048 |
| 3.209* | 235.048 | 1.462 ± 0.020 |
| 3.254 | 227.399 | 1.340 ± 0.045 |
| 3.254 | 229.505 | 1.338 ± 0.043 |
| 3.254 | 240.581 | 1.321 ± 0.093 |
| 3.254 | 242.698 | 1.360 ± 0.048 |
| 3.254* | 235.048 | 1.322 ± 0.025 |
| 4.093 | 227.399 | 1.300 ± 0.041 |
| 4.093 | 229.505 | 1.442 ± 0.041 |
| 4.093 | 240.581 | 1.386 ± 0.057 |
| 4.093 | 242.698 | 1.495 ± 0.059 |
| 4.093* | 235.048 | 1.393 ± 0.026 |
| 1.080 | 90.5 | 2.668 ± 0.051 |
| 1.080 | 92.5 | 2.758 ± 0.053 |
| 1.080 | 102.5 | 2.533 ± 0.052 |
| 1.080 | 104.5 | 2.524 ± 0.056 |
| 1.080* | 97.5 | 2.618 ± 0.027 |
| 4.130 | 90.5 | 1.711 ± 0.052 |
| 4.130 | 92.5 | 1.764 ± 0.049 |
| 4.130 | 102.5 | 1.618 ± 0.050 |
| 4.130 | 104.5 | 1.557 ± 0.052 |
| 4.130* | 97.5 | 1.682 ± 0.029 |
| 10.240 | 90.5 | 1.189 ± 0.054 |
| 10.240 | 92.5 | 0.948 ± 0.062 |
| 10.240 | 102.5 | 0.984 ± 0.055 |
| 10.240 | 104.5 | 0.911 ± 0.060 |
| 10.240* | 97.5 | 1.005 ± 0.032 |
| 45.5* | 97.5 | <0.14 |
ALMA observing log of the afterglow of GRB 190114C. For each epoch, we provide photometric measurements performed in the four side bands, as well as the combined photometry of all the bands, indicated with a *.
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.240 | 227.399 | 1.459 ± 0.043 |
| 2.240 | 229.505 | 1.443 ± 0.045 |
| 2.240 | 240.581 | 1.559 ± 0.048 |
| 2.240 | 242.698 | 1.480 ± 0.057 |
| 2.240* | 235.048 | 1.480 ± 0.026 |
| 2.301 | 227.399 | 1.180 ± 0.056 |
| 2.301 | 229.505 | 1.261 ± 0.061 |
| 2.301 | 240.581 | 1.132 ± 0.061 |
| 2.301 | 242.697 | 1.475 ± 0.071 |
| 2.301* | 235.048 | 1.267 ± 0.034 |
| 3.209 | 227.399 | 1.468 ± 0.092 |
| 3.209 | 229.505 | 1.459 ± 0.099 |
| 3.209 | 240.581 | 1.382 ± 0.044 |
| 3.209 | 242.698 | 1.510 ± 0.048 |
| 3.209* | 235.048 | 1.462 ± 0.020 |
| 3.254 | 227.399 | 1.340 ± 0.045 |
| 3.254 | 229.505 | 1.338 ± 0.043 |
| 3.254 | 240.581 | 1.321 ± 0.093 |
| 3.254 | 242.698 | 1.360 ± 0.048 |
| 3.254* | 235.048 | 1.322 ± 0.025 |
| 4.093 | 227.399 | 1.300 ± 0.041 |
| 4.093 | 229.505 | 1.442 ± 0.041 |
| 4.093 | 240.581 | 1.386 ± 0.057 |
| 4.093 | 242.698 | 1.495 ± 0.059 |
| 4.093* | 235.048 | 1.393 ± 0.026 |
| 1.080 | 90.5 | 2.668 ± 0.051 |
| 1.080 | 92.5 | 2.758 ± 0.053 |
| 1.080 | 102.5 | 2.533 ± 0.052 |
| 1.080 | 104.5 | 2.524 ± 0.056 |
| 1.080* | 97.5 | 2.618 ± 0.027 |
| 4.130 | 90.5 | 1.711 ± 0.052 |
| 4.130 | 92.5 | 1.764 ± 0.049 |
| 4.130 | 102.5 | 1.618 ± 0.050 |
| 4.130 | 104.5 | 1.557 ± 0.052 |
| 4.130* | 97.5 | 1.682 ± 0.029 |
| 10.240 | 90.5 | 1.189 ± 0.054 |
| 10.240 | 92.5 | 0.948 ± 0.062 |
| 10.240 | 102.5 | 0.984 ± 0.055 |
| 10.240 | 104.5 | 0.911 ± 0.060 |
| 10.240* | 97.5 | 1.005 ± 0.032 |
| 45.5* | 97.5 | <0.14 |
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.240 | 227.399 | 1.459 ± 0.043 |
| 2.240 | 229.505 | 1.443 ± 0.045 |
| 2.240 | 240.581 | 1.559 ± 0.048 |
| 2.240 | 242.698 | 1.480 ± 0.057 |
| 2.240* | 235.048 | 1.480 ± 0.026 |
| 2.301 | 227.399 | 1.180 ± 0.056 |
| 2.301 | 229.505 | 1.261 ± 0.061 |
| 2.301 | 240.581 | 1.132 ± 0.061 |
| 2.301 | 242.697 | 1.475 ± 0.071 |
| 2.301* | 235.048 | 1.267 ± 0.034 |
| 3.209 | 227.399 | 1.468 ± 0.092 |
| 3.209 | 229.505 | 1.459 ± 0.099 |
| 3.209 | 240.581 | 1.382 ± 0.044 |
| 3.209 | 242.698 | 1.510 ± 0.048 |
| 3.209* | 235.048 | 1.462 ± 0.020 |
| 3.254 | 227.399 | 1.340 ± 0.045 |
| 3.254 | 229.505 | 1.338 ± 0.043 |
| 3.254 | 240.581 | 1.321 ± 0.093 |
| 3.254 | 242.698 | 1.360 ± 0.048 |
| 3.254* | 235.048 | 1.322 ± 0.025 |
| 4.093 | 227.399 | 1.300 ± 0.041 |
| 4.093 | 229.505 | 1.442 ± 0.041 |
| 4.093 | 240.581 | 1.386 ± 0.057 |
| 4.093 | 242.698 | 1.495 ± 0.059 |
| 4.093* | 235.048 | 1.393 ± 0.026 |
| 1.080 | 90.5 | 2.668 ± 0.051 |
| 1.080 | 92.5 | 2.758 ± 0.053 |
| 1.080 | 102.5 | 2.533 ± 0.052 |
| 1.080 | 104.5 | 2.524 ± 0.056 |
| 1.080* | 97.5 | 2.618 ± 0.027 |
| 4.130 | 90.5 | 1.711 ± 0.052 |
| 4.130 | 92.5 | 1.764 ± 0.049 |
| 4.130 | 102.5 | 1.618 ± 0.050 |
| 4.130 | 104.5 | 1.557 ± 0.052 |
| 4.130* | 97.5 | 1.682 ± 0.029 |
| 10.240 | 90.5 | 1.189 ± 0.054 |
| 10.240 | 92.5 | 0.948 ± 0.062 |
| 10.240 | 102.5 | 0.984 ± 0.055 |
| 10.240 | 104.5 | 0.911 ± 0.060 |
| 10.240* | 97.5 | 1.005 ± 0.032 |
| 45.5* | 97.5 | <0.14 |
3.4 GMRT
We observed GRB 190114C in band-4 (550−850 MHz) and band-5 (1050−1450 MHz) of the uGMRT between 2019 January 17 and March 25 (∼2.8–68.6 d since burst) under the approved ToO program 35_018 (P.I.: Kuntal Misra). Either 3C 147 or 3C 148 was used as flux calibrator and 0423-013 was used as phase calibrator.
We used a customized pipeline developed in casa by Ishwar-Chandra et al. (in preparation) for analysing the data. For both band 4 and band 5, about 26–28′ arcmin2 large regions centred on the GRB coordinates were imaged for the analysis, with a cell-size of 1|${_{.}^{\prime\prime}}$|24 and 0|${_{.}^{\prime\prime}}$|5, respectively. To measure the flux at the GRB position, we used the task JMFIT in the Astronomical Image Processing System. We ran the fits on a small region around the radio transient position as measured by the VLA (Alexander et al. 2019), using a two-component model consisting of an elliptical Gaussian and a flat baseline function. On all images except the last two epochs of band 4, the fitting procedure resulted in a confident detection of an unresolved point source at the GRB position. See Table 4 for the observation log. Errors quoted are obtained from the JMFIT fitting routine. The upper limits for the last two epochs of band 4 observations correspond to three times the mean flux measured in an empty region of the map. The synthesized beam is typically (5 − 8) × 3 arcsec2 for the maps. The value presented for the band 5 observation on 2019 January 17 is an improvement of the measurement reported in Cherukuri et al. (2019) and MAGIC Collaboration (2019), which was from a preliminary analysis. Self-calibration of the data in our refined analysis improved the quality of the image and the confidence of the detection. The measurements are not corrected for the host-galaxy which was detected in the pre-explosion images obtained with MeerKAT data (Tremou et al. 2019).
uGMRT observing log of the afterglow of GRB 190114C. Measurements are not corrected for the flux of the host galaxy detected in MeerKAT pre-explosion images.
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.815 | 1.26 | 0.144 ± 0.017 |
| 9.710 | 1.26 | 0.303 ± 0.012 |
| 49.690 | 1.26 | 0.153 ± 0.015 |
| 68.669 | 1.26 | 0.162 ± 0.012 |
| 21.752 | 0.65 | 0.104 ± 0.030 |
| 48.544 | 0.65 | <0.12 |
| 66.565 | 0.65 | <0.18 |
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.815 | 1.26 | 0.144 ± 0.017 |
| 9.710 | 1.26 | 0.303 ± 0.012 |
| 49.690 | 1.26 | 0.153 ± 0.015 |
| 68.669 | 1.26 | 0.162 ± 0.012 |
| 21.752 | 0.65 | 0.104 ± 0.030 |
| 48.544 | 0.65 | <0.12 |
| 66.565 | 0.65 | <0.18 |
uGMRT observing log of the afterglow of GRB 190114C. Measurements are not corrected for the flux of the host galaxy detected in MeerKAT pre-explosion images.
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.815 | 1.26 | 0.144 ± 0.017 |
| 9.710 | 1.26 | 0.303 ± 0.012 |
| 49.690 | 1.26 | 0.153 ± 0.015 |
| 68.669 | 1.26 | 0.162 ± 0.012 |
| 21.752 | 0.65 | 0.104 ± 0.030 |
| 48.544 | 0.65 | <0.12 |
| 66.565 | 0.65 | <0.18 |
| T-T0 . | Frequency . | Flux density . |
|---|---|---|
| (d) . | (GHz) . | (mJy) . |
| 2.815 | 1.26 | 0.144 ± 0.017 |
| 9.710 | 1.26 | 0.303 ± 0.012 |
| 49.690 | 1.26 | 0.153 ± 0.015 |
| 68.669 | 1.26 | 0.162 ± 0.012 |
| 21.752 | 0.65 | 0.104 ± 0.030 |
| 48.544 | 0.65 | <0.12 |
| 66.565 | 0.65 | <0.18 |
4 MULTIBAND LIGHT CURVES
In Fig. 1, we show the multiband evolution of the afterglow of GRB 190114C constructed using our ATCA, ALMA, GMRT, GIT, DFOT, and HCT data and supplemented with the X-ray lightcurve obtained from the Swift XRT archive1 (Evans et al. 2007, 2009) and using available optical and radio data in the literature (Bolmer & Schady 2019; D’Avanzo et al. 2019; Izzo et al. 2019; Kim et al. 2019; Kim & Im 2019; Kumar et al. 2019b; Laskar et al. 2019; Mazaeva et al. 2019a,b,c,d; Ragosta et al. 2019; Selsing et al. 2019; Singh et al. 2019; Watson et al. 2019a,b). We adopt the X-ray light curve from the Swift XRT archive considering that there is no photon index evolution. However, The Swift Burst Analyser page2 (Evans et al. 2010) for this burst shows that the X-ray photon index changes over time between 105 and 106 s. In order to address this issue, we performed our own spectral fits to estimate the photon index. We binned the count rate light curve using Bayesian block binning (Scargle 1998) and generated the spectra in these time bins. The spectra are fitted with an absorbed simple power law model (phabs) using two absorption components - one for Galactic and one for host. The NH values for our galaxy and host are fixed at 7.54 × 1019 and 8.0 × 1022 cm−2 (taken from XRT spectrum repository) respectively and z of the absorber is fixed at 0.42. We compare our estimated photon index with that of the burst analyser. Our results are consistent with the photon index of 1.94 (+0.11, −0.10) within error bars given in the XRT repository and no spectral evolution is evident. A comparison of the photon index values from burst analyser and our estimates along with the XRT repository photon index is shown in Fig. 2. Based on these results, we adopt the XRT repository light curve for the rest of the analysis presented in this paper.
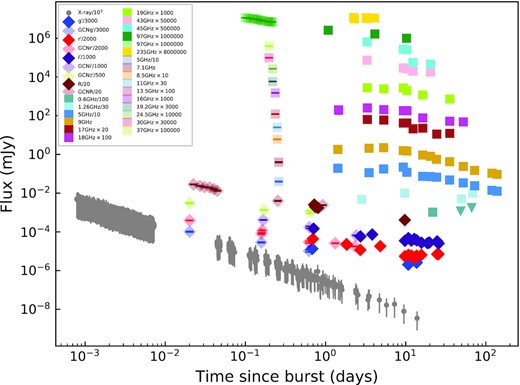
Multiband light curves of the afterglow of GRB 190114C from X-ray to the radio/mm bands. The solid symbols represent our data and the light shaded symbols represent the data from the literature.
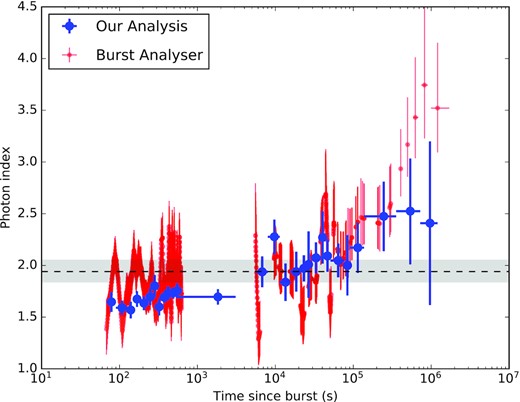
Comparison of the X-ray photon index values from burst analyser (red) and our estimates (blue) along with the photon index value (grey horizontal bar) reported in the XRT repository.
The multiband evolution of the GRB 190114C afterglow is complex as seen from Fig. 1. The temporal evolution of the X-ray light curve is consistent with a single power-law following a decay index of |$\alpha _\rm {X}=-1.344\pm 0.003$| from 68 s to ∼10 d, and shows a hint of a steeper decline thereafter.
ATCA 9 and 5.5 GHz data offer a temporal coverage of two orders of magnitude. The late-time temporal slope of 9 GHz (t > 10 d) is −1.07 ± 0.04 and of 5.5 GHz (t > 25 d) is −1.00 ± 0.03. Millimetre data presented in this paper along with that of Laskar et al. (2019) give a wide temporal coverage at 97 GHz. For t < 0.3 d, the 97 GHz light curve decays as t−(0.71 ± 0.02), the temporal coverage is sparse afterwards, however our last observation yielding a 3σ upper limit of 0.14 mJy indicates a steeper decay. In Fig. 3, we present the power-law fits in the X-ray, R, 97 GHz, and 9 GHz bands mentioned above.
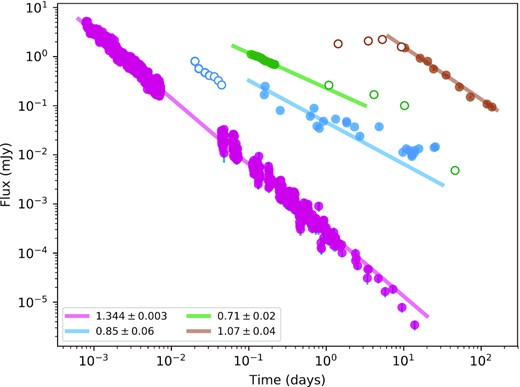
Empirical fits to a selected set of multiband light curve data, used to aid the physical modelling (see text). X-ray (violet), R band (blue), 97 GHz (green), and 9 GHz (brown). For 9 GHz, 97 GHz and the R band, data excluded from the fit are shown with open symbols.
To construct a broadband multicolour optical/NIR light curve, we take data from the following sources: this paper, MAGIC Collaboration (2019); de Ugarte Postigo et al. (2020); Jordana-Mitjans et al. (2020); Melandri et al., in preparation; and GCNs (Bikmaev et al. 2019; Im, Paek & Choi 2019; Kim & Im 2019; Mazaeva et al. 2019b; Watson et al. 2019b). We correct for Galactic extinction along the line of sight (E(B − V) = 0.0107 ± 0.0004 mag; Schlafly & Finkbeiner 2011), remove outliers and fit the data set, spanning from the uvw2 to the K band, with a set of smoothly broken power-laws. Hereby, we assume achromaticity3 and share the fit parameters early steep slope αs, pre-break slope α1, post-break slope α2, break times tb, s, tb and break smoothness ns, n among all bands, whereas the normalizations and host-galaxy magnitudes are individual parameters for each band. We exclude any data beyond 7 d (except for late host observations at >50 d), as they may be influenced by a rising supernova component.
We find that the earliest observations are far brighter than a back-extrapolation of the data beyond 0.1 d, likely due to a steeply decaying RS component (Jordana-Mitjans et al. 2020). Fitting the data up to 0.8 d yields (|$\chi ^2{\rm {/d.o.f.}} = 1.86$|) αs = −2.076 ± 0.023, α1 = −0.544 ± 0.011, and tb, s = 0.00508 ± 0.0003 d (tb, s = 439 ± 26 s); hereby n = −0.5 was fixed, a soft steep-to-shallow transition between slopes.
Between 0.06 and 7 d, the multicolour light curve is well-described (some remaining scatter leads to |$\chi ^2{\rm {/d.o.f.}} = 3.35$|) by a broken power-law with α1 = −0.530 ± 0.017, α2 = −1.067 ± 0.011, and tb = 0.576 ± 0.028 d; hereby n = 10 was fixed. The normalization of each band, formally the magnitude at break time for n = ∞ (Zeh, Klose & Kann 2006), then represents the UV/optical/NIR Spectral Energy Distribution (SED), based not just on a small number of data points, but on all data involved in the fit. As only the first fit covers all bands, we use the values derived from it. The direct values are measured at break time ∼0.005 d, but are valid over the entire temporal range if scaled according to the light-curve evolution.
4.1 Extinction in the host galaxy and intrinsic afterglow spectrum
Using the broadband UV-to-NIR SED derived in Section 4, we can derive the intrinsic host-galaxy extinction using the parametrization of Pei (1992) and following the method of e.g. Kann, Klose & Zeh (2006). A fit without any extinction yields a very steep spectral slope β0 = −2.90 ± 0.03 (usual intrinsic values range from |$\approx -0.5\, \mathrm{ to}\, -1.1$|), immediately indicative of dust along the line of sight in the host galaxy. The SED shows some scatter and strong curvature combined with small errors, leading to large χ2 values despite a visually good fit when a dust model is included. For Milky Way (MW), Large Magellanic Cloud (LMC), and Small Magellanic Cloud (SMC) dust, we derive positive intrinsic β values, indicating it is unlikely that the host galaxy has dust similar to these local galaxies. Such positive values, with the flux density rising from the red to the blue, are not expected from afterglow theory. Of all three dust models, MW dust yields the best fit, with χ2 = 1.36, β = 0.32 ± 0.14, and AV = 3.07 ± 0.14 mag. The two other dust models represent the SED less well (LMC: χ2 = 3.61, β = 0.61 ± 0.14, and AV = 3.21 ± 0.14 mag; SMC: χ2 = 5.91, β = 0.39 ± 0.13, and AV = 2.95 ± 0.13 mag), neither being able to adapt to the large u − b colour and the relatively bright UVOT UV detections. Especially noteworthy is the failure of SMC dust, which is most often able to fit GRB sightlines well (e.g. Kann et al. 2006, 2010).
In addition to the three different fits with the intrinsic slope as a free parameter, we also fix the slope to two values based on the X-ray fit from the Swift XRT archive, βX = βopt = −0.81 and βX − 0.5 = βopt = −0.31. For these fits and MW dust, we derive AV = 1.93 ± 0.03 mag and AV = 2.41 ± 0.04 mag, respectively, indicating that AV = 1.9 − 2.4 mag is a realistic range. Such large values of extinction had already been hinted at from spectroscopy (Kann et al. 2019), a result in qualitative agreement with the independent analysis of MAGIC Collaboration (2019).
The SED fits are shown in Fig. 4. It can be clearly seen that the three dust extinction laws differ little at Fν ≲ 1015 Hz, implying that if low-z bursts are only observed in the observer-frame B band and redder, the dust model can not be determined (Kann et al. 2006). However, the detections in the UV clearly allow a distinction – and in this case, actually none of the three models fits the data well, however, the MW dust model yields the best of the three fits. While the detections in the three Swift UVOT UV bands are low-S/N, they follow the afterglow decay as determined from the optical bands well, and the host galaxy is not luminous in these bands (de Ugarte Postigo et al. 2020). A more detailed analysis of the SED with a more free parametrization than the curves of Pei (1992) provide, following e.g. the methods of Zafar et al. (2018a), Zafar et al. (2018b), is beyond the scope of this paper.
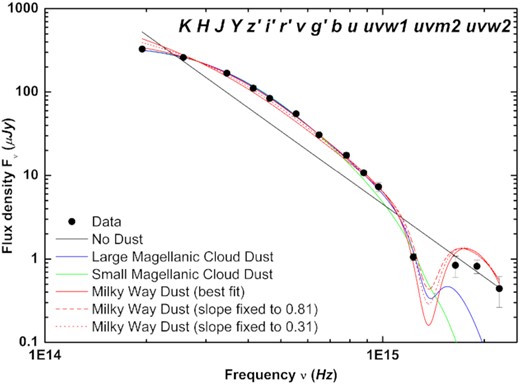
SED of GRB 190114C as derived from a multiwavelength joint fit. It stretches from the UV (right) to the NIR (left). We have fit the SED with different dust-extinction laws. It can be seen that at ≲ 1015 Hz, all three dust models fit about equally well, whereas there are large differences in the rest-frame far-UV; here, none of the dust models fits well, however, the Milky-Way dust fit fits the SED significantly better than the other two dust models. All fits indicate strong dust attenuation. For the MW fit, we also show two fits with fixed spectral slope β derived from X-ray data (see text for more details).
4.2 The afterglow of 190114C in the context of other GRB afterglows
To put the X-ray emission in the context of other GRB afterglows, we retrieved the X-ray light curves of all Swift GRBs until the end of February 2019 with detected X-ray afterglows (detected in at least two epochs) and known redshifts from the Swift XRT archive. The density plot in Fig. 5 displays the parameter space occupied by these 415 bursts (using the method described in Schulze et al. 2014). GRB 190114C, displayed in green, has a luminosity that is similar to the majority of the GRB population.
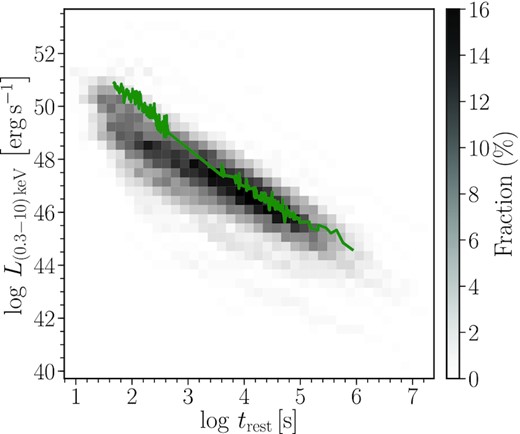
The X-ray light curve of GRB 190114C in the context of the X-ray afterglows of Swift GRBs with known redshifts. The luminosity of GRB 190114C is comparable to the bulk of the GRB population.
To compare the optical afterglow light curves of GRB 190114C with other GRB afterglows, we follow the steps described below. We use the SED derived for the afterglow of GRB 190114C to shift the data of individual bands to the R band, after subtracting the individual host-galaxy contributions, and then clean this composite light curve of outliers. Hereby, we use only NIR data at t > 7 d as this is expected to not be affected by the SN contribution as much. We then use our knowledge of the redshift and the host-galaxy extinction with the method of Kann et al. (2006) to determine the magnitude shift dRc. This shift (together with the time shift determined from the redshift) moves the light curve in such a way as it would appear if the GRB occurred at z = 1 in a completely transparent universe – the host-galaxy extinction is corrected for. The time, however, is still given in the observer frame. Applied to a large sample, this allows for a direct luminosity comparison. For GRB 190114C, the high extinction and low redshift essentially cancel each other out. For the two fits with MW dust coupled to the X-ray spectral slope, we find |$dRc=-0.944^{+0.054}_{-0.055}$| mag for the high-extinction case (β = −0.31) and |$dRc=-0.169^{+0.051}_{-0.053}$| mag for the low-extinction one (β = −0.81).
In Fig. 6, we show the observed and corrected light curves of GRB 190114C in comparison to a large afterglow sample (Kann et al. 2006, 2010, 2011, 2018). The early steep decay likely resulting from a reverse-shock flash is clearly visible. At early times, the afterglow of GRB 190114C is one of the brightest detected so far observationally, despite the high line-of-sight extinction. However, in the z = 1 frame (we plot the high-extinction case), it is seen to be of only average luminosity initially, making it once again similar to the ‘nearby ordinary monster’ GRB 130427A (Maselli et al. 2014), and mirroring the result we find in the X-rays. At late times, the slow decay and lack of any visible jet break to t > 10 d, which is unusual behaviour for GRB afterglows, leads it to become comparably more and more luminous. We caution this also stems from our choice of a high extinction correction, though, conversely, that is the better SED fit. We can also compare the afterglow of GRB 190114C with the two other cases4 of known GRB with VHE detections, namely GRB 180720B (Abdalla et al. 2019) and GRB 190829A (de Naurois & H. E. S. S. Collaboration 2019). Observationally, the afterglow of GRB 180720B (based on data from Crouzet & Malesani 2018; Horiuchi et al. 2018; Itoh et al. 2018; Lipunov et al. 2018; Martone et al. 2018; Reva et al. 2018; Sasada et al. 2018; Schmalz et al. 2018; Watson et al. 2018; Zheng & Filippenko 2018 as well as Kann et al., in preparation) is seen to be even brighter, it is one of the few GRB afterglows detected at <10 mag at very early times. Despite its proximity, the afterglow of GRB 190829A (a preliminary analysis based on the data presented in Hu et al. 2021) is seen to be of average brightness, fainter than the more distant one of GRB 190114C. We find a straight SED for the GRB 180720B afterglow, with no evidence for dust. This is very different from the two other VHE-detected GRBs, as we also find evidence for large line-of-sight extinction, AV ≈ 3 mag, for GRB 190829A. Shifting both afterglows to z = 1, we find the afterglow of GRB 180720B to be quite similar to that of GRB 190114C in terms of luminosity (albeit with a steeper decay at late times), and being an average afterglow in the context of the whole sample. The afterglow of GRB 190829A, on the other hand, despite the large extinction correction, is found to be less luminous than most of the sample, thereby being similar to those of other low-luminosity GRBs in the local Universe (Kann et al. 2010). The detectCion of VHE emission is therefore neither linked inextricably to the extinction along the line of sight, nor to the luminosity of the afterglow.
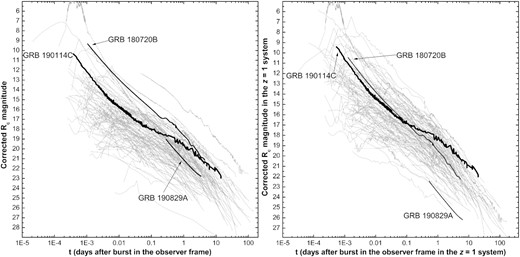
The optical light curve of the afterglow of GRB 190114C in comparison to a large afterglow sample. Left: Afterglows in the observer frame. These have been corrected for Galactic extinction, as well as being host- and, where possible, supernova-subtracted, but are otherwise as observed. GRB 190114C is seen to have one of the brightest known early afterglows however, it is outshone by that of GRB 180720B. The third known GRB with a VHE detection, GRB 190829A, is seen to be of average brightness despite its proximity. Right: Afterglows shifted to the z = 1 frame (see text for more details), corrected for host-galaxy extinction. Despite the large correction for extinction, the afterglow of GRB 190114C is seen to be of average nature at early times, but becomes one of the most luminous afterglows later on, stemming from the slow decay which is untypical for GRBs at t > a few days. The other two VHE-detected GRBs are also plotted. The afterglow of GRB 180720B is seen to be similar to that of GRB 190114C, especially at early times. The afterglow of GRB 190829A, despite the correction for the large line-of-sight extinction, is seen to be underluminous, similar to other afterglows of nearby GRBs.
Fig. 7 shows a comparison of the peak flux densities of GRB 190114C with other events at millimetre and centimetre wavelengths, as a function of the redshift. Although GRB 190114C is bright at radio and millimetre wavelengths, this is mostly due to its low redshift. Comparing its peak luminosity with these samples of bursts, we yet again observe an average event. We note that the peak luminosity in millimetre wavelengths is dominated by the RS, detected through very early ALMA observations by Laskar et al. (2019).
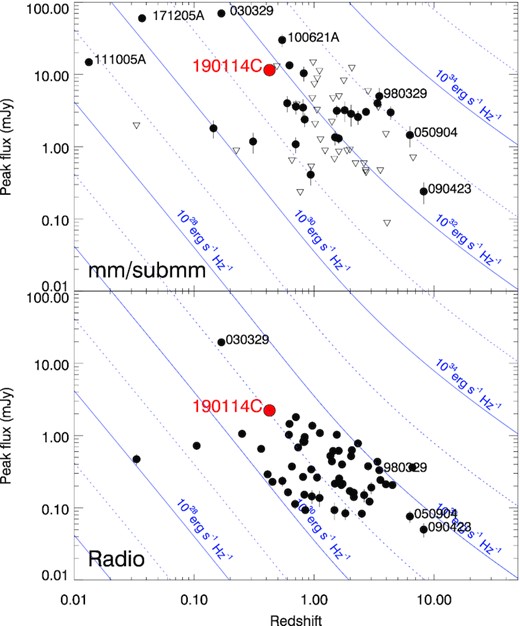
Peak flux densities of GRB 190114C in the context of the mm/submm and radio samples of de Ugarte Postigo et al. (2012) and Chandra & Frail (2012), plotted as a function of redshift. Blue lines indicate equal luminosity, with the most luminous events being found in the top right corner. Some prominent events have been highlighted.
5 INTERSTELLAR SCINTILLATION IN RADIO BANDS
Inhomogeneities in the electron density distribution in the MW along the GRB line-of-sight scatter radio photons. This effect, called ISS, results in variations in measured flux density of the source at low frequencies (≲ 10 GHz; Rickett 1990; Goodman 1997; Walker 1998; Goodman & Narayan 2006; Granot & van der Horst 2014). GRBs often display a similar behaviour in their radio light curves (see e.g. Frail et al. 1997; Goodman 1997; Frail, Waxman & Kulkarni 2000) with the variations occurring between observations on time-scales ranging between hours and days.
In all regimes, the strength of scattering ξ decreases with time at all frequencies as the size of the emitting region expands, with diffractive ISS quenching before refractive ISS. The source expansion also increases the typical time-scale of the variations for both diffractive and refractive ISS (Resmi 2017). In this complex scenario, the contribution of ISS for each regime is defined by the modulation index m, defined as the rms fractional flux-density variation (e.g. Walker 1998; Granot & van der Horst 2014).
In our analysis, we estimated the ISS effects on GRB 190114C through a dedicated fitting function that includes both diffractive and refractive contributions (Goodman & Narayan 2006). The values of νtrans = 8.14 GHz and dscr = 0.76 kpc and SM = 1.79 × 10−4 kpc m−20/3 are estimated through the NE20015 model for the Galactic electron distribution (Cordes & Lazio 2002). We estimated the ISS contribution in our radio data summing this effect to the uncertainty of flux densities; this contribution is very important in C (ATCA 5.5 GHz) and X (ATCA 9 GHz) bands (|$\sim 50 {{\ \rm per\ cent}}$| of the flux density), whereas it is very low for L (GMRT 1.26 GHz) band and ALMA frequencies (|$\lesssim 5{{\ \rm per\ cent}}$|).
6 X-RAY, MILLIMETRE, AND RADIO OBSERVATIONS WITHIN THE STANDARD AFTERGLOW MODEL
We used the framework of the standard afterglow model (see Kumar & Zhang 2015 for a review) to reproduce the multiband afterglow evolution. We primarily considered the radio/mm data presented in this paper for the modelling, along with the publicly available Swift XRT observations. We used the specific flux at 3 keV for the model, obtained by converting the integrated flux in the 0.3–10 keV band using an average spectral index of −0.81 quoted at the XRT spectral repository.6 We excluded the optical/IR light curves because of the large host extinction (see Section 4.2), which introduces an additional parameter in the problem. We show optical predictions from parameters estimated by using X-ray and radio bands.
The basic physical parameters of the afterglow fireball, isotropic equivalent energy Eiso, ambient density (n0 for ISM and A⋆ for wind), fractional energy content in electrons (ϵe), and magnetic field (ϵB) translate to the basic parameters of the synchrotron spectrum which are the characteristic frequency (νm), cooling frequency (νc), self-absorption frequency (νa), and the flux normalization at the SED peak (fm) at a given epoch (Wijers & Galama 1999). In addition, the model also depends on the electron energy spectral index p and the fraction ζe of electrons going into the non-thermal pool. We use a uniform top-hat jet with half-opening angle θj.
We do not consider synchrotron self-Comtpon (SSC) emission in our model and hence we exclude MAGIC and Fermi LAT data from our analysis.
6.1 A challenge to the standard model
As mentioned in Section 4, the XRT light curve decays with a slope of αX = −1.344 ± 0.003 at t ≤ 10 d and the ATCA light curves decay with a slope of αradio ∼ −1 at t ≥ 10 d. The last XRT detection at 13.86 d mildly deviates from the single power-law while the 3σ upper limit at 27.5 d can not place any further constraints on a potential break. This may indicate the onset of jet effects at ∼10 d, either due to a change in the dynamical regime or due to relativistic effects in case of a non-expanding jet (Rhoads 1999; Sari, Piran & Halpern 1999). However, to begin with, we consider both light-curve slopes to be devoid of jet effects (see Section 6.1.1 below for a discussion considering jet side effects).
The difference Δα in the temporal indices of the two light curves is consistent with 0.25, the expected number if the synchrotron cooling break νc remains between the bands. Under this assumption, light-curve slopes αX and αradio imply p ∼ 2.45 and a constant density ambient medium. However, this picture demands that the XRT spectral index should be ∼−1.23, which is not consistent with the value of βX = −0.81 ± 0.1 reported in the Swift XRT spectral repository. Moreover, if νc is between radio and X-ray frequencies, the spectral slope between radio (say 9 GHz as a representative frequency) and XRT should lie between −(p − 1)/2 ∼ −0.73 and −p/2 ∼ −1.2, with the exact value decided by the position of νc at the epoch at which the spectral slope is measured. To test the possibility of the X-ray light curve originating in the ν > νc segment and the decaying part of the radio light curve belonging to the νm < ν < νc segment, we constructed a synthesized simultaneous spectrum at 10 d, extrapolated from single power-law fits to the light curves at 5 GHz, 9 GHz, and 7.26 × 1017 Hz (3 keV). We found that the ratio of the extrapolated fluxes is FX/F9GHz = (νX/ν9GHz)−0.64, which is even smaller than ν−0.73, completely ruling out the possibility of a p ∼ 2.45.
Next we examine if the radio-XRT SED at 10 d agrees with a smooth double power-law of asymptotic slopes β1 and β2 = β1 + 0.5 (to mimic the synchrotron spectrum around νc). We found the SED can be reproduced if β1 = −0.52 ± 0.02 and |$\nu _c = 3.1^{+3.1}_{-1.5} \times 10^{15}$| Hz (Fig. 8). The smoothing index is set at 2.0. Due to the scatter in the radio/mm data at this epoch, we have used the scintillation correction described in Section 5 to do the fitting. The fitting results are sensitive to the choice of data, such that without scintillation correction in 9 and 5 GHz, the spectral index is flatter. Both the β1 and the observed XRT spectral index are consistent with p ∼ 2.0. Therefore, we conclude that while p ∼ 2, both the radio and X-ray light curves decay at much steeper rate than expected, and the most likely solution is to relax the assumption that ϵe and ϵB are constants in time. It is to be noted that the best-fitting host extinction correction leads to a flatter UV/optical/NIR SED. However, due to the uncertainties in inferring the host extinction (see Section 4.1), we have ignored this inconsistency in future discussions and also chose not to include UV/optical/NIR data for further analysis.
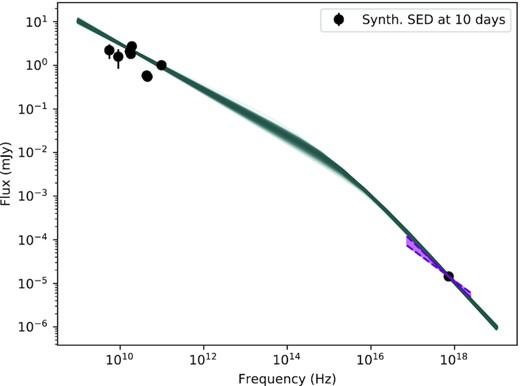
The synthesized radio-XRT spectrum at ∼10 d. The smooth double power-law model assumes νc = 3.1 × 1015 Hz and β1 = 0.52. The observed spectral index from XRT spectral repository is shown in purple.
Nevertheless, in Appendix B we give a detailed description of how the radio/X-ray data compare with the standard afterglow model with constant ϵe and ϵB. Before proceeding with the time-evolving microphysics model, we however explore the validity of a model with jet break at ∼10 d in the next section.
6.1.1 Can a jet break save the standard model?
The last XRT observation at 27.5 d yielded an upper limit, which (within 3σ) falls above the extrapolation of the single power-law light curve. Yet, it is possible that there indeed is a break at ∼10 d in the XRT light curve. More sensitive late-time observations by XMM-Newton or Chandra could yield conclusive evidence of this possibility. Considering the fact that the ATCA light curves also show a change of slope at about 10 d, such a break can likely be due to jet effects, though achromaticity of jet breaks is debated Zhang et al. (2006).
We consider two asymptotic examples, an exponentially expanding jet such as in Rhoads (1999) and a non-expanding jet. For the former, as the radial velocity is negligible post jet break, the temporal decay indices are insensitive to the density profile (Rhoads 1999). In this case, for the spectral regimes ν < νa, νa < ν < νm, νm < ν < νa, (νm, νa) < ν < νc, and (νm, νc) < ν, the temporal indices are 0, −1/3, 1, −p, and −p, respectively. However, the observed temporal decay of the ATCA light curves does not agree with any of these values, therefore this possibility is ruled out. Moreover, a smoothly varying double power-law fit to the XRT light curve (smoothing index of 2) shows that the post-break slope α2, X = −1.76 ± 0.06. This does not conform to the predictions of the simple model of exponentially expanding jets where the post break slope of the optically thin light curve is always −p.
For the latter case, the flux is reduced as the solid angle accessible to the observer increases beyond the jet edge. Therefore, the expression for the observed flux picks up an additional factor of Γ2 (where Γ is the bulk Lorentz factor of the jet) to account for the deficit in solid angle (Kumar & Zhang 2015). Here, for an adiabatic blast-wave in a constant density ambient medium (Γ∝t−3/8; Wijers & Galama 1999), post-break temporal indices are −1/4, −1/4, +1/2, −3p/4, and −(3p + 1)/4, respectively for the above-mentioned set of spectral regimes. For a wind-blown density profile (Γ∝t−1/4; Chevalier & Li 2000), the temporal indices become +1/2, −1/2, +1/2, −(3p + 1)/4, and −3p/4, respectively. None of these values for a range of 2 < p < 3 are in agreement with the radio light-curve slope of ∼−1. Therefore, we rule out the possibility of a jet break saving the standard afterglow model.
We conclude that even if there is an achromatic break in the light curves at ∼10 d, non-standard effects are required to explain the multi-band flux evolution. In the next section, we describe the time-evolving shock micro-physics model.
6.2 Time-evolving shock micro-physics
The standard afterglow model assumes that the fractional energy content in non-thermal electrons and the magnetic field, ϵe and ϵB, respectively, remain constant across the evolution of the shock. However, this need not necessarily be valid and there have been afterglows where micro-physical parameters have to be time evolving (Filgas et al. 2011a; van der Horst et al. 2014).
To derive the equations governing the spectral parameters, we used the definitions given in Wijers & Galama (1999). For optical depth to self-absorption, we used the expression given in Panaitescu & Kumar (2002), |$\tau _m = \frac{5}{3-s} \frac{e n(r) r \zeta _e}{B \gamma _m^5}$|, where e is the electric charge, n(r) is the ambient density as a function of the fireball radius r, ζe is the fraction of electrons in the power-law distribution, B is the magnetic field, and γm is the minimum Lorentz factor of the power-law electrons. For the dynamics of the blastwave in a constant density medium, we used the temporal evolution of bulk Lorentz factor and radius of the fireball given in Wijers & Galama (1999) and for the wind driven medium, we used the same given in Chevalier & Li (2000).
We first attempted ι = 0 (constant ϵe). The light-curve slope α2 for the spectral segment (ν > νc) then reduces to (2 + p(λ − 3) − 2λ)/4 independent of the value of s, which equals the observed αX only if p > 2.4. Therefore, we conclude that time evolution of ϵB alone can not reproduce the observations.
We attempted Bayesian parameter estimation using Markov Chain Monte Carlo sampling under this model, but convergence could not be achieved perhaps due to the large dimension and degeneracy of the parameter space (see below). Therefore, we visually inspected the light curves to freeze the parameters which are sensitive to the light-curve indices (s, p, λ, and ι).
Using the results of the XRT, optical, and XRT/radio SED analysis, we fixed p = 2.01. We used a value above 2 to avoid the addition of yet another parameter to the problem, the upper cut off of the electron distribution. When p ∼ 2, α2 becomes a function of ι alone (dependence on λ is weak for p close to 2 and zero for p = 2) and we find that ι of −0.4 to −0.3 can reproduce the observed XRT light-curve decay slope. For a fixed p and ι, a region of the s − λ space can reproduce α9GHz (see Fig. 9). For a constant density medium, we fix λ = 0.1 and for a wind-driven density profile, we fix λ = 0.76.
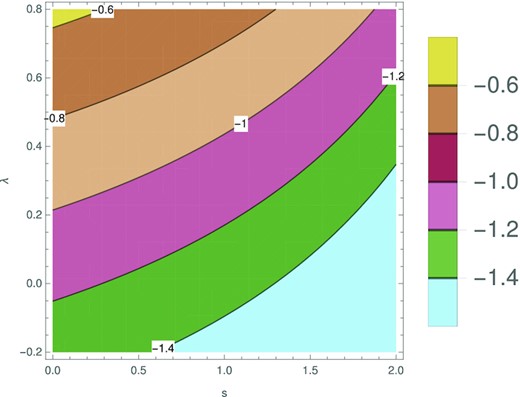
Predicted light-curve decay slopes for the spectral segment νm < ν < νc, as contours in the plane of s − λ. p and ι are fixed at 2.01 and −0.4, respectively. The observed radio decay index of −1.0 to −1.1 can be reproduced by a range of s and λ values. In this paper, we have presented models for (s = 0, λ = 0.1) and (s = 2, λ = 0.76).
We attempted Bayesian parameter estimation in the spectral parameter regime, where the remaining parameters of the problem are νm, νc, fm and the optical depth τm at ν = νm. All values correspond to a specific epoch which we fixed to be t = 65 s. We employed the Bayesian parameter estimation package pyMultinest (Buchner et al. 2014) based on the Nested Sampling Monte Carlo algorithm Multinest (Feroz, Hobson & Bridges 2009). Multinest is an efficient Bayesian inference tool which also produces reliable estimates of the posterior distribution.
uGMRT measurements imply that the fireball is optically thick below 1.4 GHz. However, as the low-frequency data are limited, we could not obtain a meaningful convergence for τm. Therefore, we ran simulations for different fixed values of τm and found that for the constant density medium, −16.5 < log τm(t = 65 s) < −15.5 is consistent with the overall evolution of the fireball at higher frequencies. For the wind medium, −17 < log τm(t = 65 s) < −12 is consistent. Nevertheless, we find that the self-absorbed light curves in 1.26 and 0.65 GHz are not in great agreement with the observations. It is likely that the evolution of νa from this model is different from what is demanded by the observations (see Figs 10 and 11). A different νa evolution could arise due to absorption by thermal electrons (our solutions indicate a low fraction of electrons in the non-thermal pool, Ressler & Laskar 2017). A different s − λ combination may also solve this discrepancy.

Light curves in the constant density model, corresponding to the peak of the posterior distribution presented in Fig. 12. Error bars in radio bands account for scintillation (see Section 5). Though we have included all the radio/mm data presented in this paper along with the XRT data in the Bayesian parameter estimation, for clarity we have only shown a few representative bands in this figure. For the uGMRT 1.25 GHz (0.65 GHz) model, we have included a host galaxy flux of 0.05 mJy (0.07 mJy). The optical bands are not included in the parameter estimation, but our model predictions, with the range of host galaxy extinction used in Section- 4.1 (Av = 1.9 − 2.4, MW extinction law) are well in agreement with the observations. In this figure, we have used Av = 1.9.
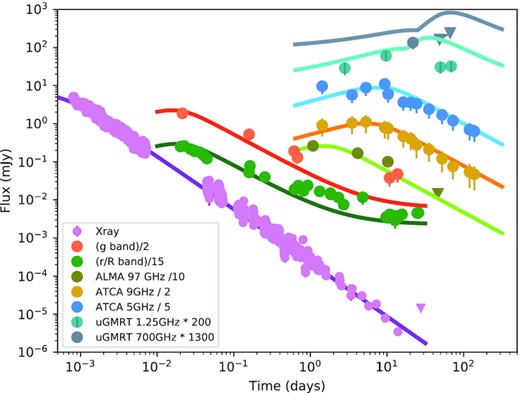
Light curves in the wind model, corresponding to the peak of the posterior distribution presented in Fig. 13. We have used host Av = 2.4 for this figure.
In Figs 10 and 11, we present multiband light curves from this model respectively for a constant density and a stratified density medium. For uGMRT 1.25 GHz predictions, we have included a host galaxy flux of 0.05 mJy (three times the average RMS in our maps) to account for the host galaxy seen in meerKAT images (Tremou et al. 2019). For uGMRT band-4 (650 MHz), we added a flux of 0.07 mJy, considering a slope of ν−0.5 for the host SED. Even though the optical data are not included in the parameter estimation, we have presented r′, R, and g′ bands in the figure to demonstrate that both models are well in agreement with the early optical observations. At late time, optical transient flux includes contribution from the associated supernova which we have not considered in the model. In addition, the late time flux also contains contribution from the host galaxy system, a close pair of interacting galaxies (de Ugarte Postigo et al. 2020). We have used host-galaxy magnitudes of 23.1 (corresponding to HST F475W as the frequencies are close) in g′ band. For r′/R band, we used a host magnitude of 22 which is in between that for F606W and F775W. It must be noted that depending on the telescope, the optical transient flux may also include contribution from the companion.
In Figs 12 and 13, we present the posterior distribution of the 3D spectral parameter space and in Tables 5 and 6, we present the fit parameters and the inferred physical parameters. To derive the physical parameters, we used the expressions given in Appendix A. The nested sampling global log-evidences are −(0.37 ± 0.44) and −(0.38 ± 0.25) for the ISM and the wind models, respectively. As the values are comparable within errorbars, we can not prefer one ambient medium to the other under the premises of our model.
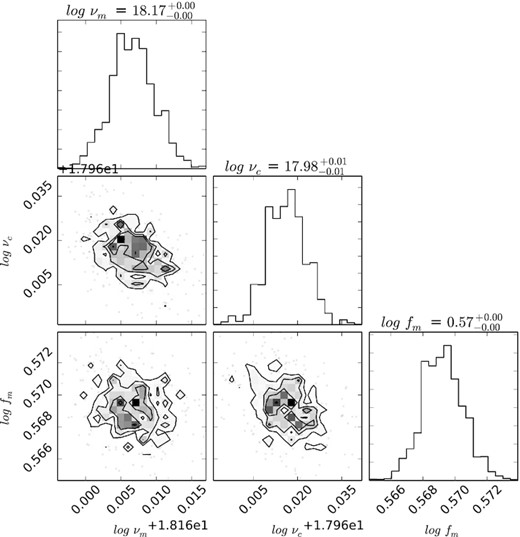
Posterior distributions of the three fit parameters, log (νm/Hz), log (νc/Hz), and log(fm/mJy) for the constant density medium. Values correspond to t = 65 s.
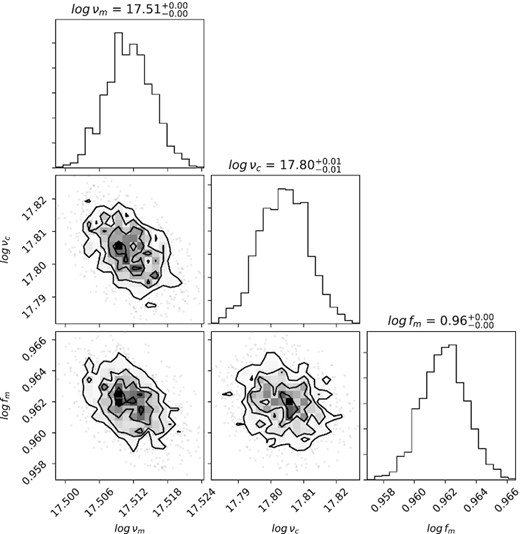
Posterior distributions of the wind model, same parameters as presented in Fig. 12.
Spectral and physical parameters of the time-varying micro-physics model. Spectral parameters are at t = 65 s. Physical parameters correspond to the peak of the posterior. Isotropic equivalent energy is normalized to 1052 ergs and number density is normalized to cm−3. ϵe0 and ϵB0 correspond to t = 1 d i.e, the final values of these parameters are |$\epsilon _e = 0.02 (\frac{t}{\rm day})^{-0.4}$| and |$\epsilon _B = 4.7 \times 10^{-5} (\frac{t}{\rm day})^{+0.1}$|. The fraction of electrons ζe in non-thermal pool is decided by requiring ϵe(t = 65) s <1.
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.1 | 0 | −16.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 18.167 ± 0.003 | 17.98 ± 0.01 | 0.569 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | n0 | ϵe0 | ϵB0 | ζe (assumed) |
| 193.4 | 23.0 | 0.02 | 4.7 × 10−5 | 0.02 |
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.1 | 0 | −16.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 18.167 ± 0.003 | 17.98 ± 0.01 | 0.569 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | n0 | ϵe0 | ϵB0 | ζe (assumed) |
| 193.4 | 23.0 | 0.02 | 4.7 × 10−5 | 0.02 |
Spectral and physical parameters of the time-varying micro-physics model. Spectral parameters are at t = 65 s. Physical parameters correspond to the peak of the posterior. Isotropic equivalent energy is normalized to 1052 ergs and number density is normalized to cm−3. ϵe0 and ϵB0 correspond to t = 1 d i.e, the final values of these parameters are |$\epsilon _e = 0.02 (\frac{t}{\rm day})^{-0.4}$| and |$\epsilon _B = 4.7 \times 10^{-5} (\frac{t}{\rm day})^{+0.1}$|. The fraction of electrons ζe in non-thermal pool is decided by requiring ϵe(t = 65) s <1.
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.1 | 0 | −16.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 18.167 ± 0.003 | 17.98 ± 0.01 | 0.569 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | n0 | ϵe0 | ϵB0 | ζe (assumed) |
| 193.4 | 23.0 | 0.02 | 4.7 × 10−5 | 0.02 |
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.1 | 0 | −16.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 18.167 ± 0.003 | 17.98 ± 0.01 | 0.569 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | n0 | ϵe0 | ϵB0 | ζe (assumed) |
| 193.4 | 23.0 | 0.02 | 4.7 × 10−5 | 0.02 |
Spectral and physical parameters for the wind model. The final values of the microphysical parameters are |$\epsilon _e = 0.02 (\frac{t}{\rm day})^{-0.4}$| and |$\epsilon _B = 4.7 \times 10^{-5} (\frac{t}{\rm day})^{+0.76}$|. The fraction of electrons ζe in non-thermal pool is decided by requiring ϵe(t = 65) s <1.
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.76 | 0 | −13.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 17.511 ± 0.004 | 17.804 ± 0.007 | 0.961 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | A⋆ | ϵe0 | ϵB0 | ζe (assumed) |
| 17.9 | 2.0 | 0.03 | 4 × 10−4 | 0.02 |
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.76 | 0 | −13.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 17.511 ± 0.004 | 17.804 ± 0.007 | 0.961 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | A⋆ | ϵe0 | ϵB0 | ζe (assumed) |
| 17.9 | 2.0 | 0.03 | 4 × 10−4 | 0.02 |
Spectral and physical parameters for the wind model. The final values of the microphysical parameters are |$\epsilon _e = 0.02 (\frac{t}{\rm day})^{-0.4}$| and |$\epsilon _B = 4.7 \times 10^{-5} (\frac{t}{\rm day})^{+0.76}$|. The fraction of electrons ζe in non-thermal pool is decided by requiring ϵe(t = 65) s <1.
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.76 | 0 | −13.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 17.511 ± 0.004 | 17.804 ± 0.007 | 0.961 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | A⋆ | ϵe0 | ϵB0 | ζe (assumed) |
| 17.9 | 2.0 | 0.03 | 4 × 10−4 | 0.02 |
| Fixed parameters | ||||
| p | ι | λ | s | log τm |
| 2.01 | −0.4 | +0.76 | 0 | −13.0 |
| Fitted parameters | ||||
| logνm/Hz | logνc/Hz | logfm/mJy | ||
| 17.511 ± 0.004 | 17.804 ± 0.007 | 0.961 ± 0.001 | ||
| Derived physical parameters | ||||
| E52 | A⋆ | ϵe0 | ϵB0 | ζe (assumed) |
| 17.9 | 2.0 | 0.03 | 4 × 10−4 | 0.02 |
Our derived Eiso = 1.93 × 1054 ergs for the constant density medium exceeds the isotropic energy release in prompt emission by nearly an order of magnitude (MAGIC Collaboration 2019), while for the wind model (Eiso = 1.8 × 1053 erg), it is nearly same as the prompt emission energetics. Lloyd-Ronning & Zhang (2004) found that the prompt efficiency is nearly unity for bursts with large kinetic energy. The constant density solution leads this burst to have a much larger kinetic energy compared to bursts with similar prompt energy release, while by using the wind solution the burst lies close to the rest of the bursts in the distribution presented by Lloyd-Ronning & Zhang (2004). There is degeneracy in the s − λ parameter space as we can see in Fig. 9. However, the extremely high value of Eiso, K may be used to disfavour the ISM medium.
Considering a lower limit at t = 100 d for the jet-break, we derive the half opening angle of the jet to be |$32.5^{\circ } \left(\frac{t_{\rm jet}}{100 \rm day} \right)^{3/8}$|, indicating a true energy release of Etot > 3 × 1053 ergs for the constant density medium. For the wind medium, the opening angle from the same consideration of a jet break leads to θ > 19.3°, and a true energy release of 1052 ergs. The inferred steep rise in ϵB for a wind environment is still consistent with it to remain within the equipartition value within the available observations. The value of ϵB reaches 0.3 only at 5000 d.
6.2.1 Reverse shock emission
We used the Eiso, 52 and the number density derived from the forward shock and searched the parameter space of the RS to explain the early VLA and ALMA data presented by Laskar et al. (2019). While the VLA data from 5 to 37 GHz can be well explained by the RS model presented in Resmi & Zhang (2016), we could not reproduce the shallow decay of the 97 GHz light curve around 0.1 d. This could be resolved by improvements in the RS model. On the other hand, this may be resolved by a different combination of the degenerate parameter pair s − λ.
6.3 Discussion on the modelling
In summary, we have found that the multiwavelength afterglow evolution is not consistent with the spectro-temporal closure relations predicted by the standard afterglow model. We have shown that a time evolution of the shock microphysical parameters can very well explain the overall behaviour of the afterglow, particularly above 1 GHz. Such a time evolution of the afterglow shock microphysics has been invoked to explain individual afterglow observations in the past, for example by Filgas et al. (2011a) to explain GRB 091127 and by van der Horst et al. (2014) to explain GRB 130427A. For GRB 091127, an ϵB increasing as t1/2 is required to explain the fast movement of the cooling break while for GRB 130427A, an ϵe∝t−0.2 is required to explain the evolution of νm. Compared to these authors, we require both ϵe and ϵB to evolve in time, and similar to our inferred evolution, van der Horst et al. (2014) also require ϵe to decrease with time (though slower by a factor of 2). Bošnjak & Daigne (2014) have invoked time evolution of shock microphysics in GRB prompt emission and have given a detailed description of the validity of this assumption in the context of particle-in-cell simulations of relativistic shocks.
Gompertz, Fruchter & Pe’er (2018) has found a scatter in the p value between light curve and spectral indices for several GRBs. A standard deviation of 0.25 found by them can accommodate the disagreement between the α and β values for this burst. However, such a modelling incorporating a distribution of p is beyond the scope of this paper.
We have not considered SSC cooling, which can modify the electron distribution and therefore cause deviation from the α − β closure relations expected under the standard model (Nakar, Ando & Sari 2009). However such a modification is expected only for the fast-cooling phase and it is highly unlikely to be relevant for late-time observations.
It is also to be noted that numerical simulations of expanding jets have shown differences from semi-analytical treatments like ours (see Granot & van der Horst 2014 for a review). For example, the jet break could be less pronounced in radio light curves. Therefore, employing results from more detailed numerical simulations may remove some of these inconsistencies.
In addition to all these points above, another important fact to note is that the radio band is known to exhibit non-standard behaviour (Frail et al. 2004), and the ATCA light curves may very well be representing the same. Detailed broadband follow-up of individual bursts in the radio band is definitely important and has promising prospects in the future era of the Square Kilometer Array and ngVLA.
7 CONCLUSIONS
In this paper, we focus particularly on the late time and low-frequency afterglow of the MAGIC-detected GRB 190114C obtained using GIT, DFOT, and HCT in the optical, ALMA, ATCA, and uGMRT in radio. GRB 190114C is one of the three bursts (other two are GRBs 180720B and 190829A) so far detected at high GeV/TeV energies. Detailed modelling of the TeV and early multiwavelength afterglow has shown that the high-energy photons arise from up-scattered synchrotron photons (MAGIC Collaboration 2019).
Multiwavelength evolution of the afterglow does not conform to the α − β closure relations expected under the standard fireball model. Mutiwavelength modelling indicates that for an adiabatic blastwave we require the microphysical parameters to evolve in time, as ϵe∝t−0.4, ϵB∝t+0.1 for constant density ambient medium and ϵB∝t+0.76 for a stellar wind driven medium. A time evolution of shock microphysics such as the one inferred here, resulting in a low ϵB and a high ϵe at early times may play a role in producing the bright TeV emission. The inferred isotropic equivalent kinetic energy in the fireball, 1.9 × 1054 ergs, exceeding that in the prompt emission as observed for several afterglows (Cenko et al. 2011). Considering 100 d as a lower limit to the jet break time, we derive the opening angle to be >32.5° and the total energy to be >3 × 1053 ergs.
Due to the inclusion of the late-time radio data, our interpretations differ from those of MAGIC Collaboration (2019) and Ajello et al. (2020). However, there are unsolved components in the evolution of the afterglow still, particularly in the early RS emission at millimetre wavelengths. More detailed models including realistic jet dynamics and lateral expansion may have to be tested against these observations. These observations show the importance of low-frequency campaigns in obtaining an exhaustive picture of GRB afterglow evolution.
ACKNOWLEDGEMENTS
We thank the referee for providing constructive comments which have improved the scientific content of the paper. We thank the staff of the GMRT that made these observations possible. GMRT is run by the National Centre for Radio Astrophysics (NCRA) of the Tata Institute of Fundamental Research (TIFR). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.01410.T, ADS/JAO.ALMA#2018.A.00020.T. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The Australia Telescope Compact Array (ATCA) is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We thank Gaurav Waratkar, Viraj Karambelkar, and Shubham Srivastava for undertaking the optical observations with the GIT. The GIT is a 70 cm telescope with a 0.7 deg field of view, set up by the Indian Institute of Astrophysics (IIA, Bengaluru) and the Indian Institute of Technology Bombay (IITB) with support from the Indo-US Science and Technology Forum (IUSSTF) and the Science and Engineering Research Board (SERB) of the Department of Science and Technology (DST), Government of India (https://sites.google.com/view/growthindia/). It is located at the Indian Astronomical Observatory (Hanle), operated by the Indian Institute of Astrophysics (IIA). This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester. LR and VKJ acknowledge support from the grant EMR/2016/007127 from Dept. of Science and Technology, India. DAK, AdUP, and CCT acknowledge support from the Spanish research project AYA2017-89384-P. AdUP and CT acknowledge support from funding associated to Ramón y Cajal fellowships (RyC-2012-09975 and RyC-2012-09984). DAK also acknowledges support from the Spanish research project RTI2018-098104-J-I00 (GRBPhot). KM, SBP, and RG acknowledge BRICS grant DST/IMRCD/BRICS/Pilotcall/ProFCheap/2017(G) for this work. V. Jaiswal and S. V. Cherukuri thank Ishwara-Chandra C. H. for kindly making GMRT data analysis pipeline available. L Resmi thanks Johannes Buchner for helpful discussions on pyMultinest. Harsh Kumar thanks the LSSTC Data Science Fellowship Program, which is funded by LSSTC, NSF Cybertraining Grant #1829740, the Brinson Foundation, and the Moore Foundation; his participation in the program has benefited this work. The Cosmic Dawn Center is funded by the DNRF. JPUF thanks the Carlsberg Foundation for support. MJM acknowledges the support of the National Science Centre, Poland through the SONATA BIS grant 2018/30/E/ST9/00208. GEA is the recipient of an Australian Research Council Discovery Early Career Researcher Award (project number DE180100346) funded by the Australian Government.
DATA AVAILABILITY
The optical, radio, and millimetre data underlying this article is available in the article.
Footnotes
Note that Jordana-Mitjans et al. (2020) find evidence at early times for colour evolution. This increases the χ2 of our fit but does not significantly influence the SED.
https://www.swift.ac.uk/xrt_spectra/00883832/ (Evans et al. 2009).
REFERENCES
,
APPENDIX A: SPECTRAL PARAMETERS FOR A MODEL WITH TIME-EVOLVING SHOCK MICRO-PHYSICS
In this section, we present the expressions for the spectral parameters used in the time-evolving microphysics model. For the adiabatic dynamics of the relativistic blastwave in a constant density medium, we used the expressions from Wijers & Galama (1999). For the wind medium, we used the dynamics given in Chevalier & Li (2000). In these expressions, E52 is the isotropic kinetic energy normalized to 1052 ergs, n0 is the ambient medium density in units of cm−3, A⋆ represents the normalized density in a stratified wind medium following Chevalier & Li (2000), ϵe0 and ϵB0 are the fractional energy in electrons and magnetic field respectively at 1 d since explosion, p is the electron energy spectral index, ζe is the fraction of electrons in the non-thermal pool, X is the hydrogen mass fraction, xp and ϕp are numerical functions of p as explained in Wijers & Galama (1999), and td is time since burst in days. t0 is the reference time where ϵe0 and ϵB0 are measured.
APPENDIX B: STANDARD MODEL FITS
In this section, we present results from our attempts to test the standard model predictions with the XRT/radio/mm data. This is an illustration that the multiwavelength data can not be explained by the model. We used both a constant density and wind-blown ambient medium for our analysis.
RS emission depends, in addition to Eiso, θj, and the ambient density, on the initial bulk Lorentz factor η of the fireball, the electron energy spectrum (characterized by pRS) and the fractional energy content in electrons and the magnetic field, parametrized as |$\epsilon _e^{\rm RS} = {\mathcal {R}}_e \epsilon _e^{\rm FS}$| and |$\epsilon _B^{\rm RS} = {\mathcal {R}}_B \epsilon _B^{\rm FS}$|, respectively.
The code used in this analysis accounts for forward and reverse (thick shell RS in a wind medium and thin shell RS in a constant-density medium) shock emission, and was developed in Resmi & Zhang (2016). We used the Bayesian parameter estimation package pyMultinest (Feroz et al. 2009; Buchner et al. 2014) to explore the 7D parameter space of (pFS, ϵe, ϵB, θJ, Eiso, 52, n0orA⋆, η). We fixed |${\mathcal {R}}_B=1$| and pRS = 2.1, as keeping them as free parameters will not give any additional advantage in explaining this data. If X-ray or radio/mm is considered alone, excellent agreement with the model is possible. However, for both types of ambient medium, models fail to reproduce the afterglow evolution if the entire data set is considered.
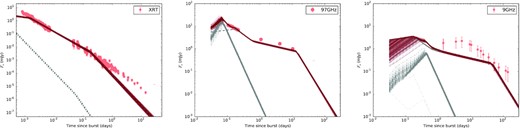
Realizations from our posterior distribution for a constant-density medium. We use the three representative bands to present the results. Grey dashed curves belong to forward shock and grey dotted curves are emission from the RS. Maroon curves represent the total flux. Scintillation is accounted for in the errors of the radio data.
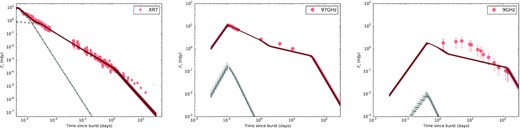
Author notes
LSSTC Data Science Fellow



