-
PDF
- Split View
-
Views
-
Cite
Cite
Emanuele Sobacchi, Joonas Nättilä, Lorenzo Sironi, A fully kinetic model for orphan gamma-ray flares in blazars, Monthly Notices of the Royal Astronomical Society, Volume 503, Issue 1, May 2021, Pages 688–693, https://doi.org/10.1093/mnras/stab562
Close - Share Icon Share
ABSTRACT
Blazars emit a highly variable non-thermal spectrum. It is usually assumed that the same non-thermal electrons are responsible for the IR-optical-UV emission (via synchrotron) and the gamma-ray emission (via inverse Compton). Hence, the light curves in the two bands should be correlated. Orphan gamma-ray flares (i.e. lacking a luminous low-frequency counterpart) challenge our theoretical understanding of blazars. By means of large-scale two-dimensional radiative particle-in-cell simulations, we show that orphan gamma-ray flares may be a self-consistent by-product of particle energization in turbulent magnetically dominated pair plasmas. The energized particles produce the gamma-ray flare by inverse Compton scattering an external radiation field, while the synchrotron luminosity is heavily suppressed since the particles are accelerated nearly along the direction of the local magnetic field. The ratio of inverse Compton to synchrotron luminosity is sensitive to the initial strength of turbulent fluctuations (a larger degree of turbulent fluctuations weakens the anisotropy of the energized particles, thus increasing the synchrotron luminosity). Our results show that the anisotropy of the non-thermal particle population is key to modelling the blazar emission.
1 INTRODUCTION
Blazars, active galactic nuclei (AGNs) launching a jet in the direction of the observer, are remarkably variable at all wavelengths. Variability at different wavelengths is usually correlated, but sometimes is not. A striking example of uncorrelated variability are the so-called ‘orphan’ gamma-ray flares. During an orphan flare, the gamma-ray flux may increase by a factor of 10–100 with respect to the quiescent level, while the IR-optical-UV flux does not show any significant variation (e.g. Krawczynski et al. 2004; Błażejowski et al. 2005; Hayashida et al. 2015; MacDonald, Jorstad & Marscher 2017). In this paper, we mostly focus on orphan GeV flares from flat spectrum radio quasars (FSRQs),1 which have been routinely reported since the launch of the Fermi Large Area Telescope (e.g. MacDonald et al. 2017).
Orphan gamma-ray flares challenge the standard one-zone blazar emission model, which assumes the same electrons to emit the IR-optical-UV radiation via synchrotron, and the gamma-rays via inverse Compton (IC) (e.g. Maraschi et al. 1992; Sikora et al. 1994). Hence, the IR-optical-UV and gamma-ray light curves should be well correlated.
Different explanations for the origin of orphan gamma-ray flares have been proposed (for a review, see e.g. Böttcher 2019), including (i) proton synchrotron emission (e.g. Weidinger & Spanier 2015); (ii) the temporary enhancement of the external radiation field at the location of the emitting region (e.g. Kusunose & Takahara 2006; MacDonald et al. 2015; Tavani, Vittorini & Cavaliere 2015); (iii) the injection of fresh non-thermal electrons into the emitting region, and the simultaneous decrease of the magnetic field (e.g. Böttcher & Baring 2019; Lewis, Finke & Becker 2019). Though associating the flare to the injection of fresh non-thermal electrons may look attractive, the lack of a detectable synchrotron counterpart constrains the magnetic field to be well below the equipartition level. This requirement challenges the widely accepted paradigm that AGN jets are magnetically dominated objects (e.g. Blandford & Znajek 1977; Komissarov et al. 2007; Tchekhovskoy, Narayan & McKinney 2011).
The need for sub-equipartition magnetic fields can be tracked back to the textbook (and ad hoc) assumption that the distribution of the synchrotron-emitting particles is isotropic. Instead, we show that energetic particles move nearly along the direction of the local magnetic field. Then the radiated synchrotron power is heavily suppressed even if the magnetic field is large, while the IC power is practically the same as in the standard isotropic case.
In magnetically dominated AGN jets, internal shocks are weak. Then viable non-thermal particle acceleration mechanisms are reconnection and turbulence. Since there is a huge separation of scales between the transverse size of the jet, which is the energy-carrying scale, and the particle Larmor radius, which is the scale where dissipation happens, we argue that dissipation proceeds through a turbulent cascade. Recently, fully kinetic particle-in-cell (PIC) simulations have reached the maturity to simulate the energization of non-thermal particles in turbulent magnetically dominated plasmas from first principles (e.g. Zhdankin et al. 2017, 2018, 2020; Comisso & Sironi 2018, 2019; Nättilä 2019; Comisso, Sobacchi & Sironi 2020). Using highly magnetized uncooled PIC simulations, Comisso & Sironi (2018, 2019) have shown that (i) particles are first energized due to strong non-ideal electric fields in large-scale reconnecting current sheets.2 Since the reconnection electric field is nearly aligned with the local magnetic field, the distribution of the reconnection-accelerated particles is strongly anisotropic, with particles preferentially moving along the magnetic field;3 (ii) particles are further accelerated by scattering off turbulent magnetic fluctuations. The distribution of the scattered particles becomes increasingly isotropic at higher energies.
Comparing the gamma-ray luminosity with the extended emission from the radio lobes suggests that blazars are extremely radiative efficient (e.g. Nemmen et al. 2012). Then turbulence should develop in the fast cooling regime, i.e. reconnection-accelerated particles should radiate most of their energy within the light crossing time of the system (otherwise, adiabatic losses become dominant and the jet is radiatively inefficient). Here, we use large-scale two-dimensional PIC simulations to study radiative turbulence in the fast cooling regime. We show that (i) the local anisotropy of the reconnection-accelerated particles may suppress the synchrotron luminosity by orders of magnitude with respect to the IC luminosity; (ii) further energization due to scattering is inhibited since it operates on a longer time-scale than cooling (see also Nättilä & Beloborodov 2020; Zhdankin et al. 2020). Hence, we argue that orphan gamma-ray flares can be a self-consistent by-product of particle energization in magnetically dominated plasmas with fast cooling.
The paper is organized as follows. In Section 2, we present our model. In Section 3, we validate our model using radiative fully kinetic simulations of turbulent magnetically dominated pair plasmas. Finally, in Section 4 we conclude.
2 PHYSICAL MODEL
Let us consider a blob filled with a turbulent plasma. In the proper frame of the blob, the characteristic physical parameters of the plasma are (i) l, the turbulence energy-carrying scale, which we assume to be comparable to the size of the emitting blob; (ii) B, the intensity of the magnetic field. We assume the turbulent component of the magnetic field to be δB ∼ B; (iii) n0, the electron number density. The available magnetic energy per electron exceeds the rest mass, i.e. the initial plasma magnetization is σ0 ≡ δB2/4πn0mc2 ≫ 1, where m is the electron mass. If the plasma has a significant proton component, we assume that a large fraction (i.e. |${\gtrsim}50{{\ \rm per\ cent}}$|) of the turbulent energy heats the plasma electrons
The emitting blob moves with a velocity βc and a Lorentz factor |$\Gamma \equiv 1/\sqrt{1-\beta ^2}$| with respect to the observer. If the viewing angle is θ ≲ 1/Γ, the Doppler factor of the blob is δ ≡ 1/[Γ(1 − βcos θ)] ∼ Γ. Throughout this paper, we take a fiducial value of δ ∼ Γ ∼ 20. For the physical parameters of blazars, such Lorentz factor typically guarantees that the gamma-rays do not annihilate with lower energy photons within the emitting blob (e.g. Dondi & Ghisellini 1995).
The blob is immersed in an external radiation field of frequency ν0 ∼ 1015 Hz and energy density Urad ∼ 0.01 erg cm−3 (which in the blob frame are Lorentz-boosted to |$\nu _0^{\prime }\sim \Gamma \nu _0$|, and |$U^{\prime }_{\rm rad}\sim \Gamma ^2 U_{\rm rad}$|), as may be produced by the Broad Line Region in FSRQ (e.g. Sikora et al. 1994, 2009; Ghisellini & Tavecchio 2009). Due to IC losses, within a dynamical time tdyn particles cool down to a Lorentz factor |$\gamma _{\rm cool}\sim \max \left[1, 3mc/4\sigma _{\rm T}U^{\prime }_{\rm rad}t_{\rm dyn}\right]$|, where σT is the Thomson cross-section.
The turbulent component of the magnetic field dissipates on a time-scale tdyn ∼ l/c (e.g. Comisso & Sironi 2018, 2019; Nättilä & Beloborodov 2020). We assume that (i) reconnection injects particles of Lorentz factor γ ∼ σ0 at a constant rate over a dynamical time, until the turbulent energy is dissipated; (ii) reconnection-accelerated particles cool efficiently within a dynamical time by IC scattering the external radiation field (i.e. as discussed in Section 2.1, we consider the fast cooling regime γcool ≪ σ0), which produces a gamma-ray flare. If the magnetic field within the emitting blob is tangled, the particle distribution is isotropic on the global scale of the blob (for example, the emitting blob may contain multiple turbulent cells, each having a random direction of the mean field). Then the IC emission is the same as in the standard isotropic case. In contrast, as we discuss below, the local particle distribution is strongly anisotropic in pitch angle. The anisotropy heavily suppresses the synchrotron emission.
2.1 Effect of the anisotropy
Uncooled PIC simulations of magnetically dominated pair plasma turbulence (e.g. Comisso & Sironi 2018, 2019; Nättilä 2019; Wong et al. 2020) have shown that (i) particles are injected at Lorentz factors γ ∼ σ0 due to strong non-ideal electric fields (Erec ∼ ηrecδB, with ηrec ∼ 0.1) in large-scale reconnecting current sheets. The injection time is tinj ∼ σ0mc/eErec, and typically tinj ≪ tdyn. Since the reconnection electric field is nearly aligned with the local magnetic field, reconnection-accelerated particles have a strong anisotropy; (ii) particles may be further accelerated (up to γ ≫ σ0) by scattering off turbulent magnetic fluctuations. Scattering operates on a longer time-scale, tscat ∼ tdyn.
For the properties of the emitting plasma estimated above, one finds that |$\gamma _{\rm cool}\sim 3mc/4\sigma _{\rm T}U^{\prime }_{\rm rad}t_{\rm dyn}\sim 4$|. The ratio of the injection to the cooling time for particles with γ ∼ σ0 is tinj/tcool ∼ (σ0/γcr)2 ∼ 10−8, where γcr is defined by the condition that IC losses balance the acceleration by the reconnection electric field, i.e. |$eE_{\rm rec}\sim 4\sigma _{\rm T}\gamma _{\rm cr}^2U^{\prime }_{\rm rad}/3$|. Since tinj ≪ tcool, particle injection in large-scale current sheet is practically unaffected by cooling (e.g. Nättilä & Beloborodov 2020; Sobacchi & Lyubarsky 2020). The ratio of the cooling to the scattering time is tcool/tscat ∼ tcool/tdyn ∼ γcool/σ0 ∼ 10−2. Since tcool ≪ tscat, further energization due to scattering is inhibited (e.g. Nättilä & Beloborodov 2020; Sironi & Beloborodov 2020; Sobacchi & Lyubarsky 2020; Zhdankin et al. 2020). Effectively, in a fast cooling system, turbulence is only able to inject particles with γ ∼ σ0 via reconnection. Particles move nearly along the local magnetic field, and cool down to γ ∼ γcool via IC scattering within a dynamical time. Then most of the particle energy is converted into radiation.
In the frame of the emitting blob, the magnetic energy density is UB ≡ δB2/8π ∼ 0.08 erg cm−3, and the radiation energy density is |$U^{\prime }_{\rm rad}\sim 4{\rm \,\, erg\,\, cm}^{-3}$|. If the particle distribution were isotropic, the synchrotron luminosity would be |$L_{\rm sync}\sim (U_{\rm B}/U^{\prime }_{\rm rad})L_{\rm obs}\sim 2\times 10^{46}{\rm \,\, erg\,\, s}^{-1}$|. However, the synchrotron luminosity is suppressed by a factor |$\sin ^2\bar{\alpha }$|, where |$\bar{\alpha }\ll 1$| is the pitch angle between the particle velocity and the local magnetic field (e.g. Comisso & Sironi 2019; Comisso et al. 2020). In the next section, we demonstrate that this effect can suppress the synchrotron luminosity by orders of magnitude, making the low-energy counterpart of the gamma-ray flare practically undetectable.
Since we are considering IC scattering off an external radiation field, our model adequately describes orphan gamma-ray flares from FSRQ. In the case of BL Lacs, the seed photons are instead produced within the jet itself via synchrotron emission (e.g. Maraschi et al. 1992). We argue that our proposed mechanism can explain orphan gamma-ray flares also in BL Lacs. Let us consider a fast cooling system, and neglect Klein–Nishina effects on IC scattering. The ratio of the synchrotron to IC power is |$P_{\rm sync}/P_{\rm IC}\sim (U_{\rm B}/U_{\rm sync})\sin ^2\bar{\alpha }$|, where Usync is the comoving energy density of the synchrotron radiation. Since only a fraction Psync/PIC ≪ 1 of the available magnetic energy is converted to synchrotron radiation when |$\bar{\alpha }\ll 1$|, one finds that Usync ∼ (Psync/PIC)UB, and therefore |$P_{\rm sync}/P_{\rm IC}\sim \sin \bar{\alpha }\ll 1$|. Numerical simulations of this process are more challenging since the radiation field should be modelled self-consistently, and are left for future work.
3 PIC SIMULATIONS
3.1 Numerical method and set-up
We perform ab initio PIC simulations employing the PIC codes tristan-mp (Buneman 1993; Spitkovsky 2005) and runko (Nättilä 2019). Simulations were performed with both the codes, finding consistent results. We conduct large-scale two-dimensional (2D) simulations in the xy plane, but all three components of particle momenta and electromagnetic fields are evolved in time.6 The computational domain is a square of size L × L, with periodic boundary conditions in all directions.
The simulation set-up is similar to our previous works on magnetically dominated plasma turbulence (Comisso & Sironi 2018, 2019; Comisso et al. 2020; Nättilä & Beloborodov 2020). We initialize a uniform electron–positron plasma with total particle density n0 and a small thermal spread θ0 = kBT0/mc2 = 10−5, where kB is the Boltzmann constant and T0 is the initial plasma temperature (we have obtained practically identical results using a thermal spread θ0 = 0.1, in which case the Debye length is resolved since the very beginning of the simulation). Turbulence develops from uncorrelated magnetic field fluctuations that are initialized in the plane perpendicular to a uniform mean magnetic field B0ez. The initial fluctuations have low wavenumbers kj = 2πnj/L, where nj ∈ {1, …, 4} and j indicates the wavenumber direction, and equal amplitude per mode. The initial magnetic energy spectrum peaks near kp = 8π/L. We use l = 2π/kp = L/4 as our unit length.
The strength of the initial magnetic field fluctuations is parametrized by the magnetization |$\sigma _0 = \delta B_{{\rm {rms}}0}^2/4\pi n_0 m c^2$|, where δBrms0 = 〈δB2(t = 0)〉1/2 is the space-averaged root-mean-square value of the initial fluctuating fields. We use a fiducial magnetization σ0 = 160, but we have obtained similar results for σ0 ≳ 40. We vary the level of turbulent fluctuations δBrms0/B0 between 0.5 (our fiducial case) and 2. This plays a significant role on the pitch angle distribution of accelerated particles, and so on the resulting synchrotron emission.
The large size of our computational domain (with L = 40 000 cells) allows to achieve asymptotically converged results. We resolve the initial plasma skin depth |$d_{e0}=c/\omega _{\rm p0}=\sqrt{{m}c^2/4\pi n_0 {e^2}}$| with three cells, and we employ four computational particles per cell. The simulation time-step is controlled by the numerical speed of light of 0.45 cells per time-step. Our earlier studies (Comisso & Sironi 2018, 2019) have demonstrated convergence with respect to these numerical parameters.
We implement IC cooling as a Compton drag term in the particle equation of motion (e.g. Werner, Philippov & Uzdensky 2019; Nättilä & Beloborodov 2020; Sironi & Beloborodov 2020; Zhdankin et al. 2020), assuming that the radiation is isotropic in the simulation frame and that Compton scattering happens in the Thomson regime. We parametrize the strength of IC cooling by defining the Lorentz factor γcr at which IC losses would prohibit further acceleration by the reconnection electric field Erec = ηrecδBrms0 (ηrec ∼ 0.1), i.e. |$eE_{\rm rec}=4\sigma _{\rm T}\gamma _{\rm cr}^2U^{\prime }_{\rm rad}/3$|. We choose a reference value of γcr = 80, which is larger than the mean Lorentz factor ∼σ0/4 = 40 at which particles are accelerated by reconnection. The Lorentz factor of the cooled particles may be written as |$\gamma _{\rm cool}\sim \max [1, (\gamma _{\rm cr}^2 / \eta _{\rm rec} \sqrt{\sigma _0})(d_{e0} / ct_{\rm dyn})]$|, where tdyn ∼ l/c. For our reference choice of |$l=L/4\simeq 3,300\, {d_{e0}}$|, one finds that γcool ∼ 1.5.
Our simulations maintain the correct ordering of the relevant time-scales (tinj < tcool < tscat ∼ tdyn), as it is expected for blazar conditions (see Section 2.1). However, reproducing the correct separation between these time-scales would require an impossibly large simulation box. Then our numerical results demonstrate that IC emission may have a negligible synchrotron counterpart as an effect of small pitch angles, but are not meant to reproduce the exact properties (e.g. peak frequency and luminosity) of blazar flares.
3.2 Results
In our simulations, turbulence develops from the initial unbalanced state, and the magnetic energy decays over time since we do not impose any continuous external driving. As shown in Fig. 1 (top panel), the turbulent cascade leads to the formation of intense current layers. Several layers become prone to fast magnetic reconnection due to the plasmoid instability (e.g. Comisso et al. 2016; Uzdensky & Loureiro 2016). Magnetic reconnection plays a crucial role in extracting particles from the thermal pool and injecting them into the acceleration process (e.g. Comisso & Sironi 2018, 2019). In the absence of cooling, particles energized by reconnection would be accelerated to even higher energies by scattering off the turbulent fluctuations. However, the rate of stochastic acceleration is slower than the IC cooling rate, so particle acceleration to γ ≫ σ0 is inhibited. Rather, at any given time the highest energy particles in the simulation are still experiencing significant reconnection-powered acceleration. In fact, the locations of high-energy particles (see the mean kinetic energy per particle in the bottom panel of Fig. 1) are well correlated with reconnection layers (compare top and bottom panels).
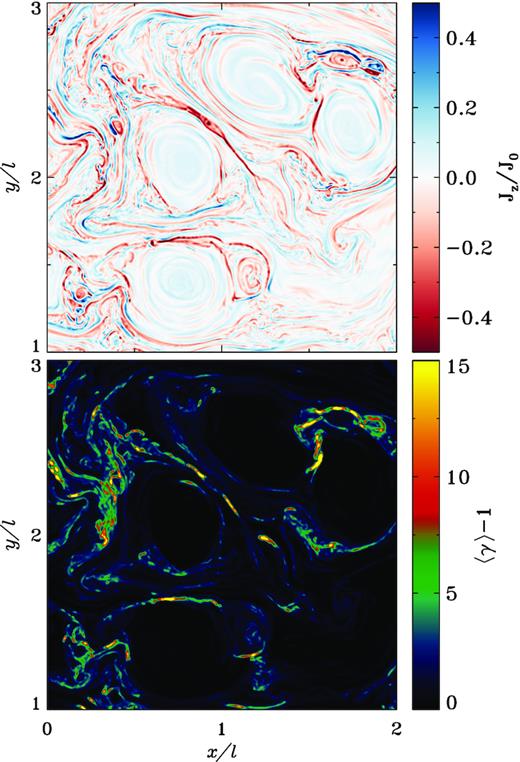
2D structure of turbulence from a simulation with σ0 = 160, δBrms0/B0 = 0.5, and L/de0 = 13 300 (with l = L/4), at time ct/l = 7 (near the peak of the light curves, see Fig. 2). We focus on a portion of the simulation domain to emphasize small-scale structures (the overall box is 4l × 4l). Top: out-of-plane current density Jz (normalized to J0 = en0c) indicating the presence of current sheets and reconnection plasmoids. Bottom: mean kinetic energy per particle (in units of mc2), showing that high-energy particles are preferentially located at reconnecting current sheets.
In Fig. 2(a), we show the time evolution of the particle spectrum dN/dlog (γ − 1). As a result of field dissipation, the spectrum shifts to energies much larger than the initial thermal energy. At late times the spectral peak is at γ ∼ 2, and it is populated by cooled particles (in fact, γcool ∼ 1 for our simulation). The highest energy part of the spectrum (at γ ≳ 16, beyond the vertical dashed line) builds up at early times, reaches the highest normalization at 5 ≲ ct/l ≲ 10, and is depleted at later times. The depletion at late times is due to the fact that in our simulation the magnetic energy decays over time (Fig. 2b), so turbulence-induced reconnection progressively becomes less efficient. The resulting decrease in magnetization is associated with an analogous drop in the high-energy spectral cut-off of the Lorentz factor of reconnection-accelerated particles, whose Lorentz factor is γ ∼ σ0/4 = 40, as seen in Fig. 2(a).
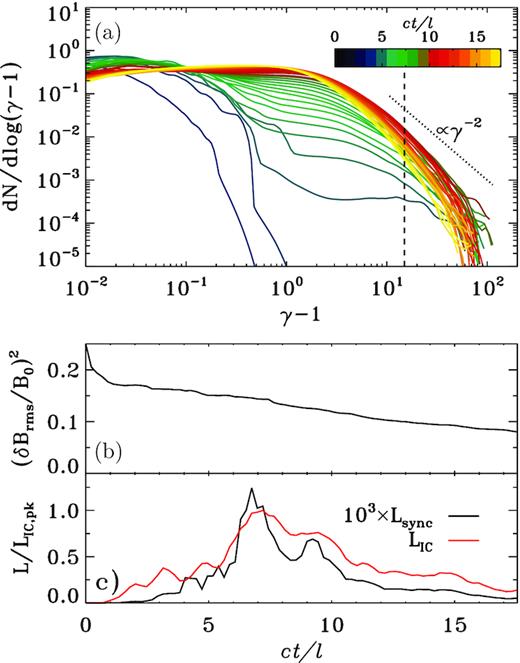
Temporal evolution of the same simulation as in Fig. 1. We show: (a) the time evolution of the particle energy spectrum; the dotted line indicates the slope dN/dlog (γ − 1) ∝ γ−2 yielding equal IC luminosity per decade in Lorentz factor. (b) the decay of the magnetic energy density in turbulent fluctuations. (c) IC (red) and synchrotron (black) light curves, normalized to the peak of the IC curve; the synchrotron emission is scaled up by a factor of 103. Both light curves are computed using particles with Lorentz factor γ ≥ 16 = σ0/10 (to the right of the dashed line in panel a).
In order to compute the IC and synchrotron light curves, we only consider particles with Lorentz factors γ ≥ 16 = σ0/10 (i.e. to the right of the vertical dashed line in Fig. 2a), which dominate the emission. For each particle, we compute the IC power as |$P_{\rm IC}\propto \gamma ^2 U^{\prime }_{\rm rad}$|, whereas the synchrotron power is |$P_{\rm sync}\propto \bar{\gamma }^2\bar{U}_B\, \sin ^2\bar{\alpha }$|. For the latter, the particle Lorentz factor |$\bar{\gamma }$|, the magnetic energy density |$\bar{U}_B$| and the pitch angle |$\bar{\alpha }$| are all computed in the local E × B frame (i.e. the frame moving with the local E × B speed). The resulting light curves are presented in Fig. 2(c), assuming equipartition of radiation and magnetic energy density in the simulation frame at the initial time (i.e. |$U^{\prime }_{\rm rad}=U_{\rm B0}=B_0^2/8 \pi$|; note that the magnetic energy is dominated by the mean field for our reference case with δBrms0/B0 = 0.5). Both light curves peak at ct/l ∼ 7, and display significant emission in the time interval 5 ≲ ct/l ≲ 10. However, as indicated in the legend, the synchrotron emission (black line) is suppressed by three orders of magnitude, as compared to the IC emission (red curve). This follows from the small pitch angles of particles accelerated by reconnection. In fact, given that we assume |$U^{\prime }_{\rm rad}=U_{\rm B0}$|, the ratio of synchrotron to IC emission is expected to be approximately equal to the mean value of |$\sin ^2\bar{\alpha }$|, which we indeed measure to be ∼10−3. In summary, the small pitch angle of reconnection-accelerated particles is responsible for a significant suppression of the synchrotron luminosity.
In Fig. 3, we present the dependence of the IC (solid) and synchrotron (dashed) light curves on the level of turbulent fluctuations δBrms0/B0, by comparing our reference case δBrms0/B0 = 0.5 (red) with two cases with stronger fluctuations: δBrms0/B0 = 1 (green) and δBrms0/B0 = 2 (blue). All curves are normalized to the peak IC luminosity of our reference case and they assume |$U^{\prime }_{\rm rad}=U_{\rm B0}$|. The figure shows that the ratio of IC to synchrotron luminosity is a strong function of δBrms0/B0. For larger fluctuations, the particles accelerated by reconnection have larger pitch angles (as also found in the uncooled simulations of Comisso et al. 2020), and so they are more efficient synchrotron emitters. In fact, the synchrotron luminosity increases by nearly two orders of magnitude from δBrms0/B0 = 0.5 to δBrms0/B0 = 1, whereas the IC luminosity is nearly unchanged. The modest increase in IC luminosity with δBrms0/B0 is in agreement with results of uncooled simulations, where higher δBrms0/B0 yielded harder particle spectra, and so more efficient particle acceleration to high energies (e.g. Comisso & Sironi 2018).
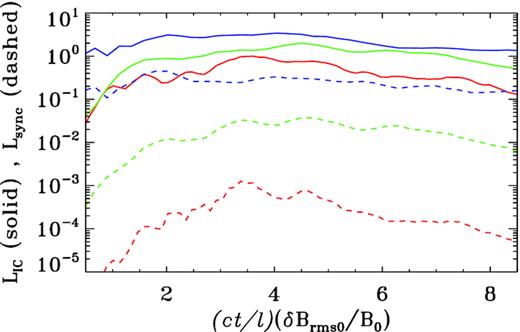
Dependence of the IC (solid) and synchrotron (dashed) light curves on the level of turbulent fluctuations δBrms0/B0, for our reference case δBrms0/B0 = 0.5 (red) and two cases with stronger fluctuations: δBrms0/B0 = 1 (green) and δBrms0/B0 = 2 (blue). Time on the horizontal axis is rescaled with δBrms0/B0 to account for the different rate of turbulence decay.
We have checked that the anisotropy and energy spectrum of high-energy particles are independent of the box size if σ0 and |$\gamma _{\rm cr}^2 (d_{e0}/l)$| are kept constant. Since also |$\gamma _{\rm cool}\sim \max [1, (\gamma _{\rm cr}^2 / \eta _{\rm rec} \sqrt{\sigma _0})(d_{e0} / ct_{\rm dyn})]$| remains constant, our results are applicable to asymptotically large astrophysical systems in the fast cooling regime.
4 CONCLUSIONS
In this work, we show that orphan gamma-ray flares can be a self-consistent by-product of the particle acceleration physics in magnetically dominated pair plasmas. We mostly focus on orphan GeV flares from flat spectrum radio quasars. Particles energized by the decaying turbulence cool down on a dynamical time by IC scattering an external photon field (e.g. the photons emitted by the Broad Line Region), thus producing the gamma-ray flare. The flare has a faint low-energy counterpart since the particles are accelerated nearly along the local magnetic field, and then the synchrotron emission is suppressed.
Even though our numerical results are based on simulations of magnetically dominated plasma turbulence, we argue that our conclusions hold more generally, for any system where particle injection is governed by reconnection in the strong guide field regime, and where fast cooling prevents further particle energization. This may happen in the non-linear stages of, e.g. the kink instability (Davelaar et al. 2020) and the Kelvin–Helmholtz instability (Sironi, Rowan & Narayan 2020).
The majority of blazar gamma-ray flares have a luminous low-energy counterpart. Our results show that the ratio of inverse Compton to synchrotron luminosity may be regulated by the initial strength of the turbulent fluctuations (the anisotropy of the accelerated particles is weaker for a larger degree of fluctuations, and the synchrotron luminosity increases). A complementary possibility, yet to be tested with PIC simulations, is that kinetic instabilities reduce the anisotropy if the rest-mass energy density of the plasma is dominated by the ions (Sobacchi & Lyubarsky 2019).
Our numerical results rely on 2D simulations. Our previous studies have demonstrated that the particle energy distribution and anisotropy are nearly the same between 2D and 3D for uncooled systems (Comisso & Sironi 2018, 2019; Comisso et al. 2020). Investigating 3D effects in fast cooling systems is a worthwhile direction for future investigation.
ACKNOWLEDGEMENTS
We thank the anonymous referee for constructive comments and suggestions that improved the paper. We are grateful to Luca Comisso for insightful discussions. L.S. acknowledges support from the Sloan Fellowship, the Cottrell Scholar Award, DoE DE-SC0021254, NASA ATP 80NSSC18K1104, and NSF PHY-1903412. The simulations have been performed at Columbia (Habanero and Terremoto), and with NERSC (Cori) and NASA (Pleiades) resources.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
In FSRQ, gamma-rays are most likely emitted as a population of non-thermal electrons inverse Compton scatters off an external photon field, which may be produced by the Broad Line Region (e.g. Sikora, Begelman & Rees 1994; Ghisellini & Tavecchio 2009; Sikora et al. 2009). In BL Lacs, gamma-rays are instead emitted as the non-thermal electrons scatter the same synchrotron photons that they emit (e.g. Maraschi, Ghisellini & Celotti 1992).
In reconnection-based models of blazar flares, it is usually assumed that the initial conditions can be modelled as a single large-scale Harris current sheet (e.g. Petropoulou, Giannios & Sironi 2016; Christie et al. 2019). Instead, in our model the properties of the large-scale current sheets are a self-consistent by-product of the turbulent plasma motions.
In relativistic reconnection with weak guide fields, the reconnection electric field is nearly perpendicular to the magnetic field. Then reconnection-accelerated particles move in the direction perpendicular to the magnetic field (i.e. pitch angles are large). During the turbulent cascade, reconnection instead occurs in the regime of strong guide field, and the reconnection electric field is directed along the guide field. Then reconnection-accelerated particles move nearly along the direction of the guide field (i.e. pitch angles are small).
Orphan flares with a variability time-scale of a few hours were recently reported by Patel et al. (2020). Variability on short time-scales (i.e. ≪1 d) may be produced by plasma clumps moving relativistically within the emitting region, as in the so-called ‘jet-in-a-jet’ models (e.g. Giannios, Uzdensky & Begelman 2009; Giannios 2013).
We remark that we have defined the magnetization with respect to the electron rest-mass energy density.
Our previous studies have demonstrated that the particle energy distribution and anisotropy are nearly the same between 2D and 3D for uncooled systems (Comisso & Sironi 2018, 2019; Comisso et al. 2020). In uncooled systems, particles are first energized by reconnection, and then by scattering off turbulent magnetic fluctuations. Energization due to scattering is arguably sensitive to 3D effects since turbulent fluctuations are anisotropic. Then we expect 3D effects to be minor in fast cooling systems, since energization due to scattering becomes ineffective.



