-
PDF
- Split View
-
Views
-
Cite
Cite
T Jayasinghe, C S Kochanek, K Z Stanek, B J Shappee, T W-S Holoien, Todd A Thompson, J L Prieto, Subo Dong, M Pawlak, O Pejcha, G Pojmanski, S Otero, N Hurst, D Will, The ASAS-SN catalogue of variable stars IX: The spectroscopic properties of Galactic variable stars, Monthly Notices of the Royal Astronomical Society, Volume 503, Issue 1, May 2021, Pages 200–235, https://doi.org/10.1093/mnras/stab114
Close - Share Icon Share
ABSTRACT
The All-Sky Automated Survey for Supernovae provides long baseline (∼4 yr) V-band light curves for sources brighter than V≲ 17 mag across the whole sky. We produced V-band light curves for a total of ∼61.5 million sources and systematically searched these sources for variability. We identified ∼426 000 variables, including ∼219 000 new discoveries. Most (|${\sim }74{ per\ cent}$|) of our discoveries are in the Southern hemisphere. Here, we use spectroscopic information from LAMOST, GALAH, RAVE, and APOGEE to study the physical and chemical properties of these variables. We find that metal-poor eclipsing binaries have orbital periods that are shorter than metal-rich systems at fixed temperature. We identified rotational variables on the main-sequence, red giant branch, and the red clump. A substantial fraction (|${\gtrsim }80{ per\ cent}$|) of the rotating giants have large |$v$|rot or large near-ultraviolet excesses also indicative of fast rotation. The rotational variables have unusual abundances suggestive of analysis problems. Semiregular variables tend to be lower metallicity (|$\rm [Fe/H]{\sim }-0.5$|) than most giant stars. We find that the APOGEE DR16 temperatures of oxygen-rich semiregular variables are strongly correlated with the WRP − WJK colour index for |$\rm T_{eff}\lesssim 3800$| K. Using abundance measurements from APOGEE DR16, we find evidence for Mg and N enrichment in the semiregular variables. We find that the Aluminum abundances of the semiregular variables are strongly correlated with the pulsation period, where the variables with |$\rm P\gtrsim 60$| d are significantly depleted in Al.
1 INTRODUCTION
Variable stars are useful astrophysical tools that can be used to study the lives and deaths of stars. Pulsating variables, including Cepheids, RR Lyrae stars, and Mira variables are used as distance indicators as they follow distinct period–luminosity relationships (e.g. Leavitt 1908; Matsunaga et al. 2006; Whitelock, Feast & Van Leeuwen 2008; Beaton et al. 2018, and references therein). Eclipsing binary stars allow for the derivation of dynamical information and fundamental stellar parameters, including the masses and radii of the stars (Torres, Andersen & Giménez 2010). The precise measurements afforded by eclipsing binaries allow for tests of stellar theory across the Hertzsprung–Russell diagram. Variable stars are also used to study stellar populations and Galactic structure (Feast & Whitelock 2014; Mateu & Vivas 2018; Matsunaga 2018).
Modern large scale sky surveys such as the All-Sky Automated Survey (ASAS; Pojmanski 2002), the All-Sky Automated Survey for SuperNovae (ASAS-SN; Shappee et al. 2014; Kochanek et al. 2017; Jayasinghe et al. 2018), the Optical Gravitational Lensing Experiment (OGLE; Udalski 2003), the Northern Sky Variability Survey (Woźniak et al. 2004), MACHO (Alcock et al. 1997), EROS (Derue et al. 2002), the Catalina Real-Time Transient Survey (CRTS; Drake et al. 2014), the Asteroid Terrestrial-impact Last Alert System (ATLAS; Heinze et al. 2018; Tonry et al. 2018a), Gaia (Gaia Collaboration 2018; Holl et al. 2018; Gaia Collaboration 2019), and the Zwicky Transient Facility (Bellm et al. 2019; Chen et al. 2020) have revolutionized the study of stellar variability. Amateur astronomers have also contributed to these discoveries over the years. As of 2020 May, the International Variable Stars Index (VSX; Watson, Henden & Price 2006) hosted by the American Association of Variable Star Observers (AAVSO) lists ∼1.4 × 106 variable stars.
In addition to these modern photometric surveys, large-scale wide-field spectroscopic surveys such as the Apache Point Observatory Galactic Evolution Experiement (APOGEE; Gunn et al. 2006; Blanton et al. 2017; Wilson et al. 2019), Large Sky Area Multi-Object Fibre Spectroscopic Telescope (LAMOST; Cui et al. 2012), GALactic Archaeology with HERMES (GALAH; De Silva et al. 2015; Buder et al. 2018), and the RAdial Velocity Experiment (RAVE; Casey et al. 2017) have been making medium-/high-resolution spectroscopic observations of millions of Galactic stars. Spectroscopic observations of Galactic stars are invaluable for deciphering the chemical evolution of our Galaxy (see e.g. Griffith, Johnson & Weinberg 2019; Weinberg et al. 2019), and for evolved stars they also provide clues to understanding chemical enrichment caused by dredge-up episodes (see e.g. Salaris et al. 2015; Shetrone et al. 2019). Variable stars that have both extensive time-series data and spectroscopic observations will allow for the study of stellar evolution to great detail.
ASAS-SN monitored the visible sky to a depth of V ≲ 17 mag with a cadence of 2–3 d using two units in Chile and Hawaii each with four telescopes from 2014 to 2018. Since then, ASAS-SN has expanded to five units with 20 telescopes and is currently monitoring the sky in the g band to a depth of g ≲ 18.5 mag with a cadence of ∼1 d. The ASAS-SN telescopes are hosted by the Las Cumbres Observatory (LCO; Brown et al. 2013) in Hawaii, Chile, Texas, and South Africa. The primary focus of ASAS-SN is the detection of bright supernovae and other transients (e.g. tidal disruption events, cataclysmic variables, AGN flares, stellar flares, etc.) with minimal bias (e.g. Holoien et al. 2014, 2016, 2017), but its excellent baseline and all-sky coverage allows for the characterization of stellar variability across the whole sky.
In Paper I (Jayasinghe et al. 2018), we discovered ∼66 000 new variables that were flagged during the search for supernovae, most of which are located in regions that were not well sampled by previous surveys. In Paper II (Jayasinghe et al. 2019b), we homogeneously analysed ∼412 000 known variables from the VSX catalogue, and developed a versatile random forest variability classifier utilizing the ASAS-SN V-band light curves and data from external catalogues. As data from the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) became available, we have explored the synergy between the two surveys. In Paper III (Jayasinghe et al. 2019a), we characterized the variability of ∼1.3 million sources within 18° of the southern ecliptic pole towards the TESS continuous viewing zone and identified ∼11 700 variables, including ∼7000 new discoveries. We have also explored the synergy between ASAS-SN and large-scale spectroscopic surveys using data from APOGEE (Holtzman et al. 2015) with the discovery of the first likely non-interacting binary composed of a black hole with a field red giant (Thompson et al. 2019) and the identification of 1924 APOGEE stars as periodic variables in Paper IV (Pawlak et al. 2019). In Paper V, we systematically searched for variable sources with V < 17 mag in the Southern hemisphere and identified ∼220 000 variable sources, of which ∼88 300 were new discoveries (Jayasinghe et al. 2019c). In Paper VI, we derived period–luminosity relationships for δ Scuti stars (Jayasinghe et al. 2020b). We studied contact binaries in Paper VII (Jayasinghe et al. 2020a). In Paper VIII, we identified 11 new ‘dipper’ stars in the Lupus star-forming region (Bredall et al. 2020).
Here, we summarize the results of our V-band variability search based on ∼61.5 million ASAS-SN light curves of sources from the AAVSO Photometric All-Sky Survey (APASS; Henden et al. 2015) DR9 catalogue with V < 17 mag and the ATLAS All-Sky Stellar Reference Catalogue (refcat2, Tonry et al. 2018b) catalogue with g < 17 mag. In this work, we describe our V-band variability catalogue of ∼426 000 variable sources, of which ∼219 000 are new discoveries. In Section 2, we discuss the ASAS-SN observations, our variable star identification and classification procedure and summarize the final V-band catalogue. Section 3 discusses the cross-matches made to various spectroscopic catalogues and the general spectroscopic properties of the ASAS-SN variable stars. In Section 4, we discuss the eclipsing binaries, rotational variables and semiregular (SR) variables in greater depth and present a summary of our work in Section 5.
2 THE ASAS-SN V-BAND CATALOGUE OF VARIABLE STARS
The ASAS-SN V-band observations used in this work were made by the ‘Brutus’ (Haleakala, Hawaii) and ‘Cassius’ (CTIO, Chile) quadruple telescopes between 2013 and 2018. Each ASAS-SN V-band field is observed to a depth of V ≲ 17 mag. The field of view of an ASAS-SN camera is 4.5 deg2, the pixel scale is 8|${^{\prime\prime}_{.}}$|0 and the full width at half-maximum (FWHM) is typically ∼2 pixels. ASAS-SN tends to saturate at ∼10−11 mag, but we attempt to correct the light curves of saturated sources for bleed trails (see Kochanek et al. 2017). The V-band light curves were extracted as described in Jayasinghe et al. (2018) using image subtraction (Alard & Lupton 1998; Alard 2000) and aperture photometry on the subtracted images with a 2 pixel radius aperture. We corrected the zero-point offsets between the different cameras as described in Jayasinghe et al. (2018). The photometric errors were recalculated as described in Jayasinghe et al. (2019a).
As we did in Paper V, we started with the APASS DR9 catalogue (Henden et al. 2015) as our input source catalogue for the Northern hemisphere. We selected ∼23.1M APASS sources with V < 17 mag in the Northern hemisphere (δ > 0°). However, there are regions towards the Galactic plane that are missing in the APASS DR9 catalogue (Henden et al. 2015; Marrese et al. 2019). To address the issue of incomplete sky coverage, we used the refcat2 catalogue (Tonry et al. 2018b) to produce light curves for the sources missing from APASS DR9. From the refcat2 catalogue, we selected ∼7.1M sources with r1 > 30″ and G < 17 mag, where r1 is the radius at which the cumulative G flux in the aperture exceeds the flux of the source being considered and is a measure of blending around a star. We use this cut in r1 to reduce the number of heavily blended sources. This does bias the selected refcat2 sources towards more isolated stars, and will reduce the completeness of the catalogue, especially towards the Galactic plane. In total, we produced ∼61.5M V-band light curves. The V-band light curves of all ∼61.5M sources are available online at the ASAS-SN Photometry Data base (https://asas-sn.osu.edu/photometry).
We applied the trained random forest classifier from Jayasinghe et al. (2019c) to identify candidate variables. From this sample, blended sources were identified and removed as described in Jayasinghe et al. (2019c). Following these procedures, we used the variability classifier implemented in Jayasinghe et al. (2019b), which consists of a random forest classifier plus several refinement steps, in order to classify the candidate variables. We applied additional quality checks to improve the purity of our catalogue (summarized in table 4 from Jayasinghe et al. 2019c). Peak-to-peak variability amplitudes were estimated by fitting a random forest regression model to the light curves (Jayasinghe et al. 2019c). We previously noted that light curves that are contaminated by systematics tend to be classified as irregular or generic variables. Thus, we visually reviewed all the sources that were classified as L, VAR, GCAS, or YSO to improve the purity of our catalogue. Following this, we identified ∼124 000 and ∼40 000 variables among the northern APASS sources and the refcat2 sources, respectively. As described in Jayasinghe et al. (2019c), we cross-matched these variables to the various catalogues of known variable stars. Following this, we identified ∼30 900 and ∼28 200 variables as new discoveries among the northern APASS sources and the refcat2 sources, respectively.
Here, we present the final catalogue of variables that we identified in the ASAS-SN V-band data. In total, we have identified ∼426 000 variables in the V-band data, out of which ∼219 000 were new ASAS-SN discoveries. The complete catalogue of ∼426 000 variables and their light curves are available at the ASAS-SN Variable Stars Data base (https://asas-sn.osu.edu/variables) along with the V-band light curves for each source. Both this data base and the VSX catalogue have included these Northern variables and light curves since 2019 September. The ASAS-SN variable stars have also been included in the VSX catalogue.1 Table 1 lists the number of sources of each variability type in the ASAS-SN V-band catalogue of variable stars.
| VSX Type . | Description . | Known . | New . | New/Known . |
|---|---|---|---|---|
| CWA | W Virginis-type variables with P > 8 d | 243 | 108 | 0.44 |
| CWB | W Virginis-type variables with P < 8 d | 182 | 72 | 0.40 |
| DCEP | Fundamental mode classical Cepheids | 1466 | 162 | 0.11 |
| DCEPS | First overtone Cepheids | 529 | 49 | 0.09 |
| DSCT | δ Scuti variables | 2203 | 2227 | 1.01 |
| EA | Detached Algol-type binaries | 21 399 | 19 329 | 0.90 |
| EB | β Lyrae-type binaries | 17 078 | 6956 | 0.41 |
| EW | W Ursae Majoris-type binaries | 56 431 | 15 415 | 0.27 |
| HADS | High amplitude δ Scuti variables | 2541 | 1626 | 0.64 |
| M | Mira variables | 4612 | 1661 | 0.36 |
| ROT | Rotational variables | 15 218 | 17 624 | 1.16 |
| RRAB | RR Lyrae variables (Type ab) | 16 683 | 5136 | 0.31 |
| RRC | First overtone RR Lyrae variables | 4380 | 1808 | 0.41 |
| RRD | Double mode RR Lyrae variables | 299 | 71 | 0.24 |
| RVA | RV Tauri variables (Subtype A) | 44 | 22 | 0.50 |
| SR | Semiregular variables | 51 270 | 115 088 | 2.24 |
| L | Irregular variables | 6584 | 21 110 | 3.21 |
| GCAS | γ Cassiopeiae variables | 146 | 258 | 1.77 |
| YSO | Young stellar objects | 2173 | 2353 | 1.08 |
| GCAS: | Uncertain γ Cassiopeiae variables | 37 | 71 | 1.92 |
| VAR | Generic variables | 2668 | 8193 | 3.07 |
| Total | 206 218 | 219 351 | 1.06 |
| VSX Type . | Description . | Known . | New . | New/Known . |
|---|---|---|---|---|
| CWA | W Virginis-type variables with P > 8 d | 243 | 108 | 0.44 |
| CWB | W Virginis-type variables with P < 8 d | 182 | 72 | 0.40 |
| DCEP | Fundamental mode classical Cepheids | 1466 | 162 | 0.11 |
| DCEPS | First overtone Cepheids | 529 | 49 | 0.09 |
| DSCT | δ Scuti variables | 2203 | 2227 | 1.01 |
| EA | Detached Algol-type binaries | 21 399 | 19 329 | 0.90 |
| EB | β Lyrae-type binaries | 17 078 | 6956 | 0.41 |
| EW | W Ursae Majoris-type binaries | 56 431 | 15 415 | 0.27 |
| HADS | High amplitude δ Scuti variables | 2541 | 1626 | 0.64 |
| M | Mira variables | 4612 | 1661 | 0.36 |
| ROT | Rotational variables | 15 218 | 17 624 | 1.16 |
| RRAB | RR Lyrae variables (Type ab) | 16 683 | 5136 | 0.31 |
| RRC | First overtone RR Lyrae variables | 4380 | 1808 | 0.41 |
| RRD | Double mode RR Lyrae variables | 299 | 71 | 0.24 |
| RVA | RV Tauri variables (Subtype A) | 44 | 22 | 0.50 |
| SR | Semiregular variables | 51 270 | 115 088 | 2.24 |
| L | Irregular variables | 6584 | 21 110 | 3.21 |
| GCAS | γ Cassiopeiae variables | 146 | 258 | 1.77 |
| YSO | Young stellar objects | 2173 | 2353 | 1.08 |
| GCAS: | Uncertain γ Cassiopeiae variables | 37 | 71 | 1.92 |
| VAR | Generic variables | 2668 | 8193 | 3.07 |
| Total | 206 218 | 219 351 | 1.06 |
| VSX Type . | Description . | Known . | New . | New/Known . |
|---|---|---|---|---|
| CWA | W Virginis-type variables with P > 8 d | 243 | 108 | 0.44 |
| CWB | W Virginis-type variables with P < 8 d | 182 | 72 | 0.40 |
| DCEP | Fundamental mode classical Cepheids | 1466 | 162 | 0.11 |
| DCEPS | First overtone Cepheids | 529 | 49 | 0.09 |
| DSCT | δ Scuti variables | 2203 | 2227 | 1.01 |
| EA | Detached Algol-type binaries | 21 399 | 19 329 | 0.90 |
| EB | β Lyrae-type binaries | 17 078 | 6956 | 0.41 |
| EW | W Ursae Majoris-type binaries | 56 431 | 15 415 | 0.27 |
| HADS | High amplitude δ Scuti variables | 2541 | 1626 | 0.64 |
| M | Mira variables | 4612 | 1661 | 0.36 |
| ROT | Rotational variables | 15 218 | 17 624 | 1.16 |
| RRAB | RR Lyrae variables (Type ab) | 16 683 | 5136 | 0.31 |
| RRC | First overtone RR Lyrae variables | 4380 | 1808 | 0.41 |
| RRD | Double mode RR Lyrae variables | 299 | 71 | 0.24 |
| RVA | RV Tauri variables (Subtype A) | 44 | 22 | 0.50 |
| SR | Semiregular variables | 51 270 | 115 088 | 2.24 |
| L | Irregular variables | 6584 | 21 110 | 3.21 |
| GCAS | γ Cassiopeiae variables | 146 | 258 | 1.77 |
| YSO | Young stellar objects | 2173 | 2353 | 1.08 |
| GCAS: | Uncertain γ Cassiopeiae variables | 37 | 71 | 1.92 |
| VAR | Generic variables | 2668 | 8193 | 3.07 |
| Total | 206 218 | 219 351 | 1.06 |
| VSX Type . | Description . | Known . | New . | New/Known . |
|---|---|---|---|---|
| CWA | W Virginis-type variables with P > 8 d | 243 | 108 | 0.44 |
| CWB | W Virginis-type variables with P < 8 d | 182 | 72 | 0.40 |
| DCEP | Fundamental mode classical Cepheids | 1466 | 162 | 0.11 |
| DCEPS | First overtone Cepheids | 529 | 49 | 0.09 |
| DSCT | δ Scuti variables | 2203 | 2227 | 1.01 |
| EA | Detached Algol-type binaries | 21 399 | 19 329 | 0.90 |
| EB | β Lyrae-type binaries | 17 078 | 6956 | 0.41 |
| EW | W Ursae Majoris-type binaries | 56 431 | 15 415 | 0.27 |
| HADS | High amplitude δ Scuti variables | 2541 | 1626 | 0.64 |
| M | Mira variables | 4612 | 1661 | 0.36 |
| ROT | Rotational variables | 15 218 | 17 624 | 1.16 |
| RRAB | RR Lyrae variables (Type ab) | 16 683 | 5136 | 0.31 |
| RRC | First overtone RR Lyrae variables | 4380 | 1808 | 0.41 |
| RRD | Double mode RR Lyrae variables | 299 | 71 | 0.24 |
| RVA | RV Tauri variables (Subtype A) | 44 | 22 | 0.50 |
| SR | Semiregular variables | 51 270 | 115 088 | 2.24 |
| L | Irregular variables | 6584 | 21 110 | 3.21 |
| GCAS | γ Cassiopeiae variables | 146 | 258 | 1.77 |
| YSO | Young stellar objects | 2173 | 2353 | 1.08 |
| GCAS: | Uncertain γ Cassiopeiae variables | 37 | 71 | 1.92 |
| VAR | Generic variables | 2668 | 8193 | 3.07 |
| Total | 206 218 | 219 351 | 1.06 |
The definition of an ASAS-SN discovery is that we could find no reference to the system as a variable star at the time we publicly released the new discoveries from papers I to IX. We directly matched to many large catalogues such as the ASAS (Pojmanski 2002), CRTS (Drake et al. 2014), and WISE (Chen et al. 2018) catalogues of variables and also to the AAVSO’s VSX catalogue (Watson et al. 2006), which attempts to be a complete summary of variable stars. Because the final accounting of ∼ 219 000 new variables comes from this series of papers that began in 2018, how they overlap with variable star catalogues published in the interim depends on which survey first released the variable. As a particular example, Paper I (Jayasinghe et al. 2018) appeared before the Gaia DR2 variable star catalogue (Gaia Collaboration 2019), so a previously unknown variable from Paper I is a new ASAS-SN variable even if it is in the later Gaia DR2 catalogue. In the later papers, the Gaia DR2 catalogue was included as one of the catalogues to check before identifying a source as a newly discovered variable. So, for example, the roughly ∼60 000 new variables released as part of this paper contain no stars in the Gaia catalogue. The same approach was taken for the ATLAS variable star catalogue (Heinze et al. 2018).
With the completion of our V-band variability survey, ASAS-SN has significantly increased the numbers of SR variables (|$+224{ per\ cent}$|), δ Scuti variables (|$+101{ per\ cent}$|), rotational variables (|$+116{ per\ cent}$|), and detached eclipsing binaries (|$+90{ per\ cent}$|). Combined, we have increased the census of SR and irregular variables by |$+235{ per\ cent}$| and δ Scuti variables (both the DSCT and HADS sub-types) by |$+81{ per\ cent}$|. The majority of the SR variables, δ Scuti variables, and rotational variables have small variability amplitudes, which make their discovery non-trivial. Furthermore, SR variables have periods between ∼10 and ∼103 d, and their detection requires long duration light curves with good cadence. The long baselines (∼500−2000 d, depending on the field) and the cadence (∼2−3 d) of the ASAS-SN V-band light curves enable the discovery of these long period variables with good efficiency. We illustrate the sky distribution of the new ASAS-SN variables in Fig. 1. Variables with large amplitudes and strong periodicity are relatively easily discovered and characterized by wide field photometric surveys and amateur astronomers, so the existing completeness of these variable types is very high. Nevertheless, we make considerable additions to the census of these variable types, with the smallest percentage increase coming from the first-overtone classical Cepheids (DCEPS) at |$+9{ per\ cent}$|. Overall, we have increased the numbers of variable stars across the entire sky with V-band magnitudes 11 < V < 17 mag by |$+106{ per\ cent}$|. We also show the sky distribution of the known variables identified in our work in Fig. 2. Most (|${\sim }74{ per\ cent}$|) of our discoveries were in the Southern hemisphere. Given the relative scarcity of wide-field photometric surveys that monitor the Southern hemisphere, this is not surprising.
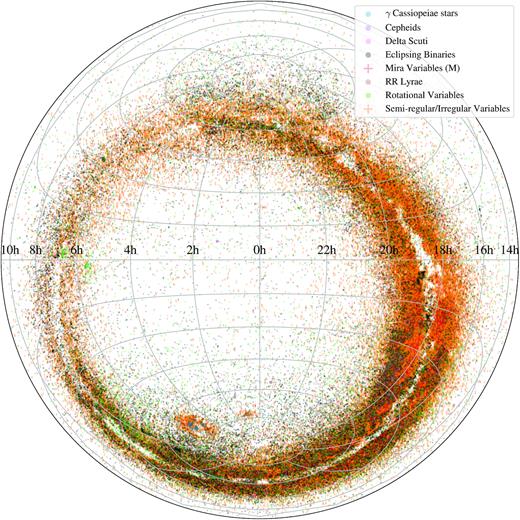
Projected distribution of the ∼219 400 new ASAS-SN discoveries in Equatorial coordinates (Lambert projection). The points are coloured by the variability type.
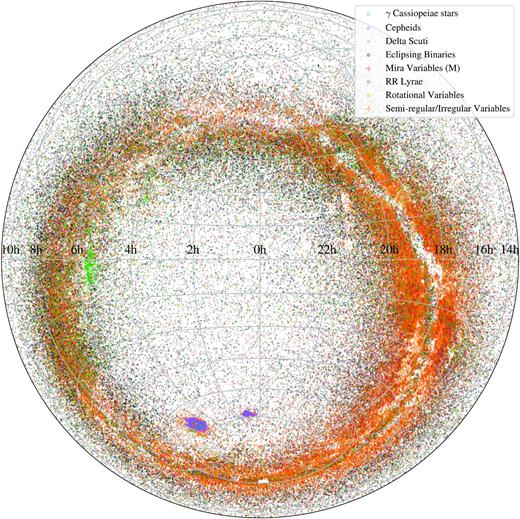
Projected distribution of the ∼ 206 200 known variable stars recovered through ASAS-SN in equatorial coordinates (Lambert projection). The points are coloured by the variability type.
Fig. 3 shows the root-mean-square (RMS) variability of a sample of V-band variables as a function of their mean brightness along with 300 000 constant sources. As expected, Mira variables have the largest RMS variability. At the bright end of the survey, ASAS-SN is able to detect variability at the level of |${\sim }1{ per\ cent}$|, dropping to |${\sim }10\rm{--}20{ per\ cent}$| at the faintest magnitudes.
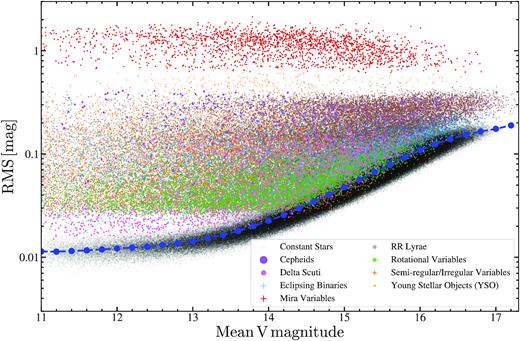
Root-mean-square (RMS) as a function of mean magnitude for the ASAS-SN V-band variable stars with |$\rm Prob\,\,\gt\,\, 0.95$|. A sample of 300 000 constant sources are shown in black. The median RMS of the constant stars is shown in blue for bins of 0.2 mag.
We can estimate the amount of flux blended with the variables using the proximity statistics from refcat2 (Tonry et al. 2018b). Fig. 4 shows the distribution of the radius at which the cumulative GaiaG-band flux in the aperture exceeds the flux of the variable source (r1). A value of 99|${^{\prime\prime}_{.}}$|9 is assigned when the star is so isolated that the cumulative flux never exceeds the required threshold within the 36|${^{\prime\prime}_{.}}$|0 search radius employed by Tonry et al. (2018b). A large fraction (|${\sim }72{ per\ cent}$|) of the V-band variables met this criterion. Another |${\sim }11{ per\ cent}$| of the variables had r1 > 30 arcsec, and are effectively isolated. Thus, in the context of blending, most (|${\sim }83{ per\ cent}$|) of the variables can be considered to be relatively isolated. However, a peak corresponding to heavily blended sources is seen at ∼3|${^{\prime\prime}_{.}}$|0 in Fig. 4. Only |${\sim }4{ per\ cent}$| and |${\sim }6{ per\ cent}$| of the variables exceed their flux within an aperture corresponding to the ASAS-SN pixel scale (∼8|${^{\prime\prime}_{.}}$|0) and FWHM (∼16|${^{\prime\prime}_{.}}$|0), respectively. The main effect of blending is to reduce the apparent variability amplitude.
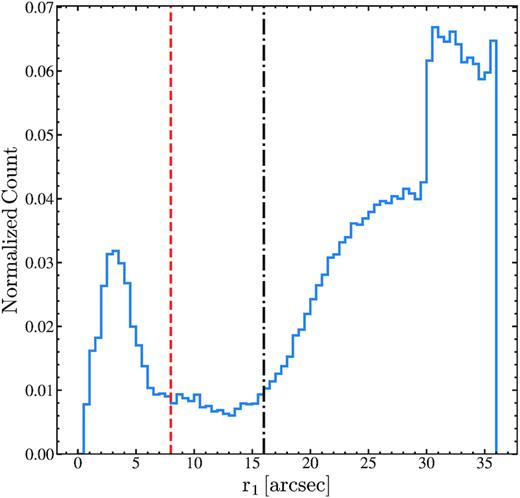
Distribution of the radius at which the cumulative GaiaG flux in the aperture exceeds the flux of the variable source (|$\rm r1$| from Tonry et al. 2018b) for the ASAS-SN V-band variable stars. The ASAS-SN pixel scale (∼8|${^{\prime\prime}_{.}}$|0) and FWHM (∼16|${^{\prime\prime}_{.}}$|0) are shown as the red-dashed and black dot–dashed lines, respectively.
The near-infrared (NIR) |$M_{K_s}$| versus J −Ks colour–magnitude diagram and the |$\rm M_{Ks}$| period–luminosity relationship (PLR) diagram for all the variables with variable type classification probabilities |$\rm Prob\gt 0.95$|, AV < 2 mag and Gaia DR2 parallaxes better than |$20{ per\ cent}$| are shown in Fig. 5. Generic and uncertain variable types are not shown. We have sorted the variables into groups to highlight the different classes of variable sources. Rotational variables in our catalogue consist of spotted stars on the main-sequence (MS) as well as evolved stars on the red giant branch (RGB). SR variables and Mira variables lie on the asymptotic giant branch (AGB). Several PLR sequences are seen in Fig. 5. We studied the PLR sequences for the δ Scuti variables and contact binaries in Papers VI and VII, respectively. The slight deficits of variables at the aliases of a sidereal day (e.g. P ≈ 1 d, P ≈ 2 d, P ≈ 30 d, etc.) are due to the quality checks from Jayasinghe et al. (2019c).
![NIR colour–magnitude (left) and period–luminosity (right) diagrams for the ASAS-SN V-band variable stars with $\rm Prob\gt 0.95$, AV < 2 mag and parallaxes better than $20{ per\ cent}$. MIST isochrones (Choi et al. 2016; Dotter 2016) for single stars with $\rm [Fe/H]=0$ at 1, 5, and 10 Gyr are shown for comparison.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig5.jpeg?Expires=1749866512&Signature=TAIP5kTkP4VRNBLaBm-O69B4CQ7TTJVbeWVqyxe07GE8r3zqOu7pvFRswThm9lw3FF-CPAoMlezWY8zQ5zTZJhIl4pgYEJMYNXSyKnzYZDD~kFVllJDTtHbE6ZlPYo0C538O0i~OiBFQrYKJGnidcbbUQRYU-UnLRE9-o~nFuq~sjNcIOkYQH6F4ucvCumtVdEsiP8ukmxsEHWI-h2lYlojM8r96gvakLJJBPw-GKQPyp7IQUEzIfr-MgqnvSFXIzVgheGoDn4BZFZJlqSXhL65~G~1jfP7IUyJzhX3TOyylnFQpI0~gczgukEvP1NPAzXqQn0zjz3q9gbeeddlwqg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
NIR colour–magnitude (left) and period–luminosity (right) diagrams for the ASAS-SN V-band variable stars with |$\rm Prob\gt 0.95$|, AV < 2 mag and parallaxes better than |$20{ per\ cent}$|. MIST isochrones (Choi et al. 2016; Dotter 2016) for single stars with |$\rm [Fe/H]=0$| at 1, 5, and 10 Gyr are shown for comparison.
The period–amplitude distribution of the periodic variables is shown in Fig. 6. Most variables (|${\sim }96{ per\ cent}$|) have amplitudes A < 1 mag. Of the variables with amplitudes A > 1 mag, |${\sim }59{ per\ cent}$| are Mira and SR variables. Eclipsing binaries (|${\sim }22{ per\ cent}$|) and RR Lyrae (|${\sim }17{ per\ cent}$|) are also prominent in this group. Variables with large amplitudes A > 2 mag are rarer (|${\sim }1{ per\ cent}$|) and these high amplitude variables are almost exclusively Mira variables.

Period–amplitude distributions of the periodic ASAS-SN V-band variables. The points are colored by the variability type as in Fig. 5. Reference amplitudes of 1 and 2 mag are shown in red and blue, respectively.
3 ASAS-SN VARIABLES IN WIDE-FIELD SPECTROSCOPIC SURVEYS
ASAS-SN significantly overlaps with modern major wide-field spectroscopic surveys owing to its all-sky coverage and the magnitude range of the survey. We cross-matched our catalogue with the APOGEE DR16 catalogue (Holtzman et al. 2015; García Pérez et al. 2016; Ahumada et al. 2019; Jönsson et al. 2020), the RAVE-on catalogue (Casey et al. 2017), the LAMOST DR5 v4 catalogue (Cui et al. 2012) and the GALAH DR2 catalogue (De Silva et al. 2015; Buder et al. 2018) using a matching radius of 5|${^{\prime\prime}_{.}}$|0. LAMOST only reports |$\rm T_{eff}$|, |$\rm \log (g)$|, and |$\rm [Fe/H]$| for A, F, G, and K stars. We identified 39811 (39036) total (unique) matches to the catalogues from the LAMOST (17381), GALAH (3067), RAVE (15050), and APOGEE (4313) spectroscopic surveys.
These spectroscopic surveys differ in their targeting strategy, spectral resolution, and data reduction. APOGEE is a NIR survey with a spectral resolving power of R ∼ 22, 500. LAMOST, RAVE, and GALAH are optical surveys with R ∼ 1800, R ∼ 7000, and R ∼ 28 000, respectively. The different pipelines that are used in the data reduction process can result in survey specific offsets in the spectroscopic parameters for similar stars. However, efforts have been made to compare the various spectroscopic parameters amongst these surveys, and the parameters are generally similar for most stars (Casey et al. 2017; Buder et al. 2018). The targeting strategies are also different, with APOGEE focusing more on observing red stars than the other surveys. Additionally, variability might impact the derivation of spectroscopic parameters, particularly when sources are in double-lined spectroscopic binaries (eclipsing binaries). Thus, we cannot rely on a single survey to study all the different classes of variable stars.
We illustrate the distribution of the ASAS-SN variable stars with classification probabilities |$\rm Prob\gt 0.95$| in |$\rm T_{eff}$| and |$\rm \log (g)$| (Kiel Diagram) across these surveys in Fig. 7. We will only consider sources with |$\rm Prob\gt 0.95$| in all of our examinations of spectroscopic properties. We have generally not implemented any cuts on the various flags that are available across these data sets. The LAMOST survey provides the only data set that samples all the major variability classes in our catalogue. Most of the cross-matches to APOGEE come from the SR variables and rotational variables. If we implement the data quality cut ASPCAPFLAG = 0, |${\sim }65{ per\ cent}$| of the APOGEE sources remain. We note that some fraction of the SR variables with temperatures |$\rm T_{eff}\,\,\lt\,\, 3800$| K in the RAVE data set have values of |$\rm \log (g)$| that are inconsistent with being evolved stars on the AGB. If we implement the quality cut QC = 0 from Casey et al. (2017), |${\sim }95{ per\ cent}$| of the RAVE sources remain, but this issue with the location of the giants persists. It is also clear that the vast majority of the SR variables in GALAH have incorrect spectroscopic parameters as they populate a non-physical locus in the Kiel diagram. Buder et al. (2018) noted this issue with their pipeline for cool giants with |$\rm T_{eff}\,\,\lt\,\, 4500 \, K$|. Implementing the data quality cut FLAG_CANNON = 0 suggested by Buder et al. (2018), eliminates all but |${\sim }5{ per\ cent}$| of the GALAH sources, which suggests that the GALAH data set is sub-optimal for our purpose of studying variable stars. We find that the data from the LAMOST and RAVE surveys are best suited to characterizing pulsators, eclipsing binaries, and rotational variables. APOGEE data are excellent for the characterization of the cooler SR and irregular variables.
![Distributions of the ASAS-SN V-band variables in $\rm \log (g)$ and $\rm T_{eff}$ across the LAMOST, APOGEE, RAVE, and GALAH data sets. The points are coloured by the variable type. Spectroscopic data quality cuts are not included. MIST isochrones (Choi et al. 2016; Dotter 2016) for single stars with $\rm [Fe/H]=-0.50$ at 1, 5, and 10 Gyr are shown for comparison.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig7.jpeg?Expires=1749866512&Signature=CT6neIX7i12-1IH1Gd1i1Wo4z8lc5Av7bySK9tcHMS5DodRj0w8xzSFqgM5GDkVPFD2HktE~CjHLtQIcI5qRwwy8ZBBFItfvZHocs-aLuvLv6TlfeLWZfENEko5s-Py4jevGXOYrp5QnmM0VEtcPWS0mEb-DnR~OizTXbHDPke7LkNkygvv67Zk30IyNZMJTzVjqRYgbIo3QE~PaYbpwvPdp6SepdfpXGUwoDHP0sL9ZpsA1CdPIbECnnWOy8IiH53rg7r-C79kexIWsoLP-9-BQ4bouhKrXw4TOeUWdcyc14KGtDqenG8E0653kym13qo5xiwdjBfWAARnJfc62lw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distributions of the ASAS-SN V-band variables in |$\rm \log (g)$| and |$\rm T_{eff}$| across the LAMOST, APOGEE, RAVE, and GALAH data sets. The points are coloured by the variable type. Spectroscopic data quality cuts are not included. MIST isochrones (Choi et al. 2016; Dotter 2016) for single stars with |$\rm [Fe/H]=-0.50$| at 1, 5, and 10 Gyr are shown for comparison.
The distribution of the variables in |$\rm T_{eff}$| and |$\rm [Fe/H]$| is shown in Fig. 8. We note that the eclipsing binaries in the GALAH sample have metallicities that are largely inconsistent with the eclipsing binaries in the other catalogues. However, only a tiny fraction of this sample passes the quality cut FLAG_CANNON = 0. In order to improve the accuracy of our work, we will only consider GALAH sources with FLAG_CANNON = 0. We also restrict the RAVE sample of SR variables to those stars with |$\rm \log (g)\,\,\lt\,\, 2$|.
![Distributions of the ASAS-SN V-band variables in $\rm T_{eff}$ and $\rm [Fe/H]$ across the LAMOST, APOGEE, RAVE, and GALAH data sets. The points are coloured by the variable type.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig8.jpeg?Expires=1749866512&Signature=a6IS3~zUKDXu4ghLZWewojHMrEI3vcRApcVOb8GT3xT2o6SaVPrFU9iFixXYtOqWVczEFtA3glXQ-VfBXT~ZRTlZYaK4LtLCyFsJ2vTHlzsJan4QG5HyxFICz8EOaxNCmESBO~9MdMxfYQJN86Vl9Ko7FZ5xdfsa49rQapT~SjTjitTLB~6j7ObptrCS7guyjBekpuO4RhuAUrzlNmd1G~fDmt7qry0T5xCX1NbLIUCqS3bYERD7Jqn2aHUlxv2LRkPpogoAIXt7KTou1nvawNVa~kmQGLks-1Ogh6c0PF0LowhK0zgIY1NMexQwk~FE1Cg67bzxVEvcZjDUAfWpBw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distributions of the ASAS-SN V-band variables in |$\rm T_{eff}$| and |$\rm [Fe/H]$| across the LAMOST, APOGEE, RAVE, and GALAH data sets. The points are coloured by the variable type.
The combined distributions of the variables in |$\rm T_{eff}$|, |$\rm \log (g)$|, |$\rm [Fe/H]$|, and |$\rm \log _{10}(P/days)$| are shown in Fig. 9. The median and standard deviation of the spectroscopic parameters for variable types with sample sizes N > 10 are also summarized in Table 2. On average, eclipsing binaries have sub-solar metallicities (|$\rm [Fe/H]{\sim }-0.2$|). Cepheid variables have metallicities consistent with Solar metallicity. δ Scuti variables and rotational variables have metallicites that are slightly sub-solar (|$\rm [Fe/H]{\sim }-0.1$|). SR variables are strongly peaked at |$\rm [Fe/H]{\sim }-0.5$|, with very few having solar or supersolar metallicities. The population II RRAB stars have very low metallicities with |$\rm [Fe/H]{\sim }-1$|. The average metallicity of the overtone RR Lyrae (RRC) variables in our sample is |$\rm [Fe/H]{\sim }-0.3$| and has a large dispersion of σ ∼ 0.8 dex. Walker & Terndrup (1991) found that, on average, both RRAB and RRC variables in Baade’s window had |$\rm [Fe/H]{\sim }-1$|. This suggests that some fraction of the sources classified as RRC variables are in fact EW-type eclipsing binaries with higher metallicities (|$\rm [Fe/H]{\sim }-0.2$|). Without spectroscopic information, there can be non-negligible confusion between these two variable groups during the classification process due to their very similar and symmetrical light-curve shapes.
![Distributions of the ASAS-SN V-band variables in $\rm T_{eff}$, $\rm \log (g)$, $\rm [Fe/H]$, and $\rm \log _{10}(P/days)$. The histograms are coloured by the variable type.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig9.jpeg?Expires=1749866512&Signature=OBx1bslyxnZn5YEpghikxPz9prRUyM4teGDeyuo0tjNmtttWybzchBh9x31eDM9hTM~dad7EvOvetIFzSv~dtOO3xcg1S09r9fl5oN4s-plVtOCwjzpnlScegCaZbupnCFWUas2r~EAOTddFs5cykbT~EA6o13Nm914gHQ8eMK9Zg~3ypZXnVomfiVHdY2mwOTQYhjPGBEVsTri3y4cYH3mF1etgF2L-DVc8zY0XwFRrFCHD9S2EYFgt~GqR~M9HVSYXqV91arRUt0vVIFDSJAJkeoc3muCWEbwEuXb4V~7q161IYzorFoGL--ctDJjfQ9JdzYDwcCZ9oC1-VNc8Ig__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distributions of the ASAS-SN V-band variables in |$\rm T_{eff}$|, |$\rm \log (g)$|, |$\rm [Fe/H]$|, and |$\rm \log _{10}(P/days)$|. The histograms are coloured by the variable type.
Distribution of |$\rm [Fe/H]$|, |$\rm T_{eff}$|, and |$\rm \log (g)$| for variable types with at least 10 members with classifications. The variable types are defined in Table 1. The median and standard deviation for each spectroscopic parameter is shown.
| VSX Type . | N . | |$\rm T_{eff}$| . | |$\rm \log (g)$| . | |$\rm [Fe/H]$| . |
|---|---|---|---|---|
| DCEP | 40 | 6094 ± 453 | 1.5 ± 0.8 | −0.02 ± 0.28 |
| DCEPS | 17 | 6618 ± 428 | 2.9 ± 0.8 | 0.01 ± 0.16 |
| DSCT | 537 | 7194 ± 408 | 4.0 ± 0.2 | −0.09 ± 0.27 |
| HADS | 267 | 7256 ± 538 | 4.1 ± 0.2 | −0.24 ± 0.34 |
| EA | 3115 | 6283 ± 851 | 4.1 ± 0.3 | −0.13 ± 0.27 |
| EB | 1948 | 6725 ± 771 | 4.1 ± 0.3 | −0.16 ± 0.27 |
| EW | 6388 | 5905 ± 656 | 4.2 ± 0.2 | −0.17 ± 0.32 |
| SR | 7232 | 3777 ± 158 | 0.6 ± 0.3 | −0.51 ± 0.24 |
| L | 371 | 3773 ± 212 | 0.5 ± 0.4 | −0.47 ± 0.24 |
| ROT | 2748 | 4616 ± 503 | 4.1 ± 0.8 | −0.14 ± 0.28 |
| YSO | 27 | 4188 ± 497 | 4.0 ± 0.9 | −0.21 ± 0.25 |
| RRAB | 1086 | 6477 ± 297 | 4.2 ± 0.2 | −1.01 ± 0.37 |
| RRC | 161 | 6960 ± 554 | 4.2 ± 0.3 | −0.33 ± 0.60 |
| VAR | 17 | 5811 ± 1262 | 4.1 ± 1.8 | −0.90 ± 0.63 |
| VSX Type . | N . | |$\rm T_{eff}$| . | |$\rm \log (g)$| . | |$\rm [Fe/H]$| . |
|---|---|---|---|---|
| DCEP | 40 | 6094 ± 453 | 1.5 ± 0.8 | −0.02 ± 0.28 |
| DCEPS | 17 | 6618 ± 428 | 2.9 ± 0.8 | 0.01 ± 0.16 |
| DSCT | 537 | 7194 ± 408 | 4.0 ± 0.2 | −0.09 ± 0.27 |
| HADS | 267 | 7256 ± 538 | 4.1 ± 0.2 | −0.24 ± 0.34 |
| EA | 3115 | 6283 ± 851 | 4.1 ± 0.3 | −0.13 ± 0.27 |
| EB | 1948 | 6725 ± 771 | 4.1 ± 0.3 | −0.16 ± 0.27 |
| EW | 6388 | 5905 ± 656 | 4.2 ± 0.2 | −0.17 ± 0.32 |
| SR | 7232 | 3777 ± 158 | 0.6 ± 0.3 | −0.51 ± 0.24 |
| L | 371 | 3773 ± 212 | 0.5 ± 0.4 | −0.47 ± 0.24 |
| ROT | 2748 | 4616 ± 503 | 4.1 ± 0.8 | −0.14 ± 0.28 |
| YSO | 27 | 4188 ± 497 | 4.0 ± 0.9 | −0.21 ± 0.25 |
| RRAB | 1086 | 6477 ± 297 | 4.2 ± 0.2 | −1.01 ± 0.37 |
| RRC | 161 | 6960 ± 554 | 4.2 ± 0.3 | −0.33 ± 0.60 |
| VAR | 17 | 5811 ± 1262 | 4.1 ± 1.8 | −0.90 ± 0.63 |
Distribution of |$\rm [Fe/H]$|, |$\rm T_{eff}$|, and |$\rm \log (g)$| for variable types with at least 10 members with classifications. The variable types are defined in Table 1. The median and standard deviation for each spectroscopic parameter is shown.
| VSX Type . | N . | |$\rm T_{eff}$| . | |$\rm \log (g)$| . | |$\rm [Fe/H]$| . |
|---|---|---|---|---|
| DCEP | 40 | 6094 ± 453 | 1.5 ± 0.8 | −0.02 ± 0.28 |
| DCEPS | 17 | 6618 ± 428 | 2.9 ± 0.8 | 0.01 ± 0.16 |
| DSCT | 537 | 7194 ± 408 | 4.0 ± 0.2 | −0.09 ± 0.27 |
| HADS | 267 | 7256 ± 538 | 4.1 ± 0.2 | −0.24 ± 0.34 |
| EA | 3115 | 6283 ± 851 | 4.1 ± 0.3 | −0.13 ± 0.27 |
| EB | 1948 | 6725 ± 771 | 4.1 ± 0.3 | −0.16 ± 0.27 |
| EW | 6388 | 5905 ± 656 | 4.2 ± 0.2 | −0.17 ± 0.32 |
| SR | 7232 | 3777 ± 158 | 0.6 ± 0.3 | −0.51 ± 0.24 |
| L | 371 | 3773 ± 212 | 0.5 ± 0.4 | −0.47 ± 0.24 |
| ROT | 2748 | 4616 ± 503 | 4.1 ± 0.8 | −0.14 ± 0.28 |
| YSO | 27 | 4188 ± 497 | 4.0 ± 0.9 | −0.21 ± 0.25 |
| RRAB | 1086 | 6477 ± 297 | 4.2 ± 0.2 | −1.01 ± 0.37 |
| RRC | 161 | 6960 ± 554 | 4.2 ± 0.3 | −0.33 ± 0.60 |
| VAR | 17 | 5811 ± 1262 | 4.1 ± 1.8 | −0.90 ± 0.63 |
| VSX Type . | N . | |$\rm T_{eff}$| . | |$\rm \log (g)$| . | |$\rm [Fe/H]$| . |
|---|---|---|---|---|
| DCEP | 40 | 6094 ± 453 | 1.5 ± 0.8 | −0.02 ± 0.28 |
| DCEPS | 17 | 6618 ± 428 | 2.9 ± 0.8 | 0.01 ± 0.16 |
| DSCT | 537 | 7194 ± 408 | 4.0 ± 0.2 | −0.09 ± 0.27 |
| HADS | 267 | 7256 ± 538 | 4.1 ± 0.2 | −0.24 ± 0.34 |
| EA | 3115 | 6283 ± 851 | 4.1 ± 0.3 | −0.13 ± 0.27 |
| EB | 1948 | 6725 ± 771 | 4.1 ± 0.3 | −0.16 ± 0.27 |
| EW | 6388 | 5905 ± 656 | 4.2 ± 0.2 | −0.17 ± 0.32 |
| SR | 7232 | 3777 ± 158 | 0.6 ± 0.3 | −0.51 ± 0.24 |
| L | 371 | 3773 ± 212 | 0.5 ± 0.4 | −0.47 ± 0.24 |
| ROT | 2748 | 4616 ± 503 | 4.1 ± 0.8 | −0.14 ± 0.28 |
| YSO | 27 | 4188 ± 497 | 4.0 ± 0.9 | −0.21 ± 0.25 |
| RRAB | 1086 | 6477 ± 297 | 4.2 ± 0.2 | −1.01 ± 0.37 |
| RRC | 161 | 6960 ± 554 | 4.2 ± 0.3 | −0.33 ± 0.60 |
| VAR | 17 | 5811 ± 1262 | 4.1 ± 1.8 | −0.90 ± 0.63 |
The temperatures and surface gravities of the SR/irregular variables are consistent with these stars being highly evolved AGB stars. Classical pulsators, such as the RR Lyraes, Cepheids, and δ Scuti variables, have temperatures that fall within the instability strip for pulsations. Overtone Cepheids and RR Lyrae are hotter than the fundamental mode pulsators at fixed temperature. The eclipsing binaries in this sample mostly have surface gravities consistent with main sequence (MS) or slightly evolved stars. Fig. 8 shows that the eclipsing binaries span a large range in effective temperature with |$\rm 4000\, K\,\,\lt\,\, Teff\,\,\lt\,\, 8000\, K$| (A-K spectral types). On average, β Lyrae-type semidetached binaries (EB) have hotter effective temperatures than both contact binaries and detached eclipsing binaries. The surface gravities of the rotational variables peak near the MS, but the dispersion of σ ∼ 0.8 dex is large because it is a much more diverse population of sources, including spotted stars on the RGB. We will further investigate the populations of eclipsing binaries and rotational variables in Section 4.
Fig. 10 shows the correlation between APOGEE and GALAH estimates of |$v$|sin (i) and the ASAS-SN |$\rm \log _{10}(P/days)$| for the variables in the spectroscopic sample. As expected for the rotational variables, |$v$|sin (i) decreases with the period. For the 32 SR variables with |$v$|sin (i) measurements from GALAH [APOGEE does not report |$v$|sin (i) for very evolved stars], the median was |$v\sin (i){\sim }8\, \rm km\,s^{ -1}$|. δ Scuti variables have a broad distribution in |$v$|sin (i), consistent with previous measurements (Solano & Fernley 1997). Most short period (|$\rm P\lt 1$| d) eclipsing binaries have |$v\sin (i){\lesssim }20\, \rm km\,s^{ -1}$|.
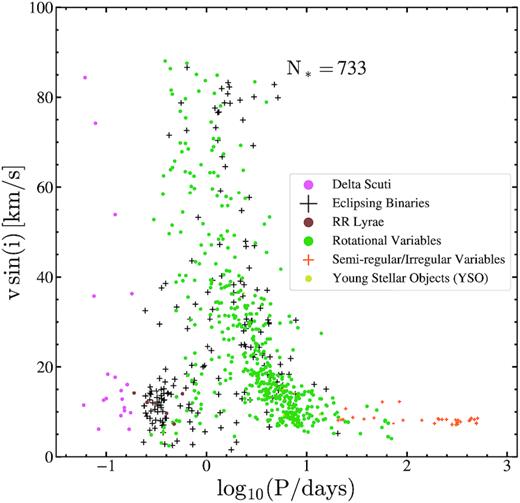
Distributions of the ASAS-SN V-band variables in |$v$|sin (i) versus |$\rm \log _{10}(P/days)$|. The points are coloured by the variable type.
4 DISCUSSION
Here, we discuss eclipsing binaries, rotational variables and SR variables using both the photometric information from ASAS-SN and other surveys (including Gaia, WISE, 2MASS, and GALEX) and spectroscopic information from the cross-matching in Section 3 in more detail. In Section 4.1, we study the temperature and metallicity dependences of the periods of eclipsing binaries. In Section 4.2, we examine our catalogue of rotational variables and particularly the rapidly rotating evolved stars. In Section 4.3, we discuss the SR variables and their chemical properties using the measurements from APOGEE DR16.
4.1 Eclipsing binaries
Eclipsing binaries are useful astrophysical tools that can be used to measure the masses and radii of stars across the Hertzsprung–Russell diagram (see Torres et al. 2010, and references therein). We classified ∼136 000 eclipsing binaries in our catalogue into the VSX types: EW (W UMa), EB (β-Lyrae), and EA (Algol). These classifications were made using a random forest classifier with features derived from light-curve characteristics, including Fourier parameters (see Jayasinghe et al. 2019b). EW binaries have light curves with similar primary/secondary eclipse depths, whereas EB binaries tend to have eclipses with significantly different depths. Both the EW and EB binaries transition smoothly from the eclipse to the out-of-eclipse state. EA (Algol) binaries are systems where the exact onset and end of the eclipses are easily defined. EA binaries may or may not have a secondary minimum.
Fig. 11 shows the distributions of the eclipsing binaries in |$\rm \log (g)$|, |$\rm T_{eff}$|, |$\rm \log _{10}(P/days)$|, and |$\rm M_{Ks}$|. The surface gravity distributions of the three sub-types are very similar. The biggest differences between the different sub-types are in their effective temperatures. On average, EW type contact binaries are significantly cooler (|$\rm T_{eff}\,\,{\sim }\,\,5900$| K) than both the EB (|$\rm T_{eff}\,\,{\sim }\,\,6700$| K) and the EA systems (|$\rm T_{eff}\,\,{\sim }\,\,6300$| K). EW binaries peak at |$\rm \log _{10}(P/days)\,\,{\sim }-0.5$| and drop sharply at both longer and shorter periods. There are very few EW systems with |$\rm \log _{10}(P/days)\,\gt\, 0$|. EB systems peak at |$\rm \log _{10}(P/days)\,{\sim }\,-0.8$| and span a larger range in period. The detached EA systems peak at |$\rm \log _{10}(P/days)\,{\sim }\,0.4$| and are more evenly distributed in their orbital periods than the EB and EW systems. EW systems are fainter, with a peak at |$\rm M_{Ks}\,{\sim }\,2.4$| mag, whereas the EB and EA systems peak at a similar |$\rm M_{Ks}\,{\sim }\,1.6$| mag.
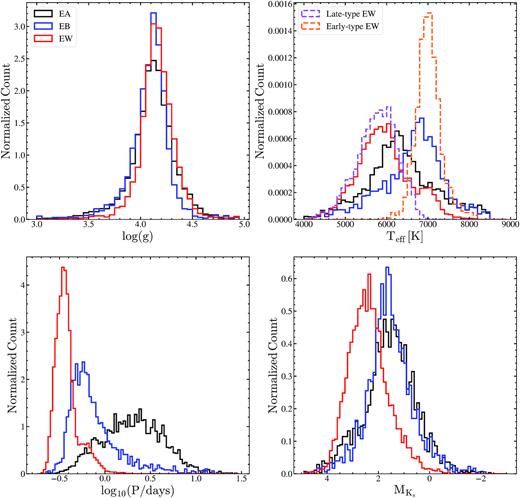
Distributions of the EW (red), EB (blue), and EA (black) binaries in |$\rm \log (g)$|, |$\rm T_{eff}$|, |$\rm \log _{10}(P/days)$|, and |$\rm M_{Ks}$|. The distributions in |$\rm T_{eff}$| for the early- (orange) and late-type (purple) EW binaries from Jayasinghe et al. (2020a) are shown as the dashed histograms.
In Paper VII (Jayasinghe et al. 2020a), we analysed a sample of ∼71 000 EW systems, and noted a clear dichotomy between the early- and late-type EW systems. We found that the period distribution had a clear minimum at |$\rm \log (\rm P/d) =-0.30$| that also corresponded to a break in the slope of the period–luminosity relation. The distinction between the populations was even clearer in the space of period and effective temperature, with a gap along the line |$\rm T_{eff}=6710K-1760K\, \log (P/0.5\, d)$|. The median temperature of the early-type contact binaries (|$\rm T_{eff}\,\,{\sim }\,\,6900$| K) was significantly hotter than the late-type contact binaries (|$\rm T_{eff}\,\,{\sim }\,\,5800$| K). We further noted that the Kraft break (Kraft 1967) appeared to determine the observed dichotomy of the contact binaries. Early-type systems form due to stellar evolution and the subsequent expansion of a more massive component that is above the Kraft break (∼1.3 M⊙). In contrast, the less massive late-type systems can come into contact due to efficient angular momentum loss during the detached phase (Yıldız 2014).
Fig. 12 shows the different sub-types of eclipsing binaries in the space of |$\rm \log (\rm P/d)$| and |$\rm T_{eff}$|. There is significant overlap in period–temperature space between the EW and EB binaries, with most EB binaries falling above the cut defined in Jayasinghe et al. (2020a) for the early-type EW systems. The overlap between the EW and EB binaries is most significant in the period–temperature space above this cut. The EA binaries are distributed randomly in this space. The distribution of EB binaries peaks at a similar temperature to the early-type EW binaries (|$\rm T_{eff}{\sim }6900$| K, see Fig. 11), which suggests that the early-type EW are drawn from the population of EB binaries. However, these two populations differ in the ratio between the primary and secondary light curve minima. The degree of thermal equilibrium between the two stars dictates the difference in eclipse depths (Paczyński et al. 2006), and the very similar eclipses seen in EW binaries suggest that these stars are in better thermal contact than the EB binaries that have different eclipse depths.
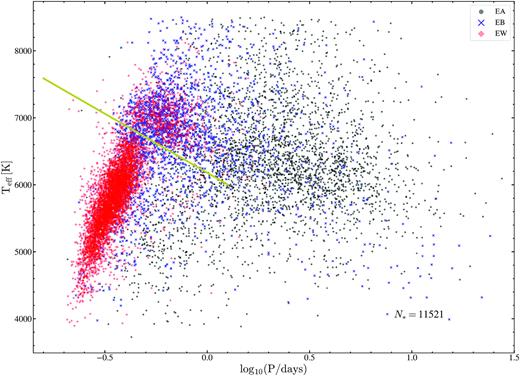
|$\rm T_{eff}$| versus |$\rm \log (\rm P/d)$| for EW (red), EB (blue), and EA (black) binaries. The yellow line in |$\rm T_{eff}$| and |$\rm \log (\rm P/d)$| that separates early- and late-type EW binaries is derived in Jayasinghe et al. (2020a).
In our previous work, we hypothesized that the early-type EW systems have a massive component above the Kraft break (≳1.3 M⊙) that is in thermal contact with the secondary. The EB systems are likely to have similar massive components, but the two components in these systems diverge significantly from thermal contact, unlike those in the late-type EW systems. Models of thermal relaxation oscillations (TRO; see e.g. Lucy 1976; Flannery 1976; Yakut & Eggleton 2005) predict a population of EB eclipsing binaries with unequal minima that overlap in period and temperature with the EW systems (Webbink 2003). In the TRO cycle, an eclipsing binary oscillates between the contact and semidetached states. The semidetached phase spans a period and temperature range that is comparable to the contact phase, and the two components develop different effective temperatures during the EB stage of the cycle (Webbink 2003). The overlap between the early-type EW and the EB systems appear to be consistent with the predictions of the TRO models for contact binaries.
![The median $\rm \log (\rm P/d)$ as a function of $\rm T_{eff}$ distributions for EW (top), EB (middle), and EA (bottom) binaries. The shaded regions correspond to the 5–95 per cent ranges of the periods. The predicted period–temperature relationships for MS Roche contact binaries with mass ratios q = 1 (light blue) and q = 0.1 (orange) is derived using the MIST isochrones (Choi et al. 2016; Dotter 2016) and are shown for metallicities of $\rm [Fe/H]=-0.50$ (dashed), $\rm [Fe/H]=0$ (dotted), and $\rm [Fe/H]=0.25$ (dot–dashed) for a 108 yr old stellar population.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig13.jpeg?Expires=1749866512&Signature=tbBEvaRZq6G8Z57rL-WYQaBnUVhIB6HqQJkcR0sKl1RMmElXdj8wgcyRWU4PCuzDAGHeAFXjZgxmOEJRWzZj14Yein7nbkimfoJUnOtrmj-Yf7vMrCKLfN1uadYzI4ODIbBBPDrbaNPiydGHBxFfpXo96i9562Zj-idGBER7pMhc4r7HC3zciok~ZbNTaqz99CQiDN0FHASMIsb2XgkoJrss4JSUPk7q9Eq9r9ta5sjgSDfZJhcC4f88VV3vuTuDkAC31oI1W8RR8IUjaKlspsSuhokfvOtN5WIFwUp5axaE0XJunMKGEGu5klMc-3AWKMQ01uOpGbuJuBMEdL5Pfg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The median |$\rm \log (\rm P/d)$| as a function of |$\rm T_{eff}$| distributions for EW (top), EB (middle), and EA (bottom) binaries. The shaded regions correspond to the 5–95 per cent ranges of the periods. The predicted period–temperature relationships for MS Roche contact binaries with mass ratios q = 1 (light blue) and q = 0.1 (orange) is derived using the MIST isochrones (Choi et al. 2016; Dotter 2016) and are shown for metallicities of |$\rm [Fe/H]=-0.50$| (dashed), |$\rm [Fe/H]=0$| (dotted), and |$\rm [Fe/H]=0.25$| (dot–dashed) for a 108 yr old stellar population.
In the MIST model shown in Fig. 13, we see that the low metallicity binaries can be more compact before reaching the Roche limit. In Fig. 14, we divide each class of eclipsing binaries into metallicity bins of |$\rm [Fe/H]\lt -0.5$|, |$\rm -0.5\lt [Fe/H]\lt 0$|, and |$\rm [Fe/H]\gt 0$|, and show the period ranges as a function of temperature for each bin. Most (|${\sim }63{ per\ cent}$|) eclipsing binaries have metallicities in the range |$\rm -0.5\lt [Fe/H]\lt 0$|. Similarly, Pawlak et al. (2019) found that the ASAS-SN eclipsing binaries had a median |$\rm [Fe/H]$| 0.2 dex lower than the entire APOGEE DR14 sample. In general, we see that the lower metallicity binaries have shorter periods than the binaries that are metal rich at fixed temperature.
![The distribution of the 5th percentile in $\rm \log (\rm P/d)$ versus $\rm T_{eff}$ for EW (top), EB (middle), and EA (bottom) binaries in metallicity bins of $\rm [Fe/H]\,\lt -0.5$ (black), $\rm -0.5\,\,\lt\,\, [Fe/H]\,\,\lt\,\, 0$ (red) and $\rm [Fe/H]\,\,\gt\,\, 0$ (blue). The shaded regions correspond to the 5–95 per cent ranges of the periods. The predicted period–temperature relationships (light blue) for equal mass MS binaries overflowing their Roche Lobes is derived using the MIST isochrones (Choi et al. 2016; Dotter 2016) and are shown for metallicities of $\rm [Fe/H]=-0.50$ (dashed), $\rm [Fe/H]=0$ (dotted), and $\rm [Fe/H]=0.25$ (dot–dashed) for a 108 yr old stellar population.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig14.jpeg?Expires=1749866512&Signature=3dm1j28XobyDbtWle~3sX1jiRfEuP5lCb1U-P~oUfJypZ2mABjv-m5wy6aFqXsWpPSFUUzwlfi4h3Ehiku0ZVMIpSg2kfIEmDSQWqavLMVtkWSeAKGzwtT8He1E3I13QYq5qJOTKqNkC8SMP7vfh54RhD12XqF8B7aJ5WHQ47QWk2bqSxFizUyO9T9lC6z0Gve~g2ROY9Ya5gyZIlaTuz2Ch-u1lh-nlVi7dI2pgkkwjk0T0vbPkc6UpbZLNxHleauOBbQTj-FiayFw5zOj9MUU3hEHZP8st46lIl7Y5YH8WOSldArQgp~gW0GK-LXGFxa4WX0Bj3IYnGqhpKqZQIA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of the 5th percentile in |$\rm \log (\rm P/d)$| versus |$\rm T_{eff}$| for EW (top), EB (middle), and EA (bottom) binaries in metallicity bins of |$\rm [Fe/H]\,\lt -0.5$| (black), |$\rm -0.5\,\,\lt\,\, [Fe/H]\,\,\lt\,\, 0$| (red) and |$\rm [Fe/H]\,\,\gt\,\, 0$| (blue). The shaded regions correspond to the 5–95 per cent ranges of the periods. The predicted period–temperature relationships (light blue) for equal mass MS binaries overflowing their Roche Lobes is derived using the MIST isochrones (Choi et al. 2016; Dotter 2016) and are shown for metallicities of |$\rm [Fe/H]=-0.50$| (dashed), |$\rm [Fe/H]=0$| (dotted), and |$\rm [Fe/H]=0.25$| (dot–dashed) for a 108 yr old stellar population.
4.2 Rotational variables
The ∼33, 000 Rotational (ROT) variables in our V-band catalogue are drawn from a variety of rotational variable types, including α2 Canum Venaticorum variables (ACV), RS Canum Venaticorum-type (RS) binary systems, BY Draconis-type variables (BY), FK Comae Berenices-type variables (FKCOM), rotating ellipsoidal variables (ELL) and spotted T Tauri stars showing periodic variability (TTS/ROT). Rotational variables are distributed across the Hertzsprung–Russell diagram, but the detectability of a rotational signal largely depends on their evolutionary state. Ceillier et al. (2017) studied ∼17, 400 Kepler red giants and noted that |${\sim }2{ per\ cent}$| of these sources had a detectable rotational signal in their light curves. They also studied ∼600 red clump (RC) stars in their sample and found that |${\sim }15{ per\ cent}$| of these sources had a detectable rotational signal. In contrast, McQuillan, Mazeh & Aigrain (2014) detected periodic rotational signals in the Kepler light curves of |${\sim }25.6{ per\ cent}$| of 133,030 MS stars. Rotational variables found by ASAS-SN must be higher amplitude than the typical examples found by Kepler, favoring spotted stars with large spot covering fractions and/or asymmetric spot coverage (Iwanek et al. 2019).
Fig. 15 shows the distributions of the ROT variables in |$\rm \log (g)$|, |$\rm T_{eff}$|, |$\rm \log _{10}(P/days)$| and |$\rm M_{Ks}$|. The rotational variables in LAMOST are shown separately, as most spectroscopic cross-matches to the rotational variables come from this catalogue. The LAMOST catalogue is incomplete for the M-dwarf rotational variables with |$\rm \log (g)\gt 4.8$|, |$\rm T_{eff}\lt 3800$| K. As expected, there are three distinct classes of rotational variables in the |$\rm \log (g)$| and |$\rm M_{Ks}$| distributions. These correspond to sources on the MS/pre-MS (|$\rm \log (g){\sim }4.5$|, |$\rm M_{Ks}{\sim }4$|), sub-giants/giants toward the base of the RGB (|$\rm \log (g){\sim }3.5$|, |$\rm M_{Ks}{\sim }1$|) and the RC (|$\rm \log (g){\sim }2.6$|, |$\rm M_{Ks}{\sim }-1.5$|). These three classes of rotational variables have been characterized in previous surveys (see e.g. McQuillan, Mazeh & Aigrain 2013; McQuillan et al. 2014; Ceillier et al. 2017). The colour–magnitude diagram shown in Fig. 5 suggests that sources with |$\rm M_{Ks}\,\,{\gtrsim }\,\,2$| mag are likely to be sub-giants or giants at the base of the RGB. Most of these stars at the base of the RGB will have a sub-giant luminosity class. RC stars have an absolute magnitude of |$\rm M_{Ks}=-1.61\pm 0.01$| mag (Hawkins et al. 2017), which is consistent with the peak in the |$\rm M_{Ks}$| distribution.
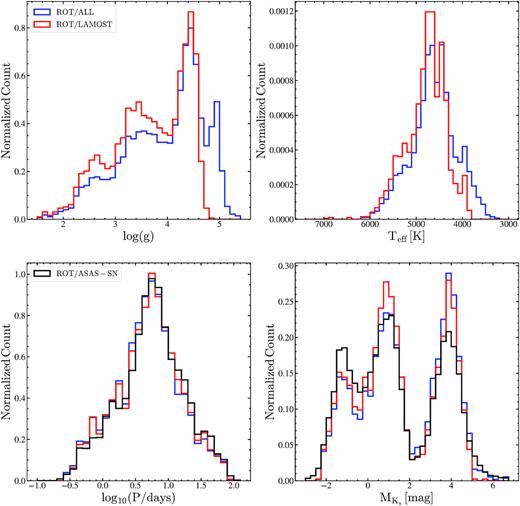
Distributions of the rotational variables for the complete spectroscopic sample (blue) and the LAMOST sample (red) in |$\rm \log (g)$|, |$\rm T_{eff}$|, |$\rm \log _{10}(P/days)$| and |$\rm M_{Ks}$|. The |$\rm \log _{10}(P/days)$| and |$\rm M_{Ks}$| distributions of the rotational variables in the entire ASAS-SN sample are shown in black.
Fig. 16 shows the distribution of rotational variables in |$\rm \log (g)$| and luminosity as a function of |$\rm T_{eff}$|. We use the calibrations from Torres et al. (2010) to derive the radii of the rotational variables using |$\rm T_{eff}$|, |$\rm \log (g)$| and |$\rm [Fe/H]$|. The Torres et al. (2010) scalings agree with asteroseismic estimates (Yu et al. 2018). The luminosities are then derived using the radius and |$\rm T_{eff}$|. We find that the rotational variables are largely distributed along the MS and the RGB, with most of the evolved rotational variables located towards the base of the RGB at |$\rm \log (g){\sim } 3.5$|. Rotational variables are also located on the sub-giant branch (SGB). Sources on the RC are also seen in both of these spaces. There are also many sources above the MS, which are likely spotted stars in binary systems or pre-MS spotted T Tauri stars (TTS/ROT). Of the rotational variables with spectroscopic information, |${\sim }53{ per\ cent}$| (|${\sim }47{ per\ cent}$|) had log (g) > 4 (log (g) < 4).

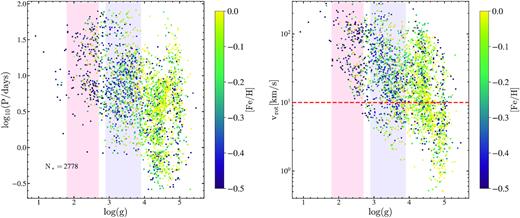
|$\rm \log _{10}(\rm P/days)$| (left) and |$v$|rot (right) as a function of |$\rm \log (g)$| for the rotational variables. The points are coloured by metallicity. Regions corresponding to the RC (|$\rm 1.8 \lesssim \log (g){\lesssim }2.8$|) and the RGB (|$\rm 2.9 \lesssim \log (g){\lesssim }3.9$|) are shaded in red and blue, respectively. The red-dashed line corresponds to the division between fast (|$v$|rot > 10 km s−1) and slow-rotating giants.
If we impose a more conservative cut on the RC sample to minimize contamination from RGB stars by restricting our sample to stars with |$\rm 2.3 \lesssim \log (g){\lesssim }2.6$|, we find that nearly all of these stars have |$v_{\rm rot}\gt 10 \rm \, km\,s^{ -1}$|, implying that rapid rotation is more common for RC stars than for stars on the RGB. To investigate the properties of intrinsically brighter RGB stars, we impose a cut on the SGB/RGB sample to only select RGB stars with |$\rm 2.8 \lesssim \log (g){\lesssim }3.2$|. These stars have a median radius and luminosity of |$R{\sim }6.3 \, R_\odot$| and |$\rm L{\sim }17.6 \, L_\odot$|, respectively. We find that |${\sim }84{ per\ cent}$| of these giants have |$v_{\rm rot}\gt 10 \rm \, km/s$|, which is comparable to the broader sample of rotational variables on the SGB/RGB.
Of the rapidly rotating RC stars, |${\sim }30{ per\ cent}$| are metal-poor with |$\rm [Fe/H]\lt -0.5$|, whereas only |${\sim }8{ per\ cent}$| are metal-rich with |$\rm [Fe/H]\,\,\gt\,\, 0$|. The multiplicity fraction is anticorrelated with metallicity (see e.g. Moe, Kratter & Badenes 2019), and the prevalence of metal-poor rapid rotators maybe a consequence of higher binary fractions at lower metallicity. Similarly, Tayar et al. (2015) found a large fraction of rapidly rotating stars on the RC. This enhancement probably appears because stars are more likely to interact as they expand going up the giant branch, and stop interacting as they descend the giant branch to the RC. The clump stars then retain the ‘memory’ of the interactions allowed by the expansion. The multiplicity fraction at the RC is also lower than that of the RGB, and is comparable to the multiplicity fraction at the tip of the RGB (Badenes et al. 2018; Price-Whelan et al. 2020). The reduced multiplicity fraction could be a sign of companion engulfment and spin-up during a common envelope phase (Ivanova et al. 2013; Price-Whelan et al. 2020).
Iwanek et al. (2019) studied 12 660 spotted stars in the Galactic bulge using OGLE data and noted the presence of two distinct groups consisting of rapidly rotating (|$\rm P_{rot}\,\,\lt \,\,2$| d) stars with low amplitude variability (A < 0.2 mag in the I band), and slowly rotating stars with large amplitudes (up to A < 0.8 mag in the I band). The sample with large amplitudes mostly consisted of giants. We investigate the V-band variability amplitudes of the ASAS-SN rotational variables with spectroscopic information as a function of |$\rm \log (g)$| and period in Fig. 18. The variability amplitudes of the rotational variables are dependent on their evolutionary state, with the MS stars having the lowest amplitudes. The variability amplitudes peak at |$\rm \log (g){\sim }3.2$|, and drop off again at lower |$\rm \log (g)$|. At any given period, the evolved rotational variables have larger amplitudes than stars on the MS. This is consistent with the results from Iwanek et al. (2019). The amplitudes of the MS and evolved rotational variables increase at longer periods. Iwanek et al. (2019) noted similar trends in the OGLE sample. Most high-amplitude MS rotators in the OGLE sample had long periods, and the spotted giants with long rotational periods showed larger brightness variations, consistent with the trends seen in Fig. 18. The large brightness variations in these stars can be attributed to large spot covering fractions and/or longitudinal asymmetries in the coverage of spots (Iwanek et al. 2019).
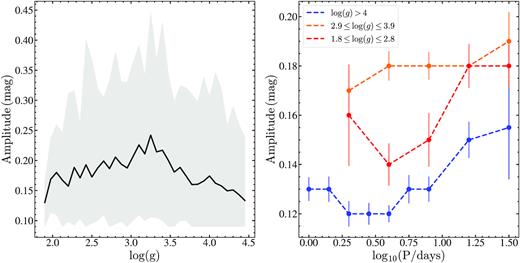
The V-band amplitude of the rotational variables in the spectroscopic sample as a function of |$\rm \log (g;$| left) and period (right). The shaded region corresponds to the |$5{ per\ cent}$| to |$95{ per\ cent}$| range of the amplitudes. The amplitude distributions with period are grouped by |$\rm \log (g)$|: log (g) > 4 (blue), 2.9 ≤ log (g) ≤ 3.9 (orange), and 1.8 ≤ log (g) ≤ 2.8 (red).
Of the MS rotational variables with log (g) > 4, |${\sim }54{ per\ cent}$| have |$v_{\rm rot}\gt 10 \rm \, km/s$|, compared to |${\sim }83{ per\ cent}$| for evolved stars with log (g) < 4. The MS rotators and evolved stars have median periods of |$\rm P_{rot}{\sim }3.5$| and |$\rm P_{rot}{\sim }8$| d, respectively. A substantial fraction (|${\sim }18{ per\ cent}$|) of the MS stars have very short periods with |$\rm P_{rot}\lt 1$| d (Fig. 17). The MS rotators are also more metal rich (|$\rm [Fe/H]{\sim }-0.08$|) than the evolved stars (|$\rm [Fe/H]{\sim }-0.23$|). The median effective temperature for these MS rotators (|$\rm T_{eff} {\sim }4460$| K) corresponds to stars with late K spectral types. This is not surprising, as it has been shown that cool MS stars typically have large variability amplitudes and are more likely to show rotational signals than hotter stars (McQuillan et al. 2014), making their detection by ground-based surveys easier. In particular, McQuillan et al. (2014) found that |${\sim }69{ per\ cent}$| of the MS stars with |$\rm 4000 \le T_{eff}/K \le 4500$| K showed periodic rotational variability in their Kepler light curves.
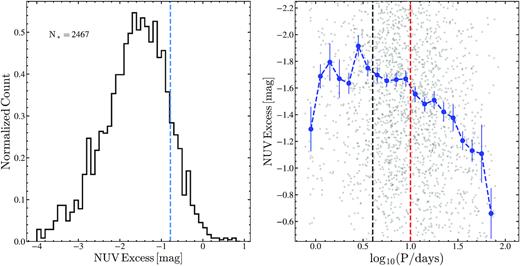
Distributions of the NUV excess (left) and its dependence on period (right) for the rotational variables with |$\rm M_{Ks}\lt 2$| mag. The blue-dashed line is the expected NUV excess (−0.78 mag) for rotating giant stars with |$v\sin (i)=10 \rm \, km\,s^{ -1}$| from Dixon et al. (2020). The red-dashed line represents the break in the period–NUV excess relationship at |$\rm P_{rot}=10$| d from Dixon et al. (2020). The period at which rotating giants reach supersaturation is shown as a black-dashed line at |$\rm P_{rot}\approx 4$| d.
Dixon et al. (2020) argued that the dependence of the NUV excess on period could be divided into a saturated and a linear regime in activity with a break at |$\rm P_{rot}=10$| d. Our sources follow a similar trend, with the median NUV excess decreasing with increasing period beyond |$\rm P_{rot}=10$| d (Fig. 19). The median NUV excess is roughly flat between |$\rm 4\lt P_{rot}/d\lt 10$|, as also found by Dixon et al. (2020). In the supersaturated regime (|$\rm P_{rot}\approx 4$| d for typical giants), active giant stars are expected to have decreased activity compared to giants in the saturated regime. We see some evidence for this supersaturated regime in Fig. 19.
Fig. 20 shows the distribution of all the 248 rotational variables in APOGEE with ASPCAP_FLAG = 0 in the |$\rm [Mg/Fe]$|–|$\rm [Fe/H]$| plane as compared to the ∼248 000 APOGEE DR16 giants with log (g) < 3.8 and ASPCAP_FLAG = 0. We also show the division from Weinberg et al. (2019) between the ‘high-α’ and ‘low-α’ sequences. The high-α population is older, kinematically hotter and is located in the thick disc, whereas the low-α population is located in the thin disc (Fuhrmann 1998; Prochaska et al. 2000; Weinberg et al. 2019). The plateau in the high-α sequence at |$\rm [Mg/Fe]\,\,{\sim }\,\,0.4$| is the average yield of core collapse supernovae and the drop to lower values of |$\rm [Mg/Fe]$| is due to later Fe production in Type Ia supernovae (Weinberg et al. 2019). The rotational variables are low-α stars strongly clustered towards |$\rm [Mg/Fe]{\sim }-0.1$| and |$\rm [Fe/H]{\sim }-0.1$|. Their distribution in Fig. 20 is very different from the typical giant stars or the SR variables and AGB stars we discuss in Section 4.3.3. The rotational variables occupy a sparsely populated area in the |$\rm [Mg/Fe]$|–|$\rm [Fe/H]$| plane, and this odd clustering of the rotational variables is very likely due to systematics in the APOGEE Stellar Parameters and Chemical Abundances Pipeline (ASPCAP) abundance pipeline when dealing with rapidly rotating stars. We also highlight 2M05215658 + 4359220, the candidate giant star-black hole binary identified by Thompson et al. (2019) in Fig. 20. 2M05215658 + 4359220 is a rapidly rotating giant with |$v\sin (i)\approx 14.1 \pm 0.6 \rm \, km\,s^{ -1}$| and is a clear outlier in the |$\rm [Mg/Fe]$|–|$\rm [Fe/H]$| plane, even compared to the ROT variables. The ASPCAP pipeline includes the flag ROTATION_WARN to warn of the presence of broadened lines in the APOGEE spectrum, suggesting that the abundances derived for this object could be suspect. The |$\rm [C/N]$| abundance of this giant is unusual for a giant with |$\rm M_{giant}\approx 3.2\pm 1.0 M_\odot$| and is more typical of a lower mass giant with |$\rm M_{giant}{\sim }1 M_\odot$| (Thompson et al. 2019). Thompson et al. (2020) cautions against the use of the APOGEE |$\rm [C/N]$| abundance in claiming a lower mass for the giant based on the systematic uncertainties in the determination of abundances for rapidly rotating giants. The distribution of the ASAS-SN rotational variables in Fig. 20 supports this argument, as their abundances are unusual and suggestive of systematic issues in the ASPCAP pipeline when dealing with rapidly rotating stars. Indeed, if we examine the individual element abundances (|$\rm [Fe/Mg]$|, |$\rm [C/Mg]$|, |$\rm [Mn/Mg]$|, and |$\rm [Ni/Mg]$|) of the rotational variables, they are almost all peculiar, and those of 2M05215658 + 4359220 are more peculiar than most.
![The distribution of all the rotational variables in APOGEE DR16 (red) and a reference sample of giants from APOGEE DR16 (2D histogram) in the $\rm [Mg/Fe]$ versus $\rm [Fe/H]$ plane. The blue line shows the division between the low-α and high-α populations from Weinberg et al. (2019). The candidate giant star-black hole binary (2M05215658 + 4359220) from Thompson et al. (2019) is shown as a orange star.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig20.jpeg?Expires=1749866512&Signature=UGviAQ6RTHB9prtjoc8b6fJu3oTTadFGXzzumZhbfF7BTFI923w-EIJxHw41tD3Z-B1kt-YnEU8a23SU-eRr~wkItQ1ZnHW68d0gHcyI9ATvxZI0dxBQK3MhajoDSSF5Oc2N08sQ5ldfNx2n7Ond5tmYX6TDsSx6cT5zhh2sUc5wxrotj2Q5Ra~93winOKPz5OvUH2Zoi25Gw-1VSNsGVaVV-CB2bjoPAq788y7pzB06Tk-D0oQbH1PtWySZhM-HvJ2vn1vGk2k9Ou2Pxk3~WgRJR8g6dFW3~0MUzrxpoT4Xfrkm02XuCVoXIMmEZ2NvJmMf5mKQ3TBU1rt8findKw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of all the rotational variables in APOGEE DR16 (red) and a reference sample of giants from APOGEE DR16 (2D histogram) in the |$\rm [Mg/Fe]$| versus |$\rm [Fe/H]$| plane. The blue line shows the division between the low-α and high-α populations from Weinberg et al. (2019). The candidate giant star-black hole binary (2M05215658 + 4359220) from Thompson et al. (2019) is shown as a orange star.
4.3 Long period variables on the asymptotic giant branch
Low- and intermediate-mass stars end their lives after reaching the AGB. During the AGB phase, stellar evolution is characterized by hydrogen and helium shell burning on top of a degenerate carbon/oxygen core (see e.g. Herwig 2005). AGB stars are cool, luminous objects that chemically enrich the interstellar medium through nucleosynthetic processes and strong mass-loss (Herwig 2005; Lebzelter et al. 2018). In particular, the thermally pulsing AGB (TP-AGB) stars are characterized by long-period pulsational variability and heavy mass-loss rates (Marigo & Girardi 2007).
The long-period variables on the TP-AGB are broadly classified into the SR variables and the Mira variables. Mira variables are luminous AGB stars (Iben & Renzini 1983) and have large variability amplitudes (A > 2.5 mag in the Vband is the AAVSO definition). Previous surveys have argued that TP-AGB stars start off as pulsating SR variables with small amplitudes and later evolve into the high-amplitude Mira variables as they reach the tip of the AGB (Wood et al. 1999; Marigo & Girardi 2007; Soszyński et al. 2009). Mira variables follow a period–luminosity relationship (Glass & Evans 1981; Whitelock et al. 2008), although some Mira variables can undergo changes in their period over time (Percy & Colivas 1999). Compared to the Mira variables, SR variables are less strictly periodic with irregularities in their light curves and multiple periods that can be used to study the dynamics of stellar interiors (Kiss et al. 1999). Microlensing surveys of the Magellanic clouds have shown that SR variables fall along five distinct period–luminosity sequences (A-E; Wood et al. 1999; Wood 2000). More recent work has shown that the five sequences from Wood et al. (1999) are a result of an overlap of 14 or more period–luminosity sequences (Soszynski et al. 2007, 2009; Trabucchi et al. 2017). In the ASAS-SN pipeline, Mira and SR variables are classified on the basis of their periods, colours (optical and NIR), and absolute magnitudes (see Jayasinghe et al. 2019b). SR variables are separated from the Mira variables using their variability amplitudes (A > 2 mag in the V-band for Miras). We chose a lower limit of A > 2 mag in amplitude when compared to the AAVSO definition (A > 2.5 mag) in order to compensate for the effects of blending that can reduce the observed variability amplitudes in ASAS-SN.
We use APOGEE DR16 data (Ahumada et al. 2019) to study the spectroscopic and chemical properties of pulsating AGB stars. The abundances come from the ASPCAP pipeline (Nidever et al. 2015). The various subsets of Mira and SR variables discussed in this section are summarized in Table 3. For comparison with the SR variables, we selected a set of RGB stars (APOGEE/RGB: |$\rm T_{eff} \le 5200$| K, |$2 \le \rm \log (g) \le 3.5$|, N ∼ 160 000) and likely AGB stars (APOGEE/AGB: |$\rm T_{eff} \le 4000$| K, |$\rm \log (g) \le 1$|, N ∼ 15 000). The sample of candidate AGB stars is likely contaminated with some lower mass stars on the upper RGB, and does not contain any ASAS-SN SR variables. For detailed studies of the APOGEE DR16 abundance ratios, we required the flag X_FE_FLAG = 0, where X = Mg, Al, C, N, or O. We calculate the |$\rm [X/Mg]$| abundance ratios as |$\rm [X/Mg]=[X/H]-[Mg/H]$|. Following Weinberg et al. (2019), we chose Mg as the reference element because it is produced almost exclusively by core-collapse supernovae and is thus a simpler tracer of chemical enrichment than Fe.
| Group . | Description . | Criteria . | Count . | Sections . |
|---|---|---|---|---|
| ALLSPEC/SR | Spectroscopic cross-matches to ASAS-SN SR variables | |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 5390 | Section 4.3.1 |
| ASAS-SN/SR | ASAS-SN SR variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 96 724 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 124 836 | Section 4.3.2 | ||
| ASAS-SN/MIRA | ASAS-SN MIRA variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 958 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 2737 | Section 4.3.2 | ||
| APOGEE/SR | ASAS-SN SR variables in APOGEE | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 991 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$| | 1615 | Sections 4.3.2, 4.3.3, 4.3.4, 4.3.5 | ||
| APOGEE/GIANTS | Giants in APOGEE | log (g) < 3.8 | 238 472 | Section 4.3.3 |
| APOGEE/AGB | AGB candidates in APOGEE | |$\rm T_{eff} \le 4000$| K, and |$\rm \log (g) \le 1$| | 15 050 | Sections 4.3.3, 4.3.4, 4.3.5 |
| APOGEE/RGB | RGB candidates in APOGEE | |$\rm T_{eff} \le 5200$| K, and |$2 \le \rm \log (g) \le 3.5$| | 159 042 | Sections 4.3.3,4.3.4, 4.3.5 |
| Group . | Description . | Criteria . | Count . | Sections . |
|---|---|---|---|---|
| ALLSPEC/SR | Spectroscopic cross-matches to ASAS-SN SR variables | |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 5390 | Section 4.3.1 |
| ASAS-SN/SR | ASAS-SN SR variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 96 724 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 124 836 | Section 4.3.2 | ||
| ASAS-SN/MIRA | ASAS-SN MIRA variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 958 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 2737 | Section 4.3.2 | ||
| APOGEE/SR | ASAS-SN SR variables in APOGEE | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 991 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$| | 1615 | Sections 4.3.2, 4.3.3, 4.3.4, 4.3.5 | ||
| APOGEE/GIANTS | Giants in APOGEE | log (g) < 3.8 | 238 472 | Section 4.3.3 |
| APOGEE/AGB | AGB candidates in APOGEE | |$\rm T_{eff} \le 4000$| K, and |$\rm \log (g) \le 1$| | 15 050 | Sections 4.3.3, 4.3.4, 4.3.5 |
| APOGEE/RGB | RGB candidates in APOGEE | |$\rm T_{eff} \le 5200$| K, and |$2 \le \rm \log (g) \le 3.5$| | 159 042 | Sections 4.3.3,4.3.4, 4.3.5 |
| Group . | Description . | Criteria . | Count . | Sections . |
|---|---|---|---|---|
| ALLSPEC/SR | Spectroscopic cross-matches to ASAS-SN SR variables | |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 5390 | Section 4.3.1 |
| ASAS-SN/SR | ASAS-SN SR variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 96 724 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 124 836 | Section 4.3.2 | ||
| ASAS-SN/MIRA | ASAS-SN MIRA variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 958 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 2737 | Section 4.3.2 | ||
| APOGEE/SR | ASAS-SN SR variables in APOGEE | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 991 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$| | 1615 | Sections 4.3.2, 4.3.3, 4.3.4, 4.3.5 | ||
| APOGEE/GIANTS | Giants in APOGEE | log (g) < 3.8 | 238 472 | Section 4.3.3 |
| APOGEE/AGB | AGB candidates in APOGEE | |$\rm T_{eff} \le 4000$| K, and |$\rm \log (g) \le 1$| | 15 050 | Sections 4.3.3, 4.3.4, 4.3.5 |
| APOGEE/RGB | RGB candidates in APOGEE | |$\rm T_{eff} \le 5200$| K, and |$2 \le \rm \log (g) \le 3.5$| | 159 042 | Sections 4.3.3,4.3.4, 4.3.5 |
| Group . | Description . | Criteria . | Count . | Sections . |
|---|---|---|---|---|
| ALLSPEC/SR | Spectroscopic cross-matches to ASAS-SN SR variables | |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 5390 | Section 4.3.1 |
| ASAS-SN/SR | ASAS-SN SR variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 96 724 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 124 836 | Section 4.3.2 | ||
| ASAS-SN/MIRA | ASAS-SN MIRA variables | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 958 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$|, Ks-band photometry available | 2737 | Section 4.3.2 | ||
| APOGEE/SR | ASAS-SN SR variables in APOGEE | |||
| |$\rm Prob\gt 0.95$| and parallaxes better than |$50\%$| | 991 | Section 4.3.1 | ||
| |$\rm Prob\gt 0.95$| | 1615 | Sections 4.3.2, 4.3.3, 4.3.4, 4.3.5 | ||
| APOGEE/GIANTS | Giants in APOGEE | log (g) < 3.8 | 238 472 | Section 4.3.3 |
| APOGEE/AGB | AGB candidates in APOGEE | |$\rm T_{eff} \le 4000$| K, and |$\rm \log (g) \le 1$| | 15 050 | Sections 4.3.3, 4.3.4, 4.3.5 |
| APOGEE/RGB | RGB candidates in APOGEE | |$\rm T_{eff} \le 5200$| K, and |$2 \le \rm \log (g) \le 3.5$| | 159 042 | Sections 4.3.3,4.3.4, 4.3.5 |
In Section 4.3.1, we study the various TP-AGB period–luminosity sequences. We identify an APOGEE temperature –WRP − WJK colour index fit to the oxygen-rich AGB stars in Section 4.3.2. We examine the α enhancements of the SR variables in Section 4.3.3. In Section 4.3.4, we study the Aluminum abundances of the SR variables and characterize the pulsation period dependent Al depletion as a result of mass-loss and dust production. We look at the Nitrogen abundances of the SR variables in Section 4.3.5 and identify a sample of likely intermediate-mass AGB stars undergoing hot-bottom burning (HBB).
4.3.1 Period–luminosity sequences
Fig. 21 shows the distributions in |$\rm \log (g)$|, |$\rm T_{eff}$|, |$\rm \log _{10}(P/days)$|, and |$\rm M_{Ks}$| of the SR variables. The SR variables in APOGEE are shown separately. The spectroscopic parameters confirm the highly evolved nature of these stars, with the SR variables having a median surface gravity of |$\rm \log (g){\sim }0.6$|, and a median effective temperature of |$\rm T_{eff}{\sim }3750$| K. The subset of SR variables in APOGEE DR16 are skewed towards cooler, more evolved SR variables when compared to the SR variables in other surveys. We will only consider the SR variables from APOGEE in the discussions below.
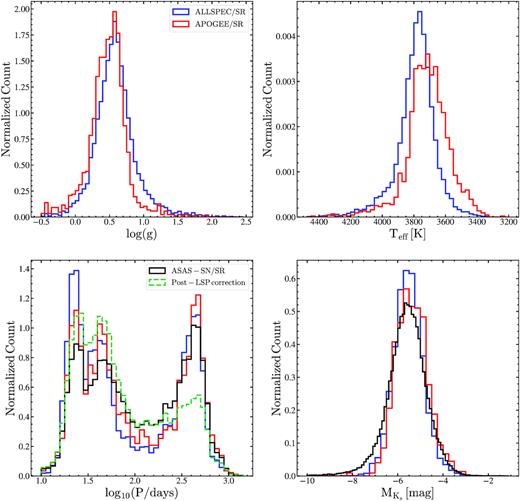
Distributions of the semiregular variables for the complete spectroscopic sample (blue) and the APOGEE sample (red) in |$\rm \log (g)$|, |$\rm T_{eff}$|, |$\rm \log _{10}(P/days)$|, and |$\rm M_{Ks}$|. The |$\rm \log _{10}(P/days)$| and |$\rm M_{Ks}$| distributions of the semiregular variables in the entire ASAS-SN sample are shown in black. The period distribution of the semiregular variables after correcting for LSPs is shown in green.
The Gaia DR2 parallaxes of these luminous giants are poor, so we cannot directly assign them to the Wood (2000)’s A-E period–luminosity relations. However, we can use the periods to roughly group them. There are three distinct peaks in the period distribution shown in Fig. 21 at |$\rm \log _{10}(P/days){\sim }1.4,\, 1.7,$| and |$\, 2.7$|. SR variables with |$1 \lesssim \rm \log _{10}(P/days) \lesssim 1.5$| (hereafter group I) fall on the Wood (2000) sequence A and have low variability amplitudes. Due to the overlap between the PLR sequences A and B, SR variables with |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$| (hereafter group II) consist of sources on both sequences A and B. In addition, SR variables on sequence E also have periods in this range, even though they are less luminous than the variables on sequences A and B. The OGLE small amplitude variable red giants (OSARGs; Soszynski et al. 2004) consist of both RGB and AGB stars, and follow a unique set of period–luminosity relations (Soszynski et al. 2007). OSARGs have periods that span group I and have amplitudes as small as ∼3 mmag (Soszynski et al. 2007; Auge et al. 2020). Note that we are not considering the much lower variability amplitudes of ASAS-SN OSARGs used by Auge et al. (2020) to determine the feasibility of ground-based asteroseismology of luminous giants. There is a paucity of SR variables with periods in the range |$1.9 \lesssim \rm \log _{10}(P/days) \lesssim 2.3$| (hereafter group III) that spans the PLR sequence C corresponding to the Mira variables. It is thought that the PLR sequence C corresponds to the fundamental mode of pulsation, while sequences A and B correspond to higher order overtone modes (Fraser et al. 2005). SR variables on sequence E are less luminous, and are thought to be on the first ascent giant branch instead of the AGB. SR variables on sequence E have periods typical of contact binaries with a giant component (Wood 2000) and will be included in groups II and III. SR variables with periods |$\rm \log _{10}(P/days) \gtrsim 2.3$| (hereafter group IV) include sources on sequences C and D.
A large fraction of the SR variables with reported periods |$\rm \log _{10}(P/days) \gtrsim 2.3$| (sequence D) are examples of SR variables with long secondary periods (LSPs) of |$\rm P_{LSP}{\sim }300-1500$| d that are ∼10−15 times longer than their actual pulsation period (Wood, Olivier & Kawaler 2004). The origin of the LSPs is debated (Wood et al. 2004; Pawlak et al. 2019). These LSPs can complicate our analysis of the pulsational properties of these variables. Thus, we re-derived the periods of the SR variables using the generalized Lomb–Scargle (GLS; Scargle 1982; Zechmeister & Kürster 2009) periodogram implemented in astrobase (Bhatti et al. 2018). From the five best periods in the periodogram, SR variables with LSPs were identified if there was a significantly shorter period |$\rm P$| in the range |$8 \le \rm P_{LSP}/P \le 30$| relative to the primary period. For SR variables identified as LSPs, we assign the shorter period as the pulsation period. Of the SR variables with |$\rm \log _{10}(P/days) \gtrsim 2.3$|, |${\sim }36{ per\ cent}$| were LSPs. This estimate of the LSP fraction at these periods agrees with the estimates (|${\sim }25\rm{--}50{ per\ cent}$|) from previous studies (see e.g. Wood et al. 2004; Soszyński 2007; Nicholls et al. 2009). Of the LSPs, |${\sim }60{ per\ cent}$| had pulsational periods in the range |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$| and the LSP was on average ∼11 times longer than the actual pulsation period. This agrees with the results from Trabucchi et al. (2017) who found that LSPs had pulsation periods between the PLR sequences B and C’ (|$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.7$|). The period distribution of the SR variables after correcting for LSPs is shown in Fig. 21. We assign the LSPs into a separate group (group V) for comparison with the other SR variables.
Fig. 22 shows the distribution of the SR variables in |$\rm M_{Ks}$| (left) and |$\rm \log (g)$| with period. SR variables on the PLR sequences A, B, and D are prominent, with sources on sequence C largely absent from this sample. The SR variables in these sequences overlap in both the period–luminosity and period–surface gravity spaces. It is difficult to disentangle the PLR sequences given the distance uncertainties – only |${\sim }15{ per\ cent}$| (|${\sim }9{ per\ cent}$|) of these sources have Gaia DR2 parallaxes better than |$20{ per\ cent}$| (|$10{ per\ cent}$|). The various spectroscopic parameters and chemical abundance ratios from APOGEE DR16 for the five groups (I–V, defined above) are summarized in Table 4.
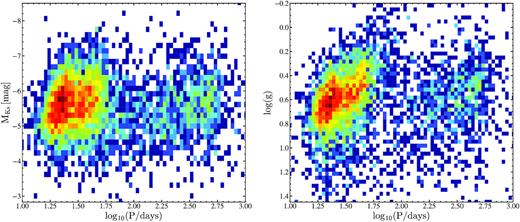
2D histograms of |$\rm M_{Ks}$| (left) and |$\rm \log (g)$| (right) as a function of period for the SR variables in APOGEE DR16 after correcting for LSPs. The bins are coloured by the number density.
Distribution of the APOGEE DR16 spectroscopic parameters and chemical abundance ratios for the SR variables, binned by period. The SR variables are sorted into period bins as described in the text. The median and standard deviation for each parameter are shown.
| . | Group I . | Group II . | Group III . | Group IV . | Group V (LSP) . |
|---|---|---|---|---|---|
| . | |$1 \lesssim \rm \log _{10}(P/days) \lesssim 1.5$| . | |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$| . | |$1.9 \lesssim \rm \log _{10}(P/days) \lesssim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . |
| N | 407 | 475 | 169 | 334 | 300 |
| |$\rm Amplitude\, [mag]$| | 0.11 ± 0.04 | 0.20 ± 0.14 | 0.29 ± 0.28 | 0.30 ± 0.27 | 0.16 ± 0.14 |
| |$\rm T_{eff}\, [K]$| | 3733 ± 106 | 3695 ± 128 | 3705 ± 176 | 3705 ± 149 | 3722 ± 126 |
| |$\rm \log (g)$| | 0.62 ± 0.20 | 0.41 ± 0.22 | 0.34 ± 0.41 | 0.41 ± 0.31 | 0.51 ± 0.24 |
| |$\rm [M/H]$| | −0.42 ± 0.23 | −0.63 ± 0.31 | −0.71 ± 0.33 | −0.66 ± 0.29 | −0.57 ± 0.25 |
| |$\rm [\alpha /M]$| | 0.10 ± 0.09 | 0.11 ± 0.10 | 0.10 ± 0.11 | 0.10 ± 0.11 | 0.10 ± 0.10 |
| |$\rm [Fe/H]$| | −0.44 ± 0.22 | −0.64 ± 0.29 | −0.71 ± 0.31 | −0.66 ± 0.28 | −0.59 ± 0.24 |
| |$\rm [Mg/Fe]$| | 0.17 ± 0.11 | 0.18 ± 0.11 | 0.15 ± 0.13 | 0.17 ± 0.12 | 0.17 ± 0.11 |
| |$\rm [C/Mg]$| | −0.13 ± 0.08 | −0.15 ± 0.15 | −0.16 ± 0.19 | −0.14 ± 0.14 | −0.15 ± 0.11 |
| |$\rm [N/Mg]$| | 0.05 ± 0.14 | 0.00 ± 0.18 | −0.00 ± 0.20 | 0.01 ± 0.20 | 0.02 ± 0.15 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.05 ± 0.06 | −0.05 ± 0.05 | −0.04 ± 0.04 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.04 | −0.12 ± 0.05 | −0.12 ± 0.07 | −0.12 ± 0.05 | −0.12 ± 0.04 |
| |$\rm [Ca/Mg]$| | −0.08 ± 0.07 | −0.07 ± 0.08 | −0.07 ± 0.11 | −0.08 ± 0.10 | −0.08 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.15 ± 0.09 | −0.27 ± 0.16 | −0.35 ± 0.15 | −0.32 ± 0.14 | −0.32 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.07 ± 0.14 | −0.09 ± 0.21 | −0.10 ± 0.26 | −0.09 ± 0.23 | −0.10 ± 0.19 |
| |$\rm [P/Mg]$| | −0.02 ± 0.13 | −0.06 ± 0.21 | −0.04 ± 0.27 | −0.03 ± 0.25 | −0.04 ± 0.16 |
| |$\rm [K/Mg]$| | 0.02 ± 0.11 | 0.01 ± 0.11 | −0.00 ± 0.12 | 0.01 ± 0.11 | 0.01 ± 0.10 |
| |$\rm [Cr/Mg]$| | −0.17 ± 0.10 | −0.16 ± 0.12 | −0.14 ± 0.17 | −0.15 ± 0.15 | −0.13 ± 0.11 |
| |$\rm [V/Mg]$| | −0.06 ± 0.08 | −0.05 ± 0.13 | −0.07 ± 0.13 | −0.06 ± 0.14 | −0.05 ± 0.10 |
| |$\rm [Co/Mg]$| | −0.09 ± 0.08 | −0.11 ± 0.09 | −0.10 ± 0.13 | −0.10 ± 0.11 | −0.10 ± 0.10 |
| |$\rm [Mn/Mg]$| | −0.06 ± 0.16 | −0.11 ± 0.18 | −0.09 ± 0.19 | −0.09 ± 0.18 | −0.09 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.16 ± 0.08 | −0.17 ± 0.08 | −0.15 ± 0.11 | −0.16 ± 0.10 | −0.17 ± 0.08 |
| |$\rm [Ti/Mg]$| | −0.03 ± 0.13 | −0.08 ± 0.14 | −0.11 ± 0.15 | −0.09 ± 0.13 | −0.07 ± 0.13 |
| |$\rm [C/N]$| | −0.17 ± 0.14 | −0.17 ± 0.23 | −0.18 ± 0.27 | −0.18 ± 0.24 | −0.18 ± 0.17 |
| |$\rm [C/O]$| | −0.10 ± 0.06 | −0.11 ± 0.12 | −0.10 ± 0.17 | −0.10 ± 0.13 | −0.11 ± 0.09 |
| |$\rm [N/O]$| | 0.07 ± 0.14 | 0.05 ± 0.17 | 0.06 ± 0.19 | 0.07 ± 0.19 | 0.07 ± 0.15 |
| |$\rm [Al/O]$| | −0.12 ± 0.08 | −0.24 ± 0.14 | −0.28 ± 0.15 | −0.27 ± 0.13 | −0.19 ± 0.12 |
| . | Group I . | Group II . | Group III . | Group IV . | Group V (LSP) . |
|---|---|---|---|---|---|
| . | |$1 \lesssim \rm \log _{10}(P/days) \lesssim 1.5$| . | |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$| . | |$1.9 \lesssim \rm \log _{10}(P/days) \lesssim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . |
| N | 407 | 475 | 169 | 334 | 300 |
| |$\rm Amplitude\, [mag]$| | 0.11 ± 0.04 | 0.20 ± 0.14 | 0.29 ± 0.28 | 0.30 ± 0.27 | 0.16 ± 0.14 |
| |$\rm T_{eff}\, [K]$| | 3733 ± 106 | 3695 ± 128 | 3705 ± 176 | 3705 ± 149 | 3722 ± 126 |
| |$\rm \log (g)$| | 0.62 ± 0.20 | 0.41 ± 0.22 | 0.34 ± 0.41 | 0.41 ± 0.31 | 0.51 ± 0.24 |
| |$\rm [M/H]$| | −0.42 ± 0.23 | −0.63 ± 0.31 | −0.71 ± 0.33 | −0.66 ± 0.29 | −0.57 ± 0.25 |
| |$\rm [\alpha /M]$| | 0.10 ± 0.09 | 0.11 ± 0.10 | 0.10 ± 0.11 | 0.10 ± 0.11 | 0.10 ± 0.10 |
| |$\rm [Fe/H]$| | −0.44 ± 0.22 | −0.64 ± 0.29 | −0.71 ± 0.31 | −0.66 ± 0.28 | −0.59 ± 0.24 |
| |$\rm [Mg/Fe]$| | 0.17 ± 0.11 | 0.18 ± 0.11 | 0.15 ± 0.13 | 0.17 ± 0.12 | 0.17 ± 0.11 |
| |$\rm [C/Mg]$| | −0.13 ± 0.08 | −0.15 ± 0.15 | −0.16 ± 0.19 | −0.14 ± 0.14 | −0.15 ± 0.11 |
| |$\rm [N/Mg]$| | 0.05 ± 0.14 | 0.00 ± 0.18 | −0.00 ± 0.20 | 0.01 ± 0.20 | 0.02 ± 0.15 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.05 ± 0.06 | −0.05 ± 0.05 | −0.04 ± 0.04 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.04 | −0.12 ± 0.05 | −0.12 ± 0.07 | −0.12 ± 0.05 | −0.12 ± 0.04 |
| |$\rm [Ca/Mg]$| | −0.08 ± 0.07 | −0.07 ± 0.08 | −0.07 ± 0.11 | −0.08 ± 0.10 | −0.08 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.15 ± 0.09 | −0.27 ± 0.16 | −0.35 ± 0.15 | −0.32 ± 0.14 | −0.32 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.07 ± 0.14 | −0.09 ± 0.21 | −0.10 ± 0.26 | −0.09 ± 0.23 | −0.10 ± 0.19 |
| |$\rm [P/Mg]$| | −0.02 ± 0.13 | −0.06 ± 0.21 | −0.04 ± 0.27 | −0.03 ± 0.25 | −0.04 ± 0.16 |
| |$\rm [K/Mg]$| | 0.02 ± 0.11 | 0.01 ± 0.11 | −0.00 ± 0.12 | 0.01 ± 0.11 | 0.01 ± 0.10 |
| |$\rm [Cr/Mg]$| | −0.17 ± 0.10 | −0.16 ± 0.12 | −0.14 ± 0.17 | −0.15 ± 0.15 | −0.13 ± 0.11 |
| |$\rm [V/Mg]$| | −0.06 ± 0.08 | −0.05 ± 0.13 | −0.07 ± 0.13 | −0.06 ± 0.14 | −0.05 ± 0.10 |
| |$\rm [Co/Mg]$| | −0.09 ± 0.08 | −0.11 ± 0.09 | −0.10 ± 0.13 | −0.10 ± 0.11 | −0.10 ± 0.10 |
| |$\rm [Mn/Mg]$| | −0.06 ± 0.16 | −0.11 ± 0.18 | −0.09 ± 0.19 | −0.09 ± 0.18 | −0.09 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.16 ± 0.08 | −0.17 ± 0.08 | −0.15 ± 0.11 | −0.16 ± 0.10 | −0.17 ± 0.08 |
| |$\rm [Ti/Mg]$| | −0.03 ± 0.13 | −0.08 ± 0.14 | −0.11 ± 0.15 | −0.09 ± 0.13 | −0.07 ± 0.13 |
| |$\rm [C/N]$| | −0.17 ± 0.14 | −0.17 ± 0.23 | −0.18 ± 0.27 | −0.18 ± 0.24 | −0.18 ± 0.17 |
| |$\rm [C/O]$| | −0.10 ± 0.06 | −0.11 ± 0.12 | −0.10 ± 0.17 | −0.10 ± 0.13 | −0.11 ± 0.09 |
| |$\rm [N/O]$| | 0.07 ± 0.14 | 0.05 ± 0.17 | 0.06 ± 0.19 | 0.07 ± 0.19 | 0.07 ± 0.15 |
| |$\rm [Al/O]$| | −0.12 ± 0.08 | −0.24 ± 0.14 | −0.28 ± 0.15 | −0.27 ± 0.13 | −0.19 ± 0.12 |
Distribution of the APOGEE DR16 spectroscopic parameters and chemical abundance ratios for the SR variables, binned by period. The SR variables are sorted into period bins as described in the text. The median and standard deviation for each parameter are shown.
| . | Group I . | Group II . | Group III . | Group IV . | Group V (LSP) . |
|---|---|---|---|---|---|
| . | |$1 \lesssim \rm \log _{10}(P/days) \lesssim 1.5$| . | |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$| . | |$1.9 \lesssim \rm \log _{10}(P/days) \lesssim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . |
| N | 407 | 475 | 169 | 334 | 300 |
| |$\rm Amplitude\, [mag]$| | 0.11 ± 0.04 | 0.20 ± 0.14 | 0.29 ± 0.28 | 0.30 ± 0.27 | 0.16 ± 0.14 |
| |$\rm T_{eff}\, [K]$| | 3733 ± 106 | 3695 ± 128 | 3705 ± 176 | 3705 ± 149 | 3722 ± 126 |
| |$\rm \log (g)$| | 0.62 ± 0.20 | 0.41 ± 0.22 | 0.34 ± 0.41 | 0.41 ± 0.31 | 0.51 ± 0.24 |
| |$\rm [M/H]$| | −0.42 ± 0.23 | −0.63 ± 0.31 | −0.71 ± 0.33 | −0.66 ± 0.29 | −0.57 ± 0.25 |
| |$\rm [\alpha /M]$| | 0.10 ± 0.09 | 0.11 ± 0.10 | 0.10 ± 0.11 | 0.10 ± 0.11 | 0.10 ± 0.10 |
| |$\rm [Fe/H]$| | −0.44 ± 0.22 | −0.64 ± 0.29 | −0.71 ± 0.31 | −0.66 ± 0.28 | −0.59 ± 0.24 |
| |$\rm [Mg/Fe]$| | 0.17 ± 0.11 | 0.18 ± 0.11 | 0.15 ± 0.13 | 0.17 ± 0.12 | 0.17 ± 0.11 |
| |$\rm [C/Mg]$| | −0.13 ± 0.08 | −0.15 ± 0.15 | −0.16 ± 0.19 | −0.14 ± 0.14 | −0.15 ± 0.11 |
| |$\rm [N/Mg]$| | 0.05 ± 0.14 | 0.00 ± 0.18 | −0.00 ± 0.20 | 0.01 ± 0.20 | 0.02 ± 0.15 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.05 ± 0.06 | −0.05 ± 0.05 | −0.04 ± 0.04 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.04 | −0.12 ± 0.05 | −0.12 ± 0.07 | −0.12 ± 0.05 | −0.12 ± 0.04 |
| |$\rm [Ca/Mg]$| | −0.08 ± 0.07 | −0.07 ± 0.08 | −0.07 ± 0.11 | −0.08 ± 0.10 | −0.08 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.15 ± 0.09 | −0.27 ± 0.16 | −0.35 ± 0.15 | −0.32 ± 0.14 | −0.32 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.07 ± 0.14 | −0.09 ± 0.21 | −0.10 ± 0.26 | −0.09 ± 0.23 | −0.10 ± 0.19 |
| |$\rm [P/Mg]$| | −0.02 ± 0.13 | −0.06 ± 0.21 | −0.04 ± 0.27 | −0.03 ± 0.25 | −0.04 ± 0.16 |
| |$\rm [K/Mg]$| | 0.02 ± 0.11 | 0.01 ± 0.11 | −0.00 ± 0.12 | 0.01 ± 0.11 | 0.01 ± 0.10 |
| |$\rm [Cr/Mg]$| | −0.17 ± 0.10 | −0.16 ± 0.12 | −0.14 ± 0.17 | −0.15 ± 0.15 | −0.13 ± 0.11 |
| |$\rm [V/Mg]$| | −0.06 ± 0.08 | −0.05 ± 0.13 | −0.07 ± 0.13 | −0.06 ± 0.14 | −0.05 ± 0.10 |
| |$\rm [Co/Mg]$| | −0.09 ± 0.08 | −0.11 ± 0.09 | −0.10 ± 0.13 | −0.10 ± 0.11 | −0.10 ± 0.10 |
| |$\rm [Mn/Mg]$| | −0.06 ± 0.16 | −0.11 ± 0.18 | −0.09 ± 0.19 | −0.09 ± 0.18 | −0.09 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.16 ± 0.08 | −0.17 ± 0.08 | −0.15 ± 0.11 | −0.16 ± 0.10 | −0.17 ± 0.08 |
| |$\rm [Ti/Mg]$| | −0.03 ± 0.13 | −0.08 ± 0.14 | −0.11 ± 0.15 | −0.09 ± 0.13 | −0.07 ± 0.13 |
| |$\rm [C/N]$| | −0.17 ± 0.14 | −0.17 ± 0.23 | −0.18 ± 0.27 | −0.18 ± 0.24 | −0.18 ± 0.17 |
| |$\rm [C/O]$| | −0.10 ± 0.06 | −0.11 ± 0.12 | −0.10 ± 0.17 | −0.10 ± 0.13 | −0.11 ± 0.09 |
| |$\rm [N/O]$| | 0.07 ± 0.14 | 0.05 ± 0.17 | 0.06 ± 0.19 | 0.07 ± 0.19 | 0.07 ± 0.15 |
| |$\rm [Al/O]$| | −0.12 ± 0.08 | −0.24 ± 0.14 | −0.28 ± 0.15 | −0.27 ± 0.13 | −0.19 ± 0.12 |
| . | Group I . | Group II . | Group III . | Group IV . | Group V (LSP) . |
|---|---|---|---|---|---|
| . | |$1 \lesssim \rm \log _{10}(P/days) \lesssim 1.5$| . | |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$| . | |$1.9 \lesssim \rm \log _{10}(P/days) \lesssim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . | |$\rm \log _{10}(P/days) \gtrsim 2.3$| . |
| N | 407 | 475 | 169 | 334 | 300 |
| |$\rm Amplitude\, [mag]$| | 0.11 ± 0.04 | 0.20 ± 0.14 | 0.29 ± 0.28 | 0.30 ± 0.27 | 0.16 ± 0.14 |
| |$\rm T_{eff}\, [K]$| | 3733 ± 106 | 3695 ± 128 | 3705 ± 176 | 3705 ± 149 | 3722 ± 126 |
| |$\rm \log (g)$| | 0.62 ± 0.20 | 0.41 ± 0.22 | 0.34 ± 0.41 | 0.41 ± 0.31 | 0.51 ± 0.24 |
| |$\rm [M/H]$| | −0.42 ± 0.23 | −0.63 ± 0.31 | −0.71 ± 0.33 | −0.66 ± 0.29 | −0.57 ± 0.25 |
| |$\rm [\alpha /M]$| | 0.10 ± 0.09 | 0.11 ± 0.10 | 0.10 ± 0.11 | 0.10 ± 0.11 | 0.10 ± 0.10 |
| |$\rm [Fe/H]$| | −0.44 ± 0.22 | −0.64 ± 0.29 | −0.71 ± 0.31 | −0.66 ± 0.28 | −0.59 ± 0.24 |
| |$\rm [Mg/Fe]$| | 0.17 ± 0.11 | 0.18 ± 0.11 | 0.15 ± 0.13 | 0.17 ± 0.12 | 0.17 ± 0.11 |
| |$\rm [C/Mg]$| | −0.13 ± 0.08 | −0.15 ± 0.15 | −0.16 ± 0.19 | −0.14 ± 0.14 | −0.15 ± 0.11 |
| |$\rm [N/Mg]$| | 0.05 ± 0.14 | 0.00 ± 0.18 | −0.00 ± 0.20 | 0.01 ± 0.20 | 0.02 ± 0.15 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.05 ± 0.06 | −0.05 ± 0.05 | −0.04 ± 0.04 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.04 | −0.12 ± 0.05 | −0.12 ± 0.07 | −0.12 ± 0.05 | −0.12 ± 0.04 |
| |$\rm [Ca/Mg]$| | −0.08 ± 0.07 | −0.07 ± 0.08 | −0.07 ± 0.11 | −0.08 ± 0.10 | −0.08 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.15 ± 0.09 | −0.27 ± 0.16 | −0.35 ± 0.15 | −0.32 ± 0.14 | −0.32 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.07 ± 0.14 | −0.09 ± 0.21 | −0.10 ± 0.26 | −0.09 ± 0.23 | −0.10 ± 0.19 |
| |$\rm [P/Mg]$| | −0.02 ± 0.13 | −0.06 ± 0.21 | −0.04 ± 0.27 | −0.03 ± 0.25 | −0.04 ± 0.16 |
| |$\rm [K/Mg]$| | 0.02 ± 0.11 | 0.01 ± 0.11 | −0.00 ± 0.12 | 0.01 ± 0.11 | 0.01 ± 0.10 |
| |$\rm [Cr/Mg]$| | −0.17 ± 0.10 | −0.16 ± 0.12 | −0.14 ± 0.17 | −0.15 ± 0.15 | −0.13 ± 0.11 |
| |$\rm [V/Mg]$| | −0.06 ± 0.08 | −0.05 ± 0.13 | −0.07 ± 0.13 | −0.06 ± 0.14 | −0.05 ± 0.10 |
| |$\rm [Co/Mg]$| | −0.09 ± 0.08 | −0.11 ± 0.09 | −0.10 ± 0.13 | −0.10 ± 0.11 | −0.10 ± 0.10 |
| |$\rm [Mn/Mg]$| | −0.06 ± 0.16 | −0.11 ± 0.18 | −0.09 ± 0.19 | −0.09 ± 0.18 | −0.09 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.16 ± 0.08 | −0.17 ± 0.08 | −0.15 ± 0.11 | −0.16 ± 0.10 | −0.17 ± 0.08 |
| |$\rm [Ti/Mg]$| | −0.03 ± 0.13 | −0.08 ± 0.14 | −0.11 ± 0.15 | −0.09 ± 0.13 | −0.07 ± 0.13 |
| |$\rm [C/N]$| | −0.17 ± 0.14 | −0.17 ± 0.23 | −0.18 ± 0.27 | −0.18 ± 0.24 | −0.18 ± 0.17 |
| |$\rm [C/O]$| | −0.10 ± 0.06 | −0.11 ± 0.12 | −0.10 ± 0.17 | −0.10 ± 0.13 | −0.11 ± 0.09 |
| |$\rm [N/O]$| | 0.07 ± 0.14 | 0.05 ± 0.17 | 0.06 ± 0.19 | 0.07 ± 0.19 | 0.07 ± 0.15 |
| |$\rm [Al/O]$| | −0.12 ± 0.08 | −0.24 ± 0.14 | −0.28 ± 0.15 | −0.27 ± 0.13 | −0.19 ± 0.12 |
The median effective temperatures are similar for all the groups, however, the median surface gravity for group I is larger than the other groups, suggesting that these sources might be less evolved. Sources in group I might be contaminated with some sources on the upper RGB or are relatively new to the TP-AGB phase. Sources in group III and IV have the largest median V-band amplitudes. This is not too surprising as these stars are fundamental-mode pulsators. Sources in group I have the smallest amplitudes, which is consistent with them being overtone pulsators. The metallicities of the sources in groups II, III, and IV are largely similar. However, group I has a slightly different chemical profile, with median abundance ratios higher than for the other groups. However, the |$\rm [X/Mg]$| abundance ratios are consistent across these groups given the reported dispersions. The biggest difference (∼0.2 dex) is seen in |$\rm [Al/Mg]$|, with the median abundance trending from |$\rm [Al/Mg]{\sim }-0.1$| for |$\rm \log _{10}(P/days)\lt 1.5$| to |$\rm [Al/Mg]{\sim }-0.3$| for |$\rm \log _{10}(P/days)\gt 1.5$|. The LSPs are less evolved than the SR variables in group IV with |$\rm \Delta \log (g) {\sim }0.1$|, and are more similar to the SR variables in groups I and II in their properties. This is not surprising given that the pulsation periods of the LSPs are consistent with the periods of SR variables in groups I and II (Trabucchi et al. 2017).
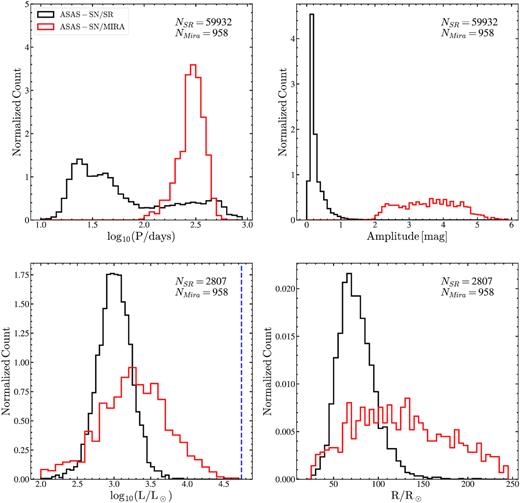
Distributions of the SR variables after correcting for LSPs (black) and Mira variables (red) with AV < 2 mag and parallaxes better than |$50{ per\ cent}$|, in |$\rm \log _{10}(P/days)$|, V-band amplitude, log (L/L⊙), and R/R⊙. The blue-dashed line corresponds to the maximum luminosity of AGB stars (log (L/L⊙) = 4.74) as calculated by Paczyński (1970).
4.3.2 A multiband photometric calibration for the temperatures of oxygen-rich AGB stars
Most AGB stars lack spectroscopic information, but well-calibrated temperatures are useful for studying these evolved stars. Here, we develop a temperature calibration based on the APOGEE temperatures, and a combination of Gaia and 2MASS photometry. Lebzelter et al. (2018) developed a multiband approach using the Wesenheit magnitudes, WRP and WJK, to distinguish between the various types of AGB stars. The intrinsic spread of red giants in the NIR colours is small, and the Wesenheit magnitudes adequately correct for the interstellar extinction. The visual colours of red giants are more sensitive to their surface temperatures and chemical compositions, resulting in a bigger spread in their optical colours. In their work, Lebzelter et al. (2018) found that the colour index WRP−WJK traces the temperature and molecular features in the stellar spectra of AGB stars and that the WRP − WJK index can be used to distinguish between carbon-rich and oxygen-rich AGB stars, with the carbon-rich (oxygen-rich) stars having WRP− WJK ≳ 0.8 mag (WRP − WJK ≲ 0.8 mag). Arnold et al. (2020) used the WRP −WJK index and the 2MASS J − Ks colours to study long period variables in the KELT survey (Pepper et al. 2007).
We illustrate the distribution of ASAS-SN Mira and SR variables in the (WRP − WJK)–(J− Ks) plane in Fig. 24. For reference, we also show the sources from the Catalogue of Galactic Carbon Stars (Alksnis et al. 2001). The carbon stars form a sharp, linear locus in this colour–colour space and have a median WRP− WJK ∼ 1.5 mag. In contrast to the carbon rich stars, the oxygen-rich sources form a broader and bluer distribution in this plane. The vast majority of the ASAS-SN Mira and SR variables have values of WRP − WJK consistent with oxygen-rich stars. Of the Mira variables and SR variables, |${\sim }97{ per\ cent}$| and |${\sim }95{ per\ cent}$| appear to be oxygen-rich AGB stars, respectively. The carbon-rich SR variables follow the tight carbon-star locus in the WRP − WJK–J − Ks plane at |$1 \, {\rm mag} \lesssim W_{RP}-W_{JK} \lesssim 2 \, {\rm mag}$|. In general, the carbon-rich SR variables with WRP − WJK ≳ 0.8 mag have longer median periods (|$\rm \log _{10}(P/days) {\sim } 2.1$|) than the oxygen-rich stars (|$\rm \log _{10}(P/days) {\sim } 1.9$|). The Mira variables have a distinct distribution in WRP− WJK that skews lower than that of the SR variables.
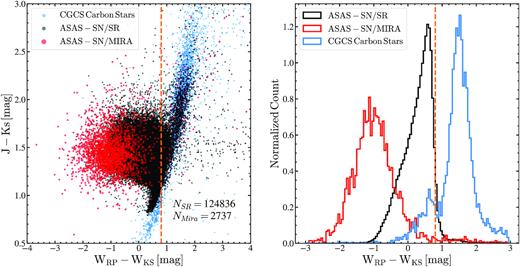
Distributions of the semiregular variables (black) and Mira variables (red) in WRP− WJK versus J − Ks (left) and WRP − WJK (right). The sources from the Catalogue of Galactic Carbon Stars (Alksnis et al. 2001; light blue) are also shown for reference. The orange-dashed line corresponds to the WRP − WJK index used to separate oxygen-rich (WRP− WJK ≲ 0.8 mag) and carbon-rich (WRP− WJK ≳ 0.8 mag) AGB stars.
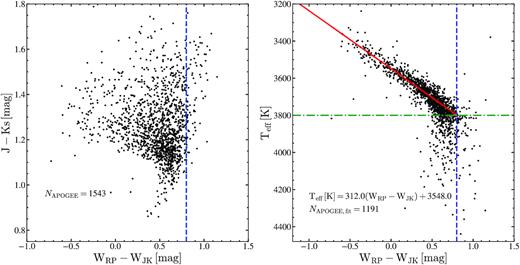
Distributions of the semiregular variables in APOGEE DR16 in WRP− WJK versus J− Ks (left) and WRP− WJK versus |$\rm T_{eff}$| (right). The blue-dashed line corresponds to the WRP− WJK index (0.8 mag) used to separate oxygen-rich and carbon-rich AGB stars. The red line shows the linear fit to the sources with |$\rm T_{eff}\lt 3800$| K and WRP−WJK < 0.8. The green-dashed line corresponds to the temperature cut-off of |$\rm T_{eff}=3800$| K used in the fit.
As a test, we use this relation to estimate the temperatures of the Mira variables shown in Fig. 24. The majority of these sources have WRP − WJK < −0.7 mag, thus they lie outside the parameter space of the sources used in the fit. Applying equation (8) to these Mira variables, we find the median temperature to be |$\rm T_{eff}{\sim }3230$| K (M5 spectral type), with the 1st percentile being |$\rm T_{eff}{\sim }2800$| K (M8 spectral type) and the 99th percentile being |$\rm T_{eff}{\sim }3687$| K (M1 spectral type). Mira variables have spectral temperatures that range from M0 to M10 (Yao et al. 2017), which is entirely consistent with the extrapolation. Furthermore, the median Gaia DR2 temperature for these Mira variables is |$\rm T_{eff}{\sim }3290$| K, which is very similar to the median temperature estimated using equation (8).
4.3.3 α-enhancements on the TP-AGB
During the TP-AGB, numerous nuclides are produced during H and He burning. The surfaces of AGB stars are chemically enriched primarily through the TDU events that follow a thermal pulse. AGB nucleosynthesis depends on the efficiency of the TDU events, the minimum core mass at which TDU begins, the size of the convective envelope, and the mass of the He intershell (Karakas, Lattanzio & Pols 2002). The efficiency of TDU increases with increasing stellar mass and decreasing metallicity (Karakas et al. 2002). In particular, the surface abundances of CNO elements are enhanced by an order of magnitude or more through successive TDU episodes (Iwamoto et al. 2004). The surfaces of AGB stars are also enriched in heavy elements that are produced by the s-process (e.g. Zr, Sr, Ba, etc., Smith & Lambert 1986, 1988). HBB in the more massive AGB stars can also further enhance the surface N abundances (Scalo, Despain & Ulrich 1975; McSaveney et al. 2007). Thus, the surface abundances of intermediate-mass AGB stars are dependent on both the TDU and HBB processes.
We show the distribution of the SR variables in the |$\rm [Mg/Fe]$|–|$\rm [Fe/H]$| plane as compared to the distribution of a reference sample of ∼238 000 giants in APOGEE DR16 with log (g) < 3.8 in Fig. 26. In the reference sample, |${\sim }27{ per\ cent}$| of the sources belong in the high-α sequence. The bimodality in |$\rm [Mg/Fe]$| at sub-solar |$\rm [Fe/H]$| is clearly seen for the SR variables as well, but |${\sim }38{ per\ cent}$| of the SR variables lie in the high-α sequence, which is an enhancement of |$+41{ per\ cent}$| compared to the overall APOGEE sample.
![The distribution of the semiregular variables in the APOGEE DR16 $\rm [Mg/Fe]$ versus $\rm [Fe/H]$ plane. The contours show the distribution of a reference sample of APOGEE giants. The red line shows the division between the low-α and high-α populations from Weinberg et al. (2019).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig26.jpeg?Expires=1749866512&Signature=LPhHAKTg9EuyQRRoBFBSuYmDOVGuVOTli73tZpAwufnXooJM6eVCzHOc74lqAMUe0IO6Nb80~pVonFXC50H7N4W6CUFKTkfGKgnvV0EyemMNP17G72~O0L9HypppatGSLOsqtO6fU6Yk42~vBu8AZ6ehLkTi7Ip2GLORZKjkAX8UMxCssPLIlVhhbpdI6mF8lIAFe34Ks7vYVsrUB6MYUrBILZWMVISuDFExEaK9RPf-zWfPBKgVMldACDdnyPhN1Qk9idmotiNULJ~hJF-lB~7G-8RKHJWM1W5klGdyzwdG6cHr6FaBomvOmb~aALldQi3pN8OU35tLv3OXpoAJqw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of the semiregular variables in the APOGEE DR16 |$\rm [Mg/Fe]$| versus |$\rm [Fe/H]$| plane. The contours show the distribution of a reference sample of APOGEE giants. The red line shows the division between the low-α and high-α populations from Weinberg et al. (2019).
We also illustrate the distributions of various surface abundances of the SR variables, APOGEE/RGB stars and APOGEE/AGB stars in Fig. 27. The SR variables and the APOGEE/AGB stars are significantly metal poor. SR variables with |$\rm [Fe/H]\gt 0$| or |$\rm [Mg/H]\gt 0$| are rare (|${\sim }3{ per\ cent}$| and |${\sim }7{ per\ cent}$|). The APOGEE/AGB stars populate the supersolar abundance bins significantly more than the SR variables, but this maybe due to the contamination from metal-rich upper RGB stars. The distributions of |$\rm [Na/Mg]$|, |$\rm [P/Mg]$|, and |$\rm [Mn/Mg]$| for the three samples are mostly similar. The SR variables and the APOGEE/AGB stars have lower |$\rm [C/Mg]$|, |$\rm [N/Mg]$|, and |$\rm [O/Mg]$| abundance ratios than the APOGEE/RGB stars. The biggest deviation from the APOGEE/RGB stars is in the distribution of |$\rm [Al/Mg]$|, with the SR variables peaking ∼− 0.3 dex below the peak of the APOGEE/RGB stars. There are virtually no APOGEE/RGB stars with |$\rm [Al/Mg]\lt -0.25$|. There are more SR variables than APOGEE/AGB stars in these lower metallicity bins, perhaps suggesting a pulsational dependence to the |$\rm [Al/Mg]$| abundance ratio. We will further investigate this phenomenon in Section 4.3.4. The SR variables and APOGEE/AGB stars also show substantial shifts relative to the APOGEE/RGB stars in the |$\rm [Si/Mg]$| (Δ ∼−0.1 dex), |$\rm [Ni/Mg]$| (Δ ∼−0.1 dex), and |$\rm [Co/Mg]$| (Δ ∼−0.1 dex) abundance ratios.
![$\rm [Fe/H]$, $\rm [Mg/H]$, and $\rm [X/Mg]$ abundance ratios, where X = C, N, O, Al, Si, P, Na, Ni, Co, and Mn, for the semiregular variables (blue), APOGEE/AGB stars (red) and APOGEE/RGB stars (black).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig27.jpeg?Expires=1749866512&Signature=5O8KELBwnbF7ZRczAfAAGgafgJsNmKbOm~1P~boY2mxpwgO98d0P1~wOjSWIF2VI6xtAIZnm3m-SnkXMLy34GB0sPY6-RXoR9TCzDAJ3fdLLpwAkOf1oTFiCDMEuZ5I5PDv2c769Ho4Dw9SYr~bNPQbcx4cKKDwV4ErQe6Rgt5dTNeqKEWQCqzA4~q-uJuzKMRSeWDiGx7LRUa~cNYIWDCqqQWP~N9T-RWkw4Khj5FIlrITJ2IJfK51SEphNpVoJmqvg6zi3PWM0Lng~AZRJgBB605Ga3XCE0HbZvmetqJoC2n1S2~eSeDJrbs35uq-e9o3-LGYofI8rYz5JjXaMqg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$\rm [Fe/H]$|, |$\rm [Mg/H]$|, and |$\rm [X/Mg]$| abundance ratios, where X = C, N, O, Al, Si, P, Na, Ni, Co, and Mn, for the semiregular variables (blue), APOGEE/AGB stars (red) and APOGEE/RGB stars (black).
While the morphology of the SR distribution in Fig. 26 is similar to the APOGEE giants, the actual metallicity and abundance distributions are shifted, as shown in Figs 27 and 28. SR variables tend to be more metal poor (peak |$\rm [Fe/H]{\sim }-0.6$| instead of |$\rm [Fe/H]{\sim }-0.2$|) and α rich (median |$\rm [Mg/Fe]{\sim }0.16$| instead of |$\rm [Mg/Fe]{\sim }0.07$|). The low-α SR variables peak at |$\rm [Mg/Fe]{\sim }+0.12$|, compared to |$\rm [Mg/Fe]{\sim }+0.03$| for the low-α APOGEE/GIANTS. We illustrate the shifts in the distribution of the |$\rm [\alpha /M]$|, |$\rm [Mg/Fe]$|, |$\rm [O/Fe]$|, and |$\rm [Si/Fe]$| abundance ratios in Fig. 28. We see significant shifts for both the low-α and high-α stars in all but the |$\rm [Si/Fe]$| abundance ratio.
![The distribution of the SR variables (blue) and giant stars from APOGEE DR16 in $\rm [\alpha /M]$, $\rm [Mg/Fe]$, $\rm [O/Fe]$, and $\rm [Si/Fe]$. The median abundance ratios of the high-α and low-α SR variables (APOGEE giants) are shown as the red (purple) dashed (dot–dashed) lines.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig28.jpeg?Expires=1749866512&Signature=gQwkZizIi1AVaFWxCCsWTS6aYX2xM~uRjfF1WCywNL87hX0jUj8WdBS1UaL38koWFpS0SDB5X77KgLJArsozqZbAjtmTimYMBrK0N-uJxwtDsoQpeTRCwwDBBVlGrRPL7FkAVvOJxHVzkK0JP1Nwpd72umm~6dPiTE9KfOBlJogOJSgQo36w6qX57GZOYnKC7Ld~hABf~pfvfITVTbb33sRqQ7T-CkBtLfiEUIWIy~R73dDWqyTfgfRaIUg5LulHdA3-zZcV8377MwXjCi16ZItZBNHhHlPKM5fh3C8GBxpe-CjwpaLOs4gjcaogn~D4Wy77iPEm1Saz-jJDg~kDuA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of the SR variables (blue) and giant stars from APOGEE DR16 in |$\rm [\alpha /M]$|, |$\rm [Mg/Fe]$|, |$\rm [O/Fe]$|, and |$\rm [Si/Fe]$|. The median abundance ratios of the high-α and low-α SR variables (APOGEE giants) are shown as the red (purple) dashed (dot–dashed) lines.
To distinguish between the contribution of (i) the initial abundances at star formation and (ii) dredge-up effects, to the |$\rm [\alpha /M]$|, |$\rm [Mg/Fe]$|, |$\rm [O/Fe]$|, and |$\rm [Si/Fe]$| abundance ratios (Fig. 28), we re-calculate the peak shifts by limiting the sample of SR variables and APOGEE giants to |$\rm -1 \le [Fe/H] \le -0.25$|. In this metallicity-limited sample of SR variables and APOGEE giants, we see that the magnitude of the abundance shifts are smaller, as summarized in Table 5. For example, the peak shift of the low-α SR variables in |$\rm [Mg/Fe]$| is now ∼+ 0.04, compared to ∼+ 0.09 for the full sample. Furthermore, the low-α SR variables appear to have significantly lower median |$\rm [Si/Fe]$| abundance ratios than the APOGEE giants. This is suggestive of Si depletion through dust formation in the winds of these AGB stars (Massalkhi et al. 2018).
The shifts in the median abundance ratios of various α elements between the SR variables and APOGEE/GIANTS. The median abundance error is ∼0.01 dex.
| Abundance . | Low-α shift . | High-α shift . | Low-α shift . | High-α shift . |
|---|---|---|---|---|
| . | All . | All . | Metallicity-limited . | Metallicity-limited . |
| |$\rm [\alpha /M]$| | + 0.06 | + 0.06 | + 0.02 | + 0.04 |
| |$\rm [Mg/Fe]$| | + 0.09 | + 0.04 | + 0.04 | + 0.01 |
| |$\rm [O/Fe]$| | + 0.08 | + 0.05 | + 0.0 | + 0.01 |
| |$\rm [Si/Fe]$| | + 0.01 | + 0.01 | −0.04 | −0.01 |
| Abundance . | Low-α shift . | High-α shift . | Low-α shift . | High-α shift . |
|---|---|---|---|---|
| . | All . | All . | Metallicity-limited . | Metallicity-limited . |
| |$\rm [\alpha /M]$| | + 0.06 | + 0.06 | + 0.02 | + 0.04 |
| |$\rm [Mg/Fe]$| | + 0.09 | + 0.04 | + 0.04 | + 0.01 |
| |$\rm [O/Fe]$| | + 0.08 | + 0.05 | + 0.0 | + 0.01 |
| |$\rm [Si/Fe]$| | + 0.01 | + 0.01 | −0.04 | −0.01 |
The shifts in the median abundance ratios of various α elements between the SR variables and APOGEE/GIANTS. The median abundance error is ∼0.01 dex.
| Abundance . | Low-α shift . | High-α shift . | Low-α shift . | High-α shift . |
|---|---|---|---|---|
| . | All . | All . | Metallicity-limited . | Metallicity-limited . |
| |$\rm [\alpha /M]$| | + 0.06 | + 0.06 | + 0.02 | + 0.04 |
| |$\rm [Mg/Fe]$| | + 0.09 | + 0.04 | + 0.04 | + 0.01 |
| |$\rm [O/Fe]$| | + 0.08 | + 0.05 | + 0.0 | + 0.01 |
| |$\rm [Si/Fe]$| | + 0.01 | + 0.01 | −0.04 | −0.01 |
| Abundance . | Low-α shift . | High-α shift . | Low-α shift . | High-α shift . |
|---|---|---|---|---|
| . | All . | All . | Metallicity-limited . | Metallicity-limited . |
| |$\rm [\alpha /M]$| | + 0.06 | + 0.06 | + 0.02 | + 0.04 |
| |$\rm [Mg/Fe]$| | + 0.09 | + 0.04 | + 0.04 | + 0.01 |
| |$\rm [O/Fe]$| | + 0.08 | + 0.05 | + 0.0 | + 0.01 |
| |$\rm [Si/Fe]$| | + 0.01 | + 0.01 | −0.04 | −0.01 |
These enhancements are suggestive of surface Mg enhancement during TDU episodes. During the AGB, isotopes of Mg are primarily created during thermal pulses through neutron capture processes, and the Ne–Mg reactions (Cristallo et al. 2011). Models of AGB stars have shown that the surface abundance of Mg is enhanced at low metallicities (Cristallo et al. 2011, 2015). For example, taking a model of a |$1.5\rm M_\odot$| AGB star, the final surface |$\rm [Mg/Fe]$| abundance ratio is 0.01 at Z = 6 × 10−3, and 0.43 at Z = 1 × 10−3 (Cristallo et al. 2011). The efficiency of dredge-up also increases with decreasing metallicity (Karakas et al. 2002; Marigo & Girardi 2007). Considering these theoretical expectations, it is not surprising to see Mg enhancements in the atmospheres of these metal-poor pulsating AGB stars.
In summary, we find that the metallicities and abundance ratios of the SR variables are distinct from the RGB stars. There are more α-rich SR variables than α-rich RGB stars. The SR variables are more metal-poor with a metallicity peak at |$\rm [Fe/H]{\sim }-0.6$|. Even after considering the initial abundances at star formation, we find some evidence of α/Mg enrichment in the atmospheres of the SR variables, which is likely the result of the third dredge-up during the AGB.
4.3.4 Surface aluminium depletion on the TP-AGB
Al is a light, odd Z element that is almost entirely produced due to core-collapse supernovae (see e.g. Weinberg et al. 2019; Griffith et al. 2019). The oxygen-rich atmospheres of most AGB stars are conducive to the formation of dust seeds close to the stellar surface, including |$\rm Al_2O_3$|, |$\rm SiO_2$|, and |$\rm TiO_2$| (Gail et al. 2013; Decin et al. 2017). The presence of alumina (|$\rm Al_2O_3$|) dust around oxygen-rich AGB stars is well known (Onaka, de Jong & Willems 1989). Banerjee et al. (2012) reported the near-IR detection of several AlO bands in the wavelength range |$1.0\rm{--}1.35\,\mu \rm m$| and rotational transitions of this molecule have also been reported (De Beck et al. 2017; Decin et al. 2017). It is thought that AlO is efficiently depleted from the gas around oxygen-rich AGB stars to form alumina dust seeds (De Beck et al. 2017). AGB stars lose mass through a slow wind (|${\sim }10\, \rm km/s$|) driven by radiation pressure on dust grains (Iben & Renzini 1983; Khouri et al. 2015). Understanding the formation of dust seeds such as alumina and silicate is a crucial consideration when studying mass-loss in AGB stars.
In Section 4.3.3, we noted that the SR variables and the sample of APOGEE/AGB stars in APOGEE DR16 had lower |$\rm [Al/Mg]$| abundance ratios than the APOGEE/RGB stars. The median |$\rm [Al/Mg]$| abundance ratios for the SR variables, APOGEE/AGB stars, and APOGEE/RGB stars are −0.25, −0.16, and −0.01, respectively. We investigate the |$\rm [Al/Mg]$| and |$\rm [Al/C]$| abundance ratios for the SR variables, APOGEE/AGB and APOGEE/RGB stars in Fig. 29. In the |$\rm [Al/Mg]$|–|$\rm [Mg/H]$| plane, both the SR variables and APOGEE/AGB stars form two distinct sequences of increasing |$\rm [Al/Mg]$| with increasing |$\rm [Mg/H]$|. In general, the APOGEE/AGB stars have higher |$\rm [Al/Mg]$| abundance ratios than the SR variables. The |$\rm [Al/Mg]$| abundance ratios of the APOGEE/RGB stars appear to follow a Gaussian distribution centred at |$\rm [Al/Mg]=0$|. Of the APOGEE/RGB stars, only |${\sim }3{ per\ cent}$| have |$\rm [Al/Mg]\lt -0.2$|, whereas |${\sim }61{ per\ cent}$| of the SR variables and |${\sim }42{ per\ cent}$| of the APOGEE/AGB stars have |$[\rm Al/Mg]\lt -0.2$|. This suggests that Al is being depleted on the AGB, with the pulsating TP-AGB stars depleting more Al than other AGB stars.
![$\rm [Al/Mg]$ (top left) and $\rm [Al/C]$ (top right) versus $\rm [Mg/H]$ for the semiregular variables ($\rm P\lt 60$d: black, $\rm P\gt 60$d: purple) and APOGEE AGB stars (orange). The distributions of the APOGEE RGB stars in these planes are shown as contours. The distributions of $\rm [Al/Mg]$ (bottom left) and $\rm [Al/C]$ (bottom right) for the semiregular variables (black) APOGEE AGB (orange) and RGB (blue) stars are shown as the histograms.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig29.jpeg?Expires=1749866512&Signature=zXNeJkh1i1LzLz7IPJ50lQDG2XSnJEEUdI2TSwlyhF3IzB2pGqD4nuFrYlltrRKI~9p~UJobLtrlIQ19f0ORuGPx1IrmivrTgPPXdqMXqc2BwkDINgyVEPqZMn3~uKva2Lg6CfTkfK0azY1n~QFysKAyESz16e14rbZaKGBQQwEeXVdgmeB9ECd3on6FifUpaM9Tbq3tnUI2pVa373M1DsjdkjgczQM67zveGOGurDbUjO54F5ZUUhPbgtyvgElLL-X5D0f4EoCxn8t~Y-IxiEerUUiI1BXufRRZAEFIgaKCsDoq0uhJtJlm5h~18ozJYXE-gupnTjIm4qlcpJn6HA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$\rm [Al/Mg]$| (top left) and |$\rm [Al/C]$| (top right) versus |$\rm [Mg/H]$| for the semiregular variables (|$\rm P\lt 60$|d: black, |$\rm P\gt 60$|d: purple) and APOGEE AGB stars (orange). The distributions of the APOGEE RGB stars in these planes are shown as contours. The distributions of |$\rm [Al/Mg]$| (bottom left) and |$\rm [Al/C]$| (bottom right) for the semiregular variables (black) APOGEE AGB (orange) and RGB (blue) stars are shown as the histograms.
The two Al sequences (hereafter the ‘high-Al’ and ‘low-Al’ sequences) are even more distinct in the |$\rm [Al/C]$|–|$\rm [Mg/H]$| plane (Fig. 29). The ‘high-Al’ and ‘low-Al’ populations are centred on |$\rm [Al/C]{\sim }0$| and |$\rm [Al/C]{\sim }-0.15$|. The APOGEE/RGB stars again appear to follow a Gaussian distribution in |$\rm [Al/C]$|, centred at |$\rm [Al/C]{\sim }+0.05$|. However, both the SR variables and APOGEE/AGB stars have a bi-modal distribution in |$\rm [Al/C]$|. The SR variables populate the ‘low-Al’ sequence relatively more than the APOGEE/AGB stars, with |${\sim }40{ per\ cent}$| of the SR variables having |$[\rm Al/C]\lt -0.1$| compared to only |${\sim }23{ per\ cent}$| of the APOGEE/AGB stars. This again hints at a correlation between Al depletion and pulsations in AGB stars.
We investigate the dependence of |$\rm [Al/X]$|, where |$\rm X=$| Mg, C, Si, O, with the pulsation period in Fig. 30. The reference elements C, Si, and O, were chosen due to their significant presence in dust grains. Previous studies have established that strong mass-loss and increased dust formation first occurs for pulsation periods of |$\rm P{\gtrsim }60$| d for Galactic AGB stars (Glass et al. 2009; McDonald et al. 2018). The |$\rm [Al/X]$| abundance ratios of the SR variables are strongly correlated with the pulsational period. On average, the |$\rm [Al/X]$| abundance ratios decrease with period up until |$\rm P{\sim }60$| d and then flatten. The most striking dependence is seen in the distribution of |$\rm [Al/O]$| with period. The |$\rm [Al/O]$| trend largely plateaus at |$\rm [Al/O]{\sim }-0.3$| beyond P ∼ 60 d. The fraction of sources with |$\rm [Al/O]\lt -0.22$| varies between the PLR groups (see Section 4.3.1), with |${\sim }16{ per\ cent}$| in group I, |${\sim }54{ per\ cent}$| in group II, |${\sim }74{ per\ cent}$| in group III, and |${\sim }69{ per\ cent}$| in group IV. The fraction of sources with |$\rm [Al/C]\lt -0.1$| follow a similar trend, with |${\sim }14{ per\ cent}$| in group I, |${\sim }45{ per\ cent}$| in group II, |${\sim }62{ per\ cent}$| in group III, and |${\sim }63{ per\ cent}$| in group IV. Of the LSPs, |${\sim }44{ per\ cent}$| and |${\sim }41{ per\ cent}$| had |$\rm [Al/O]\lt -0.22$| and |$\rm [Al/C]\lt -0.1$|, respectively. These period trends were far less obvious when we assigned stars their LSPs, which strongly supports the argument that the shorter periods are more physically important.
![$\rm [Al/Mg]$, $\rm [Al/C]$, $\rm [Al/Si]$, and $\rm [Al/O]$ versus $\rm \log _{10}(P/days)$ for the semiregular variables. The binned median abundance ratios are shown in blue. The red-dashed line shows the period at which increased dust formation first occurs for Galactic AGB stars ($\rm P{\,\,\gtrsim\,\, }60$ d). These correlations are far less clear if we use the LSP periods.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig30.jpeg?Expires=1749866512&Signature=ylue1D13qugmeIJA268vavZn5hgABQl5zrVAuymfKaUQeliPqC4Me2mTvzkQXpnal4ymzmKNkKHrJb7og7ojp5qmU3NfKQyvPYLKUVY2nzw-a2Q1PM1ifewPvaurZ5QCq87AwEmno-zzRJEK~HtLraDOrPGQzG93cYqgc2~CwGK8N4RsRduRGmE4A1e3M1CNsT4K0YqWWnI9NcTTYPx9DiA8vKkeLggTYnYmczAAW9wWr8uQ-sgvVqntqbMS3z8w79IhgeBR8qt0D8kZ6QyQlLsOaL3O9GsD-4~FVxCnBxSO8nAx~u999vLJyqUd~0eXTww8e92m9iV6XRRkY65Mxg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$\rm [Al/Mg]$|, |$\rm [Al/C]$|, |$\rm [Al/Si]$|, and |$\rm [Al/O]$| versus |$\rm \log _{10}(P/days)$| for the semiregular variables. The binned median abundance ratios are shown in blue. The red-dashed line shows the period at which increased dust formation first occurs for Galactic AGB stars (|$\rm P{\,\,\gtrsim\,\, }60$| d). These correlations are far less clear if we use the LSP periods.
Fig. 31 shows the dependence of |$\rm [Al/X]$|, where |$\rm X=$| Mg, C, Si, and O, with effective temperature for the SR variables. The high-Al and low-Al sequences that were identified in the |$\rm [Al/Mg]$|–|$\rm [Mg/H]$| and |$\rm [Al/C]$|–|$\rm [Mg/H]$| planes are also apparent in temperature-abundance space. Furthermore, we see evidence of the period dependence on the Al abundance ratios, with short period sources falling into the high-Al sequence. Cuts of |$\rm [Al/Mg]=-0.25$|, |$\rm [Al/C]=-0.1$|, |$\rm [Al/O]=-0.22$|, or |$\rm [Al/Si]=-0.13$| roughly separate the high-Al and low-Al sequences. The Al abundance ratios of the high-Al stars decrease with increasing temperature, and is best seen in the trends of the |$\rm [Al/O]$| and |$\rm [Al/Si]$| abundance ratios with |$\rm T_{eff}$|. In contrast, the Al abundances of the low-Al stars are not correlated with temperature.
![The dependence of $\rm [Al/Mg]$, $\rm [Al/C]$,$\rm [Al/Si]$, and $\rm [Al/O]$ on $\rm T_{eff}$ for the semiregular variables. The points are coloured by $\rm \log _{10}(P/days)$ with the changes in hue at periods near 60 d. The trends in the Al abundance ratios with $\rm T_{eff}$ for the high-Al and low-Al sequences are shown in orange and green, respectively. The black-dashed line shows the suggested abundance cuts ($\rm [Al/Mg]=-0.25$, $\rm [Al/C]=-0.1$, $\rm [Al/O]=-0.22$, or $\rm [Al/Si]=-0.13$) for separating the high-Al and low-Al sequences.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig31.jpeg?Expires=1749866512&Signature=F~235TW1iR8BpIqzFLIJH5whRKnyBFoiK0eWIs7XyTkw7NS5jI8ZMDeIr7z9SlfWA2JvIZ4WgbXM4zRrVHXHBHJsU3p3v1AyUoaIdQyzyG5KNblka356HVAdicFNbVLF1DXHkXp1CjTrx4mgY6VbiGYh53nRyYk-jQGfZfj1QhBy19wMcmBsojiiiQMEDjRQHNo~t9yepp6ShQtF2p8ENiVDcR8M9N8nQTMJ5p59ueffymCrAgd~51l1aFWi5JDEf~A7dRYVrecw6KQThffBn91KXuBVvLj~q81~ZOSiMPlERn6Bhs0yQmvdv15-T5raVtfuMX5B7bEC9lZYkpaXyA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The dependence of |$\rm [Al/Mg]$|, |$\rm [Al/C]$|,|$\rm [Al/Si]$|, and |$\rm [Al/O]$| on |$\rm T_{eff}$| for the semiregular variables. The points are coloured by |$\rm \log _{10}(P/days)$| with the changes in hue at periods near 60 d. The trends in the Al abundance ratios with |$\rm T_{eff}$| for the high-Al and low-Al sequences are shown in orange and green, respectively. The black-dashed line shows the suggested abundance cuts (|$\rm [Al/Mg]=-0.25$|, |$\rm [Al/C]=-0.1$|, |$\rm [Al/O]=-0.22$|, or |$\rm [Al/Si]=-0.13$|) for separating the high-Al and low-Al sequences.
Separating based on their |$\rm [Al/C]$| abundance ratio, we find that the high-Al variables have a median period of |$\rm \log _{10}(P/days) {\sim } 1.5\pm 0.4$|, whereas the low-Al variables have a median period of |$\rm \log _{10}(P/days) {\sim } 1.8\pm 0.5$|. In general, the high-Al variables have periods that fall below the period at which dust formation and mass-loss is significant for AGB stars (|$\rm \log _{10}(P/days) {\sim } 1.75$|). Most low-Al stars have periods above the canonical threshold (|$\rm P{\,\,\gtrsim\,\, }60$| d) for dust formation in Galactic AGB stars (Fig. 30). This suggests that the low-Al sequence could be the result of significant Al depletion through the formation of dust grains containing Al (for example, alumina) in the stellar winds of AGB stars.
The various APOGEE DR16 spectroscopic parameters and chemical abundance ratios for the high-Al and low-Al sequences are summarized in Table 6 for these two groups. The median V-band amplitudes of the low-Al stars are more than twice that of the high-Al stars. The high-Al stars have |$\rm [\alpha /M]$| abundance ratios that are consistent with being on the low-α sequence, whereas the low-Al stars have |$\rm [\alpha /M]$| consistent with being high-α stars. Based on the division in Weinberg et al. (2019), we find that |${\sim }54{ per\ cent}$| of the low-Al stars are high-α stars, whereas only |${\sim }34{ per\ cent}$| of the high-Al variables are on the high-α sequence.
Distribution of the APOGEE DR16 spectroscopic parameters and chemical abundances for the SR variables grouped by their abundances. The SR variables are sorted into these groups based on their |$\rm [Al/O]$| and |$\rm [N/O]$| abundances. The median and standard deviation for each parameter are shown.
| . | High Al . | Low Al . | High N . | Low N . | HBB . |
|---|---|---|---|---|---|
| . | |$\rm [Al/O]\gt -0.22$| . | |$\rm [Al/O]\lt -0.22$| . | |$\rm 0.02 \le [N/O]\le 0.3$| . | |$\rm [N/O]\lt 0.02$| . | |$\rm [N/O]\gt 0.30$| . |
| N | 874 | 812 | 872 | 728 | 86 |
| |$\rm \log _{10}(P/days)$| | 1.5 ± 0.4 | 1.8 ± 0.5 | 1.6 ± 0.5 | 1.6 ± 0.5 | 2.0 ± 0.6 |
| |$\rm Amplitude\, [mag]$| | 0.13 ± 0.13 | 0.26 ± 0.23 | 0.15 ± 0.19 | 0.20 ± 0.21 | 0.17 ± 0.21 |
| |$\rm T_{eff}\, [K]$| | 3730 ± 126 | 3683 ± 139 | 3727 ± 126 | 3677 ± 120 | 3822 ± 194 |
| |$\rm \log (g)$| | 0.54 ± 0.29 | 0.42 ± 0.25 | 0.46 ± 0.28 | 0.55 ± 0.21 | 0.07 ± 0.55 |
| |$\rm [M/H]$| | −0.50 ± 0.26 | −0.68 ± 0.29 | −0.57 ± 0.31 | −0.63 ± 0.28 | −0.52 ± 0.31 |
| |$\rm [\alpha /M]$| | 0.08 ± 0.09 | 0.22 ± 0.11 | 0.07 ± 0.05 | 0.25 ± 0.06 | −0.03 ± 0.07 |
| |$\rm [Fe/H]$| | −0.52 ± 0.25 | −0.69 ± 0.28 | −0.59 ± 0.30 | −0.64 ± 0.27 | −0.56 ± 0.30 |
| |$\rm [Mg/Fe]$| | 0.14 ± 0.10 | 0.24 ± 0.12 | 0.13 ± 0.07 | 0.30 ± 0.08 | 0.03 ± 0.09 |
| |$\rm [C/Mg]$| | −0.14 ± 0.09 | −0.15 ± 0.16 | −0.14 ± 0.13 | −0.15 ± 0.14 | −0.22 ± 0.18 |
| |$\rm [N/Mg]$| | 0.08 ± 0.16 | −0.07 ± 0.18 | 0.10 ± 0.08 | −0.13 ± 0.09 | 0.36 ± 0.19 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.05 ± 0.05 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.05 | −0.12 ± 0.06 | −0.11 ± 0.05 | −0.12 ± 0.05 | −0.08 ± 0.06 |
| |$\rm [Ca/Mg]$| | −0.07 ± 0.07 | −0.10 ± 0.10 | −0.06 ± 0.06 | −0.14 ± 0.08 | 0.05 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.16 ± 0.09 | −0.34 ± 0.11 | −0.20 ± 0.14 | −0.31 ± 0.14 | −0.31 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.04 ± 0.15 | −0.14 ± 0.24 | −0.02 ± 0.16 | −0.17 ± 0.20 | 0.10 ± 0.17 |
| |$\rm [P/Mg]$| | −0.01 ± 0.15 | −0.07 ± 0.25 | 0.01 ± 0.17 | −0.11 ± 0.20 | 0.18 ± 0.23 |
| |$\rm [K/Mg]$| | 0.02 ± 0.10 | −0.01 ± 0.11 | 0.03 ± 0.10 | −0.02 ± 0.11 | 0.09 ± 0.11 |
| |$\rm [Cr/Mg]$| | −0.11 ± 0.11 | −0.21 ± 0.15 | −0.08 ± 0.11 | −0.25 ± 0.09 | 0.02 ± 0.12 |
| |$\rm [V/Mg]$| | −0.04 ± 0.09 | −0.07 ± 0.13 | −0.03 ± 0.12 | −0.09 ± 0.09 | −0.05 ± 0.13 |
| |$\rm [Co/Mg]$| | −0.08 ± 0.09 | −0.12 ± 0.11 | −0.06 ± 0.10 | −0.14 ± 0.08 | −0.09 ± 0.12 |
| |$\rm [Mn/Mg]$| | −0.04 ± 0.16 | −0.17 ± 0.18 | −0.02 ± 0.14 | −0.24 ± 0.14 | 0.02 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.13 ± 0.08 | −0.20 ± 0.09 | −0.11 ± 0.07 | −0.23 ± 0.06 | −0.12 ± 0.10 |
| |$\rm [Ti/Mg]$| | −0.06 ± 0.14 | −0.10 ± 0.12 | −0.07 ± 0.16 | −0.09 ± 0.11 | −0.01 ± 0.11 |
| |$\rm [C/N]$| | −0.20 ± 0.18 | −0.11 ± 0.24 | −0.23 ± 0.12 | −0.02 ± 0.14 | −0.60 ± 0.32 |
| |$\rm [C/O]$| | −0.10 ± 0.07 | −0.11 ± 0.14 | −0.10 ± 0.11 | −0.11 ± 0.11 | −0.17 ± 0.17 |
| |$\rm [N/O]$| | 0.11 ± 0.15 | −0.03 ± 0.17 | 0.13 ± 0.06 | −0.09 ± 0.07 | 0.41 ± 0.19 |
| |$\rm [Al/O]$| | −0.12 ± 0.07 | −0.29 ± 0.10 | −0.14 ± 0.12 | −0.27 ± 0.12 | −0.27 ± 0.20 |
| . | High Al . | Low Al . | High N . | Low N . | HBB . |
|---|---|---|---|---|---|
| . | |$\rm [Al/O]\gt -0.22$| . | |$\rm [Al/O]\lt -0.22$| . | |$\rm 0.02 \le [N/O]\le 0.3$| . | |$\rm [N/O]\lt 0.02$| . | |$\rm [N/O]\gt 0.30$| . |
| N | 874 | 812 | 872 | 728 | 86 |
| |$\rm \log _{10}(P/days)$| | 1.5 ± 0.4 | 1.8 ± 0.5 | 1.6 ± 0.5 | 1.6 ± 0.5 | 2.0 ± 0.6 |
| |$\rm Amplitude\, [mag]$| | 0.13 ± 0.13 | 0.26 ± 0.23 | 0.15 ± 0.19 | 0.20 ± 0.21 | 0.17 ± 0.21 |
| |$\rm T_{eff}\, [K]$| | 3730 ± 126 | 3683 ± 139 | 3727 ± 126 | 3677 ± 120 | 3822 ± 194 |
| |$\rm \log (g)$| | 0.54 ± 0.29 | 0.42 ± 0.25 | 0.46 ± 0.28 | 0.55 ± 0.21 | 0.07 ± 0.55 |
| |$\rm [M/H]$| | −0.50 ± 0.26 | −0.68 ± 0.29 | −0.57 ± 0.31 | −0.63 ± 0.28 | −0.52 ± 0.31 |
| |$\rm [\alpha /M]$| | 0.08 ± 0.09 | 0.22 ± 0.11 | 0.07 ± 0.05 | 0.25 ± 0.06 | −0.03 ± 0.07 |
| |$\rm [Fe/H]$| | −0.52 ± 0.25 | −0.69 ± 0.28 | −0.59 ± 0.30 | −0.64 ± 0.27 | −0.56 ± 0.30 |
| |$\rm [Mg/Fe]$| | 0.14 ± 0.10 | 0.24 ± 0.12 | 0.13 ± 0.07 | 0.30 ± 0.08 | 0.03 ± 0.09 |
| |$\rm [C/Mg]$| | −0.14 ± 0.09 | −0.15 ± 0.16 | −0.14 ± 0.13 | −0.15 ± 0.14 | −0.22 ± 0.18 |
| |$\rm [N/Mg]$| | 0.08 ± 0.16 | −0.07 ± 0.18 | 0.10 ± 0.08 | −0.13 ± 0.09 | 0.36 ± 0.19 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.05 ± 0.05 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.05 | −0.12 ± 0.06 | −0.11 ± 0.05 | −0.12 ± 0.05 | −0.08 ± 0.06 |
| |$\rm [Ca/Mg]$| | −0.07 ± 0.07 | −0.10 ± 0.10 | −0.06 ± 0.06 | −0.14 ± 0.08 | 0.05 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.16 ± 0.09 | −0.34 ± 0.11 | −0.20 ± 0.14 | −0.31 ± 0.14 | −0.31 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.04 ± 0.15 | −0.14 ± 0.24 | −0.02 ± 0.16 | −0.17 ± 0.20 | 0.10 ± 0.17 |
| |$\rm [P/Mg]$| | −0.01 ± 0.15 | −0.07 ± 0.25 | 0.01 ± 0.17 | −0.11 ± 0.20 | 0.18 ± 0.23 |
| |$\rm [K/Mg]$| | 0.02 ± 0.10 | −0.01 ± 0.11 | 0.03 ± 0.10 | −0.02 ± 0.11 | 0.09 ± 0.11 |
| |$\rm [Cr/Mg]$| | −0.11 ± 0.11 | −0.21 ± 0.15 | −0.08 ± 0.11 | −0.25 ± 0.09 | 0.02 ± 0.12 |
| |$\rm [V/Mg]$| | −0.04 ± 0.09 | −0.07 ± 0.13 | −0.03 ± 0.12 | −0.09 ± 0.09 | −0.05 ± 0.13 |
| |$\rm [Co/Mg]$| | −0.08 ± 0.09 | −0.12 ± 0.11 | −0.06 ± 0.10 | −0.14 ± 0.08 | −0.09 ± 0.12 |
| |$\rm [Mn/Mg]$| | −0.04 ± 0.16 | −0.17 ± 0.18 | −0.02 ± 0.14 | −0.24 ± 0.14 | 0.02 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.13 ± 0.08 | −0.20 ± 0.09 | −0.11 ± 0.07 | −0.23 ± 0.06 | −0.12 ± 0.10 |
| |$\rm [Ti/Mg]$| | −0.06 ± 0.14 | −0.10 ± 0.12 | −0.07 ± 0.16 | −0.09 ± 0.11 | −0.01 ± 0.11 |
| |$\rm [C/N]$| | −0.20 ± 0.18 | −0.11 ± 0.24 | −0.23 ± 0.12 | −0.02 ± 0.14 | −0.60 ± 0.32 |
| |$\rm [C/O]$| | −0.10 ± 0.07 | −0.11 ± 0.14 | −0.10 ± 0.11 | −0.11 ± 0.11 | −0.17 ± 0.17 |
| |$\rm [N/O]$| | 0.11 ± 0.15 | −0.03 ± 0.17 | 0.13 ± 0.06 | −0.09 ± 0.07 | 0.41 ± 0.19 |
| |$\rm [Al/O]$| | −0.12 ± 0.07 | −0.29 ± 0.10 | −0.14 ± 0.12 | −0.27 ± 0.12 | −0.27 ± 0.20 |
Distribution of the APOGEE DR16 spectroscopic parameters and chemical abundances for the SR variables grouped by their abundances. The SR variables are sorted into these groups based on their |$\rm [Al/O]$| and |$\rm [N/O]$| abundances. The median and standard deviation for each parameter are shown.
| . | High Al . | Low Al . | High N . | Low N . | HBB . |
|---|---|---|---|---|---|
| . | |$\rm [Al/O]\gt -0.22$| . | |$\rm [Al/O]\lt -0.22$| . | |$\rm 0.02 \le [N/O]\le 0.3$| . | |$\rm [N/O]\lt 0.02$| . | |$\rm [N/O]\gt 0.30$| . |
| N | 874 | 812 | 872 | 728 | 86 |
| |$\rm \log _{10}(P/days)$| | 1.5 ± 0.4 | 1.8 ± 0.5 | 1.6 ± 0.5 | 1.6 ± 0.5 | 2.0 ± 0.6 |
| |$\rm Amplitude\, [mag]$| | 0.13 ± 0.13 | 0.26 ± 0.23 | 0.15 ± 0.19 | 0.20 ± 0.21 | 0.17 ± 0.21 |
| |$\rm T_{eff}\, [K]$| | 3730 ± 126 | 3683 ± 139 | 3727 ± 126 | 3677 ± 120 | 3822 ± 194 |
| |$\rm \log (g)$| | 0.54 ± 0.29 | 0.42 ± 0.25 | 0.46 ± 0.28 | 0.55 ± 0.21 | 0.07 ± 0.55 |
| |$\rm [M/H]$| | −0.50 ± 0.26 | −0.68 ± 0.29 | −0.57 ± 0.31 | −0.63 ± 0.28 | −0.52 ± 0.31 |
| |$\rm [\alpha /M]$| | 0.08 ± 0.09 | 0.22 ± 0.11 | 0.07 ± 0.05 | 0.25 ± 0.06 | −0.03 ± 0.07 |
| |$\rm [Fe/H]$| | −0.52 ± 0.25 | −0.69 ± 0.28 | −0.59 ± 0.30 | −0.64 ± 0.27 | −0.56 ± 0.30 |
| |$\rm [Mg/Fe]$| | 0.14 ± 0.10 | 0.24 ± 0.12 | 0.13 ± 0.07 | 0.30 ± 0.08 | 0.03 ± 0.09 |
| |$\rm [C/Mg]$| | −0.14 ± 0.09 | −0.15 ± 0.16 | −0.14 ± 0.13 | −0.15 ± 0.14 | −0.22 ± 0.18 |
| |$\rm [N/Mg]$| | 0.08 ± 0.16 | −0.07 ± 0.18 | 0.10 ± 0.08 | −0.13 ± 0.09 | 0.36 ± 0.19 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.05 ± 0.05 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.05 | −0.12 ± 0.06 | −0.11 ± 0.05 | −0.12 ± 0.05 | −0.08 ± 0.06 |
| |$\rm [Ca/Mg]$| | −0.07 ± 0.07 | −0.10 ± 0.10 | −0.06 ± 0.06 | −0.14 ± 0.08 | 0.05 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.16 ± 0.09 | −0.34 ± 0.11 | −0.20 ± 0.14 | −0.31 ± 0.14 | −0.31 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.04 ± 0.15 | −0.14 ± 0.24 | −0.02 ± 0.16 | −0.17 ± 0.20 | 0.10 ± 0.17 |
| |$\rm [P/Mg]$| | −0.01 ± 0.15 | −0.07 ± 0.25 | 0.01 ± 0.17 | −0.11 ± 0.20 | 0.18 ± 0.23 |
| |$\rm [K/Mg]$| | 0.02 ± 0.10 | −0.01 ± 0.11 | 0.03 ± 0.10 | −0.02 ± 0.11 | 0.09 ± 0.11 |
| |$\rm [Cr/Mg]$| | −0.11 ± 0.11 | −0.21 ± 0.15 | −0.08 ± 0.11 | −0.25 ± 0.09 | 0.02 ± 0.12 |
| |$\rm [V/Mg]$| | −0.04 ± 0.09 | −0.07 ± 0.13 | −0.03 ± 0.12 | −0.09 ± 0.09 | −0.05 ± 0.13 |
| |$\rm [Co/Mg]$| | −0.08 ± 0.09 | −0.12 ± 0.11 | −0.06 ± 0.10 | −0.14 ± 0.08 | −0.09 ± 0.12 |
| |$\rm [Mn/Mg]$| | −0.04 ± 0.16 | −0.17 ± 0.18 | −0.02 ± 0.14 | −0.24 ± 0.14 | 0.02 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.13 ± 0.08 | −0.20 ± 0.09 | −0.11 ± 0.07 | −0.23 ± 0.06 | −0.12 ± 0.10 |
| |$\rm [Ti/Mg]$| | −0.06 ± 0.14 | −0.10 ± 0.12 | −0.07 ± 0.16 | −0.09 ± 0.11 | −0.01 ± 0.11 |
| |$\rm [C/N]$| | −0.20 ± 0.18 | −0.11 ± 0.24 | −0.23 ± 0.12 | −0.02 ± 0.14 | −0.60 ± 0.32 |
| |$\rm [C/O]$| | −0.10 ± 0.07 | −0.11 ± 0.14 | −0.10 ± 0.11 | −0.11 ± 0.11 | −0.17 ± 0.17 |
| |$\rm [N/O]$| | 0.11 ± 0.15 | −0.03 ± 0.17 | 0.13 ± 0.06 | −0.09 ± 0.07 | 0.41 ± 0.19 |
| |$\rm [Al/O]$| | −0.12 ± 0.07 | −0.29 ± 0.10 | −0.14 ± 0.12 | −0.27 ± 0.12 | −0.27 ± 0.20 |
| . | High Al . | Low Al . | High N . | Low N . | HBB . |
|---|---|---|---|---|---|
| . | |$\rm [Al/O]\gt -0.22$| . | |$\rm [Al/O]\lt -0.22$| . | |$\rm 0.02 \le [N/O]\le 0.3$| . | |$\rm [N/O]\lt 0.02$| . | |$\rm [N/O]\gt 0.30$| . |
| N | 874 | 812 | 872 | 728 | 86 |
| |$\rm \log _{10}(P/days)$| | 1.5 ± 0.4 | 1.8 ± 0.5 | 1.6 ± 0.5 | 1.6 ± 0.5 | 2.0 ± 0.6 |
| |$\rm Amplitude\, [mag]$| | 0.13 ± 0.13 | 0.26 ± 0.23 | 0.15 ± 0.19 | 0.20 ± 0.21 | 0.17 ± 0.21 |
| |$\rm T_{eff}\, [K]$| | 3730 ± 126 | 3683 ± 139 | 3727 ± 126 | 3677 ± 120 | 3822 ± 194 |
| |$\rm \log (g)$| | 0.54 ± 0.29 | 0.42 ± 0.25 | 0.46 ± 0.28 | 0.55 ± 0.21 | 0.07 ± 0.55 |
| |$\rm [M/H]$| | −0.50 ± 0.26 | −0.68 ± 0.29 | −0.57 ± 0.31 | −0.63 ± 0.28 | −0.52 ± 0.31 |
| |$\rm [\alpha /M]$| | 0.08 ± 0.09 | 0.22 ± 0.11 | 0.07 ± 0.05 | 0.25 ± 0.06 | −0.03 ± 0.07 |
| |$\rm [Fe/H]$| | −0.52 ± 0.25 | −0.69 ± 0.28 | −0.59 ± 0.30 | −0.64 ± 0.27 | −0.56 ± 0.30 |
| |$\rm [Mg/Fe]$| | 0.14 ± 0.10 | 0.24 ± 0.12 | 0.13 ± 0.07 | 0.30 ± 0.08 | 0.03 ± 0.09 |
| |$\rm [C/Mg]$| | −0.14 ± 0.09 | −0.15 ± 0.16 | −0.14 ± 0.13 | −0.15 ± 0.14 | −0.22 ± 0.18 |
| |$\rm [N/Mg]$| | 0.08 ± 0.16 | −0.07 ± 0.18 | 0.10 ± 0.08 | −0.13 ± 0.09 | 0.36 ± 0.19 |
| |$\rm [O/Mg]$| | −0.03 ± 0.04 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.04 ± 0.05 | −0.05 ± 0.05 |
| |$\rm [Si/Mg]$| | −0.11 ± 0.05 | −0.12 ± 0.06 | −0.11 ± 0.05 | −0.12 ± 0.05 | −0.08 ± 0.06 |
| |$\rm [Ca/Mg]$| | −0.07 ± 0.07 | −0.10 ± 0.10 | −0.06 ± 0.06 | −0.14 ± 0.08 | 0.05 ± 0.08 |
| |$\rm [Al/Mg]$| | −0.16 ± 0.09 | −0.34 ± 0.11 | −0.20 ± 0.14 | −0.31 ± 0.14 | −0.31 ± 0.14 |
| |$\rm [Na/Mg]$| | −0.04 ± 0.15 | −0.14 ± 0.24 | −0.02 ± 0.16 | −0.17 ± 0.20 | 0.10 ± 0.17 |
| |$\rm [P/Mg]$| | −0.01 ± 0.15 | −0.07 ± 0.25 | 0.01 ± 0.17 | −0.11 ± 0.20 | 0.18 ± 0.23 |
| |$\rm [K/Mg]$| | 0.02 ± 0.10 | −0.01 ± 0.11 | 0.03 ± 0.10 | −0.02 ± 0.11 | 0.09 ± 0.11 |
| |$\rm [Cr/Mg]$| | −0.11 ± 0.11 | −0.21 ± 0.15 | −0.08 ± 0.11 | −0.25 ± 0.09 | 0.02 ± 0.12 |
| |$\rm [V/Mg]$| | −0.04 ± 0.09 | −0.07 ± 0.13 | −0.03 ± 0.12 | −0.09 ± 0.09 | −0.05 ± 0.13 |
| |$\rm [Co/Mg]$| | −0.08 ± 0.09 | −0.12 ± 0.11 | −0.06 ± 0.10 | −0.14 ± 0.08 | −0.09 ± 0.12 |
| |$\rm [Mn/Mg]$| | −0.04 ± 0.16 | −0.17 ± 0.18 | −0.02 ± 0.14 | −0.24 ± 0.14 | 0.02 ± 0.16 |
| |$\rm [Ni/Mg]$| | −0.13 ± 0.08 | −0.20 ± 0.09 | −0.11 ± 0.07 | −0.23 ± 0.06 | −0.12 ± 0.10 |
| |$\rm [Ti/Mg]$| | −0.06 ± 0.14 | −0.10 ± 0.12 | −0.07 ± 0.16 | −0.09 ± 0.11 | −0.01 ± 0.11 |
| |$\rm [C/N]$| | −0.20 ± 0.18 | −0.11 ± 0.24 | −0.23 ± 0.12 | −0.02 ± 0.14 | −0.60 ± 0.32 |
| |$\rm [C/O]$| | −0.10 ± 0.07 | −0.11 ± 0.14 | −0.10 ± 0.11 | −0.11 ± 0.11 | −0.17 ± 0.17 |
| |$\rm [N/O]$| | 0.11 ± 0.15 | −0.03 ± 0.17 | 0.13 ± 0.06 | −0.09 ± 0.07 | 0.41 ± 0.19 |
| |$\rm [Al/O]$| | −0.12 ± 0.07 | −0.29 ± 0.10 | −0.14 ± 0.12 | −0.27 ± 0.12 | −0.27 ± 0.20 |
The high-Al stars have enhanced N, Na, P, Cr, Mn, Ni, and Ti abundances when compared to the low-Al stars. The low-Al stars tend to have larger Mg abundances (|$\rm [Mg/Fe]_{~low~Al}=0.24\pm 0.12$|) and lower metallicities (|$\rm [Fe/H]_{~low~Al}=-0.69\pm 0.28$|) when compared to the high-Al stars (|$\rm [Mg/Fe]_{~high~Al}=0.14\pm 0.10$|, |$\rm [Fe/H]_{~high~Al}=-0.52\pm 0.25$|). The |$\rm [Mg/Fe]$| abundance ratios (at star formation) for both the high-α and low-α sequences tend to increase with decreasing metallicity. In addition, models of both low-mass and intermediate-mass AGB stars show that surface |$\rm [Mg/Fe]$| is enhanced at low metallicities due to dredge-up processes (Cristallo et al. 2011, 2015). In Section 4.3.3, we showed that the SR variables could be enhanced in Mg through dredge-up. Therefore, the larger Mg abundances observed for the low-Al stars can be explained by their birth |$\rm [Mg/Fe]$| distribution and possibly with a contribution from dredge-up processes in AGB stars.
In summary, an analysis of the |$\rm [Al/X]$| abundance ratios of the SR variables shows that the Al abundances are correlated with the pulsation period. We identified two distinct sequences amongst the SR variables corresponding to SR variables with high- and low-Al abundances. The trends of the Al abundances with pulsation period and temperature suggest that the low-Al sequence is likely the result of significant Al depletion through the formation of dust grains containing Al in the stellar winds of AGB stars. The low-Al sequence likely consists of pulsating AGB stars that lose mass through dust-driven winds.
4.3.5 Nitrogen abundances on the TP-AGB
Nitrogen production during the AGB phase is dominated by hot bottom burning (HBB) in intermediate mass stars with M ≳ 3 M⊙ (Scalo et al. 1975; McSaveney et al. 2007). During HBB, proton-capture nucelosynthesis occcurs at the base of the outer envelope, favoring the conversion of C–N through the CN cycle (Boothroyd & Sackmann 1992) where the |$^{12}\rm C,^{15}\rm N$|, |$^{16}\rm O$|, and |$^{18}\rm O$| isotopes are destroyed to produce |$^{14}\rm N$| (Lattanzio et al. 1996). This can only happen if the temperature at the bottom of the envelope exceeds ∼50 × 106 K (García-Hernández et al. 2013). In these intermediate mass stars, the combination of third dredge-up and HBB results in increased N abundances (McSaveney et al. 2007). At the onset of the thermal pulses, HBB reduces the |$^{12}\rm C$| abundance to ∼1/15 of the MS value and increases the |$^{14}\rm N$| abundance to ∼5−6 times the MS value (Lattanzio & Wood 2004). TDU episodes can continue after HBB ceases to operate, allowing the C abundances to again increase (Frost & Lattanzio 1996).
We investigate the |$\rm [C/Mg]$| and |$\rm [C/N]$| abundance ratios for the SR variables, APOGEE AGB and RGB stars in Fig. 32. The |$\rm [C/Mg]$| abundance ratios for both the SR variables and APOGEE/AGB stars are positively correlated with |$\rm [Mg/H]$|. The APOGEE/AGB stars and SR variables tend to be carbon poor when compared to the APOGEE/RGB stars. Only |${\sim }20{ per\ cent}$| of the APOGEE/RGB stars have |$\rm [C/Mg]{\lesssim }-0.1$|, whereas |${\sim }75{ per\ cent}$| of the SR variables and |${\sim }64{ per\ cent}$| of the APOGEE/AGB stars have |$\rm [C/Mg]{\lesssim }-0.1$|. The APOGEE/AGB stars form three distinct clusters in the |$\rm [C/N]$|–|$\rm [Mg/H]$| plane at (−0.4, −0.25), (−0.25, 0), and (0.25, −0.25). However, the vast majority of the SR variables only populate the two clusters with |$\rm [Mg/H]\,\,\lt\,\, 0$|. This is not too surprising as SR variables with |$\rm [Mg/H]\,\,\gt\,\, 0$| are rare in our catalogue. The distribution of the APOGEE/RGB stars overlap the metal-rich cluster of APOGEE/AGB stars at (0.25, −0.25) that is devoid of SR variables, suggesting that the sample of APOGEE/AGB stars is likely contaminated with stars on the RGB. The distribution of |$\rm [C/N]$| is strongly bi-modal for both the SR variables and the APOGEE/AGB stars (|$\rm [C/N]{\sim }-0.2$| and |$\rm [C/N]{\sim }0$|), whereas the APOGEE/RGB stars form a continuous distribution in |$\rm [C/N]$|, peaking at |$\rm [C/N]{\sim }-0.2$|. Compared to the APOGEE/RGB stars, there is a small enhancement in the distribution of APOGEE/AGB stars and SR variables with |$\rm [C/N]{\lesssim }-0.5$|. These are potentially sources with significant N enhancement due to HBB.
![$\rm [C/Mg]$ (top left) and $\rm [C/N]$ (top right) versus $\rm [Mg/H]$ for the semiregular variables (black) and APOGEE AGB stars (orange). The distributions of the APOGEE RGB stars in these planes are shown as contours. The distributions of $\rm [C/Mg]$ (bottom left) and $\rm [C/N]$ (bottom right) for the semiregular variables (black) APOGEE AGB (orange) and RGB (blue) stars are shown as the histograms.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig32.jpeg?Expires=1749866512&Signature=CebGDvlC1R2A6aqDn3KWbFWxCeQZhyMyZiaOI1WjTdib5qT~LdeLIM4mJVOvgB760pQ2NzjqlpiNDLWI~m31XyK7grHA56EldpFbj~YrkTMOLZHbY~IJRUqVn7dDA1XP~gqD7AWGdlkAk52lNyCNWjgqk0lI4Ag9rbkztFKJmKSmmzQSa2Gf1RJ7T1QJ0MnQfOzziiNHfp~NblgZw1PBRqH4UKNn84ESdDR3-R7cxEbmfuPhXcVbrEDRcoIb1BSyl8wPwVXj9~f1V38He93i88LUQGj6ei1R20gtwkOg0ap1wRZqkQM-dRw8NL~7rNa2q2e1SOrY7BaIxNoL9vhhtw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$\rm [C/Mg]$| (top left) and |$\rm [C/N]$| (top right) versus |$\rm [Mg/H]$| for the semiregular variables (black) and APOGEE AGB stars (orange). The distributions of the APOGEE RGB stars in these planes are shown as contours. The distributions of |$\rm [C/Mg]$| (bottom left) and |$\rm [C/N]$| (bottom right) for the semiregular variables (black) APOGEE AGB (orange) and RGB (blue) stars are shown as the histograms.
In the |$\rm [N/Mg]$|–|$\rm [Mg/H]$| plane (Fig. 33), the APOGEE/AGB stars and SR variables form clusters at (−0.4, 0.1) and (−0.25, −0.15). Similarly, in the |$\rm [Mg/H]$|–|$\rm [N/O]$| plane, the APOGEE/AGB stars form three distinct clusters at (−0.25, −0.1), (−0.4, 0.15), and (0.25,0.15), with the SR variables populating the two clusters with |$\rm [Mg/H]\,\,\lt\,\, 0$|. The distribution of APOGEE/RGB stars in |$\rm [N/Mg]$| appears to be bi-modal, with peaks that are similar to those seen for the SR variables and APOGEE/AGB stars. Unlike the APOGEE/RGB stars, the distribution in |$\rm [N/O]$| is strongly bi-modal for both the SR variables and APOGEE/AGB stars. We also note the presence of some stars with large |$\rm [N/Mg]$| (|$\rm [N/Mg]\gtrsim 0.25$|) and |$\rm [N/O]$| (|$\rm [N/O]{\gtrsim }0.3$|) abundance ratios. These N-rich sources are candidates for intermediate-mass AGB stars where the surface abundances of N are greatly enhanced due to HBB.
![$\rm [N/Mg]$ (top left) and $\rm [N/O]$ (top right) versus $\rm [Mg/H]$ for the semiregular variables (black) and APOGEE AGB stars (orange). The distributions of the APOGEE RGB stars in these planes are shown as the contours. The distributions of $\rm [N/Mg]$ (bottom left) and $\rm [N/O]$ (bottom right) for the semiregular variables (black) APOGEE AGB (orange) and RGB (blue) stars are shown as the histograms.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/503/1/10.1093_mnras_stab114/1/m_stab114fig33.jpeg?Expires=1749866512&Signature=Nh5MIxcJN6~UhMvrMSNep3K6GAu2hRJQDTXIIHIe4dLMuFvDYUmjd0ZMqtGYrSn9GPZA7Hk5fv~xVtxj0I6xpSqfJYh~tNg362Riq757dBIDRAVt1-5edHWTPjfSZXM6OOhOvY64DB4BBq3GdJVqwQXu3EMyg0gu0p9yx0F5dO~Zf5wlsll1G5VmDHUXVJK8qpi0MkbsAvqqcivmM3~m8Tnn2pMZRP0GVHPQuuPs-wgK5f2Px-DsuTD3hu0zzWZmztDHiR4rmJ5ip5ISqBAejyz7wwpwbOzxsan3LMPwF~0~4Xa-KC6EmSFQMBkV0-m~q4mZ5p9LUZdIqv2h3tr0hw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$\rm [N/Mg]$| (top left) and |$\rm [N/O]$| (top right) versus |$\rm [Mg/H]$| for the semiregular variables (black) and APOGEE AGB stars (orange). The distributions of the APOGEE RGB stars in these planes are shown as the contours. The distributions of |$\rm [N/Mg]$| (bottom left) and |$\rm [N/O]$| (bottom right) for the semiregular variables (black) APOGEE AGB (orange) and RGB (blue) stars are shown as the histograms.
SR variables and APOGEE/AGB stars with |$\rm [N/Mg]{\lesssim }-0.3$| are very rare. Similarly, there is a sharp cut-off in |$\rm [N/O]$| for both the SR variables and APOGEE/AGB stars at |$\rm [N/O]{\sim }-0.3$|. Only |${\sim }0.7{ per\ cent}$| of the SR variables and |${\sim }0.5{ per\ cent}$| of the APOGEE/AGB stars have |$\rm [N/O]{\lesssim }-0.3$|, whereas |${\sim }4.7{ per\ cent}$| of the APOGEE/RGB stars have |$\rm [N/O]{\lesssim }-0.3$|. While the N abundances are enhanced and the O abundances are depleted due to the CN cycle, the Mg–Al chain also operates during HBB, destroying the Mg isotopes |$\rm ^{24}Mg$| and |$\rm ^{25}Mg$|. In a scenario where HBB operates in an AGB star, the surface abundances of |$\rm [N/Mg]$| and |$\rm [N/O]$| will increase due to N enrichment and Mg/O depletion. Thus, the observed cut-offs in the |$\rm [N/Mg]$| and |$\rm [N/O]$| abundance ratios could potentially be related to the nucelosynthetic processes that occur during HBB.
Based on their |$\rm [N/O]$| abundance ratios, we group the SR variables into the ‘high-N’ group (|$\rm 0.02 \le [N/O]\le 0.3$|), ‘low-N’ group (|$\rm [N/O]\lt 0.02$|), and intermediate-mass AGB stars that are candidates for HBB (|$\rm [N/O]\gt 0.30$|). The various APOGEE DR16 spectroscopic parameters and chemical abundance ratios for these groups are summarized in Table 6.
The HBB candidates with |$\rm [N/O]\gt 0.30$| are distinct from the high-N and low-N stars. They have significantly lower |$\rm \log (g){\sim }0.07$|, when compared to the high-N (|$\rm \log (g){\sim }0.46$|) and low-N (|$\rm \log (g){\sim }0.55$|) groups. The HBB candidates are generally hotter than the high-N and low-N stars, with a median temperature of |$\rm T_{eff}\, {\sim }3822\pm 194$| K. The HBB candidates have a median period of |$\rm \log _{10}(P/days)\,\,{\sim }\,\,2$|, which is consistent with these stars pulsating in the fundamental mode (Fadeyev 2017). Much like the high-N stars, the HBB candidates also have low |$\rm [\alpha /M]$| abundance ratios (|$\rm [\alpha /M]{\sim }-0.04$|) consistent with the low-α sequence. The HBB stars have average |$\rm [Al/Mg]$| and |$\rm [Al/O]$| abundance ratios (|$\rm [Al/Mg]{\sim }-0.3$|, |$\rm [Al/O]{\sim }-0.3$|) that are consistent with the low-Al sequence identified in Section 4.3.4. Compared to both the high-N and low-N groups, the HBB candidates are poor in Mg and C and they have enhanced N, Ca, Na, P, K, Cr, Mn, and Ti abundances compared to both the high-N and low-N groups. The |$\rm [C/N]$| abundance ratios of the HBB candidates are significantly different – these HBB candidates have |$\rm [C/N]{\simeq }-0.6\pm 0.3$|, compared to |$\rm [C/N]{\simeq }-0.2\pm 0.1$| for the high-N and |$\rm [C/N]{\simeq }0.0\pm 0.1$| for the low-N stars.
The high-N and low-N stars have similar periods, temperatures, and |$\rm \log (g)$|. The slight differences in these measures(|$\rm \Delta Teff {\sim }50$| K, |$\rm \Delta \log (g) {\sim }0.1$|) might suggest that the high-N stars are somewhat more evolved and hotter than the low-N stars. The high-N stars have |$\rm [\alpha /M]$| abundance ratios that are consistent with them being on the low-α sequence, whereas the low-N stars have |$\rm [\alpha /M]$| consistent with them being high-α stars. The low-N stars have larger Mg abundances (|$\rm \Delta [Mg/Fe]{\sim }0.2$| dex) than the high-N stars. The |$\rm [Al/Mg]$| and |$\rm [Al/O]$| abundance ratios of the low-N stars are lower than that of the high-N stars and possibly indicate that these stars are undergoing mass-loss. The high-N stars have enhanced N, Ca, Na, P, K, Cr, V, Co, Mn, and Ni abundances when compared to the low-N stars.
In summary, we identified a ‘high-N’ group (|$\rm 0.02 \le [N/O]\le 0.3$|), and a ‘low-N’ group (|$\rm [N/O]\lt 0.02$|) amongst the SR variables. The high-N stars differ in their chemical profiles when compared to the low-N stars. We also identified a sample of N-enhanced, likely intermediate-mass AGB stars (|$\rm [N/O]\gt 0.30$|) going through significant HBB. We also find that the HBB candidates are carbon poor with |$\rm [C/N]{\sim }-0.6$|.
5 CONCLUSIONS
We systematically searched for variable sources in ASAS-SN with V < 17 mag in the V-band light curves of ∼61.5 million sources. Through our search which first began in 2018, we identified ∼426 000 variable sources, of which ∼219 000 are new discoveries. The V-band light curves of all the ∼61.5M sources studied in this work are available online at the ASAS-SN Photometry Data base (https://asas-sn.osu.edu/photometry). The V-band light curves and other information on the variable stars identified in our work are available on the ASAS-SN variable stars data base (https://asas-sn.osu.edu/variables). ASAS-SN has significantly improved the census of SR/irregular variables (|$+235{ per\ cent}$|), δ Scuti variables (|$+81{ per\ cent}$|), rotational variables (|$+116{ per\ cent}$|), and detached eclipsing binaries (|$+90{ per\ cent}$|) with V < 17 mag. Most (|${\sim }74{ per\ cent}$|) of our discoveries were in the Southern hemisphere.
Due to the overlap between ASAS-SN and modern major wide-field spectroscopic surveys, we are able to utilize spectroscopic information to closely study various variable types. We cross-matched our catalogue of variables with the APOGEE DR16 catalogue, the RAVE-on catalogue, the LAMOST DR5 v4 catalogue and the GALAH DR2 catalogue, and identified ∼39 000 unique cross-matches. We find that data from the LAMOST and RAVE surveys are best suited to the characterization of pulsators, eclipsing binaries, and rotational variables. APOGEE data are excellent for the characterization of the cooler SR and irregular variables. Our main results for eclipsing binaries, rotational variables, and SR variables are summarized below.
Eclipsing binaries:
EW-type contact binaries are significantly cooler (|$\rm T_{eff}{\sim }5900$| K) than both the semidetached EB binaries (|$\rm T_{eff}{\sim }6700$| K) and the detached EA systems (|$\rm T_{eff}{\sim }6300$| K).
There is significant overlap in period–temperature space between the early-type EW and EB binaries. This overlap is consistent with the predictions of the TRO models for contact binaries, where systems can transition between the semidetached and contact phases.
Most (|${\sim }63{ per\ cent}$|) eclipsing binaries have metallicities |$\rm -0.5\lt [Fe/H]\lt 0$|. This is consistent with recent findings of higher binary fractions at lower metallicity (Badenes et al. 2018; El-Badry & Rix 2019; Moe et al. 2019).
The period–temperature distributions depend on metallicity, with lower metallicity binaries having shorter periods at fixed temperature.
Contact binaries have an observed period–temperature relationship that falls below that of the semidetached and detached binaries at any given temperature and tracks Roche expectations.
Rotational variables:
We find rotational variables on the MS/pre-MS (|$\rm \log (g){\sim }4.5$|, |$\rm M_{Ks}{\sim }4$| mag), the base of the RGB (|$\rm \log (g){\sim }3.5$|, |$\rm M_{Ks}{\sim }1$| mag) and the RC (|$\rm \log (g){\sim }2.6$|, |$\rm M_{Ks}{\sim }-1.5$| mag).
Approximately |$81{ per\ cent}$| of the rotating giants with spectroscopic |$v$|sin (i) were rapid rotators with |$v\sin (i)\gt 10 \rm \, km\,s^{ -1}$|.
Approximately |$80{ per\ cent}$| of the giants have |$v_{\rm rot}\,\,\gt\,\, 10 \rm \, km\,s^{ -1}$|, consistent with the estimate of rapid rotators with spectroscopic |$v$|sin (i).
Approximately |$98{ per\ cent}$| of the rotational variables on the RC have |$v_{\rm rot}\gt 10 \rm \, km\,s^{ -1}$|.
Approximately |$30{ per\ cent}$| of the rapidly rotating RC stars are metal-poor with |$\rm [Fe/H]\lt -0.5$|, whereas only |${\sim }8{ per\ cent}$| are metal-rich with |$\rm [Fe/H]\gt 0$|.
Approximately |$87{ per\ cent}$| of the rotating giants had NUV excesses from Dixon et al. (2020) consistent with |$v\sin (i)\gt 10 \rm \, km\,s^{ -1}$|. This is consistent with our other estimates of the fraction of sources with rapid rotation (|$v\sin (i)\gt 10 \rm \, km\,s^{ -1}$|).
Evolved rotating giants have larger amplitudes than MS rotational variables at any given period, with the variability amplitudes peaking at |$\rm \log (g){\sim }3.2$|.
The NUV excesses of these rotating giants follow a similar trend with period to the work of Dixon et al. (2020).
The rotational variables in APOGEE are low-α stars strongly clustered towards |$\rm [Mg/Fe]{\sim }-0.1$| and |$\rm [Fe/H]{\sim }-0.1$|, distinct from the typical giant stars or the SR variables and AGB stars. These abundances are unusual and suggestive of systematic issues in the ASPCAP pipeline when dealing with rapidly rotating stars.
Semiregular variables and Miras:
SR variables tend to be lower metallicity (|$\rm [Fe/H]{\sim }-0.5$|) than most giant stars.
Of the SR variables with |$\rm \log _{10}(P/days) \gtrsim 2.3$|, |${\sim }36{ per\ cent}$| were LSPs. Approximately |$60{ per\ cent}$| of the LSPs had pulsational periods in the range |$1.5 \lesssim \rm \log _{10}(P/days) \lesssim 1.9$|. The LSP was on average ∼11 times longer than the actual pulsation period.
Many SR variables have LSPs, and while it seems clear that the shorter period rather than the LSP is more closely related to the physical properties of the star, we could identify no spectroscopic property (|$\rm T_{eff}$|, |$\rm \log (g)$|, abundances, etc.) which distinguished SR variables with LSPs from those without.
The vast majority of the ASAS-SN Mira (|${\sim }97{ per\ cent}$|) and SR variables (|${\sim }95{ per\ cent}$|) are oxygen-rich AGB stars.
We fit a temperature –WRP− WJK relation that returns temperatures that are, on average, within |$\pm 0.7{ per\ cent}$| of the APOGEE temperatures for the oxygen-rich SR variables with |$\rm T_{eff}\lt 3800$| K and |$-0.7 {\, \rm mag} \le W_{RP}-W_{JK}\le 0.8 {\, \rm mag}$|. We tested an extrapolation of this temperature – WRP − WJK relation to estimate the temperatures of the Mira variables with WRP − WJK < −0.7 mag. We find the results of our extrapolation consistent with the expected temperatures of Miras (Yao et al. 2017).
The peak shifts in the |$\rm [Mg/Fe]$| and |$\rm [\alpha /M]$| abundance ratios for the high-α and low-α stars relative to the APOGEE giants indicate possible α-enhancements due to the effects of the third dredge-up in AGB stars.
The |$\rm [Al/X]$| abundance ratios of the SR variables are correlated with the pulsation period. These abundance ratios decrease with period and plateau beyond the canonical period of P ∼ 60 d where dust formation first occurs.
We identified a ‘high-Al’ and a ‘low-Al’ sequence amongst the SR variables. The Al depleted ‘low-Al’ sequence likely corresponds to AGB stars with significant dust production and mass-loss. Cuts of |$\rm [Al/Mg]=-0.25$|, |$\rm [Al/C]=-0.1$|, |$\rm [Al/O]=-0.22$|, or |$\rm [Al/Si]=-0.13$| roughly separate the high-Al and low-Al sequences.
We identified a ‘high-N’ group (|$\rm 0.02 \le [N/O]\le 0.3$|), and a ‘low-N’ group (|$\rm [N/O]\lt 0.02$|) amongst the SR variables. The high-N stars have enhanced Ca, N, Na, P, K, Cr, V, Co, Mn, and Ni abundances when compared to the low-N stars.
We identified a sample of likely intermediate-mass AGB stars going through significant HBB using the cut-off |$\rm [N/O]\gt 0.30$|. The HBB candidates are poor in Mg and C (|$\rm [C/N]{\sim }-0.6$|), but have enhanced N, Ca, Na, P, K, Cr, Mn, and Ti abundances compared to both the high-N and low-N groups.
This work is a first exploration of the powerful synergy between wide-field photometric and spectroscopic surveys towards deciphering the various properties of variable stars. As the number of stars with spectroscopic measurements increases by orders of magnitude over the coming years, it will be possible to study much larger samples of variable stars in greater detail. While we have not examined it here, larger samples with models of selection effects can be used to examine the detailed fractions of variable types as a function of their spectroscopic properties, similar to the recent studies of the dependence of binary fraction on metallicity (Badenes et al. 2018; El-Badry & Rix 2019; Moe et al. 2019).
ACKNOWLEDGEMENTS
This work is dedicated to the memory of our friend and colleague David Will, whose enduring support enabled the success of the ASAS-SN project.
We thank the anonymous referee for the very useful comments that improved our presentation of this work. We thank Dr. Jamie Tayar for her help with interpreting the APOGEE data used in this analysis. We thank the LCO and its staff for its continuing support of the ASAS-SN project. We also thank the Ohio State University College of Arts and Sciences Technology Services for helping us set up and maintain the ASAS-SN variable stars and photometry data bases.
ASAS-SN is supported by the Gordon and Betty Moore Foundation through grant GBMF5490 to the Ohio State University, and NSF grants AST-1515927 and AST-1908570. Development of ASAS-SN has been supported by NSF grant AST-0908816, the Mt. Cuba Astronomical Foundation, the Center for Cosmology and AstroParticle Physics at the Ohio State University, the Chinese Academy of Sciences South America Center for Astronomy (CAS-SACA), the Villum Foundation, and George Skestos.
KZS and CSK are supported by NSF grants AST-1515927, AST-1814440, and AST-1908570. BJS is supported by NSF grants AST-1908952, AST-1920392, and AST-1911074. TAT acknowledges support from a Simons Foundation Fellowship and from an IBM Einstein Fellowship from the Institute for Advanced Study, Princeton. Support for JLP is provided in part by the Ministry of Economy, Development, and Tourism’s Millennium Science Initiative through grant IC120009, awarded to The Millennium Institute of Astrophysics, MAS. Support for MP and OP has been provided by INTER-EXCELLENCE grant LTAUSA18093 from the Czech Ministry of Education, Youth, and Sports. The research of OP has also been supported by Horizon 2020 ERC Starting Grant ‘Cat-In-hAT’ (grant #803158) and PRIMUS/SCI/17 award from Charles University. This work was partly supported by NSFC 11721303.
Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colourado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
This work has used data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium. This publication has used data products from the Two Micron All Sky Survey, as well as data products from the Wide-field Infrared Survey Explorer. This research was also made possible through the use of the AAVSO Photometric All-Sky Survey (APASS), funded by the Robert Martin Ayers Sciences Fund.
This research has used the VizieR catalogue access tool, CDS, Strasbourg, France. This research also used astropy, a community-developed core python package for Astronomy (Astropy Collaboration 2013).
DATA AVAILABILITY
The ASAS-SN photometric data underlying this article are available on the ASAS-SN Photometry Data base (https://asas-sn.osu.edu/photometry) and the ASAS-SN variable stars data base (https://asas-sn.osu.edu/variables). The external photometric data underlying this article were accessed from sources in the public domain: Gaia (https://www.cosmos.esa.int/gaia), 2MASS (https://old.ipac.caltech.edu/2mass/overview/access.html), AllWISE (http://wise2.ipac.caltech.edu/docs/release/allwise/), and GALEX (https://archive.stsci.edu/missions-and-data/galex-1/). The spectroscopic data sets underlying this article were accessed from sources in the public domain: APOGEE (https://www.sdss.org/dr16/), LAMOST (http://dr5.lamost.org/), GALAH (https://galah-survey.org/publicdata/), and RAVE (https://www.rave-survey.org/).



