-
PDF
- Split View
-
Views
-
Cite
Cite
K L Malanchev, M V Pruzhinskaya, V S Korolev, P D Aleo, M V Kornilov, E E O Ishida, V V Krushinsky, F Mondon, S Sreejith, A A Volnova, A A Belinski, A V Dodin, A M Tatarnikov, S G Zheltoukhov, (The SNAD Team), Anomaly detection in the Zwicky Transient Facility DR3, Monthly Notices of the Royal Astronomical Society, Volume 502, Issue 4, April 2021, Pages 5147–5175, https://doi.org/10.1093/mnras/stab316
Close - Share Icon Share
ABSTRACT
We present results from applying the SNAD anomaly detection pipeline to the third public data release of the Zwicky Transient Facility (ZTF DR3). The pipeline is composed of three stages: feature extraction, search of outliers with machine learning algorithms, and anomaly identification with followup by human experts. Our analysis concentrates in three ZTF fields, comprising more than 2.25 million objects. A set of four automatic learning algorithms was used to identify 277 outliers, which were subsequently scrutinized by an expert. From these, 188 (68 per cent) were found to be bogus light curves – including effects from the image subtraction pipeline as well as overlapping between a star and a known asteroid, 66 (24 per cent) were previously reported sources whereas 23 (8 per cent) correspond to non-catalogued objects, with the two latter cases of potential scientific interest (e.g. one spectroscopically confirmed RS Canum Venaticorum star, four supernovae candidates, one red dwarf flare). Moreover, using results from the expert analysis, we were able to identify a simple bi-dimensional relation that can be used to aid filtering potentially bogus light curves in future studies. We provide a complete list of objects with potential scientific application so they can be further scrutinised by the community. These results confirm the importance of combining automatic machine learning algorithms with domain knowledge in the construction of recommendation systems for astronomy. Our code is publicly available.1
1 INTRODUCTION
The meaning of astronomical discovery has changed throughout history, but it has always been highly correlated with the technological development of the era and the sociological construct that accompanies it. In astronomy, the discovery of new or unexpected astronomical sources was often serendipitous (Dick 2013), for example, the discovery of gamma-ray bursts in the late 1960s by the Vela satellites (Klebesadel, Strong & Olson 1973) or the discovery of the cosmic microwave background radiation by Robert Wilson and Arno Penzias (Penzias & Wilson 1965). The advent of the CCD highly increased our ability to gather photometric data, and allowed programmed systematic searches for scientifically interesting objects (Filippenko 1992; Perlmutter et al. 1992; Richmond, Treffers & Filippenko 1993). Nevertheless, manual screening continued to play a central role in the discovery of new sources (e.g. Cardamone et al. 2009; Borisov 2019).
The arrival of large-scale sky surveys like the Sloan Digital Sky Survey (SDSS; Blanton et al. 2017) and, more recently, the Zwicky Transient Facility (ZTF; Bellm et al. 2019; Masci et al. 2019) pushed this paradigm even further. Confronted with data sets holding observational data from around a billion sources, the use of automated machine learning methods to search for new physics was unavoidable (Ball & Brunner 2010). This trend, shifting the astronomical data analysis towards data-driven approaches, is highly recognized in supervised learning tasks (e.g. photometric classification of transients, Ishida 2019), but it is as crucial for unsupervised ones. Given that new astronomical surveys are always accompanied by technological developments that allow them to probe different epochs in the evolution of the Universe, or different regions within our own galaxy, every new instrument has a high probability of observing previously non-catalogued phenomena. At the same time, every new data set is more complex and bigger than its precedents. In the absence of appropriate unsupervised learning pipelines, we may miss the discovery opportunity which is in the root of all scientific endeavour.
This key aspect of unsupervised learning in astronomical research has been recognized by the research community with some extent, producing interesting illustrative examples: Rebbapragada et al. (2009) discovered periodic variable stars using a Phased k-means algorithm; Hoyle et al. (2015) isolated and removed problematic objects for photometric redshift estimation with an Elliptical Envelope routine; Nun et al. (2016) selected five different algorithms for an ensemble method tested on three MACHO fields and confirmed some objects belonging to rare classes; Baron & Poznanski (2017) identified anomalous galaxy spectra based on an Unsupervised Random Forest (URF); Solarz et al. (2017) used One-Class Support Vector Machine (O-SVM) to find weird objects in photometric data, including a few misclassifications; Reyes & Estévez (2020) used a geometric transformation-based model to highlight artefacts’ properties from real objects in ZTF images; and Soraisam et al. (2020, 2021) identified novel events in variable source population by computing distributions of magnitude changes over time intervals for a given filter.
The task of applying machine learning algorithms to real data also requires the data to be translated into an acceptable format for automatic learning applications, for example each light curve could be transformed to a vector of features. Modern astronomical data are frequently composed of a large number of correlated features that must be simplified and/or homogenized. Several works provide details on efforts in the dimensionality reduction stage. For example: Pruzhinskaya et al. (2019) located both novel and misclassified transient events light curves in the Open Supernova Catalog (Guillochon et al. 2017) after applying t-SNE to Gaussian-process approximated light curves, combined with an isolation forest (IF) and confirmed by expert analysis. Martínez-Galarza et al. (2020) implemented tree-based algorithms (IF, URF) and two manifold-based algorithms (t-SNE, UMAP) to identify anomalies, using their bona fide anomaly Boyajian’s star (KIC 8462852; Boyajian et al. 2016) as reference, and investigated how an ensemble of such methods can be used to find objects of similar phenomenology or astrophysical characteristics. This work was built off of Giles & Walkowicz (2019), who used t-SNE to visually represent cluster membership designations of Kepler light curve data (including Boyajian’s star as a ‘ground truth’ anomaly) from DBSCAN. The same authors applied the same technique to range Kepler objects by their outlier score (Giles & Walkowicz 2020). Similarly, Webb et al. (2020) used t-SNE to visually represent HDBSCAN cluster membership designations of Deeper, Wider, Faster program light curves combined with anomaly scores assigned by an IF algorithm in their interactive astronomaly package (Lochner & Bassett 2020).
In this work, we present detailed description of a complete anomaly detection pipeline and its results when applied to three fields from ZTF Data Release 3 (DR3).1 The SNAD2 pipeline was built with the goal of exploiting the potential of modern astronomical data sets for discovery and under the hypothesis that, although automatic learning algorithms have a crucial role to play in this task, the scientific discovery is only completely realized when such systems are designed to boost the impact of domain knowledge experts. Our approach combines a diverse set of machine learning algorithms, tailored feature extraction procedures, and domain knowledge experts who validate the results of the machine learning pipeline (Ishida et al. 2019; Kornilov et al. 2019; Pruzhinskaya et al. 2019; Aleo et al. 2020; Malanchev et al. 2020).
In what follows, Section 2 describes the ZTF data and the adopted preprocessing steps. Section 3 details the outlier detection algorithms, follow-up observations and expert analysis employed in this work. Section 4 lists the outliers found by the complete pipeline and Section 5 reports numerical efficiency of our pipeline in identifying fake light curves. Section 6 provides a deeper analysis of our feature parameter space. Our conclusions are outlined in Section 7. We also provide further details of our analysis in the appendices: Appendix A mathematically defines the extracted light curve features, and Appendix B describes the SNAD ZTF DR object web-viewer and cross-match tool, constructed to help the experts in their critical evaluation of each outlier. Appendix C illustrates results from the light-curve fit of the supernova candidates and Appendix D lists properties of each anomaly candidate discovered from this work.
Our code, zwad, is publicly available at https://github.com/snad-space/zwad, and the SNAD team’s ZTF DR3 object viewer can be found at https://ztf.snad.space/.
2 ZTF DATA
The ZTF is a 48-inch Schmidt telescope on Mount Palomar, equipped with a 47 deg2 camera, which allows rapid scanning of the entire north sky. The ZTF survey started on 2018 March and during its initial phase has observed around a billion objects (Bellm et al. 2019). Beyond representing the current state of the art in rapid photometric observations, ZTF also has the crucial role of being the predecessor of the next generation of large-scale surveys like the Vera Rubin Observatory Legacy Survey of Space and Time3 (LSST). Many of its data protocols are being used as test-bench for LSST systems.
In this work, we analysed data from the first 9.4 months of the ZTF survey, between 2018 March 17 and December 31 (58194 ≤ MJD ≤ 58483). This period includes data from ZTF private survey, thus having a better cadence than the rest of DR3. We selected only perfectly clean extractions at every epoch (|$\tt {catflag} = 0$|) obtained in passband zr, which encloses more than half of all objects.
Light curves from ZTF DR3 are spread over 1020 fields, with objects within the same field being sampled with a similar cadence – on average ∼1 d for the Galactic plane and ∼3 d for the Northern-equatorial sky. In order to minimize effects due to different cadences, we performed our analysis in three separate fields: ‘M 31’ (a part of ZTF field 695), which includes the Andromeda galaxy (Messier 1781), ‘deep’ (ZTF field 795), located far from the Galactic plane, and ‘disk’ (ZTF field 805), located in the Galaxy plane. The Andromeda galaxy region is a well-studied part of the sky, thus allowing further scrutiny of candidates with external information. The Andromeda galaxy is fully imaged by only one CCD, thus the M 31 field of view (FOV) is only 1/16 of ZTF light-sensitive area (∼3 deg2), and does not contain as many objects as the two other fields. For disk and deep, we chose fields with high declination, which allow easier follow-up observations by Northern hemisphere facilities, and which maximize the number of field objects.
We imposed a final selection cut by choosing light curves with at least 100 observations in M 31 and deep, and at least 500 observations in disk. All data were downloaded from IRSA IPAC.4 The number of light curves passed through the selection cuts are shown in Table 1 along with a few other properties of these fields.
| Field name . | ZTF field . | Centre (α, δ) . | Centre (l, b) . | FOV . | N . | Object count . |
|---|---|---|---|---|---|---|
| M 31 | Field 695, ccdid 11 | 10|${_{.}^{\circ}}$|72, 41|${_{.}^{\circ}}$|34 | 121|${_{.}^{\circ}}$|20, −21|${_{.}^{\circ}}$|51 | 3 deg2 | ≥100 | 57 546 |
| deep | Field 795 | 246|${_{.}^{\circ}}$|72, 54|${_{.}^{\circ}}$|88 | 83|${_{.}^{\circ}}$|91, 42|${_{.}^{\circ}}$|45 | 55 deg2 | ≥100 | 406 611 |
| disk | Field 807 | 19|${_{.}^{\circ}}$|99, 62|${_{.}^{\circ}}$|05 | 126|${_{.}^{\circ}}$|27, −0|${_{.}^{\circ}}$|63 | 55 deg2 | ≥500 | 1790 565 |
| Field name . | ZTF field . | Centre (α, δ) . | Centre (l, b) . | FOV . | N . | Object count . |
|---|---|---|---|---|---|---|
| M 31 | Field 695, ccdid 11 | 10|${_{.}^{\circ}}$|72, 41|${_{.}^{\circ}}$|34 | 121|${_{.}^{\circ}}$|20, −21|${_{.}^{\circ}}$|51 | 3 deg2 | ≥100 | 57 546 |
| deep | Field 795 | 246|${_{.}^{\circ}}$|72, 54|${_{.}^{\circ}}$|88 | 83|${_{.}^{\circ}}$|91, 42|${_{.}^{\circ}}$|45 | 55 deg2 | ≥100 | 406 611 |
| disk | Field 807 | 19|${_{.}^{\circ}}$|99, 62|${_{.}^{\circ}}$|05 | 126|${_{.}^{\circ}}$|27, −0|${_{.}^{\circ}}$|63 | 55 deg2 | ≥500 | 1790 565 |
| Field name . | ZTF field . | Centre (α, δ) . | Centre (l, b) . | FOV . | N . | Object count . |
|---|---|---|---|---|---|---|
| M 31 | Field 695, ccdid 11 | 10|${_{.}^{\circ}}$|72, 41|${_{.}^{\circ}}$|34 | 121|${_{.}^{\circ}}$|20, −21|${_{.}^{\circ}}$|51 | 3 deg2 | ≥100 | 57 546 |
| deep | Field 795 | 246|${_{.}^{\circ}}$|72, 54|${_{.}^{\circ}}$|88 | 83|${_{.}^{\circ}}$|91, 42|${_{.}^{\circ}}$|45 | 55 deg2 | ≥100 | 406 611 |
| disk | Field 807 | 19|${_{.}^{\circ}}$|99, 62|${_{.}^{\circ}}$|05 | 126|${_{.}^{\circ}}$|27, −0|${_{.}^{\circ}}$|63 | 55 deg2 | ≥500 | 1790 565 |
| Field name . | ZTF field . | Centre (α, δ) . | Centre (l, b) . | FOV . | N . | Object count . |
|---|---|---|---|---|---|---|
| M 31 | Field 695, ccdid 11 | 10|${_{.}^{\circ}}$|72, 41|${_{.}^{\circ}}$|34 | 121|${_{.}^{\circ}}$|20, −21|${_{.}^{\circ}}$|51 | 3 deg2 | ≥100 | 57 546 |
| deep | Field 795 | 246|${_{.}^{\circ}}$|72, 54|${_{.}^{\circ}}$|88 | 83|${_{.}^{\circ}}$|91, 42|${_{.}^{\circ}}$|45 | 55 deg2 | ≥100 | 406 611 |
| disk | Field 807 | 19|${_{.}^{\circ}}$|99, 62|${_{.}^{\circ}}$|05 | 126|${_{.}^{\circ}}$|27, −0|${_{.}^{\circ}}$|63 | 55 deg2 | ≥500 | 1790 565 |
3 METHODOLOGY
Our anomaly detection pipeline is composed of three stages: feature extraction (Section 3.1), outlier detection using machine learning (Section 3.2), and domain expert analysis (Section 3.3).
We consider as outliers all the objects which result from the machine learning algorithms. Among the outliers we define two groups of objects, i.e. ‘bogus outliers’ and ‘anomaly candidates’. To the former case, we assign all artefacts of image processing, bad columns on CCDs, tracks from satellites, diffraction spikes, and other cases of non-astrophysical variability. To the latter case, we attribute the objects whose variability is proved to be astrophysically real and related either to the internal properties of the source or to the environmental effects, e.g. present of a companion. All the anomaly candidates have a potential to be interesting for the experts in the corresponding domain. If after thorough expert investigation an object is shown to behave unusually for its suspected astrophysical type, has unknown nature of variability, or represents a rare class of objects, then we deem it an ‘anomaly’. It has to be stressed that the experts can miss some anomalies from the anomaly candidates due to insufficient knowledge in a particular domain of variable stars or transients or the lack of opportunity to perform the additional observations with required facilities. Therefore, presenting the results of this work in Table D, we show not only anomalies confirmed by us, but the other anomaly candidates that have a potential to be proved as anomalies by other experts in the field.
All light-curve data sets were submitted to the same feature extraction procedure before being used as input to different machine learning algorithms.
3.1 Feature extraction
We extracted 42 features from each light curve. Some of them probe magnitude properties (e.g. Amplitude, Von Neumann η, Standard Deviation), while others are specific summary statistics for periodic signals (e.g. Periodogram Amplitude, Periodogram η, Periodogram Standard Deviation). This ensemble of features describe different aspects of the light-curve shape, with the tails of feature distributions indicating objects with less common light curve properties, or potential outliers. A detailed description of each feature is given in Appendix A. Light-curve feature data within each field were standardized by shifting to zero mean and re-scaling to unity standard deviation. This ensures the results from outlier detection strategies will not depend on the units of the input variables.
3.2 Outlier detection algorithms
This section describes the outlier detection algorithms used in this study, which are aimed to select objects located in sparse regions of the feature space. Our pipeline profits from the Python scikit-learn (Pedregosa et al. 2011) implementation for all strategies.
3.2.1 Isolation forest
IF is an unsupervised outlier detection algorithm first proposed by Liu, Ting & Zhou (2008). It considers that outliers are normally isolated from nominal data in the input parameter space, hence requiring less number of random partitions to be separated from it. Its scores are based on the inverse distance from root to leave node in an ensemble of decision trees built with random split points. Outliers are identified as objects with shorter path-length from root to leaf node and the score is inversely proportional to the average path root-to-leaf among all trees in the forest.
The two main parameters that describe an IF are: the number of trees and the sub-sample size used to train each tree. In what follows all results were obtained using sub-samples of 1000 elements and a forest containing 1000 trees.
3.2.2 Local Outlier Factor
The Local Outlier Factor (LOF; Breunig et al. 2000) algorithm detects outliers in a data set based on comparative local density estimation. For each object in the data set, its local density is calculated using the distance between the object and its k-th nearest neighbour and the total number of neighbours it encloses (k). The average local density is calculated over all k neighbours and the score is defined as the ratio between the individual and average local densities. Normal objects are expected to have similar local density to that of its neighbours, while outliers will show significant differences.
The behaviour of the LOF algorithm is dictated by two main parameters: the number of neighbours k and the metric used to calculate the distance between instances. The number of neighbours, k, in particular is an important criterion, since too high a value of k might cause the algorithm to miss outliers while too small a value results in a narrow focus that might be especially problematic in the case of noisy data sets. In what follows, all results were obtained using k = 100 with the distances given by the Euclidean metric.
3.2.3 Gaussian Mixture Model
A Gaussian Mixture Model (GMM; McLachlan & Peel 2000) is a parametric description of the data which assumes that multiple classes can be modelled as a superposition of multivariate Gaussian distributions. An object is considered to belong to a group according to its probability of being generated by one of the Gaussians within the model. Alternatively, an outlier is defined as an object for which all Gaussians within the mixture assign a low probability. The most important variable that defines the GMM is the number of components, or groups, to consider. In what follows, we used 10 isotropic Gaussian components.
3.2.4 One-class Support Vector Machines
Support Vector Machines (Cristianini et al. 2000; Hastie, Tibshirani & Friedman 2009) were originally formulated to tackle supervised binary classification scenarios. This is achieved by defining a hyperplane that separates points belonging to different classes. If the different classes are not linearly separable in a given feature space, they are projected into a higher dimensional feature space where they can be linearly separated using a kernel (‘kernel trick’). Scholkopf et al. (1999) proposed a modification to this method for novelty/outlier detection called One-class SVM. Analogously to its supervised learning counterpart, O-SVM identifies a decision boundary, by defining the smallest hypersphere containing the bulk part of the data. The model has two parameters: ν, often called the margin that defines the probability of finding a new but normal point outside the decision boundary, and the kernel. In this work, we used ν = 0.01 and a Gaussian radial basis function kernel.
3.3 Domain expert analysis
Outlier detection algorithms are, in general, able to identify statistical abnormalities within a large data set, e.g. objects from sparse regions of the feature space or which do not conform with the general statistical description of the data. However, these may not be of astrophysical interest. Our approach to mining scientifically significant peculiarities admits that the light curve itself is typically not enough to determine the scientific content of a given source. Therefore, each outlier automatically identified is subjected to analysis by a human expert with the goal of scrutinizing its characteristics and determining the degree of its astrophysical content. In this context, all automatic learning algorithms can be seen as recommendation systems whose goal is to perform a first triage which is subsequently confirmed by a human. The expert analysis includes literature and community search, cross-matching with known data bases and catalogues, analysis of compatibility with theoretical models and, when possible, additional photometric and/or spectroscopic observations. The final aim of the last stage is identification of anomalies (scientifically interesting objects confirmed by the expert) from outliers (candidates identified with high scores by the machine learning algorithms).
3.3.1 The ZTF viewer
In order to provide a smooth experience for the experts in charge of analysing outliers, we constructed a specially designed web-interface that allows smooth visualization of several light curve characteristics: the SNAD ZTF viewer5 (Fig. B1). It enables easy access to the individual exposure images; to the Aladin Sky Atlas (Bonnarel et al. 2000; Boch & Fernique 2014) and to various catalogues of variable stars and transients, including the General Catalogue of Variable Stars (GCVS; Samus’ et al. 2017), the American Association of Variable Star Observers’ Variable Star Index (AAVSO VSX; Watson, Henden & Price 2006), the Asteroid Terrestrial-impact Last Alert System (ATLAS; Heinze et al. 2018), the ZTF Catalog of Periodic Variable Stars (Chen et al. 2020), astrocats,6 the OGLE-III On-line Catalog of Variable Stars (Soszynski et al. 2008), and the simbad database (Wenger et al. 2000).
In ZTF DR3 each OID corresponds to an object in a particular field and passband, therefore the same source can have several OIDs. Our viewer allows the user to perform fast coordinate cross-match to associate a given OID with others from different fields and passbands, under a user-defined cross-match radius. Full description of the SNAD ZTF viewer is given in Appendix B.
3.3.2 Additional observations
For a few anomaly candidates, we also performed additional observations with the telescopes at the Caucasus Mountain Observatory that belongs to the Sternberg Astronomical Institute, Lomonosov Moscow State University (CMO SAI MSU; Shatsky et al. 2020).
Photometric observations were carried with the 60-cm Ritchie–Chretien telescope in g′, r′, i′ passbands (Fukugita et al. 1996), in remote control mode (RC600, Berdnikov et al. 2020). Photometric reductions were performed using standard methods of dark frames and twilight sky flat-fields. Fluxes were extracted with the aperture photometry technique using fixed aperture radius ≈2.5 full width at half-maximum (FWHM) of the stellar point spread function of the frame. We used an ensemble of 400 nearby stars from Pan-STARRS DR1 catalogue (Chambers et al. 2016; Flewelling et al. 2016) to derive the linear solution between instrumental and Pan-STARRS DR1 magnitudes. Some stars were ejected from ensemble due to 3σ-clipping. The final number of comparison stars in each ensemble was ∼ 200–300 for different objects.
Spectra were obtained with the Transient Double-beam Spectrograph (TDS) of the 2.5-m telescope (Potanin et al. 2017). The general characteristics of the TDS and the data reduction methods are described in Potanin et al. (2020). The slit was oriented vertically in order to reduce wavelength dependent slit losses caused by atmospheric dispersion. The wavelength calibration was performed with a Ne-Al-Si lamp and corrected by using night-sky emission lines that allowed us to achieve an accuracy of ≲10 km s−1. The spectra were extracted with an aperture of 4.5 arcsec. The flux calibration was performed by dividing the extracted spectra by the response curve, calculated with the spectrophotometric standard BD+28d4211. However, the photometric accuracy was lost due to the narrow slit, which was used to achieve a higher spectral resolution. Barycentric radial velocity corrections were applied.
4 RESULTS
We applied the outlier detection algorithms separately to each field. M 31 and deep fields were scrutinized by all four algorithms, while for disk we used only IF, GMM, and O-SVM (LOF had a prohibitively high computation cost given the number of objects in this field). For all machine learning algorithms, the 40 objects with largest values of outlier score were submitted to the expert analysis. Taking into account that a few objects were assigned high anomaly scores by more than one algorithm, the final list of unique outliers contained 277 objects: 101 in M 31, 113 in deep, and 63 in disk. Each one of the 277 was subjected to the expert analysis using the utilities described in Section 3.3. A summary of the properties describing anomaly candidates is given in Table D1. The first column is the object identifier from ZTF DR3. The second column contains alternative nomenclature by which the object is known. The equatorial coordinates (α, δ) in degrees are presented in the third column. The fourth and fifth columns show the minimum and maximum zr magnitudes derived from the entire public light curve of ZTF DR3. The line-of-sight reddening in our galaxy E(B − V) is given in column 6 (Schlafly & Finkbeiner 2011). The seventh column indicates the distance to the object (D) in parsec according to Bailer-Jones et al. (2018); for objects belonging to M 31 we adopt a distance of ∼780 kpc (Makarov et al. 2014). The eighth column gives the approximate absolute zr magnitude derived as |$M_{r, {\rm max}} = m_{r, {\rm max}} - 5\log _{10}\, D + 5 - A_r$|, where Ar is the Milky Way foreground absorption in zr passband. Column 9 contains the best period P0, in days, extracted from either the Lomb–Scargle periodogram (see Appendix A) or one of the catalogues listed in the ZTF-viewer or determined by us. In case of previously catalogued objects, their types and the source of classification are listed in columns 10 and 11, respectively.
4.1 M 31
Among the 101 outliers automatically identified in the M 31 field, there are 80 bogus light curves and 21 objects of astrophysical nature, 7 of which are not listed in known catalogues and/or data bases of variable sources. As expected, a large part of anomaly candidates in this field belongs to the M 31 galaxy. Further information about these objects is given in Table D1.
The known variables from our list are distributed by types as follows: three classical Cepheids (M 31), two red supergiants (RSG, M 31), one eclipsing binary (EB, MW), two possible novae (PNV, M 31), one RS Canum Venaticorum-type binary system (RSCVN, MW), and five objects of unknown nature of variability.
4.1.1 695211200019653 – RSCVN
The object 695211200019653 (Fig. 1) was previously classified as a star with sine-like variability and period P = 7.696 d in the ATLAS catalogue of variable stars (Heinze et al. 2018). The ASAS-SN Catalog of Variable Stars (Jayasinghe et al. 2020) classifies it as a rotation variable with P = 7.709 d and the ZTF Catalog of Periodic Variable Stars (Chen et al. 2020) considers it a RSCVN with period P = 7.734 d based on an automatic DBSCAN classifier. Moreover, this object is also marked as X-ray and UV source by ROSAT, XMM–Newton, and Swift/UVOT. According to the Gaia DR2 (Gaia Collaboration 2018), it is a Milky Way object at the distance D ≈ 1640 pc, R ≈ 2.34 R⊙, Teff ≈ 4500 K, and L ≈ 2 L⊙.
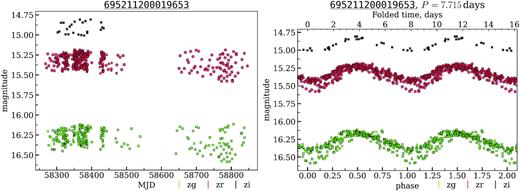
The light curve of RS Canum Venaticorum-type variable. Left: observed ZTF light curve. Right: folded light curve using P = 7.715 d obtained using our feature extraction code (see Appendix A). Note the minimum depth change after MJD ≳ 58750 (left) and the two outlier zg observations in the folded light curve (right). OIDs: 695111200008124, 695211200019653, 695311200027644, 1735101200013615, 1735201200018614. Different colours denote the different ZTF passbands. Red circles correspond to the outlier OID, squares show data from other OIDs corresponding to the same source but found in different passbands and ZTF fields.
Its ZTF DR3 light curves are characterized by amplitude variability, e.g. around |$\rm MJD\simeq 58750\!-\!58850$| when the minimums become deeper. Moreover, its zg light curve shows two observations at |$\rm MJD\simeq 58368.4$| which could be a flare with an amplitude of ≳0.1 mag. The Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014) observed 695211200019653 continuously during ∼3 periods. Its light curve shows an asymmetric sine-like variability with amplitude of ≈3 per cent, significant inter-period changing (typical for stars with spot activity) and ∼0.05 mag flare near |$\rm MJD\simeq 58779.5$|. The estimated period is 7.662 d. The difference in periods estimation from different surveys can be explained by the low signal to noise ratio of ASAS-SN data, irregular sampling of ZTF and ATLAS data, and by the short observation sequence of TESS. Alternatively, the difference could also be explained by a real fluctuation in period due to changing of positions and temperatures of stellar spots.
We obtained two spectra of 6952112007019653 with a resolution of ∼1500 and a signal to noise ratio of ∼50 on 2020 August 22 and November 12 (MJD = 59083.9651 and MJD = 59165.7250) with a 1 arcsec slit and total exposure times of 1500 s and 1800 s, correspondingly (see Fig. 2). Spectral classification was done by comparing with the spectral library (Valdes et al. 2004). We determined the spectral class as K3. Strong variable Balmer and Ca ii H-K emissions are present in all spectra, indicating chromospheric activity (Wilson 1968). Velocities of the emission lines correspond to the absorption lines. The radial velocity shift between two spectra is 46 ± 10 km s−1, that points out to the presence of a second companion. However, we did not detect any obvious spectral signs of a companion in the spectra. Based on overall analysis, distance estimation, photometric and spectral data, we definitely classified 695211200019653 as RS Canum Venaticorum-type binary system (Berdyugina 2005).
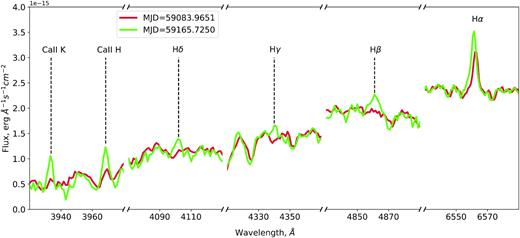
Ca ii H-K and Balmer series emissions on two spectra of 695211200019653 obtained with the 2.5-m telescope of CMO SAI MSU.
4.1.2 695211200075348 – unclassified variable
The object M31N 2013-11b was first discovered by Ovcharov et al. (2013) on 2013 November 7.780 ut (MJD = 56603.780) with R ≃ 20.3 mag and classified as probable nova in M31. Later on, 2013 November–December, Hornoch (2013) observed the object using the 0.65-m telescope at Ondrejov and the Danish 1.54-m telescope at La Silla. The observations revealed a significant red colour that is not typical for a classical nova unless the object is highly reddened, which is not expected for its line of sight. Hornoch (2013) concluded that it is more likely a red long-period variable which is supported also by its very slow brightening.
On MJD = 57633.1234 MASTER-IAC autodetection system discovered the optical transient source, MASTER OT J004126.22+414350.0, at the same position with unfiltered magnitude ∼19.7 mag (Shumkov et al. 2016). Williams et al. (2016) performed spectroscopic and additional photometric observations with the 2-m Liverpool Telescope on 2016 September 9 ut. The spectrum revealed no obvious emission or absorption lines, but the continuum was clearly detected. Spectroscopic and photometric observations of the transient implied it is unlikely to be a recurrent nova eruption in M 31. The colour of the transient also suggests it is unlikely to be a Galactic dwarf nova outburst. The ZTF object light curve is given in Fig. 3.
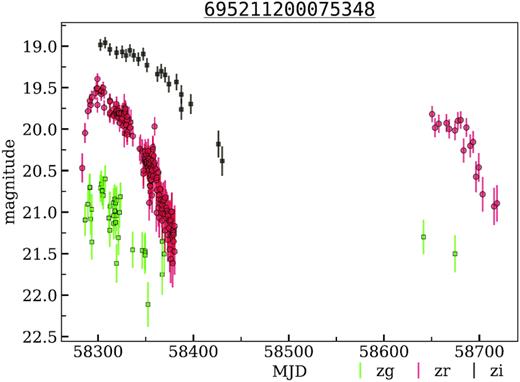
The light curves of M31N 2013-11b/MASTER OT J004126.22+414350.0 – unclassified variable object from the M 31 field. OIDs: 695111200015523, 695211200075348, 695311200020148, 1735101200009309, 1735201200040725.
4.1.3 695211100022045 – nova candidate
According to the Transient Name Server7 (TNS), the object 695211100022045 was first seen on 2017-10-29 (MJD = 58055) as AT 2017ixs. It was detected a second time on 2017-12-15 (MJD = 58102) with 19.5 mag in Clear filter and classified as a possible nova (Carey 2017) in M 31. Six months later, on 2018-06-20 (MJD = 58289), MASTER-Kislovodsk autodetection system discovered MASTER OT J004355.89+413209.9 with an unfiltered magnitude of 19.0 mag at AT 2017ixs position (Balanutsa et al. 2018). The behaviour of its light curve is not typical for a dwarf nova or a cataclysmic variable, therefore AT 2017ixs is the interesting anomaly for the further study. The ZTF object light curve is given in Fig. 4.
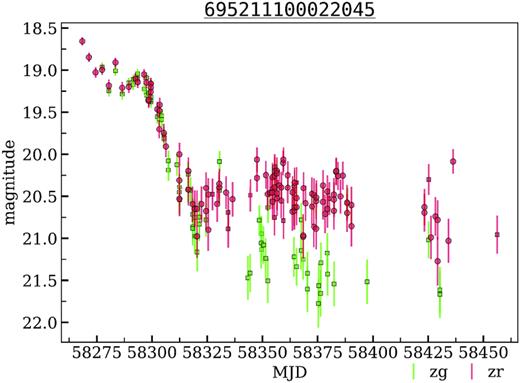
The light curves of AT 2017ixs/MASTER OT J004355.89+413209.9 – nova candidate from the M 31 field. OIDs: 695111100031492, 695211100022045, 1735101200034700, 1735201200049286.
4.1.4 695211100131796 – LBV candidate
The object 695211100131796 (Fig. 5) is located near the ionized hydrogen region [AMB2011] H ii 2692 (Azimlu, Marciniak & Barmby 2011). It was previously detected as an object of unknown nature PSO J011.0457+41.5548 (Lee et al. 2014). Based on the spectra of PSO J011.0457+41.5548, which is turned to be typical of B- and A-type supergiants, Humphreys et al. (2017) concluded that the available information is insufficient to confirm it as a luminous blue variable (LBV). We consider it a luminous blue variable or variable of the S Doradus type (SDOR) candidate.
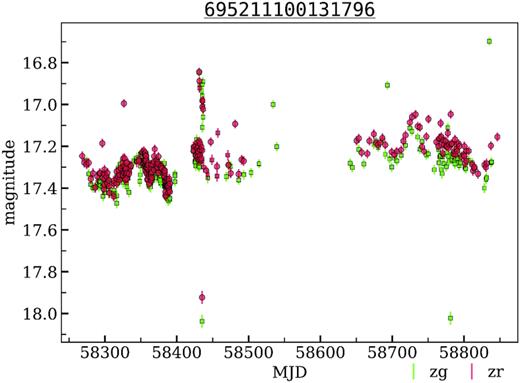
The light curves of PSO J011.0457+41.5548 – luminous blue variable candidate from the M 31 field. OIDs: 695111100014264, 695211100131796, 1735101200058759, 1735201200018887.
4.2 DEEP
Among the 113 outliers in the deep field there are 95 bogus light curves and 18 objects of astrophysical nature, eight of which are not listed in known catalogues and/or data bases of variable sources. The information about these objects is given in Table D1.
The known variables from our list are distributed by types as follows: two eclipsing binaries, two semiregular variables, one Mira variable, one RR Lyrae variable with asymmetric light curve (steep ascending branches), one polar, one Type Ia supernova (SN), two supernova candidates.
4.2.1 795214300016648 – red dwarf flare
Among the unclassified objects we would like to mention, 795214300016648 is a possible red dwarf flare (Fig. 6). It is a relatively nearby object at a distance of ∼400 pc (Bailer-Jones et al. 2018), with a high proper motion |$\rm PM_{R.A.} = 8.122\pm 0.502$| mas yr−1, |$\rm PM_{Dec.} = -29.269\pm 0.596$| mas yr−1 (Gaia Collaboration 2018). Despite the fact that such objects are quite common in our galaxy, their detection is rare because of the small duration and low luminosity of its flares. Their study is of great scientific interest due to the potential habitability associated with the planets it hosts (e.g. Segura et al. 2010; France et al. 2013).
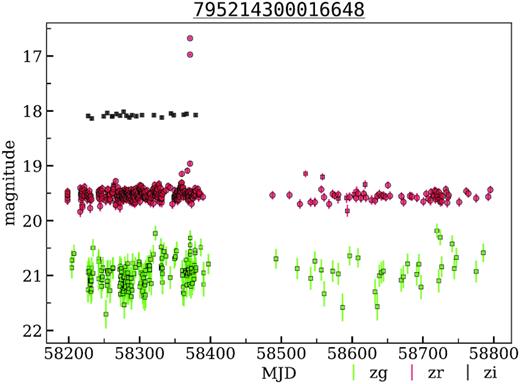
The light curves of 795214300016648 from the deep field classified by us as red dwarf flare. OIDs: 795114300008349, 795214300016648, 795314300011499, 1829206200019338.
4.2.2 Supernova candidates
In the outlier list from deep, there are six objects that are possibly of extragalactic origin – 795202100005941, 795204100013041, 795205100007271, 795209200003484, 795212100007964, 795213200000671. Two of them appeared in the data bases as known supernova candidates: 795213200000671 (AT 2018afr/Gaia18apj8) and 795202100005941 (MLS180307:163438+521642; Drake et al. 2009). Considering the photometric redshift of the possible host galaxy, 795202100005941 absolute magnitude is ∼−22.4, making it a potential superluminous supernova (SLSN) candidate. The four remaining objects are not catalogued.
We use the python library sncosmo 9 to fit their light curves with several supernova models: Peter Nugent’s spectral templates10 that cover the main supernova types (Ia, Ib/c, IIP, IIL, IIn) and SALT2 model of Type Ia supernovae (Guy et al. 2007). Each model is characterized by a set of parameters. Nugent’s models are the simple spectral time series that can be scaled up and down. The parameters of the models are the redshift z, the observer-frame time corresponding to the zero source’s phase, t0, and the amplitude. The zero phase is defined relative to the explosion moment and the observed time t is related to phase via t = t0 + phase × (1 + z).
The SALT2 model is more sophisticated and contains the parameters that affect the shape of the spectrum at each phase. In addition to the redshift, t0, and amplitude, the light curves are also characterized by x1 (stretch) and c (colour) parameters. The x1 parameter describes the time-stretching of the light curve. The c parameter corresponds to the colour offset with respect to the average at the date of maximum luminosity in B-band, i.e. c = (B − V)max − 〈B − V〉. In SALT2 models, the zero phase is defined relative to the maximum in B-band.
For each object, we extracted photometry in zg, zr, zi passbands from deep field only. In a few cases, due to insufficient number of photometrical points in zi, we added to the zi-light curve observations from other fields. Then, we subtracted the reference magnitude from ZTF light curves to roughly account for the host galaxy contamination. In order to perform the fit, we determined the redshift bounds for each supernova candidate. For three objects (see Table 2), there are known SDSS galaxies at the source position with measured photometric redshift with errors, which we used for the redshift bounds. For the remaining ones, we adopted [−15; −22] as an acceptable region for the supernovae absolute magnitude (Richardson et al. 2014) and, then, using the apparent maximum magnitude, roughly transform it to the possible redshift range.
Results of the light-curve fit with the SALT2 model for supernova candidates from the deep field.
| OID . | Host galaxy* . | zph . | z . | t0 . | x1 . | c . | Comments† . |
|---|---|---|---|---|---|---|---|
| 795202100005941/ZTF18aanbnjh | SDSS J163437.92+521642.2 | 0.424 ± 0.103 | – | – | – | – | Blazar |
| 795204100013041/ZTF18abgvctp | SDSS J160913.83+521251.3 | 0.375 ± 0.138 | ∼0.24 | 58320.9336 ± 0.4389 | 1.71 ± 0.51 | −0.044 ± 0.035 | – |
| 795205100007271/ZTF18aayatjf | – | – | ∼0.20 | 58285.8334 ± 0.1810 | −0.54 ± 0.18 | −0.075 ± 0.021 | SN Ia |
| 795209200003484/ZTF18abbpebf | – | – | ∼0.11 | 58299.7269 ± 0.0008 | 0.60 ± 0.12 | −0.013 ± 0.012 | SN Ia |
| 795212100007964/ZTF18aanbksg | SDSS J161144.90+555740.7 | 0.288 ± 0.122 | ∼0.18 | 58214.4470 ± 0.0002 | 0.40 ± 0.20 | −0.282 ± 0.020 | Blazar |
| 795213200000671/ZTF18aaincjv | – | – | – | – | – | – | AGN-I |
| OID . | Host galaxy* . | zph . | z . | t0 . | x1 . | c . | Comments† . |
|---|---|---|---|---|---|---|---|
| 795202100005941/ZTF18aanbnjh | SDSS J163437.92+521642.2 | 0.424 ± 0.103 | – | – | – | – | Blazar |
| 795204100013041/ZTF18abgvctp | SDSS J160913.83+521251.3 | 0.375 ± 0.138 | ∼0.24 | 58320.9336 ± 0.4389 | 1.71 ± 0.51 | −0.044 ± 0.035 | – |
| 795205100007271/ZTF18aayatjf | – | – | ∼0.20 | 58285.8334 ± 0.1810 | −0.54 ± 0.18 | −0.075 ± 0.021 | SN Ia |
| 795209200003484/ZTF18abbpebf | – | – | ∼0.11 | 58299.7269 ± 0.0008 | 0.60 ± 0.12 | −0.013 ± 0.012 | SN Ia |
| 795212100007964/ZTF18aanbksg | SDSS J161144.90+555740.7 | 0.288 ± 0.122 | ∼0.18 | 58214.4470 ± 0.0002 | 0.40 ± 0.20 | −0.282 ± 0.020 | Blazar |
| 795213200000671/ZTF18aaincjv | – | – | – | – | – | – | AGN-I |
Results of the light-curve fit with the SALT2 model for supernova candidates from the deep field.
| OID . | Host galaxy* . | zph . | z . | t0 . | x1 . | c . | Comments† . |
|---|---|---|---|---|---|---|---|
| 795202100005941/ZTF18aanbnjh | SDSS J163437.92+521642.2 | 0.424 ± 0.103 | – | – | – | – | Blazar |
| 795204100013041/ZTF18abgvctp | SDSS J160913.83+521251.3 | 0.375 ± 0.138 | ∼0.24 | 58320.9336 ± 0.4389 | 1.71 ± 0.51 | −0.044 ± 0.035 | – |
| 795205100007271/ZTF18aayatjf | – | – | ∼0.20 | 58285.8334 ± 0.1810 | −0.54 ± 0.18 | −0.075 ± 0.021 | SN Ia |
| 795209200003484/ZTF18abbpebf | – | – | ∼0.11 | 58299.7269 ± 0.0008 | 0.60 ± 0.12 | −0.013 ± 0.012 | SN Ia |
| 795212100007964/ZTF18aanbksg | SDSS J161144.90+555740.7 | 0.288 ± 0.122 | ∼0.18 | 58214.4470 ± 0.0002 | 0.40 ± 0.20 | −0.282 ± 0.020 | Blazar |
| 795213200000671/ZTF18aaincjv | – | – | – | – | – | – | AGN-I |
| OID . | Host galaxy* . | zph . | z . | t0 . | x1 . | c . | Comments† . |
|---|---|---|---|---|---|---|---|
| 795202100005941/ZTF18aanbnjh | SDSS J163437.92+521642.2 | 0.424 ± 0.103 | – | – | – | – | Blazar |
| 795204100013041/ZTF18abgvctp | SDSS J160913.83+521251.3 | 0.375 ± 0.138 | ∼0.24 | 58320.9336 ± 0.4389 | 1.71 ± 0.51 | −0.044 ± 0.035 | – |
| 795205100007271/ZTF18aayatjf | – | – | ∼0.20 | 58285.8334 ± 0.1810 | −0.54 ± 0.18 | −0.075 ± 0.021 | SN Ia |
| 795209200003484/ZTF18abbpebf | – | – | ∼0.11 | 58299.7269 ± 0.0008 | 0.60 ± 0.12 | −0.013 ± 0.012 | SN Ia |
| 795212100007964/ZTF18aanbksg | SDSS J161144.90+555740.7 | 0.288 ± 0.122 | ∼0.18 | 58214.4470 ± 0.0002 | 0.40 ± 0.20 | −0.282 ± 0.020 | Blazar |
| 795213200000671/ZTF18aaincjv | – | – | – | – | – | – | AGN-I |
Since dust in the Galaxy also affects the shape of an observed spectrum, we accounted for it as an additional effect during the fitting procedure. We used Cardelli, Clayton & Mathis (1989) extinction model and the individual object’s colour excess E(B − V) (see Table D1).
Results from the light-curve fit are presented in Figs C1, C2, C3, and C4. We do not show the fitted light curves for 795202100005941, 795213200000671 since both supernova candidates were discovered after the maximum light and only descending part of the light curves is available. The analysis of four non-catalogued supernova candidates revealed that their light curves are similar to those of Type Ia supernovae. The determined x1 and c parameters are typical for SNe Ia. We summarized the main fit parameters using the SALT2 model in Table 2.
4.3 DISK
Among the 63 outliers in the disk field, there are 13 bogus light curves and 50 variable objects of astrophysical nature, eight of which are not listed in known catalogues and/or data bases of variable sources. The information about these objects is given in Table D1.
Among the known variables from our list there are three dwarf novae, five eclipsing systems, one Orion variable with rapid light variations, 28 Mira variables, one other long-period variable of unspecified type, and four candidates to pre-main-sequence (PMS) stars. These objects are considered anomaly candidates, and therefore, interesting sources to study more carefully. For example, some of these Mira variables have asymmetric light curves that may indicate the presence of a companion (e.g. 807206200023036, Fig. 7).
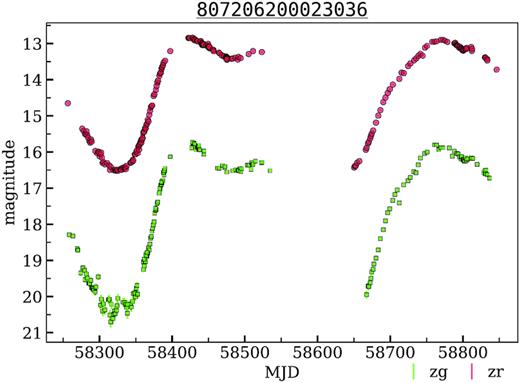
The light curves of NSVS J0122238+611352 – Mira variable from the disk field. OIDs: 807106200016307, 807206200023036, 1810114300003360, 1810214300006290.
4.3.1 Pre-main-sequence candidates
We identified four objects (807206200003542, 807206200004116, 807206200014645, 807210200026027) previously classified as PMS candidates (Vioque et al. 2020). For these objects, we gathered additional observations with the RC600 telescope of CMO SAI MSU in g′, r′, i′ passbands (Table 3) and confirmed that the variability is still present. Three of them are located at a distance of 800–1000 pc, and the last one (807210200026027) is significantly further, at 1700 pc (Bailer-Jones et al. 2018). In particular, 807210200026027 can be also found among the AGN candidates reported by Edelson & Malkan (2012). In order to identify AGN candidates, Edelson & Malkan (2012) used the colour information from the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010), the Two Micron All-Sky Survey (2MASS; Skrutskie et al. 2006), and checked their presence in X-rays data with ROSAT All-Sky Survey (RASS; Voges et al. 1999). However, 807210200026027 was assigned as an AGN solely based on infrared observations, making it a weak candidate, and in contradiction with Gaia parallax (Gaia Collaboration 2018). Based on ML techniques, the object was also classified as a young stellar object (YSO; Marton et al. 2016). However, the light curve seems to be typical for slow red irregular variables, LB type, according to the GCVS classification system (Fig. 8), which does not contradict the Gaia parallax.
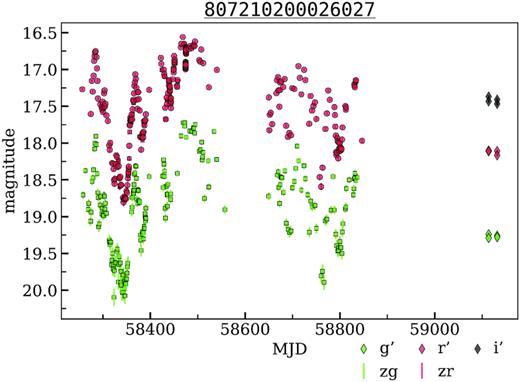
The light curves of poorly classified variable object – PMS star or slow red irregular variable candidate from the disk field. OIDs: 807110200025843, 807210200026027, 1840103100026721, 1840203100059097. Diamonds show the additional g′, r′, i′ observations performed with RC600 telescope of CMO SAI MSU.
Photometric observations of the candidates to PMS sources with RC600 telescope of the Caucasus Mountain Observatory, SAI MSU.
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807206200003542 | |||
| 59114.06219 | g′ | 16.916 | 0.010 |
| 59114.06499 | g′ | 16.930 | 0.010 |
| 59114.06780 | g′ | 16.911 | 0.011 |
| 59132.84609 | g′ | 16.046 | 0.006 |
| 59132.84720 | g′ | 16.052 | 0.006 |
| 59114.06319 | r′ | 15.592 | 0.006 |
| 59114.06600 | r′ | 15.597 | 0.006 |
| 59114.06881 | r′ | 15.588 | 0.006 |
| 59132.84437 | r′ | 14.900 | 0.004 |
| 59132.84514 | r′ | 14.901 | 0.004 |
| 59114.06403 | i′ | 14.833 | 0.005 |
| 59114.06683 | i′ | 14.823 | 0.005 |
| 59114.06964 | i′ | 14.830 | 0.005 |
| 59132.84283 | i′ | 14.249 | 0.004 |
| 59132.84359 | i′ | 14.252 | 0.004 |
| 807206200004116 | |||
| 59114.07549 | g′ | 20.150 | 0.180 |
| 59132.82983 | g′ | 20.587 | 0.160 |
| 59132.83456 | g′ | 20.480 | 0.096 |
| 59132.83812 | g′ | 20.310 | 0.087 |
| 59114.07953 | r′ | 18.534 | 0.047 |
| 59114.08100 | r′ | 18.546 | 0.055 |
| 59132.82603 | r′ | 18.949 | 0.059 |
| 59132.82783 | r′ | 18.887 | 0.054 |
| 59114.08235 | i′ | 17.587 | 0.047 |
| 59114.08347 | i′ | 17.529 | 0.049 |
| 59132.82239 | i′ | 18.369 | 0.106 |
| 59132.82420 | i′ | 18.195 | 0.057 |
| 807206200014645 | |||
| 59114.03133 | g′ | 17.780 | 0.016 |
| 59114.03279 | g′ | 17.782 | 0.016 |
| 59114.03426 | g′ | 17.805 | 0.016 |
| 59132.81479 | g′ | 18.379 | 0.058 |
| 59132.81625 | g′ | 18.285 | 0.066 |
| 59132.81771 | g′ | 18.358 | 0.075 |
| 59114.03544 | r′ | 16.997 | 0.013 |
| 59114.03621 | r′ | 17.031 | 0.014 |
| 59114.03699 | r′ | 16.992 | 0.013 |
| 59132.81127 | r′ | 17.535 | 0.034 |
| 59132.81238 | r′ | 17.532 | 0.034 |
| 59132.81349 | r′ | 17.506 | 0.040 |
| 59114.03781 | i′ | 16.386 | 0.013 |
| 59114.03859 | i′ | 16.391 | 0.013 |
| 59114.03936 | i′ | 16.384 | 0.012 |
| 59132.80879 | i′ | 16.832 | 0.034 |
| 59132.80955 | i′ | 16.829 | 0.037 |
| 59132.81031 | i′ | 16.905 | 0.038 |
| 807210200026027 | |||
| 59113.8449916 | g′ | 19.240 | 0.033 |
| 59113.8485605 | g′ | 19.290 | 0.034 |
| 59131.8365898 | g′ | 19.259 | 0.039 |
| 59131.8401575 | g′ | 19.280 | 0.039 |
| 59113.8513134 | r′ | 18.103 | 0.022 |
| 59113.8531301 | r′ | 18.111 | 0.022 |
| 59131.8430829 | r′ | 18.109 | 0.023 |
| 59131.8452469 | r′ | 18.167 | 0.024 |
| 59113.8549981 | i′ | 17.369 | 0.019 |
| 59113.8568122 | i′ | 17.433 | 0.020 |
| 59131.8472884 | i′ | 17.467 | 0.024 |
| 59131.8491064 | i′ | 17.409 | 0.025 |
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807206200003542 | |||
| 59114.06219 | g′ | 16.916 | 0.010 |
| 59114.06499 | g′ | 16.930 | 0.010 |
| 59114.06780 | g′ | 16.911 | 0.011 |
| 59132.84609 | g′ | 16.046 | 0.006 |
| 59132.84720 | g′ | 16.052 | 0.006 |
| 59114.06319 | r′ | 15.592 | 0.006 |
| 59114.06600 | r′ | 15.597 | 0.006 |
| 59114.06881 | r′ | 15.588 | 0.006 |
| 59132.84437 | r′ | 14.900 | 0.004 |
| 59132.84514 | r′ | 14.901 | 0.004 |
| 59114.06403 | i′ | 14.833 | 0.005 |
| 59114.06683 | i′ | 14.823 | 0.005 |
| 59114.06964 | i′ | 14.830 | 0.005 |
| 59132.84283 | i′ | 14.249 | 0.004 |
| 59132.84359 | i′ | 14.252 | 0.004 |
| 807206200004116 | |||
| 59114.07549 | g′ | 20.150 | 0.180 |
| 59132.82983 | g′ | 20.587 | 0.160 |
| 59132.83456 | g′ | 20.480 | 0.096 |
| 59132.83812 | g′ | 20.310 | 0.087 |
| 59114.07953 | r′ | 18.534 | 0.047 |
| 59114.08100 | r′ | 18.546 | 0.055 |
| 59132.82603 | r′ | 18.949 | 0.059 |
| 59132.82783 | r′ | 18.887 | 0.054 |
| 59114.08235 | i′ | 17.587 | 0.047 |
| 59114.08347 | i′ | 17.529 | 0.049 |
| 59132.82239 | i′ | 18.369 | 0.106 |
| 59132.82420 | i′ | 18.195 | 0.057 |
| 807206200014645 | |||
| 59114.03133 | g′ | 17.780 | 0.016 |
| 59114.03279 | g′ | 17.782 | 0.016 |
| 59114.03426 | g′ | 17.805 | 0.016 |
| 59132.81479 | g′ | 18.379 | 0.058 |
| 59132.81625 | g′ | 18.285 | 0.066 |
| 59132.81771 | g′ | 18.358 | 0.075 |
| 59114.03544 | r′ | 16.997 | 0.013 |
| 59114.03621 | r′ | 17.031 | 0.014 |
| 59114.03699 | r′ | 16.992 | 0.013 |
| 59132.81127 | r′ | 17.535 | 0.034 |
| 59132.81238 | r′ | 17.532 | 0.034 |
| 59132.81349 | r′ | 17.506 | 0.040 |
| 59114.03781 | i′ | 16.386 | 0.013 |
| 59114.03859 | i′ | 16.391 | 0.013 |
| 59114.03936 | i′ | 16.384 | 0.012 |
| 59132.80879 | i′ | 16.832 | 0.034 |
| 59132.80955 | i′ | 16.829 | 0.037 |
| 59132.81031 | i′ | 16.905 | 0.038 |
| 807210200026027 | |||
| 59113.8449916 | g′ | 19.240 | 0.033 |
| 59113.8485605 | g′ | 19.290 | 0.034 |
| 59131.8365898 | g′ | 19.259 | 0.039 |
| 59131.8401575 | g′ | 19.280 | 0.039 |
| 59113.8513134 | r′ | 18.103 | 0.022 |
| 59113.8531301 | r′ | 18.111 | 0.022 |
| 59131.8430829 | r′ | 18.109 | 0.023 |
| 59131.8452469 | r′ | 18.167 | 0.024 |
| 59113.8549981 | i′ | 17.369 | 0.019 |
| 59113.8568122 | i′ | 17.433 | 0.020 |
| 59131.8472884 | i′ | 17.467 | 0.024 |
| 59131.8491064 | i′ | 17.409 | 0.025 |
Photometric observations of the candidates to PMS sources with RC600 telescope of the Caucasus Mountain Observatory, SAI MSU.
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807206200003542 | |||
| 59114.06219 | g′ | 16.916 | 0.010 |
| 59114.06499 | g′ | 16.930 | 0.010 |
| 59114.06780 | g′ | 16.911 | 0.011 |
| 59132.84609 | g′ | 16.046 | 0.006 |
| 59132.84720 | g′ | 16.052 | 0.006 |
| 59114.06319 | r′ | 15.592 | 0.006 |
| 59114.06600 | r′ | 15.597 | 0.006 |
| 59114.06881 | r′ | 15.588 | 0.006 |
| 59132.84437 | r′ | 14.900 | 0.004 |
| 59132.84514 | r′ | 14.901 | 0.004 |
| 59114.06403 | i′ | 14.833 | 0.005 |
| 59114.06683 | i′ | 14.823 | 0.005 |
| 59114.06964 | i′ | 14.830 | 0.005 |
| 59132.84283 | i′ | 14.249 | 0.004 |
| 59132.84359 | i′ | 14.252 | 0.004 |
| 807206200004116 | |||
| 59114.07549 | g′ | 20.150 | 0.180 |
| 59132.82983 | g′ | 20.587 | 0.160 |
| 59132.83456 | g′ | 20.480 | 0.096 |
| 59132.83812 | g′ | 20.310 | 0.087 |
| 59114.07953 | r′ | 18.534 | 0.047 |
| 59114.08100 | r′ | 18.546 | 0.055 |
| 59132.82603 | r′ | 18.949 | 0.059 |
| 59132.82783 | r′ | 18.887 | 0.054 |
| 59114.08235 | i′ | 17.587 | 0.047 |
| 59114.08347 | i′ | 17.529 | 0.049 |
| 59132.82239 | i′ | 18.369 | 0.106 |
| 59132.82420 | i′ | 18.195 | 0.057 |
| 807206200014645 | |||
| 59114.03133 | g′ | 17.780 | 0.016 |
| 59114.03279 | g′ | 17.782 | 0.016 |
| 59114.03426 | g′ | 17.805 | 0.016 |
| 59132.81479 | g′ | 18.379 | 0.058 |
| 59132.81625 | g′ | 18.285 | 0.066 |
| 59132.81771 | g′ | 18.358 | 0.075 |
| 59114.03544 | r′ | 16.997 | 0.013 |
| 59114.03621 | r′ | 17.031 | 0.014 |
| 59114.03699 | r′ | 16.992 | 0.013 |
| 59132.81127 | r′ | 17.535 | 0.034 |
| 59132.81238 | r′ | 17.532 | 0.034 |
| 59132.81349 | r′ | 17.506 | 0.040 |
| 59114.03781 | i′ | 16.386 | 0.013 |
| 59114.03859 | i′ | 16.391 | 0.013 |
| 59114.03936 | i′ | 16.384 | 0.012 |
| 59132.80879 | i′ | 16.832 | 0.034 |
| 59132.80955 | i′ | 16.829 | 0.037 |
| 59132.81031 | i′ | 16.905 | 0.038 |
| 807210200026027 | |||
| 59113.8449916 | g′ | 19.240 | 0.033 |
| 59113.8485605 | g′ | 19.290 | 0.034 |
| 59131.8365898 | g′ | 19.259 | 0.039 |
| 59131.8401575 | g′ | 19.280 | 0.039 |
| 59113.8513134 | r′ | 18.103 | 0.022 |
| 59113.8531301 | r′ | 18.111 | 0.022 |
| 59131.8430829 | r′ | 18.109 | 0.023 |
| 59131.8452469 | r′ | 18.167 | 0.024 |
| 59113.8549981 | i′ | 17.369 | 0.019 |
| 59113.8568122 | i′ | 17.433 | 0.020 |
| 59131.8472884 | i′ | 17.467 | 0.024 |
| 59131.8491064 | i′ | 17.409 | 0.025 |
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807206200003542 | |||
| 59114.06219 | g′ | 16.916 | 0.010 |
| 59114.06499 | g′ | 16.930 | 0.010 |
| 59114.06780 | g′ | 16.911 | 0.011 |
| 59132.84609 | g′ | 16.046 | 0.006 |
| 59132.84720 | g′ | 16.052 | 0.006 |
| 59114.06319 | r′ | 15.592 | 0.006 |
| 59114.06600 | r′ | 15.597 | 0.006 |
| 59114.06881 | r′ | 15.588 | 0.006 |
| 59132.84437 | r′ | 14.900 | 0.004 |
| 59132.84514 | r′ | 14.901 | 0.004 |
| 59114.06403 | i′ | 14.833 | 0.005 |
| 59114.06683 | i′ | 14.823 | 0.005 |
| 59114.06964 | i′ | 14.830 | 0.005 |
| 59132.84283 | i′ | 14.249 | 0.004 |
| 59132.84359 | i′ | 14.252 | 0.004 |
| 807206200004116 | |||
| 59114.07549 | g′ | 20.150 | 0.180 |
| 59132.82983 | g′ | 20.587 | 0.160 |
| 59132.83456 | g′ | 20.480 | 0.096 |
| 59132.83812 | g′ | 20.310 | 0.087 |
| 59114.07953 | r′ | 18.534 | 0.047 |
| 59114.08100 | r′ | 18.546 | 0.055 |
| 59132.82603 | r′ | 18.949 | 0.059 |
| 59132.82783 | r′ | 18.887 | 0.054 |
| 59114.08235 | i′ | 17.587 | 0.047 |
| 59114.08347 | i′ | 17.529 | 0.049 |
| 59132.82239 | i′ | 18.369 | 0.106 |
| 59132.82420 | i′ | 18.195 | 0.057 |
| 807206200014645 | |||
| 59114.03133 | g′ | 17.780 | 0.016 |
| 59114.03279 | g′ | 17.782 | 0.016 |
| 59114.03426 | g′ | 17.805 | 0.016 |
| 59132.81479 | g′ | 18.379 | 0.058 |
| 59132.81625 | g′ | 18.285 | 0.066 |
| 59132.81771 | g′ | 18.358 | 0.075 |
| 59114.03544 | r′ | 16.997 | 0.013 |
| 59114.03621 | r′ | 17.031 | 0.014 |
| 59114.03699 | r′ | 16.992 | 0.013 |
| 59132.81127 | r′ | 17.535 | 0.034 |
| 59132.81238 | r′ | 17.532 | 0.034 |
| 59132.81349 | r′ | 17.506 | 0.040 |
| 59114.03781 | i′ | 16.386 | 0.013 |
| 59114.03859 | i′ | 16.391 | 0.013 |
| 59114.03936 | i′ | 16.384 | 0.012 |
| 59132.80879 | i′ | 16.832 | 0.034 |
| 59132.80955 | i′ | 16.829 | 0.037 |
| 59132.81031 | i′ | 16.905 | 0.038 |
| 807210200026027 | |||
| 59113.8449916 | g′ | 19.240 | 0.033 |
| 59113.8485605 | g′ | 19.290 | 0.034 |
| 59131.8365898 | g′ | 19.259 | 0.039 |
| 59131.8401575 | g′ | 19.280 | 0.039 |
| 59113.8513134 | r′ | 18.103 | 0.022 |
| 59113.8531301 | r′ | 18.111 | 0.022 |
| 59131.8430829 | r′ | 18.109 | 0.023 |
| 59131.8452469 | r′ | 18.167 | 0.024 |
| 59113.8549981 | i′ | 17.369 | 0.019 |
| 59113.8568122 | i′ | 17.433 | 0.020 |
| 59131.8472884 | i′ | 17.467 | 0.024 |
| 59131.8491064 | i′ | 17.409 | 0.025 |
4.3.2 Eclipsing binaries
Among the unclassified objects, we identified six new eclipsing binaries (807203200013118, 807204200004799, 807204400014494, 807208400036953, 807211400009493, 807216400013229). As an example, Fig. 9 shows the folded light curve of the object 807204200004799 in zr, zg passbands.
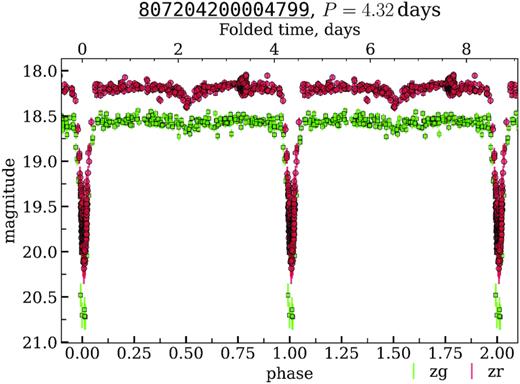
The folded light curves of 807204200004799 from the disk field classified by us as an eclipsing binary. OIDs: 807104200003543, 807204200004799, 1809109100009148, 1809209100012225, 1810112100013288, 1810212100046961.
4.3.3 Unclassified variables
Two other unclassified objects – 807212100012737, 807210200004045 – show non-periodic variability with an amplitude >1 mag. Their light curves are shown in Figs 10 and 11. We also obtained the observations with the RC600 telescope of CMO SAI MSU in g′, r′, i′ passbands (Table 4). The variability is still present. Both objects do not have a significant IR excess. The distance to 807212100012737 is ∼1000 pc. Based on this distance, brightness, and colours, we can make a dubious assumption that 807212100012737 is a red dwarf with strong spot activity. The distance to 807210200004045 is poorly defined; the Gaia parallax to error ratio is 1.14. Therefore, we do not make any assumption about its nature.
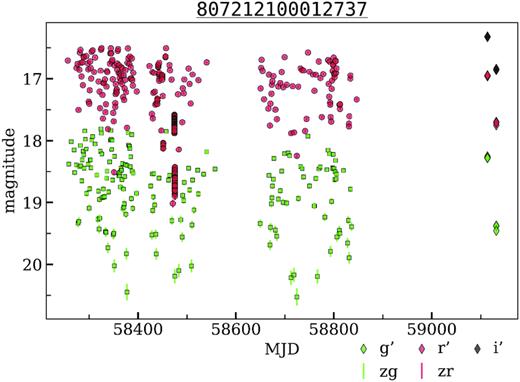
The light curves of unclassified variable object from the disk field. OIDs: 807112100008284, 807212100012737. Diamonds show the additional g′, r′, i′ observations performed with RC600 telescope of CMO SAI MSU.
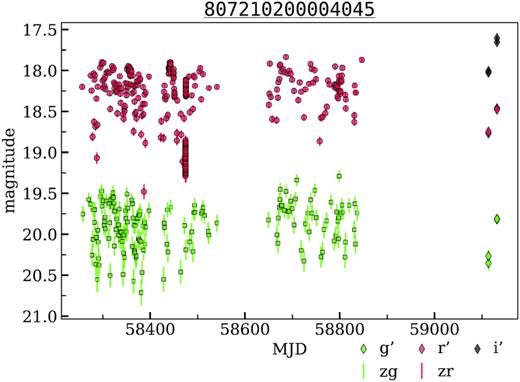
The light curves of unclassified variable object from the disk field. OIDs: 807110200019782, 807210200004045. Diamonds show the additional g′, r′, i′ observations performed with RC600 telescope of CMO SAI MSU.
Photometric observations of unclassified variable objects with RC600 telescope of the Caucasus Mountain Observatory, SAI MSU.
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807210200004045 | |||
| 59113.82463 | g′ | 20.352 | 0.091 |
| 59113.82820 | g′ | 20.268 | 0.084 |
| 59131.79666 | g′ | 19.818 | 0.048 |
| 59131.80022 | g′ | 19.813 | 0.049 |
| 59113.83096 | r′ | 18.769 | 0.039 |
| 59113.83277 | r′ | 18.746 | 0.038 |
| 59131.80315 | r′ | 18.462 | 0.027 |
| 59131.80531 | r′ | 18.478 | 0.028 |
| 59113.83464 | i′ | 18.007 | 0.034 |
| 59113.83645 | i′ | 18.027 | 0.035 |
| 59131.80736 | i′ | 17.654 | 0.027 |
| 59131.80917 | i′ | 17.605 | 0.026 |
| 807212100012737 | |||
| 59113.79655 | g′ | 18.256 | 0.026 |
| 59113.79802 | g′ | 18.278 | 0.026 |
| 59113.79948 | g′ | 18.281 | 0.026 |
| 59131.77430 | g′ | 19.380 | 0.058 |
| 59131.77697 | g′ | 19.376 | 0.043 |
| 59131.77937 | g′ | 19.457 | 0.045 |
| 59113.80083 | r′ | 16.960 | 0.012 |
| 59113.80194 | r′ | 16.948 | 0.012 |
| 59113.80305 | r′ | 16.946 | 0.012 |
| 59131.78118 | r′ | 17.697 | 0.020 |
| 59131.78230 | r′ | 17.751 | 0.022 |
| 59131.78342 | r′ | 17.711 | 0.021 |
| 59113.80422 | i′ | 16.325 | 0.011 |
| 59113.80533 | i′ | 16.321 | 0.011 |
| 59113.80644 | i′ | 16.320 | 0.011 |
| 59131.78459 | i′ | 16.857 | 0.017 |
| 59131.78571 | i′ | 16.856 | 0.017 |
| 59131.78683 | i′ | 16.841 | 0.016 |
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807210200004045 | |||
| 59113.82463 | g′ | 20.352 | 0.091 |
| 59113.82820 | g′ | 20.268 | 0.084 |
| 59131.79666 | g′ | 19.818 | 0.048 |
| 59131.80022 | g′ | 19.813 | 0.049 |
| 59113.83096 | r′ | 18.769 | 0.039 |
| 59113.83277 | r′ | 18.746 | 0.038 |
| 59131.80315 | r′ | 18.462 | 0.027 |
| 59131.80531 | r′ | 18.478 | 0.028 |
| 59113.83464 | i′ | 18.007 | 0.034 |
| 59113.83645 | i′ | 18.027 | 0.035 |
| 59131.80736 | i′ | 17.654 | 0.027 |
| 59131.80917 | i′ | 17.605 | 0.026 |
| 807212100012737 | |||
| 59113.79655 | g′ | 18.256 | 0.026 |
| 59113.79802 | g′ | 18.278 | 0.026 |
| 59113.79948 | g′ | 18.281 | 0.026 |
| 59131.77430 | g′ | 19.380 | 0.058 |
| 59131.77697 | g′ | 19.376 | 0.043 |
| 59131.77937 | g′ | 19.457 | 0.045 |
| 59113.80083 | r′ | 16.960 | 0.012 |
| 59113.80194 | r′ | 16.948 | 0.012 |
| 59113.80305 | r′ | 16.946 | 0.012 |
| 59131.78118 | r′ | 17.697 | 0.020 |
| 59131.78230 | r′ | 17.751 | 0.022 |
| 59131.78342 | r′ | 17.711 | 0.021 |
| 59113.80422 | i′ | 16.325 | 0.011 |
| 59113.80533 | i′ | 16.321 | 0.011 |
| 59113.80644 | i′ | 16.320 | 0.011 |
| 59131.78459 | i′ | 16.857 | 0.017 |
| 59131.78571 | i′ | 16.856 | 0.017 |
| 59131.78683 | i′ | 16.841 | 0.016 |
Photometric observations of unclassified variable objects with RC600 telescope of the Caucasus Mountain Observatory, SAI MSU.
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807210200004045 | |||
| 59113.82463 | g′ | 20.352 | 0.091 |
| 59113.82820 | g′ | 20.268 | 0.084 |
| 59131.79666 | g′ | 19.818 | 0.048 |
| 59131.80022 | g′ | 19.813 | 0.049 |
| 59113.83096 | r′ | 18.769 | 0.039 |
| 59113.83277 | r′ | 18.746 | 0.038 |
| 59131.80315 | r′ | 18.462 | 0.027 |
| 59131.80531 | r′ | 18.478 | 0.028 |
| 59113.83464 | i′ | 18.007 | 0.034 |
| 59113.83645 | i′ | 18.027 | 0.035 |
| 59131.80736 | i′ | 17.654 | 0.027 |
| 59131.80917 | i′ | 17.605 | 0.026 |
| 807212100012737 | |||
| 59113.79655 | g′ | 18.256 | 0.026 |
| 59113.79802 | g′ | 18.278 | 0.026 |
| 59113.79948 | g′ | 18.281 | 0.026 |
| 59131.77430 | g′ | 19.380 | 0.058 |
| 59131.77697 | g′ | 19.376 | 0.043 |
| 59131.77937 | g′ | 19.457 | 0.045 |
| 59113.80083 | r′ | 16.960 | 0.012 |
| 59113.80194 | r′ | 16.948 | 0.012 |
| 59113.80305 | r′ | 16.946 | 0.012 |
| 59131.78118 | r′ | 17.697 | 0.020 |
| 59131.78230 | r′ | 17.751 | 0.022 |
| 59131.78342 | r′ | 17.711 | 0.021 |
| 59113.80422 | i′ | 16.325 | 0.011 |
| 59113.80533 | i′ | 16.321 | 0.011 |
| 59113.80644 | i′ | 16.320 | 0.011 |
| 59131.78459 | i′ | 16.857 | 0.017 |
| 59131.78571 | i′ | 16.856 | 0.017 |
| 59131.78683 | i′ | 16.841 | 0.016 |
| MJD . | Filter . | Magnitude . | Error . |
|---|---|---|---|
| 807210200004045 | |||
| 59113.82463 | g′ | 20.352 | 0.091 |
| 59113.82820 | g′ | 20.268 | 0.084 |
| 59131.79666 | g′ | 19.818 | 0.048 |
| 59131.80022 | g′ | 19.813 | 0.049 |
| 59113.83096 | r′ | 18.769 | 0.039 |
| 59113.83277 | r′ | 18.746 | 0.038 |
| 59131.80315 | r′ | 18.462 | 0.027 |
| 59131.80531 | r′ | 18.478 | 0.028 |
| 59113.83464 | i′ | 18.007 | 0.034 |
| 59113.83645 | i′ | 18.027 | 0.035 |
| 59131.80736 | i′ | 17.654 | 0.027 |
| 59131.80917 | i′ | 17.605 | 0.026 |
| 807212100012737 | |||
| 59113.79655 | g′ | 18.256 | 0.026 |
| 59113.79802 | g′ | 18.278 | 0.026 |
| 59113.79948 | g′ | 18.281 | 0.026 |
| 59131.77430 | g′ | 19.380 | 0.058 |
| 59131.77697 | g′ | 19.376 | 0.043 |
| 59131.77937 | g′ | 19.457 | 0.045 |
| 59113.80083 | r′ | 16.960 | 0.012 |
| 59113.80194 | r′ | 16.948 | 0.012 |
| 59113.80305 | r′ | 16.946 | 0.012 |
| 59131.78118 | r′ | 17.697 | 0.020 |
| 59131.78230 | r′ | 17.751 | 0.022 |
| 59131.78342 | r′ | 17.711 | 0.021 |
| 59113.80422 | i′ | 16.325 | 0.011 |
| 59113.80533 | i′ | 16.321 | 0.011 |
| 59113.80644 | i′ | 16.320 | 0.011 |
| 59131.78459 | i′ | 16.857 | 0.017 |
| 59131.78571 | i′ | 16.856 | 0.017 |
| 59131.78683 | i′ | 16.841 | 0.016 |
4.4 Bogus
The ZTF data processing pipeline includes a procedure to separate the astrophysical events from bogus, i.e. false positive detections (Masci et al. 2019). However, among the outliers, we encountered a significant fraction of bogus light curves (80/101, 95/113, 13/63 for the M 31, deep, disk fields, respectively). A few examples are
a point sharply dropping up or down by several magnitudes – possibly due to satellite/plane tracks, double star in one aperture due to defocusing, bad columns on CCDs, or cosmic particles;
a random spread within several magnitudes due to ghosts, diffraction spikes, bright stars haloes, cosmic rays or wrong background subtraction (close to M 31 centre);
a combination of (i) and (ii).
Bogus examples with suggested classification are given in Fig. 12. We discuss below some interesting cases.

Cases of bogus detections found among the outliers. The outlier is located in the image centre. The size of the cutout showing a cosmic ray is 70 × 70 CCD pixels, for the others the image size is 100 × 100 CCD pixels.
4.4.1 795205400022890 and its echoes
In our outlier list, there are four variables with the same phase and period. We found that one of them, known as IW Dra, is a typical Mira variable, while three others are located in ∼20 arcsec region around it. It turned out that these three neighbours are artefacts of the automatic ZTF photometry arising from incorrect background subtraction of the halo of a bright variable star that overlaps with the light from the nearby objects. The light curves of IW Dra and its echoes are shown in Fig. 13.
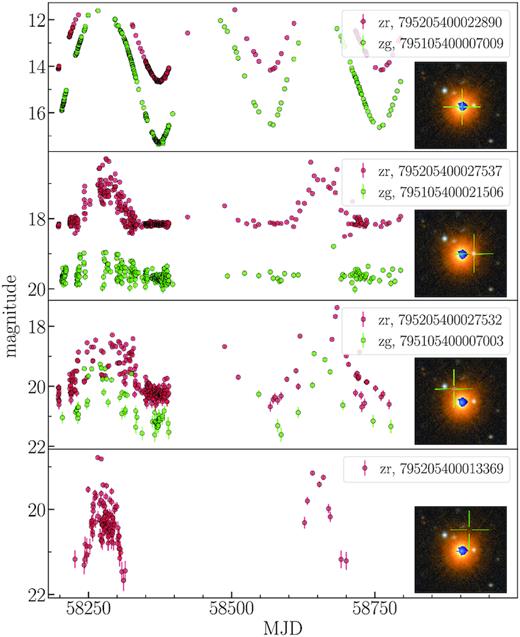
IW Dra and its echoes. SDSS image shows the position of IW Dra and three ZTF sources showing the correlated variability.
4.4.2 807203300039547 – overlap of star and known asteroid
One short transient was identified as a conjunction of asteroid 945 (Barcelona) and a weak star in the disk field (Fig. 14). The identification of the asteroid was performed with SkyBot (Berthier et al. 2006).

Asteroid Barcelona overlapping object 807203300039547. The blue crosses mark the location of the ZTF transient detection. An animated version is available in the electronic version.
4.4.3 695211200077906 – double star artefact
We found several objects that show bogus variability, and identified them as double stars with ∼2 arcsec separation. We assume that bogus measurements occur due defocusing when the FWHM becomes significantly larger than the separation between the components of the double star, which leads to overstatement of the object brightness. The example of such a bogus light curve is 695211200077906, see Fig. 15, where positions are given by the ZTF Lightcurve API.11
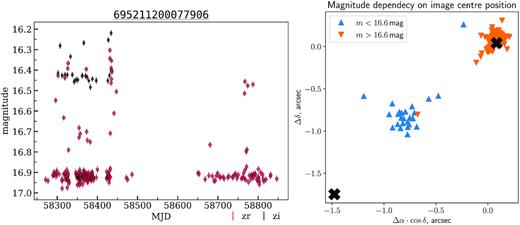
The light curves and the image centre positions of 695211200077906. Left: light curves, OIDs: 695211200077906 (zr, red circles), 695311200089204 (zi, black squares). Right: spatial distribution of observations relative to the average object position, black crosses show Gaia DR2 positions of the double star components. Note that the small brightness (m > 16.6 mag) of the object corresponds to the position of one of the components, while the large brightness (m < 16.6 mag) corresponds to the position somewhere between the components. We assume that the reason of such correlation between magnitude and position is in different FWHM of point spread function in different observations: for the first case FWHM is ∼2 arcsec and photometry counts signal from one component only, but for the other case FWHM is ∼4 arcsec and both components are being described by the common integrating area that makes measured magnitude closer to the integral magnitude of the double star and position to be near the double star centre.
5 PIPELINE VALIDATION
In order to access the efficiency of our pipeline in identifying light curves with significantly different properties than those already present in the bulk of ZTF DR3 data, we created validation test-sets adding a few artificially generated light curves to the real data. This set of enclosed light curves is inspired by potentially interesting astrophysical sources, as well as example cases of non-existing objects. The last case includes a perfectly plateau ‘Flat Without Noise’ light curve, ‘Flat With Noise’ that represents non-variable source, ‘Point Up’, ‘Point Down’, ‘Step Up’, and ‘Step Down’ mimicking a rapid magnitude change or bad column. The astrophysically motivated fakes were built from (1) confirmed binary microlensing events Gaia16aye (three different parts of its r light curve; Wyrzykowski et al. 2016), and candidates ZTF18ablruzq and ZTF18acskgwu (zr passband; Mróz et al. 2020), (2) single microlensing events ZTF18aaztjyd and ZTF18abaqxrt (zr passband; Mróz et al. 2020), (3) r light curve of kilonova 170817 (Villar et al. 2017), (4) V light curve of cepheid in eclipsing binary OGLE-LMC-CEP-0227 (Soszynski et al. 2008).
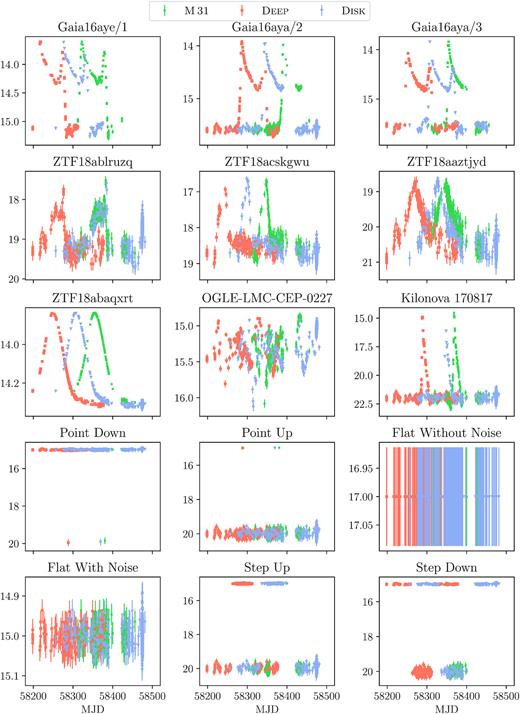
Fake zr light curves. Time-shift between different fields is caused by different initial observational date for each field. We show the light curves following cadences of M 31 (green), deep (orange), and disk (blue) fields.
We built three validation data sets adding 15 fake anomalous light curves to each of them and applied the same outlier detection algorithms as used for the ZTF data. The resulting detection rates are shown in Fig. 17, where ‘union’ denotes the total rate of all used algorithms run in parallel. M 31 field is the smallest one, so the per cent of outliers the expert can examine is the largest. This is why the very first 32 outliers contain 13 of 15 fake anomalies, while OGLE-LMC-CEP-0227 is the 408th and ‘Flat With Noise’ the 3630th outlier. We use only three algorithms (IF, GMM, and O-SVM) for deep field, but the fake detection rate is still very high, probably because its light curves are less diverse and the fake anomalies are more different. The first 30 outliers contain 11 fakes, while ZTF18ablruzq and ZTF18acskgwu are found within the first 700 outliers, OGLE-LMC-CEP-0227 and ‘Flat With Noise’ are within the first 6000 objects. The disk field contains ∼1.8 million objects and we used IF and GMM only, but the fake performance is quite acceptable: first eight fakes are found within the first 90 outliers, 14 of 15 fakes are found within the first 1200 outliers, and only ‘Flat With Noise’ was not detected until the 400 000th outlier. These results show that the outlier detection pipeline shows good anomaly detection rate and could detect physically interesting events. The ‘Flat With Noise’ object is the hardest fake light curve to detect by all algorithms in all fields. This is possibly due to its location in a dense region of feature space which is also populated with low-variable sources and variable sources below ZTF’s threshold of detectability, or even stochastic variance stemming from a small subset of objects marked as variable from within a large distribution of non-variable objects.
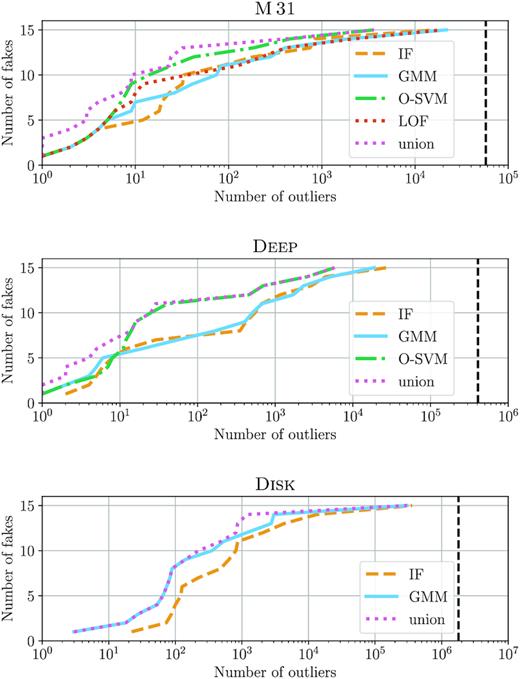
Fake detection rate. ‘Union’ shows the total performance of all algorithms being run in parallel. Vertical dashed line shows the total number of light curves.
6 EXPLORATORY DATA ANALYSIS
Once the experts finished their investigation, we can now use the accumulated knowledge to identify simple strategies that would allow us to quickly separate interesting anomaly candidates from bogus light curves. We start with an exploratory data analysis (EDA) of our feature space. Fig. A1 shows histograms for all features and fields. In what follows, we give an example EDA performed over the incremented parameter space, which includes features as well as the expert judgement.
Fig. A2 shows the separate feature distribution for bogus objects and anomaly candidates in the M 31 field. From this, it is evident that Periodogram Amplitude and Reduced χ2 possess complementary dissimilar distributions between the two classes. Analysing the relationship between these two features (Fig. 18), we see that it is possible to identify bogus light curves as those presenting low Periodogram Amplitude (frequently caused by chaotic signals) and high Reduced χ2 values (when one or more images of some real source is overlapping with another source, such as a bad column or a glare, which mimics a constant light curve with bright outbursts).
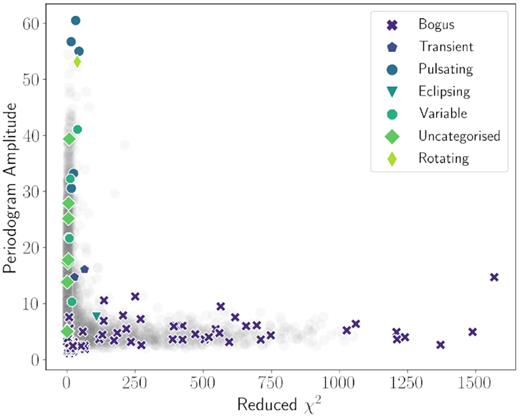
A scatter plot of the 101 M 31 expert-tagged outliers in a Periodogram Amplitude–Reduced χ2 phase-space. The bogus objects can be well separated from anomaly candidates. All 57 546 M 31 objects are shown as grey circles.
We emphasize that the expert-tagging of objects was performed prior to the EDA, and the overall near-orthogonal distribution of objects in the M 31 field did not influence the expert’s analysis.
Although we do not expect a 2D parameter space to completely enclose the complexity of a real/bogus separation pipeline, it is reasonable to assume that, for each data set, some low-dimensional representation will enable quick identification of these two classes – even if we do not expect the final classification to be perfect. This is a direct example of how we can harvest expert knowledge to optimize further automatic identifications. Similar approaches may be used to construct powerful alert stream filters in the context of real-time alert brokers like ANTARES (Narayan et al. 2018; Matheson et al. 2020), ALeRCE (Förster et al. 2020), and Fink (Möller et al. 2021). Further exploration of feature phase-space anomaly detection is currently a main focus in Aleo et al. (in preparation).
6.1 Principal Components
Principal Component Analysis (PCA; Jolliffe 2013) is a dimensionality-reduction technique whereby multidimensional data are decomposed into an orthogonal basis following the directions of maximum data variance. We implemented the PCA module using the sklearn Python package (Pedregosa et al. 2011), and normalized the feature values across all objects using the StandardScaler module. Subsequently, we calculated 42 Principal Components (PCs), ordered by those which explain the most variance. For the M 31 field, the first two PCs together explain 47.1 per cent of the variance, with the first 15 explaining 90.4 per cent. Likewise, for the deep and disk fields the first two PCs together explain 49.7 per cent, and 50.2 per cent of the variance, respectively.
The contribution to the first two PCs (loadings) from each of the 42 features are shown in Fig. 19. For PC 1, shown in black, Standard Deviation, Inter Percentile Range 10 per cent, and Percent Difference Magnitude Percentile 5 per cent are the highest contributors. For PC 2, shown in magenta, Periodogram Amplitude, Periodogram Percent Amplitude, and Periodogram Beyond 2 Standard Deviations are those which contribute the most. From this, we note that PC 1 favours magnitude-based differences, and PC 2 favours periodogram-based features across all three fields. This is expected, since the two categories of information are complementary.
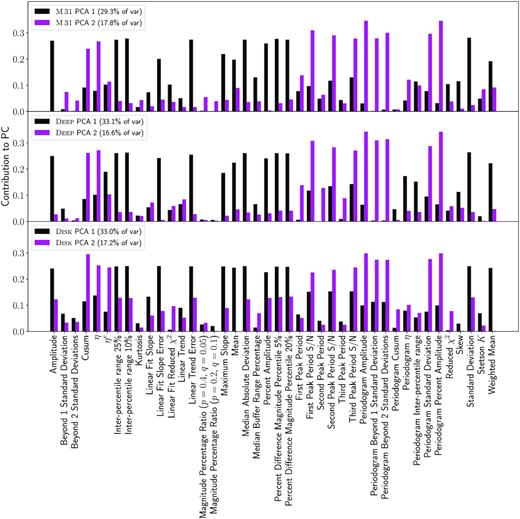
The first two principal components with ascribed feature loadings plotted for the M 31 field (top panel, 47.1 per cent of variance), deep field (middle panel, 49.7 per cent of variance), and disk field (bottom panel, 50.2 per cent of variance). Notice that one PC favours magnitude-based features (black), and the other favours periodogram and temporally based features (magenta).
This complementarity is also evident in the correlation matrix of normalized feature values (Fig. A3). We see clearly two separate sets of features highly correlated between themselves and weakly correlated with members from the other group. This may be indicative that some features are degenerate. In fact, in Fig. A1, those features with similar correlation vectors share similar distributions, albeit different values. However, since no singular feature had a consistently negligible contribution across all PCs and given the fluctuation in contribution by each feature to successive PCs (19), we decided to keep all 42 features as input in our anomaly detection algorithm pipeline.
We show in Fig. 20 distributions for the features with largest contribution to the first three PCs (PC 1–Standard Deviation, PC 2–Periodogram Amplitude, PC 3–Reduced χ2) across all fields considering only objects identified as uncategorized anomaly candidates. All uncategorized anomaly candidates across the three fields are contained within, but do not constitute the edges of, their parent field distribution. That is, they are not in the tail of the distribution where the feature value is greatest, and are sometimes dwarfed in number by other objects in their field that make up their parent distribution. This could explain why such anomaly candidates were not yet categorized. These interesting, uncategorized candidates are high priority targets for future follow-up. See Section 4 and Table D1 for their listings.
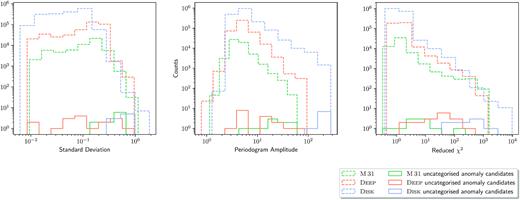
Distribution of features with largest contribution to the first three PCs for objects in M 31 (dashed green), deep (dashed orange), and disk (dashed blue) fields, as well as expert-identified uncategorized anomaly candidates (solid contours).
7 CONCLUSIONS
Despite all the expected scientific results that inspired the construction of modern astronomical observatories, there is little doubt about the potential of the resulting data sets for new discoveries. In the era of systematic large-scale sky surveys, a telescope that only fulfils its science goals cannot be considered successful (Norris 2017). In this context, the use of automatic machine learning tools is unavoidable. They provide important insights into the statistical properties and limits of the data set at hand, and can be optimized to be good recommendation systems. Nevertheless, the discovery itself will always be a profoundly human experience. In this context, the identification of scientifically interesting sources is a product of the combination of data-driven machine learning and human-acquired domain knowledge. The SNAD anomaly detection pipeline, presented in this work, and its accompany results, are a concrete example of how powerful such a system can be when applied to a rich data set as the ZTF DR3.
The pipeline consists of three separate stages: feature extraction, automatic outlier detection based on machine learning, and anomaly confirmation by human experts. The infrastructure put in place to enable such detailed analysis includes not only the software pipeline12 for feature extraction and outlier detection, but also a web-viewer13 allowing cross-match with multiple catalogues and external data source – specifically designed to help the expert in forming a global view of specific candidates. We apply the complete anomaly detection pipeline to three ZTF fields, corresponding to more than 2.25 million objects. Four outlier detection algorithms (IF, GMM, O-SVM, and LOF) were used to identify the top 277 outliers. From these, the expert analysis concluded that 188 (68 per cent) were bogus light curves and 89 (32 per cent) real astrophysical sources – 66 of them being previously reported sources and 23 corresponding to non-catalogued objects.
For a few of the most interesting anomaly candidates, the expert analysis included gathering additional observational data. This allowed us to spectroscopically classify one anomaly candidate as an RS Canum Venaticorum star – a close detached binary whose variability outside the eclipse is due to stellar spots. Such objects are rare in ZTF DR3 therefore we consider it an anomaly. Other found anomalies that belong to the rare types of objects are polar, supernovae, and red dwarf flare. The interesting anomalies we found also include a few unclassified variable stars with controversial reports in the literature, among them the objects for which we performed the photometric observations. Nevertheless, additional studies are still required. We also found the sources that behave unusually for their suspected astrophysical type, e.g. the burst frequency of AT 2017ixs – possible nova in M 31. Even among the bogus light curves, we were able to identify interesting events, like the IW Dra star and its three companion echoes or the interaction of an asteroid with a background star.
Given the high incidence of bogus light curves, we searched for a simple rule which could allow us to easy estimate the likelihood of a given object being bogus. A quick EDA, over the data accumulated by the expert, showed that bogus light curves are more likely to have a high reduced χ2 and low period amplitude (at least for data in the M 31 field). At this point, this result should be seen only as an indication that a careful exploitation of the parameter space by the expert can potentially lead to useful relations. If confirmed, such a relation could be used in the construction of alert stream filters for future telescopes.
Despite the encouraging results reported in this work, the incidence of bogus among the automatic identified outliers is still relatively high (68 per cent). In order to use similar techniques in the context of future surveys like the Vera Rubin Observatory Legacy Survey of Space and Time or the Nancy G. Roman Space Telescope,14 it is necessary to reinforce and optimize the interaction between the domain expert and the machine learning algorithm. We are currently working on adaptive strategies that are proven to perform well in such scenarios (Ishida et al. 2019) and intend to add similar capabilities to the SNAD pipeline. Nevertheless, this experiment confirms the potential of machine learning techniques in pointing non-standard elements within a large data set. The list of anomaly candidates provided here may be of use for scientists working in a broad range of domains and consists of a concrete example of the crucial role to be played by automatic pipelines in the future of astronomical discovery.
ACKNOWLEDGEMENTS
We are grateful to L. N. Berdnikov and S. V. Antipin for the helpful discussion on the physical nature of anomaly candidates.
MVK, VSK, KLM, AAV, and MVP were supported by Russian Foundation for Basic Research (RFBR) grant according to the research project 20-02-00779 for preparing ZTF data, implementation of the anomaly detection algorithm, and analysis of outliers. We used the equipment funded by the Lomonosov Moscow State University Program of Development. The authors acknowledge the support by the Interdisciplinary Scientific and Educational School of Moscow University ‘Fundamental and Applied Space Research’. PDA was supported by the Center for Astrophysical Surveys (CAPS) at the National Center for Supercomputing Applications (NCSA) as an Illinois Survey Science Graduate Fellow. V.V.K. is supported by the Ministry of science and higher education of Russian Federation, topic? FEUZ-2020-0038. EEOI and SS acknowledge support from Centre national de la recherche scientifique (CNRS) 2017 MOMENTUM grant under project Active Learning for Large Scale Sky Surveys. Observations with TDS and data reduction (SGZ, AVD) were supported by the Ministry of Science and Higher Education of the Russian Federation under the contract 075-15-2020-778 in the framework of the Large scientific projects program within the national project ‘Science’.
This research has made use of the International Variable Star Index (VSX) data base, operated at AAVSO, Cambridge, Massachusetts, USA. This research has made use of data and/or software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC. This research has made use of ‘Aladin sky atlas’ developed at CDS, Strasbourg Observatory, France. This research has made use of the SIMBAD data base, operated at CDS, Strasbourg, France. We acknowledge the usage of the HyperLeda data base.16 This research has made use of NASA’s Astrophysics Data System Bibliographic Services and following Python software packages: numpy (van der Walt, Colbert & Varoquaux 2011), matplotlib (Hunter 2007), scipy (Jones et al. 2001), pandas (Virtanen 2020; Pandas Development Team 2020), scikit-learn (Pedregosa et al. 2011), astropy (Astropy Collaboration 2013, 2018), and astroquery (Ginsburg et al. 2019).
DATA AVAILABILITY
The ZTF light-curve data underlying this article are available in NASA/IPAC Infrared Science Archive.15 Light-curve feature set is available in Zenodo, at https://doi.org/10.5281/zenodo.4318700. Other data underlying this article are available in the source code GitHub repository at https://github.com/snad-space/zwad.
Footnotes
In this particular case, we used the API because the individual observations coordinates are missed in the bulk-downloadable files. API description page is https://irsa.ipac.caltech.edu/docs/program_interface/ztf_lightcurve_api.html.
REFERENCES
APPENDIX A: FEATURES
We extracted 42 features from every light curve. For this purpose, the library on Rust programming language was developed.17
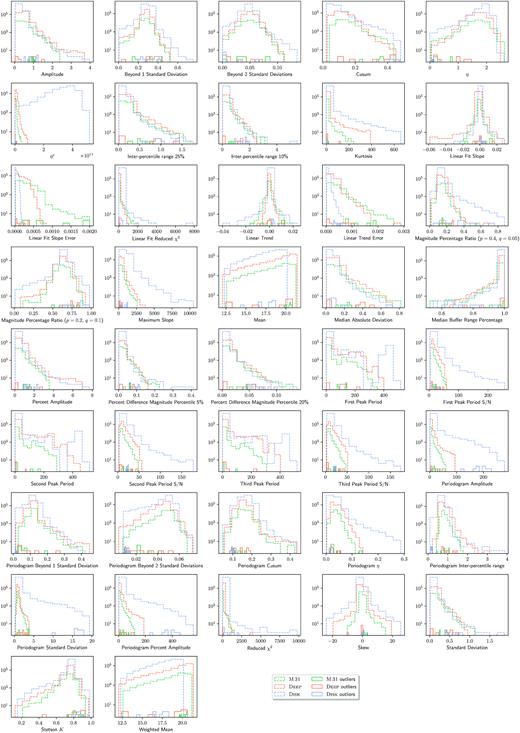
Histogram of all 42 light curve features for objects in M 31 (dashed green), deep (dashed orange), and disk (dashed blue), as well as outliers in M 31 (solid green), deep (solid orange), and disk (solid blue) fields.
Histogram of all 42 light curve features in M 31 field for both bogus (dashed purple) and anomaly candidates (solid red).
A1 Auxiliary definitions
A1.1 Light curve
We define light curve as a list of triples of magnitude mi, its error δi, and observation time ti, where i = 0...N − 1 and N is the number of observations.
A1.2 Mean
A1.3 Weighted mean
A1.4 Standard deviation
A1.5 Indicator function
The indicator function of a set A IA(x) is a function that equals unity when x ∈ A and equals zero when x∉A. For instance, Ix > 0 equals unity for positive numbers and zero for non-positive.
A1.6 Distribution quantile
We define Qx(p) to be the R-518 pth quantile (100 × p percentile) of {xi}.
A1.7 Median
We define Median(x) ≡ Qx(0.5).
A1.8 Periodogram
A2 Feature description
We follow feature names from the original papers when possible.
A2.1 Amplitude
A2.2 Beyond n Std
A2.3 Cusum
A2.4 Von Neummann η
A2.5 ηe
A2.6 Inter-percentile range
We use p = 0.1 and p = 0.25 in our analysis.
A2.7 Kurtosis
A2.8 Linear Trend
A2.9 Linear Fit
A2.10 Magnitude percentage ratio
A2.11 Maximum slope
A2.12 Mean
See A1.2.
A2.13 Median absolute deviation
A2.14 Median Buffer Range Percentage
A2.15 Percent Amplitude
A2.16 Percent Difference Magnitude Percentile
A2.17 Periodogram Amplitude
Same as Amplitude (see A2.1) but for {Pk}.
A2.18 Periodogram Beyond n Std
Same as Beyond n Std (see A2.2) but for {Pk}. We used n = 1 and n = 2 in our analysis.
A2.19 Periodogram Cusum
Same as Cusum (see A2.3) but for {Pk}.
A2.20 Periodogram η
Same as Von Neummann η (see A2.4) but for {Pk}.
A2.21 Periodogram Inter-Percentile range
Same as Inter-Percentile range (see A2.6) but for {Pk}. We used p = 0.25 in our analysis.
A2.22 Periodogram peaks
Three highest periodogram peaks’ period and Ppeak/σP (‘signal-to-noise’ ratio; Kim et al. 2014), where σP is periodogram values standard deviation (see A2.23).
A2.23 Periodogram standard deviation
Same as Standard Deviation (see A2.27) but for {Pk}.
A2.24 Peridogram Percent Amplitude
Same as Percent Amplitude (see A2.3) but for {Pk}.
A2.25 Reduced χ2
A2.26 Skew
A2.27 Standard deviation
σm, see A1.4.
A2.28 Stetson K
A2.29 Weighted mean
|$\bar{m}$|, see A1.3.
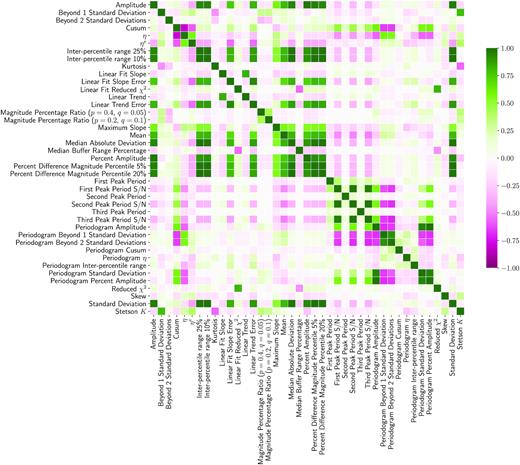
A correlation matrix of all 42 light curve features on a combined data set of the M 31, deep, and disk fields.
APPENDIX B: ZTF DR OBJECTS WEB-VIEWER
We developed web-based graphical user interface for expert analysis of outliers, however, it can be used by any researcher working with ZTF DRs as a light-curve viewer and cross-match tool. We use ClickHouse19 column-based relation data base management system as a storage for ZTF DR light curves. A column-based data base is sub-optimal for querying a small number of objects which is required by a web-service, but in our case the main purpose of the data base was selecting of batches of objects for feature extraction for anomaly detection, while an opportunity of getting of individual objects is a useful by-product. The web-viewer is written on Dash20 Python framework which is suitable for interactive data visualization. A ZTF object page shows the main properties, light curve and result of cross-matching with different catalogues. Due to the fact that several ZTF DR3 objects (OIDs) can represent the same source, the viewer shows not only light curve of the current object, but also finds all neighbour ZTF DR light curves within some radius, the default value is one arcsec. A user can interact with the plot, changing this search radius, turn-off and turn on light curves, click on an observation to load image into embedded FITS viewer powered by JS9 library.21 Also a user can see folded light-curve that can be useful for periodic variable star analysis. The object page contains cross-matching information with various variable star and transient catalogues, has embedded Aladin (Boch & Fernique 2014) Sky Atlas where object position is marked. Feature set that is presented in this paper (see Section A) is listed on the object page too. Web-viewer supports SIMBAD-powered (Wenger et al. 2000) object cone search that allows a user to find ZTF DR3 objects by common source name or by sky coordinates. A screenshot of the web-viewer is presented in Fig. B1 and its source code is available on Github.22
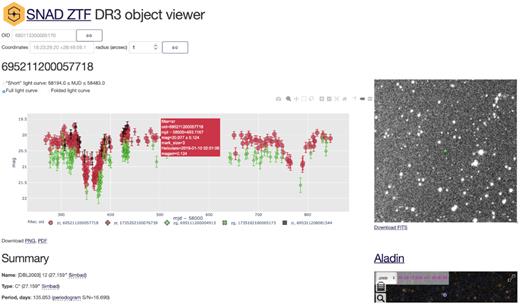
APPENDIX C: LIGHT-CURVE FIT OF SUPERNOVA CANDIDATES
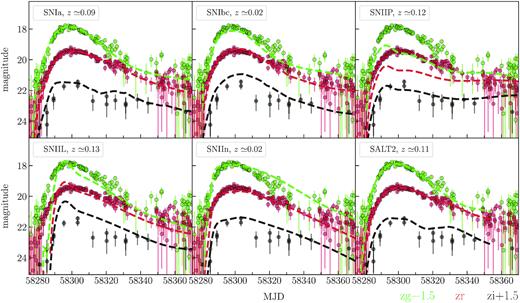
Results of light-curve fit of 795209200003484 by Nugent’s supernova models and SALT2 model. Observational data correspond to OIDs: 795109200001660 (zg), 795209200003484 (zr), 795309200004249 (zi), 796312200003601 (zi).
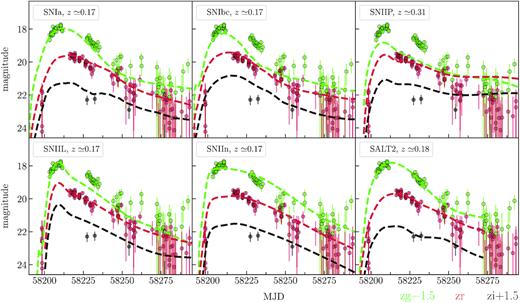
Results of light-curve fit of 795212100007964 by Nugent’s supernova models and SALT2 model. Observational data correspond to OIDs: 795112100014865 (zg), 795212100007964 (zr), 795312100008834 (zi).
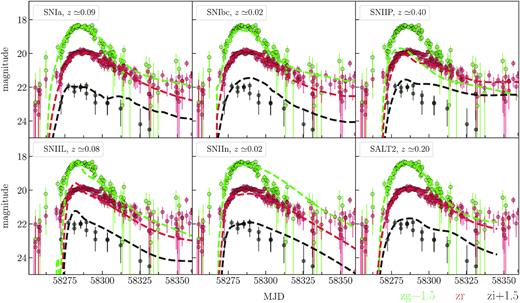
Results of light-curve fit of 795205100007271 by Nugent’s supernova models and SALT2 model. Observational data correspond to OIDs: 795105100002903 (zg), 795205100007271 (zr), 795305100008092 (zi), 796308200008245 (zi).
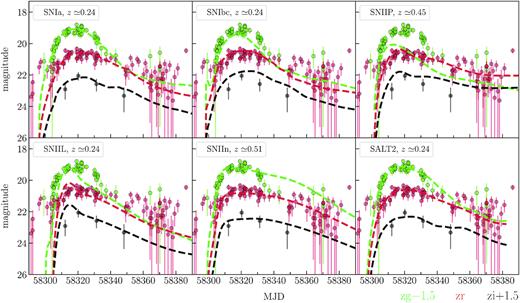
Results of light-curve fit of 795204100013041 by Nugent’s supernova models and SALT2 model. Observational data correspond to OIDs: 795104100011724 (zg), 795204100013041 (zr), 795304100015672 (zi).
APPENDIX D: ANOMALY CANDIDATES
| OID . | Other identifiers . | α, δ (deg) . | mr, min . | mr, max . | E(B − V) . | D (pc) . | Mr, max . | |$P_0^\dagger$| (d) . | Type⋆ . | References . |
|---|---|---|---|---|---|---|---|---|---|---|
| M 31 | ||||||||||
| 695211100003383 | 2MASS J00452494+4207269 | 11.35388 42.12427 | 20.87 ± 0.25 | 18.71 ± 0.05 | 0.117 | M 31 | −6.05 | – | RSG | [14] |
| 695211100015190 | 11.79716 41.78059 | 21.45 ± 0.31 | 19.49 ± 0.09 | 0.078 | M 31 | −5.17 | – | – | ||
| 695211100022045 | AT 2017ixs | 10.98339 41.53641 | 21.27 ± 0.29 | 18.66 ± 0.05 | 0.268 | M 31 | −6.50 | – | PNV | [15] |
| 695211100131796 | PSO J011.0457+41.5548 | 11.04581 41.55487 | 17.92 ± 0.03 | 16.84 ± 0.02 | 0.287 | M 31 | −8.36 | – | VAR | [16,17] |
| 695211200018901 | 2MASS J00421755+4135039 | 10.57313 41.58447 | 18.54 ± 0.04 | 17.78 ± 0.02 | 0.143 | M 31 | −7.06 | 214.6 | RSG | [14] |
| 695211200019653 | 2MASS J00415491+4133323, | 10.47879 41.55899 | 15.58 ± 0.01 | 15.19 ± 0.01 | 0.100 | 1642 | 3.85 | 7.715 | MSINE, | [2,3] |
| ZTFJ004154.90+413332.3 | RSCVN | |||||||||
| 695211200022958 | PSO J010.4744+41.4515 | 10.47441 41.45149 | 18.86 ± 0.05 | 18.30 ± 0.03 | 0.171 | M 31 | −6.61 | 90.54 | Delta Cep | [18] |
| 695211200035023 | 10.50601 41.81453 | 21.17 ± 0.25 | 19.33 ± 0.07 | 0.061 | M 31 | −5.29 | 132.9 | – | ||
| 695211200046528 | [MAP97] 55 | 10.63267 41.48622 | 18.51 ± 0.04 | 17.85 ± 0.02 | 0.308 | M 31 | −7.41 | 74.29 | Delta Cep | [19] |
| 695211200057718 | 9.82489 41.76983 | 21.56 ± 0.29 | 19.71 ± 0.09 | 0.056 | M 31 | −4.90 | >200 | – | ||
| 695211200058391 | 9.98496 41.74939 | 22.18 ± 0.35 | 20.02 ± 0.12 | 0.058 | M 31 | −4.59 | – | – | ||
| 695211200075348 | M31N 2013-11b, | 10.35917 41.73029 | 21.61 ± 0.29 | 19.40 ± 0.07 | 0.060 | M 31 | −5.22 | 168.4 | VAR | [20,21] |
| MASTER OTJ004126.22+414350.0 | ||||||||||
| 695211300004359 | PNV J00414894+4109173 | 10.45371 41.15395 | 20.61 ± 0.21 | 17.56 ± 0.03 | 0.261 | M 31 | −7.58 | – | PNV | [22] |
| 695211300006331 | CSS_J003827.1+410334 | 9.61336 41.05944 | 15.03 ± 0.01 | 14.30 ± 0.02 | 0.067 | 1546 | 3.18 | 3.138 | EA | [1] |
| 695211300007276 | SV* SON 10726 | 10.19874 41.03242 | 18.51 ± 0.05 | 17.78 ± 0.03 | 0.275 | M 31 | −7.40 | 58.00 | Delta Cep | [23] |
| 695211400009049 | 11.11946 40.99692 | 21.47 ± 0.31 | 19.72 ± 0.12 | 0.076 | M 31 | −4.94 | – | – | ||
| 695211400025927 | 11.44201 41.25969 | 21.82 ± 0.34 | 20.07 ± 0.16 | 0.072 | M 31 | −4.58 | – | – | ||
| 695211400027347 | 2MASS J00434749+4112585 | 10.94775 41.21573 | 21.50 ± 0.31 | 19.57 ± 0.11 | 0.332 | M 31 | −5.76 | >200 | VAR | [24] |
| 695211400046832 | 11.26142 40.57456 | 22.17 ± 0.37 | 20.21 ± 0.18 | 0.063 | M 31 | −4.41 | – | – | ||
| 695211400070144 | 2MASS J00443180+4119083 | 11.13252 41.31898 | 19.63 ± 0.12 | 18.10 ± 0.04 | 0.275 | M 31 | −7.07 | – | VAR | [25] |
| 695211400121607 | [JPN2003] V206 | 10.87915 41.09875 | 21.42 ± 0.30 | 19.33 ± 0.09 | 0.181 | M 31 | −5.60 | – | VAR | [24] |
| Deep | ||||||||||
| 795202100005941 | MLS180307:163438+521642, | 248.65767 52.27841 | 21.90 ± 0.27 | 19.45 ± 0.07 | 0.026 | – | – | – | SN candidate | [11] |
| ZTF18aanbnjh | ||||||||||
| 795202300001087 | NSVS 5270259 | 247.70051 51.96916 | 13.84 ± 0.01 | 12.99 ± 0.01 | 0.022 | 957 | 3.03 | 0.674 | EA | [1] |
| 795203200009604 | DDE 32 | 244.89910 52.77552 | 20.39 ± 0.14 | 16.50 ± 0.01 | 0.019 | 439 | 8.24 | – | AM | [1] |
| 795204100013041 | ZTF18abgvctp | 242.30742 52.21426 | 21.87 ± 0.27 | 20.02 ± 0.11 | 0.016 | – | – | – | – | |
| 795204200006882 | CSS_J160450.1+520159 | 241.20883 52.03324 | 20.67 ± 0.18 | 17.20 ± 0.02 | 0.014 | 3909 | 4.20 | 316.8 | EA | [1] |
| 795205100007271 | ZTF18aayatjf | 252.30216 54.11178 | 21.45 ± 0.23 | 19.51 ± 0.08 | 0.021 | – | – | – | – | |
| 795205400001697 | SDSS J164749.77+534217.3, | 251.95740 53.70487 | 12.48 ± 0.01 | 12.35 ± 0.01 | 0.051 | 924 | 2.39 | 2.217 | – | |
| ZTF18aajsmrd | ||||||||||
| 795205400022890 | IW Dra | 251.56278 53.19847 | 14.69 ± 0.01 | 11.57 ± 0.01 | 0.047 | 4888 | −1.99 | 193.2 | Mira | [1] |
| 795205400035251 | SDSS J164533.41+531522.6 | 251.38937 53.25627 | 16.37 ± 0.01 | 15.99 ± 0.01 | 0.046 | 1353 | 5.21 | 230.3 | – | |
| 795209200003484 | ZTF18abbpebf | 251.54866 56.33124 | 21.33 ± 0.22 | 18.96 ± 0.05 | 0.015 | – | – | – | – | |
| 795209300012791 | CSS_J164050.1+552654 | 250.20916 55.44835 | 16.27 ± 0.01 | 15.17 ± 0.01 | 0.015 | 5138 | 1.58 | 0.458 | RRAB | [1] |
| 795210400001565 | SDSS J163331.55+554406.1 | 248.38139 55.73513 | 12.50 ± 0.01 | 12.43 ± 0.01 | 0.006 | 240 | 5.52 | 3.731 | – | |
| 795211200035931 | SN 2018coi | 244.74136 56.71714 | 20.35 ± 0.15 | 18.04 ± 0.03 | 0.009 | – | −19.07 | – | SN Ia | [12] |
| 795212100007964 | ZTF18aanbksg | 242.93762 55.96133 | 21.72 ± 0.27 | 19.28 ± 0.07 | 0.007 | – | – | – | – | |
| 795213200000671 | AT2018afr, Gaia18apj, | 251.93077 58.50559 | 20.46 ± 0.17 | 18.86 ± 0.05 | 0.012 | – | – | – | SN candidate | [13] |
| ZTF18aaincjv | ||||||||||
| 795213300001714 | ASASSN-V J164454.40+573232.3 | 251.22667 57.54232 | 13.02 ± 0.01 | 12.41 ± 0.01 | 0.016 | 4974 | −1.11 | 52.90 | SR | [1] |
| 795213400008053 | NSVS J1647409+565803 | 251.91816 56.96779 | 14.98 ± 0.01 | 13.25 ± 0.01 | 0.017 | 8363 | −1.40 | 111.3 | SR | [1] |
| 795214300016648 | 248.03423 57.75695 | 19.84 ± 0.10 | 16.68 ± 0.01 | 0.010 | 403 | 8.62 | – | – | ||
| disk | ||||||||||
| 807201100022915 | V0476 Cas | 25.84085 59.36414 | 15.93 ± 0.01 | 12.79 ± 0.01 | 0.512 | 3256 | −1.11 | 227.1 | Mira | [1] |
| 807202100027080 | J022.6771+60.0173, | 22.67713 60.01735 | 16.61 ± 0.01 | 15.44 ± 0.01 | 0.441 | 1875 | 2.93 | 0.824 | DBF, EA | [2,3] |
| ZTFJ013042.51+600102.4 | ||||||||||
| 807202300038681 | MGAB-V574 | 20.22254 58.82538 | 20.74 ± 0.22 | 17.24 ± 0.02 | 0.474 | 2830 | 3.75 | – | UG | [1] |
| 807202400015654 | V0420 Cas | 22.80860 58.79127 | 14.82 ± 0.01 | 13.72 ± 0.01 | 0.419 | 2717 | 0.46 | 13.78 | EA | [1] |
| 807203200013118 | J017.9869+59.7407, | 17.98693 59.74082 | 17.73 ± 0.03 | 16.14 ± 0.01 | 0.553 | 1026 | 4.65 | 2.185 | – | |
| ZTF18abfyqzh | ||||||||||
| 807203300044912 | V0890 Cas | 16.93576 59.05054 | 20.79 ± 0.24 | 14.32 ± 0.01 | 0.747 | 4536 | −0.90 | 421.8 | Mira | [1] |
| 807203400031819 | Romanov V28 | 19.30153 58.46788 | 19.28 ± 0.08 | 16.09 ± 0.01 | 0.414 | 1485 | 4.15 | >20 | UGSS | [1] |
| 807203400037050 | Dauban V254, | 19.20494 59.08340 | 16.74 ± 0.02 | 14.17 ± 0.01 | 0.491 | 2625 | 0.80 | 256.0 | Mira | [3] |
| ZTFJ011649.18+590500.2 | ||||||||||
| 807204200004799 | 14.29017 59.90208 | 20.19 ± 0.17 | 18.05 ± 0.03 | 0.435 | 4891 | 3.47 | 4.320 | – | ||
| 807204400014494 | ZTF18abhakel | 16.16915 58.85506 | 14.88 ± 0.01 | 13.86 ± 0.01 | 0.607 | 1514 | 1.38 | 6.017 | – | |
| 807205200017536 | V0367 Cas | 25.29686 61.25982 | 16.30 ± 0.01 | 13.48 ± 0.01 | 0.964 | 1955 | −0.48 | 3.709 | EA | [1] |
| 807206200003542 | ASASSN-V J012356.42+615458.8 | 20.98505 61.91633 | 17.18 ± 0.02 | 14.74 ± 0.01 | 10.394 | 793 | −21.81 | – | VAR, YSO, | [1,4,5] |
| PMS | ||||||||||
| 807206200004116 | MGAB-V1397 | 21.18448 61.89163 | 20.17 ± 0.16 | 17.63 ± 0.02 | 1.411 | 984 | 3.99 | – | YSO, PMS | [1,5] |
| 807206200014645 | MGAB-V1388 | 20.49273 61.50519 | 18.45 ± 0.04 | 16.28 ± 0.01 | 0.887 | 935 | 4.11 | – | YSO, PMS | [1,5] |
| 807206200023036 | NSVS J0122238+611352 | 20.59913 61.23097 | 16.53 ± 0.01 | 12.84 ± 0.01 | 0.626 | 4401 | −2.01 | 325.1 | Mira | [1] |
| 807206300013468 | II Cas | 21.67063 60.77933 | 15.62 ± 0.01 | 12.32 ± 0.01 | 0.560 | 2997 | −1.52 | 282.0 | Mira | [1] |
| 807206400014916 | Mis V1358 | 22.34756 60.74668 | 17.36 ± 0.02 | 12.92 ± 0.01 | 0.489 | 2911 | −0.67 | 310.0 | Mira: | [1] |
| 807207100005929 | IRAS 01145+6132, | 19.45793 61.80168 | 17.80 ± 0.03 | 14.25 ± 0.01 | 1.013 | 3247 | −0.95 | 278.0 | LPV, Mira | [3,6] |
| ZTFJ011749.90+614805.9 | ||||||||||
| 807207300036103 | BMAM-V362 | 16.98932 60.35615 | 20.46 ± 0.18 | 17.79 ± 0.03 | 0.540 | 2311 | 4.57 | – | UGZ | [1] |
| 807208200059506 | V0450 Cas | 12.87116 61.64957 | 16.42 ± 0.01 | 13.93 ± 0.01 | 1.223 | 560 | 2.01 | – | INS | [1] |
| 807208300012891 | OU Cas | 13.32034 60.69593 | 16.80 ± 0.02 | 15.17 ± 0.01 | 0.542 | 2434 | 1.82 | 1.265 | EA | [1] |
| 807208300016714 | OT Cas | 13.26166 60.59657 | 16.10 ± 0.01 | 12.49 ± 0.01 | 0.496 | 3145 | −1.29 | 292.0 | Mira | [1] |
| 807208400015695 | AV Cas | 14.89163 60.72181 | 15.72 ± 0.01 | 11.95 ± 0.01 | 0.570 | 1695 | −0.68 | 330.0 | Mira | [1] |
| 807208400036953 | ZTF18abflqpt | 14.44257 60.25802 | 20.01 ± 0.14 | 17.48 ± 0.02 | 0.445 | 2553 | 4.29 | 1.544 | – | |
| 807209100042420 | Dauban V252, | 27.07326 63.12797 | 18.25 ± 0.04 | 13.44 ± 0.01 | 1.031 | 3624 | −2.03 | 327.6 | Mira | [3] |
| ZTFJ014817.58+630740.6 | ||||||||||
| 807209300012026 | WISE J014237.7+623700 | 25.65734 62.61680 | 14.32 ± 0.01 | 13.20 ± 0.01 | 1.294 | 3020 | −2.57 | 6.399 | EA | [1] |
| 807209300037143 | NSVS J0141549+623406 | 25.47716 62.56828 | 16.89 ± 0.02 | 12.32 ± 0.01 | 1.349 | 4302 | −4.36 | 297.0 | Mira | [1] |
| 807209400037670 | IRAS 01438+6208 | 26.85197 62.38822 | 18.56 ± 0.05 | 12.56 ± 0.01 | 1.426 | 3518 | −3.88 | 286.0 | Mira | [7] |
| 807210100028861 | NSVS J0129109+631249, | 22.29801 63.21435 | 16.28 ± 0.01 | 12.70 ± 0.01 | 1.357 | 5972 | −4.71 | 454.2 | LPV, | [1,7] |
| IRAS 01257+6257 | SR+L, C | |||||||||
| 807210200004045 | 21.24037 63.85572 | 19.48 ± 0.09 | 17.84 ± 0.03 | 1.550 | 3353 | 1.18 | – | – | ||
| 807210200026027 | 21.96268 63.28808 | 18.81 ± 0.06 | 16.56 ± 0.01 | 1.451 | 1704 | 1.63 | 421.7 | YSO, PMS, | [4,5,8] | |
| AGN | ||||||||||
| 807211100059466 | V0724 Cas | 18.72328 63.61240 | 15.55 ± 0.01 | 12.54 ± 0.01 | 1.488 | 5475 | −5.03 | 280.0 | Mira | [1] |
| 807211300006190 | Mis V0818, | 16.17487 62.88210 | 17.33 ± 0.02 | 13.02 ± 0.01 | 1.332 | 4768 | −3.85 | 315.0 | Mira | [3] |
| ZTFJ010441.96+625255.5 | ||||||||||
| 807211300012948 | ZTFJ010526.59+624324.4 | 16.36079 62.72345 | 16.09 ± 0.01 | 14.31 ± 0.01 | 1.463 | 2785 | −1.72 | 302.9 | Mira | [3] |
| 807211400009493 | ZTF18abjcvcb | 18.74697 62.83884 | 20.08 ± 0.15 | 17.63 ± 0.02 | 1.472 | 3334 | 1.18 | 2.546 | – | |
| 807212100012737 | ZTF17aaaeesd | 15.01403 63.61420 | 19.01 ± 0.07 | 16.51 ± 0.01 | 1.196 | 1087 | 3.22 | – | – | |
| 807212100020830 | ZTFJ005605.95+632426.8 | 14.02475 63.40745 | 16.80 ± 0.02 | 13.26 ± 0.01 | 1.016 | 3188 | −1.90 | 394.4 | Mira | [3] |
| 807212200034055 | [I81] M 633 | 13.10185 63.06180 | 16.83 ± 0.02 | 13.64 ± 0.01 | 1.039 | 2171 | −0.75 | 364.0 | Mira | [9] |
| 807212300038616 | NSVS J0053173+623614, | 13.32484 62.60320 | 19.61 ± 0.11 | 14.55 ± 0.01 | 1.306 | 3530 | −1.59 | 311.0 | L, Mira | [1,9] |
| [I81] M 644 | ||||||||||
| 807214100007080 | [WWV2004] J0129273+653917 | 22.37209 65.65551 | 18.30 ± 0.04 | 13.00 ± 0.01 | 1.051 | 3655 | −2.55 | 295.2 | Mira | [7] |
| 807214100026393 | Dauban V269, | 22.36480 65.19663 | 20.94 ± 0.27 | 16.75 ± 0.02 | 1.074 | 3884 | 1.00 | 454.2 | Mira | [3] |
| ZTFJ012927.55+651147.8 | ||||||||||
| 807214100042070 | MGAB-V1402 | 24.06955 65.31108 | 20.11 ± 0.16 | 18.24 ± 0.04 | 1.125 | 3876 | 2.37 | 600.0 | Mira | [1] |
| 807214300010833 | NSVS 1695145 | 21.24271 64.77038 | 16.53 ± 0.01 | 13.84 ± 0.01 | 1.315 | 4633 | −2.91 | 560.0 | Mira: | [1] |
| 807214300051120 | ZTFJ012430.53+641432.2 | 21.12717 64.24230 | 17.69 ± 0.03 | 15.41 ± 0.01 | 1.194 | 3852 | −0.62 | 325.0 | Mira | [3] |
| 807215100019764 | VSX J011759.4+652153 | 19.49756 65.36491 | 19.37 ± 0.09 | 14.03 ± 0.01 | 1.593 | 4243 | −3.26 | 320.0 | Mira: | [1] |
| 807215200006611 | NSVS J0108368+653701 | 17.15140 65.61674 | 16.78 ± 0.02 | 12.71 ± 0.01 | 1.580 | 5238 | −5.00 | 309.0 | Mira | [1] |
| 807216100038423 | IPHAS J005934.24+651815.1, | 14.89278 65.30412 | 18.25 ± 0.04 | 14.47 ± 0.01 | 1.412 | 2598 | −1.27 | 295.2 | AGB, Mira | [3,10] |
| ZTFJ005934.27+651814.9 | ||||||||||
| 807216200026731 | NSV 15193 | 13.35496 65.03225 | 16.29 ± 0.01 | 12.10 ± 0.01 | 1.305 | 2681 | −3.44 | 507.0 | Mira | [1] |
| 807216200045725 | NSVS 1633482 | 11.72349 65.61549 | 21.30 ± 0.34 | 15.52 ± 0.01 | 1.411 | 3882 | −1.10 | 390.0 | Mira | [1] |
| 807216400013229 | 14.15960 64.56684 | 17.41 ± 0.02 | 16.29 ± 0.01 | 1.381 | 2530 | 0.69 | 2.160 | – | ||
| OID . | Other identifiers . | α, δ (deg) . | mr, min . | mr, max . | E(B − V) . | D (pc) . | Mr, max . | |$P_0^\dagger$| (d) . | Type⋆ . | References . |
|---|---|---|---|---|---|---|---|---|---|---|
| M 31 | ||||||||||
| 695211100003383 | 2MASS J00452494+4207269 | 11.35388 42.12427 | 20.87 ± 0.25 | 18.71 ± 0.05 | 0.117 | M 31 | −6.05 | – | RSG | [14] |
| 695211100015190 | 11.79716 41.78059 | 21.45 ± 0.31 | 19.49 ± 0.09 | 0.078 | M 31 | −5.17 | – | – | ||
| 695211100022045 | AT 2017ixs | 10.98339 41.53641 | 21.27 ± 0.29 | 18.66 ± 0.05 | 0.268 | M 31 | −6.50 | – | PNV | [15] |
| 695211100131796 | PSO J011.0457+41.5548 | 11.04581 41.55487 | 17.92 ± 0.03 | 16.84 ± 0.02 | 0.287 | M 31 | −8.36 | – | VAR | [16,17] |
| 695211200018901 | 2MASS J00421755+4135039 | 10.57313 41.58447 | 18.54 ± 0.04 | 17.78 ± 0.02 | 0.143 | M 31 | −7.06 | 214.6 | RSG | [14] |
| 695211200019653 | 2MASS J00415491+4133323, | 10.47879 41.55899 | 15.58 ± 0.01 | 15.19 ± 0.01 | 0.100 | 1642 | 3.85 | 7.715 | MSINE, | [2,3] |
| ZTFJ004154.90+413332.3 | RSCVN | |||||||||
| 695211200022958 | PSO J010.4744+41.4515 | 10.47441 41.45149 | 18.86 ± 0.05 | 18.30 ± 0.03 | 0.171 | M 31 | −6.61 | 90.54 | Delta Cep | [18] |
| 695211200035023 | 10.50601 41.81453 | 21.17 ± 0.25 | 19.33 ± 0.07 | 0.061 | M 31 | −5.29 | 132.9 | – | ||
| 695211200046528 | [MAP97] 55 | 10.63267 41.48622 | 18.51 ± 0.04 | 17.85 ± 0.02 | 0.308 | M 31 | −7.41 | 74.29 | Delta Cep | [19] |
| 695211200057718 | 9.82489 41.76983 | 21.56 ± 0.29 | 19.71 ± 0.09 | 0.056 | M 31 | −4.90 | >200 | – | ||
| 695211200058391 | 9.98496 41.74939 | 22.18 ± 0.35 | 20.02 ± 0.12 | 0.058 | M 31 | −4.59 | – | – | ||
| 695211200075348 | M31N 2013-11b, | 10.35917 41.73029 | 21.61 ± 0.29 | 19.40 ± 0.07 | 0.060 | M 31 | −5.22 | 168.4 | VAR | [20,21] |
| MASTER OTJ004126.22+414350.0 | ||||||||||
| 695211300004359 | PNV J00414894+4109173 | 10.45371 41.15395 | 20.61 ± 0.21 | 17.56 ± 0.03 | 0.261 | M 31 | −7.58 | – | PNV | [22] |
| 695211300006331 | CSS_J003827.1+410334 | 9.61336 41.05944 | 15.03 ± 0.01 | 14.30 ± 0.02 | 0.067 | 1546 | 3.18 | 3.138 | EA | [1] |
| 695211300007276 | SV* SON 10726 | 10.19874 41.03242 | 18.51 ± 0.05 | 17.78 ± 0.03 | 0.275 | M 31 | −7.40 | 58.00 | Delta Cep | [23] |
| 695211400009049 | 11.11946 40.99692 | 21.47 ± 0.31 | 19.72 ± 0.12 | 0.076 | M 31 | −4.94 | – | – | ||
| 695211400025927 | 11.44201 41.25969 | 21.82 ± 0.34 | 20.07 ± 0.16 | 0.072 | M 31 | −4.58 | – | – | ||
| 695211400027347 | 2MASS J00434749+4112585 | 10.94775 41.21573 | 21.50 ± 0.31 | 19.57 ± 0.11 | 0.332 | M 31 | −5.76 | >200 | VAR | [24] |
| 695211400046832 | 11.26142 40.57456 | 22.17 ± 0.37 | 20.21 ± 0.18 | 0.063 | M 31 | −4.41 | – | – | ||
| 695211400070144 | 2MASS J00443180+4119083 | 11.13252 41.31898 | 19.63 ± 0.12 | 18.10 ± 0.04 | 0.275 | M 31 | −7.07 | – | VAR | [25] |
| 695211400121607 | [JPN2003] V206 | 10.87915 41.09875 | 21.42 ± 0.30 | 19.33 ± 0.09 | 0.181 | M 31 | −5.60 | – | VAR | [24] |
| Deep | ||||||||||
| 795202100005941 | MLS180307:163438+521642, | 248.65767 52.27841 | 21.90 ± 0.27 | 19.45 ± 0.07 | 0.026 | – | – | – | SN candidate | [11] |
| ZTF18aanbnjh | ||||||||||
| 795202300001087 | NSVS 5270259 | 247.70051 51.96916 | 13.84 ± 0.01 | 12.99 ± 0.01 | 0.022 | 957 | 3.03 | 0.674 | EA | [1] |
| 795203200009604 | DDE 32 | 244.89910 52.77552 | 20.39 ± 0.14 | 16.50 ± 0.01 | 0.019 | 439 | 8.24 | – | AM | [1] |
| 795204100013041 | ZTF18abgvctp | 242.30742 52.21426 | 21.87 ± 0.27 | 20.02 ± 0.11 | 0.016 | – | – | – | – | |
| 795204200006882 | CSS_J160450.1+520159 | 241.20883 52.03324 | 20.67 ± 0.18 | 17.20 ± 0.02 | 0.014 | 3909 | 4.20 | 316.8 | EA | [1] |
| 795205100007271 | ZTF18aayatjf | 252.30216 54.11178 | 21.45 ± 0.23 | 19.51 ± 0.08 | 0.021 | – | – | – | – | |
| 795205400001697 | SDSS J164749.77+534217.3, | 251.95740 53.70487 | 12.48 ± 0.01 | 12.35 ± 0.01 | 0.051 | 924 | 2.39 | 2.217 | – | |
| ZTF18aajsmrd | ||||||||||
| 795205400022890 | IW Dra | 251.56278 53.19847 | 14.69 ± 0.01 | 11.57 ± 0.01 | 0.047 | 4888 | −1.99 | 193.2 | Mira | [1] |
| 795205400035251 | SDSS J164533.41+531522.6 | 251.38937 53.25627 | 16.37 ± 0.01 | 15.99 ± 0.01 | 0.046 | 1353 | 5.21 | 230.3 | – | |
| 795209200003484 | ZTF18abbpebf | 251.54866 56.33124 | 21.33 ± 0.22 | 18.96 ± 0.05 | 0.015 | – | – | – | – | |
| 795209300012791 | CSS_J164050.1+552654 | 250.20916 55.44835 | 16.27 ± 0.01 | 15.17 ± 0.01 | 0.015 | 5138 | 1.58 | 0.458 | RRAB | [1] |
| 795210400001565 | SDSS J163331.55+554406.1 | 248.38139 55.73513 | 12.50 ± 0.01 | 12.43 ± 0.01 | 0.006 | 240 | 5.52 | 3.731 | – | |
| 795211200035931 | SN 2018coi | 244.74136 56.71714 | 20.35 ± 0.15 | 18.04 ± 0.03 | 0.009 | – | −19.07 | – | SN Ia | [12] |
| 795212100007964 | ZTF18aanbksg | 242.93762 55.96133 | 21.72 ± 0.27 | 19.28 ± 0.07 | 0.007 | – | – | – | – | |
| 795213200000671 | AT2018afr, Gaia18apj, | 251.93077 58.50559 | 20.46 ± 0.17 | 18.86 ± 0.05 | 0.012 | – | – | – | SN candidate | [13] |
| ZTF18aaincjv | ||||||||||
| 795213300001714 | ASASSN-V J164454.40+573232.3 | 251.22667 57.54232 | 13.02 ± 0.01 | 12.41 ± 0.01 | 0.016 | 4974 | −1.11 | 52.90 | SR | [1] |
| 795213400008053 | NSVS J1647409+565803 | 251.91816 56.96779 | 14.98 ± 0.01 | 13.25 ± 0.01 | 0.017 | 8363 | −1.40 | 111.3 | SR | [1] |
| 795214300016648 | 248.03423 57.75695 | 19.84 ± 0.10 | 16.68 ± 0.01 | 0.010 | 403 | 8.62 | – | – | ||
| disk | ||||||||||
| 807201100022915 | V0476 Cas | 25.84085 59.36414 | 15.93 ± 0.01 | 12.79 ± 0.01 | 0.512 | 3256 | −1.11 | 227.1 | Mira | [1] |
| 807202100027080 | J022.6771+60.0173, | 22.67713 60.01735 | 16.61 ± 0.01 | 15.44 ± 0.01 | 0.441 | 1875 | 2.93 | 0.824 | DBF, EA | [2,3] |
| ZTFJ013042.51+600102.4 | ||||||||||
| 807202300038681 | MGAB-V574 | 20.22254 58.82538 | 20.74 ± 0.22 | 17.24 ± 0.02 | 0.474 | 2830 | 3.75 | – | UG | [1] |
| 807202400015654 | V0420 Cas | 22.80860 58.79127 | 14.82 ± 0.01 | 13.72 ± 0.01 | 0.419 | 2717 | 0.46 | 13.78 | EA | [1] |
| 807203200013118 | J017.9869+59.7407, | 17.98693 59.74082 | 17.73 ± 0.03 | 16.14 ± 0.01 | 0.553 | 1026 | 4.65 | 2.185 | – | |
| ZTF18abfyqzh | ||||||||||
| 807203300044912 | V0890 Cas | 16.93576 59.05054 | 20.79 ± 0.24 | 14.32 ± 0.01 | 0.747 | 4536 | −0.90 | 421.8 | Mira | [1] |
| 807203400031819 | Romanov V28 | 19.30153 58.46788 | 19.28 ± 0.08 | 16.09 ± 0.01 | 0.414 | 1485 | 4.15 | >20 | UGSS | [1] |
| 807203400037050 | Dauban V254, | 19.20494 59.08340 | 16.74 ± 0.02 | 14.17 ± 0.01 | 0.491 | 2625 | 0.80 | 256.0 | Mira | [3] |
| ZTFJ011649.18+590500.2 | ||||||||||
| 807204200004799 | 14.29017 59.90208 | 20.19 ± 0.17 | 18.05 ± 0.03 | 0.435 | 4891 | 3.47 | 4.320 | – | ||
| 807204400014494 | ZTF18abhakel | 16.16915 58.85506 | 14.88 ± 0.01 | 13.86 ± 0.01 | 0.607 | 1514 | 1.38 | 6.017 | – | |
| 807205200017536 | V0367 Cas | 25.29686 61.25982 | 16.30 ± 0.01 | 13.48 ± 0.01 | 0.964 | 1955 | −0.48 | 3.709 | EA | [1] |
| 807206200003542 | ASASSN-V J012356.42+615458.8 | 20.98505 61.91633 | 17.18 ± 0.02 | 14.74 ± 0.01 | 10.394 | 793 | −21.81 | – | VAR, YSO, | [1,4,5] |
| PMS | ||||||||||
| 807206200004116 | MGAB-V1397 | 21.18448 61.89163 | 20.17 ± 0.16 | 17.63 ± 0.02 | 1.411 | 984 | 3.99 | – | YSO, PMS | [1,5] |
| 807206200014645 | MGAB-V1388 | 20.49273 61.50519 | 18.45 ± 0.04 | 16.28 ± 0.01 | 0.887 | 935 | 4.11 | – | YSO, PMS | [1,5] |
| 807206200023036 | NSVS J0122238+611352 | 20.59913 61.23097 | 16.53 ± 0.01 | 12.84 ± 0.01 | 0.626 | 4401 | −2.01 | 325.1 | Mira | [1] |
| 807206300013468 | II Cas | 21.67063 60.77933 | 15.62 ± 0.01 | 12.32 ± 0.01 | 0.560 | 2997 | −1.52 | 282.0 | Mira | [1] |
| 807206400014916 | Mis V1358 | 22.34756 60.74668 | 17.36 ± 0.02 | 12.92 ± 0.01 | 0.489 | 2911 | −0.67 | 310.0 | Mira: | [1] |
| 807207100005929 | IRAS 01145+6132, | 19.45793 61.80168 | 17.80 ± 0.03 | 14.25 ± 0.01 | 1.013 | 3247 | −0.95 | 278.0 | LPV, Mira | [3,6] |
| ZTFJ011749.90+614805.9 | ||||||||||
| 807207300036103 | BMAM-V362 | 16.98932 60.35615 | 20.46 ± 0.18 | 17.79 ± 0.03 | 0.540 | 2311 | 4.57 | – | UGZ | [1] |
| 807208200059506 | V0450 Cas | 12.87116 61.64957 | 16.42 ± 0.01 | 13.93 ± 0.01 | 1.223 | 560 | 2.01 | – | INS | [1] |
| 807208300012891 | OU Cas | 13.32034 60.69593 | 16.80 ± 0.02 | 15.17 ± 0.01 | 0.542 | 2434 | 1.82 | 1.265 | EA | [1] |
| 807208300016714 | OT Cas | 13.26166 60.59657 | 16.10 ± 0.01 | 12.49 ± 0.01 | 0.496 | 3145 | −1.29 | 292.0 | Mira | [1] |
| 807208400015695 | AV Cas | 14.89163 60.72181 | 15.72 ± 0.01 | 11.95 ± 0.01 | 0.570 | 1695 | −0.68 | 330.0 | Mira | [1] |
| 807208400036953 | ZTF18abflqpt | 14.44257 60.25802 | 20.01 ± 0.14 | 17.48 ± 0.02 | 0.445 | 2553 | 4.29 | 1.544 | – | |
| 807209100042420 | Dauban V252, | 27.07326 63.12797 | 18.25 ± 0.04 | 13.44 ± 0.01 | 1.031 | 3624 | −2.03 | 327.6 | Mira | [3] |
| ZTFJ014817.58+630740.6 | ||||||||||
| 807209300012026 | WISE J014237.7+623700 | 25.65734 62.61680 | 14.32 ± 0.01 | 13.20 ± 0.01 | 1.294 | 3020 | −2.57 | 6.399 | EA | [1] |
| 807209300037143 | NSVS J0141549+623406 | 25.47716 62.56828 | 16.89 ± 0.02 | 12.32 ± 0.01 | 1.349 | 4302 | −4.36 | 297.0 | Mira | [1] |
| 807209400037670 | IRAS 01438+6208 | 26.85197 62.38822 | 18.56 ± 0.05 | 12.56 ± 0.01 | 1.426 | 3518 | −3.88 | 286.0 | Mira | [7] |
| 807210100028861 | NSVS J0129109+631249, | 22.29801 63.21435 | 16.28 ± 0.01 | 12.70 ± 0.01 | 1.357 | 5972 | −4.71 | 454.2 | LPV, | [1,7] |
| IRAS 01257+6257 | SR+L, C | |||||||||
| 807210200004045 | 21.24037 63.85572 | 19.48 ± 0.09 | 17.84 ± 0.03 | 1.550 | 3353 | 1.18 | – | – | ||
| 807210200026027 | 21.96268 63.28808 | 18.81 ± 0.06 | 16.56 ± 0.01 | 1.451 | 1704 | 1.63 | 421.7 | YSO, PMS, | [4,5,8] | |
| AGN | ||||||||||
| 807211100059466 | V0724 Cas | 18.72328 63.61240 | 15.55 ± 0.01 | 12.54 ± 0.01 | 1.488 | 5475 | −5.03 | 280.0 | Mira | [1] |
| 807211300006190 | Mis V0818, | 16.17487 62.88210 | 17.33 ± 0.02 | 13.02 ± 0.01 | 1.332 | 4768 | −3.85 | 315.0 | Mira | [3] |
| ZTFJ010441.96+625255.5 | ||||||||||
| 807211300012948 | ZTFJ010526.59+624324.4 | 16.36079 62.72345 | 16.09 ± 0.01 | 14.31 ± 0.01 | 1.463 | 2785 | −1.72 | 302.9 | Mira | [3] |
| 807211400009493 | ZTF18abjcvcb | 18.74697 62.83884 | 20.08 ± 0.15 | 17.63 ± 0.02 | 1.472 | 3334 | 1.18 | 2.546 | – | |
| 807212100012737 | ZTF17aaaeesd | 15.01403 63.61420 | 19.01 ± 0.07 | 16.51 ± 0.01 | 1.196 | 1087 | 3.22 | – | – | |
| 807212100020830 | ZTFJ005605.95+632426.8 | 14.02475 63.40745 | 16.80 ± 0.02 | 13.26 ± 0.01 | 1.016 | 3188 | −1.90 | 394.4 | Mira | [3] |
| 807212200034055 | [I81] M 633 | 13.10185 63.06180 | 16.83 ± 0.02 | 13.64 ± 0.01 | 1.039 | 2171 | −0.75 | 364.0 | Mira | [9] |
| 807212300038616 | NSVS J0053173+623614, | 13.32484 62.60320 | 19.61 ± 0.11 | 14.55 ± 0.01 | 1.306 | 3530 | −1.59 | 311.0 | L, Mira | [1,9] |
| [I81] M 644 | ||||||||||
| 807214100007080 | [WWV2004] J0129273+653917 | 22.37209 65.65551 | 18.30 ± 0.04 | 13.00 ± 0.01 | 1.051 | 3655 | −2.55 | 295.2 | Mira | [7] |
| 807214100026393 | Dauban V269, | 22.36480 65.19663 | 20.94 ± 0.27 | 16.75 ± 0.02 | 1.074 | 3884 | 1.00 | 454.2 | Mira | [3] |
| ZTFJ012927.55+651147.8 | ||||||||||
| 807214100042070 | MGAB-V1402 | 24.06955 65.31108 | 20.11 ± 0.16 | 18.24 ± 0.04 | 1.125 | 3876 | 2.37 | 600.0 | Mira | [1] |
| 807214300010833 | NSVS 1695145 | 21.24271 64.77038 | 16.53 ± 0.01 | 13.84 ± 0.01 | 1.315 | 4633 | −2.91 | 560.0 | Mira: | [1] |
| 807214300051120 | ZTFJ012430.53+641432.2 | 21.12717 64.24230 | 17.69 ± 0.03 | 15.41 ± 0.01 | 1.194 | 3852 | −0.62 | 325.0 | Mira | [3] |
| 807215100019764 | VSX J011759.4+652153 | 19.49756 65.36491 | 19.37 ± 0.09 | 14.03 ± 0.01 | 1.593 | 4243 | −3.26 | 320.0 | Mira: | [1] |
| 807215200006611 | NSVS J0108368+653701 | 17.15140 65.61674 | 16.78 ± 0.02 | 12.71 ± 0.01 | 1.580 | 5238 | −5.00 | 309.0 | Mira | [1] |
| 807216100038423 | IPHAS J005934.24+651815.1, | 14.89278 65.30412 | 18.25 ± 0.04 | 14.47 ± 0.01 | 1.412 | 2598 | −1.27 | 295.2 | AGB, Mira | [3,10] |
| ZTFJ005934.27+651814.9 | ||||||||||
| 807216200026731 | NSV 15193 | 13.35496 65.03225 | 16.29 ± 0.01 | 12.10 ± 0.01 | 1.305 | 2681 | −3.44 | 507.0 | Mira | [1] |
| 807216200045725 | NSVS 1633482 | 11.72349 65.61549 | 21.30 ± 0.34 | 15.52 ± 0.01 | 1.411 | 3882 | −1.10 | 390.0 | Mira | [1] |
| 807216400013229 | 14.15960 64.56684 | 17.41 ± 0.02 | 16.29 ± 0.01 | 1.381 | 2530 | 0.69 | 2.160 | – | ||
†The best period extracted from either the Lomb–Scargle periodogram or one of the catalogues listed in the ZTF-viewer or determined by us.
⋆AM – AM Herculis-type variable.
AGB – Asymptotic Giant Branch Star.
C – Carbon star.
DBF – Distant binary, full period.
Delta Cep – Classical Cepheid.
EA – β Persei-type (Algol) eclipsing system.
INS – Orion variable with rapid light variations.
L – Slow irregular variable, stars are often attributed to this type because of being insufficiently studied.
LPV – Long Period Variable.
Mira – o (omicron) Ceti-type variable.
MSINE – Star showing modulated sinusoids.
PNV – Possible nova.
RRAB – RR Lyrae variable with asymmetric light curves.
RSCVN – RS Canum Venaticorum-type binary system.
RSG – Red supergiant.
SN – Supernova.
SR – Semiregular variable.
UG – U Geminorum-type variable, quite often called dwarf nova.
UGSS – SS Cygni-type variable.
UGZ – Z Camelopardalis-type star.
VAR – Variable of unspecified type.
YSO – Young stellar Object of unspecified variable type.
[1] – Watson et al. 2006; [2] – Heinze et al. 2018; [3] – Chen et al. 2020; [4] – Marton et al. 2016; [5] – Vioque et al. 2020; [6] – Usatov & Nosulchik 2008; [7] – Woźniak et al. 2004; [8] – Edelson & Malkan 2012; [9] – Nesci et al. 2018; [10] – Wright et al. 2009; [11] – Drake et al. 2009; [12] – Graham et al. 2018; [13] – Delgado et al. 2018; [14] – Massey et al. 2009; [15] – Carey 2017; [16] – Lee et al. 2014; [17] – Humphreys et al. 2017; [18] – Kodric et al. 2018; [19] – Magnier et al. 1997; [20] – Ovcharov et al. 2013; [21] – Shumkov et al. 2016; [22] – Hornoch & Kucakova 2015; [23] – Kodric et al. 2013; [24] – Joshi et al. 2003; [25] – Kaluzny et al. 1999.
| OID . | Other identifiers . | α, δ (deg) . | mr, min . | mr, max . | E(B − V) . | D (pc) . | Mr, max . | |$P_0^\dagger$| (d) . | Type⋆ . | References . |
|---|---|---|---|---|---|---|---|---|---|---|
| M 31 | ||||||||||
| 695211100003383 | 2MASS J00452494+4207269 | 11.35388 42.12427 | 20.87 ± 0.25 | 18.71 ± 0.05 | 0.117 | M 31 | −6.05 | – | RSG | [14] |
| 695211100015190 | 11.79716 41.78059 | 21.45 ± 0.31 | 19.49 ± 0.09 | 0.078 | M 31 | −5.17 | – | – | ||
| 695211100022045 | AT 2017ixs | 10.98339 41.53641 | 21.27 ± 0.29 | 18.66 ± 0.05 | 0.268 | M 31 | −6.50 | – | PNV | [15] |
| 695211100131796 | PSO J011.0457+41.5548 | 11.04581 41.55487 | 17.92 ± 0.03 | 16.84 ± 0.02 | 0.287 | M 31 | −8.36 | – | VAR | [16,17] |
| 695211200018901 | 2MASS J00421755+4135039 | 10.57313 41.58447 | 18.54 ± 0.04 | 17.78 ± 0.02 | 0.143 | M 31 | −7.06 | 214.6 | RSG | [14] |
| 695211200019653 | 2MASS J00415491+4133323, | 10.47879 41.55899 | 15.58 ± 0.01 | 15.19 ± 0.01 | 0.100 | 1642 | 3.85 | 7.715 | MSINE, | [2,3] |
| ZTFJ004154.90+413332.3 | RSCVN | |||||||||
| 695211200022958 | PSO J010.4744+41.4515 | 10.47441 41.45149 | 18.86 ± 0.05 | 18.30 ± 0.03 | 0.171 | M 31 | −6.61 | 90.54 | Delta Cep | [18] |
| 695211200035023 | 10.50601 41.81453 | 21.17 ± 0.25 | 19.33 ± 0.07 | 0.061 | M 31 | −5.29 | 132.9 | – | ||
| 695211200046528 | [MAP97] 55 | 10.63267 41.48622 | 18.51 ± 0.04 | 17.85 ± 0.02 | 0.308 | M 31 | −7.41 | 74.29 | Delta Cep | [19] |
| 695211200057718 | 9.82489 41.76983 | 21.56 ± 0.29 | 19.71 ± 0.09 | 0.056 | M 31 | −4.90 | >200 | – | ||
| 695211200058391 | 9.98496 41.74939 | 22.18 ± 0.35 | 20.02 ± 0.12 | 0.058 | M 31 | −4.59 | – | – | ||
| 695211200075348 | M31N 2013-11b, | 10.35917 41.73029 | 21.61 ± 0.29 | 19.40 ± 0.07 | 0.060 | M 31 | −5.22 | 168.4 | VAR | [20,21] |
| MASTER OTJ004126.22+414350.0 | ||||||||||
| 695211300004359 | PNV J00414894+4109173 | 10.45371 41.15395 | 20.61 ± 0.21 | 17.56 ± 0.03 | 0.261 | M 31 | −7.58 | – | PNV | [22] |
| 695211300006331 | CSS_J003827.1+410334 | 9.61336 41.05944 | 15.03 ± 0.01 | 14.30 ± 0.02 | 0.067 | 1546 | 3.18 | 3.138 | EA | [1] |
| 695211300007276 | SV* SON 10726 | 10.19874 41.03242 | 18.51 ± 0.05 | 17.78 ± 0.03 | 0.275 | M 31 | −7.40 | 58.00 | Delta Cep | [23] |
| 695211400009049 | 11.11946 40.99692 | 21.47 ± 0.31 | 19.72 ± 0.12 | 0.076 | M 31 | −4.94 | – | – | ||
| 695211400025927 | 11.44201 41.25969 | 21.82 ± 0.34 | 20.07 ± 0.16 | 0.072 | M 31 | −4.58 | – | – | ||
| 695211400027347 | 2MASS J00434749+4112585 | 10.94775 41.21573 | 21.50 ± 0.31 | 19.57 ± 0.11 | 0.332 | M 31 | −5.76 | >200 | VAR | [24] |
| 695211400046832 | 11.26142 40.57456 | 22.17 ± 0.37 | 20.21 ± 0.18 | 0.063 | M 31 | −4.41 | – | – | ||
| 695211400070144 | 2MASS J00443180+4119083 | 11.13252 41.31898 | 19.63 ± 0.12 | 18.10 ± 0.04 | 0.275 | M 31 | −7.07 | – | VAR | [25] |
| 695211400121607 | [JPN2003] V206 | 10.87915 41.09875 | 21.42 ± 0.30 | 19.33 ± 0.09 | 0.181 | M 31 | −5.60 | – | VAR | [24] |
| Deep | ||||||||||
| 795202100005941 | MLS180307:163438+521642, | 248.65767 52.27841 | 21.90 ± 0.27 | 19.45 ± 0.07 | 0.026 | – | – | – | SN candidate | [11] |
| ZTF18aanbnjh | ||||||||||
| 795202300001087 | NSVS 5270259 | 247.70051 51.96916 | 13.84 ± 0.01 | 12.99 ± 0.01 | 0.022 | 957 | 3.03 | 0.674 | EA | [1] |
| 795203200009604 | DDE 32 | 244.89910 52.77552 | 20.39 ± 0.14 | 16.50 ± 0.01 | 0.019 | 439 | 8.24 | – | AM | [1] |
| 795204100013041 | ZTF18abgvctp | 242.30742 52.21426 | 21.87 ± 0.27 | 20.02 ± 0.11 | 0.016 | – | – | – | – | |
| 795204200006882 | CSS_J160450.1+520159 | 241.20883 52.03324 | 20.67 ± 0.18 | 17.20 ± 0.02 | 0.014 | 3909 | 4.20 | 316.8 | EA | [1] |
| 795205100007271 | ZTF18aayatjf | 252.30216 54.11178 | 21.45 ± 0.23 | 19.51 ± 0.08 | 0.021 | – | – | – | – | |
| 795205400001697 | SDSS J164749.77+534217.3, | 251.95740 53.70487 | 12.48 ± 0.01 | 12.35 ± 0.01 | 0.051 | 924 | 2.39 | 2.217 | – | |
| ZTF18aajsmrd | ||||||||||
| 795205400022890 | IW Dra | 251.56278 53.19847 | 14.69 ± 0.01 | 11.57 ± 0.01 | 0.047 | 4888 | −1.99 | 193.2 | Mira | [1] |
| 795205400035251 | SDSS J164533.41+531522.6 | 251.38937 53.25627 | 16.37 ± 0.01 | 15.99 ± 0.01 | 0.046 | 1353 | 5.21 | 230.3 | – | |
| 795209200003484 | ZTF18abbpebf | 251.54866 56.33124 | 21.33 ± 0.22 | 18.96 ± 0.05 | 0.015 | – | – | – | – | |
| 795209300012791 | CSS_J164050.1+552654 | 250.20916 55.44835 | 16.27 ± 0.01 | 15.17 ± 0.01 | 0.015 | 5138 | 1.58 | 0.458 | RRAB | [1] |
| 795210400001565 | SDSS J163331.55+554406.1 | 248.38139 55.73513 | 12.50 ± 0.01 | 12.43 ± 0.01 | 0.006 | 240 | 5.52 | 3.731 | – | |
| 795211200035931 | SN 2018coi | 244.74136 56.71714 | 20.35 ± 0.15 | 18.04 ± 0.03 | 0.009 | – | −19.07 | – | SN Ia | [12] |
| 795212100007964 | ZTF18aanbksg | 242.93762 55.96133 | 21.72 ± 0.27 | 19.28 ± 0.07 | 0.007 | – | – | – | – | |
| 795213200000671 | AT2018afr, Gaia18apj, | 251.93077 58.50559 | 20.46 ± 0.17 | 18.86 ± 0.05 | 0.012 | – | – | – | SN candidate | [13] |
| ZTF18aaincjv | ||||||||||
| 795213300001714 | ASASSN-V J164454.40+573232.3 | 251.22667 57.54232 | 13.02 ± 0.01 | 12.41 ± 0.01 | 0.016 | 4974 | −1.11 | 52.90 | SR | [1] |
| 795213400008053 | NSVS J1647409+565803 | 251.91816 56.96779 | 14.98 ± 0.01 | 13.25 ± 0.01 | 0.017 | 8363 | −1.40 | 111.3 | SR | [1] |
| 795214300016648 | 248.03423 57.75695 | 19.84 ± 0.10 | 16.68 ± 0.01 | 0.010 | 403 | 8.62 | – | – | ||
| disk | ||||||||||
| 807201100022915 | V0476 Cas | 25.84085 59.36414 | 15.93 ± 0.01 | 12.79 ± 0.01 | 0.512 | 3256 | −1.11 | 227.1 | Mira | [1] |
| 807202100027080 | J022.6771+60.0173, | 22.67713 60.01735 | 16.61 ± 0.01 | 15.44 ± 0.01 | 0.441 | 1875 | 2.93 | 0.824 | DBF, EA | [2,3] |
| ZTFJ013042.51+600102.4 | ||||||||||
| 807202300038681 | MGAB-V574 | 20.22254 58.82538 | 20.74 ± 0.22 | 17.24 ± 0.02 | 0.474 | 2830 | 3.75 | – | UG | [1] |
| 807202400015654 | V0420 Cas | 22.80860 58.79127 | 14.82 ± 0.01 | 13.72 ± 0.01 | 0.419 | 2717 | 0.46 | 13.78 | EA | [1] |
| 807203200013118 | J017.9869+59.7407, | 17.98693 59.74082 | 17.73 ± 0.03 | 16.14 ± 0.01 | 0.553 | 1026 | 4.65 | 2.185 | – | |
| ZTF18abfyqzh | ||||||||||
| 807203300044912 | V0890 Cas | 16.93576 59.05054 | 20.79 ± 0.24 | 14.32 ± 0.01 | 0.747 | 4536 | −0.90 | 421.8 | Mira | [1] |
| 807203400031819 | Romanov V28 | 19.30153 58.46788 | 19.28 ± 0.08 | 16.09 ± 0.01 | 0.414 | 1485 | 4.15 | >20 | UGSS | [1] |
| 807203400037050 | Dauban V254, | 19.20494 59.08340 | 16.74 ± 0.02 | 14.17 ± 0.01 | 0.491 | 2625 | 0.80 | 256.0 | Mira | [3] |
| ZTFJ011649.18+590500.2 | ||||||||||
| 807204200004799 | 14.29017 59.90208 | 20.19 ± 0.17 | 18.05 ± 0.03 | 0.435 | 4891 | 3.47 | 4.320 | – | ||
| 807204400014494 | ZTF18abhakel | 16.16915 58.85506 | 14.88 ± 0.01 | 13.86 ± 0.01 | 0.607 | 1514 | 1.38 | 6.017 | – | |
| 807205200017536 | V0367 Cas | 25.29686 61.25982 | 16.30 ± 0.01 | 13.48 ± 0.01 | 0.964 | 1955 | −0.48 | 3.709 | EA | [1] |
| 807206200003542 | ASASSN-V J012356.42+615458.8 | 20.98505 61.91633 | 17.18 ± 0.02 | 14.74 ± 0.01 | 10.394 | 793 | −21.81 | – | VAR, YSO, | [1,4,5] |
| PMS | ||||||||||
| 807206200004116 | MGAB-V1397 | 21.18448 61.89163 | 20.17 ± 0.16 | 17.63 ± 0.02 | 1.411 | 984 | 3.99 | – | YSO, PMS | [1,5] |
| 807206200014645 | MGAB-V1388 | 20.49273 61.50519 | 18.45 ± 0.04 | 16.28 ± 0.01 | 0.887 | 935 | 4.11 | – | YSO, PMS | [1,5] |
| 807206200023036 | NSVS J0122238+611352 | 20.59913 61.23097 | 16.53 ± 0.01 | 12.84 ± 0.01 | 0.626 | 4401 | −2.01 | 325.1 | Mira | [1] |
| 807206300013468 | II Cas | 21.67063 60.77933 | 15.62 ± 0.01 | 12.32 ± 0.01 | 0.560 | 2997 | −1.52 | 282.0 | Mira | [1] |
| 807206400014916 | Mis V1358 | 22.34756 60.74668 | 17.36 ± 0.02 | 12.92 ± 0.01 | 0.489 | 2911 | −0.67 | 310.0 | Mira: | [1] |
| 807207100005929 | IRAS 01145+6132, | 19.45793 61.80168 | 17.80 ± 0.03 | 14.25 ± 0.01 | 1.013 | 3247 | −0.95 | 278.0 | LPV, Mira | [3,6] |
| ZTFJ011749.90+614805.9 | ||||||||||
| 807207300036103 | BMAM-V362 | 16.98932 60.35615 | 20.46 ± 0.18 | 17.79 ± 0.03 | 0.540 | 2311 | 4.57 | – | UGZ | [1] |
| 807208200059506 | V0450 Cas | 12.87116 61.64957 | 16.42 ± 0.01 | 13.93 ± 0.01 | 1.223 | 560 | 2.01 | – | INS | [1] |
| 807208300012891 | OU Cas | 13.32034 60.69593 | 16.80 ± 0.02 | 15.17 ± 0.01 | 0.542 | 2434 | 1.82 | 1.265 | EA | [1] |
| 807208300016714 | OT Cas | 13.26166 60.59657 | 16.10 ± 0.01 | 12.49 ± 0.01 | 0.496 | 3145 | −1.29 | 292.0 | Mira | [1] |
| 807208400015695 | AV Cas | 14.89163 60.72181 | 15.72 ± 0.01 | 11.95 ± 0.01 | 0.570 | 1695 | −0.68 | 330.0 | Mira | [1] |
| 807208400036953 | ZTF18abflqpt | 14.44257 60.25802 | 20.01 ± 0.14 | 17.48 ± 0.02 | 0.445 | 2553 | 4.29 | 1.544 | – | |
| 807209100042420 | Dauban V252, | 27.07326 63.12797 | 18.25 ± 0.04 | 13.44 ± 0.01 | 1.031 | 3624 | −2.03 | 327.6 | Mira | [3] |
| ZTFJ014817.58+630740.6 | ||||||||||
| 807209300012026 | WISE J014237.7+623700 | 25.65734 62.61680 | 14.32 ± 0.01 | 13.20 ± 0.01 | 1.294 | 3020 | −2.57 | 6.399 | EA | [1] |
| 807209300037143 | NSVS J0141549+623406 | 25.47716 62.56828 | 16.89 ± 0.02 | 12.32 ± 0.01 | 1.349 | 4302 | −4.36 | 297.0 | Mira | [1] |
| 807209400037670 | IRAS 01438+6208 | 26.85197 62.38822 | 18.56 ± 0.05 | 12.56 ± 0.01 | 1.426 | 3518 | −3.88 | 286.0 | Mira | [7] |
| 807210100028861 | NSVS J0129109+631249, | 22.29801 63.21435 | 16.28 ± 0.01 | 12.70 ± 0.01 | 1.357 | 5972 | −4.71 | 454.2 | LPV, | [1,7] |
| IRAS 01257+6257 | SR+L, C | |||||||||
| 807210200004045 | 21.24037 63.85572 | 19.48 ± 0.09 | 17.84 ± 0.03 | 1.550 | 3353 | 1.18 | – | – | ||
| 807210200026027 | 21.96268 63.28808 | 18.81 ± 0.06 | 16.56 ± 0.01 | 1.451 | 1704 | 1.63 | 421.7 | YSO, PMS, | [4,5,8] | |
| AGN | ||||||||||
| 807211100059466 | V0724 Cas | 18.72328 63.61240 | 15.55 ± 0.01 | 12.54 ± 0.01 | 1.488 | 5475 | −5.03 | 280.0 | Mira | [1] |
| 807211300006190 | Mis V0818, | 16.17487 62.88210 | 17.33 ± 0.02 | 13.02 ± 0.01 | 1.332 | 4768 | −3.85 | 315.0 | Mira | [3] |
| ZTFJ010441.96+625255.5 | ||||||||||
| 807211300012948 | ZTFJ010526.59+624324.4 | 16.36079 62.72345 | 16.09 ± 0.01 | 14.31 ± 0.01 | 1.463 | 2785 | −1.72 | 302.9 | Mira | [3] |
| 807211400009493 | ZTF18abjcvcb | 18.74697 62.83884 | 20.08 ± 0.15 | 17.63 ± 0.02 | 1.472 | 3334 | 1.18 | 2.546 | – | |
| 807212100012737 | ZTF17aaaeesd | 15.01403 63.61420 | 19.01 ± 0.07 | 16.51 ± 0.01 | 1.196 | 1087 | 3.22 | – | – | |
| 807212100020830 | ZTFJ005605.95+632426.8 | 14.02475 63.40745 | 16.80 ± 0.02 | 13.26 ± 0.01 | 1.016 | 3188 | −1.90 | 394.4 | Mira | [3] |
| 807212200034055 | [I81] M 633 | 13.10185 63.06180 | 16.83 ± 0.02 | 13.64 ± 0.01 | 1.039 | 2171 | −0.75 | 364.0 | Mira | [9] |
| 807212300038616 | NSVS J0053173+623614, | 13.32484 62.60320 | 19.61 ± 0.11 | 14.55 ± 0.01 | 1.306 | 3530 | −1.59 | 311.0 | L, Mira | [1,9] |
| [I81] M 644 | ||||||||||
| 807214100007080 | [WWV2004] J0129273+653917 | 22.37209 65.65551 | 18.30 ± 0.04 | 13.00 ± 0.01 | 1.051 | 3655 | −2.55 | 295.2 | Mira | [7] |
| 807214100026393 | Dauban V269, | 22.36480 65.19663 | 20.94 ± 0.27 | 16.75 ± 0.02 | 1.074 | 3884 | 1.00 | 454.2 | Mira | [3] |
| ZTFJ012927.55+651147.8 | ||||||||||
| 807214100042070 | MGAB-V1402 | 24.06955 65.31108 | 20.11 ± 0.16 | 18.24 ± 0.04 | 1.125 | 3876 | 2.37 | 600.0 | Mira | [1] |
| 807214300010833 | NSVS 1695145 | 21.24271 64.77038 | 16.53 ± 0.01 | 13.84 ± 0.01 | 1.315 | 4633 | −2.91 | 560.0 | Mira: | [1] |
| 807214300051120 | ZTFJ012430.53+641432.2 | 21.12717 64.24230 | 17.69 ± 0.03 | 15.41 ± 0.01 | 1.194 | 3852 | −0.62 | 325.0 | Mira | [3] |
| 807215100019764 | VSX J011759.4+652153 | 19.49756 65.36491 | 19.37 ± 0.09 | 14.03 ± 0.01 | 1.593 | 4243 | −3.26 | 320.0 | Mira: | [1] |
| 807215200006611 | NSVS J0108368+653701 | 17.15140 65.61674 | 16.78 ± 0.02 | 12.71 ± 0.01 | 1.580 | 5238 | −5.00 | 309.0 | Mira | [1] |
| 807216100038423 | IPHAS J005934.24+651815.1, | 14.89278 65.30412 | 18.25 ± 0.04 | 14.47 ± 0.01 | 1.412 | 2598 | −1.27 | 295.2 | AGB, Mira | [3,10] |
| ZTFJ005934.27+651814.9 | ||||||||||
| 807216200026731 | NSV 15193 | 13.35496 65.03225 | 16.29 ± 0.01 | 12.10 ± 0.01 | 1.305 | 2681 | −3.44 | 507.0 | Mira | [1] |
| 807216200045725 | NSVS 1633482 | 11.72349 65.61549 | 21.30 ± 0.34 | 15.52 ± 0.01 | 1.411 | 3882 | −1.10 | 390.0 | Mira | [1] |
| 807216400013229 | 14.15960 64.56684 | 17.41 ± 0.02 | 16.29 ± 0.01 | 1.381 | 2530 | 0.69 | 2.160 | – | ||
| OID . | Other identifiers . | α, δ (deg) . | mr, min . | mr, max . | E(B − V) . | D (pc) . | Mr, max . | |$P_0^\dagger$| (d) . | Type⋆ . | References . |
|---|---|---|---|---|---|---|---|---|---|---|
| M 31 | ||||||||||
| 695211100003383 | 2MASS J00452494+4207269 | 11.35388 42.12427 | 20.87 ± 0.25 | 18.71 ± 0.05 | 0.117 | M 31 | −6.05 | – | RSG | [14] |
| 695211100015190 | 11.79716 41.78059 | 21.45 ± 0.31 | 19.49 ± 0.09 | 0.078 | M 31 | −5.17 | – | – | ||
| 695211100022045 | AT 2017ixs | 10.98339 41.53641 | 21.27 ± 0.29 | 18.66 ± 0.05 | 0.268 | M 31 | −6.50 | – | PNV | [15] |
| 695211100131796 | PSO J011.0457+41.5548 | 11.04581 41.55487 | 17.92 ± 0.03 | 16.84 ± 0.02 | 0.287 | M 31 | −8.36 | – | VAR | [16,17] |
| 695211200018901 | 2MASS J00421755+4135039 | 10.57313 41.58447 | 18.54 ± 0.04 | 17.78 ± 0.02 | 0.143 | M 31 | −7.06 | 214.6 | RSG | [14] |
| 695211200019653 | 2MASS J00415491+4133323, | 10.47879 41.55899 | 15.58 ± 0.01 | 15.19 ± 0.01 | 0.100 | 1642 | 3.85 | 7.715 | MSINE, | [2,3] |
| ZTFJ004154.90+413332.3 | RSCVN | |||||||||
| 695211200022958 | PSO J010.4744+41.4515 | 10.47441 41.45149 | 18.86 ± 0.05 | 18.30 ± 0.03 | 0.171 | M 31 | −6.61 | 90.54 | Delta Cep | [18] |
| 695211200035023 | 10.50601 41.81453 | 21.17 ± 0.25 | 19.33 ± 0.07 | 0.061 | M 31 | −5.29 | 132.9 | – | ||
| 695211200046528 | [MAP97] 55 | 10.63267 41.48622 | 18.51 ± 0.04 | 17.85 ± 0.02 | 0.308 | M 31 | −7.41 | 74.29 | Delta Cep | [19] |
| 695211200057718 | 9.82489 41.76983 | 21.56 ± 0.29 | 19.71 ± 0.09 | 0.056 | M 31 | −4.90 | >200 | – | ||
| 695211200058391 | 9.98496 41.74939 | 22.18 ± 0.35 | 20.02 ± 0.12 | 0.058 | M 31 | −4.59 | – | – | ||
| 695211200075348 | M31N 2013-11b, | 10.35917 41.73029 | 21.61 ± 0.29 | 19.40 ± 0.07 | 0.060 | M 31 | −5.22 | 168.4 | VAR | [20,21] |
| MASTER OTJ004126.22+414350.0 | ||||||||||
| 695211300004359 | PNV J00414894+4109173 | 10.45371 41.15395 | 20.61 ± 0.21 | 17.56 ± 0.03 | 0.261 | M 31 | −7.58 | – | PNV | [22] |
| 695211300006331 | CSS_J003827.1+410334 | 9.61336 41.05944 | 15.03 ± 0.01 | 14.30 ± 0.02 | 0.067 | 1546 | 3.18 | 3.138 | EA | [1] |
| 695211300007276 | SV* SON 10726 | 10.19874 41.03242 | 18.51 ± 0.05 | 17.78 ± 0.03 | 0.275 | M 31 | −7.40 | 58.00 | Delta Cep | [23] |
| 695211400009049 | 11.11946 40.99692 | 21.47 ± 0.31 | 19.72 ± 0.12 | 0.076 | M 31 | −4.94 | – | – | ||
| 695211400025927 | 11.44201 41.25969 | 21.82 ± 0.34 | 20.07 ± 0.16 | 0.072 | M 31 | −4.58 | – | – | ||
| 695211400027347 | 2MASS J00434749+4112585 | 10.94775 41.21573 | 21.50 ± 0.31 | 19.57 ± 0.11 | 0.332 | M 31 | −5.76 | >200 | VAR | [24] |
| 695211400046832 | 11.26142 40.57456 | 22.17 ± 0.37 | 20.21 ± 0.18 | 0.063 | M 31 | −4.41 | – | – | ||
| 695211400070144 | 2MASS J00443180+4119083 | 11.13252 41.31898 | 19.63 ± 0.12 | 18.10 ± 0.04 | 0.275 | M 31 | −7.07 | – | VAR | [25] |
| 695211400121607 | [JPN2003] V206 | 10.87915 41.09875 | 21.42 ± 0.30 | 19.33 ± 0.09 | 0.181 | M 31 | −5.60 | – | VAR | [24] |
| Deep | ||||||||||
| 795202100005941 | MLS180307:163438+521642, | 248.65767 52.27841 | 21.90 ± 0.27 | 19.45 ± 0.07 | 0.026 | – | – | – | SN candidate | [11] |
| ZTF18aanbnjh | ||||||||||
| 795202300001087 | NSVS 5270259 | 247.70051 51.96916 | 13.84 ± 0.01 | 12.99 ± 0.01 | 0.022 | 957 | 3.03 | 0.674 | EA | [1] |
| 795203200009604 | DDE 32 | 244.89910 52.77552 | 20.39 ± 0.14 | 16.50 ± 0.01 | 0.019 | 439 | 8.24 | – | AM | [1] |
| 795204100013041 | ZTF18abgvctp | 242.30742 52.21426 | 21.87 ± 0.27 | 20.02 ± 0.11 | 0.016 | – | – | – | – | |
| 795204200006882 | CSS_J160450.1+520159 | 241.20883 52.03324 | 20.67 ± 0.18 | 17.20 ± 0.02 | 0.014 | 3909 | 4.20 | 316.8 | EA | [1] |
| 795205100007271 | ZTF18aayatjf | 252.30216 54.11178 | 21.45 ± 0.23 | 19.51 ± 0.08 | 0.021 | – | – | – | – | |
| 795205400001697 | SDSS J164749.77+534217.3, | 251.95740 53.70487 | 12.48 ± 0.01 | 12.35 ± 0.01 | 0.051 | 924 | 2.39 | 2.217 | – | |
| ZTF18aajsmrd | ||||||||||
| 795205400022890 | IW Dra | 251.56278 53.19847 | 14.69 ± 0.01 | 11.57 ± 0.01 | 0.047 | 4888 | −1.99 | 193.2 | Mira | [1] |
| 795205400035251 | SDSS J164533.41+531522.6 | 251.38937 53.25627 | 16.37 ± 0.01 | 15.99 ± 0.01 | 0.046 | 1353 | 5.21 | 230.3 | – | |
| 795209200003484 | ZTF18abbpebf | 251.54866 56.33124 | 21.33 ± 0.22 | 18.96 ± 0.05 | 0.015 | – | – | – | – | |
| 795209300012791 | CSS_J164050.1+552654 | 250.20916 55.44835 | 16.27 ± 0.01 | 15.17 ± 0.01 | 0.015 | 5138 | 1.58 | 0.458 | RRAB | [1] |
| 795210400001565 | SDSS J163331.55+554406.1 | 248.38139 55.73513 | 12.50 ± 0.01 | 12.43 ± 0.01 | 0.006 | 240 | 5.52 | 3.731 | – | |
| 795211200035931 | SN 2018coi | 244.74136 56.71714 | 20.35 ± 0.15 | 18.04 ± 0.03 | 0.009 | – | −19.07 | – | SN Ia | [12] |
| 795212100007964 | ZTF18aanbksg | 242.93762 55.96133 | 21.72 ± 0.27 | 19.28 ± 0.07 | 0.007 | – | – | – | – | |
| 795213200000671 | AT2018afr, Gaia18apj, | 251.93077 58.50559 | 20.46 ± 0.17 | 18.86 ± 0.05 | 0.012 | – | – | – | SN candidate | [13] |
| ZTF18aaincjv | ||||||||||
| 795213300001714 | ASASSN-V J164454.40+573232.3 | 251.22667 57.54232 | 13.02 ± 0.01 | 12.41 ± 0.01 | 0.016 | 4974 | −1.11 | 52.90 | SR | [1] |
| 795213400008053 | NSVS J1647409+565803 | 251.91816 56.96779 | 14.98 ± 0.01 | 13.25 ± 0.01 | 0.017 | 8363 | −1.40 | 111.3 | SR | [1] |
| 795214300016648 | 248.03423 57.75695 | 19.84 ± 0.10 | 16.68 ± 0.01 | 0.010 | 403 | 8.62 | – | – | ||
| disk | ||||||||||
| 807201100022915 | V0476 Cas | 25.84085 59.36414 | 15.93 ± 0.01 | 12.79 ± 0.01 | 0.512 | 3256 | −1.11 | 227.1 | Mira | [1] |
| 807202100027080 | J022.6771+60.0173, | 22.67713 60.01735 | 16.61 ± 0.01 | 15.44 ± 0.01 | 0.441 | 1875 | 2.93 | 0.824 | DBF, EA | [2,3] |
| ZTFJ013042.51+600102.4 | ||||||||||
| 807202300038681 | MGAB-V574 | 20.22254 58.82538 | 20.74 ± 0.22 | 17.24 ± 0.02 | 0.474 | 2830 | 3.75 | – | UG | [1] |
| 807202400015654 | V0420 Cas | 22.80860 58.79127 | 14.82 ± 0.01 | 13.72 ± 0.01 | 0.419 | 2717 | 0.46 | 13.78 | EA | [1] |
| 807203200013118 | J017.9869+59.7407, | 17.98693 59.74082 | 17.73 ± 0.03 | 16.14 ± 0.01 | 0.553 | 1026 | 4.65 | 2.185 | – | |
| ZTF18abfyqzh | ||||||||||
| 807203300044912 | V0890 Cas | 16.93576 59.05054 | 20.79 ± 0.24 | 14.32 ± 0.01 | 0.747 | 4536 | −0.90 | 421.8 | Mira | [1] |
| 807203400031819 | Romanov V28 | 19.30153 58.46788 | 19.28 ± 0.08 | 16.09 ± 0.01 | 0.414 | 1485 | 4.15 | >20 | UGSS | [1] |
| 807203400037050 | Dauban V254, | 19.20494 59.08340 | 16.74 ± 0.02 | 14.17 ± 0.01 | 0.491 | 2625 | 0.80 | 256.0 | Mira | [3] |
| ZTFJ011649.18+590500.2 | ||||||||||
| 807204200004799 | 14.29017 59.90208 | 20.19 ± 0.17 | 18.05 ± 0.03 | 0.435 | 4891 | 3.47 | 4.320 | – | ||
| 807204400014494 | ZTF18abhakel | 16.16915 58.85506 | 14.88 ± 0.01 | 13.86 ± 0.01 | 0.607 | 1514 | 1.38 | 6.017 | – | |
| 807205200017536 | V0367 Cas | 25.29686 61.25982 | 16.30 ± 0.01 | 13.48 ± 0.01 | 0.964 | 1955 | −0.48 | 3.709 | EA | [1] |
| 807206200003542 | ASASSN-V J012356.42+615458.8 | 20.98505 61.91633 | 17.18 ± 0.02 | 14.74 ± 0.01 | 10.394 | 793 | −21.81 | – | VAR, YSO, | [1,4,5] |
| PMS | ||||||||||
| 807206200004116 | MGAB-V1397 | 21.18448 61.89163 | 20.17 ± 0.16 | 17.63 ± 0.02 | 1.411 | 984 | 3.99 | – | YSO, PMS | [1,5] |
| 807206200014645 | MGAB-V1388 | 20.49273 61.50519 | 18.45 ± 0.04 | 16.28 ± 0.01 | 0.887 | 935 | 4.11 | – | YSO, PMS | [1,5] |
| 807206200023036 | NSVS J0122238+611352 | 20.59913 61.23097 | 16.53 ± 0.01 | 12.84 ± 0.01 | 0.626 | 4401 | −2.01 | 325.1 | Mira | [1] |
| 807206300013468 | II Cas | 21.67063 60.77933 | 15.62 ± 0.01 | 12.32 ± 0.01 | 0.560 | 2997 | −1.52 | 282.0 | Mira | [1] |
| 807206400014916 | Mis V1358 | 22.34756 60.74668 | 17.36 ± 0.02 | 12.92 ± 0.01 | 0.489 | 2911 | −0.67 | 310.0 | Mira: | [1] |
| 807207100005929 | IRAS 01145+6132, | 19.45793 61.80168 | 17.80 ± 0.03 | 14.25 ± 0.01 | 1.013 | 3247 | −0.95 | 278.0 | LPV, Mira | [3,6] |
| ZTFJ011749.90+614805.9 | ||||||||||
| 807207300036103 | BMAM-V362 | 16.98932 60.35615 | 20.46 ± 0.18 | 17.79 ± 0.03 | 0.540 | 2311 | 4.57 | – | UGZ | [1] |
| 807208200059506 | V0450 Cas | 12.87116 61.64957 | 16.42 ± 0.01 | 13.93 ± 0.01 | 1.223 | 560 | 2.01 | – | INS | [1] |
| 807208300012891 | OU Cas | 13.32034 60.69593 | 16.80 ± 0.02 | 15.17 ± 0.01 | 0.542 | 2434 | 1.82 | 1.265 | EA | [1] |
| 807208300016714 | OT Cas | 13.26166 60.59657 | 16.10 ± 0.01 | 12.49 ± 0.01 | 0.496 | 3145 | −1.29 | 292.0 | Mira | [1] |
| 807208400015695 | AV Cas | 14.89163 60.72181 | 15.72 ± 0.01 | 11.95 ± 0.01 | 0.570 | 1695 | −0.68 | 330.0 | Mira | [1] |
| 807208400036953 | ZTF18abflqpt | 14.44257 60.25802 | 20.01 ± 0.14 | 17.48 ± 0.02 | 0.445 | 2553 | 4.29 | 1.544 | – | |
| 807209100042420 | Dauban V252, | 27.07326 63.12797 | 18.25 ± 0.04 | 13.44 ± 0.01 | 1.031 | 3624 | −2.03 | 327.6 | Mira | [3] |
| ZTFJ014817.58+630740.6 | ||||||||||
| 807209300012026 | WISE J014237.7+623700 | 25.65734 62.61680 | 14.32 ± 0.01 | 13.20 ± 0.01 | 1.294 | 3020 | −2.57 | 6.399 | EA | [1] |
| 807209300037143 | NSVS J0141549+623406 | 25.47716 62.56828 | 16.89 ± 0.02 | 12.32 ± 0.01 | 1.349 | 4302 | −4.36 | 297.0 | Mira | [1] |
| 807209400037670 | IRAS 01438+6208 | 26.85197 62.38822 | 18.56 ± 0.05 | 12.56 ± 0.01 | 1.426 | 3518 | −3.88 | 286.0 | Mira | [7] |
| 807210100028861 | NSVS J0129109+631249, | 22.29801 63.21435 | 16.28 ± 0.01 | 12.70 ± 0.01 | 1.357 | 5972 | −4.71 | 454.2 | LPV, | [1,7] |
| IRAS 01257+6257 | SR+L, C | |||||||||
| 807210200004045 | 21.24037 63.85572 | 19.48 ± 0.09 | 17.84 ± 0.03 | 1.550 | 3353 | 1.18 | – | – | ||
| 807210200026027 | 21.96268 63.28808 | 18.81 ± 0.06 | 16.56 ± 0.01 | 1.451 | 1704 | 1.63 | 421.7 | YSO, PMS, | [4,5,8] | |
| AGN | ||||||||||
| 807211100059466 | V0724 Cas | 18.72328 63.61240 | 15.55 ± 0.01 | 12.54 ± 0.01 | 1.488 | 5475 | −5.03 | 280.0 | Mira | [1] |
| 807211300006190 | Mis V0818, | 16.17487 62.88210 | 17.33 ± 0.02 | 13.02 ± 0.01 | 1.332 | 4768 | −3.85 | 315.0 | Mira | [3] |
| ZTFJ010441.96+625255.5 | ||||||||||
| 807211300012948 | ZTFJ010526.59+624324.4 | 16.36079 62.72345 | 16.09 ± 0.01 | 14.31 ± 0.01 | 1.463 | 2785 | −1.72 | 302.9 | Mira | [3] |
| 807211400009493 | ZTF18abjcvcb | 18.74697 62.83884 | 20.08 ± 0.15 | 17.63 ± 0.02 | 1.472 | 3334 | 1.18 | 2.546 | – | |
| 807212100012737 | ZTF17aaaeesd | 15.01403 63.61420 | 19.01 ± 0.07 | 16.51 ± 0.01 | 1.196 | 1087 | 3.22 | – | – | |
| 807212100020830 | ZTFJ005605.95+632426.8 | 14.02475 63.40745 | 16.80 ± 0.02 | 13.26 ± 0.01 | 1.016 | 3188 | −1.90 | 394.4 | Mira | [3] |
| 807212200034055 | [I81] M 633 | 13.10185 63.06180 | 16.83 ± 0.02 | 13.64 ± 0.01 | 1.039 | 2171 | −0.75 | 364.0 | Mira | [9] |
| 807212300038616 | NSVS J0053173+623614, | 13.32484 62.60320 | 19.61 ± 0.11 | 14.55 ± 0.01 | 1.306 | 3530 | −1.59 | 311.0 | L, Mira | [1,9] |
| [I81] M 644 | ||||||||||
| 807214100007080 | [WWV2004] J0129273+653917 | 22.37209 65.65551 | 18.30 ± 0.04 | 13.00 ± 0.01 | 1.051 | 3655 | −2.55 | 295.2 | Mira | [7] |
| 807214100026393 | Dauban V269, | 22.36480 65.19663 | 20.94 ± 0.27 | 16.75 ± 0.02 | 1.074 | 3884 | 1.00 | 454.2 | Mira | [3] |
| ZTFJ012927.55+651147.8 | ||||||||||
| 807214100042070 | MGAB-V1402 | 24.06955 65.31108 | 20.11 ± 0.16 | 18.24 ± 0.04 | 1.125 | 3876 | 2.37 | 600.0 | Mira | [1] |
| 807214300010833 | NSVS 1695145 | 21.24271 64.77038 | 16.53 ± 0.01 | 13.84 ± 0.01 | 1.315 | 4633 | −2.91 | 560.0 | Mira: | [1] |
| 807214300051120 | ZTFJ012430.53+641432.2 | 21.12717 64.24230 | 17.69 ± 0.03 | 15.41 ± 0.01 | 1.194 | 3852 | −0.62 | 325.0 | Mira | [3] |
| 807215100019764 | VSX J011759.4+652153 | 19.49756 65.36491 | 19.37 ± 0.09 | 14.03 ± 0.01 | 1.593 | 4243 | −3.26 | 320.0 | Mira: | [1] |
| 807215200006611 | NSVS J0108368+653701 | 17.15140 65.61674 | 16.78 ± 0.02 | 12.71 ± 0.01 | 1.580 | 5238 | −5.00 | 309.0 | Mira | [1] |
| 807216100038423 | IPHAS J005934.24+651815.1, | 14.89278 65.30412 | 18.25 ± 0.04 | 14.47 ± 0.01 | 1.412 | 2598 | −1.27 | 295.2 | AGB, Mira | [3,10] |
| ZTFJ005934.27+651814.9 | ||||||||||
| 807216200026731 | NSV 15193 | 13.35496 65.03225 | 16.29 ± 0.01 | 12.10 ± 0.01 | 1.305 | 2681 | −3.44 | 507.0 | Mira | [1] |
| 807216200045725 | NSVS 1633482 | 11.72349 65.61549 | 21.30 ± 0.34 | 15.52 ± 0.01 | 1.411 | 3882 | −1.10 | 390.0 | Mira | [1] |
| 807216400013229 | 14.15960 64.56684 | 17.41 ± 0.02 | 16.29 ± 0.01 | 1.381 | 2530 | 0.69 | 2.160 | – | ||
†The best period extracted from either the Lomb–Scargle periodogram or one of the catalogues listed in the ZTF-viewer or determined by us.
⋆AM – AM Herculis-type variable.
AGB – Asymptotic Giant Branch Star.
C – Carbon star.
DBF – Distant binary, full period.
Delta Cep – Classical Cepheid.
EA – β Persei-type (Algol) eclipsing system.
INS – Orion variable with rapid light variations.
L – Slow irregular variable, stars are often attributed to this type because of being insufficiently studied.
LPV – Long Period Variable.
Mira – o (omicron) Ceti-type variable.
MSINE – Star showing modulated sinusoids.
PNV – Possible nova.
RRAB – RR Lyrae variable with asymmetric light curves.
RSCVN – RS Canum Venaticorum-type binary system.
RSG – Red supergiant.
SN – Supernova.
SR – Semiregular variable.
UG – U Geminorum-type variable, quite often called dwarf nova.
UGSS – SS Cygni-type variable.
UGZ – Z Camelopardalis-type star.
VAR – Variable of unspecified type.
YSO – Young stellar Object of unspecified variable type.
[1] – Watson et al. 2006; [2] – Heinze et al. 2018; [3] – Chen et al. 2020; [4] – Marton et al. 2016; [5] – Vioque et al. 2020; [6] – Usatov & Nosulchik 2008; [7] – Woźniak et al. 2004; [8] – Edelson & Malkan 2012; [9] – Nesci et al. 2018; [10] – Wright et al. 2009; [11] – Drake et al. 2009; [12] – Graham et al. 2018; [13] – Delgado et al. 2018; [14] – Massey et al. 2009; [15] – Carey 2017; [16] – Lee et al. 2014; [17] – Humphreys et al. 2017; [18] – Kodric et al. 2018; [19] – Magnier et al. 1997; [20] – Ovcharov et al. 2013; [21] – Shumkov et al. 2016; [22] – Hornoch & Kucakova 2015; [23] – Kodric et al. 2013; [24] – Joshi et al. 2003; [25] – Kaluzny et al. 1999.
Author notes
Center for Astrophysical Surveys Fellow, National Center for Supercomputing Applications, USA.



