Probing frequency-dependent half-wave plate systematics for CMB experiments with full-sky beam convolution simulations

Duivenvoorden, Adriaan J; Adler, Alexandre E; Billi, Matteo; Dachlythra, Nadia; Gudmundsson, Jon E

doi:10.1093/mnras/stab317

ABSTRACT

We study systematic effects from half-wave plates (HWPs) for cosmic microwave background (CMB) experiments using full-sky time-domain beam convolution simulations. Using an optical model for a fiducial spaceborne two-lens refractor telescope, we investigate how different HWP configurations optimized for dichroic detectors centred at 95 and 150 GHz impact the reconstruction of primordial B-mode polarization. We pay particular attention to possible biases arising from the interaction of frequency-dependent HWP non-idealities with polarized Galactic dust emission and the interaction between the HWP and the instrumental beam. To produce these simulations, we have extended the capabilities of the publicly available beamconv code. To our knowledge, we produce the first time-domain simulations that include both HWP non-idealities and realistic full-sky beam convolution. Our analysis shows how certain achromatic HWP configurations produce significant systematic polarization angle offsets that vary for sky components with different frequency dependence. Our analysis also demonstrates that once we account for interactions with HWPs, realistic beam models with non-negligible cross-polarization and sidelobes will cause significant B-mode residuals that will have to be extensively modelled in some cases.

polarization, methods: numerical, techniques: polarimetric, telescopes, cosmic background radiation, cosmology: observations

1 INTRODUCTION

The measured temperature anisotropies of the cosmic microwave background (CMB) provide a large part of the empirical basis for ΛCDM, the current standard model of cosmology (MacTavish et al. 2006; Bennett et al. 2013; Planck Collaboration VI 2020a). Additional cosmological information from the CMB will mainly come from accurate characterization of the polarized component of the anisotropies. Although many cosmological constraints will benefit from polarization measurements (Galli et al. 2014), the most notable advance is perhaps seen in the search for primordial gravitational waves, which might have a distinctive signature in the B-mode component of the CMB polarization (Kamionkowski, Kosowsky & Stebbins 1997; Zaldarriaga & Seljak 1997).

Experiments have to minimize spurious polarization in order to measure the weak CMB polarization. An attractive approach is the use of a half-wave plate (HWP): a birefringent optical element that shifts the polarization angle of linearly polarized light that passes through. The shift depends on the orientation of the plate, which allows modulation of the polarized sky signal by rotation of the HWP. An ideal rotating HWP only modulates the linearly polarized sky signal and therefore allows one to cleanly separate this desired signal from unpolarized sky signal. Unfortunately, non-ideal HWPs impede perfectly controlled modulation and indirectly cause spurious polarized signal of their own. The merit of an HWP has to be carefully weighed against the downsides.

Multiple polarimetric experiments have employed HWPs. Examples include MAXIPOL (Johnson et al. 2007); POLARBEAR (The Polarbear Collaboration 2010; Hill et al. 2016); ABS (Kusaka et al. 2014); SPIDER (Rahlin et al. 2014); PILOT (Misawa et al. 2014); BLAST (Galitzki et al. 2016); and EBEX (Aboobaker et al. 2018). In addition, several upcoming B-mode experiments are planning to use HWPs; see e.g. the Simons Observatory small-aperture telescopes (Galitzki et al. 2018) and the proposed LiteBIRD satellite (Suzuki et al. 2018; Sugai et al. 2020). Consequently, there exists a rich body of literature describing the optical impact of HWPs, including descriptions of various HWP non-idealities (Bryan et al. 2010b; Kusaka et al. 2014; Pisano et al. 2014; CMB-S4 Collaboration 2017) and mitigation strategies (Bao et al. 2012; Matsumura 2014; Bao et al. 2016; Vergès, Errard & Stompor 2020).

In order to separate astrophysical foregrounds from the CMB signal, experiments observe in several frequency bands. For example, the proposed LiteBIRD satellite effort currently proposes to deploy 15 frequency bands in three telescope modules spanning 34–448 GHz (Suzuki et al. 2018; Sugai et al. 2020). Successful implementation of wide-band polarization modulation is arguably quite technically challenging: the modulation efficiency of simple birefringent crystals is constant over a relatively small frequency range and the plate will cause loss in linear polarization for signals outside that frequency range. In order to efficiently modulate polarization over a wide frequency range, for example, to support the use of dichroic or even trichroic bolometers (Suzuki et al. 2014), an achromatic half-wave plate (AHWP) is likely required (Hill et al. 2016; Komatsu et al. 2018). AHWPs largely remove the frequency-dependent loss in polarization modulation efficiency, but they can also rotate the polarization angle of linearly polarized light by a frequency-dependent angle. This angle offset, which can be significant for certain AHWP configurations, is potentially troublesome. When present, an observer needs prior knowledge of the spatial and spectral energy distribution (SED) of various astrophysical sources in order to correctly interpret the modulated sky signal. For instance, a sky region dominated by polarized dust requires a different angle correction compared to one dominated by the polarized CMB (Bao et al. 2012; Abitbol et al. 2020).

In this paper, we investigate how non-idealities from a collection of (A)HWP configurations optimized for dichroic detectors sensitive to both 95 and 150 GHz limit our ability to reconstruct primordial B-mode polarization. We pay particular attention to the frequency-dependent polarization rotation angle for these different configurations. It has been pointed out, see e.g. Vergès et al. (2020), that such angle offsets will inevitably lead to biased sky maps that require different correcting polarization angles for each sky component. Here, we provide a realistic example of this effect to judge its importance. We also simulate the interaction between the HWP non-idealities and a realistic polarized beam and point out the importance of this potential systematic. To produce these simulations, we extend the beamconv ¹ code, first described in Duivenvoorden, Gudmundsson & Rahlin (2019). The new code allows us to simulate the effects of non-ideal HWPs on the time-ordered data (TOD) of CMB experiments. To our knowledge, this is the first time that a publicly available code can perform realistic time-domain simulations that include both HWP non-idealities and all-sky beam convolution with asymmetric beams.

This paper is organized as follows: in Section 2, we introduce the mathematical framework and the data model used for the simulations. The description of our fiducial instrument, the HWP properties, the proposed scanning strategy, and the input sky models are presented in Section 3. Results are given in Section 4. We discuss the results and formulate our conclusions in Section 5.

2 MATHEMATICAL FRAMEWORK

In this section, we derive a data model for a typical CMB polarization experiment (see Section 2.2). The model describes the effects of a non-ideal HWP combined with beam convolution on the TOD. We generalize the model presented in Bryan et al. (2010b) to multilayer HWPs and arbitrary shaped and non-trivially polarized beams. First, however, we briefly discuss the Mueller matrix description of an HWP. See Hecht (2002) or Gil Pérez & Ossikovski (2016) for general introductions to the Mueller matrix formalism and Bryan, Montroy & Ruhl (2010a), Essinger-Hileman (2013), Moncelsi et al. (2014), Salatino, de Bernardis & Masi (2017), and Salatino et al. (2018) for applications to HWPs for CMB experiments.

Throughout this section, we make use of the Einstein summation convention: pairs of upper and lower indices are implicitly summed over. We use θ and ϕ to denote the polar and azimuthal angles of the standard spherical coordinate system. The metric of the sphere is given by g_ij = diag(1, sin ²θ) in these coordinates.

2.1 Half-wave plate Mueller matrix

We start by describing the polarized sky signal incident from direction |$\hat{\boldsymbol {n}}$| and at frequency ν as a Stokes vector:

$$\begin{eqnarray*} \boldsymbol {S}_{\mathrm{sky}}(\hat{\boldsymbol {n}}, \nu) = {\begin{pmatrix}I \\ Q \\ U \\ V \end{pmatrix}} (\hat{\boldsymbol {n}}, \nu) \, . \end{eqnarray*}$$

(1)

Here, I represents the total intensity of the radiation, while Q and U describe the linearly polarized part of the radiation and V describes the circularly polarized component. Stokes vectors have real elements that obey

$$\begin{eqnarray*} I \ge \sqrt{Q^2 + U^2 + V^2} \, . \end{eqnarray*}$$

(2)

The above inequality is saturated for completely polarized light, while the right-hand side of the equality goes to zero for unpolarized light.

Mueller matrices describe the set of linear transformations that transform Stokes vectors to other valid Stokes vectors. Linear optical media such as HWPs is described by Mueller matrices. Multiplying a Stokes vector by such a Mueller matrix describes how the HWP alters the polarization properties of the radiation described by the Stokes vector.

A traditional HWP design involves a single layer of birefringent crystal cut to a thickness such that the phase shift incurred from a particular wavelength at normal incidence is exactly half a period. In the Mueller formalism, an HWP comprised of a single layer of birefringent material and any number of layers of isotropic dielectric materials can be represented through a matrix characterized by four parameters:

$$\begin{eqnarray*} \boldsymbol{\sf M}_{\mathrm{HWP}}(\nu) = {\begin{pmatrix}T & \quad \rho & \quad 0 & \quad 0\\ \rho & \quad T & \quad 0 & \quad 0\\ 0 & \quad 0 & \quad c & \quad -s\\ 0 & \quad 0 & \quad s & \quad c \end{pmatrix}} (\nu) \quad \quad \mathrm{(single\ layer)} \, , \end{eqnarray*}$$

(3)

where T can be interpreted as the total transmission, ρ as the difference in transmission between the fast and the slow axes, c as the linear polarization response, and s as the coupling to circular polarization. The values of these parameters can be directly linked to the Fresnel coefficients for reflection and transmission. For an ideal HWP, we note that T = 1 = −c and ρ = s = 0. For a real single-layer HWP, these elements are instead variable and dependent on the frequency and the incidence angle of the incoming radiation. Fig. 1 shows how the angle of incidence made by light hitting the HWP changes significantly as one moves across the focal plane. For wide field-of-view telescopes, this incidence angle can be as large as 17° (Galitzki et al. 2018).

Figure 1.

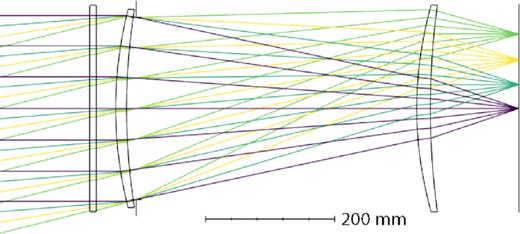
Sketch of telescope model used for this study. Light coming in from the left interacts with an HWP before hitting the primary lens. Light from the primary lens then gets further focused by the secondary lens before hitting the focal plane (on the right). The edge pixel has a beam centroid of 14° relative to boresight (see ray bundle emitted from top right corner).

Open in new tab Download slide

Pancharatnam (1955) showed that there exist combinations of layers of birefringent materials that, unlike the single-layer HWPs, can behave in an almost achromatic manner. The resulting AHWPs have a low frequency dependence in polarization modulation efficiency across a broad frequency range. This is achieved by introducing a relative rotation angle for one or several of the birefringent layers such that not all of the fast optical axes are aligned. The set-up is discussed in detail in Title (1975). A complication of AHWPs is their effective frequency-dependent rotation angle offset. We will come back to this issue in Section 3.4.

The Mueller matrix of an AHWP, being composed of more than one birefringent layer, cannot be adequately described by the four parameters in equation (3). Instead, the transfer matrix method (TMM) can be used to generate an appropriate Mueller matrix. The TMM formalism captures the response of materials that are composed of any collection of dielectric and birefringent media. For the work presented here, we use the publicly available code described in Essinger-Hileman (2013) to calculate the Mueller matrices of the HWPs that we study.²

2.2 Data model

We model the TOD of a single detector of a CMB polarimeter as follows:

$$\begin{eqnarray*} d_t = \int \mathrm{d}\nu \, F(\nu) \int \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \, I_{\mathrm{tot}}^{(t)}(\hat{\boldsymbol {n}}, \nu) + n_t \, . \end{eqnarray*}$$

(4)

The signal incident on the detector |$\smash{I_{\mathrm{tot}}^{(t)}}$| depends on the Stokes vector of the sky |$\boldsymbol {S}_{\mathrm{sky}}$|⁠, but is a scalar quantity; the detector is ultimately only sensitive to total intensity. The signal is time varying, the index t runs over the number of recorded time samples. The frequency passband of the detector and the additive noise are denoted by F(ν) and n_t, respectively.

To describe how the polarization of the sky couples to the instrument, we express |$\smash{I_{\mathrm{tot}}^{(t)}}$| in terms of the trace of the product of two density matrices: one that describes the polarization state of the sky |$\boldsymbol{\sf W}_{\mathrm{sky}}$| and one time-varying density matrix |$\smash{\boldsymbol{\sf W}_{\mathrm{instr}}^{(t)}}$| that describes the instrumental response on the sky (Hu, Hedman & Zaldarriaga 2003; Kamionkowski & Kovetz 2016; Hivon, Mottet & Ponthieu 2017):

$$\begin{eqnarray*} I_{\mathrm{tot}}^{(t)}(\hat{\boldsymbol {n}}, \nu) = 2 \, \mathrm{tr} \left(\boldsymbol{\sf W}_{\mathrm{instr}}^{(t)} \boldsymbol{\sf W}_{\mathrm{sky}}\right) (\hat{\boldsymbol {n}}, \nu) \, . \end{eqnarray*}$$

(5)

The density matrices are rank 2 tensor fields defined on the sphere that contain the same polarization state information as the Stokes vectors. In fact, it is possible to express a density matrix |$\boldsymbol{\sf W}$| in terms of a Stokes vector S^μ = {I, Q, U, V} using

$$\begin{eqnarray*} \boldsymbol{\sf W} (\hat{\boldsymbol {n}}, \nu) &= S^{\mu } (\hat{\boldsymbol {n}}, \nu) \boldsymbol {\mathsf {\sigma }}_{\mu } (\hat{\boldsymbol {n}}) \, , \end{eqnarray*}$$

(6)

where |$\boldsymbol {\mathsf {\sigma }}_{\mu }$| is given by the identity matrix and the (permuted) Pauli matrices defined on the sphere: |$\boldsymbol {\mathsf {\sigma }}_{\mu } = \lbrace \boldsymbol {\mathsf {\sigma }}_0, \boldsymbol {\mathsf {\sigma }}_3, \boldsymbol {\mathsf {\sigma }}_1, \boldsymbol {\mathsf {\sigma }}_2 \rbrace$|⁠, see equations (A20)–(A23). The tensor nature of the polarization state is explicit in the density matrix formulation, it is implicit in the Stokes vector formulation. Using the standard spherical coordinate system, the elements of the sky density matrix are given by

$$\begin{eqnarray*} \big (W_{\mathrm{sky}}\big)_{ij} (\hat{\boldsymbol {n}}, \nu) = \frac{1}{2}{\begin{pmatrix}I + Q & \quad (U - \mathrm{i} V) \sin \theta\\ (U + \mathrm{i} V) \sin \theta & \quad (I - Q) \sin ^2 \theta \end{pmatrix}} (\hat{\boldsymbol {n}}, \nu). \end{eqnarray*}$$

(7)

The time-dependent instrumental density matrix is similarly expressed as

$$\begin{eqnarray*} && \big (W_{\mathrm{instr}}^{(t)}\big)_{ij} (\hat{\boldsymbol {n}}, \nu) \nonumber \\ && \quad = \frac{1}{2} {\begin{pmatrix}\widetilde{I}^{\, (t)}_{\mathrm{i}} + \widetilde{Q}^{\, (t)}_{\mathrm{i}} & \quad \big (\widetilde{U}^{\, (t)}_{\mathrm{i}} - \mathrm{i} \widetilde{V}^{\, (t)}_{\mathrm{i}}\big) \sin \theta \\ \big (\widetilde{U}^{\, (t)}_{\mathrm{i}} + \mathrm{i} \widetilde{V}^{\, (t)}_{\mathrm{i}}\big) \sin \theta & \quad \big (\widetilde{I}^{\, (t)}_{\mathrm{i}} - \widetilde{Q}^{\, (t)}_{\mathrm{i}}\big) \sin ^2 \theta \end{pmatrix}}\! (\hat{\boldsymbol {n}}, \nu), \end{eqnarray*}$$

(8)

where we have used a tilde to distinguish these Stokes parameters from those of the sky. The t and i indices denote that the parameters are time dependent and correspond to the instrument (i.e. the combination of beam and HWP), respectively.

Both density matrices in equation (5) are defined with respect to the same coordinate basis that is fixed relative to the sky. As a result, the instrumental density matrix |$\smash{\boldsymbol{\sf W}^{(t)}_{\mathrm{instr}}}$| is time dependent due to the continuous rotation of the instrument with respect to the sky (another time dependence is due to the HWP rotation, which is kept implicit for now). This time dependence can be factored out by considering the instrumental density matrix in a coordinate system fixed relative to the instrument. Let us denote the density matrix in the instrument frame by |$\smash{\boldsymbol{\sf W}^{(0)}_{\mathrm{instr}}}$|⁠. The two frames are connected by a 3D rotation |$\boldsymbol{\sf R}_t$| that we define as the rotation that would align the instrument frame to the frame fixed relative to the sky. We can thus perform an active rotation of the |$\smash{\boldsymbol{\sf W}^{(0)}_{\mathrm{instr}}}$| tensor by |$\boldsymbol{\sf R}_t$| to get back |$\smash{\boldsymbol{\sf W}^{(t)}_{\mathrm{instr}}}$|⁠:

$$\begin{eqnarray*} \big (W_{\mathrm{instr}}^{(0)}\big)_{ij} (\hat{\boldsymbol {n}}, \nu) &\mapsto & \big (W_{\mathrm{instr}}^{(t)}\big)_{ij} (\hat{\boldsymbol {n}}, \nu) \nonumber\\ &&= \Lambda _{i}^{\phantom{a}k} (\boldsymbol{\sf R}_t) \Lambda _{j}^{\phantom{a}l} (\boldsymbol{\sf R}_t) \big (W^{(0)}_{\mathrm{instr}}\big)_{kl} (\boldsymbol{\sf R}_t^{-1} \hat{\boldsymbol {n}}, \nu). \end{eqnarray*}$$

(9)

The |$\boldsymbol {\Lambda }$| matrices are matrix representations of the 3D rotation |$\boldsymbol{\sf R}_t$| (Challinor et al. 2000).

The 3D rotation from the instrument frame to the sky frame can be parametrized using three time-dependent Euler angles:

$$\begin{eqnarray*} \boldsymbol{\sf R}_t = \boldsymbol{\sf R}(\psi _t, \theta _t, \phi _t) \, . \end{eqnarray*}$$

(10)

The ψ_t, θ_t, and ϕ_t angles can be understood as follows. Imagine a right-handed 3D Cartesian coordinate frame with X-, Y-, and Z-axes centred at the origin of the spherical coordinate system. Let the Z axis point towards the centre of the instrumental response, i.e. the beam centre. The 3D rotation is then achieved by a sequence of three right-handed rotations: first rotating around the Z-axis by the first Euler angle ψ_t, then rotating around the Y-axis by θ_t, and finally rotating around the Z-axis again by ϕ_t.

Under the rotation |$\smash{\boldsymbol{\sf R}_t}$|⁠, the |$\smash{\boldsymbol{\sf W}^{(0)}_{\mathrm{instr}}}$| tensor transforms as equation (9). While it is possible to evaluate the transformation directly, we follow Challinor et al. (2000) and Wandelt & Górski (2001) and perform the transformation in the spherical harmonic domain instead. In the harmonic domain, the data model of equation (4) is expressed as follows:

$$\begin{eqnarray*} d_t &=& \int \mathrm{d}\nu F(\nu) \!\sum _{\ell , m, s} \Big \lbrace b^{\widetilde{I}^{(0)}_{\mathrm{i}}}_{\ell s}\!(\nu , \alpha _t) a^{I}_{\ell m}(\nu) + b^{\widetilde{V}^{(0)}_{\mathrm{i}}}_{\ell s}\!(\nu , \alpha _t) a^{V}_{\ell m}(\nu) \nonumber \\ && +\, \frac{1}{2} \Big [ {}_{-2}b^{\widetilde{P}^{(0)}_{\mathrm{i}}}_{\ell s}\!(\nu , \alpha _t) {}_{2}a^{P}_{\ell m} (\nu) + {}_{2}b^{\widetilde{P}^{(0)}_{\mathrm{i}}}_{\ell s}\!(\nu , \alpha _t) {}_{-2}a^{P}_{\ell m} (\nu) \Big ] \Big \rbrace \nonumber \\ && \times \, \sqrt{\frac{4 \pi }{2 \ell + 1}} \mathrm{e}^{- \mathrm{i} s \psi _t} {}_s Y_{\ell m} (\theta _t, \phi _t) + n_t , \end{eqnarray*}$$

(11)

where the _sY_ℓm function is a spin-weighted spherical harmonic (SWSH) and the ψ_t, θ_t, and ϕ_t Euler angles describe the instrumental pointing. The different b coefficients are SWSH coefficients that describe |$\smash{\boldsymbol{\sf W}_{\mathrm{instr}}^{(0)}}$|⁠, while the different a SWSH coefficients correspond to |$\smash{\boldsymbol{\sf W}_{\mathrm{sky}}}$|⁠. The sum over ℓ runs from 0 to the harmonic band limit of the beams: ℓ_max, while the sums over m and s run from −ℓ to ℓ. It should be noted that the sum over s can be truncated drastically for an approximately symmetric instrumental response. For perfectly symmetric beams, only s = 0 and s = ±2 are needed for the |$\smash{\widetilde{I}^{\, (0)}_{\mathrm{i}}}$|⁠, |$\smash{\widetilde{V}^{(0)}_{\mathrm{i}}}$|⁠, and |$\smash{\widetilde{P}^{(0)}_{\mathrm{i}}}$| coefficients, respectively (Challinor et al. 2000; Hivon et al. 2017). Exact definitions of the SWSH coefficients are given below and a full derivation is provided in Appendix A. The expression matches that of a general CMB polarimeter derived in Challinor et al. (2000), but is generalized to have an explicit dependence on frequency and the HWP rotation angle α_t.

The b harmonic coefficients that describe the instrument in equation (11) are given by combinations of the Stokes parameters of the beam, denoted with the subscript b, and the elements of the HWP Mueller matrix. For the sake of brevity, we use a complex representation of the Stokes parameters to describe the linearly polarized beam:

$$\begin{eqnarray*} \widetilde{P}^{(0)}_{\mathrm{b}} = \widetilde{Q}^{(0)}_{\mathrm{b}} + \mathrm{i} \widetilde{U}^{(0)}_{\mathrm{b}} \, . \end{eqnarray*}$$

(12)

Additionally, we replace the standard HWP Mueller matrix with a complex representation |$\boldsymbol{\sf C}$| that is indexed by {I, P, P*, V}. The two matrices are related by the following unitary transformation:

$$\begin{eqnarray*} \boldsymbol{\sf C} = \boldsymbol{\sf T} \boldsymbol{\sf M}_{\mathrm{HWP}} \boldsymbol{\sf T}^{\dagger } \, , \end{eqnarray*}$$

(13)

where |$\boldsymbol{\sf M}_{\mathrm{HWP}}$| is the unrotated Mueller matrix and |$\boldsymbol{\sf T}$| is given by

$$\begin{eqnarray*} \boldsymbol{\sf T} = {\begin{pmatrix}1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad \frac{1}{\sqrt{2}} & \quad \frac{\mathrm{i}}{\sqrt{2}} & \quad 0 \\ 0 & \quad \frac{1}{\sqrt{2}} & \quad \frac{-\mathrm{i}}{\sqrt{2}} & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{pmatrix}} . \end{eqnarray*}$$

(14)

The complex representation allows us to cleanly separate terms with different dependence on the HWP rotation angle α_t. The harmonic coefficients that describe the instrumental response in equation (11) are then given by

$$\begin{eqnarray*} {}_{\phantom{2}}b^{\widetilde{I}^{(0)}_{\mathrm{i}}}_{\ell s}\!(\nu , \alpha) &=& \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \Big [\widetilde{I}^{\, (0)}_{\mathrm{b}}(\hat{\boldsymbol {n}}, \nu) C_{II}(\nu) \nonumber \\ && + \widetilde{V}^{(0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{VI}(\nu) \nonumber\\ &&+ \sqrt{2} \mathrm{Re} \Big (\widetilde{P}^{(0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{P^* I}(\nu)\mathrm{e}^{-2i\alpha } \Big) \Big ] Y_{\ell s}^* (\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(15)

$$\begin{eqnarray*} {}_{\pm 2}b^{\widetilde{P}^{(0)}_{\mathrm{i}}}_{\ell s}(\nu , \alpha) &=& \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \Big [ \widetilde{I}^{\, (0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{IP}(\nu) \sqrt{2} \, \mathrm{e}^{-2\mathrm{i}\alpha } \nonumber \\ &&+ \widetilde{V}^{(0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{VP}(\nu) \sqrt{2} \mathrm{e}^{-2\mathrm{i}\alpha } \nonumber\\ && + \widetilde{P}^{(0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{P^* P} (\nu) \mathrm{e}^{-4\mathrm{i}\alpha } \nonumber\\ &&+ \widetilde{P}^{(0)*}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{P P}(\nu) \Big ]{}_{2}Y_{\ell s}^* (\hat{\boldsymbol {n}}), \end{eqnarray*}$$

(16)

$$\begin{eqnarray*} {}_{\phantom{2}}b^{\widetilde{V}^{(0)}_{\mathrm{i}}}_{\ell s} (\nu , \alpha) &=& \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \Big [\widetilde{I}^{\, (0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{IV}(\nu)\nonumber \\ && + \widetilde{V}^{(0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{VV}(\nu) \nonumber \\ &&+ \sqrt{2} \mathrm{Re} \Big (\widetilde{P}^{\, (0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{P^* V}(\nu)\mathrm{e}^{-2\mathrm{i}\alpha } \Big) \Big ] Y_{\ell s}^* (\hat{\boldsymbol {n}}). \end{eqnarray*}$$

(17)

The elements of the |$\boldsymbol{\sf C}$| HWP matrix are given in equation (A36). Note that the |$\smash{{}_{-2}b_{\ell s}}$| coefficients can be obtained using the following symmetry relation:

$$\begin{eqnarray*} {}_{-2}b^{\widetilde{P}^{(0)}_{\mathrm{i}}}_{\ell s}(\alpha) = \big [{}_{2}b^{\widetilde{P}^{(0)}_{\mathrm{i}}}_{\ell -s}(\alpha)\big ]^* (-1)^{s} . \end{eqnarray*}$$

(18)

The harmonic coefficients that represent the Stokes parameters of the sky in equation (11) are given by

$$\begin{eqnarray*} a^{I}_{\ell m}(\nu) = \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) I(\hat{\boldsymbol {n}}, \nu) Y^*_{\ell m} (\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(19)

$$\begin{eqnarray*} {}_{\pm 2}a^{P}_{\ell m}(\nu) = \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) (Q \pm \mathrm{i} U)(\hat{\boldsymbol {n}}, \nu) {}_{\pm 2}Y^*_{\ell m} (\hat{\boldsymbol {n}}), \end{eqnarray*}$$

(20)

$$\begin{eqnarray*} a^{V}_{\ell m}(\nu) = \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) V(\hat{\boldsymbol {n}}, \nu) Y^*_{\ell m} (\hat{\boldsymbol {n}}). \end{eqnarray*}$$

(21)

Fig. 2 helps to qualify the rather verbose expressions for the above harmonic coefficients. It illustrates the effect of a non-ideal HWP on the TOD by comparing the corresponding power spectrum densities for two cases: without an HWP and with a non-ideal HWP (see Section 3.3). Recall that ideal HWP modulation will only modulate the Q and U sky signal, which it will do at a modulation frequency 4ν_α, where ν_α is the HWP rotation frequency. It can be seen that the non-ideal HWP introduces an additional spurious 2ν_α modulation of the I sky (second line of equation 15), a 2ν_α modulation of the Q and U sky (first and second line of equation 16), and a 2ν_α modulation of the V sky (second line of equation 17, not shown in the figure). Finally, the non-ideal HWP also introduces a spurious constant 0ν_α modulation of the Q and U sky (fourth line of equation 16). Note that Fig. 2 omits the case of an input V sky. The ν_α dependence of the V-input case will be the same, qualitatively, as the Stokes I-input case.

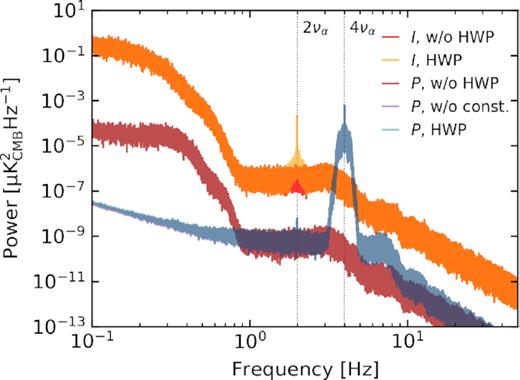
$Power spectral densities (PSDs) corresponding to a typical 2-h segment of noiseless TOD for a single detector. The curves labelled I (P) correspond to scans over an I-only ((Q, U)-only) simulated CMB sky. The curves labelled HWP include HWP modulation using the three-layer BR3 HWP configuration (to be discussed in Section 3) spinning at a frequency να of 1 Hz. The curve labelled P, w/o const. (overlapping with P, HWP but slightly different below $\sim {2}{\, \mathrm{Hz}}$) incorporates the same HWP modulation, but does not include the HWP systematic that is constant with HWP angle α, see equation (16). The curves labelled w/o HWP do not include HWP modulation. The simulated data are recorded at a monochromatic frequency of 90 GHz using a Gaussian beam with a full width at half-maximum of 32.2 arcmin. Each curve is the average of 10 PSDs corresponding to successive 2-h scans. The scan strategy is described in Section 3.1.$

Figure 2.

Power spectral densities (PSDs) corresponding to a typical 2-h segment of noiseless TOD for a single detector. The curves labelled I (P) correspond to scans over an I-only ((Q, U)-only) simulated CMB sky. The curves labelled HWP include HWP modulation using the three-layer BR3 HWP configuration (to be discussed in Section 3) spinning at a frequency ν_α of 1 Hz. The curve labelled P, w/o const. (overlapping with P, HWP but slightly different below |$\sim {2}{\, \mathrm{Hz}}$|⁠) incorporates the same HWP modulation, but does not include the HWP systematic that is constant with HWP angle α, see equation (16). The curves labelled w/o HWP do not include HWP modulation. The simulated data are recorded at a monochromatic frequency of 90 GHz using a Gaussian beam with a full width at half-maximum of 32.2 arcmin. Each curve is the average of 10 PSDs corresponding to successive 2-h scans. The scan strategy is described in Section 3.1.

Open in new tab Download slide

The dependence on HWP angle α of the different terms in the data model is relevant because this dependence is used by the subsequent map-making procedure to distinguish between I, Q, U, (and possibly V) sky signal. Leakage between the Stokes parameters will occur when the data model used by the map maker does not capture the full α modulation of the TOD. For the experimental configuration considered in this work, see Section 3, we find that the I → (Q, U) leakage that is caused by ignoring the 2ν_α terms during map making is subdominant to the Q↔U leakage that is caused by ignoring non-idealities in the 4ν_α term.

It should be noted that in the derivation of equations (15)–(17) in Appendix A, we have assumed that the instrumental Stokes vector, which is related to |$\smash{\boldsymbol{\sf W}^{(0)}_{\mathrm{instr}}}$| by equation (6), can be factored into a Stokes vector describing the beam and a Mueller matrix describing the skywards HWP:

$$\begin{eqnarray*} \boldsymbol {S}^{(0) \mathsf {T}}_{\mathrm{instr}}(\hat{\boldsymbol {n}}, \nu , \alpha _t, \vartheta _\mathrm{inc}) = \boldsymbol {S}^{(0) \mathsf {T}}_{\mathrm{beam}} (\hat{\boldsymbol {n}}, \nu) \, \boldsymbol{\sf M}_{\mathrm{HWP}} (\nu , \alpha _t, \vartheta _\mathrm{inc}) \, . \end{eqnarray*}$$

(22)

The Stokes vector describing the beam has an angular dependence that describes the finite resolution of the experiment, but it is constant with time. On the other hand, the Mueller matrix of the HWP depends on the time-varying HWP angle α_t but is assumed to have no angular dependence. Note that the Mueller matrix varies between detectors based on their position on the focal plane (see Fig. 1). This dependence on detector incidence angle is captured by the ϑ_inc parameter. The factorization of the beam and HWP response in equation (22) is an approximation. It allows for separate modelling of the HWP and the instrumental beam. Strictly speaking, the factorization is only valid when the radiation in between the HWP and the beam-forming optical elements is described by plane waves propagating along |$\hat{\boldsymbol {n}}$|⁠. The interaction between the near-field beam and the HWP would in reality also be sensitive to the longitudinal component of the electric field in between the elements. On top of that, the near-field beam is different than the far-field beam described by |$\smash{\boldsymbol {S}^{(0)}_{\mathrm{beam}}}$|⁠. Accounting for such near-field effects is beyond the scope of current analysis and simulation infrastructures. We expect that our approximation describes the interaction between the HWP and the beam sufficiently well.

The data model described by equations (11)–(21) is now implemented in the beamconv library. The frequency dependence of the model is handled by approximating the integral over the instrumental frequency band with a small number (n_ν = 7 for the results in Section 4) of monochromatic input skies, beams, and HWP Mueller matrices. The memory costs and computational scaling of the algorithm have thus gained a linear scaling with n_ν compared to the algorithm in Duivenvoorden et al. (2019) but are unchanged otherwise. The algorithm allows for efficient time-domain simulations that include all-sky beam convolution with asymmetric beams and non-ideal HWPs.

3 SIMULATION SET-UP

We consider a telescope similar to the one described in Duivenvoorden et al. (2019), but with an HWP in front of the primary lens. Incoming radiation passes through the HWP followed by a pair of lenses before being absorbed by the detectors on the focal plane (see Fig. 1). A beam profile for a typical 150-GHz detector used in this analysis is shown in Fig. 3. We model 50 dichroic detectors sensitive to two 30-GHz-wide frequency windows centred at 95 and 150 GHz. The detectors are evenly distributed on a square grid of a focal plane fed by a 30- cm aperture telescope. The field of view of this square grid is only 7° compared to the 28° that can be supported by this telescope; the detectors therefore only cover a fraction of the focal plane. The spectral response of the detectors is assumed to be represented by a top-hat function within each band. In order to test frequency-dependent effects, we run simulations at seven subfrequencies within a band. These subfrequencies are 80, 85, 90, 95, 100, 105, and 110 GHz for the 95-GHz band and 135, 140, 145, 150, 155, 160, and 165 GHz for the 150-GHz band (see hatched regions in Fig. 4).

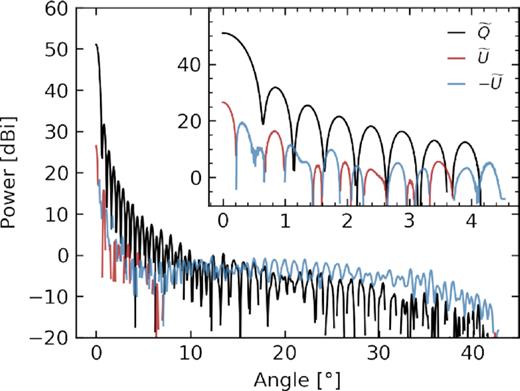
$Azimuthally averaged beam profiles (dBi units) for a representative detector of one of the 50 used in this analysis. Shown are the Stokes $\widetilde{Q}$ and $\widetilde{U}$ beam components. For this figure, we have defined the Stokes parameters with respect to the Ludwig-3 basis (Ludwig 1973). This basis is approximately Cartesian around the beam centre and has been aligned with the polarized element of the detector. As a result, the $\pm \widetilde{U}$ profile quantifies the amount of non-aligned (or ‘cross-polar’) polarized sensitivity of the beam. It can be seen that $|\widetilde{U}|$ is subdominant close to the centre of the beam (see inset) while having a relatively large contribution at large opening angles.$

Figure 3.

Azimuthally averaged beam profiles (dBi units) for a representative detector of one of the 50 used in this analysis. Shown are the Stokes |$\widetilde{Q}$| and |$\widetilde{U}$| beam components. For this figure, we have defined the Stokes parameters with respect to the Ludwig-3 basis (Ludwig 1973). This basis is approximately Cartesian around the beam centre and has been aligned with the polarized element of the detector. As a result, the |$\pm \widetilde{U}$| profile quantifies the amount of non-aligned (or ‘cross-polar’) polarized sensitivity of the beam. It can be seen that |$|\widetilde{U}|$| is subdominant close to the centre of the beam (see inset) while having a relatively large contribution at large opening angles.

Open in new tab Download slide

Figure 4.

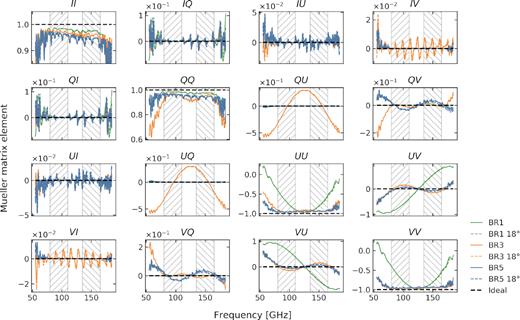
HWP Mueller matrix elements as a function of frequency in the normal incidence case (solid lines) and for an incidence angle ϑ_inc of 18° (dashed lines, virtually indistinguishable from solid lines) simulated using the TMM. The three HWP configurations described in Table 1 are shown. A 31.4° HWP rotation angle offset is applied to the three-layer BR3 model. The black dashed line represents the ideal HWP (T = −c = 1, ρ = s = 0 in equation 3). The grey hatched bands illustrate the two instrumental frequency bands used in this work.

Open in new tab Download slide

3.1 Simulated scanning

Using the updated version of beamconv, we simulate 1 yr of satellite scanning for 50 detectors. We use a similar scan strategy as in Duivenvoorden et al. (2019), which is based on Gorski (2008) and Wallis et al. (2017). The satellite spins around its principal axis with a period of 600 s. It precesses about the boresight axis with a period of 90 min. The two axes are separated by 50°. We set the HWP rotation frequency ν_α to 1 Hz (angular frequency of |${2 \pi }{\, \mathrm{rad\, s}^{-1}}$|⁠) and sample the data at 12.01 Hz. Although the sampling frequency is likely an order of magnitude below that of a real experiment, we find that this rate suffices for our noiseless simulations. The resulting angular coverage is excellent and allows for simultaneous per-pixel recovery of I, Q, and U over the full sky. Even without a continuously spinning HWP, the average condition number of the per-pixel (I, Q, U) covariance matrix, which is inverted as part of the solution (Duivenvoorden et al. 2019), is approximately 2.9 for a N_side = 256 map. In comparison, the condition number approaches 2.0 (the minimum value) for all pixels when the HWP is spun with a 1-Hz rotation frequency.

3.2 Input maps

We generate statistically isotropic random Gaussian Stokes I, Q, and U CMB maps (with a vanishing B-mode component) using the synfast utility in healpix’s (Górski et al. 2005) python implementation, healpy ^3,4 and the best-fitting 2018 Planck power spectra (Planck Collaboration VI 2020a). To probe how frequency-dependent HWP systematics interact with the different components of the microwave sky, we also simulate polarized Galactic dust using the python Sky Model (pysm) code (Thorne et al. 2017). Other foreground sources, including synchrotron radiation, are subdominant in our 95 and 150 GHz frequency bands. pysm provides different templates for dust emission, all based on the high-frequency Planck data (Planck Collaboration X 2016b).⁵ We use six different pysm dust models: d0 to d5. The first four models are directly based on a modified blackbody distribution. In units of CMB brightness temperature, these models all follow the same parametrization:

$$\begin{eqnarray*} {\begin{pmatrix}Q \\ U \end{pmatrix}} (\hat{\boldsymbol {n}}, \nu) ={\begin{pmatrix}A_{Q} \\ A_{U} \end{pmatrix}} \! (\hat{\boldsymbol {n}}) \times \left(\frac{\nu }{\nu _0}\right)^{\beta (\hat{\boldsymbol {n}}) + 1} \frac{\mathrm{e}^{h\nu _0 / k_{\mathrm{B}}T(\hat{\boldsymbol {n}}) }-1}{\mathrm{e}^{h\nu / k_{\mathrm{B}}T(\hat{\boldsymbol {n}}) }-1} \, , \end{eqnarray*}$$

(23)

There are four parameters: the spectral index β, the dust temperature T, and the A_Q/U amplitudes at the reference frequency |$\nu _0 = {353}{\, \mathrm{GHz}}$|⁠. A brief description of each model follows, see Thorne et al. (2017) for more details.

d0 uses a fixed spectral index (β = 1.54), a fixed temperature (⁠|$T={20}{\, \mathrm{K}}$|⁠), and the Commander dust template from Planck Collaboration IX (2016a) for A_Q/U.
d1 extends the d0 model with spatially varying spectral index and temperature that are both given by the Commander templates from Planck Collaboration IX (2016a).
d2 modifies the d1 model with a spectra index that varies randomly on degree scales, following a Gaussian distribution: |$\beta \sim \mathcal {N}(\mu =1.59, \sigma ^2 = 0.04)$|⁠.
d3 is the same as d2 except that |$\beta \sim \mathcal {N}(\mu =1.59, \sigma ^2 = 0.09)$|⁠.
d4 models two dust populations as two modified blackbodies with different but spatially constant spectral indices and two different spatially varying temperatures and dust amplitudes (Meisner & Finkbeiner 2015).
d5 is a more physically motivated model based on the physical properties of two populations of dust grains (silicate and carbonaceous) (Hensley 2015; Hensley & Bull 2018).

The inclusion of these six models in our analysis serves to roughly bracket the current uncertainty in dust modelling. We note that the d3 model is designed to match the largest variation in spectral index allowed by the Planck data. We study the interplay between the HWP non-idealities and these different foreground models in Section 4.3.

3.3 Selection of HWPs

A wide range of HWP designs have been described and studied in the literature (Bryan et al. 2010b; The Polarbear Collaboration 2010; Hill et al. 2016; Aboobaker et al. 2018; Komatsu et al. 2018). HWP design involves a complex optimization problem where absorptive and reflective losses from materials with high index of refraction need to be balanced against the desire for unity polarization efficiency across a wide band. We choose to study three HWP configurations, which are loosely based on Bryan et al. (2010b) as a model of a one layer HWP, (Hill et al. 2016) for the three-layer HWP, and a five-layer HWP model taken from Komatsu et al. (2020). Some key properties of these three HWP configurations, which we denote as BR1, BR3, and BR5, are shown in Table 1.

Table 1.

Open in new tab

HWP configurations adopted for the analysis presented in this paper. Orientation angles are those of the fast axis of the birefringent layers relative to the plane of incoming vertically polarized radiation. The rotation angle offset is given in each band following equation (24), for CMB and dust weights as defined in equation (25).

Model	Orientation	Phase 95 GHz	Phase 150 GHz
		CMB/dust	CMB/dust
BR1	0°	0°/0°	0°/0°
BR3	{0°, 54°, 0°}	30.75° / 31.16°	32.51° / 32.30°
BR5	{22.9°, −50°, 0°
	50°, −22.9°}	0°/0°	0°/0°

Model	Orientation	Phase 95 GHz	Phase 150 GHz
		CMB/dust	CMB/dust
BR1	0°	0°/0°	0°/0°
BR3	{0°, 54°, 0°}	30.75° / 31.16°	32.51° / 32.30°
BR5	{22.9°, −50°, 0°
	50°, −22.9°}	0°/0°	0°/0°

Table 1.

Open in new tab

HWP configurations adopted for the analysis presented in this paper. Orientation angles are those of the fast axis of the birefringent layers relative to the plane of incoming vertically polarized radiation. The rotation angle offset is given in each band following equation (24), for CMB and dust weights as defined in equation (25).

Model	Orientation	Phase 95 GHz	Phase 150 GHz
		CMB/dust	CMB/dust
BR1	0°	0°/0°	0°/0°
BR3	{0°, 54°, 0°}	30.75° / 31.16°	32.51° / 32.30°
BR5	{22.9°, −50°, 0°
	50°, −22.9°}	0°/0°	0°/0°

Model	Orientation	Phase 95 GHz	Phase 150 GHz
		CMB/dust	CMB/dust
BR1	0°	0°/0°	0°/0°
BR3	{0°, 54°, 0°}	30.75° / 31.16°	32.51° / 32.30°
BR5	{22.9°, −50°, 0°
	50°, −22.9°}	0°/0°	0°/0°

We adopt a fixed thickness, |$d={3.75}{\, \mathrm{mm}}$|⁠, for the individual sapphire plate layers for all three polarization modulators. This thickness was found using the traditional formula for HWPs made of a single layer of birefringent material d = c/[2ν(n_e − n_o)], where n_o and n_e correspond to the index of refraction for the ordinary and extraordinary axes, respectively. The selected thickness is optimal for |$\nu = {126}{\, \mathrm{GHz}}$|⁠, near the average of our two band centres. We adopt an antireflection coating similar to the one described in Coughlin et al. (2018) that is optimized for 75–170 GHz. We settle on three AR layers with thicknesses |$d_\mathrm{AR} = 0.5, 0.31, {0.257}{\, \mathrm{mm}}$| and individual indices n_AR = (1.268, 1.979, 2.855). The above parameters are used as input to the TMM formalism to calculate the Mueller matrices of the HWPs. We produce a unique set of Mueller matrices for each unique HWP incidence angle ϑ_inc.

Fig. 4 shows the Mueller matrix elements for our three HWP configurations as function of frequency. It can be seen that the additional layers of the BR3 and BR5 HWPs improve the frequency uniformity of the polarization efficiency (see the UU elements) compared to the BR1 case. Describing the efficiency loss for the different Stokes parameters is a rather complicated task. Although the efficiency loss of Stokes I is easy to understand, as the II elements decrease in value with additional layers, the same is not true for the polarization efficiency.⁶ Because of these complications, we do not directly use the HWP Mueller matrix elements to correct our results for the efficiency loss. As will be detailed in Section 4, we settle for a more robust and simpler power spectrum based calibration method. Such an approach will likely also be taken by a real experiment. Finally, we note that the Mueller matrix models that we use do not include systematic effects caused by non-ideal manufacturing or material non-uniformity, which are likely to exist at some non-negligible level even in next-generation experiments.

3.4 Determining the AHWP induced rotation offset

AHWPs, such as the three- and five-layer configurations discussed in this paper, tend to have higher polarization efficiency over a given frequency range compared to a single-layer HWP. However, they also introduce an undesirable frequency-dependent phase between the in-going and out-going electric field that manifests itself as a frequency-dependent HWP rotation angle offset. Fig. 5 shows our HWP Mueller matrices, integrated over the two frequency bands, as a function of the HWP angle α. From the inner two-by-two set of panels it is clear that the three-layer HWP has a relatively large rotation angle offset. It turns out that the offset angle of the three-layer model also displays the largest variation with frequency. While the average value of this offset angle can be simply calibrated out, this large variation with frequency poses a difficulty: sky components with different frequency characteristics will require different offset angles after integration over the instrumental frequency band.

Figure 5.

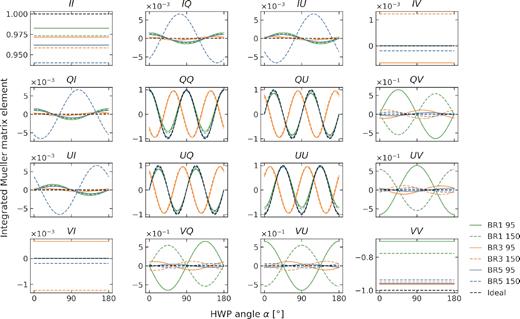
Mueller matrix elements for the three HWP models described in Table 1, integrated over the instrumental frequency bands (95: solid lines, 80–110 GHz; 150: dashed lines, 135–165 GHz) as a function of the HWP rotation angle. The dashed black lines represent the behaviour of the ideal HWP (T = −c = 1, ρ = s = 0 in equation 3). It can be seen that the BR3 configuration (orange lines) is out of phase with the other HWP configurations.

Open in new tab Download slide

We can determine an optimal rotation angle offset for a specific sky component as the HWP rotation angle, α_min, that minimizes the difference between the QQ, QU, UQ, UU submatrices of the Mueller matrices of the HWP and the ideal HWP. The α_min angle is found by minimizing

$$\begin{eqnarray*} R(\alpha) = \sum _{i,j \in \lbrace Q, U \rbrace } \left[ \sum _{k=1}^{n_{\nu }} w(\nu _k) \: M_{\mathrm{HWP},ij}(\nu _k) - D_{ij}(\alpha) \right]^2 \, , \end{eqnarray*}$$

(24)

where |$\boldsymbol{\sf M}_{\mathrm{HWP}}(\nu _k)$| is the same as in equation (22) with normally incident light and |$\boldsymbol{\sf D}(\alpha)$| is the Mueller matrix of the ideal HWP rotated by an angle α. The ν_k are a set of subfrequencies within the band, and w(ν_k) are weights applied to model the SED. Because we work in units of CMB brightness temperature, we use uniform weighting for the CMB. If we assume that Galactic dust follows a modified blackbody distribution with a fixed temperature and spectral index across the sky, the weights can be derived from equation (23):

$$\begin{eqnarray*} w(\nu _k) = \left(\sum _{i=1}^{n_{\nu }} \frac{\nu _i^{\beta +1}}{\mathrm{e}^{h\nu _i / k_{\mathrm{B}} T} -1 } \right)^{-1} \frac{\nu _k^{\beta +1}}{\mathrm{e}^{h\nu _k / k_{\mathrm{B}}T}-1 } \, . \end{eqnarray*}$$

(25)

Note, however, that these assumptions about the dust SED are only valid for the d0 pysm model (with |$T={20}{\, \mathrm{K}}$| and β = 1.54). The optimal offset angles for the CMB and the above dust weights are given in Table 1. The three-layer configuration shows a significantly different optimal offset angle for the CMB versus dust.

The optimal HWP rotation angle correction will vary across the sky for foregrounds models that include spatial SED variations. We can determine an optimal per-pixel correction for a given foreground component by applying equation (24) on a pixel-by-pixel basis. In Fig. 6, we compare the distribution of the optimal HWP rotation offset angles for the d1–d5 pysm dust models to the d0 value given by equation (25). We only show results for BR3 in Fig. 6. The BR1 and BR5 configurations have a near-constant rotation angle offset over the range of frequencies that we consider and show no appreciable deviation from an isotropic angle offset. Calculating the distributions in Fig. 6 requires knowledge on the per-pixel SED weights w(ν_k) in equation (24). Although we lack a closed-form expression for all of the SEDs of our dust models, we can make use of the pysm predictions at each subfrequency ν_k to determine the SED weights using

$$\begin{eqnarray*} w(\hat{\boldsymbol {n}}, \nu _k) = \Bigg (\sum _{j=1}^{n_{\nu }} \vert P(\hat{\boldsymbol {n}}, \nu _j) \vert \Bigg)^{-1} \vert P(\hat{\boldsymbol {n}}, \nu _k) \vert \, , \end{eqnarray*}$$

(26)

where |$\vert P(\hat{\boldsymbol {n}}, \nu _k) \vert$| is the amplitude of linear polarization at subfrequency ν_k in direction |$\hat{\boldsymbol {n}}$|⁠.

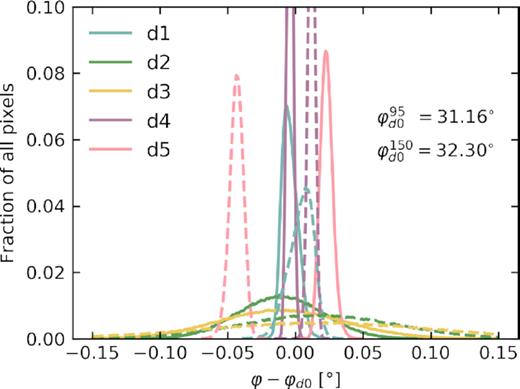
$Distribution of optimal BR3 HWP rotation angle offset φ in the 95 GHz (solid lines) and 150 GHz (dashed lines) bands for the pysm Galactic dust models based on their per-pixel spectral energy distribution at Nside = 512. The distributions are given for the 40 per cent sky mask used in our analysis. The abscissa is expressed as the difference between the rotation angle offset φ and the reference angle φd0 corresponding to a modified blackbody with $T={20}{\, \mathrm{K}}$ and β = 1.54 as in Table 1.$

Figure 6.

Distribution of optimal BR3 HWP rotation angle offset φ in the 95 GHz (solid lines) and 150 GHz (dashed lines) bands for the pysm Galactic dust models based on their per-pixel spectral energy distribution at N_side = 512. The distributions are given for the 40 per cent sky mask used in our analysis. The abscissa is expressed as the difference between the rotation angle offset φ and the reference angle φ_d0 corresponding to a modified blackbody with |$T={20}{\, \mathrm{K}}$| and β = 1.54 as in Table 1.

Open in new tab Download slide

4 ANALYSIS RESULTS

To test the capabilities of the updated beamconv code, we run a number of simulations that probe the different HWP configurations, sky models, and instrumental beams. Each simulation batch is based on seven subfrequency maps per frequency band that are combined assuming a top-hat passband. Seven subfrequencies represent the lowest adequate sampling of the frequency variation of the HWP Mueller matrices. The simulated TOD are binned on the sphere using the standard map-making scheme that ignores the instrumental beam and assumes the following data model for each detector:

$$\begin{eqnarray*} \begin{split} d_{t} = I(\hat{\boldsymbol {n}}_t) + Q(\hat{\boldsymbol {n}}_t) \cos &\big [2 (\psi _t + \gamma) + 4 (\alpha _t + \varphi)\big ] \\ + U(\hat{\boldsymbol {n}}_t) \sin &\big [2 (\psi _t + \gamma) + 4 (\alpha _t + \varphi)\big ] + n_t\, . \end{split} \end{eqnarray*}$$

(27)

Here, |$\hat{\boldsymbol {n}}_t$|⁠, ψ_t, and α_t describe the instrumental pointing and HWP rotation angle at time-sample t while γ and φ describe the detector polarization angle and HWP rotation angle offset, respectively. The map maker solves for I, Q, and U per pixel, uses uniform weighting of the TOD and does not explicitly use detector pair differencing, see e.g. Duivenvoorden et al. (2019).

For every simulated systematic effect, the same simulation is performed using an ideal HWP (T = −c = 1, ρ = s = 0 in equation 3). With ideal and non-ideal maps in hand, we can calculate difference maps that quantify signal residuals due to HWP-related systematics. The resulting difference maps cover the entire sky, but we use a 40 per cent sky mask (gal040; Planck Collaboration IX 2016a) before calculating power spectra using polspice (Challinor et al. 2011).

4.1 Calibration

To correct for the non-ideal polarization efficiency of each HWP model, we calibrate each map on a map obtained by scanning with an ideal HWP. This is performed using the EE angular power spectrum at degree angular scales, 50 ≤ ℓ ≤ 200. The choice of angular scales roughly coincides with the peak in the expected primordial gravitational wave power spectrum. Note that the calibration procedure could instead be performed using lab measurements or simulated HWP (and other optical component) material properties (Pisano et al. 2006; Bryan et al. 2010a, b; Hill et al. 2016). The EE calibration approach uses the following factor:

$$\begin{eqnarray*} g = \frac{1}{151} \sum _{\ell = 50}^{200} \frac{C^{EE, \mathrm{ideal}}_{\ell }}{C_\ell ^{EE}}\, , \end{eqnarray*}$$

(28)

where the denominator (numerator) is the E-mode power spectrum estimated from the output maps created with a non-ideal (ideal) HWP. The final difference maps are formed by subtracting the calibrated output of the non-ideal simulation from the ideal simulation’s output:

$$\begin{eqnarray*} {\begin{pmatrix}Q \\ U \end{pmatrix}}_\mathrm{diff}= {\begin{pmatrix}Q \\ U \end{pmatrix}}_\mathrm{ideal} -\sqrt{g} {\begin{pmatrix}Q \\ U \end{pmatrix}} \, . \end{eqnarray*}$$

(29)

The residual B-mode power spectrum caused by the non-ideal HWP is then estimated from these calibrated difference maps.

Finally, we divide out a beam window function to correct the power spectrum for the azimuthally symmetric part of the beam. This allows us to directly compare the residual to theory spectra. For each simulation, we use a window function that corresponds to the averaged symmetric part of the input detector beams.

4.2 Scanning with an ideal Gaussian beam

We start by exploring effects that are purely caused by non-ideal HWPs. This is achieved by choosing a copolar polarized and azimuthally symmetric Gaussian beam model, see e.g. Duivenvoorden et al. (2019). Using this beam, we scan the CMB with the different HWP configurations; we summarize our results in Fig. 7. We find that only the BR3 configuration shows an appreciable B-mode residual in this case. All three HWP configurations outperform the case without HWP modulation, which shows a relatively large white-noise spectrum caused by small conditioning problems in the map-making solution that are approximately uncorrelated between pixels. It is instructive to determine which terms of the data model in equations (15)–(17) are causing the BR3 residual. It turns out that this spurious signal is due to E → B leakage from the 4ν_α terms, i.e. non-idealities in the inner two-by-two part of the HWP Mueller matrix. We have checked that the residual is not caused by I → (Q, U) leakage due to the 2ν_α term in equation (15) that couples the linearly polarized beam to the I sky signal: we obtain virtually identical residuals when the input Stokes I signal is artificially set to zero. The insignificance of the 2ν_α term can be attributed to the smallness of the IQ and IU elements in the HWP Mueller matrices (see Fig. 5), the lack of a strong atmospheric I signal, and most importantly, the rather good conditioning of the map-making solution. Even without modification, the map maker corresponding to equation (27) accurately distinguishes between time-ordered signal that is modulated at 2ν_α and 4ν_α.

Figure 7.

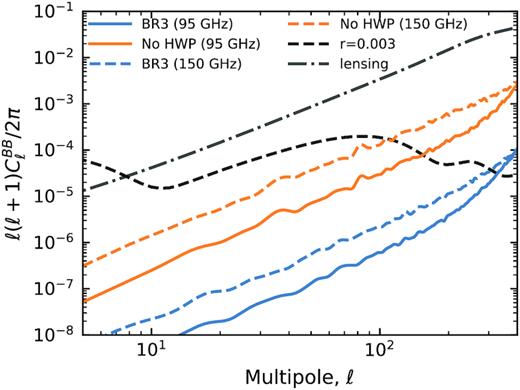
Residual B-mode power spectra obtained by observing the CMB with the BR3 configurations presented in Table 1 (including the rotation angle offset optimized for the CMB). The beams are Gaussian. We omit the BR1 and BR5 HWP configurations since their residuals fall below the limits on the vertical axis. The no-HWP case is also shown (orange curves).

Open in new tab Download slide

Using the same set-up, we then explore the addition of a foreground component. Specifically, we simulate what happens when a map maker that uses an HWP angle offset φ (see equation 27) that is optimized for the CMB encounters polarized signal from Galactic dust. Fig. 8 shows the B-mode residual for this hypothetical situation as well as for the opposite case in which the CMB is observed with φ optimized for the SED of dust. We again only show the BR3 HWP configuration. The error in φ causes E → B leakage: the residual clearly traces the shape of the input E-mode spectrum. The effect is identical to that of a systematic polarization angle calibration error. It can be seen that for both cases the residual is larger for 95 GHz than for 150 GHz. This is due to the fact that the optimal BR3 offset angle for dust in the 95 GHz band differs from the optimal angle offset for the CMB by about 0.4° while the difference at 150 GHz is only half that.

Figure 8.

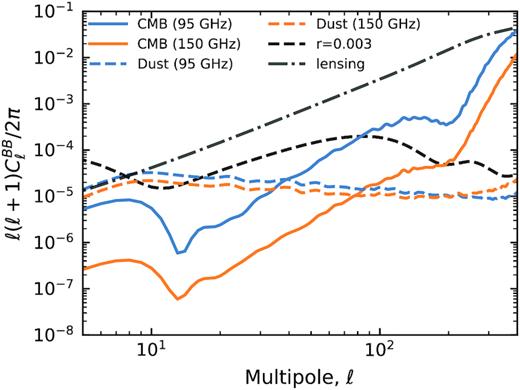
Residual B-mode power spectra generated when the CMB is observed using the BR3 HWP with a rotation angle offset optimized for the pysm Galactic dust model d1 (solid curves) and vice versa (dashed curves).

Open in new tab Download slide

From this section it becomes clear that in the presence of multiple sky components a single HWP offset angle φ will not effectively reduce B-mode residual caused by HWP non-idealities. The remaining spurious signal for the BR3 HWP configuration is at a level that would be unacceptable for upcoming B-mode experiments. A correction angle per sky component seems to be necessary. We further explore this point in the next section.

4.3 Foreground dependence

To investigate how the HWP-induced systematics depend on foreground emission, we scan the different pysm Galactic dust models (d0–d5) with Gaussian beams (using the same set-up as in the previous section). Data from the Planck satellite have provided a wealth of information on Galactic dust emission, but there remains considerable uncertainty regarding both its frequency scaling and spatial variation (Planck Collaboration XI 2020b). It is therefore natural to ask whether this uncertainty is large enough to impact the modelling of HWP systematics. We are particularly interested in seeing if spatial variation in the effective spectral index invalidates the use of a single HWP rotation angle offset. Recall that in Fig. 6 the offset angles for the various pysm dust models are compared to the offset angle determined for the simplest modified blackbody model d0. The offset angle distributions of the more involved dust models are both biased from the d0 value and show a dispersion. The model with the greatest dispersion (d3) predicts that a significant number of sky pixels will have an optimal offset angle that is more than 0.1° away from the mean value for the BR3 HWP configuration.

Fig. 9 shows the effect of ignoring the spatial SED variations of the various pysm models. We scan the dust models using the BR3 HWP and correct for the HWP-induced rotation offset using an angle that corresponds to the mean of each distribution in Fig. 6. As expected, we see that the d2 and d3 models, which both have a relatively large spread in spectral index over the sky, give the largest residuals. However, the amplitude of the spurious signal is still well below any detectable B-mode power spectrum amplitude. It thus seems that any realistic spatial variation in the dust SED can be safely ignored when determining the optimal HWP rotation angle correction for the dust component.

Figure 9.

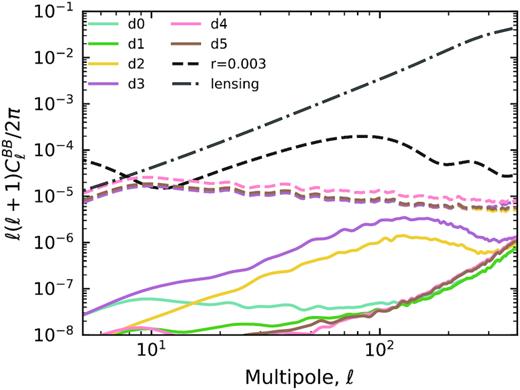
Residual B-mode power spectra for the different pysm Galactic dust models in the 150 GHz frequency band scanned using the BR3 HWP configuration. The solid lines use a value of the HWP angle offset that is tailored to each dust model (the median of the distributions shown in Fig. 6). The dashed coloured lines use the median of the rotation angle offsets calculated for the case of an SED given by the combination of CMB and dust.

Open in new tab Download slide

Similar to the previous section, we also explore the case in which a single angle calculated for the SED of the combination of CMB and dust is used to correct for the HWP-induced rotation angle. These residuals are given by the dashed lines in Fig. 9. We again see that this choice of correction angle would produce significant residual and we see that this result is insensitive to the choice of dust model.

4.4 Scanning with a non-ideal beam

The simulation framework presented in this paper enables studies of the complicated interplay between non-ideal HWPs and non-ideal beams. For this purpose, we can use physical optics (PO) simulations that include extended beam sidelobes with non-negligible cross-polar response; features that could be present in an optical configuration shown in Fig. 1. The azimuthally averaged beam profiles for the Stokes Q and U beams of a representative beam used in this analysis are shown in Fig. 3. We study two cases, one where we apodize the beam maps at 3° away from the beam centre (no far-sidelobes) and one where we extend our beam maps out to 30° (with far-sidelobes). In order to focus on effects from the interplay between the beam and the HWP, we calculate difference maps by subtracting a map generated using the same beam model but with an ideal HWP.

Fig. 10 shows the resultant B-mode residuals; the input sky is the d1 dust model, the amplitude of the curves should be compared to the solid d1 curve in Fig. 9. The effect of the more complex beam model is two-fold. The increased solid angle of the beam, i.e. the sidelobe, brings in E-mode dust signal from behind the Galactic mask. Given that we use a correction for the HWP rotation angle offset φ that has been calculated for unmasked pixels, the correction that we apply is not quite appropriate for this extra signal. The result is E → B leakage close to the edges of the mask. The second, more significant, effect is due to the cross-polar beam. This is especially obvious in the right-hand panel of Fig. 10 that was made with the beam model that extends out to 30° and includes a relatively large cross-polar component. The impact of the cross-polar beam can be understood as an ℓ-dependent polarization rotation that, given the shape of the cross-polar component in Fig. 3, is larger at lower ℓ. One might wonder why the resulting E → B leakage is not cancelled in our set-up when we subtract the ideal-HWP maps that were created using the same cross-polar beam. The reason is that the dominant HWP non-ideality couples directly to the cross-polar beam component: the two effects are not additive but multiplicative. This can be seen in the third line of equation (16): the dominant 4ν_α term of the data model contains a term proportional to |$\smash{\widetilde{U}^{(0)}_{\mathrm{b}}C_{P^* P}}$|⁠, i.e. the product of the cross-polar beam and the P*P component of the HWP Mueller matrix in equation (A36). Roughly speaking, the difference maps used to create the spectra in Fig. 10 are thus proportional to the cross-polar beam times |$(1 - C_{P^* P})$|⁠, the deviation from the ideal HWP Mueller element. The outcome is E → B leakage from the HWP non-ideality that is modulated by the cross-polar beam, resulting in the leaking of a redder version of the original E-mode dust spectrum to the B-mode spectrum, as can be observed in the right-hand panel of Fig. 10.

Figure 10.

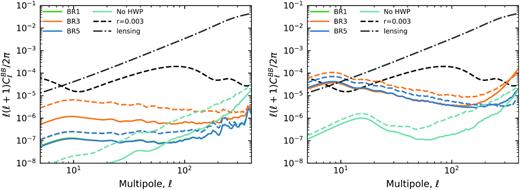
Left: Residual B-mode power spectra at 95 GHz (solid lines) and 150 GHz (dashed lines) derived from the band-averaged difference maps obtained by observing the pysm d1 dust model using all of the HWP configurations presented in Table 1 for scans with a PO beam truncated at 3°. Right: The same, but now observing the sky with a PO beam that extends to 30° and therefore includes a higher contribution from sidelobes (see Fig. 3). Note that the BR1 curves are almost completely hidden behind the BR5 curves.

Open in new tab Download slide

4.5 Polarization sensitivity

Given the results that we have discussed so far, there does not seem to be much difference between the BR1 and BR5 performance. Both outperform the BR3 HWP configuration in all the tests we presented and in Fig. 10 the BR1 and BR5 curves overlap almost perfectly. However, the calibration process that we described in Section 4.1 masks the fact that the BR5 configuration has much greater polarization modulation efficiency than the BR1 configuration. For example, in the case when we scan the CMB with a Gaussian beam (see Section 4.2, Fig. 7), we find that the calibration coefficients based on the E-mode power spectrum are 1.44, 1.10, 1.09, and 1.00 for the BR1, BR3, BR5, and no HWP configurations, respectively. In comparison, the calibration procedure that uses the temperature power spectrum gives 1.04, 1.05, 1.08, and 1.00, for the BR1, BR3, BR5, and no-HWP configurations, respectively. This shows that even though the BR5 configuration has lower optical efficiency because of the larger number of optical elements, and therefore a greater number of both loss and reflection mechanisms, its polarization modulation efficiency, and therefore sensitivity, is approximately 15 per cent higher than that of the BR1 configuration when integrated over the 95-GHz band.

5 CONCLUSIONS

We formulated an extension of the harmonic beam convolution algorithm originally described by Wandelt & Górski (2001) that adds the capability of simulating systematics due to non-ideal HWPs. The generalized algorithm allows for numerically efficient generation of simulated time-domain data that include spurious signal from non-ideal HWPs and asymmetric and/or non-trivially polarized beams. Such time-domain simulations are a crucial part of ‘end-to-end’ analysis pipeline validation efforts for CMB experiments. As multiple current and upcoming CMB instruments employ HWPs, it is timely to include the associated non-idealities in our simulations. The new simulator also allows us to investigate the importance of HWP-related systematics, some of which we have investigated in this paper. The extended algorithm is implemented as part of the publicly available beamconv code, which has also been used to derive the results in this paper.

For our investigation into HWP systematics, we included three different HWP configurations: a one-, three-, and five-layer model. With this selection, we simulated data for a representative CMB B-mode satellite experiment that employs a spinning HWP as polarization modulator. Particular attention was paid to the frequency dependence of the system. Our simulated experiment employs dichroic detectors and is thus especially sensitive to frequency-dependent HWP systematics given the wide frequency band of the detectors.

We find that the choice of HWP configuration significantly impacts the B-mode reconstruction fidelity. In particular, the three-layer HWP that we study comes with a significant frequency-dependent rotation angle offset, which, if not corrected for, acts as a polarization angle offset that leaks E-mode to B-mode polarization by an amount that would be problematic for an experiment aiming to constrain the tensor-to-scalar ratio r to a level of r < 0.003. Correcting for the rotation offset requires a correcting HWP angle offset φ that is dependent on the SED of the observed signal; we demonstrate that φ varies significantly between the CMB signal and the Galactic dust signal. This introduces a challenge for the standard CMB data analysis paradigm, which aims to compress an experiment’s TOD into unbiased sky maps before component separation and cosmological analysis is performed. During this map-making procedure one typically has no knowledge of the relative contribution of each sky component to the TOD. As a result, the map-making procedure can only be given a single φ angle, based on some combination of the optimal φ of each of the sky components, which will necessary lead to biased maps. Parametric algorithms for component separation, starting from a prior on the SEDs of the various sky components, could use φ as a parameter per sky component and forward propagate the polarization rotation. Such algorithms might attempt to divine the φ angles from the observed amount of EB signal in the non-component separated maps, as no significant EB power has until now been observed for either dust or the CMB (Planck Collaboration XI 2020b).

In light of HWP rotation angle offsets that vary between sky components, we investigate how well one would need to know the SED of polarized Galactic dust when modelling the angle offset of this component. We find that the current understanding of the dust SED will likely suffice for this procedure. We determine offset angles for a range of different dust models and find that the resulting angles vary by an insignificant amount. Spatial variations in the dust SED also seem to be of relatively minor importance.

Finally, we leverage the potential of the new code by simulating data using non-ideal HWPs and non-ideal instrumental beams. We point out that there exist an interplay between the cross-polar component of the beam and certain HWP non-idealities. We find significant B-mode residual for all three HWP configurations when this interplay is not modelled correctly. We can conclude that a thorough understanding of the instrumental beam will be necessary for future experiments attempting to model or correct for HWP non-idealities.

ACKNOWLEDGEMENTS

We are grateful to Aurelien Fraisse, Brandon Hensley, Jo Dunkley, Tomotake Matsumura, and Hans Kristian Eriksen for helpful comments. Computations have been performed at the Owl Cluster funded by the University of Oslo and the Research Council of Norway through grant 250672. MB acknowledges the financial support from the COSMOS network (www.cosmosnet.it) through the ASI (Italian Space Agency) Grants 2016-24-H.0 and 2016-24-H.1-2018. JEG acknowledges support from the Swedish National Space Agency (SNSA/Rymdstyrelsen) and the Swedish Research Council (Reg. no. 2019-03959). Some of the results in this paper have been derived using the healpix (Górski et al. 2005) package.

DATA AVAILABILITY STATEMENT

The data underlying this article will be shared on reasonable request to the corresponding author.

Footnotes

1

https://github.com/AdriJD/beamconv

2

https://github.com/tomessingerhileman/birefringent_transfer_matrix

3

http://healpix.sf.net

4

https://github.com/healpy/healpy

5

https://pysm3.readthedocs.io/en/latest/

6

The amplitude of incoming linear polarization |$\sqrt{Q^2 + U^2}$| will be changed based on the QQ, QU, UQ, UU submatrix. The change in amplitude will be bounded by the singular values of this matrix. Note that the amplitude change will generally be different per pixel and frequency. Furthermore, the input I and V signal will also alter the linear polarization amplitude due to leakage caused by the QI, UI, QV, and UV terms.

REFERENCES

Abitbol

M. H.

et al. ,

2020

,

preprint (arXiv:2011.02449)

Aboobaker

A. M.

et al. ,

2018

,

ApJS

,

239

,

7

10.3847/1538-4365/aae434

Crossref

Bao

C.

et al. ,

2012

,

ApJ

,

747

,

97

10.1088/0004-637X/747/2/97

Crossref

Bao

C.

,

Baccigalupi

C.

,

Gold

B.

,

Hanany

S.

,

Jaffe

A.

,

Stompor

R.

,

2016

,

ApJ

,

819

,

12

10.3847/0004-637X/819/1/12

Crossref

Bennett

C. L.

et al. ,

2013

,

ApJS

,

208

,

20

10.1088/0067-0049/208/2/20

Crossref

Bryan

S. A.

,

Montroy

T. E.

,

Ruhl

J. E.

,

2010a

,

Appl. Opt.

,

49

,

6313

10.1364/AO.49.006313

Crossref

Bryan

S. A.

et al. ,

2010b

, in

Holland

W. S.

,

Zmuidzinas

J.

, eds,

Proc. SPIE Conf. Ser. Vol. 7741, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy V

.

SPIE

,

Bellingham

, p.

77412B

Challinor

A.

,

Fosalba

P.

,

Mortlock

D.

,

Ashdown

M.

,

Wandelt

B.

,

Górski

K.

,

2000

,

Phys. Rev. D

,

62

,

123002

10.1103/PhysRevD.62.123002

Crossref

Challinor

A.

,

Chon

G.

,

Colombi

S.

,

Hivon

E.

,

Prunet

S.

,

Szapudi

I.

,

2011

,

Astrophysics Source Code Library

, record ascl:1109.005

CMB-S4 Collaboration

,

2017

,

preprint (arXiv:1706.02464)

Coughlin

K. P.

,

McMahon

J. J.

,

Crowley

K. T.

,

Koopman

B. J.

,

Miller

K. H.

,

Simon

S. M.

,

Wollack

E. J.

,

2018

,

J. Low Temp. Phys.

,

193

,

876

10.1007/s10909-018-1955-7

Crossref

Duivenvoorden

A. J.

,

Gudmundsson

J. E.

,

Rahlin

A. S.

,

2019

,

MNRAS

,

486

,

5448

10.1093/mnras/stz1143

Crossref

Essinger-Hileman

T.

,

2013

,

Appl. Opt.

,

52

,

212

10.1364/AO.52.000212

Crossref

Galitzki

N.

et al. ,

2016

, in

Holland

W. S.

,

Zmuidzinas

J.

, eds,

Proc. SPIE Conf. Ser. Vol. 9914, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VIII

.

SPIE

,

Bellingham

, p.

99140J

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Galitzki

N.

et al. ,

2018

, in

Zmuidzinas

J.

,

Gao

J.-R.

, eds,

Proc. SPIE Conf. Ser. Vol. 10708, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy IX

.

SPIE

,

Bellingham

, p.

1070804

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Galli

S.

et al. ,

2014

,

Phys. Rev. D

,

90

,

063504

10.1103/PhysRevD.90.063504

Crossref

Gil Pérez

J. J.

,

Ossikovski

R.

,

2016

,

Polarized Light and the Mueller Matrix Approach

.

CRC Press, Taylor & Francis Group

,

Boca Raton

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Goldberg

J. N.

,

Macfarlane

A. J.

,

Newman

E. T.

,

Rohrlich

F.

,

Sudarshan

E. C. G.

,

1967

,

J. Math. Phys.

,

8

,

2155

10.1063/1.1705135

Crossref

Gorski

K. M.

,

2008

,

Presentation at ‘Mitigating Systematic Errors in Space-Based CMB Polarization Measurements’

.

Annapolis, Maryland, USA

(accessed July 9, 2020)

OpenURL Placeholder Text

WorldCat

Górski

K. M.

,

Hivon

E.

,

Banday

A. J.

,

Wand elt

B. D.

,

Hansen

F. K.

,

Reinecke

M.

,

Bartelmann

M.

,

2005

,

ApJ

,

622

,

759

10.1086/427976

Crossref

Hecht

E.

,

2002

,

Optics

.

Addison-Wesley

,

Reading

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Hensley

B.

,

2015

,

PhD thesis

,

Princeton University

Hensley

B. S.

,

Bull

P.

,

2018

,

ApJ

,

853

,

127

10.3847/1538-4357/aaa489

Crossref

Hill

C. A.

et al. ,

2016

, in

Holland

W. S.

,

Zmuidzinas

J.

, eds,

Proc. SPIE Conf. Ser. Vol. 9914, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VIII

.

SPIE

,

Bellingham

, p.

99142U

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Hivon

E.

,

Mottet

S.

,

Ponthieu

N.

,

2017

,

A&A

,

598

,

A25

10.1051/0004-6361/201629626

Crossref

Hu

W.

,

Hedman

M. M.

,

Zaldarriaga

M.

,

2003

,

Phys. Rev. D.

,

67

,

043004

10.1103/PhysRevD.67.043004

Crossref

Johnson

B. R.

et al. ,

2007

,

ApJ

,

665

,

42

10.1086/518105

Crossref

Kamionkowski

M.

,

Kovetz

E. D.

,

2016

,

ARA&A

,

54

,

227

10.1146/annurev-astro-081915-023433

Crossref

Kamionkowski

M.

,

Kosowsky

A.

,

Stebbins

A.

,

1997

,

Phys. Rev. Lett.

,

78

,

2058

10.1103/PhysRevLett.78.2058

Crossref

Komatsu

K.

et al. ,

2018

, in

Zmuidzinas

J.

,

Gao

J.-R

, eds,

Proc. SPIE Conf. Ser. Vol. 10708, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy IX

.

SPIE

,

Bellingham

, p.

1070847

10.1117/12.2312431

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Crossref

Komatsu

K.

,

Ishino

H.

,

Katayama

N.

,

Matsumura

T.

,

Sakurai

Y.

,

Takaku

R.

,

2020

, in

Zmuidzinas

J.

,

Gao

J.-R.

, eds,

Proc. SPIE Conf. Ser. Vol. 11453, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy X

.

SPIE

,

Bellingham

, p.

114534B

Kusaka

A.

et al. ,

2014

,

Rev. Sci. Instrum.

,

85

,

039901

10.1063/1.4867655

Crossref

Ludwig

A. C.

,

1973

,

IEEE Trans. Antennas Propag.

,

21

,

116

10.1109/TAP.1973.1140406

Crossref

MacTavish

C. J.

et al. ,

2006

,

ApJ

,

647

,

799

10.1086/505558

Crossref

Matsumura

T.

,

2014

,

preprint (arXiv:1404.5795)

Meisner

A. M.

,

Finkbeiner

D. P.

,

2015

,

ApJ

,

798

,

88

10.1088/0004-637X/798/2/88

Crossref

Misawa

R.

et al. ,

2014

, in

Holland

W. S.

,

Zmuidzinas

J.

, eds,

Proc. SPIE Conf. Ser. Vol. 9153, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII

.

SPIE

,

Bellingham

, p.

91531H

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Moncelsi

L.

et al. ,

2014

,

MNRAS

,

437

,

2772

10.1093/mnras/stt2090

Crossref

Newman

E. T.

,

Penrose

R.

,

1966

,

J. Math. Phys.

,

7

,

863

10.1063/1.1931221

Crossref

Pancharatnam

S.

,

1955

,

Proc. Indian Acad. Sci. A

,

41

,

137

Pisano

G.

,

Savini

G.

,

Ade

P. A. R.

,

Haynes

V.

,

Gear

W. K.

,

2006

,

Appl. Opt.

,

45

,

6982

10.1364/AO.45.006982

Crossref

Pisano

G.

et al. ,

2014

, in

Holland

W. S.

,

Zmuidzinas

J.

, eds,

Proc. SPIE Conf. Ser. Vol. 9153, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII

.

SPIE

,

Bellingham

, p.

915317

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Planck Collaboration IX

,

2016a

,

A&A

,

594

,

A9

10.1051/0004-6361/201525936

Crossref

Planck Collaboration X

,

2016b

,

A&A

,

594

,

A10

10.1051/0004-6361/201525967

Crossref

Planck Collaboration VI

,

2020a

,

A&A

,

641

,

A6

10.1051/0004-6361/201833910

Crossref

Planck Collaboration XI

,

2020b

,

A&A

,

641

,

A11

10.1051/0004-6361/201832618

Crossref

Rahlin

A. S.

et al. ,

2014

, in

Holland

W. S.

,

Zmuidzinas

J.

, eds,

Proc. SPIE Conf. Ser. Vol. 915313, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII

. p.

915313

,

SPIE

,

Bellingham

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Salatino

M.

,

de Bernardis

P.

,

Masi

S.

,

2017

,

J. Infrared Millim. Terahertz Waves

,

38

,

215

10.1007/s10762-016-0320-7

Crossref

Salatino

M.

et al. ,

2018

, in

Zmuidzinas

J.

,

Gao

J.-R.

, eds,

Proc. SPIE Conf. Ser. Vol. 10708, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy IX

.

SPIE

,

Bellingham

, p.

1070848

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Sugai

H.

et al. ,

2020

,

J. Low Temp. Phys.

,

199

,

1107

10.1007/s10909-019-02329-w

Crossref

Suzuki

A.

et al. ,

2014

,

J. Low Temp. Phys.

,

176

,

650

10.1007/s10909-013-1049-5

Crossref

Suzuki

A.

et al. ,

2018

,

J. Low Temp. Phys.

,

193

,

1048

10.1007/s10909-018-1947-7

Crossref

The Polarbear Collaboration

,

2010

,

preprint (arXiv:1011.0763)

Thorne

B.

,

Dunkley

J.

,

Alonso

D.

,

Næss

S.

,

2017

,

MNRAS

,

469

,

2821

10.1093/mnras/stx949

Crossref

Title

A. M.

,

1975

,

Appl. Opt.

,

14

,

229

10.1364/AO.14.000229

Crossref

Vergès

C.

,

Errard

J.

,

Stompor

R.

,

2020

,

preprint (arXiv:2009.07814)

Wallis

C. G. R.

,

Brown

M. L.

,

Battye

R. A.

,

Delabrouille

J.

,

2017

,

MNRAS

,

466

,

425

10.1093/mnras/stw2577

Crossref

Wandelt

B. D.

,

Górski

K. M.

,

2001

,

Phys. Rev. D

,

63

,

123002

10.1103/PhysRevD.63.123002

Crossref

Zaldarriaga

M.

,

Seljak

U.

,

1997

,

Phys. Rev. D

,

55

,

1830

10.1103/PhysRevD.55.1830

Crossref

APPENDIX A: EXPANDING ON THE MATHEMATICAL FRAMEWORK

The aim of this appendix is to give a more exhaustive explanation of the mathematical framework used in Section 2. In particular, we will derive the harmonic-domain version of the data model of equation (11) and derive the harmonic coefficients in equations (15)–(17).

We express the data model in terms of the Stokes parameters of the instrument and the sky by inserting equation (5) in equation (4):

$$\begin{eqnarray*} d_t &=& \int \mathrm{d}\nu \, F(\nu) \int \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \Big ( I \widetilde{I}^{\, (t)}_{\mathrm{i}} + Q \widetilde{Q}^{\, (t)}_{\mathrm{i}} \nonumber \\ && +\, U \widetilde{U}^{\, (t)}_{\mathrm{i}} + V\widetilde{V}^{\, (t)}_{\mathrm{i}} \Big) (\hat{\boldsymbol {n}}, \nu) . \end{eqnarray*}$$

(A1)

Note that we omit the noise term for brevity. The instrumental Stokes parameters in the above equation are defined in a basis fixed to the sky and thus change continuously as the telescope scans over the sky. The transformation between sky and instrument coordinate frame is given by equation (9). In this derivation, we will, however, first express the data model in the harmonic domain before performing the transformation.

By working in the harmonic domain we can make use of the fact that a generic set of SWSH coefficients |$\smash{f^{(0)}_{\ell m}}$| defined with respect to the coordinate basis fixed to the instrument transform as follows:

$$\begin{eqnarray*} f^{(0)}_{\ell m} \mapsto f^{(t)}_{\ell m} = \sqrt{\frac{4 \pi }{2 \ell + 1}} \sum _{s=-\ell }^{\ell } f^{(0)}_{\ell s} \, {}_{s} Y_{\ell -m}(\theta _t, \phi _t) \mathrm{e}^{-\mathrm{i} s \psi _t} \, , \end{eqnarray*}$$

(A2)

when we instead define the coefficients with respect to the coordinate frame fixed relative to the sky. Here, ψ_i, θ_i, and ϕ_i are the three Euler angles that describe |$\boldsymbol{\sf R}_t$|⁠, the rotation between the two frames, and _sY_ℓm is a spin-s spherical harmonic (Newman & Penrose 1966; Goldberg et al. 1967).

To make use of equation (A2) it is necessary to know the SWSH coefficients for each of the different Stokes parameters in equation (A1). Using the transformation rule for the density matrix in equation (9), we may illustrate why |$\smash{\widetilde{I}^{\, (t)}_{\mathrm{i}}}$|⁠, and |$\smash{\widetilde{V}^{\, (t)}_{\mathrm{i}}}$| should be expanded into regular (spin-0) spherical harmonics and why

$$\begin{eqnarray*} \widetilde{P}^{\, (t)}_{\mathrm{i}} = \widetilde{Q}^{\, (t)}_{\mathrm{i}} + \mathrm{i} \widetilde{U}^{\, (t)}_{\mathrm{i}} \, , \end{eqnarray*}$$

(A3)

ought to be expanded in spin-2 spherical harmonics. We note that the |$\boldsymbol {\Lambda }$| matrices in equation (9) generally depend on the ψ_t, θ_t, and ϕ_t angles that describe |$\boldsymbol{\sf R}_t$| but that in the case where |$\boldsymbol{\sf R}_t$| describes a right-handed rotation around |$\hat{\boldsymbol {n}}$| by an angle ψ_t the matrices are simply given by

$$\begin{eqnarray*} \Lambda _{i}^{\phantom{a}j} \left(\boldsymbol{\sf R}_{\hat{\boldsymbol {n}}}(\psi _t)\right) = {\begin{pmatrix}\cos \psi _t & \quad \sin \psi _t \\ -\sin \psi _t & \quad \cos \psi _t \end{pmatrix}} . \end{eqnarray*}$$

(A4)

It is straightforward to check that when this specific rotation is applied to |$\smash{\boldsymbol{\sf W}_{\mathrm{instr}}^{(t)} }$|⁠, the |$\smash{\widetilde{I}^{\, (t)}_{\mathrm{i}}}$| and |$\smash{\widetilde{V}^{\, (t)}_{\mathrm{i}}}$| elements remain invariant, while the elements of the symmetric trace-free part, |$\smash{\widetilde{Q}^{\, (t)}_{\mathrm{i}}}$| and |$\smash{\widetilde{U}^{\, (t)}_{\mathrm{i}}}$|⁠, transform as a spin-2 field:

$$\begin{eqnarray*} \big (\widetilde{Q}^{\, (t)}_{\mathrm{i}} \pm \mathrm{i} \widetilde{U}^{\, (t)}_{\mathrm{i}}\big) (\hat{\boldsymbol {n}}) \mapsto \mathrm{e}^{\mp 2 \mathrm{i} \psi _t} \big (\widetilde{Q}^{\, (t)}_{\mathrm{i}} \pm \mathrm{i} \widetilde{U}^{\, (t)}_{\mathrm{i}}\big)(\hat{\boldsymbol {n}}) \, . \end{eqnarray*}$$

(A5)

We now expand the instrumental Stokes parameters into the appropriate spin-weighted spherical harmonics:

$$\begin{eqnarray*} \widetilde{I}^{\, (t)}_{\mathrm{i}}\!(\hat{\boldsymbol {n}}, \nu , \alpha _t) = \sum _{\ell =0}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } b^{\widetilde{I}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\nu , \alpha _t) Y_{\ell m}(\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(A6)

$$\begin{eqnarray*} \widetilde{P}^{\, (t)}_{\mathrm{i}}\, (\hat{\boldsymbol {n}}, \nu , \alpha _t) = \sum _{\ell =2}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } {}_{2}b^{\widetilde{P}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\nu , \alpha _t) {}_{2}Y_{\ell m}(\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(A7)

$$\begin{eqnarray*} \widetilde{V}^{\, (t)}_{\mathrm{i}}\, (\hat{\boldsymbol {n}}, \nu , \alpha _t) = \sum _{\ell =0}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } b^{\widetilde{V}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\nu , \alpha _t) Y_{\ell m}(\hat{\boldsymbol {n}}) . \end{eqnarray*}$$

(A8)

The Stokes parameters of the sky are expanded in a similar manner:

$$\begin{eqnarray*} I(\hat{\boldsymbol {n}}, \nu) = \sum _{\ell =0}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } a^{I}_{\ell m}(\nu) Y_{\ell m}(\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(A9)

$$\begin{eqnarray*} P(\hat{\boldsymbol {n}}, \nu) = \sum _{\ell =2}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } {}_{2}a^{P}_{\ell m}(\nu) {}_{2}Y_{\ell m}(\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(A10)

$$\begin{eqnarray*} V(\hat{\boldsymbol {n}}, \nu) = \sum _{\ell =0}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } a^{V}_{\ell m}(\nu) Y_{\ell m}(\hat{\boldsymbol {n}}) , \end{eqnarray*}$$

(A11)

where we have used the following definition:

$$\begin{eqnarray*} P = Q + \mathrm{i} U . \end{eqnarray*}$$

(A12)

We insert equations (A6)–(A11) into equation (A1) to produce the following version of the data model:

$$\begin{eqnarray*} d_t &=& \int \mathrm{d}\nu F(\nu) \sum _{\ell =0}^{\ell _{\mathrm{max}}} \sum _{m=-\ell }^{\ell } \Big \lbrace \big [b^{\widetilde{I}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\nu , \alpha _t)\big ]^* \, a^{I}_{\ell m}(\nu) \nonumber \\ && +\, \mathrm{Re}\Big (\! \big [{}_{2}b^{\widetilde{P}^{\, (t)}_{\mathrm{i}}}_{\ell m}\!\!(\nu , \alpha _t)\big ]^* {}_{2}a^{P}_{\ell m} (\nu) \Big) \nonumber \\ && +\, \big [b^{\widetilde{V}^{\, (t)}_{\mathrm{i}}}_{\ell m}\!\!(\nu , \alpha _t)\big ]^* a^{V}_{\ell m}(\nu)\Big \rbrace . \end{eqnarray*}$$

(A13)

To obtain this expression, we have made use of the orthogonality of the SWSH:

$$\begin{eqnarray*} \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) {}_sY_{\ell m}(\hat{\boldsymbol {n}}) {}_sY^*_{\ell ^{\prime } m^{\prime }}(\hat{\boldsymbol {n}}) = \delta _{\ell , \ell ^{\prime }} \delta _{m, m^{\prime }} \, . \end{eqnarray*}$$

(A14)

Note that the |$\smash{b^{\widetilde{I}^{(t)}_{\mathrm{i}}}_{\ell m}}$|⁠, |$\smash{{}_{2}b^{\widetilde{P}^{(t)}_{\mathrm{i}}}_{\ell m}}$|⁠, and |$\smash{b^{\widetilde{V}^{(t)}_{\mathrm{i}}}_{\ell m}}$| coefficients in equation (A13) are still defined on the basis fixed to the sky, so they are time dependent (they change as the telescope scans over the sky). We may now use equation (A2) to relate these time-varying coefficients to the |$\smash{b^{\widetilde{I}}_{\ell s}}$|⁠, |$\smash{{}_{\pm 2}b^{\widetilde{P}}_{\ell s}}$|⁠, and |$\smash{b^{\widetilde{V}}_{\ell s}}$| coefficients in equation (11) that are defined with respect to the coordinate frame fixed to the instrument. Under the rotation |$\boldsymbol{\sf R}_t$| the following relationships hold:

$$\begin{eqnarray*} b^{\widetilde{I}^{\, (0)}_{\mathrm{i}}}_{\ell m}(\alpha _t) &\mapsto & b^{\widetilde{I}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\alpha _t) \nonumber \\ &&= q_{\ell } \sum _{s=-\ell }^{\ell } b^{\widetilde{I}^{\, (0)}_{\mathrm{i}}}_{\ell s}(\alpha _t) \, {}_{s} Y_{\ell -m}(\theta _t, \phi _t) \mathrm{e}^{-\mathrm{i} s \psi _t}, \end{eqnarray*}$$

(A15)

$$\begin{eqnarray*} {}_{2}b^{\widetilde{P}^{\, (0)}_{\mathrm{i}}}_{\ell m}(\alpha _t) &\mapsto & {}_{2}b^{\widetilde{P}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\alpha _t) \nonumber \\ &&= q_{\ell } \sum _{s=-\ell }^{\ell } {}_{2}b^{\widetilde{P}^{\, (0)}_{\mathrm{i}}}_{\ell s}(\alpha _t) \, {}_{s} Y_{\ell -m}(\theta _t, \phi _t) \mathrm{e}^{-\mathrm{i} s \psi _t}, \end{eqnarray*}$$

(A16)

$$\begin{eqnarray*} b^{\widetilde{V}^{\, (0)}_{\mathrm{i}}}_{\ell m}(\alpha _t) &\mapsto & b^{\widetilde{V}^{\, (t)}_{\mathrm{i}}}_{\ell m}(\alpha _t) \nonumber\\ &&= q_{\ell } \sum _{s=-\ell }^{\ell } b^{\widetilde{V}^{\, (0)}_{\mathrm{i}}}_{\ell s}(\alpha _t) \, {}_{s} Y_{\ell -m}(\theta _t, \phi _t) \mathrm{e}^{-\mathrm{i} s \psi _t}, \end{eqnarray*}$$

(A17)

where we have defined the shorthand:

$$\begin{eqnarray*} q_{\ell } = \sqrt{\frac{4 \pi }{2 \ell + 1}} \, . \end{eqnarray*}$$

(A18)

Inserting the above into equation (A13) yields the final expression for the data model in equation (11).

To derive the harmonic coefficients in equations (15)–(17), we need to compute the instrumental Stokes parameters in the coordinate frame fixed to the instrument. We make use of equation (22) that expresses these parameters in terms of a Stokes vector representing the beam and the HWP Mueller matrix, rotated by an angle α_t:

$$\begin{eqnarray*} \boldsymbol {S}^{(0)\mathsf {T}}_{\mathrm{instr}}(\hat{\boldsymbol {n}}, \nu , \alpha _t) = \boldsymbol {S}^{(0) \mathsf {T}}_{\mathrm{beam}} (\hat{\boldsymbol {n}}, \nu) \, \boldsymbol{\sf M}_{\mathrm{HWP}} (\nu , \alpha _t) \, . \end{eqnarray*}$$

(A19)

The instrumental Stokes vector contains the same information as the instrumental density matrix |$\boldsymbol{\sf W}^{(0)}_{\mathrm{instr}}$| in equation (9). We may use equation (6) to transform the between density matrix and Stokes vector using the following Pauli matrices:

$$\begin{eqnarray*} (\sigma _0)_{ij} = {\begin{pmatrix}1 & \quad 0 \\ 0 & \quad \sin ^2\theta \end{pmatrix}} , \end{eqnarray*}$$

(A20)

$$\begin{eqnarray*} (\sigma _3)_{ij} = {\begin{pmatrix}1 & \quad 0 \\ 0 & \quad -\sin ^2\theta \end{pmatrix}} , \end{eqnarray*}$$

(A21)

$$\begin{eqnarray*} (\sigma _1)_{ij} = {\begin{pmatrix}0 & \quad \sin \theta \\ \sin \theta & \quad 0 \end{pmatrix}} , \end{eqnarray*}$$

(A22)

$$\begin{eqnarray*} (\sigma _2)_{ij} = {\begin{pmatrix}0 & \quad -\mathrm{i}\sin \theta \\ \mathrm{i}\sin \theta & \quad 0 \end{pmatrix}} . \end{eqnarray*}$$

(A23)

The additional factors of sin θ compared to the standard Pauli matrices are a consequence of the metric of the assumed spherical coordinates: g_ij = diag(1, sin ²θ).

We start by rewriting equation (A19) as follows:

$$\begin{eqnarray*} \boldsymbol {S}^{(0) \mathsf {T}}_{\mathrm{instr}}(\hat{\boldsymbol {n}}, \nu , \alpha _t) \boldsymbol{\sf T}^{\dagger } = \boldsymbol {S}^{(0)\mathsf {T}}_{\mathrm{beam}} (\hat{\boldsymbol {n}}, \nu) \boldsymbol{\sf T}^{\dagger } \boldsymbol{\sf T} \boldsymbol{\sf M}_{\mathrm{HWP}} (\nu , \alpha _t)\boldsymbol{\sf T}^{\dagger } \, , \end{eqnarray*}$$

(A24)

where we have introduced the following complex transformation matrix:

$$\begin{eqnarray*} \boldsymbol{\sf T} = {\begin{pmatrix}1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad \frac{1}{\sqrt{2}} & \quad \frac{\mathrm{i}}{\sqrt{2}} & \quad 0 \\ 0 & \quad \frac{1}{\sqrt{2}} & \quad \frac{-\mathrm{i}}{\sqrt{2}} & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{pmatrix}} \, , \end{eqnarray*}$$

(A25)

that should be understood as transforming the real Stokes parameter basis to a complex basis spanned by I, |$(Q + \mathrm{i}U)/\sqrt{2}$|⁠, |$(Q - \mathrm{i}U)/\sqrt{2}$|⁠, and V. Note that |$\boldsymbol{\sf T}$| is unitary:

$$\begin{eqnarray*} \boldsymbol{\sf T}^{\dagger } \boldsymbol{\sf T} = \boldsymbol{\sf T} \boldsymbol{\sf T}^{\dagger } = \boldsymbol{\sf 1} \, . \end{eqnarray*}$$

(A26)

Next, we factor the rotated HWP Mueller matrix into the unrotated matrix and two Mueller rotation matrices:

$$\begin{eqnarray*} \boldsymbol{\sf M}_{\mathrm{HWP}}(\alpha) = \boldsymbol{\sf M}_{\alpha }^{\mathsf {T}} \boldsymbol{\sf M}_{\mathrm{HWP}} \boldsymbol{\sf M}_{\alpha } \, , \end{eqnarray*}$$

(A27)

with:

$$\begin{eqnarray*} \boldsymbol{\sf M}_{\alpha } = {\begin{pmatrix}1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad \cos 2\alpha & \quad \sin 2 \alpha & \quad 0 \\ 0 & \quad -\sin 2 \alpha & \quad \cos 2 \alpha & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{pmatrix}} \, . \end{eqnarray*}$$

(A28)

Note that the |$\boldsymbol{\sf T}$| matrix diagonalizes the rotation matrix:

$$\begin{eqnarray*} \boldsymbol{\sf T} \boldsymbol{\sf M}_{\alpha } \boldsymbol{\sf T}^{\dagger } = {\begin{pmatrix}1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad \mathrm{e}^{-2\mathrm{i}\alpha } & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad \mathrm{e}^{2\mathrm{i}\alpha } & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \end{pmatrix}} \, . \end{eqnarray*}$$

(A29)

Putting everything together yields:

$$\begin{eqnarray*} &&\boldsymbol {S}^{(0) \mathsf {T}}_{\mathrm{instr}}(\hat{\boldsymbol {n}}, \nu , \alpha _t) \boldsymbol{\sf T}^{\dagger } \nonumber \\ && \quad \quad = \boldsymbol {S}^{(0) \mathsf {T}}_{\mathrm{beam}}(\hat{\boldsymbol {n}}, \nu) \boldsymbol{\sf T}^{\dagger } \boldsymbol{\sf T} \boldsymbol{\sf M}_{\alpha }^{\mathsf {T}} \boldsymbol{\sf T}^{\dagger } \boldsymbol{\sf T} \boldsymbol{\sf M}_{\mathrm{HWP}}(\nu) \boldsymbol{\sf T}^{\dagger } \boldsymbol{\sf T} \boldsymbol{\sf M}_{\alpha } \boldsymbol{\sf T}^{\dagger }. \end{eqnarray*}$$

(A30)

Evaluating this expression provides us with the instrumental Stokes parameters in terms of the beam Stokes parameters and the HWP:

$$\begin{eqnarray*} \widetilde{I}^{\, (0)}_{\mathrm{i}}(\hat{\boldsymbol {n}}, \alpha _t, \nu) &=& \widetilde{I}^{\, (0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{IV}(\nu) + \widetilde{V}^{(0)}_{\mathrm{b}} \! (\hat{\boldsymbol {n}}, \nu) C_{VV}(\nu) \nonumber\\ &&+\, \sqrt{2} \mathrm{Re} \Big (\widetilde{P}^{\, (0)}_{\mathrm{b}} \! (\hat{\boldsymbol {n}}, \nu) C_{P^* V}(\nu)\mathrm{e}^{-2\mathrm{i}\alpha } \Big), \end{eqnarray*}$$

(A31)

$$\begin{eqnarray*} \widetilde{P}^{(0)}_{\mathrm{i}} (\hat{\boldsymbol {n}}, \alpha , \nu) &=& \widetilde{I}^{\, (0)}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{IP}(\nu) \sqrt{2} \, \mathrm{e}^{-2\mathrm{i}\alpha } \nonumber \\ &&+\, \widetilde{V}^{(0)}_{\mathrm{b}} \!(\hat{\boldsymbol {n}}, \nu) C_{VP}(\nu) \sqrt{2} \mathrm{e}^{-2\mathrm{i}\alpha } \nonumber\\ &&+\, \widetilde{P}^{(0)}_{\mathrm{b}} \!(\hat{\boldsymbol {n}}, \nu) C_{P^* P} (\nu) \mathrm{e}^{-4\mathrm{i}\alpha } \nonumber\\ && +\, \widetilde{P}^{(0)*}_{\mathrm{b}} (\hat{\boldsymbol {n}}, \nu) C_{P P}(\nu), \end{eqnarray*}$$

(A32)

$$\begin{eqnarray*} \widetilde{V}^{(0)}_{\mathrm{i}} (\hat{\boldsymbol {n}}, \alpha , \nu) &=& \widetilde{I}^{\, (0)}_{\mathrm{b}} \!(\hat{\boldsymbol {n}}, \nu) C_{IV}(\nu) + \widetilde{V}^{(0)}_{\mathrm{b}} \! (\hat{\boldsymbol {n}}, \nu) C_{VV}(\nu) \nonumber\\ &&+\, \sqrt{2} \mathrm{Re} \Big (\widetilde{P}^{\, (0)}_{\mathrm{b}} \! (\hat{\boldsymbol {n}}, \nu) C_{P^* V}(\nu)\mathrm{e}^{-2\mathrm{i}\alpha } \Big), \end{eqnarray*}$$

(A33)

where

$$\begin{eqnarray*} \widetilde{P}^{\, (0)}_{\mathrm{i}} = \widetilde{Q}^{\, (0)}_{\mathrm{i}} + \mathrm{i} \widetilde{U}^{\, (0)}_{\mathrm{i}} \, , \end{eqnarray*}$$

(A34)

and where we have used the following shorthand for the unrotated HWP Mueller matrix expressed in the complex basis:

$$\begin{eqnarray*} \boldsymbol{\sf C} = \boldsymbol{\sf T} \boldsymbol{\sf M}_{\mathrm{HWP}} \boldsymbol{\sf T}^{\dagger } \, , \end{eqnarray*}$$

(A35)

that, in terms of the original HWP Mueller matrix elements, is given by

$$\begin{eqnarray*} \boldsymbol{\sf C} &= &\left({\begin{array}{*{10}c}M_{II} & \frac{M_{IQ}- \mathrm{i} M_{IU}}{\sqrt{2}} \nonumber\\ \frac{M_{QI}+\mathrm{i}M_{UI}}{\sqrt{2}} & \frac{M_{QQ} + M_{UU} - \mathrm{i} (M_{QU} - M_{UQ})}{2} \nonumber\\ \frac{M_{QI}-\mathrm{i}M_{UI}}{\sqrt{2}} & \frac{M_{QQ} - M_{UU} - \mathrm{i} (M_{QU} + M_{UQ})}{2} \nonumber\\ M_{VI} & \frac{M_{VQ}-\mathrm{i}M_{VU}}{\sqrt{2}} \end{array}} \right. \nonumber\\ &&\quad \left. \times \, {\begin{array}{*{10}c}\frac{M_{IQ}+\mathrm{i}M_{IU}}{\sqrt{2}} & M_{IV}\\ \frac{M_{QQ} - M_{UU} + \mathrm{i} (M_{QU} + M_{UQ})}{2} & \frac{M_{QV}+\mathrm{i}M_{UV}}{\sqrt{2}}\\ \frac{M_{QQ} + M_{UU} + \mathrm{i} (M_{QU} - M_{UQ})}{2} & \frac{M_{QV}-\mathrm{i}M_{UV}}{\sqrt{2}}\\ \frac{(M_{VQ}+\mathrm{i}M_{VU})}{\sqrt{2}} & M_{VV} \end{array}} \right). \end{eqnarray*}$$

(A36)

Finally, we plug the instrumental Stokes parameters in equations (A31)–(A33) into the transformations below:

$$\begin{eqnarray*} \begin{split} b^{\widetilde{I}^{\, (0)}_{\mathrm{i}}}_{\ell m}(\nu) &= \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \widetilde{I}^{\, (0)}_{\mathrm{i}}(\hat{\boldsymbol {n}}, \alpha _t, \nu) Y_{\ell m}^* (\hat{\boldsymbol {n}}), \end{split} \end{eqnarray*}$$

(A37)

$$\begin{eqnarray*} \begin{split} {}_{2}b^{\widetilde{P}^{\, (0)}_{\mathrm{i}}}_{\ell m}(\nu) &= \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \widetilde{P}^{\, (0)}_{\mathrm{i}}(\hat{\boldsymbol {n}}, \alpha _t, \nu) {}_{2}Y_{\ell m}^* (\hat{\boldsymbol {n}}) \, , \end{split} \end{eqnarray*}$$

(A38)

$$\begin{eqnarray*} \begin{split} b^{\widetilde{V}^{\, (0)}_{\mathrm{i}}}_{\ell m}(\nu) &= \int _{S^2} \mathrm{d}\Omega (\hat{\boldsymbol {n}}) \widetilde{V}^{\, (0)}_{\mathrm{i}}(\hat{\boldsymbol {n}}, \alpha _t, \nu) Y_{\ell m}^* \, , \end{split} \end{eqnarray*}$$

(A39)

to obtain the harmonic coefficients given in equations (15)–(17).

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
February 2021	4
March 2021	15
April 2021	9
May 2021	3
June 2021	12
July 2021	7
August 2021	4
September 2021	4
October 2021	5
November 2021	7
December 2021	3
January 2022	12
February 2022	12
March 2022	9
April 2022	4
May 2022	10
June 2022	5
July 2022	10
September 2022	1
October 2022	6
November 2022	1
December 2022	8
January 2023	3
February 2023	2
March 2023	8
May 2023	3
June 2023	12
July 2023	5
September 2023	15
October 2023	2
November 2023	1
December 2023	4
January 2024	29
February 2024	17
March 2024	13
April 2024	10
May 2024	26
June 2024	16
July 2024	25
August 2024	22
September 2024	7
October 2024	17
November 2024	24
December 2024	6
January 2025	27
February 2025	2
March 2025	15
April 2025	3
May 2025	12

Article Contents

Probing frequency-dependent half-wave plate systematics for CMB experiments with full-sky beam convolution simulations

ABSTRACT

1 INTRODUCTION

2 MATHEMATICAL FRAMEWORK

2.1 Half-wave plate Mueller matrix

2.2 Data model

3 SIMULATION SET-UP

3.1 Simulated scanning

3.2 Input maps

3.3 Selection of HWPs

3.4 Determining the AHWP induced rotation offset

4 ANALYSIS RESULTS

4.1 Calibration

4.2 Scanning with an ideal Gaussian beam

4.3 Foreground dependence

4.4 Scanning with a non-ideal beam

4.5 Polarization sensitivity

5 CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY STATEMENT

Footnotes

REFERENCES

APPENDIX A: EXPANDING ON THE MATHEMATICAL FRAMEWORK

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Probing frequency-dependent half-wave plate systematics for CMB experiments with full-sky beam convolution simulations Free

ABSTRACT

1 INTRODUCTION

2 MATHEMATICAL FRAMEWORK

2.1 Half-wave plate Mueller matrix

2.2 Data model

3 SIMULATION SET-UP

3.1 Simulated scanning

3.2 Input maps

3.3 Selection of HWPs

3.4 Determining the AHWP induced rotation offset

4 ANALYSIS RESULTS

4.1 Calibration

4.2 Scanning with an ideal Gaussian beam

4.3 Foreground dependence

4.4 Scanning with a non-ideal beam

4.5 Polarization sensitivity

5 CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY STATEMENT

Footnotes

REFERENCES

APPENDIX A: EXPANDING ON THE MATHEMATICAL FRAMEWORK

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Probing frequency-dependent half-wave plate systematics for CMB experiments with full-sky beam convolution simulations