On the formation and stability of fermionic dark matter haloes in a cosmological framework Free

ABSTRACT

1 INTRODUCTION

The thermodynamics of self-gravitating systems is a vast subject of research with deep implications in astrophysics. It includes the long-standing problems of relaxation in collisionless/collisional stellar systems, to the issue of virialization of dark matter (DM) haloes and structure formation. Depending on the initial conditions of the system at virialization (such as total mass, size, degree of concentration, etc.), they may become thermodynamically unstable, experience a gravothermal catastrophe, suffer phase transitions, or even undergo core collapse towards a massive black hole (BH).

The first dynamical and thermodynamical studies were developed for classical point masses within Newtonian gravity, and applied to the case of stars in globular clusters or galaxies in Antonov (1962), Michie (1963), King (1966), Lynden-Bell (1967), Lynden-Bell & Wood (1968), Katz (1980, 2003), Padmanabhan (1990), and Chavanis (2006).¹ Contemporaneously to such earliest works, the attention was directed to self-gravitating quantum particles in Ruffini & Bonazzola (1969), mainly focusing on the mathematical aspects of the solutions at hydrostatic equilibrium. The role of the quantum pressure at the centre of the configurations was evidenced within a fully general relativistic (GR) treatment, distinguishing between the bosonic and fermionic nature of the particles. In the case of fermions, such self-gravitating models (either at zero or at the more realistic finite temperature) were further investigated by different authors, with applications to the morphology of DM haloes at equilibrium and/or to the mass of the DM particles (Zel'dovich et al. 1980; Doroshkevich et al. 1980; Baldeschi, Gelmini & Ruffini 1983; Ruffini & Stella 1983; Gao, Merafina & Ruffini 1990; Ingrosso et al. 1992; Bilic et al. 2002; Bilic, Tupper & Viollier 2003; Argüelles et al. 2014, 2018, 2019a, b; de Vega, Salucci & Sanchez 2014; Chavanis, Lemou & Méhats 2015a, b; Ruffini, Argüelles & Rueda 2015; Gómez et al. 2016; Randall, Scholtz & Unwin 2017; Becerra-Vergara et al. 2020), though lacking a thermodynamic stability analysis (with the exception of Chavanis et al. 2015a, b).

In the case of galactic structures, a central question in the field is precisely how a self-gravitating system of collisionless particles (either stars or DM particles) reaches the steady state we observe. The complex evolution of the coarse-grained phase-space distribution of such a system is driven by the mean-field Vlasov–Poisson (VP) equation. It involves rapid fluctuations in the overall time-varying gravitational field, able to redistribute the energy between the particles in few dynamical times, even faster than collisional relaxation time-scales (Binney & Tremaine 2008). Such a process is known as violent relaxation, and is the main mechanism able to lead the averaged phase-space distribution function (DF) towards a quasi-stationary state (qSS).

A typical stationary coarse-grained DF that is a possible solution of the mean-field VP equation was originally predicted to be of a Fermi–Dirac type in the seminal work of Lynden-Bell (1967), from a statistical description. Such an approach for violent relaxation was developed for distinguishable classical particles, and three decades later extended to indistinguishable particles such as massive neutrinos in Kull, Treumann & Boehringer (1996). Those results were later formalized and extended out of equilibrium (e.g. allowing for the escape of particle effects) within thermodynamical and kinetic theory approaches in Chavanis (1998, 2004), respectively. Such a generalization leads to a tidally truncated Fermi–Dirac DF at equilibrium, naturally implying finite-sized systems as the ones applied here to model fermionic haloes.

However, as recognized by Lynden-Bell himself (Lynden-Bell 1967), the violent relaxation mechanism is likely to be incomplete towards the outer and low-density halo regions. This discrepancy was traditionally associated with the short dynamical time-scales involved, which together with the long-range nature of the interactions imply that the entire system does not have enough time to explore the full phase space to reach a most likely final state. Contrary to this expectation, in Levin, Pakter & Rizzato (2008) it was shown that when the initial phase-space distribution (prior to relaxation) satisfies the virial theorem, then the resulting qSS is close to ergodic and so the Lynden-Bell statistics works well to reproduce the numerical simulations.² However, if the virial condition is violated, parametric resonances arise and the mean-field gravitational potential oscillations lead to ergodicity breaking with partial mass evaporation towards the halo (Levin et al. 2008). This more general case implies a qSS with a dense core–diluted halo behaviour, as arising within numerical simulations, which according to Levin et al. (2014) cannot be well explained in the traditional Lynden-Bell theory. However, more general core–halo distributions can arise as well within generalized Lynden-Bell statistics (as e.g. successfully applied here for fermionic haloes with equation 1), which still remain to be contrasted against numerical simulations of violent relaxation.

On general grounds, as first recognized in the original work of Lynden-Bell (1967) for classical particles, there is an effective ‘exclusion principle’ acting in such relaxation processes due to the incompressibility of the VP equation in phase space; that is, the coarse-grained DF cannot exceed a maximum initial value after some evolution. This may be considered as a classical counterpart of the Pauli exclusion principle for self-gravitating fermions, both leading to degeneracy effects in the matter distribution of the collisionless systems. This degeneracy, either of quantum or of classical origin, when large enough implies a richer dense core–diluted halo morphology for the qSS (regardless of any possible incompleteness of violent relaxation that would only affect the outer halo). Explicit realizations of such a novel profile morphology were solved in Chavanis & Sommeria (1998) for stars, and in Gao et al. (1990), Bilic et al. (2002), Ruffini et al. (2015), Chavanis et al. (2015b), Argüelles et al. (2018, 2019a), and Becerra-Vergara et al. (2020) for fermions. Such distributions differentiate with respect to the traditional King profiles (typically applied to globular clusters), the latter being based on a Boltzmannian DF inherent to collisional systems (Binney & Tremaine 2008).

The manifestation of such a core–halo profile in astrophysics is yet an open issue, though several key results have been reported from theoretical as well as phenomenological fronts. They include (i) the avoidance of the traditional gravothermal catastrophe, thanks to the arising of the central degeneracy (Chavanis & Sommeria 1998; Chavanis et al. 2015b), not present in Boltzmannian distributions; (ii) the possibility for the degenerate fermion core to mimic the massive BHs at the centre of galaxies, while the outer halo can explain the rotation curves (Ruffini et al. 2015; Argüelles et al. 2018, 2019a); and (iii) the fact that astrophysical core–halo DM profiles can be thermodynamically (and dynamically) stable, as well as long-lived as proven here. These issues can be addressed through a thermodynamic stability analysis for self-gravitating systems with a given particle number (see e.g. Chavanis et al. 2015b, for a recent study within Newtonian gravity). Indeed, it is the aim of this work to make, for the first time, such an analysis in full GR, and apply it to realistic DM haloes of fermionic nature at virialization within a realistic cosmological framework.

On the realm of fermionic self-gravitating systems, the bulk of the works in the field (besides the ones done by P. H. Chavanis) were developed assuming hydrostatic equilibrium, without analysing the thermodynamic stability of the solutions. Interestingly, stationary phase-space solutions of the VP equation [of the form f(ϵ) with f^′(ϵ) < 0 and ϵ the particles energy], such as (13) or (1) implemented here, are always VP dynamically stable (Binney & Tremaine 2008; Lemou, Méhats & Raphaël 2011). However, this stability analysis does not explain how such a collisionless self-gravitating system reaches the required steady state, nor whether they minimize the free energy (or maximize the coarse-grained entropy), or whether they are just transitional (unstable/unreachable) states.

Indeed, a proper answer to this problem requires the introduction of relaxation processes such as violent relaxation and Landau damping, where the qSS is reached upon a maximization (coarse-grained) entropy problem. Moreover, as it is explained in Chavanis et al. (2015b), the VP equation has an infinite number of conserved integrals (e.g. the so-called Casimir integrals), while the maximization entropy problem holds only for a given total mass and energy (two integrals). Therefore, VP dynamical stability does not necessarily imply thermodynamical stability (see, however, Chavanis 2019, and references therein for general conclusions in the relativistic case). Thus, some VP dynamically stable solutions in hydrostatic equilibrium are more likely to occur in nature than others.

A first thermodynamic study of self-gravitating systems of elementary fermions in a fully relativistic framework was given in Bilić & Viollier (1999), paying attention mainly to the occurrence of gravitational phase transitions between gaseous and semidegenerate (neutral) fermion stars. They worked in the canonical ensemble, and analysed only (i) systems with total number of fermions below the Oppenheimer–Volkoff value (i.e. N < N_OV) where no relativistic collapse to a BH is possible and (ii) very low spherical-box sizes R up to R ∼ 10¹R_OV not applicable to any astrophysical DM halo system.

Only recently, a more extensive fully relativistic, thermodynamic stability analysis for self-gravitating fermions was done in Alberti & Chavanis (2018), Roupas & Chavanis (2019), and Chavanis & Alberti (2019), complementing to the case N > N_OV (where core collapse towards a BH may arise). In the latter, such an analysis was done either in the microcanonical or in the canonical ensembles, enlarging to spherical-box sizes about an order of magnitude above the original work of Bilić & Viollier (1999), yet orders of magnitude below any realistic DM halo size. An analogous non-relativistic (e.g. Newtonian) thermodynamical study was done in Chavanis et al. (2015b) within the more realistic fermionic King model. There, much larger bounded system sizes were reached, with potential applicability to realistic DM haloes for particles masses of |$mc^2 \sim {1}\, {\rm keV}$| (results that are here compared against our relativistic approach in Section 3.4). However, the works cited above were mainly focused on the mathematical aspects and characterization of the solutions in full dimensionless units, and only applied to astrophysical objects in a qualitative fashion.

It is the purpose of this work to make a detailed thermodynamic stability analysis of a self-gravitating system of fermions in GR, at the moment of DM halo formation in a realistic cosmological set-up, and for particle masses of |$mc^2 \sim \mathcal {O}({10}\, {\rm keV})$|⁠. The novelty of this work with respect to other similar analysis recently given in the literature (Chavanis et al. 2015b; Alberti & Chavanis 2018; Roupas & Chavanis 2019) relies on the fact that it is the first time such a thermodynamical analysis of fermionic matter is developed in GR, for realistic DM halo configurations that are tidally truncated (i.e. by including the escape of particle effects) in a warm dark matter (WDM) cosmology. In particular, we emphasize on the possible different shapes of the DM profiles, and analyse their thermodynamical stability, from dwarf to larger halo sizes, making a direct link with the core–halo Ruffini–Argüelles–Rueda (RAR) profiles presented in Ruffini et al. (2015), Argüelles et al. (2018, 2019a), and Becerra-Vergara et al. (2020).

In the following, we summarize the content of this work. In Section 2, we write the hydrostatic and thermodynamic equilibrium equations of a self-gravitating system of massive fermions at finite temperature in GR. In Section 3, we develop for the first time a thermodynamic stability analysis for systems with a given particle number N at halo virialization (with initial conditions consistent with a Press–Schechter analysis within a WDM cosmology as given in Appendix  B), and for a particle mass of |$mc^2 \sim \mathcal {O}({10}\, {\rm keV})$|⁠. We first assume (a) spherical-box-confined configurations with size R and (b) tidally truncated systems. We work in the microcanonical ensemble, which is more appropriate for astrophysical applications as explained in Chavanis et al. (2015b). Details on the stability criterion used here, as well as the calculation of the lifetime of metastable states, are given in Appendix  A.

The main conclusion of Section 3 can be summarized as follows: For spherical-box-confined configurations, there are no thermodynamically stable core–halo solutions that are of astrophysical interest when applied to DM haloes, while the opposite is true for tidally truncated systems. This is the first time that a dense core–diluted halo solution, which is successfully applied to model realistic DM haloes (as in Argüelles et al. 2018, 2019a; Becerra-Vergara et al. 2020), is proven to be thermodynamically stable (i.e. entropy maxima) and extremely long-lived.

In Section 3.4 and Appendix  A, we compare our results with other similar works in the literature. In Section 4, we explain the mathematical and physical characteristics of the turning point (TP) instability, while further showing the existence of a gravitational core collapse for solutions with N > N_OV, and its implications for supermassive BH (SMBH) formation in the high-redshift Universe. In Section 5, we draw our conclusions.

2 SELF-GRAVITATING FERMIONS AT FINITE TEMPERATURE IN GR

Importantly, the quantum phase-space function equation (1) can be obtained from a maximum entropy production principle as first shown for fermions in Chavanis (1998). Indeed, there it is shown to be a stationary solution of a generalized Fokker–Planck equation for fermions including the physics of violent relaxation and evaporation, appropriate within the non-linear stages of structure formation. As explained in Section 1, these results were first conceptualized in the pioneer work of D. Lynden-Bell for collisionless stellar systems (Lynden-Bell 1967), and formalized and generalized much later for quantum (collisionless) particles (Kull et al. 1996; Chavanis 1998, 2004). Indeed, maximum entropy principles applied to DM halo formation in terms of self-gravitating systems are being recently reconsidered in the literature, as in the case of dwarf galaxies in Sánchez Almeida, Trujillo & Plastino (2020).

The above coupled system of ordinary (highly non-linear) differential equations (8)–(12) implies a boundary condition problem to be solved numerically. It was first solved in Argüelles et al. (2018) for regular conditions at the centre of the configuration [M(0) = 0, θ(0) = θ₀, β(0) = β₀, ν(0) = ν₀, W(0) = W₀], for a given DM particle mass m, to find solutions consistent with the DM halo observables of the Galaxy. For positive central degeneracy parameter θ₀ > 0, the DM profiles (fulfilling with fixed halo boundary conditions inferred from observables) develop a dense core–diluted halo morphology where the central core is sensitive to the particle mass (Ruffini et al. 2015; Argüelles et al. 2018). While the central core is governed by Fermi-degeneracy pressure, the outer halo holds against gravity by thermal pressure and resembles the King profile or Burkert profile (see Argüelles et al. 2018, 2019a, for details).

A model built upon the above considerations is usually called as the RAR model, in honour of the authors in Ruffini et al. (2015),³ and then extended in Argüelles et al. (2018) including for the escape of particles (or tidal effects). Importantly, such a DM halo model is the more general of its kind, given it does not work in the fully Fermi-degeneracy regime θ₀ ≫ 1 (as in Randall et al. 2017), nor in the diluted Fermi regime θ₀ ≪ −1 (as in de Vega et al. 2014). However, in the next sections, we will cover all regimes and check along the full set of equilibrium configurations that are thermodynamically stable or unstable, and analyse if they are of astrophysical interest regarding the DM halo phenomenology.

The main advantages of fermionic DM profiles with a core–halo morphology (e.g. as in Argüelles et al. 2018) over the diluted ones (e.g. Boltzmannian-like) can be summarized as follows:

• The arising of the fermion-degeneracy pressure developed through the centre of the DM halo is able to stop the gravitational core collapse to a singularity, thus preventing the gravothermal catastrophe typical of Boltzmannian phase-space DF. Such a result was first demonstrated in Chavanis & Sommeria (1998) in Newtonian gravity, and further shown here as well as in Alberti & Chavanis (2018) and Chavanis & Alberti (2020) in full GR.

• Thermodynamically metastable (i.e. local maxima of entropy) core–halo solutions of self-gravitating fermions are extremely long-lived, and shown to be of astrophysical relevance when applied to DM haloes as demonstrated in this work. Besides, they are more likely to arise in Nature than global entropy maximum (King-like) solutions (Chavanis 2005).

• Such a core–halo DM distribution is in good agreement with overall rotation curve data from dwarf to elliptical galaxies, while the dense core can be an alternative for the central massive BH scenario (Argüelles et al. 2019a), including the case of our own Galaxy (Argüelles et al. 2018; Becerra-Vergara et al. 2020) and for the same particle mass in the keV regime.

3 THERMODYNAMIC STABILITY ANALYSIS OF DM HALOES AT VIRIALIZATION

In the former section, we set the necessary equations to obtain a system of self-gravitating fermions in hydrostatic equilibrium, which can be successfully applied to model DM haloes as in the RAR model. However, such stability equations do not explain how these kinds of collisionless systems reach the steady state in a given cosmological set-up. Indeed, the relaxation of collisionless self-gravitating particles represents a rather complicated problem that involves complex processes such as violent relaxation and non-linear Landau damping (Binney & Tremaine 2008). As first shown in the seminal paper of Lynden-Bell (1967), it is possible to obtain a qSS resulting from a violent relaxation process, by solving a maximization (coarse-grained) entropy problem at fixed total energy and particle number. The concept of thermodynamical stability, at difference to dynamical stability, is thus understood in terms of such a maximization problem. Moreover, it can be shown that if an equilibrium state in GR is thermodynamically stable (i.e. coarse-grained entropy maxima) then it is always dynamically stable (Ipser 1980), while in general, the reciprocal is incorrect (see Chavanis 2019, for a detailed discussion in Newtonian gravity as well as in GR).

Historically, the main motivation to study the stability of dense clusters composed by self-gravitating objects was linked to the appealing idea that the formation of massive BHs at the centre of active galactic nuclei could be the result of the collapse of such clusters (Rees 1984). The bulk of the works in the field were aimed at the analysis of the relativistic instability (i.e. collapse) of dense stellar clusters following Maxwellian energy distributions with specific cut-offs in energy a la Zeldovich–Podurets (see e.g. Bisnovatyi-Kogan et al. 1998, and references therein). Such stability analysis was pursued by approximate methods such as the fractional binding energy criterion or the search for maxima in an M(ρ₀) curve, with ρ₀ the central density and M the total mass of the configuration.

In this work, we reconsider the problem of collapse of dense and relativistic clusters with application to massive BH formation, though the cluster is now a degenerate compact core made of neutral keV DM fermions, surrounded by a diluted halo composed of the very same particles. Such DM fermions follow a much richer energy DF such as the generalized Fermi–Dirac DF in equation (1), including for central degeneracy, generic cut-off energy, and (effective) temperature free parameters, which is well motivated since it arises from a maximum entropy production principle (see Section 2). We use a rigorous approach to analyse the thermodynamic (and dynamical) stability of the fermionic distributions as the one developed by Katz (1978) (see Appendix  A), which was not applied in Bisnovatyi-Kogan et al. (1998) nor in similar contemporary works. Such an analysis is properly compared and connected in Section 4 with the TP criterion in terms of the traditional M(ρ₀) curve. Even if the stability results presented here show some similitude with respect to the ones done in the past for Maxwellian DFs, they cannot be compared on an equal footing; that is, the more general quantum DFs used here imply a double-spiralling shape in the caloric curves as in Fig. 7, one of gravothermal catastrophic nature including for degeneracy effects (not present in the classical DF) and the other of relativistic nature.

As mentioned above, we will use throughout this work the Katz criterion (detailed in Appendix  A) to find the full set of thermodynamical-stable solutions along the series of (hydrostatic) equilibrium. This is a powerful and rigorous method that relies only on the derivatives of specific caloric curves (e.g. total energy versus 1/T_∞), without the need to explicitly calculate the (rather involving) second-order variations in entropy.⁴ Indeed, this is a commonly used method in the context of self-gravitating systems as can be seen in recent works (Chavanis et al. 2015a; Alberti & Chavanis 2018). In next subsections, we work on the microcanonical ensemble, applied for isolated systems so that its energy E is conserved. In this ensemble, the relevant thermodynamic potential to be extremized is the coarse-grained entropy S.⁵ This choice is justified, the microcanonical ensemble being the more appropriate for astrophysical applications as carefully explained in Chavanis et al. (2015b).

Self-gravitating solutions with a given particle number N and total energy E = c²M(R), which extremize the coarse-grained entropy, must be bounded in radius. Otherwise, as the total mass of the system has no upper bound, the maximization entropy problem is not well defined and the entropy will never reach a maximum (Binney & Tremaine 2008).

In this section, we formally perform two thermodynamic stability analysis, under two different choices of the fermionic phase-space DFs. In Section 3.1, we assume a DF given by equation (13). Under this choice, the solutions obtained from equations (8) to (12) have no spatial boundaries, implying DM density profiles scaling as ρ ∝ r⁻² at large distances (see Fig. 2 and e.g. Ruffini et al. 2015, for more details). Thus, as it is customary, we confine such a self-gravitating system within a spherical box of total radius R in order to avoid an entropy runaway.

In Section 3.2 instead, we assume a DF given by equation (1), corresponding to the more realistic tidally truncated self-gravitating system, naturally bounded in radius (R ≡ r_b) thanks to the particle-energy cut-off condition.

3.1 Box-confined DM haloes

1. |$\hat{N}=0.38, \hat{R}_{\rm vir}=1.4 \times 10^{7}$|

2. |$\hat{N}=3.67, \hat{R}_{\rm vir}=3.8 \times 10^{7}$|⁠.

Such values imply, in dimensionfull units, the following virial mass and radius: a typically small DM halo with |$M_{\rm vir} \equiv M(R_{\rm vir}) \approx 6.2 \times 10^{9}{\, \mathrm{M}_\odot}$| and |$R_{\rm vir} = {11.1}\, \mathrm{kpc}$| corresponding to the example (1) and an average-sized DM halo with |$M_{\rm vir} \equiv M(R_{\rm vir}) \approx 5.9 \times 10^{10}{\, \mathrm{M}_\odot}$| and |$R_{\rm vir} = {29.7}\, \mathrm{kpc}$| for (2); that is, each pair (R_vir, M_vir) is consistent with the values obtained from the Press–Schechter formalism as required (see Fig. B2).

The values for |$\hat{N}$| are chosen this way in order to have one case, i.e. item (1), with |$\hat{N}=0.38 \lt \hat{N}_{\rm OV}$|⁠, and the other, i.e. item (2), with |$\hat{N}=3.67 \gt \hat{N}_{\rm OV}$|⁠, |$\hat{N}_{\rm OV} \approx 0.4$| being the Oppenheimer–Volkoff critical particle number (Oppenheimer & Volkoff 1939). Such a critical value triggering core collapse can be written in a more familiar way in terms of the Planck mass m_p and the fermion mass m as |$N_{\rm OV}=0.398\, m_{\mathrm{ p}}^3/m^3$|⁠, corresponding to a critical mass |$M_{\rm OV}=0.384\, m_{\mathrm{ p}}^3/m^2$| that for |$mc^2={10}\, {\rm keV}$| reads |$M_{\rm OV}\approx 6 \times 10^{9}{\, \mathrm{M}_\odot}$|⁠. Thus, any equilibrium configuration of fermions at finite T_∞ with |$M \gtrsim 6 \times 10^{9}{\, \mathrm{M}_\odot}$| may undergo (under certain conditions) a core collapse towards an SMBH as explained in Section 4. The astrophysical and cosmological consequences of such a core collapse in terms of the typical DM halo examples considered here are further commented in Sections 4 and 5.

We next apply the Katz criterion (see Appendix  A for the details) to find all the thermodynamically stable branches of solutions along the microcanonical caloric curve |$1/\hat{T}_\infty$| versus |$\hat{E}$|⁠, with |$1/\hat{T}_\infty =\partial S/\partial \hat{E}$| and |$\hat{E}=\hat{M}(\hat{R})$|⁠.⁶ Thermodynamically stable solutions are maxima of entropy S (either local or global) at fixed E and N, while the unstable solutions are either minimum or saddle point of entropy. Importantly, thermodynamically stable solutions (associated with second-order variations of S) are only a reduced subset along the full set of (hydrostatic) equilibrium solutions. Indeed, the latter corresponds with solutions arising from the system of given equations (8)–(12), (18), and (19), which are simply an extremum of entropy (i.e. to first order δS = 0 for given N and E) as demonstrated in Chavanis (2019). This last statement clearly justifies the need to apply the Katz criterion to make a stability analysis.

3.1.1 |$M_{\rm vir} \approx 6.2 \times 10^{9}{\, \mathrm{M}_\odot}$|⁠, |$R_{\rm vir} = {11.1}\, \mathrm{kpc}$|

The numerical problem consists in solving equations (8)–(12) under the choice of the DF given by equation (13), with the specific boundary condition equations (18) and (19) at virialization. As a first example, we consider a rather small halo with |$M_{\rm vir} \approx 6.2 \times 10^{9}{\, \mathrm{M}_\odot}$| and |$R_{\rm vir} = {11.1}\, \mathrm{kpc}$|⁠. We solve this problem for a wide range of control parameters (ν₀, β₀, and θ₀), for fixed |$mc^2={10}\, {\rm keV}$|⁠, and plot in Fig. 1 all the equilibrium solutions (i.e. extremum of S) along the caloric curve (i.e. |$-\hat{M}$| versus |$1/\hat{T}_\infty$|⁠) as customary. This problem implies a monoparametric family of solutions, since for a fixed particle mass m we have three free model parameters and two given boundary conditions given by equations (18) and (19)

Figure 1.

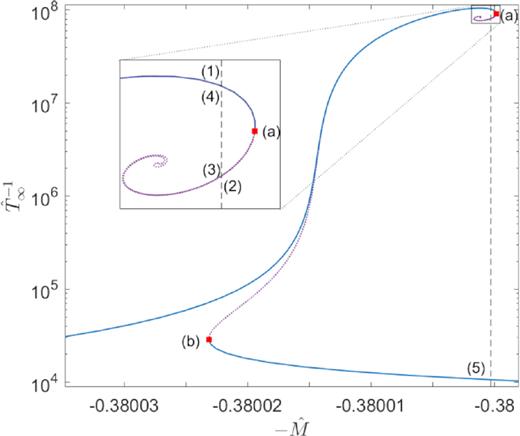
Series of equilibrium solutions along the caloric curve for box-confined configurations of |$mc^2={10}\, {\rm keV}$| fermions fulfilling the boundary conditions (1) at halo virialization. For this large value of |$\hat{R}\sim 10^7$|⁠, the curve spirals inwards several turns until it starts unwinding just when the quantum degeneracy (i.e. Pauli principle) sets in at θ₀ ≳ 10. The states within the continuous-blue branches are thermodynamically (and dynamically) stable (i.e. either local or global entropy maxima), while the dotted-purple branch – between (a) and (b) – is unstable (i.e. either minimum or saddle point of entropy), according to the stability criterion of Appendix  A.

Open in new tabDownload slide

We differentiate in Fig. 1 among the full family set of thermodynamically stable solutions (in continuous-blue line), from the thermodynamically unstable ones that are shown in dotted violet. We then analyse in detail all the different kinds of density profiles (extremum of S) for a fixed value of the total energy |$\hat{M}$| inside the spiral structure (see vertical dashed line in Fig. 1). The main conclusions out of this stability analysis can be summarized as follows:

• Upper continuous-blue branch contains solutions that are entropy maxima (either local or global; see Appendix  A), until the point where the caloric curve starts to rotate clockwise (i.e. first point where the curve |$1/\hat{T}_{\infty}$| versus |$-\hat{M}$| is tangent to a vertical line), labelled as a red square (a). Interestingly, all the solutions lying in this stable branch belong to the diluted Fermi regime, with θ₀ ≪ −1 (i.e. Boltzmannian-like). The associated density profiles resemble pseudo-isothermal spheres, with a density tail behaviour of ρ ∝ r⁻² at large distances (see curve 1 in Fig. 2).

• From this point all along the dotted-violet branch ending in point (b), solutions are thermodynamically unstable (either minimum or saddle point of S). Hydrostatic equilibrium solutions well inside the spiral start to transition from diluted Fermi [see e.g. the density profile (2) in Fig. 2 with θ₀ ≲ −1] to semidegenerate Fermi [see e.g. density profile (3) with θ₀ ≳ 10], just when the caloric curve starts to rotate anticlockwise. Precisely at this point, the central core becomes degeneracy-pressure supported; that is, the thermal de Broglie wavelength (λ_B) is larger than the interparticle mean distance at the core λ_B > l_c. This unwinding within the upper spiral of the caloric curve proves that the Pauli exclusion principle halts the classical gravothermal catastrophe, as first realized within Newtonian gravity in Chavanis & Sommeria (1998). In the ‘unrolled’ side of the curve, the profiles develop a core–halo behaviour, such that the larger θ₀ ≳ 10 the more compact and degenerate is the central core while the more diluted and extended is the outer halo. Unstable core–halo solutions like (4) are similar to the ones applied to DM haloes in Ruffini et al. (2015) within the original RAR model (see Section 3.4 for further relevant implications).

• For larger energies [at the right of point (b), where the amount of anticlockwise rotations of the caloric curve equals the number of clockwise rotations], a lower branch of entropy maximum (either local or global) arises, labelled in continuous-blue. The thermodynamically metastable solutions of this branch (i.e. local entropy maxima) have a tremendously long-lived lifetime much larger than the age of the Universe as calculated in Appendix  A. The interesting connection between metastability and long-liveness of self-gravitating systems with long-range interactions was originally demonstrated in Chavanis (2005). Typical stable density profiles [see e.g. density profile (5) of Fig. 2] develop highly compact core sizes below Mpc scales, surrounded by a very extended and diluted halo with no relevant astrophysical application as further discussed below.

• We recognize the existence of a spiral feature in the caloric curve, with the absence of the monotonic inspiralling typical of Boltzmannian DF (see e.g. Padmanabhan 1990). This necessarily implies that the gravothermal catastrophe is avoided, since the singular isothermal sphere is never present along our fermionic family of solutions. Such a result was first demonstrated in Chavanis & Sommeria (1998) for the Fermi–Dirac DF in Newtonian gravity and generalized here within GR for realistic DM halo sizes (see also Alberti & Chavanis 2018).

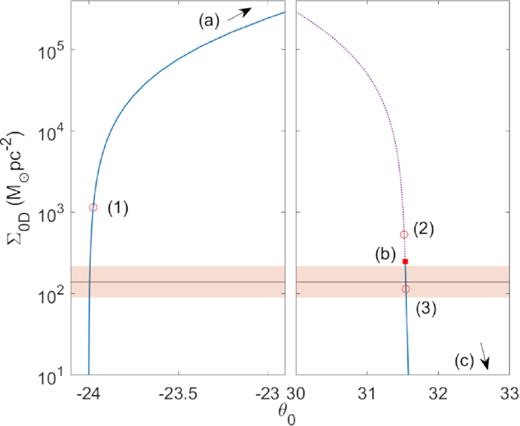
• By comparing the observationally inferred DM surface density |$\Sigma _{0{\rm D}}^{\rm obs} \sim 10^{2}{\, \mathrm{M}_\odot \, \mathrm{ pc}^{-2}}$| (Donato et al. 2009) (including 3σ errors in orange band) with the theoretical prediction⁷ from the corresponding fermionic density profiles along the caloric curve, we conclude the following:

  • There are no thermodynamically stable core–halo solutions of astrophysical interest when applied to low-mass (⁠|${\sim} 10^{9}{\, \mathrm{M}_\odot}$|⁠) DM haloes (box-confined). Either they can fit DM halo observables [like the solution (4) as obtained within the RAR model in Ruffini et al. 2015] but are saddle points of entropy or they are (local) maxima of entropy as solution (5), but the halo is too diluted to match the observational Σ_0D relation.

  • There exist diluted Fermi DM profiles [like solution (1) resembling pseudo-isothermal spheres] that are stable (i.e. maxima of entropy), and at the same time they match the observational Σ_0D relation. These statements can be directly checked by comparing the information in Figs 1–3.

Figure 2.

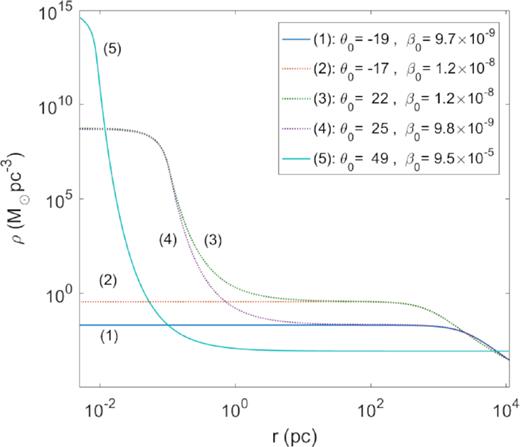
Density profiles for |$mc^2={10}\, {\rm keV}$| corresponding to the equilibrium states of the caloric curve in Fig. 1 with energy |$\hat{M}\approx 0.38$|⁠. Only the profile (1) (resembling a pseudo-isothermal sphere) and the core–halo one (5) are stable, while profiles (2)–(4) are thermodynamically unstable. Solutions like (4) were applied to describe DM haloes in galaxies in Ruffini et al. (2015), though they are very unlikely to occur in Nature (i.e. unstable), at difference with the more realistic core–halo solutions analysed in Section 3.2.

Open in new tabDownload slide

Figure 3.

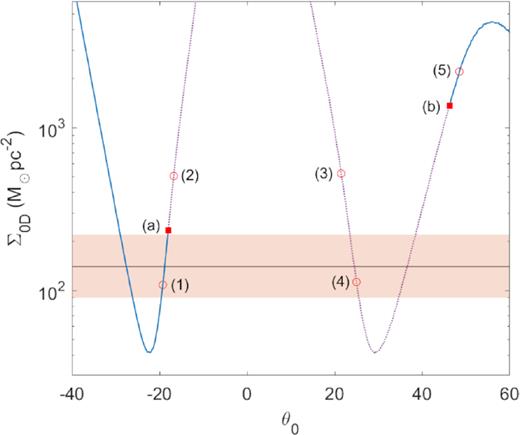
The observationally inferred DM surface density |$\Sigma _{0{\rm D}}^{\rm obs} \sim 10^{2}{\, \mathrm{M}_\odot \, \mathrm{ pc}^{-2}}$| (including 3σ errors in orange band; Donato et al. 2009) is compared with the theoretical prediction Σ_0D ∝ ρ_pr_h (see footnote 7), for the full series of equilibrium along the caloric curve of Fig. 1. Only pseudo-isothermal-like solutions such as (1) (see Fig. 2) are stable and agree with |$\Sigma _{0{\rm D}}^{\rm obs}$| at the same time.

Open in new tabDownload slide

3.1.2 |$M_{\rm vir}\approx 5.9 \times 10^{10}{\, \mathrm{M}_\odot}$|⁠, |$R_{\rm vir} = {29.7}\, \mathrm{kpc}$|

We repeat here the same analysis done in the above example, but in this case the total particle number corresponds to larger haloes, exceeding the OV limit (as e.g. |$\hat{N} = 3.67 \gt \hat{N}_{\rm OV}$|⁠). This implies a novel qualitative behaviour in the lower end of the caloric curve, towards the more degenerate and relativistic (i.e. higher T_∞) configurations, while for lower values of such parameters the situation is similar than in the above |$\hat{N} \lt \hat{N}_{\rm OV}$| case. Indeed, by comparing Figs 4–6 with respect to the analogous Figs 1–3, it can be directly concluded that the main five results drawn in the above example with |$\hat{N} \lt \hat{N}_{\rm OV}$| hold here as well, as we summarize below:

• Starting with stable (entropy maxima) states corresponding to solutions with θ₀ ≪ −1 (in upper continuous-blue branch of Fig. 4), there is an equal amount of times the caloric curve rotates clockwise starting at (a) (i.e. gaining an instability mode) as rotates anticlockwise (i.e. recovering a stability mode). This process continues until point (b), where the thermodynamic stability is restored. In between the points (a) and (b), the solutions are either minimum or saddle points of entropy, and progressively increase their central degeneracy until a typical core–halo profile (i.e. with θ₀ ≳ 10) is obtained just after the spiral unwinds.

• After point (b) and up to (c), the solutions are entropy maxima (either local or global) and therefore thermodynamically metastable or stable, respectively. Metastable solutions are shown to be extremely long-lived as calculated in Appendix  A, and thus can be considered as stable and even more likely to occur in Nature than global entropy maxima as explained in Chavanis (2005). Similarly as in the above case, these stable core–halo solutions are of no astrophysical interest when applied to typical DM halo masses (⁠|${\sim} 10^{10}{\, \mathrm{M}_\odot}$|⁠), since their halo densities are too diluted (and their sizes too extended) to match the observational Σ_0D relation [see e.g. solution (3) in Figs 5 and 6].

• At difference with the former case (⁠|$\hat{N} \lt \hat{N}_{\rm OV}$|⁠), a turn-over occurs in the caloric curve at the ending point of the stable branch where the continuous-blue line is tangent to a vertical line [labelled (c) in Fig. 4]). According to the Katz criterion (see Appendix  A), a new instability mode is gained because at (c) an extra clockwise rotation takes place in the thermodynamic curve. On the left of this point arises a new branch of thermodynamically unstable solutions, plotted in Fig. 4 in dotted-violet, which extends indefinitely into the second spiral in the caloric curve.⁸ Importantly, at the bottom-left end of this unstable branch we recognize the so-called ‘TP’ instability (labelled with an empty red circle), whose mathematical, physical, and astrophysical properties are discussed in Section 4.

Figure 4.

Series of equilibrium solutions along the caloric curve for box-confined configurations of |$mc^2={10}\, {\rm keV}$| fermions fulfilling the boundary conditions (2) at halo virialization. The states within the continuous-blue branches are thermodynamically (and dynamically) stable (i.e. either local or global entropy maxima), while the dotted-violet branches – between (a) and (b) and after (c) – are unstable (i.e. either minimum or saddle point of entropy), according to the stability criterion explained in Appendix  A. The arising of the second spiral of relativistic origin for high T_∞ is characteristic of caloric curves at a fixed N within GR, and implies the existence of a TP in an M(ρ₀) curve (see Section 4).

Open in new tabDownload slide

Figure 5.

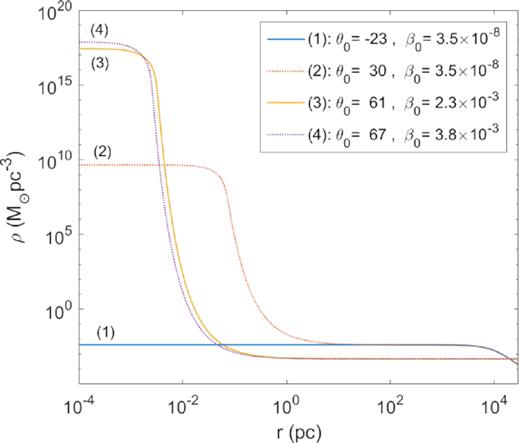
Density profiles for |$mc^2={10}\, {\rm keV}$| corresponding to the equilibrium states of the caloric curve in Fig. 4 with energy |$\hat{M}\approx 3.672$|⁠. Only the profiles (1) (resembling a pseudo-isothermal sphere) and the core–halo one (3) are stable, while profiles (2) and (4) are thermodynamically unstable. Solutions like (2) were applied to describe DM haloes in galaxies similar to the Milky Way in Ruffini et al. (2015), though they are very unlikely to occur in Nature (i.e. unstable), at difference with the more realistic core–halo solutions analysed in Section 3.2.

Open in new tabDownload slide

Figure 6.

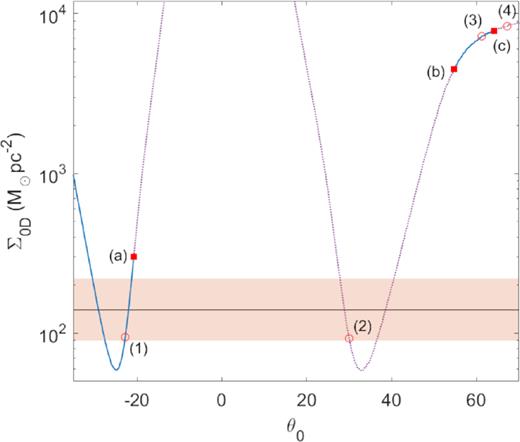
The observationally inferred DM surface density |$\Sigma _{0{\rm D}}^{\rm obs} \sim 10^{2}{\, \mathrm{M}_\odot \, \mathrm{ pc}^{-2}}$| (including 3σ errors in orange band; Donato et al. 2009) is compared with the theoretical prediction Σ_0D ∝ ρ_pr_h (see footnote 7), for the full series of equilibrium along the caloric curve of Fig. 4. Only pseudo-isothermal-like solutions such as (1) (see Fig. 5) are stable and agree with |$\Sigma _{0{\rm D}}^{\rm obs}$| at the same time.

Open in new tabDownload slide

Remark 1: The pseudo-isothermal sphere-like behaviour (belonging to the diluted Fermi class of stable configurations) implies density halo tails going as ρ ∼ r⁻² for large r, until the abrupt end of the boundary-box radius R sets in. Though such a slope is in tension with standard DM halo phenomenology, which indicates sharper halo trends such as ∼r⁻³ as in the Burkert or NFW profiles. Importantly, halo tails more similar to this phenomenologically suitable one can be obtained in the more realistic tidally truncated scenario, while at the same time belonging to stable branch, shown in the following Section 3.2.

Remark 2: As shown in Alberti & Chavanis (2018), for box-confined configurations of fermions, the larger the box size |$\hat{R}$| (as compared to R_OV), the less relevant are the GR effects in the overall distribution when compared with Newtonian gravity. As we are using very large values of |$\hat{R}\sim 10^7$| in order to reach realistic galactic sizes for |$\mathcal {O}({10}\, {\rm keV})$| particles, very similar conclusions about the stability should be obtained within Newtonian equations as well. However, we notice that appreciable differences should arise towards the high-|$\hat{T}_\infty$| end of the caloric curve, since the radius of the degenerate core is close to the critical one before collapse⁹ [i.e. notice that r_c ∼ R_OV close to point (c) of Fig. 4; see also Section 4].

3.2 Tidally truncated DM haloes

In tidally truncated systems, the tidal radius R, which is naturally set by the escape energy condition in Section 2, is not fixed along the series of equilibrium. Indeed, it must be sensitive to the free parameters of the system that vary along the caloric curve, including T_∞. What remains constant instead is a combination of the Klein and escape energy conditions, as explicited in Section 2 and equation (12).

In other words, at difference with the box-confined case, the factor W₀ − θ₀ = (ϵ_c − μ)/(k_BT) is the one to be kept constant here, together with N. It is only by fixing this factor (and not R) that the Katz criterion applies, and that the changes of stability in the thermodynamic curve (e.g. in the microcanonical ensemble) correspond to the maximization entropy problem (Katz 1980; Chavanis et al. 2015b).¹⁰

In tidally truncated systems, the spanning of the caloric curve (either in temperature or in energy) is sensitive to the constant W₀ − θ₀, affecting as a consequence the different locations of the solutions in such curve. Given such solutions may be of astrophysical interest for DM halo applications, it is thus convenient to have an educated guess on which W₀ − θ₀ value to start with, in order not to make (undesired) blind trials.

Fortunately, the phenomenology of different observationally inferred DM haloes (from dwarf all the way to elliptical galaxies) in terms of a self-gravitating system of fermions given by equations (8)–(12) was already worked out in Argüelles et al. (2019a) within the RAR model. In that work, a particle mass of |$mc^2={48}\, {\rm keV}$| was used as a relevant example, in views of the successful Milky Way phenomenology developed within the same model in Argüelles et al. (2018). For haloes with density tails eventually acquiring a power law r⁻ⁿ with n > 2 (i.e. close to the ones provided by N-body simulations), we obtain from Argüelles et al. (2019a) typical W₀ − θ₀ values between 20 and 28 (and reaching up to 40 or larger for isothermal sphere density tails ∝ r⁻²).

Therefore, we consider next the boundary condition problem (⁠|$\hat{N}, W_0-\theta _0$|⁠), and perform the corresponding thermodynamic stability analysis (for |$mc^2={48}\, {\rm keV}$| as motivated in the comment above), with the following values: |$\hat{N}=76.25$| and W₀ − θ₀ = 24.

The chosen value for |$\hat{N}=76.25 \gt \hat{N}_{\rm OV}$|⁠) implies, in dimensionfull units, the virial mass of an average DM halo mass |$M_{\rm vir} \equiv M(R_{\rm vir}) \approx 5.4 \times 10^{10}{\, \mathrm{M}_\odot}$|⁠. That value is chosen this way in order to properly compare the thermodynamical stability results of this section with the ones of Section 3.1.2.

With the educated choice of W₀ − θ₀ = 24, it is expected to find along the series of equilibrium a solution with a halo size at virialization of |$R_{\rm vir} \approx {29}\, \mathrm{kpc}$| (as dictated from Fig. B2 within the Press–Schechter formalism of Appendix  B). Besides that, it is further pursued to check if such an expected solution may be both thermodynamically stable and of astrophysical interest or otherwise.

The numerical problem is analogous as the one of Section   3.1.2. Indeed, for the tidally truncated haloes under consideration (i.e. with |$\hat{N} \gt \hat{N}_{\rm OV}$|⁠), it is expected that the caloric curve is qualitatively similar to the one in the box-confined case (see Chavanis et al. 2015b, for an analogous comparison in Newtonian gravity reaching the same conclusion). However, it is clear that the precise locations of the points where stability changes, as well as the stability branch extensions along the caloric curve, should shift with respect to one another. It is thus worthy to make here a detailed investigation to search for a new family of solutions, with the hope to find profiles that are thermodynamically stable as well as of astrophysical interest (not possible for the box-confined case as shown in Section 3.1).

We solve the system of equations (8)–(12) though this time under the more realistic DF given by equation (1), with the specific fixed constraints (⁠|$\hat{N}=76.25$|⁠, W₀ − θ₀ = 24) and for |$mc^2 = {48}\, {\rm keV}$|⁠. We solve it for a wide range of control parameters [ν₀, β₀, and θ₀], and plot in Fig. 7 all the equilibrium solutions (i.e. extremum of S) along the |$-\hat{M}$| versus |$1/\hat{T}_\infty$| caloric curve as customary.¹¹ This problem implies a monoparametric family of solutions, since we have three free model parameters (notice that W₀ is not independent of θ₀) for two given boundary conditions. We differentiate in Fig. 7 among the full family set of thermodynamically stable solutions (in continuous-blue line), from the thermodynamically unstable ones that are shown in dotted-violet. We then analyse in detail all the different kinds of density profiles for a fixed value of the total energy |$\hat{M}$| as an example (see vertical dashed line in Figs 7 and 8 for the profiles).

Figure 7.

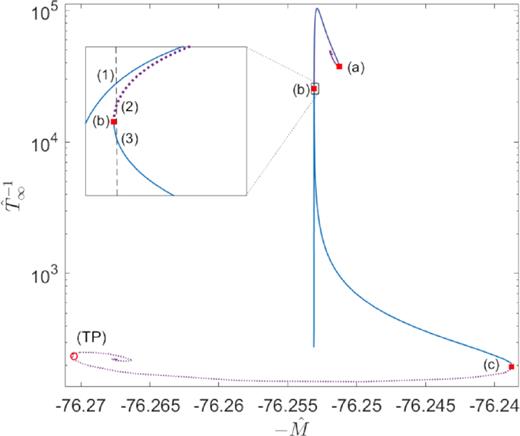
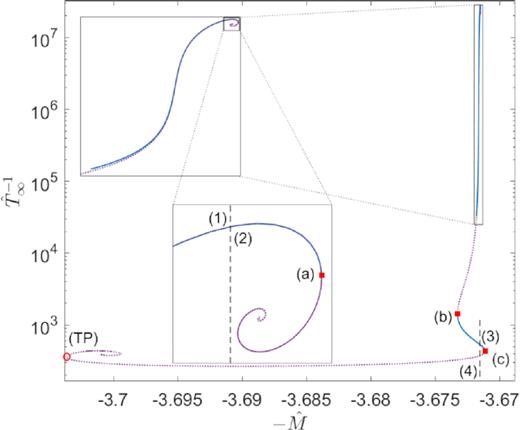
Series of equilibrium solutions along the caloric curve for tidally truncated configurations of |$mc^2={48}\, {\rm keV}$| fermions fulfilling (⁠|$\hat{N}=76.25$|⁠, W₀ − θ₀ = 24). The states within the continuous-blue branches are thermodynamically (and dynamically) stable (i.e. either local or global entropy maxima), while the dotted-violet branches – between (a) and (b) and after (c) – are unstable (i.e. either minimum or saddle point of entropy), according to the Katz criterion. Solution (3) is stable and fulfils the virialization conditions as required from the Press–Schechter formalism of Appendix  B. The arising of the second spiral of relativistic origin for high T_∞ is characteristic of caloric curves at a fixed N within GR, and implies the existence of a TP in an M(ρ₀) curve (see Section 4).

Open in new tabDownload slide

Figure 8.

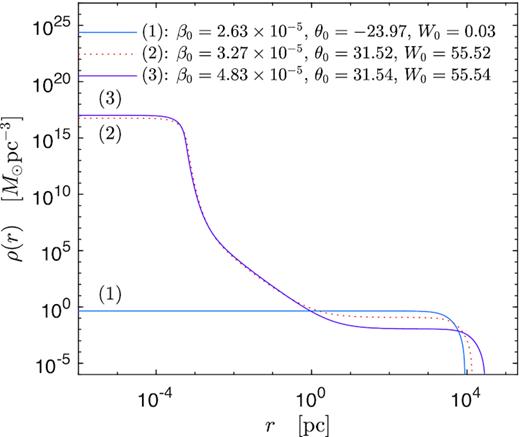
Density profiles for |$mc^2={48}\, {\rm keV}$| corresponding to the equilibrium states of the caloric curve in Fig. 7 with energy |$\hat{M}=76.25308$|⁠. Only the profiles (1) (resembling a King distribution) and the core–halo one (3) are stable, while profile (2) is thermodynamically unstable. Interestingly, solutions like (3) were successfully applied to explain the DM halo in the Milky Way in Argüelles et al. (2018). They are stable, extremely long-lived, and fulfil the |$\Sigma _{0{\rm D}}^{\rm obs}$| relation as shown in Fig. 9, as well as the expected value of the dispersion velocity σ_h in CDM N-body simulations as shown in Fig. 10.

Open in new tabDownload slide

The main conclusions out of this stability analysis can be summarized as follows:

• Analogously as in Section 3.1.2, the entropy maximum states (either local or global) correspond to solutions with θ₀ ≪ −1 lying in the upper continuous-blue branch of Fig. 7, and ending at point (a) where the first instability branch starts. Solutions in this unstable branch (labelled in dotted-violet) are either minimum or saddle points of entropy, and progressively increase their central degeneracy from negative to positive until a core–halo profile arises (for θ₀ ≳ 10). More precisely, exactly at the point where the spiral starts to unwind, a mild degenerate core with θ₀ = 6.7 becomes quantum pressure supported being λ_B = 2l_c. Confirming once more that the gravothermal catastrophe typical of Boltzmannian distributions, is avoided when the fermion degeneracy comes into play through the Pauli exclusion principle. Solutions obtained for 10 ≲ θ₀ ≲ 28, prior to point (b), have a core–halo behaviour qualitatively similar as the ones obtained in Ruffini et al. (2015), falling all within the unstable branch. The unstable branch ends at (b), once the caloric curve has rotated as many anticlockwise times as clockwise rotations, and the thermodynamic stability is recovered. Metastable solutions in this new stable branch [as solution (3) within the continuous-blue curve] are shown to be of astrophysical interest [see point (iii) below]. Such a stability is lost at point (c) when the curve rotates clockwise once again, thus becoming thermodynamically unstable all the way to the second spiral of relativistic origin. The TP instability at the left end of such a spiral, and the concept of gravitational collapse of the core at the last stable point (c), is discussed in detail in Section 4.

• The key difference with respect to the Section 3.1.2 case is precisely in the second stable branch: It is much more extended in energy and |$\hat{T}_\infty$| and therefore implies a larger family of metastable (and stable) states. More importantly, it starts at (b) with central degeneracies θ₀ ≈ 30 and β₀ ∼ 10⁻⁵ typical of astrophysical density profiles (Argüelles et al. 2018, 2019a; Becerra-Vergara et al. 2020) for such average halo mass. Indeed, the metastable solution (3) plotted in Fig. 8 is of a perfect astrophysical applicability (see also the item below), since it is similar to that of a Milky Way RAR DM halo for |$mc^2={48}\, {\rm keV}$|⁠, shown to perfectly fit the rotation curve data (Argüelles et al. 2018, 2019b; Becerra-Vergara et al. 2020).

  This is a remarkable result, since for the first time a core–halo solution like (3) known to be of astrophysical applicability has now been proven to fall inside the metastable branch while being extremely long-lived (as calculated in Appendix  A) and thus reachable in Nature. We believe this is not a coincidence; i.e. the fact that in Argüelles et al. (2018, 2019b) and Becerra-Vergara et al. (2020) it was shown that the existence of a DM core–halo profile where the core can mimic a massive BH while the outer halo can explain the rotation curve was already a smoking gun for its plausibility in Nature.

• There is a full family of solutions in the second stable branch between (b) and (c) (corresponding to θ₀ ≈ 31.5 and β₀ ∈ [3.3 × 10⁻⁵, 5 × 10⁻⁵]), which are found to be of astrophysical interest; that is, they lie within the allowed DM surface density |$\Sigma ^{\rm obs}_{0{\rm D}}$| strip as shown in Fig. 9, and agree with the expected N-body dispersion velocities (σ_h) as shown in Fig. 10. Interestingly, they cover inner-halo densities at plateau roughly |$\rho _\mathrm{ p} \approx 10^{-3}\!-\!10^{-1}\, \mathrm{M}_\odot \, \mathrm{pc}^{-3}$| and total sizes of |$R \approx 10\!-\!50\, \mathrm{kpc}$|⁠. In particular, the solution (3) in Fig. 8 is the one having the value of |$R_{\rm vir} \approx {29}\, \mathrm{kpc}$| as required from the Press–Schechter analysis within a self-consistent WDM cosmology (Appendix  B). Finally, solutions with larger |$\hat{T}_\infty$| (i.e. β₀ ≳ 5 × 10⁻⁵) towards the relativistic regime approaching point (c) are all of no astrophysical interest: The haloes are too diluted and extended to fit within the allowed Σ_0D as explicitly shown in Fig. 9.

Figure 9.

The observationally inferred DM surface density |$\Sigma _{0{\rm D}}^{\rm obs} \sim 10^{2}{\, \mathrm{M}_\odot \, \mathrm{ pc}^{-2}}$| (including 3σ errors in orange band; Donato et al. 2009) is compared with the theoretically prediction Σ_0D ∝ ρ(r_pl)r_h, for the full series of equilibrium along the caloric curve of Fig. 7. Only King-like profiles similar to (1) (see Fig. 8) and core–halo profiles like (3) are stable and agree with |$\Sigma _{0{\rm D}}^{\rm obs}$| at the same time.

Open in new tabDownload slide

Figure 10.

The dispersion velocity σ_h of fermionic haloes with a core–halo morphology lying along Fig. 7 is plotted against their effective temperature. It is compared with the traditional isothermal relation (k_BT/m)^1/2, and with the predicted σ_h values arising from N-body simulations within a CDM cosmology. Importantly, there exists a window of T around 10⁴ K where the fermionic core–halo profiles are thermodynamically stable, long-lived, and astrophysically allowed in the sense of both the DM surface density relation |$\Sigma _{0{\rm D}}^{\rm obs}$| and the expected σ_h from (CDM) N-body simulations.

Open in new tabDownload slide

Remark: Even if the above conclusions apply for average-sized DM haloes, i.e. |$M_{\rm vir} \sim 10^{10}{\, \mathrm{M}_\odot}$|⁠, with fixed W₀ − θ₀ = 24, we have repeated the stability analysis for other values of W₀ − θ₀ between 20 and 28 (for the same |$\hat{N}$|⁠). We have found that for W₀ − θ₀ ≲ 20 there are no astrophysical solutions within the metastable branch: They acquire inner-halo densities at plateau |$\rho _\mathrm{ p} \gtrsim 1{\, \mathrm{M}_\odot \, \mathrm{pc}^{-3}}$| above any reasonable value even for the smallest haloes (totally in line with the analysis done in Argüelles et al. 2019a).

Interestingly, for W₀ − θ₀ = 24 there are no stable core–halo solutions with a quantum core mass |$M_\mathrm{ c} \lesssim 10^{7}{\, \mathrm{M}_\odot}$|⁠. Nevertheless, for larger values of 24 < W₀ − θ₀ < 28 (and for the same |$\hat{N}$|⁠), it is possible to obtain lower (stable) core masses of |${\sim} 10^{6}{\, \mathrm{M}_\odot}$|⁠. The relevance of such (smaller) fermionic core mass is obvious when comparing with our Galaxy (though with a larger N by an order of magnitude than the one adopted here), given it may represent an alternative to the central BH scenario as proven in Argüelles et al. (2018) and Becerra-Vergara et al. (2020).

Finally, there exists a threshold value of W₀ − θ₀ somewhere between 20 and 22 where the metastable branch extends only up to an energy value |$\hat{M}$|  smaller than that of point (a) before becoming unstable [i.e. last stable point (c) is to the left of point (a) in energy]. This may imply important consequences regarding the possible gravitational collapse (of gravothermal catastrophic nature) of DM cores towards a BH as can be concluded from the remark in Section 4.

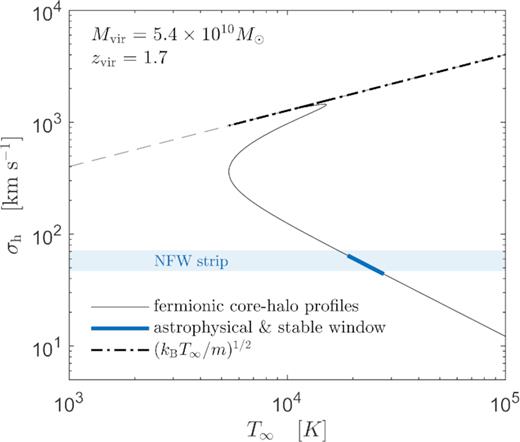
3.3 The σ_h–T relation of fermionic haloes

The dispersion velocity of the fermionic haloes (calculated as the root-mean-square velocity at a given halo-scale) is a relevant magnitude that can be compared with the one coming from N-body simulations at virialization. Indeed, within the Lambda cold dark matter (ΛCDM) cosmology, in Taylor & Navarro (2001) it was calculated a phenomenological expression for the dispersion velocity of the DM haloes as a function of the halo mass inside the radius where the rotation curve peaks (dubbed here as σ_h). Thus, in Fig. 10 we compare the behaviour of such a dispersion velocity (labelled in light blue, within the NFW concentration parameters c as reported in Taylor & Navarro 2001), with respect to the one of fermionic haloes lying along the caloric curve of Fig. 7, and having |$M(R_{\rm vir}) \approx 5.4 \times 10^{10}{\, \mathrm{M}_\odot}$| occurring at z_vir ∼ 2 (see  B and the above section). The fermionic σ_h values are plotted as a function of its (effective) temperature T_∞ ≡ T, and calculated for tidally truncated fermionic solutions with a phase-space DF given by equation (1). Such a σ_h–T relation is explicitly shown in Fig. 10 for core–halo solutions (i.e. θ₀ ≳ 10) lying along the caloric curve of Fig. 7; the very same relation exists for the branch of diluted (King-like) solutions with θ₀ < −1. The reason for the existence of both branches of solutions with the same σ_h–T relation is that for each core–halo solution along Fig. 7, there exists another one in the diluted regime that closely matches the halo part of the former, inside which the dispersion velocity is evaluated [see e.g. the behaviours between solutions (1) and (3) in Fig.   8].

One important result from this analysis is the fact that the σ_h–Trelation of fermionic haloes does not follow the traditional isothermal trend σ ∝ (k_BT/m)^1/2. Instead, it deviates from it according to the different behaviour of the caloric curve of Fig. 7 in which the temperature covers a wide range of regimes, from relatively hot to relatively cold, depending on the central degeneracy and cut-off parameter (the latter two not present in the traditional isothermal scenario); that is, for core–halo solutions starting with θ₀ = 10 in the caloric curve (just after the spiralling out at the top of Fig. 7), the temperature increases with corresponding increase of σ_h closely following the Boltzmannian relation. This trend continues until the first anticlockwise turn of the caloric curve [in the inner part of the location of point (a)], where T decreases (and so does σ_h). This second trend ends when the caloric curve reaches the maximum (from the inside curve), and so T starts to rise once more (in this case with decreasing σ_h), all the way until the onset of instability at point (c).

The main conclusion from this analysis is that there exists a window of effective T ∼ few |$10^{4}\, \mathrm{K}$| falling within the range of thermodynamically stable core–halo solutions, with corresponding σ_h  values that roughly agree with the predicted window arising from N-body simulations within a CDM cosmology as given in Taylor & Navarro (2001). Interestingly, such very same range of T practically coincides with the one of the astrophysical family of solutions (shown in thick-blue in Fig. 10) in the sense of the DM surface density relation of Fig. 9.

This dispersion velocity analysis allows us to link the temperature of the DM fermions prior and after virialization, and to know which values are the realistic ones (for a given particle mass) in the sense of the expected σ_h from simulations. Indeed, while typical DM redshifting temperature of the fermions just prior halo formation is about few Kelvin (i.e. at z_vir = 10 as calculated from  B for resonantly produced sterile neutrinos), the effective T of the very same particles in the fermionic haloes of |${\sim} 5 \times 10^{10}{\, \mathrm{M}_\odot}$| must be |${\sim} 10^{4}\, \mathrm{K}$|⁠. That temperature gap between prior and after relaxation can be understood in terms of the violent relaxation mechanism. It mixes the fermion gas and makes the (effective) temperature of the quasi-relaxed halo hotter as expected from the negative specific heat acting on these kinds of self-gravitating systems.

3.4 Comparison with other works

We start by emphasizing that the stability results presented in this section are completely original, since it is the first time they are obtained for tidally truncated self-gravitating fermions at finite temperature in GR, with realistic boundary conditions at virialization. Nevertheless, it is important to compare the main conclusions obtained in Section 3.2, with those of a similar stability analysis done for self-gravitating fermions within Newtonian gravity in Chavanis et al. (2015b) (see Appendix  A for comparisons with other works using the box-confined ansatz for fermions in GR).

In fig. 30 of that work, Chavanis et al. obtained a similar caloric curve as the one obtained here in Fig. 7, though without the second spiral of relativistic origin since they applied the Newtonian (non-relativistic) theory of gravity. The importance of this comparison is that both caloric curves have the similar features: Both (microcanonical) stable branches are of similar features and are both applicable to relatively large haloes. Indeed, in Chavanis et al. (2015b) they did the analysis for a dimensionless parameter μ = 10⁹ (not the chemical potential), which can be easily shown to be equal to |${\rm e}^{W_0-\theta _0}$|⁠, thus implying a value for W₀ − θ₀ ≈ 21 close to the one chosen in Section 3.2.

In fig. 45 of that work, they provided all the possible density profiles at a given energy, similarly as done here in Fig. 8, though they did for an energy value already within the spiral feature. They showed basically three different kinds of profiles: (i) a King-like profile belonging to the first stable branch dubbed as the ‘gaseous-phase’ [similar to solution (1) in Fig. 8]; (ii) a core–halo profile belonging to the unstable branch dubbed as the ‘embrionic-phase’; and (iii) another kind of core–halo profile belonging to the second stable branch and dubbed by Chavanis et al. as the ‘condensed-phase’ [similar to solution (3) in Fig. 8].

Up to this point both qualitative results about the thermodynamic stability (i.e. the one given in Chavanis et al. 2015b and the one from Section 3.2) are somewhat in line, though Chavanis et al. attempted a very different conclusion with respect to the one obtained here regarding the applicability to DM haloes. They concluded that (i) either you have core–halo solutions belonging to the ‘embrionic-phase’ (qualitatively similar as the ones obtained in Ruffini et al. 2015) but are thermodynamically unstable (i.e. unreachable) or (ii) you get stable core–halo profiles belonging to the ‘condensed-phase’, but cannot explain the DM content in large galaxies since the halo is too extended and diluted for such a goal. While we generally agree on conclusion (i) as shown in Sections 3.1 and 3.2, we totally disagree with conclusion (ii). Moreover, we have proven in Section 3.2 that such a conclusion is indeed wrong.

Such a discrepancy in the interpretation of the results is understood when introducing a proper quantitative and dimensionfull analysis of the profiles in relation to DM halo observables, together with the quest for a full coverage of the energy values |$\hat{M}$| along the metastable branch (not developed in Chavanis et al. 2015b); that is, for a particle mass |$mc^2 \sim {50}\, {\rm keV}$| there exists an accessible energy window |$\hat{M}$| in which there are metastable (and long-lived) core–halo profiles that acquire the observationally inferred inner-halo densities (⁠|${\sim} 10^{-2}{\, \mathrm{M}_\odot \, \mathrm{pc}^{-3}}$|⁠) and virial radii (∼ few |${10}\, \mathrm{kpc}$|⁠) typical of average-sized galaxies. Indeed, this observational correspondence is evidenced through the Σ_0D relation shown in Fig. 9 and further explained in Section 3.2.

These kinds of thermodynamically stable core–halo profiles correspond to the so-called ‘condensed-phase’ introduced in Chavanis et al. (2015b), and have been already implemented in Argüelles et al. (2018, 2019b) to provide an excellent fit to the Milky Way rotation curve. Remarkably enough, the degenerate core of this last kind of solutions (for particle masses in the range of |${\sim} 10^{1}\!-\!10^{2}\, {\rm keV}$|⁠) can mimic the massive BH in SgrA* (Argüelles et al. 2018; Becerra-Vergara et al. 2020) as well, a result that is not possible for ‘embrionic-phase’ solutions as shown in Ruffini et al. (2015) (by the way unstable).

Remark: In Chavanis et al. (2015b), the highly degenerate core (i.e. T → 0) belonging to the ‘condensed-phase’ kind of stable solutions was used as a potential candidate to explain the DM haloes in dwarf galaxies for particle masses of |${\sim} {1}\, {\rm keV}$| (as motivated by the results in Destri, de Vega & Sanchez 2013).¹² However, we notice that from the discussion above, there is a priori no necessity to go to such low fermion masses of |${\sim} {1}\, {\rm keV}$| (or below) in order to explain the DM haloes in dwarf galaxies. In other words, it is absolutely possible to provide good fits to dispersion velocity data in such galaxy types, using the overall stable core–halo profiles [like solution (3) in Fig. 8 but for lower |$M_{\rm vir} \sim 10^{8}{\, \mathrm{M}_\odot}$|], as shown in Argüelles et al. (2019a). We thus claim, in views of the results here presented together with the phenomenology for DM haloes made in Argüelles et al. (2018, 2019a) and Becerra-Vergara et al. (2020), that the semidegenerate fermion regime (i.e. leading either to diluted or to core–halo profiles) is enough to explain the plethora of DM haloes without the need to invoke the (extreme) fully degenerate (T → 0) regime.

Moreover, such fully degeneracy paradigm for |$mc^2\lesssim {1}\, {\rm keV}$| aimed to be applicable to dSph DM haloes, and suffers from many problems or tensions such as (a) Ly α forest constraints (Yèche et al. 2017), (b) phase-space bounds and MW satellite counts (Horiuchi et al. 2014), and even (c) dispersion velocity fits in dwarfs since an extra isothermal halo component has been shown in Randall et al. (2017) to be needed in order to agree with data. Problems that naturally disappear within our |$\mathcal {O}({10}\,\, {\rm keV})$| fermionic approach.

4 GRAVITATIONAL COLLAPSE AND TP INSTABILITY

Fermionic core–halo solutions with N > N_OV at virialization may eventually become unstable (either thermodynamically and dynamically) and undergo a gravitational core collapse as we show below. Historically, the gravitational collapse of a degenerate and relativistic ‘star’ at a specific central density ρ₀ was understood in terms of the onset of thermodynamical (and dynamical) instability at a TP (Harrison et al. 1965; Sorkin 1981; Friedman, Ipser & Sorkin 1988). Such a TP is defined as the point where the total mass is a maximum with respect to ρ₀, i.e. |$\rm dM/\rm d\rho _0=0$|⁠. Importantly, in Sorkin (1981) and Schiffrin & Wald (2014) it was demonstrated that for any EoS (e.g. not necessarily isentropic) the existence of a TP along a smooth sequence of GR equilibrium states implies the presence of a thermodynamic instability on one side of the TP.

However, TPs do not provide a necessary condition for thermodynamic instability, and the onset of such an instability could occur even without the existence of a TP at all [see point (a) in Fig. 1 with N < N_OV for an explicit example, and Schiffrin & Wald 2014 for a general theoretical result]. Moreover, the onset of thermodynamical (and dynamical) instability can occur prior to the TP in the ρ₀ versus M curve, as first shown numerically in Takami, Rezzolla & Yoshida (2011) for rotating perfect-fluid ‘stars’ (contrary to what is historically expected in Friedman et al. 1988).

Importantly, for the first time we confirm such a conclusion but for a perfect-fluid (neutral) fermionic non-rotating ‘star’, with an EoS including for temperature effects as demonstrated below and in Figs 11 and 7.

Figure 11.

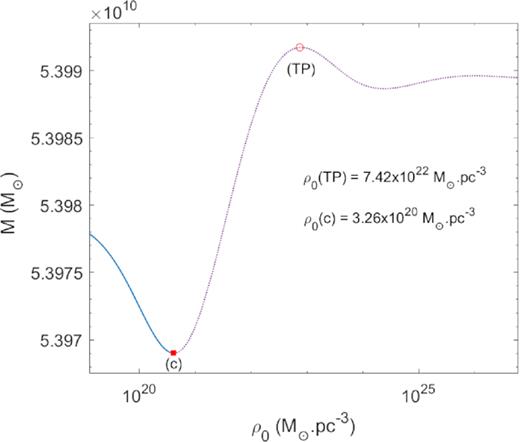
Series of equilibrium states with N > N_OV are shown along a ρ₀ versus M curve, in correspondence with the relativistic and degenerate end of the caloric curve of Fig. 7. At difference with standard degenerate fermion ‘stars’, the last stable configuration (c) of self-gravitating fermions at finite T_∞ occurs just at the minimum of the curve and prior to the TP instability.

Open in new tabDownload slide

Moreover, we are able to localize the TP instability (i.e. the maximum in a ρ₀ versus M curve as in Fig. 11) in the left-lower end of the caloric curve, where the spiral of relativistic origin rotates clockwise (see the open red circle in Fig. 7). Clearly, such TP occurs at a different energy with respect to the last stable configuration (c) along the unstable branch of the caloric curve.

Thus, we have proven that for self-gravitating systems at finite T_∞ in GR, the TP instability does not coincide with the last stable configuration occurring at (c). This original result bares an important consequence regarding the concept of critical mass for gravitational core collapse |$M_\mathrm{ c}^{\rm cr}\propto m_{\mathrm{ p}}^3/m^2$|⁠, where m_p is the Planck mass,¹³ traditionally explained in terms of the TP instability for fully degenerate stars (see e.g. Shapiro & Teukolsky 1983). Such a correspondence does not apply here, and instead, the |$M_\mathrm{ c}^{\rm cr}$| value is achieved at the last stable configuration (c) placed at the minimum of the ρ₀ versus M curve, thus occurring prior to the TP as can be directly checked by comparing Figs 7 and 11.

Interestingly, such a last stable configuration acquiring the critical core mass occurs instead at the maximum, but in a ρ₀ versus M_c curve as shown in Fig. 12. Indeed, the value of the core mass at the TP is near an order of magnitude below the critical |$M_\mathrm{ c}^{\rm cr}$| as can be seen directly by comparing Figs 12 and 11. The right value of the critical mass |$M_\mathrm{ c}^{\rm cr}$| (i.e. the one associated with the last stable configuration and not with the TP) is of central importance for SMBH formation and astrophysics in general. As a clear example, for |$mc^2 = {48}\, {\rm keV}$| it is possible to form an SMBH of |$M_\mathrm{ c}^{\rm cr}\approx 2 \times 10^{8}{\, \mathrm{M}_\odot}$| (see Fig. 12) at the centre of a realistic DM halo as explained in Section 3.2 and in the remark below. The relevance of such a DM core-collapse scenario is that it can occur in the high-redshift (z ∼ 10) Universe at halo virialization (see Appendix  B), without the need of prior star formation or other BH seed mechanisms involving super-Eddington accretion rates; that is, the thermodynamics of tidally truncated self-gravitating fermions in a cosmological set-up can offer a powerful tool for SMBH formation worthy for further investigation.

Figure 12.

The last stable configuration (c) at the onset of the core collapse [corresponding to point (c) in Fig. 7] is acquired at the maximum of a central density versus core mass, and having a critical core mass of |$M_\mathrm{ c}^{\rm cr}\approx {2E8}{\, \mathrm{M}_\odot}$| for |$mc^2={48}\, {\rm keV}$|⁠. The core mass at the TP is nearly an order of magnitude below the critical mass.

Open in new tabDownload slide

We have further calculated the central redshift [z₀ = e^−ν(0)/2 − 1] of a light source at rest at the centre of a DM core (for all the solutions along the caloric curve of Fig. 7), as a measure of how relativistic they are. For the critical solution (c), it gives |$z_0^{\mathrm{ cr}}=0.478$| (at |$\hat{T}_{\infty }=5.11\times 10^{-3}$|⁠), while for the TP (unstable) core it gives |$z_0^{\mathrm{ TP}}=3.16$| (at |$\hat{T}_{\infty }=4.24\times 10^{-3}$|⁠). The arising of thermodynamically (and dynamically) unstable (i.e. collapsing to a BH) solutions for |$z_0^{\mathrm{ cr}}\gtrsim 0.5$| found here for tidally truncated configurations of keV fermions (with N > N_OV in the high T regime) is in line with former results found in Rasio, Shapiro & Teukolsky (1989) for relativistic clusters.

Remark 1: Since we do not solve the time evolution of the fermionic configurations once they become thermodynamically (and dynamically) unstable, the concept of gravitational collapse deserves further explanation. In the caloric curves with N > N_OV under study, there are two kinds of possible gravitational collapses that may arise. For a system starting at virialization in the diluted (stable) regime before point (a), one can think that such a state evolves quasi-stationary in time while it loses energy due to evaporation and (long-range) collisions, until reaching the threshold energy of point (a). At this critical energy, the configuration will evolve directly towards the next accessible stable state just below (a) in the metastable branch, and lead to the new core–halo configuration. Such limiting phase transition, i.e. from diluted to a semidegenerate one occurring at such critical energy, is usually called as a collapse of gravothermal catastrophic nature (Chavanis & Alberti 2020).

If it keeps losing energy along the second stable branch, it will eventually reach the last stable configuration at (c) (see Fig. 7), below which there is no possible accessible state, and the system must collapse towards a massive BH (according to the core-collapse criterion of relativistic origin explained above). For a further discussion including the different time-scales involved between the two different collapsing processes, i.e. between the gravothermal catastrophe at point (a) and the gravitational collapse of relativistic origin occurring at (c), see Chavanis & Alberti (2020) and references therein.

Remark 2: We notice that a complementary mathematical proof about the onset of thermodynamical (and dynamical) stability in the microcanonical ensemble may be obtained by explicitly calculating the second-order variations of entropy and their sign changes, following the work of Roupas (2013). However, even if in that work it was explicitly calculated the expressions for δ²S for a self-gravitating system of particles in GR under a perfect-fluid assumption, it was done only for barotropic equations of state. The fermionic equations of states used in this paper are of more general form, written only parametrically; thus, more sophisticated calculations are needed in the present case (if at all possible) in order to attempt such a complementary proof.

5 CONCLUSIONS

We have studied the formation and stability of collisionless self-gravitating system of fermions at finite T in GR, with applications to the problem of virialization of DM haloes in a realistic cosmological framework. Unlike the N-body numerical simulation approach, we have assessed these issues by means of a thermodynamical approach for self-gravitating fermions, which eventually maximize its coarse-grained entropy. In particular, we have performed a thermodynamic stability analysis in the microcanonical ensemble for solutions with a given particle number N, at the moment of halo virialization in a WDM cosmology, and further calculate the lifetime of the metastable equilibrium states.

The advantage of our numerical approach is that it allows for a detailed description of the relaxed haloes from the very centre to periphery, not possible in N-body simulations due to finite inner-halo resolution. In addition, it includes richer physical ingredients such as (i) general relativity – necessary for a proper gravitational DM core collapse to an SMBH, (ii) the quantum nature of the particles – allowing for an explicit fermion mass dependence on the profiles, and (iii) the Pauli principle self-consistently included in the phase-space DF – giving place to novel core–halo profiles at (violent) relaxation.

Our approach allows us to link the behaviour and evolution of the DM particles from the early Universe all the way to the late stages of non-linear structure formation at virialization; that is, we start by calculating the linear matter power spectrum for an |$\mathcal {O}({10}\, {\rm keV})$| DM sterile neutrino, and then use the corresponding Press–Schechter formalism to obtain the virial halo mass, M_vir, with associated redshift z_vir (see Appendix  B). The fermionic haloes are assumed to be formed by fulfilling a maximum entropy production principle at virialization. It allows us to obtain a most likely DF of Fermi–Dirac type as first shown in Chavanis (1998) (generalizing Lynden-Bell results), which is here applied to explain DM haloes. Moreover, such a DF is used here to calculate the full family (from King-like to core–halo-like) of fermionic equilibrium profiles in full GR, in agreement with prior virial constraints. Finally, the stability, typical lifetime of such equilibrium states, and their possible astrophysical applications are studied within a thermodynamic approach.

The disadvantage of our procedure is that it does not explicitly include for the accretion and merger processes in a time-dependent manner as achieved in numerical simulations. However, we recall that the violent relaxation mechanism (as the one applying here within a maximum entropy production assumption) takes place subsequent times at each merging process event, probabilistically included in the Press–Schechter formalism through the mass variance σ(M).

Our approach is self-consistent, in the sense that the nature and mass of the DM particle involved in the linear matter power spectrum calculations (obtained within a class code for WDM) are the very same building block on the basis of virialized DM configurations with its inherent effects in the core–halo profiles. It applies to spherical and rather isolated DM configurations that just underwent a violent relaxation process within an |$\mathcal {O}({10}\, {\rm keV})$| WDM cosmology. Such configurations can start forming in the high-z (∼10) Universe, though they take place more ubiquitously at z ∼ 2, with boundary halo conditions consistent with a Press–Schechter theory of non-linear structure formation (see Appendix  B).

We outline all the main theoretical results and their astrophysical consequences obtained in this work as follows:

• Among all the GR spherically symmetric self-gravitating systems of|$\mathcal {O}({10}\, {\rm keV})$|fermions confined in a spherical box, which maximize the coarse-grained entropy at halo virialization in a WDM cosmology, there does not exist any thermodynamically stable core–halo configuration with halo masses of |${\sim} 10^{9}\!-\!10^{10}{\, \mathrm{M}_\odot}$|, that is able to agree with the observed DM surface density relation Σ_0D. Instead, diluted Fermi configurations (resembling pseudo-isothermal spheres) do fulfil both the thermodynamic stability and the DM halo Σ_0D phenomenology in the above DM halo mass range.¹⁴ See Section 3.1 for details.

• Among all the GR spherically symmetric and tidally truncated self-gravitating systems of |$\mathcal {O}({10}\, {\rm keV})$| fermions, which maximize the coarse-grained entropy at halo virialization in a WDM cosmology, there exist thermodynamically metastable core–halo configurations that are long-lived and agree with the observed DM surface density relation Σ_0D and with the expected N-body dispersion velocities (σ_h) for |${\sim} 10^{10}{\, \mathrm{M}_\odot}$| haloes. Such kind of stable core–halo fermionic profiles have effective temperatures of few |$10^{4}\, \mathrm{K}$|⁠, and are precisely of the same kind as the ones applied recently in Argüelles et al. (2018, 2019a) and Becerra-Vergara et al. (2020) to explain the rotation curve data in galaxies, with the DM core able to mimic the SMBHs at their centres. See Section 3.2 for details.

• The thermodynamic formalism for self-gravitating |$\mathcal {O}({10}\, {\rm keV})$| fermions introduced here allows for an SMBH formation mechanism through the DM core collapse of relativistic origin (see Section 4). Interestingly, it can start within the high-z (∼10) Universe, without the need of prior star formation or any BH seed mechanisms involving (likely unrealistic) super-Eddington accretion rates. More generally, a dense quantum core (i.e. without the singularity) at the centre of a stable and average-sized DM halo can reach masses between |${\sim} 10^{6}\hbox{ and }10^{8}{\, \mathrm{M}_\odot}$| (see Section 3.2), which may provide an alternative for the traditional SMBH scenario (Argüelles et al. 2018, 2019a, b; Becerra-Vergara et al. 2020).

• We have calculated for the first time the caloric curves for self-gravitating tidally truncated |$\mathcal {O}({10}\, {\rm keV})$| fermions at finite T within GR, and applied to realistic DM haloes (i.e. sizes and masses). Our results confirm and extend the double-spiral feature (the first of quantum nature and the second of relativistic origin) in the caloric curves with fixed N as recently obtained in Alberti & Chavanis (2018) and Chavanis & Alberti (2020). With the precise shape of the caloric curves, we have applied the Katz criterion for thermodynamic stability (Appendix  A), finding different families of stable as well as astrophysical DM profiles. They either are King-like (similar to Burkert) or develop a core–halo morphology able to fit the rotation curve in galaxies (Argüelles et al. 2018, 2019a). In the first case, the fermions are in the dilute regime (i.e. θ₀ ≪ −1) and correspond to a global maximum of entropy, while in the second case, the degeneracy pressure (i.e. Pauli principle) is holding the quantum core against gravity, and corresponds to a local maximum of entropy. Such metastable states are extremely long-lived as shown in Appendix  A, and more likely to arise in Nature than the former as argued in Chavanis (2005).

• We proved for the first time that for tidally truncated self-gravitating systems of neutral fermions at finite T in GR, the thermodynamical (and dynamical) instability occurs prior to the TP in the ρ₀ versus M curve, as explicited in Section 4. Indeed, the critical mass of gravitational core collapse |$M_\mathrm{ c}^{\rm cr}$| is achieved at the last stable configuration (with lower energy with respect to the TP), which interestingly coincides with the maximum but in a core mass M_c versus ρ₀ curve. Given that the value of M_c at the TP can differ by an order of magnitude below the real |$M_\mathrm{ c}^{\rm cr}$|⁠, it shows the importance of this result regarding the SMBH mass estimates, when applied to astrophysics.

The DM fermion mass of |$\mathcal {O}({10}\, {\rm keV})$| used in this work produces, down to Mpc scales, the same ΛCDM power spectrum, hence providing the expected large-scale structure (Boyarsky, Ruchayskiy & Shaposhnikov 2009a). Moreover, since the fermion mass is |${\gt} {5}\, {\rm keV}$|⁠, it is not in tension with constraints from the Lyman-α forest (Boyarsky et al. 2009b; Viel et al. 2013; Iršič et al. 2017), nor with the number of Milky Way satellites (Tollerud et al. 2008). Finally, on inner halo scales, our |$\mathcal {O}({10}\, {\rm keV})$| fermionic density profiles develope an extended plateau (similar to Burkert profiles), thus not suffering from the core-cusp problem associated to the standard ΛCDM cosmology (Bullock et al. 2017).

To conclude, we believe that the results shown in this paper may provide new insights into the formation and evolution of galaxies. Moreover, the degeneracy-pressure-supported core at the centre of the stable DM profile, and its eventual core collapse, may play crucial roles in helping us to understand the formation of SMBHs in the high-z Universe or in mimicking its effects without the need of the singularity at all. The astrophysical consequences of the analysis here developed – together with the results recently presented in Argüelles et al. (2018, 2019a) and Becerra-Vergara et al. (2020) – strongly suggest that such DM core–halo morphologies may be a plausible scenario within the late stages of non-linear structure formation, which should start to be seriously considered in the field.

ACKNOWLEDGEMENTS

The authors thank G. V. Vereshchagin for a critical reading of this paper, and J. A. Rueda, C. Llinares, and C. A. Vega-Martínez for useful discussions about different aspects of the work. CRA was supported by CONICET and MINCyT (code: PICT-2018-03743), and by the Secretary of Science and Technology of the Facultad de Ciencias Astronómicas y Geofísicas, UNLP. MID was partially supported by the University of Buenos Aires, and by the ANR project MOMA (France). RY was supported by Università La Sapienza (Rome) and by the International Center for Relativistic Astrophysics Network (ICRANet).

DATA AVAILABILITY

The data underlying this article will be shared on reasonable request to the corresponding author.

Footnotes

REFERENCES

APPENDIX A: THERMODYNAMIC STABILITY CRITERION AND LIFETIMES OF METASTABLE STATES

A1 Thermodynamic stability: the Katz criterion

The thermodynamic stability analysis pertinent to this work (valid either in the microcanonical or in the canonical ensembles) is carried out following the criterion described by Katz (1978, 1979). This is a powerful method based on the theory developed by Poincaré (1885), which allows us to obtain the number of unstable modes only from the topological properties of the series of equilibrium, without the need to calculate the full eigenvalue problem of the perturbed system. In this section, we first summarize the method in a rather generic and formal manner, and then we provide a ‘rule of thumb’ on how to apply it in an easy way depending on the ensemble under consideration.

Following Katz (1978, 1979), let f be some relevant function of the configuration that finds itself at an extremum, say a maximum, when the system is in a stable equilibrium, and x as a parameter that runs continuously through the series of equilibria. Then, it is there demonstrated that changes of stability for any individual perturbative mode will occur, at a given point in the series, if and only if the following two specific conditions are met:

• the slope of the ∂_xf versus x curve is infinite (i.e. the tangent is a vertical line), and

• the sign of said slope shifts at that point.

Note that this will usually mean the presence of a multivalued ∂_xf.

A vertical tangent at a specific point in the series is equivalent to a mode eigenvalue being zero (Katz 1978, 1979). Near that point, the sign of the eigenvalue is equal to that of the slope. A positive (negative) eigenvalue means that the system is stable (unstable) regarding perturbations in that mode. It is then immediate that when conditions (i) and (ii) are met, a shift in stability occurs at the single mode level.

A configuration is considered to be at a stable equilibrium whenever all of the modes are stable. Conversely, instability of a single mode suffices to make the whole configuration unstable. Therefore, knowledge of the total number of unstable modes for one single equilibrium is sufficient to determine the stability of all the other equilibria in the family. The procedure thus consists in simply locating a known stable point in the ∂_xf versus x diagram, and then following the curve, locating the points where conditions (i) and (ii) are met, while counting the resulting number of unstable modes.

When working in the microcanonical ensemble, it is natural to define f as the entropy of the system (f ≡ S) and x as the thermodynamic parameter of the ensemble, the energy, which in GR is equal to the (dimensionless) total mass of the system (⁠|$x\equiv \hat{M}$|⁠). This yields the derivative |$\partial _x f \equiv \frac{\partial S}{\partial \hat{M}}=\hat{T}_{\infty }^{-1}$| (the inverse temperature). Thus, the relevant curves in this context must be displayed through a |$T_{\infty }^{-1}$| versus M plot. However, in order to keep with conventions and more easily compare with other works, we choose to plot |$\hat{T}_{\infty }^{-1}$| versus |$-\hat{M}$| instead throughout the paper. This simple reverses the meaning of the sign of the slope near a vertical TP; a negative (positive) slope now means a stable (unstable) mode.

Following the explained above (as e.g. in the microcanonical ensemble) as well as Chavanis & Sommeria (1998) and Chavanis et al. (2015b), we can state as a practical ‘rule of thumb’ the following: (a) The arising of an unstable mode (when the negative slope in the |$T_{\infty }^{-1}$| versus −M curve becomes infinite just before turning into positive) is equivalent to say that the caloric curve ‘rotates clockwise’ and vice versa and (b) when the same curve ‘rotates anticlockwise’, it implies that a stable mode has been regained (the latter implying that a positive slope turned into negative just after becoming vertical). In this sense, once in a given unstable branch of the caloric curve (coming from an originally stable branch), it is necessary as many anticlockwise turns of the curve as clockwise passed, to regain the thermodynamic stability.

We exemplify this process for a box-confined case (i.e. |$\hat{N}=0.38 \lt N_{\rm OV}$| and |$\hat{R}=1000$|⁠) in Fig. A1, where the stable branches of solutions are plotted in continuous-blue, and the unstable branches are displayed in dotted-violet. A qualitative analysis in the microcanonical ensemble that is sequential in its nature proceeds as follows. When θ₀ ≪ −1, the systems behave like a classical Boltzmannian self-gravitating gas, robust in its stability (Lynden-Bell & Wood 1968). Such solutions lie in upper continuous-blue curve identified as the stable branch, up until the first clockwise turn takes place (i.e. gaining an instability mode; see Fig. A1). At this point, the caloric curve spirals inwards in the unstable branch, corresponding to the semidegenerate regime of solutions when θ₀ is just turning into positive. For this small |$\hat{R}$| case, this trend continues until the curve rotates anticlockwise and the stability mode is regained.¹⁵ From this point and on (which for this rather small |$\hat{R}$| occurs at θ₀ ≳ 10), solutions acquire a dense core – diluted halo morphology (see solution (3) in Fig. A3), where the central core is degeneracy-pressure supported (due to the Pauli principle) and the atmosphere is thermal-pressure supported. For N < N_OV, this stability trend continues for all accessible values of energy and temperature as θ₀ increases.

Figure A1.

Series of equilibrium solutions along the caloric curve for box-confined configurations of fermions with |$\hat{N}=0.38 \lt N_{\rm OV}$| and |$\hat{R}=10^3$|⁠. For such relatively small value of |$\hat{R}$|⁠, the curve develops a ‘dinosaur’s neck’, where the gravothermal catastrophe typical of Boltzmannian systems is avoided thanks to central degeneracy, as first shown in Newtonian gravity in Chavanis & Sommeria (1998). Every time the curve rotates clockwise [point (a) in the microcanonical ensemble], it loses a stability mode, which is regained when it rotates anticlockwise [at point (b)] according to the Katz criterion of thermodynamic stability. The stable (unstable) branches in relation with the entropy maxima (minimum/saddle points) are shown in Fig. A2.

Open in new tabDownload slide

Finding stable and metastable solutions via this procedure equates to proving that such a solution corresponds either to a global or to a local maximum of the entropy, respectively. Unstable solutions correspond either to a minimum or saddle point of entropy. The distinction between different entropy maxima can be ultimately made by explicitly comparing entropy values for a given energy, as done here in Fig. A2 in correspondence with Fig. A1. Metastable fermionic solutions (i.e. local entropy maxima) are of great importance in astrophysics as pointed out in Chavanis (2005). In particular, they are shown to be extremely long-lived and thus reachable in Nature, as proven here as well in Section A2 for the case of realistic DM haloes in a cosmological set-up.

Figure A2.

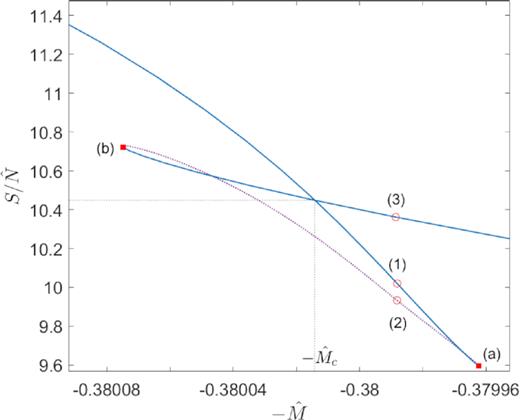
Normalized entropy |$S/\hat{N}$| (according to equation 17) with respect to total energy |$-\hat{M}$|⁠. Global entropy maxima are clearly distinguished from local entropy maxima, indicating the stable and metastable branches of solutions in Fig. A1. Minimum or saddle points of entropy correspond to the dotted-violet part of the curve, in correspondence with the thermodynamically unstable branch of Fig. A1. At the critical energy |$\hat{M}_\mathrm{ c}$|⁠, a gravitational (first-order) phase transition from a stable gaseous state - like solution (1)- to a stable core–halo one -like solution (3)- may take place.

Open in new tabDownload slide

Figure A3.

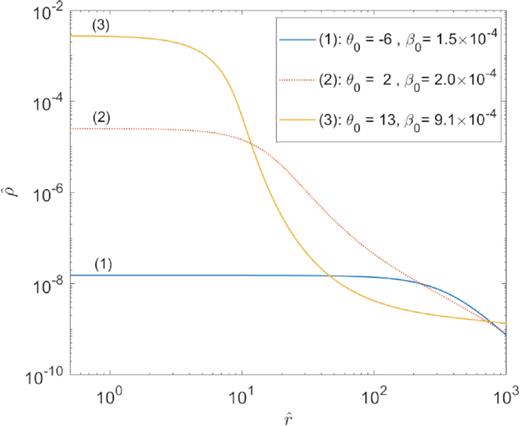
Density profiles corresponding to the equilibrium states of the caloric curve in Fig. A1 with energy |$\hat{M}\approx 0.38$|⁠. Only the profiles like (1) and the core–halo ones like (3) are thermodynamically stable, while profile (2) is thermodynamically unstable. This profile has no application to DM haloes since its boundary value |$\hat{R}$| is orders of magnitude below any realistic halo size.

Open in new tabDownload slide

Finally, we make a short description of the gravitational phase transitions occurring in these kinds of self-gravitating systems of fermions at finite T_∞, while we refer the reader to Bilić & Viollier (1999), Chavanis (2006), and Chavanis & Alberti (2020) for a broader discussion on the topic (where most of the examples in this Appendix, as the ones displayed in Figs. A1-A6., were already shown). Generally, the phase transitions (from a gaseous state to another composed by a degenerate core surrounded by a diluted halo) are manifested in the microcanonical (or canonical) ensembles, through the presence of a multivaluation in the entropy S (or free energy F), respectively. For relatively small-size systems as studied here (⁠|$\hat{R}=10^{3}$|⁠), we show in Fig. A2 the triangle-like shape with the consequent multivaluation in S implying the existence of a (microcanonical) first-order phase transition, occurring at a critical energy of about ∼0.5 in dimensionless units. Interestingly, for smaller size configurations (⁠|$\hat{R}=100$|⁠) and similar |$\hat{N}$|⁠, we show in Fig. A6 that such a microcanonical phase transition is no longer present, and S increases continuously with energy, while instead, in the canonical ensemble of the same system, the free energy does show a multivaluated shape. Indeed, in Fig. A5 we see that the free energies of both stable branches equate at the critical temperature |$\hat{T}_\mathrm{ c}=0.0044$|⁠, which indicates that a first-order phase transition takes place at that point. Such an apparent discrepancy in the existence (or not) of a gravitational phase transition is an explicit manifestation of the famous ensemble inequivalence, typical of long-range interaction systems.

A2 Lifetime of metastable configurations

Due to the long-range nature of the interaction among the self-gravitating particles, it can be shown that the lifetime (τ) of metastable states (i.e. local entropy maxima) scales as e^N, and therefore they are extremely long-lived for astrophysical systems with large N, and cannot be ignored with respect to global entropy maximum states (Chavanis 2005).

Next, we provide the explicit calculations of the lifetimes of the metastable states in different scenarios: First, we give the value of τ_c from equation () in terms of the caloric curve given in Fig. A4, as a pedagogical example. We do it under the choice of |$\hat{R}=100$| and |$\hat{N}=0.38$| (i.e. not applicable to DM haloes), for particular unstable and metastable states (labelled with U and M, respectively) with a temperature of |$\hat{T}=0.0053$| (or |$T=6.4E5\, \mathrm{K}$|⁠) as shown in Fig. A5. This gives as a result a tremendously long-lived metastable state with |$\tau _\mathrm{ c} = 7.8 \times 10^{-28}\, {\rm e}^{4.2 \times 10^{71}}\, \mathrm{s}$|⁠, which can be considered as ∞, being Δj = 4.2 × 10⁻³ and N = 10⁷⁴ fermions.

Figure A4.

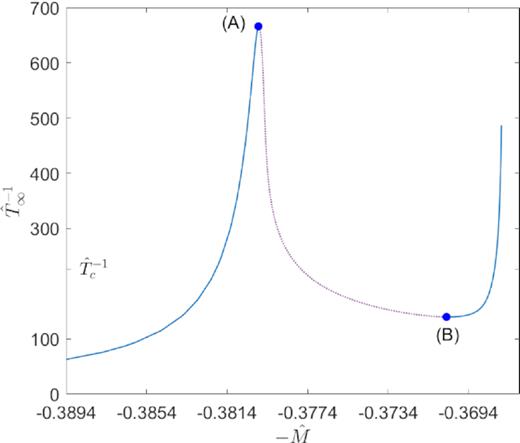
Series of equilibrium solutions along the caloric curve for box-confined configurations of fermions with |$\hat{N}=0.38 \lt N_{\rm OV}$| and |$\hat{R}=10^2$|⁠. According to the Katz criterion (canonical ensemble), at the maximum (A) of the caloric curve, it loses a stability mode, which is regained at the minimum (B) of the curve. The stable (unstable) branches in relation with the minimum (maximum/saddle points) of free energy are shown in Fig. A5. For such a low boundary size |$\hat{R}$|⁠, the curve develops a N-shape showing no microcanonical phase transition at all (at difference with Fig. A1).

Open in new tabDownload slide

Figure A5.

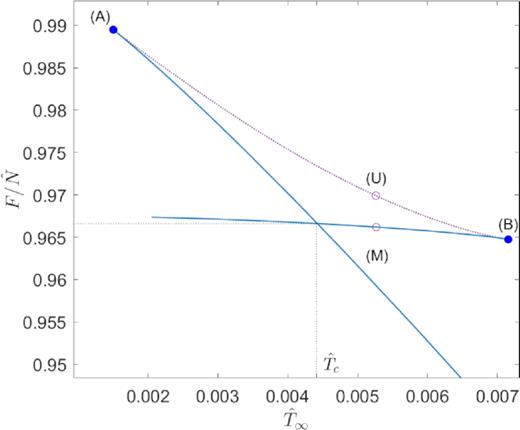
Normalized free energy |$F/\hat{N}$| (according to equation 16) with respect to dimensionless temperature |$\hat{T}_\infty$|⁠. The critical temperature |$\hat{T}_\infty$| indicates the place in the caloric curve in Fig. A4 where a (first-order) canonical phase transition may occur. This very result was first found in Bilić & Viollier (1999).

Open in new tabDownload slide

Figure A6.

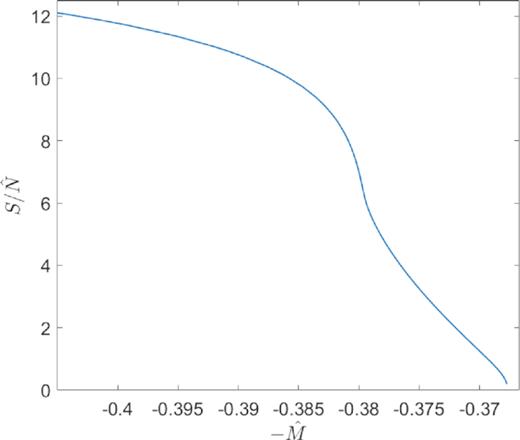
Normalized entropy |$S/\hat{N}$| with respect to dimensionless energy |$-\hat{M}$| corresponding to the caloric curve of Fig. A4. The continuous (not multivaluated) trend of the entropy indicates that no microcanonical phase transition is present at difference with the canonical ensemble (see Fig. A5), evidencing the ensemble inequivalence typical of long-range interaction systems.

Open in new tabDownload slide

Finally, we estimate the lifetimes τ_μ ∼ e^NΔs of the metastable states selected in the three cases analysed within the microcanonical ensemble in Section 3. They are labelled as (5) for the case of Fig. 1, and (3) in the cases of Figs 4 and 7, with the corresponding unstable ones forming the entropic barrier as mentioned above. We first calculate the barrier of entropy per particle Δs between the selected states using equation (17), and then multiply by N. Interestingly, in all the three cases of astrophysical interest studied here Δs ≳ 0.2 (rising up to ∼10³ in the case of Fig. 4, while reaching a much lower value of 0.24 in Fig. 7 given the rather close position between the given unstable and metastable states), and |$N\sim \mathcal {O}(10^{70})$|⁠, thus making the lifetimes τ_μ of these metastable states essentially infinite for all the cases here studied.

APPENDIX B: DM HALO FORMATION WITHIN A WDM PARADIGM

A thermodynamical stability analysis of a quasi-relaxed system of self-gravitating fermions has been performed in the microcanonical ensemble within GR in Section 3. As explained in the introduction, violent relaxation is the main underlying relaxation process able to lead the fermionic halo into the steady state we observe, a process occurring at late stages on non-linear structure formation. The boundary conditions for the thermodynamical analysis of these self-gravitating systems, e.g. particle number and total radius, are valid after the virialization of the structure in the context of hierarchical structure formation. Given a cosmological evolution model, the Press–Schechter (PS) theory (Press & Schechter 1974) or its subsequent extensions (see e.g. Mo, van den Bosch & White 2010) can be used to get the relevant astrophysical magnitudes at formation such as virial mass and radius at a given collapse redshift z* (z* ≡ z_vir). Relating the mass of a given DM halo with its spatial extent follows directly from the definitions of a virial radius and the background density of the universe. However, estimating a typical redshift in which the structure is formed becomes key to the analysis, as the density is a time-dependent quantity. So, our objective for this appendix is, given a (total) halo mass scale M ≡ M_vir, to obtain an approximation to the spatial extent of the system right after virialization is complete: r_vir measured at the most probable gravitational collapse time t_vir. We use the Press–Schechter formalism to obtain a good estimation on the most probable collapse time for a given mass scale t_PS(M). Then, we use this estimate to obtain the virial radius of the system right after it virialized r_vir[M, t_PS(M)].

So, at redshift z haloes are formed in significant numbers for masses M ≤ M*. We can invert this relation so that, for a given substructure mass M, we can obtain a typical collapse redshift z*(M): This relation can be seen in Fig. B1, together with two selected values of M_vir = 6.2 × 10⁹ M_⊙ (blue dot) and M_vir = 5.9 × 10¹⁰ M_⊙ (green triangle) for a WDM cosmology with |$mc^2 = {10}\, {\rm keV}$|⁠, corresponding with the values used in Section 3.1. The value of M_vir = 5.4 × 10¹⁰M_⊙, at z* = 1.7 in the case of a WDM cosmology with |$mc^2 = {48}\, {\rm keV}$| (not displayed in the plot), is used in Section 3.2 and in Fig. 10. As the collapse mass M* indicates the z in which most structures of such mass are collapsed, we also plot in Fig. B1 the 3σ collapse mass defined as |$3 \sigma (M^{*}_{3\sigma }) = \delta _\mathrm{ c} (t)$| to indicate the expected formation redshift of the earliest haloes (see e.g. Binney & Tremaine 2008). For average- to low-mass haloes such as the ones considered in Sections 3.1 and 3.2, the PS formalism expects early halo formation at a redshift up to z ≈ 10 as shown in Fig. B1.

Figure B1.

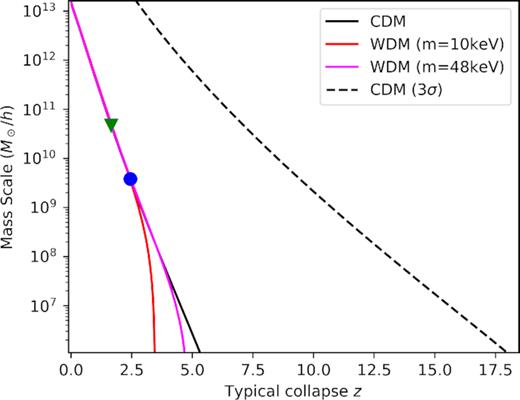
Characteristic collapse redshift z* as a function of substructure mass M_vir. CDM models in black line and WDM thermal relic models with |$mc^2 = {10}\, {\rm keV}$| and |$mc^2 = {48}\, {\rm keV}$| in red and magenta, respectively. An additional dotted line represents the collapse redshift of 3σ overdensities in CDM. The mass–virial radius combinations used for DM halo models in Section 3 are marked on the plot with a green triangle and a blue dot.

Open in new tabDownload slide

Once this typical collapse redshift is obtained, it is possible to evaluate the relation between scale mass and radius (B1), using z*(M) to obtain an estimation of the virial radius of substructure of mass M, evaluated at the time in which most of this substructure is already collapsed. This is shown in Fig. B2 for the above selected values of M_vir, implying r_vir ≡ r₂₀₀ = 11.1 kpc (blue dot), r_vir = 29.7 kpc (green triangle, for an |$mc^2 = {10}\, {\rm keV}$| cosmology), and r_vir = 28.5 kpc (for an |$mc^2 = {48}\, {\rm keV}$| cosmology, not displayed in the plot).

Figure B2.

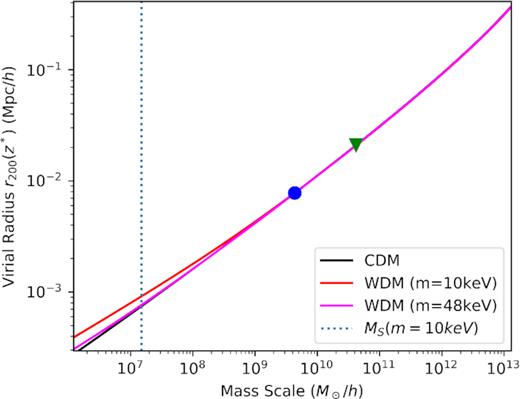
Virial radius r₂₀₀ at virialization time as a function of substructure mass M_vir. CDM models in black line and WDM thermal relic models with |$mc^2 = {10}\, {\rm keV}$| and |$mc^2 = {48}\, {\rm keV}$| in red and magenta, respectively. In blue dotted line, the free streaming mass scale |$M_{\mathrm{ S}} = 2 \times 10^{7}{\, \mathrm{M}_\odot}$|⁠. The green triangle and blue dot correspond to the ones selected in Fig. B1 for the astrophysical application of Section 3.

Open in new tabDownload slide

In Figs B2 and B1, the results obtained here using several different cosmological models are compared. For ΛCDM models, we simulate the power spectrum P(k) using best-fitting parameters from Planck’s 2018 data release (Planck Collaboration VI 2020), and compare these results with the ones obtained by replacing CDM for sterile neutrino WDM components of |${10}$| and |${48}\, {\rm keV}$|⁠, leaving all other cosmology parameters equal. In the latter, the power spectra are simulated using class version 2.7.2 (Lesgourgues & Tram 2011) and sterile neutrino WDM phase-space distribution at production is simulated using Venumadhav et al. (2016) with mixing angles of θ² = 5 × 10⁻¹¹ and 10⁻¹² for the |${10}$| and |${48}\, {\rm keV}$| models, respectively. We can see in Fig. B2 that differences between CDM and WDM models are insignificant with respect to this relation.

Also plotted in Fig. B2, we can see the corresponding free streaming scale of the |$mc^2={10}\, {\rm keV}$| WDM model, indicating the smallest non-suppressed structures in the power spectrum. Typically, WDM models establish a cut-off in the power spectrum of metric perturbations due to free steaming of particles. This implies that the formation of objects under a certain length-scale is suppressed and the number of small, low-mass haloes and satellite galaxies is significantly lower. We plot an estimate to this mass scale using the prescription in Viel et al. (2005) for sterile neutrino free streaming.