-
PDF
- Split View
-
Views
-
Cite
Cite
P R B Oliveira, R Martinez, D Fulvio, E F da Silveira, Energetic ion irradiation of N2O ices relevant for Solar system surfaces, Monthly Notices of the Royal Astronomical Society, Volume 502, Issue 1, March 2021, Pages 1423–1432, https://doi.org/10.1093/mnras/stab083
Close - Share Icon Share
ABSTRACT
Ices are the dominant surface material of many Solar system objects, such as comets and trans-Neptunian objects. They are continuously exposed to ion bombardment by solar wind ions and cosmic rays, which trigger secondary ion emission, contributing to the exosphere formation. Laboratory studies demonstrated the effects of energetic processing of ices at low temperature, showing the production of molecules and free radicals of astrophysical interest. Nitrous oxide (N2O) is one of the molecular species observed in star-forming sites, reason why it may be present in the ices covering some minor bodies in the outer Solar system. In the current work, N2O ice at 10 K was irradiated by energetic (MeV/u) multicharged heavy ions (e.g. 105Rh and 140Ba); the sputtered species were detected and analysed by the TOF-PDMS technique (time-of-flight plasma desorption mass spectrometry). Small positive and negative secondary ions were identified: N+, N2+, NO+, O+, and O−. The bombardment also induces production of ion cluster series: (N2)nR|$_{m}^+$|, (NO)nR|$_{m}^+$|, (N2O)nR|$_{m}^+$|, where R = N+, N2+, NO+, N2O+, Om+ (n up to ∼ 10, m = 1−3). Their yield distributions follow the sum of two decreasing exponentials, one fast -F and another slow -S, suggesting a two-regime formation. Most of the yield distributions have the same pair of exponential decay constants, around kF ∼ 1.4 and kS ∼ 0.15 u−1. Based on this behavior, an emission description for aggregates is proposed, useful to understand the processes by which neutral and ionized molecular species are delivery to the gas phase in space.
1 INTRODUCTION
Ices are ubiquitous present in the outer Solar system, for instance on the surface of comets, trans-Neptunian objects (TNOs) as well as on planets and their moons (e.g. Schmitt, de Bergh & Festou 1998; Barucci 2008; Strazzulla 2011; Mastrapa, Grundy & Gudipati 2013). Moreover, icy mantles cover dust grains in dense molecular clouds in the interstellar medium (ISM), where the grain temperature may be as low as 10 K therefore allowing gas phase atomic and molecular species to condense on them (e.g. Boogert, Gerakines & Whittet 2015; McGuire 2018). Among the ices of astrophysical interest, those containing nitrogen are particularly important due to their reactivity and are considered potential precursors of prebiotic molecules (e.g. Charnley & Rodgers 2002; de Barros et al. 2017; Fulvio et al. 2019); indeed, among all the known molecules detected in the gas phase of the ISM, almost 40 |${{\ \rm per\ cent}}$| are nitrogen bearing (e.g. Jamieson et al. 2005). This is a consequence of the nitrogen rich chemistry, which produces a variety of complex molecules, although the great majority of interstellar nitrogen is likely to exist in the diatomic form (e.g. Womack, Ziurys & Wyckoff 1992; Snow 2004). Due to the fact that N2-containing molecules are inactive in the microwave and infrared spectral regions, our knowledge of the abundance of diatomic nitrogen in space is still limited. Even so, N2 ice was identified as the primary surface component of Pluto and Triton, in the solid state, thanks to the 4656 cm−1 stretching mode (e.g. Bernstein & Sandford 1999; Sandford et al. 2001). The NASA New Horizons mission confirmed the N2 ice presence in trans-Neptunian objects (TNOs), as well as on Pluto surface (e.g. Cruikshank et al. 2015).
Concerning the interstellar medium (ISM), measurements using the NRAO 12-m telescope revealed significant concentrations of N2O (a relative fractional abundance of 10−9 to molecular hydrogen H2) in the high-mass star-forming site SgrB2(M) (e.g. Ziurys et al. 1994). More recently, N2O (nitrous oxide) was detected, for the first time, towards the low-mass protostar IRAS 16293−2422B, through confirmation with the single-dish TIMASSS survey (e.g. Ligterink et al. 2018). Observations suggest that presence of nitrous oxide is related to NO (e.g. Ziurys et al. 1994; Halfen, Apponi & Ziurys 2001).
Even though the N2O molecule has not yet been detected in any object of the outer Solar system, it has been shown by several laboratory experiments that either energetic processing and non-energetic surface reactions of different icy mixtures of planetary interest (such as those mixtures containing N2, H2O, and O2 or N2 and CO or the studies where NO2 reacts with H, O, or N) may lead to the appearance of N2O (e.g. Boduch et al. 2012; Sicilia et al. 2012; Ioppolo et al. 2014). Simpler condensed gases, like N2 and O2 mixtures, irradiated at 34 K with energetic (∼0.5 MeV u−1) heavy multicharged ions (105Rh and 140Ba as well as other 252Cf fission fragments) also conducted to the formation and emission of new hybrid species like N2O (e.g. Ponciano et al. 2008). In addition, experiments of nitrogen implantation in pure H2O ice have shown the N2O formation (e.g. Strazzulla 2011). Their results indicate that N2O and NO species are produced from reactions between the implanted projectiles and the ions within the target.
Accordingly, solid N2O which sublimation temperature, at 10−7 mbar, is ∼75 K (e.g. Pereira et al. 2019), may also be formed on the surface of outer Solar system objects, in low temperature environments like on Triton and Pluto surfaces, at about 40 K (e.g. Tryka et al. 1993, 1994). In fact, such surfaces are subjected to constant solar wind and cosmic rays irradiation (e.g. Strazzulla & Johnson 1991; Palumbo et al. 2008; Fulvio et al. 2019), therefore experiencing the same sort of processing studied in the laboratory works above mentioned, where common ices like H2O, N2, CO2, and CO may undergo molecular dissociation, followed by reactions between constituent atoms/ions, to generate N2O. Similarly, non-energetic surface reactions may also induce the formation of N2O. For what said, according to Hudson et al. (2008), N2O is one of the species most likely to exist on the surfaces of TNOs.
Irradiations of N2O ices have also been performed. For instance, Almeida et al. (2017) investigated the irradiation of frozen N2O molecules by energetic (1.5 MeV) 14N+ ion irradiation, aiming to estimate their half-life in astrophysical environments. Electron beams were also used to study chemical processing induced by 1 keV e− irradiation of a solid N2O ice sample at 25 K (e.g. Sivaraman et al. 2008). Besides the production of ozone, they observed the appearance of several oxides of nitrogen (NO2, N2O2, N2O3, N2O4, and N2O5). Fulvio et al. (2019) studied the effects of 200 keV protons irradiation on N2O ices and NO2:N2O4 = 1:1 ice mixtures at 16 and 50/60 K and showed that within 105−108 yr may be produced amounts of NO ice detectable by the James Webb Space Telescope.
Cosmic rays, solar wind, and also magnetospheric ion irradiation cause, among other effects, ejection of atoms and molecules from the irradiated surface (e.g. Grasset et al. 2013). Sputtering of atoms, molecules, ions, and radicals from icy surfaces may populate and maintain exospheres of those objects in the Solar system (e.g. Plainaki et al. 2015; Martinez et al. 2017, 2019). The interactions of cosmic rays and of solar wind with icy surfaces are different from each other since they have distinct energy distributions. As a consequence, the projectile energy loss per unit path-length (stopping power) is higher at energies where inelastic collisions occur. At these conditions, the electronic stopping power dominates (in this regime, both energy and momentum from the ion projectile are transferred to the target atoms by ion–electron interactions). Those interactions influence very likely the way those exospheres are formed; as the formation and presence of molecular clusters in the Hermean exosphere reported by Killen, Bida & Morgan (2005) and Killen et al. (2014).
The experiments of this work were performed to understand the interaction of cosmic rays with the surface of TNOs, Galilean moons, or Saturn’s inner satellites, where icy N2O may be present. For this objective, N2O ices were irradiated with energetic heavy ions, which are fission fragments (FF) emitted by 252Cf source, simulating heavy constituent ions of cosmic rays (e.g. Farenzena et al. 2006; Martinez et al. 2006). The interaction yields an electronic stopping power of about ∼5 keV nm−1, situation in which the electronic stopping power of heavy ions on N2O is higher than the nuclear one.
2 SPUTTERING – EXPERIMENTAL METHOD
N2O ice was irradiated by energetic (∼0.5 MeV u−1) heavy multicharged ions emitted by a 252Cf source (fission fragments) at the Van de Graaff Laboratory of the Pontifical Catholic University of Rio de Janeiro (PUC-Rio), Brazil. Secondary ion desorption was studied using the time-of-flight plasma desorption mass spectrometry (TOF-PDMS) technique. Experiments were performed inside a high vacuum chamber (base pressure of the order of 10−7 mbar). The experimental setup consists of a copper substrate mounted on a JANIS Closed Cycle Refrigerator Helium Cryostat, a 252Cf ionization source (inside a protection capsule), and a time-of-flight mass spectrometer (TOF; Fig. 1). Details about the experimental setup were presented in previous works (e.g. Collado et al. 2004b; Farenzena et al. 2006).
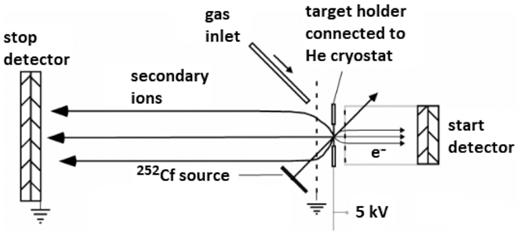
Schematic representation of the PDMS-TOF-SIMS experimental set-up (adapted from Martinez et al. 2006). The ion beam impinges at an angle of 45○ on the deposited ice film.
Inside the high vacuum chamber, the N2O ice was grown on to a copper substrate previously cooled to 10 K. By using a needle valve, a weak flow of gas was directed to the substrate where it is condensed. To reduce contamination by residual gas in the experimental chamber, the upper ice layers of the target were renewed continuously through the constant deposition of N2O gas on to the substrate. The base pressure at these conditions was of the order of 10−5 mbar.
Nitrous oxide molecules are deposited at low temperature on to a Cu substrate and at constant pressure deposition of 10−5 mbar. The heterogeneous ice nucleation process is influenced by physico-chemical properties of both the substrate and the gas to be condensed. The nucleation and growth processes happen by random adsorption and desorption of vapour molecules, while growth and decay of small clusters of molecules proceed on the surface. Only the clusters larger than the critical size grow stably (e.g. Seki & Hasegawa 1983). Thus, the formed N2O ice is an amorphous solid with ‘preformed clusters’ of N2O inside.
Due to ion–surface interactions, close to the impact site (infratrack, r ∼ 1.5 Å) molecular dissociation and recombination processes occur, generating a temporary plasma. Around it, a negative region (called ultratrack, r ∼ 15 Å) is formed. Several species are emitted from the surface. Around the impact site, emission of light ions such as H+ happens. In adition, the subsequent recombination tends to synthesize stable clusters with small number of constituents (fast regime). The next stage is the track relaxation, when fragmentation causes the emission of small and large fractured parts of the solid surface (slow regime). Consequently, preformed or newly formed larger chemical species are desorbed (e.g. Andrade et al. 2008)
252Cf fission fragments, having average energy of about 65 MeV after passing the protection foil, were used for the heavy ion bombardment of the N2O ice target. The interaction of fission fragments with the solid induces the emission of neutrals and secondary ions from the bombarded target. In order to transport the secondary ions ejected from the sample towards the TOF spectrometer, an electrical potential of ±5 kV is applied to bring out the desorbed ions: the positive electrical potential for cations, and the negative electrical potential for anions.
The secondary ions were driven, by polarizing the electron grid with +6.2 kV for cations or −3.8 kV for anions, towards a Micro-Channel-Plate (MCP) detector, that gives the STOP signal for the time-of-flight spectrometer. The START signal was given by a second MCP detector when reached by secondary electrons emitted at the copper substrate’s backside and accelerated to 2.2 keV. Using these START and STOP signals, time-of-flight spectra were obtained; the calibration of the mass spectrum was performed from the knowledge of low mass desorbed ions. Detection efficiency is estimated to be about 50 |${{\ \rm per\ cent}}$| (e.g. Collado et al. 2004b).
Note that the 5 kV potential is not necessary to extract the ions from the ice. Instead, it is used to conduct the ejected ions towards the detector and to increase their kinetic energy for a more efficient detection. In a more sophisticated technique called delayed extraction (not used in the current work), this potential is only applied nanoseconds after the projectile impact, aiming to accelerate only final products. The technique consists in waiting the complete decay of metastable emitted species and then start to accelerate stable ionic fragments (e.g. Collado et al. 2004a).
The main line of the ion desorption process is the following. Whenever a MeV projectile impinge an insulator surface, electronic excitation is the first phenomenon that occurs, which may be followed by (secondary) electron emission. The inner part of the projectile’s track becomes electron-depleted (therefore positively charged) and repels away from the solid the formed cations in its surface. Local electric fields are coulombian atomic ones, of the order of E ∼ K e2/r, where e is the electron charge and r is the atomic radius. Alternatively, E ∼ ionization potential/Bohr radius = 10 V/5 × 10−11 m = 2 × 1011 V m−1. These fields decrease very fast, either because the track neutralizes quickly or because the distance between charges increases during ejection (e.g. Iza et al. 2005).
On the other hand, electric fields used in TOF mass spectrometry correspond, for instance, to 5 kV difference of potential applied between electrodes placed 5 mm apart. This means ETOF = 5 × 103 V/5 × 10−3 m = 1 × 106 V m−1, five orders of magnitude lesser than the electric fields responsible for the electronic sputtering. The conclusion is that the so called extraction potential generates electric fields near the impact site that are negligible compared with local atomic fields. Extraterrestrial sputtering yields are the same as their analogues in laboratory.
3 SECONDARY ION FORMATION
Experiments with swift multicharged heavy ions, such as fission fragments having atomic numbers higher than that of iron, are indeed very practical to analyse ion desorption and allow mimicking the effects produced by the heavy ion fraction of cosmic rays. Even though heavy ions constitute a few per cent of cosmic rays, it has been demonstrated that processing effects of these particles in ices are by far more efficient than protons or alpha particles with the same velocity (e.g. Seperuelo Duarte et al. 2010), or even by photons (e.g. Gerakines, Moore & Hudson 2001), because of their high stopping power and energy deposition processes.
Energetic processing of N2O ices has been the subject of recent laboratory studies, with experiments performed with different N2O ice temperatures (in the range 10–75 K), different projectile energies (1 keV electrons; 200 keV protons; 1.5 MeV N+; 90 MeV Xe23 +), or by considering different sources of processing, i.e. ions (H+, N+, Xe23+) rather than electrons (e.g. Sivaraman et al. 2008; Almeida et al. 2017; de Barros et al. 2017; Fulvio et al. 2019; Pereira et al. 2019). All these studies focus on the new molecules formed within the ice by the irradiation processing and showed that, despite some identification discrepancies and abundance variations among different studies, the main species are: NO, (NO)2, NO2, N2O3, N2O4, N2O5, and O3. To form them within the processed ice, one should start considering that the dissociation of N2O delivers (i) O and N2 or (ii) N and NO for chemical reactions. Starting from this point and simplifying the discussion without including here neither the bond’s dissociation energy nor statistical consideration on the probability of each dissociation and recombination reaction, several chemical pathways become possible. Considering for instance the free O atom formed in (i), it may recombine to form O2 which, in turn, could subsequently react with an atomic O to form O3. Alternatively, the free O atom formed in (i) may recombine with N2O to form two NO molecules, the nitric oxide dimer (NO)2, or the pair O2 + N2. A free O atom may then recombine with a NO monomer to form NO2, which may react with another NO2 to form N2O4 or which may also react with a third NO to form N2O2. This last molecule can alternatively be formed by the reaction of a free O atom to N2O2 or by the reaction of molecular O2 directly to N2O. Two NO2 molecules may also react with O3 to form N2O5 (and O2). Alternatively, N2O5 may be formed by the reaction of N2O with 2O2 or by the reaction N2O + O3 + O.
A similar reasoning could be repeated with the other primary dissociation products available in (i) and (ii), such as the free N atoms, further analysis are outside the purpose of the current study. For detailed discussion on the possible chemical pathways related to the dissociation of N2O by irradiation processing, the interested reader is invited to read the previously mentioned works, such as Sivaraman et al. (2008), Almeida et al. (2017), and references therein.
The goal of this brief description is to point out that the N2O dissociation and the multiple recombination pathways of the dissociation products may explain the presence of: (i) all the main species identified within the ice in previous irradiation experiments of solid N2O; (ii) those identified as secondary ions and clusters emitted from the irradiated N2O ice.
3.1 Sputtering of positive ions
Fig. 2 shows the mass distribution of positive secondary ions with mass-to-charge ratio up to 60 u, emitted from N2O ice at 10 K when irradiated by swift multicharged FF. The lower panel of Fig. 2 shows, in a semilog plot, the sputtered positive ion yield (PIY), i.e. the number of desorbed ions per impact for each ion’s mass (e.g. Vestal 1983; Usmanov et al. 2017). Actually, this numbers should be regarded as the minimum values, since the efficiency of the ‘stop’ detector is lesser than unity.
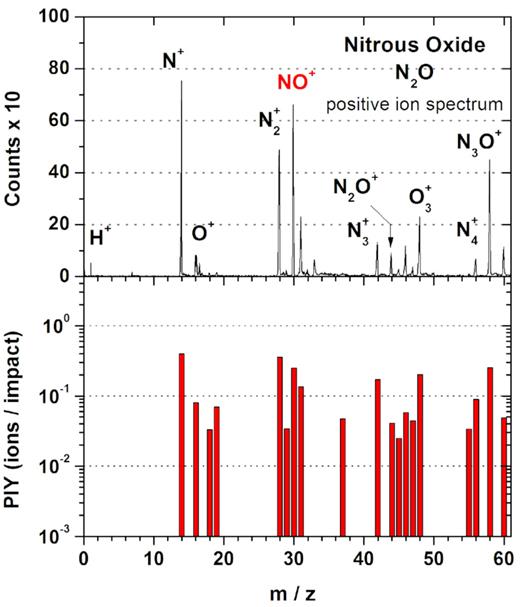
Top panel: Mass spectrum of positive secondary ions desorbed from the nitrous oxide (N2O) ice at 10 K. Bottom panel: PIY (ions/impact) for each fragment and hybrid desorbed species, from TOF mass spectra.
The positive mass distribution shows a small peak of the hydrogen ion (H+), which means that the surface contamination may be considered negligible. The general fragmentation pattern for the nitrous oxide includes nitrogen (atomic and molecular), oxygen, and nitric oxide ions: the mass spectrum is characterized by relatively intense peaks corresponding to masses 14, 28, and 30 u, attributed to N+, N2+, and NO+, respectively. Surprisingly, the desorption yield of the O+ (16 u) and N2O+ (44 u) species are low. On the other hand, the recombination pattern for the N2O irradiated by swift heavy ions comprises mainly aggregates of the fragments like the ozone ion O3+, at mass 48 u, and the cluster series Nn+ (with n = 3 and 4) at masses 42 and 56 u. Mass 60 u, may be attributed to N3O+ ion, a member of a new series, as will be seen in next sections. Possible cluster attributions for the observed mass peaks are treated in Section 3.3.
3.2 Sputtering of negative ions
Similarly to the positive ion spectrum analysis, Fig. 3 shows the spectrum of negative secondary ions with mass-to-charge ratio up to 60 u. They have desorbed from 10 K N2O ice irradiated by FF. As well, the lower panel of Fig. 3 shows the sputtered negative ion yield (NIY), i.e. the desorption yield.

Top panel: Mass spectrum of negative secondary ions desorbed from the nitrous oxide (N2O) ice at 10 K. Bottom panel: NIY (ions/impact) for each fragment and hybrid desorbed species, from TOF mass spectra.
Once again, the hydrogen peak appears in the negative secondary spectrum as H−, with a very weak intensity, confirming the low surface contamination. Another hydrogen-containing peak is the OH− ion, at 17 u, which is small too. The most intense secondary ion in the spectrum is O−, at 16 u. In addition, it is important to note the relatively high desorption yields of the O2− and O3− ions, at 32 and 48 u, which are aggregates of the oxygen ion. These observed cluster series will be analysed in Section 3.3. Concerning the N–O containing species, the most relevant one occurs at mass 60 u: the N2O2−. Also the NO2− ion peak should be noted at 46 u. Interestingly, the charged NO species peak is also present in the negative spectrum, but with intensity much lower than that in the positive one.
Although the sputtering yields of positive ions are expected to be higher than those of negative ions due the secondary electron emission, the dissociation of the N2O molecule into a cation and an anion may be energetically favourable. This is the case for the N2O → N2+ + O− channel, which is open at 12.2 eV of electronic excitation (determined by DFT calculations), a lower value than the N2O ionization energy (12. 9 eV) or than the dissociation energy of any other cation + neutral + electron channel. This explains why the O− desorption yield is the highest (Fig. 3).
3.3 Sputtering of charged molecular clusters
The N2O ice radiolysis induced by swift heavy ions forms small and large fractured parts of the solid in the surface; a fraction of them desorb. According to the emission model discussed by Martinez et al. (2006), these physical–chemical processes occur in a small cylinder around the projectile trajectory inside the material, called ultratrack; moreover, in a region very close to the surface (a few molecular layers), emission of molecular aggregates happens. These emitted species may be neutral and/or charged, positive or negative, including hybrid aggregates. The emission of charged particles, called ion desorption, has already been observed before for many other condensed gases (e.g. Johnson 1990; Betts, da Silveira & Schweikert 1995; Hudson & Moore 2001; Farenzena et al. 2005; Martinez et al. 2006; Andrade et al. 2007; Andrade et al. 2009).
For instance, the formation of new species, like N2O, NO and aggregates, were observed when a mixture of O2 and N2 ices was irradiated by energetic heavy ions (e.g. Ponciano et al. 2008). Concerning cluster formation due to N2O irradiation, only gas phase experiments were accomplished. The authors reported the formation of negative cluster ions NO–(N2O) with n = 1, 2 (e.g. Coe et al. 1987; Jones & Csizmadia 1994). In the current experiment performed with solid N2O, besides several ionic hybrid species containing N2 and O2, various ionic cluster series are identified. To better observe the mass distribution of ionic clusters, Figs 4 and 5 show the spectra for positive and negative ions with mass-to-charge ratio up to 300 u, desorbed form the N2O ice.
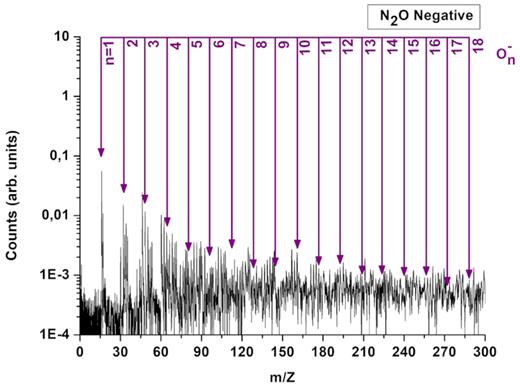
Mass spectrum of negative secondary ions desorbed from the N2O ice at 10 K showing the principal negative cluster series (O)n−.
The cluster series in the mass spectrum of positive ions can be classified in two main groups: the oxygen pure series On+ and the cluster series (N2)nRm+, (NO)nRm+, (N2O)nRm+, where the driving positive ion Rm+ is N+, N2+, NO+, N2O+, Om+ (m = 1 − 3). Thus, the cluster series in the mass spectrum of positive ions are mainly three (N2)n, (NO)n, and (N2O)n, with five different driving positive ions or radicals (N+, N2+, NO+, N2O+, Om+). The pure oxygen series will be analysed together with the negative one (On−), since both show similarities and interesting properties.
For the nitrogen clusters (N2)n, and for a better understanding and analysis, we decided to consider the radical Rm+ as N2N2+ instead of N2+. At first glance, the nitrogen clusters (N2)nN2N2+ and mostly (N2)nN+ appear to be the most abundant positive series, mainly due to the high concentration of nitrogen atoms in the target and consequently in the expanding plasma formed right after the interaction. Nevertheless, as analysed in the next section, they all have similar intensities. In fact, the N–O bearing clusters are the most abundant since there are 10 different clusters, product of the atomization–recombination emission mechanisms of precursor atoms.
On the other hand, the cluster series in the mass spectrum of negative ions (Fig. 5) is mainly characterized by the oxygen ion clusters (On−). Due to the relative low background, the observation of ionic species up to mass 300 u for positives and 500 u for negatives is possible. This means that On cluster ions up to n = 18 for positive and n = 30 for negative ions were detected and identified. The ion desorption yields in both spectra oscillate with a periodicity of two and three oxygen atoms (suggesting ozone clustering), feature also reported by Ponciano et al. (2008). They observed the same periodicity irradiating O2 pure ice. Before, Stulik et al. (1983) and Tonuma et al. (1994) reported the same effect for positive and negative cluster ions.
Electronic excitation is the main energy transfer mechanism from MeV projectile to target atoms. For the cases where the transferred energy is higher than the ionization energy, secondary electron emission occurs. If the emitted electron has low kinetic energy (up to a few eV) very likely it will be captured by nearby molecular species – forming anions; if it has tens of eV, new ionizations occur – forming cations. Provided that these anions or cations are produced near the target surface, they may escape from the solid as secondary ions (e.g. Iza et al. 2006).
4 SPUTTERING DEPENDENCE ON NUCLEARITY
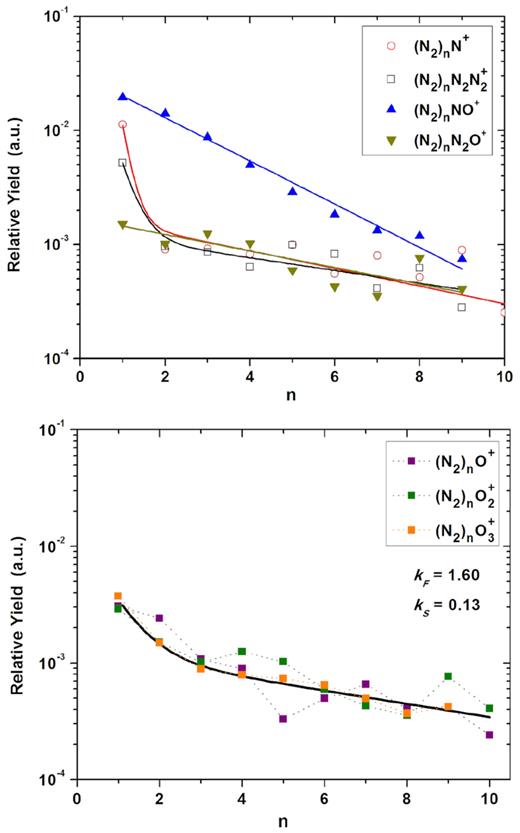
Relative Desorption Yield as a function of the nuclearity (n) for the (N2)n ionic cluster series. Top panel: with N-bearing radical Rm+. Bottom panel: with O-pure radical Rm+. The exponential slope constants k are determined depending on whether the data are fitted by a single or double exponential fitting.
The discussion on fast and low emission regimes is related to a model proposed for cluster emission based on two simultaneous and independent regimes. The energy transferred to the sample due to the ion-target interaction produces secondary electrons along the ion trajectory, creating a typical electric field of ∼1 V/Å. As discussed earlier, this phenomenon allows us defining two regions: the infratrack (r ∼ 1.5 Å), a positive region since the produced secondary electrons are moved radially away from the track. And the ultratrack (r ∼ 15 Å), a negative region around it.
Close to the impact site (infratrack) and tens of picoseconds after the impact, molecular dissociation and recombination processes happen, generating a temporary plasma. The subsequent recombination tends to synthesize stable clusters with small number of constituents (fast regime). In fact, the production of large clusters in this region is unlikely, since there is a relatively small quantity of ejecta (thousands of atoms) with high emission velocities (∼30 km/s). Thus a fast decreasing slope distribution (i.e. large kF values) is expected. After 10−13 s, the track relaxation takes place and fragmentation causes the emission of small and large fractured parts of the solid surface (slow regime). Generally, the cluster yield distribution shapes (the kS-slope) are fairly the same, which may indicate that the solid fragmentation pattern is rather insensitive to stopping power dependence (e.g. Hedin et al. 1985; Martinez et al. 2006; Ponciano et al. 2008).
Hereinafter, the three different cluster series [(N2)n, (NO)n, (N2O)n] are presented individually, each one with their radical ion (R = N+, N2+, NO+, N2O+, Om+ m = 1 − 3). For a better visualization and understanding, each radical is represented by the same colour and symbol along the different distributions, which is repeated for all series (Figs 6–8). Those that do not have an oxygen atom are represented by an open symbol, while a filled one represents those that have.
4.1 The (N2)n ion cluster series
Data of the seven clusters identified in this series are distributed in two graphics according to R+. In Fig. 6 the relative desorption yields for the cluster series (N2)n R+, with R+ = N+, N2N2+, NO+, N2O+ are presented. In the lower panel (Fig. 6) the Om+ (m = 1 − 3) clusters series desorption yields are showed.
On the one hand, the (N2)nN+ and (N2)nN2N2+ ionic cluster series show proportional distributions, with the two decreasing exponential curves almost parallel in the semi-log plot. This characteristic feature suggests that the same processes control the formation of these two cluster series. Also intensities are quite similar, which means that emission sputtering yields are about the same. On the other hand, the (N2)nNO+ and (N2)nN2O+ ion cluster series, despite their very different intensities, show proportional distributions but with only one exponential decay. This suggests a single formation process that would be the slow-decay regime, different from the former. Lastly, in Fig. 6 the three clusters containing oxygen radicals (N2)nOm+ (m = 1 − 3) are presented together because, as can be seen, they show similar behaviour with two decreasing exponential curves and yields on the same order.
The slope parameters (kF and kS) obtained from the fitting curve of equation (1), describing the cluster ion populations of ion-induced desorbed species, reflect the physical processes related to emission mechanisms. The kF / kS values for the (N2)nN+ and (N2)nN2N2+ clusters are 5.18 / 0.18 and 3.13 / 0.13 respectively, while for the (N2)nNO+ and (N2)nN2O+ clusters, which only shows the kS parameter, the values are 0.43 and 0.17, respectively. Moreover, the slope parameters for the (N2)nOm+ (m = 1 − 3) clusters are similar with the mean values of: |$\overline{k}_F$| = 1.60 and |$\overline{k}_S$| = 0.13.
It is interesting to draw attention to the (N2)nN2N2+ cluster data, for which the value of the constant kS is very similar to the cluster series (N2)n reported by Farenzena et al. (2005), kS = 0.17 (see fig. 10 therein), which shows that both findings should have the same origin.
4.2 The (NO)n ion cluster series
The relative desorption yields for the (NO)nR+ cluster series are presented in Fig. 7, in two panels. In the top panel (Fig. 7) the relative desorption yields for the cluster series with R+ = N+, N2+, NO+, N2O+ are presented. In the lower panel the Om+ (m = 1 − 3) clusters series desorption yields are showed.
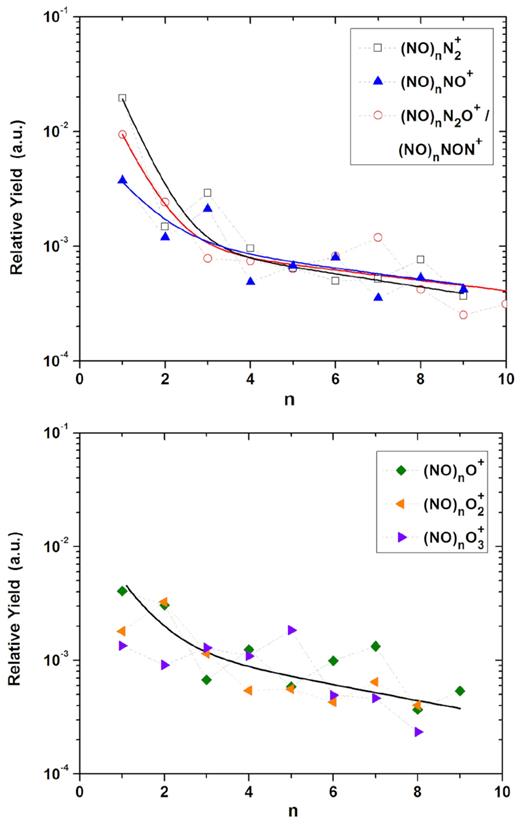
Relative desorption yield as a function of the nuclearity (n) for the (NO)n ionic cluster series. Top panel: with N-bearing radical Rm+. Bottom panel: with O-pure radical Rm+. The exponential slope constants k are determined by a double exponential fitting.
Because the (NO)nNON+ and (NO)nN2O+ hybrid clusters have the same mass, their mass distributions in mass spectrometry cannot be differentiated (top panel Fig. 7). Whereas considering the (NO)nN2+ and (NO)nNO+ clusters, a zigzag trend appears as the number of NO monomers grows. Even though all those differences along the distribution of each cluster, all the (NO)n ion cluster series have almost the same fitting parameters (slope and yield coefficients) with values |$\overline{k}_F$| = 1.72 and |$\overline{k}_S$| = 0.12. It is interesting to note that the mean slow coefficient (|$\overline{k}_S$|) is also similar as the one for (N2)nOm+ clusters. This suggests that larger masses of these clusters are formed by the same processes, whereas formation of the lighter ones is different, which is probably linked to the reaction N2O + N2O* |$\longrightarrow$| N2 + 2NO.
Finally, the ion cluster series (NO)nOm+ (m = 1 − 3) are presented in lower panel (Fig. 7). As in the case of (N2)nOm+ cluster series, here the three cluster series are exhibited together because they show quite similar decreasing exponential curves. Also interesting is that the slope parameters for these clusters, with mean values of: |$\overline{k}_F$| = 1.47 and |$\overline{k}_S$| = 0.16, are similar as for the (N2)nOm+ ones; this indicates, once again, similar processes of formation/emission.
4.3 The (N2O)n ion cluster series
The relative desorption yields for the seven clusters identified in the (N2O)n series are presented in Fig. 8. As before and for a better observation and analyses, cluster series with R+ = N+, N2+, NO+, N2O+ are presented in the top panel (Fig. 8) and the cluster series with R+ = Om+ (m = 1−3) are showed in the bottom panel. All the distributions are decreasing exponential curves but their behaviours are somehow different.
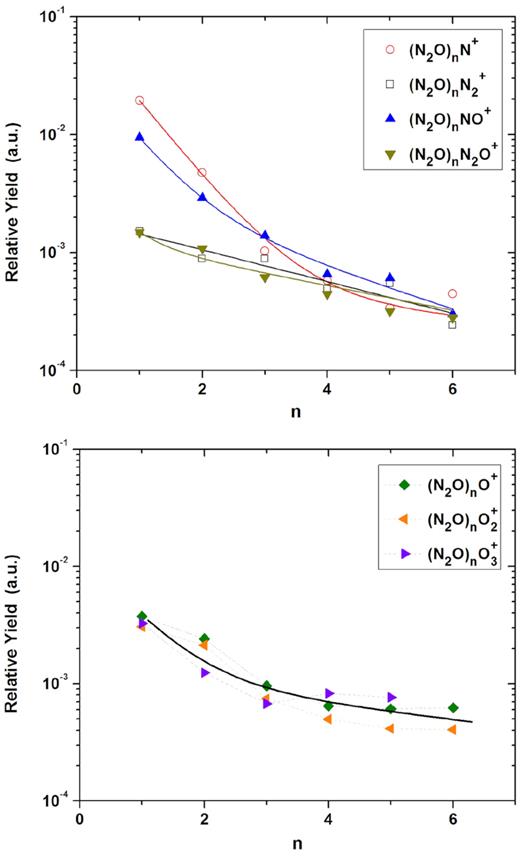
Relative desorption yield as a function of the nuclearity (n) for the (N2O)n ionic cluster series. Top panel: with N-bearing radical Rm+. Bottom panel: with O-pure radical Rm+. The exponential slope constants k are determined by a double exponential fitting.
At first glance, all (N2O)n ion cluster series in Fig. 8 (with R+ ≠ Om+) present roughly the same behaviour for n ≥ 3. For lower n, two tendencies are observed: (N2O)nN+ and (N2O)nNO+ cluster series show relative yields higher than the (N2O)nN2+ and (N2O)nN2O+ ones. This causes the fast (-F) slope parameter be higher for the first two series ((N2O)nN+ and (N2O)nNO+) and the second pair of clusters ((N2O)nN2+ and (N2O)nN2O+) show distributions with, apparently, only one decreasing exponential curve.
Although slope parameters for the slow regime for the four cluster series seem to be very similar, numerical values show differences varying around the mean value |$\overline{k}_S$| = 0.32 (see Table 1). On the other hand, for the fast regime, slope parameters are different for the two trends described before: |$\overline{k}_F$| = 1.60 for the (N2O)nN+ and (N2O)nNO+ cluster series and no |$\overline{k}_F$| for the (N2O)nN2+ and (N2O)nN2O+ cluster series. This finding indicates a single formation process in the slow-decay regime, where bigger clusters are formed, different from the former.
Decay constants values (kF and kS) for the nitrous oxide clusters obtained when N2O ice is irradiated by energetic multicharged heavy ions.
| Ionic cluster . | Cluster . | kF . | kS . | Yi, tot . |
|---|---|---|---|---|
| Series . | . | (u−1) . | (u−1) . | (au) . |
| (N2)n | (N2)nN+ | 5.18 | 0.18 | 0.001 |
| (N2)nN2N2+ | 3.13 | 0.13 | 0.021 | |
| (N2)nNO+ | – | 0.43 | 0.046 | |
| (N2)nN2O+ | – | 0.17 | 0.009 | |
| (N2)nOm+ | 1.60 | 0.13 | 0.011 | |
| (NO)n | (NO)nN2+ | 1.98 | 0.13 | 0.015 |
| (NO)nNO+ | 1.25 | 0.11 | 0.012 | |
| (NO)nN2O+ / | 1.94 | 0.11 | 0.016 | |
| (NO)nNON+ | ||||
| (NO)nOm+ | 1.47 | 0.16 | 0.008 | |
| (N2O)n | (N2O)nN+ | 1.51 | 0.12 | 0.017 |
| (N2O)nN2+ | – | 0.31 | 0.005 | |
| (N2O)nNO+ | 1.69 | 0.39 | 0.010 | |
| (N2O)nN2O+ | – | 0.45 | 0.005 | |
| (N2O)nOm+ | 1.45 | 0.15 | 0.009 | |
| On | On+ | 1.06 | 0.10 | 0.020 |
| On− | 1.17 | 0.12 | 0.019 |
| Ionic cluster . | Cluster . | kF . | kS . | Yi, tot . |
|---|---|---|---|---|
| Series . | . | (u−1) . | (u−1) . | (au) . |
| (N2)n | (N2)nN+ | 5.18 | 0.18 | 0.001 |
| (N2)nN2N2+ | 3.13 | 0.13 | 0.021 | |
| (N2)nNO+ | – | 0.43 | 0.046 | |
| (N2)nN2O+ | – | 0.17 | 0.009 | |
| (N2)nOm+ | 1.60 | 0.13 | 0.011 | |
| (NO)n | (NO)nN2+ | 1.98 | 0.13 | 0.015 |
| (NO)nNO+ | 1.25 | 0.11 | 0.012 | |
| (NO)nN2O+ / | 1.94 | 0.11 | 0.016 | |
| (NO)nNON+ | ||||
| (NO)nOm+ | 1.47 | 0.16 | 0.008 | |
| (N2O)n | (N2O)nN+ | 1.51 | 0.12 | 0.017 |
| (N2O)nN2+ | – | 0.31 | 0.005 | |
| (N2O)nNO+ | 1.69 | 0.39 | 0.010 | |
| (N2O)nN2O+ | – | 0.45 | 0.005 | |
| (N2O)nOm+ | 1.45 | 0.15 | 0.009 | |
| On | On+ | 1.06 | 0.10 | 0.020 |
| On− | 1.17 | 0.12 | 0.019 |
Decay constants values (kF and kS) for the nitrous oxide clusters obtained when N2O ice is irradiated by energetic multicharged heavy ions.
| Ionic cluster . | Cluster . | kF . | kS . | Yi, tot . |
|---|---|---|---|---|
| Series . | . | (u−1) . | (u−1) . | (au) . |
| (N2)n | (N2)nN+ | 5.18 | 0.18 | 0.001 |
| (N2)nN2N2+ | 3.13 | 0.13 | 0.021 | |
| (N2)nNO+ | – | 0.43 | 0.046 | |
| (N2)nN2O+ | – | 0.17 | 0.009 | |
| (N2)nOm+ | 1.60 | 0.13 | 0.011 | |
| (NO)n | (NO)nN2+ | 1.98 | 0.13 | 0.015 |
| (NO)nNO+ | 1.25 | 0.11 | 0.012 | |
| (NO)nN2O+ / | 1.94 | 0.11 | 0.016 | |
| (NO)nNON+ | ||||
| (NO)nOm+ | 1.47 | 0.16 | 0.008 | |
| (N2O)n | (N2O)nN+ | 1.51 | 0.12 | 0.017 |
| (N2O)nN2+ | – | 0.31 | 0.005 | |
| (N2O)nNO+ | 1.69 | 0.39 | 0.010 | |
| (N2O)nN2O+ | – | 0.45 | 0.005 | |
| (N2O)nOm+ | 1.45 | 0.15 | 0.009 | |
| On | On+ | 1.06 | 0.10 | 0.020 |
| On− | 1.17 | 0.12 | 0.019 |
| Ionic cluster . | Cluster . | kF . | kS . | Yi, tot . |
|---|---|---|---|---|
| Series . | . | (u−1) . | (u−1) . | (au) . |
| (N2)n | (N2)nN+ | 5.18 | 0.18 | 0.001 |
| (N2)nN2N2+ | 3.13 | 0.13 | 0.021 | |
| (N2)nNO+ | – | 0.43 | 0.046 | |
| (N2)nN2O+ | – | 0.17 | 0.009 | |
| (N2)nOm+ | 1.60 | 0.13 | 0.011 | |
| (NO)n | (NO)nN2+ | 1.98 | 0.13 | 0.015 |
| (NO)nNO+ | 1.25 | 0.11 | 0.012 | |
| (NO)nN2O+ / | 1.94 | 0.11 | 0.016 | |
| (NO)nNON+ | ||||
| (NO)nOm+ | 1.47 | 0.16 | 0.008 | |
| (N2O)n | (N2O)nN+ | 1.51 | 0.12 | 0.017 |
| (N2O)nN2+ | – | 0.31 | 0.005 | |
| (N2O)nNO+ | 1.69 | 0.39 | 0.010 | |
| (N2O)nN2O+ | – | 0.45 | 0.005 | |
| (N2O)nOm+ | 1.45 | 0.15 | 0.009 | |
| On | On+ | 1.06 | 0.10 | 0.020 |
| On− | 1.17 | 0.12 | 0.019 |
Concerning the clusters with R+ = Om+, they show distributions with the two decreasing exponential curves. In addition, they present very close yields. As for the two previous series with R+ = Om+, the slope parameters for these clusters are approximately the same ( |$\overline{k}_F$| = 1.45 and |$\overline{k}_S$| = 0.15); indicating – once again – similar processes of formation/emission.
4.4 The (O)n ion cluster series
The relative desorption yields for the cluster series On+ and On− are presented in Fig. 9. Both, positive and negative cluster series, follow roughly the same yield distribution (same shape and values). Similar results were found by Ponciano et al. (2008) they measured oxygen cluster distributions, positive and negative, proportional to each other; nevertheless, they reported relative yields of positive cluster ions about 20 times higher than those of the corresponding negative ones.
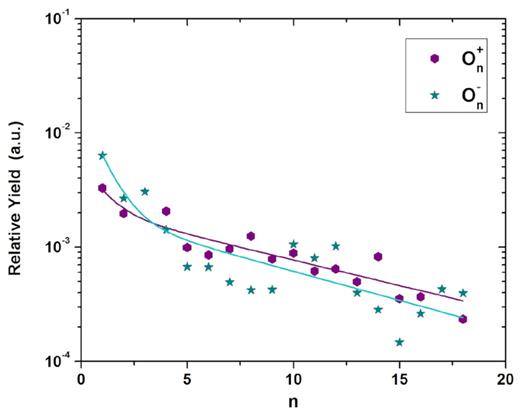
Relative desorption yield as a function of the nuclearity (n) for the (O)n ionic cluster series, positive and negative. The exponential slope constants k are determined by a double exponential fitting.
Thus, On+ and On− cluster series show proportional slope parameters: |$\overline{k}_F$| = 1.12 and |$\overline{k}_S$| = 0.11. Ponciano et al. (2008), regardless of relative yields, also found comparable slope parameters: kF = 0.9 and kS = 0.05. These features strongly suggest that the production of ionic clusters On+ and On− is determined by the formation of the neutral cluster On, which in turn indicates the same formation processes. In general, the yield of neutral secondary particles is estimated to be 2–3 orders of magnitude higher than the yield of the charged ones (e.g. Ponciano et al. 2008; de Barros et al. 2011).
The positive and negative desorption yields as a function of n fluctuate with certain periodicity because they depend: (i) on the emitted neutral cluster population and (ii) on an eventual n-dependence probability for an O± ion be attached to (O2)n and/or (O3)n clusters; this behaviour suggests molecular oxygen and/or ozone clustering (e.g. Ponciano et al. 2008). Stulik et al. (1983) and Tonuma et al. (1994) have also reported these oscillations for positive and negative cluster ions. respectively.
Table 1 shows the fast (-F) and slow (-S) decay values for the nitrous oxide clusters obtained when N2O ice is irradiated by energetic multicharged heavy ions.
In addition, the total ion desorption yields (Yi, tot) for the positive and negative ionic clusters are presented in Table 1. Yi, tot is defined as the number of ionic species (atoms and molecules) ejected per projectile impact as a sequence of events after the projectile impacts on to the surface. The employed technique (TOF-PDMS) is suitable to the study of fragmentation patterns formed during prompt induced desorption (i.e. sputtering), which occurs on time-scales of ∼10−11 s after the projectile impact (e.g. Martinez et al. 2014). The dependence of the ion desorption yield on the nuclearity is used to discuss the emission process of the desorbed ions. Thus, the Yi, tot analysis shows that the (N2)n ionic clusters are the most abundant species, particularly the (N2)nNO+ and (N2)nN2N2+, with desorption yields of 0.046 and 0.021 ions impact−1, respectively. On the other hand, the least abundant clusters are the (N2O)n ones, for instance, the (N2O)nN2+ and (N2O)nN2O+ clusters, both with 0.005 ions impact−1 as desorption yields.
5 ASTROPHYSICAL IMPLICATIONS
It is well known that bombardment of ices by energetic ions leads, among other effects, to the sputtering of atoms, molecules, and clusters from the irradiated surface (e.g. Wagner et al. 1993; Betts et al. 1995; Grasset et al. 2013; Martinez et al. 2006, 2019). A similar effect is expected by considering the bombardment of ices in space by cosmic rays, solar wind, and magnetospheric ion. As a consequence, the sputtering of atoms, molecules, ions, and clusters from the surface of icy bodies in the Solar system may populate and maintain their exospheres (e.g. Johnson et al. 2004; Strazzulla 2011; Plainaki et al. 2015; Martinez et al. 2017).
When considering the sputtering of positive ions (Section 3.1), it was observed among the main results that the mass spectrum presents relatively intense peaks attributed to N+, N2+, and NO+. The ion species O+ and N2O+ show low sputtering yields similarly to other aggregates, resulting from the recombination of fragments, like N3O+, O3+, and the series Nn+ (with n = 3 and 4). Interestingly enough, N2 ice was already found in the outer Solar system, due to the low temperatures in that region (e.g. Gudipati & Castillo-Rogez 2012), and the New Horizons mission confirmed the presence of N2 on the surface of Pluto (e.g. Bagenal et al. 2016; Gladstone et al. 2016; Grundy et al. 2016; Stern et al. 2015). Also, Rubin et al. (2015) reported the N2 identification in the coma of comet 67P/Churyumov–Gerasimenko by the ROSINA mass spectrometer onboard the Rosetta spacecraft. Other N–O containing molecules may be present in the solid phase on the surface of minor bodies in the outer Solar system, such as Pluto and Triton (e.g. Fulvio et al. 2019). In addition, the Cassini Plasma Spectrometer (CAPS) instrument made measurements of Titan’s plasma environment when the Cassini Orbiter flew through the moon’s plasma. Among the detected ion species from Titan’s magnetic tail, N2+ was found. The relative abundance of these ions is consistent with the densities of the corresponding neutral exosphere sources. The principal ions inferred from CAPS measurements are H+, H2+, N+, CH4+, and N2+ (e.g. Hartle et al. 2006).
The analysis of negative ion sputtering (Section 3.2) reveals that, among the most intense peaks, the ones related to O− were observed (and, at lower intensity, its aggregates O2− and O3+); the species N2O2− and NO2−. NO− are also present but with lower intensity. The Cassini–Huygens mission reported the detection of anions in Titan’s atmosphere (e.g. Coates et al. 2007; Wellbrock et al. 2019). Different mechanisms for the formation of negative ions have been proposed, being probably the most important the electron attachment, which is initiated by a free electron (e.g. Millar, Walsh & Field 2017). According to these authors, free electron energies in astrophysical environments vary from ∼0.9 to 90 meV, reflecting local temperatures from 10 to 1000 K. In the Solar system, the main electron source is the Sun with a flux neither radial nor isotropic and sensitive to magnetic fields (e.g. in the Van Allen belt). Most of electrons emitted by the Sun have a Maxwellian distribution corresponding to an average energy of ∼10 eV, which is too low to allow them induce ionization and form cations. Although having an energy too high to be captured in primary interactions, these electrons may impinge on cosmic bodies where, after some collisions, have their energy decreased down to below 2 eV when electron attachment starts (e.g. Matejcik et al. 1996). Desorption of preformed anions becomes possible for a certain time up to the local site be discharged. In laboratory experiments, energetic secondary electrons are generated in the region surrounding the projectile trajectory due to the ion–solid interaction, which may in turn leave the target surface with enough energy to form anions with the desorbed atoms and molecules de Castro, Bitensky & da Silveira (1997) and Iza, Farenzena & da Silveira (2007).
In addition to what said, the presence of O2 in Europa and Ganymede’s tenuous atmospheres was already detected via Hubble Space Telescope (HST) by observations of atomic oxygen emissions at 1304 and 1356 Å (e.g. Hall et al. 1995, 1998; Plainaki et al. 2015). It is thought that the energetic magnetospheric ions and electrons may produce the O2 by radiolytic decomposition of water ice (e.g. Johnson 1990).
Finally, the current work demonstrates that N2O ice sputtering produces a great variety of clusters and aggregates, as the result of the recombination of the N2O fragments. A detailed physico-chemical discussion on these clusters and aggregates is done in Sections 3.3 and 4. It is expected that this analysis may be useful as the starting point for further discussion as some of these species become observed in space.
6 CONCLUSIONS
The N2O pure ice was irradiated at 10 K by energetic (MeV u−1) multicharged heavy ions (e.g. 105Rh and 140Ba), sputtering small positive and negative secondary ions, particularly ionic clusters. A similar process is expected to occur in space when cosmic rays, solar wind, and magnetospheric ions bombard icy surfaces. Among small sputtered ionic species, N+, N2+ NO+, O+, O− are identified. Furthermore, abundant ejection of ion cluster are observed: (N2)nRm+, (NO)nRm+, (N2O)nRm+, with Rm+ = N+, N2+, NO+, N2O+, Om+ (n up to ∼ 10, m = 1–3). Several of the detected ions in the current experiment are present in many minor bodies of the Solar system objects. For instance, N2 ice is found in the outer Solar system, due to the local low temperatures (e.g. Gudipati & Castillo-Rogez 2012). Also, they were detected in the ISM, towards the molecular cloud Sgr B2 using the NRAO telescope: Liszt & Turner (1978) reported the identification of NO and Ziurys et al. (1994) reported the detection of N2O.
The relative yield distributions of the sputtered species are determined. The cluster yields distributions of the positive and negative cluster ions, plotted as a function of the number of monomers (nuclearity), are well fitted by the sum of two-exponential decay functions. This double exponential behaviour has already been reported for other ices bombarded by heavy ions in high stopping power conditions and may explain emission mechanisms (e.g. Hedin et al. 1985; Martinez et al. 2006; Ponciano et al. 2008). In addition, the total ion desorption yields (Yi, tot) for positive and negative ionic clusters are determined. The Yi, tot analysis shows that the (N2)n ionic clusters are the most abundant species, particularly the (N2)nNO+ and (N2)nN2N2+ ones, with desorption yields of 0.046 and 0.021 ions impact−1, respectively. On the other hand, the (N2O)n species are the least abundant clusters, for instance, the (N2O)nN2+ and (N2O)nN2O+ clusters, both with 0.005 ions impact−1 as desorption yields.
The N2O ice has not yet been detected in the Solar system, in any object. Nevertheless, such surfaces are constantly irradiated by solar wind and cosmic rays causing dissociation and ionization of molecules by radiolysis. As N-bearing radiolysis of ices in laboratory has shown the production of nitrous oxide, N2O molecules may be formed on surfaces of outer Solar system objects, at low temperature environments like on Triton and Pluto surfaces. Here, irradiation of N2O was performed to help to understand the cosmic ray interaction with surfaces of TNOs, Galilean moons, or Saturn’s inner satellites, where N2O may be present. Several of those N-bearing molecules were detected. According to Hudson et al. (2008), N2O molecule is one of the species most likely to exist on TNO surfaces.
ACKNOWLEDGEMENTS
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brazil (CAPES) – Finance Code 001. The authors wish to thank the partial support by Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ). RM is grateful to FAPERJ agency (PDS – 2020 program).
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.




