-
PDF
- Split View
-
Views
-
Cite
Cite
N Ndugu, B Bitsch, A Morbidelli, A Crida, E Jurua, Probing the impact of varied migration and gas accretion rates for the formation of giant planets in the pebble accretion scenario, Monthly Notices of the Royal Astronomical Society, Volume 501, Issue 2, February 2021, Pages 2017–2028, https://doi.org/10.1093/mnras/staa3629
Close - Share Icon Share
ABSTRACT
The final orbital position of growing planets is determined by their migration speed, which is essentially set by the planetary mass. Small mass planets migrate in type-I migration, while more massive planets migrate in type-II migration, which is thought to depend mostly on the viscous evolution rate of the disc. A planet is most vulnerable to inward migration before it reaches type-II migration and can lose a significant fraction of its semimajor axis at this stage. We investigated the influence of different disc viscosities, the dynamical torque, and gas accretion from within the horseshoe region as mechanisms for slowing down planet migration. Our study confirms that planets growing in low viscosity environments migrate less, due to the earlier gap opening and slower type-II migration rate. We find that taking the gas accretion from the horseshoe region into account allows an earlier gap opening and this results in less inward migration of growing planets. Furthermore, this effect increases the planetary mass compared to simulations that do not take the effect of gas accretion from the horseshoe region. Moreover, combining the effect of the dynamical torque with the effect of gas accretion from the horseshoe region, significantly slows down inward migration. Taking these effects into account could allow the formation of cold Jupiters (a > 1 au) closer to the water ice line region compared to previous simulations that did not take these effects into account. We, thus, conclude that gas accretion from within the horseshoe region and the dynamical torque play crucial roles in shaping planetary systems.
1 INTRODUCTION
The number of observed extrasolar planets has tremendously grown over the last decades, since the discovery of the first exoplanet around a main-sequence star (Mayor et al. 1995). These observed extrasolar planets are very diverse in their properties (e.g. mass, semimajor axis, eccentricity, etc). In particular, it is now clear that the hot jupiters are a minority, and that most giant planets orbit a few aus from their host star (Howard et al. 2010). Nevertheless, giant planets are the minority, instead the population of planets is dominated by close-in hot super-Earths (Fressin et al. 2013) and by ice giants orbiting around the ice-line (Cassan et al. 2012; Suzuki et al. 2016). Matching all of these different populations of planets is a challenge for planet formation theories.
Studies of giant exoplanet occurrences show that giant planets are seen more frequently around high metallicity and massive stars (Santos et al. 2004; Fischer & Valenti 2005; Johnson et al. 2010), which is in agreement with core accretion paradigms (Pollack et al. 1996). Recently, a gas giant has been identified orbiting a low-mass star (Morales et al. 2019), presenting a challenge to planetary growth and migration models, but in support of gravitational instability model (Nayakshin 2015). Therefore, there is still no clear global understanding to explain the rich diversity of the observed extrasolar planets.
The first attempts to explain the distribution of exoplanets have been done in the so-called population synthesis studies that started about a decade ago (Ida & Lin 2004). Planet population synthesis models have become progressively more complex over the years (Alibert et al. 2005; Ida & Lin 2008a, b; Mordasini, Alibert & Benz 2009; Alibert, Mordasini & Benz 2011; Miguel, Guilera & Brunini 2011; Fortier et al. 2013; Ida, Lin & Nagasawa 2013; Dittkrist et al. 2014; Bitsch & Johansen 2017; Ronco, Guilera & de Elía 2017; Brügger et al. 2018; Chambers 2018; Ida et al. 2018; Ndugu, Bitsch & Jurua 2018, 2019; Cridland, Eistrup & van Dishoeck 2019; Johansen, Ida & Brasser 2019). Most of these planet population synthesis simulations model the planetary growth phase due to the accretion of planetesimals (e.g. Alibert et al. 2005, 2011; Ida & Lin 2008a, b; Mordasini et al. 2009; Miguel et al. 2011; Fortier et al. 2013; Ida et al. 2013; Dittkrist et al. 2014; Ronco et al. 2017). However, the accretion of planetesimals is inefficient if most of the mass is carried by planetesimals larger than a few 10 km in size (e.g. Tanaka & Ida 1999; Thommes, Duncan & Levison 2003; Levison, Thommes & Duncan 2010; Johansen & Bitsch 2019). Most of the planetesimal-based planet population synthesis studies, thus, make use of small planetesimals (below 1 km in size) to achieve a fast enough growth of planets (e.g. Mordasini et al. 2009), even though there is no evidence in the Solar system that planetesimals were that small in the inner regions (Bottke et al. 2005; Morbidelli et al. 2009; Singer et al. 2019).
A fresh attempt to model planet population synthesis via pebble accretion appeared in the recent years (e.g. Ali-Dib 2017; Bitsch & Johansen 2017; Brügger et al. 2018; Chambers 2018; Ida et al. 2018; Ndugu et al. 2018, 2019; Johansen et al. 2019). In these planet population syntheses models, solid accretion is solely from accretion of mm-cm sized particles (Johansen & Lacerda 2010; Ormel & Klahr 2010; Lambrechts & Johansen 2012, 2014). These models include type-I (Paardekooper, Baruteau & Kley 2011) and type-II migration (Baruteau et al. 2014), as well as gas accretion (Machida et al. 2010; Piso & Youdin 2014). Ndugu et al. (2018, 2019) follow the disc model of Bitsch et al. (2015a). Johansen et al. (2019) used a modified pebble-accretion approach with relatively smaller pebble sizes than used in previous studies (Bitsch & Johansen 2017; Brügger et al. 2018; Chambers 2018; Ndugu et al. 2018, 2019), showing how planetary growth can out perform planet migration. The pebble-based planet population synthesis models compute the final mass and location of planets depending on the initial time when the planetary embryo was placed in the disc, the location at which they started to grow and the disc parameters.
Most of the models preferentially reproduce some of the subsets of the observed exoplanets, but not the full statistics of the observed extrasolar planets. The planet population synthesis models mainly suffer from a mismatch between the migration and the growth speed. Johansen et al. (2019) found that planets could be saved from being lost to the host star via radial migration by using smaller pebble size and using slower type-II migration following the simulations of Kanagawa, Tanaka & Szuszkiewicz (2018).
Bitsch, Lambrechts & Johansen (2015b, hereafter B15) used a pebble based planet formation model with a high viscosity disc and found a quite surprising result. They find that for a Jupiter-mass planet to be at a few au from the central star at the end of the protoplanetary disc lifetime, its seed has to form beyond 20 au, towards the end of the disc’s evolution (i.e. at t = 1.5–2 Myr, for a disc’s lifetime of 3 Myr). However, the most favourable place for giant planet formation is presumably the water ice line region (at most ∼7 au from the central star in a young disc; Bitsch et al. 2015a), where planetesimals can form rapidly due to the local pile-up of pebbles at this location (Ida & Guillot 2016; Drążkowska & Alibert 2017; Schoonenberg & Ormel 2017) and where the subsequent pebble-accretion process is the most efficient (Morbidelli 2015). How could the seeds of the giant planets form beyond 20 au and not at the water ice line? A possibility is that all planets forming within 20 au or earlier than ∼2/3 of the disc’s lifetime ended by migration into the Sun. But, there is no evidence in the Solar system for the migration of massive planets through the terrestrial planet region. Moreover, it is questionable whether planets can be engulfed by the parent star. The discovery of many systems of close-in super-Earths argues that protoplanetary discs have inner edges, where planet migration is stopped (Masset et al. 2006; Ogihara, Morbidelli & Guillot 2015; Flock et al. 2019). Thus, it is difficult to accept the idea that many planets formed in the Solar system but disappeared into the Sun, and that the present giant planets are just the “last of the Mohicans” (Laughlin & Adams 1997; Lin & Ida 1997).
The reason why in the model of B15 the giant planets have to start forming far and late is that planet migration, at face values, is too fast. Unlike in earlier works, type-I migration of solid cores does not appear to be the critical phenomenon. This is because, in the pebble accretion scenario, the solid cores of planets grow very quickly, and therefore they do not have the time to migrate far away from their initial location. Moreover, there are in the disc some outward migration zones (Paardekooper et al. 2011; Bitsch et al. 2014, 2015a), that block inward type-I migration for moderate-mass planets. Instead, the most dangerous phases in terms of migration occur when the planet is already very massive. The first critical phase occurs when the planet exceeds the so-called pebble isolation mass (Lambrechts, Johansen & Morbidelli 2014). When the planet exceeds a mass of the order of 20 Earth masses [this value scales as (H/r/0.05)3, where H/r is the local scale height of the disc], the planet stops accreting pebbles because the latter remain blocked at the pressure bump generated outside of the planet’s orbit by the the opening of a shallow gap in the disc. Hence, the accretion of the planet slows down considerably, because only gas accretion remains possible. Inward migration is fast in this phase. In fact, the entropy-driven corotation torque that drives outward migration of medium-mass planets (Paardekooper et al. 2011) is not operational for planets of tens of Earth masses, because the corotation torque becomes saturated, particularly in late discs (Bitsch et al. 2014, 2015a).
The second critical phase is that of type-II migration, occurring when the planet becomes massive enough to open a deep gap in the disc. Although type-II migration occurs at the viscous accretion rate of the disc, for realistic rates consistent with observations (Hartmann et al. 1998; Manara et al. 2012) type-II migration is fast enough to move giant planets by several aus on a Myr time-scale. Nelson et al. (2000) also identified type-II migration to be mostly responsible for bringing giant planets too close to the star compared to observations.
Recently, Crida & Bitsch (2017, CB hereafter) have shown that a planet accreting gas at a high enough rate can open a gap in the disc before its mass exceeds the nominal value for gap opening through planetary torques (Crida, Morbidelli & Masset 2006). This may allow the planet to transition to type-II migration at lower masses than envisioned in B15. In this phase, the planet accretes gas mostly from its co-orbital region and therefore it can grow faster than the rate at which the disc supplies mass through radial transport, until the horseshoe region is depleted, which then marks the transition to type-II migration.
Another important result originating from recent studies (Nelson, Gressel & Umurhan 2013; Stoll & Kley 2014) is the fact that discs may have a very small mid-plane viscosity (α of the order of 10−4 or less, where α is the parameter governing the viscosity in the Shakura & Sunyaev 1973 prescription) because the Magneto-Rotational Instability (MRI) is quenched at all scale heights in the disc (Turner et al. 2014).
The goal of this paper is thus to investigate the potential impact of lower disc viscosity, gap opening by gas accretion (CB; Bergez-Casalou et al. 2020) and the influence of dynamical torques (Paardekooper 2014) on the formation of planets. The target is to find in the disc where and when the dynamical torque and gap opening by gas accretion becomes important.
Planet population synthesis simulations should aim to explain all the data available from exoplanet observations at once. This requires not only to include all processes relevant for planet formation (e.g. disc evolution, solid and gas accretion, planet migration), but also to vary the initial conditions within each simulation (e.g. alpha viscosity parameter, dust-to-gas ratio, disc mass and size, embryo starting time and position). In our study, we focused to understand the impact of a new recipe for gas accretion and for planet migration on planet formation via global planetary evolution map approach of Bitsch et al. (2015b). We, thus, limited ourselves to one simple disc model and a controlled change in the alpha viscosity parameter to understand when and how our new recipes for gas accretion and planet migration affect the picture of planet formation, which might not be possible if all parameters are drawn at random as done in comprehensive planet population synthesis models.
This paper is organized as follows. In Section 2, we highlight the disc model and planet formation model used. In Section 3, we introduce the concept of gap opening by accretion, following CB. We additionally introduce a prescription for the dynamical torques in the last part of Section 3 with the goal of reducing the fast inward type-I migration in low viscosity environments. All the results will be presented showing individual evolution of planets in terms of their mass and semimajor axis, as well as global maps like those of B15, showing the final location and mass of planets as a function of the time and the location at which they started to grow. In Section 4, we explore where and when the CB formalism and the dynamical torque becomes effective in gas giant planet formation. Section 5 summarizes the results, putting them into perspectives for future investigations.
2 METHODS
2.1 Disc model
We note that throughout this work, our nominal disc model uses h0 = 0.025. The herein adopted flared disc model removes the outward migration regions for small-mass planets due to the entropy-driven corotation torque. Here, one should note that the disc temperature is not influenced by the disc viscosity since the Chiang & Goldreich (1997) prescription does not account for viscous heating. Therefore, our model deviates significantly from a viscously heated model in the inner regions of the disc (e.g. Bitsch et al. 2015a). However, because in this study, we will mostly deal with low viscosities in the disc, the Chiang & Goldreich (1997) temperature profile is an acceptable approximation.
2.2 Planet formation model
Here, we start by presenting similar growth tracks as used in Ndugu et al. (2018, hereafter NN) but utilizing the simple flared disc profile from Chiang & Goldreich (1997) as the reference model for the rest of this paper. In our model, the planetary embryos that grow and migrate through the disc start at the pebble transition mass (when Hill accretion becomes efficient, see Lambrechts & Johansen 2012).
At low α values, type-I migration is increasingly fast with increasing planetary mass due to early saturation of corotation torques. However, the speed of type-I migration can be reduced if we consider the dynamical corotation torque (Paardekooper 2014) or thermal torque due to heating by the accreting pebbles (Benítez-Llambay et al. 2015).2 The dynamical corotation torque is particularly effective in reducing type-I migration in low-viscosity discs with surface density profile shallower than 1/r3/2, like the one assumed here. We discussed the detailed implementation of dynamical corotation torque in appendix A. We remind the reader that type-I migration changes in inviscid disc, where the Paardekooper et al. (2011) prescription might not hold. The focus of our paper is not inviscid discs, but to probe the impact of lower migration rates via lower viscosities in discs. We acknowledge that at lower visocities, although type-II migration is slowed, type-I migration is too fast for forming large planets due to early saturation of corotational torques. We, however, reduced this by invoking the dynamical corotation torque in our migration prescription.
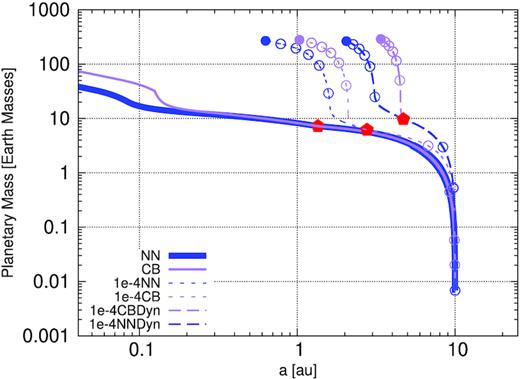
Evolution of planets implanted at 10 au in a disc of lifetime of 3 Myr at 0.1 Myr using the different models described in Table 1 with the α parameters stated therein. The simulation was terminated when the planet reached 0.04 au or evolved for 3 Myr (marked by a solid dot). The circles on the curves are placed at t0, 2t0, 3t0, 5t0, 10t0, 15t0, 20t0, 25t0, and 30t0 Myr, respectively. The pebble isolation mass is depicted by the red filled polygonal mark. The solid blue NN track was made thick for a clear differentiation with the solid CB track which basically follows exactly the same growth trajectory.
We stop the simulation when the planet either (i) reaches 0.04 au, where we assume migrating planets are trapped at the inner disc edge (Masset et al. 2006; Flock et al. 2019) or (ii) at the time of disc dispersion for the planets that do not reach the inner edge. All the models studied in this paper are described in Table 1.
Model descriptions used in the planet formation simulations. The acronym NN, CB, and Dyn describes the models of NN, CB, and Paardekooper (2014), respectively, where Paardekooper (2014) describes the model of the dynamical torques. α is the viscosity used in the simulation. The rest of the symbols of the model are derived from a combination of the aforementioned models. The nom abbreviation symbolizes the nominal migration and gas accretion parameter values as in Bitsch et al. (2015b) and NN.
| Model . | α . | Gas accretion . | Torque . |
|---|---|---|---|
| NN | 0.005 | nom | nom |
| |$\rm 5e-4$| NN | 0.0005 | nom | nom |
| |$\rm 1e-4$|NN | 0.0001 | nom | nom |
| CB | 0.005 | CB | nom |
| |$\rm 1e-3$| CB | 0.001 | CB | nom |
| |$\rm 5e-4$|CB | 0.0005 | CB | nom |
| |$\rm 1e-4$|CB | 0.0001 | CB | nom |
| NNDyn | 0.005 | nom | nom+Dyn |
| |$\rm 1e-4$|NNDyn | 0.0001 | nom | nom+Dyn |
| CBDyn | 0.005 | CB | nom+Dyn |
| |$\rm 1e-3$|CBDyn | 0.001 | CB | nom+Dyn |
| |$\rm 5e-4$|CBDyn | 0.0005 | CB | nom+Dyn |
| |$\rm 1e-4$|CBDyn | 0.0001 | CB | nom+Dyn |
| Model . | α . | Gas accretion . | Torque . |
|---|---|---|---|
| NN | 0.005 | nom | nom |
| |$\rm 5e-4$| NN | 0.0005 | nom | nom |
| |$\rm 1e-4$|NN | 0.0001 | nom | nom |
| CB | 0.005 | CB | nom |
| |$\rm 1e-3$| CB | 0.001 | CB | nom |
| |$\rm 5e-4$|CB | 0.0005 | CB | nom |
| |$\rm 1e-4$|CB | 0.0001 | CB | nom |
| NNDyn | 0.005 | nom | nom+Dyn |
| |$\rm 1e-4$|NNDyn | 0.0001 | nom | nom+Dyn |
| CBDyn | 0.005 | CB | nom+Dyn |
| |$\rm 1e-3$|CBDyn | 0.001 | CB | nom+Dyn |
| |$\rm 5e-4$|CBDyn | 0.0005 | CB | nom+Dyn |
| |$\rm 1e-4$|CBDyn | 0.0001 | CB | nom+Dyn |
Model descriptions used in the planet formation simulations. The acronym NN, CB, and Dyn describes the models of NN, CB, and Paardekooper (2014), respectively, where Paardekooper (2014) describes the model of the dynamical torques. α is the viscosity used in the simulation. The rest of the symbols of the model are derived from a combination of the aforementioned models. The nom abbreviation symbolizes the nominal migration and gas accretion parameter values as in Bitsch et al. (2015b) and NN.
| Model . | α . | Gas accretion . | Torque . |
|---|---|---|---|
| NN | 0.005 | nom | nom |
| |$\rm 5e-4$| NN | 0.0005 | nom | nom |
| |$\rm 1e-4$|NN | 0.0001 | nom | nom |
| CB | 0.005 | CB | nom |
| |$\rm 1e-3$| CB | 0.001 | CB | nom |
| |$\rm 5e-4$|CB | 0.0005 | CB | nom |
| |$\rm 1e-4$|CB | 0.0001 | CB | nom |
| NNDyn | 0.005 | nom | nom+Dyn |
| |$\rm 1e-4$|NNDyn | 0.0001 | nom | nom+Dyn |
| CBDyn | 0.005 | CB | nom+Dyn |
| |$\rm 1e-3$|CBDyn | 0.001 | CB | nom+Dyn |
| |$\rm 5e-4$|CBDyn | 0.0005 | CB | nom+Dyn |
| |$\rm 1e-4$|CBDyn | 0.0001 | CB | nom+Dyn |
| Model . | α . | Gas accretion . | Torque . |
|---|---|---|---|
| NN | 0.005 | nom | nom |
| |$\rm 5e-4$| NN | 0.0005 | nom | nom |
| |$\rm 1e-4$|NN | 0.0001 | nom | nom |
| CB | 0.005 | CB | nom |
| |$\rm 1e-3$| CB | 0.001 | CB | nom |
| |$\rm 5e-4$|CB | 0.0005 | CB | nom |
| |$\rm 1e-4$|CB | 0.0001 | CB | nom |
| NNDyn | 0.005 | nom | nom+Dyn |
| |$\rm 1e-4$|NNDyn | 0.0001 | nom | nom+Dyn |
| CBDyn | 0.005 | CB | nom+Dyn |
| |$\rm 1e-3$|CBDyn | 0.001 | CB | nom+Dyn |
| |$\rm 5e-4$|CBDyn | 0.0005 | CB | nom+Dyn |
| |$\rm 1e-4$|CBDyn | 0.0001 | CB | nom+Dyn |
Each of the blue curves in Fig. 1 traces a single evolution for a planet and differ for the choice of α, and the inclusion or not of gas accretion from the horseshoe region and of the dynamical torque. Repeating the solid blue curve simulation in Fig. 1 for a range of planetary injection time and positions, we come up with a growth evolution map shown in the first column of the top panel of Fig. 2. For this approach, we vary the initial assumptions: starting time [0.1 Myr, 2.9 Myr] and starting position [0.2 au, 50 au]. We remind the reader that the initial time is a free parameter of the model, because it corresponds to the time when the planet seed achieves a mass corresponding to the transition between the Bondi and the Hill regime in the pebble accretion process at the planet location in the disc.
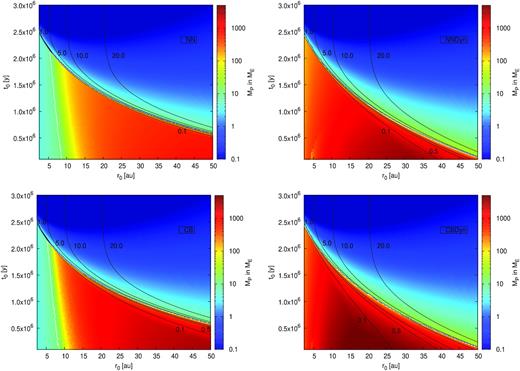
Final masses of planets as a function of initial time (t0) and and initial location (r0) of their planetary embryos. Here, the colours indicate final planetary masses. The black curves depict the final orbital positions, the blue line marks the pebble isolation mass, where planets below the line have reached pebble isolation mass. All planets inside the white line are in the runaway gas accretion regime with Mcore < Menv. The first row plots feature NN (first column plot) and NNDyn (second column plot). The second row plots feature CB (first column plot) and CBDyn (second column plot).
3 GAP OPENING BY ACCRETION
Previous studies of planet-disc interactions only considered gap opening via gravitational perturbations (Lin & Papaloizou 1986; Crida et al. 2006; Crida & Morbidelli 2007). Studies by CB, and subsequently by Bergez-Casalou et al. (2020), found that gas accretion by the planet in the runaway regime (third phase of the Pollack et al. 1996 scheme) can change the picture of planet formation significantly, in particular, in terms of gap opening and accretion rate. They found using 2D isothermal hydrodynamical simulations that the accretion flow on to the planet comes from the neighbourhood of the separatrix around the horseshoe region. This has two consequences that change the picture of the transition from type-I to type-II migration.
As the separatrix empties because of the accretion by the planet, the horseshoe region becomes partially isolated from the inner and outer discs. The flow from the inner and outer discs towards the separatrix is intercepted and accreted by the planet before it can reach the horseshoe region, if the accretion rates on to the planet are large. Hence, if the horseshoe region empties (because of the planetary accretion, see below), a gap is maintained, even if the planet is not massive enough to maintain a gap opened by its sole gravity according to the Crida et al. (2006) criterion.
As the separatrix empties, the horseshoe region diffuses viscously and tends to replenish the separatrix. This empties progressively the horseshoe region while its mass is transferred to the planet. In fact, the horseshoe material can be seen as a reservoir of mass that the planet can easily accrete, before being limited to what the disc can provide.
These two effects combine to limit the transition phase between type-I and type-II migration, which is the most dangerous phase in terms of amplitude of inward migration. Not only can a planet reach the gap opening mass more rapidly, but it can actually open a gap before the classical gap opening mass, if the accretion rate is fast enough. Our model allows an inflow into an expanding horsehoe region by adding fresh material in the horseshoe mass reservoir. For a rapid expansion of the horseshoe region, like in 3D hydrodynamic simulations, new neighbouring gas might be included in the horseshoe region. Accreting this gas instantaneously on to the planet would not be physical. By adding it into the HS region, we allow for its accretion on to the planet on a synodic time-scale. We explain the implementation of this finding in the following subsection.
3.1 Implementation of the new gap opening and accretion model
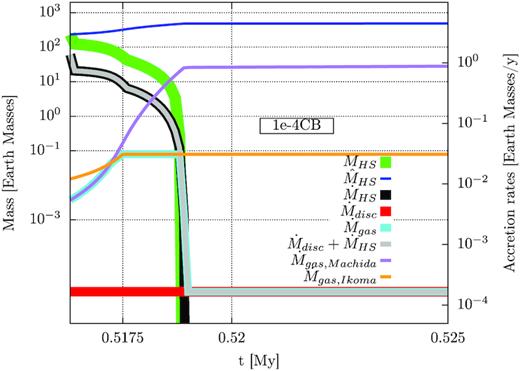
Time evolution of horseshoe gas mass (green curve) and the relevant gas accretion rates (from the horseshoe region – black; from the disc’s viscous accretion – red; the sum of the two – grey; the effective gas accretion rate on to the planet – light blue). For simplicity, we assumed that the planet has a fixed position of a = 10 au and the disc does not evolve over time. The plots feature α-viscosity value of 0.0001 and core mass of 16.56 Earth masses. The dark blue curve depicts the mass inside the horseshoe region without taking any depletion by accretion into account.
3.2 Consequences on planet formation
Using the previous outlined modifications, we plot the growth track of a planet starting at a0 = 10 au and t0 = 0.1 Myr as a purple line in Fig. 1. For the nominal α viscosity reported in this work (0.005), the discussed new prescription of gas accretion appears irrelevant, especially in slowing the overall migrating distance to the star. We attribute this result to the faster type-II migration rates due to the high α-viscosity. In addition, the high α-viscosity means high pebble scale height, therefore the pebbles are not in the efficient accretion zones of the planetary embryo. Therefore, migration wins over growth, with the planet starting to carve a gap when the cores is approaching 1 au from the star and migrates even further inwards before transitioning fully into slower type-II regime. We test the importance of core location in the disc by implanting cores at 20 au in Fig. 4. As expected, the core now starts carving gap just outside of 2 au but the planets still migrate all the way to the disc’s inner edge. We therefore conclude that, within the framework of the simple power-law disc model we used, the difference between NN and CB in slowing inward migration is not very significant for higher α viscosity.
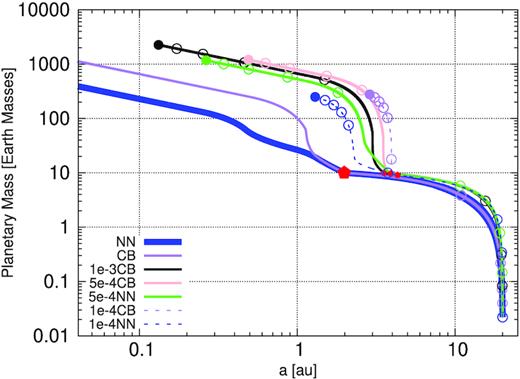
Growth track showing the impact of α-viscosity on the mass-distance distribution of forming planets. With the exception of planetary embryos implanted at 20 au, the plots are obtained with the same initial starting time (0.1 Myr) and disc dispersion time (3 Myr) as in Fig. 1. The marks on the curves have same meaning as in Fig. 1. The sub models are defined in Table 1.
Assuming a lower α-viscosity (0.0001) in the disc, we clearly see differences appearing between NN and CB model in Fig. 1. Both 1e-4NN and the 1e-4CB simulations now accrete pebbles in the efficient 2D regime. This allows the early formation of a gap, before the planet is driven to the inner edge of the disc. The 1e-4CB curve (short dashed purple) starts to diverge relative to the 1e-4NN model (short dashed blue curve), when the planet starts its runaway gas accretion. From this point on, the growth is faster in the 1e-4CB case, because gas accretion is not limited by the disc accretion as long as the horseshoe region is not empty. As soon as the horseshoe region empties, the growth slows down and becomes limited by what the disc can provide. At the same time, the planet transitions into type-II migration. Therefore, the intermediate phase between type-I and type-II migration is very short. At the end of the disc lifetime, the planet following the 1e-4CB track ends just outside 1 au and with a mass of around 300 Earth masses. For these particular growth tracks (Fig. 1), an important difference between 1e-4NN and 1e-4CB is noted in the final planetary orbital positions, but only a small difference is seen in terms of the final planetary mass. Comparing Figs 1 and 4, we note that the difference between NN and CB prescriptions scales with: (i) α viscosity and (ii) injection positions of planetary embryos in the discs. The effect of the CB prescription is clearly highlighted for cores implanted in the outer disc. In this prescription, the gas surface density of the protoplanetary disc plays a crucial role in the final mass of the planet, as it determines how much material the planet can accrete from its horseshoe region.3 This is a clear difference with respect to the NN model, where the final planetary mass depends only on the mass accretion rate through the disc and not on the total gas surface density. Planets that formed earlier, when the disc is more massive, can grow larger than planets formed later. In addition, if planets are formed late, the differences between CB and NN should be very small due to the limited material available in the horseshoe region [see the global maps (Figs 2, 6, and 7) for more illustration]. The corresponding global map for NN and CB models are shown in the first column of the top and the bottom panel of Fig. 2, respectively. We see that there are many more super Jupiters in hot/warm orbits with respect to the nominal case (first column of the top panel of Fig. 2), because the more rapid transition to type-II migration reduces the overall migration of the planet towards the star. The planets, moreover, are a bit more massive than in the nominal case.
We show in Fig. 5 the overall sequence of major events in the track 1e-4CB (short-dashed purple curve) of Fig. 1. It is clear from Fig. 5 that the planetary migration rate occurs in three regimes (marked by different colours). The type-I migration rate scales linearly with planetary mass until it opens a gap. The planet then gradually transitions into the constant slower type-II migration rate. We remind the reader that the onset of our horseshoe gas mass depletion corresponds to the intermediate type-I/type-II regime. In addition, our effective gap parameter profile (black curve) follows the horseshoe gas mass profile (green curve) and is only marginally determined by the gravitational gap opening, highlighting the role of gas accretion for gap opening.
![The left-hand panel shows the time dependency of the horseshoe gas mass (green curve) from equation (20), gap depth parameter due to horseshoe gas accretion (pink curve) and due to gravitational pushing (light blue curve), effective gap depth parameter (red curve) from equation (19), and the inward migration rates (deep blue curve) for the 1e-4CB track displayed in Fig. 1. The left-hand panel plot also shows the m−t relationship for 1e-4CB track [pebble accretion (black curve), horseshoe gas depletion (dashed green curve) and when the disc’s accretion rate limits the accretion on to the planet (orange dashed curves)]. The right-hand panel shows the main sequence of events occurring in the m−a trajectory of the 1e-4CB displayed in Fig. 1. The planet accretes pebbles and concurrently undergoes migration in the type-I regime (black curve). After the planet reached the pebble isolation mass (red triangle), the planet starts accreting gas from the horseshoe region, causing its depletion (green curve). The depletion regime of horseshoe gas corresponds closely to the transition to type-II migration. The core then undergoes runaway gas accretion in the regime marked by the dashed orange curve with the migration rates in this regime corresponding to the type-II migration.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/501/2/10.1093_mnras_staa3629/1/m_staa3629fig5.jpeg?Expires=1750577544&Signature=X2id1ieTm3k93X-6XWi9ZvhcYAYkJuCWOy7xAaYra~aIQNVEDeNz0LfU5x9r6igd5o~8PMxAZdL-TBdD4rkRLvEFF-IZAAzex8vFILcaq7DWR9SnWkIurQC2gZoPwhNPiTpPYVTewoW0-giypG4YOW3hK2-sRblC~ZaAwRzcpAXlSB1t0j2dytEtXwF8tAOzb0maMtgF7C19~tWlXxzls1deOZ0s2E4riPTlDk9xWdc2FlVfxE2Ti0q5aF4MHLiQ4pgj8Pfh79VWzxGAg3-r3b59sYcJiusOLScxpiCN-njOe8aYxIs39H6BLEGVovHE60vLBd62y4t3KmqpnMb18Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The left-hand panel shows the time dependency of the horseshoe gas mass (green curve) from equation (20), gap depth parameter due to horseshoe gas accretion (pink curve) and due to gravitational pushing (light blue curve), effective gap depth parameter (red curve) from equation (19), and the inward migration rates (deep blue curve) for the 1e-4CB track displayed in Fig. 1. The left-hand panel plot also shows the m−t relationship for 1e-4CB track [pebble accretion (black curve), horseshoe gas depletion (dashed green curve) and when the disc’s accretion rate limits the accretion on to the planet (orange dashed curves)]. The right-hand panel shows the main sequence of events occurring in the m−a trajectory of the 1e-4CB displayed in Fig. 1. The planet accretes pebbles and concurrently undergoes migration in the type-I regime (black curve). After the planet reached the pebble isolation mass (red triangle), the planet starts accreting gas from the horseshoe region, causing its depletion (green curve). The depletion regime of horseshoe gas corresponds closely to the transition to type-II migration. The core then undergoes runaway gas accretion in the regime marked by the dashed orange curve with the migration rates in this regime corresponding to the type-II migration.
We stress that the formula of Crida & Morbidelli (2007) for the gap depth would predict the opening of a gap with 50 per cent depth at ∼5 Earth masses, determining the end of pure type-I migration. However, such a gap would cause the blockage of the flux of pebbles at the outer edge of the gap. In other words, opening a gap at 5 Earth masses is inconsistent with estimate of the pebble isolation mass at ∼20 Earth masses at disc location with |$\frac{H}{r} = 0.05$| (Bitsch et al. 2018). We think that the Crida & Morbidelli (2007) formula, calibrated for giant planets in viscous discs, is not quantitatively reliable for small planets in disc of vanishing viscosity, as stated in Bitsch et al. (2018). Instead, the pebble isolation mass criterion has been investigated in the proper regime by recent hydrodynamical simulations (Lambrechts & Johansen 2014; Ataiee et al. 2018; Bitsch et al. 2018). Thus, we assume that type-I migration operates until the pebble isolation mass.
In the transition period between type-I and type-II migration, the planet implanted at 10 au and at 0.1 Myr in a disc with α = 0.0001 using the CB accretion prescription (short dashed-purple line in Fig. 1) achieves 90 per cent orbital decay. Applying the dynamic co-rotation torque, we obtain the tracks depicted by the long dashed curves in Fig. 1. Following the purple long dashed curve (1e-4CBDyn track) in Fig. 1, type-I migration now brings the planet to ∼3 au. Runaway gas accretion therefore starts just before 0.4 Myr, when the planet is still beyond 4 au, bringing the planet into the type-II migration regime. Then, as expected, due to the low viscosity of the disc, the migration is slow. In the subsequent 2.6 Myr, the planet moves radially by ∼1 au, finding itself at ∼300 Earth masses just inside of 3 au at the end of the disc’s lifetime. This result confirms the relevance of the dynamical torque in planet formation.
4 WHEN ARE THE CB ACCRETION AND THE DYNAMICAL TORQUES RELEVANT IN PLANET FORMATION?
The previous section showed that, in the CB prescription and accounting for the dynamical corotation torque, the viscosity of the disc and the location and time of injection of the planetary seed in the disc play a major role. In this section, we show when and where the CB prescription and the dynamical torque become important in planet formation using a global evolution map of planet formation like those of Fig. 2. We start by exploring the impact of α viscosity in the disc on the global planet formation map. The α viscosity in our model controls the migration and accretion speed, for example at a higher α viscosity, inward migration is fast and the gas accretion rate of a planet exceeding the pebble isolation mass is high. In addition, a lower viscosity reduces the pebble scale height, allowing faster growth during the pebble accretion stage.
It is clear from the simulations with α = 0.0001 that the lower migration speeds and faster pebble-accretion rates allow the formation of gas giants also in the inner parts of the protoplanetary disc (see the first column plots in Fig. 6). On the contrary, for higher α viscosity, the gas giant planets have to start forming in the disc outskirts due to the fast inward migration speed that outperforms growth rates (see the first column plots in Fig. 2).
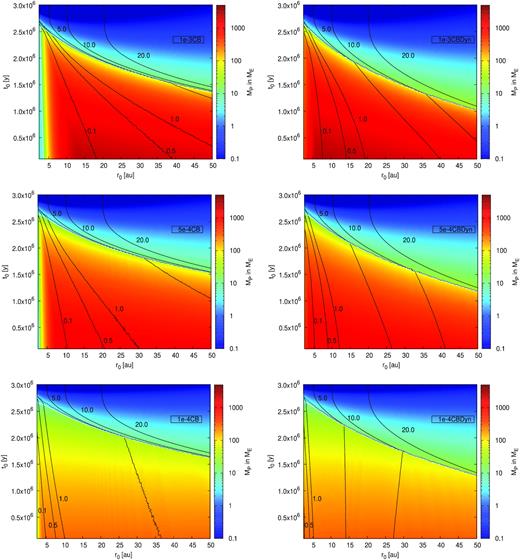
Growth map showing the impact of the disc’s α-viscosity parameter on planets growing with the CB prescription. The top, middle, and bottom plots feature the 1e-3CB, 5e-4CB, and 1e-4CB models. All the lines have the same meaning as in Fig. 2, but we now feature different α values (top to bottom panels) and include the effect of the dynamical torques (left-hand panel plots).
The effects of the CB prescription become enhanced at low viscosities. This results in earlier gap opening, less inward migration, and slightly larger gas giants (e.g. Figs 1 and 4). However, in the case of α = 10−4, the gas accretion rate in itself is very low, resulting in planets that barely reach super Jupiter mass, indicating that a higher viscosity might be needed to explain very massive giant planets. In addition, the effects of the CB prescription depends on the injection time of the planetary embryo. In particular, an early injection time of the planetary embryo results in a stronger effect of the CB accretion compared to later planetary embryo injection times. This is caused due to the fact that the mass of gas in the planet’s horseshoe region is larger at earlier times.
We show in Fig. 6 (second column plots) the influence of the dynamical torque on the final masses and positions of planets formed in our model. Quite clearly, the dynamical torque becomes more efficient in slowing-down migration if the disc’s viscosity is smaller (Paardekooper 2014). At high viscosities, the dynamical torque only affects planetary embryos growing initially in the very outer regions of the disc. Cores forming in the inner region (a < 5 au) of the disc are only barely affected. At low viscosites, the effect of the dynamical torque increases significantly. At α = 0.0001, if the dynamical torque is not accounted for, early forming planets have to originate outside of 30 au to stay exterior of 5 au, while planets can form as close as 15 au if the effects of the dynamical torque is included.
We show in Fig. 7 the result of planet formation simulations using α = 0.0001 for discs with higher aspect ratio (h0 = 0.033). The higher aspect ratio of the disc reduce the pebble accretion rates due to the higher scale height. The high aspect ratio also results in a higher pebble isolation mass resulting in larger planetary cores. This shortens the envelope contraction phase resulting in higher planetary masses, if the planets reach the pebble isolation mass and transition into gas accretion.
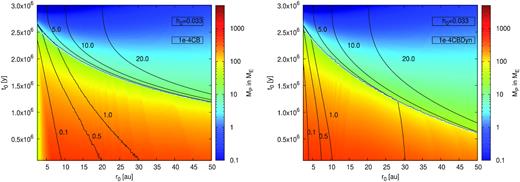
Growth map of planets growing in a disc with a higher aspect ratio (h0 = 0.033). We show the results of the 1e-4CB (left-hand panel) and 1e-4CBDyn (right-hand panel) models. All lines have the same meaning as in Fig. 6.
Our simulation results hold no surprise in this case, as a higher aspect ratio clearly results in higher planetary masses and at the same time also in faster inward migration. In addition, it seems that the effects of the dynamical torque are less enhanced, because for a given planet mass, the width of the horseshoe region decreases with increasing disc’s aspect ratio.
Our results indicate that the effects of the CB accretion mechanism and the dynamical torque greatly reduce inward migration in low viscosity environments. As such, these effects are important for future planet formation simulations.
5 CONCLUSION
In this paper, we have revisited the work of Bitsch et al. (2015b) and NN on the accretion and migration of planets in a simple approach where pebble accretion is modelled with a constant Stokes number of 0.1. Bitsch et al. (2015b) concluded that giant planets that are at a few au from the central star at the end of the disc’s lifetime must have started forming beyond 20 au. This conclusion appears inconsistent with the expectation that the most favourable place for the accretion of a giant planet’s core should be the water ice line, which is probably not beyond 7 au in young protoplanetary discs (Savvidou, Bitsch & Lambrechts 2020). This large-scale inward migration is driven by the high viscosity of the disc assumed in Bitsch et al. (2015b), leading to fast inward migration also in the type-II regime.
An obvious solution to reduce inward migration, is the reduction of the disc’s viscosity. For low mid-α viscosity, we have shown that the planet covers a smaller radial distance in type-II migration, as shown also by previous studies. In the case of low viscosities, the entropy driven corotation torque is fully saturated (e.g. Paardekooper et al. 2011), preventing outward migration. Instead, the low viscosity allows a transition into the slower type-II migration at lower planetary masses. The low viscosity of the disc limits also the gas accretion rate on to the planet, resulting in lower mass planets in discs with lower viscosity.
Our simulations show that the dynamical torque (Paardekooper 2014) reduces the inward migration before the planet opens a deep gap in the disc. Furthermore, we find that accreting material directly from the horseshoe region (CB) can help in opening a deep gap, allowing an earlier transition into type-II migration and retaining the planet at larger distances from the star.
As already shown by Paardekooper (2014), a viscosity of below a few times 10−4 is needed for the dynamical torque to operate and slow down migration effectively. If the dynamical torque is as efficient as shown in our work, it could allow giant planets to form close to the water ice line and remain in the outer disc. We thus conclude that the incorporation of the dynamical torques and the accretion from the horseshoe region can have significant influence on the resulting planet population and should be taken into account in future comprehensive planet population synthesis simulation.
ACKNOWLEDGEMENTS
NN acknowledges financial support from the International Science Program (ISP) and the Poincaré junior fellowship. EJ appreciates the financial support from the International Science Program (ISP). BB thanks the European Research Council (ERC Starting Grant 757448-PAMDORA) for their financial support. We thank an anonymous referee whose comments helped to improve this manuscript.
DATA AVAILABILITY
The codes used to obtain the results in this paper is available upon reasonable request.
Footnotes
This approximation results in an increase of the physical particle sizes from 0.9 to 29 cm from the outer to the inner disc.
The maximal accretion rates for our planets are around 10−4 Earth masses year–1, which is a factor of a few lower than what is needed for the heating torque to operate (Baumann & Bitsch 2020). We therefore do not incorporate the contribution of thermal torque in our simulations.
The amount of materials in the core’s horseshoe region depends on the accretional viscosity and the core’s location in the disc.
REFERENCES
APPENDIX A: IMPLEMENTATION OF DYNAMICAL COROTATION TORQUE
APPENDIX B: INFLUENCE OF STOKES NUMBER
In protoplanetary discs, the small micrometer dust grains can grow to form larger particles by coagulation (e.g. Brauer, Dullemond & Henning 2008) or condensation (e.g Ros & Johansen 2013). These growth processes result in different Stokes numbers of particles, which are probably also not uniform in the disc. This has important consequences for the solid accretion rates via pebble accretion. For a fixed pebble surface density, larger Stokes number should lead to faster growth. However, in our model, the pebble surface density increases with reduction in Stokes number (equation 4) for a fixed pebble flux. Therefore, from equation (5), cores accrete pebbles at a rate proportional to |${\tau _{\rm }}^{\frac{-1}{3}}$|, leading to faster growth with lower Stokes numbers.
We show the impact of different Stokes numbers in our model in Fig. B1. Our results clearly indicate that planets growing in environments with larger/small Stokes numbers grow slower/faster and thus smaller/bigger. This can be clearly seen in Fig. B1, where the simulations with lower Stokes numbers produce relatively massive giant planets compared to the simulations with larger Stokes numbers. On the other hand, it seems that the influence of Stokes number on the final position of the formed gas giants is not that pronounced at the inner parts of the disc (Fig. B1).
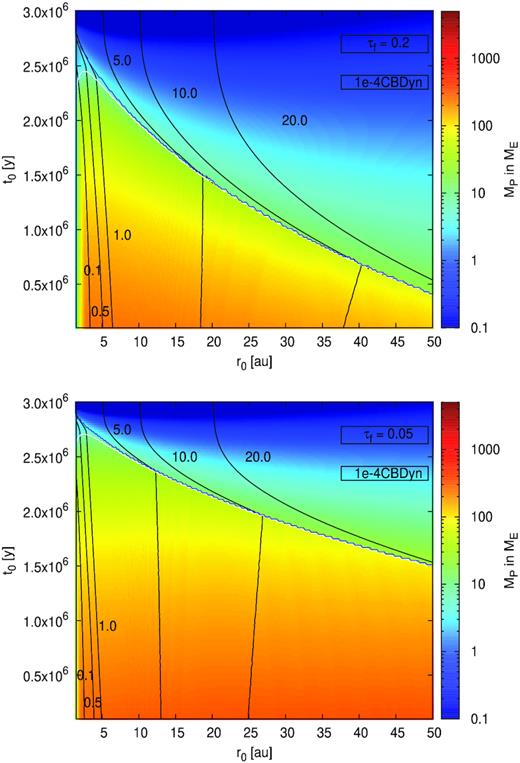
Growth maps showing the influence of different Stokes numbers of the pebbles for the growth of planets. We show the results of the 1e-4CBDyn model using a Stokes number of 0.2 (top) and 0.05 (bottom). The lines have the same meaning as in Fig. 2.
We therefore conclude that the Stokes number has an important influence on the outcome of our simulations. However, the effects discussed in the main paper, namely the influence of the CB accretion mechanism and of the dynamical torques are untouched by the difference in Stokes number. In future simulations that aim to reproduce all planet populations from different Stokes numbers should be taken into account.



