-
PDF
- Split View
-
Views
-
Cite
Cite
Julian E Bautista, Romain Paviot, Mariana Vargas Magaña, Sylvain de la Torre, Sebastien Fromenteau, Hector Gil-Marín, Ashley J Ross, Etienne Burtin, Kyle S Dawson, Jiamin Hou, Jean-Paul Kneib, Arnaud de Mattia, Will J Percival, Graziano Rossi, Rita Tojeiro, Cheng Zhao, Gong-Bo Zhao, Shadab Alam, Joel Brownstein, Michael J Chapman, Peter D Choi, Chia-Hsun Chuang, Stéphanie Escoffier, Axel de la Macorra, Hélion du Mas des Bourboux, Faizan G Mohammad, Jeongin Moon, Eva-Maria Müller, Seshadri Nadathur, Jeffrey A Newman, Donald Schneider, Hee-Jong Seo, Yuting Wang, The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: measurement of the BAO and growth rate of structure of the luminous red galaxy sample from the anisotropic correlation function between redshifts 0.6 and 1, Monthly Notices of the Royal Astronomical Society, Volume 500, Issue 1, January 2021, Pages 736–762, https://doi.org/10.1093/mnras/staa2800
Close - Share Icon Share
ABSTRACT
We present the cosmological analysis of the configuration-space anisotropic clustering in the completed Sloan Digital Sky Survey IV extended Baryon Oscillation Spectroscopic Survey (eBOSS) Data Release 16 galaxy sample. This sample consists of luminous red galaxies (LRGs) spanning the redshift range 0.6 < |$z$| < 1, at an effective redshift of |$z$|eff = 0.698. It combines 174 816 eBOSS and 202 642 BOSS LRGs. We extract and model the baryon acoustic oscillation (BAO) and redshift-space distortion (RSD) features from the galaxy two-point correlation function to infer geometrical and dynamical cosmological constraints. The adopted methodology is extensively tested on a set of realistic simulations. The correlations between the inferred parameters from the BAO and full-shape correlation function analyses are estimated. This allows us to derive joint constraints on the three cosmological parameter combinations: DM(|$z$|)/rd, DH(|$z$|)/rd, and fσ8(|$z$|), where DM is the comoving angular diameter distance, DH is the Hubble distance, rd is the comoving BAO scale, f is the linear growth rate of structure, and σ8 is the amplitude of linear matter perturbations. After combining the results with those from the parallel power spectrum analysis of Gil-Marin et al., we obtain the constraints: DM/rd = 17.65 ± 0.30, DH/rd = 19.77 ± 0.47, and fσ8 = 0.473 ± 0.044. These measurements are consistent with a flat Lambda cold dark matter model with standard gravity.
1 INTRODUCTION
The large-scale structure (LSS) in the late Universe is a fundamental probe of the cosmological model, sensitive to both universal expansion and structure growth, and complementary to early Universe observations from the cosmic microwave background. The LSS can be mapped by large redshift surveys through systematic measurements of the three-dimensional positions of matter tracers such as galaxies or quasars. Because the observed LSS is the result of the growth of initial matter perturbations through gravity in an expanding universe, it gives the possibility of both testing the expansion and structure growth histories,which in turn puts us in a unique position to solve the question of the origin of the late acceleration of the expansion and dark energy (Clifton et al. 2012; Weinberg et al. 2013; Zhai et al. 2017b; Ferreira 2019).
Over the last two decades, redshift surveys have explored increasingly larger volumes of the Universe at different cosmic times. The methodology to extract the cosmological information from those redshift surveys has evolved and has now reached maturity. Particularly, the baryon acoustic oscillations (BAOs) and the redshift-space distortions (RSDs) in the two-point and three-point statistics of the galaxy spatial distribution are now key observables to constrain cosmological models. The BAO horizon scale imprinted in the matter distribution was frozen in the LSS at the drag epoch, slightly after matter–radiation decoupling. This characteristic scale can still be seen in the large-scale distribution of galaxies at late times and be used as a standard ruler to measure the expansion history. At the same time, the galaxy peculiar velocities distorting the line-of-sight cosmological distances based on observed redshifts are sensitive on large scales to the coherent motions induced by the growth rate of structure, which in turn depends on the strength of gravity. BAO and RSD are highly complementary, as they allow both geometrical and dynamical cosmological constraints from the same observations.
The signature of baryons in the clustering of galaxies was first detected in the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2005) and 2dF Galaxy Redshift Survey (2dFGRS; Percival et al. 2001; Cole et al. 2005). Since then, further measurements using the 2dFGRS, SDSS, and additional surveys have improved the accuracy of BAO measurements and extended the range of redshifts covered from |$z$| = 0 to 1. Examples of analyses include those of the SDSS-II (Percival et al. 2010), 6dFGS (Beutler et al. 2011), WiggleZ (Kazin et al. 2014), and SDSS-MGS (Ross et al. 2015a) galaxy surveys. An important milestone was achieved with the Baryon Oscillation Spectroscopic Survey (BOSS; Dawson et al. 2013), part of the third generation of the SDSS (Eisenstein et al. 2011). This allowed the most precise measurements of BAO using galaxies achieved to date using galaxies as direct tracers (Alam et al. 2017) and Lyman-α forest measurements (Bautista et al. 2017; du Mas des Bourboux et al. 2017), reaching a relative precision of 1 per cent on the distance relative to the sound horizon at the drag epoch.
Although RSDs have been understood and measured since the late 1980s (Kaiser 1987), it is only in the last decade, when there has been significant interest in deviations from standard gravity that would explain the apparent late-time acceleration of the expansion of the Universe, that the ability of RSD measurements to provide such tests has been explored (Guzzo et al. 2008; Song & Percival 2009). This has resulted in renewed interest in RSD with examples of RSD measurement from the WiggleZ (Blake et al. 2011), 6dFGRS (Beutler et al. 2012), SDSS-II (Samushia, Percival & Raccanelli 2012), SDSS-MGS (Howlett et al. 2015), FastSound (Okumura et al. 2016), and VIPERS (Pezzotta et al. 2017) galaxy surveys, with BOSS achieving the best precision of ∼6 per cent on the parameter combination fσ8 (Beutler et al. 2017; Grieb et al. 2017; Sánchez et al. 2017; Satpathy et al. 2017), which is commonly used to quantify the amplitude of the velocity power spectrum.
The extended Baryon Oscillation Spectroscopic Survey (eBOSS; Dawson et al. 2016) programme is the successor of BOSS in the fourth generation of the SDSS (Blanton et al. 2017). It maps the LSS using four main tracers: luminous red galaxies (LRGs), emission line galaxies (ELGs), quasars used as direct tracers of the density field, and quasars from whose spectra we can measure the Ly α forest. With respect to BOSS, it explores galaxies at higher redshifts, covering the range 0.6 < |$z$| < 2.2. Using the first 2 yr of data from Data Release 14 (DR14), BAO and RSD measurements have been performed using different tracers and methods: LRG BAO (Bautista et al. 2018), LRG RSD (Icaza-Lizaola et al. 2020), quasar BAO (Ata et al. 2018), quasar BAO with redshift weights (Zhu et al. 2018), quasar BAO Fourier space (Wang et al. 2018), quasar RSD Fourier space (Gil-Marín et al. 2018), quasar RSD Fourier space with redshift weights (Ruggeri et al. 2017, 2019), quasar RSD in configuration space (Hou et al. 2018; Zarrouk et al. 2018), and quasar tomographic RSD in Fourier space with redshift weights (Zhao et al. 2019).
In this paper, we perform the BAO and RSD analyses in configuration space of the completed eBOSS LRG sample, part of DR16. This work is part of a series of papers using different tracers and methods.1 The official SDSS-IV DR16 quasar catalogue is described in Lyke et al. (2020). The production of the catalogues specific for large-scale clustering measurements of the quasar and LRG sample (input for this work) is described in Ross et al. (2020), while the analogous work for the ELG sample is described in Raichoor et al. (2020). From the same LRG catalogue, Gil-Marín et al. (2020) report the BAO and RSD analyses in Fourier space. The BAO and RSD constraints from the quasar sample are presented by Hou et al. (2020) in configuration space and by Neveux & Burtin (2020) in Fourier space. The clustering from the ELG sample is described by de Mattia et al. (2020) in Fourier space and by Amelie et al. (2020) in configuration space. Finally, a series of articles describes the simulations used to test the different methodologies for each tracer. The approximate mocks used to estimate covariance matrices and assess observational systematics for the LRG, ELG, and quasar samples are described in Zhao et al. (2020) (see also Lin et al. 2020, for an alternative method for ELGs), while realistic N-body simulations were produced by Rossi et al. (2020) for the LRG sample, by Smith et al. (2020) for the quasar sample, and by Alam et al. (2020) for the ELG sample. In Ávila et al. (2020), halo occupation models for ELGs are studied. A machine-learning method to remove systematics caused by photometry was applied to the ELG sample (Kong et al. 2020) and a new method to account for fibre collisions in the eBOSS sample is described in Mohammad et al. (2020). The BAO analysis of the Lyman-α forest sample is presented by du Mas des Bourboux et al. (2020). The final cosmological implications from all these clustering analyses are presented in eBOSS Collaboration (2020).
The paper is organized as follows: Section 2 describes the LRG data set and simulations used in this analysis. Section 3 presents the adopted methodology and particularly BAO and RSD theoretical models. We estimate biases and systematic errors from different sources in Section 4. We present BAO and RSD results in Section 5 and finally conclude in Section 6.
2 DATA SET
In this section, we summarize the observations, catalogues, and mock data sets that are used to test our methodology, as well as the clustering statistics used in this work.
2.1 Spectroscopic observations and reductions
The fourth generation of the SDSS (SDSS-IV; Blanton et al. 2017) employed the two multi-object BOSS spectrographs (Smee et al. 2013) installed on the 2.5-m telescope (Gunn et al. 2006) at the Apache Point Observatory in New Mexico, USA, to carry out spectroscopic observations for eBOSS. The target sample of LRGs, the analysis of which is our focus, was selected from the optical SDSS photometry from DR13 (Albareti et al. 2017), with additional infrared information from the Wide-field Infrared Survey Explorer satellite (Lang, Hogg & Schlegel 2014). The final targeting algorithm is described in detail in Prakash et al. (2016) and produced about 60 deg−2 LRG targets over the 7500 deg2 of the eBOSS footprint, of which 50 deg−2 were observed spectroscopically. The selection was tested over 466 deg2 covered during the Sloan Extended Quasar, ELG, and LRG Survey (SEQUELS), confirming that more than 41 deg−2 LRGs have 0.6 < |$z$| < 1.0 (Dawson et al. 2016).
The raw CCD images were converted to one-dimensional, wavelength and flux calibrated spectra using version v5_13_0 of the SDSS spectroscopic pipeline idlspec2d.2 Two main improvements of this pipeline since its previous release (DR14; Abolfathi et al. 2018) include a new library of stellar templates for flux calibration and a more stable extraction procedure. Ahumada et al. (2020) provide a summary of all improvements of the spectroscopic pipeline since SDSS-III.
The redshift of each LRG was estimated with the redrock algorithm.3 This algorithm improves classification rates with respect to its predecessor redmonster (Hutchinson et al. 2016). redrock uses templates derived from principal component analysis of the SDSS data to classify spectra, which is followed by a redshift refinement procedure that uses stellar population models for galaxies. On average, 96.5 per cent of spectra yield a confident redshift estimate with redrock compared to 90 per cent with redmonster, with less than 1 per cent of catastrophic redshift errors (details can be found in Ross et al. 2020).
2.2 Survey geometry and observational features
The full procedure to model the survey geometry and correct for observational features is described in detail in the companion paper Ross et al. (2020). We summarize it in the following.
The random catalogue allows estimating the survey geometry and number density of galaxies in the observed sample. It contains a random population of objects with the same radial and angular selection functions as the data. A random uniform sample of points is drawn over the angular footprint of eBOSS targets to model its geometry. We use random samples with 50 times more objects than in the data to minimize the shot noise contribution in the estimated correlation function, and redshifts are randomly taken from galaxy redshifts in the data. A series of masks are then applied to both data and random samples in order to eliminate regions with bad photometric properties, targets that collide with quasar spectra (which had priority in fibre assignment), and the central region of the plates where it is physically impossible to put a fibre. All masks combined cover 17 per cent of the initial footprint, with the quasar collision mask accounting for 11 per cent. The spectroscopic information is finally matched to the remaining targets.
About 4 per cent of the LRG targets were not observed due to fibre collisions; i.e. when a group of two or more galaxies are closer than 62 arcsec, they cannot all receive a fibre. On regions of the sky observed more than once, some collisions could be resolved. These collisions can bias the clustering measurements, so we applied the following correction: Ntarg objects in a given collision group for which Nspec have a spectrum, all objects are up-weighted by |$w$|cp = Ntarg/Nspec. This is different compared to Bautista et al. (2018), where the weight of the collided object without spectrum was transferred to its nearest neighbour with valid spectrum. Both corrections are only approximations valid on scales larger than 62 arcsec. An unbiased correction method is described in Bianchi & Percival (2017) and applied to eBOSS samples in Mohammad et al. (2020). We show in Appendix B that our results are insensitive to the correction method since it affects mostly the smallest scales.
A similar procedure as in Bautista et al. (2018) was used to account for the 3.5 per cent of LRG targets without reliable redshift estimate. The redshift-failure weight |$w$|noz acts as an inverse probability weight, boosting galaxies with good redshifts such that this weighted sample is an unbiased sampling of the full population. This assumes that the probability of a given galaxy being selected is a function of both its trace position on the CCD and the overall signal-to-noise ratio of the spectrograph in which this target was observed, and that the galaxies not observed are statistically equivalent to the observed galaxies. Spurious fluctuations in the target selection caused by the photometry are corrected by weighting each galaxy by |$w$|sys. These weights are computed with a multilinear regression on the observed relations between the angular overdensities of galaxies versus stellar density, seeing, and galactic extinction. Fitting all quantities simultaneously automatically accounts for their correlations. The weights |$w$|noz and |$w$|sys are computed independently.
The observational completeness creates artificial angular variations of the density that are accounted for using the random catalogue. The completeness is defined as the ratio of the number of weighted spectra (including those classified as stars or quasars) to the number of targets (equation 11 in Ross et al. 2020). This quantity is computed per sky sector, i.e. a connected region observed by a unique set of plates. We downweight each point in the random catalogue by the completeness of its corresponding sky sector.
Optimal weights for large-scale correlations, known as FKP weights (Feldman, Kaiser & Peacock 1994), are computed with the estimated comoving density of tracers |$\bar{n}(z)$| as a function of redshift using our fiducial cosmology in Table 1. The final weight for each galaxy is defined4 as |$w$| = |$w$|noz|$w$|cp|$w$|syst|$w$|FKP. The weight for each galaxy from the random catalogue is the same, with the completeness information already included in |$w$|sys.
Sets of cosmological models used in this work. All models are parametrized by their fraction of the total energy density in form of total matter Ωm, cold dark matter Ωc, baryons Ωb, and neutrinos Ων, the Hubble constant h = H0/(100 km s−1 Mpc−1), the primordial spectral index ns, and primordial amplitude of power spectrum As. With these parameters, we compute the normalization of the linear power spectrum σ8 at |$z$| = 0 and the comoving sound horizon scale at drag epoch rdrag. The different labels refer to our baseline choice (Base), the EZmocks (EZ), the Nseries (NS), the OuterRim (OR) cosmologies, and an additional model (X) with larger value for Ωm.
| . | Base . | ez . | ns . | or . | X . |
|---|---|---|---|---|---|
| Ωm | 0.310 | 0.307 | 0.286 | 0.265 | 0.350 |
| Ωc | 0.260 | 0.259 | 0.239 | 0.220 | 0.300 |
| Ωb | 0.048 | 0.048 | 0.047 | 0.045 | 0.048 |
| Ων | 0.0014 | 0 | 0 | 0 | 0.0014 |
| h | 0.676 | 0.678 | 0.700 | 0.710 | 0.676 |
| ns | 0.970 | 0.961 | 0.960 | 0.963 | 0.970 |
| As (10−9) | 2.041 | 2.116 | 2.147 | 2.160 | 2.041 |
| σ8 (|$z$| = 0) | 0.800 | 0.823 | 0.820 | 0.800 | 0.874 |
| rdrag (Mpc) | 147.78 | 147.66 | 147.15 | 149.35 | 143.17 |
| . | Base . | ez . | ns . | or . | X . |
|---|---|---|---|---|---|
| Ωm | 0.310 | 0.307 | 0.286 | 0.265 | 0.350 |
| Ωc | 0.260 | 0.259 | 0.239 | 0.220 | 0.300 |
| Ωb | 0.048 | 0.048 | 0.047 | 0.045 | 0.048 |
| Ων | 0.0014 | 0 | 0 | 0 | 0.0014 |
| h | 0.676 | 0.678 | 0.700 | 0.710 | 0.676 |
| ns | 0.970 | 0.961 | 0.960 | 0.963 | 0.970 |
| As (10−9) | 2.041 | 2.116 | 2.147 | 2.160 | 2.041 |
| σ8 (|$z$| = 0) | 0.800 | 0.823 | 0.820 | 0.800 | 0.874 |
| rdrag (Mpc) | 147.78 | 147.66 | 147.15 | 149.35 | 143.17 |
Sets of cosmological models used in this work. All models are parametrized by their fraction of the total energy density in form of total matter Ωm, cold dark matter Ωc, baryons Ωb, and neutrinos Ων, the Hubble constant h = H0/(100 km s−1 Mpc−1), the primordial spectral index ns, and primordial amplitude of power spectrum As. With these parameters, we compute the normalization of the linear power spectrum σ8 at |$z$| = 0 and the comoving sound horizon scale at drag epoch rdrag. The different labels refer to our baseline choice (Base), the EZmocks (EZ), the Nseries (NS), the OuterRim (OR) cosmologies, and an additional model (X) with larger value for Ωm.
| . | Base . | ez . | ns . | or . | X . |
|---|---|---|---|---|---|
| Ωm | 0.310 | 0.307 | 0.286 | 0.265 | 0.350 |
| Ωc | 0.260 | 0.259 | 0.239 | 0.220 | 0.300 |
| Ωb | 0.048 | 0.048 | 0.047 | 0.045 | 0.048 |
| Ων | 0.0014 | 0 | 0 | 0 | 0.0014 |
| h | 0.676 | 0.678 | 0.700 | 0.710 | 0.676 |
| ns | 0.970 | 0.961 | 0.960 | 0.963 | 0.970 |
| As (10−9) | 2.041 | 2.116 | 2.147 | 2.160 | 2.041 |
| σ8 (|$z$| = 0) | 0.800 | 0.823 | 0.820 | 0.800 | 0.874 |
| rdrag (Mpc) | 147.78 | 147.66 | 147.15 | 149.35 | 143.17 |
| . | Base . | ez . | ns . | or . | X . |
|---|---|---|---|---|---|
| Ωm | 0.310 | 0.307 | 0.286 | 0.265 | 0.350 |
| Ωc | 0.260 | 0.259 | 0.239 | 0.220 | 0.300 |
| Ωb | 0.048 | 0.048 | 0.047 | 0.045 | 0.048 |
| Ων | 0.0014 | 0 | 0 | 0 | 0.0014 |
| h | 0.676 | 0.678 | 0.700 | 0.710 | 0.676 |
| ns | 0.970 | 0.961 | 0.960 | 0.963 | 0.970 |
| As (10−9) | 2.041 | 2.116 | 2.147 | 2.160 | 2.041 |
| σ8 (|$z$| = 0) | 0.800 | 0.823 | 0.820 | 0.800 | 0.874 |
| rdrag (Mpc) | 147.78 | 147.66 | 147.15 | 149.35 | 143.17 |
Values for the comoving angular diameter distance DM and the Hubble distance DH = c/H(|$z$|) in units of the sound horizon scale at drag epoch rd, and the normalized growth rate of structures fσ8. These values are predictions from the cosmological models in Table 1 computed at typical redshifts used in this work.
| Model . | |$z$|eff . | |$\frac{D_\mathrm{ M}}{r_{\rm drag}}$| . | |$\frac{D_\mathrm{ H}}{r_{\rm drag}}$| . | fσ8 . |
|---|---|---|---|---|
| Base | 0.698 | 17.436 | 20.194 | 0.456 |
| Base | 0.560 | 14.529 | 21.960 | 0.465 |
| ez | 0.698 | 17.429 | 20.211 | 0.467 |
| ns | 0.560 | 14.221 | 21.692 | 0.469 |
| or | 0.695 | 16.717 | 19.866 | 0.447 |
| X | 0.698 | 17.685 | 20.146 | 0.504 |
| X | 0.560 | 14.778 | 22.019 | 0.518 |
| Model . | |$z$|eff . | |$\frac{D_\mathrm{ M}}{r_{\rm drag}}$| . | |$\frac{D_\mathrm{ H}}{r_{\rm drag}}$| . | fσ8 . |
|---|---|---|---|---|
| Base | 0.698 | 17.436 | 20.194 | 0.456 |
| Base | 0.560 | 14.529 | 21.960 | 0.465 |
| ez | 0.698 | 17.429 | 20.211 | 0.467 |
| ns | 0.560 | 14.221 | 21.692 | 0.469 |
| or | 0.695 | 16.717 | 19.866 | 0.447 |
| X | 0.698 | 17.685 | 20.146 | 0.504 |
| X | 0.560 | 14.778 | 22.019 | 0.518 |
Values for the comoving angular diameter distance DM and the Hubble distance DH = c/H(|$z$|) in units of the sound horizon scale at drag epoch rd, and the normalized growth rate of structures fσ8. These values are predictions from the cosmological models in Table 1 computed at typical redshifts used in this work.
| Model . | |$z$|eff . | |$\frac{D_\mathrm{ M}}{r_{\rm drag}}$| . | |$\frac{D_\mathrm{ H}}{r_{\rm drag}}$| . | fσ8 . |
|---|---|---|---|---|
| Base | 0.698 | 17.436 | 20.194 | 0.456 |
| Base | 0.560 | 14.529 | 21.960 | 0.465 |
| ez | 0.698 | 17.429 | 20.211 | 0.467 |
| ns | 0.560 | 14.221 | 21.692 | 0.469 |
| or | 0.695 | 16.717 | 19.866 | 0.447 |
| X | 0.698 | 17.685 | 20.146 | 0.504 |
| X | 0.560 | 14.778 | 22.019 | 0.518 |
| Model . | |$z$|eff . | |$\frac{D_\mathrm{ M}}{r_{\rm drag}}$| . | |$\frac{D_\mathrm{ H}}{r_{\rm drag}}$| . | fσ8 . |
|---|---|---|---|---|
| Base | 0.698 | 17.436 | 20.194 | 0.456 |
| Base | 0.560 | 14.529 | 21.960 | 0.465 |
| ez | 0.698 | 17.429 | 20.211 | 0.467 |
| ns | 0.560 | 14.221 | 21.692 | 0.469 |
| or | 0.695 | 16.717 | 19.866 | 0.447 |
| X | 0.698 | 17.685 | 20.146 | 0.504 |
| X | 0.560 | 14.778 | 22.019 | 0.518 |
The eBOSS sample of LRGs overlaps in area and redshift range with the highest redshift bin of the CMASS sample (0.5 < |$z$| < 0.75). We combine the eBOSS LRG sample with all the |$z$| > 0.6 BOSS CMASS galaxies and their corresponding random catalogue (including the non-overlapping with eBOSS), making sure that the data-to-random number ratio is the same for both samples. This combination is beneficial for two reasons. First, the combined sample supersedes the last redshift bin of BOSS measurements while being completely independent of the first two lower redshift bins. Secondly, the reconstruction technique applied to this sample (see the next section) benefits from a higher density of tracers, reducing potential noise introduced by the procedure. The new eBOSS LRG sample covers 4242 deg2 of the total BOSS CMASS footprint of 9494 deg2 (NGC and SGC combined). Considering their spectroscopic weights, the new eBOSS sample has 185 295 new redshifts over 0.6 < |$z$| < 1.0 while CMASS contributes with 104 865 redshifts in the overlapping area and 111 892 in the non-overlapping area. A total of 402 052 LRGs over 0.6 < |$z$| < 1.0 contribute to this measurement, with a total effective comoving volume of 2.72 Gpc3 (1.43 Gpc3 from the CMASS sample and 1.28 Gpc3 from the new eBOSS sample). A detailed description of these numbers is given in Ross et al. (2020). In the following, we simply refer to the combined CMASS+LRG sample as the eBOSS LRG sample. The number density of CMASS galaxies, LRGs, and combined CMASS+LRG sample are presented in Fig. 1.
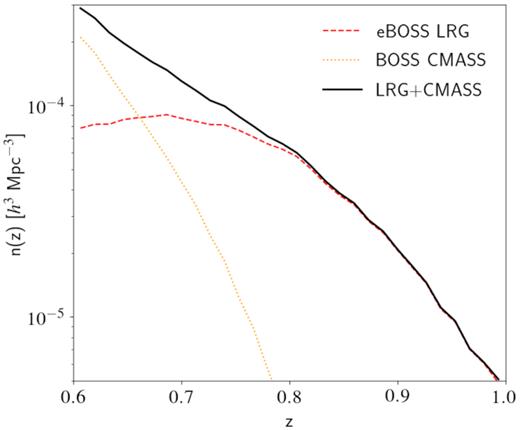
The observed number density of eBOSS LRGs (dashed curve), BOSS CMASS galaxies (dotted curve), and combined CMASS+LRG sample galaxies (solid curve) at 0.6 < |$z$| < 1. This combines NGC and SGC fields.
2.3 Reconstruction
While constraints on the growth rate of structure are obtained using the information from the full shape of the correlation function, BAO analyses extract the cosmological information only from the position of the BAO peak. In our BAO analysis, we applied the reconstruction technique of Burden et al. (2014) and Burden, Percival & Howlett (2015) to the observed galaxy density field in order to remove a fraction of the RSDs, as well as non-linear motions of galaxies that smeared out the BAO peak. This technique sharpens the BAO feature in the two-point statistics in Fourier and configuration space, increasing the precision of the measurement of the acoustic scale. Reconstruction is applied on actual data and on mock catalogues using a publicly available5 code (Bautista et al. 2018). Our final BAO results are solely based on reconstructed catalogues, while full-shape results use the pre-reconstruction sample.
We apply reconstruction to the full eBOSS+CMASS final LRG catalogue. We use our fiducial cosmology from Table 1 to convert redshifts to comoving distances. For the reconstruction, we fix the bias value to b = 2.3 and assume the standard gravity relation between the growth rate of structure and Ωm, i.e. |$f = \Omega _\mathrm{ m}^{6/11}(z=0.7) = 0.815$|. We use a smoothing scale of 15 h−1 Mpc. The BAO results are not sensitive to small variations of those parameter choices as studied in Carter et al. (2020).
2.4 Mocks
In order to test the overall methodology and study the impact of systematic effects, we have constructed several sets of mock samples. Approximate methods are considered to be sufficient for covariance matrix estimates and to derive systematic biases in BAO measurements. However, the full-shape analysis of the correlation function requires more realistic N-body simulations, particularly in order to test the modelling. In this study, our synthetic data sets are the following:
1000 realizations of the LRG eBOSS+CMASS survey geometry using the EZmock method (Chuang et al. 2015), which employs the Zel’dovich approximation to compute the density field at a given redshift and populates it with galaxies. This method is fast and has been calibrated to reproduce the two- and three-point statistics of the given galaxy sample, to a good approximation and up to mildly non-linear scales. The angular and redshift distributions of the eBOSS LRG sample in combination with the |$z$| > 0.6 CMASS sample were reproduced in these mock catalogues. The full description of the EZmock LRG samples can be found in the companion paper Zhao et al. (2020). We use these mocks in several steps of our analysis: to infer the error covariance matrix of our clustering measurements in the data, to study the impact of observational systematic effects on cosmology, and to estimate the correlations between different methods for the calculation of the consensus results.
84 realizations of the Nseries mocks, which are N-body simulation snapshots populated with a single halo occupation distribution (HOD) model. These mock catalogues reproduce the angular and redshift distributions of the North Galactic Cap of the BOSS CMASS sample within the redshift range 0.43 < |$z$| < 0.70 (Alam et al. 2017). While this data set is not fully representative of the eBOSS LRG sample, we use these N-body mocks to test the RSD models down to the non-linear regime. The number of available realizations and their large volume are ideal to test model accuracy in the high-precision regime. The covariance matrix for these mocks is computed from 2048 realizations of the same volume with the MD-Patchy approximated method (Kitaura, Yepes & Prada 2014). The redshift of those mocks is |$z$| = 0.55.
27 realizations extracted from the OuterRim N-body simulation (Heitmann et al. 2019), and corresponding to cubical mocks of 1 h−3 Gpc3 each. The dark matter haloes have been populated with galaxies using four different HODs (Zheng, Coil & Zehavi 2007; Leauthaud et al. 2011; Tinker et al. 2013; Hearin, Watson & van den Bosch 2015) at three different luminosity thresholds to cover a large range of galaxy populations. These mocks are part of our internal MockChallenge and aimed at quantifying potential systematic errors originating from the HODs. A detailed description of these simulations and the MockChallenge can be found in the companion paper Rossi et al. (2020). The redshift of those mocks is |$z$| = 0.695.
2.5 Fiducial cosmologies
The redshift of each galaxy is converted into radial comoving distances for clustering measurements by means of a fiducial cosmology. The fiducial cosmologies employed in this work are shown in Table 1. Our baseline choice, named ‘Base’, is a flat Lambda cold dark matter (ΛCDM) model matching the cosmology used in previous BOSS analyses (Alam et al. 2017) with parameters within 1σ of Planck best-fitting parameters (Planck Collaboration I 2018a). Some of these cosmologies were used to produce the mock data sets described in Section 2.4. A choice of fiducial cosmology is also needed when computing the linear power spectrum Plin(k), input for all our correlation function models in this work (see Sections 3.1 and 3.2). In Sections 4.1 and 4.2, we study the dependence of our results on the choice of fiducial cosmology.
2.6 Galaxy clustering estimation
The measured anisotropic correlation function, where the galaxy separation vector |$\boldsymbol{r}$| has been decomposed into line-of-sight and transverse separations (r⊥, r∥), is presented in the left-hand panel of Fig. 2. A clear BAO feature is seen at r ≈ 100 h−1 Mpc as well as the impact of RSD, which squashes the contours along the line of sight on large scales. In the right-hand panel of Fig. 2, we show the post-reconstruction correlation function where some of the isotropy is recovered and the BAO feature is sharpened.
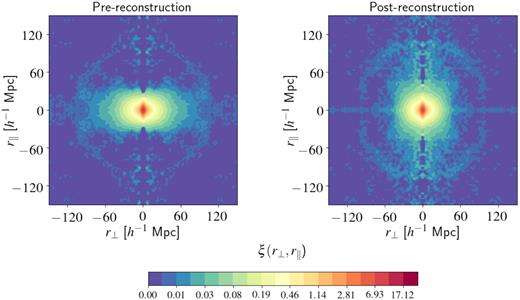
Anisotropic two-point correlation function of eBOSS LRG+CMASS galaxies at 0.6 < |$z$| < 1. The left-hand (right) panel shows the pre-reconstruction (post-reconstruction) two-point correlation function in bins of r⊥ and r∥. Bins of size 1.25 h−1 Mpc and a bi-cubic spline interpolation have been used to produce the contours.
The red points with error bars in Fig. 3 show the even multipoles of the correlation function from the eBOSS LRG sample. The solid, dashed, and dotted black curves display the average multipoles in the different mock data sets used in this study: EZmocks, Nseries, and MockChallenge. The error bars are obtained from the dispersion of the 1000 EZmocks multipoles around their mean. By construction, the amplitude of the EZmock multipoles matches the data at separations s < 70 h−1 Mpc. A slight mismatch in the BAO peak amplitudes between data and EZmocks is visible. This mismatch does not impact cosmological results from the data since the covariance matrix dependence on the peak amplitude is small. However, the comparison of the precision of BAO peak measurements between mocks and data needs to account for this mismatch: The expected errors of our BAO measurement are smaller for data than those for the ensemble of EZmocks. For comparison, the average multipoles of the Nseries mocks, also shown in Fig. 3, are a better match to the peak amplitude seen in the data.
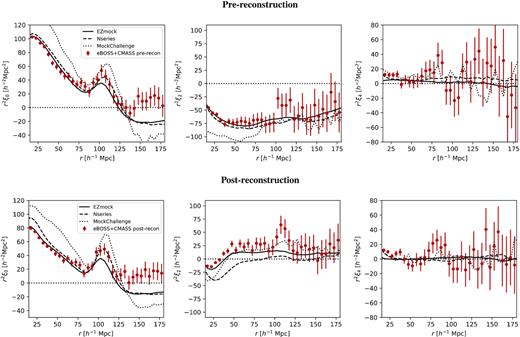
Multipoles of the correlation function of data compared to the mock catalogues. The data are the combined eBOSS LRG+CMASS (NGC+SGC) samples and the mocks are the average multipoles of 1000 EZmocks realizations (solid line), 84 Nseries realizations (dashed line), and 27 MockChallenge mocks populated with L11 HOD model (dotted lines). The top panels show the monopole, quadrupole, and hexadecapole of the pre-reconstruction samples while the bottom panels show the same for the post-reconstruction case.
3 METHODOLOGY
In this section, we describe the BAO and RSD modelling, fitting procedure, and how errors on cosmological parameters are estimated.
3.1 BAO modelling
We employ the standard approach used in previous SDSS publications for measuring the BAO scale in configuration space (e.g. Anderson et al. 2014; Alam et al. 2017; Ross et al. 2017; Bautista et al. 2018). The code that produces the model and performs the fitting to the data is publicly available.6
We follow the procedure from Kirkby et al. (2013) to decompose the BAO peak component Ppeak from the linear power spectrum Plin. We start by computing the correlation function by Fourier transforming Plin, and then we replace the correlations over the peak region by a polynomial function fitted using information outside the peak region (50 < r < 80 and 160 < r < 190 h−1 Mpc). The resulting correlation function is then Fourier transformed back to get Pno peak. The linear power spectrum Plin is computed using the code camb 7 (Lewis, Challinor & Lasenby 2000) with cosmological parameters of our fiducial cosmology (Table 1). The analysis in Fourier space uses the same procedure (see Gil-Marín et al. 2020). Previous BOSS and eBOSS analyses making BAO measurements from direct tracer galaxies used the approximate formulae from Eisenstein, Hu & Tegmark (1998) for decomposing the peak. We have checked that both methods yield only negligibly different results.
Our baseline BAO analysis uses the monopole ξ0 and the quadrupole ξ2 of the correlation function. We performed fits on mock multipoles including the hexadecapole ξ4, finding that it does not add information (see Table 6). We fix β = 0.35 and fit b with a flat prior between b = 1.0 and 4. For all fits, the broad-band parameters are free, while both dilation parameters are allowed to vary between 0.5 and 1.5. A total of nine parameters are fitted simultaneously.
3.2 RSD modelling
We describe the apparent distortions introduced by galaxy peculiar velocities in the redshift-space galaxy clustering pattern using two different analytical models: the combined Gaussian streaming (GS) and Convolutional Lagrangian Perturbation Theory (CLPT) formalism developed by Reid & White (2011), Carlson, Reid & White (2013), Wang, Reid & White (2014), and the Taruya, Nishimichi & Saito (2010) model (TNS) supplemented with a non-linear galaxy bias prescription. These two models, frequently used in the literature, partially account for RSD non-linearities and describe the anisotropic clustering down to the quasi-linear regime. We use both models to fit the multipoles of the correlation function and later combine their results to provide more robust estimates of the growth rate of structure and geometrical parameters. This procedure should reduce the residual theoretical systematic errors. In this section, we briefly describe the two models and assess in Section 4.2 their performance in the recovery of unbiased cosmological parameters using mock data sets.
3.2.1 CLPT with GS
The kernels |$M_{1,2}(\boldsymbol{r}, \boldsymbol{q})$| also depend on the first two non-local derivatives of the Lagrangian bias 〈F′〉 and 〈F″〉, which are free parameters in addition to the linear growth rate f in our model. Hereafter, we eliminate the angle brackets around the Lagrangian bias terms to simplify the notation in the following sections.
Although CLPT is more accurate than Lagrangian Resummation Theory from Matsubara (2008) in real space, we still have to improve the small-scale modelling in order to study RSDs. This is particularly important considering that part of peculiar velocities is generated by interactions that occur at the typical scales of clusters of galaxies (∼1 Mpc). This is achieved by mapping the real-space CLPT model of the two-point statistics into redshift space with the GS model proposed by Reid & White (2011). The pairwise velocity distribution of tracers is assumed to have a Gaussian distribution that depends on both the separation r and the angle between the separation vector and the line of sight μ.
3.2.2 TNS model
The input linear power spectrum Plin is obtained with camb, while the non-linear power spectrum Pδδ is calculated from the respresso code (Nishimichi, Bernardeau & Taruya 2017). This non-linear power spectrum prediction does agree very well with successful perturbation theory-based predictions such as RegPT, but extend their validity to k ≃ 0.4 (Nishimichi et al. 2017). This is very relevant for configuration-space analysis, where one needs to have both a correct BAO amplitude and a non-vanishing signal at high k to avoid aliasing in the transformation from Fourier to configuration space.
In total, this model has either four or five free parameters, [f, b1, b2, σ|$v$|] or |$[f,b_1,b_2,b_{\Gamma _{3}},\sigma _v]$|, depending on the number of bias parameters that are let free. Finally, the multipole moments of the anisotropic correlation function are obtained by performing the Hankel transform of the model |$P_\ell ^s(k)$|.
3.2.3 Alcock–Paczynski effect
3.2.4 The fiducial scale at which σ8 is measured
3.3 Parameter inference
In the BAO analysis, the best-fitting parameters (α⊥, α∥) are found by minimizing |$-2\ln \mathcal {L} = \chi ^2$| using a quasi-Newton minimum finder algorithm iMinuit.9 The errors in α∥ and α⊥ are found by computing the intervals where χ2 increases by unity. Gaussianity is not assumed in the error calculation, but we find that on average, errors are symmetric and correctly described by a Gaussian. The 2D errors in (α⊥, α∥), such as those presented in Fig. 13, are found by scanning χ2 values in a regular grid in α⊥ and α∥. In the case of the full-shape analysis, we explore the likelihood with the Markov chain Monte Carlo (MCMC) ensemble sampler emcee.10 The input power spectrum shape parameters are fixed at the fiducial cosmology and any deviations are accounted for through the Alcock–Paczynski parameters α⊥ and α∥. We assume the uniform priors on model parameters given in Table 3.
List of fitter parameters and their priors used in full-shape analysis for the two models.
| Par. TNS . | Prior TNS . | Par. CLPT-GS . | Prior CLPT-GS . |
|---|---|---|---|
| α⊥ | [0.5, 1.5] | α⊥ | [0.5, 1.5] |
| α∥ | [0.5, 1.5] | α∥ | [0.5, 1.5] |
| f | [0, 2] | f | [0, 2] |
| b1 | [0.2, 4] | 〈F′〉 | [0, 3] |
| b2 | [−10, 10] | 〈F″〉 | [−10, 10] |
| |$b_{\Gamma _3}$| | [−2, 4] | σFoG | [0, 40] |
| σ|$v$| | [0.1, 8] | – | – |
| Par. TNS . | Prior TNS . | Par. CLPT-GS . | Prior CLPT-GS . |
|---|---|---|---|
| α⊥ | [0.5, 1.5] | α⊥ | [0.5, 1.5] |
| α∥ | [0.5, 1.5] | α∥ | [0.5, 1.5] |
| f | [0, 2] | f | [0, 2] |
| b1 | [0.2, 4] | 〈F′〉 | [0, 3] |
| b2 | [−10, 10] | 〈F″〉 | [−10, 10] |
| |$b_{\Gamma _3}$| | [−2, 4] | σFoG | [0, 40] |
| σ|$v$| | [0.1, 8] | – | – |
List of fitter parameters and their priors used in full-shape analysis for the two models.
| Par. TNS . | Prior TNS . | Par. CLPT-GS . | Prior CLPT-GS . |
|---|---|---|---|
| α⊥ | [0.5, 1.5] | α⊥ | [0.5, 1.5] |
| α∥ | [0.5, 1.5] | α∥ | [0.5, 1.5] |
| f | [0, 2] | f | [0, 2] |
| b1 | [0.2, 4] | 〈F′〉 | [0, 3] |
| b2 | [−10, 10] | 〈F″〉 | [−10, 10] |
| |$b_{\Gamma _3}$| | [−2, 4] | σFoG | [0, 40] |
| σ|$v$| | [0.1, 8] | – | – |
| Par. TNS . | Prior TNS . | Par. CLPT-GS . | Prior CLPT-GS . |
|---|---|---|---|
| α⊥ | [0.5, 1.5] | α⊥ | [0.5, 1.5] |
| α∥ | [0.5, 1.5] | α∥ | [0.5, 1.5] |
| f | [0, 2] | f | [0, 2] |
| b1 | [0.2, 4] | 〈F′〉 | [0, 3] |
| b2 | [−10, 10] | 〈F″〉 | [−10, 10] |
| |$b_{\Gamma _3}$| | [−2, 4] | σFoG | [0, 40] |
| σ|$v$| | [0.1, 8] | – | – |
The final parameter constraints are obtained by marginalizing the full posterior likelihood over the nuisance parameters. The marginal posterior is approximated by a multivariate Gaussian distribution with central values given by best-fitting parameter values θ* = (α⊥, α∥, fσ8) and parameter covariance matrix Cθ. Since the covariance matrix is computed from a finite number of mock realizations, we need to apply correction factors to the obtained Cθ. These factors are equations (18) and (22) from Percival et al. (2014) to be applied to uncertainties and to the scatter over best-fitting values, respectively. These factors, which depend on the number of mocks, parameters, and bins in the data vectors, are presented in Table 4. The final parameter constraints from this work are available to the public in this format.11
Characteristics of the baseline fits for all models in this work, where Nmock is the number of mocks used in the estimation of the covariance matrix, Npar is the total number of parameters fitted, Nbins is the total size of the data vector, (1 − D) is the correction factor to the precision matrix (Hartlap et al. 2007), m1 is the factor to be applied to the estimated error matrix, and m2 is the factor that scales the scatter of best-fitting parameters of a set of mocks (if these were used in the calculation of the covariance matrix). The derivation of m1 and m2 can be found in Percival et al. (2014).
| . | BAO . | RSD TNS . | RSD CLPT-GS . |
|---|---|---|---|
| Nmock | 1000 | 1000 | 1000 |
| Npar | 9 | 7 | 6 |
| Nbins | 40 | 65 | 63 |
| (1 − D) | 0.96 | 0.93 | 0.94 |
| m1 | 1.022 | 1.053 | 1.053 |
| m2 | 1.065 | 1.128 | 1.125 |
| . | BAO . | RSD TNS . | RSD CLPT-GS . |
|---|---|---|---|
| Nmock | 1000 | 1000 | 1000 |
| Npar | 9 | 7 | 6 |
| Nbins | 40 | 65 | 63 |
| (1 − D) | 0.96 | 0.93 | 0.94 |
| m1 | 1.022 | 1.053 | 1.053 |
| m2 | 1.065 | 1.128 | 1.125 |
Characteristics of the baseline fits for all models in this work, where Nmock is the number of mocks used in the estimation of the covariance matrix, Npar is the total number of parameters fitted, Nbins is the total size of the data vector, (1 − D) is the correction factor to the precision matrix (Hartlap et al. 2007), m1 is the factor to be applied to the estimated error matrix, and m2 is the factor that scales the scatter of best-fitting parameters of a set of mocks (if these were used in the calculation of the covariance matrix). The derivation of m1 and m2 can be found in Percival et al. (2014).
| . | BAO . | RSD TNS . | RSD CLPT-GS . |
|---|---|---|---|
| Nmock | 1000 | 1000 | 1000 |
| Npar | 9 | 7 | 6 |
| Nbins | 40 | 65 | 63 |
| (1 − D) | 0.96 | 0.93 | 0.94 |
| m1 | 1.022 | 1.053 | 1.053 |
| m2 | 1.065 | 1.128 | 1.125 |
| . | BAO . | RSD TNS . | RSD CLPT-GS . |
|---|---|---|---|
| Nmock | 1000 | 1000 | 1000 |
| Npar | 9 | 7 | 6 |
| Nbins | 40 | 65 | 63 |
| (1 − D) | 0.96 | 0.93 | 0.94 |
| m1 | 1.022 | 1.053 | 1.053 |
| m2 | 1.065 | 1.128 | 1.125 |
3.4 Combining BAO and RSD constraints
From the same input LRG catalogue, we produced BAO-only and full-shape RSD constraints, both in configuration and Fourier space (Gil-Marín et al. 2020). Each measurement yields a marginal posterior on (α⊥, α∥) for BAO-only or (α⊥, α∥, fσ8) for the full-shape RSD analyses. In the following, we describe the procedure to combine all these posteriors into a single consensus constraint, while correctly accounting for their covariances. This consensus result is the one used for the final cosmological constraints described in eBOSS Collaboration (2020).
We use the method described above to perform all the constraint combinations, except for the combination of results from CLPT-GS and TNS RSD models, which use the same input data vector (pre-reconstruction multipoles in configuration space). For this particular combination, we simply assume that |$C_c^{-1} = 0.5(C_{mm}^{-1}+C_{nn}^{-1})$| and |$x_c = 2 C_c^{-1}\left(C_{mm}^{-1} x_{m} + C_{nn}^{-1} x_{n}\right)$|. For all combinations, we chose to use the results from at most two methods at once (M = 2) in order to reduce the potential noise introduced by the procedure.
Denoting ξℓ the results from the configuration-space analysis and Pℓ that from the Fourier-space analysis, our recipe to obtain the consensus result for the LRG sample is as follows:
Combine RSD ξℓ TNS and RSD ξℓ CLPT-GS results into RSD ξℓ,
Combine BAO ξℓ with BAO Pℓ into BAO (ξℓ + Pℓ),
Combine RSD ξℓ with RSD Pℓ into RSD (ξℓ + Pℓ),
Combine BAO (ξℓ + Pℓ) with RSD (ξℓ + Pℓ) into BAO+RSD (ξℓ + Pℓ).
Alternatively, we can proceed as
Combine BAO ξℓ with RSD ξℓ into (BAO+RSD) ξℓ,
Combine BAO Pℓ with RSD Pℓ into (BAO+RSD) Pℓ,
Combine BAO+RSD ξℓ with BAO+RSD Pℓ into (BAO+RSD) ξℓ + Pℓ.
In Section 4.3, we test this procedure on the mock catalogues.
4 ROBUSTNESS OF THE ANALYSIS AND SYSTEMATIC ERRORS
4.1 Systematics in the BAO analysis
The methodology described in Section 3.1 was tested using the 1000 EZmocks mock survey realizations and 84 Nseries realizations. For each realization, we compute the correlation function and its multipoles, and fit for the BAO peak position to determine the dilation parameters α∥, α⊥ and associated errors. We compare the best-fitting α⊥, α∥ to their expected values, which are obtained from the cosmological models described in Table 1. The effective redshift of the EZmocks is |$z$|eff = 0.698 and |$z$|eff = 0.56 for Nseries.
In Fig. 4, we summarize the systematic biases from pre- and post-reconstruction mocks for a few choices of fiducial cosmology, parametrized by |$\Omega _\mathrm{ m}^{\rm fid}$|. In pre-reconstruction mocks, biases in the recovered α values reach up to 0.5 per cent in α⊥ and 1.0 per cent in α∥. These biases are expected due to the impact of non-linear effects on the position of the peak that cannot be correctly accounted for with the Gaussian damping terms in equation (4) at this level of precision (Seo et al. 2016). We recall that we are fitting the average of all realizations. The reconstruction procedure removes in part the non-linear effects and this is seen as a reduction of the biases to less than 0.2 per cent. The bias reduction is also seen in the Nseries mocks, particularly on α⊥, confirming that the bias reduction is not related to a feature of the mocks induced by the approximate method used to build them.
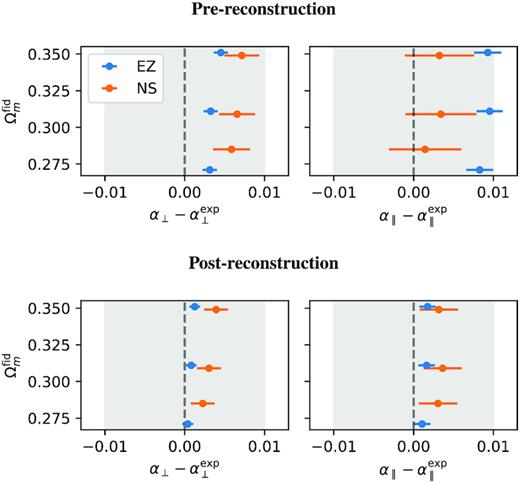
Impact of choice of fiducial cosmology in the recovered values of α∥ and α⊥ from the stacks of 1000 multipoles from the EZmocks (blue) and 84 Nseries mocks (orange), for pre- (top panels) and post-reconstruction (bottom panels). Associated error bars correspond to the error on the mean of the mocks. The grey shaded areas correspond to 1 per cent errors. For comparison, the error on real data is near 1.9 per cent for α⊥ and 2.6 per cent for α∥ in the post-reconstruction case.
Table 5 shows results from Fig. 4 for the post-reconstruction case only, including the fits with the hexadecapole ξℓ = 4. The impact of the hexadecapole is negligible even in this very low-noise regime, for both types of mocks. The reported dilation parameters for almost all cases are consistent with expected value within 2σ. We see a 2.6σ deviation on α⊥ for the Nseries case analysed with |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$|. However, this choice of |$\Omega _\mathrm{ m}^{\rm fid}$| is the most distant from the true value of the simulation and its observed bias is still less than half a per cent, which is small compared to the statistical power of our sample. For the EZmocks, which have smaller errors, the biases are up to 0.13 per cent for α⊥ and 0.18 per cent for α∥. These biases are much smaller than the expected statistical errors in our data, i.e. ∼1.9 per cent for α⊥ and ∼2.6 per cent for α∥, showing that our methodology is robust at this statistical level. In these fits, all parameters except Σrec = 15 h−1 Mpc were left free. The best-fitting values of Σ⊥, Σ∥, and Σs were used and held fixed in the fits of individual realizations.
Average biases from BAO fits on the stacked multipoles of 1000 EZmocks and 84 Nseries realizations. All results are based on post-reconstruction correlation functions.
| Sample . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | ℓmax . | |$\alpha _\perp - \alpha _\perp ^{\rm exp} \ [10^{-3}]$| . | |$\alpha _\parallel - \alpha _\parallel ^{\rm exp} \ [10^{-3}]$| . |
|---|---|---|---|---|
| ez | 0.27 | 2 | 0.4 ± 0.7 | 1.1 ± 1.0 |
| ez | 0.27 | 4 | 0.5 ± 0.7 | 1.4 ± 1.0 |
| ez | 0.31 | 2 | 0.9 ± 0.7 | 0.3 ± 1.1 |
| ez | 0.31 | 4 | 1.0 ± 0.7 | 0.4 ± 1.1 |
| ez | 0.35 | 2 | 1.3 ± 0.7 | 1.8 ± 1.0 |
| ez | 0.35 | 4 | 1.2 ± 0.7 | 1.5 ± 1.0 |
| ns | 0.286 | 2 | 2.3 ± 1.5 | 3.1 ± 2.4 |
| ns | 0.286 | 4 | 2.2 ± 1.5 | 3.0 ± 2.4 |
| ns | 0.31 | 2 | 3.0 ± 1.5 | 3.6 ± 2.4 |
| ns | 0.31 | 4 | 3.0 ± 1.5 | 3.7 ± 2.4 |
| ns | 0.35 | 2 | 3.9 ± 1.5 | 3.2 ± 2.4 |
| ns | 0.35 | 4 | 3.9 ± 1.5 | 3.5 ± 2.4 |
| Sample . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | ℓmax . | |$\alpha _\perp - \alpha _\perp ^{\rm exp} \ [10^{-3}]$| . | |$\alpha _\parallel - \alpha _\parallel ^{\rm exp} \ [10^{-3}]$| . |
|---|---|---|---|---|
| ez | 0.27 | 2 | 0.4 ± 0.7 | 1.1 ± 1.0 |
| ez | 0.27 | 4 | 0.5 ± 0.7 | 1.4 ± 1.0 |
| ez | 0.31 | 2 | 0.9 ± 0.7 | 0.3 ± 1.1 |
| ez | 0.31 | 4 | 1.0 ± 0.7 | 0.4 ± 1.1 |
| ez | 0.35 | 2 | 1.3 ± 0.7 | 1.8 ± 1.0 |
| ez | 0.35 | 4 | 1.2 ± 0.7 | 1.5 ± 1.0 |
| ns | 0.286 | 2 | 2.3 ± 1.5 | 3.1 ± 2.4 |
| ns | 0.286 | 4 | 2.2 ± 1.5 | 3.0 ± 2.4 |
| ns | 0.31 | 2 | 3.0 ± 1.5 | 3.6 ± 2.4 |
| ns | 0.31 | 4 | 3.0 ± 1.5 | 3.7 ± 2.4 |
| ns | 0.35 | 2 | 3.9 ± 1.5 | 3.2 ± 2.4 |
| ns | 0.35 | 4 | 3.9 ± 1.5 | 3.5 ± 2.4 |
Average biases from BAO fits on the stacked multipoles of 1000 EZmocks and 84 Nseries realizations. All results are based on post-reconstruction correlation functions.
| Sample . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | ℓmax . | |$\alpha _\perp - \alpha _\perp ^{\rm exp} \ [10^{-3}]$| . | |$\alpha _\parallel - \alpha _\parallel ^{\rm exp} \ [10^{-3}]$| . |
|---|---|---|---|---|
| ez | 0.27 | 2 | 0.4 ± 0.7 | 1.1 ± 1.0 |
| ez | 0.27 | 4 | 0.5 ± 0.7 | 1.4 ± 1.0 |
| ez | 0.31 | 2 | 0.9 ± 0.7 | 0.3 ± 1.1 |
| ez | 0.31 | 4 | 1.0 ± 0.7 | 0.4 ± 1.1 |
| ez | 0.35 | 2 | 1.3 ± 0.7 | 1.8 ± 1.0 |
| ez | 0.35 | 4 | 1.2 ± 0.7 | 1.5 ± 1.0 |
| ns | 0.286 | 2 | 2.3 ± 1.5 | 3.1 ± 2.4 |
| ns | 0.286 | 4 | 2.2 ± 1.5 | 3.0 ± 2.4 |
| ns | 0.31 | 2 | 3.0 ± 1.5 | 3.6 ± 2.4 |
| ns | 0.31 | 4 | 3.0 ± 1.5 | 3.7 ± 2.4 |
| ns | 0.35 | 2 | 3.9 ± 1.5 | 3.2 ± 2.4 |
| ns | 0.35 | 4 | 3.9 ± 1.5 | 3.5 ± 2.4 |
| Sample . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | ℓmax . | |$\alpha _\perp - \alpha _\perp ^{\rm exp} \ [10^{-3}]$| . | |$\alpha _\parallel - \alpha _\parallel ^{\rm exp} \ [10^{-3}]$| . |
|---|---|---|---|---|
| ez | 0.27 | 2 | 0.4 ± 0.7 | 1.1 ± 1.0 |
| ez | 0.27 | 4 | 0.5 ± 0.7 | 1.4 ± 1.0 |
| ez | 0.31 | 2 | 0.9 ± 0.7 | 0.3 ± 1.1 |
| ez | 0.31 | 4 | 1.0 ± 0.7 | 0.4 ± 1.1 |
| ez | 0.35 | 2 | 1.3 ± 0.7 | 1.8 ± 1.0 |
| ez | 0.35 | 4 | 1.2 ± 0.7 | 1.5 ± 1.0 |
| ns | 0.286 | 2 | 2.3 ± 1.5 | 3.1 ± 2.4 |
| ns | 0.286 | 4 | 2.2 ± 1.5 | 3.0 ± 2.4 |
| ns | 0.31 | 2 | 3.0 ± 1.5 | 3.6 ± 2.4 |
| ns | 0.31 | 4 | 3.0 ± 1.5 | 3.7 ± 2.4 |
| ns | 0.35 | 2 | 3.9 ± 1.5 | 3.2 ± 2.4 |
| ns | 0.35 | 4 | 3.9 ± 1.5 | 3.5 ± 2.4 |
Fig. 5 displays the distribution of recovered α⊥, α∥ and their respective errors measured from each of the individual EZmocks. The error distribution shows that reconstruction improves the constraints on α⊥ or α∥ in 94 per cent of the realizations (89 per cent have both errors improved). As expected, realizations with smaller errors generally exhibit larger values of |$\Delta \chi ^2 = \chi ^2_{\rm no \ peak} - \chi ^2_{\rm peak}$|, meaning a more pronounced BAO peak and higher detection significance. We see no particular trend in the best-fitting α values with Δχ2 in the two top panels. The red stars in Fig. 5 indicate the values obtained in real data. The error in α⊥ in the data is typical of what is found in mocks, although for α∥ it is found at the extreme of the mocks distribution. As discussed in Section 2.4 and displayed in Fig. 3, the BAO peak amplitude in the data multipoles is slightly larger than the one seen in this EZmock sample. A similar behaviour is observed in the eBOSS QSO sample (Hou et al. 2020; Neveux & Burtin 2020), who also use EZmocks from Zhao et al. (2020), and in the BOSS DR12 CMASS sample (see fig. 12 of Ross et al. 2017).
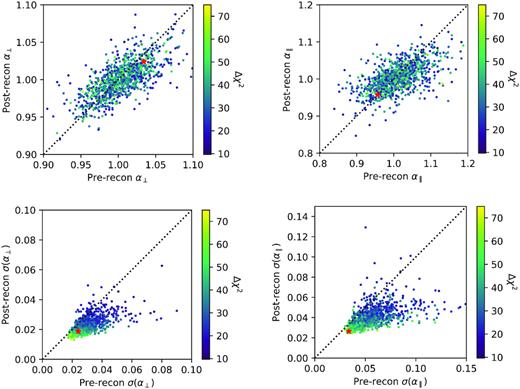
Distribution of dilation parameters α⊥ and α∥ and its estimated errors for pre- and post-reconstruction EZmock catalogues with systematic effects. The colour scale indicates the difference in χ2 values between a model with and without BAO peak. The red stars show results with real data. There is a known mismatch in the BAO peak amplitude between data and EZmocks causing the accuracy of the data point to be slightly smaller than the error distribution in the EZmocks (see Section 2.4).
Table 6 presents a statistical summary of the fits performed on the EZmocks. We tested several changes to our baseline analysis: include the hexadecapole, change the separation range [rmin, rmax], allow BAO damping parameters Σ⊥ and Σ∥ to vary within a Gaussian prior (5.5 ± 2 h−1 Mpc), and fit the pre-reconstruction multipoles. We remove realizations with fits that did not converge or with extreme error values (more than 5σ of their distribution, where σ is defined as the half the range covered by 68 per cent of values). The total number of valid realizations is given by Ngood in Table 6. In most cases studied, the observed standard deviation of the best-fitting parameters σ(α) is consistent with the average per-mock error estimates 〈σα〉, indicating that our errors are correctly estimated. We also see that the dispersion of dilation parameters is not significantly reduced when adding the hexadecapole ξ4 to the BAO fits, showing that most of the BAO information is contained in the monopole and quadrupole at this level of precision. The mean and dispersion of the pull parameter, defined as Zα = (α − 〈α〉)/σα, are consistent with a unit Gaussian for almost all cases, which further validates our error estimates.
Statistics on errors from BAO fits on 1000 EZmocks realizations. All results are based on post-reconstruction correlation functions. σ is the scatter of best-fitting values xi among the Ngood realizations with confident detection or non-extreme values or errors (out of the 1000), 〈σi〉 is the mean estimated error per mock, Z = (xi − 〈xi〉)/σi is the pull quantity for which we show the mean 〈Zi〉 and standard deviation σ(Z). The first row corresponds to our baseline analysis.
| Analysis . | Ngood . | α⊥ . | α∥ . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . |
| baseline | 990 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.036 | −0.03 | 0.96 |
| ℓmax = 4 | 995 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.035 | −0.03 | 0.97 |
| pre-recon | 968 | 0.030 | 0.030 | −0.05 | 1.07 | 0.055 | 0.056 | −0.06 | 0.97 |
| pre-recon ℓmax = 4 | 968 | 0.029 | 0.028 | −0.03 | 1.04 | 0.054 | 0.054 | −0.07 | 1.02 |
| rmin = 20 h−1 Mpc | 979 | 0.023 | 0.026 | −0.01 | 0.93 | 0.035 | 0.040 | 0.04 | 1.26 |
| rmin = 30 h−1 Mpc | 987 | 0.023 | 0.024 | −0.02 | 0.95 | 0.036 | 0.038 | −0.02 | 0.92 |
| rmin = 40 h−1 Mpc | 995 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.02 | 0.94 |
| rmax = 160 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 170 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 180 h−1 Mpc | 990 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.03 | 0.95 |
| Prior Σ⊥, ∥ | 993 | 0.022 | 0.023 | −0.02 | 1.00 | 0.035 | 0.035 | −0.03 | 0.96 |
| Analysis . | Ngood . | α⊥ . | α∥ . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . |
| baseline | 990 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.036 | −0.03 | 0.96 |
| ℓmax = 4 | 995 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.035 | −0.03 | 0.97 |
| pre-recon | 968 | 0.030 | 0.030 | −0.05 | 1.07 | 0.055 | 0.056 | −0.06 | 0.97 |
| pre-recon ℓmax = 4 | 968 | 0.029 | 0.028 | −0.03 | 1.04 | 0.054 | 0.054 | −0.07 | 1.02 |
| rmin = 20 h−1 Mpc | 979 | 0.023 | 0.026 | −0.01 | 0.93 | 0.035 | 0.040 | 0.04 | 1.26 |
| rmin = 30 h−1 Mpc | 987 | 0.023 | 0.024 | −0.02 | 0.95 | 0.036 | 0.038 | −0.02 | 0.92 |
| rmin = 40 h−1 Mpc | 995 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.02 | 0.94 |
| rmax = 160 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 170 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 180 h−1 Mpc | 990 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.03 | 0.95 |
| Prior Σ⊥, ∥ | 993 | 0.022 | 0.023 | −0.02 | 1.00 | 0.035 | 0.035 | −0.03 | 0.96 |
Statistics on errors from BAO fits on 1000 EZmocks realizations. All results are based on post-reconstruction correlation functions. σ is the scatter of best-fitting values xi among the Ngood realizations with confident detection or non-extreme values or errors (out of the 1000), 〈σi〉 is the mean estimated error per mock, Z = (xi − 〈xi〉)/σi is the pull quantity for which we show the mean 〈Zi〉 and standard deviation σ(Z). The first row corresponds to our baseline analysis.
| Analysis . | Ngood . | α⊥ . | α∥ . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . |
| baseline | 990 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.036 | −0.03 | 0.96 |
| ℓmax = 4 | 995 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.035 | −0.03 | 0.97 |
| pre-recon | 968 | 0.030 | 0.030 | −0.05 | 1.07 | 0.055 | 0.056 | −0.06 | 0.97 |
| pre-recon ℓmax = 4 | 968 | 0.029 | 0.028 | −0.03 | 1.04 | 0.054 | 0.054 | −0.07 | 1.02 |
| rmin = 20 h−1 Mpc | 979 | 0.023 | 0.026 | −0.01 | 0.93 | 0.035 | 0.040 | 0.04 | 1.26 |
| rmin = 30 h−1 Mpc | 987 | 0.023 | 0.024 | −0.02 | 0.95 | 0.036 | 0.038 | −0.02 | 0.92 |
| rmin = 40 h−1 Mpc | 995 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.02 | 0.94 |
| rmax = 160 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 170 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 180 h−1 Mpc | 990 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.03 | 0.95 |
| Prior Σ⊥, ∥ | 993 | 0.022 | 0.023 | −0.02 | 1.00 | 0.035 | 0.035 | −0.03 | 0.96 |
| Analysis . | Ngood . | α⊥ . | α∥ . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| . | . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . |
| baseline | 990 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.036 | −0.03 | 0.96 |
| ℓmax = 4 | 995 | 0.022 | 0.023 | −0.02 | 0.99 | 0.035 | 0.035 | −0.03 | 0.97 |
| pre-recon | 968 | 0.030 | 0.030 | −0.05 | 1.07 | 0.055 | 0.056 | −0.06 | 0.97 |
| pre-recon ℓmax = 4 | 968 | 0.029 | 0.028 | −0.03 | 1.04 | 0.054 | 0.054 | −0.07 | 1.02 |
| rmin = 20 h−1 Mpc | 979 | 0.023 | 0.026 | −0.01 | 0.93 | 0.035 | 0.040 | 0.04 | 1.26 |
| rmin = 30 h−1 Mpc | 987 | 0.023 | 0.024 | −0.02 | 0.95 | 0.036 | 0.038 | −0.02 | 0.92 |
| rmin = 40 h−1 Mpc | 995 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.02 | 0.94 |
| rmax = 160 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 170 h−1 Mpc | 989 | 0.022 | 0.023 | −0.02 | 0.99 | 0.036 | 0.036 | −0.03 | 0.96 |
| rmax = 180 h−1 Mpc | 990 | 0.022 | 0.023 | −0.02 | 0.98 | 0.035 | 0.036 | −0.03 | 0.95 |
| Prior Σ⊥, ∥ | 993 | 0.022 | 0.023 | −0.02 | 1.00 | 0.035 | 0.035 | −0.03 | 0.96 |
All the tests performed in this section show that our BAO analysis is unbiased and provides correct error estimates. We apply our baseline analysis to the real data and report results in Section 5.1.
4.2 Systematics in the RSD analysis
We present in this section the systematic error budget of the full-shape RSD analysis. Particularly, we discuss the impact of the choice of scales used in the fit, the bias introduced by each model, the bias introduced by varying the fiducial cosmology, the bias associated with the choice of the LRG HOD model, and the impact of observational effects. These are quantified through the analysis of the various sets of mocks with both TNS and CLPT-GS models, which are described in Section 3.2.
4.2.1 Optimal fitting range of scales
We first study the optimal range of scales in the fit for the two RSD models considered in this work (see Section 3). It is worth noting that the optimal range of scales is not necessarily the same for the two models. Generally, full-shape RSD analyses use scales going from tens of h−1 Mpc to about |$130\!-\!150\,$|h−1 Mpc. Including smaller scales potentially increases the precision of the constraints but at the expense of stronger biases on the recovered parameters. This is related to the limitations of current RSD models to fully describe the non-linear regime. On the other hand, including scales larger than ∼130 h−1 Mpc does not significantly improve the precision, since the variations of the model on those scales are small.
In order to determine the optimal range of scales for our RSD models, we performed fits to the mean correlation function of the Nseries mocks, which are those that most accurately predict the expected RSD in the data. Fig. 6 shows the best-fitting values of fσ8, α∥, and α⊥ as a function of the minimum scale used in the fit, rmin. In each panel, the grey bands show 1 per cent errors in α⊥, α∥ and 3 per cent errors in fσ8 for reference. The top panels present the measurements from the TNS model when the parameter bΓ3 is fixed to the value given by equation (26), while in the mid-panels this parameter is let free. The bottom panels show best-fitting values for the CLPT-GS model as studied in Icaza-Lizaola et al. (2020). As noted in Zarrouk et al. (2018), the hexadecapole is more sensitive to the difference between the true and fiducial cosmologies and is generally less well modelled on small scales compared to the monopole and quadrupole. We therefore consider the possibility of having a different minimum fitting scale for the hexadecapole with respect to the monopole and quadrupole that share the same rmin. For consistency with the other systematic tests, we performed this analysis using two choices of fiducial cosmologies, |$\Omega ^{\rm fid}_\mathrm{ m} = 0.286$| (blue) and |$\Omega ^{\rm fid}_\mathrm{ m} = 0.31$| (red). The maximum separation in all cases is rmax = 130 h−1 Mpc, as we find that using larger rmax has a negligible impact on the recovered parameter values and associated errors.
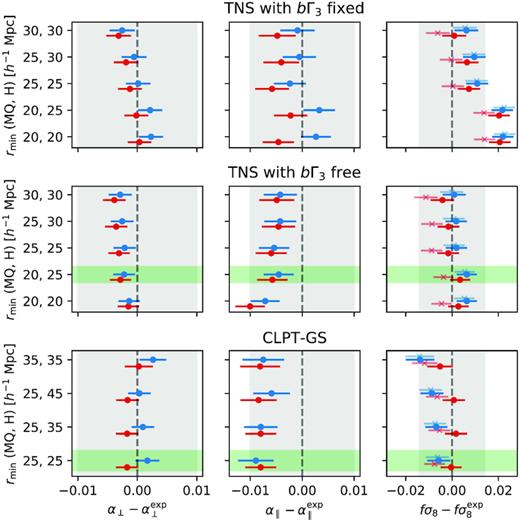
Biases in the measurement of fσ8, α∥, α⊥ obtained from full-shape fits to the average of 84 multipoles from the Nseries mocks as a function of the separation range used. The y-axis displays the value of the minimal separation rmin used in fits of the monopole, quadrupole (MQ), and hexadecapole (H). The top and middle rows display results for the TNS model when fixing or letting free the parameter bΓ3, respectively. The bottom row presents results for the CLPT-GS model. The blue circles correspond to the analysis using |$\Omega _\mathrm{ m}^{\rm fid} = 0.286$| (the true value of simulations) while the red squares correspond to |$\Omega _\mathrm{ m}^{\rm fid} = 0.31$|. The grey shaded areas correspond to 1 per cent errors in α⊥, α∥ and to 3 per cent in fσ8. The green shared area shows our choice for baseline analysis for TNS and CLPT-GS models.
In the case of the TNS model, we consider two different cases that correspond to when bΓ3 is fixed to its Lagrangian prediction and when bΓ3 is allowed to vary. In the case of |$\Omega ^{\rm fid}_\mathrm{ m} = 0.286$| and when bΓ3 is fixed, in the top panels of Fig. 6, we can see that fσ8 is overestimated by 1.5 per cent when using scales above 25 h−1 Mpc and by 2 per cent below. Using rmin > 25 h−1 Mpc reduces the bias to about 1 per cent on fσ8. For α∥ and α⊥ parameters, biases range from 0.3 to 0.5 per cent and are all statistically consistent with zero. When bΓ3 is let free, in the middle panels of Fig. 6, the model provides more robust measurements of fσ8 at all tested ranges. The biases in fσ8 over all ranges do not exceed 0.6σ, compared to approx. 2.5σ for the fixed bΓ3 case. We also remark that letting |$b_{\Gamma _3}$| free also provides a better fit to the BAO amplitude and the hexadecapole on the scales of 20–25 h−1 Mpc. We see a 1 per cent bias on α∥ when rmin = 20 h−1 Mpc for all three multipoles. This bias is, however, reduced by increasing the hexadecapole minimum scale to rmin = 25 h−1 Mpc. The most optimal configuration for the TNS model is to let bΓ3 free and fit the monopole and quadrupole in the range 20 ≤ r ≤ 130 h−1 Mpc and the hexadecapole in the range 25 ≤ r ≤ 130 h−1 Mpc, as marked by the green band in Fig. 6. If we use |$\Omega ^{\rm fid}_\mathrm{ m}=0.31$|, the trends and quantitative results are similar to the case with |$\Omega ^{\rm fid}_\mathrm{ m}=0.286$|.
For the CLPT-GS model, an exploration of the optimal fitting range was done in Icaza-Lizaola et al. (2020). Two sets of tests have been performed. The first set consisted of fitting the mean of the mocks when varying rmin and the second, fitting the 84 individual mocks and measuring the bias and variance of the best fits when varying rmin. We revisit the first set of tests, but this time performing a full MCMC analysis to determine best fits and errors. The bottom panels of Fig. 6 summarize the results. In the case of |$\Omega ^{\rm fid}_\mathrm{ m} = 0.286$|, we see that using rmin = 25 h−1 Mpc for all multipoles yields biases of 0.1, 1.1, and 1.6 per cent in α⊥, α∥, and fσ8, respectively. Increasing rmin for the hexadecapole while fixing rmin = 25 h−1 Mpc for the monopole and quadrupole does not change the results significantly; the biases are 0.1 per cent for all ranges in α⊥, and 1 per cent also for all ranges in α∥. For fσ8 variation of 0.1–0.2 per cent arises when varying the range, but this variation in statistically consistent with zero. In the case of |$\Omega ^{\rm fid}_\mathrm{ m} = 0.31$|, we find very similar trends. Using rmin = 25 h−1 Mpc for all multipoles yields biases of 0.2, 0.9, and 1.6 in α⊥, α∥, and fσ8, respectively. When we decrease the range of the fits, the biases on (α⊥, α∥, fσ8) vary by (0.1–0.2, 0.2–0.3, 0.3–0.4) per cent. These variations are not significant and we decide to keep the lowest considered minimum scales on the hexadecapole in the fits.
Compared with previous BOSS full-shape RSD analysis in configuration space, we used for CLPT-GS model the same minimum scale for the monopole and quadrupole (Alam et al. 2017; Satpathy et al. 2017). The hexadecapole was not included in BOSS analyses. The exploration for the optimal minimum scale to be used for the hexadecapole was done in Icaza-Lizaola et al. (2020) and revisited in this work. The systematic error associated with the adopted fitting range is also consistent with previous results for the case where only the monopole and quadrupole are used, as reported in Icaza-Lizaola et al. (2020). The TNS model was not used in configuration space for analysing previous SDSS samples. However, as we describe in Section 4.2.2, the bias associated with both models when using their optimal fitting range is consistent between them, as well as consistent with previous BOSS results.
Overall, these tests performed on the Nseries mocks allow us to define the optimal fitting ranges of scales for both RSD models. Minimizing the bias of the models while keeping rmin as small as possible, we eventually adopt the following optimal ranges:
TNS model: 20 < r < 130 h−1 Mpc for ξ0 and ξ2, and 25 < r < 130 h−1 Mpc for ξ4,
CLPT-GS model: 25 < r < 130 h−1 Mpc for all multipoles,
which serve as baseline in the following. We compare the performance of the two models using these ranges in the following sections.
4.2.2 Systematic errors from RSD modelling and adopted fiducial cosmology
We quantify in this section the systematic error introduced by the RSD modelling and the choice of fiducial cosmology. For this, we used the Nseries mocks.12 The measurements of α⊥, α∥, and fσ8 from fits to the average multipoles are given in Table 7 and shown in Fig. 7. The shaded area in the figure corresponds to 1 per cent deviation for α⊥, α∥ expected values and 3 per cent for fσ8 expected value. We used both TNS (red) and CLPT-GS (blue) models and consider three choices of fiducial cosmologies parametrized by their value of |$\Omega _\mathrm{ m}^{\rm fid}$|. Note that, as for the BAO analysis, we only test flat ΛCDM models close to the most probable one. We expect the full-shape analysis to be biased if the fiducial cosmology is too different from the truth (the parametrization with α⊥ and α∥ would not fully account for the distortions and the template power spectrum would differ significantly).
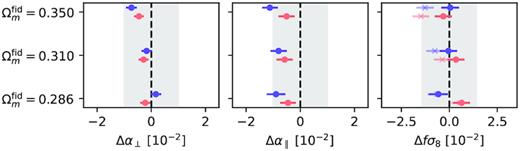
Biases in best-fitting parameters for both CLPT-GS (blue) and TNS (red) models from fits to the average multipoles of 84 Nseries mocks. Shaded grey areas show the equivalent of 1 per cent error for α⊥, α∥ and 3 per cent for fσ8. In the right-hand panel, crosses indicate fσ8 values when σ8 is not recomputed as described in Section 3.2.4. The true cosmology of the mocks is Ωm = 0.286. For reference, the errors on our data sample are ∼2, 3, and 10 per cent for α⊥, α∥, and fσ8, respectively.
Performance of the two full-shape models on the Nseries mocks. Fits were performed on the average of 84 multipoles. We report the shifts of best-fitting parameters relative to their expected values. For |$\Omega _\mathrm{ m}^{\rm fid} = 0.286$|, we expect that both the α parameters are equal to 1. For |$\Omega _\mathrm{ m}^{\rm fid} = 0.31$|, |$\alpha _\perp ^{\rm exp} = 0.9788$|, |$\alpha _\parallel ^{\rm exp}= 0.9878$| while for |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$| we expect |$\alpha _\perp ^{\rm exp} = 0.9623$|, |$\alpha _\parallel ^{\rm exp}= 0.9851$|. Since the growth rate of structures does not depend on the assumed cosmology, we expect to recover |$f\sigma _8^{\rm exp} = 0.469$| for all cases.
| Model . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| CLPT-GS | 0.286 | 0.2 ± 0.2 | −0.9 ± 0.3 | −0.6 ± 0.5 |
| CLPT-GS | 0.31 | −0.2 ± 0.2 | −0.8 ± 0.3 | −0.0 ± 0.5 |
| CLPT-GS | 0.35 | −0.7 ± 0.2 | −1.1 ± 0.3 | 0.0 ± 0.5 |
| TNS | 0.286 | −0.2 ± 0.2 | −0.5 ± 0.3 | 0.6 ± 0.4 |
| TNS | 0.31 | −0.3 ± 0.2 | −0.6 ± 0.3 | 0.3 ± 0.4 |
| TNS | 0.35 | −0.5 ± 0.2 | −0.5 ± 0.3 | −0.3 ± 0.4 |
| Model . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| CLPT-GS | 0.286 | 0.2 ± 0.2 | −0.9 ± 0.3 | −0.6 ± 0.5 |
| CLPT-GS | 0.31 | −0.2 ± 0.2 | −0.8 ± 0.3 | −0.0 ± 0.5 |
| CLPT-GS | 0.35 | −0.7 ± 0.2 | −1.1 ± 0.3 | 0.0 ± 0.5 |
| TNS | 0.286 | −0.2 ± 0.2 | −0.5 ± 0.3 | 0.6 ± 0.4 |
| TNS | 0.31 | −0.3 ± 0.2 | −0.6 ± 0.3 | 0.3 ± 0.4 |
| TNS | 0.35 | −0.5 ± 0.2 | −0.5 ± 0.3 | −0.3 ± 0.4 |
Performance of the two full-shape models on the Nseries mocks. Fits were performed on the average of 84 multipoles. We report the shifts of best-fitting parameters relative to their expected values. For |$\Omega _\mathrm{ m}^{\rm fid} = 0.286$|, we expect that both the α parameters are equal to 1. For |$\Omega _\mathrm{ m}^{\rm fid} = 0.31$|, |$\alpha _\perp ^{\rm exp} = 0.9788$|, |$\alpha _\parallel ^{\rm exp}= 0.9878$| while for |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$| we expect |$\alpha _\perp ^{\rm exp} = 0.9623$|, |$\alpha _\parallel ^{\rm exp}= 0.9851$|. Since the growth rate of structures does not depend on the assumed cosmology, we expect to recover |$f\sigma _8^{\rm exp} = 0.469$| for all cases.
| Model . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| CLPT-GS | 0.286 | 0.2 ± 0.2 | −0.9 ± 0.3 | −0.6 ± 0.5 |
| CLPT-GS | 0.31 | −0.2 ± 0.2 | −0.8 ± 0.3 | −0.0 ± 0.5 |
| CLPT-GS | 0.35 | −0.7 ± 0.2 | −1.1 ± 0.3 | 0.0 ± 0.5 |
| TNS | 0.286 | −0.2 ± 0.2 | −0.5 ± 0.3 | 0.6 ± 0.4 |
| TNS | 0.31 | −0.3 ± 0.2 | −0.6 ± 0.3 | 0.3 ± 0.4 |
| TNS | 0.35 | −0.5 ± 0.2 | −0.5 ± 0.3 | −0.3 ± 0.4 |
| Model . | |$\Omega _\mathrm{ m}^{\rm fid}$| . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| CLPT-GS | 0.286 | 0.2 ± 0.2 | −0.9 ± 0.3 | −0.6 ± 0.5 |
| CLPT-GS | 0.31 | −0.2 ± 0.2 | −0.8 ± 0.3 | −0.0 ± 0.5 |
| CLPT-GS | 0.35 | −0.7 ± 0.2 | −1.1 ± 0.3 | 0.0 ± 0.5 |
| TNS | 0.286 | −0.2 ± 0.2 | −0.5 ± 0.3 | 0.6 ± 0.4 |
| TNS | 0.31 | −0.3 ± 0.2 | −0.6 ± 0.3 | 0.3 ± 0.4 |
| TNS | 0.35 | −0.5 ± 0.2 | −0.5 ± 0.3 | −0.3 ± 0.4 |
The biases on the recovered parameters shown in Fig. 7 induced by the choice of fiducial cosmology remain within 1, 1, and 3 per cent for α⊥, α∥, and fσ8, respectively. For α⊥, both CLPT-GS and TNS models produce biases lower than 2σ for all cosmologies except |$\Omega _\mathrm{ m}^{\rm fid}=0.35$|, which is the most distant value from the true cosmology of the simulation Ωm = 0.286. For α∥, all biases are consistent with zero at 2σ level for the TNS model, while CLPT-GS shows biases slightly larger than 2σ for all |$\Omega _\mathrm{ m}^{\rm fid}$|.
4.2.3 Systematic errors from HOD
We quantify in this section the potential systematic errors introduced by the models with respect to how LRGs occupy dark matter haloes. This is done by analysing mock catalogues produced with different HOD models that mimic different underlying galaxy clustering properties. The same input dark matter field is used when varying the HOD model. We use the OuterRim mocks described in Section 2.4 and in Rossi et al. (2020). Specifically, we analysed the mocks constructed using the ‘Threshold 2’ for the HOD models from Leauthaud et al. (2011), Tinker et al. (2013), and Hearin et al. (2015) and performed fits to the average multipoles over the 27 realizations available for each HOD model.
Fig. 8 and Table 8 show the results. In this figure, each best-fitting parameter is compared to the average best fit over all HOD models in order to quantify the relative impact of each HOD (instead of comparing with their true value). The biases with respect to the true values were quantified in the previous section. The shaded regions represent 1 per cent error for α⊥ and α∥, and 3 per cent error for fσ8.
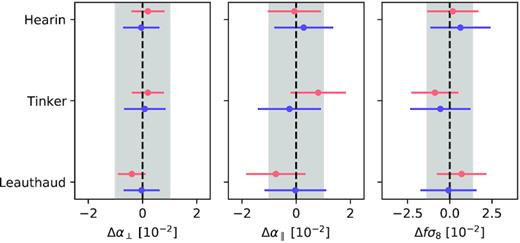
Best-fitting values of α⊥, α∥, and fσ8 from fitting the average multipoles of the OuterRim mocks compared to their average over all HOD models. Blue points show results for the CLPT-GS model and red points show results for the TNS model. The shaded area shows 1 per cent error for α⊥, α∥ and 3 per cent for fσ8.
Performance of the full-shape analyses on the Outerim mocks produced using different HOD recipes. For each HOD (Leauthaud et al. 2011; Tinker et al. 2013; Hearin et al. 2015), we display results obtained from our two RSD models (CLPT-GS and TNS). All results are from fits to the average multipoles of 27 realizations. Each row displays the shift of best-fitting parameters with respect to the average parameters over the three HOD models: Δx = x − 〈x〉HOD. We found that these shifts are not significant and therefore do not contribute to systematic errors.
| HOD . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| L11 | CLPT-GS | 0.0 ± 0.7 | 0.0 ± 1.1 | −0.1 ± 1.7 |
| T13 | CLPT-GS | 0.1 ± 0.8 | −0.2 ± 1.2 | −0.6 ± 1.8 |
| H15 | CLPT-GS | 0.0 ± 0.7 | 0.3 ± 1.1 | 0.6 ± 1.8 |
| L11 | TNS | −0.4 ± 0.5 | −0.7 ± 1.1 | 0.7 ± 1.5 |
| T13 | TNS | 0.2 ± 0.6 | 0.8 ± 1.0 | −0.9 ± 1.4 |
| H15 | TNS | 0.2 ± 0.6 | −0.1 ± 1.0 | 0.2 ± 1.5 |
| HOD . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| L11 | CLPT-GS | 0.0 ± 0.7 | 0.0 ± 1.1 | −0.1 ± 1.7 |
| T13 | CLPT-GS | 0.1 ± 0.8 | −0.2 ± 1.2 | −0.6 ± 1.8 |
| H15 | CLPT-GS | 0.0 ± 0.7 | 0.3 ± 1.1 | 0.6 ± 1.8 |
| L11 | TNS | −0.4 ± 0.5 | −0.7 ± 1.1 | 0.7 ± 1.5 |
| T13 | TNS | 0.2 ± 0.6 | 0.8 ± 1.0 | −0.9 ± 1.4 |
| H15 | TNS | 0.2 ± 0.6 | −0.1 ± 1.0 | 0.2 ± 1.5 |
Performance of the full-shape analyses on the Outerim mocks produced using different HOD recipes. For each HOD (Leauthaud et al. 2011; Tinker et al. 2013; Hearin et al. 2015), we display results obtained from our two RSD models (CLPT-GS and TNS). All results are from fits to the average multipoles of 27 realizations. Each row displays the shift of best-fitting parameters with respect to the average parameters over the three HOD models: Δx = x − 〈x〉HOD. We found that these shifts are not significant and therefore do not contribute to systematic errors.
| HOD . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| L11 | CLPT-GS | 0.0 ± 0.7 | 0.0 ± 1.1 | −0.1 ± 1.7 |
| T13 | CLPT-GS | 0.1 ± 0.8 | −0.2 ± 1.2 | −0.6 ± 1.8 |
| H15 | CLPT-GS | 0.0 ± 0.7 | 0.3 ± 1.1 | 0.6 ± 1.8 |
| L11 | TNS | −0.4 ± 0.5 | −0.7 ± 1.1 | 0.7 ± 1.5 |
| T13 | TNS | 0.2 ± 0.6 | 0.8 ± 1.0 | −0.9 ± 1.4 |
| H15 | TNS | 0.2 ± 0.6 | −0.1 ± 1.0 | 0.2 ± 1.5 |
| HOD . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| L11 | CLPT-GS | 0.0 ± 0.7 | 0.0 ± 1.1 | −0.1 ± 1.7 |
| T13 | CLPT-GS | 0.1 ± 0.8 | −0.2 ± 1.2 | −0.6 ± 1.8 |
| H15 | CLPT-GS | 0.0 ± 0.7 | 0.3 ± 1.1 | 0.6 ± 1.8 |
| L11 | TNS | −0.4 ± 0.5 | −0.7 ± 1.1 | 0.7 ± 1.5 |
| T13 | TNS | 0.2 ± 0.6 | 0.8 ± 1.0 | −0.9 ± 1.4 |
| H15 | TNS | 0.2 ± 0.6 | −0.1 ± 1.0 | 0.2 ± 1.5 |
We find that the biases for both RSD models are all within 1σ from the mean, although statistical errors are quite large (around 1 per cent for α⊥, α∥) compared to Nseries mocks for instance. Also, the observed shifts are all smaller than the systematic errors estimated in the previous section. If we were to use the same definition for the systematic error introduced in Section 4, the relatively large errors from these measurements would produce a significant contribution to the error budget. Therefore, we consider that HOD has a negligible contribution to the total systematic error budget.
4.2.4 Systematic errors from observational effects
We investigate in this section the observational systematics. We used a set of 100 EZmocks to quantify their impact on our measurements. From the same set, we added different observational effects. For simplicity, those samples were made from mocks reproducing only the eBOSS component of the survey, neglecting the CMASS component. We consider that the systematic errors estimated this way can be extrapolated to the full eBOSS+CMASS sample by assuming that their contribution is the same over the CMASS volume. We thus produced the following samples:
no observational effects included, which we use as reference,
including the effect of the radial integral constraint (RIC; de Mattia & Ruhlmann-Kleider 2019), where the redshifts of the random catalogue are randomly chosen from the redshifts of the data catalogue,
including RIC and all angular features: fibre collisions, redshift failures, and photometric corrections.
For each set, we computed the average multipoles and fitted them using our two RSD models. The covariance matrix is held fixed between cases. Table 9 summarizes the biases in α⊥, α∥, and fσ8 caused by the different observational effects. The shifts are relative to results of mocks without observational effects. We find that the RIC produces the greatest effect, particularly for the CLPT-GS model for which the deviation on fσ8 is slightly larger than 2σ. Indeed, the quadrupole for mocks with RIC has smaller absolute amplitude, which translates into small fσ8 values. However, when adding angular observational effects the shifts are all broadly consistent with zero, which indicates that the two effects partially cancel each other.
Impact of observational effects on the full-shape analysis using Ezmocks. Each row displays the shifts of best-fitting parameters with respect to the case without observational effects (‘no syst’): Δx = x − xno syst. Fits are performed on the average multipoles of 100 realizations. We test the cases of mocks with RIC and mocks with the combination of RIC and all angular observational effects (fibre collisions, redshift failures, and photometric fluctuations). The angular effects introduced in mocks are corrected using the same procedure used in data. For simplicity, the mocks used here are only for the eBOSS part of the survey.
| Type . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| RIC | CLPT-GS | −0.3 ± 0.5 | 1.1 ± 0.6 | −1.7 ± 0.8 |
| +Ang. Sys. | CLPT-GS | 0.0 ± 0.4 | 0.3 ± 0.6 | 0.0 ± 0.9 |
| RIC | TNS | 0.6 ± 0.5 | −0.1 ± 0.7 | −0.8 ± 0.9 |
| +Ang. Sys. | TNS | 0.8 ± 0.5 | −0.2 ± 0.7 | 0.1 ± 0.9 |
| Type . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| RIC | CLPT-GS | −0.3 ± 0.5 | 1.1 ± 0.6 | −1.7 ± 0.8 |
| +Ang. Sys. | CLPT-GS | 0.0 ± 0.4 | 0.3 ± 0.6 | 0.0 ± 0.9 |
| RIC | TNS | 0.6 ± 0.5 | −0.1 ± 0.7 | −0.8 ± 0.9 |
| +Ang. Sys. | TNS | 0.8 ± 0.5 | −0.2 ± 0.7 | 0.1 ± 0.9 |
Impact of observational effects on the full-shape analysis using Ezmocks. Each row displays the shifts of best-fitting parameters with respect to the case without observational effects (‘no syst’): Δx = x − xno syst. Fits are performed on the average multipoles of 100 realizations. We test the cases of mocks with RIC and mocks with the combination of RIC and all angular observational effects (fibre collisions, redshift failures, and photometric fluctuations). The angular effects introduced in mocks are corrected using the same procedure used in data. For simplicity, the mocks used here are only for the eBOSS part of the survey.
| Type . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| RIC | CLPT-GS | −0.3 ± 0.5 | 1.1 ± 0.6 | −1.7 ± 0.8 |
| +Ang. Sys. | CLPT-GS | 0.0 ± 0.4 | 0.3 ± 0.6 | 0.0 ± 0.9 |
| RIC | TNS | 0.6 ± 0.5 | −0.1 ± 0.7 | −0.8 ± 0.9 |
| +Ang. Sys. | TNS | 0.8 ± 0.5 | −0.2 ± 0.7 | 0.1 ± 0.9 |
| Type . | Model . | Δα⊥ [10−2] . | Δα∥ [10−2] . | Δfσ8 [10−2] . |
|---|---|---|---|---|
| RIC | CLPT-GS | −0.3 ± 0.5 | 1.1 ± 0.6 | −1.7 ± 0.8 |
| +Ang. Sys. | CLPT-GS | 0.0 ± 0.4 | 0.3 ± 0.6 | 0.0 ± 0.9 |
| RIC | TNS | 0.6 ± 0.5 | −0.1 ± 0.7 | −0.8 ± 0.9 |
| +Ang. Sys. | TNS | 0.8 ± 0.5 | −0.2 ± 0.7 | 0.1 ± 0.9 |
4.2.5 Total systematic error of the full-shape RSD analysis
Table 10 summarizes all systematic error contributions to the full-shape measurements discussed in the previous sections. We show the results for our two configuration-space RSD models TNS and CLPT-GS and for the Fourier-space analysis of Gil-Marín et al. (2020). We compute the total systematic error σsyst by summing up all the contributions in quadrature, assuming that they are all independent. By comparing the systematic errors with the statistical error from the baseline fits to the data (see Section 5.2), we find that the systematic errors are far from being negligible: more than 50 per cent of the statistical errors for all parameters. The systematic errors are in quadrature to the diagonal of the covariance of each measurement. We do not attempt to compute the covariance between systematic errors and this approach is more conservative (it does not underestimate errors).
Summary of systematic errors obtained from tests with mock catalogues. The total systematic error σsyst is the quadratic sum of each contribution. We compare the systematic errors to the statistical errors from our baseline fits on real data. The last rows display the final error that is a quadratic sum of statistical and systematic errors.
| Type . | Model . | |$\sigma _{\alpha _\perp }$| . | |$\sigma _{\alpha _\parallel }$| . | |$\sigma _{f{\sigma _8}}$| . |
|---|---|---|---|---|
| Modelling | CLPT-GS | 0.004 | 0.009 | 0.010 |
| TNS | 0.004 | 0.006 | 0.009 | |
| Fid. cosmology | CLPT-GS | 0.009 | 0.010 | 0.014 |
| TNS | 0.005 | 0.008 | 0.012 | |
| Obs. effects | CLPT-GS | 0.009 | 0.012 | 0.017 |
| TNS | 0.010 | 0.014 | 0.018 | |
| σsyst | CLPT-GS | 0.013 | 0.018 | 0.024 |
| TNS | 0.012 | 0.017 | 0.023 | |
| Pℓ | 0.012 | 0.013 | 0.024 | |
| σstat | CLPT-GS | 0.020 | 0.028 | 0.045 |
| TNS | 0.018 | 0.031 | 0.040 | |
| Pℓ | 0.027 | 0.036 | 0.042 | |
| σsyst/σstat | CLPT-GS | 0.66 | 0.63 | 0.54 |
| TNS | 0.65 | 0.55 | 0.58 | |
| Pℓ | 0.43 | 0.37 | 0.58 | |
| |$\sigma _{\rm tot} = \sqrt{\sigma _{\rm syst}^2+\sigma _{\rm stat}^2}$| | CLPT-GS | 0.024 | 0.033 | 0.051 |
| TNS | 0.021 | 0.035 | 0.046 | |
| Pℓ | 0.029 | 0.038 | 0.048 |
| Type . | Model . | |$\sigma _{\alpha _\perp }$| . | |$\sigma _{\alpha _\parallel }$| . | |$\sigma _{f{\sigma _8}}$| . |
|---|---|---|---|---|
| Modelling | CLPT-GS | 0.004 | 0.009 | 0.010 |
| TNS | 0.004 | 0.006 | 0.009 | |
| Fid. cosmology | CLPT-GS | 0.009 | 0.010 | 0.014 |
| TNS | 0.005 | 0.008 | 0.012 | |
| Obs. effects | CLPT-GS | 0.009 | 0.012 | 0.017 |
| TNS | 0.010 | 0.014 | 0.018 | |
| σsyst | CLPT-GS | 0.013 | 0.018 | 0.024 |
| TNS | 0.012 | 0.017 | 0.023 | |
| Pℓ | 0.012 | 0.013 | 0.024 | |
| σstat | CLPT-GS | 0.020 | 0.028 | 0.045 |
| TNS | 0.018 | 0.031 | 0.040 | |
| Pℓ | 0.027 | 0.036 | 0.042 | |
| σsyst/σstat | CLPT-GS | 0.66 | 0.63 | 0.54 |
| TNS | 0.65 | 0.55 | 0.58 | |
| Pℓ | 0.43 | 0.37 | 0.58 | |
| |$\sigma _{\rm tot} = \sqrt{\sigma _{\rm syst}^2+\sigma _{\rm stat}^2}$| | CLPT-GS | 0.024 | 0.033 | 0.051 |
| TNS | 0.021 | 0.035 | 0.046 | |
| Pℓ | 0.029 | 0.038 | 0.048 |
Summary of systematic errors obtained from tests with mock catalogues. The total systematic error σsyst is the quadratic sum of each contribution. We compare the systematic errors to the statistical errors from our baseline fits on real data. The last rows display the final error that is a quadratic sum of statistical and systematic errors.
| Type . | Model . | |$\sigma _{\alpha _\perp }$| . | |$\sigma _{\alpha _\parallel }$| . | |$\sigma _{f{\sigma _8}}$| . |
|---|---|---|---|---|
| Modelling | CLPT-GS | 0.004 | 0.009 | 0.010 |
| TNS | 0.004 | 0.006 | 0.009 | |
| Fid. cosmology | CLPT-GS | 0.009 | 0.010 | 0.014 |
| TNS | 0.005 | 0.008 | 0.012 | |
| Obs. effects | CLPT-GS | 0.009 | 0.012 | 0.017 |
| TNS | 0.010 | 0.014 | 0.018 | |
| σsyst | CLPT-GS | 0.013 | 0.018 | 0.024 |
| TNS | 0.012 | 0.017 | 0.023 | |
| Pℓ | 0.012 | 0.013 | 0.024 | |
| σstat | CLPT-GS | 0.020 | 0.028 | 0.045 |
| TNS | 0.018 | 0.031 | 0.040 | |
| Pℓ | 0.027 | 0.036 | 0.042 | |
| σsyst/σstat | CLPT-GS | 0.66 | 0.63 | 0.54 |
| TNS | 0.65 | 0.55 | 0.58 | |
| Pℓ | 0.43 | 0.37 | 0.58 | |
| |$\sigma _{\rm tot} = \sqrt{\sigma _{\rm syst}^2+\sigma _{\rm stat}^2}$| | CLPT-GS | 0.024 | 0.033 | 0.051 |
| TNS | 0.021 | 0.035 | 0.046 | |
| Pℓ | 0.029 | 0.038 | 0.048 |
| Type . | Model . | |$\sigma _{\alpha _\perp }$| . | |$\sigma _{\alpha _\parallel }$| . | |$\sigma _{f{\sigma _8}}$| . |
|---|---|---|---|---|
| Modelling | CLPT-GS | 0.004 | 0.009 | 0.010 |
| TNS | 0.004 | 0.006 | 0.009 | |
| Fid. cosmology | CLPT-GS | 0.009 | 0.010 | 0.014 |
| TNS | 0.005 | 0.008 | 0.012 | |
| Obs. effects | CLPT-GS | 0.009 | 0.012 | 0.017 |
| TNS | 0.010 | 0.014 | 0.018 | |
| σsyst | CLPT-GS | 0.013 | 0.018 | 0.024 |
| TNS | 0.012 | 0.017 | 0.023 | |
| Pℓ | 0.012 | 0.013 | 0.024 | |
| σstat | CLPT-GS | 0.020 | 0.028 | 0.045 |
| TNS | 0.018 | 0.031 | 0.040 | |
| Pℓ | 0.027 | 0.036 | 0.042 | |
| σsyst/σstat | CLPT-GS | 0.66 | 0.63 | 0.54 |
| TNS | 0.65 | 0.55 | 0.58 | |
| Pℓ | 0.43 | 0.37 | 0.58 | |
| |$\sigma _{\rm tot} = \sqrt{\sigma _{\rm syst}^2+\sigma _{\rm stat}^2}$| | CLPT-GS | 0.024 | 0.033 | 0.051 |
| TNS | 0.021 | 0.035 | 0.046 | |
| Pℓ | 0.029 | 0.038 | 0.048 |
4.3 Statistical properties of the LRG sample
We can also use the EZmocks for evaluating the statistical properties of the LRG sample, in particular to quantify how typical is our data compared with EZmocks, but also for measuring the correlations among the different methods and globally validating our error estimation.
The left-hand panel of the Fig. 9 presents a comparison between the best fit (α⊥, α∥, fσ8) and their estimated errors from fits of the TNS and CLPT-GS models. The confidence contours contain approximately 68 per cent and 95 per cent of the results around the mean. The contours and histograms reveal a good agreement for the two models. Stars indicate the corresponding best-fitting values obtained from the data. The correlations between best-fitting parameters of both models are 86, 83, and 93 per cent for α⊥, α∥, and fσ8, respectively. A similar comparison for the errors is presented in the right-hand panel of the Fig. 9. The errors inferred from the data analysis, shown as stars, are in good agreement with the 2D distributions from the mocks, lying within the 68 per cent contours. The histograms comparing the distributions of errors for both methods also show a good agreement, in particular for α∥ and fσ8. For α⊥, we observe that the distribution from CLPT-GS is slightly peaked towards smaller errors, while for TNS the error distribution has a larger dispersion for this parameter. The correlation coefficients between estimated errors from the two models are: 56, 38, and 39 per cent for α⊥, α∥, and fσ8, respectively.
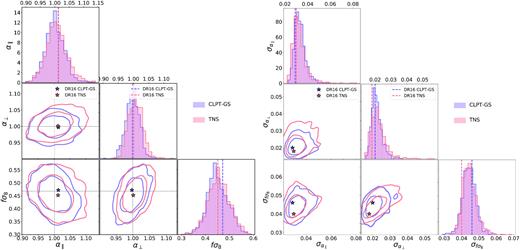
Comparison between best-fitting values (left-hand panels) and estimated errors (right-hand panel) for (α⊥, α∥, fσ8) using 1000 realizations of EZmocks fitted with the TNS and CLPT-GS models. The values obtained with real data are indicated by stars in each panel or as coloured vertical lines in the histograms. The thin black dashed line on the 2D plots refers to the true values of each parameter in the EZmocks.
Table 11 summarizes the statistical properties of errors for α⊥, α∥, and fσ8 for both BAO and full-shape RSD analysis in configuration space (noted ξℓ). We also include for reference the results from Fourier-space analysis of Gil-Marín et al. (2020), noted Pℓ. For each parameter, we show the standard deviation of the best-fitting values, σ, the mean estimated error 〈σ〉, the mean of the pull, Zi = (xi − 〈x〉)/σx, where x = α⊥, α∥, fσ8, and its standard deviation σ(Z). If errors are correctly estimated and follow a Gaussian distribution, we expect that σ = 〈σi〉, 〈Zi〉 = 0, and σ(Z) = 1. For method, we remove results from non-converged chains and 5σ outliers in both best-fitting values and errors (with σ defined as half of the range covered by the central 68 per cent values). Table 11 also shows the results from combining different methods employing the procedure described in Section 3.4. For each combination, we create the covariance matrix C (equation 40) from the correlation coefficients obtained from 1000 EZmocks fits, with small adjustments to account for the observed errors of a given realization. The correlation coefficients (before this adjustment) are shown in Fig. 10 for all five methods. The BAO measurements from configuration and Fourier spaces are 87 and 88 per cent correlated for α⊥ and α∥, respectively. In RSD analyses, these correlations reduce to slightly less than 80 per cent between α⊥ and α∥ of both spaces, while fσ8 correlations reach 84 per cent. The fact that these correlations are not exactly 100 per cent indicates that there is potential gain combining them.
Statistics on errors from consensus results on 1000 EZmocks realizations. For each parameter, we show the standard deviation of best-fitting values, σ(xi), the mean estimated error 〈σi〉, the mean of the pull, Zi = (xi − 〈xi〉)/σi, and its standard deviation σ(Zi). Ngood shows the number of valid realizations for each case after removing extreme values and errors at 5σ level.
| Observable . | Ngood . | α⊥ . | α∥ . | fσ8 . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | . |
| BAO ξℓ | 987 | 0.023 | 0.023 | −0.02 | 0.98 | 0.036 | 0.035 | −0.02 | 0.96 | – | – | – | – |
| BAO Pℓ | 978 | 0.024 | 0.024 | −0.02 | 0.95 | 0.039 | 0.040 | 0.00 | 0.90 | – | – | – | – |
| BAO ξℓ + Pℓ | 970 | 0.022 | 0.022 | −0.02 | 1.01 | 0.034 | 0.034 | −0.02 | 0.97 | – | – | – | – |
| RSD ξℓ CLPT | 819 | 0.023 | 0.021 | 0.01 | 1.03 | 0.033 | 0.033 | −0.04 | 0.95 | 0.046 | 0.045 | −0.01 | 0.97 |
| RSD ξℓ TNS | 951 | 0.024 | 0.023 | −0.05 | 1.03 | 0.037 | 0.033 | −0.05 | 1.07 | 0.046 | 0.045 | −0.01 | 0.95 |
| RSD ξℓ | 781 | 0.021 | 0.021 | −0.01 | 0.99 | 0.031 | 0.032 | −0.03 | 0.96 | 0.042 | 0.045 | −0.01 | 0.95 |
| RSD Pℓ | 977 | 0.025 | 0.026 | 0.02 | 0.94 | 0.037 | 0.036 | −0.04 | 1.00 | 0.046 | 0.046 | 0.01 | 0.96 |
| RSD ξℓ + Pℓ | 767 | 0.019 | 0.020 | 0.00 | 0.98 | 0.030 | 0.031 | −0.03 | 0.97 | 0.041 | 0.043 | −0.00 | 0.97 |
| BAO+RSD ξℓ | 772 | 0.018 | 0.019 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.043 | 0.040 | −0.02 | 1.06 |
| BAO+RSD Pℓ | 955 | 0.019 | 0.020 | 0.00 | 0.96 | 0.028 | 0.029 | −0.03 | 0.96 | 0.044 | 0.042 | −0.01 | 1.05 |
| BAO×RSD Pℓ | 986 | 0.019 | 0.019 | 0.03 | 0.99 | 0.029 | 0.028 | −0.06 | 1.02 | 0.041 | 0.045 | −0.01 | 0.92 |
| BAO (ξℓ + Pℓ) + | 747 | 0.017 | 0.018 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.042 | 0.039 | −0.02 | 1.09 |
| RSD (ξℓ + Pℓ) | – | – | – | – | – | – | – | – | – | – | – | – | – |
| (BAO+RSD) ξℓ + | 747 | 0.017 | 0.018 | −0.01 | 1.01 | 0.024 | 0.025 | −0.03 | 0.99 | 0.042 | 0.039 | −0.02 | 1.09 |
| (BAO+RSD) Pℓ | – | – | – | – | – | – | – | – | – | – | – | – | – |
| Observable . | Ngood . | α⊥ . | α∥ . | fσ8 . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | . |
| BAO ξℓ | 987 | 0.023 | 0.023 | −0.02 | 0.98 | 0.036 | 0.035 | −0.02 | 0.96 | – | – | – | – |
| BAO Pℓ | 978 | 0.024 | 0.024 | −0.02 | 0.95 | 0.039 | 0.040 | 0.00 | 0.90 | – | – | – | – |
| BAO ξℓ + Pℓ | 970 | 0.022 | 0.022 | −0.02 | 1.01 | 0.034 | 0.034 | −0.02 | 0.97 | – | – | – | – |
| RSD ξℓ CLPT | 819 | 0.023 | 0.021 | 0.01 | 1.03 | 0.033 | 0.033 | −0.04 | 0.95 | 0.046 | 0.045 | −0.01 | 0.97 |
| RSD ξℓ TNS | 951 | 0.024 | 0.023 | −0.05 | 1.03 | 0.037 | 0.033 | −0.05 | 1.07 | 0.046 | 0.045 | −0.01 | 0.95 |
| RSD ξℓ | 781 | 0.021 | 0.021 | −0.01 | 0.99 | 0.031 | 0.032 | −0.03 | 0.96 | 0.042 | 0.045 | −0.01 | 0.95 |
| RSD Pℓ | 977 | 0.025 | 0.026 | 0.02 | 0.94 | 0.037 | 0.036 | −0.04 | 1.00 | 0.046 | 0.046 | 0.01 | 0.96 |
| RSD ξℓ + Pℓ | 767 | 0.019 | 0.020 | 0.00 | 0.98 | 0.030 | 0.031 | −0.03 | 0.97 | 0.041 | 0.043 | −0.00 | 0.97 |
| BAO+RSD ξℓ | 772 | 0.018 | 0.019 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.043 | 0.040 | −0.02 | 1.06 |
| BAO+RSD Pℓ | 955 | 0.019 | 0.020 | 0.00 | 0.96 | 0.028 | 0.029 | −0.03 | 0.96 | 0.044 | 0.042 | −0.01 | 1.05 |
| BAO×RSD Pℓ | 986 | 0.019 | 0.019 | 0.03 | 0.99 | 0.029 | 0.028 | −0.06 | 1.02 | 0.041 | 0.045 | −0.01 | 0.92 |
| BAO (ξℓ + Pℓ) + | 747 | 0.017 | 0.018 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.042 | 0.039 | −0.02 | 1.09 |
| RSD (ξℓ + Pℓ) | – | – | – | – | – | – | – | – | – | – | – | – | – |
| (BAO+RSD) ξℓ + | 747 | 0.017 | 0.018 | −0.01 | 1.01 | 0.024 | 0.025 | −0.03 | 0.99 | 0.042 | 0.039 | −0.02 | 1.09 |
| (BAO+RSD) Pℓ | – | – | – | – | – | – | – | – | – | – | – | – | – |
Statistics on errors from consensus results on 1000 EZmocks realizations. For each parameter, we show the standard deviation of best-fitting values, σ(xi), the mean estimated error 〈σi〉, the mean of the pull, Zi = (xi − 〈xi〉)/σi, and its standard deviation σ(Zi). Ngood shows the number of valid realizations for each case after removing extreme values and errors at 5σ level.
| Observable . | Ngood . | α⊥ . | α∥ . | fσ8 . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | . |
| BAO ξℓ | 987 | 0.023 | 0.023 | −0.02 | 0.98 | 0.036 | 0.035 | −0.02 | 0.96 | – | – | – | – |
| BAO Pℓ | 978 | 0.024 | 0.024 | −0.02 | 0.95 | 0.039 | 0.040 | 0.00 | 0.90 | – | – | – | – |
| BAO ξℓ + Pℓ | 970 | 0.022 | 0.022 | −0.02 | 1.01 | 0.034 | 0.034 | −0.02 | 0.97 | – | – | – | – |
| RSD ξℓ CLPT | 819 | 0.023 | 0.021 | 0.01 | 1.03 | 0.033 | 0.033 | −0.04 | 0.95 | 0.046 | 0.045 | −0.01 | 0.97 |
| RSD ξℓ TNS | 951 | 0.024 | 0.023 | −0.05 | 1.03 | 0.037 | 0.033 | −0.05 | 1.07 | 0.046 | 0.045 | −0.01 | 0.95 |
| RSD ξℓ | 781 | 0.021 | 0.021 | −0.01 | 0.99 | 0.031 | 0.032 | −0.03 | 0.96 | 0.042 | 0.045 | −0.01 | 0.95 |
| RSD Pℓ | 977 | 0.025 | 0.026 | 0.02 | 0.94 | 0.037 | 0.036 | −0.04 | 1.00 | 0.046 | 0.046 | 0.01 | 0.96 |
| RSD ξℓ + Pℓ | 767 | 0.019 | 0.020 | 0.00 | 0.98 | 0.030 | 0.031 | −0.03 | 0.97 | 0.041 | 0.043 | −0.00 | 0.97 |
| BAO+RSD ξℓ | 772 | 0.018 | 0.019 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.043 | 0.040 | −0.02 | 1.06 |
| BAO+RSD Pℓ | 955 | 0.019 | 0.020 | 0.00 | 0.96 | 0.028 | 0.029 | −0.03 | 0.96 | 0.044 | 0.042 | −0.01 | 1.05 |
| BAO×RSD Pℓ | 986 | 0.019 | 0.019 | 0.03 | 0.99 | 0.029 | 0.028 | −0.06 | 1.02 | 0.041 | 0.045 | −0.01 | 0.92 |
| BAO (ξℓ + Pℓ) + | 747 | 0.017 | 0.018 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.042 | 0.039 | −0.02 | 1.09 |
| RSD (ξℓ + Pℓ) | – | – | – | – | – | – | – | – | – | – | – | – | – |
| (BAO+RSD) ξℓ + | 747 | 0.017 | 0.018 | −0.01 | 1.01 | 0.024 | 0.025 | −0.03 | 0.99 | 0.042 | 0.039 | −0.02 | 1.09 |
| (BAO+RSD) Pℓ | – | – | – | – | – | – | – | – | – | – | – | – | – |
| Observable . | Ngood . | α⊥ . | α∥ . | fσ8 . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | σ . | 〈σi〉 . | 〈Zi〉 . | σ(Zi) . | . |
| BAO ξℓ | 987 | 0.023 | 0.023 | −0.02 | 0.98 | 0.036 | 0.035 | −0.02 | 0.96 | – | – | – | – |
| BAO Pℓ | 978 | 0.024 | 0.024 | −0.02 | 0.95 | 0.039 | 0.040 | 0.00 | 0.90 | – | – | – | – |
| BAO ξℓ + Pℓ | 970 | 0.022 | 0.022 | −0.02 | 1.01 | 0.034 | 0.034 | −0.02 | 0.97 | – | – | – | – |
| RSD ξℓ CLPT | 819 | 0.023 | 0.021 | 0.01 | 1.03 | 0.033 | 0.033 | −0.04 | 0.95 | 0.046 | 0.045 | −0.01 | 0.97 |
| RSD ξℓ TNS | 951 | 0.024 | 0.023 | −0.05 | 1.03 | 0.037 | 0.033 | −0.05 | 1.07 | 0.046 | 0.045 | −0.01 | 0.95 |
| RSD ξℓ | 781 | 0.021 | 0.021 | −0.01 | 0.99 | 0.031 | 0.032 | −0.03 | 0.96 | 0.042 | 0.045 | −0.01 | 0.95 |
| RSD Pℓ | 977 | 0.025 | 0.026 | 0.02 | 0.94 | 0.037 | 0.036 | −0.04 | 1.00 | 0.046 | 0.046 | 0.01 | 0.96 |
| RSD ξℓ + Pℓ | 767 | 0.019 | 0.020 | 0.00 | 0.98 | 0.030 | 0.031 | −0.03 | 0.97 | 0.041 | 0.043 | −0.00 | 0.97 |
| BAO+RSD ξℓ | 772 | 0.018 | 0.019 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.043 | 0.040 | −0.02 | 1.06 |
| BAO+RSD Pℓ | 955 | 0.019 | 0.020 | 0.00 | 0.96 | 0.028 | 0.029 | −0.03 | 0.96 | 0.044 | 0.042 | −0.01 | 1.05 |
| BAO×RSD Pℓ | 986 | 0.019 | 0.019 | 0.03 | 0.99 | 0.029 | 0.028 | −0.06 | 1.02 | 0.041 | 0.045 | −0.01 | 0.92 |
| BAO (ξℓ + Pℓ) + | 747 | 0.017 | 0.018 | −0.01 | 1.00 | 0.024 | 0.025 | −0.03 | 0.97 | 0.042 | 0.039 | −0.02 | 1.09 |
| RSD (ξℓ + Pℓ) | – | – | – | – | – | – | – | – | – | – | – | – | – |
| (BAO+RSD) ξℓ + | 747 | 0.017 | 0.018 | −0.01 | 1.01 | 0.024 | 0.025 | −0.03 | 0.99 | 0.042 | 0.039 | −0.02 | 1.09 |
| (BAO+RSD) Pℓ | – | – | – | – | – | – | – | – | – | – | – | – | – |
For the BAO results (top three rows of Table 11), we see good agreement between σx and 〈σ〉 for all the parameters in both the spaces. The mean of the pull 〈Zi〉 is consistent with zero (their errors are roughly 0.02) and the standard deviation σ(Zi) is slightly smaller than unity for all variables, indicating that errors might be slightly overestimated. The combined BAO results of (ξℓ + Pℓ) have errors slightly reduced to 2.2 per cent for α⊥ and 3.4 per cent in α∥ (based on the scatter σ of the best-fitting values). The σ(Zi) are both closer to 1.0, indicating better estimate of errors for the combined case. As a conservative approach, the BAO errors on data (Section 5.1) are therefore not corrected by this overestimation.
Full-shape RSD results (fourth to eighth rows in Table 11) also show good agreement between σx and 〈σ〉 for all the parameters for both models and both spaces. Fig. 11 shows the pull distributions for both CLPT-GS and TNS models. The mean of the pull for α⊥ and fσ8 is consistent with zero in all cases though the mean pull for α∥ is negative, indicating a slightly skewed distribution. The σ(Zi) values for CLPT-GS and TNS models are consistent with one for α⊥ and slightly different than one for α∥ and fσ8. Their combination (sixth row) with inverse variance weighing slightly compensates for these differences, yielding better estimated errors, with σ(Zi) closer to one for all three parameters. The full-shape measurements in Fourier space (seventh row) show similar behaviour than the ones in configuration space, with errors larger than measurements in configuration space. This is due to the larger number of nuisance parameters in the Fourier-space analysis and to the choice of scales used in the Fourier-space fits (0.02 ≤ k ≤ 0.15 h Mpc−1), which do not exactly translate to the range in separation used in our fits (25 < r < 130 h−1 Mpc), and may contain less information on average. The combined ξℓ + Pℓ full-shape results in the eighth row present smaller dispersion on all parameters relative to each individual method. The pull values indicating slightly overestimated errors, which we do not attempt to correct.
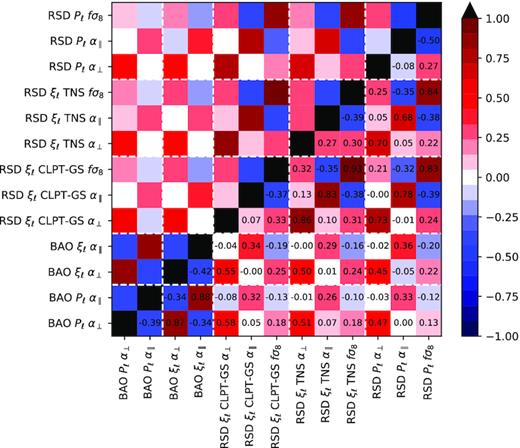
Correlation coefficients between α⊥, α∥, and fσ8 for all methods and models obtained from fits to 1000 EZmock realizations of the eBOSS LRG+CMASS sample. The values of fσ8 have been corrected with the procedure described in Section 3.2.4.
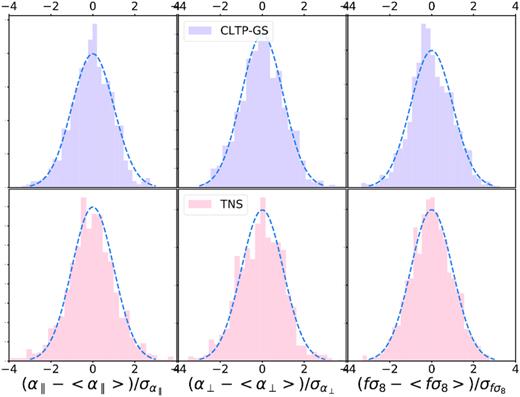
Normalized distributions of the pull for the α∥, α⊥, and fσ8 from fits of TNS and CLPT-GS models on EZmocks. The blue dashed lines represent the centred normalized Gaussian distribution.
The ninth and tenth rows of Table 11 show results of combining BAO and full-shape RSD results for a given space, ξℓ or Pℓ, while fully accounting for their large covariance as described in Section 3.4. We see that the scatter of α⊥ and α∥ is reduced by ∼20 and 30 per cent, respectively, relative to their BAO-only analyses. For fσ8 the scatter of best-fitting values is the same as the full-shape-only analyses, as expected (BAO only do not provide extra information on fσ8). The values of σ(Zi) for the combined results are consistent with one for α⊥, α∥, though for fσ8 they are more than 5 per cent larger than unity for both configuration and Fourier space. This would indicate that our combination procedure from Section 3.4 produces slightly underestimated errors for fσ8. In Gil-Marín et al. (2020), an alternative method was suggested to extract the consensus results from BAO and RSD analysis: a simultaneous fit. Both BAO and RSD models are fitted simultaneously to the concatenation of the pre- and post-reconstruction data vectors. This fit requires the full covariance matrix between pre- and post-reconstruction multipoles and is estimated from 1000 EZmocks. Results of simultaneous fits on mocks are shown in the eleventh row of Table 11 and are noted ‘BAO×RSD Pℓ’. These are to be compared with our usual method of combining posteriors, noted ‘BAO+RSD’ and shown in the tenth row. First, we see good agreement between the scatter of best-fitting values of all three parameters between BAO×RSD and BAO+RSD. However, the simultaneous fit overestimates the errors in fσ8 by 8 per cent, based on its σ(Zi) value. While in theory the simultaneous fit is a better procedure, accounting for all correlations, in practice we only use 1000 mocks to estimate a larger covariance matrix with large off-diagonal terms. Therefore, we cannot conclude from this test which method leads to better estimated errors. We use BAO+RSD entries for the consensus results.
The last two rows of Table 11 show statistics on the final consensus results from the LRG sample when combining BAO and full shape from both Fourier and configuration spaces. These results reflect the full statistical power of the LRG sample. The excellent agreement between the statistics of these two rows shows that the order of combination does not impact results. The dispersion σ on α⊥ and α∥ is reduced to 1.8 and 2.6 per cent, respectively, while we had 2.2 and 3.4 per cent for only BAO, and 2.0 and 3.2 per cent for only full shape. The pull distributions for α⊥ and α∥ are consistent with a Gaussian distribution. The scatter in fσ8 is not reduced compared to individual methods, which is expected since BAO does not add information on this parameter, so the consensus error should be equal to the one obtained from the full-shape fits. However, the σ(Zi) for fσ8 indicates that our consensus errors on this parameter might be underestimated by 10 per cent. While this seems to be significant, this result can be a consequence of the Gaussian assumption of all individual likelihoods not holding for all realizations, or the combination procedure itself might lead to underestimated errors (as seen with fσ8 in the ninth and tenth rows), though we would need more mocks to test these hypotheses carefully.
For this work, we consider the underestimation on fσ8 consensus errors (last two rows of Table 11) as another source of systematic error. The simplest correction to this underestimation is to scale the estimated errors of fσ8 in each realization by σ(Zi) = 1.09. We proceed to apply this correction factor to the consensus fσ8 errors with our data sample. This factor is to be applied only to statistical errors. In Section 5.3, we describe how we apply with this scaling in the presence of systematic errors.
5 RESULTS
We provide in this section the results of the BAO analysis, the full-shape RSD analysis, and the combination of the two for the eBOSS LRG sample. The analysis assumes an effective redshift for the sample of |$z$|eff = 0.698.
5.1 Result from the BAO analysis
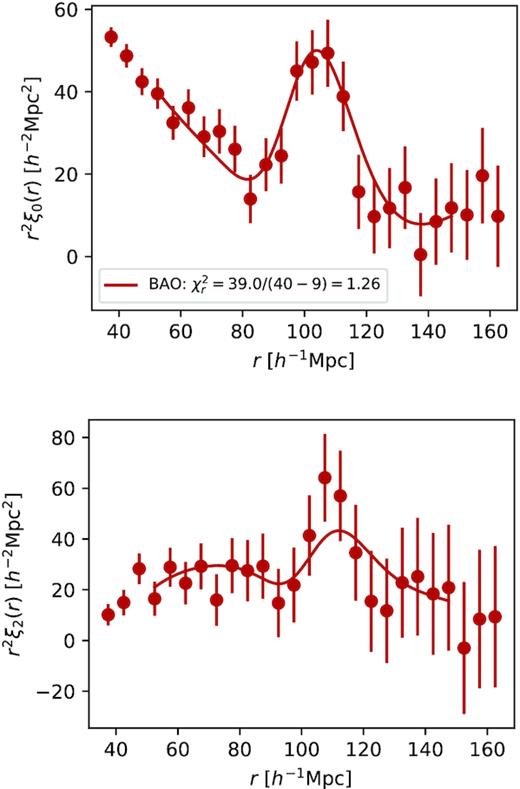
Best-fitting BAO model to the monopole (top) and quadrupole (bottom) of the post-reconstruction correlation function of the eBOSS+CMASS LRG sample. The legend displays the χ2 value of the fit.
Fig. 13 shows in blue the 68 and 95 per cent confidence contours in the (DM/rd, DH/rd) space for the BAO measurement in configuration space. Our best-fitting values are consistent within 1.26σ to the prediction of a flat ΛCDM model given by Planck 2018 best-fitting parameters (Planck Collaboration VI 2018b) assuming a χ2 distribution with 2 degrees of freedom. This measurement is also in excellent agreement with the BAO analysis performed in Fourier space (Gil-Marín et al. 2020), shown as red contours in Fig. 13. Since Fourier- and configuration-space analyses use the same data, final measurements are highly correlated. Based on measurements of the same 1000 realizations of EZmocks, we obtain correlation coefficients of 0.86 for both DM/rd and DH/rd. As these correlations are not unity, there is some gain, in combining both measurements. Using the methods presented in Section 3.4, we compute the combined BAO measurements between Fourier and configuration space. The result is displayed as grey contours in Fig. 13 and in Table 14 as ‘BAO ξℓ + Pℓ’. The error of the combined result is only 2 per cent smaller than the error of the configuration-space analysis alone.
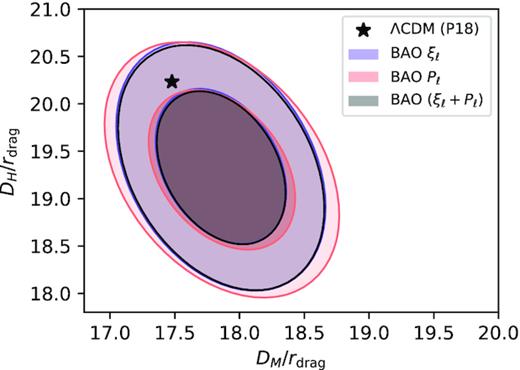
Constraints on DM/rd and DH/rd at |$z$|eff = 0.698 from the BAO analysis of the eBOSS LRG sample post-reconstruction. Contours show 68 and 95 per cent confidence regions for the configuration-space analysis in blue (this work), the Fourier-space analysis from Gil-Marín et al. (2020) in salmon, and the consensus BAO result in grey. The expected values in a flat ΛCDM model with Planck 2018 best-fitting parameters, shown by the black star, lie at 1.26σ from our best-fitting parameters of the configuration-space analysis.
Table 12 shows the impact on the BAO results in configuration space of different modifications in the methodology around the baseline configuration. The middle part of the table shows that our result is reasonably insensitive to some of these changes. Setting all systematic weights to unity causes only mild shifts to best-fitting parameters while estimated errors are unchanged. Removing the corrections by weights significantly distorts the broad shape of the correlation function. The fact that our BAO results are insensitive to these corrections proves that practically all information comes uniquely from the BAO peak and not from the full shape of the correlation function. This is a strong robustness validation of our BAO measurement. When leaving BAO damping parameters (Σ⊥, Σ∥) free or constrained within a Gaussian prior, the best-fitting values barely change while their errors are smaller than our baseline analysis. As observed on mocks, some realizations present sharper peaks due to noise and a sharper model could be considered as a better fit. However, we prefer to be conservative and not allow for this artificial increase in precision in our BAO analysis. Including the hexadecapole or changing the fiducial cosmology shifts alphas by less than one error bar, which is consistent to what is observed in mocks. We performed the BAO fits using the methods used in the BOSS DR12 analysis (Alam et al. 2017), which gives results in excellent agreement with our baseline method, with a slight better χ2. In the third part of Table 12, we present the pre-reconstruction result with similar best-fitting α⊥ and α∥ but with errors larger by factors of 1.3 and 1.5, which is typical as seen in mocks (Fig. 5). Pre-reconstruction BAO-only fits using our methodology show biases of about 1 per cent in the mocks; therefore, we do not recommend using pre-reconstruction results without accounting for these biases. The NGC and SGC results are two independent samples and their best-fitting α⊥ and α∥ are 0.25 and 0.53σ from each other, respectively, therefore not representing a significant difference among hemispheres.
The BAO measurement with the DR16 eBOSS+CMASS LRG data set using the standard pipeline described in Section 3.1 and other analysis choices. Note that for cases with different |$\Omega _\mathrm{ m}^{\rm fid}$|, we scale the obtained α⊥, α∥ by the distance ratios in order to make them comparable with the case where |$\Omega _\mathrm{ m}^{\rm fid} = 0.31$|.
| case . | α⊥ . | α∥ . | χ2/d.o.f. . |
|---|---|---|---|
| Baseline | 1.024 ± 0.019 | 0.956 ± 0.023 | 39.0/(40 − 9) |
| |$w$|sys|$w$|cp|$w$|noz = 1 | 1.022 ± 0.018 | 0.954 ± 0.023 | 30.1/(40 − 9) |
| Σ⊥, Σ∥ free | 1.027 ± 0.016 | 0.947 ± 0.019 | 31.9/(40 − 11) |
| Σ⊥, Σ∥ prior | 1.025 ± 0.017 | 0.952 ± 0.021 | 36.2/(40 − 11) |
| +ξ4 | 1.031 ± 0.019 | 0.949 ± 0.024 | 53.5/(60 − 12) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.27$| | 1.026 ± 0.020 | 0.950 ± 0.023 | 33.3/(40 − 9) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$| | 1.026 ± 0.019 | 0.951 ± 0.022 | 39.6/(40 − 9) |
| DR12 method | 1.023 ± 0.019 | 0.955 ± 0.024 | 34.5/(40 − 10) |
| Pre-recon | 1.035 ± 0.025 | 0.957 ± 0.035 | 42.0/(40 − 9) |
| NGC only | 1.038 ± 0.024 | 0.943 ± 0.024 | 42.3/(40 − 9) |
| SGC only | 0.993 ± 0.032 | 0.982 ± 0.070 | 44.5/(40 − 9) |
| case . | α⊥ . | α∥ . | χ2/d.o.f. . |
|---|---|---|---|
| Baseline | 1.024 ± 0.019 | 0.956 ± 0.023 | 39.0/(40 − 9) |
| |$w$|sys|$w$|cp|$w$|noz = 1 | 1.022 ± 0.018 | 0.954 ± 0.023 | 30.1/(40 − 9) |
| Σ⊥, Σ∥ free | 1.027 ± 0.016 | 0.947 ± 0.019 | 31.9/(40 − 11) |
| Σ⊥, Σ∥ prior | 1.025 ± 0.017 | 0.952 ± 0.021 | 36.2/(40 − 11) |
| +ξ4 | 1.031 ± 0.019 | 0.949 ± 0.024 | 53.5/(60 − 12) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.27$| | 1.026 ± 0.020 | 0.950 ± 0.023 | 33.3/(40 − 9) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$| | 1.026 ± 0.019 | 0.951 ± 0.022 | 39.6/(40 − 9) |
| DR12 method | 1.023 ± 0.019 | 0.955 ± 0.024 | 34.5/(40 − 10) |
| Pre-recon | 1.035 ± 0.025 | 0.957 ± 0.035 | 42.0/(40 − 9) |
| NGC only | 1.038 ± 0.024 | 0.943 ± 0.024 | 42.3/(40 − 9) |
| SGC only | 0.993 ± 0.032 | 0.982 ± 0.070 | 44.5/(40 − 9) |
The BAO measurement with the DR16 eBOSS+CMASS LRG data set using the standard pipeline described in Section 3.1 and other analysis choices. Note that for cases with different |$\Omega _\mathrm{ m}^{\rm fid}$|, we scale the obtained α⊥, α∥ by the distance ratios in order to make them comparable with the case where |$\Omega _\mathrm{ m}^{\rm fid} = 0.31$|.
| case . | α⊥ . | α∥ . | χ2/d.o.f. . |
|---|---|---|---|
| Baseline | 1.024 ± 0.019 | 0.956 ± 0.023 | 39.0/(40 − 9) |
| |$w$|sys|$w$|cp|$w$|noz = 1 | 1.022 ± 0.018 | 0.954 ± 0.023 | 30.1/(40 − 9) |
| Σ⊥, Σ∥ free | 1.027 ± 0.016 | 0.947 ± 0.019 | 31.9/(40 − 11) |
| Σ⊥, Σ∥ prior | 1.025 ± 0.017 | 0.952 ± 0.021 | 36.2/(40 − 11) |
| +ξ4 | 1.031 ± 0.019 | 0.949 ± 0.024 | 53.5/(60 − 12) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.27$| | 1.026 ± 0.020 | 0.950 ± 0.023 | 33.3/(40 − 9) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$| | 1.026 ± 0.019 | 0.951 ± 0.022 | 39.6/(40 − 9) |
| DR12 method | 1.023 ± 0.019 | 0.955 ± 0.024 | 34.5/(40 − 10) |
| Pre-recon | 1.035 ± 0.025 | 0.957 ± 0.035 | 42.0/(40 − 9) |
| NGC only | 1.038 ± 0.024 | 0.943 ± 0.024 | 42.3/(40 − 9) |
| SGC only | 0.993 ± 0.032 | 0.982 ± 0.070 | 44.5/(40 − 9) |
| case . | α⊥ . | α∥ . | χ2/d.o.f. . |
|---|---|---|---|
| Baseline | 1.024 ± 0.019 | 0.956 ± 0.023 | 39.0/(40 − 9) |
| |$w$|sys|$w$|cp|$w$|noz = 1 | 1.022 ± 0.018 | 0.954 ± 0.023 | 30.1/(40 − 9) |
| Σ⊥, Σ∥ free | 1.027 ± 0.016 | 0.947 ± 0.019 | 31.9/(40 − 11) |
| Σ⊥, Σ∥ prior | 1.025 ± 0.017 | 0.952 ± 0.021 | 36.2/(40 − 11) |
| +ξ4 | 1.031 ± 0.019 | 0.949 ± 0.024 | 53.5/(60 − 12) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.27$| | 1.026 ± 0.020 | 0.950 ± 0.023 | 33.3/(40 − 9) |
| |$\Omega _\mathrm{ m}^{\rm fid} = 0.35$| | 1.026 ± 0.019 | 0.951 ± 0.022 | 39.6/(40 − 9) |
| DR12 method | 1.023 ± 0.019 | 0.955 ± 0.024 | 34.5/(40 − 10) |
| Pre-recon | 1.035 ± 0.025 | 0.957 ± 0.035 | 42.0/(40 − 9) |
| NGC only | 1.038 ± 0.024 | 0.943 ± 0.024 | 42.3/(40 − 9) |
| SGC only | 0.993 ± 0.032 | 0.982 ± 0.070 | 44.5/(40 − 9) |
5.2 Results from the full-shape RSD analysis
We present in Fig. 14 the best-fitting TNS (red) and CLPT-GS (blue) RSD models to the pre-reconstruction eBOSS LRG multipoles. The associated reduced chi-squared values are χ2/dof = 85.2/(65 − 7) = 1.47 for TNS and χ2/dof = 83.7/(63 − 6) = 1.47 for CLPT-GS. While these values are unlikely explained by statistical fluctuations, we verified that the values reported for the χ2 for both models are within EZmock χ2 distributions. Both models perform similarly on data, but some differences are visible in Fig. 14. The TNS model produces a slightly sharper BAO peak than the CLPT-GS model, clearly visible in the monopole. This is due the fact that, intrinsically, the CLPT-GS model tends to predict a slighter higher BAO damping compared to Eulerian perturbation theory, as implemented here in the TNS model with respresso prescription. The CLPT-GS model has a slightly higher hexadecapole amplitude than the TNS model but both models seem to underestimate the hexadecapole amplitude below 35 h−1 Mpc by 1σ of the statistical uncertainties of the data. This underestimation in the amplitude of the hexadecapole is also present in the mocks for both the Nseries and EZmocks and was already reported in Icaza-Lizaola et al. (2020) explaining the relative high χ2 of the data.
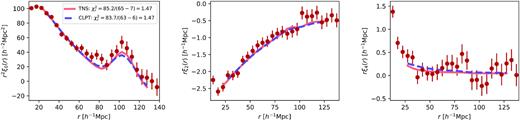
Best-fitting full-shape models to the eBOSS+CMASS multipoles. The left-hand, middle, and right-hand panels display mono, quad, and hexadecapole, respectively. The monopole is scaled by r2 while the other two are scaled by r. The CLPT-GS model is shown by the blue dashed line while the TNS model is shown by the red solid line. Note the baseline ranges used for each model are slightly different (see Fig. 6).
Table 13 shows the impact of different modifications in the methodology around the baseline configuration. First, if we change the range of scales used in the hexadecapole by changing rmin from 25 to 35 h−1 Mpc. We see a decrease of the reduced chi-squared as we remove these scales from the hexadecapole, which are underestimated by the models. Removing those scales impact the measured cosmological parameters, particularly α∥, which is shifted by about 1σ. We performed the same cuts on the analysis of EZmocks, finding that such a shift lies at about 2.3σ of the shifts observed in 1000 mocks (see details in Appendix A). The NGC and SGC fields are two independent samples and we find that their individual best-fitting α⊥ and α∥, and fσ8 are 0.7σ, 0.5σ, and 0.3σ from each other, respectively, for CLPT-GS and 0.7σ, 0.8σ, and 0.1σ for TNS, which is not a significant difference.
The full-shape measurements with the DR16 eBOSS+CMASS LRG data set from our baseline analysis described in Section 3.2 followed by results from other analysis choices. The presented errors are purely statistical and do not include systematic errors.
| Model . | Analysis . | α⊥ . | α∥ . | fσ8 . | χ2/d.o.f. . |
|---|---|---|---|---|---|
| CLPT-GS | baseline | 0.997 ± 0.020 | 1.013 ± 0.028 | 0.471 ± 0.045 | 83.7/(63 − 6) = 1.47 |
| CLPT-GS | rmin = 35 h−1 Mpc for ξ4 | 1.017 ± 0.022 | 0.971 ± 0.031 | 0.499 ± 0.046 | 79.3/(61 − 6) = 1.44 |
| CLPT-GS | NGC only | 1.015 ± 0.025 | 1.009 ± 0.031 | 0.464 ± 0.055 | 81.1/(63 − 6) = 1.40 |
| CLPT-GS | SGC only | 0.985 ± 0.036 | 1.041 ± 0.062 | 0.439 ± 0.078 | 71.3/(63 − 6) = 1.25 |
| TNS | baseline | 1.001 ± 0.018 | 1.013 ± 0.031 | 0.451 ± 0.040 | 85.2/(65 − 7) = 1.47 |
| TNS | rmin = 35 h−1 Mpc for ξ4 | 1.013 ± 0.016 | 0.976 ± 0.027 | 0.458 ± 0.036 | 73.7/(63 − 7) = 1.32 |
| TNS | Without ξ4 | 1.019 ± 0.019 | 0.963 ± 0.035 | 0.472 ± 0.044 | 50.1/(44 − 7) = 1.35 |
| TNS | NGC only | 1.024 ± 0.029 | 1.013 ± 0.036 | 0.436 ± 0.053 | 80.6/(65 − 7) = 1.39 |
| TNS | SGC only | 0.993 ± 0.034 | 1.076 ± 0.070 | 0.423 ± 0.076 | 69.1/(65 − 7) = 1.19 |
| Model . | Analysis . | α⊥ . | α∥ . | fσ8 . | χ2/d.o.f. . |
|---|---|---|---|---|---|
| CLPT-GS | baseline | 0.997 ± 0.020 | 1.013 ± 0.028 | 0.471 ± 0.045 | 83.7/(63 − 6) = 1.47 |
| CLPT-GS | rmin = 35 h−1 Mpc for ξ4 | 1.017 ± 0.022 | 0.971 ± 0.031 | 0.499 ± 0.046 | 79.3/(61 − 6) = 1.44 |
| CLPT-GS | NGC only | 1.015 ± 0.025 | 1.009 ± 0.031 | 0.464 ± 0.055 | 81.1/(63 − 6) = 1.40 |
| CLPT-GS | SGC only | 0.985 ± 0.036 | 1.041 ± 0.062 | 0.439 ± 0.078 | 71.3/(63 − 6) = 1.25 |
| TNS | baseline | 1.001 ± 0.018 | 1.013 ± 0.031 | 0.451 ± 0.040 | 85.2/(65 − 7) = 1.47 |
| TNS | rmin = 35 h−1 Mpc for ξ4 | 1.013 ± 0.016 | 0.976 ± 0.027 | 0.458 ± 0.036 | 73.7/(63 − 7) = 1.32 |
| TNS | Without ξ4 | 1.019 ± 0.019 | 0.963 ± 0.035 | 0.472 ± 0.044 | 50.1/(44 − 7) = 1.35 |
| TNS | NGC only | 1.024 ± 0.029 | 1.013 ± 0.036 | 0.436 ± 0.053 | 80.6/(65 − 7) = 1.39 |
| TNS | SGC only | 0.993 ± 0.034 | 1.076 ± 0.070 | 0.423 ± 0.076 | 69.1/(65 − 7) = 1.19 |
The full-shape measurements with the DR16 eBOSS+CMASS LRG data set from our baseline analysis described in Section 3.2 followed by results from other analysis choices. The presented errors are purely statistical and do not include systematic errors.
| Model . | Analysis . | α⊥ . | α∥ . | fσ8 . | χ2/d.o.f. . |
|---|---|---|---|---|---|
| CLPT-GS | baseline | 0.997 ± 0.020 | 1.013 ± 0.028 | 0.471 ± 0.045 | 83.7/(63 − 6) = 1.47 |
| CLPT-GS | rmin = 35 h−1 Mpc for ξ4 | 1.017 ± 0.022 | 0.971 ± 0.031 | 0.499 ± 0.046 | 79.3/(61 − 6) = 1.44 |
| CLPT-GS | NGC only | 1.015 ± 0.025 | 1.009 ± 0.031 | 0.464 ± 0.055 | 81.1/(63 − 6) = 1.40 |
| CLPT-GS | SGC only | 0.985 ± 0.036 | 1.041 ± 0.062 | 0.439 ± 0.078 | 71.3/(63 − 6) = 1.25 |
| TNS | baseline | 1.001 ± 0.018 | 1.013 ± 0.031 | 0.451 ± 0.040 | 85.2/(65 − 7) = 1.47 |
| TNS | rmin = 35 h−1 Mpc for ξ4 | 1.013 ± 0.016 | 0.976 ± 0.027 | 0.458 ± 0.036 | 73.7/(63 − 7) = 1.32 |
| TNS | Without ξ4 | 1.019 ± 0.019 | 0.963 ± 0.035 | 0.472 ± 0.044 | 50.1/(44 − 7) = 1.35 |
| TNS | NGC only | 1.024 ± 0.029 | 1.013 ± 0.036 | 0.436 ± 0.053 | 80.6/(65 − 7) = 1.39 |
| TNS | SGC only | 0.993 ± 0.034 | 1.076 ± 0.070 | 0.423 ± 0.076 | 69.1/(65 − 7) = 1.19 |
| Model . | Analysis . | α⊥ . | α∥ . | fσ8 . | χ2/d.o.f. . |
|---|---|---|---|---|---|
| CLPT-GS | baseline | 0.997 ± 0.020 | 1.013 ± 0.028 | 0.471 ± 0.045 | 83.7/(63 − 6) = 1.47 |
| CLPT-GS | rmin = 35 h−1 Mpc for ξ4 | 1.017 ± 0.022 | 0.971 ± 0.031 | 0.499 ± 0.046 | 79.3/(61 − 6) = 1.44 |
| CLPT-GS | NGC only | 1.015 ± 0.025 | 1.009 ± 0.031 | 0.464 ± 0.055 | 81.1/(63 − 6) = 1.40 |
| CLPT-GS | SGC only | 0.985 ± 0.036 | 1.041 ± 0.062 | 0.439 ± 0.078 | 71.3/(63 − 6) = 1.25 |
| TNS | baseline | 1.001 ± 0.018 | 1.013 ± 0.031 | 0.451 ± 0.040 | 85.2/(65 − 7) = 1.47 |
| TNS | rmin = 35 h−1 Mpc for ξ4 | 1.013 ± 0.016 | 0.976 ± 0.027 | 0.458 ± 0.036 | 73.7/(63 − 7) = 1.32 |
| TNS | Without ξ4 | 1.019 ± 0.019 | 0.963 ± 0.035 | 0.472 ± 0.044 | 50.1/(44 − 7) = 1.35 |
| TNS | NGC only | 1.024 ± 0.029 | 1.013 ± 0.036 | 0.436 ± 0.053 | 80.6/(65 − 7) = 1.39 |
| TNS | SGC only | 0.993 ± 0.034 | 1.076 ± 0.070 | 0.423 ± 0.076 | 69.1/(65 − 7) = 1.19 |
The marginal posteriors on α⊥, α∥, and fσ8 and associated 68 per cent and 95 per cent confidence contours are shown in Fig. 15. The posteriors obtained from both models are in good agreement. Entries denoted as ‘RSD ξℓ CLPT-GS’ and ‘RSD ξℓ TNS’ in Table 14 give the best-fitting parameters and 1σ error (including systematic errors), translated into DM/rd, DH/rd, and fσ8. We find an excellent agreement in the best-fitting parameters and errors between the two RSD models, as expected from the posteriors. The full posteriors including all nuisance parameters can be found in Appendix C.
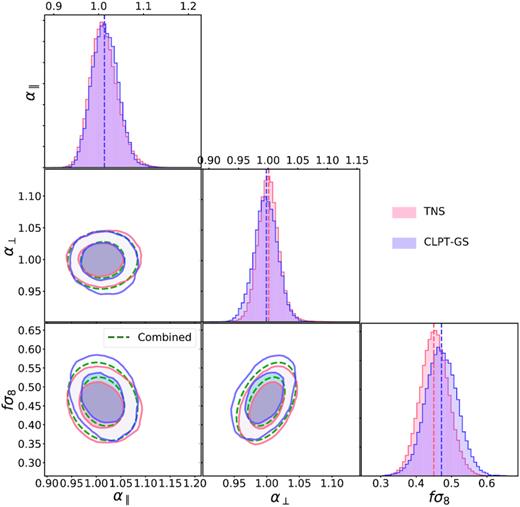
Comparison between the TNS and CLPT-GS final posterior distributions over the three main parameters using the DR16 data. The distributions are in good agreement for the two models. The vertical dashed lines on the 1D distributions refer to the mean. Dashed line contours show the combined result from the two models, assuming Gaussian errors. The full posteriors including nuisance parameters can be found in Appendix C.
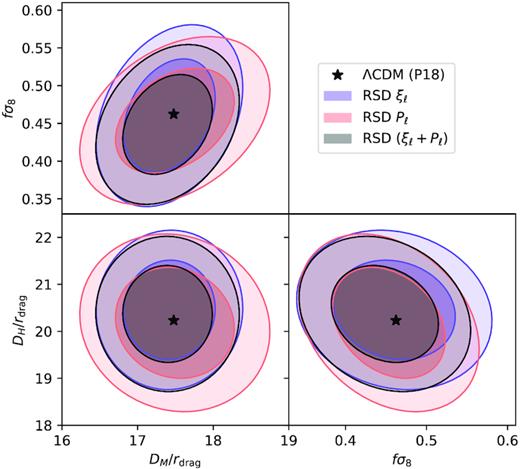
Constraints on DM/rd, DH/rd, and fσ8 |$z$|eff = 0.698 from the full-shape RSD analysis of the completed eBOSS LRG sample pre-reconstruction. Contours show 68 and 95 per cent confidence regions for the analyses in configuration space (blue), Fourier space (red), and the combined (grey). The expected values in a flat ΛCDM model with best-fitting parameters from Planck 2018 results are indicated as a black star.
Summary table with results from this work, from Gil-Marín et al. (2020), and their combination. All reported errors include the systematic component. The effective redshift of all measurements is |$z$|eff = 0.698.
| Method . | DM/rd . | DH/rd . | fσ8 . |
|---|---|---|---|
| BAO ξℓ | 17.86 ± 0.33 | 19.34 ± 0.54 | – |
| BAO Pℓ | 17.86 ± 0.37 | 19.30 ± 0.56 | – |
| BAO ξℓ + Pℓ | 17.86 ± 0.33 | 19.33 ± 0.53 | – |
| RSD ξℓ CLPT | 17.39 ± 0.43 | 20.46 ± 0.68 | 0.471 ± 0.052 |
| RSD ξℓ TNS | 17.45 ± 0.38 | 20.45 ± 0.72 | 0.451 ± 0.047 |
| RSD ξℓ | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| RSD Pℓ | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| RSD ξℓ + Pℓ | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| BAO+RSD ξℓ | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| BAO+RSD Pℓ | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| BAO (ξℓ + Pℓ) + | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
| RSD (ξℓ + Pℓ) | – | – | – |
| (BAO+RSD) ξℓ + | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| (BAO+RSD) Pℓ | – | – | – |
| Method . | DM/rd . | DH/rd . | fσ8 . |
|---|---|---|---|
| BAO ξℓ | 17.86 ± 0.33 | 19.34 ± 0.54 | – |
| BAO Pℓ | 17.86 ± 0.37 | 19.30 ± 0.56 | – |
| BAO ξℓ + Pℓ | 17.86 ± 0.33 | 19.33 ± 0.53 | – |
| RSD ξℓ CLPT | 17.39 ± 0.43 | 20.46 ± 0.68 | 0.471 ± 0.052 |
| RSD ξℓ TNS | 17.45 ± 0.38 | 20.45 ± 0.72 | 0.451 ± 0.047 |
| RSD ξℓ | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| RSD Pℓ | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| RSD ξℓ + Pℓ | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| BAO+RSD ξℓ | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| BAO+RSD Pℓ | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| BAO (ξℓ + Pℓ) + | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
| RSD (ξℓ + Pℓ) | – | – | – |
| (BAO+RSD) ξℓ + | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| (BAO+RSD) Pℓ | – | – | – |
Summary table with results from this work, from Gil-Marín et al. (2020), and their combination. All reported errors include the systematic component. The effective redshift of all measurements is |$z$|eff = 0.698.
| Method . | DM/rd . | DH/rd . | fσ8 . |
|---|---|---|---|
| BAO ξℓ | 17.86 ± 0.33 | 19.34 ± 0.54 | – |
| BAO Pℓ | 17.86 ± 0.37 | 19.30 ± 0.56 | – |
| BAO ξℓ + Pℓ | 17.86 ± 0.33 | 19.33 ± 0.53 | – |
| RSD ξℓ CLPT | 17.39 ± 0.43 | 20.46 ± 0.68 | 0.471 ± 0.052 |
| RSD ξℓ TNS | 17.45 ± 0.38 | 20.45 ± 0.72 | 0.451 ± 0.047 |
| RSD ξℓ | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| RSD Pℓ | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| RSD ξℓ + Pℓ | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| BAO+RSD ξℓ | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| BAO+RSD Pℓ | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| BAO (ξℓ + Pℓ) + | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
| RSD (ξℓ + Pℓ) | – | – | – |
| (BAO+RSD) ξℓ + | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| (BAO+RSD) Pℓ | – | – | – |
| Method . | DM/rd . | DH/rd . | fσ8 . |
|---|---|---|---|
| BAO ξℓ | 17.86 ± 0.33 | 19.34 ± 0.54 | – |
| BAO Pℓ | 17.86 ± 0.37 | 19.30 ± 0.56 | – |
| BAO ξℓ + Pℓ | 17.86 ± 0.33 | 19.33 ± 0.53 | – |
| RSD ξℓ CLPT | 17.39 ± 0.43 | 20.46 ± 0.68 | 0.471 ± 0.052 |
| RSD ξℓ TNS | 17.45 ± 0.38 | 20.45 ± 0.72 | 0.451 ± 0.047 |
| RSD ξℓ | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| RSD Pℓ | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| RSD ξℓ + Pℓ | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| BAO+RSD ξℓ | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| BAO+RSD Pℓ | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| BAO (ξℓ + Pℓ) + | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
| RSD (ξℓ + Pℓ) | – | – | – |
| (BAO+RSD) ξℓ + | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| (BAO+RSD) Pℓ | – | – | – |
We combine the results from our two RSD models using a weighted average based on the individual covariance matrices (see Section 3.4). The combined measurement is indicated by ‘RSD ξℓ’ in Table 14 and shown with dashed contours in Fig. 15. Central values and errors of the combined result fall approximately in between the values of each individual measurement.
5.3 Consensus results
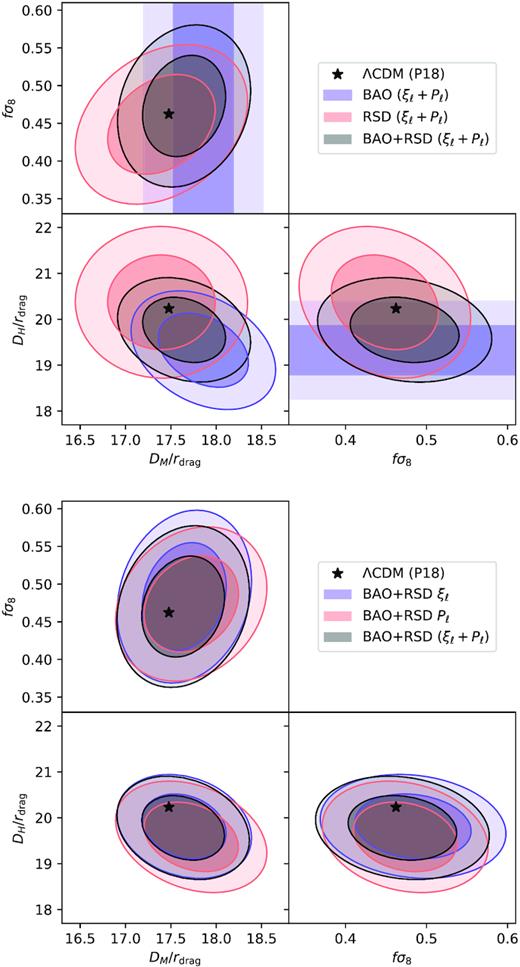
Final measurements of DM/rd, DH/rd, fσ8 from the completed eBOSS LRG sample at |$z$|eff = 0.698. The top and bottom panels show two possible procedures for obtaining the final result. The grey contours show the final results, which are virtually the same in both panels (two bottom lines in Table 14). The black star indicates the prediction in a flat ΛCDM model with parameters from Planck 2018 results.
Systematic errors originating from observational effects, modelling, and combination methods were carefully included in our measurements and are responsible for inflating final errors by 6, 13, and 20 per cent, respectively, on DM/rd, DH/rd, and fσ8. In Section 4.3, we found that our statistical errors on the consensus fσ8 were slightly underestimated. To apply this correction on the data consensus, we proceed as follows. First, we compute consensus with and without accounting for systematic errors from Table 10. The difference between their error matrices gives us the additive systematic matrix. Then, we scale the statistical errors on fσ8 by 1.09 and we add back the additive systematic matrix. This procedure yields the results reported in equations (56) and (57).
5.4 Comparison with previous results
Our final consensus result for the DR16 LRG sample is shown in equations (56) and (57), and used a total of 402 052 (weighted) galaxies over 9463 deg2 (with 4242 deg2 observed by eBOSS). Bautista et al. (2018) and Icaza-Lizaola et al. (2020) describe, respectively, the BAO and full-shape RSD measurements using the DR14 LRG sample, which contains 126 557 galaxies over 1844 deg2. In the DR14 sample, CMASS galaxies outside of the eBOSS footprint were not used. Because of that, the effective redshift of the DR14 measurements is slightly higher, at |$z$|eff = 0.72.
Bautista et al. (2018) reported a 2.5 per cent measurement of the ratio of the spherically averaged distance to the sound horizon scale, |$D_\mathrm{ V}(z=0.72)/r_\mathrm{ d} = 16.08^{+0.41}_{-0.40}$|. This result was obtained with isotropic fits to the monopole of the post-reconstruction correlation function. The statistical power of the DR14 sample is relatively low for anisotropic BAO constraints and has large non-Gaussian errors. Converting our DR16 anisotropic measurement of equation (56) into spherically averaged distances, we obtain: DV(|$z$| = 0.698)/rd = 16.26 ± 0.20, which is well within 1σ from the DR14 value. The error on DV has reduced by a factor of 2, slightly more than the square root of the increase in effective volume, which gives a factor of |$\sqrt{ V_{\rm eff, DR16}/V_{\rm eff, DR14}} = \sqrt{2.73/0.9} \sim 1.74$|. Note that in DR16 we combine BAO and full-shape analysis in Fourier and configuration spaces, which maximizes the amount of extracted cosmological information.
Icaza-Lizaola et al. (2020) presented the full-shape RSD analysis in the DR14 LRG sample in configuration space, yielding fσ8 = 0.454 ± 0.134, DM/rd = 17.07 ± 1.55, and DH/rd = 19.17 ± 2.84. All values are consistent within 1σ of DR16 results, even though errors for DR14 are quite large given the even lower significance of the BAO peak in the pre-reconstruction multipoles. The error on the growth rate of structure fσ8 reduces by a factor of 3 in DR16 compared to DR14, clearly benefiting from the larger sample and the combination with post-reconstruction BAO results that help breaking model degeneracies.
Our DR16 LRG results at 0.6 < |$z$| < 1.0 supersede the highest redshift results of the DR12 BOSS sample at 0.5 < |$z$| < 0.75, which has an effective redshift of |$z$|eff = 0.61. Alam et al. (2017) report 1.4, 2.2, and 7.8 per cent measurements of DM/rd, DH/rd, and fσ8, respectively. While the errors in the high-redshift bin are slightly smaller than our DR16 result, it has a large correlation with the intermediate-redshift bin at 0.4 < |$z$| < 0.6. Our DR16 measurement is thus virtually independent of the first two DR12 BOSS redshift bins, and has effectively more weight in the final joint cosmological constraints. The cosmological implications of our DR16 LRG measurements are fully described in eBOSS Collaboration (2020).
6 CONCLUSION
This work presented the cosmological analysis of the configuration-space anisotropic clustering in the DR16 eBOSS LRG sample, which is used for the final cosmological analysis of the completed eBOSS survey. We extracted and model the BAO and RSD features from the galaxy two-point correlation function monopole, quadrupole, and hexadecapole moments. We used the reconstruction technique to sharpen the BAO peak and mitigate associated non-linearities. The pre- and post-reconstruction multipole moments were used to perform a full-shape RSD analysis and a BAO-only analysis, respectively. In the RSD analysis, we considered two different RSD models, whose results were later combined to increase the robustness and accuracy of the measurements. The combination of the BAO-only and full-shape RSD analyses allowed us to derive joint constraints on the three cosmological parameter combinations: DH(|$z$|)/rd, DM(|$z$|)/rd, and fσ8(|$z$|). This analysis is complementary to that performed in Fourier space and presented in Gil-Marin et al. (2020). We found an excellent agreement between the inferred parameters in both spaces, both for BAO-only and full-shape RSD analyses. After combining the results with those from that in Fourier space, we obtain the following final constraints: DM/rd = 17.65 ± 0.30, DH/rd = 19.77 ± 0.47, and fσ8 = 0.473 ± 0.044, which are currently the most accurate at |$z$|eff = 0.698.
The adopted methodology has been extensively tested on a set of realistic simulations and shown to be very robust against systematics. In particular, we investigated different potential sources of systematic errors: inaccuracy in the modelling of both BAO/RSD and intrinsic galaxy clustering, arbitrary choice of reference cosmology, and systematic errors from observational effects such as redshift failures, fibre collision, incompleteness, or the RIC. We quantified the associated systematic error contributions and included them on the final cosmological parameter constraints. Overall, we found that the total systematic error inflates errors by 6, 13, and 20 per cent for α⊥, α∥, and fσ8.
The cosmological parameters inferred from the DR16 eBOSS LRG sample are in good agreement with the predictions from General Relativity in a flat ΛCDM cosmological model with parameters set to Planck 2018 results. These measurements complement those obtained from the other eBOSS tracers (de Mattia et al. 2020; du Mas des Bourboux et al. 2020; Hou et al. 2020; Neveux & Burtin 2020; Raichoor et al. 2020). The full cosmological interpretation of all eBOSS tracer results combined with previous BOSS results is presented in eBOSS Collaboration (2020).
Future large spectroscopic surveys such as DESI or Euclid will probe much larger volumes of the Universe. This will allow reducing the statistical errors on the cosmological parameters considerably, at the per cent level or below. For those, it will be crucial to control the level of systematics at an extremely low level. This is today a challenge and the work presented here has shown the current state-of-the-art methodology, which will have to be further developed and improved in view of the optimal exploitation of next-generation surveys.
ACKNOWLEDGEMENTS
RP, SdlT, and SE acknowledge the support from the French National Research Agency (ANR) under contract ANR-16-CE31-0021, eBOSS. SdlT and SE acknowledge the support of the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the ‘Investissements d’Avenir’ French government programme managed by the ANR. MVM and SF are partially supported by Programa de Apoyo a Proyectos de Investigación e Inovación ca Teconológica (PAPITT) no. IA101518, no. IA101619, Proyecto LANCAD-UNAM-DGTIC-319, and LANCAD-UNAM-DGTIC-136. HGM acknowledges the support from la Caixa Foundation (ID 100010434) code LCF/BQ/PI18/11630024. SA is supported by the European Research Council through the COSFORM Research Grant (#670193). GR, PDC, and JM acknowledge support from the National Research Foundation of Korea (NRF) through Grant Nos. 2017R1E1A1A01077508 and 2020R1A2C1005655 funded by the Korean Ministry of Education, Science and Technology (MoEST), and from the faculty research fund of Sejong University.
Numerical computations were done on the Sciama High Performance Compute (HPC) cluster, which is supported by the ICG, SEPNet, and the University of Portsmouth. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This research also uses resources of the HPC cluster ATOCATL-IA-UNAM México. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 693024).
Funding for the SDSS IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
DATA AVAILABILITY
The correlation functions, covariance matrices, and resulting likelihoods for cosmological parameters are (will be made) available (after acceptance) via the SDSS Science Archive Server (https://sas.sdss.org/), with the exact address tbd.
Footnotes
A summary of all SDSS BAO and RSD measurements with accompanying legacy figures can be found at sdss.org/science/final-bao-and-rsd-measurements/ and the cosmological interpretation of these measurements can be found at sdss.org/science/cosmology-results-from-eboss/.
Publicly available at sdss.org/dr16/software/products.
Publicly available at github.com/desihub/redrock.
Note that this definition differs from the one used in BOSS, where |$w$| = (|$w$|noz + |$w$|cp − 1)|$w$|sys|$w$|FKP.
Given the mismatch between the clustering of the MockChallenge mocks and data, and its larger cosmic variance compared to Nseries mocks, we decided to use MockChallenge only for the quantification of systematic errors related to the halo occupation models.
REFERENCES
APPENDIX A: IMPACT OF SCALES USED FROM THE HEXADECAPOLE
We present in Fig. A1 the distribution in the EZmocks of the difference on parameter constraints and reduced χ2 induced by including or not the smallest scales of the hexadecapole in the fit. We find that the distribution for each of the parameters is centred on zero with a standard deviation of 0.006, 0.015, and 0.01 for α⊥, α∥, and fσ8, respectively, which correspond to 0.3, 0.4, and 0.2 |${{\ \rm per\ cent}}$| of the uncertainties on the RSD TNS measurements in the data. This demonstrates that cosmological constraints are stable to the choice of the truncation scale for the hexadecapole. The vertical line shows the corresponding shift in the data. This shift remains within 1σ of the EZmocks distribution for fσ8 and reaches up to 2.3σ for α∥. For the reduced χ2, the observed difference is on the edge of the EZmocks distribution. Even if few EZmocks realizations exhibit the same variation as in the data, the observed shifts are still statistically consistent.
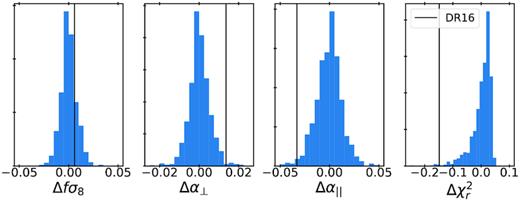
Variation of the cosmological parameters and the reduced chi-squared as a function of the truncation scale of the hexadecapole for the TNS model. The normalized distributions correspond to 1000 EZmocks while the vertical lines correspond to the shift for the data.
Fig. A2 displays the difference on the geometrical distortion parameters between the BAO post-reconstruction and RSD TNS measurements in the EZmocks. Similarly as in the previous figure, the vertical line shows the difference found in the data. While the differences for α⊥ and α∥ are smaller when the smallest scales of the hexadecapole are removed from the RSD fits, both measurements seem to be consistent with BAO post-reconstruction measurements similarly as in the mocks. Both distributions are centred on zero with a standard deviation between BAO and RSD measurements of 0.04 and 0.06 for α⊥ and α∥, respectively. This shows that as expected RSD measurements provide a more uncertain determination of the geometrical distortion parameters than BAO measurements.
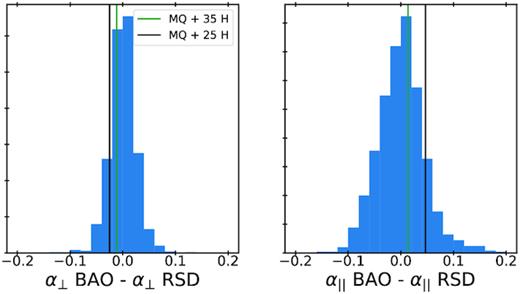
Absolute difference between TNS and BAO post-recon constraint on the alphas. The normalized distributions correspond to 1000 EZmocks, while the two vertical lines correspond to the two different truncation scales for the hexadecapole.
APPENDIX B: IMPACT OF FIBRE COLLISION CORRECTION SCHEME
Mohammad et al. (2020) present an improved correction scheme for fibre collisions for the eBOSS LRG sample but without CMASS galaxies. It is based on the method of Bianchi & Percival (2017), commonly referred to as the pair inverse probability (PIP) weighting. We performed fits of our BAO and full-shape RSD models to the multipoles for this restricted sample. Note that this sample is about two-thirds of the full sample used in our work. Table B1 compares the results on α⊥, α∥, and fσ8 obtained with our baseline fibre collision correction to those using PIP weights. We see that the changes are small compared to the statistical errors for all methods and models. This is expected since PIP weights mostly impact the clustering on the smallest scales not used in our analysis (r < 20 h−1 Mpc), while the baseline correction already well accounts for large-scale effects.
Impact of the choice of fibre collision correction scheme on the recovered α⊥, α∥, and fσ8 parameters in the eBOSS LRG sample without CMASS galaxies.
| Model . | Par . | Base . | PIP . |
|---|---|---|---|
| α⊥ | 1.189 ± 0.062 | 1.199 ± 0.070 | |
| BAO | α∥ | 0.850 ± 0.071 | 0.843 ± 0.074 |
| χ2/dof | 47.7/48 = 0.99 | 51.7/48 = 1.08 | |
| α⊥ | 1.009 ± 0.046 | 0.980 ± 0.044 | |
| CLPT-GS | α∥ | 1.027 ± 0.056 | 1.035 ± 0.055 |
| fσ8 | 0.473 ± 0.066 | 0.446 ± 0.066 | |
| χ2/dof | 67.8/54 = 1.26 | 71.5/54 = 1.32 | |
| α⊥ | 1.024 ± 0.044 | 1.001 ± 0.041 | |
| TNS | α∥ | 1.038 ± 0.050 | 1.032 ± 0.046 |
| fσ8 | 0.451 ± 0.068 | 0.420 ± 0.065 | |
| χ2/dof | 71.1/58 = 1.23 | 74.8/58 = 1.29 |
| Model . | Par . | Base . | PIP . |
|---|---|---|---|
| α⊥ | 1.189 ± 0.062 | 1.199 ± 0.070 | |
| BAO | α∥ | 0.850 ± 0.071 | 0.843 ± 0.074 |
| χ2/dof | 47.7/48 = 0.99 | 51.7/48 = 1.08 | |
| α⊥ | 1.009 ± 0.046 | 0.980 ± 0.044 | |
| CLPT-GS | α∥ | 1.027 ± 0.056 | 1.035 ± 0.055 |
| fσ8 | 0.473 ± 0.066 | 0.446 ± 0.066 | |
| χ2/dof | 67.8/54 = 1.26 | 71.5/54 = 1.32 | |
| α⊥ | 1.024 ± 0.044 | 1.001 ± 0.041 | |
| TNS | α∥ | 1.038 ± 0.050 | 1.032 ± 0.046 |
| fσ8 | 0.451 ± 0.068 | 0.420 ± 0.065 | |
| χ2/dof | 71.1/58 = 1.23 | 74.8/58 = 1.29 |
Impact of the choice of fibre collision correction scheme on the recovered α⊥, α∥, and fσ8 parameters in the eBOSS LRG sample without CMASS galaxies.
| Model . | Par . | Base . | PIP . |
|---|---|---|---|
| α⊥ | 1.189 ± 0.062 | 1.199 ± 0.070 | |
| BAO | α∥ | 0.850 ± 0.071 | 0.843 ± 0.074 |
| χ2/dof | 47.7/48 = 0.99 | 51.7/48 = 1.08 | |
| α⊥ | 1.009 ± 0.046 | 0.980 ± 0.044 | |
| CLPT-GS | α∥ | 1.027 ± 0.056 | 1.035 ± 0.055 |
| fσ8 | 0.473 ± 0.066 | 0.446 ± 0.066 | |
| χ2/dof | 67.8/54 = 1.26 | 71.5/54 = 1.32 | |
| α⊥ | 1.024 ± 0.044 | 1.001 ± 0.041 | |
| TNS | α∥ | 1.038 ± 0.050 | 1.032 ± 0.046 |
| fσ8 | 0.451 ± 0.068 | 0.420 ± 0.065 | |
| χ2/dof | 71.1/58 = 1.23 | 74.8/58 = 1.29 |
| Model . | Par . | Base . | PIP . |
|---|---|---|---|
| α⊥ | 1.189 ± 0.062 | 1.199 ± 0.070 | |
| BAO | α∥ | 0.850 ± 0.071 | 0.843 ± 0.074 |
| χ2/dof | 47.7/48 = 0.99 | 51.7/48 = 1.08 | |
| α⊥ | 1.009 ± 0.046 | 0.980 ± 0.044 | |
| CLPT-GS | α∥ | 1.027 ± 0.056 | 1.035 ± 0.055 |
| fσ8 | 0.473 ± 0.066 | 0.446 ± 0.066 | |
| χ2/dof | 67.8/54 = 1.26 | 71.5/54 = 1.32 | |
| α⊥ | 1.024 ± 0.044 | 1.001 ± 0.041 | |
| TNS | α∥ | 1.038 ± 0.050 | 1.032 ± 0.046 |
| fσ8 | 0.451 ± 0.068 | 0.420 ± 0.065 | |
| χ2/dof | 71.1/58 = 1.23 | 74.8/58 = 1.29 |
APPENDIX C: FULL PARAMETER SPACE POSTERIOR DISTRIBUTIONS
For the sake of readability, we do not present the full parameter space posterior distribution of our chains in the main text. However, it could be of interest to see the full information. Due to some differences between parameters in the two models we use, we separately present the full posterior distributions for TNS and CLPT-GS in Figs C1 and C2, respectively.
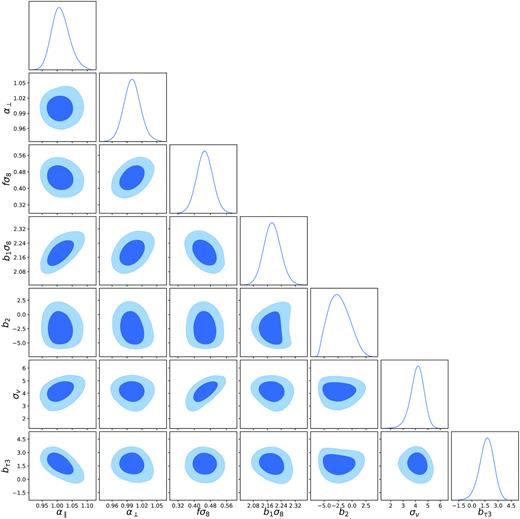
Full posterior distribution of the MCMC chain for the TNS model.
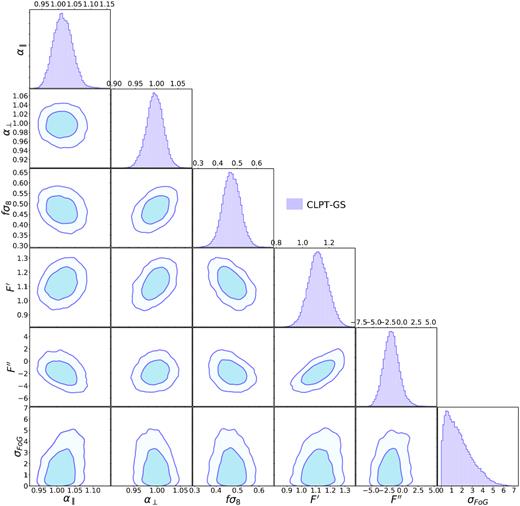
Full posterior distribution of the MCMC chain for the CLPT-GS model.



