-
PDF
- Split View
-
Views
-
Cite
Cite
G Dudziński, E Podlewska-Gaca, P Bartczak, S Benseguane, M Ferrais, L Jorda, J Hanuš, P Vernazza, N Rambaux, B Carry, F Marchis, M Marsset, M Viikinkoski, M Brož, R Fetick, A Drouard, T Fusco, M Birlan, E Jehin, J Berthier, J Castillo-Rogez, F Cipriani, F Colas, C Dumas, A Kryszczynska, P Lamy, H Le Coroller, A Marciniak, T Michalowski, P Michel, T Santana-Ros, P Tanga, F Vachier, A Vigan, O Witasse, B Yang, Volume uncertainty of (7) Iris shape models from disc-resolved images, Monthly Notices of the Royal Astronomical Society, Volume 499, Issue 3, December 2020, Pages 4545–4560, https://doi.org/10.1093/mnras/staa3153
Close - Share Icon Share
ABSTRACT
High angular resolution disc-resolved images of (7) Iris collected by VLT/SPHERE instrument are allowed for the detailed shape modelling of this large asteroid revealing its surface features. If (7) Iris did not suffer any events catastrophic enough to disrupt the body (which is very likely) by studying its topography, we might get insights into the early Solar system’s collisional history. When it comes to internal structure and composition, thoroughly assessing the volume and density uncertainties is necessary. In this work, we propose a method of uncertainty calculation of asteroid shape models based on light curve and adaptive optics (AO) images. We apply this method on four models of (7) Iris produced from independent Shaping Asteroids using Genetic Evolution and All-Data Asteroid Modelling inversion techniques and multiresolution photoclinometry by deformation. Obtained diameter uncertainties stem from both the observations from which the models were scaled and the models themselves. We show that despite the availability of high-resolution AO images, the volume and density of (7) Iris have substantial error bars that were underestimated in the previous studies.
1 INTRODUCTION
In 2017, asteroid (7) Iris was observed by the VLT/ SPHERE/ ZIMPOL instrument (Hanuš et al. 2019) as part of an ESO Large program (Vernazza et al. 2018). Because of the angular resolution of ∼20 mas at 600 nm (Schmid et al. 2017) and the large diameter of the target (D ∼ 200 km), the adaptive optics (AO) images had a spectacular resolution of 2.35 km per pixel. They did not only reveal the global shape of the body, but also some topographic features like large craters. The 2017 data supported by AO images and light curves from previous years yielded a detailed 3D shape model (Hanuš et al. 2019) using All-Data Asteroid Modelling (ADAM) algorithm (Viikinkoski, Kaasalainen & Durech 2015). This model’s volume together with an average of mass estimates from the literature yields a density of 2.7 ± 0.3 g cm−3, which is consistent with LL ordinary chondrites, which match Iris’ surface composition (Vernazza et al. 2014). The identification of a large excavation near the equator of the body indicates a large collision in the past, however, no asteroid family has yet been associated with (7) Iris.
Still, the 2017 AO images were obtained only under a single aspect angle, i.e. ∼150°, showing only the Southern hemisphere. Other AO images of Iris collected in previous years either covered roughly the same region or had much worse resolution. The global shape of the model, hence the volume and density estimates, could be affected by the fact that major parts of the body might have been poorly represented in the data. It is hard to judge the reliability of the density value reported by Hanuš et al. (2019) given that its uncertainty is based only in mass estimation uncertainty.
The method we use for calculating uncertainties of physical parameters of asteroid models, including volume, has been proposed by Bartczak & Dudziński (2019). However, the later study dealt only with visual disc-integrated photometry. The authors concluded that the least known parameter of light curve-based models is the extent of the body along the spin axis (i.e. z-scale), which has a huge impact on the volume estimate. The success of determining this parameter strongly depends on the coverage of aspect angles in supplementary absolute disc-integrated or disc-resolved observations.
Adding to the already impressive pool of AO images of (7) Iris, especially the ones that revealed surface features, the ESO Large programme allocated additional observation time in 2019. Although the resolution achieved in that campaign was not as spectacular as in 2017, observations were carried under a different aspect angle of close to 20°. This new data led to the creation of new models using adam, Shaping Asteroids using Genetic Evolution (sage; Bartczak & Dudziński 2018) and Multiresolution Photoclinometry by Deformation (mpcd; Capanna et al. 2013; Jorda et al. 2016) methods. The sage method has been extended in this work to incorporate AO images alongside light curves. In addition, the uncertainty assessment method presented in Bartczak & Dudziński (2019) has also been modified to include disc-resolved data, thus enabling to test (7) Iris models created independently with all three methods. As a result, the volume error bars reported here offer new insights into the density of this large asteroid.
In Section 2, we describe the methods used to assess the uncertainty and calculate the size of the shape models based on AO images. Section 3 describes the light-curve observations used in this study and images obtained with VLT/SPHERE instrument. The uncertainties in the shape model, sizes, and densities are presented in Section 4, which is followed by the conclusions in Section 5.
2 METHODS
2.1 sage method extension
For the purposes of this study, the sage algorithm (Bartczak & Dudziński 2018) has been extended to include AO images alongside light curves. Using genetic algorithm, the method gradually forms the resultant shape and spin state. The discrepancy between the synthetic data (created based on intermediate models) and observations expressed in root-mean-square deviaiton (RMSD) value is used as the measure of fitness in the modelling procedure.
Combining two types of observations (light curves and AO images) in one minimalization procedure is challenging due to the existence of two separate criteria: RMSDLC in magnitudes and RMSDAO in pixels. In order to combine the two, the observations’ weighting procedure of sage method has been modified. In short, for every observation obtained with a given technique, a minimal value of the fit found in the history of a model’s evolution is stored and used to calculate a weighting factor for normalization. After normalization, a single fitness function can be used in the evolution process.
2.2 Uncertainty assessment
The method for uncertainty assessment used in this work is a direct extension of the one presented in Bartczak & Dudziński (2019). It was augmented with a module for comparing AO images with asteroids’ shape models, and the uncertainty calculation procedure has been updated.
In brief, the method is a modelling-technique independent sensitivity analysis of an asteroid model’s parameters: shape, pole, rotational period, and rotational phase at the reference epoch. It transforms deterministic model into a stochastic one by introducing random changes to the model’s parameters yielding a uniform population of clones. The vertices of the shape are moved inwards or outwards in a range between 0.5 and 1.5 of the nominal distance to the center of a model, whereas the pole’s longitude and latitude are modified up to 30°. Then, some fraction of the clones is either accepted or rejected based on the confidence level of the nominal model. Parameters’ uncertainty values are then calculated from the range of values found in the accepted clones population. This population also serves as the basis for determining the size of a model by taking into account both observations’ and model’s uncertainties in result offering volume and density with reliable errorbars.
The AO images were converted into binary form, i.e. pixel values are set either at 0 for the background, or 1 where the target is visible. The binary images were created by thresholding operation with iterative procedure implemented in imagej 1 image processing software, and based on isodata algorithm (Ridler & S. 1978).
The corresponding synthetic per clone images were made by rendering a computer-generated scene simulating observations’ viewing and illumination geometries. These images are also binary. That way, during the comparison, the whole emphasis is put on the silhouettes while ignoring the flux changes on the surface of the body, which can be strongly affected by the deconvolution procedure, small and unknown local topographic features beyond the image resolution, and by the choice of the scattering law in synthetic images.
For more technical details of the method, please refer to section 4 in Bartczak & Dudziński (2019).
2.3 Size determination
Once a population of accepted clones is created, its members can be used to determine the size of the target. One size measurement is performed by comparing a synthetic image based on a accepted clone with an AO image. The synthetic image is scaled and moved in x and y axes in search of the best fit, i.e. the smallest number of pixels that have different values on both images. The obtained model projection’s scale in pixels combined with the distance to the target yields a mesh with vertex positions expressed in physical units. The volume of a scaled mesh is then used to determine its equivalent sphere diameter D, i.e. the diameter of a sphere with the same volume. The collection of diameters of all the accepted clones for all of the AO images gives a range of diameters that target body could have.
2.4 Observations’ weighting
Each clone-image pair has a different size associated with it. Images have varied resolutions (expressed in km per pixel) and different clone shapes will yield different results. Moreover, observations have been obtained under different geometries showing different parts of the body. To get the final diameter, a weighting procedure based on image resolution and aspect angle is introduced.
In the set of images |$\mathcal {I}$|, an ith image has been taken under ξi aspect angle with a resolution δi. When a projection of a clone c is compared with an ith image we get an equivalent sphere diameter Di, c. When all of the clones are compared to an ith image, we get a range of diameters between |$D^{min}_{i}$| and |$D^{max}_{i}$|. For the nominal model we get Di, nom.
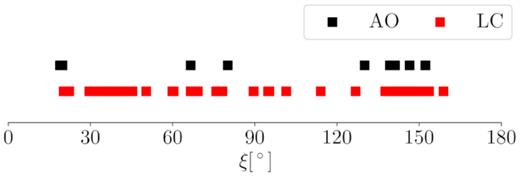
The coverage of aspect angles ξ of (7) Iris for the sets of used light curves (in red) and AO images (in black). Nominal pole solutions were used in calculations.
When Di = Di, nom in equation (3), we get the nominal diameter value. When Di = Di, c and when we perform calculations for all of the clones, we get a set of diameters from which error bars can be extracted, i.e. the maximum Dmax and the minimum Dmin values found in this set.
2.5 Multiresolution Photoclinometry by Deformation
Apart from sage and adam, the mpcd method was used as well to extract even more details from AO images. Additionally, this method has been modified for the purposes of this work as well to allow the calculation of errors from the fitting procedure.
The mpcd method of 3D shape reconstruction takes an initial shape model (in our case the model produced with the adam method) and then further modifies it to give the best fit to the AO images. The details can be found in Capanna et al. (2013) and Jorda et al. (2016). In the case of the mpcd model presented in this work, the error bars on the parameters associated with the reconstructed shape model were additionally calculated with a different method than the one described above.
The process involves two steps. First, the residuals (square of the difference between the observed and the synthetic pixel values, expressed in DN) are calculated for each pixel of the images used during the reconstruction. In this process, we exclude all the pixels located at the limbs and terminators on the images. These residuals are then reprojected on to the triangular facets of the reconstructed shape model. This leads to a residual for all the facets illuminated and visible on a given image. We then compute the change of the signal in DN associated with a small variation of the direction of the normal vector of the facet. This allows us to derive the slope error of the facet (in degrees) associated with its residual value (in DN). Multiplying the slope error of the facet by the mean length of its edges leads us to a height error estimate (in km). For a given facet, these height error estimates are averaged to provide an ‘error map’ (in km) associated with the facets of the shape model.
In the second step, we convert this local error map into uncertainties on integrated parameters such as the volume of the model. Applying a random displacement to the vertices of the model from the above error map would lead to physically unrealistic models with very high slopes.2 As a result, we apply instead a ‘fractal deformation’ to the reconstructed shape model. The deformation follows a fractal law in which the sigma of the Gaussian random displacement distribution follows a power law with respect to the sampling of the multiresolution models used in the mpcd method (Capanna et al. 2013). The sampling of each model is calculated as the mean edge length of all triangles. In order to ensure that our displacements match the error map calculated in the first step, the sigma value of the fractal law applied to the latest (highest resolution) model is set equal to the standard deviation of the map values. The fractal dimension is taken between 2.1 and 2.3, following the analysis of NEAR/NRL laser altimetry measurements performed by NEAR for the surface of asteroid (433) Eros (Cheng et al. 2002). A large number (10000) of such ‘fractal random models’ are generated in this way. The physical parameters are calculated for each model and the calculated values represent their error distribution, which is fitted by a Gaussian curve. The adopted error associated with each parameter is the fitted sigma value of the Gaussian.
3 OBSERVATIONS
This study uses 133 light curves in total, which were obtained at phase angles between 2.6° and 31.9° spanning 62 yr (1950–2012) with amplitudes ranging from 0.02 to 0.35 mag. Observation characteristics are shown in Table A1. In addition, 57 AO images were used. Of which, 35 were obtained by the VLT/SPHERE/ZIMPOL instrument, reduced and deconvoluted with the ESO pipeline. This process is described in Vernazza et al. (2018). More information on the AO images is provided in Table A2.
The coverage of aspect angles for all of the data is shown in Fig. 1. In Fig. 2, the resolution of AO images is shown against their aspect angles. The best quality images from VLT/SPHERE in 2017 with 2.35 km per pixel resolution were accompanied by Keck observations with aspect angles between 130° and 146°, but with significantly worse resolution. Another set of VLT/SPHERE observations in 2019 at aspect 20° covered the asteroid’s Northern hemisphere, a part of the body not visible earlier. Unfortunately, due to the greater distance to the target than in 2017, the resolution of ∼5 km per pixel did not allow distinguishing topographical features on the surface. Also, the fact that the aspects of two of the best quality image sets are 130° from each other looking at the target from opposite poles limits proper shape determination mostly at the low-latitude regions. When it comes to putting the limits on the z-scale of the (7) Iris models, the 2009 and 2010 data sets are critical as they were obtained at aspects 80° and 67°. Their resolution, however, is rather low (>8 km per pixel).
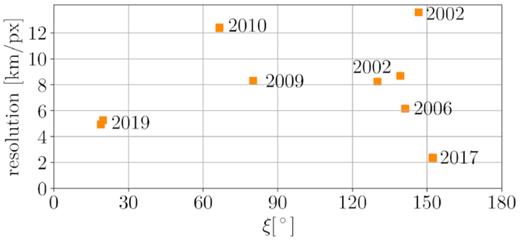
Resolution of AO images in km per pixel against aspect angle ξ.
4 RESULTS
4.1 Models of (7) Iris
Light curve and AO data of (7) Iris were used to analyse four models of this object denoted hereafter as adam,adam_2, sage, and mpcd. The first model was created by Hanuš et al. (2019) with the adam technique and did not utilize the 2019 AO images. In this work, we created three additional models (denoted as adam_2, sage, and mpcd) with the adam, sage, and mpcd methods. The adam_2 and sage models are based on the full data set including 2019 images. The sage method was developed to create light-curve-based models of asteroids (Bartczak & Dudziński 2018) and extended here to include AO images as well. The mpcd model was created with the adam model as a starting point that was modified to give the best fit to the subset of AO images from 2017 to 2019. (see Tables 1 and A2 for the exact epochs). The rotational periods of the models are almost identical, and the pole solutions differ only by a few degrees. These values are shown in Table 2.
Summary of the input data used to create the models. Note that mpcd model uses adam model as a starting point. The usage of individual AO images is shown in Table A2.
| . | sage . | adam . | adam_2 . | mpcd . |
|---|---|---|---|---|
| Light curves | ✓ | ✓ | ✓ | ✗ |
| AO (2002) | ✓ | ✓ | ✓ | ✗ |
| AO (2006) | ✓ | ✓ | ✓ | ✗ |
| AO (2009) | ✓ | ✓ | ✓ | ✗ |
| AO (2010) | ✓ | ✓ | ✓ | ✗ |
| AO (2017) | ✓ | ✓ | ✓ | ✓ |
| AO (2019) | ✓ | ✗ | ✓ | ✓ |
| . | sage . | adam . | adam_2 . | mpcd . |
|---|---|---|---|---|
| Light curves | ✓ | ✓ | ✓ | ✗ |
| AO (2002) | ✓ | ✓ | ✓ | ✗ |
| AO (2006) | ✓ | ✓ | ✓ | ✗ |
| AO (2009) | ✓ | ✓ | ✓ | ✗ |
| AO (2010) | ✓ | ✓ | ✓ | ✗ |
| AO (2017) | ✓ | ✓ | ✓ | ✓ |
| AO (2019) | ✓ | ✗ | ✓ | ✓ |
Summary of the input data used to create the models. Note that mpcd model uses adam model as a starting point. The usage of individual AO images is shown in Table A2.
| . | sage . | adam . | adam_2 . | mpcd . |
|---|---|---|---|---|
| Light curves | ✓ | ✓ | ✓ | ✗ |
| AO (2002) | ✓ | ✓ | ✓ | ✗ |
| AO (2006) | ✓ | ✓ | ✓ | ✗ |
| AO (2009) | ✓ | ✓ | ✓ | ✗ |
| AO (2010) | ✓ | ✓ | ✓ | ✗ |
| AO (2017) | ✓ | ✓ | ✓ | ✓ |
| AO (2019) | ✓ | ✗ | ✓ | ✓ |
| . | sage . | adam . | adam_2 . | mpcd . |
|---|---|---|---|---|
| Light curves | ✓ | ✓ | ✓ | ✗ |
| AO (2002) | ✓ | ✓ | ✓ | ✗ |
| AO (2006) | ✓ | ✓ | ✓ | ✗ |
| AO (2009) | ✓ | ✓ | ✓ | ✗ |
| AO (2010) | ✓ | ✓ | ✓ | ✗ |
| AO (2017) | ✓ | ✓ | ✓ | ✓ |
| AO (2019) | ✓ | ✗ | ✓ | ✓ |
Uncertainty values of models’ parameters in reference to the nominal model; Deq – equivalent sphere diameter, u(Deq) – relative diameter uncertainty, u(V) – relative volume uncertainty, P – rotational period, λ and β – coordinates of the spin axis. The relative uncertainties were calculated according to the formula: |$u_{rel}(x) = \frac{1}{2}(\delta ^+_x - \delta ^-_x)/x \cdot 100\%$|, where |$\delta ^+_x$| and |$\delta ^-_x$| are the upper and lower uncertainties of x. The mpcd* corresponds to the values produced independently using the mpcd method (see Section 2.5).
| Method . | Deq (km) . | u(Deq) (%) . | u(V) (%) . | P . | λ (°) . | β (°) . |
|---|---|---|---|---|---|---|
| sage | |$199^{+10}_{-8}$| | 4.5 | 13.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$21^{+1}_{-1}$| | |$23^{+1}_{-2}$| |
| adam | |$199^{+12}_{-9}$| | 5.5 | 16.6 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-2}$| | |$26^{+3}_{-3}$| |
| adam_2 | |$200^{+10}_{-18}$| | 6.8 | 19.7 | |$7.138844^{+0.000004}_{-0.00001}$| | |$20^{+1}_{-5}$| | |$23^{+3}_{-3}$| |
| mpcd | |$198^{+19}_{-17}$| | 9.2 | 27.9 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-6}$| | |$26^{+8}_{-1}$| |
| mpcd* | |$204^{+10}_{-10}$| | 4.9 | 14.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$19^{+3}_{-3}$| | |$26^{+3}_{-3}$| |
| Method . | Deq (km) . | u(Deq) (%) . | u(V) (%) . | P . | λ (°) . | β (°) . |
|---|---|---|---|---|---|---|
| sage | |$199^{+10}_{-8}$| | 4.5 | 13.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$21^{+1}_{-1}$| | |$23^{+1}_{-2}$| |
| adam | |$199^{+12}_{-9}$| | 5.5 | 16.6 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-2}$| | |$26^{+3}_{-3}$| |
| adam_2 | |$200^{+10}_{-18}$| | 6.8 | 19.7 | |$7.138844^{+0.000004}_{-0.00001}$| | |$20^{+1}_{-5}$| | |$23^{+3}_{-3}$| |
| mpcd | |$198^{+19}_{-17}$| | 9.2 | 27.9 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-6}$| | |$26^{+8}_{-1}$| |
| mpcd* | |$204^{+10}_{-10}$| | 4.9 | 14.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$19^{+3}_{-3}$| | |$26^{+3}_{-3}$| |
Uncertainty values of models’ parameters in reference to the nominal model; Deq – equivalent sphere diameter, u(Deq) – relative diameter uncertainty, u(V) – relative volume uncertainty, P – rotational period, λ and β – coordinates of the spin axis. The relative uncertainties were calculated according to the formula: |$u_{rel}(x) = \frac{1}{2}(\delta ^+_x - \delta ^-_x)/x \cdot 100\%$|, where |$\delta ^+_x$| and |$\delta ^-_x$| are the upper and lower uncertainties of x. The mpcd* corresponds to the values produced independently using the mpcd method (see Section 2.5).
| Method . | Deq (km) . | u(Deq) (%) . | u(V) (%) . | P . | λ (°) . | β (°) . |
|---|---|---|---|---|---|---|
| sage | |$199^{+10}_{-8}$| | 4.5 | 13.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$21^{+1}_{-1}$| | |$23^{+1}_{-2}$| |
| adam | |$199^{+12}_{-9}$| | 5.5 | 16.6 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-2}$| | |$26^{+3}_{-3}$| |
| adam_2 | |$200^{+10}_{-18}$| | 6.8 | 19.7 | |$7.138844^{+0.000004}_{-0.00001}$| | |$20^{+1}_{-5}$| | |$23^{+3}_{-3}$| |
| mpcd | |$198^{+19}_{-17}$| | 9.2 | 27.9 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-6}$| | |$26^{+8}_{-1}$| |
| mpcd* | |$204^{+10}_{-10}$| | 4.9 | 14.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$19^{+3}_{-3}$| | |$26^{+3}_{-3}$| |
| Method . | Deq (km) . | u(Deq) (%) . | u(V) (%) . | P . | λ (°) . | β (°) . |
|---|---|---|---|---|---|---|
| sage | |$199^{+10}_{-8}$| | 4.5 | 13.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$21^{+1}_{-1}$| | |$23^{+1}_{-2}$| |
| adam | |$199^{+12}_{-9}$| | 5.5 | 16.6 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-2}$| | |$26^{+3}_{-3}$| |
| adam_2 | |$200^{+10}_{-18}$| | 6.8 | 19.7 | |$7.138844^{+0.000004}_{-0.00001}$| | |$20^{+1}_{-5}$| | |$23^{+3}_{-3}$| |
| mpcd | |$198^{+19}_{-17}$| | 9.2 | 27.9 | |$7.138843^{+0.0001}_{-0.0001}$| | |$19^{+1}_{-6}$| | |$26^{+8}_{-1}$| |
| mpcd* | |$204^{+10}_{-10}$| | 4.9 | 14.7 | |$7.138843^{+0.000003}_{-0.000009}$| | |$19^{+3}_{-3}$| | |$26^{+3}_{-3}$| |
The adam and mpcd models were created with the goal to reproduce surface details. In the first case, the model was created in two steps. In the first one, light curves and AO data had the same weights giving preliminary model. Then, the weights of the data were lowered with the exception of VLT/SPHERE images. In result, the topographical features were reproduced at the cost of the fit to the light curves. This model was fed to the mpcd method, which used 2017 and 2019 AO images alone to reproduce topographical features, and their reliability, in even more detail. The adam_2 and sage models focused on explaining light curves and AO images simultaneously, meaning that the weights for light curves and AO data were not altered. Therefore, the first two models have worse fits to the light curves (0.0301 mag for adam and 0.0304 mag for mpcd) compared to the latter two (0.0254 mag for adam_2 and 0.0252 mag for sage), but they reproduce topographical features much better. The light-curve comparison is featured in Fig. B1, while the comparison of AO images and the models’ projections is featured in Figs B2 and B3.
4.2 Uncertainty assessment
All four models were subjected to uncertainty assessment using the complete data set of light curves and AO images. It should be mentioned that the 2019 VLT/SPHERE observations were not used to create the adam model of (7) Iris, and the mpcd model used the adam model as a starting point and used a subset of 2017 and 2019 images only. The population of accepted clones is the basis of the uncertainty of all physical parameters reported in this section.
The projections of the models with the uncertainty of the shape colour-coded on the surface are presented in Fig. 3. The colours correspond to the level of deviation of a given vertex from the nominal position in the clone population.
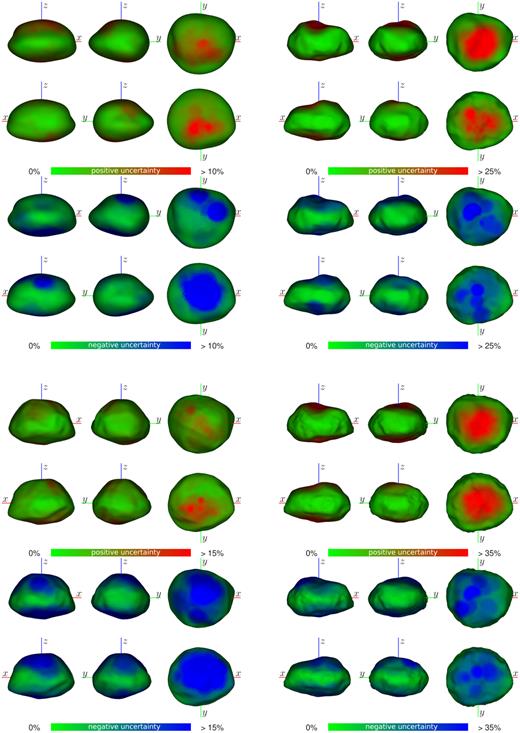
Projections of (7) Iris sage (top left), adam (top right), adam_2 (bottom left), and mpcd (bottom right) models. Colours represent positive (red) and negative (blue) local surface uncertainties expressed as percentage of the length of the longest vector in the model. These values come from the discrepancy of vertex positions in the population of accepted clones. Note different ranges of values for each model.
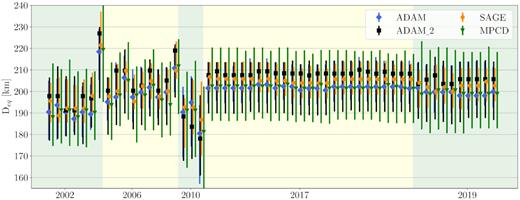
To incorporate the models’ uncertainties in the size determination, the dimensionless clones were fitted to the AO images. From those fits, a range of values was extracted and compared with the sizes of nominal models. The diameters from different images were weighted as described in Section 2.4. The resulting equivalent sphere diameters for the models are D|$^{\text{SAGE}}_{\mathrm{ eq}} = 199^{+10}_{-8}$| km, D|$^{\text{ADAM}}_{\mathrm{ eq}} = 199^{+12}_{-9}$| km, D|$^{\text{ADAM_2}}_{\mathrm{ eq}} = 200^{+10}_{-18}$| km, and D|$^{\text{MPCD}}_{\mathrm{ eq}} = 198^{+19}_{-17}$| km. The fits to individual images are shown in Fig. 4, while uncertainties of the diameter, volume, rotational period, and pole solution are given in Table 2.
4.3 Uncertainty reported by mpcd method
The uncertainty values for mpcd model were also obtained independently based on AO images alone and using the method described in Section 2.5. The resulting values and uncertainties diverge from the one reported in the previous section because both the method and data set used were different.
The Northern and Southern hemispheres of (7) Iris were observed at different resolutions during two distinct apparitions in 2017 and 2019. We thus applied the process separately for the two resolutions and added the resulting uncertainties quadratically. Finally, we doubled the uncertainty along the rotation axis because no images with an equatorial view were used.
The uncertainties on the spin-vector coordinates correspond to an offset of ∼1px at the limbs. The associated χ2 (square of the difference between the observed and synthetic images, in units of the instrumental noise) are also within 30 per cent from the χ2 of the best-fitting solution.
The resulting model parameters with uncertainties are Deq = 204 ± 10 km, λ = 19 ± 3°, and β = 26 ± 3°.
4.4 Density
Finally, the models’ volumes were combined with the mass estimates available in the literature to calculate densities. The values are shown in Table C1 and plotted in Fig. 5. The density uncertainties come both from mass estimates’ and model uncertainties. The values vary significantly: from 1.52 to 11.51 g cm−3, averaging at 4 g cm−3 (or 3.28 g cm−3 when four outliers above 6 g cm−3 are disregarded). Fig. 6 shows the ratios of mass to volume uncertainties as contributing factors to the overall density uncertainty. The ratio for a given density puts it into one of two categories, i.e. mass and volume dominant, when the ratio is above or below 1, respectively.
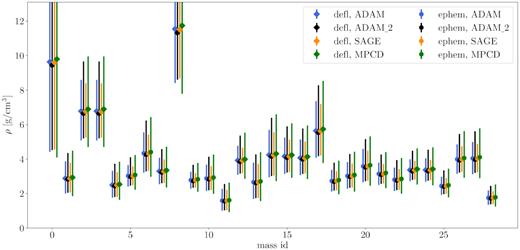
Densities of (7) Iris models. Masses obtained via deflection method are marked by the diamond shapes, while the circles mark the ones obtained with the ephemeris method. Density and mass values with references can be found in Table C1.
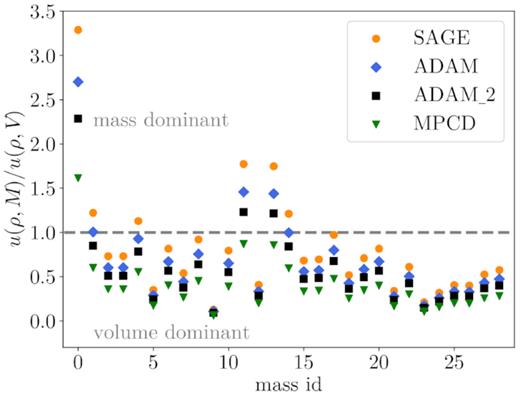
The ratios of mass to volume uncertainties u(ρ, M)/u(ρ, V) as contributing factors to the overall density uncertainty. The values above or below 1 indicate that the density uncertainty is dominated by mass or volume uncertainty, respectively.
To give per model density of (7) Iris, we used the procedure described in Hanuš et al. (2019), i.e. we took the median mass value from the values reported in the literature after excluding five estimates with the highest uncertainties. The value with 1σ confidence level is (13.75 ± 1.3) × 1018 kg. The mass and diameter uncertainties were added in quadrature, yielding ρsage = 3.27 ± 0.54, ρadam = 3.25 ± 0.61, |$\rho ^{\text{ADAM_2}} = 3.47 \pm 0.80$|, and ρmpcd = 3.33 ± 0.97 g cm−3. The values are shown in Fig. 7.
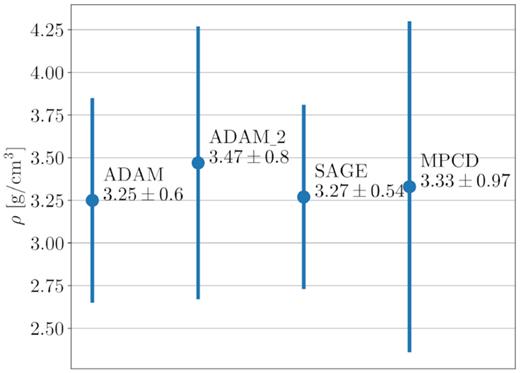
Density values of the models based on the median mass value (13.75 ± 1.3) × 1018 kg.
5 CONCLUSIONS
We have developed the method to assess the uncertainties of an asteroid shape modelled from light curves and AO images. The method was used to test three models of (7) Iris produced independently by the sage,adam, and mpcd modelling techniques. As a result, we calculated the uncertainties of physical parameters of the models (volume, rotational period, pole coordinates). The population of accepted clones was then used to scale the models by comparing the clones’ projections with AO images and infer the diameter of (7) Iris taking into account models’ uncertainties. The values were then used to calculate the densities.
When establishing the size of the models, the fits were weighted based on observations’ aspect angles and image resolutions to balance the information content in the data. We found the equivalent sphere diameters to be D|$^{\text{SAGE}}_{\mathrm{ eq}} = 199^{+10}_{-8}$| km, D|$^{\text{ADAM}}_{\mathrm{ eq}} = 199^{+12}_{-9}$| km, D|$^{\text{ADAM_2}}_{\mathrm{ eq}} = 200^{+10}_{-18}$| km, and D|$^{\text{MPCD}}_{\mathrm{ eq}} = 198^{+19}_{-17}$| km. The relative diameter uncertainties of these models are 4.5 per cent, 5.5 per cent, 6.8 per cent, and 9.2 per cent, respectively, which translate into 13.7 per cent, 16.6 per cent, 19.7 per cent, and 27.9 per cent relative uncertainties in the volume. An independent uncertainty assessment with mpcd method based on a subset of AO images alone yielded Deq = 204 ± 10 km. The size of (7) Iris established in this work lies within the error bars of the one presented in Hanuš et al. (2019), i.e. 214 ± 5 km. However, the relative uncertainty is more than four times greater.
A closer look at the models’ projections (Fig. 3) indicates that the equatorial regions are well determined while the biggest source of uncertainty comes from the pole regions. This is consistent with the fact that relative light curves in practice carry close to zero information about the z-scale. Hence, the resulting z-scale was for the most part dependent on AO images with aspect angles near 90°; since the resolution of those was poor, there was a significant amount of free play for models’ parameters at high latitudes. It is also not surprising that the Northern hemisphere modelled in the sage model has smaller uncertainty than in the adam model since the data from 2019 covering the Northern hemisphere were not used in modelling of the latter. The adam_2 model is taller in z-axis from the others but has larger negative uncertainty values. This reflects the fact that the weight put on AO data compared to light curves in this example was smaller than in the adam model.
The differences between the level of detail on the surfaces of the models are due to the different weights put on the data during the modelling. The adam model favoured VLT/SPHERE images sacrificing the goodness of the fit of the light curves. This indicates some inconsistency among the two data types, which could be a result of several factors, e.g. albedo variations on the surface of (7) Iris or particular scattering law used during the modelling, both influencing the light curves and AO images in different ways. The light curves and AO images also covered different epochs, hence different aspect and phase angles. The reliability of the topographical features should be therefore interpreted with this in mind. However, the results of the mpcd method, that used AO images alone with success, indicate that the topographical features are at least consistent among AO images themselves. The presence of topographical features does not influence the volume of the body in significant way, though, and do not alter our results on volume and density uncertainties.
The densities were calculated based on the mass estimates available in the literature (Table C1). The results are rather humbling in regards to what is possible to be known about the internal structure and composition of (7) Iris. First, the mass estimates are not consistent with each other, hence, the computed densities vary greatly between 1.56 and 11.74 g cm−3. However, the great variability in mass estimates indicates that the error bars for the masses are vastly underestimated, thus clouding our judgement. Secondly, despite the use of a big number of light curves and excellent quality AO images, the uncertainty method used in this work revealed that the models themselves are a source of considerable ambiguity as well. The majority of densities’ uncertainties are still volume dominant, as shown in Fig. 6.
If we consider the median mass after discarding five mass values with the greatest error bars and calculating 1σ confidence level, i.e. (13.75 ± 1.3) × 1018 kg, we get ρsage = 3.27 ± 0.54, ρadam = 3.25 ± 0.61, |$\rho ^{\text{ADAM_2}} = 3.47 \pm 0.80$| and ρmpcd = 3.33 ± 0.97 g cm−3 density values. The use of the median mass is dictated by the use of different methods and data sets when producing the masses. Also, because of that, the confidence level of the median comes from the dispersion of the mass values rather than the combination of uncertainties reported in the literature.
The sage model has the smallest uncertainty of the four models. The uncertainty was calculated with the use of all of the available light curves and AO images, and the sage model was produced with the same data set. Moreover, the surface details were not reproduced the aim of this model being to explain all of the data as well as possible simultaneously and focusing on the volume. Because the craters and other topographic features have minimal impact on the volume, the opposite happened for the mpcd model. This model reproduces the surface features with great detail, while not being considerate of the light curves as much. Each data type has its pitfalls and careful uncertainty assessment is essential in evaluating the results. The analysis can also be very useful in planning the future observations, e.g. to aim at the epochs that will potentially contribute new information on the target.
ACKNOWLEDGEMENTS
Based on observations collected at the European Organization for Astronomical Research in the Southern hemisphere under ESO programme 199.C-0074 (principal investigator: P. Vernazza). This work has been supported by the Czech Science Foundation through grant 20-08218S (JH, MB) and by the Charles University Research program No. UNCE/SCI/023. This work has been partially supported by Horizon 2020 grant no. 871149 ‘EPN-2024-RI’.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
This also is why a ‘smoothness’ regularization term is very often added to the objective function in clinometry methods.
REFERENCES
APPENDIX A: OBSERVATIONS
Details of the light curves used in the modelling process. Np denotes the number of photometric points in a light curve and φ denotes the phase angle.
| Date . | Np . | φ (°) . | Reference . |
|---|---|---|---|
| 1950-08-12.2 | 34 | 17.4 | Groeneveld & Kuiper (1954) |
| 1950-08-13.2 | 25 | 17.7 | Groeneveld & Kuiper (1954) |
| 1950-08-14.2 | 22 | 18.0 | Groeneveld & Kuiper (1954) |
| 1950-08-16.2 | 9 | 18.6 | Groeneveld & Kuiper (1954) |
| 1952-01-28.3 | 82 | 5.2 | Groeneveld & Kuiper (1954) |
| 1955-12-28.5 | 39 | 23.4 | van Houten-Groeneveld & van Houten (1958) |
| 1955-12-29.4 | 39 | 23.3 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-02.5 | 35 | 22.7 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-05.5 | 18 | 22.1 | van Houten-Groeneveld & van Houten (1958) |
| 1956-03-08.4 | 64 | 4.3 | van Houten-Groeneveld & van Houten (1958) |
| 1958-11-05.2 | 62 | 8.7 | Gehrels & Owings (1962) |
| 1963-02-02.7 | 63 | 13.0 | Chang & Chang (1963) |
| 1963-02-03.6 | 99 | 13.4 | Chang & Chang (1963) |
| 1968-06-12.2 | 18 | 8.4 | Taylor (1977) |
| 1968-06-13.3 | 45 | 8.8 | Taylor (1977) |
| 1973-10-28.4 | 27 | 29.1 | Taylor (1977) |
| 1973-12-15.3 | 46 | 8.8 | Taylor (1977) |
| 1973-12-16.3 | 58 | 8.2 | Taylor (1977) |
| 1974-02-16.3 | 17 | 22.8 | Taylor (1977) |
| 1974-02-17.2 | 7 | 23.0 | Taylor (1977) |
| 1980-10-14.6 | 49 | 14.3 | Zhou, Yang & Wu (1982) |
| 1980-11-08.6 | 40 | 24.8 | Zhou et al. (1982) |
| 1984-09-29.4 | 52 | 31.9 | Lagerkvist & Williams (1987) |
| 1989-01-02.9 | 18 | 18.7 | Hoffmann & Geyer (1993) |
| 1989-01-04.1 | 538 | 18.4 | Hoffmann & Geyer (1993) |
| 1989-04-29.9 | 70 | 23.4 | Hoffmann & Geyer (1993) |
| 1989-05-02.9 | 42 | 23.4 | Hoffmann & Geyer (1993) |
| 1990-02-05.2 | 33 | 19.4 | Hoffmann & Geyer (1993) |
| 1990-02-06.2 | 15 | 19.5 | Hoffmann & Geyer (1993) |
| 1991-08-19.0 | 38 | 12.6 | Hoffmann & Geyer (1993) |
| 1991-09-03.0 | 75 | 6.4 | Hoffmann & Geyer (1993) |
| 1991-09-04.0 | 26 | 6.1 | Hoffmann & Geyer (1993) |
| 1991-09-05.0 | 40 | 5.9 | Hoffmann & Geyer (1993) |
| 1991-09-18.0 | 44 | 7.7 | Hoffmann & Geyer (1993) |
| 1991-11-01.9 | 9 | 26.4 | Foglia (1992) |
| 1991-11-06.9 | 23 | 27.7 | Foglia (1992) |
| 2010-12-10.1 | 623 | 22.9 | Gerald Rousseau |
| 2010-12-11.1 | 589 | 22.5 | Gerald Rousseau |
| 2013-08-15.0 | 173 | 4.4 | Patrick Sogorb |
| 2006-10-11 | 47 | 20.2 | Grice et al. (2017) |
| 2006-11-27 | 40 | 8.8 | Grice et al. (2017) |
| 2006-11-28 | 41 | 9.3 | Grice et al. (2017) |
| 2006-11-29 | 42 | 9.9 | Grice et al. (2017) |
| 2006-11-30 | 92 | 10.5 | Grice et al. (2017) |
| 2006-12-05 | 72 | 13.3 | Grice et al. (2017) |
| 2006-12-06 | 76 | 13.8 | Grice et al. (2017) |
| 2008-01-31 | 47 | 20.3 | Grice et al. (2017) |
| 2008-02-21 | 87 | 17.0 | Grice et al. (2017) |
| 2008-02-27 | 39 | 15.5 | Grice et al. (2017) |
| 2008-02-28 | 42 | 15.3 | Grice et al. (2017) |
| 2008-02-28 | 44 | 15.3 | Grice et al. (2017) |
| 2008-03-01 | 59 | 14.8 | Grice et al. (2017) |
| 2008-03-01 | 74 | 14.8 | Grice et al. (2017) |
| 2008-03-02 | 56 | 14.5 | Grice et al. (2017) |
| 2008-03-02 | 81 | 14.5 | Grice et al. (2017) |
| 2008-03-10 | 67 | 12.1 | Grice et al. (2017) |
| 2008-03-13 | 57 | 11.1 | Grice et al. (2017) |
| 2008-03-19 | 58 | 8.9 | Grice et al. (2017) |
| 2008-06-10 | 95 | 18.9 | Grice et al. (2017) |
| 2008-06-22 | 39 | 20.0 | Grice et al. (2017) |
| 2008-06-24 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-25 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-26 | 45 | 20.2 | Grice et al. (2017) |
| 2010-10-25 | 39 | 30.6 | Grice et al. (2017) |
| 2010-10-26 | 91 | 30.5 | Grice et al. (2017) |
| 2010-12-12 | 127 | 21.8 | Grice et al. (2017) |
| 2010-12-13 | 55 | 21.4 | Grice et al. (2017) |
| 2010-12-27 | 75 | 15.5 | Grice et al. (2017) |
| 2010-12-31 | 76 | 13.5 | Grice et al. (2017) |
| 2011-01-01 | 52 | 13.0 | Grice et al. (2017) |
| 2011-01-02 | 79 | 12.5 | Grice et al. (2017) |
| 2011-01-03 | 56 | 12.0 | Grice et al. (2017) |
| 2011-01-04 | 63 | 11.4 | Grice et al. (2017) |
| 2011-01-05 | 65 | 10.9 | Grice et al. (2017) |
| 2011-01-06 | 50 | 10.4 | Grice et al. (2017) |
| 2011-01-07 | 50 | 9.9 | Grice et al. (2017) |
| 2011-01-10 | 48 | 8.3 | Grice et al. (2017) |
| 2011-02-18 | 119 | 13.6 | Grice et al. (2017) |
| 2011-02-19 | 86 | 14.1 | Grice et al. (2017) |
| 2011-02-20 | 72 | 14.5 | Grice et al. (2017) |
| 2011-02-21 | 99 | 14.9 | Grice et al. (2017) |
| 2011-02-22 | 103 | 15.2 | Grice et al. (2017) |
| 2011-02-23 | 103 | 15.6 | Grice et al. (2017) |
| 2011-02-24 | 103 | 16.0 | Grice et al. (2017) |
| 2011-02-25 | 77 | 16.3 | Grice et al. (2017) |
| 2011-03-01 | 95 | 17.7 | Grice et al. (2017) |
| 2011-03-02 | 91 | 18.0 | Grice et al. (2017) |
| 2012-02-19 | 41 | 19.6 | Grice et al. (2017) |
| 2012-02-20 | 43 | 19.5 | Grice et al. (2017) |
| 2012-02-21 | 43 | 19.4 | Grice et al. (2017) |
| 2012-02-23 | 47 | 19.3 | Grice et al. (2017) |
| 2012-02-24 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-25 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-26 | 43 | 19.1 | Grice et al. (2017) |
| 2012-03-01 | 47 | 18.7 | Grice et al. (2017) |
| 2012-03-02 | 51 | 18.6 | Grice et al. (2017) |
| 2012-03-03 | 51 | 18.4 | Grice et al. (2017) |
| 2012-03-06 | 65 | 18.0 | Grice et al. (2017) |
| 2012-03-07 | 51 | 17.9 | Grice et al. (2017) |
| 2012-03-07 | 75 | 17.9 | Grice et al. (2017) |
| 2012-03-08 | 81 | 17.7 | Grice et al. (2017) |
| 2012-03-08 | 89 | 17.8 | Grice et al. (2017) |
| 2012-03-09 | 82 | 17.6 | Grice et al. (2017) |
| 2012-03-13 | 79 | 16.9 | Grice et al. (2017) |
| 2012-03-17 | 63 | 16.1 | Grice et al. (2017) |
| 2012-03-18 | 71 | 15.9 | Grice et al. (2017) |
| 2012-03-19 | 72 | 15.7 | Grice et al. (2017) |
| 2012-03-20 | 43 | 15.5 | Grice et al. (2017) |
| 2012-03-20 | 52 | 15.5 | Grice et al. (2017) |
| 2012-03-25 | 56 | 14.3 | Grice et al. (2017) |
| 2012-03-25 | 59 | 14.3 | Grice et al. (2017) |
| 2012-03-31 | 44 | 12.7 | Grice et al. (2017) |
| 2012-04-01 | 79 | 12.4 | Grice et al. (2017) |
| 2012-04-01 | 93 | 12.4 | Grice et al. (2017) |
| 2012-04-02 | 87 | 12.1 | Grice et al. (2017) |
| 2012-04-02 | 101 | 12.1 | Grice et al. (2017) |
| 2012-04-03 | 79 | 11.7 | Grice et al. (2017) |
| 2012-04-03 | 89 | 11.8 | Grice et al. (2017) |
| 2012-04-04 | 54 | 11.4 | Grice et al. (2017) |
| 2012-04-05 | 47 | 11.1 | Grice et al. (2017) |
| 2012-04-05 | 84 | 11.1 | Grice et al. (2017) |
| 2012-04-10 | 125 | 9.5 | Grice et al. (2017) |
| 2012-04-11 | 121 | 9.1 | Grice et al. (2017) |
| 2012-04-11 | 131 | 9.1 | Grice et al. (2017) |
| 2012-04-12 | 99 | 8.8 | Grice et al. (2017) |
| 2012-04-12 | 109 | 8.8 | Grice et al. (2017) |
| 2012-04-15 | 98 | 7.7 | Grice et al. (2017) |
| 2012-04-20 | 55 | 5.8 | Grice et al. (2017) |
| 2012-04-23 | 43 | 4.7 | Grice et al. (2017) |
| 2012-04-29 | 55 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 57 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 59 | 2.6 | Grice et al. (2017) |
| 2012-06-06 | 58 | 12.6 | Grice et al. (2017) |
| Date . | Np . | φ (°) . | Reference . |
|---|---|---|---|
| 1950-08-12.2 | 34 | 17.4 | Groeneveld & Kuiper (1954) |
| 1950-08-13.2 | 25 | 17.7 | Groeneveld & Kuiper (1954) |
| 1950-08-14.2 | 22 | 18.0 | Groeneveld & Kuiper (1954) |
| 1950-08-16.2 | 9 | 18.6 | Groeneveld & Kuiper (1954) |
| 1952-01-28.3 | 82 | 5.2 | Groeneveld & Kuiper (1954) |
| 1955-12-28.5 | 39 | 23.4 | van Houten-Groeneveld & van Houten (1958) |
| 1955-12-29.4 | 39 | 23.3 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-02.5 | 35 | 22.7 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-05.5 | 18 | 22.1 | van Houten-Groeneveld & van Houten (1958) |
| 1956-03-08.4 | 64 | 4.3 | van Houten-Groeneveld & van Houten (1958) |
| 1958-11-05.2 | 62 | 8.7 | Gehrels & Owings (1962) |
| 1963-02-02.7 | 63 | 13.0 | Chang & Chang (1963) |
| 1963-02-03.6 | 99 | 13.4 | Chang & Chang (1963) |
| 1968-06-12.2 | 18 | 8.4 | Taylor (1977) |
| 1968-06-13.3 | 45 | 8.8 | Taylor (1977) |
| 1973-10-28.4 | 27 | 29.1 | Taylor (1977) |
| 1973-12-15.3 | 46 | 8.8 | Taylor (1977) |
| 1973-12-16.3 | 58 | 8.2 | Taylor (1977) |
| 1974-02-16.3 | 17 | 22.8 | Taylor (1977) |
| 1974-02-17.2 | 7 | 23.0 | Taylor (1977) |
| 1980-10-14.6 | 49 | 14.3 | Zhou, Yang & Wu (1982) |
| 1980-11-08.6 | 40 | 24.8 | Zhou et al. (1982) |
| 1984-09-29.4 | 52 | 31.9 | Lagerkvist & Williams (1987) |
| 1989-01-02.9 | 18 | 18.7 | Hoffmann & Geyer (1993) |
| 1989-01-04.1 | 538 | 18.4 | Hoffmann & Geyer (1993) |
| 1989-04-29.9 | 70 | 23.4 | Hoffmann & Geyer (1993) |
| 1989-05-02.9 | 42 | 23.4 | Hoffmann & Geyer (1993) |
| 1990-02-05.2 | 33 | 19.4 | Hoffmann & Geyer (1993) |
| 1990-02-06.2 | 15 | 19.5 | Hoffmann & Geyer (1993) |
| 1991-08-19.0 | 38 | 12.6 | Hoffmann & Geyer (1993) |
| 1991-09-03.0 | 75 | 6.4 | Hoffmann & Geyer (1993) |
| 1991-09-04.0 | 26 | 6.1 | Hoffmann & Geyer (1993) |
| 1991-09-05.0 | 40 | 5.9 | Hoffmann & Geyer (1993) |
| 1991-09-18.0 | 44 | 7.7 | Hoffmann & Geyer (1993) |
| 1991-11-01.9 | 9 | 26.4 | Foglia (1992) |
| 1991-11-06.9 | 23 | 27.7 | Foglia (1992) |
| 2010-12-10.1 | 623 | 22.9 | Gerald Rousseau |
| 2010-12-11.1 | 589 | 22.5 | Gerald Rousseau |
| 2013-08-15.0 | 173 | 4.4 | Patrick Sogorb |
| 2006-10-11 | 47 | 20.2 | Grice et al. (2017) |
| 2006-11-27 | 40 | 8.8 | Grice et al. (2017) |
| 2006-11-28 | 41 | 9.3 | Grice et al. (2017) |
| 2006-11-29 | 42 | 9.9 | Grice et al. (2017) |
| 2006-11-30 | 92 | 10.5 | Grice et al. (2017) |
| 2006-12-05 | 72 | 13.3 | Grice et al. (2017) |
| 2006-12-06 | 76 | 13.8 | Grice et al. (2017) |
| 2008-01-31 | 47 | 20.3 | Grice et al. (2017) |
| 2008-02-21 | 87 | 17.0 | Grice et al. (2017) |
| 2008-02-27 | 39 | 15.5 | Grice et al. (2017) |
| 2008-02-28 | 42 | 15.3 | Grice et al. (2017) |
| 2008-02-28 | 44 | 15.3 | Grice et al. (2017) |
| 2008-03-01 | 59 | 14.8 | Grice et al. (2017) |
| 2008-03-01 | 74 | 14.8 | Grice et al. (2017) |
| 2008-03-02 | 56 | 14.5 | Grice et al. (2017) |
| 2008-03-02 | 81 | 14.5 | Grice et al. (2017) |
| 2008-03-10 | 67 | 12.1 | Grice et al. (2017) |
| 2008-03-13 | 57 | 11.1 | Grice et al. (2017) |
| 2008-03-19 | 58 | 8.9 | Grice et al. (2017) |
| 2008-06-10 | 95 | 18.9 | Grice et al. (2017) |
| 2008-06-22 | 39 | 20.0 | Grice et al. (2017) |
| 2008-06-24 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-25 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-26 | 45 | 20.2 | Grice et al. (2017) |
| 2010-10-25 | 39 | 30.6 | Grice et al. (2017) |
| 2010-10-26 | 91 | 30.5 | Grice et al. (2017) |
| 2010-12-12 | 127 | 21.8 | Grice et al. (2017) |
| 2010-12-13 | 55 | 21.4 | Grice et al. (2017) |
| 2010-12-27 | 75 | 15.5 | Grice et al. (2017) |
| 2010-12-31 | 76 | 13.5 | Grice et al. (2017) |
| 2011-01-01 | 52 | 13.0 | Grice et al. (2017) |
| 2011-01-02 | 79 | 12.5 | Grice et al. (2017) |
| 2011-01-03 | 56 | 12.0 | Grice et al. (2017) |
| 2011-01-04 | 63 | 11.4 | Grice et al. (2017) |
| 2011-01-05 | 65 | 10.9 | Grice et al. (2017) |
| 2011-01-06 | 50 | 10.4 | Grice et al. (2017) |
| 2011-01-07 | 50 | 9.9 | Grice et al. (2017) |
| 2011-01-10 | 48 | 8.3 | Grice et al. (2017) |
| 2011-02-18 | 119 | 13.6 | Grice et al. (2017) |
| 2011-02-19 | 86 | 14.1 | Grice et al. (2017) |
| 2011-02-20 | 72 | 14.5 | Grice et al. (2017) |
| 2011-02-21 | 99 | 14.9 | Grice et al. (2017) |
| 2011-02-22 | 103 | 15.2 | Grice et al. (2017) |
| 2011-02-23 | 103 | 15.6 | Grice et al. (2017) |
| 2011-02-24 | 103 | 16.0 | Grice et al. (2017) |
| 2011-02-25 | 77 | 16.3 | Grice et al. (2017) |
| 2011-03-01 | 95 | 17.7 | Grice et al. (2017) |
| 2011-03-02 | 91 | 18.0 | Grice et al. (2017) |
| 2012-02-19 | 41 | 19.6 | Grice et al. (2017) |
| 2012-02-20 | 43 | 19.5 | Grice et al. (2017) |
| 2012-02-21 | 43 | 19.4 | Grice et al. (2017) |
| 2012-02-23 | 47 | 19.3 | Grice et al. (2017) |
| 2012-02-24 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-25 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-26 | 43 | 19.1 | Grice et al. (2017) |
| 2012-03-01 | 47 | 18.7 | Grice et al. (2017) |
| 2012-03-02 | 51 | 18.6 | Grice et al. (2017) |
| 2012-03-03 | 51 | 18.4 | Grice et al. (2017) |
| 2012-03-06 | 65 | 18.0 | Grice et al. (2017) |
| 2012-03-07 | 51 | 17.9 | Grice et al. (2017) |
| 2012-03-07 | 75 | 17.9 | Grice et al. (2017) |
| 2012-03-08 | 81 | 17.7 | Grice et al. (2017) |
| 2012-03-08 | 89 | 17.8 | Grice et al. (2017) |
| 2012-03-09 | 82 | 17.6 | Grice et al. (2017) |
| 2012-03-13 | 79 | 16.9 | Grice et al. (2017) |
| 2012-03-17 | 63 | 16.1 | Grice et al. (2017) |
| 2012-03-18 | 71 | 15.9 | Grice et al. (2017) |
| 2012-03-19 | 72 | 15.7 | Grice et al. (2017) |
| 2012-03-20 | 43 | 15.5 | Grice et al. (2017) |
| 2012-03-20 | 52 | 15.5 | Grice et al. (2017) |
| 2012-03-25 | 56 | 14.3 | Grice et al. (2017) |
| 2012-03-25 | 59 | 14.3 | Grice et al. (2017) |
| 2012-03-31 | 44 | 12.7 | Grice et al. (2017) |
| 2012-04-01 | 79 | 12.4 | Grice et al. (2017) |
| 2012-04-01 | 93 | 12.4 | Grice et al. (2017) |
| 2012-04-02 | 87 | 12.1 | Grice et al. (2017) |
| 2012-04-02 | 101 | 12.1 | Grice et al. (2017) |
| 2012-04-03 | 79 | 11.7 | Grice et al. (2017) |
| 2012-04-03 | 89 | 11.8 | Grice et al. (2017) |
| 2012-04-04 | 54 | 11.4 | Grice et al. (2017) |
| 2012-04-05 | 47 | 11.1 | Grice et al. (2017) |
| 2012-04-05 | 84 | 11.1 | Grice et al. (2017) |
| 2012-04-10 | 125 | 9.5 | Grice et al. (2017) |
| 2012-04-11 | 121 | 9.1 | Grice et al. (2017) |
| 2012-04-11 | 131 | 9.1 | Grice et al. (2017) |
| 2012-04-12 | 99 | 8.8 | Grice et al. (2017) |
| 2012-04-12 | 109 | 8.8 | Grice et al. (2017) |
| 2012-04-15 | 98 | 7.7 | Grice et al. (2017) |
| 2012-04-20 | 55 | 5.8 | Grice et al. (2017) |
| 2012-04-23 | 43 | 4.7 | Grice et al. (2017) |
| 2012-04-29 | 55 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 57 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 59 | 2.6 | Grice et al. (2017) |
| 2012-06-06 | 58 | 12.6 | Grice et al. (2017) |
Details of the light curves used in the modelling process. Np denotes the number of photometric points in a light curve and φ denotes the phase angle.
| Date . | Np . | φ (°) . | Reference . |
|---|---|---|---|
| 1950-08-12.2 | 34 | 17.4 | Groeneveld & Kuiper (1954) |
| 1950-08-13.2 | 25 | 17.7 | Groeneveld & Kuiper (1954) |
| 1950-08-14.2 | 22 | 18.0 | Groeneveld & Kuiper (1954) |
| 1950-08-16.2 | 9 | 18.6 | Groeneveld & Kuiper (1954) |
| 1952-01-28.3 | 82 | 5.2 | Groeneveld & Kuiper (1954) |
| 1955-12-28.5 | 39 | 23.4 | van Houten-Groeneveld & van Houten (1958) |
| 1955-12-29.4 | 39 | 23.3 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-02.5 | 35 | 22.7 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-05.5 | 18 | 22.1 | van Houten-Groeneveld & van Houten (1958) |
| 1956-03-08.4 | 64 | 4.3 | van Houten-Groeneveld & van Houten (1958) |
| 1958-11-05.2 | 62 | 8.7 | Gehrels & Owings (1962) |
| 1963-02-02.7 | 63 | 13.0 | Chang & Chang (1963) |
| 1963-02-03.6 | 99 | 13.4 | Chang & Chang (1963) |
| 1968-06-12.2 | 18 | 8.4 | Taylor (1977) |
| 1968-06-13.3 | 45 | 8.8 | Taylor (1977) |
| 1973-10-28.4 | 27 | 29.1 | Taylor (1977) |
| 1973-12-15.3 | 46 | 8.8 | Taylor (1977) |
| 1973-12-16.3 | 58 | 8.2 | Taylor (1977) |
| 1974-02-16.3 | 17 | 22.8 | Taylor (1977) |
| 1974-02-17.2 | 7 | 23.0 | Taylor (1977) |
| 1980-10-14.6 | 49 | 14.3 | Zhou, Yang & Wu (1982) |
| 1980-11-08.6 | 40 | 24.8 | Zhou et al. (1982) |
| 1984-09-29.4 | 52 | 31.9 | Lagerkvist & Williams (1987) |
| 1989-01-02.9 | 18 | 18.7 | Hoffmann & Geyer (1993) |
| 1989-01-04.1 | 538 | 18.4 | Hoffmann & Geyer (1993) |
| 1989-04-29.9 | 70 | 23.4 | Hoffmann & Geyer (1993) |
| 1989-05-02.9 | 42 | 23.4 | Hoffmann & Geyer (1993) |
| 1990-02-05.2 | 33 | 19.4 | Hoffmann & Geyer (1993) |
| 1990-02-06.2 | 15 | 19.5 | Hoffmann & Geyer (1993) |
| 1991-08-19.0 | 38 | 12.6 | Hoffmann & Geyer (1993) |
| 1991-09-03.0 | 75 | 6.4 | Hoffmann & Geyer (1993) |
| 1991-09-04.0 | 26 | 6.1 | Hoffmann & Geyer (1993) |
| 1991-09-05.0 | 40 | 5.9 | Hoffmann & Geyer (1993) |
| 1991-09-18.0 | 44 | 7.7 | Hoffmann & Geyer (1993) |
| 1991-11-01.9 | 9 | 26.4 | Foglia (1992) |
| 1991-11-06.9 | 23 | 27.7 | Foglia (1992) |
| 2010-12-10.1 | 623 | 22.9 | Gerald Rousseau |
| 2010-12-11.1 | 589 | 22.5 | Gerald Rousseau |
| 2013-08-15.0 | 173 | 4.4 | Patrick Sogorb |
| 2006-10-11 | 47 | 20.2 | Grice et al. (2017) |
| 2006-11-27 | 40 | 8.8 | Grice et al. (2017) |
| 2006-11-28 | 41 | 9.3 | Grice et al. (2017) |
| 2006-11-29 | 42 | 9.9 | Grice et al. (2017) |
| 2006-11-30 | 92 | 10.5 | Grice et al. (2017) |
| 2006-12-05 | 72 | 13.3 | Grice et al. (2017) |
| 2006-12-06 | 76 | 13.8 | Grice et al. (2017) |
| 2008-01-31 | 47 | 20.3 | Grice et al. (2017) |
| 2008-02-21 | 87 | 17.0 | Grice et al. (2017) |
| 2008-02-27 | 39 | 15.5 | Grice et al. (2017) |
| 2008-02-28 | 42 | 15.3 | Grice et al. (2017) |
| 2008-02-28 | 44 | 15.3 | Grice et al. (2017) |
| 2008-03-01 | 59 | 14.8 | Grice et al. (2017) |
| 2008-03-01 | 74 | 14.8 | Grice et al. (2017) |
| 2008-03-02 | 56 | 14.5 | Grice et al. (2017) |
| 2008-03-02 | 81 | 14.5 | Grice et al. (2017) |
| 2008-03-10 | 67 | 12.1 | Grice et al. (2017) |
| 2008-03-13 | 57 | 11.1 | Grice et al. (2017) |
| 2008-03-19 | 58 | 8.9 | Grice et al. (2017) |
| 2008-06-10 | 95 | 18.9 | Grice et al. (2017) |
| 2008-06-22 | 39 | 20.0 | Grice et al. (2017) |
| 2008-06-24 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-25 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-26 | 45 | 20.2 | Grice et al. (2017) |
| 2010-10-25 | 39 | 30.6 | Grice et al. (2017) |
| 2010-10-26 | 91 | 30.5 | Grice et al. (2017) |
| 2010-12-12 | 127 | 21.8 | Grice et al. (2017) |
| 2010-12-13 | 55 | 21.4 | Grice et al. (2017) |
| 2010-12-27 | 75 | 15.5 | Grice et al. (2017) |
| 2010-12-31 | 76 | 13.5 | Grice et al. (2017) |
| 2011-01-01 | 52 | 13.0 | Grice et al. (2017) |
| 2011-01-02 | 79 | 12.5 | Grice et al. (2017) |
| 2011-01-03 | 56 | 12.0 | Grice et al. (2017) |
| 2011-01-04 | 63 | 11.4 | Grice et al. (2017) |
| 2011-01-05 | 65 | 10.9 | Grice et al. (2017) |
| 2011-01-06 | 50 | 10.4 | Grice et al. (2017) |
| 2011-01-07 | 50 | 9.9 | Grice et al. (2017) |
| 2011-01-10 | 48 | 8.3 | Grice et al. (2017) |
| 2011-02-18 | 119 | 13.6 | Grice et al. (2017) |
| 2011-02-19 | 86 | 14.1 | Grice et al. (2017) |
| 2011-02-20 | 72 | 14.5 | Grice et al. (2017) |
| 2011-02-21 | 99 | 14.9 | Grice et al. (2017) |
| 2011-02-22 | 103 | 15.2 | Grice et al. (2017) |
| 2011-02-23 | 103 | 15.6 | Grice et al. (2017) |
| 2011-02-24 | 103 | 16.0 | Grice et al. (2017) |
| 2011-02-25 | 77 | 16.3 | Grice et al. (2017) |
| 2011-03-01 | 95 | 17.7 | Grice et al. (2017) |
| 2011-03-02 | 91 | 18.0 | Grice et al. (2017) |
| 2012-02-19 | 41 | 19.6 | Grice et al. (2017) |
| 2012-02-20 | 43 | 19.5 | Grice et al. (2017) |
| 2012-02-21 | 43 | 19.4 | Grice et al. (2017) |
| 2012-02-23 | 47 | 19.3 | Grice et al. (2017) |
| 2012-02-24 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-25 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-26 | 43 | 19.1 | Grice et al. (2017) |
| 2012-03-01 | 47 | 18.7 | Grice et al. (2017) |
| 2012-03-02 | 51 | 18.6 | Grice et al. (2017) |
| 2012-03-03 | 51 | 18.4 | Grice et al. (2017) |
| 2012-03-06 | 65 | 18.0 | Grice et al. (2017) |
| 2012-03-07 | 51 | 17.9 | Grice et al. (2017) |
| 2012-03-07 | 75 | 17.9 | Grice et al. (2017) |
| 2012-03-08 | 81 | 17.7 | Grice et al. (2017) |
| 2012-03-08 | 89 | 17.8 | Grice et al. (2017) |
| 2012-03-09 | 82 | 17.6 | Grice et al. (2017) |
| 2012-03-13 | 79 | 16.9 | Grice et al. (2017) |
| 2012-03-17 | 63 | 16.1 | Grice et al. (2017) |
| 2012-03-18 | 71 | 15.9 | Grice et al. (2017) |
| 2012-03-19 | 72 | 15.7 | Grice et al. (2017) |
| 2012-03-20 | 43 | 15.5 | Grice et al. (2017) |
| 2012-03-20 | 52 | 15.5 | Grice et al. (2017) |
| 2012-03-25 | 56 | 14.3 | Grice et al. (2017) |
| 2012-03-25 | 59 | 14.3 | Grice et al. (2017) |
| 2012-03-31 | 44 | 12.7 | Grice et al. (2017) |
| 2012-04-01 | 79 | 12.4 | Grice et al. (2017) |
| 2012-04-01 | 93 | 12.4 | Grice et al. (2017) |
| 2012-04-02 | 87 | 12.1 | Grice et al. (2017) |
| 2012-04-02 | 101 | 12.1 | Grice et al. (2017) |
| 2012-04-03 | 79 | 11.7 | Grice et al. (2017) |
| 2012-04-03 | 89 | 11.8 | Grice et al. (2017) |
| 2012-04-04 | 54 | 11.4 | Grice et al. (2017) |
| 2012-04-05 | 47 | 11.1 | Grice et al. (2017) |
| 2012-04-05 | 84 | 11.1 | Grice et al. (2017) |
| 2012-04-10 | 125 | 9.5 | Grice et al. (2017) |
| 2012-04-11 | 121 | 9.1 | Grice et al. (2017) |
| 2012-04-11 | 131 | 9.1 | Grice et al. (2017) |
| 2012-04-12 | 99 | 8.8 | Grice et al. (2017) |
| 2012-04-12 | 109 | 8.8 | Grice et al. (2017) |
| 2012-04-15 | 98 | 7.7 | Grice et al. (2017) |
| 2012-04-20 | 55 | 5.8 | Grice et al. (2017) |
| 2012-04-23 | 43 | 4.7 | Grice et al. (2017) |
| 2012-04-29 | 55 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 57 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 59 | 2.6 | Grice et al. (2017) |
| 2012-06-06 | 58 | 12.6 | Grice et al. (2017) |
| Date . | Np . | φ (°) . | Reference . |
|---|---|---|---|
| 1950-08-12.2 | 34 | 17.4 | Groeneveld & Kuiper (1954) |
| 1950-08-13.2 | 25 | 17.7 | Groeneveld & Kuiper (1954) |
| 1950-08-14.2 | 22 | 18.0 | Groeneveld & Kuiper (1954) |
| 1950-08-16.2 | 9 | 18.6 | Groeneveld & Kuiper (1954) |
| 1952-01-28.3 | 82 | 5.2 | Groeneveld & Kuiper (1954) |
| 1955-12-28.5 | 39 | 23.4 | van Houten-Groeneveld & van Houten (1958) |
| 1955-12-29.4 | 39 | 23.3 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-02.5 | 35 | 22.7 | van Houten-Groeneveld & van Houten (1958) |
| 1956-01-05.5 | 18 | 22.1 | van Houten-Groeneveld & van Houten (1958) |
| 1956-03-08.4 | 64 | 4.3 | van Houten-Groeneveld & van Houten (1958) |
| 1958-11-05.2 | 62 | 8.7 | Gehrels & Owings (1962) |
| 1963-02-02.7 | 63 | 13.0 | Chang & Chang (1963) |
| 1963-02-03.6 | 99 | 13.4 | Chang & Chang (1963) |
| 1968-06-12.2 | 18 | 8.4 | Taylor (1977) |
| 1968-06-13.3 | 45 | 8.8 | Taylor (1977) |
| 1973-10-28.4 | 27 | 29.1 | Taylor (1977) |
| 1973-12-15.3 | 46 | 8.8 | Taylor (1977) |
| 1973-12-16.3 | 58 | 8.2 | Taylor (1977) |
| 1974-02-16.3 | 17 | 22.8 | Taylor (1977) |
| 1974-02-17.2 | 7 | 23.0 | Taylor (1977) |
| 1980-10-14.6 | 49 | 14.3 | Zhou, Yang & Wu (1982) |
| 1980-11-08.6 | 40 | 24.8 | Zhou et al. (1982) |
| 1984-09-29.4 | 52 | 31.9 | Lagerkvist & Williams (1987) |
| 1989-01-02.9 | 18 | 18.7 | Hoffmann & Geyer (1993) |
| 1989-01-04.1 | 538 | 18.4 | Hoffmann & Geyer (1993) |
| 1989-04-29.9 | 70 | 23.4 | Hoffmann & Geyer (1993) |
| 1989-05-02.9 | 42 | 23.4 | Hoffmann & Geyer (1993) |
| 1990-02-05.2 | 33 | 19.4 | Hoffmann & Geyer (1993) |
| 1990-02-06.2 | 15 | 19.5 | Hoffmann & Geyer (1993) |
| 1991-08-19.0 | 38 | 12.6 | Hoffmann & Geyer (1993) |
| 1991-09-03.0 | 75 | 6.4 | Hoffmann & Geyer (1993) |
| 1991-09-04.0 | 26 | 6.1 | Hoffmann & Geyer (1993) |
| 1991-09-05.0 | 40 | 5.9 | Hoffmann & Geyer (1993) |
| 1991-09-18.0 | 44 | 7.7 | Hoffmann & Geyer (1993) |
| 1991-11-01.9 | 9 | 26.4 | Foglia (1992) |
| 1991-11-06.9 | 23 | 27.7 | Foglia (1992) |
| 2010-12-10.1 | 623 | 22.9 | Gerald Rousseau |
| 2010-12-11.1 | 589 | 22.5 | Gerald Rousseau |
| 2013-08-15.0 | 173 | 4.4 | Patrick Sogorb |
| 2006-10-11 | 47 | 20.2 | Grice et al. (2017) |
| 2006-11-27 | 40 | 8.8 | Grice et al. (2017) |
| 2006-11-28 | 41 | 9.3 | Grice et al. (2017) |
| 2006-11-29 | 42 | 9.9 | Grice et al. (2017) |
| 2006-11-30 | 92 | 10.5 | Grice et al. (2017) |
| 2006-12-05 | 72 | 13.3 | Grice et al. (2017) |
| 2006-12-06 | 76 | 13.8 | Grice et al. (2017) |
| 2008-01-31 | 47 | 20.3 | Grice et al. (2017) |
| 2008-02-21 | 87 | 17.0 | Grice et al. (2017) |
| 2008-02-27 | 39 | 15.5 | Grice et al. (2017) |
| 2008-02-28 | 42 | 15.3 | Grice et al. (2017) |
| 2008-02-28 | 44 | 15.3 | Grice et al. (2017) |
| 2008-03-01 | 59 | 14.8 | Grice et al. (2017) |
| 2008-03-01 | 74 | 14.8 | Grice et al. (2017) |
| 2008-03-02 | 56 | 14.5 | Grice et al. (2017) |
| 2008-03-02 | 81 | 14.5 | Grice et al. (2017) |
| 2008-03-10 | 67 | 12.1 | Grice et al. (2017) |
| 2008-03-13 | 57 | 11.1 | Grice et al. (2017) |
| 2008-03-19 | 58 | 8.9 | Grice et al. (2017) |
| 2008-06-10 | 95 | 18.9 | Grice et al. (2017) |
| 2008-06-22 | 39 | 20.0 | Grice et al. (2017) |
| 2008-06-24 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-25 | 63 | 20.1 | Grice et al. (2017) |
| 2008-06-26 | 45 | 20.2 | Grice et al. (2017) |
| 2010-10-25 | 39 | 30.6 | Grice et al. (2017) |
| 2010-10-26 | 91 | 30.5 | Grice et al. (2017) |
| 2010-12-12 | 127 | 21.8 | Grice et al. (2017) |
| 2010-12-13 | 55 | 21.4 | Grice et al. (2017) |
| 2010-12-27 | 75 | 15.5 | Grice et al. (2017) |
| 2010-12-31 | 76 | 13.5 | Grice et al. (2017) |
| 2011-01-01 | 52 | 13.0 | Grice et al. (2017) |
| 2011-01-02 | 79 | 12.5 | Grice et al. (2017) |
| 2011-01-03 | 56 | 12.0 | Grice et al. (2017) |
| 2011-01-04 | 63 | 11.4 | Grice et al. (2017) |
| 2011-01-05 | 65 | 10.9 | Grice et al. (2017) |
| 2011-01-06 | 50 | 10.4 | Grice et al. (2017) |
| 2011-01-07 | 50 | 9.9 | Grice et al. (2017) |
| 2011-01-10 | 48 | 8.3 | Grice et al. (2017) |
| 2011-02-18 | 119 | 13.6 | Grice et al. (2017) |
| 2011-02-19 | 86 | 14.1 | Grice et al. (2017) |
| 2011-02-20 | 72 | 14.5 | Grice et al. (2017) |
| 2011-02-21 | 99 | 14.9 | Grice et al. (2017) |
| 2011-02-22 | 103 | 15.2 | Grice et al. (2017) |
| 2011-02-23 | 103 | 15.6 | Grice et al. (2017) |
| 2011-02-24 | 103 | 16.0 | Grice et al. (2017) |
| 2011-02-25 | 77 | 16.3 | Grice et al. (2017) |
| 2011-03-01 | 95 | 17.7 | Grice et al. (2017) |
| 2011-03-02 | 91 | 18.0 | Grice et al. (2017) |
| 2012-02-19 | 41 | 19.6 | Grice et al. (2017) |
| 2012-02-20 | 43 | 19.5 | Grice et al. (2017) |
| 2012-02-21 | 43 | 19.4 | Grice et al. (2017) |
| 2012-02-23 | 47 | 19.3 | Grice et al. (2017) |
| 2012-02-24 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-25 | 49 | 19.2 | Grice et al. (2017) |
| 2012-02-26 | 43 | 19.1 | Grice et al. (2017) |
| 2012-03-01 | 47 | 18.7 | Grice et al. (2017) |
| 2012-03-02 | 51 | 18.6 | Grice et al. (2017) |
| 2012-03-03 | 51 | 18.4 | Grice et al. (2017) |
| 2012-03-06 | 65 | 18.0 | Grice et al. (2017) |
| 2012-03-07 | 51 | 17.9 | Grice et al. (2017) |
| 2012-03-07 | 75 | 17.9 | Grice et al. (2017) |
| 2012-03-08 | 81 | 17.7 | Grice et al. (2017) |
| 2012-03-08 | 89 | 17.8 | Grice et al. (2017) |
| 2012-03-09 | 82 | 17.6 | Grice et al. (2017) |
| 2012-03-13 | 79 | 16.9 | Grice et al. (2017) |
| 2012-03-17 | 63 | 16.1 | Grice et al. (2017) |
| 2012-03-18 | 71 | 15.9 | Grice et al. (2017) |
| 2012-03-19 | 72 | 15.7 | Grice et al. (2017) |
| 2012-03-20 | 43 | 15.5 | Grice et al. (2017) |
| 2012-03-20 | 52 | 15.5 | Grice et al. (2017) |
| 2012-03-25 | 56 | 14.3 | Grice et al. (2017) |
| 2012-03-25 | 59 | 14.3 | Grice et al. (2017) |
| 2012-03-31 | 44 | 12.7 | Grice et al. (2017) |
| 2012-04-01 | 79 | 12.4 | Grice et al. (2017) |
| 2012-04-01 | 93 | 12.4 | Grice et al. (2017) |
| 2012-04-02 | 87 | 12.1 | Grice et al. (2017) |
| 2012-04-02 | 101 | 12.1 | Grice et al. (2017) |
| 2012-04-03 | 79 | 11.7 | Grice et al. (2017) |
| 2012-04-03 | 89 | 11.8 | Grice et al. (2017) |
| 2012-04-04 | 54 | 11.4 | Grice et al. (2017) |
| 2012-04-05 | 47 | 11.1 | Grice et al. (2017) |
| 2012-04-05 | 84 | 11.1 | Grice et al. (2017) |
| 2012-04-10 | 125 | 9.5 | Grice et al. (2017) |
| 2012-04-11 | 121 | 9.1 | Grice et al. (2017) |
| 2012-04-11 | 131 | 9.1 | Grice et al. (2017) |
| 2012-04-12 | 99 | 8.8 | Grice et al. (2017) |
| 2012-04-12 | 109 | 8.8 | Grice et al. (2017) |
| 2012-04-15 | 98 | 7.7 | Grice et al. (2017) |
| 2012-04-20 | 55 | 5.8 | Grice et al. (2017) |
| 2012-04-23 | 43 | 4.7 | Grice et al. (2017) |
| 2012-04-29 | 55 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 57 | 2.6 | Grice et al. (2017) |
| 2012-04-29 | 59 | 2.6 | Grice et al. (2017) |
| 2012-06-06 | 58 | 12.6 | Grice et al. (2017) |
Details of adaptive optics observations used in the modelling process. φ – phase angle, ξ – aspect angle, δ – resolution. A letter corresponding to a model appears in the ‘usage’ column if an image has been used during the modelling: S – sage, a – adam, A – adam_2, M – mpcd.
| Time . | Instrument . | φ (°) . | ξ (°) . | δ (km px−1) . | Usage . | Reference . |
|---|---|---|---|---|---|---|
| 2002-08-05 14:42:06 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:45:29 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:48:25 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:11:44 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:14:34 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-09-27 09:54:15 | Keck/NIRC2 | 17.5 | 130.1 | 8.23 | SaA | Viikinkoski et al. (2017) |
| 2002-12-29 04:35:18 | Keck/NIRC2 | 30.4 | 146.6 | 13.59 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:06:23 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:13:20 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:18:58 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:53:59 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:57:52 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:02:23 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:24:30 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:27:22 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:30:57 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 07:50:06 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 08:15:57 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2010-12-13 06:05:38 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-13 06:55:02 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-14 05:24:30 | VLT/NaCo | 21.4 | 66.6 | 12.35 | SaA | 086.C-0785 |
| 2017-10-10 3:56:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 3:57:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:58:33 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:59:43 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:00:55 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:07:50 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:09:01 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:10:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:11:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:12:32 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-11 4:40:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:41:53 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:43:05 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:44:16 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:45:26 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:34:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:35:52 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:37:04 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:38:15 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:39:25 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:28:33 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:29:45 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:30:57 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:32:07 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:33:18 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2019-02-25 03:50:05 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:52:55 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:55:45 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-02-25 03:58:34 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 04:01:22 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-03-15 02:53:44 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 02:56:33 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 02:59:23 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 03:02:13 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 03:05:03 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| Time . | Instrument . | φ (°) . | ξ (°) . | δ (km px−1) . | Usage . | Reference . |
|---|---|---|---|---|---|---|
| 2002-08-05 14:42:06 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:45:29 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:48:25 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:11:44 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:14:34 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-09-27 09:54:15 | Keck/NIRC2 | 17.5 | 130.1 | 8.23 | SaA | Viikinkoski et al. (2017) |
| 2002-12-29 04:35:18 | Keck/NIRC2 | 30.4 | 146.6 | 13.59 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:06:23 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:13:20 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:18:58 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:53:59 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:57:52 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:02:23 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:24:30 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:27:22 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:30:57 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 07:50:06 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 08:15:57 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2010-12-13 06:05:38 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-13 06:55:02 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-14 05:24:30 | VLT/NaCo | 21.4 | 66.6 | 12.35 | SaA | 086.C-0785 |
| 2017-10-10 3:56:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 3:57:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:58:33 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:59:43 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:00:55 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:07:50 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:09:01 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:10:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:11:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:12:32 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-11 4:40:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:41:53 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:43:05 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:44:16 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:45:26 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:34:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:35:52 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:37:04 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:38:15 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:39:25 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:28:33 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:29:45 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:30:57 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:32:07 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:33:18 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2019-02-25 03:50:05 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:52:55 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:55:45 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-02-25 03:58:34 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 04:01:22 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-03-15 02:53:44 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 02:56:33 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 02:59:23 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 03:02:13 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 03:05:03 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
Details of adaptive optics observations used in the modelling process. φ – phase angle, ξ – aspect angle, δ – resolution. A letter corresponding to a model appears in the ‘usage’ column if an image has been used during the modelling: S – sage, a – adam, A – adam_2, M – mpcd.
| Time . | Instrument . | φ (°) . | ξ (°) . | δ (km px−1) . | Usage . | Reference . |
|---|---|---|---|---|---|---|
| 2002-08-05 14:42:06 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:45:29 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:48:25 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:11:44 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:14:34 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-09-27 09:54:15 | Keck/NIRC2 | 17.5 | 130.1 | 8.23 | SaA | Viikinkoski et al. (2017) |
| 2002-12-29 04:35:18 | Keck/NIRC2 | 30.4 | 146.6 | 13.59 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:06:23 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:13:20 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:18:58 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:53:59 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:57:52 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:02:23 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:24:30 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:27:22 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:30:57 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 07:50:06 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 08:15:57 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2010-12-13 06:05:38 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-13 06:55:02 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-14 05:24:30 | VLT/NaCo | 21.4 | 66.6 | 12.35 | SaA | 086.C-0785 |
| 2017-10-10 3:56:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 3:57:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:58:33 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:59:43 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:00:55 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:07:50 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:09:01 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:10:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:11:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:12:32 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-11 4:40:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:41:53 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:43:05 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:44:16 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:45:26 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:34:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:35:52 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:37:04 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:38:15 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:39:25 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:28:33 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:29:45 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:30:57 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:32:07 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:33:18 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2019-02-25 03:50:05 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:52:55 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:55:45 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-02-25 03:58:34 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 04:01:22 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-03-15 02:53:44 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 02:56:33 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 02:59:23 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 03:02:13 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 03:05:03 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| Time . | Instrument . | φ (°) . | ξ (°) . | δ (km px−1) . | Usage . | Reference . |
|---|---|---|---|---|---|---|
| 2002-08-05 14:42:06 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:45:29 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 14:48:25 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:11:44 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-08-05 15:14:34 | Keck/NIRC2 | 12.3 | 139.3 | 8.69 | SaA | N10N2 |
| 2002-09-27 09:54:15 | Keck/NIRC2 | 17.5 | 130.1 | 8.23 | SaA | Viikinkoski et al. (2017) |
| 2002-12-29 04:35:18 | Keck/NIRC2 | 30.4 | 146.6 | 13.59 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:06:23 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:13:20 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:18:58 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:53:59 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 07:57:52 | Keck/NIRC2 | 3.3 | 141.2 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:02:23 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:24:30 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:27:22 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2006-11-17 08:30:57 | Keck/NIRC2 | 3.3 | 141.3 | 6.14 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 07:50:06 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2009-08-16 08:15:57 | Keck/NIRC2 | 18.1 | 80.1 | 8.2 | SaA | Viikinkoski et al. (2017) |
| 2010-12-13 06:05:38 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-13 06:55:02 | VLT/NaCo | 21.7 | 66.6 | 12.41 | SaA | 086.C-0785 |
| 2010-12-14 05:24:30 | VLT/NaCo | 21.4 | 66.6 | 12.35 | SaA | 086.C-0785 |
| 2017-10-10 3:56:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 3:57:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:58:33 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 3:59:43 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:00:55 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:07:50 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaAM | 199.C-0074 |
| 2017-10-10 4:09:01 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:10:12 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:11:22 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-10 4:12:32 | VLT/SPHERE | 13.2 | 152.2 | 2.36 | SaA | 199.C-0074 |
| 2017-10-11 4:40:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:41:53 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:43:05 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 4:44:16 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 4:45:26 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:34:41 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:35:52 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:37:04 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 5:38:15 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 5:39:25 | VLT/SPHERE | 12.7 | 152.3 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:28:33 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:29:45 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:30:57 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2017-10-11 6:32:07 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaAM | 199.C-0074 |
| 2017-10-11 6:33:18 | VLT/SPHERE | 12.7 | 152.4 | 2.35 | SaA | 199.C-0074 |
| 2019-02-25 03:50:05 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:52:55 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 03:55:45 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-02-25 03:58:34 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SA | 199.C-0074 |
| 2019-02-25 04:01:22 | VLT/SPHERE | 12.7 | 19.8 | 5.26 | SAM | 199.C-0074 |
| 2019-03-15 02:53:44 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 02:56:33 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 02:59:23 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
| 2019-03-15 03:02:13 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SA | 199.C-0074 |
| 2019-03-15 03:05:03 | VLT/SPHERE | 12.7 | 18.9 | 4.93 | SAM | 199.C-0074 |
APPENDIX B: OBSERVATIONS’ COMPARISON
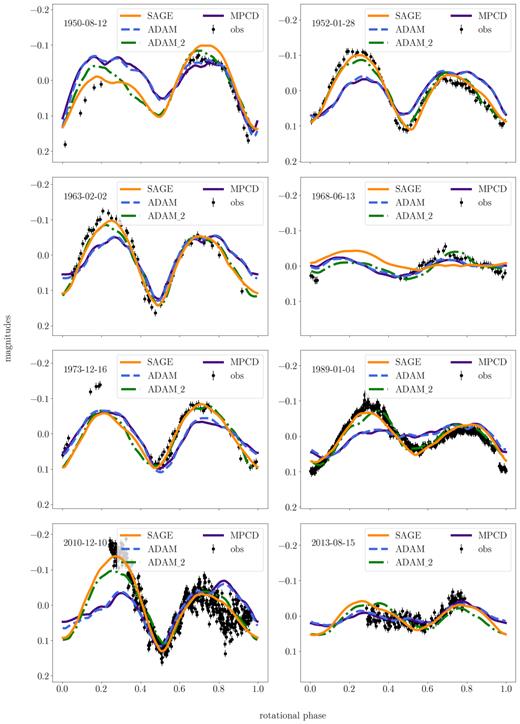
Comparison of synthetic models’ light curves with selected observations of (7) Iris.
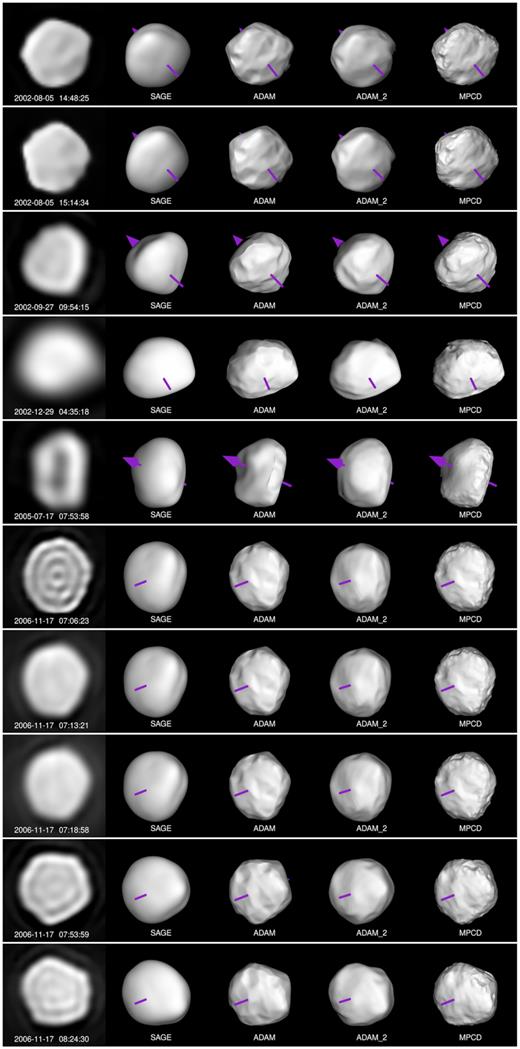
Comparison of the models’ projections with some of the AO images used in the study.
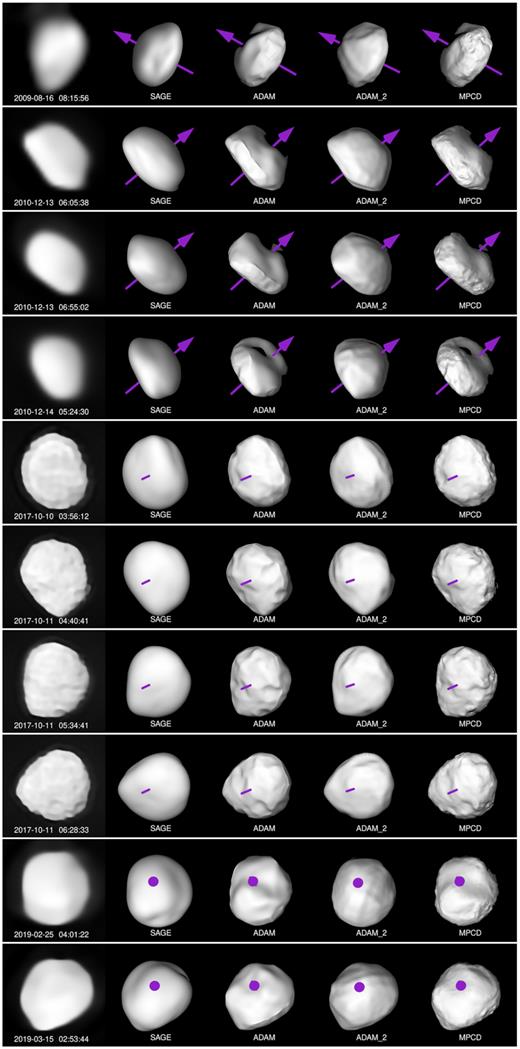
Comparison of the models’ projections with some of the AO images used in the study.
APPENDIX C: DENSITIES
Compilation of density values ρ of (7) Irisbased on various mass estimates. Indexes S, A, A2, and M refer to sage, adam, adam_2, and mpcd models, respectively. Column ‘meth.’ denotes a method used for mass calculation: D – deflection, E – ephemeris.
| id . | ρS (g cm−3) . | ρA . | ρA2 . | ρM . | M (kg) . | u(M) (kg) . | Meth. . | Mass reference . |
|---|---|---|---|---|---|---|---|---|
| 0 | |$9.6^{+6.13}_{-5.04}$| | |$9.63^{+6.47}_{-5.21}$| | |$9.44^{+8.47}_{-5.11}$| | |$9.79^{+9.02}_{-5.54}$| | 3.98 × 1019 | 1.79 × 1019 | D | Vasilyev & Yagudina (1999) |
| 1 | |$2.87^{+0.92}_{-0.81}$| | |$2.88^{+1.0}_{-0.88}$| | |$2.82^{+1.48}_{-0.84}$| | |$2.93^{+1.61}_{-1.03}$| | 1.19 × 1019 | 1.99 × 1018 | D | Krasinsky et al. (2001) |
| 2 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Chernetenko & Kochetova (2002) |
| 3 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Kochetova (2004) |
| 4 | |$2.49^{+0.75}_{-0.68}$| | |$2.49^{+0.83}_{-0.73}$| | |$2.44^{+1.24}_{-0.69}$| | |$2.53^{+1.35}_{-0.87}$| | 1.03 × 1019 | 1.59 × 1018 | D | Pitjeva (2004) |
| 5 | |$3.02^{+0.55}_{-0.54}$| | |$3.02^{+0.63}_{-0.62}$| | |$2.97^{+1.09}_{-0.57}$| | |$3.08^{+1.22}_{-0.8}$| | 1.25 × 1019 | 6.0 × 1017 | E | Pitjeva (2005) |
| 6 | |$4.32^{+1.1}_{-1.01}$| | |$4.33^{+1.22}_{-1.12}$| | |$4.25^{+1.91}_{-1.05}$| | |$4.4^{+2.1}_{-1.36}$| | 1.79 × 1019 | 2.0 × 1018 | E | Aslan et al. (2007) |
| 7 | |$3.28^{+0.7}_{-0.66}$| | |$3.29^{+0.78}_{-0.75}$| | |$3.23^{+1.29}_{-0.69}$| | |$3.35^{+1.43}_{-0.94}$| | 1.36 × 1019 | 1.0 × 1018 | D | Baer et al. (2008) |
| 8 | |$11.51^{+3.13}_{-2.83}$| | |$11.54^{+3.44}_{-3.13}$| | |$11.32^{+5.3}_{-2.94}$| | |$11.74^{+5.82}_{-3.76}$| | 4.77 × 1019 | 6.0 × 1018 | D | Ivantsov (2008) |
| 9 | |$2.78^{+0.41}_{-0.43}$| | |$2.78^{+0.48}_{-0.5}$| | |$2.73^{+0.89}_{-0.45}$| | |$2.83^{+1.0}_{-0.67}$| | 1.15 × 1019 | 2.0 × 1017 | E | Fienga et al. (2008) |
| 10 | |$2.87^{+0.72}_{-0.66}$| | |$2.88^{+0.8}_{-0.74}$| | |$2.82^{+1.26}_{-0.69}$| | |$2.93^{+1.38}_{-0.9}$| | 1.19 × 1019 | 1.29 × 1018 | E | Folkner, Williams & Boggs (2009) |
| 11 | |$1.58^{+0.64}_{-0.55}$| | |$1.59^{+0.68}_{-0.59}$| | |$1.56^{+0.97}_{-0.56}$| | |$1.61^{+1.04}_{-0.66}$| | 6.56 × 1018 | 1.59 × 1018 | E | Pitjeva (2009) |
| 12 | |$3.91^{+0.75}_{-0.72}$| | |$3.92^{+0.85}_{-0.83}$| | |$3.84^{+1.44}_{-0.76}$| | |$3.99^{+1.61}_{-1.07}$| | 1.62 × 1019 | 9.0 × 1017 | D | Baer, Chesley & Matson (2011) |
| 13 | |$2.65^{+1.06}_{-0.91}$| | |$2.66^{+1.14}_{-0.97}$| | |$2.61^{+1.61}_{-0.93}$| | |$2.71^{+1.75}_{-1.1}$| | 1.1 × 1019 | 2.63 × 1018 | E | Konopliv et al. (2011) |
| 14 | |$4.22^{+1.34}_{-1.18}$| | |$4.23^{+1.46}_{-1.29}$| | |$4.15^{+2.17}_{-1.22}$| | |$4.31^{+2.37}_{-1.51}$| | 1.75 × 1019 | 2.9 × 1018 | D | Zielenbach (2011) |
| 15 | |$4.15^{+0.97}_{-0.9}$| | |$4.16^{+1.09}_{-1.01}$| | |$4.08^{+1.74}_{-0.94}$| | |$4.23^{+1.92}_{-1.25}$| | 1.72 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 16 | |$4.05^{+0.96}_{-0.88}$| | |$4.07^{+1.06}_{-1.01}$| | |$3.99^{+1.7}_{-0.93}$| | |$4.13^{+1.88}_{-1.23}$| | 1.68 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 17 | |$5.62^{+1.58}_{-1.41}$| | |$5.64^{+1.73}_{-1.57}$| | |$5.53^{+2.64}_{-1.47}$| | |$5.73^{+2.89}_{-1.87}$| | 2.33 × 1019 | 3.1 × 1018 | D | Zielenbach (2011) |
| 18 | |$2.73^{+0.57}_{-0.54}$| | |$2.73^{+0.65}_{-0.61}$| | |$2.68^{+1.07}_{-0.56}$| | |$2.78^{+1.18}_{-0.77}$| | 1.13 × 1019 | 8.0 × 1017 | E | Fienga et al. (2011) |
| 19 | |$3.02^{+0.72}_{-0.67}$| | |$3.02^{+0.81}_{-0.74}$| | |$2.97^{+1.28}_{-0.69}$| | |$3.08^{+1.41}_{-0.91}$| | 1.25 × 1019 | 1.21 × 1018 | E | Fienga et al. (2013) |
| 20 | |$3.57^{+0.91}_{-0.83}$| | |$3.58^{+1.01}_{-0.93}$| | |$3.51^{+1.58}_{-0.87}$| | |$3.64^{+1.74}_{-1.13}$| | 1.48 × 1019 | 1.65 × 1018 | E | Kuchynka & Folkner (2013) |
| 21 | |$3.14^{+0.57}_{-0.56}$| | |$3.15^{+0.64}_{-0.65}$| | |$3.08^{+1.12}_{-0.59}$| | |$3.2^{+1.25}_{-0.84}$| | 1.3 × 1019 | 6.0 × 1017 | E | Pitjeva (2013) |
| 22 | |$2.8^{+0.63}_{-0.59}$| | |$2.81^{+0.7}_{-0.67}$| | |$2.75^{+1.13}_{-0.62}$| | |$2.85^{+1.25}_{-0.83}$| | 1.16 × 1019 | 9.7 × 1017 | E | Fienga et al. (2014) |
| 23 | |$3.35^{+0.55}_{-0.54}$| | |$3.36^{+0.63}_{-0.64}$| | |$3.3^{+1.13}_{-0.58}$| | |$3.42^{+1.26}_{-0.84}$| | 1.39 × 1019 | 4.0 × 1017 | D | Goffin (2014) |
| 24 | |$3.35^{+0.6}_{-0.58}$| | |$3.36^{+0.69}_{-0.68}$| | |$3.3^{+1.19}_{-0.62}$| | |$3.42^{+1.33}_{-0.88}$| | 1.39 × 1019 | 6.0 × 1017 | D | Kochetova & Chernetenko (2014) |
| 25 | |$2.44^{+0.47}_{-0.45}$| | |$2.44^{+0.53}_{-0.52}$| | |$2.4^{+0.9}_{-0.47}$| | |$2.49^{+1.01}_{-0.66}$| | 1.01 × 1019 | 5.6 × 1017 | E | Viswanathan et al. (2017) |
| 26 | |$3.98^{+0.76}_{-0.73}$| | |$3.99^{+0.86}_{-0.84}$| | |$3.92^{+1.47}_{-0.77}$| | |$4.06^{+1.64}_{-1.08}$| | 1.65 × 1019 | 9.0 × 1017 | E | Baer & Chesley (2017) |
| 27 | |$4.03^{+0.85}_{-0.8}$| | |$4.04^{+0.95}_{-0.91}$| | |$3.96^{+1.57}_{-0.84}$| | |$4.11^{+1.75}_{-1.15}$| | 1.67 × 1019 | 1.2 × 1018 | E | Baer & Chesley (2017) |
| 28 | |$1.75^{+0.38}_{-0.36}$| | |$1.75^{+0.43}_{-0.41}$| | |$1.72^{+0.7}_{-0.37}$| | |$1.78^{+0.77}_{-0.51}$| | 7.24 × 1018 | 5.7 × 1017 | E | A. Fienga, 2018, priv. com |
| id . | ρS (g cm−3) . | ρA . | ρA2 . | ρM . | M (kg) . | u(M) (kg) . | Meth. . | Mass reference . |
|---|---|---|---|---|---|---|---|---|
| 0 | |$9.6^{+6.13}_{-5.04}$| | |$9.63^{+6.47}_{-5.21}$| | |$9.44^{+8.47}_{-5.11}$| | |$9.79^{+9.02}_{-5.54}$| | 3.98 × 1019 | 1.79 × 1019 | D | Vasilyev & Yagudina (1999) |
| 1 | |$2.87^{+0.92}_{-0.81}$| | |$2.88^{+1.0}_{-0.88}$| | |$2.82^{+1.48}_{-0.84}$| | |$2.93^{+1.61}_{-1.03}$| | 1.19 × 1019 | 1.99 × 1018 | D | Krasinsky et al. (2001) |
| 2 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Chernetenko & Kochetova (2002) |
| 3 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Kochetova (2004) |
| 4 | |$2.49^{+0.75}_{-0.68}$| | |$2.49^{+0.83}_{-0.73}$| | |$2.44^{+1.24}_{-0.69}$| | |$2.53^{+1.35}_{-0.87}$| | 1.03 × 1019 | 1.59 × 1018 | D | Pitjeva (2004) |
| 5 | |$3.02^{+0.55}_{-0.54}$| | |$3.02^{+0.63}_{-0.62}$| | |$2.97^{+1.09}_{-0.57}$| | |$3.08^{+1.22}_{-0.8}$| | 1.25 × 1019 | 6.0 × 1017 | E | Pitjeva (2005) |
| 6 | |$4.32^{+1.1}_{-1.01}$| | |$4.33^{+1.22}_{-1.12}$| | |$4.25^{+1.91}_{-1.05}$| | |$4.4^{+2.1}_{-1.36}$| | 1.79 × 1019 | 2.0 × 1018 | E | Aslan et al. (2007) |
| 7 | |$3.28^{+0.7}_{-0.66}$| | |$3.29^{+0.78}_{-0.75}$| | |$3.23^{+1.29}_{-0.69}$| | |$3.35^{+1.43}_{-0.94}$| | 1.36 × 1019 | 1.0 × 1018 | D | Baer et al. (2008) |
| 8 | |$11.51^{+3.13}_{-2.83}$| | |$11.54^{+3.44}_{-3.13}$| | |$11.32^{+5.3}_{-2.94}$| | |$11.74^{+5.82}_{-3.76}$| | 4.77 × 1019 | 6.0 × 1018 | D | Ivantsov (2008) |
| 9 | |$2.78^{+0.41}_{-0.43}$| | |$2.78^{+0.48}_{-0.5}$| | |$2.73^{+0.89}_{-0.45}$| | |$2.83^{+1.0}_{-0.67}$| | 1.15 × 1019 | 2.0 × 1017 | E | Fienga et al. (2008) |
| 10 | |$2.87^{+0.72}_{-0.66}$| | |$2.88^{+0.8}_{-0.74}$| | |$2.82^{+1.26}_{-0.69}$| | |$2.93^{+1.38}_{-0.9}$| | 1.19 × 1019 | 1.29 × 1018 | E | Folkner, Williams & Boggs (2009) |
| 11 | |$1.58^{+0.64}_{-0.55}$| | |$1.59^{+0.68}_{-0.59}$| | |$1.56^{+0.97}_{-0.56}$| | |$1.61^{+1.04}_{-0.66}$| | 6.56 × 1018 | 1.59 × 1018 | E | Pitjeva (2009) |
| 12 | |$3.91^{+0.75}_{-0.72}$| | |$3.92^{+0.85}_{-0.83}$| | |$3.84^{+1.44}_{-0.76}$| | |$3.99^{+1.61}_{-1.07}$| | 1.62 × 1019 | 9.0 × 1017 | D | Baer, Chesley & Matson (2011) |
| 13 | |$2.65^{+1.06}_{-0.91}$| | |$2.66^{+1.14}_{-0.97}$| | |$2.61^{+1.61}_{-0.93}$| | |$2.71^{+1.75}_{-1.1}$| | 1.1 × 1019 | 2.63 × 1018 | E | Konopliv et al. (2011) |
| 14 | |$4.22^{+1.34}_{-1.18}$| | |$4.23^{+1.46}_{-1.29}$| | |$4.15^{+2.17}_{-1.22}$| | |$4.31^{+2.37}_{-1.51}$| | 1.75 × 1019 | 2.9 × 1018 | D | Zielenbach (2011) |
| 15 | |$4.15^{+0.97}_{-0.9}$| | |$4.16^{+1.09}_{-1.01}$| | |$4.08^{+1.74}_{-0.94}$| | |$4.23^{+1.92}_{-1.25}$| | 1.72 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 16 | |$4.05^{+0.96}_{-0.88}$| | |$4.07^{+1.06}_{-1.01}$| | |$3.99^{+1.7}_{-0.93}$| | |$4.13^{+1.88}_{-1.23}$| | 1.68 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 17 | |$5.62^{+1.58}_{-1.41}$| | |$5.64^{+1.73}_{-1.57}$| | |$5.53^{+2.64}_{-1.47}$| | |$5.73^{+2.89}_{-1.87}$| | 2.33 × 1019 | 3.1 × 1018 | D | Zielenbach (2011) |
| 18 | |$2.73^{+0.57}_{-0.54}$| | |$2.73^{+0.65}_{-0.61}$| | |$2.68^{+1.07}_{-0.56}$| | |$2.78^{+1.18}_{-0.77}$| | 1.13 × 1019 | 8.0 × 1017 | E | Fienga et al. (2011) |
| 19 | |$3.02^{+0.72}_{-0.67}$| | |$3.02^{+0.81}_{-0.74}$| | |$2.97^{+1.28}_{-0.69}$| | |$3.08^{+1.41}_{-0.91}$| | 1.25 × 1019 | 1.21 × 1018 | E | Fienga et al. (2013) |
| 20 | |$3.57^{+0.91}_{-0.83}$| | |$3.58^{+1.01}_{-0.93}$| | |$3.51^{+1.58}_{-0.87}$| | |$3.64^{+1.74}_{-1.13}$| | 1.48 × 1019 | 1.65 × 1018 | E | Kuchynka & Folkner (2013) |
| 21 | |$3.14^{+0.57}_{-0.56}$| | |$3.15^{+0.64}_{-0.65}$| | |$3.08^{+1.12}_{-0.59}$| | |$3.2^{+1.25}_{-0.84}$| | 1.3 × 1019 | 6.0 × 1017 | E | Pitjeva (2013) |
| 22 | |$2.8^{+0.63}_{-0.59}$| | |$2.81^{+0.7}_{-0.67}$| | |$2.75^{+1.13}_{-0.62}$| | |$2.85^{+1.25}_{-0.83}$| | 1.16 × 1019 | 9.7 × 1017 | E | Fienga et al. (2014) |
| 23 | |$3.35^{+0.55}_{-0.54}$| | |$3.36^{+0.63}_{-0.64}$| | |$3.3^{+1.13}_{-0.58}$| | |$3.42^{+1.26}_{-0.84}$| | 1.39 × 1019 | 4.0 × 1017 | D | Goffin (2014) |
| 24 | |$3.35^{+0.6}_{-0.58}$| | |$3.36^{+0.69}_{-0.68}$| | |$3.3^{+1.19}_{-0.62}$| | |$3.42^{+1.33}_{-0.88}$| | 1.39 × 1019 | 6.0 × 1017 | D | Kochetova & Chernetenko (2014) |
| 25 | |$2.44^{+0.47}_{-0.45}$| | |$2.44^{+0.53}_{-0.52}$| | |$2.4^{+0.9}_{-0.47}$| | |$2.49^{+1.01}_{-0.66}$| | 1.01 × 1019 | 5.6 × 1017 | E | Viswanathan et al. (2017) |
| 26 | |$3.98^{+0.76}_{-0.73}$| | |$3.99^{+0.86}_{-0.84}$| | |$3.92^{+1.47}_{-0.77}$| | |$4.06^{+1.64}_{-1.08}$| | 1.65 × 1019 | 9.0 × 1017 | E | Baer & Chesley (2017) |
| 27 | |$4.03^{+0.85}_{-0.8}$| | |$4.04^{+0.95}_{-0.91}$| | |$3.96^{+1.57}_{-0.84}$| | |$4.11^{+1.75}_{-1.15}$| | 1.67 × 1019 | 1.2 × 1018 | E | Baer & Chesley (2017) |
| 28 | |$1.75^{+0.38}_{-0.36}$| | |$1.75^{+0.43}_{-0.41}$| | |$1.72^{+0.7}_{-0.37}$| | |$1.78^{+0.77}_{-0.51}$| | 7.24 × 1018 | 5.7 × 1017 | E | A. Fienga, 2018, priv. com |
Compilation of density values ρ of (7) Irisbased on various mass estimates. Indexes S, A, A2, and M refer to sage, adam, adam_2, and mpcd models, respectively. Column ‘meth.’ denotes a method used for mass calculation: D – deflection, E – ephemeris.
| id . | ρS (g cm−3) . | ρA . | ρA2 . | ρM . | M (kg) . | u(M) (kg) . | Meth. . | Mass reference . |
|---|---|---|---|---|---|---|---|---|
| 0 | |$9.6^{+6.13}_{-5.04}$| | |$9.63^{+6.47}_{-5.21}$| | |$9.44^{+8.47}_{-5.11}$| | |$9.79^{+9.02}_{-5.54}$| | 3.98 × 1019 | 1.79 × 1019 | D | Vasilyev & Yagudina (1999) |
| 1 | |$2.87^{+0.92}_{-0.81}$| | |$2.88^{+1.0}_{-0.88}$| | |$2.82^{+1.48}_{-0.84}$| | |$2.93^{+1.61}_{-1.03}$| | 1.19 × 1019 | 1.99 × 1018 | D | Krasinsky et al. (2001) |
| 2 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Chernetenko & Kochetova (2002) |
| 3 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Kochetova (2004) |
| 4 | |$2.49^{+0.75}_{-0.68}$| | |$2.49^{+0.83}_{-0.73}$| | |$2.44^{+1.24}_{-0.69}$| | |$2.53^{+1.35}_{-0.87}$| | 1.03 × 1019 | 1.59 × 1018 | D | Pitjeva (2004) |
| 5 | |$3.02^{+0.55}_{-0.54}$| | |$3.02^{+0.63}_{-0.62}$| | |$2.97^{+1.09}_{-0.57}$| | |$3.08^{+1.22}_{-0.8}$| | 1.25 × 1019 | 6.0 × 1017 | E | Pitjeva (2005) |
| 6 | |$4.32^{+1.1}_{-1.01}$| | |$4.33^{+1.22}_{-1.12}$| | |$4.25^{+1.91}_{-1.05}$| | |$4.4^{+2.1}_{-1.36}$| | 1.79 × 1019 | 2.0 × 1018 | E | Aslan et al. (2007) |
| 7 | |$3.28^{+0.7}_{-0.66}$| | |$3.29^{+0.78}_{-0.75}$| | |$3.23^{+1.29}_{-0.69}$| | |$3.35^{+1.43}_{-0.94}$| | 1.36 × 1019 | 1.0 × 1018 | D | Baer et al. (2008) |
| 8 | |$11.51^{+3.13}_{-2.83}$| | |$11.54^{+3.44}_{-3.13}$| | |$11.32^{+5.3}_{-2.94}$| | |$11.74^{+5.82}_{-3.76}$| | 4.77 × 1019 | 6.0 × 1018 | D | Ivantsov (2008) |
| 9 | |$2.78^{+0.41}_{-0.43}$| | |$2.78^{+0.48}_{-0.5}$| | |$2.73^{+0.89}_{-0.45}$| | |$2.83^{+1.0}_{-0.67}$| | 1.15 × 1019 | 2.0 × 1017 | E | Fienga et al. (2008) |
| 10 | |$2.87^{+0.72}_{-0.66}$| | |$2.88^{+0.8}_{-0.74}$| | |$2.82^{+1.26}_{-0.69}$| | |$2.93^{+1.38}_{-0.9}$| | 1.19 × 1019 | 1.29 × 1018 | E | Folkner, Williams & Boggs (2009) |
| 11 | |$1.58^{+0.64}_{-0.55}$| | |$1.59^{+0.68}_{-0.59}$| | |$1.56^{+0.97}_{-0.56}$| | |$1.61^{+1.04}_{-0.66}$| | 6.56 × 1018 | 1.59 × 1018 | E | Pitjeva (2009) |
| 12 | |$3.91^{+0.75}_{-0.72}$| | |$3.92^{+0.85}_{-0.83}$| | |$3.84^{+1.44}_{-0.76}$| | |$3.99^{+1.61}_{-1.07}$| | 1.62 × 1019 | 9.0 × 1017 | D | Baer, Chesley & Matson (2011) |
| 13 | |$2.65^{+1.06}_{-0.91}$| | |$2.66^{+1.14}_{-0.97}$| | |$2.61^{+1.61}_{-0.93}$| | |$2.71^{+1.75}_{-1.1}$| | 1.1 × 1019 | 2.63 × 1018 | E | Konopliv et al. (2011) |
| 14 | |$4.22^{+1.34}_{-1.18}$| | |$4.23^{+1.46}_{-1.29}$| | |$4.15^{+2.17}_{-1.22}$| | |$4.31^{+2.37}_{-1.51}$| | 1.75 × 1019 | 2.9 × 1018 | D | Zielenbach (2011) |
| 15 | |$4.15^{+0.97}_{-0.9}$| | |$4.16^{+1.09}_{-1.01}$| | |$4.08^{+1.74}_{-0.94}$| | |$4.23^{+1.92}_{-1.25}$| | 1.72 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 16 | |$4.05^{+0.96}_{-0.88}$| | |$4.07^{+1.06}_{-1.01}$| | |$3.99^{+1.7}_{-0.93}$| | |$4.13^{+1.88}_{-1.23}$| | 1.68 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 17 | |$5.62^{+1.58}_{-1.41}$| | |$5.64^{+1.73}_{-1.57}$| | |$5.53^{+2.64}_{-1.47}$| | |$5.73^{+2.89}_{-1.87}$| | 2.33 × 1019 | 3.1 × 1018 | D | Zielenbach (2011) |
| 18 | |$2.73^{+0.57}_{-0.54}$| | |$2.73^{+0.65}_{-0.61}$| | |$2.68^{+1.07}_{-0.56}$| | |$2.78^{+1.18}_{-0.77}$| | 1.13 × 1019 | 8.0 × 1017 | E | Fienga et al. (2011) |
| 19 | |$3.02^{+0.72}_{-0.67}$| | |$3.02^{+0.81}_{-0.74}$| | |$2.97^{+1.28}_{-0.69}$| | |$3.08^{+1.41}_{-0.91}$| | 1.25 × 1019 | 1.21 × 1018 | E | Fienga et al. (2013) |
| 20 | |$3.57^{+0.91}_{-0.83}$| | |$3.58^{+1.01}_{-0.93}$| | |$3.51^{+1.58}_{-0.87}$| | |$3.64^{+1.74}_{-1.13}$| | 1.48 × 1019 | 1.65 × 1018 | E | Kuchynka & Folkner (2013) |
| 21 | |$3.14^{+0.57}_{-0.56}$| | |$3.15^{+0.64}_{-0.65}$| | |$3.08^{+1.12}_{-0.59}$| | |$3.2^{+1.25}_{-0.84}$| | 1.3 × 1019 | 6.0 × 1017 | E | Pitjeva (2013) |
| 22 | |$2.8^{+0.63}_{-0.59}$| | |$2.81^{+0.7}_{-0.67}$| | |$2.75^{+1.13}_{-0.62}$| | |$2.85^{+1.25}_{-0.83}$| | 1.16 × 1019 | 9.7 × 1017 | E | Fienga et al. (2014) |
| 23 | |$3.35^{+0.55}_{-0.54}$| | |$3.36^{+0.63}_{-0.64}$| | |$3.3^{+1.13}_{-0.58}$| | |$3.42^{+1.26}_{-0.84}$| | 1.39 × 1019 | 4.0 × 1017 | D | Goffin (2014) |
| 24 | |$3.35^{+0.6}_{-0.58}$| | |$3.36^{+0.69}_{-0.68}$| | |$3.3^{+1.19}_{-0.62}$| | |$3.42^{+1.33}_{-0.88}$| | 1.39 × 1019 | 6.0 × 1017 | D | Kochetova & Chernetenko (2014) |
| 25 | |$2.44^{+0.47}_{-0.45}$| | |$2.44^{+0.53}_{-0.52}$| | |$2.4^{+0.9}_{-0.47}$| | |$2.49^{+1.01}_{-0.66}$| | 1.01 × 1019 | 5.6 × 1017 | E | Viswanathan et al. (2017) |
| 26 | |$3.98^{+0.76}_{-0.73}$| | |$3.99^{+0.86}_{-0.84}$| | |$3.92^{+1.47}_{-0.77}$| | |$4.06^{+1.64}_{-1.08}$| | 1.65 × 1019 | 9.0 × 1017 | E | Baer & Chesley (2017) |
| 27 | |$4.03^{+0.85}_{-0.8}$| | |$4.04^{+0.95}_{-0.91}$| | |$3.96^{+1.57}_{-0.84}$| | |$4.11^{+1.75}_{-1.15}$| | 1.67 × 1019 | 1.2 × 1018 | E | Baer & Chesley (2017) |
| 28 | |$1.75^{+0.38}_{-0.36}$| | |$1.75^{+0.43}_{-0.41}$| | |$1.72^{+0.7}_{-0.37}$| | |$1.78^{+0.77}_{-0.51}$| | 7.24 × 1018 | 5.7 × 1017 | E | A. Fienga, 2018, priv. com |
| id . | ρS (g cm−3) . | ρA . | ρA2 . | ρM . | M (kg) . | u(M) (kg) . | Meth. . | Mass reference . |
|---|---|---|---|---|---|---|---|---|
| 0 | |$9.6^{+6.13}_{-5.04}$| | |$9.63^{+6.47}_{-5.21}$| | |$9.44^{+8.47}_{-5.11}$| | |$9.79^{+9.02}_{-5.54}$| | 3.98 × 1019 | 1.79 × 1019 | D | Vasilyev & Yagudina (1999) |
| 1 | |$2.87^{+0.92}_{-0.81}$| | |$2.88^{+1.0}_{-0.88}$| | |$2.82^{+1.48}_{-0.84}$| | |$2.93^{+1.61}_{-1.03}$| | 1.19 × 1019 | 1.99 × 1018 | D | Krasinsky et al. (2001) |
| 2 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Chernetenko & Kochetova (2002) |
| 3 | |$6.76^{+1.63}_{-1.51}$| | |$6.78^{+1.81}_{-1.7}$| | |$6.64^{+2.88}_{-1.58}$| | |$6.89^{+3.18}_{-2.08}$| | 2.8 × 1019 | 2.8 × 1018 | D | Kochetova (2004) |
| 4 | |$2.49^{+0.75}_{-0.68}$| | |$2.49^{+0.83}_{-0.73}$| | |$2.44^{+1.24}_{-0.69}$| | |$2.53^{+1.35}_{-0.87}$| | 1.03 × 1019 | 1.59 × 1018 | D | Pitjeva (2004) |
| 5 | |$3.02^{+0.55}_{-0.54}$| | |$3.02^{+0.63}_{-0.62}$| | |$2.97^{+1.09}_{-0.57}$| | |$3.08^{+1.22}_{-0.8}$| | 1.25 × 1019 | 6.0 × 1017 | E | Pitjeva (2005) |
| 6 | |$4.32^{+1.1}_{-1.01}$| | |$4.33^{+1.22}_{-1.12}$| | |$4.25^{+1.91}_{-1.05}$| | |$4.4^{+2.1}_{-1.36}$| | 1.79 × 1019 | 2.0 × 1018 | E | Aslan et al. (2007) |
| 7 | |$3.28^{+0.7}_{-0.66}$| | |$3.29^{+0.78}_{-0.75}$| | |$3.23^{+1.29}_{-0.69}$| | |$3.35^{+1.43}_{-0.94}$| | 1.36 × 1019 | 1.0 × 1018 | D | Baer et al. (2008) |
| 8 | |$11.51^{+3.13}_{-2.83}$| | |$11.54^{+3.44}_{-3.13}$| | |$11.32^{+5.3}_{-2.94}$| | |$11.74^{+5.82}_{-3.76}$| | 4.77 × 1019 | 6.0 × 1018 | D | Ivantsov (2008) |
| 9 | |$2.78^{+0.41}_{-0.43}$| | |$2.78^{+0.48}_{-0.5}$| | |$2.73^{+0.89}_{-0.45}$| | |$2.83^{+1.0}_{-0.67}$| | 1.15 × 1019 | 2.0 × 1017 | E | Fienga et al. (2008) |
| 10 | |$2.87^{+0.72}_{-0.66}$| | |$2.88^{+0.8}_{-0.74}$| | |$2.82^{+1.26}_{-0.69}$| | |$2.93^{+1.38}_{-0.9}$| | 1.19 × 1019 | 1.29 × 1018 | E | Folkner, Williams & Boggs (2009) |
| 11 | |$1.58^{+0.64}_{-0.55}$| | |$1.59^{+0.68}_{-0.59}$| | |$1.56^{+0.97}_{-0.56}$| | |$1.61^{+1.04}_{-0.66}$| | 6.56 × 1018 | 1.59 × 1018 | E | Pitjeva (2009) |
| 12 | |$3.91^{+0.75}_{-0.72}$| | |$3.92^{+0.85}_{-0.83}$| | |$3.84^{+1.44}_{-0.76}$| | |$3.99^{+1.61}_{-1.07}$| | 1.62 × 1019 | 9.0 × 1017 | D | Baer, Chesley & Matson (2011) |
| 13 | |$2.65^{+1.06}_{-0.91}$| | |$2.66^{+1.14}_{-0.97}$| | |$2.61^{+1.61}_{-0.93}$| | |$2.71^{+1.75}_{-1.1}$| | 1.1 × 1019 | 2.63 × 1018 | E | Konopliv et al. (2011) |
| 14 | |$4.22^{+1.34}_{-1.18}$| | |$4.23^{+1.46}_{-1.29}$| | |$4.15^{+2.17}_{-1.22}$| | |$4.31^{+2.37}_{-1.51}$| | 1.75 × 1019 | 2.9 × 1018 | D | Zielenbach (2011) |
| 15 | |$4.15^{+0.97}_{-0.9}$| | |$4.16^{+1.09}_{-1.01}$| | |$4.08^{+1.74}_{-0.94}$| | |$4.23^{+1.92}_{-1.25}$| | 1.72 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 16 | |$4.05^{+0.96}_{-0.88}$| | |$4.07^{+1.06}_{-1.01}$| | |$3.99^{+1.7}_{-0.93}$| | |$4.13^{+1.88}_{-1.23}$| | 1.68 × 1019 | 1.6 × 1018 | D | Zielenbach (2011) |
| 17 | |$5.62^{+1.58}_{-1.41}$| | |$5.64^{+1.73}_{-1.57}$| | |$5.53^{+2.64}_{-1.47}$| | |$5.73^{+2.89}_{-1.87}$| | 2.33 × 1019 | 3.1 × 1018 | D | Zielenbach (2011) |
| 18 | |$2.73^{+0.57}_{-0.54}$| | |$2.73^{+0.65}_{-0.61}$| | |$2.68^{+1.07}_{-0.56}$| | |$2.78^{+1.18}_{-0.77}$| | 1.13 × 1019 | 8.0 × 1017 | E | Fienga et al. (2011) |
| 19 | |$3.02^{+0.72}_{-0.67}$| | |$3.02^{+0.81}_{-0.74}$| | |$2.97^{+1.28}_{-0.69}$| | |$3.08^{+1.41}_{-0.91}$| | 1.25 × 1019 | 1.21 × 1018 | E | Fienga et al. (2013) |
| 20 | |$3.57^{+0.91}_{-0.83}$| | |$3.58^{+1.01}_{-0.93}$| | |$3.51^{+1.58}_{-0.87}$| | |$3.64^{+1.74}_{-1.13}$| | 1.48 × 1019 | 1.65 × 1018 | E | Kuchynka & Folkner (2013) |
| 21 | |$3.14^{+0.57}_{-0.56}$| | |$3.15^{+0.64}_{-0.65}$| | |$3.08^{+1.12}_{-0.59}$| | |$3.2^{+1.25}_{-0.84}$| | 1.3 × 1019 | 6.0 × 1017 | E | Pitjeva (2013) |
| 22 | |$2.8^{+0.63}_{-0.59}$| | |$2.81^{+0.7}_{-0.67}$| | |$2.75^{+1.13}_{-0.62}$| | |$2.85^{+1.25}_{-0.83}$| | 1.16 × 1019 | 9.7 × 1017 | E | Fienga et al. (2014) |
| 23 | |$3.35^{+0.55}_{-0.54}$| | |$3.36^{+0.63}_{-0.64}$| | |$3.3^{+1.13}_{-0.58}$| | |$3.42^{+1.26}_{-0.84}$| | 1.39 × 1019 | 4.0 × 1017 | D | Goffin (2014) |
| 24 | |$3.35^{+0.6}_{-0.58}$| | |$3.36^{+0.69}_{-0.68}$| | |$3.3^{+1.19}_{-0.62}$| | |$3.42^{+1.33}_{-0.88}$| | 1.39 × 1019 | 6.0 × 1017 | D | Kochetova & Chernetenko (2014) |
| 25 | |$2.44^{+0.47}_{-0.45}$| | |$2.44^{+0.53}_{-0.52}$| | |$2.4^{+0.9}_{-0.47}$| | |$2.49^{+1.01}_{-0.66}$| | 1.01 × 1019 | 5.6 × 1017 | E | Viswanathan et al. (2017) |
| 26 | |$3.98^{+0.76}_{-0.73}$| | |$3.99^{+0.86}_{-0.84}$| | |$3.92^{+1.47}_{-0.77}$| | |$4.06^{+1.64}_{-1.08}$| | 1.65 × 1019 | 9.0 × 1017 | E | Baer & Chesley (2017) |
| 27 | |$4.03^{+0.85}_{-0.8}$| | |$4.04^{+0.95}_{-0.91}$| | |$3.96^{+1.57}_{-0.84}$| | |$4.11^{+1.75}_{-1.15}$| | 1.67 × 1019 | 1.2 × 1018 | E | Baer & Chesley (2017) |
| 28 | |$1.75^{+0.38}_{-0.36}$| | |$1.75^{+0.43}_{-0.41}$| | |$1.72^{+0.7}_{-0.37}$| | |$1.78^{+0.77}_{-0.51}$| | 7.24 × 1018 | 5.7 × 1017 | E | A. Fienga, 2018, priv. com |



