Two-fluid simulations of the magnetic field evolution in neutron star cores in the weak-coupling regime

Castillo, F; Reisenegger, A; Valdivia, J A

doi:10.1093/mnras/staa2543

ABSTRACT

In a previous paper, we reported simulations of the evolution of the magnetic field in neutron star (NS) cores through ambipolar diffusion, taking the neutrons as a motionless uniform background. However, in real NSs, neutrons are free to move, and a strong composition gradient leads to stable stratification (stability against convective motions) both of which might impact on the time-scales of evolution. Here, we address these issues by providing the first long-term two-fluid simulations of the evolution of an axially symmetric magnetic field in a neutron star core composed of neutrons, protons, and electrons with density and composition gradients. Again, we find that the magnetic field evolves towards barotropic ‘Grad–Shafranov equillibria’, in which the magnetic force is balanced by the degeneracy pressure gradient and gravitational force of the charged particles. However, the evolution is found to be faster than in the case of motionless neutrons, as the movement of charged particles (which are coupled to the magnetic field, but are also limited by the collisional drag forces exerted by neutrons) is less constrained, since neutrons are now allowed to move. The possible impact of non-axisymmetric instabilities on these equilibria, as well as beta decays, proton superconductivity, and neutron superfluidity, are left for future work.

MHD, methods: numerical, magnetic fields

1 INTRODUCTION

Neutron stars (NSs) are classified in several types based on their substantially different observational properties, which appear to be determined mainly by their rotation rates, magnetic field strengths, and presence or absence of accretion from a binary companion. In particular, the magnetic fields control the torque that slows down their rotation, can have a crucial effect on the free energy budget and radiation processes, and influence the flow of accreted matter on and around these stars. On the other hand, the structure and evolution of these magnetic fields is far from understood as different classes of NSs have very different magnetic field strengths, which appear to be correlated with their age. Young NSs; such as magnetars, classical radio pulsars, and high-mass X-ray binaries; have strong surface magnetic fields ∼10^11–15 G; while the much older low-mass X-ray binaries and millisecond pulsars have weaker fields ∼10^8–9 G (Kaspi 2010; Viganò et al. 2013). This suggests a magnetic field decay, which is usually attributed to the accretion process (Backer et al. 1982; Bhattacharya 1991, 1995; Tauris & van den Heuvel 2006), but might also be explainable through its own dynamics and spontaneous decay as the NS cools and ages (Cruces, Reisenegger & Tauris 2019). Furthermore, the high time-averaged luminosity of magnetars is thought to be linked to the decay of their magnetic field, since their rotational energy loss is insufficient to account for it. Since these objects appear to be isolated, their field decay must be attributed to processes intrinsic to the NSs (Thompson & Duncan 1995, 1996). Therefore, understanding the mechanisms that drive the long-term evolution of the magnetic field in NSs may help us unveil the relation between their different classes.

The physics of the evolution of the magnetic field varies in different regions of the NS (Goldreich & Reisenegger 1992). For example, in the solid crust, ions have very restricted mobility, so the currents are carried by electrons. Therefore the long-term mechanisms that control the evolution of the field in this region are Ohmic diffusion, i.e. current dissipation by electric resistivity; and Hall drift which corresponds to the transport of the magnetic flux by the electron motion. Since the magnetic field dynamics is intrinsically non-linear, its recent studies have mainly taken a numerical point of view (Hollerbach & Rüdiger 2002; Pons & Geppert 2007; Pons, Miralles & Geppert 2009; Viganò, Pons & Miralles 2012; Gourgouliatos et al. 2013; Viganò et al. 2013; Lander & Gourgouliatos 2019), finding that the magnetic field evolves towards stable ‘attractor’ configurations (Gourgouliatos & Cumming 2014; Marchant et al. 2014).

In this work, we concentrate on the long-term magnetic field dynamics in the core of NSs, which is conceptually much more involved than in the crust. Indeed, the core of an NS is a fluid mixture of neutrons, protons, and electrons, joined by other species at increasing densities. The mechanisms for field evolution in this region are strongly dependent on the star’s core temperature T. Shortly after the NS is formed, neutrons and charged particles are strongly coupled by collisions, behaving essentially as a single fluid, coupled to the magnetic flux. This fluid is stably stratified by its composition gradient (due to the different density profiles of charged particles and neutrons) (Pethick 1992; Goldreich & Reisenegger 1992; Reisenegger 2009); thus, strong buoyancy forces oppose convective motions. However, as noted by Reisenegger (2007), weak interaction processes (so-called ‘Urca reactions’; Gamow & Schoenberg 1941; Haensel 1995) can quickly adjust the composition of a fluid element, overcoming stable stratification and allowing the fluid to transport the magnetic flux. In this ‘strong-coupling’ regime, the matter can be regarded as a single, stably stratified, non-barotropic fluid (i.e. pressure depends on the non-uniform chemical composition in addition to density). However, as weak interactions are strongly temperature dependent, this regime applies only for a very short time after the NS birth (while T ≳ 5 × 10⁸ K). As the star cools, the progressive reduction of the collisional coupling makes relative motions possible, so the charged particles can carry the magnetic flux with a different velocity field than that of the neutrons, a process called ‘ambipolar diffusion’ (Pethick 1992; Goldreich & Reisenegger 1992). Hence, on long time-scales, the NS core is in a ‘weak-coupling’ regime, in which neutrons and charged particles act as independent barotropic fluids (assuming charged particles other than p and e can be ignored), with only the charged particles coupling significantly to the magnetic field. It has been argued that ambipolar diffusion may be relevant to explain the activity of magnetars due to its strong dependence on the magnetic field intensity (Thompson & Duncan 1995, 1996).

In Castillo, Reisenegger & Valdivia (2017) (hereafter paper I), we provided the first simulations that evolve simultaneously and consistently the structure of the magnetic field and the small density perturbations it induces on the charged particles (taken to be a nearly uniform, locally neutral mix of protons and electrons) inside the core of an isolated, spherical NS through ambipolar diffusion in axial symmetry. We modelled the neutrons as a motionless uniform background that produces a frictional drag on the charged particles (see Goldreich & Reisenegger 1992) and neglected the currents in the crust, assuming it has a very low conductivity. We also ignored the effects of superfluidity, superconductivity, and weak interactions (‘Urca reactions’).

We found that the magnetic field evolves in the expected time-scales, eventually reaching equillibrium states in which the magnetic forces are balanced by the degeneracy pressure gradient and gravitational force of charged particles. The latter, being a homogeneous mixture of protons and electrons, can be regarded as a barotropic fluid (with a one-to-one relation between pressure and density), so these equilibrium states satisfy the Grad–Shafranov equation (Grad & Rubin 1958; Shafranov 1966), strongly constraining the magnetic field configuration. The toroidal field is confined to regions of closed poloidal field lines forming ‘twisted tori’ whose number is conserved by the evolution, since ambipolar diffusion by itself cannot produce magnetic reconnection. Outside these tori, i.e. along poloidal field lines that extend beyond the star, the toroidal field disappears through ‘unwinding’ of the field lines by a toroidal component of the ambipolar velocity. We also confirmed that previously found solutions of the Grad–Shafranov equation (e.g. Armaza, Reisenegger & Valdivia 2015) are stable in axial symmetry.

We must remark that barotropic axially symmetric equillibria (as the ones found in paper I, and eventually in this work) are likely to become unstable under non-axisymmetric perturbations, as there are numerous magneto-hydrodynamic instabilities identified for axially symmetric magnetic fields, all of which break the axial symmetry (Tayler 1973; Markey & Tayler 1973; Wright 1973). Additionally, stable stratification (non-barotropy) appears to be required to stabilize magnetic field configurations (Braithwaite 2009; Reisenegger 2009; Mitchell et al. 2015). Such instabilities might lead to a complete dissipation of the field, unless the charged particle fluid is stably stratified by a gradient of muons or other particle species, in addition to protons and electrons. Addressing 3D motions, as well as the high temperature ‘strong-coupling’ regime (in which collisional coupling and weak interactions between species become important) is left for future work.

Paper I was a starting point, but contains several simplifications that must be considered. For instance, we modelled the neutrons as a motionless, uniform background with the only effect of providing a frictional force on the charged particles. However, in real NSs, neutrons can move, and both neutrons and charged particles have strong, but different density gradients, so their velocity fields must also be different, as long as their relative abundances cannot be adjusted ‘in real time’ by Urca reactions, as is the case at high temperatures. Thus, there will both be a bulk motion and a relative motion of neutrons and charged particles, setting time-scales that might be somewhat shorter than those previously found. This has been recently studied by Ofengeim & Gusakov (2018), who evaluated the different instantaneous particle velocities for a fixed magnetic field configuration, finding that the magnetic field may lead to the generation of a macroscopic fluid velocity that is substantially larger than the relative velocities between species. The impact of the neutron motion on an evolving magnetic field has been previously studied by Hoyos, Reisenegger & Valdivia (2008, 2010); however, their one-dimensional simulations cannot capture all the relevant physics of the process. Therefore, in this work we address those issues by numerically evolving the magnetic field, including the motion of neutrons, in a spherical star with an axially symmetric magnetic field.

In this paper, we neglect the effects of superfluidity and superconductivity, which should at the very least change the couplings between superfluid neutrons and superconducting protons, thus modifying the time-scales for the processes simulated here, and possibly change the equillibrium configurations found. These issues have been studied by several authors in the last years (e.g. Glampedakis, Jones & Samuelsson 2011; Graber et al. 2015; Elfritz et al. 2016; Passamonti et al. 2017a; Bransgrove, Levin & Beloborodov 2018), and the discussion has not been exempt from controversy (Gusakov & Dommes 2016; Dommes & Gusakov 2017; Passamonti et al. 2017b). Until recently, the impact of superfluidity and superconductivity was thought to be well understood only in particularly simple situations, such as the one studied by Kantor & Gusakov (2018). However, it was not until very recently that an expression for the force on proton vortices in superfluid and superconducting matter (Gusakov 2019) was proposed, which is a key ingredient for studying the long-term magnetic evolution. Thus, performing magneto-hydrodynamic simulations including such effects is left for future work.

This paper is organized as follows. In Section 2, we discuss the physical model and construct the equations to be solved in axial symmetry. Here, we also discuss the relevant time-scales and describe our toy model for the equation of state. In Section 3.1, we test the impact of including an extra artificial friction, which is used in our simulations to keep the magnetic field close to a magneto-hydrostatic quasi-equillibrium throughout its evolution. In Section 3.2, we check if the simulations are in agreement with the analytically expected time-scales. In Section 3.3, we study the equillibrium configurations found. Finally, in Section 4, our results are summarized and conclusions are outlined.

2 PHYSICAL MODEL

2.1 Basic equations

As in Paper I, we model the interior of an isolated NS as a plasma composed of neutrons, protons, and electrons. The species are coupled by collisions and electromagnetic forces, and their equations of motion are written as

$$\begin{eqnarray*} n_i\frac{\mu _i}{c^2}\frac{\mathrm{ d}\boldsymbol{v_i}}{\mathrm{ d}t}&=& n_i q_i\left(\boldsymbol{E} +\frac{\boldsymbol{v_i}}{c}\times \boldsymbol{B} \right) -n_i\boldsymbol{\nabla }\mu _i - \frac{n_i\mu _i}{c^2}\boldsymbol{\nabla }\Psi \nonumber\\ &&-\, \sum _{j\ne i}\gamma _{ij}n_i n_j \left(\boldsymbol{v_i} - \boldsymbol{v_j}\right), \end{eqnarray*}$$

(1)

where n_i and μ_i (i = n, p, e) are the number density and chemical potential of species i, respectively; μ_i/c² is the effective mass of each species, which could include corrections due to interactions and relativistic effects (Akmal, Pandharipande & Ravenhall 1998); q_i is the electric charge of the respective particles; and |$\boldsymbol{v_i}$| is the velocity of the ith species. We assume charge neutrality, so that at all times n_p = n_e ≡ n_c. The forces acting on each particle are, from left to right, the Lorentz force (where |$\boldsymbol{E}$| and |$\boldsymbol{B}$| are the electric and magnetic fields), the degeneracy-pressure gradient of species i, the gravitational force acting on each fluid species (where Ψ is the gravitational potential), and the frictional drag forces due to collisions between particles of different species. The later are parametrized by rate coefficients γ_ij, so that momentum conservation implies γ_ij = γ_ji.

Under any perturbation, the star very quickly reaches a magneto-hydrostatic quasi-equilibrium state in which all the forces on a fluid element are close to balancing each other. The time-scale to reach this state is a few Alfvén times, t_Alf ∼ (10¹⁴G/B) s. Since we are interested in the long-term evolution of the field, which happens on much longer time-scales, ∼10^3–10 yr, we do not intend to follow the propagation of sound waves, gravity (buoyancy) waves, and Alfvén waves in detail. Instead, we filter them out by replacing the inertial terms on the left-hand side of the equations of motion by an artificial frictional force acting on the neutrons, of the form |$\boldsymbol{f_\zeta }\equiv -\zeta n_\mathrm{ n} \boldsymbol{v_\mathrm{ n}}$| (Hoyos et al. 2008). The balance between this and the other forces acting on a fluid element determines the velocity field |$\boldsymbol{v_\mathrm{ n}}$|⁠, which quickly restores the hydro-magnetic quasi-equilibrium by rearranging the particles and magnetic field on a time-scale set by the parameter ζ. The value of this parameter is chosen to be small enough so its associated time-scale is much longer than the dynamical time-scales (∼Alfvén times), but shorter than the time-scales relevant to us (see discussion in Section 2.6).

In paper I, we did not need to explicitly introduce such mechanism. As we froze the neutrons, their friction with the charged particles provided a mechanism ensuring that the latter would evolve through successive quasi-equilibrium states. In contrast, in this work we are allowing neutrons to move and rearrange in a way in which they help to maintain a hydro-magnetic quasi-equilibrium, which might be much closer to reality.

The equations of motion then become:

$$\begin{eqnarray*} 0&=&-n_\mathrm{ n}\boldsymbol{\nabla }\mu _\mathrm{ n} - \frac{n_\mathrm{ n}\mu _\mathrm{ n}}{c^2}\boldsymbol{\nabla }\Psi - \gamma _{\mathrm{ ne}}n_\mathrm{ n} n_\mathrm{ c} \left(\boldsymbol{v_\mathrm{ n}} - \boldsymbol{v_\mathrm{ e}}\right)\nonumber\\ &&-\, \gamma _{\mathrm{ np}}n_\mathrm{ n} n_\mathrm{ c} \left(\boldsymbol{v_\mathrm{ n}} - \boldsymbol{v_\mathrm{ p}}\right) - \zeta n_\mathrm{ n}\boldsymbol{v_\mathrm{ n}}, \end{eqnarray*}$$

(2)

$$\begin{eqnarray*} 0&=&+ n_\mathrm{ c} e\left(\boldsymbol{E} +\frac{\boldsymbol{v_\mathrm{ p}}}{c}\times \boldsymbol{B} \right)-n_\mathrm{ c}\boldsymbol{\nabla }\mu _\mathrm{ p} - \frac{n_\mathrm{ c}\mu _\mathrm{ p}}{c^2}\boldsymbol{\nabla }\Psi \nonumber\\ &&-\,\gamma _{\mathrm{ pe}}n_\mathrm{ c}^2 \left(\boldsymbol{v_\mathrm{ p}} - \boldsymbol{v_\mathrm{ e}}\right) - \gamma _{\mathrm{ pn}}n_\mathrm{ c} n_\mathrm{ n} \left(\boldsymbol{v_\mathrm{ p}} - \boldsymbol{v_\mathrm{ n}}\right), \end{eqnarray*}$$

(3)

$$\begin{eqnarray*} 0&=&- n_\mathrm{ c} e\left(\boldsymbol{E} +\frac{\boldsymbol{v_\mathrm{ e}}}{c}\times \boldsymbol{B} \right)-n_\mathrm{ c}\boldsymbol{\nabla }\mu _\mathrm{ e} - \frac{n_\mathrm{ c}\mu _\mathrm{ e}}{c^2}\boldsymbol{\nabla }\Psi \nonumber\\ &&-\, \gamma _{\mathrm{ ep}}n_\mathrm{ c}^2 \left(\boldsymbol{v_\mathrm{ e}} - \boldsymbol{v_\mathrm{ p}}\right) - \gamma _{\mathrm{ en}}n_\mathrm{ c} n_\mathrm{ n} \left(\boldsymbol{v_\mathrm{ e}} - \boldsymbol{v_\mathrm{ n}}\right). \end{eqnarray*}$$

(4)

By taking the product of equation (3) with γ_en and equation (4) with γ_pn, and then subtracting them, we get

$$\begin{eqnarray*} \boldsymbol{E}&=& - \frac{\gamma _{\mathrm{ pn}}\boldsymbol{v_\mathrm{ e}} +\gamma _{\mathrm{ en}}\boldsymbol{v_\mathrm{ p}}}{c\gamma _{\mathrm{ cn}}} \times \boldsymbol{B} +\frac{\boldsymbol{J}}{\sigma } \nonumber\\ &&+\,\frac{\gamma _{\mathrm{ en}}\boldsymbol{\nabla }\mu _\mathrm{ p}-\gamma _{\mathrm{ pn}}\boldsymbol{\nabla }\mu _\mathrm{ e}}{e\gamma _{\mathrm{ cn}}} + \frac{\gamma _{\mathrm{ en}}\mu _\mathrm{ p}-\gamma _{\mathrm{ pn}}\mu _\mathrm{ e}}{ec^2\gamma _{\mathrm{ cn}}} \boldsymbol{\nabla }\Psi . \end{eqnarray*}$$

(5)

where γ_cn = γ_pn + γ_en is the net collisional coupling between charged particles and neutrons

$$\begin{eqnarray*} \sigma = e^2\left(\gamma _{\mathrm{ pe}}+\frac{\gamma _{\mathrm{ en}}\gamma _{\mathrm{ pn}}}{\gamma _{\mathrm{ cn}}}\frac{n_\mathrm{ n}}{n_\mathrm{ c}} \right)^{-1}, \end{eqnarray*}$$

(6)

is the electric conductivity, and |$\boldsymbol{J}$| is the electric current density |$\boldsymbol{J}=n_\mathrm{ ce}(\boldsymbol{v_\mathrm{ p}}-\boldsymbol{v_\mathrm{ e}})=c\boldsymbol{\nabla }\!\times \!\boldsymbol{B}/4\pi$|⁠.

We define the ‘ambipolar diffusion velocity’, which represents the joint motion of the two charged particle species relative to the neutrons, as

$$\begin{eqnarray*} \boldsymbol{v_{\mathrm{ ad}\mathrm{ }}} = \frac{\gamma _{\mathrm{ pn}}(\boldsymbol{v_\mathrm{ p}} -\boldsymbol{v_\mathrm{ n}})+\gamma _{\mathrm{ en}}(\boldsymbol{v_\mathrm{ e}} -\boldsymbol{v_\mathrm{ n}})}{\gamma _{\mathrm{ cn}}}, \end{eqnarray*}$$

(7)

and the ‘Hall drift velocity’, which is proportional to the electric current, as

$$\begin{eqnarray*} \boldsymbol{v_\mathrm{ H}} = - \frac{\gamma _{\mathrm{ pn}}-\gamma _{\mathrm{ en}}}{\gamma _{\mathrm{ cn}}} (\boldsymbol{v_\mathrm{ p}} -\boldsymbol{v_\mathrm{ e}}) = - \frac{\gamma _{\mathrm{ pn}}-\gamma _{\mathrm{ en}}}{\gamma _{\mathrm{ cn}}}\frac{\boldsymbol{J}}{n_\mathrm{ c} e}. \end{eqnarray*}$$

(8)

Hence, |$\left(\gamma _{\mathrm{ pn}}\boldsymbol{v_\mathrm{ e}}+\gamma _{\mathrm{ en}}\boldsymbol{v_\mathrm{ p}}\right)/\gamma _{\mathrm{ cn}}=\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}+\boldsymbol{v_\mathrm{ H}}$|⁠, so the evolution equation for the magnetic field is obtained from Faraday’s law as

$$\begin{eqnarray*} \frac{\partial \boldsymbol{B}}{\partial t} &=& \boldsymbol{\nabla }\!\times \!\left[\left(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}+\boldsymbol{v_\mathrm{ H}}\right)\times \boldsymbol{B} -\frac{c}{\sigma }\boldsymbol{J}\right]\nonumber\\ &&-\,\boldsymbol{\nabla }\left(\frac{c\gamma _{\mathrm{ en}}}{e\gamma _{\mathrm{ cn}}}\right) \times \boldsymbol{\nabla }\mu _\mathrm{ c} -\boldsymbol{\nabla }\left(\frac{\mu _\mathrm{ p}\gamma _{\mathrm{ en}}-\mu _\mathrm{ e}\gamma _{\mathrm{ pn}}}{ec\gamma _{\mathrm{ cn}}}\right) \times \boldsymbol{\nabla }\Psi, \end{eqnarray*}$$

(9)

where we defined a total chemical potential for the charged particles, μ_c ≡ μ_p + μ_e. The last term inside the curl represents Ohmic dissipation, and the two last terms represent battery effects.

As discussed in Goldreich & Reisenegger (1992), in the core of NSs the effects of Hall drift and Ohmic decay can be orders of magnitude smaller than the ambipolar diffusion, hence we neglect those terms. Also, as shown in paper I, the time-scale on which the battery terms are relevant is roughly the same as the Hall time-scale, therefore we also neglect those terms, obtaining

$$\begin{eqnarray*} \frac{\partial \boldsymbol{B}}{\partial t}= \boldsymbol{\nabla }\!\times \!\left(\boldsymbol{v_\mathrm{ c}}\times \boldsymbol{B} \right), \end{eqnarray*}$$

(10)

where |$\boldsymbol{v_\mathrm{ c}}\equiv \boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}$| is the velocity of the charged particles.

The relevant velocities can be computed from the equations of motion. By adding equations (2), (3), and (4), we get the velocity field of the neutrons, parametrized by the fictitious friction coefficient ζ, which replaces the very small inertial terms

$$\begin{eqnarray*} \boldsymbol{v_\mathrm{ n}}&=&\frac{1}{\zeta n_\mathrm{ n}}\left[\frac{\boldsymbol{J}}{c}\times \boldsymbol{B} -n_\mathrm{ c}\left(\boldsymbol{\nabla }\mu _\mathrm{ c} +\frac{\mu _\mathrm{ c}}{c^2}\boldsymbol{\nabla }\Psi \right)\right.\nonumber\\ &&\left.-\,n_\mathrm{ n}\left(\boldsymbol{\nabla }\mu _\mathrm{ n} +\frac{\mu _\mathrm{ n}}{c^2}\boldsymbol{\nabla }\Psi \right) \right]. \end{eqnarray*}$$

(11)

From equations (3), (4), and (7) we obtain the ambipolar diffusion velocity

$$\begin{eqnarray*} \boldsymbol{v_{\mathrm{ ad}}} = \frac{1}{\gamma _{\mathrm{ cn}}n_\mathrm{ c} n_\mathrm{ n}}\left[\frac{\boldsymbol{J}\times \boldsymbol{B}}{c} - n_\mathrm{ c}\left(\boldsymbol{\nabla }\mu _\mathrm{ c}+\mu _\mathrm{ c}\frac{\boldsymbol{\nabla }\Psi }{c^2}\right)\right], \end{eqnarray*}$$

(12)

which is proportional to the imbalance between the forces, including (from left to right) the magnetic force density, the gradient of the degeneracy pressure of the charged particles, and the gravitational force on the charged particles. Thus, the ambipolar diffusion is driven by the magnetic force, controlled by the pressure gradient and gravitational forces acting on the charged particles, and opposed by the collisional drag of the neutrons. The terms in equation (11) have an analogous interpretation.

To evolve the particle densities, we use the continuity equations

$$\begin{eqnarray*} \frac{\partial n_\mathrm{ c}}{\partial t} + \boldsymbol{\nabla }\cdot \left(n_\mathrm{ c}\boldsymbol{v_\mathrm{ c}}\right) = -\Delta \Gamma, \end{eqnarray*}$$

(13)

$$\begin{eqnarray*} \frac{\partial n_\mathrm{ n}}{\partial t} + \boldsymbol{\nabla }\cdot \left(n_\mathrm{ n}\boldsymbol{v_\mathrm{ n}}\right) = +\Delta \Gamma, \end{eqnarray*}$$

(14)

where ΔΓ is the net rate per unit volume of conversion of charged particles to neutrons by weak interactions, i.e. the difference between the rates for the (direct or modified) Urca processes, p + e → n + ν_e and |$n\rightarrow p+e+\bar{\nu }_\mathrm{ e}$|⁠, where ν_e and |$\bar{\nu }_\mathrm{ e}$| denote electron neutrinos and electron antineutrinos, respectively. This quantity becomes very small in the low-temperature regime (T ≲ 5 × 10⁸ K) of interest here (Goldreich & Reisenegger 1992; Reisenegger 1995), therefore we ignore it in this work.

2.2 Background NS model

As in paper I, we consider the (realistic) situation where the magnetic field induces only small perturbations with respect to a hypothetical non-magnetized stellar structure (see also Reisenegger 2009). Thus, we split the particle densities, and hence the chemical potentials, in two:

time-independent background densities n_i(r) and chemical potentials μ_i(r) determined by the conditions of chemical (beta) equillibrium,
$$\begin{eqnarray*} \mu _{\mathrm{ n}}=\mu _{\mathrm{ c}}\equiv \mu (r), \end{eqnarray*}$$
(15)
and hydrostatic equilibrium in the absence of the magnetic field
$$\begin{eqnarray*} \boldsymbol{\nabla }\mu +\mu \boldsymbol{\nabla }\Psi /c^2=0, \end{eqnarray*}$$
(16)
and
much smaller time-dependent perturbations δn_c, δn_n, δμ_c, and δμ_n, respectively, induced by the evolving magnetic field (to be discussed in Section 2.3).

An important improvement of this work over paper I is that we consider the non-magnetized background star to have non-uniform particle densities, with different radial gradients for the neutrons and charged particles, as imposed by beta equilibrium.

For simplicity, we ignore strong interactions, treating neutrons and protons (with the same mass m) as non-relativistic Fermi gases and electrons as an extremely relativistic (massless) Fermi gas. Thus, the chemical potentials are related to the particle densities by

$$\begin{eqnarray*} \mu _\mathrm{ n}(r) = m c^2 + \frac{p_{\mathrm{ Fn}}(r)^2}{2m}, \end{eqnarray*}$$

(17)

$$\begin{eqnarray*} \mu _\mathrm{ c}(r) = m c^2 + \frac{p_{\mathrm{ Fc}}(r)^2}{2m} + p_{\mathrm{ Fc}}(r)c, \end{eqnarray*}$$

(18)

where |$p_{\mathrm{ Fi}}(r) = \hbar \left[3\pi ^2n_i(r)\right]^{1/3}\,$| are the Fermi momenta of neutrons (i = n) and charged particles (i = c). Since we assume charge neutrality, the densities (and thus the Fermi momenta) of protons and electrons are the same. Thus, the condition of chemical equilibrium (equation 15) allows to write the density of neutrons in terms of that of the charged particles,

$$\begin{eqnarray*} n_\mathrm{ n}(r)=\left[\frac{2mc}{\hbar (3\pi ^2)^{1/3}}n_\mathrm{ c}(r)^{1/3} + n_\mathrm{ c}(r)^{2/3}\right]^{3/2}. \end{eqnarray*}$$

(19)

For the background number density of charged particles, we use the simple analytical approximation

$$\begin{eqnarray*} n_\mathrm{ c}(r)=n_{\mathrm{ c}0}\left[\frac{\sin (0.7\pi r/R)}{0.7\pi r/R}\right]^6, \end{eqnarray*}$$

(20)

where R is the radius of the core, taken as |$70{{\ \rm per\ cent}}$| of the stellar radius. As can be seen in Fig. 1, this relation closely resembles the numerical solution obtained by imposing Newtonian hydrostatic equilibrium equation (16) on this Fermi gas, and we adjusted the central density so ξ ≡ n_n(0)/n_c(0) = 10, yielding a star of mass 1.58 M_⊙ and radius 8.2 km.

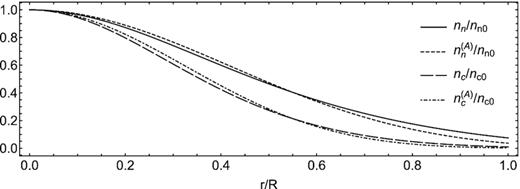
$Comparison between nn/nn(0) and nc/nc(0) (obtained by numerically solving the hydrostatic equilibrium equation 16), and the simple analytical approximations $n_\mathrm{ n}^{(A)}/n_\mathrm{ n}(0)$ and $n_\mathrm{ c}^{(A)}/n_\mathrm{ c}(0)$, respectively. Here, $n_\mathrm{ n}^{(A)}$ is computed from equation (19), using $n_\mathrm{ c}^{(A)}$, the analytical expression for nc given by equation (20).$

Figure 1.

Comparison between n_n/n_n(0) and n_c/n_c(0) (obtained by numerically solving the hydrostatic equilibrium equation 16), and the simple analytical approximations |$n_\mathrm{ n}^{(A)}/n_\mathrm{ n}(0)$| and |$n_\mathrm{ c}^{(A)}/n_\mathrm{ c}(0)$|⁠, respectively. Here, |$n_\mathrm{ n}^{(A)}$| is computed from equation (19), using |$n_\mathrm{ c}^{(A)}$|⁠, the analytical expression for n_c given by equation (20).

Open in new tab Download slide

The transport coefficients γ_ij(r, T) between species i and j are computed for the relations derived for τ_ij(r, T) by Yakovlev & Shalybkov (1990), where T denotes the core temperature.

This stellar model, although very simplified, allows us to capture the effects of radial density gradients, gravity, and stable stratification into our simulations, which is a vast improvement over paper I, where the background densities were treated as fixed radially independent numbers.

2.3 Linearization

Since the density perturbations are small, we can linearize δμ_n = K_nnδn_n (where K_nn = dμ_n/dn_n), and δμ_c = K_ccδn_c (where K_cc = dμ_c/dn_c). In our model, as there are no strong interactions, the cross-derivatives K_cn = ∂μ_c/∂n_n and K_nc = ∂μ_n/∂n_c vanish.

Dropping higher order terms, we can write the full set of equations to be solved as

$$\begin{eqnarray*} \frac{\partial \boldsymbol{B}}{\partial t}= \boldsymbol{\nabla }\!\times \!\left[\left(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}\right)\times \boldsymbol{B} \right], \end{eqnarray*}$$

(21)

$$\begin{eqnarray*} \frac{\partial \delta n_\mathrm{ n}}{\partial t} + \boldsymbol{\nabla }\cdot \left(n_\mathrm{ n}\boldsymbol{v_\mathrm{ n}}\right) = 0, \end{eqnarray*}$$

(22)

$$\begin{eqnarray*} \frac{\partial \delta n_\mathrm{ c}}{\partial t} + \boldsymbol{\nabla }\cdot \left[n_\mathrm{ c}(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}})\right] = 0, \end{eqnarray*}$$

(23)

$$\begin{eqnarray*} \boldsymbol{v_\mathrm{ n}}=\frac{1}{\zeta n_\mathrm{ n}}\left(\boldsymbol{f_B}+\boldsymbol{f_\mathrm{ n}}+\boldsymbol{f_\mathrm{ c}}\right), \end{eqnarray*}$$

(24)

$$\begin{eqnarray*} \boldsymbol{v_{\mathrm{ ad}}} = \frac{1}{\gamma _{\mathrm{ cn}}n_\mathrm{ c} n_\mathrm{ n}}\left(\boldsymbol{f_B}+\boldsymbol{f_\mathrm{ c}}\right), \end{eqnarray*}$$

(25)

$$\begin{eqnarray*} \boldsymbol{f_B}=\frac{(\boldsymbol{\nabla }\!\times \!\boldsymbol{B})\times \boldsymbol{B}}{4\pi }, \end{eqnarray*}$$

(26)

$$\begin{eqnarray*} \boldsymbol{f_\mathrm{ n}}=-n_\mathrm{ n}\mu \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ n}}{\mu }\right), \end{eqnarray*}$$

(27)

$$\begin{eqnarray*} \boldsymbol{f_\mathrm{ c}}=-n_\mathrm{ c}\mu \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ c}}{\mu }\right), \end{eqnarray*}$$

(28)

$$\begin{eqnarray*} \delta \mu _\mathrm{ n} = K_{\mathrm{ nn}}\delta n_\mathrm{ n}, \end{eqnarray*}$$

(29)

$$\begin{eqnarray*} \delta \mu _\mathrm{ c} = K_{\mathrm{ cc}}\delta n_\mathrm{ c}, \end{eqnarray*}$$

(30)

where the degeneracy pressure gradients and the gravitational forces for each species have been combined into the ‘fluid forces’ (more precisely, force densities) |$\boldsymbol{f_\mathrm{ n}}$| and |$\boldsymbol{f_\mathrm{ c}}$| using the hydrostatic equilibrium condition of the background, equation (16).

2.4 Boundary conditions

For simplicity, we assume that currents in the crust decay much faster than typical evolution time-scales in the core, so we can treat the crust as a vacuum whose magnetic field at any time is fully determined by the field in the core (see discussion and more detail on the imposed boundary conditions in paper I). This external current-free magnetic field is computed at all time-steps as a multipolar expansion, whose coefficients (a_ℓ, with ℓ = 1, 2, ...) are determined by the value of the radial component of the magnetic field at the crust–core interface. These coefficients also determine the energy stored in the external magnetic field (see details in paper I), namely

$$\begin{eqnarray*} U_{\text{ext}}\equiv \sum _{\ell =1}^\infty U_{\text{ext},\ell }=\sum _{\ell =1}^\infty \frac{\ell +1}{2\ell +1}\frac{a_\ell ^2}{2}, \end{eqnarray*}$$

(31)

where U_{ext, ℓ} is the energy stored in the ℓ-th component of the external field. Also, at the crust–core interface we assume that the radial components of both the neutron velocity |$\boldsymbol{v}_\mathrm{ n}$| and the charged-particle velocity |$\boldsymbol{v}_\mathrm{ c}$| are null. Therefore, at the crust–core interface we have

$$\begin{eqnarray*} \frac{\partial }{\partial r}\left(\frac{\delta \mu _\mathrm{ c}}{\mu }\right) =\frac{f_B^r}{n_\mathrm{ c}\mu }, \end{eqnarray*}$$

(32)

$$\begin{eqnarray*} \frac{\partial }{\partial r}\left(\frac{\delta \mu _\mathrm{ n}}{\mu }\right)=0. \end{eqnarray*}$$

(33)

2.5 Axial symmetry

Lastly, we restrict ourselves to axial symmetry, so the magnetic field can be decomposed as

$$\begin{eqnarray*} \boldsymbol{B}=\boldsymbol{\nabla }\alpha \times \boldsymbol{\nabla }\phi + \beta \boldsymbol{\nabla }\phi. \end{eqnarray*}$$

(34)

Here, the scalar potentials α(t, r, θ) and β(t, r, θ) generate the poloidal and toroidal magnetic field, respectively, where t denotes time, r is the radial coordinate, and θ and ϕ are the polar and azimuthal angles, respectively, so |$\boldsymbol{\nabla }\phi =\hat{\phi }/(r\sin \theta)$|⁠. An explicit form for the evolution of the magnetic potentials can be derived from equation (21), where we get

$$\begin{eqnarray*} \frac{\partial \alpha }{\partial t}=r\sin \theta \left[\left(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}\right)\times \boldsymbol{B}\right]\cdot \hat{\phi }, \end{eqnarray*}$$

(35)

$$\begin{eqnarray*} \frac{\partial \beta }{\partial t}=r^2\sin ^2\theta \boldsymbol{\nabla }\cdot \left\lbrace \frac{\left[\left(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}\right)\times \boldsymbol{B} \right]\times \hat{\phi }}{r\sin \theta } \right\rbrace. \end{eqnarray*}$$

(36)

2.6 Time-scale estimates

2.6.1 Short-term relaxation through fictitious friction

In order to mimic the quick hydro-magnetic relaxation due to the propagation and damping of sound waves, gravity waves, and Alfvén waves, which happens much faster than ambipolar diffusion, the fictitious friction parameter introduced in equation (2) must satisfy ζ ≪ γ_cnn_c, so a net force imbalance on a fluid element (in round brackets on the right-hand side of equation 24) is reduced by bulk motions (with velocity |$\boldsymbol{v}_\mathrm{ n}$|⁠) much more quickly than an imbalance of the partial forces on the charged-particle component (in round brackets on the right-hand side of equation 25) is reduced by ambipolar diffusion (with relative velocity |$\boldsymbol{v}_{\mathrm{ ad}}$|⁠). Thus, for an arbitrary, non-equilibrium initial condition, the dynamics is initially dominated by a bulk motion with the neutron velocity, |$\boldsymbol{v}_\mathrm{ n}$|⁠. For a characteristic spatial scale L ≲ R of the magnetic field, the time-scales for the evolution of the density perturbations, ∼(δn_n/n_n)(L/v_n) (from equation 22) and ∼(δn_c/n_c)(L/v_n) (from equation 23) are much shorter than that for the magnetic field, ∼L/v_n (from equation 21). Thus, for t ≪ L/v_n, the magnetic field can be regarded as fixed, and only the density perturbations evolve.¹

For an axially symmetric magnetic field configuration, the Lorentz force density (equation 26) can be decomposed as

$$\begin{eqnarray*} \boldsymbol{f}_B=\boldsymbol{f}_B^{\mathrm{Pol}}+\boldsymbol{f}_B^{\mathrm{Tor}}, \end{eqnarray*}$$

(37)

where |$\boldsymbol{f}_B^{\mathrm{Pol}}$| and |$\boldsymbol{f}_B^{\mathrm{Tor}}$| are its poloidal and a toroidal components. On the other hand, the fluid forces given by equations (27) and (28) are purely poloidal, therefore they cannot balance |$\boldsymbol{f}_B^{\mathrm{Tor}}$|⁠. Furthermore, each of the fluid forces is proportional to the gradient of a single scalar function, therefore an arbitrary |$\boldsymbol{f}_B^{\mathrm{Pol}}$| can only be balanced for a particular, non-trivial combination of chemical potential perturbations, δμ_n(r, θ) and δμ_c(r, θ).

For definiteness, let us assume an initial condition with vanishing density perturbations, δn_n(t = 0) = δn_c(t = 0) = 0. In this case, the initial poloidal bulk velocity is |$\boldsymbol{v}_\mathrm{ n}^{\mathrm{Pol}}(t=0)=\boldsymbol{f}_B^{\mathrm{Pol}}/(\zeta n_\mathrm{ n})$|⁠, and the density perturbations grow roughly as |$|\delta n_\mathrm{ n}/n_\mathrm{ n}|\sim |\delta n_\mathrm{ c}/n_\mathrm{ c}|\sim v_\mathrm{ n}^{\mathrm{Pol}} t/L$|⁠. This causes a growth of the fluid forces, |$f_\mathrm{ n}\sim K_{\mathrm{ nn}}n_\mathrm{ n}^2v_\mathrm{ n}^{\mathrm{Pol}} t/L^2$| and |$f_\mathrm{ c}\sim K_{\mathrm{ cc}}n_\mathrm{ c}^2v_\mathrm{ n}^{\mathrm{Pol}} t/L^2$|⁠, until the larger of these, namely |$\boldsymbol{f}_\mathrm{ n}$| (because K_nnn_n ∼ K_ccn_c, whereas n_c ≪ n_n) approaches the magnitude of |$\boldsymbol{f}_B^{\mathrm{Pol}}$|⁠. This happens on a time-scale

$$\begin{eqnarray*} t_{\zeta \mathrm{ p}}\sim \frac{\zeta L^2}{K_{\mathrm{ nn}}n_\mathrm{ n}}, \end{eqnarray*}$$

(38)

the analogue of the propagation time of sound waves (p-modes) when inertial effects are taken into account. However, as discussed in the previous paragraph, |$\boldsymbol{f}_\mathrm{ n}$| alone cannot balance an arbitrary (poloidal) vector field |$\boldsymbol{f}_B^{\mathrm{Pol}}(r,\theta)$|⁠. Thus, |$\boldsymbol{v}_\mathrm{ n}$| might now be a very different vector field than |$\boldsymbol{f}_B/(\zeta n_\mathrm{ n})$|⁠, but it will still be roughly of the same order of magnitude, further modifying the density perturbations until |$\boldsymbol{f}_B^{\mathrm{Pol}}+\boldsymbol{f}_\mathrm{ n}+\boldsymbol{f}_\mathrm{ c}\approx 0,$| at which point the density perturbations reach the (still very small) fractional magnitudes |$|\delta n_\mathrm{ n}|/n_\mathrm{ n}\sim B^2/(4\pi K_{\mathrm{ nn}}n_\mathrm{ n}^2)$| and |$|\delta n_\mathrm{ c}|/n_\mathrm{ c}\sim B^2/(4\pi K_{\mathrm{ cc}}n_\mathrm{ c}^2)$|⁠. The latter happens on a time-scale

$$\begin{eqnarray*} t_{\zeta g}\sim \frac{L}{v_\mathrm{ n}}\frac{|\delta n_\mathrm{ c}|}{n_\mathrm{ c}}\sim \frac{\zeta n_\mathrm{ n} L^2}{K_{\mathrm{ cc}}n_\mathrm{ c}^2}, \end{eqnarray*}$$

(39)

which should be roughly identified with the propagation time of gravity waves (g-modes), i.e. the buoyancy (Brunt–Väisälä) period in a realistic NS (Reisenegger & Goldreich 1992), since balancing an arbitrary |$\boldsymbol{f}_B^{\mathrm{Pol}}$| will generally require non-parallel vector fields |$\boldsymbol{\nabla }[\delta \mu _\mathrm{ n}(r,\theta ,t)/\mu (r)]$| and |$\boldsymbol{\nabla }[\delta \mu _\mathrm{ c}(r,\theta ,t)/\mu (r)]$|⁠, i.e. a baroclinic (non-barotropic) configuration.

On the other hand, |$\boldsymbol{f}_B^{\mathrm{Tor}}$| cannot be canceled by fluid forces and must thus decay to zero, which occurs on a longer time-scale

$$\begin{eqnarray*} t_{\zeta B}\sim \frac{L}{v_\mathrm{ n}}\sim \frac{4\pi \zeta n_\mathrm{ n} L^2}{B^2}, \end{eqnarray*}$$

(40)

which should be identified with an Alfvén-like time. The latter evolution clearly also modifies |$\boldsymbol{f}_B^{\mathrm{Pol}}$|⁠, but the fluid displacements can keep up, always maintaining the balance between |$\boldsymbol{f}_B^{\mathrm{Pol}}$| and the gradient terms and eventually leading to a nearly complete cancellation of the forces on the right-hand side of equation (24), thus making |$|\boldsymbol{v}_\mathrm{ n}|$| comparable to |$|\boldsymbol{v}_{\mathrm{ ad}}|$|⁠.

These arguments remain valid when removing the restriction of axial symmetry. As two gradient forces can only balance two different components of the magnetic force (in a time-scale t_ζg), one component will always remain unbalanced. Therefore, reaching a state of hydro-magnetic quasi-equilibrium will always require the magnetic field to adjust so that the latter component vanishes, which will happen on a time-scale ∼t_ζB. Since we are interested in an evolution on a time-scale many orders of magnitude longer than an Alfvén-like time, we only need ζ to be small enough to make t_ζB sufficiently short to maintain the hydro-magnetic quasi-equilibrium discussed above.

Gusakov, Kantor & Ofengeim (2017) used the time-derivative of the toroidal component of the quasi-equilibrium condition, |$\partial \boldsymbol{f}_B^{\mathrm{Tor}}/\partial t=0$|⁠, to obtain the macroscopic toroidal velocity of the particle flow. However, solving this equation at all time-steps in a simulation is unpractical, as it would require high spatial resolution to properly resolve the fourth-order derivatives over |$\boldsymbol{B}$|⁠. Our approach is simpler, as we do not attempt to solve this equation directly, rather, we let the system relax to this condition through the addition of the fictitious friction force.

2.6.2 Long-term evolution through ambipolar diffusion

As the magnetic force acts only on the charged particles (which are coupled to the neutrons only by collisions), it induces a slow relative motion with velocity |$\boldsymbol{v}_{\mathrm{ ad}}$| in which the magnetic field lines are carried along with the charged particles. This process slowly modifies the hydro-magnetic quasi-equilibrium, eventually reaching a state in which the magnetic force is balanced mainly by the fluid force of the charged particles, while the contribution of the neutrons becomes negligible. During this process, the magnetic field has to adjust, since it has to transition from a state in which |$\boldsymbol{f}_B^{\mathrm{Pol}}$| is balanced by the sum of two different gradients to a state in which only one gradient is available. While the charged particles diffuse through neutrons at a velocity v_ad ∼ B²/4|$\pi$|Lγ_cnn_cn_n, the neutrons have to adjust accordingly. Therefore, the velocity of the neutrons is also controlled by γ_cn and independent of the value given to ζ (granted that ζ is sufficiently small, so t_ζB is much shorter than the ambipolar diffusion time-scale).

At this stage, we expect |$|\partial \delta n_\mathrm{ c}/\partial t|\sim |\delta n_\mathrm{ c}|v_{ad}/L\ll n_\mathrm{ c} v_{\mathrm{ ad}}/L\sim |\boldsymbol{\nabla }\cdot (n_\mathrm{ c}\boldsymbol{v_{\mathrm{ ad}}})|$|⁠, and therefore |$\boldsymbol{\nabla }\cdot \left(n_\mathrm{ c}\boldsymbol{v_{\mathrm{ ad}}}\right)\approx -\boldsymbol{\nabla }\cdot \left(n_\mathrm{ c}\boldsymbol{v_\mathrm{ n}}\right)$|⁠. This imposes a restriction on the irrotational component of |$n_\mathrm{ c}\boldsymbol{v_{\mathrm{ ad}}}$| and |$n_\mathrm{ c}\boldsymbol{v_\mathrm{ n}}$|⁠, so we expect |$\boldsymbol{v_{\mathrm{ ad}}}$| and |$\boldsymbol{v_\mathrm{ n}}$| to be of similar order of magnitude. The magnetic field will evolve under this process until the fluid force of the charged particles balances the magnetic force, reaching an equilibrium state (which may not be stable in the presence of not axially symmetric instabilities, and can also be very slowly eroded by Ohmic decay and other processes neglected in this analysis). This dissipative process sets the long time-scale for magnetic field evolution, which can be estimated as

$$\begin{eqnarray*} t_{\mathrm{ ad}} &\sim& \frac{L}{|\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}|} \lesssim \frac{4\pi \gamma _{\mathrm{ cn}}n_\mathrm{ c}n_\mathrm{ n}L^2}{B^2} \nonumber\\ &\sim& 3\times 10^{3} \, \left(\frac{10^{15}\text{G}}{B}\right)^{2}\left(\frac{T}{10^8\,\text{K}}\right)^{2}\left(\frac{L}{1\,\text{km}}\right)^{2}\, \text{yr}, \end{eqnarray*}$$

(41)

where v_n ∼ v_ad. (See Ofengeim & Gusakov 2018 for analytic relations between these two velocity fields.)

2.7 Dimensionless equations

We have written the equations in dimensionless form

$$\begin{eqnarray*} \frac{\partial \alpha }{\partial t}=r\sin \theta \left[\left(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}\right)\times \boldsymbol{B}\right]\cdot \hat{\phi }, \end{eqnarray*}$$

(42)

$$\begin{eqnarray*} \frac{\partial \beta }{\partial t}=r^2\sin ^2\theta \boldsymbol{\nabla }\cdot \left\lbrace \frac{\left[\left(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}\right)\times \boldsymbol{B} \right]\times \hat{\phi }}{r\sin \theta } \right\rbrace, \end{eqnarray*}$$

(43)

$$\begin{eqnarray*} \frac{\partial \delta n_\mathrm{ n}}{\partial t} + \boldsymbol{\nabla }\cdot \left(n_\mathrm{ n}\boldsymbol{v_\mathrm{ n}}\right) = 0, \end{eqnarray*}$$

(44)

$$\begin{eqnarray*} \frac{\partial \delta n_\mathrm{ c}}{\partial t} + \boldsymbol{\nabla }\cdot \left[n_\mathrm{ c}(\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}})\right] = 0, \end{eqnarray*}$$

(45)

$$\begin{eqnarray*} \boldsymbol{v_\mathrm{ n}}=\frac{\xi }{\zeta n_\mathrm{ n}}\left[b^2\left(\boldsymbol{\nabla }\!\times \!\boldsymbol{B}\right)\times \boldsymbol{B} -n_\mathrm{ c}\mu \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ c}}{\mu }\right) -n_\mathrm{ n}\mu \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ n}}{\mu }\right) \right], \nonumber\\ \end{eqnarray*}$$

(46)

$$\begin{eqnarray*} \boldsymbol{v_{\mathrm{ ad}}} = \frac{\xi }{\gamma _{\mathrm{ cn}}n_\mathrm{ c} n_\mathrm{ n}}\left[b^2\left(\boldsymbol{\nabla }\!\times \!\boldsymbol{B}\right)\times \boldsymbol{B}-n_\mathrm{ c}\mu \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ c}}{\mu }\right) \right], \end{eqnarray*}$$

(47)

$$\begin{eqnarray*} \delta \mu _\mathrm{ c} = K_{\mathrm{ cc}}\delta n_\mathrm{ c}, \end{eqnarray*}$$

(48)

$$\begin{eqnarray*} \delta \mu _\mathrm{ n} = K_{\mathrm{ nn}}\delta n_\mathrm{ n}, \end{eqnarray*}$$

(49)

where distances have been normalized to the core radius R, number densities n_n and n_c are in units of n_c0, K_nn, and K_cc are in units of K_cc0 = K_cc(r = 0), γ_cn is in units of γ_cn0 = γ_cn(r = 0), time has been normalized to t₀ = ξR²γ_cn0/K_cc0, chemical potentials are in units of K_cc0n_c0, ζ is in units of γ_cn0n_c0, velocities are normalized to R/t₀, and the magnetic field is in units of B₀ (the root mean square of the initial magnetic field in the volume of the star). α and β are in units of R²B₀ and RB₀, respectively. We control the strength of the magnetic field adjusting the parameter

$$\begin{eqnarray*} b^2 \equiv \frac{B_0^2}{4\pi K_{\mathrm{ cc}0}n_{c0}^2}, \end{eqnarray*}$$

(50)

which is of the order of the (very small) ratio between the magnetic pressure and the degeneracy pressure of the charged particles. Thus, for our NS model, |$B_0 = n_{\mathrm{ c}0}\sqrt{4\pi K_{\mathrm{ cc}0}}\:b = 2\times 10^{18}b\, \text{G}$|⁠.

Hereafter, we take the value of the different time-scales at the centre of the NS as reference values, which, in dimensionless units read, from the shortest to the longest,

$$\begin{eqnarray*} t_{\zeta \mathrm{ p}} \equiv \left.\frac{K_{\mathrm{ cc}}n_\mathrm{ c}^2}{K_{\mathrm{ nn}}n_\mathrm{ n}^2}\right|_{r=0}\zeta x^2=\frac{\zeta x^2}{16.45}, \end{eqnarray*}$$

(51)

$$\begin{eqnarray*} t_{\zeta \mathrm{ g}} \equiv \zeta x^2, \end{eqnarray*}$$

(52)

$$\begin{eqnarray*} t_{\zeta B} \equiv \frac{\zeta x^2}{ b^2}, \end{eqnarray*}$$

(53)

$$\begin{eqnarray*} t_{\mathrm{ ad}} \equiv \frac{x^2}{b^2}, \end{eqnarray*}$$

(54)

where x ≡ L/R, and we take x = 1/4, since it roughly fits the structure of the initial condition of our simulations. In order to properly resolve all four time-scales in our simulations without having to use a prohibitively small time-step, we use unrealistically large values for the magnetic field (fixed by b) and ζ, so the four time-scales are in the correct order of sizes, but get much closer to each other than in reality.

In order to evolve the magnetic field in the NS core, we upgraded the code described in paper I to include the motion of neutrons and the radial density gradients, so it evolves the set of equations (42)–(49). This is done by discretizing the values of the variables over a staggered polar grid composed of N_r points inhomogeneously distributed in the radial direction inside the core and N_θ points equally spaced in the polar direction, while the external multipolar expansion of α(r, θ) is truncated to the first N_Exp terms. The numerical computation is done conservatively for the evolution of the toroidal magnetic field and the density perturbations of the charged particles and neutrons, using a finite-volume scheme. The time derivative of the poloidal potential is computed using finite differences, and the system is evolved to second-order accuracy in time. This scheme guarantees that the |$\boldsymbol{\nabla }\cdot \boldsymbol{B}=0$| condition, as well as the total number of particles, are conserved at all times to machine precision. Details on the numerical code can be seen in paper I.

3 RESULTS

3.1 Dependence on the artificial friction

In our model, the fictitious friction force is a device to allow the particle densities and the magnetic field configuration to reach a hydro-magnetic equilibrium on time-scales ≲t_ζB shorter than the ambipolar diffusion time t_ad, but close enough to the latter for the numerical simulation to be feasible. Thus, the friction parameter ζ needs to be chosen to satisfy this compromise, and its value should not affect the long-term evolution of the magnetic field on scales ∼t_ad. In order to estimate its optimal value, we compare three simulations that differ only by their value of ζ. Since the total integration time is proportional to t_ad/t_ζp = 16.45/ζb², decreasing the values of ζ and b increases the integration time very quickly. Therefore, to keep it manageable, we perform this test with an unrealistically large value of b², namely, 10⁻². For ζ, we take the values ζ₁ = 10⁻², ζ₂ = 10⁻³, and ζ₃ = 10⁻⁴, which yield ratios t_ad/t_ζB = 10², 10³, and 10⁴, respectively.

As initial condition, we choose the purely poloidal magnetic field generated by the potential

$$\begin{eqnarray*} \alpha _1(r,\theta)=\alpha _{01}r^2\left(1 -\frac{6}{5}r^2 +\frac{3}{7}r^4 \right)\sin ^2\theta, \end{eqnarray*}$$

(55)

where α₀₁ = 1.336 is a normalization constant, fixed by the condition 〈B〉 = 1 on the normalized magnetic field, where 〈.〉 denotes rms in the volume of the core. We chose this configuration, as it is one of the simplest analytic expressions matching all the constraints required for |$\boldsymbol{B}$|⁠, and it has been widely used in the literature (Akgün et al. 2013; Passamonti et al. 2017a; Ofengeim & Gusakov 2018). As in the discussion of Section 2.6.1, we take the initial conditions δn_n = δn_c = 0 for the density perturbations.

Our results are summarized in Fig. 2. Panel (a) shows that during the early stages (∝t_ζB), there is a small adjustment of the magnetic field. This is expected, as growing the density perturbations up to |δn_i|/n_i ∼ b² (for i = n, c) implies spatial displacements of a fraction ∼b² of the core radius thus the magnetic field strength is expected to be reduced by a similar fraction. We also see that, while the early dynamics is dominated by the artificial friction, the three simulations converge to the same curve at t ∼ t_ζB∝ζ. This can be seen more clearly in panel (b). The convergence of |$\boldsymbol{v_\mathrm{ n}}$| for simulations with very different values of ζ confirms that the scheme is indeed yielding the expected results, namely f_ζ∝ζ, thus reproducing the correct ‘physical’ neutron velocity on time-scales t ∼ t_ζB, independent of the value used for ζ (as long as it is sufficiently small). The good agreement of the three curves after this time suggests that all three values chosen for ζ are adequate for our purpose. To be on the safe side, we will use ζ ∼ 10⁻³ to perform long-term simulations (reaching t ∼ t_ad), as it still yields manageable integration times.

$Comparison of the evolution of simulations using the initial condition from equation (55) and three different values of ζ (10−2, 10−3, and 10−4), which yield the following ratios between the different relevant time-scales at the centre of the star: tζp: tζg: tζB: tad = 1: 16.45: 1645: 1.645 × 105 (continuous line), =1: 16.45: 1645: 1.645 × 106 (dashed), and =1: 16.45: 1645: 1.645 × 107 (dotted), respectively. The vertical lines show the value of the time-scale tζB for each simulation. We show the time evolution of (a) the magnetic field $\langle \boldsymbol{B} \rangle$ in units of B0, where 〈.〉 denotes rms in the volume of the core, (b) the neutron velocity $\langle \boldsymbol{v_\mathrm{ n}} \rangle$, (c) the ambipolar diffusion velocity $\langle \boldsymbol{v_{\mathrm{ ad}}} \rangle$, and (d) the ratio $\langle \boldsymbol{\nabla }\cdot (n_i\boldsymbol{v_{i}})\rangle /\langle [\boldsymbol{\nabla }\!\times \!(n_i\boldsymbol{v_{i}})]_\phi \rangle$ for neutrons (i = n, black lines), and charged particles (i = c, grey lines).$

Figure 2.

Comparison of the evolution of simulations using the initial condition from equation (55) and three different values of ζ (10⁻², 10⁻³, and 10⁻⁴), which yield the following ratios between the different relevant time-scales at the centre of the star: t_ζp: t_ζg: t_ζB: t_ad = 1: 16.45: 1645: 1.645 × 10⁵ (continuous line), =1: 16.45: 1645: 1.645 × 10⁶ (dashed), and =1: 16.45: 1645: 1.645 × 10⁷ (dotted), respectively. The vertical lines show the value of the time-scale t_ζB for each simulation. We show the time evolution of (a) the magnetic field |$\langle \boldsymbol{B} \rangle$| in units of B₀, where 〈.〉 denotes rms in the volume of the core, (b) the neutron velocity |$\langle \boldsymbol{v_\mathrm{ n}} \rangle$|⁠, (c) the ambipolar diffusion velocity |$\langle \boldsymbol{v_{\mathrm{ ad}}} \rangle$|⁠, and (d) the ratio |$\langle \boldsymbol{\nabla }\cdot (n_i\boldsymbol{v_{i}})\rangle /\langle [\boldsymbol{\nabla }\!\times \!(n_i\boldsymbol{v_{i}})]_\phi \rangle$| for neutrons (i = n, black lines), and charged particles (i = c, grey lines).

Open in new tab Download slide

It is usually assumed in the literature that during the long-term evolution of the field, the time derivatives in the continuity equations are negligible (Goldreich & Reisenegger 1992; Gusakov et al. 2017). Since in our approach we are explicitly evolving the fluid perturbations, it is interesting to see if our scheme confirms this assumption. Neglecting time derivatives in equations (22) and (23) implies that both |$n_\mathrm{ n}\boldsymbol{v_\mathrm{ n}}$| and |$n_\mathrm{ c}\boldsymbol{v_\mathrm{ c}}$| will be perfectly solenoidal during the long-term evolution. The simulation shown in the next subsection (see Figs. 3d and e at t = t_ζB) suggests that |$\boldsymbol{v_\mathrm{ n}}$| and |$\boldsymbol{v_\mathrm{ c}}=\boldsymbol{v_\mathrm{ n}}+\boldsymbol{v_{\mathrm{ ad}}}$| are indeed mostly solenoidal. This becomes even clearer from Fig. 2(d). For neutrons

$$\begin{eqnarray*} \frac{\boldsymbol{\nabla }\cdot (n_\mathrm{ n}\boldsymbol{v_{\mathrm{ n}}})}{[\boldsymbol{\nabla }\!\times \!(n_\mathrm{ n}\boldsymbol{v_{\mathrm{ n}}})]_\phi }\sim \frac{\delta n_\mathrm{ n}/t_{\zeta B}}{n_\mathrm{ n} v_{\mathrm{ n}}/L}\sim \frac{\delta n_\mathrm{ n}}{n_\mathrm{ n}} \sim \frac{B^2}{4\pi K_{\mathrm{ nn}}n_\mathrm{ n}^2}\sim \frac{b^2}{16}, \end{eqnarray*}$$

(56)

which roughly agrees with our results. Similarly, for charged particles, |$\boldsymbol{\nabla }\cdot (n_\mathrm{ c}\boldsymbol{v_{\mathrm{ c}}})/[\boldsymbol{\nabla }\!\times \!(n_\mathrm{ c}\boldsymbol{v_{\mathrm{ c}}})]_\phi \sim \delta n_\mathrm{ c}/n_\mathrm{ c}\sim b^2$|⁠. These estimates are in agreement with the arguments used in the literature to neglect the time derivatives (Goldreich & Reisenegger 1992; Gusakov et al. 2017). As δn_i/n_i scales with b² (i = n, c), it is expected that both approaches are equivalent when running simulations using realistic values of b (10⁻²⁰ < b² < 10⁻⁴); however, this is not possible at the moment, due to computing time constraints.

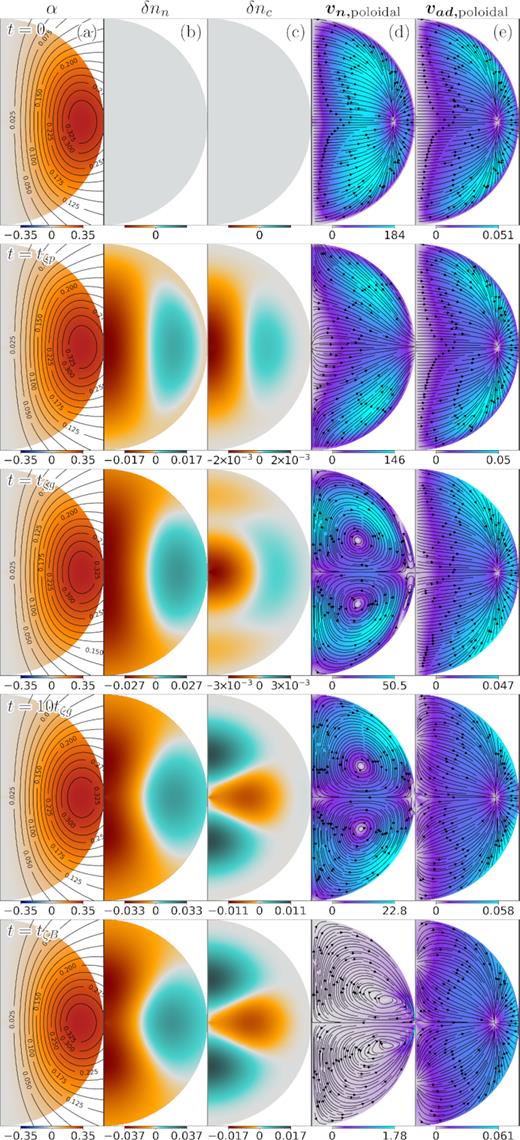
$Evolution of the magnetic field discussed in Section 3.2.1, with initial conditions set by α from equation (55) and β = 0, and parameters ζ = 10−4 and b2 = 10−2, yielding time-scales at the centre of the star in proportions tζp: tζg: tζB: tad = 1: 16.45: 1645: 1.645 × 107. We used a grid of Nr = 60 radial steps and Nθ = 91 polar steps inside the core, as well as NExp = 27 external multipoles. From left to right: (a) Configuration of the magnetic field, where lines represent the poloidal magnetic field and the colours the poloidal potential α; (b) and (c) density perturbations δnn and δnc, respectively, normalized to nc0; (d) and (e) poloidal component of the neutron velocity, $\boldsymbol{v_{\mathrm{ n}}}$, and ambipolar diffusion velocity, $\boldsymbol{v_{\mathrm{ ad}}}$, where arrows represent the direction and colours the magnitude normalized to R/t0. Rows correspond to different times: t = 0, tζp, tζg, 10tζg, and tζB.$

Figure 3.

Evolution of the magnetic field discussed in Section 3.2.1, with initial conditions set by α from equation (55) and β = 0, and parameters ζ = 10⁻⁴ and b² = 10⁻², yielding time-scales at the centre of the star in proportions t_ζp: t_ζg: t_ζB: t_ad = 1: 16.45: 1645: 1.645 × 10⁷. We used a grid of N_r = 60 radial steps and N_θ = 91 polar steps inside the core, as well as N_Exp = 27 external multipoles. From left to right: (a) Configuration of the magnetic field, where lines represent the poloidal magnetic field and the colours the poloidal potential α; (b) and (c) density perturbations δn_n and δn_c, respectively, normalized to n_c0; (d) and (e) poloidal component of the neutron velocity, |$\boldsymbol{v_{\mathrm{ n}}}$|⁠, and ambipolar diffusion velocity, |$\boldsymbol{v_{\mathrm{ ad}}}$|⁠, where arrows represent the direction and colours the magnitude normalized to R/t₀. Rows correspond to different times: t = 0, t_ζp, t_ζg, 10t_ζg, and t_ζB.

Open in new tab Download slide

It remains to be seen if the fictitious force is indeed negligible during the long-term evolution of the field, and if our estimates for the different time-scales of evolution are in agreement with our results. This will be addressed in the following section.

3.2 Hydro-magnetic evolution

3.2.1 Reaching hydro-magnetic quasi-equilibrium with a purely poloidal configuration

In this section, we study the process in which the fictitious friction rearranges the particle densities and magnetic field to reach hydro-magnetic quasi-equilibrium, checking if the associated time-scales agree with the analytical estimates of Section 2.6. For this purpose, we perform a simulation using the same initial condition as in the previous section (see equation 55). The initial condition and some snapshots of its evolution are shown in Fig. 3.

The short time-scales t_ζp and t_ζg (equations 38 and 39, respectively) are associated with a quick adjustment of the densities in the presence of a magnetic force, nevertheless they do not explicitly depend on the magnetic field strength. As they are much shorter than the time-scales for magnetic field evolution, the magnetic field remains essentially unchanged during this process. Although in our simulations we use an unrealistically high value of b, the value chosen is still small enough to understand the dynamics of the fluid motion, since t_ζp/t_ζB = 6 × 10⁻⁴. Also, here we are only interested in the dynamics on time-scales ∼t_ζB, thus we can use small values of ζ without changing the total integration time as the required number of time-steps will be ∝t_ζB/t_ζp, independent of ζ. Therefore, we will focus, as suggested before, on the simulation with ζ = ζ₃ = 10⁻⁴.

We can see that, as expected, at short times (∼t_ζp), the magnetic field pushes the fluid, which grows density perturbations δn_n(r, θ) and δn_c(r, θ) with similar structure, in particular the same sign, as would happen in sound waves (p-modes, in asteroseismology jargon). At later times (∼t_ζg), although by construction the two species are still mostly moving together (as |$\boldsymbol{v_{\mathrm{ n}}} \gg \boldsymbol{v_{\mathrm{ ad}}}$|⁠, since we are still out of quasi-equilibrium, implying |$\boldsymbol{v_\mathrm{ n}} \approx \boldsymbol{v_\mathrm{ c}}$|⁠), their different background density profiles (n_c(r)/n_n(r) ≠ constant) together with a non-trivial velocity field |$\boldsymbol{v}_\mathrm{ n}(r,\theta)$| allow their continuity equations (44) and (45) to create density perturbations not necessarily of the same signs (as they would have in so-called ‘gravity waves’ or ‘g modes’, e.g. Reisenegger & Goldreich 1992), allowing their different fluid forces to jointly balance both components of the poloidal magnetic force (see panels at t = t_ζg and t = 10t_ζg). This leads joint radial motions to be opposed by strong buoyancy forces (Pethick 1992; Goldreich & Reisenegger 1992). Thus, the two components jointly behave as a single, stably stratified, non-barotropic fluid.

The strength of the magnetic and fluid forces throughout the simulation can be seen in Fig. 4. At early stages (∼t_ζp), the magnetic force is partially balanced by the fluid force of the neutrons, while the contribution of the charged particles is much smaller. This is because at this stage the charged particles and neutrons at any point in the star are jointly compressed or expanded by the magnetic force (with δn_c(r, θ)/n_c(r) ∼ δn_n(r, θ)/n_n(r)). Since there are many more neutrons than charged particles present, they represent the main contribution to the pressure of the fluid. At later times (∼t_ζg), the neutron and charged-particle density perturbations become very different and the latter also contribute substantially to the fluid force. At first, it may be surprising that the two fluid forces do not act in the same direction, opposite to the magnetic force. Instead, they grow very different density perturbations that, acting together, balance the magnetic force (see the red line). It is clear from Section 2.6.1 that to reach this kind of force balance, density perturbations of similar magnitude (but not necessarily of the same sign) are required. The relative smallness of f_ζ in Fig. 5(d), shows that this force balance is being reached. Nevertheless, as the magnetic flux is slowly being carried by the motion of the fluid, a perfect force balance cannot be reached, as seen in Fig. 4: After their fast initial growth (in a time-scale ∼t_ζg), the fluid forces reach a plateau. However, as the magnetic field evolves (on a much slower time-scale), the particles have to keep up, thus evolving at the same rate as the magnetic field, until the latter reaches a new quasi-equilibrium configuration at times ∼t_ζB. At this point, all forces are close to balancing, and the fictitious friction becomes negligible compared to all of the physical forces (|f_ζ|/min{|f_B|, |f_c|, |f_n|}∝ζ/γ_cnn_c). Thus, at this point the fictitious force plays no significant role in the evolution of the field, other than giving us a way of computing the neutron velocity field needed to maintain the quasi-equilibrium condition f_ζ ∼ 0. It is also worth noting that the topology of the velocity fields at this point is consistent with the results from Ofengeim & Gusakov (2018) (see Fig. 3d and e at t = t_ζB), although a quantitative comparison is not possible since our toy-model equation of state does not consider entrainment.

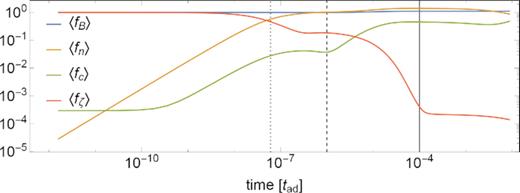
$For the simulation of Fig. 3: Time evolution of the force densities $\langle \boldsymbol{f_B} \rangle$, $\langle \boldsymbol{f_\mathrm{ n}} \rangle$, $\langle \boldsymbol{f_\mathrm{ c}} \rangle$ and $\langle \boldsymbol{f_\zeta } \rangle$, all of them normalized by $\langle \boldsymbol{f_B}(t=0)\rangle$, where 〈.〉 denotes rms in the volume of the core. Time is in units of tad. The vertical lines show, from left to right, the values of the time-scales tζp, tζg, and tζB.$

Figure 4.

For the simulation of Fig. 3: Time evolution of the force densities |$\langle \boldsymbol{f_B} \rangle$|⁠, |$\langle \boldsymbol{f_\mathrm{ n}} \rangle$|⁠, |$\langle \boldsymbol{f_\mathrm{ c}} \rangle$| and |$\langle \boldsymbol{f_\zeta } \rangle$|⁠, all of them normalized by |$\langle \boldsymbol{f_B}(t=0)\rangle$|⁠, where 〈.〉 denotes rms in the volume of the core. Time is in units of t_ad. The vertical lines show, from left to right, the values of the time-scales t_ζp, t_ζg, and t_ζB.

Open in new tab Download slide

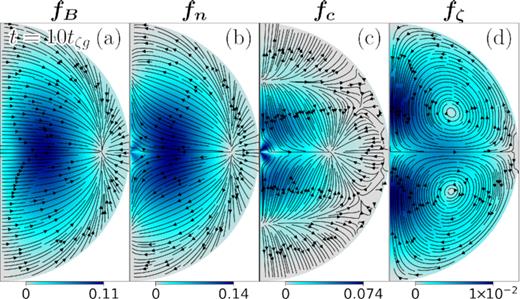
$From left to right: Snapshot of (a) $\boldsymbol{f_B}$, (b) $\boldsymbol{f_\mathrm{ n}}$, (c) $\boldsymbol{f_\mathrm{ c}}$, and (d) $\boldsymbol{f_\zeta }$ for the simulation of Fig. 3 at t = 10tζg. Arrows represent the direction of the forces at each point, and colours their magnitudes.$

Figure 5.

From left to right: Snapshot of (a) |$\boldsymbol{f_B}$|⁠, (b) |$\boldsymbol{f_\mathrm{ n}}$|⁠, (c) |$\boldsymbol{f_\mathrm{ c}}$|⁠, and (d) |$\boldsymbol{f_\zeta }$| for the simulation of Fig. 3 at t = 10t_ζg. Arrows represent the direction of the forces at each point, and colours their magnitudes.

Open in new tab Download slide

3.2.2 Long-term magnetic field evolution of a poloidal and toroidal configuration

In the previous sections, we studied simulations of a purely poloidal magnetic field, which is known to be unstable to non-axisymmetric perturbations (Markey & Tayler 1973; Flowers & Ruderman 1977; Marchant, Reisenegger & Akgün 2011). Thus, in order to study the long-term evolution, we now consider a simulation for the much more realistic case of a field with poloidal and toroidal components. This allows us to check whether the time-scales for the magnetic field evolution from Section 2.6 (equations 40 and 41) are in agreement with our numerical scheme, but mainly, it allows us to study the impact of the neutron motions on the long-term evolution of the magnetic field.

In addition to the dipolar potential α₁ defined in Section 3.1, we now consider an additional quadrupolar poloidal potential,

$$\begin{eqnarray*} \alpha _2(r,\theta)=\alpha _{02}r^3\left(1 -\frac{10}{7}r^2 +\frac{5}{9}r^4 \right)\sin ^2\theta \cos \theta, \end{eqnarray*}$$

(57)

where α₀₂ = 1.239 is a normalization constant, fixed by the condition 〈B_Pol〉 = 1, and a toroidal potential

$$\begin{eqnarray*} \beta _1(r,\theta)=\beta _{01}r^5(1 -r)^2\sin ^2\theta \sin (\theta -\pi /5), \end{eqnarray*}$$

(58)

where β₀₁ = 112.546 is fixed by the condition 〈B_Tor〉 = 1. We choose the initial condition as

$$\begin{eqnarray*} \alpha (r,\theta) = \sqrt{0.18}\alpha _1(r,\theta)+\sqrt{0.42}\alpha _2(r,\theta), \end{eqnarray*}$$

(59)

$$\begin{eqnarray*} \beta (r,\theta) = \sqrt{0.4}\beta _1(r,\theta), \end{eqnarray*}$$

(60)

so the toroidal magnetic field has 40 per cent of the initial internal magnetic energy. The artificial friction is set to ζ = 3 × 10⁻³, which yields an initial ratio 〈v_n〉/〈v_ad〉 ∼ 130.

The initial configuration, as well as some snapshots of its evolution, are shown in Fig. 6. We see how at t = t_ζp the density perturbations grow together following δn_c/n_c ∼ δn_n/n_n, while at t = t_ζg they are evolving towards a state in which their signs are not correlated, thus reproducing the results from the previous section. This can also be observed in Fig. 7(a), which shows the rms of the different fluid forces throughout the simulation. During the first stages of the evolution (t ∼ t_ζp–t_ζg), the magnetic force is partially balanced by the fluid forces, which are dominated by the neutrons.

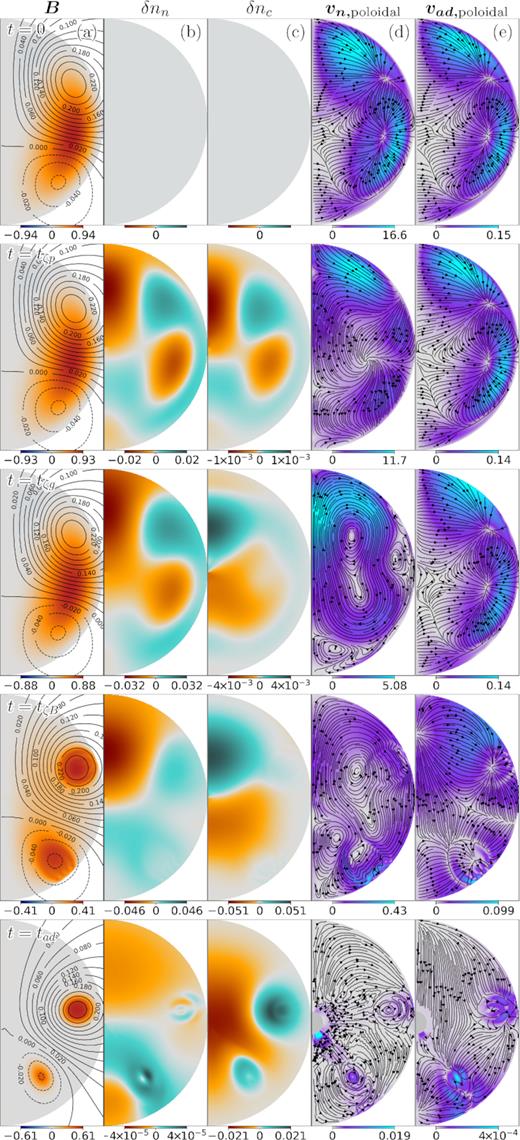
$Evolution of the magnetic field discussed in Section 3.2.2 with initial conditions given by equations (59) and (60) (so the poloidal component has 60 per cent of the initial internal magnetic energy), and parameters ζ = 3 × 10−3 and b2 = 10−2. Thus, the time-scales at the centre of the star satisfy tζp: tζg: tζB: tad = 1: 16.45: 1645: 548500. We used a grid of Nr = 60 radial steps and Nθ = 91 polar steps inside the core, as well as NExp = 27 external multipoles. From left to right: (a) Configuration of the magnetic field, where lines represent the poloidal magnetic field (labelled by the magnitude of α) and colours the toroidal potential β; (b) and (c) density perturbations δnn and δnc, respectively, both normalized to nc0; (d) and (e) poloidal component of the neutron velocity, $\boldsymbol{v_\mathrm{ n}}$, and ambipolar diffusion velocity, $\boldsymbol{v_{\mathrm{ ad}}}$, where arrows represent the direction and colours the magnitude normalized to R/t0. Rows correspond to different times: t = 0, tζp, tζg, tζB, and tad.$

Figure 6.

Evolution of the magnetic field discussed in Section 3.2.2 with initial conditions given by equations (59) and (60) (so the poloidal component has 60 per cent of the initial internal magnetic energy), and parameters ζ = 3 × 10⁻³ and b² = 10⁻². Thus, the time-scales at the centre of the star satisfy t_ζp: t_ζg: t_ζB: t_ad = 1: 16.45: 1645: 548500. We used a grid of N_r = 60 radial steps and N_θ = 91 polar steps inside the core, as well as N_Exp = 27 external multipoles. From left to right: (a) Configuration of the magnetic field, where lines represent the poloidal magnetic field (labelled by the magnitude of α) and colours the toroidal potential β; (b) and (c) density perturbations δn_n and δn_c, respectively, both normalized to n_c0; (d) and (e) poloidal component of the neutron velocity, |$\boldsymbol{v_\mathrm{ n}}$|⁠, and ambipolar diffusion velocity, |$\boldsymbol{v_{\mathrm{ ad}}}$|⁠, where arrows represent the direction and colours the magnitude normalized to R/t₀. Rows correspond to different times: t = 0, t_ζp, t_ζg, t_ζB, and t_ad.

Open in new tab Download slide

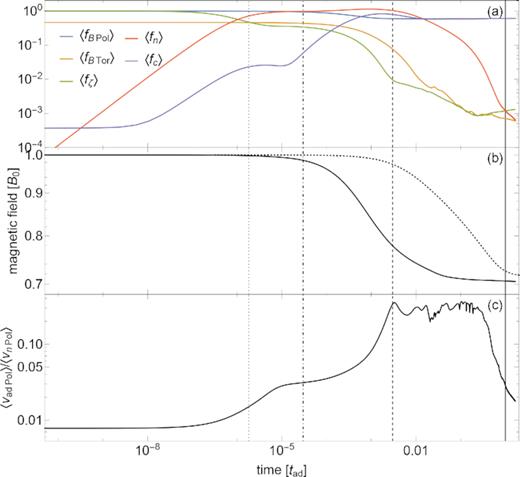
$For the simulation of Fig. 6: Time evolution of (a) the rms force densities $\langle \boldsymbol{f_{B\, \text{Pol}}} \rangle$, $\langle \boldsymbol{f_{B\, \text{Tor}}} \rangle$, $\langle \boldsymbol{f_\mathrm{ n}} \rangle$, $\langle \boldsymbol{f_\mathrm{ c}} \rangle$, and $\langle \boldsymbol{f_\zeta } \rangle$, all normalized by $\langle \boldsymbol{f_{B\, \text{Pol}}}(t=0)\rangle$, where 〈.〉 denotes rms in the volume of the core; (b) the rms magnetic field $\langle \boldsymbol{B} \rangle$ (in units of its initial value B0) in the NS core. The dotted line corresponds to $\langle \boldsymbol{B} \rangle$ on a simulation using the same initial condition, but taking ζ → ∞ (fixed neutrons); and (c) $\langle v_{\mathrm{ ad}\, \text{Pol}}\rangle /\langle v_{n\, \text{Pol}}\rangle$. For all panels, time is in units of tad. The vertical lines show, from left to right, the time-scales tζp, tζg, tζB, and tad.$

Figure 7.

For the simulation of Fig. 6: Time evolution of (a) the rms force densities |$\langle \boldsymbol{f_{B\, \text{Pol}}} \rangle$|⁠, |$\langle \boldsymbol{f_{B\, \text{Tor}}} \rangle$|⁠, |$\langle \boldsymbol{f_\mathrm{ n}} \rangle$|⁠, |$\langle \boldsymbol{f_\mathrm{ c}} \rangle$|⁠, and |$\langle \boldsymbol{f_\zeta } \rangle$|⁠, all normalized by |$\langle \boldsymbol{f_{B\, \text{Pol}}}(t=0)\rangle$|⁠, where 〈.〉 denotes rms in the volume of the core; (b) the rms magnetic field |$\langle \boldsymbol{B} \rangle$| (in units of its initial value B₀) in the NS core. The dotted line corresponds to |$\langle \boldsymbol{B} \rangle$| on a simulation using the same initial condition, but taking ζ → ∞ (fixed neutrons); and (c) |$\langle v_{\mathrm{ ad}\, \text{Pol}}\rangle /\langle v_{n\, \text{Pol}}\rangle$|⁠. For all panels, time is in units of t_ad. The vertical lines show, from left to right, the time-scales t_ζp, t_ζg, t_ζB, and t_ad.

Open in new tab Download slide

In the fourth row of Fig. 6 (at t = t_ζB), it can be seen how the magnetic field unwinds, eliminating most of the toroidal component, except in the regions of closed poloidal field lines. As discussed in paper I, such ‘twisted-torus’ configurations are expected in axially symmetric hydro-magnetic equilibria, because there is no toroidal pressure gradient or gravitational force available to balance a toroidal component of the Lorentz force. This implies the restriction β = β(α) on the potentials, which is also verified in the figure (see also Fig. 8). This state corresponds to a non-barotropic quasi-equilibrium, as both charged particles and neutrons, which have different fluid forces, are contributing to balance the magnetic force. This can be seen more clearly in Fig. 7(a), where the poloidal magnetic force and fluid forces are all of the same order, but the poloidal force imbalance |$\langle \boldsymbol{f_{\zeta ,\text{Pol}}} \rangle$| is much smaller, meaning that in the poloidal component there is a balance between the magnetic force and the induced fluid forces. In the toroidal component, |$\boldsymbol{f_{\zeta ,\text{Tor}}}=\boldsymbol{f_{B,\text{Tor}}}$| always, but at t_ζB this force has become much smaller than its initial value. Thus, the configuration at t ∼ t_ζB is very close to a (non-barotropic) hydro-magnetic quasi-equilibrium where even the toroidal component of friction force has become small.

Figure 8.

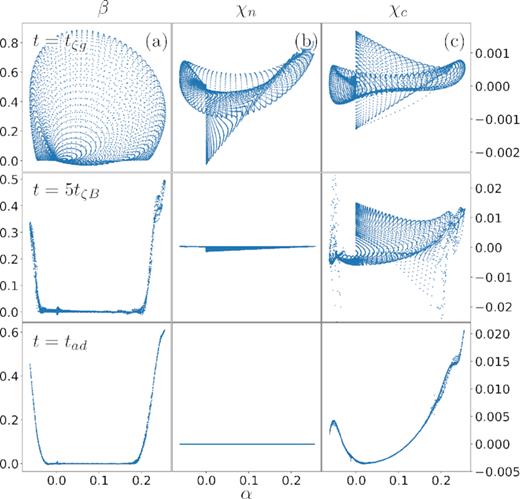
For the simulation of Fig. 6: Scatter plot of α versus (a) β, (b) χ_n, and (c) χ_c, showing all of the grid points at t = t_ζg, t = 5t_ζB, and t = t_ad, respectively. The axis label on the left side of the figure corresponds to plot (a), while that on the right corresponds to (b) and (c).

Open in new tab Download slide

On a much longer time-scale, this quasi-equilibrium is slowly eroded by ambipolar diffusion. Charged particles, pushed by the magnetic force, carry the magnetic flux relative to the neutrons until the magnetic force can be balanced by the force due to the density perturbations of the charged particles alone, choking the motion. This can be seen in the last row of Fig. 6 (t = t_ad), where the ambipolar velocity is much smaller than at t_ζB. Also, |δn_c|/n_c ≫ |δn_n|/n_n, confirming that the magnetic force is mostly balanced by the charged particles. This is further supported by Fig. 7(a), which shows a transition from t = t_ζB, where the magnetic force is balanced by the combined force from charged particles and neutrons, to t = t_ad, where it is balanced mostly by the charged particles, while the contribution from the neutrons becomes negligible.

However, this does not mean that the neutron motion is irrelevant to the long-term evolution. While ambipolar diffusion pushes the charged particles relative to the neutrons, all components (neutrons, charged particles, and the magnetic field) have to keep adjusting to successive quasi-equilibria, thus inducing a slow macroscopic motion of the fluid. This motion (controlled by the drag force between neutrons and charged particles) gives the charged particles an extra push, shortening the time-scale for the long-term magnetic evolution (∼L/v_c). This can be seen in Fig. 7(b), where the decay of the magnetic field in the simulation with mobile neutrons is much faster than in a simulation with the same initial condition, but with fixed neutrons.

As discussed in Section 2.6, we expect that in the quasi-stationary state |∂δn_c/∂t| is much smaller than both |$|\boldsymbol{\nabla }\cdot \left(n_\mathrm{ c}\boldsymbol{v_{\mathrm{ ad}}}\right)|$| and |$|\boldsymbol{\nabla }\cdot \left(n_\mathrm{ c}\boldsymbol{v_\mathrm{ n}}\right)|$|⁠. Thus, the irrotational components of |$n_\mathrm{ c}\boldsymbol{v_\mathrm{ n}}$|⁠, and |$n_\mathrm{ c}\boldsymbol{v_{\mathrm{ ad}}}$| are of the same order. However, as pointed out in Section 3.1, both vector fields are dominated by their solenoidal component, and Fig. 7(c) shows that, during the long-term evolution from t_ζB to t_ad, v_n becomes larger than v_ad by a factor ∼4. Similar fractions were found for different simulations in our tests. This is in agreement with the results of Ofengeim & Gusakov (2018). In Fig. 7(c) we also see that, towards the end on the simulation, the core is reaching equilibrium, thus |$\boldsymbol{v_{\mathrm{ ad}}}$| gets progressively smaller, faster than |$\boldsymbol{v_\mathrm{ n}}$|⁠. Sadly, at this point the numerical noise starts to become dominant towards the centre of the star, where the coordinate system is singular (see Fig. 6[d] at t = t_ad).

3.3 Grad–Shafranov equilibria

We saw that, within a few t_ζB, the NS core reaches a hydro-magnetic quasi-equilibrium in which all forces are close to balance. As described in the previous section, this implies that the toroidal magnetic force must vanish, since there are no other azimuthal forces available to balance it, so

$$\begin{eqnarray*} \boldsymbol{\nabla }\alpha \times \boldsymbol{\nabla }\beta =0, \end{eqnarray*}$$

(61)

requiring (at least locally) a relation β = β(α). This can be verified in Fig. 8, where at early times (∼t_ζg) there is no clear relation between the variables, while at ∼t_ζB there is an evident dependence of β on α. However, at that time, no similar relations are found for other variables, such as δn_i or δμ_i (i = n, c).

At later times (∼t_ad), the velocities become much smaller than their initial value, suggesting that the system is approaching an equilibrium state in which both |$\boldsymbol{v_\mathrm{ n}}=0$| and |$\boldsymbol{v_{\mathrm{ ad}}}=0$|⁠. The first condition implies |$\boldsymbol{f_{B}}+\boldsymbol{f_{\mathrm{ n}}}+\boldsymbol{f_{\mathrm{ c}}}=0$|⁠, while the second implies |$\boldsymbol{f_{B}}+\boldsymbol{f_{\mathrm{ c}}}=0$| (see equations 24 and 25). As the toroidal magnetic force is already negligible at this point, this requires

$$\begin{eqnarray*} \frac{\boldsymbol{J}}{c}\times \boldsymbol{B}-n_\mathrm{ c}\mu \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ c}}{\mu }\right)=0, \end{eqnarray*}$$

(62)

$$\begin{eqnarray*} \boldsymbol{\nabla }\left(\frac{\delta \mu _\mathrm{ n}}{\mu }\right)=0, \end{eqnarray*}$$

(63)

implying that the neutrons are in diffusive equilibrium (unperturbed by the presence of the magnetic field), while the forces due to the charged-particle density perturbations must balance the Lorentz force. This, together with equation (61), implies that χ_c ≡ δμ_c/μ must also be a function of α (while χ_n ≡ δμ_n/μ must be uniform). This can be verified in Fig. 8, where at early times (∼t_ζg and ∼t_ζB) there is no clear relation between the variables, while at later times (∼t_ad) there is an evident dependence on α for β and χ_c, while χ_n ≈ 0.

As discussed previously (Lander & Jones 2009, 2012; Reisenegger 2009; Armaza et al. 2015; Castillo et al. 2017), equation (61) can be used to rewrite equation (62) as a ‘Grad–Shafranov (GS) equation’ (Grad & Rubin 1958; Shafranov 1966)

$$\begin{eqnarray*} \Delta ^*\alpha +\beta \beta ^{\prime } + 4\pi r^2\sin ^2\theta \, n_\mathrm{ c}(r)\mu (r)\chi _\mathrm{ c}^{\prime } = 0, \end{eqnarray*}$$

(64)

where

$$\begin{eqnarray*} \Delta ^* &\equiv& r^2\sin ^2\theta \boldsymbol{\nabla }\cdot \left(\frac{\boldsymbol{\nabla }}{r^2\sin ^2\theta }\right) \nonumber\\ &=& \frac{\partial ^2}{\partial r^2} + \frac{\sin \theta }{r^2} \frac{\partial }{\partial \theta }\left(\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\right), \end{eqnarray*}$$

(65)

is the ‘GS operator’, β and χ_c are functions of α(r, θ), and primes denote derivatives with respect to α. We emphasize that (as seen in Fig. 8) this equation is generally not satisfied in the previous stage (at t ∼ t_ζB), which is also a hydro-magnetic quasi-equilibrium, but with neutrons and charged particles collisionally coupled and thus jointly balancing the Lorentz force.

In order to check if our simulations lead to configurations in which the GS equation (64) is satisfied in the expected time-scale (a few t_ad), we evaluate the ‘GS integral’

$$\begin{eqnarray*} \Gamma =\frac{\int _V \mathrm{ d}^3x\left|\Delta ^*\alpha +\beta \beta ^{\prime } + 4\pi r^2\sin ^2\theta \, n_\mathrm{ c}\mu \chi ^{\prime } \right|}{V\max \left|\Delta ^*\alpha \right|}, \end{eqnarray*}$$

(66)

where the derivatives on α are computed from our simulations taking |$\beta ^{\prime }=(\boldsymbol{\nabla }\beta \cdot \boldsymbol{\nabla }\alpha)/|\boldsymbol{\nabla }\alpha |^2$|⁠, and |$\chi _\mathrm{ c}^{\prime }=(\boldsymbol{\nabla }\chi _\mathrm{ c}\cdot \boldsymbol{\nabla }\alpha)/|\boldsymbol{\nabla }\alpha |^2$|⁠. Figs 7(b) and 9(a) show that, in the time interval t_ζB < t < t_ad the rms magnetic field strength (and thus square root of the internal magnetic energy) decays only from |$78{{\ \rm per\ cent}}$| to |$71{{\ \rm per\ cent}}$|⁠, the external magnetic energy decays from |$87{{\ \rm per\ cent}}$| to |$48{{\ \rm per\ cent}}$| of its initial value, and Γ decays from |$30{{\ \rm per\ cent}}$| to |$0.5{{\ \rm per\ cent}}$| of its initial value, clearly showing that the magnetic field configuration approaches a GS equilibrium in t ∼ t_ad. Fig. 9(b) shows that during this process the poloidal magnetic field, which is initially a combination of dipolar (ℓ = 1) and quadrupolar (ℓ = 2) components, evolves towards a mostly dipolar configuration, where the quadrupolar component becomes progressively smaller, as an octupolar (ℓ = 3) component increases, reaching a similar magnitude in the final equilibrium. It can also be seen that the contribution of higher multipoles is negligible. Further simulations are required to check if this behaviour is generic. The results provided here may be a valuable resource for improving crustal magnetic field evolution models, which usually use boundary conditions relying on unphysical assumptions, such as crust confinement.

Figure 9.

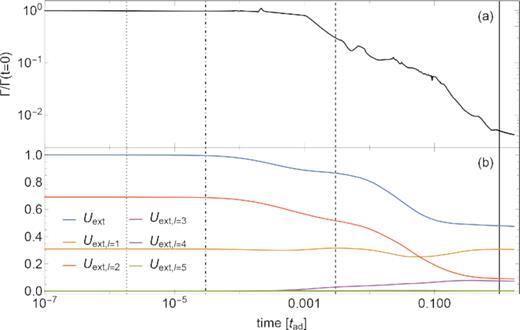
For the simulation of Fig. 6: Time evolution of (a) the ‘Grad–Shafranov integral’ Γ (defined in equation 66) and (b) the magnetic energy stored in the ℓ-th component of the external magnetic field (see equation 31). The vertical lines show, from left to right, the time-scales t_ζp, t_ζg, t_ζB, and t_ad.

Open in new tab Download slide

4 CONCLUSIONS

In paper I, we studied the long-term evolution of the magnetic field of an NS through ambipolar diffusion, modelling its core as a charged-particle fluid of protons and electrons, which carries the magnetic flux through a motionless uniform background of neutrons. In this paper, we addressed two of the main shortcomings of that work by allowing neutrons to move as well as including different density gradients for neutrons and charged particles, thus accounting for their stable stratification.

We know that the star can reach a hydro-magnetic quasi-equilibrium many orders of magnitude faster than the magnetic field evolution time-scales. To maintain quasi-equilibrium realistically during the evolution of the field would require following the propagation of sound, gravity, and Alfvén waves. Resolving such processes would make it impossible to simulate the long-term evolution of the field. We have addressed this issue by adding a fictitious friction force to the equation of motion of the neutrons (Hoyos et al. 2008). This force, which causes a neutron velocity proportional to the net force imbalance at each point, replaces the very small inertial terms present in the equations of motions, and provides a mechanism to maintain the hydro-magnetic quasi-equilibrium.

Our results can be summarized as follows:

The addition of the fictitious friction in our simulations was found to be a useful method to quickly reach and then maintain the hydro-magnetic quasi-equilibrium of the star without having to resolve the propagation of sound, gravity, and Alfvén waves, leading to the same kind of non-barotropic ‘twisted torus’ quasi-equilibrium previously found in MHD simulations (Braithwaite & Spruit 2004; Braithwaite & Nordlund 2006) in a time-scale t_ζB that can be adjusted to make the simulations both doable and physically interesting.
We found good agreement between different expected time-scales involved in this process (t_ζp, t_ζg, and t_ζB), and simulations. The long-term evolution of the magnetic field is not significantly affected by the fictitious friction force if the ratio between the time-scale in which the hydro-magnetic quasi-equilibrium is restored by this artificial friction and the time-scale of ambipolar diffusion is small enough (t_ζB/t_ad ∼ ζ/γ_cnn_c ≲ 10⁻³ in our simulations).
Relaxing the unrealistic assumption of fixed neutrons was found to impact the long-term evolution of the magnetic field in the following way: Since the density profiles of neutrons and charged particles are different, joint motion of the two species is strongly constrained by buoyancy forces. Thus, there will always be relative motions between species (i.e. ambipolar diffusion). This process, in which the magnetic force pushes the charged particles and magnetic flux relative to the neutrons, slowly erodes the hydro-magnetic quasi-equilibrium; therefore neutrons, charged particles, and the magnetic field have to continuously adjust to restore it. This motion makes the charged particles (and thus the magnetic flux) move faster than in the case of fixed neutrons, thus shortening the time-scale for magnetic evolution. In our simulations we find that the speed of neutrons and charged particles can be ∼1–10 times larger than their relative velocity, yielding a time-scale
$$\begin{eqnarray*} t_{\mathrm{ ad}} \sim (0.3 - 3)\times 10^{3} \, \left(\frac{10^{15}\text{G}}{B}\right)^{2}\left(\frac{T}{10^8\,\text{K}}\right)^{2}\left(\frac{L}{1\,\text{km}}\right)^{2}\, \text{yr} \end{eqnarray*}$$
(67)
for the long-term evolution of the field.
The process described above leads to a final equilibrium state in which the magnetic force is balanced by the pressure and gravitational forces of the charged particles, while the neutron density perturbations become negligible, thus recovering the barotropic ‘Grad–Shafranov equilibria’ from paper I.

The following two main caveats need to be addressed by future work:

It is likely that the magnetic equilibria found may become unstable if we relax the axial symmetry restriction, as previous works indicate that there are no stable hydro-magnetic equilibria in barotropic stars (Braithwaite 2009; Akgün et al. 2013; Mitchell et al. 2015). In that case ambipolar diffusion might dissipate all the magnetic flux, so the low magnetic field of millisecond pulsars might be explained by magnetic flux dissipation prior to accretion (Cruces et al. 2019). However, if the charged particles also include muons, the charged fluid will no longer be barotropic, which may help to stabilize the magnetic field.
NS matter is expected to be superfluid and superconducting at the temperatures of interest, which might have a major impact on the time-scales described here, as the coupling between the different species should, in principle, be many orders of magnitude smaller. The dynamics of the field evolution might also be quite different from what we presented here, as the macroscopic effect of the dynamics and interactions between quantized neutron vortices and magnetic flux tubes needs to be taken into account.
In this work, we assumed a potential solution for the crustal and external magnetic field, thus assuming that the crust adjusts instantaneously to the evolution in the core. However, if the crust is highly conductive, this may not be the case as currents may keep circulating in the crust, leading to non-trivial configurations (see for instance Cumming, Arras & Zweibel 2004; Pons & Geppert 2007; Gourgouliatos, Wood & Hollerbach 2016; Akgün et al. 2018). Ultimately, this might indicate that it is the crust which sets the time-scale for the evolution of the external field, leading to more restrictive equilibrium configurations in the core.

ACKNOWLEDGEMENTS

We are very grateful to M. Gusakov, J. Pons, and the ANSWERS group in Santiago de Chile for useful discussions. This work was supported by the National Fund for Scientific and Technological Development (FONDECYT) projects 3180700 (FC), 1201582 (AR), and 1190703 (JAV), and the Center for Astrophysics and Associated Technologies (CATA; CONICYT/ANID project Basal AFB-170002). JAV thanks for the support of the Center for the Development of Nanoscience and Nanotechnology (CEDENNA) under CONICYT/ANID grant FB0807.

DATA AVAILABILITY

The data underlying this article will be shared on reasonable request to the corresponding author.

Footnotes

1

Formally, equations (22) to (30) can be rewritten as a system of two coupled diffusion equations for δn_n and δn_c with an inhomogeneous term linear in |$\boldsymbol{f_B}$| (which can be taken as a constant in this regime) and diffusion coefficients (and thus characteristic time-scales) independent of |$\boldsymbol{B}$|⁠.

REFERENCES

Akgün

T.

,

Reisenegger

A.

,

Mastrano

A.

,

Marchant

P.

,

2013

,

MNRAS

,

433

,

2445

10.1093/mnras/stt913

Crossref

Search ADS

Akgün

T.

,

Cerdá-Durán

P.

,

Miralles

J. A.

,

Pons

J. A.

,

2018

,

MNRAS

,

481

,

5331

10.1093/mnras/sty2669

Crossref

Search ADS

Akmal

A.

,

Pandharipande

V. R.

,

Ravenhall

D. G.

,

1998

,

Phys. Rev. C

,

58

,

1804

10.1103/PhysRevC.58.1804

Crossref

Search ADS

Armaza

C.

,

Reisenegger

A.

,

Valdivia

J. A.

,

2015

,

ApJ

,

802

,

121

10.1088/0004-637X/802/2/121

Crossref

Search ADS

Backer

D. C.

,

Kulkarni

S. R.

,

Heiles

C.

,

Davis

M. M.

,

Goss

W. M.

,

1982

,

Nature

,

300

,

615

10.1038/300615a0

Crossref

Search ADS

Bhattacharya

D.

,

1991

,

Phys. Rep.

,

203

,

1

10.1016/0370-1573(91)90064-S

Crossref

Search ADS

Bhattacharya

D.

,

1995

, in

Lewin

W. H. G.

,

van Paradijs

J.

,

van den Heuvel

E. P. J.

, eds,

X-Ray Binaries

.

Cambridge Univ. Press

,

Cambridge

, p.

233

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Braithwaite

J.

,

2009

,

MNRAS

,

397

,

763

10.1111/j.1365-2966.2008.14034.x

Crossref

Search ADS

Braithwaite

J.

,

Nordlund

Å.

,

2006

,

A&A

,

450

,

1077

10.1051/0004-6361:20041980

Crossref

Search ADS

Braithwaite

J.

,

Spruit

H. C.

,

2004

,

Nature

,

431

,

819

Bransgrove

A.

,

Levin

Y.

,

Beloborodov

A.

,

2018

,

MNRAS

,

473

,

2771

10.1093/mnras/stx2508

Crossref

Search ADS

Castillo

F.

,

Reisenegger

A.

,

Valdivia

J. A.

,

2017

,

MNRAS

,

471

,

507

(paper I)

10.1093/mnras/stx1604

Crossref

Search ADS

Cruces

M.

,

Reisenegger

A.

,

Tauris

T. M.

,

2019

,

MNRAS

,

490

,

2013

10.1093/mnras/stz2701

Crossref

Search ADS

Cumming

A.

,

Arras

P.

,

Zweibel

E.

,

2004

,

ApJ

,

609

,

999

10.1086/421324

Crossref

Search ADS

Dommes

V. A.

,

Gusakov

M. E.

,

2017

,

MNRAS

,

467

,

L115

10.1093/mnrasl/slx011

Crossref

Elfritz

J. G.

,

Pons

J. A.

,

Rea

N.

,

Glampedakis

K.

,

Viganò

D.

,

2016

,

MNRAS

,

456

,

4461

10.1093/mnras/stv2963

Crossref

Search ADS

Flowers

E.

,

Ruderman

M. A.

,

1977

,

ApJ

,

215

,

302

10.1086/155359

Crossref

Search ADS

Gamow

G.

,

Schoenberg

M.

,

1941

,

Phys. Rev.

,

59

,

539

10.1103/PhysRev.59.539

Crossref

Search ADS

Glampedakis

K.

,

Jones

D. I.

,

Samuelsson

L.

,

2011

,

MNRAS

,

413

,

2021

10.1111/j.1365-2966.2011.18278.x

Crossref

Search ADS

Goldreich

P.

,

Reisenegger

A.

,

1992

,

ApJ

,

395

,

250

10.1086/171646

Crossref

Search ADS

Gourgouliatos

K. N.

,

Cumming

A.

,

2014

,

MNRAS

,

446

,

1121

10.1093/mnras/stu2140

Crossref

Search ADS

Gourgouliatos

K. N.

,

Cumming

A.

,

Reisenegger

A.

,

Armaza

C.

,

Lyutikov

M.

,

Valdivia

J. A.

,

2013

,

MNRAS

,

434

,

2480

10.1093/mnras/stt1195

Crossref

Search ADS

Gourgouliatos

K. N.

,

Wood

T. S.

,

Hollerbach

R.

,

2016

,

Proc. Natl. Acad. Sci.

,

113

,

1522363113

10.1073/pnas.1522363113

Crossref

Search ADS

Graber

V.

,

Andersson

N.

,

Glampedakis

K.

,

Lander

S. K.

,

2015

,

MNRAS

,

453

,

671

10.1093/mnras/stv1648

Crossref

Search ADS

Grad

H.

,

Rubin

H.

,

1958

,

J. Nucl. Energy

,

7

,

284

10.1016/0891-3919(58)90139-6

Crossref

Gusakov

M. E.

,

2019

,

MNRAS

,

485

,

4936

10.1093/mnras/stz657

Crossref

Search ADS

Gusakov

M. E.

,

Dommes

V. A.

,

2016

,

Phys. Rev. D

,

94

,

083006

10.1103/PhysRevD.94.083006

Crossref

Search ADS

Gusakov

M. E.

,

Kantor

E. M.

,

Ofengeim

D. D.

,

2017

,

Phys. Rev. D

,

96

,

103012

10.1103/PhysRevD.96.103012

Crossref

Search ADS

Haensel

P.

,

1995

,

Space Sci. Rev.

,

74

,

427

10.1007/BF00751429

Crossref

Search ADS

Hollerbach

R.

,

Rüdiger

G.

,

2002

,

MNRAS

,

337

,

216

10.1046/j.1365-8711.2002.05905.x

Crossref

Search ADS

Hoyos

J.

,

Reisenegger

A.

,

Valdivia

J. A.

,

2008

,

A&A

,

487

,

789

10.1051/0004-6361:200809466

Crossref

Search ADS

Hoyos

J.

,

Reisenegger

A.

,

Valdivia

J. A.

,

2010

,

MNRAS

,

408

,

1730

10.1111/j.1365-2966.2010.17237.x

Crossref

Search ADS

Kantor

E. M.

,

Gusakov

M. E.

,

2018

,

MNRAS

,

473

,

4272

10.1093/mnras/stx2682

Crossref

Search ADS

Kaspi

V. M.

,

2010

,

Proc. Natl. Acad. Sci.

,

107

,

7147

10.1073/pnas.1000812107

Crossref

Search ADS

Lander

S. K.

,

Gourgouliatos

K. N.

,

2019

,

MNRAS

,

486

,

4130

10.1093/mnras/stz1042

Crossref

Search ADS

Lander

S. K.

,

Jones

D. I.

,

2009

,

MNRAS

,

395

,

2162

10.1111/j.1365-2966.2009.14667.x

Crossref

Search ADS

Lander

S. K.

,

Jones

D. I.

,

2012

,

MNRAS

,

424

,

482

10.1111/j.1365-2966.2012.21213.x

Crossref

Search ADS

Marchant

P.

,

Reisenegger

A.

,

Akgün

T.

,

2011

,

MNRAS

,

415

,

2426

10.1111/j.1365-2966.2011.18874.x

Crossref

Search ADS

Marchant

P.

,

Reisenegger

A.

,

Valdivia

J. A.

,

Hoyos

J. H.

,

2014

,

ApJ

,

796

,

94

10.1088/0004-637X/796/2/94

Crossref

Search ADS

Markey

P.

,

Tayler

R. J.

,

1973

,

MNRAS

,

163

,

77

10.1093/mnras/163.1.77

Crossref

Search ADS

Mitchell

J. P.

,

Braithwaite

J.

,

Reisenegger

A.

,

Spruit

H.

,

Valdivia

J. A.

,

Langer

N.

,

2015

,

MNRAS

,

447

,

1213

10.1093/mnras/stu2514

Crossref

Search ADS

Ofengeim

D. D.

,

Gusakov

M. E.

,

2018

,

Phys. Rev. D

,

98

,

043007

10.1103/PhysRevD.98.043007

Crossref

Search ADS

Passamonti

A.

,

Akgün

T.

,

Pons

J. A.

,

Miralles

J. A.

,

2017a

,

MNRAS

,

465

,

3416

10.1093/mnras/stw2936

Crossref

Search ADS

Passamonti

A.

,

Akgün

T.

,

Pons

J. A.

,

Miralles

J. A.

,

2017b

,

MNRAS

,

469

,

4979

10.1093/mnras/stx1192

Crossref

Search ADS

Pethick

C.

,

1992

, in

Pines

D.

,

Tamagaki

R.

,

Tsuruta

S.

, eds,

Structure and Evolution of Neutron Stars

,

Addison-Wesley

,

Redwood City

, p.

115

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Pons

J. A.

,

Geppert

U.

,

2007

,

A&A

,

470

,

303

10.1051/0004-6361:20077456

Crossref

Search ADS

Pons

J. A.

,

Miralles

J. A.

,

Geppert

U.

,

2009

,

A&A

,

496

,

207

10.1051/0004-6361:200811229

Crossref

Search ADS

Reisenegger

A.

,

1995

,

ApJ

,

442

,

749

10.1086/175480

Crossref

Search ADS

Reisenegger

A.

,

2007

,

Astron. Nachr.

,

328

,

1173

10.1002/asna.200710848

Crossref

Search ADS

Reisenegger

A.

,

2009

,

A&A

,

499

,

557

10.1051/0004-6361/200810895

Crossref

Search ADS

Reisenegger

A.

,

Goldreich

P.

,

1992

,

ApJ

,

395

,

240

10.1086/171645

Crossref

Search ADS

Shafranov

V. D.

,

1966

,

Rev. Plasma Phys.

,

2

,

103

Tauris

T. M.

,

van den Heuvel

E. P. J.

,

2006

, in

Lewin

W.

,

van der Klis

M.

, eds,

Compact Stellar X-ray Sources

,

Cambridge Univ. Press

,

Cambridge

, p.

623

Tayler

R. J.

,

1973

,

MNRAS

,

161

,

365

10.1093/mnras/161.4.365

Crossref

Search ADS

Thompson

C.

,

Duncan

R. C.

,

1995

,

MNRAS

,

275

,

255

10.1093/mnras/275.2.255

Crossref

Search ADS

Thompson

C.

,

Duncan

R. C.

,

1996

,

ApJ

,

473

,

322

10.1086/178147

Crossref

Search ADS

Viganò

D.

,

Pons

J. A.

,

Miralles

J. A.

,

2012

,

Comput. Phys. Commun.

,

183

,

2042

10.1016/j.cpc.2012.04.029

Crossref

Search ADS

Viganò

D.

,

Rea

N.

,

Pons

J. A.

,

Perna

R.

,

Aguilera

D. N.

,

Miralles

J. A.

,

2013

,

MNRAS

,

434

,

123

10.1093/mnras/stt1008

Crossref

Search ADS

Wright

G. A. E.

,

1973

,

MNRAS

,

162

,

339

10.1093/mnras/162.4.339

Crossref

Search ADS

Yakovlev

D. G.

,

Shalybkov

D. A.

,

1990

,

SvA

,

16

,

86

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
August 2020	4
September 2020	12
October 2020	17
November 2020	13
December 2020	8
January 2021	2
February 2021	1
March 2021	3
April 2021	1
May 2021	1
June 2021	9
July 2021	2
August 2021	5
September 2021	3
November 2021	2
December 2021	2
February 2022	2
March 2022	2
April 2022	7
May 2022	1
June 2022	3
July 2022	2
August 2022	1
September 2022	2
October 2022	2
November 2022	2
December 2022	5
January 2023	5
February 2023	2
March 2023	11
May 2023	6
July 2023	1
September 2023	1
October 2023	1
November 2023	9
December 2023	11
January 2024	5
February 2024	8
March 2024	19
April 2024	12
May 2024	14
June 2024	12
July 2024	9
August 2024	9
September 2024	9
October 2024	10
November 2024	4
December 2024	1
January 2025	7
February 2025	2
March 2025	16
April 2025	4
May 2025	2

Article Contents

Two-fluid simulations of the magnetic field evolution in neutron star cores in the weak-coupling regime

ABSTRACT

1 INTRODUCTION

2 PHYSICAL MODEL

2.1 Basic equations

2.2 Background NS model

2.3 Linearization

2.4 Boundary conditions

2.5 Axial symmetry

2.6 Time-scale estimates

2.6.1 Short-term relaxation through fictitious friction

2.6.2 Long-term evolution through ambipolar diffusion

2.7 Dimensionless equations

3 RESULTS

3.1 Dependence on the artificial friction

3.2 Hydro-magnetic evolution

3.2.1 Reaching hydro-magnetic quasi-equilibrium with a purely poloidal configuration

3.2.2 Long-term magnetic field evolution of a poloidal and toroidal configuration

3.3 Grad–Shafranov equilibria

4 CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Two-fluid simulations of the magnetic field evolution in neutron star cores in the weak-coupling regime Free

ABSTRACT

1 INTRODUCTION

2 PHYSICAL MODEL

2.1 Basic equations

2.2 Background NS model

2.3 Linearization

2.4 Boundary conditions

2.5 Axial symmetry

2.6 Time-scale estimates

2.6.1 Short-term relaxation through fictitious friction

2.6.2 Long-term evolution through ambipolar diffusion

2.7 Dimensionless equations

3 RESULTS

3.1 Dependence on the artificial friction

3.2 Hydro-magnetic evolution

3.2.1 Reaching hydro-magnetic quasi-equilibrium with a purely poloidal configuration

3.2.2 Long-term magnetic field evolution of a poloidal and toroidal configuration

3.3 Grad–Shafranov equilibria

4 CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Two-fluid simulations of the magnetic field evolution in neutron star cores in the weak-coupling regime