-
PDF
- Split View
-
Views
-
Cite
Cite
A Travascio, A Bongiorno, P Tozzi, R Fassbender, F De Gasperin, V F Cardone, L Zappacosta, G Vietri, E Merlin, M Bischetti, E Piconcelli, F Duras, F Fiore, N Menci, P Mazzotta, A Nastasi, Multiple AGN activity during the BCG assembly of XDCPJ0044.0-2033 at z ∼ 1.6, Monthly Notices of the Royal Astronomical Society, Volume 498, Issue 2, October 2020, Pages 2719–2733, https://doi.org/10.1093/mnras/staa2495
Close - Share Icon Share
ABSTRACT
Undisturbed galaxy clusters are characterized by a massive and large elliptical galaxy at their centre, i.e. the brightest cluster galaxy (BCG). How these central galaxies form is still debated. According to most models, a typical epoch for their assembly is |$z$| ∼ 1–2. We have performed a detailed multiwavelength analysis of the core of XMM–Newton Distant Cluster Project (XDCP) J0044.0-2033 (XDCP0044), one of the most massive and densest galaxy clusters currently known at redshift |$z$| ∼ 1.6, whose central galaxy population shows high star formation compared to lower z clusters and an X-ray active galactic nuclei (AGN) located close to its centre. SINFONI J-, H-, and KMOS YJ-, H-bands spectroscopic data have been analysed, together with deep archival HST photometric data in F105W, F140W, and F160W bands, Chandra X-ray, radio JVLA data at 1–2 GHz, and ALMA band-6 observations. In the very central region of the cluster (∼70 kpc × 70 kpc), two systems of interacting galaxies have been identified and studied (Complex A and B), with a total of seven confirmed cluster members. These galaxies show perturbed morphologies and three of them show signs of AGN activity. In particular, two type-1 AGN with typical broad lines have been found at the centre of each complex (both of them X-ray obscured and highly accreting with |$\rm \lambda _{Edd}\sim 0.4-0.6$|), while a type-2 AGN has been discovered in Complex A. The AGN at the centre of Complex B is also detected in X-ray, while the other two are spatially related to radio emission. The three AGN provide one of the closest AGN triple at |$z$| > 1 revealed so far with a minimum (maximum) projected distance of 10 (40) kpc. The observation of high star formation, merger signatures, and nuclear activity in the core of XDCP0044 suggests that all these processes are key ingredients in shaping the nascent BCG. According to our data, XDCP0044 could form a typical massive galaxy of |$M_{\star }\sim 10^{12} \, \mathrm{M}_{\odot }$|, hosting a black hole of |$\rm 2 \times 10^8\!-\!10^9 \, \mathrm{M}_{\odot }$|, in a time-scale of the order of ∼2.5 Gyr.
1 INTRODUCTION
Brightest cluster galaxies (BCGs) are the most massive (|$M_{\star } \sim 10^{12} \, \mathrm{M}_{\odot }$|) and luminous (Mv ≈ −23) galaxies and reside at the centre of relaxed, virialized and undisturbed galaxy clusters in the local Universe (Sandage, Kristian & Westphal 1976; Lin, Ostriker & Miller 2010). BCGs are usually located at the minimum of the cluster potential well, close to the peak of the X-ray emission (Jones & Forman 1984). At low redshift, they appear like red, quiescent, massive, and large (Carter 1977; Bernardi et al. 2007, up to 100 kpc) elliptical galaxies (Dubinski 1998) and they often show radio nuclear activity and jet emissions, able to affect the gas in the intracluster medium (ICM; Best et al. 2007; Hogan et al. 2015; Moravec et al. 2020). On the contrary, most observations of galaxy cluster cores at |$z$| >1 do not show the presence of a single BCG but are instead characterized by star-forming galaxies (SFGs) with disturbed morphology (Zhao et al. 2017). Moreover, although in some cases galaxies exhibiting early-type morphology are also found in |$z$| ≥ 1.4 cluster cores (Strazzullo et al. 2013; Cooke et al. 2016), evidence is reported by several authors for an increase of the SFGs fraction in these distant environments (Bai et al. 2007, 2009; Krick et al. 2009). Specifically, in high-z systems, a reversal star formation (SF)–density relation has been observed, i.e. while at |$z$| < 1.4 the number of SFGs increases towards the cluster outskirts, at |$z$| > 1.4 the SFGs fraction is higher in the cluster cores (Brodwin et al. 2013; Santos et al. 2015). To date, the process responsible for the transition between the unquenched and quenched eras in such environments is still not clear and its understanding is fundamental not only for explaining the formation of local BCGs but also for both cluster and galaxy evolution theory (Lin & Mohr 2004; Rudick, Mihos & McBride 2011; Contini et al. 2014).
Because the BCGs are located in privileged places in the cluster cores, these are expected to experience SF processes, active galactic nuclei (AGN) feedback, and multiple mergers. According to many cosmological simulations and semi-analytic models (e.g. Springel, Di Matteo & Hernquist 2005; Croton 2006; De Lucia & Blaizot 2007; Cooke et al. 2016; Lee-Brown et al. 2017; Pillepich et al. 2018; Ragone-Figueroa et al. 2018), the BCG progenitors form most (∼50 per cent) of their stars at |$z$| > 2.5. This mass is then assembled at |$z$| ∼ 1–2 through mergers and, later (z < 1), through multiple accretion of small galaxies, to form the final BCG (Stott 2008; Laporte et al. 2013; Lidman et al. 2013). On the other hand, recent IR and sub-mm observations of molecular cold gas in galaxy clusters at 1 < z < 2, found a significant star formation rate (SFR; tens and hundreds |$\rm \, \mathrm{M}_{\odot }~yr^{-1}$|) in BCG (Webb et al. 2015; McDonald et al. 2016) and this is mainly attributed to wet major and minor mergers (Bonaventura et al. 2017; Webb et al. 2017). According to these works, |$z$| ∼ 1–2 should be a crucial epoch during which we expect a high rate of merger activity among galaxies (the BCG progenitors) residing in the core of massive galaxy clusters. These mergers will eventually lead to deposit large reservoir of gas in cluster cores and induce dust-obscured starburst events (Cooke et al. 2019).
Most of the studies found indeed an enhancement of the merger activity in high-z galaxy clusters with respect to the low-redshift systems and the field ones (Fassbender et al. 2011; Mancone et al. 2012; Lidman et al. 2013; Lotz et al. 2013; Mei et al. 2015). In particular, Alberts et al. (2016) found an excess of SF and merger activity in the cores of massive (|$M \gt 10^{14} \, \mathrm{M}_{\odot }$|) galaxy clusters at |$z$| > 1. Conversely, other works found the merger fraction in galaxy clusters (Andreon 2013) and/or their cores (Delahaye et al. 2017) comparable to the field one. Interestingly, Alberts et al. (2016) also found an excess of AGN activity in such high-z systems, highlighting the key role of dense environments in triggering nuclear activity at this epoch and pointing towards a co-evolution between SF and black hole (BH) accretion (Galametz et al. 2009; Martini et al. 2013). Moreover, the excess of both SF and AGN activity in high-z galaxy clusters relative to the field one, supports a scenario in which (i) the increase in the merging rate at |$z$| >1 is responsible for triggering both formation of stars and BH accretion, and (ii) the subsequent possible AGN feedback could be one of the mechanisms able to quench SF in massive galaxies, leading to the formation of red and dead elliptical galaxies, as observed in local galaxy cluster cores (Springel et al. 2005; Hopkins et al. 2008; Narayanan et al. 2010). This would also explain the inversion of the SF–density relation observed in |$z$| > 1.4 clusters (see fig. 6 in Brodwin et al. 2013). In fact, while the higher normalization of the relation at higher redshift is easily explained with the higher number of mergers, the change in the slope implies a mechanism able to stop SF (e.g. AGN feedback) in shorter time-scales in galaxies located in the cluster core than in the outer region.
In this paper, we studied the core of the X-ray detected galaxy cluster XDCP J0044.0-2033 (hereafter XDCP0044; Fassbender et al. 2011; Santos et al. 2011) at |$z$| ∼ 1.6. XDCP0044 is one of the most massive galaxy clusters discovered at |$z$| > 1.4 with M2001|$\rm \approx 4.4 _{-0.8} ^{+1.3} \times 10^{14} \, \mathrm{M}_{\odot }$|. It has been detected in low-resolution XMM archival data within the XMM–Newton Distant Cluster Project (XDCP; Fassbender et al. 2011) thanks to its extended X-ray emission (RA=00:44:05.2, Dec = -20:33:59.7), and confirmed by deep Chandra observation to have strong diffuse emission typical of virialized clusters. XDCP0044 is in a quite advanced state of dynamical relaxation, with evidence of ongoing cluster-scale major-merger activity (Fassbender et al. 2014; Tozzi et al. 2015) and of a reversal SF–density relation (Santos et al. 2015). Fig. 1 (left-hand panel) shows the HST RGB (as a combination of F105W, F140W, and F160W filters) image of XDCP0044 with overlaid the X-ray Chandra soft [(0.5–2) keV, magenta] and hard [(2–7) keV, green] bands contours. The red circles indicate the five point-like sources (AGN) identified by Tozzi et al. (2015) within 30 arcsec (∼250 kpc) from the cluster centre. XDCP0044 is a unique laboratory to study the building up of the BCG and the interplay between galaxies, nuclear activity, and the intergalactic gas in the core of massive high-redshift galaxy clusters. In this work, we have conducted a detailed multiwavelength study of the very central region (∼70 kpc × 70 kpc) of the XDCP0044 core (right-hand panel of Fig. 1).
![Left-hand panel:: HST RGB (F105W + F140W + F160W bands) image of the galaxy cluster XDCP0044. The yellow cross indicates the centroid of the extended X-ray emission (RA 00:44:05.2, Dec. −20:33:59.8), while in yellow is reported a circle of radius ∼30 arcsec, corresponding to 250 kpc. The green and magenta contours are the Chandra hard [$\rm (2\!-\!7)\, keV$] and soft [$\rm (0.5-2)\, keV$] X-ray emissions, respectively, while the red circles mark the unresolved X-ray sources as identified by Tozzi et al. (2015). Finally, the red and blue squares delimit the region analysed in this paper, corresponding to the SINFONI and the KMOS field of views. Right-hand Panel: zoom-in of the analysed central region. The magenta-dashed lines mark the two detected complex of galaxies. Specifically, the complex in the upper left corner of the SINFONI field (Complex A) is the BCG as identified by Fassbender et al. (2014), while the central complex (Complex B) is the X-ray AGN identified by Tozzi et al. (2015; the red circle).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2495/1/m_staa2495fig1.jpeg?Expires=1750566919&Signature=nHk5WWzYcufbNKLF5sbbg8fajvdv-QEW~9ng8uTx3MIPEYEiBlMJLMIlk3mufsnIhjBWgMwsd60N8ctMjpAUND-o1wzppNa8GhbMU8J7IcdtnXwxs37qZ4Pun~vfD6MXntxFwCXT07AR09VW6jWpQpYLwEQ8VUMsazbEyvL5mnPw61ziZ4w-T7OnYVt7KlJvzQxymGcIcTNXMiPkaMtZBpZm0ZtrY8qWUY4k38liUJIAs44aVHGnygr7KlDdcFrcGJEobc6Ltya5-pDy1-SufYBhdSZF9tBjo9DofuAkNfN~yIPUjBBYOdJW~zxjxJ~93PHll-q0GrSl8SC~GEOqsw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Left-hand panel:: HST RGB (F105W + F140W + F160W bands) image of the galaxy cluster XDCP0044. The yellow cross indicates the centroid of the extended X-ray emission (RA 00:44:05.2, Dec. −20:33:59.8), while in yellow is reported a circle of radius ∼30 arcsec, corresponding to 250 kpc. The green and magenta contours are the Chandra hard [|$\rm (2\!-\!7)\, keV$|] and soft [|$\rm (0.5-2)\, keV$|] X-ray emissions, respectively, while the red circles mark the unresolved X-ray sources as identified by Tozzi et al. (2015). Finally, the red and blue squares delimit the region analysed in this paper, corresponding to the SINFONI and the KMOS field of views. Right-hand Panel: zoom-in of the analysed central region. The magenta-dashed lines mark the two detected complex of galaxies. Specifically, the complex in the upper left corner of the SINFONI field (Complex A) is the BCG as identified by Fassbender et al. (2014), while the central complex (Complex B) is the X-ray AGN identified by Tozzi et al. (2015; the red circle).
The paper is organized as follows: Section 2 describes the observations and data reduction, while Section 3 presents the photometric and spectroscopic analysis of the galaxies in the analysed region. We then focus on the AGN and SF activity in Section 4. Discussion, summary, and conclusions are presented in Sections 5 and 6.
Throughout the paper, we will assume a cosmology with |$\Omega _\Lambda =0.6842$| and |$H_0=67.32 \, \mathrm{ km\, s^{-1}\, Mpc}^{-1}$| (Planck Collaboration 2018), and the errors will be quoted at 1σ and upper/lower limits at |$90{{\ \rm per\ cent}}$| confidence level, unless otherwise stated.
2 OBSERVATIONS AND DATA REDUCTION
In this paper, we combine and study the information derived from several photometric and spectroscopic multiwavelength observations of the inner region of XDCP0044, from X-ray to optical, near-infrared (NIR) and radio bands, that have been obtained in the recent years. A summary of the analysed data is presented in this section.
2.1 Proprietary data
2.1.1 SINFONI observations and data reduction
Integral field unit (IFU) SINFONI observations in J and H band of the central region of XDCP0044 (program ID 094.A-0713(A); PI A. Bongiorno), have been obtained in 2014. At the redshift of the cluster, J band corresponds to the rest-frame [O iii] and H β emission lines (∼ 4496–5230 Å), while H-band samples the H α emission line with a resolution of R = 2000 and R = 3000, respectively.
The data have been taken in seeing limited mode (average seeing ∼ 0.8 arcsec) in a 8 arcsec × 8 arcsec field of view (FOV) that corresponds to ∼70 kpc × 70 kpc. The observed FOV (centred at RA = 00:44:05.420, Dec. = −20:33:57.16) is shown in the right-hand panel of Fig. 1 with a red square. Observations consist of six Observing Blocks (OBs) in J band and two OBs in H band. We performed observations of 300 s per frame both on objects (O) and on sky (S), following the scheme ‘OOSSOOSSOO’, in addition to the observations of the standard and telluric stars. The total on target integration time is ∼4 h in Jband and 1.5 h in H band. SINFONI data reduction was performed using the ESO pipeline esorex (Modigliani et al. 2007), with the improved sky subtraction proposed by Davies (2007). After flat-fielding, dark correction, correction for distortions, cosmic rays removal, and wavelength calibration, each frame within a single OB was corrected for the sky emission lines, using the idl routine skysub.pro (Davies 2007). The science frames within each OB were combined considering the offsets of the object in each frame and, finally, flux calibrated according to the standard stars. Moreover, a further flux correction in J band was applied by rescaling the continuum flux to the HAWK-I J-band photometric point published in Fassbender et al. (2014). The flux-calibrated exposures of the different OBs were then combined together by measuring and applying the relative offset between the peak emissions of the most luminous sources in the fields. The final result of the data reduction procedure was a 3D flux-calibrated data cube having a point spread function (PSF) full width at half-maximum (FWHM) ∼ 0.7 and 0.6 arcsec in J and in H band, respectively.
2.1.2 KMOS observations and data reduction
KMOS IFU observations in JY and H bands have been obtained in 2013 (Program ID: 092.A-0114(A); PI R. Fassbender). In this work, we focused on the analysis of the KMOS data centred on the BCG candidate identified by Fassbender et al. (2014). At the redshift of the cluster, JY-band samples the [O iii] and H β emission lines with a resolving power |$\rm R\simeq$|3600, while H-band samples the H α region with |$\rm R\simeq$| 4000. The data have been taken with an average seeing of ∼ 1 arcsec in a 2.8 arcsec × 2.8 arcsec FOV. The observed FOV, centred at RA = 00:44:05.600, Dec. = −20:33:54.716, is shown in Fig. 1 with a blue square. Observations consist of seven OBs in YJ band and two OBs in H band. Each OB is made of five frames, each of 450 s integration time, for both sky (S) and science observations (O). The total on target integration time is ∼4.4 h in YJ band and ∼1.25 h in H band.
The data were reduced using the pipeline with the software package for astronomical reduction with KMOS (Davies et al. 2013), which includes dark correction, flat fielding, illumination correction, wavelength calibration, and the sky subtraction (Davies et al. 2011). Data were then combined according to the spatial shift of the object in each frame. The final datacubes in JY and H bands have a PSF FWHM of ∼0.8 and 0.9 arcsec, respectively.
2.1.3 JVLA observations and data reduction
JVLA data have been taken in 2016 in the L band (1–2 GHz) in A, B, and C configuration (with |$\rm t_{exp}$| of 5 h each) as part of the project 16A-082 (PI F. De Gasperin). The data were reduced using the casa2 package. The visibilities were Hanning-smoothed, bandpass-calibrated, and then flagged using the automatic tool AOflagger (Offringa, van de Gronde & Roerdink 2012). We used 3C 147 as flux calibrator and the point source J2357–1125 as phase calibrator. The flux scale has been set to Perley & Butler (2013). Bandpass, scalar delays, cross-hand delays, and polarization angle corrections were transferred to the target and the phase calibrator. Then, phase and rescaled amplitude from the phase calibrator were transferred to the target field. Finally, a few cycles of phase-only self-calibration was applied on the target field. We obtained final images in A, B, and C configurations with resolution of 2 arcsec × 1 arcsec, 6 arcsec × 3 arcsec and 16 arcsec × 8 arcsec and noise of 15, 20, and 25 |$\rm \mu Jy\, beam^{-1}$|, respectively. The data sets were finally combined to obtain single image used for the scientific analysis.
We note that all flux density errors for extended emission were computed as |$S_{\rm err} = \sigma \cdot \sqrt{N_{\rm beam}}$|, where σ is the local image rms and Nbeam is the number of beams covering the source extension.
2.2 Archival data
HST data of the XDCP0044 galaxy cluster have been obtained in 2015 (Program 13677; PI S. Perlmutter) in F105W, F140W, F160W, and F814W bands, with the following exposure times: 2 h in F105W and F140W, 1 h in F160W, and 47 min in F814W. In our analysis, we used the images obtained by combining the archival drizzled (DRZ) frames, after performing the astrometry and aligning them. Due to the low S/N, the F814W band has not been included in the analysis.
Chandra/ACIS-S X-ray observation of the cluster has been performed in 2013 October–December and carried out in six exposures for a total time of ∼370 ks (PI P. Tozzi). Details on observations and data reduction can be found in Tozzi et al. (2015). In Section 3.4 we present a detailed spectral analysis.
ALMA band 6 data from project 2017.1.01387.S (PI S. Stach), covering the FOV of our SINFONI data, are also included in our study. These observations span the frequency range 221.5–225.3 GHz and 236.3–240.7 GHz for a total bandwidth of ∼7.5 GHz, and a spectral resolution of |$\rm \sim 40~km~s^{-1}$|. Given the redshift of the cluster, the ALMA coverage corresponds to the rest-frame ∼600 GHz continuum and CO(5–4) emission line (|$\rm \nu _{rest}$| = 576.27 GHz). ALMA data were calibrated with the casa 5.1.1 version in pipeline mode using the default calibrators provided by the Observatory. The continuum map was created by averaging the visibilities over the whole bandwidth. Specifically, we applied the standard non-interactive cleaning, with clark algorithm and natural weighting. This resulted into an rms sensitivity of 0.024 mJy beam−1 and an angular resolution of 0.98 × 0.78 |$\rm arcsec^2$|. The resulting sensitivity to the native spectral resolution of the observations (|$\sim 10\rm ~km~s^{-1}$|) is 1.5 mJy beam−1 and the beam is 0.82 × 0.63 arcsec2.
3 ANALYSIS
3.1 Optical/NIR source identification
We limited our analysis of HST data to the central region of the cluster, where spectroscopic SINFONI and KMOS observations have been taken (right-hand panel of Fig. 1) and we used sextractor (Bertin & Arnouts 1996) to detect and deblend the sources. We chose F105W as detection band, identifying a total of 16 sources (see Fig. 2). Interestingly, two main galaxies complexes have been identified:
Complex A, in the top left corner of the XDCP0044 core (Fig. 2), consists of several sources identified in HST data. This complex includes what was identified by Fassbender et al. (2014) in the HAWK-I images as a single source and classified as the BCG, although with several extensions, interpreted as sign of ongoing or recent mergers.
Complex B in the central region of the SINFONI field. This complex includes the X-ray AGN discovered by Tozzi et al. (2015; source b1 in Fig. 2). The HST photometric analysis revealed the presence of a second source (b2) very close to the central one.
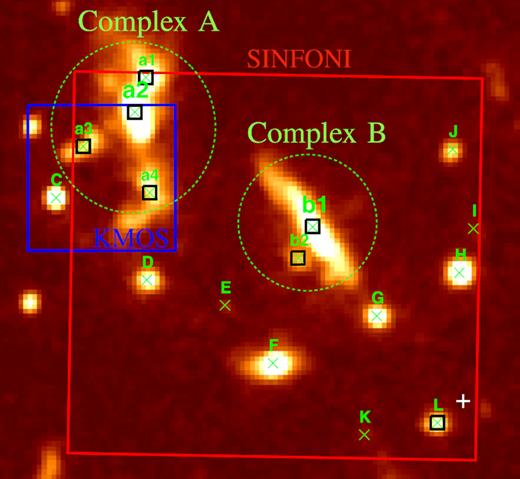
HST F105W image of the core of XDCP0044, where two complexes (A and B) are highlighted with the green-dashed line. The green crosses mark the sources identified in the HST images and listed in Table 1. The black squares mark the sources for which a redshift has been measured, while the white cross is the X-ray centroid.
For the 16 sources, aperture photometry was performed in dual mode on the available bands. We did not PSF-match the images, as the FWHMs in all images are comparable (∼0.130 arcsec, 0.137 arcsec, and 0.145 arcsec in F105W, F140W, and F160W bands, respectively). We took the isophotal flux3 as the best photometric estimate, since the severe blending of sources would make photometric measurements in larger areas unreliable. In particular, we do not attempt to estimate total fluxes using Kron apertures 4 (FLUX_AUTO), as they would be strongly contaminated by light coming from neighbouring sources. AB system magnitudes (listed in Table 1) have been estimated from the isophotal flux using zero-points zp = (26.2, 26.4, 25.9) for (F105W, F140W, F160) band, respectively.
| ID . | RA . | Dec. . | mF105W . | mF140W . | mF160W . |
|---|---|---|---|---|---|
| a1 | 00:44:05.595 | −20:33:53.61 | 22.756 ± 0.140 | 22.087 ± 0.097 | 21.858 ± 0.162 |
| a2 | 00:44:05.607 | −20:33:54.51 | 22.288 ± 0.113 | 21.600 ± 0.077 | 21.363 ± 0.129 |
| a3 | 00:44:05.680 | −20:33:54.92 | 23.602 ± 0.206 | 23.217 ± 0.163 | 23.214 ± 0.303 |
| a4 | 00:44:05.590 | −20:33:55.80 | 22.465 ± 0.123 | 21.962 ± 0.092 | 21.776 ± 0.156 |
| b1 | 00:44:05.369 | −20:33:56.45 | 21.717 ± 0.086 | 21.014 ± 0.059 | 20.815 ± 0.100 |
| b2 | 00:44:05.388 | −20:33:57.04 | 25.225 ± 0.435 | 24.340 ± 0.274 | 24.058 ± 0.446 |
| C | 00:44:05.717 | −20:33:55.90 | 23.277 ± 0.178 | 23.123 ± 0.156 | 23.032 ± 0.279 |
| D | 00:44:05.594 | −20:33:57.46 | 23.357 ± 0.186 | 22.797 ± 0.135 | 22.620 ± 0.231 |
| E | 00:44:05.488 | −20:33:57.94 | 25.974 ± 0.647 | 25.441 ± 0.479 | 25.295 ± 0.824 |
| F | 00:44:05.423 | −20:33:59.04 | 22.466 ± 0.123 | 21.569 ± 0.077 | 21.367 ± 0.129 |
| G | 00:44:05.282 | −20:33:58.14 | 23.368 ± 0.188 | 22.492 ± 0.118 | 22.290 ± 0.198 |
| H | 00:44:05.170 | −20:33:57.32 | 23.049 ± 0.161 | 22.436 ± 0.115 | 22.248 ± 0.195 |
| I | 00:44:05.151 | −20:33:56.48 | 27.047 ± 1.028 | 27.042 ± 0.980 | 26.666 ± 1.502 |
| J | 00:44:05.179 | −20:33:54.97 | 24.162 ± 0.274 | 23.763 ± 0.217 | 23.514 ± 0.354 |
| K | 00:44:05.299 | −20:34:00.40 | 26.192 ± 0.702 | 25.833 ± 0.566 | 25.490 ± 0.883 |
| L | 00:44:05.200 | −20:34:00.17 | 24.106 ± 0.264 | 23.684 ± 0.205 | 23.554 ± 0.357 |
| ID . | RA . | Dec. . | mF105W . | mF140W . | mF160W . |
|---|---|---|---|---|---|
| a1 | 00:44:05.595 | −20:33:53.61 | 22.756 ± 0.140 | 22.087 ± 0.097 | 21.858 ± 0.162 |
| a2 | 00:44:05.607 | −20:33:54.51 | 22.288 ± 0.113 | 21.600 ± 0.077 | 21.363 ± 0.129 |
| a3 | 00:44:05.680 | −20:33:54.92 | 23.602 ± 0.206 | 23.217 ± 0.163 | 23.214 ± 0.303 |
| a4 | 00:44:05.590 | −20:33:55.80 | 22.465 ± 0.123 | 21.962 ± 0.092 | 21.776 ± 0.156 |
| b1 | 00:44:05.369 | −20:33:56.45 | 21.717 ± 0.086 | 21.014 ± 0.059 | 20.815 ± 0.100 |
| b2 | 00:44:05.388 | −20:33:57.04 | 25.225 ± 0.435 | 24.340 ± 0.274 | 24.058 ± 0.446 |
| C | 00:44:05.717 | −20:33:55.90 | 23.277 ± 0.178 | 23.123 ± 0.156 | 23.032 ± 0.279 |
| D | 00:44:05.594 | −20:33:57.46 | 23.357 ± 0.186 | 22.797 ± 0.135 | 22.620 ± 0.231 |
| E | 00:44:05.488 | −20:33:57.94 | 25.974 ± 0.647 | 25.441 ± 0.479 | 25.295 ± 0.824 |
| F | 00:44:05.423 | −20:33:59.04 | 22.466 ± 0.123 | 21.569 ± 0.077 | 21.367 ± 0.129 |
| G | 00:44:05.282 | −20:33:58.14 | 23.368 ± 0.188 | 22.492 ± 0.118 | 22.290 ± 0.198 |
| H | 00:44:05.170 | −20:33:57.32 | 23.049 ± 0.161 | 22.436 ± 0.115 | 22.248 ± 0.195 |
| I | 00:44:05.151 | −20:33:56.48 | 27.047 ± 1.028 | 27.042 ± 0.980 | 26.666 ± 1.502 |
| J | 00:44:05.179 | −20:33:54.97 | 24.162 ± 0.274 | 23.763 ± 0.217 | 23.514 ± 0.354 |
| K | 00:44:05.299 | −20:34:00.40 | 26.192 ± 0.702 | 25.833 ± 0.566 | 25.490 ± 0.883 |
| L | 00:44:05.200 | −20:34:00.17 | 24.106 ± 0.264 | 23.684 ± 0.205 | 23.554 ± 0.357 |
| ID . | RA . | Dec. . | mF105W . | mF140W . | mF160W . |
|---|---|---|---|---|---|
| a1 | 00:44:05.595 | −20:33:53.61 | 22.756 ± 0.140 | 22.087 ± 0.097 | 21.858 ± 0.162 |
| a2 | 00:44:05.607 | −20:33:54.51 | 22.288 ± 0.113 | 21.600 ± 0.077 | 21.363 ± 0.129 |
| a3 | 00:44:05.680 | −20:33:54.92 | 23.602 ± 0.206 | 23.217 ± 0.163 | 23.214 ± 0.303 |
| a4 | 00:44:05.590 | −20:33:55.80 | 22.465 ± 0.123 | 21.962 ± 0.092 | 21.776 ± 0.156 |
| b1 | 00:44:05.369 | −20:33:56.45 | 21.717 ± 0.086 | 21.014 ± 0.059 | 20.815 ± 0.100 |
| b2 | 00:44:05.388 | −20:33:57.04 | 25.225 ± 0.435 | 24.340 ± 0.274 | 24.058 ± 0.446 |
| C | 00:44:05.717 | −20:33:55.90 | 23.277 ± 0.178 | 23.123 ± 0.156 | 23.032 ± 0.279 |
| D | 00:44:05.594 | −20:33:57.46 | 23.357 ± 0.186 | 22.797 ± 0.135 | 22.620 ± 0.231 |
| E | 00:44:05.488 | −20:33:57.94 | 25.974 ± 0.647 | 25.441 ± 0.479 | 25.295 ± 0.824 |
| F | 00:44:05.423 | −20:33:59.04 | 22.466 ± 0.123 | 21.569 ± 0.077 | 21.367 ± 0.129 |
| G | 00:44:05.282 | −20:33:58.14 | 23.368 ± 0.188 | 22.492 ± 0.118 | 22.290 ± 0.198 |
| H | 00:44:05.170 | −20:33:57.32 | 23.049 ± 0.161 | 22.436 ± 0.115 | 22.248 ± 0.195 |
| I | 00:44:05.151 | −20:33:56.48 | 27.047 ± 1.028 | 27.042 ± 0.980 | 26.666 ± 1.502 |
| J | 00:44:05.179 | −20:33:54.97 | 24.162 ± 0.274 | 23.763 ± 0.217 | 23.514 ± 0.354 |
| K | 00:44:05.299 | −20:34:00.40 | 26.192 ± 0.702 | 25.833 ± 0.566 | 25.490 ± 0.883 |
| L | 00:44:05.200 | −20:34:00.17 | 24.106 ± 0.264 | 23.684 ± 0.205 | 23.554 ± 0.357 |
| ID . | RA . | Dec. . | mF105W . | mF140W . | mF160W . |
|---|---|---|---|---|---|
| a1 | 00:44:05.595 | −20:33:53.61 | 22.756 ± 0.140 | 22.087 ± 0.097 | 21.858 ± 0.162 |
| a2 | 00:44:05.607 | −20:33:54.51 | 22.288 ± 0.113 | 21.600 ± 0.077 | 21.363 ± 0.129 |
| a3 | 00:44:05.680 | −20:33:54.92 | 23.602 ± 0.206 | 23.217 ± 0.163 | 23.214 ± 0.303 |
| a4 | 00:44:05.590 | −20:33:55.80 | 22.465 ± 0.123 | 21.962 ± 0.092 | 21.776 ± 0.156 |
| b1 | 00:44:05.369 | −20:33:56.45 | 21.717 ± 0.086 | 21.014 ± 0.059 | 20.815 ± 0.100 |
| b2 | 00:44:05.388 | −20:33:57.04 | 25.225 ± 0.435 | 24.340 ± 0.274 | 24.058 ± 0.446 |
| C | 00:44:05.717 | −20:33:55.90 | 23.277 ± 0.178 | 23.123 ± 0.156 | 23.032 ± 0.279 |
| D | 00:44:05.594 | −20:33:57.46 | 23.357 ± 0.186 | 22.797 ± 0.135 | 22.620 ± 0.231 |
| E | 00:44:05.488 | −20:33:57.94 | 25.974 ± 0.647 | 25.441 ± 0.479 | 25.295 ± 0.824 |
| F | 00:44:05.423 | −20:33:59.04 | 22.466 ± 0.123 | 21.569 ± 0.077 | 21.367 ± 0.129 |
| G | 00:44:05.282 | −20:33:58.14 | 23.368 ± 0.188 | 22.492 ± 0.118 | 22.290 ± 0.198 |
| H | 00:44:05.170 | −20:33:57.32 | 23.049 ± 0.161 | 22.436 ± 0.115 | 22.248 ± 0.195 |
| I | 00:44:05.151 | −20:33:56.48 | 27.047 ± 1.028 | 27.042 ± 0.980 | 26.666 ± 1.502 |
| J | 00:44:05.179 | −20:33:54.97 | 24.162 ± 0.274 | 23.763 ± 0.217 | 23.514 ± 0.354 |
| K | 00:44:05.299 | −20:34:00.40 | 26.192 ± 0.702 | 25.833 ± 0.566 | 25.490 ± 0.883 |
| L | 00:44:05.200 | −20:34:00.17 | 24.106 ± 0.264 | 23.684 ± 0.205 | 23.554 ± 0.357 |
3.2 NIR spectroscopy
In this section, we present the spectroscopic analysis of VLT/SINFONI and KMOS IFU data.
A first extraction of the spectra of the sources identified in HST was performed using a fixed aperture diameter of 7 pixels in SINFONI (0.875 arcsec) and 5 pixels in KMOS (1 arcsec) and each spectrum was normalized using the HST photometry. For 7 of the 16 galaxies, a clear H |$\alpha \lambda 6563\, \mathring{\rm A}$| line, one of the strongest line expected, has been identified together with few other lines [e.g. (O iii) |$\lambda \lambda 4959\, \mathring{\rm A}5007\, \mathring{\rm A}$| doublet, H|$\beta \lambda 4861\, \mathring{\rm A}$|, (O ii) |$\lambda 3727\, \mathring{\rm A}$|, and (N ii) |$\lambda \lambda 6550\, \mathring{\rm A},6585\, \mathring{\rm A}$|], which confirmed the redshift. The spectra are shown in Figs A1 and A2 and their redshifts, listed in Table 2, range from |$z$| = 1.5567 to |$z$| = 1.5904 (Δ|$z$| ≃ 0.0337), consistently with the redshift of the cluster. All 7 galaxies (shown with a black square in Fig. 2) are therefore spectroscopically confirmed cluster members. Four of them (a1, a2, a3, and a4) belong to Complex A, other two are instead part of Complex B, and the L is close to the X-ray centroid. The spectroscopic analysis confirms that Complex A and Complex B are indeed interacting galaxies of at least four galaxies at a projected distance of 20 kpc in Complex A and 2 galaxies at ∼5 kpc in Complex B. The two complexes are very close to each other, i.e. ∼ 35 kpc. Moreover, as detailed later, in two of the analysed sources, a2 in Complex A and b1 in Complex B, the H α emission line is broad (|$\rm FWHM\gt 1800~\rm {km~s^{-1}}$|). These sources have been therefore classified as broad line AGN (BL–AGN).
Properties derived from the spectral analysis. Columns are object ID, redshifts, FWHM, and flux of the H α line, luminosity at 5100 Å and V-band absolute magnitude Mv. Upper limits are given at 3σ.
| |$\rm ID$| . | |$z$| . | |$\rm FWHM$| (H α) . | |$\rm F(H \,\alpha)$| . | |$\rm F[(N\,\rm{\small{II}}) \lambda 6549 \mathring{\rm A}]$| . | |$\rm F[(N\, \rm{\small{II}}) \lambda 6585 \mathring{\rm A}]$| . | |$\rm F[(O\, \rm{\small{III}}) \lambda 5070 \mathring{\rm A}]$| . | |$\rm F(H \beta)$| . | |$\rm log(L_{5100})$| . | Mv . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | (erg s−1) . | . |
| a1 | 1.5567 | 339 ± 28 | 3.23 ± 0.40 | 8.2 ± 1.0 | 24.7 ± 3.1 | <0.04 | <0.27 | 44.25 ± 0.21 | −23.1 |
| a2 | 1.5577 | 1880 ± 321 a | 16.62 ± 4.36 a | 6.1 ± 1.1 | 18.0 ± 3.2 | 1.96 ± 0.30 | 10.8 ± 1.65 | 44.45 ± 0.17 | −23.6 |
| a3 | 1.5831 | 175 ± 82 | 3.13 ± 1.53 | 7.3 ± 3.6 | 21.7 ± 10.6 | 1.83 ± 0.50 | 3.66 ± 0.97 | 43.83 ± 0.36 | −22.1 |
| a4 | 1.5609 | 311 ± 108 | 7.67 ± 4.00 | 9.3 ± 4.8 | 27.5 ± 14.3 | <0.11 | <0.48 | 44.31 ± 0.20 | −23.2 |
| b1 | 1.5904 | 2205 ± 383 a | 40.23 ± 10.72 a | 4.0 ± 1.4 | 11.7 ± 4.1 | <0.03 | <0.38 | 44.71 ± 0.13 | −24.2 |
| b2 | 1.5659 | 100 ± 62 | 0.39 ± 0.31 | <0.70 | <1.95 | <0.07 | <0.44 | 43.35 ± 0.71 | −20.8 |
| L | 1.5848 | 290 ± 99 | 5.55 ± 2.80 | 7.2 ± 3.7 | 21.2 ± 10.8 | <0.15 | <0.67 | 43.65 ± 0.47 | −21.6 |
| |$\rm ID$| . | |$z$| . | |$\rm FWHM$| (H α) . | |$\rm F(H \,\alpha)$| . | |$\rm F[(N\,\rm{\small{II}}) \lambda 6549 \mathring{\rm A}]$| . | |$\rm F[(N\, \rm{\small{II}}) \lambda 6585 \mathring{\rm A}]$| . | |$\rm F[(O\, \rm{\small{III}}) \lambda 5070 \mathring{\rm A}]$| . | |$\rm F(H \beta)$| . | |$\rm log(L_{5100})$| . | Mv . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | (erg s−1) . | . |
| a1 | 1.5567 | 339 ± 28 | 3.23 ± 0.40 | 8.2 ± 1.0 | 24.7 ± 3.1 | <0.04 | <0.27 | 44.25 ± 0.21 | −23.1 |
| a2 | 1.5577 | 1880 ± 321 a | 16.62 ± 4.36 a | 6.1 ± 1.1 | 18.0 ± 3.2 | 1.96 ± 0.30 | 10.8 ± 1.65 | 44.45 ± 0.17 | −23.6 |
| a3 | 1.5831 | 175 ± 82 | 3.13 ± 1.53 | 7.3 ± 3.6 | 21.7 ± 10.6 | 1.83 ± 0.50 | 3.66 ± 0.97 | 43.83 ± 0.36 | −22.1 |
| a4 | 1.5609 | 311 ± 108 | 7.67 ± 4.00 | 9.3 ± 4.8 | 27.5 ± 14.3 | <0.11 | <0.48 | 44.31 ± 0.20 | −23.2 |
| b1 | 1.5904 | 2205 ± 383 a | 40.23 ± 10.72 a | 4.0 ± 1.4 | 11.7 ± 4.1 | <0.03 | <0.38 | 44.71 ± 0.13 | −24.2 |
| b2 | 1.5659 | 100 ± 62 | 0.39 ± 0.31 | <0.70 | <1.95 | <0.07 | <0.44 | 43.35 ± 0.71 | −20.8 |
| L | 1.5848 | 290 ± 99 | 5.55 ± 2.80 | 7.2 ± 3.7 | 21.2 ± 10.8 | <0.15 | <0.67 | 43.65 ± 0.47 | −21.6 |
Note. FWHM reported in table has been corrected for the instrumental.
a refers to the broad H α component.
Properties derived from the spectral analysis. Columns are object ID, redshifts, FWHM, and flux of the H α line, luminosity at 5100 Å and V-band absolute magnitude Mv. Upper limits are given at 3σ.
| |$\rm ID$| . | |$z$| . | |$\rm FWHM$| (H α) . | |$\rm F(H \,\alpha)$| . | |$\rm F[(N\,\rm{\small{II}}) \lambda 6549 \mathring{\rm A}]$| . | |$\rm F[(N\, \rm{\small{II}}) \lambda 6585 \mathring{\rm A}]$| . | |$\rm F[(O\, \rm{\small{III}}) \lambda 5070 \mathring{\rm A}]$| . | |$\rm F(H \beta)$| . | |$\rm log(L_{5100})$| . | Mv . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | (erg s−1) . | . |
| a1 | 1.5567 | 339 ± 28 | 3.23 ± 0.40 | 8.2 ± 1.0 | 24.7 ± 3.1 | <0.04 | <0.27 | 44.25 ± 0.21 | −23.1 |
| a2 | 1.5577 | 1880 ± 321 a | 16.62 ± 4.36 a | 6.1 ± 1.1 | 18.0 ± 3.2 | 1.96 ± 0.30 | 10.8 ± 1.65 | 44.45 ± 0.17 | −23.6 |
| a3 | 1.5831 | 175 ± 82 | 3.13 ± 1.53 | 7.3 ± 3.6 | 21.7 ± 10.6 | 1.83 ± 0.50 | 3.66 ± 0.97 | 43.83 ± 0.36 | −22.1 |
| a4 | 1.5609 | 311 ± 108 | 7.67 ± 4.00 | 9.3 ± 4.8 | 27.5 ± 14.3 | <0.11 | <0.48 | 44.31 ± 0.20 | −23.2 |
| b1 | 1.5904 | 2205 ± 383 a | 40.23 ± 10.72 a | 4.0 ± 1.4 | 11.7 ± 4.1 | <0.03 | <0.38 | 44.71 ± 0.13 | −24.2 |
| b2 | 1.5659 | 100 ± 62 | 0.39 ± 0.31 | <0.70 | <1.95 | <0.07 | <0.44 | 43.35 ± 0.71 | −20.8 |
| L | 1.5848 | 290 ± 99 | 5.55 ± 2.80 | 7.2 ± 3.7 | 21.2 ± 10.8 | <0.15 | <0.67 | 43.65 ± 0.47 | −21.6 |
| |$\rm ID$| . | |$z$| . | |$\rm FWHM$| (H α) . | |$\rm F(H \,\alpha)$| . | |$\rm F[(N\,\rm{\small{II}}) \lambda 6549 \mathring{\rm A}]$| . | |$\rm F[(N\, \rm{\small{II}}) \lambda 6585 \mathring{\rm A}]$| . | |$\rm F[(O\, \rm{\small{III}}) \lambda 5070 \mathring{\rm A}]$| . | |$\rm F(H \beta)$| . | |$\rm log(L_{5100})$| . | Mv . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | ×10−17(erg s−1 cm−2) . | ×10−18(erg s−1 cm−2) . | (erg s−1) . | . |
| a1 | 1.5567 | 339 ± 28 | 3.23 ± 0.40 | 8.2 ± 1.0 | 24.7 ± 3.1 | <0.04 | <0.27 | 44.25 ± 0.21 | −23.1 |
| a2 | 1.5577 | 1880 ± 321 a | 16.62 ± 4.36 a | 6.1 ± 1.1 | 18.0 ± 3.2 | 1.96 ± 0.30 | 10.8 ± 1.65 | 44.45 ± 0.17 | −23.6 |
| a3 | 1.5831 | 175 ± 82 | 3.13 ± 1.53 | 7.3 ± 3.6 | 21.7 ± 10.6 | 1.83 ± 0.50 | 3.66 ± 0.97 | 43.83 ± 0.36 | −22.1 |
| a4 | 1.5609 | 311 ± 108 | 7.67 ± 4.00 | 9.3 ± 4.8 | 27.5 ± 14.3 | <0.11 | <0.48 | 44.31 ± 0.20 | −23.2 |
| b1 | 1.5904 | 2205 ± 383 a | 40.23 ± 10.72 a | 4.0 ± 1.4 | 11.7 ± 4.1 | <0.03 | <0.38 | 44.71 ± 0.13 | −24.2 |
| b2 | 1.5659 | 100 ± 62 | 0.39 ± 0.31 | <0.70 | <1.95 | <0.07 | <0.44 | 43.35 ± 0.71 | −20.8 |
| L | 1.5848 | 290 ± 99 | 5.55 ± 2.80 | 7.2 ± 3.7 | 21.2 ± 10.8 | <0.15 | <0.67 | 43.65 ± 0.47 | −21.6 |
Note. FWHM reported in table has been corrected for the instrumental.
a refers to the broad H α component.
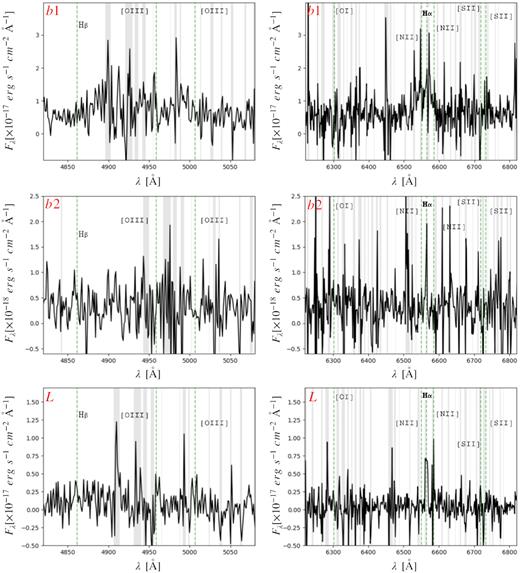
Given the low quality of the data, for these seven sources, we built the integrated signal-to-noise ratio (SNR) map of the H α emission lines and we extracted the spectra using a region centred on the H α line SNR peak, with a radius of ∼0.4 arcsec. Fig. 3 reports a zoom-in of the H α spectral region together with the best fit to the data (the red line) consisting of a power law for the continuum, plus up to four Gaussian components that model the narrow and broad H α line and the doublet [N ii] |$\lambda \lambda 6550\, \mathring{\rm A},6585\, \mathring{\rm A}$| emission lines. In the fit, we constrained the intensity of [N ii] |$\lambda 6585\, \mathring{\rm A}$| to be 2.96 times the [N ii] |$\lambda 6550\, \mathring{\rm A}$| one (Acker et al. 1989) and we set all three narrow lines to have the same dispersion. The results of the best-fitting model, i.e FWHM corrected for the instrumental resolution, H α and [N ii] (if detected) fluxes, are reported in Table 2. Uncertainties were computed following Lenz & Ayres (1992) for noisy emission line spectra.
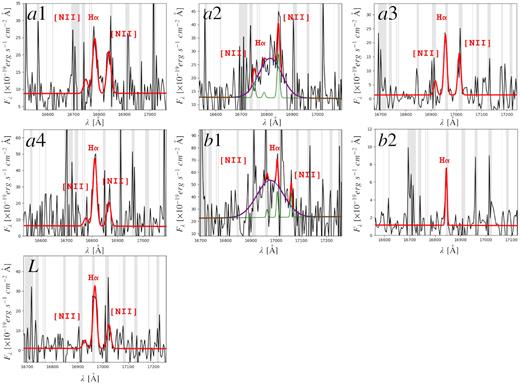
Zoom-in of the spectra (smoothed at ∼70 |$\rm km~s^{-1}$|) around the H α line of the seven confirmed cluster members. The red line represents the total best-fitting model consisting of a power law for the continuum plus up to four Gaussian components to model the emission lines. The fit to the continuum and the narrow lines are shown in green, while the broad components in blue.
For two sources, i.e. a2 (one of the BLAGN) and a3, we also detect H β and the [O iii] λ5007 emission lines in the J-band SINFONI and KMOS spectrum, respectively, as shown in Fig. 4. This allowed us to confirm their redshifts and reveal the nature of a3 through the BPT diagram (Baldwin, Phillips & Terlevich 1981). The estimated integrated flux of the emission lines lead to ratios |$\rm log(F_{[O\, \rm{\small{III}}]}/F_{H \beta }) = 0.7 \pm 0.2$| and |$\rm log(F_{[N\, \rm{\small{II}}]}/F_{H \alpha }) = -0.2 _{-0.5} ^{+0.2}$|. According to the separation criterion between AGN and SF galaxies in the BPT diagram by Kauffmann et al. (2003), a3 is therefore classified as a Type-2 AGN.
![Zoom-in of the spectra (smoothed at 70 $\rm ~km~s^{-1}$) around the H β line of the sources a2 (J-band SINFONI) and a3 (JY-band KMOS): in red the fit to the H β and [O iii] λλ4959,5007Å emission lines.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2495/1/m_staa2495fig4.jpeg?Expires=1750566919&Signature=wmdOcrgVyGCXuu8Xi978GkxX68ALOHtDBqKYu0TfYMsPCeS7y1n1QY2yCVGRkXToPyueoy-W5z0iRTxpXrtHbiSzhWQgIMR-VjtQ8zXzaBwfR9~5KuAPK0UNMVG8y5cJjFBzfqMGkDCgJgg3W5zwsIsRukrdbsdkgHnZey2V7N01uymFYsipEHQmbb6-Ir5d6iuG0fLovpVahvBzJf-XYio-gxpnjAgOsOkB3fDhkNDRfOeqLoBnh9cUAYwo~NVneT~N14FlOdi5EaMFRX25HhW1AoQcn8MiJEKeOrN2DFbQsn~876L9vM~mYDcPPjERYYFhGycWxj0YIOTkqpj3kA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Zoom-in of the spectra (smoothed at 70 |$\rm ~km~s^{-1}$|) around the H β line of the sources a2 (J-band SINFONI) and a3 (JY-band KMOS): in red the fit to the H β and [O iii] λλ4959,5007Å emission lines.
Finally, for all seven galaxies for which a redshift has been measured, we estimated the rest-frame luminosity at 5100 Å (|$\rm L_{5100}$|) and the V-band absolute magnitudes from the flux measured by interpolating the HST photometric points (i.e. F105W and F140W). The values, reported in Table 2, indicate that such galaxies have high luminosities, i.e. a2 and b1 are the most powerful sources with |$\rm log[L_{5100\mathring{\rm A}}/erg~s^{-1}]\gt 44.4$| and Mv < −23.5, in agreement with the fact that they host an unobscured AGN. All other sources show slightly lower luminosities, brighter than typical normal galaxies but consistent with what found for galaxies in |$z$| ∼ 1.0 clusters (i.e. close to the knee of the cluster galaxy luminosity function, Martinet et al. 2015).
3.3 Dynamics of the galaxy cluster
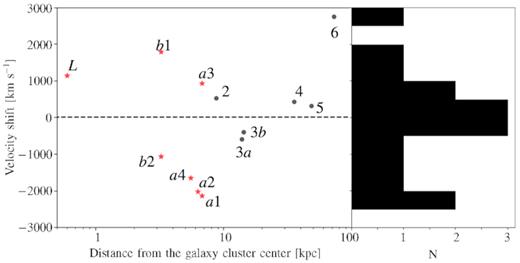
Velocity shift of all cluster members as a function of their distance from the X-ray centroid. The histogram of the velocity shifts (binned at 500 |$\rm ~km~s^{-1}$|) is reported on the right. The red stars and the black dots indicate the cluster members identified in this paper and in Fassbender et al. (2014), respectively.
Coordinates, redshift, and velocity shift of the SINFONI, KMOS, and FORS2 spectroscopic cluster members.
| ID . | RA . | Dec. . | z . | v . |
|---|---|---|---|---|
| SINFONI and KMOS data | ||||
| a1 | 00:44:05.595 | −20:33:53.61 | 1.5567 | −2094 |
| a2 | 00:44:05.607 | −20:33:54.51 | 1.5577 | −1988 |
| a3 | 00:44:05.680 | −20:33:54.92 | 1.5831 | 972 |
| a4 | 00:44:05.590 | −20:33:55.80 | 1.5609 | −1609 |
| b1 | 00:44:05.369 | −20:33:56.45 | 1.5904 | 1342 |
| b2 | 00:44:05.388 | −20:33:57.04 | 1.5659 | −1026 |
| L | 00:44:05.200 | −20:34:00.17 | 1.5848 | 1173 |
| FORS2 data | ||||
| 2 | 0:44:04.737 | −20:34:09.43 | 1.5795 | 556 |
| 3a | 0:44:05.450 | −20:34:16.78 | 1.5699 | −562 |
| 3b | 0:44:05.531 | −20:34:16.78 | 1.5716 | −364 |
| 4 | 0:44:05.325 | −20:33:14.28 | 1.5787 | 463 |
| 5 | 0:44:05.611 | −20:32:58.55 | 1.5778 | 358 |
| 6 | 0:44:03.015 | −20:32:31.84 | 1.5986 | 2780 |
| ID . | RA . | Dec. . | z . | v . |
|---|---|---|---|---|
| SINFONI and KMOS data | ||||
| a1 | 00:44:05.595 | −20:33:53.61 | 1.5567 | −2094 |
| a2 | 00:44:05.607 | −20:33:54.51 | 1.5577 | −1988 |
| a3 | 00:44:05.680 | −20:33:54.92 | 1.5831 | 972 |
| a4 | 00:44:05.590 | −20:33:55.80 | 1.5609 | −1609 |
| b1 | 00:44:05.369 | −20:33:56.45 | 1.5904 | 1342 |
| b2 | 00:44:05.388 | −20:33:57.04 | 1.5659 | −1026 |
| L | 00:44:05.200 | −20:34:00.17 | 1.5848 | 1173 |
| FORS2 data | ||||
| 2 | 0:44:04.737 | −20:34:09.43 | 1.5795 | 556 |
| 3a | 0:44:05.450 | −20:34:16.78 | 1.5699 | −562 |
| 3b | 0:44:05.531 | −20:34:16.78 | 1.5716 | −364 |
| 4 | 0:44:05.325 | −20:33:14.28 | 1.5787 | 463 |
| 5 | 0:44:05.611 | −20:32:58.55 | 1.5778 | 358 |
| 6 | 0:44:03.015 | −20:32:31.84 | 1.5986 | 2780 |
Coordinates, redshift, and velocity shift of the SINFONI, KMOS, and FORS2 spectroscopic cluster members.
| ID . | RA . | Dec. . | z . | v . |
|---|---|---|---|---|
| SINFONI and KMOS data | ||||
| a1 | 00:44:05.595 | −20:33:53.61 | 1.5567 | −2094 |
| a2 | 00:44:05.607 | −20:33:54.51 | 1.5577 | −1988 |
| a3 | 00:44:05.680 | −20:33:54.92 | 1.5831 | 972 |
| a4 | 00:44:05.590 | −20:33:55.80 | 1.5609 | −1609 |
| b1 | 00:44:05.369 | −20:33:56.45 | 1.5904 | 1342 |
| b2 | 00:44:05.388 | −20:33:57.04 | 1.5659 | −1026 |
| L | 00:44:05.200 | −20:34:00.17 | 1.5848 | 1173 |
| FORS2 data | ||||
| 2 | 0:44:04.737 | −20:34:09.43 | 1.5795 | 556 |
| 3a | 0:44:05.450 | −20:34:16.78 | 1.5699 | −562 |
| 3b | 0:44:05.531 | −20:34:16.78 | 1.5716 | −364 |
| 4 | 0:44:05.325 | −20:33:14.28 | 1.5787 | 463 |
| 5 | 0:44:05.611 | −20:32:58.55 | 1.5778 | 358 |
| 6 | 0:44:03.015 | −20:32:31.84 | 1.5986 | 2780 |
| ID . | RA . | Dec. . | z . | v . |
|---|---|---|---|---|
| SINFONI and KMOS data | ||||
| a1 | 00:44:05.595 | −20:33:53.61 | 1.5567 | −2094 |
| a2 | 00:44:05.607 | −20:33:54.51 | 1.5577 | −1988 |
| a3 | 00:44:05.680 | −20:33:54.92 | 1.5831 | 972 |
| a4 | 00:44:05.590 | −20:33:55.80 | 1.5609 | −1609 |
| b1 | 00:44:05.369 | −20:33:56.45 | 1.5904 | 1342 |
| b2 | 00:44:05.388 | −20:33:57.04 | 1.5659 | −1026 |
| L | 00:44:05.200 | −20:34:00.17 | 1.5848 | 1173 |
| FORS2 data | ||||
| 2 | 0:44:04.737 | −20:34:09.43 | 1.5795 | 556 |
| 3a | 0:44:05.450 | −20:34:16.78 | 1.5699 | −562 |
| 3b | 0:44:05.531 | −20:34:16.78 | 1.5716 | −364 |
| 4 | 0:44:05.325 | −20:33:14.28 | 1.5787 | 463 |
| 5 | 0:44:05.611 | −20:32:58.55 | 1.5778 | 358 |
| 6 | 0:44:03.015 | −20:32:31.84 | 1.5986 | 2780 |
3.4 Chandra X-ray spectroscopy
Sources a2, a3, and b1 have been spectroscopically identified as AGN, although only b1 has been detected in the Chandra image, as already reported by Tozzi et al. (2015).
To measure the nuclear properties of b1, we extracted the X-ray spectrum of this source. The source and local background spectral extractions were performed separately in each observation, using circular regions of 1.5 arcsec radius and annular regions with inner and outer radii of 3 and 7.5 arcsec, respectively.6 The spectral extractions and response files production were performed with the CIAO script specextract. The spectra were finally co-added using the FTOOLS7 script addascaspec. The resulting spectrum has been grouped to 1 count per bin, and modelled in xspec v. 12.9.0 in the 0.3–8 keV (0.8–20 keV rest-frame) band and using the Cash statistics implementation with direct background subtraction (Cash 1976; Wachter, Leach & Kellogg 1979). The X-ray spectrum of b1 consists of 268 ± 21 (90 |${{\ \rm per\ cent}}$| C.l.) background-subtracted counts, in the 0.3–8 keV energy band and is shown in Fig. 6. It has been modelled with an intrinsically absorbed power law (the dashed line) with a thermal emission (apec model in XSPEC, the dotted line) at low energies (<0.6 keV) to account for residual excess. The latter component can either parametrize a possible hot thermal corona associated with the quasar host galaxy or may account for the improper background subtraction at these energies due to inhomogeneous distribution of the ICM in the spectral extraction regions. The best-fitting model (C − stat/dof = 125/173) gives a |$\rm \Gamma = 1.4\pm 0.2$| and |$\rm log[N_{H}/cm^{-2}] = 22.7^{+0.1}_{-0.2}$| with a best fit |$\rm kT\approx 0.7$| keV (assuming solar abundance). The latter is unconstrained given that the thermal component affects a restricted spectral region at energies <0.6−0.7 keV of low SNR. The resulting unabsorbed 2–10 keV luminosity is |$\rm log [L_{[2-10]\, keV}/erg~s^{-1}] = 44.1 \pm 0.2$|. A fit with a canonical |$\rm \Gamma = 1.9$| requires slightly higher column densities of |$\rm log[N_{H}/cm^{-2}] = 23.0 \pm 0.1$| and results in |$\rm log [L_{[2-10]\, keV}/erg~s^{-1}] = 44.2$|. b1 is therefore a luminous and moderately obscured source.
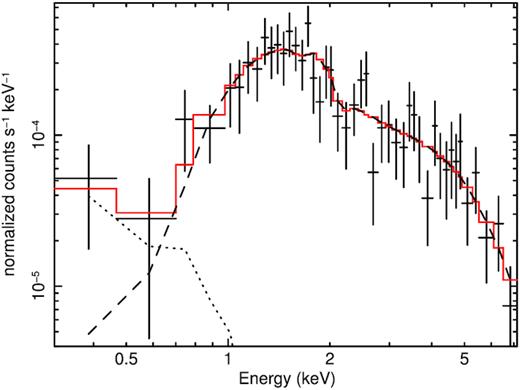
X-ray spectrum and best-fitting model (red) of b1. The dotted and dashed lines represent the thermal and absorbed power-law model component, respectively.
AGN a2 and a3 have not been detected in Chandra. While this is not at odd for a3, which is classified as a type-2 AGN and its X-ray emission is indeed obscured, a2 shows a broad emission line. We derived a 3σ observed luminosity upper limit at the position of these sources (whose distance is less than Chandra resolution) finding |$\rm log[L_{[2-10]\, keV}/erg~s^{-1}]\lt 43$|, assuming an unabsorbed power law with typical Γ = 1.9. If we consider the bolometric luminosity of a2 derived from |$\rm L_{5100 \, \mathring{\rm A} }$| (i.e. |$\rm log [L_{bol}/erg~s^{-1}] \simeq 45.3$|; see Section 4.1 and Table 4), by applying a bolometric correction |$\rm k_{bol,[2-10keV]}\simeq 18.96 \pm 0.24$| (Duras et al. 2020) we expect an intrinsic luminosity |$\rm log[L_{[2-10]\, keV}/ erg~s^{-1}] \sim 44.01$|. This means that, to satisfy the upper limit on |$\rm log[L_{[2-10]\, keV}/ erg~s^{-1}]$|, a high level of obscuration (|$\rm log[N_{H}/cm^{-2}] \gtrsim 23.8$|) would be required. This is consistent with its optical properties. Indeed, while the source b1 has an H α emission line clearly broad (|$\rm FWHM_{H\alpha }\gt 2000~km\, s^{-1}$|), a2 has an FWHM that is close to the typical value used as threshold to distinguish between Type-1 and Type-2 AGN (|$\rm FWHM_{H\alpha } \sim 1900~km\, s^{-1}$|). The same calculation cannot be made for the a3 source since its host galaxy emission is expected to dominate the 5100 Å continuum luminosity and therefore no bolometric correction can be applied. The derived X-ray properties are reported in Table 4.
| . | |$\log L_{\rm bol} ^{a }$| . | |$\rm logM_{BH}$| . | |$\rm \lambda _{Edd}$| . | |$\log L_{\rm X}^{b}$| . | |$\rm logN_{H}$| . | Γ . |
|---|---|---|---|---|---|---|
| . | |$\rm (erg\, s^{-1})$| . | (M⊙) . | . | |$\rm (erg\, s^{-1})$| . | |$\rm (cm^{-2})$| . | . |
| a2 | 45.4 ± 0.2 | |$7.55 _{-0.38} ^{+0.35}$| | |$0.51 _{-0.35} ^{+0.68}$| | 44.0 | ≳ 23.8 | 1.9 |
| b1 | 45.6 ± 0.2 | |$7.86 _{-0.37}^{+0.34}$| | |$0.46_{-0.30} ^{+0.57}$| | 44.1 | 22.7 | 1.4 ± 0.2 |
| . | |$\log L_{\rm bol} ^{a }$| . | |$\rm logM_{BH}$| . | |$\rm \lambda _{Edd}$| . | |$\log L_{\rm X}^{b}$| . | |$\rm logN_{H}$| . | Γ . |
|---|---|---|---|---|---|---|
| . | |$\rm (erg\, s^{-1})$| . | (M⊙) . | . | |$\rm (erg\, s^{-1})$| . | |$\rm (cm^{-2})$| . | . |
| a2 | 45.4 ± 0.2 | |$7.55 _{-0.38} ^{+0.35}$| | |$0.51 _{-0.35} ^{+0.68}$| | 44.0 | ≳ 23.8 | 1.9 |
| b1 | 45.6 ± 0.2 | |$7.86 _{-0.37}^{+0.34}$| | |$0.46_{-0.30} ^{+0.57}$| | 44.1 | 22.7 | 1.4 ± 0.2 |
a derived from |$L_{5100\, \mathrm{\mathring{\rm A}}|}$| following Runnoe et al. (2012)
b the values of |$\log L_{\rm [2-10]\, keV}$| reported are intrinsic (unabsorbed). This value has been computed from the X-ray spectrum for b1, while for a2 has been derived from the bolometric luminosity.
| . | |$\log L_{\rm bol} ^{a }$| . | |$\rm logM_{BH}$| . | |$\rm \lambda _{Edd}$| . | |$\log L_{\rm X}^{b}$| . | |$\rm logN_{H}$| . | Γ . |
|---|---|---|---|---|---|---|
| . | |$\rm (erg\, s^{-1})$| . | (M⊙) . | . | |$\rm (erg\, s^{-1})$| . | |$\rm (cm^{-2})$| . | . |
| a2 | 45.4 ± 0.2 | |$7.55 _{-0.38} ^{+0.35}$| | |$0.51 _{-0.35} ^{+0.68}$| | 44.0 | ≳ 23.8 | 1.9 |
| b1 | 45.6 ± 0.2 | |$7.86 _{-0.37}^{+0.34}$| | |$0.46_{-0.30} ^{+0.57}$| | 44.1 | 22.7 | 1.4 ± 0.2 |
| . | |$\log L_{\rm bol} ^{a }$| . | |$\rm logM_{BH}$| . | |$\rm \lambda _{Edd}$| . | |$\log L_{\rm X}^{b}$| . | |$\rm logN_{H}$| . | Γ . |
|---|---|---|---|---|---|---|
| . | |$\rm (erg\, s^{-1})$| . | (M⊙) . | . | |$\rm (erg\, s^{-1})$| . | |$\rm (cm^{-2})$| . | . |
| a2 | 45.4 ± 0.2 | |$7.55 _{-0.38} ^{+0.35}$| | |$0.51 _{-0.35} ^{+0.68}$| | 44.0 | ≳ 23.8 | 1.9 |
| b1 | 45.6 ± 0.2 | |$7.86 _{-0.37}^{+0.34}$| | |$0.46_{-0.30} ^{+0.57}$| | 44.1 | 22.7 | 1.4 ± 0.2 |
a derived from |$L_{5100\, \mathrm{\mathring{\rm A}}|}$| following Runnoe et al. (2012)
b the values of |$\log L_{\rm [2-10]\, keV}$| reported are intrinsic (unabsorbed). This value has been computed from the X-ray spectrum for b1, while for a2 has been derived from the bolometric luminosity.
4 AGN AND SF ACTIVITY IN THE CLUSTER CORE
4.1 Bolometric luminosity, BH masses, and Eddington ratios
The values obtained for the bolometric luminosity are of the order of 1045−1046 |$\rm erg~s^{-1}$| (see Table 4). For the source b1, we could also estimate the bolometric luminosity from the [2–10] keV band by assuming the bolometric correction from Duras et al. (2020). The derived value is log[L|$\rm _{bol}/ erg~s^{-1}$|] = 45.4, very close to the one computed from the 5100 Å luminosity [i.e. log(L|$\rm _{bol}/ erg~s^{-1}$|) = 45.6]. This agreement confirms that the 5100 Å luminosity is AGN dominated and therefore can be used in the BH mass computation. Indeed, from the broad H α line, we estimated the BH mass of the two BLAGN (a2 and b1) using the virial formula by Greene & Ho (2005).
Sources a2 and b1 are therefore luminous, massive, highly accreting, and obscured AGN. We caution the reader that the values obtained for the BH masses can be underestimated due to the high |$\rm N_H$|, which might extinguish the H α emission line and the |$\rm L_{5100}$|. Bolometric luminosities, black hole masses, and Eddington ratios are reported in Table 4.
4.2 Star formation activity
Santos et al. (2015) derived the SFR in the cluster core galaxies through Herschel far-IR data (the red contour in Fig. 7), finding an SFR |$\rm \simeq 450 \pm 60 ~M_{\odot } ~yr^{-1}$|. Unfortunately, given the SPIRE point spread function ranging from 17.6 arcsec at 250 |$\mu$|m to 35.2 arcsec at 500 |$\mu$|m, this value includes all sources studied here plus an additional very bright object to the north of the studied region. On the contrary, ALMA observations provide sufficient angular resolution (0.98 arcsec × 0.78 arcsec) to distinguish the single sources within the observed ALMA field shown in cyan in Fig. 7.
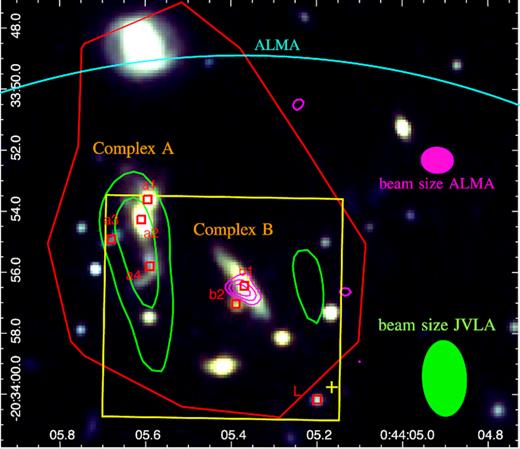
HST RGB image of the XDCP0044 core, with overplotted the 3σ 1–2 GHz JVLA radio contours (green), the Herschel FIR 3σ detection (red), and the 230 GHz ALMA continuum at 5σ (magenta). The cyan line indicates the ALMA FOV, while the green and magenta ellipses are the JVLA and ALMA beam, respectively.
The analysis of the ALMA data did not spot emission lines in the region covered by the SINFONI FOV. On the contrary, in the ALMA continuum map observed at 230 GHz with an rms sensitivity of 0.024 mJy beam−1 (the magenta contours in Fig. 7), we detected the source b1 at 5σ significance with a rest-frame 600 GHz flux of 0.80 ± 0.15 mJy. No emission is associated to a2, a 3σ upper limit on the flux has been computed to be <0.59 mJy.
For the source b1, we derived the SFR by assuming a typical QSO SED, i.e. Mrk 231 template, and normalizing it to the observed ALMA flux. The derived value obtained by integrating from 8 to 1000|$\rm ~\mu m$|, is |$\rm 490~M_{\odot }~yr^{-1}$|. This value is consistent with the SFR derived from IR Herschel data by Santos et al. (2015) for the entire central region, suggesting that most of the IR emission, and therefore of the SF, might be associated to b1. However, if we consider a different modelization for the dust emission and we assume, e.g. a simple blackbody template normalized to the ALMA flux with dust temperature of 40 K, the SFR we obtain is lower, i.e. ∼150 M⊙ yr−1. Also, for source a2 we computed an upper limit on the SFR (1) using the Mrk 231 template, finding SFR < 285 |$\rm M_{\odot }~yr^{-1}$| and (2) by fitting with a simple blackbody template with different temperatures, finding a best fit with T = 30 K and a SFR < 240 |$\rm M_{\odot }~yr^{-1}$|.
JVLA data reveal an extended radio emission associated to Complex A with a flux density of |$\rm S_{1.5~GHz} = 0.22 \pm 0.3~mJy$| (green contours in Fig. 7). Its luminosity is |$\rm L_{1.5~GHz} = 3.6\pm 0.5\times 10^{24}\, W\, Hz^{-1}$| and under the assumption that the radio signal is produced by a single source, its power (|$\rm log [P_{1.5GHz}/W~Hz^{-1}~sr^{-1}]$| = 23.45) would be just above the threshold at |$z$| ∼ 1.6, introduced by Magliocchetti et al. (2014; |$\rm log P_{cross} (z)$| = 21.7 + z), to discriminate SF processes from AGN, suggesting therefore a likely AGN powered radio emission. However, since the value is slightly above |$\rm P_{cross}(z)$| but below |$\rm P_{cross}(z)+0.2$|, there is a 20–40 |${{\ \rm per\ cent}}$| probability that the radio emission is on the contrary due to SF processes (Magliocchetti et al. 2018). In this case, the measured radio luminosity would translate into an |$\rm SFR \sim 100~ ~M_{\odot } ~yr^{-1}$| according to the relation by Brown et al. (2017), in agreement with the upper limit estimated from the ALMA data.
We then estimated an upper limit on the CO flux, producing a velocity-integrated map by assuming an FWHM = 500 |$\rm ~km~s^{-1}$|, typically expected for CO emission lines of AGN (e.g. Brusa et al. 2018; Herrera-Camus et al. 2019), centred at the redshift of the cluster. This translates into a 3σ upper limit on the CO integrated flux for a point source of ∼0.27 Jy beam−1 km s−1, equivalent to |$\sim 0.585 \rm ~mJy$|. This value corresponds to a |$\rm L^{\prime }_{CO} = 4.9 \times 10^{11} K~km\, s^{-1}~pc^2$| following the relation from Solomon & Vanden Bout (2005) and assuming the ratio CO(5-4) to CO(1-0) given by Carilli & Walter (2013). According to the values found by Accurso et al. (2017) for massive galaxies (|$M_{\star } \gt 10^{11} \, \mathrm{M}_{\odot }$|), this value results in |$\rm M(CO)\lt 3.5-4 \times 10^9 M_{\odot }$|, in agreement with what recently found for galaxies in high-z clusters (e.g. Hayashi et al. 2018; Pulido et al. 2018).
5 DISCUSSION
5.1 Multiple AGN activity in the cluster core
As a very interesting result, we found that three of the seven galaxies in the core of XDCP0044 host an obscured AGN and that such galaxies are located at a minimum (maximum) projected distance of ∼10 kpc (40 kpc). This evidence seems to suggest a crucial role of AGN in the galaxy evolution at this epoch and for these environments. The discovery of multiple AGN activity is common in proto-clusters, where large centrally overdensity of AGN are frequently found (Digby-North et al. 2010; Galametz et al. 2010; Krishnan et al. 2017; Casasola et al. 2018), but up to now only few works reported multiple AGN activity in high-z galaxy cluster cores, although not at such small distances. For example, Hilton et al. (2010) reported the detection of two central X-ray cluster member AGN at a projected distance of ≈90 kpc in the z = 1.46 galaxy cluster XMMXCS J2215.9-1738 and, at higher redshift (|$z$| ∼ 2), Gobat et al. (2013) found two X-ray AGN at a projected distance of ∼100 kpc in CL J1449 + 0856. The newly discovered AGN in XDCP0044 are among the closest AGN found at |$z$| > 1 (De Rosa et al. 2020, and references therein) and their proximity implies a future merger between them. In addition, these AGN are located in merger systems and exhibit high luminosity, high/intermediate obscuration, and high accretion rates. Specifically, two of them show broad lines and are mildly (|$\rm log(N_H/cm^2) = 22.7$|) or highly (|$\rm log(N_H/cm^2) \gt 23.8$|) X-ray obscured, while the third one is also optically obscured (type-2 AGN).
Semi-analytical models suggest that mergers between gas-rich galaxies can destabilize the gas and cause its inflow towards the inner regions, thus providing potential accreting material for the central BH and triggering starburst activity (e.g. Granato et al. 2004; Hopkins et al. 2008). This scenario is confirmed by several statistical works (e.g. Martini et al. 2013; Alberts et al. 2016) who observed a correlation between AGN and merger activity in both proto-clusters and galaxy clusters. Moreover, according to this scenario, in this phase the AGN is expected to be highly accreting and obscured (e.g. Koss et al. 2018), in agreement with our findings.
For the two discovered AGN showing broad lines, we also studied their location in the |$\rm M_{BH}$|–|$\rm M_{*}$| plane. Stellar masses of the AGN host galaxies were computed, as detailed in Section 5.2, finding |$\rm log (M_{\star }) \approx 11.3~M_{\odot }$| and |$\rm 11.6~M_{\odot }$| for a2 and b1, respectively. As shown in Bongiorno et al. (2019), we found that both of them lie below the Kormendy & Ho (2013) relation for local inactive galaxies, i.e. at ∼2σ from it with Δlog(|$\rm M_{BH}/M_{\star }$|) computed perpendicular to the relation. On the contrary, the |$\rm M_{BH}/M_{\star }$| ratios seem to be more in agreement with the recent local scaling relation computed for active galaxies at z < 0.055 by Reines & Volonteri (2015) and with the unbiased |$\rm M_{BH}$|–M⋆ relation derived by Shankar et al. (2016).
5.2 Mass assembly and time-scales for the BCG formation
How the BCG form is still an open question due to the difficulty in identifying the BCG progenitors at |$z$| > 1.5. To test the scenario predicting the BCG formation at this epoch through mergers (Stott 2008; Laporte et al. 2013; Lidman et al. 2013; Webb et al. 2015), we estimated the time-scale for merging all galaxies discovered to be in the cluster core and the final mass of the possible newly formed galaxy. We first computed the stellar masses of each galaxy resolved by HAWK-I images (see Fassbender et al. 2014) by performing an SED-fitting procedure on the HST photometry, HAWK-I J- and K|$\rm s$|-bands. We used the zphot code (Fontana et al. 2000), with Bruzual & Charlot (2003) templates, Salpeter (1959) initial mass function and Calzetti et al. (2000) extinction. We adopted exponentially declining SF histories (τ-models) and approximated the redshift of all the sources to |$z$|c = 1.578. Assuming that the seven confirmed cluster members (all 16 galaxies detected by HST) will be forming the BCG, their best-fitting masses would sum up to a final stellar mass of |$\rm \sim 1.0\, (2.3) \times 10^{12} M_{\odot }$|, consistent with the mass range observed for local BCGs (Zhao, Aragón-Salamanca & Conselice 2015).
The BCG assembly time-scale is computed according to the average time for a major merger of close pairs reported in Kitzbichler & White (2008). We considered the case in which Complex A and Complex B are cluster’s sub-clumps, each of which will aggregate to form a cD-like galaxy through a gravitational phase transition. In Complex B, this process seems to be already in an advanced state, with b1 dominating the system, while in Complex A, several galaxies with similar mass are still visible. However, the resulting merging time (|$\rm t_{merge}$|) is similar for both complexes, i.e. of the order of ∼1–1.5 Gyr. This process will lead to the formation of two massive galaxies (galaxy A from Complex A and galaxy B from Complex B) at the centre of the galaxy cluster that will possibly merge to form the final BCG. We then assumed that these two galaxies and the L source will move towards the X-ray centroid in a dynamical friction time (Binney & Tremaine 1987) of the order of |$\rm \sim$|1.2–2.5 Gyr. Therefore, according to this scenario, all these galaxies will merge in |$\rm \simeq$| 2.5 Gyr.
A different scenario has also been considered in which Complex A and Complex B do not represent subgroups of the cluster core and therefore all galaxies will directly merge close to the X-ray centroid to form the final BCG in a friction time-scale. In this case, we estimated the mass of the single galaxies resolved by HST observations by assuming a constant mass-to-light ratio in the HST F160W-band, which is the closest to the rest-frame K band considered as a good indicator of the mass with a 1σ scatter of about 0.1 dex (Madau, Pozzetti & Dickinson 1998; Bell et al. 2003). According to this scenario, which does not imply the formation of sub-groups, the central QSO b1 and the L source are found to have shorter merger times (|$\rm \lt 600~Myr$|) compared to all other galaxies, whose friction time ranges from 3.2 to 6 Gyr. Galaxy a3 needs more than 10 Gyr to reach the X-ray centroid and therefore would not merge.
Summarizing, we find that in a time-scale of a couple of Gyr, all galaxies in the core of XDCP0044 will experience several major mergers, forming a massive central galaxy with |$M_{\star }\sim 10^{12}\, \mathrm{M}_{\odot }$| at |$z$| ∼ 1, in agreement with what predicted by semi-analytic models (De Lucia & Blaizot 2007) and found observationally (Prieto & Eliche-Moral 2015; Sawicki et al. 2020). The BCG will then keep slowly growing its mass at z ≤ 1 through minor mergers (e.g. Lidman et al. 2013; Liu et al. 2015).
The newly formed BCG will host a central SMBH, whose lower limit to the mass is |$\rm M_{BH} \gt 2 \times 10^8 \, \mathrm{M}_{\odot }$|, obtained by summing the masses of the two AGN, a2 and b1. Stellar and BH masses of the final BCG as well as merging time-scales have to be considered as lower limits. In our computation, we have indeed conservatively considered only spectroscopically confirmed galaxies. However, additional cluster complexes [e.g. galaxies complex 3(a + b) identified in Fassbender et al. 2014] might also take part in the formation of the BCG.
6 SUMMARY AND CONCLUSIONS
In this paper, we have investigated the properties of the galaxy population in the very central region (∼70 × 70 kpc2) of XDCP0044, one of the most massive galaxy clusters at |$z$| ∼1.6. We have analysed high-resolution HST images in F105W, F140W, and F160W-bands, IFU spectroscopy obtained with SINFONI in J and H band, and KMOS in JY and H band, together with JVLA at 1–2 GHz and ALMA band 6 observations at 288 GHz.
The main results of our analysis are summarized as follows:
High-resolution HST F105W, F140W, and F160W images reveal the presence of 16 sources in the core of XDCP0044. We find that most of such galaxies are grouped, forming two complexes, i.e. Complex A and Complex B. The first one includes the BCG identified by Fassbender et al. (2014) through HAWK-I images, while the second contains the central X-ray AGN identified by Tozzi et al. (2015).
Through SINFONI and KMOS spectroscopy, we have confirmed seven cluster members with redshifts ranging from |$z$| = 1.5567 to |$z$| = 1.5904 (Δ|$z$| ≃ 0.0337), consistently with the redshift of the cluster. In particular, we find that Complex A consists of at least four cluster members at a projected distance of ∼20 kpc, while the central AGN b1, and the nearby (∼5 kpc) galaxy b2, belong to the Complex B.
In 2 of the 7 confirmed cluster members (a2 in Complex A and b1 in Complex B), we detect a broad (|$\rm \gtrsim 2000~km~ s^{-1}$|) H α emission line. These sources have been therefore classified as BL-AGN, hosting massive (|$\rm \gt 10^7\!-\!10^8 \, \mathrm{M}_{\odot }$|) and highly accreting (|$\rm \sim 0.4-0.5$|) BHs. Moreover, the analysis of the BPT diagram pointed out the presence of an additional AGN that does not show broad lines (a3 in Complex A). The minimum distance in this AGN triple is 10 kpc between a2 and a3, while the maximum distance between a3 and b1 is 40 kpc.
One of the BLAGN, i.e. b1, was already identified as AGN from its unresolved X-ray emission by Tozzi et al. (2015). The analysis of the spectrum reveals that b1 is a luminous and moderately obscured AGN, with X-ray luminosity |$\rm L_{[2-10]\, keV} = 1.2_{-0.6} ^{+1.4}\times 10^{44}\rm erg\, s^{-1}$| and column density |$\rm N_H \simeq 5.4 \times 10^{22} cm ^{-2}$|. The other two objects (the BLAGN a2 and the NLAGN a3), on the contrary, are not detected in the Chandra data, implying a high level of obscuration. In particular, source a2, for which the intrinsic X-ray luminosity could be derived from the bolometric one, is found to be X-ray luminous (|$\rm L_{[2-10]\, keV} \sim 10^{44} ~erg~s^{-1}$|) and obscured (|$\rm log [N_{\rm H}/cm^{-2}] \gtrsim 23.8$|).
The integrated SFR of the whole central region of XDCP0044 is |$\rm \simeq 450 \pm 60 ~M_{\odot } ~yr^{-1}$|. This value has been derived by Santos et al. (2015) using Herschel data that, however, do not allow us to distinguish the different sources. Because of the higher resolution ALMA observations, we derive the SFR of the single observed sources finding that the central AGN b1 alone contributes to this value with an SFR ranging from 150 to 490 |$\rm M_{\odot }\,yr^{ -1}$|, depending on the assumed SED, while a2 might contribute less than ∼285 |$\rm M_{\odot }$| yr−1, in agreement with the radio emission of Complex A.
In conclusion, XDCP0044 allows us to witness the BCG assembly in one of the densest galaxy cluster core at z ∼ 1.6, which is thought to be in a crucial formation epoch, when both SF and nuclear activity are at their peak (Madau & Dickinson 2014; Aird et al. 2015). We confirm that high-z galaxy cluster cores show different properties compared to the |$z$| = 0 ones. Indeed, no single, early-type BCG has been detected in the core of XDCP0044, which is found to host a large number (at least seven confirmed) of highly star-forming interacting galaxies grouped in two main complexes, both hosting multiple AGN activity. The discovered AGN triple is one of the closest revealed so far at |$z$| >1 (De Rosa et al. 2020), with a projected distance ranging from 10 to 40 kpc. Moreover, these results lead to a scenario in which obscured AGN activity is triggered during the formation of the cluster BCG, when mergers between gas-rich galaxies provide the fuel for the AGN and for triggering starburst activity. According to our data, we expect to form a typical massive galaxy of |$M_{\star }\sim 10^{12} \, \mathrm{M}_{\odot }$|, hosting an SMBH with mass |$\gt 2 \times 10^8 ~\, \mathrm{M}_{\odot }$|, in a time-scale of few Gyr.
ACKNOWLEDGEMENTS
We thank Andrea Biviano, Claudio Ricci, and Alessandra Lamastra for useful discussions. This work is based on observations collected at the European Southern Observatory under ESO programmes 094.A-0713(A) and 092.A-0114(A). AB, EP, LZ, and MB acknowledge the support from ASI–INAF 2017-14-H.0. PT acknowledges support from the Istituto Nazionale di Astrofisica (INAF) PRIN-SKA 2017 program 1.05.01.88.04 (ESKAPE). This paper uses the following ALMA data: ADS/JAO.ALMA #2017.1.01387.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ.
DATA AVAILABILITY
All raw data used in this paper are publicly available in the telescopes archives. Further information on the storage of these data is given in Section 2. The reprocessed data we have produced in this work are available on request.
Footnotes
The mass that encloses an overdensity of 200 times the critical density of the Universe, computed by Tozzi et al. (2015) by modelling the X-ray data.
sextractorFLUX_ISO, namely the summation of the fluxes in all the pixel assigned to each object in the segmentation map.
Elliptical aperture defined by the second-order moments of the object’s light distribution in sextractor routine.
For both methods, the uncertainties are computed by adopting the bootstrapping, which is a statistical robust estimator when dealing with small samples (<50).
From this region, we excluded a circular region of 1.5 arcsec radius centred on the HST detected position of the BCG galaxy in order to avoid possible, unresolved, contributions from it.
Defined as Sν ∝ να.
REFERENCES
APPENDIX A: SINFONI AND KMOS SPECTRA OF CLUSTER MEMBERS
Zoom-in of the SINFONI J and H band and KMOS JY- and H-band (for a3) rest-frame spectra of the galaxies in the field of interest classified as cluster members.
![Zoom-in of the SINFONI J- and H-band (KMOS JY- and H-band for a3) rest-frame spectra of the galaxies in Complex A in spectral regions in which (left-hand panels) [O iii] doublet and H β emission lines and (right-hand panels) [N ii] and [S ii] doublet, [O i] and H α emission lines, are expected to be observed. The expected position for each emission line is marked with a dashed green line and bold labels correspond to the detected lines. The grey vertical bands indicate the wavelength regions contaminated by the sky emission lines. All the spectra are binned at 70 $\rm km~s^{-1}$.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2495/1/m_staa2495figa1.jpeg?Expires=1750566919&Signature=xUnZ3pbDKBuqn2dxVp0LgTF3myozt4v-CM0h4dDlNNoNUtCpevKlKtCdohOmktR8JGykyb65fgy1GRnlhSdgBNyiMc6oR~B-hQC1Y5mrkZCwSg80CUOBwiXpM8-2AnNot-Ga48NiVv6buTM57x6Lj6jmh2pDuDIOT-CCKmRgleZi496XHU4YFjhOy3Vril9EDi7Mdt2HZwwVXmxVXfOJWQtRLm8n0B~We6KiDSNZqhEPxw2MXmnnaCryF6YZqS1aHgJORxFvDPev3GBmEO5OfBMeYwAfjOFJxZC~Xr4deNRpr9WdRZOVphdZrwl4tFLT0ib~pr2QMuzOi8PeoDezSg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Zoom-in of the SINFONI J- and H-band (KMOS JY- and H-band for a3) rest-frame spectra of the galaxies in Complex A in spectral regions in which (left-hand panels) [O iii] doublet and H β emission lines and (right-hand panels) [N ii] and [S ii] doublet, [O i] and H α emission lines, are expected to be observed. The expected position for each emission line is marked with a dashed green line and bold labels correspond to the detected lines. The grey vertical bands indicate the wavelength regions contaminated by the sky emission lines. All the spectra are binned at 70 |$\rm km~s^{-1}$|.
APPENDIX B: JVLA RADIO DETECTED SOURCES IN XDCP0044
Radio JVLA data include the whole galaxy cluster field. Here, we briefly summarize the radio sources detected in XDCP0044. Fig. B1 shows the HST RGB image of the cluster with overlapped the 3σ radio JVLA contours in green at 1.5 GHz and the soft X-ray emission in magenta. In addition to the extended radio emission associated with Complex A and described in Section 4.2 (i.e. r2), four radio sources have been detected, i.e. three compact radio sources in the south region of the galaxy cluster (r3, r4, and r5) and an extended emission, r1, in the north part. We report the JVLA fluxes of the identified radio sources in Table B1.
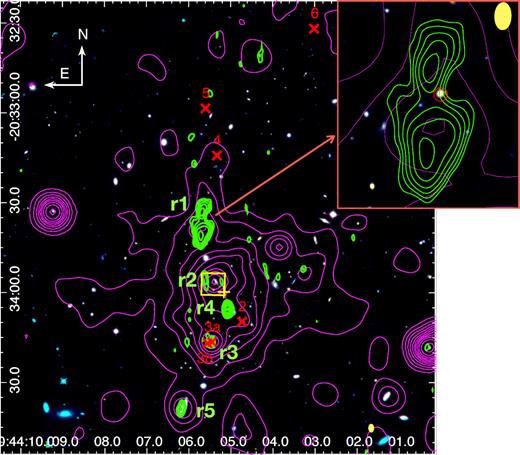
HST RGB image of XDCP0044 with |$\rm 3\sigma$| 1–2 GHz JVLA radio emissions contours (green) and soft X-ray emission (magenta). The yellow filled ellipse corresponds to the beam size of the JVLA data. The red crosses indicate the confirmed cluster members from FORS2 spectroscopy by Fassbender et al. (2014). Five radio sources are indicated with r1, r2, r3, r4, and r5. The top right-hand panel shows a zoom-in of the radio source r1 and its most probable optical counterpart (marked with a red circle), which was identified by Fassbender et al. (2014) as a passive galaxy. The yellow ellipse represents the beam size of the JVLA observations.
| |$\rm Radio\, source$| . | |$\rm S_{[1.5~GHz]}$| . |
|---|---|
| . | |$\rm (mJy)$| . |
| r1 | 3.19 ± 0.07 |
| r2 | 0.22 ± 0.03 |
| r3 | 0.16 ± 0.02 |
| r4 | 0.85 ± 0.03 |
| r5 | 0.28 ± 0.03 |
| |$\rm Radio\, source$| . | |$\rm S_{[1.5~GHz]}$| . |
|---|---|
| . | |$\rm (mJy)$| . |
| r1 | 3.19 ± 0.07 |
| r2 | 0.22 ± 0.03 |
| r3 | 0.16 ± 0.02 |
| r4 | 0.85 ± 0.03 |
| r5 | 0.28 ± 0.03 |
| |$\rm Radio\, source$| . | |$\rm S_{[1.5~GHz]}$| . |
|---|---|
| . | |$\rm (mJy)$| . |
| r1 | 3.19 ± 0.07 |
| r2 | 0.22 ± 0.03 |
| r3 | 0.16 ± 0.02 |
| r4 | 0.85 ± 0.03 |
| r5 | 0.28 ± 0.03 |
| |$\rm Radio\, source$| . | |$\rm S_{[1.5~GHz]}$| . |
|---|---|
| . | |$\rm (mJy)$| . |
| r1 | 3.19 ± 0.07 |
| r2 | 0.22 ± 0.03 |
| r3 | 0.16 ± 0.02 |
| r4 | 0.85 ± 0.03 |
| r5 | 0.28 ± 0.03 |
The compact radio sources r5 and r4 are associated with optically detected galaxies for which the redshift is unknown. However, the optical counterpart of r5 is probably a foreground galaxy, since its size at z ≥ 1.5 would be too large (∼35–50 kpc) compared to a typical galaxy. On the contrary, the compact radio emission r3 is associated to a group of interacting galaxies hosting an X-ray AGN found to be part of the cluster (object 3 in Tozzi et al. 2015). Its radio luminosity is |$\rm L_{1.5~GHz} = 2.6\pm 0.3 \times 10^{24}~W~Hz^{-1}$|, not k-corrected.
Finally, the hourglass-like extended emission , r1, does not show a radio core or a central radio galaxy. It might be associated with one or multiple optical counterparts located in the central narrowing, none of which has a known redshift. The most probable candidate seems the passive galaxy identified by Fassbender et al. 2014 (see zoom-in of Fig. B1). This radio source is spatially correlated to an X-ray north–south elongation reported by Tozzi et al. (2015) and described as evidence of mass accretion on to the cluster. This claim is supported by the presence of three spectroscopically confirmed cluster members (the red crosses in figure) located along the north axis (Fassbender et al. 2014).
We extracted the radio spectral index8 α of this source combining JVLA data at 1.5 GHz with a detection from the TGSS at 150 MHz (Intema et al. 2017). We found α = −1.3 ± 0.1, steeper than the average spectral index associated with radio galaxy lobes. This might be interpreted as a signature of aged plasma from a remnant radio galaxy. Assuming this radio source at the distance of the cluster, its radio luminosity at 1.5 GHz would be 7.0 ± 0.2 × 1025 W Hz−1, k-corrected assuming the measured α. This luminosity is high if compared with typical radio galaxies in local clusters (van Velzen et al. 2012). However, to date we know very little about the typical luminosities of high-redshift radio galaxies in cluster environments. Alternatively, this source might be directly associated to the ICM, possibly generated by compression of old plasma bubbles from merging induced shock waves (the so-called ‘radio phoenixes’; Ensslin & Brüggen 2001). This would explain the steep spectrum of the source. However, the high luminosity is at odds with what expected for these kind of sources (van Weeren et al. 2019).



