-
PDF
- Split View
-
Views
-
Cite
Cite
Héctor Gil-Marín, Julián E Bautista, Romain Paviot, Mariana Vargas-Magaña, Sylvain de la Torre, Sebastien Fromenteau, Shadab Alam, Santiago Ávila, Etienne Burtin, Chia-Hsun Chuang, Kyle S Dawson, Jiamin Hou, Arnaud de Mattia, Faizan G Mohammad, Eva-Maria Müller, Seshadri Nadathur, Richard Neveux, Will J Percival, Anand Raichoor, Mehdi Rezaie, Ashley J Ross, Graziano Rossi, Vanina Ruhlmann-Kleider, Alex Smith, Amélie Tamone, Jeremy L Tinker, Rita Tojeiro, Yuting Wang, Gong-Bo Zhao, Cheng Zhao, Jonathan Brinkmann, Joel R Brownstein, Peter D Choi, Stephanie Escoffier, Axel de la Macorra, Jeongin Moon, Jeffrey A Newman, Donald P Schneider, Hee-Jong Seo, Mariappan Vivek, The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: measurement of the BAO and growth rate of structure of the luminous red galaxy sample from the anisotropic power spectrum between redshifts 0.6 and 1.0, Monthly Notices of the Royal Astronomical Society, Volume 498, Issue 2, October 2020, Pages 2492–2531, https://doi.org/10.1093/mnras/staa2455
Close - Share Icon Share
ABSTRACT
We analyse the clustering of the Sloan Digital Sky Survey IV extended Baryon Oscillation Spectroscopic Survey Data Release 16 luminous red galaxy sample (DR16 eBOSS LRG) in combination with the high redshift tail of the Sloan Digital Sky Survey III Baryon Oscillation Spectroscopic Survey Data Release 12 (DR12 BOSS CMASS). We measure the redshift space distortions (RSD) and also extract the longitudinal and transverse baryonic acoustic oscillation (BAO) scale from the anisotropic power spectrum signal inferred from 377 458 galaxies between redshifts 0.6 and 1.0, with the effective redshift of zeff = 0.698 and effective comoving volume of |$2.72\, {\rm Gpc}^3$|. After applying reconstruction, we measure the BAO scale and infer DH(zeff)/rdrag = 19.30 ± 0.56 and DM(zeff)/rdrag = 17.86 ± 0.37. When we perform an RSD analysis on the pre-reconstructed catalogue on the monopole, quadrupole, and hexadecapole we find, DH(zeff)/rdrag = 20.18 ± 0.78, DM(zeff)/rdrag = 17.49 ± 0.52 and fσ8(zeff) = 0.454 ± 0.046. We combine both sets of results along with the measurements in configuration space and report the following consensus values: DH(zeff)/rdrag = 19.77 ± 0.47, DM(zeff)/rdrag = 17.65 ± 0.30 and fσ8(zeff) = 0.473 ± 0.044, which are in full agreement with the standard ΛCDM and GR predictions. These results represent the most precise measurements within the redshift range 0.6 ≤ z ≤ 1.0 and are the culmination of more than 8 yr of SDSS observations.
1 INTRODUCTION
The large-scale structure (LSS) of the Universe contains valuable information of how the Universe has been evolving in the last ∼7 × 109 yr, when the dark-energy-domination era started. The current state-of-the-art spectroscopic LSS observations allow to utilize the standard ruler baryon acoustic oscillations (BAO), first detected in Eisenstein et al. (2005) on the Sloan Digital Sky Survey (SDSS) data set and Cole et al. (2005) on the Two-Degree Field Survey (2dF, Colless et al. 2003), to determine with precision the background expansion history of the Universe at late-time. During the last decade, the BAO technique has evolved in both precision and accuracy becoming mature. Consequently, a plethora of measurements has been performed on spectroscopic galaxy surveys at different epochs: 6-degree Field Survey (6dF; Jones et al. 2009; Beutler et al. 2011) at z = 0.106, WiggleZ (Drinkwater et al. 2010; Blake et al. 2011b; Kazin et al. 2014) at |$z=0.44,\, 0.6,\, 0.73$|, and Baryon Oscillation Spectroscopic Survey (BOSS) galaxies (Anderson et al. 2012, 2014a, b; Dawson et al. 2013; Alam et al. 2017) at |$z=0.38,\, 0.51,\, 0.61$|, and BOSS Lyman α forests (Bautista et al. 2017; du Mas des Bourboux et al. 2017) at z = 2.40. Additionally, if we want to obtain a direct measurement of the growth of structures from these same spectroscopic surveys we need to measure the effect of redshift space distortions (RSD; Kaiser 1987). Consequently, we obtain both an expansion history and a growth of structure measurement from the same data set. Parallel to the BAO technique development, RSD analyses have also matured both in modelling and observational systematics treatment during the last decade: RSD in 2dF (Percival et al. 2004), in 6dF (Beutler et al. 2012), in WiggleZ (Blake et al. 2011a), in VIPERS (de la Torre et al. 2013; Guzzo et al. 2014; Pezzotta et al. 2017), in FastSound (Okumura et al. 2016), as well in BOSS galaxies (Alam et al. 2017).
Anisotropic BAO studies provide a direct measurement of the background expansion at the epoch of the observed galaxies, z, through the absolute and relative BAO peak position in the anisotropic multipoles of the power spectrum or correlation function. Under the assumption of a functional form of the background expansion, H(z; Ωm) one can obtain a direct measurement of the density of matter in the Universe Ωm. Note that the BAO peak position is not directly sensitive to H(z), but to H(z)rdrag, and to the comoving angular diameter distance over the comoving sound horizon at the epoch where the baryon-drag optical depth equals unity, DM(z)/rdrag. From these measurements, one can either infer Ωm from the product of the two (which is independent of rdrag), or assume an extra prior on rdrag, which can either come from cosmic microwave background (CMB) measurements, or from a functional form of rdrag given by priors on the baryon, Ωb and radiation density |$\boldsymbol{\Theta }_{\rm rad}$| (which are typically not measured by LSS), and infer H0 (see for e.g. Addison et al. 2018). Within the SDSS collaboration, we opt to analyse these results under the less restrictive set of priors, and thus only assume a functional form for H(z), but no restriction on rdrag as a function of cosmology. The motivation for proceeding this way is the robustness of the cosmological interpretation under potential changes of the cosmological paradigm if, for example, the state-of-the-art value of rdrag changes significantly in the future or ΛCDM is ruled out, as one would just only need to re-interpret the quantities H(z)rdrag and DM(z)/rdrag rather than reanalysing the data. In this paper, we choose to work with the ‘Hubble distance’, DH, defined as DH(z) ≡ c/H(z), where c is the speed of light. The parameter DH(z)/rdrag has the advantage of being dimensionless, of the order of unity and directly proportional to the scale factor, which is actually measured.
RSD are a measurement of the peculiar velocity field of the galaxies along the line-of-sight (LOS). As this velocity field is only detected along the LOS, it generates an anisotropic signal in the power spectrum expansion as a function of the cosine of the LOS with the vector separation of the galaxy pair. This velocity field is generated by overdensities of matter, and therefore is coherent with the growth of these density perturbations. Thus, by measuring the redshift space distortion effect on the power spectrum of galaxies one can set constraints on the logarithmic growth of structure parameter, f. For the two-point statistics, this parameter is degenerate with the parameter σ8, the amplitude of dark matter fluctuations at the scale of |$8\, \, h^{-1}\, {\rm Mpc}$|. For this reason power spectrum or correlation function redshift space distortion analyses are sensitive to the combination, f times σ8, which we just refer as fσ8.
In this paper, we perform two complementary analyses, BAO and full shape analyses in order to extract DM(z)/rdrag, DH(z)/rdrag and fσ8 from the power spectrum of the final Data Release 16 (DR16) SDSS-IV eBOSS LRG catalogue in combination with the high redshift tail of the Data Release 12 (DR12) SDSS-III BOSS LRG catalogue (for simplicity we refer to this combined catalogue as the DR16 CMASS + eBOSS LRG catalogue). The catalogue consists of 377 458 galaxies between redshifts 0.6 and 1.0, with effective redshift of zeff = 0.698 and effective comoving volume of |$2.72\, {\rm Gpc}^3$|. The BAO analysis is focused exclusively on identifying the position of the BAO features in the power spectrum, whereas the full shape analysis models the anisotropic power spectrum shape to extract information. In order to enhance the BAO detection, we utilize the standard reconstruction algorithm (Eisenstein et al. 2007; Burden et al. 2014). Thanks to reconstruction we are able to remove most of the non-linear bulk flow effect and enhance the significance of the BAO features. For the BAO analysis, we therefore perform the standard analysis on the reconstructed catalogues, whereas the full shape analysis is performed on the original, pre-reconstructed catalogues. The results extracted from the analysis of the same sample in configuration space are presented in the companion paper (Bautista et al. 2020). Since these two results are expected to be highly correlated (as they are both extracted from the exact same catalogue) we perform a consensus results which is presented at the end of both papers.
The cosmological implication is presented instead in the companion paper (eBOSS Collaboration et al. 2020) along with the measurements of the rest of the galaxy and Lyman α samples of BOSS and eBOSS. These samples correspond to the following:1
luminous red galaxy sample (LRG), 0.6 < z < 1.0, power spectrum analysis (this paper) and correlation function analysis (Bautista et al. 2020)
emission-line galaxy sample (ELG), 0.6 < z < 1.1, power spectrum analysis (de Mattia et al. 2020), correlation function analysis (Tamone et al. 2020) and catalogue description (Raichoor et al. 2020)
quasar-clustering sample (QSO), 0.8 < z < 2.2, power spectrum analysis (Neveux et al. 2020), and correlation function analysis (Hou et al. 2020)
lyman α cross-correlation and autocorrelation analysis (des Mas du Bourboux et al. 2020) with quasars z > 2.1.
In addition, eBOSS Collaboration et al. (2020) include as well the results from the two low- and middle-redshift overlapping bins from SDSS-III BOSS (Alam et al. 2017), as they do not overlap with any of the eBOSS samples. An essential component of these studies is the generation of data catalogues (Lyke et al. 2020; Ross et al. 2020), mock catalogues (Lin et al. 2020; Zhao et al. 2020a), and N-body simulations for assessing systematic errors on the LRG (Rossi et al. 2020; Smith et al. 2020) and ELG samples (Alam et al. 2020; Avila et al. 2020). Additionally, in Wang et al. (2020) and Zhao et al. (2020b), the cross-correlation signal between LRG and ELG samples is presented and studied.
Previous to the final DR16 analysis, these samples were already studied for the two-year observation catalogues Data Release 14 (DR14): DR14 eBOSS LRG BAO (Bautista et al. 2018), DR14 eBOSS LRG RSD (Icaza-Lizaola et al. 2019), DR14 eBOSS quasar BAO (Ata et al. 2018), DR14 eBOSS quasar RSD (Hou et al. (Gil-Marín et al. 2018; Hou et al. 2018; Zarrouk et al. 2018) and DR14 Lyman α (de Sainte Agathe (Blomqvist et al. 2019; de Sainte Agathe et al. 2019). Other studies that included redshift-weighting techniques of the DR14 quasar sample were also presented by Ruggeri et al. (2019), Wang et al. (2018), Zhao et al. (2019), and Zhu et al. (2018).
This paper is organized as follows. In Section 2, we briefly present the actual and synthetic galaxy catalogues used in this paper. In Section 3, we describe the methodology followed for performing the power spectrum estimation and the models used for both BAO and full shape analysis. In Section 4, we present the results of this paper as well as the consensus along with the complementary configuration space analysis. In Section 5, we perform an exhaustive systematic study to quantify the potential systematic effect that could affect the inferred cosmological parameters. In Section 6, we present the Fourier and configuration space consensus results and in Section 7 we compare our findings with the standard Lambda cold dark matter (ΛCDM) model predictions. Finally, in Section 8, we present the conclusions of this work.
2 DATA SET
We briefly describe the DR16 LRG data set along with the synthetic mock catalogues we use. A detailed description of the DR16 data set is presented in Ross et al. (2020); the synthetic fast EZmocks used for estimating the covariance are fully described in Zhao et al. (2020a); and the mocks based on OuterRimN-body simulation used for validating the pipeline are described in Rossi et al. (2020). Additionally, we make use of a series of N-body simulations used for previous BOSS analyses (Alam et al. 2017), which we refer as Nseries mocks.
2.1 LRG galaxy sample
The SDSS fourth-generation spectroscopic observations (SDSS-IV, Blanton et al. 2017) employ two multi-object spectrographs (Smee et al. 2013) installed on the Apache Point Observatory 2.5-m telescope located in New Mexico, USA (Gunn et al. 2006), to carry out spectroscopic measurements from a photometrically selected eBOSS LRGs sample (Dawson et al. 2016). Such LRGs were previously selected from the optical SDSS photometry DR13 (Albareti et al. 2017) with the supplementary infrared photometry from the WISE satellite (Lang, Hogg & Schlegel 2016). The same instrument was already used for the previous BOSS program.
A description of the final targeting algorithm is presented in Prakash et al. (2016), which produced 60 LRG targets per square-degree over a sky footprint of 7500 deg2, of which ∼50 deg-2 were spectroscopically observed. Such observations returned mainly objects between 0.6 ≤ z ≤ 1.0 as tested by The Sloan Extended Quasar, ELG and LRG Survey (Dawson et al. 2016).
The estimation of the redshift of each LRG spectrum was performed using the publicly available RedRock algorithm,2 which improved the redshift efficiency of its predecessor, RedMonster (Hutchinson et al. 2016), from 90 up to 96.5 per cent in terms of objects with a confident redshift estimate, with less than 1 per cent catastrophic redshift errors.
The density of objects with spectroscopic information per sky-area in the galaxy catalogues is not constant over the eBOSS sky footprint, due to both observational systematics (varying observational features across the imaging survey) and geometrical effects (for example whether a region has been simultaneously observed by more than one plate). We refer to this whole effect as completeness, without separating the observational and geometrical contributions. Qualitatively, the completeness generates spurious signals, we need to filter out in order to measure the intrinsic clustering. Within the eBOSS collaboration, we define the completeness as the ratio of the number of weighted spectra (including also objects classified as stars and quasars) to the number of targets, which is computed per sky sector, this is, a connected region of the sky observed by a unique set of plates. In order to account for the effect of completeness, we downsample each object of the random catalogue by the completeness of its corresponding sky sector. In this way, the definition of completeness includes the systematic weight, wsys, as well as other effects, including the variation of the mean density as a function of stellar density and galactic extinction. For further details on the catalogue creation, we refer the reader to Ross et al. (2020).
Additionally, a minimum variance weight is also applied, the FKP weight (Feldman, Kaiser & Peacock 1994). This accounts for the radial mean density dependence, wFKP(z) = 1/[1 + n(z)P0], where P0 is chosen to be the amplitude of the power spectrum P(k) at the scales of BAO, |$k\sim 0.1\, \, h\, {\rm Mpc}^{-1}$|, |$P_0=10\, 000\, (\, h^{-1}\, {\rm Mpc})^3$|.
Fig. 1 displays the mean density of objects as a function of redshift for the eBOSS-only LRG (blue) and CMASS (red) galaxies, and the combined CMASS + eBOSS LRG catalogue (black). The solid lines stand for the density of the north galactic cap (NGC) and the dashed lines for the south galactic cap (SGC).
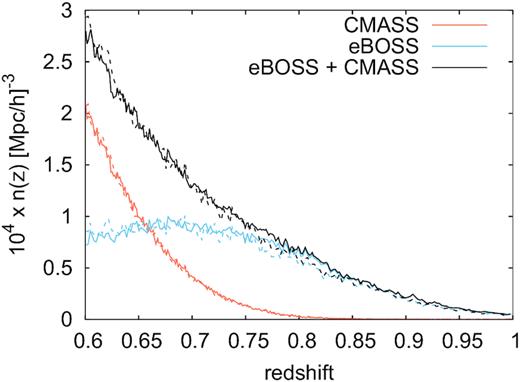
Number density of objects with spectroscopic observations for DR12 BOSS CMASS LRGs (in blue) and DR16 eBOSS LRGs (in orange), for the NGC (solid lines) and SGC (dashed lines). In black is shown the addition of CMASS and eBOSS densities. Note that such additions only correspond to those regions with overlapping area between eBOSS and BOSS CMASS galaxies, which approximately correspond to the whole eBOSS LRG area. The effective redshift of the combined sample corresponds to zeff = 0.698 according to the definition of equation (4).
We have quantified the difference between the NGC and SGC using the mocks to infer the errors and covariance among redshift bins. Unlike the CMASS sample, we find that CMASS + eBOSS LRG n(z) distribution between NGC and SGC is significantly different, which we have imprinted in the EZmocks.
2.2 Synthetic catalogues
In this paper, we employ several type of mocks in order to estimate the covariance, quantify the impact of systematic errors and to validate the pipeline and methods employed on the data.
2.2.1 EZMOCKS
The EZmocks consist of a set of 1000 independent realizations using the fast approximative method based on Zeldovich approximation (Chuang et al. 2015) with the main purpose of estimating the covariance of the data. Such mocks consist of light-cones with the radial and angular geometry of the CMASS + eBOSS LRG data set, with observational effects, such as fibre collision, redshift failures, and completeness. These light-cones are drawn from four and five snapshots at different redshifts, for CMASS and eBOSS galaxies, respectively. A full description of these mocks is presented in Zhao et al. (2020a). These mocks are generated using fast-techniques, which are a good approximation of an actual N-body simulation at large scales, but which eventually fail to reproduce the complex gravity interaction and peculiar motions at small scales. Because of this, we use them to estimate the covariance matrix of the data, but their performance for reproducing physical effects such as BAO and RSD is not guaranteed at sub- per cent precision level. Thus, we do not estimate the potential modelling systematics based on these mocks, but on full N-body mocks. However, these mocks are useful to estimate the relative change on cosmological parameters when applying each of these observational features. We use them to quantify the potential impact of observational systematics in the final data results. In order to analyse these mocks, we use the covariance drawn from themselves.
2.2.2 Nseries mocks
The Nseries mocks are full N-body mocks populated with a fixed halo occupation distribution (HOD) model similar to the one corresponding to the DR12 BOSS NGC CMASS LRGs. Their effective redshift, zeff = 0.56 is slightly smaller compared to the effective redshift of the DR16 CMASS + eBOSS LRG sample, zeff = 0.698, as they were initially designed to test the potential systematics on the modelling used for the BOSS CMASS sample. They were generated out of seven independent periodic boxes of |$2.6\, h^{-1}{\rm Gpc}$| side, projected through 12 different orientations and cuts, per box. In total, after these projections and cuts 84 pseudo-independent realizations were produced. The mass resolution of these boxes is |$1.5\times 10^{11}\, {\rm M}_\odot {\it \,h}^{-1}$| and with 20483 particles per box. The large effective volume, |$84\times 3.67\, [{\rm Gpc}]^3$| makes them ideal to test potential BAO and RSD systematics generated by the analysis pipeline, as to test the response of the arbitrary choice of reference cosmology on the BAO and full shape model templates, in the galaxy catalogues when converting redshifts into distances, and its impact on the inferred cosmological parameters. We use the NGC MD-Patchy mocks (Kitaura et al. 2016) to describe the covariance of these mocks. We rescale the covariance terms by 10 per cent based on the ratio of particles, as the MD-Patchy mocks have fewer particles than the Nseries mocks due to veto effects on DR12 CMASS data, which was also imprinted into the MD-Patchy mocks but not into Nseries mocks. When we run reconstruction on the Nseries mocks, we consistently also use the covariance from reconstructed MD-Patchy mocks.
2.2.3 OuterRim–HOD mocks
The OuterRim-HOD mocks are drawn from the OuterRimN-body simulation (Heitmann et al. 2019) and populated with different types of HOD models (see Rossi et al. 2020 for a full description), some of them similar to the LRG sample, but also others having different properties. The original simulation corresponds to a single cubic box realization with periodic boundary conditions whose size is |$3\, h^{-1}{\rm Gpc}$|. This box is divided into 27 cubic sub-boxes of |$1\, h^{-1}{\rm Gpc}$| per side, without the periodicity of cubic-boxes. For those galaxy catalogues, whose HOD models are close to the actual data sample studied here (those labelled ‘Hearin-Threshold-2’, ‘Leauthaud-Threshold-2’, and ‘Tinker-Threshold-2’, see Rossi et al. 2020 for a description of all models), we place the galaxies in a larger box of |$3\, h^{-1}{\rm Gpc}$| per side with empty space between the galaxies and the box edges, and generate a random catalogue with the same distribution but with no clustering. In this way, when performing the discrete Fourier transform (FT) the non-periodicity conditions do not impact the results. We refer to this process as padding. Additionally, we also apply reconstruction on these padded catalogues.
The effective volume of each sub-box of the ‘Hearin-Threshold-2’, ‘Leauthaud-Threshold-2’, and ‘Tinker-Threshold-2’, corresponds to |$\sim 1.1\, {\rm Gpc}^3$|. For the rest of the HOD-models, the effective volume varies between 2.1 and |$2.7\, {\rm Gpc}^3$|, as the number density of objects, and consequently |$\bar{n}P$|, is much higher.
In order to deal with the covariance of these mocks, we have used the covariance derived from the EZmocks and re-scaled by the difference in particle number. These rescalings correspond to the factors of 1.0, 0.64, and 9 for ‘Standard’, ‘Threshold-1’, and ‘Threshold-2’, respectively, for Hearin, Leauthaud and Tinker HOD-types. For Zheng HOD-type, we use 0.60, 2.37, and 0.60, for ‘Standard’, ‘Threshold 1’, and ‘Threshold 2’, respectively.
2.3 Reference cosmology
In this paper, we choose a set of cosmological parameters within the flat ΛCDM model to define a reference cosmology, which is used to (i) transform the redshifts of galaxies into comoving distances; and (ii) produce a linear template used to build a fitting model. We use as our main baseline analysis the fiducial set of parameters, |$\boldsymbol{\Theta }_{\rm fid}$|, listed in the first row of Table 1 as a reference cosmology. In addition, we also analyse the mocks and data using other sets of reference cosmologies to check the impact of this arbitrary choice. Among these cosmologies, we choose to use as reference cosmology the underlying cosmology of the Nseries mocks, |$\boldsymbol{\Theta }_{\rm Nseries}$|, the OuterRim derived mocks, |$\boldsymbol{\Theta }_{\rm OR}$| and three high-Ωm cosmologies, |$\boldsymbol{\Theta }_X$|, |$\boldsymbol{\Theta }_Y$|, and |$\boldsymbol{\Theta }_Z$|, whose properties are listed in Table 1. In particular, |$\boldsymbol{\Theta }_{Y}$| and |$\boldsymbol{\Theta }_{Z}$| have a very different rdrag value compared to the one inferred from the usual CMB-anisotropy experiments (Hinshaw et al. 2013; Aghanim et al. 2018). In case of |$\boldsymbol{\Theta }_Y$|, this is driven by a large value of the total number of neutrino species, and for |$\boldsymbol{\Theta }_Z$| by a high value of the baryon density. The |$\boldsymbol{\Theta }_Y$| and |$\boldsymbol{\Theta }_Z$| correspond to a very disfavoured cosmologies compared to the state-of-the art CMB observations. However, our LSS results are presented in a compressed set of variables which do not depend on these CMB priors. Consequently, the results inferred from LSS observations by assuming any of the tested cosmologies as ‘reference-cosmology’ are valid, as we will demonstrate in Section 5.
List of reference cosmology models used along the paper. For our baseline analysis of mocks and data, we use the fiducial set of cosmology parameters, |$\boldsymbol{\Theta }_{\rm fid}$|, as a reference cosmology. For all cosmologies, Ωk = 0.
| Model . | Ωm . | Ωmh2 . | Ωb . | Ωbh2 . | 103 × Ων . | h . | ns . | As × 109 . | |$\sigma _8^0$| . | |$r_{\rm drag}\, ({\rm Mpc})$| . | Neff . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm fid}$| | 0.310 | 0.1417 | 0.0481 | 0.0220 | 1.400 | 0.676 | 0.97 | 2.040 | 0.8 | 147.78 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm EZ}$| | 0.307 | 0.1411 | 0.0482 | 0.0220 | 0 | 0.678 | 0.96 | 2.115 | 0.8225 | 147.66 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | 0.286 | 0.1401 | 0.0470 | 0.0230 | 0 | 0.700 | 0.96 | 2.146 | 0.82 | 147.15 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm OR}$| | 0.265 | 0.1335 | 0.0448 | 0.0226 | 0 | 0.710 | 0.96 | 2.159 | 0.8 | 149.35 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm X}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 1.767 | 0.814 | 143.17 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Y}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 2.040 | 0.814 | 138.77 | 4.046 |
| |$\boldsymbol{\Theta }_{\rm Z}$| | 0.365 | 0.2053 | 0.0658 | 0.0370 | 0 | 0.750 | 0.96 | 2.146 | 0.9484 | 123.97 | 3.046 |
| Model . | Ωm . | Ωmh2 . | Ωb . | Ωbh2 . | 103 × Ων . | h . | ns . | As × 109 . | |$\sigma _8^0$| . | |$r_{\rm drag}\, ({\rm Mpc})$| . | Neff . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm fid}$| | 0.310 | 0.1417 | 0.0481 | 0.0220 | 1.400 | 0.676 | 0.97 | 2.040 | 0.8 | 147.78 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm EZ}$| | 0.307 | 0.1411 | 0.0482 | 0.0220 | 0 | 0.678 | 0.96 | 2.115 | 0.8225 | 147.66 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | 0.286 | 0.1401 | 0.0470 | 0.0230 | 0 | 0.700 | 0.96 | 2.146 | 0.82 | 147.15 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm OR}$| | 0.265 | 0.1335 | 0.0448 | 0.0226 | 0 | 0.710 | 0.96 | 2.159 | 0.8 | 149.35 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm X}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 1.767 | 0.814 | 143.17 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Y}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 2.040 | 0.814 | 138.77 | 4.046 |
| |$\boldsymbol{\Theta }_{\rm Z}$| | 0.365 | 0.2053 | 0.0658 | 0.0370 | 0 | 0.750 | 0.96 | 2.146 | 0.9484 | 123.97 | 3.046 |
List of reference cosmology models used along the paper. For our baseline analysis of mocks and data, we use the fiducial set of cosmology parameters, |$\boldsymbol{\Theta }_{\rm fid}$|, as a reference cosmology. For all cosmologies, Ωk = 0.
| Model . | Ωm . | Ωmh2 . | Ωb . | Ωbh2 . | 103 × Ων . | h . | ns . | As × 109 . | |$\sigma _8^0$| . | |$r_{\rm drag}\, ({\rm Mpc})$| . | Neff . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm fid}$| | 0.310 | 0.1417 | 0.0481 | 0.0220 | 1.400 | 0.676 | 0.97 | 2.040 | 0.8 | 147.78 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm EZ}$| | 0.307 | 0.1411 | 0.0482 | 0.0220 | 0 | 0.678 | 0.96 | 2.115 | 0.8225 | 147.66 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | 0.286 | 0.1401 | 0.0470 | 0.0230 | 0 | 0.700 | 0.96 | 2.146 | 0.82 | 147.15 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm OR}$| | 0.265 | 0.1335 | 0.0448 | 0.0226 | 0 | 0.710 | 0.96 | 2.159 | 0.8 | 149.35 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm X}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 1.767 | 0.814 | 143.17 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Y}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 2.040 | 0.814 | 138.77 | 4.046 |
| |$\boldsymbol{\Theta }_{\rm Z}$| | 0.365 | 0.2053 | 0.0658 | 0.0370 | 0 | 0.750 | 0.96 | 2.146 | 0.9484 | 123.97 | 3.046 |
| Model . | Ωm . | Ωmh2 . | Ωb . | Ωbh2 . | 103 × Ων . | h . | ns . | As × 109 . | |$\sigma _8^0$| . | |$r_{\rm drag}\, ({\rm Mpc})$| . | Neff . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm fid}$| | 0.310 | 0.1417 | 0.0481 | 0.0220 | 1.400 | 0.676 | 0.97 | 2.040 | 0.8 | 147.78 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm EZ}$| | 0.307 | 0.1411 | 0.0482 | 0.0220 | 0 | 0.678 | 0.96 | 2.115 | 0.8225 | 147.66 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | 0.286 | 0.1401 | 0.0470 | 0.0230 | 0 | 0.700 | 0.96 | 2.146 | 0.82 | 147.15 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm OR}$| | 0.265 | 0.1335 | 0.0448 | 0.0226 | 0 | 0.710 | 0.96 | 2.159 | 0.8 | 149.35 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm X}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 1.767 | 0.814 | 143.17 | 3.046 |
| |$\boldsymbol{\Theta }_{\rm Y}$| | 0.350 | 0.1599 | 0.0481 | 0.0220 | 1.313 | 0.676 | 0.97 | 2.040 | 0.814 | 138.77 | 4.046 |
| |$\boldsymbol{\Theta }_{\rm Z}$| | 0.365 | 0.2053 | 0.0658 | 0.0370 | 0 | 0.750 | 0.96 | 2.146 | 0.9484 | 123.97 | 3.046 |
2.4 Reconstruction
The BAO peak detection significance can be enhanced by applying the reconstruction technique (Eisenstein et al. 2007). We use the algorithm described by Burden et al. (2014), Burden, Percival & Howlett (2015) in which the underlying dark matter density field is inferred from the actual galaxy field by assuming a value of the growth of structure and bias, which can be estimated from a full shape-analysis on the pre-reconstruction catalogue, and used to remove both the non-linear motions and the redshift-space distortions of galaxies.
We make use of the publicly available code4 employed for performing reconstruction of the DR14 LRG sample (Bautista et al. 2018). In this paper, we apply this code to the combined CMASS + eBOSS sample, by assuming a bias value of b = 2.3 and a growth rate consistent with |$f(z)=\Omega _{\rm m}^\gamma (z)$|, which in this case is f = 0.82, and using a smoothing scale of |$15\, \, h^{-1}\, {\rm Mpc}$|. Recently, Carter et al. (2019) showed how the inferred cosmological parameters were not sensitive to these arbitrary choices. Potential systematics arising from reconstruction are checked in Section 5.
2.5 Power Spectrum estimator
In this work, we use 50 times more density for the random catalogue of the actual LRG data set and 20 times more for the randoms of the EZmocks. The difference in the estimated power spectrum using the 20 and 50 times random catalogue is smaller than 0.5 per cent per k-bin in the power spectrum monopole with no systematic offset. As described previously, both data and mocks catalogues total weight wtot is made by the product of the systematic weight, wsys which contains both completeness and imaging weight, the collision weight wcol, which contains both failures and close pairs collisions, and the FKP-weight. Further details of how these weights were constructed are given in Ross et al. (2020). The normalization factor |$I_2^{1/2}$| normalizes the amplitude of the observed power spectrum and is defined as, |$I_2\equiv \int {\rm d}{\boldsymbol r}\, [n_{\rm gal}w_{\rm tot}({\boldsymbol r})]^2$|. Later in this section, we will comment on how this parameter is inferred and its impact on the final results.
In order to measure the power spectrum multipoles of the galaxy distribution, we follow the same procedure described in previous works (Gil-Marín et al. 2017). Briefly, we assign the objects of the data and random catalogues to a regular Cartesian grid, which allows the use of FT-based algorithms. We embed the full survey volume into a cubic box of side |$L_b=5000\, \, h^{-1}\, {\rm Mpc}$|, and subdivide it into |$N_g^3=512^3$| cubic cells, whose resolution and Nyqvist frequency are |$9.8\, \, h^{-1}\, {\rm Mpc}$| and |$k_{\rm Ny}=0.322\, \, h\, {\rm Mpc}^{-1}$|, respectively. We assign the particles to the cubic grid cells using a third-order B-spline mass interpolation scheme, usually referred to as Piecewise cubic shape (PCS), where each data or random particle is distributed among 53 grid-cells. Additionally, we interlace two identical grid-cells schemes displaced by 1/2 of the size of the grid-cell; this allows us to reduce the aliasing effect below 0.1 per cent at scales below the Nyqvist frequency (Hockney & Eastwood 1981, Sefusatti et al. 2016).
Unless stated otherwise, we perform the measurement of the power spectrum linearly binning k in bins of |$\Delta k=0.01\, \, h\, {\rm Mpc}^{-1}$| up to |$k_{\rm max}=0.32\, \, h\, {\rm Mpc}^{-1}$|, although not all the k-elements will be necessarily used in the final analysis. The resulting power spectrum multipoles for the combined CMASS + eBOSS LRG sample are displayed in Fig. 2. We observe a significant mismatch between the amplitude of the mocks and data. This difference is caused by an early version of the mocks (with no completeness) being fitted to reproduce an early version of the data (with completeness). The normalization of the data was initially set in such a way that the overall amplitude depended on the value of the overall completeness. As a consequence, when the completeness was applied in the final version of the mocks, mocks, and data did not match. This mismatching only appears to be evident in Fourier space, but not in configuration space (see e.g. fig. 2 of Bautista et al. 2020). Therefore, this effect must correspond to a mismatch at scales of around |$s\sim 1-5\, \mathrm{Mpc}\, {h}^{-1}$| in configuration space. We conclude that this effect has no impact on the final covariance of the data. On the other hand, the overall normalization of the data has no impact on the cosmological signal extracted, as it is appropriately modelled by the window function as we describe below.
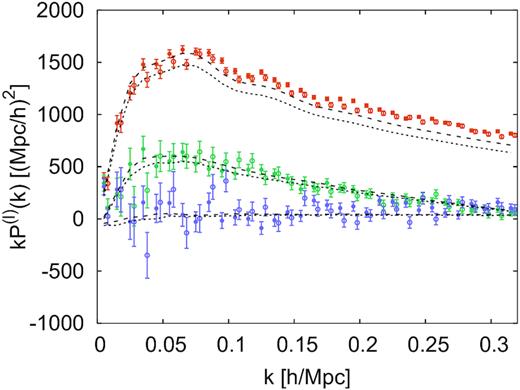
Power spectrum multipoles measured from the DR16 CMASS + eBOSS LRG sample, monopole (orange symbols), quadrupole (green symbols) and hexadecapole (purple symbols). The filled and empty symbols correspond to measurements from the NGC and SGC, respectively. The empty symbols are displaced horizontally for visibility. The black dashed and dotted lines correspond to the clustering of the mean of the 1000 realizations of the EZmocks with all the systematics applied, for NGC and SGC, respectively. The amplitude mismatch, more evident for the monopole, is due to the effect of completeness on the normalization factor of the power for data and mocks.
In Appendix D, we explicitly write how the selection effect is included in the power spectrum model.
3 METHODOLOGY
In this paper, we perform two parallel analyses: the analysis of the position of the BAO peak in the anisotropic power spectrum (hereafter BAO analysis), and on the RSD and Alcock–Paczynski effect (AP effect) using the full shape information in the power spectrum (hereafter Full Shape analysis or simply FS analysis).
The BAO analysis consists of using a fixed and arbitrary template to compare the relative BAO peak positions in the power spectrum multipoles. Such analysis can be performed on both pre- and post-reconstruction catalogues. The analysis performed on the reconstructed catalogue measurements has a higher probability of providing a larger significance detection, and consequently, smaller error bars than the pre-reconstruction measurement. The BAO peak position along and across the LOS direction is then linked to the expansion history and angular diameter distance at the redshift-bin of the measurement.
The FS analysis consists of a full modelling of the shape and amplitude of the power spectrum multipoles, taking into account non-linear dark matter effects, galaxy bias, and RSD, and is only performed over the pre-reconstructed catalogues. In order to do so, we choose an underlying linear power spectrum template at fixed cosmological parameters and infer the scale dilations and the amplitudes of the power spectrum multipoles. With this we are able to infer not only the expansion history and angular diameter distance, but as well the logarithmic growth of structure times the fluctuations of the dark matter field filtered by a top-hat function of |$8\, \, h^{-1}\, {\rm Mpc}$|, fσ8.
Unlike ΛCDM-model based analyses, the previously described FS and BAO analyses do not guarantee a consistent relation between the expansion history and the angular diameter distance within a ΛCDM model. In this sense, our analysis goes beyond such assumption and can be used to actually test the validity of the model.
Pre- and post-reconstruction catalogues are considered to contain independent, although correlated, cosmological information. In this fashion, we maximize the amount of cosmological information if we combine them with the appropriate covariance.
3.1 Modelling the BAO signal
We fit the data by considering independent NGC and SGC broad-band and bias parameters, both on the power spectra monopole and quadrupole. Thus, in the standard fit we consider two physical parameters, {α∥, α⊥} and 15 nuisance parameters, |$\lbrace \beta , B_{\rm N}, {A_i^{(0)}}_{\rm N}, {A_i^{(2)}}_{\rm N}, B_{\rm S}, {A_i^{(0)}}_{\rm S}, {A_i^{(2)}}_{\rm S} \rbrace$|, where i = 1, …, n, and |${\rm N},\, {\rm S}$| stand for NGC and SGC, respectively.
The main difference between the above isotropic template and the anisotropic template of Equations (20) and (21) is the effect of the BAO damping parameter Σnl. In the anisotropic template, the exponential argument has an explicit μ-dependence through the damping terms along and across the LOS, Σ⊥ and Σ∥. In this case, the monopole and quadrupole contain an effective weighted-averaged damping parameter, Σ0, Σ2, and Σ4. The main advantage of the isotropic template is that (i) it is faster to evaluate, as it does not require an integration over the LOS, and (ii) the broad-band parameters are in linear combination and therefore an analytical solver can be applied without the need of running an Markov chain Monte Carlo (MCMC) solver to explore the likelihood. The drawback is that the BAO damping is not as accurately described as in the anisotropic BAO template, especially for the anisotropic signal.
In Section 4, we test this effect on the mean of the mocks and in Table 3, we present an alternative analysis using this template. We show that the differences observed among these templates are sufficiently small to not be relevant for the precision of the measurements of this paper.
3.2 Modelling the RSD and galaxy bias
The FS analysis model employed to describe the power spectrum multipoles is the same to the one used in previous analyses of the BOSS survey for the redshift range 0.15 < z < 0.70 (Gil-Marín et al. 2015, Gil-Marín et al. 2016a) and for DR14 eBOSS quasars 0.8 ≤ z ≤ 1.2 (Gil-Marín et al. 2018), so we briefly present it here to avoid repetition.
3.2.1 Galaxy bias model
We follow the Eulerian non-linear bias model presented by McDonald & Roy (2009). The model consists of four bias parameters: the linear galaxy bias b1, the non-linear galaxy bias b2, and two non-local galaxy bias parameters, bs2 and b3nl. We always consider the local biases b1 and b2 as nuisance and free parameters of the model. Unless stated otherwise, the non-local bias parameters are constrained by assuming the local bias relations from Lagrangian space, |$b_{s^2}=-4/7\, (b_1-1)$| (Baldauf et al. 2012) and |$b_{3{\rm nl}}=32/315\, (b_1-1)$| (Saito et al. 2014).
3.2.2 Real-space spectra
3.2.3 Redshift space distortions
3.3 Parameter inference
In this paper, we infer the covariance matrix from 1000 realizations of the EZmocks (Zhao et al. 2020a). Due to the finite number of mock catalogues when estimating the covariance, we expect a noise term arising when inverting the covariance. We apply the corrections described in Hartlap, Simon & Schneider (2007) which for the current sample is |$\sim 6{{\ \rm per\ cent}}$| factor in the χ2 values for BAO analysis and |$4{{\ \rm per\ cent}}$| for FS when the hexadecapole is used. Extra corrections, such as the ones described in Percival et al. (2014), have a minor contribution to the final errors. They represent a |$2$| and |$1.4{{\ \rm per\ cent}}$| increase for the BAO and FS analyses, respectively. We include them only on the last stage of the analysis along with other systematic contributions.
In order to explore the full likelihood surface of a given set of parameters, we run Markov-chains (mcmc-chains). We use Brass11 based on the Metropolis–Hasting algorithm with a proposal covariance and ensure its convergence performing the Gelman–Rubin convergence test, R − 1 < 0.005, on each parameter. We apply the flat priors listed in Table 2 otherwise stated.
Flat prior ranges on the parameters used in the MCMC analyses. The priors on α∥ and α⊥ apply both to FS and BAO analyses. β, B, and Ai priors correspond to BAO type of analyses; whereas, f, b1, b2, σP, and Anoise correspond to FS type. For the Anoise term, we try two type of priors, as we describe in Section 4.
| Parameter . | Flat-prior range . |
|---|---|
| α∥ | |${}[0.5,\, 1.5]$| |
| α⊥ | |${}[0.5,\, 1.5]$| |
| β | [0 , 30] |
| B | |${}[0,\, 20]$| |
| |$A_i\times 10^{-3}[(\, h^{-1}\, {\rm Mpc})^{5-i}]$| | [−20, + 20] |
| f | |${}[0,\, 10]$| |
| b1 | |${}[0,\, 30]$| |
| b2 | |${}[-10,\, 10]$| |
| |$\sigma _P\, [\, h^{-1}\, {\rm Mpc}]$| | |${}[0,\, 20]$| |
| Anoise | |${}[-5,\, 5]$| or |${}[0.5,\, 1.5]$| |
| Parameter . | Flat-prior range . |
|---|---|
| α∥ | |${}[0.5,\, 1.5]$| |
| α⊥ | |${}[0.5,\, 1.5]$| |
| β | [0 , 30] |
| B | |${}[0,\, 20]$| |
| |$A_i\times 10^{-3}[(\, h^{-1}\, {\rm Mpc})^{5-i}]$| | [−20, + 20] |
| f | |${}[0,\, 10]$| |
| b1 | |${}[0,\, 30]$| |
| b2 | |${}[-10,\, 10]$| |
| |$\sigma _P\, [\, h^{-1}\, {\rm Mpc}]$| | |${}[0,\, 20]$| |
| Anoise | |${}[-5,\, 5]$| or |${}[0.5,\, 1.5]$| |
Flat prior ranges on the parameters used in the MCMC analyses. The priors on α∥ and α⊥ apply both to FS and BAO analyses. β, B, and Ai priors correspond to BAO type of analyses; whereas, f, b1, b2, σP, and Anoise correspond to FS type. For the Anoise term, we try two type of priors, as we describe in Section 4.
| Parameter . | Flat-prior range . |
|---|---|
| α∥ | |${}[0.5,\, 1.5]$| |
| α⊥ | |${}[0.5,\, 1.5]$| |
| β | [0 , 30] |
| B | |${}[0,\, 20]$| |
| |$A_i\times 10^{-3}[(\, h^{-1}\, {\rm Mpc})^{5-i}]$| | [−20, + 20] |
| f | |${}[0,\, 10]$| |
| b1 | |${}[0,\, 30]$| |
| b2 | |${}[-10,\, 10]$| |
| |$\sigma _P\, [\, h^{-1}\, {\rm Mpc}]$| | |${}[0,\, 20]$| |
| Anoise | |${}[-5,\, 5]$| or |${}[0.5,\, 1.5]$| |
| Parameter . | Flat-prior range . |
|---|---|
| α∥ | |${}[0.5,\, 1.5]$| |
| α⊥ | |${}[0.5,\, 1.5]$| |
| β | [0 , 30] |
| B | |${}[0,\, 20]$| |
| |$A_i\times 10^{-3}[(\, h^{-1}\, {\rm Mpc})^{5-i}]$| | [−20, + 20] |
| f | |${}[0,\, 10]$| |
| b1 | |${}[0,\, 30]$| |
| b2 | |${}[-10,\, 10]$| |
| |$\sigma _P\, [\, h^{-1}\, {\rm Mpc}]$| | |${}[0,\, 20]$| |
| Anoise | |${}[-5,\, 5]$| or |${}[0.5,\, 1.5]$| |
Since σ8 is very degenerate with f and b1 this is equivalent to treat the terms |$f\sigma _8^{n+1}$| in the Equations (27)–(30), as two independent parameters:12fσ8 and |$\sigma _8^n$|, where fσ8 is freely fit, whereas |$\sigma _8^n$| is kept fixed. For large scales n = 0, so this approach is exact. At smaller scales n > 0 terms arise, but the systematic effect of fixing this part to a constant is very small. We have checked that varying σ8 on the |$\sigma _8^n$| terms by 15 per cent, only shifts fσ8 by 0.2 per cent. In Section 4, we present a fit to the data where both f and σ8 are varied freely and we show how this has no effect on the final results, although the convergence time for such runs is larger.
For the standard BAO case, we apply equation (21) and leave free |$\lbrace \alpha _\parallel ,\, \alpha _\perp ,\beta \rbrace$| and the broadband parameters |$\lbrace B,A_i^{(\ell)} \rbrace$|, which we fit separately for NGC and SGC. This corresponds to 17 free parameters. In some cases, we also leave the damping terms, Σ∥ and Σ⊥, free, and treat them as independent.
For both BAO and FS cases the covariances from NGC and SGC are drawn from two independent sets of mocks and are assumed to be fully independent, as these are two disconnected patches of the Universe. In this fashion, the total likelihood is just the product of NGC and SGC likelihoods: |$\mathcal {L}=\mathcal {L}_{\rm NGC}\times \mathcal {L}_{\rm SGC}$|. We expect that only for very large modes (k much smaller than |$0.02\, \, h^{-1}\, {\rm Mpc}$|) this assumption loses validity.
In this paper, we report the mean of the mcmc chain when converged, R − 1 < 0.005, except for the burn-in part which we discard (the first 104 steps), and report its rms as the 1σ error. This matches the 68 per cent confident level in case of having a Gaussian distribution. For the mocks, we run six independent sub-chains where after convergence, we concatenate and treat as a single chain when calculating the mean and rms. We also test that running different set of chains on the same data set report the same values within the statistical precision required, which indicates that the chain noise is below the statistical precision of the sample. In Appendix B, we show how the contours drawn from the mcmc chain of the data are in very good agreement with the inferred Gaussian contours.
The isotropic BAO template described by equations (22) and (23) can be solved analytically for most of its parameters using the least-squares method. Given a fixed α∥, α⊥, and Σnl, ℓ, the rest of variables, B, and |$A_i^{(\ell)}$| can be solved analytically so a full MCMC run is not required. One therefore only needs to perform subsequent fits changing α∥, α⊥, and Σnl, ℓ within a fixed array, in order to resolve the likelihood shape, and then interpolate to find the best fit and its error.
4 RESULTS
In this section, we describe the results obtained when applying the BAO and FS pipeline described in the previous section. We perform these two analyses separately, and later in Section 6, we discuss how to combine them. The error bars reported in this section only contain the statistical error budget. Later, in Section 5, we discuss qualitatively and quantitatively the systematic error budget of such approaches.
4.1 BAO analysis
Fig. 3 displays the BAO oscillatory features measured from the CMASS + eBOSS LRG data with respect to the broadband, for the isotropic signal, in orange symbols, and the anisotropic μ2-moment, in green symbols. The black solid lines represent the best fit and the lower panel the model-data deviations in units of statistical 1σ error. The left-hand panel displays the pre-reconstructed results and the right-hand panel the post-reconstructed results. Reconstruction enhances significantly the BAO signal both in the isotropic and anisotropic power spectrum signal. Note that the actual BAO analysis is performed on the monopole and quadrupole, although we visually report the μ2-moment, as defined by equation (25) instead of the quadrupole, as the BAO feature is more evident there.
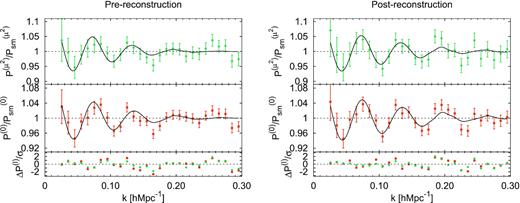
DR16 CMASS + eBOSS LRG power spectrum measurements for the pre- (left-hand panel) and post-reconstructed catalogue (right-hand panel). The orange points display the power spectrum monopole and the green points the μ2-moment (see equation 25 for definition). The associated errors are drawn from the covariance of 1000 mocks and the black solid line represent the best-fitting solution (quoted in Table 3 using the anisotropic templated at the fixed values of |$\Sigma _\parallel =7.0\, \, h^{-1}\, {\rm Mpc}$| and |$\Sigma _\perp =2.0\, \, h^{-1}\, {\rm Mpc}$| for post-recon and |$\Sigma _\parallel =9.4\, \, h^{-1}\, {\rm Mpc}$| and |$\Sigma _\perp =4.8\, \, h^{-1}\, {\rm Mpc}$| for pre-recon). The bottom sub-panels show the difference between model and measurement divided by the 1σ errors.
Table 3 presents the main results from the BAO analysis of the data in terms of the scaling parameters, α∥ and α⊥. We perform the BAO analysis keeping the Σ∥ and Σ⊥ variables fixed at their best-fitting values on the mean of the pre- and post-reconstructed mocks. These values are |$\Sigma _\parallel =9.4\, \, h^{-1}\, {\rm Mpc}$| and |$\Sigma _\perp =4.8\, \, h^{-1}\, {\rm Mpc}$| for the pre-reconstructed and |$\Sigma _\parallel =7.0$| and |$\Sigma _\perp =2.0\, \, h^{-1}\, {\rm Mpc}$| for the post-reconstructed catalogues.13 The first two rows of Table 3 report the BAO analysis on the pre- and post-reconstructed data in the Fourier space (matching the performance displayed by Fig. 3) and in configuration space of the same data set (presented in Bautista et al. 2020). Along with those the consensus between Fourier and gonfiguration space is also presented. The technique used to infer this value is described later in Section 6. The rest of the rows represent the values obtained from the pre- or post-reconstructed analysis on Fourier space with variations of the standard pipeline analysis, to show the sensitivity of the results under certain assumptions. Among these cases, we present analyses when: NGC and SGC are the only-fitted regions, ignoring the effect of the selection function in the modelling (no-mask case), turning off the systematic and collision weights on the data (no-wsyswcol), using the isotropic template of equation (22) with three- (Isotropic template) and five-parameter broad-band (Isotropic template order-5), using the anisotropic template of equation (20) with five parameters (Order-5), allowing Σ∥ and Σ⊥ to be free parameters (|$\Sigma _{\parallel ,\, \perp }$| Free), or free but with a Gaussian prior, |$\bar{x}\pm \sigma _x$|,14 Σ∥ = 7 ± 3, and Σ⊥ = 2 ± 3 (|$\Sigma _{\parallel ,\, \perp }$| Gaussian prior), using the hexadecapole along with the monopole and quadrupole on the BAO fit (+ hexadecapole), using a different reference cosmology for the BAO fitting template (|$\boldsymbol{\Theta }_{\rm OR}$|, |$\boldsymbol{\Theta }_X$|, |$\boldsymbol{\Theta }_Y$|, and |$\boldsymbol{\Theta }_{Z}$|; see Table 1 and the top panel of Fig 10 for a description of these cosmologies) and finally using only 500 realizations of the EZmocks to estimate the covariance (500 real.). When using different x-reference cosmologies, we re-scale the obtained α-parameters by the appropriate factor, |$(D_{\rm H,M}^x/r_{\rm drag})/(D_{\rm H,M}^{\rm fid}/r_{\rm drag}^{\rm fid})$|, to match the results one would have obtained if a fiducial cosmology would have been used as reference cosmology instead. In this way, all the α-parameters of the different rows are comparable, regardless of the template cosmology used.
Impact of different parameters and data-vectors choices when performing a BAO analysis on the DR16 CMASS + eBOSS LRG data set using the pipeline described in Section 3.1. The Fourier space post-recon represent the main BAO results of this paper and correspond to the model displayed in the right-hand panel of Fig 3. The configuration space results correspond to the analysis described in Bautista et al. 2020. The rest of the cases (see the text for a full description) represent variations of the standard pipeline. For each case, we only report the physical BAO scaling parameters and their corresponding χ2. For the cases, where the Σ∥ and Σ⊥ are varied, we find that when these are treated as free parameters (with a wide uninformative prior), we obtain |$\Sigma _\parallel ^{\rm free}=2.2\pm 1.7$|, |$\Sigma _\perp ^{\rm free}=2.3\pm 1.7$|; whereas under the Gaussian prior, we find |$\Sigma _\parallel ^{\rm Gauss}=3.5 \pm 1.9$| (Gaussian prior: 7 ± 3) and |$\Sigma _\perp ^{\rm Gauss}= 2.0 \pm 1.4$| (Gaussian prior: 2 ± 3). The error bars correspond to 1σ and only include the statistical error budget.
| Case . | α∥ . | α⊥ . | χ2/dof . |
|---|---|---|---|
| Pk pre-recon | 0.939 ± 0.036 | 1.043 ± 0.032 | 96/(112 − 17) |
| Pk post-recon | 0.956 ± 0.024 | 1.025 ± 0.019 | 108/(112 − 17) |
| ξs pre-recon | 0.954 ± 0.035 | 1.034 ± 0.025 | 41/(40 − 9) |
| ξs post-recon | 0.958 ± 0.026 | 1.024 ± 0.019 | 41/(40 − 9) |
| (Pk + ξs) post-recon | 0.956 ± 0.024 | 1.024 ± 0.018 | − |
| NGC-only pre-recon | 0.932 ± 0.046 | 1.054 ± 0.043 | 46/(56 − 10) |
| NGC-only post-recon | 0.947 ± 0.026 | 1.042 ± 0.024 | 65/(56 − 10) |
| SGC-only pre-recon | 0.928 ± 0.088 | 1.058 ± 0.091 | 46/(56 − 10) |
| SGC-only post-recon | 0.996 ± 0.113 | 0.992 ± 0.038 | 40/(56 − 10) |
| No-mask post-recon | 0.953 ± 0.022 | 1.030 ± 0.016 | 109/(112 − 17) |
| No-wsyswcol post-recon | 0.950 ± 0.027 | 1.023 ± 0.020 | 87/(112 − 17) |
| Isotropic template post-recon | 0.941 ± 0.027 | 1.030 ± 0.023 | 126/(112 − 18) |
| Isotropic template order-5 post-recon | 0.941 ± 0.027 | 1.027 ± 0.024 | 102/(112 − 26) |
| Order-5 post-recon | 0.959 ± 0.024 | 1.018 ± 0.021 | 99/(112 − 25) |
| |$\Sigma _{\parallel ,\, \perp }$| Free post-recon | 0.949 ± 0.019 | 1.027 ± 0.019 | 101/(112 − 19) |
| |$\Sigma _{\parallel ,\, \perp }$| Gaussian prior post-recon | 0.950 ± 0.020 | 1.027 ± 0.019 | 100/(112 − 19) |
| + Hexadecapole pre-recon | 0.914 ± 0.035 | 1.054 ± 0.031 | 190/(168 − 22) |
| + Hexadecapole post-recon | 0.949 ± 0.026 | 1.025 ± 0.020 | 157/(168 − 22) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (re-scaled to fiducial) | 0.962 ± 0.026 | 1.009 ± 0.018 | 120/(112 − 17) |
| |$\boldsymbol{\Theta }_{X}$| (re-scaled to fiducial) | 0.959 ± 0.025 | 1.022 ± 0.020 | 109/(112 − 17) |
| |$\boldsymbol{\Theta }_{Y}$| (re-scaled to fiducial) | 0.962 ± 0.025 | 1.024 ± 0.020 | 106/(112 − 17) |
| |$\boldsymbol{\Theta }_{Z}$| (re-scaled to fiducial) | 0.956 ± 0.024 | 1.017 ± 0.017 | 112/(112 − 17) |
| 500 real. in covariance | 0.955 ± 0.025 | 1.029 ± 0.019 | 106/(112 − 17) |
| Case . | α∥ . | α⊥ . | χ2/dof . |
|---|---|---|---|
| Pk pre-recon | 0.939 ± 0.036 | 1.043 ± 0.032 | 96/(112 − 17) |
| Pk post-recon | 0.956 ± 0.024 | 1.025 ± 0.019 | 108/(112 − 17) |
| ξs pre-recon | 0.954 ± 0.035 | 1.034 ± 0.025 | 41/(40 − 9) |
| ξs post-recon | 0.958 ± 0.026 | 1.024 ± 0.019 | 41/(40 − 9) |
| (Pk + ξs) post-recon | 0.956 ± 0.024 | 1.024 ± 0.018 | − |
| NGC-only pre-recon | 0.932 ± 0.046 | 1.054 ± 0.043 | 46/(56 − 10) |
| NGC-only post-recon | 0.947 ± 0.026 | 1.042 ± 0.024 | 65/(56 − 10) |
| SGC-only pre-recon | 0.928 ± 0.088 | 1.058 ± 0.091 | 46/(56 − 10) |
| SGC-only post-recon | 0.996 ± 0.113 | 0.992 ± 0.038 | 40/(56 − 10) |
| No-mask post-recon | 0.953 ± 0.022 | 1.030 ± 0.016 | 109/(112 − 17) |
| No-wsyswcol post-recon | 0.950 ± 0.027 | 1.023 ± 0.020 | 87/(112 − 17) |
| Isotropic template post-recon | 0.941 ± 0.027 | 1.030 ± 0.023 | 126/(112 − 18) |
| Isotropic template order-5 post-recon | 0.941 ± 0.027 | 1.027 ± 0.024 | 102/(112 − 26) |
| Order-5 post-recon | 0.959 ± 0.024 | 1.018 ± 0.021 | 99/(112 − 25) |
| |$\Sigma _{\parallel ,\, \perp }$| Free post-recon | 0.949 ± 0.019 | 1.027 ± 0.019 | 101/(112 − 19) |
| |$\Sigma _{\parallel ,\, \perp }$| Gaussian prior post-recon | 0.950 ± 0.020 | 1.027 ± 0.019 | 100/(112 − 19) |
| + Hexadecapole pre-recon | 0.914 ± 0.035 | 1.054 ± 0.031 | 190/(168 − 22) |
| + Hexadecapole post-recon | 0.949 ± 0.026 | 1.025 ± 0.020 | 157/(168 − 22) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (re-scaled to fiducial) | 0.962 ± 0.026 | 1.009 ± 0.018 | 120/(112 − 17) |
| |$\boldsymbol{\Theta }_{X}$| (re-scaled to fiducial) | 0.959 ± 0.025 | 1.022 ± 0.020 | 109/(112 − 17) |
| |$\boldsymbol{\Theta }_{Y}$| (re-scaled to fiducial) | 0.962 ± 0.025 | 1.024 ± 0.020 | 106/(112 − 17) |
| |$\boldsymbol{\Theta }_{Z}$| (re-scaled to fiducial) | 0.956 ± 0.024 | 1.017 ± 0.017 | 112/(112 − 17) |
| 500 real. in covariance | 0.955 ± 0.025 | 1.029 ± 0.019 | 106/(112 − 17) |
Impact of different parameters and data-vectors choices when performing a BAO analysis on the DR16 CMASS + eBOSS LRG data set using the pipeline described in Section 3.1. The Fourier space post-recon represent the main BAO results of this paper and correspond to the model displayed in the right-hand panel of Fig 3. The configuration space results correspond to the analysis described in Bautista et al. 2020. The rest of the cases (see the text for a full description) represent variations of the standard pipeline. For each case, we only report the physical BAO scaling parameters and their corresponding χ2. For the cases, where the Σ∥ and Σ⊥ are varied, we find that when these are treated as free parameters (with a wide uninformative prior), we obtain |$\Sigma _\parallel ^{\rm free}=2.2\pm 1.7$|, |$\Sigma _\perp ^{\rm free}=2.3\pm 1.7$|; whereas under the Gaussian prior, we find |$\Sigma _\parallel ^{\rm Gauss}=3.5 \pm 1.9$| (Gaussian prior: 7 ± 3) and |$\Sigma _\perp ^{\rm Gauss}= 2.0 \pm 1.4$| (Gaussian prior: 2 ± 3). The error bars correspond to 1σ and only include the statistical error budget.
| Case . | α∥ . | α⊥ . | χ2/dof . |
|---|---|---|---|
| Pk pre-recon | 0.939 ± 0.036 | 1.043 ± 0.032 | 96/(112 − 17) |
| Pk post-recon | 0.956 ± 0.024 | 1.025 ± 0.019 | 108/(112 − 17) |
| ξs pre-recon | 0.954 ± 0.035 | 1.034 ± 0.025 | 41/(40 − 9) |
| ξs post-recon | 0.958 ± 0.026 | 1.024 ± 0.019 | 41/(40 − 9) |
| (Pk + ξs) post-recon | 0.956 ± 0.024 | 1.024 ± 0.018 | − |
| NGC-only pre-recon | 0.932 ± 0.046 | 1.054 ± 0.043 | 46/(56 − 10) |
| NGC-only post-recon | 0.947 ± 0.026 | 1.042 ± 0.024 | 65/(56 − 10) |
| SGC-only pre-recon | 0.928 ± 0.088 | 1.058 ± 0.091 | 46/(56 − 10) |
| SGC-only post-recon | 0.996 ± 0.113 | 0.992 ± 0.038 | 40/(56 − 10) |
| No-mask post-recon | 0.953 ± 0.022 | 1.030 ± 0.016 | 109/(112 − 17) |
| No-wsyswcol post-recon | 0.950 ± 0.027 | 1.023 ± 0.020 | 87/(112 − 17) |
| Isotropic template post-recon | 0.941 ± 0.027 | 1.030 ± 0.023 | 126/(112 − 18) |
| Isotropic template order-5 post-recon | 0.941 ± 0.027 | 1.027 ± 0.024 | 102/(112 − 26) |
| Order-5 post-recon | 0.959 ± 0.024 | 1.018 ± 0.021 | 99/(112 − 25) |
| |$\Sigma _{\parallel ,\, \perp }$| Free post-recon | 0.949 ± 0.019 | 1.027 ± 0.019 | 101/(112 − 19) |
| |$\Sigma _{\parallel ,\, \perp }$| Gaussian prior post-recon | 0.950 ± 0.020 | 1.027 ± 0.019 | 100/(112 − 19) |
| + Hexadecapole pre-recon | 0.914 ± 0.035 | 1.054 ± 0.031 | 190/(168 − 22) |
| + Hexadecapole post-recon | 0.949 ± 0.026 | 1.025 ± 0.020 | 157/(168 − 22) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (re-scaled to fiducial) | 0.962 ± 0.026 | 1.009 ± 0.018 | 120/(112 − 17) |
| |$\boldsymbol{\Theta }_{X}$| (re-scaled to fiducial) | 0.959 ± 0.025 | 1.022 ± 0.020 | 109/(112 − 17) |
| |$\boldsymbol{\Theta }_{Y}$| (re-scaled to fiducial) | 0.962 ± 0.025 | 1.024 ± 0.020 | 106/(112 − 17) |
| |$\boldsymbol{\Theta }_{Z}$| (re-scaled to fiducial) | 0.956 ± 0.024 | 1.017 ± 0.017 | 112/(112 − 17) |
| 500 real. in covariance | 0.955 ± 0.025 | 1.029 ± 0.019 | 106/(112 − 17) |
| Case . | α∥ . | α⊥ . | χ2/dof . |
|---|---|---|---|
| Pk pre-recon | 0.939 ± 0.036 | 1.043 ± 0.032 | 96/(112 − 17) |
| Pk post-recon | 0.956 ± 0.024 | 1.025 ± 0.019 | 108/(112 − 17) |
| ξs pre-recon | 0.954 ± 0.035 | 1.034 ± 0.025 | 41/(40 − 9) |
| ξs post-recon | 0.958 ± 0.026 | 1.024 ± 0.019 | 41/(40 − 9) |
| (Pk + ξs) post-recon | 0.956 ± 0.024 | 1.024 ± 0.018 | − |
| NGC-only pre-recon | 0.932 ± 0.046 | 1.054 ± 0.043 | 46/(56 − 10) |
| NGC-only post-recon | 0.947 ± 0.026 | 1.042 ± 0.024 | 65/(56 − 10) |
| SGC-only pre-recon | 0.928 ± 0.088 | 1.058 ± 0.091 | 46/(56 − 10) |
| SGC-only post-recon | 0.996 ± 0.113 | 0.992 ± 0.038 | 40/(56 − 10) |
| No-mask post-recon | 0.953 ± 0.022 | 1.030 ± 0.016 | 109/(112 − 17) |
| No-wsyswcol post-recon | 0.950 ± 0.027 | 1.023 ± 0.020 | 87/(112 − 17) |
| Isotropic template post-recon | 0.941 ± 0.027 | 1.030 ± 0.023 | 126/(112 − 18) |
| Isotropic template order-5 post-recon | 0.941 ± 0.027 | 1.027 ± 0.024 | 102/(112 − 26) |
| Order-5 post-recon | 0.959 ± 0.024 | 1.018 ± 0.021 | 99/(112 − 25) |
| |$\Sigma _{\parallel ,\, \perp }$| Free post-recon | 0.949 ± 0.019 | 1.027 ± 0.019 | 101/(112 − 19) |
| |$\Sigma _{\parallel ,\, \perp }$| Gaussian prior post-recon | 0.950 ± 0.020 | 1.027 ± 0.019 | 100/(112 − 19) |
| + Hexadecapole pre-recon | 0.914 ± 0.035 | 1.054 ± 0.031 | 190/(168 − 22) |
| + Hexadecapole post-recon | 0.949 ± 0.026 | 1.025 ± 0.020 | 157/(168 − 22) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (re-scaled to fiducial) | 0.962 ± 0.026 | 1.009 ± 0.018 | 120/(112 − 17) |
| |$\boldsymbol{\Theta }_{X}$| (re-scaled to fiducial) | 0.959 ± 0.025 | 1.022 ± 0.020 | 109/(112 − 17) |
| |$\boldsymbol{\Theta }_{Y}$| (re-scaled to fiducial) | 0.962 ± 0.025 | 1.024 ± 0.020 | 106/(112 − 17) |
| |$\boldsymbol{\Theta }_{Z}$| (re-scaled to fiducial) | 0.956 ± 0.024 | 1.017 ± 0.017 | 112/(112 − 17) |
| 500 real. in covariance | 0.955 ± 0.025 | 1.029 ± 0.019 | 106/(112 − 17) |
In general, we see that most of these arbitrary choices produce no significant variation (<0.5σ) with respect to the standard pipeline, demonstrating a strong robustness on the BAO results. Some exceptions are when the data vector is different (pre- versus post-) or when the NGC and SGC are analysed independently. However, in these cases the cosmic variance has a much larger impact and therefore a larger shift is expected. The highest shift we observe (when the data vector is unchanged) is on the variable α⊥ when the reference cosmology is varied from |$\boldsymbol{\Theta }_{\rm fid}$| to |$\boldsymbol{\Theta }_{\rm OR}$|. In such case, α⊥ changes by 0.85σ. Note that these α-values have been re-scaled after the actual fit to be both with respect to the same reference cosmology, so in the absence of noise and systematics both α-value should be the same. Later, in Section 5.1.2 and in Table 5, we investigate such effect using the EZmocks and the Nseries mocks, and find no strong shift when the template cosmology is changed, concluding that the difference we observe for the data is exclusively due to a statistical fluctuation.
The reader could think that the results obtained by adding the hexadecapole to the standard monopole plus quadrupole analysis should have reported larger BAO information and smaller statistical error component. Previously, Ross, Percival & Manera (2015a) demonstrated that the amount of BAO information that higher-than-quadrupole moments add in terms of anisotropic BAO is very small. Indeed, we report as well such findings later in Table 5 when we apply our analysis to the mocks. However, this is not the case for an FS analysis, where the hexadecapole is key to break degeneracies between the anisotropy generated by AP and RSD. We therefore conclude that the difference between the BAO analyses with and without hexadecapole are exclusively due to noise fluctuations, and do not correspond to any significant extra BAO information. Because of this, we take as our main BAO results those in which only the monopole and quadrupole are analysed.
Fig. 4 displays the likelihood posteriors for 1σ and 2σ for the BAO analysis using the pre- (orange) and post-reconstruction (blue) catalogues, in terms of the physical variables, DM/rdrag – DH/rdrag. In both cases, the agreement is very good. The statistical errors on the cosmological parameters inferred from the post-reconstructed catalogues present are a factor of 1.5 smaller than those obtained from the pre-reconstructed catalogues. Later, in Section 5, we study how typical this gain factor is by using the results from individual mocks.
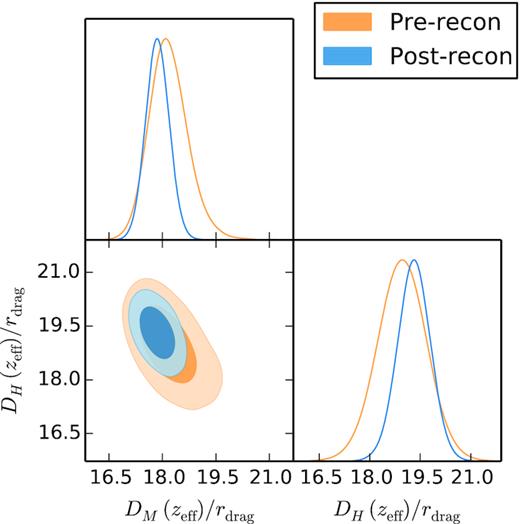
Likelihood posterior for 1σ and 2σ contours (only statistical contribution), from the BAO type of analysis on the DR16 CMASS + eBOSS LRG data for the pre-reconstructed catalogues (in orange) and the post-reconstructed catalogues (in blue) in terms of DM(zeff)/rdrag and DH(zeff)/rdrag variables, at zeff = 0.698. Results corresponding to the first two rows of Table 3.
4.2 Full shape analysis
We run the FS pipeline on the power spectrum monopole, quadrupole, and hexadecapole measured from the CMASS + eBOSS galaxies for the k-range |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le 0.15$|, as described in Section 3.2. The covariance among k-bins is estimated from the analysis of 1000 EZmocks.
Fig. 5 displays the monopole (round orange symbols), quadrupole (square green symbols), and hexadecapole (triangle purple symbols) for the results of the CMASS + eBOSS LRG data used for the FS analysis. The black solid lines display the performance of the best-fitting model when the three multipoles are simultaneously fitted, whereas the black-dashed lines when only the monopole and quadrupole are used.
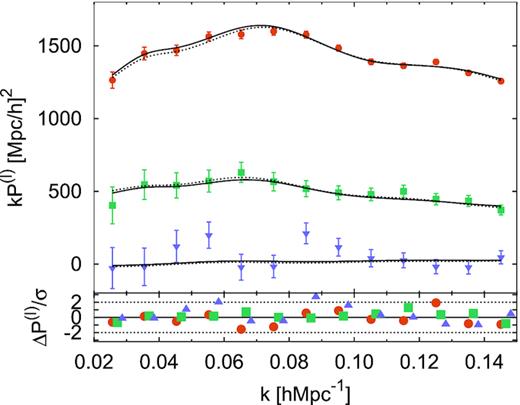
Power spectrum multipoles measured from the DR16 CMASS + eBOSS LRG sample (weight-averaged between NGC and SGC), monopole (circular orange symbols), quadrupole (square green symbols), and hexadecapole (triangle purple symbols), along with the error bars predicted by the rms of the 1000 EZmocks. The solid and dashed black lines represent the FS best-fitting model (weight-averaged between NGC and SGC) when the monopole and quadrupole only are fitting (black dashed lines) and when the hexadecapole is also used (black solid line). In the bottom sub-panel, the differences between the measurement and the model, relative to the value of 1σ error bar, are also displayed using the same colour notation. The results for the best-fitting parameters are reported in Table F3 for the narrow prior on the amplitude of shot noise, 0.5 ≤ Anoise ≤ 1.5.
Table 4 displays the results for FS analysis under different cases. The first two rows represent the case where the monopole (M), quadrupole (Q), and hexadecapole (H) are fitted up to a |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$| with a wide and flat uninformative prior on the amplitude of shot noise (first row) and with a more restrictive prior allowing for such amplitude to vary within |$50{{\ \rm per\ cent}}$| of its Poisson prediction (second row). The third row displays the result from the configuration space analysis reported in Bautista et al. (2020) and the fourth row the consensus between Fourier and configuration space, as described in Section 6. The rest of the rows are variations of the above pipeline (with a wide uninformative prior on the amplitude of shot noise as a default option): using only the monopole and quadrupole (M+Q), fitting to NGC- and SGC-only (NGC, SGC M+Q + H), fitting to the weighted mean signal of NGC and SGC (NGC+SGC M+Q + H), setting a hard prior on b2 to be positive (b2 > 0 prior), using the monopole, quadrupole, and hexadecapole with a different k-range, computing the hexadecapole using a different decomposition on the LOS (hexadecapole as |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1)\mathcal {L}_0(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_2)$|), ignoring the ATNS and BTNS in the modelling of equation (31) (no-TNS terms), only using one-loop correction in the modelling of equation (27) (only one-loop terms), using SPT predictions instead of RPT for the terms of equation (27) (SPT 2-loop), using the Gaussian form of equation (33) for FoG (FoG Gaussian), setting the fiducial σ8 to a 15 per cent higher value than the predicted by the reference cosmology at z = 0.70 (σ8 15 per cent high), treating f and σ8 as free independent parameters (σ8 free), using a different cosmology as a reference cosmology (|$\boldsymbol{\Theta }_{\rm OR}$|, |$\boldsymbol{\Theta }_{\rm X}$|, |$\boldsymbol{\Theta }_{\rm Y}$|, and |$\boldsymbol{\Theta }_{\rm Z}$|15), turning off the systematics and/or collision weights (wsys off, wcol off, wsyswcol off), and using only 500 EZmock realization to estimate the covariance (500 real. in covariance).
Impact of different parameters and data-vector choices when performing an FS analysis on the DR16 CMASS + eBOSS LRG data set using the pipeline described in Section 3.2. The second row with the 0.5 ≤ Anoise ≤ 1.5 prior on the amplitude of shot noise represents the main result of FS analysis of this paper and correspond to the model (in solid black lines) displayed in Fig 5. The configuration space results are main results reported by Bautista et al. (2020). The rest of the cases (see the text for a full description) represent variations of the standard pipeline or data-vector choices. For each case, we do not report all the nuisance parameters, only the physical BAO scaling parameters, fσ8, and their corresponding χ2. The error bars correspond to 1σ and only include the statistical error budget.
| Case . | α∥ . | α⊥ . | fσ8 . | χ2/dof . |
|---|---|---|---|---|
| Pk, kmax = 0.15, M+Q + H | 1.017 ± 0.045 | 1.006 ± 0.027 | 0.469 ± 0.046 | 77/(78 − 11) |
| Pk, 0.5 ≤ Anoise ≤ 1.5 prior | 0.999 ± 0.036 | 1.003 ± 0.027 | 0.454 ± 0.042 | 77/(78 − 11) |
| ξs | 1.016 ± 0.029 | 1.004 ± 0.019 | 0.461 ± 0.042 | – |
| Pk + ξs | 1.008 ± 0.027 | 1.002 ± 0.018 | 0.449 ± 0.039 | – |
| M+Q | 0.977 ± 0.054 | 1.032 ± 0.037 | 0.511 ± 0.065 | 38/(52 − 11) |
| M+Q, 0.5 ≤ A ≤ 1.5 prior | 0.972 ± 0.050 | 1.026 ± 0.036 | 0.496 ± 0.062 | 38/(52 − 11) |
| NGC M+Q + H | 0.983 ± 0.049 | 1.045 ± 0.036 | 0.495 ± 0.059 | 28/(39 − 7) |
| SGC M+Q + H | 1.174 ± 0.109 | 0.955 ± 0.042 | 0.375 ± 0.093 | 45/(39 − 7) |
| NGC + SGC M+Q + H | 1.007 ± 0.044 | 1.004 ± 0.027 | 0.459 ± 0.046 | 34/(39 − 7) |
| 0 ≤ b2 prior | 1.002 ± 0.036 | 1.007 ± 0.026 | 0.455 ± 0.043 | 78/(78 − 11) |
| kmax = 0.20, M+Q | 1.006 ± 0.045 | 1.013 ± 0.027 | 0.499 ± 0.053 | 58/(72 − 11) |
| |$k_{\rm max}=(0.20, {\rm M+Q})+(\, 0.15,\, {\rm H})$| | 1.025 ± 0.035 | 0.999 ± 0.021 | 0.481 ± 0.041 | 97/(98 − 11) |
| |$k_{\rm max}=(0.15, {\rm M+Q})+(\, 0.10,\, {\rm H})$| | 1.052 ± 0.062 | 0.989 ± 0.029 | 0.449 ± 0.052 | 68/(68 − 11) |
| kmax = 0.20, M+Q + H | 1.041 ± 0.033 | 0.989 ± 0.021 | 0.450 ± 0.041 | 124/(108 − 11) |
| Hexadecapole as |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1)\mathcal {L}_0(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_2)$| | 1.017 ± 0.046 | 1.006 ± 0.028 | 0.471 ± 0.047 | 78/(78 − 11) |
| No-TNS terms | 1.007 ± 0.034 | 0.996 ± 0.025 | 0.446 ± 0.040 | 76/(78 − 11) |
| Only 1-loop terms | 1.009 ± 0.042 | 1.007 ± 0.027 | 0.470 ± 0.046 | 76/(78 − 11) |
| SPT 2-loop | 1.012 ± 0.043 | 1.007 ± 0.027 | 0.466 ± 0.047 | 77/(72 − 11) |
| FoG Gaussian | 1.020 ± 0.046 | 1.003 ± 0.028 | 0.467 ± 0.045 | 76/(78 − 11) |
| σ8 free | 0.989 ± 0.039 | 1.005 ± 0.026 | 0.452 ± 0.043 | 77/(78 − 12) |
| σ8 free, 0.5 ≤ A ≤ 1.5 prior | 0.979 ± 0.034 | 1.005 ± 0.026 | 0.445 ± 0.039 | 77/(78 − 12) |
| σ8 15% high | 1.021 ± 0.044 | 1.008 ± 0.028 | 0.468 ± 0.047 | 76/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (αs re-scaled to fiducial) | 1.008 ± 0.038 | 1.013 ± 0.026 | 0.453 ± 0.040 | 85/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm X}$| (αs re-scaled to fiducial) | 1.015 ± 0.042 | 1.008 ± 0.028 | 0.472 ± 0.053 | 77/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Y}$| (αs re-scaled to fiducial) | 1.041 ± 0.048 | 1.015 ± 0.029 | 0.474 ± 0.053 | 74/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Z}$| (αs re-scaled to fiducial) | 1.026 ± 0.048 | 1.005 ± 0.027 | 0.495 ± 0.058 | 75/(78 − 11) |
| wsys off | 1.037 ± 0.049 | 0.992 ± 0.028 | 0.426 ± 0.047 | 82/(78 − 11) |
| wcol off | 1.002 ± 0.040 | 1.003 ± 0.028 | 0.468 ± 0.048 | 64/(78 − 11) |
| wsyswcol off | 1.019 ± 0.044 | 0.990 ± 0.028 | 0.431 ± 0.047 | 69/(78 − 11) |
| 500 real. in covariance | 1.020 ± 0.042 | 0.996 ± 0.027 | 0.464 ± 0.047 | 79/(78 − 11) |
| Case . | α∥ . | α⊥ . | fσ8 . | χ2/dof . |
|---|---|---|---|---|
| Pk, kmax = 0.15, M+Q + H | 1.017 ± 0.045 | 1.006 ± 0.027 | 0.469 ± 0.046 | 77/(78 − 11) |
| Pk, 0.5 ≤ Anoise ≤ 1.5 prior | 0.999 ± 0.036 | 1.003 ± 0.027 | 0.454 ± 0.042 | 77/(78 − 11) |
| ξs | 1.016 ± 0.029 | 1.004 ± 0.019 | 0.461 ± 0.042 | – |
| Pk + ξs | 1.008 ± 0.027 | 1.002 ± 0.018 | 0.449 ± 0.039 | – |
| M+Q | 0.977 ± 0.054 | 1.032 ± 0.037 | 0.511 ± 0.065 | 38/(52 − 11) |
| M+Q, 0.5 ≤ A ≤ 1.5 prior | 0.972 ± 0.050 | 1.026 ± 0.036 | 0.496 ± 0.062 | 38/(52 − 11) |
| NGC M+Q + H | 0.983 ± 0.049 | 1.045 ± 0.036 | 0.495 ± 0.059 | 28/(39 − 7) |
| SGC M+Q + H | 1.174 ± 0.109 | 0.955 ± 0.042 | 0.375 ± 0.093 | 45/(39 − 7) |
| NGC + SGC M+Q + H | 1.007 ± 0.044 | 1.004 ± 0.027 | 0.459 ± 0.046 | 34/(39 − 7) |
| 0 ≤ b2 prior | 1.002 ± 0.036 | 1.007 ± 0.026 | 0.455 ± 0.043 | 78/(78 − 11) |
| kmax = 0.20, M+Q | 1.006 ± 0.045 | 1.013 ± 0.027 | 0.499 ± 0.053 | 58/(72 − 11) |
| |$k_{\rm max}=(0.20, {\rm M+Q})+(\, 0.15,\, {\rm H})$| | 1.025 ± 0.035 | 0.999 ± 0.021 | 0.481 ± 0.041 | 97/(98 − 11) |
| |$k_{\rm max}=(0.15, {\rm M+Q})+(\, 0.10,\, {\rm H})$| | 1.052 ± 0.062 | 0.989 ± 0.029 | 0.449 ± 0.052 | 68/(68 − 11) |
| kmax = 0.20, M+Q + H | 1.041 ± 0.033 | 0.989 ± 0.021 | 0.450 ± 0.041 | 124/(108 − 11) |
| Hexadecapole as |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1)\mathcal {L}_0(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_2)$| | 1.017 ± 0.046 | 1.006 ± 0.028 | 0.471 ± 0.047 | 78/(78 − 11) |
| No-TNS terms | 1.007 ± 0.034 | 0.996 ± 0.025 | 0.446 ± 0.040 | 76/(78 − 11) |
| Only 1-loop terms | 1.009 ± 0.042 | 1.007 ± 0.027 | 0.470 ± 0.046 | 76/(78 − 11) |
| SPT 2-loop | 1.012 ± 0.043 | 1.007 ± 0.027 | 0.466 ± 0.047 | 77/(72 − 11) |
| FoG Gaussian | 1.020 ± 0.046 | 1.003 ± 0.028 | 0.467 ± 0.045 | 76/(78 − 11) |
| σ8 free | 0.989 ± 0.039 | 1.005 ± 0.026 | 0.452 ± 0.043 | 77/(78 − 12) |
| σ8 free, 0.5 ≤ A ≤ 1.5 prior | 0.979 ± 0.034 | 1.005 ± 0.026 | 0.445 ± 0.039 | 77/(78 − 12) |
| σ8 15% high | 1.021 ± 0.044 | 1.008 ± 0.028 | 0.468 ± 0.047 | 76/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (αs re-scaled to fiducial) | 1.008 ± 0.038 | 1.013 ± 0.026 | 0.453 ± 0.040 | 85/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm X}$| (αs re-scaled to fiducial) | 1.015 ± 0.042 | 1.008 ± 0.028 | 0.472 ± 0.053 | 77/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Y}$| (αs re-scaled to fiducial) | 1.041 ± 0.048 | 1.015 ± 0.029 | 0.474 ± 0.053 | 74/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Z}$| (αs re-scaled to fiducial) | 1.026 ± 0.048 | 1.005 ± 0.027 | 0.495 ± 0.058 | 75/(78 − 11) |
| wsys off | 1.037 ± 0.049 | 0.992 ± 0.028 | 0.426 ± 0.047 | 82/(78 − 11) |
| wcol off | 1.002 ± 0.040 | 1.003 ± 0.028 | 0.468 ± 0.048 | 64/(78 − 11) |
| wsyswcol off | 1.019 ± 0.044 | 0.990 ± 0.028 | 0.431 ± 0.047 | 69/(78 − 11) |
| 500 real. in covariance | 1.020 ± 0.042 | 0.996 ± 0.027 | 0.464 ± 0.047 | 79/(78 − 11) |
Impact of different parameters and data-vector choices when performing an FS analysis on the DR16 CMASS + eBOSS LRG data set using the pipeline described in Section 3.2. The second row with the 0.5 ≤ Anoise ≤ 1.5 prior on the amplitude of shot noise represents the main result of FS analysis of this paper and correspond to the model (in solid black lines) displayed in Fig 5. The configuration space results are main results reported by Bautista et al. (2020). The rest of the cases (see the text for a full description) represent variations of the standard pipeline or data-vector choices. For each case, we do not report all the nuisance parameters, only the physical BAO scaling parameters, fσ8, and their corresponding χ2. The error bars correspond to 1σ and only include the statistical error budget.
| Case . | α∥ . | α⊥ . | fσ8 . | χ2/dof . |
|---|---|---|---|---|
| Pk, kmax = 0.15, M+Q + H | 1.017 ± 0.045 | 1.006 ± 0.027 | 0.469 ± 0.046 | 77/(78 − 11) |
| Pk, 0.5 ≤ Anoise ≤ 1.5 prior | 0.999 ± 0.036 | 1.003 ± 0.027 | 0.454 ± 0.042 | 77/(78 − 11) |
| ξs | 1.016 ± 0.029 | 1.004 ± 0.019 | 0.461 ± 0.042 | – |
| Pk + ξs | 1.008 ± 0.027 | 1.002 ± 0.018 | 0.449 ± 0.039 | – |
| M+Q | 0.977 ± 0.054 | 1.032 ± 0.037 | 0.511 ± 0.065 | 38/(52 − 11) |
| M+Q, 0.5 ≤ A ≤ 1.5 prior | 0.972 ± 0.050 | 1.026 ± 0.036 | 0.496 ± 0.062 | 38/(52 − 11) |
| NGC M+Q + H | 0.983 ± 0.049 | 1.045 ± 0.036 | 0.495 ± 0.059 | 28/(39 − 7) |
| SGC M+Q + H | 1.174 ± 0.109 | 0.955 ± 0.042 | 0.375 ± 0.093 | 45/(39 − 7) |
| NGC + SGC M+Q + H | 1.007 ± 0.044 | 1.004 ± 0.027 | 0.459 ± 0.046 | 34/(39 − 7) |
| 0 ≤ b2 prior | 1.002 ± 0.036 | 1.007 ± 0.026 | 0.455 ± 0.043 | 78/(78 − 11) |
| kmax = 0.20, M+Q | 1.006 ± 0.045 | 1.013 ± 0.027 | 0.499 ± 0.053 | 58/(72 − 11) |
| |$k_{\rm max}=(0.20, {\rm M+Q})+(\, 0.15,\, {\rm H})$| | 1.025 ± 0.035 | 0.999 ± 0.021 | 0.481 ± 0.041 | 97/(98 − 11) |
| |$k_{\rm max}=(0.15, {\rm M+Q})+(\, 0.10,\, {\rm H})$| | 1.052 ± 0.062 | 0.989 ± 0.029 | 0.449 ± 0.052 | 68/(68 − 11) |
| kmax = 0.20, M+Q + H | 1.041 ± 0.033 | 0.989 ± 0.021 | 0.450 ± 0.041 | 124/(108 − 11) |
| Hexadecapole as |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1)\mathcal {L}_0(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_2)$| | 1.017 ± 0.046 | 1.006 ± 0.028 | 0.471 ± 0.047 | 78/(78 − 11) |
| No-TNS terms | 1.007 ± 0.034 | 0.996 ± 0.025 | 0.446 ± 0.040 | 76/(78 − 11) |
| Only 1-loop terms | 1.009 ± 0.042 | 1.007 ± 0.027 | 0.470 ± 0.046 | 76/(78 − 11) |
| SPT 2-loop | 1.012 ± 0.043 | 1.007 ± 0.027 | 0.466 ± 0.047 | 77/(72 − 11) |
| FoG Gaussian | 1.020 ± 0.046 | 1.003 ± 0.028 | 0.467 ± 0.045 | 76/(78 − 11) |
| σ8 free | 0.989 ± 0.039 | 1.005 ± 0.026 | 0.452 ± 0.043 | 77/(78 − 12) |
| σ8 free, 0.5 ≤ A ≤ 1.5 prior | 0.979 ± 0.034 | 1.005 ± 0.026 | 0.445 ± 0.039 | 77/(78 − 12) |
| σ8 15% high | 1.021 ± 0.044 | 1.008 ± 0.028 | 0.468 ± 0.047 | 76/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (αs re-scaled to fiducial) | 1.008 ± 0.038 | 1.013 ± 0.026 | 0.453 ± 0.040 | 85/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm X}$| (αs re-scaled to fiducial) | 1.015 ± 0.042 | 1.008 ± 0.028 | 0.472 ± 0.053 | 77/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Y}$| (αs re-scaled to fiducial) | 1.041 ± 0.048 | 1.015 ± 0.029 | 0.474 ± 0.053 | 74/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Z}$| (αs re-scaled to fiducial) | 1.026 ± 0.048 | 1.005 ± 0.027 | 0.495 ± 0.058 | 75/(78 − 11) |
| wsys off | 1.037 ± 0.049 | 0.992 ± 0.028 | 0.426 ± 0.047 | 82/(78 − 11) |
| wcol off | 1.002 ± 0.040 | 1.003 ± 0.028 | 0.468 ± 0.048 | 64/(78 − 11) |
| wsyswcol off | 1.019 ± 0.044 | 0.990 ± 0.028 | 0.431 ± 0.047 | 69/(78 − 11) |
| 500 real. in covariance | 1.020 ± 0.042 | 0.996 ± 0.027 | 0.464 ± 0.047 | 79/(78 − 11) |
| Case . | α∥ . | α⊥ . | fσ8 . | χ2/dof . |
|---|---|---|---|---|
| Pk, kmax = 0.15, M+Q + H | 1.017 ± 0.045 | 1.006 ± 0.027 | 0.469 ± 0.046 | 77/(78 − 11) |
| Pk, 0.5 ≤ Anoise ≤ 1.5 prior | 0.999 ± 0.036 | 1.003 ± 0.027 | 0.454 ± 0.042 | 77/(78 − 11) |
| ξs | 1.016 ± 0.029 | 1.004 ± 0.019 | 0.461 ± 0.042 | – |
| Pk + ξs | 1.008 ± 0.027 | 1.002 ± 0.018 | 0.449 ± 0.039 | – |
| M+Q | 0.977 ± 0.054 | 1.032 ± 0.037 | 0.511 ± 0.065 | 38/(52 − 11) |
| M+Q, 0.5 ≤ A ≤ 1.5 prior | 0.972 ± 0.050 | 1.026 ± 0.036 | 0.496 ± 0.062 | 38/(52 − 11) |
| NGC M+Q + H | 0.983 ± 0.049 | 1.045 ± 0.036 | 0.495 ± 0.059 | 28/(39 − 7) |
| SGC M+Q + H | 1.174 ± 0.109 | 0.955 ± 0.042 | 0.375 ± 0.093 | 45/(39 − 7) |
| NGC + SGC M+Q + H | 1.007 ± 0.044 | 1.004 ± 0.027 | 0.459 ± 0.046 | 34/(39 − 7) |
| 0 ≤ b2 prior | 1.002 ± 0.036 | 1.007 ± 0.026 | 0.455 ± 0.043 | 78/(78 − 11) |
| kmax = 0.20, M+Q | 1.006 ± 0.045 | 1.013 ± 0.027 | 0.499 ± 0.053 | 58/(72 − 11) |
| |$k_{\rm max}=(0.20, {\rm M+Q})+(\, 0.15,\, {\rm H})$| | 1.025 ± 0.035 | 0.999 ± 0.021 | 0.481 ± 0.041 | 97/(98 − 11) |
| |$k_{\rm max}=(0.15, {\rm M+Q})+(\, 0.10,\, {\rm H})$| | 1.052 ± 0.062 | 0.989 ± 0.029 | 0.449 ± 0.052 | 68/(68 − 11) |
| kmax = 0.20, M+Q + H | 1.041 ± 0.033 | 0.989 ± 0.021 | 0.450 ± 0.041 | 124/(108 − 11) |
| Hexadecapole as |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1)\mathcal {L}_0(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_2)$| | 1.017 ± 0.046 | 1.006 ± 0.028 | 0.471 ± 0.047 | 78/(78 − 11) |
| No-TNS terms | 1.007 ± 0.034 | 0.996 ± 0.025 | 0.446 ± 0.040 | 76/(78 − 11) |
| Only 1-loop terms | 1.009 ± 0.042 | 1.007 ± 0.027 | 0.470 ± 0.046 | 76/(78 − 11) |
| SPT 2-loop | 1.012 ± 0.043 | 1.007 ± 0.027 | 0.466 ± 0.047 | 77/(72 − 11) |
| FoG Gaussian | 1.020 ± 0.046 | 1.003 ± 0.028 | 0.467 ± 0.045 | 76/(78 − 11) |
| σ8 free | 0.989 ± 0.039 | 1.005 ± 0.026 | 0.452 ± 0.043 | 77/(78 − 12) |
| σ8 free, 0.5 ≤ A ≤ 1.5 prior | 0.979 ± 0.034 | 1.005 ± 0.026 | 0.445 ± 0.039 | 77/(78 − 12) |
| σ8 15% high | 1.021 ± 0.044 | 1.008 ± 0.028 | 0.468 ± 0.047 | 76/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm OR}$| (αs re-scaled to fiducial) | 1.008 ± 0.038 | 1.013 ± 0.026 | 0.453 ± 0.040 | 85/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm X}$| (αs re-scaled to fiducial) | 1.015 ± 0.042 | 1.008 ± 0.028 | 0.472 ± 0.053 | 77/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Y}$| (αs re-scaled to fiducial) | 1.041 ± 0.048 | 1.015 ± 0.029 | 0.474 ± 0.053 | 74/(78 − 11) |
| |$\boldsymbol{\Theta }_{\rm Z}$| (αs re-scaled to fiducial) | 1.026 ± 0.048 | 1.005 ± 0.027 | 0.495 ± 0.058 | 75/(78 − 11) |
| wsys off | 1.037 ± 0.049 | 0.992 ± 0.028 | 0.426 ± 0.047 | 82/(78 − 11) |
| wcol off | 1.002 ± 0.040 | 1.003 ± 0.028 | 0.468 ± 0.048 | 64/(78 − 11) |
| wsyswcol off | 1.019 ± 0.044 | 0.990 ± 0.028 | 0.431 ± 0.047 | 69/(78 − 11) |
| 500 real. in covariance | 1.020 ± 0.042 | 0.996 ± 0.027 | 0.464 ± 0.047 | 79/(78 − 11) |
Except for some extreme cases, such as those when the systematic weights are not applied, we do not observe any strong dependence of the inferred cosmological parameters with any of the studied variations. In particular, we observe very mild changes when the underlying linear power spectrum template is changed. We also note the change in the size of errors of α∥ and fσ8 when the 50 per cent prior on Anoise is set (first versus second row). In this last case the 2σ, contours do hit the higher boundary of Anoise = 1.5, and therefore the reduction of error is a direct consequence of this. The amplitude of shot noise is very correlated with b2 which is poorly constrained without higher order moments as the bispectrum (Gil-Marín et al. 2017). In particular, the Anoise ≃ 1 solution also corresponds to b2 > 0, whereas Anoise > 1.5 corresponds to b2 < 0 (see Fig. E2). From the power spectrum and bispectrum analysis of BOSS DR12 CMASS sample 0.43 < z < 0.70, we expect that b2 for these type of galaxies is close to the value reported in Gil-Marín et al. (2017), b2σ8 = 0.606 ± 0.069, which agrees with the solution of shot noise being close to the Poisson prediction. Thus, we find plausible that the shot noise should not differ by more than 50 per cent (which is already quite a large amount) from the Poissonian prediction and we decide to take as the FS analysis main result of this paper the cosmological parameters inferred when this |$50{{\ \rm per\ cent}}$| prior is applied. In Appendix E, we further comment on this effect (see also Fig. E1).
In Fig. 6, we display the derived DH/rdrag, DM/rdrag, and fσ8 cosmological parameters from the FS and BAO analysis on the pre- and post-reconstructed catalogues, respectively. Both measurements rely on very correlated pre- and post-recon catalogues, and therefore it is not straightforward to resolve the level of agreement between them. Later in Section 6, we come back to this question and also compare these findings with the quantities inferred from configuration space. For now, we just note that the reconstructed-BAO analysis provides tighter constrains on both DH/rdrag and DM/rdrag than the FS analysis. This feature is actually expected due to the enhancement that reconstruction provides in the measurement of the BAO peak oscillatory features. We also note that the reconstructed-BAO analysis favours higher values of both DM/rdrag and DH/rdrag with respect to the FS analysis on pre-reconstructed data. In fact, if we were looking at the pair of variables α0 and ϵ we would notice that such difference arises from the AP variable, ϵ or Fϵ, where the results inferred from reconstructed data present an ∼2σ deviation from the null-AP behaviour, which is what we observe for the pre-reconstructed catalogue. We will fully discuss these differences later in Section 6.

Comparison of the cosmological inferred parameters from the FS and BAO analysis (on post-reconstructed catalogues), respectively, from the power spectrum multipoles. In this case, the FS derived results have been computed from the power spectrum monopole, quadrupole, and hexadecapole under the analysis with |$50{{\ \rm per\ cent}}$| priors on Anoise reported by the second row of Table 4. The BAO reconstructed results come from the standard analysis on power spectrum monopole and quadrupole, as it is reported by the second row of Table 3. In all cases, the contours represent only the statistical contribution.
5 SYSTEMATIC TESTS
In this section, we aim to run the BAO and FS pipeline analyses on different sets of mocks to check the performance and to identify potential systematic errors. In total, we use NEZ = 1000 realizations of the EZmocks, NNseries = 84 realizations of the Nseries mocks and NOR = 27 realizations of the OuterRim-HOD mocks.
5.1 BAO systematics
We start by running the BAO pipeline described in Section 3.1 on the pre- and post-reconstructed EZmocks, Nseries and OuterRim +‘Hearin-Threshold-2’, +‘Leauthaud-Threshold-2’ and + ‘Tinker-Threshold-2’ HOD mocks. We run the BAO pipeline on the power spectrum monopole and quadrupole for |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.30$|. Smaller and larger scales do not contain relevant BAO information.
In this section we aim to
check how typical the data is with respect to the EZmocks;
determine the systematic budget of the pipeline;
check whether the arbitrary choice of the BAO reference template has an impact on the inferred cosmological parameters; and
determine whether the underlying galaxy HOD has an impact on the recovered parameters.
The top panels of Fig. 7 display the recovered α∥ and α⊥ scaling parameters on the pre- (left-hand panels) and post-reconstructed (right-hand panel) 1000 EZmocks realizations (green points). The corresponding bottom panels display the distribution of errors inferred from the rms of the individual MCMC chains. In addition, we represent with a red cross the values for the actual data catalogue, and with a black dot the values obtained when fitting the average power spectrum of 1000 EZmocks realizations. The error of this last case is expected to scale with the square root of the total volume, and therefore we re-scale it by the |$\sqrt{N_{\rm EZ}}$| factor in order to match the value of the error of a single realization. For all the cases, the results inferred from the mean of the mocks are in excellent agreement with the results of the individual cases, suggesting that the mean of the fits is close to the fit of the mean (shown later in Table 5). We find that the values of α∥ and α⊥ inferred from the data catalogue are also consistent with the intrinsic scatter observed from the mocks. However, we obtain atypically small errors when analysing the data catalogue, both for the pre- and post-reconstructed cases of α∥. In particular, for the post-reconstruction case, we have only found a total of ∼10/1000 realizations whose error on α∥ is comparable to the one found in the data, which certainly suggest a |$\sim 1{{\ \rm per\ cent}}$| probability of being in such situation. As we show later (see Fig. 15 in Section 6), this result is perfectly compatible with what we find in the complementary BAO analysis in configuration space performed in Bautista et al. (2020). The χ2 value of the data is not small with respect to the typical value obtained by the mocks, which suggests that this small BAO error on α∥ may be caused by noise fluctuations, which enhance the BAO signal in the data along the LOS, with respect to the typical noise level predicted by the mocks. Given the number of physical parameters (α∥, α⊥, pre- and post-reconstructed catalogues, fσ8 and their corresponding errors: 10 variables in total) it is not very unlikely that at least one of them is atypical at 3σ level, which is known as ‘the look-elsewhere effect’.
![The top sub-panels display the distribution of best-fitting α∥ and α⊥, for the pre- (left-hand panels) and post-reconstructed (right-hand panels) power spectrum monopole and quadrupole for $0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le 0.30$, for the 1000 realizations of the EZmocks catalogues (green points), for the DR16 CMASS + eBOSS LRG data catalogue (red cross) and for the best-fit to the mean of the 1000 mock power spectra (black dot). The horizontal and vertical black dotted lines represent the expected α values for the EZmocks. The distribution of χ2 values is also shown for each case. The bottom sub-panels display analogous plots for the errors of α∥ and α⊥, instead. In this case, the error of the mean has been re-scaled by the square root of number of realizations.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2455/1/m_staa2455fig7.jpeg?Expires=1750266550&Signature=kYA68-RS~hBZK36GXfOls7jzqdK9v1W9BZn8XPm4Zrq1UJbR2p8diXBNy-G0EEzpivWePgRyJbKf6mI64qpZyqmb8Vm0TUqTkgYhBIHdb7~dXYS0lYIJntfHW6E5XItXU-S4pIJ8JvARrdFIdAj~75OTPDF-8ndW1WOBTeMGkqCnTqhDa0HjnF3Cr0ObfYf0N~lXkha0hFGopkHEzC~6Ph8ZcrUPU~iC5WotTA92NCBXx74tYxjdCQWTUldkokc~Rn4eh5ckXzAu3LzKzPkcyZgpjp-iNI4rrz6lrlQMNDxsa4x8c~iI-uK9r~D-qAwLvRLZ~xnX~RZfbf~fTDLkrQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The top sub-panels display the distribution of best-fitting α∥ and α⊥, for the pre- (left-hand panels) and post-reconstructed (right-hand panels) power spectrum monopole and quadrupole for |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le 0.30$|, for the 1000 realizations of the EZmocks catalogues (green points), for the DR16 CMASS + eBOSS LRG data catalogue (red cross) and for the best-fit to the mean of the 1000 mock power spectra (black dot). The horizontal and vertical black dotted lines represent the expected α values for the EZmocks. The distribution of χ2 values is also shown for each case. The bottom sub-panels display analogous plots for the errors of α∥ and α⊥, instead. In this case, the error of the mean has been re-scaled by the square root of number of realizations.
Performance of the BAO template of equation (21) in different set of mocks. For The EZmocks expected values are |$\alpha _\parallel ^{\rm exp}=1+8.853\times 10^{-4}$| and |$\alpha _\perp ^{\rm exp}=1-3.650\times 10^{-4}$| as the mocks are not analysed in their underlying true cosmology (except for those where the cosmology is explicitly varied, |$\boldsymbol{\Theta }_{\rm OR,X,Y,Z}$|). For the rest of the mocks, these values are 1, as they are, respectively, analysed in their own underlying true cosmology. For each set of mocks, the results from both pre- and post-recon catalogues are presented. We display the results of fitting the mean of all the mocks, indicated with ‘Mean’, and the mean of the individual fits on the mocks, indicated with ‘Individual’. For the fit to the mean, the error quoted is the 1σ of the error on this fit, where in order to do so, we have scaled the covariances by the number of realizations used to take the mean, which in all the cases is the maximum number of realizations available, Ntot, 1000, 84, and 27 for EZmocks, Nseries, and OuterRim-HOD mocks, respectively. For the OuterRim-HOD type of mocks only the ‘Threshold 2’ flavour is represented, where a padding has been applied to the original non-periodic cubic sub-box in order avoid spurious non-periodic effects. For the mean of individual best-fits, the error quoted is rms divided by |$\sqrt{N_{\rm det}}$|, where Ndet is the number of BAO detections (those fits with α∥ and α⊥ were both between 0.8 and 1.2, for EZmocks, Nseries, and 0.7 and 1.3 for OuterRim-HOD). Fig. 9 visually displays the results of this table.
| Mock name . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| Mean EZmocks | Pre-recon | −0.0003 ± 0.0015 | −0.004 80 ± 0.000 92 | 1/1 |
| Individual EZmocks | Pre-recon | −0.0165 ± 0.0019 | 0.0025 ± 0.0010 | 982/1000 |
| Mean EZmocks | Post-recon | 0.0060 ± 0.0010 | −0.00024 ± 0.000 68 | 1/1 |
| Individual EZmocks | Post-recon | 0.0017 ± 0.0012 | 0.00071 ± 0.000 73 | 999/1000 |
| Mean EZmocks (+ Hexadecapole) | Pre-recon | −0.0039 ± 0.0015 | −0.009 46 ± 0.000 96 | 1/1 |
| Mean EZmocks (+ Hexadecapole) | Post-recon | −0.0022 ± 0.0011 | −0.003 67 ± 0.000 66 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm OR}$|) | Post-recon | −0.0015 ± 0.0013 | 0.001 18 ± 0.000 75 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm X}$|) | Post-recon | 0.0044 ± 0.0013 | −0.004 01 ± 0.000 76 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Y}$|) | Post-recon | 0.0032 ± 0.0012 | 0.000 89 ± 0.000 78 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Z}$|) | Post-recon | −0.0004 ± 0.0011 | −0.008 38 ± 0.000 72 | 1/1 |
| Mean Nseries | Pre-recon | −0.0045 ± 0.0041 | −0.0021 ± 0.0020 | 1/1 |
| Individual Nseries | Pre-recon | −0.0062 ± 0.0051 | 0.0000 ± 0.0026 | 84/84 |
| Mean Nseries | Post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| Individual Nseries | Post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| Mean OuterRim-HOD-Hearin | Pre-recon | −0.022 ± 0.014 | 0.0108 ± 0.0099 | 1/1 |
| Individual OuterRim-HOD-Hearin | Pre-recon | −0.021 ± 0.016 | 0.016 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Hearin | Post-recon | 0.000 ± 0.011 | 0.0122 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Hearin | Post-recon | 0.009 ± 0.015 | 0.0167 ± 0.0061 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Pre-recon | −0.011 ± 0.018 | 0.003 ± 0.011 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Pre-recon | 0.000 ± 0.018 | 0.011 ± 0.012 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Post-recon | −0.006 ± 0.010 | −0.0024 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Post-recon | 0.002 ± 0.013 | −0.0093 ± 0.0074 | 27/27 |
| Mean OuterRim-HOD-Tinker | Pre-recon | 0.002 ± 0.018 | −0.005 ± 0.012 | 1/1 |
| Individual OuterRim-HOD-Tinker | Pre-recon | −0.011 ± 0.016 | 0.023 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Tinker | Post-recon | −0.002 ± 0.012 | −0.0025 ± 0.0088 | 1/1 |
| Individual OuterRim-HOD-Tinker | Post-recon | 0.0038 ± 0.0097 | −0.0006 ± 0.0072 | 27/27 |
| Mock name . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| Mean EZmocks | Pre-recon | −0.0003 ± 0.0015 | −0.004 80 ± 0.000 92 | 1/1 |
| Individual EZmocks | Pre-recon | −0.0165 ± 0.0019 | 0.0025 ± 0.0010 | 982/1000 |
| Mean EZmocks | Post-recon | 0.0060 ± 0.0010 | −0.00024 ± 0.000 68 | 1/1 |
| Individual EZmocks | Post-recon | 0.0017 ± 0.0012 | 0.00071 ± 0.000 73 | 999/1000 |
| Mean EZmocks (+ Hexadecapole) | Pre-recon | −0.0039 ± 0.0015 | −0.009 46 ± 0.000 96 | 1/1 |
| Mean EZmocks (+ Hexadecapole) | Post-recon | −0.0022 ± 0.0011 | −0.003 67 ± 0.000 66 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm OR}$|) | Post-recon | −0.0015 ± 0.0013 | 0.001 18 ± 0.000 75 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm X}$|) | Post-recon | 0.0044 ± 0.0013 | −0.004 01 ± 0.000 76 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Y}$|) | Post-recon | 0.0032 ± 0.0012 | 0.000 89 ± 0.000 78 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Z}$|) | Post-recon | −0.0004 ± 0.0011 | −0.008 38 ± 0.000 72 | 1/1 |
| Mean Nseries | Pre-recon | −0.0045 ± 0.0041 | −0.0021 ± 0.0020 | 1/1 |
| Individual Nseries | Pre-recon | −0.0062 ± 0.0051 | 0.0000 ± 0.0026 | 84/84 |
| Mean Nseries | Post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| Individual Nseries | Post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| Mean OuterRim-HOD-Hearin | Pre-recon | −0.022 ± 0.014 | 0.0108 ± 0.0099 | 1/1 |
| Individual OuterRim-HOD-Hearin | Pre-recon | −0.021 ± 0.016 | 0.016 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Hearin | Post-recon | 0.000 ± 0.011 | 0.0122 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Hearin | Post-recon | 0.009 ± 0.015 | 0.0167 ± 0.0061 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Pre-recon | −0.011 ± 0.018 | 0.003 ± 0.011 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Pre-recon | 0.000 ± 0.018 | 0.011 ± 0.012 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Post-recon | −0.006 ± 0.010 | −0.0024 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Post-recon | 0.002 ± 0.013 | −0.0093 ± 0.0074 | 27/27 |
| Mean OuterRim-HOD-Tinker | Pre-recon | 0.002 ± 0.018 | −0.005 ± 0.012 | 1/1 |
| Individual OuterRim-HOD-Tinker | Pre-recon | −0.011 ± 0.016 | 0.023 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Tinker | Post-recon | −0.002 ± 0.012 | −0.0025 ± 0.0088 | 1/1 |
| Individual OuterRim-HOD-Tinker | Post-recon | 0.0038 ± 0.0097 | −0.0006 ± 0.0072 | 27/27 |
Performance of the BAO template of equation (21) in different set of mocks. For The EZmocks expected values are |$\alpha _\parallel ^{\rm exp}=1+8.853\times 10^{-4}$| and |$\alpha _\perp ^{\rm exp}=1-3.650\times 10^{-4}$| as the mocks are not analysed in their underlying true cosmology (except for those where the cosmology is explicitly varied, |$\boldsymbol{\Theta }_{\rm OR,X,Y,Z}$|). For the rest of the mocks, these values are 1, as they are, respectively, analysed in their own underlying true cosmology. For each set of mocks, the results from both pre- and post-recon catalogues are presented. We display the results of fitting the mean of all the mocks, indicated with ‘Mean’, and the mean of the individual fits on the mocks, indicated with ‘Individual’. For the fit to the mean, the error quoted is the 1σ of the error on this fit, where in order to do so, we have scaled the covariances by the number of realizations used to take the mean, which in all the cases is the maximum number of realizations available, Ntot, 1000, 84, and 27 for EZmocks, Nseries, and OuterRim-HOD mocks, respectively. For the OuterRim-HOD type of mocks only the ‘Threshold 2’ flavour is represented, where a padding has been applied to the original non-periodic cubic sub-box in order avoid spurious non-periodic effects. For the mean of individual best-fits, the error quoted is rms divided by |$\sqrt{N_{\rm det}}$|, where Ndet is the number of BAO detections (those fits with α∥ and α⊥ were both between 0.8 and 1.2, for EZmocks, Nseries, and 0.7 and 1.3 for OuterRim-HOD). Fig. 9 visually displays the results of this table.
| Mock name . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| Mean EZmocks | Pre-recon | −0.0003 ± 0.0015 | −0.004 80 ± 0.000 92 | 1/1 |
| Individual EZmocks | Pre-recon | −0.0165 ± 0.0019 | 0.0025 ± 0.0010 | 982/1000 |
| Mean EZmocks | Post-recon | 0.0060 ± 0.0010 | −0.00024 ± 0.000 68 | 1/1 |
| Individual EZmocks | Post-recon | 0.0017 ± 0.0012 | 0.00071 ± 0.000 73 | 999/1000 |
| Mean EZmocks (+ Hexadecapole) | Pre-recon | −0.0039 ± 0.0015 | −0.009 46 ± 0.000 96 | 1/1 |
| Mean EZmocks (+ Hexadecapole) | Post-recon | −0.0022 ± 0.0011 | −0.003 67 ± 0.000 66 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm OR}$|) | Post-recon | −0.0015 ± 0.0013 | 0.001 18 ± 0.000 75 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm X}$|) | Post-recon | 0.0044 ± 0.0013 | −0.004 01 ± 0.000 76 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Y}$|) | Post-recon | 0.0032 ± 0.0012 | 0.000 89 ± 0.000 78 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Z}$|) | Post-recon | −0.0004 ± 0.0011 | −0.008 38 ± 0.000 72 | 1/1 |
| Mean Nseries | Pre-recon | −0.0045 ± 0.0041 | −0.0021 ± 0.0020 | 1/1 |
| Individual Nseries | Pre-recon | −0.0062 ± 0.0051 | 0.0000 ± 0.0026 | 84/84 |
| Mean Nseries | Post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| Individual Nseries | Post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| Mean OuterRim-HOD-Hearin | Pre-recon | −0.022 ± 0.014 | 0.0108 ± 0.0099 | 1/1 |
| Individual OuterRim-HOD-Hearin | Pre-recon | −0.021 ± 0.016 | 0.016 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Hearin | Post-recon | 0.000 ± 0.011 | 0.0122 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Hearin | Post-recon | 0.009 ± 0.015 | 0.0167 ± 0.0061 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Pre-recon | −0.011 ± 0.018 | 0.003 ± 0.011 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Pre-recon | 0.000 ± 0.018 | 0.011 ± 0.012 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Post-recon | −0.006 ± 0.010 | −0.0024 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Post-recon | 0.002 ± 0.013 | −0.0093 ± 0.0074 | 27/27 |
| Mean OuterRim-HOD-Tinker | Pre-recon | 0.002 ± 0.018 | −0.005 ± 0.012 | 1/1 |
| Individual OuterRim-HOD-Tinker | Pre-recon | −0.011 ± 0.016 | 0.023 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Tinker | Post-recon | −0.002 ± 0.012 | −0.0025 ± 0.0088 | 1/1 |
| Individual OuterRim-HOD-Tinker | Post-recon | 0.0038 ± 0.0097 | −0.0006 ± 0.0072 | 27/27 |
| Mock name . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| Mean EZmocks | Pre-recon | −0.0003 ± 0.0015 | −0.004 80 ± 0.000 92 | 1/1 |
| Individual EZmocks | Pre-recon | −0.0165 ± 0.0019 | 0.0025 ± 0.0010 | 982/1000 |
| Mean EZmocks | Post-recon | 0.0060 ± 0.0010 | −0.00024 ± 0.000 68 | 1/1 |
| Individual EZmocks | Post-recon | 0.0017 ± 0.0012 | 0.00071 ± 0.000 73 | 999/1000 |
| Mean EZmocks (+ Hexadecapole) | Pre-recon | −0.0039 ± 0.0015 | −0.009 46 ± 0.000 96 | 1/1 |
| Mean EZmocks (+ Hexadecapole) | Post-recon | −0.0022 ± 0.0011 | −0.003 67 ± 0.000 66 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm OR}$|) | Post-recon | −0.0015 ± 0.0013 | 0.001 18 ± 0.000 75 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm X}$|) | Post-recon | 0.0044 ± 0.0013 | −0.004 01 ± 0.000 76 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Y}$|) | Post-recon | 0.0032 ± 0.0012 | 0.000 89 ± 0.000 78 | 1/1 |
| Mean EZmocks (|$\boldsymbol{\Theta }_{\rm Z}$|) | Post-recon | −0.0004 ± 0.0011 | −0.008 38 ± 0.000 72 | 1/1 |
| Mean Nseries | Pre-recon | −0.0045 ± 0.0041 | −0.0021 ± 0.0020 | 1/1 |
| Individual Nseries | Pre-recon | −0.0062 ± 0.0051 | 0.0000 ± 0.0026 | 84/84 |
| Mean Nseries | Post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| Individual Nseries | Post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| Mean OuterRim-HOD-Hearin | Pre-recon | −0.022 ± 0.014 | 0.0108 ± 0.0099 | 1/1 |
| Individual OuterRim-HOD-Hearin | Pre-recon | −0.021 ± 0.016 | 0.016 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Hearin | Post-recon | 0.000 ± 0.011 | 0.0122 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Hearin | Post-recon | 0.009 ± 0.015 | 0.0167 ± 0.0061 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Pre-recon | −0.011 ± 0.018 | 0.003 ± 0.011 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Pre-recon | 0.000 ± 0.018 | 0.011 ± 0.012 | 27/27 |
| Mean OuterRim-HOD-Leauthaud | Post-recon | −0.006 ± 0.010 | −0.0024 ± 0.0075 | 1/1 |
| Individual OuterRim-HOD-Leauthaud | Post-recon | 0.002 ± 0.013 | −0.0093 ± 0.0074 | 27/27 |
| Mean OuterRim-HOD-Tinker | Pre-recon | 0.002 ± 0.018 | −0.005 ± 0.012 | 1/1 |
| Individual OuterRim-HOD-Tinker | Pre-recon | −0.011 ± 0.016 | 0.023 ± 0.011 | 27/27 |
| Mean OuterRim-HOD-Tinker | Post-recon | −0.002 ± 0.012 | −0.0025 ± 0.0088 | 1/1 |
| Individual OuterRim-HOD-Tinker | Post-recon | 0.0038 ± 0.0097 | −0.0006 ± 0.0072 | 27/27 |
The panels in Fig. 8 display how the reconstruction algorithm performs on the EZmocks, for the errors of α∥ and α⊥. Reconstruction significantly helps to improve the determination of the αs in almost all the realizations of the mocks, where the typical improvement (ratio between pre- and post-recon errors) is |$\sim 40{{\ \rm per\ cent}}$| for α∥ and |$20{{\ \rm per\ cent}}$| on α⊥. This behaviour is expected for cosmic variance limited samples, like the LRGs and ELGs, unlike other more sparse samples like the quasars. We find that for the data, the improvement on α⊥ is expected and typical with respect to what is observed in the mocks, whereas for α∥ the values are atypical as we have commented above, but the improvement ratio is typical.
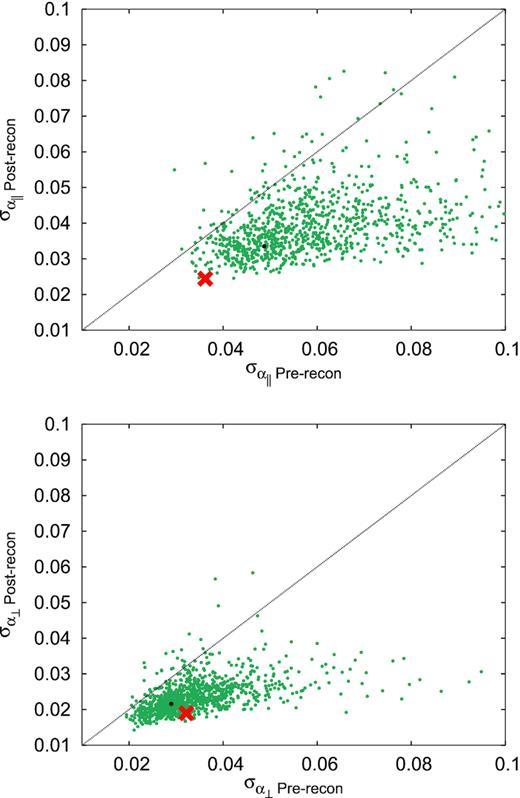
Performance of the reconstruction on the DR16 CMASS + eBOSS LRG catalogues, the green symbols represent the 1000 realizations of the EZmocks, the red cross the actual DR16 CMASS + eBOSS LRG data catalogue. The x-axis represents the pre-reconstructed quantity and the y-axis the post-reconstructed quantity. For reference, a black dashed line, x = y is also shown. The top and bottom panels display the 1σ errors of α∥ and α⊥, respectively. The black dot represents the mean of 1000 realizations re-scaled by the square root of the 1000 realizations.
5.1.1 Performance of BAO template
We start by applying the BAO anisotropic template described by equation (21) on the different sets of mocks. Table 5 displays the results when fitting the mean power spectra of all available realizations for a given type of mock (rows labelled ‘Mean’); and the mean of the fits of individual realizations (rows labelled ‘Individual’).
Fig. 9 graphically represents the data contained in Table 5. For each sub-panel, the difference between the measured α∥ and α⊥, and their expected value are inferred for the pre- (left-hand side) and post-reconstructed (right-hand side) catalogues. The individual results on the mocks are shown in grey, the results of the mean of the mocks are represented by a △-symbol in green (for the pre-reconstructed catalogues) and in orange (for post-reconstructed catalogues). The associated errors are consistently the errors of the mean, obtained by re-scaling the covariance by a factor the number of realizations, NEZ, NNseries, and NOR. Therefore, these errors are a factor |$\sqrt{N_i}$| smaller than the error we obtain for a single realization of these mocks. The mean of the individual fits is represented by a \space-symbol in pink (for pre-reconstructed catalogues) and in purple (for post-reconstructed catalogues). In this case, the error associated is the rms of all the individual fits, which is |$\sim \sqrt{N_i}$| larger than the error associated to the mean. The sub-panels show the difference between the measured and the expected value of α∥ and α⊥ in terms of number of statisticalσ of the error of the mean, and the |${\rm rms}/\sqrt{N_i}$|. Note that for the EZmocks the effective volume is so large (|$\simeq 2,650\, {\rm Gpc}^3$|) that in some cases the result is totally dominated by systematics and the symbols are off the scale of ±3σ.
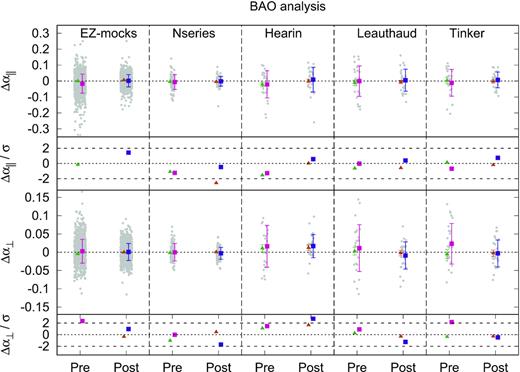
Performance of the BAO type of analysis for α∥ (top panel) and α⊥ (bottom panel) as indicated. Each of the five vertical sub-panels corresponds to the results on the EZmocks, Nseries, and the OuterRim-HOD mocks by Hearin+threshold2, Leauthaud+threshold2, and Tinker + threshold2, as indicated. A padding has been applied to the original non-periodic OuterRim-HOD cubic sub-box in order avoid spurious non-periodic effects. For each α, we display the panels Δα ≡ α − αexp and Δα/σ. For each of these sub-panels, we display the pre- (left-hand panel) and post-recon results (right-hand panel). The grey points correspond to the individual best-fitting parameters. The green (for pre-recon) and orange (for post-recon) triangles symbols correspond to the results of fitting the mean of the mocks, and its error corresponds to the error of the mean. The pink (for pre-recon) and purple (for post-recon) squares symbols display the results of taking the mean of Ndet individual fits, and the reported error is its rms. Consequently, the error of the mean of the fits is |$\sqrt{N_{\rm det}}$| times the error of the mean. In the Δα/σ sub-panels, σ represents the error of the mean for the fit to the mean (orange and green triangles), and the rms/|$\sqrt{N_{\rm det}}$| for the mean of the individual fits. The numerical results of this plot are also listed in Table 5.
The EZmocks ‘Mean’ results on post-reconstruction catalogues reveal that the α∥ variable is significantly shifted by |$0.6{{\ \rm per\ cent}}$| with respect to their expected quantity, which corresponds to 6σ deviation from the expected value; whereas for α⊥, mocks and model agree to within |$0.068{{\ \rm per\ cent}}$| (1σ level). It is also worth mentioning that at this sub-per cent level of precision, we would require full N-body mocks to actually validate this kind of systematic shifts, as the EZmocks have not been designed to be accurate at this level of precision. Therefore, we cannot discern whether this observed |$0.6{{\ \rm per\ cent}}$| shift in α∥ is due to a limitation of the model of equation (21), a limitation of the EZmocks themselves, or an effect arising from the reconstruction technique. From the remaining N-body mocks, we do not observe any significant BAO peak position shift with respect to their corresponding expected value in any of the post-reconstructed catalogues analysed. The BAO pipeline is able to deal with different kinds of HOD models. We do see some fluctuations, but these are always below ±2.5σ limit, so we do not take them as significant shifts. However, the statistical errors associated to these catalogues are not as small as those corresponding to the EZmocks, so we can only state that we have not detected any systematic above the statistical threshold of |$1{-}2{{\ \rm per\ cent}}$| for OuterRim-HOD, and |$0.1{-}0.5{{\ \rm per\ cent}}$| for Nseries. Such upper limits are below the statistical precision of our sample: for post-reconstructed catalogues we obtain a statistical precision of |$\sim 2.4{{\ \rm per\ cent}}$| for α∥ and |$\sim 1.9{{\ \rm per\ cent}}$| for α⊥. From the Nseries results, we conclude that there are no strong modelling-systematic errors associated when determining αs, which validates our modelling pipeline, including the reconstruction technique. From the OuterRim-HOD results, we conclude that we do not detect any relative systematic due to different HOD modelling, although the statistical precision reached on these mocks is comparable to the statistical precision of our sample.
5.1.2 Effect of reference cosmology on BAO
We are interested in testing the potential impact of the arbitrary choice of reference cosmology. For simplicity, we use the same cosmology to (i) produce the BAO template, and (ii) convert redshifts into distances in both random and galaxy catalogues. The BAO analysis measures relative differences between the BAO peak position in the power spectrum with respect to the template. Therefore, a priori the specific choice of reference cosmology should not impact this result. In this section, we explicitly check this by analysing the Nseries mocks in five different cosmologies: their own cosmology, |$\boldsymbol{\Theta }_{\rm Nseries}$|; the fiducial cosmology which is used for the baseline analysis of the actual data catalogue, |$\boldsymbol{\Theta }_{\rm fid}$|; and three extra cosmologies with a higher value of Ωm: |$\boldsymbol{\Theta }_X$|, |$\boldsymbol{\Theta }_Y$|, and |$\boldsymbol{\Theta }_Z$|, all listed in Table 1. The oscillatory features of these cosmologies are plotted in the top panel of Fig. 10. The expected values of α∥ and α⊥ are therefore different among these cosmologies. We do not analyse these mocks on the |$\boldsymbol{\Theta }_{\rm OR}$| cosmology, as this cosmology is very similar to the |$\boldsymbol{\Theta }_{\rm Nseries}$|. Inputing the values of the true |$\boldsymbol{\Theta }_{\rm Nseries}$| and these four cosmologies into equations (14) and (15), we determine the expected values of the scaling factors. For the |$\boldsymbol{\Theta }_{\rm fid}$| cosmology, we find that |$\alpha ^{\rm exp}_\parallel =0.9875$| and |$\alpha _\perp ^{\rm exp}=0.9787$|; for the |$\boldsymbol{\Theta }_X$| cosmology, we find that |$\alpha _\parallel ^{\rm exp} = 0.9846$| and |$\alpha _\perp ^{\rm exp} = 0.9620$|; for the |$\boldsymbol{\Theta }_Y$| cosmology, we find that |$\alpha _\parallel ^{\rm exp} = 0.9543$| and |$\alpha _\perp ^{\rm exp} = 0.9325$|; for the |$\boldsymbol{\Theta }_Z$| cosmology, we find that |$\alpha _\parallel ^{\rm exp} = 0.9557$| and |$\alpha _\perp ^{\rm exp} = 0.9291$|; and of course when the mocks are analysed in their own cosmology the expected values are unity.
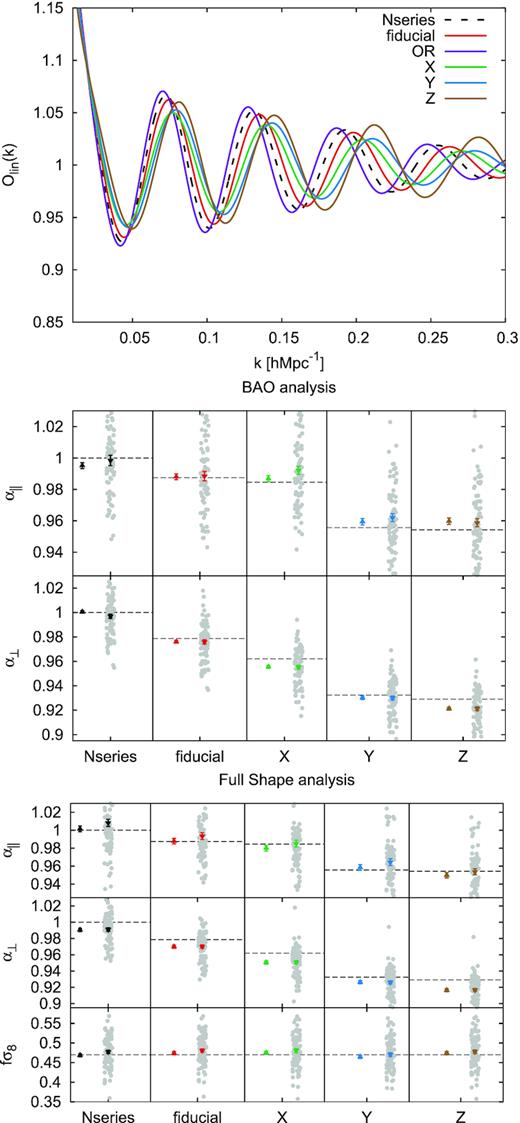
Top panel: BAO signal, |$\mathcal {O}_{\rm lin}(k)$| of the cosmologies listed in Table 1 (except for |$\boldsymbol{\Theta }_{\rm EZ}$|), used to test the cosmology dependence of the BAO and FS analyses with the reference cosmology displayed in the middle panel (BAO analysis on post-recon catalogues and listed in Table F4) and in the bottom panel (FS analysis on pre-recon catalogues listed in Table F5). Middle panel: BAO scale factors along (α∥) and across (α⊥) the LOS measured on the reconstructed Nseries mocks. The △ symbols display the fit on the mean of the 84 realizations, the grey symbols display the fit on the individual 84 realizations, and the ▽ symbols the mean of the 84 individual fits. The error associated is the error of the mean and the rms among the 84 realizations divided by |$\sqrt{84}$|, respectively. Bottom panel: same notation than the middle panel applied to FS analysis on the same mocks. The x-axis shows the results for different cosmologies used for the template (and for mapping redshifts into comoving distances when computing the power spectrum). The horizontal dashed lines mark the expected value of |$\alpha _{\parallel ,\, \perp }$|, and fσ8.
The results of the fits on the mean of the mocks and on the individual fits are reported in Table F4, for post-reconstruction analyses, where reconstruction has been performed using the true value of f and b1. We follow this approach because in this test we aim to check the impact of the arbitrary choice of the reference cosmology when recovering the BAO parameters, rather than to test the efficiency of reconstruction as a function of the assumed parameters (see Carter et al. 2019 for such a study). The middle panel of Fig. 10 displays the post-reconstruction results from Table F4, where the horizontal dashed lines represent the expected values for αs in each cosmology. For each case, we display the fit to the mean of the NNseries realizations along with the error of the mean, the individual fit to these NNseries realizations, and mean of the fit of these NNseries realizations, along with the rms divided by |$N_{\rm Nseries}^{1/2}$|. When studying the post-reconstructed catalogues, we find that for both α∥ and α⊥ the highest shift, relative to those parameters inferred from |$\boldsymbol{\Theta }_{\rm Nseries}$|, are those inferred using the templates of |$\boldsymbol{\Theta }_Z$|, which show a deviation of |$1{{\ \rm per\ cent}}$| in α∥ and |$0.8{{\ \rm per\ cent}}$| for α⊥. We note that |$\boldsymbol{\Theta }_Z$| represents a very distinct cosmology with respect to the true cosmology of Nseries, with shifts of ΔΩm = 0.08 and ΔΩb = 0.019, which are 10σ and 50σ away, respectively, from the results reported by Planck (Aghanim et al. 2018). On the other hand, if a closer-to-standard ΛCDM reference cosmology is used, such as |$\boldsymbol{\Theta }_{\rm fid}$|, these shifts reduce to |$0.5{{\ \rm per\ cent}}$| on α∥ and |$0.3{{\ \rm per\ cent}}$| for α⊥.
5.1.3 Effect of non-periodicity on BAO measurements
The OuterRim-HOD mocks comes from a single OuterRim dark matter simulation, split into 27 non-periodic cubic sub-boxes and populated with different types of HOD models and flavours. In this section, we aim to quantify the impact of analysing the non-periodic sub-boxes when DFT algorithms are used to obtain the power spectra, which implicitly assume periodic boundary conditions. In this case, and across the paper we only consider wave numbers between |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.30$| for BAO analyses. In order to test this impact within such scale-range, we only focus on the set of HOD types and flavours closer to the LRG galaxy sample. We refer to such padded catalogues as ‘sky-cuts’. In Table F1, we display the results on the mean of the 27 mocks, for both cubic non-periodic and sky-cut case. Note that the non-periodic cubic and sky-cut contain the same galaxies, therefore, the information content should be the same in the absence of spurious non-periodic effects. We do not observe any significant changes in α⊥ parameter, but a consistent shift of α∥ by |$2{-}3{{\ \rm per\ cent}}$|: for the non-periodic cubic box, we find an excess in the value of α∥ with respect to what is expected, whereas for the sky-cut case the results are in agreement (within 2σ error bars) with the expected values. We conclude that (1) the non-periodic effects are important when determining α∥, but not α⊥ (2) we do not observe relative shifts in any of the α parameters when the HOD model or flavour is varied.
5.1.4 Impact of HOD modelling in BAO
In this section, we aim to explore the impact of different HODs and flavours when recovering the scaling parameters. Ideally, we should pad as well around these catalogues in order to remove the effect of non-periodicity. However, since the galaxy catalogues can be very large for some of the HODs studied (five million galaxies for threshold1), and the random catalogues need to be at least 20 to 50 times larger, this is not feasible. Since the spurious effects of non-periodicity have a geometrical origin, they should be independent of the intrinsic clustering, and we are only interested in the relative effect of the HOD modelling, we opt to analyse the OuterRim-HOD mocks as if they were periodic boxes, and compare only the relative recovered values among them, bearing in mind that we expect an |$\sim 2-3{{\ \rm per\ cent}}$| offset on α∥. These results are listed in Table F2 for the mean of 27 mocks and graphically represented in Fig. 11, where the filled black symbols are the results for the cubic boxes (affected by the non-periodicity) and the empty black symbols the results where the boxes have been padded (not affected by non-periodicity). For all the HODs, we consistently see that there is the expected |$3{{\ \rm per\ cent}}$| offset on α∥ as an effect of the non-periodicity of the box, whereas α⊥ is well recovered in all the cases. We therefore conclude that within the statistical errors of |$1{-}2{{\ \rm per\ cent}}$| the AP parameters recovered from the BAO type of analysis are not affected by the HOD model for LRGs. These findings are in agreement with the recent study by Duan & Eisenstein (2019).
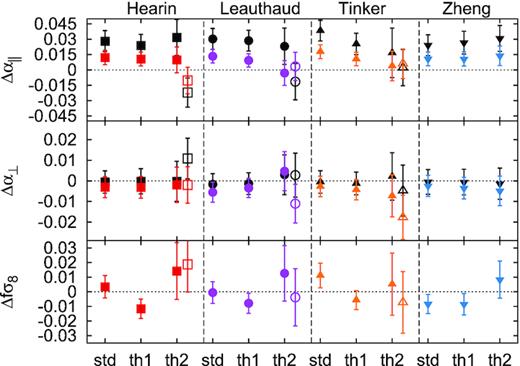
Inferred scaling parameters, α∥ and α⊥, and fσ8 using a BAO (black symbols) and FS (coloured symbols) type of analysis from the pre-reconstructed OuterRim-HOD mocks, for different types of HOD models and flavours (listed in the x-axis). Red, purple, orange, and blue colours correspond to Hearin, Leauthaud, Tinker and Zheng HOD models for the FS type of analysis, respectively. For each of these models three flavours have been implemented: standard (std), threshold 1 (th1), and threshold2 (th2), as labelled. The filled symbols correspond to |$1\, h^{-1}{\rm Gpc}$|-size cubic box without periodic boundary conditions. The empty symbols correspond to the results obtained from a padded and larger box corresponding to |$3\, h^{-1}{\rm Gpc}$|-size, where the non-periodicity impact is negligible. All results correspond to fitting the mean of 27 mocks, and the reported error is 1σ of the error of the mean.
5.2 RSD systematics
We repeat the same strategy used for BAO systematics in the previous Section 5.1. We run the standard FS pipeline described previously in Section 3.2 on the pre-reconstructed mocks. We aim to check the typicality of the data with respect to the EZmocks under the FS analysis, how such analysis responses to change in the HOD of the mocks, the impact of the arbitrary choice of the reference template used to compute the FS model, and to calibrate the optimal k-range to be used on FS in order to maximize the statistical error and minimize the systematic budget.
The panels of Fig. 12 display the recovered parameters, α∥, α⊥, and fσ8 (top panels), and their errors (bottom panels) from an FS analysis on the power spectrum monopole, quadrupole, and hexadecapole using |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$|. Later, we justify the choice of these specific scales. As in Fig. 7, the red cross displays the performance of the DR16 CMASS + eBOSS LRG data catalogue, and the black dots the performance on the mean of the 1000 realizations of EZmocks. In the bottom panels, the error of the mean has been re-scaled by the factor |$\sqrt{1000}$| to match the typical error of one single realization. We note that the re-scaled error of the mean of the mocks is displaced from the centre of the cloud of errors from individual mocks. This behaviour is caused by the 50 per cent prior on Anoise on the individual mocks (this prior has no effect when fitting the mean of the mocks) which shrinks the distribution tail towards smaller errors, especially for α∥ and fσ8. The values and errors of α∥, α⊥, and fσ8 inferred from the data catalogue are consistent with the intrinsic scatter observed from the mocks; and also the χ2 value of the data is probable given the distribution of the mocks.
![The top sub-panels display the distribution of inferred α∥, α⊥, and fσ8 parameters using an FS analysis of the power spectrum monopole, quadrupole, and hexadecapole for the 1000 realizations of the EZmocks catalogues (blue points), DR16 CMASS + eBOSS LRG data catalogue (red cross) and the best-fit to the mean of the 1000 mock power spectra. The horizontal and vertical black dashed lines represent the expected αs and fσ8 values for the EZmocks. The scales fitted are in all cases $0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$. In each panel, the distribution of χ2 values is also shown. The bottom sub-panels display an analogous plots for the errors of α∥, α⊥, and fσ8 instead. In this case, the error of the mean have been re-scaled by the square root of number of realizations.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2455/1/m_staa2455fig12.jpeg?Expires=1750266550&Signature=AAyovLRPFekvgbX1HYnA4wGsmVk-HqlfMAHffDlu9ZMI1E31HEA-l7oZnsauueqJea2A9KKJaukv6KMgeOp28XqNo6KNrd~KgJ6GiXn~owUgyeBSN6hOXKPKZ6qRbvfdDdcTL5IwWZDHcphrul5e7sde1nU3Oto27eDoZbBoJbDNwBQX776p1Zy~3-LnWMQ3jndgassOi6OHXYeUFOt2NK9rE~EIS4HmYhpkF8FabaTllMv1MDNDD~5e8UXLVkZ4SYQvKFZvdoTW6sHyRaeGS1pmOBwV5oEdQWFcCCj3n0jqOHbEHM-QFJD~Xo7Dv9MfLeROLeQ5rGBX3dq35-YVlA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The top sub-panels display the distribution of inferred α∥, α⊥, and fσ8 parameters using an FS analysis of the power spectrum monopole, quadrupole, and hexadecapole for the 1000 realizations of the EZmocks catalogues (blue points), DR16 CMASS + eBOSS LRG data catalogue (red cross) and the best-fit to the mean of the 1000 mock power spectra. The horizontal and vertical black dashed lines represent the expected αs and fσ8 values for the EZmocks. The scales fitted are in all cases |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$|. In each panel, the distribution of χ2 values is also shown. The bottom sub-panels display an analogous plots for the errors of α∥, α⊥, and fσ8 instead. In this case, the error of the mean have been re-scaled by the square root of number of realizations.
5.2.1 Optimal range of scales for the FS analysis
We aim to determine the range of scales, we should be using when performing an FS analysis. Ideally, the wider this range, the smaller the statistical uncertainty in the inferred cosmological parameters should be. We expect that at very small scales the amount of information on cosmological parameters saturates, although the state-of-the art FS techniques have not reached that limit yet (Hand et al. 2017). Thus, we set the small scale truncation limit based on the ability of the FS model to recover unbiased cosmological parameters. In order to determine this limit, we apply the FS analysis on the full N-body Nseries mocks truncating the model at different scales. Fig. 13 shows the response of α∥, α⊥, and fσ8 on the truncation scale, kmax, when the monopole and quadrupole are used (denoted MQ) and when the hexadecapole is also used (MQH).

Test of performance when recovering cosmological parameters for the FS analysis described in Section 3.2 as a function of the range of scales used in each power spectrum multipole, where Δx ≡ x − xexp for α∥, α⊥, and fσ8 for the three different panels. The symbols represent the response on the mean of the 84 realizations of the Nseries mocks when the fiducial cosmology is used as reference template (red △ symbol), when the |$\boldsymbol{\Theta }_Y$|–cosmology template is used (blue ▽ symbol), and when the true cosmology template is used (black • points). The x-axis labels indicate the combination of multipoles (monopole, quadrupole, hexadecapole) used, and the value of kmax in |$\, h\, {\rm Mpc}^{-1}$|. The results do not show any particular trend with the template. Note that in some cases the value of kmax is different for the hexadecapole compared to that for the monopole and quadrupole. For all cases, the value of kmin is set to |$0.02\, \, h\, {\rm Mpc}^{-1}$|. The horizontal dotted lines represent the |$1{{\ \rm per\ cent}}$| deviation for αs and |$2{{\ \rm per\ cent}}$| for fσ8. The numerical results of this plot are displayed in Table F5.
We study the following cases: using only the power spectrum monopole and quadrupole for |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le k_{\rm max}$| (labelled MQ kmax); using monopole, quadrupole, and hexadecapole with the same-scale truncation |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le k_{\rm max}$| for all three (labelled MQH kmax); and truncation of multipoles at different scales, |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le k_{\rm max}^{(1)}$| for monopole and quadrupole and |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le k_{\rm max}^{(2)}$| for hexadecapole (labelled MQ |$k_{\rm max}^{(1)}$| + H |$k_{\rm max}^{(2)}$|). The hexadecapole is more sensitive to RSD than the other multipoles, as the modes parallel to the LOS are relatively more weighted than the transverse ones. Therefore, a potential μ-dependent systematic could appear as a parameter-shift when kmax grows for the hexadecapole, but not necessarily when it grows for lower multipoles.
For completeness, we perform such analysis using three different templates, corresponding to |$\boldsymbol{\Theta }_{\rm fid}$| at z = 0.70 (red symbols), |$\boldsymbol{\Theta }_Y$| at z = 0.55 (blue symbols) and to |$\boldsymbol{\Theta }_{\rm Nseries}$| at z = 0.55 (black symbols). The difference in redshift among these templates (and in particular for z = 0.70 which is different from the effective redshift of the Nseries mocks, zeff = 0.55) only enters in the model through the fixed σ8 value in the second-order terms of the model, and the difference between the σ8 values at these two redshift is |$\sim 11{{\ \rm per\ cent}}$|. From the results of Fig. 13, there is no significant difference among these templates, suggesting that, (i) the shape of the template for the reference cosmology has a negligible impact on the inferred cosmological parameters (we test this later in Section 5.2.3 for a wider range of templates); and (ii) the redshift at which this template is computed (which solely regulates its amplitude) has an impact on fσ8 which is |$\lt 1{{\ \rm per\ cent}}$| when the truncation scale is |$\le 0.15\, \, h\, {\rm Mpc}^{-1}$| and |$\simeq 1{{\ \rm per\ cent}}$| when the truncation scale is |$0.20\, \, h\, {\rm Mpc}^{-1}$|. This happens due to the non-linear terms proportional to |$f\times \sigma _8^n$| for n > 1 in the non-linear terms of the model as already discussed in Section 3.3. The statistical error on the fσ8 measurement is about 10 per cent for this sample and consequently this effect is completely negligible.
The results reported in Fig. 13 suggest that the effect of the truncation scale on α∥ is of the order of |$\le 1{{\ \rm per\ cent}}$| for the k-ranges studied here. For α⊥, we find that the effect of increasing the value of kmax and including the hexadecapole tend to underpredict its value by |$1{-}1.5{{\ \rm per\ cent}}$| depending on the truncation option. On fσ8 the effect of increasing kmax can be either overpredict and underpredict, depending on which template is being used, but the effects are always below |$2{-}3{{\ \rm per\ cent}}$|.
As a fiducial choice, we opt to truncate the FS analysis at |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$| for all three multipoles, (MHQ 0.15). This option shows no detected systematic on α∥ and |$1{{\ \rm per\ cent}}$| systematic on α⊥ and fσ8. Alternatively, we could also have considered to use only the monopole and quadrupole at the same truncation scale (MQ 0.15), which shows no significant systematic in any of the three variables. However, not using the hexadecapole significantly increases the statistical errors (see Fig. 17), which does not compensate for the reduction of systematic errors. Therefore, our main analysis relies on the choice MQH 0.15.
We have not shown any results with kmax below |$0.15\, \, h\, {\rm Mpc}^{-1}$|. The reason is that doing this actually also introduces systematics. This paradoxical effect is caused by worsening the BAO detection. If kmax is reduced down to |$0.10\, \, h\, {\rm Mpc}^{-1}$|, although the power spectrum and RSD behave closer to linear physics (which is better modelled), the lost BAO information between |$0.10$| and |$0.15\, \, h\, {\rm Mpc}^{-1}$| makes it hard to distinguish the RSD signal from the AP signal, which ends up introducing very long degeneracy tails between fσ8, α∥, and α⊥, which in the end introduce other type of systematics. This effect even appears in a BAO-only analysis, suggesting that there is an intrinsic effect of the data vector not related to the specific model, BAO or FS, used. On the other hand, we do not explore scales above |$k_{\rm min}=0.02\, \, h\, {\rm Mpc}^{-1}$|, as they are usually more contaminated by large-scale systematics, and they barely contain extra information on α∥, α⊥, and fσ8.
In Beutler et al. (2017) DR12 CMASS LRG galaxies, and in particular those between 0.5 ≤ z ≤ 0.75 were analysed under the truncation scheme ‘MQ 0.15 H 0.10’ using a very similar model. In this work, we have not found significant differences in terms of systematics between ‘MQ 0.15 H 0.10’ and ‘MQH 0.15’, and therefore we have decided to also include those hexadecapole modes between |$0.10\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$|.
5.2.2 Performance of the RSD modelling
We apply the FS template pipeline described in Section 3.2 for |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le 0.15$| on the different set of mocks: the results are displayed in Fig. 14 for EZmocks, Nseries, and OuterRim-HOD mocks (for threshold2 flavour only and with padding included), as labelled, when the monopole and quadrupole are used (MQ) and when the hexadecapole is also used (MQH). The green and orange symbols display the results when fitting the mean of the mocks and report the error of the mean. The pink and purple symbols display the average of the individual fits (displayed in grey) and report the rms in the error bars. Consequently, the error on the mean of the fits is a factor |$\sqrt{N_{i}}$| larger than the error on the fit of the mean. We stress that the error bars associated to both measurements should be the same, as they are both inferred from the same volume (except for large-scale modes and cases where the BAO is not detected), although the latter may suffer from extra systematic effects if the individual fits do not have a sufficiently high signal-to-noise ratio. In Fig. 14 (as in Fig. 9), we opt to display the rms for the mean of the individual fits as an error bar, along with the individual fits in grey, for visualization purposes. These results are also presented in Table 6, using the same notation and format of Table 5, where the error reported for the mean of individual fits is the rms divided by |$\sqrt{N_{\rm det}}$|, matching the error of the mean. The results displayed in Fig. 14 for the EZmocks and Nseries present a good agreement between the fit of the mean and the mean of individual fits. For the Nseries mocks α∥ and fσ8 are recovered with no systematics, for both MQ and MQH. For the Nseries mocks, we are able to recover the expected α⊥ when the monopole and quadrupole are used, whereas when we add the hexadecapole there is a systematic offset of |$\sim 1{{\ \rm per\ cent}}$|, as was reported in the previous section and in Fig. 13. As we have already mentioned, the EZmocks are not full N-body mocks, and therefore they should not be used to validate our pipeline in terms of systematics of the model. However, as a general trend, we observe that the response these mocks have is very similar to the one observed for the Nseries, which serves as a validation of these mocks reproducing the clustering properties of full N-body mocks, and therefore for producing a reliable covariance.
![Performance of the FS type of analyses on different type of mocks, with a similar notation as in Fig. 9. In this case, we analyse only pre-reconstruction catalogues using monopole and quadrupole only (MQ) and also including the hexadecapole (MQH). In all cases, the range of scales used are $0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$, motivated the findings of Fig. 13. The corresponding numerical results for this figure can be found in Table 6.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2455/1/m_staa2455fig14.jpeg?Expires=1750266550&Signature=3pTtokX5JQuBH3278aAJwKTIPi8awf50ljcq7SOGUhyL6qeqrizqhM98Q~9IkaCjG2vWgdtqSrKxUpImb4t2boCJxB-uLYT1U4at~vlEWlPZGqpRxJJreO4PSRvGnkj0XjiidoRpuYxLeu-lXy1CrC05cBkqUwj6ZFlMXVQviFbyJxEhr9QkSbcgTL7eIaH2U5PHROlxGqj-P6AFD9hTDejdwJte5C~gXRttHrB16FDALeR3wfC2r0E8m7Ec2WHNTK4vgZATwPH-CbZsCs3w1xXmA6aeQTWcAURtE3sQd9I3v0n1AoUisGXiYRbu8kGZqsQMjgTRl-TGhRnVqqswOQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Performance of the FS type of analyses on different type of mocks, with a similar notation as in Fig. 9. In this case, we analyse only pre-reconstruction catalogues using monopole and quadrupole only (MQ) and also including the hexadecapole (MQH). In all cases, the range of scales used are |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$|, motivated the findings of Fig. 13. The corresponding numerical results for this figure can be found in Table 6.
Performance of the FS model of equation (21) in different set of mocks. For The EZmocks |$\alpha _\parallel ^{\rm exp}=1+8.853\times 10^{-4}$|, |$\alpha _\perp ^{\rm exp}=1-3.650\times 10^{-4}$|, and |$f\sigma _8^{\rm exp}=0.467\,81$|. For the rest, the α expected values are 1 as they are, respectively, analysed in their own cosmology. For the Nseries mocks, |$f\sigma _8^{\rm exp}=0.470\,166$|, and for the OuterRim-HOD mocks, |$f\sigma _8^{\rm exp}=0.4475$|. For the OuterRim-HOD type of mocks only the threshold2 flavour is represented, where a padding has been applied to the original non-periodic cubic sub-box in order avoid spurious non-periodic effects. We follow the same notation presented in Table 5. Fig. 14 visually displays the results of this table. All results at |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$|.
| Mock name . | Multipoles . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean EZmocks | M+Q + H | 0.0040 ± 0.0011 | −0.014 81 ± 0.000 81 | −0.0096 ± 0.0015 | 1/1 |
| Individual EZmocks | M+Q + H | 0.0079 ± 0.0011 | −0.014 44 ± 0.000 80 | −0.0124 ± 0.0014 | 1000/1000 |
| Mean EZmocks | M + Q | 0.0025 ± 0.0016 | −0.0075 ± 0.0011 | −0.0053 ± 0.0021 | 1/1 |
| Individual EZmocks | M + Q | 0.0043 ± 0.0020 | −0.0055 ± 0.0012 | 0.0003 ± 0.0023 | 985/1000 |
| Mean EZmocks (raw) | M+Q + H | 0.0108 ± 0.0011 | −0.016 80 ± 0.000 78 | −0.0161 ± 0.0014 | 1/1 |
| Mean EZmocks (raw) | M + Q | 0.0011 ± 0.0016 | −0.005 68 ± 0.000 98 | −0.0016 ± 0.0019 | 1/1 |
| Mean EZmocks (no-RIC) | M+Q + H | 0.0073 ± 0.0011 | −0.017 91 ± 0.000 81 | −0.0170 ± 0.0015 | 1/1 |
| Mean EZmocks (no-RIC) | M + Q | 0.0020 ± 0.0016 | −0.0080 ± 0.0011 | −0.0077 ± 0.0020 | 1/1 |
| Mean Nseries | M+Q + H | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | M+Q + H | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | M + Q | −0.0031 ± 0.0046 | −0.0011 ± 0.0024 | 0.0047 ± 0.0054 | 1/1 |
| Individual Nseries | M + Q | 0.0045 ± 0.0070 | 0.0001 ± 0.0029 | 0.0201 ± 0.0061 | 84/84 |
| Mean HOD-Hearin | M+Q + H | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 | 1/1 |
| Individual HOD-Hearin | M+Q + H | 0.045 ± 0.017 | 0.0001 ± 0.0093 | 0.026 ± 0.022 | 27/27 |
| Mean HOD-Hearin | M + Q | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 | 1/1 |
| Individual HOD-Hearin | M + Q | 0.154 ± 0.022 | 0.005 ± 0.014 | 0.022 ± 0.031 | 27/27 |
| Mean HOD-Leauthaud | M+Q + H | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 | 1/1 |
| Individual HOD-Leauthaud | M+Q + H | 0.061 ± 0.014 | −0.0195 ± 0.0087 | 0.006 ± 0.016 | 27/27 |
| Mean HOD-Leauthaud | M + Q | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 | 1/1 |
| Individual HOD-Leauthaud | M + Q | 0.182 ± 0.026 | 0.009 ± 0.019 | 0.025 ± 0.037 | 27/27 |
| Mean HOD-Tinker | M+Q + H | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 | 1/1 |
| Individual HOD-Tinker | M+Q + H | 0.097 ± 0.024 | −0.0047 ± 0.0097 | 0.014 ± 0.022 | 27/27 |
| Mean HOD-Tinker | M + Q | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 | 1/1 |
| Individual HOD-Tinker | M + Q | 0.162 ± 0.027 | 0.056 ± 0.026 | 0.095 ± 0.046 | 27/27 |
| Mock name . | Multipoles . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean EZmocks | M+Q + H | 0.0040 ± 0.0011 | −0.014 81 ± 0.000 81 | −0.0096 ± 0.0015 | 1/1 |
| Individual EZmocks | M+Q + H | 0.0079 ± 0.0011 | −0.014 44 ± 0.000 80 | −0.0124 ± 0.0014 | 1000/1000 |
| Mean EZmocks | M + Q | 0.0025 ± 0.0016 | −0.0075 ± 0.0011 | −0.0053 ± 0.0021 | 1/1 |
| Individual EZmocks | M + Q | 0.0043 ± 0.0020 | −0.0055 ± 0.0012 | 0.0003 ± 0.0023 | 985/1000 |
| Mean EZmocks (raw) | M+Q + H | 0.0108 ± 0.0011 | −0.016 80 ± 0.000 78 | −0.0161 ± 0.0014 | 1/1 |
| Mean EZmocks (raw) | M + Q | 0.0011 ± 0.0016 | −0.005 68 ± 0.000 98 | −0.0016 ± 0.0019 | 1/1 |
| Mean EZmocks (no-RIC) | M+Q + H | 0.0073 ± 0.0011 | −0.017 91 ± 0.000 81 | −0.0170 ± 0.0015 | 1/1 |
| Mean EZmocks (no-RIC) | M + Q | 0.0020 ± 0.0016 | −0.0080 ± 0.0011 | −0.0077 ± 0.0020 | 1/1 |
| Mean Nseries | M+Q + H | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | M+Q + H | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | M + Q | −0.0031 ± 0.0046 | −0.0011 ± 0.0024 | 0.0047 ± 0.0054 | 1/1 |
| Individual Nseries | M + Q | 0.0045 ± 0.0070 | 0.0001 ± 0.0029 | 0.0201 ± 0.0061 | 84/84 |
| Mean HOD-Hearin | M+Q + H | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 | 1/1 |
| Individual HOD-Hearin | M+Q + H | 0.045 ± 0.017 | 0.0001 ± 0.0093 | 0.026 ± 0.022 | 27/27 |
| Mean HOD-Hearin | M + Q | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 | 1/1 |
| Individual HOD-Hearin | M + Q | 0.154 ± 0.022 | 0.005 ± 0.014 | 0.022 ± 0.031 | 27/27 |
| Mean HOD-Leauthaud | M+Q + H | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 | 1/1 |
| Individual HOD-Leauthaud | M+Q + H | 0.061 ± 0.014 | −0.0195 ± 0.0087 | 0.006 ± 0.016 | 27/27 |
| Mean HOD-Leauthaud | M + Q | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 | 1/1 |
| Individual HOD-Leauthaud | M + Q | 0.182 ± 0.026 | 0.009 ± 0.019 | 0.025 ± 0.037 | 27/27 |
| Mean HOD-Tinker | M+Q + H | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 | 1/1 |
| Individual HOD-Tinker | M+Q + H | 0.097 ± 0.024 | −0.0047 ± 0.0097 | 0.014 ± 0.022 | 27/27 |
| Mean HOD-Tinker | M + Q | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 | 1/1 |
| Individual HOD-Tinker | M + Q | 0.162 ± 0.027 | 0.056 ± 0.026 | 0.095 ± 0.046 | 27/27 |
Performance of the FS model of equation (21) in different set of mocks. For The EZmocks |$\alpha _\parallel ^{\rm exp}=1+8.853\times 10^{-4}$|, |$\alpha _\perp ^{\rm exp}=1-3.650\times 10^{-4}$|, and |$f\sigma _8^{\rm exp}=0.467\,81$|. For the rest, the α expected values are 1 as they are, respectively, analysed in their own cosmology. For the Nseries mocks, |$f\sigma _8^{\rm exp}=0.470\,166$|, and for the OuterRim-HOD mocks, |$f\sigma _8^{\rm exp}=0.4475$|. For the OuterRim-HOD type of mocks only the threshold2 flavour is represented, where a padding has been applied to the original non-periodic cubic sub-box in order avoid spurious non-periodic effects. We follow the same notation presented in Table 5. Fig. 14 visually displays the results of this table. All results at |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$|.
| Mock name . | Multipoles . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean EZmocks | M+Q + H | 0.0040 ± 0.0011 | −0.014 81 ± 0.000 81 | −0.0096 ± 0.0015 | 1/1 |
| Individual EZmocks | M+Q + H | 0.0079 ± 0.0011 | −0.014 44 ± 0.000 80 | −0.0124 ± 0.0014 | 1000/1000 |
| Mean EZmocks | M + Q | 0.0025 ± 0.0016 | −0.0075 ± 0.0011 | −0.0053 ± 0.0021 | 1/1 |
| Individual EZmocks | M + Q | 0.0043 ± 0.0020 | −0.0055 ± 0.0012 | 0.0003 ± 0.0023 | 985/1000 |
| Mean EZmocks (raw) | M+Q + H | 0.0108 ± 0.0011 | −0.016 80 ± 0.000 78 | −0.0161 ± 0.0014 | 1/1 |
| Mean EZmocks (raw) | M + Q | 0.0011 ± 0.0016 | −0.005 68 ± 0.000 98 | −0.0016 ± 0.0019 | 1/1 |
| Mean EZmocks (no-RIC) | M+Q + H | 0.0073 ± 0.0011 | −0.017 91 ± 0.000 81 | −0.0170 ± 0.0015 | 1/1 |
| Mean EZmocks (no-RIC) | M + Q | 0.0020 ± 0.0016 | −0.0080 ± 0.0011 | −0.0077 ± 0.0020 | 1/1 |
| Mean Nseries | M+Q + H | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | M+Q + H | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | M + Q | −0.0031 ± 0.0046 | −0.0011 ± 0.0024 | 0.0047 ± 0.0054 | 1/1 |
| Individual Nseries | M + Q | 0.0045 ± 0.0070 | 0.0001 ± 0.0029 | 0.0201 ± 0.0061 | 84/84 |
| Mean HOD-Hearin | M+Q + H | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 | 1/1 |
| Individual HOD-Hearin | M+Q + H | 0.045 ± 0.017 | 0.0001 ± 0.0093 | 0.026 ± 0.022 | 27/27 |
| Mean HOD-Hearin | M + Q | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 | 1/1 |
| Individual HOD-Hearin | M + Q | 0.154 ± 0.022 | 0.005 ± 0.014 | 0.022 ± 0.031 | 27/27 |
| Mean HOD-Leauthaud | M+Q + H | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 | 1/1 |
| Individual HOD-Leauthaud | M+Q + H | 0.061 ± 0.014 | −0.0195 ± 0.0087 | 0.006 ± 0.016 | 27/27 |
| Mean HOD-Leauthaud | M + Q | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 | 1/1 |
| Individual HOD-Leauthaud | M + Q | 0.182 ± 0.026 | 0.009 ± 0.019 | 0.025 ± 0.037 | 27/27 |
| Mean HOD-Tinker | M+Q + H | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 | 1/1 |
| Individual HOD-Tinker | M+Q + H | 0.097 ± 0.024 | −0.0047 ± 0.0097 | 0.014 ± 0.022 | 27/27 |
| Mean HOD-Tinker | M + Q | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 | 1/1 |
| Individual HOD-Tinker | M + Q | 0.162 ± 0.027 | 0.056 ± 0.026 | 0.095 ± 0.046 | 27/27 |
| Mock name . | Multipoles . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean EZmocks | M+Q + H | 0.0040 ± 0.0011 | −0.014 81 ± 0.000 81 | −0.0096 ± 0.0015 | 1/1 |
| Individual EZmocks | M+Q + H | 0.0079 ± 0.0011 | −0.014 44 ± 0.000 80 | −0.0124 ± 0.0014 | 1000/1000 |
| Mean EZmocks | M + Q | 0.0025 ± 0.0016 | −0.0075 ± 0.0011 | −0.0053 ± 0.0021 | 1/1 |
| Individual EZmocks | M + Q | 0.0043 ± 0.0020 | −0.0055 ± 0.0012 | 0.0003 ± 0.0023 | 985/1000 |
| Mean EZmocks (raw) | M+Q + H | 0.0108 ± 0.0011 | −0.016 80 ± 0.000 78 | −0.0161 ± 0.0014 | 1/1 |
| Mean EZmocks (raw) | M + Q | 0.0011 ± 0.0016 | −0.005 68 ± 0.000 98 | −0.0016 ± 0.0019 | 1/1 |
| Mean EZmocks (no-RIC) | M+Q + H | 0.0073 ± 0.0011 | −0.017 91 ± 0.000 81 | −0.0170 ± 0.0015 | 1/1 |
| Mean EZmocks (no-RIC) | M + Q | 0.0020 ± 0.0016 | −0.0080 ± 0.0011 | −0.0077 ± 0.0020 | 1/1 |
| Mean Nseries | M+Q + H | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | M+Q + H | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | M + Q | −0.0031 ± 0.0046 | −0.0011 ± 0.0024 | 0.0047 ± 0.0054 | 1/1 |
| Individual Nseries | M + Q | 0.0045 ± 0.0070 | 0.0001 ± 0.0029 | 0.0201 ± 0.0061 | 84/84 |
| Mean HOD-Hearin | M+Q + H | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 | 1/1 |
| Individual HOD-Hearin | M+Q + H | 0.045 ± 0.017 | 0.0001 ± 0.0093 | 0.026 ± 0.022 | 27/27 |
| Mean HOD-Hearin | M + Q | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 | 1/1 |
| Individual HOD-Hearin | M + Q | 0.154 ± 0.022 | 0.005 ± 0.014 | 0.022 ± 0.031 | 27/27 |
| Mean HOD-Leauthaud | M+Q + H | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 | 1/1 |
| Individual HOD-Leauthaud | M+Q + H | 0.061 ± 0.014 | −0.0195 ± 0.0087 | 0.006 ± 0.016 | 27/27 |
| Mean HOD-Leauthaud | M + Q | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 | 1/1 |
| Individual HOD-Leauthaud | M + Q | 0.182 ± 0.026 | 0.009 ± 0.019 | 0.025 ± 0.037 | 27/27 |
| Mean HOD-Tinker | M+Q + H | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 | 1/1 |
| Individual HOD-Tinker | M+Q + H | 0.097 ± 0.024 | −0.0047 ± 0.0097 | 0.014 ± 0.022 | 27/27 |
| Mean HOD-Tinker | M + Q | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 | 1/1 |
| Individual HOD-Tinker | M + Q | 0.162 ± 0.027 | 0.056 ± 0.026 | 0.095 ± 0.046 | 27/27 |
The results on the OuterRim-HOD mocks present a significant difference between the fit of the mean (green and orange symbols) and the mean of the fits (pink and purple symbols). In general, for the fit of the mean the cosmological parameters α∥, α⊥ and fσ8 are recovered within the statistical uncertainty, which is |$1{-}3{{\ \rm per\ cent}}$|. However, the individual fits and its mean present systematic shifts, overestimating α∥ and fσ8. These shifts are larger for MQ than MQH. Since these effects are not shown in the mean of the fits, we conclude that they are caused by the low signal of individual realizations. Indeed, the volume of the realizations of each of these mocks is not high enough to have good BAO detections, in particular for α∥ which is always the worse-detected scaling factor. In such low-signal-to noise conditions, the model tends to shift the BAO scale to larger scales (recall that k′ = k/α in Fourier space, or s′ = sα in configuration space), where the noise-per-k-mode is higher. This effect is partially mitigated by adding the hexadecapole, as the signal of the data vector is increased. The reason why this effect is only present in the OuterRim-HOD mocks, and not in the Nseries or EZmocks has to do with the effective volume per mock, which is |$1.10\, {\rm Gpc}^3$| for the OuterRim-HOD mocks, |$3.67\, {\rm Gpc}^3$| for the Nseries, and |$2.72\, {\rm Gpc}^3$| for the EZmocks.
In summary, (i) the results displayed in Fig. 14 show no systematic shift as a consequence to the change in the HOD models on any of the cosmological parameters; (ii) the statistical limit of the previous statement only applies to potential systematics larger than the statistical limit of the OuterRim-HOD mocks, which is |$1{-}3{{\ \rm per\ cent}}$|; and (iii) we observe a systematic shift of |$\sim 1{{\ \rm per\ cent}}$| on α⊥ when the Nseries mocks are analysed and no strong systematic shift on α∥ or fσ8 above the statistical uncertainty, which for these mocks is |$\sim 0.5{{\ \rm per\ cent}}$|.
In Table 6, we also display two additional results on potential observational systematics. We perform the FS analysis on the EZmocks before, labelled EZmocks (raw), and after, labelled EZmocks, applying the observational effects (which includes completeness and collision weights) followed by the corresponding correction applied in the data catalogue and described in Section 2.1. These effects are redshift failures, close-pair collisions (only in the eBOSS LRGs) and completeness. The relative systematic shift of all these effects can be estimated by the difference of the inferred cosmological parameters from the EZmocks before and after applying them. For the fiducial case of MQH, we obtain that these shifts are of the order of |$0.7{{\ \rm per\ cent}}$| for α∥; of the order of |$0.2{{\ \rm per\ cent}}$| for α⊥; and of the order of |$0.6{{\ \rm per\ cent}}$| for fσ8. Individually, such shifts are sub-dominant with respect to the statistical error of the data.
We also check the effect of the radial integral constraint (RIC; see de Mattia et al. 2020 for a description of this effect). We turn on and off this effect by computing the power spectra of the individual mocks with and without a random catalogue that matches the n(z) of the galaxy catalogue. The best-fitting parameters to the mean of the mocks without the RIC is shown in Table 6. The effect of RIC on α∥ and α⊥ is about |$0.3$| and |$1.6{{\ \rm per\ cent}}$| on fσ8.
5.2.3 Impact of reference template
In the bottom panel of Fig. 10, we display the recovered cosmological parameters for the Nseries mocks when they are analysed assuming five reference templates: |$\boldsymbol{\Theta }_{\rm Nseries}$|, |$\boldsymbol{\Theta }_{\rm fid}$|, |$\boldsymbol{\Theta }_X$|, |$\boldsymbol{\Theta }_Y$|, and |$\boldsymbol{\Theta }_{Z}.$|16 As before, we display both the fit on the mean, and the mean of the individual fits (which are also shown in grey). Table F5 lists these results. The horizontal dashed lines are the expected values, for each of these cosmologies. Note that the expected α∥ and α⊥ change with Ωm and h, but fσ8 does not, as the latter is an absolute variable, which does not depend on the choice of template.
For a displacement in the reference cosmology from |$\boldsymbol{\Theta }_{\rm Nseries}$| and |$\boldsymbol{\Theta }_{\rm fid}$|, we do not observe any shift larger than the 1σ error bar of one of the measurements. As the reference cosmology moves away from the true cosmology, we observe a mild rise of systematics, which reaches |$0.6$| and |$0.4{{\ \rm per\ cent}}$| for α∥ and α⊥, respectively, for |$\boldsymbol{\Theta }_Z$|, although the significance of detection given the statistics of Nseries is not very high. For fσ8 the largest deviation appears for |$\boldsymbol{\Theta }_X$|, which reaches Δfσ8 = 0.009, which is about a |$2{{\ \rm per\ cent}}$| shift. As for the scaling variables, the significance of detection of this shift is well within a 2σ fluctuation.
Bear in mind that the |$\boldsymbol{\Theta }_X,\, \boldsymbol{\Theta }_Y,\, \boldsymbol{\Theta }_Z\,$| templates are very extreme cases with shifts of the order of ΔΩ ≃ 0.065. In addition, for |$\boldsymbol{\Theta }_Z$| the baryon density is ∼50σ above the Planck-inferred value and for |$\boldsymbol{\Theta }_Y$| the number of neutrino species is Neff = 4.046. Even in such cases the systematics on the α’s stay well below |$1{{\ \rm per\ cent}}$|. These findings demonstrate how insensitive LSS structure data is to Ωb. Alternatively, one could put priors on Ωb by assuming a ΛCDM model through the horizon scale, which also set tight constraints on the relation between α∥ and α⊥ (D’Amico et al. 2019; Ivanov, Simonović & Zaldarriaga 2019; Tröster et al. 2020). By taking this approach one would increase the precision in measuring α∥ and α⊥ at the expense of assuming the functional form that a generic ΛCDM imposes between these two-scale factors.
5.2.4 HOD and periodicity
In Section 5.1.3, we have already tested the impact of the non-periodicity of the 27 sub-boxes generated from the OuterRim mocks for a BAO type of analysis. In this section, we do the same for the FS analysis. We use the same catalogues as before (Hearin, Leauthaud and Tinker with threshold2 flavour), and we compare how embedding the non-periodic |$1\, h^{-1}{\rm Gpc}$| box into a |$3\, h^{-1}{\rm Gpc}$| box changes the results. Table F6 displays the results on performing an FS on the padded and unpadded catalogues. These results can also be seen in Fig. 11, where the empty symbols display the padded results, for FS analysis on the Hearin+threshold2 (red), Leauthaud+threshold2 (purple), and Tinker + threshold2 (orange). As was found for BAO fits (in black symbols in the same figure), only α∥ presents a significant shift for the Hearin case, whereas α⊥ and fσ8 seem barely altered by this effect. In the same panel, and also along Table F7, the results using other flavours (standard and threshold 1 as labelled), as well an extra HOD model (Zheng in blue symbols) are also displayed for FS. The full picture from BAO and RSD fits is that only α∥ is affected by the non-periodicity of the box. The systematic shift is of the order of |$1.5{{\ \rm per\ cent}}$| for the FS analysis (unlike the |$2{-}3{{\ \rm per\ cent}}$| for BAO analysis). This disparity can be due to the variation in the scales fitted, as well as the intrinsic modelling. As for the BAO analysis, we do not detect any significant relative shift on the cosmological parameters when either the HOD model or the flavour is varied. Such results put constrains in the upper limit of systematic errors in the modelling as a result of different HOD models. Such upper limits are of the order of |$0.5{-}1{{\ \rm per\ cent}}$| systematic shifts.
5.3 Systematic error budget
In this section, we summarize all the potential systematic error contributions described above, for both BAO and FS analyses, and describe how the total systematic budget of the main results of this paper is computed. Additionally, we also quantify the systematic errors when a simultaneous BAO and FS fit is performed (see Section 6 for details on how the simultaneous fit is performed). We consider the BAO-type of analysis on the post-recon catalogue in the scale range |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le 0.30$|, and the FS analysis on the pre-recon catalogue using monopole, quadrupole, and hexadecapole in the scale range |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}] \le 0.15$|. We consider the following systematics:
Modelling systematics: Associated with the inaccuracies in the theoretical or phenomenological model used. We test these by comparing the inferred value from the Nseries mocks and the expected value, when the mocks are analysed using their own true cosmology as a reference cosmology. These results have been presented in Tables 5 and 6 for BAO and FS, respectively.
Reference cosmology systematics: We test the arbitrary choice of the reference cosmology (both to convert redshift into distances and to choose the modelling template), for both BAO and FS analysis. We test the relative differences between Δx = x − x0 for four different reference cosmologies, and take the highest observed deviation (noted as ‘limit’ in Table 7), where the super-index ‘0’ corresponds to the parameters inferred using its own true cosmology as reference cosmology. In particular, we test the differences between |$\boldsymbol{\Theta }_{\rm Nseries}$| and |$\boldsymbol{\Theta }_{\rm fid}$|, |$\boldsymbol{\Theta }_{X}$|, |$\boldsymbol{\Theta }_{Y}$|, |$\boldsymbol{\Theta }_{Z}$|. These results can be found in Tables F4 and F5 for BAO and FS analysis, respectively.
Observational systematics: Such as the effect of redshift failures, collisions, and completeness, and systematics derived from the RIC. In order to test these types of systematics, we take the difference between the fit on the EZmocks, when these effects are applied, with respect to the fit to those raw EZmocks previous to the appliance of the effect. We consider two separate cases, (i) collisions, failures, and completeness effects (FCC); and (ii) the RIC effect.17 We only compute the contribution of the FCC and RIC systematics for the FS and consensus FS + BAO cases, as the BAO peak position is very insensitive to such effects. These results have been presented in Table 6.
Systematic error budget summary for cosmological parameters of interest: |$\alpha _\parallel ^{\rm post}$| and |$\alpha _\perp ^{\rm post}$| from a BAO analysis on the post-reconstructed catalogues; |$\alpha _\parallel ^{\rm FS},\, \alpha _\perp ^{\rm FS}$|, and fσ8FS for an FS analysis and |$\alpha _\parallel ^{\rm sim},\, \alpha _\perp ^{\rm sim}$|, and fσ8sim for the simultaneous BAO + FS fit, in all cases using the standard pipelines described in Sections 3.1 and 3.2. The results show the observed relative systematic shift, along with two times the statistical precision inferred from the mean of the mocks. We consider a detection of systematic error when the deviation with respect to the expected value is larger than 2σ. If no systematic shift is found within this limit, we adopt as a systematic contribution the 2σ value, as a conservative resolution limit. The potential sources for systematic studied are: modelling, the arbitrary choice of reference cosmology, and the observational weights: redshift failures, collisions and completeness (FCC), and RIC. σX represents the total systematic contribution: |$\sigma _X^2=\sum _i \sigma _i^2$|, where σi are the individual systematic contributions. The total error budget includes the statistical contribution, σsta, added in quadrature with σX.
| Case . | Modelling . | Reference cosmology (limit) . | FCC . | RIC . | σX/σsta . | |$\sqrt{\sigma _{\rm X}^2+\sigma _{\rm est}^2}$| . |
|---|---|---|---|---|---|---|
| |$\Delta \alpha _\parallel ^{\rm post}\pm 2\sigma$| | −0.0048 ± 0.0038 | |$0.0106 \pm 0.0057\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.012/0.024 | 0.027 |
| |$\Delta \alpha _\perp ^{\rm post}\pm 2\sigma$| | 0.0005 ± 0.0021 | |$-0.0089 \pm 0.0032\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.0091/0.020 | 0.021 |
| |$\Delta \alpha _\parallel ^{\rm FS}\pm 2\sigma$| | 0.0016 ± 0.0064 | |$-0.0063 \pm 0.0089\, (\boldsymbol{\Theta }_{\rm Z})$| | 0.0068 ± 0.0031 | 0.0033 ± 0.0030 | 0.013/0.036 | 0.039 |
| |$\Delta \alpha _\perp ^{\rm FS}\pm 2\sigma$| | −0.0095 ± 0.0040 | |$-0.0041 \pm 0.0056\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0020 ± 0.0023 | −0.0031 ± 0.0023 | 0.012/0.027 | 0.030 |
| |$\Delta f{\sigma _8}_{\rm res}^{\rm FS}\pm 2\sigma$| | −0.0038 ± 0.0082 | |$0.009 \pm 0.012\, (\boldsymbol{\Theta }_{\rm X})$| | −0.0065 ± 0.0042 | −0.0074 ± 0.0043 | 0.017/0.042 | 0.046 |
| |$\Delta \alpha _\parallel ^{\rm sim}\pm 2\sigma$| | −0.0008 ± 0.0034 | |$0.0078 \pm 0.0048\, (\boldsymbol{\Theta }_{\rm Y})$| | 0.0033 ± 0.0021 | 0.0024 ± 0.0022 | 0.0094/0.023 | 0.025 |
| |$\Delta \alpha _\perp ^{\rm sim}\pm 2\sigma$| | −0.0017 ± 0.0022 | |$-0.0071 \pm 0.0030\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0024 ± 0.0017 | −0.0018 ± 0.0017 | 0.0080/0.017 | 0.019 |
| Δfσ8sim ± 2σ | 0.0181 ± 0.0074 | |$-0.011 \pm 0.011\, (\boldsymbol{\Theta }_{\rm Y})$| | −0.0050 ± 0.0037 | −0.0076 ± 0.0039 | 0.023/0.037 | 0.043 |
| Case . | Modelling . | Reference cosmology (limit) . | FCC . | RIC . | σX/σsta . | |$\sqrt{\sigma _{\rm X}^2+\sigma _{\rm est}^2}$| . |
|---|---|---|---|---|---|---|
| |$\Delta \alpha _\parallel ^{\rm post}\pm 2\sigma$| | −0.0048 ± 0.0038 | |$0.0106 \pm 0.0057\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.012/0.024 | 0.027 |
| |$\Delta \alpha _\perp ^{\rm post}\pm 2\sigma$| | 0.0005 ± 0.0021 | |$-0.0089 \pm 0.0032\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.0091/0.020 | 0.021 |
| |$\Delta \alpha _\parallel ^{\rm FS}\pm 2\sigma$| | 0.0016 ± 0.0064 | |$-0.0063 \pm 0.0089\, (\boldsymbol{\Theta }_{\rm Z})$| | 0.0068 ± 0.0031 | 0.0033 ± 0.0030 | 0.013/0.036 | 0.039 |
| |$\Delta \alpha _\perp ^{\rm FS}\pm 2\sigma$| | −0.0095 ± 0.0040 | |$-0.0041 \pm 0.0056\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0020 ± 0.0023 | −0.0031 ± 0.0023 | 0.012/0.027 | 0.030 |
| |$\Delta f{\sigma _8}_{\rm res}^{\rm FS}\pm 2\sigma$| | −0.0038 ± 0.0082 | |$0.009 \pm 0.012\, (\boldsymbol{\Theta }_{\rm X})$| | −0.0065 ± 0.0042 | −0.0074 ± 0.0043 | 0.017/0.042 | 0.046 |
| |$\Delta \alpha _\parallel ^{\rm sim}\pm 2\sigma$| | −0.0008 ± 0.0034 | |$0.0078 \pm 0.0048\, (\boldsymbol{\Theta }_{\rm Y})$| | 0.0033 ± 0.0021 | 0.0024 ± 0.0022 | 0.0094/0.023 | 0.025 |
| |$\Delta \alpha _\perp ^{\rm sim}\pm 2\sigma$| | −0.0017 ± 0.0022 | |$-0.0071 \pm 0.0030\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0024 ± 0.0017 | −0.0018 ± 0.0017 | 0.0080/0.017 | 0.019 |
| Δfσ8sim ± 2σ | 0.0181 ± 0.0074 | |$-0.011 \pm 0.011\, (\boldsymbol{\Theta }_{\rm Y})$| | −0.0050 ± 0.0037 | −0.0076 ± 0.0039 | 0.023/0.037 | 0.043 |
Systematic error budget summary for cosmological parameters of interest: |$\alpha _\parallel ^{\rm post}$| and |$\alpha _\perp ^{\rm post}$| from a BAO analysis on the post-reconstructed catalogues; |$\alpha _\parallel ^{\rm FS},\, \alpha _\perp ^{\rm FS}$|, and fσ8FS for an FS analysis and |$\alpha _\parallel ^{\rm sim},\, \alpha _\perp ^{\rm sim}$|, and fσ8sim for the simultaneous BAO + FS fit, in all cases using the standard pipelines described in Sections 3.1 and 3.2. The results show the observed relative systematic shift, along with two times the statistical precision inferred from the mean of the mocks. We consider a detection of systematic error when the deviation with respect to the expected value is larger than 2σ. If no systematic shift is found within this limit, we adopt as a systematic contribution the 2σ value, as a conservative resolution limit. The potential sources for systematic studied are: modelling, the arbitrary choice of reference cosmology, and the observational weights: redshift failures, collisions and completeness (FCC), and RIC. σX represents the total systematic contribution: |$\sigma _X^2=\sum _i \sigma _i^2$|, where σi are the individual systematic contributions. The total error budget includes the statistical contribution, σsta, added in quadrature with σX.
| Case . | Modelling . | Reference cosmology (limit) . | FCC . | RIC . | σX/σsta . | |$\sqrt{\sigma _{\rm X}^2+\sigma _{\rm est}^2}$| . |
|---|---|---|---|---|---|---|
| |$\Delta \alpha _\parallel ^{\rm post}\pm 2\sigma$| | −0.0048 ± 0.0038 | |$0.0106 \pm 0.0057\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.012/0.024 | 0.027 |
| |$\Delta \alpha _\perp ^{\rm post}\pm 2\sigma$| | 0.0005 ± 0.0021 | |$-0.0089 \pm 0.0032\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.0091/0.020 | 0.021 |
| |$\Delta \alpha _\parallel ^{\rm FS}\pm 2\sigma$| | 0.0016 ± 0.0064 | |$-0.0063 \pm 0.0089\, (\boldsymbol{\Theta }_{\rm Z})$| | 0.0068 ± 0.0031 | 0.0033 ± 0.0030 | 0.013/0.036 | 0.039 |
| |$\Delta \alpha _\perp ^{\rm FS}\pm 2\sigma$| | −0.0095 ± 0.0040 | |$-0.0041 \pm 0.0056\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0020 ± 0.0023 | −0.0031 ± 0.0023 | 0.012/0.027 | 0.030 |
| |$\Delta f{\sigma _8}_{\rm res}^{\rm FS}\pm 2\sigma$| | −0.0038 ± 0.0082 | |$0.009 \pm 0.012\, (\boldsymbol{\Theta }_{\rm X})$| | −0.0065 ± 0.0042 | −0.0074 ± 0.0043 | 0.017/0.042 | 0.046 |
| |$\Delta \alpha _\parallel ^{\rm sim}\pm 2\sigma$| | −0.0008 ± 0.0034 | |$0.0078 \pm 0.0048\, (\boldsymbol{\Theta }_{\rm Y})$| | 0.0033 ± 0.0021 | 0.0024 ± 0.0022 | 0.0094/0.023 | 0.025 |
| |$\Delta \alpha _\perp ^{\rm sim}\pm 2\sigma$| | −0.0017 ± 0.0022 | |$-0.0071 \pm 0.0030\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0024 ± 0.0017 | −0.0018 ± 0.0017 | 0.0080/0.017 | 0.019 |
| Δfσ8sim ± 2σ | 0.0181 ± 0.0074 | |$-0.011 \pm 0.011\, (\boldsymbol{\Theta }_{\rm Y})$| | −0.0050 ± 0.0037 | −0.0076 ± 0.0039 | 0.023/0.037 | 0.043 |
| Case . | Modelling . | Reference cosmology (limit) . | FCC . | RIC . | σX/σsta . | |$\sqrt{\sigma _{\rm X}^2+\sigma _{\rm est}^2}$| . |
|---|---|---|---|---|---|---|
| |$\Delta \alpha _\parallel ^{\rm post}\pm 2\sigma$| | −0.0048 ± 0.0038 | |$0.0106 \pm 0.0057\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.012/0.024 | 0.027 |
| |$\Delta \alpha _\perp ^{\rm post}\pm 2\sigma$| | 0.0005 ± 0.0021 | |$-0.0089 \pm 0.0032\, (\boldsymbol{\Theta }_{\rm Z})$| | − | − | 0.0091/0.020 | 0.021 |
| |$\Delta \alpha _\parallel ^{\rm FS}\pm 2\sigma$| | 0.0016 ± 0.0064 | |$-0.0063 \pm 0.0089\, (\boldsymbol{\Theta }_{\rm Z})$| | 0.0068 ± 0.0031 | 0.0033 ± 0.0030 | 0.013/0.036 | 0.039 |
| |$\Delta \alpha _\perp ^{\rm FS}\pm 2\sigma$| | −0.0095 ± 0.0040 | |$-0.0041 \pm 0.0056\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0020 ± 0.0023 | −0.0031 ± 0.0023 | 0.012/0.027 | 0.030 |
| |$\Delta f{\sigma _8}_{\rm res}^{\rm FS}\pm 2\sigma$| | −0.0038 ± 0.0082 | |$0.009 \pm 0.012\, (\boldsymbol{\Theta }_{\rm X})$| | −0.0065 ± 0.0042 | −0.0074 ± 0.0043 | 0.017/0.042 | 0.046 |
| |$\Delta \alpha _\parallel ^{\rm sim}\pm 2\sigma$| | −0.0008 ± 0.0034 | |$0.0078 \pm 0.0048\, (\boldsymbol{\Theta }_{\rm Y})$| | 0.0033 ± 0.0021 | 0.0024 ± 0.0022 | 0.0094/0.023 | 0.025 |
| |$\Delta \alpha _\perp ^{\rm sim}\pm 2\sigma$| | −0.0017 ± 0.0022 | |$-0.0071 \pm 0.0030\, (\boldsymbol{\Theta }_{\rm Z})$| | −0.0024 ± 0.0017 | −0.0018 ± 0.0017 | 0.0080/0.017 | 0.019 |
| Δfσ8sim ± 2σ | 0.0181 ± 0.0074 | |$-0.011 \pm 0.011\, (\boldsymbol{\Theta }_{\rm Y})$| | −0.0050 ± 0.0037 | −0.0076 ± 0.0039 | 0.023/0.037 | 0.043 |
For simplicity, we consider only the results from the fit to the mean of the mocks, as it is less sensitive to noise effects compared to the mean of individual fits. We also consider that a systematic is detected if the deviation between the expected and measured variable is higher than 2σ. In case of no detection, we assign as a systematic contribution the corresponding 2σ value, which sets a limit in sensitivity. Note that 2σ corresponds to the |$95{{\ \rm per\ cent}}$| confidence level of the mean of the mocks, whose effective volume is 113 times larger, for the Nseries mocks, and 1000 times larger for the EZmocks, than the DR16 CMASS + eBOSS LRG data set. Table 7 displays the full systematic contribution on the variables of interest.
For the post-reconstruction BAO analysis, we detect an |$\sim 0.5{{\ \rm per\ cent}}$| systematic shift induced by the modelling systematic on α∥, and none for α⊥, with a resolution limit of |$\sim 0.2{{\ \rm per\ cent}}$|. The choice of reference cosmology places an error of about |$\sim 1$| and |$\sim 0.9{{\ \rm per\ cent}}$| on α∥ and α⊥. Such shifts are observed to be higher for the |$\boldsymbol{\Theta }_Z$| cosmology. When both effects are taken into account we find that the total systematic contribution increases by |$\sim 10{{\ \rm per\ cent}}$| for both α∥ and α⊥. The reader might think that these error bars are unrealistically inflated as the |$\boldsymbol{\Theta }_Z$| cosmology represents a cosmology strongly disfavoured by state-of-the-art CMB measurements. If we only consider |$\boldsymbol{\Theta }_{\rm fid}$| and |$\boldsymbol{\Theta }_{X}$| as acceptable templates instead, the systematic shifts are reduced to |$0.5$| and |$0.3{{\ \rm per\ cent}}$| for α∥ and α⊥, respectively (similar to what was found in Gil-Marín et al. 2016b for the DR12 LRG sample). In this less conservative case, the error bars would increase by |$7{{\ \rm per\ cent}}$|, instead. Therefore, the total systematic error budget is not strongly modified by these ‘priors’ on the selection of reference cosmologies. As a conservative choice, we keep the total error budget as the most conservative one, where all four studied templates are considered.
When we look at the variables of the FS analysis, we find that, for α∥ the dominant source of systematics are FCC and the choice of reference cosmology, both contributing to about |$\sim 0.7{{\ \rm per\ cent}}$|. The RIC contributes |$0.3{{\ \rm per\ cent}}$| and we do not resolve any modelling systematic contribution (|$\lt 0.6{{\ \rm per\ cent}}$|). The total systematic contribution enlarges the error budget by |$7{{\ \rm per\ cent}}$|. For α⊥ the dominant source of systematics is the modelling, with about |$1{{\ \rm per\ cent}}$| systematic contribution. The other sources of systematics correspond to |$0.2$| and |$0.3{{\ \rm per\ cent}}$| for FCC and RIC, respectively. We do not detect any systematic related to the choice of the reference cosmology below the resolution limit (|$\lt 0.5{{\ \rm per\ cent}}$|). The total error contribution of α⊥ increases by |$8{{\ \rm per\ cent}}$| due to systematics. For fσ8 the dominant source of systematic is the reference cosmology, which represents a shift of Δfσ8 ≃ 0.009 (about |$2{{\ \rm per\ cent}}$|), which corresponds to the |$\boldsymbol{\Theta }_X$| reference cosmology. The FCC and RIC generate shifts of around 0.007, and we observe no significant shift caused by modelling systematics. In total, the errors are increased by 8 per cent due to the systematic contribution.
When we analyse BAO and FS simultaneously, we obtain systematic shifts, which are comparable to those obtained by considering these analyses individually. For the scaling parameters, the most important source of systematics is the choice of reference cosmology, which produces systematic shifts of about |$0.7{{\ \rm per\ cent}}$|, which corresponds to the |$\boldsymbol{\Theta }_Y$| and |$\boldsymbol{\Theta }_Z$| cosmologies. If only the |$\boldsymbol{\Theta }_{\rm fid}$| and |$\boldsymbol{\Theta }_{X}$| reference cosmologies were considered, these shifts would be reduced to |$0.6{{\ \rm per\ cent}}$| and |$0.4{{\ \rm per\ cent}}$| for α∥ and α⊥, respectively. As before, we take the conservative choice where all the reference cosmologies are considered, which does not modify significantly the final errors. We find that the total errors on α∥ and α⊥ are increased by 8 and 10 per cent, respectively. For fσ8, we find that the dominant source of systematic is the modelling, with a shift of 0.018 (about |$4{{\ \rm per\ cent}}$|). The total error budget increases by |$15{{\ \rm per\ cent}}$| due to systematics.
We have not included any BAO-type systematic from the OuterRim-HOD mocks in this section. The reason is that in any of the cases studied no such systematic shift was detected. However, the resolution limit of these mocks is poor given their low effective volume (|$\sim 27\, {\rm Gpc}^3$| for Threshold2 HOD types). Consequently, according to our detection criterion, only shifts of the order of |$2{-}6{{\ \rm per\ cent}}$| would be detected. These figures would set limits for potential systematic, which are above a reasonable value, as these models (both for BAO and FS) have been tested in the past using different sets of tracers, and such large systematics would have been already identified. Also, adding a 2σ resolution effect would have artificially inflated our systematic errors, simply due to poor statistical power in these mocks rather than a reasonable limitation of our modelling.
We modify the error covariance of the different data vectors by replacing the statistical contribution only in the diagonal elements, by the total systematic plus statistical contribution. In other words, the total covariance elements, |$c^{\rm tot}_{ij}$|, become, |$c^{\rm tot}_{ij}=c^{\rm sta}_{ij}+c^{\rm sys}_{i}\delta ^{\rm Kr.}_{ij}$|, where |$c^{\rm sta}_{ij}$| are the elements only accounting for the statistical contribution, and the |$c^{\rm sys}_{i}$| terms correspond to |$\sigma _X^2$| according to Table 7. We note that by doing this we assume that the systematic errors are uncorrelated among them, as they are only added on the diagonal of the covariance. This is probably not accurate, but we take this as a conservative choice, as correlation among systematics would reduce their effect in the final covariance matrix.
Table 8 presents the final cosmology results with and without the full error budget for the different DR16 CMASS + eBOSS LRG type of analysis performed, both in this work and in Bautista et al. (2020).
Summary of the cosmology parameters inferred from the DR16 CMASS + eBOSS LRG catalogue using BAO and FS analyses, in Fourier space (this paper) and in configuration space (Bautista et al. 2020). Fourier space, configuration space, BAO, and FS results can be combined (using the parameter-level covariance inferred from EZmocks), which we denote as ‘+’. For the Fourier space, we additionally display the result of the simultaneous BAO and FS fit (using the covariance at the k-bin level inferred from EZmocks), which we denote as ‘×’. The reported error bars correspond to 1σ and contain only the statistical error budget (first half of the table) and the full error budget (second half of the table). Full resolution data vectors and covariances can be found on-line.
| Probe . | DM/rdrag . | DH/rdrag . | fσ8 . |
|---|---|---|---|
| Without systematic error budget | |||
| BAO Pk | 17.86 ± 0.34 | 19.30 ± 0.50 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.32 | 19.31 ± 0.49 | − |
| FS Pk | 17.49 ± 0.48 | 20.18 ± 0.73 | 0.454 ± 0.042 |
| FS ξs | 17.42 ± 0.34 | 20.46 ± 0.60 | 0.460 ± 0.044 |
| FS (Pk + ξs) | 17.37 ± 0.32 | 20.39 ± 0.59 | 0.448 ± 0.040 |
| (BAO + FS) Pk | 17.72 ± 0.31 | 19.58 ± 0.45 | 0.476 ± 0.038 |
| (BAO × FS) Pk | 17.58 ± 0.30 | 19.96 ± 0.47 | 0.466 ± 0.037 |
| (BAO + FS) ξs | 17.57 ± 0.29 | 19.95 ± 0.44 | 0.491 ± 0.040 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.39 ± 0.27 | 19.88 ± 0.43 | 0.475 ± 0.037 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.55 ± 0.28 | 19.88 ± 0.42 | 0.481 ± 0.037 |
| With systematic error budget | |||
| BAO Pk | 17.86 ± 0.37 | 19.30 ± 0.56 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.33 | 19.33 ± 0.53 | − |
| FS Pk | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| FS ξs | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| FS (Pk + ξs) | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| (BAO + FS) Pk | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| (BAO × FS) Pk | 17.58 ± 0.33 | 19.96 ± 0.50 | 0.466 ± 0.043 |
| (BAO + FS) ξs | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
| Probe . | DM/rdrag . | DH/rdrag . | fσ8 . |
|---|---|---|---|
| Without systematic error budget | |||
| BAO Pk | 17.86 ± 0.34 | 19.30 ± 0.50 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.32 | 19.31 ± 0.49 | − |
| FS Pk | 17.49 ± 0.48 | 20.18 ± 0.73 | 0.454 ± 0.042 |
| FS ξs | 17.42 ± 0.34 | 20.46 ± 0.60 | 0.460 ± 0.044 |
| FS (Pk + ξs) | 17.37 ± 0.32 | 20.39 ± 0.59 | 0.448 ± 0.040 |
| (BAO + FS) Pk | 17.72 ± 0.31 | 19.58 ± 0.45 | 0.476 ± 0.038 |
| (BAO × FS) Pk | 17.58 ± 0.30 | 19.96 ± 0.47 | 0.466 ± 0.037 |
| (BAO + FS) ξs | 17.57 ± 0.29 | 19.95 ± 0.44 | 0.491 ± 0.040 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.39 ± 0.27 | 19.88 ± 0.43 | 0.475 ± 0.037 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.55 ± 0.28 | 19.88 ± 0.42 | 0.481 ± 0.037 |
| With systematic error budget | |||
| BAO Pk | 17.86 ± 0.37 | 19.30 ± 0.56 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.33 | 19.33 ± 0.53 | − |
| FS Pk | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| FS ξs | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| FS (Pk + ξs) | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| (BAO + FS) Pk | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| (BAO × FS) Pk | 17.58 ± 0.33 | 19.96 ± 0.50 | 0.466 ± 0.043 |
| (BAO + FS) ξs | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
Summary of the cosmology parameters inferred from the DR16 CMASS + eBOSS LRG catalogue using BAO and FS analyses, in Fourier space (this paper) and in configuration space (Bautista et al. 2020). Fourier space, configuration space, BAO, and FS results can be combined (using the parameter-level covariance inferred from EZmocks), which we denote as ‘+’. For the Fourier space, we additionally display the result of the simultaneous BAO and FS fit (using the covariance at the k-bin level inferred from EZmocks), which we denote as ‘×’. The reported error bars correspond to 1σ and contain only the statistical error budget (first half of the table) and the full error budget (second half of the table). Full resolution data vectors and covariances can be found on-line.
| Probe . | DM/rdrag . | DH/rdrag . | fσ8 . |
|---|---|---|---|
| Without systematic error budget | |||
| BAO Pk | 17.86 ± 0.34 | 19.30 ± 0.50 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.32 | 19.31 ± 0.49 | − |
| FS Pk | 17.49 ± 0.48 | 20.18 ± 0.73 | 0.454 ± 0.042 |
| FS ξs | 17.42 ± 0.34 | 20.46 ± 0.60 | 0.460 ± 0.044 |
| FS (Pk + ξs) | 17.37 ± 0.32 | 20.39 ± 0.59 | 0.448 ± 0.040 |
| (BAO + FS) Pk | 17.72 ± 0.31 | 19.58 ± 0.45 | 0.476 ± 0.038 |
| (BAO × FS) Pk | 17.58 ± 0.30 | 19.96 ± 0.47 | 0.466 ± 0.037 |
| (BAO + FS) ξs | 17.57 ± 0.29 | 19.95 ± 0.44 | 0.491 ± 0.040 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.39 ± 0.27 | 19.88 ± 0.43 | 0.475 ± 0.037 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.55 ± 0.28 | 19.88 ± 0.42 | 0.481 ± 0.037 |
| With systematic error budget | |||
| BAO Pk | 17.86 ± 0.37 | 19.30 ± 0.56 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.33 | 19.33 ± 0.53 | − |
| FS Pk | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| FS ξs | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| FS (Pk + ξs) | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| (BAO + FS) Pk | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| (BAO × FS) Pk | 17.58 ± 0.33 | 19.96 ± 0.50 | 0.466 ± 0.043 |
| (BAO + FS) ξs | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
| Probe . | DM/rdrag . | DH/rdrag . | fσ8 . |
|---|---|---|---|
| Without systematic error budget | |||
| BAO Pk | 17.86 ± 0.34 | 19.30 ± 0.50 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.32 | 19.31 ± 0.49 | − |
| FS Pk | 17.49 ± 0.48 | 20.18 ± 0.73 | 0.454 ± 0.042 |
| FS ξs | 17.42 ± 0.34 | 20.46 ± 0.60 | 0.460 ± 0.044 |
| FS (Pk + ξs) | 17.37 ± 0.32 | 20.39 ± 0.59 | 0.448 ± 0.040 |
| (BAO + FS) Pk | 17.72 ± 0.31 | 19.58 ± 0.45 | 0.476 ± 0.038 |
| (BAO × FS) Pk | 17.58 ± 0.30 | 19.96 ± 0.47 | 0.466 ± 0.037 |
| (BAO + FS) ξs | 17.57 ± 0.29 | 19.95 ± 0.44 | 0.491 ± 0.040 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.39 ± 0.27 | 19.88 ± 0.43 | 0.475 ± 0.037 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.55 ± 0.28 | 19.88 ± 0.42 | 0.481 ± 0.037 |
| With systematic error budget | |||
| BAO Pk | 17.86 ± 0.37 | 19.30 ± 0.56 | − |
| BAO ξs | 17.86 ± 0.33 | 19.34 ± 0.54 | − |
| BAO (Pk + ξs) | 17.86 ± 0.33 | 19.33 ± 0.53 | − |
| FS Pk | 17.49 ± 0.52 | 20.18 ± 0.78 | 0.454 ± 0.046 |
| FS ξs | 17.42 ± 0.40 | 20.46 ± 0.70 | 0.460 ± 0.050 |
| FS (Pk + ξs) | 17.40 ± 0.39 | 20.37 ± 0.68 | 0.449 ± 0.044 |
| (BAO + FS) Pk | 17.72 ± 0.34 | 19.58 ± 0.50 | 0.474 ± 0.042 |
| (BAO × FS) Pk | 17.58 ± 0.33 | 19.96 ± 0.50 | 0.466 ± 0.043 |
| (BAO + FS) ξs | 17.65 ± 0.31 | 19.81 ± 0.47 | 0.483 ± 0.047 |
| (BAO + FS) ξs + (BAO+FS) Pk | 17.64 ± 0.30 | 19.78 ± 0.46 | 0.470 ± 0.044 |
| BAO (Pk + ξs) + FS (Pk + ξs) | 17.65 ± 0.30 | 19.77 ± 0.47 | 0.473 ± 0.044 |
6 CONSENSUS RESULTS
The DR16 CMASS + eBOSS LRG data has been analysed performing four different types of analyses: (i) FS in Fourier space, (ii) BAO post-reconstruction in Fourier space, and (iii) FS in configuration space, and (iv) BAO post-reconstruction in configuration space. Analyses (i) and (ii) are fully described in this paper, whereas analyses (iii) and (iv) are presented in Bautista et al. (2020). Although all analyses rely on the same underlying catalogues (pre-recon for FS and post-recon for BAO) their information content is not the same. This happens because (1) each space data vector is computed directly from the catalogue and not as an FT of the complementary-space data vector; and (2) because data-vectors do not cover an infinite range of scales, and therefore the DFT of a finite set of elements in configuration space will never match the elements in Fourier space, and vice versa. Since we intend to produce a single inferred set of cosmological parameters per catalogue, we aim to combine Fourier and configuration space measurements into a single consensus set of parameters.
In order to do so, we use a similar approach to the one described in Sánchez et al. (2017), which was used to produce the consensus results of BOSS (Alam et al. 2017). This approach, known as the ‘best linear unbiased estimator’, consists of building a linear estimator of the consensus parameters (|$\alpha _\parallel ^{\rm cons},\, \alpha _\perp ^{\rm cons}\, f\sigma _8^{\rm cons}$|) as a function of the individual parameters estimated in Fourier and configuration space with certain coefficients. These coefficients are determined by imposing a minimum variance on the resulting consensus parameters. Thus, we require a covariance that describes the full correlation among all parameters. This matrix is given by the individual covariances among parameters of the same space. Note that the individual covariances are effectively different for each realization of the mocks, as the noise content of each realization is a stochastic process. However, we still need to determine those elements of the full covariance corresponding to the blocks describing the correlation between different spaces. Such coefficients can be estimated from the mocks, by inferring the data vector in each mock realization. There are some choices to be made in the details of building the final covariance. One can take only the diagonal elements from the actual data catalogues and the remaining elements from the mocks, or take the diagonal blocks corresponding to the same space from the data, and only the off-diagonal blocks across spaces from the mocks, just as two examples. We have tested that the impact of these choices is minimal. In this work, we take the approach described in section 3.4 of Bautista et al. (2020).
Fig. 15 displays the comparison between the Fourier space results presented in this paper and the configuration space results presented in Bautista et al. (2020) for BAO analysis using the post-recon catalogues from the EZmocks (green points) and the DR16 CMASS + eBOSS LRG data catalogue (red cross). The panels display the comparison between the two analyses for α∥ and α⊥ and for their corresponding errors, as indicated. The black dot displays the result on the mean of the 1000 EZmocks, and for the error case, this quantity has been re-scaled by the factor |$\sqrt{N_{\rm EZ}}$| to match the typical error of an individual mock. We find an excellent agreement, both for measurements and errors, for both mocks and data. This agreement motivates the combination of both results as they are fully consistent. The consensus results among BAO-Fourier space and BAO-configuration space are displayed in Table 8. We note that when both spaces are combined there is a slight reduction of errors on both DH/rdrag and DM/rdrag parameters. The extra information driving this improvement in precision is related to the fact that Fourier and configuration space data-vectors do not contain the exact same information, although the amount of correlation is very high, with cross-correlation parameters between the αs of the different spaces of ρ = 0.88.
Comparison of the of the BAO measurement on the post-reconstructed catalogues in Fourier space (this work) and in Configuration space (Bautista et al. 2020). The x-axes represent the Fourier space quantities and the y-axes configuration space quantities. The left sub-panels display the performance on α∥ (top left-hand panel) and α⊥ (bottom left-hand panel), whereas the right-hand panels display the performance on the 1σ error of the corresponding quantities. The green symbols display the performance on the individual 1000 mocks, the black dot the performance on the mean power spectra of the 1000 mocks, and the red cross the performance on the DR16 CMASS + eBOSS LRG data. The errors correspond to 1σ and only represent the statistical contribution.
Fig. 16 displays an analogous set of panels corresponding to FS-type of analysis. In this case, a third pair of panels is added to account for the fσ8 variable. As for the BAO type of analysis both Fourier and configuration show a strong correlation, for both errors and measurements. We also observe that the DR16 CMASS + eBOSS LRG catalogue behaves as expected given the performance of the mocks. We note that for α⊥ there is an offset between the Fourier and configuration space inferred values. This is caused by the |$1{{\ \rm per\ cent}}$| systematic shift identified already in Section 5.2.2. Also, as a general trend we see that configuration space errors on the scaling parameters tend to be smaller than the Fourier space one. This trend is not present in the BAO type of analysis (Fig. 15). We think that this difference is caused by the shortening of the k-range of analysis, |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$|, with respect to the BAO, which reaches |$k_{\rm max}=0.30\, {\, h\, {\rm Mpc}^{-1}}$|, which we believe adds extra BAO information. In configuration space, this effect is not present as the BAO feature is very localized at scales of |$\sim 100\, \, h^{-1}\, {\rm Mpc}$|.

Comparison of the of the RSD measurement in Fourier space (this work) and in configuration space (Bautista et al. 2020). The x-axes represent the Fourier space quantities and the y-axes configuration space quantities. The left sub-panels display the performance on α∥ (top left-hand panel), α⊥ (middle-left panel) and fσ8 (bottom left-hand panel), whereas the right-hand panels display the performance on the 1σ error of the corresponding quantities. The blue symbols display the performance on the individual 1000 mocks and the red cross the performance on the DR16 CMASS + eBOSS LRG data.
6.1 BAO–FS simultaneous fit
In this section, we aim to perform a simultaneous fit using the BAO type of analysis on reconstructed catalogues and FS type on pre-reconstructed catalogues. From the point of view of information content, we are allowed to do so, because the pre- and post-reconstructed catalogues are essentially different, and there is an actual gain of information in the process of using them when extracting cosmological information.
We start by comparing all Fourier-space BAO analyses (pre- and post-reconstruction) with the FS analysis with and without the hexadecapole, and using the 50 per cent-prior on Anoise. Fig. 17 displays the posterior likelihoods for all the Fourier space analyses presented in this paper: FS using MQ (green), FS using MQH (red), BAO on the pre-reconstructed catalogues (orange), and BAO on post-reconstructed catalogues (blue). Note that the BAO pre-reconstruction and FS M + Q data vectors are the same, except that the BAO pre-recon data vector contains k-elements up to smaller scales than the FS. The agreement between all analyses is very good for all variables of interest. In particular, we see that performing an FS analysis adding the hexadecapole helps to remove the strong correlation between the scaling factors and fσ8.
![Likelihood posterior for 1σ and 2σ, from the BAO and FS type of analysis on the DR16 CMASS + eBOSS LRG: BAO type of analysis on the pre-reconstructed catalogues (yellow contours) and on the post-reconstructed catalogues (blue contours), FS type of analysis when the monopole and quadrupole are the only multipoles being used (green contours), and when the hexadecapole is also included (red contours). For BAO type of analysis, we use $0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.30$, whereas for FS analysis $0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$. For all cases, the contours only account for the statistical error budget. These contours correspond to the results presented in the first half (without systematics) of Table 8.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/498/2/10.1093_mnras_staa2455/1/m_staa2455fig17.jpeg?Expires=1750266550&Signature=yoI0n6rhTvx0-r7HurJrmupge0HX8C32veubV6ZP1I5iey40Exlp3C45RMKUt1X-75KFN6~dRFHMeSyrtb3bHNdaRDCIP2m-qd4nbeV47B--VONZDqQm~CF1C5OpKwRM~Ucqi2P~hawaFLCxzKxic3UnftB3DdacTP7fhBR0LjSBzi2PgRVp9bxym9xd7u-Fs0kYLC8zt~kJbUjssh5bMcBBpOKMj413HpHV12~b2wGEE39kf2xJN8LZ~BTcFbLIGE5JXBw2dGaeyCtmawpX0qLVBIfwbCrYAI5h81DWEL8mWyn0Qt5kddTbDq4tc5St~LO9fCMaE2jzWR7i-Zq0Kw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Likelihood posterior for 1σ and 2σ, from the BAO and FS type of analysis on the DR16 CMASS + eBOSS LRG: BAO type of analysis on the pre-reconstructed catalogues (yellow contours) and on the post-reconstructed catalogues (blue contours), FS type of analysis when the monopole and quadrupole are the only multipoles being used (green contours), and when the hexadecapole is also included (red contours). For BAO type of analysis, we use |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.30$|, whereas for FS analysis |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]\le 0.15$|. For all cases, the contours only account for the statistical error budget. These contours correspond to the results presented in the first half (without systematics) of Table 8.
Fig. 18 presents in purple contours the result of combining BAO post-recon (blue contours) and FS (red contours) Fourier space analyses. This result has been obtained by applying the same technique used to the corresponding Fourier-space and configuration-space results. As before this approach suffers from having to estimate cross-method coefficients from the mocks. This may have an impact on the final contours, as it could fail to accurately describe the exact correlation that variables among the two spaces have for a specific realization. The numerical results of this Fourier consensus are presented in Table 8, as ‘(BAO + FS) Pk’.
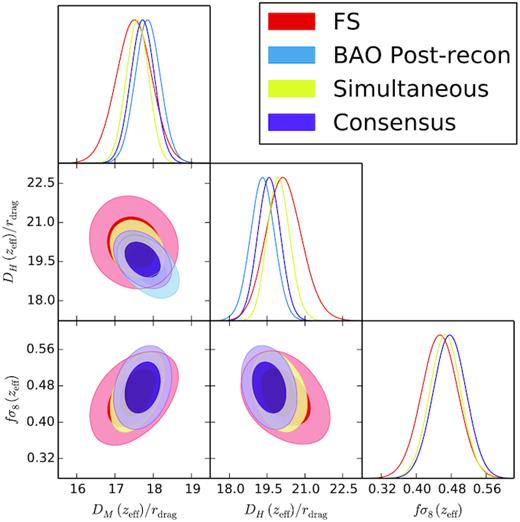
Likelihood posterior for 1σ and 2σ contour for the Fourier space BAO and FS consensus (purple contours) and simultaneous fit (yellow contours). For reference, the individual BAO post-recon (blue contours) and FS pre-recon (red contours) have also been included. In all cases, the contours only account for the statistical error budget. These contours correspond to the results presented in the first half (without systematics) of Table 8.
We follow an alternative analysis of extracting the combined BAO post-recon and FS pre-recon information without relying on the cross-coefficients of parameters estimated from the mocks. We do so by performing a simultaneous fit on both reconstructed and pre-reconstructed data vectors using the BAO and FS analysis respectively, simultaneously fitting α∥ and α⊥. As for the individual BAO and FS analyses, we estimate the full covariance matrix using the EZmocks. In Appendix C, we show what the off-diagonal elements of this matrix look like. Since the data-vectors differ, this matrix is not singular and can be safely inverted. However, the off-diagonal cross-correlation coefficients describing the pre- and post-data-vector elements with the same k-bin and ℓ-multipole, can be as high as ∼0.9, which inevitably will introduce some noise when inverting the matrix. We validate this approach by applying this pipeline to the Nseries mocks. Table F8 displays the performance of the simultaneous BAO and FS fit, along with the individual BAO and FS analyses, for both a fit on the mean of the mocks and the mean of the 84 individual fits. In both cases, the result is very similar. We see how this combined analysis can actually recover well the expected cosmological parameters with better precision than the individual BAO and FS analyses. Also the rms and error of the mean for the combined fit is smaller than any of the individual fits, confirming the gain of information. In particular, we note that by performing the consensus fits we obtain lower systematic shifts in the scaling factor variables than by performing the FS analysis alone. In fact, we observe an |$\sim 1{{\ \rm per\ cent}}$| systematic shift on α⊥ on the FS-alone, whereas for the simultaneous fit this shift is smaller than |$0.5{{\ \rm per\ cent}}$|. Conversely, for fσ8, FS-alone reported a shift of ∼−0.004 and for the FS × BAO this has been increased up to ∼0.018.
Employing the Nseries and EZmocks mocks, we find that using a third-order polynomial to perform the BAO part of the combined fit is not sufficient to achieve a sufficiently high accuracy on fσ8. This is caused by small inaccuracies in reproducing the BAO post-reconstruction broad-band, which are severely leaked into the FS analysis through the cross-covariance terms of the matrix. As a consequence, these BAO broad-band inaccuracies produced biased results on fσ8 as well as a bad-χ2 fits. This behaviour was also reported in the companion paper by de Mattia et al. (2020) when performing a similar combined fit. We increase the BAO polynomial order up to five and find that such behaviour vanishes and we are able to recover the expected fσ8 in mocks.
The results of applying this combined fit methodology to the data are shown by the yellow contours in Fig. 18 with only the statistical error contribution, as well reported in Table 8, under the notation ‘(BAO × FS) Pk’. We observe some differences between the two approaches of using both FS and BAO data, but the overall result is very similar, especially for fσ8. We observe that for the consensus result DM/rdrag and DH/rdrag are closer to the BAO-only results, opposite to the behaviour observed when the final results are produced by using the simultaneous fit. Also, bear in mind that when combining BAO and FS analysis, either by doing a consensus or a simultaneous fit, we do improve the fσ8 measurement. This might seem paradoxical as BAO analysis do not constrain fσ8 information. However, we obtain an indirect gain on this variable through a better measurement of the BAO scaling parameters, α∥ and α⊥, which are significantly correlated with fσ8. In terms of information content, the reconstructed catalogue is produced under the assumption of GR in order to undo the non-linear physics that degrade the BAO-peak significance. In this sense, the results on fσ8 coming from either combined or simultaneous fit, have stronger priors on gravity than those derived from the FS analysis on its own.
The general agreement between the simultaneous and consensus fit in Fourier space serves as a validation of the consensus methodology applied to combine result from both spaces.
6.2 Consensus final LRG results from BOSS and eBOSS
In this section, we present the most relevant results and corresponding covariance matrices of this paper.18 For reference, all the results correspond to those including the full systematic budget and represented by the second half of Table 8.
Legacy BOSS + eBOSS LRG cosmological measurements and covariance matrix within the redshift range 0.2 < z < 1.0. The table presents the results of the low- (|$0.2\lt z\lt 0.5,\, z_{\rm eff}=0.38$|) and middle-redshift bin (|$0.4\lt z\lt 0.6,\, z_{\rm eff}=0.51$|) of the DR12 BOSS galaxies. The new high-redshift bin (|$0.6\lt z\lt 1.0,\, z_{\rm eff}=0.698$|) is inferred from the DR16 CMASS + eBOSS LRG galaxies. Note that the low- and middle-redshift bins are overlapping in z, and therefore correlated, whereas the highest redshift bin does not overlap with any of the other two, and therefore is considered uncorrelated. The results are drawn from the combination of BAO post-reconstruction and Full Shape analyses, both in Fourier and configuration spaces. The covariance matrix elements include the full systematic budget. The low- and middle-redshift bin figures are inferred from those presented in table 8 of Alam et al. 2017. fσ8 values of BOSS DR12 redshift bins have been rescaled by equation (40) to use the same methodology as for the result of the high redshift bin.
| . | Mean . | . | . | . | cij × 104 . | . | . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|
| DM(0.38)/rdrag | 10.274 | 228.97 | −200.70 | 26.481 | 134.87 | −81.402 | 10.292 | 0 | 0 | 0 |
| DH(0.38)/rdrag | 24.888 | − | 3384.9 | −85.213 | −160.24 | 1365.2 | −38.002 | 0 | 0 | 0 |
| fσ8(0.38) | 0.49729 | − | − | 20.319 | 13.250 | −23.012 | 8.14158 | 0 | 0 | 0 |
| DM(0.51)/rdrag | 13.381 | − | − | − | 321.58 | −200.91 | 26.409 | 0 | 0 | 0 |
| DH(0.51)/rdrag | 22.429 | − | − | − | − | 2319.2 | −55.377 | 0 | 0 | 0 |
| fσ8(0.51) | 0.45902 | − | − | − | − | − | 14.322 | 0 | 0 | 0 |
| DM(0.698)/rdrag | 17.646 | − | − | − | − | − | − | 911.40 | −337.89 | 24.686 |
| DH(0.698)/rdrag | 19.770 | − | − | − | − | − | − | − | 2200.9 | −36.088 |
| fσ8(0.698) | 0.47300 | − | − | − | − | − | − | − | − | 19.616 |
| . | Mean . | . | . | . | cij × 104 . | . | . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|
| DM(0.38)/rdrag | 10.274 | 228.97 | −200.70 | 26.481 | 134.87 | −81.402 | 10.292 | 0 | 0 | 0 |
| DH(0.38)/rdrag | 24.888 | − | 3384.9 | −85.213 | −160.24 | 1365.2 | −38.002 | 0 | 0 | 0 |
| fσ8(0.38) | 0.49729 | − | − | 20.319 | 13.250 | −23.012 | 8.14158 | 0 | 0 | 0 |
| DM(0.51)/rdrag | 13.381 | − | − | − | 321.58 | −200.91 | 26.409 | 0 | 0 | 0 |
| DH(0.51)/rdrag | 22.429 | − | − | − | − | 2319.2 | −55.377 | 0 | 0 | 0 |
| fσ8(0.51) | 0.45902 | − | − | − | − | − | 14.322 | 0 | 0 | 0 |
| DM(0.698)/rdrag | 17.646 | − | − | − | − | − | − | 911.40 | −337.89 | 24.686 |
| DH(0.698)/rdrag | 19.770 | − | − | − | − | − | − | − | 2200.9 | −36.088 |
| fσ8(0.698) | 0.47300 | − | − | − | − | − | − | − | − | 19.616 |
Legacy BOSS + eBOSS LRG cosmological measurements and covariance matrix within the redshift range 0.2 < z < 1.0. The table presents the results of the low- (|$0.2\lt z\lt 0.5,\, z_{\rm eff}=0.38$|) and middle-redshift bin (|$0.4\lt z\lt 0.6,\, z_{\rm eff}=0.51$|) of the DR12 BOSS galaxies. The new high-redshift bin (|$0.6\lt z\lt 1.0,\, z_{\rm eff}=0.698$|) is inferred from the DR16 CMASS + eBOSS LRG galaxies. Note that the low- and middle-redshift bins are overlapping in z, and therefore correlated, whereas the highest redshift bin does not overlap with any of the other two, and therefore is considered uncorrelated. The results are drawn from the combination of BAO post-reconstruction and Full Shape analyses, both in Fourier and configuration spaces. The covariance matrix elements include the full systematic budget. The low- and middle-redshift bin figures are inferred from those presented in table 8 of Alam et al. 2017. fσ8 values of BOSS DR12 redshift bins have been rescaled by equation (40) to use the same methodology as for the result of the high redshift bin.
| . | Mean . | . | . | . | cij × 104 . | . | . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|
| DM(0.38)/rdrag | 10.274 | 228.97 | −200.70 | 26.481 | 134.87 | −81.402 | 10.292 | 0 | 0 | 0 |
| DH(0.38)/rdrag | 24.888 | − | 3384.9 | −85.213 | −160.24 | 1365.2 | −38.002 | 0 | 0 | 0 |
| fσ8(0.38) | 0.49729 | − | − | 20.319 | 13.250 | −23.012 | 8.14158 | 0 | 0 | 0 |
| DM(0.51)/rdrag | 13.381 | − | − | − | 321.58 | −200.91 | 26.409 | 0 | 0 | 0 |
| DH(0.51)/rdrag | 22.429 | − | − | − | − | 2319.2 | −55.377 | 0 | 0 | 0 |
| fσ8(0.51) | 0.45902 | − | − | − | − | − | 14.322 | 0 | 0 | 0 |
| DM(0.698)/rdrag | 17.646 | − | − | − | − | − | − | 911.40 | −337.89 | 24.686 |
| DH(0.698)/rdrag | 19.770 | − | − | − | − | − | − | − | 2200.9 | −36.088 |
| fσ8(0.698) | 0.47300 | − | − | − | − | − | − | − | − | 19.616 |
| . | Mean . | . | . | . | cij × 104 . | . | . | . | . | . |
|---|---|---|---|---|---|---|---|---|---|---|
| DM(0.38)/rdrag | 10.274 | 228.97 | −200.70 | 26.481 | 134.87 | −81.402 | 10.292 | 0 | 0 | 0 |
| DH(0.38)/rdrag | 24.888 | − | 3384.9 | −85.213 | −160.24 | 1365.2 | −38.002 | 0 | 0 | 0 |
| fσ8(0.38) | 0.49729 | − | − | 20.319 | 13.250 | −23.012 | 8.14158 | 0 | 0 | 0 |
| DM(0.51)/rdrag | 13.381 | − | − | − | 321.58 | −200.91 | 26.409 | 0 | 0 | 0 |
| DH(0.51)/rdrag | 22.429 | − | − | − | − | 2319.2 | −55.377 | 0 | 0 | 0 |
| fσ8(0.51) | 0.45902 | − | − | − | − | − | 14.322 | 0 | 0 | 0 |
| DM(0.698)/rdrag | 17.646 | − | − | − | − | − | − | 911.40 | −337.89 | 24.686 |
| DH(0.698)/rdrag | 19.770 | − | − | − | − | − | − | − | 2200.9 | −36.088 |
| fσ8(0.698) | 0.47300 | − | − | − | − | − | − | − | − | 19.616 |
7 DISCUSSION
In this section, we present a brief interpretation of the results inferred from the DR16 CMASS + eBOSS LRG samples presented in this paper in combination with the configuration space counterpart presented in Bautista et al. (2020). A full and consistent cosmological analysis is discussed in eBOSS Collaboration et al. (2020).
Fig. 19 displays the comparison between the DR16 CMASS + eBOSS LRG analyses on Fourier space (blue contours), configuration space (yellow contours) and its combination (red contours), for the BAO-only analysis on reconstructed catalogues (top panel) and FS analyses (bottom panel). Additionally, in the bottom panel, we display the full BAO and FS consensus (grey contours). In green, we display the prediction of a flat-ΛCDM model using the values reported by Planck (Aghanim et al. 2018). For the fσ8 panel, the additional relation set by GR is used to infer |$f(z)=\Omega _{\rm m}^{6/11}(z)$| and the linear growth factor D(z), which propagates σ8(z) = D(z)σ8(z = 0) to the redshift of interest, z = 0.698.
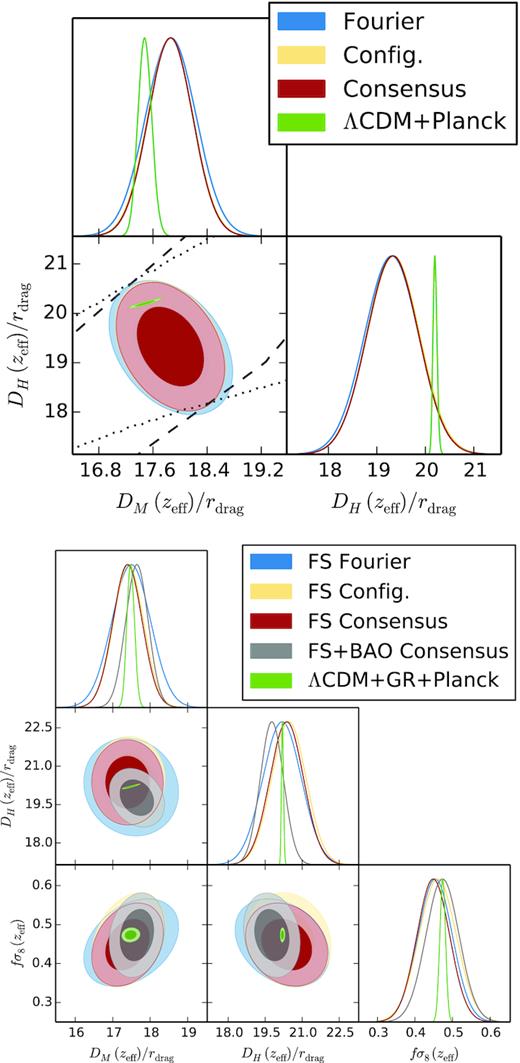
Top panel: Likelihood posteriors from BAO reconstruction analysis , inferred from Fourier space (this work), configuration space (Bautista et al. 2020), and its consensus. The black dashed and dotted lines show the limits imposed by a flat-ΛCDM model with two sets of wide priors (see the text). Bottom panel: same as the top panel but from FS analysis, additionally a full consensus between Fourier space, configuration space, BAO, and FS analysis is added. In all cases, the contours do include the systematic error budget. For reference, we include the prediction of flat-ΛCDM and GR using Planck measurements.
The agreement between Fourier and configuration space is very good, as we already reported in Tables 8 and 6. When BAO reconstructed information is used in combination with FS-only analyses, we obtain the tighter constrains of this paper. In all cases, the agreement with the flat-ΛCDM + GR model prediction is excellent.
We remark that the methodology used in this paper to infer DM(zeff)/rdrag and DH(zeff)/rdrag(z) does not assume the internal ΛCDM prior: |$D_{\rm M}(z)=\int _0^z {\rm d}z^{\prime }\, D_{\rm H}(z^{\prime })$|. This relation sets additional limits on the DH/rdrag−DM/rdrag parameter space, which in the top panel of Fig. 19 is shown as black lines when the following hard priors are used: |$\lbrace 135\lt r_{\rm drag}\, [{\rm Mpc}]\lt 165;\, 0.25\lt \Omega _{\rm m}\lt 0.90;\, 0.55\lt h\lt 0.80\rbrace$| in dashed lines; and |$\lbrace 135\lt r_{\rm drag}\, [{\rm Mpc}]\lt 165;\, 0.145\lt \Omega _{\rm m}h^2\lt 0.200\rbrace$|19 in dotted lines. Using the wide Ωx-type of ΛCDM priors (dashed lines) is not the optimal approach, as it easily hits the LSS contours even in this wide-prior scenario. This situation can be partially solved by imposing Ωxh2-type of priors instead (dotted lines). However, one has to control the effect that priors on Ωbh2 and Ωmh2 has on rdrag, which we do not study here. Therefore, those LSS analyses that iteratively change the shape of the power spectrum according to ΛCDM templates (see for e.g. D’Amico et al. 2019; Ivanov et al. 2019; Tröster et al. 2020) have to carefully asses the impact of these type priors on their analyses. Fig. 20 displays the predicted evolution with redshift of the parameters DM(z)/rdrag, DH(z)/rdrag, and fσ8(z) predicted by the ΛCDM model and GR using the Planck measurements (green contours) for the 1σ and 2σ confidence levels. The symbols show the measurements by the main galaxy sample (MGS, Howlett et al. 2015), DR12 BOSS LRG sample (Alam et al. 2017), DR14 eBOSS LRG sample (Icaza-Lizaola et al. 2019), and DR16 CMASS + eBOSS LRG sample (this work in combination with Bautista et al. 2020) at z = 0.698, for the FS analysis (empty symbol), and for the FS + BAO analysis (filled symbol).
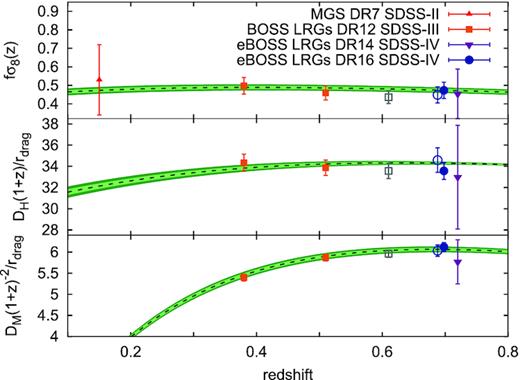
Cosmology measurements based on low-redshift galaxies, for the DR7 MGS (Howlett et al. 2015) at z = 0.15, DR12 BOSS LRG sample (Alam et al. 2017) at |$z=\lbrace 0.38,\, 0.51,\, 0.61\rbrace$|, DR14 eBOSS LRG sample (Icaza-Lizaola et al. 2019) at z = 0.72, and DR16 CMASS + eBOSS LRG sample (this work in combination with Bautista et al. 2020) at z = 0.698. The DR16 CMASS + eBOSS LRG empty symbol correspond to the values inferred from the FS-only analysis, whereas the filled symbol to the full consensus of FS + BAO reconstruction. Note that (i) the low and middle DR12 BOSS LRG sample measurements are correlated; (ii) the high redshift bin of DR12 BOSS LRG sample (in grey) is fully contained by the DR16 CMASS + eBOSS LRG sample and the middle redshift bin of DR12 BOSS LRG sample, and therefore, does not add any extra information. For reference in green bands, the constraints inferred by flat-ΛCDM and GR using Planck measurements (Aghanim et al. 2018) is also shown.
We see the great improvement in the constraining power between the former DR14 eBOSS LRG analysis and the current work. Part of this gain is explained by the larger volume of the DR16 sample, a factor of ∼3 larger, which explains a reduction of about a factor of 2 in the error bars. The additional reduction is provided by the use of the hexadecapole signal in the DR16 analysis, which helps to break degeneracies between parameters, and can explain the further observed gain.
The results from the DR12 BOSS LRG sample are shown in orange for the two lowest redshift bins, and in grey for the highest redshift bin. We remind the reader that with the current DR16 CMASS+eBOSS LRG sample in play, all the LRG galaxies contained in the BOSS high redshift bin are also contained either by either the BOSS middle redshift bin catalogue, or by the DR16 CMASS+eBOSS LRG catalogue. As a consequence, the high redshift bin of BOSS is highly correlated with the adjacent redshift bins, and therefore it barely contains extra information. Therefore, we reorganize the whole set of LRG galaxies observed by BOSS + eBOSS galaxies in three redshift bins: the low- (|$0.2\lt z\lt 0.5,\, z_{\rm eff}=0.38$|) and middle-redshift bin (|$0.4\lt z\lt 0.6,\, z_{\rm eff}=0.51$|), both from the DR12 BOSS analysis, and a new high redshift bin (|$0.6\lt z\lt 1.0,\, z_{\rm eff}=0.698$|) containing BOSS and eBOSS LRG galaxies. Table 9 summarizes these measurements and correlations.
Fig. 20 displays a very good agreement between the measured quantities and model predictions in the redshift range 0.2 < z < 1.0, showing no significant discrepancy in any of the variables.
8 CONCLUSIONS
We have performed BAO and full shape analyses in Fourier space of the final DR16 CMASS + eBOSS LRG catalogue, consisting of 377 458 galaxies in the redshift range 0.6 < z < 1.0. In order to increase the BAO signal, we have applied the density-field reconstruction technique in order to remove the non-linear gravitational physics, and enhance BAO peak detection. We have extracted the monopole, quadrupole, and hexadecapole signal of the pre- and post-reconstructed galaxy catalogues and employed them to measure the comoving angular diameter distance over the horizon scale at drag epoch, DM(zeff)/rdrag, the Hubble distance over the horizon scale at drag epoch, DH(zeff)/rdrag and the logarithmic growth factor times the amplitude of dark matter fluctuations at scales of |$8\, \, h^{-1}\, {\rm Mpc}$|, fσ8(zeff), at the effective redshift of the sample, zeff = 0.698. These analyses are complementary to those performed in configuration space and presented in Bautista et al. (2020). We have found an excellent agreement between the Fourier space and configuration space inferred parameters, both for BAO and FS-type of analysis.
We have combined the cosmological results produced in both spaces to generate a set of consensus parameters, which represents the most precise and accurate cosmological measurements at this epoch: DM(zeff)/rdrag = 17.65 ± 0.30, DH(zeff)/rdrag = 19.77 ± 0.47, fσ8(zeff) = 0.473 ± 0.044.
We have tested the validity of the approaches used in this paper employing realistic N-body simulation catalogues. We have quantified four types of sources of potential systematic errors: (i) systematic errors arising from the inaccuracy of the modelling; (ii) systematic errors produced by the arbitrary choice of reference cosmology, and systematic errors produced by (iii) observational effects such has redshift failures, collisions, completeness effects, and (iv) the RIC. The total systematic error budget that results is sub-dominant compared to the statistical errors. After propagating the systematic error into the total error budget, we have observed that the error bars of the cosmological parameters have increased by about 10 per cent.
We have also tested the BAO and FS models with galaxy catalogues for different types of using different types of HOD models. We have observed no significant effect on the cosmological parameters of interest, although the precision on these catalogues does not allow to resolve changes of more than few per cent in the cosmological parameters of interest.
The inferred cosmological parameters from the DR16 CMASS+eBOSS LRG sample show an excellent agreement with the predictions by the standard cosmological model, flat-ΛCDM + GR, using the cosmological parameters inferred by Planck. These observations complement those based on ELGs (de Mattia et al. 2020; Tamone et al. 2020), quasars (Hou et al. 2020; Neveux et al. 2020) and Ly-α (des Mas du Bourboux et al. 2020). A full cosmology interpretation using these and previous BOSS analyses (Alam et al. 2017) is presented in eBOSS Collaboration et al. (2020).
Next generation galaxy surveys, such as the Dark Energy Spectroscopic Instrument (DESI, DESI Collaboration et al. 2016a, b), EUCLID (Amendola et al. 2018), the Large Synoptic Survey Telescope (LSST, LSST Science Collaboration et al. 2009) or the Square Kilometer Array (SKA, Square Kilometre Array Cosmology Science Working Group et al. 2020), will extensively re-probe the redshift range 0 < z < 4 with an unprecedented level of precision never reached before, and in some cases will extend this range up to z ≃ 6.
The SDSS-I and -II (2004–2009), the BOSS (2009–2014), and finally the eBOSS observations (2014–2019) have probed for first time the physics of the late-time Universe using galaxies as dark matter tracers. These experiments have demonstrated that the BAO and RSD techniques can effectively be used to measure expansion and logarithmic growth rate, opening a new window for the next-generation of experiments, which potentially will reveal hints of new physics phenomena occurring in our Universe.
ACKNOWLEDGEMENTS
HG-M acknowledges the support from la Caixa Foundation (ID 100010434) which code LCF/BQ/PI18/11630024. RP, SdlT, and SE acknowledge support from the ANR eBOSS project (ANR-16-CE31-0021) of the French National Research Agency. SdlT and SE acknowledge the support of the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the ‘Investissements d’Avenir’ French government program managed by the ANR. MV-M and SF are partially supported by Programa de Apoyo a Proyectos de Investigación e Inovación Teconológica (PAPITT) no. IA101518, no. IA101619 and Proyecto LANCAD-UNAM-DGTIC-136. GR acknowledges support from the National Research Foundation of Korea (NRF) through Grants No. 2017R1E1A1A01077508 and No. 2020R1A2C1005655 funded by the Korean Ministry of Education, Science and Technology (MoEST), and from the faculty research fund of Sejong University. SA is supported by the European Research Council through the COSFORM Research Grant (#670193). E-MM is supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 693024).
The numerical computations presented in this work were done on Hipatia and Aganice ICC-UB BULLx High Performance ComputingCluster at the University of Barcelona. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231. This research also uses resources of the HPC cluster ATOCATL-IA-UNAM México.
In addition, this research relied on resources provided to the eBOSS Collaboration by the National Energy Research Scientific Computing Center (NERSC). NERSC is a US Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.
Funding for the SDSS IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
DATA AVAILABILITY
The power spectra, covariance matrices, and resulting likelihoods for cosmological parameters are available at the SDSS Science Archive Server (https://data.sdss.org/sas/dr16/eboss/lss/).
Footnotes
A summary of all SDSS BAO and RSD measurements with accompanying legacy figures can be found here: sdss.org/science/final-bao-and-rsd-measurements/. The full cosmological interpretation of these measurements can be found here: sdss.org/science/cosmology-results-from-eboss/
RedRock is available at sdss.org/dr16/software/products
For the NGC sample, we find zeff = 0.695 and for SGC we find zeff = 0.704. For the combined NGC–SGC sample, we simply approximate zeff = 0.70 in the power spectrum linear templates.
Reconstruction code available at github.com/julianbautista/eboss_clustering
Rapid foUrier STatIstics COde github.com/hectorgil/rustico.
Fastest FT in the West: fftw.org
The angular diameter distance, DA(z) and the comoving angular diameter distance are related by DM(z) = (1 + z)DA(z).
In this paper, these two reference cosmologies, the cosmology chosen to convert redshift into distance and the cosmology chosen for the model-template, are chosen to be the same for simplicity.
We do not attempt any physical interpretation of β as the ratio of the logarithmic growth of structure f and the linear bias parameter b1.
When analysing other type of mocks, such Nseries or OuterRim-derived mocks, we set Σ∥ and Σ⊥ to the best-fitting values of the mean of these mocks, respectively.
Bao and Rsd Algorithm for Spectroscopic Surveys, github.com/hectorgil/Brass.
In these equations, σ8 is not explicitly written, but it is hidden within the linear power spectra, |$P_{\rm lin}\propto \sigma _8^2$|.
When the reference template is modified, these values are accordingly changed.
Here, |$\bar{x}$| and |$\sigma _x^2$| represent the mean and the variance, respectively, of the normal distribution used as a prior.
As in Table 3, the obtained α-parameters are re-scaled after the fit to match the prediction of the fiducial cosmology when used as a reference cosmology.
We consistently map the redshifts into comoving distances in the catalogues using the cosmology of these templates.
In order to remove the RIC, we generate a common random catalogue from all the individual 1000 random catalogues, taking a random |$0.1{{\ \rm per\ cent}}$| fraction of the objects.
The results of all the cases can be found online.
The hard low prior on Ωmh2 seems to exclude the value preferred by Planck + ΛCDM. This effect is caused by the wide prior on rdrag. When the prior on rdrag is tightened, the prior on Ωmh2 needs to be relaxed to maintain the same limits on the DH/rdrag−DM/rdrag plane, which would make the Ωmh2 prior consistent with Planck best fit.
REFERENCES
APPENDIX A: EFFECT OF ISOTROPIC TEMPLATE ON BAO DETERMINATION
In this appendix, we aim to show the performance of the isotropic BAO template described by equations (22) and (23) when is applied on the analysis the full anisotropic signal, compared to the standard approach, described by equations (20) and (21). In principle, the standard approach is more complete as it describe better the damping of the BAO signal in an explicit μ-dependent way, whereas the isotropic template takes only the average of this dependence for each multipole into account. However, for the post-reconstructed data, the BAO damping is weak (as most of it is removed by the reconstruction process) and both approaches converge: In the limit, |$\Sigma _{\perp ,\, \parallel }\rightarrow 0$| both approaches are equivalent. Fig. A1 displays the performance on the mean of the EZmocks for the reconstructed catalogue when the isotropic template is used using three (orange contours) and five (red contours) polynomial terms in the broadband; and when the anisotropic is also used in the same catalogue for three (turquoise contours which corresponds to the standard approach used in the paper) and five (blue contours) polynomial terms in the broadband. In all the cases, |$\Sigma _0,\, \Sigma _2$| (in the isotropic template), as well as |$\Sigma _\parallel ,\, \Sigma _\perp$| (in the anisotropic template) have been freely fit to the mean of the mocks. For reference we also show the performance on the pre-recon catalogue of the anisotropic template with three terms in the polynomial broadband function. The horizontal and vertical dashed lines show the expected values given the difference between the reference (in this case the fiducial) and underlying true cosmology of the mocks.
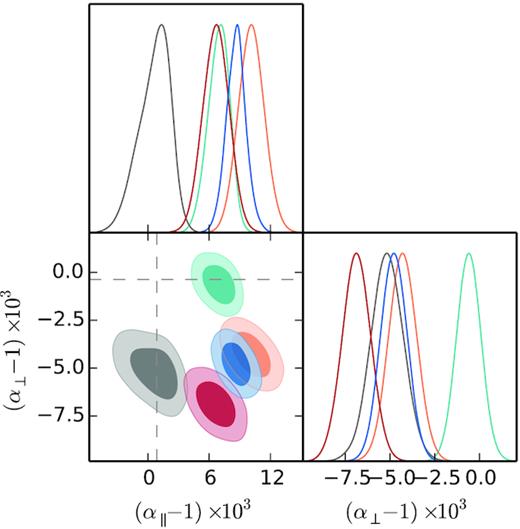
BAO template comparison: pre-recon anisotropic third order (grey), post-recon isotropic of 3rd order, (orange), post-recon isotropic of fifth order (red), post-recon anisotropic of third-order (turquoise), post-recon anisotropic of fifth order (blue).
We see that all the post-reconstructed analyses perform very similarly on the determination of the α∥ variable, which shows an about |$0.6{{\ \rm per\ cent}}$| shift with respect to the expected value, for all the studied cases. On the other hand, the different templates display a different performance when determining the α⊥ variable. The isotropic template tends to consistently underestimate α⊥ by about |$0.5{-}0.75{{\ \rm per\ cent}}$|, regardless of the polynomial order of the broadband. On the other hand, when the anisotropic template is used, having three broadband parameters shows unbiased results, whereas when we add two extra parameters, we bias the results in about |$0.5{{\ \rm per\ cent}}$|. Finally, we recall that these studies are performed on fast EZmocks, and therefore, such conclusions should be validated with full N-body simulations.
APPENDIX B: GAUSSIAN TEST
We perform a comparison between the outcome of the MCMC on the DR16 CMASS + eBOSS LRG data set and its Gaussian approximation, given by the parameters of Table 3 for BAO and Table 4 for FS analysis. The comparison is displayed by Fig. B1, for BAO reconstructed chains (blue contours), FS chains (red contours); and their corresponding Gaussian contours (black lines), where no systematic error budget has been taken into account for simplicity.
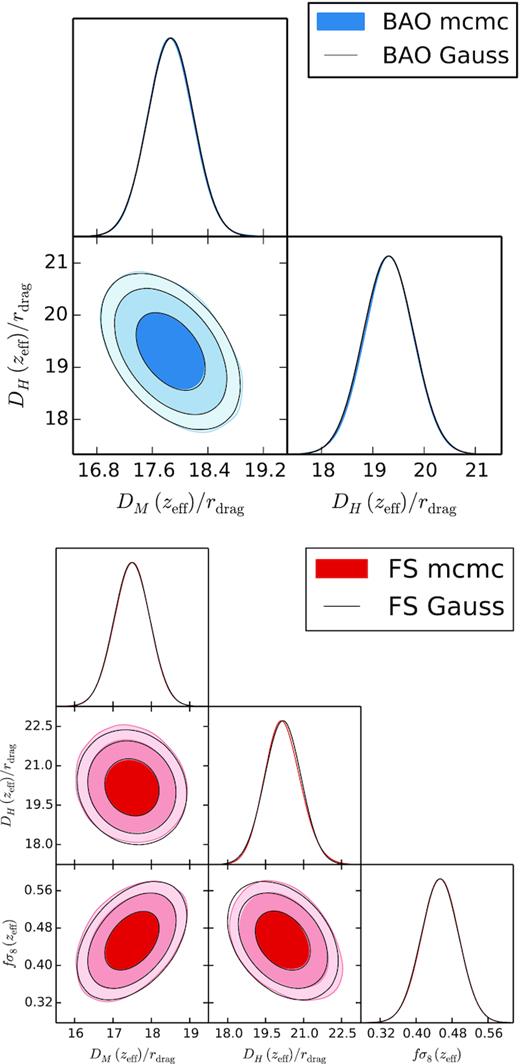
FS and BAO Gaussian test. The top and bottom panel displays the posterior of the BAO post-reconstruction and FS analysis, respectively. The black curves display the Gaussian prediction, for 1σ, 2σ, and 3σ confidence levels. In all cases only the statistical error contribution is shown.
We conclude that the Gaussian approximation is very good for BAO type of analysis up to 3σ confidence levels. The FS analysis displays some degree of non-Gaussianity at 3σ, specially for DH/rdrag. This kind of behaviour is expected as the modes along the LOS present a higher level of noise, which typically induces non-Gaussian tails. However, such features only appears at the edges of the likelihood shape and have a very small impact in the cosmological constrains.
APPENDIX C: COVARIANCE
The top panel of Fig. C1 display the cross-correlation coefficients of the covariance matrix inferred from the 1000 realizations of the EZmocks. The matrix is divided in five blocks corresponding to the post-reconstructed monopole and quadrupole, between |$k=0.02\,$| and |$0.30\, \, h\, {\rm Mpc}^{-1}$|; and the pre-reconstructed monopole, quadrupole, and hexadecapole, between |$k=0.02\,$| and |$0.15\, \, h\, {\rm Mpc}^{-1}$|. The high values of the off-diagonal terms corresponding to those elements cross-correlating elements with equal k and ℓ, but corresponding to pre- and post-catalogues. In order to perform the BAO type of analysis, we only invert the first first blocks, whereas for the M+Q + H FS analysis we invert the three last blocks. Only when the simultaneous fit is performed we invert the five blocks all-together.
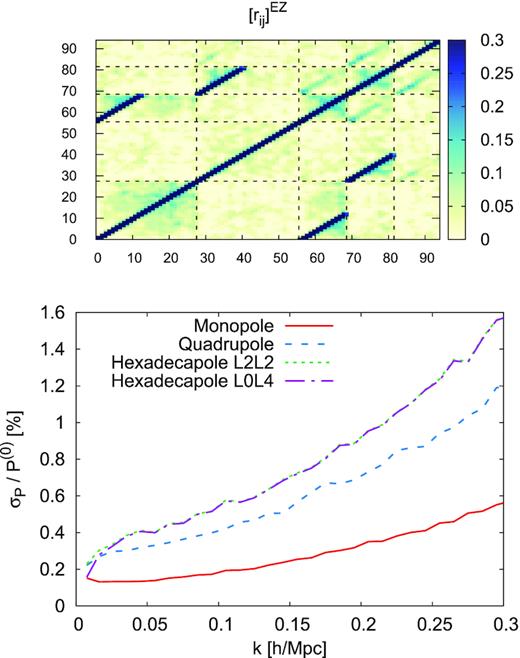
The top panel shows the cross-correlation elements of the covariance matrix corresponding to the full power spectrum data vector. The dashed lines mark the different blocks of the covariance: P(0), P(2) (for reconstructed catalogues), P(0), P(2), and P(4) (for pre-reconstructed catalogues). Note that reconstructed elements are two times larger than the pre-reconstructed ones due to the difference in k-range. The bottom panel shows the statistical error estimated from 1000 realizations of the EZmocks of P(ℓ)(k) relative to P(0)(k) for |$\ell =0,\, 2,\, 4$|, as a function of k. For the hexadecapole, two errors are displayed, depending on the LOS treatment (see Section 2.5). In all cases, only the NGC contribution is shown.
The bottom panel of Fig. C1 display the error of P(ℓ) relative to the value of P(0) as a function of k. For the hexadecapole, ℓ = 4, we report the error of the two estimators according to the expansions |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_h)\rightarrow \mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1)$| (L0L4) and |$\mathcal {L}_4(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_h)\rightarrow \mathcal {L}_2(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_1) \mathcal {L}_2(\hat{\boldsymbol k}\cdot \hat{\boldsymbol r}_2)$| (L2L2), in equation (6). We see that the variance of these two estimators of the hexadecapole is very close for the k-range used here, |$0.02\le k\, [\, h\, {\rm Mpc}^{-1}]$|, which implies that the wide-angle effects are in effect negligible.
APPENDIX D: WINDOW FUNCTION
Fig. D1 display the |$W_\ell ^2(r)$| functions for the NGC/SGC DR16 CMASS + eBOSS LRG sample (solid lines/dashed lines).
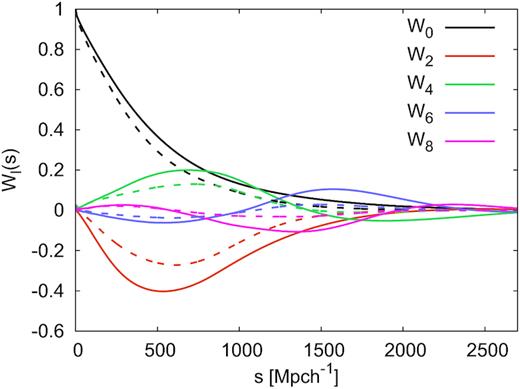
Selection function multipoles according to equation (13) for the DR16 CMASS + eBOSS LRG catalogue within 0.6 ≤ z ≤ 1.0. The solid lines represent the NGC and the dashed lines the SGC. The different colours display the performance for the even ℓ-multipoles as indicated in the key.
APPENDIX E: EFFECT OF THE PRIORS IN THE AMPLITUDE OF SHOT NOISE
Fig. E1 displays the effect of the 50 per cent-noise prior, 0.5 < Anoise < 1.5 (purple contours) on the likelihood posterior of the cosmological parameters of interest, DH/rdrag, DM/rdrag, and fσ8, for the DR16 CMASS + eBOSS LRG sample. For reference, we show in red contours the posterior corresponding to a wider and uninformative prior on Anoise. The effect of the 50 per cent-noise prior prior is almost uninformative for DM/rdrag and remove the non-Gaussian tail on the higher side of the likelihood and posteriors of DH/rdrag and fσ8, which are highly correlated.
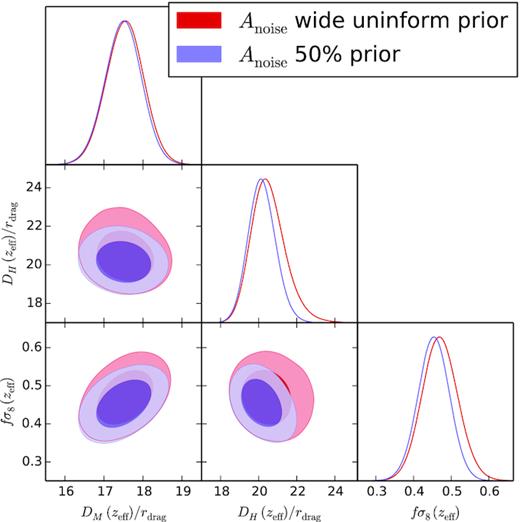
Effect of the noise prior on the likelihood posteriors of the variables of cosmological interest for the FS analysis. The red contours show the posteriors with an uninformative prior on the amplitude of shot noise; the purple contours show the same when a hard prior has been applied to this amplitude to not differ more than 50 per cent from the Poissonian prediction. The effect on the rest of the model parameters is displayed in Table E2.
Fig. E2 displays the same effect but extended to the full parameter-vector of the FS type of analysis. Some of the variables show a highly non-Gaussian behaviour. This is the case of b2, which is poorly constrained by the power spectrum. In this case, we observe a strong banana-shape type of correlation between b2 and Anoise. This effect is leaked through correlations to the rest of parameters, in particular into α∥ and f, which causes the non-Gaussian tails showed in Fig. E2. We can partly solves this spurious behaviour by imposing the 50 per cent-noise prior on Anoise (purple contours). Alternatively, including bispectrum data would also help to constrain b2 and naturally help to keep Anoise posterior around values of 1, which is the Poisson prediction.
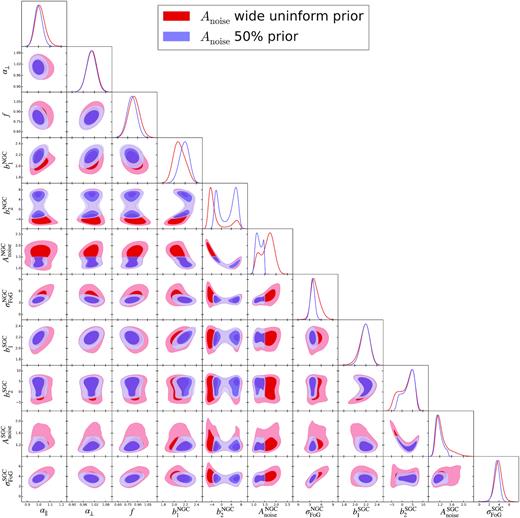
Posterior likelihood for all the 11 parameters of the FS fit with M+Q + H and kmax = 0.15 to the DR16 LRG CMASS + eBOSS data set, with an uninformative prior on Anoise (red contours) and with the prior 0.5 < Anoise < 1.5 (the main result for FS in this paper) in purple. Note at the strong correlation between b2 and Anoise, which drive Anoise to take unphysical values Anoise ∼ 2.
APPENDIX F: TABLES
In this section, we include a series of tables, which can be helpful for the reader to cross-check some values of the plots displayed in the main text. We list them below briefly.
Table F1 accounts for the impact of non-periodic boundary conditions of the |$1\, h^{-1}{\rm Gpc}$| cubic boxes from the OuterRim-HOD mocks by comparing them with the |$3\, h^{-1}{\rm Gpc}$| padded sky-cut samples.
Impact of non-periodicity in OuterRim-HOD-mocks for pre-recon catalogues. The cubic box catalogues consist of non-periodic cubic boxes of |$1\, h^{-1}{\rm Gpc}$|. The sky-cuts catalogues mimic a sky-mock geometry (i.e. non-uniform n(z)), where galaxies and randoms are placed in cubic boxes of |$3\, h^{-1}{\rm Gpc}$|, where two-thirds of the volume is empty). The periodicity of the box is implicitly assumed under any discrete Fourier space calculation. We expect that the non-periodic effects are negligible for the sky-cuts mocks, but not for the cubic boxes. For simplicity only the fit to the mean is provided.
| HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Sky-cut | −0.022 ± 0.014 | 0.0108 ± 0.0099 |
| Hearin | Cubic box | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Sky-cut | −0.011 ± 0.018 | 0.003 ± 0.011 |
| Leauthaud | Cubic box | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Sky-cut | 0.002 ± 0.018 | −0.005 ± 0.012 |
| Tinker | Cubic box | 0.017 ± 0.024 | 0.002 ± 0.012 |
| HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Sky-cut | −0.022 ± 0.014 | 0.0108 ± 0.0099 |
| Hearin | Cubic box | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Sky-cut | −0.011 ± 0.018 | 0.003 ± 0.011 |
| Leauthaud | Cubic box | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Sky-cut | 0.002 ± 0.018 | −0.005 ± 0.012 |
| Tinker | Cubic box | 0.017 ± 0.024 | 0.002 ± 0.012 |
Impact of non-periodicity in OuterRim-HOD-mocks for pre-recon catalogues. The cubic box catalogues consist of non-periodic cubic boxes of |$1\, h^{-1}{\rm Gpc}$|. The sky-cuts catalogues mimic a sky-mock geometry (i.e. non-uniform n(z)), where galaxies and randoms are placed in cubic boxes of |$3\, h^{-1}{\rm Gpc}$|, where two-thirds of the volume is empty). The periodicity of the box is implicitly assumed under any discrete Fourier space calculation. We expect that the non-periodic effects are negligible for the sky-cuts mocks, but not for the cubic boxes. For simplicity only the fit to the mean is provided.
| HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Sky-cut | −0.022 ± 0.014 | 0.0108 ± 0.0099 |
| Hearin | Cubic box | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Sky-cut | −0.011 ± 0.018 | 0.003 ± 0.011 |
| Leauthaud | Cubic box | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Sky-cut | 0.002 ± 0.018 | −0.005 ± 0.012 |
| Tinker | Cubic box | 0.017 ± 0.024 | 0.002 ± 0.012 |
| HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Sky-cut | −0.022 ± 0.014 | 0.0108 ± 0.0099 |
| Hearin | Cubic box | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Sky-cut | −0.011 ± 0.018 | 0.003 ± 0.011 |
| Leauthaud | Cubic box | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Sky-cut | 0.002 ± 0.018 | −0.005 ± 0.012 |
| Tinker | Cubic box | 0.017 ± 0.024 | 0.002 ± 0.012 |
Table F2 lists the effect of different HOD models and flavours of the |$1\, h^{-1}{\rm Gpc}$| cubic sub-boxes drawn from the OuterRim-HOD mocks on BAO pre-recon analysis.
Impact of different HOD types and ‘flavours’ on pre-recon BAO fits on cubic boxes without periodic boundary conditions. For simplicity only fit on the mean is provided.
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Standard | 0.028 ± 0.010 | −0.0005 ± 0.0054 |
| Hearin | Threshold 1 | 0.024 ± 0.011 | −0.0002 ± 0.0061 |
| Hearin | Threshold 2 | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Standard | 0.030 ± 0.010 | −0.0016 ± 0.0052 |
| Leauthaud | Threshold 1 | 0.029 ± 0.010 | −0.0013 ± 0.0052 |
| Leauthaud | Threshold 2 | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Standard | 0.038 ± 0.010 | −0.0005 ± 0.0054 |
| Tinker | Threshold 1 | 0.025 ± 0.010 | −0.0013 ± 0.0055 |
| Tinker | Threshold 2 | 0.017 ± 0.024 | 0.002 ± 0.012 |
| Zheng | Standard | 0.024 ± 0.010 | −0.0005 ± 0.0060 |
| Zheng | Threshold 1 | 0.027 ± 0.011 | −0.0006 ± 0.0062 |
| Zheng | Threshold 2 | 0.031 ± 0.013 | −0.0014 ± 0.0075 |
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Standard | 0.028 ± 0.010 | −0.0005 ± 0.0054 |
| Hearin | Threshold 1 | 0.024 ± 0.011 | −0.0002 ± 0.0061 |
| Hearin | Threshold 2 | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Standard | 0.030 ± 0.010 | −0.0016 ± 0.0052 |
| Leauthaud | Threshold 1 | 0.029 ± 0.010 | −0.0013 ± 0.0052 |
| Leauthaud | Threshold 2 | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Standard | 0.038 ± 0.010 | −0.0005 ± 0.0054 |
| Tinker | Threshold 1 | 0.025 ± 0.010 | −0.0013 ± 0.0055 |
| Tinker | Threshold 2 | 0.017 ± 0.024 | 0.002 ± 0.012 |
| Zheng | Standard | 0.024 ± 0.010 | −0.0005 ± 0.0060 |
| Zheng | Threshold 1 | 0.027 ± 0.011 | −0.0006 ± 0.0062 |
| Zheng | Threshold 2 | 0.031 ± 0.013 | −0.0014 ± 0.0075 |
Impact of different HOD types and ‘flavours’ on pre-recon BAO fits on cubic boxes without periodic boundary conditions. For simplicity only fit on the mean is provided.
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Standard | 0.028 ± 0.010 | −0.0005 ± 0.0054 |
| Hearin | Threshold 1 | 0.024 ± 0.011 | −0.0002 ± 0.0061 |
| Hearin | Threshold 2 | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Standard | 0.030 ± 0.010 | −0.0016 ± 0.0052 |
| Leauthaud | Threshold 1 | 0.029 ± 0.010 | −0.0013 ± 0.0052 |
| Leauthaud | Threshold 2 | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Standard | 0.038 ± 0.010 | −0.0005 ± 0.0054 |
| Tinker | Threshold 1 | 0.025 ± 0.010 | −0.0013 ± 0.0055 |
| Tinker | Threshold 2 | 0.017 ± 0.024 | 0.002 ± 0.012 |
| Zheng | Standard | 0.024 ± 0.010 | −0.0005 ± 0.0060 |
| Zheng | Threshold 1 | 0.027 ± 0.011 | −0.0006 ± 0.0062 |
| Zheng | Threshold 2 | 0.031 ± 0.013 | −0.0014 ± 0.0075 |
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . |
|---|---|---|---|
| Hearin | Standard | 0.028 ± 0.010 | −0.0005 ± 0.0054 |
| Hearin | Threshold 1 | 0.024 ± 0.011 | −0.0002 ± 0.0061 |
| Hearin | Threshold 2 | 0.032 ± 0.018 | −0.0002 ± 0.0097 |
| Leauthaud | Standard | 0.030 ± 0.010 | −0.0016 ± 0.0052 |
| Leauthaud | Threshold 1 | 0.029 ± 0.010 | −0.0013 ± 0.0052 |
| Leauthaud | Threshold 2 | 0.023 ± 0.018 | 0.0030 ± 0.0097 |
| Tinker | Standard | 0.038 ± 0.010 | −0.0005 ± 0.0054 |
| Tinker | Threshold 1 | 0.025 ± 0.010 | −0.0013 ± 0.0055 |
| Tinker | Threshold 2 | 0.017 ± 0.024 | 0.002 ± 0.012 |
| Zheng | Standard | 0.024 ± 0.010 | −0.0005 ± 0.0060 |
| Zheng | Threshold 1 | 0.027 ± 0.011 | −0.0006 ± 0.0062 |
| Zheng | Threshold 2 | 0.031 ± 0.013 | −0.0014 ± 0.0075 |
Table F3 provides the FS best-fitting parameters to the DR16 CMASS+eBOSS LRG catalogues, for M+Q and M+Q + H cases. Note that these are the raw results, performed at a given fixed template amplitude. Therefore, the f and biases values need to be re-scaled the template amplitude, to be physically interpreted as cosmology-reference invariant parameters. The rescaling factors are given in the table caption.
Parameters from FS analysis corresponding to |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$| using the power spectrum monopole and quadrupole (M+Q); and also the hexadecapole (M+Q + H) which is the main FS result of this paper. In both cases, the results are obtained with with 50 per cent prior on Anoise. f should be rescaled by the fiducial σ8(α0) value according to equation (40), which for the used template is σ8(α0 = 1.0020) = 0.558 25 (for M+Q + H fit); and σ8(α0 = 1.0081) = 0.555 90 (for the M + Q fit). For reference the σ8(α0 = 1) = 0.559 01.
| Parameter . | Value M + Q . | Value M+Q + H . |
|---|---|---|
| α∥ | 0.9724 ± 0.0496 | 0.9994 ± 0.0357 |
| α⊥ | 1.0265 ± 0.0363 | 1.0033 ± 0.0269 |
| f | 0.892 ± 0.111 | 0.8125 ± 0.0749 |
| |$b_1^{\rm NGC}$| | 2.1466 ± 0.0942 | 2.1851 ± 0.0891 |
| |$b_1^{\rm SGC}$| | 2.1488 ± 0.0881 | 2.1896 ± 0.0828 |
| |$b_2^{\rm NGC}$| | 3.16 ± 3.69 | 2.42 ± 3.71 |
| |$b_2^{\rm SGC}$| | 3.07 ± 2.68 | 3.06 ± 2.71 |
| |$A_{\rm noise}^{\rm NGC}$| | 1.257 ± 0.133 | 1.254 ± 0.140 |
| |$A_{\rm noise}^{\rm SGC}$| | 1.188 ± 0.119 | 1.172 ± 0.120 |
| |$\sigma _{\rm FoG}^{\rm NGC}$| | 3.658 ± 0.604 | 3.757 ± 0.598 |
| |$\sigma _{\rm FoG}^{\rm SGC}$| | 3.563 ± 0.605 | 3.525 ± 0.606 |
| χ2/dof | 38/(52 − 11) | 77/(78 − 11) |
| Parameter . | Value M + Q . | Value M+Q + H . |
|---|---|---|
| α∥ | 0.9724 ± 0.0496 | 0.9994 ± 0.0357 |
| α⊥ | 1.0265 ± 0.0363 | 1.0033 ± 0.0269 |
| f | 0.892 ± 0.111 | 0.8125 ± 0.0749 |
| |$b_1^{\rm NGC}$| | 2.1466 ± 0.0942 | 2.1851 ± 0.0891 |
| |$b_1^{\rm SGC}$| | 2.1488 ± 0.0881 | 2.1896 ± 0.0828 |
| |$b_2^{\rm NGC}$| | 3.16 ± 3.69 | 2.42 ± 3.71 |
| |$b_2^{\rm SGC}$| | 3.07 ± 2.68 | 3.06 ± 2.71 |
| |$A_{\rm noise}^{\rm NGC}$| | 1.257 ± 0.133 | 1.254 ± 0.140 |
| |$A_{\rm noise}^{\rm SGC}$| | 1.188 ± 0.119 | 1.172 ± 0.120 |
| |$\sigma _{\rm FoG}^{\rm NGC}$| | 3.658 ± 0.604 | 3.757 ± 0.598 |
| |$\sigma _{\rm FoG}^{\rm SGC}$| | 3.563 ± 0.605 | 3.525 ± 0.606 |
| χ2/dof | 38/(52 − 11) | 77/(78 − 11) |
Parameters from FS analysis corresponding to |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$| using the power spectrum monopole and quadrupole (M+Q); and also the hexadecapole (M+Q + H) which is the main FS result of this paper. In both cases, the results are obtained with with 50 per cent prior on Anoise. f should be rescaled by the fiducial σ8(α0) value according to equation (40), which for the used template is σ8(α0 = 1.0020) = 0.558 25 (for M+Q + H fit); and σ8(α0 = 1.0081) = 0.555 90 (for the M + Q fit). For reference the σ8(α0 = 1) = 0.559 01.
| Parameter . | Value M + Q . | Value M+Q + H . |
|---|---|---|
| α∥ | 0.9724 ± 0.0496 | 0.9994 ± 0.0357 |
| α⊥ | 1.0265 ± 0.0363 | 1.0033 ± 0.0269 |
| f | 0.892 ± 0.111 | 0.8125 ± 0.0749 |
| |$b_1^{\rm NGC}$| | 2.1466 ± 0.0942 | 2.1851 ± 0.0891 |
| |$b_1^{\rm SGC}$| | 2.1488 ± 0.0881 | 2.1896 ± 0.0828 |
| |$b_2^{\rm NGC}$| | 3.16 ± 3.69 | 2.42 ± 3.71 |
| |$b_2^{\rm SGC}$| | 3.07 ± 2.68 | 3.06 ± 2.71 |
| |$A_{\rm noise}^{\rm NGC}$| | 1.257 ± 0.133 | 1.254 ± 0.140 |
| |$A_{\rm noise}^{\rm SGC}$| | 1.188 ± 0.119 | 1.172 ± 0.120 |
| |$\sigma _{\rm FoG}^{\rm NGC}$| | 3.658 ± 0.604 | 3.757 ± 0.598 |
| |$\sigma _{\rm FoG}^{\rm SGC}$| | 3.563 ± 0.605 | 3.525 ± 0.606 |
| χ2/dof | 38/(52 − 11) | 77/(78 − 11) |
| Parameter . | Value M + Q . | Value M+Q + H . |
|---|---|---|
| α∥ | 0.9724 ± 0.0496 | 0.9994 ± 0.0357 |
| α⊥ | 1.0265 ± 0.0363 | 1.0033 ± 0.0269 |
| f | 0.892 ± 0.111 | 0.8125 ± 0.0749 |
| |$b_1^{\rm NGC}$| | 2.1466 ± 0.0942 | 2.1851 ± 0.0891 |
| |$b_1^{\rm SGC}$| | 2.1488 ± 0.0881 | 2.1896 ± 0.0828 |
| |$b_2^{\rm NGC}$| | 3.16 ± 3.69 | 2.42 ± 3.71 |
| |$b_2^{\rm SGC}$| | 3.07 ± 2.68 | 3.06 ± 2.71 |
| |$A_{\rm noise}^{\rm NGC}$| | 1.257 ± 0.133 | 1.254 ± 0.140 |
| |$A_{\rm noise}^{\rm SGC}$| | 1.188 ± 0.119 | 1.172 ± 0.120 |
| |$\sigma _{\rm FoG}^{\rm NGC}$| | 3.658 ± 0.604 | 3.757 ± 0.598 |
| |$\sigma _{\rm FoG}^{\rm SGC}$| | 3.563 ± 0.605 | 3.525 ± 0.606 |
| χ2/dof | 38/(52 − 11) | 77/(78 − 11) |
Table F4 corresponds to the middle panel of Fig. 10 and displays the impact of the arbitrary choice of cosmology on the post-reconstructed Nseries mocks on the BAO analysis, for both the fit to the mean of the mocks, and the mean of the 84 individual fits.
Impact of the reference cosmology on Nseries mocks. The different cosmology models are listed in Table 1. For |$\boldsymbol{\Theta }_{\rm Nseries}$|, we expect that both α-parameters are 1; for |$\boldsymbol{\Theta }_{\rm fid}$|, we expect |$\alpha _\parallel ^{\rm exp}=0.9875$| and |$\alpha _\perp ^{\rm exp}=0.9787$|; for |$\boldsymbol{\Theta }_X$|, we expect |$\alpha _\parallel ^{\rm exp} = 0.9846$| and |$\alpha _\perp ^{\rm exp} = 0.9620$|; for |$\boldsymbol{\Theta }_Y$|, we expect |$\alpha _\parallel ^{\rm exp} = 0.9543$| and |$\alpha _\perp ^{\rm exp} = 0.9325$|; for |$\boldsymbol{\Theta }_Z$|, we expect |$\alpha _\parallel ^{\rm exp} = 0.9557$| and |$\alpha _\perp ^{\rm exp} = 0.9291$|. We use the same notation of Table 5 where Mean catalogue display the fits to the mean with the error on the mean, and Individual catalogue display the mean of the 84 individual fits reporting the |${\rm rms}/\sqrt{N}$|. The bottom panel of Fig. 10 displays the performance of the results.
| Reference cosmology . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean post-recon | 0.0006 ± 0.0018 | −0.0026 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual post-recon | 0.0010 ± 0.0030 | −0.0027 ± 0.0017 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean post-recon | 0.0023 ± 0.0020 | −0.0065 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual post-recon | 0.0076 ± 0.0026 | −0.0068 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean post-recon | 0.0037 ± 0.0021 | −0.0022 ± 0.0015 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual post-recon | 0.0078 ± 0.0025 | −0.0024 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean post-recon | 0.0055 ± 0.0020 | −0.0078 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual post-recon | 0.0031 ± 0.0026 | −0.0078 ± 0.0016 | 84/84 |
| Reference cosmology . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean post-recon | 0.0006 ± 0.0018 | −0.0026 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual post-recon | 0.0010 ± 0.0030 | −0.0027 ± 0.0017 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean post-recon | 0.0023 ± 0.0020 | −0.0065 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual post-recon | 0.0076 ± 0.0026 | −0.0068 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean post-recon | 0.0037 ± 0.0021 | −0.0022 ± 0.0015 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual post-recon | 0.0078 ± 0.0025 | −0.0024 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean post-recon | 0.0055 ± 0.0020 | −0.0078 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual post-recon | 0.0031 ± 0.0026 | −0.0078 ± 0.0016 | 84/84 |
Impact of the reference cosmology on Nseries mocks. The different cosmology models are listed in Table 1. For |$\boldsymbol{\Theta }_{\rm Nseries}$|, we expect that both α-parameters are 1; for |$\boldsymbol{\Theta }_{\rm fid}$|, we expect |$\alpha _\parallel ^{\rm exp}=0.9875$| and |$\alpha _\perp ^{\rm exp}=0.9787$|; for |$\boldsymbol{\Theta }_X$|, we expect |$\alpha _\parallel ^{\rm exp} = 0.9846$| and |$\alpha _\perp ^{\rm exp} = 0.9620$|; for |$\boldsymbol{\Theta }_Y$|, we expect |$\alpha _\parallel ^{\rm exp} = 0.9543$| and |$\alpha _\perp ^{\rm exp} = 0.9325$|; for |$\boldsymbol{\Theta }_Z$|, we expect |$\alpha _\parallel ^{\rm exp} = 0.9557$| and |$\alpha _\perp ^{\rm exp} = 0.9291$|. We use the same notation of Table 5 where Mean catalogue display the fits to the mean with the error on the mean, and Individual catalogue display the mean of the 84 individual fits reporting the |${\rm rms}/\sqrt{N}$|. The bottom panel of Fig. 10 displays the performance of the results.
| Reference cosmology . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean post-recon | 0.0006 ± 0.0018 | −0.0026 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual post-recon | 0.0010 ± 0.0030 | −0.0027 ± 0.0017 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean post-recon | 0.0023 ± 0.0020 | −0.0065 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual post-recon | 0.0076 ± 0.0026 | −0.0068 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean post-recon | 0.0037 ± 0.0021 | −0.0022 ± 0.0015 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual post-recon | 0.0078 ± 0.0025 | −0.0024 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean post-recon | 0.0055 ± 0.0020 | −0.0078 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual post-recon | 0.0031 ± 0.0026 | −0.0078 ± 0.0016 | 84/84 |
| Reference cosmology . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean post-recon | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual post-recon | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean post-recon | 0.0006 ± 0.0018 | −0.0026 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual post-recon | 0.0010 ± 0.0030 | −0.0027 ± 0.0017 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean post-recon | 0.0023 ± 0.0020 | −0.0065 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual post-recon | 0.0076 ± 0.0026 | −0.0068 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean post-recon | 0.0037 ± 0.0021 | −0.0022 ± 0.0015 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual post-recon | 0.0078 ± 0.0025 | −0.0024 ± 0.0016 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean post-recon | 0.0055 ± 0.0020 | −0.0078 ± 0.0012 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual post-recon | 0.0031 ± 0.0026 | −0.0078 ± 0.0016 | 84/84 |
Table F5 corresponds to the bottom panel of Fig. 10 and lists the impact of the arbitrary choice of cosmology on the Nseries catalogues on the FS type of analysis, for both the fit to the mean of the mocks, and the mean of the 84 individual fits.
Impact of reference cosmology on Nseries mocks for FS analyses. The different cosmology models are listed in Table 1. The expected α values are the same as those from Table F4. In all the cases, we expect to recover the same expected growth of structure, |$f\sigma _8^{\rm exp}=0.4702$|. We use the same notation of Table 5 where Mean catalogue display the fits to the mean with the error on the mean, and individual catalogue display the mean of the 84 individual fits reporting the |${\rm rms}/\sqrt{N}$|. The bottom panel of Fig. 10 displays the performance of the results.
| Reference cosmology . | catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean | 0.0003 ± 0.0031 | −0.0087 ± 0.0019 | −0.0055 ± 0.0040 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual | 0.0060 ± 0.0039 | −0.0084 ± 0.0020 | 0.0107 ± 0.0042 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean | −0.0046 ± 0.0031 | −0.0115 ± 0.0020 | −0.0050 ± 0.0042 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual | 0.0005 ± 0.0039 | −0.0111 ± 0.0019 | 0.0106 ± 0.0049 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean | 0.0028 ± 0.0032 | −0.0062 ± 0.0019 | −0.0054 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual | 0.0102 ± 0.0038 | −0.0064 ± 0.0019 | 0.0004 ± 0.0046 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean | −0.0045 ± 0.0030 | −0.0126 ± 0.0018 | 0.0039 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual | −0.0020 ± 0.0032 | −0.0123 ± 0.0018 | 0.0077 ± 0.0045 | 84/84 |
| Reference cosmology . | catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean | 0.0003 ± 0.0031 | −0.0087 ± 0.0019 | −0.0055 ± 0.0040 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual | 0.0060 ± 0.0039 | −0.0084 ± 0.0020 | 0.0107 ± 0.0042 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean | −0.0046 ± 0.0031 | −0.0115 ± 0.0020 | −0.0050 ± 0.0042 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual | 0.0005 ± 0.0039 | −0.0111 ± 0.0019 | 0.0106 ± 0.0049 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean | 0.0028 ± 0.0032 | −0.0062 ± 0.0019 | −0.0054 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual | 0.0102 ± 0.0038 | −0.0064 ± 0.0019 | 0.0004 ± 0.0046 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean | −0.0045 ± 0.0030 | −0.0126 ± 0.0018 | 0.0039 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual | −0.0020 ± 0.0032 | −0.0123 ± 0.0018 | 0.0077 ± 0.0045 | 84/84 |
Impact of reference cosmology on Nseries mocks for FS analyses. The different cosmology models are listed in Table 1. The expected α values are the same as those from Table F4. In all the cases, we expect to recover the same expected growth of structure, |$f\sigma _8^{\rm exp}=0.4702$|. We use the same notation of Table 5 where Mean catalogue display the fits to the mean with the error on the mean, and individual catalogue display the mean of the 84 individual fits reporting the |${\rm rms}/\sqrt{N}$|. The bottom panel of Fig. 10 displays the performance of the results.
| Reference cosmology . | catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean | 0.0003 ± 0.0031 | −0.0087 ± 0.0019 | −0.0055 ± 0.0040 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual | 0.0060 ± 0.0039 | −0.0084 ± 0.0020 | 0.0107 ± 0.0042 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean | −0.0046 ± 0.0031 | −0.0115 ± 0.0020 | −0.0050 ± 0.0042 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual | 0.0005 ± 0.0039 | −0.0111 ± 0.0019 | 0.0106 ± 0.0049 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean | 0.0028 ± 0.0032 | −0.0062 ± 0.0019 | −0.0054 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual | 0.0102 ± 0.0038 | −0.0064 ± 0.0019 | 0.0004 ± 0.0046 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean | −0.0045 ± 0.0030 | −0.0126 ± 0.0018 | 0.0039 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual | −0.0020 ± 0.0032 | −0.0123 ± 0.0018 | 0.0077 ± 0.0045 | 84/84 |
| Reference cosmology . | catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Mean | 0.0016 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm Nseries}$| | Individual | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Mean | 0.0003 ± 0.0031 | −0.0087 ± 0.0019 | −0.0055 ± 0.0040 | 1/1 |
| |$\boldsymbol{\Theta }_{\rm fid}$| | Individual | 0.0060 ± 0.0039 | −0.0084 ± 0.0020 | 0.0107 ± 0.0042 | 84/84 |
| |$\boldsymbol{\Theta }_X$| | Mean | −0.0046 ± 0.0031 | −0.0115 ± 0.0020 | −0.0050 ± 0.0042 | 1/1 |
| |$\boldsymbol{\Theta }_X$| | Individual | 0.0005 ± 0.0039 | −0.0111 ± 0.0019 | 0.0106 ± 0.0049 | 84/84 |
| |$\boldsymbol{\Theta }_Y$| | Mean | 0.0028 ± 0.0032 | −0.0062 ± 0.0019 | −0.0054 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Y$| | Individual | 0.0102 ± 0.0038 | −0.0064 ± 0.0019 | 0.0004 ± 0.0046 | 84/84 |
| |$\boldsymbol{\Theta }_Z$| | Mean | −0.0045 ± 0.0030 | −0.0126 ± 0.0018 | 0.0039 ± 0.0041 | 1/1 |
| |$\boldsymbol{\Theta }_Z$| | Individual | −0.0020 ± 0.0032 | −0.0123 ± 0.0018 | 0.0077 ± 0.0045 | 84/84 |
Table F6 shows an analogous result displayed by Table F1, but for the FS type of analysis.
Impact of non-periodicity in HOD-mocks for pre-recon catalogues or FS analyses. For simplicity only the fit to the mean is provided.
| Multipoles . | HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|---|
| M+Q + H | Hearin | Sky-cut | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 |
| M+Q + H | Hearin | Cubic box | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| M + Q | Hearin | Sky-cut | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 |
| M + Q | Hearin | Cubic box | 0.022 ± 0.016 | −0.0010 ± 0.0092 | 0.005 ± 0.023 |
| M+Q + H | Leauthaud | Sky-cut | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 |
| M+Q + H | Leauthaud | Cubic box | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| M + Q | Leauthaud | Sky-cut | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 |
| M + Q | Leauthaud | Cubic box | 0.002 ± 0.016 | 0.010 ± 0.010 | 0.022 ± 0.023 |
| M+Q + H | Tinker | Sky-cut | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 |
| M+Q + H | Tinker | Cubic box | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| M + Q | Tinker | Sky-cut | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 |
| M + Q | Tinker | Cubic box | −0.004 ± 0.019 | 0.004 ± 0.011 | 0.025 ± 0.025 |
| Multipoles . | HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|---|
| M+Q + H | Hearin | Sky-cut | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 |
| M+Q + H | Hearin | Cubic box | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| M + Q | Hearin | Sky-cut | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 |
| M + Q | Hearin | Cubic box | 0.022 ± 0.016 | −0.0010 ± 0.0092 | 0.005 ± 0.023 |
| M+Q + H | Leauthaud | Sky-cut | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 |
| M+Q + H | Leauthaud | Cubic box | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| M + Q | Leauthaud | Sky-cut | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 |
| M + Q | Leauthaud | Cubic box | 0.002 ± 0.016 | 0.010 ± 0.010 | 0.022 ± 0.023 |
| M+Q + H | Tinker | Sky-cut | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 |
| M+Q + H | Tinker | Cubic box | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| M + Q | Tinker | Sky-cut | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 |
| M + Q | Tinker | Cubic box | −0.004 ± 0.019 | 0.004 ± 0.011 | 0.025 ± 0.025 |
Impact of non-periodicity in HOD-mocks for pre-recon catalogues or FS analyses. For simplicity only the fit to the mean is provided.
| Multipoles . | HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|---|
| M+Q + H | Hearin | Sky-cut | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 |
| M+Q + H | Hearin | Cubic box | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| M + Q | Hearin | Sky-cut | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 |
| M + Q | Hearin | Cubic box | 0.022 ± 0.016 | −0.0010 ± 0.0092 | 0.005 ± 0.023 |
| M+Q + H | Leauthaud | Sky-cut | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 |
| M+Q + H | Leauthaud | Cubic box | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| M + Q | Leauthaud | Sky-cut | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 |
| M + Q | Leauthaud | Cubic box | 0.002 ± 0.016 | 0.010 ± 0.010 | 0.022 ± 0.023 |
| M+Q + H | Tinker | Sky-cut | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 |
| M+Q + H | Tinker | Cubic box | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| M + Q | Tinker | Sky-cut | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 |
| M + Q | Tinker | Cubic box | −0.004 ± 0.019 | 0.004 ± 0.011 | 0.025 ± 0.025 |
| Multipoles . | HOD-type . | Catalogue . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|---|
| M+Q + H | Hearin | Sky-cut | −0.010 ± 0.013 | −0.0020 ± 0.0089 | 0.019 ± 0.019 |
| M+Q + H | Hearin | Cubic box | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| M + Q | Hearin | Sky-cut | −0.002 ± 0.017 | −0.001 ± 0.011 | 0.009 ± 0.023 |
| M + Q | Hearin | Cubic box | 0.022 ± 0.016 | −0.0010 ± 0.0092 | 0.005 ± 0.023 |
| M+Q + H | Leauthaud | Sky-cut | 0.003 ± 0.014 | −0.0111 ± 0.0094 | −0.004 ± 0.020 |
| M+Q + H | Leauthaud | Cubic box | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| M + Q | Leauthaud | Sky-cut | 0.007 ± 0.018 | −0.006 ± 0.011 | −0.001 ± 0.024 |
| M + Q | Leauthaud | Cubic box | 0.002 ± 0.016 | 0.010 ± 0.010 | 0.022 ± 0.023 |
| M+Q + H | Tinker | Sky-cut | 0.006 ± 0.014 | −0.018 ± 0.011 | −0.007 ± 0.021 |
| M+Q + H | Tinker | Cubic box | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| M + Q | Tinker | Sky-cut | 0.012 ± 0.019 | −0.012 ± 0.013 | −0.005 ± 0.026 |
| M + Q | Tinker | Cubic box | −0.004 ± 0.019 | 0.004 ± 0.011 | 0.025 ± 0.025 |
Table F7 displays the effect on the FS analysis of a broad type of HOD and ‘flavours’ using the OuterRim-HOD mocks, analogously to the results displayed on Table F2 for the BAO type of analysis.
Impact of different HOD types and ‘flavours’ on pre-recon FS fits on cubic boxes without periodic boundary conditions. For simplicity, only fit on the mean is provided where monopole, quadrupole, and hexadecapole are used up to |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$|.
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|
| Hearin | standard | 0.0121 ± 0.0069 | −0.0031 ± 0.0051 | 0.0040 ± 0.0077 |
| Hearin | Threshold 1 | 0.0106 ± 0.0068 | −0.0032 ± 0.0052 | −0.0112 ± 0.0066 |
| Hearin | Threshold 2 | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| Leauthaud | standard | 0.0133 ± 0.0066 | −0.0055 ± 0.0049 | −0.0003 ± 0.0074 |
| Leauthaud | Threshold 1 | 0.0093 ± 0.0064 | −0.0035 ± 0.0046 | −0.0076 ± 0.0069 |
| Leauthaud | Threshold 2 | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| Tinker | standard | 0.0178 ± 0.0068 | −0.0027 ± 0.0050 | 0.0124 ± 0.0084 |
| Tinker | Threshold 1 | 0.0107 ± 0.0066 | −0.0043 ± 0.0049 | −0.0055 ± 0.0065 |
| Tinker | Threshold 2 | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| Zheng | standard | 0.0108 ± 0.0067 | −0.0025 ± 0.0051 | −0.0083 ± 0.0065 |
| Zheng | Threshold 1 | 0.0107 ± 0.0069 | −0.0035 ± 0.0052 | −0.0085 ± 0.0073 |
| Zheng | Threshold 2 | 0.0138 ± 0.0095 | −0.0049 ± 0.0072 | 0.008 ± 0.013 |
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|
| Hearin | standard | 0.0121 ± 0.0069 | −0.0031 ± 0.0051 | 0.0040 ± 0.0077 |
| Hearin | Threshold 1 | 0.0106 ± 0.0068 | −0.0032 ± 0.0052 | −0.0112 ± 0.0066 |
| Hearin | Threshold 2 | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| Leauthaud | standard | 0.0133 ± 0.0066 | −0.0055 ± 0.0049 | −0.0003 ± 0.0074 |
| Leauthaud | Threshold 1 | 0.0093 ± 0.0064 | −0.0035 ± 0.0046 | −0.0076 ± 0.0069 |
| Leauthaud | Threshold 2 | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| Tinker | standard | 0.0178 ± 0.0068 | −0.0027 ± 0.0050 | 0.0124 ± 0.0084 |
| Tinker | Threshold 1 | 0.0107 ± 0.0066 | −0.0043 ± 0.0049 | −0.0055 ± 0.0065 |
| Tinker | Threshold 2 | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| Zheng | standard | 0.0108 ± 0.0067 | −0.0025 ± 0.0051 | −0.0083 ± 0.0065 |
| Zheng | Threshold 1 | 0.0107 ± 0.0069 | −0.0035 ± 0.0052 | −0.0085 ± 0.0073 |
| Zheng | Threshold 2 | 0.0138 ± 0.0095 | −0.0049 ± 0.0072 | 0.008 ± 0.013 |
Impact of different HOD types and ‘flavours’ on pre-recon FS fits on cubic boxes without periodic boundary conditions. For simplicity, only fit on the mean is provided where monopole, quadrupole, and hexadecapole are used up to |$k_{\rm max}=0.15\, \, h\, {\rm Mpc}^{-1}$|.
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|
| Hearin | standard | 0.0121 ± 0.0069 | −0.0031 ± 0.0051 | 0.0040 ± 0.0077 |
| Hearin | Threshold 1 | 0.0106 ± 0.0068 | −0.0032 ± 0.0052 | −0.0112 ± 0.0066 |
| Hearin | Threshold 2 | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| Leauthaud | standard | 0.0133 ± 0.0066 | −0.0055 ± 0.0049 | −0.0003 ± 0.0074 |
| Leauthaud | Threshold 1 | 0.0093 ± 0.0064 | −0.0035 ± 0.0046 | −0.0076 ± 0.0069 |
| Leauthaud | Threshold 2 | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| Tinker | standard | 0.0178 ± 0.0068 | −0.0027 ± 0.0050 | 0.0124 ± 0.0084 |
| Tinker | Threshold 1 | 0.0107 ± 0.0066 | −0.0043 ± 0.0049 | −0.0055 ± 0.0065 |
| Tinker | Threshold 2 | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| Zheng | standard | 0.0108 ± 0.0067 | −0.0025 ± 0.0051 | −0.0083 ± 0.0065 |
| Zheng | Threshold 1 | 0.0107 ± 0.0069 | −0.0035 ± 0.0052 | −0.0085 ± 0.0073 |
| Zheng | Threshold 2 | 0.0138 ± 0.0095 | −0.0049 ± 0.0072 | 0.008 ± 0.013 |
| HOD-type . | HOD-flavour . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . |
|---|---|---|---|---|
| Hearin | standard | 0.0121 ± 0.0069 | −0.0031 ± 0.0051 | 0.0040 ± 0.0077 |
| Hearin | Threshold 1 | 0.0106 ± 0.0068 | −0.0032 ± 0.0052 | −0.0112 ± 0.0066 |
| Hearin | Threshold 2 | 0.010 ± 0.013 | −0.0019 ± 0.0085 | 0.015 ± 0.019 |
| Leauthaud | standard | 0.0133 ± 0.0066 | −0.0055 ± 0.0049 | −0.0003 ± 0.0074 |
| Leauthaud | Threshold 1 | 0.0093 ± 0.0064 | −0.0035 ± 0.0046 | −0.0076 ± 0.0069 |
| Leauthaud | Threshold 2 | −0.003 ± 0.012 | 0.0047 ± 0.0095 | 0.013 ± 0.019 |
| Tinker | standard | 0.0178 ± 0.0068 | −0.0027 ± 0.0050 | 0.0124 ± 0.0084 |
| Tinker | Threshold 1 | 0.0107 ± 0.0066 | −0.0043 ± 0.0049 | −0.0055 ± 0.0065 |
| Tinker | Threshold 2 | 0.004 ± 0.014 | −0.007 ± 0.010 | 0.004 ± 0.021 |
| Zheng | standard | 0.0108 ± 0.0067 | −0.0025 ± 0.0051 | −0.0083 ± 0.0065 |
| Zheng | Threshold 1 | 0.0107 ± 0.0069 | −0.0035 ± 0.0052 | −0.0085 ± 0.0073 |
| Zheng | Threshold 2 | 0.0138 ± 0.0095 | −0.0049 ± 0.0072 | 0.008 ± 0.013 |
Table F8 displays the fits on the Nseries mocks of the BAO post-recon analysis, the FS analysis, and a simultaneous FS and BAO analysis. The reference cosmology chosen in this case is the Nseries own cosmology.
Results from the BAO post-recon only analysis, FS pre-reconstruction analysis, and simultaneous BAO + FS fit (BAO × FS); on the. Nseries mocks. The Nseries cosmology has been used as a reference cosmology. BAO stands for post-recon. For the individual fits, we report the mean and the rms / |$\sqrt{84 }$|, whereas for the ‘Mean’ we report the best fit and the error of the mean. For the BAO only analysis, we use three polynomial terms for describing the broadband. When the simultaneous BAO + FS fit is performed we use five polynomial terms for describing the BAO broadband (see the main text for the full motivation of this approach).
| Mock name . | Type of fit . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean Nseries | BAO × FS | −0.0008 ± 0.0017 | −0.0017 ± 0.0011 | 0.0181 ± 0.0037 | 1/1 |
| Individual Nseries | BAO × FS | 0.0062 ± 0.0024 | −0.0068 ± 0.0015 | 0.0193 ± 0.0041 | 84/84 |
| Mean Nseries | FS only | 0.0015 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | FS only | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | BAO only | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | – | 1/1 |
| Individual Nseries | BAO only | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | – | 84/84 |
| Mock name . | Type of fit . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean Nseries | BAO × FS | −0.0008 ± 0.0017 | −0.0017 ± 0.0011 | 0.0181 ± 0.0037 | 1/1 |
| Individual Nseries | BAO × FS | 0.0062 ± 0.0024 | −0.0068 ± 0.0015 | 0.0193 ± 0.0041 | 84/84 |
| Mean Nseries | FS only | 0.0015 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | FS only | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | BAO only | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | – | 1/1 |
| Individual Nseries | BAO only | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | – | 84/84 |
Results from the BAO post-recon only analysis, FS pre-reconstruction analysis, and simultaneous BAO + FS fit (BAO × FS); on the. Nseries mocks. The Nseries cosmology has been used as a reference cosmology. BAO stands for post-recon. For the individual fits, we report the mean and the rms / |$\sqrt{84 }$|, whereas for the ‘Mean’ we report the best fit and the error of the mean. For the BAO only analysis, we use three polynomial terms for describing the broadband. When the simultaneous BAO + FS fit is performed we use five polynomial terms for describing the BAO broadband (see the main text for the full motivation of this approach).
| Mock name . | Type of fit . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean Nseries | BAO × FS | −0.0008 ± 0.0017 | −0.0017 ± 0.0011 | 0.0181 ± 0.0037 | 1/1 |
| Individual Nseries | BAO × FS | 0.0062 ± 0.0024 | −0.0068 ± 0.0015 | 0.0193 ± 0.0041 | 84/84 |
| Mean Nseries | FS only | 0.0015 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | FS only | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | BAO only | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | – | 1/1 |
| Individual Nseries | BAO only | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | – | 84/84 |
| Mock name . | Type of fit . | |$\alpha _\parallel -\alpha _\parallel ^{\rm exp}$| . | |$\alpha _\perp -\alpha _\perp ^{\rm exp}$| . | |$f\sigma _8-f\sigma _8^{\rm exp}$| . | Ndet/Ntot . |
|---|---|---|---|---|---|
| Mean Nseries | BAO × FS | −0.0008 ± 0.0017 | −0.0017 ± 0.0011 | 0.0181 ± 0.0037 | 1/1 |
| Individual Nseries | BAO × FS | 0.0062 ± 0.0024 | −0.0068 ± 0.0015 | 0.0193 ± 0.0041 | 84/84 |
| Mean Nseries | FS only | 0.0015 ± 0.0032 | −0.0095 ± 0.0020 | −0.0038 ± 0.0041 | 1/1 |
| Individual Nseries | FS only | 0.0082 ± 0.0040 | −0.0089 ± 0.0021 | 0.0073 ± 0.0043 | 84/84 |
| Mean Nseries | BAO only | −0.0048 ± 0.0019 | 0.0005 ± 0.0010 | – | 1/1 |
| Individual Nseries | BAO only | −0.0016 ± 0.0033 | −0.0030 ± 0.0018 | – | 84/84 |



