-
PDF
- Split View
-
Views
-
Cite
Cite
Hajime Fukushima, Hidenobu Yajima, Kazuyuki Sugimura, Takashi Hosokawa, Kazuyuki Omukai, Tomoaki Matsumoto, Star cluster formation and cloud dispersal by radiative feedback: dependence on metallicity and compactness, Monthly Notices of the Royal Astronomical Society, Volume 497, Issue 3, September 2020, Pages 3830–3845, https://doi.org/10.1093/mnras/staa2062
Close - Share Icon Share
ABSTRACT
We study star cluster formation in various environments with different metallicities and column densities by performing a suite of 3D radiation hydrodynamics simulations. We find that the photoionization feedback from massive stars controls the star formation efficiency (SFE) in a star-forming cloud, and its impact sensitively depends on the gas metallicity Z and initial cloud surface density Σ. At Z = 1 Z⊙, SFE increases as a power law from 0.03 at Σ = 10 M⊙ pc−2 to 0.3 at |$\Sigma = 300\,\mathrm{M}_{\odot }\, {\rm pc^{-2}}$|. In low-metallicity cases |$10^{-2}\!-\!10^{-1}\, \mathrm{Z}_{\odot }$|, star clusters form from atomic warm gases because the molecule formation time is not short enough with respect to the cooling or dynamical time. In addition, the whole cloud is disrupted more easily by expanding H ii bubbles that have higher temperature owing to less efficient cooling. With smaller dust attenuation, the ionizing radiation feedback from nearby massive stars is stronger and terminate star formation in dense clumps. These effects result in inefficient star formation in low-metallicity environments: the SFE drops by a factor of ∼3 at Z = 10−2 Z⊙ compared to the results for Z = 1 Z⊙, regardless of Σ. Newborn star clusters are also gravitationally less bound. We further develop a new semi-analytical model that can reproduce the simulation results well, particularly the observed dependencies of the SFEs on the cloud surface densities and metallicities.
1 INTRODUCTION
The formation of massive stars is an essential factor in understanding the cosmic star formation history (Madau & Dickinson 2014) and galactic dynamics (Pillepich et al. 2018). Stellar feedback from them regulates the total star formation rate within a galaxy (e.g. Schaye et al. 2010; Wise et al. 2012; Hasegawa & Semelin 2013; Yajima et al. 2017) and induce galactic outflow (e.g. Heckman, Armus & Miley 1990; Heckman et al. 2015). Ionizing radiation from them destroys parent clouds and leaks out to the interstellar and intergalactic space (Kim, Kim & Ostriker 2019; He, Ricotti & Geen 2020). Most massive stars are known to be born as members of clusters in the Milky Way (e.g. Gvaramadze & Bomans 2008; Schilbach & Röser 2008). On the other hand, the origin of field massive stars in dwarf galaxies, such as Small Magellanic Cloud, is still debated (e.g. Lamb et al. 2016; Ramachandran et al. 2019). The formation processes of star clusters and massive stars have not been fully understood yet.
The star formation efficiency (SFE) is a pivotal quantity in the star-cluster formation, as it determines whether a newborn cluster remains gravitationally bound after the cloud dispersal. As suggested by observations of nearby galaxies, the star formation in the entire galaxy proceeds slowly with the depletion time-scale ∼1 Gyr (e.g. Kennicutt 1998; Bigiel et al. 2008; Momose et al. 2013). On the other hand, the star formation in an individual giant molecular cloud only lasts for ∼10 Myr (Hartmann, Ballesteros-Paredes & Bergin 2001; Fukui & Kawamura 2010) by considering observed numbers of GMCs in local galaxies (e.g. Chevance et al. 2020). This implies that only a small fraction of the molecular gas is converted into stars and the rest returns into an interstellar or intergalactic medium. Recently, Kruijssen et al. (2019) showed that the lifetime of GMCs are about one dynamical time, and the SFE is only a few per cent, by analysing the spatial de-correlation between young stars and star-forming regions in the spiral galaxy NGC 300. They indicated that GMCs are disrupted before the end of the lifetimes of OB stars, and thus pre-supernova feedback, such as ultraviolet (UV) radiation feedback or stellar winds, regulated star formation in GMCs.
Extreme ultraviolet (EUV; 13.6 eV ≤ hν ≲ 1 keV) radiation from massive stars creates H ii bubbles and heat up the gas to ∼104 K. The H ii bubbles expand rapidly because of the high thermal pressure so that heated materials are photoevaporated against the gravitational pull from the gas and stars. Based on simple analytical models, previous studies suggested that the radiative feedback suppresses star formation in GMCs, resulting in the low SFEs (e.g. Williams & McKee 1997; Matzner 2002; Krumholz, Matzner & McKee 2006; Kim, Kim & Ostriker 2016). Fall, Krumholz & Matzner (2010) derived an analytical expression for the SFE as a function of the surface density of the clouds. In reality, however, the supersonic turbulent motion shapes hierarchical cloud structures. H ii regions forming around newborn clusters expand across such complex structures and finally destroy the GMCs.
Numerical simulations have been utilized (e.g. Vázquez-Semadeni et al. 2010; Dale, Ercolano & Bonnell 2012) to investigate the star cluster formation and cloud dispersal through the realistic evolution. Geen, Soler & Hennebelle (2017) showed the disruption of molecular clouds due to the radiative feedback by using radiation hydrodynamics (RHD) simulations with a diffuse approximation for the radiative transfer (ramses-rt: Rosdahl et al. 2013). They showed that the radiative feedback quenches the star formation immediately, and the SFE increases with increasing cloud column density. Using the same simulation code, He, Ricotti & Geen (2019) investigated this problem in a wider parameter range of initial gas clouds and showed that the massive-end slope of simulated sink mass function was similar to that of Salpeter-like initial mass function.
Recently, Kim, Kim & Ostriker (2018) showed the cloud dispersal occurred within 2–10 Myr after the onset of radiative feedback using the RHD simulations with a ray-tracing scheme. They found a close relationship between the SFEs and the surface densities of gas clouds. However, their simulations were limited to the clouds with metallicity Z = 1 Z⊙. Varying the metallicity potentially changes the star formation and feedback processes. For instance, a smaller amount of dust grains results in less attenuation of the stellar UV radiation, which strengthens the feedback effect (e.g. Fukushima et al. 2020).
In this paper, we study the star-cluster formation and resulting cloud dispersal for various cases with metallicities Z = 10−2−1 Z⊙. We perform 3D RHD simulations with sfumato-rt (Sugimura et al. 2020), an Eulerian adaptive mesh refinement (AMR) hydrodynamics code (Matsumoto 2007) coupled with the radiative transfer solver using the ray-tracing method. Also, we calculate the gas temperature considering metal and dust cooling, while Kim et al. (2018) assumed the temperature with an approximation based on local ionization degree. The temperature of ionized gas decreases as the metallicity increases due to the metal-line cooling, e.g. O ii and O iii (Osterbrock & Ferland 2006). As discussed in He et al. (2019), an H ii bubble expands earlier at lower metallicities, resulting in the shorter lifetime of the clouds.
In this work, we consistently solve the thermal and chemical states of the neutral and molecular gases, from which stars form. With Z ≳ 10−2 Z⊙, CO molecules (nH < 105 cm−3) and dust grains (nH > 105 cm−3) are efficient coolant for the molecular gas (e.g. Omukai et al. 2005), with which the temperature could drop to the CMB value. The atomic gas also cools mainly via O i and C ii fine-structure line emission. Far-ultraviolet (FUV; 6.0 eV ≤ hν ≤ 13.6 eV) photons are the dominant heating sources for the neutral gas via the photodissociation of hydrogen molecules and photoelectric heating of dust grains. As a result, the H ii bubbles are surrounded by a warm neutral layer where the temperature is raised up to a few 100 K in the case of Z = Z⊙ (so-called the photodissociation region or PDR; e.g. Hollenbach & Tielens 1999; Hosokawa & Inutsuka 2005, 2006). Our simulations show that at very low metallicity of Z = 10−2 Z⊙ the whole star-forming clouds are mostly dominated by such warm atomic gases, and that massive star clusters directly form from the atomic clouds.
We organize the rest of the paper as follows. In Section 2, we describe the numerical method and set-up of our simulations. We present our simulation results in Section 3. We then develop a semi-analytical model that helps us to interpret numerical results in Section 4. Section 5 is for summary and discussions. We describe the details of the numerical simulations and the fitting formula of the fraction of hydrogen ionization in an H ii region in Appendices A and B.
2 NUMERICAL METHOD
We perform RHD simulations with sfumato-rt (Sugimura et al. 2020), a modified version of the self-gravitational magnetohydrodynamics code with AMR, sfumato (Matsumoto 2007; Matsumoto, Dobashi & Shimoikura 2015). sfumato-rt has been developed to solve radiative transfer with the adaptive ray-tracing method (Abel & Wandelt 2002) and non-equilibrium chemistry of the primordial gas. For the current purpose, we further add the effects of heavy elements (e.g. dust grains, atomic carbon, oxygen, etc.) as described in Section 2.1.
2.1 Chemical and thermal processes
We update the chemistry module of sfumato-rt to calculate the chemical and thermal evolution of the gas. We consider the chemical network of 11 species: |$\rm H$|, |$\rm H_2$|, |$\rm H^{-}$|, |$\rm H^{+}$|, |$\rm H_{2}^{+}$|, |$\rm e$|, |$\rm CO$|, C ii, O i, O ii, and O iii. To follow the CO formation, we adopt the simple chemical network of Nelson & Langer (1997). In this model, we only explicitly include C ii and CO as carbon species. CO is assumed to form via hydrocarbon radicals without C i in the chemical network. Glover & Clark (2012b) and Gong, Ostriker & Wolfire (2017) showed limitations of such a simplified treatment and provided the alternative extended network. However, our qualitative results of the cluster formation and cloud dispersal do not rely on those details because C ii becomes the dominant coolant instead of CO molecules (e.g. Glover & Clark 2012a). As in Fukushima et al. (2020), we assume that the neutral fraction of oxygen is the same as hydrogen and that O ii and O iii are in the chemical equilibrium with photoionization and recombination. The metal-line cooling by O ii and O iii becomes the dominant coolant in H ii regions at metallicity as high as Z = 1 Z⊙.
We set the temperature floor at T = 10 K in our simulations, supposing the CMB temperature at the redshift z ≃ 2.5. This floor does not affect our results because the gas temperature is normally much higher than the floor value, particularly in low-metallicity cases. We do not consider stellar UV background radiation, which would permeate into the cloud externally. We discuss this effect later in Section 4.1.
2.2 Sink particles and radiation sources
We employ the sink particle technique to follow long-term evolution without resolving very dense structures by adding finer grid refinement levels. We insert a sink particle in a mesh that satisfies the following conditions (Federrath et al. 2010; Matsumoto et al. 2015): (1) the gas density is above the threshold value; (2) the gravitational potential is a local minimum, (3) the velocity divergence |$\nabla \cdot \boldsymbol {v}$| and all the eigenvalues of the velocity gradient tensor |$\nabla \boldsymbol {v}$| are negative; and (4) the sum of the thermal, kinetic, and gravitational energies inside the sink radius is negative (Eth + Ekin + Egr < 0). We determine the density threshold in a way proposed by Gong & Ostriker (2013), as in Kim et al. (2018). Assuming the density profile of Larson–Penston solution (Larson 1969; Penston 1969) around the density peak, we set the density threshold as |$\rho _{\rm thr} = 8.86 c_{\rm s}^2/(\pi G \Delta x^2)=5.34\times 10^{-19}\,{\rm g \, cm^{-3}}$|, where Δx is the minimum mesh size (Δx = 0.078 pc) and cs is the sound speed of gas with temperature T = 20 K. In practice, if the gas temperature is higher than 20 K, the condition (4) of the sink creation is not satisfied at ρthr and the gas density becomes higher than ρthr until all of the conditions are fulfilled. Therefore, the threshold density ρthr should be regarded as the lower limit for the sink creation. We set the sink radius rsink = 2Δx and merge nearby sink particles if their separation distances are smaller than 2rsink. The velocity of the merged sink particles is determined from momentum conservation.
We regard each sink particle as a star cluster, as we cannot resolve individual stars due to high computational cost, and calculate the transfer of radiation emitted from each cluster particle. To evaluate the luminosity and spectrum of the star cluster, we take the average of the stellar isochrone given by Chen et al. (2015), where the Chabrier IMF (Chabrier 2003) with a stellar-mass range from 0.1 to 150 M⊙ is used. In our simulations, the duration time of star formation is on the order of Myr, and thus we use their isochrone at t = 1 Myr. We assume that low-mass cluster particles with <50 M⊙ do not emit ionizing photons, neglecting the weak contributions from the smaller clusters. This is a reasonable approximation as the expected number of massive stars (≳10 M⊙) is less than unity for such small clusters. With this procedure, we significantly reduce the computational costs of solving radiation transfer.
2.3 Initial conditions
Table 1 summarizes the models considered in this paper. We set uniform density spheres with turbulent velocities as the initial conditions. We consider five different clouds with masses Mcl = 104 and 105 M⊙ and size |$R_{\rm cl}=10\, \!-\!\, 40\,{\rm pc}$|, which are consistent with the observed properties of galactic and extragalactic GMCs (e.g. Faesi, Lada & Forbrich 2018). In Table 1, the surface density is defined as |$\Sigma = M_{\rm cl}/ (\pi R_{\rm cl}^2)$|. The gas metallicity is assumed to be the solar value in the fiducial model, but we also consider lower metallicity environments with 10−2 and 10−1 Z⊙. To see the impact of the individual feedback effect, we also simulate the cases where we only consider either photoionization (M5R20Z0PI) or radiation pressure induced by dust grains (M5R20Z0RP) for a star-forming cloud with (Mcl, Rcl, Z) = (105M⊙, 20pc, 1Z⊙). We set the initial gas temperature of 20 K irrespective of metallicity, which is the approximate value of collapsing clouds when the central density reaches |$n_{\rm ini}\sim 10 \, \!-\!\, 10^3 \,{\rm cm^{-3}}$| (Omukai et al. 2005), the initial values in our simulations. Note, however, that the initial turbulent velocity is supersonic, as we will describe next, and thus the dynamics of the clouds are almost independent of the initial gas temperature. We also assume the atomic gas at the initial state. We set the abundance of hydrogen molecules is |$y_{\rm H_2} = 10^{-3}$|,1 and other species are in atomic states. This assumption is motivated by theoretical prediction for low-metallicity star-forming regions (Krumholz 2012). On the other hand, observations show that the star-forming clouds are almost fully molecular at Z = 1 Z⊙. In our simulations, molecules rapidly form in high-density parts within the clouds before the first cluster particle appears. The star formation then mostly occurs in the molecular clouds surrounded by rarefied atomic envelope. We also show that this is not necessarily the case for lower metallicity cases, where star clusters are formed in almost atomic clouds.
| Model . | |$M_{\rm cl} \, ( \, \mathrm{M}_{\odot } \, )$| . | |$R_{\rm cl}\, ( \, {\rm pc} \, )$| . | |$Z \, ( \, \mathrm{Z}_{\odot } \, )$| . | |$n_{\rm ini} \, ( \, {\rm cm^{-3}} \, )$| . | |$\Sigma \, (\, \mathrm{M}_{\odot } \, {\rm pc^{-2}} \, )$| . | |$\sigma _0 \, ( \, {\rm km s^{-1}} \, )$| . | |$t_{\rm ff} \, ( \, {\rm Myr} \, )$| . | lmax . | Feedback . |
|---|---|---|---|---|---|---|---|---|---|
| M4R10Z0 | 104 | 10 | 1 | 70 | 32 | 1.1 | 5.2 | 3 | PIa, RPb |
| M4R20Z0 | 104 | 20 | 1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z0 | 105 | 10 | 1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z0 | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z0 | 105 | 40 | 1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-1 | 104 | 10 | 10−1 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-1 | 104 | 20 | 10−1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-1 | 105 | 10 | 10−1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-1 | 105 | 20 | 10−1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-1 | 105 | 40 | 10−1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-2 | 104 | 10 | 10−2 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-2 | 104 | 20 | 10−2 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-2 | 105 | 10 | 10−2 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-2 | 105 | 20 | 10−2 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-2 | 105 | 40 | 10−2 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M5R20Z0PI | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI |
| M5R20Z0RP | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | RP |
| Model . | |$M_{\rm cl} \, ( \, \mathrm{M}_{\odot } \, )$| . | |$R_{\rm cl}\, ( \, {\rm pc} \, )$| . | |$Z \, ( \, \mathrm{Z}_{\odot } \, )$| . | |$n_{\rm ini} \, ( \, {\rm cm^{-3}} \, )$| . | |$\Sigma \, (\, \mathrm{M}_{\odot } \, {\rm pc^{-2}} \, )$| . | |$\sigma _0 \, ( \, {\rm km s^{-1}} \, )$| . | |$t_{\rm ff} \, ( \, {\rm Myr} \, )$| . | lmax . | Feedback . |
|---|---|---|---|---|---|---|---|---|---|
| M4R10Z0 | 104 | 10 | 1 | 70 | 32 | 1.1 | 5.2 | 3 | PIa, RPb |
| M4R20Z0 | 104 | 20 | 1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z0 | 105 | 10 | 1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z0 | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z0 | 105 | 40 | 1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-1 | 104 | 10 | 10−1 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-1 | 104 | 20 | 10−1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-1 | 105 | 10 | 10−1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-1 | 105 | 20 | 10−1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-1 | 105 | 40 | 10−1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-2 | 104 | 10 | 10−2 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-2 | 104 | 20 | 10−2 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-2 | 105 | 10 | 10−2 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-2 | 105 | 20 | 10−2 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-2 | 105 | 40 | 10−2 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M5R20Z0PI | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI |
| M5R20Z0RP | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | RP |
Notes. Column 1: model names, Column 2: cloud masses, Column 3: cloud radii, Column 4: metallicities, Column5: initial number densities, Column 6: surface densities, Column 7: 3D velocity dispersions, Column 8: free fall times, Column 9: maximum refinement levels.
a‘PI’ represents photoionization feedback.
b‘RP’ represents radiation-pressure feedback.
| Model . | |$M_{\rm cl} \, ( \, \mathrm{M}_{\odot } \, )$| . | |$R_{\rm cl}\, ( \, {\rm pc} \, )$| . | |$Z \, ( \, \mathrm{Z}_{\odot } \, )$| . | |$n_{\rm ini} \, ( \, {\rm cm^{-3}} \, )$| . | |$\Sigma \, (\, \mathrm{M}_{\odot } \, {\rm pc^{-2}} \, )$| . | |$\sigma _0 \, ( \, {\rm km s^{-1}} \, )$| . | |$t_{\rm ff} \, ( \, {\rm Myr} \, )$| . | lmax . | Feedback . |
|---|---|---|---|---|---|---|---|---|---|
| M4R10Z0 | 104 | 10 | 1 | 70 | 32 | 1.1 | 5.2 | 3 | PIa, RPb |
| M4R20Z0 | 104 | 20 | 1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z0 | 105 | 10 | 1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z0 | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z0 | 105 | 40 | 1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-1 | 104 | 10 | 10−1 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-1 | 104 | 20 | 10−1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-1 | 105 | 10 | 10−1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-1 | 105 | 20 | 10−1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-1 | 105 | 40 | 10−1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-2 | 104 | 10 | 10−2 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-2 | 104 | 20 | 10−2 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-2 | 105 | 10 | 10−2 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-2 | 105 | 20 | 10−2 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-2 | 105 | 40 | 10−2 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M5R20Z0PI | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI |
| M5R20Z0RP | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | RP |
| Model . | |$M_{\rm cl} \, ( \, \mathrm{M}_{\odot } \, )$| . | |$R_{\rm cl}\, ( \, {\rm pc} \, )$| . | |$Z \, ( \, \mathrm{Z}_{\odot } \, )$| . | |$n_{\rm ini} \, ( \, {\rm cm^{-3}} \, )$| . | |$\Sigma \, (\, \mathrm{M}_{\odot } \, {\rm pc^{-2}} \, )$| . | |$\sigma _0 \, ( \, {\rm km s^{-1}} \, )$| . | |$t_{\rm ff} \, ( \, {\rm Myr} \, )$| . | lmax . | Feedback . |
|---|---|---|---|---|---|---|---|---|---|
| M4R10Z0 | 104 | 10 | 1 | 70 | 32 | 1.1 | 5.2 | 3 | PIa, RPb |
| M4R20Z0 | 104 | 20 | 1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z0 | 105 | 10 | 1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z0 | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z0 | 105 | 40 | 1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-1 | 104 | 10 | 10−1 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-1 | 104 | 20 | 10−1 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-1 | 105 | 10 | 10−1 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-1 | 105 | 20 | 10−1 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-1 | 105 | 40 | 10−1 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M4R10Z-2 | 104 | 10 | 10−2 | 70 | 32 | 1.1 | 5.2 | 3 | PI, RP |
| M4R20Z-2 | 104 | 20 | 10−2 | 8.7 | 8 | 0.80 | 15 | 4 | PI, RP |
| M5R10Z-2 | 105 | 10 | 10−2 | 700 | 320 | 3.6 | 1.7 | 3 | PI, RP |
| M5R20Z-2 | 105 | 20 | 10−2 | 87 | 80 | 2.5 | 4.7 | 4 | PI, RP |
| M5R40Z-2 | 105 | 40 | 10−2 | 11 | 20 | 1.8 | 13 | 5 | PI, RP |
| M5R20Z0PI | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | PI |
| M5R20Z0RP | 105 | 20 | 1 | 87 | 80 | 2.5 | 4.7 | 4 | RP |
Notes. Column 1: model names, Column 2: cloud masses, Column 3: cloud radii, Column 4: metallicities, Column5: initial number densities, Column 6: surface densities, Column 7: 3D velocity dispersions, Column 8: free fall times, Column 9: maximum refinement levels.
a‘PI’ represents photoionization feedback.
b‘RP’ represents radiation-pressure feedback.
3 RESULTS
We describe the results of our simulations in this section. In Section 3.1, we show the time evolution of the cloud being destroyed by the radiative feedback from a newborn star cluster, first for the fiducial solar-metallicity model and then for the low-metallicity model with Z = 10−2 Z⊙ (models M5R20Z0 and M5R20Z-2 in Table 1). In Section 3.2, we present the dependences of the SFEs and the time-scale until star formation ceases on the cloud surface density and metallicity, obtained from all the examined cases. In Section 3.3, we show the time evolution of the half-mass radius and the mass distribution of star cluster particles to investigate the metallicity dependence of the gravitational boundness of the newborn clusters.
3.1 Star cluster formation and cloud dispersal
3.1.1 Fiducial solar-metallicity model
We first present the case with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1Z⊙) as the fiducial model, which has the moderate initial cloud surface density Σ ≃ 80 M⊙ pc−2 (see M5R20Z0 in Table 1). Fig. 1 shows the evolution of the surface density Σ, temperature T on the xy-plane of z = 0, the column densities of |$\rm H_{2}$| (|$N_{\rm H_2}$|) and |$\rm CO$| (NCO). In Fig. 2, we show the volume rendering of the number density, together with the positions of star cluster particles and ionization front at the same snapshots as in Fig. 1.
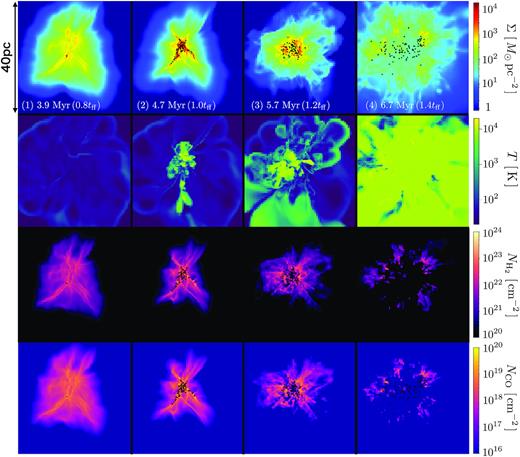
The cloud dispersal and formation of the star cluster for the fiducial model with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1Z⊙). We plot the surface density, temperature (on a slice) and the column densities of |$\rm H_{2}$| and |$\rm CO$| molecules from top to bottom. The four panels at each row show the snapshots at the epochs of t = 3.9, 4.7, 5.7, and 6.3 Myr. The black dots represent the positions of the star cluster particles.

3D volume rendering of the density field, together with the ionization fronts (green surface) where the ionization degree is 0.8, for the same case as in Fig. 1 with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1 Z⊙). Each panel shows the snapshot at the same epochs as in Fig. 1. The white dots in the panel (4) represent the positions of the star cluster particles. The box size is 40 pc on a side.
Early on, the turbulent motions and self-gravity control the evolution of the cloud. Sheet-like structures are induced by turbulent motions. At the intersection of these sheets, filamentary density structures appear. Then, the gas density gradually increases along the filaments due to self-gravity. At this time, the gas temperature is generally less than 30 K because of the cooling by heavy elements (C ii, O i, and CO). The first star-cluster particle forms in the central region of the cloud when the elapsed time of the simulation is 3.8 Myr (Figs 1-1, 2-1). After that, stars continuously form along the filaments in the central 10 pc region of the cloud, as shown in the snapshot at 4.7 Myr, which is equal to one free-fall time of the cloud, tff (Figs 1-2, 2-2). Ionizing photons emitted by the stars begin to form H ii regions, which expand outwards due to enhanced thermal pressure of the ionized gas with 8000–104 K. The ionization fronts propagate in gap regions between the filament structures since H ii regions expand more quickly at lower densities. The filamentary structures are not disrupted by photoionization, but the expansion of H ii regions starts to push them out (5.7 Myr, Figs 1-3, 2-3). Finally, most of them are swept out and the star formation is quenched at 6.7 Myr (Figs 1-4, 2-4). Even though the total emissivity of ionizing photons is large enough to completely ionize all the gas in the initial homogeneous cloud, H ii regions cannot spread to the entire domains, and some filamentary structures survive until the final time of the simulation.
As the collapse of the cloud proceeds, |$\rm H_2$| and CO molecules gradually form in dense regions. In the snapshots at 3.9 and 4.7 Myr of Fig. 1, |$\rm H_2$| and CO molecules form in the entire region of the cloud. These molecules, however, cannot survive except in dense structures after FUV photons from stars begin to photodissociate them. Therefore, the column densities of |$\rm H_2$| and CO molecules only trace the dense filamentary structures in the snapshots at 5.7 and 6.7 Myr of Fig. 1.
The top panel of Fig. 3 shows the time evolution of the mass in each component, i.e. the stars, neutral, molecular, and ionized gases. Here, the neutral gas is defined as the neutral fraction of hydrogen is higher than 0.9. Hydrogen molecules form via the dust surface reaction, which increases the amount of |$\rm H_2$| to 0.6 times the cloud mass at 4.5 Myr. After that, the stellar mass grows while the |$\rm H_2$| mass decreases due to the photodissociation by stellar FUV radiation. The ionized gas emerges as soon as the star formation begins, but its mass is kept small until it rapidly increases at 6.5 Myr as the H ii regions expand and quench the star formation. At the final step of the simulation, clumps that contain the residual neutral component are being ionized gradually, without forming stars anymore within them.
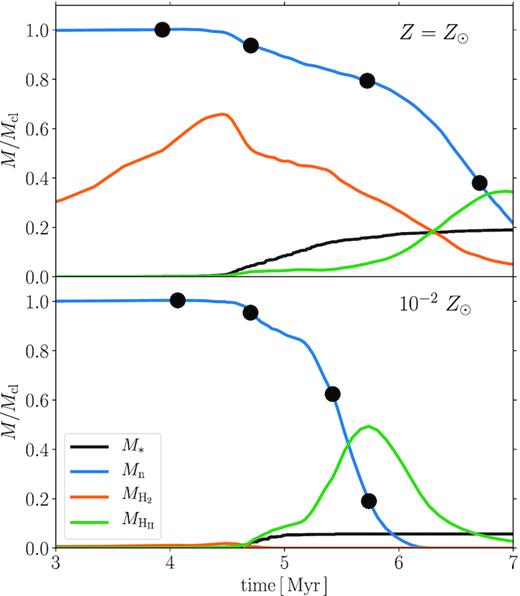
The time evolution of the mass of each component in the cluster-forming clouds with mass Mcl = 105 M⊙, radius Rcl = 20 pc, and metallicity Z = 1 Z⊙ (top) and 10−2 Z⊙ (bottom). Each line represents the total stellar mass M* (black), neutral gas mass Mn (blue), |$\rm H_2$| molecule mass (orange), and ionized gas mass |$M_{\rm H\,{\small II}}$| (green). The filled circles mark the four epochs for which we show the snapshots in Figs 1 and 2.
In the above case, star formation starts at 3.8 Myr and is quenched at 6.7 Myr. Hence, the duration of the star formation (∼3 Myr) is less than the free-fall time of the cloud (∼4.7 Myr). The SFE defined by the final stellar mass normalized by the initial cloud mass is 19 per cent. Kim et al. (2018) adopted a similar set-up, although they use α = 2.0 (see equation 8) as the initial condition. The stronger turbulent field suppresses the star formation more effectively, but the resulting SFE is in the same order of 10 per cent. On the other hand, He et al. (2019) adopted centrally concentrated density profiles and considered magnetic fields. Nevertheless, the SFEs in their simulations have similar values to ours. In our simulations, the clouds collapse in a self-similar fashion (Larson 1969) in the early stages because the turbulent motion cannot support the collapsing clouds with α = 0.5. When the star formation takes place, the density structure resembles the power-law profile with the high-density core at the centre as in the initial set-up of He et al. (2019). Besides, they adopted very similar strength of turbulent motions to our simulations (α = 0.4) and magnetic fields weaker than the turbulence. Therefore, the small difference in the SFEs might be attributable to the similar virial parameter α.
3.1.2 Low-metallicity model with Z = 10−2 Z⊙
Next, we consider the low-metallicity case (M5R20Z-2 in Table 1) with Z = 10−2 Z⊙ to examine the metallicity dependence of the evolution. Figs 4 and 5 illustrate the evolution for this case in the same styles as in Figs 1 and 2, respectively. In the early epoch, the turbulent motion gives the dominant contribution. The overall evolution looks similar to that in the fiducial case with Z = 1 Z⊙ until the first star particle forms at 4.0 Myr (Figs 4-1, 5-1), even though the metal cooling is inefficient. Once star formation occurs, H ii regions start to expand into low-density regions at 4.7 Myr (Figs 4-2, 5-2). Unlike the case with Z = 1 Z⊙, dense filaments are easily photoionized, and they cannot survive around the H ii region. The neutral gas is pushed out all at once, and star formation is completely quenched at 5.4 Myr (Figs 4-3, 5-3). Finally, the H ii regions spread over the entire cloud and complete the photoevaporation of the gas inside the cloud at 5.7 Myr (Figs 4-4, 5-4).
Only small amounts of |$\rm H_2$| and CO molecules form along the filaments in the early phase of the cloud collapse, but the stellar FUV photons easily dissociate them. As shown in Fig. 4, |$\rm H_2$| and CO molecules completely disappear after one free-fall time unlike for the cloud with Z = 1 Z⊙ (see Fig. 4-2). The cloud becomes dark in CO lines soon after the star formation begins.
In the bottom panel of Fig. 3, we show the time evolution of the mass in each component for the case with Z = 10−2 Z⊙. We see that the |$\rm H_2$| mass is much lower than that for the case with Z = 1 Z⊙ throughout the evolution. Since |$\rm H_2$| formation on the dust grains is inefficient due to lower metallicity (and hence lower dust abundance), most of the gas remains atomic from the beginning of the simulation. In this case, the star cluster formation occurs in an almost atomic cloud rather than in a molecular cloud (Krumholz 2012). Meanwhile, the ionized gas mass increases until the ionized gas is finally evaporated from the cloud. The star formation stops at 5 Myr, with the duration of star formation ∼1 Myr, much shorter than in the case with Z = 1 Z⊙. The SFE is 5 per cent and smaller than that for Z = 1 Z⊙ by a factor of ∼3. He et al. (2019) also performed one simulation run assuming Z = 1/40 Z⊙, and they obtained a similar reduction rate of the SFE.
3.1.3 Radiation pressure on dust grains
In Sections 3.1.1 and 3.1.2, we have seen that the expansion of H ii regions quenches star formation, while the radiation pressure on dust grains also affects the gas motion. Here, we investigate the individual effects of photoionization and radiation pressure on star formation separately. Fig. 6 shows the time evolution of total stellar masses in the cases where we only consider either photoionization (M5R20Z0PI, the dashed line) or radiation pressure (M5R20Z0RP, the dot–dashed line). With only photoionization, star formation starts at ∼4.5 Myr, and continues until ∼7 Myr. The star formation history is almost the same as in the fiducial case, where we include both photoionization and radiation pressure effects. On the other hand, with only radiation pressure effect the SFE is very high exceeding 0.8. This result is consistent with the simulation of Raskutti, Ostriker & Skinner (2016) at α = 0.4. This demonstrates that the photoionization feedback plays the leading role in regulating star formation.
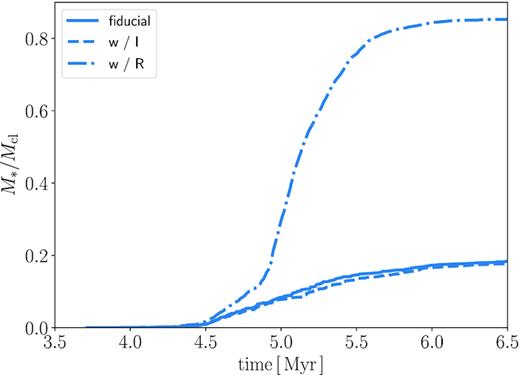
Impact of photoionization and radiation pressure on star formation. Each line shows the time evolution of the total stellar mass in the cloud with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1 Z⊙). The solid line represents the fiducial case (M5R20Z0) as shown in Fig. 3. Other lines shows the cases where we only consider either photoionization (the dashed line, M5R20Z0PI) or radiation pressure (the dot–dashed line, M5R20Z0RP).
If Z ≪ 1 Z⊙, the cloud is not optically thick (see also, Section 4.2), and the radiation pressure has little impact. Thus, we take only the photoionization feedback into account in developing a semi-analytical model in Section 4.
3.2 Variations among models with different cloud properties
3.2.1 Star formation efficiency
For the models with various Mcl, Rcl, and Z, we obtain the SFE ϵ* ≡ M*/Mcl from the simulations, where M* is the final total stellar mass. Fig. 7 shows the SFE as a function of the initial surface density of the clouds. The SFE increases with the surface density, consistently with previous studies (e.g. Raskutti et al. 2016; Kim et al. 2018; He et al. 2019). For the case with Z = 1 Z⊙, the SFE increases from 2 to 30 per cent as Σ increases from 8 to 300 M⊙ pc−2. At each metallicity, the SFE is well approximated by a power-law function of the surface density except for the case with the lowest surface density (Σ ∼ 8 M⊙ pc−2). At Σ ∼ 8 M⊙ pc−2, a single or a few star clusters easily photoionize the entire region of the cloud. In these cases, the SFEs do not follow the power-law relations, regardless of metallicity.
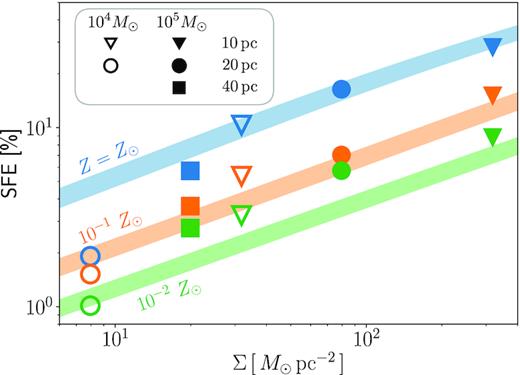
The star formation efficiency (SFE) as a function of the cloud surface density Σ, mass Mcl, and metallicity Z. The symbols represent the simulation results for the clouds with the different radii Rcl = 10 pc (the square), 20 pc (the circle), and 40 pc (the triangle), and with the different masses Mcl = 105 M⊙ (filled) and 104 M⊙ (open). The shaded stripes show our analytical estimate of the SFE for the clouds with mass between Mcl = 104 and 105 M⊙ given by equation (20). The different colours represent different metallicities of Z = 1 Z⊙ (blue), 10−1 Z⊙ (orange), and 10−2 Z⊙ (green) for both the symbols and stripes.
Note that the EUV/FUV emissivity of an individual cluster particle should also fluctuate when the mass is small, owing to the stochastic sampling of high-mass stars. Kim et al. (2016) showed that the assumption of a constant emissivity was valid for M* ≳ 104 M⊙, but the stochasticity appears if the cluster mass was lower. In low-mass clusters with M* ≲ 102 M⊙, furthermore, the averaged emissivity of EUV/FUV photons should be smaller than the constant value we currently assume because of the scarcity of high-mass stars (Inoguchi et al. 2020). We expect that, for the low-surface density clouds, the above effects enhance the SFEs and reduce the deviations from the power-law relation on average, albeit with some scatters.
The SFE also increases with the metallicity. This is because the photoionization feedback that disrupts the star-forming clouds becomes stronger at lower metallicity from the following two reasons. First, the temperature in the H ii regions, where the main coolant is the metal lines of O ii and O iii (Osterbrock & Ferland 2006), is higher in lower metallicity cases: its typical value increases from 9 × 103 K at Z = 1 Z⊙ to 2.0 × 104 K at Z = 10−2 Z⊙. The resultant higher pressure causes more rapid expansion of the H ii regions and thus stronger feedback to the star-forming clouds. Secondly, the ionizing photons are less attenuated by dust grains in lower metallicity cases. As discussed in Section 3.1, in the case with Z = 1 Z⊙, the star-forming filaments can survive even after the H ii regions begin to expand because dust grains shield the neutral gas from the photoionization. For the case with Z = 10−2 Z⊙, however, the filaments are easily photoionized and soon disrupted. From the reasons above, the duration of star formation is short, and thus the SFE is low in lower metallicity environments. The dust shielding of the filaments will be discussed analytically in Section 4.2.
3.2.2 Lifetime of the clouds
In Fig. 8, we show the lifetime of cluster-forming clouds tlife as a function of the surface density. In the numerical simulations, we define the cloud lifetime as elapsed time since the start of the simulations until the total stellar mass reaches 90 per cent of the final value. In low surface-density cases with Σ ≲ 30 M⊙ pc−2, the duration of the star formation is much shorter than the free-fall time of the clouds, and hence the lifetime is almost equal to the latter. In high surface-density cases with Σ ≳ 70 M⊙ pc−2, however, the lifetime is slightly longer than the free-fall time because of the longer expansion time of the H ii regions. In some cases, the lifetimes of clouds can be longer than that of massive stars (∼3 Myr). However, the duration time from the onset of star formation to the disruption is much shorter than the lifetime of massive stars in all the cases. Therefore, our modelling of the luminosity from a sink particle can be justified.
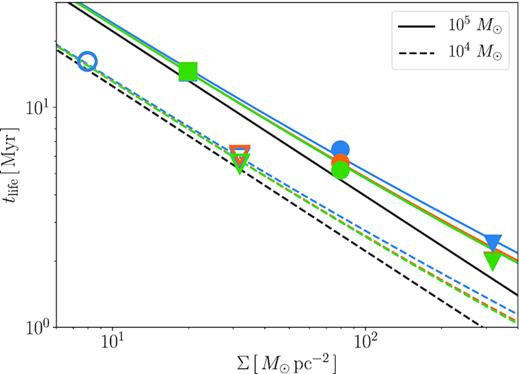
The lifetime of star-forming clouds as a function of the surface density. We use the same symbols and colours as in Fig. 7 to indicate the different conditions of Rcl, Mcl, and Z. The analytical estimations of the lifetime for the clouds with Mcl = 105 M⊙ (solid) and 104 M⊙ (dashed) and Z = 1 Z⊙ (blue), 10−1 Z⊙ (orange) and 10−2 Z⊙ (green) are also shown with the lines, which are calculated from |$t_{\rm life} = t_{\rm ff} + t_{\rm H\,{\small II}}$| with the free-fall time of the clouds tff (shown with the black lines) and the analytical estimate of the duration of star formation |$t_{\rm H\,{\small II}, cl}$| (equation 21).
3.3 Evolution of cluster particles
The early evolution of newborn star clusters depends on the initial cloud surface density and metallicity. In a more compact and higher metallicity cloud, the SFE and the total stellar mass are higher. Thus, the star cluster formed there tends to remain gravitationally bound. In our case, the star clusters remain gravitationally bound until the end of the simulation only in cases with metallicity Z = 1 Z⊙ and with initial surface density |$\Sigma \gtrsim 80\,{\mathrm{M}_{\odot }\, {\rm pc^{-2}}}$|. In Fig. 9, the time evolution of the half-mass radius of the star clusters formed in our simulations is shown in some cases. In the case with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1Z⊙), where |$\Sigma \simeq 80\,{\mathrm{M}_{\odot }\, {\rm pc^{-2}}}$|, the half-mass radius remains constant at 1.5 pc (∼0.075 Rcl) after the quenching of the star formation, and the star clusters remain gravitationally bound. We see that even with the same Σ, the clusters finally dissolve at lower metallicities. In other cases with |$\Sigma \simeq 32\,{\mathrm{M}_{\odot }\, {\rm pc^{-2}}}$|, the half-mass radii increase monotonously and the star clusters become unbound regardless of Σ. In these cases, the time-scale of dissolving the clusters corresponds to that of the H ii-region expansion. Before the disruption of the clouds, the star cluster is trapped in the central region due to the gravitational potential of the gas. However, it becomes shallower after the H ii-region expansion and the star cluster comes apart if the gravitational binding is not sufficient, as shown in Fig. 9. The above trend may be consistent with the high ‘infant mortality’ of embedded clusters (e.g. Lada & Lada 2003). Note that, individual stars modeled in a sink particle can also be dispersed as a result of the cloud photoevaporation and the properties of star clusters change via the interaction between individual stars (Kroupa, Aarseth & Hurley 2001; Banerjee & Kroupa 2013, 2017). Following these processes is out of the scope in this work.
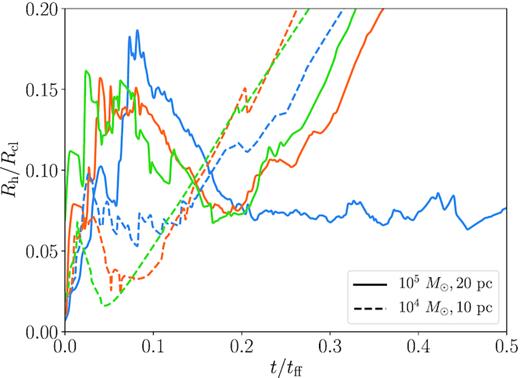
The time evolution of the half-mass radius Rh of the cluster particles for the cases with (Mcl, Rcl) = (105 M⊙, 20 pc) (‘M5R20’ models, the solid line) and (104 M⊙, 10 pc) (‘M4R10’ models, the dashed line) as a function of the time normalized by the free fall time of the clouds tff. The initial surface density Σ is 80 M⊙ pc−2 for the former cases and 32 M⊙ pc−2 for the latter. The line colours indicate the metallicity: Z = 1 Z⊙ (blue), 10−1 Z⊙ (orange), and 10−2 Z⊙ (green).
In Fig. 10, the mass distribution of the cluster particles are shown for cases with metallicities Z = 1 Z⊙ and 10−2 Z⊙. We see that the mass spectrum at Z = 10−2 Z⊙ is much flatter than that at Z = 1 Z⊙. The mass distribution at Z = 1 Z⊙ is well fitted by a power law |$\mathrm{ d}N/\mathrm{ d}M_*\propto M_*^{-2}$|, which is consistent with observed mass functions of nearby open and young massive clusters (e.g. Portegies Zwart, McMillan & Gieles 2010; Krumholz, McKee & Bland-Hawthorn 2019). We argue that this dependence on metallicity comes from how tight the system is gravitationally bound. In the case with Z = 10−2 Z⊙, the cluster particles are only loosely bound at birth and immediately dissolve through the cloud dispersal as described above. Mergers between cluster particles hardly occur. We have confirmed that, although not presented, the flat mass distribution is broadly observed in the other cases where the particles become unbound after the cloud dispersal. At Z = 1 Z⊙, on the other hand, the cluster particles are more tightly bound for long enough time, resulting in more frequent merger events. It appears that the power-law mass distribution is a result of such difference in the evolution.
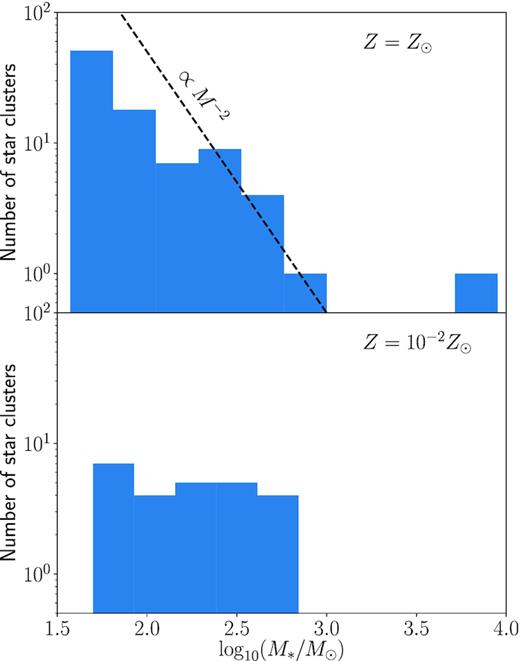
The mass distribution of the cluster particles at the end of the simulations. Top and bottom panels show the cases with (Mcl, Rcl, Z) = (105M⊙, 20pc, 1 Z⊙) and (105M⊙, 20pc, 10−2 Z⊙). The dashed line indicates the relation |$\propto M_*^{-2}$|.
4 SEMI-ANALYTICAL ARGUMENT
4.1 Dependence of SFE on physical conditions of clouds
As shown in the previous section, the SFE and the cloud lifetime vary with the initial surface density and metallicity in our simulations. In previous works, semi-analytical models have been developed to interpret the simulation results, particularly the variation of the SFE. Kim et al. (2018) considered the total momentum of the neutral and ionized gases ejected from photoevaporating clouds, using their simulation results. He et al. (2019) evaluated the SFE using the star formation rate and the sound crossing time of H ii regions calibrated with their simulation results, although limited only to the case of Z = 1 Z⊙. In this section, we construct a new semi-analytical model in a different approach, paying special attention to the metallicity dependence of photoionization feedback. We consider the propagation time of ionizing front |$t_{\rm H\,{\small II}}$| as the duration of star formation because the star formation continues until the expanding H ii bubbles terminate gas supply by inflows to dense star-forming regions. Then, the total stellar mass M* = ϵ*Mcl is obtained by multiplying |$t_{\rm H\,{\small II}}$| with the star formation rate |$\dot{M}_*$|. In our model, |$t_{\rm H\,{\small II}}$| also depends on the total stellar mass of radiation sources. Besides, the star formation rate |$\dot{M}_*$| varies with metallicity because the cooling time of gas becomes longer in low-metallicity environments. Therefore, we need to calculate the SFEs ϵ*, the propagation time |$t_{\rm H\,{\small II}}$|, and the star formation rate |$\dot{M}_*$| consistently. In the following, we consider the conversion rate of the neutral gas to stars to formulate the star formation rate |$\dot{M}_*$| in Section 4.1.1. We then construct a model for the SFE ϵ* and the propagation time |$t_{\rm H\,{\small II}}$| in Section 4.1.2.
4.1.1 Fraction of star-forming gas around star clusters
We find that only a part of neutral gas around stars is used for the subsequent star formation in our simulations. We thus first estimate the amount of cold gas as a reservoir for the star formation. As shown in Figs 2 and 5, the neutral and ionized regions coexist around star clusters. The neutral gas is vulnerable to compressional heating by the expanding H ii bubbles and the feedback by FUV photons is secondary. At Z = 1 Z⊙, those dense regions are shielded from EUV/FUV photons by dust grains (see Sec 4.2), and the photodissociation of molecules and photoelectric heating are inefficient. At low metallicities, on the other hand, UV radiation can penetrate the clouds, but the clouds consist of atomic gas originally, and the dust content is low. Thus, both the photodissociation and photoelectric heating are not important in the neutral gas around the H ii regions. Main cooling processes are the dust cooling and line emission of CO, C ii, and O i. From the thermal balance among these processes, the gas temperature can be higher than a few 100 K, depending on metallicity. With higher temperatures, the collapse of a dense part is delayed until its mass exceeds the higher value of Jeans mass by accreting more surrounding gas. In this case, a warm gas can be evacuated due to photoionization instead of collapse. Only the gas with temperature below the threshold value collapses promptly, resulting in star formation. Here, we assume the critical temperature Tcr = 200 K above which the gas is supposed to be heated up due to the feedback as described above.
Fig. 12 shows the gas mass distribution on the number density and temperature plane for the cases with (Mcl, Rcl) = (105 M⊙, 20 pc) at t = tff (4.7 Myr). With Z = 1 Z⊙, dense star-forming gas with nH ≳ 104 cm−3 has low temperature of 30 K < T < 200 K. Most of this component is in the molecular state. At low metallicity of Z = 10−2 Z⊙, on the other hand, there is few dense and cold gas with T < 100 K because of inefficient radiative cooling. Star clusters directly form from such warm and atomic gases. The above features are also highlighted in Fig. 13, showing the density-integrated temperature distribution for the same cases. Two peaks at 40–50 K and 100 K are observable in both cases corresponding to the different main cooling processes, the dust and [C ii] cooling, respectively. The lower (higher) temperature peak is higher for Z = Z⊙ (Z = 10−2 Z⊙, respectively). At Z = 10−2 Z⊙, more neutral gas distributes above 102 K owing to less efficient [C ii] cooling than in the solar metallicity case. In each case, plenty of gas accumulates around the peak temperature because the cooling becomes inefficient below that. Even if the gas is not affected by heating from the newborn stars, it stays at these temperatures for a long time. Thus, we consider the gas with T < 200 K as the star-forming gas in both cases.

The gas mass distributions on the nH − T plane within the star-forming region rsf (see text) at the epoch of t = tff. The top and bottom panels represent the cases with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1 Z⊙) and (105 M⊙, 20 pc, 10−2 Z⊙). In each panel the colours show the mass ratio of each bin to the total mass.
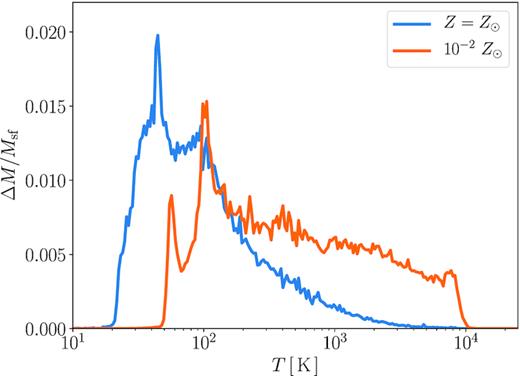
The mass distribution against the temperature within the star-forming region r < rsf at the epoch of t = tff. Plotted is the mass fraction at each temperature bin ΔM/Msf, where Msf is the total mass contained within the radius rsf. Only the non-ionized gas is considered for the plots. The blue and orange lines represent the cases with (Mcl, Rcl, Z) = (105 M⊙, 20 pc, 1 Z⊙) and (105 M⊙, 20 pc, 10−2 Z⊙).
4.1.2 Star formation efficiencies
4.2 Conditions of dust shielding
Turbulent motions create sheet-like density fluctuations as shown in Figs 2 and 5. These structures survive even after the H ii region expansion in the case of Z = 1 Z⊙ (Fig. 2-3) while they completely disappear in the case of Z = 10−2 Z⊙ (Fig. 5-3). This difference comes from the fact that the optical depth of such structures against ionizing photons depends on metallicity as the dust grains are the main source of opacity. In the shade of optically thick sheets, the gas can flow into the star-forming regions, and the star formation continues until the sheets are disrupted by the H ii-region expansion. Next, we analytically estimate the optical depth of such sheets and clumps, and consider under what conditions such dense structures are protected against UV photons by dust attenuation. This is useful to understand the simulation results because these quantities should be related to the metallicity dependence of the cold gas mass fraction Rn (equation 11), which is higher with higher metallicity.
5 SUMMARY AND DISCUSSION
We have performed 3D RHD simulations to systematically study the star cluster formation and cloud dispersal in various environments, including very low-metallicity cases. Our simulations include radiative feedback from massive stars, such as photoionization of hydrogen atoms, photoelectric heating, and photodissociation of molecules. We have investigated the cluster-forming clouds with different surface densities and metallicities, |$\Sigma = 10\!-\!300\,\mathrm{M}_{\odot }\, {\rm pc^{-2}}$| and Z = 10−2−1 Z⊙. We have also developed a semi-analytical model that reproduces well the simulation results, e.g. the dependence of the SFE on the cloud surface density and metallicity. Our findings are summarized as follows:
Overall evolution in the simulation is qualitatively similar among all the examined cases. As a cloud collapses, the initial turbulent velocity field creates the dense gas filaments, which fragment to form stars. As the mass in stars increases, UV radiation from newborn massive stars creates H ii bubbles, which expands due to its high thermal pressure and eventually blow away surrounding non-ionized gas. Once the radiative feedback becomes effective, the star formation is quenched within a free-fall time. That is, the natal cloud is promptly disrupted after the massive star formation.
At each metallicity, the SFE ϵ* increases with increasing initial surface density Σ. At Z = 1 Z⊙, for instance, ϵ* = 0.02 for |$\Sigma = 10\,{\rm \mathrm{M}_{\odot }\, {\rm pc^{-2}}}$| and ϵ* = 0.3 for |$\Sigma = 300\,{\rm \mathrm{M}_{\odot }\, {\rm pc^{-2}}}$|. At low metallicity, clusters form in atomic clouds as the molecule formation time is longer than the cooling or dynamical time. We have found that the SFE is systematically lower for lower metallicity with the reduction factor ≃0.3 at Z = 10−2 Z⊙, regardless of Σ. In low-metallicity environments, the temperature of the photoionized gas is high due to ineffective radiative cooling and dust attenuation of ionizing photons. This leads to more rapid expansion of the H ii regions, which terminates the star formation over the cloud in a shorter time-scale. The newborn clusters are less gravitationally bound after the cloud dispersal than those at the solar metallicity.
To understand the dependence of SFE on cloud properties and metallicity, we have developed a semi-analytical model that gives SFE agreeing excellently with the simulation results.
CO molecules are the standard tracer of the molecular clouds, i.e. the star-forming cold gas. Since we have consistently solved the thermal and chemical states of the atomic and molecular gas in our simulations, we could follow the time evolution of the CO-to-H2 conversion factor of the cluster-forming clouds (e.g. Inoguchi et al. 2020), although not focused above. In our simulations for Z = 1 Z⊙, the formation of CO and |$\rm H_{2}$| molecules occurs in the dense filaments, in which newborn clusters are formed. In the cases of Z = 10−2 Z⊙, molecule formation hardly proceeds and the star formation occurs directly from almost atomic gas (Krumholz 2012). Observations suggest a high value of the CO-to-H2 conversion factor for GMCs with sub-solar metallicity associated with massive star-forming regions (Leroy et al. 2009). Our simulations should potentially provide such metallicity dependence even for very metal-poor cases with Z = 10−2 Z⊙, which will be considered in our future studies.
In our simulations, we only considered radiative feedback and did not include kinematic feedback effects, such as outflows, stellar winds, and supernovae. Outflows alone would not suppress star formation in star-forming clouds whose escape velocities are typically larger than |$1\,{\rm km\, s^{-1}}$| (Matzner & Jumper 2015; Krumholz et al. 2019). However, outflows inject momentum to the surrounding medium and maintain turbulent motions in cluster-forming clouds (Li & Nakamura 2006; Nakamura & Li 2007). This is likely to suppress the SFE. Stellar winds can also push the neutral gas away. The SFEs may further be reduced due to the combined effects of stellar winds and photoionization (e.g. Dale et al. 2014). When the duration of star formation in clouds is longer than the lifetime of OB stars, supernovae also contribute to destruction of the clouds (e.g. Geen et al. 2016). In future works, we will take those feedback effects into account in our numerical simulations.
Our simulations show that the cluster formation and cloud dispersal proceed in the filamentary gas. Given that a strong magnetic field exists in the cloud, the gas structure will change significantly (e.g. Inoue & Inutsuka 2012; Inutsuka et al. 2015). Also, the magnetic fields give support to collapsing GMCs and delay the star formation (Geen et al. 2015). We plan to study the impact of magnetic fields combined with the radiative feedback on star formation in GMCs in future work.
ACKNOWLEDGEMENTS
The authors wish to express their cordial thanks to Profs. Masayuki Umemura and Ken Ohsuga for their continual interest, advice, and encouragement. This work is supported by the Grants-in-Aid for Basic Research by the Ministry of Education, Science and Culture of Japan (HY: 17H04827, 18H04570, 20H04727, TH: 19H01934, KO: 25287040, 17H01102, 17H02869), and NAOJ ALMA Scientific Research Grant Numbers 2019-11A. The numerical simulations were performed on the Cray XC50 (Aterui II) at the Center for Computational Astrophysics of National Astronomical Observatory of Japan and the Cray XC40 at Yukawa Institute for Theoretical Physics in Kyoto University.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
The abundance of species i is given as yi that is the ratio of the number density of the species i to that of atomic hydrogen.
REFERENCES
APPENDIX A: RADIATIVE PROCESS
As discussed in Section 2.1, we use the adoptive ray-tracing method for radiation transfer (Abel & Wandelt 2002). In this method, we calculate the equation of radiation transfer from each radiation source, discretizing the solid angle with healpix (Górski et al. 2005). In the regions far from the radiation sources, we split the ray to ensure that three rays always cross each cell.
In chemical and thermal solvers, we consider photoionization (H i and O ii), photodissociation (|$\rm H_{2}$| and CO), photoelectric heating and dust heating as follows.
To obtain the dust temperature, we calculate the balance among the dust thermal emission, absorption of the direct light (EUV, FUV, and continuum), and energy transport from gases. We use the energy transport rate between dust grains and gases given by Hollenbach & McKee (1979). Further details are shown in Fukushima et al. (2020).






