-
PDF
- Split View
-
Views
-
Cite
Cite
Benjamin E Stahl, Jorge Martínez-Palomera, WeiKang Zheng, Thomas de Jaeger, Alexei V Filippenko, Joshua S Bloom, deepSIP: linking Type Ia supernova spectra to photometric quantities with deep learning, Monthly Notices of the Royal Astronomical Society, Volume 496, Issue 3, August 2020, Pages 3553–3571, https://doi.org/10.1093/mnras/staa1706
Close - Share Icon Share
ABSTRACT
We present deepSIP (deep learning of Supernova Ia Parameters), a software package for measuring the phase and – for the first time using deep learning – the light-curve shape of a Type Ia supernova (SN Ia) from an optical spectrum. At its core, deepSIP consists of three convolutional neural networks trained on a substantial fraction of all publicly available low-redshift SN Ia optical spectra, on to which we have carefully coupled photometrically derived quantities. We describe the accumulation of our spectroscopic and photometric data sets, the cuts taken to ensure quality, and our standardized technique for fitting light curves. These considerations yield a compilation of 2754 spectra with photometrically characterized phases and light-curve shapes. Though such a sample is significant in the SN community, it is small by deep-learning standards where networks routinely have millions or even billions of free parameters. We therefore introduce a data-augmentation strategy that meaningfully increases the size of the subset we allocate for training while prioritizing model robustness and telescope agnosticism. We demonstrate the effectiveness of our models by deploying them on a sample unseen during training and hyperparameter selection, finding that Model I identifies spectra that have a phase between −10 and 18 d and light-curve shape, parametrized by Δm15, between 0.85 and 1.55 mag with an accuracy of 94.6 per cent. For those spectra that do fall within the aforementioned region in phase–Δm15 space, Model II predicts phases with a root-mean-square error (RMSE) of 1.00 d and Model III predicts Δm15 values with an RMSE of 0.068 mag.
1 INTRODUCTION
The optical spectra of Type Ia supernovae (SNe Ia) are rich with information (for a review, see e.g. Filippenko 1997). In addition to probing ejecta dynamics and chemical composition, spectral features have been found to encode the phase of an SN Ia in its temporal evolution (e.g. Riess et al. 1997; Foley et al. 2005; Howell et al. 2005; Blondin & Tonry 2007; Muthukrishna, Parkinson & Tucker 2019a), and to a somewhat less quantitatively formalized extent, its peak luminosity (Nugent et al. 1995; Arsenijevic et al. 2008; Bailey et al. 2009; Blondin, Mandel & Kirshner 2011; Silverman et al. 2012b; Zheng, Kelly & Filippenko 2018; Siebert et al. 2019). The ability to extract the former (henceforth, the ‘phase’) and the latter (or something that correlates with it via a width–luminosity relation, such as Δm15 or Δ; Phillips 1993; Riess, Press & Kirshner 1996, respectively) from optical spectra is of particular significance because both are conventionally derived from photometry. As the requisite light curves must consist of numerous individual observations conducted over at least several weeks, the ability to measure the aforementioned quantities from perhaps just a single observation (i.e. a spectrum) is of great value when allocating limited observing resources to optimize for specific science goals.
The SuperNova IDentification code (SNID; Blondin & Tonry 2007) has become the de facto1 tool for classifying the type and phase of an SN from spectra, though alternatives do exist (e.g. Superfit; Howell et al. 2005). To determine the phase of an SN Ia, such conventional approaches compare2 an input spectrum to a large data base of spectra with known phases and then perform an aggregation of the phases from the best-matching templates. This approach has the advantage of being easy to understand (‘SN X is most similar to SN Y at Z days relative to maximum brightness’), but it has the disadvantage of being inherently slow – prediction time scales linearly with the number of template spectra in the data base.
Machine learning (ML; see Ivezić et al. 2014, for an overview of use cases in astronomy) provides an interesting and fundamentally different approach to these tasks. In particular, phase and light-curve-shape determination can both be treated within the ‘supervised learning’ paradigm, where a robust mapping between inputs and outputs is derived from a training set of input–output pairs. Subject to passing user-defined efficacy criteria when applied to a distinct testing set, the derived map can then be deployed to characterize new, unseen data. This approach leads to predictions that are fast (i.e. based on features themselves instead of comparisons against a large data base) and therefore scalable. Accordingly, supervised ML has become increasingly prevalent in astronomical research campaigns (e.g. Bloom et al. 2012; Masci et al. 2014; Goldstein et al. 2015; Wright et al. 2015; Kim & Brunner 2017; Miller et al. 2017; Zhang & Bloom 2020).
Indeed, ML has proven to be a viable approach to photometric SN classification (e.g. Richards et al. 2012; Lochner et al. 2016; Möller et al. 2016; Charnock & Moss 2017; Narayan et al. 2018; Muthukrishna et al. 2019b), but only several studies thus far have applied such techniques to SN spectra. Sasdelli et al. (2016) use unsupervised ML techniques to explore the spectroscopic diversity of SNe Ia, and find that much of the spectral variability, including that of the peculiar SN 1991bg-like (Filippenko et al. 1992; Leibundgut et al. 1993) and SN 2002cx-like (now known as the distinct ‘SN Iax’ class; Filippenko 2003; Li et al. 2003; Foley et al. 2013) objects, can be parametrized by a carefully constructed five-dimensional space. As a much faster alternative to the aforementioned template-matching options (i.e. SNID and Superfit), Muthukrishna et al. (2019a) have used a deep convolutional neural network (CNN; see e.g. LeCun, Bengio & Hinton 2015) to develop DASH, a software package that classifies the type, phase, redshift, and host galaxy (but not light-curve shape) of an SN from optical spectra.
Motivated by this and the well-documented ability of CNNs to extract representative low-dimensional features from input signals, we formulate our approach as a set of three models, each of which utilizes a similar CNN architecture to (Model I) determine if an input spectrum belongs to an SN Ia within a specific domain in a space defined by phase and light-curve shape, (Model II) calculate the phase if it is within the domain, and (Model III) calculate a measure of the light-curve shape (Δm15; Burns et al. 2011) if the same criterion is met. Although Model II shares a common objective and architectural elements with DASH (i.e. phase determination via a CNN architecture), we optimize specifically for SNe Ia that fall within certain thresholds, treat the problem as one of regression (not classification), and utilize dropout variational inference as a method by which to model uncertainties (Gal & Ghahramani 2015; Leung & Bovy 2019). Moreover, our development of a CNN to predict the light-curve shape of an SN Ia from its spectrum is novel.
We use the following sections to present the development of the aforementioned models. Section 2 details the accumulation of our data set, including how we process and prepare spectra for ingestion by our models. We outline our model architecture and discuss training and hyperparameter selection procedures in Section 3, and we provide model-specific results in Section 4. Concluding remarks are then given in Section 5.
2 DATA
2.1 Spectra
We source the spectra used herein from the three largest low-redshift SN Ia spectral data sets currently in existence: the Berkeley SuperNova Ia Program (BSNIP; Silverman et al. 2012a; Stahl et al. 2020, henceforth S12 and S20, respectively) sample with a total of 1935 spectra covering the period from 1989 through 2018 (see S12 for 1989–2008 and S20 for 2009–2018), the Harvard-Smithsonian Center for Astrophysics (CfA) sample with a total of 2603 spectra from observations spanning 1993–2008 (Blondin et al. 2012), and the Carnegie Supernova Program (CSP) sample with 630 spectra observed in the range 2004–2009 (Folatelli et al. 2013). From this initial compilation of 5168 spectra, we perform two modest ‘usability’ cuts that reduce our sample to 4941 (these cuts, in addition to those that are introduced below, are outlined in Fig. 1). First, we drop the small fraction without a redshift listed in their associated publication, thereby yielding 5110 spectra, and secondly, we remove a further 169 that lack full coverage3 of the Si ii λ6355 feature that is ubiquitous in near-maximum-light SN Ia spectra.
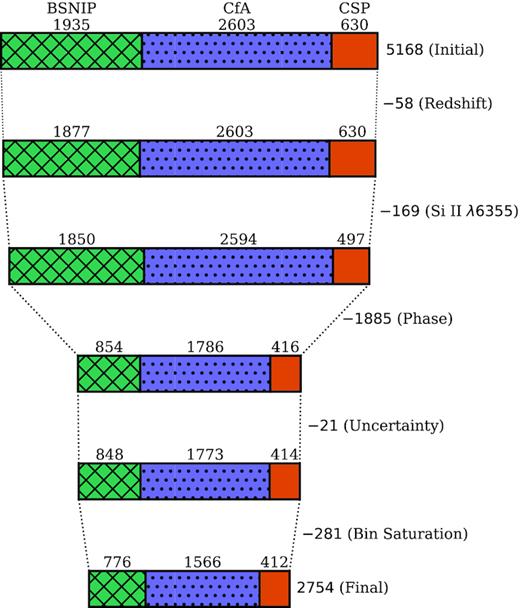
Full accounting of all cuts made in distilling our initial set of 5168 spectra down to the 2754 in our final compilation (1113 of which are within the ‘domain’ defined in Section 2.3). We delineate the source of each spectrum in the top row. By a wide margin, the lack of suitable photometric observations is responsible for the most severe cut (indicated with ‘Phase’).
In addition to the high quality and sheer size of these data sets, the BSNIP and CfA sets were specifically selected for their complementarity – whereas the observing strategy employed by the BSNIP is generally to prioritize the total number of SNe observed instead of the number of spectra per SN, the CfA data set covers fewer SNe but with higher cadence. This is clearly seen in the distribution of the number of spectra per SN in the top panel of Fig. 2: The BSNIP sample spans many more SNe with several observations than does the CfA (or CSP) sample, but beyond ∼6 spectra per object, the CfA sample wins out. Together, then, these data sets offer comprehensive coverage of the spectral diversity of SNe Ia at both the individual and population levels.
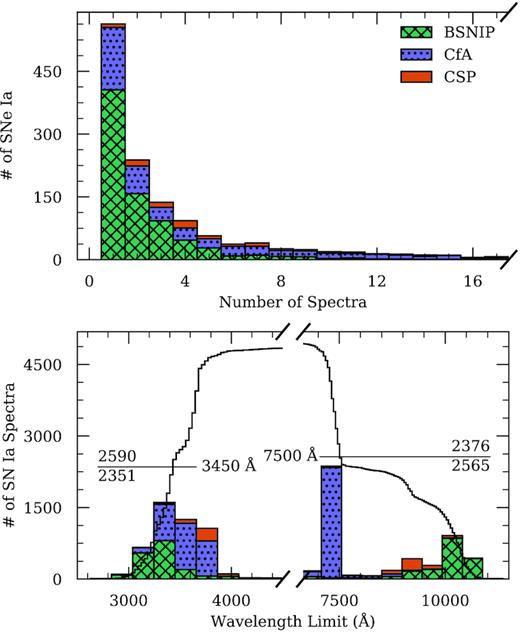
Stacked distributions of data set parameters for our spectral compilation, distinguished by source. The top panel shows the number of spectroscopic observations per object (the tail extends to higher numbers of spectra, but is truncated for clarity) and the bottom panel displays the blue and red wavelength limits of the spectra. Overlaid on the bottom panel is the cumulative (inverse-cumulative) distribution of blue (red) wavelength limits, and the intersecting horizontal lines reflect the bounds defined in Section 2.3.2. The numbers of spectra above and below each intersecting line are also labelled.
We show the distribution of blue (red) wavelength limits for the spectra in our compilation in the lower panel of Fig. 2. The superior red-wavelength coverage of the Kast double spectrograph on the 3 m Shane telescope at Lick Observatory (responsible for |${\sim} 79{{\ \rm per\ cent}}$| of the BSNIP sample; Miller & Stone 1993) to that of the FAST spectrograph on the 1.5 m Tillinghast telescope at Whipple Observatory (responsible for |${\sim} 94{{\ \rm per\ cent}}$| of the CfA sample; Fabricant et al. 1998) is evident. The Lick spectra as well as most from CSP have good relative spectrophotometry owing to the slit being placed at the parallactic angle (Filippenko 1982), but the continuum shapes of the FAST spectra may be inaccurate in some cases since the slit could not be rotated to arbitrary parallactic angles. Because any heterogeneities in the inputs to our models should reflect only physically significant information, we formulate our data pre-processing and augmentation procedures (see Sections 2.3.2 and 2.3.3, respectively) to obscure as much source-specific information and contamination (e.g. wavelength limits and inaccurate continuum shapes) as possible.
2.2 Light curves
As the purpose of this study is to identify and therefore derive, through supervised learning, certain photometrically derived properties encoded in SN Ia spectra, the aforementioned spectral compilation must be coupled to photometric observations (i.e. light curves), thereby allowing for the desired properties to be measured. To this end, we collect the requisite information from data releases by the same groups responsible for our compilation of spectra (Riess et al. 1999; Jha et al. 2006; Hicken et al. 2009; Ganeshalingam et al. 2010; Krisciunas et al. 2017; Stahl et al. 2019, henceforth G10 and S19 for the Berkeley sample, CfA1-3 for the CfA sample, and CSP3 for the CSP sample, respectively), as well as publish several new light curves (see Appendix A). We use the E(B − V) model implemented within the SNooPy package (Burns et al. 2011; see Appendix B for additional details) to fit the aforementioned light curves (except for those from S19 and CSP3, who have published fits using the same procedure along with their photometry), allowing us to measure the time of maximum B-band brightness (and hence the phase4) and the decline-rate parameter,5 Δm15.
2.3 Final compilation
All told, 3056 spectra are linked to light curves with successful SNooPy fits, but as shown in Fig. 1, we remove 21 spectra having a phase uncertainty in excess of 1 day (d) and/or a Δm15 uncertainty exceeding 0.1 mag, thus yielding 3035 spectra. We visualize this compilation within the photometric parameter space of interest (namely, Δm15 and phase) in Fig. 3. Unsurprisingly, the densest coverage – by a wide margin – occurs for Δm15 ≈ 1.1 mag (reflecting that of a prototypical SN Ia), but particularly impressive is the coverage within the region defined by −10 ≲ phase ≲ 18 d and 0.85 ≲ Δm15 ≲ 1.55 mag (albeit a bit sparse for the more rapidly declining objects within this region).
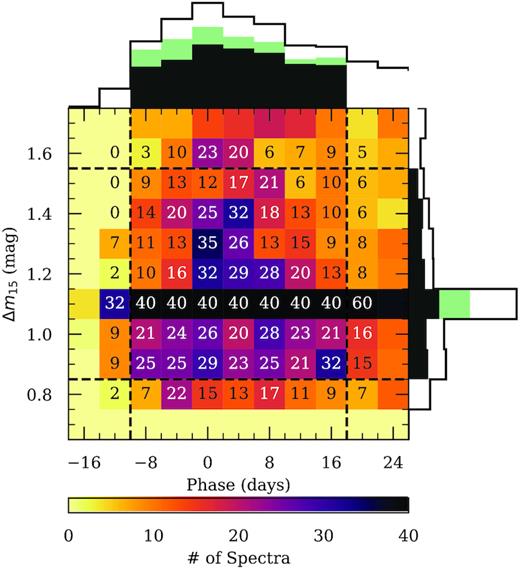
Distribution of Δm15 and phase for the spectra in our compilation, with axes truncated to focus on the domain of interest. The empty-black one-dimensional projections reflect the full set of 3035 spectra, the green components consider only those 1394 spectra that are within the domain of interest, and the filled-black components show the same once spectra are removed to enforce the saturation criteria of 40 examples per bin (leaving 1113 in-domain spectra). The number of spectra falling within each in-domain bin and their immediate neighbours is labelled.
Motivated by this coverage, we impose the aforementioned region as a ‘domain’ on our models in the following way: Model I is tasked with classifying whether an input spectrum lies within its boundaries, while Model II and Model III determine the phase and Δm15 (respectively) for spectra within this restricted domain. To mitigate the imbalance caused by the dominance of samples with Δm15 ≈ 1.1 mag, we enforce a ‘saturation point’ of 40 samples for each in-domain bin in Fig. 3. According to this policy, overly dense bins are brought into compliance by removing spectra with the largest Δm15 uncertainties until only 40 remain. A total of 281 spectra are removed by this action, leaving 2754 examples (1113 of which are in-domain and thus relevant to Models II and III) in what will henceforth be referred to as our final compilation (see the bottom row of Fig. 1). Though this runs contrary to the common dogma that more data are always better, we have found our choice to be empirically superior in this specific application.
A cursory inspection of Fig. 3 reveals that our coverage does not drop off significantly at larger phase and Δm15 values than those that terminate our selected domain. It is therefore tempting to consider expanding the domain until such a drop is achieved (so as to make predictions over a wider swath of parameter space), but we choose not to do so for a myriad of reasons, the bulk of which are conveyed in the sequences of variance spectra presented in Fig. 4. If we assume that the spectral energy distribution (SED) of an SN Ia is predominantly6 determined by its phase and light-curve shape, then considering sequences of variance spectra – whereby one of the aforementioned parameters is discretized into narrow bins and the variations within those bins are studied – allows us to infer which regions in SN Ia spectra vary the most at a given point in the sequence. If our assumption that the SED is largely a function of these two parameters holds, then such regions of large variation encode the most discriminating information about the non-discretized parameter.
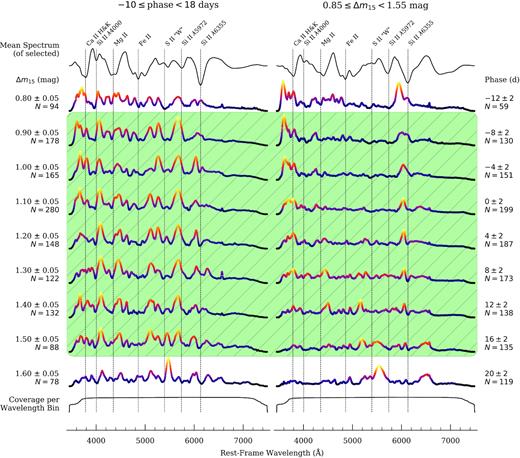
Sequences of variance spectra progressing through equally spaced Δm15 (left column) and phase (right column) bins. Each column begins with the selection criteria for the spectra in it and the mean spectrum of all those that are selected. Prominent spectral features are indicated. After advancing through the indicated variance sequence, the column terminates with the coverage per wavelength bin of the selected spectra. The same vertical scaling is applied to all variance spectra, but the colour map is normalized to each and is used to emphasize regions of significant variation. Our selected domain of interest is covered by the green region with diagonal hatching. All spectra used in generating the sequences have been pre-processed according to the specifications of Section 2.3.2. The narrow spike that appears redward of the Si ii λ6355 line in some variance spectra is due to nebular H α emission from the host galaxy.
With this interpretation established, we note that for spectra with phases between −10 and 18 d, the variance spectra in the left column of Fig. 4 show notably similar structure for Δm15 bins ranging from 0.90 to 1.50 mag. We interpret this as an indication that, at least within this range of Δm15 values, phases between −10 and 18 d are encoded by a common – or ‘slowly’ evolving – set of features. A consequence of this is that a fairly simple CNN should be able to learn these features without much difficulty (we discuss our network architecture, including the way in which Fig. 4 motives it, in more detail in Section 3.1), and although a sophisticated network may well be able to learn ‘when’ to weight certain features more heavily – in addition to the features themselves – we are content with the range of Δm15 values afforded by our selected domain. Indeed, our coverage drops off sharply for lower Δm15 and the more rapidly declining SNe Ia in our data set (i.e. those with Δm15 ≳ 1.6 mag) are likely to be SN 1991bg-like objects that do not follow the Phillips relation (or its derivatives).
The aforementioned arguments do not perfectly carry over when we consider the phase-binned variance spectra for those SNe Ia in our sample having 0.85 ≤ Δm15 < 1.55 mag. Before maximum light, the blue wing of the Ca ii H&K feature exhibits the most variability and thus offers the best discrimination of Δm15, but beyond peak, this variability fades and the dominant variation is observed in the blue wing of the Si ii λ6355 feature. At phases ≳10 d, this too begins to fade and variability is strongest at intermediate wavelengths, typically those in the vicinity of the S ii ‘W’ feature. It is beyond the scope of this study to speculate about – or offer an explanation of – the physical mechanism(s) that gives rise to these observations, but we note that Nugent et al. (1995) identified these features in particular as a probe of SN Ia luminosity, with the cause ascribed to temperature differences (and thus, to the total amount of 56Ni produced) between explosions. We do not pursue earlier phases owing to a paucity of data (indeed, Fig. 3 reveals that doing so would result in several empty bins), and while our compilation may well support an extension to later phases, we do not undertake such an addition here because Model III would have to become very robust to evolving features.
2.3.1 Training, validation, and testing sets
In developing a neural network (or any supervised ML model), one typically divides the available data into three distinct subsets: a ‘training’ set used to derive the decision path between features and outputs, a ‘validation’ set to assess model performance during training and tune externally assigned hyperparameters, and finally, a completely separate ‘testing’ set, which is used to probe the efficacy of the final model against unseen data, and not used for either the optimization of the network or the assignment of hyperparameters. In light of the small absolute size of our compilation (by modern ML standards), we intentionally set the validation and testing splits (10 per cent each) to be smaller than conventional allocations so as to keep our training set as large as possible.
We take a nuanced approach to ensure that our proportionally smaller validation and testing sets provide a realistic representation of our final compilation. Specifically, we sample according to a pseudo-stratified scheme for the 1113 in-domain spectra in our compilation, whereby we select random subsets of the appropriate size from each bin in Fig. 3. In this way, the Model II and III training, validation, and testing sets have approximately the same bin-wise distribution. We impose a floor so that even bins with fewer than 10 total instances have at least one sample for each of the validation and testing sets. As a result, the actual validation and testing ratios are elevated slightly higher than the targeted 10 per cent. The Model I sets are generated by randomly sampling all out-of-domain spectra at the prescribed ratios and then adding them to the pseudo-stratified in-domain sets. This ensures that all spectra in the Model II/III sets are just subsets of the corresponding Model I sets. Therefore, we can holistically assess deepSIP (deep learning of Supernova Ia Parameters; the software package that encapsulates our models) via the Model I testing set without fear of Model II or III inadvertently being asked to characterize spectra that occur in their training or validation sets.
2.3.2 Pre-processing
Our models should be sensitive only to the physical characteristics encoded in the spectra they are trained on, not to any peculiarities relating to how the spectra were collected or reduced. Furthermore, it is imperative that each spectrum is processed in a carefully controlled and systematic way to avoid inadvertent biases. We therefore perform the following pre-processing steps to homogenize input spectra prior to ingestion by our models:
Each spectrum is de-redshifted – that is, the redshift is removed. This step is skipped for augmented spectra (see Section 2.3.3) that are already in (or near) the rest frame.
Each spectrum is smoothed using a Savitzky–Golay filter (Savitzky & Golay 1964) with a window equivalent to 100 Å, though the window is varied for augmented spectra.
The pseudo-continuum is modelled by again smoothing the spectrum, but with a much wider window of 3000 Å (unless this exceeds the range of the spectrum, in which case we use a dynamically determined value corresponding to |${\sim} 70{{\ \rm per\ cent}}$| of the available wavelength range). We then subtract it from the spectrum.
The spectrum is binned on to a log-wavelength scale consisting of 1024 points between 3450 and 7500 Å. As shown in Fig. 2, these endpoints are such that ∼50 per cent of our global compilation (i.e. including those without phase information) have additional spectral information either below 3450 Å or above 7500 Å that is disregarded. This painful step of throwing away potentially useful information is necessary to avoid inducing significant biases between our data sources. If a spectrum does not have signal all the way to the blue or red ends of this range, we set it to zero in the missing end(s). In addition to ensuring that all spectra are represented by vectors of the same length, this transformation has the useful consequence that redshifting corresponds to a linear translation (see Section 2.3.3 for more details).
We scale the signal so that it has a range of unity and then translate it such that it has a mean of zero.
The first and last 5 per cent of the signal in the spectrum is tapered using a Cosine Bell (i.e. a Hanning window) so that it smoothly goes to zero at the ends.
Finally, we add 0.5 to the signal so that it is positive everywhere. Henceforth, we refer to this quantity as ‘scaled flux’.
We show an example of the intermediate stages and final result derived from our pre-processing procedure in Fig. 5.
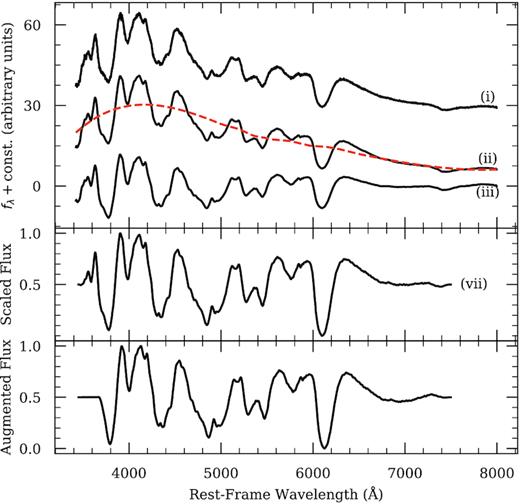
Snapshots showing various stages of our pre-processing routine as applied to a spectrum of SN 2016coj at +1.3 d. The numerals indicate the last pre-processing step to have been performed on the plotted spectrum, and the dashed orange line illustrates the fitted (and subsequently removed) pseudo-continuum. The bottom panel shows an example of the spectrum after data augmentation steps have been applied.
2.3.3 Augmentation
Though we have taken care to assemble a significant fraction of all publicly available low-redshift SN Ia optical spectra currently in existence, our final compilation is still rather small by modern standards in deep learning (especially for the domain-restricted subset that is relevant for Models II and III). For this reason, we formulate a data-augmentation strategy (i.e. a method for extending our training set beyond its limited size while preserving its characteristics; e.g. Dieleman, Willett & Dambre 2015; Cabrera-Vives et al. 2017; Martínez-Palomera et al. 2018; Boone 2019) that generates a training set of substantially increased size. To accomplish this, we randomly sample data from the Model I (II/III) training set, with replacement, until we have a collection whose size, when combined with the non-augmented training set, equals 5000 examples (an ∼4-to-1 ratio of augmented to original training samples for the Model II/III set). After obtaining samples according to this prescription, we transform each sampled spectrum using the following operations:
Redshifting: As noted in Section 2.3.2, we remove the redshift from all spectra that are fed into our models. However, we expect our models to be robust to small redshift errors that propagate into the rest-wavelength transformation. To this end, we perturb the rest-wavelength array of each sampled spectrum by a multiplicative factor of (1 + δz), where δz is drawn from a uniform distribution, |$\delta z \sim \mathcal {U}(-0.004, 0.004)$|, motivated by the mean uncertainty in the SNID-derived redshifts reported by S20 for their data set. Coupled with log-binning (which converts redshifting/de-redshifting into a linear offset; see Section 2.3.2), this allows us to reinforce and exploit the invariance to small translations that CNN architectures exhibit (LeCun et al. 2015).
Noise: To encourage our models to be robust to variations in the signal-to-noise ratios of input spectra, we vary the degree of smoothing applied to each sampled spectrum during our pre-processing procedures (see Section 2.3.2). We do this by randomly selecting the smoothing window, |$w \sim \mathcal {U}(50, 150)$| Å, with these bounds chosen to be roughly consistent with the range of wavelength-space extents of the high-variance regions identified in Fig. 4.
Trimming: We expect our models to be insensitive to any information about the observing apparatus and configuration that might be encoded in a spectrum. For example, the median phase of the BSNIP-collected spectra in our compilation is ∼18 d, while for the CfA-collected spectra it is ∼9 d, but our models should not form a decision path that preferentially associates spectra having extensive red-wavelength coverage (namely, the BSNIP spectra) with later phases – this correlation is purely a consequence of exogenous biases in our compilation. Therefore, in addition to the pre-processing steps outlined in Section 2.3.2, we remove a random proportion, f, from the blue and red ends of each sampled spectrum, where |$f \sim \mathcal {U}(0, 0.1)$|, with the upper bound chosen so as to maintain full coverage of the characteristic Si ii λ6355 feature that we require for spectra in our compilation to possess.
We show an example of the results of the aforementioned augmentation procedures in the bottom panel of Fig. 5.
3 MODELS
As noted, we have constructed three models to ultimately determine the phase and light-curve shape parameter, Δm15, of an SN Ia from an optical spectrum. The first model determines if the input is from an SN Ia with a phase of −10 ≤ phase < 18 d that has a light-curve-shape parameter of 0.85 ≤ Δm15 < 1.55 mag. The second model determines the phase, and the third, Δm15, both only within the domain for which Model I discerns. We formulate the first model as a binary classification problem – either a spectrum belongs to an SN Ia subject to the aforementioned photometric restrictions or it does not. The remaining models can be construed as a regression problem, where a continuous quantity (e.g. phase or Δm15) is to be predicted. Despite their differing applications, each model uses a similar neural network architecture, and much of the work flow of training and evaluating them is common. We therefore devote the following subsections to discussing the underlying architecture employed in our models and the common aspects of our work flow. We present model-specific results in Section 4.
3.1 Architecture
At the heart of our models is a deep (i.e. multilayer) CNN, but whereas the prototypical use-case is two-dimensional (2D) – deep 2D CNNs have a storied history in image classification (e.g. LeCun et al. 1990, 1998; Szegedy et al. 2014) and even Muthukrishna et al. (2019a) resorted to tiling 1D SN spectra into 2D ‘images’ to formulate their problem as one of image identification – we follow the inherent dimensionality of our data by using a 1D implementation (for a summary of 1D CNNs, see Kiranyaz et al. 2019). In addition to being more conceptually compatible with our application, our use of a 1D CNN gives us much more control over the degree to which non-local features are aggregated through pooling operations.
We present a schematic of our neural architecture, which utilizes a total of four convolutional layers to extract representative features from input spectra, in Fig. 6. We apply the Rectified Linear Unit (ReLU; Nair & Hinton 2010) activation function to the output of each convolutional and fully connected layer. Following each convolutional layer, we apply max pooling to reduce computational complexity and remove irrelevant features. Finally, we conclude each ‘block’ (i.e. convolution + ReLU + max pool + dropout) in our network with a dropout layer to assist in the prevention of overfitting (Srivastava et al. 2014). Each convolutional and fully connected layer has its weights initialized with zero-centred Gaussian noise and its bias to a small, positive value. All of our models are implemented using PyTorch 1.0 (Paszke et al. 2019), and we make our trained models and framework available as deepSIP,7 an open-source Python package (see Appendix C for guidelines on basic usage).
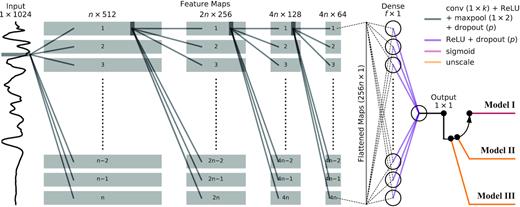
Schematic of the common neural network architecture used by each of the three fully independent networks that constitute Models I–III (which collectively comprise deepSIP). A set of n feature maps is computed from the pre-processed input spectrum and down-sampled using max pooling (the resulting maps are indicated by grey boxes). This operation is then recursively applied to the down-sampled feature maps a total of three additional times, with the number of feature maps doubling for all but the last set. The final set of down-sampled feature maps is then flattened into a vector of length 256n and fed through a fully connected layer consisting of f neurons before reaching the output neuron. Then, depending on the model, a final operation is performed to transform the raw output of the network into the appropriate context (‘probabilities’ in the case of Model I or dimensional phase or Δm15 values for Models II and III, respectively). The convolution kernel, k, the number of feature maps generated by the first convolutional layer, n, and the number of neurons in the fully connected layer, f, are all hyperparameters whose preferred value depends on the specific model. A dropout layer with dropout probability p follows each weight layer aside from the output neuron.
Our selected architecture is largely motivated by insights gleaned from the sequences of variance spectra presented in Fig. 4. As noted earlier, the Δm15-binned sequence shows more or less the same structure over our selected range of values. This homogeneity supports the use of a simple feed-forward network in the case of Model II, but the depth of the network (i.e. how many convolutional layers are used) and the progression in the number of filters computed per layer are motivated by the heterogeneity in features as they progress through the sequence. For example, the blue wing of the Si ii λ6355 feature shows variation throughout the sequence, but the exact ‘shape’ of that variation as a function of wavelength varies. For this reason, we use multiple convolutional layers and increase the number of convolutional kernels per layer in all but the last so that our networks have the capacity to make decisions based on many complex, highly specialized features that are computed from a smaller number of basic features supplied by the earlier layers. The situation is mostly the same for Model III, but the relevant variance spectra (i.e. those in the right column of Fig. 4) exhibit fewer common features and more extreme evolution in their shapes as the sequence progresses through phase bins. Motivated by this, we did carry out experiments with several architectures capable of predicting the phase in tandem with Δm15, but none performed substantively better than our set of simple, independent networks. We do expect, however, that in addition to requiring much more high-quality training data, a specialized architecture would be crucial in expanding the output domain of Models II and III. Indeed, extending the sequences of Fig. 4 out to larger phase and Δm15 values reveals significant feature evolution. A network capable of providing feedback between phase and Δm15 predictions would allow for this evolution to be properly modelled.
The aforementioned dropout layers – each of which randomly drops elements from their input with Bernoulli-distributed probability, p, and (in our implementation) rescales outputs by a factor of 1/(1 − p) during training – serve a secondary purpose in our networks. Namely, the purpose is to make the networks probabilistic (Gal & Ghahramani 2015): Each forward pass with dropout enabled in training mode produces a different prediction, and thus, it is straightforward to quantitatively describe not only a point estimate (the prediction of a model) but also an estimate of its uncertainty. To do so when generating predictions, we make N stochastic (i.e. with dropout turned on) forward passes8 for a given input and assign the mean and standard deviation of the resulting collection of predictions as the final model prediction and an estimate of its uncertainty.
3.2 Training
To train each of our models, we supply the appropriate training set in small batches and utilize an adaptive gradient descent algorithm (ADAM; Kingma & Ba 2014) to minimize the appropriate objective function by updating the weights and biases in each layer of the network. For Model I, we employ the binary cross-entropy loss as our objective function, while for Models II and III we use the mean squared error (MSE) loss. We also scale training outputs that are continuous (i.e. phase and Δm15) such that they range from 0 to 1 using a transformation of the form |$\mathbf {y}^\prime = (\mathbf {y} - y_{\rm min}) / (y_{\rm max} - y_{\rm min})$|, where (ymin, ymax) represent the domain boundary (as shown in Fig. 3) along the output’s dimension. Subsequent predictions by these models are then unscaled using the inverse of this transformation. Model I predictions are transformed into ‘probabilities’ using the sigmoid function.
We train each of our models for a total of 75 epochs, with the learning rate set to step down by a multiplicative factor of 0.1 after thresholds of 45, 60, and 70 epochs are reached. In testing, we found these choices to yield stable convergences without requiring excessive training time. At the culmination of each epoch, we compute success metrics against the relevant validation set, thereby affording a specific measure of model-performance evolution in terms of the metrics we care most about (e.g. in dimensional, unscaled units for Models II and III). For Model I, we primarily use the area under the curve (AUC) of the Receiver Operating Characteristic (ROC) curve,9 whereas for Models II and III, we primarily use the root-mean-square error (RMSE). We emphasize that although these are the primary metrics, we consider secondary indicators as well (see Sections 4.1 and 4.2 for Models I and II/III, respectively).
3.3 Hyperparameter selection
There are several external parameters (i.e. not determined through backpropagation; henceforth, referred to as ‘hyperparameters’) that must be selected specifically for each of our models. Some are architectural (e.g. k, the size of each convolutional kernel; n, the number of distinct feature maps computed by the first convolutional layer; f, the number of neurons in the fully connected layer; and p, the dropout probability used for training; see Fig. 6), and some have to do with our training algorithm (e.g. training batch size, learning rate, and weight decay). The optimal choice of such parameters is not known a priori and is application dependent (e.g. we find that Model II performs best when k is less than the value that maximizes Model III performance; see Table 1). We note that the dropout probability used during training need not be the same as that used when generating predictions. We therefore consider them separately as follows: The dropout probability for training is chosen as part of our hyperparameter selection process and the dropout probability used for generating predictions is separately chosen in tandem with N (see Section 4.2.1).
| Hyperparameter . | Valuesa . |
|---|---|
| Convolution kernelb (k) | 5, 15, 25I, II, 35III |
| Filters in first convolution (n) | 8I, II, III, 16, 32 |
| Fully connected neurons (f) | 16I, II, 32, 64, 128III |
| Training dropout probability (p) | 0.01I, II, III, 0.05, 0.1 |
| Batch sizec | 2, 4, 8, 16I, II, 32III |
| Learning rate | 0.0005II, III, 0.001I |
| Weight decay | 0.000 01III, 0.0001I, II |
| Hyperparameter . | Valuesa . |
|---|---|
| Convolution kernelb (k) | 5, 15, 25I, II, 35III |
| Filters in first convolution (n) | 8I, II, III, 16, 32 |
| Fully connected neurons (f) | 16I, II, 32, 64, 128III |
| Training dropout probability (p) | 0.01I, II, III, 0.05, 0.1 |
| Batch sizec | 2, 4, 8, 16I, II, 32III |
| Learning rate | 0.0005II, III, 0.001I |
| Weight decay | 0.000 01III, 0.0001I, II |
Notes. aSuperscripts mark the preferred hyperparameter of the denoted model.
bThough small (e.g. 3 × 3) kernels are typical in 2D scenarios, significantly larger kernels have proven optimal in some 1D applications to astrophysical signals (e.g. quasar spectra; Parks et al. 2018).
cMasters & Luschi (2018) have suggested that batch sizes between 2 and 32 yield the best performance.
| Hyperparameter . | Valuesa . |
|---|---|
| Convolution kernelb (k) | 5, 15, 25I, II, 35III |
| Filters in first convolution (n) | 8I, II, III, 16, 32 |
| Fully connected neurons (f) | 16I, II, 32, 64, 128III |
| Training dropout probability (p) | 0.01I, II, III, 0.05, 0.1 |
| Batch sizec | 2, 4, 8, 16I, II, 32III |
| Learning rate | 0.0005II, III, 0.001I |
| Weight decay | 0.000 01III, 0.0001I, II |
| Hyperparameter . | Valuesa . |
|---|---|
| Convolution kernelb (k) | 5, 15, 25I, II, 35III |
| Filters in first convolution (n) | 8I, II, III, 16, 32 |
| Fully connected neurons (f) | 16I, II, 32, 64, 128III |
| Training dropout probability (p) | 0.01I, II, III, 0.05, 0.1 |
| Batch sizec | 2, 4, 8, 16I, II, 32III |
| Learning rate | 0.0005II, III, 0.001I |
| Weight decay | 0.000 01III, 0.0001I, II |
Notes. aSuperscripts mark the preferred hyperparameter of the denoted model.
bThough small (e.g. 3 × 3) kernels are typical in 2D scenarios, significantly larger kernels have proven optimal in some 1D applications to astrophysical signals (e.g. quasar spectra; Parks et al. 2018).
cMasters & Luschi (2018) have suggested that batch sizes between 2 and 32 yield the best performance.
Thus, for each of Models I, II, and III, we perform a randomized search whereby we select preferred hyperparameter values by training and validating the models on many combinations of hyperparameters that are randomly drawn from a grid. A total of 12 h of compute time on a single of NVIDIA Tesla K80 GPU was allocated, per model, for these searches. We increase efficiency by automatically stopping training after 20 epochs when a performance threshold is not achieved on the validation set, and as a result, we are able to explore a significant portion of the selected hyperparameter space. Table 1 details the full hyperparameter grid, and summarizes the final set for each model. We discuss our selection criteria for determining these final, preferred sets in Sections 4.1 and 4.2 for Models I and II/III, respectively.
4 RESULTS
4.1 Model I: domain classification
4.1.1 Preferred hyperparameters
Our first model is designed to determine if an input spectrum belongs to an SN Ia having −10 ≤ phase < 18 d and 0.85 ≤ Δm15 < 1.55 mag. If a spectrum satisfies these criteria, it is said to be in the domain of interest; otherwise it is out. In this way, Model I serves as a precursor to Models II and III: The subsequent predictions for spectra that it classifies as being outside the domain of interest should be carefully scrutinized, if not disregarded altogether. From our Model I hyperparameter search (as discussed in Section 3.3 and summarized in Table 1), we find that the highest achieved validation ROC AUC score is 0.992 (see Fig. 7), and on the basis of this score, we select the hyperparameters that yield it as the final, preferred set. These hyperparameters produce a network with a relatively modest number (∼75k) of trainable parameters. Though we currently do not consider uncertainty estimates for Model I, we still use the full machinery of our probabilistic architecture with settings aligned to those of Models II and III (i.e. N = 30 and p = 0.02; see Section 4.2.1) for consistency and to grant straightforward extensibility in the future.
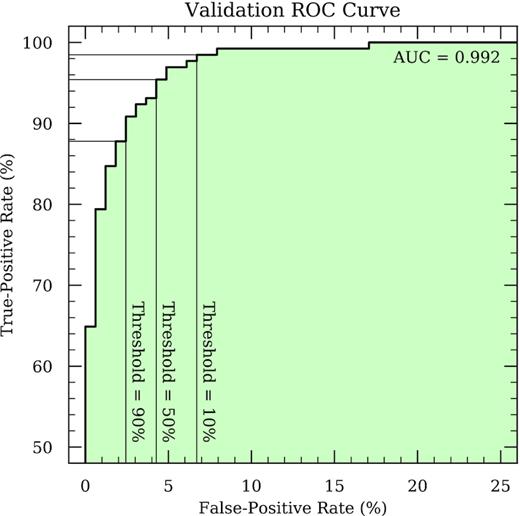
ROC curve for Model I deployed on its validation set. The locations that correspond to various decision thresholds are indicated.
4.1.2 Decision threshold
With the information afforded by Fig. 7, we are also able to tune the decision threshold of our model (i.e. the minimum ‘probability’ of being in to be classified as such). While many opt to use a default threshold of 50 per cent without further consideration, the optimal choice depends on striking an application-specific balance between the extent to which false positives can be tolerated and true positives can be missed. Taking a holistic view and recalling the aforementioned role of Model I in the overall output of deepSIP, it becomes obvious that the quality of Model II and III predictions should be given the utmost priority. The optimal decision threshold in our case is therefore the one that yields the best Model II and III performance on spectra that Model I classifies as in-domain (which will be a mixture of true positives and false positives). This criterion is much more important than the overall classification accuracy10 given the ‘blurry’ nature of the domain boundary – individual spectra can and do fall so close to it that the particular side they end up on is determined by statistical variations.
To identify the optimal threshold, then, we use the Model I validation11 set to study, as a function of decision threshold, Model II/III RMSE scores segmented, based on the classifications of Model I, into false negatives (FN), false positives (FP), true positives (TP), and all positives (P = FP + TP). We find that the Model II scores belonging to FN and FP both follow a trend of decrease with rising decision threshold, and that those for FN are generally larger by a modest (∼0.5 d) amount. The corresponding FN scores for Model III also follow a decreasing trend (with rising threshold) but are significantly lower than those for the FP, which remain roughly constant at ∼0.2 mag until a dip forms between ∼90 and 95 per cent. While one could argue that the FP scores for Model II are acceptable over a wide range of thresholds (∼2–2.5 d for thresholds of ∼5–80 per cent, and lower thereafter), the aforementioned Model III scores over a similar range are prohibitive. We simply cannot tolerate any significant contamination by FP with such high RMSE scores. This constrains the range of acceptable decision thresholds to just ∼90–95 per cent, even at the expense of more FN with reasonable Model II/III performance.
As the P scores are fairly flat between these bounds, we err to the low side (thereby minimizing the number of incorrect classifications) and set our Model I decision threshold to 90 per cent. This yields 13 FN (with RMSE scores of 1.91 d and 0.080 mag from Models II and III, respectively) and 122 P (with scores of 1.05 d and 0.068 mag, respectively) of which 4 are FP (with scores of 1.39 d and 0.160 mag, respectively) from the 295 spectra (including 160 true negatives) in our validation set. Though this results in an accuracy score (|$94.2{{\ \rm per\ cent}}$|) that is slightly suboptimal to the peak value of 95.9 per cent achieved at a different threshold, it is still vastly in excess of the baseline score yielded by picking the most popular class every time (|$55.6{{\ \rm per\ cent}}$|) and it gives us confidence that the positives Model I passes on to Models II and III are sufficiently ‘pure’.
4.1.3 Performance on testing set
With the decision threshold determined, we now make predictions on the testing set (which, as outlined in Section 2.3.1, has not been used to optimize the network or hyperparameters) and assess the efficacy of Model I by comparing predicted labels to true labels. We find a similarly high ROC AUC of 0.989 and note that Model I achieves a TP rate of 90.8 per cent at an FP rate of 2.4 per cent for our selected threshold of 90 per cent. From the 295 spectra in the testing set, Model I delivers 160 true negatives, 12 FN, 4 FP, and 119 TP, collectively yielding an accuracy score of 94.6 per cent (as compared to the 55.6 per cent baseline score obtained by picking the most popular class every time). Of those marked as in-domain (i.e. P), Models II and III yield RMSE scores of 1.06 d and 0.072 mag, respectively, while the TP subset performs even better at 1.00 d and 0.064 mag. These measures give us a high level of satisfaction with Model I, and we therefore consider it complete.
4.2 Models II and III: photometric quantity estimation
4.2.1 Preferred hyperparameters
Models II and III are intended to determine the rest-frame phase and Δm15, respectively, of an SN Ia from its spectrum, assuming that it is within the phase and light-curve shape bounds that Model I identifies (i.e. the spectrum is in the relevant domain). As previously stated, our primary metric for regression tasks is the RMSE, but we consider two secondary indicators when selecting the final hyperparameter values: (i) the slope of a linear fit to predictions as a function of ground truth values, and (ii) the maximum absolute difference between predictions and labels (henceforth MR, for maximum residual). The first diagnoses the directionality of prediction errors – systematic overestimates for low values and underestimates for high values are conveyed in a fitted slope of less than unity (and vice versa, though our models only bias in the aforementioned direction; see Section 4.2.5), and the second gives an indication of how homogeneous the absolute residuals are (when compared with the corresponding RMSE score). It is not sufficient for a set of hyperparameters to yield a competitive RMSE score; they must yield competitive scores across each of these three metrics.
We therefore identify the preferred hyperparameters for Models II and III using a tiered approach to our search results. First, we filter to select only those results that have a slope above and an MR below a fiducial value when evaluated against the relevant validation set. Then, from the resulting subset, we select the entry with the lowest RMSE score. In this way, the final, preferred Model II hyperparameters are chosen for yielding an RMSE of 1.15 d, a slope of 0.96, and an MR of 4.32 d and the Model III hyperparameters on the basis of yielding scores of 0.065 mag, 0.823, and 0.206 mag, respectively. The final networks have ∼75k and ∼320k trainable parameters, respectively. Although it is beyond the scope of this study to make any definitive or in-depth statements about the significance of the final hyperparameters, it is interesting to note the differences between those that yield the best observed performance in Models II and III. For example, we find that Model III performs best with a larger convolution kernel, k, than does Model II (35 for Model III versus 25 for Model II); this may indicate that features encoding phase information are generally narrower than those that encode Δm15. At the same time, Model II requires fewer neurons in the fully connected layer than does Model III. This is consistent with our general intuition that phases are more ‘simply’ codified in spectral features than Δm15 (or other luminosity indicators), which may be best parametrized by ratios of non-local features (as suggested by Nugent et al. 1995).
As a final refinement to the parameters that govern Models II and III, we study the effect of varying the number of stochastic forward passes (N) and dropout probability (p) when the models are used to generate predictions. To do so, we use Models II and III to generate predictions from the relevant validation set over a grid of (N, p) values and then tabulate the RMSE and mean estimated uncertainty at each point. The results (visualized in Fig. 8) are generally consistent with our expectations: mean predicted uncertainties steadily grow with p as do RMSE values, albeit at a much less significant rate. For Model III, both metrics show minimal dependence on N, but for Model II there are ‘bands’ of improved RMSE performance at N = 30–80, 140–160, and beyond 180 (though they only outperform their surroundings by ≲0.2 d). While our primary concern is optimizing model performance (i.e. achieving low RMSE scores and ‘reasonable’ uncertainty estimates), it is desirable from a compute-time perspective to use the lowest N value possible. We therefore select (N, p) = (30, 0.02) for all deepSIP predictions. As Fig. 8 clearly shows, this yields the desired low N (for fast prediction times) without compromising the quality of model predictions.
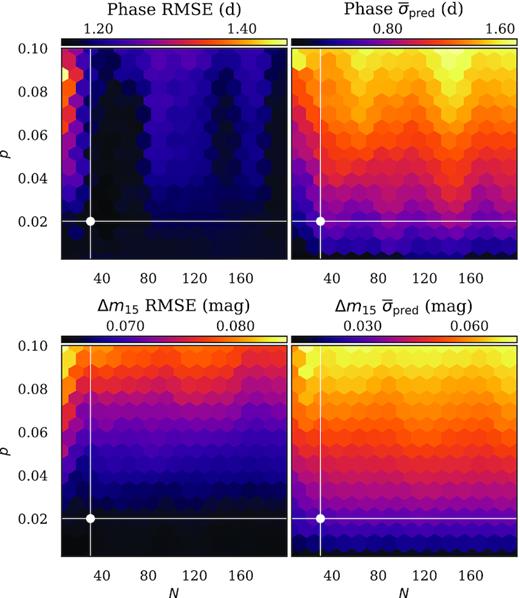
Validation RMSE and mean predicted uncertainty values for Models II and III over a grid of N and p values. A separate colour bar is provided for each panel, and the selected (N, p) set is indicated.
4.2.2 Performance on testing set
Having selected the final hyperparameters for each model, we make predictions on the relevant testing sets. As shown in Fig. 9, we find strong agreement when we compare predictions to ground truth labels, achieving RMSE, slope, and MR scores of 1.00 d, 0.97, and 3.22 d; and 0.068 mag, 0.809, and 0.228 mag, respectively. For the 131 samples in each testing set, the median phase (Δm15) residual is −0.19 d (0.001 mag); also, 94 (94) are within one standard deviation of the median, 122 (123) are within two, and 130 (129) are within three.
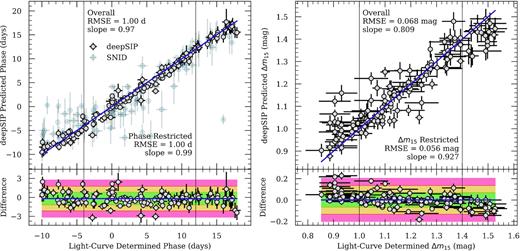
Phase (left-hand panel) and Δm15 (right-hand panel) determined by deepSIP versus ground truth values from the respective Model II and III testing sets, with residuals in the lower panels. The indigo line in each upper plot shows the one-to-one correspondence for ground truth values, while in the lower plots, it indicates the median residual. The green, yellow, and red regions indicate the 1σ, 2σ, and 3σ bounds about the median residual, respectively. We mark the relevant RSME and slope, both globally and for a restricted subset (see Section 4.2.5) in each panel. SNID-based phase predictions are presented as an overlay to the upper left panel, but they are omitted from the residuals for clarity.
In Section 4.2.6, we investigate the quality of the uncertainty estimates produced by our models, which serve as a systematic error probe by quantifying the dispersion between N realizations drawn (for each input spectrum) from the underlying distribution that is each of our models. Here we do the opposite in an attempt to quantify statistical error: We remove the stochasticity from our models (by disabling dropout) and assess prediction robustness when they are fed perturbed inputs. We generate such inputs using our data-augmentation strategy (see Section 2.3.3) to bootstrap our Model II and III testing sets up to 5000 instances, each of which is slightly perturbed in redshift, noise, and signal length. The results, which we assess by means of the RMSE, are highly satisfactory: Model II yields 1.05 d and Model III delivers 0.080 mag, both broadly consistent with the corresponding measures reported above. One could potentially use a variation of this strategy to generate a unique statistical uncertainty estimate for each input spectrum and include that with each prediction, but we defer that task to future study and development.
4.2.3 Comparison with SNID-derived phases
To contextualize the level of performance of Model II with regard to phase predictions, we attempt to characterize the spectra in the testing set using a series of SNID runs that adhere to the specifications12 laid out by S20. When we do so, we find that deepSIP performs significantly better than SNID in virtually every way. Whereas the SNID-based scheme (consisting of a total of four runs per spectrum, all of which are controlled and read using a Python script and hence subject to small Python overheads) takes ∼7 min to process all 131 testing samples on a server with a modern CPU, our Model II (which entails a total of 30 stochastic forward passes per spectrum) takes under 1 s on a single NVIDIA Tesla K80 GPU to characterize pre-processed spectra (<1 min on a modern, four-core CPU), with <1 s for pre-processing. Moreover, the SNID approach fails to derive a phase in 18/131 instances while deepSIP is successful in making a prediction in all cases. Perhaps most significantly, the RMSE between those instances where SNID successfully predicts a phase and the true phases is 3.48 d, a factor of ∼3.5 times worse (in RMSE; ∼12 times worse in MSE) than that for our deepSIP-derived results. The SNID results are also much more afflicted by a bias to overestimate the earliest phases (a tendency that has been observed and discussed by S20 and others); the mean residual (predicted minus true) at phases from −10 to −5 d is +3.30 d for SNID-derived results, but just +0.31 d for those from deepSIP. This bias is also exhibited in the aforementioned fitted-slope metric, with SNID yielding a value of 0.80 compared to 0.97 for Model II.
4.2.4 Δm15 consistency
Unfortunately, we are unable to perform an analogous SNID-based comparison for Δm15 values, but we can exploit a unique feature that the Δm15 labels possess to perform a separate test on the validity of Model III. Unlike phases that are unique to individual spectra, Δm15 values are unique to individual SNe Ia. As a result, it is not uncommon for multiple spectra in the training, validation, or testing sets to map to the same Δm15 value. We can test how well Model III deals with this degeneracy by looking at the scatter (parametrized by the standard deviation) in Δm15 predictions in the testing set, grouped by distinct Δm15 label (and therefore, by distinct object).
When we do so, we find encouraging results that we summarize with the following observations: (i) as compared to the global scatter in predicted Δm15 values (0.161 mag), the median scatter in predicted values per distinct Δm15 label is just 0.018 mag; (ii) the observed distribution is positively skewed so that the majority of the scatter is near zero (e.g. the 25th percentile is 0.007 mag while the 75th percentile is 0.045 mag); and (iii) of the two examples with scatter >0.07 mag, both are at or near the extremes of the predicted Δm15 values (i.e. where the model’s predictions are typically the most uncertain and the training data are sparsest).
4.2.5 Biases
Though mitigated by our selection criteria (namely, our choice to enforce a 40 spectrum-per-bin saturation policy), Model II and (especially) Model III do exhibit some bias towards the more central values in their prediction ranges. This is unfortunate, but expected given the non-uniformity of our training data (e.g. see Figs 3 and 10). We emphasize that despite this bias, the residual distributions are approximately symmetric. Still, it is useful to quantify the extent of this bias, and we choose to do so by means of the previously mentioned slope of a linear fit to the results presented in Fig. 9.
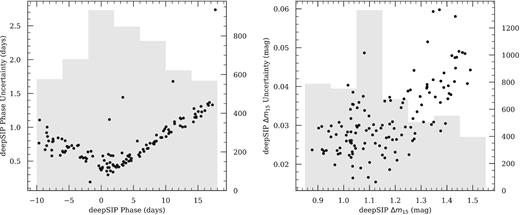
deepSIP-determined phase (left-hand panel) and Δm15 (right-hand panel) uncertainties versus predicted values from the respective Model II and III testing sets. The grey distributions behind each convey the relevant training data (including those from the augmented training set).
In doing so, we find a slope of 0.97 for phases and 0.809 for Δm15 values, confirming our suspicion that the bias is present (and more pronounced in Model III). However, if we select a more restrictive subset to exclude the biased ends (taken to be the equivalent of 1.5 bins from Fig. 3, i.e. 6 d and 0.15 mag from each end), the fitted slopes improve to 0.99 and 0.927, respectively. The Model III RMSE value improves as well, dropping to 0.056 mag. Users of deepSIP may therefore choose to give more weight to results within these restricted ranges. Such improvements reinforce our belief that more performance could be extracted from our models with a larger and more balanced training set.
4.2.6 Estimated uncertainties
To further probe the quality of our estimated uncertainties, one might be tempted to study the relationship between estimated and true uncertainties (i.e. those derived from light-curve fits). This, however, would not be appropriate because the true uncertainties were not accounted for by our loss function during model training (nor anywhere else aside from selection cuts). Instead, we can ask a more appropriate question of our estimated uncertainties: How do they behave relative to the data our models were trained on? The answer, depicted in Fig. 10, is encouraging. We see that our estimated uncertainties for both models are generally smallest in the region where training data are most abundant, and that the uncertainties grow steadily as the training data become more scarce. This captures the general behaviour we desire, though the uncertainties may be modestly underestimated (given the lower panels in Fig. 9, but we defer an extensive study of this to future work). Thus, on the basis of this desired behaviour and all prior points elucidated above, we consider Models II and III ready for deployment.
5 CONCLUSION
In this paper, we present and characterize the performance of deepSIP, an open-source software package that encapsulates a set of three CNNs that collectively map optical SN Ia spectra to their corresponding phases and light-curve shapes (parametrized by Δm15). The treatment of these tasks with supervised learning – and the specific use of a CNN architecture – is a natural choice in many regards. This choice is rewarded with highly satisfactory performance.
To train, validate, and test our models, we compile a significant collection of low-redshift SN Ia spectra by drawing from public data releases from the CfA, CSP, and our own BSNIP. These spectra form, after pre-processing, the inputs of the input–output pairs that our models learn to map. To assemble the corresponding outputs (i.e. phases and light-curve shapes), we draw from the photometric data releases of the same research campaigns, supplementing with five SNe Ia for which we publish light curves that have recently become available in our own archives. We fit all light curves (except for those from S19 and CSP3, who performed the same fits) using the SNooPyE(B − V) model, ensuring systematic consistency between all phase and Δm15 values used herein. After all cuts are accounted for, our final compilation consists of 2754 spectra with photometrically derived phase and Δm15 values, and of these, 1113 are within the phase and Δm15 constrained domain of interest for Models II and III.
Because we draw spectra from multiple sources, we take great care to both understand and mitigate systematic differences between sources so that our models form decision paths exclusively from physically significant features encoded in the spectra. Our mitigation strategy manifests chiefly in our pre-processing procedure that, among other things, discards any spectral information below 3450 Å or above 7500 Å. Though painful, this prevents our models from being affected by the presence or absence of signal at more extreme wavelengths – a distinction that on the red end almost perfectly segments CfA, CSP, and BSNIP spectra. We also let our desire for telescope agnosticism guide the data-augmentation strategy that we employ to increase our modest sample size. In addition to a redshift perturbation, we vary the extent to which augmented spectra are smoothed and randomly drop signal from the ends. The latter two actions serve to blur out the signature imparted by the specific equipment used to collect a given spectrum.
We describe the common neural network architecture that underlies each of our models and whose organization and layout are largely motivated by our consideration of sequences of variance spectra. Under the assumption that spectral variations in SNe Ia are mostly a result of phase and light-curve shape (i.e. luminosity, via a width–luminosity relation), such sequences inform us about which regions in spectra most strongly encode a given target. Our observation of a relatively consistent set of features in such sequences has informed our adoption of a rather simple feed-forward network. To estimate uncertainties alongside point values for our targets, we use a probabilistic model provided by dropout variational inference. We employ a randomized grid search to determine the preferred set of hyperparameters for each of Models I–III, and upon doing so, set out to assess their performance.
To do so, we deploy each model against a distinct (i.e. unused during training and hyperparameter selection) testing set. In the case of Model I (a binary classifier of ‘in/out’ with regard to a domain defined by −10 ≤ phase < 18 d and 0.85 ≤ Δm15 < 1.55 mag), we achieve an accuracy score of 94.6 per cent and ROC AUC of 0.989. At a false-positive rate of 2.4 per cent, Model I has an in-domain detection rate of 90.8 per cent. With Model II (a continuous predictor of phases from −10 to 18 d), we achieve an RMSE (wRMSE) of 1.00 d (0.92 d), a marked improvement over SNID-derived predictions on the same spectra. Finally, for Model III (a continuous predictor of Δm15 values from 0.85 to 1.55 mag), we achieve an RMSE (wRMSE) of 0.068 mag (0.065 mag). These final, trained models are publicly available through deepSIP, which provides an easy-to-use API for deploying them to characterize new SN Ia spectra. We strongly encourage public use of deepSIP for this purpose.
Looking to the future, we expect that the performance of deepSIP could be significantly improved as more spectra with corresponding light curves become available. Indeed, the dominant factor in our selection of the phase–Δm15 domain inside of which Models II and III offer predictions is the paucity of data available with more extreme light-curve shapes. As such data become more prevalent, the networks that underlie deepSIP can easily be retrained and if necessary, modified to accommodate feedback between predicted phase and Δm15 values that may be necessary given the substantial feature evolution observed beyond the domain boundary. We welcome community involvement on these fronts (accumulating more data and designing more sophisticated network architectures), and intend to continue active, transparent development on our publicly hosted GitHub repository.
SUPPORTING INFORMATION
photometry.txt
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
We thank our referee, Tom Charnock, whose exceptionally insightful comments and suggestions improved the manuscript. BES thanks Marc J. Staley for generously providing fellowship funding and D. Muthukrishna for helpful discussions about CNN architecture choices. JMP and JSB were partially supported by a Gordon and Betty Moore Foundation Data-Driven Discovery grant. Support for AVF’s SN group has been provided by U.S. National Science Foundation (NSF) grant AST–1211916, the Richard and Rhoda Goldman Fund, the TABASGO Foundation, Gary and Cynthia Bengier (TdJ is a Bengier Postdoctoral Fellow), the Christopher R. Redlich Fund, and the Miller Institute for Basic Research in Science (U.C. Berkeley). Katzman Automatic Imaging Telescope (KAIT) and its ongoing operation were made possible by donations from Sun Microsystems, Inc., the Hewlett-Packard Company, AutoScope Corporation, Lick Observatory, the NSF, the University of California, the Sylvia & Jim Katzman Foundation, and the TABASGO Foundation. Research at Lick Observatory is partially supported by a generous gift from Google. In addition, we greatly appreciate contributions from numerous individuals, including Charles Baxter and Jinee Tao, George and Sharon Bensch, Firmin Berta, Marc and Cristina Bensadoun, Frank and Roberta Bliss, Eliza Brown and Hal Candee, Kathy Burck and Gilbert Montoya, Alan and Jane Chew, David and Linda Cornfield, Michael Danylchuk, Jim and Hildy DeFrisco, William and Phyllis Draper, Luke Ellis and Laura Sawczuk, Jim Erbs and Shan Atkins, Alan Eustace and Kathy Kwan, Peter and Robin Frazier, David Friedberg, Harvey Glasser, Charles and Gretchen Gooding, Alan Gould and Diane Tokugawa, Thomas and Dana Grogan, Timothy and Judi Hachman, Alan and Gladys Hoefer, Charles and Patricia Hunt, Stephen and Catherine Imbler, Adam and Rita Kablanian, Roger and Jody Lawler, Kenneth and Gloria Levy, Peter Maier, DuBose and Nancy Montgomery, Rand Morimoto and Ana Henderson, Sunil Nagaraj and Mary Katherine Stimmler, Peter and Kristan Norvig, James and Marie O’Brient, Emilie and Doug Ogden, Paul and Sandra Otellini, Jeanne and Sanford Robertson, Sissy Sailors and Red Conger, Stanley and Miriam Schiffman, Thomas and Alison Schneider, Ajay Shah and Lata Krishnan, Alex and Irina Shubat, the Silicon Valley Community Foundation, Mary-Lou Smulders and Nicholas Hodson, Hans Spiller, Alan and Janet Stanford, the Hugh Stuart Center Charitable Trust, Clark and Sharon Winslow, Weldon and Ruth Wood, David and Angie Yancey, and many others.
We thank Stanley Browne, Sanyum Channa, Ian Crossfield, Edward Falcon, Tatiana Gibson, Ellen Glad, Christopher Griffith, Julia Hestenes, Benjamin Jeffers, Charles Kilpatrick, Michelle Kislak, Laura Langland, Joel Leja, Gary Li, Michael Ross, Timothy Ross, Costas Soler, Samantha Stegman, Kevin Tang, Patrick Thrasher, Priscilla West, Sameen Yunus, and Keto Zhang, for their effort in obtaining data with the 1 m Nickel telescope at Lick Observatory.
This research used the Savio computational cluster resource provided by the Berkeley Research Computing program at U.C. Berkeley (supported by the U.C. Berkeley Chancellor, Vice Chancellor for Research, and Chief Information Officer). This research has made use of the CfA Supernova Archive, which is funded in part by the NSF through grant AST–0907903. The Pan-STARRS1 Surveys (PS1) and the PS1 public science archive have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, the Johns Hopkins University, Durham University, the University of Edinburgh, Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration (NASA) under grant NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, NSF grant AST–1238877, the University of Maryland, Eötvös Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation.
DATA AVAILABILITY
The data published herein are available in the article and in its online supplementary material.
Footnotes
As assessed from its prevalence in spectroscopic classifications issued by the Central Bureau of Electronic Telegrams (CBET) and in International Astronomical Union Circulars (IAUCs).
SNID uses cross-correlation (Tonry & Davis 1979) for comparison while Superfit uses χ2 minimization.
We consider an SN Ia spectrum to have full coverage of the Si ii λ6355 feature if it has a minimum wavelength of less than 5750 Å and a maximum in excess of 6600 Å. These values represent the minimum and maximum extremes of the domains S20 use to search for the feature’s blue and red endpoints, respectively.
The phase of a spectrum is the time interval between when it is observed and when its SN reaches maximum B-band brightness, as derived in Appendix B and listed in Table B1, divided by a factor of (1 + z) to correct for time dilation. The adopted redshift was listed in the original publication for that spectrum.
Our selected implementation of the SN Ia width–luminosity relation uses a generalized light-curve shape parameter, Δm15, which is similar to – but distinct from – the more popular Δm15(B) used in the Phillips relation (i.e. the decline in magnitudes of an SN Ia over the first 15 d of its post-maximum B-band evolution). Indeed, the two may deviate randomly and systematically (see section 3.4.2 of Burns et al. 2011).
We emphasize that ‘predominantly’ does not mean ‘exclusively’ – other factors such as Galactic and host-galaxy extinction have an effect on an observed SN Ia SED; our assumption is merely that those factors are of secondary significance to phase and light-curve shape, especially for spectra that have already been pre-processed in accordance with Section 2.3.2.
An ROC curve shows the true-positive rate (ordinate) versus the false-positive rate (see Fig. 7). The most optimal AUC score is 1, corresponding to a false-positive rate of 0 and a TP rate of 1.
The accuracy score is the fraction of all predicted labels that are correct.
As discussed in Section 2.3.1, our careful preparation of the Model I validation and testing sets ensures that they are supersets of the corresponding sets for Models II and III. Because of this, we can make predictions with the latter models on the former sets without concern for contamination.
The SNID procedure is minimally intrusive, but intended to increase reliability by determining the type, subtype, redshift, and phase from an SN Ia spectrum in consecutive runs that progressively refine the set of templates used for comparison.
REFERENCES
APPENDIX A: SUPPLEMENTARY LIGHT CURVES
In the time since the photometric data set presented by S19 was published, we have continued to obtain host-galaxy template images for the unpublished SNe Ia in our archives. With these new observations, we are able to process five additional SNe Ia (SN 2007S, SN 2008hv, SN 2010kg, SN 2017hpa, and SN 2018oh) of utility to this work. We therefore present their BVRI light curves (some also have unfiltered observations, which we refer to as Clear). All processing steps are identical to those described by S19, so we provide only a brief summary of the methodology before delivering results.
All images were collected using either the 0.76 m KAIT (Li et al. 2000; Filippenko et al. 2001) or the 1 m Nickel telescope, both of which are located at Lick Observatory where the seeing averages ∼2 arcsec. After removing bias and dark current, flat-field correcting, and deriving an astrometric solution, we pass images to our automated photometry pipeline13 (LOSSPhotPypeline; see S19), which handles all aspects of the remaining processing.
We present the final Landolt-system light curves derived from the aforementioned processing steps in Fig. A1. The final light curves are publicly available through our U.C. Berkeley SuperNova DataBase15 (SNDB; S12; Shivvers et al. 2016) and in the Supplementary Materials included with this article. We describe our method for (and results from) fitting these light curves (and the others in our compilation) using SNooPy in the following section.
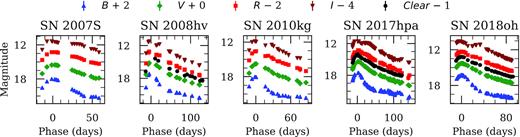
Observed light curves for the previously unpublished SNe Ia in our archives. In most cases, the error bars are smaller than the points themselves. All dates have been shifted relative to the time of maximum B-band brightness. The light curves are available in a tabular form through our SNDB and are also accessible as online supplementary material.
APPENDIX B: LIGHT-CURVE FITTING
We use the E(B − V) model as implemented by the SNooPy package to simultaneously fit the BVRI (or subset thereof) light curves in our photometry compilation. The model assumes a peak B-band magnitude and B − X colours parametrized by the decline rate, and the results from fitting are the time of maximum B-band light (tmax), decline-rate parameter16 (Δm15), host-galaxy reddening, and distance modulus. We use the fitting results obtained by S19 and CSP for their data sets, and employ the strategy of the former to fit the remaining SNe Ia in our photometry compilation (i.e. those from G10 and CfA1-3). We give the resulting values of tmax and Δm15 for all SNe that pass a visual inspection for fit quality in Table B1, and defer a more thorough explanation of the fitting process to S19 (and their listed references).
| SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1993ac | CfA1 | 49269.34 ± 0.70 | 1.098 ± 0.040 | 2001bg | G10 | 52039.95 ± 0.24 | 1.155 ± 0.029 | 2004dt | G10 | 53240.19 ± 0.18 | 1.136 ± 0.022 |
| 1993ae | CfA1 | 49289.15 ± 0.19 | 1.480 ± 0.022 | 2001br | G10 | 52051.78 ± 0.16 | 1.435 ± 0.024 | 2004fu | CfA3 | 53325.28 ± 0.48 | 1.170 ± 0.063 |
| 1994M | CfA1 | 49474.56 ± 0.29 | 1.331 ± 0.021 | 2001cj | G10 | 52064.98 ± 0.11 | 0.903 ± 0.013 | 2004fz | G10 | 53333.53 ± 0.10 | 1.473 ± 0.027 |
| 1994Q | CfA1 | 49495.35 ± 0.40 | 1.093 ± 0.020 | 2001ck | G10 | 52072.10 ± 0.12 | 1.079 ± 0.017 | 2005bc | G10 | 53469.96 ± 0.12 | 1.646 ± 0.028 |
| 1994S | CfA1 | 49517.90 ± 0.36 | 1.021 ± 0.038 | 2001cp | G10 | 52087.82 ± 0.08 | 0.884 ± 0.009 | 2005bo | G10 | 53478.10 ± 0.16 | 1.270 ± 0.008 |
| 1994ae | CfA1 | 49685.19 ± 0.10 | 1.058 ± 0.011 | 2001da | G10 | 52107.02 ± 0.19 | 1.149 ± 0.021 | 2005cf | G10 | 53533.85 ± 0.08 | 1.123 ± 0.008 |
| 1995D | CfA1 | 49767.78 ± 0.16 | 0.886 ± 0.012 | 2001dl | G10 | 52130.58 ± 0.12 | 1.022 ± 0.023 | 2005de | G10 | 53598.65 ± 0.10 | 1.216 ± 0.012 |
| 1995E | CfA1 | 49774.49 ± 0.22 | 1.069 ± 0.018 | 2001eh | G10 | 52168.42 ± 0.16 | 0.837 ± 0.006 | 2005eu | G10 | 53659.81 ± 0.12 | 1.099 ± 0.018 |
| 1995ac | CfA1 | 49992.44 ± 0.30 | 0.941 ± 0.036 | 2001en | G10 | 52192.43 ± 0.10 | 1.282 ± 0.005 | 2005hf | CfA3 | 53660.68 ± 0.95 | 1.449 ± 0.053 |
| 1995ak | CfA1 | 50022.22 ± 0.50 | 1.278 ± 0.018 | 2001ep | G10 | 52199.65 ± 0.17 | 1.133 ± 0.023 | 2005ls | CfA3 | 53714.40 ± 0.31 | 0.930 ± 0.033 |
| 1995al | CfA1 | 50028.26 ± 0.19 | 0.910 ± 0.014 | 2001ex | G10 | 52204.27 ± 0.28 | 1.813 ± 0.029 | 2005lz | CfA3 | 53735.82 ± 0.39 | 1.276 ± 0.031 |
| 1995bd | CfA1 | 50086.33 ± 0.15 | 0.937 ± 0.030 | 2001fe | CfA3 | 52229.01 ± 0.30 | 0.956 ± 0.019 | 2005mc | CfA3 | 53733.83 ± 0.22 | 1.733 ± 0.026 |
| 1996C | CfA1 | 50127.77 ± 0.33 | 0.965 ± 0.019 | 2002G | G10 | 52297.43 ± 0.43 | 1.145 ± 0.050 | 2005ms | CfA3 | 53744.16 ± 0.10 | 1.079 ± 0.018 |
| 1996X | CfA1 | 50190.73 ± 0.13 | 1.225 ± 0.009 | 2002aw | G10 | 52324.57 ± 0.25 | 1.123 ± 0.017 | 2005mz | CfA3 | 53745.01 ± 0.13 | 1.864 ± 0.003 |
| 1996ai | CfA1 | 50256.52 ± 0.38 | 1.112 ± 0.036 | 2002bf | G10 | 52335.09 ± 0.00 | 1.093 ± 0.032 | 2006X | G10 | 53786.01 ± 0.55 | 0.971 ± 0.038 |
| 1996bk | CfA1 | 50369.07 ± 0.55 | 1.758 ± 0.010 | 2002bo | G10 | 52356.29 ± 0.12 | 1.105 ± 0.014 | 2006ac | G10 | 53779.74 ± 0.51 | 1.199 ± 0.029 |
| 1996bl | CfA1 | 50376.23 ± 0.19 | 1.100 ± 0.019 | 2002bz | CfA3 | 52368.19 ± 0.53 | 1.366 ± 0.045 | 2006al | CfA3 | 53789.06 ± 0.35 | 1.569 ± 0.044 |
| 1996bo | CfA1 | 50386.51 ± 0.38 | 1.156 ± 0.036 | 2002cd | G10 | 52384.39 ± 0.23 | 1.101 ± 0.024 | 2006az | CfA3 | 53826.76 ± 0.13 | 1.354 ± 0.027 |
| 1996bv | CfA1 | 50403.42 ± 0.39 | 0.930 ± 0.023 | 2002cf | G10 | 52384.39 ± 0.10 | 1.823 ± 0.001 | 2006bb | CfA3 | 53815.83 ± 0.48 | 1.615 ± 0.018 |
| 1997bp | CfA2 | 50550.08 ± 0.43 | 1.114 ± 0.049 | 2002cr | G10 | 52409.07 ± 0.09 | 1.260 ± 0.007 | 2006bt | G10 | 53857.71 ± 0.23 | 1.091 ± 0.036 |
| 1997bq | CfA2 | 50558.43 ± 0.31 | 1.136 ± 0.031 | 2002cs | G10 | 52410.26 ± 0.17 | 1.097 ± 0.020 | 2006cc | CfA3 | 53874.13 ± 0.13 | 1.044 ± 0.030 |
| 1997br | CfA2 | 50559.90 ± 0.27 | 1.122 ± 0.027 | 2002cu | G10 | 52416.12 ± 0.10 | 1.461 ± 0.022 | 2006cp | G10 | 53896.91 ± 0.31 | 1.130 ± 0.054 |
| 1997cw | CfA2 | 50627.98 ± 0.44 | 0.811 ± 0.020 | 2002de | G10 | 52432.99 ± 0.16 | 1.071 ± 0.021 | 2006dm | G10 | 53928.20 ± 0.09 | 1.523 ± 0.017 |
| 1997do | CfA2 | 50766.18 ± 0.23 | 1.088 ± 0.023 | 2002dj | G10 | 52450.79 ± 0.35 | 1.149 ± 0.046 | 2006ef | G10 | 53968.14 ± 0.22 | 1.273 ± 0.012 |
| 1997dt | CfA2 | 50786.77 ± 0.23 | 1.341 ± 0.054 | 2002dl | G10 | 52451.92 ± 0.09 | 1.759 ± 0.007 | 2006ej | G10 | 53975.67 ± 0.17 | 1.498 ± 0.037 |
| 1998ab | CfA2 | 50914.39 ± 0.19 | 1.103 ± 0.021 | 2002do | G10 | 52441.42 ± 0.47 | 1.718 ± 0.010 | 2006em | G10 | 53976.32 ± 0.24 | 1.823 ± 0.001 |
| 1998bp | CfA2 | 50936.36 ± 0.18 | 1.800 ± 0.012 | 2002dp | G10 | 52450.38 ± 0.11 | 1.214 ± 0.008 | 2006en | G10 | 53970.97 ± 0.34 | 0.974 ± 0.021 |
| 1998de | G10 | 51025.70 ± 0.12 | 1.821 ± 0.001 | 2002eb | G10 | 52494.31 ± 0.08 | 1.067 ± 0.012 | 2006gr | G10 | 54012.41 ± 0.13 | 1.084 ± 0.017 |
| 1998dh | G10 | 51029.00 ± 0.12 | 1.118 ± 0.015 | 2002ef | G10 | 52489.88 ± 0.17 | 1.144 ± 0.019 | 2006hb | G10 | 54000.62 ± 0.29 | 1.693 ± 0.011 |
| 1998dk | CfA2 | 51057.17 ± 0.29 | 1.135 ± 0.015 | 2002el | G10 | 52507.93 ± 0.07 | 1.367 ± 0.020 | 2006le | G10 | 54047.74 ± 0.16 | 1.082 ± 0.018 |
| 1998dm | G10 | 51060.25 ± 0.12 | 1.008 ± 0.015 | 2002er | G10 | 52524.49 ± 0.16 | 1.140 ± 0.018 | 2006lf | G10 | 54045.03 ± 0.17 | 1.459 ± 0.032 |
| 1998ec | G10 | 51088.65 ± 0.93 | 1.146 ± 0.072 | 2002eu | G10 | 52520.22 ± 0.24 | 1.731 ± 0.010 | 2006mo | CfA3 | 54048.02 ± 0.35 | 1.653 ± 0.047 |
| 1998ef | G10 | 51113.19 ± 0.10 | 1.280 ± 0.007 | 2002fb | G10 | 52529.02 ± 0.09 | 1.824 ± 0.000 | 2006mp | CfA3 | 54053.92 ± 0.12 | 0.995 ± 0.019 |
| 1998eg | G10 | 51110.13 ± 0.70 | 1.117 ± 0.047 | 2002fk | G10 | 52547.13 ± 0.10 | 1.027 ± 0.010 | 2006oa | CfA3 | 54066.52 ± 0.19 | 0.953 ± 0.054 |
| 1998es | G10 | 51142.61 ± 0.07 | 0.925 ± 0.010 | 2002ha | G10 | 52580.77 ± 0.04 | 1.362 ± 0.008 | 2006qo | CfA3 | 54082.94 ± 0.15 | 1.054 ± 0.014 |
| 1999aa | G10 | 51231.89 ± 0.13 | 0.886 ± 0.014 | 2002he | G10 | 52585.40 ± 0.06 | 1.439 ± 0.011 | 2006sr | CfA3 | 54092.38 ± 0.14 | 1.279 ± 0.011 |
| 1999ac | G10 | 51249.98 ± 0.19 | 1.104 ± 0.022 | 2002hu | CfA3 | 52592.12 ± 0.13 | 1.089 ± 0.015 | 2006td | CfA3 | 54099.32 ± 0.14 | 1.422 ± 0.020 |
| 1999by | G10 | 51307.95 ± 0.10 | 1.824 ± 0.000 | 2002hw | CfA3 | 52595.63 ± 0.12 | 1.552 ± 0.027 | 2006te | CfA3 | 54096.89 ± 0.40 | 1.130 ± 0.021 |
| 1999cc | CfA2 | 51315.33 ± 0.18 | 1.344 ± 0.028 | 2002jg | G10 | 52609.62 ± 0.07 | 1.417 ± 0.019 | 2007O | G10 | 54122.77 ± 0.40 | 1.139 ± 0.041 |
| 1999cl | G10 | 51340.88 ± 0.22 | 1.144 ± 0.026 | 2002jy | CfA3 | 52634.02 ± 0.37 | 0.881 ± 0.026 | 2007S | this | 54144.73 ± 0.24 | 0.836 ± 0.005 |
| 1999cp | G10 | 51362.61 ± 0.12 | 1.032 ± 0.021 | 2002kf | CfA3 | 52638.27 ± 0.43 | 1.236 ± 0.016 | 2007al | CfA3 | 54169.59 ± 0.25 | 1.857 ± 0.016 |
| 1999da | G10 | 51369.79 ± 0.09 | 1.823 ± 0.001 | 2003W | G10 | 52679.65 ± 0.23 | 1.130 ± 0.029 | 2007ap | CfA3 | 54168.31 ± 0.15 | 1.490 ± 0.018 |
| 1999dg | G10 | 51392.64 ± 0.32 | 1.509 ± 0.049 | 2003Y | G10 | 52676.54 ± 0.12 | 1.822 ± 0.001 | 2007au | G10 | 54183.75 ± 0.17 | 1.754 ± 0.017 |
| 1999dk | G10 | 51414.72 ± 0.13 | 1.103 ± 0.014 | 2003cg | G10 | 52729.24 ± 0.14 | 1.136 ± 0.015 | 2007bj | G10 | 54199.92 ± 0.70 | 0.905 ± 0.039 |
| 1999dq | G10 | 51435.95 ± 0.10 | 1.090 ± 0.012 | 2003ch | CfA3 | 52725.42 ± 0.35 | 1.274 ± 0.019 | 2007bz | CfA3 | 54213.68 ± 0.50 | 0.888 ± 0.051 |
| 1999ej | G10 | 51482.78 ± 0.06 | 1.565 ± 0.010 | 2003cq | G10 | 52737.64 ± 0.33 | 1.170 ± 0.023 | 2007ci | G10 | 54246.24 ± 0.18 | 1.732 ± 0.015 |
| 1999ek | CfA2 | 51481.16 ± 0.39 | 1.164 ± 0.016 | 2003du | G10 | 52765.71 ± 0.11 | 1.055 ± 0.007 | 2007co | G10 | 54264.07 ± 0.13 | 1.108 ± 0.020 |
| 1999gd | CfA2 | 51518.85 ± 0.53 | 1.168 ± 0.025 | 2003fa | G10 | 52806.74 ± 0.08 | 1.072 ± 0.009 | 2007cq | G10 | 54280.01 ± 0.16 | 1.148 ± 0.018 |
| 1999gh | CfA2 | 51513.29 ± 0.37 | 1.737 ± 0.008 | 2003gn | G10 | 52852.44 ± 0.09 | 1.399 ± 0.028 | 2007fr | G10 | 54301.70 ± 0.16 | 1.755 ± 0.013 |
| 1999gp | G10 | 51549.68 ± 0.12 | 1.076 ± 0.014 | 2003gs | G10 | 52847.65 ± 0.25 | 1.820 ± 0.001 | 2007qe | G10 | 54429.37 ± 0.24 | 1.128 ± 0.029 |
| 2000ce | CfA2 | 51666.53 ± 0.46 | 1.015 ± 0.034 | 2003gt | G10 | 52861.61 ± 0.06 | 1.095 ± 0.008 | 2007sr | G10 | 54447.66 ± 0.33 | 1.085 ± 0.015 |
| 2000cf | CfA2 | 51671.86 ± 0.29 | 1.144 ± 0.022 | 2003he | G10 | 52875.89 ± 0.11 | 0.956 ± 0.016 | 2008C | G10 | 54463.84 ± 0.53 | 1.100 ± 0.019 |
| 2000cn | G10 | 51706.76 ± 0.08 | 1.713 ± 0.008 | 2003hv | G10 | 52890.04 ± 0.09 | 1.554 ± 0.008 | 2008L | G10 | 54493.79 ± 0.14 | 1.545 ± 0.023 |
| 2000cp | G10 | 51719.52 ± 0.68 | 1.158 ± 0.070 | 2003ic | CfA3 | 52906.73 ± 0.71 | 1.425 ± 0.058 | 2008Q | G10 | 54504.62 ± 0.23 | 1.029 ± 0.090 |
| 2000cu | G10 | 51743.78 ± 0.10 | 1.502 ± 0.017 | 2003it | CfA3 | 52934.97 ± 0.21 | 1.435 ± 0.029 | 2008Z | G10 | 54514.74 ± 0.21 | 1.020 ± 0.043 |
| 2000cw | G10 | 51747.89 ± 0.17 | 1.153 ± 0.022 | 2003iv | CfA3 | 52933.94 ± 0.20 | 1.527 ± 0.047 | 2008af | CfA3 | 54503.68 ± 0.73 | 1.532 ± 0.041 |
| 2000cx | G10 | 51752.60 ± 0.15 | 1.265 ± 0.011 | 2003kf | G10 | 52980.13 ± 0.22 | 1.025 ± 0.025 | 2008ar | G10 | 54534.35 ± 0.17 | 1.113 ± 0.023 |
| 2000dk | G10 | 51811.79 ± 0.05 | 1.712 ± 0.005 | 2004E | G10 | 53014.95 ± 0.43 | 1.121 ± 0.023 | 2008dr | G10 | 54649.53 ± 0.22 | 1.463 ± 0.035 |
| 2000dm | G10 | 51815.25 ± 0.11 | 1.535 ± 0.017 | 2004S | G10 | 53039.57 ± 0.26 | 1.115 ± 0.013 | 2008ec | G10 | 54673.78 ± 0.09 | 1.341 ± 0.016 |
| 2000dn | G10 | 51824.52 ± 0.15 | 1.107 ± 0.023 | 2004as | G10 | 53084.66 ± 0.18 | 1.133 ± 0.037 | 2008ei | G10 | 54670.78 ± 0.75 | 1.142 ± 0.058 |
| 2000dr | G10 | 51833.97 ± 0.00 | 1.753 ± 0.007 | 2004at | G10 | 53091.65 ± 0.07 | 1.092 ± 0.009 | 2008hv | this | 54817.01 ± 0.08 | 1.276 ± 0.007 |
| 2000fa | G10 | 51891.78 ± 0.12 | 0.974 ± 0.012 | 2004bd | G10 | 53096.93 ± 0.39 | 1.736 ± 0.007 | 2010kg | this | 55543.89 ± 0.19 | 1.269 ± 0.014 |
| 2001E | G10 | 51926.16 ± 0.41 | 1.021 ± 0.058 | 2004bg | G10 | 53108.35 ± 0.22 | 1.024 ± 0.018 | 2017hpa | this | 58066.66 ± 0.05 | 1.101 ± 0.005 |
| 2001V | G10 | 51971.43 ± 0.30 | 0.849 ± 0.013 | 2004bk | G10 | 53111.45 ± 0.46 | 0.892 ± 0.019 | 2018oh | this | 58163.16 ± 0.07 | 1.064 ± 0.008 |
| 2001ah | G10 | 52005.19 ± 0.21 | 0.921 ± 0.036 | 2004br | G10 | 53147.60 ± 0.23 | 0.880 ± 0.022 | SNF20071021-000 | G10 | 54406.73 ± 0.18 | 1.180 ± 0.017 |
| 2001az | CfA3 | 52031.82 ± 0.59 | 1.016 ± 0.043 | 2004bv | G10 | 53160.48 ± 0.10 | 1.083 ± 0.010 | SNF20080514-002 | G10 | 54611.84 ± 0.13 | 1.393 ± 0.015 |
| 2001bf | G10 | 52044.66 ± 0.00 | 0.921 ± 0.025 | 2004bw | G10 | 53162.66 ± 0.11 | 1.323 ± 0.012 | SNF20080909-030 | G10 | 54730.08 ± 0.62 | 0.926 ± 0.032 |
| SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1993ac | CfA1 | 49269.34 ± 0.70 | 1.098 ± 0.040 | 2001bg | G10 | 52039.95 ± 0.24 | 1.155 ± 0.029 | 2004dt | G10 | 53240.19 ± 0.18 | 1.136 ± 0.022 |
| 1993ae | CfA1 | 49289.15 ± 0.19 | 1.480 ± 0.022 | 2001br | G10 | 52051.78 ± 0.16 | 1.435 ± 0.024 | 2004fu | CfA3 | 53325.28 ± 0.48 | 1.170 ± 0.063 |
| 1994M | CfA1 | 49474.56 ± 0.29 | 1.331 ± 0.021 | 2001cj | G10 | 52064.98 ± 0.11 | 0.903 ± 0.013 | 2004fz | G10 | 53333.53 ± 0.10 | 1.473 ± 0.027 |
| 1994Q | CfA1 | 49495.35 ± 0.40 | 1.093 ± 0.020 | 2001ck | G10 | 52072.10 ± 0.12 | 1.079 ± 0.017 | 2005bc | G10 | 53469.96 ± 0.12 | 1.646 ± 0.028 |
| 1994S | CfA1 | 49517.90 ± 0.36 | 1.021 ± 0.038 | 2001cp | G10 | 52087.82 ± 0.08 | 0.884 ± 0.009 | 2005bo | G10 | 53478.10 ± 0.16 | 1.270 ± 0.008 |
| 1994ae | CfA1 | 49685.19 ± 0.10 | 1.058 ± 0.011 | 2001da | G10 | 52107.02 ± 0.19 | 1.149 ± 0.021 | 2005cf | G10 | 53533.85 ± 0.08 | 1.123 ± 0.008 |
| 1995D | CfA1 | 49767.78 ± 0.16 | 0.886 ± 0.012 | 2001dl | G10 | 52130.58 ± 0.12 | 1.022 ± 0.023 | 2005de | G10 | 53598.65 ± 0.10 | 1.216 ± 0.012 |
| 1995E | CfA1 | 49774.49 ± 0.22 | 1.069 ± 0.018 | 2001eh | G10 | 52168.42 ± 0.16 | 0.837 ± 0.006 | 2005eu | G10 | 53659.81 ± 0.12 | 1.099 ± 0.018 |
| 1995ac | CfA1 | 49992.44 ± 0.30 | 0.941 ± 0.036 | 2001en | G10 | 52192.43 ± 0.10 | 1.282 ± 0.005 | 2005hf | CfA3 | 53660.68 ± 0.95 | 1.449 ± 0.053 |
| 1995ak | CfA1 | 50022.22 ± 0.50 | 1.278 ± 0.018 | 2001ep | G10 | 52199.65 ± 0.17 | 1.133 ± 0.023 | 2005ls | CfA3 | 53714.40 ± 0.31 | 0.930 ± 0.033 |
| 1995al | CfA1 | 50028.26 ± 0.19 | 0.910 ± 0.014 | 2001ex | G10 | 52204.27 ± 0.28 | 1.813 ± 0.029 | 2005lz | CfA3 | 53735.82 ± 0.39 | 1.276 ± 0.031 |
| 1995bd | CfA1 | 50086.33 ± 0.15 | 0.937 ± 0.030 | 2001fe | CfA3 | 52229.01 ± 0.30 | 0.956 ± 0.019 | 2005mc | CfA3 | 53733.83 ± 0.22 | 1.733 ± 0.026 |
| 1996C | CfA1 | 50127.77 ± 0.33 | 0.965 ± 0.019 | 2002G | G10 | 52297.43 ± 0.43 | 1.145 ± 0.050 | 2005ms | CfA3 | 53744.16 ± 0.10 | 1.079 ± 0.018 |
| 1996X | CfA1 | 50190.73 ± 0.13 | 1.225 ± 0.009 | 2002aw | G10 | 52324.57 ± 0.25 | 1.123 ± 0.017 | 2005mz | CfA3 | 53745.01 ± 0.13 | 1.864 ± 0.003 |
| 1996ai | CfA1 | 50256.52 ± 0.38 | 1.112 ± 0.036 | 2002bf | G10 | 52335.09 ± 0.00 | 1.093 ± 0.032 | 2006X | G10 | 53786.01 ± 0.55 | 0.971 ± 0.038 |
| 1996bk | CfA1 | 50369.07 ± 0.55 | 1.758 ± 0.010 | 2002bo | G10 | 52356.29 ± 0.12 | 1.105 ± 0.014 | 2006ac | G10 | 53779.74 ± 0.51 | 1.199 ± 0.029 |
| 1996bl | CfA1 | 50376.23 ± 0.19 | 1.100 ± 0.019 | 2002bz | CfA3 | 52368.19 ± 0.53 | 1.366 ± 0.045 | 2006al | CfA3 | 53789.06 ± 0.35 | 1.569 ± 0.044 |
| 1996bo | CfA1 | 50386.51 ± 0.38 | 1.156 ± 0.036 | 2002cd | G10 | 52384.39 ± 0.23 | 1.101 ± 0.024 | 2006az | CfA3 | 53826.76 ± 0.13 | 1.354 ± 0.027 |
| 1996bv | CfA1 | 50403.42 ± 0.39 | 0.930 ± 0.023 | 2002cf | G10 | 52384.39 ± 0.10 | 1.823 ± 0.001 | 2006bb | CfA3 | 53815.83 ± 0.48 | 1.615 ± 0.018 |
| 1997bp | CfA2 | 50550.08 ± 0.43 | 1.114 ± 0.049 | 2002cr | G10 | 52409.07 ± 0.09 | 1.260 ± 0.007 | 2006bt | G10 | 53857.71 ± 0.23 | 1.091 ± 0.036 |
| 1997bq | CfA2 | 50558.43 ± 0.31 | 1.136 ± 0.031 | 2002cs | G10 | 52410.26 ± 0.17 | 1.097 ± 0.020 | 2006cc | CfA3 | 53874.13 ± 0.13 | 1.044 ± 0.030 |
| 1997br | CfA2 | 50559.90 ± 0.27 | 1.122 ± 0.027 | 2002cu | G10 | 52416.12 ± 0.10 | 1.461 ± 0.022 | 2006cp | G10 | 53896.91 ± 0.31 | 1.130 ± 0.054 |
| 1997cw | CfA2 | 50627.98 ± 0.44 | 0.811 ± 0.020 | 2002de | G10 | 52432.99 ± 0.16 | 1.071 ± 0.021 | 2006dm | G10 | 53928.20 ± 0.09 | 1.523 ± 0.017 |
| 1997do | CfA2 | 50766.18 ± 0.23 | 1.088 ± 0.023 | 2002dj | G10 | 52450.79 ± 0.35 | 1.149 ± 0.046 | 2006ef | G10 | 53968.14 ± 0.22 | 1.273 ± 0.012 |
| 1997dt | CfA2 | 50786.77 ± 0.23 | 1.341 ± 0.054 | 2002dl | G10 | 52451.92 ± 0.09 | 1.759 ± 0.007 | 2006ej | G10 | 53975.67 ± 0.17 | 1.498 ± 0.037 |
| 1998ab | CfA2 | 50914.39 ± 0.19 | 1.103 ± 0.021 | 2002do | G10 | 52441.42 ± 0.47 | 1.718 ± 0.010 | 2006em | G10 | 53976.32 ± 0.24 | 1.823 ± 0.001 |
| 1998bp | CfA2 | 50936.36 ± 0.18 | 1.800 ± 0.012 | 2002dp | G10 | 52450.38 ± 0.11 | 1.214 ± 0.008 | 2006en | G10 | 53970.97 ± 0.34 | 0.974 ± 0.021 |
| 1998de | G10 | 51025.70 ± 0.12 | 1.821 ± 0.001 | 2002eb | G10 | 52494.31 ± 0.08 | 1.067 ± 0.012 | 2006gr | G10 | 54012.41 ± 0.13 | 1.084 ± 0.017 |
| 1998dh | G10 | 51029.00 ± 0.12 | 1.118 ± 0.015 | 2002ef | G10 | 52489.88 ± 0.17 | 1.144 ± 0.019 | 2006hb | G10 | 54000.62 ± 0.29 | 1.693 ± 0.011 |
| 1998dk | CfA2 | 51057.17 ± 0.29 | 1.135 ± 0.015 | 2002el | G10 | 52507.93 ± 0.07 | 1.367 ± 0.020 | 2006le | G10 | 54047.74 ± 0.16 | 1.082 ± 0.018 |
| 1998dm | G10 | 51060.25 ± 0.12 | 1.008 ± 0.015 | 2002er | G10 | 52524.49 ± 0.16 | 1.140 ± 0.018 | 2006lf | G10 | 54045.03 ± 0.17 | 1.459 ± 0.032 |
| 1998ec | G10 | 51088.65 ± 0.93 | 1.146 ± 0.072 | 2002eu | G10 | 52520.22 ± 0.24 | 1.731 ± 0.010 | 2006mo | CfA3 | 54048.02 ± 0.35 | 1.653 ± 0.047 |
| 1998ef | G10 | 51113.19 ± 0.10 | 1.280 ± 0.007 | 2002fb | G10 | 52529.02 ± 0.09 | 1.824 ± 0.000 | 2006mp | CfA3 | 54053.92 ± 0.12 | 0.995 ± 0.019 |
| 1998eg | G10 | 51110.13 ± 0.70 | 1.117 ± 0.047 | 2002fk | G10 | 52547.13 ± 0.10 | 1.027 ± 0.010 | 2006oa | CfA3 | 54066.52 ± 0.19 | 0.953 ± 0.054 |
| 1998es | G10 | 51142.61 ± 0.07 | 0.925 ± 0.010 | 2002ha | G10 | 52580.77 ± 0.04 | 1.362 ± 0.008 | 2006qo | CfA3 | 54082.94 ± 0.15 | 1.054 ± 0.014 |
| 1999aa | G10 | 51231.89 ± 0.13 | 0.886 ± 0.014 | 2002he | G10 | 52585.40 ± 0.06 | 1.439 ± 0.011 | 2006sr | CfA3 | 54092.38 ± 0.14 | 1.279 ± 0.011 |
| 1999ac | G10 | 51249.98 ± 0.19 | 1.104 ± 0.022 | 2002hu | CfA3 | 52592.12 ± 0.13 | 1.089 ± 0.015 | 2006td | CfA3 | 54099.32 ± 0.14 | 1.422 ± 0.020 |
| 1999by | G10 | 51307.95 ± 0.10 | 1.824 ± 0.000 | 2002hw | CfA3 | 52595.63 ± 0.12 | 1.552 ± 0.027 | 2006te | CfA3 | 54096.89 ± 0.40 | 1.130 ± 0.021 |
| 1999cc | CfA2 | 51315.33 ± 0.18 | 1.344 ± 0.028 | 2002jg | G10 | 52609.62 ± 0.07 | 1.417 ± 0.019 | 2007O | G10 | 54122.77 ± 0.40 | 1.139 ± 0.041 |
| 1999cl | G10 | 51340.88 ± 0.22 | 1.144 ± 0.026 | 2002jy | CfA3 | 52634.02 ± 0.37 | 0.881 ± 0.026 | 2007S | this | 54144.73 ± 0.24 | 0.836 ± 0.005 |
| 1999cp | G10 | 51362.61 ± 0.12 | 1.032 ± 0.021 | 2002kf | CfA3 | 52638.27 ± 0.43 | 1.236 ± 0.016 | 2007al | CfA3 | 54169.59 ± 0.25 | 1.857 ± 0.016 |
| 1999da | G10 | 51369.79 ± 0.09 | 1.823 ± 0.001 | 2003W | G10 | 52679.65 ± 0.23 | 1.130 ± 0.029 | 2007ap | CfA3 | 54168.31 ± 0.15 | 1.490 ± 0.018 |
| 1999dg | G10 | 51392.64 ± 0.32 | 1.509 ± 0.049 | 2003Y | G10 | 52676.54 ± 0.12 | 1.822 ± 0.001 | 2007au | G10 | 54183.75 ± 0.17 | 1.754 ± 0.017 |
| 1999dk | G10 | 51414.72 ± 0.13 | 1.103 ± 0.014 | 2003cg | G10 | 52729.24 ± 0.14 | 1.136 ± 0.015 | 2007bj | G10 | 54199.92 ± 0.70 | 0.905 ± 0.039 |
| 1999dq | G10 | 51435.95 ± 0.10 | 1.090 ± 0.012 | 2003ch | CfA3 | 52725.42 ± 0.35 | 1.274 ± 0.019 | 2007bz | CfA3 | 54213.68 ± 0.50 | 0.888 ± 0.051 |
| 1999ej | G10 | 51482.78 ± 0.06 | 1.565 ± 0.010 | 2003cq | G10 | 52737.64 ± 0.33 | 1.170 ± 0.023 | 2007ci | G10 | 54246.24 ± 0.18 | 1.732 ± 0.015 |
| 1999ek | CfA2 | 51481.16 ± 0.39 | 1.164 ± 0.016 | 2003du | G10 | 52765.71 ± 0.11 | 1.055 ± 0.007 | 2007co | G10 | 54264.07 ± 0.13 | 1.108 ± 0.020 |
| 1999gd | CfA2 | 51518.85 ± 0.53 | 1.168 ± 0.025 | 2003fa | G10 | 52806.74 ± 0.08 | 1.072 ± 0.009 | 2007cq | G10 | 54280.01 ± 0.16 | 1.148 ± 0.018 |
| 1999gh | CfA2 | 51513.29 ± 0.37 | 1.737 ± 0.008 | 2003gn | G10 | 52852.44 ± 0.09 | 1.399 ± 0.028 | 2007fr | G10 | 54301.70 ± 0.16 | 1.755 ± 0.013 |
| 1999gp | G10 | 51549.68 ± 0.12 | 1.076 ± 0.014 | 2003gs | G10 | 52847.65 ± 0.25 | 1.820 ± 0.001 | 2007qe | G10 | 54429.37 ± 0.24 | 1.128 ± 0.029 |
| 2000ce | CfA2 | 51666.53 ± 0.46 | 1.015 ± 0.034 | 2003gt | G10 | 52861.61 ± 0.06 | 1.095 ± 0.008 | 2007sr | G10 | 54447.66 ± 0.33 | 1.085 ± 0.015 |
| 2000cf | CfA2 | 51671.86 ± 0.29 | 1.144 ± 0.022 | 2003he | G10 | 52875.89 ± 0.11 | 0.956 ± 0.016 | 2008C | G10 | 54463.84 ± 0.53 | 1.100 ± 0.019 |
| 2000cn | G10 | 51706.76 ± 0.08 | 1.713 ± 0.008 | 2003hv | G10 | 52890.04 ± 0.09 | 1.554 ± 0.008 | 2008L | G10 | 54493.79 ± 0.14 | 1.545 ± 0.023 |
| 2000cp | G10 | 51719.52 ± 0.68 | 1.158 ± 0.070 | 2003ic | CfA3 | 52906.73 ± 0.71 | 1.425 ± 0.058 | 2008Q | G10 | 54504.62 ± 0.23 | 1.029 ± 0.090 |
| 2000cu | G10 | 51743.78 ± 0.10 | 1.502 ± 0.017 | 2003it | CfA3 | 52934.97 ± 0.21 | 1.435 ± 0.029 | 2008Z | G10 | 54514.74 ± 0.21 | 1.020 ± 0.043 |
| 2000cw | G10 | 51747.89 ± 0.17 | 1.153 ± 0.022 | 2003iv | CfA3 | 52933.94 ± 0.20 | 1.527 ± 0.047 | 2008af | CfA3 | 54503.68 ± 0.73 | 1.532 ± 0.041 |
| 2000cx | G10 | 51752.60 ± 0.15 | 1.265 ± 0.011 | 2003kf | G10 | 52980.13 ± 0.22 | 1.025 ± 0.025 | 2008ar | G10 | 54534.35 ± 0.17 | 1.113 ± 0.023 |
| 2000dk | G10 | 51811.79 ± 0.05 | 1.712 ± 0.005 | 2004E | G10 | 53014.95 ± 0.43 | 1.121 ± 0.023 | 2008dr | G10 | 54649.53 ± 0.22 | 1.463 ± 0.035 |
| 2000dm | G10 | 51815.25 ± 0.11 | 1.535 ± 0.017 | 2004S | G10 | 53039.57 ± 0.26 | 1.115 ± 0.013 | 2008ec | G10 | 54673.78 ± 0.09 | 1.341 ± 0.016 |
| 2000dn | G10 | 51824.52 ± 0.15 | 1.107 ± 0.023 | 2004as | G10 | 53084.66 ± 0.18 | 1.133 ± 0.037 | 2008ei | G10 | 54670.78 ± 0.75 | 1.142 ± 0.058 |
| 2000dr | G10 | 51833.97 ± 0.00 | 1.753 ± 0.007 | 2004at | G10 | 53091.65 ± 0.07 | 1.092 ± 0.009 | 2008hv | this | 54817.01 ± 0.08 | 1.276 ± 0.007 |
| 2000fa | G10 | 51891.78 ± 0.12 | 0.974 ± 0.012 | 2004bd | G10 | 53096.93 ± 0.39 | 1.736 ± 0.007 | 2010kg | this | 55543.89 ± 0.19 | 1.269 ± 0.014 |
| 2001E | G10 | 51926.16 ± 0.41 | 1.021 ± 0.058 | 2004bg | G10 | 53108.35 ± 0.22 | 1.024 ± 0.018 | 2017hpa | this | 58066.66 ± 0.05 | 1.101 ± 0.005 |
| 2001V | G10 | 51971.43 ± 0.30 | 0.849 ± 0.013 | 2004bk | G10 | 53111.45 ± 0.46 | 0.892 ± 0.019 | 2018oh | this | 58163.16 ± 0.07 | 1.064 ± 0.008 |
| 2001ah | G10 | 52005.19 ± 0.21 | 0.921 ± 0.036 | 2004br | G10 | 53147.60 ± 0.23 | 0.880 ± 0.022 | SNF20071021-000 | G10 | 54406.73 ± 0.18 | 1.180 ± 0.017 |
| 2001az | CfA3 | 52031.82 ± 0.59 | 1.016 ± 0.043 | 2004bv | G10 | 53160.48 ± 0.10 | 1.083 ± 0.010 | SNF20080514-002 | G10 | 54611.84 ± 0.13 | 1.393 ± 0.015 |
| 2001bf | G10 | 52044.66 ± 0.00 | 0.921 ± 0.025 | 2004bw | G10 | 53162.66 ± 0.11 | 1.323 ± 0.012 | SNF20080909-030 | G10 | 54730.08 ± 0.62 | 0.926 ± 0.032 |
| SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1993ac | CfA1 | 49269.34 ± 0.70 | 1.098 ± 0.040 | 2001bg | G10 | 52039.95 ± 0.24 | 1.155 ± 0.029 | 2004dt | G10 | 53240.19 ± 0.18 | 1.136 ± 0.022 |
| 1993ae | CfA1 | 49289.15 ± 0.19 | 1.480 ± 0.022 | 2001br | G10 | 52051.78 ± 0.16 | 1.435 ± 0.024 | 2004fu | CfA3 | 53325.28 ± 0.48 | 1.170 ± 0.063 |
| 1994M | CfA1 | 49474.56 ± 0.29 | 1.331 ± 0.021 | 2001cj | G10 | 52064.98 ± 0.11 | 0.903 ± 0.013 | 2004fz | G10 | 53333.53 ± 0.10 | 1.473 ± 0.027 |
| 1994Q | CfA1 | 49495.35 ± 0.40 | 1.093 ± 0.020 | 2001ck | G10 | 52072.10 ± 0.12 | 1.079 ± 0.017 | 2005bc | G10 | 53469.96 ± 0.12 | 1.646 ± 0.028 |
| 1994S | CfA1 | 49517.90 ± 0.36 | 1.021 ± 0.038 | 2001cp | G10 | 52087.82 ± 0.08 | 0.884 ± 0.009 | 2005bo | G10 | 53478.10 ± 0.16 | 1.270 ± 0.008 |
| 1994ae | CfA1 | 49685.19 ± 0.10 | 1.058 ± 0.011 | 2001da | G10 | 52107.02 ± 0.19 | 1.149 ± 0.021 | 2005cf | G10 | 53533.85 ± 0.08 | 1.123 ± 0.008 |
| 1995D | CfA1 | 49767.78 ± 0.16 | 0.886 ± 0.012 | 2001dl | G10 | 52130.58 ± 0.12 | 1.022 ± 0.023 | 2005de | G10 | 53598.65 ± 0.10 | 1.216 ± 0.012 |
| 1995E | CfA1 | 49774.49 ± 0.22 | 1.069 ± 0.018 | 2001eh | G10 | 52168.42 ± 0.16 | 0.837 ± 0.006 | 2005eu | G10 | 53659.81 ± 0.12 | 1.099 ± 0.018 |
| 1995ac | CfA1 | 49992.44 ± 0.30 | 0.941 ± 0.036 | 2001en | G10 | 52192.43 ± 0.10 | 1.282 ± 0.005 | 2005hf | CfA3 | 53660.68 ± 0.95 | 1.449 ± 0.053 |
| 1995ak | CfA1 | 50022.22 ± 0.50 | 1.278 ± 0.018 | 2001ep | G10 | 52199.65 ± 0.17 | 1.133 ± 0.023 | 2005ls | CfA3 | 53714.40 ± 0.31 | 0.930 ± 0.033 |
| 1995al | CfA1 | 50028.26 ± 0.19 | 0.910 ± 0.014 | 2001ex | G10 | 52204.27 ± 0.28 | 1.813 ± 0.029 | 2005lz | CfA3 | 53735.82 ± 0.39 | 1.276 ± 0.031 |
| 1995bd | CfA1 | 50086.33 ± 0.15 | 0.937 ± 0.030 | 2001fe | CfA3 | 52229.01 ± 0.30 | 0.956 ± 0.019 | 2005mc | CfA3 | 53733.83 ± 0.22 | 1.733 ± 0.026 |
| 1996C | CfA1 | 50127.77 ± 0.33 | 0.965 ± 0.019 | 2002G | G10 | 52297.43 ± 0.43 | 1.145 ± 0.050 | 2005ms | CfA3 | 53744.16 ± 0.10 | 1.079 ± 0.018 |
| 1996X | CfA1 | 50190.73 ± 0.13 | 1.225 ± 0.009 | 2002aw | G10 | 52324.57 ± 0.25 | 1.123 ± 0.017 | 2005mz | CfA3 | 53745.01 ± 0.13 | 1.864 ± 0.003 |
| 1996ai | CfA1 | 50256.52 ± 0.38 | 1.112 ± 0.036 | 2002bf | G10 | 52335.09 ± 0.00 | 1.093 ± 0.032 | 2006X | G10 | 53786.01 ± 0.55 | 0.971 ± 0.038 |
| 1996bk | CfA1 | 50369.07 ± 0.55 | 1.758 ± 0.010 | 2002bo | G10 | 52356.29 ± 0.12 | 1.105 ± 0.014 | 2006ac | G10 | 53779.74 ± 0.51 | 1.199 ± 0.029 |
| 1996bl | CfA1 | 50376.23 ± 0.19 | 1.100 ± 0.019 | 2002bz | CfA3 | 52368.19 ± 0.53 | 1.366 ± 0.045 | 2006al | CfA3 | 53789.06 ± 0.35 | 1.569 ± 0.044 |
| 1996bo | CfA1 | 50386.51 ± 0.38 | 1.156 ± 0.036 | 2002cd | G10 | 52384.39 ± 0.23 | 1.101 ± 0.024 | 2006az | CfA3 | 53826.76 ± 0.13 | 1.354 ± 0.027 |
| 1996bv | CfA1 | 50403.42 ± 0.39 | 0.930 ± 0.023 | 2002cf | G10 | 52384.39 ± 0.10 | 1.823 ± 0.001 | 2006bb | CfA3 | 53815.83 ± 0.48 | 1.615 ± 0.018 |
| 1997bp | CfA2 | 50550.08 ± 0.43 | 1.114 ± 0.049 | 2002cr | G10 | 52409.07 ± 0.09 | 1.260 ± 0.007 | 2006bt | G10 | 53857.71 ± 0.23 | 1.091 ± 0.036 |
| 1997bq | CfA2 | 50558.43 ± 0.31 | 1.136 ± 0.031 | 2002cs | G10 | 52410.26 ± 0.17 | 1.097 ± 0.020 | 2006cc | CfA3 | 53874.13 ± 0.13 | 1.044 ± 0.030 |
| 1997br | CfA2 | 50559.90 ± 0.27 | 1.122 ± 0.027 | 2002cu | G10 | 52416.12 ± 0.10 | 1.461 ± 0.022 | 2006cp | G10 | 53896.91 ± 0.31 | 1.130 ± 0.054 |
| 1997cw | CfA2 | 50627.98 ± 0.44 | 0.811 ± 0.020 | 2002de | G10 | 52432.99 ± 0.16 | 1.071 ± 0.021 | 2006dm | G10 | 53928.20 ± 0.09 | 1.523 ± 0.017 |
| 1997do | CfA2 | 50766.18 ± 0.23 | 1.088 ± 0.023 | 2002dj | G10 | 52450.79 ± 0.35 | 1.149 ± 0.046 | 2006ef | G10 | 53968.14 ± 0.22 | 1.273 ± 0.012 |
| 1997dt | CfA2 | 50786.77 ± 0.23 | 1.341 ± 0.054 | 2002dl | G10 | 52451.92 ± 0.09 | 1.759 ± 0.007 | 2006ej | G10 | 53975.67 ± 0.17 | 1.498 ± 0.037 |
| 1998ab | CfA2 | 50914.39 ± 0.19 | 1.103 ± 0.021 | 2002do | G10 | 52441.42 ± 0.47 | 1.718 ± 0.010 | 2006em | G10 | 53976.32 ± 0.24 | 1.823 ± 0.001 |
| 1998bp | CfA2 | 50936.36 ± 0.18 | 1.800 ± 0.012 | 2002dp | G10 | 52450.38 ± 0.11 | 1.214 ± 0.008 | 2006en | G10 | 53970.97 ± 0.34 | 0.974 ± 0.021 |
| 1998de | G10 | 51025.70 ± 0.12 | 1.821 ± 0.001 | 2002eb | G10 | 52494.31 ± 0.08 | 1.067 ± 0.012 | 2006gr | G10 | 54012.41 ± 0.13 | 1.084 ± 0.017 |
| 1998dh | G10 | 51029.00 ± 0.12 | 1.118 ± 0.015 | 2002ef | G10 | 52489.88 ± 0.17 | 1.144 ± 0.019 | 2006hb | G10 | 54000.62 ± 0.29 | 1.693 ± 0.011 |
| 1998dk | CfA2 | 51057.17 ± 0.29 | 1.135 ± 0.015 | 2002el | G10 | 52507.93 ± 0.07 | 1.367 ± 0.020 | 2006le | G10 | 54047.74 ± 0.16 | 1.082 ± 0.018 |
| 1998dm | G10 | 51060.25 ± 0.12 | 1.008 ± 0.015 | 2002er | G10 | 52524.49 ± 0.16 | 1.140 ± 0.018 | 2006lf | G10 | 54045.03 ± 0.17 | 1.459 ± 0.032 |
| 1998ec | G10 | 51088.65 ± 0.93 | 1.146 ± 0.072 | 2002eu | G10 | 52520.22 ± 0.24 | 1.731 ± 0.010 | 2006mo | CfA3 | 54048.02 ± 0.35 | 1.653 ± 0.047 |
| 1998ef | G10 | 51113.19 ± 0.10 | 1.280 ± 0.007 | 2002fb | G10 | 52529.02 ± 0.09 | 1.824 ± 0.000 | 2006mp | CfA3 | 54053.92 ± 0.12 | 0.995 ± 0.019 |
| 1998eg | G10 | 51110.13 ± 0.70 | 1.117 ± 0.047 | 2002fk | G10 | 52547.13 ± 0.10 | 1.027 ± 0.010 | 2006oa | CfA3 | 54066.52 ± 0.19 | 0.953 ± 0.054 |
| 1998es | G10 | 51142.61 ± 0.07 | 0.925 ± 0.010 | 2002ha | G10 | 52580.77 ± 0.04 | 1.362 ± 0.008 | 2006qo | CfA3 | 54082.94 ± 0.15 | 1.054 ± 0.014 |
| 1999aa | G10 | 51231.89 ± 0.13 | 0.886 ± 0.014 | 2002he | G10 | 52585.40 ± 0.06 | 1.439 ± 0.011 | 2006sr | CfA3 | 54092.38 ± 0.14 | 1.279 ± 0.011 |
| 1999ac | G10 | 51249.98 ± 0.19 | 1.104 ± 0.022 | 2002hu | CfA3 | 52592.12 ± 0.13 | 1.089 ± 0.015 | 2006td | CfA3 | 54099.32 ± 0.14 | 1.422 ± 0.020 |
| 1999by | G10 | 51307.95 ± 0.10 | 1.824 ± 0.000 | 2002hw | CfA3 | 52595.63 ± 0.12 | 1.552 ± 0.027 | 2006te | CfA3 | 54096.89 ± 0.40 | 1.130 ± 0.021 |
| 1999cc | CfA2 | 51315.33 ± 0.18 | 1.344 ± 0.028 | 2002jg | G10 | 52609.62 ± 0.07 | 1.417 ± 0.019 | 2007O | G10 | 54122.77 ± 0.40 | 1.139 ± 0.041 |
| 1999cl | G10 | 51340.88 ± 0.22 | 1.144 ± 0.026 | 2002jy | CfA3 | 52634.02 ± 0.37 | 0.881 ± 0.026 | 2007S | this | 54144.73 ± 0.24 | 0.836 ± 0.005 |
| 1999cp | G10 | 51362.61 ± 0.12 | 1.032 ± 0.021 | 2002kf | CfA3 | 52638.27 ± 0.43 | 1.236 ± 0.016 | 2007al | CfA3 | 54169.59 ± 0.25 | 1.857 ± 0.016 |
| 1999da | G10 | 51369.79 ± 0.09 | 1.823 ± 0.001 | 2003W | G10 | 52679.65 ± 0.23 | 1.130 ± 0.029 | 2007ap | CfA3 | 54168.31 ± 0.15 | 1.490 ± 0.018 |
| 1999dg | G10 | 51392.64 ± 0.32 | 1.509 ± 0.049 | 2003Y | G10 | 52676.54 ± 0.12 | 1.822 ± 0.001 | 2007au | G10 | 54183.75 ± 0.17 | 1.754 ± 0.017 |
| 1999dk | G10 | 51414.72 ± 0.13 | 1.103 ± 0.014 | 2003cg | G10 | 52729.24 ± 0.14 | 1.136 ± 0.015 | 2007bj | G10 | 54199.92 ± 0.70 | 0.905 ± 0.039 |
| 1999dq | G10 | 51435.95 ± 0.10 | 1.090 ± 0.012 | 2003ch | CfA3 | 52725.42 ± 0.35 | 1.274 ± 0.019 | 2007bz | CfA3 | 54213.68 ± 0.50 | 0.888 ± 0.051 |
| 1999ej | G10 | 51482.78 ± 0.06 | 1.565 ± 0.010 | 2003cq | G10 | 52737.64 ± 0.33 | 1.170 ± 0.023 | 2007ci | G10 | 54246.24 ± 0.18 | 1.732 ± 0.015 |
| 1999ek | CfA2 | 51481.16 ± 0.39 | 1.164 ± 0.016 | 2003du | G10 | 52765.71 ± 0.11 | 1.055 ± 0.007 | 2007co | G10 | 54264.07 ± 0.13 | 1.108 ± 0.020 |
| 1999gd | CfA2 | 51518.85 ± 0.53 | 1.168 ± 0.025 | 2003fa | G10 | 52806.74 ± 0.08 | 1.072 ± 0.009 | 2007cq | G10 | 54280.01 ± 0.16 | 1.148 ± 0.018 |
| 1999gh | CfA2 | 51513.29 ± 0.37 | 1.737 ± 0.008 | 2003gn | G10 | 52852.44 ± 0.09 | 1.399 ± 0.028 | 2007fr | G10 | 54301.70 ± 0.16 | 1.755 ± 0.013 |
| 1999gp | G10 | 51549.68 ± 0.12 | 1.076 ± 0.014 | 2003gs | G10 | 52847.65 ± 0.25 | 1.820 ± 0.001 | 2007qe | G10 | 54429.37 ± 0.24 | 1.128 ± 0.029 |
| 2000ce | CfA2 | 51666.53 ± 0.46 | 1.015 ± 0.034 | 2003gt | G10 | 52861.61 ± 0.06 | 1.095 ± 0.008 | 2007sr | G10 | 54447.66 ± 0.33 | 1.085 ± 0.015 |
| 2000cf | CfA2 | 51671.86 ± 0.29 | 1.144 ± 0.022 | 2003he | G10 | 52875.89 ± 0.11 | 0.956 ± 0.016 | 2008C | G10 | 54463.84 ± 0.53 | 1.100 ± 0.019 |
| 2000cn | G10 | 51706.76 ± 0.08 | 1.713 ± 0.008 | 2003hv | G10 | 52890.04 ± 0.09 | 1.554 ± 0.008 | 2008L | G10 | 54493.79 ± 0.14 | 1.545 ± 0.023 |
| 2000cp | G10 | 51719.52 ± 0.68 | 1.158 ± 0.070 | 2003ic | CfA3 | 52906.73 ± 0.71 | 1.425 ± 0.058 | 2008Q | G10 | 54504.62 ± 0.23 | 1.029 ± 0.090 |
| 2000cu | G10 | 51743.78 ± 0.10 | 1.502 ± 0.017 | 2003it | CfA3 | 52934.97 ± 0.21 | 1.435 ± 0.029 | 2008Z | G10 | 54514.74 ± 0.21 | 1.020 ± 0.043 |
| 2000cw | G10 | 51747.89 ± 0.17 | 1.153 ± 0.022 | 2003iv | CfA3 | 52933.94 ± 0.20 | 1.527 ± 0.047 | 2008af | CfA3 | 54503.68 ± 0.73 | 1.532 ± 0.041 |
| 2000cx | G10 | 51752.60 ± 0.15 | 1.265 ± 0.011 | 2003kf | G10 | 52980.13 ± 0.22 | 1.025 ± 0.025 | 2008ar | G10 | 54534.35 ± 0.17 | 1.113 ± 0.023 |
| 2000dk | G10 | 51811.79 ± 0.05 | 1.712 ± 0.005 | 2004E | G10 | 53014.95 ± 0.43 | 1.121 ± 0.023 | 2008dr | G10 | 54649.53 ± 0.22 | 1.463 ± 0.035 |
| 2000dm | G10 | 51815.25 ± 0.11 | 1.535 ± 0.017 | 2004S | G10 | 53039.57 ± 0.26 | 1.115 ± 0.013 | 2008ec | G10 | 54673.78 ± 0.09 | 1.341 ± 0.016 |
| 2000dn | G10 | 51824.52 ± 0.15 | 1.107 ± 0.023 | 2004as | G10 | 53084.66 ± 0.18 | 1.133 ± 0.037 | 2008ei | G10 | 54670.78 ± 0.75 | 1.142 ± 0.058 |
| 2000dr | G10 | 51833.97 ± 0.00 | 1.753 ± 0.007 | 2004at | G10 | 53091.65 ± 0.07 | 1.092 ± 0.009 | 2008hv | this | 54817.01 ± 0.08 | 1.276 ± 0.007 |
| 2000fa | G10 | 51891.78 ± 0.12 | 0.974 ± 0.012 | 2004bd | G10 | 53096.93 ± 0.39 | 1.736 ± 0.007 | 2010kg | this | 55543.89 ± 0.19 | 1.269 ± 0.014 |
| 2001E | G10 | 51926.16 ± 0.41 | 1.021 ± 0.058 | 2004bg | G10 | 53108.35 ± 0.22 | 1.024 ± 0.018 | 2017hpa | this | 58066.66 ± 0.05 | 1.101 ± 0.005 |
| 2001V | G10 | 51971.43 ± 0.30 | 0.849 ± 0.013 | 2004bk | G10 | 53111.45 ± 0.46 | 0.892 ± 0.019 | 2018oh | this | 58163.16 ± 0.07 | 1.064 ± 0.008 |
| 2001ah | G10 | 52005.19 ± 0.21 | 0.921 ± 0.036 | 2004br | G10 | 53147.60 ± 0.23 | 0.880 ± 0.022 | SNF20071021-000 | G10 | 54406.73 ± 0.18 | 1.180 ± 0.017 |
| 2001az | CfA3 | 52031.82 ± 0.59 | 1.016 ± 0.043 | 2004bv | G10 | 53160.48 ± 0.10 | 1.083 ± 0.010 | SNF20080514-002 | G10 | 54611.84 ± 0.13 | 1.393 ± 0.015 |
| 2001bf | G10 | 52044.66 ± 0.00 | 0.921 ± 0.025 | 2004bw | G10 | 53162.66 ± 0.11 | 1.323 ± 0.012 | SNF20080909-030 | G10 | 54730.08 ± 0.62 | 0.926 ± 0.032 |
| SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . | SN . | Sourcea . | tmax (MJD) . | Δm15 (mag) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1993ac | CfA1 | 49269.34 ± 0.70 | 1.098 ± 0.040 | 2001bg | G10 | 52039.95 ± 0.24 | 1.155 ± 0.029 | 2004dt | G10 | 53240.19 ± 0.18 | 1.136 ± 0.022 |
| 1993ae | CfA1 | 49289.15 ± 0.19 | 1.480 ± 0.022 | 2001br | G10 | 52051.78 ± 0.16 | 1.435 ± 0.024 | 2004fu | CfA3 | 53325.28 ± 0.48 | 1.170 ± 0.063 |
| 1994M | CfA1 | 49474.56 ± 0.29 | 1.331 ± 0.021 | 2001cj | G10 | 52064.98 ± 0.11 | 0.903 ± 0.013 | 2004fz | G10 | 53333.53 ± 0.10 | 1.473 ± 0.027 |
| 1994Q | CfA1 | 49495.35 ± 0.40 | 1.093 ± 0.020 | 2001ck | G10 | 52072.10 ± 0.12 | 1.079 ± 0.017 | 2005bc | G10 | 53469.96 ± 0.12 | 1.646 ± 0.028 |
| 1994S | CfA1 | 49517.90 ± 0.36 | 1.021 ± 0.038 | 2001cp | G10 | 52087.82 ± 0.08 | 0.884 ± 0.009 | 2005bo | G10 | 53478.10 ± 0.16 | 1.270 ± 0.008 |
| 1994ae | CfA1 | 49685.19 ± 0.10 | 1.058 ± 0.011 | 2001da | G10 | 52107.02 ± 0.19 | 1.149 ± 0.021 | 2005cf | G10 | 53533.85 ± 0.08 | 1.123 ± 0.008 |
| 1995D | CfA1 | 49767.78 ± 0.16 | 0.886 ± 0.012 | 2001dl | G10 | 52130.58 ± 0.12 | 1.022 ± 0.023 | 2005de | G10 | 53598.65 ± 0.10 | 1.216 ± 0.012 |
| 1995E | CfA1 | 49774.49 ± 0.22 | 1.069 ± 0.018 | 2001eh | G10 | 52168.42 ± 0.16 | 0.837 ± 0.006 | 2005eu | G10 | 53659.81 ± 0.12 | 1.099 ± 0.018 |
| 1995ac | CfA1 | 49992.44 ± 0.30 | 0.941 ± 0.036 | 2001en | G10 | 52192.43 ± 0.10 | 1.282 ± 0.005 | 2005hf | CfA3 | 53660.68 ± 0.95 | 1.449 ± 0.053 |
| 1995ak | CfA1 | 50022.22 ± 0.50 | 1.278 ± 0.018 | 2001ep | G10 | 52199.65 ± 0.17 | 1.133 ± 0.023 | 2005ls | CfA3 | 53714.40 ± 0.31 | 0.930 ± 0.033 |
| 1995al | CfA1 | 50028.26 ± 0.19 | 0.910 ± 0.014 | 2001ex | G10 | 52204.27 ± 0.28 | 1.813 ± 0.029 | 2005lz | CfA3 | 53735.82 ± 0.39 | 1.276 ± 0.031 |
| 1995bd | CfA1 | 50086.33 ± 0.15 | 0.937 ± 0.030 | 2001fe | CfA3 | 52229.01 ± 0.30 | 0.956 ± 0.019 | 2005mc | CfA3 | 53733.83 ± 0.22 | 1.733 ± 0.026 |
| 1996C | CfA1 | 50127.77 ± 0.33 | 0.965 ± 0.019 | 2002G | G10 | 52297.43 ± 0.43 | 1.145 ± 0.050 | 2005ms | CfA3 | 53744.16 ± 0.10 | 1.079 ± 0.018 |
| 1996X | CfA1 | 50190.73 ± 0.13 | 1.225 ± 0.009 | 2002aw | G10 | 52324.57 ± 0.25 | 1.123 ± 0.017 | 2005mz | CfA3 | 53745.01 ± 0.13 | 1.864 ± 0.003 |
| 1996ai | CfA1 | 50256.52 ± 0.38 | 1.112 ± 0.036 | 2002bf | G10 | 52335.09 ± 0.00 | 1.093 ± 0.032 | 2006X | G10 | 53786.01 ± 0.55 | 0.971 ± 0.038 |
| 1996bk | CfA1 | 50369.07 ± 0.55 | 1.758 ± 0.010 | 2002bo | G10 | 52356.29 ± 0.12 | 1.105 ± 0.014 | 2006ac | G10 | 53779.74 ± 0.51 | 1.199 ± 0.029 |
| 1996bl | CfA1 | 50376.23 ± 0.19 | 1.100 ± 0.019 | 2002bz | CfA3 | 52368.19 ± 0.53 | 1.366 ± 0.045 | 2006al | CfA3 | 53789.06 ± 0.35 | 1.569 ± 0.044 |
| 1996bo | CfA1 | 50386.51 ± 0.38 | 1.156 ± 0.036 | 2002cd | G10 | 52384.39 ± 0.23 | 1.101 ± 0.024 | 2006az | CfA3 | 53826.76 ± 0.13 | 1.354 ± 0.027 |
| 1996bv | CfA1 | 50403.42 ± 0.39 | 0.930 ± 0.023 | 2002cf | G10 | 52384.39 ± 0.10 | 1.823 ± 0.001 | 2006bb | CfA3 | 53815.83 ± 0.48 | 1.615 ± 0.018 |
| 1997bp | CfA2 | 50550.08 ± 0.43 | 1.114 ± 0.049 | 2002cr | G10 | 52409.07 ± 0.09 | 1.260 ± 0.007 | 2006bt | G10 | 53857.71 ± 0.23 | 1.091 ± 0.036 |
| 1997bq | CfA2 | 50558.43 ± 0.31 | 1.136 ± 0.031 | 2002cs | G10 | 52410.26 ± 0.17 | 1.097 ± 0.020 | 2006cc | CfA3 | 53874.13 ± 0.13 | 1.044 ± 0.030 |
| 1997br | CfA2 | 50559.90 ± 0.27 | 1.122 ± 0.027 | 2002cu | G10 | 52416.12 ± 0.10 | 1.461 ± 0.022 | 2006cp | G10 | 53896.91 ± 0.31 | 1.130 ± 0.054 |
| 1997cw | CfA2 | 50627.98 ± 0.44 | 0.811 ± 0.020 | 2002de | G10 | 52432.99 ± 0.16 | 1.071 ± 0.021 | 2006dm | G10 | 53928.20 ± 0.09 | 1.523 ± 0.017 |
| 1997do | CfA2 | 50766.18 ± 0.23 | 1.088 ± 0.023 | 2002dj | G10 | 52450.79 ± 0.35 | 1.149 ± 0.046 | 2006ef | G10 | 53968.14 ± 0.22 | 1.273 ± 0.012 |
| 1997dt | CfA2 | 50786.77 ± 0.23 | 1.341 ± 0.054 | 2002dl | G10 | 52451.92 ± 0.09 | 1.759 ± 0.007 | 2006ej | G10 | 53975.67 ± 0.17 | 1.498 ± 0.037 |
| 1998ab | CfA2 | 50914.39 ± 0.19 | 1.103 ± 0.021 | 2002do | G10 | 52441.42 ± 0.47 | 1.718 ± 0.010 | 2006em | G10 | 53976.32 ± 0.24 | 1.823 ± 0.001 |
| 1998bp | CfA2 | 50936.36 ± 0.18 | 1.800 ± 0.012 | 2002dp | G10 | 52450.38 ± 0.11 | 1.214 ± 0.008 | 2006en | G10 | 53970.97 ± 0.34 | 0.974 ± 0.021 |
| 1998de | G10 | 51025.70 ± 0.12 | 1.821 ± 0.001 | 2002eb | G10 | 52494.31 ± 0.08 | 1.067 ± 0.012 | 2006gr | G10 | 54012.41 ± 0.13 | 1.084 ± 0.017 |
| 1998dh | G10 | 51029.00 ± 0.12 | 1.118 ± 0.015 | 2002ef | G10 | 52489.88 ± 0.17 | 1.144 ± 0.019 | 2006hb | G10 | 54000.62 ± 0.29 | 1.693 ± 0.011 |
| 1998dk | CfA2 | 51057.17 ± 0.29 | 1.135 ± 0.015 | 2002el | G10 | 52507.93 ± 0.07 | 1.367 ± 0.020 | 2006le | G10 | 54047.74 ± 0.16 | 1.082 ± 0.018 |
| 1998dm | G10 | 51060.25 ± 0.12 | 1.008 ± 0.015 | 2002er | G10 | 52524.49 ± 0.16 | 1.140 ± 0.018 | 2006lf | G10 | 54045.03 ± 0.17 | 1.459 ± 0.032 |
| 1998ec | G10 | 51088.65 ± 0.93 | 1.146 ± 0.072 | 2002eu | G10 | 52520.22 ± 0.24 | 1.731 ± 0.010 | 2006mo | CfA3 | 54048.02 ± 0.35 | 1.653 ± 0.047 |
| 1998ef | G10 | 51113.19 ± 0.10 | 1.280 ± 0.007 | 2002fb | G10 | 52529.02 ± 0.09 | 1.824 ± 0.000 | 2006mp | CfA3 | 54053.92 ± 0.12 | 0.995 ± 0.019 |
| 1998eg | G10 | 51110.13 ± 0.70 | 1.117 ± 0.047 | 2002fk | G10 | 52547.13 ± 0.10 | 1.027 ± 0.010 | 2006oa | CfA3 | 54066.52 ± 0.19 | 0.953 ± 0.054 |
| 1998es | G10 | 51142.61 ± 0.07 | 0.925 ± 0.010 | 2002ha | G10 | 52580.77 ± 0.04 | 1.362 ± 0.008 | 2006qo | CfA3 | 54082.94 ± 0.15 | 1.054 ± 0.014 |
| 1999aa | G10 | 51231.89 ± 0.13 | 0.886 ± 0.014 | 2002he | G10 | 52585.40 ± 0.06 | 1.439 ± 0.011 | 2006sr | CfA3 | 54092.38 ± 0.14 | 1.279 ± 0.011 |
| 1999ac | G10 | 51249.98 ± 0.19 | 1.104 ± 0.022 | 2002hu | CfA3 | 52592.12 ± 0.13 | 1.089 ± 0.015 | 2006td | CfA3 | 54099.32 ± 0.14 | 1.422 ± 0.020 |
| 1999by | G10 | 51307.95 ± 0.10 | 1.824 ± 0.000 | 2002hw | CfA3 | 52595.63 ± 0.12 | 1.552 ± 0.027 | 2006te | CfA3 | 54096.89 ± 0.40 | 1.130 ± 0.021 |
| 1999cc | CfA2 | 51315.33 ± 0.18 | 1.344 ± 0.028 | 2002jg | G10 | 52609.62 ± 0.07 | 1.417 ± 0.019 | 2007O | G10 | 54122.77 ± 0.40 | 1.139 ± 0.041 |
| 1999cl | G10 | 51340.88 ± 0.22 | 1.144 ± 0.026 | 2002jy | CfA3 | 52634.02 ± 0.37 | 0.881 ± 0.026 | 2007S | this | 54144.73 ± 0.24 | 0.836 ± 0.005 |
| 1999cp | G10 | 51362.61 ± 0.12 | 1.032 ± 0.021 | 2002kf | CfA3 | 52638.27 ± 0.43 | 1.236 ± 0.016 | 2007al | CfA3 | 54169.59 ± 0.25 | 1.857 ± 0.016 |
| 1999da | G10 | 51369.79 ± 0.09 | 1.823 ± 0.001 | 2003W | G10 | 52679.65 ± 0.23 | 1.130 ± 0.029 | 2007ap | CfA3 | 54168.31 ± 0.15 | 1.490 ± 0.018 |
| 1999dg | G10 | 51392.64 ± 0.32 | 1.509 ± 0.049 | 2003Y | G10 | 52676.54 ± 0.12 | 1.822 ± 0.001 | 2007au | G10 | 54183.75 ± 0.17 | 1.754 ± 0.017 |
| 1999dk | G10 | 51414.72 ± 0.13 | 1.103 ± 0.014 | 2003cg | G10 | 52729.24 ± 0.14 | 1.136 ± 0.015 | 2007bj | G10 | 54199.92 ± 0.70 | 0.905 ± 0.039 |
| 1999dq | G10 | 51435.95 ± 0.10 | 1.090 ± 0.012 | 2003ch | CfA3 | 52725.42 ± 0.35 | 1.274 ± 0.019 | 2007bz | CfA3 | 54213.68 ± 0.50 | 0.888 ± 0.051 |
| 1999ej | G10 | 51482.78 ± 0.06 | 1.565 ± 0.010 | 2003cq | G10 | 52737.64 ± 0.33 | 1.170 ± 0.023 | 2007ci | G10 | 54246.24 ± 0.18 | 1.732 ± 0.015 |
| 1999ek | CfA2 | 51481.16 ± 0.39 | 1.164 ± 0.016 | 2003du | G10 | 52765.71 ± 0.11 | 1.055 ± 0.007 | 2007co | G10 | 54264.07 ± 0.13 | 1.108 ± 0.020 |
| 1999gd | CfA2 | 51518.85 ± 0.53 | 1.168 ± 0.025 | 2003fa | G10 | 52806.74 ± 0.08 | 1.072 ± 0.009 | 2007cq | G10 | 54280.01 ± 0.16 | 1.148 ± 0.018 |
| 1999gh | CfA2 | 51513.29 ± 0.37 | 1.737 ± 0.008 | 2003gn | G10 | 52852.44 ± 0.09 | 1.399 ± 0.028 | 2007fr | G10 | 54301.70 ± 0.16 | 1.755 ± 0.013 |
| 1999gp | G10 | 51549.68 ± 0.12 | 1.076 ± 0.014 | 2003gs | G10 | 52847.65 ± 0.25 | 1.820 ± 0.001 | 2007qe | G10 | 54429.37 ± 0.24 | 1.128 ± 0.029 |
| 2000ce | CfA2 | 51666.53 ± 0.46 | 1.015 ± 0.034 | 2003gt | G10 | 52861.61 ± 0.06 | 1.095 ± 0.008 | 2007sr | G10 | 54447.66 ± 0.33 | 1.085 ± 0.015 |
| 2000cf | CfA2 | 51671.86 ± 0.29 | 1.144 ± 0.022 | 2003he | G10 | 52875.89 ± 0.11 | 0.956 ± 0.016 | 2008C | G10 | 54463.84 ± 0.53 | 1.100 ± 0.019 |
| 2000cn | G10 | 51706.76 ± 0.08 | 1.713 ± 0.008 | 2003hv | G10 | 52890.04 ± 0.09 | 1.554 ± 0.008 | 2008L | G10 | 54493.79 ± 0.14 | 1.545 ± 0.023 |
| 2000cp | G10 | 51719.52 ± 0.68 | 1.158 ± 0.070 | 2003ic | CfA3 | 52906.73 ± 0.71 | 1.425 ± 0.058 | 2008Q | G10 | 54504.62 ± 0.23 | 1.029 ± 0.090 |
| 2000cu | G10 | 51743.78 ± 0.10 | 1.502 ± 0.017 | 2003it | CfA3 | 52934.97 ± 0.21 | 1.435 ± 0.029 | 2008Z | G10 | 54514.74 ± 0.21 | 1.020 ± 0.043 |
| 2000cw | G10 | 51747.89 ± 0.17 | 1.153 ± 0.022 | 2003iv | CfA3 | 52933.94 ± 0.20 | 1.527 ± 0.047 | 2008af | CfA3 | 54503.68 ± 0.73 | 1.532 ± 0.041 |
| 2000cx | G10 | 51752.60 ± 0.15 | 1.265 ± 0.011 | 2003kf | G10 | 52980.13 ± 0.22 | 1.025 ± 0.025 | 2008ar | G10 | 54534.35 ± 0.17 | 1.113 ± 0.023 |
| 2000dk | G10 | 51811.79 ± 0.05 | 1.712 ± 0.005 | 2004E | G10 | 53014.95 ± 0.43 | 1.121 ± 0.023 | 2008dr | G10 | 54649.53 ± 0.22 | 1.463 ± 0.035 |
| 2000dm | G10 | 51815.25 ± 0.11 | 1.535 ± 0.017 | 2004S | G10 | 53039.57 ± 0.26 | 1.115 ± 0.013 | 2008ec | G10 | 54673.78 ± 0.09 | 1.341 ± 0.016 |
| 2000dn | G10 | 51824.52 ± 0.15 | 1.107 ± 0.023 | 2004as | G10 | 53084.66 ± 0.18 | 1.133 ± 0.037 | 2008ei | G10 | 54670.78 ± 0.75 | 1.142 ± 0.058 |
| 2000dr | G10 | 51833.97 ± 0.00 | 1.753 ± 0.007 | 2004at | G10 | 53091.65 ± 0.07 | 1.092 ± 0.009 | 2008hv | this | 54817.01 ± 0.08 | 1.276 ± 0.007 |
| 2000fa | G10 | 51891.78 ± 0.12 | 0.974 ± 0.012 | 2004bd | G10 | 53096.93 ± 0.39 | 1.736 ± 0.007 | 2010kg | this | 55543.89 ± 0.19 | 1.269 ± 0.014 |
| 2001E | G10 | 51926.16 ± 0.41 | 1.021 ± 0.058 | 2004bg | G10 | 53108.35 ± 0.22 | 1.024 ± 0.018 | 2017hpa | this | 58066.66 ± 0.05 | 1.101 ± 0.005 |
| 2001V | G10 | 51971.43 ± 0.30 | 0.849 ± 0.013 | 2004bk | G10 | 53111.45 ± 0.46 | 0.892 ± 0.019 | 2018oh | this | 58163.16 ± 0.07 | 1.064 ± 0.008 |
| 2001ah | G10 | 52005.19 ± 0.21 | 0.921 ± 0.036 | 2004br | G10 | 53147.60 ± 0.23 | 0.880 ± 0.022 | SNF20071021-000 | G10 | 54406.73 ± 0.18 | 1.180 ± 0.017 |
| 2001az | CfA3 | 52031.82 ± 0.59 | 1.016 ± 0.043 | 2004bv | G10 | 53160.48 ± 0.10 | 1.083 ± 0.010 | SNF20080514-002 | G10 | 54611.84 ± 0.13 | 1.393 ± 0.015 |
| 2001bf | G10 | 52044.66 ± 0.00 | 0.921 ± 0.025 | 2004bw | G10 | 53162.66 ± 0.11 | 1.323 ± 0.012 | SNF20080909-030 | G10 | 54730.08 ± 0.62 | 0.926 ± 0.032 |
APPENDIX C: USAGE
In tandem with this paper, we provide a well-documented17 and easy-to-use Python package called deepSIP. The final, trained models presented herein are shipped with the code base, and hence, it is ready for deployment on new spectra. To use deepSIP for this purpose, one must prepare spectra as a pandas DataFrame with three mandatory columns: SN, filename, and z for the for name(s) of the SN(e) Ia, their filenames, and their redshifts (it is assumed that the spectra need to be de-redshifted), respectively. Generating predictions is then accomplished as follows:
from deepSIP import deepSIP
ds = deepSIP()
predictions = ds.predict(spectra, status = True)
All necessary spectral pre-processing steps are performed automatically prior to generating predictions. No arguments are necessary to instantiate deepSIP under normal use cases (though one may give the keyword argument drop_rate to change the dropout probability). When generating predictions from spectra, three keyword arguments can – but need not – be invoked: (i) threshold sets the decision threshold for Model I (0.9 by default), (ii) mcnum sets the number of stochastic forward passes (30 by default), and (iii) status can be used to enable status bars. The returned predictions are provided as a pandas DataFrame with five columns: Domain, prob_Domain, Phase, e_Phase, dm15, and e_dm15, corresponding to the respective predictions of Models I–III. Each row in predictions corresponds to the spectrum from the same row in spectra.
Author notes
Marc J. Staley Graduate Fellow.
Bengier Postdoctoral Fellow.
Miller Senior Fellow.



