A hint on the metal-free star formation rate density from 21-cm-EDGES data Free

ABSTRACT

1 INTRODUCTION

The past few years have seen enormous advances in peering back to the era of early star formation (for a recent review see Dayal & Ferrara 2018), with instruments such as the Hubble Space Telescope proving glimpses of star formation at redshifts as high as z ∼ 11 (Oesch et al. 2016) with a resolution of a few parsecs (e.g. Bouwens et al. 2017; Vanzella et al. 2019). However, the first metal-free (Population III; Pop III) stars postulated to explain the metallicity gap from big bang nucleosynthesis to the metal-rich (Population II; Pop II) stars seen in high-redshift galaxies or in the low-metallicity tail of the metallicity distribution function of Galactic halo stars remain elusive. The fact that the first stars lasted only a few Myr, if their initial mass function is pre-dominantly top-heavy (see Bromm 2013 for a thorough review) coupled with their predicted low star formation efficiency (Tornatore, Ferrara & Schneider 2007; Maio et al. 2010, 2011; Johnson, Dalla Vecchia & Khochfar 2013; Xu et al. 2016; de Bennassuti et al. 2017; Jaacks et al. 2018; Sarmento, Scannapieco & Côté 2019), has, so far, not resulted in the detection of any metal-free stars at high-z (see however Vanzella et al. 2020 for a strongly lensed candidate Pop III star complex at z = 6.6). Indeed, models require an instantaneous Pop III burst of |$\sim 10^5 \, {\rm \rm M_\odot }$| for such first stars to be visible with the James Webb Space Telescope (e.g. Zackrisson et al. 2015).

However, recently, another avenue has opened up with regard to studying star formation at extremely high redshifts (⁠|$z \lower.5ex\hbox{$\,\, \buildrel\gt \over \sim \,\,$}16$|⁠). This is the result provided by the EDGES (Experiment to Detect the Global Epoch of Reionization Signature) collaboration (Bowman et al. 2018). These authors have measured a sky-averaged 21-cm absorption signal (from neutral hydrogen) at a central frequency ν = 78 ± 1 MHz corresponding to z ≈ 17.2. While this redshift is consistent with expectations of Ly α photons coupling the spin temperature of neutral hydrogen to the gas kinetic temperature in the standard cold dark matter paradigm, the differential brightness temperature ∼−500 ± 200  mK is about twice as strong as that expected from any ‘standard’ model (Barkana 2018). Explaining the strength of this signal either requires gas colder than expected or a radiation background higher than expected (Bowman et al. 2018). Indeed, given its possible origin from within the first 250 Myr of the Universe, this signal has already been proposed to test new dark matter physics (Barkana 2018; Fraser et al. 2018; Pospelov et al. 2018; Slatyer & Wu 2018; Chatterjee et al. 2019). On the other hand, the excess radio background solution (Feng & Holder 2018; Fialkov & Barkana 2019) could point to populations of early black holes/micro-quasars (Ewall-Wice et al. 2018; Mirabel 2019), Pop III stars (Jana, Nath & Biermann 2019; Schauer, Liu & Bromm 2019), or extremely efficient star formation in low-mass haloes (Mirocha & Furlanetto 2019).

In this work, we carry out a proof-of-concept calculation assuming that the EDGES signal is driven by a combination of Pop II and Pop III stars. Our aim is to provide the first data-constrained estimate of the star formation rate density (SFRD) at such high-z, using a Markov Chain Monte Carlo (MCMC) approach, which results in a 21-cm signal at the right redshift with an amplitude and shape compatible with the EDGES result.

The cosmological parameters used in this work correspond to Ω_m = 0.3089, Ω_Λ = 0.6911, Ω_b = 0.049, h = 0.67, n_s = 0.96, and σ₈ = 0.81 (Planck Collaboration 2016).

2 THEORETICAL MODEL

We start by describing our calculation of the coupling coefficients before discussing the kinetic temperature in equation (2). The collisional coupling coefficient, x_c, is determined by three different channels, namely, hydrogen–hydrogen (H–H), hydrogen–electron (H–e), and hydrogen–proton (H–p) collisions.

Though the collisional coefficients do not play any important role at epochs relevant to this work we include them in our numerical code for completeness.

As seen from this discussion, the only z-dependent quantities entering the equations explicitly are the SFRDs for Pop II and Pop III stars. As already noted, for Pop II stars we use the SFRD and Ly α photon production rate results from the Delphi semi-analytic model that has been shown to reproduce all key observables for galaxies and active galactic nuclei (AGNs; including their UV luminosity functions, stellar mass/black hole mass densities, SFRDs, the stellar/black hole mass function) at |$z \lower.5ex\hbox{$\,\, \buildrel\gt \over \sim \,\,$}5$| (Dayal et al. 2014, 2019). From this model, we find that the redshift evolution of the Pop II SFRD is well described by |$\log (\dot{\rho }_{*}^{\mathrm{ II}} / \rm M_\odot ~Mpc^{-3}~\text{yr}^{-1})=-0.008(1+z)^2+0.047(1+z)-0.995$|⁠.

To summarize, our model has a total of seven free parameters: four for the Pop III SFRD (a₁–a₄) and three for the temperature contribution for Pop III stars (⁠|$f_{X,h}^{\mathrm{ III}}$|⁠, |$f_{\mathrm{ R}}^{\mathrm{ III}}$|⁠, |$f_{\alpha }^{\mathrm{ III}}$|⁠). Additionally, we have assumed |$f_\mathrm{ R}^{\mathrm{ II}}=1$| and |$f_{X,h}^{\mathrm{ II}}=0.2$|⁠. Finally, while the value of |$\dot{\rho }_{*}^{\mathrm{ II}}$| is obtained from the Delphi semi-analytic model, we use a normalization of |$\dot{\rho }_{*}^{\mathrm{ III}}(z_{\rm mean}) = 10^{-4.5}~\rm M_\odot ~{\rm yr^{-1}~Mpc^{-3}}$|⁠.

By comparing the predictions of our model with EDGES data, we constrain the values of these parameters and consequently study the implications of the Pop III star formation at high-z. The constraints on the parameters, i.e. their posterior probability distributions are computed using a Bayesian statistical method based on MCMC. We make use of the publicly available emcee package (Foreman-Mackey et al. 2013) for this purpose.

3 RESULTS

As already shown in Chatterjee et al. (2019), simultaneously matching to the shape and amplitude of the EDGES signal requires an Ly α background already in place by z ∼ 20 that can couple the spin temperature to the gas temperature, an excess radio background at z ∼ 20 that yields a signal of the depth required and that falls off steeply at |$z \lower.5ex\hbox{$\,\, \buildrel\lt \over \sim \,\,$}17$|⁠, and an X-ray background by z ∼ 17 that heats the gas so as to reduce the absorption amplitude.

We start by quantifying the 1-D and 2-D projections of the posterior probability distributions of all the seven Pop III free-parameter values required to yield these trends in Fig. 1. First, the increasing Pop III SFRD values at z > z_mean are essentially driven by the positive a₃(z − z_mean)³ term; the remaining three terms (with coefficients a₁, a₂, and a₄ in equation 11) are responsible for the steep downturn seen at |$z\lower.5ex\hbox{$\,\, \buildrel\lt \over \sim \,\,$}16$|⁠. Moving to the fourth row of the same figure, we find |$f_\alpha ^{\mathrm{ III}} \sim 200 \times 10^{25}$|⁠. As seen in what follows, this results in a situation where Pop III stars dominate the Ly α background between z ∼ 21 − 15. Further, as seen from these plots, per unit SFRD, Pop III stars are required to provide a radio background that is about 400 times higher than that provided by Pop II stars (where |$f_R^{\mathrm{ II}}=1$|⁠), assuming the normalization |$\dot{\rho }_{*}^{\mathrm{ III}}(z_{\rm mean}) = 10^{-4.5}~\rm M_\odot ~{\rm yr^{-1}~Mpc^{-3}}$|⁠. This naturally results in a radio background that is predominantly driven by Pop III stars. Indeed, this is the key factor that determines the fall-off of the Pop III SFRD. Finally, we find that Pop II stars dominate the X-ray background at all z with Pop III stars providing almost no contribution. This is required to maintain the spin temperature being coupled to the gas temperature between z ∼ 16 and 19 and yield the EDGES absorption trough. Indeed, the earlier the X-ray background arises, the faster the spin temperature saturates to the CMB temperature.

Figure 1.

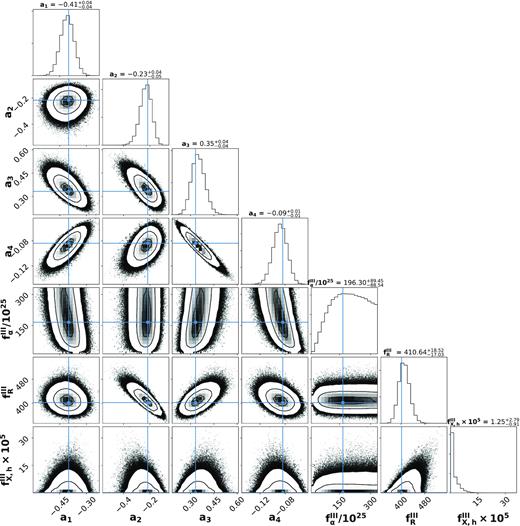
The posterior distribution of the seven free parameters associated with Pop III stars obtained by matching to the EDGES data (using the normalization |$\dot{\rho }_{*}^{\mathrm{ III}}(z_{\rm mean})=10^{-4.5}~\rm M_\odot ~{\rm yr^{-1}~Mpc^{-3}}$|⁠, see Section 2 for details). The 2-D plots show the joint probability distribution of any two parameters while the diagonal plots show the corresponding 1-D distributions. The values above the 1-D histograms show the median value along with the ±1σ range (i.e. the 16th and 84th percentiles). Contours in the 2-D plots correspond to the 1σ, 2σ, and 3σ ranges. The blue straight lines show the median values of the parameters.

Open in new tabDownload slide

Next, we focus on analysing the contribution of Pop II and Pop III stars to the EDGES signal, as shown in Fig. 2. In addition to the best-fitting values for Pop III, we also show results for 1000 random points sampled from the chains; the region spanned by these sampled curves should be thought of as the range of histories that are allowed by the EDGES data. From panel (a), we see that our model results are in reasonable agreement with the EDGES data with the match being particularly good at z ≳ 16. We find that the match degrades at z ≲ 16 where our models evolve somewhat slower than what is required by the data. This part of the evolution is driven by X-ray heating from Pop II stars, which in turn is fixed by the Delphi output; a better match would require steeper evolution in the Pop II star formation rate.²

Figure 2.

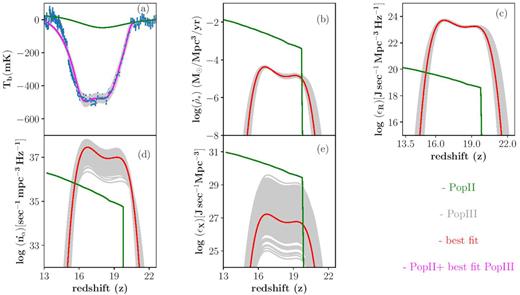
As a function of redshift, the panels show the results for Pop II stars and Pop III stars for models that fit the EDGES brightness temperature for: (a) the differential brightness temperature where the blue points show the EDGES data, (b) the star formation rate densities, (c) the radio emissivity, (d) the Ly α photon production rate, and (e) the X-ray emissivity. We artificially force the Pop II SFRD to be zero at z > 19.5 because the formation of Pop II stars cannot precede that of Pop III stars. In all panels, the green and red lines show the results for Pop II (based on Delphi) and Pop III stars (the best-fitting model obtained from MCMC) respectively. The grey shaded regions show 1000 random samples from the joint posterior distribution, i.e. they represent models that are consistent with the EDGES data.

Open in new tabDownload slide

Panel (b) in the same figure shows the Pop III SFRD which is always subdominant compared to the Pop II stars. This is mainly because of the normalization we have chosen. However, as noted before, our key results concerns the shape of the Pop III SFRD. The data requires a rise in Pop III stars at z ∼ 20–21 followed by a sharp fall at z ∼ 15–16. The evolution of |$\dot{\rho }_{*}^{\mathrm{ III}}(z)$| also shows a ‘kink’-like feature at z ∼ 18 which is due to a similar feature in the absorption profile as observed by EDGES. This is only to be expected - since our model of Pop III stars is entirely driven by data, any feature present in the data would show up in the model predictions as well.

In panel (d), we see that the Ly α emissivity is completely dominated by Pop III stars at redshifts relevant for the EDGES observations. Note that, unlike |$\dot{\rho }_{*}^{\mathrm{ III}}(z)$|⁠, this emissivity does not depend on the normalization; this is because as seen from equation (6), the emissivity depends on the product of |$\dot{\rho }_{*}^{\mathrm{ III}}(z)$| and |$f_\alpha ^{\mathrm{ III}}$| which absorb all the uncertainties. On the other hand, the X-ray emissivity from Pop III stars is always subdominant compared to the Pop II stars. This implies that the amount of heating required to match the EDGES data can be contributed solely by the Pop II stars (as modelled in Delphi). Indeed, a larger contribution from Pop III stars would lead to a faster coupling between the spin and CMB temperatures, resulting in a higher redshift at which the signal would tend to 0. Finally, in all panels, we also show by the grey shaded regions the models that are consistent with the EDGES data. As expected, while the range of histories naturally shows a dispersion, their redshift-evolution remains unaffected. The Pop III SFRD and the radio emissivity show the least dispersion (since they effectively govern the brightness temperature from Pop III stars) while, given their negligible contribution to the X-ray emissivity, the value of |$f_X^{\mathrm{ III}}$| shows the largest dispersion.

It is worth pointing out here that the depth of the EDGES signal is highly controversial (see, e.g. Hills et al. 2018; Sims & Pober 2020). In case the amplitude of the signal turns out to be much smaller than what is assumed in this work (say |δT_b| ≲ 100 mK), then the Pop II stars with conventional choice of efficiency parameters are sufficient to explain the observations. Hence our conclusions on the Pop III stars hold only in the case where the amplitude and redshift extent of the 21-cm signal are similar to those reported by the EDGES experiment.

Finally, we compare our predicted redshift evolution of the Pop III SFRD with some theoretical models in Fig. 3. Most models predict a Pop III SFRD that either rises between z ∼ 22 and 13 (Jaacks et al. 2018; Sarmento et al. 2019) or shows a relatively constant behaviour for z ∼ 20 − 13 (Johnson et al. 2013). The only exceptions are the predictions by Valiante et al. (2016), Valiante et al. (2018), whose amplitude and redshift dependence are very similar to our predicted shape. Interestingly, the Valiante et al. (2016), Valiante et al. (2018) models aim to describe the formation histories of z ∼ 6–7 quasars and their host galaxies. They therefore describe rapidly evolving and biased regions of the Universe. In these models, Pop III stars (and their black hole remnants) start to form at z > 20 in dark matter mini-haloes with mass [10⁶–10⁷]M_⊙. However, their formation efficiency is small, as Lyman-Werner radiation limits gas cooling due to H₂ photo-dissociation. Because of this, the bulk of Pop III stars form at redshift 15 < z < 20 in metal poor (Z < Z_cr = 10^−3.8Z_⊙) Ly α-cooling haloes, with mass [10^7.5 − 10^8.5]M_⊙ that are able to self-shield and cool the gas more efficiently (see the top panel of Fig. 1 in Valiante et al. 2018). At z ≤ 15 Pop III star formation is suppressed by metal enrichment, as Z < Z_cr = 10^−3.8Z_⊙ star forming regions become increasingly rare. Hence, the shape of the EDGES signal suggests that the rapid coupling between the spin temperature and the gas kinetic temperature is driven by Ly α photons produced by Pop III stars that form in relatively massive and rare haloes, whose abundance grows fast, due to the exponential growth of the massive-end of the halo mass function, before the quick rise of the gas temperature rapidly erases the signal at z ≲ 16. Interestingly, these considerations are very consistent with the results of Kaurov et al. (2018), who also suggest that the shape of the EDGES signal can be best explained if the bulk of the UV photons are produced by rare and massive haloes, and explore the implications for the amplitude of the 21-cm power spectrum.

Figure 3.

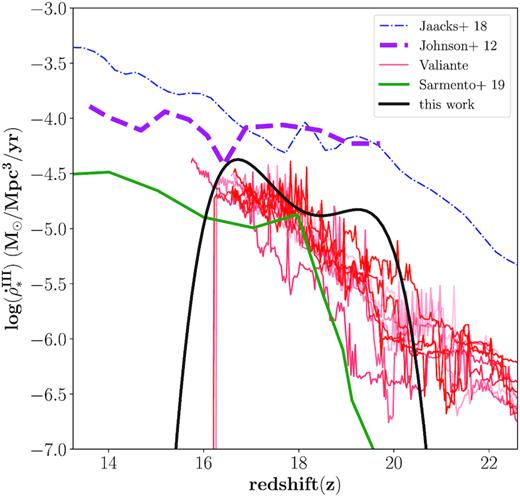
The redshift evolution of the Pop III star formation rate density. The black line (best-fitting model from this work) is compared to other theoretical estimates from Johnson et al. (2013, dashed purple line), Jaacks et al. (2018, dot–dashed blue line), and Sarmento et al. (2019, solid green line). Finally, the thin red lines show the results for 10 different simulations by Valiante et al. (2016), which aim to reproduce the observed properties of z ∼ 6–7 quasars and their host galaxies (see the text).

Open in new tabDownload slide

4 CONCLUSIONS AND DISCUSSION

In this work, we aim to provide an estimate of the Pop III SFRD required at high redshifts (⁠|$z \lower.5ex\hbox{$\,\, \buildrel\gt \over \sim \,\,$}16$|⁠) in order to reproduce both the amplitude and the redshift of the EDGES 21-cm global signal. This essentially requires a rapidly rising Ly α background at z ∼ 20 (to couple the spin temperature to the gas temperature), an excess radio background at z ∼ 20 that falls off steeply at |$z \lower.5ex\hbox{$\,\, \buildrel\lt \over \sim \,\,$}17$| (to match to the depth and subsequent increase of the EDGES signal), and an X-ray background by z ∼ 17 (to heat the gas so as to reduce the absorption amplitude). Our model has a total of seven free parameters: four for the Pop III SFRD (a₁–a₄) and three for the temperature contribution for Pop III stars (⁠|$f_{X,h}^{\mathrm{ III}}$|⁠, |$f_{R}^{\mathrm{ III}}$|⁠, |$f_{\alpha }^{\mathrm{ III}}$|⁠); we use a normalization of |$\dot{\rho }_{*}^{\mathrm{ III}}(z_{\rm mean}) = 10^{-4.5}~\rm M_\odot ~{\rm yr^{-1}~Mpc^{-3}}$| motivated by simulation results of Valiante et al. (2016). These seven parameters are constrained using the emcee package, a Bayesian statistical method based on MCMC. As for Pop II stars, the SFRD and Ly α photon production rate are obtained directly from the Delphi semi-analytic model that has been shown to reproduce all key observables for galaxies and AGNs at |$z \lower.5ex\hbox{$\,\, \buildrel\gt \over \sim \,\,$}5$| (Dayal et al. 2014, 2019). Finally, we use |$f_R^{\mathrm{ II}}=1$| and |$f_{X,h}^{\mathrm{ II}}=0.2$| in order to be consistent with low-redshift observations. This results in a first estimate of the redshift evolution of the Pop III SFRD whose form is solely constrained using data. Our key results are:

• Our model predicts a Pop III SFRD that while increasing from z ∼ 21 to 16 thereafter show a sharp decline. While this is in excellent agreement with the results of Valiante et al. (2016, 2018), there is a disparity with the results of most other models that predict a Pop III SFRD that either rises between z ∼ 22 and 13 (Jaacks et al. 2018; Sarmento et al. 2019) or shows a relatively constant behaviour for z ∼ 20–13 (Johnson et al. 2013).

• Pop III stars dominate the Ly α background between z ∼ 21 and 15.

• Pop III stars are required to provide a radio background that is about 3–4 orders of magnitude higher than that provided by Pop II stars, resulting in a radio background that is predominantly driven by Pop III stars.

• Pop II stars dominate the X-ray background at all z (where |$f_{X,h}^{\mathrm{ II}}=0.2$|⁠) with Pop III stars providing almost no contribution.

The above findings suggest that the rapidly rising Ly α background implied by the EDGES signal is dominated by the emission of Pop III stars formed in metal-poor Ly α-cooling haloes with mass 10^7.5–10^8.5 M_⊙ (Valiante et al. 2016, 2018). These systems are massive enough to provide a rapidly growing contribution at z ∼ 21–19, due to the exponential growth of the massive end of the halo mass function (see also Kaurov et al. 2018), but their number is large enough to ensure that the spin temperature and the gas kinetic temperature are coupled in a large fraction of the Universe.³ In an earlier work, Mebane, Mirocha & Furlanetto (2020) have studied the effects of Pop III remnants on the 21-cm signal and compared their results with the EDGES data. Analogous to this work, they have also found that the subset of their Pop III SFRD models that are able to match the timing and position of depth of the EDGES signal always prefer larger radio emission and small X-ray emission. In another recent (similar) work, using a more physically motivated model of Pop III stars, Schauer et al. (2019) find that Pop III stars are crucial in providing the necessary Ly α flux at high redshifts in order to agree with the EDGES data, consistent with our conclusions regarding the Ly α flux.

We should also mention that our galaxy formation model (Delphi) and also the quantities |$f_{X}^{\mathrm{ II}}$| and |$f_R^{\mathrm{ II}}$| for Pop II stars are calibrated to lower redshift observations and could be different at higher redshift. However, in the absence of any rigorous model or observation at high redshifts, we have taken the most conservative approach and kept the values of these parameters constant. This also ensures that the number of free parameters does not increase beyond control

However, the question that remains is: how can Pop III stars dominate the Ly α and radio backgrounds and be completely subdominant for the X-ray background? Pop III stars can give rise to a radio background as a result of synchrotron emission from high-energy cosmic ray (CR) electrons accelerated in SN explosions, but the signal is accompanied by substantial IGM heating due to CR protons (Jana et al. 2019). Hence, even without including the effect of X-ray heating, the associated CR proton heating limits the contribution of Pop III SNe to the radio background required to explain the depth of the absorption trough in the EDGES signal, unless the ratio of the CR electrons to protons energy is substantially larger than usually assumed. An additional contribution to the radio background at cosmic dawn could come from accreting black hole remnants of Pop III stars. Again, to avoid the associated X-ray heating of the IGM, the X-rays must be absorbed by a substantial column of gas, with N_H ∼ 5 × 10²³ cm⁻², for ∼100 Myr (Ewall-Wice et al. 2018). This requirement allows to have escape fractions of ionizing photons f_esc ∼ 0 to avoid exceeding the Planck constraint on the Thompson scattering optical depth (Planck Collaboration 2016) and boosting-up the emission of Ly α photons.

Whatever the true physical explanation is, it is clear that the shape of the 21-cm signal measured by EDGES has offered a first glimpse on the potential of 21-cm observations to constrain the properties of the Universe at cosmic dawn.

ACKNOWLEDGEMENTS

We warmly thank Rosa Valiante for providing her estimates of the Pop III star formation rate densities. AC and TRC acknowledge support of the Department of Atomic Energy, Government of India, under project no. 12-R&D-TFR-5.02-0700. PD acknowledges support from the European Research Council’s starting grant ERC StG-717001 (‘DELPHI’), from the NWO grant 016.VIDI.189.162 (‘ODIN’), and from the European Commission’s and University of Groningen’s CO-FUND Rosalind Franklin program. PD also thanks La Sapienza for their hospitality and thanks the Sexten centre of Astrophysics where a huge part of this work was carried out. RS acknowledges support from the Amaldi Research Center funded by the MIUR program ‘Dipartimento di Eccellenza’ (CUP:B81I18001170001).

Footnotes

REFERENCES