-
PDF
- Split View
-
Views
-
Cite
Cite
C P Gutiérrez, M Sullivan, L Martinez, M C Bersten, C Inserra, M Smith, J P Anderson, Y-C Pan, A Pastorello, L Galbany, P Nugent, C R Angus, C Barbarino, D Carollo, T-W Chen, T M Davis, M Della Valle, R J Foley, M Fraser, C Frohmaier, S González-Gaitán, M Gromadzki, E Kankare, R Kokotanekova, J Kollmeier, G F Lewis, M R Magee, K Maguire, A Möller, N Morrell, M Nicholl, M Pursiainen, J Sollerman, N E Sommer, E Swann, B E Tucker, P Wiseman, M Aguena, S Allam, S Avila, E Bertin, D Brooks, E Buckley-Geer, D L Burke, A Carnero Rosell, M Carrasco Kind, J Carretero, M Costanzi, L N da Costa, J De Vicente, S Desai, H T Diehl, P Doel, T F Eifler, B Flaugher, P Fosalba, J Frieman, J García-Bellido, D W Gerdes, D Gruen, R A Gruendl, J Gschwend, G Gutierrez, S R Hinton, D L Hollowood, K Honscheid, D J James, K Kuehn, N Kuropatkin, O Lahav, M Lima, M A G Maia, M March, F Menanteau, R Miquel, E Morganson, A Palmese, F Paz-Chinchón, A A Plazas, M Sako, E Sanchez, V Scarpine, M Schubnell, S Serrano, I Sevilla-Noarbe, M Soares-Santos, E Suchyta, M E C Swanson, G Tarle, D Thomas, T N Varga, A R Walker, R Wilkinson, (DES Collaboration), DES16C3cje: A low-luminosity, long-lived supernova, Monthly Notices of the Royal Astronomical Society, Volume 496, Issue 1, July 2020, Pages 95–110, https://doi.org/10.1093/mnras/staa1452
Close - Share Icon Share
ABSTRACT
We present DES16C3cje, a low-luminosity, long-lived type II supernova (SN II) at redshift 0.0618, detected by the Dark Energy Survey (DES). DES16C3cje is a unique SN. The spectra are characterized by extremely narrow photospheric lines corresponding to very low expansion velocities of ≲1500 km s−1, and the light curve shows an initial peak that fades after 50 d before slowly rebrightening over a further 100 d to reach an absolute brightness of Mr ∼ −15.5 mag. The decline rate of the late-time light curve is then slower than that expected from the powering by radioactive decay of 56Co, but is comparable to that expected from accretion power. Comparing the bolometric light curve with hydrodynamical models, we find that DES16C3cje can be explained by either (i) a low explosion energy (0.11 foe) and relatively large 56Ni production of 0.075 M⊙ from an ∼15 M⊙ red supergiant progenitor typical of other SNe II, or (ii) a relatively compact ∼40 M⊙ star, explosion energy of 1 foe, and 0.08 M⊙ of 56Ni. Both scenarios require additional energy input to explain the late-time light curve, which is consistent with fallback accretion at a rate of ∼0.5 × 10−8 M⊙ s−1.
1 INTRODUCTION
Recent wide-field sky surveys have revealed a significant diversity in the observed properties of supernovae (SNe). These events have covered a wide range of observed characteristics: transients with extremely bright luminosities (e.g. superluminous SNe, Gal-Yam 2012); transients with a rapid temporal evolution spanning a range of luminosities (e.g. Perets et al. 2010; Kasliwal et al. 2012; Drout et al. 2014; Pursiainen et al. 2018), and a heterogeneous population of transients with a slow temporal evolution (e.g. Taddia et al. 2016; Arcavi et al. 2017; Terreran et al. 2017). These new SN discoveries have in turn created new challenges for the SN field, particularly concerning the SN progenitor and the physics of the explosion.
In the canonical picture of a core-collapse SN, the explosion releases ∼1051 erg of energy (1 foe), and a fraction of the progenitor’s material is burned into various intermediate-mass and iron-peak elements. The early emission from SNe, defined as the cooling phase, is powered by the release of shock deposited energy, while the power source from the peak to late-phases is provided by the decay of 56Ni into 56Co and subsequently 56Fe. In slow- and fast-declining hydrogen-rich SNe (historical SNe IIP and SNe IIL, respectively), the cooling phase is followed by a hydrogen recombination phase, where the luminosity evolves more slowly until it becomes dominated by the energy released during the decay of radioactive material. However, some core-collapse SNe have larger luminosities, which typically require an additional source of energy to explain them (see review, and references therein, of Moriya, Sorokina & Chevalier 2018a). Pair-Instability SNe (PISNe; e.g. Heger & Woosley 2002; Gal-Yam et al. 2009), magnetars (e.g. Kasen & Bildsten 2010; Bersten & Benvenuto 2016), accretion power (e.g. Moriya et al. 2010; Dexter & Kasen 2013), and pulsational pair-instability (PPI; e.g. Woosley, Blinnikov & Heger 2007; Woosley 2017) have all been proposed as a source of additional energy, but as yet there is no clear consensus about the relative importance of each source nor associations to specific transients.
Recently, two peculiar type II SNe (SNe II) have been studied in detail: iPTF14hls (Arcavi et al. 2017; Sollerman et al. 2019) and OGLE-2014-SN-073 (Terreran et al. 2017). iPTF14hls is an SN with very little spectral evolution over ∼600 d, and with a light curve that shows multiple re-brightening events. OGLE-2014-SN-073 is a very bright SN with an unusually broad light curve, combined with high ejecta velocities in its spectra. Both objects exploded in low-luminosity galaxies and require an extra source of power (beyond shock energy and radioactivity) to explain their unusual evolution.
Popular scenarios invoked to explain the peculiar behaviour of these two transients are a magnetar (Dessart 2018; Orellana, Bersten & Moriya 2018; Woosley 2018), PISNe (Woosley 2018), circumstellar interaction (Andrews & Smith 2018; Woosley 2018), and fallback accretion (Arcavi et al. 2017; Moriya, Terreran & Blinnikov 2018b; Wang et al. 2018). Moriya et al. (2018b) found the latter scenario can reproduce the shape of the light curve, luminosity, and photospheric velocities of OGLE-2014-SN-073, while Arcavi et al. (2017) and Wang et al. (2018) proposed that iPTF14hls may be powered by intermittent fallback accretion. The idea of fallback in SNe was introduced by Colgate (1971), and has been broadly studied to determine its effects on the central remnant (e.g. Chevalier 1989; Woosley & Weaver 1995; Fryer 1999), and on SN light curves (e.g. Fryer et al. 2009; Moriya et al. 2010; Dexter & Kasen 2013). Dexter & Kasen (2013) showed that the accretion power may be relevant to explain peculiar and rare SNe.
In this paper, we present the photometry and spectra of DES16C3cje, an unusual SN II discovered by the Dark Energy Survey Supernova Program (DES-SN; Bernstein et al. 2012). We discuss its peculiar characteristics and examine the late-time light curve under the fallback scenario. In Section 2 we describe our observations of DES16C3cje and measurements. We analyse the spectral and photometric properties and compare them with other similar events in Section 3, and then discuss the progenitor scenarios that could explain the event in Section 4. We discuss and conclude in Section 5. Throughout, we assume a flat ΛCDM universe, with a Hubble constant of H0 = 70 km s−1 Mpc−1, and Ωm = 0.3.
2 OBSERVATIONS
DES16C3cje was detected by DES using the wide-field Dark Energy Camera (DECam; Flaugher et al. 2015) instrument in an r-band image taken on 2016 October 11 (JD = 2457673.3) with an apparent magnitude of r = 23.26 mag. The transient was located at |$\alpha =03^{\mathrm{h}}28^{\mathrm{m}}35{{_{.}^{\rm s}}}29$|, δ = −27°09′06|${_{.}^{\prime\prime}}$|6 (J2000.0) in a faint host galaxy (Mr ∼ −18.5 mag) at a redshift of 0.0616. The previous non-detection with DES was obtained on 2016 October 7 (MJD = 57667.6), with a detection limit of z ∼ 25.1 mag. This limit places a constraint on the explosion epoch of ±2.6 d; we adopt 2016 October 9 (the intermediate epoch; MJD = 57670.2 ± 2.6 d) as the explosion date. Further information on the DES-SN difference-imaging search pipeline and machine-learning algorithms to identify transient objects can be found in Kessler et al. (2015) and Goldstein et al. (2015).
Photometric coverage of DES16C3cje was acquired by DES-SN in griz filters from 2016 October until 2017 February, and then from 2017 August to 2018 February. Between 2017 February and 2017 July, additional photometric data were obtained by the extended Public European Southern Observatory (ESO) Spectroscopic Survey for Transient Objects (ePESSTO; Smartt et al. 2015) and other collaborators with the ESO Faint Object Spectrograph and Camera 2 (EFOSC2; Buzzoni et al. 1984) at the 3.6m ESO New Technology Telescope (NTT), with the FOcal Reducer/low dispersion Spectrograph 2 (FORS2; Appenzeller et al. 1998) at the ESO Very Large Telescope (VLT), with the Low Dispersion Survey Spectrograph 3 (LDSS3; Osip et al. 2004) on the Magellan Clay 6.5-m telescope, and with the the Gamma-Ray Burst Optical/Near-Infrared Detector (GROND; Greiner et al. 2008), at the 2.2-m MPG telescope at the European Southern Observatory (ESO) La Silla Observatory.
The NTT data were reduced using the PESSTO pipeline (Smartt et al. 2015), while for the FORS2 images we used the esoreflex pipeline (Freudling et al. 2013). Reductions for data obtained with LDSS3 were performed with Image Reduction and Analysis Facility (iraf; Tody 1986) using standard routines. Images from the MPG were reduced with the GROND pipeline (Krühler et al. 2008). The DES photometric measurements were made using the pipeline discussed by Papadopoulos et al. (2015) and Smith et al. (2016), which has also been extensively used in the literature (e.g. Firth et al. 2015, and references therein). This pipeline subtracts a deep template image from each individual DES image to remove the host-galaxy light using a point-spread-function (PSF) matching routine. SN photometry is then measured from the difference image using a PSF-fitting technique. The photometry of DES16C3cje is reported in Appendix A1.
DES16C3cje was observed spectroscopically on six epochs from +47 to +403 d (throughout the paper, we give all epochs relative to the explosion epoch). These observations were obtained with four different instruments: The AAOmega spectrograph at the Anglo-Australian Telescope (AAT), X-SHOOTER (Vernet et al. 2011) and FORS2 at the VLT, and Gemini Multi-Object Spectrograph (GMOS-S; Hook et al. 2004) at the Gemini Observatory. A log of the spectroscopic observations of DES16C3cje is reported in Table 1. Spectroscopic reductions for X-SHOOTER were performed using the esoreflex pipeline, FORS2 data were reduced with iraf using standard routines, while for GMOS-S we used the Gemini iraf package, combined with idl routines to flux calibrate the data and remove telluric lines.
| UT date . | MJD . | Rest-frame phase⋆ . | Telescope . | Range . | Grism/Grating/ . |
|---|---|---|---|---|---|
| . | (d) . | (d) . | + Instrument . | (Å) . | Arm . |
| 20161127 | 57719.7 | 47 | AAT + AAOmega | 3750–9000 | 580V + 385R |
| 20170102 | 57755.6 | 80 | Gemini + GMOS-S | 5700–7500 | R400-G5305 |
| 20170129 | 57782.0 | 105 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170221 | 57805.0 | 127 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170731 | 57965.3 | 278 | VLT + FORS2 | 4300–9500 | 300V + GG435 |
| 20171116 | 58074.2 | 380 | VLT + XSHOOTER | 3600–9600 | UV/VIS/NIR |
| UT date . | MJD . | Rest-frame phase⋆ . | Telescope . | Range . | Grism/Grating/ . |
|---|---|---|---|---|---|
| . | (d) . | (d) . | + Instrument . | (Å) . | Arm . |
| 20161127 | 57719.7 | 47 | AAT + AAOmega | 3750–9000 | 580V + 385R |
| 20170102 | 57755.6 | 80 | Gemini + GMOS-S | 5700–7500 | R400-G5305 |
| 20170129 | 57782.0 | 105 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170221 | 57805.0 | 127 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170731 | 57965.3 | 278 | VLT + FORS2 | 4300–9500 | 300V + GG435 |
| 20171116 | 58074.2 | 380 | VLT + XSHOOTER | 3600–9600 | UV/VIS/NIR |
Note. ⋆The phase is relative to the estimated explosion date, MJD = 57670.2 ± 2.6 d.
| UT date . | MJD . | Rest-frame phase⋆ . | Telescope . | Range . | Grism/Grating/ . |
|---|---|---|---|---|---|
| . | (d) . | (d) . | + Instrument . | (Å) . | Arm . |
| 20161127 | 57719.7 | 47 | AAT + AAOmega | 3750–9000 | 580V + 385R |
| 20170102 | 57755.6 | 80 | Gemini + GMOS-S | 5700–7500 | R400-G5305 |
| 20170129 | 57782.0 | 105 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170221 | 57805.0 | 127 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170731 | 57965.3 | 278 | VLT + FORS2 | 4300–9500 | 300V + GG435 |
| 20171116 | 58074.2 | 380 | VLT + XSHOOTER | 3600–9600 | UV/VIS/NIR |
| UT date . | MJD . | Rest-frame phase⋆ . | Telescope . | Range . | Grism/Grating/ . |
|---|---|---|---|---|---|
| . | (d) . | (d) . | + Instrument . | (Å) . | Arm . |
| 20161127 | 57719.7 | 47 | AAT + AAOmega | 3750–9000 | 580V + 385R |
| 20170102 | 57755.6 | 80 | Gemini + GMOS-S | 5700–7500 | R400-G5305 |
| 20170129 | 57782.0 | 105 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170221 | 57805.0 | 127 | VLT + XSHOOTER | 3100–10400 | UV/VIS/NIR |
| 20170731 | 57965.3 | 278 | VLT + FORS2 | 4300–9500 | 300V + GG435 |
| 20171116 | 58074.2 | 380 | VLT + XSHOOTER | 3600–9600 | UV/VIS/NIR |
Note. ⋆The phase is relative to the estimated explosion date, MJD = 57670.2 ± 2.6 d.
3 CHARACTERIZING DES16C3CJE
3.1 Host galaxy properties
The host galaxy of DES16C3cje was identified as PGC3243310, a low-luminosity galaxy (M|$_B^\mathrm{host}=-18.26\pm 0.50$| mag1) at a redshift of 0.0618.2 Adopting the recessional velocity corrected into the CMB frame3 (v = 18465 ± 89 km s−1), we obtain a distance of 275.95 Mpc, which corresponds to μ = 37.20. The galactic reddening in the direction of PGC3243310 is E(B − V) = 0.01 mag (Schlafly & Finkbeiner 2011). Due to the faintness of the galaxy and the absence of the absorption Na i D lines in the SN spectra, we assume the host extinction negligible.
Using a spectrum obtained by OzDES with the AAOmega at the AAT (see Section 3.4) and a spectrum from the 2dF Galaxy Redshift Survey (Colless et al. 2003), we estimate the integrated oxygen abundance. The lack of [N ii] suggests a very low metallicity. Setting the upper limits of the flux ratio of H α/[[N ii]λ6583 and measuring the ratio of [O iii]λ5007/H β, we estimate the upper limit of the metallicity. Applying the O3N2 diagnostic method from Marino et al. (2013), we obtain an oxygen abundance of 12 + log (O/H) < 8.19 ± 0.02. With the luminosity of H α and the equation of Kennicutt & Evans (2012), we calculate the SFR to be 0.042 M⊙ yr−1.
3.2 Light curves
The unusual photometric evolution of DES16C3cje from ∼+2 to +450 d is presented in Fig. 1 (top panel). The light curves show an initial increase in brightness for the first 20 d followed by a decrease, particularly in the bluer filters, as observed in some SNe II (e.g. SN 2004em, SN 2004ek; Taddia et al. 2016). In the redder bands, the luminosity increase monotonically, with a change in the slope at ∼60d. After 60 d, the g-band increases ∼1.4 mag over 70 d versus ∼1.0 mag in riz.

Upper: griz light curves of DES16C3cje. The filled symbols represent the data obtained with DES, while open stars show the data obtained with EFOSC2, LDSS3, FORS2, and GROND. Only corrections for Milky Way extinction have been made. The last non-detection is presented as a green arrow. The vertical purple arrows represent epochs of optical spectroscopy. The solid lines show the Gaussian process (GP) interpolation. Middle: Colour curves of DES16C3cje. The solid lines show the GP interpolation. The vertical green arrows represent epochs of minimum, peak, and the beginning of the tail in the optical light curves. Lower: Bolometric (pink) and pseudo-bolometric (dark cyan) light curves of DES16C3cje. The dashed line shows the luminosity expected from 56Co (assuming full trapping) and the solid line the luminosity expected from accretion power.
We use Gaussian processes (GPs) to interpolate the observed light curves (see de Jaeger et al. 2017; Inserra et al. 2018b; Angus et al. 2019, for more details). The interpolation was performed with the Python package GEORGE (Ambikasaran et al. 2015) using the Matern 3/2 kernel. We find that DES16C3cje reaches a peak brightness of ∼−15.75 ± 0.10 mag at 152 ± 5 d in the r-band. The long rise is reminiscent of SN 1987A, but over a longer scale; this behaviour has not previously been observed in an SN II light curve. During the later phases (after ∼300 d), the light curves show a linear decline in riz and a flat evolution in the g-band. The slope of the decline in the r-band light curve is 0.70 mag per 100 d, smaller than that expected from the full trapping of gamma-ray photons and positrons from the decay of 56Co (0.98 mag per 100 d; Woosley, Pinto & Hartmann 1989).
In the middle panel of Fig. 1, the colour curves are presented. During the first 65 d (in the plateau), DES16C3cje becomes redder, changing from g − r = 0.37 to g − r = 0.85. The SN then evolves to bluer colours. At late-phases (>+300 d), the object has a redder colour than during the first two months, but its evolution is relatively flat.
3.3 Bolometric luminosity and Nickel mass
Using the griz photometric data, we compute the pseudobolometric and bolometric light curves for DES16C3cje (Fig. 1, bottom panel) following the prescriptions presented by Inserra et al. (2018a). In this method, the griz bands are converted into fluxes at the effective filter wavelengths, and then corrected for the Milky Way extinction (presented in Section 3.1). A spectral energy distribution (SED) is then computed over the wavelengths covered and the flux under the SED is integrated assuming zero flux beyond the integration limits. Fluxes are converted to luminosities using the adopted distance (275.95 Mpc). We determined the points on the pseudobolometric light curves at epochs when griz were available simultaneously. Magnitudes from the missing bands were generally estimated by interpolating or extrapolating the light curves using low-order polynomials (n ≤ 3) and assuming constant colours from nearest epochs. Therefore, we obtain a peak luminosity of Lbol = (4.96 ± 0.10) × 1041 erg s−1, and Lgriz = (2.33 ± 0.08) × 1041 erg s−1.
3.4 Spectral evolution
In Fig. 2, we present the optical spectra obtained for DES16C3cje between +47 d and +380 d. At 47 d, the spectrum is completely dominated by the emission lines from the host galaxy, with no traces of the SN. From 80 d, the spectra show that DES16C3cje is a SN II with very narrow photospheric lines. At 80 d and 127 d, DES16C3cje presents characteristic P-Cygni profiles of H α, H β, Fe ii λ4924, Fe ii λ5018, Fe ii λ5169, Na i D λ5893, and the Ca ii near-IR triplet, together with a lack of Sc ii and Ba ii lines. The ‘Cachito’ feature, related to high velocity (HV) spectra components (Gutiérrez et al. 2017), are also visible at these epochs, suggesting an interaction between the SN ejecta and circumstellar material (CSM). The later spectra are dominated by H α, with a weak contribution of the Ca ii near-IR triplet in emission. There is no evidence of forbidden lines (e.g. [O i] λλ6300, 6363, [Fe ii] λ7155, and [Ca ii] λ7291, 7323), which are typical of core-collapse SNe at late phases. The lack of these lines could suggest either a high density associated with a large mass and low-velocity or an interaction between the SN ejecta and the CSM (Section 5).

Left-hand panel: Optical spectra of DES16C3cje from 80 to 380 d after explosion. Each spectrum has been corrected for Milky Way reddening and shifted by an arbitrary amount for presentation. The phases are labelled on the right. Right-hand panel: Zoom around the H α P-Cygni profile in velocity space.
DES16C3cje shows a complex H α P-cygni profile (Fig. 2, right-hand panel). At early times (spectra between 80 d and 127 d), the absorption component increases in strength with time, from 3.8 ± 0.5 Å to 8.5 ± 1.2 Å; however, at 278 d and 380 d, this component is absent. The emission component at earlier times shows a Gaussian profile with an extra narrow emission line, caused by a contaminating H ii region. At late times, the H α emission has a Lorentzian profile with a full width at half-maximum (FWHM) velocity of 815 ± 65 km s−1 at 295 d, increasing to 980 ± 55 km s−1 at 403 d. The absence of the absorption component, and the Lorentzian profile in emission, further indicate interaction between the ejecta and the CSM (Chugai et al. 2004). At 380 d, on the top of the emission component of the H α, a small notch is observed; upon close examination this was revealed to be residuals from the galaxy subtraction.4
Based on the width of the lines observed in the SN spectra, we infer very low expansion velocities. The velocity obtained for H α decreases from ∼1500 km s−1 at 80 d, to ∼1300 km s−1 at 127 d. The velocities found for other lines show a similar behaviour: low expansion velocities (<2000 km s−1), and little evolution.
3.5 Comparison to other supernovae
The slow rise of DES16C3cje is reminiscent of SN 1987A-like objects, whereas its low luminosity and low expansion velocities are a common characteristic in low luminosity (LL) SNe II. In Fig. 3, we show the photometric and spectral comparison of DES16C3cje with these two classes of events. For the SN 1987A-like objects we compared with SN 1987A (Bouchet et al. 1989; Hamuy & Suntzeff 1990), which is the best observed and studied SN II; SN 2004ek (Taddia et al. 2016) and SN 2004em (Taddia et al. 2016), which both show a plateau before the main peak; SN 2005ci (Taddia et al. 2016) and SN 2009E (Pastorello et al. 2012), which are the faintest clones of SN 1987A. For the LL SNe II, we select objects with spectra at around 110 d: SN 1999br (Pastorello et al. 2004; Galbany et al. 2016; Gutiérrez et al. 2017), which is the faintest slowly declining SN II; SN2003Z (Faran et al. 2014; Spiro et al. 2014), SN 2005cs (Pastorello et al. 2006, 2009), and SN 2013K (Tomasella et al. 2018), which all have good photometric coverage in the first 150 d. The long rise to peak is common between the SN1987A-like events and DES16C3cje; however, the rise is even longer for DES16C3cje.

Left-hand panel: Comparison of the r/R-band light curve of DES16C3cje with well-observed SNe II. Upper panel: Comparison with 87A-like objects: SN 1987A (Bouchet et al. 1989; Hamuy & Suntzeff 1990), SN 2004ek (Taddia et al. 2016), SN 2004em (Taddia et al. 2016), SN 2005ci (Taddia et al. 2016), and SN 2009E (Pastorello et al. 2012). Lower panel: Comparison with LLSNe II: SN 1999br (Pastorello et al. 2004; Galbany et al. 2016), SN2003Z (Faran et al. 2014; Spiro et al. 2014), SN 2005cs (Pastorello et al. 2009), and SN 2013K (Tomasella et al. 2018). Right-hand panel: Spectral comparison around 110 d for DES16C3cje. Upper panel: Comparison with SN1987A-like objects: SN 1987A (Phillips et al. 1988), SN 2004ek (Taddia et al. 2016), and SN 2009E (Pastorello et al. 2012). Lower panel: Comparison with LLSNe II: SN 1999br (Gutiérrez et al. 2017), SN2003Z (Spiro et al. 2014), SN 2005cs (Pastorello et al. 2009), and SN 2013K (Tomasella et al. 2018).
The full light curve evolution shows that DES16C3cje, from explosion to 60 d, exhibits a initial ‘plateau’. Although this plateau is not common in SN1987A-like objects, two other SNe do show it: SN 2004ek (in the V and R-bands) and SN 2004em (in the I-band, Taddia et al. 2016). Taddia et al. (2016) suggest that these two SNe are an intermediate case between SN 1987A and normal SNe II. Pastorello et al. (2012) argue that these plateaus are due to shock cooling. DES16C3cje also has the lowest luminosity within the SN1987A-like group, around 1 mag fainter than SN 1987A and ∼0.5 mag fainter than the low-luminosity SN 2009E.
Comparing to the LL-SNe II sample, the initial evolution of DES16C3cje is consistent with typical SNe II for ∼60 d; however a sudden increase in luminosity transforms a ‘typical SN II’ to an SN1987A-like event. The post-peak light curve evolution also differs, where all SN1987A-like and LL-SNe follow the rate of 56Co decay. In the case of DES16C3cje, the decay at late-times is slower, again suggesting an extra source of energy is needed. We also note that SN 2005cs shows a slow decline soon after the plateau (between 140 and ∼320 d; Pastorello et al. 2009). One possible explanation for this flattening was given by Utrobin (2007), who suggested that it is produced by a residual contribution from radiation energy. Giving that this effect is predicted for typical slow-declining SNe II soon after the plateau phase, we explore an alternative scenario to explain the decay at the late-times in DES16C3cje.
To distinguish between the scenarios of 56Co decay and accretion power (L ∝ t−5/3) as explanations for the light curves, we compare the reduced chi-squared (χ2) values (shown in Table A2) of the corresponding fits to the SNe with data at late-time (between 280 and 500 d; DES16C3cje, SN 1987A, SN 2005cs, and SN 2009E). Out of these, only for DES16C3cje does the power law provides a better fit (χ2 = 0.71), supporting the idea of an extra source of energy. Because of the large uncertainties in the bolometric light curve of DES16C3cje, we test this result using a Monte Carlo resampling with 105 random draws (assuming a Gaussian distribution). The results obtained support our previous findings.
Fig. 3 also presents the spectral comparison at ∼105 d from explosion. The comparison with SN1987A-like objects and LL-SNe II again shows that DES16C3cje is a unique object. None of the other SNe have lines as narrow as DES16C3cje. SN 1999br has the narrowest lines, but its spectrum also shows Ba ii and Sc ii, together with a multiple component H α P-Cygni profile, characteristic of LL-SNe II.
4 LIGHT-CURVE MODELLING
We now consider some models that can be used to understand and explain the physical origin and unusual features of DES16C3cje. For these models, we use the 1D Lagrangian hydrodynamical code presented in Bersten, Benvenuto & Hamuy (2011). This code simulates an SN explosion, and produces bolometric light curves and photospheric velocities to characterize the progenitor and explosion properties. There are two particular challenges to this modelling: the early photometric behaviour (before peak) and the low expansion velocities, and the late-time decline rate. We begin with the former.
There is a degree of degeneracy between the progenitor (pre-SN) mass and radius (M, R) and the explosion energy (E), which can be partially reduced by modelling the luminosity evolution together with the expansion velocity evolution. For DES16C3cje, the expansion velocities imply a low E/M ratio. We found that for a progenitor with similar characteristics to those used for SN 1987A (i.e. a blue supergiant star with R ∼ 50 R⊙, MZAMS = 20 M⊙, and E = 1 foe), there is no model that simultaneously matches the light curve and velocity evolution, as a low energy is needed to reproduce the latter. The low energy required leads to a much fainter and broader light curve than that observed. We found that explosion energies of ∼0.1 foe are needed to reproduce the expansion velocities of DES16C3cje.
Therefore, we calculated a grid of hydrodynamical models with values of E close to 0.1 foe. Our pre-SN models were computed using the stellar evolution code mesa version 10398 (Paxton et al. 2011, 2013, 2015, 2018). The stars were evolved from the pre-main-sequence to the time of core collapse, defined as when any part of the collapsing core exceeds an infall velocity of 1000 km s−1, and assuming solar metallicity. Our models cover the MZAMS range of 9–25 M⊙ in intervals of 1 M⊙(which corresponds to progenitor radii between 480 and 1050 R⊙), and explosion energies between 0.1 and 0.5 foe with the exception of the largest masses and lower energies due to numerical difficulties.
After exploring several configurations (see Fig. B1 in the Appendix), we found a model that reproduced the observations relatively well. This model is presented on the left-hand panel of Fig. 4 and has the following physical parameters: a MZAMS = 15 M⊙, a pre-SN mass of 13.3 M⊙, R = 830 R⊙, and E = 0.11 foe. We also consider 56Ni masses in the range of 0.01 and 0.1 M⊙ and find that a relatively large 56Ni mass of 0.095 M⊙ is required to reproduce the light curve observed after the initial plateau. This material was mixed up to 0.75 of the pre-SN mass, and therefore a not too extreme mixing was required as is common in several 87A-like objects in order to produce the initial plateau and the long rise to the peak. In this scenario, the peculiar light curve shape of DES16C3cje can be understood as a combination of a low explosion energy and a relatively large 56Ni production, while its progenitor has a red supergiant (RSG) structure typical of other SN II objects.

Bolometric light curve of DES16C3cje (stars) compared with the results of the light curve calculations from hydrodynamic models (Section 4). A core-collapse explosion (powered only by 56Ni) is presented in green on the left-hand panel and in cyan on the right. Explosions powered by both 56Ni and fallback (i.e. with an extra contribution of energy coming from accretion in the central region) are presented in blue and black in each panel. The parameters used for each model are given in the legends.
We now turn to the late-time light curve. Despite the good agreement between the model and observations at early times, there are clear differences in the slopes during the light curve tail (green curve in Fig. 4). As discussed above, DES16C3cje does not follow the behaviour expected by radioactive decay of 56Co, but instead is consistent with a power law ∝t−5/3, compatible with the decline rate expected from accretion power (or ‘fallback’5; Michel 1988; Chevalier 1989). Under some conditions, for example if the SN explosion is not powerful enough, some material may not acquire sufficient energy to escape and will eventually be accreted on to the compact remnant. These accretions are usually associated with powerful energy outflows. A fraction of this energy can be thermalized within the SN ejecta and thus power the light curve (Dexter & Kasen 2013).
We have included this extra energy in our 1D Lagrangian code to explore if this can improve the differences between the model and observations during the latter part of the light curve. The rate input of energy due to the accretion can be written as: L|$_{\rm fb}={\dot{E}}= \eta \, \dot{M}\, c^2$| where |$\dot{M}$| is the fallback accretion rate, c is the speed of light, and η is the efficiency factor, estimated to be of the order of 10−3 (Dexter & Kasen 2013). Analytic estimates (Chevalier 1989), as well as numerical simulations (Zhang, Woosley & Heger 2008; Dexter & Kasen 2013), have shown that the accretion rate can be assumed to be |$\dot{M}= \dot{M_0} (t/t_0)^{-5/3}$|, where |$\dot{M_0}$| is the accretion rate on to the remnant at a time t0 when the fallback episode begins. The fallback energy is instantaneously deposited after the explosion, near the centre of the progenitor, and we assume full trapping.
In our treatment, |$\dot{M_0}$| and t0 are free parameters to be determined by comparison with the observations. We again calculate a grid of simulations, but this time vary |$\dot{M}$| in the range of 10−7 − 10−9 and t0 between 0.1 and 50 d after the onset of the simulation, finding a set of parameters that can reproduce the behaviour of the light-curve tail of DES16C3cje. In the lower panel of Fig. B1, we show the effect on the light curve and velocities as a result of the variation of |$\dot{M_0}$|, while in Fig. B2, the changes in the light curve produced by different t0 are presented. The fallback parameters found are: |$\dot{M_0}=0.5\times 10^{-8}$| M⊙ s−1 and t0 = 1 d. These calculations were performed assuming the same progenitor and explosion energy as the RSG model presented above, and the combined model is shown in Fig. 4 (left-hand panel). The inclusion of fallback energy clearly improves the modelling during the tail, with almost no effect in other phases. However, we note a slightly smaller amount of 56Ni is needed when fallback energy is added; a good match is found using 0.075 M⊙ of 56Ni. The value of |$\dot{M_0}$| is small compared with that usually found in the literature (Zhang et al. 2008; Moriya et al. 2018a). The reason is the low luminosity of this SN: larger accretion rates inject more energy and produce brighter light curves.
We emphasize that even though we try to model the light curve peak assuming that it was powered by fallback accretion instead of 56Ni, we are unable to find any set of fallback parameters that can reproduce it. Larger accretion rates produce more luminous light curves and earlier plateaus than observed. In addition, a delayed deposition of the fallback energy is not a solution as despite the low accretion rate, a time delay factor produces an extremely luminous plateau (similar to fig. 2 of Moriya et al. 2019) and a brighter light curve tail.
The parameters of our preferred model point to a normal RSG progenitor that has experienced a low energy explosion leading to the fallback process. The peculiar light-curve shape of DES16C3cje can then be explained as a combination of a low explosion energy, a relatively large 56Ni mass but not extremely mixing, and extra energy due to the accretion of material on to the compact remnant.
There is strong evidence of the existence of a correlation between the explosion energy and the amount of 56Ni (see for example Pejcha & Prieto 2015), in the sense that more energetic events produce larger amount of 56Ni. This relation is also supported by theoretical studies. The low explosion energy and the relatively large 56Ni production found in our modelling does not follow the expected correlation. We note a low explosion energy was mainly required to reproduce the low-expansion velocities.
DES16C3cje has only two measurements of the expansion velocity available at ∼105 d and ∼127 d, and thus the expansion velocity during the first weeks of evolution is not unambiguously known, and the measurements around ∼100 d may not represent the photospheric velocities of the ejecta. We experiment with relaxing the condition to reproduce the expansion velocity, and find an alternative model that reproduces relatively well the observed light curve with a progenitor with ∼40 M⊙, an explosion energy of 1 foe and 0.08 M⊙ of 56Ni (Fig. 4). Here, we used a polytropic model to describe the structure of the star before explosion. The fallback parameters needed to reproduce the tail are similar to that in the previous model, i.e., |$\dot{M_0}=0.4\times 10^{-8}$| M⊙ s−1 and t0 = 1 d. The higher energy of this model is then more consistent with known correlations between 56Ni production and explosion energy. Fig. B3 shows the different configurations explored for this case. The parameters of the best-fitting models are presented in Table A3.
5 DISCUSSION AND CONCLUSIONS
DES16C3cje is a low-luminosity and low-velocity type II supernova (SN II). Its light curves show a plateau for ∼60 d, followed by a long rise time, reminiscent of SN 1987A, but on a longer time-scale. The initial faint plateau can be explained by hydrogen recombination, while the broad peak is powered by radioactive decay. After 300 d, the tail presents a decline rate comparable to that expected from accretion power (∝t−5/3). The narrow lines observed in the spectra imply low expansion velocities, and thus, low explosion energies. Taken together, these characteristics suggest an unusual explosion.
Modelling the light curve of DES16C3cje and its velocity evolution with hydrodynamical calculations, we have shown that the SN is consistent with the explosion of an RSG star with a mass of 15 M⊙, an energy of 0.11 foe, and synthesizing a 56Ni mass of 0.075 M⊙. Because of the low energy in the explosion, some material is accreted by the compact remnant with an accretion rate of ∼0.5 × 10−8 M⊙ s−1. Although this scenario reproduces the light curve and velocities, at first sight the required 56Ni mass appears relatively large for two main reasons: (1) low energy explosions are observed to produce small amounts of 56Ni, and (2) in the fallback scenario, some amount of the 56Ni is expected to be accreted on to the central remnant.
However, Chevalier (1989) discussed the expectation that an ejection of substantial 56Ni would imply little mass fallback, and showed this is not valid for accretion after the passage of the reverse shock wave, when the 56Ni is expected to mix with outer core layers. Heger & Woosley (2010) further showed that a considerable amount of 56Ni comes out when mixing precedes fallback. The mixing in RSGs is larger than in compact objects as perturbations have more time to grow before freezing out. Under these considerations, it is not unusual to find SNe that both experienced some fallback and have a relatively large amount of 56Ni.
Nonetheless, we also consider an alternative scenario by assuming that the velocities measured from the absorption lines at 105 and 126 d do not represent the photospheric velocities of the ejecta. We then find that DES16C3cje can be modelled as the explosion of a relatively compact star (R = 100 R⊙), with a mass of ∼40 M⊙, an explosion energy of 1 foe, and a 56Ni mass of 0.08 M⊙.
Both models can reproduce the overall evolution of the light curve of DES16C3cje; however, the low-energy explosion of an RSG fits the early part of the light curve better, and provides a good agreement with expansion velocities.
A further possibility to explain the late-time light curve of DES16C3cje is interaction with CSM. Interacting objects (e.g. SNe IIn, SN 2009ip-like objects; Stritzinger et al. 2012; Fraser et al. 2015; Elias-Rosa et al. 2016; Pastorello et al. 2018) often have flattened late-time light curves, with decline rates slower than that expected for 56Co decay. The flat evolution in the light curves of DES16C3cje, together with the lack of [O ii] λλ6300, 6363, [Fe ii] λ7155, and [Ca ii] λ7291, 7323 emission lines, offer some support for this scenario. However, this evidence for interaction only appears at around 300 d from explosion with no evidence for interaction prior to this epoch, in turn suggesting a significant mass-loss during the progenitor star evolution.
Theoretical models have also shown that stars with masses below 40 M⊙ at low-metallicities undergo very little mass-loss due to stellar winds (e.g. Woosley et al. 2007; Meynet et al. 2013). Assuming that the progenitor mass favoured by our hydrodynamical models (15 and 40 M⊙) is correct, we would expect a low mass-loss. The location of our object supports this argument: DES16C3cje exploded in a low-luminosity (low-metallicity, Section 3.1) host, and models predict low-metallicity stars have less mass-loss and bigger hydrogen envelopes when they explode (e.g. Heger et al. 2003).
While the late-time light curve of DES16C3cje is following a decline rate close to t−5/3, we cannot rule out a scenario involving interaction with CSM. Moriya et al. (2019) briefly discuss the possibility of CSM interaction in fallback SN and the need to study this issue in the future.
In summary, we have shown that the fallback SN scenario can naturally explain the slow decline in the late-time light curve. However, further investigations are needed to interpret the origin of these peculiar objects, the signatures required to identify the explosion scenario, and the role of the 56Ni mass and interaction with CSM.
ACKNOWLEDGEMENTS
We are grateful to Pedro Lacerda for performing some of the observations used in this work. We thank the anonymous referee for useful suggestions.
CPG and MS acknowledge support from EU/FP7-ERC grant No. [615929]. LG was funded by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 839090. TWC acknowledgments the funding provided by the Alexander von Humboldt Foundation. MF is supported by a Royal Society–Science Foundation Ireland University Research Fellowship. MG is supported by the Polish NCN MAESTRO grant 2014/14/A/ST9/00121. MN is supported by a Royal Astronomical Society Research Fellowship.
This work used data collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile, under program IDs: 299.D-5040(A), 299.D-5040(B), 0100.D-0461(A), 194.C-0207(I), and as part of PESSTO, (the Public ESO Spectroscopic Survey for Transient Objects Survey) ESO program 197.D-1075, 199.D-0143.
Some of the data presented here were obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina), and Ministério da Ciência, Tecnologia e Inovação (Brazil). Gemini observations were obtained under programme NOAO GS-2016B-Q-9.
Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft and the Collaborating Institutions in the Dark Energy Survey.
The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, The Ohio State University, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, Texas A&M University, and the OzDES Membership Consortium.
Based in part on observations at Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.
Part of the funding for GROND (both hardware as well as personnel) was generously granted from the Leibniz-Prize to Prof. G. Hasinger (DFG grant HA 1850/28-1).
This paper includes data gathered with the 6.5 m Magellan Clay Telescope located at Las Campanas Observatory, Chile under the programme 100type IA Supernovae (100IAS) survey.
This work has been partially supported by the Spanish grant PGC2018-095317-B-C21 within the European Funds for Regional Development (FEDER).
The DES data management system is supported by the National Science Foundation under Grant Numbers AST-1138766 and AST-1536171. The DES participants from Spanish institutions are partially supported by MINECO under grants AYA2015-71825, ESP2015-66861, FPA2015-68048, SEV-2016-0588, SEV-2016-0597, and MDM-2015-0509, some of which include ERDF funds from the European Union. IFAE is partially funded by the CERCA program of the Generalitat de Catalunya. Research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013) including ERC grant agreements 240672, 291329, and 306478. We acknowledge support from the Brazilian Instituto Nacional de Ciênciae Tecnologia (INCT) e-Universe (CNPq grant 465376/2014-2).
This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.
This manuscript has been authored by Fermi Research Alliance, LLC under Contract No. DE-AC02-07CH11359 with the U.S. Department of Energy, Office of Science, Office of High Energy Physics. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes.
Footnotes
Redshift obtained from the narrow emission lines of the host galaxy.
The expansion velocities and the pseudo-equivalent-widths were measured removing the contribution of the host galaxy.
The canonical power-law index, n = −5/3, is produced by a simple ballistic fallback model (Rees 1988). However, standard viscous disc descriptions extend the duration of the emission, with an index closer to n = −1.2 (see Balbus & Mummery 2018, and references therein). This suggests that the index value n changes depending on the conditions of the disc.
REFERENCES
APPENDIX A: TABLES
| UT date . | MJD . | Rest-frame phase . | g . | r . | i . | z . | Instrument . |
|---|---|---|---|---|---|---|---|
| . | . | (d) . | (mag) . | (mag) . | (mag) . | (mag) . | . |
| 20161011 | 57673.3 | 2.9 | – | – | – | 23.26 ± 0.08 | DECam |
| 20161018 | 57680.3 | 9.5 | – | 22.71 ± 0.13 | – | – | DECam |
| 20161019 | 57681.1 | 10.3 | 23.31 ± 0.24 | – | 22.86 ± 0.26 | 23.01 ± 0.08 | DECam |
| 20161020 | 57682.1 | 11.2 | – | 22.78 ± 0.06 | 22.87 ± 0.05 | – | DECam |
| 20161024 | 57686.3 | 15.2 | 23.22 ± 0.08 | 22.85 ± 0.05 | – | 22.86 ± 0.08 | DECam |
| 20161025 | 57687.2 | 16.0 | 23.24 ± 0.08 | – | 22.91 ± 0.07 | – | DECam |
| 20161101 | 57694.1 | 22.5 | 23.23 ± 0.07 | 22.71 ± 0.03 | 22.71 ± 0.06 | 22.73 ± 0.06 | DECam |
| 20161108 | 57701.1 | 29.1 | 23.21 ± 0.08 | 22.68 ± 0.03 | 22.67 ± 0.03 | 22.62 ± 0.03 | DECam |
| 20161115 | 57708.2 | 35.8 | 23.28 ± 0.10 | 22.60 ± 0.04 | 22.61 ± 0.05 | 22.54 ± 0.05 | DECam |
| 20161121 | 57714.1 | 41.3 | 23.43 ± 0.13 | 22.61 ± 0.05 | 22.57 ± 0.04 | 22.50 ± 0.04 | DECam |
| 20161122 | 57715.1 | 42.3 | 23.84 ± 0.18 | – | – | – | DECam |
| 20161123 | 57716.2 | 43.3 | 23.42 ± 0.09 | – | – | – | DECam |
| 20161126 | 57719.2 | 46.1 | 23.42 ± 0.08 | 22.70 ± 0.03 | 22.54 ± 0.03 | 22.48 ± 0.03 | DECam |
| 20161201 | 57724.1 | 50.8 | 23.47 ± 0.08 | 22.66 ± 0.03 | 22.54 ± 0.05 | 22.46 ± 0.04 | DECam |
| 20161207 | 57730.1 | 56.4 | 23.42 ± 0.17 | 22.57 ± 0.03 | 22.50 ± 0.04 | 22.31 ± 0.04 | DECam |
| 20161216 | 57739.2 | 65.0 | 23.37 ± 0.15 | 22.57 ± 0.03 | 22.40 ± 0.03 | 22.28 ± 0.04 | DECam |
| 20161223 | 57746.1 | 71.5 | 23.26 ± 0.04 | 22.41 ± 0.02 | 22.27 ± 0.02 | 22.24 ± 0.02 | DECam |
| 20161227 | 57750.2 | 75.3 | 23.12 ± 0.06 | 22.29 ± 0.03 | 22.10 ± 0.04 | – | DECam |
| 20161228 | 57751.1 | 76.2 | – | – | 22.25 ± 0.03 | 22.11 ± 0.03 | DECam |
| 20170102 | 57756.1 | 80.9 | 23.02 ± 0.06 | 22.25 ± 0.02 | 22.11 ± 0.02 | 22.02 ± 0.03 | DECam |
| 20170109 | 57763.1 | 87.5 | – | 22.04 ± 0.03 | 21.96 ± 0.02 | – | DECam |
| 20170116 | 57770.1 | 94.1 | 22.60 ± 0.03 | 21.88 ± 0.01 | 21.85 ± 0.01 | 21.76 ± 0.02 | DECam |
| 20170121 | 57775.2 | 98.9 | 22.51 ± 0.04 | – | – | – | DECam |
| 20170124 | 57778.1 | 101.6 | – | 21.82 ± 0.02 | – | 21.65 ± 0.02 | DECam |
| 20170125 | 57779.1 | 102.6 | 22.31 ± 0.04 | – | 21.68 ± 0.01 | – | DECam |
| 20170128 | 57782.1 | 105.4 | – | 21.74 ± 0.02 | – | 21.58 ± 0.02 | DECam |
| 20170130 | 57784.1 | 107.3 | 22.27 ± 0.03 | – | 21.59 ± 0.02 | – | DECam |
| 20170204 | 57789.1 | 112.0 | – | 21.73 ± 0.05 | – | 21.54 ± 0.02 | DECam |
| 20170206 | 57791.1 | 113.9 | 22.62 ± 0.19 | – | 21.53 ± 0.02 | – | DECam |
| 20170215 | 57800.1 | 122.3 | 22.09 ± 0.03 | 21.58 ± 0.02 | – | – | DECam |
| 20170218 | 57803.5 | 125.5 | – | – | 21.39 ± 0.01 | – | DECam |
| 20170227 | 57811.5 | 133.1 | – | 21.55 ± 0.20 | – | – | EFOSC2 |
| 20170325 | 57837.5 | 157.6 | 21.94 ± 0.10 | 21.93 ± 0.10 | 20.90 ± 0.10 | – | EFOSC2 |
| 20170402 | 57845.5 | 165.1 | – | 21.66 ± 0.22 | – | – | EFOSC2 |
| 20170412 | 57855.5 | 174.5 | >20.47 | >20.85 | >20.52 | >20.68 | GROND |
| 20170531 | 57905.4 | 221.5 | – | 22.00 ± 0.10 | – | – | EFOSC2 |
| 20170601 | 57906.4 | 222.5 | – | 22.07 ± 0.22 | – | – | EFOSC2 |
| 20170603 | 57908.4 | 224.3 | – | 22.14 ± 0.15 | 21.55 ± 0.15 | – | EFOSC2 |
| 20170720 | 57955.9 | 269.1 | – | 23.04 ± 0.20 | 22.88 ± 0.06 | – | LDSS3 |
| 20170727 | 57962.4 | 275.2 | 22.93 ± 0.05 | 23.41 ± 0.30 | 23.27 ± 0.31 | 23.30 ± 0.30 | FORS2 |
| 20170821 | 57987.3 | 298.6 | 24.87 ± 0.27 | 23.39 ± 0.06 | 23.76 ± 0.10 | 23.36 ± 0.09 | DECam |
| 20170826 | 57992.3 | 303.4 | 24.80 ± 0.23 | 23.51 ± 0.06 | 23.81 ± 0.11 | 23.33 ± 0.12 | DECam |
| 20170831 | 57997.3 | 308.1 | – | – | 23.76 ± 0.31 | – | DECam |
| 20170901 | 57998.2 | 308.9 | – | – | 23.53 ± 0.24 | 23.11 ± 0.24 | DECam |
| 20170902 | 57999.3 | 309.9 | – | 23.49 ± 0.13 | – | 23.47 ± 0.19 | DECam |
| 20170906 | 58003.3 | 313.7 | – | 23.44 ± 0.17 | 23.95 ± 0.19 | 23.37 ± 0.08 | DECam |
| 20170910 | 58007.4 | 317.6 | – | 23.51 ± 0.09 | 23.63 ± 0.12 | – | DECam |
| 20170912 | 58009.4 | 319.5 | – | – | 23.68 ± 0.12 | 23.35 ± 0.06 | DECam |
| 20170917 | 58014.2 | 324.0 | 24.68 ± 0.20 | 23.50 ± 0.05 | – | – | DECam |
| 20170923 | 58020.3 | 329.7 | 24.88 ± 0.28 | 23.64 ± 0.08 | 24.06 ± 0.10 | 23.33 ± 0.06 | DECam |
| 20171001 | 58028.2 | 337.2 | – | 23.52 ± 0.11 | – | 23.37 ± 0.09 | DECam |
| 20171009 | 58036.3 | 344.8 | – | 23.26 ± 0.11 | 23.93 ± 0.12 | 23.48 ± 0.09 | DECam |
| 20171013 | 58040.3 | 348.6 | – | 23.74 ± 0.07 | – | 23.66 ± 0.10 | DECam |
| 20171018 | 58045.3 | 353.3 | 24.90 ± 0.25 | 23.74 ± 0.07 | 24.04 ± 0.12 | 23.64 ± 0.11 | DECam |
| 20171025 | 58052.1 | 359.7 | 25.00 ± 0.24 | 23.85 ± 0.10 | 24.00 ± 0.15 | 23.54 ± 0.10 | DECam |
| 20171030 | 58057.2 | 364.5 | – | 23.70 ± 0.09 | 24.02 ± 0.12 | 23.55 ± 0.08 | DECam |
| 20171106 | 58064.2 | 371.1 | – | 23.53 ± 0.12 | 24.19 ± 0.16 | 23.67 ± 0.11 | DECam |
| 20171113 | 58071.2 | 377.7 | – | 23.79 ± 0.06 | 23.93 ± 0.10 | 23.62 ± 0.09 | DECam |
| 20171118 | 58076.3 | 382.5 | 25.17 ± 0.32 | 23.93 ± 0.10 | 24.19 ± 0.18 | – | DECam |
| 20171121 | 58079.1 | 385.1 | – | – | – | 23.79 ± 0.12 | DECam |
| 20171124 | 58082.2 | 388.0 | – | 23.92 ± 0.08 | 24.34 ± 0.17 | – | DECam |
| 20171126 | 58084.3 | 390.0 | 25.02 ± 0.36 | – | – | 23.75 ± 0.11 | DECam |
| 20171204 | 58092.2 | 397.4 | – | – | – | 23.90 ± 0.15 | DECam |
| 20171210 | 58098.2 | 403.1 | 24.56 ± 0.24 | 23.93 ± 0.10 | 24.33 ± 0.17 | 23.85 ± 0.14 | DECam |
| 20171213 | 58101.2 | 405.9 | – | 24.09 ± 0.10 | 24.49 ± 0.17 | – | DECam |
| 20171219 | 58107.2 | 411.6 | 24.97 ± 0.24 | 24.05 ± 0.07 | 24.73 ± 0.16 | 23.96 ± 0.13 | DECam |
| 20171229 | 58117.1 | 420.9 | – | 23.97 ± 0.31 | 24.70 ± 0.32 | 24.01 ± 0.22 | DECam |
| 20180105 | 58124.1 | 427.5 | – | 24.34 ± 0.08 | 24.65 ± 0.14 | 24.05 ± 0.11 | DECam |
| 20180112 | 58131.1 | 434.1 | – | 24.47 ± 0.30 | 25.17 ± 0.33 | 24.11 ± 0.12 | DECam |
| 20180118 | 58137.1 | 439.7 | – | 24.55 ± 0.14 | – | 24.37 ± 0.24 | DECam |
| 20180122 | 58141.1 | 443.5 | – | 24.65 ± 0.28 | – | – | DECam |
| 20180203 | 58153.1 | 454.8 | – | 24.48 ± 0.12 | – | – | DECam |
| 20180210 | 58160.0 | 461.3 | – | 24.76 ± 0.20 | – | – | DECam |
| UT date . | MJD . | Rest-frame phase . | g . | r . | i . | z . | Instrument . |
|---|---|---|---|---|---|---|---|
| . | . | (d) . | (mag) . | (mag) . | (mag) . | (mag) . | . |
| 20161011 | 57673.3 | 2.9 | – | – | – | 23.26 ± 0.08 | DECam |
| 20161018 | 57680.3 | 9.5 | – | 22.71 ± 0.13 | – | – | DECam |
| 20161019 | 57681.1 | 10.3 | 23.31 ± 0.24 | – | 22.86 ± 0.26 | 23.01 ± 0.08 | DECam |
| 20161020 | 57682.1 | 11.2 | – | 22.78 ± 0.06 | 22.87 ± 0.05 | – | DECam |
| 20161024 | 57686.3 | 15.2 | 23.22 ± 0.08 | 22.85 ± 0.05 | – | 22.86 ± 0.08 | DECam |
| 20161025 | 57687.2 | 16.0 | 23.24 ± 0.08 | – | 22.91 ± 0.07 | – | DECam |
| 20161101 | 57694.1 | 22.5 | 23.23 ± 0.07 | 22.71 ± 0.03 | 22.71 ± 0.06 | 22.73 ± 0.06 | DECam |
| 20161108 | 57701.1 | 29.1 | 23.21 ± 0.08 | 22.68 ± 0.03 | 22.67 ± 0.03 | 22.62 ± 0.03 | DECam |
| 20161115 | 57708.2 | 35.8 | 23.28 ± 0.10 | 22.60 ± 0.04 | 22.61 ± 0.05 | 22.54 ± 0.05 | DECam |
| 20161121 | 57714.1 | 41.3 | 23.43 ± 0.13 | 22.61 ± 0.05 | 22.57 ± 0.04 | 22.50 ± 0.04 | DECam |
| 20161122 | 57715.1 | 42.3 | 23.84 ± 0.18 | – | – | – | DECam |
| 20161123 | 57716.2 | 43.3 | 23.42 ± 0.09 | – | – | – | DECam |
| 20161126 | 57719.2 | 46.1 | 23.42 ± 0.08 | 22.70 ± 0.03 | 22.54 ± 0.03 | 22.48 ± 0.03 | DECam |
| 20161201 | 57724.1 | 50.8 | 23.47 ± 0.08 | 22.66 ± 0.03 | 22.54 ± 0.05 | 22.46 ± 0.04 | DECam |
| 20161207 | 57730.1 | 56.4 | 23.42 ± 0.17 | 22.57 ± 0.03 | 22.50 ± 0.04 | 22.31 ± 0.04 | DECam |
| 20161216 | 57739.2 | 65.0 | 23.37 ± 0.15 | 22.57 ± 0.03 | 22.40 ± 0.03 | 22.28 ± 0.04 | DECam |
| 20161223 | 57746.1 | 71.5 | 23.26 ± 0.04 | 22.41 ± 0.02 | 22.27 ± 0.02 | 22.24 ± 0.02 | DECam |
| 20161227 | 57750.2 | 75.3 | 23.12 ± 0.06 | 22.29 ± 0.03 | 22.10 ± 0.04 | – | DECam |
| 20161228 | 57751.1 | 76.2 | – | – | 22.25 ± 0.03 | 22.11 ± 0.03 | DECam |
| 20170102 | 57756.1 | 80.9 | 23.02 ± 0.06 | 22.25 ± 0.02 | 22.11 ± 0.02 | 22.02 ± 0.03 | DECam |
| 20170109 | 57763.1 | 87.5 | – | 22.04 ± 0.03 | 21.96 ± 0.02 | – | DECam |
| 20170116 | 57770.1 | 94.1 | 22.60 ± 0.03 | 21.88 ± 0.01 | 21.85 ± 0.01 | 21.76 ± 0.02 | DECam |
| 20170121 | 57775.2 | 98.9 | 22.51 ± 0.04 | – | – | – | DECam |
| 20170124 | 57778.1 | 101.6 | – | 21.82 ± 0.02 | – | 21.65 ± 0.02 | DECam |
| 20170125 | 57779.1 | 102.6 | 22.31 ± 0.04 | – | 21.68 ± 0.01 | – | DECam |
| 20170128 | 57782.1 | 105.4 | – | 21.74 ± 0.02 | – | 21.58 ± 0.02 | DECam |
| 20170130 | 57784.1 | 107.3 | 22.27 ± 0.03 | – | 21.59 ± 0.02 | – | DECam |
| 20170204 | 57789.1 | 112.0 | – | 21.73 ± 0.05 | – | 21.54 ± 0.02 | DECam |
| 20170206 | 57791.1 | 113.9 | 22.62 ± 0.19 | – | 21.53 ± 0.02 | – | DECam |
| 20170215 | 57800.1 | 122.3 | 22.09 ± 0.03 | 21.58 ± 0.02 | – | – | DECam |
| 20170218 | 57803.5 | 125.5 | – | – | 21.39 ± 0.01 | – | DECam |
| 20170227 | 57811.5 | 133.1 | – | 21.55 ± 0.20 | – | – | EFOSC2 |
| 20170325 | 57837.5 | 157.6 | 21.94 ± 0.10 | 21.93 ± 0.10 | 20.90 ± 0.10 | – | EFOSC2 |
| 20170402 | 57845.5 | 165.1 | – | 21.66 ± 0.22 | – | – | EFOSC2 |
| 20170412 | 57855.5 | 174.5 | >20.47 | >20.85 | >20.52 | >20.68 | GROND |
| 20170531 | 57905.4 | 221.5 | – | 22.00 ± 0.10 | – | – | EFOSC2 |
| 20170601 | 57906.4 | 222.5 | – | 22.07 ± 0.22 | – | – | EFOSC2 |
| 20170603 | 57908.4 | 224.3 | – | 22.14 ± 0.15 | 21.55 ± 0.15 | – | EFOSC2 |
| 20170720 | 57955.9 | 269.1 | – | 23.04 ± 0.20 | 22.88 ± 0.06 | – | LDSS3 |
| 20170727 | 57962.4 | 275.2 | 22.93 ± 0.05 | 23.41 ± 0.30 | 23.27 ± 0.31 | 23.30 ± 0.30 | FORS2 |
| 20170821 | 57987.3 | 298.6 | 24.87 ± 0.27 | 23.39 ± 0.06 | 23.76 ± 0.10 | 23.36 ± 0.09 | DECam |
| 20170826 | 57992.3 | 303.4 | 24.80 ± 0.23 | 23.51 ± 0.06 | 23.81 ± 0.11 | 23.33 ± 0.12 | DECam |
| 20170831 | 57997.3 | 308.1 | – | – | 23.76 ± 0.31 | – | DECam |
| 20170901 | 57998.2 | 308.9 | – | – | 23.53 ± 0.24 | 23.11 ± 0.24 | DECam |
| 20170902 | 57999.3 | 309.9 | – | 23.49 ± 0.13 | – | 23.47 ± 0.19 | DECam |
| 20170906 | 58003.3 | 313.7 | – | 23.44 ± 0.17 | 23.95 ± 0.19 | 23.37 ± 0.08 | DECam |
| 20170910 | 58007.4 | 317.6 | – | 23.51 ± 0.09 | 23.63 ± 0.12 | – | DECam |
| 20170912 | 58009.4 | 319.5 | – | – | 23.68 ± 0.12 | 23.35 ± 0.06 | DECam |
| 20170917 | 58014.2 | 324.0 | 24.68 ± 0.20 | 23.50 ± 0.05 | – | – | DECam |
| 20170923 | 58020.3 | 329.7 | 24.88 ± 0.28 | 23.64 ± 0.08 | 24.06 ± 0.10 | 23.33 ± 0.06 | DECam |
| 20171001 | 58028.2 | 337.2 | – | 23.52 ± 0.11 | – | 23.37 ± 0.09 | DECam |
| 20171009 | 58036.3 | 344.8 | – | 23.26 ± 0.11 | 23.93 ± 0.12 | 23.48 ± 0.09 | DECam |
| 20171013 | 58040.3 | 348.6 | – | 23.74 ± 0.07 | – | 23.66 ± 0.10 | DECam |
| 20171018 | 58045.3 | 353.3 | 24.90 ± 0.25 | 23.74 ± 0.07 | 24.04 ± 0.12 | 23.64 ± 0.11 | DECam |
| 20171025 | 58052.1 | 359.7 | 25.00 ± 0.24 | 23.85 ± 0.10 | 24.00 ± 0.15 | 23.54 ± 0.10 | DECam |
| 20171030 | 58057.2 | 364.5 | – | 23.70 ± 0.09 | 24.02 ± 0.12 | 23.55 ± 0.08 | DECam |
| 20171106 | 58064.2 | 371.1 | – | 23.53 ± 0.12 | 24.19 ± 0.16 | 23.67 ± 0.11 | DECam |
| 20171113 | 58071.2 | 377.7 | – | 23.79 ± 0.06 | 23.93 ± 0.10 | 23.62 ± 0.09 | DECam |
| 20171118 | 58076.3 | 382.5 | 25.17 ± 0.32 | 23.93 ± 0.10 | 24.19 ± 0.18 | – | DECam |
| 20171121 | 58079.1 | 385.1 | – | – | – | 23.79 ± 0.12 | DECam |
| 20171124 | 58082.2 | 388.0 | – | 23.92 ± 0.08 | 24.34 ± 0.17 | – | DECam |
| 20171126 | 58084.3 | 390.0 | 25.02 ± 0.36 | – | – | 23.75 ± 0.11 | DECam |
| 20171204 | 58092.2 | 397.4 | – | – | – | 23.90 ± 0.15 | DECam |
| 20171210 | 58098.2 | 403.1 | 24.56 ± 0.24 | 23.93 ± 0.10 | 24.33 ± 0.17 | 23.85 ± 0.14 | DECam |
| 20171213 | 58101.2 | 405.9 | – | 24.09 ± 0.10 | 24.49 ± 0.17 | – | DECam |
| 20171219 | 58107.2 | 411.6 | 24.97 ± 0.24 | 24.05 ± 0.07 | 24.73 ± 0.16 | 23.96 ± 0.13 | DECam |
| 20171229 | 58117.1 | 420.9 | – | 23.97 ± 0.31 | 24.70 ± 0.32 | 24.01 ± 0.22 | DECam |
| 20180105 | 58124.1 | 427.5 | – | 24.34 ± 0.08 | 24.65 ± 0.14 | 24.05 ± 0.11 | DECam |
| 20180112 | 58131.1 | 434.1 | – | 24.47 ± 0.30 | 25.17 ± 0.33 | 24.11 ± 0.12 | DECam |
| 20180118 | 58137.1 | 439.7 | – | 24.55 ± 0.14 | – | 24.37 ± 0.24 | DECam |
| 20180122 | 58141.1 | 443.5 | – | 24.65 ± 0.28 | – | – | DECam |
| 20180203 | 58153.1 | 454.8 | – | 24.48 ± 0.12 | – | – | DECam |
| 20180210 | 58160.0 | 461.3 | – | 24.76 ± 0.20 | – | – | DECam |
Note. The magnitudes have not been corrected for extinction. DECam: Dark Energy Camera at Blanco 4-m telescope; EFOSC2: ESO Faint Object Spectrograph and Camera at the 3.5-m ESO New Technology Telescope (NTT); GROND: Gamma-Ray Burst Optical/Near-Infrared Detector at the 2.2-m MPG telescope; LDSS3: Low Dispersion Survey Spectrograph at the Magellan Clay 6.5-m telescope; FORS2: FOcal Reducer/low dispersion Spectrograph 2 at the ESO Very Large Telescope (VLT).
| UT date . | MJD . | Rest-frame phase . | g . | r . | i . | z . | Instrument . |
|---|---|---|---|---|---|---|---|
| . | . | (d) . | (mag) . | (mag) . | (mag) . | (mag) . | . |
| 20161011 | 57673.3 | 2.9 | – | – | – | 23.26 ± 0.08 | DECam |
| 20161018 | 57680.3 | 9.5 | – | 22.71 ± 0.13 | – | – | DECam |
| 20161019 | 57681.1 | 10.3 | 23.31 ± 0.24 | – | 22.86 ± 0.26 | 23.01 ± 0.08 | DECam |
| 20161020 | 57682.1 | 11.2 | – | 22.78 ± 0.06 | 22.87 ± 0.05 | – | DECam |
| 20161024 | 57686.3 | 15.2 | 23.22 ± 0.08 | 22.85 ± 0.05 | – | 22.86 ± 0.08 | DECam |
| 20161025 | 57687.2 | 16.0 | 23.24 ± 0.08 | – | 22.91 ± 0.07 | – | DECam |
| 20161101 | 57694.1 | 22.5 | 23.23 ± 0.07 | 22.71 ± 0.03 | 22.71 ± 0.06 | 22.73 ± 0.06 | DECam |
| 20161108 | 57701.1 | 29.1 | 23.21 ± 0.08 | 22.68 ± 0.03 | 22.67 ± 0.03 | 22.62 ± 0.03 | DECam |
| 20161115 | 57708.2 | 35.8 | 23.28 ± 0.10 | 22.60 ± 0.04 | 22.61 ± 0.05 | 22.54 ± 0.05 | DECam |
| 20161121 | 57714.1 | 41.3 | 23.43 ± 0.13 | 22.61 ± 0.05 | 22.57 ± 0.04 | 22.50 ± 0.04 | DECam |
| 20161122 | 57715.1 | 42.3 | 23.84 ± 0.18 | – | – | – | DECam |
| 20161123 | 57716.2 | 43.3 | 23.42 ± 0.09 | – | – | – | DECam |
| 20161126 | 57719.2 | 46.1 | 23.42 ± 0.08 | 22.70 ± 0.03 | 22.54 ± 0.03 | 22.48 ± 0.03 | DECam |
| 20161201 | 57724.1 | 50.8 | 23.47 ± 0.08 | 22.66 ± 0.03 | 22.54 ± 0.05 | 22.46 ± 0.04 | DECam |
| 20161207 | 57730.1 | 56.4 | 23.42 ± 0.17 | 22.57 ± 0.03 | 22.50 ± 0.04 | 22.31 ± 0.04 | DECam |
| 20161216 | 57739.2 | 65.0 | 23.37 ± 0.15 | 22.57 ± 0.03 | 22.40 ± 0.03 | 22.28 ± 0.04 | DECam |
| 20161223 | 57746.1 | 71.5 | 23.26 ± 0.04 | 22.41 ± 0.02 | 22.27 ± 0.02 | 22.24 ± 0.02 | DECam |
| 20161227 | 57750.2 | 75.3 | 23.12 ± 0.06 | 22.29 ± 0.03 | 22.10 ± 0.04 | – | DECam |
| 20161228 | 57751.1 | 76.2 | – | – | 22.25 ± 0.03 | 22.11 ± 0.03 | DECam |
| 20170102 | 57756.1 | 80.9 | 23.02 ± 0.06 | 22.25 ± 0.02 | 22.11 ± 0.02 | 22.02 ± 0.03 | DECam |
| 20170109 | 57763.1 | 87.5 | – | 22.04 ± 0.03 | 21.96 ± 0.02 | – | DECam |
| 20170116 | 57770.1 | 94.1 | 22.60 ± 0.03 | 21.88 ± 0.01 | 21.85 ± 0.01 | 21.76 ± 0.02 | DECam |
| 20170121 | 57775.2 | 98.9 | 22.51 ± 0.04 | – | – | – | DECam |
| 20170124 | 57778.1 | 101.6 | – | 21.82 ± 0.02 | – | 21.65 ± 0.02 | DECam |
| 20170125 | 57779.1 | 102.6 | 22.31 ± 0.04 | – | 21.68 ± 0.01 | – | DECam |
| 20170128 | 57782.1 | 105.4 | – | 21.74 ± 0.02 | – | 21.58 ± 0.02 | DECam |
| 20170130 | 57784.1 | 107.3 | 22.27 ± 0.03 | – | 21.59 ± 0.02 | – | DECam |
| 20170204 | 57789.1 | 112.0 | – | 21.73 ± 0.05 | – | 21.54 ± 0.02 | DECam |
| 20170206 | 57791.1 | 113.9 | 22.62 ± 0.19 | – | 21.53 ± 0.02 | – | DECam |
| 20170215 | 57800.1 | 122.3 | 22.09 ± 0.03 | 21.58 ± 0.02 | – | – | DECam |
| 20170218 | 57803.5 | 125.5 | – | – | 21.39 ± 0.01 | – | DECam |
| 20170227 | 57811.5 | 133.1 | – | 21.55 ± 0.20 | – | – | EFOSC2 |
| 20170325 | 57837.5 | 157.6 | 21.94 ± 0.10 | 21.93 ± 0.10 | 20.90 ± 0.10 | – | EFOSC2 |
| 20170402 | 57845.5 | 165.1 | – | 21.66 ± 0.22 | – | – | EFOSC2 |
| 20170412 | 57855.5 | 174.5 | >20.47 | >20.85 | >20.52 | >20.68 | GROND |
| 20170531 | 57905.4 | 221.5 | – | 22.00 ± 0.10 | – | – | EFOSC2 |
| 20170601 | 57906.4 | 222.5 | – | 22.07 ± 0.22 | – | – | EFOSC2 |
| 20170603 | 57908.4 | 224.3 | – | 22.14 ± 0.15 | 21.55 ± 0.15 | – | EFOSC2 |
| 20170720 | 57955.9 | 269.1 | – | 23.04 ± 0.20 | 22.88 ± 0.06 | – | LDSS3 |
| 20170727 | 57962.4 | 275.2 | 22.93 ± 0.05 | 23.41 ± 0.30 | 23.27 ± 0.31 | 23.30 ± 0.30 | FORS2 |
| 20170821 | 57987.3 | 298.6 | 24.87 ± 0.27 | 23.39 ± 0.06 | 23.76 ± 0.10 | 23.36 ± 0.09 | DECam |
| 20170826 | 57992.3 | 303.4 | 24.80 ± 0.23 | 23.51 ± 0.06 | 23.81 ± 0.11 | 23.33 ± 0.12 | DECam |
| 20170831 | 57997.3 | 308.1 | – | – | 23.76 ± 0.31 | – | DECam |
| 20170901 | 57998.2 | 308.9 | – | – | 23.53 ± 0.24 | 23.11 ± 0.24 | DECam |
| 20170902 | 57999.3 | 309.9 | – | 23.49 ± 0.13 | – | 23.47 ± 0.19 | DECam |
| 20170906 | 58003.3 | 313.7 | – | 23.44 ± 0.17 | 23.95 ± 0.19 | 23.37 ± 0.08 | DECam |
| 20170910 | 58007.4 | 317.6 | – | 23.51 ± 0.09 | 23.63 ± 0.12 | – | DECam |
| 20170912 | 58009.4 | 319.5 | – | – | 23.68 ± 0.12 | 23.35 ± 0.06 | DECam |
| 20170917 | 58014.2 | 324.0 | 24.68 ± 0.20 | 23.50 ± 0.05 | – | – | DECam |
| 20170923 | 58020.3 | 329.7 | 24.88 ± 0.28 | 23.64 ± 0.08 | 24.06 ± 0.10 | 23.33 ± 0.06 | DECam |
| 20171001 | 58028.2 | 337.2 | – | 23.52 ± 0.11 | – | 23.37 ± 0.09 | DECam |
| 20171009 | 58036.3 | 344.8 | – | 23.26 ± 0.11 | 23.93 ± 0.12 | 23.48 ± 0.09 | DECam |
| 20171013 | 58040.3 | 348.6 | – | 23.74 ± 0.07 | – | 23.66 ± 0.10 | DECam |
| 20171018 | 58045.3 | 353.3 | 24.90 ± 0.25 | 23.74 ± 0.07 | 24.04 ± 0.12 | 23.64 ± 0.11 | DECam |
| 20171025 | 58052.1 | 359.7 | 25.00 ± 0.24 | 23.85 ± 0.10 | 24.00 ± 0.15 | 23.54 ± 0.10 | DECam |
| 20171030 | 58057.2 | 364.5 | – | 23.70 ± 0.09 | 24.02 ± 0.12 | 23.55 ± 0.08 | DECam |
| 20171106 | 58064.2 | 371.1 | – | 23.53 ± 0.12 | 24.19 ± 0.16 | 23.67 ± 0.11 | DECam |
| 20171113 | 58071.2 | 377.7 | – | 23.79 ± 0.06 | 23.93 ± 0.10 | 23.62 ± 0.09 | DECam |
| 20171118 | 58076.3 | 382.5 | 25.17 ± 0.32 | 23.93 ± 0.10 | 24.19 ± 0.18 | – | DECam |
| 20171121 | 58079.1 | 385.1 | – | – | – | 23.79 ± 0.12 | DECam |
| 20171124 | 58082.2 | 388.0 | – | 23.92 ± 0.08 | 24.34 ± 0.17 | – | DECam |
| 20171126 | 58084.3 | 390.0 | 25.02 ± 0.36 | – | – | 23.75 ± 0.11 | DECam |
| 20171204 | 58092.2 | 397.4 | – | – | – | 23.90 ± 0.15 | DECam |
| 20171210 | 58098.2 | 403.1 | 24.56 ± 0.24 | 23.93 ± 0.10 | 24.33 ± 0.17 | 23.85 ± 0.14 | DECam |
| 20171213 | 58101.2 | 405.9 | – | 24.09 ± 0.10 | 24.49 ± 0.17 | – | DECam |
| 20171219 | 58107.2 | 411.6 | 24.97 ± 0.24 | 24.05 ± 0.07 | 24.73 ± 0.16 | 23.96 ± 0.13 | DECam |
| 20171229 | 58117.1 | 420.9 | – | 23.97 ± 0.31 | 24.70 ± 0.32 | 24.01 ± 0.22 | DECam |
| 20180105 | 58124.1 | 427.5 | – | 24.34 ± 0.08 | 24.65 ± 0.14 | 24.05 ± 0.11 | DECam |
| 20180112 | 58131.1 | 434.1 | – | 24.47 ± 0.30 | 25.17 ± 0.33 | 24.11 ± 0.12 | DECam |
| 20180118 | 58137.1 | 439.7 | – | 24.55 ± 0.14 | – | 24.37 ± 0.24 | DECam |
| 20180122 | 58141.1 | 443.5 | – | 24.65 ± 0.28 | – | – | DECam |
| 20180203 | 58153.1 | 454.8 | – | 24.48 ± 0.12 | – | – | DECam |
| 20180210 | 58160.0 | 461.3 | – | 24.76 ± 0.20 | – | – | DECam |
| UT date . | MJD . | Rest-frame phase . | g . | r . | i . | z . | Instrument . |
|---|---|---|---|---|---|---|---|
| . | . | (d) . | (mag) . | (mag) . | (mag) . | (mag) . | . |
| 20161011 | 57673.3 | 2.9 | – | – | – | 23.26 ± 0.08 | DECam |
| 20161018 | 57680.3 | 9.5 | – | 22.71 ± 0.13 | – | – | DECam |
| 20161019 | 57681.1 | 10.3 | 23.31 ± 0.24 | – | 22.86 ± 0.26 | 23.01 ± 0.08 | DECam |
| 20161020 | 57682.1 | 11.2 | – | 22.78 ± 0.06 | 22.87 ± 0.05 | – | DECam |
| 20161024 | 57686.3 | 15.2 | 23.22 ± 0.08 | 22.85 ± 0.05 | – | 22.86 ± 0.08 | DECam |
| 20161025 | 57687.2 | 16.0 | 23.24 ± 0.08 | – | 22.91 ± 0.07 | – | DECam |
| 20161101 | 57694.1 | 22.5 | 23.23 ± 0.07 | 22.71 ± 0.03 | 22.71 ± 0.06 | 22.73 ± 0.06 | DECam |
| 20161108 | 57701.1 | 29.1 | 23.21 ± 0.08 | 22.68 ± 0.03 | 22.67 ± 0.03 | 22.62 ± 0.03 | DECam |
| 20161115 | 57708.2 | 35.8 | 23.28 ± 0.10 | 22.60 ± 0.04 | 22.61 ± 0.05 | 22.54 ± 0.05 | DECam |
| 20161121 | 57714.1 | 41.3 | 23.43 ± 0.13 | 22.61 ± 0.05 | 22.57 ± 0.04 | 22.50 ± 0.04 | DECam |
| 20161122 | 57715.1 | 42.3 | 23.84 ± 0.18 | – | – | – | DECam |
| 20161123 | 57716.2 | 43.3 | 23.42 ± 0.09 | – | – | – | DECam |
| 20161126 | 57719.2 | 46.1 | 23.42 ± 0.08 | 22.70 ± 0.03 | 22.54 ± 0.03 | 22.48 ± 0.03 | DECam |
| 20161201 | 57724.1 | 50.8 | 23.47 ± 0.08 | 22.66 ± 0.03 | 22.54 ± 0.05 | 22.46 ± 0.04 | DECam |
| 20161207 | 57730.1 | 56.4 | 23.42 ± 0.17 | 22.57 ± 0.03 | 22.50 ± 0.04 | 22.31 ± 0.04 | DECam |
| 20161216 | 57739.2 | 65.0 | 23.37 ± 0.15 | 22.57 ± 0.03 | 22.40 ± 0.03 | 22.28 ± 0.04 | DECam |
| 20161223 | 57746.1 | 71.5 | 23.26 ± 0.04 | 22.41 ± 0.02 | 22.27 ± 0.02 | 22.24 ± 0.02 | DECam |
| 20161227 | 57750.2 | 75.3 | 23.12 ± 0.06 | 22.29 ± 0.03 | 22.10 ± 0.04 | – | DECam |
| 20161228 | 57751.1 | 76.2 | – | – | 22.25 ± 0.03 | 22.11 ± 0.03 | DECam |
| 20170102 | 57756.1 | 80.9 | 23.02 ± 0.06 | 22.25 ± 0.02 | 22.11 ± 0.02 | 22.02 ± 0.03 | DECam |
| 20170109 | 57763.1 | 87.5 | – | 22.04 ± 0.03 | 21.96 ± 0.02 | – | DECam |
| 20170116 | 57770.1 | 94.1 | 22.60 ± 0.03 | 21.88 ± 0.01 | 21.85 ± 0.01 | 21.76 ± 0.02 | DECam |
| 20170121 | 57775.2 | 98.9 | 22.51 ± 0.04 | – | – | – | DECam |
| 20170124 | 57778.1 | 101.6 | – | 21.82 ± 0.02 | – | 21.65 ± 0.02 | DECam |
| 20170125 | 57779.1 | 102.6 | 22.31 ± 0.04 | – | 21.68 ± 0.01 | – | DECam |
| 20170128 | 57782.1 | 105.4 | – | 21.74 ± 0.02 | – | 21.58 ± 0.02 | DECam |
| 20170130 | 57784.1 | 107.3 | 22.27 ± 0.03 | – | 21.59 ± 0.02 | – | DECam |
| 20170204 | 57789.1 | 112.0 | – | 21.73 ± 0.05 | – | 21.54 ± 0.02 | DECam |
| 20170206 | 57791.1 | 113.9 | 22.62 ± 0.19 | – | 21.53 ± 0.02 | – | DECam |
| 20170215 | 57800.1 | 122.3 | 22.09 ± 0.03 | 21.58 ± 0.02 | – | – | DECam |
| 20170218 | 57803.5 | 125.5 | – | – | 21.39 ± 0.01 | – | DECam |
| 20170227 | 57811.5 | 133.1 | – | 21.55 ± 0.20 | – | – | EFOSC2 |
| 20170325 | 57837.5 | 157.6 | 21.94 ± 0.10 | 21.93 ± 0.10 | 20.90 ± 0.10 | – | EFOSC2 |
| 20170402 | 57845.5 | 165.1 | – | 21.66 ± 0.22 | – | – | EFOSC2 |
| 20170412 | 57855.5 | 174.5 | >20.47 | >20.85 | >20.52 | >20.68 | GROND |
| 20170531 | 57905.4 | 221.5 | – | 22.00 ± 0.10 | – | – | EFOSC2 |
| 20170601 | 57906.4 | 222.5 | – | 22.07 ± 0.22 | – | – | EFOSC2 |
| 20170603 | 57908.4 | 224.3 | – | 22.14 ± 0.15 | 21.55 ± 0.15 | – | EFOSC2 |
| 20170720 | 57955.9 | 269.1 | – | 23.04 ± 0.20 | 22.88 ± 0.06 | – | LDSS3 |
| 20170727 | 57962.4 | 275.2 | 22.93 ± 0.05 | 23.41 ± 0.30 | 23.27 ± 0.31 | 23.30 ± 0.30 | FORS2 |
| 20170821 | 57987.3 | 298.6 | 24.87 ± 0.27 | 23.39 ± 0.06 | 23.76 ± 0.10 | 23.36 ± 0.09 | DECam |
| 20170826 | 57992.3 | 303.4 | 24.80 ± 0.23 | 23.51 ± 0.06 | 23.81 ± 0.11 | 23.33 ± 0.12 | DECam |
| 20170831 | 57997.3 | 308.1 | – | – | 23.76 ± 0.31 | – | DECam |
| 20170901 | 57998.2 | 308.9 | – | – | 23.53 ± 0.24 | 23.11 ± 0.24 | DECam |
| 20170902 | 57999.3 | 309.9 | – | 23.49 ± 0.13 | – | 23.47 ± 0.19 | DECam |
| 20170906 | 58003.3 | 313.7 | – | 23.44 ± 0.17 | 23.95 ± 0.19 | 23.37 ± 0.08 | DECam |
| 20170910 | 58007.4 | 317.6 | – | 23.51 ± 0.09 | 23.63 ± 0.12 | – | DECam |
| 20170912 | 58009.4 | 319.5 | – | – | 23.68 ± 0.12 | 23.35 ± 0.06 | DECam |
| 20170917 | 58014.2 | 324.0 | 24.68 ± 0.20 | 23.50 ± 0.05 | – | – | DECam |
| 20170923 | 58020.3 | 329.7 | 24.88 ± 0.28 | 23.64 ± 0.08 | 24.06 ± 0.10 | 23.33 ± 0.06 | DECam |
| 20171001 | 58028.2 | 337.2 | – | 23.52 ± 0.11 | – | 23.37 ± 0.09 | DECam |
| 20171009 | 58036.3 | 344.8 | – | 23.26 ± 0.11 | 23.93 ± 0.12 | 23.48 ± 0.09 | DECam |
| 20171013 | 58040.3 | 348.6 | – | 23.74 ± 0.07 | – | 23.66 ± 0.10 | DECam |
| 20171018 | 58045.3 | 353.3 | 24.90 ± 0.25 | 23.74 ± 0.07 | 24.04 ± 0.12 | 23.64 ± 0.11 | DECam |
| 20171025 | 58052.1 | 359.7 | 25.00 ± 0.24 | 23.85 ± 0.10 | 24.00 ± 0.15 | 23.54 ± 0.10 | DECam |
| 20171030 | 58057.2 | 364.5 | – | 23.70 ± 0.09 | 24.02 ± 0.12 | 23.55 ± 0.08 | DECam |
| 20171106 | 58064.2 | 371.1 | – | 23.53 ± 0.12 | 24.19 ± 0.16 | 23.67 ± 0.11 | DECam |
| 20171113 | 58071.2 | 377.7 | – | 23.79 ± 0.06 | 23.93 ± 0.10 | 23.62 ± 0.09 | DECam |
| 20171118 | 58076.3 | 382.5 | 25.17 ± 0.32 | 23.93 ± 0.10 | 24.19 ± 0.18 | – | DECam |
| 20171121 | 58079.1 | 385.1 | – | – | – | 23.79 ± 0.12 | DECam |
| 20171124 | 58082.2 | 388.0 | – | 23.92 ± 0.08 | 24.34 ± 0.17 | – | DECam |
| 20171126 | 58084.3 | 390.0 | 25.02 ± 0.36 | – | – | 23.75 ± 0.11 | DECam |
| 20171204 | 58092.2 | 397.4 | – | – | – | 23.90 ± 0.15 | DECam |
| 20171210 | 58098.2 | 403.1 | 24.56 ± 0.24 | 23.93 ± 0.10 | 24.33 ± 0.17 | 23.85 ± 0.14 | DECam |
| 20171213 | 58101.2 | 405.9 | – | 24.09 ± 0.10 | 24.49 ± 0.17 | – | DECam |
| 20171219 | 58107.2 | 411.6 | 24.97 ± 0.24 | 24.05 ± 0.07 | 24.73 ± 0.16 | 23.96 ± 0.13 | DECam |
| 20171229 | 58117.1 | 420.9 | – | 23.97 ± 0.31 | 24.70 ± 0.32 | 24.01 ± 0.22 | DECam |
| 20180105 | 58124.1 | 427.5 | – | 24.34 ± 0.08 | 24.65 ± 0.14 | 24.05 ± 0.11 | DECam |
| 20180112 | 58131.1 | 434.1 | – | 24.47 ± 0.30 | 25.17 ± 0.33 | 24.11 ± 0.12 | DECam |
| 20180118 | 58137.1 | 439.7 | – | 24.55 ± 0.14 | – | 24.37 ± 0.24 | DECam |
| 20180122 | 58141.1 | 443.5 | – | 24.65 ± 0.28 | – | – | DECam |
| 20180203 | 58153.1 | 454.8 | – | 24.48 ± 0.12 | – | – | DECam |
| 20180210 | 58160.0 | 461.3 | – | 24.76 ± 0.20 | – | – | DECam |
Note. The magnitudes have not been corrected for extinction. DECam: Dark Energy Camera at Blanco 4-m telescope; EFOSC2: ESO Faint Object Spectrograph and Camera at the 3.5-m ESO New Technology Telescope (NTT); GROND: Gamma-Ray Burst Optical/Near-Infrared Detector at the 2.2-m MPG telescope; LDSS3: Low Dispersion Survey Spectrograph at the Magellan Clay 6.5-m telescope; FORS2: FOcal Reducer/low dispersion Spectrograph 2 at the ESO Very Large Telescope (VLT).
χ2 for the power-law and exponential fits at late-time (between 280 and 500 d from explosion).
| SN . | χ2 Power law . | χ2 Exponential . |
|---|---|---|
| . | (accretion power) . | (56Co decay) . |
| DES16C3cje | 0.710 | 2.384 |
| SN 1987A | 14.060 | 2.551 |
| SN 2005cs | 5.871 | 0.249 |
| SN 2009E | 2.510 | 0.116 |
| SN . | χ2 Power law . | χ2 Exponential . |
|---|---|---|
| . | (accretion power) . | (56Co decay) . |
| DES16C3cje | 0.710 | 2.384 |
| SN 1987A | 14.060 | 2.551 |
| SN 2005cs | 5.871 | 0.249 |
| SN 2009E | 2.510 | 0.116 |
χ2 for the power-law and exponential fits at late-time (between 280 and 500 d from explosion).
| SN . | χ2 Power law . | χ2 Exponential . |
|---|---|---|
| . | (accretion power) . | (56Co decay) . |
| DES16C3cje | 0.710 | 2.384 |
| SN 1987A | 14.060 | 2.551 |
| SN 2005cs | 5.871 | 0.249 |
| SN 2009E | 2.510 | 0.116 |
| SN . | χ2 Power law . | χ2 Exponential . |
|---|---|---|
| . | (accretion power) . | (56Co decay) . |
| DES16C3cje | 0.710 | 2.384 |
| SN 1987A | 14.060 | 2.551 |
| SN 2005cs | 5.871 | 0.249 |
| SN 2009E | 2.510 | 0.116 |
| Model . | Mass . | Radius . | Energy . | Ni mass . | |$\dot{M_0}$| . | Reference . |
|---|---|---|---|---|---|---|
| . | (M⊙) . | (R⊙) . | (Foe) . | (M⊙) . | (M⊙ s−1) . | (Colour) . |
| RSG | 15 | 830 | 0.11 | 0.095 | ... | Green line |
| RSG | 15 | 830 | 0.11 | 0.095 | 0.5 × 10−8 | Blue line |
| BSG | 40 | 100 | 1.0 | 0.085 | ... | Cyan line |
| BSG | 40 | 100 | 1.0 | 0.080 | 0.4 × 10−8 | Black line |
| Model . | Mass . | Radius . | Energy . | Ni mass . | |$\dot{M_0}$| . | Reference . |
|---|---|---|---|---|---|---|
| . | (M⊙) . | (R⊙) . | (Foe) . | (M⊙) . | (M⊙ s−1) . | (Colour) . |
| RSG | 15 | 830 | 0.11 | 0.095 | ... | Green line |
| RSG | 15 | 830 | 0.11 | 0.095 | 0.5 × 10−8 | Blue line |
| BSG | 40 | 100 | 1.0 | 0.085 | ... | Cyan line |
| BSG | 40 | 100 | 1.0 | 0.080 | 0.4 × 10−8 | Black line |
| Model . | Mass . | Radius . | Energy . | Ni mass . | |$\dot{M_0}$| . | Reference . |
|---|---|---|---|---|---|---|
| . | (M⊙) . | (R⊙) . | (Foe) . | (M⊙) . | (M⊙ s−1) . | (Colour) . |
| RSG | 15 | 830 | 0.11 | 0.095 | ... | Green line |
| RSG | 15 | 830 | 0.11 | 0.095 | 0.5 × 10−8 | Blue line |
| BSG | 40 | 100 | 1.0 | 0.085 | ... | Cyan line |
| BSG | 40 | 100 | 1.0 | 0.080 | 0.4 × 10−8 | Black line |
| Model . | Mass . | Radius . | Energy . | Ni mass . | |$\dot{M_0}$| . | Reference . |
|---|---|---|---|---|---|---|
| . | (M⊙) . | (R⊙) . | (Foe) . | (M⊙) . | (M⊙ s−1) . | (Colour) . |
| RSG | 15 | 830 | 0.11 | 0.095 | ... | Green line |
| RSG | 15 | 830 | 0.11 | 0.095 | 0.5 × 10−8 | Blue line |
| BSG | 40 | 100 | 1.0 | 0.085 | ... | Cyan line |
| BSG | 40 | 100 | 1.0 | 0.080 | 0.4 × 10−8 | Black line |
APPENDIX B: FIGURES
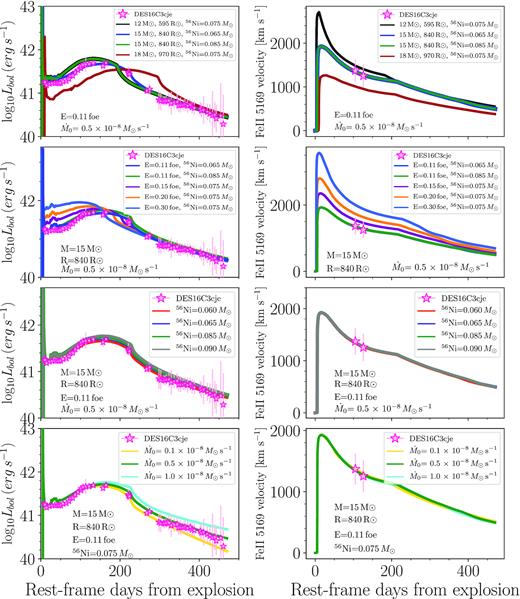
Left-hand panel: Bolometric light curve of DES16C3cje (stars) compared with the results of the light curve calculations from hydrodynamic models. For each plot, the legend shows the differences in the models, while the parameters with similar values are presented next to the curves. Right-hand panel: Evolution of the photospheric velocity for the models presented in the left-hand panel compared with measured Fe II 5169 Åline velocities of DES16C3cje.

Bolometric light curve of DES16C3cje (stars) compared with the results of the light curve calculations from hydrodynamic models. The continuous lines show the effect of t0 in the 15 M⊙ model. The used parameters are presented on the bottom.

Same as Fig. B1 but for more massive and relatively compact progenitors.



