-
PDF
- Split View
-
Views
-
Cite
Cite
Isabel M E Santos-Santos, Julio F Navarro, Andrew Robertson, Alejandro Benítez-Llambay, Kyle A Oman, Mark R Lovell, Carlos S Frenk, Aaron D Ludlow, Azadeh Fattahi, Adam Ritz, Baryonic clues to the puzzling diversity of dwarf galaxy rotation curves, Monthly Notices of the Royal Astronomical Society, Volume 495, Issue 1, June 2020, Pages 58–77, https://doi.org/10.1093/mnras/staa1072
Close - Share Icon Share
ABSTRACT
We use a compilation of disc galaxy rotation curves to assess the role of the luminous component (‘baryons’) in the rotation curve diversity problem. As in earlier work, we find that rotation curve shape correlates with baryonic surface density: high surface density galaxies have rapidly rising rotation curves consistent with cuspy cold dark matter haloes; slowly rising rotation curves (characteristic of galaxies with inner mass deficits or ‘cores’) occur only in low surface density galaxies. The correlation, however, seems too weak to be the main driver of the diversity. In addition, dwarf galaxies exhibit a clear trend, from ‘cuspy’ systems where baryons are unimportant in the inner mass budget to ‘cored’ galaxies where baryons actually dominate. This trend constrains the various scenarios proposed to explain the diversity, such as (i) baryonic inflows and outflows during galaxy formation; (ii) dark matter self-interactions; (iii) variations in the baryonic mass structure coupled to rotation velocities through the ‘mass discrepancy–acceleration relation’ (MDAR); or (iv) non-circular motions in gaseous discs. Together with analytical modelling and cosmological hydrodynamical simulations, our analysis shows that each of these scenarios has promising features, but none seems to fully account for the observed diversity. The MDAR, in particular, is inconsistent with the observed trend between rotation curve shape and baryonic importance; either the trend is caused by systematic errors in the data or the MDAR does not apply. The origin of the dwarf galaxy rotation curve diversity and its relation to the structure of cold dark matter haloes remains an open issue.
1 INTRODUCTION
The non-linear structure of dark matter haloes is a solid prediction of the Λ cold dark matter (ΛCDM) paradigm for structure formation. Numerical ‘dark-matter-only’ (DMO) simulations have consistently shown that the density profiles of ΛCDM haloes are approximately self-similar, so that the full mass profile of a halo depends on a single parameter, such as the virial1 mass of the system (Navarro, Frenk & White 1996b, 1997, hereafter NFW). This prediction may be contrasted with observation using the rotation curves of dark matter-dominated systems, such as dwarf galaxies.
In ΛCDM, dwarf galaxy rotation curve shapes are expected to be nearly identical for systems with similar maximum circular velocity, Vmax, which is a reliable proxy for the halo virial mass. Observed rotation curves, however, deviate from this simple prediction, and show great diversity at fixed Vmax. We illustrate this in Fig. 1, where the rotation curves of four galaxies with Vmax ∼ 80 km s−1 are compared with the circular velocity profile of an NFW halo with parameters as expected for a Planck-normalized ΛCDM cosmology (Ludlow et al. 2016).
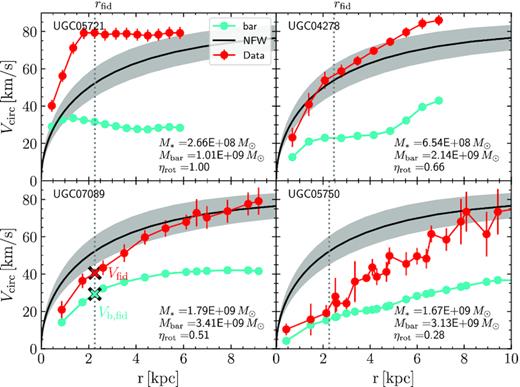
Examples of rotation curves of dwarf galaxies from the SPARC data set with Vmax ∼ 80 km s−1. The four galaxies have been chosen to span a range of rotation curve shapes, from fast-rising (top left) to slow-rising (bottom right) relative to the ΛCDM predictions, shown by the black line and grey shaded area. Observed rotation speeds are shown in red; the baryonic contribution (gas+stars) is shown in cyan. Dotted vertical lines indicate rfid, the inner fiducial radius adopted in our analysis (see equation 1). The red and cyan crosses in the bottom left-hand panel illustrate two of the characteristic velocities used in our study; the rotation velocity at rfid, Vfid ≡ Vrot(rfid) and the baryonic contribution to the circular velocity are rfid, Vb,fid ≡ Vbar(rfid). The total stellar and baryonic masses, as well as the rotation curve shape parameter ηrot = Vfid/Vmax, are given in the legends of each panel.
All of these galaxies are heavily dark matter dominated in the outskirts, where they reach approximately the same Vmax, but the shapes of their rotation curves vary greatly. Although UGC 04278 (the top right-hand panel of Fig. 1) follows roughly the expected NFW circular velocity profile, the other three deviate from this prediction. Rotation curves that rise more sharply than the NFW curve (UGC 05721; top-left) are not unexpected, and may arise, in principle, from the accumulation of baryons (i.e. stars plus gas) in the inner regions and the ensuing contraction of the halo.
On the other hand, the two galaxies in the bottom panels of Fig. 1 are more problematic, as they have inner velocities well below the expected values. This implies a sizable ‘inner deficit’ of matter relative to ΛCDM, a feature that is often associated with a constant-density ‘core’ in the dark matter distribution. These two galaxies are thus clear examples of the well-known ‘cusp-core’ controversy (Flores & Primack 1994; Moore 1994; de Blok et al. 2001; Gentile et al. 2004; de Blok 2010), which, as argued by Oman et al. (2015), is best characterized as an inner mass deficit relative to the ΛCDM predictions. Note that this deficit affects only some galaxies and that others are actually quite consistent with ΛCDM, at least according to this measure.
The origin of the diversity illustrated in Fig. 1 is still unclear, and has elicited a number of proposals that are being actively debated in the literature. These proposals may be grouped into four broad categories. One is that the diversity is caused by the effects of baryonic inflows and outflows during the formation of the galaxy, which lead to gravitational potential fluctuations that may rearrange the inner dark matter profiles (see e.g. Navarro, Eke & Frenk 1996a; Read & Gilmore 2005; Mashchenko, Couchman & Wadsley 2006; Brook et al. 2012; Governato et al. 2012; Pontzen & Governato 2012; Chan et al. 2015). In this scenario, ‘cores’ are created by feedback-driven blowouts that remove baryons from the inner regions, leading to a reduction of the inner dark matter content. These cores can, in principle, be reversed, and dark matter cusps may be recreated by subsequent baryonic (or dark) mass infall (Laporte & Penarrubia 2015; Tollet et al. 2016; Benítez-Llambay et al. 2019). This ‘baryon-induced core and cusp (BICC)’ mechanism offers in principle an appealing potential explanation for the observed diversity.
A second scenario argues that dark matter self-interactions are responsible for ‘heating up’ the inner regions of a CDM halo into a core, thus reducing the central densities and allowing for slowly-rising rotation curves such as those in the bottom panels of Fig. 1 (Spergel & Steinhardt 2000). Galaxies with rapidly rising rotation curves are more difficult to accommodate in this self-interacting dark matter scenario (hereafter SIDM), where they are ascribed to either systems that were originally so dense that the resulting core is negligibly small, or to systems where the central baryonic potential is deep enough to affect the SIDM density profile (e.g. Rocha et al. 2013; Kaplinghat, Tulin & Yu 2016; Kamada et al. 2017; Ren et al. 2019).
A third possibility is that the diversity is generated by variations in the spatial distribution of the baryonic component. Indeed, it has been argued that galaxy rotation speeds at all radii may be inferred directly from the baryonic matter distribution via the ‘mass discrepancy–acceleration relation’ (hereafter, MDAR,2 McGaugh 2004; McGaugh, Lelli & Schombert 2016; Lelli, McGaugh & Schombert 2016). In this scenario, the radial acceleration associated with circular motion, |$g_{\rm obs}(r)=V_{\rm rot}^2(r)/r$|, is linked to the baryonic contribution to such acceleration, |$g_{\rm bar}=V_{\rm bar}^2(r)/r$|, through a simple function, gobs(gbar), with small scatter. Thus, the diversity in the rotation curve shapes would result simply from the diverse contribution of baryons to the acceleration in the inner regions of galaxies with similar Vmax.
Finally, the possibility has been raised that, at least in part, the diversity may be due to uncertainties in the circular velocities inferred from observations. The recent work of Marasco et al. (2018) and Oman et al. (2019) argues that the triaxiality of the dark matter halo may induce non-circular (i.e. elliptical) closed orbits in gaseous discs (see also Hayashi & Navarro 2006). Depending on how the kinematic principal axes of a particular galaxy are aligned relative to the major and minor axes of the orbital ellipses, the inferred velocities may over- or underestimate the true circular velocity, sometimes by large amounts. This could also, in principle, explain the observed diversity.
How can we tell these scenarios apart? The papers cited in the above discussion have already shown that each of these mechanisms can, in principle, modify the ΛCDM mass profiles enough to account for the observed diversity. Therefore, assessing the viability of each of these scenarios must rely on a more detailed elaboration of their predictions as well as on the use of ancillary data and diagnostics. This is what we attempt in this paper, where we use cosmological hydrodynamical simulations of galaxy formation in these scenarios, as well as a more detailed analysis of the role of baryons on different measures of rotation curve diversity to gauge the success of each of the above scenarios.
We begin with a brief description of the observational data sets (Section 2), followed by a description of the cosmological simulations adopted for our analysis (Section 3). We present our main results in Section 4 and summarize our main conclusions in Section 5.
As we were preparing this paper for submission, we became aware of a recent preprint by Kaplinghat, Ren & Yu (2019), who analyse many of the same issues we address here. Some of our conclusions agree with theirs, others do not. We discuss briefly similarities and differences in Section 5.
2 OBSERVATIONAL DATA
Our compilation of rotation curves from the literature includes data sets from the Spitzer Photometry & Accurate Rotation Curves project (SPARC; Lelli et al. 2016); from The HI Nearby Galaxy Survey (THINGS; de Blok et al. 2008); from the Local Irregulars That Trace Luminosity Extremes, The HI Nearby Galaxy Survey (LITTLE THINGS ; Oh et al. 2015); as well as from the work of Adams et al. (2014) and Relatores et al. (2019).
All rotation curves in this compilation were inferred from high-resolution H i and/or H α velocity fields, and include asymmetric drift corrections when needed. In all cases the velocity field data has been combined with photometry to construct mass models that include the stellar, gaseous, and dark matter components. In particular, the SPARC, THINGS, and LITTLE THINGS data make use of Spitzer 3.6 μm surface photometry, while Adams et al. (2014) and Relatores et al. (2019) use r-band images from a variety of sources. If the same galaxy is common to more than one survey, we adopt the SPARC data, because the majority of galaxies in our sample come from that compilation.
We note that in most cases Vlast ≈ Vmax and that the scaling of rfid with Vmax ensures that the ratio ηrot = Vfid/Vmax (where Vfid ≡ Vrot(rfid)) is a simple but reliable indicator of the shape of the rotation curve for dwarf and massive galaxies alike. Rapidly rising rotation curves have high values of ηrot, approaching unity for rotation curves that remain approximately flat from the inner to the outermost regions.
Because sharply rising rotation curves are expected from cuspy dark matter profiles, we shall at times loosely refer to rotation curves with ηrot ∼ 1 as ‘cuspy’. On the other hand, systems with ηrot ≪ 1 have very slowly rising rotation curves, consistent with ‘cores’. We shall occasionally refer to such systems as having ‘cored’ mass profiles or ‘cored’ rotation curves.
Our compilation retains a total of 160 galaxies, spanning a wide range in Vmax (from ∼20 to ∼380 km s−1) and in stellar mass (from |$M_{\rm star}\sim 1.6\times 10^6\, {\rm M}_\odot$| to |${\sim}2.5 \times 10^{11} \, {\rm M}_\odot$|). Our analysis makes use of published mass models, which include the combined gravitational effect of gas and stars – which we shall hereafter refer to as ‘baryons’–, on the rotation curve. In practice, we shall use |$V_{\rm bar}^2(r)=V_{\rm gas}^2(r)+V_{\rm stars}^2(r)$|, where the latter two terms are the contributions to the circular velocity of gas and stars reported in the literature. We have also computed baryonic half-mass radii, rb,half, assuming spherical symmetry (i.e. |$M_{\rm bar}({\lt}r)=r V_{\rm bar}^2(r) /G$|) and that the baryonic component does not extend beyond rlast.
When necessary, we estimate virial masses, M200, for each system assuming an NFW profile of the same maximum circular velocity and a concentration parameter, c, taken from Ludlow et al. (2016)’s median M200(c) relation. We list, for each galaxy in our sample, the specific structural and velocity parameters used in our analysis in Table A1. Although this compilation contains most galaxies with high-quality rotation curves inferred from 2D velocity fields, it is important to note that our sample may be subject to substantial selection biases that are not easy to quantify. We shall hereafter assume that these galaxies are representative of the galaxy population as a whole, but this is an assumption that may require revision once better, more complete data sets become available.
3 NUMERICAL SIMULATIONS
3.1 ΛCDM simulations: EAGLE/APOSTLE
The APOSTLE project is a set of 12 zoom-in simulations of ‘Local Group’ (LG)-like regions selected from a 1003 Mpc3 DMO cosmological box run in a WMAP-7 cosmology. These LG regions are defined by the presence of a pair of haloes that meet mass, relative velocity, and isolation criteria that match observed constraints on the Milky Way–Andromeda pair (Fattahi et al. 2016; Sawala et al. 2016). These LG volumes have been run at three different levels of resolution. We shall use for this analysis the highest resolution set (labelled ‘AP-L1’), with particle masses |$m_{\rm dm}\sim 5\times 10^4\, {\rm M}_\odot$|, |$m_{\rm gas}\sim 10^4\, {\rm M}_\odot$|, and a maximum physical gravitational softening length of 134 pc. Our analysis will use isolated (i.e. not satellites) systems found at z = 0 within ∼2.5 Mpc from the barycentre of the two main galaxies in each volume.
3.2 ΛCDM simulations: NIHAO
The NIHAO (Numerical Investigation of a Hundred Astrophysical Objects) project is a set of ∼100 cosmological zoom-in hydrodynamical simulations of isolated galaxies performed using the ESF-Gasoline2 code (Wadsley, Stadel & Quinn 2004; Wang et al. 2015) and run in a flat ΛCDM cosmology with parameters from Planck Collaboration XVI (2014). These simulations span a wide range of halo virial masses, from ∼5 × 109 to |$2\times 10^{12} \, {\rm M}_\odot$|. All NIHAO have spatial resolution high enough to resolve the mass profile of all systems reliably down to |$1{{\ \rm per\ cent}}$| of the virial radius. Particle masses scale with halo virial mass so that all haloes are resolved with similar numbers of particles. As an example, they are |$m_{\rm dm}\sim 2\times 10^4\, {\rm M}_\odot$| and |$m_{\rm gas}\sim 3.5\times 10^3\, {\rm M}_\odot$| for a 10|$^{10}\, {\rm M}_\odot$| halo.
Subgrid physics include a recipe for star formation that matches the Kennicutt–Schmidt law in regions with a temperature below 15 000 K and density above a threshold, nthr > 10.3 cm−3. The algorithm includes stellar feedback from supernovae (implemented through a blast-wave formalism; Stinson et al. 2006) and from massive stars prior to their explosion as SNe (‘early stellar feedback’; Stinson et al. 2013).
The star formation and feedback algorithms are such that NIHAO dark matter haloes can expand to form cores, with the degree of expansion depending mainly on the stellar-to-halo mass ratio (Tollet et al. 2016; Dutton et al. 2016, 2019b). As a result, NIHAO galaxies show a fairly wide diversity of rotation curves, as discussed by Santos-Santos et al. (2018).
3.3 ΛCDM simulations: EAGLE-CHT10
This simulation series, first presented in Benítez-Llambay et al. (2019), evolves cosmological boxes 12 Mpc on a side, and are run with the same code and cosmology as the EAGLE/APOSTLE project (see Section 3.1). The main difference is that they adopt a higher threshold for star formation, independent of metallicity. In this paper, we consider a run with constant nthr = 10 cm−3, which is roughly 100× higher than that used in APOSTLE. Mass resolution is given by |$m_{\rm dm}\sim 4\times 10^5\, {\rm M}_\odot$| and |$m_{\rm gas}\sim 8\times 10^4\, {\rm M}_\odot$|. As reported in Benítez-Llambay et al. (2019), a higher star formation threshold allows gas to collapse and become gravitationally dominant at the centre of a halo. Baryonic outflows driven by supernova feedback are then able to modify the inner DM density profile, just as in the NIHAO simulations, which adopt a similar value of nthr.
3.4 SIDM simulations: SIDM10
We use two re-simulations of one of the APOSTLE volumes (AP01-L1 in the notation of Fattahi et al. 2016). One re-simulation is DMO, the other includes the same subgrid physical treatment of star formation and feedback as APOSTLE, except that it uses the EAGLE-Recal model parameters rather than the EAGLE-Ref parameters that were used in the APOSTLE runs (Lovell et al. 2020). Mass and spatial resolution are the same as in that series (Section 3.1). The only difference is that the EAGLE code has been modified to include a collisional term for dark matter particle pairwise interactions in order to model the effects of a ssi = σSIDM/m = 10 cm2 g−1 velocity-independent self-interaction cross-section. The code modifications are described in detail in Robertson, Massey & Eke (2017) and Robertson et al. (2018).
4 RESULTS
4.1 Rotation curve diversity: observational results
4.1.1 Rotation curve shape versus mass
The parameter ηrot = Vfid/Vmax is a useful measure of the shape of a rotation curve. It contrasts the measured rotation speeds in the inner regions of the galaxy (Vfid) with the maximum rotation speed (Vmax), which is generally similar to the velocity at the outermost measured point, Vlast. We note that in some cases the rotation curve may still be rising at the last measured point, in which case Vmax may be underestimated. This, however, should have a relatively minor effect on ηrot because a change in Vmax would lead to a change in the inner fiducial radius, rfid (see equation 1). Recall as well that we only retain systems where |$r_{\rm last}\gt 2\, r_{\rm fid}$|, which should minimize any bias introduced by this effect.
The scaling of rfid with Vmax means that our measure of the inner rotation curve adjusts to the total mass of a system. This is preferable to using a fixed physical radius, and allows for a proper comparison of the inner and outer regions of the rotation curve of a galaxy, regardless of mass. For ΛCDM haloes, rfid is in the rising part of the circular velocity curve, and one would expect a roughly constant value of Vfid/Vmax ∼ 0.65. We plot these two parameters for all galaxies in our sample in Fig. 2.
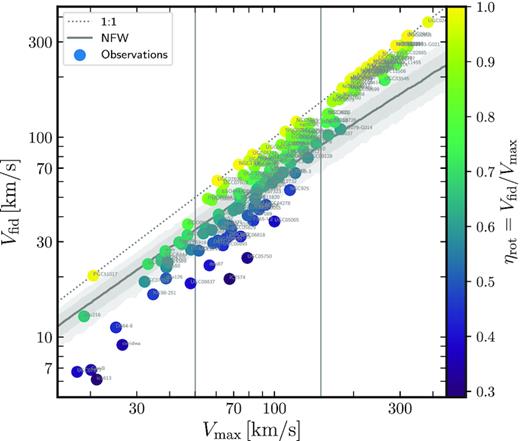
Rotation speed at the inner fiducial radius versus maximum rotation speed for all galaxies in our observational sample. Galaxies with rapidly rising rotation curves lie near the 1:1 dotted line. Rotation curves with (Vfid, Vmax) values consistent with dark matter-only ΛCDM haloes lie along the grey curve and shaded area, computed using the median M200(c) relation (plus 10–90 and 1–99 percentiles) for a Planck-normalized cosmology (Ludlow et al. 2016). Slowly rising rotation curves (i.e. ‘cored’ galaxies with a substantial inner mass deficit relative to ΛCDM) lie below the grey-shaded area. Each galaxy is labelled with its name and coloured according to ηrot, which we adopt as a simple measure of rotation curve shape.
Fig. 2 illustrates a few interesting points. One is that the evidence for ‘cores’, defined by an inner mass deficit relative to ΛCDM at rfid, affects only a fraction of all galaxies and is restricted to dwarf systems. Indeed, no galaxy with Vmax > 150 km s−1 is found below the grey-shaded band that tracks the expected loci of dark matter haloes in ΛCDM. Most massive galaxies closely hug the 1:1 line, suggesting rotation curves that rise actually more rapidly than expected for ΛCDM haloes and stay flat out to their last measured radius. As we shall discuss below (Section 4.1.3), this is due to the effect of baryons, which accumulate at the centre and drive the circular velocity at rfid to higher values than expected from the dark matter alone.
Galaxies with Vmax < 150 km s−1, on the other hand, show a wide diversity of rotation curve shapes, from rapidly rising, nearly flat rotation curve galaxies near the dotted 1:1 line, to very slowly rising curves well below the grey band. The latter are systems where the evidence for an inner mass deficit, or a ‘core’, is most compelling.
As discussed in Section 1, four different scenarios have been proposed to explain the rotation curve diversity illustrated in Fig. 2, identifying which one is most consistent with existing data is the main goal of this paper. Since baryons play an important role in several of the proposed scenarios, it is important to check how the diversity correlates with the gravitational contribution of baryons. We discuss this next.
4.1.2 Rotation curve shape and baryon surface density
The role of baryons in determining the shape of the rotation curve has long been predicated on the basis that the shape of the inner rotation curve seems to correlate with galaxy surface brightness (e.g. de Blok, McGaugh & van der Hulst 1996; Swaters et al. 2009, 2012; Lelli, Fraternali & Verheijen 2013). We shall use here baryonic surface density rather than (stellar) surface brightness, since baryons are mainly in gaseous form in many galaxies of our sample. We explore this in Fig. 3, where we plot the rotation curve shape parameter, ηrot, as a function of the ‘effective’ baryonic surface mass density, |$\Sigma _{\rm bar}=M_{\rm bar}/2\pi r_{\rm b,half}^2$|. (Mbar and rb,half are the total baryonic mass and half-mass radius of a galaxy, respectively.)

Rotation curve shape parameter, ηrot, versus effective baryonic surface density, Σbar. The correlation between the two reflects the ηrot dependence on galaxy mass (or Vmax), which in turn correlates strongly with surface density. Massive galaxies (high Σbar) do not show evidence for cores, which only occur in dwarfs, which have low Σbar. In the dwarf galaxy regime, the ηrot–Σbar is actually quite weak and unlikely to be the cause of the diversity. See the text for further discussion.
There is indeed a correlation between ηrot and Σbar, but it is largely a reflection of the galaxy mass-surface density relation: massive galaxies (none of which have cores, as discussed in the previous subsection) have higher surface density than dwarfs (some of which have cores and others which do not). Aside from this overall trend, when considering only dwarfs (i.e. Vmax < 150 km s−1) Fig. 3 shows that the correlation between ηrot and Σbar is rather weak. Although all ‘cored’ galaxies (i.e. |$\eta _{\rm rot} \lesssim 0.55$|) are low surface density systems, the converse is not true: there are indeed a number of low surface density galaxies with ‘cuspy’ rotation curves. Baryonic surface density alone is thus not a reliable indicator of the presence of a core or cusp in a dwarf galaxy and, therefore, unlikely to be the origin of the diversity. This is an issue to which we will return repeatedly throughout our discussion below.
4.1.3 Rotation curve shape and baryon central dominance
Although, overall, dwarf galaxy rotation curve shapes correlate only weakly with the effective baryon surface density, it is possible that baryons shape rotation curves through their role in setting the inner gravitational potential. We explore this in Fig. 4, where we plot ηrot versus ηbar, where the latter is defined as ηbar ≡ (Vbar(rfid)/Vfid)2. [We hereafter define Vb,fid ≡ Vbar(rfid) for ease of notation.] The (squared) ratio between the baryonic contribution and the measured rotation velocity at rfid is roughly equivalent to the ratio between the enclosed baryonic and total mass within the inner fiducial radius, rfid.

Rotation curve shape parameter, ηrot, as a function of the gravitational importance of the baryonic component at the inner fiducial radius, ηbar. The latter is approximately the ratio between baryonic and total enclosed masses within rfid. Galaxies are coloured by maximum circular velocity, as indicated by the colourbar. DMO ΛCDM haloes have, on average, ηrot ∼ 0.65, with 10:90 percentile scatter as indicated by the grey band. The rotation curves of the four galaxies highlighted with black circles are shown in Fig. 5. Systems with ηbar < 0.09 are shown at that value for clarity.
Fig. 4 illustrates a few interesting points. The first is that in massive discs (i.e. Vmax > 150 km s−1) rotation curves are approximately flat (i.e. ηrot ∼ 1) and baryons, as expected, play an important role (i.e. |$\eta _{\rm bar} \gtrsim 0.4$|–0.5). An example of this kind of galaxy (UGC 03205) is shown in the top right-hand panel of Fig. 5. The rotation curve in this case rises actually more rapidly than expected for an ΛCDM halo of the same Vmax (black curve in the same panel) because of the gravitational importance of the baryons at rfid.

Rotation curves of four galaxies in different regions of Fig. 4, where they are marked with black circles. Symbols, colours, and lines are as in Fig. 1. The inner fiducial radius, rfid, is indicated by the vertical dashed line in each panel. Top panels show galaxies with rapidly rising rotation curves, where baryons play an important (right) or negligible (left) role at rfid. Bottom panels are ‘cored’ galaxies with slowly rising rotation curves, where, as in top, baryons are gravitationally important (right) or negligible (left) at rfid.
For less massive systems, the interpretation is less clear: most dwarf galaxies (defined as having Vmax < 150 km s−1) scatter from the top-left to bottom-right corners in Fig. 4, a surprising trend for scenarios that envision the importance of baryons as the main driver of the rotation curve diversity.
Indeed, take, for example, systems at the top-left corner of Fig. 4: these are galaxies with rapidly rising (‘cuspy’) rotation curves but where baryons play a negligible role at the inner fiducial radius rfid. An example (NGC 1705) is shown in the top left-hand panel of Fig. 5. As we shall see below, systems like this are difficult to reproduce in scenarios like BICC and SIDM, where all or most haloes have cores and cuspy rotation curves are assumed to occur only in systems where baryons dominate the central potential.
A similar comment applies to galaxies at the bottom-right corner of Fig. 4: these galaxies have the largest ‘cores’, which, in the BICC scenario, would correspond to systems that have suffered the effects of explosive baryonic outflows, and where few baryons should have remained in the galaxy. An example (IC 2574) is shown in the bottom right-hand panel of Fig. 5. In this galaxy, as well as in most systems with the largest cores, baryons are actually as dominant at rfid as in massive, high surface brightness discs (i.e. ηbar > 0.5).
This discussion illustrates how Fig. 4 provides a useful tool to judge the viability of the various scenarios that aim to explain the rotation curve diversity. In other words, it is not enough to identify a mechanism that may modify the inner regions of a halo to create diversity in the rotation curves of dwarf galaxies; the same mechanism must also allow galaxies to exhibit the observed diversity in the importance of baryons in the inner regions and must reproduce the trends in the ηrot–ηbar plane shown in Fig. 4. This is the key argument of the analysis that follows, where we shall examine, in turn, the successes and shortcomings of each of the four scenarios identified in Section 1.
4.2 Diversity and BICC (baryon-induced cores/cusps)
We shall use several ΛCDM cosmological hydrodynamical simulations to compare with observed rotation curves. The first corresponds to simulations from the APOSTLE project (Sawala et al. 2016), which used the code developed for the EAGLE project (Crain et al. 2015; Schaye et al. 2015) to simulate volumes selected to resemble the LG.
Rotation curves from these simulations have been analysed in a number of papers (e.g. Oman et al. 2015; Sales et al. 2017; Bose et al. 2019), who report that the inner cuspy structure of the haloes is largely unaltered by the assembly of the galaxy, except for some halo contraction caused by the accumulation of baryons at the centre (see also Schaller et al. 2015). No dark matter ‘cores’ are formed in APOSTLE, in the sense that there is no obvious reduction in the inner dark matter content compared to what would be expected from a DMO simulation. We shall use galaxies selected from the ‘high-resolution’ APOSTLE volumes, referred to as AP-L1 for short (Fattahi et al. 2016).
The lack of cores in the EAGLE/APOSTLE simulations has been traced to the relatively low (minimum) gas density threshold for star formation adopted in that code (equation 2). This prevents the gas that condenses at the centres of dark matter haloes from dominating gravitationally, minimizing the effects that baryonic inflows and outflows may have on the dark matter (Pontzen & Governato 2012). Cores do form in simulations run with the same EAGLE code but with a raised threshold (Benítez-Llambay et al. 2019). For that reason, we shall also use here results from a simulation with nthr = 10 cm−3, labelled EAGLE-CHT10.
Dark matter cores have also been reported in simulations from the NIHAO project (Wang et al. 2015), a series of zoom-in resimulations of galaxies spanning a wide range in mass. Like EAGLE-CHT10, these simulations adopt a high star formation threshold, but a rather different implementation of the star formation and feedback algorithms. Details for this and other simulations may be found in Section 3 and references listed there.
How well do each of these simulation series reproduce the observed diversity and, importantly, the relation between rotation curve shape and baryonic importance? We contrast the Vfid–Vmax results with observational data in Fig. 6. Simulated galaxies are only included if the Power et al. (2003) convergence radius is smaller than rfid. Except when otherwise explicitly noted, we shall estimate circular velocities in simulated galaxies assuming spherical symmetry; i.e. |$V_{\rm circ}^2(R)=GM(\lt r)/r$|.
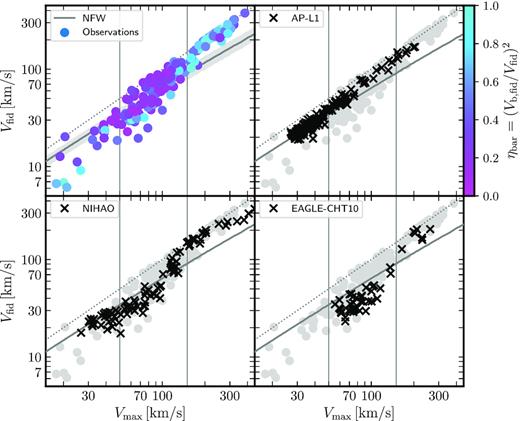
Rotation velocity at the inner fiducial radius versus maximum circular velocity, for observations and ΛCDM simulations. Symbols and lines in each panel are as Fig. 2. Top left-hand panel presents the observational sample, coloured by ηbar, which measures the gravitational importance of baryons at rfid. Other panels not only indicate the results of simulations (crosses) but also include the observations, for reference, as grey circles. Legends in each panel identify the simulation series. Simulated galaxies are only included if the Power et al. (2003) convergence radius is smaller than rfid. See discussion in text.
The top left-hand panel reproduces the observational data presented in Fig. 2, coloured this time by the baryon importance parameter, ηbar. The same observational data is reproduced in the other panels, for reference, with grey circles. Legends in each panel label the simulation series it corresponds to.
Fig. 7 is similar in concept to Fig. 6, but for the ηrot–ηbar relation. Observed galaxies are shown in the top left-hand panel of Fig. 7 and are coloured by Vmax. We shall use these two figures to discuss next the results of each simulation series.
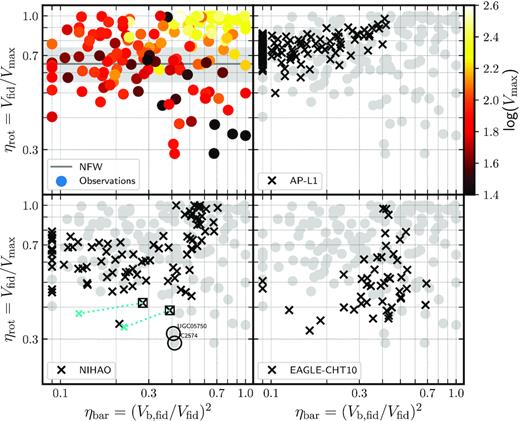
Rotation curve shape parameter, ηrot, versus baryonic importance parameter, ηbar, for observations and ΛCDM simulations. Symbols and lines in each panel are as in Fig. 4. Top left-hand panel presents the observational sample, coloured by the maximum circular velocity, Vmax. Other panels not only indicate the results of simulations (crosses) but also include observations, for reference, as grey circles. Legends in each panel identify the simulation series. Systems with ηbar < 0.09 are shown at that value for clarity. See the text in Section 4.2.2 for a discussion of the systems highlighted in the bottom left-hand panel.
4.2.1 APOSTLE
As expected from the discussion above, APOSTLE galaxies (the top right-hand panel in Fig. 6) show little diversity in their rotation curve shapes, which track closely the loci of DMO ΛCDM haloes (grey line/shaded band in the top left-hand panel). The upturn relative to the ΛCDM/NFW line in massive galaxies results from the contribution of baryons in the inner regions. Note that because of the relatively small simulated volume there are few massive galaxies in APOSTLE. The APOSTLE sample contains no slowly-rising, large core dwarf galaxies (i.e. systems well below the grey line), in disagreement with the observational data set considered here.
In terms of rotation curve shape versus baryon importance, we see from the top right-hand panel of Fig. 7 that few APOSTLE galaxies are heavily dominated by baryons in the inner regions. APOSTLE is able to reproduce fairly well rapidly rising rotation curves in galaxies where baryons are unimportant (i.e. top left-hand corner of the ηrot–ηbar panel); these correspond to NFW-like haloes where the initial cusp has been, if anything, slightly strengthened by the accumulation of baryons at the centre.
Slowly rising rotation curves (i.e. |$\eta _{\rm rot} \lesssim 0.55$|), as well as heavily baryon-dominated galaxies (|$\eta _{\rm bar} \gtrsim 0.4$|) are not present in these simulations. This comparison briefly summarizes the known shortcomings of EAGLE/APOSTLE simulations to reproduce the observed diversity of dwarf galaxy rotation curves (e.g. Oman et al. 2015).
4.2.2 NIHAO
The comparison with NIHAO is shown in the bottom left-hand panels of Figs 6 and 7. Starting with Fig. 6, NIHAO galaxies exhibit more slowly rising rotation curves than APOSTLE in the Vmax range of 40–100 km s−1. This is the result of the cores created by baryonic outflows in these runs. More massive galaxies have rapidly rising rotation curves, and thus no obvious cores, presumably because baryonic outflows are less efficient in the deep potential wells of these systems. Cores do not form in very low-mass galaxies either (i.e. Vmax < 40 km s−1), in this case because too few stars form in these systems to power the needed outflows (e.g. Di Cintio et al. 2014a,b).
The cores in NIHAO help to reconcile ΛCDM with some of the slowly-rising rotation curve systems that APOSTLE fails to reproduce. Note, however, that because core formation is quite efficient in the 40 < Vmax/km s−1 <100 range, NIHAO seems unable to reproduce rapidly rising rotation curves in that range (see also Santos-Santos et al. 2018). Indeed, judging from the lower left-hand panel of Fig. 6, NIHAO’s result do not seem to capture the full diversity of dwarf galaxy rotation curves. In addition, there is some evidence for cores in observed galaxies at the lowest mass end (i.e. Vmax < 40 km s−1) again at odds with NIHAO’s results.
These shortcomings are also apparent in the bottom left-hand panel of Fig. 7, where we see that NIHAO does not reproduce the observed systems with ‘cuspy’ rotation curves and negligible baryon contribution (top left-hand corner), nor baryon-dominated galaxies with large cores (bottom right).
Regarding the latter (two examples of which, UGC05750 and IC2574, are highlighted with circles in the bottom-left panel of Fig. 7), Santos-Santos et al. (2018) have suggested that the disagreement may have been caused by the assumption of spherical symmetry when estimating circular velocities in simulations (see also Dutton, Obreja & Macciò 2019a).
Indeed, these authors show in their fig. 6 that the inner circular velocities of two NIHAO galaxies (highlighted with squares in the bottom left-hand panel of Fig. 7) could be substantially reduced by taking into account the actual flattened geometry of the baryons when computing the gravitational potential on the disc plane. This reduction could, in principle, lead to lower values of ηrot, as shown by the cyan dashed lines in the bottom left-hand panel of Fig. 7.
However, because the NIHAO galaxies are actually dark matter dominated at rfid, the reduction in ηrot is accompanied by an even more substantial reduction in ηbar, shifting the galaxies to the bottom-left corner of the panel, rather than closer to the observed galaxies. In other words, NIHAO galaxies may come close to matching the shape of the rotation curves of UGC05750 and IC2574, but are unable to reproduce, simultaneously, the importance of baryons in their inner regions. This discussion highlights the power of using both ηrot and ηbar as diagnostics of the viability of a particular scenario meant to explain the rotation curve diversity.
4.2.3 EAGLE-CHT10
Finally, we consider an alternative ΛCDM simulation run with the EAGLE code, but where a higher star formation threshold allows baryonic outflows to transform cusps into cores. The star formation and feedback algorithm is quite different from NIHAO’s so, in principle, we do not expect the same results. However, as may be seen in the bottom right-hand panel of Fig. 6, the results for EAGLE-CHT10 are not too dissimilar to NIHAO’s. There is, again, a shortage of ‘cuspy’ systems in the 70 < Vmax/km s−1<150 range. We are unable to check for the presence of cores in Vmax < 40 km s−1 galaxies because of limited numerical resolution.
In terms of ηrot versus ηbar (Fig. 7), we see that, as in the case of NIHAO, EAGLE-CHT10 has difficulty reproducing ‘cuspy’ galaxies where the baryon contribution is negligible. EAGLE-CHT10 fares a bit better in terms of the largest cores, especially those with high values of ηbar, but the difference with NIHAO in this respect is small.
4.2.4 Summary
It is clear that baryonic outflows can produce cores in dwarf galaxies, reconciling in the process ΛCDM with systems with slowly rising rotation curves. However, this mechanism, at least as implemented in the NIHAO and EAGLE-CHT10 simulations we analysed here, is unable to account simultaneously for galaxies with ‘cuspy’ rotation curves where the inner contribution of baryons is negligible.
The observed diversity seems to demand a mechanism that forms cores in some galaxies only, while others retain (or re-form) a cusp, independently of the baryonic mass contribution. This feature seems to elude current simulations of this mechanism. It is unclear whether this signals a fundamental shortcoming of the models, or just a need to ‘fine tune’ the numerical implementations. What is clear, however, is that any successful explanation of the rotation curve diversity should provide a natural explanation for the apparent presence of cusps and cores in dwarfs and for their peculiar relation to the importance of baryons in the inner regions.
4.3 Diversity and SIDM
Self-interacting dark matter is a distinct scenario for explaining the rotation curve diversity, where cores in the inner dark matter density profiles form not through baryonic outflows, but, rather, because of the inward ‘heat transfer’ driven by collisions (‘self-interactions’) between dark matter particles.3 The simplest example of SIDM corresponds to elastic, velocity-independent interactions where the magnitude of the effect is controlled by a single parameter; the self-interacting cross-section, ssi (see; e.g. Rocha et al. 2013). This is, in principle, a free parameter, but values between 0.1 and 1 cm2 g−1 lead to tangible changes in the inner density profiles of dark matter haloes (see e.g. the recent review by Tulin & Yu 2018).
An exploration of all SIDM alternatives is beyond the scope of this paper, which adopts a single value of ssi = 10 cm2 g−1. This is a rather extreme value that, however, allows us to explore the maximal effect of this mechanism without promoting a ‘core collapse’ of the inner regions (e.g. Elbert et al. 2015). This model, which we shall refer to hereafter as SIDM10, should be regarded as a limiting case where cores are as large as this mechanism may be plausibly expected to yield.
We emphasize that more realistic SIDM models would include a velocity-dependent cross-section, which is needed to reduce the effective cross-section in galaxy clusters, where a cross-section as large as assumed here is clearly ruled out (see; e.g. Tulin & Yu 2018, and references therein). Velocity dependence is indeed generic with light force mediators, as would be expected for large cross-sections. We shall ignore these complications in our analysis, which is not meant to rule in or out SIDM as a class, but rather to identify further observational diagnostics useful for assessing the relative performance of different scenarios.
4.3.1 SIDM10: DMO
We begin by exploring the effect of SIDM on the inner mass distribution of dark matter haloes in the DMO case. As discussed above, interactions reduce the inner dark matter density and promote the formation of a constant density core. This has little effect on the maximum circular velocity of a halo, but can reduce substantially the circular velocity at the inner fiducial radius.
We may see the resulting effect on the top right-hand panel of Fig. 8, where we plot the results of the DMO ΛCDM AP-L1 runs (in red), together with results from the DMO SIDM10 run (blue). Clearly, the values of Vfid at fixed Vmax are substantially lower in the case of SIDM10 than for ΛCDM.
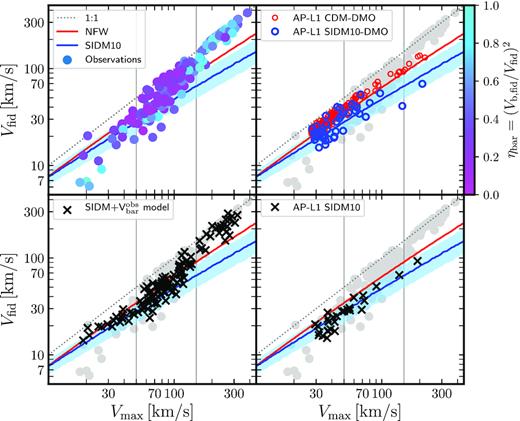
As Fig. 6, but for observations and SIDM. Top left-hand panel presents the observational sample, coloured by the inner baryon importance parameter, ηbar. Other panels indicate the results of simulations, but also include observations, for reference, as grey circles. Legends in each panel identify the simulation series. See the discussion in the text.
We can use the results of the AP-L1 and SIDM10 DMO runs to model the DMO SIDM10 Vfid–Vmax relation, as well as its scatter, starting from the ΛCDM M200–concentration relation (and its scatter; Ludlow et al. 2016). Details of the procedure are given in the Appendix (Sections A2 and A1), but we describe it briefly for completeness.
The inner mass profile of an SIDM halo is well approximated by a non-singular isothermal sphere, which is fully described by a pair of parameters (see e.g. page 228 of Binney & Tremaine 1987). These may be taken to be the central density, ρ0, and a scale radius, r0, or, alternatively, a velocity dispersion, σ0. For SIDM10, these parameters correlate closely with the corresponding ΛCDM parameters: for example, there is a close relation between the Vmax of an ΛCDM halo and the characteristic σ0 of the counterpart SIDM halo that forms when the same initial conditions are evolved with self-interactions turned on.
Likewise, there is a strong correlation between r0 and the characteristic radial scale of an ΛCDM halo, best expressed through r1, the radius where, on average, one interaction per particle is expected per Hubble time. These correlations are sensitive to the value of ssi adopted; we show them for ssi = 10 cm2 g−1 in Fig. A2 for matching halo pairs identified in ΛCDM and SIDM DMO simulations of one of the AP-L1 volumes.
These same correlations may be used to generate a population of SIDM10 haloes that include both the original scatter in the ΛCDM mass–concentration relation but also the scatter in the relations that link ΛCDM and SIDM10. The results of this procedure, in terms of Vfid and Vmax, are shown by the blue thick line (and shaded area, which delineate the 10:90 percentiles) in the top right-hand panel of Fig. 8. To make further progress, we need to model the effect of baryons into this population of SIDM10 haloes, either through modelling or direct simulation. We pursue this below.
4.3.2 SIDM10+baryons: a model
As baryons accumulate at the centre of an SIDM halo, they are expected to deepen the central gravitational potential. This should cause the surrounding dark matter to respond by contracting and, for large enough perturbations, by rebuilding the inner cusp. This process has been explored using analytical techniques and simulations of isolated systems in prior work (Kaplinghat et al. 2014; Kamada et al. 2017; Ren et al. 2019; Creasey et al. 2017), which argue that the effect should be strong enough in practice to produce cuspy and cored rotation curves, and may account for the observed rotation curve diversity.
In this scenario, slowly rising rotation curves reflect systems where self-interactions have carved a core, and where the baryons are not important enough to rebuild the cusp. At the other extreme, rapidly rising rotation curves should generally correspond to systems where baryons deepened the central potential and are gravitationally important enough to rebuild the central dark matter cusp. These two features are, at first glance, at odds with the trends for dwarf galaxies highlighted in Fig. 4, where it is clear that there are many ‘cuspy’ systems where baryons are unimportant and, in addition, that baryons actually do play an important role at the centre of systems with the largest cores. Can SIDM models resolve this apparent disagreement?
We explore this by using an analytical model, described in detail in the Appendix (Section A3), to estimate the response of SIDM haloes to the accumulation of baryons at the centre, and to compare the resulting rotation curves with observations. In particular, we use the actual baryonic mass profile of individual galaxies and place them in randomly selected SIDM haloes of the appropriate Vmax to verify whether the resulting rotation curves reproduce the observed diversity.
Our modelling proceeds as follows. For each observed galaxy in our sample, we choose a random SIDM10 halo of matching Vmax (Section 4.3.1) and compute the change in the inner dark matter distribution expected from the addition of the baryons. The procedure uses the full baryonic distribution of each galaxy [given by Vbar(r)] to compute the response of the dark matter (see the details in Section A3), and results in a new rotation curve for the galaxy. The procedure preserves Vmax and Vbar(r) of each galaxy, but modifies its rotation speed at the inner fiducial radius, Vfid.
The results of this modelling are presented in the bottom left-hand panel of Fig. 8. At first glance, this results in a wider range of rotation curve shapes compared with the ΛCDM simulations shown in Fig. 6. This is, however, partly a result of the wider diversity of baryonic profiles probed here, which matches, by construction, exactly those of the observed sample.
In particular, the SIDM10 model successfully reproduces the steeply rising rotation curves of massive galaxies (i.e. Vmax > 150 km s−1), despite the fairly large cores imposed by SIDM. In lower mass systems, the diversity is reproduced less well, with fewer systems near the 1:1 line and, despite the extreme value of ssi adopted, few cores as large as observed. This is especially true at the very low-mass end, where SIDM cores seem too small to affect the rotation curve at rfid.
This conclusion is supported by the distribution of galaxies in the ηrot–ηbar plane (the left-hand panel of Fig. 9), where it is clear that there are few galaxies in the upper-left and bottom-right corners of this plot. Like the BICC models discussed in Section 4.2, SIDM10 has difficulty in accounting for both the observed population of sharply rising rotation curves without a dominant inner baryonic contribution (top-left corner), and for the very slowly rising rotation curves where baryons play an important role near the centre (bottom-right corner). On its own, the SIDM hypothesis seems thus unable to explain fully the observed diversity of rotation curve shapes.

Rotation curve shape parameter, ηrot, versus baryonic importance parameter, ηbar, for observations and SIDM simulations. Left-hand panel shows observations (grey circles) and the results of the analytical model discussed in Section 4.3.2 (crosses). Right-hand panel corresponds to the SIDM10+baryon simulation discussed in Section 4.3.3. Systems with ηbar < 0.05 are shown at that value for clarity. See the discussion in the text.
Note that our analysis addresses whether observed galaxies, if placed in SIDM haloes of randomly sampled concentration (and not particular haloes chosen to fit the observed rotation curves), would exhibit the observed diversity. This differs from earlier work on this topic, which addressed whether it is possible to obtain adequate fits to individual rotation curves in SIDM haloes by allowing the size of the core (which is intimately linked to the assumed concentration) to vary as a free parameter (see e.g. Ren et al. 2019 and references therein). Such work reproduces the diversity by construction, by carefully choosing concentration values for the haloes of individual galaxies so as to fit their rotation curves. The distribution of required concentrations, however, is quite different from what would be expected from randomly sampling the halo mass–concentration relation (see Creasey et al. 2017 for a similar argument).
We illustrate this in Fig. 10, where we contrast the probability distribution of concentrations adopted by Ren et al. (2019) (i.e. their ‘MCMC best-fitting’ model; see their table S2) with the concentration distribution used in our work (pink histogram). Clearly, the two distributions are substantially and significantly different.
![Distribution of halo concentrations about the mean expected in ΛCDM for haloes of given Vmax[(red solid curve; from Ludlow et al. (2016)’s M200(c) relation plus scatter]. The concentrations adopted in the SIDM model used in this work is shown by the pink histogram; those used in the SIDM model of Ren et al. (2019) are shown by the purple histogram. See the text for further details.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/495/1/10.1093_mnras_staa1072/1/m_staa1072fig10.jpeg?Expires=1750339519&Signature=3s8XWSgUJIsQQvjWTg6sojIMxEp6OJCLuaC-E3iEcZ5JSGOG~nzfK7yS6CFMWPsVJR-1ZUmmx7M9edW56sSjoDVw2qmGNdNG43fjG0zYGgVA4OJOE7w2i~-TvJRegocH3qGp8wHzNLX7YbZTy41t477tNwiVrp0zFQUPGJLef3fFpUQdKoer2ldH0iU9AeaZvFbx7LgKUR7ub9-qFiJV4C00kxjUp-wM-r9WlK91aIgOLR5sLPgF6oD9hvmwoUsTH8nKxQeIalp97BI3uGDDBVVnIYBEqPVIN97PSVSnk9WXJ3Cb8qDZQJwKmF~4XptMAty1Yll2ck0bymHiVpFGvg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of halo concentrations about the mean expected in ΛCDM for haloes of given Vmax[(red solid curve; from Ludlow et al. (2016)’s M200(c) relation plus scatter]. The concentrations adopted in the SIDM model used in this work is shown by the pink histogram; those used in the SIDM model of Ren et al. (2019) are shown by the purple histogram. See the text for further details.
In other words, fitting the observed rotation curve diversity with SIDM requires carefully chosen concentrations which, taken as an ensemble, are quite unlike what is expected from cosmological simulations (Gaussian curve in Fig. 10). While it remains possible to match rotation curves with SIDM, the improbable distribution of required concentrations detracts, in our opinion, from the appeal of the SIDM scenario as an explanation of the diversity of dwarf galaxy rotation curves.
4.3.3 SIDM10+baryons: a simulation
The results of a cosmological hydrodynamical simulation that includes a self-interaction cross-section of ssi = 10 cm2 g−1 and the EAGLE/APOSTLE star formation/feedback implementation are presented in the bottom right-hand panel of Fig. 8. (Details of the simulation are given in Section 3.) Recall that, because of the low star formation density threshold adopted in this model, we do not expect baryonic outflows to effect large changes in the inner dark matter density profile. Indeed, the simulation results show that, in terms of Vfid–Vmax, the simulated galaxies follow approximately the dark matter-only results (indicated by the blue shaded area). As for the analytic model discussed in the previous subsection, low-mass simulated galaxies fail to populate the rapidly rising (1:1) rotation curve regime and to account for the largest observed cores.
These conclusions are again supported by inspection of the ηrot–ηbar plane, shown in the right-hand panel of Fig. 9. There is again a clear dearth of ‘cuspy’ systems where the baryons are gravitationally unimportant (upper-left corner) and of ‘cored’ systems where baryons dominate the inner regions (bottom-right corner). Indeed, baryons do not seem to play an important role in any simulated SIDM10 galaxy, although this is likely a result of the particular star formation algorithm adopted in the EAGLE/APOSTLE code. These conclusions echo those of the previous subsection and highlight the difficulty faced by models like SIDM, where most haloes develop cores, to account naturally for the observed rotation curve diversity.
4.4 Diversity and non-circular motions
We consider next the effects that non-circular motions may have on the interpretation of the rotation curve diversity. As discussed by Oman et al. (2019) and Marasco et al. (2018), the triaxial potential of ΛCDM haloes may induce non-circular motions in the gaseous discs of dwarf galaxies. In the simplest case, closed orbits in the disc plane become elliptical and the azimuthal speed of the gas varies along the orbit, from maxima along the orbital minor axis (pericentres) of the ellipse to minima along the orbital major axis (apocentres). This may lead to different rotation curves for the same galaxy, depending on how the line of nodes of a particular sky projection aligns with the orbital principal axis (see also Hayashi & Navarro 2006). In particular, large underestimates of the inner circular velocity may result when the projected kinematic major axis is aligned with the orbital apocentres, mimicking the effect of a core.
Non-circular motions may affect the inferred values of both Vfid and Vmax, introducing scatter in the tight relation between these two parameters expected in ΛCDM simulations where cores do not form, such as APOSTLE. We show the effect by selecting two dwarf galaxies from the AP-L1 sample and projecting them along 24 different lines of sight at fixed inclination, i = 60°. Synthetic HI data cubes are constructed for each projection, which are then modelled using 3DBAROLO, a publicly available tilted-ring processing tool (Di Teodoro & Fraternali 2015; Iorio et al. 2017). Details of the modelling as applied to the APOSTLE galaxies may be found in Oman et al. (2019).
Each of the two galaxies is shown with different colours in Fig. 11, illustrating the dramatic impact that non-circular motions may have on the Vfid–Vmax and ηrot–ηbar correlations. At least for these two galaxies the effects of non-circular motions are quite substantial. For galaxy AP-L1-V6-5-0 (shown in blue; notation as in Oman et al. 2019), the maximum circular velocity may vary from 70 km s−1 to slightly over 100 km s−1 and the inferred rotation speed at the inner fiducial radius from ∼30 to 100 km s−1, depending on projection. Non-circular motions of this magnitude can clearly explain much of the observed diversity in the Vfid–Vmax plane.
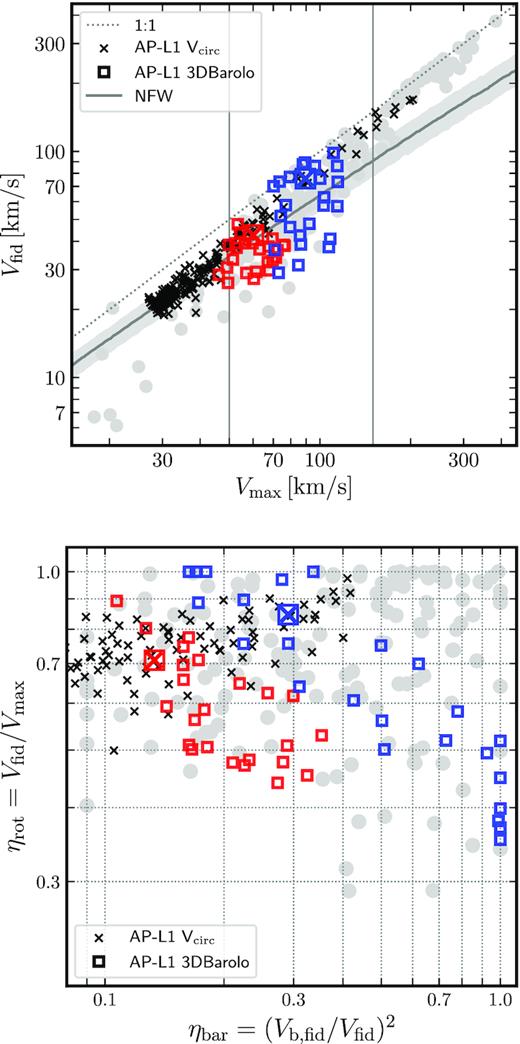
Top: Same as the top-right panel of Fig. 6, but including the results of mock HI observations of two simulated galaxies from APOSTLE, analysed with 3DBAROLO (Di Teodoro & Fraternali 2015; Oman et al. 2019). AP-L1-V6-5-0 is shown in blue, AP-L1-V4-14-0 in red. The results of 24 different lines of sight at fixed inclination (i = 60°) are shown, with different colours for each of the two galaxies. Bottom: Same as the top right-hand panel of Fig. 7, for the same two galaxies as in top panel. The large boxes with a cross indicate the values obtained from the circular velocity curve rather than from 3DBAROLO.
In particular, the same galaxy could end up being classified either as a rapidly rising rotation curve where baryons are relatively unimportant (top-left corner in the bottom panel of Fig. 11), or as a galaxy with a large core where baryons dominate the inner regions (bottom-right corner of the same panel). This is because non-circular motions tend to scatter galaxies along the same band in the ηrot–ηbar plane traced by dwarf galaxies (see galaxies with Vmax < 150 km s−1 in Fig. 4). Non-circular motions thus provide an appealing explanation for this puzzling trend, which, as we have discussed, is not reproduced well in other scenarios.
Although attractive, the non-circular motion explanation of the diversity also suffers from shortcomings. In particular, it may be argued that the magnitude of non-circular motions required to spread galaxies across the whole ηrot–ηbar plane is quite substantial, whereas many observed galaxies show quieter velocity fields, without clear obvious distortions (Trachternach et al. 2008). However, Oman et al. (2019) report that at least two galaxies with obvious ‘cores’ (DDO 47 and DDO 87) show clear signs of non-circular motions and emphasize that these may be difficult to detect because of the large number of free parameters involved in tilted-ring model fits.
A second difficulty refers to our earlier discussion of Fig. 3, which shows that ‘cores’ are only manifest in low surface brightness/density galaxies. If diversity were due mostly to non-circular motions, why would they only affect low surface brightness galaxies? There is no clear answer to this, but one possibility is that in galaxies with highly concentrated baryonic components the halo responds by becoming more spherical, reducing the importance of non-circular motions (e.g. Abadi et al. 2010, and references therein). For the same reason, we emphasize that non-circular motions of the kind described here would only be expected in ΛCDM haloes that have preserved their original cusp and triaxiality, since mechanisms that erase the cusp are also likely to sphericalize the halo. This is a well-known feature of SIDM (e.g. Miralda-Escudé 2002) that is likely to apply as well to baryon-induced cores.
A detailed re-analysis of all ‘cored’ galaxies designed specifically to test the non-circular-motion hypothesis, together with a concerted effort to infer rotation curves from synthetic 2D velocity fields for more simulated galaxies is clearly needed in order to assess the true viability of this scenario. However, at least from the evidence presented in Fig. 11, it would be premature to rule out non-circular motions as one of the driving causes of the observed diversity.
4.5 Diversity and MDAR
Finally, we explore whether the observed rotation curve shape diversity could be a consequence of the ‘mass discrepancy–acceleration relation’ (MDAR) proposed by McGaugh et al. (2016). The MDAR posits that, at all radii, and for all galaxies, observed accelerations, |$g_{\rm obs}(r)=V_{\rm rot}^2(r)/r$| are uniquely determined by the accelerations expected from the baryonic distribution, |$g_{\rm bar}(r)=V_{\rm bar}^2(r)/r$|. This, of course, implies a unique relation between Vbar and Vrot at all radii, so that the full rotation curve may be derived solely from the distribution of baryons.
In this scenario, the diversity of rotation curve shapes must therefore follow from variations in the baryonic mass distribution, which may in principle induce a large spread of inner acceleration values in galaxies of given Vmax. This issue has been studied by Ghari et al. (2019), who considered the original SPARC data set as well as revisions to the SPARC data set proposed by Li et al. (2018),4 and concluded that, if the MDAR does indeed hold, a sizable scatter in Vfid is indeed expected, mainly driven by the structural diversity of galaxies of given Vmax.
We show this in the top panel of Fig. 12, where the coloured circles correspond to re-deriving the values of Vfid and Vmax for each galaxy using only the Vbar(r) profile and the MDAR (assuming negligible scatter). The grey circles in the same figure are the original data, as presented in Fig. 2. Note that although the main trends remain, the diversity in the dwarf galaxy regime has been reduced, and most dwarfs now lie closer to the ΛCDM prediction, indicated by the ‘NFW’ band in the same figure. We have explicitly checked that using the Li et al. (2018) revisions to Vbar(r) for SPARC galaxies does not change appreciably this conclusion; if anything, it reduces the diversity even further.

Top: Same as Fig. 2, but with the original data shown in grey. The coloured circles correspond to re-deriving Vfid and Vmax for each galaxy using solely the Vbar(r) profile and the MDAR. Bottom: Same as Fig. 4, with the original data in grey. Coloured circles correspond to re-deriving ηrot and ηbar using only the Vbar(r) profile and the MDAR. The MDAR forces galaxies of given Vmax to lie along curves such as those shown in this panel, for a few select values of Vmax.
In the context of our discussion, we note that the MDAR is incompatible with the trends between inner baryon dominance and rotation curve shape (ηrot versus ηbar) highlighted when discussing dwarf galaxies in Fig. 4. Indeed, it is straightforward to show that the MDAR links these two parameters so that galaxies must follow curves in the ηrot–ηbar plane like those shown in the bottom panel of Fig. 12, depending solely on their Vmax. Dwarf galaxies, in particular, are constrained to the top-left and are excluded from the bottom-right region of this panel. In other words, dwarf galaxies with slowly rising rotation curves (‘cores’) and where baryons dominate the inner regions should not exist in the MDAR scenario.
This is illustrated by the coloured circles in the bottom panel of Fig. 12, which correspond to assuming that the MDAR holds (with negligible scatter), so that only Vbar(r) is used to compute ηrot and ηbar for each observed galaxy. As is clear, the trend from top-left to bottom-right drawn by dwarf galaxies in Fig. 4 is not present anymore, and no dwarfs are found at the bottom-right region of the plot. The aforementioned trend must therefore arise, in the MDAR interpretation, as a consequence of (substantial) errors in the rotation velocities.
This is reminiscent of the discussion in the preceding subsection (Section 4.4), where we argued that errors in the observed rotation speeds (due, in that case, to non-circular motions) may reconcile the ΛCDM AP-L1 results with the observed diversity. Indeed, note that there is a strong similarity between dwarf galaxies in Fig. 12 and ΛCDM galaxies in the AP-L1 runs (see e.g. the crosses in the bottom panel of Fig. 11): in both cases, dwarf cluster at the upper-left corner of this figure. This similarity has already been hinted at by Navarro et al. (2017) and Ludlow et al. (2017), who argued that the MDAR relation is actually readily reproduced in ΛCDM: since dwarf galaxies with large ‘cores’ are unexpected in ΛCDM, they should also deviate systematically from the MDAR, at least in their inner regions.
We may see this directly in Fig. 13, where we show how closely the total and baryonic accelerations correlate at the inner fiducial radius for all galaxies in our sample. The MDAR relation from McGaugh et al. (2016), including its quoted scatter, is shown by the light blue shaded region. Observed galaxies are coloured by the shape parameter, ηrot, and are seen to follow only approximately the MDAR relation at rfid. Indeed, the rms scatter in gobs is 0.24 dex, substantially larger than the 0.13 dex obtained by McGaugh et al. (2016) by combining data for all galaxies and radii. In addition, most galaxies with large ‘cores’ (i.e. ηrot < 0.5) fall systematically off and below the MDAR relation (see also Santos-Santos et al. 2016; Ren et al. 2019, who report a similar result).

Observed radial acceleration at the inner fiducial radius, |$g_{\rm obs,fid}=V_{\rm fid}^2/r_{\rm fid}$|, versus the baryonic acceleration at the same radius, |$g_{\rm b,fid}=V_{\rm b,fid}^2/r_{\rm fid}$| for all galaxies in our observational sample. Each galaxy is coloured by the rotation curve shape parameter, ηrot. Note that ‘cored’ galaxies with slowly rising rotation curves (i.e. |$\eta _{\rm rot} \lesssim 0.55$|) typically fall outside of the MDAR relation proposed by McGaugh et al. (2016), shown by the blue shaded area. The diversity in observed rotation curves is thus not caused by the MDAR through variations in the gravitational acceleration at rfid induced by the baryonic component.
In conclusion, although variations in the baryonic distribution of galaxies may lead to some diversity in rotation curve shapes, the subtler trends between such shapes and the importance of baryons in the inner regions implied by the data are incompatible with the MDAR. On the other hand, if the MDAR actually holds, then the baryonic trends must result from errors in the data. Since the same data was actually used to derive the MDAR in the first place, this reduces, in our opinion, the appeal of the MDAR as a possible explanation for the diversity of dwarf galaxy rotation curve shapes.
5 SUMMARY AND CONCLUSIONS
Dwarf galaxy rotation curves are challenging to reproduce in the standard ΛCDM cosmogony. In some galaxies, rotation speeds rise rapidly to their maximum value, consistent with the circular velocity curves expected of cuspy ΛCDM haloes. In others, however, rotation speeds rise more slowly, revealing large ‘inner mass deficits’ or ‘cores’ when compared with ΛCDM haloes (e.g. de Blok 2010). This diversity is unexpected in ΛCDM, where, in the absence of modifications by baryons, circular velocity curves are expected to be simple, self-similar functions of the total halo mass (Navarro et al. 1996b, 1997; Oman et al. 2015). We examine in this paper the viability of different scenarios proposed to explain the diversity, and, in particular, the apparent presence of both cusps and cores in dwarfs.
A first scenario (BICC – ‘baryon-induced cores/cusps’) envisions the diversity as caused by the effect of baryonic inflows and outflows during the formation of the galaxy, which may rearrange the inner dark matter profiles: cores are created by baryonic blowouts but cusps can be recreated by further baryonic infall (see e.g. Navarro et al. 1996a; Pontzen & Governato 2012; Di Cintio et al. 2014b; Tollet et al. 2016; Benítez-Llambay et al. 2019). A third scenario (SIDM) argues that dark matter self-interactions may reduce the central DM densities relative to CDM, creating cores. As in BICC, cusps may be re-formed in galaxies where baryons are gravitationally important enough to deepen substantially the central potential (see e.g. Tulin & Yu 2018 for a recent review).
We have analysed cosmological simulations of these two scenarios and find that, although both of them show promise explaining systems with cores, neither reproduces the observed diversity in full detail. Indeed, both scenarios have difficulty in reproducing an intriguing feature of the observed diversity, namely the existence of galaxies with fast-rising rotation curves where the gravitational effects of baryons in the inner regions is unimportant. They also face difficulty explaining slowly rising rotation curves where baryons actually dominate in the inner regions, which are also present in the observational sample we analyse.
We argue that these issues present a difficult problem for any scenario where most haloes are expected to develop a sizable core and where baryons are supposed to be responsible for the observed diversity. This is especially so because the relation between baryon surface density and rotation curve shape is quite weak in the dwarf galaxy regime, and thus unlikely to drive the diversity. We emphasize that, strictly speaking, this conclusion applies only to the particular implementations of BICC and SIDM we have tested here. These are by no means the only possible realizations of these scenarios, and it is definitely possible that further refinements may lead to improvements in their accounting of the rotation curve diversity.
Our conclusions regarding a second scenario, SIDM, may seem at odds with recent work that reports good agreement between SIDM predictions and dwarf galaxy rotation curves (see e.g. the recent preprint of Kaplinghat et al. 2019, which appeared as we were readying this paper for submission, and references therein). That work, however, was meant to address whether observed rotation curves can be reproduced by adjusting the SIDM halo parameters freely in the fitting procedure, with promising results. Our analysis, on the other hand, explores whether the observed galaxies, if placed in average (random) SIDM haloes, would exhibit the observed diversity. Our results do show, in agreement with earlier work, that SIDM leads to a wide distribution of rotation curve shapes. However they also highlight the fact that outliers, be they large cores or cuspy systems, are not readily accounted for in this scenario, an issue that was also raised by Creasey et al. (2017). Whether this is a critical flaw of the SIDM scenario, or just signals the need for further elaboration, is still unclear.
In a third scenario, the diversity is caused by variations in the baryonic contribution to the acceleration in the inner regions, which is linked to rotation velocities through the ‘mass discrepancy–acceleration relation’ (MDAR; McGaugh et al. 2016). Earlier work has already shown that such variations may indeed induce substantial diversity in rotation curve shapes (Ghari et al. 2019). However, the MDAR is incompatible with the trend between shape and baryonic importance and, in particular, with the existence of galaxies with slowly rising rotation curves where baryons are important in the inner regions. Reconciling these with the MDAR requires assuming that the inner rotation velocities in those galaxies are in error. This is an unappealing solution, since the MDAR was actually derived from such data in the first place.
We end by noting that the rather peculiar relation between inner baryon dominance and rotation curve shapes could be naturally explained if non-circular motions were a driving cause of the diversity. For this scenario to succeed, however, it would need to explain why such motions affect solely low surface brightness galaxies, the systems where the evidence for ‘cores’ is most compelling. Further progress in this regard would require a detailed reanalysis of the data to uncover evidence for non-circular motions, and a clear elaboration of the reason why non-circular motions do not affect massive, high surface brightness galaxies. Until then, we would argue that the dwarf galaxy rotation curve diversity problem remains, for the time being, open.
ACKNOWLEDGEMENTS
We thank the NIHAO collaboration for kindly sharing their simulation data. ISS and AR are supported by the Arthur B. McDonald Canadian Astroparticle Physics Research Institute. JFN is a Fellow of the Canadian Institute for Advanced Research and acknowledges useful discussions with Laura Sales. MRL and AF had support from Marie Curie COFUND-Durham Junior Research Fellowship under EU grant agreement no. 609412. MRL is funded by a Grant of Excellence from the Icelandic Research Fund (grant no. 173929-051). AF and CSF are supported by the Science and Technology Facilities Council (STFC) (grant nos ST/F001166/1, ST/I00162X/1, ST/P000541/1). KO received support from VICI grant no. 016.130.338 of the Netherlands Foundation for Scientific Research (NWO). AR is supported by the European Research Council (ERC-StG-716532-PUNCA) and the STFC (ST/N001494/1). This work used the DiRAC@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grant nos ST/K00042X/1, ST/P002293/1, ST/R002371/1, and ST/S002502/1, Durham University and STFC operation grant no. ST/R000832/1. DiRAC is part of the National e-Infrastructure. ISS dedicates this work to her Abuelita, who was fascinated by the Universe and outer space.
Footnotes
We define the virial quantities of a system as those defined by a mean density of 200× the critical density for closure. Virial parameters are identified by a ‘200’ subscript.
This relation is also known as the ‘radial acceleration relation’, or RAR.
In principle, baryonic inflows and outflows may also affect the inner regions of SIDM haloes, a complication that we shall ignore in this paper.
Assuming that the MDAR is indeed valid, these authors adjust the distances, inclinations, and mass-to-light ratios of SPARC galaxies so as to derive a much tighter relation than originally presented by McGaugh et al. (2016). With these adjustments the overall scatter in the MDAR may be reduced from ∼0.130 to ∼0.057 dex.
REFERENCES
APPENDIX: SIDM TRANSFORMATION OF ΛCDM HALOES
A1 Analytical model
The solid black line in the top panel of Fig. A1 shows the NFW fit to the density profile of an ΛCDM halo of virial mass |$M_{200}=1.2 \times 10^{11}\, {\rm M}_\odot$| (solid black circles) selected from the AP-L1 DMO run. The fit has concentration c = r200/rs = 17.3; rs = 6.06 kpc; and |$\rho _{\rm s}=5.62\times 10^6\, {\rm M}_\odot /$|kpc3. Assuming isotropy, the NFW fit may be used to predict the velocity dispersion profile, which is shown in the bottom panel of Fig. A1.
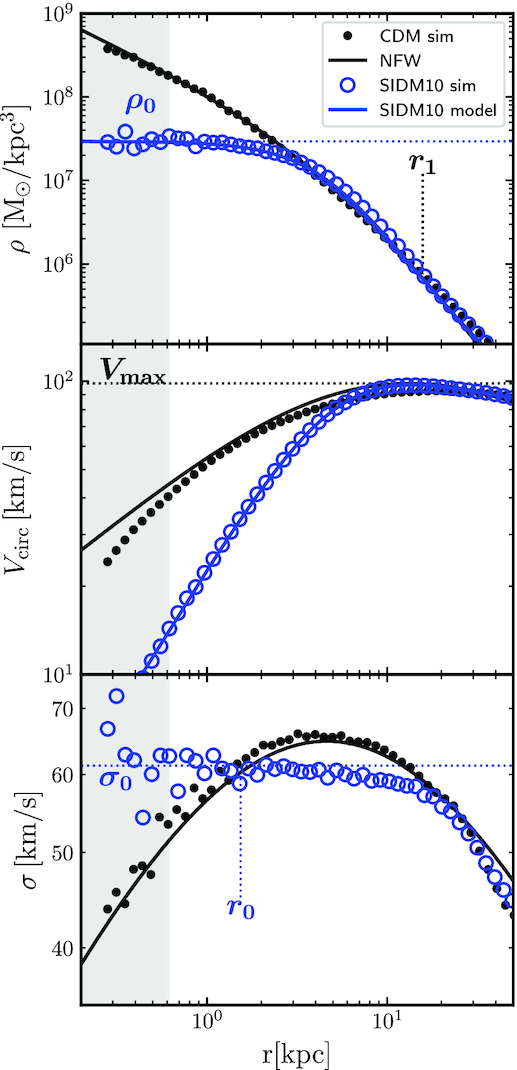
Density (top), circular velocity (middle), and radial velocity dispersion (bottom) profiles for a low mass ΛCDM halo (black) and its SIDM counterpart evolved assuming ssi = 10 cm2 g−1 (blue). Thin solid black lines correspond to the best NFW fit to the ΛCDM halo profiles. Thin solid blue lines indicate the best-fitting SIDM profile, computed as described in Section A1. Some of the characteristic halo parameters are indicated in the profiles, such the central SIDM density, ρ0; core radius, r0; and central velocity dispersion, σ0. The characteristic r1 radius (equation A2) and maximum velocity, Vmax, of the NFW fit are also indicated. The grey area indicates the region inside the Power et al. (2003) convergence radius.
| Name . | Sample . | Vmax (km s−1) . | Vb,max (km s−1) . | Vfid (km s−1) . | Vb,fid (km s−1) . | Mbar (M⊙) . | rb,half (kpc) . | M200 (M⊙) . |
|---|---|---|---|---|---|---|---|---|
| CamB | S | 20.10 | 13.85 | 6.85 | 10.08 | 5.35e+07 | 0.86 | 1.23e+09 |
| D512-2 | S | 37.20 | 16.34 | 24.04 | 11.80 | 2.70e+08 | 1.94 | 8.50e+09 |
| D564-8 | S | 25.00 | 9.24 | 11.17 | 6.66 | 5.51e+07 | 1.50 | 2.43e+09 |
| D631-7 | S | 58.50 | 24.51 | 29.50 | 23.54 | 4.84e+08 | 2.03 | 3.55e+10 |
| DDO064 | S | 46.90 | 25.29 | 36.67 | 16.28 | 3.59e+08 | 1.86 | 1.76e+10 |
| DDO154 | S | 48.20 | 18.73 | 27.37 | 13.90 | 3.92e+08 | 2.71 | 1.92e+10 |
| DDO161 | S | 67.50 | 35.35 | 32.14 | 25.01 | 2.11e+09 | 5.59 | 5.58e+10 |
| DDO168 | S | 55.00 | 25.90 | 35.00 | 23.08 | 6.45e+08 | 2.12 | 2.92e+10 |
| ESO079-G014 | S | 178.00 | 100.77 | 109.73 | 64.21 | 3.00e+10 | 9.46 | 1.21e+12 |
| ESO116-G012 | S | 112.00 | 52.33 | 83.47 | 47.73 | 3.59e+09 | 4.07 | 2.78e+11 |
| ESO444-G084 | S | 63.10 | 21.89 | 52.73 | 21.31 | 2.15e+08 | 1.38 | 4.51e+10 |
| ESO563-G021 | S | 321.00 | 200.92 | 286.19 | 176.36 | 1.88e+11 | 12.00 | 7.95e+12 |
| F565-V2 | S | 83.10 | 30.16 | 38.28 | 15.53 | 1.21e+09 | 6.13 | 1.08e+11 |
| F568-3 | S | 120.00 | 52.15 | 66.15 | 29.09 | 8.42e+09 | 10.60 | 3.46e+11 |
| F568-V1 | S | 118.00 | 44.75 | 91.59 | 28.75 | 5.23e+09 | 9.82 | 3.28e+11 |
| F571-8 | S | 144.00 | 81.10 | 93.14 | 70.96 | 7.45e+09 | 2.04 | 6.18e+11 |
| F574-1 | S | 99.70 | 46.48 | 68.23 | 29.70 | 7.96e+09 | 8.73 | 1.92e+11 |
| F583-1 | S | 86.90 | 41.35 | 44.55 | 13.55 | 3.32e+09 | 10.70 | 1.24e+11 |
| F583-4 | S | 69.90 | 31.15 | 43.05 | 23.48 | 1.71e+09 | 4.12 | 6.23e+10 |
| IC2574 | S | 67.50 | 32.02 | 19.54 | 12.57 | 1.89e+09 | 7.24 | 5.58e+10 |
| IC4202 | S | 250.00 | 181.45 | 231.32 | 165.39 | 1.06e+11 | 9.07 | 3.58e+12 |
| KK98-251 | S | 34.60 | 20.25 | 16.35 | 10.59 | 1.95e+08 | 1.83 | 6.76e+09 |
| NGC 0024 | S | 110.00 | 52.54 | 106.73 | 51.90 | 2.84e+09 | 2.53 | 2.62e+11 |
| NGC 0055 | S | 87.40 | 50.19 | 43.53 | 33.96 | 4.40e+09 | 6.74 | 1.26e+11 |
| NGC 0100 | S | 91.20 | 40.75 | 56.83 | 36.27 | 4.26e+09 | 3.72 | 1.45e+11 |
| NGC 0247 | S | 108.00 | 53.09 | 66.63 | 29.91 | 5.99e+09 | 8.02 | 2.48e+11 |
| NGC 0289 | S | 194.00 | 160.25 | 174.05 | 156.00 | 7.26e+10 | 16.54 | 1.60e+12 |
| NGC 0300 | S | 97.00 | 41.87 | 66.19 | 35.13 | 2.71e+09 | 4.56 | 1.76e+11 |
| NGC 0801 | S | 238.00 | 199.22 | 233.82 | 195.75 | 1.87e+11 | 15.86 | 3.06e+12 |
| NGC 0891 | S | 234.00 | 265.08 | 224.00 | 214.65 | 7.51e+10 | 2.79 | 2.90e+12 |
| NGC 1003 | S | 115.00 | 59.35 | 74.39 | 55.38 | 1.12e+10 | 12.36 | 3.02e+11 |
| NGC 1090 | S | 176.00 | 121.39 | 154.59 | 108.35 | 4.77e+10 | 8.68 | 1.17e+12 |
| NGC 1705 | S | 73.20 | 35.42 | 72.84 | 29.77 | 4.51e+08 | 0.95 | 7.21e+10 |
| NGC 2366 | S | 53.70 | 28.57 | 32.98 | 20.62 | 9.79e+08 | 3.25 | 2.71e+10 |
| NGC 2403 | S | 136.00 | 75.85 | 117.48 | 75.48 | 9.28e+09 | 5.07 | 5.15e+11 |
| NGC 2683 | S | 212.00 | 171.90 | 211.40 | 169.48 | 4.21e+10 | 3.45 | 2.12e+12 |
| NGC 2841 | S | 323.00 | 231.30 | 322.93 | 214.81 | 1.07e+11 | 7.98 | 8.11e+12 |
| NGC 2903 | S | 216.00 | 213.11 | 207.86 | 176.97 | 4.43e+10 | 2.58 | 2.25e+12 |
| NGC 2915 | S | 86.50 | 35.40 | 77.83 | 27.64 | 9.96e+08 | 4.97 | 1.22e+11 |
| NGC 2955 | S | 276.00 | 252.60 | 245.59 | 246.68 | 1.98e+11 | 8.12 | 4.91e+12 |
| NGC 2998 | S | 214.00 | 157.58 | 204.14 | 150.74 | 1.07e+11 | 11.13 | 2.18e+12 |
| NGC 3109 | S | 67.30 | 21.72 | 36.06 | 15.30 | 7.31e+08 | 3.92 | 5.52e+10 |
| NGC 3198 | S | 157.00 | 101.32 | 118.91 | 85.11 | 3.36e+10 | 10.54 | 8.13e+11 |
| NGC 3521 | S | 220.00 | 200.33 | 214.79 | 174.16 | 4.79e+10 | 2.99 | 2.38e+12 |
| NGC 3726 | S | 169.00 | 131.38 | 119.56 | 111.65 | 4.37e+10 | 6.73 | 1.03e+12 |
| NGC 3741 | S | 51.60 | 14.28 | 27.05 | 11.19 | 2.56e+08 | 3.79 | 2.39e+10 |
| NGC 3769 | S | 126.00 | 98.81 | 106.57 | 98.43 | 1.67e+10 | 4.28 | 4.04e+11 |
| NGC 3877 | S | 171.00 | 145.67 | 157.15 | 109.76 | 3.82e+10 | 6.22 | 1.07e+12 |
| NGC 3893 | S | 194.00 | 152.06 | 193.30 | 149.89 | 3.70e+10 | 3.83 | 1.60e+12 |
| NGC 3917 | S | 138.00 | 80.96 | 104.05 | 57.20 | 1.35e+10 | 6.35 | 5.40e+11 |
| NGC 3953 | S | 224.00 | 176.03 | 211.67 | 159.61 | 7.44e+10 | 7.33 | 2.52e+12 |
| NGC 3972 | S | 134.00 | 79.21 | 105.02 | 62.09 | 8.79e+09 | 4.75 | 4.91e+11 |
| NGC 4010 | S | 129.00 | 77.65 | 86.12 | 68.91 | 1.24e+10 | 5.15 | 4.35e+11 |
| NGC 4013 | S | 198.00 | 166.75 | 197.26 | 161.12 | 4.35e+10 | 5.49 | 1.70e+12 |
| NGC 4051 | S | 161.00 | 141.36 | 131.17 | 103.88 | 5.12e+10 | 6.35 | 8.81e+11 |
| NGC 4088 | S | 182.00 | 189.42 | 161.40 | 170.20 | 6.46e+10 | 5.21 | 1.30e+12 |
| NGC 4100 | S | 195.00 | 147.99 | 185.05 | 132.10 | 3.38e+10 | 5.13 | 1.62e+12 |
| NGC 4138 | S | 195.00 | 171.38 | 193.22 | 142.04 | 2.40e+10 | 2.61 | 1.62e+12 |
| NGC 4157 | S | 201.00 | 182.02 | 194.60 | 174.37 | 6.38e+10 | 4.96 | 1.79e+12 |
| NGC 4183 | S | 115.00 | 66.98 | 83.39 | 43.71 | 1.01e+10 | 7.10 | 3.02e+11 |
| NGC 4217 | S | 191.00 | 234.50 | 177.25 | 205.45 | 4.61e+10 | 2.69 | 1.52e+12 |
| NGC 4559 | S | 124.00 | 83.97 | 98.55 | 78.38 | 1.74e+10 | 7.55 | 3.84e+11 |
| NGC 5033 | S | 225.00 | 241.63 | 224.72 | 185.97 | 7.03e+10 | 3.56 | 2.56e+12 |
| NGC 5055 | S | 206.00 | 198.71 | 201.57 | 196.38 | 9.21e+10 | 5.53 | 1.93e+12 |
| NGC 5371 | S | 242.00 | 213.77 | 214.79 | 173.23 | 1.85e+11 | 11.10 | 3.23e+12 |
| NGC 5585 | S | 92.30 | 44.82 | 62.65 | 40.75 | 3.71e+09 | 4.59 | 1.50e+11 |
| NGC 5907 | S | 235.00 | 165.49 | 218.01 | 139.96 | 1.16e+11 | 11.24 | 2.94e+12 |
| NGC 5985 | S | 305.00 | 165.00 | 288.80 | 140.14 | 1.20e+11 | 12.81 | 6.75e+12 |
| NGC 6015 | S | 166.00 | 106.26 | 151.16 | 106.20 | 2.38e+10 | 5.11 | 9.71e+11 |
| NGC 6195 | S | 258.00 | 235.77 | 233.45 | 235.70 | 2.23e+11 | 10.62 | 3.96e+12 |
| NGC 6503 | S | 121.00 | 101.33 | 119.67 | 91.08 | 8.74e+09 | 2.16 | 3.55e+11 |
| NGC 6674 | S | 291.00 | 177.58 | 285.98 | 175.67 | 1.50e+11 | 10.19 | 5.81e+12 |
| NGC 6946 | S | 181.00 | 195.85 | 176.12 | 149.58 | 4.06e+10 | 4.39 | 1.28e+12 |
| NGC 7331 | S | 257.00 | 275.82 | 257.00 | 255.45 | 1.40e+11 | 4.40 | 3.91e+12 |
| NGC 7793 | S | 116.00 | 72.47 | 102.82 | 72.45 | 4.67e+09 | 2.55 | 3.11e+11 |
| NGC 7814 | S | 265.00 | 290.19 | 226.72 | 163.25 | 3.87e+10 | 1.66 | 4.31e+12 |
| PGC51017 | S | 20.50 | 18.81 | 20.27 | 12.47 | 3.45e+08 | 1.58 | 1.31e+09 |
| UGC00128 | S | 134.00 | 55.39 | 78.98 | 35.06 | 1.59e+10 | 18.83 | 4.91e+11 |
| UGC00191 | S | 83.85 | 42.19 | 71.49 | 30.11 | 2.79e+09 | 5.41 | 1.11e+11 |
| UGC00731 | S | 74.00 | 37.19 | 46.52 | 10.43 | 2.56e+09 | 7.30 | 7.46e+10 |
| UGC00891 | S | 63.75 | 26.57 | 28.75 | 17.86 | 7.56e+08 | 3.50 | 4.65e+10 |
| UGC02259 | S | 90.00 | 36.92 | 76.15 | 29.49 | 1.52e+09 | 4.01 | 1.39e+11 |
| UGC02455 | S | 61.00 | 57.14 | 30.44 | 56.18 | 2.89e+09 | 1.93 | 4.05e+10 |
| UGC02487 | S | 383.00 | 251.56 | 376.62 | 250.17 | 2.69e+11 | 10.67 | 1.40e+13 |
| UGC02885 | S | 305.00 | 231.80 | 260.15 | 210.89 | 2.55e+11 | 21.76 | 6.75e+12 |
| UGC02916 | S | 218.00 | 237.95 | 209.71 | 197.65 | 9.30e+10 | 8.55 | 2.31e+12 |
| UGC02953 | S | 319.00 | 247.65 | 319.00 | 238.35 | 1.40e+11 | 5.31 | 7.79e+12 |
| UGC03205 | S | 237.00 | 174.00 | 236.00 | 173.49 | 6.97e+10 | 5.94 | 3.02e+12 |
| UGC03546 | S | 262.00 | 330.90 | 193.03 | 167.97 | 5.42e+10 | 2.52 | 4.16e+12 |
| UGC03580 | S | 131.00 | 97.26 | 96.63 | 84.30 | 1.24e+10 | 5.84 | 4.57e+11 |
| UGC04278 | S | 92.80 | 46.03 | 45.88 | 21.46 | 2.14e+09 | 5.70 | 1.53e+11 |
| UGC04305 | S | 37.30 | 33.87 | 24.47 | 19.17 | 1.29e+09 | 3.21 | 8.57e+09 |
| UGC04325 | S | 92.70 | 44.02 | 87.71 | 37.41 | 1.91e+09 | 3.14 | 1.52e+11 |
| UGC04499 | S | 74.30 | 39.87 | 49.06 | 27.20 | 2.24e+09 | 4.77 | 7.56e+10 |
| UGC05005 | S | 100.00 | 43.08 | 37.87 | 25.08 | 6.16e+09 | 15.24 | 1.94e+11 |
| UGC05253 | S | 248.00 | 238.24 | 246.00 | 208.09 | 1.08e+11 | 6.08 | 3.49e+12 |
| UGC05414 | S | 61.40 | 33.68 | 41.04 | 26.20 | 1.32e+09 | 2.52 | 4.13e+10 |
| UGC05716 | S | 74.70 | 31.57 | 49.52 | 20.96 | 1.75e+09 | 6.86 | 7.69e+10 |
| UGC05721 | S | 82.60 | 34.76 | 81.92 | 29.52 | 1.01e+09 | 3.33 | 1.06e+11 |
| UGC05750 | S | 78.90 | 41.46 | 24.89 | 15.88 | 3.13e+09 | 13.59 | 9.14e+10 |
| UGC05764 | S | 55.80 | 22.22 | 49.25 | 16.24 | 2.59e+08 | 2.08 | 3.05e+10 |
| UGC05829 | S | 68.60 | 37.43 | 34.69 | 12.54 | 1.64e+09 | 5.10 | 5.87e+10 |
| UGC05918 | S | 44.50 | 19.72 | 29.16 | 9.21 | 5.12e+08 | 3.04 | 1.49e+10 |
| UGC05986 | S | 116.00 | 56.04 | 98.38 | 51.27 | 5.89e+09 | 3.44 | 3.11e+11 |
| UGC06399 | S | 87.60 | 38.86 | 58.74 | 27.28 | 2.04e+09 | 4.54 | 1.27e+11 |
| UGC06446 | S | 84.90 | 38.55 | 64.44 | 24.16 | 2.33e+09 | 6.00 | 1.15e+11 |
| UGC06614 | S | 205.00 | 209.41 | 184.29 | 186.91 | 9.13e+10 | 13.15 | 1.90e+12 |
| UGC06667 | S | 85.70 | 30.25 | 54.81 | 12.29 | 1.77e+09 | 5.12 | 1.19e+11 |
| UGC06786 | S | 229.00 | 175.04 | 219.00 | 155.28 | 4.34e+10 | 4.47 | 2.71e+12 |
| UGC06787 | S | 276.00 | 271.81 | 243.26 | 170.76 | 5.58e+10 | 2.77 | 4.91e+12 |
| UGC06818 | S | 74.40 | 32.73 | 31.86 | 28.59 | 2.23e+09 | 3.73 | 7.59e+10 |
| UGC06917 | S | 111.00 | 56.30 | 79.59 | 43.25 | 6.11e+09 | 6.44 | 2.70e+11 |
| UGC06923 | S | 81.10 | 47.91 | 61.65 | 43.56 | 2.52e+09 | 2.88 | 9.97e+10 |
| UGC06930 | S | 109.00 | 60.56 | 78.67 | 41.51 | 8.77e+09 | 8.06 | 2.55e+11 |
| UGC06983 | S | 113.00 | 51.91 | 90.67 | 43.65 | 6.60e+09 | 7.81 | 2.86e+11 |
| UGC07089 | S | 79.10 | 42.06 | 40.58 | 29.31 | 3.41e+09 | 5.01 | 9.22e+10 |
| UGC07125 | S | 65.60 | 44.56 | 31.20 | 24.34 | 7.51e+09 | 10.46 | 5.10e+10 |
| UGC07151 | S | 76.20 | 44.10 | 64.66 | 36.63 | 1.96e+09 | 3.54 | 8.19e+10 |
| UGC07323 | S | 85.60 | 51.74 | 52.58 | 35.03 | 3.01e+09 | 3.91 | 1.18e+11 |
| UGC07399 | S | 106.00 | 33.87 | 91.53 | 32.51 | 1.57e+09 | 3.27 | 2.33e+11 |
| UGC07524 | S | 83.80 | 43.92 | 44.96 | 19.35 | 3.58e+09 | 7.73 | 1.11e+11 |
| UGC07559 | S | 32.10 | 19.76 | 18.91 | 13.18 | 2.79e+08 | 1.79 | 5.34e+09 |
| UGC07577 | S | 17.80 | 12.60 | 6.69 | 5.52 | 8.10e+07 | 1.10 | 8.39e+08 |
| UGC07603 | S | 64.00 | 27.55 | 58.22 | 27.15 | 5.31e+08 | 1.56 | 4.71e+10 |
| UGC07690 | S | 60.70 | 36.49 | 60.65 | 35.71 | 9.48e+08 | 1.59 | 3.99e+10 |
| UGC07866 | S | 33.10 | 18.42 | 23.18 | 12.75 | 2.19e+08 | 1.53 | 5.88e+09 |
| UGC08286 | S | 84.30 | 35.34 | 72.65 | 29.57 | 1.48e+09 | 3.94 | 1.13e+11 |
| UGC08490 | S | 80.10 | 35.71 | 76.29 | 35.55 | 1.47e+09 | 2.96 | 9.59e+10 |
| UGC08550 | S | 57.80 | 24.64 | 48.45 | 23.06 | 5.28e+08 | 3.96 | 3.41e+10 |
| UGC08699 | S | 202.00 | 214.73 | 170.49 | 125.86 | 3.01e+10 | 3.85 | 1.82e+12 |
| UGC08837 | S | 48.00 | 29.32 | 18.56 | 13.25 | 6.76e+08 | 2.82 | 1.90e+10 |
| UGC09037 | S | 160.00 | 116.33 | 102.52 | 107.36 | 5.97e+10 | 10.23 | 8.64e+11 |
| UGC09133 | S | 289.00 | 283.20 | 287.52 | 244.07 | 1.86e+11 | 8.06 | 5.69e+12 |
| UGC10310 | S | 73.20 | 40.86 | 52.31 | 24.84 | 2.46e+09 | 4.84 | 7.21e+10 |
| UGC11455 | S | 291.00 | 232.15 | 232.60 | 204.66 | 2.05e+11 | 10.36 | 5.81e+12 |
| UGC11820 | S | 84.45 | 38.77 | 49.23 | 20.19 | 3.11e+09 | 8.75 | 1.13e+11 |
| UGC12506 | S | 255.00 | 134.55 | 210.25 | 101.90 | 1.17e+11 | 18.78 | 3.82e+12 |
| UGC12632 | S | 73.20 | 36.66 | 44.04 | 18.21 | 2.97e+09 | 7.28 | 7.21e+10 |
| UGC12732 | S | 98.00 | 46.29 | 59.03 | 23.06 | 5.70e+09 | 11.78 | 1.82e+11 |
| UGCA442 | S | 57.80 | 24.49 | 34.31 | 18.27 | 4.20e+08 | 2.18 | 3.41e+10 |
| UGCA444 | S | 38.30 | 16.18 | 25.38 | 14.49 | 9.51e+07 | 1.19 | 9.32e+09 |
| U11707 | A | 103.74 | 32.33 | 63.19 | 22.91 | 2.24e+09 | 5.99 | 2.18e+11 |
| N2552 | A | 96.10 | 35.28 | 68.53 | 30.81 | 1.78e+09 | 3.43 | 1.71e+11 |
| wlm | LT | 38.53 | 14.84 | 26.93 | 10.86 | 1.73e+08 | 2.22 | 9.49e+09 |
| ddo87 | LT | 56.63 | 18.79 | 22.83 | 4.92 | 5.85e+08 | 4.68 | 3.20e+10 |
| ddo50 | LT | 38.84 | 33.88 | 22.29 | 7.38 | 1.67e+09 | 4.62 | 9.74e+09 |
| ddo52 | LT | 61.72 | 22.52 | 38.71 | 10.70 | 6.30e+08 | 3.80 | 4.20e+10 |
| ngc1569 | LT | 39.28 | 38.68 | 23.57 | 20.45 | 1.12e+09 | 2.84 | 1.01e+10 |
| haro29 | LT | 43.49 | 12.00 | 29.82 | 9.69 | 1.68e+08 | 4.36 | 1.39e+10 |
| cvnidwa | LT | 26.45 | 8.89 | 9.14 | 8.43 | 4.53e+07 | 1.68 | 2.91e+09 |
| ddo133 | LT | 46.73 | 18.84 | 32.36 | 11.48 | 2.87e+08 | 2.28 | 1.74e+10 |
| ic1613 | LT | 21.13 | 15.29 | 6.13 | 5.03 | 1.47e+08 | 1.82 | 1.44e+09 |
| ddo216 | LT | 18.91 | 8.45 | 12.69 | 6.90 | 1.73e+07 | 0.60 | 1.01e+09 |
| ddo126 | LT | 38.74 | 18.70 | 19.63 | 10.07 | 2.91e+08 | 2.44 | 9.66e+09 |
| NGC 925 | TH | 114.50 | 75.56 | 54.41 | 46.03 | 1.73e+10 | 9.65 | 2.98e+11 |
| NGC 3621 | TH | 159.20 | 118.03 | 130.41 | 116.23 | 3.48e+10 | 6.38 | 8.50e+11 |
| ngc4396 | R | 99.46 | 30.63 | 79.58 | 30.13 | 1.12e+09 | 2.71 | 1.91e+11 |
| ngc6106 | R | 124.75 | 68.67 | 114.06 | 68.32 | 5.46e+09 | 2.58 | 3.91e+11 |
| ugc4169 | R | 97.72 | 46.37 | 74.84 | 38.39 | 3.11e+09 | 3.65 | 1.80e+11 |
| ugc3371 | R | 64.01 | 15.95 | 36.79 | 10.54 | 3.98e+08 | 4.26 | 4.71e+10 |
| Name . | Sample . | Vmax (km s−1) . | Vb,max (km s−1) . | Vfid (km s−1) . | Vb,fid (km s−1) . | Mbar (M⊙) . | rb,half (kpc) . | M200 (M⊙) . |
|---|---|---|---|---|---|---|---|---|
| CamB | S | 20.10 | 13.85 | 6.85 | 10.08 | 5.35e+07 | 0.86 | 1.23e+09 |
| D512-2 | S | 37.20 | 16.34 | 24.04 | 11.80 | 2.70e+08 | 1.94 | 8.50e+09 |
| D564-8 | S | 25.00 | 9.24 | 11.17 | 6.66 | 5.51e+07 | 1.50 | 2.43e+09 |
| D631-7 | S | 58.50 | 24.51 | 29.50 | 23.54 | 4.84e+08 | 2.03 | 3.55e+10 |
| DDO064 | S | 46.90 | 25.29 | 36.67 | 16.28 | 3.59e+08 | 1.86 | 1.76e+10 |
| DDO154 | S | 48.20 | 18.73 | 27.37 | 13.90 | 3.92e+08 | 2.71 | 1.92e+10 |
| DDO161 | S | 67.50 | 35.35 | 32.14 | 25.01 | 2.11e+09 | 5.59 | 5.58e+10 |
| DDO168 | S | 55.00 | 25.90 | 35.00 | 23.08 | 6.45e+08 | 2.12 | 2.92e+10 |
| ESO079-G014 | S | 178.00 | 100.77 | 109.73 | 64.21 | 3.00e+10 | 9.46 | 1.21e+12 |
| ESO116-G012 | S | 112.00 | 52.33 | 83.47 | 47.73 | 3.59e+09 | 4.07 | 2.78e+11 |
| ESO444-G084 | S | 63.10 | 21.89 | 52.73 | 21.31 | 2.15e+08 | 1.38 | 4.51e+10 |
| ESO563-G021 | S | 321.00 | 200.92 | 286.19 | 176.36 | 1.88e+11 | 12.00 | 7.95e+12 |
| F565-V2 | S | 83.10 | 30.16 | 38.28 | 15.53 | 1.21e+09 | 6.13 | 1.08e+11 |
| F568-3 | S | 120.00 | 52.15 | 66.15 | 29.09 | 8.42e+09 | 10.60 | 3.46e+11 |
| F568-V1 | S | 118.00 | 44.75 | 91.59 | 28.75 | 5.23e+09 | 9.82 | 3.28e+11 |
| F571-8 | S | 144.00 | 81.10 | 93.14 | 70.96 | 7.45e+09 | 2.04 | 6.18e+11 |
| F574-1 | S | 99.70 | 46.48 | 68.23 | 29.70 | 7.96e+09 | 8.73 | 1.92e+11 |
| F583-1 | S | 86.90 | 41.35 | 44.55 | 13.55 | 3.32e+09 | 10.70 | 1.24e+11 |
| F583-4 | S | 69.90 | 31.15 | 43.05 | 23.48 | 1.71e+09 | 4.12 | 6.23e+10 |
| IC2574 | S | 67.50 | 32.02 | 19.54 | 12.57 | 1.89e+09 | 7.24 | 5.58e+10 |
| IC4202 | S | 250.00 | 181.45 | 231.32 | 165.39 | 1.06e+11 | 9.07 | 3.58e+12 |
| KK98-251 | S | 34.60 | 20.25 | 16.35 | 10.59 | 1.95e+08 | 1.83 | 6.76e+09 |
| NGC 0024 | S | 110.00 | 52.54 | 106.73 | 51.90 | 2.84e+09 | 2.53 | 2.62e+11 |
| NGC 0055 | S | 87.40 | 50.19 | 43.53 | 33.96 | 4.40e+09 | 6.74 | 1.26e+11 |
| NGC 0100 | S | 91.20 | 40.75 | 56.83 | 36.27 | 4.26e+09 | 3.72 | 1.45e+11 |
| NGC 0247 | S | 108.00 | 53.09 | 66.63 | 29.91 | 5.99e+09 | 8.02 | 2.48e+11 |
| NGC 0289 | S | 194.00 | 160.25 | 174.05 | 156.00 | 7.26e+10 | 16.54 | 1.60e+12 |
| NGC 0300 | S | 97.00 | 41.87 | 66.19 | 35.13 | 2.71e+09 | 4.56 | 1.76e+11 |
| NGC 0801 | S | 238.00 | 199.22 | 233.82 | 195.75 | 1.87e+11 | 15.86 | 3.06e+12 |
| NGC 0891 | S | 234.00 | 265.08 | 224.00 | 214.65 | 7.51e+10 | 2.79 | 2.90e+12 |
| NGC 1003 | S | 115.00 | 59.35 | 74.39 | 55.38 | 1.12e+10 | 12.36 | 3.02e+11 |
| NGC 1090 | S | 176.00 | 121.39 | 154.59 | 108.35 | 4.77e+10 | 8.68 | 1.17e+12 |
| NGC 1705 | S | 73.20 | 35.42 | 72.84 | 29.77 | 4.51e+08 | 0.95 | 7.21e+10 |
| NGC 2366 | S | 53.70 | 28.57 | 32.98 | 20.62 | 9.79e+08 | 3.25 | 2.71e+10 |
| NGC 2403 | S | 136.00 | 75.85 | 117.48 | 75.48 | 9.28e+09 | 5.07 | 5.15e+11 |
| NGC 2683 | S | 212.00 | 171.90 | 211.40 | 169.48 | 4.21e+10 | 3.45 | 2.12e+12 |
| NGC 2841 | S | 323.00 | 231.30 | 322.93 | 214.81 | 1.07e+11 | 7.98 | 8.11e+12 |
| NGC 2903 | S | 216.00 | 213.11 | 207.86 | 176.97 | 4.43e+10 | 2.58 | 2.25e+12 |
| NGC 2915 | S | 86.50 | 35.40 | 77.83 | 27.64 | 9.96e+08 | 4.97 | 1.22e+11 |
| NGC 2955 | S | 276.00 | 252.60 | 245.59 | 246.68 | 1.98e+11 | 8.12 | 4.91e+12 |
| NGC 2998 | S | 214.00 | 157.58 | 204.14 | 150.74 | 1.07e+11 | 11.13 | 2.18e+12 |
| NGC 3109 | S | 67.30 | 21.72 | 36.06 | 15.30 | 7.31e+08 | 3.92 | 5.52e+10 |
| NGC 3198 | S | 157.00 | 101.32 | 118.91 | 85.11 | 3.36e+10 | 10.54 | 8.13e+11 |
| NGC 3521 | S | 220.00 | 200.33 | 214.79 | 174.16 | 4.79e+10 | 2.99 | 2.38e+12 |
| NGC 3726 | S | 169.00 | 131.38 | 119.56 | 111.65 | 4.37e+10 | 6.73 | 1.03e+12 |
| NGC 3741 | S | 51.60 | 14.28 | 27.05 | 11.19 | 2.56e+08 | 3.79 | 2.39e+10 |
| NGC 3769 | S | 126.00 | 98.81 | 106.57 | 98.43 | 1.67e+10 | 4.28 | 4.04e+11 |
| NGC 3877 | S | 171.00 | 145.67 | 157.15 | 109.76 | 3.82e+10 | 6.22 | 1.07e+12 |
| NGC 3893 | S | 194.00 | 152.06 | 193.30 | 149.89 | 3.70e+10 | 3.83 | 1.60e+12 |
| NGC 3917 | S | 138.00 | 80.96 | 104.05 | 57.20 | 1.35e+10 | 6.35 | 5.40e+11 |
| NGC 3953 | S | 224.00 | 176.03 | 211.67 | 159.61 | 7.44e+10 | 7.33 | 2.52e+12 |
| NGC 3972 | S | 134.00 | 79.21 | 105.02 | 62.09 | 8.79e+09 | 4.75 | 4.91e+11 |
| NGC 4010 | S | 129.00 | 77.65 | 86.12 | 68.91 | 1.24e+10 | 5.15 | 4.35e+11 |
| NGC 4013 | S | 198.00 | 166.75 | 197.26 | 161.12 | 4.35e+10 | 5.49 | 1.70e+12 |
| NGC 4051 | S | 161.00 | 141.36 | 131.17 | 103.88 | 5.12e+10 | 6.35 | 8.81e+11 |
| NGC 4088 | S | 182.00 | 189.42 | 161.40 | 170.20 | 6.46e+10 | 5.21 | 1.30e+12 |
| NGC 4100 | S | 195.00 | 147.99 | 185.05 | 132.10 | 3.38e+10 | 5.13 | 1.62e+12 |
| NGC 4138 | S | 195.00 | 171.38 | 193.22 | 142.04 | 2.40e+10 | 2.61 | 1.62e+12 |
| NGC 4157 | S | 201.00 | 182.02 | 194.60 | 174.37 | 6.38e+10 | 4.96 | 1.79e+12 |
| NGC 4183 | S | 115.00 | 66.98 | 83.39 | 43.71 | 1.01e+10 | 7.10 | 3.02e+11 |
| NGC 4217 | S | 191.00 | 234.50 | 177.25 | 205.45 | 4.61e+10 | 2.69 | 1.52e+12 |
| NGC 4559 | S | 124.00 | 83.97 | 98.55 | 78.38 | 1.74e+10 | 7.55 | 3.84e+11 |
| NGC 5033 | S | 225.00 | 241.63 | 224.72 | 185.97 | 7.03e+10 | 3.56 | 2.56e+12 |
| NGC 5055 | S | 206.00 | 198.71 | 201.57 | 196.38 | 9.21e+10 | 5.53 | 1.93e+12 |
| NGC 5371 | S | 242.00 | 213.77 | 214.79 | 173.23 | 1.85e+11 | 11.10 | 3.23e+12 |
| NGC 5585 | S | 92.30 | 44.82 | 62.65 | 40.75 | 3.71e+09 | 4.59 | 1.50e+11 |
| NGC 5907 | S | 235.00 | 165.49 | 218.01 | 139.96 | 1.16e+11 | 11.24 | 2.94e+12 |
| NGC 5985 | S | 305.00 | 165.00 | 288.80 | 140.14 | 1.20e+11 | 12.81 | 6.75e+12 |
| NGC 6015 | S | 166.00 | 106.26 | 151.16 | 106.20 | 2.38e+10 | 5.11 | 9.71e+11 |
| NGC 6195 | S | 258.00 | 235.77 | 233.45 | 235.70 | 2.23e+11 | 10.62 | 3.96e+12 |
| NGC 6503 | S | 121.00 | 101.33 | 119.67 | 91.08 | 8.74e+09 | 2.16 | 3.55e+11 |
| NGC 6674 | S | 291.00 | 177.58 | 285.98 | 175.67 | 1.50e+11 | 10.19 | 5.81e+12 |
| NGC 6946 | S | 181.00 | 195.85 | 176.12 | 149.58 | 4.06e+10 | 4.39 | 1.28e+12 |
| NGC 7331 | S | 257.00 | 275.82 | 257.00 | 255.45 | 1.40e+11 | 4.40 | 3.91e+12 |
| NGC 7793 | S | 116.00 | 72.47 | 102.82 | 72.45 | 4.67e+09 | 2.55 | 3.11e+11 |
| NGC 7814 | S | 265.00 | 290.19 | 226.72 | 163.25 | 3.87e+10 | 1.66 | 4.31e+12 |
| PGC51017 | S | 20.50 | 18.81 | 20.27 | 12.47 | 3.45e+08 | 1.58 | 1.31e+09 |
| UGC00128 | S | 134.00 | 55.39 | 78.98 | 35.06 | 1.59e+10 | 18.83 | 4.91e+11 |
| UGC00191 | S | 83.85 | 42.19 | 71.49 | 30.11 | 2.79e+09 | 5.41 | 1.11e+11 |
| UGC00731 | S | 74.00 | 37.19 | 46.52 | 10.43 | 2.56e+09 | 7.30 | 7.46e+10 |
| UGC00891 | S | 63.75 | 26.57 | 28.75 | 17.86 | 7.56e+08 | 3.50 | 4.65e+10 |
| UGC02259 | S | 90.00 | 36.92 | 76.15 | 29.49 | 1.52e+09 | 4.01 | 1.39e+11 |
| UGC02455 | S | 61.00 | 57.14 | 30.44 | 56.18 | 2.89e+09 | 1.93 | 4.05e+10 |
| UGC02487 | S | 383.00 | 251.56 | 376.62 | 250.17 | 2.69e+11 | 10.67 | 1.40e+13 |
| UGC02885 | S | 305.00 | 231.80 | 260.15 | 210.89 | 2.55e+11 | 21.76 | 6.75e+12 |
| UGC02916 | S | 218.00 | 237.95 | 209.71 | 197.65 | 9.30e+10 | 8.55 | 2.31e+12 |
| UGC02953 | S | 319.00 | 247.65 | 319.00 | 238.35 | 1.40e+11 | 5.31 | 7.79e+12 |
| UGC03205 | S | 237.00 | 174.00 | 236.00 | 173.49 | 6.97e+10 | 5.94 | 3.02e+12 |
| UGC03546 | S | 262.00 | 330.90 | 193.03 | 167.97 | 5.42e+10 | 2.52 | 4.16e+12 |
| UGC03580 | S | 131.00 | 97.26 | 96.63 | 84.30 | 1.24e+10 | 5.84 | 4.57e+11 |
| UGC04278 | S | 92.80 | 46.03 | 45.88 | 21.46 | 2.14e+09 | 5.70 | 1.53e+11 |
| UGC04305 | S | 37.30 | 33.87 | 24.47 | 19.17 | 1.29e+09 | 3.21 | 8.57e+09 |
| UGC04325 | S | 92.70 | 44.02 | 87.71 | 37.41 | 1.91e+09 | 3.14 | 1.52e+11 |
| UGC04499 | S | 74.30 | 39.87 | 49.06 | 27.20 | 2.24e+09 | 4.77 | 7.56e+10 |
| UGC05005 | S | 100.00 | 43.08 | 37.87 | 25.08 | 6.16e+09 | 15.24 | 1.94e+11 |
| UGC05253 | S | 248.00 | 238.24 | 246.00 | 208.09 | 1.08e+11 | 6.08 | 3.49e+12 |
| UGC05414 | S | 61.40 | 33.68 | 41.04 | 26.20 | 1.32e+09 | 2.52 | 4.13e+10 |
| UGC05716 | S | 74.70 | 31.57 | 49.52 | 20.96 | 1.75e+09 | 6.86 | 7.69e+10 |
| UGC05721 | S | 82.60 | 34.76 | 81.92 | 29.52 | 1.01e+09 | 3.33 | 1.06e+11 |
| UGC05750 | S | 78.90 | 41.46 | 24.89 | 15.88 | 3.13e+09 | 13.59 | 9.14e+10 |
| UGC05764 | S | 55.80 | 22.22 | 49.25 | 16.24 | 2.59e+08 | 2.08 | 3.05e+10 |
| UGC05829 | S | 68.60 | 37.43 | 34.69 | 12.54 | 1.64e+09 | 5.10 | 5.87e+10 |
| UGC05918 | S | 44.50 | 19.72 | 29.16 | 9.21 | 5.12e+08 | 3.04 | 1.49e+10 |
| UGC05986 | S | 116.00 | 56.04 | 98.38 | 51.27 | 5.89e+09 | 3.44 | 3.11e+11 |
| UGC06399 | S | 87.60 | 38.86 | 58.74 | 27.28 | 2.04e+09 | 4.54 | 1.27e+11 |
| UGC06446 | S | 84.90 | 38.55 | 64.44 | 24.16 | 2.33e+09 | 6.00 | 1.15e+11 |
| UGC06614 | S | 205.00 | 209.41 | 184.29 | 186.91 | 9.13e+10 | 13.15 | 1.90e+12 |
| UGC06667 | S | 85.70 | 30.25 | 54.81 | 12.29 | 1.77e+09 | 5.12 | 1.19e+11 |
| UGC06786 | S | 229.00 | 175.04 | 219.00 | 155.28 | 4.34e+10 | 4.47 | 2.71e+12 |
| UGC06787 | S | 276.00 | 271.81 | 243.26 | 170.76 | 5.58e+10 | 2.77 | 4.91e+12 |
| UGC06818 | S | 74.40 | 32.73 | 31.86 | 28.59 | 2.23e+09 | 3.73 | 7.59e+10 |
| UGC06917 | S | 111.00 | 56.30 | 79.59 | 43.25 | 6.11e+09 | 6.44 | 2.70e+11 |
| UGC06923 | S | 81.10 | 47.91 | 61.65 | 43.56 | 2.52e+09 | 2.88 | 9.97e+10 |
| UGC06930 | S | 109.00 | 60.56 | 78.67 | 41.51 | 8.77e+09 | 8.06 | 2.55e+11 |
| UGC06983 | S | 113.00 | 51.91 | 90.67 | 43.65 | 6.60e+09 | 7.81 | 2.86e+11 |
| UGC07089 | S | 79.10 | 42.06 | 40.58 | 29.31 | 3.41e+09 | 5.01 | 9.22e+10 |
| UGC07125 | S | 65.60 | 44.56 | 31.20 | 24.34 | 7.51e+09 | 10.46 | 5.10e+10 |
| UGC07151 | S | 76.20 | 44.10 | 64.66 | 36.63 | 1.96e+09 | 3.54 | 8.19e+10 |
| UGC07323 | S | 85.60 | 51.74 | 52.58 | 35.03 | 3.01e+09 | 3.91 | 1.18e+11 |
| UGC07399 | S | 106.00 | 33.87 | 91.53 | 32.51 | 1.57e+09 | 3.27 | 2.33e+11 |
| UGC07524 | S | 83.80 | 43.92 | 44.96 | 19.35 | 3.58e+09 | 7.73 | 1.11e+11 |
| UGC07559 | S | 32.10 | 19.76 | 18.91 | 13.18 | 2.79e+08 | 1.79 | 5.34e+09 |
| UGC07577 | S | 17.80 | 12.60 | 6.69 | 5.52 | 8.10e+07 | 1.10 | 8.39e+08 |
| UGC07603 | S | 64.00 | 27.55 | 58.22 | 27.15 | 5.31e+08 | 1.56 | 4.71e+10 |
| UGC07690 | S | 60.70 | 36.49 | 60.65 | 35.71 | 9.48e+08 | 1.59 | 3.99e+10 |
| UGC07866 | S | 33.10 | 18.42 | 23.18 | 12.75 | 2.19e+08 | 1.53 | 5.88e+09 |
| UGC08286 | S | 84.30 | 35.34 | 72.65 | 29.57 | 1.48e+09 | 3.94 | 1.13e+11 |
| UGC08490 | S | 80.10 | 35.71 | 76.29 | 35.55 | 1.47e+09 | 2.96 | 9.59e+10 |
| UGC08550 | S | 57.80 | 24.64 | 48.45 | 23.06 | 5.28e+08 | 3.96 | 3.41e+10 |
| UGC08699 | S | 202.00 | 214.73 | 170.49 | 125.86 | 3.01e+10 | 3.85 | 1.82e+12 |
| UGC08837 | S | 48.00 | 29.32 | 18.56 | 13.25 | 6.76e+08 | 2.82 | 1.90e+10 |
| UGC09037 | S | 160.00 | 116.33 | 102.52 | 107.36 | 5.97e+10 | 10.23 | 8.64e+11 |
| UGC09133 | S | 289.00 | 283.20 | 287.52 | 244.07 | 1.86e+11 | 8.06 | 5.69e+12 |
| UGC10310 | S | 73.20 | 40.86 | 52.31 | 24.84 | 2.46e+09 | 4.84 | 7.21e+10 |
| UGC11455 | S | 291.00 | 232.15 | 232.60 | 204.66 | 2.05e+11 | 10.36 | 5.81e+12 |
| UGC11820 | S | 84.45 | 38.77 | 49.23 | 20.19 | 3.11e+09 | 8.75 | 1.13e+11 |
| UGC12506 | S | 255.00 | 134.55 | 210.25 | 101.90 | 1.17e+11 | 18.78 | 3.82e+12 |
| UGC12632 | S | 73.20 | 36.66 | 44.04 | 18.21 | 2.97e+09 | 7.28 | 7.21e+10 |
| UGC12732 | S | 98.00 | 46.29 | 59.03 | 23.06 | 5.70e+09 | 11.78 | 1.82e+11 |
| UGCA442 | S | 57.80 | 24.49 | 34.31 | 18.27 | 4.20e+08 | 2.18 | 3.41e+10 |
| UGCA444 | S | 38.30 | 16.18 | 25.38 | 14.49 | 9.51e+07 | 1.19 | 9.32e+09 |
| U11707 | A | 103.74 | 32.33 | 63.19 | 22.91 | 2.24e+09 | 5.99 | 2.18e+11 |
| N2552 | A | 96.10 | 35.28 | 68.53 | 30.81 | 1.78e+09 | 3.43 | 1.71e+11 |
| wlm | LT | 38.53 | 14.84 | 26.93 | 10.86 | 1.73e+08 | 2.22 | 9.49e+09 |
| ddo87 | LT | 56.63 | 18.79 | 22.83 | 4.92 | 5.85e+08 | 4.68 | 3.20e+10 |
| ddo50 | LT | 38.84 | 33.88 | 22.29 | 7.38 | 1.67e+09 | 4.62 | 9.74e+09 |
| ddo52 | LT | 61.72 | 22.52 | 38.71 | 10.70 | 6.30e+08 | 3.80 | 4.20e+10 |
| ngc1569 | LT | 39.28 | 38.68 | 23.57 | 20.45 | 1.12e+09 | 2.84 | 1.01e+10 |
| haro29 | LT | 43.49 | 12.00 | 29.82 | 9.69 | 1.68e+08 | 4.36 | 1.39e+10 |
| cvnidwa | LT | 26.45 | 8.89 | 9.14 | 8.43 | 4.53e+07 | 1.68 | 2.91e+09 |
| ddo133 | LT | 46.73 | 18.84 | 32.36 | 11.48 | 2.87e+08 | 2.28 | 1.74e+10 |
| ic1613 | LT | 21.13 | 15.29 | 6.13 | 5.03 | 1.47e+08 | 1.82 | 1.44e+09 |
| ddo216 | LT | 18.91 | 8.45 | 12.69 | 6.90 | 1.73e+07 | 0.60 | 1.01e+09 |
| ddo126 | LT | 38.74 | 18.70 | 19.63 | 10.07 | 2.91e+08 | 2.44 | 9.66e+09 |
| NGC 925 | TH | 114.50 | 75.56 | 54.41 | 46.03 | 1.73e+10 | 9.65 | 2.98e+11 |
| NGC 3621 | TH | 159.20 | 118.03 | 130.41 | 116.23 | 3.48e+10 | 6.38 | 8.50e+11 |
| ngc4396 | R | 99.46 | 30.63 | 79.58 | 30.13 | 1.12e+09 | 2.71 | 1.91e+11 |
| ngc6106 | R | 124.75 | 68.67 | 114.06 | 68.32 | 5.46e+09 | 2.58 | 3.91e+11 |
| ugc4169 | R | 97.72 | 46.37 | 74.84 | 38.39 | 3.11e+09 | 3.65 | 1.80e+11 |
| ugc3371 | R | 64.01 | 15.95 | 36.79 | 10.54 | 3.98e+08 | 4.26 | 4.71e+10 |
| Name . | Sample . | Vmax (km s−1) . | Vb,max (km s−1) . | Vfid (km s−1) . | Vb,fid (km s−1) . | Mbar (M⊙) . | rb,half (kpc) . | M200 (M⊙) . |
|---|---|---|---|---|---|---|---|---|
| CamB | S | 20.10 | 13.85 | 6.85 | 10.08 | 5.35e+07 | 0.86 | 1.23e+09 |
| D512-2 | S | 37.20 | 16.34 | 24.04 | 11.80 | 2.70e+08 | 1.94 | 8.50e+09 |
| D564-8 | S | 25.00 | 9.24 | 11.17 | 6.66 | 5.51e+07 | 1.50 | 2.43e+09 |
| D631-7 | S | 58.50 | 24.51 | 29.50 | 23.54 | 4.84e+08 | 2.03 | 3.55e+10 |
| DDO064 | S | 46.90 | 25.29 | 36.67 | 16.28 | 3.59e+08 | 1.86 | 1.76e+10 |
| DDO154 | S | 48.20 | 18.73 | 27.37 | 13.90 | 3.92e+08 | 2.71 | 1.92e+10 |
| DDO161 | S | 67.50 | 35.35 | 32.14 | 25.01 | 2.11e+09 | 5.59 | 5.58e+10 |
| DDO168 | S | 55.00 | 25.90 | 35.00 | 23.08 | 6.45e+08 | 2.12 | 2.92e+10 |
| ESO079-G014 | S | 178.00 | 100.77 | 109.73 | 64.21 | 3.00e+10 | 9.46 | 1.21e+12 |
| ESO116-G012 | S | 112.00 | 52.33 | 83.47 | 47.73 | 3.59e+09 | 4.07 | 2.78e+11 |
| ESO444-G084 | S | 63.10 | 21.89 | 52.73 | 21.31 | 2.15e+08 | 1.38 | 4.51e+10 |
| ESO563-G021 | S | 321.00 | 200.92 | 286.19 | 176.36 | 1.88e+11 | 12.00 | 7.95e+12 |
| F565-V2 | S | 83.10 | 30.16 | 38.28 | 15.53 | 1.21e+09 | 6.13 | 1.08e+11 |
| F568-3 | S | 120.00 | 52.15 | 66.15 | 29.09 | 8.42e+09 | 10.60 | 3.46e+11 |
| F568-V1 | S | 118.00 | 44.75 | 91.59 | 28.75 | 5.23e+09 | 9.82 | 3.28e+11 |
| F571-8 | S | 144.00 | 81.10 | 93.14 | 70.96 | 7.45e+09 | 2.04 | 6.18e+11 |
| F574-1 | S | 99.70 | 46.48 | 68.23 | 29.70 | 7.96e+09 | 8.73 | 1.92e+11 |
| F583-1 | S | 86.90 | 41.35 | 44.55 | 13.55 | 3.32e+09 | 10.70 | 1.24e+11 |
| F583-4 | S | 69.90 | 31.15 | 43.05 | 23.48 | 1.71e+09 | 4.12 | 6.23e+10 |
| IC2574 | S | 67.50 | 32.02 | 19.54 | 12.57 | 1.89e+09 | 7.24 | 5.58e+10 |
| IC4202 | S | 250.00 | 181.45 | 231.32 | 165.39 | 1.06e+11 | 9.07 | 3.58e+12 |
| KK98-251 | S | 34.60 | 20.25 | 16.35 | 10.59 | 1.95e+08 | 1.83 | 6.76e+09 |
| NGC 0024 | S | 110.00 | 52.54 | 106.73 | 51.90 | 2.84e+09 | 2.53 | 2.62e+11 |
| NGC 0055 | S | 87.40 | 50.19 | 43.53 | 33.96 | 4.40e+09 | 6.74 | 1.26e+11 |
| NGC 0100 | S | 91.20 | 40.75 | 56.83 | 36.27 | 4.26e+09 | 3.72 | 1.45e+11 |
| NGC 0247 | S | 108.00 | 53.09 | 66.63 | 29.91 | 5.99e+09 | 8.02 | 2.48e+11 |
| NGC 0289 | S | 194.00 | 160.25 | 174.05 | 156.00 | 7.26e+10 | 16.54 | 1.60e+12 |
| NGC 0300 | S | 97.00 | 41.87 | 66.19 | 35.13 | 2.71e+09 | 4.56 | 1.76e+11 |
| NGC 0801 | S | 238.00 | 199.22 | 233.82 | 195.75 | 1.87e+11 | 15.86 | 3.06e+12 |
| NGC 0891 | S | 234.00 | 265.08 | 224.00 | 214.65 | 7.51e+10 | 2.79 | 2.90e+12 |
| NGC 1003 | S | 115.00 | 59.35 | 74.39 | 55.38 | 1.12e+10 | 12.36 | 3.02e+11 |
| NGC 1090 | S | 176.00 | 121.39 | 154.59 | 108.35 | 4.77e+10 | 8.68 | 1.17e+12 |
| NGC 1705 | S | 73.20 | 35.42 | 72.84 | 29.77 | 4.51e+08 | 0.95 | 7.21e+10 |
| NGC 2366 | S | 53.70 | 28.57 | 32.98 | 20.62 | 9.79e+08 | 3.25 | 2.71e+10 |
| NGC 2403 | S | 136.00 | 75.85 | 117.48 | 75.48 | 9.28e+09 | 5.07 | 5.15e+11 |
| NGC 2683 | S | 212.00 | 171.90 | 211.40 | 169.48 | 4.21e+10 | 3.45 | 2.12e+12 |
| NGC 2841 | S | 323.00 | 231.30 | 322.93 | 214.81 | 1.07e+11 | 7.98 | 8.11e+12 |
| NGC 2903 | S | 216.00 | 213.11 | 207.86 | 176.97 | 4.43e+10 | 2.58 | 2.25e+12 |
| NGC 2915 | S | 86.50 | 35.40 | 77.83 | 27.64 | 9.96e+08 | 4.97 | 1.22e+11 |
| NGC 2955 | S | 276.00 | 252.60 | 245.59 | 246.68 | 1.98e+11 | 8.12 | 4.91e+12 |
| NGC 2998 | S | 214.00 | 157.58 | 204.14 | 150.74 | 1.07e+11 | 11.13 | 2.18e+12 |
| NGC 3109 | S | 67.30 | 21.72 | 36.06 | 15.30 | 7.31e+08 | 3.92 | 5.52e+10 |
| NGC 3198 | S | 157.00 | 101.32 | 118.91 | 85.11 | 3.36e+10 | 10.54 | 8.13e+11 |
| NGC 3521 | S | 220.00 | 200.33 | 214.79 | 174.16 | 4.79e+10 | 2.99 | 2.38e+12 |
| NGC 3726 | S | 169.00 | 131.38 | 119.56 | 111.65 | 4.37e+10 | 6.73 | 1.03e+12 |
| NGC 3741 | S | 51.60 | 14.28 | 27.05 | 11.19 | 2.56e+08 | 3.79 | 2.39e+10 |
| NGC 3769 | S | 126.00 | 98.81 | 106.57 | 98.43 | 1.67e+10 | 4.28 | 4.04e+11 |
| NGC 3877 | S | 171.00 | 145.67 | 157.15 | 109.76 | 3.82e+10 | 6.22 | 1.07e+12 |
| NGC 3893 | S | 194.00 | 152.06 | 193.30 | 149.89 | 3.70e+10 | 3.83 | 1.60e+12 |
| NGC 3917 | S | 138.00 | 80.96 | 104.05 | 57.20 | 1.35e+10 | 6.35 | 5.40e+11 |
| NGC 3953 | S | 224.00 | 176.03 | 211.67 | 159.61 | 7.44e+10 | 7.33 | 2.52e+12 |
| NGC 3972 | S | 134.00 | 79.21 | 105.02 | 62.09 | 8.79e+09 | 4.75 | 4.91e+11 |
| NGC 4010 | S | 129.00 | 77.65 | 86.12 | 68.91 | 1.24e+10 | 5.15 | 4.35e+11 |
| NGC 4013 | S | 198.00 | 166.75 | 197.26 | 161.12 | 4.35e+10 | 5.49 | 1.70e+12 |
| NGC 4051 | S | 161.00 | 141.36 | 131.17 | 103.88 | 5.12e+10 | 6.35 | 8.81e+11 |
| NGC 4088 | S | 182.00 | 189.42 | 161.40 | 170.20 | 6.46e+10 | 5.21 | 1.30e+12 |
| NGC 4100 | S | 195.00 | 147.99 | 185.05 | 132.10 | 3.38e+10 | 5.13 | 1.62e+12 |
| NGC 4138 | S | 195.00 | 171.38 | 193.22 | 142.04 | 2.40e+10 | 2.61 | 1.62e+12 |
| NGC 4157 | S | 201.00 | 182.02 | 194.60 | 174.37 | 6.38e+10 | 4.96 | 1.79e+12 |
| NGC 4183 | S | 115.00 | 66.98 | 83.39 | 43.71 | 1.01e+10 | 7.10 | 3.02e+11 |
| NGC 4217 | S | 191.00 | 234.50 | 177.25 | 205.45 | 4.61e+10 | 2.69 | 1.52e+12 |
| NGC 4559 | S | 124.00 | 83.97 | 98.55 | 78.38 | 1.74e+10 | 7.55 | 3.84e+11 |
| NGC 5033 | S | 225.00 | 241.63 | 224.72 | 185.97 | 7.03e+10 | 3.56 | 2.56e+12 |
| NGC 5055 | S | 206.00 | 198.71 | 201.57 | 196.38 | 9.21e+10 | 5.53 | 1.93e+12 |
| NGC 5371 | S | 242.00 | 213.77 | 214.79 | 173.23 | 1.85e+11 | 11.10 | 3.23e+12 |
| NGC 5585 | S | 92.30 | 44.82 | 62.65 | 40.75 | 3.71e+09 | 4.59 | 1.50e+11 |
| NGC 5907 | S | 235.00 | 165.49 | 218.01 | 139.96 | 1.16e+11 | 11.24 | 2.94e+12 |
| NGC 5985 | S | 305.00 | 165.00 | 288.80 | 140.14 | 1.20e+11 | 12.81 | 6.75e+12 |
| NGC 6015 | S | 166.00 | 106.26 | 151.16 | 106.20 | 2.38e+10 | 5.11 | 9.71e+11 |
| NGC 6195 | S | 258.00 | 235.77 | 233.45 | 235.70 | 2.23e+11 | 10.62 | 3.96e+12 |
| NGC 6503 | S | 121.00 | 101.33 | 119.67 | 91.08 | 8.74e+09 | 2.16 | 3.55e+11 |
| NGC 6674 | S | 291.00 | 177.58 | 285.98 | 175.67 | 1.50e+11 | 10.19 | 5.81e+12 |
| NGC 6946 | S | 181.00 | 195.85 | 176.12 | 149.58 | 4.06e+10 | 4.39 | 1.28e+12 |
| NGC 7331 | S | 257.00 | 275.82 | 257.00 | 255.45 | 1.40e+11 | 4.40 | 3.91e+12 |
| NGC 7793 | S | 116.00 | 72.47 | 102.82 | 72.45 | 4.67e+09 | 2.55 | 3.11e+11 |
| NGC 7814 | S | 265.00 | 290.19 | 226.72 | 163.25 | 3.87e+10 | 1.66 | 4.31e+12 |
| PGC51017 | S | 20.50 | 18.81 | 20.27 | 12.47 | 3.45e+08 | 1.58 | 1.31e+09 |
| UGC00128 | S | 134.00 | 55.39 | 78.98 | 35.06 | 1.59e+10 | 18.83 | 4.91e+11 |
| UGC00191 | S | 83.85 | 42.19 | 71.49 | 30.11 | 2.79e+09 | 5.41 | 1.11e+11 |
| UGC00731 | S | 74.00 | 37.19 | 46.52 | 10.43 | 2.56e+09 | 7.30 | 7.46e+10 |
| UGC00891 | S | 63.75 | 26.57 | 28.75 | 17.86 | 7.56e+08 | 3.50 | 4.65e+10 |
| UGC02259 | S | 90.00 | 36.92 | 76.15 | 29.49 | 1.52e+09 | 4.01 | 1.39e+11 |
| UGC02455 | S | 61.00 | 57.14 | 30.44 | 56.18 | 2.89e+09 | 1.93 | 4.05e+10 |
| UGC02487 | S | 383.00 | 251.56 | 376.62 | 250.17 | 2.69e+11 | 10.67 | 1.40e+13 |
| UGC02885 | S | 305.00 | 231.80 | 260.15 | 210.89 | 2.55e+11 | 21.76 | 6.75e+12 |
| UGC02916 | S | 218.00 | 237.95 | 209.71 | 197.65 | 9.30e+10 | 8.55 | 2.31e+12 |
| UGC02953 | S | 319.00 | 247.65 | 319.00 | 238.35 | 1.40e+11 | 5.31 | 7.79e+12 |
| UGC03205 | S | 237.00 | 174.00 | 236.00 | 173.49 | 6.97e+10 | 5.94 | 3.02e+12 |
| UGC03546 | S | 262.00 | 330.90 | 193.03 | 167.97 | 5.42e+10 | 2.52 | 4.16e+12 |
| UGC03580 | S | 131.00 | 97.26 | 96.63 | 84.30 | 1.24e+10 | 5.84 | 4.57e+11 |
| UGC04278 | S | 92.80 | 46.03 | 45.88 | 21.46 | 2.14e+09 | 5.70 | 1.53e+11 |
| UGC04305 | S | 37.30 | 33.87 | 24.47 | 19.17 | 1.29e+09 | 3.21 | 8.57e+09 |
| UGC04325 | S | 92.70 | 44.02 | 87.71 | 37.41 | 1.91e+09 | 3.14 | 1.52e+11 |
| UGC04499 | S | 74.30 | 39.87 | 49.06 | 27.20 | 2.24e+09 | 4.77 | 7.56e+10 |
| UGC05005 | S | 100.00 | 43.08 | 37.87 | 25.08 | 6.16e+09 | 15.24 | 1.94e+11 |
| UGC05253 | S | 248.00 | 238.24 | 246.00 | 208.09 | 1.08e+11 | 6.08 | 3.49e+12 |
| UGC05414 | S | 61.40 | 33.68 | 41.04 | 26.20 | 1.32e+09 | 2.52 | 4.13e+10 |
| UGC05716 | S | 74.70 | 31.57 | 49.52 | 20.96 | 1.75e+09 | 6.86 | 7.69e+10 |
| UGC05721 | S | 82.60 | 34.76 | 81.92 | 29.52 | 1.01e+09 | 3.33 | 1.06e+11 |
| UGC05750 | S | 78.90 | 41.46 | 24.89 | 15.88 | 3.13e+09 | 13.59 | 9.14e+10 |
| UGC05764 | S | 55.80 | 22.22 | 49.25 | 16.24 | 2.59e+08 | 2.08 | 3.05e+10 |
| UGC05829 | S | 68.60 | 37.43 | 34.69 | 12.54 | 1.64e+09 | 5.10 | 5.87e+10 |
| UGC05918 | S | 44.50 | 19.72 | 29.16 | 9.21 | 5.12e+08 | 3.04 | 1.49e+10 |
| UGC05986 | S | 116.00 | 56.04 | 98.38 | 51.27 | 5.89e+09 | 3.44 | 3.11e+11 |
| UGC06399 | S | 87.60 | 38.86 | 58.74 | 27.28 | 2.04e+09 | 4.54 | 1.27e+11 |
| UGC06446 | S | 84.90 | 38.55 | 64.44 | 24.16 | 2.33e+09 | 6.00 | 1.15e+11 |
| UGC06614 | S | 205.00 | 209.41 | 184.29 | 186.91 | 9.13e+10 | 13.15 | 1.90e+12 |
| UGC06667 | S | 85.70 | 30.25 | 54.81 | 12.29 | 1.77e+09 | 5.12 | 1.19e+11 |
| UGC06786 | S | 229.00 | 175.04 | 219.00 | 155.28 | 4.34e+10 | 4.47 | 2.71e+12 |
| UGC06787 | S | 276.00 | 271.81 | 243.26 | 170.76 | 5.58e+10 | 2.77 | 4.91e+12 |
| UGC06818 | S | 74.40 | 32.73 | 31.86 | 28.59 | 2.23e+09 | 3.73 | 7.59e+10 |
| UGC06917 | S | 111.00 | 56.30 | 79.59 | 43.25 | 6.11e+09 | 6.44 | 2.70e+11 |
| UGC06923 | S | 81.10 | 47.91 | 61.65 | 43.56 | 2.52e+09 | 2.88 | 9.97e+10 |
| UGC06930 | S | 109.00 | 60.56 | 78.67 | 41.51 | 8.77e+09 | 8.06 | 2.55e+11 |
| UGC06983 | S | 113.00 | 51.91 | 90.67 | 43.65 | 6.60e+09 | 7.81 | 2.86e+11 |
| UGC07089 | S | 79.10 | 42.06 | 40.58 | 29.31 | 3.41e+09 | 5.01 | 9.22e+10 |
| UGC07125 | S | 65.60 | 44.56 | 31.20 | 24.34 | 7.51e+09 | 10.46 | 5.10e+10 |
| UGC07151 | S | 76.20 | 44.10 | 64.66 | 36.63 | 1.96e+09 | 3.54 | 8.19e+10 |
| UGC07323 | S | 85.60 | 51.74 | 52.58 | 35.03 | 3.01e+09 | 3.91 | 1.18e+11 |
| UGC07399 | S | 106.00 | 33.87 | 91.53 | 32.51 | 1.57e+09 | 3.27 | 2.33e+11 |
| UGC07524 | S | 83.80 | 43.92 | 44.96 | 19.35 | 3.58e+09 | 7.73 | 1.11e+11 |
| UGC07559 | S | 32.10 | 19.76 | 18.91 | 13.18 | 2.79e+08 | 1.79 | 5.34e+09 |
| UGC07577 | S | 17.80 | 12.60 | 6.69 | 5.52 | 8.10e+07 | 1.10 | 8.39e+08 |
| UGC07603 | S | 64.00 | 27.55 | 58.22 | 27.15 | 5.31e+08 | 1.56 | 4.71e+10 |
| UGC07690 | S | 60.70 | 36.49 | 60.65 | 35.71 | 9.48e+08 | 1.59 | 3.99e+10 |
| UGC07866 | S | 33.10 | 18.42 | 23.18 | 12.75 | 2.19e+08 | 1.53 | 5.88e+09 |
| UGC08286 | S | 84.30 | 35.34 | 72.65 | 29.57 | 1.48e+09 | 3.94 | 1.13e+11 |
| UGC08490 | S | 80.10 | 35.71 | 76.29 | 35.55 | 1.47e+09 | 2.96 | 9.59e+10 |
| UGC08550 | S | 57.80 | 24.64 | 48.45 | 23.06 | 5.28e+08 | 3.96 | 3.41e+10 |
| UGC08699 | S | 202.00 | 214.73 | 170.49 | 125.86 | 3.01e+10 | 3.85 | 1.82e+12 |
| UGC08837 | S | 48.00 | 29.32 | 18.56 | 13.25 | 6.76e+08 | 2.82 | 1.90e+10 |
| UGC09037 | S | 160.00 | 116.33 | 102.52 | 107.36 | 5.97e+10 | 10.23 | 8.64e+11 |
| UGC09133 | S | 289.00 | 283.20 | 287.52 | 244.07 | 1.86e+11 | 8.06 | 5.69e+12 |
| UGC10310 | S | 73.20 | 40.86 | 52.31 | 24.84 | 2.46e+09 | 4.84 | 7.21e+10 |
| UGC11455 | S | 291.00 | 232.15 | 232.60 | 204.66 | 2.05e+11 | 10.36 | 5.81e+12 |
| UGC11820 | S | 84.45 | 38.77 | 49.23 | 20.19 | 3.11e+09 | 8.75 | 1.13e+11 |
| UGC12506 | S | 255.00 | 134.55 | 210.25 | 101.90 | 1.17e+11 | 18.78 | 3.82e+12 |
| UGC12632 | S | 73.20 | 36.66 | 44.04 | 18.21 | 2.97e+09 | 7.28 | 7.21e+10 |
| UGC12732 | S | 98.00 | 46.29 | 59.03 | 23.06 | 5.70e+09 | 11.78 | 1.82e+11 |
| UGCA442 | S | 57.80 | 24.49 | 34.31 | 18.27 | 4.20e+08 | 2.18 | 3.41e+10 |
| UGCA444 | S | 38.30 | 16.18 | 25.38 | 14.49 | 9.51e+07 | 1.19 | 9.32e+09 |
| U11707 | A | 103.74 | 32.33 | 63.19 | 22.91 | 2.24e+09 | 5.99 | 2.18e+11 |
| N2552 | A | 96.10 | 35.28 | 68.53 | 30.81 | 1.78e+09 | 3.43 | 1.71e+11 |
| wlm | LT | 38.53 | 14.84 | 26.93 | 10.86 | 1.73e+08 | 2.22 | 9.49e+09 |
| ddo87 | LT | 56.63 | 18.79 | 22.83 | 4.92 | 5.85e+08 | 4.68 | 3.20e+10 |
| ddo50 | LT | 38.84 | 33.88 | 22.29 | 7.38 | 1.67e+09 | 4.62 | 9.74e+09 |
| ddo52 | LT | 61.72 | 22.52 | 38.71 | 10.70 | 6.30e+08 | 3.80 | 4.20e+10 |
| ngc1569 | LT | 39.28 | 38.68 | 23.57 | 20.45 | 1.12e+09 | 2.84 | 1.01e+10 |
| haro29 | LT | 43.49 | 12.00 | 29.82 | 9.69 | 1.68e+08 | 4.36 | 1.39e+10 |
| cvnidwa | LT | 26.45 | 8.89 | 9.14 | 8.43 | 4.53e+07 | 1.68 | 2.91e+09 |
| ddo133 | LT | 46.73 | 18.84 | 32.36 | 11.48 | 2.87e+08 | 2.28 | 1.74e+10 |
| ic1613 | LT | 21.13 | 15.29 | 6.13 | 5.03 | 1.47e+08 | 1.82 | 1.44e+09 |
| ddo216 | LT | 18.91 | 8.45 | 12.69 | 6.90 | 1.73e+07 | 0.60 | 1.01e+09 |
| ddo126 | LT | 38.74 | 18.70 | 19.63 | 10.07 | 2.91e+08 | 2.44 | 9.66e+09 |
| NGC 925 | TH | 114.50 | 75.56 | 54.41 | 46.03 | 1.73e+10 | 9.65 | 2.98e+11 |
| NGC 3621 | TH | 159.20 | 118.03 | 130.41 | 116.23 | 3.48e+10 | 6.38 | 8.50e+11 |
| ngc4396 | R | 99.46 | 30.63 | 79.58 | 30.13 | 1.12e+09 | 2.71 | 1.91e+11 |
| ngc6106 | R | 124.75 | 68.67 | 114.06 | 68.32 | 5.46e+09 | 2.58 | 3.91e+11 |
| ugc4169 | R | 97.72 | 46.37 | 74.84 | 38.39 | 3.11e+09 | 3.65 | 1.80e+11 |
| ugc3371 | R | 64.01 | 15.95 | 36.79 | 10.54 | 3.98e+08 | 4.26 | 4.71e+10 |
| Name . | Sample . | Vmax (km s−1) . | Vb,max (km s−1) . | Vfid (km s−1) . | Vb,fid (km s−1) . | Mbar (M⊙) . | rb,half (kpc) . | M200 (M⊙) . |
|---|---|---|---|---|---|---|---|---|
| CamB | S | 20.10 | 13.85 | 6.85 | 10.08 | 5.35e+07 | 0.86 | 1.23e+09 |
| D512-2 | S | 37.20 | 16.34 | 24.04 | 11.80 | 2.70e+08 | 1.94 | 8.50e+09 |
| D564-8 | S | 25.00 | 9.24 | 11.17 | 6.66 | 5.51e+07 | 1.50 | 2.43e+09 |
| D631-7 | S | 58.50 | 24.51 | 29.50 | 23.54 | 4.84e+08 | 2.03 | 3.55e+10 |
| DDO064 | S | 46.90 | 25.29 | 36.67 | 16.28 | 3.59e+08 | 1.86 | 1.76e+10 |
| DDO154 | S | 48.20 | 18.73 | 27.37 | 13.90 | 3.92e+08 | 2.71 | 1.92e+10 |
| DDO161 | S | 67.50 | 35.35 | 32.14 | 25.01 | 2.11e+09 | 5.59 | 5.58e+10 |
| DDO168 | S | 55.00 | 25.90 | 35.00 | 23.08 | 6.45e+08 | 2.12 | 2.92e+10 |
| ESO079-G014 | S | 178.00 | 100.77 | 109.73 | 64.21 | 3.00e+10 | 9.46 | 1.21e+12 |
| ESO116-G012 | S | 112.00 | 52.33 | 83.47 | 47.73 | 3.59e+09 | 4.07 | 2.78e+11 |
| ESO444-G084 | S | 63.10 | 21.89 | 52.73 | 21.31 | 2.15e+08 | 1.38 | 4.51e+10 |
| ESO563-G021 | S | 321.00 | 200.92 | 286.19 | 176.36 | 1.88e+11 | 12.00 | 7.95e+12 |
| F565-V2 | S | 83.10 | 30.16 | 38.28 | 15.53 | 1.21e+09 | 6.13 | 1.08e+11 |
| F568-3 | S | 120.00 | 52.15 | 66.15 | 29.09 | 8.42e+09 | 10.60 | 3.46e+11 |
| F568-V1 | S | 118.00 | 44.75 | 91.59 | 28.75 | 5.23e+09 | 9.82 | 3.28e+11 |
| F571-8 | S | 144.00 | 81.10 | 93.14 | 70.96 | 7.45e+09 | 2.04 | 6.18e+11 |
| F574-1 | S | 99.70 | 46.48 | 68.23 | 29.70 | 7.96e+09 | 8.73 | 1.92e+11 |
| F583-1 | S | 86.90 | 41.35 | 44.55 | 13.55 | 3.32e+09 | 10.70 | 1.24e+11 |
| F583-4 | S | 69.90 | 31.15 | 43.05 | 23.48 | 1.71e+09 | 4.12 | 6.23e+10 |
| IC2574 | S | 67.50 | 32.02 | 19.54 | 12.57 | 1.89e+09 | 7.24 | 5.58e+10 |
| IC4202 | S | 250.00 | 181.45 | 231.32 | 165.39 | 1.06e+11 | 9.07 | 3.58e+12 |
| KK98-251 | S | 34.60 | 20.25 | 16.35 | 10.59 | 1.95e+08 | 1.83 | 6.76e+09 |
| NGC 0024 | S | 110.00 | 52.54 | 106.73 | 51.90 | 2.84e+09 | 2.53 | 2.62e+11 |
| NGC 0055 | S | 87.40 | 50.19 | 43.53 | 33.96 | 4.40e+09 | 6.74 | 1.26e+11 |
| NGC 0100 | S | 91.20 | 40.75 | 56.83 | 36.27 | 4.26e+09 | 3.72 | 1.45e+11 |
| NGC 0247 | S | 108.00 | 53.09 | 66.63 | 29.91 | 5.99e+09 | 8.02 | 2.48e+11 |
| NGC 0289 | S | 194.00 | 160.25 | 174.05 | 156.00 | 7.26e+10 | 16.54 | 1.60e+12 |
| NGC 0300 | S | 97.00 | 41.87 | 66.19 | 35.13 | 2.71e+09 | 4.56 | 1.76e+11 |
| NGC 0801 | S | 238.00 | 199.22 | 233.82 | 195.75 | 1.87e+11 | 15.86 | 3.06e+12 |
| NGC 0891 | S | 234.00 | 265.08 | 224.00 | 214.65 | 7.51e+10 | 2.79 | 2.90e+12 |
| NGC 1003 | S | 115.00 | 59.35 | 74.39 | 55.38 | 1.12e+10 | 12.36 | 3.02e+11 |
| NGC 1090 | S | 176.00 | 121.39 | 154.59 | 108.35 | 4.77e+10 | 8.68 | 1.17e+12 |
| NGC 1705 | S | 73.20 | 35.42 | 72.84 | 29.77 | 4.51e+08 | 0.95 | 7.21e+10 |
| NGC 2366 | S | 53.70 | 28.57 | 32.98 | 20.62 | 9.79e+08 | 3.25 | 2.71e+10 |
| NGC 2403 | S | 136.00 | 75.85 | 117.48 | 75.48 | 9.28e+09 | 5.07 | 5.15e+11 |
| NGC 2683 | S | 212.00 | 171.90 | 211.40 | 169.48 | 4.21e+10 | 3.45 | 2.12e+12 |
| NGC 2841 | S | 323.00 | 231.30 | 322.93 | 214.81 | 1.07e+11 | 7.98 | 8.11e+12 |
| NGC 2903 | S | 216.00 | 213.11 | 207.86 | 176.97 | 4.43e+10 | 2.58 | 2.25e+12 |
| NGC 2915 | S | 86.50 | 35.40 | 77.83 | 27.64 | 9.96e+08 | 4.97 | 1.22e+11 |
| NGC 2955 | S | 276.00 | 252.60 | 245.59 | 246.68 | 1.98e+11 | 8.12 | 4.91e+12 |
| NGC 2998 | S | 214.00 | 157.58 | 204.14 | 150.74 | 1.07e+11 | 11.13 | 2.18e+12 |
| NGC 3109 | S | 67.30 | 21.72 | 36.06 | 15.30 | 7.31e+08 | 3.92 | 5.52e+10 |
| NGC 3198 | S | 157.00 | 101.32 | 118.91 | 85.11 | 3.36e+10 | 10.54 | 8.13e+11 |
| NGC 3521 | S | 220.00 | 200.33 | 214.79 | 174.16 | 4.79e+10 | 2.99 | 2.38e+12 |
| NGC 3726 | S | 169.00 | 131.38 | 119.56 | 111.65 | 4.37e+10 | 6.73 | 1.03e+12 |
| NGC 3741 | S | 51.60 | 14.28 | 27.05 | 11.19 | 2.56e+08 | 3.79 | 2.39e+10 |
| NGC 3769 | S | 126.00 | 98.81 | 106.57 | 98.43 | 1.67e+10 | 4.28 | 4.04e+11 |
| NGC 3877 | S | 171.00 | 145.67 | 157.15 | 109.76 | 3.82e+10 | 6.22 | 1.07e+12 |
| NGC 3893 | S | 194.00 | 152.06 | 193.30 | 149.89 | 3.70e+10 | 3.83 | 1.60e+12 |
| NGC 3917 | S | 138.00 | 80.96 | 104.05 | 57.20 | 1.35e+10 | 6.35 | 5.40e+11 |
| NGC 3953 | S | 224.00 | 176.03 | 211.67 | 159.61 | 7.44e+10 | 7.33 | 2.52e+12 |
| NGC 3972 | S | 134.00 | 79.21 | 105.02 | 62.09 | 8.79e+09 | 4.75 | 4.91e+11 |
| NGC 4010 | S | 129.00 | 77.65 | 86.12 | 68.91 | 1.24e+10 | 5.15 | 4.35e+11 |
| NGC 4013 | S | 198.00 | 166.75 | 197.26 | 161.12 | 4.35e+10 | 5.49 | 1.70e+12 |
| NGC 4051 | S | 161.00 | 141.36 | 131.17 | 103.88 | 5.12e+10 | 6.35 | 8.81e+11 |
| NGC 4088 | S | 182.00 | 189.42 | 161.40 | 170.20 | 6.46e+10 | 5.21 | 1.30e+12 |
| NGC 4100 | S | 195.00 | 147.99 | 185.05 | 132.10 | 3.38e+10 | 5.13 | 1.62e+12 |
| NGC 4138 | S | 195.00 | 171.38 | 193.22 | 142.04 | 2.40e+10 | 2.61 | 1.62e+12 |
| NGC 4157 | S | 201.00 | 182.02 | 194.60 | 174.37 | 6.38e+10 | 4.96 | 1.79e+12 |
| NGC 4183 | S | 115.00 | 66.98 | 83.39 | 43.71 | 1.01e+10 | 7.10 | 3.02e+11 |
| NGC 4217 | S | 191.00 | 234.50 | 177.25 | 205.45 | 4.61e+10 | 2.69 | 1.52e+12 |
| NGC 4559 | S | 124.00 | 83.97 | 98.55 | 78.38 | 1.74e+10 | 7.55 | 3.84e+11 |
| NGC 5033 | S | 225.00 | 241.63 | 224.72 | 185.97 | 7.03e+10 | 3.56 | 2.56e+12 |
| NGC 5055 | S | 206.00 | 198.71 | 201.57 | 196.38 | 9.21e+10 | 5.53 | 1.93e+12 |
| NGC 5371 | S | 242.00 | 213.77 | 214.79 | 173.23 | 1.85e+11 | 11.10 | 3.23e+12 |
| NGC 5585 | S | 92.30 | 44.82 | 62.65 | 40.75 | 3.71e+09 | 4.59 | 1.50e+11 |
| NGC 5907 | S | 235.00 | 165.49 | 218.01 | 139.96 | 1.16e+11 | 11.24 | 2.94e+12 |
| NGC 5985 | S | 305.00 | 165.00 | 288.80 | 140.14 | 1.20e+11 | 12.81 | 6.75e+12 |
| NGC 6015 | S | 166.00 | 106.26 | 151.16 | 106.20 | 2.38e+10 | 5.11 | 9.71e+11 |
| NGC 6195 | S | 258.00 | 235.77 | 233.45 | 235.70 | 2.23e+11 | 10.62 | 3.96e+12 |
| NGC 6503 | S | 121.00 | 101.33 | 119.67 | 91.08 | 8.74e+09 | 2.16 | 3.55e+11 |
| NGC 6674 | S | 291.00 | 177.58 | 285.98 | 175.67 | 1.50e+11 | 10.19 | 5.81e+12 |
| NGC 6946 | S | 181.00 | 195.85 | 176.12 | 149.58 | 4.06e+10 | 4.39 | 1.28e+12 |
| NGC 7331 | S | 257.00 | 275.82 | 257.00 | 255.45 | 1.40e+11 | 4.40 | 3.91e+12 |
| NGC 7793 | S | 116.00 | 72.47 | 102.82 | 72.45 | 4.67e+09 | 2.55 | 3.11e+11 |
| NGC 7814 | S | 265.00 | 290.19 | 226.72 | 163.25 | 3.87e+10 | 1.66 | 4.31e+12 |
| PGC51017 | S | 20.50 | 18.81 | 20.27 | 12.47 | 3.45e+08 | 1.58 | 1.31e+09 |
| UGC00128 | S | 134.00 | 55.39 | 78.98 | 35.06 | 1.59e+10 | 18.83 | 4.91e+11 |
| UGC00191 | S | 83.85 | 42.19 | 71.49 | 30.11 | 2.79e+09 | 5.41 | 1.11e+11 |
| UGC00731 | S | 74.00 | 37.19 | 46.52 | 10.43 | 2.56e+09 | 7.30 | 7.46e+10 |
| UGC00891 | S | 63.75 | 26.57 | 28.75 | 17.86 | 7.56e+08 | 3.50 | 4.65e+10 |
| UGC02259 | S | 90.00 | 36.92 | 76.15 | 29.49 | 1.52e+09 | 4.01 | 1.39e+11 |
| UGC02455 | S | 61.00 | 57.14 | 30.44 | 56.18 | 2.89e+09 | 1.93 | 4.05e+10 |
| UGC02487 | S | 383.00 | 251.56 | 376.62 | 250.17 | 2.69e+11 | 10.67 | 1.40e+13 |
| UGC02885 | S | 305.00 | 231.80 | 260.15 | 210.89 | 2.55e+11 | 21.76 | 6.75e+12 |
| UGC02916 | S | 218.00 | 237.95 | 209.71 | 197.65 | 9.30e+10 | 8.55 | 2.31e+12 |
| UGC02953 | S | 319.00 | 247.65 | 319.00 | 238.35 | 1.40e+11 | 5.31 | 7.79e+12 |
| UGC03205 | S | 237.00 | 174.00 | 236.00 | 173.49 | 6.97e+10 | 5.94 | 3.02e+12 |
| UGC03546 | S | 262.00 | 330.90 | 193.03 | 167.97 | 5.42e+10 | 2.52 | 4.16e+12 |
| UGC03580 | S | 131.00 | 97.26 | 96.63 | 84.30 | 1.24e+10 | 5.84 | 4.57e+11 |
| UGC04278 | S | 92.80 | 46.03 | 45.88 | 21.46 | 2.14e+09 | 5.70 | 1.53e+11 |
| UGC04305 | S | 37.30 | 33.87 | 24.47 | 19.17 | 1.29e+09 | 3.21 | 8.57e+09 |
| UGC04325 | S | 92.70 | 44.02 | 87.71 | 37.41 | 1.91e+09 | 3.14 | 1.52e+11 |
| UGC04499 | S | 74.30 | 39.87 | 49.06 | 27.20 | 2.24e+09 | 4.77 | 7.56e+10 |
| UGC05005 | S | 100.00 | 43.08 | 37.87 | 25.08 | 6.16e+09 | 15.24 | 1.94e+11 |
| UGC05253 | S | 248.00 | 238.24 | 246.00 | 208.09 | 1.08e+11 | 6.08 | 3.49e+12 |
| UGC05414 | S | 61.40 | 33.68 | 41.04 | 26.20 | 1.32e+09 | 2.52 | 4.13e+10 |
| UGC05716 | S | 74.70 | 31.57 | 49.52 | 20.96 | 1.75e+09 | 6.86 | 7.69e+10 |
| UGC05721 | S | 82.60 | 34.76 | 81.92 | 29.52 | 1.01e+09 | 3.33 | 1.06e+11 |
| UGC05750 | S | 78.90 | 41.46 | 24.89 | 15.88 | 3.13e+09 | 13.59 | 9.14e+10 |
| UGC05764 | S | 55.80 | 22.22 | 49.25 | 16.24 | 2.59e+08 | 2.08 | 3.05e+10 |
| UGC05829 | S | 68.60 | 37.43 | 34.69 | 12.54 | 1.64e+09 | 5.10 | 5.87e+10 |
| UGC05918 | S | 44.50 | 19.72 | 29.16 | 9.21 | 5.12e+08 | 3.04 | 1.49e+10 |
| UGC05986 | S | 116.00 | 56.04 | 98.38 | 51.27 | 5.89e+09 | 3.44 | 3.11e+11 |
| UGC06399 | S | 87.60 | 38.86 | 58.74 | 27.28 | 2.04e+09 | 4.54 | 1.27e+11 |
| UGC06446 | S | 84.90 | 38.55 | 64.44 | 24.16 | 2.33e+09 | 6.00 | 1.15e+11 |
| UGC06614 | S | 205.00 | 209.41 | 184.29 | 186.91 | 9.13e+10 | 13.15 | 1.90e+12 |
| UGC06667 | S | 85.70 | 30.25 | 54.81 | 12.29 | 1.77e+09 | 5.12 | 1.19e+11 |
| UGC06786 | S | 229.00 | 175.04 | 219.00 | 155.28 | 4.34e+10 | 4.47 | 2.71e+12 |
| UGC06787 | S | 276.00 | 271.81 | 243.26 | 170.76 | 5.58e+10 | 2.77 | 4.91e+12 |
| UGC06818 | S | 74.40 | 32.73 | 31.86 | 28.59 | 2.23e+09 | 3.73 | 7.59e+10 |
| UGC06917 | S | 111.00 | 56.30 | 79.59 | 43.25 | 6.11e+09 | 6.44 | 2.70e+11 |
| UGC06923 | S | 81.10 | 47.91 | 61.65 | 43.56 | 2.52e+09 | 2.88 | 9.97e+10 |
| UGC06930 | S | 109.00 | 60.56 | 78.67 | 41.51 | 8.77e+09 | 8.06 | 2.55e+11 |
| UGC06983 | S | 113.00 | 51.91 | 90.67 | 43.65 | 6.60e+09 | 7.81 | 2.86e+11 |
| UGC07089 | S | 79.10 | 42.06 | 40.58 | 29.31 | 3.41e+09 | 5.01 | 9.22e+10 |
| UGC07125 | S | 65.60 | 44.56 | 31.20 | 24.34 | 7.51e+09 | 10.46 | 5.10e+10 |
| UGC07151 | S | 76.20 | 44.10 | 64.66 | 36.63 | 1.96e+09 | 3.54 | 8.19e+10 |
| UGC07323 | S | 85.60 | 51.74 | 52.58 | 35.03 | 3.01e+09 | 3.91 | 1.18e+11 |
| UGC07399 | S | 106.00 | 33.87 | 91.53 | 32.51 | 1.57e+09 | 3.27 | 2.33e+11 |
| UGC07524 | S | 83.80 | 43.92 | 44.96 | 19.35 | 3.58e+09 | 7.73 | 1.11e+11 |
| UGC07559 | S | 32.10 | 19.76 | 18.91 | 13.18 | 2.79e+08 | 1.79 | 5.34e+09 |
| UGC07577 | S | 17.80 | 12.60 | 6.69 | 5.52 | 8.10e+07 | 1.10 | 8.39e+08 |
| UGC07603 | S | 64.00 | 27.55 | 58.22 | 27.15 | 5.31e+08 | 1.56 | 4.71e+10 |
| UGC07690 | S | 60.70 | 36.49 | 60.65 | 35.71 | 9.48e+08 | 1.59 | 3.99e+10 |
| UGC07866 | S | 33.10 | 18.42 | 23.18 | 12.75 | 2.19e+08 | 1.53 | 5.88e+09 |
| UGC08286 | S | 84.30 | 35.34 | 72.65 | 29.57 | 1.48e+09 | 3.94 | 1.13e+11 |
| UGC08490 | S | 80.10 | 35.71 | 76.29 | 35.55 | 1.47e+09 | 2.96 | 9.59e+10 |
| UGC08550 | S | 57.80 | 24.64 | 48.45 | 23.06 | 5.28e+08 | 3.96 | 3.41e+10 |
| UGC08699 | S | 202.00 | 214.73 | 170.49 | 125.86 | 3.01e+10 | 3.85 | 1.82e+12 |
| UGC08837 | S | 48.00 | 29.32 | 18.56 | 13.25 | 6.76e+08 | 2.82 | 1.90e+10 |
| UGC09037 | S | 160.00 | 116.33 | 102.52 | 107.36 | 5.97e+10 | 10.23 | 8.64e+11 |
| UGC09133 | S | 289.00 | 283.20 | 287.52 | 244.07 | 1.86e+11 | 8.06 | 5.69e+12 |
| UGC10310 | S | 73.20 | 40.86 | 52.31 | 24.84 | 2.46e+09 | 4.84 | 7.21e+10 |
| UGC11455 | S | 291.00 | 232.15 | 232.60 | 204.66 | 2.05e+11 | 10.36 | 5.81e+12 |
| UGC11820 | S | 84.45 | 38.77 | 49.23 | 20.19 | 3.11e+09 | 8.75 | 1.13e+11 |
| UGC12506 | S | 255.00 | 134.55 | 210.25 | 101.90 | 1.17e+11 | 18.78 | 3.82e+12 |
| UGC12632 | S | 73.20 | 36.66 | 44.04 | 18.21 | 2.97e+09 | 7.28 | 7.21e+10 |
| UGC12732 | S | 98.00 | 46.29 | 59.03 | 23.06 | 5.70e+09 | 11.78 | 1.82e+11 |
| UGCA442 | S | 57.80 | 24.49 | 34.31 | 18.27 | 4.20e+08 | 2.18 | 3.41e+10 |
| UGCA444 | S | 38.30 | 16.18 | 25.38 | 14.49 | 9.51e+07 | 1.19 | 9.32e+09 |
| U11707 | A | 103.74 | 32.33 | 63.19 | 22.91 | 2.24e+09 | 5.99 | 2.18e+11 |
| N2552 | A | 96.10 | 35.28 | 68.53 | 30.81 | 1.78e+09 | 3.43 | 1.71e+11 |
| wlm | LT | 38.53 | 14.84 | 26.93 | 10.86 | 1.73e+08 | 2.22 | 9.49e+09 |
| ddo87 | LT | 56.63 | 18.79 | 22.83 | 4.92 | 5.85e+08 | 4.68 | 3.20e+10 |
| ddo50 | LT | 38.84 | 33.88 | 22.29 | 7.38 | 1.67e+09 | 4.62 | 9.74e+09 |
| ddo52 | LT | 61.72 | 22.52 | 38.71 | 10.70 | 6.30e+08 | 3.80 | 4.20e+10 |
| ngc1569 | LT | 39.28 | 38.68 | 23.57 | 20.45 | 1.12e+09 | 2.84 | 1.01e+10 |
| haro29 | LT | 43.49 | 12.00 | 29.82 | 9.69 | 1.68e+08 | 4.36 | 1.39e+10 |
| cvnidwa | LT | 26.45 | 8.89 | 9.14 | 8.43 | 4.53e+07 | 1.68 | 2.91e+09 |
| ddo133 | LT | 46.73 | 18.84 | 32.36 | 11.48 | 2.87e+08 | 2.28 | 1.74e+10 |
| ic1613 | LT | 21.13 | 15.29 | 6.13 | 5.03 | 1.47e+08 | 1.82 | 1.44e+09 |
| ddo216 | LT | 18.91 | 8.45 | 12.69 | 6.90 | 1.73e+07 | 0.60 | 1.01e+09 |
| ddo126 | LT | 38.74 | 18.70 | 19.63 | 10.07 | 2.91e+08 | 2.44 | 9.66e+09 |
| NGC 925 | TH | 114.50 | 75.56 | 54.41 | 46.03 | 1.73e+10 | 9.65 | 2.98e+11 |
| NGC 3621 | TH | 159.20 | 118.03 | 130.41 | 116.23 | 3.48e+10 | 6.38 | 8.50e+11 |
| ngc4396 | R | 99.46 | 30.63 | 79.58 | 30.13 | 1.12e+09 | 2.71 | 1.91e+11 |
| ngc6106 | R | 124.75 | 68.67 | 114.06 | 68.32 | 5.46e+09 | 2.58 | 3.91e+11 |
| ugc4169 | R | 97.72 | 46.37 | 74.84 | 38.39 | 3.11e+09 | 3.65 | 1.80e+11 |
| ugc3371 | R | 64.01 | 15.95 | 36.79 | 10.54 | 3.98e+08 | 4.26 | 4.71e+10 |
The main effect of self-interactions is to ‘transfer heat’ from the outside in, ‘thermalizing’ in the process the inner velocity dispersion profile. This is demonstrated by the blue circles in the bottom panel of Fig. A1, which corresponds to the same ΛCDM halo, but evolved with the DMO SIDM code (Section 3.4), with ssi = 10 cm2 g−1.
Note that, in principle, this equation permits a family of solutions for ρ(r), many of which have cuspy inner profiles. (A simple example is, of course, the singular isothermal sphere.) Integrating equation (A7) numerically, therefore, requires that appropriate boundary conditions are set.
Motivated by the density profile of the numerical SIDM halo shown in the top panel of Fig. A1, we may set the conditions y(0) = 0 (i.e. finite central density) and dy/dx(r = 0) = 0 (i.e. a flat density slope at the centre or ‘constant density core’) to solve for y(x).
This solution gives a unique ρ(r) profile that may be scaled for any particular pair of values chosen from ρ0, r0, and σ0. The thin blue lines in the top two panels of Fig. A1 show one of these profiles and demonstrate that it provides an excellent fit to the actual inner density profile of simulated SIDM haloes. This analytical model is similar to that of Kaplinghat et al. (2014).
A2 Empirical relations
As described above, describing the inner mass profile of an SIDM halo requires that two parameters be specified. These parameters are expected to be closely related to the NFW parameters of its corresponding ΛCDM halo. We show this in Fig. A2 for matching pairs of haloes identified in DMO ΛCDM and SIDM runs of one of the AP-L1 volumes. The SIDM run assumes ssi = 10 cm2 g−1.

Empirical relations between the characteristic parameters of CDM and SIDM (ssi = 10 cm2 g−1) matched halo pairs in the APOSTLE L1-V1 simulation. Left: Central SIDM velocity dispersion, σ0, versus ΛCDM Vmax. Right: Characteristic SIDM core radius r0 versus the characteristic ΛCDM radius, r1, given by equation (A2).
The blue bands shown in Fig. 8 were computed this way, after transforming thousands of Planck-normalized ΛCDM haloes with M200 and c sampled from the mass–concentration relation of Ludlow et al. (2016). We emphasize that the relations shown in Fig. A2 are sensitive to the assumed value of ssi = 10 cm2 g−1.
A3 Including baryons in SIDM haloes
We impose this condition when solving equation (A9) to find the dark matter density profile in the presence of baryons. The final dark matter profile is renormalized by the universal baryon fraction to take into account the fact that the SIDM halo parameters computed as described in Section A2 were computed from a DMO simulation. We also make a small adjustment to account for the fact that the potential wells of low-mass haloes in cosmological hydrodyamical simulations are systematically less deep than in DMO runs (see e.g. Sawala et al. 2016). These adjustments have a minor effect on our results, but help to reconcile our analytical model with the results of the SIDM cosmological hydrodynamical run shown in the bottom right-hand panels of Figs 8 and 9.
For illustration, we show two examples of our procedure in Fig. A3. This illustrates the effect on the inner dark matter profile of two rather different baryonic distributions; that of NGC 1075 (left) and that of IC 2574 (right), when added to two randomly drawn SIDM haloes with maximum velocities matching the observed values of each of these galaxies. The solid black lines indicate the DMO SIDM profile; the dashed black lines are the resulting profiles after the baryons have been added. Note that the dashed-line profiles have less dark matter in total because of the baryonic mass renormalization described in the preceding paragraph. The addition of baryons leads, as expected, to dark matter profiles that are denser near the centre and that drop more sharply than their DMO counterparts.
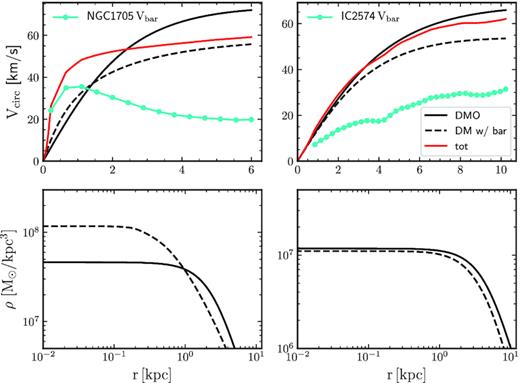
Baryon-induced transformation of an SIDM halo, according to the model described in Section A3. Two examples are given, where the baryonic mass profiles of NGC 1075 (left) and IC 2574 (right) are added to randomly selected SIDM haloes with matching Vmax (73 km s−1 for NGC 1075 and 68 km s−1 for IC 2574). The DMO SIDM halo profiles are shown with solid lines. The resulting profiles induced by the baryonic component and the rescaling/normalization procedure described in Section A3 are shown with dashed lines. Note that the dark matter profile is less affected in the case of IC 2574 than for NGC 1075 because the baryonic mass distribution is more extended in the former and has a smaller effect on the central gravitational potential.



