-
PDF
- Split View
-
Views
-
Cite
Cite
Antonio D Montero-Dorta, L Raul Abramo, Benjamin R Granett, Sylvain de la Torre, Luigi Guzzo, The Multi-Tracer Optimal Estimator applied to VIPERS, Monthly Notices of the Royal Astronomical Society, Volume 493, Issue 4, April 2020, Pages 5257–5272, https://doi.org/10.1093/mnras/staa405
Close - Share Icon Share
ABSTRACT
We use mock galaxy data from the VIMOS Public Extragalactic Redshift Survey (VIPERS) to test the performance of the Multi-Tracer Optimal Estimator (MTOE) of Abramo et al. as a tool to measure the monopoles of the power spectra of multiple tracers of the large-scale structure, |$P^{(0)}_\alpha (\mathbf {k})$|. We show that MTOE provides more accurate measurements than the standard technique of Feldman, Kaiser & Peacock (FKP), independently of the tracer-selection strategy adopted, on both small and large scales. The largest improvements on individual |$P^{(0)}_\alpha (\mathbf {k})$| are obtained on small scales, using a colour–magnitude selection, due to MTOE being naturally better equipped to deal with shot noise: we report an average error reduction with respect to FKP of |$\sim 30{{\ \rm per\ cent}}$| at |$0.3 \lt k \, [h$| Mpc−1] < 0.5, with improvements exceeding 40–50 |${{\ \rm per\ cent}}$| for some tracers. On large scales (k[h Mpc−1] ≲ 0.1), the gain in accuracy resulting from cosmic-variance cancellation is ∼10 |${{\ \rm per\ cent}}$| for the ratios of |$P^{(0)}_\alpha (\mathbf {k})$|. We have carried out a Markov chain Monte Carlo analysis to determine the impact of these gains on several quantities derived from |$P^{(0)}_\alpha (\mathbf {k})$|. If we pushthat the estimated power spectra are themselves the measurement to scales |$0.3 \lt k \, [h$| Mpc−1] < 0.5, the average improvements are |$\sim 30{{\ \rm per\ cent}}$| for the amplitudes of the monopoles, |$\sim 75{{\ \rm per\ cent}}$| for the monopole ratios, and |$\sim 20{{\ \rm per\ cent}}$| for the linear galaxy biases. Our results highlight the potential of MTOE to shed light upon the physics that operate both on large and small cosmological scales. The effect of MTOE on cosmological constraints using VIPERS data will be addressed in a separate paper.
1 INTRODUCTION
Upcoming dark-energy surveys such as Euclid,1 the Dark Energy Spectroscopic Instrument (DESI2), the Dark Energy Survey (DES3), the Javalambre Physics of the Accelerated Universe Astrophysical Survey (J-PAS4), the Prime Focus Spectroscopy survey (PFS5), the Large Synoptic Spectroscopic Telescope (LSST6), or SPHEREx7 will collect data from tens to hundreds of millions of galaxies and quasars over enormous cosmological volumes. These data sets will map the large-scale structure of the Universe (LSS) over vast distances and time-scales, allowing highly accurate measurements of the accelerated expansion, the growth rate of structure, and many other cosmological parameters. In addition to their statistical power, some of these upcoming dark-energy surveys such as J-PAS are also advantageous, as compared to previous experiments, in that they employ wider galaxy selections that are not based on a few specific LSS tracers – such as the luminous red galaxies and quasars selected for the Baryon Acoustic Oscillation Spectroscopic Survey (BOSS; Eisenstein et al. 2011; Dawson et al. 2013). Other data sets will partially overlap in some cosmological volumes (e.g. J-PAS, DESI, and Euclid).
This upcoming wealth of cosmological-survey data naturally poses the question of how clustering information from different galaxy populations or data sets can be combined in an optimal way. Importantly, different LSS maps are not independent, since different species of galaxies trace the same underlying dark matter density field, albeit in slightly different ways (Benoist et al. 1996; Guzzo et al. 1997). This imposes a constraint between different tracers that can be exploited in order to realize the full potential of overlapping data sets. However, the inclusion of this additional information brings with it the correlations that exist between the distributions of those different tracers, which arise primarily as a consequence of cosmic variance – i.e. the fact that local patterns of matter overdensities and underdensities propagate to the number counts of all tracers.
Despite this limitation, the strict bounds imposed by cosmic variance do not apply to many key cosmological quantities (McDonald 2008; Seljak 2009). By comparing the clustering of different tracers we can beat cosmic variance, i.e. we can measure some quantities with an accuracy that is basically unconstrained by cosmic variance. One of the quantities of interest is bias, which broadly describes the relation between the spatial distribution of galaxies (or haloes) and that of the underlying matter density field. The cancellation of cosmic variance can serve not only to measure bias, but also to improve our constraints on the matter growth rate, reflected in the redshift-space distortions (RSDs; see Kaiser 1987; Hamilton 1998), as well as the non-gaussianity parameters fNL and gNL, and in general any parameters that affect the relative clustering of different tracers (see e.g. Slosar 2009; Gil-Marín et al. 2010; Hamaus, Seljak & Desjacques 2011; Smith, Desjacques & Marian 2011; Cai & Bernstein 2012; Hamaus, Seljak & Desjacques 2012; Abramo & Leonard 2013; Blake et al. 2013; Ferramacho et al. 2014; Bull et al. 2015; Fonseca et al. 2015; Abramo & Bertacca 2017; Alarcon, Eriksen & Gaztañaga 2018; Witzemann et al. 2019, for more information)
In this paper, we apply the Multi-Tracer Optimal Estimator (hereafter, MTOE) to mock data that mimic the VIMOS Public Extragalactic Redshift Survey (Guzzo et al. 2014) in the redshift range 0.55 < z < 1.1. The MTOE for the redshift-space power spectra of an arbitrary number of LSS tracers was derived in Abramo, Secco & Loureiro (2016). The technique, which is a generalization of the standard weighting scheme of Feldman, Kaiser & Peacock (1994; henceforth FKP), is based on the Fisher matrix for multiple tracers (Abramo 2012; Abramo & Leonard 2013), which encapsulates the information contained in multi-tracer cosmological surveys.
The goal of this paper is to evaluate the performance of MTOE as compared to the traditional FKP approach in the context of the measurement of galaxy power spectra and galaxy biases. Note that FKP does not necessarily imply a single-tracer approach: we will compare MTOE with FKP in a multi-tracer fashion, i.e. in both cases splitting our sample in multiple galaxy populations. The latter approach was employed by Blake et al. (2013), who analysed multiple tracers in the Galaxy And Mass Assembly (GAMA) survey. The authors employed FKP weighting in a multi-tracer context, reporting improvements of 10–20 |${{\ \rm per\ cent}}$| in measurements of the gravitational growth rate compared to a single-tracer analysis. The added value of MTOE is that it employs a multi-tracer weighting scheme, which is optimal for measuring the power spectra of the individual tracers. It is important to stress that, in the context of our analysis, ‘optimal’ always refers to this ‘optimal weighting scheme’ for the determination of the density field of each tracer. Although, we will discuss different strategies for tracer selection, it is outside the scope of this work to provide an optimal tracer selection scheme, which largely depends on the galaxy information available.
The first multi-tracer weighting scheme was proposed by Percival, Verde & Peacock (2004). The PVP method provides optimal weights for a minimum-variance estimator of the combined matter power spectrum |$P_\mathrm{ m}(\mathbf {k})$| in situations where several different biased tracers are considered – see also Cai, Bernstein & Sheth (2011) and Granett et al. (2015). As compared to PVP, the advantage of MTOE resides in the fact that it is optimal both in terms of the estimation of the matter power spectrum, as well as the redshift-space auto-power spectra of each individual tracer. In fact, as shown in Abramo et al. (2016), when the individual power spectra of the tracers estimated with the MTOE method are combined to obtain the matter power spectrum, the result is identical to that obtained using the PVP method.
We have successfully applied MTOE to the determination of the power spectra and the ratios of biases for different subsets of haloes in the context of the study of halo assembly bias (or more generally, secondary bias). In Sato-Polito et al. (2019), we show that MTOE provides a significant improvement in the signal-to-noise of the secondary-bias measurement. In Sato-Polito et al. (2019), each subset of haloes is regarded as a different tracer, and a total of 32 tracers per simulation box are considered. Applying the method to a real galaxy data set is, however, beset by two difficulties which can potentially reduce the ‘gain signal’. First, the natural stochasticity in the way galaxies populate haloes – i.e. how a particular subset of galaxies might typically occupy certain types of haloes, but only in a statistical sense. Secondly, the observational limitations associated with real data, such as incompleteness or a tracer-dependent selection function.
VIPERS is an excellent data set to test the performance of MTOE, due to a combination of large volume, broad galaxy selection, and high completeness (see e.g. Granett et al. 2015; de la Torre et al. 2017; Pezzotta et al. 2017; Rota et al. 2017; Mohammad et al. 2018 for other cosmological analyses using VIPERS). In order to partially circumvent the second obstacle mentioned above, i.e. the fact that unaccounted observational effects can reduce the potential gain provided by MTOE, in this first paper we concentrate on mock galaxy data. This allows us to build the machinery and to identify the particular cases where MTOE is more advantageous than the standard FKP analysis.
The paper is organized as follows. In Section 2, we summarize the MTOE and FKP techniques by describing their weighting schemes and the treatment of the window functions. Section 3 describes the VIPERS mock data, and Section 4 presents our tracer selection schemes. Section 5 provides practical information on the implementation of the MTOE method. In Section 6, we present the main results of this analysis: the improvements provided by MTOE as compared to FKP on the estimation of the power spectra of multiple tracers and derived quantities such as galaxy biases. Finally, we discuss the implications of our results and summarize our main conclusions in Section 7. Throughout this work, we assume the standard lambda cold dark matter (ΛCDM) cosmology (Planck Collaboration I 2014), with parameters h = 0.677, Ωm = 0.307, ΩΛ = 0.693, ns = 0.96, and σ8 = 0.823.
2 OPTIMAL ESTIMATORS OF THE POWER SPECTRUM
2.1 The optimal weights
Galaxy surveys are not only limited to finite regions of space, both in the angular and radial direction, but also they typically have modulations in the mean number densities of galaxies across the survey volume. These variations in the mean density of galaxies (the selection functions, |$\bar{n}_\mu$|) can be due to an intrinsic redshift-dependent abundance of these objects, but they can also arise as a consequence of the depth of the survey, or because of varying observing conditions across different patches of the sky.
Given that selection functions are in general inhomogeneous, some regions of the survey are expected to carry more weight than others: typically, regions with higher densities of galaxies have better clustering signal compared with regions of low number densities. Since this is ultimately a matter of signal versus noise, not only the weights applied to each region in the survey volume must know about the mean density of galaxies in that region, but also about the signal that we are trying to measure – i.e. the strength of the clustering of the tracers.
However, if there are two or more distinct biased tracers occupying the same survey volume, the signal and the noise for all possible auto- and cross-correlations should now be taken into account, leading to a generalization of the FKP weights. If the goal is to compute the matter power spectrum |$P_\mathrm{ m}(\mathbf {k})$|, the generalized weights that lead to a minimum-variance estimator of |$P_\mathrm{ m} (\mathbf {k})$| were first found by Percival et al. (2004) – see also Cai et al. (2011) for a minimum-variance estimator of the mass density field. However, if the goal is to compute the redshift-space power spectra of all the individual tracers (which can then be combined to find the matter power spectrum), then the optimal weights are those derived in Abramo et al. (2016). In what follows, we employ both this latter method, which we call the MTOE, and the standard method (FKP).
2.2 Estimators versus theory: the window functions
The power spectra estimated either by equation (3) or equation (6) are based on the Fourier transforms of the weighted fields, not on the density contrasts. Since the weighting is applied in configuration space, the Fourier transforms of the weighted fields are convolutions of the Fourier transforms of the weights and of the density contrasts. This means that the estimated power spectra are themselves convolutions of the putative power spectrum – i.e. there is mode coupling.
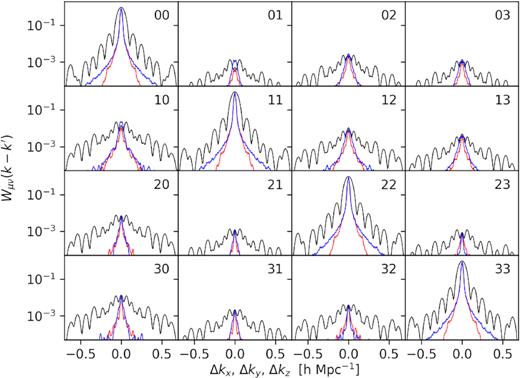
Survey window functions |$W_{\mu \nu } (\mathbf {k}-\mathbf {k}^{\prime })$| for each tracer, as a function of kx (black), ky (blue), and kz (red), normalized at the value of Wμμ(0). Rows correspond to μ, columns to ν.
In addition to the survey window function, the mass assignment (MA) method, whereby an object (a galaxy, in our case) is associated to a given cell in the grid, may also distort the original power spectrum. In order to deconvolve the effects of the MA on the estimated power spectra we employ the procedure outlined in Jing (2005). For all modes of interest, which lie well below the Nyquist frequency of the grid, the MA convolution is well approximated by a normalization factor, |$P(\mathbf {k}) \simeq P(\mathbf {k}) \times W^2_{\mathrm{ MA}}(\mathbf {k})$|. We compute the window function following the standard prescription (Jing 2005), using a theoretical matter power spectrum from camb9 (Lewis & Bridle 2002) to account for the shape of the power spectrum.
Finally, we allow for anisotropies in the power spectra through redshift-space distortions. Even though in this first paper we only employ the angle-averaged spectra (i.e. the monopoles), we have also computed the higher order multipoles. We follow the method proposed by Bianchi et al. (2015) and Scoccimarro (2015), which makes use of the physical (configuration space) multipoles of the galaxy maps and avoids having to fix a single direction to the survey in order to define the angles of the Fourier modes (|$\mu \rightarrow \hat{\mathbf {k}} \cdot \hat{\mathbf {r}}$|).
3 THE MOCK DATA
In order to test the performance of MTOE, we use mock data from the VIMOS Public Extragalactic Redshift Survey (VIPERS; Guzzo et al. 2014; Scodeggio et al. 2018), which provides high-fidelity galaxy maps at high redshift. The survey measured 90 000 galaxies with moderate-resolution spectroscopy within the nominal redshift range 0.5 ≲ z ≲ 1.1, using the Visible Multi-Object Spectrograph (VIMOS) at VLT. Targets were selected to a limiting magnitude of iAB = 22.5 in 24 square degrees of the CFHTLS Wide imaging survey. This area is divided in two fields, W1 and W4, with 16 and 8 square degrees, respectively. The low-redshift limit was imposed by a pre-selection based upon colour that effectively removed foreground galaxies while ensuring a robust flux-limited selection at z > 0.5. For more information on the Public Data Release 2 (PDR-2), the one used in this paper, refer to Scodeggio et al. (2018). Detailed descriptions of the data reduction and management infrastructure are presented in Garilli et al. (2014). For information on the survey design and target selection, see Guzzo et al. (2014).
We employ a set of 153 independent VIPERS-like mock catalogues (de la Torre et al. 2013, 2017; Mohammad et al. 2018) that mimic the VIPERS survey geometry and the application of the slit-assignment algorithm and redshift measurement error. As discussed in Mohammad et al. (2018), these mocks represent very well the global properties of the galaxy population targeted by VIPERS. However, they were not built to simultaneously and precisely reproduce the measured bias and number density of multiple subpopulations defined in colour–magnitude space.10 In order to avoid inconsistencies in the computation of errors, we restrict our analysis to the mocks themselves. In this way, we can better isolate the improvements provided by MTOE and build the machinery for the application of the method to the actual VIPERS data.
The VIPERS mocks were built from the Big MultiDark Planck (Klypin et al. 2016) N-body cosmological simulation, which assumes the standard ΛCDM cosmology (Planck Collaboration et al. 2014), with parameters h = 0.677, Ωm = 0.307, ΩΛ = 0.693, ns = 0.96, and σ8 = 0.823. Dark matter haloes were populated with galaxies using the technique of halo occupation distributions (HOD). The parameters of the HOD were calibrated using clustering measurements as a function of luminosity from the preliminary data release of VIPERS (see de la Torre et al. 2013, 2017 for a detailed description of the procedure). Importantly, since the resolution of the box is not good enough to match the typical halo masses probed by VIPERS, a population of low-mass haloes were subsequently added following the method presented in de la Torre & Peacock (2013). In essence, central galaxies were placed at the centre of haloes assuming no peculiar velocities with respect to the hosting-halo rest frame, whereas satellite galaxies were disposed around haloes following an NFW profile (Navarro, Frenk & White 1997). For satellite galaxies, a random velocity component was added to the hosting-halo peculiar velocity.
Luminosities in the B band and colours were assigned to galaxies following the methodology presented in Skibba et al. (2006) and Skibba (2009). First, an analytical luminosity- and redshift-dependent HOD parametrization was derived by fitting the observed projected correlation functions in several samples defined using luminosity thresholds (de la Torre et al. 2013). Secondly, galaxies were placed in haloes following the observed conditional colour distribution (<U − V|MB >) of VIPERS, which was fit with a double Gaussian model. A detailed description on how these assignments were performed can be found in Skibba et al. (2006) and Skibba (2009). A summary of the procedure can be found in Mohammad et al. (2018). The redshift distribution of the mocks is shown in Fig. 2.
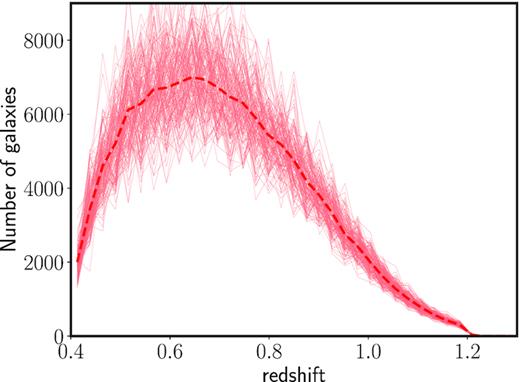
Redshift distribution of the 153 VIPERS mocks used in this work in bins of Δz = 0.025. The mean of all mocks is represented by a thick dashed line.
4 TRACER SELECTION
The selection of the LSS tracers is a key part of the multi-tracer analysis, since the performance of the method ultimately depends on our ability to discriminate between different galaxy populations with different biases and number densities (i.e. shot noise).
Here, we define several selection schemes in order to test the performance of MTOE in different plausible configurations where the number densities and biases of the tracers differ. Our fiducial selection scheme is based on colour and luminosity, which, in principle, should allow for a good separation of tracers in terms of their clustering properties. A total of four tracers in this scheme, which we call LC (luminosity–colour), are defined, as follows, in each redshift:
Redshift slice 0.55 < z < 0.7:
T1: blue colour and MI > −20.3
T2: red colour and MI > −20.3
T3: blue colour and MI < −20.3
T4: red colour and MI < −20.3
Redshift slice 0.7 < z < 0.9:
T1: blue colour and MI > −21
T2: red colour and MI > −21
T3: blue colour and MI < −21
T4: red colour and MI < −21
Redshift slice 0.9 < z < 1.1:
T1: blue colour and MI > −21.5
T2: red colour and MI > −21.5
T3: blue colour and MI < −21.5
T4: red colour and MI < −21.5
In the VIPERS mocks, a colour type (0:‘red’, 1:‘blue’) is defined from the (U–B) colour, which is in turn computed by matching the colour bimodality of the data (see de la Torre et al. 2013). In Fig. 3, I-band absolute magnitudes are shown as a function of redshift for a randomly chosen mock, in order to illustrate the LC cuts adopted. The abundances of red and blue galaxies are represented by contours; blue mock galaxies are typically less luminous than red galaxies, at fixed redshift. The LC selection employs an absolute-magnitude cut at the peak of the absolute magnitude distribution at the corresponding redshift. This demarcation is, to some extent, arbitrary, since we are not interested in measuring the evolution of clustering for the same population of galaxies as a function of redshift. Instead, our goal is to compare MTOE and FKP in different redshift slices.
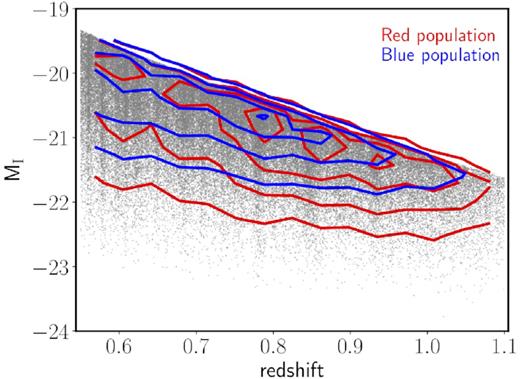
The I-band absolute magnitude as a function of redshift for a randomly selected mock. The red and blue mock galaxy distributions are represented by red and blue contours, respectively.
It is interesting to analyse how the performance of MTOE depends on the complexity of the selection scheme. To this end, we define a simple 4-tracer scheme where selection is performed by splitting the sample only by luminosity (the L selection). For the sake of simplicity, only the first redshift slice is used for this test. In this case the four tracers are defined as
Redshift slice 0.55 < z < 0.7:
T1 : MI > −20.3
T2 : −20.3 < MI < −20.8
T3 : −20.8 < MI < −21.4
T4 : MI < −21.4
Finally, we will also consider the most basic selection criterion, i.e. only two tracers defined by luminosity:
Redshift slice 0.55 < z < 0.7:
T1 : MI > −20.5
T2 : MI < −20.5
We call this scheme L0 selection. The resulting number density for different tracers in each redshift slice after applying the above selection schemes are listed in Table 1.
Number densities |$\bar{n}$| in units of [ h−1Mpc] −3 for the three tracer selection schemes considered in this analysis. As a reference, the shot-noise level for each subset is typically |$\sim 1/\bar{n}$|.
| Selection scheme . | Criteria . | Redshift range . | |$\bar{n}_{T1}(\times 10^{-4}$|) . | |$\bar{n}_{T2}(\times 10^{-4}$|) . | |$\bar{n}_{T3}(\times 10^{-4}$|) . | |$\bar{n}_{T4}(\times 10^{-4}$|) . |
|---|---|---|---|---|---|---|
| L0 | MI | 0.55 < z < 0.7 | 36.6 | 46.6 | – | – |
| L | MI | 0.55 < z < 0.7 | 24.3 | 27.7 | 19.9 | 11.4 |
| LC | MI and (U–B) colour | 0.55 < z < 0.7 | 31 | 5.6 | 36.8 | 9.8 |
| 0.7 < z < 0.9 | 17 | 3.5 | 20.4 | 7.6 | ||
| 0.9 < z < 1.1 | 5.2 | 1.7 | 6.7 | 4 |
| Selection scheme . | Criteria . | Redshift range . | |$\bar{n}_{T1}(\times 10^{-4}$|) . | |$\bar{n}_{T2}(\times 10^{-4}$|) . | |$\bar{n}_{T3}(\times 10^{-4}$|) . | |$\bar{n}_{T4}(\times 10^{-4}$|) . |
|---|---|---|---|---|---|---|
| L0 | MI | 0.55 < z < 0.7 | 36.6 | 46.6 | – | – |
| L | MI | 0.55 < z < 0.7 | 24.3 | 27.7 | 19.9 | 11.4 |
| LC | MI and (U–B) colour | 0.55 < z < 0.7 | 31 | 5.6 | 36.8 | 9.8 |
| 0.7 < z < 0.9 | 17 | 3.5 | 20.4 | 7.6 | ||
| 0.9 < z < 1.1 | 5.2 | 1.7 | 6.7 | 4 |
Number densities |$\bar{n}$| in units of [ h−1Mpc] −3 for the three tracer selection schemes considered in this analysis. As a reference, the shot-noise level for each subset is typically |$\sim 1/\bar{n}$|.
| Selection scheme . | Criteria . | Redshift range . | |$\bar{n}_{T1}(\times 10^{-4}$|) . | |$\bar{n}_{T2}(\times 10^{-4}$|) . | |$\bar{n}_{T3}(\times 10^{-4}$|) . | |$\bar{n}_{T4}(\times 10^{-4}$|) . |
|---|---|---|---|---|---|---|
| L0 | MI | 0.55 < z < 0.7 | 36.6 | 46.6 | – | – |
| L | MI | 0.55 < z < 0.7 | 24.3 | 27.7 | 19.9 | 11.4 |
| LC | MI and (U–B) colour | 0.55 < z < 0.7 | 31 | 5.6 | 36.8 | 9.8 |
| 0.7 < z < 0.9 | 17 | 3.5 | 20.4 | 7.6 | ||
| 0.9 < z < 1.1 | 5.2 | 1.7 | 6.7 | 4 |
| Selection scheme . | Criteria . | Redshift range . | |$\bar{n}_{T1}(\times 10^{-4}$|) . | |$\bar{n}_{T2}(\times 10^{-4}$|) . | |$\bar{n}_{T3}(\times 10^{-4}$|) . | |$\bar{n}_{T4}(\times 10^{-4}$|) . |
|---|---|---|---|---|---|---|
| L0 | MI | 0.55 < z < 0.7 | 36.6 | 46.6 | – | – |
| L | MI | 0.55 < z < 0.7 | 24.3 | 27.7 | 19.9 | 11.4 |
| LC | MI and (U–B) colour | 0.55 < z < 0.7 | 31 | 5.6 | 36.8 | 9.8 |
| 0.7 < z < 0.9 | 17 | 3.5 | 20.4 | 7.6 | ||
| 0.9 < z < 1.1 | 5.2 | 1.7 | 6.7 | 4 |
5 IMPLEMENTATION OF THE METHOD
In this section, we provide some practical information regarding the main steps in the implementation of the power spectrum estimation methods.
5.1 Formatting the data
The practical computation of the power spectrum estimators of equation (3) (FKP) and (6) (MTOE) involves binning the galaxy coordinates on a Cartesian grid and using a Fast Fourier Transform (FFT) algorithm. To implement the Fourier-transform approach, galaxies in each of the three redshift slices considered are placed on to three separate grids, of 63 × 14 × 76, 73 × 16 × 70, and 84 × 18 × 84 cells, respectively, with grid cells of H = 4 h−1 Mpc on a side. The total volumes of the cuboids are 4.29, 5.23, and 8.13 × 10−3 [ h−1Gpc] −3, respectively. These dimensions have been chosen so that the maximum fraction of the VIPERS volume is taken under consideration. We will consider wavenumbers up to k = 0.5 h Mpc−1 – well below the Nyquist frequency of the system, which is π/H ∼ 0.8 h Mpc−1.
A cell size of 4 h−1 Mpc captures the main small-scale features of galaxy clustering and avoids potential issues resulting from very low tracer counts per cell. We have checked that the main conclusions of the analysis remain unaltered when 8 h−1 Mpc cells are employed. We note that a smaller 2 h−1 Mpc cell was used before in the context of the VIPERS power spectrum measurement (Rota et al. 2017), but only for the combined sample.
5.2 Selection function
The matter power spectrum is defined through the expectation value (or, in this context, the ensemble average) |$\langle \delta _\mathrm{ m} (\mathbf {k},z) \delta _\mathrm{ m}^*(\mathbf {k}^{\prime },z) \rangle = (2\pi)^3 P_\mathrm{ m}(\mathbf {k},z) \delta _\mathrm{ D} (\mathbf {k}-\mathbf {k}^{\prime })$|, where |$\delta _\mathrm{ m}(\mathbf {k})$| is the matter density contrast, and δD is the Dirac delta function. For a given tracer with counts per unit volume |$n_\alpha (\mathbf {x})$|, the density contrast is |$\delta _\alpha (\mathbf {x}) = n_\alpha (\mathbf {x})/\bar{n}_\alpha (\mathbf {x}) -1$|. Here, the mean number densities |$\bar{n}_\alpha$| should reflect the spatial modulations in the observed numbers of galaxies which are due to the instrument, the strategy and schedule of observations, as well as any other factors unrelated to the redshift-space cosmological fluctuations. For simplicity, instead of using random maps or a selection function defined on subgrid scales, we compute the selection function of each tracer, |$\bar{n}_\alpha$|, by taking the mean of all mocks. The approximation implied by this procedure can affect the small-scale clustering of sparse samples when the number of mocks is not large enough (i.e. the selection function can be 0 in cells that belong to unmasked survey regions). We have checked that this is not an issue given the size of our cells and the number of mocks available.
5.3 Normalization of the power spectrum
5.4 Fiducial model
Throughout this paper, we use a theoretical model for the matter power spectrum |$P_\mathrm{ m}(\mathbf {k})$| obtained from the Boltzmann code CAMB11 (Lewis & Bridle 2002), at the corresponding median redshift of the particular redshift slice considered, and assuming the Planck cosmology.
For the galaxy power spectrum of a tracer, the camb model is combined with halofit (Smith et al. 2003), which implements non-linear corrections in the clustering. We have checked that our results, in terms of the FKP versus MTOE comparison, remain unaltered when a linear power spectrum is employed.
Fiducial values for the galaxy biases of the subpopulations are obtained iteratively. To initiate the process, we use values that roughly follow the magnitude and colour dependence of bias that was previously measured from VIPERS (see fig. 8 from Granett et al. 2015). These biases are used to generate the MTOE weights that are subsequently applied to the density field in order to compute |$P(\mathbf {k})$|. This computation is performed for all mocks, which allows us to obtain the covariance matrix. From the covariance matrix, we determine best-fitting biases by means of a likelihood maximization technique (such as χ2 minimization or MCMC). These updated biases are injected back into equation (5) in order to compute the MTOE weights, and the procedure is iterated until convergence. See Fig. 4 for a simple diagram describing the process.
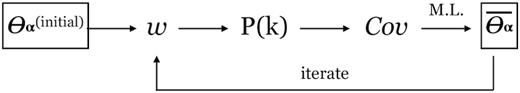
A simple diagram describing the iterative procedure for the estimation of the power spectra. In the first step, the MTOE weights are computed given an initial set of parameters |$\theta _{\alpha }^{(\mathrm{ initial})}$| (i.e. the galaxy biases, matter power spectrum, and matter growth rate). We then use these weights to compute the monopoles of the power spectra of each tracer for each mock. The monopoles of the mocks are then used to determine their covariance matrix. With that covariance matrix we are able, by means of maximum likelihood techniques (i.e. MCMC or χ2 minimization), to find updated best-fitting values for the parameters, which can then be used to re-compute the weights and start the process over again. The process is iterated until it converges.
We have checked that the convergence is rather fast (a few iterations suffice), and that the procedure is robust, even in cases where the initial fiducial values (the ones that we used to initialize the process) are completely off (e.g. all biases set to 1). As a reference, for the first redshift slice and the W1 field (LC selection), if we initialize the process with all bias values equal to unity, the procedure takes three iterations to converge at a 2 |${{\ \rm per\ cent}}$| level. Note that this convergence level is significantly below the final errors that we obtain for the biases.
6 RESULTS
In this section, we evaluate the performance of MTOE as compared to FKP in the context of the determination of the power spectra (the basic measurement) and the galaxy biases of multiple tracers. The posterior probability density function of the linear galaxy biases and related quantities is obtained using a Markov chain Monte Carlo (MCMC) procedure.
6.1 The power spectrum
Fig. 5 presents the monopole of the normalized power spectra (see equation 20) of the four tracers of the LC selection, in each of the three redshift bins considered, i.e. 0.6 < z < 0.75, 0.75 < z < 0.9, and 0.9 < z < 1.1, respectively, for both the W1 and the W4 fields. The symbols correspond to the means of the mocks, and the error bars are obtained from the diagonal of the (sample) covariance matrix. In each panel, both the FKP and the MTOE estimates are shown for comparison, along with the fiducial theoretical model (assuming the best-fitting bias values obtained through the MCMC procedure, see Section 6.2 below). One of our nuisance parameters is a constant additional shot noise term, which only makes a (small) difference in the case of very sparse tracers, and on small scales.
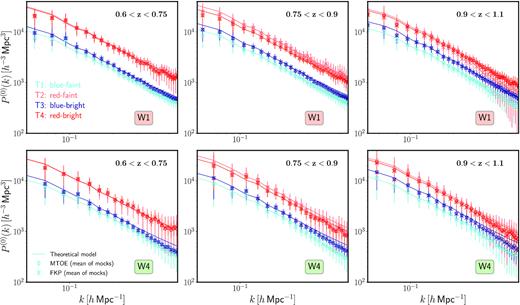
The normalized monopoles of the power spectrum, |$P^{(0)}(\mathbf {k})$|, for each of the four tracers of the LC (luminosity and colour) selection in the three redshift slices considered (for both the W1 and the smaller W4 field). In each panel, the MTOE measurement is shown in circles, whereas the FKP estimate is represented by crosses. For each tracer, a theoretical (halofit + camb) model assuming the estimated bias value is shown in solid lines (see text).
Importantly, the mean values of |$P^{(0)}(\mathbf {k})$| measured using the two estimates are almost identical within the entire range of scales considered, which confirms that MTOE is statistically unbiased with respect to the standard approach (see Abramo et al. 2016), even when the method is applied to a realistic mock catalogue. Note that differences are only barely noticeable in the highest redshift slice, and on very small scales (where uncertainties are very large). In addition, results from the two VIPERS fields are totally consistent with each other, with only small discrepancies that are also subdominant with respect to the estimated errors. Note that the volume covered by the W4 field is significantly smaller than that of the W1 field, which explains the larger errors associated with the W4 measurements.
MTOE provides a significantly more precise measurement of the monopoles |$P^{(0)}(\mathbf {k})$|, especially on smaller scales. This effect can be glimpsed from Fig. 5, but is more clearly illustrated by Fig. 6, which displays the complete correlation matrix for the four tracers considered as part of the LC selection in the first redshift slice (0.6 < z < 0.75) in the W1 field. The upper-diagonal terms correspond to the FKP correlation matrix, whereas the lower diagonal ones show the MTOE measurement. Visually, it becomes obvious that the correlation between Fourier modes (the off-diagonal terms) is significantly higher in the FKP case compared with MTOE. The diagonal of the matrix, which allow us to compare the autocorrelations for each tracer as computed from MTOE and FKP, reveals that the MTOE measurement is also significantly more precise on scales k ≳ 0.25 h Mpc−1. Although the strength of the effect depends on the particular tracer, redshift slice, and field, the same qualitative behaviour is found for all cases considered.
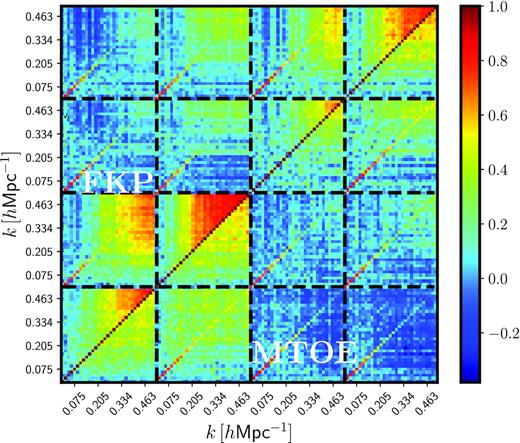
The complete correlation matrix for the entire set of tracers of the LC selection in the first redshift slice, i.e. 0.6 < z < 0.75 (W1 field). The MTOE method consistently provides a less-correlated measurement than FKP, especially on small scales.
The fact that FKP is noisier than the MTOE approach on small scales is due to the influence of shot noise. The FKP estimator for the power spectrum of any given tracer only takes into account those tracers. The MTOE method, on the other hand, not only employs the autocorrelation of that tracer with itself, but also takes into account the cross-correlations of that tracer with all the other tracers in the estimation of the spectrum. Since shot noise affects more the small scales (where the amplitude of the spectrum is lower), the upshot is that MTOE is less noisy on small scales, effectively lowering the threshold imposed by shot noise. We have found qualitatively similar behaviours for the other redshift slices, and also when the simple L and L0 selections are imposed. We proceed now to quantify the magnitude of the effect.
Of course, on very small scales the galaxy distribution is dominated by intrahalo effects such as those arising from the halo density profile and stochasticity (McDonald & Seljak 2009), hence there is no cosmic variance to cancel anymore. However, the fact that, as we approach that regime, the FKP and MTOE estimators remain unbiased with respect to each other but MTOE still has lower uncertainties shows the advantage of combining the tracers to measure clustering not only on large, but also on smaller scales – even if the MTOE may not be ‘optimal’ as we go deeper into the non-linear regime. Although, it is difficult to exploit the information on those smaller scales in order to constrain cosmological parameters, these improvements are useful in terms of exploring how galaxies are connected to their environments.
In Fig. 7, we show the ratios of the fractional errors (i.e. the standard deviations divided by the mean of all mocks) obtained from FKP and MTOE, as a function of k, for the first redshift slice in the W1 field. This quantity reflects the relative gain in accuracy and is computed for both the individual power spectra (left-hand column) and the ratios of individual spectra (right-hand column). Each row in this figure represents a different tracer selection, in increasing order of complexity from top to bottom, i.e. L0, L, and LC, respectively. Several conclusions can be extracted from this figure, which are consistent with results from Abramo et al. (2016). First, increasing the number of tracers (at least within some reasonable limits) tends to improve the performance of MTOE, as compared to FKP. Secondly, the advantages are observed both in terms of the individual power spectra, and on the ratios of individual spectra. Thirdly, considering additional ways of discriminating between different populations is beneficial. This can be seen in the last row of Fig. 7, where colour is used as a second discriminator. Note that it is not the number of parameters what ultimately matters, but the combined discriminating capabilities of the parameter set.
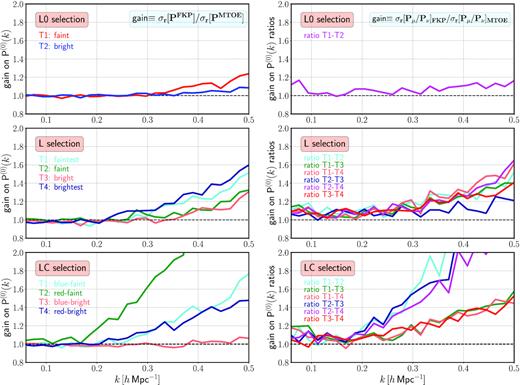
The relative gain in accuracy provided by MTOE as compared to the standard FKP weighting for different tracer selections in the redshift range 0.55 < z < 0.7. From top to bottom, increasingly more complicated selections are shown: L0 selection (two tracers selected in luminosity), L-selection (four tracers selected in luminosity), and LC-selection (four tracers selected in colour and luminosity). In each row, the left-hand plot displays the gain for each individual |$P^{(0)}(\mathbf {k})$| as a function of k, whereas the right-hand plot shows this effect on the ratios of individual spectra. Here, the relative gain is defined as the ratio between the corresponding fractional errors, obtained dividing the standard deviations (taken from the diagonal of the sample covariance matrix) by the mean values of the spectra or ratios of spectra.
In the W1 field, the average relative error reduction at |$0.3 \lt k[h \,$| Mpc−1] < 0.5 for the spectra of LC tracers is around 30 per cent in the three redshift slices considered, whereas for the ratios of individual spectra the improvements raise to ∼35 |${{\ \rm per\ cent}}$|. A similar gain is achieved for individual spectra in the W4 field. The relative error reduction for the ratios of spectra in this field can, however, reach 40–50 |${{\ \rm per\ cent}}$| on average at |$0.3 \lt k[h \,$| Mpc−1] < 0.5. Note that these are averaged and integrated gains; as shown in Fig. 7, the improvement for a particular tracer can significantly exceed these values as we move towards smaller scales.
It is important to note that the gains reported in Fig. 7 show up in scales that are, typically, still larger than the characteristic ‘shot noise scale’ for each tracer, i.e. k < kSN, where |$P(k_{\rm SN}) \sim 1/\bar{n_i}$|. In fact, only for the second tracer in the LC selection (i.e. ‘red-faint’) does kSN lie within the k-range considered (kSN ∼ 0.4 h Mpc−1).
Fig. 7 also reflects the most salient advantage of using multi-tracer techniques: the cancellation of cosmic variance on large scales. This effect can be seen most clearly in the ratios of spectra – which MTOE has been shown to measure with higher accuracy (Abramo et al. 2016). The right-hand panels of Fig. 7 show an average increase in the precision of this measurement of around |$10{{\ \rm per\ cent}}$| at k ≲ 0.1 h Mpc−1 when MTOE is employed. The improvement is a little higher (|$\sim 15{{\ \rm per\ cent}}$|) for the smaller W4 field.
The improvement that MTOE provides depends strongly on the number density of the particular tracer considered: the scarcer the tracer, the larger the improvement on individual spectra, and the smaller the scale at which the effect becomes significant. To demonstrate this, we draw attention to the left-bottom panel of Fig. 7, which displays the gain on individual spectra for the LC scheme. The number densities of the tracers are, respectively, 31 (T1), 5.6 (T2), 36.8 (T3), and 9.8 (T4) 10−4 [ h-1Mpc] −3, as listed in Table 1. The scale at which the improvement reaches 20 |${{\ \rm per\ cent}}$| is, respectively, k ≃ 0.35 (T1), ≃ 0.2 (T2), > 0.5 (T3), ≃ 0.35 (T4). Qualitatively, this general trend applies for any given selection and redshift slice – even though the particular gain will also depend on other factors, including the distribution of biases for a particular population.
In summary, the large increase in the signal-to-noise provided by MTOE on small scales for individual power spectra (and for the ratios of spectra) is a reflection of the method being better equipped to deal with shot noise, since MTOE combines information from all tracers. This feature is especially beneficial for sparse samples and on small scales, where the lack of signal becomes more severe. On the other hand, the improvement in the measurement of the ratios of spectra on large scales is due to the cancellation of cosmic variance, a feature that the MTOE is naturally designed to enhance.
6.2 Derived quantities: Markov chain Monte Carlo
The multipoles of the redshift-space power spectra constitute the basic measurements from which constraints on the galaxy biases and cosmological parameters can be obtained. Here, we employ an MCMC algorithm to fit the normalized monopole |$P^{(0)}(\mathbf {k})$|, and derive posterior probability distributions for the amplitudes of the monopoles, the ratios of the amplitudes of the monopoles and the linear biases of tracers, at fixed cosmology. Since the main motivation for this analysis is to evaluate the performance of MTOE in a variety of configurations, we opt to present results from the W1 and W4 fields, separately.
In this section, we show how the improvement on |$P^{(0)}(\mathbf {k})$| translates into Mα, Mαβ, and bα, for all redshift slices and selections. In order to provide a more complete view of the problem, we have opted to treat the W1 and W4 fields, separately. We have checked, however, that our gains are similar, on average, when the measurements of the monopoles of |$P(\mathbf {k})$| from W1 and W4 are combined in the MCMC.
A critical aspect in the MCMC is the integration range. As seen in Fig. 7, MTOE is especially advantageous on small scales. However, these are also the k-ranges where uncertainties, mode couplings and non-linearities are larger, independently of the estimation method. Hence, we start by choosing a conservative range 0.1 < k[h Mpc−1] < 0.3.
Fig. 8 shows the posterior probability distributions for the amplitudes of the monopoles of the LC-selected tracers in the redshift range 0.75 < z < 0.9 (second redshift slice), W1 field. In this case, an additional (constant) shot-noise term was used as a nuisance parameter, but the cosmology was fixed. Results for the monopole ratios and for the biases are displayed in Figs 9 and 10, respectively. Although, the extent of the effect depends on the particular tracer, the improvement in the accuracy of the measurements, in terms of narrower posterior probability distributions, is observed, on average, for all parameters.
![Posterior probability distributions for the amplitudes of the monopoles (see equation 22) estimated using both MTOE and FKP for the four tracers considered as part of the LC selection in the redshift range 0.75 < z < 0.9 (W1 field). The MCMC is performed within the wavenumber range 0.1 < k[h Mpc−1] < 0.3.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/493/4/10.1093_mnras_staa405/1/m_staa405fig8.jpeg?Expires=1750039625&Signature=SWPxFKGeBz0ZhX-R7J90Xa4N5Z~MHxXpkUaFeWPyxNcsXw6DkPxTByW5SHTYQaKKnFmg-B1Iyra0xuNvHNF3E70MvCqaF3rBUMO~ApifY8rIeGLgTkSLDG1Mz5vpTQ3Cis1pICFwcBSGP2aEnG8u-NQDWB6r2yzTnelP7y7tG2-cgsXM4pDdqdFa0kO0zH3GR4PoWMOPKRehjxaUvkaa8Mf4yeWsbKQHRtCLerdtCroqra61Ie8qOVSJ-br~AOJFmDljO8Zh4gU17RxRokd8iAKQDa1sWeswSUHWc0Dnfhf1xuuAW-va1~pxsgf-wk4SjGsdce21WeAOMIvNv8lLvw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Posterior probability distributions for the amplitudes of the monopoles (see equation 22) estimated using both MTOE and FKP for the four tracers considered as part of the LC selection in the redshift range 0.75 < z < 0.9 (W1 field). The MCMC is performed within the wavenumber range 0.1 < k[h Mpc−1] < 0.3.
![Posterior probability distributions for the ratios of the monopoles for the four tracers considered as part of the LC selection in the redshift range 0.75 < z < 0.9 (W1 field), estimated using both MTOE and FKP. The MCMC is performed within the wavenumber range 0.1 < k[h Mpc−1] < 0.3.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/493/4/10.1093_mnras_staa405/1/m_staa405fig9.jpeg?Expires=1750039625&Signature=Prt-y7FjEMmrjgCsTA3e-0Sz97SrMWkorPlaxhcdClYXcx4Nafu5ciSvrBKU8WffD7zdcs96pmeZCtzODFTr--E9N1HQdB~ccgijf5tHFJQbjpHhAhV9c-9rEHmG1YlUJ768Oqvc8qQfUjQ6841~4DeWqsggOgB5w49gZOrGk0Nvltfbnk-5aEPSg8NhwVlWq2tOiqQN7AfJBc8ihyWaKsABgPN3jqpzy~JTleNprMJ0Ab-3rYWfv~HlwEqtxLWkkZxMyVI~jnmJG7RPE0Am9ZAwbzgbvzqhOld1c3zwgvr26yRjS4MygyzyRPq7ZGbvWbjKWKHQ1M~mPQl7UaCt0A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Posterior probability distributions for the ratios of the monopoles for the four tracers considered as part of the LC selection in the redshift range 0.75 < z < 0.9 (W1 field), estimated using both MTOE and FKP. The MCMC is performed within the wavenumber range 0.1 < k[h Mpc−1] < 0.3.
![Posterior probability distributions for the linear galaxy biases of the four tracers considered as part of the LC selection in the redshift range 0.75 < z < 0.9 (W1 field), estimated using both FKP and MTOE. The MCMC is performed within the wavenumber range 0.1 < k[h Mpc−1] < 0.3.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/493/4/10.1093_mnras_staa405/1/m_staa405fig10.jpeg?Expires=1750039625&Signature=i45PV2OkFKiprVoTac~GKLLQ5hcjcBighMj29YVvC2CfJnhgXK5CGa8aVXaLtu6WZm16lMIgYZSs599UZJ5ykcJ15p~KpONe-EgKNJy0zerJMvAt5nUDmsd7Unn0eaDFQLmnpf3Jbv3hGE-3GhHNWD2~mmPC3ZPoZ9RCrJHg2Xg3KTbQ3EZTnM5i3cFOLDeM~ySOOY2jCABzS9sMm5hzzo1YcTeTEdqPmTKzx0xzzCrdc8KjpxtAc5U38pQTgyKt5J782UBrlkP1Ux7IM4m7RH~-kSaoOnduvmm4MvIsV7qNU73XASS03TW-se4ak5iYioL-IWJ3-iWcHk39a~ttIg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Posterior probability distributions for the linear galaxy biases of the four tracers considered as part of the LC selection in the redshift range 0.75 < z < 0.9 (W1 field), estimated using both FKP and MTOE. The MCMC is performed within the wavenumber range 0.1 < k[h Mpc−1] < 0.3.
The question that arises is how much we can further gain by pushing the measurements to higher values of k – a question that depends on the scientific purpose of the analysis. The answer to this question is illustrated in Fig. 11, which displays the posterior probability distributions for the monopoles of the same tracers of Fig. 8, but now measured at the wavenumber range 0.3 < k[h Mpc−1] < 0.5. The difference between MTOE and FKP becomes apparent here, as expected from the improvements in the accuracy of the |$P(\mathbf {k})$| measurement shown in Fig. 7.
![The same as Fig. 8 but assuming an integration range 0.3 < k[h Mpc−1] < 0.5.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/493/4/10.1093_mnras_staa405/1/m_staa405fig11.jpeg?Expires=1750039625&Signature=kMcajDTtswHRi4exsMuxcl02yH~9j6c0H3iz5gzTtMzpg9k6xgAP9xNwfM9zAxWiJG1k5YYsm6o2enZMPLnrZu2~VqR~7JMTOf4~BBSRrsZ4JYp1cxNdb18jvSiLtEXzFvlbrYGUYFynXwa0tZuoKEFNpO5RCMf0YzM0IIrVgaGU0DXWctbtn-4Yd5C0lMdZ4-xkY88QnVE5uaA37ZkbWwGmNYqGn3XDoLOvkB~OnBtWjalXt-eI006WbbgyG-G0xmuvAYChSNmEpjvHJsmsZ1apk4518Tq~G0-fvthnZWi~GB3l3AA1zLtjwsfqYFalyNCPT-oTtYfSQpe03aHtNg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The same as Fig. 8 but assuming an integration range 0.3 < k[h Mpc−1] < 0.5.
In order to quantify the improvements, we define the ‘relative gain’ provided by MTOE as the percentage difference between the relative confidence intervals derived from both methods, i.e. |$100\times (\sigma ^{(r)}_{\rm FKP}-\sigma ^{(r)}_{\rm MTOE})/\sigma ^{(r)}_{\rm MTOE}$| (where relative indicates that the confidence intervals are divided by the best-fitting values12). In Fig. 12, we show these gains in a colour-coded diagram for all tracers and redshift slices, and for the two different integration ranges: 0.1 < k[h Mpc−1] < 0.3 and 0.3 < k[h Mpc−1] < 0.5. Redder colours indicate a positive gain (improvement), whereas bluer colours show a decrease in the accuracy of the measurement. The first thing to notice is that MTOE provides a more accurate measurement than FKP in the great majority of cases, i.e. ∼80 |${{\ \rm per\ cent}}$|, with significant loss of precision (gain |$\lt -5{{\ \rm per\ cent}}$|) in less than 10 |${{\ \rm per\ cent}}$| of cases. Also, the gains are notably larger for the much smaller W4 field. This is again a consequence of MTOE being more equipped to deal with small-number statistics and noisier samples.
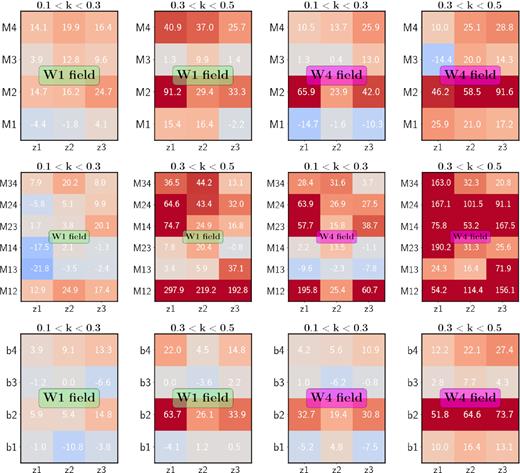
The improvement provided by MTOE with respect to FKP for the amplitude of the monopoles, monopole ratios, and biases of the four tracers of the fiducial LC selection over the three redshift slices considered, in theW1 and W4 fields. The colour code corresponds to the percentage difference in the relative confidence intervals of the estimated parameters, i.e. |$100\times (\sigma ^{(r)}_{\rm FKP}-\sigma ^{(r)}_{\rm MTOE})/\sigma ^{(r)}_{\rm MTOE}$| (where relative indicates that the confidence intervals are divided by the best-fitting values). Redder colours indicate an increase in the accuracy, whereas bluer colours represent a decrease. The actual values of the percentage difference are provided inside each cell.
In the wavenumber range 0.1 < k[h Mpc−1] < 0.3, the gain is, on average, |$\sim 12.5{{\ \rm per\ cent}}$| for the amplitudes of the monopoles, |$\sim 18{{\ \rm per\ cent}}$| for the monopole ratios, and |$\sim 5{{\ \rm per\ cent}}$| for the linear biases (combining both fields). Individual cases, however, can reach much larger improvements. If we opt for a more aggressive take on small scales, the difference is boosted significantly. The average gain increases to |$\sim 27{{\ \rm per\ cent}}$| for the amplitudes, |$\sim 75{{\ \rm per\ cent}}$| for the monopole ratios, and |$\sim 19{{\ \rm per\ cent}}$| for the linear biases. In the Appendix, we list the mean values, confidence intervals, and gains for all cases considered.
Since MTOE is mostly advantageous on small scales, for tracers with low number density, we must ensure that the method is robust for this configuration. As mentioned before, we have checked that the improvement shown in Figs 7–11 persists (qualitatively) when cells of 8 h−1 Mpc are employed (instead of 4 h−1 Mpc). In addition, we also computed the power spectra using a selection function smoothed with a Gaussian kernel, to check whether small-scale variations in the selection function could change the power – and we verified that this had no effect whatsoever on our measurements.
7 DISCUSSION AND CONCLUSIONS
When multiple biased tracers occupy the same survey volume, the signal and the noise for all possible auto- and cross-correlations should be taken into account. The standard weighting scheme of FKP (Feldman et al. 1994) was designed to be used in the context of the Fourier analysis of surveys based on a single population of LSS tracers. The PVP scheme (Percival et al. 2004), on the other hand, provides optimal weights that lead to a minimum-variance estimator of the matter power spectrum |$P_\mathrm{ m}(\mathbf {k})$| in situations where several different biased tracers are considered – see also Cai et al. (2011). The MTOE (Abramo et al. 2016), which we describe and apply in this paper, is optimal both to estimate the matter power spectrum, as well as the redshift-space auto-power spectra of each individual tracer.
The purpose of this work is threefold. First, to provide a compact, simplified and self-contained description of MTOE that can be easily implemented. Secondly, to evaluate the performance of the method on simulated but realistic galaxy data, and quantify the improvement with respect to the standard FKP approach. Thirdly, to lay the foundations for the implementation of the method on the VIPERS data set, in order to improve constraints not only on the power spectra and galaxy biases, but also on the cosmological parameters.
On the theoretical side, the description of the method that we provide incorporates an analytic derivation of the window functions of the auto-power spectra – a result that was not known previously. We show that the MTOE window functions conserve the total power of the measurement: they are normalized to unity in terms of the modes, and the mean mixing between the different tracers vanishes when averaged over all the modes.
We have shown that MTOE provides significant advantages when applied to a data set split in multiple galaxy populations. It is unbiased with respect to the standard FKP approach, and improves upon its performance. In the case of VIPERS, this gain is more pronounced on small scales. We report an average increase in the signal-to-noise of the monopoles of the auto-power spectra of ∼ 30 |${{\ \rm per\ cent}}$| at 0.3 < k[h Mpc−1] < 0.5, with improvements increasing towards smaller scales – the specific values depending on the particular tracer and on the characteristics of the survey. The improvements on small scales are also large for the ratios of power spectra. We have also implemented an MCMC procedure in order to explore the probability density space of derived fitting quantities such as the amplitudes of the monopoles, the monopole ratios, and the linear galaxy biases. If we can push the measurement to a wavenumber range 0.3 < k[h Mpc−1] < 0.5, the gain on these quantities reaches, on average, 30, 75, and 20 |${{\ \rm per\ cent}}$|, respectively.
The particular extent of the improvement for a given tracer subsample is determined, to a large degree, by the survey volume, the number density, and the bias of the tracer. We illustrate this with a summary plot in Fig. 13. Here, tracers from different selections and redshifts are shown together, and the corresponding gains plotted as a function of number density and number of objects. For abundant tracers, the advantage of using MTOE is very mild. For scarcer tracer, the gain is very significant, depending strongly on the type of tracer: redder tracers, which are more strongly bias, benefit more from the MTOE weighting.
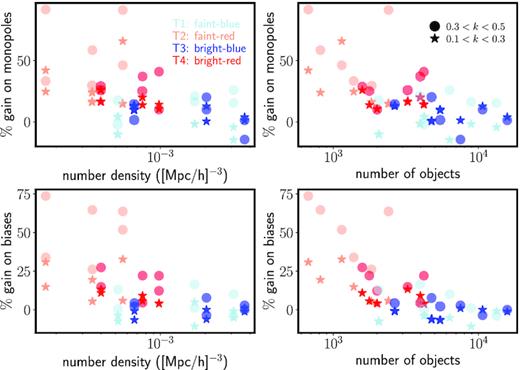
The percentage relative gain in precision (see text) provided by MTOE with respect to FKP on the amplitude of the monopoles and biases as a function of the number density and total number of objects of the particular tracer subpopulation. Here, tracers in different redshift slices and fields are shown in order to illustrate the dependence of the improvement on the abundance and type of tracer.
The improvement provided by MTOE is not restricted to small scales. As expected from the very foundation of the method, which is based on combining different measurements in order minimize cosmic variance, we find an average gain of ∼10 |${{\ \rm per\ cent}}$| on scales k[h Mpc−1] ≲ 0.1 for the ratios of spectra. Importantly, the application of the method to larger cosmological volumes in the future will allow us to test whether we can achieve larger improvements on even larger scales.
The second paper of this series will focus on the application of the method to the VIPERS data set, as well as the inclusion of all cross-spectra of the tracers. In particular, it is still to be determined how much of the reported gains can be recovered when other sources of uncertainties, associated with a real data set, are present. The most relevant issue that we can anticipate is the fidelity of the mocks with respect to the data, in the context of a multi-tracer analysis. It is important to stress that MTOE can be applied on data only without mocks. However, mocks are needed to estimate errors. Mocks (including the VIPERS mocks) are typically built to reproduce the clustering of a combined data set, or, in some cases, the dependence of clustering on stellar mass or luminosity. As we have shown, the ideal situation for a multi-tracer approach involves having multiple ways of selecting galaxy populations (e.g. luminosity and colour). If mocks do not reproduce the bias and number density of these subpopulations, the derived errors can be inaccurate. Accurate ‘multi-tracer mocks’ are thus needed.
This paper shows that MTOE is also a powerful tool to explore the physics that takes place on small cosmological scales from the perspective of the power spectrum measurement. On scales ≲10 h−1 Mpc, the effect of the 1-halo term (Cooray & Sheth 2002), which describes the clustering of galaxies inside haloes, starts to become dominant and can become degenerate with shot noise. MTOE provides a route into the astrophysics of multiple galaxy populations, since it can be used to place tighter constraints on HOD models on small scales.
From the perspective of the halo-galaxy connection, improving on our ability to measure galaxy biases is advantageous in the context of assembly bias studies (see e.g. Lin et al. 2016; Miyatake et al. 2016; Montero-Dorta et al. 2017; Niemiec et al. 2018; Montero-Dorta et al. 2020). In Sato-Polito et al. (2019), we show how applying the MTOE to multiple subsets of haloes increases the signal-to-noise ratio of the secondary bias (i.e. ‘halo assembly bias’) measurement to a level that can only be achieved if the underlying dark matter density field of the simulation is known. This convenient ‘trick’ is not attainable with real data, therefore the usefulness of MTOE.
The unprecedented wealth of cosmological survey data that will soon be available to the community motivates us to continue developing MTOE. Experiments such as J-PAS, DESI, Euclid, or the LSST will map huge volumes of the high-redshift universe with broad galaxy selections, seeking accurate cosmological measurements over unexplored redshift ranges. MTOE and other multi-tracer approaches, applied to a single data set or a combination of multiple surveys, can help us push the limits of the clustering measurement to scales that were not accessible before.
ACKNOWLEDGEMENTS
ADMD thanks the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for financial support. LRA thanks both FAPESP and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for financial support. BRG and LG acknowledge support of the Agenzia Spaziale Italiana (ASI), through contract no. 2018-23-HH.0 ‘Euclid’. SdlT acknowledges the support of the Origins, Constituents and EVolution of the Universe Laboratory of Excellence (OCEVU Labex, ANR-11-LABX-0060) and the Aix-Marseille Initiative of Excellence (A*MIDEX) project (ANR-11-IDEX-0001-02) funded by the ‘Investissements d’Avenir’ French government program managed by the Agence Nationale de la Recherche (ANR).
We also thank S. Vitenti, M. Penna-Lima, and C. Doux for the use of their Numerical Cosmology package, NumCosmo.13
Footnotes
This holds if the bandpowers |$\mathbf {k}_i$| and |$\mathbf {k}_j$| are sufficiently wide – see e.g. Abramo (2012) for a more detailed discussion.
Ideally, constructing mocks of such multi-tracer accuracy could be done via an iterative process in which the measured biases/number densities for any chosen set of galaxy tracers are reinforced back into the mock generator until the estimation and mock generation procedures converge. This is computationally very costly, but it is conceivable that next-generation mocks are specifically built to reproduce multiple clustering dependencies simultaneously, such as those on colour and stellar mass/luminosity.
Note that, in practice, since MTOE is statistically unbiased with respect to FKP, our results only marginally change when the comparison is performed on the basis of the absolute, not fractional, confidence intervals.
REFERENCES
APPENDIX A: BEST-FITTING VALUES
We provide here best-fitting values for the amplitudes of the monopoles, monopole ratios, and linear biases of the LC tracers estimated using both the FKP and MTOE methods, in the three redshift slices considered. Tables A1 and A2 display results for integration ranges of 0.1 < k[h Mpc−1] < 0.3 and 0.3 < k[h Mpc−1] < 0.5, respectively, in the W1 field. Results for the W4 field are listed in Tables A3 and A4.
The best-fitting FKP and MTOE estimates of the amplitudes of the monopoles, monopole ratios, and biases of the LC tracers along with the percentage relative reduction of the uncertainty provided by MTOE (|$100\times \sigma ^{(r)}_{\mathrm{ FKP}}-\sigma ^{(r)}_{\mathrm{ MTOE}}/\sigma ^{(r)}_{\mathrm{ MTOE}}$|), for an integration range 0.1 < k[h Mpc−1] < 0.3, in the W1 field.
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.671 ± 0.145 | 1.629 ± 0.136 | −4.4 | 1.948 ± 0.151 | 2.010 ± 0.153 | −1.8 | 2.367 ± 0.251 | 2.345 ± 0.259 | +4.1 |
| M2 | 4.838 ± 0.569 | 4.947 ± 0.667 | +14.7 | 5.920 ± 0.708 | 5.754 ± 0.799 | +16.2 | 5.739 ± 0.564 | 5.603 ± 0.686 | +24.7 |
| M3 | 1.990 ± 0.098 | 1.961 ± 0.100 | +3.9 | 2.572 ± 0.126 | 2.564 ± 0.142 | +12.8 | 3.265 ± 0.192 | 3.273 ± 0.210 | +9.6 |
| M4 | 4.404 ± 0.330 | 4.293 ± 0.367 | +14.1 | 4.722 ± 0.342 | 4.854 ± 0.421 | +19.9 | 5.352 ± 0.351 | 5.386 ± 0.411 | +16.4 |
| M1, 2 | 0.332 ± 0.031 | 0.330 ± 0.035 | +12.9 | 0.332 ± 0.028 | 0.322 ± 0.034 | +24.9 | 0.412 ± 0.040 | 0.401 ± 0.046 | +17.4 |
| M1, 3 | 0.851 ± 0.078 | 0.822 ± 0.059 | −21.8 | 0.767 ± 0.054 | 0.759 ± 0.051 | −3.5 | 0.722 ± 0.070 | 0.716 ± 0.068 | −2.4 |
| M1, 4 | 0.366 ± 0.044 | 0.367 ± 0.036 | −17.5 | 0.406 ± 0.028 | 0.405 ± 0.029 | +2.1 | 0.431 ± 0.048 | 0.446 ± 0.050 | −1.3 |
| M2, 3 | 2.451 ± 0.292 | 2.366 ± 0.287 | +1.7 | 2.314 ± 0.245 | 2.339 ± 0.257 | +3.8 | 1.764 ± 0.158 | 1.749 ± 0.189 | +20.1 |
| M2, 4 | 1.105 ± 0.139 | 1.128 ± 0.134 | −5.8 | 1.192 ± 0.115 | 1.220 ± 0.124 | +5.1 | 1.061 ± 0.102 | 1.049 ± 0.111 | +9.9 |
| M3, 4 | 0.443 ± 0.024 | 0.453 ± 0.027 | +7.9 | 0.528 ± 0.026 | 0.526 ± 0.032 | +20.2 | 0.599 ± 0.037 | 0.603 ± 0.040 | +8.0 |
| b1 | 0.952 ± 0.116 | 0.941 ± 0.114 | −1.0 | 1.059 ± 0.119 | 1.155 ± 0.116 | −10.8 | 1.197 ± 0.137 | 1.217 ± 0.134 | −3.8 |
| b2 | 1.911 ± 0.164 | 1.877 ± 0.171 | +5.9 | 2.111 ± 0.177 | 2.147 ± 0.190 | +5.4 | 2.048 ± 0.153 | 2.089 ± 0.180 | +14.8 |
| b3 | 1.126 ± 0.105 | 1.134 ± 0.104 | −1.2 | 1.202 ± 0.0 | 1.364 ± 0.112 | – | 1.408 ± 0.118 | 1.524 ± 0.119 | −6.6 |
| b4 | 1.782 ± 0.117 | 1.790 ± 0.122 | +3.9 | 1.891 ± 0.123 | 1.912 ± 0.136 | +9.1 | 2.008 ± 0.123 | 1.992 ± 0.138 | +13.3 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.671 ± 0.145 | 1.629 ± 0.136 | −4.4 | 1.948 ± 0.151 | 2.010 ± 0.153 | −1.8 | 2.367 ± 0.251 | 2.345 ± 0.259 | +4.1 |
| M2 | 4.838 ± 0.569 | 4.947 ± 0.667 | +14.7 | 5.920 ± 0.708 | 5.754 ± 0.799 | +16.2 | 5.739 ± 0.564 | 5.603 ± 0.686 | +24.7 |
| M3 | 1.990 ± 0.098 | 1.961 ± 0.100 | +3.9 | 2.572 ± 0.126 | 2.564 ± 0.142 | +12.8 | 3.265 ± 0.192 | 3.273 ± 0.210 | +9.6 |
| M4 | 4.404 ± 0.330 | 4.293 ± 0.367 | +14.1 | 4.722 ± 0.342 | 4.854 ± 0.421 | +19.9 | 5.352 ± 0.351 | 5.386 ± 0.411 | +16.4 |
| M1, 2 | 0.332 ± 0.031 | 0.330 ± 0.035 | +12.9 | 0.332 ± 0.028 | 0.322 ± 0.034 | +24.9 | 0.412 ± 0.040 | 0.401 ± 0.046 | +17.4 |
| M1, 3 | 0.851 ± 0.078 | 0.822 ± 0.059 | −21.8 | 0.767 ± 0.054 | 0.759 ± 0.051 | −3.5 | 0.722 ± 0.070 | 0.716 ± 0.068 | −2.4 |
| M1, 4 | 0.366 ± 0.044 | 0.367 ± 0.036 | −17.5 | 0.406 ± 0.028 | 0.405 ± 0.029 | +2.1 | 0.431 ± 0.048 | 0.446 ± 0.050 | −1.3 |
| M2, 3 | 2.451 ± 0.292 | 2.366 ± 0.287 | +1.7 | 2.314 ± 0.245 | 2.339 ± 0.257 | +3.8 | 1.764 ± 0.158 | 1.749 ± 0.189 | +20.1 |
| M2, 4 | 1.105 ± 0.139 | 1.128 ± 0.134 | −5.8 | 1.192 ± 0.115 | 1.220 ± 0.124 | +5.1 | 1.061 ± 0.102 | 1.049 ± 0.111 | +9.9 |
| M3, 4 | 0.443 ± 0.024 | 0.453 ± 0.027 | +7.9 | 0.528 ± 0.026 | 0.526 ± 0.032 | +20.2 | 0.599 ± 0.037 | 0.603 ± 0.040 | +8.0 |
| b1 | 0.952 ± 0.116 | 0.941 ± 0.114 | −1.0 | 1.059 ± 0.119 | 1.155 ± 0.116 | −10.8 | 1.197 ± 0.137 | 1.217 ± 0.134 | −3.8 |
| b2 | 1.911 ± 0.164 | 1.877 ± 0.171 | +5.9 | 2.111 ± 0.177 | 2.147 ± 0.190 | +5.4 | 2.048 ± 0.153 | 2.089 ± 0.180 | +14.8 |
| b3 | 1.126 ± 0.105 | 1.134 ± 0.104 | −1.2 | 1.202 ± 0.0 | 1.364 ± 0.112 | – | 1.408 ± 0.118 | 1.524 ± 0.119 | −6.6 |
| b4 | 1.782 ± 0.117 | 1.790 ± 0.122 | +3.9 | 1.891 ± 0.123 | 1.912 ± 0.136 | +9.1 | 2.008 ± 0.123 | 1.992 ± 0.138 | +13.3 |
The best-fitting FKP and MTOE estimates of the amplitudes of the monopoles, monopole ratios, and biases of the LC tracers along with the percentage relative reduction of the uncertainty provided by MTOE (|$100\times \sigma ^{(r)}_{\mathrm{ FKP}}-\sigma ^{(r)}_{\mathrm{ MTOE}}/\sigma ^{(r)}_{\mathrm{ MTOE}}$|), for an integration range 0.1 < k[h Mpc−1] < 0.3, in the W1 field.
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.671 ± 0.145 | 1.629 ± 0.136 | −4.4 | 1.948 ± 0.151 | 2.010 ± 0.153 | −1.8 | 2.367 ± 0.251 | 2.345 ± 0.259 | +4.1 |
| M2 | 4.838 ± 0.569 | 4.947 ± 0.667 | +14.7 | 5.920 ± 0.708 | 5.754 ± 0.799 | +16.2 | 5.739 ± 0.564 | 5.603 ± 0.686 | +24.7 |
| M3 | 1.990 ± 0.098 | 1.961 ± 0.100 | +3.9 | 2.572 ± 0.126 | 2.564 ± 0.142 | +12.8 | 3.265 ± 0.192 | 3.273 ± 0.210 | +9.6 |
| M4 | 4.404 ± 0.330 | 4.293 ± 0.367 | +14.1 | 4.722 ± 0.342 | 4.854 ± 0.421 | +19.9 | 5.352 ± 0.351 | 5.386 ± 0.411 | +16.4 |
| M1, 2 | 0.332 ± 0.031 | 0.330 ± 0.035 | +12.9 | 0.332 ± 0.028 | 0.322 ± 0.034 | +24.9 | 0.412 ± 0.040 | 0.401 ± 0.046 | +17.4 |
| M1, 3 | 0.851 ± 0.078 | 0.822 ± 0.059 | −21.8 | 0.767 ± 0.054 | 0.759 ± 0.051 | −3.5 | 0.722 ± 0.070 | 0.716 ± 0.068 | −2.4 |
| M1, 4 | 0.366 ± 0.044 | 0.367 ± 0.036 | −17.5 | 0.406 ± 0.028 | 0.405 ± 0.029 | +2.1 | 0.431 ± 0.048 | 0.446 ± 0.050 | −1.3 |
| M2, 3 | 2.451 ± 0.292 | 2.366 ± 0.287 | +1.7 | 2.314 ± 0.245 | 2.339 ± 0.257 | +3.8 | 1.764 ± 0.158 | 1.749 ± 0.189 | +20.1 |
| M2, 4 | 1.105 ± 0.139 | 1.128 ± 0.134 | −5.8 | 1.192 ± 0.115 | 1.220 ± 0.124 | +5.1 | 1.061 ± 0.102 | 1.049 ± 0.111 | +9.9 |
| M3, 4 | 0.443 ± 0.024 | 0.453 ± 0.027 | +7.9 | 0.528 ± 0.026 | 0.526 ± 0.032 | +20.2 | 0.599 ± 0.037 | 0.603 ± 0.040 | +8.0 |
| b1 | 0.952 ± 0.116 | 0.941 ± 0.114 | −1.0 | 1.059 ± 0.119 | 1.155 ± 0.116 | −10.8 | 1.197 ± 0.137 | 1.217 ± 0.134 | −3.8 |
| b2 | 1.911 ± 0.164 | 1.877 ± 0.171 | +5.9 | 2.111 ± 0.177 | 2.147 ± 0.190 | +5.4 | 2.048 ± 0.153 | 2.089 ± 0.180 | +14.8 |
| b3 | 1.126 ± 0.105 | 1.134 ± 0.104 | −1.2 | 1.202 ± 0.0 | 1.364 ± 0.112 | – | 1.408 ± 0.118 | 1.524 ± 0.119 | −6.6 |
| b4 | 1.782 ± 0.117 | 1.790 ± 0.122 | +3.9 | 1.891 ± 0.123 | 1.912 ± 0.136 | +9.1 | 2.008 ± 0.123 | 1.992 ± 0.138 | +13.3 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.671 ± 0.145 | 1.629 ± 0.136 | −4.4 | 1.948 ± 0.151 | 2.010 ± 0.153 | −1.8 | 2.367 ± 0.251 | 2.345 ± 0.259 | +4.1 |
| M2 | 4.838 ± 0.569 | 4.947 ± 0.667 | +14.7 | 5.920 ± 0.708 | 5.754 ± 0.799 | +16.2 | 5.739 ± 0.564 | 5.603 ± 0.686 | +24.7 |
| M3 | 1.990 ± 0.098 | 1.961 ± 0.100 | +3.9 | 2.572 ± 0.126 | 2.564 ± 0.142 | +12.8 | 3.265 ± 0.192 | 3.273 ± 0.210 | +9.6 |
| M4 | 4.404 ± 0.330 | 4.293 ± 0.367 | +14.1 | 4.722 ± 0.342 | 4.854 ± 0.421 | +19.9 | 5.352 ± 0.351 | 5.386 ± 0.411 | +16.4 |
| M1, 2 | 0.332 ± 0.031 | 0.330 ± 0.035 | +12.9 | 0.332 ± 0.028 | 0.322 ± 0.034 | +24.9 | 0.412 ± 0.040 | 0.401 ± 0.046 | +17.4 |
| M1, 3 | 0.851 ± 0.078 | 0.822 ± 0.059 | −21.8 | 0.767 ± 0.054 | 0.759 ± 0.051 | −3.5 | 0.722 ± 0.070 | 0.716 ± 0.068 | −2.4 |
| M1, 4 | 0.366 ± 0.044 | 0.367 ± 0.036 | −17.5 | 0.406 ± 0.028 | 0.405 ± 0.029 | +2.1 | 0.431 ± 0.048 | 0.446 ± 0.050 | −1.3 |
| M2, 3 | 2.451 ± 0.292 | 2.366 ± 0.287 | +1.7 | 2.314 ± 0.245 | 2.339 ± 0.257 | +3.8 | 1.764 ± 0.158 | 1.749 ± 0.189 | +20.1 |
| M2, 4 | 1.105 ± 0.139 | 1.128 ± 0.134 | −5.8 | 1.192 ± 0.115 | 1.220 ± 0.124 | +5.1 | 1.061 ± 0.102 | 1.049 ± 0.111 | +9.9 |
| M3, 4 | 0.443 ± 0.024 | 0.453 ± 0.027 | +7.9 | 0.528 ± 0.026 | 0.526 ± 0.032 | +20.2 | 0.599 ± 0.037 | 0.603 ± 0.040 | +8.0 |
| b1 | 0.952 ± 0.116 | 0.941 ± 0.114 | −1.0 | 1.059 ± 0.119 | 1.155 ± 0.116 | −10.8 | 1.197 ± 0.137 | 1.217 ± 0.134 | −3.8 |
| b2 | 1.911 ± 0.164 | 1.877 ± 0.171 | +5.9 | 2.111 ± 0.177 | 2.147 ± 0.190 | +5.4 | 2.048 ± 0.153 | 2.089 ± 0.180 | +14.8 |
| b3 | 1.126 ± 0.105 | 1.134 ± 0.104 | −1.2 | 1.202 ± 0.0 | 1.364 ± 0.112 | – | 1.408 ± 0.118 | 1.524 ± 0.119 | −6.6 |
| b4 | 1.782 ± 0.117 | 1.790 ± 0.122 | +3.9 | 1.891 ± 0.123 | 1.912 ± 0.136 | +9.1 | 2.008 ± 0.123 | 1.992 ± 0.138 | +13.3 |
Same as Table A1 for an integration range 0.3 < k[h Mpc−1] < 0.5 (W1 field).
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.675 ± 0.154 | 1.600 ± 0.170 | +15.4 | 1.981 ± 0.198 | 1.932 ± 0.225 | +16.4 | 2.297 ± 0.387 | 2.269 ± 0.374 | −2.2 |
| M2 | 4.828 ± 0.561 | 4.633 ± 1.029 | +91.2 | 5.639 ± 0.829 | 5.913 ± 1.125 | +29.4 | 5.765 ± 0.944 | 5.726 ± 1.250 | +33.3 |
| M3 | 1.997 ± 0.098 | 1.974 ± 0.098 | +1.3 | 2.558 ± 0.156 | 2.515 ± 0.169 | +9.9 | 3.274 ± 0.307 | 3.239 ± 0.307 | +1.4 |
| M4 | 4.480 ± 0.318 | 4.387 ± 0.439 | +40.9 | 4.746 ± 0.373 | 4.829 ± 0.520 | +37.0 | 5.483 ± 0.474 | 5.444 ± 0.592 | +25.7 |
| M1, 2 | 0.335 ± 0.034 | 0.293 ± 0.119 | +297.9 | 0.319 ± 0.036 | 0.336 ± 0.123 | +219.2 | 0.396 ± 0.082 | 0.404 ± 0.246 | +192.8 |
| M1, 3 | 0.840 ± 0.089 | 0.834 ± 0.091 | +3.4 | 0.774 ± 0.079 | 0.759 ± 0.082 | +5.9 | 0.708 ± 0.197 | 0.724 ± 0.277 | +37.1 |
| M1, 4 | 0.362 ± 0.048 | 0.367 ± 0.052 | +7.8 | 0.399 ± 0.041 | 0.393 ± 0.049 | +20.4 | 0.415 ± 0.081 | 0.436 ± 0.084 | −0.8 |
| M2, 3 | 2.438 ± 0.292 | 2.472 ± 0.518 | +74.7 | 2.218 ± 0.309 | 2.359 ± 0.410 | +24.9 | 1.784 ± 0.366 | 1.710 ± 0.410 | +16.8 |
| M2, 4 | 1.070 ± 0.138 | 1.102 ± 0.236 | +64.6 | 1.220 ± 0.138 | 1.232 ± 0.200 | +43.4 | 1.068 ± 0.165 | 1.050 ± 0.215 | +32.0 |
| M3, 4 | 0.447 ± 0.027 | 0.454 ± 0.037 | +36.5 | 0.524 ± 0.034 | 0.518 ± 0.048 | +44.2 | 0.608 ± 0.064 | 0.596 ± 0.071 | +13.1 |
| b1 | 0.946 ± 0.113 | 1.003 ± 0.114 | −4.1 | 1.046 ± 0.129 | 1.035 ± 0.129 | +1.2 | 1.200 ± 0.162 | 1.240 ± 0.168 | +0.5 |
| b2 | 1.878 ± 0.148 | 1.946 ± 0.251 | +63.7 | 2.119 ± 0.200 | 2.119 ± 0.252 | +26.1 | 2.140 ± 0.220 | 2.078 ± 0.286 | +33.9 |
| b3 | 1.050 ± 0.103 | 1.194 ± 0.0 | – | 1.357 ± 0.117 | 1.357 ± 0.113 | −3.6 | 1.489 ± 0.135 | 1.508 ± 0.140 | +2.2 |
| b4 | 1.786 ± 0.112 | 1.818 ± 0.139 | +22.0 | 1.868 ± 0.134 | 1.946 ± 0.146 | +4.5 | 1.997 ± 0.140 | 2.002 ± 0.161 | +14.8 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.675 ± 0.154 | 1.600 ± 0.170 | +15.4 | 1.981 ± 0.198 | 1.932 ± 0.225 | +16.4 | 2.297 ± 0.387 | 2.269 ± 0.374 | −2.2 |
| M2 | 4.828 ± 0.561 | 4.633 ± 1.029 | +91.2 | 5.639 ± 0.829 | 5.913 ± 1.125 | +29.4 | 5.765 ± 0.944 | 5.726 ± 1.250 | +33.3 |
| M3 | 1.997 ± 0.098 | 1.974 ± 0.098 | +1.3 | 2.558 ± 0.156 | 2.515 ± 0.169 | +9.9 | 3.274 ± 0.307 | 3.239 ± 0.307 | +1.4 |
| M4 | 4.480 ± 0.318 | 4.387 ± 0.439 | +40.9 | 4.746 ± 0.373 | 4.829 ± 0.520 | +37.0 | 5.483 ± 0.474 | 5.444 ± 0.592 | +25.7 |
| M1, 2 | 0.335 ± 0.034 | 0.293 ± 0.119 | +297.9 | 0.319 ± 0.036 | 0.336 ± 0.123 | +219.2 | 0.396 ± 0.082 | 0.404 ± 0.246 | +192.8 |
| M1, 3 | 0.840 ± 0.089 | 0.834 ± 0.091 | +3.4 | 0.774 ± 0.079 | 0.759 ± 0.082 | +5.9 | 0.708 ± 0.197 | 0.724 ± 0.277 | +37.1 |
| M1, 4 | 0.362 ± 0.048 | 0.367 ± 0.052 | +7.8 | 0.399 ± 0.041 | 0.393 ± 0.049 | +20.4 | 0.415 ± 0.081 | 0.436 ± 0.084 | −0.8 |
| M2, 3 | 2.438 ± 0.292 | 2.472 ± 0.518 | +74.7 | 2.218 ± 0.309 | 2.359 ± 0.410 | +24.9 | 1.784 ± 0.366 | 1.710 ± 0.410 | +16.8 |
| M2, 4 | 1.070 ± 0.138 | 1.102 ± 0.236 | +64.6 | 1.220 ± 0.138 | 1.232 ± 0.200 | +43.4 | 1.068 ± 0.165 | 1.050 ± 0.215 | +32.0 |
| M3, 4 | 0.447 ± 0.027 | 0.454 ± 0.037 | +36.5 | 0.524 ± 0.034 | 0.518 ± 0.048 | +44.2 | 0.608 ± 0.064 | 0.596 ± 0.071 | +13.1 |
| b1 | 0.946 ± 0.113 | 1.003 ± 0.114 | −4.1 | 1.046 ± 0.129 | 1.035 ± 0.129 | +1.2 | 1.200 ± 0.162 | 1.240 ± 0.168 | +0.5 |
| b2 | 1.878 ± 0.148 | 1.946 ± 0.251 | +63.7 | 2.119 ± 0.200 | 2.119 ± 0.252 | +26.1 | 2.140 ± 0.220 | 2.078 ± 0.286 | +33.9 |
| b3 | 1.050 ± 0.103 | 1.194 ± 0.0 | – | 1.357 ± 0.117 | 1.357 ± 0.113 | −3.6 | 1.489 ± 0.135 | 1.508 ± 0.140 | +2.2 |
| b4 | 1.786 ± 0.112 | 1.818 ± 0.139 | +22.0 | 1.868 ± 0.134 | 1.946 ± 0.146 | +4.5 | 1.997 ± 0.140 | 2.002 ± 0.161 | +14.8 |
Same as Table A1 for an integration range 0.3 < k[h Mpc−1] < 0.5 (W1 field).
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.675 ± 0.154 | 1.600 ± 0.170 | +15.4 | 1.981 ± 0.198 | 1.932 ± 0.225 | +16.4 | 2.297 ± 0.387 | 2.269 ± 0.374 | −2.2 |
| M2 | 4.828 ± 0.561 | 4.633 ± 1.029 | +91.2 | 5.639 ± 0.829 | 5.913 ± 1.125 | +29.4 | 5.765 ± 0.944 | 5.726 ± 1.250 | +33.3 |
| M3 | 1.997 ± 0.098 | 1.974 ± 0.098 | +1.3 | 2.558 ± 0.156 | 2.515 ± 0.169 | +9.9 | 3.274 ± 0.307 | 3.239 ± 0.307 | +1.4 |
| M4 | 4.480 ± 0.318 | 4.387 ± 0.439 | +40.9 | 4.746 ± 0.373 | 4.829 ± 0.520 | +37.0 | 5.483 ± 0.474 | 5.444 ± 0.592 | +25.7 |
| M1, 2 | 0.335 ± 0.034 | 0.293 ± 0.119 | +297.9 | 0.319 ± 0.036 | 0.336 ± 0.123 | +219.2 | 0.396 ± 0.082 | 0.404 ± 0.246 | +192.8 |
| M1, 3 | 0.840 ± 0.089 | 0.834 ± 0.091 | +3.4 | 0.774 ± 0.079 | 0.759 ± 0.082 | +5.9 | 0.708 ± 0.197 | 0.724 ± 0.277 | +37.1 |
| M1, 4 | 0.362 ± 0.048 | 0.367 ± 0.052 | +7.8 | 0.399 ± 0.041 | 0.393 ± 0.049 | +20.4 | 0.415 ± 0.081 | 0.436 ± 0.084 | −0.8 |
| M2, 3 | 2.438 ± 0.292 | 2.472 ± 0.518 | +74.7 | 2.218 ± 0.309 | 2.359 ± 0.410 | +24.9 | 1.784 ± 0.366 | 1.710 ± 0.410 | +16.8 |
| M2, 4 | 1.070 ± 0.138 | 1.102 ± 0.236 | +64.6 | 1.220 ± 0.138 | 1.232 ± 0.200 | +43.4 | 1.068 ± 0.165 | 1.050 ± 0.215 | +32.0 |
| M3, 4 | 0.447 ± 0.027 | 0.454 ± 0.037 | +36.5 | 0.524 ± 0.034 | 0.518 ± 0.048 | +44.2 | 0.608 ± 0.064 | 0.596 ± 0.071 | +13.1 |
| b1 | 0.946 ± 0.113 | 1.003 ± 0.114 | −4.1 | 1.046 ± 0.129 | 1.035 ± 0.129 | +1.2 | 1.200 ± 0.162 | 1.240 ± 0.168 | +0.5 |
| b2 | 1.878 ± 0.148 | 1.946 ± 0.251 | +63.7 | 2.119 ± 0.200 | 2.119 ± 0.252 | +26.1 | 2.140 ± 0.220 | 2.078 ± 0.286 | +33.9 |
| b3 | 1.050 ± 0.103 | 1.194 ± 0.0 | – | 1.357 ± 0.117 | 1.357 ± 0.113 | −3.6 | 1.489 ± 0.135 | 1.508 ± 0.140 | +2.2 |
| b4 | 1.786 ± 0.112 | 1.818 ± 0.139 | +22.0 | 1.868 ± 0.134 | 1.946 ± 0.146 | +4.5 | 1.997 ± 0.140 | 2.002 ± 0.161 | +14.8 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.675 ± 0.154 | 1.600 ± 0.170 | +15.4 | 1.981 ± 0.198 | 1.932 ± 0.225 | +16.4 | 2.297 ± 0.387 | 2.269 ± 0.374 | −2.2 |
| M2 | 4.828 ± 0.561 | 4.633 ± 1.029 | +91.2 | 5.639 ± 0.829 | 5.913 ± 1.125 | +29.4 | 5.765 ± 0.944 | 5.726 ± 1.250 | +33.3 |
| M3 | 1.997 ± 0.098 | 1.974 ± 0.098 | +1.3 | 2.558 ± 0.156 | 2.515 ± 0.169 | +9.9 | 3.274 ± 0.307 | 3.239 ± 0.307 | +1.4 |
| M4 | 4.480 ± 0.318 | 4.387 ± 0.439 | +40.9 | 4.746 ± 0.373 | 4.829 ± 0.520 | +37.0 | 5.483 ± 0.474 | 5.444 ± 0.592 | +25.7 |
| M1, 2 | 0.335 ± 0.034 | 0.293 ± 0.119 | +297.9 | 0.319 ± 0.036 | 0.336 ± 0.123 | +219.2 | 0.396 ± 0.082 | 0.404 ± 0.246 | +192.8 |
| M1, 3 | 0.840 ± 0.089 | 0.834 ± 0.091 | +3.4 | 0.774 ± 0.079 | 0.759 ± 0.082 | +5.9 | 0.708 ± 0.197 | 0.724 ± 0.277 | +37.1 |
| M1, 4 | 0.362 ± 0.048 | 0.367 ± 0.052 | +7.8 | 0.399 ± 0.041 | 0.393 ± 0.049 | +20.4 | 0.415 ± 0.081 | 0.436 ± 0.084 | −0.8 |
| M2, 3 | 2.438 ± 0.292 | 2.472 ± 0.518 | +74.7 | 2.218 ± 0.309 | 2.359 ± 0.410 | +24.9 | 1.784 ± 0.366 | 1.710 ± 0.410 | +16.8 |
| M2, 4 | 1.070 ± 0.138 | 1.102 ± 0.236 | +64.6 | 1.220 ± 0.138 | 1.232 ± 0.200 | +43.4 | 1.068 ± 0.165 | 1.050 ± 0.215 | +32.0 |
| M3, 4 | 0.447 ± 0.027 | 0.454 ± 0.037 | +36.5 | 0.524 ± 0.034 | 0.518 ± 0.048 | +44.2 | 0.608 ± 0.064 | 0.596 ± 0.071 | +13.1 |
| b1 | 0.946 ± 0.113 | 1.003 ± 0.114 | −4.1 | 1.046 ± 0.129 | 1.035 ± 0.129 | +1.2 | 1.200 ± 0.162 | 1.240 ± 0.168 | +0.5 |
| b2 | 1.878 ± 0.148 | 1.946 ± 0.251 | +63.7 | 2.119 ± 0.200 | 2.119 ± 0.252 | +26.1 | 2.140 ± 0.220 | 2.078 ± 0.286 | +33.9 |
| b3 | 1.050 ± 0.103 | 1.194 ± 0.0 | – | 1.357 ± 0.117 | 1.357 ± 0.113 | −3.6 | 1.489 ± 0.135 | 1.508 ± 0.140 | +2.2 |
| b4 | 1.786 ± 0.112 | 1.818 ± 0.139 | +22.0 | 1.868 ± 0.134 | 1.946 ± 0.146 | +4.5 | 1.997 ± 0.140 | 2.002 ± 0.161 | +14.8 |
Same as Table A1 for an integration range 0.1 < k[h Mpc−1] < 0.3 in the W4 field.
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.538 ± 0.199 | 1.553 ± 0.172 | −14.7 | 1.946 ± 0.222 | 1.964 ± 0.220 | −1.6 | 2.386 ± 0.364 | 2.443 ± 0.334 | −10.3 |
| M2 | 3.256 ± 0.590 | 2.870 ± 0.863 | +65.9 | 5.377 ± 0.881 | 5.248 ± 1.065 | +23.9 | 5.650 ± 0.983 | 5.402 ± 1.335 | +42.0 |
| M3 | 2.019 ± 0.184 | 1.958 ± 0.181 | +1.3 | 2.454 ± 0.203 | 2.414 ± 0.201 | 0.4 | 5.650 ± 0.983 | 5.402 ± 1.335 | +13.0 |
| M4 | 3.134 ± 0.451 | 3.078 ± 0.490 | +10.5 | 4.560 ± 0.534 | 4.783 ± 0.637 | +13.7 | 5.319 ± 0.546 | 5.135 ± 0.663 | +25.9 |
| M1, 2 | 0.489 ± 0.083 | 0.474 ± 0.240 | +195.8 | 0.363 ± 0.059 | 0.359 ± 0.074 | +25.4 | 0.405 ± 0.062 | 0.416 ± 0.102 | +60.7 |
| M1, 3 | 0.769 ± 0.098 | 0.736 ± 0.085 | −9.6 | 0.800 ± 0.089 | 0.793 ± 0.087 | −2.3 | 0.693 ± 0.101 | 0.729 ± 0.098 | −7.8 |
| M1, 4 | 0.476 ± 0.078 | 0.476 ± 0.077 | +2.2 | 0.424 ± 0.055 | 0.425 ± 0.063 | +13.5 | 0.443 ± 0.070 | 0.459 ± 0.072 | −1.1 |
| M2, 3 | 1.629 ± 0.275 | 1.566 ± 0.417 | +57.7 | 2.242 ± 0.336 | 2.224 ± 0.386 | +15.8 | 1.661 ± 0.272 | 1.562 ± 0.355 | +38.7 |
| M2, 4 | 0.981 ± 0.160 | 0.951 ± 0.254 | +63.9.9 | 1.156 ± 0.159 | 1.160 ± 0.203 | +26.9 | 1.042 ± 0.159 | 1.102 ± 0.215 | +27.5 |
| M3, 4 | 0.636 ± 0.070 | 0.644 ± 0.091 | +28.4 | 0.521 ± 0.049 | 0.515 ± 0.063 | +31.6 | 0.611 ± 0.063 | 0.640 ± 0.069 | +3.7 |
| b1 | 0.977 ± 0.134 | 0.916 ± 0.119 | −5.2 | 1.086 ± 0.132 | 1.034 ± 0.132 | 4.8 | 1.251 ± 0.162 | 1.228 ± 0.147 | −7.5 |
| b2 | 1.418 ± 0.197 | 1.490 ± 0.274 | +32.7 | 1.984 ± 0.215 | 1.974 ± 0.255 | +19.4 | 2.083 ± 0.227 | 2.099 ± 0.299 | +30.8 |
| b3 | 1.181 ± 0.119 | 1.116 ± 0.114 | +1.0 | 1.194 ± 0.123 | 1.280 ± 0.124 | −6.2 | 1.490 ± 0.128 | 1.481 ± 0.126 | −0.8 |
| b4 | 1.478 ± 0.158 | 1.497 ± 0.167 | +4.2 | 1.769 ± 0.158 | 1.863 ± 0.175 | +5.6 | 2.001 ± 0.152 | 2.005 ± 0.169 | +10.9 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.538 ± 0.199 | 1.553 ± 0.172 | −14.7 | 1.946 ± 0.222 | 1.964 ± 0.220 | −1.6 | 2.386 ± 0.364 | 2.443 ± 0.334 | −10.3 |
| M2 | 3.256 ± 0.590 | 2.870 ± 0.863 | +65.9 | 5.377 ± 0.881 | 5.248 ± 1.065 | +23.9 | 5.650 ± 0.983 | 5.402 ± 1.335 | +42.0 |
| M3 | 2.019 ± 0.184 | 1.958 ± 0.181 | +1.3 | 2.454 ± 0.203 | 2.414 ± 0.201 | 0.4 | 5.650 ± 0.983 | 5.402 ± 1.335 | +13.0 |
| M4 | 3.134 ± 0.451 | 3.078 ± 0.490 | +10.5 | 4.560 ± 0.534 | 4.783 ± 0.637 | +13.7 | 5.319 ± 0.546 | 5.135 ± 0.663 | +25.9 |
| M1, 2 | 0.489 ± 0.083 | 0.474 ± 0.240 | +195.8 | 0.363 ± 0.059 | 0.359 ± 0.074 | +25.4 | 0.405 ± 0.062 | 0.416 ± 0.102 | +60.7 |
| M1, 3 | 0.769 ± 0.098 | 0.736 ± 0.085 | −9.6 | 0.800 ± 0.089 | 0.793 ± 0.087 | −2.3 | 0.693 ± 0.101 | 0.729 ± 0.098 | −7.8 |
| M1, 4 | 0.476 ± 0.078 | 0.476 ± 0.077 | +2.2 | 0.424 ± 0.055 | 0.425 ± 0.063 | +13.5 | 0.443 ± 0.070 | 0.459 ± 0.072 | −1.1 |
| M2, 3 | 1.629 ± 0.275 | 1.566 ± 0.417 | +57.7 | 2.242 ± 0.336 | 2.224 ± 0.386 | +15.8 | 1.661 ± 0.272 | 1.562 ± 0.355 | +38.7 |
| M2, 4 | 0.981 ± 0.160 | 0.951 ± 0.254 | +63.9.9 | 1.156 ± 0.159 | 1.160 ± 0.203 | +26.9 | 1.042 ± 0.159 | 1.102 ± 0.215 | +27.5 |
| M3, 4 | 0.636 ± 0.070 | 0.644 ± 0.091 | +28.4 | 0.521 ± 0.049 | 0.515 ± 0.063 | +31.6 | 0.611 ± 0.063 | 0.640 ± 0.069 | +3.7 |
| b1 | 0.977 ± 0.134 | 0.916 ± 0.119 | −5.2 | 1.086 ± 0.132 | 1.034 ± 0.132 | 4.8 | 1.251 ± 0.162 | 1.228 ± 0.147 | −7.5 |
| b2 | 1.418 ± 0.197 | 1.490 ± 0.274 | +32.7 | 1.984 ± 0.215 | 1.974 ± 0.255 | +19.4 | 2.083 ± 0.227 | 2.099 ± 0.299 | +30.8 |
| b3 | 1.181 ± 0.119 | 1.116 ± 0.114 | +1.0 | 1.194 ± 0.123 | 1.280 ± 0.124 | −6.2 | 1.490 ± 0.128 | 1.481 ± 0.126 | −0.8 |
| b4 | 1.478 ± 0.158 | 1.497 ± 0.167 | +4.2 | 1.769 ± 0.158 | 1.863 ± 0.175 | +5.6 | 2.001 ± 0.152 | 2.005 ± 0.169 | +10.9 |
Same as Table A1 for an integration range 0.1 < k[h Mpc−1] < 0.3 in the W4 field.
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.538 ± 0.199 | 1.553 ± 0.172 | −14.7 | 1.946 ± 0.222 | 1.964 ± 0.220 | −1.6 | 2.386 ± 0.364 | 2.443 ± 0.334 | −10.3 |
| M2 | 3.256 ± 0.590 | 2.870 ± 0.863 | +65.9 | 5.377 ± 0.881 | 5.248 ± 1.065 | +23.9 | 5.650 ± 0.983 | 5.402 ± 1.335 | +42.0 |
| M3 | 2.019 ± 0.184 | 1.958 ± 0.181 | +1.3 | 2.454 ± 0.203 | 2.414 ± 0.201 | 0.4 | 5.650 ± 0.983 | 5.402 ± 1.335 | +13.0 |
| M4 | 3.134 ± 0.451 | 3.078 ± 0.490 | +10.5 | 4.560 ± 0.534 | 4.783 ± 0.637 | +13.7 | 5.319 ± 0.546 | 5.135 ± 0.663 | +25.9 |
| M1, 2 | 0.489 ± 0.083 | 0.474 ± 0.240 | +195.8 | 0.363 ± 0.059 | 0.359 ± 0.074 | +25.4 | 0.405 ± 0.062 | 0.416 ± 0.102 | +60.7 |
| M1, 3 | 0.769 ± 0.098 | 0.736 ± 0.085 | −9.6 | 0.800 ± 0.089 | 0.793 ± 0.087 | −2.3 | 0.693 ± 0.101 | 0.729 ± 0.098 | −7.8 |
| M1, 4 | 0.476 ± 0.078 | 0.476 ± 0.077 | +2.2 | 0.424 ± 0.055 | 0.425 ± 0.063 | +13.5 | 0.443 ± 0.070 | 0.459 ± 0.072 | −1.1 |
| M2, 3 | 1.629 ± 0.275 | 1.566 ± 0.417 | +57.7 | 2.242 ± 0.336 | 2.224 ± 0.386 | +15.8 | 1.661 ± 0.272 | 1.562 ± 0.355 | +38.7 |
| M2, 4 | 0.981 ± 0.160 | 0.951 ± 0.254 | +63.9.9 | 1.156 ± 0.159 | 1.160 ± 0.203 | +26.9 | 1.042 ± 0.159 | 1.102 ± 0.215 | +27.5 |
| M3, 4 | 0.636 ± 0.070 | 0.644 ± 0.091 | +28.4 | 0.521 ± 0.049 | 0.515 ± 0.063 | +31.6 | 0.611 ± 0.063 | 0.640 ± 0.069 | +3.7 |
| b1 | 0.977 ± 0.134 | 0.916 ± 0.119 | −5.2 | 1.086 ± 0.132 | 1.034 ± 0.132 | 4.8 | 1.251 ± 0.162 | 1.228 ± 0.147 | −7.5 |
| b2 | 1.418 ± 0.197 | 1.490 ± 0.274 | +32.7 | 1.984 ± 0.215 | 1.974 ± 0.255 | +19.4 | 2.083 ± 0.227 | 2.099 ± 0.299 | +30.8 |
| b3 | 1.181 ± 0.119 | 1.116 ± 0.114 | +1.0 | 1.194 ± 0.123 | 1.280 ± 0.124 | −6.2 | 1.490 ± 0.128 | 1.481 ± 0.126 | −0.8 |
| b4 | 1.478 ± 0.158 | 1.497 ± 0.167 | +4.2 | 1.769 ± 0.158 | 1.863 ± 0.175 | +5.6 | 2.001 ± 0.152 | 2.005 ± 0.169 | +10.9 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.538 ± 0.199 | 1.553 ± 0.172 | −14.7 | 1.946 ± 0.222 | 1.964 ± 0.220 | −1.6 | 2.386 ± 0.364 | 2.443 ± 0.334 | −10.3 |
| M2 | 3.256 ± 0.590 | 2.870 ± 0.863 | +65.9 | 5.377 ± 0.881 | 5.248 ± 1.065 | +23.9 | 5.650 ± 0.983 | 5.402 ± 1.335 | +42.0 |
| M3 | 2.019 ± 0.184 | 1.958 ± 0.181 | +1.3 | 2.454 ± 0.203 | 2.414 ± 0.201 | 0.4 | 5.650 ± 0.983 | 5.402 ± 1.335 | +13.0 |
| M4 | 3.134 ± 0.451 | 3.078 ± 0.490 | +10.5 | 4.560 ± 0.534 | 4.783 ± 0.637 | +13.7 | 5.319 ± 0.546 | 5.135 ± 0.663 | +25.9 |
| M1, 2 | 0.489 ± 0.083 | 0.474 ± 0.240 | +195.8 | 0.363 ± 0.059 | 0.359 ± 0.074 | +25.4 | 0.405 ± 0.062 | 0.416 ± 0.102 | +60.7 |
| M1, 3 | 0.769 ± 0.098 | 0.736 ± 0.085 | −9.6 | 0.800 ± 0.089 | 0.793 ± 0.087 | −2.3 | 0.693 ± 0.101 | 0.729 ± 0.098 | −7.8 |
| M1, 4 | 0.476 ± 0.078 | 0.476 ± 0.077 | +2.2 | 0.424 ± 0.055 | 0.425 ± 0.063 | +13.5 | 0.443 ± 0.070 | 0.459 ± 0.072 | −1.1 |
| M2, 3 | 1.629 ± 0.275 | 1.566 ± 0.417 | +57.7 | 2.242 ± 0.336 | 2.224 ± 0.386 | +15.8 | 1.661 ± 0.272 | 1.562 ± 0.355 | +38.7 |
| M2, 4 | 0.981 ± 0.160 | 0.951 ± 0.254 | +63.9.9 | 1.156 ± 0.159 | 1.160 ± 0.203 | +26.9 | 1.042 ± 0.159 | 1.102 ± 0.215 | +27.5 |
| M3, 4 | 0.636 ± 0.070 | 0.644 ± 0.091 | +28.4 | 0.521 ± 0.049 | 0.515 ± 0.063 | +31.6 | 0.611 ± 0.063 | 0.640 ± 0.069 | +3.7 |
| b1 | 0.977 ± 0.134 | 0.916 ± 0.119 | −5.2 | 1.086 ± 0.132 | 1.034 ± 0.132 | 4.8 | 1.251 ± 0.162 | 1.228 ± 0.147 | −7.5 |
| b2 | 1.418 ± 0.197 | 1.490 ± 0.274 | +32.7 | 1.984 ± 0.215 | 1.974 ± 0.255 | +19.4 | 2.083 ± 0.227 | 2.099 ± 0.299 | +30.8 |
| b3 | 1.181 ± 0.119 | 1.116 ± 0.114 | +1.0 | 1.194 ± 0.123 | 1.280 ± 0.124 | −6.2 | 1.490 ± 0.128 | 1.481 ± 0.126 | −0.8 |
| b4 | 1.478 ± 0.158 | 1.497 ± 0.167 | +4.2 | 1.769 ± 0.158 | 1.863 ± 0.175 | +5.6 | 2.001 ± 0.152 | 2.005 ± 0.169 | +10.9 |
Same as Table A1 for an integration range 0.3 < k[h Mpc−1] < 0.5 in the W4 field.
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.500 ± 0.180 | 1.591 ± 0.240 | +25.9 | 1.927 ± 0.235 | 1.877 ± 0.278 | +21.0 | 2.379 ± 0.529 | 2.462 ± 0.641 | +17.2 |
| M2 | 3.096 ± 0.914 | 3.374 ± 1.456 | +46.2 | 5.258 ± 1.096 | 5.537 ± 1.829 | +58.5 | 5.599 ± 1.258 | 4.964 ± 2.137 | +91.6 |
| M3 | 1.956 ± 0.174 | 2.030 ± 0.154 | −14.4 | 2.386 ± 0.191 | 2.387 ± 0.230 | +20.0 | 3.398 ± 0.367 | 3.357 ± 0.414 | +14.3 |
| M4 | 3.119 ± 0.601 | 3.081 ± 0.654 | +10.0 | 4.510 ± 0.589 | 4.553 ± 0.745 | +25.1 | 5.140 ± 0.682 | 5.151 ± 0.880 | +28.8 |
| M1, 2 | 0.491 ± 0.252 | 0.465 ± 0.368 | +54.2 | 0.373 ± 0.144 | 0.211 ± 0.175 | +114.4 | 0.412 ± 0.130 | 0.432 ± 0.350 | +156.1 |
| M1, 3 | 0.725 ± 0.108 | 0.720 ± 0.133 | +24.3 | 0.813 ± 0.109 | 0.761 ± 0.119 | +16.4 | 0.693 ± 0.155 | 0.697 ± 0.269 | +71.9 |
| M1, 4 | 0.464 ± 0.118 | 0.474 ± 0.352 | +190.2 | 0.413 ± 0.067 | 0.409 ± 0.087 | +31.3 | 0.436 ± 0.106 | 0.460 ± 0.141 | +25.6 |
| M2, 3 | 1.515 ± 0.426 | 1.467 ± 0.725 | +75.8 | 2.153 ± 0.437 | 2.297 ± 0.714 | +53.2 | 1.707 ± 0.529 | 1.476 ± 1.224 | +167.5 |
| M2, 4 | 0.990 ± 0.298 | 0.930 ± 0.750 | +167.1 | 1.177 ± 0.203 | 1.108 ± 0.385 | +101.5 | 1.079 ± 0.240 | 0.955 ± 0.407 | +91.1 |
| M3, 4 | 0.612 ± 0.130 | 0.431 ± 0.241 | +163.0 | 0.513 ± 0.061 | 0.508 ± 0.080 | +32.3 | 0.635 ± 0.084 | 0.645 ± 0.103 | +20.8 |
| b1 | 0.933 ± 0.124 | 0.940 ± 0.138 | +10.0 | 1.070 ± 0.127 | 1.035 ± 0.144 | +16.4 | 1.200 ± 0.207 | 1.219 ± 0.238 | +13.1 |
| b2 | 1.484 ± 0.269 | 1.628 ± 0.449 | +51.8 | 2.019 ± 0.254 | 2.026 ± 0.420 | +64.6 | 2.083 ± 0.287 | 1.973 ± 0.473 | +73.7 |
| b3 | 1.142 ± 0.110 | 1.162 ± 0.115 | +2.8 | 1.319 ± 0.121 | 1.293 ± 0.128 | +7.7 | 1.475 ± 0.149 | 1.466 ± 0.155 | +4.3 |
| b4 | 1.474 ± 0.188 | 1.496 ± 0.214 | +12.2 | 1.823 ± 0.169 | 1.786 ± 0.202 | +22.1 | 1.949 ± 0.179 | 1.850 ± 0.217 | +27.4 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.500 ± 0.180 | 1.591 ± 0.240 | +25.9 | 1.927 ± 0.235 | 1.877 ± 0.278 | +21.0 | 2.379 ± 0.529 | 2.462 ± 0.641 | +17.2 |
| M2 | 3.096 ± 0.914 | 3.374 ± 1.456 | +46.2 | 5.258 ± 1.096 | 5.537 ± 1.829 | +58.5 | 5.599 ± 1.258 | 4.964 ± 2.137 | +91.6 |
| M3 | 1.956 ± 0.174 | 2.030 ± 0.154 | −14.4 | 2.386 ± 0.191 | 2.387 ± 0.230 | +20.0 | 3.398 ± 0.367 | 3.357 ± 0.414 | +14.3 |
| M4 | 3.119 ± 0.601 | 3.081 ± 0.654 | +10.0 | 4.510 ± 0.589 | 4.553 ± 0.745 | +25.1 | 5.140 ± 0.682 | 5.151 ± 0.880 | +28.8 |
| M1, 2 | 0.491 ± 0.252 | 0.465 ± 0.368 | +54.2 | 0.373 ± 0.144 | 0.211 ± 0.175 | +114.4 | 0.412 ± 0.130 | 0.432 ± 0.350 | +156.1 |
| M1, 3 | 0.725 ± 0.108 | 0.720 ± 0.133 | +24.3 | 0.813 ± 0.109 | 0.761 ± 0.119 | +16.4 | 0.693 ± 0.155 | 0.697 ± 0.269 | +71.9 |
| M1, 4 | 0.464 ± 0.118 | 0.474 ± 0.352 | +190.2 | 0.413 ± 0.067 | 0.409 ± 0.087 | +31.3 | 0.436 ± 0.106 | 0.460 ± 0.141 | +25.6 |
| M2, 3 | 1.515 ± 0.426 | 1.467 ± 0.725 | +75.8 | 2.153 ± 0.437 | 2.297 ± 0.714 | +53.2 | 1.707 ± 0.529 | 1.476 ± 1.224 | +167.5 |
| M2, 4 | 0.990 ± 0.298 | 0.930 ± 0.750 | +167.1 | 1.177 ± 0.203 | 1.108 ± 0.385 | +101.5 | 1.079 ± 0.240 | 0.955 ± 0.407 | +91.1 |
| M3, 4 | 0.612 ± 0.130 | 0.431 ± 0.241 | +163.0 | 0.513 ± 0.061 | 0.508 ± 0.080 | +32.3 | 0.635 ± 0.084 | 0.645 ± 0.103 | +20.8 |
| b1 | 0.933 ± 0.124 | 0.940 ± 0.138 | +10.0 | 1.070 ± 0.127 | 1.035 ± 0.144 | +16.4 | 1.200 ± 0.207 | 1.219 ± 0.238 | +13.1 |
| b2 | 1.484 ± 0.269 | 1.628 ± 0.449 | +51.8 | 2.019 ± 0.254 | 2.026 ± 0.420 | +64.6 | 2.083 ± 0.287 | 1.973 ± 0.473 | +73.7 |
| b3 | 1.142 ± 0.110 | 1.162 ± 0.115 | +2.8 | 1.319 ± 0.121 | 1.293 ± 0.128 | +7.7 | 1.475 ± 0.149 | 1.466 ± 0.155 | +4.3 |
| b4 | 1.474 ± 0.188 | 1.496 ± 0.214 | +12.2 | 1.823 ± 0.169 | 1.786 ± 0.202 | +22.1 | 1.949 ± 0.179 | 1.850 ± 0.217 | +27.4 |
Same as Table A1 for an integration range 0.3 < k[h Mpc−1] < 0.5 in the W4 field.
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.500 ± 0.180 | 1.591 ± 0.240 | +25.9 | 1.927 ± 0.235 | 1.877 ± 0.278 | +21.0 | 2.379 ± 0.529 | 2.462 ± 0.641 | +17.2 |
| M2 | 3.096 ± 0.914 | 3.374 ± 1.456 | +46.2 | 5.258 ± 1.096 | 5.537 ± 1.829 | +58.5 | 5.599 ± 1.258 | 4.964 ± 2.137 | +91.6 |
| M3 | 1.956 ± 0.174 | 2.030 ± 0.154 | −14.4 | 2.386 ± 0.191 | 2.387 ± 0.230 | +20.0 | 3.398 ± 0.367 | 3.357 ± 0.414 | +14.3 |
| M4 | 3.119 ± 0.601 | 3.081 ± 0.654 | +10.0 | 4.510 ± 0.589 | 4.553 ± 0.745 | +25.1 | 5.140 ± 0.682 | 5.151 ± 0.880 | +28.8 |
| M1, 2 | 0.491 ± 0.252 | 0.465 ± 0.368 | +54.2 | 0.373 ± 0.144 | 0.211 ± 0.175 | +114.4 | 0.412 ± 0.130 | 0.432 ± 0.350 | +156.1 |
| M1, 3 | 0.725 ± 0.108 | 0.720 ± 0.133 | +24.3 | 0.813 ± 0.109 | 0.761 ± 0.119 | +16.4 | 0.693 ± 0.155 | 0.697 ± 0.269 | +71.9 |
| M1, 4 | 0.464 ± 0.118 | 0.474 ± 0.352 | +190.2 | 0.413 ± 0.067 | 0.409 ± 0.087 | +31.3 | 0.436 ± 0.106 | 0.460 ± 0.141 | +25.6 |
| M2, 3 | 1.515 ± 0.426 | 1.467 ± 0.725 | +75.8 | 2.153 ± 0.437 | 2.297 ± 0.714 | +53.2 | 1.707 ± 0.529 | 1.476 ± 1.224 | +167.5 |
| M2, 4 | 0.990 ± 0.298 | 0.930 ± 0.750 | +167.1 | 1.177 ± 0.203 | 1.108 ± 0.385 | +101.5 | 1.079 ± 0.240 | 0.955 ± 0.407 | +91.1 |
| M3, 4 | 0.612 ± 0.130 | 0.431 ± 0.241 | +163.0 | 0.513 ± 0.061 | 0.508 ± 0.080 | +32.3 | 0.635 ± 0.084 | 0.645 ± 0.103 | +20.8 |
| b1 | 0.933 ± 0.124 | 0.940 ± 0.138 | +10.0 | 1.070 ± 0.127 | 1.035 ± 0.144 | +16.4 | 1.200 ± 0.207 | 1.219 ± 0.238 | +13.1 |
| b2 | 1.484 ± 0.269 | 1.628 ± 0.449 | +51.8 | 2.019 ± 0.254 | 2.026 ± 0.420 | +64.6 | 2.083 ± 0.287 | 1.973 ± 0.473 | +73.7 |
| b3 | 1.142 ± 0.110 | 1.162 ± 0.115 | +2.8 | 1.319 ± 0.121 | 1.293 ± 0.128 | +7.7 | 1.475 ± 0.149 | 1.466 ± 0.155 | +4.3 |
| b4 | 1.474 ± 0.188 | 1.496 ± 0.214 | +12.2 | 1.823 ± 0.169 | 1.786 ± 0.202 | +22.1 | 1.949 ± 0.179 | 1.850 ± 0.217 | +27.4 |
| . | 0.6 < z < 0.75 . | 0.75 < z < 0.9 . | 0.9 < z < 1.1 . | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Param. . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . | MTOE . | FKP . | Gain (per cent) . |
| M1 | 1.500 ± 0.180 | 1.591 ± 0.240 | +25.9 | 1.927 ± 0.235 | 1.877 ± 0.278 | +21.0 | 2.379 ± 0.529 | 2.462 ± 0.641 | +17.2 |
| M2 | 3.096 ± 0.914 | 3.374 ± 1.456 | +46.2 | 5.258 ± 1.096 | 5.537 ± 1.829 | +58.5 | 5.599 ± 1.258 | 4.964 ± 2.137 | +91.6 |
| M3 | 1.956 ± 0.174 | 2.030 ± 0.154 | −14.4 | 2.386 ± 0.191 | 2.387 ± 0.230 | +20.0 | 3.398 ± 0.367 | 3.357 ± 0.414 | +14.3 |
| M4 | 3.119 ± 0.601 | 3.081 ± 0.654 | +10.0 | 4.510 ± 0.589 | 4.553 ± 0.745 | +25.1 | 5.140 ± 0.682 | 5.151 ± 0.880 | +28.8 |
| M1, 2 | 0.491 ± 0.252 | 0.465 ± 0.368 | +54.2 | 0.373 ± 0.144 | 0.211 ± 0.175 | +114.4 | 0.412 ± 0.130 | 0.432 ± 0.350 | +156.1 |
| M1, 3 | 0.725 ± 0.108 | 0.720 ± 0.133 | +24.3 | 0.813 ± 0.109 | 0.761 ± 0.119 | +16.4 | 0.693 ± 0.155 | 0.697 ± 0.269 | +71.9 |
| M1, 4 | 0.464 ± 0.118 | 0.474 ± 0.352 | +190.2 | 0.413 ± 0.067 | 0.409 ± 0.087 | +31.3 | 0.436 ± 0.106 | 0.460 ± 0.141 | +25.6 |
| M2, 3 | 1.515 ± 0.426 | 1.467 ± 0.725 | +75.8 | 2.153 ± 0.437 | 2.297 ± 0.714 | +53.2 | 1.707 ± 0.529 | 1.476 ± 1.224 | +167.5 |
| M2, 4 | 0.990 ± 0.298 | 0.930 ± 0.750 | +167.1 | 1.177 ± 0.203 | 1.108 ± 0.385 | +101.5 | 1.079 ± 0.240 | 0.955 ± 0.407 | +91.1 |
| M3, 4 | 0.612 ± 0.130 | 0.431 ± 0.241 | +163.0 | 0.513 ± 0.061 | 0.508 ± 0.080 | +32.3 | 0.635 ± 0.084 | 0.645 ± 0.103 | +20.8 |
| b1 | 0.933 ± 0.124 | 0.940 ± 0.138 | +10.0 | 1.070 ± 0.127 | 1.035 ± 0.144 | +16.4 | 1.200 ± 0.207 | 1.219 ± 0.238 | +13.1 |
| b2 | 1.484 ± 0.269 | 1.628 ± 0.449 | +51.8 | 2.019 ± 0.254 | 2.026 ± 0.420 | +64.6 | 2.083 ± 0.287 | 1.973 ± 0.473 | +73.7 |
| b3 | 1.142 ± 0.110 | 1.162 ± 0.115 | +2.8 | 1.319 ± 0.121 | 1.293 ± 0.128 | +7.7 | 1.475 ± 0.149 | 1.466 ± 0.155 | +4.3 |
| b4 | 1.474 ± 0.188 | 1.496 ± 0.214 | +12.2 | 1.823 ± 0.169 | 1.786 ± 0.202 | +22.1 | 1.949 ± 0.179 | 1.850 ± 0.217 | +27.4 |



