-
PDF
- Split View
-
Views
-
Cite
Cite
Rukaiya Khatoon, Zahir Shah, Ranjeev Misra, Rupjyoti Gogoi, Study of long-term flux and photon index distributions of blazars using RXTE observations, Monthly Notices of the Royal Astronomical Society, Volume 491, Issue 2, January 2020, Pages 1934–1940, https://doi.org/10.1093/mnras/stz3108
Close - Share Icon Share
ABSTRACT
We present a detailed study of flux and index distributions of three blazars [one flat-spectrum radio quasar (FSRQ) and two BL Lacertae objects (BL Lacs)] by using 16 yr of Rossi X-ray Timing Explorer (RXTE) archival data. The three blazars were chosen such that their flux and index distributions have sufficient number of data points (≥90) with relatively less uncertainty |$\left(\overline{\sigma _{\rm err}^{2}}/\sigma ^{2} < 0.2\right)$| in light curves. Anderson–Darling (AD) test and histogram fitting show that flux distribution of FSRQ 3C 273 is lognormal, while its photon index distribution is Gaussian. This result is consistent with linear Gaussian perturbation in the particle acceleration time-scale, which produces lognormal distribution in flux. However, for two BL Lacs, viz. Mrk 501 and Mrk 421, AD test shows that their flux distributions are neither Gaussian nor lognormal, and their index distributions are non-normal. The histogram fitting of Mrk 501 and Mrk 421 suggests that their flux distributions are more likely to be a bimodal, and their index distributions are double Gaussian. Since, Sinha et al. had shown that Gaussian distribution of index produces a lognormal distribution in flux, double Gaussian distribution of index in Mrk 501 and Mrk 421 indicates that their flux distributions are probably double lognormal. Observation of double lognormal flux distribution with double Gaussian distribution in index reaffirms two flux states hypothesis. Further, the difference observed in the flux distribution of FSRQ (3C 273) and BL Lacs (Mrk 501 and Mrk 421) at X-rays suggests that the low-energy emitting electrons have a single lognormal flux distribution, while the high-energy ones have a double lognormal flux distribution.
1 INTRODUCTION
Blazars are the class of radio-loud active galactic nuclei (AGNs), with relativistic jets oriented close to the observer’s line of sight (Urry & Padovani 1995). The non-thermal emission from blazars extends from radio to γ-ray energies. Blazars are characterized by their extreme properties like luminous core, rapid variability, high polarization, superluminal motion, occasional spectacular flares, etc. These extreme properties are usually attributed to the Doppler boosting of the emission that occurs from the relativistic regions in the jet. Blazars are broadly classified into two subclasses, namely BL Lacertae objects (BL Lacs) and flat-spectrum radio quasars (FSRQs). The difference between these two subclasses is based on the presence or absence of emission/absorption line features in their optical spectrum, such that FSRQs show strong emission lines, whereas for BL Lacs, the emission lines are weak/absent (Urry & Padovani 1995; Fan 2003). The non-thermal emission originating from blazar jet produces a double humped spectral energy distribution (SED; Fossati et al. 1998), with the low-energy component peaking at optical/ultraviolet (UV)/soft X-ray energies, while the high-energy component peaks at GeV energies. The low-energy component is well established to be produced by synchrotron emission from relativistic electrons gyrating in the magnetic field of the jet, whereas the high-energy component is usually attributed either to the inverse Compton (IC) scattering of low-energy photons (Dermer, Schlickeiser & Mastichiadis 1992; Maraschi, Ghisellini & Celotti 1992; Shah et al. 2017) or to the hadronic cascades initiated in the jet (Böttcher 2007). Based on the location of the peak frequency in the low-energy component, blazars are further classified into three subclasses namely, high-energy peaked BL Lac (HBL; νp > 1015.3 Hz; Padovani & Giommi 1995), intermediate-energy peaked BL Lac (IBL; 1014 < νp ≤ 1015.3 Hz), and low-energy peaked BL Lac (LBL; νp ≤ 1014 Hz; Fan et al. 2016).
The light curves of blazars show unpredictable variations over a broad range of time-scales ranging from minutes to years across the entire electromagnetic spectrum. The clue to the mechanism causing such variations can be obtained by studying their long-term flux distributions. Typically, a Gaussian distribution of fluxes suggests additive processes, which is obtained when the flux variation is stochastic and linear. However, if the stochastic flux variation is non-linear, a Gaussian distribution in logarithmic flux values is expected, and such distributions are known as lognormal, which are often found in galactic and extragalactic sources, like X-ray binaries, gamma-ray bursts, and AGNs (Lyubarskii 1997; Uttley & McHardy 2001; Negoro & Mineshige 2002; Quilligan et al. 2002; Giebels & Degrange 2009). In the case of AGNs, the lognormal behaviour is observed on time-scales ranging from minutes to days (Gaskell 2004), whereas for X-ray binaries such behaviour is seen in subsecond time-scales (Uttley, McHardy & Vaughan 2005). Among blazars, BL Lac is the first blazar in which lognormal distribution of X-ray flux was observed (Giebels & Degrange 2009). Subsequently, such lognormal behaviour in fluxes with the excess rms correlating linearly with the average flux has been found in different energy bands for a HBL, PKS 2155−304 (H.E.S.S. Collaboration et al. 2017). Recently, a lognormal distribution of flux was shown in PKS 2155−304 at X-ray and optical bands by using 10 yr of data (Chevalier et al. 2019). In the very high energy (VHE) γ-ray band, the lognormal behaviour of flux distribution has been detected in the well-known high-synchrotron peaked BL Lac objects Mrk 501 (Tluczykont et al. 2010; Romoli et al. 2018) and PKS 2155−304 (Aharonian et al. 2009; H.E.S.S. Collaboration et al. 2010). The brightest blazar sources seen by Fermi-Large Area Telescope (LAT) show a similar trend in their long-term monthly binned γ-ray light curves (Shah et al. 2018). Also, using the Fermi-LAT observations, the long-term γ-ray flux variability of the VHE source 1ES 1011+496 is independently confirmed to be lognormal by Sinha et al. (2017). In addition to single lognormal distribution, the double lognormal profile has also been revealed at multiwavelength bands for some blazars (Kushwaha et al. 2016; Shah et al. 2018).
The lognormal behaviour of these astrophysical sources is generally explained in terms of variations from the accretion disc, which is multiplicative in nature (Uttley et al. 2005; McHardy 2010). However, the fluctuations in the accretion disc may not produce minute scale variability as seen in most of the blazar sources (Gaidos et al. 1996; Albert et al. 2007; Paliya et al. 2015). Therefore, as an alternative to the accretion disc model, the lognormal flux distribution in blazars has also been explained in terms of a sum of emission from a large collection of minijets, which are randomly oriented inside the relativistic jet (Biteau & Giebels 2012). Moreover, recently it has been shown that a linear Gaussian perturbation in the particle acceleration time-scale can produce the lognormal flux distribution (Sinha et al. 2018). They showed that perturbation in the acceleration time-scale produces a Gaussian distribution in the index that in turn results in a lognormal distribution of the flux, whereas the perturbation in the particle cooling rate produces neither a Gaussian nor a lognormal flux distribution.
In this work, we study the flux and photon index distribution properties of blazar sources having statistically significant light curves in the 16 yr of Rossi X-ray Timing Explorer(RXTE) observation. The sample selection criteria from the RXTE AGN catalogue are described in Section 2. Characterization of flux/index distribution and correlation study between the flux and photon index are described in Section 3. The physical interpretations of the obtained flux distributions are discussed in Section 4.
2 RXTE ARCHIEVE AND SAMPLE SELECTION
The RXTE public data base provides the systematically analysed long-term light curves and spectral information of AGN sources, for the period from 1996 January to 2012 January. RXTE has two co-aligned instruments, the Proportional Counter Array (PCA; 2–60 keV; Jahoda et al. 2006) and the High-Energy X-ray Timing Experiment (HEXTE; 15–250 keV; Rothschild et al. 1998). It provides light curves in the energy range 2–10 keV. In these light curves, the sampling of data is uneven as different periods had been proposed for various scientific goals. However, despite the time gaps in the light curves, the 16 yr of RXTE observation provides a large data set, which is sometimes statistically suitable to investigate the variability behaviour.
Light-curve significance fraction R values for the unbinned/binned flux and index light curves. Column 1: selected blazars satisfying the conditions R < 0.2 and length of binned flux/index light curve ≥90; column 2: number of data points in the distributions; column 3: R value for index light curve; and column 4: Rvalue for the flux light curve.
| Blazar name . | Number of . | |$R_\Gamma$| . | RFlux . |
|---|---|---|---|
| . | data points . | . | . |
| 3C 273 | 1960 (unbinned) | 0.22 | 2.0 × 10−3 |
| 1151 (2-d binned) | 0.19 | 1.5 × 10−3 | |
| Mrk 501 | 496 (unbinned) | 0.05 | 1.0 × 10−4 |
| 188 (2-d binned) | 0.06 | 1.0 × 10−4 | |
| Mrk 421 | 1182 (unbinned) | 0.75 | 6.8 × 10−5 |
| 93 (10-d binned) | 0.17 | 9.6 × 10−6 |
| Blazar name . | Number of . | |$R_\Gamma$| . | RFlux . |
|---|---|---|---|
| . | data points . | . | . |
| 3C 273 | 1960 (unbinned) | 0.22 | 2.0 × 10−3 |
| 1151 (2-d binned) | 0.19 | 1.5 × 10−3 | |
| Mrk 501 | 496 (unbinned) | 0.05 | 1.0 × 10−4 |
| 188 (2-d binned) | 0.06 | 1.0 × 10−4 | |
| Mrk 421 | 1182 (unbinned) | 0.75 | 6.8 × 10−5 |
| 93 (10-d binned) | 0.17 | 9.6 × 10−6 |
Light-curve significance fraction R values for the unbinned/binned flux and index light curves. Column 1: selected blazars satisfying the conditions R < 0.2 and length of binned flux/index light curve ≥90; column 2: number of data points in the distributions; column 3: R value for index light curve; and column 4: Rvalue for the flux light curve.
| Blazar name . | Number of . | |$R_\Gamma$| . | RFlux . |
|---|---|---|---|
| . | data points . | . | . |
| 3C 273 | 1960 (unbinned) | 0.22 | 2.0 × 10−3 |
| 1151 (2-d binned) | 0.19 | 1.5 × 10−3 | |
| Mrk 501 | 496 (unbinned) | 0.05 | 1.0 × 10−4 |
| 188 (2-d binned) | 0.06 | 1.0 × 10−4 | |
| Mrk 421 | 1182 (unbinned) | 0.75 | 6.8 × 10−5 |
| 93 (10-d binned) | 0.17 | 9.6 × 10−6 |
| Blazar name . | Number of . | |$R_\Gamma$| . | RFlux . |
|---|---|---|---|
| . | data points . | . | . |
| 3C 273 | 1960 (unbinned) | 0.22 | 2.0 × 10−3 |
| 1151 (2-d binned) | 0.19 | 1.5 × 10−3 | |
| Mrk 501 | 496 (unbinned) | 0.05 | 1.0 × 10−4 |
| 188 (2-d binned) | 0.06 | 1.0 × 10−4 | |
| Mrk 421 | 1182 (unbinned) | 0.75 | 6.8 × 10−5 |
| 93 (10-d binned) | 0.17 | 9.6 × 10−6 |
3C 273 is a well-studied FSRQ source located at a redshift |$z$| ∼ 0.158. The RXTE X-ray spectra of this source is fitted with a power-law model with an average power-law index of Γ = 1.70 ± 0.01 (Rivers et al. 2013). The obtained RXTE flux/index light curves of 3C 273 are shown in Fig. 1. The two BL Lac objects, viz. Mrk 501 and Mrk 421 at a redshift of 0.033 and 0.031, respectively, are very well-known high synchrotron peaked BL Lac (HBL) objects, with the low-energy SED component peaking at frequency νp > 1015.3 Hz. The RXTE spectra of these sources are fitted better with a broken power-law model (Rivers et al. 2013). For Mrk 501, the average values of power-law photon index before break energy (Γ1) and after break energy (Γ2) are obtained as 1.97 ± 0.02 and 2.02 ± 0.01, respectively, with a break energy at 6.9 ± 1.2 keV, whereas for Mrk 421, the average values of Γ1 and Γ2 are obtained as 2.41 ± 0.09 and 2.75 ± 0.01, respectively, with break energy of 6.6 ± 0.4 keV. The RXTE flux and Γ1 light curves of Mrk 501 and Mrk 421 are shown in Figs 2 and 3.
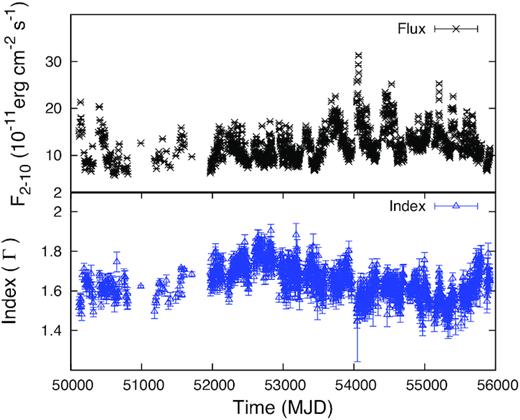
The X-ray flux/index light curves of 3C 273 obtained by using the 16 yr of RXTE archive data. Top panel: 2-d time binned flux light curve obtained in the energy range 2–10 keV. Bottom panel: 2-d time binned index light curve.
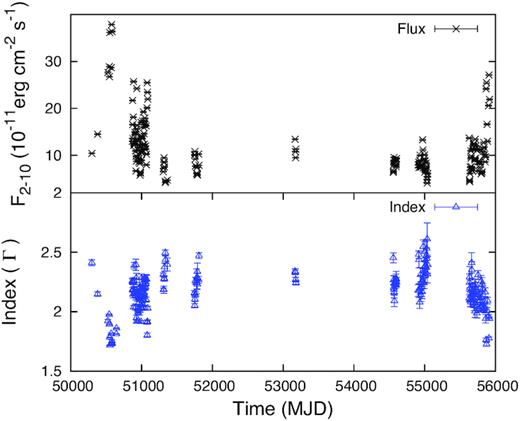
The X-ray flux and Γ1 light curves of Mrk 501 obtained by using the 16 yr of RXTE archive data. Top panel and bottom panel are the same as in Fig. 1.
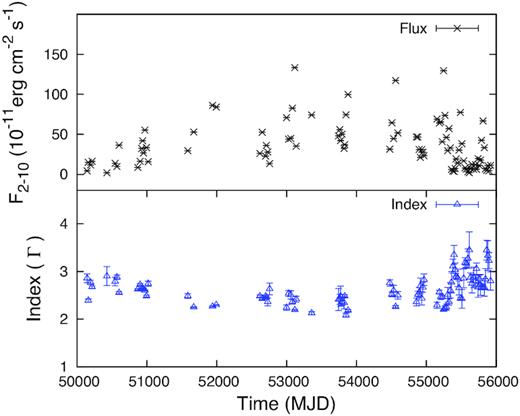
The X-ray flux and Γ1 light curves of Mrk 421 obtained by using the 16 yr of RXTE archive data. Top panel: 10-d time binned flux light curve obtained in the energy range 2–10 keV. Bottom panel: 10-d time binned Γ1 light curve.
Moreover, since RATSD provides light curves from a pointing instrument (PCA), there is a possibility of bias being introduced in the flux distributions, if the sources were preferentially observed in the high flux states. To check for this, we looked for correlation between the flux and time gap (time between two observations) with the Spearman’s rank correlation test. The null hypothesis probability values (P-value) for 3C 273, Mrk 501, and Mrk 421 are obtained as 0.07, 0.15, and 0.08, respectively. In the case of Spearman’s correlation, the null hypothesis (H0) is that there is no correlation between two variables, and we reject the null hypothesis if P < 0.01. Therefore, the obtained P-values indicate that there is no significant correlation between flux and time gap.
3 DISTRIBUTION STUDY FOR BLAZARS
3.1 AD test
Generally, the flux distribution of blazar light curves shows an asymmetric/tailed trend. Anderson–Darling (AD) test statistic is a useful tool for the normality test, which is sensitive towards the tails of a distribution (Press et al. 1992). The null hypothesis (H0) of the AD test is that the data sample is drawn from a particular distribution (say normal distribution in our case). The AD test calculates the null hypothesis probability value (p-value) such that p-value < 0.01 would indicate the deviation from the normality of the sample.
The AD test for 3C 273 shows that the p-values for flux in log-scale and index in normal-scale are larger than 0.01, which suggests the flux distribution is consistent with a lognormal and the index distribution with a normal one. However, for the two BL Lac objects, viz. Mrk 501 and Mrk 421, p-values for flux in linear-scale and log-scale are much smaller than 0.01, which indicates that the flux distribution will be neither normal nor lognormal. Moreover, the p-value of index distribution also suggests a non-normal distribution of index in Mrk 501 and Mrk 421. The AD test results of 3C 273, Mrk 501, and Mrk 421 are summarized in Table 2.
AD test results for the flux/index distribution of three selected blazars, viz. 3C 273, Mrk 501, and Mrk 421. Column 1: selected blazars satisfying the conditions R < 0.2 and length of binned flux/index light curve is ≥90; column 2: number of data points in the distributions; columns 3 and 4: AD statistics for flux and logarithm of flux distribution; and column 5: AD statistics for index distribution.
| Blazar name . | Number of . | Normal (flux) . | Lognormal (flux) . | Normal (spectral index) . |
|---|---|---|---|---|
| . | data points . | AD (p-value) . | AD (p-value) . | AD (p-value) . |
| 3C 273 | 1151 (2-d binned) | 13.02 (<2.2 × 10−16) | 0.76 (0.06) | 0.57 (0.14) |
| Mrk 501 | 188 (2-d binned) | 15.89 (<2.2 × 10−16) | 2.78 (4.96 × 10−7) | 1.24 (3.0 × 10−3) |
| Mrk 421 | 93 (10-d binned) | 2.29 (7.44 × 10−6) | 1.27 (2.5 × 10−3) | 1.09 (7.0 × 10−3) |
| Blazar name . | Number of . | Normal (flux) . | Lognormal (flux) . | Normal (spectral index) . |
|---|---|---|---|---|
| . | data points . | AD (p-value) . | AD (p-value) . | AD (p-value) . |
| 3C 273 | 1151 (2-d binned) | 13.02 (<2.2 × 10−16) | 0.76 (0.06) | 0.57 (0.14) |
| Mrk 501 | 188 (2-d binned) | 15.89 (<2.2 × 10−16) | 2.78 (4.96 × 10−7) | 1.24 (3.0 × 10−3) |
| Mrk 421 | 93 (10-d binned) | 2.29 (7.44 × 10−6) | 1.27 (2.5 × 10−3) | 1.09 (7.0 × 10−3) |
AD test results for the flux/index distribution of three selected blazars, viz. 3C 273, Mrk 501, and Mrk 421. Column 1: selected blazars satisfying the conditions R < 0.2 and length of binned flux/index light curve is ≥90; column 2: number of data points in the distributions; columns 3 and 4: AD statistics for flux and logarithm of flux distribution; and column 5: AD statistics for index distribution.
| Blazar name . | Number of . | Normal (flux) . | Lognormal (flux) . | Normal (spectral index) . |
|---|---|---|---|---|
| . | data points . | AD (p-value) . | AD (p-value) . | AD (p-value) . |
| 3C 273 | 1151 (2-d binned) | 13.02 (<2.2 × 10−16) | 0.76 (0.06) | 0.57 (0.14) |
| Mrk 501 | 188 (2-d binned) | 15.89 (<2.2 × 10−16) | 2.78 (4.96 × 10−7) | 1.24 (3.0 × 10−3) |
| Mrk 421 | 93 (10-d binned) | 2.29 (7.44 × 10−6) | 1.27 (2.5 × 10−3) | 1.09 (7.0 × 10−3) |
| Blazar name . | Number of . | Normal (flux) . | Lognormal (flux) . | Normal (spectral index) . |
|---|---|---|---|---|
| . | data points . | AD (p-value) . | AD (p-value) . | AD (p-value) . |
| 3C 273 | 1151 (2-d binned) | 13.02 (<2.2 × 10−16) | 0.76 (0.06) | 0.57 (0.14) |
| Mrk 501 | 188 (2-d binned) | 15.89 (<2.2 × 10−16) | 2.78 (4.96 × 10−7) | 1.24 (3.0 × 10−3) |
| Mrk 421 | 93 (10-d binned) | 2.29 (7.44 × 10−6) | 1.27 (2.5 × 10−3) | 1.09 (7.0 × 10−3) |
3.2 Histogram of flux and index
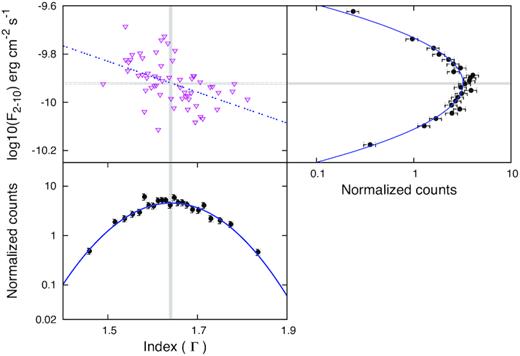
Multiplot for the characterization of flux/index distribution of 3C 273. Left-hand top panel is the logarithm of flux versus index scatter plot along with the best-fitting line (dotted line). Right-hand top panel is the histogram of logarithmic of flux distribution. Bottom panel is the histogram of index distribution. The solid curve in the right-hand top panel and bottom panel indicates the best-fitting PDF (equation 2). The vertical and horizontal grey bands indicate the 1σ error range on the centroid (μ) of the PDF (equation 2) fitted to the index distribution and logarithm of flux distribution, respectively.
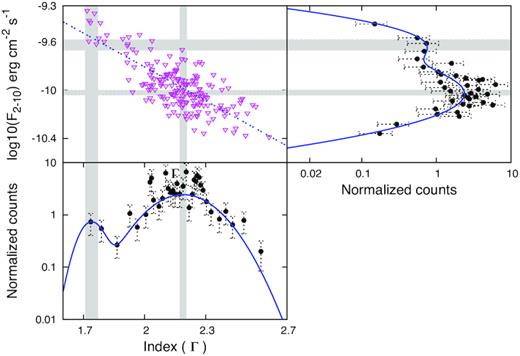
Multiplot for the characterization of flux/index distribution of Mrk 501. Left-hand top panel is the logarithm of flux versus index scatter plot along with the best-fitting line (dotted line). Right-hand top panel is the histogram of logarithm of flux distribution. Bottom panel is the histogram of index distribution. The solid curve in the right-hand top panel and bottom panel indicates the best-fitting double PDF (equation 3). The vertical and horizontal grey bands indicate the 1σ error range on the centroids (μ1, μ2) of the double PDF (equation 3) fitted to the index distribution and logarithm of flux distribution, respectively.
Best-fitting parameter values of the PDF (equation 2) fitted to the logarithm of flux and index histograms. Column 2: histogram obtained from the logarithm of flux and linear index distribution; columns 3 and 4: best-fitting values of μ and σ; column 5: degrees of freedom; and column 6: reduced χ2.
| Blazar name . | Histogram . | μ . | σ . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|
| 3C 273 | Log10(flux) | −9.922 ± 0.004 | 0.124 ± 0.003 | 21 | 0.92 |
| Index | 1.642 ± 0.003 | 0.088 ± 0.002 | 21 | 1.22 |
| Blazar name . | Histogram . | μ . | σ . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|
| 3C 273 | Log10(flux) | −9.922 ± 0.004 | 0.124 ± 0.003 | 21 | 0.92 |
| Index | 1.642 ± 0.003 | 0.088 ± 0.002 | 21 | 1.22 |
Best-fitting parameter values of the PDF (equation 2) fitted to the logarithm of flux and index histograms. Column 2: histogram obtained from the logarithm of flux and linear index distribution; columns 3 and 4: best-fitting values of μ and σ; column 5: degrees of freedom; and column 6: reduced χ2.
| Blazar name . | Histogram . | μ . | σ . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|
| 3C 273 | Log10(flux) | −9.922 ± 0.004 | 0.124 ± 0.003 | 21 | 0.92 |
| Index | 1.642 ± 0.003 | 0.088 ± 0.002 | 21 | 1.22 |
| Blazar name . | Histogram . | μ . | σ . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|
| 3C 273 | Log10(flux) | −9.922 ± 0.004 | 0.124 ± 0.003 | 21 | 0.92 |
| Index | 1.642 ± 0.003 | 0.088 ± 0.002 | 21 | 1.22 |
Best-fitting parameter values of the double PDF (equation 3) fitted to the logarithm of flux and index histograms. Column 2: histogram obtained from the logarithm of flux and linear index distribution; columns 3–6: best-fitting values of μ1, σ1, μ2, and σ2; column 7: normalization fraction; column 8: degrees of freedom; and column 9: reduced χ2.
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −9.62 ± 0.04 | 0.10 ± 0.03 | −10.02 ± 0.02 | 0.14 ± 0.02 | 0.83 ± 0.06 | 33 | 1.16 |
| Index | 1.74 ± 0.03 | 0.09 ± 0.02 | 2.19 ± 0.02 | 0.15 ± 0.01 | 0.83 | 34 | 1.15 | |
| Mrk 421 | Log10(flux) | −9.36 ± 0.05 | 0.26 ± 0.05 | −10.10 ± 0.08 | 0.29 ± 0.08 | 0.3 | 15 | 0.79 |
| Index | 2.54 ± 0.05 | 0.21 ± 0.04 | 3.09 ± 0.48 | 0.51 ± 0.31 | 0.3 | 14 | 1.21 |
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −9.62 ± 0.04 | 0.10 ± 0.03 | −10.02 ± 0.02 | 0.14 ± 0.02 | 0.83 ± 0.06 | 33 | 1.16 |
| Index | 1.74 ± 0.03 | 0.09 ± 0.02 | 2.19 ± 0.02 | 0.15 ± 0.01 | 0.83 | 34 | 1.15 | |
| Mrk 421 | Log10(flux) | −9.36 ± 0.05 | 0.26 ± 0.05 | −10.10 ± 0.08 | 0.29 ± 0.08 | 0.3 | 15 | 0.79 |
| Index | 2.54 ± 0.05 | 0.21 ± 0.04 | 3.09 ± 0.48 | 0.51 ± 0.31 | 0.3 | 14 | 1.21 |
Best-fitting parameter values of the double PDF (equation 3) fitted to the logarithm of flux and index histograms. Column 2: histogram obtained from the logarithm of flux and linear index distribution; columns 3–6: best-fitting values of μ1, σ1, μ2, and σ2; column 7: normalization fraction; column 8: degrees of freedom; and column 9: reduced χ2.
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −9.62 ± 0.04 | 0.10 ± 0.03 | −10.02 ± 0.02 | 0.14 ± 0.02 | 0.83 ± 0.06 | 33 | 1.16 |
| Index | 1.74 ± 0.03 | 0.09 ± 0.02 | 2.19 ± 0.02 | 0.15 ± 0.01 | 0.83 | 34 | 1.15 | |
| Mrk 421 | Log10(flux) | −9.36 ± 0.05 | 0.26 ± 0.05 | −10.10 ± 0.08 | 0.29 ± 0.08 | 0.3 | 15 | 0.79 |
| Index | 2.54 ± 0.05 | 0.21 ± 0.04 | 3.09 ± 0.48 | 0.51 ± 0.31 | 0.3 | 14 | 1.21 |
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −9.62 ± 0.04 | 0.10 ± 0.03 | −10.02 ± 0.02 | 0.14 ± 0.02 | 0.83 ± 0.06 | 33 | 1.16 |
| Index | 1.74 ± 0.03 | 0.09 ± 0.02 | 2.19 ± 0.02 | 0.15 ± 0.01 | 0.83 | 34 | 1.15 | |
| Mrk 421 | Log10(flux) | −9.36 ± 0.05 | 0.26 ± 0.05 | −10.10 ± 0.08 | 0.29 ± 0.08 | 0.3 | 15 | 0.79 |
| Index | 2.54 ± 0.05 | 0.21 ± 0.04 | 3.09 ± 0.48 | 0.51 ± 0.31 | 0.3 | 14 | 1.21 |
Best-fitting parameter values of the double PDF (lognormal+Gaussian) fitted to the logarithm of flux histogram. Column 2: histogram obtained from the logarithm of flux distribution; columns 3–6: best-fitting values of μ1, σ1, μ2, and σ2; column 7: normalization fraction; column 8: degrees of freedom; and column 9: reduced χ2.
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −10.03 ± 0.03 | 0.14 ± 0.02 | 2.26e–10 ± 3.998e–11 | 6.51e–11 ± 2.10e–11 | 0.79 ± 0.09 | 33 | 1.163 |
| Mrk 421 | Log10(flux) | −10.10 ± 0.08 | 0.28 ± 0.08 | 4.07e–10 ± 5.20e–11 | 2.48e–10 ± 4.43e–11 | 0.3 | 15 | 0.85 |
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −10.03 ± 0.03 | 0.14 ± 0.02 | 2.26e–10 ± 3.998e–11 | 6.51e–11 ± 2.10e–11 | 0.79 ± 0.09 | 33 | 1.163 |
| Mrk 421 | Log10(flux) | −10.10 ± 0.08 | 0.28 ± 0.08 | 4.07e–10 ± 5.20e–11 | 2.48e–10 ± 4.43e–11 | 0.3 | 15 | 0.85 |
Best-fitting parameter values of the double PDF (lognormal+Gaussian) fitted to the logarithm of flux histogram. Column 2: histogram obtained from the logarithm of flux distribution; columns 3–6: best-fitting values of μ1, σ1, μ2, and σ2; column 7: normalization fraction; column 8: degrees of freedom; and column 9: reduced χ2.
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −10.03 ± 0.03 | 0.14 ± 0.02 | 2.26e–10 ± 3.998e–11 | 6.51e–11 ± 2.10e–11 | 0.79 ± 0.09 | 33 | 1.163 |
| Mrk 421 | Log10(flux) | −10.10 ± 0.08 | 0.28 ± 0.08 | 4.07e–10 ± 5.20e–11 | 2.48e–10 ± 4.43e–11 | 0.3 | 15 | 0.85 |
| Blazar name . | Histogram . | μ1 . | σ1 . | μ2 . | σ2 . | a . | dof . | |$\rm \chi ^2/dof$| . |
|---|---|---|---|---|---|---|---|---|
| Mrk 501 | Log10(flux) | −10.03 ± 0.03 | 0.14 ± 0.02 | 2.26e–10 ± 3.998e–11 | 6.51e–11 ± 2.10e–11 | 0.79 ± 0.09 | 33 | 1.163 |
| Mrk 421 | Log10(flux) | −10.10 ± 0.08 | 0.28 ± 0.08 | 4.07e–10 ± 5.20e–11 | 2.48e–10 ± 4.43e–11 | 0.3 | 15 | 0.85 |
3.3 Correlation study
The three blazars selected from RXTE catalogue have a sufficient number of data points to study the correlation between the photon index and the flux in the 2–10 keV energy band. We have used the Spearman’s rank correlation method to assess the correlation behaviour between the index and flux. The obtained Spearman’s rank correlation coefficient (rs), its chance correlation probability (P), and the correlation slope (A) are summarized in Table 6. The correlation parameters show a significant negative correlation between the flux and index in all the three blazars, which is the usual trend blazars show across the electromagnetic spectrum (Brown & Adams 2011; Wierzcholska et al. 2015; Pandey, Gupta & Wiita 2017). In the correlation plots (top left-hand panel in Figs 4–6), grey bands represent the 1σ error on the centroids of the logarithm of flux and index distributions (Figs 4–6). In the bottom panel of Fig. 6, the error on higher index centroid is large, so a single vertical line is shown instead of a grey band.
Spearman correlation results obtained by comparing flux and index distribution of three selected blazars. Column 1: selected blazar sources; column 2: Spearman’s rank correlation coefficient (rs); column 3: probability chances for correlation (P); and column 4: slope of the best-fitting line to correlation plots (A).
| Blazar name . | rs . | P . | A . |
|---|---|---|---|
| 3C 273 | −0.60 | 2.0 × 10−4 | −0.61 ± 0.22 |
| Mrk 501 | −0.65 | 2.96 × 10−24 | −0.94 ± 0.06 |
| Mrk 421 | −0.86 | 7.25 × 10−29 | −1.21 ± 0.07 |
| Blazar name . | rs . | P . | A . |
|---|---|---|---|
| 3C 273 | −0.60 | 2.0 × 10−4 | −0.61 ± 0.22 |
| Mrk 501 | −0.65 | 2.96 × 10−24 | −0.94 ± 0.06 |
| Mrk 421 | −0.86 | 7.25 × 10−29 | −1.21 ± 0.07 |
Spearman correlation results obtained by comparing flux and index distribution of three selected blazars. Column 1: selected blazar sources; column 2: Spearman’s rank correlation coefficient (rs); column 3: probability chances for correlation (P); and column 4: slope of the best-fitting line to correlation plots (A).
| Blazar name . | rs . | P . | A . |
|---|---|---|---|
| 3C 273 | −0.60 | 2.0 × 10−4 | −0.61 ± 0.22 |
| Mrk 501 | −0.65 | 2.96 × 10−24 | −0.94 ± 0.06 |
| Mrk 421 | −0.86 | 7.25 × 10−29 | −1.21 ± 0.07 |
| Blazar name . | rs . | P . | A . |
|---|---|---|---|
| 3C 273 | −0.60 | 2.0 × 10−4 | −0.61 ± 0.22 |
| Mrk 501 | −0.65 | 2.96 × 10−24 | −0.94 ± 0.06 |
| Mrk 421 | −0.86 | 7.25 × 10−29 | −1.21 ± 0.07 |
4 DISCUSSION
After selecting three blazars, viz. 3C 273, Mrk 501, and Mrk 421, from the sample of blazars in the RXTE catalogue, we used the AD test and histogram fitting to characterize their flux and index distributions. We found that the flux distribution of FSRQ 3C 273 follows a lognormal distribution, while its index is Gaussian distributed. The lognormal distribution of flux in 3C 273 is also observed in the monthly binned γ-ray light curve (Shah et al. 2018). Since the variations in the index are related to the fluctuations in acceleration and escape time-scales of the emitting particles in the acceleration region, the observed Gaussian distribution in index therefore indicate a linear normal fluctuations in the intrinsic time-scales in the acceleration region. This result is consistent with the study by Sinha et al. (2018), where they showed that the linear normal fluctuation in the intrinsic particle acceleration time-scale in the acceleration region can produce a lognormal flux distribution. The connection of lognormal flux distribution with the Gaussian index variation indicates that the source of X-ray flux variation in 3C 273 is not from the accretion disc, instead, the perturbations are mostly local to the jet.
Using the AD test, we found that the flux and index distributions of two BL Lacs, viz. Mrk 501 and Mrk 421, are not consistent with a single distribution, and their histograms can be fitted with a double distribution. Interestingly, the overlapping of the centroids (within 1σ error – grey bands in Figs 5 and 6) of the double distributions in the log of flux and index distribution on the best-fitting correlation line (blue dotted line in the correlation plots), with same normalization fraction values for both the distributions (Section 3.3, Table 4), implies that the double distribution in photon index is connected to the double distribution in flux. The reduced χ2 test shows that the flux distributions of Mrk 501 and Mrk 421 are either double lognormal or combination of lognormal and Gaussian, while their index distributions are double Gaussian. However, using the interpretation of Sinha et al. (2018), the double Gaussian distribution in the index would preferably indicate double lognormal distribution in flux. Sinha et al. (2018) showed that Gaussian distribution in the index can be initiated through linear fluctuations in the particle acceleration rate, and hence the lognormal flux distribution may carry information regarding the acceleration processes in the blazar jets.
In the study of multiwavelength flux variations in PKS 1510−089, the two distinct lognormal profiles found in the flux distribution at near-infrared (NIR), optical, and γ-ray energies are connected to two possible flux states in the source (Kushwaha et al. 2016). In our work, the observation of double Gaussian distribution in index with bi-lognormal flux distribution in Mrk 501 and Mrk 421 further confirms the two flux states hypothesis. Moreover, contrary to double lognormal flux distribution in Mrk 501 and Mrk 421 in X-ray, the study of the γ-ray flux distribution of brightest Fermi blazars shows a single lognormal flux distribution at γ-ray energy (Shah et al. 2018). However, it should be noted that the results of Shah et al. (2018) are obtained from light curves with a bin size of a month, which is longer than those used in this work. A longer binning might remove the second component of the distribution. In case of HBL sources like Mrk 501 and Mrk 421, the X-ray spectrum lies beyond the synchrotron peak and hence is mainly emitted by the high-energy end of the electron distribution. While in FSRQs, the X-ray emission is mainly due to the low-energy tail of the electron distribution. Further, in the case of HBL sources, the low-energy γ-ray spectrum occurs before the break energy of the inverse Compton component. Therefore, the differences observed in the flux distribution of FSRQ 3C 273 and HBLs (Mrk 501 and Mrk 421) at X-rays may possibly be related to the energy of emitting particles. Thus, it seems that low-energy emitting particles produce a single lognormal flux distribution, while the high-energy tail of the electron distribution produces double lognormal flux distribution. However, such inference can be confirmed by carrying out a detailed flux distribution study for a sample of sources with more statistically significant light curves. In this direction, a systematic regular long-term monitoring of blazars with Monitor of All-sky X-ray Image (MAXI) would be important to probe such information. It will be interesting and important to quantify the flux distribution of these sources in other wavebands, as that may strengthen the results presented here. However, continuous significant and reliable detection of flux and index at other bands is not available at present. We note that the upcoming Cherenkov Telescope Array (CTA; CTA Consortium & Ong 2019) may provide such high-quality light curves in γ-rays.
ACKNOWLEDGEMENTS
We thank the anonymous referee for valuable comments and suggestions. This work has made use of light curves provided by the University of California, San Diego Center for Astrophysics and Space Sciences, X-ray Group (R. E. Rothschild, A. G. Markowitz, E. S. Rivers, and B. A. McKim), obtained at https://cass.ucsd.edu/ rxteagn/. RK and RG would like to thank CSIR, New Delhi (03(1412)/17/EMR-II) for financial support. RK would like to thank IUCAA, Pune, for the hospitality. RG would like to thank IUCAA for associateship.




