-
PDF
- Split View
-
Views
-
Cite
Cite
L Ji, V Doroshenko, A Santangelo, C Güngör, S Zhang, L Ducci, S-N Zhang, M-Y Ge, L J Qu, Y P Chen, Q C Bu, C Cai, X L Cao, Z Chang, G Chen, L Chen, T X Chen, Y Chen, Y B Chen, W Cui, W W Cui, J K Deng, Y W Dong, Y Y Du, M X Fu, G H Gao, H Gao, M Gao, Y D Gu, J Guan, C C Guo, D W Han, Y Huang, J Huo, S M Jia, L H Jiang, W C Jiang, J Jin, L D Kong, B Li, C K Li, G Li, M S Li, T P Li, W Li, X Li, X B Li, X F Li, Y G Li, Z W Li, X H Liang, J Y Liao, C Z Liu, G Q Liu, H W Liu, X J Liu, Y N Liu, B Lu, F J Lu, X F Lu, Q Luo, T Luo, X Ma, B Meng, Y Nang, J Y Nie, G Ou, N Sai, L M Song, X Y Song, L Sun, Y Tan, L Tao, Y L Tuo, C Wang, G F Wang, J Wang, W S Wang, Y S Wang, X Y Wen, B B Wu, B Y Wu, M Wu, G C Xiao, S Xiao, S L Xiong, Y P Xu, Y J Yang, J W Yang, S Yang, Y J Yang, Q B Yi, Q Q Yin, Y You, A M Zhang, C M Zhang, F Zhang, H M Zhang, J Zhang, T Zhang, W Zhang, W C Zhang, W Z Zhang, Y Zhang, Y Zhang, Y F Zhang, Y J Zhang, Z Zhang, Z L Zhang, H S Zhao, X F Zhao, S J Zheng, D K Zhou, J F Zhou, Y Zhu, Y X Zhu, Timing analysis of 2S 1417−624 observed with NICER and Insight-HXMT, Monthly Notices of the Royal Astronomical Society, Volume 491, Issue 2, January 2020, Pages 1851–1856, https://doi.org/10.1093/mnras/stz2745
Close - Share Icon Share
ABSTRACT
We present a study of timing properties of the accreting pulsar 2S 1417−624 observed during its 2018 outburst, based on Swift/BAT, Fermi/GBM, Insight-HXMT, and NICER observations. We report a dramatic change of the pulse profiles with luminosity. The morphology of the profile in the range 0.2–10.0 keV switches from double to triple peaks at ∼2.5|$\rm \times 10^{37}{\it D}_{10}^2\ erg\ s^{-1}$|and from triple to quadruple peaks at ∼7|$\rm \times 10^{37}{\it D}_{10}^2\ erg\ s^{-1}$|. The profile at high energies (25–100 keV) shows significant evolutions as well. We explain this phenomenon according to existing theoretical models. We argue that the first change is related to the transition from the sub to the supercritical accretion regime, while the second to the transition of the accretion disc from the gas-dominated to the radiation pressure-dominated state. Considering the spin-up as well due to the accretion torque, this interpretation allows to estimate the magnetic field self-consistently at ∼7 × 1012 G.
1 INTRODUCTION
X-ray pulsars are highly magnetized neutron stars in binary systems with B ∼1012 G, fed by accretion of matter from a donor star. Accretion is one of the most efficient mechanisms known to produce energy, and in fact the observed luminosity of these objects can reach |$\sim 10^{40} \rm erg\ s^{-1}$|, making them natural ‘laboratories’ to study properties of matter under extreme conditions, such as very high temperatures and ultrastrong magnetic fields. Pulsations arise because plasma from the accretion disc is channelled by the magnetic field lines on to the magnetic poles, producing beamed radiation, which changes the orientation with respect to observers as the neutron star rotates. Interaction of the accretion flow with the magnetic field thus defines the geometry of the emission region and plays a key role in X-ray pulsars (e.g. Basko & Sunyaev 1975; Becker & Wolff 2007; Mushtukov et al. 2015b).
In particular, two regimes of accretion can be identified. If the radiation pressure can be ignored and the luminosity is smaller than a critical value Lcrit, i.e. in the sub-Eddington regime, the accreted plasma falls on to the surface of the neutron star-forming accretion mounds. Otherwise, a radiation-dominated shock appears at some distance above the neutron star surface (see e.g. Basko & Sunyaev 1975; Becker et al. 2012; Mushtukov et al. 2015a). The radiation pressure and consequently the transitional luminosity are defined by the geometry of the emission region, and thus by the magnetic field strength and structure. Observations of the transition between the two regimes and the study of the properties of X-ray pulsars in the two states is essential to understand the complex interplay between the ram pressure, the radiation structure, and the intensity and geometry of the magnetic field.
2S 1417−624 is a transient source discovered with SAS-3 in 1978 (Apparao et al. 1980). Several outbursts from the source have been observed by BATSE and Rossi X-ray Timing Explorer (RXTE;Finger, Wilson & Chakrabarty 1996; İnam et al. 2004; Gupta et al. 2018). The spin period was found to be ∼17.5 s, while the spin-up rate was measured to be in the order of magnitude of 10−11 Hz s−1, and correlated with the pulsed flux. The optical counterpart has been identified as a B1 Ve star. Its orbital period of the source has been estimated by Finger et al. (1996) as ∼42 d. Using the optical properties of the donor star, Grindlay, Petro & McClintock (1984) estimated the distance of the binary system to be between 1.4 to 11.1 kpc. Recently, Gaia provided a distance measurement of |$9.9_{-2.4}^{+3.1}$| kpc (68 per cent confidence level;1 Bailer-Jones et al. 2018). Using Chandra data, Tsygankov et al. (2017) detected a quiescence flux of |$F_{(0.5-10\, keV)} \sim 5\times 10^{-13}$| erg s−1cm−2, and modelled the Chandra spectrum with a blackbody-like function with a temperature of ∼1.5 keV. The derived high temperature suggests that in the low-luminosity state the source might still accrete matter without entering the propeller regime in which centrifugal forces inhibit accretion (Tsygankov et al. 2016; Güngör et al. 2017).
In this paper, we report a study of timing properties of 2S 1417−624 during the outburst in 2018 using high cadence observations in a broad range of energy obtained with several facilities. This paper is organized as follows: the details of the observations and data reduction are introduced in Section 2; the results are presented in Section 3; and finally our arguments to explain the observed phenomenology are discussed in Section 4.
2 DATA ANALYSIS AND RESULTS
The Burst Alert Telescope (BAT) onboard the Swift observatory (Gehrels et al. 2004) is an all-sky hard X-ray monitor aimed at studying transient phenomena, such as gamma-ray bursts. We have used the daily light curve (15–50 keV) of the source provided by the BAT hard X-ray transient monitor2 as an indicator of the bolometric flux during the outbursts. Another estimate of the source flux in the hard band is provided by Fermi/Gamma-ray Burst Monitor (GBM;3 Meegan et al. 2009). We have also used the spin-frequency and frequency derivative estimated by the GBM. The pulsed flux reported is in the energy band of 12–50 keV, which only includes the first and second harmonics.
We have also used dedicated observations of the source obtained by the Hard X-ray Modulation Telescope (Insight-HMXT; Zhang et al. 2014) in the hard band and the Neutron Star Interior Composition Explorer (NICER; Gendreau et al. 2016) in the soft band. China launched Insight-HMXT in 2017. The mission has a wide energy coverage in the energy range 1–250 keV and large effective area, especially at hard X-rays (>25 keV). There are 29 Insight-HMXT pointing observations during the outburst of 2S 1417−624, in both the rising and decay phases. Green vertical lines in the upper panel of Fig. 1 show observational times of Insight-HXMT. In this paper, we have used Insight-HXMT data to estimate the bolometric flux, and the pulsed fraction at high energies (25–100 keV). This allowed a cross check of the Fermi/GBM’s results. The data analysis was performed with hxmtdas v2.01 following the recommended procedures in the user’s guide.4 An extensive study of the Insight-HXMT observations aimed at fully characterizing the spectral-timing behaviour as a function of luminosity is in preparation (Güngör et al., in preparation). The estimated bolometric fluxes are well correlated with the Swift/BAT count rate in the 15–50 keV range, which thus appears to be a good tracer of the bolometric flux. The conversion factor (A) was calculated by using the broad-band spectra of Insight-HXMT. In fact the spectral shape of the source is relatively steady, and can be fitted as a cut-off power-law model, with a photon index of ∼0.25 and a cut-off at ∼16 keV. We conclude that the bolometric flux can be estimated by multiplying the observed Swift/BAT count rate by the conversion factor A |$\rm \approx 1.13 \times 10^{-7}\ erg\,cts^{ -1}$|.
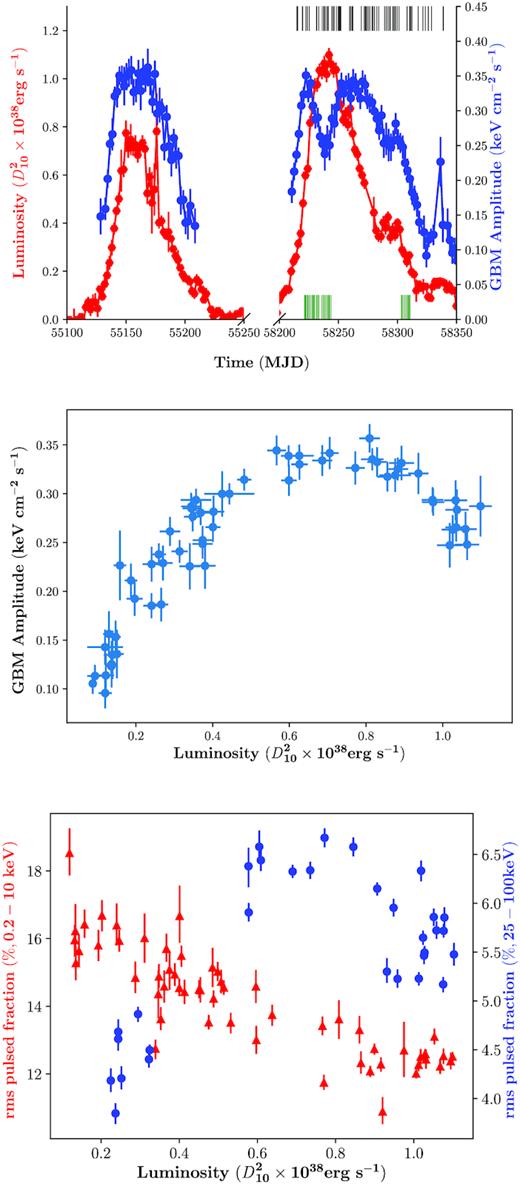
Upper panel: the luminosity of outbursts in 2009 and 2018 observed with Swift/BAT, after considering the bolometric correction performed by Insight-HXMT, and the pulsed flux observed with Fermi/GBM (12–150 keV). The black and green vertical lines represent the observational time of NICER and Insight-HXMT, respectively. Middle panel: the luminosity versus the pulsed flux mentioned above for the 2018 outburst. Bottom panel: the rms pulsed fraction observed with NICER (red triangles; 0.2–10.0 keV) and Insight-HXMT (blue points; 25–100 keV) for the outburst in 2018.
NICER is an external payload on-board the International Space Station (Gendreau et al. 2016). In this work, we used the X-ray Timing Instrument (XTI), which operates in the range 0.2–10.0 keV. NICER performed 83 observations during the outburst of 2S 1417−624 in 2018. Among them we selected 57 observations (Table 1) with effective exposure longer than the 300 s required to obtain meaningful estimate of the source pulse profiles in each observation. Black vertical lines in the upper panel of Fig. 1 represent the observational times. We followed the standard analysis procedures outlined in instruments’ documentation and used heasoft v6.25 to extract source light curves.
The columns denote numbers, ObsIDs, time, luminosity, and pulsed fractions at 0.2–10.0 keV of NICER observations for the outburst in 2018.
| No. . | ObsID . | Time . | Luminosity . | PF . |
|---|---|---|---|---|
| . | . | (MJD) . | (|$\rm {\it D}_{10}^2 \times 10^{38} erg\ s^{-1}$|) . | (%) . |
| 1 | 1200 130 177 | 58 328.83 | 0.12 ± 0.02 | |$18.59_{-0.69}^{+0.68}$| |
| 2 | 1200 130 175 | 58 326.13 | 0.13 ± 0.02 | |$15.96_{-0.47}^{+0.44}$| |
| 3 | 1200 130 173 | 58 323.69 | 0.13 ± 0.02 | |$16.13_{-0.77}^{+0.86}$| |
| 4 | 1200 130 171 | 58 321.56 | 0.14 ± 0.03 | |$15.31_{-0.48}^{+0.46}$| |
| 5 | 1200 130 169 | 58 317.70 | 0.14 ± 0.01 | |$15.63_{-0.48}^{+0.49}$| |
| 6 | 1200 130 181 | 58 338.84 | 0.16 ± 0.02 | |$16.45_{-0.42}^{+0.41}$| |
| 7 | 1200 130 167 | 58 311.34 | 0.19 ± 0.02 | |$15.79_{-0.49}^{+0.42}$| |
| 8 | 1200 130 168 | 58 312.44 | 0.20 ± 0.02 | |$16.65_{-0.45}^{+0.52}$| |
| 9 | 1200 130 166 | 58 310.32 | 0.24 ± 0.02 | |$16.39_{-0.57}^{+0.62}$| |
| 10 | 1200 130 165 | 58 308.25 | 0.25 ± 0.02 | |$15.95_{-0.35}^{+0.31}$| |
| 11 | 1200 130 104 | 58 214.77 | 0.29 ± 0.02 | |$14.90_{-0.45}^{+0.44}$| |
| 12 | 1200 130 105 | 58 215.45 | 0.31 ± 0.02 | |$15.97_{-0.78}^{+0.70}$| |
| 13 | 1200 130 149 | 58 282.67 | 0.34 ± 0.02 | |$12.75_{-0.29}^{+0.27}$| |
| 14 | 1200 130 154 | 58 293.76 | 0.35 ± 0.02 | |$14.40_{-0.70}^{+0.72}$| |
| 15 | 1200 130 156 | 58 297.46 | 0.35 ± 0.02 | |$14.84_{-0.34}^{+0.33}$| |
| 16 | 1200 130 155 | 58 296.28 | 0.36 ± 0.03 | |$13.61_{-0.36}^{+0.36}$| |
| 17 | 1200 130 157 | 58 298.46 | 0.36 ± 0.02 | |$14.55_{-0.51}^{+0.51}$| |
| 18 | 1200 130 150 | 58 284.00 | 0.37 ± 0.03 | |$15.72_{-0.42}^{+0.43}$| |
| 19 | 1200 130 160 | 58 301.48 | 0.37 ± 0.03 | |$15.06_{-0.58}^{+0.58}$| |
| 20 | 1200 130 151 | 58 289.16 | 0.39 ± 0.02 | |$14.94_{-0.35}^{+0.34}$| |
| 21 | 1200 130 158 | 58 299.72 | 0.40 ± 0.02 | |$16.67_{-0.81}^{+0.80}$| |
| 22 | 1200 130 148 | 58 280.49 | 0.40 ± 0.04 | |$14.55_{-0.26}^{+0.28}$| |
| 23 | 1200 130 152 | 58 290.71 | 0.41 ± 0.02 | |$15.48_{-0.31}^{+0.30}$| |
| 24 | 1200 130 153 | 58 292.16 | 0.41 ± 0.03 | |$14.40_{-0.37}^{+0.34}$| |
| 25 | 1200 130 147 | 58 279.27 | 0.45 ± 0.05 | |$14.49_{-0.30}^{+0.27}$| |
| 26 | 1200 130 146 | 58 278.66 | 0.46 ± 0.05 | |$14.48_{-0.41}^{+0.40}$| |
| 27 | 1200 130 145 | 58 276.61 | 0.48 ± 0.04 | |$13.52_{-0.19}^{+0.21}$| |
| 28 | 1200 130 106 | 58 219.56 | 0.49 ± 0.02 | |$15.14_{-0.63}^{+0.58}$| |
| 29 | 1200 130 144 | 58 275.38 | 0.49 ± 0.03 | |$14.21_{-0.26}^{+0.27}$| |
| 30 | 1200 130 143 | 58 274.42 | 0.50 ± 0.03 | |$15.05_{-0.29}^{+0.29}$| |
| 31 | 1200 130 142 | 58 273.39 | 0.51 ± 0.02 | |$14.72_{-0.36}^{+0.34}$| |
| 32 | 1200 130 141 | 58 272.75 | 0.52 ± 0.02 | |$14.57_{-0.23}^{+0.21}$| |
| 33 | 1200 130 140 | 58 271.88 | 0.53 ± 0.02 | |$13.52_{-0.29}^{+0.27}$| |
| 34 | 1200 130 107 | 58 222.43 | 0.60 ± 0.03 | |$13.01_{-0.46}^{+0.44}$| |
| 35 | 1200 130 139 | 58 269.48 | 0.60 ± 0.02 | |$14.56_{-0.48}^{+0.47}$| |
| 36 | 1200 130 108 | 58 223.63 | 0.64 ± 0.04 | |$13.71_{-0.32}^{+0.35}$| |
| 37 | 1200 130 135 | 58 262.28 | 0.77 ± 0.03 | |$13.42_{-0.29}^{+0.25}$| |
| 38 | 1200 130 134 | 58 261.46 | 0.77 ± 0.02 | |$11.75_{-0.22}^{+0.21}$| |
| 39 | 1200 130 110 | 58 225.43 | 0.81 ± 0.03 | |$13.58_{-0.57}^{+0.61}$| |
| 40 | 1200 130 132 | 58 259.44 | 0.86 ± 0.04 | |$13.31_{-0.37}^{+0.39}$| |
| 41 | 1200 130 130 | 58 252.13 | 0.87 ± 0.04 | |$12.35_{-0.35}^{+0.32}$| |
| 42 | 1200 130 133 | 58 260.30 | 0.89 ± 0.05 | |$12.07_{-0.16}^{+0.17}$| |
| 43 | 1200 130 129 | 58 251.31 | 0.90 ± 0.04 | |$12.73_{-0.18}^{+0.17}$| |
| 44 | 1200 130 128 | 58 250.74 | 0.92 ± 0.04 | |$12.27_{-0.20}^{+0.24}$| |
| 45 | 1200 130 127 | 58 249.95 | 0.92 ± 0.03 | |$10.87_{-0.38}^{+0.39}$| |
| 46 | 1200 130 113 | 58 231.53 | 0.98 ± 0.03 | |$12.68_{-0.83}^{+0.83}$| |
| 47 | 1200 130 126 | 58 248.40 | 1.01 ± 0.03 | |$12.01_{-0.15}^{+0.15}$| |
| 48 | 1200 130 118 | 58 239.44 | 1.01 ± 0.03 | |$12.28_{-0.19}^{+0.18}$| |
| 49 | 1200 130 115 | 58 236.38 | 1.02 ± 0.03 | |$12.51_{-0.24}^{+0.24}$| |
| 50 | 1200 130 124 | 58 246.34 | 1.03 ± 0.03 | |$12.58_{-0.14}^{+0.15}$| |
| 51 | 1200 130 114 | 58 233.31 | 1.03 ± 0.03 | |$12.59_{-0.14}^{+0.14}$| |
| 52 | 1200 130 123 | 58 245.47 | 1.03 ± 0.03 | |$12.43_{-0.28}^{+0.27}$| |
| 53 | 1200 130 122 | 58 244.34 | 1.05 ± 0.03 | |$13.10_{-0.22}^{+0.24}$| |
| 54 | 1200 130 116 | 58 237.60 | 1.07 ± 0.03 | |$12.21_{-0.22}^{+0.22}$| |
| 55 | 1200 130 117 | 58 238.22 | 1.08 ± 0.04 | |$12.52_{-0.23}^{+0.24}$| |
| 56 | 1200 130 119 | 58 240.86 | 1.10 ± 0.04 | |$12.37_{-0.24}^{+0.26}$| |
| 57 | 1200 130 120 | 58 241.36 | 1.10 ± 0.03 | |$12.50_{-0.14}^{+0.13}$| |
| No. . | ObsID . | Time . | Luminosity . | PF . |
|---|---|---|---|---|
| . | . | (MJD) . | (|$\rm {\it D}_{10}^2 \times 10^{38} erg\ s^{-1}$|) . | (%) . |
| 1 | 1200 130 177 | 58 328.83 | 0.12 ± 0.02 | |$18.59_{-0.69}^{+0.68}$| |
| 2 | 1200 130 175 | 58 326.13 | 0.13 ± 0.02 | |$15.96_{-0.47}^{+0.44}$| |
| 3 | 1200 130 173 | 58 323.69 | 0.13 ± 0.02 | |$16.13_{-0.77}^{+0.86}$| |
| 4 | 1200 130 171 | 58 321.56 | 0.14 ± 0.03 | |$15.31_{-0.48}^{+0.46}$| |
| 5 | 1200 130 169 | 58 317.70 | 0.14 ± 0.01 | |$15.63_{-0.48}^{+0.49}$| |
| 6 | 1200 130 181 | 58 338.84 | 0.16 ± 0.02 | |$16.45_{-0.42}^{+0.41}$| |
| 7 | 1200 130 167 | 58 311.34 | 0.19 ± 0.02 | |$15.79_{-0.49}^{+0.42}$| |
| 8 | 1200 130 168 | 58 312.44 | 0.20 ± 0.02 | |$16.65_{-0.45}^{+0.52}$| |
| 9 | 1200 130 166 | 58 310.32 | 0.24 ± 0.02 | |$16.39_{-0.57}^{+0.62}$| |
| 10 | 1200 130 165 | 58 308.25 | 0.25 ± 0.02 | |$15.95_{-0.35}^{+0.31}$| |
| 11 | 1200 130 104 | 58 214.77 | 0.29 ± 0.02 | |$14.90_{-0.45}^{+0.44}$| |
| 12 | 1200 130 105 | 58 215.45 | 0.31 ± 0.02 | |$15.97_{-0.78}^{+0.70}$| |
| 13 | 1200 130 149 | 58 282.67 | 0.34 ± 0.02 | |$12.75_{-0.29}^{+0.27}$| |
| 14 | 1200 130 154 | 58 293.76 | 0.35 ± 0.02 | |$14.40_{-0.70}^{+0.72}$| |
| 15 | 1200 130 156 | 58 297.46 | 0.35 ± 0.02 | |$14.84_{-0.34}^{+0.33}$| |
| 16 | 1200 130 155 | 58 296.28 | 0.36 ± 0.03 | |$13.61_{-0.36}^{+0.36}$| |
| 17 | 1200 130 157 | 58 298.46 | 0.36 ± 0.02 | |$14.55_{-0.51}^{+0.51}$| |
| 18 | 1200 130 150 | 58 284.00 | 0.37 ± 0.03 | |$15.72_{-0.42}^{+0.43}$| |
| 19 | 1200 130 160 | 58 301.48 | 0.37 ± 0.03 | |$15.06_{-0.58}^{+0.58}$| |
| 20 | 1200 130 151 | 58 289.16 | 0.39 ± 0.02 | |$14.94_{-0.35}^{+0.34}$| |
| 21 | 1200 130 158 | 58 299.72 | 0.40 ± 0.02 | |$16.67_{-0.81}^{+0.80}$| |
| 22 | 1200 130 148 | 58 280.49 | 0.40 ± 0.04 | |$14.55_{-0.26}^{+0.28}$| |
| 23 | 1200 130 152 | 58 290.71 | 0.41 ± 0.02 | |$15.48_{-0.31}^{+0.30}$| |
| 24 | 1200 130 153 | 58 292.16 | 0.41 ± 0.03 | |$14.40_{-0.37}^{+0.34}$| |
| 25 | 1200 130 147 | 58 279.27 | 0.45 ± 0.05 | |$14.49_{-0.30}^{+0.27}$| |
| 26 | 1200 130 146 | 58 278.66 | 0.46 ± 0.05 | |$14.48_{-0.41}^{+0.40}$| |
| 27 | 1200 130 145 | 58 276.61 | 0.48 ± 0.04 | |$13.52_{-0.19}^{+0.21}$| |
| 28 | 1200 130 106 | 58 219.56 | 0.49 ± 0.02 | |$15.14_{-0.63}^{+0.58}$| |
| 29 | 1200 130 144 | 58 275.38 | 0.49 ± 0.03 | |$14.21_{-0.26}^{+0.27}$| |
| 30 | 1200 130 143 | 58 274.42 | 0.50 ± 0.03 | |$15.05_{-0.29}^{+0.29}$| |
| 31 | 1200 130 142 | 58 273.39 | 0.51 ± 0.02 | |$14.72_{-0.36}^{+0.34}$| |
| 32 | 1200 130 141 | 58 272.75 | 0.52 ± 0.02 | |$14.57_{-0.23}^{+0.21}$| |
| 33 | 1200 130 140 | 58 271.88 | 0.53 ± 0.02 | |$13.52_{-0.29}^{+0.27}$| |
| 34 | 1200 130 107 | 58 222.43 | 0.60 ± 0.03 | |$13.01_{-0.46}^{+0.44}$| |
| 35 | 1200 130 139 | 58 269.48 | 0.60 ± 0.02 | |$14.56_{-0.48}^{+0.47}$| |
| 36 | 1200 130 108 | 58 223.63 | 0.64 ± 0.04 | |$13.71_{-0.32}^{+0.35}$| |
| 37 | 1200 130 135 | 58 262.28 | 0.77 ± 0.03 | |$13.42_{-0.29}^{+0.25}$| |
| 38 | 1200 130 134 | 58 261.46 | 0.77 ± 0.02 | |$11.75_{-0.22}^{+0.21}$| |
| 39 | 1200 130 110 | 58 225.43 | 0.81 ± 0.03 | |$13.58_{-0.57}^{+0.61}$| |
| 40 | 1200 130 132 | 58 259.44 | 0.86 ± 0.04 | |$13.31_{-0.37}^{+0.39}$| |
| 41 | 1200 130 130 | 58 252.13 | 0.87 ± 0.04 | |$12.35_{-0.35}^{+0.32}$| |
| 42 | 1200 130 133 | 58 260.30 | 0.89 ± 0.05 | |$12.07_{-0.16}^{+0.17}$| |
| 43 | 1200 130 129 | 58 251.31 | 0.90 ± 0.04 | |$12.73_{-0.18}^{+0.17}$| |
| 44 | 1200 130 128 | 58 250.74 | 0.92 ± 0.04 | |$12.27_{-0.20}^{+0.24}$| |
| 45 | 1200 130 127 | 58 249.95 | 0.92 ± 0.03 | |$10.87_{-0.38}^{+0.39}$| |
| 46 | 1200 130 113 | 58 231.53 | 0.98 ± 0.03 | |$12.68_{-0.83}^{+0.83}$| |
| 47 | 1200 130 126 | 58 248.40 | 1.01 ± 0.03 | |$12.01_{-0.15}^{+0.15}$| |
| 48 | 1200 130 118 | 58 239.44 | 1.01 ± 0.03 | |$12.28_{-0.19}^{+0.18}$| |
| 49 | 1200 130 115 | 58 236.38 | 1.02 ± 0.03 | |$12.51_{-0.24}^{+0.24}$| |
| 50 | 1200 130 124 | 58 246.34 | 1.03 ± 0.03 | |$12.58_{-0.14}^{+0.15}$| |
| 51 | 1200 130 114 | 58 233.31 | 1.03 ± 0.03 | |$12.59_{-0.14}^{+0.14}$| |
| 52 | 1200 130 123 | 58 245.47 | 1.03 ± 0.03 | |$12.43_{-0.28}^{+0.27}$| |
| 53 | 1200 130 122 | 58 244.34 | 1.05 ± 0.03 | |$13.10_{-0.22}^{+0.24}$| |
| 54 | 1200 130 116 | 58 237.60 | 1.07 ± 0.03 | |$12.21_{-0.22}^{+0.22}$| |
| 55 | 1200 130 117 | 58 238.22 | 1.08 ± 0.04 | |$12.52_{-0.23}^{+0.24}$| |
| 56 | 1200 130 119 | 58 240.86 | 1.10 ± 0.04 | |$12.37_{-0.24}^{+0.26}$| |
| 57 | 1200 130 120 | 58 241.36 | 1.10 ± 0.03 | |$12.50_{-0.14}^{+0.13}$| |
The columns denote numbers, ObsIDs, time, luminosity, and pulsed fractions at 0.2–10.0 keV of NICER observations for the outburst in 2018.
| No. . | ObsID . | Time . | Luminosity . | PF . |
|---|---|---|---|---|
| . | . | (MJD) . | (|$\rm {\it D}_{10}^2 \times 10^{38} erg\ s^{-1}$|) . | (%) . |
| 1 | 1200 130 177 | 58 328.83 | 0.12 ± 0.02 | |$18.59_{-0.69}^{+0.68}$| |
| 2 | 1200 130 175 | 58 326.13 | 0.13 ± 0.02 | |$15.96_{-0.47}^{+0.44}$| |
| 3 | 1200 130 173 | 58 323.69 | 0.13 ± 0.02 | |$16.13_{-0.77}^{+0.86}$| |
| 4 | 1200 130 171 | 58 321.56 | 0.14 ± 0.03 | |$15.31_{-0.48}^{+0.46}$| |
| 5 | 1200 130 169 | 58 317.70 | 0.14 ± 0.01 | |$15.63_{-0.48}^{+0.49}$| |
| 6 | 1200 130 181 | 58 338.84 | 0.16 ± 0.02 | |$16.45_{-0.42}^{+0.41}$| |
| 7 | 1200 130 167 | 58 311.34 | 0.19 ± 0.02 | |$15.79_{-0.49}^{+0.42}$| |
| 8 | 1200 130 168 | 58 312.44 | 0.20 ± 0.02 | |$16.65_{-0.45}^{+0.52}$| |
| 9 | 1200 130 166 | 58 310.32 | 0.24 ± 0.02 | |$16.39_{-0.57}^{+0.62}$| |
| 10 | 1200 130 165 | 58 308.25 | 0.25 ± 0.02 | |$15.95_{-0.35}^{+0.31}$| |
| 11 | 1200 130 104 | 58 214.77 | 0.29 ± 0.02 | |$14.90_{-0.45}^{+0.44}$| |
| 12 | 1200 130 105 | 58 215.45 | 0.31 ± 0.02 | |$15.97_{-0.78}^{+0.70}$| |
| 13 | 1200 130 149 | 58 282.67 | 0.34 ± 0.02 | |$12.75_{-0.29}^{+0.27}$| |
| 14 | 1200 130 154 | 58 293.76 | 0.35 ± 0.02 | |$14.40_{-0.70}^{+0.72}$| |
| 15 | 1200 130 156 | 58 297.46 | 0.35 ± 0.02 | |$14.84_{-0.34}^{+0.33}$| |
| 16 | 1200 130 155 | 58 296.28 | 0.36 ± 0.03 | |$13.61_{-0.36}^{+0.36}$| |
| 17 | 1200 130 157 | 58 298.46 | 0.36 ± 0.02 | |$14.55_{-0.51}^{+0.51}$| |
| 18 | 1200 130 150 | 58 284.00 | 0.37 ± 0.03 | |$15.72_{-0.42}^{+0.43}$| |
| 19 | 1200 130 160 | 58 301.48 | 0.37 ± 0.03 | |$15.06_{-0.58}^{+0.58}$| |
| 20 | 1200 130 151 | 58 289.16 | 0.39 ± 0.02 | |$14.94_{-0.35}^{+0.34}$| |
| 21 | 1200 130 158 | 58 299.72 | 0.40 ± 0.02 | |$16.67_{-0.81}^{+0.80}$| |
| 22 | 1200 130 148 | 58 280.49 | 0.40 ± 0.04 | |$14.55_{-0.26}^{+0.28}$| |
| 23 | 1200 130 152 | 58 290.71 | 0.41 ± 0.02 | |$15.48_{-0.31}^{+0.30}$| |
| 24 | 1200 130 153 | 58 292.16 | 0.41 ± 0.03 | |$14.40_{-0.37}^{+0.34}$| |
| 25 | 1200 130 147 | 58 279.27 | 0.45 ± 0.05 | |$14.49_{-0.30}^{+0.27}$| |
| 26 | 1200 130 146 | 58 278.66 | 0.46 ± 0.05 | |$14.48_{-0.41}^{+0.40}$| |
| 27 | 1200 130 145 | 58 276.61 | 0.48 ± 0.04 | |$13.52_{-0.19}^{+0.21}$| |
| 28 | 1200 130 106 | 58 219.56 | 0.49 ± 0.02 | |$15.14_{-0.63}^{+0.58}$| |
| 29 | 1200 130 144 | 58 275.38 | 0.49 ± 0.03 | |$14.21_{-0.26}^{+0.27}$| |
| 30 | 1200 130 143 | 58 274.42 | 0.50 ± 0.03 | |$15.05_{-0.29}^{+0.29}$| |
| 31 | 1200 130 142 | 58 273.39 | 0.51 ± 0.02 | |$14.72_{-0.36}^{+0.34}$| |
| 32 | 1200 130 141 | 58 272.75 | 0.52 ± 0.02 | |$14.57_{-0.23}^{+0.21}$| |
| 33 | 1200 130 140 | 58 271.88 | 0.53 ± 0.02 | |$13.52_{-0.29}^{+0.27}$| |
| 34 | 1200 130 107 | 58 222.43 | 0.60 ± 0.03 | |$13.01_{-0.46}^{+0.44}$| |
| 35 | 1200 130 139 | 58 269.48 | 0.60 ± 0.02 | |$14.56_{-0.48}^{+0.47}$| |
| 36 | 1200 130 108 | 58 223.63 | 0.64 ± 0.04 | |$13.71_{-0.32}^{+0.35}$| |
| 37 | 1200 130 135 | 58 262.28 | 0.77 ± 0.03 | |$13.42_{-0.29}^{+0.25}$| |
| 38 | 1200 130 134 | 58 261.46 | 0.77 ± 0.02 | |$11.75_{-0.22}^{+0.21}$| |
| 39 | 1200 130 110 | 58 225.43 | 0.81 ± 0.03 | |$13.58_{-0.57}^{+0.61}$| |
| 40 | 1200 130 132 | 58 259.44 | 0.86 ± 0.04 | |$13.31_{-0.37}^{+0.39}$| |
| 41 | 1200 130 130 | 58 252.13 | 0.87 ± 0.04 | |$12.35_{-0.35}^{+0.32}$| |
| 42 | 1200 130 133 | 58 260.30 | 0.89 ± 0.05 | |$12.07_{-0.16}^{+0.17}$| |
| 43 | 1200 130 129 | 58 251.31 | 0.90 ± 0.04 | |$12.73_{-0.18}^{+0.17}$| |
| 44 | 1200 130 128 | 58 250.74 | 0.92 ± 0.04 | |$12.27_{-0.20}^{+0.24}$| |
| 45 | 1200 130 127 | 58 249.95 | 0.92 ± 0.03 | |$10.87_{-0.38}^{+0.39}$| |
| 46 | 1200 130 113 | 58 231.53 | 0.98 ± 0.03 | |$12.68_{-0.83}^{+0.83}$| |
| 47 | 1200 130 126 | 58 248.40 | 1.01 ± 0.03 | |$12.01_{-0.15}^{+0.15}$| |
| 48 | 1200 130 118 | 58 239.44 | 1.01 ± 0.03 | |$12.28_{-0.19}^{+0.18}$| |
| 49 | 1200 130 115 | 58 236.38 | 1.02 ± 0.03 | |$12.51_{-0.24}^{+0.24}$| |
| 50 | 1200 130 124 | 58 246.34 | 1.03 ± 0.03 | |$12.58_{-0.14}^{+0.15}$| |
| 51 | 1200 130 114 | 58 233.31 | 1.03 ± 0.03 | |$12.59_{-0.14}^{+0.14}$| |
| 52 | 1200 130 123 | 58 245.47 | 1.03 ± 0.03 | |$12.43_{-0.28}^{+0.27}$| |
| 53 | 1200 130 122 | 58 244.34 | 1.05 ± 0.03 | |$13.10_{-0.22}^{+0.24}$| |
| 54 | 1200 130 116 | 58 237.60 | 1.07 ± 0.03 | |$12.21_{-0.22}^{+0.22}$| |
| 55 | 1200 130 117 | 58 238.22 | 1.08 ± 0.04 | |$12.52_{-0.23}^{+0.24}$| |
| 56 | 1200 130 119 | 58 240.86 | 1.10 ± 0.04 | |$12.37_{-0.24}^{+0.26}$| |
| 57 | 1200 130 120 | 58 241.36 | 1.10 ± 0.03 | |$12.50_{-0.14}^{+0.13}$| |
| No. . | ObsID . | Time . | Luminosity . | PF . |
|---|---|---|---|---|
| . | . | (MJD) . | (|$\rm {\it D}_{10}^2 \times 10^{38} erg\ s^{-1}$|) . | (%) . |
| 1 | 1200 130 177 | 58 328.83 | 0.12 ± 0.02 | |$18.59_{-0.69}^{+0.68}$| |
| 2 | 1200 130 175 | 58 326.13 | 0.13 ± 0.02 | |$15.96_{-0.47}^{+0.44}$| |
| 3 | 1200 130 173 | 58 323.69 | 0.13 ± 0.02 | |$16.13_{-0.77}^{+0.86}$| |
| 4 | 1200 130 171 | 58 321.56 | 0.14 ± 0.03 | |$15.31_{-0.48}^{+0.46}$| |
| 5 | 1200 130 169 | 58 317.70 | 0.14 ± 0.01 | |$15.63_{-0.48}^{+0.49}$| |
| 6 | 1200 130 181 | 58 338.84 | 0.16 ± 0.02 | |$16.45_{-0.42}^{+0.41}$| |
| 7 | 1200 130 167 | 58 311.34 | 0.19 ± 0.02 | |$15.79_{-0.49}^{+0.42}$| |
| 8 | 1200 130 168 | 58 312.44 | 0.20 ± 0.02 | |$16.65_{-0.45}^{+0.52}$| |
| 9 | 1200 130 166 | 58 310.32 | 0.24 ± 0.02 | |$16.39_{-0.57}^{+0.62}$| |
| 10 | 1200 130 165 | 58 308.25 | 0.25 ± 0.02 | |$15.95_{-0.35}^{+0.31}$| |
| 11 | 1200 130 104 | 58 214.77 | 0.29 ± 0.02 | |$14.90_{-0.45}^{+0.44}$| |
| 12 | 1200 130 105 | 58 215.45 | 0.31 ± 0.02 | |$15.97_{-0.78}^{+0.70}$| |
| 13 | 1200 130 149 | 58 282.67 | 0.34 ± 0.02 | |$12.75_{-0.29}^{+0.27}$| |
| 14 | 1200 130 154 | 58 293.76 | 0.35 ± 0.02 | |$14.40_{-0.70}^{+0.72}$| |
| 15 | 1200 130 156 | 58 297.46 | 0.35 ± 0.02 | |$14.84_{-0.34}^{+0.33}$| |
| 16 | 1200 130 155 | 58 296.28 | 0.36 ± 0.03 | |$13.61_{-0.36}^{+0.36}$| |
| 17 | 1200 130 157 | 58 298.46 | 0.36 ± 0.02 | |$14.55_{-0.51}^{+0.51}$| |
| 18 | 1200 130 150 | 58 284.00 | 0.37 ± 0.03 | |$15.72_{-0.42}^{+0.43}$| |
| 19 | 1200 130 160 | 58 301.48 | 0.37 ± 0.03 | |$15.06_{-0.58}^{+0.58}$| |
| 20 | 1200 130 151 | 58 289.16 | 0.39 ± 0.02 | |$14.94_{-0.35}^{+0.34}$| |
| 21 | 1200 130 158 | 58 299.72 | 0.40 ± 0.02 | |$16.67_{-0.81}^{+0.80}$| |
| 22 | 1200 130 148 | 58 280.49 | 0.40 ± 0.04 | |$14.55_{-0.26}^{+0.28}$| |
| 23 | 1200 130 152 | 58 290.71 | 0.41 ± 0.02 | |$15.48_{-0.31}^{+0.30}$| |
| 24 | 1200 130 153 | 58 292.16 | 0.41 ± 0.03 | |$14.40_{-0.37}^{+0.34}$| |
| 25 | 1200 130 147 | 58 279.27 | 0.45 ± 0.05 | |$14.49_{-0.30}^{+0.27}$| |
| 26 | 1200 130 146 | 58 278.66 | 0.46 ± 0.05 | |$14.48_{-0.41}^{+0.40}$| |
| 27 | 1200 130 145 | 58 276.61 | 0.48 ± 0.04 | |$13.52_{-0.19}^{+0.21}$| |
| 28 | 1200 130 106 | 58 219.56 | 0.49 ± 0.02 | |$15.14_{-0.63}^{+0.58}$| |
| 29 | 1200 130 144 | 58 275.38 | 0.49 ± 0.03 | |$14.21_{-0.26}^{+0.27}$| |
| 30 | 1200 130 143 | 58 274.42 | 0.50 ± 0.03 | |$15.05_{-0.29}^{+0.29}$| |
| 31 | 1200 130 142 | 58 273.39 | 0.51 ± 0.02 | |$14.72_{-0.36}^{+0.34}$| |
| 32 | 1200 130 141 | 58 272.75 | 0.52 ± 0.02 | |$14.57_{-0.23}^{+0.21}$| |
| 33 | 1200 130 140 | 58 271.88 | 0.53 ± 0.02 | |$13.52_{-0.29}^{+0.27}$| |
| 34 | 1200 130 107 | 58 222.43 | 0.60 ± 0.03 | |$13.01_{-0.46}^{+0.44}$| |
| 35 | 1200 130 139 | 58 269.48 | 0.60 ± 0.02 | |$14.56_{-0.48}^{+0.47}$| |
| 36 | 1200 130 108 | 58 223.63 | 0.64 ± 0.04 | |$13.71_{-0.32}^{+0.35}$| |
| 37 | 1200 130 135 | 58 262.28 | 0.77 ± 0.03 | |$13.42_{-0.29}^{+0.25}$| |
| 38 | 1200 130 134 | 58 261.46 | 0.77 ± 0.02 | |$11.75_{-0.22}^{+0.21}$| |
| 39 | 1200 130 110 | 58 225.43 | 0.81 ± 0.03 | |$13.58_{-0.57}^{+0.61}$| |
| 40 | 1200 130 132 | 58 259.44 | 0.86 ± 0.04 | |$13.31_{-0.37}^{+0.39}$| |
| 41 | 1200 130 130 | 58 252.13 | 0.87 ± 0.04 | |$12.35_{-0.35}^{+0.32}$| |
| 42 | 1200 130 133 | 58 260.30 | 0.89 ± 0.05 | |$12.07_{-0.16}^{+0.17}$| |
| 43 | 1200 130 129 | 58 251.31 | 0.90 ± 0.04 | |$12.73_{-0.18}^{+0.17}$| |
| 44 | 1200 130 128 | 58 250.74 | 0.92 ± 0.04 | |$12.27_{-0.20}^{+0.24}$| |
| 45 | 1200 130 127 | 58 249.95 | 0.92 ± 0.03 | |$10.87_{-0.38}^{+0.39}$| |
| 46 | 1200 130 113 | 58 231.53 | 0.98 ± 0.03 | |$12.68_{-0.83}^{+0.83}$| |
| 47 | 1200 130 126 | 58 248.40 | 1.01 ± 0.03 | |$12.01_{-0.15}^{+0.15}$| |
| 48 | 1200 130 118 | 58 239.44 | 1.01 ± 0.03 | |$12.28_{-0.19}^{+0.18}$| |
| 49 | 1200 130 115 | 58 236.38 | 1.02 ± 0.03 | |$12.51_{-0.24}^{+0.24}$| |
| 50 | 1200 130 124 | 58 246.34 | 1.03 ± 0.03 | |$12.58_{-0.14}^{+0.15}$| |
| 51 | 1200 130 114 | 58 233.31 | 1.03 ± 0.03 | |$12.59_{-0.14}^{+0.14}$| |
| 52 | 1200 130 123 | 58 245.47 | 1.03 ± 0.03 | |$12.43_{-0.28}^{+0.27}$| |
| 53 | 1200 130 122 | 58 244.34 | 1.05 ± 0.03 | |$13.10_{-0.22}^{+0.24}$| |
| 54 | 1200 130 116 | 58 237.60 | 1.07 ± 0.03 | |$12.21_{-0.22}^{+0.22}$| |
| 55 | 1200 130 117 | 58 238.22 | 1.08 ± 0.04 | |$12.52_{-0.23}^{+0.24}$| |
| 56 | 1200 130 119 | 58 240.86 | 1.10 ± 0.04 | |$12.37_{-0.24}^{+0.26}$| |
| 57 | 1200 130 120 | 58 241.36 | 1.10 ± 0.03 | |$12.50_{-0.14}^{+0.13}$| |
The first result was obtained through the simple comparison of the Swift/BAT and Fermi/GBM light curves of the 2009 and 2018 outbursts (see Fig. 1). The duration of the two outbursts is similar, e.g. ∼350 d, but the second outburst is significantly brighter. We note the striking difference between the BAT and GBM light curves. While during the outburst in 2009 the pulsed flux measured by GBM is strongly correlated with the BAT rate, which is clearly not the case for the 2018 outburst (the middle panel of Fig. 1). Here the pulsed flux increases with the BAT rate when the source is relatively faint (≲5 ×|$\rm 10^{37}$||$D_{10}^{2}$||$\rm \, erg\ s^{-1}$|). However, for a luminosity higher than ∼8 ×|$\rm 10^{37}$||$D_{10}^{2}$||$\rm \, erg\ s^{-1}$|, the correlation breaks, and the pulsed flux starts to drop while the bolometric flux traced by BAT increases. We note that the 2009 outburst also shows some sign of the saturation of the increasing GBM pulsed flux at the same flux.
This difference can only be due to a dramatic decrease of the pulsed fraction close to the peak of the second outburst. Such a dramatic change is also expected to affect the observed pulse profile shape. To investigate that in more detail, we folded the events observed with NICER/XTI based on the spin history and the orbital ephemeris reported by the Fermi/GBM team. We aligned the pulse profiles by cross-correlating pairs of the pulse profiles sorted by flux to obtain a ’phase-luminosity’ matrix shown in Fig. 2. Here the fluxes of the NICER observations were estimated, using the contemporary BAT data and converting the observed BAT count rate to the bolometric flux as described above.
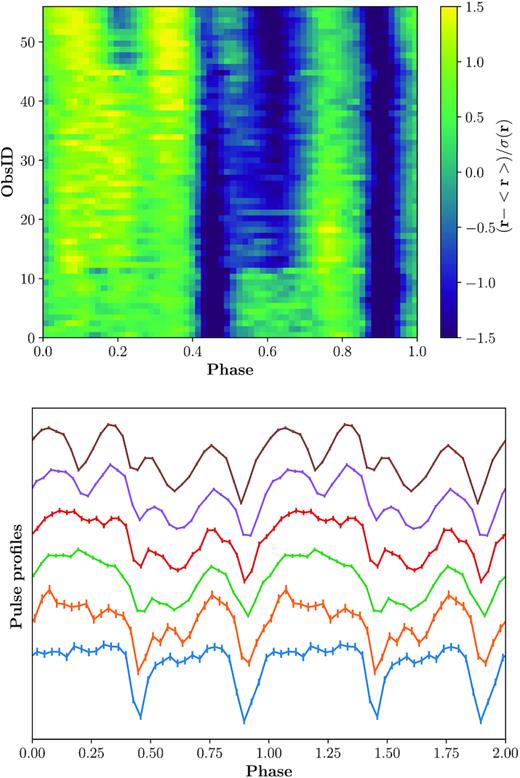
Upper panel: the evolution of pulse profiles of NICER observations, where the ObsID is sorted (in an ascending order) according to the flux. The flux is estimated by using the Swift/BAT count rate after taking into account the bolometric correction provided by Insight-HXMT. Lower panel: representative pulse profiles at different flux levels (ObsID 6, 16, 26, 36, 46, and 56 from bottom to top).
Thanks to NICER’s high-cadence monitoring, the smooth evolution of the pulse profile morphology with luminosity can be observed. For a luminosity below ∼2.5 ×|$\rm 10^{37} {\it D_{\rm 10}^2} \, erg\ s^{-1}$|(obsID ∼10), the pulse profile at 0.2–10.0 keV shows two broad peaks. At a higher luminosity an additional peak appears, and a second transition of the morphology to even four peaks is observed when the luminosity is larger than ∼7 ×|$\rm 10^{37} {\it D_{\rm 10}^2} \, erg\ s^{-1}$|. This result is consistent with the NuSTAR observation at the outburst peak (Gupta, Naik & Jaisawal 2019).For hard X-rays (25–100 keV) observed with Insight-HXMT/HE, the pulse profile also exhibits significant changes with luminosity. For example, in Fig. 3 we show pulse profiles at low, intermediate, and high states (3,7,10 × |$\rm 10^{37} {\it D_{\rm 10}^2} \, erg\ s^{-1}$|), respectively. The pulse profile has two broad peaks at the low state, and one of them evolves into a narrower structure at a higher luminosity. When the luminosity is larger than ∼7 ×|$\rm 10^{37} {\it D_{\rm 10}^2} \, erg\ s^{-1}$|, a triple-peak profile is gradually shown. We note that changes of the pulse profiles observed with Insight-HXMT correspond to the variability of the GBM pulsed flux shown in Fig. 1.
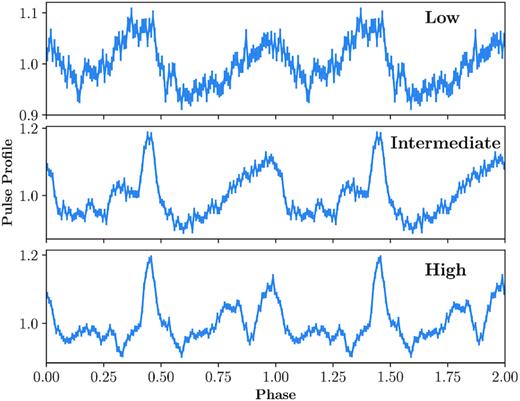
Examples of pulse profiles in the energy range of 25–100 keV observed with Insight-HXMT/HE in the low, intermediate, and high states, respectively.
We show the rms pulsed fractions (PF) for both soft (0.2–10.0 keV) and hard (25–100 keV) X-rays observed with NICER and Insight-HXMT in Fig. 1. The pulsed fraction is calculated as |$\sqrt{\Sigma _{j=1}^{m} (a_{\rm j}^2 + b_{\rm j}^2 - \sigma _{\rm a, j}^2 - \sigma _{\rm b, j}^2) / (a_{0}^2 + b_{0}^2)}$|, where aj and bj are the Fourier coefficient, σa,jand σb,j are the corresponding uncertainties, and m is the number of phase bins (Archibald et al. 2015). The pulsed fraction both in the hard (25–100 keV) and soft (0.2–10.0 keV) bands appears to change with luminosity; however, the dependence is different. In the soft band the pulsed fraction decreases with luminosity, whereas in hard X-rays it actually increases with the luminosity up to 7×|$\rm 10^{37} {\it D_{\rm 10}^2} \, erg\ s^{-1}$|, and then decreases. The pulsed fraction luminosity dependence in the hard band revealed by Insight-HXMT, thus confirms the already noted drop of the pulsed flux at the peak of the second outburst based on the comparison of Fermi/GBM and BAT fluxes. It is also interesting to note that the drop of the pulsed fraction in the hard band occurred simultaneously with the transition of the soft X-ray pulse profiles from three peaked to four peaked shape.
3 DISCUSSION
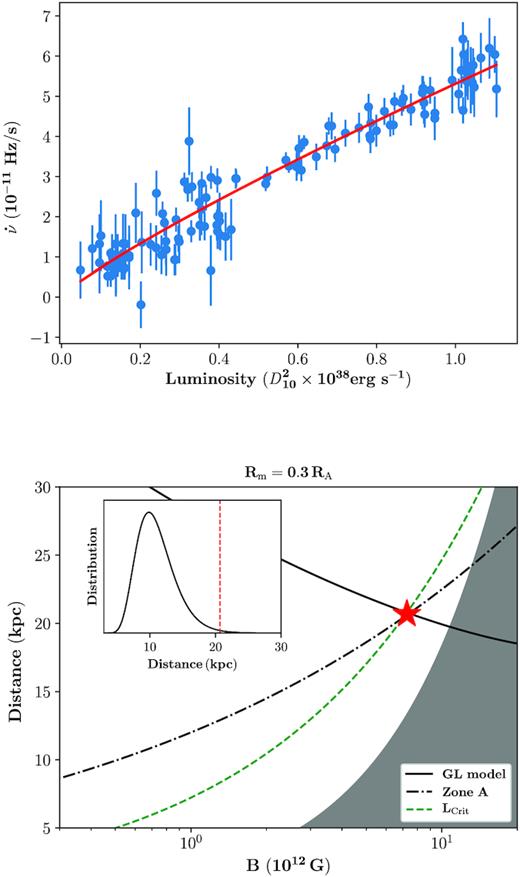
Upper panel: the luminosity versus the frequency derivative, where the red line is the fitting by using GL model. Lower panel: the estimation of the magnetic field and distance of 2S 1417−624 (shown as a red star). The solid black line shows the fitting result by using the GL model. The green dashed line is obtained by assuming |$\rm F_{\rm crit1}$| is the critical luminosity between accretion regimes. The dash–dotted line shows the condition if |$\rm F_{\rm crit2}$| corresponds to the changes of the accretion disc between the gas and radiation pressure dominated states. The grey region represents the forbidden parameter space obtained from the propeller effect, only above which the source is able to accrete in the quiescence state as observed by Tsygankov et al. (2017). The inset shows the distribution of the distance suggested by Gaia (Bailer-Jones et al. 2018), where the vertical line is the estimation in this work.
This condition is shown as a dotted line in Fig. 4. The distance and magnetic field inferred above are consistent with the parameter space where the accretion is allowed in the quiescence state.
No cyclotron resonance scattering features (CRSFs) have been found in 2S 1417−624 with RXTE and NuSTAR observations (Gupta et al. 2018; Gupta et al. 2019). The high value of the estimates of the magnetic field obtained above ∼7 × 1012 G could explain the lack of detection as the CRSF could be expected to have energy ≳80 keV in this case. Unfortunately, the counting statistics does not allow to put robust detection of an absorption line at these energies (Güngör et al., in preparation). The inferred distance is ∼20 kpc, which is, however, larger than the Gaia’s estimation at a nearly 3 σ significance level. We note that this discrepancy mainly originates from the torque model, which does not allow a closer distance. Other torque models cannot solve this problem either because they predict a similar behaviour for slow rotators, like the case in 2S 1417−624 (see e.g. Wang 1987; Kluźniak & Rappaport 2007; Shi, Zhang & Li 2015). If the distance measured by Gaia is correct, a torque which is ∼3 times larger than GL model is required to explain the observed spin-up. This may bring a challenge for the current torque models, and other effects, for example, the quadrupolar magnetic field, might be important. Furthermore, the Lcrit is also highly uncertain (Becker et al. 2012; Mushtukov et al. 2015b), and its effect is discussed by Doroshenko (2019). Nevertheless, a deep study that contains both the spin-up rate and the variability of pulse profiles provides a new measure and a self-consistent solution to understand the magnetic field of 2S 1417−624. On the other hand, independent estimate of the magnetic field, for instance by detection of a cyclotron line, would allow to verify theoretical assumptions we used above. Observing similar phenomenology in more sources is also required to ensure the robustness of these interpretations, particularly in ultraluminous X-ray sources.
ACKNOWLEDGEMENTS
This work made use of the data from the Insight-HXMT mission, a project funded by China National Space Administration (CNSA) and the Chinese Academy of Sciences (CAS). The Insight-HXMT team gratefully acknowledges the support from the National Program on Key Research and Development Project (Grant No. 2016YFA0400800) from the Minister of Science and Technology of China (MOST) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB23040400). The authors thank supports from the National Natural Science Foundation of China under Grants No. 11503027, 11673023, 11733009, U1838201, and U1838202. We acknowledge the use of public data and products from the Swift, NICER, and Fermi data archive.
Footnotes
source_id = 5854 175 187 710 795 136.



