-
PDF
- Split View
-
Views
-
Cite
Cite
L Löbling, T Rauch, M M Miller Bertolami, H Todt, F Friederich, M Ziegler, K Werner, J W Kruk, Spectral analysis of the hybrid PG 1159-type central stars of the planetary nebulae Abell 43 and NGC 7094, Monthly Notices of the Royal Astronomical Society, Volume 489, Issue 1, October 2019, Pages 1054–1071, https://doi.org/10.1093/mnras/stz1994
Close - Share Icon Share
Abstract
Stellar post asymptotic giant branch (post-AGB) evolution can be completely altered by a final thermal pulse (FTP) which may occur when the star is still leaving the AGB (AFTP), at the departure from the AGB at still constant luminosity (late TP, LTP) or after the entry to the white-dwarf cooling sequence (very late TP, VLTP). Then convection mixes the He-rich material with the H-rich envelope. According to stellar evolution models the result is a star with a surface composition of |$\mathrm{H}\approx \, 20$| per cent by mass (AFTP), ≈ 1 per cent (LTP), or (almost) no H (VLTP). Since FTP stars exhibit intershell material at their surface, spectral analyses establish constraints for AGB nucleosynthesis and stellar evolution. We performed a spectral analysis of the so-called hybrid PG 1159-type central stars (CS) of the planetary nebulae Abell 43 and NGC 7094 by means of non-local thermodynamical equilibrium models. We confirm the previously determined effective temperatures of |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000\pm 5\, 000 \, \mathrm{K}$| and determine surface gravities of |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2} )) = 5.6\pm 0.1$| for both. From a comparison with AFTP evolutionary tracks, we derive stellar masses of |$0.57^{+0.07}_{-0.04}$| M⊙ and determine the abundances of H, He, and metals up to Xe. Both CS are likely AFTP stars with a surface H mass fraction of 0.25 ± 0.03 and 0.15 ± 0.03, respectively, and an Fe deficiency indicating subsolar initial metallicities. The light metals show typical PG 1159-type abundances and the elemental composition is in good agreement with predictions from AFTP evolutionary models. However, the expansion ages do not agree with evolution time-scales expected from the AFTP scenario and alternatives should be explored.
1 INTRODUCTION
Asymptotic giant branch (AGB) stars are important contributors to the formation of elements heavier than iron (trans-iron elements, TIEs). Schematically, the internal structure of an AGB star is illustrated in Fig. 1. It is composed of an inner C/O core, the two burning shells with an He, C, and O rich intershell region in between and an H-rich convective envelope on top. These stars experience several thermal pulses (TPs) during which the intershell region becomes convectively unstable and C-rich both due to He burning and to dredge up from the core. Additionally, small amounts of H can be partially mixed into the intershell region during the expansion and cooling of the envelope that follows a TP. The presence of large amounts of 12C mixed with traces of H at high temperatures leads to the formation of 13C that acts as a neutron source for the slow neutron capture process (s-process). The intershell region of AGB stars is the main astrophysical site for the s-process. The stellar post-AGB evolution divides into two major channels of H-rich and H-deficient stars. The latter comprise about a quarter of all post-AGB stars and include He- and C-dominated stars. While the He-dominated, H-deficient stars may be the result of stellar mergers (Reindl et al. 2014b), it is commonly accepted that the C-rich are the outcome of a (very) late He-shell flash (late thermal pulse, LTP, cf. Werner & Herwig 2006). The occurrence of a thermal pulse in a post-AGB star or white dwarf was predicted by, e.g. Paczyński (1970), Schönberner (1979), Iben et al. (1983). The particular timing of the final thermal pulse (FTP), determines the amount of remaining photospheric H (cf. Herwig 2001). Still on the AGB (AGB final thermal pulse, AFTP), flash-induced mixing of the H-rich envelope (|$\approx 10^{-2}\, {\rm M}_\odot$|) with the He-rich intershell layer (|$\approx 10^{-2}\, {\rm M}_\odot$|) reduces the H abundance to about 10–20 per cent but H i lines remain detectable. After the departure from the AGB, the H-rich envelope is less massive (|$10^{-4}\, {\rm M}_\odot$|). If the nuclear burning is still ‘on’, i.e. the star evolves at constant luminosity, the mixing due to a late thermal pulse (LTP) reduces H below the detection limit (about 10 per cent by mass at the relatively high surface gravity). After the star has entered the white-dwarf cooling sequence and the nuclear burning is ‘off’, a very late thermal pulse (VLTP) will produce convective mixing of the entire H-rich envelope (no entropy barrier due to the H-burning shell) down to the bottom of the He-burning shell where H is burned. In that case, the star will become H free at that time. The internal structure of such a post-AGB star that underwent a FTP scenario is illustrated in Fig. 1.

Left: Internal structure (not to scale) of an AGB star during a thermal pulse. Right: Internal structure of a post-AGB star after having experienced a final thermal pulse that caused flash induced mixing of the envelope and the intershell region.
The spectroscopic class of PG 1159 stars (effective temperatures of |$75\, 000\, \mathrm{K} \lesssim \mbox{$T_\mathrm{eff}$}\, \lesssim 250\, 000\, \mathrm{K}$| and surface gravities of |$5.5 \lesssim \log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}) ) \lesssim 8.0$|) belongs to the H-deficient, C-rich evolutionary channel (e.g. Werner & Herwig 2006), with the sequence AGB → [WC]-type Wolf-Rayet stars → PG 1159 stars → DO-type white dwarfs (WDs). In the AFTP and LTP scenarios with any remaining H, the stars will turn into DA-type WDs. In PG 1159 star photospheres, He, C, and O are dominant with mass fractions of He = [0.30,0.92], C = [0.08,0.60], and O = [0.02,0.20] (Werner, Rauch & Kruk 2016).
Napiwotzki & Schönberner (1991) discovered the spectroscopic sub-class of so-called hybrid PG 1159 stars. They found that WD 1822 + 008 (McCook & Sion 1999), the central star (CS) of the planetary nebula (PN) Sh 2 − 68 exhibits strong Balmer lines in its spectrum. The hybrid PG 1159 stars are thought to be AFTP stars. Presently, only five of them are known, namely the CSPNe of Abell 43, NGC 7094, Sh 2 − 68, HS 2324 + 3944, and SDSS 152116.00 + 251437.46 (Werner & Herwig 2006; Werner, Rauch & Kepler 2014).
Abell 43 (PN G036.0 + 17.6) was discovered by Abell (1955, object No. 31) and classified as PN (Abell 1966, No. 43). NGC 7094 (PN G066.7 − 28.2) was discovered in 1885 by Swift (1885). Kohoutek (1963) identified it as a PN (K 1 − 19). Narrow-band imaging of Abell 43 and NGC 7094 (Rauch 1999) revealed apparent sizes (in west-east and north-south direction) of 1′28″ × 1′20″and 1′45″ × 1′46″, respectively.
Abell 43 and NGC 7094 belong to the group of so-called ‘Galactic Soccerballs’ (Rauch 1999) because they exhibit filamentary structures that remind of the seams of a traditional leather soccer ball. These structures may be explained by instabilities in the dense, moving nebular shell (Vishniac 1983). While Abell 43 is almost perfectly round and most likely expanded into a void in the ISM, NGC 7094 shows some deformation that may be a hint for ISM interaction.
Another recently discovered member of this group is the PN Kn 61 (SDSS J192138.93 + 381857.2, Kronberger et al. 2012; De Marco et al. 2015). García-Díaz et al. (2014) compared medium-resolution optical spectra of the CSPN Kn 61 with spectra published by Werner et al. (2014) and found a particularly close resemblance of the CSPN Kn 61 to SDSS 075415.12 + 085232.18, an H-deficient PG 1159-type star with |$\mbox{$T_\mathrm{eff}$}\, = 120\, 000 \pm 10\, 000 \, \mathrm{K}$|, |$\log g = 7.0 \pm 0.3$|, and a mass ratio C/He = 1. Other members and candidates to become a Galactic Soccerball nebula are known, e.g. the PN NGC 1501 (PN G144.5 + 06.5). An investigation on the three-dimensional ionization structure by Ragazzoni et al. (2001) had shown that it might resemble a Soccerball nebula in a couple of thousands of years. The CSPN, however, is of spectral type [WC4] (Koesterke & Hamann 1997) and cannot resemble a progenitor star of the CSs of Abell 43 and NGC 7094. In this paper, we analyse the hybrid PG 1159-type CSs of Abell 43 and NGC 7094, that we introduce briefly in the following paragraphs.
A first spectral analysis of the CSs of Abell 43 and NGC 7094, namely WD 1751 + 106 and WD 2134 + 125 (McCook & Sion 1999), respectively, with non-local thermodynamical equilibrium (NLTE) model atmospheres that considered opacities of H, He, and C was presented by Dreizler, Werner & Heber (1995). They analysed medium-resolution optical spectra and found that their synthetic spectra, calculated with |$\mbox{$T_\mathrm{eff}$}\, = 110\, 000 \, \mathrm{K}$|, |$\log g = 5.7$|, and a surface-abundance pattern of H/He/C = 42/51/5 (by mass, H is uncertain), reproduced equally good the observations of both stars making them a pair of spectroscopic twins.
Napiwotzki (1999) used medium-resolution optical spectra and an extended H + He-composed NLTE model-atmosphere grid. With a statistical (χ2) approach, he found |$\mbox{$T_\mathrm{eff}$}\, = 116\, 900 \pm 5500 \, \mathrm{K}$| and |$\log g = 5.51 \pm 0.22$| for WD 1751 + 106 and |$\mbox{$T_\mathrm{eff}$}\, = 125\, 900 \pm 7700 \, \mathrm{K}$| and |$\log g = 5.45 \pm 0.23$| for WD 2134 + 125. An attempt to measure the Fe abundance of WD 2134 + 125 from far ultraviolet (FUV) observations performed with Far Ultraviolet Spectroscopic Explorer (FUSE) revealed a strong Fe underabundance of 1–2 dex (Miksa et al. 2002). This was not in line with expectations from stellar evolution theory (e.g. Busso, Gallino & Wasserburg 1999). Ziegler et al. (2009) found also an underabundance of Ni of about 1 dex for both stars. The transformation of Fe to Ni seems therefore unlikely to be the reason for the Fe deficiency. They reanalysed Teff and log g of WD 2134 + 125 and found |$\mbox{$T_\mathrm{eff}$}\, = 100\, 000 \pm 15\, 000 \, \mathrm{K}$| and |$\log g = 5.5 \pm 0.2$| with an improved abundance ratio of H/He = 17/69 (by mass). Furthermore, the element abundances of the C – Ne, Si, P, and S were determined. Ringat et al. (2011) reanalysed WD 1751 + 106 and found |$\mbox{$T_\mathrm{eff}$}\, = 105\, 000 \pm 10\, 000 \, \mathrm{K}$| and |$\log g = 5.6 \pm 0.3$|. Also the element abundances of C – Ne, Si, P, and S were determined and agree with the values of Friederich (2010). Löbling (2018) found |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \pm 5000 \, \mathrm{K}$| for both stars and |$\log g = 5.4 \pm 0.1$| and |$\log g = 5.5 \pm 0.1$| for WD 2134 + 125 and WD 1751 + 106 , respectively. She considered 31 elements in her analysis and determined abundances in individual line-formation calculations. This work is a continuative analysis giving a more extensive description.
For NLTE model-atmosphere calculations, reliable atomic data is mandatory to construct detailed model atoms to represent individual elements. In the last decade, the availability of such atomic data improved, e.g. Kurucz’s line lists for iron-group elements (IGEs), namely Ca–Ni, were strongly extended in 2009 (Kurucz 2009, 2011) by about a factor of 10. In addition, transition probabilities and oscillator strengths for many TIEs were calculated recently (Table A3, available online). Therefore, we decided to perform a detailed spectral analysis of the hybrid PG 1159-type CSPNe Abell 43 and NGC 7094, by means of state-of-the-art NLTE model-atmosphere techniques. We describe the available observations and our model atmospheres in Sections 2 and 3, respectively. The spectral analyses follow in Sections 4 and 5. We investigate on the stellar wind of both stars in Section 6 and determine stellar masses, distances, and luminosities in Section 7. We summarize the results and conclude in Section 8.
2 OBSERVATIONS
Our spectral analysis is based on high signal-to-noise ratio (S/N) and high-resolution observations from the far ultraviolet (FUV) to the optical wavelength range. UV spectra were retrieved from the Barbara A. Mikulski Archive for Space Telescopes (MAST). To improve the S/N, multiple observations in the same set-up were co-added. The spectra were partly processed with a low-pass filter (Savitzky & Golay 1964). To simulate the instruments’ resolutions, all synthetic spectra shown in this paper are convolved with respective Gaussians. The observation log for all space- and ground-based observations of WD 1751 + 106 and WD 2134 + 125 used for this work is given in Table A2, available online.
Radial and rotational velocity. We measured radial velocity shifts for all observations using prominent lines of He ii, C iv, O v and O vi, Si v, and Fe vii and shifted the spectra to rest wavelength.
The observed line profiles are broadened but the quality of the spectra does not unambiguously allow to decide whether it is due to stellar rotation or caused by some wind related macro turbulence. For WD 1751 + 106 , we selected O vi |$\lambda \lambda \, 1124.7, 1124.9$| Å and S vi|$\lambda \, 1117.8$| Å (Fig. 2) to determine a rotational velocity of |$v_\mathrm{rot} \sin i = 18 \pm 5\, \mathrm{km}\, \mathrm{s}^{-1}$|. This new determination revises the previous higher value of |$v_\mathrm{rot} \sin i = 42 \pm 13\, \mathrm{km}\, \mathrm{s}^{-1}$| (Rauch et al. 2004). The profiles of these lines also agree with broadening with radial-tangential macro turbulence profiles (Gray 1975) with the same velocity (Fig. 2). For WD 2134 + 125 , we used O vi|$\lambda \lambda \, 1122.4, 1122.6, 1124.7, 1124.9$| and N v |$\lambda \, 1242.6$| Å (Fig. 2) to determine |$v_\mathrm{rot} \sin i = 28 \pm 5\, \mathrm{km}\, \mathrm{s}^{-1}$|. This value agrees within the error limits with the value of |$46 \pm 16\, \mathrm{km}\, \mathrm{s}^{-1}$| from Rauch et al. (2004). Again, we cannot claim this broadening to be rotation alone because the profiles can also be reproduced with radial-tangential macro turbulence profiles with |$v_\mathrm{macro} = 35 \pm 5\, \mathrm{km}\, \mathrm{s}^{-1}$|.

Synthetic spectra (red) convolved with rotational profiles (|$v_\mathrm{rot} = 18\, \mathrm{km}\, \mathrm{s}^{-1}$| for WD 1751 + 106 , upper panels and |$v_\mathrm{rot} = 28\, \mathrm{km}\, \mathrm{s}^{-1}$| for WD 2134 + 125 , lower panels) and convolved with radial-tangential macro turbulence profiles (blue, |$v_\mathrm{macro}=18\, \mathrm{km}\, \mathrm{s}^{-1}$| for WD 1751 + 106 , upper panels and |$v_\mathrm{macro} = 35\, \mathrm{km}\, \mathrm{s}^{-1}$| for WD 2134 + 125 , lower panels) around O vi, N v, and S vi lines (marked with their wavelengths at the top of the panels) calculated from our final models compared with observations (gray). A model without extra broadening (red, dashed) and one without interstellar absorption (green, dashed) are shown. Interstellar absorption lines are indicated by blue marks.
Interstellar reddening. It was measured by a comparison of observed UV fluxes and optical and infrared brightnesses with our synthetic spectra. The latter were normalized to the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006; Cutri et al. 2003) brightnesses and then, Fitzpatrick’s law (Fitzpatrick 1999) was applied to match the observed UV continuum flux level (Fig. A1, available online). We determined |$\mbox{$E_{B-V}$}= 0.265 \pm 0.01$| and |$\mbox{$E_{B-V}$}= 0.135 \pm 0.01$| for WD 1751 + 106 and WD 2134 + 125, respectively.
We determined the interstellar neutral H column density from the comparison of theoretical line profiles of Ly α with the observations (Fig. A9, available online). These are best reproduced at |$n_{\mathrm{H\,{\small I}}}= 1.0 \pm 0.1 \times 10^{21}\, \mathrm{cm^{-2}}$| and |$n_{\mathrm{H\,{\small I}}}= 6.5 \pm 0.1 \times 10^{20}\, \mathrm{cm^{-2}}$| for WD 1751 + 106 and WD 2134 + 125 , respectively. Our values of |$\log\,(n_{\mathrm{H\,{\small I}}}/\mbox{$E_{B-V}$}) = 21.58 \pm 0.02$| and |$\log\,(n_{\mathrm{H\,{\small I}}}/\mbox{$E_{B-V}$}) = 21.68 \pm 0.03$|, respectively, agree well with the prediction from the Galactic reddening law of Groenewegen & Lamers (1989, |$\log\,(n_{\mathrm{H\,{\small I}}}/\mbox{$E_{B-V}$}) = 21.58\pm 0.1$|).
Interstellar line absorption. This absorption in the FUSE observations was modelled with the line-profile fitting procedure OWENS (Hébrard et al. 2002; Lemoine et al. 2002; Hébrard & Moos 2003). It allows to consider several individual clouds in the interstellar medium (ISM) with individual chemical compositions, column densities for each of the included molecules and ions, radial and turbulent velocities, and temperatures. The FUV observations are strongly contaminated by ISM line absorption and, thus, it is necessary to reproduce these lines well to unambiguously identify photospheric lines (cf. Ziegler et al. 2007, 2012). In the FUSE spectra of WD 1751 + 106 and WD 2134 + 125 , ISM absorption lines from H 2 (J = 0 − 5), HD, C i-iii, N i-ii, O i, Si ii, P ii, S iii, Ar i, and Fe ii were identified and simulated.
3 MODEL ATMOSPHERES AND ATOMIC DATA
To calculate synthetic spectra, we used the Tübingen NLTE Model Atmosphere Package (TMAP1; Werner et al. 2003; Werner, Dreizler & Rauch 2012). The models assume plane-parallel geometry, are chemically homogeneous, and in hydrostatic and radiative equilibrium. TMAP considers level dissolution (pressure ionization) following Hummer & Mihalas (1988) and Hubeny, Hummer & Lanz (1994). Stark-broadening tables of Tremblay & Bergeron (2009, extended tables of 2015, private communication) and Schöning & Butler (1989) are used to calculate the theoretical profiles of H i and He ii lines, respectively. To represent the elements considered by TMAP, model atoms were retrieved from the Tübingen Model Atom Database (TMAD; Rauch & Deetjen 2003) that has been constructed as part of the Tübingen contribution to the German Astrophysical Virtual Observatory (GAVO2). For IGEs and TIEs (atomic weight Z ≥ 29), we used Kurucz’s line lists3 (Kurucz 2009, 2011) and recently calculated data for Zn, Ga, Ge, Se, Kr, Sr, Zr, Mo, Te, I, Xe, and Ba (Table A3, available online) that is available via the Tübingen Oscillator Strengths Service (TOSS). For the elements with Z ≥ 20, we created model atoms using a statistical approach that calculates super levels and super lines (Rauch & Deetjen 2003). The statistics of all elements considered in our model-atmosphere calculations are summarized in Table A1, available online.
To simulate prominent P Cygni profiles in the observations, we used the Potsdam Wolf–Rayet (PoWR) code that has been developed for expanding atmospheres and considers mass loss due to a stellar wind (Section 6). These models are used to determine mass-loss rates and terminal wind velocities.
4 EFFECTIVE TEMPERATURE AND SURFACE GRAVITY
Model atmospheres grids (|$\Delta \mbox{$\mbox{$T_\mathrm{eff}$}\, = 5000 \, \mathrm{K}$}$| and |$\Delta \mbox{$\log g = 0.1$}$|) were calculated around the literature values of Löbling (2018). These models consider opacities of 31 elements from H to Ba for which the ionization fractions of the considered ions are shown in Fig. A8, available online. The abundances used for the calculation of the atmospheric structure are given in Table A4, available online. The best agreement for the line width and depth increment for the observed He ii |$\lambda\lambda\,4025.6, 4100.1, 4199.8, 4338.7, 4859.3, 5411.5$| Å , and H i |$\lambda \lambda \, 4101.7, 4340.5, 4861.3$| Å was obtained for surface gravity values of |$\log g = 5.6\pm 0.1$| for WD 1751 + 106 (Fig. A2, available online) and WD 2134 + 125 (Fig. A3, available online). The value for WD 2134 + 125 is also verified by the depth increment of the He II Fowler series (Fig. A4, available online). The lower surface gravity values of Löbling (2018) were based on model atmospheres assuming the abundances found by Friederich (2010). Using new models with a revised He/H ratio and including opacities of more elements, these previous values appear too low. Higher values for log g have an impact on the final masses which are lower compared to previous values (Section 7). We confirm the temperature determination of |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000\pm 5\, 000 \, \mathrm{K}$| for both stars by Löbling (2018) by the evaluation of the O v/O vi ionization equilibrium using O v λλ1371.3, 1506.7, 1506.7, 1506.8, 4930.2, 4930.3 Å and O vi|$\lambda \lambda \, 1124.7, 1124.9, 3811.3, 3834.2$| Å (Fig. A5, available online). We adopt |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \, \mathrm{K}$| and |$\log g = 5.6$| for WD 1751 + 106 and WD 2134 + 125 for our further analysis.
5 METAL ABUNDANCES
In the following paragraphs, we discuss all elements, that were considered in this analysis. To determine the abundances, we varied them in subsequent line formation calculations in steps of 0.2 dex or smaller. The abundances were derived by line-profile fits and evaluation by eye. For illustration, some representative spectral lines are shown in Figs 3–7. These values are affected by typical errors estimated to 0.3 dex by redoing the abundance determination for models at the edges of the error range for Teff and log g (we used a model with |$\mbox{$T_\mathrm{eff}$}\, = 120\, 000 \, \mathrm{K}$|, |$\log g = 5.5$| and one with |$\mbox{$T_\mathrm{eff}$}\, = 110\, 000 \, \mathrm{K}$| and |$\log g = 5.7$|). If no line identification was possible, we determined upper limits by reducing the abundance until the strongest computed lines become undetectable within the noise of the spectrum. The results are summarized in Table 3. The whole FUSE spectra compared with our final models are shown in Fig. A6, available online, and the GHRS spectrum of WD 1751 + 106 as well as the STIS spectrum of WD 2134 + 125 in Fig. A7, available online. The solar abundances are taken from Asplund et al. (2009), Scott et al. (2015b,a), and Grevesse et al. (2015).
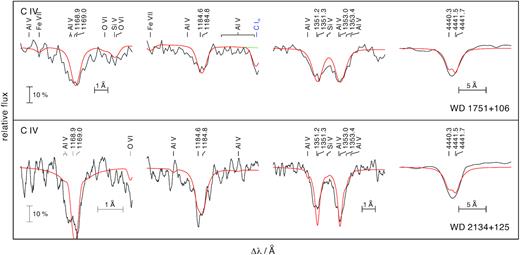
Synthetic spectra (red) around C iv lines calculated from our final model compared with observations (gray).
Carbon. Detailed line-profile fits were performed for C iv |$\lambda \lambda \, 1168.9, 1169.0, 1184.6$| Å in the FUSE observations, C iv |$\lambda \lambda \, 1351.2, 1351.3, 1353.0$| Å in the GHRS or STIS observations, and the C iv lines at 3685–3691 Å, 4440–4442 Å, 4785–4790 Å, 5016–5019 Å, and 6591–6593 Å in the UVES SPY observations (Fig. 3). We achieve |${}[\mathrm{C}]= \log \, \mathrm{(abundance/solar\ abundance)} ={2.0}$| for WD 1751 + 106 and [C] = 2.1 for WD 2134 + 125.
Nitrogen. The photospheric N v |$\lambda \lambda \, 1238.8, 1242.8$| Å resonance doublet in the STIS spectrum of WD 2134 + 125 is blended by strong interstellar absorption. Therefore, we used N v |$\lambda \lambda \, 4943.2, 4944.0, 4945.3 4945.6, 4945.7$| Å in addition (Fig. 4) and determined [N] = 0.6 for WD 1751 + 106 and [N] = − 0.3 for WD 2134 + 125.

Oxygen. The determination of the O abundance in WD 2134 + 125 is hampered by the fact that all useful lines in the UV and FUV are either blended with interstellar lines or display strong P Cygni profiles (e.g., O v |$\lambda \, 1371.3$| Å and O vi |$\lambda \lambda \, 1031.9, 1037.6$| Å). We used O vi |$\lambda \lambda \, 1122.4, 1122.6, 1124.7, 1124.9$| Å in the FUSE spectra and O vi |$\lambda \lambda \, 5289.5, 5289.8, 5290.7, 5292.0$| Å in the UVES SPY spectra (Fig. 4) to determine [O] = − 0.2 for WD 1751 + 106 and [O] = − 0.1 for WD 2134 + 125. Furthermore, we employed PoWR to calculate wind profiles. Details on the wind models are given in Section 6.
Fluorine. The strong line F vi |$\lambda \, 1139.5$| Å shows a P Cygni profile. For an abundance determination with our static models, we analysed F v |$\lambda \lambda \, 1082.3, 1087.8, 1088.4$| Å (Fig. 4), which are reproduced best with an abundance of [F] = 1.0 for WD 1751 + 106 and [F] = 1.5 for WD 2134 + 125 (the same value was measured by Werner, Rauch & Kruk 2005). These abundances exceed the values of Ringat et al. (2011) and Ziegler et al. (2009) but agree with the value of [F] = 1.2 (Reiff et al. 2008) for WD 2134 + 125 , who employed a wind model for their analysis. We examined the profile of F vi |$\lambda \, 1139.5$| Å in our PoWR wind model and verified the newly determined abundances.
Neon. All lines of Ne v with observed wavelengths in the FUSE and STIS wavelength range that are available from the National Institute for Standards and Technology (NIST) Atomic Spectra Database4 (Kramida et al. 2018) are affected by a wavelength uncertainty of 1.5 Å or blended with interstellar absorption like Ne v |$\lambda \, 946.9$| Å . Ne vi |$\lambda \lambda \, 1645.1, 1645.6, 1666.2, 1667.8, 1679.7$| Å are visible in the STIS spectrum of WD 2134 + 125 and used for an estimate of the Ne abundance (Fig. 4). Ne vii |$\lambda \, 1319.8$| Å is also detectable but blended with Si v |$\lambda \, 1319.6$| Å . The optical lines Ne vii |$\lambda \lambda \, 3643.6$|, 3853.5, 3866.7, 3873.3, 3894.0, 3905.3, 3912.0 Å are very weak. We determine [Ne] = 1.2 for WD 2134 + 125 and pose an upper limit of [Ne] < 1.5 for WD 1751 + 106 owing to the resolution of the GHRS observation and the fact that the strong Ne vi lines are not within the GHRS range. Ne vii |$\lambda \, 973.3$| Å exhibits a strong P Cygni profile. The wind profile of this line in the PoWR model confirms the Ne abundance.
Magnesium. No Mg line can be identified in the observations. Based on the computed lines of Mg iv |$\lambda \lambda \, 1346.5$|, 1346.6, 1382.5, 1385.7, 1387.5 Å (Fig. 5), we find upper limits of [Mg] < 0.5 for WD 2134 + 125 and [Mg] < 0.8 for WD 1751 + 106. The latter value is higher due to the lower resolution of the GHRS observation compared to the one obtained with STIS.
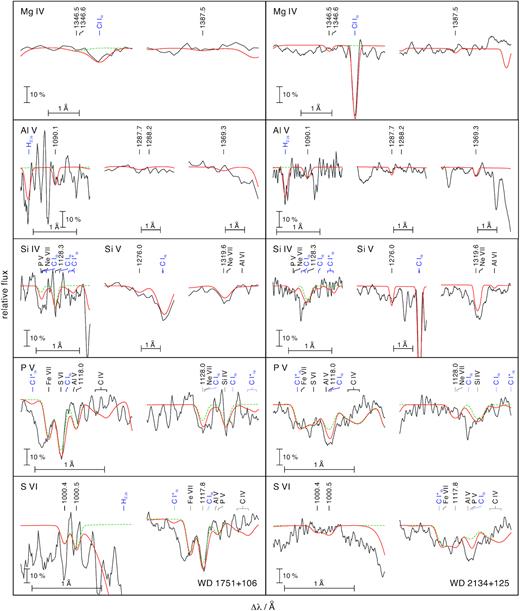
Aluminum. Al v |$\lambda \lambda \, 1090.1, 1287.7, 1288.2, 1369.3$| Å are the most prominent Al lines in the synthetic spectra (Fig. 5). We determined an abundance of [Al] = 0.6 for WD 2134 + 125 and an upper limit of [Al] < 0.7 for WD 1751 + 106.
Silicon. In the STIS and GHRS observations of both stars, the Si iv |$\lambda \lambda \, 1393.8, 1402.8$| Å resonance doublet is blended by interstellar absorption lines. Thus, our abundance determination is based on Si iv |$\lambda \, 1128.3$| Å and Si v |$\lambda \lambda \, 1118.8$|, 1251.4, 1276.0, 1291.4, 1319.6 Å (Fig. 5). These lines indicate [Si] = − 0.6 for WD 1751 + 106. For WD 2134 + 125, we used the same lines as well as Si v |$\lambda \lambda \, 1465.5, 1582.7$| Å and measured [Si] = − 0.7.
Phosphorus. We used the strongest P lines, namely P V |$\lambda \lambda \, 1118.0, 1128.0$| Å , in the theoretical spectra to establish upper limits of [P] < 0.3 for WD 1751 + 106 and [P] < 0.4 for WD 2134 + 125 (Fig. 5).
Sulfur. The most prominent S lines in the FUSE spectrum of WD 1751 + 106 and WD 2134 + 125, S vi |$\lambda\lambda\, 933.4, 944.5\,{\mathring{\rm A}}$| are both blended by interstellar H2 lines and thus it is uncertain to derive the S abundance. From S vi |$\lambda \lambda \, 1000.4$|, 1000.5, 1117.8 Å (Fig. 5), we determine [S] = − 0.1 and [S] ≤ − 0.6 for WD 1751+106 and WD 2134 + 125 , respectively.
Chlorine. Cl vii |$\lambda \lambda \, 949.0, 949.1, 996.7, 997.0$| Å are present in the synthetic spectra but cannot be identified in the FUSE observations of both stars. Based on these lines, we determined upper limits of [Cl] < 1.1 and [Cl] < 1.0 for WD 1751 + 106 and WD 2134 + 125, respectively.
Argon. The strong Ar viii |$\lambda \, 1063.6$| Å line is blended by interstellar absorption and thus can not be used to derive an abundance value for argon. We used Ar viii |$\lambda \, 1164.1$| Å to derive an upper limit of [Ar] < 0.3 for WD 1751 + 106 and [Ar] < − 0.3 for WD 2134 + 125 (Fig. 6).
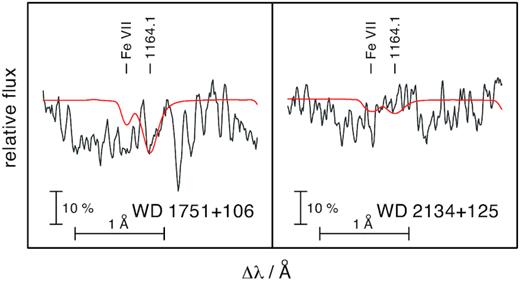
Synthetic spectra around Ar viii |$\lambda \, 1164.1$| Å calculated from our final models compared with the FUSE observations.
Calcium. The strongest line in the synthetic spectra, namely Ca ix |$\lambda \, 1116.0$| Å , is blended with a strong interstellar H2 absorption feature. For WD 1751 + 106 , this line appears in the wing of the H2 line and is used to derive an upper limit of [Ca] < 0.0.
Chromium. None of the Cr vii lines appearing in the synthetic spectrum has been identified in the observation. We used Cr vii |$\lambda \lambda \, 1170.1, 1186.6, 1187.3$| Å to determine upper limits of [Cr] < 2.0 for WD 1751 + 106 and WD 2134 + 125.
Iron. In previous analysis of NGC 7094, Miksa et al. (2002) found subsolar values of at least 1 dex for Fe. For the CS of Abell 43, they found a solar upper limit for Fe. With extended model atoms, Löbling (2018) checked and correct this result and determined [Fe] = −0.4 for WD 1751 + 106 and [Fe] = −0.8 for WD 2134 + 125. These values are supported also by our final model including all opacities of 31 elements (Fig. 7). Previous analyses that assumed a larger deficiency, did not take line broadening due to stellar rotation or macro turbulence into account explaining the lower Fe abundances. A solar Fe abundance can be ruled out since the computed lines of Fe vii appear too strong (Fig. 7)
![Synthetic spectra around Fe vii and viii lines calculated from our final models with [Fe] = −0.4 (red, full) and solar (blue, dashed) compared with the FUSE observation.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/489/1/10.1093_mnras_stz1994/1/m_stz1994fig7.jpeg?Expires=1750290729&Signature=4wvLUsI5hebke2kYzvX5q4NMkVcHyDTJXvQNYn0qrft-9z82l-zooy8J17aBaLKrfr7PXedIaLUy2e74BokyGxlc64OD6COU70on0aCWPzqHJJKvrivmYf-4R3EKwuvXt8C8fIUyNA4k5geB2BuqiDhQW0eORKM4elaAZedZzbUJmcb34foapQyGAEvfMMHmDrVP2a-RvFAde1nUfF1uofGCrIZrPeHmAvjRUp00GbOtunizD0nCYenQrqYqfTLcZ0Nw-EhgnmrogqKjZOT7tlL1OPuJjFl4buuGiTGGGngOpSdzlUOduuvRiVT-9gnmF-Y1~8yPQ2oG5F-qRMMYkQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Synthetic spectra around Fe vii and viii lines calculated from our final models with [Fe] = −0.4 (red, full) and solar (blue, dashed) compared with the FUSE observation.
Nickel. The dominating ionization stages of the IGEs in the expected parameter regime are vii and viii. Due to the lack of POS lines of Ni in these stages in Kurucz’s line list (Kurucz 1991, 2009) for the spectral ranges of FUSE, STIS, and GHRS, no Ni lines could be detected and identified. In their analysis, Ziegler et al. (2009) used Ni vi lines and determined upper Ni abundance limits only. Their subsolar values may again be a result of not taking additional broadening due to rotation or macro turbulence into account. Furthermore, they assumed lower temperatures and higher gravities for both stars. The Ni vi lines are very sensitive to Teff and are significantly stronger for a model with Teff reduced by 10 kK (Fig. 8).
![Top panel: Synthetic spectra around Ni vi lines calculated from our final models for WD 1751 + 106 with $\mbox{$T_\mathrm{eff}$}\, = 115$ kK and [Ni] = − 0.4 (red, full) and 1 dex supersolar (blue, dashed) and $\mbox{$T_\mathrm{eff}$}\, = 105$ kK and Ni 1 dex supersolar (green, dotted). Bottom: For WD 2134 + 125 with $\mbox{$T_\mathrm{eff}$}\, = 115$ kK and [Ni] = − 0.8 (red, full) and 1 dex supersolar (blue, dashed) and $\mbox{$T_\mathrm{eff}$}\, = 105$ kK and Ni 1 dex supersolar (green, dotted).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/489/1/10.1093_mnras_stz1994/1/m_stz1994fig8.jpeg?Expires=1750290729&Signature=L1bgc~eKR49t5mUvEwTNMo3jtiemZUOe8hA4HYw~VJGCH3ZJJXiE1wv6A55YqOwxDQ3gemAJrqHqNwi5UkO4~gDnSU70uYbasKZOa3E9GzxdToQcUji8GHZ83FQ4RZoJksuMJxZPM-qzLzqNtitrcYkLWFj6XTJgdC0ma1N5XeEunw9MWVjTrw7EY1dn4mUy1ZZhffWS2szwkbcRTjH4Xam322382esjW3hTbhJKr0SUWkUV0AtA7LGMOyKBZFIYscrceKQJvPqEg2dd95G437M9VeTTrrgSmrjSzQ-aGfMw5o9nof~mFU3pL4QdIj67P1QMZ1m7UxtfCzQwMcRlzg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Top panel: Synthetic spectra around Ni vi lines calculated from our final models for WD 1751 + 106 with |$\mbox{$T_\mathrm{eff}$}\, = 115$| kK and [Ni] = − 0.4 (red, full) and 1 dex supersolar (blue, dashed) and |$\mbox{$T_\mathrm{eff}$}\, = 105$| kK and Ni 1 dex supersolar (green, dotted). Bottom: For WD 2134 + 125 with |$\mbox{$T_\mathrm{eff}$}\, = 115$| kK and [Ni] = − 0.8 (red, full) and 1 dex supersolar (blue, dashed) and |$\mbox{$T_\mathrm{eff}$}\, = 105$| kK and Ni 1 dex supersolar (green, dotted).
No strong lines in the spectra of both stars were found from the elements Sc, Ti, V, Mn, Ni, and Co. Therefore, these elements were combined to a generic model atom (Rauch & Deetjen 2003). All IGEs were taken into account with solar abundances ratios normalized to the Fe abundance in the final model calculations.
Zinc. The strong lines Zn v |$\lambda \lambda \, 1132.3, 1123.7, 1133.0, 1133.1,$| 1133.3, 1133.5, 1174.3, 1180.0 Å appear in the synthetic spectra but could not be identified in the observations. Thus, we can only derive an upper limit of [Zn] < 1.0 for both stars.
Gallium. We used the strongest line Ga vi |$\lambda \, 1006.9$| Å to determine an upper limit of [Ga] < 2.0 for WD 1751 + 106 and WD 2134 + 125.
Germanium. Ge VI |$\lambda \lambda \, 920.5, 926.8, 988.2$| Å are partly blended by interstellar absorption features. The analysis yields an upper limit of [Ge] < 2.0 for both stars.
Krypton. Kr vii |$\lambda \lambda \, 1166.9, 1169.6, 1195.6, 1284.6$| Å are present in the models. We used these lines to measure an upper limit of [Kr] < 3.5 for both stars.
Zirconium. By analysing STIS observation of WD 2134 + 125 around the computed lines Zr vii |$\lambda \lambda \, 1233.6$|, 1235.0, 1376.6 Å, we derived an upper limit of [Zr] < 3.0. Due to the fact that these lines are located in the range of the lower resolution GHRS observation of WD 1751 + 106, we were not able to derive a reasonable value for this star.
Tellurium. We used Te vi |$\lambda \, 1071.4$| Å , the strongest computed line in the FUSE range, to ascertain [Te] ≤ 4.0 for WD 1751 + 106 and [Te] ≤ 3.5 for WD 2134 + 125.
Iodine. The strongest computed lines I vi |$\lambda \lambda \, 911.2$|, 915.4, 919.2 Å are useless for the abundance measurement, since they are blended by interstellar absorption. Based on I vi |$\lambda \lambda \, 1045.4, 1120.3,1153.3$| Å , we derived upper limits of [I] < 4.6 and [I] < 5.0 for WD 1751 + 106 and WD 2134 + 125, respectively.
Xenon. We used the strongest line Xe vii |$\lambda \, 995.5$| Å to determine an upper limit of [Xe] < 4.0 for WD 2134 + 125. The quality of the FUSE observation of WD 1751 + 106 around this line does not suffice to determine the Xe abundance.
Selenium, strontium, molybdenum, and barium. Even if we increase the Se, Sr, Mo, and Ba abundances in the synthetic models to thousand times solar, no lines of these elements appear in the computed spectra.
In our final models, all TIEs are taken into account with solar abundance ratios normalized to the determined Fe abundance value. The temperature and density structure and the ionization fractions of all ions considered in the final model for WD 2134 + 125 are shown in Fig. A8, available online.
6 STELLAR WIND AND MASS LOSS
At |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \, \mathrm{K}$| and |$\log g = 5.6$| the stars have luminosities of almost 4 000 L⊙ (Section 7). They are located close to the Eddington limit and experience mass loss due to a radiation-driven wind (cf. Pauldrach et al. 1988) and, hence, exhibit prominent P Cygni profiles in their UV spectra (Fig. 9). Koesterke & Werner (1998) and Koesterke, Dreizler & Rauch (1998) investigated the wind properties of WD 2134 + 125 by means of NLTE models for spherically expanding atmospheres and determined the mass-loss rate |$\dot{M}$| and the terminal wind velocity v∞ from HST/GHRS and ORFEUS-SPAS II5 observations, respectively. They found |$\log [\dot{M}\, /\, ({\rm M}_\odot \mathrm{yr{^{-1}}})]=-7.3$| from C iv |$\lambda \lambda \, 1548.20, 1550.77$| Å and |$\log [\dot{M}\, /\, ({\rm M}_\odot \mathrm{yr{^{-1}}})]=-7.7$| from O vi |$\lambda \lambda \, 1031.91, 1037.61$| Å and |$v_\infty =3\, 500\, \mathrm{km\, s}^{-1}$|, which is slightly lower than the former value of |$v_\infty =3\, 900\, \mathrm{km\, s}^{-1}$| of Kaler & Feibelman (1985) based on the analysis of spectra obtained with IUE. Guerrero & De Marco (2013) used lines of O vi and found 3610 km s−1 for WD 2134 + 125 and 3000–3600 km s−1 from the analysis of O vi and Ne vii lines for WD 1751 + 106 .
![Comparison of synthetic spectra calculated with PoWR (blue line, dotted) compared with the FUSE observation of WD 1751 + 106 (left) and WD 2134 + 125 (right). In red a combined wind + ISM spectrum is shown. The wind models are calculated with a mass-loss rate of $\log [\dot{M}\, /\, ({\rm M}_\odot\, \mathrm{yr{^{-1}}})] =-8.1$, and $v_\infty =3500\, \mathrm{km\, s}^{-1}$ for WD 1751 + 106 and $v_\infty =3300\, \mathrm{km\, s}^{-1}$ for WD 2134 + 125 . Upper panel: around Ne vii $\lambda \, 973.33$ Å , lower: around O vi $\lambda \lambda \, 1031.91, 1037.61$ Å. The green marks at the bottom of each panel indicate wavelengths of strong interstellar H2 lines.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/489/1/10.1093_mnras_stz1994/1/m_stz1994fig9.jpeg?Expires=1750290729&Signature=4J30~cR56a2FxY6ae5eWcVYYHCAQlG3ydl7NERI8611YCozMK6yITzRw~A1lkRxBcq7uejNJoz4Xd20EQrmx11ZbeQpMgAK7pmlPqEtC05JnkBmdzPVMhvDEKcTQT6a3kcSxfjNZoj9CL9KLXHRalFJ8bjbPWlMX65MxvfWREp~nK5VHLF3nPRM9Kqwy9sg60YXtZHK3PYEeduF6n8Q~26IcdRnL80-EQw7PCkfX0RFaOU4lHrhcQOyWg2CNmRuvQawyRYrytCCwtc6x4qbWF~6kOpCKn13uKTMZqv-VV7Fc6P1zuzeeGevcCZpF8gSQ8gc7-tjs5Z2iSOYJfCGZPg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Comparison of synthetic spectra calculated with PoWR (blue line, dotted) compared with the FUSE observation of WD 1751 + 106 (left) and WD 2134 + 125 (right). In red a combined wind + ISM spectrum is shown. The wind models are calculated with a mass-loss rate of |$\log [\dot{M}\, /\, ({\rm M}_\odot\, \mathrm{yr{^{-1}}})] =-8.1$|, and |$v_\infty =3500\, \mathrm{km\, s}^{-1}$| for WD 1751 + 106 and |$v_\infty =3300\, \mathrm{km\, s}^{-1}$| for WD 2134 + 125 . Upper panel: around Ne vii |$\lambda \, 973.33$| Å , lower: around O vi |$\lambda \lambda \, 1031.91, 1037.61$| Å. The green marks at the bottom of each panel indicate wavelengths of strong interstellar H2 lines.
For the analysis of the wind lines in the UV range we used the PoWR model atmosphere code. This is a state-of-the-art NLTE code that accounts for mass loss, line blanketing, and wind clumping. It can be employed for a wide range of hot stars at arbitrary metallicities (e.g. Oskinova et al. 2011; Hainich et al. 2014, 2015; Reindl et al. 2014a; Shenar et al. 2015; Reindl et al. 2017), since the hydrostatic and wind regimes of the atmosphere are treated consistently (Sander et al. 2015). The NLTE radiative transfer is calculated in the co-moving frame. Any model can be specified by its luminosity L, stellar temperature Teff, surface gravity g, and mass-loss rate |$\dot{M}$| as main parameters. In the subsonic region, the velocity field is defined such that a hydrostatic density stratification is approached (Sander et al. 2015). In the supersonic region, the wind velocity field v(r) is pre-specified assuming the so-called β-law (Castor, Abbott & Klein 1975). Wind clumping is taken into account in first-order approximation (Hamann & Gräfener 2004) with a density contrast D = ϱcl/〈ϱ〉 between the clumps and a smooth wind of same mass-loss rate. As we do not assume an interclump medium, |$D=f_V^{-1}$|.
We adopted the stellar parameters from the TMAP analysis as given in Table 3. Our calculations include complex model atoms for H, He, C, N, O, F, Ne, Si, P, S, and the iron group elements Sc, Ti, V, Cr, Mn, Fe, Co, Ni.
The only P Cygni line that is not saturated and is sensitive enough to the mass-loss rate is C iv |$\lambda \lambda \, 1548,1551$| Å . For WD 1751 + 106 the quality of the UV observation in this wavelength range is very poor. However, we found that the mass-loss rate must be |$\log [\dot{M}\, /\, ({\rm M}_\odot\, \mathrm{yr}^{-1})] \lesssim -8.1$| to obtain a model that is compatible with the observation. The STIS spectrum of WD 2134 + 125 in this wavelength range has a much better quality. We obtained the best fit to the complicated line profile of C IV |$\lambda \lambda \, 1548,1551$| Å by models with a mass-loss rate of |$\log [\dot{M}\, /\, (M_\odot /\mathrm{yr})] \approx -8.1$|. In both cases, we assumed a density contrast of D = 10, which is typically found for H-deficient CSPNe winds (Todt, Hamann & Gräfener 2008).
The blue edges of the P Cygni profiles of O vi |$\lambda \lambda \, 1032,1038$| Å and C iv |$\lambda \lambda \, 1548,1551$| Å were used to estimate the terminal wind velocity for WD 2134 + 125 of about |$v_\infty = 3300 \pm 100\,$| km s−1 and a β = 0.6. Additional broadening due to depth dependent microturbulence with |$v_\text{D} = 20\,$| km s−1 in the photosphere, estimated from, e.g. the F vi |$\, \lambda 1140$| line, up to |$v_\text{D} = 230\,$| km s−1 in the outer wind was taken into account and allows to fit the width of the O vi (Fig. 9) and the C iv resonance lines simultaneously. Similar values have been obtained for WD 1751 + 106, i.e. |$v_\infty = 3500 \pm 100\,$| km s−1 and |$v_\text{D} = 50\,$| km s−1 in the photosphere up to |$v_\text{D} = 180\,$| km s−1 in the outer wind. At these high mass-loss rates, the stellar wind is coupled and the photosphere is chemically homogeneous (Unglaub 2007, 2008).
7 MASS, LUMINOSITY, AND DISTANCE
The determination of the mass of WD 1751 + 106 and WD 2134 + 125 is difficult since their evolutionary history is not unambiguous. If they are AFTP stars no appropriate set of evolutionary tracks is available in the literature to compare with. Lawlor & MacDonald (2006) presented a variety of calculations for the evolution of H-deficient post-AGB stars. The so-called AGB departure type V scenario (departure from the AGB during an He flash) and the type IV scenario appear to be in the transition between AFTP and LTP (Table 1). A different H/He ratio should have an influence on the result (cf. Miller Bertolami & Althaus 2007). To decide which grid of post-AGB tracks should be used, we calculated some AFTP models with LPCODE (Althaus et al. 2003, 2005) (Table 1). This was done by recomputing the end of the AGB evolution of three models presented in Miller Bertolami (2016) and tuning the mass loss at the end of the AGB phase as to enforce an AFTP event. These sequences have (MZAMS, ZZAMS, Mf) = (1.25M⊙, 0.01, 0.566M⊙), (1.00M⊙, 0.001, 0.550M⊙), (1.50M⊙, 0.001, 0.594M⊙) (Table 1). At the location of the stars in the log g –Teff diagram, the tracks for VLTP and AFTP stars coincide (Fig. 10). Thus, the approach of using VLTP tracks for the determination of the mass is acceptable.
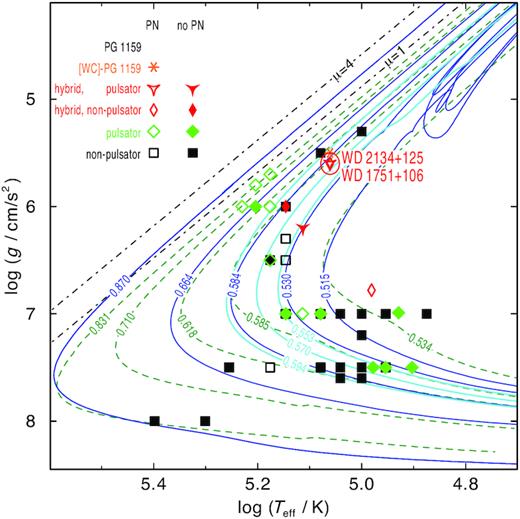
Positions of WD 1751 + 106 (Abell 43) and WD 2134 + 125 (NGC 7094) with their error ellipses and related objects in the |$\log \mbox{$T_\mathrm{eff}$}\, - \mbox{$\log g$}\,$| plane compared with evolutionary tracks (labelled with the respective masses in M⊙) of VLTP stars (Miller Bertolami & Althaus 2006, blue full lines), of H-burning post-AGB stars (calculated with initial solar metallicity, Miller Bertolami 2016, green dashed lines), and of AFTP stars (cyan, thick lines).The dash–dotted μ = 1 and 4 lines indicate the Eddington limits for pure H and He atmospheres, respectively.
Photospheric abundances of WD 1751 + 106 and WD 2134 + 125 compared with evolutionary models.
| Teff . | . | H . | He . | C . | N . | O . | Ne . | . |
|---|---|---|---|---|---|---|---|---|
| . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | . | Comment . |
| (K) . | . | (Mass fraction) . | . | |||||
| 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 3 | 0.001 9 | WD 2134 + 125 , our atmosphere model |
| 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | 0.012 | WD 1751 + 106 , our atmosphere model |
| 84 000 | 5.0 | 0.444 | 0.539 | 0.012 | 0.002 | 0.002 | 0.000 8 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 140 000 | 6.0 | 0.106 | 0.794 | 0.085 | 0.002 | 0.012 | 0.003 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 87 000 | 5.0 | 0.565 | 0.427 | 0.005 | 0.000 9 | 0.000 9 | 0.000 4 | Lawlor & MacDonald (2006, AGB departure type V) |
| 150 000 | 6.0 | 0.164 | 0.775 | 0.051 | 0.001 4 | 0.005 7 | 0.002 | Lawlor & MacDonald (2006, AGB departure type V) |
| 0.197 | 0.450 | 0.296 | 0.000 1 | 0.056 | 0.000 78 | AFTP model Mf = 0.550, Z = 0.001 | ||
| 0.137 | 0.390 | 0.357 | 0.000 6 | 0.104 | 0.008 5 | AFTP model Mf = 0.566, Z = 0.01 | ||
| 0.219 | 0.445 | 0.258 | 0.000 7 | 0.055 | 0.021 | AFTP model Mf = 0.594, Z = 0.001 | ||
| Teff . | . | H . | He . | C . | N . | O . | Ne . | . |
|---|---|---|---|---|---|---|---|---|
| . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | . | Comment . |
| (K) . | . | (Mass fraction) . | . | |||||
| 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 3 | 0.001 9 | WD 2134 + 125 , our atmosphere model |
| 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | 0.012 | WD 1751 + 106 , our atmosphere model |
| 84 000 | 5.0 | 0.444 | 0.539 | 0.012 | 0.002 | 0.002 | 0.000 8 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 140 000 | 6.0 | 0.106 | 0.794 | 0.085 | 0.002 | 0.012 | 0.003 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 87 000 | 5.0 | 0.565 | 0.427 | 0.005 | 0.000 9 | 0.000 9 | 0.000 4 | Lawlor & MacDonald (2006, AGB departure type V) |
| 150 000 | 6.0 | 0.164 | 0.775 | 0.051 | 0.001 4 | 0.005 7 | 0.002 | Lawlor & MacDonald (2006, AGB departure type V) |
| 0.197 | 0.450 | 0.296 | 0.000 1 | 0.056 | 0.000 78 | AFTP model Mf = 0.550, Z = 0.001 | ||
| 0.137 | 0.390 | 0.357 | 0.000 6 | 0.104 | 0.008 5 | AFTP model Mf = 0.566, Z = 0.01 | ||
| 0.219 | 0.445 | 0.258 | 0.000 7 | 0.055 | 0.021 | AFTP model Mf = 0.594, Z = 0.001 | ||
Photospheric abundances of WD 1751 + 106 and WD 2134 + 125 compared with evolutionary models.
| Teff . | . | H . | He . | C . | N . | O . | Ne . | . |
|---|---|---|---|---|---|---|---|---|
| . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | . | Comment . |
| (K) . | . | (Mass fraction) . | . | |||||
| 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 3 | 0.001 9 | WD 2134 + 125 , our atmosphere model |
| 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | 0.012 | WD 1751 + 106 , our atmosphere model |
| 84 000 | 5.0 | 0.444 | 0.539 | 0.012 | 0.002 | 0.002 | 0.000 8 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 140 000 | 6.0 | 0.106 | 0.794 | 0.085 | 0.002 | 0.012 | 0.003 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 87 000 | 5.0 | 0.565 | 0.427 | 0.005 | 0.000 9 | 0.000 9 | 0.000 4 | Lawlor & MacDonald (2006, AGB departure type V) |
| 150 000 | 6.0 | 0.164 | 0.775 | 0.051 | 0.001 4 | 0.005 7 | 0.002 | Lawlor & MacDonald (2006, AGB departure type V) |
| 0.197 | 0.450 | 0.296 | 0.000 1 | 0.056 | 0.000 78 | AFTP model Mf = 0.550, Z = 0.001 | ||
| 0.137 | 0.390 | 0.357 | 0.000 6 | 0.104 | 0.008 5 | AFTP model Mf = 0.566, Z = 0.01 | ||
| 0.219 | 0.445 | 0.258 | 0.000 7 | 0.055 | 0.021 | AFTP model Mf = 0.594, Z = 0.001 | ||
| Teff . | . | H . | He . | C . | N . | O . | Ne . | . |
|---|---|---|---|---|---|---|---|---|
| . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | . | Comment . |
| (K) . | . | (Mass fraction) . | . | |||||
| 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 3 | 0.001 9 | WD 2134 + 125 , our atmosphere model |
| 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | 0.012 | WD 1751 + 106 , our atmosphere model |
| 84 000 | 5.0 | 0.444 | 0.539 | 0.012 | 0.002 | 0.002 | 0.000 8 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 140 000 | 6.0 | 0.106 | 0.794 | 0.085 | 0.002 | 0.012 | 0.003 | Lawlor & MacDonald (2006, AGB departure type IV) |
| 87 000 | 5.0 | 0.565 | 0.427 | 0.005 | 0.000 9 | 0.000 9 | 0.000 4 | Lawlor & MacDonald (2006, AGB departure type V) |
| 150 000 | 6.0 | 0.164 | 0.775 | 0.051 | 0.001 4 | 0.005 7 | 0.002 | Lawlor & MacDonald (2006, AGB departure type V) |
| 0.197 | 0.450 | 0.296 | 0.000 1 | 0.056 | 0.000 78 | AFTP model Mf = 0.550, Z = 0.001 | ||
| 0.137 | 0.390 | 0.357 | 0.000 6 | 0.104 | 0.008 5 | AFTP model Mf = 0.566, Z = 0.01 | ||
| 0.219 | 0.445 | 0.258 | 0.000 7 | 0.055 | 0.021 | AFTP model Mf = 0.594, Z = 0.001 | ||
We find |$M=0.57^{+0.07}_{-0.04}\, {\rm M}_\odot$| for WD 1751 + 106 and WD 2134 + 125. Using the initial–final mass relation of Cummings et al. (2018), these stars originate from progenitors with initial mass of about 1.0–1.1 |${\rm M}_\odot$|. From the 0.515, 0,530, 0,542, 0,565, 0.584, 0.609, and 0.664 |${\rm M}_\odot$| tracks (Fig. 10), we determine the luminosity of |$\log L\, / \, {\rm L}_\odot = 3.77 ^{+0.23}_{-0.24}$| for WD 1751 + 106 and WD 2134 + 125.
8 DISCUSSION
Our aim was to determine the element abundances of WD 1751 + 106 and WD 2134 + 125 beyond He and H. The results are shown in Table 3. By comparing our results to the abundances of other post-AGB stars and evolutionary models, we are able to conclude constraints for nucleosynthesis processes and evolutionary channels. The H-deficient nature of WD 1751 + 106 and WD 2134 + 125 suggests that here, as in other H-deficient stars, we see nuclear processed material on the surface that has formed either during the progenitor AGB phase or the same mixing and burning processes that lead to the H-deficiency in the first place. Fig. 11 illustrates the following sections.
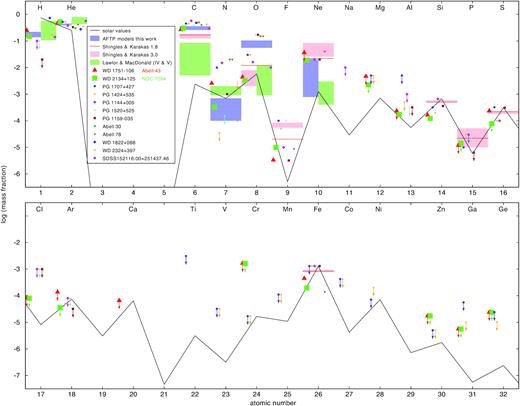
Photospheric abundances for a set of PG 1195 stars and calculated ranges from evolutionary models. For the models of Shingles & Karakas (2013), the initial mass of the star in M⊙ is given in the legend box. Upper limits are indicated with arrows. The solid black lines indicates solar abundances.
8.1 Comparison to other hybrid PG 1159 stars
The group of known hybrid PG 1159 stars comprises the CS of Sh 2 – 68 and HS 2324 + 3944 (WD 1822 + 008 and WD 2324 + 397, respectively, McCook & Sion 1999) and SDSS 152116.00 + 251437.46 (Werner & Herwig 2006; Werner et al. 2014), besides the two program stars of this work. The known atmospheric parameters for these objects are summarized in Table 2. For WD 1822 + 008, Gianninas et al. (2010) found |$T_\mathrm{eff} = 84\, 460$| K and log g = 7.24. Its position in the log Teff–log g diagram (Fig. 10) suggests that the star is already located close to the beginning of the WD cooling track and is thus further evolved than the two stars of this work. The large distance of 1000 ± 400 pc (Binnendijk 1952) was reduced and better constrained to |$399.7^{+11.8}_{-12.5}$| pc (Bailer-Jones et al. 2018) using Gaia data. With its a diameter of 400 arcsec ± 70 arcsec (Fesen, Gull & Heckathorn 1983), the PN has a radius of |$0.388^{+0.082}_{-0.078}$| pc. Considering an expansion velocity of 7.5 km s−1 (Hippelein & Weinberger 1990), this yields a dynamic time-scale of |$50\, 600 ^{+10\, 700}_{-10\, 200}$| yr, which confirms the suggestion from the location in the log Teff–log g diagram and assigns Sh 2 − 68 to the group of oldest and largest PNe. It has a lower element ratio of He/H compared to WD 1751 + 106 and WD 2134 + 125 . This might result from ongoing depletion of heavier elements from the atmosphere due to gravitational settling.
Photospheric abundances of WD 1751 + 106 and WD 2134 + 125 with other hybrid PG 1159 stars and the CSPNe Abell 30 and Abell 78.
| . | Teff . | . | H . | He . | C . | N . | O . | . |
|---|---|---|---|---|---|---|---|---|
| Object . | . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | Reference . |
| . | (K) . | . | (Mass fraction) . | . | ||||
| WD 2134 + 125 | 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 2 | This work |
| WD 1751 + 106 | 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | This work |
| WD 1822 + 008 | 84 460 | 7.24 | 0.66 | 0.34 | Gianninas et al. (2010) | |||
| WD 2324 + 397 | 130 000 | 6.2 | 0.17 | 0.35 | 0.42 | 0.000 1 | 0.06 | Dreizler et al. (1996); Dreizler (1999) |
| SDSS 152116.00 + 251437.46 | 140 000 | 6.0 | 0.14 | 0.56 | 0.29 | 0.01 | Werner et al. (2014) | |
| Abell 30 | 115 000 | 5.5 | 0.41 | 0.40 | 0.04 | 0.15 | Leuenhagen, Koesterke & Hamann (1993) | |
| Abell 78 | 117 000 | 5.5 | 0.30 | 0.50 | 0.02 | 0.15 | Toalá et al. (2015); Werner & Koesterke (1992) | |
| . | Teff . | . | H . | He . | C . | N . | O . | . |
|---|---|---|---|---|---|---|---|---|
| Object . | . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | Reference . |
| . | (K) . | . | (Mass fraction) . | . | ||||
| WD 2134 + 125 | 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 2 | This work |
| WD 1751 + 106 | 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | This work |
| WD 1822 + 008 | 84 460 | 7.24 | 0.66 | 0.34 | Gianninas et al. (2010) | |||
| WD 2324 + 397 | 130 000 | 6.2 | 0.17 | 0.35 | 0.42 | 0.000 1 | 0.06 | Dreizler et al. (1996); Dreizler (1999) |
| SDSS 152116.00 + 251437.46 | 140 000 | 6.0 | 0.14 | 0.56 | 0.29 | 0.01 | Werner et al. (2014) | |
| Abell 30 | 115 000 | 5.5 | 0.41 | 0.40 | 0.04 | 0.15 | Leuenhagen, Koesterke & Hamann (1993) | |
| Abell 78 | 117 000 | 5.5 | 0.30 | 0.50 | 0.02 | 0.15 | Toalá et al. (2015); Werner & Koesterke (1992) | |
Photospheric abundances of WD 1751 + 106 and WD 2134 + 125 with other hybrid PG 1159 stars and the CSPNe Abell 30 and Abell 78.
| . | Teff . | . | H . | He . | C . | N . | O . | . |
|---|---|---|---|---|---|---|---|---|
| Object . | . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | Reference . |
| . | (K) . | . | (Mass fraction) . | . | ||||
| WD 2134 + 125 | 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 2 | This work |
| WD 1751 + 106 | 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | This work |
| WD 1822 + 008 | 84 460 | 7.24 | 0.66 | 0.34 | Gianninas et al. (2010) | |||
| WD 2324 + 397 | 130 000 | 6.2 | 0.17 | 0.35 | 0.42 | 0.000 1 | 0.06 | Dreizler et al. (1996); Dreizler (1999) |
| SDSS 152116.00 + 251437.46 | 140 000 | 6.0 | 0.14 | 0.56 | 0.29 | 0.01 | Werner et al. (2014) | |
| Abell 30 | 115 000 | 5.5 | 0.41 | 0.40 | 0.04 | 0.15 | Leuenhagen, Koesterke & Hamann (1993) | |
| Abell 78 | 117 000 | 5.5 | 0.30 | 0.50 | 0.02 | 0.15 | Toalá et al. (2015); Werner & Koesterke (1992) | |
| . | Teff . | . | H . | He . | C . | N . | O . | . |
|---|---|---|---|---|---|---|---|---|
| Object . | . | |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| . | . | . | . | . | . | Reference . |
| . | (K) . | . | (Mass fraction) . | . | ||||
| WD 2134 + 125 | 115 000 | 5.6 | 0.15 | 0.52 | 0.31 | 0.000 3 | 0.003 2 | This work |
| WD 1751 + 106 | 115 000 | 5.6 | 0.25 | 0.46 | 0.27 | 0.002 6 | 0.004 4 | This work |
| WD 1822 + 008 | 84 460 | 7.24 | 0.66 | 0.34 | Gianninas et al. (2010) | |||
| WD 2324 + 397 | 130 000 | 6.2 | 0.17 | 0.35 | 0.42 | 0.000 1 | 0.06 | Dreizler et al. (1996); Dreizler (1999) |
| SDSS 152116.00 + 251437.46 | 140 000 | 6.0 | 0.14 | 0.56 | 0.29 | 0.01 | Werner et al. (2014) | |
| Abell 30 | 115 000 | 5.5 | 0.41 | 0.40 | 0.04 | 0.15 | Leuenhagen, Koesterke & Hamann (1993) | |
| Abell 78 | 117 000 | 5.5 | 0.30 | 0.50 | 0.02 | 0.15 | Toalá et al. (2015); Werner & Koesterke (1992) | |
Parameters of WD 1751 + 106 and WD 2134 + 125 compared with literature values.
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||
|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . |
| Teff ( kK) | 115 ± 5 a | 115 ± 5 | 115 ± 5 a | 115 ± 5 |
| |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| | 5.5 ± 0.1 a | 5.6 ± 0.1 | 5.4 ± 0.1 a | 5.6 ± 0.1 |
| EB–V | 0.265 ± 0.035 b | 0.265 ± 0.010 | 0.150 ± 0.040 c | 0.135 ± 0.010 |
| |$n_{\mathrm{H\,{\small I}}}$| (cm−2) | (1.0 ± 0.2) × 1021 b | (1.0 ± 0.1) × 1021 | (7.0 ± 0.1) × 1020 c | (6.5 ± 0.1) × 1020 |
| vrad (km s−1) | −42.0 ± 11.5 d | −100 ± 10 | −101.1 ± 30.8 d | −53 ± 10 |
| d (kpc) | 2.47 ± 0.30 e | |$2.23^{+0.31}_{-0.33}$| | 1.75 ± 0.36 e | |$1.65^{+0.32}_{-0.31}$| |
| |$M\, /\, {\rm M}_\odot$| | |$0.53^{+0.10}_{-0.02}$| b | |$0.57^{+0.07}_{-0.04}$| | |$0.53^{+0.06}_{-0.06}$| c | |$0.57^{+0.07}_{-0.04}$| |
| |${\rm log} \ (L\, /\, {\rm L}_\odot)$| | |$3.44^{+0.50}_{-0.58}$| b | |$3.77^{+0.23}_{-0.24}$| | |$3.77^{+0.23}_{-0.24}$| | |
| RPN (pc) | 0.51 f | |$0.48^{+0.07}_{-0.07}$| | 0.51 f | |$0.42^{+0.08}_{-0.08}$| |
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||
|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . |
| Teff ( kK) | 115 ± 5 a | 115 ± 5 | 115 ± 5 a | 115 ± 5 |
| |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| | 5.5 ± 0.1 a | 5.6 ± 0.1 | 5.4 ± 0.1 a | 5.6 ± 0.1 |
| EB–V | 0.265 ± 0.035 b | 0.265 ± 0.010 | 0.150 ± 0.040 c | 0.135 ± 0.010 |
| |$n_{\mathrm{H\,{\small I}}}$| (cm−2) | (1.0 ± 0.2) × 1021 b | (1.0 ± 0.1) × 1021 | (7.0 ± 0.1) × 1020 c | (6.5 ± 0.1) × 1020 |
| vrad (km s−1) | −42.0 ± 11.5 d | −100 ± 10 | −101.1 ± 30.8 d | −53 ± 10 |
| d (kpc) | 2.47 ± 0.30 e | |$2.23^{+0.31}_{-0.33}$| | 1.75 ± 0.36 e | |$1.65^{+0.32}_{-0.31}$| |
| |$M\, /\, {\rm M}_\odot$| | |$0.53^{+0.10}_{-0.02}$| b | |$0.57^{+0.07}_{-0.04}$| | |$0.53^{+0.06}_{-0.06}$| c | |$0.57^{+0.07}_{-0.04}$| |
| |${\rm log} \ (L\, /\, {\rm L}_\odot)$| | |$3.44^{+0.50}_{-0.58}$| b | |$3.77^{+0.23}_{-0.24}$| | |$3.77^{+0.23}_{-0.24}$| | |
| RPN (pc) | 0.51 f | |$0.48^{+0.07}_{-0.07}$| | 0.51 f | |$0.42^{+0.08}_{-0.08}$| |
Parameters of WD 1751 + 106 and WD 2134 + 125 compared with literature values.
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||
|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . |
| Teff ( kK) | 115 ± 5 a | 115 ± 5 | 115 ± 5 a | 115 ± 5 |
| |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| | 5.5 ± 0.1 a | 5.6 ± 0.1 | 5.4 ± 0.1 a | 5.6 ± 0.1 |
| EB–V | 0.265 ± 0.035 b | 0.265 ± 0.010 | 0.150 ± 0.040 c | 0.135 ± 0.010 |
| |$n_{\mathrm{H\,{\small I}}}$| (cm−2) | (1.0 ± 0.2) × 1021 b | (1.0 ± 0.1) × 1021 | (7.0 ± 0.1) × 1020 c | (6.5 ± 0.1) × 1020 |
| vrad (km s−1) | −42.0 ± 11.5 d | −100 ± 10 | −101.1 ± 30.8 d | −53 ± 10 |
| d (kpc) | 2.47 ± 0.30 e | |$2.23^{+0.31}_{-0.33}$| | 1.75 ± 0.36 e | |$1.65^{+0.32}_{-0.31}$| |
| |$M\, /\, {\rm M}_\odot$| | |$0.53^{+0.10}_{-0.02}$| b | |$0.57^{+0.07}_{-0.04}$| | |$0.53^{+0.06}_{-0.06}$| c | |$0.57^{+0.07}_{-0.04}$| |
| |${\rm log} \ (L\, /\, {\rm L}_\odot)$| | |$3.44^{+0.50}_{-0.58}$| b | |$3.77^{+0.23}_{-0.24}$| | |$3.77^{+0.23}_{-0.24}$| | |
| RPN (pc) | 0.51 f | |$0.48^{+0.07}_{-0.07}$| | 0.51 f | |$0.42^{+0.08}_{-0.08}$| |
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||
|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . |
| Teff ( kK) | 115 ± 5 a | 115 ± 5 | 115 ± 5 a | 115 ± 5 |
| |$\log\,(g\,/\,(\mathrm{cm}\,\mathrm{s}^{-2}))$| | 5.5 ± 0.1 a | 5.6 ± 0.1 | 5.4 ± 0.1 a | 5.6 ± 0.1 |
| EB–V | 0.265 ± 0.035 b | 0.265 ± 0.010 | 0.150 ± 0.040 c | 0.135 ± 0.010 |
| |$n_{\mathrm{H\,{\small I}}}$| (cm−2) | (1.0 ± 0.2) × 1021 b | (1.0 ± 0.1) × 1021 | (7.0 ± 0.1) × 1020 c | (6.5 ± 0.1) × 1020 |
| vrad (km s−1) | −42.0 ± 11.5 d | −100 ± 10 | −101.1 ± 30.8 d | −53 ± 10 |
| d (kpc) | 2.47 ± 0.30 e | |$2.23^{+0.31}_{-0.33}$| | 1.75 ± 0.36 e | |$1.65^{+0.32}_{-0.31}$| |
| |$M\, /\, {\rm M}_\odot$| | |$0.53^{+0.10}_{-0.02}$| b | |$0.57^{+0.07}_{-0.04}$| | |$0.53^{+0.06}_{-0.06}$| c | |$0.57^{+0.07}_{-0.04}$| |
| |${\rm log} \ (L\, /\, {\rm L}_\odot)$| | |$3.44^{+0.50}_{-0.58}$| b | |$3.77^{+0.23}_{-0.24}$| | |$3.77^{+0.23}_{-0.24}$| | |
| RPN (pc) | 0.51 f | |$0.48^{+0.07}_{-0.07}$| | 0.51 f | |$0.42^{+0.08}_{-0.08}$| |
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . | ||||||||
| Abundances . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . |
| H | − 0.483 g | 2.43 × 10−1 | − 0.5 | 2.5 × 10−1 | 6.4 × 10−1 | −0.0 | − 0.62 h | 1.77 × 10−1 | − 0.7 | 1.5 × 10−1 | 4.9 × 10−1 | 0.1 |
| He | 0.350 g | 5.59 × 10−1 | 0.3 | 4.6 × 10−1 | 3.0 × 10−1 | 0.7 | 0.45 h | 7.03 × 10−1 | 0.3 | 5.2 × 10−1 | 4.3 × 10−1 | 1.1 |
| C | 1.909 g | 1.75 × 10−1 | 2.1 | 2.7 × 10−1 | 5.8 × 10−2 | 2.5 | 1.76 h | 1.24 × 10−1 | 2.1 | 3.1 × 10−1 | 8.4 × 10−2 | 2.9 |
| N | − 0.491 g | 2.00 × 10−4 | 0.6 | 2.6 × 10−3 | 4.8 × 10−4 | 1.0 | − 0.85 h | 8.73 × 10−5 | − 0.3 | 3.3 × 10−4 | 7.7 × 10−5 | 0.5 |
| O | − 0.516 g | 1.63 × 10−3 | − 0.1 | 4.4 × 10−3 | 7.2 × 10−4 | 0.3 | − 1.81 h | 8.20 × 10−5 | − 0.2 | 3.2 × 10−3 | 6.7 × 10−4 | 0.6 |
| F | 0.694 g | 2.50 × 10−6 | 1.0 | 3.3 × 10−6 | 4.5 × 10−7 | 1.3 | 0.34 h | 1.11 × 10−6 | 1.5 | 9.9 × 10−6 | 1.7 × 10−6 | 2.1 |
| Ne | ≤ 1.5 | ≤3.6 × 10−2 | ≤4.7 × 10−3 | ≤ 1.9 | 0.00 h | 1.02 × 10−3 | 1.2 | 1.9 × 10−3 | 3.1 × 10−3 | 2.0 | ||
| Mg | ≤ 0.108 b | ≤ 7.74 × 10−4 | ≤ 0.8 | ≤4.7 × 10−3 | ≤5.0 × 10−4 | ≤1.3 | ≤ 0.5 | ≤2.2 × 10−3 | ≤3.0 × 10−4 | ≤ 1.3 | ||
| Al | ≤ 0.797 b | ≤ 2.90 × 10−4 | ≤ 0.6 | ≤2.3 × 10−4 | ≤2.2 × 10−5 | ≤1.1 | 0.5 | 1.7 × 10−4 | 2.1 × 10−5 | 1.3 | ||
| Si | − 0.560 g | 1.83 × 10−4 | − 0.6 | 1.6 × 10−4 | 1.5 × 10−5 | −0.2 | − 0.21 h | 4.10 × 10−4 | − 0.7 | 1.2 × 10−4 | 1.4 × 10−5 | 0.1 |
| P | − 0.593 g | 1.33 × 10−6 | ≤ 0.3 | ≤1.2 × 10−5 | ≤1.0 × 10−6 | ≤0.8 | − 1.15 h | 3.70 × 10−7 | ≤ 0.4 | ≤1.4 × 10−5 | ≤1.5 × 10−6 | ≤ 1.2 |
| S | − 0.378 g | 1.36 × 10−4 | − 0.1 | 2.4 × 10−4 | 1.9 × 10−5 | 0.3 | 0.16 h | 4.69 × 10−4 | ≤− 0.6 | ≤7.8 × 10−5 | ≤8.0 × 10−6 | ≤ 0.2 |
| Cl | ≤ 1.0 | ≤8.3 × 10−5 | ≤6.1 × 10−6 | ≤ 1.5 | ≤ 1.0 | ≤8.1 × 10−5 | ≤7.5 × 10−6 | ≤ 1.8 | ||||
| Ar | ≤ 1.307 b | ≤ 1.04 × 10−3 | ≤ 0.3 | ≤1.4 × 10−4 | ≤8.8 × 10−6 | ≤0.7 | 0.00 c | 4.43 × 10−5 | ≤− 0.3 | ≤3.5 × 10−5 | ≤2.9 × 10−6 | ≤ 0.5 |
| Ca | ≤ 0.0 | ≤6.5 × 10−5 | ≤4.5 × 10−6 | ≤ 0.5 | ||||||||
| Cr | ≤ 2.0 | ≤1.7 × 10−3 | ≤8.1 × 10−5 | ≤ 2.5 | ≤ 2.0 | ≤1.6 × 10−3 | ≤1.0 × 10−4 | ≤ 2.8 | ||||
| Fe | − 0.691b | 2.35 × 10−4 | − 0.4 | 4.5 × 10−4 | 2.1 × 10−5 | 0.0 | ≤− 1.00 h | ≤ 1.15 × 10−4 | − 0.8 | 2.0 × 10−4 | 1.2 × 10−5 | 0.0 |
| Ni | ≤− 1.000 b | ≤ 7.30 × 10−6 | ≤− 1.00 h | ≤ 7.30 × 10−6 | ||||||||
| Zn | ≤ 1.0 | ≤1.7 × 10−5 | ≤7.2 × 10−7 | ≤1.5 | ≤ 1.0 | ≤1.7 × 10−5 | ≤9.1 × 10−7 | ≤ 1.8 | ||||
| Ga | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.2 × 10−7 | ≤2.5 | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.8 × 10−7 | ≤ 2.8 | ||||
| Ge | ≤ 2.0 | ≤2.4 × 10−5 | ≤8.9 × 10−7 | ≤2.5 | ≤ 2.0 | ≤2.4 × 10−5 | ≤1.1 × 10−6 | ≤ 2.8 | ||||
| Kr | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.1 × 10−5 | ≤4.0 | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.4 × 10−5 | ≤ 4.3 | ||||
| Zr | ≤ 3.0 | ≤2.5 × 10−5 | ≤9.6 × 10−7 | ≤ 3.8 | ||||||||
| Te | ≤ 4.0 | ≤1.4 × 10−4 | ≤3.8 × 10−6 | ≤4.6 | ≤ 3.5 | ≤4.5 × 10−5 | ≤1.2 × 10−6 | ≤ 4.3 | ||||
| I | ≤ 4.6 | ≤1.3 × 10−4 | ≤3.6 × 10−6 | ≤5.2 | ≤ 5.0 | ≤3.3 × 10−4 | ≤8.9 × 10−6 | ≤ 5.8 | ||||
| Xe | ≤ 4.0 | ≤1.7 × 10−4 | ≤4.4 × 10−6 | ≤ 4.8 | ||||||||
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . | ||||||||
| Abundances . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . |
| H | − 0.483 g | 2.43 × 10−1 | − 0.5 | 2.5 × 10−1 | 6.4 × 10−1 | −0.0 | − 0.62 h | 1.77 × 10−1 | − 0.7 | 1.5 × 10−1 | 4.9 × 10−1 | 0.1 |
| He | 0.350 g | 5.59 × 10−1 | 0.3 | 4.6 × 10−1 | 3.0 × 10−1 | 0.7 | 0.45 h | 7.03 × 10−1 | 0.3 | 5.2 × 10−1 | 4.3 × 10−1 | 1.1 |
| C | 1.909 g | 1.75 × 10−1 | 2.1 | 2.7 × 10−1 | 5.8 × 10−2 | 2.5 | 1.76 h | 1.24 × 10−1 | 2.1 | 3.1 × 10−1 | 8.4 × 10−2 | 2.9 |
| N | − 0.491 g | 2.00 × 10−4 | 0.6 | 2.6 × 10−3 | 4.8 × 10−4 | 1.0 | − 0.85 h | 8.73 × 10−5 | − 0.3 | 3.3 × 10−4 | 7.7 × 10−5 | 0.5 |
| O | − 0.516 g | 1.63 × 10−3 | − 0.1 | 4.4 × 10−3 | 7.2 × 10−4 | 0.3 | − 1.81 h | 8.20 × 10−5 | − 0.2 | 3.2 × 10−3 | 6.7 × 10−4 | 0.6 |
| F | 0.694 g | 2.50 × 10−6 | 1.0 | 3.3 × 10−6 | 4.5 × 10−7 | 1.3 | 0.34 h | 1.11 × 10−6 | 1.5 | 9.9 × 10−6 | 1.7 × 10−6 | 2.1 |
| Ne | ≤ 1.5 | ≤3.6 × 10−2 | ≤4.7 × 10−3 | ≤ 1.9 | 0.00 h | 1.02 × 10−3 | 1.2 | 1.9 × 10−3 | 3.1 × 10−3 | 2.0 | ||
| Mg | ≤ 0.108 b | ≤ 7.74 × 10−4 | ≤ 0.8 | ≤4.7 × 10−3 | ≤5.0 × 10−4 | ≤1.3 | ≤ 0.5 | ≤2.2 × 10−3 | ≤3.0 × 10−4 | ≤ 1.3 | ||
| Al | ≤ 0.797 b | ≤ 2.90 × 10−4 | ≤ 0.6 | ≤2.3 × 10−4 | ≤2.2 × 10−5 | ≤1.1 | 0.5 | 1.7 × 10−4 | 2.1 × 10−5 | 1.3 | ||
| Si | − 0.560 g | 1.83 × 10−4 | − 0.6 | 1.6 × 10−4 | 1.5 × 10−5 | −0.2 | − 0.21 h | 4.10 × 10−4 | − 0.7 | 1.2 × 10−4 | 1.4 × 10−5 | 0.1 |
| P | − 0.593 g | 1.33 × 10−6 | ≤ 0.3 | ≤1.2 × 10−5 | ≤1.0 × 10−6 | ≤0.8 | − 1.15 h | 3.70 × 10−7 | ≤ 0.4 | ≤1.4 × 10−5 | ≤1.5 × 10−6 | ≤ 1.2 |
| S | − 0.378 g | 1.36 × 10−4 | − 0.1 | 2.4 × 10−4 | 1.9 × 10−5 | 0.3 | 0.16 h | 4.69 × 10−4 | ≤− 0.6 | ≤7.8 × 10−5 | ≤8.0 × 10−6 | ≤ 0.2 |
| Cl | ≤ 1.0 | ≤8.3 × 10−5 | ≤6.1 × 10−6 | ≤ 1.5 | ≤ 1.0 | ≤8.1 × 10−5 | ≤7.5 × 10−6 | ≤ 1.8 | ||||
| Ar | ≤ 1.307 b | ≤ 1.04 × 10−3 | ≤ 0.3 | ≤1.4 × 10−4 | ≤8.8 × 10−6 | ≤0.7 | 0.00 c | 4.43 × 10−5 | ≤− 0.3 | ≤3.5 × 10−5 | ≤2.9 × 10−6 | ≤ 0.5 |
| Ca | ≤ 0.0 | ≤6.5 × 10−5 | ≤4.5 × 10−6 | ≤ 0.5 | ||||||||
| Cr | ≤ 2.0 | ≤1.7 × 10−3 | ≤8.1 × 10−5 | ≤ 2.5 | ≤ 2.0 | ≤1.6 × 10−3 | ≤1.0 × 10−4 | ≤ 2.8 | ||||
| Fe | − 0.691b | 2.35 × 10−4 | − 0.4 | 4.5 × 10−4 | 2.1 × 10−5 | 0.0 | ≤− 1.00 h | ≤ 1.15 × 10−4 | − 0.8 | 2.0 × 10−4 | 1.2 × 10−5 | 0.0 |
| Ni | ≤− 1.000 b | ≤ 7.30 × 10−6 | ≤− 1.00 h | ≤ 7.30 × 10−6 | ||||||||
| Zn | ≤ 1.0 | ≤1.7 × 10−5 | ≤7.2 × 10−7 | ≤1.5 | ≤ 1.0 | ≤1.7 × 10−5 | ≤9.1 × 10−7 | ≤ 1.8 | ||||
| Ga | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.2 × 10−7 | ≤2.5 | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.8 × 10−7 | ≤ 2.8 | ||||
| Ge | ≤ 2.0 | ≤2.4 × 10−5 | ≤8.9 × 10−7 | ≤2.5 | ≤ 2.0 | ≤2.4 × 10−5 | ≤1.1 × 10−6 | ≤ 2.8 | ||||
| Kr | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.1 × 10−5 | ≤4.0 | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.4 × 10−5 | ≤ 4.3 | ||||
| Zr | ≤ 3.0 | ≤2.5 × 10−5 | ≤9.6 × 10−7 | ≤ 3.8 | ||||||||
| Te | ≤ 4.0 | ≤1.4 × 10−4 | ≤3.8 × 10−6 | ≤4.6 | ≤ 3.5 | ≤4.5 × 10−5 | ≤1.2 × 10−6 | ≤ 4.3 | ||||
| I | ≤ 4.6 | ≤1.3 × 10−4 | ≤3.6 × 10−6 | ≤5.2 | ≤ 5.0 | ≤3.3 × 10−4 | ≤8.9 × 10−6 | ≤ 5.8 | ||||
| Xe | ≤ 4.0 | ≤1.7 × 10−4 | ≤4.4 × 10−6 | ≤ 4.8 | ||||||||
Notes: [X] = log (abundance/solar abundance), [X/Fe] = log (nX/nFe) − log (nX, ⊙/nFe, ⊙) with the number fraction nX for element X, the error of our abundance determination is ±0.3 dex.
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . | ||||||||
| Abundances . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . |
| H | − 0.483 g | 2.43 × 10−1 | − 0.5 | 2.5 × 10−1 | 6.4 × 10−1 | −0.0 | − 0.62 h | 1.77 × 10−1 | − 0.7 | 1.5 × 10−1 | 4.9 × 10−1 | 0.1 |
| He | 0.350 g | 5.59 × 10−1 | 0.3 | 4.6 × 10−1 | 3.0 × 10−1 | 0.7 | 0.45 h | 7.03 × 10−1 | 0.3 | 5.2 × 10−1 | 4.3 × 10−1 | 1.1 |
| C | 1.909 g | 1.75 × 10−1 | 2.1 | 2.7 × 10−1 | 5.8 × 10−2 | 2.5 | 1.76 h | 1.24 × 10−1 | 2.1 | 3.1 × 10−1 | 8.4 × 10−2 | 2.9 |
| N | − 0.491 g | 2.00 × 10−4 | 0.6 | 2.6 × 10−3 | 4.8 × 10−4 | 1.0 | − 0.85 h | 8.73 × 10−5 | − 0.3 | 3.3 × 10−4 | 7.7 × 10−5 | 0.5 |
| O | − 0.516 g | 1.63 × 10−3 | − 0.1 | 4.4 × 10−3 | 7.2 × 10−4 | 0.3 | − 1.81 h | 8.20 × 10−5 | − 0.2 | 3.2 × 10−3 | 6.7 × 10−4 | 0.6 |
| F | 0.694 g | 2.50 × 10−6 | 1.0 | 3.3 × 10−6 | 4.5 × 10−7 | 1.3 | 0.34 h | 1.11 × 10−6 | 1.5 | 9.9 × 10−6 | 1.7 × 10−6 | 2.1 |
| Ne | ≤ 1.5 | ≤3.6 × 10−2 | ≤4.7 × 10−3 | ≤ 1.9 | 0.00 h | 1.02 × 10−3 | 1.2 | 1.9 × 10−3 | 3.1 × 10−3 | 2.0 | ||
| Mg | ≤ 0.108 b | ≤ 7.74 × 10−4 | ≤ 0.8 | ≤4.7 × 10−3 | ≤5.0 × 10−4 | ≤1.3 | ≤ 0.5 | ≤2.2 × 10−3 | ≤3.0 × 10−4 | ≤ 1.3 | ||
| Al | ≤ 0.797 b | ≤ 2.90 × 10−4 | ≤ 0.6 | ≤2.3 × 10−4 | ≤2.2 × 10−5 | ≤1.1 | 0.5 | 1.7 × 10−4 | 2.1 × 10−5 | 1.3 | ||
| Si | − 0.560 g | 1.83 × 10−4 | − 0.6 | 1.6 × 10−4 | 1.5 × 10−5 | −0.2 | − 0.21 h | 4.10 × 10−4 | − 0.7 | 1.2 × 10−4 | 1.4 × 10−5 | 0.1 |
| P | − 0.593 g | 1.33 × 10−6 | ≤ 0.3 | ≤1.2 × 10−5 | ≤1.0 × 10−6 | ≤0.8 | − 1.15 h | 3.70 × 10−7 | ≤ 0.4 | ≤1.4 × 10−5 | ≤1.5 × 10−6 | ≤ 1.2 |
| S | − 0.378 g | 1.36 × 10−4 | − 0.1 | 2.4 × 10−4 | 1.9 × 10−5 | 0.3 | 0.16 h | 4.69 × 10−4 | ≤− 0.6 | ≤7.8 × 10−5 | ≤8.0 × 10−6 | ≤ 0.2 |
| Cl | ≤ 1.0 | ≤8.3 × 10−5 | ≤6.1 × 10−6 | ≤ 1.5 | ≤ 1.0 | ≤8.1 × 10−5 | ≤7.5 × 10−6 | ≤ 1.8 | ||||
| Ar | ≤ 1.307 b | ≤ 1.04 × 10−3 | ≤ 0.3 | ≤1.4 × 10−4 | ≤8.8 × 10−6 | ≤0.7 | 0.00 c | 4.43 × 10−5 | ≤− 0.3 | ≤3.5 × 10−5 | ≤2.9 × 10−6 | ≤ 0.5 |
| Ca | ≤ 0.0 | ≤6.5 × 10−5 | ≤4.5 × 10−6 | ≤ 0.5 | ||||||||
| Cr | ≤ 2.0 | ≤1.7 × 10−3 | ≤8.1 × 10−5 | ≤ 2.5 | ≤ 2.0 | ≤1.6 × 10−3 | ≤1.0 × 10−4 | ≤ 2.8 | ||||
| Fe | − 0.691b | 2.35 × 10−4 | − 0.4 | 4.5 × 10−4 | 2.1 × 10−5 | 0.0 | ≤− 1.00 h | ≤ 1.15 × 10−4 | − 0.8 | 2.0 × 10−4 | 1.2 × 10−5 | 0.0 |
| Ni | ≤− 1.000 b | ≤ 7.30 × 10−6 | ≤− 1.00 h | ≤ 7.30 × 10−6 | ||||||||
| Zn | ≤ 1.0 | ≤1.7 × 10−5 | ≤7.2 × 10−7 | ≤1.5 | ≤ 1.0 | ≤1.7 × 10−5 | ≤9.1 × 10−7 | ≤ 1.8 | ||||
| Ga | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.2 × 10−7 | ≤2.5 | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.8 × 10−7 | ≤ 2.8 | ||||
| Ge | ≤ 2.0 | ≤2.4 × 10−5 | ≤8.9 × 10−7 | ≤2.5 | ≤ 2.0 | ≤2.4 × 10−5 | ≤1.1 × 10−6 | ≤ 2.8 | ||||
| Kr | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.1 × 10−5 | ≤4.0 | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.4 × 10−5 | ≤ 4.3 | ||||
| Zr | ≤ 3.0 | ≤2.5 × 10−5 | ≤9.6 × 10−7 | ≤ 3.8 | ||||||||
| Te | ≤ 4.0 | ≤1.4 × 10−4 | ≤3.8 × 10−6 | ≤4.6 | ≤ 3.5 | ≤4.5 × 10−5 | ≤1.2 × 10−6 | ≤ 4.3 | ||||
| I | ≤ 4.6 | ≤1.3 × 10−4 | ≤3.6 × 10−6 | ≤5.2 | ≤ 5.0 | ≤3.3 × 10−4 | ≤8.9 × 10−6 | ≤ 5.8 | ||||
| Xe | ≤ 4.0 | ≤1.7 × 10−4 | ≤4.4 × 10−6 | ≤ 4.8 | ||||||||
| . | WD 1751 + 106 . | WD 2134 + 125 . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | Literature . | This work . | Literature . | This work . | ||||||||
| Abundances . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . | [X] . | Mass fraction . | [X] . | Mass fraction . | Number fraction . | [X/Fe] . |
| H | − 0.483 g | 2.43 × 10−1 | − 0.5 | 2.5 × 10−1 | 6.4 × 10−1 | −0.0 | − 0.62 h | 1.77 × 10−1 | − 0.7 | 1.5 × 10−1 | 4.9 × 10−1 | 0.1 |
| He | 0.350 g | 5.59 × 10−1 | 0.3 | 4.6 × 10−1 | 3.0 × 10−1 | 0.7 | 0.45 h | 7.03 × 10−1 | 0.3 | 5.2 × 10−1 | 4.3 × 10−1 | 1.1 |
| C | 1.909 g | 1.75 × 10−1 | 2.1 | 2.7 × 10−1 | 5.8 × 10−2 | 2.5 | 1.76 h | 1.24 × 10−1 | 2.1 | 3.1 × 10−1 | 8.4 × 10−2 | 2.9 |
| N | − 0.491 g | 2.00 × 10−4 | 0.6 | 2.6 × 10−3 | 4.8 × 10−4 | 1.0 | − 0.85 h | 8.73 × 10−5 | − 0.3 | 3.3 × 10−4 | 7.7 × 10−5 | 0.5 |
| O | − 0.516 g | 1.63 × 10−3 | − 0.1 | 4.4 × 10−3 | 7.2 × 10−4 | 0.3 | − 1.81 h | 8.20 × 10−5 | − 0.2 | 3.2 × 10−3 | 6.7 × 10−4 | 0.6 |
| F | 0.694 g | 2.50 × 10−6 | 1.0 | 3.3 × 10−6 | 4.5 × 10−7 | 1.3 | 0.34 h | 1.11 × 10−6 | 1.5 | 9.9 × 10−6 | 1.7 × 10−6 | 2.1 |
| Ne | ≤ 1.5 | ≤3.6 × 10−2 | ≤4.7 × 10−3 | ≤ 1.9 | 0.00 h | 1.02 × 10−3 | 1.2 | 1.9 × 10−3 | 3.1 × 10−3 | 2.0 | ||
| Mg | ≤ 0.108 b | ≤ 7.74 × 10−4 | ≤ 0.8 | ≤4.7 × 10−3 | ≤5.0 × 10−4 | ≤1.3 | ≤ 0.5 | ≤2.2 × 10−3 | ≤3.0 × 10−4 | ≤ 1.3 | ||
| Al | ≤ 0.797 b | ≤ 2.90 × 10−4 | ≤ 0.6 | ≤2.3 × 10−4 | ≤2.2 × 10−5 | ≤1.1 | 0.5 | 1.7 × 10−4 | 2.1 × 10−5 | 1.3 | ||
| Si | − 0.560 g | 1.83 × 10−4 | − 0.6 | 1.6 × 10−4 | 1.5 × 10−5 | −0.2 | − 0.21 h | 4.10 × 10−4 | − 0.7 | 1.2 × 10−4 | 1.4 × 10−5 | 0.1 |
| P | − 0.593 g | 1.33 × 10−6 | ≤ 0.3 | ≤1.2 × 10−5 | ≤1.0 × 10−6 | ≤0.8 | − 1.15 h | 3.70 × 10−7 | ≤ 0.4 | ≤1.4 × 10−5 | ≤1.5 × 10−6 | ≤ 1.2 |
| S | − 0.378 g | 1.36 × 10−4 | − 0.1 | 2.4 × 10−4 | 1.9 × 10−5 | 0.3 | 0.16 h | 4.69 × 10−4 | ≤− 0.6 | ≤7.8 × 10−5 | ≤8.0 × 10−6 | ≤ 0.2 |
| Cl | ≤ 1.0 | ≤8.3 × 10−5 | ≤6.1 × 10−6 | ≤ 1.5 | ≤ 1.0 | ≤8.1 × 10−5 | ≤7.5 × 10−6 | ≤ 1.8 | ||||
| Ar | ≤ 1.307 b | ≤ 1.04 × 10−3 | ≤ 0.3 | ≤1.4 × 10−4 | ≤8.8 × 10−6 | ≤0.7 | 0.00 c | 4.43 × 10−5 | ≤− 0.3 | ≤3.5 × 10−5 | ≤2.9 × 10−6 | ≤ 0.5 |
| Ca | ≤ 0.0 | ≤6.5 × 10−5 | ≤4.5 × 10−6 | ≤ 0.5 | ||||||||
| Cr | ≤ 2.0 | ≤1.7 × 10−3 | ≤8.1 × 10−5 | ≤ 2.5 | ≤ 2.0 | ≤1.6 × 10−3 | ≤1.0 × 10−4 | ≤ 2.8 | ||||
| Fe | − 0.691b | 2.35 × 10−4 | − 0.4 | 4.5 × 10−4 | 2.1 × 10−5 | 0.0 | ≤− 1.00 h | ≤ 1.15 × 10−4 | − 0.8 | 2.0 × 10−4 | 1.2 × 10−5 | 0.0 |
| Ni | ≤− 1.000 b | ≤ 7.30 × 10−6 | ≤− 1.00 h | ≤ 7.30 × 10−6 | ||||||||
| Zn | ≤ 1.0 | ≤1.7 × 10−5 | ≤7.2 × 10−7 | ≤1.5 | ≤ 1.0 | ≤1.7 × 10−5 | ≤9.1 × 10−7 | ≤ 1.8 | ||||
| Ga | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.2 × 10−7 | ≤2.5 | ≤ 2.0 | ≤5.6 × 10−6 | ≤2.8 × 10−7 | ≤ 2.8 | ||||
| Ge | ≤ 2.0 | ≤2.4 × 10−5 | ≤8.9 × 10−7 | ≤2.5 | ≤ 2.0 | ≤2.4 × 10−5 | ≤1.1 × 10−6 | ≤ 2.8 | ||||
| Kr | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.1 × 10−5 | ≤4.0 | ≤ 3.5 | ≤3.4 × 10−4 | ≤1.4 × 10−5 | ≤ 4.3 | ||||
| Zr | ≤ 3.0 | ≤2.5 × 10−5 | ≤9.6 × 10−7 | ≤ 3.8 | ||||||||
| Te | ≤ 4.0 | ≤1.4 × 10−4 | ≤3.8 × 10−6 | ≤4.6 | ≤ 3.5 | ≤4.5 × 10−5 | ≤1.2 × 10−6 | ≤ 4.3 | ||||
| I | ≤ 4.6 | ≤1.3 × 10−4 | ≤3.6 × 10−6 | ≤5.2 | ≤ 5.0 | ≤3.3 × 10−4 | ≤8.9 × 10−6 | ≤ 5.8 | ||||
| Xe | ≤ 4.0 | ≤1.7 × 10−4 | ≤4.4 × 10−6 | ≤ 4.8 | ||||||||
Notes: [X] = log (abundance/solar abundance), [X/Fe] = log (nX/nFe) − log (nX, ⊙/nFe, ⊙) with the number fraction nX for element X, the error of our abundance determination is ±0.3 dex.
WD 2324 + 397 (|$T_\mathrm{eff}= 130\, 000 \pm 10\, 000$| K and log g = 6.2 ± 0.2; Dreizler et al. 1996) and SDSS 152116.00 + 251437.46 (|$T_\mathrm{eff}= 140\, 000 \pm 15\, 000$| K and log g = 6.0 ± 0.3; Werner et al. 2014) are members of this group without an ambient PN (Werner et al. 1997). The C abundance is similar to the values determined for our two program stars. Considering the C/H ratio, the value for SDSS 152116.00 + 251437.46 is close to the one of WD 2134 + 125 while the one for WD 2324 + 397 is slightly higher. Both their O/H ratios exceeds the values of our two program stars by a factor of 2 or even more. The N/H ratio of the stars for which it is known is very low. The He/H ratio of WD 2324 + 397 resembles the value of WD 1751 + 106 whereas WD 2134 + 125 has a higher He content similar to SDSS 152116.00 + 251437.46.
8.2 Comparison to Abell 30 and Abell 78
Comparing the results of our analysis to the parameters known for the CSs of the PNe Abell 30 and Abell 78 is of special interest, because these objects are located at almost the same position in the log Teff–log g diagram. Both are [WC]-PG 1159 transition objects with |$T_\mathrm{eff} = 115\, 000$| K and log g = 5.5 (Leuenhagen et al. 1993) and |$T_\mathrm{eff} = 117\, 000 \pm 5000$| K and log g = 5.5 (Werner & Koesterke 1992; Toalá et al. 2015). Their element mass fractions are also included in Table 2. Obvious are the higher He and lower C, N, and O abundances in our two hybrid PG 1159 stars. This may result from different evolutionary channels. The CSs of Abell 30 and Abell 78 both underwent a born-again scenario (Iben et al. 1983) resulting in a return to the AGB, whereas the hybrid PG 1159 stars experience a final He-shell flash at the departure from the AGB. This AFTP evolution may be the reason for the smaller amount of C, N, and O in the atmosphere in contrast to a (V)LTP scenario. Toalá et al. (2015) found an Fe deficiency of about one dex for Abell 78. This subsolar Fe abundance is in good agreement with the results for WD 1751 + 106 and WD 2134 + 125, although they show a smaller Fe deficiency. The high Ne abundance of 4 per cent by mass of the CS of Abell 78 (Toalá et al. 2015) and the revised N abundance of 1.5 per cent by mass for both CSPNe (Guerrero et al. 2012; Toalá et al. 2015) exceed the values determined for our two hybrid stars and are also an indicator for different evolutionary channels, namely VLTP and AFTP evolution. In common with the CS of Abell 78 is the high abundance of F (25 times solar; Toalá et al. 2015) compared to 9.3 and 29 times solar, for WD 1751 + 106 and WD 2134 + 125 respectively). Their mass-loss rates of |$\dot{M} / {\rm M}_{\odot } = 2.0 \times 10^{-8}\, \mathrm{yr}^{-1}$| (Guerrero et al. 2012) and |$\dot{M} / {\rm M}_{\odot } = 1.6 \times 10^{-8}\, \mathrm{yr}^{-1}$| (Toalá et al. 2015) are about a factor 2 higher than the ones determined for WD 1751 + 106 and WD 2134 + 125 (Section 6). The PNe Abell 30 and Abell 78 look very similar in shape but appear different to the ‘Galactic Soccerballs’.
8.3 Comparison to PG 1159 stars, hot post-AGB stars, and nucleosynthesis models
Karakas & Lugaro (2016) presented a grid of evolutionary models for different initial masses and metallicities. For stars with initial masses |$M \le 3\, {\rm M}_\odot$|, they predict an enhanced production of C, N, F, Ne, and Na compared to solar values and normalized to the value for Fe. This prediction for the surface abundances of post-AGB stars is in line with our abundance determinations (Fig. 12). Another set of evolutionary models for initial masses of |$1.8 - 6\, {\rm M}_\odot$| was calculated by Shingles & Karakas (2013) to investigate the resulting element yields of the species He, C, O, F, Ne, Si, P, S, and Fe depending on uncertainties in nucleosynthesis processes. They present the intershell abundances of their stellar models that should represent the surface abundances of PG 1159 stars. As described in (Section 1), the surface abundances of hybrid PG 1159 stars should reflect a mixture of the abundances of the former H-rich envelope and the intershell.
![Photospheric abundance ratio [X/Fe] = log (nX/nFe) − log (nX, ⊙/nFe, ⊙) with the number fraction nX for element X of WD 1751 + 106 and WD 2134 + 125 determined from detailed line-profile fits. Upper limits are indicated with arrows. Predictions of Karakas & Lugaro ( 2016, Mini = 1.5 and 3.0 (see legend); metallicity Z = 0.014 (green) and 0.007 (cyan)) are shown for comparison.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/489/1/10.1093_mnras_stz1994/1/m_stz1994fig12.jpeg?Expires=1750290729&Signature=bknF3POwbm7nSfao-UpKybNHCR9oM5ZQ8veB~TFI3J70yQezQz~AYJdIr-5SEwDQuItzCK6hdKuWlisNXa24GFtuK8WcuQzStnu043wyQc8Ip7q3NgxL~4Y~RFRhtcTzWhSSOGrjQwzXluZsTOprIhtjcrpHw2sLzWLrL-hHkCnD0JkeHByuw5Mir3GQVOBRd0rndU3NbV2mXcj4IDDeVKIla~Sig9zWVnrDp6jIjyHJAdhrCT3IusqKuGtkfAB9XG2Hvi5GOG0X5xOn6SFqRLKTde28a4Ghk9XSnpw~S8UbCZeMHqluSYpLFFbL3dAyd8s5hURd6d325weVQr9kmQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Photospheric abundance ratio [X/Fe] = log (nX/nFe) − log (nX, ⊙/nFe, ⊙) with the number fraction nX for element X of WD 1751 + 106 and WD 2134 + 125 determined from detailed line-profile fits. Upper limits are indicated with arrows. Predictions of Karakas & Lugaro ( 2016, Mini = 1.5 and 3.0 (see legend); metallicity Z = 0.014 (green) and 0.007 (cyan)) are shown for comparison.
The C abundances of our two program stars resemble the values of other PG 1159 stars like for example the prototype star PG 1159 − 035 (Jahn et al. 2007), the hot PG 1159 stars PG 1520 + 525 and PG 1144 + 005 (Werner et al. 2016) and the ‘cooler’ PG 1707 + 427 and PG 1424 + 535 (Werner, Rauch & Kruk 2015).
The subsolar O abundances of the two stars analysed in this work are significantly lower than the supersolar values of the stars mentioned above. However, the O abundance of the hybrid PG 1159 stars lie within the predicted range of Shingles & Karakas (2013) (O mass fraction between 0.2 and 1.2 per cent) and Lawlor & MacDonald (2006) in comparison to the PG 1159 stars. The large range in O abundances may be caused by different effectiveness of convective boundary mixing of the pulse-driven convection zone into the C/O core in the thermal pulses on the AGB.
An N enrichment is predicted for PG 1159 stars that experienced a VLTP scenario due to a large production of 14N in an H-ingestion flash (HIF; cf. Werner & Herwig 2006). WD 1751 + 106 and WD 2134 + 125 experienced an AFTP without HIF what corresponds to their comparatively low N abundance. The value for WD 2134 + 125 lies within the range that is predicted by AFTP models whereas the value for WD 1751 + 106 is higher.
The set of PG 1159 stars shows a large range of F abundances from low mass fractions of 3.2 × 10−6 for the prototype PG 1159 − 035 to values of 1.0 × 10−4 for PG 1707 − 427. The values of WD 1751 + 106 and WD 2134 + 125 lie within this range but below the predictions of Shingles & Karakas (2013) (F mass fractions between 2.0 × 10−5 and 2.7 × 10−4). The F production in the intershell region is very sensitive on the temperature and therefore on the initial mass (Lugaro et al. 2004). They predict the highest F abundances for stars with initial masses of |$2-4\, {\rm M}_\odot$| at solar metallicity (F intershell mass fractions of 3–7 × 10−5). Again, the values of WD 2134 + 125 and WD 1751 + 106 are about 3–10 times lower than these predictions.
The Ne abundances for the set of mentioned PG 1159 stars are all supersolar and in agreement with evolutionary models. The determined values for the Si, P, and S abundances are at the lower border or slightly below the predictions from evolutionary models. The same holds for the solar upper abundance limit for P in PG 1159 − 035.
The Fe deficiency is not explained by nucleosynthesis calculations like those of Karakas & Lugaro (2016) that predict solar Fe abundances for stars with an initial solar composition, which is due to the fact that iron is not strongly depleted in nuclear processes in AGB stars with masses ranging from 0.8 to 8.0 |${\rm M}_\odot$| as it is the case for the precursor AGB stars of Abell 43 and NGC 7094. The models of Shingles & Karakas (2013) yield a slightly subsolar Fe abundances but still cannot explain the observed deficiency. For some of the PG 1159 stars of the set used for comparison here, the Fe abundance has been measured and all are found to be solar. The only other star in Fig. 11 which, besides WD 1751 + 106 and WD 2134 + 125 , shows an Fe deficiency is the CSPN of Abell 78 (Section 8.2). The Fe deficiency of 0.4 and 0.8 dex for WD 1751 + 106 and WD 2134 + 125 , respectively, does not include solar values within the error ranges. Löbling (2018) discuss the speculation of Herwig, Lugaro & Werner (2003) that this underabundance can be caused by neutron capture during the former AGB phase leading to a transformation of Fe into Ni and heavier elements. Probably the low Fe abundances determined in WD 1751 + 106 and WD 2134 + 125 are just a consequence of a low initial metal content for these objects. This subsolar metallicity does not rule out a thick or even thin disc membership (Recio-Blanco et al. 2014). Also their location and distance to the Galactic plane support that these are disc objects. The models of Karakas & Lugaro (2016) predict a strong enhancement of the TIEs in the atmospheres of post-AGB stars. Unfortunately, no abundance determination was possible for the TIEs but due to the determined upper abundance limits for Zn, Ga, Ge, Kr, and Te of both stars and Zr for WD 2134 + 125 a strong enhancement can be ruled out. This is consistent with our determination of the wind intensity for which the wind is coupled. Thus, this prevents diffusion and disrupts the equilibrium balance between radiative levitation and gravitational settling. To improve the analysis of TIEs, spectra with much better S/N and the calculation of reliable atomic data are highly desirable.
9 CONCLUSION
Regarding the evolutionary scenario for WD 1751 + 106 and WD 2134 + 125, an AFTP remains the best available candidate. The AFTP models presented here (Fig. 10 and Table 1) are able to reproduce qualitatively the observed trends. Abundances of H, He, C, N, and Ne are reasonably well reproduced by AFTP models. However AFTP models computed from sequences that include convective boundary mixing at the bottom of the pulse driven convective zone (as those presented here) display O abundances much larger than those of our program stars. In fact, the O abundances shown by our stars are in good agreement with those predicted by Lawlor & MacDonald (2006), using AGB models that do not include any type of convective boundary mixing at the bottom of the pulse driven convective zone. These models, however, underestimate the C and Ne abundance, while the H and He abundances reproduce the observed values. Yet, the main argument against the AFTP scenario comes from the expansion ages of the nebulae. According to stellar evolution computations, AFTP models reach the location of our program stars in the HRD less than 2000 yrs after departing from the AGB, while the expansion ages are several times larger than this. This is true regardless the mass-loss prescription adopted in the post-AGB evolution. Unless the masses of the CSPNe are much lower than derived here, the AFTP scenario is unable to reproduce this key observational feature.
It is desirable to determine the iron abundance and the abundances of heavier elements of the ambient PN to investigate on the photospheric composition of Abell 43 and NGC 7094 at the time of the PN’s ejection and to analyse the elements produced and ejected during the preceding AGB phase (cf. Lugaro et al. 2017) but this is out of the focus of this paper.
SUPPORTING INFORMATION
Figure A1. Determination of EB–V.
Figure A2. Synthetic spectra calculated with |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \, \mathrm{K}$| and different log g , compared with the UVES SPY observations of He ii and H i lines for WD 1751 + 106 (gray).
Figure A3. Synthetic spectra calculated with |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \, \mathrm{K}$| and different log g , compared with the UVES SPY observations of He ii and H i lines for WD 2134 + 125 (gray). ( log g is indicated in panel 6).
Figure A4. Section of the HST/STIS spectrum of WD 2134 + 125 (black) compared with synthetic spectra calculated with |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \, \mathrm{K}$| and different log g of 6.1 (green dashed), 5.6 (red solid), and 5.1 (blue dotted).
Figure A5. Synthetic spectra calculated with |$\log g = 5.6$| for WD 1751 + 106 (top panel) and WD 2134 + 125 (bottom) and different Teff (red: |$\mbox{$T_\mathrm{eff}$}\, = 125\, 000 \, \mathrm{K}$|, purple: |$\mbox{$T_\mathrm{eff}$}\, = 115\, 000 \, \mathrm{K}$|, blue: |$\mbox{$T_\mathrm{eff}$}\, = 105\, 000 \, \mathrm{K}$|), compared with the STIS observation of O v |$\lambda \, 1371.3$| Å and the FUSE observation of O vi |$\lambda \lambda \, 1124.7, 1124.9$| Å (gray).
Figure A6. FUSE observation (gray) compared with the best static model including ISM line absorption (red).
Figure A7. GHRS and STIS observation (gray) for WD 1751+106 (top) and WD 2134 + 125 (bottom), respectively, compared with the best model (red).
Figure A8. Temperature and density structures and ionization fractions of all ions which are considered in our final model for WD 2134 + 125 .
Figure A9. Synthetic spectra of our best models (red lines) for WD 1751 + 106 (top panel) and WD 2134 + 125 (bottom) around H i Ly α calculated with |$n_\mathrm{H\, I} = 1.0 \times 10^{21}\, \mathrm{cm^{-2}}$| and |$6.5 \times 10^{20}\, \mathrm{cm^{-2}}$|, respectively, compared with the observations (gray).
Table A1. Statistics of the H – Ara and Ca – Bab model atoms used in our model-atmosphere calculations.
Table A2. Observation log for WD 1751 + 106 and WD 2134 + 125 .
Table A3. Ions with recently calculated oscillator strengths.
Table A4. Abundances used for the calculation of the atmospheric structures.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
LL has been supported by the German Research Foundation (DFG, grant WE 1312/49-1). M3B is supported by the PICT 2016-0053 from the Agencia National de Promotión Científica e Tecnológica (ANPCyT), Argentina. This work was partially funded by DA/16/07 grant from the German Academic Exchange Service - Ministerio de Ciencia, Tecnología e Innovación Productiva (DAAD-MinCyT) bilateral cooperation program. This work is based on observations with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26666, and on observations made with the NASA-CNES-CSA Far Ultraviolet Spectroscopic Explorer. Also this is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 167.D-0407 . We were supported by the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC, and the DFG (grant INST 37/935-1 FUGG). The GAVO project had been supported by the Federal Ministry of Education and Research (BMBF) at Tübingen (05 AC 6 VTB, 05 AC 11 VTB). We thank the referee Ralf Napiwotzki for his many useful comments that improved this paper. This work used the profile-fitting procedure OWENS developed by M. Lemoine and the FUSE French Team. We thank Falk Herwig, Timothy Lawlor, and James MacDonald for helpful comments and discussion, Ralf Napiwotzki for putting the reduced VLT spectra at our disposal. The TIRO (http://astro-uni-tuebingen.de/ TIRO), TMAD (http://astro-uni-tuebingen.de/ TMAD), and TOSS (http://astro-uni-tuebingen.de/ TOSS) services used for this paper were constructed as part of the activities of the German Astrophysical Virtual Observatory. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts. This research has made use of NASA’s Astrophysics Data System and the SIMBAD database, operated at CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Footnotes
Orbiting and Retrievable Far and Extreme Ultraviolet Spectrometer – Space Pallet Satellite II.



