-
PDF
- Split View
-
Views
-
Cite
Cite
Christopher M Irwin, Xiaping Tang, Tsvi Piran, Ehud Nakar, Jet-driven bubbles in Fanaroff–Riley type-I sources, Monthly Notices of the Royal Astronomical Society, Volume 488, Issue 4, October 2019, Pages 4926–4936, https://doi.org/10.1093/mnras/stz2075
Close - Share Icon Share
Abstract
Observations of several Fanaroff–Riley (FR) type-I sources reveal outflowing bipolar bubbles of hot gas surrounded by a weak forward shock. We consider the possibility that these bubbles were driven by choked relativistic jets that failed to penetrate the ambient intracluster medium. Using new results on choked jets linking the geometry of the forward shock to the jet properties, we infer robust limits on the radius Rch at which the jet was quenched in five well-studied FR type-I sources, finding typically Rch ∼ 10 kpc. We further show that, in order to reach this radius in less than the current age of the system, the jet must have been tightly collimated, with the jet head subtending an angle of |$\theta _{\rm h}\lesssim 2^{\circ }$|. The ambient pressure is not high enough to explain this collimation, suggesting that the jet was collimated by interaction with its own cocoon. Although the choking radius is well-constrained, we find a degeneracy between the initial jet opening angle before collimation, θ0, and the duration of jet activity, tb, with |$(t_{\rm b}/1\rm Myr)(\theta _0/5^{\circ })^{-2}\sim 0.1$|. We speculate that the working time and/or opening angle of the jet may be important factors contributing to the FR type-I/type- II morphology in galaxy clusters, with short-lived or wide jets being choked to form bipolar bubbles filled with diffuse radio emission, and longer-lived or narrow jets successfully escaping the cluster core to produce cocoons with radio hotspots.
1 INTRODUCTION
With high-resolution X-ray imaging, the Chandra and XMM–Newton space telescopes have identified many cavities with a depression of surface brightness in galaxies, galaxy groups, and galaxy clusters (e.g. Bîrzan et al. 2004; Dunn & Fabian 2006; Diehl et al. 2008; Dong, Rasmussen & Mulchaey 2010; Shin, Woo & Mulchaey 2016). The X-ray cavities are often filled with radio lobes and are thought to be inflated by active galactic nucleus (AGN) jets (e.g. Churazov et al. 2000; McNamara et al. 2000; Fabian et al. 2002; McNamara et al. 2005). Weak shocks surrounding the cavity are also observed in several well-studied objects like the Perseus cluster and M87 (e.g. Graham, Fabian & Sanders 2008; Forman et al. 2017), which further supports the connection with jet activity. The jet energy required to produce the X-ray cavities can balance the cooling of the hot gas (e.g. Bîrzan et al. 2004; Rafferty et al. 2006), which becomes an important sign of radio mode AGN feedback [see e.g. Fabian (2012) for a recent review].
Some Fanaroff–Riley (FR) type-I sources (Fanaroff & Riley 1974) that contain X-ray cavities also show clear evidence for bipolar relativistic jets. Examples include M87 (e.g. Hines, Owen & Eilek 1989; Owen, Eilek & Kassim 2000; Marshall et al. 2002; Forman et al. 2007, 2017) and Perseus (e.g. Boehringer et al. 1993; Churazov et al. 2000; Fabian et al. 2000). It is therefore natural to consider whether the bipolar bubbles we observe could be relics of past jet activity. If this is the case, what can we learn about the jet by observing the relic bubbles it leaves behind? Thanks to the wealth of observational data available, it is often possible to obtain robust estimates for the age (tage) of the bubbles,1 as well as the total energy (E) injected into the system (Tang & Churazov 2017, see also Section 3.3). However, the properties of the engine responsible for driving the outflow are more uncertain. For example, we do not know whether energy injection is still ongoing, or ceased long ago. Likewise, it is not clear whether the energy was injected quasi-spherically, or concentrated into a narrow angle.
Motivated by these questions, we investigate a choked relativistic jet model for the bubbles in FR type-I objects. In the choked jet scenario, we assume that the bubbles were driven by a relativistic jet that was quenched sometime in the past, so that we no longer observe it (see Sections 2 and 3.2). We demonstrate how four observed bubble properties (the radius of the forward shock, Rs; the location of the contact discontinuity, Rc; the shock Mach number, M; and the bubble’s apparent aspect ratio) can be used to constrain the four parameters of our model (the total injected energy, E; the age of the system, tage; the duration of the jet outburst, tb; and the initial jet opening angle, θ0).2
The possibility that the bubbles in FR type-I sources were driven by quenched outbursts has been studied analytically before by, e.g., Tang & Churazov (2017) and references therein. Our model differs from theirs in two key ways. First, whereas they assume quasi-spherical energy injection, we assume that the energy was injected by a jet into a nozzle of opening angle θ0. Secondly, we make use of an additional observable, the apparent aspect ratio of the forward shock. In other words, our model has one additional free parameter and one additional observational constraint.
In applying our model, we focus on five FR type-I sources – the Perseus cluster (Zhuravleva et al. 2016), M87 (Forman et al. 2017), MS 0735.6+7421 (Vantyghem et al. 2014), NGC 4552 (Machacek et al. 2006), and NGC 5813 (Randall et al. 2015) – which have a pair of bubbles close to the central AGN surrounded by a clearly visible forward shock [see e.g. fig. 6 of Zhuravleva et al. (2016) for an X-ray image of the relevant features]. In these cases, Rs, Rc, M, and the shock aspect ratio are all reliably measured. Each object has a low Mach number (M < 2) and Rs ∼ Rc, although the size of the systems varies across two orders of magnitude, from Rs ∼ 3 kpc in NGC 4552, to Rs ∼ 300 kpc in MS 0735.6+7421. In all but one of the systems, the apparent aspect ratio of the forward shock is ∼1.5, and the projected distance between the black hole and the centre of each bubble is comparable to the bubble’s size. (M87 is the exception; see Section 4 for further discussion.) The ambient gas density (ρa) and pressure (Pa) in these environments are also well-constrained, with typical values of |$\rho _{\rm a}\sim 10^{-25} \rm g\, cm^{-3}$| and |$P_{\rm a}\sim 0.1 \rm keV\, cm^{-3}$|. In addition, we make use of the density profile power-law index (α) reported in the ACCEPT data base (Cavagnolo et al. 2009). The values of α range from 0 to 1.5. All the observational data are summarized in Table 2.
| Observables . | |
|---|---|
| Rs | Observed radius of the forward shock along the major axis |
| Rc | Observed radius of the contact discontinuity along the major axis |
| M | Mach number of the forward shock |
| z∥/x⊥ | Observed aspect ratio of the forward shock |
| nt | Total number density of the ambient medium at r = Rs |
| ρa | Mass density of the ambient medium at r = Rs |
| Pa | Pressure of the ambient medium at r = Rs |
| α | Power-law index of the ambient density profile |
| Model parameters | |
| E | Total energy injected by the jet |
| tage | Age of the system |
| tb | Duration of jet activity |
| θ0 | Opening angle of the injected jet |
| Lj | One-sided jet luminosity, i.e. Lj = E/2tb |
| Evolutionary time-scales | |
| tsp | Time for the forward shock to become spherical |
| tbuoy | Time-scale for buoyancy to pull the bubbles apart |
| tE | Time when the outflow reaches pressure equilibrium with the ambient medium |
| Properties of the outflow upon choking | |
| Rch | Radius at which the jet is choked |
| tch | Time at which the jet is choked |
| ζ | Dimensionless ratio of Rch/Rs |
| η | Dimensionless ratio of tch/tage |
| ρch | Density of the ambient medium at Rch |
| βh | Velocity of the jet head upon choking |
| βc | Velocity of the cocoon shock upon choking |
| βh/βc | Estimate for the aspect ratio of the forward shock upon choking |
| Σh | Surface area of the jet head upon choking |
| θh | Angle subtended by the jet head upon choking |
| Vfs,ch | Volume enclosed by the forward shock upon choking |
| Pc,ch | Pressure in the cocoon upon choking |
| Λ(Rch) | Parameter determining susceptibility to the magnetic kink instability |
| Observables . | |
|---|---|
| Rs | Observed radius of the forward shock along the major axis |
| Rc | Observed radius of the contact discontinuity along the major axis |
| M | Mach number of the forward shock |
| z∥/x⊥ | Observed aspect ratio of the forward shock |
| nt | Total number density of the ambient medium at r = Rs |
| ρa | Mass density of the ambient medium at r = Rs |
| Pa | Pressure of the ambient medium at r = Rs |
| α | Power-law index of the ambient density profile |
| Model parameters | |
| E | Total energy injected by the jet |
| tage | Age of the system |
| tb | Duration of jet activity |
| θ0 | Opening angle of the injected jet |
| Lj | One-sided jet luminosity, i.e. Lj = E/2tb |
| Evolutionary time-scales | |
| tsp | Time for the forward shock to become spherical |
| tbuoy | Time-scale for buoyancy to pull the bubbles apart |
| tE | Time when the outflow reaches pressure equilibrium with the ambient medium |
| Properties of the outflow upon choking | |
| Rch | Radius at which the jet is choked |
| tch | Time at which the jet is choked |
| ζ | Dimensionless ratio of Rch/Rs |
| η | Dimensionless ratio of tch/tage |
| ρch | Density of the ambient medium at Rch |
| βh | Velocity of the jet head upon choking |
| βc | Velocity of the cocoon shock upon choking |
| βh/βc | Estimate for the aspect ratio of the forward shock upon choking |
| Σh | Surface area of the jet head upon choking |
| θh | Angle subtended by the jet head upon choking |
| Vfs,ch | Volume enclosed by the forward shock upon choking |
| Pc,ch | Pressure in the cocoon upon choking |
| Λ(Rch) | Parameter determining susceptibility to the magnetic kink instability |
| Observables . | |
|---|---|
| Rs | Observed radius of the forward shock along the major axis |
| Rc | Observed radius of the contact discontinuity along the major axis |
| M | Mach number of the forward shock |
| z∥/x⊥ | Observed aspect ratio of the forward shock |
| nt | Total number density of the ambient medium at r = Rs |
| ρa | Mass density of the ambient medium at r = Rs |
| Pa | Pressure of the ambient medium at r = Rs |
| α | Power-law index of the ambient density profile |
| Model parameters | |
| E | Total energy injected by the jet |
| tage | Age of the system |
| tb | Duration of jet activity |
| θ0 | Opening angle of the injected jet |
| Lj | One-sided jet luminosity, i.e. Lj = E/2tb |
| Evolutionary time-scales | |
| tsp | Time for the forward shock to become spherical |
| tbuoy | Time-scale for buoyancy to pull the bubbles apart |
| tE | Time when the outflow reaches pressure equilibrium with the ambient medium |
| Properties of the outflow upon choking | |
| Rch | Radius at which the jet is choked |
| tch | Time at which the jet is choked |
| ζ | Dimensionless ratio of Rch/Rs |
| η | Dimensionless ratio of tch/tage |
| ρch | Density of the ambient medium at Rch |
| βh | Velocity of the jet head upon choking |
| βc | Velocity of the cocoon shock upon choking |
| βh/βc | Estimate for the aspect ratio of the forward shock upon choking |
| Σh | Surface area of the jet head upon choking |
| θh | Angle subtended by the jet head upon choking |
| Vfs,ch | Volume enclosed by the forward shock upon choking |
| Pc,ch | Pressure in the cocoon upon choking |
| Λ(Rch) | Parameter determining susceptibility to the magnetic kink instability |
| Observables . | |
|---|---|
| Rs | Observed radius of the forward shock along the major axis |
| Rc | Observed radius of the contact discontinuity along the major axis |
| M | Mach number of the forward shock |
| z∥/x⊥ | Observed aspect ratio of the forward shock |
| nt | Total number density of the ambient medium at r = Rs |
| ρa | Mass density of the ambient medium at r = Rs |
| Pa | Pressure of the ambient medium at r = Rs |
| α | Power-law index of the ambient density profile |
| Model parameters | |
| E | Total energy injected by the jet |
| tage | Age of the system |
| tb | Duration of jet activity |
| θ0 | Opening angle of the injected jet |
| Lj | One-sided jet luminosity, i.e. Lj = E/2tb |
| Evolutionary time-scales | |
| tsp | Time for the forward shock to become spherical |
| tbuoy | Time-scale for buoyancy to pull the bubbles apart |
| tE | Time when the outflow reaches pressure equilibrium with the ambient medium |
| Properties of the outflow upon choking | |
| Rch | Radius at which the jet is choked |
| tch | Time at which the jet is choked |
| ζ | Dimensionless ratio of Rch/Rs |
| η | Dimensionless ratio of tch/tage |
| ρch | Density of the ambient medium at Rch |
| βh | Velocity of the jet head upon choking |
| βc | Velocity of the cocoon shock upon choking |
| βh/βc | Estimate for the aspect ratio of the forward shock upon choking |
| Σh | Surface area of the jet head upon choking |
| θh | Angle subtended by the jet head upon choking |
| Vfs,ch | Volume enclosed by the forward shock upon choking |
| Pc,ch | Pressure in the cocoon upon choking |
| Λ(Rch) | Parameter determining susceptibility to the magnetic kink instability |
| Name . | |$n_{\rm t}(\, \rm cm^{-3})$| . | |$P(\rm keV\, cm^{-3})$| . | |$R_{\rm c}(\, \rm kpc)$| . | |$R_{\rm s}(\, \rm kpc)$| . | Mach number . | α . | z∥/x⊥ . | Reference . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 0.10 | 0.33 | 15.0 | 22.5 | 1.16 | 0.0 | 1.5 | Zhuravleva et al. (2016) |
| M87 | 0.03 | 0.06 | 3.0 | 13.0 | 1.2 | 1.0 | ∼1 | Forman et al. (2017) |
| MS 0735.6+7421a | 0.01 | 0.04 | 259.0 | 320.0 | 1.3 | 1.7 | 1.4 | Vantyghem et al. (2014) |
| NGC 4552 | 0.10 | 0.04 | 1.0 | 1.3 | 1.7 | 1.3 | 1.5 | Machacek et al. (2006) |
| NGC 5813 | 0.06 | 0.04 | 11.6 | 14.9 | 1.5 | 1.5 | 1.4 | Randall et al. (2015) |
| Name . | |$n_{\rm t}(\, \rm cm^{-3})$| . | |$P(\rm keV\, cm^{-3})$| . | |$R_{\rm c}(\, \rm kpc)$| . | |$R_{\rm s}(\, \rm kpc)$| . | Mach number . | α . | z∥/x⊥ . | Reference . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 0.10 | 0.33 | 15.0 | 22.5 | 1.16 | 0.0 | 1.5 | Zhuravleva et al. (2016) |
| M87 | 0.03 | 0.06 | 3.0 | 13.0 | 1.2 | 1.0 | ∼1 | Forman et al. (2017) |
| MS 0735.6+7421a | 0.01 | 0.04 | 259.0 | 320.0 | 1.3 | 1.7 | 1.4 | Vantyghem et al. (2014) |
| NGC 4552 | 0.10 | 0.04 | 1.0 | 1.3 | 1.7 | 1.3 | 1.5 | Machacek et al. (2006) |
| NGC 5813 | 0.06 | 0.04 | 11.6 | 14.9 | 1.5 | 1.5 | 1.4 | Randall et al. (2015) |
| Name . | |$n_{\rm t}(\, \rm cm^{-3})$| . | |$P(\rm keV\, cm^{-3})$| . | |$R_{\rm c}(\, \rm kpc)$| . | |$R_{\rm s}(\, \rm kpc)$| . | Mach number . | α . | z∥/x⊥ . | Reference . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 0.10 | 0.33 | 15.0 | 22.5 | 1.16 | 0.0 | 1.5 | Zhuravleva et al. (2016) |
| M87 | 0.03 | 0.06 | 3.0 | 13.0 | 1.2 | 1.0 | ∼1 | Forman et al. (2017) |
| MS 0735.6+7421a | 0.01 | 0.04 | 259.0 | 320.0 | 1.3 | 1.7 | 1.4 | Vantyghem et al. (2014) |
| NGC 4552 | 0.10 | 0.04 | 1.0 | 1.3 | 1.7 | 1.3 | 1.5 | Machacek et al. (2006) |
| NGC 5813 | 0.06 | 0.04 | 11.6 | 14.9 | 1.5 | 1.5 | 1.4 | Randall et al. (2015) |
| Name . | |$n_{\rm t}(\, \rm cm^{-3})$| . | |$P(\rm keV\, cm^{-3})$| . | |$R_{\rm c}(\, \rm kpc)$| . | |$R_{\rm s}(\, \rm kpc)$| . | Mach number . | α . | z∥/x⊥ . | Reference . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 0.10 | 0.33 | 15.0 | 22.5 | 1.16 | 0.0 | 1.5 | Zhuravleva et al. (2016) |
| M87 | 0.03 | 0.06 | 3.0 | 13.0 | 1.2 | 1.0 | ∼1 | Forman et al. (2017) |
| MS 0735.6+7421a | 0.01 | 0.04 | 259.0 | 320.0 | 1.3 | 1.7 | 1.4 | Vantyghem et al. (2014) |
| NGC 4552 | 0.10 | 0.04 | 1.0 | 1.3 | 1.7 | 1.3 | 1.5 | Machacek et al. (2006) |
| NGC 5813 | 0.06 | 0.04 | 11.6 | 14.9 | 1.5 | 1.5 | 1.4 | Randall et al. (2015) |
We begin our discussion with an overview of the evolution of the system, first considering the behaviour while the central engine is active in Section 2, in both the case where the jet is collimated by its own cocoon (Section 2.1) and the case where it is collimated by the ambient pressure (Section 2.2). We then address what happens once the jet switches off in Section 3, reviewing several important time-scales for bubble evolution in Section 3.1, then showing how available observations of relic bubbles constrain the jet geometry (Section 3.2) and the duration of engine activity (Section 3.3). As the specific objects we consider are all located in clusters, we focus here on the propagation in cluster environments. However, much of the discussion is generic and applies also to isolated radio galaxies. In Section 4, we present our results for each individual object and consider possible implications for the FR type-I/FR type-II dichotomy, before concluding in Section 5.
2 JET PROPAGATION AND COLLIMATION
A relativistic AGN jet drives a strong forward shock into the ambient medium, while at the same time a reverse shock is driven back into the jet ejecta. The resulting double shock structure is known as the ‘jet head.’ As the jet propagates, jet material entering the head through the reverse shock is pushed out to the sides, forming a hot ‘cocoon’ that surrounds the jet. The subsequent evolution of the jet-and-cocoon system depends on the relationship between the thermal pressure in the cocoon, Pc, and the sum of all pressures in the ambient medium at the jet head’s location. We suppose that the ambient density and pressure are power laws in radius, with ρ ∝ R−α and P ∝ R−λ, and denote the ambient density and pressure at the location of the forward shock along the axis as ρa and Pa, respectively. At any given time, the relevant behaviour is then determined by comparing the values of Pc and Pa.
2.1 Collimation by the cocoon
If Pc ≫ Pa, the cocoon expands supersonically, driving a strong shock into the external medium; we call this shock the ‘cocoon shock.’ At the same time, the cocoon exerts pressure on the conical jet outflow, reducing its opening angle. A self-consistent analytical solution for the dynamics of the jet and cocoon in this regime is given by Bromberg et al. (2011, hereafter B11). The resulting evolution depends on the ambient density ρa, as well as the jet’s luminosity Lj and injection angle θ0, but it is independent of the ambient pressure.
The Pc ≫ Pa regime can be further subdivided based on the ratio of the jet energy density at the head, Lj/Σhc (where Σh is the cross-section of the jet head and c is the speed of light), to the ambient rest-mass energy density, ρac2. Following B11, we call this dimensionless ratio |$\tilde{L} \equiv L_{\rm j}/(\Sigma _{\rm h}\rho _{\rm a}c^3)$|. As |$\tilde{L}$| increases, the pressure in the cocoon grows, but the pressure required to collimate the jet grows even faster. Consequently, there is a critical value of |$\tilde{L}$| (or, equivalently, a critical value of Pc) above which the cocoon pressure is no longer sufficient to collimate the jet. If |$\tilde{L} \gg \theta _0^{-4/3}$| (or |$P_{\rm c}\gg \rho _{\rm a}c^2 \theta _0^{2/3}$|), the cocoon pressure is not high enough to significantly alter the jet opening angle. (Note that for a typical jet opening angle of ∼ several degrees and an intracluster medium (ICM) temperature of ∼ a few keV, |$\rho _{\rm a}c^2 \theta _0^{2/3} \gg P_{\rm a}$|.) In this case, the jet outflow remains conical with an opening angle ≈θ0, as in the leftmost panel of Fig. 1. We refer to this as the ‘uncollimated’ regime. On the other hand, if |$\tilde{L} \ll \theta _0^{-4/3}$| (or |$P_{\rm c}\ll \rho _{\rm a}c^2 \theta _0^{2/3}$|), the cocoon pressure is sufficient to collimate the jet, transforming it from a conical to a cylindrical flow, as in the middle panel of Fig. 1. Deflection of the flow is achieved via an oblique ‘collimation shock’ that forms near the base of the jet, as indicated by the heavy black line in the figure. The cylindrical shape of the jet in this ‘cocoon-collimated’ regime is a consequence of the near-uniform pressure within the cocoon (B11).
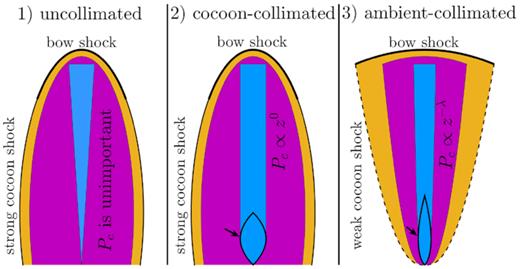
Possible regimes of jet collimation. The jet, cocoon, and shocked ambient mediums are coloured blue, purple, and yellow, respectively. The collimation shock is indicated with an arrow. In the cocoon-collimated case, the cocoon pressure Pc is spatially uniform, but in the ambient-collimated case, it is a power law in the height z.
2.2 Collimation by the ambient pressure
Because Pc, Pa, and ρa all change over time, the system may transition between the different collimation regimes as it evolves. Assuming that the jet head advances non-relativistically, the head position evolves as zh ∝ t3/(5 − α) (B11). Accordingly, the ambient density at the head scales as |$\rho _{\rm a}\propto z_{\rm h}^{-\alpha } \propto t^{-3\alpha /(5-\alpha)}$|, while the ambient pressure at the head’s location obeys |$P_{\rm a}\propto z_{\rm h}^{-\lambda } \propto t^{-3\lambda /(5-\alpha)}$|. Meanwhile, the cocoon pressure falls of as Pc ∝ t−(4 + α)/(5 − α), as discussed above. If the density and pressure profiles are relatively flat, as is typical for ICM environments, then (4 + α) is larger than both 3α and 3λ, and Pc falls off faster than ρa and Pa. In this case, the jet starts out uncollimated, then goes through a cocoon-collimated phase, and finally ends up in the ambient-collimated regime at late times.
On kiloparsec length scales, the jet is firmly in the collimated regime for typical AGN parameters (B11; see also Section 3.2), so we do not further consider the case of an uncollimated jet. However, whether the jet is collimated by the cocoon (as in panel 2 of Fig. 1) or by the ambient pressure (as in panel 3) is less clear. AGN bubble observations impose constraints on the jet properties that offer new insight into the collimation process. We will revisit this discussion in Section 3.2.
We stress that the above discussion is only relevant far from the central black hole, where the jet is propagating into the ICM. The environment close to the central AGN (i.e. within the Bondi radius) is likely considerably different, and this can affect the collimation on scales of ∼ tens of parsecs. Accretion disc winds, in particular, have been shown to impact the jet geometry over these scales (e.g. Globus & Levinson 2016, and references therein). High-resolution observations of M87 (Junor, Biretta & Livio 1999; Asada & Nakamura 2012) have also revealed changes in the jet opening angle within ∼30 pc of the central source. Our model applies to kiloparsec scales where these effects are unimportant. The injection opening angle θ0 adopted here refers to the opening angle of the jet when it escapes the central region and starts to interact with the ICM.
3 BUBBLE EVOLUTION
In an outburst, the central AGN launches bipolar jets into the surrounding medium. The subsequent evolution of the system can be divided into three morphological phases, based on the relation between the age of the system (tage), the burst duration (tb), the time it takes for the outflow to become spherical (tsp), and the time-scale for buoyancy to pull the bubbles apart (tbuoy). These three phases, which we refer to as the jet phase, the bipolar lobes phase, and the quasi-spherical phase, are illustrated in Fig. 2. Two evolutionary paths are possible, depending on whether tbuoy < tsp or tbuoy > tsp.
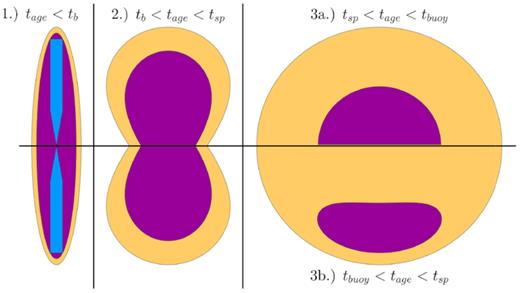
The three phases of evolution for AGN-driven bubbles and shocks. Panel (1) is the jet phase, and panel (2) is the bipolar lobes phase. Panels (3a) and (3b) show the quasi-spherical phase, respectively, for the case of no buoyancy (top) and appreciable buoyancy (bottom). Blue is the collimated jet, purple is the cocoon, and yellow is the shocked ambient medium.
In the initial jet phase (left-hand panel), the collimated jet (blue) inflates a narrow shocked region along the axis. We assume that the jet has a constant one-sided luminosity Lj, so that the total energy injected by the bipolar jets is E = 2Ljtb. The purple and the yellow regions represent the shocked jet material and the shocked ambient medium, respectively, which are separated by a contact discontinuity. The X-ray cavities, or ‘bubbles,’ seen in observations correspond to the region inside the contact discontinuity, which is filled with light jet exhaust and is ultimately affected by buoyancy. (For the rest of the paper, we use the terms ‘bubble’ and ‘cocoon’ interchangeably, with both referring to the shocked jet ejecta.)
We suppose that the jet that drove the bubbles did not persist for long enough to penetrate the surrounding cluster medium. Instead, the jet shut off and was choked at a distance Rch from the central AGN. (We consider the jet to be ‘choked’ once all of the jet ejecta have flown through the jet head and entered the cocoon.) We define the duration tb as the time when the jet shuts off, and the choking time tch as the time when the last of the jet material catches up to the jet head. If the jet material below the head is relativistic, tb and tch are related by tch ≈ tb/(1 − βh) (Nakar 2015), where βh is the velocity of the jet head scaled to c. We work in the limit of a Newtonian jet head, with βh ≪ 1 (we will verify this assumption in Section 3.2). In this case, the non-relativistic jet head does not have time to advance much before the relativistic ejecta catch up, and as a result tch ≈ tb.
After the jet is choked, the initially narrow and elongated jet-driven outflow gradually widens and transforms into a bipolar structure with two distinct lobes (Irwin, Nakar & Piran 2019, hereafter I19), as shown in the middle panel of Fig. 2. In Fig. 3, we illustrate the geometry of the system during this bipolar lobes phase and label the features and length scales of interest. 4
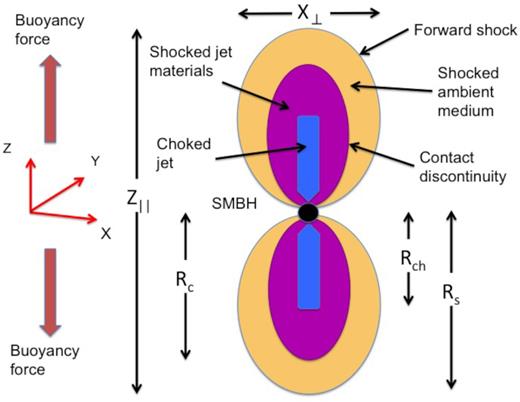
Schematic figure for the choked jet model during the bipolar lobes phase.
Once the forward shock has expanded over a length scale of ∼ tens of Rch, the system enters the quasi-spherical phase (I19). In this phase, the forward shock becomes effectively spherical. However, the evolution of the bubbles depends on whether or not buoyancy is important. In the absence of buoyancy, the bipolar bubbles also merge into a quasi-spherical shape, and the outflow resembles a spherical point explosion, as shown in panel (3a) of Fig. 2. On the other hand, if buoyancy becomes important, the bipolar bubbles are pulled apart and gradually drift away from the central AGN, as shown in panel (3b) of Fig. 2.
3.1 Evolutionary time-scales
The fact that tbuoy and tE are comparable is not a coincidence. As long as the cocoon is expanding more rapidly than the terminal velocity vt, the expansion overcomes buoyancy to keep the bubbles connected. Only once the expansion speed drops below vt can the bubbles be pulled apart by buoyancy. Now, since we consider connected bubbles with Rc ∼ Rs, vt and vk are comparable. Additionally, it is straightforward to show that an ambient medium in virial equilibrium satisfies vk ∼ cs, where cs is the ambient sound speed. Thus, we see that vt ∼ cs, which means that the time tbuoy when the bubbles separate is about the same as the time tE when pressure equilibrium is achieved and the Mach number becomes order-unity.
3.2 Choking radius and jet geometry
In this paper, we focus on bubbles and forward shocks which are in the bipolar lobes phase and are not strongly affected by buoyancy, as illustrated in panel 2 of Fig. 2. Bubbles uplifted by the buoyancy force are deformed and are more difficult to study due to projection effects. In general, the requirement for finding a system in the bipolar lobes phase is tage < min (tE, tbuoy, tsp). However, our need for reliable measurements of the bubble geometry and ICM properties resulted in a sample of five well-studied, fairly evolved systems with sufficiently good spatial resolution. In each object we consider, we find that the shocks driven by the bubbles have a low Mach number (M < 2), indicating that they are close to reaching pressure equilibrium with the ambient medium, i.e. tage ∼ tE. Since tE and tbuoy are also comparable (as discussed above), all the systems studied here satisfy tage ∼ tE ∼ tbuoy < tsp.
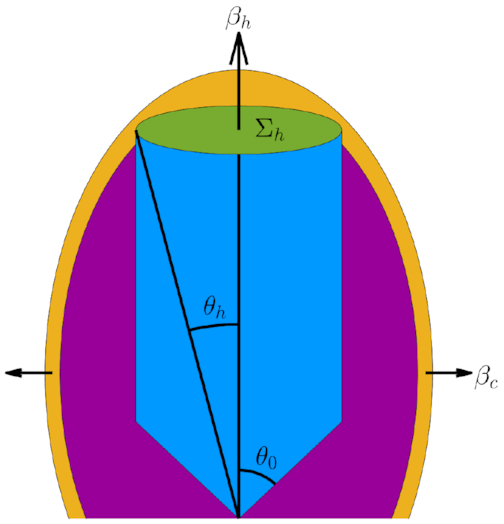
Geometry of the jet prior to choking, depicting the collimated jet (blue), jet head (green), cocoon (purple), and shocked ambient gas (yellow). The head velocity βh, the cocoon shock velocity βc, the jet injection angle θ0, and the head’s cross-section Σh and angular size θh are indicated.
Comparing Pc,ch to the observed ambient pressure, we find that |$P_{\rm c,ch}\gtrsim P_{\rm a}$|, indicating that the jet was in the cocoon-collimated regime. This is not too surprising, since all our objects have tage ∼ tE, which suggests that external pressure is just now becoming important.
3.3 Jet duration and opening angle
A possible way to break the degeneracy is to compare the relative size and shape of the X-ray cavity and the forward-shocked region. As time goes on, the contact discontinuity moves inward relative to the forward shock, and therefore Rc/Rs is smaller for older outflows. As a first approximation, we apply the point explosion model in Tang & Churazov (2017) to estimate E, tage, and tb. The model assumes that each bubble is spherically symmetric and that the energy is injected non-relativistically.
While the values of E and tage estimated from the spherical model are most likely reliable, tb could be much smaller than what is inferred from the spherical model if the bubbles were inflated by a narrow, relativistic jet, instead of a wide, non-relativistic wind. There are two reasons for this. First, a jet will always reach a given radius faster than a spherical outflow with the same energy. Secondly, a jet has Rc/Rs ≈ 1 up to the moment of choking, whereas a wind could already have Rc/Rs < 1 when energy injection ends. For these reasons, the value of tb obtained in the spherical model should be considered as an upper limit. More detailed modelling is needed to understand how the contact discontinuity evolves in the choked jet case and improve the constraints on tb.
The limits on ζ and η can be tightened further by considering the geometry of the outflow. For each object, we first estimate the aspect ratio of the forward shock, z∥/x⊥, from observations (see Fig. 3 for the definition of z∥ and x⊥). Due to projection effects, we can only place a lower limit on z∥/x⊥. We then compare the observations to a model for the shape of the forward shock in a choked jet outflow (I19). In the I19 model, the aspect ratio of the forward shock and the parameter ζ are computed as functions of η using the Kompaneets approximation, for a given initial aspect ratio and injected energy (see their figs 10 and 12). We assume that the initial aspect ratio of the forward shock upon choking was |$\approx [12/(3-\alpha)]^{1/2} \theta _0^{-1}$|, as is appropriate for a jet with a non-relativistic head (B11). Then, for different choices of θ0, we evolve the I19 model until the aspect ratio is equal to the observed aspect ratio, and compute the corresponding value of ζ at that time. Repeating this process for many choices of θ0 gives the minimum value of ζ needed to reproduce the observed aspect ratio of the forward shock, as a function of η. (Models with smaller ζ would result in a smaller aspect ratio than the observed one, even if viewed edge-on.) The lower limit on ζ inferred in this way is tighter than the one given in equation (9), particularly as η approaches unity.
The resulting constraints are illustrated in Fig. 5, using Perseus as an example. For this object, we estimate |$z_\parallel /x_\bot \gtrsim 1.5$| and Rc/Rs ≈ 0.67, which constrains the object to lie in the pink region in the figure. For reference, we also show several lines of constant θ0. Although ζ is confined to a narrow range 0.33 < ζ < 0.67, we can only place upper limits on η and θ0 due to degeneracy. We find that η < 0.36 and θ0 < 58°. The upper limit on tb is similar to the one obtained from the spherical model discussed above. Since E is well-constrained, the maximum value of η implies a minimum value for the jet luminosity, |$L_{\rm j}\gt 6.8 \times 10^{44}\rm erg\, s^{-1}$|.
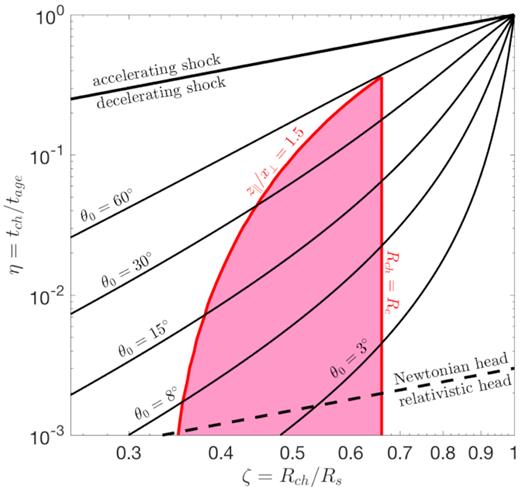
Constraints on ζ and η from the geometry of Perseus. The parameters are constrained to the pink region beneath the two red curves. The vertical red line represents the fact that the choking radius, Rch, must be less than the observed radius of the contact discontinuity, Rc. The curved red line is a curve of constant aspect ratio, z∥/r⊥ = 1.5, derived using the model of I19 (see their fig. 10). Above this line, the forward shock would be too spherical to explain the observations. The dividing lines between an accelerating and decelerating shock, and between a Newtonian and relativistic jet head, are respectively indicated by the solid and dashed heavy black lines. The thin black lines show the evolution of ζ versus η for several choices of the jet opening angle θ0.
The bound on θ0 corresponds to an aspect ratio of |$\gtrsim\!2.0$| when the jet was choked. Note that this minimum value applies to the most favourable case, where the jet axis is perpendicular to the line of sight. For a jet axis inclined by an angle i with respect to the line of sight, the minimum aspect ratio becomes |$2.0 \csc i$|, further strengthening the case for a jetted outflow.
Because we assumed a non-relativistic jet head, our model is only valid above the dashed line in Fig. 5. This requirement can only be satisfied for |$\theta _0 \gtrsim 1 ^{\circ }$| and |$\eta \gtrsim 10^{-3}$|. However, while a Newtonian head seems likely according to equation (15), the possibility of a relativistic head with smaller θ0 and/or η cannot be ruled out.
Although the model permits a wide range of jet opening angles, there are a few reasons to prefer a narrower θ0. First, the results of Section 3.2 suggest that the jet was strongly collimated by the cocoon, with |$\theta _{\rm h}\lesssim 2^{\circ }$|. It may not be possible for wide-angle outflows to become so tightly collimated. Models for collimation by the cocoon (e.g. B11) typically assume that θ0 is small, but when θ0 is ∼ tens of degrees, the physics are less well understood. Secondly, for typical parameters, the ram pressure of the jet is much larger than the ambient pressure. Therefore, a collimated jet is expected to produce strong shocks, at least on the axis. The fact that we only see low Mach number shocks in every object argues against a recently quenched jet.
4 RESULTS AND DISCUSSION
For each object in our sample, we repeat the process outlined in Section 3.3. The resulting constraints on ζ and η are plotted in Fig. 6, with each object constrained to lie under the respective coloured curve. The upper limits on tb and θ0 and the lower limit on Lj inferred from the choked jet model are reported in Table 3. For all the objects, we find similar constraints on the choking radius, with ζ residing in the range |$0.1 \lesssim \zeta \lesssim 0.8$|. On the other hand, for most of our sample the opening angle and jet duration are only weakly constrained. M87, which seems to prefer a narrow jet that was choked a long time ago, is an exception. The tighter constraints on this object are partly due to the smaller size of the bubble compared to the forward shock, and partly due to the slightly larger inferred aspect ratio (see below).
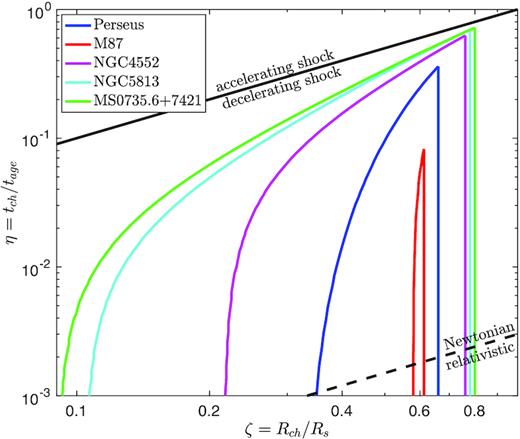
Constraints on ζ and η based on the bubble geometry, as in Fig. 5, but for all the objects in our sample. For each object, the parameters are constrained to lie under the respective coloured curve.
| Name . | |$t_{\rm age}(\, \rm Myr)$| . | |$E (10^{57} \rm erg)$| . | |$R_{\rm ch}(\, \rm kpc)$| . | βh/βc . | |$L_{\rm j}(10^{42} \rm erg\, s^{-1})$| . | |$t_{\rm b}(\, \rm Myr)$| . | θ0 . | Λ(Rch) . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 13.5 | 2.10e+02 | 7.5–15.0 | |$\gtrsim\!2.0$| | |$\gtrsim$| 680 | |$\lesssim\!4.9$| | |$\lesssim$|58° | 0.3–0.5 |
| M87 | 15.3 | 9.27e+00 | 7.5–8.1 | |$\gtrsim\!6.7$| | |$\gtrsim\!120$| | |$\lesssim\!1.2$| | |$\lesssim\!21^{\circ }$| | – |
| MS 0735.6+7421a | 97.6 | 7.71e+04 | 29–259 | |$\gtrsim\!1.4$| | |$\gtrsim$| 1.9e4 | |$\lesssim\!66$| | |$\lesssim\!90^{\circ }$| | 0.2–0.3 |
| NGC 4552 | 2.3 | 7.45e–02 | 0.3–1.0 | |$\gtrsim\!1.6$| | |$\gtrsim$| 0.82 | |$\lesssim\!1.4$| | |$\lesssim\!85^{\circ }$| | 0.2–0.4 |
| NGC 5813 | 14.2 | 1.17e+01 | 1.6–11.6 | |$\gtrsim\!1.5$| | |$\gtrsim$| 21 | |$\lesssim\!8.7$| | |$\lesssim\!90^{\circ }$| | 0.1–0.3 |
| Name . | |$t_{\rm age}(\, \rm Myr)$| . | |$E (10^{57} \rm erg)$| . | |$R_{\rm ch}(\, \rm kpc)$| . | βh/βc . | |$L_{\rm j}(10^{42} \rm erg\, s^{-1})$| . | |$t_{\rm b}(\, \rm Myr)$| . | θ0 . | Λ(Rch) . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 13.5 | 2.10e+02 | 7.5–15.0 | |$\gtrsim\!2.0$| | |$\gtrsim$| 680 | |$\lesssim\!4.9$| | |$\lesssim$|58° | 0.3–0.5 |
| M87 | 15.3 | 9.27e+00 | 7.5–8.1 | |$\gtrsim\!6.7$| | |$\gtrsim\!120$| | |$\lesssim\!1.2$| | |$\lesssim\!21^{\circ }$| | – |
| MS 0735.6+7421a | 97.6 | 7.71e+04 | 29–259 | |$\gtrsim\!1.4$| | |$\gtrsim$| 1.9e4 | |$\lesssim\!66$| | |$\lesssim\!90^{\circ }$| | 0.2–0.3 |
| NGC 4552 | 2.3 | 7.45e–02 | 0.3–1.0 | |$\gtrsim\!1.6$| | |$\gtrsim$| 0.82 | |$\lesssim\!1.4$| | |$\lesssim\!85^{\circ }$| | 0.2–0.4 |
| NGC 5813 | 14.2 | 1.17e+01 | 1.6–11.6 | |$\gtrsim\!1.5$| | |$\gtrsim$| 21 | |$\lesssim\!8.7$| | |$\lesssim\!90^{\circ }$| | 0.1–0.3 |
| Name . | |$t_{\rm age}(\, \rm Myr)$| . | |$E (10^{57} \rm erg)$| . | |$R_{\rm ch}(\, \rm kpc)$| . | βh/βc . | |$L_{\rm j}(10^{42} \rm erg\, s^{-1})$| . | |$t_{\rm b}(\, \rm Myr)$| . | θ0 . | Λ(Rch) . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 13.5 | 2.10e+02 | 7.5–15.0 | |$\gtrsim\!2.0$| | |$\gtrsim$| 680 | |$\lesssim\!4.9$| | |$\lesssim$|58° | 0.3–0.5 |
| M87 | 15.3 | 9.27e+00 | 7.5–8.1 | |$\gtrsim\!6.7$| | |$\gtrsim\!120$| | |$\lesssim\!1.2$| | |$\lesssim\!21^{\circ }$| | – |
| MS 0735.6+7421a | 97.6 | 7.71e+04 | 29–259 | |$\gtrsim\!1.4$| | |$\gtrsim$| 1.9e4 | |$\lesssim\!66$| | |$\lesssim\!90^{\circ }$| | 0.2–0.3 |
| NGC 4552 | 2.3 | 7.45e–02 | 0.3–1.0 | |$\gtrsim\!1.6$| | |$\gtrsim$| 0.82 | |$\lesssim\!1.4$| | |$\lesssim\!85^{\circ }$| | 0.2–0.4 |
| NGC 5813 | 14.2 | 1.17e+01 | 1.6–11.6 | |$\gtrsim\!1.5$| | |$\gtrsim$| 21 | |$\lesssim\!8.7$| | |$\lesssim\!90^{\circ }$| | 0.1–0.3 |
| Name . | |$t_{\rm age}(\, \rm Myr)$| . | |$E (10^{57} \rm erg)$| . | |$R_{\rm ch}(\, \rm kpc)$| . | βh/βc . | |$L_{\rm j}(10^{42} \rm erg\, s^{-1})$| . | |$t_{\rm b}(\, \rm Myr)$| . | θ0 . | Λ(Rch) . |
|---|---|---|---|---|---|---|---|---|
| Perseus | 13.5 | 2.10e+02 | 7.5–15.0 | |$\gtrsim\!2.0$| | |$\gtrsim$| 680 | |$\lesssim\!4.9$| | |$\lesssim$|58° | 0.3–0.5 |
| M87 | 15.3 | 9.27e+00 | 7.5–8.1 | |$\gtrsim\!6.7$| | |$\gtrsim\!120$| | |$\lesssim\!1.2$| | |$\lesssim\!21^{\circ }$| | – |
| MS 0735.6+7421a | 97.6 | 7.71e+04 | 29–259 | |$\gtrsim\!1.4$| | |$\gtrsim$| 1.9e4 | |$\lesssim\!66$| | |$\lesssim\!90^{\circ }$| | 0.2–0.3 |
| NGC 4552 | 2.3 | 7.45e–02 | 0.3–1.0 | |$\gtrsim\!1.6$| | |$\gtrsim$| 0.82 | |$\lesssim\!1.4$| | |$\lesssim\!85^{\circ }$| | 0.2–0.4 |
| NGC 5813 | 14.2 | 1.17e+01 | 1.6–11.6 | |$\gtrsim\!1.5$| | |$\gtrsim$| 21 | |$\lesssim\!8.7$| | |$\lesssim\!90^{\circ }$| | 0.1–0.3 |
This is not the only way in which M87 is exceptional. Although most of the objects in our sample have an aspect ratio of ∼1.5, in M87 the observed aspect ratio of the shock is close to unity. However, comparing our estimated age for this object to the time-scales from Section 3.1, we find that tage < tbuoy ≪ tsp. If the M87 bubble was driven by a jet, then this suggests that it is still in the bipolar phase of Fig. 2. One explanation for the system appearing nearly spherical is that we are viewing the system along the axis. If this is the case, we cannot directly constrain the aspect ratio from observations, but we can constrain the bubbles’ width. We therefore take a different approach to estimate z∥/x⊥ for this object. For the same explosion energy and ambient density, a bipolar outflow is always more extended along the axis than a spherical blast wave. Thus, we must have z∥ > 2Rbw, where |$R_{\rm bw} \sim (Et_{\rm age}^2/\rho _{\rm a})^{1/5}$| is the radius expected for a spherical blast wave (Taylor 1950; Sedov 1959). For a system viewed along the axis, we also have x⊥ = 2Rs. Therefore, the aspect ratio must satisfy |$z_\parallel /x_\bot \gt R_{\rm bw}/R_{\rm s}\sim (E t_{\rm age}^2/\rho _{\rm a}R_{\rm s}^5)^{1/5}$|. Applying this method to M87, we infer a minimum aspect ratio of z∥/x⊥ ≃ 2.6, somewhat larger than what is observed for the rest of the objects. Another complication is that the apparent ratio of Rc/Rs is smaller for a system observed along the axis than for a system observed edge-on. To estimate the true value of Rc/Rs that would be observed in the edge-on case, we assume that the bubble is roughly spherical and that its centre lies approximately halfway between the origin and the forward shock along the major axis (as is observed for the individual bubbles in our other systems). We then find a true value of Rc/Rs ≃ 0.6 for M87, which is comparable with observations of the other four objects.
M87 is also special among the objects in our sample in that it contains both a relic bubble and a well-studied active jet. We can therefore consider whether the jet which inflated the bubble in M87 was similar to the currently active jet. Interestingly, the observed jet lies nearly along the line of sight (Biretta, Sparks & Macchetto 1999; Wang & Zhou 2009), which is compatible with the orientation inferred from the bubble geometry. The observed half-opening angle of the M87 jet is ∼30° near the base, and decreases to a steady value of about 3.5° beyond |$10 \,$| pc (Junor et al. 1999). The bolometric jet luminosity currently measured in M87 is |$2.7\times 10^{42}\, \rm erg\, s^{-1}$| (Prieto et al. 2016), but a considerably higher mechanical luminosity of 1–3|$\times 10^{44}\,\rm erg\, s^{-1}$| is inferred from studying the kinematics of knots in the jet (Bicknell & Begelman 1996). The inferred mechanical luminosity is close to the minimum value of |$\sim 1 \times 10^{44}\, \rm erg\, s^{-1}$| allowed in the bubble model, but to match this luminosity a larger jet opening angle of ∼20° would be required. On the other hand, if we assume an opening angle of θ0 = 3.5°, as observed, we find that a much larger jet luminosity, |$\sim 2 \times 10^{45} \,\rm erg\, s^{-1}$|, would be needed to inflate the observed bubble. In conclusion, although the jet which drove the observed relic bubble had a similar orientation as the jet that we observe today, it must have been either wider or more luminous. The difference in jet properties is consistent with the picture that the jet responsible for inflating the bubble in M87 was quenched a long time ago. It is hard to say whether the similar orientation indicates a connection between the two episodes of jet activity, or is just a coincidence.
So far, we have considered a scenario where the jet is choked because the central engine driving it is switched off. An alternative possibility is that the jet is disrupted by the 3D magnetic kink instability, as proposed by Tchekhovskoy & Bromberg (2016). For a given galaxy density and pressure profile, there is a critical jet power, above which the jets remain stable and are able to penetrate the surrounding medium, forming powerful backflows. Below the critical power, on the other hand, the jets become kink-unstable and eventually break apart. After disruption, the magnetic field dissolves and the outflow becomes effectively hydrodynamic. The collimated magnetic jets are thus transformed into wide-angle hydrodynamic outflows that inflate bubbles of relativistic plasma. This scenario differs from the model discussed in Section 3 in that the jet power is continuous, rather than being switched off at tb. However, the shape of the forward shock produced by a continuous, wide-angle (|$\gtrsim$|1 radian) outflow emanating from Rch can be approximated in our model by adopting tb ∼ tage and Lj ∼ E/2tage. (In this picture, Rch refers to the radius where the jet breaks apart.) As discussed above, continuous energy injection is disfavoured for M87, but for the other objects in our sample it is plausible that tb and tage are comparable, to within a factor of ∼2 (see Fig. 6).
5 CONCLUSION
We consider relic bubbles in 5 FR type-I AGN systems: Perseus, M87, MS 0735.6+7421, NGC 4552, and NGC 5813. Motivated by the lack of spherical symmetry in most of these systems, we explore a choked jet model in which the bubbles were inflated by bipolar jets that are no longer active, and investigate how available bubble observations constrain the properties of these jets.
Unlike previous analytical works that assumed spherical symmetry of the bubbles, we take their asymmetry into account and show that the quasi-ellipsoidal shape of the forward shock places tight constraints on the radius Rch at which the jet was quenched. In every object, we find that Rch is several tenths of the current radius of the bubbles. Combining this result with the assumption of a decelerating forward shock, we show that the jet must have been tightly collimated prior to quenching, with the jet head subtending an angle of |$\theta _{\rm h}\lesssim 2 ^{\circ }$|. Furthermore, our results suggest that the jet was collimated by its own cocoon, and was not influenced much by the ambient pressure while it was active.
The tight limits on the choking radius place strong constraints on the allowed properties of the jet, with the jet duration tb and initial opening angle θ0 obeying equation (20). This implies that if the jet was injected with a wide angle (∼tens of degrees), then it must have been active for a time comparable to the age of the system (∼10 Myr). On the other hand, if the jet was narrow at injection (∼a few degrees), it must have been very short-lived, lasting only ∼0.1 Myr. Wide, short-lived jets are ruled out because they would produce a forward shock that is more spherical than what we observe. Narrow, long-lived jets are also excluded because in that case the reverse shock would have already propagated beyond the observed location of the contact discontinuity.
These results may have interesting implications for the FR morphological dichotomy. We speculate that diffuse radio bubbles, like the ones considered here, originate from jets that could not traverse the cluster’s core before turning off, because they were unusually wide and/or unusually short-lived. An alternative possibility – that the bubbles were inflated by jets disrupted by the magnetic kink instability, as suggested by Tchekhovskoy & Bromberg (2016) – also seems broadly consistent with the available data. Since this second scenario involves a wide outflow, it can only work if the jet was disrupted on a time-scale comparable with the age of the bubbles.
The choked jet model we consider provides a time-dependent alternative to the traditional, steady-state picture of a turbulently flaring FR type-I jet continuously feeding its lobes (e.g. Bicknell 1984, 1995; Hardee, Clarke & Howell 1995; Laing & Bridle 2014). In this picture, internal shocks and entrainment cause the jet to decelerate and transition from laminar to turbulent flow. This picture bears similarities to the Tchekhovskoy & Bromberg (2016) model discussed above, except that the jet is disrupted by turbulence rather than the development of the kink instability. In comparing our model with the Tchekhovskoy & Bromberg (2016) scenario, we concluded that a wide-angle jet with a duration tb comparable to the current age tage is difficult to tell apart from a magnetically disrupted jet, and the same holds true in regards to the classical picture. That is to say, in cases where it is not clear whether the X-ray cavities are relics (i.e. when tb ∼ tage), we expect the choked jet model and the turbulently flaring jet model to be difficult to distinguish observationally. However, at least in some cases, our model suggests that tb is considerably shorter than tage, lending confidence to the idea that these bubbles are indeed relics of past jet activity.
An important caveat to the above discussion is that we only consider cases in which the outflow is injected at a relativistic speed. We cannot exclude the possibility that the bubbles were inflated by quasi-spherical, non-relativistic outflows, as considered previously by, e.g. Tang & Churazov (2017) and references therein. However, in Perseus and M87, we estimate that the aspect ratio of the outflow was |$\gtrsim\!2$| when energy injection ended. While this is not conclusive proof of a jet, it may be difficult to achieve via a non-relativistic wind.
Among the objects we investigate, M87 serves as a useful case study, because it contains both a bubble inflated by past jet activity and a currently active jet. Comparing the observed jet properties to the constraints that we infer from the bubble geometry gives valuable insight into the system’s history. The shock surrounding the bubble in M87 is unique because of its apparent spherical symmetry. However, we find that the age of the system, tage ∼ 15 Myr, is much smaller than the time it would take for the forward shock to become spherical, tsp ∼ 13 Gyr. Based on this, we suggest that the bubble is not truly spherical, but rather is a bipolar structure viewed along the symmetry axis. This idea aligns well with previous studies by Biretta et al. (1999) and Wang & Zhou (2009), who suggested that the jet axis in M87 lies nearly along the line of sight. Due to the small size of the bubble relative to the forward shock in M87, we infer that the outburst that drove the bubbles was quenched long ago, after no more than ∼1.5 Myr of activity, in agreement with Tang & Churazov (2017). However, if we adopt the luminosity and opening angle of the currently observed jet, we are unable to reproduce the measured bubble properties. We conclude that the bubble in M87 was inflated by a previous episode of jet activity that ended roughly ∼15 Myr ago, and that during that time the jet was either wider or more luminous than the jet we observe today.
Unfortunately, for the rest of the objects in our sample, we are unable to distinguish between a narrow, short-lived jet and a wider, longer-lived one. This situation may be improved by a more complete theory. The present model is limited in that it only considers the shape of the forward shock; a more sophisticated model that also treats the shape of the contact discontinuity in choked jet outflows is needed. By comparing the relative size and shape of the bubble and forward shock, the degeneracy between tb and θ0 can potentially be resolved. Catching a system during the early evolution (i.e. during the transition from the jet phase to the bipolar lobes phase of Fig. 2) would also go a long way towards improving our understanding of jet-inflated AGN bubbles.
ACKNOWLEDGEMENTS
We thank O. Bromberg and E. Churazov for helpful discussions. We also thank the anonymous referee for valuable comments and suggestions that improved the paper. This research is supported by the CHE-ISF I-Core Center for Excellence in Astrophysics. TP is supported by an advanced ERC grant TReX. This work was supported in part by the Zuckerman STEM Leadership Program.
Footnotes
We define tage as the time since the jet was launched.
To help keep track of the meanings of symbols introduced throughout the paper, we provide a glossary in Table 1.
Throughout the paper, we adopt solar abundance and a mean molecular weight of 0.6.
Note that we define Rc and Rs as distances measured from the central black hole along the major axis, whereas Tang & Churazov (2017) defined them as distances measured from the centre of the bubbles.
The time-scale tsp is defined as the time when the width of the outflow becomes 90 per cent of its height.
The values of Rs and Rc defined here are roughly twice the values given in Churazov et al. (2001).
E defined here is two times that in Tang & Churazov (2017).



