Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

ABSTRACT

We present a general method to compute the non-linear matter power spectrum for dark energy (DE) and modified gravity scenarios with per cent-level accuracy. By adopting the halo model and non-linear perturbation theory, we predict the reaction of a lambda cold dark matter (ΛCDM) matter power spectrum to the physics of an extended cosmological parameter space. By comparing our predictions to N-body simulations we demonstrate that with no-free parameters we can recover the non-linear matter power spectrum for a wide range of different w0–wa DE models to better than 1 per cent accuracy out to k ≈ 1 |$h \,{\rm Mpc}^{-1}$|⁠. We obtain a similar performance for both DGP and f(R) gravity, with the non-linear matter power spectrum predicted to better than 3 per cent accuracy over the same range of scales. When including direct measurements of the halo mass function from the simulations, this accuracy improves to 1 per cent. With a single suite of standard ΛCDM N-body simulations, our methodology provides a direct route to constrain a wide range of non-standard extensions to the concordance cosmology in the high signal-to-noise non-linear regime.

methods: analytical, large-scale structure of Universe, cosmology: theory

1 INTRODUCTION

General relativity (GR) has been put under intense scrutiny in the Solar system, where it has successfully passed all tests (Will 2014). Its application to cosmology, however, involves vastly different length-scales and is comparable in orders of magnitude to an extrapolation from an atomic nucleus to the scale of human experience. It is therefore important to perform independent tests of our theory of gravity in the cosmological regime. Further motivation for a thorough inspection of cosmological gravity can be drawn from the necessity of a large dark sector in the energy budget of our Universe to explain large-scale observations with GR (Riess et al. 1998; Perlmutter et al. 1999; Hildebrandt et al. 2017; Abbott et al. 2018; Aghanim et al. 2018). In particular the late-time accelerated expansion of the cosmos has traditionally been an important driver for the development of alternative theories of gravity, a concept that has, however, become strongly challenged with the confirmation of the luminal speed of gravity (Lombriser & Taylor 2016; Abbott et al. 2017b; Baker et al. 2017; Creminelli & Vernizzi 2017; Lombriser & Lima 2017; María Ezquiaga & Zumalacárregui 2017; Sakstein & Jain 2017; Battye, Pace & Trinh 2018; Creminelli et al. 2018; de Rham & Melville 2018). Nevertheless, cosmic acceleration could be the result of a dark energy (DE) field permeating the Universe that may well be coupled to matter with an observable impact on cosmological scales. Importantly, should that coupling be universal, i.e. affecting baryons and dark matter equally, the corresponding models must then rely on the employment of screening mechanisms to comply with the stringent Solar system bounds (Vainshtein 1972; Khoury & Weltman 2004; Babichev, Deffayet & Ziour 2009; Hinterbichler & Khoury 2010). Signatures of screening are naturally to be expected in the non-linear cosmological small-scale structure, where modified gravity transitions to GR, and for some models are even exclusively confined to these scales (Wang, Hui & Khoury 2012; Heymans & Zhao 2018). The increasing wealth of high-quality data at these scales (Laureijs et al. 2011; LSST Dark Energy Science Collaboration 2012; Hildebrandt et al. 2017; Abbott et al. 2018) renders cosmological tests of gravity a very timely enterprize. At the same time, cosmological structure formation proves notoriously difficult to model to sufficient accuracy in this regime, where high-signal-to-noise measurements have the potential to distinguish a few per cent deviation from GR (Heymans & Zhao 2018).

For any given theory of gravity or DE model, our current best predictions for the statistical properties of the resulting matter distribution come from large-volume high-resolution N-body simulations (Oyaizu 2008; Schmidt 2009b; Zhao, Li & Koyama 2011; Baldi 2012; Brax et al. 2012; Li et al. 2012; Barreira et al. 2013; Puchwein, Baldi & Springel 2013; Wyman, Jennings & Lima 2013; Li et al. 2013b; Llinares, Mota & Winther 2014; Winther et al. 2015). Running these, however, can take up to thousands of node-hours on dedicated cluster facilities, and although methods to partially alleviate this drawback exist (see e.g. Barreira, Bose & Li 2015; Mead et al. 2015a; Bose et al. 2017; Llinares 2017; Valogiannis & Bean 2017; Winther et al. 2017) exploring vast swathes of the theory space remains currently unfeasible. Alternatively, analytical and semi-analytical methods can be used to swiftly predict specific large-scale structure observables, such as the matter power spectrum (Koyama, Taruya & Hiramatsu 2009; Schmidt et al. 2009; Schmidt, Hu & Lima 2010; Li & Hu 2011; Fedeli, Dolag & Moscardini 2012; Brax & Valageas 2013; Lombriser, Koyama & Li 2014; Zhao 2014; Barreira et al. 2014a, b; Achitouv et al. 2016; Mead et al. 2016; Aviles & Cervantes-Cota 2017; Bose et al. 2018; Cusin, Lewandowski & Vernizzi 2018; Hu, Liu & Cai 2018), with the important caveat that they have limited accuracy in the non-linear regime of structure formation, and often involve some level of fitting to the same quantity measured in simulations. These approaches are therefore inadequate for future applications to high-quality data from Stage IV surveys (Laureijs et al. 2011; LSST Dark Energy Science Collaboration 2012; Levi et al. 2013; Koopmans et al. 2015), where per cent level accuracy over a wide range of scales will be necessary to obtain tight and unbiased constraints on departures from GR (Alonso et al. 2017; Casas et al. 2017; Reischke et al. 2018; Spurio Mancini et al. 2018; Taylor, Bernardeau & Kitching 2018b) and the nature of DE (Albrecht et al. 2006). Matter power spectrum emulators can provide a solution to this problem for particular modified gravity or DE models (Heitmann et al. 2014; Lawrence et al. 2017; Euclid Collaboration 2018; Winther et al. 2019), but still rely on the availability of large quantities of computational resources to determine the properties of the matter power spectrum at the location of the emulator nodes. The absence of a clear attractive alternative to the ΛCDM paradigm calls for a more general framework, one easily adaptable to non-standard cosmologies beyond the handful of well-studied cases.

Here we take an important step in this direction by extending the method proposed in Mead (2017), where the halo model is used to compute matter power spectrum ratios with respect to a convenient baseline cosmology. Mead (2017) showed that by determining these ratios, rather than the absolute value of the matter power spectrum, the shortcomings of the halo model are mitigated. The initial conditions of the baseline cosmology are designed so that under GR + ΛCDM evolution the linear clustering of matter at some given redshift exactly reproduces that of the target cosmology of interest, whose evolution is instead governed by non-standard laws of gravity and/or background expansion. Assuming one can generate an accurate non-linear matter power spectrum for the reference cosmology (e.g. with a suitable emulator), recovery of the target power spectrum then hinges on the computation of a ‘correction’ factor that incorporates the non-linear effects of fifth forces, screening mechanisms, and deviations from the cosmological constant. We use the halo model and non-linear perturbation theory to obtain such corrections, and refer to this quantity as the reaction.

The paper is organized as follows. In Section 2 we briefly describe popular modified gravity and DE models used here as test beds for our methodology. Section   3 reviews the halo model formalism and introduces the matter power spectrum reactions. The cosmological simulations used to validate our approach are described in Section 4, and Section 5 presents the capability of the halo model reactions to predict the non-linear matter power spectrum. We summarize our conclusions in Section 6. We provide details of the spherical collapse and perturbation theory calculations employed in this work in Appendices  A and  B, respectively. Additional tests to gauge the importance of the halo mass function and halo concentration in our predictions are presented in Appendix  C.

2 DARK ENERGY AND MODIFIED GRAVITY THEORY

The most general four dimensional scalar–tensor theory with second-order equations of motion is described by the action (Horndeski 1974; Deffayet et al. 2011; Kobayashi, Yamaguchi & Yokoyama 2011)
(1)
where g is the determinant of the metric gμν minimally coupled to a generic matter field ψ (Jordan frame), |${\cal L}_{\rm m}$| is the matter Lagrangian, ϕ is the scalar degree of freedom, and the terms entering the Einstein–Hilbert Lagrangian are
(2)
Here, K and Gi are arbitrary functions of ϕ and X ≡ −∇νϕ∇νϕ/2, and the subscripts X and ϕ denote derivatives.
The nearly simultaneous detection of gravitational waves and electromagnetic signals emitted from two colliding neutron stars (Abbott et al. 2017a) imposes tight constraints on the present-day speed of gravitational waves cT, i.e. |cT/c − 1| ≲ 10−15, where c is the speed of light (Abbott et al. 2017b). Restricting ourselves to theories of gravity with non-evolving cT, and requiring this not to be achieved by extreme fine tuning of the G4 and G5 functions (Lombriser & Taylor 2016; Baker et al. 2017; Creminelli & Vernizzi 2017; Lombriser & Lima 2017; María Ezquiaga & Zumalacárregui 2017; Sakstein & Jain 2017; Battye et al. 2018; de Rham & Melville 2018), implies that the remaining Horndeski Lagrangian takes the form (McManus, Lombriser & Peñarrubia 2016)
(3)
In this paper we focus on well-studied models of modified gravity and DE, each exploring the effects introduced by the individual terms in equation (3). Quintessence and k-essence DE models are described by a contribution of K only (Section 2.3). G4 introduces a coupling of this field to the metric that modifies gravity. The class of models described by this term encompasses the chameleon (Khoury & Weltman 2004), symmetron (Hinterbichler & Khoury 2010), and k-mouflage (Babichev et al. 2009) screening mechanisms, and we will study a particular example of this action with chameleon screening in Section 2.1 when considering a realization in f(R) gravity. The G3 term appears, for instance, in the four-dimensional effective scalar–tensor theory of DGP braneworld gravity (Section 2.2) and gives rise to the Vainshtein screening mechanism (Vainshtein 1972). Either G3 or non-canonical kinetic contributions in K produce a non-luminal sound speed of the scalar field fluctuations that can yield observable scale-dependent effects beyond the sound horizon. The mass scale associated with a scalar field potential in K can furthermore introduce a scale-dependent growth of structure below the sound horizon. With cT = 1, a genuine self-acceleration of the cosmological background that is directly attributed to modified gravity must arise from G4 (Lombriser & Taylor 2016), which is however in tension with observations (Lombriser & Lima 2017). A self-acceleration from K or G3 that dispenses with the need of a cosmological constant is, in contrast, still observationally feasible.
Throughout, we assume a flat Friedmann–Robertson–Walker (FRW) background, and the perturbed metric in the Newtonian gauge reads1
(4)
where Ψ and Φ denote the two gravitational potentials, and a is the scale factor. The evolution of non-relativistic matter perturbations is determined by Ψ, whereas photons follow the null geodesics defined by the lensing potential Φ− = (Ψ − Φ)/2 (see e.g. Carroll 2004). For all models considered here Φ− = ΨN, where ΨN is the standard Newtonian potential.

2.1 f(R) gravity

In f(R) gravity the Einstein–Hilbert action is modified to contain an additional non-linear function of the Ricci scalar R, that is
(5)
The f(R) Lagrangian is a particular case of equation (3) with the Horndeski functions (see e.g. de Felice, Kobayashi & Tsujikawa 2011)
(6)
(7)
(8)
where we defined the scalaron field fR ≡ df/dR, and used |$\phi = (1 + f_R)/\sqrt{8\pi G}$|⁠. In the quasi-static regime,2 structure formation is governed by the following coupled equations (e.g. Oyaizu 2008):
(9)
(10)
where |$\delta \rho _{\rm m} = \rho _{\rm m} - \bar{\rho }_{\rm m}$|⁠, |$\delta R = R - \bar{R}$|⁠, and |$\delta f_R = f_R - \bar{f}_R$| are the matter density, curvature, and scalaron perturbations with respect to their background averaged values, respectively. Equations (9) and (10) can be combined to give
(11)
which explicitly shows that the scalar field fluctuations source an additional fifth force.
Since GR accurately describes gravity in our Solar system, viable modifications must also be compatible with local constraints. In f(R) gravity this is achieved by means of the chameleon screening mechanism (Khoury & Weltman 2004), which suppresses departures from standard gravity for large enough potential wells ΨN. In practice, structures are screened if the thin shell condition,
(12)
is satisfied. Stable theories require fR < 0 (Hu & Sawicki 2007), thus the chameleon screening activates throughout an isolated object if |$|\delta f_R| \le |\bar{f}_R| \ll |\Psi _{\rm N}|$|⁠. Assuming that the Milky Way is placed in the cosmological background, and knowing that |ΨMW| ∼ 10−6, this in turn imposes |$|\bar{f}_{R0}| \lt 10^{-6}$| for the present-day value of the background scalaron field.
Hereafter, we adopt the following f(R) functional form (Hu & Sawicki 2007)
(13)
where Λ is an effective cosmological constant driving the background cosmic acceleration, and |$\bar{R}_0$| corresponds to the background Ricci scalar today. We will work with values |$|\bar{f}_{R0}| = 10^{-5}$| (F5) and |$|\bar{f}_{R0}| = 10^{-6}$| (F6), for which cosmological structures are, respectively, partially unscreened or largely screened throughout the cosmic history. Note that deviations from the ΛCDM expansion history are of order |$\bar{f}_{R0}$| (Hu & Sawicki 2007). Hence, for the f(R) models considered here the background evolution is in effect equivalent to that of the concordance cosmology, with the Hubble parameter given by
(14)
where |$\bar{\rho }_\Lambda$| is the energy density of the cosmological constant. The large-scale structure data currently available allows amplitudes |$|\bar{f}_{R0}| \lesssim 10^{-5}$| (Lombriser 2014; Terukina et al. 2014; Cataneo et al. 2015; Alam, Ho & Silvestri 2016; Liu et al. 2016), thus placing the F5 model on the edge of the region of parameter space still relevant for cosmological applications3 if other effects degenerate with the enhanced growth of structure are ignored. Accounting for massive neutrinos (Baldi et al. 2014) and baryonic feedback (Puchwein et al. 2013; Hammami et al. 2015; Arnold et al. 2019) will loosen the existing constraints (see e.g. Hagstotz et al. 2019; Giocoli, Baldi & Moscardini 2018). In addition, alternative functional forms to equation (13) can lead to different upper bounds on |$|\bar{f}_{R0}|$| (see e.g. Cataneo et al. 2015).

2.2 DGP

In the DGP braneworld model the matter fields live on a four-dimensional brane embedded in a five-dimensional Minkowski space (Dvali, Gabadadze & Porrati 2000). In this model the dimensionality of the gravitational interaction is controlled by the crossover scale parameter rc, such that on scales smaller than rc DGP becomes a four-dimensional scalar–tensor theory described by an effective Lagrangian with terms (Nicolis & Rattazzi 2004; Park et al. 2010)
(15)
(16)
(17)
where the brane-bending mode φ represents the scalar field. Hereafter we will be working with the normal branch DGP model (nDGP), which despite being a stable solution of the theory is also incompatible with the observed late-time cosmic acceleration. To obviate this problem the Lagrangian given by equations (15)–(17) is extended to include a smooth, quintessence-type DE with a potential conveniently designed to match the expansion history of a flat ΛCDM cosmology (Schmidt 2009b).4 Therefore, the Friedmann equation (14) applies here as well.
The scalar field φ couples to non-relativistic matter by sourcing the dynamical potential Ψ, which in turn produces a gravitational force given by
(18)
where the second term on the right-hand side is the attractive fifth force contribution. On length-scales λ ≪ H−1, rc, and in the quasi-static regime (Schmidt 2009a; Brito et al. 2014; Winther & Ferreira 2015), the evolution of the brane-bending mode is described by (Koyama & Silva 2007)
(19)
with the function β(a) defined as
(20)
where overdots denote derivatives with respect to cosmic time. The derivative self-interactions in equation (19) suppress the field in high-density regions, where the matter density field is non-linear, effectively restoring GR. This is the so-called Vainshtein screening. To explicitly illustrate how this mechanism works we shall consider a spherically symmetric overdensity with mass
(21)
Then, for this system the gradient of φ reads (Koyama & Silva 2007; Schmidt et al. 2010)
(22)
where we defined the Vainshtein radius
(23)
The scale introduced in equation (23) sets the distance from the centre of the spherical mass distribution above which fifth force effects are observable. For instance, for a top-hat overdensity of radius |$R_{\rm \scriptscriptstyle TH}$| one has the two limiting cases
\begin{eqnarray*} \left\lbrace \begin{array}{l{@}{\quad}l}\displaystyle\frac{{\rm d}\varphi }{{\rm d}r} = \displaystyle\frac{2}{3\beta }\frac{{\rm d}\Psi _{\rm N}}{{\rm d}r} & r \gg r_{\rm V}\gt R_{\rm \scriptscriptstyle TH}, \\ \displaystyle \frac{{\rm d}\varphi }{{\rm d}r} \approx 0 & R_{\rm \scriptscriptstyle TH} \lt r \ll r_{\rm V} . \end{array} \right. \end{eqnarray*}

In the following we will consider the medium and weak nDGP variants used in Barreira, Sánchez & Schmidt (2016), with crossover scales rcH0 = 0.5 (nDGPm) and rcH0 = 2 (nDGPw) in units of the present-day Hubble horizon |$H_0^{-1}$|⁠. Note that, at present, of these two cases nDGPw is the only one compatible with growth rate data (Barreira et al. 2016). Hence, similarly to F5, the use of nDGPm will serve as a test bed for our methodology in conditions of relatively strong departures from GR.

2.3 Dark energy

The simplest models described by the Lagrangian in equation (3) are those in which the scalar field is minimally coupled to gravity, that is
(24)
(25)
(26)
In this scenario, the field ϕ is associated with a fluid called DE with energy density and pressure (see e.g. Amendola & Tsujikawa 2010)
(27)
(28)
respectively. Its background evolution is controlled by the equation of state parameter |$w \equiv \bar{P}_{\rm \scriptscriptstyle DE}/\bar{\rho }_{\rm \scriptscriptstyle DE}$|⁠, and the solution to the continuity equation
(29)
is given by
(30)
where |$\bar{\rho }_{{\rm \scriptscriptstyle DE},0}$| is the present-day DE density.
Popular models of DE, such as quintessence (Ratra & Peebles 1988; Wetterich 1988), k-essence (Armendariz-Picon, Mukhanov & Steinhardt 2000), and clustering quintessence (Creminelli et al. 2009), belong to this subclass of theories. In this paper we restrict our discussion to a quintessence-like dark fluid with rest-frame sound speed |$c_{\rm s}^2=1$| and equation of state (Chevallier & Polarski 2001; Linder 2003)
(31)
where {w0, wa} are free phenomenological parameters. The relativistic sound speed washes out the DE perturbations on sub-horizon scales, resulting in modifications to the growth of structure tied solely to the different expansion history compared to ΛCDM. Our methodology can, in principle, also be applied to forms of DE clustering on small scales.

Table 1 summarizes the DE models selected for this work, which have been chosen to roughly enclose the 2σ region of parameter space allowed by the Planck 2015 temperature and polarization data in combination with baryon acoustic oscillations, supernova Ia, and H0 measurements (Planck Collaboration XIV 2016).

Table 1.
Open in new tab

Equation-of-state parameters defining the DE models used in this work.

Modelw0wa
DE1−0.70
DE2−1.30
DE3−10.5
DE4−1−0.5
DE5−0.7−1.5
DE6−1.30.5
Modelw0wa
DE1−0.70
DE2−1.30
DE3−10.5
DE4−1−0.5
DE5−0.7−1.5
DE6−1.30.5
Table 1.
Open in new tab

Equation-of-state parameters defining the DE models used in this work.

Modelw0wa
DE1−0.70
DE2−1.30
DE3−10.5
DE4−1−0.5
DE5−0.7−1.5
DE6−1.30.5
Modelw0wa
DE1−0.70
DE2−1.30
DE3−10.5
DE4−1−0.5
DE5−0.7−1.5
DE6−1.30.5

3 MATTER POWER SPECTRUM REACTION

In Sections 3.1 and 3.2 we briefly review the spherical collapse model and the halo model formalism, which we use to predict the non-linear matter power spectrum for the range of cosmological models listed in Section 2. The halo model assumes that all matter in the Universe is localized in virialized structures, called haloes. In this approach, the spatial distribution of these objects and their density profiles determine the statistics of the matter density field on all scales. It is typically assumed that each mass element belongs to one halo only, i.e. haloes are spatially exclusive. Below we introduce the ingredients entering the halo model prescription, and refer the interested reader to the Cooray & Sheth (2002) review on the topic for more details. In Section 3.3 we then detail our new approach to reach per cent level accuracy on these power spectra over a range of scales where the halo model alone is known to fail.

3.1 Spherical collapse model

The Press–Schechter formalism (Press & Schechter 1974) approximates halo formation following the evolution of a spherical top-hat overdensity of radius |$R_{\rm \scriptscriptstyle TH}$| and mass |$M=4\pi R_{\rm \scriptscriptstyle TH}^3 \bar{\rho }_{\rm m}(1+\delta)/3$| in an otherwise homogenous background. Mass conservation and the Euler equations imply (see e.g. Schmidt et al. 2009)
(32)
Here, |$\bar{\rho }_{\rm eff}$| and w are, respectively, the background energy density and equation of state of an effective DE component causing the late-time cosmic acceleration. Hence, in f(R) gravity and nDGP, |$\bar{\rho }_{\rm eff} = \bar{\rho }_\Lambda$|⁠, and w = −1. For the smooth DE models in Section 2.3 we have |$\bar{\rho }_{\rm eff} = \bar{\rho }_{\rm \scriptscriptstyle DE}$| and w given by equation (31). Modifications of gravity enter through the potential term in equation (32), which we parametrize as
(33)
where |$\mathcal {F}$| can depend on time, mass, and environment. Equation (33) reduces to the standard Poisson equation for |$\mathcal {F}=0$|⁠, and expressions for |$\mathcal {F}$| in f(R) and nDGP cosmologies are given in Appendix  A.
The mass fluctuation δi at the initial time ai within |$R_{\rm \scriptscriptstyle TH}$| evolves as
(34)
where Ri is the initial top-hat radius. Using equations (32)–(34) we then find δi such that collapse (i.e. |$R_{\rm \scriptscriptstyle TH}=0$|⁠) occurs at a chosen time a = acoll. The Press–Schechter approach assumes that all regions in the initial density field with overdensities larger than δi have collapsed into haloes by acoll. Equivalently, one can compare the linearly evolved initial fluctuations to the linearly extrapolated collapse overdensity |$\delta _{\rm c}(a_{\rm coll}) \equiv D_\Lambda (a_{\rm coll})\delta _i/a_i$|⁠, with (see e.g. Dodelson 2003)
(35)
being the linear growth factor in ΛCDM,5 and |$\Omega _{\rm m} \equiv 8\pi G\bar{\rho }_{\rm m,0}/3H_0^2$|⁠.
In the idealized top-hat scenario, the spherical mass collapses to a point of infinite density. However, processes in the real Universe act so that, after turnaround, the overdensity eventually reaches virial equilibrium (see e.g. Mo, van den Bosch & White 2010). Following Schmidt et al. (2010) (for an earlier work see also Maor & Lahav 2005), we do not assume energy conservation during collapse, and compute the time of virialization, avir, from the virial theorem alone (see Appendix  A for details). This approach differs from previous works where changes induced by DE (Mead 2017) or modified gravity (Lombriser et al. 2014) were neglected. The virial comoving radius Rvir of the formed halo can be derived from its virial mass
(36)
knowing that the virial overdensity is given by
(37)
with the mass fluctuation δ obtained from equation (34).

3.2 Halo model

The simplest statistics describing the clustering properties of the matter density field ρm(x) is the 2-point correlation function or, its Fourier transform, the power spectrum P(k) defined as
(38)
where δD denotes the Dirac delta function, and |$\tilde{\delta }({\bf k})$| represents the Fourier transform of the matter density fluctuations relative to the background mean density, |$\delta ({\bf x}) = \rho _{\rm m}({\bf x})/\bar{\rho }_{\rm m}-1$|⁠. Note that equation (38) assumes statistical homogeneity and isotropy.
In the halo model the matter power spectrum results from the contribution of correlations between haloes (⁠|$P_{2\rm h}$|⁠) and those within haloes (⁠|$P_{1\rm h}$|⁠), and can be written as6
(39)
To properly account for these correlations we need to know the abundance of such haloes. For any redshift z, the halo mass function provides the comoving number density of haloes of mass Mvir, and it is defined as
(40)
where the peak height ν ≡ δc/σ, and we adopt the Sheth–Tormen (ST) multiplicity function (Sheth & Tormen 1999, 2002)
(41)
Here, the normalization constant A is found imposing that all mass in the Universe is confined into haloes, i.e. ∫dνf(ν) = 1, and the remaining parameters take the ΛCDM standard values q = 0.75 and p = 0.3, unless stated otherwise. The variance of the linear density field smoothed with a top-hat filter of comoving radius R enclosing a mass |$M=4\pi R^3\bar{\rho }_{\rm m,0}/3$| is given by
(42)
where |$\tilde{W}$| is the Fourier transform of the top-hat filter, and |$P_{\rm \scriptscriptstyle L}(k,z)$| is the ΛCDM linear power spectrum. At this point it is worth emphasizing that in some GR extensions, besides its usual dependence on background cosmology and redshift, the spherical collapse threshold δc can also vary with halo mass and environment (Li & Efstathiou 2012; Li & Lam 2012; Lam & Li 2012; Lombriser et al. 2013, 2014). When appropriate we include both these dependencies in our modelling by following the approach of Cataneo et al. (2016), where the initial value of the environmental overdensity is derived from the peak of the environment probability distribution.
Haloes are biased tracers of the underlying dark matter density field, and at the linear level the halo and matter density fields are connected by the relation |$\delta _{\rm h} = b_{\rm \scriptscriptstyle L} \delta$|⁠. Adopting the ST mass function, the peak-background split formalism predicts the linear halo bias7 (Sheth & Tormen 1999)
(43)
The last piece of information required by the halo model is a description of the matter distribution within haloes. We adopt Navarro–Frenk–White (NFW) halo profiles (Navarro et al. 1996)
(44)
where the scale radius rs is parametrized through the virial concentration cvir ≡ Rvir/rs, and the normalization ρs follows from the virial mass as
(45)
Inside the virial radius, and for all cosmological models studied here, the NFW profiles are a good representation of the averaged halo profiles measured in simulations (Schmidt et al. 2009; Schmidt 2009b; Zhao et al. 2011; Lombriser et al. 2012; Kwan et al. 2013; Shi et al. 2015; Achitouv et al. 2016).
In ΛCDM, f(R) gravity and nDGP we model the c–M relation as the power law
(46)
fixing c0 = 9 and α = 0.13 (Bullock et al. 2001), and M* is defined by ν(M*) = 1. In particular, for f(R) gravity M* depends itself on the halo mass (Lombriser et al. 2014), which means the c–M relation for these models is no longer described by a simple power law (Shi et al. 2015). For the smooth DE models in Section 2.3 we correct for the different expansion histories following Dolag et al. (2004), that is
(47)
where |$g_{\rm \scriptscriptstyle X}$| is the linear growth factor normalized to z = 0 (see Appendix  B). This correction reflects that haloes collapse at different times in cosmological models with different growth histories. In cosmological models where haloes collapse earlier these haloes will be more concentrated compared to the same mass haloes if they form later. In Appendix  C we demonstrate that our results are insensitive to the correct shape of the c–M relation on scales k ≲ 0.5 |$h {\rm Mpc}^{-1}$|⁠.
We can now predict the non-linear matter power spectrum, and rewrite equation (39) as
(48)
where, more explicitly,
(49)
(50)
In the equations above, u(k, M) corresponds to the Fourier transform of an NFW profile truncated at Rvir, normalized such that u(k → 0, M) → 1. Note that from equations (41) and (43) it follows that limk → 0I(k) = 1.

3.3 Halo model reactions

The apparent simplicity and versatility of the halo model has contributed to its widespread use as a method to predict the non-linear matter power spectrum in diverse scenarios. Examples include the ΛCDM cosmology (Peacock & Smith 2000; Seljak 2000; Giocoli et al. 2010; Valageas & Nishimichi 2011; Valageas, Nishimichi & Taruya 2013; Mohammed & Seljak 2014; Seljak & Vlah 2015; van Daalen & Schaye 2015; Mead et al. 2015b; Schmidt 2016), DE and modified gravity models (Schmidt et al. 2009, 2010; Li & Hu 2011; Fedeli et al. 2012; Brax & Valageas 2013; Lombriser et al. 2014; Barreira et al. 2014a, b; Achitouv et al. 2016; Mead et al. 2016; Hu et al. 2018), massive neutrinos (Abazajian et al. 2005; Massara, Villaescusa-Navarro & Viel 2014; Mead et al. 2016), baryonic physics (Fedeli 2014; Fedeli et al. 2014; Mohammed & Seljak 2014; Mead et al. 2015b), alternatives to cold dark matter (Dunstan et al. 2011; Schneider et al. 2012; Marsh 2016), and primordial non-Gaussianity (Smith, Desjacques & Marian 2011). Its imperfect underlying assumptions are however responsible for inaccuracies that limit its applicability to future high-quality data (see e.g. fig. 1 in Massara et al. 2014), where per cent level accuracy is required in order to obtain unbiased cosmological constraints (Huterer & Takada 2005; Eifler 2011; Hearin, Zentner & Ma 2012; Taylor, Kitching & McEwen 2018a).

To mitigate these downsides one can add complexity to the model at the expense of introducing new free parameters (see e.g. Seljak & Vlah 2015), fitting the existing ones to the matter power spectrum measured in simulations (see e.g. Mead et al. 2015b), or sensibly increasing the computational costs by going beyond linear order in perturbation theory (see e.g. Valageas & Nishimichi 2011). Here, instead, we follow and extend the approach presented in Mead (2017), which we shall refer to as halo model reactions.8

Our goal is to model the non-linear power spectrum of fairly general extensions to the standard cosmology, a flat ΛCDM Universe with massless neutrinos. These cosmologies equipped with beyond-ΛCDM physics are what we will call real cosmologies. We use the halo model to determine the change (i.e. the reaction) that this new physics induces in a reference ΛCDM cosmology, for which simulations are considerably cheaper. Key to the success of our method is how this reference cosmology is defined, which is what we will call the pseudo cosmology. Essentially, this is a ΛCDM cosmology evolved with standard gravity up to a final redshift zf, with the additional property that its linear clustering of matter exactly matches that of the target real cosmology of interest at zf. In other words, the cold dark matter and the cosmological constant determine the expansion history and growth of structure of the pseudo cosmology, but the initial conditions (see Section 4) are adjusted so that
(51)
The reaction function is then defined as the ratio of the non-linear matter power spectrum in the real cosmology to that in the pseudo cosmology,
(52)
and our corresponding halo model prediction takes the heuristic form9
(53)
Here, |$\mathcal {E} \sim 1$| and k⋆ > 0 are parameters introduced to improve the accuracy of the halo model reactions in modified gravity theories. These are not free parameters, and we shall derive them using the halo model and standard perturbation theory (SPT) below. However, let us first examine the general behaviour of equation (53):

  • On large linear scales |$\mathcal {R} \rightarrow 1$| by definition;10

  • On small non-linear scales |$\mathcal {R} \approx P_{1\rm h}^{\rm real}/P_{1\rm h}^{\rm pseudo}$|⁠;

  • Quasi-linear scales |$0.01 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 0.1$| are well described by perturbation theory, while intermediate scales |$0.1 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 1$| are primarily controlled by the halo mass function ratio |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$|⁠.

Fixing the real and pseudo linear power spectra to be identical (as in equation 51) forces the corresponding mass functions to be somewhat similar. Therefore, owing to (iii), reaction functions can overcome the typical inaccuracies that plague the halo model in the transition region between large and small scales.

To assign a value to the boost/suppression term |$\mathcal {E}$|⁠, it is important to realize that we would like to preserve the smoothness in the transition from the linear to the non-linear regime. In turn, this is tied to the shape of the one-halo terms on scales |$0.5 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 1$|⁠, where the two-halo contribution becomes subdominant. In this regime the one-halo terms are well approximated by their large-scale limit |$P_{1\rm h}(k \rightarrow 0)$|⁠, thus suggesting that
(54)
is a good choice, one that only depends on the ratio |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$|⁠.
In equation (53), the transition rate from linear to non-linear scales is governed by the parameter k⋆:11 for k⋆ → 0 the halo model reaction collapses to the ratio of one-halo terms; in the opposite case, k⋆ → ∞, the parameter |$\mathcal {E}$| loses any role, and the reaction reduces to its definition in Mead (2017). We determine this scale using SPT (Koyama et al. 2009; Brax & Valageas 2013; Bose & Koyama 2016) by solving the equation
(55)
where
(56)
and we set k0 = 0.06 |$h \, {\rm Mpc}^{-1}$|⁠, which we found to be the largest wavenumber that can both ensure reliable perturbative predictions and keep the inaccuracies induced by the exponential sensitivity to k⋆ under control (see Appendix  B and Carlson, White & Padmanabhan 2009). Expressions for the second order corrections P22, P13, and |$P_{13}^\Psi$| to the linear power spectrum are given in Appendix  B. Note that alternative perturbation schemes can also be used in equation (55), such as the Lagrangian perturbation theory for modified gravity recently developed in Aviles & Cervantes-Cota (2017).

The role of the two-halo correction factor in equation (53) becomes clear in the limiting case k⋆ → ∞, where it goes to unity. Mead (2017) showed that this form of the reactions matches smooth DE simulations at per cent level or better on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|for z = 0 (see also Section 5 below). On quasi-linear scales this remarkable agreement can be understood in terms of SPT. Schematically, the non-linear matter power spectrum is a non-trivial function of the linear power spectrum obtained through some operator |$\mathcal {K}$|⁠, i.e. |$P(k) = \mathcal {K}[P_{\rm \scriptscriptstyle L}(k)]$| (Bernardeau et al. 2002). Provided that gravitational forces remain unchanged, then equation (51) enforces Preal ≈ Ppseudo on linear and quasi-linear scales. This is no longer true for modifications of gravity, since the structure of the |$\mathcal {K}_{\rm MG}$| operator is altered by different mode-couplings and screening mechanisms. We correct for this fact by including the two-halo pre-factor in equation (53), so that finite k⋆ roughly encapsulates the extent of the mismatch between |$\mathcal {K}_{\rm MG}$| and |$\mathcal {K}_{\rm GR}$|⁠. For comparison, in F5 at z = 0 we have k⋆ = 0.3 |$h \, {\rm Mpc}^{-1}$|⁠, whereas in nDGPm it becomes k⋆ = 0.95 |$h \, {\rm Mpc}^{-1}$|⁠, which reflects the different screening efficiency on large scales between the chameleon and Vainshtein mechanisms.

Although our choice of k0 is commonly regarded as well within the quasi-linear regime, screening mechanisms in modified gravity induce non-linearities on large scales that can be more important than in GR. For this, the determination of k⋆ can be complicated by inaccuracies specific to the perturbation theory employed, and to reduce their impact on the halo model reactions we take advantage of the following two facts: (i) on large scales we expect |$P_{\rm NoScr}^{\rm real} \approx P^{\rm pseudo}$|⁠, where |$P_{\rm NoScr}^{\rm real}$| denotes the non-linear matter power spectrum of the real cosmology assuming there is no screening mechanism; (ii) the kernel operators |$\mathcal {K}_{\rm MG}^{\rm Scr}$| and |$\mathcal {K}_{\rm MG}^{\rm NoScr}$| for the screened and unscreened real cosmology, respectively, have a similar structure (see Appendix  B). Therefore, at least in principle, the ratio |$P_{\rm Scr,SPT}^{\rm real}/P_{\rm NoScr,SPT}^{\rm real}$| could give a better description of the reaction on large scales than the obvious candidate |$P_{\rm Scr,SPT}^{\rm real}/P_{\rm SPT}^{\rm pseudo}$|⁠. Hereafter we will use |$P_{\rm NoScr,SPT}^{\rm real}$| instead of |$P_{\rm SPT}^{\rm pseudo}$| in equation (55), which in spite of being a sub-optimal strategy in some cases (see right-hand panel of Fig. B1) produces the most consistent behaviour across the cosmological models we have tested, as shown in Section 5.

In summary, halo model reactions provide a fast (we only need one-loop SPT for a single wavenumber) and general framework to map accurate non-linear matter power spectra in ΛCDM to other non-standard cosmologies. We apply this method to f(R) gravity, nDGP, and evolving DE, and test its performance in Section 5 against the cosmological simulations described in the next section.

4 SIMULATIONS

The simulations of f(R) gravity and DGP models used in this work were run using ecosmog (Li et al. 2012; Li, Zhao & Koyama 2013a; Li et al. 2013b), which has been developed to simulate the structure formation in various subclasses of models within the Horndeski family of theories. ecosmog is an extension of the simulation code ramses (Teyssier 2002), which is a particle-mesh code employing adaptive mesh refinement to achieve high force resolution. The simulations are dark matter only and run in boxes with comoving size |$512 \, h^{-1}$|Mpc using 10243 simulation particles. Other basic information can be found in Table 2. The initial conditions of the simulations are generated using 2lptic (Crocce, Pueblas & Scoccimarro 2006), which calculates the particle initial displacements and peculiar velocities up to second order in Lagrangian perturbations, allowing us to start from a relative low initial redshift zini = 49. To isolate the effect of non-linearities we use identical phases for the initial density field in all cases. The linear power spectra used to generate the initial conditions are computed using camb (Lewis, Challinor & Lasenby 2000), with Ωm = 0.3072, |$\Omega _\Lambda =0.6928$|⁠, h = 0.68, Ωb = 0.0481 for all simulations. Importantly, following equation (51) the normalization – and shape in f(R) gravity – of the initial linear power spectra are different in the real and pseudo simulations. Since at early times deviations from GR are negligible, simulations in ΛCDM and modified gravity share the same initial conditions set by the ΛCDM power spectrum,
(57)
with σ8(z = 0) = 0.8205. The pseudo runs (to which we will apply the halo model reactions) have different initial conditions, generated using modified gravity linear power spectra at the final redshift, zf, and then rescaled with the ΛCDM linear growth to the starting redshift as
(58)
where in this work zf = 0 or 1. By evolving the initial real and pseudo power spectra, equations (57) and (58), with the modified and standard laws of gravity, respectively, equation (51) will be automatically satisfied at zf. We extract the non-linear matter power spectrum from our particle snapshots using the public code powmes (Colombi et al. 2009).
Table 2.
Open in new tab

Main technical details of the simulations employed in this work. The Nyquist frequency kNy = πNp/Lbox, ϵ is the force resolution, and mp the particle mass. The standard cosmological parameters for the real f(R) and nDGP simulations, as well as for their standard ΛCDM counterparts, are ωb ≡ Ωbh2 = 0.02225, ωc ≡ Ωch2 = 0.1198, H0 = 100 h = 68 km s−1 Mpc−1, As = 2.085 × 10−9, and ns = 0.9645. For the evolving DE models we have instead ωb = 0.0245, ωc = 0.1225, H0 = 70 km s−1 Mpc−1, σ8 = 0.8, and ns = 0.96.

ModelLbox|$N_p^3$|kNyϵmpRealizationsCode
f(R)512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
nDGP512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
DE200 |${\rm Mpc}\, h^{-1}$|51238 |$h \, {\rm Mpc}^{-1}$|7.8 kpc|$\, h^{-1}$||$5 \times 10^{9} \, \mathrm{ M}_\odot h^{-1}$|3gadget-2
ModelLbox|$N_p^3$|kNyϵmpRealizationsCode
f(R)512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
nDGP512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
DE200 |${\rm Mpc}\, h^{-1}$|51238 |$h \, {\rm Mpc}^{-1}$|7.8 kpc|$\, h^{-1}$||$5 \times 10^{9} \, \mathrm{ M}_\odot h^{-1}$|3gadget-2
Table 2.
Open in new tab

Main technical details of the simulations employed in this work. The Nyquist frequency kNy = πNp/Lbox, ϵ is the force resolution, and mp the particle mass. The standard cosmological parameters for the real f(R) and nDGP simulations, as well as for their standard ΛCDM counterparts, are ωb ≡ Ωbh2 = 0.02225, ωc ≡ Ωch2 = 0.1198, H0 = 100 h = 68 km s−1 Mpc−1, As = 2.085 × 10−9, and ns = 0.9645. For the evolving DE models we have instead ωb = 0.0245, ωc = 0.1225, H0 = 70 km s−1 Mpc−1, σ8 = 0.8, and ns = 0.96.

ModelLbox|$N_p^3$|kNyϵmpRealizationsCode
f(R)512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
nDGP512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
DE200 |${\rm Mpc}\, h^{-1}$|51238 |$h \, {\rm Mpc}^{-1}$|7.8 kpc|$\, h^{-1}$||$5 \times 10^{9} \, \mathrm{ M}_\odot h^{-1}$|3gadget-2
ModelLbox|$N_p^3$|kNyϵmpRealizationsCode
f(R)512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
nDGP512 |${\rm Mpc}\, h^{-1}$|102436.3 |$h \, {\rm Mpc}^{-1}$|15.6 kpc|$\, h^{-1}$||$1.1 \times 10^{10} \, \mathrm{ M}_\odot h^{-1}$|1ecosmog
DE200 |${\rm Mpc}\, h^{-1}$|51238 |$h \, {\rm Mpc}^{-1}$|7.8 kpc|$\, h^{-1}$||$5 \times 10^{9} \, \mathrm{ M}_\odot h^{-1}$|3gadget-2

Simulations of DE models were run using a modified version of gadget-2 that allows for the {w0, wa} parametrization under the assumption that the DE is homogeneous. Initial conditions were generated at zini = 199 using n-genic (Springel 2015), a code that calculates initial particle displacements and peculiar velocities based on the Zeldovich approximation. Our simulations take place in 200 |${\rm Mpc}\, h^{-1}$| boxes and use 5123 particles. Note that since we are concerned only with ratios of power spectra the overall resolution requirements on the simulations are less stringent than if we were interested in the absolute power spectra. We checked that our simulated reactions were insensitive to the realization, box size, particle number, and softening up to the wavenumbers we show.

Differently from the modified gravity runs, we fix σ8 = 0.8 for all the evolving DE models. Then, for the real cosmologies the amplitudes of the initial density field are determined by
(59)
where DDE(z) is the linear growth of a specific DE model, while for the pseudo counterparts one simply replaces |$P_{\rm \rm \scriptscriptstyle L}^{\rm MG}$| with |$P_{\rm \rm \scriptscriptstyle L}^{\rm DE}$| in equation (58).

5 RESULTS

Here we test our halo model reactions (see Section 3.3) against the same quantities constructed from the real and pseudo cosmological simulations described in Section 4. To help get a better sense of the performance of our method, for each real cosmology |$\mathcal {C}$| we also compute the standard ratios |$P_{\mathcal {C}}^{\rm real}(k)/P_{\Lambda {\rm CDM}}(k)$|⁠, where our theoretical prediction for the real non-linear power spectrum is obtained as
(60)
where |$\mathcal {R}(k)$| is given by equation (53). To test our modified gravity predictions we calculate |$P_{\mathcal {C}}^{\rm pseudo}(k)$| from hmcode (Mead et al. 2015b, 2016) or using the measurement from the simulations directly. For evolving DE, instead, we use the pseudo non-linear power spectrum given by the Coyote Universe emulator (Heitmann et al. 2014), and in so doing we illustrate how one could predict the real power spectrum for cosmologies beyond the concordance model with the aid of a carefully designed ΛCDM-like emulator (Giblin et al. 2019).

5.1 f(R) gravity

Fig. 1 shows the matter power spectrum reactions calculated using equation (53) for the F5 cosmology at z = 0 (left-hand panel) and z = 1 (right-hand panel) in comparison to the measured reactions in the N-body simulations. For the virial halo mass function entering |$P_{1\rm h}$| (see equation 49) we first adopt the approach developed in Lombriser et al. (2013), which incorporates both self- and environmental-screening in the spherical collapse (see Appendix  A). At z = 0 the halo concentrations, virial radii, and mass functions are good enough to give per cent level predictions on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠. A deviation of a few per cent is however visible at z = 1 starting on scales as large as k ≈ 0.2 |$h \, {\rm Mpc}^{-1}$|⁠. In Appendix  C we show that changes in the halo profiles only affect scales k ≳ 0.5 |$h \, {\rm Mpc}^{-1}$|⁠, suggesting that the observed inaccuracies could be caused by a mismatch between the predicted virial mass function ratio |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$| and the same quantity measured in simulations. Indeed, Cataneo et al. (2016) found that, for halo masses defined by spherical regions with an average matter density 300 times the mean matter density of the Universe, the halo mass function of Lombriser et al. (2013) can deviate up to 10 per cent from the simulations.

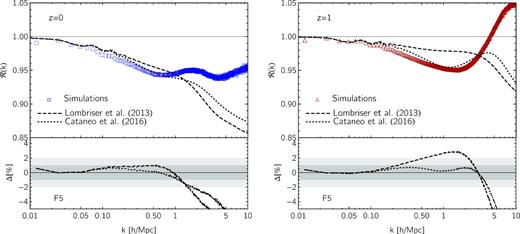
Matter power spectrum reactions in f(R) gravity for $|\bar{f}_{R0}|=10^{-5}$. In each panel the data points represent the reactions measured from simulations; lines denote the corresponding halo model predictions identified by the halo mass function used for the one-halo contributions in f(R) gravity, that is either Lombriser et al. (2013) (dashed) or Cataneo et al. (2016) fits (dotted). Lower panels present the fractional deviation of the halo model relative to the simulations, with grey bands marking the $1\, {\rm per\, cent}$ and $2\, {\rm per\, cent}$ uncertainty regions. Left: reaction at z = 0 with both halo mass functions providing predictions within $1\, {\rm per\, cent}$ from the simulations for k ≲ 1 $h \, {\rm Mpc}^{-1}$, as shown in the lower panel. Right: z = 1 reaction. The lower panel shows that thanks to the improved semi-analytical prescription for the halo abundances in Cataneo et al. (2016) the agreement between halo model and simulations reaches per cent-level on scales k ≲ 1 $h \, {\rm Mpc}^{-1}$.
Figure 1.

Matter power spectrum reactions in f(R) gravity for |$|\bar{f}_{R0}|=10^{-5}$|⁠. In each panel the data points represent the reactions measured from simulations; lines denote the corresponding halo model predictions identified by the halo mass function used for the one-halo contributions in f(R) gravity, that is either Lombriser et al. (2013) (dashed) or Cataneo et al. (2016) fits (dotted). Lower panels present the fractional deviation of the halo model relative to the simulations, with grey bands marking the |$1\, {\rm per\, cent}$| and |$2\, {\rm per\, cent}$| uncertainty regions. Left: reaction at z = 0 with both halo mass functions providing predictions within |$1\, {\rm per\, cent}$| from the simulations for k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠, as shown in the lower panel. Right: z = 1 reaction. The lower panel shows that thanks to the improved semi-analytical prescription for the halo abundances in Cataneo et al. (2016) the agreement between halo model and simulations reaches per cent-level on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠.

Open in new tabDownload slide

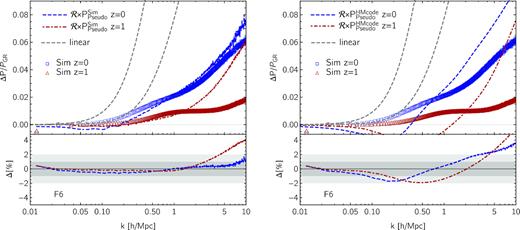
Given the complexity of measuring the virial halo mass function in f(R) simulations,12 we investigate changes in the reactions induced by a more accurate description of the halo abundances with the fits provided in Cataneo et al. (2016). There, however, the calibration of the |$n_\Delta ^{f(R)}/n_\Delta ^{\rm \Lambda CDM}$| ratios was performed for Δ = 300, whereas for our purposes we need Δ = Δvir. We go from one mass definition to the other with the scaling relations outlined in Hu & Kravtsov (2003) (for a first application to f(R) gravity see Schmidt et al. 2009). Inevitably, this transformation suffers from inaccuracies in cvir and Δvir, which we attempt to compensate for by adjusting the M300(Mvir) relation so that the new rescaled mass function provides a present-day halo model reaction that is at least as good as the reaction obtained when using the Lombriser et al. (2013) virial mass function (dotted line in the left-hand panel of Fig. 1).13 We then take the ratio of the Cataneo et al. (2016) rescaled mass function to that of Lombriser et al. (2013), and treat this quantity as a correction factor for the latter. To find the required adjustment at high redshifts we shift the z = 0 correction by an amount Δlog10Mvir inferred from the redshift evolution of the ratio of the two halo mass functions over the range z ∈ [0, 0.5] (see central panel of fig. 4 in Cataneo et al. 2016). A simple extrapolation to z = 1 gives Δlog10Mvir = 1. Although far from being a rigorous transformation, the resulting halo model reaction now agrees to better than 1 per cent down to k ≈ 3 |$h \, {\rm Mpc}^{-1}$|⁠, as shown in the right-hand panel of Fig. 1. Fig. 2 illustrates that similar considerations are also valid for the F6 cosmology, where we use the same mass shift Δlog10Mvir = 1 to go from the z = 0 to the z = 1 mass function correction. In all cases, deviations in the highly non-linear regime are most likely caused by inaccurate c–M relations. We leave the study of f(R) gravity reactions on small scales derived from proper virial quantities for future work.

Same as Fig. 1 with the amplitude of the background scalaron field now fixed to $|\bar{f}_{R0}|=10^{-6}$. For this cosmology both halo mass functions perform very well regardless of redshift, which can be explained by their similarity as shown in Cataneo et al. (2016).
Figure 2.

Same as Fig. 1 with the amplitude of the background scalaron field now fixed to |$|\bar{f}_{R0}|=10^{-6}$|⁠. For this cosmology both halo mass functions perform very well regardless of redshift, which can be explained by their similarity as shown in Cataneo et al. (2016).

Open in new tabDownload slide

Figs 3 and 4 show the relative change of the matter power spectrum in f(R) gravity with respect to GR for the F5 and F6 models, respectively. The left-hand panels present the best-case scenario, that is, when ‘perfect’ knowledge of the pseudo power spectrum is available. In this case, since the uncertainties come entirely from our halo model predictions, we can obviously reproduce the power spectrum ratios at the same level of accuracy of our reactions. For now the pseudo information comes directly from our simulations, but it is not hard to imagine a specifically designed emulator capable of generating the non-linear matter power spectrum of ΛCDM cosmologies with non-standard initial conditions. We will analyse the requirements for such emulator in a future work (Giblin et al. in preparation). In the right-hand panels we compute Ppseudo with hmcode to demonstrate that currently, together with publicly available codes, our method can achieve 2 per cent accuracy on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|in modified gravity theories characterized by scale-dependent linear growth.

Matter power spectrum fractional enhancements relative to GR for f(R) gravity with $|\bar{f}_{R0}|=10^{-5}$. As in the previous figures, the data points correspond to the results from simulations at z = 0 (blue squares) and z = 1 (red triangles). Coloured lines denote predictions based on the halo model reactions at z = 0 (dashed blue) and z = 1 (dot–dashed red). To emphasize the impact of non-linearities we include the linear theory predictions as dashed grey lines. Lower panels show the fractional deviation of the non-linear predictions from the simulations, $\Delta \equiv \left(\mathcal {R} \times P_{\rm Pseudo}^{\rm Sim/HMcode}/P_{\rm GR}^{\rm Sim/HMcode} \right)/\left(P_{\rm Real}^{\rm Sim}/P_{\rm GR}^{\rm Sim} \right)-1$, with grey bands marking $1\, {\rm per\, cent}$ and $2\, {\rm per\, cent}$ uncertainty regions. Left: for our theoretical estimates we use pseudo cosmology matter power spectra measured from simulations as the baseline, which we then rescale with the halo model reactions employing the Cataneo et al. (2016) halo mass functions. The lower panel illustrates that with future codes, eventually capable of reaching per cent-level accuracy on the matter power spectra for the ΛCDM-evolved pseudo cosmologies, high-accuracy non-linear matter power spectra in modified gravity will also be accessible. Right: same as left-hand panel with the difference that the pseudo cosmology matter power spectra computed with hmcode are now adopted as the baseline. This implies that applying our halo model reaction methodology to baseline ΛCDM predictions from existing codes we can achieve ${\lesssim}2\, {\rm per\, cent}$ precision on scales k ≲ 1 $h \, {\rm Mpc}^{-1}$.
Figure 3.

Matter power spectrum fractional enhancements relative to GR for f(R) gravity with |$|\bar{f}_{R0}|=10^{-5}$|⁠. As in the previous figures, the data points correspond to the results from simulations at z = 0 (blue squares) and z = 1 (red triangles). Coloured lines denote predictions based on the halo model reactions at z = 0 (dashed blue) and z = 1 (dot–dashed red). To emphasize the impact of non-linearities we include the linear theory predictions as dashed grey lines. Lower panels show the fractional deviation of the non-linear predictions from the simulations, |$\Delta \equiv \left(\mathcal {R} \times P_{\rm Pseudo}^{\rm Sim/HMcode}/P_{\rm GR}^{\rm Sim/HMcode} \right)/\left(P_{\rm Real}^{\rm Sim}/P_{\rm GR}^{\rm Sim} \right)-1$|⁠, with grey bands marking |$1\, {\rm per\, cent}$| and |$2\, {\rm per\, cent}$| uncertainty regions. Left: for our theoretical estimates we use pseudo cosmology matter power spectra measured from simulations as the baseline, which we then rescale with the halo model reactions employing the Cataneo et al. (2016) halo mass functions. The lower panel illustrates that with future codes, eventually capable of reaching per cent-level accuracy on the matter power spectra for the ΛCDM-evolved pseudo cosmologies, high-accuracy non-linear matter power spectra in modified gravity will also be accessible. Right: same as left-hand panel with the difference that the pseudo cosmology matter power spectra computed with hmcode are now adopted as the baseline. This implies that applying our halo model reaction methodology to baseline ΛCDM predictions from existing codes we can achieve |${\lesssim}2\, {\rm per\, cent}$| precision on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠.

Open in new tabDownload slide
Same as Fig. 3 with the background field amplitude set to $|\bar{f}_{R0}|=10^{-6}$.
Figure 4.

Same as Fig. 3 with the background field amplitude set to |$|\bar{f}_{R0}|=10^{-6}$|⁠.

Open in new tabDownload slide

For a comparison to a range of other methods for modelling the non-linear matter power spectrum in f(R) and other chameleon gravity models, we refer to fig. 4 and 5 in Lombriser (2014), noting that the majority of these methods rely on fitting parameters in contrast to the approach discussed here.

5.2 DGP

Spherical collapse dynamics is much simpler in nDGP (Schmidt et al. 2010), with both the linear overdensity threshold for collapse, δc, and the corresponding average virial halo overdensity, Δvir, being only functions of redshift. For instance, in GR one has Δvir(z = 0) = 335 and Δvir(z = 1) = 200 for Ωm = 0.3072, whereas these values become Δvir(z = 0) = 283 and Δvir(z = 1) = 178 in our nDGPm cosmology. This fact allows us to extract the virial halo mass function directly from our simulations, and test that accurate |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$| ratios do indeed produce accurate halo model reactions. Figs 5 and 6 show that, after refitting the virial ST mass function to the same quantity from simulations, halo model predictions reach per cent level accuracy on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|(see Appendix  C for details on the halo mass function calibration to simulations). Moreover, since the Vainshtein radius (equation 23) for the most massive haloes is of order a few megaparsecs, we expect small changes caused by the screening mechanism on large scales, i.e. k ≲ 0.1 |$h \, {\rm Mpc}^{-1}$|⁠. In other words, although in our calculations we keep the two-halo correction factor in equation (53), it contributes only marginally to improving the performance of our reaction functions. This is evident from the perturbation theory predictions shown in Fig. B2. Once again, deviations on scales k ≳ 1 |$h \, {\rm Mpc}^{-1}$|could be primarily sourced by inaccurate real and pseudo halo concentrations, and is the subject of future investigation.

Matter power spectrum reactions in an nDGP cosmology with crossover scale rcH0 = 0.5. In each panel the data points represent the reactions measured from simulations; lines denote the corresponding halo model predictions defined by the halo mass function used for the one-halo contributions in nDGP gravity, that is based on either the standard ST fits (dashed) or on fits to our simulations presented in Appendix C (dotted). Lower panels present the fractional deviation of the halo model relative to the simulations, with grey bands marking the $1\, {\rm per\, cent}$ and $2\, {\rm per\, cent}$ uncertainty regions. Left: reaction at z = 0 with the refitted halo mass function significantly improving the predictions for k ≲ 1 $h \, {\rm Mpc}^{-1}$, as shown in the lower panel. Right: z = 1 reaction. The lower panel shows similar performance for the two halo mass function fits, with our refitted version matching the simulations within $1\, {\rm per\, cent}$ over a wider range of scales.
Figure 5.

Matter power spectrum reactions in an nDGP cosmology with crossover scale rcH0 = 0.5. In each panel the data points represent the reactions measured from simulations; lines denote the corresponding halo model predictions defined by the halo mass function used for the one-halo contributions in nDGP gravity, that is based on either the standard ST fits (dashed) or on fits to our simulations presented in Appendix  C (dotted). Lower panels present the fractional deviation of the halo model relative to the simulations, with grey bands marking the |$1\, {\rm per\, cent}$| and |$2\, {\rm per\, cent}$| uncertainty regions. Left: reaction at z = 0 with the refitted halo mass function significantly improving the predictions for k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠, as shown in the lower panel. Right: z = 1 reaction. The lower panel shows similar performance for the two halo mass function fits, with our refitted version matching the simulations within |$1\, {\rm per\, cent}$| over a wider range of scales.

Open in new tabDownload slide
Same as Fig. 5 with the crossover scale set to rcH0 = 2. Here both halo mass function fits exhibit excellent performance independent of redshift, which can be explained by the similarity of their $n_{\rm vir}^{\rm DGP}/n_{\rm vir}^{\rm Pseudo}$ ratios shown in Fig. C2.
Figure 6.

Same as Fig. 5 with the crossover scale set to rcH0 = 2. Here both halo mass function fits exhibit excellent performance independent of redshift, which can be explained by the similarity of their |$n_{\rm vir}^{\rm DGP}/n_{\rm vir}^{\rm Pseudo}$| ratios shown in Fig. C2.

Open in new tabDownload slide

We study the ability of the halo model reactions to reproduce the relative difference of the nDGP power spectrum from that of standard gravity when combined with the pseudo matter power spectrum from either hmcode or the simulations. Figs 7 and 8 confirm that with current codes also scale-independent modifications of gravity can be predicted within 2 per cent over the range of scales relevant for this work.

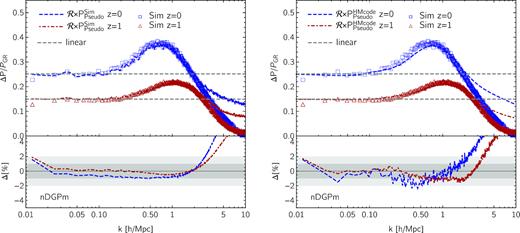
Matter power spectrum fractional enhancements relative to GR for nDGP with rcH0 = 0.5. The data points correspond to the results from simulations at z = 0 (blue squares) and z = 1 (red triangles). Coloured lines represent predictions based on the halo model responses at z = 0 (dashed blue) and z = 1 (dot–dashed red). To emphasize the impact of non-linearities we include the linear theory predictions as dashed grey lines. Lower panels show the fractional deviation of the non-linear predictions from the simulations, $\Delta \equiv \left(\mathcal {R} \times P_{\rm Pseudo}^{\rm Sim/HMcode}/P_{\rm GR}^{\rm Sim/HMcode} \right)/\left(P_{\rm Real}^{\rm Sim}/P_{\rm GR}^{\rm Sim} \right)-1$, with grey bands marking $1\, {\rm per\, cent}$ and $2\, {\rm per\, cent}$ uncertainty regions. Left: for our theoretical estimates we use pseudo cosmology matter power spectra measured from simulations as the baseline, which we then rescale with the halo model reactions employing our refitted halo mass functions in Appendix C. As for f(R) gravity, the lower panel illustrates that with future codes eventually capable of reaching per cent-level accuracy on the matter power spectra for the ΛCDM-evolved pseudo cosmologies, high-accuracy non-linear matter power spectra for scale-independent modifications of gravity will also be within reach. Right: same as the left-hand panel with the difference that the pseudo cosmology matter power spectra computed with hmcode are now adopted as the baseline. Current available codes can achieve ${\lesssim}2\, {\rm per\, cent}$ precision on scales k ≲ 1 $h \, {\rm Mpc}^{-1}$when used in combination with accurate halo model reactions.
Figure 7.

Matter power spectrum fractional enhancements relative to GR for nDGP with rcH0 = 0.5. The data points correspond to the results from simulations at z = 0 (blue squares) and z = 1 (red triangles). Coloured lines represent predictions based on the halo model responses at z = 0 (dashed blue) and z = 1 (dot–dashed red). To emphasize the impact of non-linearities we include the linear theory predictions as dashed grey lines. Lower panels show the fractional deviation of the non-linear predictions from the simulations, |$\Delta \equiv \left(\mathcal {R} \times P_{\rm Pseudo}^{\rm Sim/HMcode}/P_{\rm GR}^{\rm Sim/HMcode} \right)/\left(P_{\rm Real}^{\rm Sim}/P_{\rm GR}^{\rm Sim} \right)-1$|⁠, with grey bands marking |$1\, {\rm per\, cent}$| and |$2\, {\rm per\, cent}$| uncertainty regions. Left: for our theoretical estimates we use pseudo cosmology matter power spectra measured from simulations as the baseline, which we then rescale with the halo model reactions employing our refitted halo mass functions in Appendix  C. As for f(R) gravity, the lower panel illustrates that with future codes eventually capable of reaching per cent-level accuracy on the matter power spectra for the ΛCDM-evolved pseudo cosmologies, high-accuracy non-linear matter power spectra for scale-independent modifications of gravity will also be within reach. Right: same as the left-hand panel with the difference that the pseudo cosmology matter power spectra computed with hmcode are now adopted as the baseline. Current available codes can achieve |${\lesssim}2\, {\rm per\, cent}$| precision on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|when used in combination with accurate halo model reactions.

Open in new tabDownload slide
Same as Fig. 7 with the crossover scale set to rcH0 = 2.
Figure 8.

Same as Fig. 7 with the crossover scale set to rcH0 = 2.

Open in new tabDownload slide

5.3 Dark energy

Fig. 9 shows the reaction functions for the evolving DE cosmologies listed in Table 1. The left-hand panel contains essentially the same z = 0 information of Fig. 2 in Mead (2017), with the notable difference that here we compute the spherical collapse virial overdensities including the DE contribution to the potential energy, and do not assume energy conservation during collapse (Schmidt et al. 2010) (expressions for the individual terms entering the virial theorem can be found in Appendix  A). The right-hand panel shows the same quantity at z = 1. At both redshifts the halo model reactions based on the standard ST mass function fits can capture very well the measurements from simulations down to the transition scale between the two- and one-halo terms. Also in this case, we attribute inaccuracies on small scales mainly to the inadequacy of the Dolag et al. (2004) and Bullock et al. (2001) halo concentration prescriptions for the real and pseudo cosmologies, respectively.

Matter power spectrum reactions for the six DE cosmologies with {w0, wa} pairs listed in Table 1. In each panel, the data points represent the mean reactions measured from simulations as the average from three realizations; lines denote the corresponding halo model predictions. Lower panels show the fractional deviation of the halo model relative to the simulations, with grey bands marking the $1\, {\rm per\, cent}$ and $2\, {\rm per\, cent}$ uncertainty regions. Left: reactions at z = 0. These are similar to those presented in Mead (2017) and only differ in the derivation of the virial overdensity Δvir, in that here we account for all relevant contributions to the potential energy and do not assume energy conservation (see equations A6–A11). On small scales agreement with the simulations is somewhat better than in modified gravity, which can be ascribed to a more accurate c–M relation at z = 0. Right: z = 1 reactions. Although per cent level accuracy is reached on scales k ≲ 1 $h \, {\rm Mpc}^{-1}$, performance on highly non-linear scales deteriorates beyond the 2 per cent level for some models. We think part of the reason for that is to be found in high-z inaccuracies of the Dolag et al. (2004) prescription for the halo concentrations in DE cosmologies.
Figure 9.

Matter power spectrum reactions for the six DE cosmologies with {w0, wa} pairs listed in Table 1. In each panel, the data points represent the mean reactions measured from simulations as the average from three realizations; lines denote the corresponding halo model predictions. Lower panels show the fractional deviation of the halo model relative to the simulations, with grey bands marking the |$1\, {\rm per\, cent}$| and |$2\, {\rm per\, cent}$| uncertainty regions. Left: reactions at z = 0. These are similar to those presented in Mead (2017) and only differ in the derivation of the virial overdensity Δvir, in that here we account for all relevant contributions to the potential energy and do not assume energy conservation (see equations A6–A11). On small scales agreement with the simulations is somewhat better than in modified gravity, which can be ascribed to a more accurate c–M relation at z = 0. Right: z = 1 reactions. Although per cent level accuracy is reached on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠, performance on highly non-linear scales deteriorates beyond the 2 per cent level for some models. We think part of the reason for that is to be found in high-z inaccuracies of the Dolag et al. (2004) prescription for the halo concentrations in DE cosmologies.

Open in new tabDownload slide

In Fig. 10 we consider two representative DE models, DE2 and DE3, and compare their matter power spectra to that of ΛCDM with the same initial conditions. Their particular equations of state enhance the growth of structure in one case and suppress it in the other. Here, we employ the Coyote Universe Emulator (Heitmann et al. 2014) not only for our baseline pseudo power spectra, but also as a substitute for the real and ΛCDM cosmology simulations. This serves as an example to illustrate a straightforward application of the reaction functions: extend the cosmological parameter space of matter power spectrum emulators designed for the concordance cosmology only, without the need to run model-dependent and expensive cosmological simulations. For the evolving equation of state of DE3 we use the emulator extension code PKequal built upon the work presented in Casarini et al. (2016). Knowing that the output from the emulator is 1–2 per cent accurate on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠, from the previous results in Fig. 9 we can expect similar agreement between our reaction-based power spectra and those obtained from the emulator itself. This is indeed the case except in the range |$0.02 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 0.5$|⁠, where the interpolation process within the emulator fails to capture the correct dependence on ωb and w because the specific values we use sit on the edge of its domain of applicability.14

Matter power spectrum fractional differences relative to ΛCDM for DE3 (left) and DE2 (right) models, where the numbers in curly brackets specify the equation-of-state pair {w0, wa}. Data points correspond to the output from the Coyote Universe emulator (Heitmann et al. 2014) at z = 0 (blue squares) and z = 1 (red triangles). For DE3, which has a non-constant w, we used the emulator extension of Casarini et al. (2016). Coloured lines represent predictions based on the halo model reactions at z = 0 (dashed blue) and z = 1 (dot–dashed red). For reference, the linear theory predictions are shown as dashed grey lines. Lower panels show the fractional deviation of the non-linear predictions from the emulator, with grey bands marking $1\, {\rm per\, cent}$ and $2\, {\rm per\, cent}$ uncertainty regions. For our theoretical estimates we use pseudo cosmology matter power spectra computed with the emulator itself as baseline, which we then rescale with the halo model reactions. Lower panels illustrate that our halo model predictions can be employed to map accurately ΛCDM cosmologies to evolving DE models. Deviations of order $2\!-\!4\, {\rm per\, cent}$ on scales $0.02 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 0.5$ are entirely due to the emulator being pushed to the edges of its domain of applicability in the plane {ωb, w}.
Figure 10.

Matter power spectrum fractional differences relative to ΛCDM for DE3 (left) and DE2 (right) models, where the numbers in curly brackets specify the equation-of-state pair {w0, wa}. Data points correspond to the output from the Coyote Universe emulator (Heitmann et al. 2014) at z = 0 (blue squares) and z = 1 (red triangles). For DE3, which has a non-constant w, we used the emulator extension of Casarini et al. (2016). Coloured lines represent predictions based on the halo model reactions at z = 0 (dashed blue) and z = 1 (dot–dashed red). For reference, the linear theory predictions are shown as dashed grey lines. Lower panels show the fractional deviation of the non-linear predictions from the emulator, with grey bands marking |$1\, {\rm per\, cent}$| and |$2\, {\rm per\, cent}$| uncertainty regions. For our theoretical estimates we use pseudo cosmology matter power spectra computed with the emulator itself as baseline, which we then rescale with the halo model reactions. Lower panels illustrate that our halo model predictions can be employed to map accurately ΛCDM cosmologies to evolving DE models. Deviations of order |$2\!-\!4\, {\rm per\, cent}$| on scales |$0.02 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 0.5$| are entirely due to the emulator being pushed to the edges of its domain of applicability in the plane {ωb, w}.

Open in new tabDownload slide

6 CONCLUSIONS

The spatial distribution of matter in the Universe and its evolution with time emerge from the interplay of gravitational and astrophysical processes, and are inextricably linked to the nature of the cosmic matter-energy constituents. The power spectrum is an essential statistic describing the clustering of matter in the Universe, and lies at the heart of probes of the growth of structure such as cosmic shear and galaxy clustering. Measurements of these quantities from the next generation of large-volume surveys are expected to reach per cent level uncertainty – upon careful control of systematics – on scales where non-linearities and baryonic physics become important. It is notoriously difficult to predict the matter power spectrum in this regime to such a degree of accuracy, yet these scales contain a wealth of information on currently unanswered questions, e.g. the nature of DE, the sum of neutrino masses, and the extent of baryonic feedback mechanisms.

In this work we focused on modelling the non-linear matter power spectrum in modified theories of gravity and evolving DE cosmologies. We extended the reaction method of Mead (2017) using the halo model to predict the non-linear effects induced by new physics on the matter power spectrum of specifically designed reference cosmologies. These fiducial – pseudo – cosmologies mimic the linear clustering of the target – real – cosmologies, yet their evolution is governed by standard gravity with ΛCDM expansion histories (which are either quick to simulate with current resources, if not already available with emulators). We showed that by applying the halo model reactions to the non-linear matter power spectrum of the pseudo cosmologies we are able to recover the real counterpart to within 1 per cent on scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|for all cases under study. Remarkably, our methodology does not involve fitting the power spectra measured in simulations at any stage. Instead, having access to accurate ratios of the halo mass function in the real cosmology to that in the pseudo cosmology is crucial to achieve the observed performance. Not including this information from the simulation degrades the accuracy to |${\lesssim} 3\, {\rm per\, cent}$|⁠. The halo model reactions can also be used to predict the matter power spectrum in the highly non-linear regime. However, this requires additional knowledge of the average structural properties of the dark matter haloes as well as the inclusion of baryonic effects (see e.g. Schneider et al. 2019). We leave these improvements for future work (Cataneo et al. in preparation).

In the case of the DE models we adopted the Coyote Universe emulator for the pseudo matter power spectrum (i.e. for w = −1), which we then combined with our halo model reaction to obtain the real expected quantity. By comparing this prediction to the real output of the emulator (i.e. for w ≠ −1) we showed that emulators trained on pure ΛCDM models can be accurately extended to non-standard cosmologies in an analytical way, thus substantially increasing their flexibility while simultaneously reducing the computational cost for their design. However, applications of this strategy to scale-dependent modifications of gravity [such as f(R) models] necessitate of a more elaborate ΛCDM emulator that takes as input also information on the linearly modified shape of the matter power spectrum (Giblin et al. in preparation). Together with suitable halo model reactions, this emulator can also be employed to predict the non-linear total matter power spectrum in massive neutrino cosmologies (Cataneo et al. in preparation), where the presence of a free streaming scale induces a scale-dependent linear growth (Lesgourgues & Pastor 2006).

Given that our method builds on the halo model, the halo mass function and the spherical collapse model are absolutely central for our predictions. Contrary to the standard halo model calculations, however, the accuracy of our reactions strongly depends on the precision of the pseudo and real halo mass functions. This opens up the possibility of combining in a novel way cosmic shear and cluster abundance measurements, for example. Moreover, quite general modifications of gravity – with their screening mechanisms – can be implemented in the spherical collapse calculations through the non-linear parametrized post-Friedmannian formalism of Lombriser (2016).

In summary, halo model reactions provide a fast, accurate, and versatile method to compute the real-space non-linear matter power spectrum in non-standard cosmologies. Successful implementations in redshift-space by Mead (2017) pave the way for applications to redshift-space distortions data as well. Altogether, these features make the halo model reactions an attractive alternative in-between perturbative analytical methods and brute force emulation, and promise to be an essential tool in future combined-probe analyses in search of new physics beyond the standard paradigm.

ACKNOWLEDGEMENTS

We thank Philippe Brax, Patrick Valageas, Alejandro Aviles, and Jorge Cervantes-Cota for crosschecking our perturbation theory calculations, and David Rapetti and Simon Foreman for useful discussions. MC and CH acknowledge support from the European Research Council under grant number 647112. LL acknowledges support by a Swiss National Science Foundation (SNSF) Professorship grant (No. 170547), an SNSF Advanced Postdoc.Mobility Fellowship (No. 161058), the Science and Technology Facilities Council Consolidated Grant for Astronomy and Astrophysics at the University of Edinburgh, and the Affiliate programme of the Higgs Centre for Theoretical Physics. AM has received funding from the European Union‘s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 702971 and acknowledges MDM-2014-0369 of ICCUB (Unidad de Excelencia Maria de Maeztu). SB is supported by Harvard University through the ITC Fellowship. BL is supported by the European Research Council via grant ERC-StG-716532-PUNCA, and by UK STFC Consolidated Grants ST/P000541/1 and ST/L00075X/1. This work used the DiRAC Data Centric system at Durham University, operated by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment was funded by BIS National E-infrastructure capital grant ST/K00042X/1, STFC capital grants ST/H008519/1, ST/K00087X/1, STFC DiRAC Operations grant ST/K003267/1 and Durham University. DiRAC is part of the National E-Infrastructure.

Footnotes

1

Here and throughout we work in natural units, and set c = 1.

2

See e.g. Noller et al. (2014), Bose, Hellwing & Li (2015), and Lagos et al. (2018) for a detailed discussion on the validity of the quasi-static approximation in modified gravity.

3

See, however, the recent work by He et al. (2018) where it was showed that deviations as small as |$|\bar{f}_{R0}| =10^{-6}$| could already be in strong tension with redshift space distortions data. At this time, the tightest constraints on f(R) gravity come from the analysis of kinematic data for the gaseous and stellar components in nearby galaxies, which only allows |$|\bar{f}_{R0}| \lesssim 10^{-8}$| (Desmond et al. 2018).

4

This is an assumption made to ease comparisons to ΛCDM simulations, and is not a strict observational requirement (cf. Lombriser et al. 2009).

5

For cosmologies with a scale-independent linear growth, such as nDGP and wCDM, using the ΛCDM growth is simply a matter of convenience. In f(R) gravity this approach has the advantage of preserving the statistics of the initial mass fluctuations. For more details see Cataneo et al. (2016).

6

In this instance, and whenever the context is clear, we omit the time-dependence from our notation. However, we reintroduce it any time this can become a source of ambiguity.

7

Valogiannis & Bean (2019) recently found that in f(R) gravity the linear halo bias contains an additional term accounting for the environmental dependence, which we omit in equation (43). Given the relative unimportance of the bias for our halo model reactions (see Sections 3.3 and 5), this choice is, in effect, inconsequential for the accuracy of our predictions.

8

Note that in Mead (2017) this is referred to as response. We use the term reaction to distinguish it from the quantities studied in Neyrinck & Yang (2013), Nishimichi, Bernardeau & Taruya (2016), or Barreira & Schmidt (2017). Our and these other definitions are all conceptually analogous, in the sense that they describe how the non-linear power spectrum responds to changes in some feature, which in our case is physics beyond the vanilla ΛCDM cosmology, e.g. fifth forces, evolving DE, massive neutrinos, baryons etc.

9

Note that we neglect the integral factor equation (50) in our two-halo terms. We checked that setting I2(k) = 1 for all scales has no measurable impact on our halo model reactions.

10

This is not strictly true in the traditional halo model implementation we adopt in this work. In fact, the one-halo terms have a constant tail in the low-k limit (see equation 54) that dominates the two-halo contributions on very large scales. In a consistent formulation of the halo model, however, where mass and momentum conservation are enforced, this tail disappears leaving only the theoretically motivated two-halo term (Schmidt 2016). For our purposes we can simply ignore this inconsistency, and restrict the use of the reaction function to scales k > 0.01 |$h \, {\rm Mpc}^{-1}$|⁠.

11

As we shall see below, k⋆ is derived from perturbation theory and is largely independent of the one-halo contribution. However, its specific value should be interpreted with caution, in that equally good alternatives to the exponential function in equation (53) can provide different solutions to equation (55).

12

Due to the nature of the chameleon screening, in f(R) gravity the virial overdensity depends on both the mass of the halo and the gravitational potential in its environment. Things are much simpler in DGP, where by virtue of the Vainshtein screening both dependencies disappear.

13

In practice, we start with the Hu & Kravtsov (2003) relation |$M_{300} = \mathcal {Q}(M_{\rm vir})M_{\rm vir}$|⁠, and make the replacement |$\mathcal {Q}(M_{\rm vir}) \rightarrow \mathcal {Q}^{\prime }(M_{\rm vir}) = \min [{\tilde{a}}\mathcal {Q}^{f(R)}({\tilde{b}}M_{\rm vir}),\mathcal {Q}^{\rm GR}(M_{\rm vir})]$|⁠, where |${\tilde{a}}$| and |${\tilde{b}}$| are |$\mathcal {O}(1)$| free parameters fine-tuned to reach the required accuracy in the halo model reaction at z = 0. The use of the minimum operator ensures that the f(R) conversion factor matches the corresponding GR value for masses large enough to fully activate the chameleon screening.

14

The Coyote Universe emulator accepts values 0.0215 < ωb < 0.0235 and −1.3 < w < −0.7, while for our two evolving DE models we have ωb = 0.0245, w(DE2) = −1.3, and |$w_{\rm eff}^{\rm (DE3)} = -0.84$|⁠. Since our background baryon density resides outside the domain of the emulator, we set it to the maximum value allowed. This has virtually no impact on our halo model responses, in that they depend only weakly on ωb.

REFERENCES

Abazajian
K.
,
Switzer
E. R.
,
Dodelson
S.
,
Heitmann
K.
,
Habib
S.
,
2005
,
Phys. Rev. D
,
71
,
043507
10.1103/PhysRevD.71.043507

Crossref

 

Abbott
B. P.
et al. .,
2017a
,
Phys. Rev. Lett.
,
119
,
161101

Crossref
Search ADS
 

Abbott
B. P.
et al. .,
2017b
,
ApJ
,
848
,
L13

Crossref
Search ADS
 

Abbott
T. M. C.
et al. .,
2018
,
Phys. Rev.
,
D98
,
043526

 

Achitouv
I.
,
Baldi
M.
,
Puchwein
E.
,
Weller
J.
,
2016
,
Phys. Rev. D
,
93
,
103522
10.1103/PhysRevD.93.103522

Crossref

 

Aghanim
N.
et al. .,
2018
,
preprint (arXiv:1807.06209)

Alam
S.
,
Ho
S.
,
Silvestri
A.
,
2016
,
MNRAS
,
456
,
3743
10.1093/mnras/stv2935

Crossref
Search ADS
 

Albrecht
A.
et al. .,
2006
,
arXiv Astrophysics e-prints
10.1088/0960-1317/16/6/S13

Crossref

Alonso
D.
,
Bellini
E.
,
Ferreira
P. G.
,
Zumalacárregui
M.
,
2017
,
Phys. Rev. D
,
95
,
063502
10.1103/PhysRevD.95.063502

Crossref

 

Amendola
L.
,
Tsujikawa
S.
,
2010
,
Dark Energy: Theory and Observations
.

 

Armendariz-Picon
C.
,
Mukhanov
V.
,
Steinhardt
P. J.
,
2000
,
Phys. Rev. Lett.
,
85
,
4438
10.1103/PhysRevLett.85.4438

Crossref
Search ADS
PubMed
 

Arnold
C.
,
Fosalba
P.
,
Springel
V.
,
Puchwein
E.
,
Blot
L.
,
2019
,
MNRAS
,
483
,
790

Crossref
Search ADS
 

Aviles
A.
,
Cervantes-Cota
J. L.
,
2017
,
Phys. Rev. D
,
96
,
123526
10.1103/PhysRevD.96.123526

Crossref

 

Babichev
E.
,
Deffayet
C.
,
Ziour
R.
,
2009
,
Int. J. Mod. Phys.
,
D18
,
2147

Crossref
Search ADS
 

Baker
T.
,
Bellini
E.
,
Ferreira
P. G.
,
Lagos
M.
,
Noller
J.
,
Sawicki
I.
,
2017
,
Phys. Rev. Lett.
,
119
,
251301
10.1103/PhysRevLett.119.251301

Crossref
Search ADS
PubMed
 

Baldi
M.
,
2012
,
Phys. Dark Univ.
,
1
,
162
10.1016/j.dark.2012.10.004

Crossref
Search ADS
 

Baldi
M.
,
Villaescusa-Navarro
F.
,
Viel
M.
,
Puchwein
E.
,
Springel
V.
,
Moscardini
L.
,
2014
,
MNRAS
,
440
,
75
10.1093/mnras/stu259

Crossref
Search ADS
 

Barreira
A.
,
Bose
S.
,
Li
B.
,
2015
,
J. Cosmol. Astropart. Phys.
,
12
,
059

Crossref
Search ADS
 

Barreira
A.
,
Li
B.
,
Hellwing
W. A.
,
Baugh
C. M.
,
Pascoli
S.
,
2013
,
J. Cosmol. Astropart. Phys.
,
10
,
027

Crossref
Search ADS
 

Barreira
A.
,
Li
B.
,
Hellwing
W. A.
,
Baugh
C. M.
,
Pascoli
S.
,
2014b
,
J. Cosmol. Astropart. Phys.
,
9
,
031

Crossref
Search ADS
 

Barreira
A.
,
Li
B.
,
Hellwing
W. A.
,
Lombriser
L.
,
Baugh
C. M.
,
Pascoli
S.
,
2014a
,
J. Cosmol. Astropart. Phys.
,
4
,
029

Crossref
Search ADS
 

Barreira
A.
,
Schmidt
F.
,
2017
,
J. Cosmol. Astropart. Phys.
,
6
,
053

Crossref
Search ADS
 

Barreira
A.
,
Sánchez
A. G.
,
Schmidt
F.
,
2016
,
Phys. Rev. D
,
94
,
084022
10.1103/PhysRevD.94.084022

Crossref

 

Battye
R. A.
,
Pace
F.
,
Trinh
D.
,
2018
,
Phys. Rev. D
,
98
,
023504

Crossref
Search ADS
 

Behroozi
P. S.
,
Wechsler
R. H.
,
Wu
H.-Y.
,
2013
,
ApJ
,
762
,
109
10.1088/0004-637X/762/2/109

Crossref
Search ADS
 

Bernardeau
F.
,
Colombi
S.
,
Gaztañaga
E.
,
Scoccimarro
R.
,
2002
,
Phys. Rep.
,
367
,
1
10.1016/S0370-1573(02)00135-7

Crossref

 

Bose
B.
,
Koyama
K.
,
2016
,
J. Cosmol. Astropart. Phys.
,
8
,
032

Crossref
Search ADS
 

Bose
B.
,
Koyama
K.
,
Lewandowski
M.
,
Vernizzi
F.
,
Winther
H. A.
,
2018
,
J. Cosmol. Astropart. Phys.
,
4
,
063

Crossref
Search ADS
 

Bose
S.
,
Hellwing
W. A.
,
Li
B.
,
2015
,
J. Cosmol. Astropart. Phys.
,
2
,
034

Crossref
Search ADS
 

Bose
S.
,
Li
B.
,
Barreira
A.
,
He
J.-h.
,
Hellwing
W. A.
,
Koyama
K.
,
Llinares
C.
,
Zhao
G.-B.
,
2017
,
J. Cosmol. Astropart. Phys.
,
2
,
050

Crossref
Search ADS
 

Brax
P.
,
Davis
A.-C.
,
Li
B.
,
Winther
H. A.
,
Zhao
G.-B.
,
2012
,
J. Cosmol. Astropart. Phys.
,
10
,
002

Crossref
Search ADS
 

Brax
P.
,
Valageas
P.
,
2012
,
Phys. Rev. D
,
86
,
063512
10.1103/PhysRevD.86.063512

Crossref

 

Brax
P.
,
Valageas
P.
,
2013
,
Phys. Rev. D
,
88
,
023527
10.1103/PhysRevD.88.023527

Crossref

 

Brito
R.
,
Terrana
A.
,
Johnson
M. C.
,
Cardoso
V.
,
2014
,
Phys. Rev. D
,
90
,
124035
10.1103/PhysRevD.90.124035

Crossref

 

Bullock
J. S.
,
Kolatt
T. S.
,
Sigad
Y.
,
Somerville
R. S.
,
Kravtsov
A. V.
,
Klypin
A. A.
,
Primack
J. R.
,
Dekel
A.
,
2001
,
MNRAS
,
321
,
559
10.1046/j.1365-8711.2001.04068.x

Crossref
Search ADS
 

Carlson
J.
,
White
M.
,
Padmanabhan
N.
,
2009
,
Phys. Rev. D
,
80
,
043531
10.1103/PhysRevD.80.043531

Crossref

 

Carroll
S. M.
,
2004
,
Spacetime and Geometry: An Introduction to General Relativity
.
10.1142/9789812562128_0011

Google Scholar

OpenURL Placeholder Text

Crossref

 

Casarini
L.
,
Bonometto
S. A.
,
Tessarotto
E.
,
Corasaniti
P.-S.
,
2016
,
J. Cosmol. Astropart. Phys.
,
8
,
008

Crossref
Search ADS
 

Casas
S.
,
Kunz
M.
,
Martinelli
M.
,
Pettorino
V.
,
2017
,
Phys. Dark Univ.
,
18
,
73
10.1016/j.dark.2017.09.009

Crossref
Search ADS
 

Cataneo
M.
,
Rapetti
D.
,
Lombriser
L.
,
Li
B.
,
2016
,
J. Cosmol. Astropart. Phys.
,
2016
,
024
10.1088/1475-7516/2016/12/024

Crossref
Search ADS
 

Cataneo
M.
et al. .,
2015
,
Phys. Rev. D
,
92
,
044009
10.1103/PhysRevD.92.044009

Crossref

 

Chevallier
M.
,
Polarski
D.
,
2001
,
Int. J. Mod. Phys. D
,
10
,
213
10.1142/S0218271801000822

Crossref
Search ADS
 

Colombi
S.
,
Jaffe
A.
,
Novikov
D.
,
Pichon
C.
,
2009
,
MNRAS
,
393
,
511
10.1111/j.1365-2966.2008.14176.x

Crossref
Search ADS
 

Cooray
A.
,
Sheth
R.
,
2002
,
Phys. Rep.
,
372
,
1
10.1016/S0370-1573(02)00276-4

Crossref

 

Creminelli
P.
,
D’Amico
G.
,
Noreña
J.
,
Vernizzi
F.
,
2009
,
J. Cosmol. Astropart. Phys.
,
2
,
018

Crossref
Search ADS
 

Creminelli
P.
,
Lewandowski
M.
,
Tambalo
G.
,
Vernizzi
F.
,
2018
;
10.1088/1475-7516/2018/12/025
,
J. Cosmol. Astropart. Phys.
,
12
,
25

Crossref
Search ADS
 

Creminelli
P.
,
Vernizzi
F.
,
2017
,
Phys. Rev. Lett.
,
119
,
251302
10.1103/PhysRevLett.119.251302

Crossref
Search ADS
PubMed
 

Crocce
M.
,
Pueblas
S.
,
Scoccimarro
R.
,
2006
,
MNRAS
,
373
,
369
10.1111/j.1365-2966.2006.11040.x

Crossref
Search ADS
 

Cusin
G.
,
Lewandowski
M.
,
Vernizzi
F.
,
2018
,
J. Cosmol. Astropart. Phys.
,
4
,
005

Crossref
Search ADS
 

de Felice
A.
,
Kobayashi
T.
,
Tsujikawa
S.
,
2011
,
Phys. Lett. B
,
706
,
123
10.1016/j.physletb.2011.11.028

Crossref
Search ADS
 

Deffayet
C.
,
Gao
X.
,
Steer
D. A.
,
Zahariade
G.
,
2011
,
Phys. Rev. D
,
84
,
064039
10.1103/PhysRevD.84.064039

Crossref
Search ADS
 

de Rham
C.
,
Melville
S.
,
2018
;
10.1007/JHEP03(2018)011
,
Phys. Rev. Lett.
,
121
,
221101

Crossref
Search ADS
PubMed
 

Desmond
H.
,
Ferreira
P. G.
,
Lavaux
G.
,
Jasche
J.
,
2018
,
MNRAS
,
474
,
3152
10.1093/mnras/stx3062

Crossref
Search ADS
 

Dodelson
S.
,
2003
,
Modern Cosmology
.
10.1086/345714

Crossref

 

Dolag
K.
,
Bartelmann
M.
,
Perrotta
F.
,
Baccigalupi
C.
,
Moscardini
L.
,
Meneghetti
M.
,
Tormen
G.
,
2004
,
A&A
,
416
,
853
10.1051/0004-6361:20031757

Crossref
Search ADS
 

Dunstan
R. M.
,
Abazajian
K. N.
,
Polisensky
E.
,
Ricotti
M.
,
2011
,
preprint (
arXiv:1109.6291)

Dvali
G.
,
Gabadadze
G.
,
Porrati
M.
,
2000
,
Phys. Lett. B
,
485
,
208
10.1016/S0370-2693(00)00669-9

Crossref
Search ADS
 

Eifler
T.
,
2011
,
MNRAS
,
418
,
536
10.1111/j.1365-2966.2011.19502.x

Crossref
Search ADS
 

Euclid Collaboration
,
2018
,
preprint (arXiv:1809.04695)
10.1016/j.pss.2017.08.002

Crossref

Fedeli
C.
,
2014
,
J. Cosmol. Astropart. Phys.
,
4
,
028

 

Fedeli
C.
,
Dolag
K.
,
Moscardini
L.
,
2012
,
MNRAS
,
419
,
1588
10.1111/j.1365-2966.2011.19821.x

Crossref
Search ADS
 

Fedeli
C.
,
Semboloni
E.
,
Velliscig
M.
,
Van Daalen
M.
,
Schaye
J.
,
Hoekstra
H.
,
2014
,
J. Cosmol. Astropart. Phys.
,
8
,
028

 

Giblin
B.
,
Cataneo
M.
,
Moews
B.
,
Heymans
C.
2019
, preprint
(arXiv:1906.02742)

Giocoli
C.
,
Baldi
M.
,
Moscardini
L.
,
2018
,
MNRAS
,
481
,
2813
10.1093/mnras/sty2465

Crossref
Search ADS
 

Giocoli
C.
,
Bartelmann
M.
,
Sheth
R. K.
,
Cacciato
M.
,
2010
,
MNRAS
,
408
,
300
10.1111/j.1365-2966.2010.17108.x

Crossref
Search ADS
 

Hagstotz
S.
,
Costanzi
M.
,
Baldi
M.
,
Weller
J.
,
2019
,
MNRAS
,
486
,
3927

Crossref
Search ADS
 

Hammami
A.
,
Llinares
C.
,
Mota
D. F.
,
Winther
H. A.
,
2015
,
MNRAS
,
449
,
3635
10.1093/mnras/stv529

Crossref
Search ADS
 

Hearin
A. P.
,
Zentner
A. R.
,
Ma
Z.
,
2012
,
J. Cosmol. Astropart. Phys.
,
4
,
034

Crossref
Search ADS
 

Heitmann
K.
,
Lawrence
E.
,
Kwan
J.
,
Habib
S.
,
Higdon
D.
,
2014
,
ApJ
,
780
,
111
10.1088/0004-637X/780/1/111

Crossref
Search ADS
 

He
J.-h.
,
Guzzo
L.
,
Li
B.
,
Baugh
C. M.
,
2018
,
Nat. Astron.
10.1038/s41550-018-0573-2
,
2
,
967

Crossref
Search ADS
 

Heymans
C.
,
Zhao
G.-B.
,
2018
,
Int. J. Mod. Phys. D
,
27
,
1848005
10.1142/S021827181848005X

Crossref
Search ADS
 

Hildebrandt
H.
et al. .,
2017
,
MNRAS
,
465
,
1454
10.1093/mnras/stw2805

Crossref
Search ADS
 

Hinterbichler
K.
,
Khoury
J.
,
2010
,
Phys. Rev. Lett.
,
104
,
231301
10.1103/PhysRevLett.104.231301

Crossref
Search ADS
PubMed
 

Horndeski
G. W.
,
1974
,
Int. J. Theor. Phys.
,
10
,
363
10.1007/BF01807638

Crossref
Search ADS
 

Hu
B.
,
Liu
X.-W.
,
Cai
R.-G.
,
2018
,
MNRAS
,
476
,
L65
10.1093/mnrasl/sly032

Crossref
Search ADS
 

Huterer
D.
,
Takada
M.
,
2005
,
Astropart. Phys.
,
23
,
369
10.1016/j.astropartphys.2005.02.006

Crossref
Search ADS
 

Hu
W.
,
Kravtsov
A. V.
,
2003
,
ApJ
,
584
,
702
10.1086/345846

Crossref
Search ADS
 

Hu
W.
,
Sawicki
I.
,
2007
,
Phys. Rev. D
,
76
,
064004
10.1103/PhysRevD.76.064004

Crossref

 

Khoury
J.
,
Weltman
A.
,
2004
,
Phys. Rev. D
,
69
,
044026
10.1103/PhysRevD.69.044026

Crossref

 

Kobayashi
T.
,
Yamaguchi
M.
,
Yokoyama
J.
,
2011
,
Prog. Theor. Phys.
,
126
,
511
10.1143/PTP.126.511

Crossref
Search ADS
 

Koopmans
L.
et al. .,
2015
,
Advancing Astrophysics with the Square Kilometre Array (AASKA14)
,
1

 

Koyama
K.
,
Silva
F. P.
,
2007
,
Phys. Rev. D
,
75
,
084040
10.1103/PhysRevD.75.084040

Crossref

 

Koyama
K.
,
Taruya
A.
,
Hiramatsu
T.
,
2009
,
Phys. Rev. D
,
79
,
123512
10.1103/PhysRevD.79.123512

Crossref

 

Kwan
J.
,
Bhattacharya
S.
,
Heitmann
K.
,
Habib
S.
,
2013
,
ApJ
,
768
,
123
10.1088/0004-637X/768/2/123

Crossref
Search ADS
 

Lagos
M.
,
Bellini
E.
,
Noller
J.
,
Ferreira
P. G.
,
Baker
T.
,
2018
,
J. Cosmol. Astropart. Phys.
,
3
,
021

Crossref
Search ADS
 

Lahav
O.
,
Lilje
P. B.
,
Primack
J. R.
,
Rees
M. J.
,
1991
,
MNRAS
,
251
,
128
10.1093/mnras/251.1.128

Crossref
Search ADS
 

Lam
T. Y.
,
Li
B.
,
2012
,
MNRAS
,
426
,
3260
10.1111/j.1365-2966.2012.21746.x

Crossref
Search ADS
 

Laureijs
R.
et al. .,
2011
,
preprint (
arXiv:1110.3193)

Lawrence
E.
et al. .,
2017
,
ApJ
,
847
,
50
10.3847/1538-4357/aa86a9

Crossref
Search ADS
 

Lesgourgues
J.
,
Pastor
S.
,
2006
,
Phys. Rep.
,
429
,
307
10.1016/j.physrep.2006.04.001

Crossref

 

Levi
M.
et al. .,
2013
,
preprint (arXiv:1308.0847)
10.1016/j.jmarsys.2012.12.010

Crossref

Lewis
A.
,
Challinor
A.
,
Lasenby
A.
,
2000
,
ApJ
,
538
,
473
10.1086/309179

Crossref
Search ADS
 

Li
B.
,
Barreira
A.
,
Baugh
C. M.
,
Hellwing
W. A.
,
Koyama
K.
,
Pascoli
S.
,
Zhao
G.-B.
,
2013b
,
J. Cosmol. Astropart. Phys.
,
1311
,
012

 

Li
B.
,
Efstathiou
G.
,
2012
,
MNRAS
,
421
,
1431
10.1111/j.1365-2966.2011.20404.x

Crossref
Search ADS
 

Li
B.
,
Lam
T. Y.
,
2012
,
MNRAS
,
425
,
730
10.1111/j.1365-2966.2012.21592.x

Crossref
Search ADS
 

Li
B.
,
Zhao
G.-B.
,
Koyama
K.
,
2013a
,
J. Cosmol. Astropart. Phys.
,
1305
,
023

Crossref
Search ADS
 

Li
B.
,
Zhao
G.-B.
,
Teyssier
R.
,
Koyama
K.
,
2012
,
J. Cosmol. Astropart. Phys.
,
1201
,
051

Crossref
Search ADS
 

Linder
E. V.
,
2003
,
Phys. Rev. Lett.
,
90
,
091301
10.1103/PhysRevLett.90.091301

Crossref
Search ADS
PubMed
 

Liu
X.
et al. .,
2016
,
Phys. Rev. Lett.
,
117
,
051101
10.1103/PhysRevLett.117.051101

Crossref
Search ADS
PubMed
 

Li
Y.
,
Hu
W.
,
2011
,
Phys. Rev. D
,
84
,
084033
10.1103/PhysRevD.84.084033

Crossref

 

Llinares
C.
,
2017
,
preprint (arXiv:1709.04703)
10.1103/PhysRevLett.118.101301

Crossref

Llinares
C.
,
Mota
D. F.
,
Winther
H. A.
,
2014
,
A&A
,
562
,
A78
10.1051/0004-6361/201322412

Crossref
Search ADS
 

Lombriser
L.
,
2014
,
Annalen Phys.
,
526
,
259

Crossref
Search ADS
 

Lombriser
L.
,
2016
,
J. Cosmol. Astropart. Phys.
,
1611
,
039

Crossref
Search ADS
 

Lombriser
L.
,
Hu
W.
,
Fang
W.
,
Seljak
U.
,
2009
,
Phys. Rev. D
,
80
,
063536

Crossref
Search ADS
 

Lombriser
L.
,
Koyama
K.
,
Li
B.
,
2014
,
J. Cosmol. Astropart. Phys.
,
3
,
021

Crossref
Search ADS
 

Lombriser
L.
,
Koyama
K.
,
Zhao
G.-B.
,
Li
B.
,
2012
,
Phys. Rev. D
,
85
,
124054
10.1103/PhysRevD.85.124054

Crossref

 

Lombriser
L.
,
Li
B.
,
Koyama
K.
,
Zhao
G.-B.
,
2013
,
Phys. Rev. D
,
87
,
123511
10.1103/PhysRevD.87.123511

Crossref
Search ADS
 

Lombriser
L.
,
Lima
N. A.
,
2017
,
Phys. Lett. B
,
765
,
382
10.1016/j.physletb.2016.12.048

Crossref
Search ADS
 

Lombriser
L.
,
Taylor
A.
,
2016
,
J. Cosmol. Astropart. Phys.
,
3
,
031

Crossref
Search ADS
 

LSST Dark Energy Science Collaboration
2012
,
preprint (arXiv:1211.0310)
10.1051/0004-6361/201117780

Crossref

Maor
I.
,
Lahav
O.
,
2005
,
J. Cosmol. Astropart. Phys.
,
7
,
003

Crossref
Search ADS
 

Marsh
D. J. E.
,
2016
,
preprint (arXiv:1605.05973)
10.1371/journal.pcbi.1004922

Crossref

María Ezquiaga
J.
,
García-Bellido
J.
,
Zumalacárregui
M.
,
2017
,
preprint (
arXiv:1710.05901)

Massara
E.
,
Villaescusa-Navarro
F.
,
Viel
M.
,
2014
,
J. Cosmol. Astropart. Phys.
,
12
,
053

Crossref
Search ADS
 

McManus
R.
,
Lombriser
L.
,
Peñarrubia
J.
,
2016
,
J. Cosmol. Astropart. Phys.
,
1611
,
006

Crossref
Search ADS
 

Mead
A. J.
,
2017
,
MNRAS
,
464
,
1282
10.1093/mnras/stw2312

Crossref
Search ADS
 

Mead
A. J.
,
Heymans
C.
,
Lombriser
L.
,
Peacock
J. A.
,
Steele
O. I.
,
Winther
H. A.
,
2016
,
MNRAS
,
459
,
1468
10.1093/mnras/stw681

Crossref
Search ADS
 

Mead
A. J.
,
Peacock
J. A.
,
Heymans
C.
,
Joudaki
S.
,
Heavens
A. F.
,
2015b
,
MNRAS
,
454
,
1958

Crossref
Search ADS
 

Mead
A. J.
,
Peacock
J. A.
,
Lombriser
L.
,
Li
B.
,
2015a
,
MNRAS
,
452
,
4203

Crossref
Search ADS
 

Mo
H.
,
van den Bosch
F. C.
,
White
S.
,
2010
,
Galaxy Formation and Evolution
.

 

Mohammed
I.
,
Seljak
U.
,
2014
,
MNRAS
,
445
,
3382
10.1093/mnras/stu1972

Crossref
Search ADS
 

Navarro
J. F.
,
Frenk
C. S.
,
White
S. D. M.
,
1996
,
ApJ
,
462
,
563
10.1086/177173

Crossref
Search ADS
 

Neyrinck
M. C.
,
Yang
L. F.
,
2013
,
MNRAS
,
433
,
1628
10.1093/mnras/stt949

Crossref
Search ADS
 

Nicolis
A.
,
Rattazzi
R.
,
2004
,
J. High Energy Phys.
,
6
,
059

Crossref
Search ADS
 

Nishimichi
T.
,
Bernardeau
F.
,
Taruya
A.
,
2016
,
Phys. Lett. B
,
762
,
247
10.1016/j.physletb.2016.09.035

Crossref
Search ADS
 

Noller
J.
,
von Braun-Bates
F.
,
Ferreira
P. G.
,
2014
,
Phys. Rev. D
,
89
,
023521
10.1103/PhysRevD.89.023521

Crossref

 

Oyaizu
H.
,
2008
,
Phys. Rev. D
,
78
,
123523
10.1103/PhysRevD.78.123523

Crossref

 

Park
M.
,
Zurek
K. M.
,
Watson
S.
,
2010
,
Phys. Rev. D
,
81
,
124008
10.1103/PhysRevD.81.124008

Crossref

 

Peacock
J. A.
,
Smith
R. E.
,
2000
,
MNRAS
,
318
,
1144
10.1046/j.1365-8711.2000.03779.x

Crossref
Search ADS
 

Perlmutter
S.
et al. .,
1999
,
ApJ
,
517
,
565
10.1086/307221

Crossref
Search ADS
 

Planck Collaboration XIV
,
2016
,
A&A
,
594
,
A14
10.1051/0004-6361/201525814

Crossref
Search ADS
 

Press
W. H.
,
Schechter
P.
,
1974
,
ApJ
,
187
,
425
10.1086/152650

Crossref
Search ADS
 

Puchwein
E.
,
Baldi
M.
,
Springel
V.
,
2013
,
MNRAS
,
436
,
348
10.1093/mnras/stt1575

Crossref
Search ADS
 

Ratra
B.
,
Peebles
P. J. E.
,
1988
,
Phys. Rev. D
,
37
,
3406
10.1103/PhysRevD.37.3406

Crossref
Search ADS
 

Reischke
R.
,
Spurio Mancini
A.
,
Schäfer
B. M.
,
Merkel
P. M.
,
2018
,
preprint (arXiv:1804.02441)
10.1103/PhysRevD.98.103507

Crossref

Riess
A. G.
et al. .,
1998
,
AJ
,
116
,
1009
10.1086/300499

Crossref
Search ADS
 

Sakstein
J.
,
Jain
B.
,
2017
,
Phys. Rev. Lett.
,
119
,
251303
10.1103/PhysRevLett.119.251303

Crossref
Search ADS
PubMed
 

Schmidt
F.
,
2009a
,
Phys. Rev. D
,
80
,
043001

 

Schmidt
F.
,
2009b
,
Phys. Rev. D
,
80
,
123003

 

Schmidt
F.
,
2016
,
Phys. Rev. D
,
93
,
063512
10.1103/PhysRevD.93.063512

Crossref

 

Schmidt
F.
,
Hu
W.
,
Lima
M.
,
2010
,
Phys. Rev. D
,
81
,
063005
10.1103/PhysRevD.81.063005

Crossref

 

Schmidt
F.
,
Lima
M.
,
Oyaizu
H.
,
Hu
W.
,
2009
,
Phys. Rev. D
,
79
,
083518
10.1103/PhysRevD.79.083518

Crossref

 

Schneider
A.
,
Smith
R. E.
,
Macciò
A. V.
,
Moore
B.
,
2012
,
MNRAS
,
424
,
684
10.1111/j.1365-2966.2012.21252.x

Crossref
Search ADS
 

Schneider
A.
,
Teyssier
R.
,
Stadel
J.
,
Chisari
N. E.
,
Le Brun
A. M. C.
,
Amara
A.
,
Refregier
A.
,
2019
,
J. Cosmol. Astropart. Phys.
,
03
,
020

Crossref
Search ADS
 

Seljak
U.
,
2000
,
MNRAS
,
318
,
203
10.1046/j.1365-8711.2000.03715.x

Crossref
Search ADS
 

Seljak
U.
,
Vlah
Z.
,
2015
,
Phys. Rev. D
,
91
,
123516
10.1103/PhysRevD.91.123516

Crossref

 

Sheth
R. K.
,
Tormen
G.
,
1999
,
MNRAS
,
308
,
119
10.1046/j.1365-8711.1999.02692.x

Crossref
Search ADS
 

Sheth
R. K.
,
Tormen
G.
,
2002
,
MNRAS
,
329
,
61
10.1046/j.1365-8711.2002.04950.x

Crossref
Search ADS
 

Shi
D.
,
Li
B.
,
Han
J.
,
Gao
L.
,
Hellwing
W. A.
,
2015
,
MNRAS
,
452
,
3179
10.1093/mnras/stv1549

Crossref
Search ADS
 

Smith
R. E.
,
Desjacques
V.
,
Marian
L.
,
2011
,
Phys. Rev. D
,
83
,
043526
10.1103/PhysRevD.83.043526

Crossref

 

Springel
V.
,
2015
,
Astrophysics Source Code Library
, record
ascl:1502.003
10.1093/mnras/stu2220

Crossref

 

Spurio Mancini
A.
,
Reischke
R.
,
Pettorino
V.
,
Schäfer
B. M.
,
Zumalacárregui
M.
,
2018
,
MNRAS
,
480
,
3725
10.1093/mnras/sty2092

Crossref
Search ADS
 

Taylor
P. L.
,
Bernardeau
F.
,
Kitching
T. D.
,
2018b
,
Phys. Rev. D
,
98
,
083514

 

Taylor
P. L.
,
Kitching
T. D.
,
McEwen
J. D.
,
2018a
,
Phys. Rev. D
,
98
,
043532

 

Terukina
A.
,
Lombriser
L.
,
Yamamoto
K.
,
Bacon
D.
,
Koyama
K.
,
Nichol
R. C.
,
2014
,
J. Cosmol. Astropart. Phys.
,
140
,
013

Crossref
Search ADS
 

Teyssier
R.
,
2002
,
A&A
,
385
,
337
10.1051/0004-6361:20011817

Crossref
Search ADS
 

Vainshtein
A. I.
,
1972
,
Phys. Lett.
,
39B
,
393

Crossref
Search ADS
 

Valageas
P.
,
Nishimichi
T.
,
2011
,
A&A
,
527
,
A87
10.1051/0004-6361/201015685

Crossref
Search ADS
 

Valageas
P.
,
Nishimichi
T.
,
Taruya
A.
,
2013
,
Phys. Rev. D
,
87
,
083522
10.1103/PhysRevD.87.083522

Crossref

 

Valogiannis
G.
,
Bean
R.
,
2017
,
Phys. Rev. D
,
95
,
103515
10.1103/PhysRevD.95.103515

Crossref

 

Valogiannis
G.
,
Bean
R.
,
2019
,
Phys. Rev. D
,
99
,
063526
10.1103/PhysRevD.99.063526

Crossref

 

van Daalen
M. P.
,
Schaye
J.
,
2015
,
MNRAS
,
452
,
2247
10.1093/mnras/stv1456

Crossref
Search ADS
 

Wang
J.
,
Hui
L.
,
Khoury
J.
,
2012
,
Phys. Rev. Lett.
,
109
,
241301
10.1103/PhysRevLett.109.241301

Crossref
Search ADS
PubMed
 

Wetterich
C.
,
1988
,
Nucl. Phys. B
,
302
,
668
10.1016/0550-3213(88)90193-9

Crossref
Search ADS
 

Will
C. M.
,
2014
,
Living Rev. Relativ.
,
17
,
4
10.12942/lrr-2014-4

Crossref
Search ADS
PubMed
 

Winther
H.
,
Casas
S.
,
Baldi
M.
,
Koyama
K.
,
Li
B.
,
Lombriser
L.
,
Zhao
G.-B.
,
2019
,
preprint (
arXiv:1903.08798)

Winther
H. A.
,
Ferreira
P. G.
,
2015
,
Phys. Rev. D
,
92
,
064005
10.1103/PhysRevD.92.064005

Crossref

 

Winther
H. A.
,
Koyama
K.
,
Manera
M.
,
Wright
B. S.
,
Zhao
G.-B.
,
2017
,
J. Cosmol. Astropart. Phys.
,
8
,
006

Crossref
Search ADS
 

Winther
H. A.
et al. .,
2015
,
MNRAS
,
454
,
4208
10.1093/mnras/stv2253

Crossref
Search ADS
 

Wyman
M.
,
Jennings
E.
,
Lima
M.
,
2013
,
Phys. Rev. D
,
88
,
084029
10.1103/PhysRevD.88.084029

Crossref

 

Zhao
G.-B.
,
2014
,
ApJS
,
211
,
23
10.1088/0067-0049/211/2/23

Crossref
Search ADS
 

Zhao
G.-B.
,
Li
B.
,
Koyama
K.
,
2011
,
Phys. Rev. D
,
83
,
044007
10.1103/PhysRevD.83.044007

Crossref

 

APPENDIX A: SPHERICAL COLLAPSE IN MODIFIED GRAVITY AND QUINTESSENCE

We shall briefly review expressions for the force enhancement |$\mathcal {F}$| in f(R) and DGP gravity used in the modified spherical collapse calculation in Section 3.1 as well as its impact and the impact of DE domination on the virial theorem.

The force enhancement |$\mathcal {F}$| adopted here for the spherical collapse calculation in f(R) gravity is given by (Lombriser et al. 2013)
(A1)
which uses the thin-shell approximation (Khoury & Weltman 2004; Li & Efstathiou 2012) with thickness |$\Delta R\ll R_{\rm \scriptscriptstyle TH}$|⁠. The expression is also adopted for the thick-shell limit and interpolates between the small-field (⁠|$\mathcal {F}=0$|⁠) and large-field (⁠|$\mathcal {F}=1/3$|⁠) regimes, which correspond to the two limiting scenarios studied in the f(R) spherical collapse calculation of Schmidt et al. (2009). Furthermore, for the f(R) functional form equation (13) one finds (Lombriser et al. 2013)
(A2)
where the normalized top-hat radius
(A3)
needs to be solved in both the halo (h) and the environment (env) using equation (32), that now becomes
(A4)
where we set |$\mathcal {F}=0$| for the ΛCDM environment and primes denote derivatives with respect to ln a. To solve equation (A4) we use the initial conditions y = 1 and y′ = −δi/3 obtained from the linear theory in an Einstein-de Sitter Universe, which at early times is an accurate description for all models in Section 2 when the contribution from radiation is ignored. We then iteratively adjust δi until the condition y(acoll) = 0 (i.e. |$R_{\rm \scriptscriptstyle TH} = 0$|⁠) is satisfied at the desired time of collapse, acoll, within some small tolerance. For the environment, instead, we follow Cataneo et al. (2016). Also note that equation (A2) can easily be generalized for the family of chameleon models (Lombriser et al. 2014).
In DGP gravity, the force modification becomes (Schmidt et al. 2010)
(A5)
where |$x\equiv R_{\rm \scriptscriptstyle TH}/R_{\rm V}$|⁠, with the Vainshtein radius and β function given in equations (23) and (20), respectively. In smooth quintessence cosmologies |$\mathcal {F}=0$|⁠, and the sole effect on the spherical collapse dynamics enters through the non-standard background expansion. In both DGP and quintessence there is no contribution from the environment, hence yh alone describes the full evolution. Moreover, |$\mathcal {F}$| can be generalized and parametrized to cover the range of different screening mechanisms (Lombriser 2016).
The virial theorem for a general metric theory of gravity remains unchanged with respect to its formulation in GR, and reads
(A6)
where W is the potential energy of the system and T its kinetic energy. However, energy is not conserved for evolving DE and modified gravity scenarios, and the virial radius cannot be related to the turnaround radius in the usual way (Lahav et al. 1991). Instead, one must find the time of virialization, avir, that satisfies equation (A6) when all contributions to W are considered. More specifically, the Newtonian, scalar field and background potential energies take the form (Schmidt et al. 2010)
(A7)
(A8)
(A9)
where
(A10)
and the kinetic energy can be written as
(A11)
Combining equations (A6)–(A11) together with equations (36)–(37) allows us to find the virial radius Rvir as a function of halo mass, and for various theories of gravity as well as expansion histories.

APPENDIX B: PERTURBATION THEORY

The non-linear evolution of matter perturbations in modified gravity has been extensively studied in Koyama et al. (2009), Brax & Valageas (2012), Brax & Valageas (2013), and Bose & Koyama (2016). Here we summarize their results and provide explicit expressions for the computation of next-to-leading-order corrections to the linear power spectrum.

The continuity and Euler equations describing the evolution of the matter density perturbations, δ, and peculiar velocity, v, are
(B1)
(B2)
where the gravitational potential Ψ in modified gravity theories with screening mechanisms depends non-linearly on the matter density perturbations, as in equations (9) and (18). Assuming vanishing vorticity, the velocity field can be fully described by its divergence θ ≡ ∇ · v/(aH). By defining the vector field
(B3)
and expanding the gravitational potential up to third order in the perturbations, the fluid equations in Fourier space read
(B4)
where primes denote derivatives with respect to η ≡ ln a, k1⋅⋅⋅n ≡ k1 + ⋅⋅⋅ + kn, and repeated indices are summed over. The left-hand side of equation (B4) controls the evolution of linear perturbations, with the matrix
(B5)
The quantity ϵ measures the time- and scale-dependent linear departure from GR, which in f(R) gravity and DGP reads
(B6)
(B7)
where the mass
(B8)
with
(B9)
and the DGP function β is given in equation (20).
The sources of non-linearities are confined to the right-hand side of equation (B4), where the second order vertices are
(B10)
(B11)
with
(B12)
(B13)
and the only modified gravity non-vanishing third order vertex is σ2; 111, with
(B14)
(B15)
The vertex γ2; 11 = 0 in standard gravity, whereas
(B16)
(B17)
The one-loop power spectrum corrections require the density and velocity fields up to third order in the perturbations, that is, we need ϖ = ϖ(1) + ϖ(2) + ϖ(3). For this, we shall first find the linear solution to equation (B4), ϖ(1), and then derive recursively the higher order solutions with the help of the retarded Green function, which is obtained by setting the right-hand side of equation (B4) to a Dirac delta function (see Brax & Valageas 2012, 2013, for more details). We can write the linear ansatz as
(B18)
where the growing mode, D+(k, η), satisfies the linear second-order equation
(B19)
with Einstein-de Sitter initial conditions |$D_{+}(\eta _{\rm i}) = D_{+}^{\prime }(\eta _{\rm i}) = e^{\eta _{\rm i}}$| at the initial time ηi. The decaying mode, D−, also satisfies this equations and can be directly computed as
(B20)
where the Wronskian of D+ and D− is given by
(B21)
By using the retarded Green function
(B22)
where Θ(η1 − η2) denotes the Heaviside function, we obtain the second- and third-order density perturbations as the convolutions
(B23)
(B24)
with the operators |$\mathcal {K}^{(2)}$| and |$\mathcal {K}^{(3)}$| built from the second- and third-order vertices, γm and σm, respectively (see Brax & Valageas 2013, for more details). In equation (B22) the matrix |$\mathcal {\tilde{G}}$| takes the explicit form
(B25)
where D+/ − i is shorthand for D+/ −(ki, ηi).
Finally, we can write the equal-time two-point correlation – equivalent to equation (56) – as
(B26)
which produces the following expressions for the one-loop integrals
(B27)
(B28)
(B29)
where all indices run from 1 to 2, the linear power spectra are taken at η = 0, and we have used the two-point linear correlator
(B30)

To deactivate the screening mechanisms we simply set γ2; 11 = σ2; 111 = 0, while keeping the linear deviation ϵ given in equations (B6)–(B7). This results in what we call the real ‘no-screening’ power spectrum, |$P_{\rm NoScr}^{\rm real}$|⁠. The pseudo power spectrum up to one-loop, instead, follows from also imposing ϵ = 0, such that the only difference compared to the standard cosmology is in the initial conditions, i.e. in the shape and/or amplitude of the linear power spectrum. Figs B1 and B2 show the SPT reaction functions on quasi-linear scales for f(R) gravity and nDGP, where the pseudo non-linear power spectrum is computed using either the pseudo (solid lines) or ‘no-screening’ (dashed lines) one-loop correction. Although the former approach is theoretically motivated, accuracy arguments make the latter preferable for all cosmologies and redshifts investigated in this work.

SPT matter power spectrum reactions in f(R) gravity with background scalaron amplitudes $|\bar{f}_{R0}|=10^{-5}$ (left) and $|\bar{f}_{R0}|=10^{-6}$ (right). The different lines illustrate the effect of computing the non-linear power spectrum for the pseudo cosmology using either the exact one-loop corrections (solid) or the real unscreened one-loop terms instead (dashed). The squares are the measurements from our simulations. In F5 the real screened and unscreened one-loop contributions err in the same direction, which makes the no-chameleon correction preferable over the theoretically motivated pseudo one-loop term. The opposite is true for F6, although the difference between the two approaches is small in this case. For consistency, throughout this work we always choose the ‘no-screening’ one-loop correction for our pseudo SPT predictions, a strategy good enough on large quasi-linear scales for all cosmologies investigated.
Figure B1.

SPT matter power spectrum reactions in f(R) gravity with background scalaron amplitudes |$|\bar{f}_{R0}|=10^{-5}$| (left) and |$|\bar{f}_{R0}|=10^{-6}$| (right). The different lines illustrate the effect of computing the non-linear power spectrum for the pseudo cosmology using either the exact one-loop corrections (solid) or the real unscreened one-loop terms instead (dashed). The squares are the measurements from our simulations. In F5 the real screened and unscreened one-loop contributions err in the same direction, which makes the no-chameleon correction preferable over the theoretically motivated pseudo one-loop term. The opposite is true for F6, although the difference between the two approaches is small in this case. For consistency, throughout this work we always choose the ‘no-screening’ one-loop correction for our pseudo SPT predictions, a strategy good enough on large quasi-linear scales for all cosmologies investigated.

Open in new tabDownload slide
Same as Fig. B1 for nDGP gravity with crossover scales rcH0 = 0.5 (left) and rcH0 = 2 (right). Here using the real unscreened one-loop corrections instead of the equivalent exact pseudo quantity has negligible impact on the SPT responses.
Figure B2.

Same as Fig. B1 for nDGP gravity with crossover scales rcH0 = 0.5 (left) and rcH0 = 2 (right). Here using the real unscreened one-loop corrections instead of the equivalent exact pseudo quantity has negligible impact on the SPT responses.

Open in new tabDownload slide

APPENDIX C: HALO MASS FUNCTION AND CONCENTRATION TESTS

In Section 3.3 we showed that the real to pseudo halo mass function ratio, |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$|⁠, controls the halo model reaction on scales k ≳ 0.1 |$h \, {\rm Mpc}^{-1}$|⁠. In particular, for the nDGP cosmologies we explicitly checked that fitting the semi-analytical halo mass functions directly to our simulations results in better performance of the halo model reactions for wavenumbers |$0.1 \lesssim k \, {\rm Mpc}\, h^{-1}\lesssim 1$|⁠. Below we briefly explain how these fits to the halo mass functions extracted from our simulations were carried out.

We measure the mean halo abundances and their uncertainties from simulations as outlined in Cataneo et al. (2016), with the important difference that, here, haloes identified with the rockstar halo finder (Behroozi, Wechsler & Wu 2013) have masses defined in spherical volumes with mean density Δvir times the background comoving matter density, as in equation (36). The virial overdensity depends on redshift, matter content, and theory of gravity through equation (37). Compared to Cataneo et al. (2016) we also use a finer mass binning, with a bin size Δlog10M = 0.1. Figs C1 and C2 present a rescaled version of the halo mass functions (i.e. the large-scale limit of the one-halo integrand equation (49)) as well as the |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$| ratios. The standard halo mass function fits for the parameters in equation (41) systematically underpredict the simulation measurements. Refitting these parameters to each real and pseudo simulation separately can change the halo mass function ratio |$n_{\rm vir}^{\rm real}/n_{\rm vir}^{\rm pseudo}$| to an extent relevant for the halo model reactions. Note that when this ratio remains largely unaffected by the refitting, the predicted reactions also show very little variation (compare the right-hand panels of Figs C2 and 6). Table C1 summarizes the refitted ST halo mass function parameters for the real and pseudo nDGP cosmologies used in this work.

$P_{1\rm h}(k \rightarrow 0)$ integrands (equation 49) at z = 0 (left) and z = 1 (right) for the nDGP cosmology with crossover scale rcH0 = 0.5. The data points with error bars are Jackknife estimates from simulations; lines correspond to semi-analytical predictions using the standard ST halo mass function fits {A, q, p} = {0.3222, 0.75, 0.3} (dashed), or to direct fits to our simulations (solid). Top panels show the results for the real nDGP cosmology, while middle panels present the outcome for the pseudo counterpart. The ratios of the real halo mass functions to the pseudo ones are illustrated in the lower panels. Combined with the information in Fig. 5, these ratios clearly stand out as the relevant quantity to achieve per cent level accuracy for the reaction function over scales k ≲ 1 $h \, {\rm Mpc}^{-1}$. In fact, the difference between the standard and refitted halo mass functions is more significant at low redshift, which reflects the performance shown in the lower panels of Fig. 5.
Figure C1.

|$P_{1\rm h}(k \rightarrow 0)$| integrands (equation 49) at z = 0 (left) and z = 1 (right) for the nDGP cosmology with crossover scale rcH0 = 0.5. The data points with error bars are Jackknife estimates from simulations; lines correspond to semi-analytical predictions using the standard ST halo mass function fits {A, q, p} = {0.3222, 0.75, 0.3} (dashed), or to direct fits to our simulations (solid). Top panels show the results for the real nDGP cosmology, while middle panels present the outcome for the pseudo counterpart. The ratios of the real halo mass functions to the pseudo ones are illustrated in the lower panels. Combined with the information in Fig. 5, these ratios clearly stand out as the relevant quantity to achieve per cent level accuracy for the reaction function over scales k ≲ 1 |$h \, {\rm Mpc}^{-1}$|⁠. In fact, the difference between the standard and refitted halo mass functions is more significant at low redshift, which reflects the performance shown in the lower panels of Fig. 5.

Open in new tabDownload slide
Same as Fig. C1 for the nDGP cosmology with crossover scale rcH0 = 2. For both selected redshifts the bottom panels show small differences between the standard and refitted halo mass function ratios. Once again, this matches the expectations from Fig. 6.
Figure C2.

Same as Fig. C1 for the nDGP cosmology with crossover scale rcH0 = 2. For both selected redshifts the bottom panels show small differences between the standard and refitted halo mass function ratios. Once again, this matches the expectations from Fig. 6.

Open in new tabDownload slide
Table C1.
Open in new tab

Refitted ST halo mass function parameters obtained from the simulation data shown in Figs C1 and C2. Fits are consistent with p = 0 in all cases. The standard values are {A, q, p} = {0.3222, 0.75, 0.3}.

ModelAq
nDGPm (z = 0)0.34270.819
nDGPm (z = 1)0.30670.757
nDGPw (z = 0)0.33470.819
nDGPw (z = 1)0.30230.754
pseudo-nDGPm (z = 0)0.34380.829
pseudo-nDGPm (z = 1)0.30570.761
pseudo-nDGPw (z = 0)0.33320.823
pseudo-nDGPw (z = 1)0.30130.753
ModelAq
nDGPm (z = 0)0.34270.819
nDGPm (z = 1)0.30670.757
nDGPw (z = 0)0.33470.819
nDGPw (z = 1)0.30230.754
pseudo-nDGPm (z = 0)0.34380.829
pseudo-nDGPm (z = 1)0.30570.761
pseudo-nDGPw (z = 0)0.33320.823
pseudo-nDGPw (z = 1)0.30130.753
Table C1.
Open in new tab

Refitted ST halo mass function parameters obtained from the simulation data shown in Figs C1 and C2. Fits are consistent with p = 0 in all cases. The standard values are {A, q, p} = {0.3222, 0.75, 0.3}.

ModelAq
nDGPm (z = 0)0.34270.819
nDGPm (z = 1)0.30670.757
nDGPw (z = 0)0.33470.819
nDGPw (z = 1)0.30230.754
pseudo-nDGPm (z = 0)0.34380.829
pseudo-nDGPm (z = 1)0.30570.761
pseudo-nDGPw (z = 0)0.33320.823
pseudo-nDGPw (z = 1)0.30130.753
ModelAq
nDGPm (z = 0)0.34270.819
nDGPm (z = 1)0.30670.757
nDGPw (z = 0)0.33470.819
nDGPw (z = 1)0.30230.754
pseudo-nDGPm (z = 0)0.34380.829
pseudo-nDGPm (z = 1)0.30570.761
pseudo-nDGPw (z = 0)0.33320.823
pseudo-nDGPw (z = 1)0.30130.753

Given the structure of the one-halo term equation (49), one might argue that inaccurate halo profiles are partially responsible for the few per cent mismatch between the predicted and measured reactions in Figs 1 and 5. If that was the case, then having accurate halo mass functions would not necessarily correspond to having accurate halo model reactions. However, Fig. C3 shows otherwise, in that even extreme variations of the halo concentrations cause important changes only on scales k ≳ 0.5 |$h \, {\rm Mpc}^{-1}$|⁠.

Impact of the c–M relation on the nDGPm halo model response at z = 0. Lines correspond to different combinations of normalization and slope in equation (46), and changes are restricted to the real cosmology only. Even significant deviations from the standard values (solid blue line) are not able to match the simulations, with virtually no effect on scales k ≲ 0.5 $h \, {\rm Mpc}^{-1}$.
Figure C3.

Impact of the c–M relation on the nDGPm halo model response at z = 0. Lines correspond to different combinations of normalization and slope in equation (46), and changes are restricted to the real cosmology only. Even significant deviations from the standard values (solid blue line) are not able to match the simulations, with virtually no effect on scales k ≲ 0.5 |$h \, {\rm Mpc}^{-1}$|⁠.

Open in new tabDownload slide

From these tests we conclude that accurate virial halo mass function ratios are central to determining |${\lesssim}1\, {\rm per\, cent}$| accuracy for the halo model reactions, and that the mean concentration of massive haloes is well described by equation (46), at least as long as this relation is employed in the reaction ratios. In future works we will investigate the implications of refitting the c–M relation to that measured in simulations, which has the potential to ameliorate our halo model predictions in the highly non-linear regime.

© 2019 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Article
Download all slides