-
PDF
- Split View
-
Views
-
Cite
Cite
Dilyar Barat, Francesco D’Eugenio, Matthew Colless, Sarah Brough, Barbara Catinella, Luca Cortese, Scott M Croom, Anne M Medling, Sree Oh, Jesse van de Sande, Sarah M Sweet, Sukyoung K Yi, Joss Bland-Hawthorn, Julia Bryant, Michael Goodwin, Brent Groves, Jon Lawrence, Matt S Owers, Samuel N Richards, Nicholas Scott, The SAMI Galaxy Survey: mass–kinematics scaling relations, Monthly Notices of the Royal Astronomical Society, Volume 487, Issue 2, August 2019, Pages 2924–2936, https://doi.org/10.1093/mnras/stz1439
Close - Share Icon Share
ABSTRACT
We use data from the Sydney-AAO Multi-object Integral-field spectroscopy (SAMI) Galaxy Survey to study the dynamical scaling relation between galaxy stellar mass M∗ and the general kinematic parameter |$S_K = \sqrt{K V_{\rm rot}^2 + \sigma ^2}$| that combines rotation velocity Vrot and velocity dispersion σ. We show that the log M∗ – log SK relation: (1) is linear above limits set by properties of the samples and observations; (2) has slightly different slope when derived from stellar or gas kinematic measurements; (3) applies to both early-type and late-type galaxies and has smaller scatter than either the Tully–Fisher relation (log M∗ − log Vrot) for late types or the Faber–Jackson relation (log M∗ − log σ) for early types; and (4) has scatter that is only weakly sensitive to the value of K, with minimum scatter for K in the range 0.4 and 0.7. We compare SK to the aperture second moment (the ‘aperture velocity dispersion’) measured from the integrated spectrum within a 3-arcsecond radius aperture (|$\sigma _{3^{\prime \prime }}$|). We find that while SK and |$\sigma _{3^{\prime \prime }}$| are in general tightly correlated, the log M∗ − log SK relation has less scatter than the |$\log M_* - \log \sigma _{3^{\prime \prime }}$| relation.
1 INTRODUCTION
Galaxy scaling relations correlate observable quantities of galaxies and capture trends among physical properties. These properties can include galaxy stellar mass (M∗), half-light radius (Re), rotation velocity (Vrot), velocity dispersion (σ), luminosity (L), surface brightness (Σ), and other measurable quantities (McGaugh et al. 2000; Pizagno et al. 2005; Courteau et al. 2007; Avila-Reese et al. 2008; Catinella et al. 2012). For example, the Faber–Jackson relation (FJ; Faber & Jackson 1976) connects σ and L while the Kormendy relation (Kormendy 1977) links Σ and Re.
Galaxy scaling relations are convenient in predicting physical galaxy properties because they do not require analytic modelling of a galaxy’s internal dynamics. Using scaling relations to estimate quantities such as distance and mass is efficient when the sample size is too large to obtain detailed observations or to perform individual analyses.
Scaling relations such as the FJ and Kormendy relations have significant intrinsic scatter that impacts the precision of their predictions. Sample pruning and target selection are necessary to produce tight relations. For morphologically defined classes of galaxies, the Tully–Fisher (TF; Tully & Fisher 1977) relation provides a tight relation between L and Vrot for disc-dominated galaxies and the Fundamental Plane relation (FP; Djorgovski & Davis 1987; Dressler et al. 1987) tightly relates Re, σ, and Σ for bulge-dominated galaxies.
Galaxy scaling relations reflect physical mechanisms at work within galaxies. They enable us to gain deeper understanding of galaxy structure, formation, and evolution. For example, Kassin et al. (2012) examined Vrot/σ across redshift and found that galaxies accrete baryons faster earlier in their life-cycles, but that as galaxies evolve their accretion rate and gas content decrease; Obreschkow & Glazebrook (2014) demonstrated that the scaling relation between baryon angular momentum (j), stellar mass (M∗), and bulge fraction (β) of spiral galaxies (Peebles 1969; Fall 1983), can produce and explain the FP (and FJ) scaling relation; Lagos et al. (2017), using cosmological simulations, later confirmed the correlation between galaxy mass and specific angular momentum, and the evolution of the M∗–j scaling relation in passive and active galaxies. Kinematic scaling relations are also useful in the study of the dark matter content of galaxies. For example, Desmond & Wechsler (2017) used the FP to predict the amount of dark matter in the central regions of elliptical galaxies and suggested the deviation of the FP from the virial prediction (also known as the tilt of the FP) can be explained by non-homology in galaxy structure and variations in mass-to-light ratios; Ouellette et al. (2017) also found that the tilt of the FP correlates with the dark matter fraction of each galaxy.
The TF relation applies to disc-dominated galaxies (Bloom et al. 2017) while the FJ and FP relations apply to spheroidal galaxies. Incorporating galaxies of other morphologies into these scaling relations not only increases the scatter, but also changes the slopes and intercepts of the relations (e.g. Neistein et al. 1999; Iodice et al. 2003; Williams, Bureau & Cappellari 2010; Tonini et al. 2014), consequently reducing the accuracy and reliability of the quantities derived.
While SK has been a popular kinematic estimator and mass proxy, there are still a number of outstanding issues: (i) while K is commonly taken to be 0.5, this value has not been quantitatively justified; (ii) C14 found a non-linearity in the log M∗–log SK relation below a stellar mass of ∼1010M⊙, but the existence and location of this change in slope (which determines the limit of validity for the scaling relation in low-mass galaxies) has not been reliably determined; and (iii) there remains the question of how SK relates to aperture velocity dispersion (σap) from single-fibre surveys.
We use the latest data release from the SAMI Survey to expand on the work of C14, and explore various aspects of the log M∗–log SK scaling relation. Our work is structured as follows. In Section 2, we describe the data reduction, kinematic measurements, and sample morphologies. In Section 3, we construct SK from the gas and stellar measurements of our sample; compare SK to aperture velocity dispersion (|$\sigma _{3^{\prime \prime }}$|) measurements; and explore the sensitivity of the scatter of the relation for different values of K. In Section 4, we compare our results to observations in the literature and discuss factors that influence the value of K. In Section 5, we summarize our findings. We assume throughout an ΛCDM cosmology with ΩM = 0.3, Ωλ = 0.7 and H0 = 70 km/s/Mpc.
2 DATA AND METHODS
The SAMI Survey uses the AAOmega dual-beam spectrograph on the Anglo-Australian Telescope at Siding Spring Observatory (Sharp, Saunders & Smith 2006). SAMI obtains integral field spectra by using 13 fused-fibre hexabundles, each containing 61 fibres (Bland-Hawthorn et al. 2011; Bryant et al. 2014). The SAMI spectra cover the wavelength range 3750–5750 Å at a resolution of R ≈ 1800, and 6300–7400 Å at a resolution of R ≈ 4300 (Scott et al. 2018). These give dispersion resolutions σres of 70 km/s in the blue arm where we obtain the stellar kinematics, and 30 km/s in the red for gas kinematics.
2.1 Data reduction and sample
SAMI data reduction consists of two stages, reducing raw data to row stacked spectra (RSS) using 2dfdr1 and data cube construction from the RSS using the SAMI Python package (Allen et al. 2014). The details of the data reduction and data cubing processes can be found in Allen et al. (2015), Sharp et al. (2015), and Scott et al. (2018).
Using the extracted SAMI stellar and gas kinematic maps, we select the spaxels as follows. First, spaxels are collected within an elliptical aperture with a semimajor axis of one effective radius. For all SAMI galaxies, their semimajor axis, position angles, and ellipticity are determined using Multi-Gaussian Expansion (MGE, Emsellem, Monnet & Bacon 1994) fitting to r-band images from either the VLT Survey Telescope (VST) ATLAS (Shanks et al. 2015; Owers et al. 2017) survey or the Sloan Digital Sky Survey (SDSS). Contrary to C14 and A18, where spaxels are selected based on the absolute errors in velocity and velocity dispersion, we do not perform spaxel-level quality cuts other than requiring galaxies to have more than five spaxels within the aperture while rejecting empty spaxels. Instead, we perform an overall relative error cut on the kinematic parameter being investigated, only keeping galaxies with relative kinematic error less than 5–10 per cent. Rotation velocity, velocity dispersion, SK, and associated error calculations are described in the next section. However, for comparison, we also produced scaling relations with similar quality criteria at the spaxel level, using only spaxels with velocity error ΔVi < 20 km/s, velocity dispersion error Δσi < 0.1σ + 25 (van de Sande et al. 2017b), on top of the 5 per cent error cut on the final kinematic quantities. Details are shown in Section 3.3.
Depending on the kinematic parameter to be studied and the selection criteria, our parent sample of 2720 galaxies is divided into five sample groups (groups A–E). The selection criteria and sample group descriptions are listed in Table 1. For investigation of the log M∗–log SK scaling relation, we used sample B. Sample B includes gas–kinematics measurements for 1256 galaxies, stellar–kinematics measurements for 1574 galaxies, and 904 galaxies have both gas and stellar measurements. Galaxies in sample B have a median of ∼70 spaxels. The stellar mass histogram in Fig. 1(a) shows that sample B is relatively complete in the high-mass (≥ 1010M⊙) range, but with sufficient numbers of galaxies in the low-mass range to constrain a scaling relation.
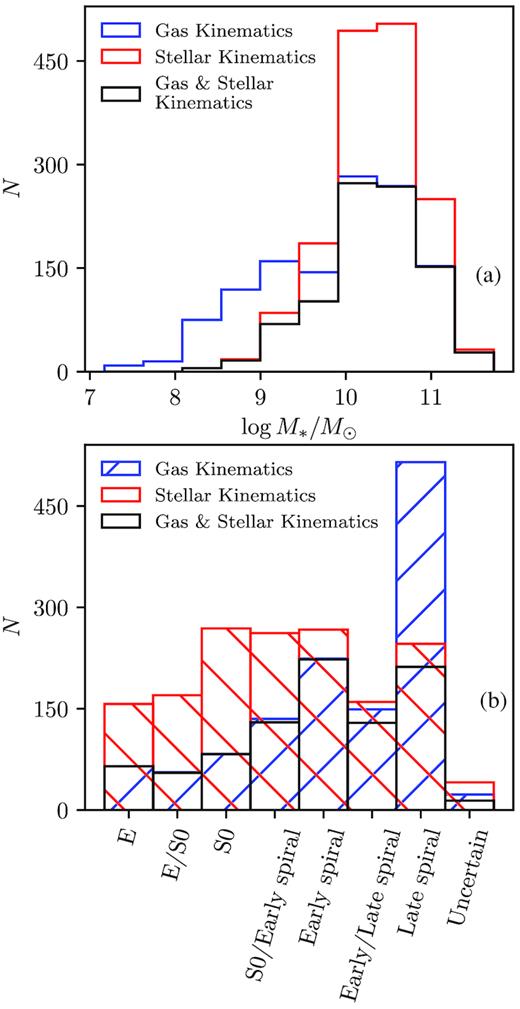
Panel (a) shows the mass distributions of sample B with various kinematic measurements available: red represents galaxies with stellar kinematics, blue represents galaxies with gas kinematics, and black represents galaxies with both gas and stellar kinematics. Panel (b) shows the visual morphology distribution of sample B: red bars represent galaxies with stellar kinematics, blue bars represent galaxies with gas kinematics, and black bars represent galaxies with both gas and stellar kinematics.
Sample selection criteria and description. All samples had the additional criterion of minor-to-major axis ratio less than 0.95.
| (1) . | (2) . | (3) . | (4) . | (5) . |
|---|---|---|---|---|
| Sample . | Selection criteria . | Number of galaxies with . | All have both gas and . | Used in . |
| . | for each galaxy . | gas/stellar measurements . | stellar measurements? . | Figure(s) . |
| A | All of Vrot, σ, S0.5 must have | 410/270 | False | 2 |
| less than 5% error for each galaxy | ||||
| B | S0.5 has error | 1256/1574 | False | 1 |
| less than 5% | 3 | |||
| B1 | ΔVi < 20 km/s, Δσi < 0.1σ + 25 km/s | 859/839 | False | 4 |
| S0.5 has error less than 5% | ||||
| C | Measurements for gas | 223/223 (Vrot) | True | 5 |
| and stellar kinematics | 961/961 (σ) | True | ||
| have error less than 5% | 904/904 (S0.5) | True | ||
| D | Both S0.5 and |$\sigma _{3^{\prime \prime }}$| | 864/1141 | False | 6 |
| have error less than 5% | 7 | |||
| E | Both Vrot and σ for both | 410/410 (ETG) | True | 8 |
| gas and stellar measurements | 232/232 (LTG) | True | ||
| have error less than 10% | 737/737 (All types) | True |
| (1) . | (2) . | (3) . | (4) . | (5) . |
|---|---|---|---|---|
| Sample . | Selection criteria . | Number of galaxies with . | All have both gas and . | Used in . |
| . | for each galaxy . | gas/stellar measurements . | stellar measurements? . | Figure(s) . |
| A | All of Vrot, σ, S0.5 must have | 410/270 | False | 2 |
| less than 5% error for each galaxy | ||||
| B | S0.5 has error | 1256/1574 | False | 1 |
| less than 5% | 3 | |||
| B1 | ΔVi < 20 km/s, Δσi < 0.1σ + 25 km/s | 859/839 | False | 4 |
| S0.5 has error less than 5% | ||||
| C | Measurements for gas | 223/223 (Vrot) | True | 5 |
| and stellar kinematics | 961/961 (σ) | True | ||
| have error less than 5% | 904/904 (S0.5) | True | ||
| D | Both S0.5 and |$\sigma _{3^{\prime \prime }}$| | 864/1141 | False | 6 |
| have error less than 5% | 7 | |||
| E | Both Vrot and σ for both | 410/410 (ETG) | True | 8 |
| gas and stellar measurements | 232/232 (LTG) | True | ||
| have error less than 10% | 737/737 (All types) | True |
Sample selection criteria and description. All samples had the additional criterion of minor-to-major axis ratio less than 0.95.
| (1) . | (2) . | (3) . | (4) . | (5) . |
|---|---|---|---|---|
| Sample . | Selection criteria . | Number of galaxies with . | All have both gas and . | Used in . |
| . | for each galaxy . | gas/stellar measurements . | stellar measurements? . | Figure(s) . |
| A | All of Vrot, σ, S0.5 must have | 410/270 | False | 2 |
| less than 5% error for each galaxy | ||||
| B | S0.5 has error | 1256/1574 | False | 1 |
| less than 5% | 3 | |||
| B1 | ΔVi < 20 km/s, Δσi < 0.1σ + 25 km/s | 859/839 | False | 4 |
| S0.5 has error less than 5% | ||||
| C | Measurements for gas | 223/223 (Vrot) | True | 5 |
| and stellar kinematics | 961/961 (σ) | True | ||
| have error less than 5% | 904/904 (S0.5) | True | ||
| D | Both S0.5 and |$\sigma _{3^{\prime \prime }}$| | 864/1141 | False | 6 |
| have error less than 5% | 7 | |||
| E | Both Vrot and σ for both | 410/410 (ETG) | True | 8 |
| gas and stellar measurements | 232/232 (LTG) | True | ||
| have error less than 10% | 737/737 (All types) | True |
| (1) . | (2) . | (3) . | (4) . | (5) . |
|---|---|---|---|---|
| Sample . | Selection criteria . | Number of galaxies with . | All have both gas and . | Used in . |
| . | for each galaxy . | gas/stellar measurements . | stellar measurements? . | Figure(s) . |
| A | All of Vrot, σ, S0.5 must have | 410/270 | False | 2 |
| less than 5% error for each galaxy | ||||
| B | S0.5 has error | 1256/1574 | False | 1 |
| less than 5% | 3 | |||
| B1 | ΔVi < 20 km/s, Δσi < 0.1σ + 25 km/s | 859/839 | False | 4 |
| S0.5 has error less than 5% | ||||
| C | Measurements for gas | 223/223 (Vrot) | True | 5 |
| and stellar kinematics | 961/961 (σ) | True | ||
| have error less than 5% | 904/904 (S0.5) | True | ||
| D | Both S0.5 and |$\sigma _{3^{\prime \prime }}$| | 864/1141 | False | 6 |
| have error less than 5% | 7 | |||
| E | Both Vrot and σ for both | 410/410 (ETG) | True | 8 |
| gas and stellar measurements | 232/232 (LTG) | True | ||
| have error less than 10% | 737/737 (All types) | True |
2.2 Galaxy kinematics
2.3 Galaxy morphologies
Galaxy morphologies in the SAMI sample vary from elliptical galaxies to late-type spiral and irregular galaxies. All SAMI galaxies are visually classified using the SDSS DR9 (Ahn et al. 2012) RGB images by 12 members of the SAMI team following the classification scheme adopted in Kelvin et al. (2014). Here, we briefly summarize the classification scheme. First, judging by the presence/absence of a disc or spiral arms, the classifier determines whether a target is an early-type or late-type galaxy. Then in each class, classifiers visually determine if the galaxy contains a bulge (for late-type galaxies) or a disc (for early-type galaxies). Early-type galaxies with only a bulge, and without any disk component, are identified as elliptical (E) galaxies; early-type galaxies that show both bulge and disc components are identified as lenticular (S0) galaxies. Late-type galaxies all have spiral arms by classification definition; if there is a prominent bulge, they are classified as early-spiral galaxies; if there are only spiral arms without a central bulge, then they are classified as late-spiral or irregular galaxies. Where the SDSS image does not show enough features, or a consensus (>67 per cent) among classifiers is lacking, the galaxy is classified as Uncertain (Cortese et al. 2016). For sample B, where we have the most galaxies for studying the log M∗–log S0.5 relation, their morphology distribution is shown in Fig. 1(b). There are relatively more early-type galaxies (E to S0 classes) in the stellar sample than the gas sample, and more late-type galaxies (early to late spiral classes) in the gas sample than the stellar sample.
Interacting galaxies, such as mergers, are typically removed from galaxy scaling relation studies. However, in our scaling relations, in order to obtain a scaling relation with minimal sample selection, we do not remove interacting galaxies from the main sample (sample B). The impact of merger galaxies is quantified further in Section 3.2.
3 SAMI SCALING RELATIONS
3.1 S0.5 reduces scatter
In this section, we demonstrate the advantage of using the S0.5 parameter in dynamical scaling relations in contrast to using Vrot and σ alone when using IFS data. In both C14 and A18, the log M∗–log S0.5 scaling relation showed significant reduction in scatter when compared to the TF relation using Vrot and FJ relation using σ. For comparison, we perform the same comparison between S0.5, Vrot, and σ using sample A (as described in Table 1). In sample A, for each of the gas and stellar kinematic measurements, all of S0.5, Vrot, and σ have less than 5 per cent error for all galaxies. Fig. 2 shows the correlation of stellar mass (M∗) with Vrot, σ, S0.5 (i.e. the stellar mass TF, FJ, and combined S0.5 scaling relations) as constructed from sample A data. We perform maximum likelihood linear fitting to all the scaling relations in Fig. 1, and measure their orthogonal median absolute deviations as their scatter. The fitting method is described in more detail in Section 3.2.1; in this case, we fit a simple linear relation with no cut-off. As can be seen from the annotated scatter values in the figure, for both the gas and stellar versions of these scaling relations, the log M∗ − log S0.5 relation consistently has less scatter than the TF and FJ relations. We also use morphologically selected samples to compare the TF relation using LTGs, the FJ relation using ETGs, and the log M∗ − log S0.5 scaling relation using both LTGs and ETGs. S0.5 continued to provide the tightest scaling relation.
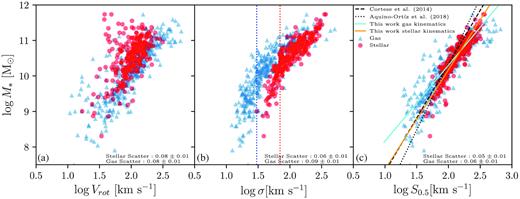
SAMI scaling relations from sample A: (a) Tully–Fisher, (b) Faber–Jackson, and (c) generalized S0.5 scaling relation. Red dots represent galaxies with stellar measurements, blue triangles represent gas measurements. The observed scatter measured from the median absolute deviation for each scaling relation is annotated in each plot. In panel (b), the red and blue vertical dotted lines represent SAMI spectral resolutions, 70 km s−1 and 30 km s−1, respectively. In panel (c) the orange solid line is the best fit line to the stellar log M∗–log S0.5 scaling relation, and the cyan solid line is the best fit line to the gas scaling relation. Relations found by C14 and A18 are included for comparison; they are represented by the black dashed line and black dotted line, respectively.
A caveat here is that our Vrot measurements for late-type spiral galaxies do not reach the peak of their rotation curves, hence they cannot accurately trace the potentials of galaxies, and so, in our ‘TF’ relation, Vrot is not as good an estimator of M∗ as S0.5.
The fits from C14 and A18 (from orthogonal fitting of the combined gas and stellar mixed sample) are shown in Fig. 2(c) by the dashed line and dotted line, respectively. There are small differences between the slopes for our gas and stellar samples, shown in orange and cyan, respectively, both with each other and with the linear relations found by C14 and A18. However, given the differences in sample selection, survey systematics, and fitting methods, it is hard to interpret the observed differences in slope as physical differences.
3.2 Linearity of the S0.5 scaling relation
C14 constructed the gas FJ and log M∗–log S0.5 scaling relations and observed that the slope became steeper for low-mass (M∗ < 1010M⊙) galaxies. This change in slope is also present in our FJ relation in Fig. 2(b), and the log M∗–log S0.5 relations in Fig. 2(c). A bend in these kinematic scaling relations is expected, as the fitted linear relations would otherwise predict zero motions for low-mass galaxies (∼105 − 106M⊙). The cause of the bend will be discussed in more detail in Section 4.1, but for now it is crucial to take the bend into consideration in fitting the scaling relation. To locate the change in slope in our log M∗–log S0.5 scaling relations more precisely, we investigate the scaling relations in detail with sample B in Fig. 3, where galaxies are selected only based on ΔS0.5/S0.5 ≤ 0.05.
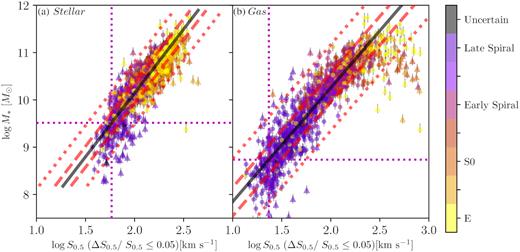
SAMI stellar and gas S0.5 scaling relations from sample B. The black solid line shows the line of best fit, with fitting parameters shown in Table 2. Red dashed and dotted lines show 1 and 3 RMS distance from the line of best fit. Triangular points are galaxies >3 RMS away from the line of best fit, and are excluded from the fitting routine. The magenta vertical and horizontal dotted lines show the location where the distribution of points deviate from a linear relation, which we fit as the sample limit. These limits occur at different S0.5 values and different stellar masses for the stellar and gas samples: S0.5, lim, stellar = 59 km s−1 for the stellar sample, S0.5, lim, gas = 23 km s−1 for the gas sample.
3.2.1 Straight line with a knee
3.2.2 The bends in the scaling relations
Following the fitting method described in the previous section, we fit the linear + cutoff model to our sample B galaxies, as shown in Fig. 3; the fitted parameters and their uncertainties are given in Table 2.
Scaling relation fitting results from hyper-fit. All scaling relations have the form as described in Equation (9).
| Sample . | Figure . | |$\rm Y$| . | Slope (a) . | Intercept (b) . | Ylim [km/s] . | |$M_{*, \rm lim}[M_{\odot }]$| . | Scatter (|$\rm MAD_{orth}$|) . |
|---|---|---|---|---|---|---|---|
| B | 3a | |$S_{0.5, \rm stellar}$| | 0.37 ± 0.01 | −1.77 ± 0.06 | 58.3 ± 1.0 | 109.56 | 0.048 ± 0.002 |
| 3b | |$S_{0.5, \rm gas}$| | 0.42 ± 0.01 | −2.26 ± 0.06 | 23.0 ± 1.0 | 108.62 | 0.070 ± 0.002 | |
| B1 | 4a | |$S_{0.5, \rm stellar}$| | 0.35 ± 0.01 | −1.60 ± 0.10 | 58.3 ± 1.0 | 109.62 | 0.041 ± 0.002 |
| 4b | |$S_{0.5, \rm gas}$| | 0.39 ± 0.01 | −1.99 ± 0.05 | 22.4 ± 1.0 | 108.56 | 0.063 ± 0.003 | |
| D | 7a | |$S_{0.5, \rm stellar}$| | 0.36 ± 0.01 | −1.59 ± 0.06 | 67.0 ± 1.2 | 109.49 | 0.049 ± 0.001 |
| 7c | |$S_{0.5, \rm gas}$| | 0.40 ± 0.01 | −2.16 ± 0.06 | 22.4 ± 1.0 | 108.73 | 0.061 ± 0.002 | |
| D | 7b | σstellar | 0.38 ± 0.01 | −1.82 ± 0.06 | 67.4 ± 1.1 | 109.61 | 0.068 ± 0.002 |
| 7d | σgas | 0.48 ± 0.01 | −2.98 ± 0.14 | 26.3 ± 1.1 | 109.17 | 0.090 ± 0.004 |
| Sample . | Figure . | |$\rm Y$| . | Slope (a) . | Intercept (b) . | Ylim [km/s] . | |$M_{*, \rm lim}[M_{\odot }]$| . | Scatter (|$\rm MAD_{orth}$|) . |
|---|---|---|---|---|---|---|---|
| B | 3a | |$S_{0.5, \rm stellar}$| | 0.37 ± 0.01 | −1.77 ± 0.06 | 58.3 ± 1.0 | 109.56 | 0.048 ± 0.002 |
| 3b | |$S_{0.5, \rm gas}$| | 0.42 ± 0.01 | −2.26 ± 0.06 | 23.0 ± 1.0 | 108.62 | 0.070 ± 0.002 | |
| B1 | 4a | |$S_{0.5, \rm stellar}$| | 0.35 ± 0.01 | −1.60 ± 0.10 | 58.3 ± 1.0 | 109.62 | 0.041 ± 0.002 |
| 4b | |$S_{0.5, \rm gas}$| | 0.39 ± 0.01 | −1.99 ± 0.05 | 22.4 ± 1.0 | 108.56 | 0.063 ± 0.003 | |
| D | 7a | |$S_{0.5, \rm stellar}$| | 0.36 ± 0.01 | −1.59 ± 0.06 | 67.0 ± 1.2 | 109.49 | 0.049 ± 0.001 |
| 7c | |$S_{0.5, \rm gas}$| | 0.40 ± 0.01 | −2.16 ± 0.06 | 22.4 ± 1.0 | 108.73 | 0.061 ± 0.002 | |
| D | 7b | σstellar | 0.38 ± 0.01 | −1.82 ± 0.06 | 67.4 ± 1.1 | 109.61 | 0.068 ± 0.002 |
| 7d | σgas | 0.48 ± 0.01 | −2.98 ± 0.14 | 26.3 ± 1.1 | 109.17 | 0.090 ± 0.004 |
Scaling relation fitting results from hyper-fit. All scaling relations have the form as described in Equation (9).
| Sample . | Figure . | |$\rm Y$| . | Slope (a) . | Intercept (b) . | Ylim [km/s] . | |$M_{*, \rm lim}[M_{\odot }]$| . | Scatter (|$\rm MAD_{orth}$|) . |
|---|---|---|---|---|---|---|---|
| B | 3a | |$S_{0.5, \rm stellar}$| | 0.37 ± 0.01 | −1.77 ± 0.06 | 58.3 ± 1.0 | 109.56 | 0.048 ± 0.002 |
| 3b | |$S_{0.5, \rm gas}$| | 0.42 ± 0.01 | −2.26 ± 0.06 | 23.0 ± 1.0 | 108.62 | 0.070 ± 0.002 | |
| B1 | 4a | |$S_{0.5, \rm stellar}$| | 0.35 ± 0.01 | −1.60 ± 0.10 | 58.3 ± 1.0 | 109.62 | 0.041 ± 0.002 |
| 4b | |$S_{0.5, \rm gas}$| | 0.39 ± 0.01 | −1.99 ± 0.05 | 22.4 ± 1.0 | 108.56 | 0.063 ± 0.003 | |
| D | 7a | |$S_{0.5, \rm stellar}$| | 0.36 ± 0.01 | −1.59 ± 0.06 | 67.0 ± 1.2 | 109.49 | 0.049 ± 0.001 |
| 7c | |$S_{0.5, \rm gas}$| | 0.40 ± 0.01 | −2.16 ± 0.06 | 22.4 ± 1.0 | 108.73 | 0.061 ± 0.002 | |
| D | 7b | σstellar | 0.38 ± 0.01 | −1.82 ± 0.06 | 67.4 ± 1.1 | 109.61 | 0.068 ± 0.002 |
| 7d | σgas | 0.48 ± 0.01 | −2.98 ± 0.14 | 26.3 ± 1.1 | 109.17 | 0.090 ± 0.004 |
| Sample . | Figure . | |$\rm Y$| . | Slope (a) . | Intercept (b) . | Ylim [km/s] . | |$M_{*, \rm lim}[M_{\odot }]$| . | Scatter (|$\rm MAD_{orth}$|) . |
|---|---|---|---|---|---|---|---|
| B | 3a | |$S_{0.5, \rm stellar}$| | 0.37 ± 0.01 | −1.77 ± 0.06 | 58.3 ± 1.0 | 109.56 | 0.048 ± 0.002 |
| 3b | |$S_{0.5, \rm gas}$| | 0.42 ± 0.01 | −2.26 ± 0.06 | 23.0 ± 1.0 | 108.62 | 0.070 ± 0.002 | |
| B1 | 4a | |$S_{0.5, \rm stellar}$| | 0.35 ± 0.01 | −1.60 ± 0.10 | 58.3 ± 1.0 | 109.62 | 0.041 ± 0.002 |
| 4b | |$S_{0.5, \rm gas}$| | 0.39 ± 0.01 | −1.99 ± 0.05 | 22.4 ± 1.0 | 108.56 | 0.063 ± 0.003 | |
| D | 7a | |$S_{0.5, \rm stellar}$| | 0.36 ± 0.01 | −1.59 ± 0.06 | 67.0 ± 1.2 | 109.49 | 0.049 ± 0.001 |
| 7c | |$S_{0.5, \rm gas}$| | 0.40 ± 0.01 | −2.16 ± 0.06 | 22.4 ± 1.0 | 108.73 | 0.061 ± 0.002 | |
| D | 7b | σstellar | 0.38 ± 0.01 | −1.82 ± 0.06 | 67.4 ± 1.1 | 109.61 | 0.068 ± 0.002 |
| 7d | σgas | 0.48 ± 0.01 | −2.98 ± 0.14 | 26.3 ± 1.1 | 109.17 | 0.090 ± 0.004 |
There are 40–50 outliers in our stellar and gas scaling relations, mostly at log S0.5 ≥ 2.5. In the stellar scaling relation, visual inspection of these galaxies shows them to be contaminated by either foreground stars or (in clusters) nearby bright galaxies. In the gas scaling relations, these galaxies are generally ETGs with relatively larger errors in their gas kinematic measurements. Thirteen of the outliers in the gas scaling relation are found to be merger galaxies. Removing these merger galaxies did not change the slope, intercept, or the scatter of the scaling relation. All of the outliers disappear when we apply a more stringent quality cut than ΔS0.5/S0.5 ≤ 0.05.
The fitted |$M_{*,\rm lim}$| for each of the gas and stellar versions of the scaling relation can be converted to |$S_{0.5,\rm lim}$| using the model. For the stellar version of the scaling relation, the bend occurs at |$({M_{*, \rm lim, stellar}},\,\,{S_{0.5, \rm lim, stellar}}) =(10^{9.6}\, M_{\odot }, 61\, {\rm km\, s^{-1}})$|, and for the gas version, |$({M_{*, \rm lim, gas}},\,\,{S_{0.5, \rm lim, gas}}) =(10^{8.9}\, M_{\odot }, 23\, {\rm km\, s^{-1}})$|. The fact that the bend in the stellar and gas scaling relations occurs at different stellar mass values suggests the nature of the bend in our scaling relation is unlikely to be a physical phenomenon.
3.3 Effect of spaxel-level quality cut
The log M∗ − log S0.5 scaling relation in our study with sample B is constructed with minimal sample selection as well as minimal quality cut on the spaxels, in order to be as inclusive as possible. This procedure is different from C14 and A18. To investigate the importance of high-quality spaxels, we perform a similar spaxel-level cut where we only keep spaxels with velocity error ΔV < 20 km s−1, velocity dispersion error Δσ < 0.1σ + 25, on top of the 5 per cent error cut on the S0.5 parameter. The velocity dispersion spaxel selection routine follows van de Sande et al. (2017b), which ensures spaxels have S/N > 3Å−1 for σ > 35 km s−1. These criteria produce sample B1. Fig. 4 shows the scaling relations produced with sample B1, and Table 2 shows the fitting results.
By introducing spaxel-level quality cuts, the slopes of both stellar and gas scaling relation decreased by 0.02 to 0.03 (i.e. by 2 to 3σ). The scatters of both scaling relations were also reduced significantly. The locations of the sample limits (Ylim, |$M_{*,\rm lim}$|) remained the same. It is clear that performing spaxel-level quality selection can increase the quality of the scaling relations. However, by applying a spaxel-level quality cut, sample sizes were reduced by 30 per cent to 50 per cent. For our study, it is better to have larger sample sizes than scaling relations with less scatter, as the sample will be divided further in later sections.
3.4 Gas and stellar S0.5 disagreement
To test whether the S0.5 parameters from the stellar and gas kinematics trace the same gravitational potentials, we compare the rotation velocities, velocity dispersions and S0.5 measurements of stellar and gas components on a per-galaxy basis with SAMI samples C (as described in Table 1). Galaxies in the sample are selected to have both gas and stellar kinematic errors less than 5 per cent for each of Vrot, σ and S0.5. Fig. 5(a), using sample C, shows that stars in general rotate more slowly than the gas. This is due to asymmetric drift, where the rotation velocity of the stars is lower than that of the gas because stars have additional pressure support against gravity from a higher dispersion (Binney & Tremaine 2008). The mean ratio between the stellar and gas rotation velocities is 〈Vrot, stellar/Vrot, gas〉 ∼ 0.77 ± 0.29 which is consistent with the value (∼0.75) obtained by C14.

Comparison between SAMI sample C gas and stellar measurements of (a) Vrot, (b) σ, and (c) S0.5. Galaxies are colour-coded by morphology. For visibility, we show 3 standard deviation error bars. Black solid lines in each panel show the one-to-one relation. The red dashed line in panel (c) is the best-fit line to the points. Horizontal and vertical magenta lines in panel (b) show the gas and stellar instrumental dispersions (30 km s−1 and 70 km s−1, respectively) and in panel (c) show the fitted gas and stellar sample limits (23 km s−1 and 59 km s−1, respectively).
Using sample C, where both gas and stellar σ measurements have less than 5 per cent error, the offset between the SAMI gas and stellar FJ relations observed in C14 is reflected in our FJ relation. The mean ratio between gas and stellar dispersions is 〈σstellar/σgas〉 ∼ 1.58 ± 0.59, as shown in Fig. 5(b), consistent with the value (∼1.55) found by C14. We note that σstellar > σgas for galaxies with log σgas < 2.5 is expected due to asymmetric drift. The galaxies with log σgas > 2.5 that lie significantly above the one-to-one line are almost entirely elliptical and S0 galaxies; these galaxies have low gas abundance, making it harder to obtain accurate σgas measurements and resulting in relatively larger uncertainties in σgas, as shown in Fig. 5(b).
In C14, the gas and stellar S0.5 parameters are found to have a mean logarithmic difference (gas − stellar) of −0.02 dex. In our sample C, the logarithmic difference is −0.05 dex. In Fig. 5c, while the one-to-one line (black) goes through our S0.5, gas − S0.5, stellar distribution, the best-fit (red–dashed) line has a slope of 1.49 ± 0.02, which suggests a systematic disagreement between S0.5, gas and S0.5, stellar. One explanation of S0.5, stellar > S0.5, gas for S0.5 < 100 km s−1 can be traced to the fact that σstellar > σgas. However, inclusion of Vrot, gas component where Vrot, gas > Vrot, stellar does not seem to sufficiently compensate S0.5gas to bring balance between S0.5, stellar and S0.5, gas. The scatter in the S0.5, gas − S0.5, stellar correlation increases for galaxies with log S0.5, gas > 2.25. As in Fig. 5(b), this increase in scatter can be explained by E and S0 galaxies having larger uncertainties in their σgas measurements. However, in the hyper-fit routine, measurements are error-weighted, reducing the impact of points with large errors; moreover, with a tighter uncertainty cut (using galaxies with <2 per cent errors) the slope remained significantly above unity (1.34 ± 0.04). Lastly, restricting the sample to only include galaxies with both gas and stellar measurements above the fitted sample limit, the slope remained steeper than unity at 1.49 ± 0.02. This disagreement between stellar and gas S0.5 parameters requires investigation on a per-galaxy basis, especially for lower mass (log M∗ < 9.5) galaxies where S0.5, stellar > S0.5, gas. This will be studied in more detail in future.
3.5 IFS and aperture kinematic measurements
While IFS data provides resolved spatial information on galaxy kinematics, compared to single fibre observations it is observationally expensive. In order to compare the effect of IFS data on the scaling relations, we constructed aperture spectra from SAMI data cubes within a 3-arcsecond-diameter (SDSS-like) aperture. Applying a 5 per cent error quality cut to the aperture velocity dispersions, we obtained |$\sigma _{3^{\prime \prime }, \rm gas}$| for 864 galaxies, and |$\sigma _{3^{\prime \prime }, \rm stellar}$| for 1141 galaxies; these form sample D (see Table 1). Fig. 6 shows a comparison between average velocity dispersion |$\sigma _{1R_e}$|, S0.5 parameter and |$\sigma _{3^{\prime \prime }}$|, and their logarithmic difference as a function of Re/3″, the galaxy size relative to the aperture diameter. Galaxies are colour coded by their |$0.5V^2_{\rm rot}/\sigma ^2$| ratio to show the balance between Vrot and σ within the S0.5 parameter, galaxies with |$0.5V^2_{\rm rot}/\sigma ^2$| ratio above and below the colour bar limits are shown in solid red and solid blue, respectively.

Direct comparison, using sample D, between S0.5 and |$\sigma _{3^{\prime \prime }}$| (the 3-arcsecond-diameter aperture velocity dispersion), and average velocity dispersion |$\sigma _{1R_e}$| within 1Re from gas and stellar kinematics. Their differences against apparent galaxy size are plotted in the inset plots. Black solid lines are the one-to-one relations; red dashed lines are the best fits; points are colour coded by |$0.5V^2_{\rm rot}/\sigma ^2$| to indicate the dominant term in the S0.5 parameter.
For stellar measurements, the kinematics is mostly pressure-supported and dominated by |$\sigma _{1R_e}$|, which is confirmed by 1098 out of 1141 galaxies having |$0.5V^2_{\rm rot}/\sigma ^2\lt 1$|. The inset residual plots comparing the residuals to galaxy size indicate that galaxies with |$0.5V^2_{\rm rot}/\sigma ^2\gt 1$| have Re > 6″, and they are furthest away from the one-to-one line in all panels. From panel a, the increasing |$0.5V^2_{\rm rot}/\sigma ^2$| ratio from the line-of-best-fit confirms that |$\sigma _{3^{\prime \prime }}$| contains a Vrot component. Comparing panel a and c, we can see that galaxies with |$0.5V^2_{\rm rot}/\sigma ^2\gt 1$| are affected the most by replacing |$\sigma _{1R_e}$| with S0.5. Since these large galaxies with high |$0.5V^2_{\rm rot}/\sigma ^2\gt 1$| ratio make up less than 5 per cent of the sample, the scatter remained the same between |$\sigma _{3^{\prime \prime }}-\sigma _{1R_e}$| and |$\sigma _{3^{\prime \prime }}-S_{0.5}$| comparisons.
The disparity due to the Vrot component between |$\sigma _{1R_e}$|, S0.5 and |$\sigma _{3^{\prime \prime }}$| is amplified for the gas kinematics, shown in the lower panels of Fig. 6. Gas has relatively more rotation support than stars; 386 out of 864 galaxies have |$0.5V^2_{rot}/\sigma ^2\gt 1$|, which makes up 44 per cent of the sample (for stellar measurements, 4 per cent). The range of |$0.5V^2_{\rm rot}/\sigma ^2$| values is larger compared to the stellar measurement, as shown by the values on the colour bar.
For both gas and stellar components, comparing |$\sigma _{3^{\prime \prime }}$| to |$\sigma _{1R_e}$| shows that |$\sigma _{3^{\prime \prime }}$| contains additional rotation support. However, by replacing |$\sigma _{1R_e}$| with S0.5 (effectively adding a |$0.5V^2_{\rm rot}$| component), S0.5 for large (Re > 6″) galaxies became significantly larger than their |$\sigma _{3^{\prime \prime }}$| values. This indicates that the rotation velocity component within |$\sigma _{3^{\prime \prime }}$| measurements is weighted less than that within the S0.5 parameter. It is clear that if one wishes to match |$\sigma _{3^{\prime \prime }}$| and S0.5, the K value in the definition of S must be less than 0.5, but greater than 0. For our particular purpose of constructing scaling relations, we compare |$\log M_* - \log \sigma _{3^{\prime \prime }}$| and log M∗ − log S0.5 in the following section.
Even though the S0.5 parameter and 3 arcsec aperture velocity dispersion |$\sigma _{3^{\prime \prime }}$| for the gas and the stars cover different parts of galaxies, they remain in broad agreement. This agreement is encouraging because while the log M∗ − log S0.5 relation applies to galaxies of all morphologies, obtaining the S0.5 parameter requires observationally-expensive IFS data, whereas the measuring the velocity dispersion in single-fibre surveys is observationally relatively cheap. The residual plots in Fig. 6(c) indicates that |$\sigma _{3^{\prime \prime }}$| is a fairly unbiased predictor of S0.5, stellar out to about Re = 3″ (rather than, as one might have expected, Re = 3″/2); moreover, the scatter only grows relatively gradually beyond Re = 3″, and more slowly for the stellar measurements than for the gas measurements.
3.6 Comparing IFS and aperture scaling relations
As both aperture σ and S0.5 are used in kinematic scaling relations, we compare variants of the FJ relation using S0.5 and |$\sigma _{3^{\prime \prime }}$| in Fig. 7. For both stellar and gas versions, using the S0.5 parameter consistently provides tighter relations with less scatter than using |$\sigma _{3^{\prime \prime }}$| (see Table 2). This confirms that S0.5 is a better mass proxy than single-aperture velocity dispersion, and suggests the promising possibility of using S0.5 to reduce the scatter in other scaling relations such as the FP relation (e.g. Graham et al. 2017). On the other hand, for many purposes the slight increase in scatter in the scaling relation that results from using the aperture dispersion rather than S0.5 (∼ 0.02 dex for stars and ∼ 0.03 dex for gas) may be an acceptable trade-off for the lower observational cost of single-fibre surveys relative to IFS surveys.
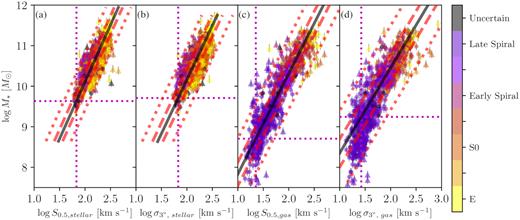
Scaling relations constructed from S0.5 kinematic parameters and aperture velocity dispersions using sample D. Panels (a), (b), (c) and (d) show scaling relations constructed between stellar mass and, respectively, S0.5, stellar, |$\sigma _{3^{\prime \prime }, \rm stellar}$|, S0.5, gas and |$\sigma _{3^{\prime \prime }, \rm gas}$| measurements. Black solid lines in each panel are lines of best fit; red dashed and dotted lines define distances 1 RMS and 3 RMS away from the line of best fit. Triangular points are measurements >3 RMS away from the line of best fit, and are excluded from the fit as outliers. Horizontal and vertical magenta dotted lines are the fitted model limits. Fit parameters and uncertainties are given in Table 2. For both gas and stellar measurements, S0.5 consistently produces scaling relations with less scatter than aperture velocity dispersion.
We notice in Fig. 7 that choosing S0.5 over |$\sigma _{3^{\prime \prime }}$| yields more outliers (triangular points, excluded from the fit) that are >3 RMS (red dotted line) away from the line-of-best-fit (black line). This is due to factors such as inclination errors and individual spaxel quality. IFS sampling radius affects the quality of the S0.5 parameter more than single-aperture velocity dispersion measurements. In SAMI |$\sigma _{3^{\prime \prime }}$| measurements, spectra from each spaxel are co-added to form the aperture spectrum, which increases the signal-to-noise ratio, and returns more reliable (albeit less accurate) kinematic measurements.
3.7 Varying K
The original SK parameter introduced by Weiner et al. (2006) combines the galaxy rotation velocity and velocity dispersion in quadrature, weighting the rotation velocity by the factor K. This is commonly taken to be K = 0.5, which is correct only for virialized systems with spherical symmetry and isotropic velocity dispersion (Kassin et al. 2007). We empirically test the effect of changing the value of K in the construction of the SK parameter by measuring the scatter about the scaling relations. In this section we use sample E, where each galaxy has both Vrot and σ with less than 10 per cent error for both gas and stellar kinematics. We chose 10 per cent error on Vrot and σ to provide a statistically large sample for determining the scatter about the scaling relation, though the results are qualitatively unaffected if we use a more stringent sample selection.
We tested K values ranging from 0 to 3 in the log M∗ − log SK scaling relation, and measured the orthogonal median absolute deviation from the scaling relation for each K value. We performed this test for both the gas and stellar versions of the scaling relation, and for all galaxies as well as separately for early-type (E and S0) and late-type (Sp and Irr) galaxies. We then measured the scatter in the scaling relation at every K value for each of these samples.
Fig. 8 shows the effect of varying K in the log M∗ − log SK scaling relation for gas and stellar measurements, for both the full sample and for early-type and late-type galaxies; the values of K that return the minimum scatter for each version of the scaling relation are listed in Table 3. For the full sample and for early-type galaxies the minimum in the scaling relation scatter is broad and spans approximately K = 0.3–0.7. Given the uncertainties in the scatter measurements, shown as shaded regions in Fig. 8, K = 0.5 returns a scatter consistent with the minimum when either ETGs or all galaxies are considered. This consistency justifies the common usage of K = 0.5 in the literature and the consistency of analyses when K is varied (e.g. Covington et al. 2010,C14,A18). However, the late-type galaxy scaling relations, whether based on stellar or gas kinematics, have scatter that is minimised over a narrower range around K = 0.2, and marginally higher scatter for K = 0.5. While this small coefficient for Vrot seems counter-intuitive given Vrot is the primary component in the TF relation for LTGs, it is apparent that for LTGs their σ component must be taken into consideration. The need for properly including the σ component can be due to effects such as beam-smearing where Vrot decreases and σ increases. In the SK parameter, σ is up-weighted by down-weighting the Vrot component, so that by using the SK parameter, the effect of beam smearing is minimised. For a broad sample of the galaxy population, the optimum value depends on the mix of morphologies in the sample; the specific factors that lead to this situation are discussed in the following section.
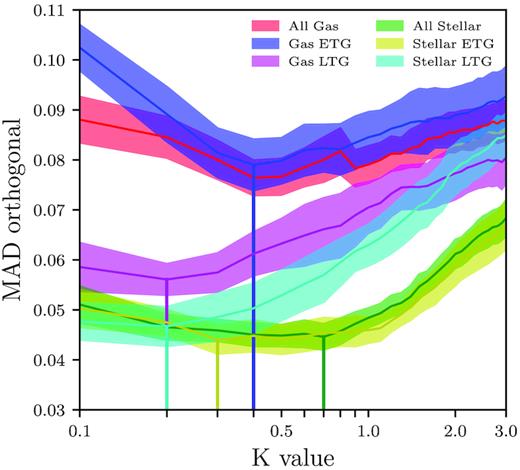
Effect of the value of K on the scatter of the SAMI gas and stellar log M∗ − log SK scaling relations. The curves show the scatter about the relation for each colour-coded galaxy sample and the shaded regions show the 1σ uncertainties. The gas and stellar samples are further divided into ETGs and LTGs to determine the effect of morphology. Where SK, gas is used, the full, ETG and LTG samples are colour-coded red, blue and purple respectively; where SK, stellar is used, the full, ETG and LTG samples are colour-coded green, yellow and cyan respectively. The vertical lines show the locations of the minimum scatter for each sample (n.b. the red and blue vertical lines are over-plotted).
Values of K that return the minimum scatter for gas and stellar scaling relations, for each morphological sample.
| . | Gas All . | Gas ETG . | Gas LTG . |
|---|---|---|---|
| Optimal K . | 0.4 . | 0.4 . | 0.2 . |
| |$\rm MAD_{orth}$| . | 0.076 . | 0.079 . | 0.057 . |
| Stellar All | Stellar ETG | Stellar LTG | |
| Optimal K | 0.7 | 0.3 | 0.2 |
| |$\rm MAD_{orth}$| | 0.045 | 0.044 | 0.047 |
| . | Gas All . | Gas ETG . | Gas LTG . |
|---|---|---|---|
| Optimal K . | 0.4 . | 0.4 . | 0.2 . |
| |$\rm MAD_{orth}$| . | 0.076 . | 0.079 . | 0.057 . |
| Stellar All | Stellar ETG | Stellar LTG | |
| Optimal K | 0.7 | 0.3 | 0.2 |
| |$\rm MAD_{orth}$| | 0.045 | 0.044 | 0.047 |
Values of K that return the minimum scatter for gas and stellar scaling relations, for each morphological sample.
| . | Gas All . | Gas ETG . | Gas LTG . |
|---|---|---|---|
| Optimal K . | 0.4 . | 0.4 . | 0.2 . |
| |$\rm MAD_{orth}$| . | 0.076 . | 0.079 . | 0.057 . |
| Stellar All | Stellar ETG | Stellar LTG | |
| Optimal K | 0.7 | 0.3 | 0.2 |
| |$\rm MAD_{orth}$| | 0.045 | 0.044 | 0.047 |
| . | Gas All . | Gas ETG . | Gas LTG . |
|---|---|---|---|
| Optimal K . | 0.4 . | 0.4 . | 0.2 . |
| |$\rm MAD_{orth}$| . | 0.076 . | 0.079 . | 0.057 . |
| Stellar All | Stellar ETG | Stellar LTG | |
| Optimal K | 0.7 | 0.3 | 0.2 |
| |$\rm MAD_{orth}$| | 0.045 | 0.044 | 0.047 |
4 DISCUSSION
4.1 SAMI scaling relations
Using integral field spectroscopy (IFS) from the SAMI Survey for a parent sample of 2720 galaxies, we re-examine the log M∗ − log S0.5 scaling relation studied in C14. We confirm that the S0.5 kinematic parameter, measured from either the stars or the gas, brings galaxies of all morphologies onto a common scaling relation with stellar mass. The slopes of the scaling relation obtained here, both for the stars (0.37 ± 0.01) and for the gas (0.42 ± 0.01), are steeper than that (0.34 ± 0.01) obtained by C14. This difference is likely due to the difference in stellar mass distributions, as our sample is skewed towards higher masses (|$M_* \gt 10^{10}\, M_{\odot }$|); C14 in fact fitted for galaxies with |$M_* \gt 10^{10}\, M_{\odot }$| and found a steeper slope. This difference in slope is slightly decreased when we performed spaxel-level quality cut which eliminated some of most massive galaxies (M∗ > 1011.5M⊙).
C14 also observed a change in slope across a mass range of 8.5 ≲ log M∗/M⊙ ≲ 11.5; this apparent change in slope is also present in our sample. C14 suggested this slope change could be due to not accounting for the mass in neutral gas; due to lack of HI data, we are unable to test this hypothesis. However, the change in slope in our log M∗ − log S0.5 scaling relation could be due to other reasons besides not accounting for the total baryonic mass. Possible causes include: a kinematic measurement limit due to the combined effects of the instrumental resolution and S/N ratio, as a reference we presented the SAMI instrument resolutions for gas and stellar kinematics in Fig. 2; the uncertainty in the low-velocity dispersion measurements positively skewing the distribution of the observed velocity dispersions; a surface brightness limit causing the low-mass sample to be biased towards brighter galaxies with relatively high-velocity dispersions; an intrinsic physical effect causing low-mass galaxies to have higher velocity dispersions than expected based on the linear relation for high-mass galaxies. Unfortunately, with the currently available SAMI data and its limitations in S/N ratio, spectral resolution and sample selection, we cannot distinguish all of these possible causes.
However, we fitted a linear scaling relation with a cutoff at a sample limit |$M_{*,\rm lim}$| (corresponding to |$S_{0.5, \rm lim})$| and found that the sample limits in the stellar and gas versions of the relation occur at different masses. This suggests the bend observed in our sample is unlikely to be caused by intrinsic properties such as stellar mass (this is not to say that there is no physical change in the slope of the scaling relation at some lower mass). A18 suggest galaxies with stellar mass below log M∗/M⊙ ∼ 9.5 have more dark matter content within the effective radius as the mass decreases, so that the dynamical mass (from S0, 5 estimation) to stellar mass ratio for low-mass galaxies increases, resulting in a change in slope in log M∗ − log S0.5. Unfortunately, while we do have galaxies in our sample with log M∗/M⊙ < 9.5, the range of low-mass galaxies does not extend down to 107–|$10^{8}\, M_{\odot }$|. For future work, high-S/N IFS observations of low-mass galaxies with higher spectral resolution (σres ∼ 10 km s−1) will be necessary to fully determine the linearity of the stellar scaling relation throughout the 7 ≲ log M∗/M⊙ ≲ 12 mass range (e.g. using Hector, Bryant et al. 2016).
4.2 IFS and aperture kinematics
In Section 3.5 and 3.6 we compared measurements of the S0.5 parameter and the aperture velocity dispersion and found surprisingly good agreement between the two kinematic tracers (as seen in Fig. 6). This agreement is interesting because, while both S0.5 and |$\sigma _{3^{\prime \prime }}$| are measures of galaxy internal motions, they measure those motions differently. By definition, |$\sigma _{3^{\prime \prime }}$| measures the second moment of the LOSVD integrated over a 3-arcsecond-diameter aperture, including the effect of rotation velocity. For S0.5, the σ component is a luminosity-averaged quantity from LOSVD dispersions measured locally over an aperture (here up to 1Re). By combining these local dispersion measurements with a global rotation measurement Vrot via a suitable scaling factor, S0.5 produces tighter scaling relations with M∗ than |$\sigma _{3^{\prime \prime }}$| (as seen in Fig. 7 and Section 3.6).
The extra information provided by IFS and the more complex calculation involved in deriving S0.5 thus provide a better understanding of this scaling relation (and others). However, IFS is observationally expensive while fibre surveys are observationally cheap. So for purposes requiring very large samples (e.g. exploring the effect of environment on scaling relations for galaxies of different morphological types or using scaling relations to derive distances and peculiar velocities) aperture dispersions may be a more efficient and economical choice.
4.3 The importance of K
The motivation for using K = 0.5 in the SK parameter originates from the virial theorem prediction of the relation between circular velocity and velocity dispersion for an isothermal sphere, |$V_{\rm circ}\propto \sqrt{\alpha } \cdot \sigma$|, where α is a constant that describes the density profile of the system. We have found empirically that the scatter depends weakly on the value of K, with minimum scatter occurring between K = 0.2 and K = 0.7.
There are a number of possible factors that can theoretically influence the value of K:
(3) Observational artefacts. Since the optimal K value is determined by comparing the scatter in the log M∗ − log S0.5 relation, the quality of kinematic parameter measurements and the scatter of the scaling relation are crucial. Covington et al. (2010) have shown with numerical simulations that instrument blurring effects such as spatial resolution and seeing, which contribute to the scatter in the TF relation, do not show significant effects on the measured S0.5 values. A18 also performed a detailed kinematic analysis with spatially resolved rotation velocity measurements. They found that the S0.5 parameter consistently reduced the scatter in scaling relations, taking into account the uncertainties in the Vrot measurement for dispersion-dominated systems. In Section 4.1, we noted that there could be multiple extrinsic causes for a non-linear scaling relation and/or increased scatter, including S/N ratios, instrument resolution, sample selection, and kinematic uncertainties. Thus the best K value is determined by a combination of intrinsic dynamical properties and observational artefacts. In order to use the log M∗ − log SK scaling relation to predict physical attributes of observed systems, it is crucial to make sure the scatter in the scaling relation is not dominated by systematic error.
5 CONCLUSIONS
In this paper we present the log M∗ − log S0.5 scaling relation constructed from the SAMI Galaxy Survey. The S0.5 parameter is useful in bringing galaxies of all morphologies onto a common relation. With no sample pruning (other than S/N quality cuts) the scatter in the log M∗ − log S0.5 relation is significantly less than the TF and FJ relations constructed from the same sample. Interestingly, applying only a relative error cut on S0.5, without any spaxel-level quality cut, still provides a tight scaling relation. Both the stellar and gas versions of the log M∗ − log S0.5 scaling relation have a sample limit where the relation deviates from a linear relation. We found the sample limits occur at different stellar masses for the gas and stellar samples, implying that the apparent non-linearity in the relation is not physical; this is emphasised by the fact that the |$S_{0.5, \rm lim }$| values corresponding to these mass cut-offs are proportional to the effective instrumental resolutions for the stellar and gas measurements.
Comparing S0.5 to single-aperture velocity dispersion |$\sigma _{3^{\prime \prime }}$| shows excellent agreement between the two parameters. For the gas measurements the residuals |$\sigma _{3^{\prime \prime }, gas}-S_{0.5, \rm gas}$| trend negatively with galaxy angular size, while for the stellar measurements the residuals |$\sigma _{3^{\prime \prime }, \rm stellar}-S_{0.5, \rm stellar}$| show no correlation with galaxy angular size. In constructing the mass scaling relations, S0.5 consistently produced less scatter than |$\sigma _{3^{\prime \prime }}$|.
In order to test the importance of choosing an optimal value of K in the construction of the Sk parameter, we measured the scatter of the scaling relations at different values of K. By investigating the correlation between the scatter of the scaling relation and the value of K in the SK parameter, we found that for both stellar and gas measurements K = 0.5 is close to producing the minimum scatter for samples containing only ETGs or mixtures of ETGs and LTGs; however, for samples containing only LTGs K = 0.2 gave significantly less scatter.
These findings are broadly consistent with previous studies by C14 using early release of SAMI data and A18 using CALIFA data.
The S0.5 kinematic parameter allows the construction of a robust and inclusive galaxy scaling relation with relatively little scatter. The tight correlation between S0.5 and |$\sigma _{3^{\prime \prime }}$| implies that a scaling relation with only slightly greater scatter can be constructed for galaxies of all morphologies using large-scale single-fibre galaxy surveys.
ACKNOWLEDGEMENTS
We thank the referee for their constructive report. The SAMI Galaxy Survey is based on observations made at the Anglo-Australian Telescope. The Sydney-AAO Multi-object Integral field spectrograph (SAMI) was developed jointly by the University of Sydney and the Australian Astronomical Observatory. The SAMI input catalogue is based on data taken from the Sloan Digital Sky Survey, the Galaxy And Mass Assembly (GAMA) Survey and the VLT Survey Telescope (VST) ATLAS Survey. The SAMI Galaxy Survey is supported by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013, the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020, and other participating institutions. The SAMI Galaxy Survey website is sami-survey.org.
DB is supported by an Australia Government Research Training Program Scholarship and ASTRO 3D. FDE acknowledges funding through the H2020 ERC Consolidator Grant 683184. JBH is supported by an ARC Laureate Fellowship that funds JvdS and an ARC Federation Fellowship that funded the SAMI prototype. JJB acknowledges support of an Australian Research Council Future Fellowship (FT180100231). JvdS is funded under Bland-Hawthorn’s ARC Laureate Fellowship (FL140100278). NS acknowledges support of a University of Sydney Postdoctoral Research Fellowship. Parts of this research were conducted by ASTRO 3D, through project number CE170100013. LC is the recipient of an Australian Research Council Future Fellowship (FT180100066) funded by the Australian Government. SB acknowledges the funding support from the Australian Research Council through a Future Fellowship (FT140101166). SMC acknowledges the support of an Australian Research Council Future Fellowship (FT100100457). BG is the recipient of an Australian Research Council Future Fellowship (FT140101202). MSO acknowledges the funding support from the Australian Research Council through a Future Fellowship (FT140100255). Support for AMM is provided by NASA through Hubble Fellowship grant #HST-HF2-51377 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. SKY acknowledges support from the Korean National Research Foundation (2017R1A2A1A05001116) and by the Yonsei University Future Leading Research Initiative (2015-22-0064). This study was performed under the umbrella of the joint collaboration between Yonsei University Observatory and the Korean Astronomy and Space Science Institute.
Footnotes
REFERENCES
Author notes
Hubble Fellow




