Energetic particles in haloes of star forming galaxies Free

Model parameters.

		r_c (kpc)	β	n (cm⁻³)	D (cm² s⁻¹)	M_g (M_⊙)
NGC 4631	Model 1	2	0.85	1	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	0.85	0.4	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	0.85	1	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.7	0.25	3 × 10³⁰	3 × 10¹⁰
NGC 4666	Model 1	2	1.05	4	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	1.05	1.3	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	1.05	4	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.85	1.1	3 × 10³⁰	3 × 10¹⁰

		r_c (kpc)	β	n (cm⁻³)	D (cm² s⁻¹)	M_g (M_⊙)
NGC 4631	Model 1	2	0.85	1	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	0.85	0.4	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	0.85	1	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.7	0.25	3 × 10³⁰	3 × 10¹⁰
NGC 4666	Model 1	2	1.05	4	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	1.05	1.3	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	1.05	4	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.85	1.1	3 × 10³⁰	3 × 10¹⁰

Table 1.

Model parameters.

		r_c (kpc)	β	n (cm⁻³)	D (cm² s⁻¹)	M_g (M_⊙)
NGC 4631	Model 1	2	0.85	1	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	0.85	0.4	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	0.85	1	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.7	0.25	3 × 10³⁰	3 × 10¹⁰
NGC 4666	Model 1	2	1.05	4	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	1.05	1.3	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	1.05	4	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.85	1.1	3 × 10³⁰	3 × 10¹⁰

		r_c (kpc)	β	n (cm⁻³)	D (cm² s⁻¹)	M_g (M_⊙)
NGC 4631	Model 1	2	0.85	1	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	0.85	0.4	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	0.85	1	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.7	0.25	3 × 10³⁰	3 × 10¹⁰
NGC 4666	Model 1	2	1.05	4	3 × 10³⁰	3 × 10¹⁰
	Model 2	3	1.05	1.3	3 × 10³⁰	3 × 10¹⁰
	Model 3	2	1.05	4	6 × 10³⁰	3 × 10¹⁰
	Model 4	2	0.85	1.1	3 × 10³⁰	3 × 10¹⁰

Based on (rough) estimates of the mean strength of the IG field, we set a lower limit of 30 nG on its value, which is relevant only in the outer halo region. These analytic distributions allow the construction of 3D emissivity grids, thereby significantly simplifying integrations along the los and convolution with a Gaussian beam to produce radio brightness profiles and volume-integrated emissivities to compute total luminosities in the radio, hard X-ray, and γ bands. The emissivity grid for the halo extends from the outer surface of the (model) disc out to x_o = y_o = _o = 200 kpc.

2.2 Particle radiative yields

The radiative yields of primary electrons, protons, and secondary electrons (and positrons) can be computed by integrating the relevant radiation emissivities over the particle distributions detailed in the previous subsection. Accordingly, the spectral radio emissivity due to a population of relativistic electrons is (Blumenthal & Gould 1970)

\begin{eqnarray*} \frac{{\rm d}E}{{\rm d}\nu \mathrm{ d}t}=\frac{\sqrt{3}ke^3B}{4\pi m_\mathrm{ e} c^2}\int \, {\rm d}\Omega _{\alpha } N_{\mathrm{ e}}\sin {\alpha }\times \int _{\gamma _1}^{\gamma _2}f(\boldsymbol{r_\mathrm{ o}},t_\mathrm{ o},\gamma) \, {\rm \mathrm{ d}}\gamma \frac{\nu }{\nu _\mathrm{ c}} \int _{\nu /\nu _\mathrm{ c}}^{\infty }K_{5/3}(\xi)\, {\rm \mathrm{ d}}\xi , \end{eqnarray*}

(13)

where the electron density N_e generally depends also on the pitch angle, α, γ₁ and γ₂ bracket the electron spectral distribution, ν_c is the cyclotron frequency, K_5/3 is the modified Bessel function of 5/3 order, and the physical constants have their usual meaning.

The (photon) emissivity due to Compton scattering of low-energy CMB photons off relativistic electrons derived in the Thomson limit is (Blumenthal & Gould 1970)

\begin{eqnarray*} \frac{{\rm d}N_{\gamma ,\epsilon }}{{\rm d}\epsilon _1\mathrm{ d}t}=\frac{\pi r_0^2c}{2\gamma ^4} \frac{n(\epsilon)d\epsilon }{\epsilon ^2}\left(2\epsilon _1 \log {\frac{\epsilon _1}{4\gamma ^2\epsilon }}+\epsilon _1+4\gamma ^2\epsilon -\frac{\epsilon _1^2}{2\gamma ^2\epsilon }\right), \end{eqnarray*}

(14)

where ϵ and ϵ₁ are the pre- and post-scattering photon energies, respectively. The electron classical radius is r₀ ≡ e²/m_ec² , and n(ϵ) is the spectral energy density of the scattering radiation fields in the disc, consisting, in addition to the CMB, of diluted Planckian distributions at temperatures 3500 K (starlight), and 30 K (dust). Some 70 per cent of the Galactic stellar radiation field originates in a ‘thin’ disc and the rest in a ‘thick’ disc, with the former modelled as an ellipsoid with semimajor and semiminor axes of 10 kpc and 300 pc (e.g. Gilmore & Reid 1983), and the latter is the remaining disc volume.

By equating the stellar luminosity (in either the optical or IR bands) with the surface-integrated flux for an isotropic diluted blackbody, F = 4δσ_bT⁴, where δ is the dilution factor and σ_b is the Stefan–Boltzmann constant, the respective dilution factors can be computed for the two disc regions. The dilution factors for the stellar and dust fields are determined based on the estimate that of the total Galactic stellar luminosity, ∼5 × 10¹⁰ L_⊙ (Strong et al. 2010), 20 per cent is processed into the IR by interstellar dust. The Compton energy loss rate in the stellar radiation field is

\begin{eqnarray*} \frac{{\rm d}E}{{\rm d}t}=\frac{4}{3}\sigma _Tc\frac{4\delta \sigma _bT^4}{c}\gamma ^2, \end{eqnarray*}

(15)

where σ_T is the Thomson cross-section. Integrating over the energy ϵ and the scattering electron population yields the total Compton emissivity

\begin{eqnarray*} \frac{{\rm d}E_{\mathrm{ tot}}(\epsilon _1,\boldsymbol{r_\mathrm{ o}})}{{\rm d}\epsilon _1\mathrm{ d}t}&=& \int _{\gamma _1}^{\gamma _2}\int _{\epsilon _1/4\gamma ^2}^{\infty } \frac{{\rm d}N_{\gamma ,\epsilon }}{{\rm d}\epsilon _1\mathrm{ d}t}\epsilon \times f(\boldsymbol{r_\mathrm{ o}},t_\mathrm{ o},\gamma) \, {\rm \mathrm{ d}}\epsilon \, {\rm \mathrm{ d}}\gamma . \end{eqnarray*}

(16)

The spectral γ-ray emission generated by π⁰ decay can be calculated as (Mannheim & Schlickeiser 1994):

\begin{eqnarray*} f_{\gamma }(E_{\gamma },\boldsymbol{r_\mathrm{ o}})&=&2E_{\gamma }\int _{E_{\gamma }+\left[\left(m_{\pi ^0}c^2)^2/ 4E_{\gamma }\right)\right]} ^{\infty }\frac{f_{\pi ^\mathrm{ 0}}(E_{\pi ^\mathrm{ 0}},\boldsymbol{r_\mathrm{ o}})\, {\rm d}E_{\pi ^\mathrm{ 0}}}{\sqrt{E_{\pi ^\mathrm{ 0}}^2-m_{\pi ^\mathrm{ 0}}^2c^4}}, \end{eqnarray*}

(17)

where (Pfrommer & Enßlin 2004)

\begin{eqnarray*} f_{\pi ^0}(E_{\pi ^\mathrm{ 0}},\boldsymbol{r_\mathrm{ o}})&=&8cnf_p(\boldsymbol{r_\mathrm{ o}},t_\mathrm{ o},\gamma)\sigma _{pp}^{\pi ^\mathrm{ 0},\pi ^{\pm }}\left(\frac{6E_{\pi ^{\pm }}}{\mathrm{GeV}}\right)^{-\frac{4}{3}(\alpha -\frac{1}{2})} \, \mathrm{GeV}^{-1}. \end{eqnarray*}

(18)

2.3 Model parameters

As noted already, our approximate description of energetic proton and electron propagation, gas density and magnetic field distributions in the Galactic disc is chosen such that it is in general agreement with the more detailed GALPROP models of Strong et al. (2010). This is affected by selecting key parameter values that are reasonably close to those of the second diffusion model which is fully specified in the latter paper. We emphasize again that the main goal in our modelling of the disc is mostly to provide a realistic basis for determining proton and electron distributions and their yields in the Galactic halo where gas and magnetic field properties are poorly known, and can only be modelled by considering reasonable ranges of the key parameters.

As can be seen in Table 1, we consider four galactic halo models, each of which is a variation of the four basic parameters (r_c, β, n, D), where M_g is the halo gas mass. We use a single model to characterize the disc, as discussed in the previous subsection.

3 RESULTS

We applied our modelling approach to predict the levels and spatial profiles of proton and electron radiative yields in the Galactic halo and in the haloes of the two star forming, edge-on galaxies NGC 4631 and NGC 4666 at the respective distances of 7.4 and 27.5 Mpc, and with star formation rates (SFRs) of 1.33 and 7.29 M_⊙ yr⁻¹ (Wiegert et al. 2015). The particle source distribution in the latter two galaxies was assumed to be as in the Galaxy, and the overall injection rates were determined by scaling up the Galactic rate, ≃ 1 M_⊙ yr⁻¹, by the respective SFR of each galaxy. As shown in Table 1, models 1–4 differ only in the value of a single parameter, with the central gas number density adjusted so as to yield the same halo gas mass of 3 × 10¹⁰M_⊙.

The spatial profiles of primary and secondary electrons at γ_e = 10⁴ (contributing most of the synchrotron emission at ν = 1.5 GHz), and protons at γ_p ≈ 12 (kinetic energy of ∼10.3 GeV, above the threshold energy for pion production), are illustrated in Fig. 1; these are essentially equations (4), (5) and (6), multiplied by the respective particle energy. The enhanced population of protons and secondary electrons above the galactic plane is clearly manifested, in clear contrast with the steeply falling profile of primary electrons.

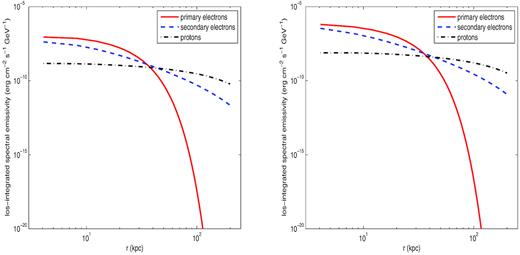
Time-averaged los-integrated particle surface emissivity profiles above the galactic plane, computed for γe = 104 (primary and secondary electrons) and γp ≈ 12 (protons). Results are shown for NGC 4631 (left-hand panel) and NGC 4666 (right-hand panel).

Figure 1.

Time-averaged los-integrated particle surface emissivity profiles above the galactic plane, computed for γ_e = 10⁴ (primary and secondary electrons) and γ_p ≈ 12 (protons). Results are shown for NGC 4631 (left-hand panel) and NGC 4666 (right-hand panel).

For each galaxy we calculated the radio, hard X-ray, and γ spectral luminosities and brightness profiles at 1.575 GHz, 20 keV, and 100 MeV, as well as spectra and bolometric luminosities in the 10–200 keV and 1 MeV–100 GeV bands. Radio brightness profiles (in mJy beam⁻¹) for the four models are plotted in Fig. 2 for NGC 4631 (left-hand panel) and NGC 4666 (right-hand panel). Intersections of the brightness contours measured by Wiegert et al. (2015) with a line perpendicular to the galactic plane and passing through its centre were read off the brightness map; for each contour above and below the plane angular distances of the intersection points were converted into physical distances and averaged. Measurement errors were estimated as the square root of the contour rms noise and thickness added in quadratures. Model predictions, smoothed with a Gaussian beam of ∼18 arcsec FWHM, were normalized either to the third (NGC 4631) or fourth (NGC 4666) data point; these refer only to the halo, and consequently the two innermost measurements for NGC 4631, which still lie in the galactic disc, are irrelevant to the halo. The change of slope apparent in the brightness profiles at ∼30–80 kpc (depending on model) marks the height above (or below) the disc where the radio-yield of secondary electrons begins to dominate over that of primary electrons.

Figure 2.

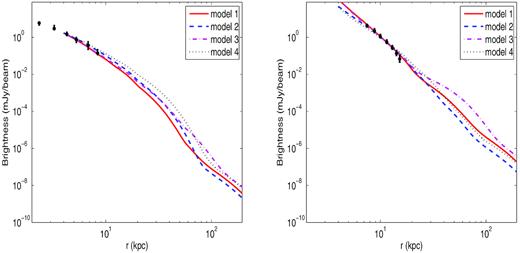
Radiobrightness profiles at ν = 1.575 GHz, smoothed with a Gaussian beam of FWHM 18 arcsec. Results are shown for NGC 4631 (left-hand panel) and NGC 4666 (right-hand panel). Parameter values are listed in Table 1.

Keeping the same total halo gas mass with a higher core radius (model 2) and lower β (model 4) implies lower central densities. This clearly results in reduced densities of secondary electrons, and consequently leads to the lower (with respect to model 1) radio brightness levels apparent in the secondary electron-dominated region of model 2; while the implied densities in model 4 are lower as well, the more moderate fall of the gas profile actually gives rise to a somewhat less steep brightness profiles, lying slightly above and below the model 1 profiles in the secondary-electron dominated zone for NGC 4631 and NGC 4666, respectively. By a qualitative comparison between the measurements and model predictions, we infer that for NGC 4631 model 2 best matches the observations, whereas model 1 provides the closest fit for NGC 4666; these are referred to as ‘fiducial’ models.

The los-integrated emissivity profile at 20 keV and the hard X-ray spectrum in the 10–200 keV band (for the fiducial models) are illustrated in Fig. 3. The profile essentially reflects that of the electrons since it primarily results from electron scattering off the (uniform) CMB. For NGC 4666 models 1, 3, and 4 are roughly similar, whereas for NGC 4631 the profile calculated for model 2 joins the models 1 and 4 profiles at ∼40 kpc. The emissivity profile for model 3 reflects the faster diffusion from the inner to the outer halo, which is clearly due to the higher diffusion coefficient in this model. As expected, the spectral X-ray luminosity in the disc and halo, shown in the lower panels of the figure, is essentially a power law in energy, with spectral indices in (the 10–100 keV band) of 0.93 and 1.00 (NGC 4631), and 0.98 and 1.01 (NGC 4666), respectively. More generally, since particle acceleration is directly related to SF, the higher luminosities of NGC 4666 exactly reflect the higher (by a factor of 5.33) SFR in this galaxy than that in NGC 4631.

Figure 3.

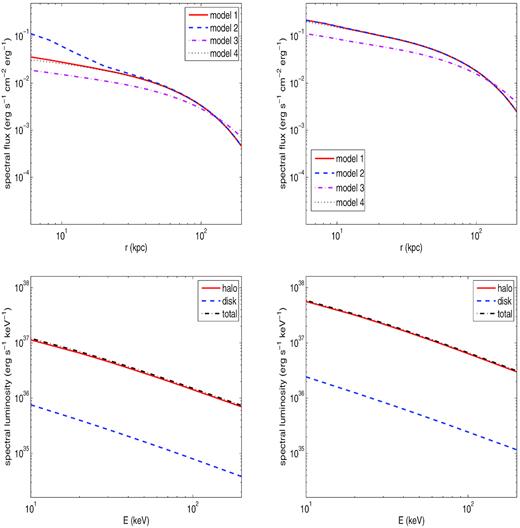
X-ray emission from NGC 4631 (left-hand panels) and NGC 4666 (right-hand panels). Upper panels: los-integrated hard X-ray emissivity profiles at 20 keV. Lower panels: 10–200 keV spectral luminosities of the disc and halo.

The los-integrated emissivity profile at 100 MeV and the γ-spectrum in the 1 MeV–100 GeV band are illustrated in Fig. 4 for the fiducial models. Up to r ∼ 40 kpc (NGC 4631) and ∼20 kpc (NGC 4666) above the galactic plane, the highest emission levels are predicted for models 1 (high central gas density) and 2 (large core radius); at larger distances the milder density slope of model 4 results in the highest emission in both galaxies. Also, the relatively low emission levels in model 3 reflect the high diffusion coefficient, which results in faster proton diffusion out of the inner higher density region of the halo. As can be clearly seen in the lower panels of the figure, the fraction of the γ emission that originates in the halo is negligible with respect to that from the disc, essentially due to the lower gas densities outside the galactic disc.

Figure 4.

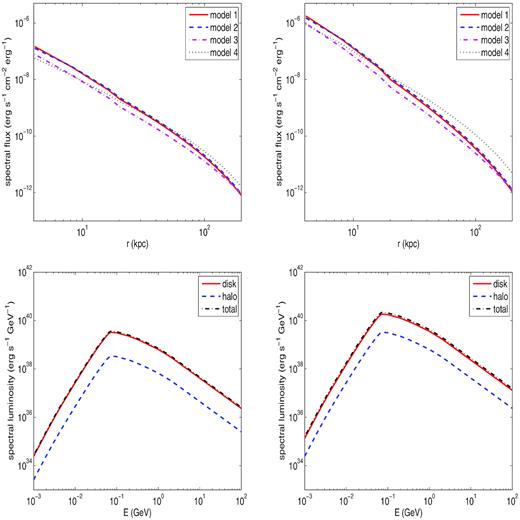
γ-ray emission from NGC 4631 (left-hand panels) and NGC 4666 (right-hand panels). Upper panels: profiles of the spectral flux at 100 MeV. Lower panels: 1 MeV–100 GeV spectral luminosities in the disc and halo.

The radio flux at 1.575 GHz, hard X-ray luminosity in the 10–200 keV, and γ-ray luminosity above 100 MeV are listed in Table 2, where the disc, halo, and total contributions are explicitly specified. These results refer to the respective fiducial model of each galaxy: model 2 for NGC 4631 and model 1 for NGC 4666. As is apparent from the table, the halo produces a non-negligible emission only in the hard X-ray band, constituting some 93–95 per cent of the total luminosity of each galaxy.

Table 2.

Computed radiative yields of NGC 4631 and NGC 4666.

		Hard X-ray (10–200 keV)	γ (≥100 MeV)	1.575 GHz flux
NGC 4631	Disc	2.5 × 10³⁷	3.2 × 10³⁹	695 mJy
	Halo	4.2 × 10³⁸	3.4 × 10³⁸	36 mJy
	Total	4.5 × 10³⁸	3.5 × 10³⁹	731 mJy
NGC 4666	Disc	7.8 × 10³⁷	1.8 × 10⁴⁰	306 mJy
	Halo	2.0 × 10³⁹	3.3 × 10³⁹	3 mJy
	Total	2.1 × 10³⁹	2.1 × 10⁴⁰	309 mJy

		Hard X-ray (10–200 keV)	γ (≥100 MeV)	1.575 GHz flux
NGC 4631	Disc	2.5 × 10³⁷	3.2 × 10³⁹	695 mJy
	Halo	4.2 × 10³⁸	3.4 × 10³⁸	36 mJy
	Total	4.5 × 10³⁸	3.5 × 10³⁹	731 mJy
NGC 4666	Disc	7.8 × 10³⁷	1.8 × 10⁴⁰	306 mJy
	Halo	2.0 × 10³⁹	3.3 × 10³⁹	3 mJy
	Total	2.1 × 10³⁹	2.1 × 10⁴⁰	309 mJy

Table 2.

Computed radiative yields of NGC 4631 and NGC 4666.

		Hard X-ray (10–200 keV)	γ (≥100 MeV)	1.575 GHz flux
NGC 4631	Disc	2.5 × 10³⁷	3.2 × 10³⁹	695 mJy
	Halo	4.2 × 10³⁸	3.4 × 10³⁸	36 mJy
	Total	4.5 × 10³⁸	3.5 × 10³⁹	731 mJy
NGC 4666	Disc	7.8 × 10³⁷	1.8 × 10⁴⁰	306 mJy
	Halo	2.0 × 10³⁹	3.3 × 10³⁹	3 mJy
	Total	2.1 × 10³⁹	2.1 × 10⁴⁰	309 mJy

		Hard X-ray (10–200 keV)	γ (≥100 MeV)	1.575 GHz flux
NGC 4631	Disc	2.5 × 10³⁷	3.2 × 10³⁹	695 mJy
	Halo	4.2 × 10³⁸	3.4 × 10³⁸	36 mJy
	Total	4.5 × 10³⁸	3.5 × 10³⁹	731 mJy
NGC 4666	Disc	7.8 × 10³⁷	1.8 × 10⁴⁰	306 mJy
	Halo	2.0 × 10³⁹	3.3 × 10³⁹	3 mJy
	Total	2.1 × 10³⁹	2.1 × 10⁴⁰	309 mJy

Finally, we calculated the radiative efficiencies for particle energy conversion to the radio and γ-radiation channels, results of which are listed in Table 3, and compared with the respective factors specified by Strong et al. (2010).

Table 3.

Radiative efficiencies for NGC 4631 and NGC 4666, compared with those determined by Strong et al. (2010) for the Milky Way.

	Radio	γ: Compton		γ: π⁰ decay
	(0.001–100 GHz)	0.01–100 MeV	100 MeV–100 GeV	0.01–100 MeV	100 MeV–100 GeV
NGC 4631	0.08	0.20	0.17	0.002	0.04
NGC 4666	0.09	0.20	0.15	0.002	0.04
Milky Way	0.16	0.14	0.14	0.0002	0.007

	Radio	γ: Compton		γ: π⁰ decay
	(0.001–100 GHz)	0.01–100 MeV	100 MeV–100 GeV	0.01–100 MeV	100 MeV–100 GeV
NGC 4631	0.08	0.20	0.17	0.002	0.04
NGC 4666	0.09	0.20	0.15	0.002	0.04
Milky Way	0.16	0.14	0.14	0.0002	0.007

Table 3.

10.1088/0004-637X/719/2/1433

Radiative efficiencies for NGC 4631 and NGC 4666, compared with those determined by Strong et al. (2010) for the Milky Way.

	Radio	γ: Compton		γ: π⁰ decay
	(0.001–100 GHz)	0.01–100 MeV	100 MeV–100 GeV	0.01–100 MeV	100 MeV–100 GeV
NGC 4631	0.08	0.20	0.17	0.002	0.04
NGC 4666	0.09	0.20	0.15	0.002	0.04
Milky Way	0.16	0.14	0.14	0.0002	0.007

	Radio	γ: Compton		γ: π⁰ decay
	(0.001–100 GHz)	0.01–100 MeV	100 MeV–100 GeV	0.01–100 MeV	100 MeV–100 GeV
NGC 4631	0.08	0.20	0.17	0.002	0.04
NGC 4666	0.09	0.20	0.15	0.002	0.04
Milky Way	0.16	0.14	0.14	0.0002	0.007

4 DISCUSSION

The main objective of our work has been a quantitative description of energetic protons and electrons in haloes of SFGs, based on detailed modelling of their SSDs in galactic discs. We adopted an approximate diffusion solution to particle distributions in the halo, normalized at the disc boundary by using detailed results from GALPROP models for the Galaxy. Our treatment provides a realistic basis for estimating the particle radiative yields in the halo for an assumed magnetic field profile, halo gas mass, gas core radius, and diffusion coefficient. Doing so we bracket the most likely ranges of spectral and spatial profiles of halo radio, hard X-ray, and γ-ray emission; these constitute a tangible basis for assessing the detection feasibility of the integrated fluxes in these spectral bands.

Results of our calculations indicate that emission from the halo of an SFG will be comparable to or higher than that of the disc only in the hard X-ray band. This clearly is due to the relatively high fraction of secondary electrons in the halo and the uniformity of the CMB (the dominant radiation field), in sharp contrast to the steeply decreasing magnetic field and gas density that determine emission levels in the radio and γ-ray, respectively. In our ‘fiducial’ models the estimated 10–200 keV halo luminosities of NGC 4631 and NGC 4666 are ∼17 and ∼26 times higher than the respective (NT) disc luminosities. For each of these galaxies the predicted luminosities in the other three models are within a factor of two of the respective values specified in Table 2. While high, the total 10–200 keV luminosity of even the (more luminous) SB galaxy NGC 4666, ≃2 × 10³⁹ erg s⁻¹, is still substantially lower than stellar X-ray emission from the disc, which is dominated by high-mass X-ray binaries (but also includes significant emission from low-mass X-ray binaries and thermal emission from diffuse IS gas). The disc emission can be estimated using the observationally deduced scaling relation (Mineo, Gilfanov & Sunyaev 2012) for the 0.5–8 keV luminosity in terms of the SFR, which for NGC 4666, yields a value that is more than a factor of 10 higher than the predicted 10–200 keV luminosity of the halo. We note that for the Galaxy, with a global SFR of ∼1 M_⊙ yr⁻¹, Strong et al. (2010) estimates for the (total) disc luminosities are |$L(10\, \mathrm{keV}\!-\!100\, \mathrm{MeV}) \simeq 2.2\times 10^{38}$| erg s⁻¹, and |$L(0.1\!-\!100\, \mathrm{GeV}) \simeq 7.2\times 10^{38}$| erg s⁻¹ for their diffusion model 2.

Our estimates of hard X-ray luminosities of the two galaxies provide sufficient motivation for dedicated searches for halo emission by the next-generation hard X-ray satellites that will likely have sufficient sensitivity and angular resolution to separate out disc and halo emission in nearby edge-on galaxies. Prime candidates for such observations are the two nearby, nearly edge-on SBGs NGC 253 and M82, which at 2.5 and 3.6 Mpc, respectively, are more than twice closer than NGC 4631, and with significantly higher SF rates, are more optimal targets for mapping X-ray emission from their haloes. The Fermi-LAT telescope detected emission above 200 MeV from NGC 253 and M82 (Abdo et al. 2010); the emission was determined to be non-varying and point-like. A recent (‘Pass 8’) analysis of 7-yr Fermi-LAT data on a sample of SFGs (Rojas-Bravo & Araya 2016) resulted only in upper limits on the emission above 100 MeV. The sample includes NGC 4631 for which a 95 per cent upper limit of 5 × 10³⁹ erg s⁻¹ was set. (This upper limit is a factor ∼1.8 lower than the value deduced by Ackermann et al. 2012 in their analysis of emission from SFGs in the 3-yr Fermi-LAT data base.) The current bound is somewhat higher than our predicted total γ-ray luminosity. Given the intense SF activity in the central disc regions in these galaxies, the measurement of high-energy X- and γ-ray emission from these closest SBGs galaxies is not surprising, and indeed was predicted based on detailed models (e.g. Goldshmidt & Rephaeli 1995, Domingo-Santamaría & Torres 2005; Persic, Rephaeli & Arieli 2008; de Cea del Pozo, Torres & Rodriguez Marrero 2009; Rephaeli, Arieli & Persic 2010).

In assessing realistic ranges of key parameters in the estimation of the predicted radiative yields of star forming galaxies, we note that in a recent analysis (Heesen et al. 2018) of radio emission profiles in nearby galaxies, higher values of the SFRs and mean disc magnetic fields were determined. The latter analysis is based on a different approach to modelling energetic electron and magnetic field distributions in the thin and thick disc regions; key differences between the respective approaches include particle source distribution (Gaussian in our treatment, uniform across the galactic disc but vanishing elsewhere in that of Heesen et al.), the duration of the transport process (time integration is performed in our approach, whereas steady state is presumed in theirs), and our inclusion of radiative emission from secondary electrons which they (apparently) have not done. Nonetheless it is still relevant to assess the net effect of the higher values of these quantities on our results. For the two galaxies considered here, NGC 4631 and NGC 4666, SFRs of 2.9 and 16.2 M_⊙ yr⁻¹ were used; these are about a factor ∼2.2 higher than the values (from Wiegert et al. 2015) adopted here. The SFR constitutes an overall normalization of particle densities in the disc, but since we normalize the predicted radio (surface) emissivity to the observed profiles, a different SFR would only affect this overall normalization factor. Mean magnetic field values in the discs of the two galaxies were taken to be 13.5 and 18.2 |$\mu$|G, higher by about ∼1.3 than our values. With the level of the overall B-dependence of the synchrotron emissivity, this difference amounts to about the same (latter) factor. Therefore, given inherent observational uncertainties, and the fact that our calculated radiative yields (for the set of models considered here) span appreciably wider ranges than that implied by the above SFR and magnetic field values, the overall impact on our predictions is small.

The ratio of the particle energy lost by interactions in IS space to the energy injected out of the acceleration sites is referred to as the calorimetric efficiency. This fraction is known to be very large (⁠|${\sim } 90{{\ \rm per\ cent}}$|⁠) for primary electrons, but quite low (⁠|${\sim } 10{{\ \rm per\ cent}}$|⁠) for protons. Obviously, additional losses in the halo result in essentially negligibly small residual primary electron component in the outer halo. Of interest is mainly the total calorimetric efficiency of protons and their residual energy content in the outer halo. For the models explored here, our estimates indicate that the total calorimetric efficiencies of protons are in the range ∼0.1–4 per cent. Propagation through the halo increases the total proton energy losses by only a few per cent over the losses in the disc.

An important consequence of the low calorimetric efficiency of protons diffusing out of SFGs is their accumulated density in clusters. In the central regions of rich clusters the gas density and magnetic fields are significantly enhanced with respect to their levels in IG space outside clusters, with typical values of O(10⁻³) cm⁻³ and O(1) μG, higher than corresponding values in the outer halo of an SFG that is not a cluster member. The higher concentration of SFGs in a cluster and stronger coupling of protons to the magnetized IC gas result in the creation of secondary electrons and the emission of significant radio and NT X-&-γ emission in the central cluster region.

We have recently carried out a first detailed assessment of galactic proton and electron in IC space (Rephaeli & Sadeh 2016) based on a calculation of the particle SSDs assuming that electrons diffuse out of radio and SF galaxies. Given the lack of unequivocal observational evidence for appreciable proton component in the lobes of radio galaxies, we conservatively ignored the contribution of radio galaxies assuming that protons originate only in SFGs. The extended distribution of SFGs, whose relative fraction increases with distance from the cluster centre, is a key feature in accounting for the large size of radio haloes. Particle escape rates were approximated by scaling to the estimated rates from the Galactic disc (Strong et al. 2010), with no account taken of propagation and energy losses in the halo. This approach was applied to conditions in the Coma cluster, where the number of SFGs was estimated from the total blue luminosity of the cluster, and only the two central powerful radio galaxies were included as electron sources.

We found that for reasonable models of the gas density and magnetic field spatial profiles, the predicted profile of the combined radio emission from primary and secondary electrons is roughly consistent with that deduced from current measurements of the Coma halo. However, in this rather conservative approach (in accounting for proton and electron sources in clusters), the level of radio emission was found to be appreciably lower than the measured emission; this suggests that there could be additional particle sources, such as AGN and lower luminosity (than that of the two strong central) radio galaxies. Also calculated were the levels of NT X-ray emission, which was predicted to be mostly by Compton scattering of electrons from radio galaxies off the CMB, and γ-ray emission from the decay of neutral pions produced in interactions of protons from SFGs with protons in IC gas. Since the predicted levels of NT X-ray and γ-ray emission from (e.g.) the Coma cluster are appreciably lower than the current upper limits, only weak constraints can at present be obtained on the steady-state proton and electron IC distributions.

In assessing the likelihood of additional proton component in clusters, we note that the low calorimetric efficiency of protons, which are clearly accelerated in the nuclei of radio galaxies, implies that these could be important proton sources. Some evidence for significant proton populations in the lobes of radio galaxies comes from Fermi-LAT measurements of emission above 100 MeV from the nearby Centaurus A (Abdo et al. 2010) and Fornax A (Ackermann et al. 2016). Based on detailed models of the radio to γ spectral energy distributions of these galaxies, it was concluded that the measured γ emission is from the π⁰ decay (produced in p–p interactions), rather than Compton up-scattering of the radio-emitting electrons off the background optical radiation field (McKinley et al. 2015, Ackermann et al. 2016). However, at least in the case of Fornax A, it was recently shown (Persic & Rephaeli 2019) that the optical radiation field in the lobes (which is dominated by the central host galaxy NGC 1316) is sufficiently intense to account for the Fermi-LAT measurements by Compton scattering. It remains to be seen if the measured emission from the Coma halo can be fully accounted for by protons and electrons from all SF and radio galaxies in the cluster. If this turns out to be unrealistic, then there would be stronger motivation to consider particle re-acceleration (in IC space) as an alternative model for maintaining the requisite level of radio-emitting electrons.

ACKNOWLEDGEMENTS

This work has been supported by a grant from JCF (San Diego, CA). The authors wish to thank Theresa Wiegert for clarifying details of the radio-map in the CHANG-ES 2015 paper, and the referee for a constructive report.

Footnotes

1

The current version of GALPROP is available at https://gitlab.mpcdf.mpg.de/aws/galprop

REFERENCES

Abdo

A. A.

et al. .,

2010

,

ApJ

,

719

,

1433

10.1088/0004-637X/755/2/164

Ackermann

M.

et al. .,

2012

,

ApJ

,

755

,

164

10.3847/0004-637X/826/1/1

Ackermann

M.

et al. .,

2016

,

ApJ

,

826

,

1

Aharonian

F. A.

,

Atoyan

A. M.

,

1996

,

A&A

,

309

,

917

Atoyan

A. M.

,

Aharonian

F. A.

,

Völk

H. J.

,

1995

,

Phys. Rev. D

,

52

,

3265

10.1103/PhysRevD.52.3265

10.1103/RevModPhys.42.237

Blumenthal

G. R.

,

Gould

R. J.

,

1970

,

Rev. Mod. Phys

.,

42

,

237

10.1088/0004-637X/698/2/1054

de Cea del Pozo

E.

,

Torres

D. F.

,

Rodriguez Marrero

A. Y.

,

2009

,

ApJ

,

698

,

1054

Domingo-Santamaría

E.

,

Torres

D. F.

,

2005

,

A&A

,

444

,

403

Gilmore

G.

,

Reid

N.

,

1983

,

MNRAS

,

202

,

1025

10.1093/mnras/202.4.1025

Goldshmidt

O.

,

Rephaeli

Y.

,

1995

,

ApJ

,

444

,

113

10.1086/175586

10.1016/0031-8914(72)90227-3

Gould

R. J.

,

1972

,

Physica

,

60

,

145

Heesen

V.

et al. .,

2018

,

MNRAS

,

476

,

158

10.1093/mnras/sty105

10.1103/PhysRevD.74.034018

Kelner

S. R.

,

Aharonian

F. A.

,

Bugayov

V. V.

,

2006

,

Phys. Rev. D

,

74

,

034018

Mannheim

K.

,

Schlickeiser

R.

,

1994

,

A&A

,

286

,

983

McKinley

B.

et al. .,

2015

,

MNRAS

,

446

,

3478

10.1093/mnras/stu2310

10.1111/j.1365-2966.2011.19862.x

Mineo

S.

,

Gilfanov

M.

,

Sunyaev

R.

,

2012

,

MNRAS

,

419

,

2095

10.1103/PhysRevD.99.043007

Orlando

E.

,

2019

,

Phys. Rev. D

,

99

,

043007

Orlando

E.

,

Strong

A.

,

2013

,

MNRAS

,

436

,

2127

10.1093/mnras/stt1718

Persic

M.

,

Rephaeli

Y.

,

Arieli

Y.

,

2008

,

A&A

,

486

,

143

Pfrommer

C.

,

Enßlin

T. A.

,

2004

,

A&A

,

426

,

777

Ramaty

R.

,

Lingenfelter

R. E.

,

1966

,

J. Geophys. Res.

,

71

,

3687

10.1029/JZ071i015p03687

10.1111/j.1365-2966.2009.15661.x

Rephaeli

Y.

,

Arieli

Y.

,

Persic

M.

,

2010

,

MNRAS

,

401

,

473

10.1103/PhysRevD.93.101301

Rephaeli

Y.

,

Sadeh

S.

,

2016

,

Phys. Rev. D

,

93

,

101301

Rojas-Bravo

C.

,

Araya

M.

,

2016

,

MNRAS

,

463

,

1068

10.1093/mnras/stw2059

Stecker F.W., Jones F.C.

,

1977

,

ApJ

,

217

, 843

Stein

Y.

,

2017

,

Magnetic Fields and Cosmic Ray Transport in Edge-On Spiral Galaxies from the CHANG-ES Sample

.

Ruh-Universität Bochum

,

Bochum

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Strong

A. W.

,

Porter

T. A.

,

Digel

S. W.

,

Jóhannesson

G.

,

Martin

P.

,

Moskalenko

I. V.

,

Murphy

E. J.

,

Orlando

E.

,

2010

,

ApJ

,

722

,

L58

10.1088/0004-6256/150/3/81

Syrovatskii

S. I.

,

1959

,

Sov. Astron.

,

3

,

22

Wiegert

T.

et al. .,

2015

,

AJ

,

150

,

81