MOVES – II. Tuning in to the radio environment of HD189733b Free

Planetary and stellar parameters of HD189733b and its host star.

Parameter	Value	Reference
Star:
Stellar mass (M_⋆)	0.78 M_\|$\odot$\|	1
Stellar radius (R_⋆)	0.76 R_\|$\odot$\|	1
Rotational period (P_rot)	11.94 d	2
Distance (d)	19.8 pc	3
Planet:
Planetary mass (M_p)	1.13 M_jup	4
Planetary radius (R_p)	1.13 R_jup	4
Orbital distance (a)	8.8 R_⋆	1
Orbital period (P_orb)	2.2 d	1

Parameter	Value	Reference
Star:
Stellar mass (M_⋆)	0.78 M_\|$\odot$\|	1
Stellar radius (R_⋆)	0.76 R_\|$\odot$\|	1
Rotational period (P_rot)	11.94 d	2
Distance (d)	19.8 pc	3
Planet:
Planetary mass (M_p)	1.13 M_jup	4
Planetary radius (R_p)	1.13 R_jup	4
Orbital distance (a)	8.8 R_⋆	1
Orbital period (P_orb)	2.2 d	1

Note. (1) Llama et al. (2013), (2) Fares et al. (2010), (3) Gaia Collaboration et al. (2018), (4) Stassun, Collins & Gaudi (2017)

Table 1.

Planetary and stellar parameters of HD189733b and its host star.

Parameter	Value	Reference
Star:
Stellar mass (M_⋆)	0.78 M_\|$\odot$\|	1
Stellar radius (R_⋆)	0.76 R_\|$\odot$\|	1
Rotational period (P_rot)	11.94 d	2
Distance (d)	19.8 pc	3
Planet:
Planetary mass (M_p)	1.13 M_jup	4
Planetary radius (R_p)	1.13 R_jup	4
Orbital distance (a)	8.8 R_⋆	1
Orbital period (P_orb)	2.2 d	1

Parameter	Value	Reference
Star:
Stellar mass (M_⋆)	0.78 M_\|$\odot$\|	1
Stellar radius (R_⋆)	0.76 R_\|$\odot$\|	1
Rotational period (P_rot)	11.94 d	2
Distance (d)	19.8 pc	3
Planet:
Planetary mass (M_p)	1.13 M_jup	4
Planetary radius (R_p)	1.13 R_jup	4
Orbital distance (a)	8.8 R_⋆	1
Orbital period (P_orb)	2.2 d	1

Note. (1) Llama et al. (2013), (2) Fares et al. (2010), (3) Gaia Collaboration et al. (2018), (4) Stassun, Collins & Gaudi (2017)

The layout of this paper is as follows: in Section 2, we present our modelling and radio emission calculation of the wind of HD189733. Then, in Section 3 we calculate the planetary radio emission. We investigate different scenarios where the planetary radio emission may be unable to propagate out of the planetary system in Section 4. We discuss our findings in Section 5, and then present a summary and conclusions in Section 6.

2 STELLAR WIND OF HD189733

2.1 Modelling the stellar wind

To model the wind of HD189733, we use the 3D magnetohydrodynamical (MHD) code BATS-R-US (Powell et al. 1999; Tóth et al. 2012), modified by Vidotto et al. (2012). BATS-R-US has been used to model stellar wind outflows in the context of low-mass and planet-hosting stars (e.g. Vidotto et al. 2012; Llama et al. 2013; Cohen et al. 2014; Alvarado-Gómez et al. 2016; Ó Fionnagáin et al. 2019).

BATS-R-US solves the ideal set of MHD equations, for conservation of mass, magnetic flux, momentum, and energy, respectively:

\begin{eqnarray*} \frac{\partial }{\partial t} \rho + \nabla \cdot (\rho \boldsymbol{u}) = 0, \end{eqnarray*}

(1)

\begin{eqnarray*} \frac{\partial }{\partial t} \boldsymbol{B} + \nabla \cdot (\boldsymbol{uB} - \boldsymbol{Bu}) = 0, \end{eqnarray*}

(2)

\begin{eqnarray*} \frac{\partial }{\partial t} (\rho \boldsymbol{u}) + \nabla \cdot \bigg [ \rho \boldsymbol{uu} + \bigg (p + \frac{B^2}{8\pi } \bigg) \boldsymbol{I} - \frac{\boldsymbol{BB}}{4\pi } \bigg ] = \rho \boldsymbol{g}, \end{eqnarray*}

(3)

\begin{eqnarray*} \frac{\partial }{\partial t} \varepsilon + \nabla \cdot \bigg [ \bigg (\varepsilon + p + \frac{B^2}{8\pi } \bigg) \boldsymbol{u} - \frac{(\boldsymbol{u} \cdot \boldsymbol{B}) \boldsymbol{B}}{4\pi } \bigg ] = \rho \boldsymbol{g} \cdot \boldsymbol{u}. \end{eqnarray*}

(4)

These equations are solved for a plasma with a mass density ρ, velocity |$\boldsymbol{u} = \lbrace u_x, u_y, u_z \rbrace$|⁠, magnetic field |$\boldsymbol{B} = \lbrace B_x, B_y, B_z \rbrace$|⁠, and thermal pressure p. Here, |$\boldsymbol{I}$| is the identity matrix, and ε is the total energy density:

\begin{eqnarray*} \varepsilon = \frac{\rho u^2}{2} + \frac{p}{\gamma - 1} + \frac{B^2}{8\pi }, \end{eqnarray*}

(5)

where γ is the polytropic index.

The inputs of BATS-R-US are the stellar mass M_⋆ and radius R_⋆, which provide the surface gravity |$\boldsymbol{g}$|⁠, coronal base temperature T₀ and number density n₀, rotational period P_rot, and surface magnetic field map. In our wind simulations, we make the following assumptions:

The wind is an ideal gas: p = nk_BT, where n = ρ/(μm_p) is the number density, k_B is Boltzmann’s constant, and T is the temperature. Here, μm_p is the mean mass per particle.
The wind is composed of fully ionised hydrogen, so we adopt a value of μ = 0.5.
The wind is polytropic: p ∝ ρ^γ.

Provided that we have derived values for the stellar mass, radius, and rotational period, we are left with the following free parameters in our models: T₀, n₀, and γ. For the coronal base temperature T₀, we adopt a value of 2 × 10⁶ K, which is typical for the coronae of K stars (Johnstone & Güdel 2015). For the base number density n₀, we assume 10¹⁰ cm⁻³. We take γ = 1.1 for the polytropic index, which is similar to the effective adiabatic index of the solar wind (Van Doorsselaere et al. 2011). This set of parameters produce a mass-loss rate of 3 × 10⁻¹² M_|$\odot$| yr⁻¹ for HD189733, which is in the range of inferred mass-loss rates for active K stars (see Wood 2004; Jardine & Collier Cameron 2019; Rodríguez et al. 2019).

To simulate the wind variability of HD189733, we implement surface magnetic field maps obtained for the star at different epochs, which were reconstructed from observations by Fares et al. (2017) using the ZDI technique. The maps implemented were obtained at the epochs 2013 June/July, 2014 September, and 2015 July, and are shown in Fig. 1. These maps allow us to estimate the yearly variability of the stellar wind properties and the planetary radio emission. The field strength at these epochs are also some of the largest observed for the star, for which we expect should drive strong radio emission from the planet. We simulate the wind with a grid that extends from −20 R_⋆ to +20 R_⋆ along the x, y, and z axes, with the star at the centre. To solve for the magnetic field in the wind, we fix the radial component B_r based on the ZDI map at each epoch, and assume an outflow or ‘float’ condition for meridional B_θ and azimuthal B_ϕ components, where we take their derivative with respect to the radial coordinate to be zero. We also incorporate adaptive mesh refinement in our grid. Our grid resolution ranges from 0.01 R_⋆ to 0.3 R_⋆, with the finest resolution occurring in the region from 1 R_⋆ to 2 R_⋆. This is equivalent to a refinement level of 10 quoted in Nicholson et al. (2016), and has a total of 39 million cells. Nicholson et al. (2016) investigated the effects of increasing the grid resolution to a refinement level of 11 on the derived global wind properties, and obtained marginally more accurate results. Given that the large number of cells in a grid of this size (300 million) is very computationally expensive, we adopt a refinement level of 10 in this work.

Figure 1.

Mollweide projections of the radial surface magnetic field of HD189733 at the three epochs 2013 June/July, 2014 September, and 2015 July (left to right), which were reconstructed from observations by Fares et al. (2017). We implement these as boundary conditions in our stellar wind simulations.

With everything in place, we set our simulation to run until a steady state is obtained. We take this to be the point where various global wind properties such as the mass-loss and angular momentum loss rates vary by |$\lt 1{{\ \rm per\ cent}}$| between iterations. The stability of these values as a function of distance from the star also indicates that a steady state has been obtained. When these conditions are satisfied, we take the wind model to be complete.

2.2 Stellar wind variability of HD189733

From our simulations, we derive the global wind properties of HD189733 at 2013 June/July, 2014 September, and 2015 July, as described by Vidotto et al. (2015). The mass-loss rate |$\dot{M}$| of the star is calculated as:

\begin{eqnarray*} \dot{M} = \oint _S \rho u_{\rm r} {\rm d}S, \end{eqnarray*}

(6)

where S is a spherical surface above the stellar surface at a specified distance. The angular momentum loss rate of the star |$\dot{J}$| is calculated as the flux of angular momentum through S:

\begin{eqnarray*} \dot{J} = \oint _S \bigg [ - \frac{\varpi B_\varphi B_{\rm r}}{4\pi } + \varpi u_\varphi \rho u_{\rm r} \bigg ] {\rm d}S, \end{eqnarray*}

(7)

where ϖ = (x² + y²)^1/2 is the cylindrical radius. The unsigned open magnetic flux of the stellar wind Φ_open is:

\begin{eqnarray*} \Phi _\text{open} = \oint _S |B_{\rm r}| {\rm d}S. \end{eqnarray*}

(8)

We compute |$\dot{M}$|⁠, |$\dot{J}$|⁠, and Φ_open at concentric spherical surfaces S around the star from 10 R_⋆ to 20 R_⋆, and take the average value in this region. Our computed values are listed in Table 2. We find that the wind properties of HD189733 vary over time in response to its changing magnetic field topology, with the mass-loss rate, angular momentum loss rate, and open magnetic flux varying by 9 per cent, 40 per cent, and 19 per cent, respectively, over the three modelled epochs, relative to the maximum over the three epochs. These results are comparable to those found by other stellar/solar wind models (Vidotto et al. 2012; Nicholson et al. 2016; Réville & Brun 2017), wherein small variations in |$\dot{M}$| (>20 per cent) and large variations in |$\dot{J}$| (50–140 per cent) are seen over time-scales of half to multiple magnetic cycles.

Table 2.

Global wind properties derived for HD189733 at different epochs. The values listed are the mass-loss rate |$\dot{M}$|⁠, angular momentum loss rate |$\dot{J}$|⁠, unsigned open magnetic flux Φ_open, and unsigned magnetic flux at the surface Φ₀.

Epoch	\|$\dot{M}$\|	\|$\dot{J}$\|	Φ_open	Φ₀
	(10⁻¹² M_\|$\odot$\| yr⁻¹)	(10³¹ erg)	(Φ₀)	(10²³ Mx)
2013 Jun/Jul	3.2	5.5	0.39	4.5
2014 Sep	3.0	5.2	0.48	3.0
2015 Jul	2.9	3.3	0.40	2.7

Epoch	\|$\dot{M}$\|	\|$\dot{J}$\|	Φ_open	Φ₀
	(10⁻¹² M_\|$\odot$\| yr⁻¹)	(10³¹ erg)	(Φ₀)	(10²³ Mx)
2013 Jun/Jul	3.2	5.5	0.39	4.5
2014 Sep	3.0	5.2	0.48	3.0
2015 Jul	2.9	3.3	0.40	2.7

Table 2.

Global wind properties derived for HD189733 at different epochs. The values listed are the mass-loss rate |$\dot{M}$|⁠, angular momentum loss rate |$\dot{J}$|⁠, unsigned open magnetic flux Φ_open, and unsigned magnetic flux at the surface Φ₀.

Epoch	\|$\dot{M}$\|	\|$\dot{J}$\|	Φ_open	Φ₀
	(10⁻¹² M_\|$\odot$\| yr⁻¹)	(10³¹ erg)	(Φ₀)	(10²³ Mx)
2013 Jun/Jul	3.2	5.5	0.39	4.5
2014 Sep	3.0	5.2	0.48	3.0
2015 Jul	2.9	3.3	0.40	2.7

Epoch	\|$\dot{M}$\|	\|$\dot{J}$\|	Φ_open	Φ₀
	(10⁻¹² M_\|$\odot$\| yr⁻¹)	(10³¹ erg)	(Φ₀)	(10²³ Mx)
2013 Jun/Jul	3.2	5.5	0.39	4.5
2014 Sep	3.0	5.2	0.48	3.0
2015 Jul	2.9	3.3	0.40	2.7

As we implement magnetic field maps with complex topologies in our wind simulations, we find that the wind of HD189733 is inhomogeneous. This can be seen in the profiles of the radial wind velocity in Fig. 2. As a result, the planet experiences a non-uniform wind as it progresses through its orbit. Table 3 lists the average values of various wind properties at the planetary orbit at 8.8 R_⋆, as well as their min/max values in the orbit. We find that the particle number density and velocity of the wind relative to the motion of the planet vary from 29–37 per cent and 25–32 per cent, respectively, throughout the orbit across the three epochs. These variations are likely to be observable in the UV transit of the planet (Lecavelier des Etangs et al. 2012; Bourrier & Lecavelier des Etangs 2013). From a previous transit of the planet in 2011, Bourrier & Lecavelier des Etangs (2013) derived a stellar wind velocity of 200 km s⁻¹ and density of 10⁶ cm⁻³ for HD189733 at the planetary orbit, based on the Ly-α absorption from the extended atmosphere of the planet in the saturation regime. These values are in good agreement with the stellar wind properties at the planetary orbit in our models. Our temperature however is a factor of 30 higher than their derived value of 3 × 10⁴ K. The cause of this discrepancy could be due the fact that our models do not consider detailed heating and cooling mechanisms for the stellar wind (Vidotto & Bourrier 2017).

Figure 2.

Simulated stellar wind of HD189733, at 2013 June/July, 2014 September, and 2015 July (left to right). Grey lines show the large-scale structure of the magnetic field of the star, which is embedded in the stellar wind. Profiles of the radial velocity (u_r) of the stellar wind in the orbital plane of the planet are shown. The orbit at 8.8 R_⋆ is shown with a black circle, and Alfvén surfaces are shown in white. The orientation in each panel is the same.

Table 3.

Average stellar wind parameters of HD189733 at the planetary orbit. The values listed are the particle number density n, velocity in the reference frame of the planet Δu, magnetic field strength B, temperature T, and total pressure p_tot of the stellar wind. The values quoted in square brackets are the min/max value of each parameter throughout the orbit, respectively.

Epoch	〈n〉	〈Δu〉	〈B〉	〈T〉	〈p_tot〉
	(10⁶ cm⁻³)	(km s⁻¹)	(mG)	(10⁶ K)	(10⁻⁴ dyn cm⁻²)
2013 Jun/Jul	4.0	235	62.1	1.03	1.71
	[3.3, 5.2]	[188, 270]	[2.2, 84.9]	[0.94, 1.22]	[<0.01, 2.87]
2014 Sep	3.8	220	55.6	0.97	1.37
	[3.0, 4.7]	[183, 271]	[1.9, 79.1]	[0.93, 1.17]	[<0.01, 2.49]
2015 Jul	3.7	212	44.6	0.95	0.86
	[3.2, 4.5]	[196, 260]	[3.9, 57.8]	[0.92, 1.05]	[0.01, 1.33]

Epoch	〈n〉	〈Δu〉	〈B〉	〈T〉	〈p_tot〉
	(10⁶ cm⁻³)	(km s⁻¹)	(mG)	(10⁶ K)	(10⁻⁴ dyn cm⁻²)
2013 Jun/Jul	4.0	235	62.1	1.03	1.71
	[3.3, 5.2]	[188, 270]	[2.2, 84.9]	[0.94, 1.22]	[<0.01, 2.87]
2014 Sep	3.8	220	55.6	0.97	1.37
	[3.0, 4.7]	[183, 271]	[1.9, 79.1]	[0.93, 1.17]	[<0.01, 2.49]
2015 Jul	3.7	212	44.6	0.95	0.86
	[3.2, 4.5]	[196, 260]	[3.9, 57.8]	[0.92, 1.05]	[0.01, 1.33]

Table 3.

Average stellar wind parameters of HD189733 at the planetary orbit. The values listed are the particle number density n, velocity in the reference frame of the planet Δu, magnetic field strength B, temperature T, and total pressure p_tot of the stellar wind. The values quoted in square brackets are the min/max value of each parameter throughout the orbit, respectively.

Epoch	〈n〉	〈Δu〉	〈B〉	〈T〉	〈p_tot〉
	(10⁶ cm⁻³)	(km s⁻¹)	(mG)	(10⁶ K)	(10⁻⁴ dyn cm⁻²)
2013 Jun/Jul	4.0	235	62.1	1.03	1.71
	[3.3, 5.2]	[188, 270]	[2.2, 84.9]	[0.94, 1.22]	[<0.01, 2.87]
2014 Sep	3.8	220	55.6	0.97	1.37
	[3.0, 4.7]	[183, 271]	[1.9, 79.1]	[0.93, 1.17]	[<0.01, 2.49]
2015 Jul	3.7	212	44.6	0.95	0.86
	[3.2, 4.5]	[196, 260]	[3.9, 57.8]	[0.92, 1.05]	[0.01, 1.33]

Epoch	〈n〉	〈Δu〉	〈B〉	〈T〉	〈p_tot〉
	(10⁶ cm⁻³)	(km s⁻¹)	(mG)	(10⁶ K)	(10⁻⁴ dyn cm⁻²)
2013 Jun/Jul	4.0	235	62.1	1.03	1.71
	[3.3, 5.2]	[188, 270]	[2.2, 84.9]	[0.94, 1.22]	[<0.01, 2.87]
2014 Sep	3.8	220	55.6	0.97	1.37
	[3.0, 4.7]	[183, 271]	[1.9, 79.1]	[0.93, 1.17]	[<0.01, 2.49]
2015 Jul	3.7	212	44.6	0.95	0.86
	[3.2, 4.5]	[196, 260]	[3.9, 57.8]	[0.92, 1.05]	[0.01, 1.33]

We also calculate the average value of the magnetic field strength at the orbit of the planet for each epoch. We find that the ambient field around the planet at the three epochs are 62.1, 55.6, and 44.6 mG, respectively, which are about twice the values calculated using the potential field source surface method (PFSS) (Fares et al. 2017). This is due to the assumption in the PFSS method that the stellar magnetic field is in its lowest energy state, which neglects that the stellar wind stresses on the stellar magnetic field lines. From the total pressure values (ram, thermal, and magnetic pressures) listed in Table 3, we also see that HD189733b is subjected to a wind pressure that varies by over 2 orders of magnitude throughout its orbit and over time.

In Fig. 2, we also show that at each epoch the planet orbits outside of the Alfvén surface, where the wind poloidal velocity equals the Alfvén velocity: |$v_\text{A} = B_\text{pol}/\sqrt{4\pi \rho }$| (B_pol is the poloidal magnetic field strength of the stellar wind). This means the planet is orbiting in the ram pressure-dominated region of the wind. As a result, we do not expect any magnetic star–planet interactions (SPI) at these epochs, as information cannot propagate back to the star (Shkolnik et al. 2008; Lanza 2012). However, due to the variability of the stellar magnetic field, there may be epochs in which the planet orbits inside the Alfvén surface, and is in direct connection to the star. During these epochs, the planet may induce hot chromospheric spots in the star. For instance, Cauley et al. (2018) recently reported Ca ii K modulations with a period coinciding with the planetary orbital period of 2.2 d in 2013 August, implying that magnetic SPI may have occurred at this epoch.

2.3 Radio emission from the stellar wind

We calculate the free–free radio emission of the stellar wind of HD189733, implementing the numerical code developed by Ó Fionnagáin et al. (2019). In this model, we solve the equations of radiative transfer for our wind models, assuming that it emits as a blackbody. The equations are solved for the line of sight of an observer placed at x = −∞, looking towards the star. The choice of the direction of the line of sight has negligible effects on the results of our calculations. We compute the free–free radio spectrum for the wind of HD189733 in the frequency range of 10 MHz–100 GHz. In this region, we find that there are negligible differences between the fluxes for each epoch. Fig. 3 shows the spectra calculated for 2013 June/July. The flux densities calculated range from 10⁻³ to 5 μJy. At such low-flux densities, this emission is unlikely to be detected with current radio telescopes. However, future developments, such as the Square Kilometre Array (SKA), are likely to allow for the detection of this emission from low-mass stars, such as HD189733 (see Section 5).

Figure 3.

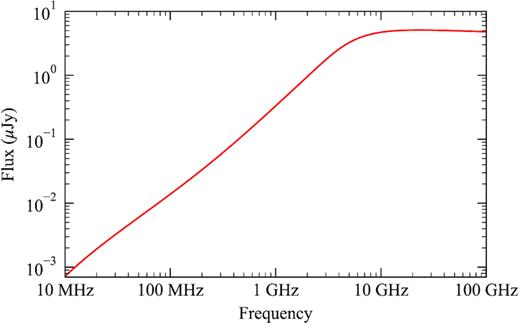
Free–free radio emission spectra of the stellar wind of HD189733 at 2013 June/July. There are negligible differences between the wind spectra for the three modelled epochs.

We also find that the wind of HD189733 becomes optically thin at 10 GHz. For frequencies less than this, regions of the wind are optically thick, which become larger towards lower frequencies. Inside these regions or ‘radio photospheres’, the wind will self-absorb its own emission. In addition to this, if the planet emits cyclotron emission and orbits within the radio photosphere for the emitted frequency, this emission would also be absorbed by the stellar wind. We investigate this scenario in Section 4.1.

We note that the free–free radio emission from the stellar wind depends on the density profile of the wind, which is determined by coronal base density n₀, a free variable in our simulations. We discuss the effects of a lower density wind on the radio emission in the Appendix.

3 PREDICTING PLANETARY RADIO EMISSION FROM HD189733B

To predict the planetary radio emission from HD189733b, we follow the description by Vidotto & Donati (2017) (see also works by Zarka 2007). Pressure balance between the stellar wind (ram, thermal, and magnetic) and the planet (magnetic) pressures gives us the size of the planetary magnetopause R_m:

\begin{eqnarray*} R_{\text{m}}= 2^{1/3} \Bigg [\frac{(B_{\text{p}}/2)^2/8\pi }{\rho {\Delta u}^2 + p + B^2/8\pi } \Bigg ]^{1/6} R_{\text{p}}, \end{eqnarray*}

(9)

where B_p is the strength of the dipolar planetary magnetic field at the poles, R_p is the planetary radius, and Δu is the magnitude of the relative velocity between the wind u and Keplerian velocity of the planet u_K: |$\boldsymbol{\Delta u} = \boldsymbol{u} - \boldsymbol{u_\text{K}}$|⁠, |$u_\text{K} = \sqrt{GM_\star /a}$|⁠. Note that we neglect the ram and thermal components of the planetary pressure. In our model, the radio emission arises from polar cap regions at co-latitudes α₀ from the poles:

\begin{eqnarray*} \alpha _0 = \sin ^{-1} \bigg [ {\Big (\frac{R_{\text{p}}}{R_{\text{m}}}\Big)}^{1/2} \bigg ]. \end{eqnarray*}

(10)

Assuming an aligned dipolar planetary magnetic field, the field strength at this co-latitude is:

\begin{eqnarray*} B(\alpha _0) = \frac{B_{\text{p}}}{2} \big (1 + 3\cos ^2\alpha _0 \big)^{1/2}. \end{eqnarray*}

(11)

Radio emission then occurs via the Cyclotron Maser instability at a maximum frequency of:

\begin{eqnarray*} f_{\text{c}}= 2.8 \bigg (\frac{B(\alpha _0)}{1\ \text{G}} \bigg)\ \text{MHz}. \end{eqnarray*}

(12)

The polar cap region where this emission originates forms a hollow cone with solid angle ω:

\begin{eqnarray*} \omega = 8\pi \sin \alpha _0 \sin \frac{\delta \alpha }{2}, \end{eqnarray*}

(13)

where δα is the thickness of the cone. We adopt a value of δα = 17.5°, which is the estimated thickness for Jupiter’s emission cone (Zarka, Cecconi & Kurth 2004).

Combining all this gives us an expression for the radio flux received from the system. The magnetic power dissipated by the wind on to the magnetosphere of the planet is given by:

\begin{eqnarray*} P_B = \frac{B_\perp ^2}{4\pi } \Delta u \pi R_{\text{m}}^2, \end{eqnarray*}

(14)

where B_⊥ is the magnitude of the magnetic field of the stellar wind perpendicular to the vector |$\boldsymbol{\Delta u}$|⁠. In our model, we compute this as:

\begin{eqnarray*} B_\perp = \sqrt{B^2 - \bigg (\frac{\boldsymbol{B} \cdot \boldsymbol{\Delta u} }{\Delta u} \bigg)^2 }. \end{eqnarray*}

(15)

The flux density received by an observer at a distance d = 19.8 pc is then given by:

\begin{eqnarray*} \Phi _\text{radio} = \frac{\eta _{\rm B} P_{\rm B}}{d^2 \omega f_{\text{c}}}. \end{eqnarray*}

(16)

Here, η_B is the efficiency ratio for the magnetic power dissipated on to the planetary magnetosphere, which we take as the Solar system value of 2 × 10⁻³ (Zarka 2007). This constant arises from the radiometric Bode’s law. Numerical studies have found that the radiometric Bode’s law is appropriate for estimating radio emission from hot Jupiters (Varela et al. 2018), while some have suggested that it may overestimate the flux densities for close-in planets (Nichols & Milan 2016). If this is indeed the case, the values we obtain here should be treated as upper limits. As we demonstrate in Section 4, there are several scenarios where in fact propagation of planetary radio emission may not be possible.

In the above equations, we use the velocity, density, pressure, and magnetic field of the stellar wind at the planetary orbit, obtained from our wind models presented in Section 2.2. In our calculations, we assume planetary magnetic field strengths of B_p = 1, 5, and 10 G, which covers the range of values predicted for extrasolar gas giants (Zaghoo & Collins 2018). Table 4 shows the calculated cyclotron frequency, magnetopause size, and co-latitude of the polar cap of HD189733b, as a function of planetary magnetic field strength. We find that these three quantities vary by small amounts throughout the orbit and between the three epochs for a given field strength. The flux densities of the radio emission however varies by around 2 orders of magnitude throughout the orbit. The variations of the fluxes calculated for B_p = 10 G throughout the orbit of the planet, and the peak fluxes at each epoch for different planetary field strengths, are shown in Fig. 4. In the top panel of Fig. 4, we see that the flux density goes to zero at points in the orbit where B_⊥ = 0 in the stellar wind (see equation 14). We also see a general trend towards lower peak fluxes from 2013 June/July to 2015 July in the bottom panel of Fig. 4. This correlates to the trend in the average magnetic field strength of the wind at the planetary orbit shown in Table 3.

Figure 4.

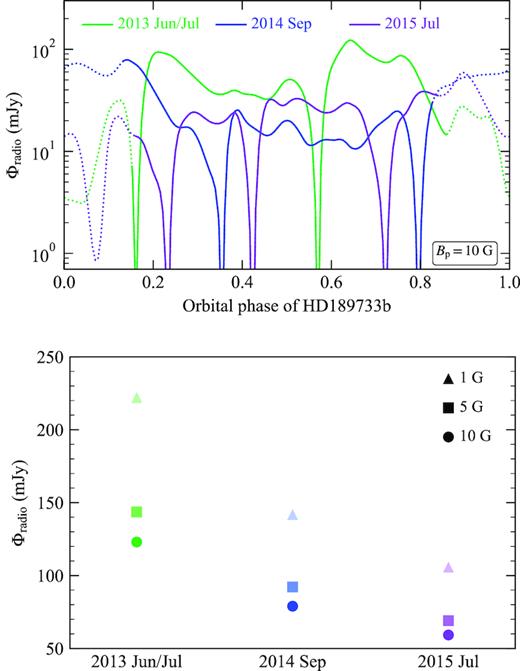
Top: Variations of the planetary radio flux throughout the orbit of HD189733b for the three epochs, for a field strength of B_p = 10 G. The dotted segment of each line represents the region of the orbit where the planetary radio emission at 25 MHz, corresponding to a planetary field strength of 10 G, cannot propagate through the stellar wind (see Section 4.1). Bottom: Peak radio flux densities calculated for HD189733b, for planetary field strengths of 1, 5, and 10 G at each epoch.

Table 4.

Emitted cyclotron frequency, magnetopause size, and co-latitude of the polar cap of HD189733b, calculated for different planetary magnetic field strengths. These values only vary by small amounts through the orbit and between each epoch.

B_p	f_c	R_m	α₀
(G)	(MHz)	(R_p)	(°)
1	2	1.6	53
5	12	2.7	38
10	25	3.3	33

Table 4.

Emitted cyclotron frequency, magnetopause size, and co-latitude of the polar cap of HD189733b, calculated for different planetary magnetic field strengths. These values only vary by small amounts through the orbit and between each epoch.

B_p	f_c	R_m	α₀
(G)	(MHz)	(R_p)	(°)
1	2	1.6	53
5	12	2.7	38
10	25	3.3	33

Comparing to recent work, Zaghoo & Collins (2018) estimated a flux of 20 mJy at a peak cyclotron frequency of 20 MHz for HD189733b. Our peak flux densities are five times larger than theirs, which is likely due to their assumption for the stellar wind power, which they extrapolated from the solar wind. As we have shown in Section 2.2, the wind strength of HD189733 is much stronger than the solar wind. As a result, we expect that HD189733b receives a higher magnetic energy from the wind of its host star, and thus higher fluxes will be emitted.

Our findings tell us that while the flux density of the planetary emission is sensitive to inhomogeneities in the stellar wind, the frequency of the emission is not. The combination of these two results could allow for planetary radio emission to be easily distinguished from other sources of radio emission in the system, such as the stellar wind. The fluxes and frequencies calculated for HD189733b also place it within the detection limit of LOFAR. We discuss this further in Section 5.

4 PROPAGATION OF THE PLANETARY RADIO EMISSION

While we have made predictions about the planetary radio emission for different assumed magnetic field strengths, the question remains: Can the emission propagate out of the planetary system? We discuss different scenarios where propagation may not be possible below.

4.1 Free–free absorption in the stellar wind

One scenario where the planetary radio emission may not propagate from the system is if the planet orbits inside the radio photosphere of the star. From the model utilized in Section 2.3, we calculate the boundary of the photospheres of the stellar wind for the calculated cyclotron frequencies of 2, 12, and 25 MHz, which we chose as they correspond to planetary field strengths of 1, 5, and 10 G (see Table 4). The radio photosphere is defined as the point where the optical depth τ = 0.399 (Panagia & Felli 1975).

Fig. 5 shows a 3D view of the radio photosphere of the wind of HD189733 at 25 MHz for 2013 June/July, as viewed by an observer at x = −∞. The radio photosphere is paraboloidal in shape. Inside the region enclosed by the surface shown, emission at 25 MHz will be absorbed by the stellar wind. We see that part of the planetary orbit is embedded in this region. In Fig. 6, we show the boundaries of these regions for the three epochs at 2, 12, and 25 MHz in the orbital plane of the planet. The thickness of these boundaries at each frequency arises from the different positions of the radio photosphere for the three epochs. From the boundaries, we find that the planetary radio emission can propagate for 41 per cent of the orbit at 12 MHz, and 67 per cent at 25 MHz. The planet’s orbit is fully embedded in the region of the wind that is optically thick at 2 MHz. This frequency is below the ionospheric cut-off of the Earth’s atmosphere. As the radio flux densities of the planet are several orders of magnitude higher than those of the stellar wind (see Fig. 8), it could be that even after the planetary emission is attenuated inside the radio photosphere of the stellar wind, a fraction of the planetary emission may still escape.

Figure 5.

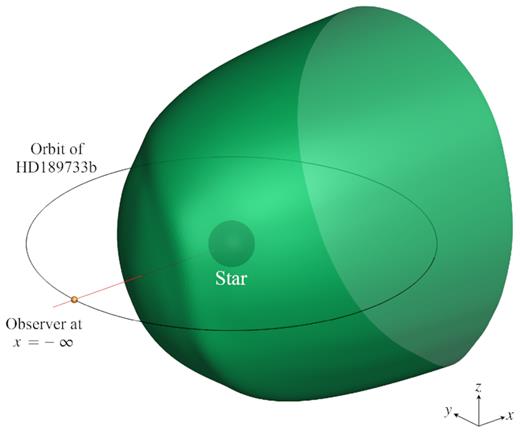
Radio photosphere of the stellar wind of HD189733 at 25 MHz for 2013 June/July, as viewed by an observer at x = −∞. The region enclosed by the surface is where planetary radio emission at 25 MHz cannot propagate without being absorbed. The red line illustrates the line connecting the planet to the star seen by the observer. Note that the size of the photosphere, star, planet and its orbit are to scale here. The radio photosphere extends back to x = 10 R_⋆.

Figure 6.

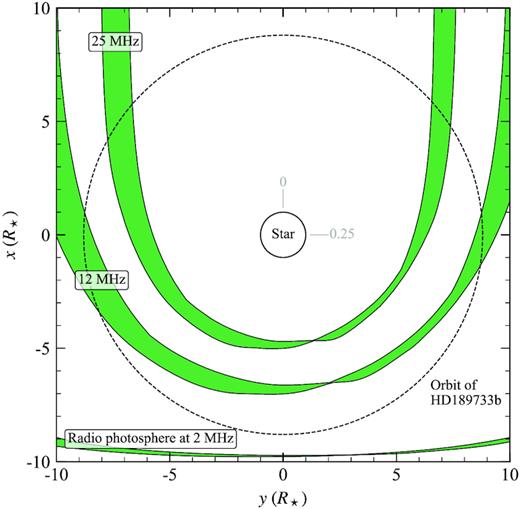
Radio photospheres of the stellar wind at the calculated frequencies of 2, 12, and 25 MHz, in the orbital plane of the planet. The planetary orbit is shown as a black dashed circle, and the star is shown in the centre. Orbital phases of 0 and 0.25 are marked near the star. In our calculation, the observer is looking along the x-axis in the positive direction.

The fraction of the orbit where the emission can propagate unattenuated to an observer at Earth corresponds to when the planet is approaching and leaving primary transit. This may be a useful signature to search for in other exoplanetary radio surveys. Indeed, Smith et al. (2009) reported a non-detection of HD189733b during secondary transit, the region where we expect the wind to be optically thick for frequencies below 10 GHz. We note however that the frequency range of their observations correspond to planetary field strengths of 100 G, which is likely to be too strong for a hot Jupiter planet such as HD189733b (see Zaghoo & Collins 2018). It is clear however that detection of planetary radio emission is more favourable for higher frequencies, which correspond to strong planetary magnetic field strengths. We caution that the size of the radio photosphere at a specific frequency scales with the density of the stellar wind, which is a free variable in our model. The effects of varying the density on the size of these regions are discussed in the Appendix.

4.2 Plasma frequency of the stellar wind

Another process by which the planetary emission may not be able to escape the system is if the cyclotron frequency is less than the plasma frequency of the stellar wind at the planetary orbit. The plasma frequency is defined as:

\begin{eqnarray*} f_{\text{p}}= 9\times 10^{-3} \sqrt{\frac{n_e}{1\ \text{cm}^{-3}}}\ \text{MHz}, \end{eqnarray*}

(17)

where n_e is the number density of free electrons. We take this to be equal to the number density of protons in our wind, as it is fully ionized.

Neglecting the presence of the planetary atmosphere, the radio emission can propagate out from the polar emission region. However, if the emitted frequency is below the plasma frequency of the stellar wind it meets, the planetary radio emission will be reflected back and hence will not propagate out of the planetary system. This is the same process which prevents sources of radio emission below 10 MHz from penetrating the Earth’s ionosphere. Fig. 7 shows the plasma frequency of the stellar wind at the planetary orbit for the three modelled epochs. We find that only cyclotron frequencies above 21 MHz will be able to propagate through the stellar wind for the entirety of the orbit at the three modelled epochs. This requires a minimum planetary field strength of 8 G, based on the values listed in Table 4.

Figure 7.

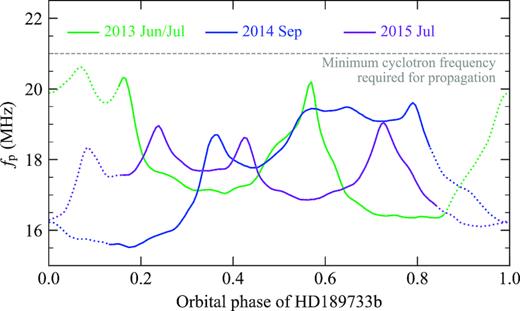
Variations of the plasma frequency of the stellar wind at the planetary orbit for each modelled epoch. The minimum cyclotron frequency of 21 MHz required for the planetary emission to propagate through the stellar wind is marked with a grey dashed line. The dotted line segments illustrate where the planetary radio emission is absorbed by the stellar wind at 25 MHz (see Section 4.1).

We note that the plasma frequency of the stellar wind will also scale with the wind density. For a wind that is 10 times less dense, the plasma frequency of the wind is reduced by a factor of |$\sqrt{10}$|⁠, thus lowering the minimum planetary field strength required for the planetary emission to propagate to 3 G.

4.3 Generation of cyclotron emission in an extended atmosphere

Another potential issue for the detection of planetary radio emission is the planetary atmosphere itself. Recently, Weber et al. (2018) suggested that while close-in hot Jupiters are exposed to more energetic winds that could boost their radio emission, they also receive much higher XUV fluxes from their host stars. As a result, their atmospheres extend far out from the planet and have a higher free electron density. From equation (17), this means that the plasma frequency of the atmosphere becomes very large. Therefore, a planetary field strength of hundreds of G would be required for the generated cyclotron frequency to be above the plasma frequency of the atmosphere. They suggest however that supermassive hot Jupiters may be more suitable targets for detection of planetary radio emission. As their atmospheres would be more tightly bound, the free electron density drops off more sharply with distance from the planet, and thus the radio emission can be generated above the plasma frequency of the atmosphere.

In our planetary radio emission model, we do not account for the presence of a planetary atmosphere, and so we were unable to test the predictions of Weber et al. (2018). Recently however, Daley-Yates & Stevens (2018) modelled the MHD equations of both the stellar and planetary winds of a solar-type star host to a hot Jupiter-type planet. They found that the generated cyclotron frequency in the planetary magnetosphere was at least a factor of 10 lower than the plasma frequency throughout the planetary atmosphere. As it is expected that the atmosphere of HD189733b is extended (Lecavelier des Etangs et al. 2012; Bourrier & Lecavelier des Etangs 2013), it could prevent the generation of cyclotron emission in the case of HD189733b.

5 DETECTION POTENTIAL WITH CURRENT AND FUTURE RADIO TELESCOPES

From our calculations of the radio emission from the planetary magnetosphere and the wind of the host star, it is clear that their radio signatures are very different. For the planet, it emits at a constant single frequency for a given planetary field strength, with the flux of its emission varying from 1 to 10² mJy as it progresses through its orbit. The stellar wind on the other hand emits at much lower fluxes across a range of frequencies. In the region of 10 MHz–100 GHz, the wind fluxes range from 10⁻³ to 5 μJy. Therefore, the peak flux from the wind emission is 4 orders of magnitude smaller than the peak flux of the planet. As a result, it should be straightforward to distinguish between the planetary and wind emission.

Fig. 8 shows a comparison between the predicted fluxes from the planet and wind of the host star, along with the sensitivities of LOFAR and SKA2. We see that for a planetary field strength of 5 G, the corresponding cyclotron frequency of 12 MHz is below the lower frequency limit of LOFAR quoted by Grießmeier, Zarka & Girard (2011). However, we determined in Section 4 that propagation of emission below 21 MHz is unlikely. For the stellar wind, we see that SKA2 is likely to have sufficient sensitivity to determine at which frequency it becomes optically thin. If so, this would allow for the base density of the stellar wind n₀ to be constrained, and consequently the mass-loss rate of the star (see the Appendix).

Figure 8.

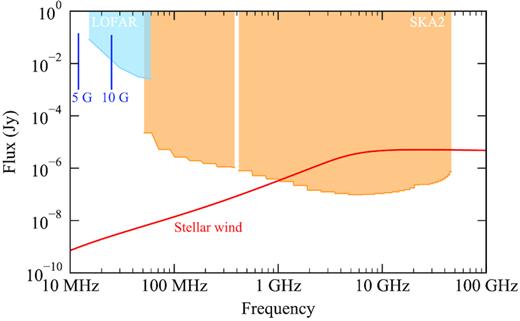
Comparison of the predicted radio flux densities and frequencies of HD189733b, for assumed planetary field strengths of 5 and 10 G, and the stellar wind of its host star. The peak planetary flux density shown is the max over the three epochs for a given field strength, with a lower limit set of 1 mJy. The stellar wind spectrum is the same as shown in Fig. 3. The sensitivities of LOFAR and SKA2 for a 1 h integration time are also shown, adapted from Grießmeier et al. (2011) and Pope et al. (2018), respectively.

10.1051/0004-6361/201527832

We note that there are likely additional sources of radio emission in planetary system, such as thermal emission from the stellar chromosphere (Villadsen et al. 2014; Fichtinger et al. 2017). However, we do not investigate this in this work.

6 SUMMARY AND CONCLUSIONS

In this work, we have characterized the radio environment of the hot Jupiter HD189733b. For its host star HD189733, we performed 3D MHD simulations of its wind, implementing surface magnetic field maps at the epochs 2013 June/July, 2014 September, and 2015 July, which were reconstructed from observations. We used our models to calculate the wind variability of HD189733, and determined that the mass-loss rate, angular momentum loss rate, and open magnetic flux vary by 9 per cent, 40 per cent, and 19 per cent over this period, respectively. We also found from our wind models that the planet experiences a non-uniform wind as it progresses through its orbit, with the wind velocity and particle number density varying by 29–37 per cent and 25–32 per cent, respectively, over the three modelled epochs. Temporal variations were observed in the extended atmosphere of HD189733b (Lecavelier des Etangs et al. 2012), which could arise from interactions with a variable stellar wind (Bourrier & Lecavelier des Etangs 2013). Our derivation of the stellar wind properties at the planetary orbit for different epochs will thus be useful to the interpretation of our MOVES observations of the upper planetary atmosphere.

Using the numerical code developed by Ó Fionnagáin et al. (2019), we calculated the free–free radio spectrum of the wind of HD189733. We found that it emits at low fluxes of 10⁻³ to 5 μJy in the frequency range of 10 MHz–100 GHz. While it is unlikely that this could be detected with current radio telescopes, future endeavours such as SKA are likely to have the sensitivity required to characterize the radio emission from the winds of stars such as HD189733. If detectable, the mass-loss rate of star could be constrained.

Our wind models provided us with the local wind properties at the planetary orbit, which in turn we used to calculate the planetary radio emission. For assumed planetary field strengths of 1, 5, and 10 G respectively, we found that the planet emits at frequencies of 2, 12, and 25 MHz, with little variation in these values over the modelled period and the orbit of the planet. The emitted flux density however varies from 1 to 10² mJy in our calculations. Therefore, a frequency corresponding to a field strength ≳10 G places HD189733b within the detection limit of LOFAR.

We investigated if our predicted planetary radio emission could propagate, and found that HD189733b orbits in and out of regions where the planetary emission will be absorbed by the stellar wind. For the calculated cyclotron frequencies of 12 and 25 MHz, we found that propagation can only occur for 41 per cent and 67 per cent of the orbit, respectively. The fraction of the orbit where propagation is possible corresponds to when the planet is approaching and leaving primary transit of the host star. This could be useful information in planning radio observing campaigns of exoplanetary systems. However, as the radio flux densities of the planet are several orders of magnitude higher than those of the stellar wind, some of the planetary emission may still escape even after being attenuated in the stellar wind. We also determined that the plasma frequency of the stellar wind at the planetary orbit is too high for propagation to occur below 21 MHz at the three modelled epochs. In addition to this, the planetary atmosphere itself may prevent the generation of radio emission, as has been recently suggested by Weber et al. (2018).

To conclude, our work has shown that the most favourable candidates for detection of planetary radio emission are hot Jupiters with large magnetic field strengths, orbiting inactive stars with low-density winds.

ACKNOWLEDGEMENTS

The authors thank the anonymous referee for their comments and suggestions. RDK acknowledges funding received from the Irish Research Council through the Government of Ireland Postgraduate Scholarship Programme. RDK and AAV also acknowledge funding received from the Irish Research Council Laureate Awards 2017/2018. VB acknowledges support by the Swiss National Science Foundation (SNSF) in the frame of the National Centre for Competence in Research PlanetS, and has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project Four Aces; grant agreement no. 724427). This work was carried out using the BATSRUS tools developed at The University of Michigan Center for Space Environment Modeling (CSEM) and made available through the NASA Community Coordinated Modeling Center (CCMC). The authors also wish to acknowledge the SFI/HEA Irish Centre for High-End Computing (ICHEC) for the provision of computational facilities and support.

REFERENCES

Alvarado-Gómez

J. D.

,

Hussain

G. A. J.

,

Cohen

O.

,

Drake

J. J.

,

Garraffo

C.

,

Grunhut

J.

,

Gombosi

T. I.

,

2016

,

A&A

,

588

,

A28

10.1051/0004-6361:20010290

Bingham

R.

,

Cairns

R. A.

,

Kellett

B. J.

,

2001

,

A&A

,

370

,

1000

10.1051/0004-6361/201628262

Boro Saikia

S.

et al. .,

2016

,

A&A

,

594

,

A29

10.1051/0004-6361/201424096

Boro Saikia

S.

,

Jeffers

S. V.

,

Petit

P.

,

Marsden

S.

,

Morin

J.

,

Folsom

C. P.

,

2015

,

A&A

,

573

,

A17

10.1051/0004-6361/201321551

Bourrier

V.

,

Lecavelier des Etangs

A.

,

2013

,

A&A

,

557

,

A124

10.1051/0004-6361/201628362

Bourrier

V.

,

Lecavelier des Etangs

A.

,

Ehrenreich

D.

,

Tanaka

Y. A.

,

Vidotto

A. A.

,

2016

,

A&A

,

591

,

A121

Cauley

P. W.

,

Shkolnik

E. L.

,

Llama

J.

,

Bourrier

V.

,

Moutou

C.

,

2018

,

AJ

,

156

,

262

10.3847/1538-3881/aae841

10.1088/0004-637X/790/1/57

Cohen

O.

,

Drake

J. J.

,

Glocer

A.

,

Garraffo

C.

,

Poppenhaeger

K.

,

Bell

J. M.

,

Ridley

A. J.

,

Gombosi

T. I.

,

2014

,

ApJ

,

790

,

57

Cuntz

M.

,

Saar

S. H.

,

Musielak

Z. E.

,

2000

,

ApJ

,

533

,

L151

10.1086/312609

Daley-Yates

S.

,

Stevens

I. R.

,

2018

,

MNRAS

,

479

,

1194

10.1093/mnras/sty1652

Donati

J.-F.

,

Semel

M.

,

Carter

B. D.

,

Rees

D. E.

,

Collier Cameron

A.

,

1997

,

MNRAS

,

291

,

658

10.1093/mnras/291.4.658

10.1111/j.1365-2966.2008.12946.x

Donati

J. F.

et al. .,

2008

,

MNRAS

,

385

,

1179

10.1111/j.1365-2966.2009.15303.x

Fares

R.

et al. .,

2009

,

MNRAS

,

398

,

1383

10.1111/j.1365-2966.2010.16715.x

Fares

R.

et al. .,

2010

,

MNRAS

,

406

,

409

Fares

R.

et al. .,

2017

,

MNRAS

,

471

,

1246

10.1093/mnras/stx1581

10.1051/0004-6361/201629886

Fichtinger

B.

,

Güdel

M.

,

Mutel

R. L.

,

Hallinan

G.

,

Gaidos

E.

,

Skinner

S. L.

,

Lynch

C.

,

Gayley

K. G.

,

2017

,

A&A

,

599

,

A127

10.1051/0004-6361/201833051

Gaia Collaboration

et al. .,

2018

,

A&A

,

616

,

A1

Grießmeier

J.-M.

,

Zarka

P.

,

Girard

J. N.

,

2011

,

Radio Sci..

,

46

,

RS0F09

10.1029/2011RS004752

10.1146/annurev.astro.40.060401.093806

Güdel

M.

,

2002

,

ARA&A

,

40

,

217

Ip

W.-H.

,

Kopp

A.

,

Hu

J.-H.

,

2004

,

ApJ

,

602

,

L53

10.1086/382274

Jardine

M.

,

Collier Cameron

A.

,

2019

,

MNRAS

,

482

,

2853

10.1093/mnras/sty2872

10.1051/0004-6361/201425283

Johnstone

C. P.

,

Güdel

M.

,

2015

,

A&A

,

578

,

A129

10.1051/0004-6361/201219002

Lanza

A. F.

,

2012

,

A&A

,

544

,

A23

10.1088/0004-6256/140/6/1929

Lazio

T. J. W.

,

Shankland

P. D.

,

Farrell

W. M.

,

Blank

D. L.

,

2010

,

AJ

,

140

,

1929

10.1051/0004-6361/201219363

Lecavelier des Etangs

A.

et al. .,

2012

,

A&A

,

543

,

L4

10.1051/0004-6361/201219789

Lecavelier des Etangs

A.

,

Sirothia

S. K.

,

Gopal-Krishna Zarka

P.

,

2013

,

A&A

,

552

,

A65

Llama

J.

,

Vidotto

A. A.

,

Jardine

M.

,

Wood

K.

,

Fares

R.

,

Gombosi

T. I.

,

2013

,

MNRAS

,

436

,

2179

10.1093/mnras/stt1725

Llama

J.

,

Jardine

M. M.

,

Wood

K.

,

Hallinan

G.

,

Morin

J.

,

2018

,

ApJ

,

854

,

7

10.3847/1538-4357/aaa59f

Nicholson

B. A.

et al. .,

2016

,

MNRAS

,

459

,

1907

10.1093/mnras/stw731

Nichols

J. D.

,

Milan

S. E.

,

2016

,

MNRAS

,

461

,

2353

10.1093/mnras/stw1430

10.1051/0004-6361/201731965

O’Gorman

E.

,

Coughlan

C. P.

,

Vlemmings

W.

,

Varenius

E.

,

Sirothia

S.

,

Ray

T. P.

,

Olofsson

H.

,

2018

,

A&A

,

612

,

A52

Ó Fionnagáin

D.

et al. .,

2019

,

MNRAS

,

483

,

873

10.1093/mnras/sty3132

10.1111/j.1365-2966.2008.13411.x

Panagia

N.

,

Felli

M.

,

1975

,

A&A

,

39

,

1

Petit

P.

et al. .,

2008

,

MNRAS

,

388

,

80

Pope

B. J. S.

,

Withers

P.

,

Callingham

J. R.

,

Vogt

M. F.

,

2018

,

MNRAS

,

484

,

648

,

Powell

K. G.

,

Roe

P. L.

,

Linde

T. J.

,

Gombosi

T. I.

,

De Zeeuw

D. L.

,

1999

,

J. Comput. Phys.

,

154

,

284

10.1006/jcph.1999.6299

Réville

V.

,

Brun

A. S.

,

2017

,

ApJ

,

850

,

45

10.3847/1538-4357/aa9218

Rodríguez

L. F.

,

Lizano

S.

,

Loinard

L.

,

Chávez-Dagostino

M.

,

Bastian

T. S.

,

Beasley

A. J.

,

2019

,

ApJ

,

871

,

172

10.3847/1538-4357/aaf9a6

Shkolnik

E.

,

Bohlender

D. A.

,

Walker

G. A. H.

,

Collier Cameron

A.

,

2008

,

ApJ

,

676

,

628

10.1086/527351

10.1051/0004-6361/201321571

Sirothia

S. K.

,

Lecavelier des Etangs

A.

,

Gopal-Krishna Kantharia

N. G.

,

Ishwar-Chandra

C. H.

,

2014

,

A&A

,

562

,

A108

10.1111/j.1365-2966.2009.14510.x

Smith

A. M. S.

,

Collier Cameron

A.

,

Greaves

J.

,

Jardine

M.

,

Langston

G.

,

Backer

D.

,

2009

,

MNRAS

,

395

,

335

Stassun

K. G.

,

Collins

K. A.

,

Gaudi

B. S.

,

2017

,

AJ

,

153

,

136

10.3847/1538-3881/aa5df3

10.1016/j.jcp.2011.02.006

Tóth

G.

et al. .,

2012

,

J. Comput. Phys.

,

231

,

870

10.1007/s00159-006-0001-y

Treumann

R. A.

,

2006

,

A&AR

,

13

,

229

10.1088/2041-8205/727/2/L32

Van Doorsselaere

T.

,

Wardle

N.

,

Del Zanna

G.

,

Jansari

K.

,

Verwichte

E.

,

Nakariakov

V. M.

,

2011

,

ApJ

,

727

,

L32

10.1051/0004-6361/201732091

Varela

J.

,

Réville

V.

,

Brun

A. S.

,

Zarka

P.

,

Pantellini

F.

,

2018

,

A&A

,

616

,

A182

Vidotto

A. A.

et al. .,

2014

,

MNRAS

,

441

,

2361

10.1093/mnras/stu728

Vidotto

A. A.

,

Bourrier

V.

,

2017

,

MNRAS

,

470

,

4026

10.1093/mnras/stx1543

10.1051/0004-6361/201629700

Vidotto

A. A.

,

Donati

J.-F.

,

2017

,

A&A

,

602

,

A39

10.1111/j.1365-2966.2012.21122.x

Vidotto

A. A.

,

Fares

R.

,

Jardine

M.

,

Donati

J.-F.

,

Opher

M.

,

Moutou

C.

,

Catala

C.

,

Gombosi

T. I.

,

2012

,

MNRAS

,

423

,

3285

Vidotto

A. A.

,

Fares

R.

,

Jardine

M.

,

Moutou

C.

,

Donati

J.-F.

,

2015

,

MNRAS

,

449

,

4117

10.1093/mnras/stv618

10.1088/0004-637X/788/2/112

Villadsen

J.

,

Hallinan

G.

,

Bourke

S.

,

Güdel

M.

,

Rupen

M.

,

2014

,

ApJ

,

788

,

112

Weber

C.

,

Erkaev

N. V.

,

Ivanov

V. A.

,

Odert

P.

,

Grießmeier

J.-M.

,

Fossati

L.

,

Lammer

H.

,

Rucker

H. O.

,

2018

,

MNRAS

,

480

,

3680

10.1093/mnras/sty2079

Wood

B. E.

,

2004

,

Living Rev. Solar Phys.

,

1

,

2

10.12942/lrsp-2004-2

Wright

A. E.

,

Barlow

M. J.

,

1975

,

MNRAS

,

170

,

41

10.1093/mnras/170.1.41

Zaghoo

M.

,

Collins

G. W.

,

2018

,

ApJ

,

862

,

19

10.3847/1538-4357/aac6e8

10.1016/j.pss.2006.05.045

Zarka

P.

,

2007

,

Planet. Space Sci.

,

55

,

598

Zarka

P.

,

Treumann

R. A.

,

Ryabov

B. P.

,

Ryabov

V. B.

,

2001

,

Ap&SS

,

277

,

293

10.1023/A:1012221527425

Zarka

P.

,

Cecconi

B.

,

Kurth

W. S.

,

2004

,

J. Geophys. Res.

,

109

,

A09S15

10.1029/2003JA010260

APPENDIX: RADIO EMISSION AND ABSORPTION FOR A LOWER DENSITY STELLAR WIND

The free–free radio emission spectrum of the stellar wind depends on the density. The density profile is primarily determined by the coronal base density in our wind simulations n₀, which is a free variable. To see the effect of a lower density wind on the free–free radio spectrum of HD189733, we divide our density values from the wind simulations by a factor of 10.

Fig. A1 shows the comparison of the spectrum shown in Fig. 3 and the spectrum calculated for the lower base density wind. We find that the lower density wind becomes optically thin at 1 GHz, as opposed to 10 GHz for the higher density wind. We also see that for the lower density wind, the radio flux densities are 1–2 orders of magnitude smaller that those for the n₀ = 10¹⁰ cm⁻³ wind. So, detection of free–free emission from the stellar wind of HD189733 is more favourable if it has a denser wind. However, the fluxes calculated for the higher density wind are still quite small. While it is unlikely that this could be detected with current radio telescopes, it is expected that future developments such as SKA will allow for radio emission from the winds of nearby low-mass stars to be detected (see Ó Fionnagáin et al. 2019). By determining the frequency at which the wind becomes optically thin, the mass-loss rate of the star could be constrained.

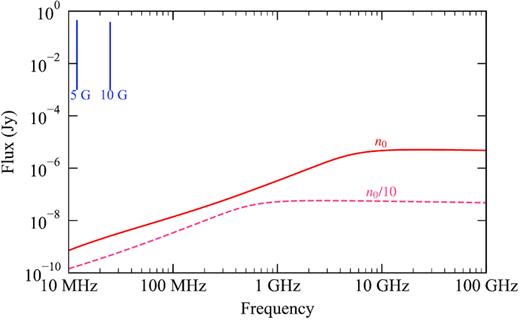
Comparison of the free–free radio spectrum of the stellar wind of HD189733 from Fig. 3 (n0), with a stellar wind that has a density which is a factor of 10 lower (n0/10). The planetary flux densities for assumed field strengths of 5 and 10 G are also shown in the upper left corner. The peak values of the planetary fluxes have been scaled for the lower density stellar wind from those shown in Fig. 8.

Figure A1.

Comparison of the free–free radio spectrum of the stellar wind of HD189733 from Fig. 3 (n₀), with a stellar wind that has a density which is a factor of 10 lower (n₀/10). The planetary flux densities for assumed field strengths of 5 and 10 G are also shown in the upper left corner. The peak values of the planetary fluxes have been scaled for the lower density stellar wind from those shown in Fig. 8.

We also show the planetary flux densities for 5 and 10 G in Fig. A1, which have been scaled for the lower density stellar wind. Assuming the planet remains orbiting in the ram-pressure dominated regime for the lower density wind, the planetary radio flux scales with n₀^−1/2 (Vidotto & Donati 2017). The frequency of the planetary emission has a very small dependence on the stellar wind density, as the magnetopause size R_m scales with n₀^−1/6 in this regime (see equations 9–12).

The sizes of the radio photospheres of the wind will also depend on the wind density. Fig. A2 shows the boundaries of these regions at the three calculated cyclotron frequencies in the orbital plane of the planet for the lower density wind. We see that for a lower density, the regions the planet orbits through where wind is optically thick to the cyclotron frequencies are smaller compared to those shown in Fig. 6 at a given frequency. Therefore, contrary to the wind radio emission, detection of planetary radio emission is more favourable for planets orbiting stars with low-density winds.

Figure A2.

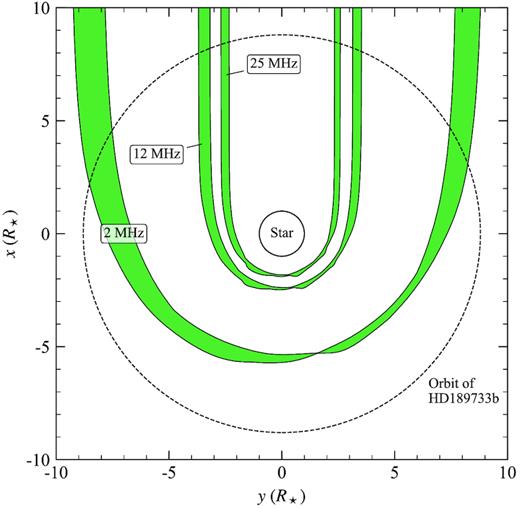
Radio photospheres of the stellar wind of HD189733, for a stellar wind that is a factor of 10 lower in density. The sizes of the radio photospheres of the lower density wind at a given frequency are smaller compared to those shown in Fig. 6.