New synthesis models of consistent extragalactic background light over cosmic time

Khaire, Vikram; Srianand, Raghunathan

doi:10.1093/mnras/stz174

ABSTRACT

We present new synthesis models of the extragalactic background light (EBL) from far infra-red (FIR) to TeV γ-rays, with an emphasis on the extreme ultraviolet (UV) background that is responsible for the observed ionization and thermal state of the intergalactic medium across the cosmic time. Our models use updated values of the star formation rate density and dust attenuation in galaxies, QSO emissivity, and the distribution of H|$\, \, {\rm {\scriptstyle I}}$| gas in the intergalactic medium. Two of the most uncertain parameters in these models, the escape fraction of H|$\, \, {\rm {\scriptstyle I}}$| ionizing photons from galaxies and the spectral energy distribution (SED) of QSOs, are determined to be consistent with the latest measurements of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| photoionization rates, the He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α effective optical depths, various constraints on H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization history, and many measurements of the local EBL from soft X-rays till γ-rays. We calculate the EBL from FIR to TeV γ-rays by using FIR emissivities from our previous work and constructing an average SED of high-energy emitting QSOs, i.e, type-2 QSOs and blazars. For public use, we also provide the EBL models obtained using different QSO SEDs at extreme-UV energies over a wide range of redshifts. These can be used to quantify uncertainties in the parameters derived from photoionization models and numerical simulations originating from the allowed variations in the UV background radiation.

galaxies: evolution, intergalactic medium, quasars: general, diffuse radiation

1 INTRODUCTION

The radiation background set-up by light emitted from all galaxies and Quasi-Stellar Objects (QSOs) throughout the cosmic time is known as extragalactic background light (EBL). The full spectrum of EBL carries imprints of cosmic structure formation; therefore, it serves as an important tool to study formation and evolution of galaxies. It is also essential for studying the propagation of high energy γ-rays from distant sources since the EBL can annihilate γ-rays upon collision (Gould & Schréder 1966; Stecker, de Jager & Salamon 1992; Ackermann et al. 2012). The EBL is playing a key role in rapidly developing γ-ray astronomy to address fundamental questions related to the production of γ-rays, their acceleration mechanism (Stecker, Baring & Summerlin 2007), and cosmic magnetic fields in the intergalactic space (Neronov & Vovk 2010; Tavecchio et al. 2011; Arlen et al. 2014; Finke et al. 2015).

A small part of this EBL at extreme-UV energies (E > 13.6 eV or λ < 912 Å) is known as the UV background (UVB). The UVB is responsible for maintaining the observed ionization and thermal state of the diffuse intergalactic medium (IGM; see reviews by Meiksin 2009; McQuinn 2016), a reservoir that is believed to contain more than 90 per cent of total baryons in the Universe.

The sources that set up the UVB also drive the major phase transitions of the IGM, the H|$\, \, {\rm {\scriptstyle I}}$|⁠, and He|$\, \, {\rm {\scriptstyle II}}$| reionization. Starting from the time when first galaxies were born, the process of H|$\, \, {\rm {\scriptstyle I}}$| reionization is believed to be completed around |$z$| ∼ 6 as suggested by various observations of H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α forest in the spectra of high redshift QSOs (e.g. Becker et al. 2001; Fan et al. 2006; Goto et al. 2011; McGreer, Mesinger & D’Odorico 2015; Bañados et al. 2018; Greig et al. 2017; Davies et al. 2018), electron scattering optical depth to the cosmic microwave background (CMB; Larson et al. 2011; Planck Collaboration XIII 2016a) and decreasing fraction of Lyman-α emitting galaxies at high redshifts (e.g. Schenker et al. 2014; Choudhury et al. 2015; Mesinger et al. 2015; Mason et al. 2018). The He|$\, \, {\rm {\scriptstyle II}}$| reionization is believed to be started by hard He|$\, \, {\rm {\scriptstyle II}}$| ionizing radiation emitted by QSOs and took longer time to complete. It was completed around |$z$| ∼ 2.8 as suggested by observations of He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α forest in a handful of QSOs (e.g. Kriss et al. 2001; Shull et al. 2004, 2010; Fechner et al. 2006; Worseck et al. 2011, 2016) and measurements of a peak in the redshift evolution of IGM temperature (Lidz et al. 2010; Becker et al. 2011; Hiss et al. 2018; Walther et al. 2018). During these reionization events, spectrum of the UVB decides the extra energy gained by photoelectrons, which gets redistributed in the IGM driving its thermal state (Hui & Gnedin 1997). Subsequently the thermal history of the IGM is driven by the UVB and adiabatic expansion of the Universe.

Thermal history of the IGM has its imprint on the small-scale structures in the IGM through pressure smoothing that can be probed by correlation analysis of closely spaced QSO sightlines (e.g. Gnedin & Hui 1998; Schaye 2001; Kulkarni et al. 2015; Rorai et al. 2017). Photoheating by the UVB can also provide negative feedback that can suppress the star formation in dwarf galaxies (Efstathiou 1992; Weinberg, Hernquist & Katz 1997) and decide the faint end shapes of the high-z luminosity functions (e.g. Samui, Srianand & Subramanian 2007). Therefore the UVB is one of the most important inputs in the cosmological simulations of structure formation and the IGM (e.g, Hernquist et al. 1996; Davé et al. 1999; Springel, Yoshida & White 2001).

Perhaps the most important and frequent application of UVB is to study the metal absorption lines ubiquitously observed in QSO absorption spectra. It is because the EBL from extreme-UV to soft X-ray ionizes not only hydrogen and helium but also several metals such as Mg, C, Si, N, O, and Ne. Therefore, the UVB serves as an essential ingredient to study the physical and chemical properties of the gas observed in the QSO absorption spectra originating either from low-density gas in the IGM or from high-density gas in the vicinity of intervening galaxies known as a circumgalactic medium (CGM). In the studies of metal absorption lines, the UVB is crucial for relating observed ionic abundances to metal abundances, in order to determine the metal production and their transport to CGM by galaxies (e.g. Ferrara, Scannapieco & Bergeron 2005; Lehner et al. 2014; Peeples et al. 2014) and the time evolution of the cosmic metal density (e.g. Songaila & Cowie 1996; Bergeron et al. 2002; Schaye et al. 2003; Aracil et al. 2004; D’Odorico et al. 2013; Shull, Danforth & Tilton 2014; Muzahid et al. 2018; Prochaska et al. 2017). At low redshifts, the UVB is essential for studying the ionization mechanism of highly ionized species such as O vi (e.g. Danforth & Shull 2005; Tripp et al. 2008; Muzahid et al. 2012; Savage et al. 2014; Pachat et al. 2016; Narayanan et al. 2018) and Ne viii (e.g. Savage et al. 2005, 2011; Narayanan, Savage & Wakker 2012; Meiring et al. 2013; Hussain et al. 2015, 2017; Pachat et al. 2017) to understand their contribution to the warm-hot IGM and missing baryons (see Shull et al. 2012).

The local EBL (⁠|$z$| = 0) at most wavelength ranges can be observed directly (e.g. Dwek & Arendt 1998; Dole et al. 2006; Ajello et al. 2008); however, there are no such direct observations of the UVB because the interstellar medium of our Milky way attenuates it completely. Therefore, one needs to model the UVB spectrum and its redshift evolution. There are, however, integral constraints on the UVB obtained from the measurements of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| photoionization rates. The H|$\, \, {\rm {\scriptstyle I}}$| photoionization rates (⁠|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$|⁠) can be measured by using the observations of 21 cm truncation and Hα fluorescence in nearby galaxies (e.g. Sunyaev 1969; Dove & Shull 1994; Adams et al. 2011; Fumagalli et al. 2017), by analyzing the incidence of Lyman-α forest lines in the proximity of QSOs (e.g. Bajtlik, Duncan & Ostriker 1988; Kulkarni & Fall 1993; Srianand & Khare 1996; Dall’Aglio, Wisotzki & Worseck 2008), and by reproducing various statistical properties of the observed Lyman-α forest in the cosmological simulations of the IGM where |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| is treated as one of the free parameters (e.g. Rauch et al. 1997; Bolton & Haehnelt 2007; Becker & Bolton 2013; Kollmeier et al. 2014; Shull et al. 2015; Gaikwad et al. 2017a,b, 2018b). One can also infer the He|$\, \, {\rm {\scriptstyle II}}$| photoionization rate (⁠|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$|⁠) using the measurements of |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| and the observed H|$\, \, {\rm {\scriptstyle I}}$| column density distribution as demonstrated in Khaire (2017). These measurements play a crucial role in calibrating the synthesis models of UVB at different redshifts.

The full synthesis model of UVB was pioneered by Haardt & Madau (1996) (see also Fardal, Giroux & Shull 1998) using cosmological radiative transfer calculations following the footsteps of the previous work (Miralda-Escude & Ostriker 1990; Shapiro, Giroux & Babul 1994; Giroux & Shapiro 1996). Over the last two decades, there are some variations of their UVB models (Haardt & Madau 2001, 2012) and the UVB models by other groups (Shull et al. 1999; Faucher-Giguère et al. 2009). Out of these, most recent models¹ are Faucher-Giguère et al. (2009, hereafter FG09) and Haardt & Madau (2012, hereafter HM12). These recent models are not completely consistent with the new observations such as |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| at |$z$| < 0.5 (Shull et al. 2015; Gaikwad et al. 2017a,b; Gurvich, Burkhart & Bird 2017; Viel et al. 2017) and |$z$| > 3 (Becker & Bolton 2013). These models also use old values of many observables relevant to UVB that are significantly different from current measurements, such as the type 1 QSO emissivity (Khaire & Srianand 2015a, hereafter KS15a), galaxy emissivity (Behroozi, Wechsler & Conroy 2013; Madau & Dickinson 2014; Khaire & Srianand 2015b, hereafter KS15b); and various constraints on H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization (Choudhury et al. 2015; Planck Collaboration XLVI 2016b; Worseck et al. 2016; Greig & Mesinger 2017). In light of all these issues, and the fact that there are only few independent UVB models available in the literature, we present new synthesis models of EBL focusing on the UVB and extending it till TeV γ-rays from far infra-red (FIR).

In our EBL models we use the updated type 1 QSO emissivity obtained from a compilation of recent QSO luminosity functions (QLFs) KS15a. Our models use galaxy emissivity till FIR wavelengths obtained from the updated star formation and dust attenuation history of the Universe from KS15b. These are determined through a large compilation of multiwavelength galaxy luminosity functions (GLFs; see KS15b, and references therein). We also use updated H|$\, \, {\rm {\scriptstyle I}}$| distribution of the IGM from Inoue et al. (2014) that is obtained from a large number of different observations (mentioned in Section 2). Apart from these, there are two additional important input parameters required to model the UVB; the average escape fraction of H|$\, \, {\rm {\scriptstyle I}}$| ionizing photons from galaxies (f_esc) and the mean spectral energy distribution (SED) of type 1 QSOs at extreme-UV wavelengths. However, the observational constraints on these are either not available or poor.

The measurement of f_esc from individual galaxies as well as large surveys has been proven to be a challenging endeavour (Vanzella et al. 2010; Mostardi et al. 2015; Siana et al. 2015). There are a handful of galaxies at |$z$| < 0.5, which show emission of H|$\, \, {\rm {\scriptstyle I}}$| ionizing photons with f_esc ranging from 2 to 46 per cent (Bergvall et al. 2006; Leitet et al. 2013; Borthakur et al. 2014; Izotov et al. 2016b,a, 2018; Leitherer et al. 2016; Puschnig et al. 2017) and only two galaxies at |$z$| > 3 with large f_esc of the order of 50 per cent (de Barros et al. 2016; Shapley et al. 2016; Vanzella et al. 2016). However, all of these are few exceptional cases, as most studies with a large number of galaxies provide only upper limits on the average f_esc (e.g. Cowie, Barger & Trouille 2009; Bridge et al. 2010; Siana et al. 2010; Guaita et al. 2016; Smith et al. 2016; Grazian et al. 2017; Japelj et al. 2017; Matthee et al. 2017; see left-hand panel of Fig. 3 and Table A1 for a summary of recent measurements). On the other hand, there are measurements of QSO SED at extreme-UV from a large number of QSOs probing rest-wavelength λ < 912 Å (e.g, Zheng et al. 1997; Telfer et al. 2002; Scott et al. 2004; Shull et al. 2012; Stevans et al. 2014; Lusso et al. 2015; Tilton et al. 2016). However, under the assumption that QSO SED follows a power law, f_ν ∝ ν^α at λ < 912 Å , the values of power-law index α obtained from these measurements show large variation (−0.56 to −1.96; see table 1 of Khaire 2017, for the summary of these measurements). Also, the smallest wavelength probed in these studies is ∼425 Å whereas the UVB model calculations extrapolate it upto soft X-rays (λ ≲ 20 Å).

Because of these uncertainties, we choose to determine f_esc(⁠|$z$|⁠) and α, which are required to consistently reproduce various observational constraints on the UVB following Khaire et al. (2016) and Khaire (2017). We obtain the f_esc(⁠|$z$|⁠) to reproduce the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements and various constraints on H|$\, \, {\rm {\scriptstyle I}}$| reionization. In our fiducial UVB model, we use α = −1.8, which was found to reproduce the measured He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α effective optical depths as a function of |$z$| and the epoch of He|$\, \, {\rm {\scriptstyle II}}$| reionization (see Khaire 2017). However, we also provide UVB models for α varying from −1.4 to −2.0 in the interval of 0.1. Moreover, following Sazonov, Ostriker & Sunyaev (2004), we modify the SED of type 1 QSOs to include the type 2 QSOs and blazars in order to calculate the X-ray and γ-ray part of the EBL consistent with various measurements of the local X-ray and γ-ray backgrounds. Our full EBL spans more than 15 orders of magnitude in wavelength from FIR to TeV γ-rays.

The paper is organized as follows. In Section 2, we briefly discuss the basic cosmological radiative transport theory used for calculating the EBL. In Section 3, we explain the emissivities used in our EBL. We discuss the QSO emissivity, their SEDs, the galaxy emissivity, f_esc(⁠|$z$|⁠), and the diffuse emissivity from the IGM. In Section 4, we discuss our fiducial model and its predictions for H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| photoionization rates, reionization histories, full spectrum of the EBL from FIR to γ-rays, and the detailed uncertainties in the UVB models. In Section 5, we summarize our main results. In the Appendix we show plots for various UVB models generated for different α and provide relevant tables of photoionization and photoheating rates and optical depths encountered by γ-ray photons due to the EBL. Throughout the paper, we have used the cosmological parameters Ω_m = 0.3, Ω_Λ = 0.7 and H₀ = 70 km s⁻¹ Mpc⁻¹ consistent with measurements from Planck Collaboration XIII (2016a). All our EBL tables in machine-readable format are publicly available to download (at http://www.iucaa.in/projects/cobra/ cobra-webpage & a http://vikramkhaire.weebly.com/downloads.html homepage) and latest version of cloudy software (last described in Ferland et al. 2017).

2 COSMOLOGICAL RADIATIVE TRANSFER

The specific intensity, |$J_{\nu _0}$|⁠, of the EBL (in units of er g cm⁻² s⁻¹ Hz⁻¹ sr⁻¹) at frequency ν₀ and redshift |$z$|₀ is obtained using the following integral (Peebles 1993; Haardt & Madau 1996):

\begin{eqnarray*} J_{\nu _{0}}(z_{0})=\frac{c}{4\pi }\int _{z_{0}}^{\infty }\mathrm{ d}z\, \frac{(1+z_{0})^{3} \, \epsilon _{\nu }(z)}{(1+z)\, {\rm H}(z)} \, {\rm e}^{-\tau _{\rm eff}(\nu _{0},\, z_{0},\, z)}. \end{eqnarray*}

(1)

Here c is the speed of light, |${\rm H} (z) = H_0 \sqrt{\Omega _m(1+z)^3+\Omega _{\Lambda}}$| is the Hubble parameter, |$\epsilon _{\nu }(z)$| is a volume averaged comoving specific emissivity at frequency ν with ν = ν₀(1 + |$z$|⁠)/(1 + |$z$|₀), and τ_eff(ν₀, |$z$|₀, |$z$|⁠) is an effective optical depth encountered by photons arriving at redshift ₀ having frequency ν₀, which were emitted at redshift |$z$| ≥ |$z$|₀ with frequency ν. τ_eff from the IGM is negligibly small for EBL at optical and higher wavelengths. However, it can be significantly larger for extreme-UV radiation due to atomic gas in the IGM. Therefore, it needs to be accurately calculated using detailed radiative transfer through hydrogen and helium gas of the IGM present in the form of discrete absorbers.

The effective optical depth is defined as τ_eff = −ln(< e^−τ >), where τ is continuum optical depth through absorbers and <e^−τ > is an average transmission over all lines of sights. Assuming that the discrete absorbers along any line of sight are Poisson distributed, τ_eff is obtained by (see Paresce, McKee & Bowyer 1980),

\begin{eqnarray*} \tau _{\rm eff}(\nu _{0}, z_{0}, z)=\int _{z_{0}}^{z}\mathrm{ d}z^{\prime }\int _{0}^{\infty } \mathrm{ d}N_{\rm H\,{\small I}}\frac{\partial ^{2}N}{\partial N_{\rm H\,{\small I}}\, \partial z^{\prime }}(1-{\rm e}^{-\tau _{\nu ^{\prime }}}). \end{eqnarray*}

(2)

Here ∂²N/∂N_H_i∂|$z$|′ = f(N_H_i, |$z$|′) is a bivariate distribution of the absorbers with respect to their redshift |$z$|′ and H|$\, \, {\rm {\scriptstyle I}}$| column density N_H_i, also known as a column density distribution function of H|$\, \, {\rm {\scriptstyle I}}$|⁠. The |$\tau _{\nu ^{\prime}}$| in equation (2) is a continuum optical depth encountered by photons arriving at redshift |$z$|₀ with frequency ν₀, which were emitted at redshift |$z$|′ ≥ |$z$|₀ with frequency ν′ = ν₀(1 + |$z$|′)/(1 + |$z$|₀). The |$\tau _{\nu ^{\prime}}$|⁠, by ignoring a negligible contribution from metals and dust in the IGM, is given by

\begin{eqnarray*} \tau _{\nu ^{\prime }}=N_{\rm H\,{\small I}}{\sigma _{\rm H\,{\small I}}(\nu ^{\prime })}+N_{\rm He\,{\small I}}{\sigma _{\rm He\,{\small I}}(\nu ^{\prime })} +N_{\rm He\,{{\small II}}}{\sigma _{\rm He\,{{\small II}}}(\nu ^{\prime })}, \end{eqnarray*}

(3)

where N_x and σ_x are the column densities and photoionization cross-sections of species x. Unlike for H|$\, \, {\rm {\scriptstyle I}}$|⁠, the column density distributions of He|$\, \, {\rm {\scriptstyle II}}$| and He|$\, \, {\rm {\scriptstyle I}}$| are not available from direct observations.

There are very few lines of sight where |$N_{\rm He\, {\rm {\scriptstyle II}}}$| has been measured (e.g. Zheng et al. 2004; Muzahid, Srianand & Petitjean 2011; McQuinn & Worseck 2014). Therefore, the amount of |$N_{\rm He\, {\rm {\scriptstyle I}}}$| and |$N_{\rm He\, {\rm {\scriptstyle II}}}$| in the H|$\, \, {\rm {\scriptstyle I}}$| absorbers needs to be inferred through photoionization modeling. For that we rewrite equation (3) as

\begin{eqnarray*} \tau _{\nu ^{\prime }}=N_{\rm H\,{\small I}}\Big [{\sigma _{\rm H\,{\small I}}(\nu ^{\prime })}+\zeta {\sigma _{\rm He\,{\small I}}(\nu ^{\prime })} +\eta {\sigma _{\rm He\,{{\small II}}}(\nu ^{\prime })}\Big ], \end{eqnarray*}

(4)

where ζ = N_He i/N_H_i and η = N_He ii/N_H_i. Under the assumption that the IGM absorbers are in photoionization equilibrium with the UVB, η is obtained by solving following quadratic equation (Fardal et al. 1998; Faucher-Giguère et al. 2009; Haardt & Madau 2012)

\begin{eqnarray*} &&{\frac{n_{\rm He}}{4n_{\rm H}}\, \frac{\Gamma _{\rm H\,{\small I}}}{n_e\alpha _{\rm H\,{\small I}}(\rm T)}\, \frac{\sigma _{912}N_{\rm H\,{\small I}}}{(1+{\rm A}\sigma _{912}N_{\rm H\,{\small I}})}}\nonumber\\ &&{\quad =\,\sigma _{228}N_{\rm He\,{{\small II}}}+ \frac{\Gamma _{\rm He\,{{\small II}}}}{n_e \alpha _{\rm He\,{{\small II}}}(\rm T)}\, \frac{\sigma _{\rm He\,{{\small II}}}N_{\rm He\,{{\small II}}}}{(1+{\rm B}\sigma _{228} N_{\rm He\,{{\small II}}})}.} \end{eqnarray*}

(5)

Here n_e is the electron density, σ₂₂₈ and σ₉₁₂ are the photoionization cross-sections of He|$\, \, {\rm {\scriptstyle II}}$| and H|$\, \, {\rm {\scriptstyle I}}$| at 228 Å and 912 Å, respectively, the constants A and B are obtained to fit the numerical results, and Γ_x is the photoionization rate for species x. Γ_x at any redshift |$z$|₀ is defined as

\begin{eqnarray*} \Gamma _{x}(z_0)=\int _{\nu _{x}}^{\infty }\mathrm{ d}\nu \, \frac{4\pi \, J_{\nu }(z_0)}{h\nu }\, \sigma _{x}(\nu)\, \, , \end{eqnarray*}

(6)

where ν_x is a threshold frequency for ionization of species x. The ionization threshold energies hν_x, where h is Planck’s constant, for H|$\, \, {\rm {\scriptstyle I}}$|⁠, He|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| are 13.6, 24.4, and 54.4 eV, respectively. Following Haardt & Madau (2012) we take A = 0.02 and B = 0.25, the relation between n_e and N_H_i as n_e = 1.024 × 10⁻⁶(N_H_iΓ_H_i)^(2/3)cm⁻³ and T = 20 000 K. We use |$\zeta = \eta n_e \, \alpha _{\rm He I}{\rm (T)}/{\Gamma _{\rm He I}}$|⁠. We verified these parameters by modeling the IGM clouds as plane-parallel slabs with the line-of-sight thickness equal to the Jeans length (Schaye 2001) using cloudy13 software (Ferland et al. 2013).

We take f(N_H_i, |$z$|⁠) from Inoue et al. (2014) at all |$z$|⁠. It has been obtained by fitting various observations over |$z$| = 0−6 such as the number distribution and column density distribution of optically thin H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α absorbers (Weymann et al. 1998; Kim, Cristiani & D’Odorico 2001; Janknecht et al. 2006; Kim et al. 2013), optically thick Lyman limit absorbers (Péroux et al. 2005; Rao, Turnshek & Nestor 2006; Prochaska, O’Meara & Worseck 2010; Songaila & Cowie 2010; Fumagalli et al. 2013; O’Meara et al. 2013) and damped Lyman-α absorbers (O’Meara et al. 2007; Noterdaeme et al. 2009, 2012; Prochaska et al. 2014), the mean transmission and optical depth of the IGM to Lyman-α photons (Fan et al. 2006; Kirkman et al. 2007; Faucher-Giguère et al. 2008; Becker et al. 2013) and the mean free path of H|$\, \, {\rm {\scriptstyle I}}$| ionizing photons through IGM (Prochaska, Worseck & O’Meara 2009; Worseck et al. 2014). The f(N_H i, |$z$|⁠) calculated at |$z$| = 5.5 and 6 from high-resolution hydrodynamic simulations for the measured |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| values match reasonably well with the f(N_H_i, |$z$|⁠) from Inoue et al. (2014), as shown in Khaire et al. (2016). This consistency motivates us to use this f(N_H_i, |$z$|⁠) even at |$z$| > 6, where direct observations are not possible because of strong Gunn–Peterson effect (Gunn & Peterson 1965). See Section 4.4.3 for uncertainties in the UVB arising when different f(N_H_i, |$z$|⁠) is used in our calculations.

3 EMISSIVITY

The comoving source emissivity |$\epsilon _{\nu}$| is the most important quantity in the EBL calculations. The |$\epsilon _{\nu}$| is contributed by photons emitted from three different sources; the QSOs (⁠|$\epsilon ^Q_{\nu }$|⁠) by accretion of matter on to supermassive blackholes, the galaxies (⁠|$\epsilon ^G_{\nu }$|⁠) from the radiation emitted by their stellar population and re-processed by dust in their interstellar medium, and the re-processed diffuse emission from the photoionized IGM (⁠|$\epsilon ^d_{\nu }$|⁠). Therefore,

\begin{eqnarray*} \epsilon _{\nu }(z)=\epsilon ^Q_{\nu }(z)+\epsilon ^G_{\nu }(z)+\epsilon ^d_{\nu }(z). \end{eqnarray*}

(7)

In the following subsections, we discuss the emissivity from these different sources used in our EBL calculations. Note that we do not consider non-standard sources such as dark-matter annihilation that has been shown to have negligible contribution to the EBL (e.g. Zavala et al. 2011; Ajello et al. 2015; Gaikwad et al. 2017a, KS15a).

3.1 QSO Emissivity

The QSO emissivity |$\epsilon ^Q_{\nu _0}(z)$| is obtained by integrating the QLF, |$\phi (L_{\nu _0}, z)$|⁠, observed at frequency ν₀ and redshift |$z$| by

\begin{eqnarray*} \epsilon ^Q_{\nu _0}(z)=\int _{L_{\nu _0}^{\rm min}}^{\infty } {L_{\nu _0}(z) \phi (L_{\nu }, z) \mathrm{ d}L_{\nu _0}}\, , \end{eqnarray*}

(8)

where |$L_{\nu _0}^{\rm min}$| is the minimum luminosity of QSOs at ν₀ used in the integration. This |$\epsilon ^Q_{\nu _0}(z)$| can be used to obtain the QSO emissivity |$\epsilon ^Q_{\nu }(z)$| at any frequency ν by using the mean SED of QSOs (k_ν) as

\begin{eqnarray*} \epsilon ^Q_{\nu }(z)=k_{\nu }\epsilon ^Q_{\nu _0}(z). \end{eqnarray*}

(9)

We use |$\epsilon ^Q_{\nu _0}(z)=\epsilon ^Q_{1000}(z)$| obtained at ν₀ = c/1000 Å (or hν₀ = 12.4 eV) from KS15a. In KS15a, the |$\epsilon ^Q_{\nu _0}(z)$| values were obtained by using a compilation of recent QLFs (of type 1 QSOs) at different wavebands (Croom et al. 2009; Schulze, Wisotzki & Husemann 2009; Glikman et al. 2011; Masters et al. 2012; McGreer et al. 2013; Palanque-Delabrouille et al. 2013; Ross et al. 2013; Kashikawa et al. 2015). For each QLF, |$\epsilon ^Q_{\nu _0}$| was obtained at the observed frequency ν₀ < c/1000 Å, by using equation (8) with |$L_{\nu }^{\rm min}=0.01L_{\nu _0}^*$|⁠, where |$L_{\nu _0}^*$| is the characteristic luminosity of that QLF. Then these |$\epsilon ^Q_{\nu _0}$| values (see table 1 of KS15a) were converted at frequency c/1000 Å using a form of QSO SED applicable at λ ≥ 1000 Å. A simple fit through the redshift evolution of |$\epsilon ^Q_{1000}(z)$| in units of |${\rm erg\, s^{-1}\, Hz^{-1} Mpc^{-3}}$| is given by²

\begin{eqnarray*} \epsilon ^Q_{1000}(z)=4.53\times 10^{24} \, (1+z)^{5.9}\, \frac{\exp (-0.36z)}{\exp (2.2z) + 25.1}\, \, . \end{eqnarray*}

(10)

In the left-hand panel of Fig. 1, we show this fit with the individual |$\epsilon ^Q_{1000}(z)$| values for each QLF compiled in KS15a. For comparison, we also show the |$\epsilon ^Q_{1000}(z)$| used by HM12, which was obtained using the QLFs compiled by Hopkins et al. (2007). At |$z$| < 3 the |$\epsilon ^Q_{1000}(z)$| by KS15a is higher than HM12 because the recent QLFs (e.g. Croom et al. 2009; Palanque-Delabrouille et al. 2013) have higher |$L_{\nu _0}^*$| and characteristic number density |$\Phi _{\nu _0}^*$|⁠. This higher QSO emissivity was crucial in resolving the photon underproduction crisis claimed by Kollmeier et al. (2014). We are using the same SED at λ > 1000 Å as used in KS15a, however, at λ < 1000 Å we use a modified form of the SED.

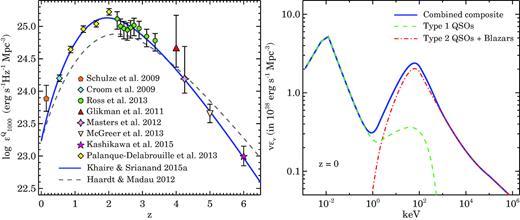
$Left-hand panel: the specific QSO emissivity at 1000 Å ($\epsilon ^Q_{\nu _{1000}}$) with $z$. Data points are taken from the compilation of recent QLFs by Khaire & Srianand (2015a, see their table 1). Blue solid curve is a simple fit through the $\epsilon ^Q_{\nu _{1000}}$ values (equation 9). Dashed curve is the $\epsilon ^Q_{\nu _{1000}}$ used by HM12, which is obtained using the compilation of QLFs by Hopkins, Richards & Hernquist (2007). Right-hand panel: $z$ = 0 QSO emissivity (solid curve) at different energies to illustrate our fiducial composite QSO SED (with α = −1.8; equation 11). Dashed curve and dot-dash curve show the adopted SED of Type 1 QSOs and high-energy emitting AGN template SED (i.e. Type 2 QSOs and blazars), respectively, normalized to get $\epsilon ^Q_{\nu _{1000}}$ at $z$ = 0.$

Figure 1.

Left-hand panel: the specific QSO emissivity at 1000 Å (⁠|$\epsilon ^Q_{\nu _{1000}}$|⁠) with |$z$|⁠. Data points are taken from the compilation of recent QLFs by Khaire & Srianand (2015a, see their table 1). Blue solid curve is a simple fit through the |$\epsilon ^Q_{\nu _{1000}}$| values (equation 9). Dashed curve is the |$\epsilon ^Q_{\nu _{1000}}$| used by HM12, which is obtained using the compilation of QLFs by Hopkins, Richards & Hernquist (2007). Right-hand panel: |$z$| = 0 QSO emissivity (solid curve) at different energies to illustrate our fiducial composite QSO SED (with α = −1.8; equation 11). Dashed curve and dot-dash curve show the adopted SED of Type 1 QSOs and high-energy emitting AGN template SED (i.e. Type 2 QSOs and blazars), respectively, normalized to get |$\epsilon ^Q_{\nu _{1000}}$| at |$z$| = 0.

Open in new tab Download slide

The QSO emissivity mentioned in equation (10) is contributed by type 1 QSOs alone. Note that to calculate the background radiation in extreme-UV, one does not need to consider the contribution from type 2 QSOs. According to the standard unification scheme of active galactic nuclei (AGNs; Antonucci 1993; Urry & Padovani 1995), different classes of QSOs arise due to differences in the orientation of QSOs along the direction of obscuring torus around their central engine with respect to us. Therefore, under the assumption of isotropic distribution of randomly oriented QSOs, to calculate the extreme-UV emissivities, it is equivalent to assume that the extreme-UV photons are emitted either isotropically by type 1 QSOs alone or only along certain directions by both type 1 and type 2 QSOs. However, in the latter assumption one needs to correctly account for the fraction of type 2 QSOs. For simplicity, to calculate the UVB, we choose the former assumption. However, to extend our EBL calculation to high-energy X-rays, which are emitted isotropically by all types of QSOs, we need to incorporate contribution from type 2 QSOs.

This contribution in X-rays can be accounted self-consistently by using type 2 QLF in soft and hard X-ray band and then modeling the distribution of different hydrogen column densities in obscuring torus, using intrinsic template of X-ray SEDs of QSOs and by fixing a contribution of extremely obscured Compton thick QSOs by comparing with measurements of the unresolved X-ray background (see e.g. Comastri et al. 1995; Treister & Urry 2005; Gilli, Comastri & Hasinger 2007; Treister, Urry & Virani 2009; Ballantyne et al. 2011). Similarly the contribution to γ-ray background from blazars can be modeled by generating the blazar luminosity function and their SED from luminosity functions of radio QSOs (e.g. Draper & Ballantyne 2009).

However, these X-ray population synthesis models require different fractions of Compton thick QSOs to generate the observed peak at ∼30 keV in X-ray background and varying degree of obscuring hydrogen column densities but still may not entirely reproduce the observed soft X-ray background (see Cappelluti et al. 2017). Although this might be the most appropriate approach, given the large uncertainties involved in it, we take a more simplistic approach that can provide an observationally consistent model of the EBL in X-ray energies useful for constructing ionization models for highly ionized metal species such as O vi, O vii, Ne viii, Ne ix, and Mg x. In particular, we follow the approach of Sazonov et al. (2004) and construct a template SED of type 1 and type 2 QSOs at X-ray energies. Our type 2 QSO SED not only accounts for the contribution of Compton thick AGNs but also includes γ-rays that mostly come from beamed sources like blazars. This SED can be thought as a template SED for high-energy emitting AGNs. These SEDs are constructed such that when used in the EBL calculations they can reproduce a complete spectrum of observed X-ray and γ-ray background. The final QSO SED constructed in this way is given below.

Our final composite QSO SED (k_ν) is a combination of the SEDs from type 1 (⁠|$k^{\rm Q1}_{\nu }$|⁠) and type 2 QSOs including blazars (⁠|$k^{\rm Q2}_{\nu }$|⁠). Therefore,

\begin{eqnarray*} k_{\nu }=k^{\rm Q1}_{\nu } + k^{\rm Q2}_{\nu } \end{eqnarray*}

(11)

We use the following SED for the type 1 QSOs:

\begin{eqnarray*} k^{\rm Q1}_{\nu }= \left\lbrace \begin{array}{@{}l@{\quad }l@{}}A_1 \Big (\frac{h\nu }{6.2 {\, \, \rm eV}} \Big)^{-0.5}, & h\nu \lt {\rm 6.2 \, \, eV} \\ A_2 \Big (\frac{h\nu }{12.4 {\, \, \rm eV}} \Big)^{-0.8}, & 6.2 \lt h\nu \lt {\rm 12.4 \, \, eV} \\ A_3 \Big (\frac{h\nu }{12.4 {\, \, \rm eV}} \Big)^{\alpha } \exp \Big (\frac{\nu }{\nu _a} \Big), & 12.4 {\rm \, \, eV}\lt h\nu \lt h\nu _a \\ A_4 \Big (\frac{\nu }{\nu _a} \Big)^{-0.8} \exp \Big (\frac{-h\nu }{{\rm 2 \, \, MeV}} \Big), & h\nu \gt h\nu _a \end{array}\right. \end{eqnarray*}

(12)

where the normalizations are

\begin{eqnarray*} A_1 &=& 2^{0.8}, \, \, \, A_2=1, \, \, \, A_3=\exp \Big (\frac{-12.4{\, \, \rm eV}}{h\nu _a}\Big), \nonumber\\ A_4 &=& A_3 \exp \Big (1 + \frac{h\nu _a}{2 {\rm \, \, MeV}}\Big)\Big (\frac{h\nu _a}{12.4 {\, \, \rm eV}} \Big)^{\alpha }. \end{eqnarray*}

The power-law SED form and the indices at hν < 12.4 eV (λ > 1000 Å) are taken from the measurements of Stevans et al. (2014). At ionizing energies, hν > 12.4 eV, we consider a range in power-law index α for our UVB models since there is no consensus on the observed value of α, as mentioned in Section 1. As shown in equation (12), this power-law SED has been multiplied by exp (ν/ν_a) to get the excess in soft X-rays and the hard X-ray bump. However, the value of ν_a depends on the assumed value of α. Therefore for each α we have used a different hν_a as given in Table 1. We calculated EBL by varying α in the interval of 0.1 from −1.4, consistent with low-z (⁠|$z$| < 1.5) measurements of Stevans et al. (2014), to α = −2, consistent with high-z (⁠|$z$| ∼ 2.5) measurements of Lusso et al. (2015) and from radio-loud QSO sample of Telfer et al. (2002). For our fiducial UVB model, we use α = −1.8, which has been shown to be consistent with the He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α effective optical depth measurements (Khaire 2017). In the right-hand panel of Fig. 1, we show the type 1 QSO SED for α = −1.8 normalized at |$\epsilon ^Q_{1000}$| at |$z$| = 0.

Table 1.

Open in new tab

Parameters of QSO SED given by equations (12) and (13).

Model Name	α	hν_a (keV)	S_k
Q14	−1.4	40	0.4
Q15	−1.5	20	0.7
Q16	−1.6	8.0	1.0
Q17	−1.7	4.0	1.3
Q18	− 1.8	2.0	1.3
Q19	−1.9	1.5	1.6
Q20	−2.0	1.0	1.4

Note: Q18 is our fiducial model.

Table 1.

Open in new tab

Parameters of QSO SED given by equations (12) and (13).

Model Name	α	hν_a (keV)	S_k
Q14	−1.4	40	0.4
Q15	−1.5	20	0.7
Q16	−1.6	8.0	1.0
Q17	−1.7	4.0	1.3
Q18	− 1.8	2.0	1.3
Q19	−1.9	1.5	1.6
Q20	−2.0	1.0	1.4

Note: Q18 is our fiducial model.

For type 2 QSOs and γ-ray emitting blazars, we adopt the following SED,

\begin{eqnarray*} k^{\rm Q2}_{\nu }= \left\lbrace \begin{array}{l{@}{\quad}l}B_1 \, p_{\nu } & h\nu \lt E_0 \\ B_2 \, p_{\nu } \Big (\frac{h\nu }{{E_0}} \Big)^{-0.24} \exp \Big (\frac{-h\nu }{{\rm 83 \, \, keV}} \Big), & E_0 \lt h\nu \lt E_1 \\ B_3 \, p_{\nu } \Big (\frac{h\nu }{E_1} \Big)^{-1.6} \, \Big [1+q\, (\frac{h\nu }{\rm 1 \, \, keV})^{0.54} \Big ], & E_1 \lt h\nu \lt E_2\\ B_4 \, p_{\nu } \Big (\frac{h\nu }{E_2} \Big)^{-1.28} \exp \Big (\frac{-h\nu }{{\rm 600 \, \, GeV}} \Big), & h\nu \gt E_2 \end{array}\right. \end{eqnarray*}

(13)

where

\begin{eqnarray*} p_{\nu } =S_k \exp \Big (-\frac{{\rm 1 \, \, keV}}{h\nu } \Big), \, \, \, q=4.1\times 10^{-3}, \, \, \, \end{eqnarray*}

\begin{eqnarray*} E_0={\rm 2 \, \, keV}, \, \, \, E_1={\rm 113 \, \, keV} \, \, \, {\rm and \, \, \, } E_2={\rm 100\, \, MeV}. \end{eqnarray*}

Here the factor S_k has been adjusted to match the hard X-ray background measurements at |$z$| = 0. Its value depends on the value of assumed α. The S_k values for different α are also given in Table 1. The normalizations in equation (13) are

\begin{eqnarray*} B_1=A_3 \Big (\frac{E_0}{12.4 {\, \, \rm eV}} \Big)^{\alpha } \exp \Big (\frac{E_0}{h\nu _a} \Big), \, \, \, B_2=B_1 \exp \Big (\frac{2}{83} \Big), \, \, \, \end{eqnarray*}

\begin{eqnarray*} B_3=9.246 \times 10^{-2} B_2 \, \, \, {\rm and} \, \, \, B_4=5.444 \times 10^{-6} B_2. \end{eqnarray*}

Note that with these normalization factors (see B₁) along with S_k, the type 2 QSO SED has been scaled with type 1 QSO emissivity. The form of type 2 QSO SED has been adopted from Sazonov et al. (2004), which we modified with different normalizations and a very high-energy part that reproduces the |$z$| = 0 X-ray and γ-ray background measurements up to TeV energies (see Section 4.3 and Fig. E3). Our type 2 QSO SED even includes γ-ray emission, therefore it serves as a combination of all high-energy emitting type of QSOs.

Note that for GeV γ-rays our constructed SED is not the intrinsic SED because we ignored the effect of the EBL on their propagation. These γ-ray photons, while traveling through the IGM, get annihilated upon collision with the EBL photons via electron–positron pair production. This phenomenon provides an effective optical depth τ_γ(ν, |$z$|⁠) for γ-rays that were emitted at redshift |$z$| with frequency ν(1 + |$z$|⁠) and observed on the Earth with frequency ν. Therefore, in our formalism the intrinsic (rest-frame) SED of γ-ray blazars at redshift |$z$| should be |$k^{\rm Q2}_{\nu } \mathrm{ e}^{\tau _{\gamma }(\nu (1+z), z)}$|⁠. In Appendix C, we provide the values of τ_γ(ν, |$z$|⁠) from our EBL models that are mostly dominated by photons having energy lower than 10 eV and therefore insensitive to the value of assumed α or the QSO emissivity (see Fig. C1). Although we choose this parametric SED approach over standard X-ray population synthesis models, in Appendix B we show that this approach reproduces soft and hard X-ray emissivity and its redshift evolution reasonably well.

In the right-hand panel of Fig. 1, we show our full composite QSO SED, which is an addition of |$k^{\rm Q1}_{\nu }$| and |$k^{\rm Q2}_{\nu }$| obtained for α = −1.8. To obtain the QSO emissivity at |$z$| = 0, the full SED is normalized to the |$\epsilon ^Q_{\nu _{1000}}$| at |$z$| = 0. As shown in the figure, the type 1 QSOs contribute mainly at E < 2 keV, type 2 QSOs at E > 2 keV till MeV and blazars at higher energies. At H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| ionizing energies, contribution from type 2 QSOs is extremely small. Therefore, 912 Å emissivity from all QSOs can be effectively written as

\begin{eqnarray*} \epsilon ^Q_{912}(z)=\Big (\frac{1000}{912}\Big)^{\alpha }\epsilon ^Q_{1000}(z)\, \, . \end{eqnarray*}

(14)

One can interpret the ratio |$k^{\rm Q2}_{\nu }/k_{\nu }$|⁠, which depends on choice of α, as the fraction of type 2 QSOs (including highly obscured Compton thick QSOs and γ-ray blazars), however such an interpretation is subject to the shape of X-ray SED assumed for type 1 QSOs. We have further discussed such an interpretation in Appendix D. We do not model QSO SED in infra-red (IR). This does not affect our background calculations since QSOs contribute negligibly to IR background (see also Sazonov et al. 2004). Galaxies are more important in the optical and IR wavelengths. We discuss the galaxy emissivity in the following subsection.

3.2 Galaxy emissivity

The galaxy emissivity |$\epsilon ^G_{\nu }$| is obtained by integrating the GLFs. To obtain this at each ν from a handful of GLF measurements, it is customary to use these GLFs to derive the star formation rate density (SFRD) first and then generate |$\epsilon ^G_{\nu }$| at each ν using stellar population synthesis models. However, most of the star formation tracers, especially the far-UV luminosity function that probes the most distant Universe, suffer from the unknown dust attenuation intrinsic to galaxies. The SFRD obtained using the far-UV GLFs is degenerate with the assumed amount of the dust attenuation in the FUV band (A_FUV). We addressed this issue in KS15b, where by using multiwavelength GLFs we lifted the degeneracy between SFRD(⁠|$z$|⁠) and A_FUV(⁠|$z$|⁠) for an assumed extinction curve. We found that for Large Magellanic Cloud Supershell (LMC2) extinction curve (from Gordon et al. 2003), our predicted A_FUV(⁠|$z$|⁠) is remarkably consistent with its measurements (see the left-hand panel of Fig. 2) obtained using IRX-β relation on FUV and FIR GLFs (Takeuchi et al. 2005; Burgarella et al. 2013). The high-|$z$| extrapolated part of our A_FUV(⁠|$z$|⁠) is also consistent with the A_FUV(⁠|$z$|⁠) measurements obtained from the UV slopes of galaxies upto |$z$| ∼ 7 (Bouwens et al. 2012). A_FUV(⁠|$z$|⁠) is crucial to get the background not only in UV-optical wavelengths but also in FIR, which is mainly dominated by the dust re-emission from galaxies.

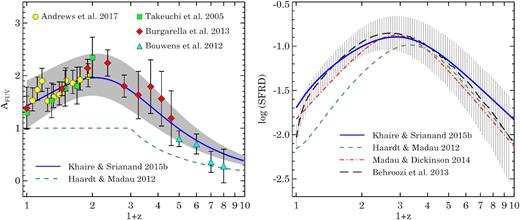
$Left-hand panel: the average dust attenuation at FUV band (AFUV) in magnitudes with $z$. The solid-curve shows AFUV($z$) used in our EBL (equation 15) and the grey-shaded region shows the range in the AFUV($z$) arising from the scatter in the FUV luminosity functions of the galaxies (KS15b). Measurements by Andrews et al. (2017, circles) are obtained by fitting SEDs of a large number of galaxies. Data points from Takeuchi, Buat & Burgarella (2005, squares) and Burgarella et al. (2013, diamonds) were obtained using IRX-β relation on IR and FUV luminosity functions of the galaxies. Bouwens et al. (2012, triangles), in the measurements, used the slopes of high-$z$ galaxy SEDs. We also show AFUV($z$) used by HM12 (dash curve) for comparison. Right-hand panel: the SFRD($z$) in units of ${\rm M_{\odot }\, yr^{-1}\, Mpc^{-3}}$. The solid curve shows our fiducial SFRD($z$) obtained using the AFUV($z$) shown in the left-hand panel (equation 16). For comparison we also show the SFRD estimated by Madau & Dickinson (2014, dot-dash curve), Behroozi et al. (2013, big-dash curve), and by HM12 (small-dash curve). The vertical-striped region shows the 1σ uncertainty in the SFRD($z$) from Behroozi et al. (2013). At $z$ < 2 HM12 SFRD($z$) is significantly different from others.$

Figure 2.

Left-hand panel: the average dust attenuation at FUV band (A_FUV) in magnitudes with |$z$|⁠. The solid-curve shows A_FUV(⁠|$z$|⁠) used in our EBL (equation 15) and the grey-shaded region shows the range in the A_FUV(⁠|$z$|⁠) arising from the scatter in the FUV luminosity functions of the galaxies (KS15b). Measurements by Andrews et al. (2017, circles) are obtained by fitting SEDs of a large number of galaxies. Data points from Takeuchi, Buat & Burgarella (2005, squares) and Burgarella et al. (2013, diamonds) were obtained using IRX-β relation on IR and FUV luminosity functions of the galaxies. Bouwens et al. (2012, triangles), in the measurements, used the slopes of high-|$z$| galaxy SEDs. We also show A_FUV(⁠|$z$|⁠) used by HM12 (dash curve) for comparison. Right-hand panel: the SFRD(⁠|$z$|⁠) in units of |${\rm M_{\odot }\, yr^{-1}\, Mpc^{-3}}$|⁠. The solid curve shows our fiducial SFRD(⁠|$z$|⁠) obtained using the A_FUV(⁠|$z$|⁠) shown in the left-hand panel (equation 16). For comparison we also show the SFRD estimated by Madau & Dickinson (2014, dot-dash curve), Behroozi et al. (2013, big-dash curve), and by HM12 (small-dash curve). The vertical-striped region shows the 1σ uncertainty in the SFRD(⁠|$z$|⁠) from Behroozi et al. (2013). At |$z$| < 2 HM12 SFRD(⁠|$z$|⁠) is significantly different from others.

Open in new tab Download slide

We use the A_FUV(⁠|$z$|⁠) magnitudes and SFRD(⁠|$z$|⁠) from the KS15b obtained for LMC2 extinction curve. These are

\begin{eqnarray*} A_{\rm FUV}(z)=\frac{1.42+0.93z}{1+(z/2.08)^{2.2}}\, \end{eqnarray*}

(15)

\begin{eqnarray*} {\rm SFRD}(z)=10^{-2}\times \frac{2.01+8.48z}{1+(z/2.5)^{3.09}} \, \, {\rm M_{\odot }\, yr^{-1}\, Mpc^{-3}} . \end{eqnarray*}

(16)

To determine A_FUV(⁠|$z$|⁠) and SFRD(⁠|$z$|⁠) in KS15b, we integrated the compiled multiwavelength GLFs down to |$0.01{\rm L_{\nu _0}^*}$| and used a stellar population synthesis code starburst99 (Leitherer et al. 1999). It uses Salpeter initial mass function (IMF; Salpeter 1955) with exponent −2.35 and the stellar mass range from 0.1 to 100 M_⊙ with a constant metallicity of 0.4 times the solar value (i.e. Z = 0.008).

In the left-hand panel of Fig. 2, we show our A_FUV(⁠|$z$|⁠) (solid-curve) along with their independent measurements obtained using the IRX-β relation (Takeuchi et al. 2005; Bouwens et al. 2012; Burgarella et al. 2013). Our A_FUV(⁠|$z$|⁠) is also remarkably consistent with the recent measurements by Andrews et al. (2017) obtained by fitting SEDs to a large number of galaxies observed in GAMA and COSMOS surveys (see also Driver et al. 2016a). The grey-shaded region shows the uncertainty in the obtained A_FUV(⁠|$z$|⁠) arising from the scatter in the reported far-UV GLFs (see KS15b). For comparison, we also show A_FUV(⁠|$z$|⁠) used in HM12 for their UVB calculations, which is significantly smaller than the measurements and our values. The difference in A_FUV(⁠|$z$|⁠) leads to different emissivities and SFRD(⁠|$z$|⁠), which can severely affect the estimates of the EBL as well as the required f_esc to be consistent with |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements. Our SFRD(⁠|$z$|⁠) obtained from the A_FUV(⁠|$z$|⁠) and stellar population synthesis models is shown in the right-hand panel of Fig. 2. For comparison we also show the SFRD(⁠|$z$|⁠) obtained by HM12, Madau & Dickinson (2014), and Behroozi et al. (2013, scaled by a factor of 1.7 to match the differences in the IMF used). SFRD(⁠|$z$|⁠) of HM12 is significantly smaller than others due to the lower A_FUV(⁠|$z$|⁠), as small as a factor of ∼3 at |$z$| < 2. At |$z$| < 6 our SFRD(⁠|$z$|⁠) agrees well with those of Behroozi et al. (2013) and Madau & Dickinson (2014) with differences smaller than 0.1 and 0.2 dex, respectively. At |$z$| > 6 our SFRD(z) is more owing to higher A_FUV(⁠|$z$|⁠); however, within the 1σ uncertainty given by Behroozi et al. (2013) as shown by the striped region in the right-hand panel of Fig. 2 and also consistent with the SFRD(⁠|$z$|⁠) from very high-|$z$| GLFs (Oesch et al. 2014; Bouwens et al. 2015; McLeod et al. 2015).

We obtain the |$\epsilon ^G_{\nu }(z)$|⁠, using A_FUV(⁠|$z$|⁠) and SFRD(⁠|$z$|⁠) from equations (15) and (16) in the following convolution integral:

\begin{eqnarray*} \epsilon ^G_{\nu } (z)=C_{\nu }(z)\int _{z}^{\infty }\frac{{\rm SFRD}(z^{\prime }) \, \, l_{\nu }[t(z)-t(z^{\prime }), Z]\, \, \mathrm{ d}z^{\prime }}{(1+z^{\prime })H(z^{\prime })}\, , \end{eqnarray*}

(17)

where l_ν[t(⁠|$z$|⁠) − t(⁠|$z$|′), Z] is a specific luminosity obtained from a simple stellar population in units of erg s⁻¹ Hz⁻¹ per unit mass of stars formed having metallicity Z and age t₀ = t(⁠|$z$|⁠) − t(⁠|$z$|′). The C_ν(⁠|$z$|⁠) is

\begin{eqnarray*} C_{\nu }(z)= \left\lbrace \begin{array}{@{}l@{\quad }l@{}}10^{-0.4\, A_{\rm FUV}(z)\frac{D_{\nu }}{D_{\rm FUV}}}, & {\, \rm at \, \, } \lambda \gt 912{\rm \, \mathring{\rm A} } \\ f_{\rm esc}(z), & {\, \rm at \, \, } 228 \lt \lambda \lt 912{\rm \, \mathring{\rm A} } \\ 0, & {\, \rm at \, \, } \lambda \lt 228{\rm \, \mathring{\rm A} }. \end{array}\right. \end{eqnarray*}

(18)

At λ > 912 Å, C_ν(⁠|$z$|⁠) is the dust correction where D_ν/D_FUV is the LMC2 extinction curve D_ν normalized at FUV band. We take C_ν = f_esc at |$228 \lt \lambda \lt 912{\rm \, \mathring{\rm A} }$|⁠, which assumes that the ionizing photons are predominantly escaping through low-density low-dust channels in the galaxies (Fujita et al. 2003; Paardekooper et al. 2011) or these photons are mostly generated by unobscured runaway stars in the outskirts of galaxies (Gnedin, Kravtsov & Chen 2008; Conroy & Kratter 2012). Note that we are treating f_esc in the same way as previous UVB calculations (such as HM12 and FG09) treated. We assume that no helium ionizing photons (⁠|$\lambda \lt 228{\rm \, \mathring{\rm A} }$|⁠) escape from galaxies. It is a reasonable assumption for galaxies at |$z$| < 6 since the stellar population generates a negligibly small amount of high-energy photons in the absence of a large number of population iii stars.

The |$\epsilon ^G_{\nu }(z)$| obtained by this method at 228 < λ < 912 Å can be approximated as a power law

\begin{eqnarray*} \epsilon ^G_{\nu }(z)= \epsilon ^G_{\nu _{912}}(z) \left (\frac{\nu }{\nu _{912}} \right)^{\beta }\, . \end{eqnarray*}

(19)

We find that β = −1.8 provides a best fit (see also Becker & Bolton 2013). We use this power-law approximation for simplicity (only for λ < 912 Å), to speed up the UVB calculations, and to smooth out the small fluctuations in |$\epsilon ^G_{\nu }$| produced by population synthesis models around ∼900 Å. We also verify that this power law with β = −1.8 reproduces the number of photons and the Γ_Hi obtained by original |$\epsilon ^G_{\nu }$|⁠. A simple fit to the redshift evolution of our |$\epsilon ^G_{\nu _{912}}$| in units of |${\rm erg\, s^{-1}\, Hz^{-1} Mpc^{-3}}$| is given by

\begin{eqnarray*} \epsilon ^G_{\nu _{912}}(z)=f_{\rm esc}(z) \times 10^{25} \frac{3.02+13.12z}{1 +(z/2.44)^{3.02}}\, . \end{eqnarray*}

(20)

The extreme-UV emissivity from galaxies depends on the value of f_esc(⁠|$z$|⁠). Therefore, an accurate estimate of this is required to model the UVB.

As mentioned in Section 1, only a handful of galaxies are detected to show emission of extreme-UV photons in large sample of galaxies. Most of the average f_esc measurements are upper limits. Therefore, we resort to deduce f_esc(⁠|$z$|⁠), which is required to be consistent with the well-measured Γ_Hi values as demonstrated in Khaire et al. (2016). We choose f_esc(⁠|$z$|⁠) to be

\begin{eqnarray*} f_{\rm esc}(z)=\frac{10^{-5}}{6.5\times 10^{-5}+\exp (-2.4z)}\, , \end{eqnarray*}

(21)

which is consistent with f_esc(⁠|$z$|⁠) from Khaire et al. (2016) and reproduce the Γ_H i(⁠|$z$|⁠) measurements (see Section 4.1 and Fig. 4). In the left-hand panel of Fig. 3, we compare our f_esc(⁠|$z$|⁠) with recent measurements from literature. The direct measurements of f_esc(⁠|$z$|⁠) are obtained using the observed ratio of flux (⁠|$f_{\lambda _{i}}$|⁠) at some extreme-UV wavelength λ_i ≤ 912 Å to the flux |$f_{\lambda _{\rm FUV}}$| at some other higher wavelength, mostly in FUV band. To get the f_esc(⁠|$z$|⁠) value, in addition to this observed ratio |$f_{\lambda _{i}}/f_{\lambda _{\rm FUV}}$|⁠, three other model-dependent quantities are required. These are the intrinsic ratio |$f_{\lambda _{i}}/f_{\lambda _{\rm FUV}}$| obtained from stellar population synthesis of the assumed galaxy model, the dust attenuation |$A_{\lambda _{\rm FUV}}$|⁠, and the correction for the transmission through IGM (⁠|$e^{\tau _{\rm eff}}$|⁠). We have corrected the measurements shown in Fig. 3 for our values of |$A_{\lambda _{\rm FUV}}$| and the intrinsic ratio |$f_{\lambda _{i}}/f_{\lambda _{\rm FUV}}$|⁠. For readers, these values are provided in Table A1. We have taken the same |$e^{\tau _{\rm eff}}$| used in the respective papers since, like us, most of them use the H|$\, \, {\rm {\scriptstyle I}}$| column-density distribution from Inoue et al. (2014). As shown in Fig. 3, our f_esc(⁠|$z$|⁠) is consistent with the measurements claimed by Marchi et al. (2017) and all other 1σ upper limits (Siana et al. 2010; Guaita et al. 2016; Rutkowski et al. 2016, 2017; Grazian et al. 2017; Japelj et al. 2017; Matthee et al. 2017; Micheva et al. 2017). Following Khaire et al. (2016), in the absence of any observational evidence for the evolution of f_esc at |$z$| > 6, our f_esc(⁠|$z$|⁠) reaches a constant asymptotic value of ∼0.15. As shown later, this f_esc value gives H|$\, \, {\rm {\scriptstyle I}}$| reionization history consistent with various observations.

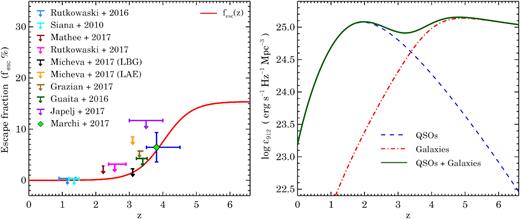
$Left-hand panel: the average escape fraction fesc($z$) of H$\, \, {\rm {\scriptstyle I}}$ ionizing photons from galaxies used in our UVB code (solid-curve, equation 21). Various data points show the recent estimates of average fesc where downward arrows indicate 1σ upper limits. These points have been converted for our fiducial galaxy emissivity models as explained in the text and provided in Table A1. Horizontal bars on each point indicate the redshift range of the galaxy sample considered for measurements. Right-hand panel: the net specific emissivity at 912 Å ($\epsilon _{\nu _{912}}$) with $z$ used in our fiducial UVB model (solid curve). The panel also shows the contribution from QSOs (dash-curve, see equation 14 for α = −1.8), galaxies (dot-dash curve, from equations 20 and 21 obtained for the fesc($z$) shown in the left-hand panel) and the addition of both (solid curve).$

Figure 3.

Left-hand panel: the average escape fraction f_esc(⁠|$z$|⁠) of H|$\, \, {\rm {\scriptstyle I}}$| ionizing photons from galaxies used in our UVB code (solid-curve, equation 21). Various data points show the recent estimates of average f_esc where downward arrows indicate 1σ upper limits. These points have been converted for our fiducial galaxy emissivity models as explained in the text and provided in Table A1. Horizontal bars on each point indicate the redshift range of the galaxy sample considered for measurements. Right-hand panel: the net specific emissivity at 912 Å (⁠|$\epsilon _{\nu _{912}}$|⁠) with |$z$| used in our fiducial UVB model (solid curve). The panel also shows the contribution from QSOs (dash-curve, see equation 14 for α = −1.8), galaxies (dot-dash curve, from equations 20 and 21 obtained for the f_esc(⁠|$z$|⁠) shown in the left-hand panel) and the addition of both (solid curve).

Open in new tab Download slide

In the right-hand panel of Fig. 3, we show the relative contribution of galaxies and QSOs to the extreme-UV emissivities, in terms of |$\epsilon_{912}(z)$|⁠. We show QSO contribution |$\epsilon ^Q_{912}(z)$| for α = −1.8 and our galaxy contribution |$\epsilon ^G_{912}(z)$| (from equations 20 and 21). QSOs dominate the extreme-UV emissivity at |$z$| < 3 (irrespective of the assumed α value) and galaxies dominate at |$z$| > 3.5. The sharp increase and then saturation in |$\epsilon ^G_{912}(z)$| result from the f_esc(⁠|$z$|⁠) adopted in our study (see the left-hand panel of Fig. 3). The rapid decrease in |$\epsilon ^Q_{912}(z)$| at |$z$| > 3 is the main reason for the required rapid increase in f_esc(⁠|$z$|⁠) and hence in the |$\epsilon ^G_{912}(z)$| at 3.5 < |$z$| < 5.5 in order to be consistent with the Γ_Hi measurements (Khaire et al. 2016). If low-luminosity AGNs contribute appreciably to the emissivity at |$z$| > 3.5, as claimed by Giallongo et al. (2015), one may not need such a rapid increase in f_esc(⁠|$z$|⁠) (see e.g. Khaire et al. 2016). We discuss the effect on UVB arising from uncertainties in galaxy emissivity in Section 4.4.2.

The galaxy emissivity obtained using equation (17) does not provide the IR and FIR emissivities since it includes only stellar radiation. Radiation from old stellar population peaks in near-IR around 1–3 μm and falls steeply at smaller wavelengths. Most of the observed FIR emissions from galaxies originate from the thermal emission of interstellar dust heated by UV and optical light from stars. We take the FIR emissivity estimated by KS15b for the same SFRD(⁠|$z$|⁠), A_FUV(⁠|$z$|⁠), and the LMC2 extinction curve used here. It has been estimated under the assumption that the energy density absorbed by dust in UV and optical wavelengths is getting emitted in IR to FIR wavelengths and the spectral shape of this emission is similar to the one observed from galaxies in local Universe. Such a spectral shape has been taken from local IR galaxy templates of Rieke et al. (2009). This FIR emissivity has been shown to be consistent with various local observations. For more details on this, we refer readers to section 5 of KS15b.

3.3 Diffuse emissivity

Most of the gas in the IGM is in photoionization equilibrium with the UVB. This gas re-emits a fraction of energy it absorbs from the UVB at different wavelengths. This re-emission happens through various recombination channels such as Lyman-series and Lyman-continuum emission of H|$\, \, {\rm {\scriptstyle I}}$|⁠, He|$\, \, {\rm {\scriptstyle I}}$|⁠, and He|$\, \, {\rm {\scriptstyle II}}$|⁠, similarly for Balmer and higher order series and continuum. Although it contributes negligibly to UVB as shown by FG09, we model few of the most dominant contributions in the extreme-UV wavelengths such as Lyman-continuum emission from H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$|⁠, Balmer-continuum emission from He|$\, \, {\rm {\scriptstyle II}}$| and the Lyman-α emission from He|$\, \, {\rm {\scriptstyle II}}$| following the procedure in FG09 and HM12. We briefly describe it here. For more details, we refer readers to the relevant sections in FG09 and HM12.

For diffuse emission from H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$|⁠, we follow analytic approximations given in FG09. The comoving recombination emissivity is obtained by solving the following equation:

\begin{eqnarray*} \epsilon ^{\rm d}_{\nu }(z)=\frac{4\pi H(z)}{(1+z)^2} \int _0^{\infty } \mathrm{ d}N_{\rm H\,{\small I}} f(N_{\rm H\,{\small I}}, z) I_{\nu }^{\rm rec} (N_{\rm H\,{\small I}}), \end{eqnarray*}

(22)

where

\begin{eqnarray*} I_{\nu }^{\rm rec} (N_x)=\frac{h\nu _{\rm rec}}{4\pi } \frac{\alpha _{\rm rec}(\rm T)}{\alpha ^A_{\rm x}(\rm T)}N_{x,\rm th}(1-\mathrm{ e}^{-N_{x}/N_{x, \rm th}}) \Gamma _{x} \phi ^{\rm rec}_{\nu }. \end{eqnarray*}

(23)

Here the subscript x denotes species (i.e H|$\, \, {\rm {\scriptstyle I}}$| or He|$\, \, {\rm {\scriptstyle II}}$|⁠), ν_rec is the line frequency of the recombination emission, α_rec is the recombination rate coefficient for the relevant transition, and |$\phi ^{\rm rec}_{\nu }$| is the recombination line profile. Following FG09, for H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| Lyman continuum emission, we use N_{H i, th} = 10^16.75 cm⁻² and N_{He ii, th} = 10^17.3 cm⁻², and for He|$\, \, {\rm {\scriptstyle II}}$| Balmer continuum emission and He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α line radiation, we use N_{He ii, th} = 2.3 × 10¹⁸ cm⁻² following HM12. For the continuum emission, we use line profile

\begin{eqnarray*} \phi ^{\rm rec}_{\nu }= \frac{(\nu /\nu _{\rm rec})^{-1} \exp (h\nu /k\rm T)}{\Gamma (0, h\nu _{\rm rec} /k\rm T)} \, \frac{\Theta (\nu -\nu _{\rm rec})}{\nu _{\rm rec}}, \end{eqnarray*}

(24)

where Θ is the Heaviside function and |$\Gamma (0, h\nu _{\rm rec} /k\rm T)$| is the incomplete gamma function. For He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α line emission, we use |$\phi ^{\rm rec}_{\nu }=\delta (\nu - \nu _{\alpha })$|⁠, where δ represents Dirac-delta function and |$\nu _{\alpha }=c/303.78\, {\rm \mathring{\rm A} }$|⁠. We do not model the H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α line emission from IGM. The contribution of H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α line emissivity to the total emissivity is negligible because the emissivity from galaxies at |$1216 \, \rm \mathring{\rm A}$| is more than an order of magnitude higher (see HM12, fig. 10). For all calculations we assume that the IGM is at |$\rm T=20\,000$| K.

We have also modeled the H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α emissivity from galaxies, which is not included in the population synthesis models. For this we followed the simple procedure used by HM12 (their section 7.1), which assumes that 68 per cent of the Lyman continuum photons that are not able to escape the galaxies [i.e. (1 − f_esc) × 0.68] are being emitted as Lyman-α photons. Unlike HM12, we multiply this H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α emissivity by |$10^{-0.4A_{\rm FUV}(z)D_{Ly\alpha }/D_{\rm FUV}}$| to capture the effect of the dust attenuation. Therefore, our UVB does not show prominent Lyman-α emission as compared to HM12. Note that such a simple method to estimate the H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α emissivity may not be consistent with the complex radiative transfer and escape of Lyman-α photons emitted by stellar population through ISM and CGM of galaxies (see e.g. Neufeld 1990, 1991; Dijkstra, Haiman & Spaans 2006; Dayal, Ferrara & Saro 2010; Gronke et al. 2016; Dijkstra 2017).

4 BASIC RESULTS

In this section we discuss basic results from our fiducial model (Q18 model with α = −1.8 used in QSO SED) for the photoionization and photoheating rates of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$|⁠, the reionization history of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$|⁠, the spectrum of local EBL from FIR to γ-rays, and the UVB spectrum along with its comparison with models of FG09 and HM12. Similar results for the models obtained with different α are presented in Appendix E. We also discuss the uncertainties in the UVB arising from different model parameters.

4.1 Photoionization and photoheating rates

The photoionization rates of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| are the only observed constraints on the UVB. Moreover, these are just integral constraints and can decide the intensity of the UVB if only the spectral shape of the UVB is known. However, unlike the direct observational constraints on EBL at wavelengths other than extreme-UV, photoionization rates are not limited to the local Universe and can be measured across a large redshift range using various observational techniques as mentioned in Section 1. In our analysis, we use the recent |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements obtained by comparing the cosmological simulations of the IGM to the observed statistics of the Ly-α forest by Gaikwad et al. (2017a) at |$z$| < 0.5, by Becker & Bolton (2013) and Bolton & Haehnelt (2007) at 2 < |$z$| < 5, and by D’Aloisio et al. (2018) and Wyithe & Bolton (2011) at 5 < |$z$| < 6. We also use the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements obtained from proximity zones of high-|$z$| QSOs by Calverley et al. (2011) at |$z$| = 5 and 6.1. In addition to |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$|⁠, we have also used the |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| measurements by Khaire (2017).

In the left-hand panel of Fig. 4, we show |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| obtained from our fiducial UVB model along with various available measurements. The remarkable agreement between our prediction and the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements at |$z$| > 3 is not surprising since we have chosen the appropriate f_esc(⁠|$z$|⁠) to match these measurements (see Khaire et al. 2016). Whereas, at |$z$| < 3, the UVB is determined by our updated QSO emissivity alone (see also KS15a) and there is no need to adjust f_esc(⁠|$z$|⁠). However, for making f_esc(⁠|$z$|⁠) as a continuous function of |$z$|⁠, we have taken negligibly small values of f_esc(⁠|$z$|⁠) at |$z$| < 2.5. At |$z$| < 0.5, our |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| is consistent not only with measurements from Gaikwad et al. (2017a) but also with Shull et al. (2015), Gurvich et al. (2017), Viel et al. (2017), Khaire et al. (2018), and Fumagalli et al. (2017), which are not shown in the figure due to shortage of space. The |$z$| = 0 Fumagalli et al. (2017) measurement is obtained using the observations of Hα fluorescence from a nearby faint disc galaxy. Note that all these |$z$| < 0.5 measurements provide ∼2.5 times smaller |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| than the measurements of Kollmeier et al. (2014). For comparison, we also show |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| obtained in UVB models of HM12, FG09,³ and a new model of Puchwein et al. (2019). At |$z$| < 0.5, unlike our models the previous two models by HM12 and FG09 underpredict |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| values compared to latest measurements. This is one of our major improvements over these previous UVB models. The differences in |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| predicted by these models at |$z$| > 2 are because of choosing different inputs in their UVB models, such as f_esc, in order to be consistent with different |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| measurements. For example, FG09 tried to be consistent with |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| from Faucher-Giguère et al. (2008), whereas HM12 with |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| from Becker, Rauch & Sargent (2007), which are quite different from the recent measurements (see Becker & Bolton 2013, for more details). Overall, our |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| values are in excellent agreement with the recent measurements at all redshifts than previous UVB models. The |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| predicted by the new UVB model of Puchwein et al. (2019) is also in very good agreement with recent measurements and our model predictions at |$z$| < 5.5. This new model has employed a novel opacity treatment to synthesize UVB in the pre-H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$|-reionization era following Madau & Fragos (2017). A sharply decreasing |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| at |$z$| > 5.8 is one of the by-products of such opacity treatment that has been shown to be important in reproducing reionization history and heating in hydrodynamical simulations of the IGM (see also Oñorbe, Hennawi & Lukić 2017a). However, the success of Puchwein et al. (2019) at |$z$| < 1 to reproduce recent |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements mainly comes from using updated QSO emissivity similar to our model (see also Madau & Haardt 2015). Note that the uncertainties in the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements are different for different measurement methods. Even for the same method, such as using flux decrement, the uncertainties depend on choice of range in the thermal state of the IGM used in calculation (see D’Aloisio et al. 2018). Therefore, the agreement between UVB models and the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements also depends on the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements considered in the model.

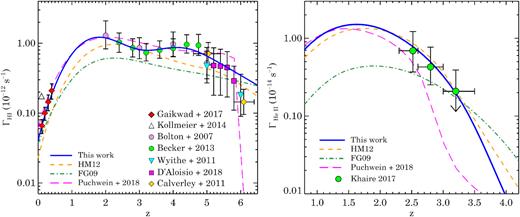
$The photoionization rate of H$\, \, {\rm {\scriptstyle I}}$ (ΓHi; left-hand panel) and He$\, \, {\rm {\scriptstyle II}}$ (ΓHe ii; right-hand panel) as a function of $z$ from our fiducial UVB model (solid curves; see Fig. E1 for UVB models with different α). For comparison we show the ΓHi from UVB models of HM12 (small-dash curve) and FG09 (dot-dash curve) and new model by Puchwein et al. (2019, big-dash curve). Various data points in the left-hand panel show the recent measurements of ΓH i. The ΓHe ii from Khaire (2017) is obtained by using the measurements of $\tau _{\alpha }^{\rm He II}$ from Worseck et al. (2016).$

Figure 4.

The photoionization rate of H|$\, \, {\rm {\scriptstyle I}}$| (Γ_Hi; left-hand panel) and He|$\, \, {\rm {\scriptstyle II}}$| (Γ_He ii; right-hand panel) as a function of |$z$| from our fiducial UVB model (solid curves; see Fig. E1 for UVB models with different α). For comparison we show the Γ_Hi from UVB models of HM12 (small-dash curve) and FG09 (dot-dash curve) and new model by Puchwein et al. (2019, big-dash curve). Various data points in the left-hand panel show the recent measurements of Γ_H i. The Γ_He ii from Khaire (2017) is obtained by using the measurements of |$\tau _{\alpha }^{\rm He II}$| from Worseck et al. (2016).

Open in new tab Download slide

UVB models with different α give slightly different values of |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| at |$z$| < 3 because at these redshifts the UVB is dominated by QSOs. However, these are still consistent with the measurements of Gaikwad et al. (2017a) as shown in the left-hand panel of Fig. E1 in the Appendix. This shows that the difference in the obtained |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| due to changing α (from −1.4 to −2) is smaller than the present uncertainties on the low-|$z$||$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements. At |$z$| > 3, |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| is dominated by galaxy emissivity, therefore the left-hand panel of Fig. E1 does not show any change in |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| with α.

In the right-hand panel of Fig. 4, we show |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| obtained from our fiducial UVB along with the values determined in Khaire (2017) at 2.5 < |$z$| < 3.5 by using the He|$\, \, {\rm {\scriptstyle II}}$| effective optical depth measurements of Worseck et al. (2016) and the f(N_H i, |$z$|⁠) from Inoue et al. (2014). For comparison, we also show the |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| from UVB models of HM12, FG09 and a new model of Puchwein et al. (2019). |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| obtained by our and HM12 UVB models match very well with the measurements. In this |$z$|-range where direct observations are available, the |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| from FG09 and Puchwein et al. (2019) are also broadly consistent with Khaire (2017) measurements. The agreement between our and HM12,|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| at 2.5 < |$z$| < 3.5, despite the fact that we are using different input parameters, is mostly coincidental and because of using different QSO SEDs. HM12 used smaller |$\epsilon ^Q_{1000}$| but steeper SED (α = −1.57), on the other hand we used higher |$\epsilon ^Q_{1000}$| but shallower SED (α = −1.8). Also, the fact that both models get almost the same |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| within 2.5 < |$z$| < 3.5 helps in getting the |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| agreement.

|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| is more sensitive to the value of α than |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$|⁠. It is because α is obtained by normalizing QSO emissivity at λ = 1000 Å. Therefore, a small change in α results in a large change for He|$\, \, {\rm {\scriptstyle II}}$| ionizing photons at more than four times smaller wavelengths. We show |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| obtained from our UVB models with different α in the right-hand panel of Fig.E1. Only −2.0 < α < −1.6 are consistent with the |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| measurements and He|$\, \, {\rm {\scriptstyle II}}$| effective optical depths (for more detailed analysis on this, refer to Khaire 2017). We note that new measurements of |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| by Worseck et al. (2018) are consistent with our UVB predictions for α = −2.0.

In Table E1 we provide the photoionization and photoheating rates for H|$\, \, {\rm {\scriptstyle I}}$|⁠, He|$\, \, {\rm {\scriptstyle I}}$|⁠, and He|$\, \, {\rm {\scriptstyle II}}$| from our fiducial UVB model with α = −1.8 and in Tables E2–E7 for UVB models with different α. Photoheating rates for different species x are obtained by

\begin{eqnarray*} {\xi }_{x}(z)=\int _{\nu _{x}}^{\infty }\mathrm{ d}\nu \, \frac{4\pi \, J_{\nu }(z)}{h\nu }\, h(\nu -\nu _x)\sigma _{x}(\nu)\, \, . \end{eqnarray*}

(25)

In Fig. E2 we show the ξ_H i(⁠|$z$|⁠) and ξ_He ii(⁠|$z$|⁠) for our UVB models obtained with different values of α. The photoheating rates follow broadly the similar redshift evolution as photoionization rates (compare Figs E1 and E2). As in the case for |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$|⁠, the ξ_He ii is also sensitive to the value of α. Note, by construct, all these models consistently reproduce |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| but differ only in |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$|⁠.

4.2 H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization

We have calculated the H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization history for the H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| ionizing emissivity used in our fiducial UVB model. The redshift evolution of volume filling factor Q_x of H|$\, \, {\rm {\scriptstyle II}}$| and He|$\, \, {\rm {\scriptstyle III}}$| is obtained by solving (see Madau, Haardt & Rees 1999; Khaire et al. 2016)

\begin{eqnarray*} Q_x(z_0) &=& \frac{1}{\langle n \rangle } \int ^{\infty }_{z_0} \mathrm{ d}z\, \frac{\dot{n}_y(z)}{(1+z)H(z)}\nonumber\\ &&\times \,\exp \left [-\alpha ^{\rm B}_y(T) \langle n \rangle \int ^{z}_{z_0}{\mathrm{ d}z^{\prime }\frac{\chi (z^{\prime }) C(z^{\prime })(1+z^{\prime })^2}{H(z^{\prime })}}\right]. \end{eqnarray*}

(26)

where 〈n〉 = 〈n_H〉 and y = H|$\, \, {\rm {\scriptstyle I}}$| when x is H|$\, \, {\rm {\scriptstyle II}}$| and 〈n〉 = 〈n_He〉 and y = He|$\, \, {\rm {\scriptstyle II}}$|⁠, when x is He|$\, \, {\rm {\scriptstyle III}}$|⁠, |$\dot{n}_y(t)$| is the comoving number density of ionizing photons per unit time for species y, C(⁠|$z$|⁠) is the clumping factor, and χ(⁠|$z$|⁠) is number of photoelectrons per hydrogen atom at redshift |$z$|⁠. We use χ(⁠|$z$|⁠) = 1.083 at |$z$| > 4 and χ(⁠|$z$|⁠) = 1.16 at |$z$| < 4 assuming that within the regions where H|$\, \, {\rm {\scriptstyle I}}$| is ionized the helium is predominantly singly ionized at |$z$| > 4 and doubly ionized at |$z$| < 4. We use the comoving number density of hydrogen 〈n_H〉 = 1.87 × 10⁻⁷ cm⁻³ and helium 〈n_He〉 = 〈n_H〉y_p/(4 − 4y_p), where y_p = 0.248 is the helium mass fraction from Planck Collaboration XIII (2016a). The |$\dot{n}_y(z)$| is obtained by

\begin{eqnarray*} \dot{n}_y(z) = \int ^{\infty }_{\nu _y}\mathrm{ d}\nu \, {\frac{\epsilon _{\nu } (z)}{h \nu }}\, \, , \end{eqnarray*}

(27)

where ν_y is threshold ionization frequency for species y. We use clumping factor C(⁠|$z$|⁠) = 9.25 − 7.21 log (1 + |$z$|⁠) obtained from the cosmological hydrodynamical simulations of the IGM from Finlator et al. (2012).

We show the Q_H_ii(⁠|$z$|⁠) and Q_He iii(⁠|$z$|⁠) results in the left-hand panel of Fig. 5. We also show recent measurements of Q_H_ii. H|$\, \, {\rm {\scriptstyle I}}$| reionization in our model completes at |$z$| = 5.8 (⁠|$z$| at which Q_x(⁠|$z$|⁠) = 1) consistent with high-|$z$| Lyman-α forest observations (Becker et al. 2001; Fan et al. 2006). Our Q_H ii(⁠|$z$|⁠) is in agreement with lower limits from McGreer et al. (2015) obtained using dark-pixel statistics of high-z QSO spectra and with measurements of Greig et al. (2017) and Bañados et al. (2018) obtained using Lyman-α damping wings of two highest redshift QSOs. Our Q_H_ii(⁠|$z$|⁠) is also consistent with the measurements obtained from the diminishing population of high-|$z$| Lyman-α emitters obtained by Schenker et al. (2014), Mason et al. (2018), and Inoue et al. (2018). We calculate the electron scattering optical depth τ_e of CMB (equation 12 from Khaire et al. 2016). The τ_e(⁠|$z$|⁠) from our reionization model is shown in the central panel of Fig. 5, which reaches asymptotic value τ_e = 0.55 consistent with the measurements of Planck Collaboration XLVI (2016b). This reiterated the results of Khaire et al. (2016) that new constraints on H|$\, \, {\rm {\scriptstyle I}}$| reionization do not require f_esc(⁠|$z$|⁠) at |$z$| > 6 to have a steep evolution and a constant value, such as 0.15 used here (equation 21), is sufficient to produce the consistent τ_e. The H|$\, \, {\rm {\scriptstyle I}}$| reionization history is same for all of our UVB models obtained with different α because in these models the H|$\, \, {\rm {\scriptstyle I}}$| reionization is driven by galaxies and QSOs contribute negligibly.

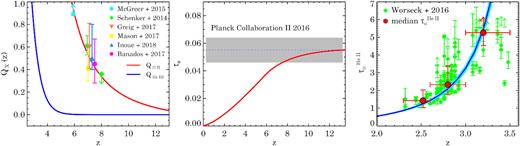
$Left-hand panel: volume filling fraction of H$\, \, {\rm {\scriptstyle II}}$ (red curve) and He$\, \, {\rm {\scriptstyle III}}$ (blue curve) obtained for our fiducial UVB model. For comparison the QHii measurements from Schenker et al. (2014), McGreer et al. (2015), Greig et al. (2017), Mason et al. (2018), Bañados et al. (2018), and Inoue et al. (2018) have been shown. We get $z$re = 5.8 for H$\, \, {\rm {\scriptstyle I}}$ and $z$re = 2.8 for He$\, \, {\rm {\scriptstyle II}}$. Central panel: electron scattering optical depth (τe) obtained from our fiducial UVB model (solid curve) shown together with the measurements from Planck Collaboration XLVI (2016b, dotted line with grey shade). Right-hand panel: the He$\, \, {\rm {\scriptstyle II}}$ Lyman-α effective optical depth ($\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$) obtained from our fiducial UVB model (solid curves with b = 28 km s−1 and cyan shade obtained by changing b from 24 to 32 km s−1) with the measurements from Worseck et al. (2016, diamonds). The red points show the median $\tau _{\alpha }^{\rm He II}$ in redshift bins indicated by horizontal bars.$

Figure 5.

Left-hand panel: volume filling fraction of H|$\, \, {\rm {\scriptstyle II}}$| (red curve) and He|$\, \, {\rm {\scriptstyle III}}$| (blue curve) obtained for our fiducial UVB model. For comparison the Q_H_ii measurements from Schenker et al. (2014), McGreer et al. (2015), Greig et al. (2017), Mason et al. (2018), Bañados et al. (2018), and Inoue et al. (2018) have been shown. We get |$z$|_re = 5.8 for H|$\, \, {\rm {\scriptstyle I}}$| and |$z$|_re = 2.8 for He|$\, \, {\rm {\scriptstyle II}}$|⁠. Central panel: electron scattering optical depth (τ_e) obtained from our fiducial UVB model (solid curve) shown together with the measurements from Planck Collaboration XLVI (2016b, dotted line with grey shade). Right-hand panel: the He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α effective optical depth (⁠|$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$|⁠) obtained from our fiducial UVB model (solid curves with b = 28 km s⁻¹ and cyan shade obtained by changing b from 24 to 32 km s⁻¹) with the measurements from Worseck et al. (2016, diamonds). The red points show the median |$\tau _{\alpha }^{\rm He II}$| in redshift bins indicated by horizontal bars.

Open in new tab Download slide

He|$\, \, {\rm {\scriptstyle II}}$| reionization in our fiducial model with α = −1.8 completes at |$z$| = 2.8. It is consistent with various measurements of He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α effective optical depths (⁠|$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$|⁠; Kriss et al. 2001; Shull et al. 2004, 2010; Fechner et al. 2006; Worseck et al. 2011, 2016), measurements of peak in the redshift evolution of mean IGM temperature (Becker et al. 2011; Hiss et al. 2018) and also with theoretical models of He|$\, \, {\rm {\scriptstyle II}}$| reionization (McQuinn et al. 2009; Compostella, Cantalupo & Porciani 2013; La Plante & Trac 2016). We also consistently reproduce |$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$| from Worseck et al. (2016), as shown in the right-hand panel of Fig. 5. It shows |$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$| calculated from our fiducial UVB model (using equations 9 and 10 from Khaire 2017) for an assumed Doppler broadening b = 28 km s⁻¹ with blue curve and the shaded cyan region provides values encompassed by changing b from 24 to 32 km s⁻¹. The red data points, shown to guide the eyes, are the median values of |$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$| (within 95 percentile errors) as obtained in three different |$z$| bins (see table 2 of Khaire 2017). Note that the He|$\, \, {\rm {\scriptstyle II}}$| reionization history and |$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$|(⁠|$z$|⁠) depends on the value of α. As shown in Khaire (2017), only −2.0 < α < −1.6 are consistent with both |$\tau _{\rm \alpha }^{\rm He\, {\scriptscriptstyle II}}$| measurements and epoch of He|$\, \, {\rm {\scriptstyle II}}$| reionization being 2.6 < |$z$| < 3.0. Similar conclusions are presented in the recent study by Gaikwad et al. (2018a) using the UVB models presented here in hydrodynamic simulations of the IGM explicitly taking into account the non-equilibrium ionization effects.

4.3 The EBL spectrum

In Fig. 6, we show our full EBL spectrum at |$z$| = 0. Our calculations cover more than 15 orders of magnitude range in wavelength from FIR to TeV energy γ-rays. The three distinct peaks in the intensity, 4πνJ_ν in units of erg s⁻¹ cm⁻², can be readily seen. These are the FIR peak arising from the dust emission around ∼100 μm (10⁶ Å), the near-IR peak dominated by old stellar population around ∼1 μm (10⁴ Å) and the hard X-ray peak from type 2 QSOs around ∼30 keV (0.4 Å). In general, the λ > 912 Å part of the EBL is dominated by emission from galaxies including their stellar and dust emission, the λ < 228 Å part is contributed by radiation only from QSOs, and the 912 > λ > 228 Å part is contributed by both galaxies and QSOs. Relative contribution to the latter is determined by f_esc, which at |$z$| = 0 is negligibly small; therefore, it is contributed by QSOs alone.

Figure 6.

The intensity of |$z$| = 0 EBL from FIR to TeV γ-rays from our fiducial model (see Fig. E3 for EBL models with different α). Various measurements shown in the figure are summarized in Section 4.3.

Open in new tab Download slide

In Fig. 6, we also show |$z$| = 0 EBL measurements at different wavelengths obtained by various methods and instruments. In the FIR wavelengths we use compiled measurements by Dwek & Krennrich (2013, their table 7) obtained from COBE. In the optical to FIR wavelengths we use compiled measurements by Kneiske & Dole (2010) and Driver et al. (2016b) obtained from integrated light from resolved galaxies in deep surveys. Our EBL models agree very well with these measurements. At 0.25 keV (λ ∼ 50 Å) the measurement is taken from Warwick & Roberts (1998) obtained using shadow measurements from ROSAT. The X-ray background measurements are taken from various instruments; Chandra (Cappelluti et al. 2017), ASCA (Gendreau et al. 1995), HEAO-1 and HEAO-4 (Gruber et al. 1999; Kinzer et al. 1997), Integral (Churazov et al. 2007), RXTE (Revnivtsev et al. 2003), Swift/BAT (Ajello et al. 2008), and Nagoya balloon (Fukada et al. 1975). Similarly γ-ray background measurements are taken from instruments: SMM (Watanabe et al. 1997), compton/Comptel (Weidenspointner et al. 2000), compton/EGRET (Strong, Moskalenko & Reimer 2003), and Fermi/LAT (Ackermann et al. 2015). Our local fiducial EBL shows remarkable match with the X-ray and γ-ray background measurements all the way upto TeV γ-rays. It is not surprising, since we have constructed type 2 QSO and blazar SED (Section 3.1) and adjusted the normalizations (see Table 1) to do so. In Fig. E3, we show our EBL models with different values of α. The normalization hν₀ and S_k are taken such that despite different α, the local EBL will consistently reproduce the X-ray and γ-ray measurements as shown in Fig. E3. However, with our assumed QSO SED shape, it becomes difficult for models with α > −1.5, to match few of the soft X-ray measurements.

The optical depth encountered by high-energy γ-rays (τ_γ) due to EBL is discussed in Appendix C. We find that τ_γ is insensitive to EBL at E < 10 eV and thus to values of α. Note that the EBL at E < 10 eV is same as the fiducial model given in KS15b (the median LMC2 model) and therefore it is consistent with many published models of optical and FIR EBL (e.g. Franceschini, Rodighiero & Vaccari 2008; Finke, Razzaque & Dermer 2010; Kneiske & Dole 2010; Domínguez et al. 2011; Gilmore et al. 2012; Helgason & Kashlinsky 2012; Inoue et al. 2013; Scully, Malkan & Stecker 2014) as shown in KS15b. We provide the updated τ_γ values calculated for our fiducial EBL model including CMB.

The UVB at z = 0, a part of the EBL at 50 < λ < 1200 Å (i.e. 10 < E < 250 eV) shown in Fig. 6, does not have any direct measurements. The measurements such as photoionization rates provide only integral constraints. Our models are consistent with them across a large |$z$|-range as shown in Fig. 4. Below we discuss the UVB spectrum and its redshift evolution in comparison with the previous UVB models. For the discussions hereafter, let us naively divide the EBL at λ < 912 Å (E > 13.6 eV) into three parts, the H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB at 13.6 < E < 54.4 eV, the He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB at 54.4 < E < 500 eV, and the X-ray background at E > 500 eV.

In Fig. 7, we compare our fiducial UVB spectrum from |$z$| = 0 to 5 with the UVB from FG09 and HM12. Two distinct features in the UVB spectrum can be readily seen; these are ionization edges of H|$\, \, {\rm {\scriptstyle I}}$| (at 13.6 eV) and He|$\, \, {\rm {\scriptstyle II}}$| (at 54.4 eV). The smoothness of these features at the bottom of the troughs is because of the inclusion of Lyman continuum emission from H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| in UVB calculations. Also, there is a small kink at 40.8 eV, prominent at |$z$| = 1 to 4 UVB, due to He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α recombination emission. Another such small kink due to H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α recombination emission from galaxies at 10.2 eV can be seen in HM12 but not in our UVB, because this emission is suppressed in our models due to dust correction. FG09 do not include H|$\, \, {\rm {\scriptstyle I}}$| Lyman-α recombination emission in their calculations. Sharp saw-tooth features due to Lyman series absorption of He|$\, \, {\rm {\scriptstyle II}}$|⁠, seen in HM12 UVB at |$z$| > 3, are not included in our and FG09 models. Note that this saw-tooth modulation only shows significant difference in UVB at high redshifts and affects a very small wavelength range.

Figure 7.

The spectrum of our fiducial UVB with energy (from 5 to 3000 eV) at |$z$| = 0, 1, 2, 3, 4, and 5. The solid blue curve shows our fiducial UVB model (see Fig. E4 for UVB models with different α). The red dash and green dot-dash curves show the UVB models from HM12 and FG09.

Open in new tab Download slide

The differences in the UVB models can be roughly mapped to the differences in their predictions of |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| and |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| (see Fig. 4). The UVB model of FG09 is significantly different from our and HM12 model at all wavelengths and redshifts. Our UVB model at |$z$| < 2 has higher H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB as compared to both FG09 and HM12 models. At |$z$| < 1, the similar He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB seen for ours and HM12 model is because of the coincidental combinations of different α and |$\epsilon _{\nu }^Q$| used in both models. At higher redshifts our He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB shows larger deviation from HM12. The similarity of X-ray background in our and HM12 at |$z$| = 0 is due to the fact that both models match the X-ray background measurements, which was not attempted by FG09. The He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB in FG09 shows comparatively smaller intensities with larger troughs at |$z$| < 2, suggesting that He|$\, \, {\rm {\scriptstyle II}}$| is recombining quickly in their model. This is not surprising given the small recombination time-scales of He|$\, \, {\rm {\scriptstyle II}}$|⁠, the ever-decreasing |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| at |$z$| < 2 and their small values at higher |$z$| > 2 (see the right-hand panel of Fig. 4). Sources of all these significant differences among the three UVB models are the differences in the input parameters used in modeling, mainly the emissivities from QSOs and galaxies along with the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements that are used to check or calibrate the models.

The significant differences in the UVB models highlight the need for routinely updating the models using ever-improving measurements of important input parameters. It is also important that the photoionization calculations that depend extensively on the assumed UVB model should use updated UVB keeping in mind all the uncertainties involved in the calculations of UVB. This is the main reason why we provide six other UVB models having different α values than our fiducial model. For these models, the differences in the obtained UVB spectrum can be seen from Fig. E4 of the Appendix. The intensity of He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB increases with α at all |$z$| since it depends only on QSO emissivity, on the other hand the H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB depends on both QSOs and galaxies, therefore it only shows clear dependences on α for |$z$| < 3 where QSOs are dominating the UVB. As mentioned earlier, the intensity of He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB is more sensitive to α than H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB, as can be seen from Fig. E4 of the Appendix for UVB at |$z$| < 3. We make all these UVBs publicly available for testing the dependence of photoionization calculation results on the assumed spectral shape of the UVB and to be able to quantify the uncertainties in the inferred quantities from these calculations. In the following section, we give a detailed account of the uncertainties involved in the UVB calculations.

4.4 Uncertainties and caveats in the UVB models

The synthesis models of EBL are affected by several assumptions and many uncertainties arising from various input parameters. Here, we discuss such uncertainties and caveats in our UV and X-ray background models (E > 13.6 eV). We refer interested readers to section 9 of KS15b for the discussion related to uncertainties in the far-UV to FIR parts (E < 13.6 eV) of the EBL.

4.4.1 QSO emissivity and SED

Uncertainties in QSO emissivity arise from how well we measure the QLF (especially at low luminosities) and how representative is the SED used in the wavelength range where there are no direct observations. At |$z$| < 2 the QLFs are relatively well measured having shallow faint end slopes. Therefore, uncertainties in the obtained emissivity at |$z$| < 2 by integrating down to faintest luminosity are small. For example, for |$z$| < 2 QLFs from Croom et al. (2009) and Palanque-Delabrouille et al. (2013), changing the minimum luminosity |$L_{\nu }^{\rm min}=0.01L^*$| to |$L_{\nu }^{\rm min}=0$| changes the emissivity by less than 5 per cent. Although we are using most recent measurements, the |$z$| > 3 QLFs at the low luminosities are not well-measured, which can make our assumed emissivities highly uncertain at these redshifts.

For a fixed type 1 QSO SED, any effect of a change in QSO emissivity will be compensated by a corresponding change in the f_esc to match the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements. However, this required change in f_esc can affect the spectral shape of the H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB depending on the differences in the type 1 QSO SED and the intrinsic SED of galaxies at E > 13.6 eV. Latter is obtained from stellar population synthesis models. For our fiducial UVB model, since the SED of QSOs (with α = −1.8) is co-incidentally same as our intrinsic SED of galaxies, using different QSO emissivity will not affect even the spectral shape of H|$\, \, {\rm {\scriptstyle I}}$|-ionizing UVB. However, the He|$\, \, {\rm {\scriptstyle II}}$|-ionizing UVB will be affected since it depends on the emission from type 1 QSOs and the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| through radiative transfer effects that determine η (see Khaire 2017).⁴ For example, there is no need to have a seemingly unrealistic sharp increase in f_esc with |$z$| (see the left-hand panel of Fig. 3) if the QSO emissivity is significantly higher than our fiducial values at |$z$| > 3.5. A much slower or no evolution in f_esc(⁠|$z$|⁠) can be easily achieved as shown in Khaire et al. (2016) when one uses high QSO emissivity models based on the QLF measurements by Giallongo et al. (2015) and assuming that the low-luminosity QSOs also have high (close to unity) escape fraction (see Grazian et al. 2018). However, such models have serious problems to reproduce the He|$\, \, {\rm {\scriptstyle II}}$| optical depth as a function of |$z$| (Khaire 2017). Moreover QLF measurements of Giallongo et al. (2015) are not supported by other similar studies (see e.g. Weigel et al. 2015; McGreer et al. 2018; Ricci et al. 2017)

Even the latest measurements of type 1 QSO SED show large variation in the measured value of power-law index α at E > 13.6 eV (from −2.3 to −0.5 within 1σ errors; Stevans et al. 2014; Lusso et al. 2015; Tilton et al. 2016). See table 1 of Khaire (2017) for a summary of α measurements till date. The change in H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB arising due to change in α can be seen in Fig. E4 for |$z$| ≤ 2, where the UVB is dominated by only type 1 QSOs. At |$z$| > 3, Fig. E4 shows no variation in H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB with change in α since it is dominated by emission from galaxies. The He|$\, \, {\rm {\scriptstyle II}}$| ionizing part of the UVB, however, shows a large variation with α at all redshifts, since it only depends on type 1 QSO emissivity. The existing measurements of α probe smallest wavelength only upto 425 Å (30 eV), therefore there are no direct observational constraints on QSO SED at He|$\, \, {\rm {\scriptstyle II}}$| ionizing wavelengths. It has been assumed that the type 1 QSO SED at λ < 912 Å (E > 13.6 eV) follows a single power law (with same α), which is normalized at 912 Å or higher wavelengths. This extrapolated power law to He|$\, \, {\rm {\scriptstyle II}}$| ionizing wavelengths gives large-intensity differences corresponding to small changes in α. Therefore, He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB and |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$| are more sensitive to α values than the H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB and |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| as can be observed from Figs E1 and E4 of the Appendix. Under the assumption of a single power law, in Khaire (2017) we find that α can have values from −1.6 to −2.0 consistent with measurements of Lusso et al. (2015) but smaller than measurements of Stevans et al. (2014) and Tilton et al. (2016). We provide UVB models with varying α from −1.4 to −2.0 in Appendix E. Using different α in the UVB models can affect the inferred properties of absorbers in the IGM and CGM, such as metallicity (Hussain et al. 2017; Muzahid et al. 2018), density (Hussain et al. 2017; Upton Sanderbeck et al. 2018), and temperatures (Gaikwad et al. in preparation).

Type 2 QSO SED and its normalizations, for different values of α used in type 1 QSO SED (see Table 1) are adjusted to be consistent with most of the X-ray and γ-ray background measurements at |$z$| = 0. These models with different α are shown in Fig. E3. For large values of α, such as −1.4 or −1.5, it is difficult to adjust normalizations to be consistent with some of the soft X-ray measurements. Nevertheless, all models are consistent with measurements at energies more than 20 keV all the way upto TeV. Although this shows a major success of such type 2 QSO and blazar SED formulation, it has been assumed to scale with type 1 QSO emissivity, with the same scaling at all redshifts. Such scaling can be justified using recent observations of QSO population (Lusso et al. 2013; Georgakakis et al. 2017; Vito et al. 2018), where the fraction of type 2 QSOs is shown to be non-evolving with redshift (however, see Gohil & Ballantyne 2018; Liu et al. 2017). Due to this scaling, all the uncertainties in type 1 QSO emissivity reflect in the normalization of type 2 QSO SED. Although it will not affect the obtained X-ray background, it will change the interpretation related to the fraction of type 2 QSOs as discussed in Appendix D. However, one should take such an interpretation with caution since the type 1 and type 2 QSO SEDs at X-ray can be adjusted arbitrarily to give different fractions of type 2 QSOs while still being consistent with local X-ray and γ-ray background measurements.

The soft-X-ray background (0.3 keV < E < 2 keV) in our EBL model is contributed only by QSOs. However, as shown in Upton Sanderbeck et al. (2018), a significant contribution at |$z$| ∼ 0 can come from hot intra-halo gas. The contribution from interstellar gas, CGM, and X-ray binary is relatively small; however, it depends on the SFRD used in the models. Upton Sanderbeck et al. (2018) used SFRD from HM12, which is a factor of ∼3 smaller than other estimates at |$z$| < 1. In our EBL models we have not included soft-X-ray background arising from these different sources that, when included in EBL models, can further constrain the SED of type 1 and 2 QSOs and can also change the interpretation of fraction of type 2 QSOs as mentioned above.

4.4.2 Galaxy emissivity and escape fraction

The emissivity of galaxies at λ < 912 Å depends, in addition to the intrinsic emissivity, on f_esc. In our model by construct f_esc is constrained to reproduce the H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB consistent with |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements. The intrinsic emissivity at λ < 912 Å depends on the derived SFRD and A_FUV as well as several parameters in the stellar population models. The derived SFRD and A_FUV alone can have systematic uncertainties of the order of 30 per cent arising due to scatter in various FUV GLFs (see e.g. figs 1 and 5 of KS15b). Uncertainties arising in SFRD and A_FUV from different parameters in stellar population models, such as using different metallicity, are smaller than this uncertainty (see section 8.2 of KS15b for more details).

As long as the intrinsic SED of galaxies at λ < 912 Å is same, the intensity of H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB remains same for different inferred values of f_esc arising from different values of SFRD, A_FUV, IMF, metallicity, or other parameters in the stellar population model. This is because in the UVB calculations the intrinsic galaxy SED has been scaled with f_esc (see also HM12, FG09), in the absence of any observational constraints on the SED of emitted light from galaxies at λ < 912 Å. Such a scaling is justified under the assumption that these photons escape through gas and dust free channels, as proposed in many theoretical models (e.g. Fujita et al. 2003; Gnedin et al. 2008; Paardekooper et al. 2011; Conroy & Kratter 2012). Although the intrinsic SED at λ < 912 Å shows reasonably small variations for different properties of stellar populations such as metallicity (see section 4 of Becker & Bolton 2013) and different synthesis models (see section 9 of HM12), different IMFs can provide quite different intrinsic SEDs.

If independent constraints on f_esc are available, then the above-mentioned uncertainties will translate to uncertainties in the UVB spectrum. In our models, for a given QSO emissivity, the f_esc values are adjusted to match |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements in the absence of strong constraints on the f_esc measurements. In future, independent constraints on f_esc or H|$\, \, {\rm {\scriptstyle I}}$| ionizing emissivity will be useful to quantify the contributions of sources other than QSOs and galaxies to the UVB.

4.4.3 H|$\, \, {\rm {\scriptstyle I}}$| distribution and other uncertainties

The column density distribution of the H|$\, \, {\rm {\scriptstyle I}}$|⁠, f(N_H i, |$z$|⁠) plays an important role in shaping the UVB model. The f(N_H_i, |$z$|⁠) affects UVB estimate through the calculation of τ_eff, especially at |$15\lt {\rm log}(N_{\rm H\,{\small I} } \, \, {\rm cm^{-2}})\lt 20.5$| for H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB (see Fig. 8) and 4/η times values for He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB. This |$N_{\rm H\,{\small I}}$| range has relatively higher measurement uncertainty as compared to log|$(N_{\rm H\,{\small I}} \, \, {\rm cm^{-2}})\lt 14$| or >20 due to saturation of the Lyman-α absorption. We have used a f(N_H_i, |$z$|⁠) fitting form provided by Inoue et al. (2014) because it has been obtained by fitting a large number of different observations covering large redshift and |$N_{\rm H\,{\small I}}$| range, as mentioned in Section 2. For comparison, in the left-hand panel of Fig. 8, we show the f(N_H i, |$z$|⁠) measurements at |$z$| = 2.5 along with the fitting forms from Inoue et al. (2014), FG09, and HM12. The fit from Inoue et al. (2014) is better than others at all |$N_{\rm H\, {\rm {\scriptstyle I}}}$|⁠. The difference in the obtained τ_eff at each |$N_{\rm H\,{\small I}}$| for different f(N_H_i, |$z$|⁠) fits are shown in the right-hand panel of Fig. 8, where a contribution of τ_eff at each |$N_{\rm H\,{\small I}}$| is represented by quantity N_H if(N_H_i, |$z$|⁠)[1 − exp(− N_H_iσ₉₁₂)]. When we use the f(N_H_i, |$z$|⁠) from HM12 instead of Inoue et al. (2014), at |$z$| < 3 our |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| reduces by 10 per cent (at |$z$| ∼ 2.5 and by 25 per cent at |$z$| ∼ 0.5) to 40 per cent (at |$z$| ∼ 0) and |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| increases by a similar amount (because of lower η due to small |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$|⁠). These changes are smaller than or comparable to the current measurement uncertainties on |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| and |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| (see fig. 16 of Gaikwad et al. 2017a). We also note that such a change in f(N_H_i, |$z$|⁠) does not affect the spectral shape of the UVB significantly (see also fig. 9 of HM12). However, note that, even if we use different f(N_H_i, |$z$|⁠) that can change the UVB, f_esc will be adjusted to get the same |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| measurements, which further reduces differences in |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| as well. The change in |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| and |$\Gamma _{\rm He \, {\scriptscriptstyle II}}$| is less than the change arising from varying the α by 0.2. Therefore, the uncertainties in f(N_H i, |$z$|⁠) have smaller impact on the UVB compared to the uncertainties in other parameters, especially the SED of type 1 QSOs.

$Left-hand panel: The f(NH i, $z$) at $z$ = 2.5 from observations at different NHi (Noterdaeme et al. 2012; Kim et al. 2013; O’Meara et al. 2013) and the fits used by HM12 and FG09 along with the updated fits given in Inoue et al. (2014). Right-hand panel: A quantity $N_{\rm H\,{\small I}}\, f(N_{\rm H\,{\small I}}, z\,) [1-\exp (-N_{\rm H\,{\small I}} \sigma _{0})]$ that determines the contribution of NH i to τeff. For f(NH i, $z$) from Inoue et al. (2014), the column density range log $N_{\rm H\,{\small I}} (\rm cm^{-2})$ from 15 to 21 (and 4/η times $N_{\rm H\,{\small I}}$) dominates the τeff for H$\, \, {\rm {\scriptstyle I}}$(and He$\, \, {\rm {\scriptstyle II}}$) ionizing photons.$

Figure 8.

Left-hand panel: The f(N_H i, |$z$|⁠) at |$z$| = 2.5 from observations at different N_H_i (Noterdaeme et al. 2012; Kim et al. 2013; O’Meara et al. 2013) and the fits used by HM12 and FG09 along with the updated fits given in Inoue et al. (2014). Right-hand panel: A quantity |$N_{\rm H\,{\small I}}\, f(N_{\rm H\,{\small I}}, z\,) [1-\exp (-N_{\rm H\,{\small I}} \sigma _{0})]$| that determines the contribution of N_H i to τ_eff. For f(N_H i, |$z$|⁠) from Inoue et al. (2014), the column density range log |$N_{\rm H\,{\small I}} (\rm cm^{-2})$| from 15 to 21 (and 4/η times |$N_{\rm H\,{\small I}}$|⁠) dominates the τ_eff for H|$\, \, {\rm {\scriptstyle I}}$|(and He|$\, \, {\rm {\scriptstyle II}}$|⁠) ionizing photons.

Open in new tab Download slide

The value of η calculated using equation (5) in optically thick He|$\, \, {\rm {\scriptstyle II}}$| regions depends on the assumption that the discrete absorbers in the IGM have line-of-sight thickness equal to the Jeans scale. Changing this thickness (by factors upto ∼ 4) can affect the estimate of He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB due to change in η, however its impact on the UVB is quite small since it affects only a small number of high column density absorbers.

4.4.4 Caveats from basic assumptions

Main caveats in the H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| ionizing part of the UVB are that the assumption of uniform and homogeneous UVB is not valid at all redshifts. It is certainly a reasonable assumption for H|$\, \, {\rm {\scriptstyle I}}$| ionizing UVB at |$z$| < 5.5 and He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB at |$z$| < 2.5 where respective reionization events are believed to be completed. Equation (1) can provide reasonable estimates of UVB only in the regime where mean free path of (H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$|⁠) ionizing photons is large. Large fluctuations in the UVB are expected at redshifts where the respective reionizations are still in progress. At these redshifts, the homogeneous H|$\, \, {\rm {\scriptstyle I}}$|(He|$\, \, {\rm {\scriptstyle II}}$|⁠) ionizing UVB calculated using equation (1) and its predictions for photoionization and photoheating rates cannot capture the effects of large fluctuations in the radiation fields. As shown by Oñorbe et al. (2017a), these rates (from FG09 and HM12) will prematurely heat the IGM and reionize the H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| very early giving observationally inconsistent reionization histories and incorrect feedback on galaxy formation. Note that, even for our UVB models the consistency with reionization constraints shown in Section 4.4.2 (left-hand and middle panels of Fig. 5) is just a sanity check on the ionizing emissivity used in UVB calculations and independent of the UVB estimates. Therefore at these redshifts, a large scatter expected in the photoheating and photoionization rates should be properly implemented in the cosmological hydrodynamic simulations. This can be achieved by modifying these rates as shown in Oñorbe et al. (2017a). Such a modification depends on how the physics of reionization is implemented in simulations, the assumed evolution of mean free path for ionizing photons, and the SED of ionizing sources (Oñorbe et al. 2017a; Puchwein et al. 2019). Moreover, in the absence of the observational constraints on the mean free paths and SEDs of ionizing sources at these redshifts, such a modification to the photoionization and photoheating rates cannot be unique. Novel methods for determining accurate timing and heat-injection during reionization (e.g. Padmanabhan, Choudhury & Srianand 2014; Oñorbe et al. 2017b) will prove valuable in future to resolve these issues.

Even after completion of the reionization, significant fluctuations in the UVB are expected (e.g. Furlanetto 2009; Furlanetto & Mesinger 2009; Davies & Furlanetto 2016; Davies, Furlanetto & Dixon 2017). In addition, the recently reionized gas may take some time to reach ionization and thermal equilibrium. Our calculations do not consider these non-equilibrium conditions (e.g. Puchwein et al. 2015). Also, most of the measurements of |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| that we used to constrain the ionizing emissivity from galaxies are obtained from observed Lyman-α forest by modeling the IGM under the assumption of ionization and thermal equilibrium. Consolidated efforts are needed to get these issues sorted out around the epoch of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization.

In the UVB calculations, several assumptions related to the input parameters are made in the absence of the concrete observational constraints. For example, the QSO SED has been assumed to be the same at all redshifts in the absence of significant observational evidence of its redshift evolution (Stevans et al. 2014; Tilton et al. 2016). Also, it has been assumed that the type 1 QSO SED follows a single power law for λ < 912 Å upto wavelengths ∼50 Å, although available observations only probe upto 425 Å. Moreover, a single power law may not be a good approximation to small wavelengths (e.g. Tilton et al. 2016; Khaire 2017). Similarly for galaxies, although mild metallicity evolution does not affect intrinsic SEDs, the IMF and other stellar population parameters have been assumed to be the same at all redshifts. The obtained f_esc and SED of galaxies can be different for top heavy IMFs (Topping & Shull 2015) and including stellar rotation (Ma et al. 2015) and binary stars (Rosdahl et al. 2018) in the population synthesis models. For galaxies, a crucial assumption, as mentioned before, is the scaling of intrinsic galaxy SED by f_esc. Because of this, our another assumption, a single dust extinction curve at all |$z$|⁠, does not affect UVB but can change EBL at FIR wavelength due to the corresponding change in A_FUV and SFRD that preserves the emissivities till near-IR wavelengths (see KS15b).

In spite of all these uncertainties, we provide EBL models that are consistent with currently available observations at all redshifts and wavelengths. Better constraints on |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| at 0.5≤|$z$| ≤2.0 and at |$z$| > 5, well-defined QLFs at low luminosity end and more measurements of τ_He ii at |$z$| > 2 will provide better constraints on the UVB models.

One of the important implications of the UVB for IGM is its thermal evolution (Oñorbe et al. 2017a; Puchwein et al. 2019). We find that our photoheating rates when used in hydrodynamical simulations of the IGM performed with explicit non-equilibrium ionization effects provide IGM thermal histories consistent with most of the recent measurements (Gaikwad et al. in preparation).

5 SUMMARY

The EBL is extensively used by the astronomical community for studying (i) spectral energy distribution of blazars in GeV energies; (ii) metal line absorption systems to derive density, metallicity, and size of the absorbing gas and their redshift evolution; and (iii) ionization and thermal state of the IGM over cosmic time. As the spectrum of EBL cannot be directly measured at all epochs, it has to be modeled using the available observations of the source emissivities and IGM opacities with appropriate cosmological radiative transport. Thus it is important to have EBL computed time to time with latest parameters that govern the source emissivities and IGM opacities. In addition, it is important to quantify the allowed variations in computed EBL at each epoch so that one can estimate systemic uncertainties arising from EBL uncertainties while interpreting the data.

With these motivations, we present new synthesis models of the EBL that cover more than 15 orders of magnitude in wavelength from FIR to TeV γ-rays (see Fig. 6 for |$z$| = 0 EBL). Our main focus of this paper is on modeling the observationally consistent extreme-UV and soft X-ray background, which is essential for studying the metal absorption lines observed in QSO spectra.

In our EBL synthesis model, we use updated inputs such as SFRD and A_FUV for galaxies, QSO emissivity, and H|$\, \, {\rm {\scriptstyle I}}$| distribution of the IGM. We determine average escape fraction (f_esc) of H|$\, \, {\rm {\scriptstyle I}}$| ionizing photons from galaxies that can reproduce the available recent measurements of the H|$\, \, {\rm {\scriptstyle I}}$| photoionization rates at |$z$| < 6.5 (the left-hand panel of Figs 3 and 4) and provide H|$\, \, {\rm {\scriptstyle I}}$| reionization history consistent with many new measurements of H|$\, \, {\rm {\scriptstyle I}}$| fraction at |$z$| > 6 and electron scattering optical depth to CMB (Fig. 5). The UVB at |$z$| < 3 is predominantly contributed by QSOs whereas galaxies contribute significantly to the H|$\, \, {\rm {\scriptstyle I}}$| ionizing emissivity at |$z$| > 3 (see also Khaire et al. 2016; Gaikwad et al. 2017a) as evident from a sharp increase in the required f_esc(⁠|$z$|⁠) (see Fig. 3).

For our fiducial EBL model, we take type 1 QSO extreme UV SED as f_ν ∝ ν^α with power-law slope α = −1.8 from Khaire (2017), which consistently reproduce the 2.5 < |$z$| < 3.5 measurements of Lyman-α effective optical depths, photoionization rates, and reionization redshift of He|$\, \, {\rm {\scriptstyle II}}$| (the right-hand panel of Figs 4 and 5). Since available measurements of α show large variation, we also provide six other EBL models (in the Appendix) calculated for different values of α from −1.4 to −2.0 consistent with recent measurements of α from Shull et al. (2012), Stevans et al. (2014), and Lusso et al. (2015). At X-ray and γ-ray energies, we modified the form of type 1 QSO SED and constructed an SED for type 2 QSOs (including γ-ray emitting blazars) following Sazonov et al. (2004) to consistently reproduce the measurements of local X-ray and γ-ray background (Fig. E3). We find that EBL models constructed in this way with α > −1.5 are not consistent with He|$\, \, {\rm {\scriptstyle II}}$| Lyman-α effective optical depths (see also Khaire 2017) and some of the soft-X-ray background measurements.

Because the UVB is an important tool to study the time evolution in physical and chemical properties of the IGM and CGM, it needs to be consistent with various observational constraints. We discuss in detail the uncertainties and caveats arising from several assumptions in the modeling of UVB (see Section 4.4). We are working on addressing some of the caveats such as non-equilibrium ionization and thermal evolution of the IGM and its impact on the UVB around the epochs of H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization (see e.g. Gaikwad et al. 2018a). Within the framework discussed here and in the previous UVB models, a major uncertainty lies in the spectral shape, therefore improved observational constraints on the QSO SEDs and escaping Lyman-continuum SEDs of galaxies are important. Also, new techniques to constrain spectral shape of the UVB by using metal absorption lines are required (e.g. Fechner 2011; Finlator et al. 2016). Our UVB models obtained for different QSO SEDs will be useful for such studies.

For public use we provide the EBL tables, the photoionization and photoheating rates of H|$\, \, {\rm {\scriptstyle I}}$|⁠, He|$\, \, {\rm {\scriptstyle I}}$|⁠, and He|$\, \, {\rm {\scriptstyle II}}$| obtained from EBL models, and γ-ray effective optical depths at all redshifts.⁵

SUPPORTING INFORMATION

ks_2018_ebl.tar.gz

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

ACKNOWLEDGEMENTS

We thank Marco Ajello, Nico Cappelluti, and Eugene Churazov for providing the X-ray background data. We thank Prakash Gaikwad, Tirthankar Roy Choudhury, Aseem Paranjape, and Kandaswamy Subramanian for helpful discussions throughout the development of this project. VK thanks Fred Davies, Jose Onorbe, Tobias Schmidt, and other http://enigma.physics.ucsb.edu/ENIGMA () group members at UCSB for valuable comments on the manuscript.

Footnotes

1

Excluding a QSO only model by Madau & Haardt (2015) and a recent Puchwein et al. (2019) model that appeared while we were finalizing the paper.

2

The |$\epsilon ^Q_{1000}(z)$| is obtained by multiplying (1000/912)^1.4 to the |$\epsilon ^Q_{912}(z)$| provided in KS15a.

3

http://galaxies.northwestern.edu/uvb/We use their December 2011 update available on web page

4

The change in f_esc can affect the He|$\, \, {\rm {\scriptstyle II}}$| ionizing UVB but only if the |$\Gamma _{\rm H \, {\scriptscriptstyle I}}$| is allowed to vary (Khaire & Srianand 2013).

5

All tables are available at http://www.iucaa.in/projects/cobra/ and http://vikramkhaire.weebly.com/downloads.html

REFERENCES

Ackermann

M.

et al. ,

2012

,

Science

,

338

,

1190

10.1126/science.1227160

Crossref

Search ADS

PubMed

Ackermann

M.

et al. ,

2015

,

ApJ

,

799

,

86

10.1088/0004-637X/799/1/86

Crossref

Search ADS

Adams

J. J.

,

Uson

J. M.

,

Hill

G. J.

,

MacQueen

P. J.

,

2011

,

ApJ

,

728

,

107

10.1088/0004-637X/728/2/107

Crossref

Search ADS

Aird

J.

,

Coil

A. L.

,

Georgakakis

A.

,

Nandra

K.

,

Barro

G.

,

Pérez-González

P. G.

,

2015

,

MNRAS

,

451

,

1892

10.1093/mnras/stv1062

Crossref

Search ADS

Ajello

M.

et al. ,

2008

,

ApJ

,

689

,

666

10.1086/592595

Crossref

Search ADS

Ajello

M.

et al. ,

2015

,

ApJ

,

800

,

L27

10.1088/2041-8205/800/2/L27

Crossref

Search ADS

Andrews

S. K.

et al. ,

2017

,

MNRAS

,

470

,

1342

10.1093/mnras/stx1279

Crossref

Search ADS

Antonucci

R.

,

1993

,

ARA&A

,

31

,

473

10.1146/annurev.aa.31.090193.002353

Crossref

Search ADS

Aracil

B.

,

Petitjean

P.

,

Pichon

C.

,

Bergeron

J.

,

2004

,

A&A

,

419

,

811

10.1051/0004-6361:20034346

Crossref

Search ADS

Arlen

T. C.

,

Vassiliev

V. V.

,

Weisgarber

T.

,

Wakely

S. P.

,

Yusef Shafi

S.

,

2014

,

ApJ

,

796

,

18

10.1088/0004-637X/796/1/18

Crossref

Bajtlik

S.

,

Duncan

R. C.

,

Ostriker

J. P.

,

1988

,

ApJ

,

327

,

570

10.1086/166217

Crossref

Search ADS

Ballantyne

D. R.

,

Draper

A. R.

,

Madsen

K. K.

,

Rigby

J. R.

,

Treister

E.

,

2011

,

ApJ

,

736

,

56

10.1088/0004-637X/736/1/56

Crossref

Search ADS

Bañados

E.

et al. ,

2018

,

Nature

,

553

,

437

10.1038/nature25180

PubMed

Becker

G. D.

,

Bolton

J. S.

,

2013

,

MNRAS

,

436

,

1023

10.1093/mnras/stt1610

Crossref

Search ADS

Becker

G. D.

,

Rauch

M.

,

Sargent

W. L. W.

,

2007

,

ApJ

,

662

,

72

10.1086/517866

Crossref

Search ADS

Becker

G. D.

,

Bolton

J. S.

,

Haehnelt

M. G.

,

Sargent

W. L. W.

,

2011

,

MNRAS

,

410

,

1096

10.1111/j.1365-2966.2010.17507.x

Crossref

Search ADS

Becker

G. D.

,

Hewett

P. C.

,

Worseck

G.

,

Prochaska

J. X.

,

2013

,

MNRAS

,

430

,

2067

10.1093/mnras/stt031

Crossref

Search ADS

Becker

R. H.

et al. ,

2001

,

AJ

,

122

,

2850

10.1086/324231

Crossref

Search ADS

Behroozi

P. S.

,

Wechsler

R. H.

,

Conroy

C.

,

2013

,

ApJ

,

770

,

57

10.1088/0004-637X/770/1/57

Crossref

Search ADS

Bergeron

J.

,

Aracil

B.

,

Petitjean

P.

,

Pichon

C.

,

2002

,

A&A

,

396

,

L11

10.1051/0004-6361:20021611

Crossref

Search ADS

Bergvall

N.

,

Zackrisson

E.

,

Andersson

B.-G.

,

Arnberg

D.

,

Masegosa

J.

,

Östlin

G.

,

2006

,

A&A

,

448

,

513

10.1051/0004-6361:20053788

Crossref

Search ADS

Bolton

J. S.

,

Haehnelt

M. G.

,

2007

,

MNRAS

,

382

,

325

10.1111/j.1365-2966.2007.12372.x

Crossref

Search ADS

Borthakur

S.

,

Heckman

T. M.

,

Leitherer

C.

,

Overzier

R. A.

,

2014

,

Science

,

346

,

216

10.1126/science.1254214

Crossref

Search ADS

PubMed

Bouwens

R. J.

et al. ,

2012

,

ApJ

,

754

,

83

10.1088/0004-637X/754/2/83

Crossref

Search ADS

Bouwens

R. J.

et al. ,

2015

,

ApJ

,

803

,

34

10.1088/0004-637X/803/1/34

Crossref

Search ADS

Bridge

C. R.

et al. ,

2010

,

ApJ

,

720

,

465

10.1088/0004-637X/720/1/465

Crossref

Search ADS

Buchner

J.

et al. ,

2015

,

ApJ

,

802

,

89

10.1088/0004-637X/802/2/89

Crossref

Search ADS

Burgarella

D.

et al. ,

2013

,

A&A

,

554

,

A70

10.1051/0004-6361/201321651

Crossref

Search ADS

Calverley

A. P.

,

Becker

G. D.

,

Haehnelt

M. G.

,

Bolton

J. S.

,

2011

,

MNRAS

,

412

,

2543

10.1111/j.1365-2966.2010.18072.x

Crossref

Search ADS

Cappelluti

N.

et al. ,

2017

,

ApJ

,

837

,

19

10.3847/1538-4357/aa5ea4

Crossref

Search ADS

Choudhury

T. R.

,

Puchwein

E.

,

Haehnelt

M. G.

,

Bolton

J. S.

,

2015

,

MNRAS

,

452

,

261

10.1093/mnras/stv1250

Crossref

Search ADS

Churazov

E.

et al. ,

2007

,

A&A

,

467

,

529

10.1051/0004-6361:20066230

Crossref

Search ADS

Comastri

A.

,

Setti

G.

,

Zamorani

G.

,

Hasinger

G.

,

1995

,

A&A

,

296

,

1

Compostella

M.

,

Cantalupo

S.

,

Porciani

C.

,

2013

,

MNRAS

,

435

,

3169

10.1093/mnras/stt1510

Crossref

Search ADS

Conroy

C.

,

Kratter

K. M.

,

2012

,

ApJ

,

755

,

123

10.1088/0004-637X/755/2/123

Crossref

Search ADS

Cowie

L. L.

,

Barger

A. J.

,

Trouille

L.

,

2009

,

ApJ

,

692

,

1476

10.1088/0004-637X/692/2/1476

Crossref

Search ADS

Croom

S. M.

et al. ,

2009

,

MNRAS

,

399

,

1755

10.1111/j.1365-2966.2009.15398.x

Crossref

Search ADS

D’Aloisio

A.

,

McQuinn

M.

,

Davies

F. B.

,

Furlanetto

S. R.

,

2018

,

MNRAS

,

473

,

560

10.1093/mnras/stx2341

Crossref

Search ADS

D’Odorico

V.

et al. ,

2013

,

MNRAS

,

435

,

1198

10.1093/mnras/stt1365

Crossref

Search ADS

Dall’Aglio

A.

,

Wisotzki

L.

,

Worseck

G.

,

2008

,

A&A

,

491

,

465

10.1051/0004-6361:200810724

Crossref

Search ADS

Danforth

C. W.

,

Shull

J. M.

,

2005

,

ApJ

,

624

,

555

10.1086/429285

Crossref

Search ADS

Davé

R.

,

Hernquist

L.

,

Katz

N.

,

Weinberg

D. H.

,

1999

,

ApJ

,

511

,

521

10.1086/306722

Crossref

Search ADS

Davies

F. B.

et al. ,

2018

,

ApJ

,

864

,

142

10.3847/1538-4357/aad6dc

Crossref

Search ADS

Davies

F. B.

,

Furlanetto

S. R.

,

2016

,

MNRAS

,

460

,

1328

10.1093/mnras/stw931

Crossref

Search ADS

Davies

F. B.

,

Furlanetto

S. R.

,

Dixon

K. L.

,

2017

,

MNRAS

,

465

,

2886

10.1093/mnras/stw2868

Crossref

Search ADS

Dayal

P.

,

Ferrara

A.

,

Saro

A.

,

2010

,

MNRAS

,

402

,

1449

10.1111/j.1365-2966.2009.15995.x

Crossref

Search ADS

de Barros

S.

et al. ,

2016

,

A&A

,

585

,

A51

10.1051/0004-6361/201527046

Crossref

Search ADS

Dijkstra

M.

,

2017

,

preprint

(http://adsabs.harvard.edu/abs/2017arXiv170403416D arXiv:1704.03416)

Dijkstra

M.

,

Haiman

Z.

,

Spaans

M.

,

2006

,

ApJ

,

649

,

14

10.1086/506243

Crossref

Search ADS

Dole

H.

et al. ,

2006

,

A&A

,

451

,

417

10.1051/0004-6361:20054446

Crossref

Search ADS

Domínguez

A.

et al. ,

2011

,

MNRAS

,

410

,

2556

10.1111/j.1365-2966.2010.17631.x

Crossref

Search ADS

Dove

J. B.

,

Shull

J. M.

,

1994

,

ApJ

,

423

,

196

10.1086/173799

Crossref

Search ADS

Draper

A. R.

,

Ballantyne

D. R.

,

2009

,

ApJ

,

707

,

778

10.1088/0004-637X/707/1/778

Crossref

Search ADS

Driver

S. P.

et al. ,

2016a

,

MNRAS

,

455

,

3911

10.1093/mnras/stv2505

Crossref

Search ADS

Driver

S. P.

et al. ,

2016b

,

ApJ

,

827

,

108

10.3847/0004-637X/827/2/108

Crossref

Search ADS

Dwek

E.

,

Arendt

R. G.

,

1998

,

ApJ

,

508

,

L9

10.1086/311714

Crossref

Search ADS

Dwek

E.

,

Krennrich

F.

,

2013

,

Astropart. Phys.

,

43

,

112

10.1016/j.astropartphys.2012.09.003

Crossref

Search ADS

Efstathiou

G.

,

1992

,

MNRAS

,

256

,

43P

10.1093/mnras/256.1.43P

Crossref

Search ADS

Fan

X.

et al. ,

2006

,

AJ

,

132

,

117

10.1086/504836

Crossref

Search ADS

Fardal

M. A.

,

Giroux

M. L.

,

Shull

J. M.

,

1998

,

AJ

,

115

,

2206

10.1086/300359

Crossref

Search ADS

Faucher-Giguère

C.-A.

,

Prochaska

J. X.

,

Lidz

A.

,

Hernquist

L.

,

Zaldarriaga

M.

,

2008

,

ApJ

,

681

,

831

10.1086/588648

Crossref

Search ADS

Faucher-Giguère

C.-A.

,

Lidz

A.

,

Zaldarriaga

M.

,

Hernquist

L.

,

2009

,

ApJ

,

703

,

1416

(FG09)

10.1088/0004-637X/703/2/1416

Crossref

Search ADS

Fechner

C.

et al. ,

2006

,

A&A

,

455

,

91

10.1051/0004-6361:20064950

Crossref

Search ADS

Fechner

C.

,

2011

,

A&A

,

532

,

A62

10.1051/0004-6361/201117080

Crossref

Search ADS

Ferland

G. J.

et al. ,

2013

,

Rev. Mex. Astron. Astrofis.

,

49

,

137

Ferland

G. J.

et al. ,

2017

,

Rev. Mex. Astron. Astrofis.

,

53

,

385

Ferrara

A.

,

Scannapieco

E.

,

Bergeron

J.

,

2005

,

ApJ

,

634

,

L37

10.1086/498845

Crossref

Search ADS

Finke

J. D.

,

Razzaque

S.

,

Dermer

C. D.

,

2010

,

ApJ

,

712

,

238

10.1088/0004-637X/712/1/238

Crossref

Search ADS

Finke

J. D.

,

Reyes

L. C.

,

Georganopoulos

M.

,

Reynolds

K.

,

Ajello

M.

,

Fegan

S. J.

,

McCann

K.

,

2015

,

ApJ

,

814

,

20

10.1088/0004-637X/814/1/20

Crossref

Search ADS

Finlator

K.

,

Oh

S. P.

,

Özel

F.

,

Davé

R.

,

2012

,

MNRAS

,

427

,

2464

10.1111/j.1365-2966.2012.22114.x

Crossref

Search ADS

Finlator

K.

,

Oppenheimer

B. D.

,

Davé

R.

,

Zackrisson

E.

,

Thompson

R.

,

Huang

S.

,

2016

,

MNRAS

,

459

,

2299

10.1093/mnras/stw805

Crossref

Franceschini

A.

,

Rodighiero

G.

,

Vaccari

M.

,

2008

,

A&A

,

487

,

837

10.1051/0004-6361:200809691

Crossref

Search ADS

Fujita

A.

,

Martin

C. L.

,

Mac Low

M.-M.

,

Abel

T.

,

2003

,

ApJ

,

599

,

50

10.1086/379276

Crossref

Search ADS

Fukada

Y.

,

Hayakawa

S.

,

Kasahara

I.

,

Makino

F.

,

Tanaka

Y.

,

Sreekantan

B. V.

,

1975

,

Nature

,

254

,

398

10.1038/254398a0

Crossref

Search ADS

Fumagalli

M.

,

O’Meara

J. M.

,

Prochaska

J. X.

,

Worseck

G.

,

2013

,

ApJ

,

775

,

78

10.1088/0004-637X/775/1/78

Crossref

Search ADS

Fumagalli

M.

,

Haardt

F.

,

Theuns

T.

,

Morris

S. L.

,

Cantalupo

S.

,

Madau

P.

,

Fossati

M.

,

2017

,

MNRAS

,

467

,

4802

10.1093/mnras/stx398

Crossref

Search ADS

Furlanetto

S. R.

,

2009

,

ApJ

,

703

,

702

10.1088/0004-637X/703/1/702

Crossref

Search ADS

Furlanetto

S. R.

,

Mesinger

A.

,

2009

,

MNRAS

,

394

,

1667

10.1111/j.1365-2966.2009.14449.x

Crossref

Search ADS

Gaikwad

P.

,

Khaire

V.

,

Choudhury

T. R.

,

Srianand

R.

,

2017a

,

MNRAS

,

466

,

838

10.1093/mnras/stw3086

Crossref

Search ADS

Gaikwad

P.

,

Srianand

R.

,

Choudhury

T. R.

,

Khaire

V.

,

2017b

,

MNRAS

,

467

,

3172

10.1093/mnras/stx248

Crossref

Search ADS

Gaikwad

P.

,

Srianand

R.

,

Khaire

V.

,

Choudhury

T. R.

,

2018a

,

preprint

(https://ui.adsabs.harvard.edu/#abs/2018arXiv181201016G arXiv:1812.01016)

Gaikwad

P.

,

Choudhury

T. R.

,

Srianand

R.

,

Khaire

V.

,

2018b

,

MNRAS

,

474

,

2233

10.1093/mnras/stx2859

Crossref

Search ADS

Gendreau

K. C.

et al. ,

1995

,

PASJ

,

47

,

L5

Georgakakis

A.

et al. ,

2017

,

MNRAS

,

469

,

3232

10.1093/mnras/stx953

Crossref

Search ADS

Giallongo

E.

et al. ,

2015

,

A&A

,

578

,

A83

10.1051/0004-6361/201425334

Crossref

Search ADS

Gilli

R.

,

Comastri

A.

,

Hasinger

G.

,

2007

,

A&A

,

463

,

79

10.1051/0004-6361:20066334

Crossref

Search ADS

Gilmore

R. C.

,

Somerville

R. S.

,

Primack

J. R.

,

Domínguez

A.

,

2012

,

MNRAS

,

422

,

3189

10.1111/j.1365-2966.2012.20841.x

Crossref

Search ADS

Giroux

M. L.

,

Shapiro

P. R.

,

1996

,

ApJS

,

102

,

191

10.1086/192257

Crossref

Search ADS

Glikman

E.

,

Djorgovski

S. G.

,

Stern

D.

,

Dey

A.

,

Jannuzi

B. T.

,

Lee

K.-S.

,

2011

,

ApJ

,

728

,

L26

10.1088/2041-8205/728/2/L26

Crossref

Search ADS

Gnedin

N. Y.

,

Hui

L.

,

1998

,

MNRAS

,

296

,

44

10.1046/j.1365-8711.1998.01249.x

Crossref

Search ADS

Gnedin

N. Y.

,

Kravtsov

A. V.

,

Chen

H.-W.

,

2008

,

ApJ

,

672

,

765

10.1086/524007

Crossref

Search ADS

Gohil

R.

,

Ballantyne

D. R.

,

2018

,

MNRAS

,

475

,

3543

10.1093/mnras/sty068

Crossref

Search ADS

Gordon

K. D.

,

Clayton

G. C.

,

Misselt

K. A.

,

Landolt

A. U.

,

Wolff

M. J.

,

2003

,

ApJ

,

594

,

279

10.1086/376774

Crossref

Search ADS

Goto

T.

,

Utsumi

Y.

,

Hattori

T.

,

Miyazaki

S.

,

Yamauchi

C.

,

2011

,

MNRAS

,

415

,

L1

10.1111/j.1745-3933.2011.01063.x

Crossref

Search ADS

Gould

R. J.

,

Schréder

G.

,

1966

,

Phys. Rev. Lett.

,

16

,

252

10.1103/PhysRevLett.16.252

Crossref

Search ADS

Grazian

A.

et al. ,

2017

,

A&A

,

602

,

A18

10.1051/0004-6361/201730447

Crossref

Search ADS

Grazian

A.

et al. ,

2018

,

A&A

,

613

,

A44

10.1051/0004-6361/201732385

Crossref

Search ADS

Greig

B.

,

Mesinger

A.

,

2017

,

MNRAS

,

465

,

4838

10.1093/mnras/stw3026

Crossref

Search ADS

Greig

B.

,

Mesinger

A.

,

Haiman

Z.

,

Simcoe

R. A.

,

2017

,

MNRAS

,

466

,

4239

10.1093/mnras/stw3351

Crossref

Search ADS

Gronke

M.

,

Dijkstra

M.

,

McCourt

M.

,

Oh

S. P.

,

2016

,

ApJ

,

833

,

L26

10.3847/2041-8213/833/2/L26

Crossref

Search ADS

Gruber

D. E.

,

Matteson

J. L.

,

Peterson

L. E.

,

Jung

G. V.

,

1999

,

ApJ

,

520

,

124

10.1086/307450

Crossref

Search ADS

Guaita

L.

et al. ,

2016

,

A&A

,

587

,

A133

10.1051/0004-6361/201527597

Crossref

Search ADS

Gunn

J. E.

,

Peterson

B. A.

,

1965

,

ApJ

,

142

,

1633

10.1086/148444

Crossref

Search ADS

Gurvich

A.

,

Burkhart

B.

,

Bird

S.

,

2017

,

ApJ

,

835

,

175

10.3847/1538-4357/835/2/175

Crossref

Search ADS

Haardt

F.

,

Madau

P.

,

1996

,

ApJ

,

461

,

20

10.1086/177035

Crossref

Search ADS

Haardt

F.

,

Madau

P.

,

2001

, in

Neumann

D. M.

,

Tran

J. T. V.

, eds,

Clusters of Galaxies and the High Redshift Universe Observed in X-rays

,

XXIst Moriond Astrophysics Meeting, held in March 10-17, 2001, Savoie, France

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Haardt

F.

,

Madau

P.

,

2012

,

ApJ

,

746

,

125

(HM12)

10.1088/0004-637X/746/2/125

Crossref

Search ADS

Helgason

K.

,

Kashlinsky

A.

,

2012

,

ApJ

,

758

,

L13

10.1088/2041-8205/758/1/L13

Crossref

Search ADS

Hernquist

L.

,

Katz

N.

,

Weinberg

D. H.

,

Miralda-Escudé

J.

,

1996

,

ApJ

,

457

,

L51

10.1086/309899

Crossref

Search ADS

Hiss

H.

,

Walther

M.

,

Hennawi

J. F.

,

Oñorbe

J.

,

O’Meara

J. M.

,

Rorai

A.

,

2018

,

ApJ

,

865

,

42

10.3847/1538-4357/aada86

Crossref

Search ADS

Hopkins

P. F.

,

Richards

G. T.

,

Hernquist

L.

,

2007

,

ApJ

,

654

,

731

10.1086/509629

Crossref

Search ADS

Hui

L.

,

Gnedin

N. Y.

,

1997

,

MNRAS

,

292

,

27

10.1093/mnras/292.1.27

Crossref

Search ADS

Hussain

T.

,

Muzahid

S.

,

Narayanan

A.

,

Srianand

R.

,

Wakker

B. P.

,

Charlton

J. C.

,

Pathak

A.

,

2015

,

MNRAS

,

446

,

2444

10.1093/mnras/stu2285

Crossref

Search ADS

Hussain

T.

,

Khaire

V.

,

Srianand

R.

,

Muzahid

S.

,

Pathak

A.

,

2017

,

MNRAS

,

466

,

3133

10.1093/mnras/stw3265

Crossref

Search ADS

Inoue

Y.

,

Inoue

S.

,

Kobayashi

M. A. R.

,

Makiya

R.

,

Niino

Y.

,

Totani

T.

,

2013

,

ApJ

,

768

,

197

10.1088/0004-637X/768/2/197

Crossref

Search ADS

Inoue

A. K.

et al. ,

2018

,

PASJ

,

70

,

55

Inoue

A. K.

,

Shimizu

I.

,

Iwata

I.

,

Tanaka

M.

,

2014

,

MNRAS

,

442

,

1805

10.1093/mnras/stu936

Crossref

Search ADS

Izotov

Y. I.

,

Schaerer

D.

,

Thuan

T. X.

,

Worseck

G.

,

Guseva

N. G.

,

Orlitová

I.

,

Verhamme

A.

,

2016a

,

MNRAS

,

461

,

3683

10.1093/mnras/stw1205

Crossref

Search ADS

Izotov

Y. I.

,

Orlitová

I.

,

Schaerer

D.

,

Thuan

T. X.

,

Verhamme

A.

,

Guseva

N. G.

,

Worseck

G.

,

2016b

,

Nature

,

529

,

178

10.1038/nature16456

Crossref

Search ADS

Izotov

Y. I.

,

Schaerer

D.

,

Worseck

G.

,

Guseva

N. G.

,

Thuan

T. X.

,

Verhamme

A.

,

Orlitová

I.

,

Fricke

K. J.

,

2018

,

MNRAS

,

474

,

4514

10.1093/mnras/stx3115

Crossref

Search ADS

Janknecht

E.

,

Reimers

D.

,

Lopez

S.

,

Tytler

D.

,

2006

,

A&A

,

458

,

427

10.1051/0004-6361:20065372

Crossref

Search ADS

Japelj

J.

et al. ,

2017

,

MNRAS

,

468

,

389

10.1093/mnras/stx477

Crossref

Search ADS

Kashikawa

N.

et al. ,

2015

,

ApJ

,

798

,

28

10.1088/0004-637X/798/1/28

Crossref

Search ADS

Khaire

V.

et al. ,

2018

,

MNRAS

,

preprint(http://adsabs.harvard.edu/abs/2018arXiv180805605K)

Khaire

V.

,

2017

,

MNRAS

,

471

,

255

10.1093/mnras/stx1487

Crossref

Search ADS

Khaire

V.

,

Srianand

R.

,

2013

,

MNRAS

,

431

,

L53

10.1093/mnrasl/slt007

Crossref

Search ADS

Khaire

V.

,

Srianand

R.

,

2015a

,

MNRAS

,

451

,

L30

(KS15a)

10.1093/mnrasl/slv060

Crossref

Search ADS

Khaire

V.

,

Srianand

R.

,

2015b

,

ApJ

,

805

,

33

(KS15b)

10.1088/0004-637X/805/1/33

Crossref

Search ADS

Khaire

V.

,

Srianand

R.

,

Choudhury

T. R.

,

Gaikwad

P.

,

2016

,

MNRAS

,

457

,

4051

10.1093/mnras/stw192

Crossref

Search ADS

Kim

T.-S.

,

Cristiani

S.

,

D’Odorico

S.

,

2001

,

A&A

,

373

,

757

10.1051/0004-6361:20010650

Crossref

Search ADS

Kim

T.-S.

,

Partl

A. M.

,

Carswell

R. F.

,

Müller

V.

,

2013

,

A&A

,

552

,

A77

10.1051/0004-6361/201220042

Crossref

Search ADS

Kinzer

R. L.

,

Jung

G. V.

,

Gruber

D. E.

,

Matteson

J. L.

,

Peterson

L. E.

,

1997

,

ApJ

,

475

,

361

10.1086/303507

Crossref

Search ADS

Kirkman

D.

,

Tytler

D.

,

Lubin

D.

,

Charlton

J.

,

2007

,

MNRAS

,

376

,

1227

10.1111/j.1365-2966.2007.11502.x

Crossref

Search ADS

Kneiske

T. M.

,

Dole

H.

,

2010

,

A&A

,

515

,

A19

10.1051/0004-6361/200912000

Crossref

Search ADS

Kollmeier

J. A.

et al. ,

2014

,

ApJ

,

789

,

L32

10.1088/2041-8205/789/2/L32

Crossref

Search ADS

Kriss

G. A.

et al. ,

2001

,

Science

,

293

,

1112

10.1126/science.1062693

Crossref

Search ADS

PubMed

Kulkarni

G.

,

Hennawi

J. F.

,

Oñorbe

J.

,

Rorai

A.

,

Springel

V.

,

2015

,

ApJ

,

812

,

30

10.1088/0004-637X/812/1/30

Crossref

Search ADS

Kulkarni

V. P.

,

Fall

S. M.

,

1993

,

ApJ

,

413

,

L63

10.1086/186960

Crossref

Search ADS

La Plante

P.

,

Trac

H.

,

2016

,

ApJ

,

828

,

90

10.3847/0004-637X/828/2/90

Crossref

Search ADS

Larson

D.

et al. ,

2011

,

ApJS

,

192

,

16

10.1088/0067-0049/192/2/16

Crossref

Search ADS

Lehner

N.

,

O’Meara

J. M.

,

Fox

A. J.

,

Howk

J. C.

,

Prochaska

J. X.

,

Burns

V.

,

Armstrong

A. A.

,

2014

,

ApJ

,

788

,

119

10.1088/0004-637X/788/2/119

Crossref

Search ADS

Leitet

E.

,

Bergvall

N.

,

Hayes

M.

,

Linné

S.

,

Zackrisson

E.

,

2013

,

A&A

,

553

,

A106

10.1051/0004-6361/201118370

Crossref

Search ADS

Leitherer

C.

et al. ,

1999

,

ApJS

,

123

,

3

10.1086/313233

Crossref

Search ADS

Leitherer

C.

,

Hernandez

S.

,

Lee

J. C.

,

Oey

M. S.

,

2016

,

ApJ

,

823

,

64

10.3847/0004-637X/823/1/64

Crossref

Search ADS

Lidz

A.

,

Faucher-Giguère

C.-A.

,

Dall’Aglio

A.

,

McQuinn

M.

,

Fechner

C.

,

Zaldarriaga

M.

,

Hernquist

L.

,

Dutta

S.

,

2010

,

ApJ

,

718

,

199

10.1088/0004-637X/718/1/199

Crossref

Search ADS

Liu

T.

et al. ,

2017

,

ApJS

,

232

,

8

10.3847/1538-4365/aa7847

Crossref

Search ADS

Lusso

E.

et al. ,

2013

,

ApJ

,

777

,

86

10.1088/0004-637X/777/2/86

Crossref

Search ADS

Lusso

E.

,

Worseck

G.

,

Hennawi

J. F.

,

Prochaska

J. X.

,

Vignali

C.

,

Stern

J.

,

O’Meara

J. M.

,

2015

,

MNRAS

,

449

,

4204

10.1093/mnras/stv516

Crossref

Search ADS

Ma

X.

,

Kasen

D.

,

Hopkins

P. F.

,

Faucher-Giguère

C.-A.

,

Quataert

E.

,

Kereš

D.

,

Murray

N.

,

2015

,

MNRAS

,

453

,

960

10.1093/mnras/stv1679

Crossref

Search ADS

Madau

P.

,

Dickinson

M.

,

2014

,

ARA&A

,

52

,

415

10.1146/annurev-astro-081811-125615

Crossref

Search ADS

Madau

P.

,

Fragos

T.

,

2017

,

ApJ

,

840

,

39

10.3847/1538-4357/aa6af9

Crossref

Search ADS

Madau

P.

,

Haardt

F.

,

2015

,

ApJ

,

813

,

L8

10.1088/2041-8205/813/1/L8

Crossref

Search ADS

Madau

P.

,

Haardt

F.

,

Rees

M. J.

,

1999

,

ApJ

,

514

,

648

10.1086/306975

Crossref

Search ADS

Marchi

F.

et al. ,

2017

,

A&A

,

601

,

A73

10.1051/0004-6361/201630054

Crossref

Search ADS

Mason

C. A.

,

Treu

T.

,

Dijkstra

M.

,

Mesinger

A.

,

Trenti

M.

,

Pentericci

L.

,

de Barros

S.

,

Vanzella

E.

,

2018

, ,

ApJ

,

856

,

2

10.3847/1538-4357/aab0a7

Crossref

Search ADS

Masters

D.

et al. ,

2012

,

ApJ

,

755

,

169

10.1088/0004-637X/755/2/169

Crossref

Search ADS

Matthee

J.

,

Sobral

D.

,

Best

P.

,

Khostovan

A. A.

,

Oteo

I.

,

Bouwens

R.

,

Röttgering

H.

,

2017

,

MNRAS

,

465

,

3637

10.1093/mnras/stw2973

Crossref

Search ADS

McGreer

I. D.

et al. ,

2013

,

ApJ

,

768

,

105

10.1088/0004-637X/768/2/105

Crossref

Search ADS

McGreer

I. D.

,

Mesinger

A.

,

D’Odorico

V.

,

2015

,

MNRAS

,

447

,

499

10.1093/mnras/stu2449

Crossref

Search ADS

McGreer

I. D.

,

Fan

X.

,

Jiang

L.

,

Cai

Z.

,

2018

,

AJ

,

155

,

131

10.3847/1538-3881/aaaab4

Crossref

Search ADS

McLeod

D. J.

,

McLure

R. J.

,

Dunlop

J. S.

,

Robertson

B. E.

,

Ellis

R. S.

,

Targett

T. A.

,

2015

,

MNRAS

,

450

,

3032

10.1093/mnras/stv780

Crossref

Search ADS

McQuinn

M.

,

2016

,

ARA&A

,

54

,

313

10.1146/annurev-astro-082214-122355

Crossref

Search ADS

McQuinn

M.

,

Worseck

G.

,

2014

,

MNRAS

,

440

,

2406

10.1093/mnras/stu242

Crossref

Search ADS

McQuinn

M.

,

Lidz

A.

,

Zaldarriaga

M.

,

Hernquist

L.

,

Hopkins

P. F.

,

Dutta

S.

,

Faucher-Giguère

C.-A.

,

2009

,

ApJ

,

694

,

842

10.1088/0004-637X/694/2/842

Crossref

Search ADS

Meiksin

A. A.

,

2009

,

Rev. Mod. Phys.

,

81

,

1405

10.1103/RevModPhys.81.1405

Crossref

Search ADS

Meiring

J. D.

,

Tripp

T. M.

,

Werk

J. K.

,

Howk

J. C.

,

Jenkins

E. B.

,

Prochaska

J. X.

,

Lehner

N.

,

Sembach

K. R.

,

2013

,

ApJ

,

767

,

49

10.1088/0004-637X/767/1/49

Crossref

Search ADS

Mesinger

A.

,

Aykutalp

A.

,

Vanzella

E.

,

Pentericci

L.

,

Ferrara

A.

,

Dijkstra

M.

,

2015

,

MNRAS

,

446

,

566

10.1093/mnras/stu2089

Crossref

Search ADS

Micheva

G.

,

Iwata

I.

,

Inoue

A. K.

,

Matsuda

Y.

,

Yamada

T.

,

Hayashino

T.

,

2017

,

MNRAS

,

465

,

316

10.1093/mnras/stw2700

Crossref

Search ADS

Miralda-Escude

J.

,

Ostriker

J. P.

,

1990

,

ApJ

,

350

,

1

10.1086/168358

Crossref

Search ADS

Mostardi

R. E.

,

Shapley

A. E.

,

Steidel

C. C.

,

Trainor

R. F.

,

Reddy

N. A.

,

Siana

B.

,

2015

,

ApJ

,

810

,

107

10.1088/0004-637X/810/2/107

Crossref

Search ADS

Muzahid

S.

,

Srianand

R.

,

Petitjean

P.

,

2011

,

MNRAS

,

410

,

2193

10.1111/j.1365-2966.2010.17592.x

Crossref

Search ADS

Muzahid

S.

,

Srianand

R.

,

Bergeron

J.

,

Petitjean

P.

,

2012

,

MNRAS

,

421

,

446

10.1111/j.1365-2966.2011.20324.x

Crossref

Muzahid

S.

,

Fonseca

G.

,

Roberts

A.

,

Rosenwasser

B.

,

Richter

P.

,

Narayanan

A.

,

Churchill

C.

,

Charlton

J.

,

2018

,

MNRAS

,

476

,

4965

10.1093/mnras/sty529

Crossref

Search ADS

Narayanan

A.

,

Savage

B. D.

,

Wakker

B. P.

,

2012

,

ApJ

,

752

,

65

10.1088/0004-637X/752/1/65

Crossref

Search ADS

Narayanan

A.

,

Savage

B. D.

,

Mishra

P. K.

,

Wakker

B. P.

,

Khaire

V.

,

Wadadekar

Y.

,

2018

,

MNRAS

,

475

,

3529

Crossref

Search ADS

Neronov

A.

,

Vovk

I.

,

2010

,

Science

,

328

,

73

10.1126/science.1184192

Crossref

Search ADS

PubMed

Neufeld

D. A.

,

1990

,

ApJ

,

350

,

216

10.1086/168375

Crossref

Search ADS

Neufeld

D. A.

,

1991

,

ApJ

,

370

,

L85

10.1086/185983

Crossref

Search ADS

Noterdaeme

P.

et al. ,

2012

,

A&A

,

547

,

L1

10.1051/0004-6361/201220259

Crossref

Search ADS

Noterdaeme

P.

,

Ledoux

C.

,

Srianand

R.

,

Petitjean

P.

,

Lopez

S.

,

2009

,

A&A

,

503

,

765

10.1051/0004-6361/200912330

Crossref

Search ADS

O’Meara

J. M.

,

Prochaska

J. X.

,

Burles

S.

,

Prochter

G.

,

Bernstein

R. A.

,

Burgess

K. M.

,

2007

,

ApJ

,

656

,

666

10.1086/510711

Crossref

Search ADS

O’Meara

J. M.

,

Prochaska

J. X.

,

Worseck

G.

,

Chen

H.-W.

,

Madau

P.

,

2013

,

ApJ

,

765

,

137

10.1088/0004-637X/765/2/137

Crossref

Search ADS

Oesch

P. A.

et al. ,

2014

,

ApJ

,

786

,

108

10.1088/0004-637X/786/2/108

Crossref

Search ADS

Oñorbe

J.

,

Hennawi

J. F.

,

Lukić

Z.

,

2017a

,

ApJ

,

837

,

106

10.3847/1538-4357/aa6031

Crossref

Search ADS

Oñorbe

J.

,

Hennawi

J. F.

,

Lukić

Z.

,

Walther

M.

,

2017b

,

ApJ

,

847

,

63

10.3847/1538-4357/aa898d

Crossref

Search ADS

Paardekooper

J.-P.

,

Pelupessy

F. I.

,

Altay

G.

,

Kruip

C. J. H.

,

2011

,

A&A

,

530

,

A87

10.1051/0004-6361/201116841

Crossref

Search ADS

Pachat

S.

,

Narayanan

A.

,

Muzahid

S.

,

Khaire

V.

,

Srianand

R.

,

Wakker

B. P.

,

Savage

B. D.

,

2016

,

MNRAS

,

458

,

733

10.1093/mnras/stw194

Crossref

Search ADS

Pachat

S.

,

Narayanan

A.

,

Khaire

V.

,

Savage

B. D.

,

Muzahid

S.

,

Wakker

B. P.

,

2017

,

MNRAS

,

471

,

792

10.1093/mnras/stx1435

Crossref

Search ADS

Padmanabhan

H.

,

Choudhury

T. R.

,

Srianand

R.

,

2014

,

MNRAS

,

443

,

3761

10.1093/mnras/stu1433

Crossref

Search ADS

Palanque-Delabrouille

N.

et al. ,

2013

,

A&A

,

551

,

A29

10.1051/0004-6361/201220379

Crossref

Search ADS

Paresce

F.

,

McKee

C. F.

,

Bowyer

S.

,

1980

,

ApJ

,

240

,

387

10.1086/158244

Crossref

Search ADS

Peebles

P. J. E.

,

1993

,

Principles of Physical Cosmology

,

Princeton University Press (Verlag)

Peeples

M. S.

,

Werk

J. K.

,

Tumlinson

J.

,

Oppenheimer

B. D.

,

Prochaska

J. X.

,

Katz

N.

,

Weinberg

D. H.

,

2014

,

ApJ

,

786

,

54

10.1088/0004-637X/786/1/54

Crossref

Search ADS

Péroux

C.

,

Dessauges-Zavadsky

M.

,

D’Odorico

S.

,

Sun Kim

T.

,

McMahon

R. G.

,

2005

,

MNRAS

,

363

,

479

10.1111/j.1365-2966.2005.09432.x

Crossref

Search ADS

Planck Collaboration

et al. ,

2016a

,

A&A

,

594

,

A13

10.1051/0004-6361/201525830

Crossref

Search ADS

Planck Collaboration

et al. ,

2016b

,

A&A

,

596

,

A107

10.1051/0004-6361/201628890

Crossref

Search ADS

Prochaska

J. X.

et al. ,

2017

,

ApJ

,

837

,

169

10.3847/1538-4357/aa6007

Crossref

Search ADS

Prochaska

J. X.

,

Worseck

G.

,

O’Meara

J. M.

,

2009

,

ApJ

,

705

,

L113

10.1088/0004-637X/705/2/L113

Crossref

Search ADS

Prochaska

J. X.

,

O’Meara

J. M.

,

Worseck

G.

,

2010

,

ApJ

,

718

,

392

10.1088/0004-637X/718/1/392

Crossref

Search ADS

Prochaska

J. X.

,

Madau

P.

,

O’Meara

J. M.

,

Fumagalli

M.

,

2014

,

MNRAS

,

438

,

476

10.1093/mnras/stt2218

Crossref

Search ADS

Puchwein

E.

,

Bolton

J. S.

,

Haehnelt

M. G.

,

Madau

P.

,

Becker

G. D.

,

Haardt

F.

,

2015

,

MNRAS

,

450

,

4081

10.1093/mnras/stv773

Crossref

Search ADS

Puchwein

E.

,

Haardt

F.

,

Haehnelt

M. G.

,

Madau

P.

,

2019

,

MNRAS

, (arXiv:1801.04931)

Puschnig

J.

et al. ,

2017

,

MNRAS

,

469

,

3252

10.1093/mnras/stx951

Crossref

Search ADS

Rao

S. M.

,

Turnshek

D. A.

,

Nestor

D. B.

,

2006

,

ApJ

,

636

,

610

10.1086/498132

Crossref

Search ADS

Rauch

M.

et al. ,

1997

,

ApJ

,

489

,

7

Crossref

Search ADS

Revnivtsev

M.

,

Gilfanov

M.

,

Sunyaev

R.

,

Jahoda

K.

,

Markwardt

C.

,

2003

,

A&A

,

411

,

329

10.1051/0004-6361:20031386

Crossref

Search ADS

Ricci

F.

,

Marchesi

S.

,

Shankar

F.

,

La Franca

F.

,

Civano

F.

,

2017

,

MNRAS

,

465

,

1915

10.1093/mnras/stw2909

Crossref

Search ADS

Rieke

G. H.

,

Alonso-Herrero

A.

,

Weiner

B. J.

,

Pérez-González

P. G.

,

Blaylock

M.

,

Donley

J. L.

,

Marcillac

D.

,

2009

,

ApJ

,

692

,

556

10.1088/0004-637X/692/1/556

Crossref

Search ADS

Rorai

A.

et al. ,

2017

,

Science

,

356

,

418

10.1126/science.aaf9346

Crossref

Search ADS

PubMed

Rosdahl

J.

et al. ,

2018

,

479

,

994

Ross

N. P.

et al. ,

2013

,

ApJ

,

773

,

14

10.1088/0004-637X/773/1/14

Crossref

Search ADS

Rutkowski

M. J.

et al. ,

2016

,

ApJ

,

819

,

81

10.3847/0004-637X/819/1/81

Crossref

Search ADS

Rutkowski

M. J.

et al. ,

2017

,

ApJ

,

841

,

L27

10.3847/2041-8213/aa733b

Crossref

Search ADS

Salpeter

E. E.

,

1955

,

ApJ

,

121

,

161

10.1086/145971

Crossref

Search ADS

Samui

S.

,

Srianand

R.

,

Subramanian

K.

,

2007

,

MNRAS

,

377

,

285

10.1111/j.1365-2966.2007.11603.x

Crossref

Search ADS

Savage

B. D.

,

Lehner

N.

,

Wakker

B. P.

,

Sembach

K. R.

,

Tripp

T. M.

,

2005

,

ApJ

,

626

,

776

10.1086/429985

Crossref

Search ADS

Savage

B. D.

,

Narayanan

A.

,

Lehner

N.

,

Wakker

B. P.

,

2011

,

ApJ

,

731

,

14

10.1088/0004-637X/731/1/14

Crossref

Search ADS

Savage

B. D.

,

Kim

T.-S.

,

Wakker

B. P.

,

Keeney

B.

,

Shull

J. M.

,

Stocke

J. T.

,

Green

J. C.

,

2014

,

ApJS

,

212

,

8

10.1088/0067-0049/212/1/8

Crossref

Search ADS

Sazonov

S. Y.

,

Ostriker

J. P.

,

Sunyaev

R. A.

,

2004

,

MNRAS

,

347

,

144

10.1111/j.1365-2966.2004.07184.x

Crossref

Search ADS

Schaye

J.

,

2001

,

ApJ

,

559

,

507

10.1086/322421

Crossref

Search ADS

Schaye

J.

,

Aguirre

A.

,

Kim

T.-S.

,

Theuns

T.

,

Rauch

M.

,

Sargent

W. L. W.

,

2003

,

ApJ

,

596

,

768

10.1086/378044

Crossref

Search ADS

Schenker

M. A.

,

Ellis

R. S.

,

Konidaris

N. P.

,

Stark

D. P.

,

2014

,

ApJ

,

795

,

20

10.1088/0004-637X/795/1/20

Crossref

Search ADS

Schulze

A.

,

Wisotzki

L.

,

Husemann

B.

,

2009

,

A&A

,

507

,

781

10.1051/0004-6361/200912730

Crossref

Search ADS

Scott

J. E.

,

Kriss

G. A.

,

Brotherton

M.

,

Green

R. F.

,

Hutchings

J.

,

Shull

J. M.

,

Zheng

W.

,

2004

,

ApJ

,

615

,

135

10.1086/422336

Crossref

Search ADS

Scully

S. T.

,

Malkan

M. A.

,

Stecker

F. W.

,

2014

,

ApJ

,

784

,

138

10.1088/0004-637X/784/2/138

Crossref

Search ADS

Shapiro

P. R.

,

Giroux

M. L.

,

Babul

A.

,

1994

,

ApJ

,

427

,

25

10.1086/174120

Crossref

Search ADS

Shapley

A. E.

,

Steidel

C. C.

,

Strom

A. L.

,

Bogosavljević

M.

,

Reddy

N. A.

,

Siana

B.

,

Mostardi

R. E.

,

Rudie

G. C.

,

2016

,

ApJ

,

826

,

L24

10.3847/2041-8205/826/2/L24

Crossref

Search ADS

Shull

J. M.

,

Roberts

D.

,

Giroux

M. L.

,

Penton

S. V.

,

Fardal

M. A.

,

1999

,

AJ

,

118

,

1450

10.1086/301053

Crossref

Search ADS

Shull

J. M.

,

Tumlinson

J.

,

Giroux

M. L.

,

Kriss

G. A.

,

Reimers

D.

,

2004

,

ApJ

,

600

,

570

10.1086/379924

Crossref

Search ADS

Shull

J. M.

,

France

K.

,

Danforth

C. W.

,

Smith

B.

,

Tumlinson

J.

,

2010

,

ApJ

,

722

,

1312

10.1088/0004-637X/722/2/1312

Crossref

Search ADS

Shull

J. M.

,

Harness

A.

,

Trenti

M.

,

Smith

B. D.

,

2012

,

ApJ

,

747

,

100

10.1088/0004-637X/747/2/100

Crossref

Search ADS

Shull

J. M.

,

Danforth

C. W.

,

Tilton

E. M.

,

2014

,

ApJ

,

796

,

49

10.1088/0004-637X/796/1/49

Crossref

Search ADS

Shull

J. M.

,

Moloney

J.

,

Danforth

C. W.

,

Tilton

E. M.

,

2015

,

ApJ

,

811

,

3

10.1088/0004-637X/811/1/3

Crossref

Search ADS

Siana

B.

et al. ,

2010

,

ApJ

,

723

,

241

10.1088/0004-637X/723/1/241

Crossref

Search ADS

Siana

B.

et al. ,

2015

,

ApJ

,

804

,

17

10.1088/0004-637X/804/1/17

Crossref

Search ADS

Smith

B. M.

et al. ,

2016

,

preprint

(http://adsabs.harvard.edu/abs/2016arXiv160201555S arXiv:1602.01555)

Songaila

A.

,

Cowie

L. L.

,

1996

,

AJ

,

112

,

335

10.1086/118018

Crossref

Search ADS

Songaila

A.

,

Cowie

L. L.

,

2010

,

ApJ

,

721

,

1448

10.1088/0004-637X/721/2/1448

Crossref

Search ADS

Springel

V.

,

Yoshida

N.

,

White

S. D. M.

,

2001

,

New Astron.

,

6

,

79

10.1016/S1384-1076(01)00042-2

Crossref

Search ADS

Srianand

R.

,

Khare

P.

,

1996

,

MNRAS

,

280

,

767

10.1093/mnras/280.3.767

Crossref

Search ADS

Stecker

F. W.

,

de Jager

O. C.

,

Salamon

M. H.

,

1992

,

ApJ

,

390

,

L49

10.1086/186369

Crossref

Search ADS

Stecker

F. W.

,

Baring

M. G.

,

Summerlin

E. J.

,

2007

,

ApJ

,

667

,

L29

10.1086/522005

Crossref

Search ADS

Stevans

M. L.

,

Shull

J. M.

,

Danforth

C. W.

,

Tilton

E. M.

,

2014

,

ApJ

,

794

,

75

10.1088/0004-637X/794/1/75

Crossref

Search ADS

Strong

A. W.

,

Moskalenko

I. V.

,

Reimer

O.

,

2003

,

Int. Cosm. Ray Conf.

,

5

,

2687

Sunyaev

R. A.

,

1969

,

Astrophys. Lett.

,

3

,

33

Takeuchi

T. T.

,

Buat

V.

,

Burgarella

D.

,

2005

,

A&A

,

440

,

L17

10.1051/0004-6361:200500158

Crossref

Search ADS

Tavecchio

F.

,

Ghisellini

G.

,

Bonnoli

G.

,

Foschini

L.

,

2011

,

MNRAS

,

414

,

3566

10.1111/j.1365-2966.2011.18657.x

Crossref

Search ADS

Telfer

R. C.

,

Zheng

W.

,

Kriss

G. A.

,

Davidsen

A. F.

,

2002

,

ApJ

,

565

,

773

10.1086/324689

Crossref

Search ADS

Tilton

E. M.

,

Stevans

M. L.

,

Shull

J. M.

,

Danforth

C. W.

,

2016

,

ApJ

,

817

,

56

10.3847/0004-637X/817/1/56

Crossref

Search ADS

Topping

M. W.

,

Shull

J. M.

,

2015

,

ApJ

,

800

,

97

10.1088/0004-637X/800/2/97

Crossref

Search ADS

Treister

E.

,

Urry

C. M.

,

2005

,

ApJ

,

630

,

115

10.1086/431892

Crossref

Search ADS

Treister

E.

,

Urry

C. M.

,

2006

,

ApJ

,

652

,

L79

10.1086/510237

Crossref

Search ADS

Treister

E.

,

Urry

C. M.

,

Virani

S.

,

2009

,

ApJ

,

696

,

110

10.1088/0004-637X/696/1/110

Crossref

Search ADS

Tripp

T. M.

,

Sembach

K. R.

,

Bowen

D. V.

,

Savage

B. D.

,

Jenkins

E. B.

,

Lehner

N.

,

Richter

P.

,

2008

,

ApJS

,

177

,

39

10.1086/587486

Crossref

Search ADS

Ueda

Y.

,

Akiyama

M.

,

Hasinger

G.

,

Miyaji

T.

,

Watson

M. G.

,

2014

,

ApJ

,

786

,

104

10.1088/0004-637X/786/2/104

Crossref

Search ADS

Upton Sanderbeck

P. R.

,

McQuinn

M.

,

D’Aloisio

A.

,

Werk

J. K.

,

2018

,

ApJ

,

869

,

159

10.3847/1538-4357/aaeff2

Crossref

Search ADS

Urry

C. M.

,

Padovani

P.

,

1995

,

PASP

,

107

,

803

10.1086/133630

Crossref

Search ADS

Vanzella

E.

et al. ,

2016

,

ApJ

,

825

,

41

10.3847/0004-637X/825/1/41

Crossref

Search ADS

Vanzella

E.

,

Siana

B.

,

Cristiani

S.

,

Nonino

M.

,

2010

,

MNRAS

,

404

,

1672

10.1111/j.1365-2966.2010.16408.x

Crossref

Viel

M.

,

Haehnelt

M. G.

,

Bolton

J. S.

,

Kim

T.-S.

,

Puchwein

E.

,

Nasir

F.

,

Wakker

B. P.

,

2017

,

MNRAS

,

467

,

L86

10.1093/mnrasl/slx004

Crossref

Vito

F.

et al. ,

2018

,

MNRAS

,

473

,

2378

10.1093/mnras/stx2486

Crossref

Search ADS

Walther

M.

,

Oñorbe

J.

,

Hennawi

J. F.

,

Lukić

Z.

,

2018

,

preprint

(http://adsabs.harvard.edu/abs/2018arXiv180804367W arXiv:1808.04367)

Warwick

R. S.

,

Roberts

T. P.

,

1998

,

Astron. Nachr.

,

319

,

59

10.1002/asna.2123190126

Crossref

Search ADS

Watanabe

K.

,

Hartmann

D. H.

,

Leising

M. D.

,

The

L.-S.

,

Share

G. H.

,

Kinzer

R. L.

,

1997

, in

Dermer

C. D.

,

Strickman

M. S.

,

Kurfess

J. D.

, eds,

AIP Conf. Ser. Vol. 410, Proceedings of the Fourth Compton Symposium

. Am. Inst. Phys., New York, p.

1223

10.1063/1.53933

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Crossref

Weidenspointner

G.

et al. ,

2000

, in

McConnell

M. L.

,

Ryan

J. M.

, eds,

AIP Conf. Ser. Vol. 510

,

The Fifth Compton Symposium

,

Am. Inst. Phys

,

New York

, p.

467

10.1063/1.1307028

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Crossref

Weigel

A. K.

,

Schawinski

K.

,

Treister

E.

,

Urry

C. M.

,

Koss

M.

,

Trakhtenbrot

B.

,

2015

,

MNRAS

,

448

,

3167

10.1093/mnras/stv184

Crossref

Search ADS

Weinberg

D. H.

,

Hernquist

L.

,

Katz

N.

,

1997

,

ApJ

,

477

,

8

10.1086/303683

Crossref

Search ADS

Weymann

R. J.

et al. ,

1998

,

ApJ

,

506

,

1

10.1086/306233

Crossref

Search ADS

Worseck

G.

et al. ,

2011

,

ApJ

,

733

,

L24

10.1088/2041-8205/733/2/L24

Crossref

Search ADS

Worseck

G.

et al. ,

2014

,

MNRAS

,

445

,

1745

10.1093/mnras/stu1827

Crossref

Search ADS

Worseck

G.

,

Prochaska

J. X.

,

Hennawi

J. F.

,

McQuinn

M.

,

2016

,

ApJ

,

825

,

144

10.3847/0004-637X/825/2/144

Crossref

Search ADS

Worseck

G.

,

Davies

F. B.

,

Hennawi

J. F.

,

Prochaska

J. X.

,

2018

,

preprint(http://adsabs.harvard.edu/abs/2018arXiv180805247W)

Wyithe

J. S. B.

,

Bolton

J. S.

,

2011

,

MNRAS

,

412

,

1926

10.1111/j.1365-2966.2010.18030.x

Crossref

Search ADS

Zavala

J.

,

Vogelsberger

M.

,

Slatyer

T. R.

,

Loeb

A.

,

Springel

V.

,

2011

,

Phys. Rev. D

,

83

,

123513

10.1103/PhysRevD.83.123513

Crossref

Search ADS

Zheng

W.

et al. ,

2004

,

ApJ

,

605

,

631

10.1086/382498

Crossref

Search ADS

Zheng

W.

,

Kriss

G. A.

,

Telfer

R. C.

,

Grimes

J. P.

,

Davidsen

A. F.

,

1997

,

ApJ

,

475

,

469

10.1086/303560

Crossref

Search ADS

APPENDIX A: ESCAPE FRACTION MEASUREMENTS

In Table A1, we provide the details of the average escape fraction measurements that are shown in the left-hand panel of Fig. 3. The f_esc is obtained using the following relation:

\begin{eqnarray*} f_{\rm esc}=f^{\rm rel}_{\rm esc}10^{-0.4A_{\rm FUV}}\left (\frac{f_{\lambda _{\rm FUV}}}{{f_{\lambda _i}}}\right)_{\rm KS15} \left (\frac{f_{\lambda _{\rm FUV}}}{{f_{\lambda _i}}}\right)^{-1} \end{eqnarray*}

(A1)

where |$f^{\rm rel}_{\rm esc}$| is the relative escape fraction provided in the respective references assuming an intrinsic value of |$(f_{\lambda _{\rm FUV}}/f_{\lambda _i}$|⁠) where λ_FUV denotes the rest wavelength at FUV and the λ_i denotes rest wavelength where ionizing photons have been observed. The |$(f_{\lambda _{\rm FUV}}/f_{\lambda _i})_{\rm KS15}$| denotes the intrinsic value of |$(f_{\lambda _{\rm FUV}}/f_{\lambda _i}$|⁠) and |$10^{-0.4A_{\rm FUV}}$| is the dust correction from our fiducial galaxy emissivity model. We use the 1σ value of f_esc given in Matthee et al. (2017) without any correction since they use an indirect method to obtain f_esc from Hα emission.

Table A1.

Open in new tab

Escape fraction measurements.

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Reference	\|$z$\|-range	\|$z$\|_mean	λ_i (Å)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)$\|	\|$f^{\rm rel}_{\rm esc}$\| (1σ)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)_{\rm KS15}$\|	\|$10^{0.4A_{\rm FUV}}$\|	f_esc (1σ)
Rutkowski et al. (2016)	0.90−1.40	1.15	900	7.0	<0.027	5.63	6.07	<0.0036
Siana et al. (2010)	1.20−1.50	1.35	700	3.0	<0.006	8.40	5.91	<0.0028
Rutkowski et al. (2017)	2.38−2.90	2.56	900	3.0	<0.07	5.26	3.88	<0.0316
Micheva et al. (2017)^a	3.06−3.13	3.1	900	4.25	<0.228	5.06	3.2	<0.0849
Micheva et al. (2017)^b	3.06−3.13	3.1	900	4.25	<0.06	5.06	3.2	<0.0223
Grazian et al. (2017)^c	3.27−3.40	3.3	900	3.0	<0.103	5.0	3.0	<0.0572
Guaita et al. (2016)	3.11−3.53	3.4	900	5.0	<0.12	5.18	2.91	<0.0427
Japelj et al. (2017)^d	3.0−4.0	3.5	900	3.0	<0.20	4.96	2.83	<0.1168
Marchi et al. (2017)	3.5−4.5	3.81	895	3.0	0.09 ± 0.04	5.6	2.6	0.065 ± 0.029
Matthee et al. (2017)^e	2.20−2.24	2.22	Hα					<0.028

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Reference	\|$z$\|-range	\|$z$\|_mean	λ_i (Å)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)$\|	\|$f^{\rm rel}_{\rm esc}$\| (1σ)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)_{\rm KS15}$\|	\|$10^{0.4A_{\rm FUV}}$\|	f_esc (1σ)
Rutkowski et al. (2016)	0.90−1.40	1.15	900	7.0	<0.027	5.63	6.07	<0.0036
Siana et al. (2010)	1.20−1.50	1.35	700	3.0	<0.006	8.40	5.91	<0.0028
Rutkowski et al. (2017)	2.38−2.90	2.56	900	3.0	<0.07	5.26	3.88	<0.0316
Micheva et al. (2017)^a	3.06−3.13	3.1	900	4.25	<0.228	5.06	3.2	<0.0849
Micheva et al. (2017)^b	3.06−3.13	3.1	900	4.25	<0.06	5.06	3.2	<0.0223
Grazian et al. (2017)^c	3.27−3.40	3.3	900	3.0	<0.103	5.0	3.0	<0.0572
Guaita et al. (2016)	3.11−3.53	3.4	900	5.0	<0.12	5.18	2.91	<0.0427
Japelj et al. (2017)^d	3.0−4.0	3.5	900	3.0	<0.20	4.96	2.83	<0.1168
Marchi et al. (2017)	3.5−4.5	3.81	895	3.0	0.09 ± 0.04	5.6	2.6	0.065 ± 0.029
Matthee et al. (2017)^e	2.20−2.24	2.22	Hα					<0.028

Notes. Corresponding to the references provided in column (1), columns (2) and (3) provide range in redshifts and the mean redshift for the observed sample of galaxies, column (4) provides rest frame extreme-UV wavelength λ_i where Lyman-continuum has been observed, column (5) gives the fiducial values of |$f_{\lambda _{\rm FUV}}/f_{\lambda _i}$| and column (6) gives the 1σ values of relative escape fraction |$f^{\rm rel}_{\rm esc}$| obtained in these references. Columns (6) and (7) provide fiducial values of |$f_{\lambda _{\rm FUV}}/f_{\lambda _i}$| denoted as |$(f_{\lambda _{\rm FUV}}/f_{\lambda _i})_{\rm KS15}$| and the dust corrections (⁠|$10^{0.4A_{\rm FUV}}$|⁠) used in our galaxy emissivity model. Column (7) provides the absolute escape fraction values relevant to our galaxy model obtained by using equation (A1). These are plotted in the left-hand panel of Fig. 3.

^aObserved for a sample of Lyman-α emitters.

^bObserved for a sample of Lyman-break galaxies.

^cObtained for the galaxies with luminosity >0.2 L*.

^dObtained for the galaxies with luminosity >0.5 L*.

^eThe measurement is obtained using the Hα emission from galaxies.

Table A1.

Open in new tab

Escape fraction measurements.

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Reference	\|$z$\|-range	\|$z$\|_mean	λ_i (Å)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)$\|	\|$f^{\rm rel}_{\rm esc}$\| (1σ)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)_{\rm KS15}$\|	\|$10^{0.4A_{\rm FUV}}$\|	f_esc (1σ)
Rutkowski et al. (2016)	0.90−1.40	1.15	900	7.0	<0.027	5.63	6.07	<0.0036
Siana et al. (2010)	1.20−1.50	1.35	700	3.0	<0.006	8.40	5.91	<0.0028
Rutkowski et al. (2017)	2.38−2.90	2.56	900	3.0	<0.07	5.26	3.88	<0.0316
Micheva et al. (2017)^a	3.06−3.13	3.1	900	4.25	<0.228	5.06	3.2	<0.0849
Micheva et al. (2017)^b	3.06−3.13	3.1	900	4.25	<0.06	5.06	3.2	<0.0223
Grazian et al. (2017)^c	3.27−3.40	3.3	900	3.0	<0.103	5.0	3.0	<0.0572
Guaita et al. (2016)	3.11−3.53	3.4	900	5.0	<0.12	5.18	2.91	<0.0427
Japelj et al. (2017)^d	3.0−4.0	3.5	900	3.0	<0.20	4.96	2.83	<0.1168
Marchi et al. (2017)	3.5−4.5	3.81	895	3.0	0.09 ± 0.04	5.6	2.6	0.065 ± 0.029
Matthee et al. (2017)^e	2.20−2.24	2.22	Hα					<0.028

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Reference	\|$z$\|-range	\|$z$\|_mean	λ_i (Å)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)$\|	\|$f^{\rm rel}_{\rm esc}$\| (1σ)	\|$\Big (\frac{f_{\lambda _{\rm FUV}}}{f_{\lambda _i}}\Big)_{\rm KS15}$\|	\|$10^{0.4A_{\rm FUV}}$\|	f_esc (1σ)
Rutkowski et al. (2016)	0.90−1.40	1.15	900	7.0	<0.027	5.63	6.07	<0.0036
Siana et al. (2010)	1.20−1.50	1.35	700	3.0	<0.006	8.40	5.91	<0.0028
Rutkowski et al. (2017)	2.38−2.90	2.56	900	3.0	<0.07	5.26	3.88	<0.0316
Micheva et al. (2017)^a	3.06−3.13	3.1	900	4.25	<0.228	5.06	3.2	<0.0849
Micheva et al. (2017)^b	3.06−3.13	3.1	900	4.25	<0.06	5.06	3.2	<0.0223
Grazian et al. (2017)^c	3.27−3.40	3.3	900	3.0	<0.103	5.0	3.0	<0.0572
Guaita et al. (2016)	3.11−3.53	3.4	900	5.0	<0.12	5.18	2.91	<0.0427
Japelj et al. (2017)^d	3.0−4.0	3.5	900	3.0	<0.20	4.96	2.83	<0.1168
Marchi et al. (2017)	3.5−4.5	3.81	895	3.0	0.09 ± 0.04	5.6	2.6	0.065 ± 0.029
Matthee et al. (2017)^e	2.20−2.24	2.22	Hα					<0.028

Notes. Corresponding to the references provided in column (1), columns (2) and (3) provide range in redshifts and the mean redshift for the observed sample of galaxies, column (4) provides rest frame extreme-UV wavelength λ_i where Lyman-continuum has been observed, column (5) gives the fiducial values of |$f_{\lambda _{\rm FUV}}/f_{\lambda _i}$| and column (6) gives the 1σ values of relative escape fraction |$f^{\rm rel}_{\rm esc}$| obtained in these references. Columns (6) and (7) provide fiducial values of |$f_{\lambda _{\rm FUV}}/f_{\lambda _i}$| denoted as |$(f_{\lambda _{\rm FUV}}/f_{\lambda _i})_{\rm KS15}$| and the dust corrections (⁠|$10^{0.4A_{\rm FUV}}$|⁠) used in our galaxy emissivity model. Column (7) provides the absolute escape fraction values relevant to our galaxy model obtained by using equation (A1). These are plotted in the left-hand panel of Fig. 3.

^aObserved for a sample of Lyman-α emitters.

^bObserved for a sample of Lyman-break galaxies.

^cObtained for the galaxies with luminosity >0.2 L*.

^dObtained for the galaxies with luminosity >0.5 L*.

^eThe measurement is obtained using the Hα emission from galaxies.

APPENDIX B: X-RAY EMISSIVITY WITH PARAMETRIC SED

To obtain the X-ray emissivity, we used a simple parametric approach to construct X-ray SED of QSOs (see Section 3.1) following Sazonov et al. (2004) than full X-ray population synthesis. Even though our simple approach consistently reproduces the local EBL measurements at X-ray and γ-ray energies, it is important to validate its predictions at different redshifts. Therefore, in this section we compare the redshift evolution of our predicted X-ray emissivity with the measurements.

We use recent X-ray luminosity functions in soft (0.5−2 keV) and hard (2−10 keV) X-ray band by Ueda et al. (2014) and Aird et al. (2015) and calculate the emissivity with |$L_{\nu _0}^{\rm min}=0.1-0.01 L_{\nu _0}^*$| in equation (8). We used their luminosity function parameters obtained for luminosity-dependent density evolution (LDDE) case. Note that these emissivities are obtained from the intrinsic luminosity functions and therefore they can be considered as upper limits for the comparison with our model. The redshift evolution of this intrinsic emissivity along with our model predictions is shown in Fig. B1.

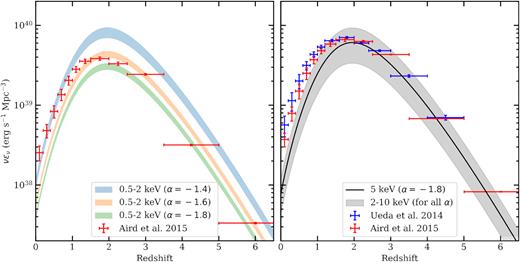
$Comparison of the X-ray emissivity obtained from X-ray luminosity functions and predicted by our parametric SED formulation as described in Section 3.1. The left-hand panel shows soft X-ray emissivity (0.5–2 keV range) and the right-hand panel shows hard X-ray emissivity (2–10 keV range). The emissivities obtained from our parametric approach are shown with colored shaded regions. The data points are obtained from the X-ray luminosity functions given in Ueda et al. (2014) and Aird et al. (2015) using their LDDE models. Vertical error-bars denote the range in emissivity calculated by setting the minimum luminosity in the range of $L_{\nu _0}^{\rm min}= 0.01 - 0.1 L_{\nu _0}^*$. Horizontal error-bars demarcate the redshift bin of the luminosity function. In soft X-ray regime our emissivity depends on the choice of α, therefore we show predictions for three values of α. At $z$ < 1, measurements are consistent with α = −1.4, while at $z$ > 1 they are more in line with α < −1.6. For hard X-ray regime our emissivity is independent of choice of α and at $z$ < 1 our predictions are systematically lower than the measurements. In both cases, our model predictions follow measured redshift evolution of X-ray emissivity reasonably well.$

Figure B1.

Comparison of the X-ray emissivity obtained from X-ray luminosity functions and predicted by our parametric SED formulation as described in Section 3.1. The left-hand panel shows soft X-ray emissivity (0.5–2 keV range) and the right-hand panel shows hard X-ray emissivity (2–10 keV range). The emissivities obtained from our parametric approach are shown with colored shaded regions. The data points are obtained from the X-ray luminosity functions given in Ueda et al. (2014) and Aird et al. (2015) using their LDDE models. Vertical error-bars denote the range in emissivity calculated by setting the minimum luminosity in the range of |$L_{\nu _0}^{\rm min}= 0.01 - 0.1 L_{\nu _0}^*$|⁠. Horizontal error-bars demarcate the redshift bin of the luminosity function. In soft X-ray regime our emissivity depends on the choice of α, therefore we show predictions for three values of α. At |$z$| < 1, measurements are consistent with α = −1.4, while at |$z$| > 1 they are more in line with α < −1.6. For hard X-ray regime our emissivity is independent of choice of α and at |$z$| < 1 our predictions are systematically lower than the measurements. In both cases, our model predictions follow measured redshift evolution of X-ray emissivity reasonably well.

Open in new tab Download slide

The left-hand panel of Fig. B1 shows soft X-ray emissivity along with our predictions for different values of α where shaded regions enclose the relevant energy range of 0.5−2 keV. At these energies our predictions depend on the choice of α. At |$z$| < 1 the measurements are consistent with α = −1.4 and higher than the predictions for α < −1.4, whereas at |$z$| > 1 they are more in line with α < −1.6. The right-hand panel of Fig. B1 shows hard X-ray emissivity along with our prediction for α = −1.8 for relevant energy range of 2−10 keV. At these energies our predictions are independent of the choice of α. At |$z$| < 1 our predictions are systematically lower than the measurements but consistent at higher-|$z$|⁠. Nevertheless, the redshift evolution of the emissivities in both soft and hard X-ray regime is reproduced quite well by our models. Note that our parametric SED does not evolve with redshift but the normalization that is anchored with respect to type 1 QSO emissivity evolves. The reasonable agreement among our predictions and the intrinsic emissivities and their redshift evolution, along with its success to reproduce the local X-ray and γ-ray background, justify our simple parametric approach.

APPENDIX C: γ-RAY OPACITY

The optical depth encountered by γ-rays depends on the energy of the γ-rays, their source redshift |$z$|₀ and the number density of the EBL photons at each |$z$| ≤ |$z$|₀. If n(E_ebl, |$z$|⁠) is the number density of the EBL photons at redshift |$z$| having energy E_ebl per unit energy then the optical depth encountered by γ-rays emitted at redshift |$z$|₀ with frequency ν_γ(1 + |$z$|₀) and observed on the Earth at frequency ν_γ is given by

\begin{eqnarray*} \tau _{\gamma }(\nu _{\gamma },z_0) &=& \frac{1}{2}\int ^{z_0}_0 \mathrm{ d}z\,\,\frac{\mathrm{ d}l}{\mathrm{ d}z}\int ^1_{-1}\mathrm{ d}(\cos \theta) \,\, (1-\cos \theta) \nonumber \\ && \times \, \int ^{\infty }_{E_{\mathrm{ min}}} \mathrm{ d}E_{\mathrm{ ebl}}\,\, n(E_{\mathrm{ ebl}},z)\,\,\sigma (E_\gamma (1+z),E_{\mathrm{ ebl}},\theta). \end{eqnarray*}

(C1)

Here E_γ = hν_γ,

\begin{eqnarray*} E_{\mathrm{ min}}=\frac{2m_e^2c^4}{h\nu _{\gamma }(1+z)(1-\cos \theta)}\, \, , \end{eqnarray*}

(C2)

and σ(E_γ(1 + |$z$|⁠), E_ebl, θ) is the cross-section for pair production (see equation 14 of KS15b).

Using the above equation, we calculate τ_γ(ν_γ, |$z$|⁠) at different |$z$| for our fiducial EBL model (Q18) and EBL model with α = −1.4. Note that to estimate τ_γ we include CMB in our EBL models. Results for three redshifts are shown in Fig. C1. The different features seen in τ_γ(ν_γ) can be naively mapped to the features seen in the EBL. For example, the γ-rays with E_γ < 20/(1 + |$z$|⁠) GeV (0.1/(1 + |$z$|⁠) GeV) are attenuated by EBL with E_ebl > 13.6 eV (500 eV), the γ-rays with E_γ > 100/(1 + |$z$|⁠) TeV are affected by CMB, and the bump in τ_γ around 100 GeV is due to rest of the EBL. The shaded region in Fig. C1 shows the observationally relevant opacities from 0.1 to 10. Within this region, EBL models with different α give same τ_γ since it is dominated by low-energy photons (E_ebl < 10 eV) that do not depend on the value of α. Fig. C1 shows that the intrinsic SED of blazars at E > 100 GeV in our formalism (Section 3) will be severely different from the one given by equation (13). The τ_γ values for our fiducial EBL model are available online.⁵

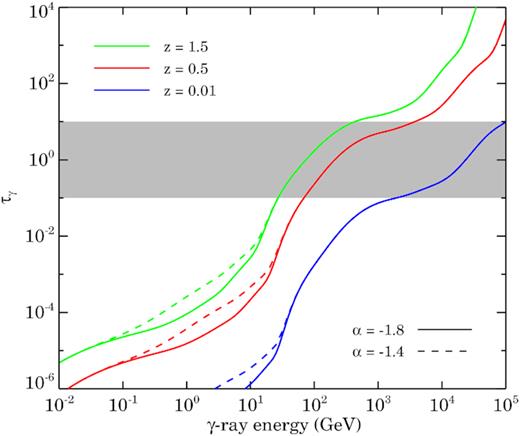
$Optical depth (τγ) encountered by γ-rays for different energy (in GeV) observed on the Earth, which were emitted from redshift $z$ = 0.01 (blue curves), $z$ = 0.5 (red curves), and $z$ = 1.5 (green curves). Solid and dashed curves are for our EBL models with α = −1.8 (fiducial) and α = −1.4 respectively. τγ is calculated by including CMB in both EBL models. Shaded region shows observationally relevant τγ values from 0.1 to 10, which are insensitive to the EBL photons with energy $E\lt 10$ eV and thus on values of assumed α.$

Figure C1.

Optical depth (τ_γ) encountered by γ-rays for different energy (in GeV) observed on the Earth, which were emitted from redshift |$z$| = 0.01 (blue curves), |$z$| = 0.5 (red curves), and |$z$| = 1.5 (green curves). Solid and dashed curves are for our EBL models with α = −1.8 (fiducial) and α = −1.4 respectively. τ_γ is calculated by including CMB in both EBL models. Shaded region shows observationally relevant τ_γ values from 0.1 to 10, which are insensitive to the EBL photons with energy |$E\lt 10$| eV and thus on values of assumed α.

Open in new tab Download slide

APPENDIX D: FRACTION OF TYPE 2 QSOs

In Section 3, the full SED of QSOs (k_ν) has been constructed to reproduce the X-ray and γ-ray background measurements. For such a constructed SED, the frequency-dependent ratio of Type-2 QSO SED and full SED, |$k^{\rm Q2}_{\nu }/k_{\nu }$|⁠, can be interpreted as the fraction of the type 2 QSOs, which is luminosity weighted and redshift independent. This fraction is decided by our constructed SED of type 1 QSOs in the X-ray energies, which depends on the value of α. Note that we have also included blazar contribution in |$k^{\rm Q2}_{\nu }$|⁠. In the left-hand panel of Fig. D1 we plot the ratio |$k^{\rm Q2}_{\nu }/k_{\nu }$| for different values of α (from equations 11–13). The α dependence can be easily seen in the plot. The small value of α leads to less emissivity from type 1 QSOs requiring more contribution from type 2 QSOs giving rise to the higher value of their fraction. At energies less than 1 keV (2 keV), the fraction of type 2 QSOs is less than 0.2 (0.5) for all α. At energies less than 500 eV, the contribution from type 2 QSOs drops below 5 per cent. Type 2 QSOs contribute significantly at hard X-ray energies around 10–100 keV consistent with the requirement of a large number of highly obscured type 2 QSOs in X-ray population synthesis models. At energies more than 1000 keV, the fraction of type 2 QSOs is unity owing to the fact that blazars are sole contributers at these energies (see also Draper & Ballantyne 2009). For comparison with the definition of the Compton thin and Compton thick type 2 QSOs, as the contribution to X-ray background at energies 2–10 keV and 10–30 keV, respectively, we plot a range in the fraction at these energies for different values of α in the right-hand panel of Fig. D1. We find that the fraction of Compton thin QSOs to vary between 0.2 and 0.8 for different α. It is 0.44–0.73 for our fiducial α = −1.8 model. For α ≤ −1.5, it varies from 0.38 to 0.78. These values are consistent with recent measurements (e.g. Buchner et al. 2015; Georgakakis et al. 2017; Vito et al. 2018) as well as with the prediction from X-ray population synthesis models (Treister & Urry 2006; Gilli et al. 2007). We need 20–30 per cent more contribution in 10–30 keV energy range from Compton thick QSOs, consistent with the predictions from Draper & Ballantyne (2009); however, it depends on the contribution of blazars that we do not resolve. All this interpretation is subject to our construction of type 1 QSO SED in X-rays. One can always adjust it to get different numbers while being consistent with the observed X-ray and γ-ray background. Note that our motivation is not to understand the fraction of type 2 QSOs but to provide an observationally consistent high-energy background.

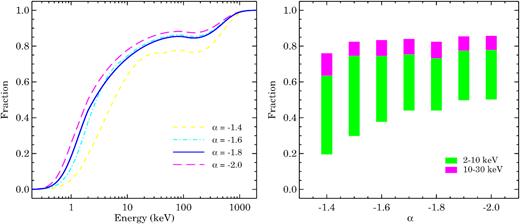
$Left-hand panel: The fraction of type 2 QSOs defined as a ratio $k^{\rm Q2}_{\nu }/k_{\nu }$ (see Section 3, equations 11–13) with energy in keV. The fraction also gives contribution of type 2 QSOs and blazars to EBL relative to type 1 QSOs for the SED templates used in our model. It depends on the extreme-UV power law index α of the type 1 QSO SED. At very high energies, fraction reaches unity due to blazar contribution included in the $k^{\rm Q2}_{\nu }$. Right-hand panel: The range in the fraction of type 2 QSOs in two energy ranges, 2–10 keV and 10–30 keV, for different values of α. The fraction in the energy range 2–10 keV and 10–30 keV can be thought as the fraction of type 2 QSOs that are Compton thin and Compton thick, respectively. Out of total type 2 QSOs, 20–30 per cent contribution comes from Compton thick QSOs.$

Figure D1.

Left-hand panel: The fraction of type 2 QSOs defined as a ratio |$k^{\rm Q2}_{\nu }/k_{\nu }$| (see Section 3, equations 11–13) with energy in keV. The fraction also gives contribution of type 2 QSOs and blazars to EBL relative to type 1 QSOs for the SED templates used in our model. It depends on the extreme-UV power law index α of the type 1 QSO SED. At very high energies, fraction reaches unity due to blazar contribution included in the |$k^{\rm Q2}_{\nu }$|⁠. Right-hand panel: The range in the fraction of type 2 QSOs in two energy ranges, 2–10 keV and 10–30 keV, for different values of α. The fraction in the energy range 2–10 keV and 10–30 keV can be thought as the fraction of type 2 QSOs that are Compton thin and Compton thick, respectively. Out of total type 2 QSOs, 20–30 per cent contribution comes from Compton thick QSOs.

Open in new tab Download slide

APPENDIX E: EBL MODELS WITH DIFFERENT VALUES OF α

Here, we provide the EBL models (plots and tables) obtained for different values of α ranging from −1.4 (Shull et al. 2012; Stevans et al. 2014) to −2.0 (Lusso et al. 2013; Khaire 2017) in the interval of 0.1. Fig. E1 shows photoionization rates |$\Gamma _{\rm H\, {\scriptscriptstyle I}}(z)$| and |$\Gamma _{\rm He \, {\scriptscriptstyle II}}(z)$|⁠, Fig. E2 shows photoheating rates ξ_H i and ξ_He ii, and Tables E1 to E7 provide these values for EBL models with different α from z = 0 to 15 including for He|$\, \, {\rm {\scriptstyle I}}$|⁠. Fig. E3 shows the local EBL from FIR to γ-rays and Fig. E4 shows UVB at redshifts |$z$| = 0–5. Refer to Section 4 for the relevant discussion on the trends seen in these plots.

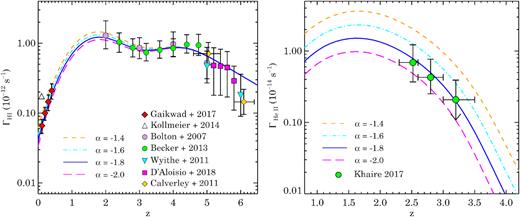
$The photoionization rates of H$\, \, {\rm {\scriptstyle I}}$ (ΓH i; left-hand panel) and He$\, \, {\rm {\scriptstyle II}}$ (ΓHe ii; right-hand panel) with $z$ from UVB models with different α. Various data points in the left-hand panel show the recent measurements of ΓH i. The ΓHe ii from Khaire (2017) is obtained by using the measurements of $\tau _{\alpha }^{\rm He II}$ from Worseck et al. (2016).$

Figure E1.

The photoionization rates of H|$\, \, {\rm {\scriptstyle I}}$| (Γ_H i; left-hand panel) and He|$\, \, {\rm {\scriptstyle II}}$| (Γ_He ii; right-hand panel) with |$z$| from UVB models with different α. Various data points in the left-hand panel show the recent measurements of Γ_H i. The Γ_He ii from Khaire (2017) is obtained by using the measurements of |$\tau _{\alpha }^{\rm He II}$| from Worseck et al. (2016).

Open in new tab Download slide

$The photoheating rates of H$\, \, {\rm {\scriptstyle I}}$ (ξH i; left-hand panel) and He$\, \, {\rm {\scriptstyle II}}$ (ξHe ii; right-hand panel) with $z$ from UVB models with different α. The dash and dot-dash curve show the results from UVB models of HM12 and FG09, respectively.$

Figure E2.

The photoheating rates of H|$\, \, {\rm {\scriptstyle I}}$| (ξ_H i; left-hand panel) and He|$\, \, {\rm {\scriptstyle II}}$| (ξ_He ii; right-hand panel) with |$z$| from UVB models with different α. The dash and dot-dash curve show the results from UVB models of HM12 and FG09, respectively.

Open in new tab Download slide

Figure E3.

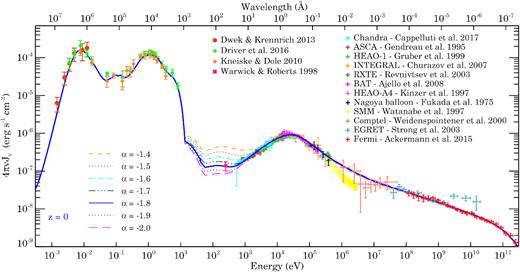
The intensity of |$z$| = 0 EBL models with different α from FIR to TeV γ-rays. For details on data points, refer to Section 4.3.

Open in new tab Download slide

Figure E4.

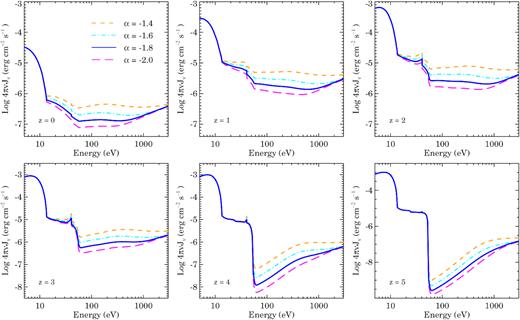
Spectrum of UVB models obtained for different values of α with energy (from 5 to 3000 eV) at |$z$| = 0, 1, 2, 3, 4, and 5. Solid blue curves show our fiducial UVB models with α = −1.8. The y-axis scales are kept same for top three panels and bottom two panels to see relative change in intensity.

Open in new tab Download slide

Table E1.

Open in new tab

Photoionization and photoheating rates for our fiducial Q18 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.058e-14	1.869e-14	6.262e-16	1.507e-13	1.494e-13	1.248e-14
0.1	6.310e-14	3.041e-14	9.453e-16	2.381e-13	2.383e-13	1.857e-14
0.2	9.353e-14	4.695e-14	1.378e-15	3.575e-13	3.640e-13	2.670e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.058e-14	1.869e-14	6.262e-16	1.507e-13	1.494e-13	1.248e-14
0.1	6.310e-14	3.041e-14	9.453e-16	2.381e-13	2.383e-13	1.857e-14
0.2	9.353e-14	4.695e-14	1.378e-15	3.575e-13	3.640e-13	2.670e-14

Table E1.

Open in new tab

Photoionization and photoheating rates for our fiducial Q18 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.058e-14	1.869e-14	6.262e-16	1.507e-13	1.494e-13	1.248e-14
0.1	6.310e-14	3.041e-14	9.453e-16	2.381e-13	2.383e-13	1.857e-14
0.2	9.353e-14	4.695e-14	1.378e-15	3.575e-13	3.640e-13	2.670e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.058e-14	1.869e-14	6.262e-16	1.507e-13	1.494e-13	1.248e-14
0.1	6.310e-14	3.041e-14	9.453e-16	2.381e-13	2.383e-13	1.857e-14
0.2	9.353e-14	4.695e-14	1.378e-15	3.575e-13	3.640e-13	2.670e-14

Table E2.

Open in new tab

Photoionization and photoheating rates for Q14 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	6.105e-14	3.709e-14	1.755e-15	2.544e-13	3.467e-13	3.675e-14
0.1	9.188e-14	5.816e-14	2.588e-15	3.895e-13	5.325e-13	5.372e-14
0.2	1.324e-13	8.706e-14	3.692e-15	5.691e-13	7.863e-13	7.588e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	6.105e-14	3.709e-14	1.755e-15	2.544e-13	3.467e-13	3.675e-14
0.1	9.188e-14	5.816e-14	2.588e-15	3.895e-13	5.325e-13	5.372e-14
0.2	1.324e-13	8.706e-14	3.692e-15	5.691e-13	7.863e-13	7.588e-14

Table E2.

Open in new tab

Photoionization and photoheating rates for Q14 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	6.105e-14	3.709e-14	1.755e-15	2.544e-13	3.467e-13	3.675e-14
0.1	9.188e-14	5.816e-14	2.588e-15	3.895e-13	5.325e-13	5.372e-14
0.2	1.324e-13	8.706e-14	3.692e-15	5.691e-13	7.863e-13	7.588e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	6.105e-14	3.709e-14	1.755e-15	2.544e-13	3.467e-13	3.675e-14
0.1	9.188e-14	5.816e-14	2.588e-15	3.895e-13	5.325e-13	5.372e-14
0.2	1.324e-13	8.706e-14	3.692e-15	5.691e-13	7.863e-13	7.588e-14

Table E3.

Open in new tab

Photoionization and photoheating rates for Q15 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	5.480e-14	3.099e-14	1.339e-15	2.214e-13	2.773e-13	2.745e-14
0.1	8.320e-14	4.907e-14	1.989e-15	3.418e-13	4.304e-13	4.039e-14
0.2	1.208e-13	7.403e-14	2.856e-15	5.031e-13	6.412e-13	5.741e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	5.480e-14	3.099e-14	1.339e-15	2.214e-13	2.773e-13	2.745e-14
0.1	8.320e-14	4.907e-14	1.989e-15	3.418e-13	4.304e-13	4.039e-14
0.2	1.208e-13	7.403e-14	2.856e-15	5.031e-13	6.412e-13	5.741e-14

Table E3.

Open in new tab

Photoionization and photoheating rates for Q15 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	5.480e-14	3.099e-14	1.339e-15	2.214e-13	2.773e-13	2.745e-14
0.1	8.320e-14	4.907e-14	1.989e-15	3.418e-13	4.304e-13	4.039e-14
0.2	1.208e-13	7.403e-14	2.856e-15	5.031e-13	6.412e-13	5.741e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	5.480e-14	3.099e-14	1.339e-15	2.214e-13	2.773e-13	2.745e-14
0.1	8.320e-14	4.907e-14	1.989e-15	3.418e-13	4.304e-13	4.039e-14
0.2	1.208e-13	7.403e-14	2.856e-15	5.031e-13	6.412e-13	5.741e-14

Table E4.

Open in new tab

Photoionization and photoheating rates for Q16 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.944e-14	2.602e-14	1.027e-15	1.938e-13	2.234e-13	2.071e-14
0.1	7.568e-14	4.162e-14	1.536e-15	3.016e-13	3.502e-13	3.064e-14
0.2	1.107e-13	6.333e-14	2.220e-15	4.472e-13	5.266e-13	4.379e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.944e-14	2.602e-14	1.027e-15	1.938e-13	2.234e-13	2.071e-14
0.1	7.568e-14	4.162e-14	1.536e-15	3.016e-13	3.502e-13	3.064e-14
0.2	1.107e-13	6.333e-14	2.220e-15	4.472e-13	5.266e-13	4.379e-14

Table E4.

Open in new tab

Photoionization and photoheating rates for Q16 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.944e-14	2.602e-14	1.027e-15	1.938e-13	2.234e-13	2.071e-14
0.1	7.568e-14	4.162e-14	1.536e-15	3.016e-13	3.502e-13	3.064e-14
0.2	1.107e-13	6.333e-14	2.220e-15	4.472e-13	5.266e-13	4.379e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.944e-14	2.602e-14	1.027e-15	1.938e-13	2.234e-13	2.071e-14
0.1	7.568e-14	4.162e-14	1.536e-15	3.016e-13	3.502e-13	3.064e-14
0.2	1.107e-13	6.333e-14	2.220e-15	4.472e-13	5.266e-13	4.379e-14

Table E5.

Open in new tab

Photoionization and photoheating rates for Q17 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.468e-14	2.194e-14	7.955e-16	1.701e-13	1.814e-13	1.586e-14
0.1	6.895e-14	3.540e-14	1.196e-15	2.670e-13	2.870e-13	2.357e-14
0.2	1.015e-13	5.425e-14	1.738e-15	3.984e-13	4.350e-13	3.382e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.468e-14	2.194e-14	7.955e-16	1.701e-13	1.814e-13	1.586e-14
0.1	6.895e-14	3.540e-14	1.196e-15	2.670e-13	2.870e-13	2.357e-14
0.2	1.015e-13	5.425e-14	1.738e-15	3.984e-13	4.350e-13	3.382e-14

Table E5.

Open in new tab

Photoionization and photoheating rates for Q17 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.468e-14	2.194e-14	7.955e-16	1.701e-13	1.814e-13	1.586e-14
0.1	6.895e-14	3.540e-14	1.196e-15	2.670e-13	2.870e-13	2.357e-14
0.2	1.015e-13	5.425e-14	1.738e-15	3.984e-13	4.350e-13	3.382e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	4.468e-14	2.194e-14	7.955e-16	1.701e-13	1.814e-13	1.586e-14
0.1	6.895e-14	3.540e-14	1.196e-15	2.670e-13	2.870e-13	2.357e-14
0.2	1.015e-13	5.425e-14	1.738e-15	3.984e-13	4.350e-13	3.382e-14

Table E6.

Open in new tab

Photoionization and photoheating rates for Q19 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.685e-14	1.586e-14	4.860e-16	1.332e-13	1.221e-13	9.640e-15
0.1	5.775e-14	2.604e-14	7.368e-16	2.121e-13	1.967e-13	1.439e-14
0.2	8.619e-14	4.048e-14	1.079e-15	3.205e-13	3.029e-13	2.075e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.685e-14	1.586e-14	4.860e-16	1.332e-13	1.221e-13	9.640e-15
0.1	5.775e-14	2.604e-14	7.368e-16	2.121e-13	1.967e-13	1.439e-14
0.2	8.619e-14	4.048e-14	1.079e-15	3.205e-13	3.029e-13	2.075e-14

Table E6.

Open in new tab

Photoionization and photoheating rates for Q19 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.685e-14	1.586e-14	4.860e-16	1.332e-13	1.221e-13	9.640e-15
0.1	5.775e-14	2.604e-14	7.368e-16	2.121e-13	1.967e-13	1.439e-14
0.2	8.619e-14	4.048e-14	1.079e-15	3.205e-13	3.029e-13	2.075e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.685e-14	1.586e-14	4.860e-16	1.332e-13	1.221e-13	9.640e-15
0.1	5.775e-14	2.604e-14	7.368e-16	2.121e-13	1.967e-13	1.439e-14
0.2	8.619e-14	4.048e-14	1.079e-15	3.205e-13	3.029e-13	2.075e-14

Table E7.

Open in new tab

Photoionization and photoheating rates for Q20 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.364e-14	1.361e-14	3.860e-16	1.187e-13	1.015e-13	7.721e-15
0.1	5.309e-14	2.250e-14	5.867e-16	1.903e-13	1.649e-13	1.152e-14
0.2	7.974e-14	3.519e-14	8.619e-16	2.893e-13	2.555e-13	1.662e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.364e-14	1.361e-14	3.860e-16	1.187e-13	1.015e-13	7.721e-15
0.1	5.309e-14	2.250e-14	5.867e-16	1.903e-13	1.649e-13	1.152e-14
0.2	7.974e-14	3.519e-14	8.619e-16	2.893e-13	2.555e-13	1.662e-14

Note: Full Tables E1–E7 in machine-readable format are available to download at http://www.iucaa.in/projects/cobra/ and at http://vikramkhaire.weebly.com/downloads.html .

Table E7.

Open in new tab

Photoionization and photoheating rates for Q20 UVB model.

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.364e-14	1.361e-14	3.860e-16	1.187e-13	1.015e-13	7.721e-15
0.1	5.309e-14	2.250e-14	5.867e-16	1.903e-13	1.649e-13	1.152e-14
0.2	7.974e-14	3.519e-14	8.619e-16	2.893e-13	2.555e-13	1.662e-14

\|$z$\|	\|$\Gamma _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\Gamma _{\rm He \, {\scriptscriptstyle II}}$\|	\|$\xi _{\rm H \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle I}}$\|	\|$\xi _{\rm He \, {\scriptscriptstyle II}}$\|
	s⁻¹	s⁻¹	s⁻¹	eV s⁻¹	eV s⁻¹	eV s⁻¹
0.0	3.364e-14	1.361e-14	3.860e-16	1.187e-13	1.015e-13	7.721e-15
0.1	5.309e-14	2.250e-14	5.867e-16	1.903e-13	1.649e-13	1.152e-14
0.2	7.974e-14	3.519e-14	8.619e-16	2.893e-13	2.555e-13	1.662e-14

Note: Full Tables E1–E7 in machine-readable format are available to download at http://www.iucaa.in/projects/cobra/ and at http://vikramkhaire.weebly.com/downloads.html .

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
February 2019	27
March 2019	29
April 2019	8
May 2019	28
June 2019	10
July 2019	12
August 2019	26
September 2019	16
October 2019	14
November 2019	6
December 2019	1
January 2020	8
February 2020	3
March 2020	3
April 2020	18
May 2020	3
June 2020	12
July 2020	4
August 2020	3
September 2020	7
October 2020	3
November 2020	1
December 2020	4
January 2021	2
March 2021	15
April 2021	2
May 2021	9
June 2021	12
July 2021	6
August 2021	3
September 2021	4
November 2021	2
December 2021	11
January 2022	5
February 2022	10
March 2022	5
April 2022	10
May 2022	18
June 2022	23
July 2022	31
August 2022	32
September 2022	32
October 2022	18
November 2022	22
December 2022	13
January 2023	19
February 2023	25
March 2023	50
April 2023	21
May 2023	20
June 2023	21
July 2023	14
August 2023	22
September 2023	22
October 2023	33
November 2023	28
December 2023	23
January 2024	65
February 2024	60
March 2024	30
April 2024	43
May 2024	25
June 2024	23
July 2024	41
August 2024	18
September 2024	28
October 2024	45
November 2024	23
December 2024	21
January 2025	17
February 2025	22
March 2025	42
April 2025	19
May 2025	10

Article Contents

New synthesis models of consistent extragalactic background light over cosmic time

ABSTRACT

1 INTRODUCTION

2 COSMOLOGICAL RADIATIVE TRANSFER

3 EMISSIVITY

3.1 QSO Emissivity

3.2 Galaxy emissivity

3.3 Diffuse emissivity

4 BASIC RESULTS

4.1 Photoionization and photoheating rates

4.2 H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization

4.3 The EBL spectrum

4.4 Uncertainties and caveats in the UVB models

4.4.1 QSO emissivity and SED

4.4.2 Galaxy emissivity and escape fraction

4.4.3 H|$\, \, {\rm {\scriptstyle I}}$| distribution and other uncertainties

4.4.4 Caveats from basic assumptions

5 SUMMARY

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

APPENDIX A: ESCAPE FRACTION MEASUREMENTS

APPENDIX B: X-RAY EMISSIVITY WITH PARAMETRIC SED

APPENDIX C: γ-RAY OPACITY

APPENDIX D: FRACTION OF TYPE 2 QSOs

APPENDIX E: EBL MODELS WITH DIFFERENT VALUES OF α

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

New synthesis models of consistent extragalactic background light over cosmic time Free

ABSTRACT

1 INTRODUCTION

2 COSMOLOGICAL RADIATIVE TRANSFER

3 EMISSIVITY

3.1 QSO Emissivity

3.2 Galaxy emissivity

3.3 Diffuse emissivity

4 BASIC RESULTS

4.1 Photoionization and photoheating rates

4.2 H|$\, \, {\rm {\scriptstyle I}}$| and He|$\, \, {\rm {\scriptstyle II}}$| reionization

4.3 The EBL spectrum

4.4 Uncertainties and caveats in the UVB models

4.4.1 QSO emissivity and SED

4.4.2 Galaxy emissivity and escape fraction

4.4.3 H|$\, \, {\rm {\scriptstyle I}}$| distribution and other uncertainties

4.4.4 Caveats from basic assumptions

5 SUMMARY

SUPPORTING INFORMATION

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

APPENDIX A: ESCAPE FRACTION MEASUREMENTS

APPENDIX B: X-RAY EMISSIVITY WITH PARAMETRIC SED

APPENDIX C: γ-RAY OPACITY

APPENDIX D: FRACTION OF TYPE 2 QSOs

APPENDIX E: EBL MODELS WITH DIFFERENT VALUES OF α

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

New synthesis models of consistent extragalactic background light over cosmic time