-
PDF
- Split View
-
Views
-
Cite
Cite
K Rice, L Malavolta, A Mayo, A Mortier, L A Buchhave, L Affer, A Vanderburg, M Lopez-Morales, E Poretti, L Zeng, A C Cameron, M Damasso, A Coffinet, D W Latham, A S Bonomo, F Bouchy, D Charbonneau, X Dumusque, P Figueira, A F Martinez Fiorenzano, R D Haywood, J Asher Johnson, E Lopez, C Lovis, M Mayor, G Micela, E Molinari, V Nascimbeni, C Nava, F Pepe, D F Phillips, G Piotto, D Sasselov, D Ségransan, A Sozzetti, S Udry, C Watson, Masses and radii for the three super-Earths orbiting GJ 9827, and implications for the composition of small exoplanets, Monthly Notices of the Royal Astronomical Society, Volume 484, Issue 3, April 2019, Pages 3731–3745, https://doi.org/10.1093/mnras/stz130
Close - Share Icon Share
Abstract
Super-Earths belong to a class of planet not found in the Solar system, but which appear common in the Galaxy. Given that some super-Earths are rocky, while others retain substantial atmospheres, their study can provide clues as to the formation of both rocky and gaseous planets, and – in particular – they can help to constrain the role of photoevaporation in sculpting the exoplanet population. GJ 9827 is a system already known to host three super-Earths with orbital periods of 1.2, 3.6, and 6.2 d. Here, we use new HARPS-N radial velocity measurements, together with previously published radial velocities, to better constrain the properties of the GJ 9827 planets. Our analysis cannot place a strong constraint on the mass of GJ 9827 c, but does indicate that GJ 9827 b is rocky with a composition that is probably similar to that of the Earth, while GJ 9827 d almost certainly retains a volatile envelope. Therefore, GJ 9827 hosts planets on either side of the radius gap that appears to divide super-Earths into pre-dominantly rocky ones that have radii below ∼1.5R⊕, and ones that still retain a substantial atmosphere and/or volatile components, and have radii above ∼2R⊕. That the less heavily irradiated of the three planets still retains an atmosphere, may indicate that photoevaporation has played a key role in the evolution of the planets in this system.
1 INTRODUCTION
One of the most exciting recent exoplanet results is the discovery that the most common type of exoplanet, with a period less than ∼100 d, is one with a radius between that of the Earth (1R⊕) and that of Neptune (∼4R⊕) (Howard et al. 2012; Batalha et al. 2013; Fulton et al. 2017; Fulton & Petigura 2018). Known as super-Earths, these appear to be common in the Galaxy, but are not found in our Solar system. It also appears that the transition from being preferentially rocky/terrestrial to having a substantial gaseous atmosphere occurs within this size range (Rogers 2015). Recent studies (Fulton et al. 2017; Zeng et al. 2017; Van Eylen et al. 2018) have suggested that there is in fact a gap in the radius distribution between 1.5 and 2R⊕, as predicted by Owen & Wu (2013) and Lopez & Fortney (2013). Planets tend to have radii less than ∼1.5R⊕ and may be pre-dominantly rocky, or they sustain a substantial gaseous envelope and have radii above 2R⊕.
Super-Earths are, therefore, an important population as they may provide clues as to both the formation of gas giants and the formation of rocky, terrestrial planets. In particular, they can help us to better understand the role that photoevaporation plays in sculpting the exoplanet population. It has been suggested that super-Earths probably formed with gas envelopes that make up at least a few per cent of their mass (Rogers et al. 2011; Lopez & Fortney 2014; Wolfgang & Lopez 2015). Those that are sufficiently strongly irradiated could then have lost their atmospheres via photoevaporation (Lopez, Fortney & Miller 2012; Owen & Wu 2013; Ehrenreich et al. 2015). Those that have not been sufficiently strongly irradiated retain their atmospheres. This could then explain the observed gap in the radius distribution (Owen & Wu 2017; Fulton et al. 2017; Lopez & Rice 2018; Van Eylen et al. 2018). There may, however, be alternative explanations for this observed radius gap, such as late giant impacts (Inamdar & Schlichting 2015) or the atmosphere being stripped by the cooling rocky core (Ginzburg, Schlichting & Sari 2016, 2018). This means that systems that have super-Earths on either side of this radius gap are particularly interesting.
In this paper, we present an analysis of one such system, the K2 target GJ 9827 (also known as K2-135, EPIC 246389858, or HIP 115752). It is already known to host 3 super-Earths with radii between 1 and ∼2R⊕, and with orbital periods of 1.21, 3.65, and 6.21 d (Niraula et al. 2017; Rodriguez et al. 2018). Rodriguez et al. (2018) and Niraula et al. (2017) suggest that GJ 9827 b has a radius of ∼1.6R⊕, GJ 9827 c has a radius of ∼1.3R⊕, while GJ 9827 d has a radius of about 2R⊕. This means that these planets have radii that approximately bracket the radius gap detected by Fulton et al. (2017) which, as already suggested, makes this a particularly interesting system for studying the origin of this gap. However, neither Rodriguez et al. (2018) nor Niraula et al. (2017) could independently estimate the planets masses and so used mass–radius relations (Weiss & Marcy 2014; Chen & Kipping 2017).
A recent radial velocity (RV) analysis (Teske et al. 2018) has, however, presented mass estimates for the GJ 9827 planets. This analysis was unable to place strong constraints on the masses of GJ 9827 c and d, but suggests that GJ 9827 b has a mass of ∼8.2 ± 1.53M⊕. With a radius of ∼1.64R⊕ (Rodriguez et al. 2018; Niraula et al. 2017), this result would make GJ 9827 b one of the densest known super-Earths. This mass and radius would suggest that GJ 9827 b has an iron core that makes up a significant fraction of its mass, and could indicate that it has undergone a mantle-stripping collision with another body of a similar mass (Marcus et al. 2010). A more recent analysis (Prieto-Arranz et al. 2018), however, suggests that the mass of GJ 9827 b is not as high as suggested by Teske et al. (2018) and, in fact, may have a composition similar to that of the Earth. This analysis also suggests that GJ 9827 c is also rocky, but that GJ 9827 d may retain a substantial, extended atmosphere.
Here, we repeat the light-curve analysis of GJ 9827 using the K2 data, which we present in Section 4. We also use the K2 light curve to constrain the stellar activity (Section 5). We then carry out an RV analysis using the same RV data as used by Teske et al. (2018), Niraula et al. (2017), and Prieto-Arranz et al. (2018), but with an additional 41 new RVs from the HARPS-N spectrograph (Cosentino et al. 2012, 2014). As we will discuss in Section 7, we were able to constrain the masses of GJ 9827 b and d to better than ‘10 per cent’ and about ‘20 per cent’, but were not able to place a strong constraint on the mass of GJ 9827 c. We also discuss what these results imply about the typical composition of planets below the radius gap (Fulton et al. 2017), a particular science goal of the HARPS-N Collaboration.
2 RADIAL VELOCITY OBSERVATIONS
2.1 HARPS-N spectroscopy
We collected a total of 43 RV spectra of GJ 9827 with the HARPS-N spectrograph (R = 115 000) installed on the 3.6-m Telescopio Nazionale Galileo at the Observatorio de los Muchachos in La Palma, Spain (Cosentino et al. 2012, 2014). We observed GJ 9827 between 2017 August and December as part of the HARPS-N Collaboration’s Guaranteed Time Observations (GTO) program. Our observational strategy consisted of taking one or two observations per night, separated by 2–3 h, for several consecutive nights in order to properly sample the RV curve of all the transiting planets.
All the observations had an exposure time of 1800s. We eliminated one observation, taken on BJD=2458048.36, as it had an anomalously low signal-to-noise ratio (S/N) of less than 20, and another, taken on BJD=2457991.62, was rejected by the data reduction software (DRS) because of abnormal flux correction.
GJ 9827 has a V-band magnitude of V = 10.25, so, with the exception of the two observations that were eliminated, we obtained spectra with signal-to-noise ratios in the range S/N = 37–121 (average S/N = 70), at 550 nm in 30 min exposures, resulting in an average RV precision of 1.9 m s−1.
The spectra were reduced with version 3.8 of the HARPS-N DRS, which includes corrections for colour systematics introduced by variations in seeing (Cosentino et al. 2014). The RVs were computed using a numerical weighted mask based on the synthetic spectrum of a K5 dwarf, following the methodology outlined in Baranne et al. (1996) and Pepe et al. (2002). The HARPS-N data are presented in TableA1 and the RVs are shown in Fig. 1. TableA1 also includes some stellar activity indicators. Specifically, the full width at half maximum (FWHM) of the cross-correlation function (CCF), the line Bisector Inverse Slope (BIS), and an activity index derived from the Calcium H and K lines (SHK).
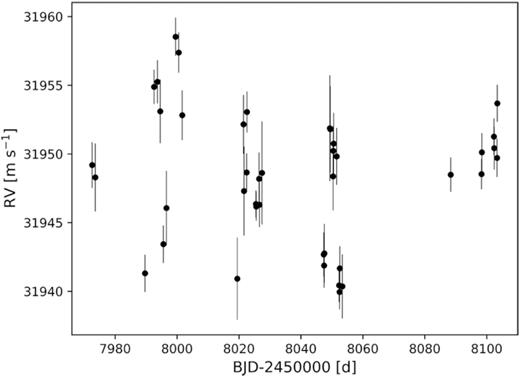
2.2 Previously published HARPS-N and HARPS spectroscopy
In our analysis, we also use the HARPS-N and HARPS spectra first presented in Prieto-Arranz et al. (2018). This additional data set includes 23 HARPS-N RV spectra, taken between 2017 July and December, and 35 HARPS spectra taken between 2017 August and October. The HARPS instrument is installed on the 3.6-m ESO telescope at La Silla and is very similar to the HARPS-N instrument, already discussed in Section 2.1. The HARPS and HARPS-N spectra were reduced with the same DRS as the HARPS-N spectra presented in Section 2.1. The HARPS-N RVs presented by Prieto-Arranz et al. (2018) have an average precision of 1.6 m s−1 and S/Ns in the range 33–95 (average S/N = 68), while the HARPS RVs have an average precision of 1.4 m s−1 and S/Ns in the range 47–100 (average S/N = 76).
The Prieto-Arranz et al. (2018) HARPS and HARPS-N data, including stellar activity indicators, can be found in their tables 2 and 3, respectively. Their HARPS-N and HARPS RVs, together with the new HARPS-N RVs presented here, are shown in the top panel of Fig. 2. The filled circles show the new HARPS-N RVs from this study, the open circles show the HARPS-N RVs from Prieto-Arranz et al. (2018), and the open squares show their HARPS RVs. We also correct for the RV offset, but assume that all the HARPS-N data has the same offset,1 while allowing the HARPS and HARPS-N data to have different offsets. This is discussed in more detail in Section 6.
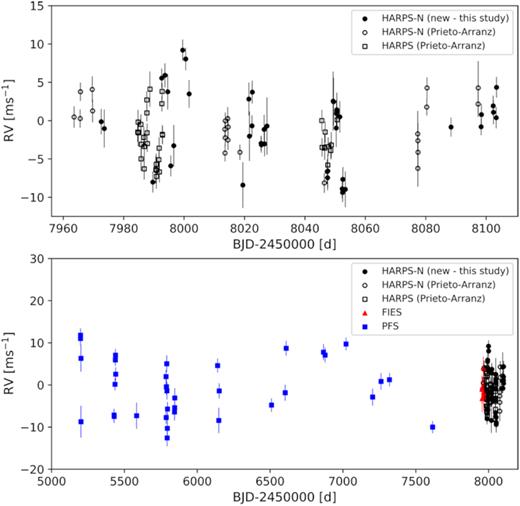
Top panel: the new HARPS-N RVs from this study (black filled circles) together with the HARPS-N and HARPS RVs presented by Prieto-Arranz et al. (2018, black open circles and black open squares, respectively). Bottom panel: PFS (blue squares) and FIES (red triangles) RVs, together with all the HARPS-N and HARPS RVs (black filled circles, black open circles, and black open squares), all corrected for offsets between the data sets.
2.3 Previously published Magellan/PFS and NOT/FIES spectroscopy
In addition to the HARPS-N and HARPS spectra, we also include in our analysis the Magellan/PFS observations first presented by Teske et al. (2018). Thirty-six PFS observations were taken between 2010 January and 2016 August, using the Planet Finder Spectrograph (PFS, Crane, Shectman & Butler 2006) on the Magellan II (Clay) Telescope. The resolution was |${\sim } 80\, 000$| and the exposure times were between 457 and 900 s. More details can be found in Teske et al. (2018), and the resulting RVs are shown in their table 1.
GJ 9827 stellar parameters showing the magnitudes, results from our SPC analysis, and the Hipparcos and Gaia parallaxes used as input to the isochrones python package for estimating the mass, M*, and radius R*. We do not show the stellar parameters from Niraula et al. (2017), Teske et al. (2018), and Rodriguez et al. (2018) that were also used in the isochrones analysis (see the text for details). Also shown are the metallicity, effective temperature, log g, and final mass and radius estimates obtained from the isochrones analysis using the Gaia parallax as a prior.
| Parameter . | Description . | Value . |
|---|---|---|
| Other | EPIC 246389858 | |
| identifiers | HIP 115752 | |
| 2MASS J23270480−0117108 | ||
| B | APASS Johnson B mag | 11.569 ± 0.034 |
| V | APASS Johnson V mag | 10.250 ± 0.138 |
| J | 2MASS J mag | 7.984 ± 0.02 |
| K | 2MASS K mag | 7.193 ± 0.02 |
| WISE2 | WISE2 mag | 7.155 ± 0.02 |
| WISE3 | WISE3 mag | 7.114 ± 0.017 |
| |$v$|sin i | Rotational velocity (SPC) | <2 km s−1 |
| [m/H] | Metallicity (SPC) | −0.5 ± 0.08 |
| Teff | Effective temperature (SPC) | 4305 ± 49 K |
| log g | Surface gravity (SPC) | 4.72 ± 0.1 (cgs) |
| πHip | Hipparcos parallax (mas) | 32.98 ± 1.76 |
| πGAIA | Gaia parallax (mas) | 33.68 ± 0.06 |
| [m/H] | Metallicity (isochrones) | −0.26 ± 0.09 |
| Teff | Effective temperature | |$4340^{+40}_{-53}$| K |
| (isochrones) | ||
| log g | Surface gravity (isochrones) | |$4.66^{+0.015}_{-0.010}$| (cgs) |
| M* | Mass (isochrones) | |$0.606^{+0.020}_{-0.014}$| M⊙ |
| R* | Radius (isochrones) | |$0.602^{+0.005}_{-0.004}$| R⊙ |
| Parameter . | Description . | Value . |
|---|---|---|
| Other | EPIC 246389858 | |
| identifiers | HIP 115752 | |
| 2MASS J23270480−0117108 | ||
| B | APASS Johnson B mag | 11.569 ± 0.034 |
| V | APASS Johnson V mag | 10.250 ± 0.138 |
| J | 2MASS J mag | 7.984 ± 0.02 |
| K | 2MASS K mag | 7.193 ± 0.02 |
| WISE2 | WISE2 mag | 7.155 ± 0.02 |
| WISE3 | WISE3 mag | 7.114 ± 0.017 |
| |$v$|sin i | Rotational velocity (SPC) | <2 km s−1 |
| [m/H] | Metallicity (SPC) | −0.5 ± 0.08 |
| Teff | Effective temperature (SPC) | 4305 ± 49 K |
| log g | Surface gravity (SPC) | 4.72 ± 0.1 (cgs) |
| πHip | Hipparcos parallax (mas) | 32.98 ± 1.76 |
| πGAIA | Gaia parallax (mas) | 33.68 ± 0.06 |
| [m/H] | Metallicity (isochrones) | −0.26 ± 0.09 |
| Teff | Effective temperature | |$4340^{+40}_{-53}$| K |
| (isochrones) | ||
| log g | Surface gravity (isochrones) | |$4.66^{+0.015}_{-0.010}$| (cgs) |
| M* | Mass (isochrones) | |$0.606^{+0.020}_{-0.014}$| M⊙ |
| R* | Radius (isochrones) | |$0.602^{+0.005}_{-0.004}$| R⊙ |
GJ 9827 stellar parameters showing the magnitudes, results from our SPC analysis, and the Hipparcos and Gaia parallaxes used as input to the isochrones python package for estimating the mass, M*, and radius R*. We do not show the stellar parameters from Niraula et al. (2017), Teske et al. (2018), and Rodriguez et al. (2018) that were also used in the isochrones analysis (see the text for details). Also shown are the metallicity, effective temperature, log g, and final mass and radius estimates obtained from the isochrones analysis using the Gaia parallax as a prior.
| Parameter . | Description . | Value . |
|---|---|---|
| Other | EPIC 246389858 | |
| identifiers | HIP 115752 | |
| 2MASS J23270480−0117108 | ||
| B | APASS Johnson B mag | 11.569 ± 0.034 |
| V | APASS Johnson V mag | 10.250 ± 0.138 |
| J | 2MASS J mag | 7.984 ± 0.02 |
| K | 2MASS K mag | 7.193 ± 0.02 |
| WISE2 | WISE2 mag | 7.155 ± 0.02 |
| WISE3 | WISE3 mag | 7.114 ± 0.017 |
| |$v$|sin i | Rotational velocity (SPC) | <2 km s−1 |
| [m/H] | Metallicity (SPC) | −0.5 ± 0.08 |
| Teff | Effective temperature (SPC) | 4305 ± 49 K |
| log g | Surface gravity (SPC) | 4.72 ± 0.1 (cgs) |
| πHip | Hipparcos parallax (mas) | 32.98 ± 1.76 |
| πGAIA | Gaia parallax (mas) | 33.68 ± 0.06 |
| [m/H] | Metallicity (isochrones) | −0.26 ± 0.09 |
| Teff | Effective temperature | |$4340^{+40}_{-53}$| K |
| (isochrones) | ||
| log g | Surface gravity (isochrones) | |$4.66^{+0.015}_{-0.010}$| (cgs) |
| M* | Mass (isochrones) | |$0.606^{+0.020}_{-0.014}$| M⊙ |
| R* | Radius (isochrones) | |$0.602^{+0.005}_{-0.004}$| R⊙ |
| Parameter . | Description . | Value . |
|---|---|---|
| Other | EPIC 246389858 | |
| identifiers | HIP 115752 | |
| 2MASS J23270480−0117108 | ||
| B | APASS Johnson B mag | 11.569 ± 0.034 |
| V | APASS Johnson V mag | 10.250 ± 0.138 |
| J | 2MASS J mag | 7.984 ± 0.02 |
| K | 2MASS K mag | 7.193 ± 0.02 |
| WISE2 | WISE2 mag | 7.155 ± 0.02 |
| WISE3 | WISE3 mag | 7.114 ± 0.017 |
| |$v$|sin i | Rotational velocity (SPC) | <2 km s−1 |
| [m/H] | Metallicity (SPC) | −0.5 ± 0.08 |
| Teff | Effective temperature (SPC) | 4305 ± 49 K |
| log g | Surface gravity (SPC) | 4.72 ± 0.1 (cgs) |
| πHip | Hipparcos parallax (mas) | 32.98 ± 1.76 |
| πGAIA | Gaia parallax (mas) | 33.68 ± 0.06 |
| [m/H] | Metallicity (isochrones) | −0.26 ± 0.09 |
| Teff | Effective temperature | |$4340^{+40}_{-53}$| K |
| (isochrones) | ||
| log g | Surface gravity (isochrones) | |$4.66^{+0.015}_{-0.010}$| (cgs) |
| M* | Mass (isochrones) | |$0.606^{+0.020}_{-0.014}$| M⊙ |
| R* | Radius (isochrones) | |$0.602^{+0.005}_{-0.004}$| R⊙ |
Similarly, we also include the seven high-resolution (|$R \sim 67\, 000$|) spectra taken using the FIbre-fed Échelle Spectrograph (FIES, Telting et al. 2014) on the 2.6-m Nordic Optical Telescope (NOT) of the Roque de los Muchachos Observatory (La Palma, Spain). More details can be found in Niraula et al. (2017), in which these observations were first presented, and the resulting RVs are shown in their table 2.
| Parameter . | GJ 9827 . |
|---|---|
| μα (mas yr−1)a | 376.02 ± 0.06 |
| μβ (mas yr−1)a | 216.07 ± 0.07 |
| ULSR (km s−1)b | −49.4 ± 0.4 |
| VLSR (km s−1)b | 22.9 ± 0.9 |
| WLSR (km s−1)b | −18.6 ± 1.1 |
| S (km s−1)b | 57.5 ± 0.6 |
| Parameter . | GJ 9827 . |
|---|---|
| μα (mas yr−1)a | 376.02 ± 0.06 |
| μβ (mas yr−1)a | 216.07 ± 0.07 |
| ULSR (km s−1)b | −49.4 ± 0.4 |
| VLSR (km s−1)b | 22.9 ± 0.9 |
| WLSR (km s−1)b | −18.6 ± 1.1 |
| S (km s−1)b | 57.5 ± 0.6 |
| Parameter . | GJ 9827 . |
|---|---|
| μα (mas yr−1)a | 376.02 ± 0.06 |
| μβ (mas yr−1)a | 216.07 ± 0.07 |
| ULSR (km s−1)b | −49.4 ± 0.4 |
| VLSR (km s−1)b | 22.9 ± 0.9 |
| WLSR (km s−1)b | −18.6 ± 1.1 |
| S (km s−1)b | 57.5 ± 0.6 |
| Parameter . | GJ 9827 . |
|---|---|
| μα (mas yr−1)a | 376.02 ± 0.06 |
| μβ (mas yr−1)a | 216.07 ± 0.07 |
| ULSR (km s−1)b | −49.4 ± 0.4 |
| VLSR (km s−1)b | 22.9 ± 0.9 |
| WLSR (km s−1)b | −18.6 ± 1.1 |
| S (km s−1)b | 57.5 ± 0.6 |
The bottom panel of Fig. 2 shows the PFS (blue squares) and FIES (red triangles) RVs, together with the new HARPS-N RVs from this study (black filled circles) and the HARPS-N and HARPS RVs presented by Prieto-Arranz et al. (2018,black open circles and black open squares, respectively). These are all corrected for offsets between the data sets based on the best RV fit for the combined data sets discussed in Section 6.
3 STELLAR PARAMETERS
Taking advantage of the high S/N, high-resolution spectra obtained using HARPS-N, we redetermined the stellar parameters of GJ 9827 using the Stellar Parameter Classification pipeline (SPC; Buchhave et al. 2014).
The high S/N needed to extract precise RVs means that these spectra are more than adequate for deriving stellar parameters. Using the spectra obtained through the HARPS-N GTO program, we ran the SPC analysis on each individual spectrum, with a prior on the surface gravity from the YY isochrone models (Spada et al. 2013). This SPC analysis yielded: Teff = 4305 ± 49 K, log g = 4.72 ± 0.10 (cgs), [m/H] =−0.50 ± 0.08, and |$v$|sin i < 2 km s−1. The formal uncertainties also take into account the model uncertainties, which primarily stem from model systematics in the atlas Kurucz stellar models and degeneracies between the derived parameters when trying to compare observed spectra to model spectra (see e.g. Buchhave et al. 2012, 2014).
To determine the mass, M⋆, and radius, R⋆, of GJ 9827, we used the isochrones python package (Morton 2015), which uses both the Mesa Isochrones and Stellar Tracks (MIST, Dotter 2016) and the Dartmouth Stellar Evolution Database (Dotter et al. 2008). In addition to Teff, log g, and [m/H], we included as priors the AAVSO Photometric All-Sky Survey B and V magnitudes (Henden et al. 2015), the 2MASS J and K magnitudes (Skrutskie et al. 2006), the WISE2 and 3 magnitudes (Cutri & et al. 2014), and the Gaia parallax from Data Release 2 (Gaia Collaboration et al. 2016, 2018). We also repeat this analysis using the Hipparcos parallax (van Leeuwen 2007), to see how this impacts the resulting mass and radius estimates. We used both the MIST and Dartmouth model grids. Posterior sampling was performed using multinest (Feroz & Hobson 2008; Feroz, Hobson & Bridges 2009; Feroz et al. 2013).
In order to investigate the systematic errors on M* and R* introduced by the spectrally derived stellar parameters when dealing with late K and cooler dwarfs, we repeated the analysis using the stellar atmosphere parameters from Niraula et al. (2017), Teske et al. (2018), and Rodriguez et al. (2018). Niraula et al. (2017) and Teske et al. (2018) used SpecMatch-Emp (Yee, Petigura & von Braun 2017), the results of which are shown in their tables 3 and 2, respectively. The stellar parameters used by Rodriguez et al. (2018) are shown in their table 1 and are taken from Houdebine et al. (2016), who used principal component analysis. The results of our analysis are shown in Fig. 3. The thin lines show the results using the Hipparcos parallax as a prior, while the thick lines are the results obtained using the Gaia parallax as a prior.
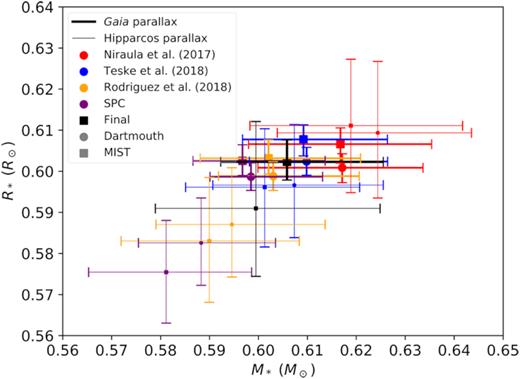
Mass (M*) against radius (R*) from our analysis using the isochrones python package. It includes results using our SPC analysis (purple), but also shows results using stellar parameters from Niraula et al. (2017, red), Teske et al. (2018, blue), and Rodriguez et al. (2018, yellow). We used both the MIST (squares) and Dartmouth (circles) model grids. We also use both the Gaia (thick lines) and Hipparcos (thin lines) parallaxes as priors. The black squares, with black error bars, show the mean M* and R*. It is clear that the Gaia parallax, which is more precise than the Hipparcos parallax, produces results that are more tightly constrained. For the rest of the analysis presented here, we will use the mean M* and R* determined using the Gaia parallax.
| Parameter . | Description . | GJ 9827 b . | GJ 9827 c . | GJ 9827 d . |
|---|---|---|---|---|
| P | Period (d) | |$1.20898190^{+0.00000693}_{-0.00000714}$| | |$3.6480957^{+0.0000633}_{-0.0000621}$| | |$6.2014698^{+0.0000626}_{-0.0000611}$| |
| Rp/R* | Radius of the planet in stellar radii | |$0.02396^{+0.00037}_{-0.00044}$| | |$0.01887^{+0.00034}_{-0.00037}$| | |$0.03073^{+0.00065}_{-0.00060}$| |
| Rp | Radius of the planet (R⊕)a | |$1.577^{+0.027}_{-0.031}$| | |$1.241^{+0.024}_{-0.026}$| | |$2.022^{+0.046}_{-0.043}$| |
| TC | Time of transit (BJD−2454833) | |$2905.82586^{+0.00026}_{-0.00026}$| | |$2909.19930^{+0.00072}_{-0.00073}$| | |$2907.96115^{+0.00044}_{-0.00045}$| |
| T14 | Transit duration (d) | |$0.05270^{+0.00093}_{-0.00083}$| | |$0.07604^{+0.00154}_{-0.00154}$| | |$0.05095^{+0.00147}_{-0.00122}$| |
| b | Impact parameter | |$0.4602^{+0.0352}_{-0.0443}$| | |$0.4428^{+0.0415}_{-0.0483}$| | |$0.8927^{+0.0071}_{-0.0090}$| |
| i | Inclination | |$86.07^{+0.41}_{-0.34}$| | |$88.19^{+0.21}_{-0.18}$| | |$87.443^{+0.045}_{-0.045}$| |
| a/R* | Semimajor axis in stellar radii | |$6.719^{+0.080}_{-0.086}$| | |$14.035^{+0.172}_{-0.171}$| | |$20.003^{+0.230}_{-0.254}$| |
| a | Semimajor axis (au)b | |$0.01880^{+0.00020}_{-0.00014}$| | |$0.03925^{+0.00042}_{-0.00029}$| | |$0.05591^{+0.00059}_{-0.00041}$| |
| Parameter . | Description . | GJ 9827 b . | GJ 9827 c . | GJ 9827 d . |
|---|---|---|---|---|
| P | Period (d) | |$1.20898190^{+0.00000693}_{-0.00000714}$| | |$3.6480957^{+0.0000633}_{-0.0000621}$| | |$6.2014698^{+0.0000626}_{-0.0000611}$| |
| Rp/R* | Radius of the planet in stellar radii | |$0.02396^{+0.00037}_{-0.00044}$| | |$0.01887^{+0.00034}_{-0.00037}$| | |$0.03073^{+0.00065}_{-0.00060}$| |
| Rp | Radius of the planet (R⊕)a | |$1.577^{+0.027}_{-0.031}$| | |$1.241^{+0.024}_{-0.026}$| | |$2.022^{+0.046}_{-0.043}$| |
| TC | Time of transit (BJD−2454833) | |$2905.82586^{+0.00026}_{-0.00026}$| | |$2909.19930^{+0.00072}_{-0.00073}$| | |$2907.96115^{+0.00044}_{-0.00045}$| |
| T14 | Transit duration (d) | |$0.05270^{+0.00093}_{-0.00083}$| | |$0.07604^{+0.00154}_{-0.00154}$| | |$0.05095^{+0.00147}_{-0.00122}$| |
| b | Impact parameter | |$0.4602^{+0.0352}_{-0.0443}$| | |$0.4428^{+0.0415}_{-0.0483}$| | |$0.8927^{+0.0071}_{-0.0090}$| |
| i | Inclination | |$86.07^{+0.41}_{-0.34}$| | |$88.19^{+0.21}_{-0.18}$| | |$87.443^{+0.045}_{-0.045}$| |
| a/R* | Semimajor axis in stellar radii | |$6.719^{+0.080}_{-0.086}$| | |$14.035^{+0.172}_{-0.171}$| | |$20.003^{+0.230}_{-0.254}$| |
| a | Semimajor axis (au)b | |$0.01880^{+0.00020}_{-0.00014}$| | |$0.03925^{+0.00042}_{-0.00029}$| | |$0.05591^{+0.00059}_{-0.00041}$| |
Notes:a Radii are derived using our estimate for the stellar radius, |$R_*=0.602^{+0.005}_{-0.004} R_{\rm \odot }$|, and the ratios Rplanet/Rstar determined here. b Semimajor axes are determined assuming that Ms + mp≅Ms and using |$a \cong [(M_{\rm s}\cdot G)^{\frac{1}{3}}\cdot P_{\rm p}^{\frac{2}{3}}]/(2\pi)^{\frac{2}{3}}$|, where G is the gravitational constant.
| Parameter . | Description . | GJ 9827 b . | GJ 9827 c . | GJ 9827 d . |
|---|---|---|---|---|
| P | Period (d) | |$1.20898190^{+0.00000693}_{-0.00000714}$| | |$3.6480957^{+0.0000633}_{-0.0000621}$| | |$6.2014698^{+0.0000626}_{-0.0000611}$| |
| Rp/R* | Radius of the planet in stellar radii | |$0.02396^{+0.00037}_{-0.00044}$| | |$0.01887^{+0.00034}_{-0.00037}$| | |$0.03073^{+0.00065}_{-0.00060}$| |
| Rp | Radius of the planet (R⊕)a | |$1.577^{+0.027}_{-0.031}$| | |$1.241^{+0.024}_{-0.026}$| | |$2.022^{+0.046}_{-0.043}$| |
| TC | Time of transit (BJD−2454833) | |$2905.82586^{+0.00026}_{-0.00026}$| | |$2909.19930^{+0.00072}_{-0.00073}$| | |$2907.96115^{+0.00044}_{-0.00045}$| |
| T14 | Transit duration (d) | |$0.05270^{+0.00093}_{-0.00083}$| | |$0.07604^{+0.00154}_{-0.00154}$| | |$0.05095^{+0.00147}_{-0.00122}$| |
| b | Impact parameter | |$0.4602^{+0.0352}_{-0.0443}$| | |$0.4428^{+0.0415}_{-0.0483}$| | |$0.8927^{+0.0071}_{-0.0090}$| |
| i | Inclination | |$86.07^{+0.41}_{-0.34}$| | |$88.19^{+0.21}_{-0.18}$| | |$87.443^{+0.045}_{-0.045}$| |
| a/R* | Semimajor axis in stellar radii | |$6.719^{+0.080}_{-0.086}$| | |$14.035^{+0.172}_{-0.171}$| | |$20.003^{+0.230}_{-0.254}$| |
| a | Semimajor axis (au)b | |$0.01880^{+0.00020}_{-0.00014}$| | |$0.03925^{+0.00042}_{-0.00029}$| | |$0.05591^{+0.00059}_{-0.00041}$| |
| Parameter . | Description . | GJ 9827 b . | GJ 9827 c . | GJ 9827 d . |
|---|---|---|---|---|
| P | Period (d) | |$1.20898190^{+0.00000693}_{-0.00000714}$| | |$3.6480957^{+0.0000633}_{-0.0000621}$| | |$6.2014698^{+0.0000626}_{-0.0000611}$| |
| Rp/R* | Radius of the planet in stellar radii | |$0.02396^{+0.00037}_{-0.00044}$| | |$0.01887^{+0.00034}_{-0.00037}$| | |$0.03073^{+0.00065}_{-0.00060}$| |
| Rp | Radius of the planet (R⊕)a | |$1.577^{+0.027}_{-0.031}$| | |$1.241^{+0.024}_{-0.026}$| | |$2.022^{+0.046}_{-0.043}$| |
| TC | Time of transit (BJD−2454833) | |$2905.82586^{+0.00026}_{-0.00026}$| | |$2909.19930^{+0.00072}_{-0.00073}$| | |$2907.96115^{+0.00044}_{-0.00045}$| |
| T14 | Transit duration (d) | |$0.05270^{+0.00093}_{-0.00083}$| | |$0.07604^{+0.00154}_{-0.00154}$| | |$0.05095^{+0.00147}_{-0.00122}$| |
| b | Impact parameter | |$0.4602^{+0.0352}_{-0.0443}$| | |$0.4428^{+0.0415}_{-0.0483}$| | |$0.8927^{+0.0071}_{-0.0090}$| |
| i | Inclination | |$86.07^{+0.41}_{-0.34}$| | |$88.19^{+0.21}_{-0.18}$| | |$87.443^{+0.045}_{-0.045}$| |
| a/R* | Semimajor axis in stellar radii | |$6.719^{+0.080}_{-0.086}$| | |$14.035^{+0.172}_{-0.171}$| | |$20.003^{+0.230}_{-0.254}$| |
| a | Semimajor axis (au)b | |$0.01880^{+0.00020}_{-0.00014}$| | |$0.03925^{+0.00042}_{-0.00029}$| | |$0.05591^{+0.00059}_{-0.00041}$| |
Notes:a Radii are derived using our estimate for the stellar radius, |$R_*=0.602^{+0.005}_{-0.004} R_{\rm \odot }$|, and the ratios Rplanet/Rstar determined here. b Semimajor axes are determined assuming that Ms + mp≅Ms and using |$a \cong [(M_{\rm s}\cdot G)^{\frac{1}{3}}\cdot P_{\rm p}^{\frac{2}{3}}]/(2\pi)^{\frac{2}{3}}$|, where G is the gravitational constant.
We then produce final estimates for each parameter by taking the median and 15.865th/84.135th percentiles of the posterior samplings for all of the sets of stellar parameters, and for both the analysis using the Gaia parallax, and the analysis using the Hipparcos parallax. The mass and radius obtained using the Hipparcos parallax as a prior are, |$M_\star = 0.60^{+0.03}_{-0.02} \, \mathrm{M}_\odot$| and |$R_\star = 0.59^{+0.02}_{-0.02} R_\odot$|, while using the Gaia parallax returns |$M_\star = 0.606^{+0.020}_{-0.014} \, \mathrm{M}_\odot$| and |$R_\star = 0.602^{+0.005}_{-0.004} R_\odot$|. It is clear that the more precise Gaia parallax produces results that are more tightly constrained than those obtained using the Hipparcos parallax. Consequently, we use the results obtained with the Gaia parallax for the rest of the analysis presented here. Similarly, using the Gaia parallax, the isochrones analysis returns |$T_{\rm eff} = 4340^{+48}_{-53}$|, [m/H] = −0.26 ± 0.09, |$\log g = 4.66^{+0.015}_{-0.010}$| (cgs), and A|$v$| = 0.22 ± 0.11 for the effective temperature, metallicity, surface gravity, and interstellar reddening, respectively. The Teff and log g results are consistent with the results from our SPC analysis, but the metallicity is discrepant at 2σ. It is, however, consistent with some earlier metallicity estimates (Niraula et al. 2017; Teske et al. 2018). The Teff, A|$v$|, and R* results are also consistent with results from Gaia Data Release 2 (Gaia Collaboration et al. 2016, 2018). The isochrone analysis also indicates that the star probably has an age of about 10 Gyr, with a lower limit (15.87th percentile) of 5Gyr.
3.1 Stellar kinematics
Stars presently near the Sun may come from a wide range of Galactic locations. Therefore, stellar space velocity, as a clue to the origin of a star in the Galaxy, is very important. The accurate Gaia parallax (see Table 1), combined with the proper motions and the stellar RV, make it possible to derive reliable space velocities for GJ 9827. The calculation of the space velocity with respect to the Sun is based on the procedure presented by Johnson & Soderblom (1987), corrected for the effect of differential galactic rotation (Scheffler, Elsässer & Armstrong 1987), by adopting a solar Galactocentric distance of 8.5 kpc and a circular velocity of 220 km s−1. The correction of space velocity to the local standard of rest is based on a solar motion,2 (U, V, W)|$\odot$| = (10.0, 5.2, 7.2) km s−1, as derived from Hipparcos data by Dehnen & Binney (1998). The peculiar space velocity S, given by S = (U2 + V2 + W2)1/2, is quoted with all kinematic data in Table 2 (with the exception of the Gaia parallax which is included in Table 1). GJ 9827, shows kinematic properties typical of the thin disc population. We have calculated the probabilities that the star belongs to a specific population, thick (TD), thin disc (D) or stellar halo (H), following the method used by Bensby, Feltzing & Lundström (2004). On account of these probabilities, we find for GJ 9827 a thick-to thin-disc probability ratio of TD/D = 0.05, implying that the star is clearly identified as a thin-disc object (typical threshold for assignment to thin disc being TD/D less than 0.1).
4 K2 PHOTOMETRY AND LIGHT-CURVE ANALYSIS
After the failure of the second of its four reaction wheels, the Kepler spacecraft was re-purposed for an extended K2 mission to obtain high-precision photometry on a set fields near the ecliptic. GJ 9827 was observed from UT 2016 December 16 until UT 2017 March 04, as part of K2 campaign 12.
Our data reduction and analysis techniques are very similar to that described in sections 2.2 and 4.1 of Mayo et al. (2018). We also provide a summary of our methods here. We first applied the method developed by Vanderburg & Johnson (2014) and Vanderburg et al. (2016a) in order to remove the roll systematics introduced by the periodic thruster firing of the Kepler Space Telescope. Next, we removed low-frequency variations from the light curve via a basis spline. Then, we used the BATMAN transit model (Kreidberg 2015) to simultaneously fit the transits of all three planets, assuming non-interaction and circular orbits. The latter assumption seems reasonable, given that the system is old enough for tidal circularization to have occurred (Barnes 2017), and that systems similar to GJ 9827 do tend to have low eccentricities (Van Eylen & Albrecht 2015). Additionally, as will be discussed in Section 6, the RV analysis is also consistent with the planets having circular orbits.
The model included four global parameters: baseline flux level, a noise parameter, and two quadratic limb-darkening coefficients parametrized according to Kipping (2013). Unlike Mayo et al. (2018), we also impose a stellar density prior of 3.92 ± 0.014 g cm−3, determined using the stellar mass and radius determined in Section 3. When imposing this prior, we also assume that the three planets each have circular orbits.
Additionally, each planet had five parameters: the initial epoch (i.e. time of first transit), the period, the inclination, the ratio of planetary to stellar radius (Rp/R*), and the semimajor axis normalized to the stellar radius (a/R*). All parameters were given a uniform prior except for each planet’s Rp/R*, for which we assumed a log-uniform prior. We estimated these model transit parameters using emcee (Foreman-Mackey et al. 2013), a python package which performs Markov Chain Monte Carlo (MCMC) simulations with an affine-invariant ensemble sampler (Goodman & Weare 2010). Using 38 walkers (i.e. twice the number of model parameters), we ran the MCMC process until convergence, which we defined as the point at which the scale-reduction factor (Gelman & Rubin 1992) dropped below 1.1 for every parameter.
The systematics corrected, normalized, and phase-folded light curves are shown in Fig. 4. The results of our light-curve analysis are shown in Table 3. For completeness, the baseline flux level is 1.000 ± 0.000002, the noise parameter is log (jitter) = −10.11 ± 0.002, and the quadratic limb-darkening parameters are |$q_1 = 0.3999^{+0.2403}_{-0.1642}$| and |$q_2 = 0.4372^{+0.3004}_{-0.2173}$|. Our results agree well with those in Rodriguez et al. (2018) and Niraula et al. (2017), and suggest that GJ 9827 b and d, with radii of |$R_{\mathrm{ p,b}} = 1.577^{+0.027}_{-0.031}$| and |$2.022^{+0.046}_{-0.043}$|, roughly lie on either side of the radius gap detected by Fulton et al. (2017). The derived quantities in Table 3 (Rp and a) were determined by sampling the posterior distributions of the dependent quantities, and presenting the median of the resulting distribution with the uncertainties being the difference between this median value and the 16th and 84th percentile values.
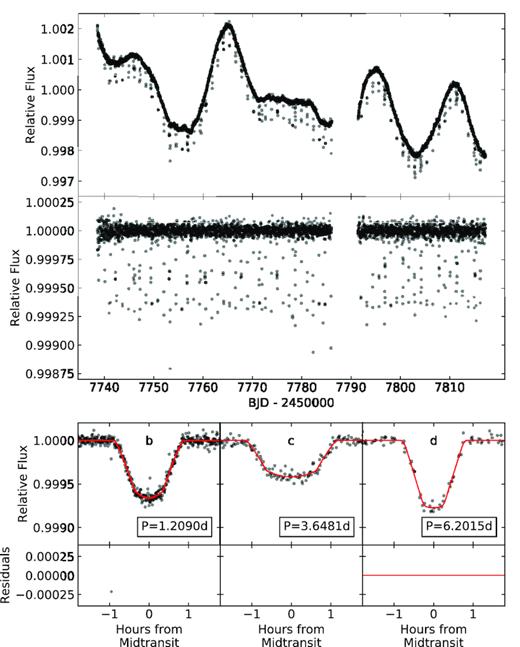
Top panel: K2 light curve after removing the roll systematics introduced by the periodic thruster fires of the Kepler Space Telescope, but without the removal of the low-frequency variations. Middle panel: K2 light curve after also removing the low-frequency variations. Bottom panel: phase-folded light curves for planets b, c, and d. The model is shown in red and the residuals are shown in the lower parts of the panel.
5 STELLAR ACTIVITY
Characterizing the activity level of the host star, and eventually modelling the activity contribution to the RV, is mandatory for accurate mass determination of small planets, even when the star is just moderately active (e.g. Haywood et al. 2018). The K2 light curve shows a strong modulation with peak-to-peak amplitude of ≃ 0.003 mag, suggesting a non-negligible level of activity for this star.
Previous analyses have estimated GJ 9827’s rotation period, but the results are not consistent. Niraula et al. (2017) suggest a rotation period of ∼17 d, while Rodriguez et al. (2018) and Teske et al. (2018) suggest a rotation period of 31 d.
Correcting for activity induced signals in the RV data requires an accurate estimate of the star’s rotational period. We use the combined HARPS and HARPS-N data set to carry out a periodogram analysis of the BIS and the FWHM of the CCF, as computed by the DRS (see Section 2.1), and the activity index derived from the Calcium H and K lines (SHK, see TableA1 and tables 2 and 3 in Prieto-Arranz et al. 2018). Specifically, we used the Bayesian formalism for the generalized Lomb–Scargle periodogram first presented by Mortier et al. (2015). The spectral window of the HARPS and HARPS-N data shows a peak at ∼27 d due to the Moon’s sidereal month. This hampers our ability to best exploit our data to derive a reliable measure of the stellar rotational period. When analysing the activity indices, a significant signal is, however, found in the SHK data at ∼34 d with another peak at around ∼15 d. We also consider correlations between the activity indices and the RVs. The Spearman’s rank correlation coefficients are all below 0.3.
Therefore, we also carry out a frequency analysis of the combined HARPS and HARPS-N RV data using the Iterative Sine-Wave Fitting (ISWF) method (Vaníček 1971). The power spectra shows clear peaks at fb = 0.827 d−1 (corresponding to the orbital period of GJ 9827 b, Pb = 1.209 d) and at fd = 0.161 d−1 (corresponding to the orbital period of GJ 9827 d, Pd = 6.21 d). The low-amplitude signal due to GJ 9827 c can be seen in the power spectrum, but it does not stand out above the noise. This frequency analysis also shows peaks at f=0.0325 d−1, 2f and 3f. The frequency f corresponds to a period of 30.8 d and is clearly related to the stellar rotation period. This would seem to indicate that the ∼15 d signal seen in the SHK data is probably the first harmonic of the stellar rotation period.
To better quantify the stellar activity, we carry out an analysis using the K2 light curve (see top panel of Fig. 4) but after removing the points affected by transits. We initially determined the autocorrelation of the K2 light-curve data, computed as described in McQuillan, Aigrain & Mazeh (2013).3 This converges to a rotational period of 29 d, which is closer to the 31 d presented in Rodriguez et al. (2018) and Teske et al. (2018), than to the ∼17 d suggested by Niraula et al. (2017).
It has, however, been suggested (Angus et al. 2018) that a Gaussian process (GP) with a quasi-periodic covariance kernel function is a more reliable method to determine the rotational period of active stars. We therefore performed an additional analysis using pyorbit4 (Malavolta et al. 2016), a package for modelling planetary and activity signals. This implements the GP quasi-periodic kernel through the george package (Ambikasaran et al. 2015). For the hyperparameters, we follow the mathematical definition introduced by Grunblatt, Howard & Haywood (2015). Hyperparameters optimization has been performed using the differential evolution code pyde,5 which provided the starting values for the affine-invariant ensemble sampler emcee (Foreman-Mackey et al. 2013). We followed the same methodology as described in Malavolta et al. (2018).
Since the GP regression typically scales with the third power of the number of data points, we binned the K2 light curve every five points, while ensuring that this did not alter the overall shape and did not change the autocorrelation result. Since there is a data gap between BJD−2450000 = 7786 and 7791, we also allow for different offsets and jitters for the two data segments. The GP analysis then suggested a rotational period of |$P_{\rm rot} = 28.72^{+0.18}_{-0.22}$| d, a decay time-scale of the active regions of |$\lambda = 33.17^{+5.90}_{-6.26}$| d, and a coherence scale of |$w$| = 0.146 ± 0.006. We also find a covariance amplitude in the K2 light-curve data of |$h_{K2} = 0.00081^{+0.00013}_{-0.00010}$| mag. These values are also presented in Table 4.
Stellar activity indicators from the GP model using the K2 light curve only.
| Parameter . | Description . | Value . |
|---|---|---|
| |$\sigma _{1, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000006^{+0.000003}_{-0.000003}$| |
| |$\sigma _{2, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000003^{+0.000003}_{-0.000002}$| |
| |$\gamma _{1, \rm K2}\, ^a$| (mag) | Offset | |$1.000237^{+0.000263}_{-0.000260}$| |
| |$\gamma _{2, \rm K2}\, ^a$| (mag) | Offset | |$0.999427^{+0.000273}_{-0.000268}$| |
| Prot (d) | Rotational period | |$28.72^{+0.18}_{-0.22}$| |
| λ (d) | Active region | |$33.17^{+5.90}_{-6.26}$| |
| decay timescale | ||
| |$w$| (m) | Coherence Scale | |$0.146^{+0.006}_{-0.006}$| |
| hK2 | Covariance amplitude | |$0.00081^{+0.00013}_{-0.00010}$| |
| Parameter . | Description . | Value . |
|---|---|---|
| |$\sigma _{1, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000006^{+0.000003}_{-0.000003}$| |
| |$\sigma _{2, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000003^{+0.000003}_{-0.000002}$| |
| |$\gamma _{1, \rm K2}\, ^a$| (mag) | Offset | |$1.000237^{+0.000263}_{-0.000260}$| |
| |$\gamma _{2, \rm K2}\, ^a$| (mag) | Offset | |$0.999427^{+0.000273}_{-0.000268}$| |
| Prot (d) | Rotational period | |$28.72^{+0.18}_{-0.22}$| |
| λ (d) | Active region | |$33.17^{+5.90}_{-6.26}$| |
| decay timescale | ||
| |$w$| (m) | Coherence Scale | |$0.146^{+0.006}_{-0.006}$| |
| hK2 | Covariance amplitude | |$0.00081^{+0.00013}_{-0.00010}$| |
Note. a The terms |$\sigma _{1, \rm jit, K2}$| and |$\gamma _{1, \rm K2}$| are for the K2 data segment ending at BJD−2450000=7786.075, while |$\sigma _{2, \rm K2}$| and |$h_{2, \rm K2}$| are for the K2 data segment starting at BJD−2450000=7791.377.
Stellar activity indicators from the GP model using the K2 light curve only.
| Parameter . | Description . | Value . |
|---|---|---|
| |$\sigma _{1, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000006^{+0.000003}_{-0.000003}$| |
| |$\sigma _{2, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000003^{+0.000003}_{-0.000002}$| |
| |$\gamma _{1, \rm K2}\, ^a$| (mag) | Offset | |$1.000237^{+0.000263}_{-0.000260}$| |
| |$\gamma _{2, \rm K2}\, ^a$| (mag) | Offset | |$0.999427^{+0.000273}_{-0.000268}$| |
| Prot (d) | Rotational period | |$28.72^{+0.18}_{-0.22}$| |
| λ (d) | Active region | |$33.17^{+5.90}_{-6.26}$| |
| decay timescale | ||
| |$w$| (m) | Coherence Scale | |$0.146^{+0.006}_{-0.006}$| |
| hK2 | Covariance amplitude | |$0.00081^{+0.00013}_{-0.00010}$| |
| Parameter . | Description . | Value . |
|---|---|---|
| |$\sigma _{1, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000006^{+0.000003}_{-0.000003}$| |
| |$\sigma _{2, \rm jit, K2}\, ^a$| (mag) | Jitter | |$0.000003^{+0.000003}_{-0.000002}$| |
| |$\gamma _{1, \rm K2}\, ^a$| (mag) | Offset | |$1.000237^{+0.000263}_{-0.000260}$| |
| |$\gamma _{2, \rm K2}\, ^a$| (mag) | Offset | |$0.999427^{+0.000273}_{-0.000268}$| |
| Prot (d) | Rotational period | |$28.72^{+0.18}_{-0.22}$| |
| λ (d) | Active region | |$33.17^{+5.90}_{-6.26}$| |
| decay timescale | ||
| |$w$| (m) | Coherence Scale | |$0.146^{+0.006}_{-0.006}$| |
| hK2 | Covariance amplitude | |$0.00081^{+0.00013}_{-0.00010}$| |
Note. a The terms |$\sigma _{1, \rm jit, K2}$| and |$\gamma _{1, \rm K2}$| are for the K2 data segment ending at BJD−2450000=7786.075, while |$\sigma _{2, \rm K2}$| and |$h_{2, \rm K2}$| are for the K2 data segment starting at BJD−2450000=7791.377.
The GP regression therefore produces a result that is consistent with that from the autocorrelation of the K2 light-curve data and with that presented in Rodriguez et al. (2018) and Teske et al. (2018). The isochrone analysis also suggests that this star has an age of ∼10 Gyr, with a lower limit of 5 Gyr. The stellar kinematics, reported in Section 3.1, indicates that GJ 9827 belongs to the galactic thin disc, but the low metallicity ([m/H] = −0.26 ± 0.09) is consistent with this being an older member of that population. A rotation period of ∼30 d is consistent with what would be expected for a star of this age (Reiners & Mohanty 2012). This would all seem to indicate that the rotation period of GJ 9827 is more likely ∼30 d than the ∼17 d suggested by Niraula et al. (2017). Therefore, we will use the results of the GP regression to correct for the stellar activity induced signals in the RV data.
6 RV ANALYSIS
The K2 light-curve analysis, the ISWF analysis of the HARPS and HARPS-N RVs, and the SHK index clearly suggest that the stellar activity of GJ 9827 may have non-negligible effects on the RVs. The approach that we have taken is to assume that the light-curve variations and activity signals in the RVs can be described by a GP with the same kernel and with common hyperparameters, except for the covariance amplitude, h, which is specific for each data set. This approach has been quite successful in confirming and improving mass determination of rocky planets (e.g. Haywood et al. 2014, Grunblatt et al. 2015), and it has delivered consistent results with respect to alternative approaches for stellar activity modelling (e.g. Malavolta et al. 2018). In the context of the GP analyis, we take the combined HARPS and HARPS-N RVs to be a single data set, with the PFS RVs and FIES RVs making up two other data sets. We do, however, allow for an offset between the HARPS and HARPS-N RVs and for independent jitter terms.
We carry out the RV analysis using the pyorbit code and, as in Section 5, assume that the quasi-periodic kernel is the best choice to model RV variations. When modelling activity signals in RVs with the help of GPs in a Bayesian framework, imposing priors obtained from the K2 light curve on the hyperparameters of the GP produces statistically indistinguishable results when compared to modelling the RVs and the light curve simultaneously (e.g. Malavolta et al. 2018).
Hence, rather than modelling the K2 light curve and the RVs simultaneously, we use the results from Section 5 to set priors on the hyperparameters, with the exception of the amplitude of the covariance h. Since the RV intensity of stellar activity depends on the wavelength range of the instrument and the RV extraction technique (e.g. Zechmeister et al. 2018), for each data set (combined HARPS and HARPS-N RVs, PFS RVs, and FIES RVs) we used an independent covariance amplitude h. For each data set, we also include a jitter term, to compensate for uncorrelated noise not included in the error estimate, and an RV offset. As mentioned above, although we treat the combined HARPS and HARPS-N RVs as a single dataset, we do allow for different offsets and jitter values for the HARPS and HARPS-N RVs. We use uniform priors for both the jitter and the RV offset. We ran two main analyses, one in which the results from Section 5 exactly define the Gaussian priors on the hyperparameters, and one in which they guide our choice of priors, but do not precisely define them. Specifically, in the second analysis, we use Gaussian priors on Prot, λ, and |$w$|, with Prot = 35 ± 10 d, λ = 36 ± 15 d, and |$w$| = 0.15 ± 0.005.
In the second analysis, we set the Prot prior to the value we would have used if only spectroscopic activity indices had been used to estimate the stellar rotation period (∼35 d from the SHK index, see Section 5), but we make the range wide enough to also incorporate the results from the analysis using the K2 light curve and to account for the photometry and RVs not being simultaneous in time.
In our model, we also assume that the orbits of all three planets are circular (eccentricity e = 0). In multiplanet systems of close-in planets, the eccentricity evolution depends on both tidal interactions and on eccentricity pumping from planet–planet interactions (Bolmont et al. 2013). However, given the age of the system (>5 Gyr), there has probably been sufficient time for the orbits of these close-in planets to have been tidally circularized (Barnes 2017), and there are indications that systems like GJ 9827 do tend to have low eccentricities (Van Eylen & Albrecht 2015). We also impose a log-uniform prior on the time of transit centre and a uniform prior on the orbital periods of the three planets, taken from the results of the analysis discussed in Section 4 (see Table 3).
Our results are shown in Table 5. The table shows the quantities derived from the RVs (radial velocity semi-amplitude, K, planet mass, Mp, and mean density, ρ) and also shows the resulting stellar activity indicators, the uncorrelated jitter, and the RV offset for each data set. The posterior distributions of some of the fitted parameters from Analysis 1 are shown in Fig. 5. For the sake of readability, only the RV semi-amplitude of the planets and the GP hyperparameters are reported. The confidence intervals of the posteriors are computed by taking the 15.87th and 84.14th percentiles of the distribution, except for Kc and hFIES, for which we report the median and the 84.14th percentile.
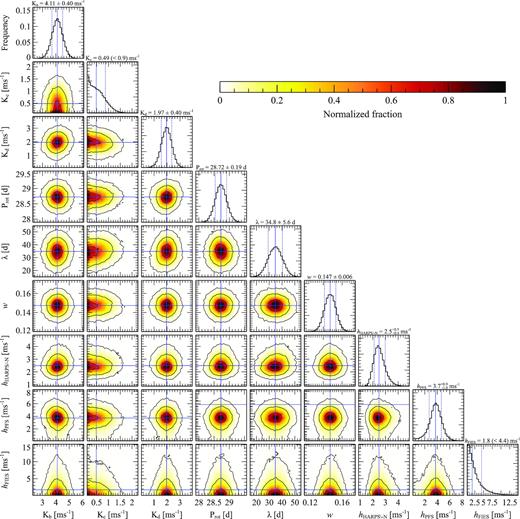
Posterior distributions of some of the fitted parameters determined by the analysis of the GJ 9827 RVs (Analysis 1 in Table 5). For the sake of readability, we only show the RV semi-amplitude of the planets and the GP hyperparameters.
| Parameter . | Best-fitting value . | |
|---|---|---|
| . | Analysis 1a . | Analysis 2b . |
| Stellar activity GP model | ||
| (Does not include those from the | ||
| K2 analysis presented in Table 4) | ||
| hHARPS-N, HARPS (m s−1) | 2.49|$^{+0.48}_{-0.39}$| | |$2.85^{+0.66}_{-0.51}$| |
| hFIES (m s−1) | 1.76|$^{+2.67}_{-1.21}$| | |$2.09^{+3.64}_{-1.46}$| |
| hPFS (m s−1) | 3.73|$^{+0.93}_{-1.03}$| | |$3.88^{+0.95}_{-0.95}$| |
| λ (d) | 34.77|$^{+5.57}_{-5.64}$| | |$30.97^{+12.47}_{-11.79}$| |
| |$w$| | 0.147 ± 0.006 | |$0.196^{+0.041}_{-0.038}$| |
| Prot (d) | |$28.72^{+0.19}_{-0.19}$| | |$30.13^{+11.11}_{-2.02}$| |
| Uncorrelated jitter | ||
| σjit, HARPS-N (m s−1) | 0.59|$^{+0.40}_{-0.37}$| | |$0.59^{+0.40}_{-0.38}$| |
| σjit, HARPS (m s−1) | 0.80|$^{+0.42}_{-0.44}$| | 0.81|$^{+0.41}_{-0.44}$| |
| σjit, FIES (m s−1) | 1.23|$^{+1.58}_{-0.85}$| | |$1.24^{+1.65}_{-0.86}$| |
| σjit, PFS (m s−1) | 2.32|$^{+1.28}_{-1.18}$| | |$2.17^{+1.17}_{-1.04}$| |
| RV offset | ||
| γHARPS-N (m s−1) | 31949.335|$^{+0.775}_{-0.753}$| | |$31949.473^{+0.970}_{-0.916}$| |
| γHARPS (m s−1) | 31948.292|$^{+0.907}_{-0.876}$| | 31948.556|$^{+1.103}_{-1.027}$| |
| γFIES (m s−1) | 31775.640|$^{+1.969}_{-1.988}$| | |$31775.623^{+2.222}_{-2.192}$| |
| γPFS (m s−1) | 0.447|$^{+0.984}_{-0.979}$| | |$0.533^{+1.019}_{-0.988}$| |
| Quantities derived from RVs | ||
| Kb (m s−1) | 4.11|$^{+0.40}_{-0.40}$| | |$4.10^{+0.37}_{-0.37}$| |
| |$K_{\rm c}\, ^1$| (m s−1) | 0.49(< 0.87) | 0.39(< 0.74) |
| Kd (m s−1) | 1.97|$^{+0.40}_{-0.40}$| | |$1.80^{+0.43}_{-0.48}$| |
| Mp, b (M⊕) | 4.91|$^{+0.49}_{-0.49}$| | |$4.90^{+0.45}_{-0.45}$| |
| |$M_{\rm p,c}\, ^1$| (M⊕) | 0.84(< 1.50) | 0.67(< 1.27) |
| Mp, d (M⊕) | 4.04|$^{+0.82}_{-0.84}$| | |$3.71^{+0.90}_{-0.99}$| |
| |$\rho _{\rm b}\, ^2$| (g cm−3) | |$6.93^{+0.82}_{-0.76}$| | |$6.90^{+0.76}_{-0.71}$| |
| |$\rho _{\rm c}\, ^{1,2}$| (g cm−3) | 2.42(< 4.35) | 1.93(< 3.66) |
| |$\rho _{\rm d}\, ^2$| (g cm−3) | |$2.69^{+0.58}_{-0.57}$| | |$2.46^{+0.63}_{-0.66}$| |
| Parameter . | Best-fitting value . | |
|---|---|---|
| . | Analysis 1a . | Analysis 2b . |
| Stellar activity GP model | ||
| (Does not include those from the | ||
| K2 analysis presented in Table 4) | ||
| hHARPS-N, HARPS (m s−1) | 2.49|$^{+0.48}_{-0.39}$| | |$2.85^{+0.66}_{-0.51}$| |
| hFIES (m s−1) | 1.76|$^{+2.67}_{-1.21}$| | |$2.09^{+3.64}_{-1.46}$| |
| hPFS (m s−1) | 3.73|$^{+0.93}_{-1.03}$| | |$3.88^{+0.95}_{-0.95}$| |
| λ (d) | 34.77|$^{+5.57}_{-5.64}$| | |$30.97^{+12.47}_{-11.79}$| |
| |$w$| | 0.147 ± 0.006 | |$0.196^{+0.041}_{-0.038}$| |
| Prot (d) | |$28.72^{+0.19}_{-0.19}$| | |$30.13^{+11.11}_{-2.02}$| |
| Uncorrelated jitter | ||
| σjit, HARPS-N (m s−1) | 0.59|$^{+0.40}_{-0.37}$| | |$0.59^{+0.40}_{-0.38}$| |
| σjit, HARPS (m s−1) | 0.80|$^{+0.42}_{-0.44}$| | 0.81|$^{+0.41}_{-0.44}$| |
| σjit, FIES (m s−1) | 1.23|$^{+1.58}_{-0.85}$| | |$1.24^{+1.65}_{-0.86}$| |
| σjit, PFS (m s−1) | 2.32|$^{+1.28}_{-1.18}$| | |$2.17^{+1.17}_{-1.04}$| |
| RV offset | ||
| γHARPS-N (m s−1) | 31949.335|$^{+0.775}_{-0.753}$| | |$31949.473^{+0.970}_{-0.916}$| |
| γHARPS (m s−1) | 31948.292|$^{+0.907}_{-0.876}$| | 31948.556|$^{+1.103}_{-1.027}$| |
| γFIES (m s−1) | 31775.640|$^{+1.969}_{-1.988}$| | |$31775.623^{+2.222}_{-2.192}$| |
| γPFS (m s−1) | 0.447|$^{+0.984}_{-0.979}$| | |$0.533^{+1.019}_{-0.988}$| |
| Quantities derived from RVs | ||
| Kb (m s−1) | 4.11|$^{+0.40}_{-0.40}$| | |$4.10^{+0.37}_{-0.37}$| |
| |$K_{\rm c}\, ^1$| (m s−1) | 0.49(< 0.87) | 0.39(< 0.74) |
| Kd (m s−1) | 1.97|$^{+0.40}_{-0.40}$| | |$1.80^{+0.43}_{-0.48}$| |
| Mp, b (M⊕) | 4.91|$^{+0.49}_{-0.49}$| | |$4.90^{+0.45}_{-0.45}$| |
| |$M_{\rm p,c}\, ^1$| (M⊕) | 0.84(< 1.50) | 0.67(< 1.27) |
| Mp, d (M⊕) | 4.04|$^{+0.82}_{-0.84}$| | |$3.71^{+0.90}_{-0.99}$| |
| |$\rho _{\rm b}\, ^2$| (g cm−3) | |$6.93^{+0.82}_{-0.76}$| | |$6.90^{+0.76}_{-0.71}$| |
| |$\rho _{\rm c}\, ^{1,2}$| (g cm−3) | 2.42(< 4.35) | 1.93(< 3.66) |
| |$\rho _{\rm d}\, ^2$| (g cm−3) | |$2.69^{+0.58}_{-0.57}$| | |$2.46^{+0.63}_{-0.66}$| |
Notes: apyorbit analysis in which we set priors on Prot, λ, and |$w$| from the stellar activity analysis using the K2 light curve only. See Section 5 and Table 4.
bpyorbit analysis in which we use the results of the activity analysis described in Section 5 to guide our choice of priors, rather than using these results exactly. Specifically, we impose Gaussian priors on Prot, λ, and |$w$| with Prot = 35 ± 10 d, λ = 36 ± 15 d, and |$w$| = 0.15 ± 0.05.
1For upper limits, we report the median and the 84th percentile.
2The density was determined by sampling the posterior distributions for the mass and radius, and presenting the median, 16th and 84th percentiles of the resulting distribution.
| Parameter . | Best-fitting value . | |
|---|---|---|
| . | Analysis 1a . | Analysis 2b . |
| Stellar activity GP model | ||
| (Does not include those from the | ||
| K2 analysis presented in Table 4) | ||
| hHARPS-N, HARPS (m s−1) | 2.49|$^{+0.48}_{-0.39}$| | |$2.85^{+0.66}_{-0.51}$| |
| hFIES (m s−1) | 1.76|$^{+2.67}_{-1.21}$| | |$2.09^{+3.64}_{-1.46}$| |
| hPFS (m s−1) | 3.73|$^{+0.93}_{-1.03}$| | |$3.88^{+0.95}_{-0.95}$| |
| λ (d) | 34.77|$^{+5.57}_{-5.64}$| | |$30.97^{+12.47}_{-11.79}$| |
| |$w$| | 0.147 ± 0.006 | |$0.196^{+0.041}_{-0.038}$| |
| Prot (d) | |$28.72^{+0.19}_{-0.19}$| | |$30.13^{+11.11}_{-2.02}$| |
| Uncorrelated jitter | ||
| σjit, HARPS-N (m s−1) | 0.59|$^{+0.40}_{-0.37}$| | |$0.59^{+0.40}_{-0.38}$| |
| σjit, HARPS (m s−1) | 0.80|$^{+0.42}_{-0.44}$| | 0.81|$^{+0.41}_{-0.44}$| |
| σjit, FIES (m s−1) | 1.23|$^{+1.58}_{-0.85}$| | |$1.24^{+1.65}_{-0.86}$| |
| σjit, PFS (m s−1) | 2.32|$^{+1.28}_{-1.18}$| | |$2.17^{+1.17}_{-1.04}$| |
| RV offset | ||
| γHARPS-N (m s−1) | 31949.335|$^{+0.775}_{-0.753}$| | |$31949.473^{+0.970}_{-0.916}$| |
| γHARPS (m s−1) | 31948.292|$^{+0.907}_{-0.876}$| | 31948.556|$^{+1.103}_{-1.027}$| |
| γFIES (m s−1) | 31775.640|$^{+1.969}_{-1.988}$| | |$31775.623^{+2.222}_{-2.192}$| |
| γPFS (m s−1) | 0.447|$^{+0.984}_{-0.979}$| | |$0.533^{+1.019}_{-0.988}$| |
| Quantities derived from RVs | ||
| Kb (m s−1) | 4.11|$^{+0.40}_{-0.40}$| | |$4.10^{+0.37}_{-0.37}$| |
| |$K_{\rm c}\, ^1$| (m s−1) | 0.49(< 0.87) | 0.39(< 0.74) |
| Kd (m s−1) | 1.97|$^{+0.40}_{-0.40}$| | |$1.80^{+0.43}_{-0.48}$| |
| Mp, b (M⊕) | 4.91|$^{+0.49}_{-0.49}$| | |$4.90^{+0.45}_{-0.45}$| |
| |$M_{\rm p,c}\, ^1$| (M⊕) | 0.84(< 1.50) | 0.67(< 1.27) |
| Mp, d (M⊕) | 4.04|$^{+0.82}_{-0.84}$| | |$3.71^{+0.90}_{-0.99}$| |
| |$\rho _{\rm b}\, ^2$| (g cm−3) | |$6.93^{+0.82}_{-0.76}$| | |$6.90^{+0.76}_{-0.71}$| |
| |$\rho _{\rm c}\, ^{1,2}$| (g cm−3) | 2.42(< 4.35) | 1.93(< 3.66) |
| |$\rho _{\rm d}\, ^2$| (g cm−3) | |$2.69^{+0.58}_{-0.57}$| | |$2.46^{+0.63}_{-0.66}$| |
| Parameter . | Best-fitting value . | |
|---|---|---|
| . | Analysis 1a . | Analysis 2b . |
| Stellar activity GP model | ||
| (Does not include those from the | ||
| K2 analysis presented in Table 4) | ||
| hHARPS-N, HARPS (m s−1) | 2.49|$^{+0.48}_{-0.39}$| | |$2.85^{+0.66}_{-0.51}$| |
| hFIES (m s−1) | 1.76|$^{+2.67}_{-1.21}$| | |$2.09^{+3.64}_{-1.46}$| |
| hPFS (m s−1) | 3.73|$^{+0.93}_{-1.03}$| | |$3.88^{+0.95}_{-0.95}$| |
| λ (d) | 34.77|$^{+5.57}_{-5.64}$| | |$30.97^{+12.47}_{-11.79}$| |
| |$w$| | 0.147 ± 0.006 | |$0.196^{+0.041}_{-0.038}$| |
| Prot (d) | |$28.72^{+0.19}_{-0.19}$| | |$30.13^{+11.11}_{-2.02}$| |
| Uncorrelated jitter | ||
| σjit, HARPS-N (m s−1) | 0.59|$^{+0.40}_{-0.37}$| | |$0.59^{+0.40}_{-0.38}$| |
| σjit, HARPS (m s−1) | 0.80|$^{+0.42}_{-0.44}$| | 0.81|$^{+0.41}_{-0.44}$| |
| σjit, FIES (m s−1) | 1.23|$^{+1.58}_{-0.85}$| | |$1.24^{+1.65}_{-0.86}$| |
| σjit, PFS (m s−1) | 2.32|$^{+1.28}_{-1.18}$| | |$2.17^{+1.17}_{-1.04}$| |
| RV offset | ||
| γHARPS-N (m s−1) | 31949.335|$^{+0.775}_{-0.753}$| | |$31949.473^{+0.970}_{-0.916}$| |
| γHARPS (m s−1) | 31948.292|$^{+0.907}_{-0.876}$| | 31948.556|$^{+1.103}_{-1.027}$| |
| γFIES (m s−1) | 31775.640|$^{+1.969}_{-1.988}$| | |$31775.623^{+2.222}_{-2.192}$| |
| γPFS (m s−1) | 0.447|$^{+0.984}_{-0.979}$| | |$0.533^{+1.019}_{-0.988}$| |
| Quantities derived from RVs | ||
| Kb (m s−1) | 4.11|$^{+0.40}_{-0.40}$| | |$4.10^{+0.37}_{-0.37}$| |
| |$K_{\rm c}\, ^1$| (m s−1) | 0.49(< 0.87) | 0.39(< 0.74) |
| Kd (m s−1) | 1.97|$^{+0.40}_{-0.40}$| | |$1.80^{+0.43}_{-0.48}$| |
| Mp, b (M⊕) | 4.91|$^{+0.49}_{-0.49}$| | |$4.90^{+0.45}_{-0.45}$| |
| |$M_{\rm p,c}\, ^1$| (M⊕) | 0.84(< 1.50) | 0.67(< 1.27) |
| Mp, d (M⊕) | 4.04|$^{+0.82}_{-0.84}$| | |$3.71^{+0.90}_{-0.99}$| |
| |$\rho _{\rm b}\, ^2$| (g cm−3) | |$6.93^{+0.82}_{-0.76}$| | |$6.90^{+0.76}_{-0.71}$| |
| |$\rho _{\rm c}\, ^{1,2}$| (g cm−3) | 2.42(< 4.35) | 1.93(< 3.66) |
| |$\rho _{\rm d}\, ^2$| (g cm−3) | |$2.69^{+0.58}_{-0.57}$| | |$2.46^{+0.63}_{-0.66}$| |
Notes: apyorbit analysis in which we set priors on Prot, λ, and |$w$| from the stellar activity analysis using the K2 light curve only. See Section 5 and Table 4.
bpyorbit analysis in which we use the results of the activity analysis described in Section 5 to guide our choice of priors, rather than using these results exactly. Specifically, we impose Gaussian priors on Prot, λ, and |$w$| with Prot = 35 ± 10 d, λ = 36 ± 15 d, and |$w$| = 0.15 ± 0.05.
1For upper limits, we report the median and the 84th percentile.
2The density was determined by sampling the posterior distributions for the mass and radius, and presenting the median, 16th and 84th percentiles of the resulting distribution.
As discussed above, the two analyses were one in which the activity priors were set by the results of Section 5, and one in which we used the results of Section 5 to set the region where we would expect the activity parameters to lie, but set the priors to have a much broader range than that suggested by the results presented in Section 5. Table 5 shows that the results of these two analyses are consistent. Since the stellar activity indicators derived from the K2 light curve, presented in Section 5, probably best represent the stellar activity, we will focus primarily on the results from Analysis 1.
Fig. 6 shows the orbital solutions and RV residuals from Analysis 1, for GJ 9827 b (top panel), GJ 9827 c (middle panel), and GJ 9827 d (lower panel), phased on the period of the corresponding planet and after removing the RV contributions from stellar activity and from the other planets. GJ 9827 b has an RV semi-amplitude of Kb = 4.11 ± 0.40 m s−1, suggesting a mass of Mp, b = 4.91 ± 0.49 M⊕. The RV semi-amplitude, Kc, for GJ 9827 c is small and suggests a mass of Mp, c = 0.84 M⊕ with an upper limit of 1.50 M⊕, while for GJ 9827 d, the RV semi amplitude is Kd = 1.97 ± 0.40 m s−1with a resulting mass estimate of |$M_{\mathrm{ p,d}} = 4.04^{+0.82}_{-0.84}$| M⊕. The mass estimate for GJ 9827 b, therefore has a precision of better than 10 per cent, while that for GJ 9827 d is close to 20 per cent.
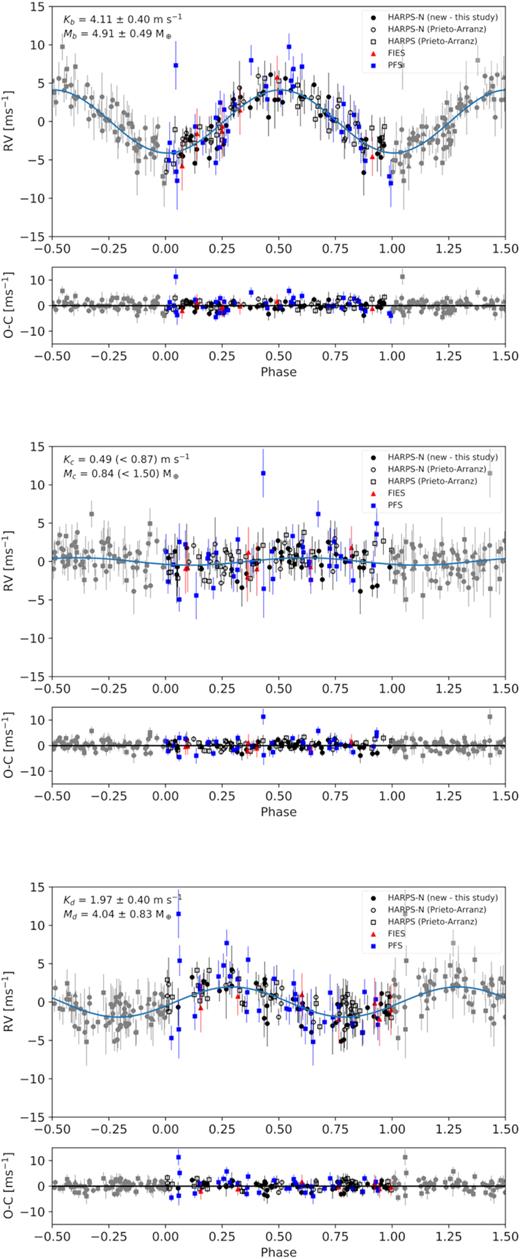
Orbital solutions and RV residuals for GJ 9827 b (top panel), GJ 9827 c (middle panel), and GJ 9827 d (lower panel), phased on the period of the corresponding planet and with the RV contributions from the other planets removed. The details are discussed in Section 6, and these figures show the results from Analysis 1.
Fig. 7 shows the HARPS-N (filled and open circles), HARPS (open squares), and FIES (red triangles) RVs, together with the best-fitting model which includes the planets’ signals and the GP model of the correlated stellar noise (light blue curve). Also shown is the GP solution (dashed blue curve) and its associated uncertainty range (grey shaded region).
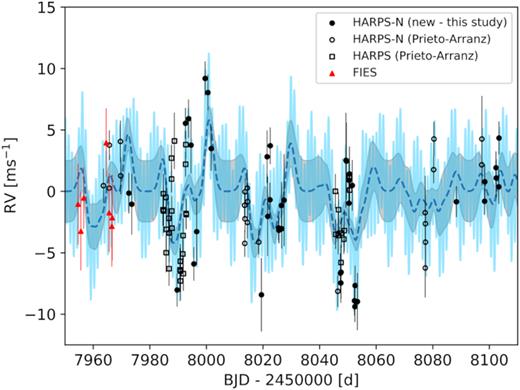
HARPS-N (filled and open circles), HARPS (open squares), and FIES (red triangles) RVs, together with the best-fitting models which includes the planets’ signals and the GP model of the correlated stellar noise (light blue curve). Also shown is the GP solution (dashed blue curve) and its associated uncertainty range (grey shaded region).
We do not, however, show the PFS RVs in Fig. 7. What Fig. 6 shows is that the RV residuals for some of the PFS data are considerably larger than that for the other data sets. This is most likely because the PFS data cover a long time interval and, during some periods, is insufficiently well sampled to constrain the stellar activity.
To test the consequences of this, we carried out two more analyses, both using the same activity priors as used by Analysis 1 in Table 5. In one, we excluded PFS data that appeared to be insufficiently well sampled to constrain the stellar activity, and in the other, we used HARPS-N and HARPS data only. In the first of these analyses, we retained the 6 PFS RVs between BJD=2455428.80 and 2455439.82, the 12 PFS RVs between BJD=2455785.72 and 2455485.70, and the 3 PFS RVs between BJD=2456139.86 and 2456150.83. In both cases, the results were consistent with, and of a similar precision to, those presented in Table 5. Consequently, we conclude that the PFS sampling does not significantly influence our results, both in terms of the best estimate or the precision.
We also carried out one additional analysis, using the same activity priors as in Analysis 1, in which we relax the constraint that the planet eccentricities are all zero. We do, however, constrain the eccentricities to be less than 0.2, which is based on pure N-body simulations using mercury6 that indicate that this is required for stability. The results from this analysis do allow for the planets to have small eccentricities, but the resulting RV semi-amplitudes, and planet masses, are very close to those produced by the equivalent analysis with circular orbits. The resulting eccentricities are also consistent with e = 0 at 2.45σ which suggests that this result is not significant (Lucy & Sweeney 1971). There is therefore no strong evidence to indicate that the orbits are non-circular.
7 DISCUSSION
Our analysis has allowed us to estimate the masses of GJ 9827 b and d with a precision of better than 10 per cent and close to 20 per cent, respectively. We cannot, however, put a strong constraint on the mass of GJ 9827 c. Our analysis suggests an upper limit (84 per cent) for GJ 9827 c’s RV semi-amplitude of <1 m s−1. If we assume an Earth-like composition (Mp ≃ 1.9M⊕, similar to Kepler-78b, Pepe et al. 2013), the RV semi-amplitude for this planet would be ≃ 1 m s−1. This might suggest that GJ9827c is unlikely to have an Earth-like composition.
Fig. 8 shows GJ 9827 b, c, and d on a mass–radius diagram which also includes all planets with a measured mass and radius from the Extrasolar Planets Encyclopaedia.6 The data points are shaded according to the precision of their mass estimate and are colour-coded according to their incident flux, relative to that of the Earth. The dashed lines show different compositions, taken from Zeng, Sasselov & Jacobsen (2016), plus one as yet unpublished track for a planet in which H2 makes up 1 per cent of its mass. The figure also shows the Earth and Venus, for reference, and indicates the approximate location of the radius gap (Fulton et al. 2017).
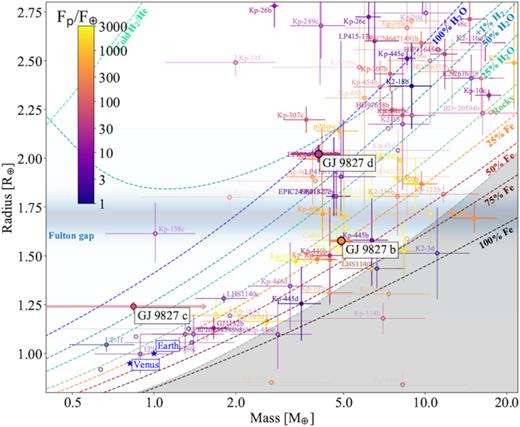
Mass–radius diagram for GJ 9827 b, GJ 9827 c, and GJ 9827 d together with all planets with a measured mass and radius from the Extrasolar Planets Encyclopaedia. The dashed lines show different compositions, taken from Zeng et al. (2016), plus one additional as yet unpublished track for a planet in which H2 makes up 1 per cent of its mass. The data points are shaded according to the precision of their mass estimate and are colour-coded according to their incident flux. Also shown are Earth and Venus, for reference, and we indicate the approximate location of the radius gap (Fulton et al. 2017).
GJ 9827 b is consistent with having a rocky, terrestrial (Earth-like) composition. The result for GJ 9827 c suggests that it is not consistent with being rocky, and that water could still make up a substantial fraction of its mass. There are, however, indications that non-detections, like that of GJ 9827 c, could return RV semi-amplitudes that are biased low with respect to the real RV semi-amplitudes (e.g. Damasso et al. 2018). Therefore, our results cannot be interpreted as strong evidence for GJ 9827 c not being rocky. GJ 9827 b, on the other hand, would seem to be composed mostly of silicates and iron. The best estimate suggests that its iron core makes up about 25 per cent of its mass, similar to that for the Earth and Venus, and the density estimate would seem to rule out GJ 9827 b having H/He on its surface, or the presence of a thick envelope of volatiles.
The bulk density of GJ 9827 d, and its location in the mass–radius diagram (Fig. 8), suggests that it probably does retain a reasonably substantial atmosphere, with water potentially making up a substantial fraction of its mass. GJ 9827 would therefore appear to host a super-Earth that is probably rocky (GJ 9827 b) and one (GJ 9827 d) that probably retains a substantial atmosphere. These two planets appear to bracket the radius gap suggested by Fulton et al. (2017) and Van Eylen et al. (2018).
The stellar fluxes received by GJ 9827 b and c are about 316 and 73 times that received by the Earth, respectively. If they are both rocky, they may still have formed with a composition similar to that of GJ 9827 d, but may have since lost their atmospheres through photoevaporation (Lopez & Fortney 2014). If, however, water still makes up a substantial fraction of GJ 9827 c’s mass, then this could have implications for the formation of this system. It could suggest that GJ 9827 c and d both formed beyond the snowline, with GJ 9287 b forming inside the snowline. Migration could then have produced the configuration we see today. That the system is in a near 1:3:5 resonance (Prieto-Arranz et al. 2018) might be consistent with this scenario. In such a scenario GJ 9827 c could still retain a water-rich atmosphere even at its current level of irradiation (Lopez 2017).
On the other hand, the stellar flux received by GJ 9827 d is about 36 times that received by the Earth, which may not be sufficient for GJ 9827 d to have lost much of its primordial atmosphere (Owen & Wu 2013; Lopez & Fortney 2013), whether water-rich or predominantly H/He (Lopez 2017). This system may therefore be consistent with photoevaporation playing a key role in generating the radius gap suggested by Owen & Wu (2013) and Lopez & Fortney (2013), and first detected by Fulton et al. (2017).
In fact, if those planets above the radius gap typically retain an H/He atmosphere, then a prediction of the photoevaporation model is that planets just above, and just below, the radius gap should have similar masses, since the envelope should make up only a small fraction of the mass of those just above the gap (Lopez & Rice 2018). The similar masses of GJ 9827 b and d are intriguingly consistent with this prediction.
There are, however, alternative explanations. For example, the luminosity of the cooling core could completely erode light envelopes, while having little impact on heavier envelopes (Ginzburg et al. 2018). This would produce a deficit of intermediate-mass planets and, hence, may also explain the observed radius gap (Fulton et al. 2017). Systems like GJ 9827 will therefore play a key role in determining which of these scenarios most likely explains this radius gap.
7.1 The composition of planets below the radius gap
One of the goals of the HARPS-N Collaboration is to try to determine the typical composition of planets with radii similar to that of the Earth. In particular, are planets below the radius gap first clearly mapped by Fulton et al. (2017) rocky? It has already been suggested (Rogers 2015) that most planets above this gap still retain significant envelopes of volatiles, but it is not yet clear if most planets below the gap are primarily composed of silicates and iron.
In Fig. 9, we plot the same data as in Fig. 8, but scale the planet masses according to the minimum mass they would need, given their radius, in order to be rocky (see composition curves in Fig. 8). As in Fig. 8, the data points are shaded according to the precision of their mass estimate and are colour-coded according to their incident flux, relative to the Earth. We also show the approximate location of the radius gap (Fulton et al. 2017).
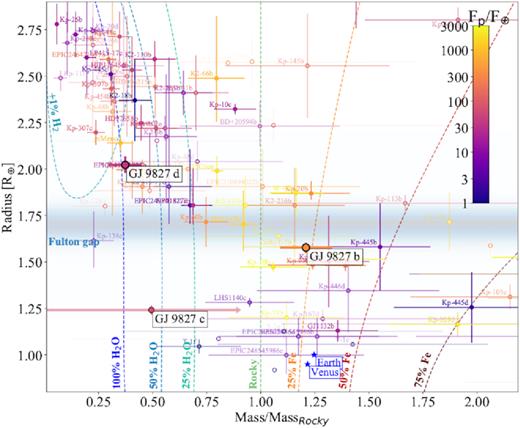
Similar to Fig. 8, except the masses are scaled according to the minimum mass they would need, given their radius, to be rocky. As in Fig. 8, the data points are shaded according to the precision of their mass estimate and colour-coded according to their incident flux, relative to that of the Earth. It also illustrates the location of the radius gap (Fulton et al. 2017).
What Fig. 9 shows quite clearly is that those with radii above the gap, including GJ 9827 d, tend to have masses below that required for them to be rocky, while those below the gap tend to have masses above the mass at which they would be rocky. Our estimate for GJ 9827 b suggests that it is clearly rocky. The upper limit for GJ 9827 c suggests that it is not rocky and that it may still retains a reasonable amount of water, and other volatiles. However, as highlighted in Damasso et al. (2018), there are indications that a result like that for GJ 9827 c could be biased low, so we really cannot rule out that GJ 9827 c is indeed rocky.
However, what Fig. 9 also shows is that the only other known planet below the radius gap that is inconsistent with being rocky at 1σ is Trappist-1f. Trappist-1f is, however, around a very low-mass star and has a low bolometric irradiation (|$M_* \sim 0.08 \, \mathrm{M}_\odot$| and Fp/F⊕ ∼ 0.382, Gillon et al. 2017). It is quite strongly irradiated in the XUV (Wheatley et al. 2017; Bolmont et al. 2017), but probably does still retain a volatile-rich envelope (Quarles et al. 2017). If GJ 9827 c does indeed still retain a substantial gaseous envelope, then it would be one of the most heavily irradiated planets below the radius gap to do so, and the only one orbiting an FGK star.
8 CONCLUSIONS
Here, we present the results of our analysis of the GJ 9827 planetary system, a system already known to contain three super-Earths (Niraula et al. 2017; Rodriguez et al. 2018). We repeat the K2 light-curve analysis and recover planetary radii that are consistent with these earlier analyses. We then carry out an RV analyses using the Magellan/PFS and FIES RVs first presented by Teske et al. (2018) and Niraula et al. (2017), respectively, the HARPS and HARPS-N RVs presented by (Prieto-Arranz et al. 2018), and with 41 additional new RV observations from HARPS-N (Cosentino et al. 2012).
Although our RV analysis cannot provide a strong constraint on the mass of GJ 9827 c, we can estimate the masses of GJ 9827 b and d with precisions of better than 10 per cent (b) and close to 20 per cent (d). We find that GJ 9827 b is probably rocky, with an iron core, but is unlikely to have a mass as high as suggested by Teske et al. (2018). GJ 9827 d, on the other hand, almost certainly retains a significant envelope of volatiles.
Using HARPS, HARPS-N, and FIES RVs, Prieto-Arranz et al. (2018) also estimated the masses of the planets in the GJ 9827 system. They conclude that GJ 9827 b is probably rocky, with an iron core, and that GJ 9827 d still retains an envelope of volatiles, which is consistent with the results presented here. However, our estimates for the mass of GJ 9827 b and GJ 9827 d are inconsistent with their estimates at the 1σ level. Our analysis suggests that both GJ 9827 b and GJ 9827 d have higher masses than suggested by Prieto-Arranz et al. (2018). Their estimate for GJ 9827 b is still consistent with an Earth-like composition, but their estimate for GJ 9827 d would seem to suggest a much lower density than is suggested by our analysis.
Prieto-Arranz et al. (2018) also claim a 2σ detection for the mass of GJ 9827 c, while we can only really set an upper limit. Although our upper limit is consistent, at 1σ, with their result, their analysis suggests that GJ 9827 c may well be rocky, whereas ours suggests that it probably is not. It would seem quite important to understand this difference, since the composition of GJ 9827 c could constrain where the planets in this system formed. If water makes up a significant fraction of its mass, then that might suggest that the outer planets in this system formed beyond the snowline. If not, then in situ formation is still a possibility (Chiang & Laughlin 2013). It is possible, however, that our non-detection has returned RV semi-amplitudes that are biased low (Damasso et al. 2018).
GJ 9827 is particularly interesting system since it hosts a rocky super-Earth near the lower boundary of the radius gap detected by Fulton et al. (2017) and one that retains a substantial atmosphere near the upper boundary of this gap. Consequently, this system could be consistent with the innermost one being sufficiently strongly irradiated to have lost its atmosphere via photoevaporation (Lopez 2017; Owen & Wu 2017). If GJ 9827 d retains a low-mass H/He envelope, rather than a water-rich atmosphere, then GJ 9827 b and d having similar masses is also consistent with the photoevaporation model. However, we cannot yet exclude alternative explanations, such as the luminosity of the cooling core eroding the lighter envelopes (Ginzburg et al. 2016, 2018). Therefore, understanding systems like GJ 9827 will help to determine which scenario is most likely.
Our results also have implications for the typical composition of planets below the radius gap detected by Fulton et al. (2017). Most planets with well-constrained masses below this radius gap have compositions consistent with them being rocky. This is indeed the case for GJ 9827 b, but our analysis cannot rule out that GJ 9827 c still retains a water-rich atmosphere. However, if this is the case, GJ 9827 c would be the one of the most heavily irradiated super-Earths below the radius gap that still retains a substantial volatile envelope. Given the faintness of the star (V = 10.3) and the expected RV amplitude (1 m s−1 for a rocky composition), it seems likely that only the next generation of high-precision velocimeters on large telescopes, such as ESPRESSO (Pepe et al. 2010) or G-CLEF (Szentgyorgyi et al. 2012), will allow a mass determination that has sufficient precision (better than ∼20 per cent) to uncover its internal composition.
As already highlighted by Rodriguez et al. (2018) and Niraula et al. (2017), GJ 9827 is bright, and cool, and hence is a potential target for atmospheric characterization via transit spectroscopy (Seager & Sasselov 2000). The expected signal can be calculated from the planet and star’s radii, and the scale height of the planet’s atmosphere (Vanderburg et al. 2016b). Our analysis suggests that if both GJ 9827 d and GJ 9827 c have predominantly H/He envelopes, the atmospheric signal could be as high as a few 100 ppm, which could be detected by the Hubble Space Telescope. However, if their atmospheres are predominantly water, a detection may require the James Webb Space Telescope. That GJ 9827 probably hosts a rocky super-Earth and one that probably retains a substantial atmosphere, and that these two planets bracket the radius gap detected by Fulton et al. (2017), makes it a particularly interesting target.
ACKNOWLEDGEMENTS
LM and DM acknowledge support from INAF/Frontiera through the ‘Progetti Premiali’ funding scheme of the Italian Ministry of Education, University, and Research. Some of this work has been carried out within the framework of the NCCR PlanetS, supported by the Swiss National Science Foundation. AV is supported by the NSF Graduate Research Fellowship, grant number DGE 1144152. This work was performed in part under contract with the California Institute of Technology (Caltech)/Jet Propulsion Laboratory (JPL) funded by NASA through the Sagan Fellowship Program executed by the NASA Exoplanet Science Institute (AV and RDH). ACC acknowledges support from STFC consolidated grant number ST/M001296/1. DWL acknowledges partial support from the Kepler mission under NASA Cooperative Agreement NNX13AB58A with the Smithsonian Astrophysical Observatory. CAW acknowledges support by STFC grant ST/P000312/1. XD is grateful to the Society in Science-Branco Weiss Fellowship for its financial support. This material is based upon work supported by the National Aeronautics and Space Administration under grants numbers NNX15AC90G and NNX17AB59G issued through the Exoplanets Research Program. This publication was made possible through the support of a grant from the John Templeton Foundation. The opinions expressed are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. The HARPS-N project has been funded by the Prodex Program of the Swiss Space Office, the Harvard University Origins of Life Initiative, the Scottish Universities Physics Alliance, the University of Geneva, the Smithsonian Astrophysical Observatory, and the Italian National Astrophysical Institute, the University of St Andrews, Queen’s University Belfast, and the University of Edinburgh. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission directorate. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5–26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX13AC07G and by other grants and contracts. This research has made use of NASA’s Astrophysics Data System and the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
Footnotes
We verified that the two HARPS-N data sets were obtained using the same instrumental setup, and analysed with the same version of the pipeline and using the same RV mask.
In the present work, |$\boldsymbol{U}$| is defined to be positive in the direction of the Galactic centre.
As implemented in https://github.com/bmorris3/interp-acf.
Version 5, available at https://github.com/LucaMalavolta/PyORBIT.
Available at https://github.com/hpparvi/PyDE
Available at http://www.exoplanet.eu
REFERENCES
APPENDIX:
| BJDUTC . | RV . | σRV . | BISspan . | FWHM . | SHK . | |$\sigma _{\rm S_{\rm HK}}$| . |
|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (m s−1) . | (km s−1) . | (dex) . | (dex) . |
| 2457972.581025 | 31949.19 | 1.66 | 54.56 | 6.16146 | 0.760934 | 0.012149 |
| 2457973.598897 | 31948.29 | 2.48 | 47.05 | 6.08261 | 0.703956 | 0.018964 |
| 2457989.650249 | 31941.31 | 1.36 | 44.43 | 6.13164 | 0.690250 | 0.008613 |
| 2457992.585770 | 31954.88 | 1.25 | 47.19 | 6.13195 | 0.712646 | 0.007336 |
| 2457993.670628 | 31955.25 | 1.57 | 52.67 | 6.13304 | 0.734660 | 0.010788 |
| 2457994.574853 | 31953.10 | 2.31 | 44.91 | 6.13740 | 0.716458 | 0.018600 |
| 2457995.576615 | 31943.43 | 1.37 | 47.27 | 6.13503 | 0.738125 | 0.008665 |
| 2457996.564509 | 31946.06 | 2.71 | 62.28 | 6.14124 | 0.703724 | 0.025410 |
| 2457999.535982 | 31958.53 | 1.39 | 46.43 | 6.14647 | 0.744546 | 0.009172 |
| 2458000.538638 | 31957.38 | 1.47 | 50.08 | 6.15661 | 0.758144 | 0.010064 |
| 2458001.680612 | 31952.82 | 1.81 | 43.66 | 6.15685 | 0.754857 | 0.013624 |
| 2458019.448280 | 31940.92 | 2.99 | 43.19 | 6.12897 | 0.680988 | 0.030242 |
| 2458021.448466 | 31952.15 | 2.14 | 50.83 | 6.12614 | 0.684284 | 0.018574 |
| 2458021.635511 | 31947.30 | 3.24 | 55.74 | 6.12959 | 0.709314 | 0.035249 |
| 2458022.469453 | 31948.65 | 1.39 | 44.09 | 6.12319 | 0.674695 | 0.008879 |
| 2458022.578398 | 31953.05 | 1.49 | 41.74 | 6.12904 | 0.692022 | 0.009983 |
| 2458025.479998 | 31946.36 | 0.99 | 49.06 | 6.13471 | 0.700214 | 0.004776 |
| 2458025.580458 | 31946.17 | 1.03 | 48.23 | 6.13419 | 0.709150 | 0.005181 |
| 2458026.500839 | 31948.19 | 1.91 | 52.53 | 6.14859 | 0.722292 | 0.014968 |
| 2458026.617340 | 31946.30 | 1.62 | 57.31 | 6.13966 | 0.715850 | 0.011669 |
| 2458027.436449 | 31948.62 | 3.75 | 49.25 | 6.13452 | 0.761666 | 0.039726 |
| 2458047.362466 | 31942.68 | 1.61 | 51.38 | 6.13719 | 0.734700 | 0.012005 |
| 2458047.488963 | 31941.88 | 1.63 | 48.83 | 6.13660 | 0.718712 | 0.011596 |
| 2458047.572523 | 31942.76 | 2.15 | 55.64 | 6.14504 | 0.719076 | 0.018844 |
| 2458049.334881 | 31951.87 | 3.86 | 55.60 | 6.13803 | 0.680903 | 0.045143 |
| 2458049.484976 | 31951.80 | 3.14 | 54.38 | 6.12018 | 0.682102 | 0.031959 |
| 2458050.373485 | 31948.37 | 2.48 | 51.30 | 6.13536 | 0.642163 | 0.022632 |
| 2458050.447982 | 31950.23 | 1.81 | 45.18 | 6.12398 | 0.686098 | 0.013886 |
| 2458050.564769 | 31950.75 | 2.24 | 47.89 | 6.12488 | 0.636900 | 0.019858 |
| 2458051.552113 | 31949.82 | 2.07 | 42.45 | 6.13584 | 0.675663 | 0.018119 |
| 2458052.333890 | 31940.43 | 1.21 | 47.34 | 6.13214 | 0.665658 | 0.007353 |
| 2458052.475119 | 31939.95 | 1.26 | 51.87 | 6.12258 | 0.650656 | 0.007588 |
| 2458052.551769 | 31941.67 | 1.61 | 50.37 | 6.11954 | 0.680874 | 0.012084 |
| 2458053.372143 | 31940.36 | 2.33 | 41.75 | 6.11748 | 0.669119 | 0.021128 |
| 2458088.371319 | 31948.49 | 1.25 | 52.18 | 6.12414 | 0.693171 | 0.006900 |
| 2458098.320396 | 31948.53 | 1.10 | 49.90 | 6.12255 | 0.702622 | 0.005724 |
| 2458098.426520 | 31950.12 | 1.40 | 45.10 | 6.11918 | 0.712788 | 0.009317 |
| 2458102.331265 | 31951.26 | 1.33 | 45.02 | 6.11895 | 0.704454 | 0.008007 |
| 2458102.409463 | 31950.42 | 1.56 | 50.57 | 6.12284 | 0.696478 | 0.010865 |
| 2458103.342309 | 31949.71 | 1.39 | 54.92 | 6.10729 | 0.749587 | 0.008941 |
| 2458103.418424 | 31953.68 | 1.35 | 49.18 | 6.11461 | 0.737197 | 0.008863 |
| BJDUTC . | RV . | σRV . | BISspan . | FWHM . | SHK . | |$\sigma _{\rm S_{\rm HK}}$| . |
|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (m s−1) . | (km s−1) . | (dex) . | (dex) . |
| 2457972.581025 | 31949.19 | 1.66 | 54.56 | 6.16146 | 0.760934 | 0.012149 |
| 2457973.598897 | 31948.29 | 2.48 | 47.05 | 6.08261 | 0.703956 | 0.018964 |
| 2457989.650249 | 31941.31 | 1.36 | 44.43 | 6.13164 | 0.690250 | 0.008613 |
| 2457992.585770 | 31954.88 | 1.25 | 47.19 | 6.13195 | 0.712646 | 0.007336 |
| 2457993.670628 | 31955.25 | 1.57 | 52.67 | 6.13304 | 0.734660 | 0.010788 |
| 2457994.574853 | 31953.10 | 2.31 | 44.91 | 6.13740 | 0.716458 | 0.018600 |
| 2457995.576615 | 31943.43 | 1.37 | 47.27 | 6.13503 | 0.738125 | 0.008665 |
| 2457996.564509 | 31946.06 | 2.71 | 62.28 | 6.14124 | 0.703724 | 0.025410 |
| 2457999.535982 | 31958.53 | 1.39 | 46.43 | 6.14647 | 0.744546 | 0.009172 |
| 2458000.538638 | 31957.38 | 1.47 | 50.08 | 6.15661 | 0.758144 | 0.010064 |
| 2458001.680612 | 31952.82 | 1.81 | 43.66 | 6.15685 | 0.754857 | 0.013624 |
| 2458019.448280 | 31940.92 | 2.99 | 43.19 | 6.12897 | 0.680988 | 0.030242 |
| 2458021.448466 | 31952.15 | 2.14 | 50.83 | 6.12614 | 0.684284 | 0.018574 |
| 2458021.635511 | 31947.30 | 3.24 | 55.74 | 6.12959 | 0.709314 | 0.035249 |
| 2458022.469453 | 31948.65 | 1.39 | 44.09 | 6.12319 | 0.674695 | 0.008879 |
| 2458022.578398 | 31953.05 | 1.49 | 41.74 | 6.12904 | 0.692022 | 0.009983 |
| 2458025.479998 | 31946.36 | 0.99 | 49.06 | 6.13471 | 0.700214 | 0.004776 |
| 2458025.580458 | 31946.17 | 1.03 | 48.23 | 6.13419 | 0.709150 | 0.005181 |
| 2458026.500839 | 31948.19 | 1.91 | 52.53 | 6.14859 | 0.722292 | 0.014968 |
| 2458026.617340 | 31946.30 | 1.62 | 57.31 | 6.13966 | 0.715850 | 0.011669 |
| 2458027.436449 | 31948.62 | 3.75 | 49.25 | 6.13452 | 0.761666 | 0.039726 |
| 2458047.362466 | 31942.68 | 1.61 | 51.38 | 6.13719 | 0.734700 | 0.012005 |
| 2458047.488963 | 31941.88 | 1.63 | 48.83 | 6.13660 | 0.718712 | 0.011596 |
| 2458047.572523 | 31942.76 | 2.15 | 55.64 | 6.14504 | 0.719076 | 0.018844 |
| 2458049.334881 | 31951.87 | 3.86 | 55.60 | 6.13803 | 0.680903 | 0.045143 |
| 2458049.484976 | 31951.80 | 3.14 | 54.38 | 6.12018 | 0.682102 | 0.031959 |
| 2458050.373485 | 31948.37 | 2.48 | 51.30 | 6.13536 | 0.642163 | 0.022632 |
| 2458050.447982 | 31950.23 | 1.81 | 45.18 | 6.12398 | 0.686098 | 0.013886 |
| 2458050.564769 | 31950.75 | 2.24 | 47.89 | 6.12488 | 0.636900 | 0.019858 |
| 2458051.552113 | 31949.82 | 2.07 | 42.45 | 6.13584 | 0.675663 | 0.018119 |
| 2458052.333890 | 31940.43 | 1.21 | 47.34 | 6.13214 | 0.665658 | 0.007353 |
| 2458052.475119 | 31939.95 | 1.26 | 51.87 | 6.12258 | 0.650656 | 0.007588 |
| 2458052.551769 | 31941.67 | 1.61 | 50.37 | 6.11954 | 0.680874 | 0.012084 |
| 2458053.372143 | 31940.36 | 2.33 | 41.75 | 6.11748 | 0.669119 | 0.021128 |
| 2458088.371319 | 31948.49 | 1.25 | 52.18 | 6.12414 | 0.693171 | 0.006900 |
| 2458098.320396 | 31948.53 | 1.10 | 49.90 | 6.12255 | 0.702622 | 0.005724 |
| 2458098.426520 | 31950.12 | 1.40 | 45.10 | 6.11918 | 0.712788 | 0.009317 |
| 2458102.331265 | 31951.26 | 1.33 | 45.02 | 6.11895 | 0.704454 | 0.008007 |
| 2458102.409463 | 31950.42 | 1.56 | 50.57 | 6.12284 | 0.696478 | 0.010865 |
| 2458103.342309 | 31949.71 | 1.39 | 54.92 | 6.10729 | 0.749587 | 0.008941 |
| 2458103.418424 | 31953.68 | 1.35 | 49.18 | 6.11461 | 0.737197 | 0.008863 |
| BJDUTC . | RV . | σRV . | BISspan . | FWHM . | SHK . | |$\sigma _{\rm S_{\rm HK}}$| . |
|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (m s−1) . | (km s−1) . | (dex) . | (dex) . |
| 2457972.581025 | 31949.19 | 1.66 | 54.56 | 6.16146 | 0.760934 | 0.012149 |
| 2457973.598897 | 31948.29 | 2.48 | 47.05 | 6.08261 | 0.703956 | 0.018964 |
| 2457989.650249 | 31941.31 | 1.36 | 44.43 | 6.13164 | 0.690250 | 0.008613 |
| 2457992.585770 | 31954.88 | 1.25 | 47.19 | 6.13195 | 0.712646 | 0.007336 |
| 2457993.670628 | 31955.25 | 1.57 | 52.67 | 6.13304 | 0.734660 | 0.010788 |
| 2457994.574853 | 31953.10 | 2.31 | 44.91 | 6.13740 | 0.716458 | 0.018600 |
| 2457995.576615 | 31943.43 | 1.37 | 47.27 | 6.13503 | 0.738125 | 0.008665 |
| 2457996.564509 | 31946.06 | 2.71 | 62.28 | 6.14124 | 0.703724 | 0.025410 |
| 2457999.535982 | 31958.53 | 1.39 | 46.43 | 6.14647 | 0.744546 | 0.009172 |
| 2458000.538638 | 31957.38 | 1.47 | 50.08 | 6.15661 | 0.758144 | 0.010064 |
| 2458001.680612 | 31952.82 | 1.81 | 43.66 | 6.15685 | 0.754857 | 0.013624 |
| 2458019.448280 | 31940.92 | 2.99 | 43.19 | 6.12897 | 0.680988 | 0.030242 |
| 2458021.448466 | 31952.15 | 2.14 | 50.83 | 6.12614 | 0.684284 | 0.018574 |
| 2458021.635511 | 31947.30 | 3.24 | 55.74 | 6.12959 | 0.709314 | 0.035249 |
| 2458022.469453 | 31948.65 | 1.39 | 44.09 | 6.12319 | 0.674695 | 0.008879 |
| 2458022.578398 | 31953.05 | 1.49 | 41.74 | 6.12904 | 0.692022 | 0.009983 |
| 2458025.479998 | 31946.36 | 0.99 | 49.06 | 6.13471 | 0.700214 | 0.004776 |
| 2458025.580458 | 31946.17 | 1.03 | 48.23 | 6.13419 | 0.709150 | 0.005181 |
| 2458026.500839 | 31948.19 | 1.91 | 52.53 | 6.14859 | 0.722292 | 0.014968 |
| 2458026.617340 | 31946.30 | 1.62 | 57.31 | 6.13966 | 0.715850 | 0.011669 |
| 2458027.436449 | 31948.62 | 3.75 | 49.25 | 6.13452 | 0.761666 | 0.039726 |
| 2458047.362466 | 31942.68 | 1.61 | 51.38 | 6.13719 | 0.734700 | 0.012005 |
| 2458047.488963 | 31941.88 | 1.63 | 48.83 | 6.13660 | 0.718712 | 0.011596 |
| 2458047.572523 | 31942.76 | 2.15 | 55.64 | 6.14504 | 0.719076 | 0.018844 |
| 2458049.334881 | 31951.87 | 3.86 | 55.60 | 6.13803 | 0.680903 | 0.045143 |
| 2458049.484976 | 31951.80 | 3.14 | 54.38 | 6.12018 | 0.682102 | 0.031959 |
| 2458050.373485 | 31948.37 | 2.48 | 51.30 | 6.13536 | 0.642163 | 0.022632 |
| 2458050.447982 | 31950.23 | 1.81 | 45.18 | 6.12398 | 0.686098 | 0.013886 |
| 2458050.564769 | 31950.75 | 2.24 | 47.89 | 6.12488 | 0.636900 | 0.019858 |
| 2458051.552113 | 31949.82 | 2.07 | 42.45 | 6.13584 | 0.675663 | 0.018119 |
| 2458052.333890 | 31940.43 | 1.21 | 47.34 | 6.13214 | 0.665658 | 0.007353 |
| 2458052.475119 | 31939.95 | 1.26 | 51.87 | 6.12258 | 0.650656 | 0.007588 |
| 2458052.551769 | 31941.67 | 1.61 | 50.37 | 6.11954 | 0.680874 | 0.012084 |
| 2458053.372143 | 31940.36 | 2.33 | 41.75 | 6.11748 | 0.669119 | 0.021128 |
| 2458088.371319 | 31948.49 | 1.25 | 52.18 | 6.12414 | 0.693171 | 0.006900 |
| 2458098.320396 | 31948.53 | 1.10 | 49.90 | 6.12255 | 0.702622 | 0.005724 |
| 2458098.426520 | 31950.12 | 1.40 | 45.10 | 6.11918 | 0.712788 | 0.009317 |
| 2458102.331265 | 31951.26 | 1.33 | 45.02 | 6.11895 | 0.704454 | 0.008007 |
| 2458102.409463 | 31950.42 | 1.56 | 50.57 | 6.12284 | 0.696478 | 0.010865 |
| 2458103.342309 | 31949.71 | 1.39 | 54.92 | 6.10729 | 0.749587 | 0.008941 |
| 2458103.418424 | 31953.68 | 1.35 | 49.18 | 6.11461 | 0.737197 | 0.008863 |
| BJDUTC . | RV . | σRV . | BISspan . | FWHM . | SHK . | |$\sigma _{\rm S_{\rm HK}}$| . |
|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (m s−1) . | (km s−1) . | (dex) . | (dex) . |
| 2457972.581025 | 31949.19 | 1.66 | 54.56 | 6.16146 | 0.760934 | 0.012149 |
| 2457973.598897 | 31948.29 | 2.48 | 47.05 | 6.08261 | 0.703956 | 0.018964 |
| 2457989.650249 | 31941.31 | 1.36 | 44.43 | 6.13164 | 0.690250 | 0.008613 |
| 2457992.585770 | 31954.88 | 1.25 | 47.19 | 6.13195 | 0.712646 | 0.007336 |
| 2457993.670628 | 31955.25 | 1.57 | 52.67 | 6.13304 | 0.734660 | 0.010788 |
| 2457994.574853 | 31953.10 | 2.31 | 44.91 | 6.13740 | 0.716458 | 0.018600 |
| 2457995.576615 | 31943.43 | 1.37 | 47.27 | 6.13503 | 0.738125 | 0.008665 |
| 2457996.564509 | 31946.06 | 2.71 | 62.28 | 6.14124 | 0.703724 | 0.025410 |
| 2457999.535982 | 31958.53 | 1.39 | 46.43 | 6.14647 | 0.744546 | 0.009172 |
| 2458000.538638 | 31957.38 | 1.47 | 50.08 | 6.15661 | 0.758144 | 0.010064 |
| 2458001.680612 | 31952.82 | 1.81 | 43.66 | 6.15685 | 0.754857 | 0.013624 |
| 2458019.448280 | 31940.92 | 2.99 | 43.19 | 6.12897 | 0.680988 | 0.030242 |
| 2458021.448466 | 31952.15 | 2.14 | 50.83 | 6.12614 | 0.684284 | 0.018574 |
| 2458021.635511 | 31947.30 | 3.24 | 55.74 | 6.12959 | 0.709314 | 0.035249 |
| 2458022.469453 | 31948.65 | 1.39 | 44.09 | 6.12319 | 0.674695 | 0.008879 |
| 2458022.578398 | 31953.05 | 1.49 | 41.74 | 6.12904 | 0.692022 | 0.009983 |
| 2458025.479998 | 31946.36 | 0.99 | 49.06 | 6.13471 | 0.700214 | 0.004776 |
| 2458025.580458 | 31946.17 | 1.03 | 48.23 | 6.13419 | 0.709150 | 0.005181 |
| 2458026.500839 | 31948.19 | 1.91 | 52.53 | 6.14859 | 0.722292 | 0.014968 |
| 2458026.617340 | 31946.30 | 1.62 | 57.31 | 6.13966 | 0.715850 | 0.011669 |
| 2458027.436449 | 31948.62 | 3.75 | 49.25 | 6.13452 | 0.761666 | 0.039726 |
| 2458047.362466 | 31942.68 | 1.61 | 51.38 | 6.13719 | 0.734700 | 0.012005 |
| 2458047.488963 | 31941.88 | 1.63 | 48.83 | 6.13660 | 0.718712 | 0.011596 |
| 2458047.572523 | 31942.76 | 2.15 | 55.64 | 6.14504 | 0.719076 | 0.018844 |
| 2458049.334881 | 31951.87 | 3.86 | 55.60 | 6.13803 | 0.680903 | 0.045143 |
| 2458049.484976 | 31951.80 | 3.14 | 54.38 | 6.12018 | 0.682102 | 0.031959 |
| 2458050.373485 | 31948.37 | 2.48 | 51.30 | 6.13536 | 0.642163 | 0.022632 |
| 2458050.447982 | 31950.23 | 1.81 | 45.18 | 6.12398 | 0.686098 | 0.013886 |
| 2458050.564769 | 31950.75 | 2.24 | 47.89 | 6.12488 | 0.636900 | 0.019858 |
| 2458051.552113 | 31949.82 | 2.07 | 42.45 | 6.13584 | 0.675663 | 0.018119 |
| 2458052.333890 | 31940.43 | 1.21 | 47.34 | 6.13214 | 0.665658 | 0.007353 |
| 2458052.475119 | 31939.95 | 1.26 | 51.87 | 6.12258 | 0.650656 | 0.007588 |
| 2458052.551769 | 31941.67 | 1.61 | 50.37 | 6.11954 | 0.680874 | 0.012084 |
| 2458053.372143 | 31940.36 | 2.33 | 41.75 | 6.11748 | 0.669119 | 0.021128 |
| 2458088.371319 | 31948.49 | 1.25 | 52.18 | 6.12414 | 0.693171 | 0.006900 |
| 2458098.320396 | 31948.53 | 1.10 | 49.90 | 6.12255 | 0.702622 | 0.005724 |
| 2458098.426520 | 31950.12 | 1.40 | 45.10 | 6.11918 | 0.712788 | 0.009317 |
| 2458102.331265 | 31951.26 | 1.33 | 45.02 | 6.11895 | 0.704454 | 0.008007 |
| 2458102.409463 | 31950.42 | 1.56 | 50.57 | 6.12284 | 0.696478 | 0.010865 |
| 2458103.342309 | 31949.71 | 1.39 | 54.92 | 6.10729 | 0.749587 | 0.008941 |
| 2458103.418424 | 31953.68 | 1.35 | 49.18 | 6.11461 | 0.737197 | 0.008863 |
Author notes
National Science Foundation Graduate Research Fellow
Fulbright Fellow
NASA Sagan Fellow



