Deep observations of the globular cluster M15 with the MAGIC telescopes Free

Abstract

1 INTRODUCTION

About 160 globular clusters (GCs) are gathered in a spherical halo around the centre of the Galaxy within a radius of ∼10 kpc (Harris 1996). GCs contain a huge number of old and low-mass stars, with a total mass up to ∼10⁶ M_⊙ in a volume with the radius of a few parsecs, and also evolved, compact objects such as millisecond pulsars (MSPs), cataclysmic variables, and low-mass X-ray binaries. Twenty GCs have been recently identified with GeV γ-ray sources discovered by the Fermi-LAT telescope (Abdo et al. 2009a, 2010; Kong, Hui & Cheng 2010; Tam et al. 2011; Zhang et al. 2016). In the case of two GCs, M28 and NGC 6624, exceptionally energetic MSPs have also been discovered: B1821-24 and J1823-3021A, respectively. The GeV γ-ray emission has been observed from these two GCs, modulated with the periods of the pulsars within the cluster (Freire et al. 2011; Johnson et al. 2013). Moreover, the spectra observed from GCs have very similar features to those observed from isolated MSPs, i.e. the spectra are flatter than −2 with a cut-off at a few GeV (Abdo et al. 2010). These observations support that the GeV γ-ray emission from GCs is very likely produced due to a cumulative emission of the MSP population, as proposed by Harding, Usov & Muslinov (2005), Venter & de Jager (2008), and Venter, de Jager & Clapson (2009). The basic features of these observations and their consequences for the MSP population in GCs are reviewed by e.g. Bednarek (2011) and Tam, Hui & Kong (2016).

MSPs are expected to inject energetic leptons from their inner magnetospheres in the form of pulsar winds as observed in the case of the pulsars formed in the core collapse supernovae (so called ‘classical pulsars’). These leptons can be injected directly with TeV energies. Alternatively, they may reach such energies as a result of re-acceleration in the pulsar wind regions, in collisions of those winds among themselves or with the winds of the GC stars. Similarities with phenomena around classical pulsars and MSPs have triggered the attention of the telescopes sensitive in the TeV γ-ray energies. However, in most of the cases only upper limits on the TeV γ-ray flux have been reported, e.g. from Omega Centauri (Kabuki et al. 2007), 47 Tuc (Aharonian et al. 2009), M13 (Anderhub et al. 2009), and M15, M13, and M5 (McCutcheon et al. 2009). The upper limits of the TeV flux for several individual GCs (and also stacked upper limits) have also been reported for the case of point-like or extended sources, mostly for the GCs not detected by Fermi-LAT in GeV γ-rays (Abramowski et al. 2013). Only in the case of GC Ter 5, longer observations (∼90 h) with the H.E.S.S. telescopes resulted in the discovery of an extended TeV γ-ray source in the direction of this GC (Abramowski et al. 2011). Surprisingly, the centre of the TeV source is shifted from the centre of Ter 5 by the distance comparable to the dimension of the GC. In fact, such asymmetry might be observed in the case of the non-spherical propagation of TeV leptons around Ter 5 (Bednarek & Sobczak 2014).

Detailed MSP models for the TeV γ-ray emission from GCs have been developed already before the above-mentioned Fermi-LAT discovery of GeV γ-ray emission from GCs. Two general models for the injection of energetic leptons were considered, either mono-energetic injection directly from the MSPs (e.g. Bednarek & Sitarek 2007; Venter et al. 2009; Cheng et al. 2010; Zajczyk, Bednarek & Rudak 2013; Bednarek, Sitarek & Sobczak 2016) or with a power-law distribution as a result of re-acceleration in the pulsar wind collision regions (e.g. Bednarek & Sitarek 2007; Kopp et al. 2013; Bednarek et al. 2016; Ndiyavala, Krüger & Venter 2018). These works assumed that TeV γ-rays originate in the Inverse Compton (IC) scattering process of low-energy radiation (optical from the GC, Cosmic Microwave Background (CMB), or the infrared and optical radiation from the Galactic disc) by leptons accelerated by MSPs. The most recent developments of numerical codes computing the γ-ray emission from GCs take into account effects related to different diffusion scenarios for energetic particles (Ndiyavala et al. 2018), the advection of leptons from GCs due to Red Giant (RG) winds and non-homogeneous injection of leptons into the GCs (Bednarek et al. 2016). Modelling results, if confronted with observations, should allow us to constrain the processes occurring in the MSP magnetospheres, acceleration of leptons within GCs, and their transport within and around GCs. Note that other phenomena, such as supernova remnants accelerating hadrons (Domainko 2011) or electrons accelerated in magnetized White Dwarfs (Bednarek 2012), might also contribute to the high-energy emission from GCs.

The IC model also predicts synchrotron emission from the same population of leptons which might be observable under favourable conditions between the radio and soft X-rays. In fact, in the Chandra observations of the GC Ter 5, the existence of an extended, non-thermal X-ray source centred on the GC core has been reported (Eger, Domainko & Clapson 2010; Clapson et al. 2011). A similar result has been reported in the case of 47 Tuc (Wu et al. 2014). Earlier observations have also reported evidence of X-ray emission from some GCs, extended over a few arcmin, which has been interpreted as a result of the interaction of the wind from the GC with the surrounding medium (Hartwick, Cowley & Grindlay 1982; Okada et al. 2007). However, such X-ray sources have not been detected in the direction of a few other GCs (Eger & Domainko 2012). Other models for the TeV γ-ray emission from GCs have been also proposed (see e.g. Cheng et al. 2010; Domainko 2011; Bednarek 2012).In summary, the production of TeV γ-rays in GCs seems to be unavoidable. However, the expected level of emission depends on several parameters, such as injection rate and spectra of leptons from the MSP magnetospheres or the propagation of energetic particles in the complex medium. These parameters are at present not well constrained. Their limitation will have important consequences for observational plans with the future generation of telescopes such as the Cherenkov Telescope Array (CTA; Acharya et al. 2013). Therefore, we performed extensive observations of the GC M15 with the MAGIC telescopes. In Section 2, we introduce the basic parameters of M15. In Section 3, we present the MAGIC observations of M15. In Section 4, we confront the results of the MAGIC observations with the model of VHE γ-ray emission of M15. We conclude the paper with final remarks in Section 5.

2 GLOBULAR CLUSTER M15

M15 belongs to the class of core collapsed, luminous GCs. Its total stellar luminosity is 7 × 10⁵ L_⊙, the core radius 0.43 pc, the half-mass radius 3.04 pc, and the distance from Earth of 10.4 kpc (Harris 1996). Eight MSPs have been discovered up to now within M15 (Freire et al. 2015).

We observed M15 with the MAGIC telescopes since it is the only GC discovered at GeV γ-ray energies by Fermi-LAT (Zhang et al. 2016), which can be observed at low zenith angles (Zd_min ∼ 16°35′) from La Palma. Its γ-ray luminosity above 0.1 GeV has been measured as |$L_\gamma ^{\rm M15} = (5.26_{-1.16}^{+1.31})\times 10^{34}$| erg s⁻¹. The spectrum is close to the power-law type with spectral index 2.84 ± 0.18, observed up to ∼5 GeV (Zhang et al. 2016). The GeV emission from a GC is interpreted as a cumulative emission from the whole population of the MSPs within the cluster. In fact, observations of nearby MSPs in the galactic plane based on the Fermi-LAT data (Abdo et al. 2009b) allow us to estimate the conversion efficiency of the MSP’s rotational energy into GeV γ-rays of η_γ ≈ 0.08 and the average luminosity of such MSP on |$\langle L_\gamma ^{\rm MSP} \rangle = 1.44\times 10^{33}$| erg s⁻¹. Based on these average values and the MSP hypothesis of the γ-ray emission from the GCs, it is possible to estimate the number of MSPs in M15 to be |$37_{-8}^{+9}$|⁠. Note that the pulsations from most of the MSPs will not be observable due to their unfavourable observation angles. We further estimated the total rotational energy loss rate by the MSPs in M15 on |$L_{\rm rot} = L_\gamma ^{\rm M15}/\eta _\gamma \approx 6.7\times 10^{35}$| erg s⁻¹.

It is expected that the winds of MSPs mix within the GC with the matter ejected by the ambient RG stars. For the expected mass-loss rates of specific RGs, estimated in the range 10⁻⁹–3 × 10⁻⁷ M_⊙ yr⁻¹ (Boyer et al. 2008; Meszaros, Avrett & Dupree 2009), and assuming the number of RGs within M15 to be of the order of 100 (for another GC, NGC 2808 137 RGs have been observed, Cacciari et al. 2004), it is possible to estimate the velocity of the mixed MSP and RG winds (see equation 1 in Bednarek et al. 2016). Assuming that MSPs provide luminosities of the order of L_rot derived above, and that the MSP winds mix with the RG material with a mixing efficiency of 0.5, we estimate the velocity of the resulting mixed wind in the range |$v$|_w ≈ (0.2–3.5) × 10⁸ cm s⁻¹. The mixing efficiency is the fraction of the rotational energy loss of the pulsars that is transmitted to the stellar winds. It depends on the geometry of all the MSP binary systems, and is only constrained to be lower than unity. Note that recent estimates of the mass-loss rate by RG stars in another massive GC, 47 Tuc, give values of about 3 × 10⁻⁶ M_⊙ yr⁻¹ (McDonald & Zijlstra 2015), with the total content of ionized gas in 47 Tuc ∼0.1 M_⊙ (Freire et al. 2001). Quite a large amount of a neutral gas, ≈0.3 M_⊙, has also been detected within M15 (Evans et al. 2003; van Loon et al. 2006).

MSPs can also distribute the magnetic field with their winds to the volume of the GC. The strength of this magnetic field can be approximated by its value at the collision region of the MSP winds (see estimates given by equations 2 and 3 in Bednarek & Sitarek 2007). For an average MSP, we assume a typical rotation period of 4 ms and the surface magnetic field of 3 × 10⁸ G. We further assume that all MSPs in M15 are confined within its core radius of |$R_{\rm c}^{M15} = 0.43$| pc. Then, the characteristic shock radius around the MSP in M15 is of the order of R_sh ≈ 2 × 10¹⁷ cm (Bednarek & Sitarek 2007). The magnetization parameter, σ which is the ratio of the Poynting flux to the relativistic particle flux, is estimated at the nebula for the winds of classical pulsars of Vela type on σ ∼ 0.1 (Sefako & de Jager 2003) and the Crab pulsar on σ ∼ 0.002 (Kennel & Coroniti 1984). On the other hand, if the wind terminated closer to the pulsar as expected in the case of the MSPs within GCs, the magnetization is expected to be higher, σ ∼ 1 (Contopoulos & Kazanas 2002). Using the above values of magnetization we estimate the magnetic field strength at the shock to be of the order of B_sh ≈ (1 − 30) × 10⁻⁶ G. In our modelling of the γ-ray emission from M15 (see Section 4) we apply the values of the mixed winds’ velocity and the magnetic field strength of the order of the ones estimated above.

3 MAGIC OBSERVATIONS OF M15

MAGIC is a system of two 17 m diameter Imaging Atmospheric Cherenkov Telescopes. The telescopes are located at the Observatorio del Roque de los Muchachos, on the Canary Island of La Palma, Spain (Aleksić et al. 2016a). MAGIC is used for observations of γ rays with energies between |${\sim }\,$|50 GeV and few tens of TeV. The telescopes reach a sensitivity of (0.66 ± 0.03) per cent of C.U. (Crab Nebula flux) in 50 h of observations for energies above 220 GeV (Aleksić et al. 2016b). The angular resolution (defined as a standard deviation of a two-dimensional Gaussian distribution) at those energies is ≲ 0.07°.

Between 2015 June and 2016 September the MAGIC telescopes performed observations of the M15 region. In total 173 h of data were collected, out of which 165 h were selected for further analysis. To assure a low-energy threshold the data have been taken mostly at low (≲30°) zenith angles. The data were analysed using the standard MAGIC analysis chain (Zanin et al. 2013; Aleksić et al. 2016b). About one third of the selected data set was taken under non-perfect atmospheric conditions (mostly due to calima, a dust wind from the Sahara desert, which affects part of the MAGIC data taken during summer). That part of the data set has been corrected using simultaneous LIDAR measurements (Fruck & Gaug 2015).

No significant signal has been observed from the direction of M15 (see Fig. 1). Also, no other significant emission is detected in the field of view covered by those observations (see Fig. 2).We compute upper limits on the flux from M15 following the approach of Rolke, López & Conrad (2005) using a 95 per cent confidence level and assuming a 30 per cent total systematic uncertainty on the collection area and a spectral index of −2.6. In addition, we require that the upper limit on the number of excess events in each energy bin is at least 3 per cent of the residual background. This ensures that, despite the long observation time, the background-induced systematic uncertainties do not exceed the assumed systematic uncertainty (see Aleksić et al. 2016b). The obtained upper limit on the integral flux above 300 GeV is equal to |$3.2\times 10^{-13}\, \mathrm{cm^{-2}\, s^{-1}}$|⁠, which corresponds to |$\lt 0.26{{\ \rm per\ cent}}$| of the Crab Nebula flux. It is a factor of a few below the previous upper limit reported from M15 by the H.E.S.S. Collaboration (equal to 7.2 × 10⁻¹³ cm⁻² s⁻¹ above 440 GeV, corresponding to 0.9 per cent of the Crab Nebula flux for a point like source; Abramowski et al. 2013). The currently most stringent constraint on the absolute TeV luminosity of a GC comes from H.E.S.S. observations of 47 Tuc. The upper limit on the integral flux of 47 Tuc above 800 GeV is |${\sim }2{{\ \rm per\ cent}}$| of the Crab Nebula flux, which translates to a luminosity limit 6.8 × 10³³ erg s⁻¹ for a distance of 4 kpc (Aharonian et al. 2009). In order to compare with the above limit on the energy flux, we compute differential flux limits and integrate them above a given energy. MAGIC observations show that the luminosity of M15 in the energy range 800 GeV–19 TeV is below 1.1 × 10³⁴ erg s⁻¹, a comparable (within a factor of 2) limit to the value for 47 Tuc, despite the ∼2.5 times larger distance to M15. Moreover, the observations with MAGIC allow us to probe the possible γ-ray emission down to lower energies without much loss of sensitivity, e.g. the luminosity of M15 in the energy range 300 GeV–19 TeV derived from the MAGIC observations is below 1.6 × 10³⁴ erg s⁻¹. The upper limits on the differential flux from M15 are compared with the model predictions in Section 4.

Figure 1.

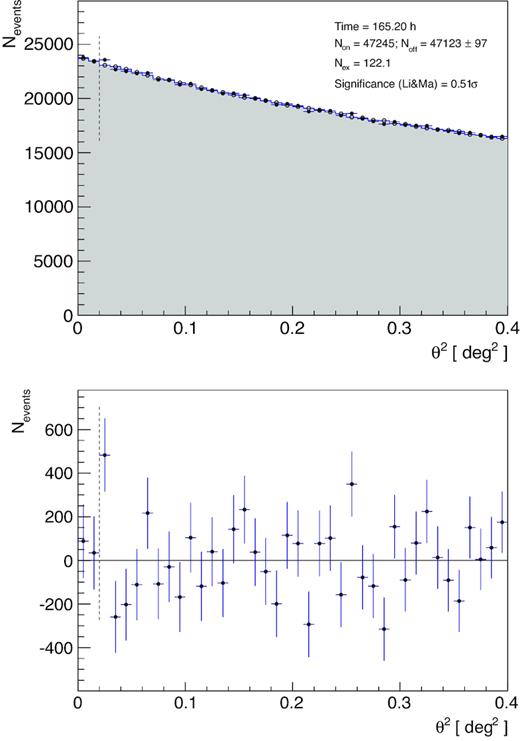
Top panel: distribution of the squared angular distance between the reconstructed event direction and the nominal source position (filled points) and the background estimation (shaded area and empty points). Bottom panel: On–Off excess distribution. The corresponding energy threshold (defined as the peak of the differential energy distribution for Monte Carlo γ rays with a spectral index of −2.6) is |${\sim }\, 75\,$|GeV. The significance of the excess was computed using equation 17 in Li & Ma (1983).

Open in new tabDownload slide

Figure 2.

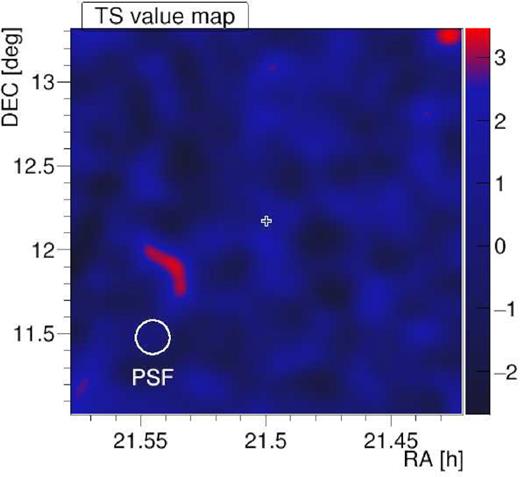
Skymap of the M15 observations. The TS value corresponds to a significance of an excess at a given location in the sky. The marker shows the nominal position of M15. The corresponding energy threshold, ∼75 GeV, is described in Fig. 1 caption.

Open in new tabDownload slide

Relativistic leptons, ejected from the inner magnetospheres of the MSPs with a quasi mono-energetic spectrum, can comptonize the optical radiation from the GC at energies affected by the Klein–Nishina regime.

As a result, strongly peaked γ-ray spectra are also expected. Therefore, we also show the upper limits on the γ-ray luminosity in narrow energy ranges (see Fig. 3). No hint of the emission has been seen from any of the energy bins (namely the significance was below 1.3σ in every of them). The upper limits, integrated in 0.2 decades in energy, reach down to a level of ∼10³³ erg s⁻¹.

Figure 3.

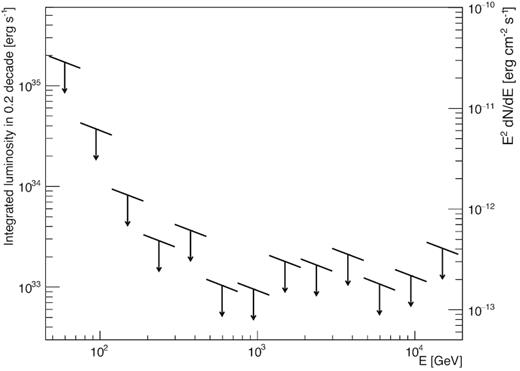
Upper limits on the γ-ray luminosity from the GC M15 (integrated in 0.2 decades in energy). The right axis shows the corresponding upper limits on the spectral energy distribution.

Open in new tabDownload slide

4 THEORETICAL EXPECTATIONS VERSUS TEV γ-RAY OBSERVATIONS

The strong upper limits on the TeV γ-ray flux from M15 are confronted with the predictions of the model for the TeV γ-ray production in GCs of Bednarek et al. (2016). In this model, the TeV γ rays are produced by leptons either injected with the mono-energetic spectra directly from the inner pulsar magnetospheres or accelerated with the power-law spectra in the MSP wind collision regions. The leptons comptonize soft radiation from the huge population of low-mass stars within the GC, from the CMB, and/or optical and infrared photons from the Galactic disc. The model also includes the synchrotron energy losses of the leptons during their propagation in the GC. The level of produced TeV γ-ray emission in a specific GC depends on the injection rate of the leptons from the MSPs and their transport through the volume of the GC. The model considers two transport processes of the leptons, i.e. diffusion process with the Bohm diffusion prescription and the advection with the wind formed within the GC. Such a wind is expected to be composed of a mixture of the energetic MSP cumulative winds and the cumulative winds from the RGs present within the GC. The range of velocities of the GC winds can be estimated to ∼10⁷–10⁸ cm s⁻¹, based on the known expected rate of the mass-loss rate by the RGs and the energy loss rate of the MSPs within the GC (see equation 1 in Bednarek et al. 2016). The energy loss rate of the MSPs within M15 is calculated for the known GeV γ-ray luminosity of the MSPs within M15 and for the known conversion efficiency of the rotational energy of isolated MSPs to the γ-ray energy range (Abdo et al. 2009a). In the calculations we do not use the estimated number of MSP in M15, but only their total luminosity measured directly by Fermi-LAT. For the applied transport model of the leptons, the observations of the TeV γ-ray emission from specific GCs allow us to estimate the basic parameters characterizing processes occurring in the MSP inner magnetospheres, such as the injection rate of the leptons and their energies and efficiency of the lepton acceleration in the wind regions around MSPs. Bednarek et al. (2016) predicted the fluxes of TeV γ rays from M15 for the range of parameters describing the transport of the leptons through the GC and for the two above mentioned spectra of injected leptons, i.e. mono-energetic electrons and electrons injected with a power-law spectrum. We use this model to interpret the results of the MAGIC observations reported in this paper.¹

4.1 Quasi-monoenergetic leptons from MSPs

We compare the differential flux upper limits, derived from MAGIC observations of M15, with the expected TeV γ-ray spectra for a variety of parameters of the mono-energetic injection of relativistic leptons from the MSP magnetospheres (see Fig. 4).

Figure 4.

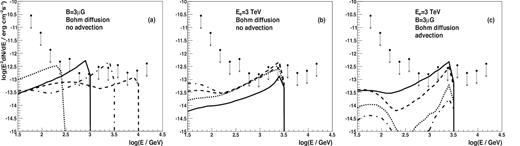
Differential flux upper limits from 165 h of MAGIC observations of M15 compared with the SED produced in the case of the isotropic injection of mono-energetic leptons from the pulsars within GC M15. We show the dependence of the IC spectra as a function of (a) the energy of injected leptons, E_e = 300 GeV (dotted), 1 TeV (solid), 3 TeV (dot–dashed), 10 TeV (dashed), for the magnetic field strength is B = 3 × 10⁻⁶ G and no advection; (b) on the magnetic field strength within the cluster, |$B = 1\, \mu$|G (dot–dashed), |$3\, \mu$|G (dashed), |$10\, \mu$|G (dotted), and |$30\, \mu$|G (solid), and the energy of leptons 3 TeV without advection; (c) the advection velocity from the GC, |$v$|_adv = 10⁷ cm s⁻¹ (dashed curve), 10⁸ cm s⁻¹ (dotted), 3 × 10⁸ cm s⁻¹ (dot–dashed), and the energy of the leptons 3 TeV, B = 3 × 10⁻⁶ G and without advection (solid). It is assumed that the power injected in leptons is equal to 1|${{\ \rm per\ cent}}$| of the rotational energy loss rate of MSPs within the GC M15 (L_e = 0.01L_rot).

Open in new tabDownload slide

The monoenergetic spectrum considered in the model, results from assuming that all pulsars have the same potential drop (and therefore the electrons are accelerated to the same energy). The expected fluxes are calculated assuming that the power in relativistic leptons is equal to |$\eta _{\rm e}=1{{\ \rm per\ cent}}$| of the rotational energy loss rate of the whole population of the MSPs within M15 (i.e. |$L_{\rm e} = 0.01L_{\rm rot} = 0.01L_\gamma ^{\rm M15}/\eta _\gamma$|⁠), where the γ-ray power, |$L_\gamma ^{\rm GC} = 5.26\times 10^{34}$| erg s⁻¹, has been derived based on the Fermi-LAT observations (see Zhang et al. 2016). The power in relativistic electrons and the observed GeV γ-ray emission can be expressed as L_e = η_eL_rotN_MSP and |$L_\gamma ^{\rm GC} = \eta _\gamma L_{\rm rot}N_{\rm MSP}$|⁠, respectively. η_e and η_γ are factors describing fractions of the MSPs rotational energy, L_rot, transferred to relativistic electrons and emitted in GeV γ-rays, and N_MSP is the number of MSPs in GC. Note that |$L_{\rm rot}\approx \langle L_\gamma ^{\rm MSP}\rangle /\eta _\gamma$|⁠, where η_γ ≈ 0.08 and |$\langle L_\gamma ^{\rm MSP} \rangle = 1.44\times 10^{33}$| erg s⁻¹ (the average luminosity of the MSPs) have been estimated based on the observations of nearby MSPs in the galactic field based on the Fermi-LAT data (Abdo et al. 2009a). Therefore, |$\eta _{\rm e} = \eta _\gamma L_{\rm e}/L_\gamma ^{\rm GC}\approx 0.08L_{\rm e}/L_\gamma ^{\rm GC}$|⁠. Then, constraints on L_e from the MAGIC observations set direct constraints on the parameter η_e. The value of this parameter is determined by the radiation processes in the inner MSP magnetospheres and its surroundings. Its value should be predicted by different models for the high-energy processes around pulsars. Note that we do not take into account the uncertainty of L_γ when computing the limits on η_e, since their effect is negligible compared to the spread of the limits due to the tested ranges of other model parameters.

Figure 5.

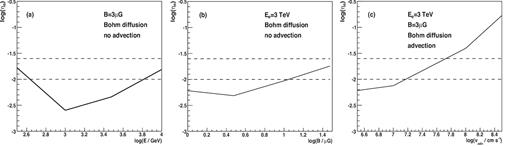
Constraints on the coefficient, η_e, of the conversion of the energy loss rate of the pulsars to relativistic leptons in GC M15 in the case of injection of monoenergetic leptons from the inner pulsar magnetospheres. The dashed lines mark the level of the conversion efficiency expected from the pulsar models (⁠|$1\text{--}2.5{{\ \rm per\ cent}}$|⁠, see text). The upper limits on η_e, obtained as a function of energy of the injected leptons, are shown in panel (a) as the solid curve. It is assumed that leptons diffuse from the GC as expected in the Bohm diffusion model and the magnetic field strength in GC is fixed on 3 |$\mu$|G. The advection of leptons is not considered. The upper limits on η_e obtained for different strengths of the magnetic field within GC are shown in (b) for the energy of the monoenergetic leptons equal to 3 TeV, assuming the Bohm diffusion prescription and neglecting the advection from the GC. In (c) we show the upper limits on η_e as a function of the advection velocity of the mixed MSP/stellar winds assuming the Bohm diffusion prescription, energy of leptons 3 TeV.

Open in new tabDownload slide

It should be noted that in the above calculations we have simplistically considered that all the MSP in M15 have the same parameters. Differences from one MSP to another are to be expected; however, are very difficult to quantify. If the emission would be divided between N MSPs of different parameters and peaking in different energy ranges the sensitivity for detection of such emission will be worse by a factor up to |$\sqrt{N}$|⁠. However, as the number of peaks increases, they will start to heavily overlap (as can be seen from Fig. 4a this would already be the case of ∼7 peaks). Moreover, not all the MSP will contribute with the same fraction of the emission, and a single dominating source can be responsible for most of the emission. GeV emission of a GC dominated by a single pulsar is the case for J1823−3021A MSP (Freire et al. 2011) in NGC 6624, and to the lesser extend also PSR B1821−24 in M28 (Johnson et al. 2013). We conclude that the conservative limits should be |${\sim }\sqrt{7}$| times larger than in Fig. 5, i.e. |$\eta _{\rm e} \lesssim \, 1.6{{\ \rm per\ cent}}$| in the broad range of the assumed parameters.

It is interesting to confront the constraints on η_e, obtained from the MAGIC observations of M15, with the expectation of some models for the acceleration and radiation processes within the MSP magnetosphere and their vicinity. For example, based on the fully 3D general-relativistic polar cap pulsar model, Venter & de Jager (2005) estimated the values of the parameter η_e to be |$1\hbox{--}2.5{{\ \rm per\ cent}}$| and η_γ to be |$2\hbox{--}9{{\ \rm per\ cent}}$| for the case of PSR J0437−4715. These estimates have been generally confirmed in the analysis of the γ-ray emission from the population of MSPs in 47 Tuc, |$\eta _{\rm e}\sim 2{{\ \rm per\ cent}}$| and |$\eta _\gamma \sim 7{{\ \rm per\ cent}}$| (Venter & de Jager 2008). The estimates of |$\eta _\gamma \sim 10{{\ \rm per\ cent}}$| are consistent with other modelling of processes in the pulsar’s inner magnetospheres based on a space charge-limited outflow polar cap model (e.g. Harding, Muslinov & Zhang 2002), the outer gap model (Takata, Wang & Cheng 2010), and with the estimates based on the Fermi-LAT observations of the population of MSPs (Abdo et al. 2009a, b, also see fig. 9 in the pulsar catalogue by Abdo et al. 2013). The upper limits on η_e derived in Fig. 5 are, for most of the parameter space, below the values expected from modelling of the processes in the pulsar magnetospheres mentioned above. However, the predictions of the pulsar models might still be consistent with the MAGIC observations provided that the mixed pulsar/stellar wind velocity is |${\gtrsim }\, 1.5\times 10^7$| cm s⁻¹ for |$\eta _{\rm e} = 1{{\ \rm per\ cent}}$| and |${\gtrsim }\, 6\times 10^7$| cm s⁻¹ for |$\eta _{\rm e} = 2.5{{\ \rm per\ cent}}$| (see Fig. 5c). Note however that a quite large amount of a neutral gas has been discovered within M15 (see Section 2). This is difficult to explain in the case of efficient removal of the matter from the volume of this GC as a result of a very fast wind from the GC. Therefore, we conclude that the present models for the high-energy processes in the inner pulsar magnetospheres are in conflict with the constraints obtained here on the injection rate of the leptons from the inner magnetospheres of the MSPs within M15 provided that the RG winds are not able to remove very efficiently the TeV leptons from the volume of the GC. The presence of such fast winds is not supported by the observations of substantial diffusive matter within M15.

The parameter η_e can be related to the parameter σ which characterizes the form of energy injected from the inner pulsar magnetosphere. σ, defined as the ratio of the Poynting flux to the particle flux, can be related to the energy carried by the magnetic field, L_B, and relativistic particles, L_e, provided that the surface area of these two flows is the same, i.e. σ = F_P/F_k = L_BS_k/L_kS_P = L_B/L_e for S_p = S_k. L_B and L_e are related to each other as L_B = L_rot − L_e. The possible contribution from heavy ions to the energy loss rate is neglected, although it has been proposed to be also important, e.g. Gallant & Arons (1994) and Coroniti (2017). σ is related to the parameter η_e in the following way, |$\sigma = (L_{\rm rot} - L_{\rm e})/L_{\rm e} = \eta _{\rm e}^{-1} - 1$|⁠. For classical pulsars, σ is expected to be of the order of ∼10⁴ close to the light cylinder radius (e.g. Cheng, Ho & Ruderman 1986; Arons 2008). The MAGIC constraints on η_e (see Fig. 5), in the case of a relatively slow advection process of leptons from M15, allow us already to constrain σ to be ≳200. Therefore, the value of the magnetization parameter for the MSPs at their light cylinder radius is also expected to be as large as in the case of classical pulsars.

4.2 Leptons with a power-law spectrum

Bednarek et al. (2016) also considered the case of injection of leptons with power-law spectra from the MSP wind regions. We have compared the results of calculations of the TeV γ-ray spectra produced in the case of the power-law injection model with the upper limits on M15 obtained from the MAGIC observations (see Fig. 6).The dependence on the TeV γ-ray emission on the spectral index of the leptons, the magnetic field strength within M15, and the advection velocity of the leptons from the GC are investigated. From confrontation of these calculations with the observed upper limits we derive upper limits on the acceleration efficiency of the leptons with a power-law spectrum (Fig. 7).The upper limits on η_e are below ∼2 × 10⁻² for negligible advection process (velocities below |$v$|_adv ∼ 10⁷ cm s⁻¹) and below ∼0.3 for fast advection process (⁠|$v$|_adv ∼ 3 × 10⁸ cm s⁻¹) and reasonable values of the magnetic field strength within the GC (⁠|$B \lt 10\, \mu$|G). The values of the parameter σ, corresponding to those acceleration velocities are estimated to be σ_MSP > 49 and σ_MSP > 2.3, respectively, for the above mentioned conditions. However, for stronger fields these limits increase reaching the values of ∼0.8 for |$B = 30\, \mu$|G. Note that the values of σ parameter in the nebulae around classical pulsars have been estimated to 0.002 (corresponding to η_e = 0.998) for the Crab Nebula (e.g. Rees & Gunn 1974; Kennel & Coroniti 1984) and ∼0.1 (η_e = 0.909) for the nebula around the Vela pulsar (Sefako & de Jager 2003). In the case of the winds, which are forced to terminate closer to the pulsar, the values of σ have been calculated to be of the order of unity (η_e = 0.5) (Contopoulos & Kazanas 2002). The lower limits on the σ parameter, constrained for the winds around MSPs within M15, are clearly above the values expected for nebulae around classical pulsars. Based on the above observations and theoretical calculations, we conclude that pulsar wind regions around MSPs are not able to accelerate leptons with the rates similar to those observed in the case of classical pulsars.

Figure 6.

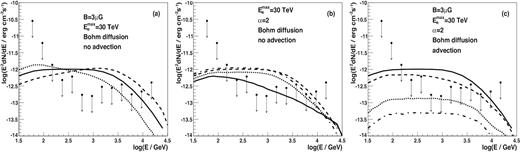
The differential flux upper limits from 165 h of M15 observations (points) compared with the SED produced in the case of the isotropic injection of the leptons with the power-law spectrum from the pulsars within GC M15. We show the dependence of the IC spectra as a function of (a) the spectral index of injected leptons, α = 1.5 (dashed), 2. (solid), 2.5 (dotted), and the cut-off energy in the spectrum at 30 TeV, the magnetic field strength |$B = 3\, \mu$|G in the case of no advection; (b) on the magnetic field strength within the cluster, |$B = 1\, \mu$|G (dot–dashed), |$3\, \mu$|G (dashed), |$10\, \mu$|G (dotted), and |$30\, \mu$|G (solid), and spectral index of leptons equal to α = 2, the cut-off energy in the lepton spectrum at 30 TeV, and without advection; (c) the advection velocity from the GC, |$v$|_adv = 10⁷ cm s⁻¹ (dashed curve), 10⁸ cm s⁻¹ (dotted), 3 × 10⁸ cm s⁻¹ (dot–dashed), and without advection (solid), the power-law spectrum of leptons with the spectral index equal to 2 and the cut-off at 30 TeV, and the magnetic field strength equal to |$B = 3\, \mu$|G. It is assumed that the power in injected leptons is equal to 10|${{\ \rm per\ cent}}$| of the rotational energy loss rate of MSPs within the GC M15.

Open in new tabDownload slide

Figure 7.

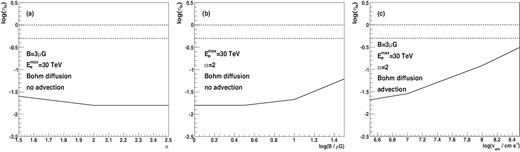
Constraints on the coefficient, η_e, of the conversion of the energy loss rate of the pulsars to relativistic leptons in the GC M15 in the case of injection of leptons with the power-law spectrum from the pulsar wind collision regions (solid curve). The upper limits on η_e are obtained for the specific propagation and injection models corresponding to the figures (a), (b), and (c) as shown in Fig. 6. The dotted lines mark the level of the energy conversion efficiency from the pulsars to leptons equal to |$50{{\ \rm per\ cent}}$| and |$100{{\ \rm per\ cent}}$|⁠.

Open in new tabDownload slide

A few explanations of the above derived constraints on the efficiency of lepton acceleration in the wind regions of the MSPs can be elaborated. The low values of η_e might indicate that the interaction of the MSP winds with a large amount of small-scale winds around classical stars (present within the GC) or with the MSP winds between themselves disrupt the wind structure preventing efficient acceleration of particles. Then, the inner regions of the pulsar winds, at distances comparable to the typical distance between the stars which is ∼10¹⁷ cm in the case of MSPs in M15, might not be able to convert efficiently energy from the magnetic field into relativistic particles. Another possible explanation can be related to the effectiveness of removal of the wind matter from the GC. If the mixed MSP/RG winds move faster than estimated above, then the upper limits derived in our modelling from the TeV γ-ray observations of M15 become much less restrictive. This explanation seems unlikely in the context of a relatively large amount of distributed matter observed in M15. Finally, the low effectiveness of lepton acceleration can be related to the assumption on the wind composition around MSPs. In the case of MSPs, the winds can be energetically dominated by hadrons. In fact, the conditions and the content of the matter at the surfaces of the classical pulsars and the MSPs within GCs differ significantly. The surface of classical pulsars is expected to contain heavy nuclei which might be strongly bounded to the surface in the strong magnetic field (Usov & Melrose 1995). On the other hand, the mildly magnetized magnetospheres of the MSPs within GCs are expected to be composed of the matter accreted from the atmospheres of low mass main-sequence stars (i.e. mainly hydrogen and helium). Therefore, the composition of particles, which dominate energetically in the neutron star’s magnetosphere, can be different. In the case of classical pulsars, leptons dominate since iron nuclei are strongly bounded to the surface. Then, the pulsar radiation processes might be well described in terms of the so-called slot gap model (Arons 1983) or pair-starved polar cap model (see Ruderman & Sutherland 1975; Muslinov & Harding 2003). In the case of MSPs, light hadrons dominate since they are not strongly bounded to the neutron star surface. Then, the pulsar energy loss rate is carried mainly by energetic hadrons. In this case leptons contribute only partially to the energy loss rate of the pulsar. Then, the high-energy emission from the MSPs can be better explained in terms of so called space charge limited outflow model (Arons & Scharlemann 1979).

We suggest that the acceleration/radiation processes within the atmospheres of classical γ-ray pulsars and the MSPs are different. Note that up to now no isolated TeV γ-ray Pulsar Wind Nebula around a MSP has been firmly detected (Ahnen, Ansoldi & Antonelli 2017; Hooper, D & Linden 2018). This, combined with the limits derived by the MAGIC observations of M15, suggests that the winds of the MSPs might not accelerate leptons as efficiently as the winds around classical pulsars.

5 CONCLUSION

Based on the deep observations of the GC M15 with the MAGIC telescopes, we obtained the most constraining upper limit on the TeV γ-ray emission of |$0.26{{\ \rm per\ cent}}$| Crab flux above 300 GeV. This upper limit has been compared with the predictions of the IC emission model in which leptons are accelerated in the inner magnetospheres (with a quasi-monoenergetic spectrum) or in the wind regions (with a power-law spectrum) of the MSPs (see Bednarek et al. 2016).

Based on the comparison of the MAGIC upper limits on M15 with the predictions of the model, we constrain the efficiency of lepton injection from the inner magnetospheres of MSPs and their vicinity. We conclude that the injection rate of leptons from the inner pulsar magnetospheres is below the rate expected from MSPs (e.g. Venter & de Jager 2005, 2008) for the expected range of the free parameters describing the IC model. We also constrained the injection rate of leptons with a power-law spectrum from the MSP wind regions. This injection rate of the leptons is also clearly below the values estimated for the injection from the wind regions around classical pulsars.

We discuss possible explanation of these very low injection rates from the MSPs within M15. The limits become less restrictive in the case of a fast advection of the leptons from the region of the GC with the velocity of the wind formed as a result of the mixture of the MSP winds with the winds from the population of the RGs within M15. This explanation is difficult to reconcile with the presence of a relatively large quantity of neutral gas within M15 (e.g. Evans et al. 2003; van Loon et al. 2006). An important difference between the wind regions around classical pulsars and those around MSPs within GCs is related to the presence of a large number of local, low mass stellar winds. Also the conditions at the termination shocks of the winds around these two types of pulsars can significantly differ since the winds around MSPs can collide between themselves. Therefore, leptons might not be able to reach large energies in the case of such earlier disrupted winds around MSPs. This suggests that leptons are only effectively accelerated in the pulsar wind regions which are terminated at relatively large distances from the pulsars.

We also speculate that the wind regions around MSPs and classical pulsars might have different compositions which results in a different mechanism for acceleration and radiation of the leptons in the vicinity of the pulsars. In fact, it is expected that the composition of matter on the surface of neutron stars, which are observed as classical pulsars and MSPs, differs significantly between MSPs and classical pulsars. MSPs are expected to contain light nuclei (hydrogen, helium) on the surface which are not strongly bound to the NS surface. On the other hand, the atmosphere of the classical pulsar is mainly composed of iron nuclei which might be strongly bound to the surface in the superstrong magnetic field. Then, the energy lost by the pulsar could be mainly carried out in the form of relativistic leptons in the case of classical pulsars (i.e. in terms of the extended polar cap model) and in the form of relativistic light nuclei in the case of MSPs (i.e. in terms of the space-charge limited outflow model). As a result, the injection rate of leptons from MSPs should be expected to be clearly lower than the injection rate of leptons from classical pulsars, in consistency with the present MAGIC observations of the GC M15.

ACKNOWLEDGEMENTS

We would like to thank the Referee for useful comments and the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The financial support of the German BMBF and MPG, the Italian INFN and INAF, the Swiss National Fund SNF, the ERDF under the Spanish Ministry of Economy and Competitiveness (MINECO) (FPA2015-69818-P, FPA2012-36668, FPA2015-68378-P, FPA2015-69210-C6-2-R, FPA2015-69210-C6-4-R, FPA2015-69210-C6-6-R, AYA2015-71042-P, AYA2016-76012-C3-1-P, ESP2015-71662-C2-2-P, FPA2017-90566-REDC), the Indian Department of Atomic Energy and the Japanese Japan Society of for the Promotion of Science (JSPS) and Ministry of Education, Culture, Sports, Science and Technology (MEXT) is gratefully acknowledged. This work was also supported by the Spanish Centro de Excelencia ‘Severo Ochoa’ SEV-2016-0588 and SEV-2015-0548, and Unidad de Excelencia ‘María de Maeztu’ MDM-2014-0369, by the Croatian Science Foundation (HrZZ) Project IP-2016-06-9782 and the University of Rijeka Project 13.12.1.3.02, by the German Research Fundation (DFG) Collaborative Research Centers SFB823/C4 and SFB876/C3, the Polish National Research Centre grant UMO-2016/22/M/ST9/00382 and by the Brazilian MCTIC, CNPq and FAPERJ. This work is also supported by the grant through the Polish National Research Centre No. 2014/15/B/ST9/04043.

Footnotes

REFERENCES