Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

ABSTRACT

We calculate the effective temperature (Teff) of ionizing star(s), the oxygen abundance of the gas phase |$(\rm O/H)$|⁠, and the ionization parameter U for a sample of H ii regions located in the discs of 59 spiral galaxies in the redshift range 0.005 < |$z$| < 0.03. We use spectroscopic data taken from the CALIFA data release 3 (DR3) and theoretical (for Teff and U) and empirical (for O/H) calibrations based on strong emission lines. We consider the spatial distribution and radial gradients of these parameters in each galactic disc for the objects in our sample. Most of the galaxies in our sample (∼70 per cent) show positive Teff radial gradients, although some exhibit negative or flat ones. The median value of the Teff radial gradient is 0.762 kK/R25. We find that the radial gradients of both log U and Teff depend on the oxygen abundance gradient, in the sense that the gradient of log U increases as the |$\log (\rm O/H)$| gradient increases while there is an anti-correlation between the gradient of Teff and the oxygen abundance gradient. Moreover, galaxies with flat oxygen abundance gradients tend to have flat log U and Teff gradients as well. Although our results are in agreement with the idea of the existence of positive Teff gradients along the disc of the majority of spiral galaxies, it seems that this is not a universal property for these objects.

ISM: abundances, H ii regions, galaxies: abundances

1 INTRODUCTION

The determination of thetend effective temperature (Teff) of ionizing star(s) belonging to H ii regions is crucial for an understanding of the processes that restrict the formation and evolution of massive stars, the physics of stellar atmospheres, the excitation of the interstellar medium (ISM) as well as the galaxy in which they reside.

For ionizing stars of nearby H ii regions, located in the Milky Way and the Magellanic Clouds, the effective temperature can be directly estimated using photometric and spectrometric data (e.g. Massey et al. 2005, 2009; Corti, Bosch & Niemela 2007; Sota et al. 2011; Morrell et al. 2014; Walborn et al. 2014; Lamb et al. 2016; Evans et al., 2015; Mohr-Smith et al. 2017; Martins & Palacios 2017; Markova, Puls & Langer 2018). For the majority of distant ionizing massive stars, however, Teff can only be indirectly estimated, for example from an analysis of emission lines emitted by the nebulae ionized by these stars. Using this methodology, which was proposed by Zanstra (1929), it is possible to estimate Teff and its behaviour along the disc of spiral galaxies (see e.g. Dors et al. 2017 and references therein).

Owing to the effects of opacity and/or line-blanketing in stellar atmospheres (Abbott & Hummer 1985; Schaerer & Schmutz 1994; Martins, Schaerer & Hillier 2005), stars with higher metallicity (Z) tend to present lower values of Teff than their counterparts with the same mass but lower Z (e.g. Mokiem et al. 2004; Martins et al. 2004). It is well known that spiral galaxies exhibit metallicity gradients, in the sense that Z decreases as the galactocentric radius increases (e.g. Pilyugin, Vílchez & Contini 2004). Therefore, assuming that stars are formed with a universal stellar upper mass limit of the initial mass function (e.g. Bastian, Covey & Meyer 2010), a positive gradient of Teff is expected in the discs of spiral galaxies. In fact, Shields & Searle (1978) suggested that the enhancement of the equivalent width of the Hβ emission line with galactocentric distance for a sample of H ii regions in M 101 could be the result of a positive Teff gradient (see also Vilchez & Pagel 1988; Henry & Howard 1995; Dors & Copetti 2003, 2005). In spite of the fact that these gradients should exist in most spiral galaxies, they were not found in early studies (e.g. Fierro, Torres-Peimbert & Peimbert 1986; Evans 1986). Recently, Dors et al. (2017) studied the Teff variation as a function of galactocentric distance for H ii regions belonging to 14 spiral galaxies using a new theoretical calibration between the observed emission-line ratio R = log([O ii](λλ3726 + 29)/[O iii]λ5007) and Teff (using the relationship proposed by Dors & Copetti 2003). These authors found positive gradients for 11 of these galaxies, null gradients for two, and a negative gradient for the remaining one (see also Pérez-Montero & Vílchez 2009). In particular, the first negative Teff gradient was found for the Milky Way by Morisset (2004). Additional analysis taking into account a larger number of galaxies is necessary in order to ascertain if the Teff gradient is a universal property of spiral galaxies.

Knowledge of the relationship between different physical parameters is essential in order to comprehend which mechanisms drive the formation and evolution of galaxies. For example, the seminal paper by Lequeux et al. (1979) calculated the metallicity (traced by the ratio between oxygen and hydrogen abundances) and the total galaxy mass (MT, obtained from atomic hydrogen velocity maps) for eight irregular and blue compact galaxies and found a clear relationship between these parameters (see also Kinman & Davidson 1981; Peimbert & Serrano 1982; Rubin, Ford & Whitmore 1984; Skillman 1992; Tremonti et al. 2004; Pilyugin et al. 2004; Sánchez et al. 2013, among others). Subsequently, Ellison et al. (2008) showed that the MT–Z relationship is affected by the dependence of the metallicity on the star formation rate (SFR), thus establishing the MT–Z–SFR relation. This result was confirmed by Lara-López et al. (2010) and Mannucci et al. (2010). In their recent study based on integral field spectroscopy data, however, Sánchez et al. (2017) did not find any significant dependence of the MT–Z relationship on the SFR, but they did not exclude the existence of such a relationship on local scales, for example in the central regions of galaxies. Therefore, the existence of the universality of Teff gradients, together with the MT–Z–SFR relationship, would produce additional and fundamental concepts of the physical processes taking place in galaxies, and important insights into the formation and evolution of massive stars as well as into their interaction with the ISM.

In this work, we use the methodology presented by Dors et al. (2017, hereafter Paper I), to estimate the Teff of extragalactic H ii regions located in a large sample of spiral galaxies. We have taken advantage of the existence of the homogeneous sample of spectroscopic data of H ii regions obtained as part of the Calar Alto Legacy Integral Field Area survey1 (CALIFA survey, Sánchez et al. 2012), which is ideal for investigating global scaling relationships between galaxy properties (see e.g. Ellison et al. 2018). The main goals of the present study are to investigate whether Teff gradients are universal properties of spiral galaxies, and the existence of any correlation between Teff and nebular parameters, such as the ionization parameter and the oxygen abundance. This paper is organized as follows. The methodology assumed to calculate Teff and the observational data used in this work are described in Section 2. The results and a discussion of the outcome are presented in Section 3. Finally, the conclusions are given in Section 4.

2 METHODOLOGY

2.1 Sample

We used publicly available spectra from the integral field spectroscopic CALIFA survey data release 3 (DR3; Sánchez et al. 2016, 2012; Walcher et al. 2014) based on observations with the PMAS/PPAK integral field spectrophotometer mounted on the Calar Alto 3.5-m telescope. CALIFA DR3 provides wide-field integral field unit (IFU) data for 667 objects in total. The data for each galaxy consist of two data cubes, which cover the spectral region of 4300–7000 Å at a spectral resolution of R ∼ 850 (setup V500) and of 3700–5000 Å at R ∼ 1650 (setup V1200). For the galaxies with both V500 and V1200 data cubes available, there are COMB data cubes for 446 galaxies that are a combination of V500 and V1200 data cubes covering the spectral range 3700–7000 Å . In this study we used these COMB data cubes.

The sample of galaxies is described in detail in Zinchenko et al. (2018, in preparation). Briefly, we selected isolated galaxies with inclination less than 60°. Galaxies with an insufficient number of spaxels with measured oxygen abundance were excluded from our sample. We also rejected from our sample galaxies with oxygen abundance measurements for fewer than 50 spaxels and/or galaxies for which spaxels with oxygen abundance measurements cover a range of galactocentric distances lower than ∼ 1/3 of the optical radius. Stellar masses, derived from ultraviolet to near-infrared photometry, have been taken from Walcher et al. (2014). Our final sample contains 59 galaxies and 49 067 spaxels.

The final spatial resolution of the CALIFA data is set by the fibre size of the PMAS/PPAK integral field spectrophotometer and is of the order of 3 arcsec (Husemann et al. 2013). Thus, the spectrum of each spaxel corresponds to the spectrum emitted by a region with a diameter varying from ∼300 pc to ∼1.5 kpc, depending on the distance to the galaxy.2 Therefore, each observed spectrum comprises the flux of a complex of H ii regions, and the physical properties derived represent an averaged value (see the discussion in Paper I).

2.2 The emission-line fluxes

The spectrum of each spaxel from the CALIFA DR3 data cubes was processed as described in Zinchenko et al. (2016). Briefly, the stellar background in all spaxels is fitted using the public version of the starlight code (Cid Fernandes et al. 2005; Mateus et al. 2006; Asari et al. 2007), adapted for execution in the NorduGrid ARC3 environment of the Ukrainian National Grid. In order to fit the stellar spectra we used 45 synthetic simple stellar population (SSP) spectra from the evolutionary synthesis models by Bruzual & Charlot (2003) with ages from 1 Myr up to 13 Gyr and metallicities Z = 0.004, 0.02 and 0.05. We adopted the reddening law of Cardelli, Clayton & Mathis (1989) with RV = 3.1. The resulting stellar radiation contribution was subtracted from the observed spectrum in order to measure and analyse the line emission from the gaseous component. The line intensities were measured using single Gaussian line-profile fittings on the pure emission spectra.

The total [O iii]λλ4959, 5007 flux was estimated as 1.33[O iii]λ5007 instead of as the sum of the fluxes of the two lines. These lines originate from transitions from the same energy level, so their flux ratio can be determined by the transition probability ratio, which is very close to 3 (Storey & Zeippen 2000). The strongest line, [O iii]λ5007, can be measured with higher precision than the weaker one. This is particularly important for high-metallicity H ii regions, which have weak high-excitation emission lines. Similarly, the [N ii]λλ6548, 6584 lines also originate from transitions from the same energy level, and the transition probability ratio for those lines is again close to 3 (Storey & Zeippen 2000). Therefore, we estimated its total flux as 1.33[N ii]λ6584. For each spectrum, we measured the fluxes of the [O ii]|$\lambda \, \lambda$|3727, 3729, Hβ, [O iii]λ5007, Hα, [N ii]λ6584 and [S ii]λ6717, 6731 lines. For further analysis we selected only those spectra for which the signal-to-noise ratio was larger than 5 for each emission line listed above. The measured line fluxes were corrected for interstellar reddening using the theoretical Hα to Hβ ratio, assuming the standard value of Hα/Hβ  = 2.86, and the analytical approximation of the Whitford interstellar reddening law from Izotov, Thuan & Lipovetsky (1994). When the measured value of Hα/Hβ is lower than 2.86, the adopted reddening is zero.

Following Paper I, we applied the log ([O iii]λ5007/Hβ) –log ([S ii]λλ6717,6731/Hα) criterion proposed by Kewley et al. (2001) to separate objects for which the main ionization source is massive stars from those whose main ionization source is shocks of gas and/or active galactic nuclei (AGNs). We consider only the objects located below the separation line defined by Kewley et al. (2001), namely 39 431 spaxels. Fig. 1 presents the BPT diagnostic diagram (Baldwin, Phillips & Terlevich 1981) for all the spaxels in our sample.

BPT diagnostic diagram (Baldwin, Phillips & Terlevich 1981) for all the spaxels in our sample. The solid line is the boundary between AGN-like and H ii-like regions defined by Kewley et al. (2001).
Figure 1.

BPT diagnostic diagram (Baldwin, Phillips & Terlevich 1981) for all the spaxels in our sample. The solid line is the boundary between AGN-like and H ii-like regions defined by Kewley et al. (2001).

Open in new tabDownload slide

2.3 Nebular parameter determinations

In order to estimate Teff, we adopted the same method as proposed in Paper I, where a new calibration between Teff and the R  = log ([O ii]λλ3727, 3729/[O iii]λ5007) ratio was proposed. The method consists of three steps: (i) estimating the metallicity Z of star-forming regions; (ii) estimating U from Z and [S ii]λλ6717, 6731 and Hα emission lines; and (iii) estimating Teff from U, Z and R.

In more detail, the first step consists of calculating the metallicity of the gas traced by the oxygen abundance in relation to the hydrogen one, in units of 12 + |$\log (\rm O/H)$|⁠. It is carried out using the R3D empirical calibration given by Pilyugin & Grebel (2016). These authors derived oxygen abundances based on direct estimations of the electron temperatures for a large sample of H ii regions and they obtained relationships between these abundances and the emission-line flux ratios of oxygen and nitrogen in relation to Hβ, defined as: R2 =[O ii]λλ3727, 3729/Hβ, R3 = [O iii]λλ4959, 5007/Hβ, N2 = [N ii]λλ6548, 6584/Hβ. In order to use this calibration it is necessary to define which branch of the curve must be considered, owing to the degeneracy in the calibrations. For H ii regions with log N2 ≥ −0.6, the upper branch is assumed and the relationship is the following:
(1)
where (O/H)R, U means 12  + log(O/H)R, U.
For H ii regions with log N2 < −0.6, the lower branch is assumed and the relationship is
(2)
where (O/H)R, L means 12  + log(O/H)R, L. In order to convert the oxygen abundance to metallicity Z/Z⊙, we assumed the solar oxygen abundance 12 + |$\log (\rm O/H)_{\odot } = 8.69$| (Allende Prieto, Lambert & Asplund 2001).
Following Paper I, the logarithm of the ionization parameter, log U, is calculated as
(3)
where S2  = log ([S ii]λλ6717, 6731/Hα), c = −0.26 (Z/Z⊙) − 1.54, and d = −3.69 (Z/Z⊙)2 + 5.11 (Z/Z⊙) − 5.26.
The Teff–R relationship derived in Paper I is
(4)
where R  = log ([O ii]λλ3727, 3729/[O iii]λ5007). Fig. 2 shows the values of the coefficientsa and b as a function of Z/Z⊙ and log U. In this figure, the values of the coefficients were calculated by interpolating the relationships given in table 2 of Paper I.
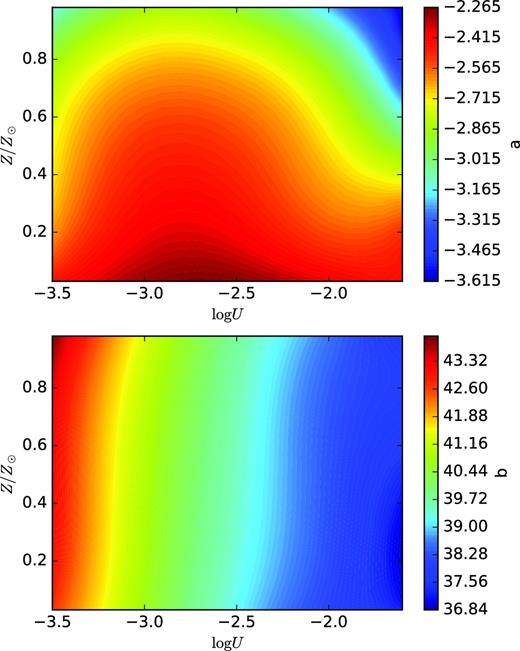
Coefficients a (upper panel) and b (lower panel) of the linear regression Teff = aR + b as a function of log U and Z/Z⊙.
Figure 2.

Coefficients a (upper panel) and b (lower panel) of the linear regression Teff = aR + b as a function of log U and Z/Z⊙.

Open in new tabDownload slide

It should be noted that the expected maximum Teff of a young stellar cluster is ∼ 50 kK (e.g. Martins et al. 2005; Simón-Díaz et al. 2014; Tramper et al. 2014; Walborn et al. 2014; Wright, Drew & Mohr-Smith 2015; Crowther et al., 2016; Martins & Palacios 2017; Holgado et al. 2018). However, the Teff −R relationship can be applied only for |$T_{\rm eff} \leqq 40$| kK, because, for higher Teff values, small variations of R produce extremely large uncertainties in Teff estimations (Dors et al. 2017). Kennicutt et al. (2000) derived a calibration between Teff and the He iiλ5876/Hβ and He iiλ6678/Hβ emission-line ratios, and they also pointed out a similar difficulty in deriving effective temperature values higher than ∼40kK. Thus, in this study we considered only objects for which we derived a Teff value lower than or equal to 40 kK. It should also be noted that Teff values higher than 40 kK were derived only for about 15 per cent of the H ii regions in our sample. Fig. 3 shows an example of the obtained maps for the Hα emission-line flux, oxygen abundance, Teff and log U for one of the galaxies in our sample (NGC 237).

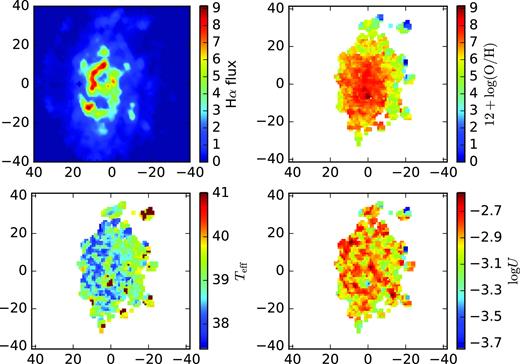
Maps of the Hα emission-line flux (top-left panel), oxygen abundance (top-right panel), Teff (bottom-left panel) and log U (bottom-right panel) for NGC 237.
Figure 3.

Maps of the Hα emission-line flux (top-left panel), oxygen abundance (top-right panel), Teff (bottom-left panel) and log U (bottom-right panel) for NGC 237.

Open in new tabDownload slide

2.4 Radial gradients

Using the methodology and the observational data presented above, we calculated radial gradients for Teff, log U and 12 + log (O/H) along the disc of the galaxies in our sample. For each galaxy, we fitted the radial distributions of these parameters using the following relationship:
(5)
where Y is a given parameter, Y0 is the extrapolated value of this parameter to the galactic centre, and|$grad\, Y$| is the slope of the distribution expressed in Y units per optical radius R25. The radial gradients were estimated using data in the galactocentric distance range 0.2 R25 < R < R25.

Fig. 4 presents the radial gradients of Teff, log U and 12 + log (O/H) for the spiral galaxy NGC 2730. This galaxy has a clear positive radial gradient of Teff and negative radial gradients of log U and 12 + log (O/H). The same plots for the radial gradients together with the 12 + log (O/H) versus log U, 12 + log (O/H) versus Teff diagrams for each galaxy in our sample are available in the Supporting Information.

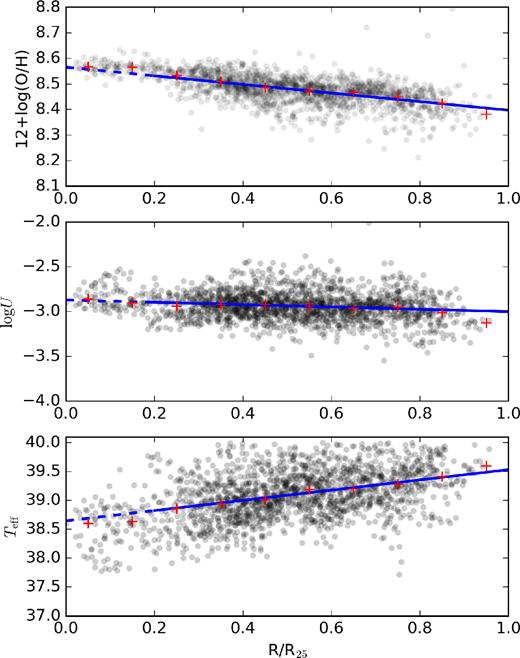
Radial gradients of the oxygen abundance (12 + log(O/H), logarithm of the ionization parameter (log U), and of the effective temperature (Teff) for NGC 2730, one galaxy of the CALIFA sample. The blue solid line is the best fit for the data, and the blue dashed line is the extrapolation to the centre. The red plus signs are median values in bins of 0.1 R25.
Figure 4.

Radial gradients of the oxygen abundance (12 + log(O/H), logarithm of the ionization parameter (log U), and of the effective temperature (Teff) for NGC 2730, one galaxy of the CALIFA sample. The blue solid line is the best fit for the data, and the blue dashed line is the extrapolation to the centre. The red plus signs are median values in bins of 0.1 R25.

Open in new tabDownload slide

Table 1 presents our sample of galaxies and the best fits of the radial distributions of Teff, log U and 12 + log (O/H) for each galaxy.

Table 1.
Open in new tab

List of the selected galaxies from the CALIFA survey.

Name12 + log (O/H)0grad log (O/H)log Ugrad log UTeffgrad Teff
[dex][dex/R25][dex][dex/R25][kK]]kK/R25]
NGC 18.615 ± 0.006−0.029 ± 0.012−2.865 ± 0.0260.073 ± 0.05238.802 ± 0.120−0.317 ± 0.234
NGC 238.730 ± 0.010−0.209 ± 0.024−3.400 ± 0.0580.751 ± 0.14639.393 ± 0.160−0.734 ± 0.369
NGC 1808.705 ± 0.034−0.217 ± 0.049−2.629 ± 0.083−0.038 ± 0.12038.088 ± 0.3370.380 ± 0.484
NGC 2348.617 ± 0.004−0.062 ± 0.009−2.696 ± 0.014−0.382 ± 0.03237.938 ± 0.0711.205 ± 0.161
NGC 2378.680 ± 0.003−0.317 ± 0.007−2.835 ± 0.011−0.165 ± 0.02338.139 ± 0.0381.405 ± 0.077
NGC 2578.696 ± 0.014−0.255 ± 0.021−2.806 ± 0.0440.020 ± 0.06838.152 ± 0.1600.585 ± 0.248
NGC 3098.781 ± 0.015−0.432 ± 0.030−2.503 ± 0.066−0.435 ± 0.13336.933 ± 0.2182.893 ± 0.439
NGC 4778.543 ± 0.010−0.058 ± 0.014−2.717 ± 0.025−0.201 ± 0.03438.193 ± 0.0850.830 ± 0.116
NGC 7768.647 ± 0.0070.002 ± 0.014−2.826 ± 0.0480.198 ± 0.10138.149 ± 0.2100.516 ± 0.440
NGC 9418.561 ± 0.006−0.394 ± 0.015−2.816 ± 0.018−0.410 ± 0.04738.698 ± 0.0501.328 ± 0.134
NGC 9918.532 ± 0.008−0.269 ± 0.019−2.951 ± 0.028−0.034 ± 0.06738.945 ± 0.0670.515 ± 0.163
NGC 10708.626 ± 0.032−0.035 ± 0.111−2.673 ± 0.103−0.150 ± 0.34938.754 ± 0.492−1.394 ± 1.669
NGC 10948.656 ± 0.004−0.117 ± 0.010−3.127 ± 0.0210.291 ± 0.05238.955 ± 0.0700.570 ± 0.170
NGC 16598.621 ± 0.006−0.184 ± 0.012−2.777 ± 0.017−0.113 ± 0.03438.233 ± 0.0530.978 ± 0.105
NGC 16678.657 ± 0.002−0.067 ± 0.005−2.847 ± 0.013−0.084 ± 0.03038.702 ± 0.0490.059 ± 0.108
NGC 23478.689 ± 0.007−0.279 ± 0.011−2.860 ± 0.0230.013 ± 0.03637.968 ± 0.0691.601 ± 0.108
NGC 24878.639 ± 0.064−0.054 ± 0.123−2.706 ± 0.166−0.041 ± 0.31839.319 ± 0.992−1.832 ± 1.900
NGC 25308.557 ± 0.006−0.251 ± 0.010−2.754 ± 0.018−0.259 ± 0.03038.098 ± 0.0461.788 ± 0.078
NGC 25408.626 ± 0.004−0.154 ± 0.006−2.904 ± 0.0150.003 ± 0.02638.434 ± 0.0540.715 ± 0.091
NGC 26048.524 ± 0.008−0.401 ± 0.020−2.834 ± 0.020−0.488 ± 0.04839.348 ± 0.0420.586 ± 0.112
NGC 27308.565 ± 0.003−0.167 ± 0.006−2.870 ± 0.012−0.129 ± 0.02138.646 ± 0.0300.886 ± 0.054
NGC 29068.643 ± 0.0050.001 ± 0.011−2.911 ± 0.0310.025 ± 0.06338.494 ± 0.1320.328 ± 0.265
NGC 29168.609 ± 0.015−0.108 ± 0.028−2.728 ± 0.043−0.085 ± 0.07637.681 ± 0.1251.895 ± 0.223
NGC 30578.318 ± 0.007−0.194 ± 0.014−3.132 ± 0.020−0.110 ± 0.03939.899 ± 0.060−0.324 ± 0.126
NGC 33818.592 ± 0.004−0.226 ± 0.009−2.927 ± 0.012−0.029 ± 0.02738.495 ± 0.0401.064 ± 0.092
NGC 36148.651 ± 0.014−0.358 ± 0.032−2.764 ± 0.038−0.272 ± 0.08737.984 ± 0.1561.789 ± 0.354
NGC 36878.697 ± 0.003−0.251 ± 0.007−3.040 ± 0.0150.368 ± 0.03738.918 ± 0.0490.052 ± 0.123
NGC 38118.649 ± 0.003−0.126 ± 0.006−2.861 ± 0.0150.040 ± 0.02637.983 ± 0.0571.382 ± 0.098
NGC 49618.533 ± 0.005−0.297 ± 0.009−2.887 ± 0.012−0.338 ± 0.02238.814 ± 0.0331.221 ± 0.070
NGC 50008.617 ± 0.012−0.075 ± 0.015−2.638 ± 0.087−0.220 ± 0.10237.199 ± 0.2151.764 ± 0.251
NGC 50168.711 ± 0.016−0.254 ± 0.029−2.620 ± 0.089−0.281 ± 0.16138.128 ± 0.2231.188 ± 0.402
NGC 52058.559 ± 0.0330.001 ± 0.065−2.723 ± 0.0840.146 ± 0.16837.566 ± 0.4350.688 ± 0.863
NGC 53208.637 ± 0.003−0.210 ± 0.006−2.817 ± 0.010−0.121 ± 0.01838.334 ± 0.0370.762 ± 0.067
NGC 54068.650 ± 0.009−0.074 ± 0.017−2.516 ± 0.046−0.458 ± 0.08437.698 ± 0.1661.248 ± 0.305
NGC 54808.601 ± 0.003−0.089 ± 0.009−2.842 ± 0.015−0.172 ± 0.03938.262 ± 0.0531.161 ± 0.135
NGC 55208.620 ± 0.002−0.097 ± 0.004−2.979 ± 0.0090.126 ± 0.01538.825 ± 0.0290.203 ± 0.044
NGC 56338.675 ± 0.003−0.166 ± 0.006−2.795 ± 0.013−0.235 ± 0.02838.295 ± 0.0480.972 ± 0.101
NGC 57208.531 ± 0.0300.021 ± 0.041−2.856 ± 0.089−0.105 ± 0.11939.715 ± 0.313−0.353 ± 0.420
NGC 57328.605 ± 0.005−0.180 ± 0.008−2.840 ± 0.012−0.017 ± 0.01838.287 ± 0.0480.944 ± 0.072
NGC 59578.688 ± 0.009−0.180 ± 0.019−2.830 ± 0.0460.006 ± 0.09938.816 ± 0.164−0.403 ± 0.353
NGC 60048.639 ± 0.007−0.039 ± 0.022−2.647 ± 0.043−0.237 ± 0.12038.085 ± 0.1731.160 ± 0.487
NGC 60638.561 ± 0.008−0.065 ± 0.010−2.940 ± 0.0190.054 ± 0.02539.200 ± 0.063−0.175 ± 0.082
NGC 61548.619 ± 0.019−0.019 ± 0.025−2.806 ± 0.093−0.153 ± 0.11939.245 ± 0.322−0.314 ± 0.410
NGC 61558.592 ± 0.005−0.088 ± 0.011−2.917 ± 0.0140.043 ± 0.03138.520 ± 0.0560.265 ± 0.120
NGC 63018.622 ± 0.016−0.086 ± 0.021−3.102 ± 0.0570.320 ± 0.07440.178 ± 0.355−1.421 ± 0.431
NGC 64978.652 ± 0.006−0.008 ± 0.009−2.785 ± 0.039−0.162 ± 0.05938.926 ± 0.144−0.102 ± 0.220
NGC 69418.581 ± 0.0190.035 ± 0.022−3.135 ± 0.0820.485 ± 0.09837.614 ± 0.4590.973 ± 0.551
NGC 73218.633 ± 0.003−0.077 ± 0.005−3.016 ± 0.0140.090 ± 0.02338.660 ± 0.0430.820 ± 0.071
NGC 74898.626 ± 0.007−0.396 ± 0.012−2.878 ± 0.016−0.156 ± 0.02638.525 ± 0.0601.287 ± 0.115
NGC 76538.673 ± 0.003−0.230 ± 0.006−2.903 ± 0.0120.118 ± 0.02638.444 ± 0.0430.400 ± 0.091
NGC 77168.613 ± 0.005−0.109 ± 0.010−2.890 ± 0.0190.064 ± 0.03938.621 ± 0.0560.615 ± 0.112
NGC 77388.689 ± 0.031−0.125 ± 0.041−3.318 ± 0.1100.316 ± 0.14440.199 ± 0.524−1.097 ± 0.684
NGC 78198.650 ± 0.009−0.272 ± 0.012−2.882 ± 0.031−0.112 ± 0.04438.088 ± 0.0871.484 ± 0.123
IC 7768.217 ± 0.008−0.074 ± 0.015−3.193 ± 0.026−0.116 ± 0.04539.860 ± 0.167−0.179 ± 0.300
IC 12568.707 ± 0.012−0.316 ± 0.019−2.871 ± 0.044−0.013 ± 0.06837.536 ± 0.1571.745 ± 0.246
IC 53098.495 ± 0.030−0.044 ± 0.043−3.015 ± 0.0660.220 ± 0.09538.759 ± 0.223−0.355 ± 0.322
UGC 87338.428 ± 0.005−0.199 ± 0.009−2.974 ± 0.017−0.172 ± 0.02839.262 ± 0.0520.896 ± 0.131
UGC 122248.587 ± 0.032−0.226 ± 0.054−2.680 ± 0.103−0.256 ± 0.17237.458 ± 0.2562.164 ± 0.427
UGC 128168.478 ± 0.010−0.187 ± 0.016−2.942 ± 0.026−0.057 ± 0.04238.799 ± 0.0670.845 ± 0.123
Name12 + log (O/H)0grad log (O/H)log Ugrad log UTeffgrad Teff
[dex][dex/R25][dex][dex/R25][kK]]kK/R25]
NGC 18.615 ± 0.006−0.029 ± 0.012−2.865 ± 0.0260.073 ± 0.05238.802 ± 0.120−0.317 ± 0.234
NGC 238.730 ± 0.010−0.209 ± 0.024−3.400 ± 0.0580.751 ± 0.14639.393 ± 0.160−0.734 ± 0.369
NGC 1808.705 ± 0.034−0.217 ± 0.049−2.629 ± 0.083−0.038 ± 0.12038.088 ± 0.3370.380 ± 0.484
NGC 2348.617 ± 0.004−0.062 ± 0.009−2.696 ± 0.014−0.382 ± 0.03237.938 ± 0.0711.205 ± 0.161
NGC 2378.680 ± 0.003−0.317 ± 0.007−2.835 ± 0.011−0.165 ± 0.02338.139 ± 0.0381.405 ± 0.077
NGC 2578.696 ± 0.014−0.255 ± 0.021−2.806 ± 0.0440.020 ± 0.06838.152 ± 0.1600.585 ± 0.248
NGC 3098.781 ± 0.015−0.432 ± 0.030−2.503 ± 0.066−0.435 ± 0.13336.933 ± 0.2182.893 ± 0.439
NGC 4778.543 ± 0.010−0.058 ± 0.014−2.717 ± 0.025−0.201 ± 0.03438.193 ± 0.0850.830 ± 0.116
NGC 7768.647 ± 0.0070.002 ± 0.014−2.826 ± 0.0480.198 ± 0.10138.149 ± 0.2100.516 ± 0.440
NGC 9418.561 ± 0.006−0.394 ± 0.015−2.816 ± 0.018−0.410 ± 0.04738.698 ± 0.0501.328 ± 0.134
NGC 9918.532 ± 0.008−0.269 ± 0.019−2.951 ± 0.028−0.034 ± 0.06738.945 ± 0.0670.515 ± 0.163
NGC 10708.626 ± 0.032−0.035 ± 0.111−2.673 ± 0.103−0.150 ± 0.34938.754 ± 0.492−1.394 ± 1.669
NGC 10948.656 ± 0.004−0.117 ± 0.010−3.127 ± 0.0210.291 ± 0.05238.955 ± 0.0700.570 ± 0.170
NGC 16598.621 ± 0.006−0.184 ± 0.012−2.777 ± 0.017−0.113 ± 0.03438.233 ± 0.0530.978 ± 0.105
NGC 16678.657 ± 0.002−0.067 ± 0.005−2.847 ± 0.013−0.084 ± 0.03038.702 ± 0.0490.059 ± 0.108
NGC 23478.689 ± 0.007−0.279 ± 0.011−2.860 ± 0.0230.013 ± 0.03637.968 ± 0.0691.601 ± 0.108
NGC 24878.639 ± 0.064−0.054 ± 0.123−2.706 ± 0.166−0.041 ± 0.31839.319 ± 0.992−1.832 ± 1.900
NGC 25308.557 ± 0.006−0.251 ± 0.010−2.754 ± 0.018−0.259 ± 0.03038.098 ± 0.0461.788 ± 0.078
NGC 25408.626 ± 0.004−0.154 ± 0.006−2.904 ± 0.0150.003 ± 0.02638.434 ± 0.0540.715 ± 0.091
NGC 26048.524 ± 0.008−0.401 ± 0.020−2.834 ± 0.020−0.488 ± 0.04839.348 ± 0.0420.586 ± 0.112
NGC 27308.565 ± 0.003−0.167 ± 0.006−2.870 ± 0.012−0.129 ± 0.02138.646 ± 0.0300.886 ± 0.054
NGC 29068.643 ± 0.0050.001 ± 0.011−2.911 ± 0.0310.025 ± 0.06338.494 ± 0.1320.328 ± 0.265
NGC 29168.609 ± 0.015−0.108 ± 0.028−2.728 ± 0.043−0.085 ± 0.07637.681 ± 0.1251.895 ± 0.223
NGC 30578.318 ± 0.007−0.194 ± 0.014−3.132 ± 0.020−0.110 ± 0.03939.899 ± 0.060−0.324 ± 0.126
NGC 33818.592 ± 0.004−0.226 ± 0.009−2.927 ± 0.012−0.029 ± 0.02738.495 ± 0.0401.064 ± 0.092
NGC 36148.651 ± 0.014−0.358 ± 0.032−2.764 ± 0.038−0.272 ± 0.08737.984 ± 0.1561.789 ± 0.354
NGC 36878.697 ± 0.003−0.251 ± 0.007−3.040 ± 0.0150.368 ± 0.03738.918 ± 0.0490.052 ± 0.123
NGC 38118.649 ± 0.003−0.126 ± 0.006−2.861 ± 0.0150.040 ± 0.02637.983 ± 0.0571.382 ± 0.098
NGC 49618.533 ± 0.005−0.297 ± 0.009−2.887 ± 0.012−0.338 ± 0.02238.814 ± 0.0331.221 ± 0.070
NGC 50008.617 ± 0.012−0.075 ± 0.015−2.638 ± 0.087−0.220 ± 0.10237.199 ± 0.2151.764 ± 0.251
NGC 50168.711 ± 0.016−0.254 ± 0.029−2.620 ± 0.089−0.281 ± 0.16138.128 ± 0.2231.188 ± 0.402
NGC 52058.559 ± 0.0330.001 ± 0.065−2.723 ± 0.0840.146 ± 0.16837.566 ± 0.4350.688 ± 0.863
NGC 53208.637 ± 0.003−0.210 ± 0.006−2.817 ± 0.010−0.121 ± 0.01838.334 ± 0.0370.762 ± 0.067
NGC 54068.650 ± 0.009−0.074 ± 0.017−2.516 ± 0.046−0.458 ± 0.08437.698 ± 0.1661.248 ± 0.305
NGC 54808.601 ± 0.003−0.089 ± 0.009−2.842 ± 0.015−0.172 ± 0.03938.262 ± 0.0531.161 ± 0.135
NGC 55208.620 ± 0.002−0.097 ± 0.004−2.979 ± 0.0090.126 ± 0.01538.825 ± 0.0290.203 ± 0.044
NGC 56338.675 ± 0.003−0.166 ± 0.006−2.795 ± 0.013−0.235 ± 0.02838.295 ± 0.0480.972 ± 0.101
NGC 57208.531 ± 0.0300.021 ± 0.041−2.856 ± 0.089−0.105 ± 0.11939.715 ± 0.313−0.353 ± 0.420
NGC 57328.605 ± 0.005−0.180 ± 0.008−2.840 ± 0.012−0.017 ± 0.01838.287 ± 0.0480.944 ± 0.072
NGC 59578.688 ± 0.009−0.180 ± 0.019−2.830 ± 0.0460.006 ± 0.09938.816 ± 0.164−0.403 ± 0.353
NGC 60048.639 ± 0.007−0.039 ± 0.022−2.647 ± 0.043−0.237 ± 0.12038.085 ± 0.1731.160 ± 0.487
NGC 60638.561 ± 0.008−0.065 ± 0.010−2.940 ± 0.0190.054 ± 0.02539.200 ± 0.063−0.175 ± 0.082
NGC 61548.619 ± 0.019−0.019 ± 0.025−2.806 ± 0.093−0.153 ± 0.11939.245 ± 0.322−0.314 ± 0.410
NGC 61558.592 ± 0.005−0.088 ± 0.011−2.917 ± 0.0140.043 ± 0.03138.520 ± 0.0560.265 ± 0.120
NGC 63018.622 ± 0.016−0.086 ± 0.021−3.102 ± 0.0570.320 ± 0.07440.178 ± 0.355−1.421 ± 0.431
NGC 64978.652 ± 0.006−0.008 ± 0.009−2.785 ± 0.039−0.162 ± 0.05938.926 ± 0.144−0.102 ± 0.220
NGC 69418.581 ± 0.0190.035 ± 0.022−3.135 ± 0.0820.485 ± 0.09837.614 ± 0.4590.973 ± 0.551
NGC 73218.633 ± 0.003−0.077 ± 0.005−3.016 ± 0.0140.090 ± 0.02338.660 ± 0.0430.820 ± 0.071
NGC 74898.626 ± 0.007−0.396 ± 0.012−2.878 ± 0.016−0.156 ± 0.02638.525 ± 0.0601.287 ± 0.115
NGC 76538.673 ± 0.003−0.230 ± 0.006−2.903 ± 0.0120.118 ± 0.02638.444 ± 0.0430.400 ± 0.091
NGC 77168.613 ± 0.005−0.109 ± 0.010−2.890 ± 0.0190.064 ± 0.03938.621 ± 0.0560.615 ± 0.112
NGC 77388.689 ± 0.031−0.125 ± 0.041−3.318 ± 0.1100.316 ± 0.14440.199 ± 0.524−1.097 ± 0.684
NGC 78198.650 ± 0.009−0.272 ± 0.012−2.882 ± 0.031−0.112 ± 0.04438.088 ± 0.0871.484 ± 0.123
IC 7768.217 ± 0.008−0.074 ± 0.015−3.193 ± 0.026−0.116 ± 0.04539.860 ± 0.167−0.179 ± 0.300
IC 12568.707 ± 0.012−0.316 ± 0.019−2.871 ± 0.044−0.013 ± 0.06837.536 ± 0.1571.745 ± 0.246
IC 53098.495 ± 0.030−0.044 ± 0.043−3.015 ± 0.0660.220 ± 0.09538.759 ± 0.223−0.355 ± 0.322
UGC 87338.428 ± 0.005−0.199 ± 0.009−2.974 ± 0.017−0.172 ± 0.02839.262 ± 0.0520.896 ± 0.131
UGC 122248.587 ± 0.032−0.226 ± 0.054−2.680 ± 0.103−0.256 ± 0.17237.458 ± 0.2562.164 ± 0.427
UGC 128168.478 ± 0.010−0.187 ± 0.016−2.942 ± 0.026−0.057 ± 0.04238.799 ± 0.0670.845 ± 0.123
Table 1.
Open in new tab

List of the selected galaxies from the CALIFA survey.

Name12 + log (O/H)0grad log (O/H)log Ugrad log UTeffgrad Teff
[dex][dex/R25][dex][dex/R25][kK]]kK/R25]
NGC 18.615 ± 0.006−0.029 ± 0.012−2.865 ± 0.0260.073 ± 0.05238.802 ± 0.120−0.317 ± 0.234
NGC 238.730 ± 0.010−0.209 ± 0.024−3.400 ± 0.0580.751 ± 0.14639.393 ± 0.160−0.734 ± 0.369
NGC 1808.705 ± 0.034−0.217 ± 0.049−2.629 ± 0.083−0.038 ± 0.12038.088 ± 0.3370.380 ± 0.484
NGC 2348.617 ± 0.004−0.062 ± 0.009−2.696 ± 0.014−0.382 ± 0.03237.938 ± 0.0711.205 ± 0.161
NGC 2378.680 ± 0.003−0.317 ± 0.007−2.835 ± 0.011−0.165 ± 0.02338.139 ± 0.0381.405 ± 0.077
NGC 2578.696 ± 0.014−0.255 ± 0.021−2.806 ± 0.0440.020 ± 0.06838.152 ± 0.1600.585 ± 0.248
NGC 3098.781 ± 0.015−0.432 ± 0.030−2.503 ± 0.066−0.435 ± 0.13336.933 ± 0.2182.893 ± 0.439
NGC 4778.543 ± 0.010−0.058 ± 0.014−2.717 ± 0.025−0.201 ± 0.03438.193 ± 0.0850.830 ± 0.116
NGC 7768.647 ± 0.0070.002 ± 0.014−2.826 ± 0.0480.198 ± 0.10138.149 ± 0.2100.516 ± 0.440
NGC 9418.561 ± 0.006−0.394 ± 0.015−2.816 ± 0.018−0.410 ± 0.04738.698 ± 0.0501.328 ± 0.134
NGC 9918.532 ± 0.008−0.269 ± 0.019−2.951 ± 0.028−0.034 ± 0.06738.945 ± 0.0670.515 ± 0.163
NGC 10708.626 ± 0.032−0.035 ± 0.111−2.673 ± 0.103−0.150 ± 0.34938.754 ± 0.492−1.394 ± 1.669
NGC 10948.656 ± 0.004−0.117 ± 0.010−3.127 ± 0.0210.291 ± 0.05238.955 ± 0.0700.570 ± 0.170
NGC 16598.621 ± 0.006−0.184 ± 0.012−2.777 ± 0.017−0.113 ± 0.03438.233 ± 0.0530.978 ± 0.105
NGC 16678.657 ± 0.002−0.067 ± 0.005−2.847 ± 0.013−0.084 ± 0.03038.702 ± 0.0490.059 ± 0.108
NGC 23478.689 ± 0.007−0.279 ± 0.011−2.860 ± 0.0230.013 ± 0.03637.968 ± 0.0691.601 ± 0.108
NGC 24878.639 ± 0.064−0.054 ± 0.123−2.706 ± 0.166−0.041 ± 0.31839.319 ± 0.992−1.832 ± 1.900
NGC 25308.557 ± 0.006−0.251 ± 0.010−2.754 ± 0.018−0.259 ± 0.03038.098 ± 0.0461.788 ± 0.078
NGC 25408.626 ± 0.004−0.154 ± 0.006−2.904 ± 0.0150.003 ± 0.02638.434 ± 0.0540.715 ± 0.091
NGC 26048.524 ± 0.008−0.401 ± 0.020−2.834 ± 0.020−0.488 ± 0.04839.348 ± 0.0420.586 ± 0.112
NGC 27308.565 ± 0.003−0.167 ± 0.006−2.870 ± 0.012−0.129 ± 0.02138.646 ± 0.0300.886 ± 0.054
NGC 29068.643 ± 0.0050.001 ± 0.011−2.911 ± 0.0310.025 ± 0.06338.494 ± 0.1320.328 ± 0.265
NGC 29168.609 ± 0.015−0.108 ± 0.028−2.728 ± 0.043−0.085 ± 0.07637.681 ± 0.1251.895 ± 0.223
NGC 30578.318 ± 0.007−0.194 ± 0.014−3.132 ± 0.020−0.110 ± 0.03939.899 ± 0.060−0.324 ± 0.126
NGC 33818.592 ± 0.004−0.226 ± 0.009−2.927 ± 0.012−0.029 ± 0.02738.495 ± 0.0401.064 ± 0.092
NGC 36148.651 ± 0.014−0.358 ± 0.032−2.764 ± 0.038−0.272 ± 0.08737.984 ± 0.1561.789 ± 0.354
NGC 36878.697 ± 0.003−0.251 ± 0.007−3.040 ± 0.0150.368 ± 0.03738.918 ± 0.0490.052 ± 0.123
NGC 38118.649 ± 0.003−0.126 ± 0.006−2.861 ± 0.0150.040 ± 0.02637.983 ± 0.0571.382 ± 0.098
NGC 49618.533 ± 0.005−0.297 ± 0.009−2.887 ± 0.012−0.338 ± 0.02238.814 ± 0.0331.221 ± 0.070
NGC 50008.617 ± 0.012−0.075 ± 0.015−2.638 ± 0.087−0.220 ± 0.10237.199 ± 0.2151.764 ± 0.251
NGC 50168.711 ± 0.016−0.254 ± 0.029−2.620 ± 0.089−0.281 ± 0.16138.128 ± 0.2231.188 ± 0.402
NGC 52058.559 ± 0.0330.001 ± 0.065−2.723 ± 0.0840.146 ± 0.16837.566 ± 0.4350.688 ± 0.863
NGC 53208.637 ± 0.003−0.210 ± 0.006−2.817 ± 0.010−0.121 ± 0.01838.334 ± 0.0370.762 ± 0.067
NGC 54068.650 ± 0.009−0.074 ± 0.017−2.516 ± 0.046−0.458 ± 0.08437.698 ± 0.1661.248 ± 0.305
NGC 54808.601 ± 0.003−0.089 ± 0.009−2.842 ± 0.015−0.172 ± 0.03938.262 ± 0.0531.161 ± 0.135
NGC 55208.620 ± 0.002−0.097 ± 0.004−2.979 ± 0.0090.126 ± 0.01538.825 ± 0.0290.203 ± 0.044
NGC 56338.675 ± 0.003−0.166 ± 0.006−2.795 ± 0.013−0.235 ± 0.02838.295 ± 0.0480.972 ± 0.101
NGC 57208.531 ± 0.0300.021 ± 0.041−2.856 ± 0.089−0.105 ± 0.11939.715 ± 0.313−0.353 ± 0.420
NGC 57328.605 ± 0.005−0.180 ± 0.008−2.840 ± 0.012−0.017 ± 0.01838.287 ± 0.0480.944 ± 0.072
NGC 59578.688 ± 0.009−0.180 ± 0.019−2.830 ± 0.0460.006 ± 0.09938.816 ± 0.164−0.403 ± 0.353
NGC 60048.639 ± 0.007−0.039 ± 0.022−2.647 ± 0.043−0.237 ± 0.12038.085 ± 0.1731.160 ± 0.487
NGC 60638.561 ± 0.008−0.065 ± 0.010−2.940 ± 0.0190.054 ± 0.02539.200 ± 0.063−0.175 ± 0.082
NGC 61548.619 ± 0.019−0.019 ± 0.025−2.806 ± 0.093−0.153 ± 0.11939.245 ± 0.322−0.314 ± 0.410
NGC 61558.592 ± 0.005−0.088 ± 0.011−2.917 ± 0.0140.043 ± 0.03138.520 ± 0.0560.265 ± 0.120
NGC 63018.622 ± 0.016−0.086 ± 0.021−3.102 ± 0.0570.320 ± 0.07440.178 ± 0.355−1.421 ± 0.431
NGC 64978.652 ± 0.006−0.008 ± 0.009−2.785 ± 0.039−0.162 ± 0.05938.926 ± 0.144−0.102 ± 0.220
NGC 69418.581 ± 0.0190.035 ± 0.022−3.135 ± 0.0820.485 ± 0.09837.614 ± 0.4590.973 ± 0.551
NGC 73218.633 ± 0.003−0.077 ± 0.005−3.016 ± 0.0140.090 ± 0.02338.660 ± 0.0430.820 ± 0.071
NGC 74898.626 ± 0.007−0.396 ± 0.012−2.878 ± 0.016−0.156 ± 0.02638.525 ± 0.0601.287 ± 0.115
NGC 76538.673 ± 0.003−0.230 ± 0.006−2.903 ± 0.0120.118 ± 0.02638.444 ± 0.0430.400 ± 0.091
NGC 77168.613 ± 0.005−0.109 ± 0.010−2.890 ± 0.0190.064 ± 0.03938.621 ± 0.0560.615 ± 0.112
NGC 77388.689 ± 0.031−0.125 ± 0.041−3.318 ± 0.1100.316 ± 0.14440.199 ± 0.524−1.097 ± 0.684
NGC 78198.650 ± 0.009−0.272 ± 0.012−2.882 ± 0.031−0.112 ± 0.04438.088 ± 0.0871.484 ± 0.123
IC 7768.217 ± 0.008−0.074 ± 0.015−3.193 ± 0.026−0.116 ± 0.04539.860 ± 0.167−0.179 ± 0.300
IC 12568.707 ± 0.012−0.316 ± 0.019−2.871 ± 0.044−0.013 ± 0.06837.536 ± 0.1571.745 ± 0.246
IC 53098.495 ± 0.030−0.044 ± 0.043−3.015 ± 0.0660.220 ± 0.09538.759 ± 0.223−0.355 ± 0.322
UGC 87338.428 ± 0.005−0.199 ± 0.009−2.974 ± 0.017−0.172 ± 0.02839.262 ± 0.0520.896 ± 0.131
UGC 122248.587 ± 0.032−0.226 ± 0.054−2.680 ± 0.103−0.256 ± 0.17237.458 ± 0.2562.164 ± 0.427
UGC 128168.478 ± 0.010−0.187 ± 0.016−2.942 ± 0.026−0.057 ± 0.04238.799 ± 0.0670.845 ± 0.123
Name12 + log (O/H)0grad log (O/H)log Ugrad log UTeffgrad Teff
[dex][dex/R25][dex][dex/R25][kK]]kK/R25]
NGC 18.615 ± 0.006−0.029 ± 0.012−2.865 ± 0.0260.073 ± 0.05238.802 ± 0.120−0.317 ± 0.234
NGC 238.730 ± 0.010−0.209 ± 0.024−3.400 ± 0.0580.751 ± 0.14639.393 ± 0.160−0.734 ± 0.369
NGC 1808.705 ± 0.034−0.217 ± 0.049−2.629 ± 0.083−0.038 ± 0.12038.088 ± 0.3370.380 ± 0.484
NGC 2348.617 ± 0.004−0.062 ± 0.009−2.696 ± 0.014−0.382 ± 0.03237.938 ± 0.0711.205 ± 0.161
NGC 2378.680 ± 0.003−0.317 ± 0.007−2.835 ± 0.011−0.165 ± 0.02338.139 ± 0.0381.405 ± 0.077
NGC 2578.696 ± 0.014−0.255 ± 0.021−2.806 ± 0.0440.020 ± 0.06838.152 ± 0.1600.585 ± 0.248
NGC 3098.781 ± 0.015−0.432 ± 0.030−2.503 ± 0.066−0.435 ± 0.13336.933 ± 0.2182.893 ± 0.439
NGC 4778.543 ± 0.010−0.058 ± 0.014−2.717 ± 0.025−0.201 ± 0.03438.193 ± 0.0850.830 ± 0.116
NGC 7768.647 ± 0.0070.002 ± 0.014−2.826 ± 0.0480.198 ± 0.10138.149 ± 0.2100.516 ± 0.440
NGC 9418.561 ± 0.006−0.394 ± 0.015−2.816 ± 0.018−0.410 ± 0.04738.698 ± 0.0501.328 ± 0.134
NGC 9918.532 ± 0.008−0.269 ± 0.019−2.951 ± 0.028−0.034 ± 0.06738.945 ± 0.0670.515 ± 0.163
NGC 10708.626 ± 0.032−0.035 ± 0.111−2.673 ± 0.103−0.150 ± 0.34938.754 ± 0.492−1.394 ± 1.669
NGC 10948.656 ± 0.004−0.117 ± 0.010−3.127 ± 0.0210.291 ± 0.05238.955 ± 0.0700.570 ± 0.170
NGC 16598.621 ± 0.006−0.184 ± 0.012−2.777 ± 0.017−0.113 ± 0.03438.233 ± 0.0530.978 ± 0.105
NGC 16678.657 ± 0.002−0.067 ± 0.005−2.847 ± 0.013−0.084 ± 0.03038.702 ± 0.0490.059 ± 0.108
NGC 23478.689 ± 0.007−0.279 ± 0.011−2.860 ± 0.0230.013 ± 0.03637.968 ± 0.0691.601 ± 0.108
NGC 24878.639 ± 0.064−0.054 ± 0.123−2.706 ± 0.166−0.041 ± 0.31839.319 ± 0.992−1.832 ± 1.900
NGC 25308.557 ± 0.006−0.251 ± 0.010−2.754 ± 0.018−0.259 ± 0.03038.098 ± 0.0461.788 ± 0.078
NGC 25408.626 ± 0.004−0.154 ± 0.006−2.904 ± 0.0150.003 ± 0.02638.434 ± 0.0540.715 ± 0.091
NGC 26048.524 ± 0.008−0.401 ± 0.020−2.834 ± 0.020−0.488 ± 0.04839.348 ± 0.0420.586 ± 0.112
NGC 27308.565 ± 0.003−0.167 ± 0.006−2.870 ± 0.012−0.129 ± 0.02138.646 ± 0.0300.886 ± 0.054
NGC 29068.643 ± 0.0050.001 ± 0.011−2.911 ± 0.0310.025 ± 0.06338.494 ± 0.1320.328 ± 0.265
NGC 29168.609 ± 0.015−0.108 ± 0.028−2.728 ± 0.043−0.085 ± 0.07637.681 ± 0.1251.895 ± 0.223
NGC 30578.318 ± 0.007−0.194 ± 0.014−3.132 ± 0.020−0.110 ± 0.03939.899 ± 0.060−0.324 ± 0.126
NGC 33818.592 ± 0.004−0.226 ± 0.009−2.927 ± 0.012−0.029 ± 0.02738.495 ± 0.0401.064 ± 0.092
NGC 36148.651 ± 0.014−0.358 ± 0.032−2.764 ± 0.038−0.272 ± 0.08737.984 ± 0.1561.789 ± 0.354
NGC 36878.697 ± 0.003−0.251 ± 0.007−3.040 ± 0.0150.368 ± 0.03738.918 ± 0.0490.052 ± 0.123
NGC 38118.649 ± 0.003−0.126 ± 0.006−2.861 ± 0.0150.040 ± 0.02637.983 ± 0.0571.382 ± 0.098
NGC 49618.533 ± 0.005−0.297 ± 0.009−2.887 ± 0.012−0.338 ± 0.02238.814 ± 0.0331.221 ± 0.070
NGC 50008.617 ± 0.012−0.075 ± 0.015−2.638 ± 0.087−0.220 ± 0.10237.199 ± 0.2151.764 ± 0.251
NGC 50168.711 ± 0.016−0.254 ± 0.029−2.620 ± 0.089−0.281 ± 0.16138.128 ± 0.2231.188 ± 0.402
NGC 52058.559 ± 0.0330.001 ± 0.065−2.723 ± 0.0840.146 ± 0.16837.566 ± 0.4350.688 ± 0.863
NGC 53208.637 ± 0.003−0.210 ± 0.006−2.817 ± 0.010−0.121 ± 0.01838.334 ± 0.0370.762 ± 0.067
NGC 54068.650 ± 0.009−0.074 ± 0.017−2.516 ± 0.046−0.458 ± 0.08437.698 ± 0.1661.248 ± 0.305
NGC 54808.601 ± 0.003−0.089 ± 0.009−2.842 ± 0.015−0.172 ± 0.03938.262 ± 0.0531.161 ± 0.135
NGC 55208.620 ± 0.002−0.097 ± 0.004−2.979 ± 0.0090.126 ± 0.01538.825 ± 0.0290.203 ± 0.044
NGC 56338.675 ± 0.003−0.166 ± 0.006−2.795 ± 0.013−0.235 ± 0.02838.295 ± 0.0480.972 ± 0.101
NGC 57208.531 ± 0.0300.021 ± 0.041−2.856 ± 0.089−0.105 ± 0.11939.715 ± 0.313−0.353 ± 0.420
NGC 57328.605 ± 0.005−0.180 ± 0.008−2.840 ± 0.012−0.017 ± 0.01838.287 ± 0.0480.944 ± 0.072
NGC 59578.688 ± 0.009−0.180 ± 0.019−2.830 ± 0.0460.006 ± 0.09938.816 ± 0.164−0.403 ± 0.353
NGC 60048.639 ± 0.007−0.039 ± 0.022−2.647 ± 0.043−0.237 ± 0.12038.085 ± 0.1731.160 ± 0.487
NGC 60638.561 ± 0.008−0.065 ± 0.010−2.940 ± 0.0190.054 ± 0.02539.200 ± 0.063−0.175 ± 0.082
NGC 61548.619 ± 0.019−0.019 ± 0.025−2.806 ± 0.093−0.153 ± 0.11939.245 ± 0.322−0.314 ± 0.410
NGC 61558.592 ± 0.005−0.088 ± 0.011−2.917 ± 0.0140.043 ± 0.03138.520 ± 0.0560.265 ± 0.120
NGC 63018.622 ± 0.016−0.086 ± 0.021−3.102 ± 0.0570.320 ± 0.07440.178 ± 0.355−1.421 ± 0.431
NGC 64978.652 ± 0.006−0.008 ± 0.009−2.785 ± 0.039−0.162 ± 0.05938.926 ± 0.144−0.102 ± 0.220
NGC 69418.581 ± 0.0190.035 ± 0.022−3.135 ± 0.0820.485 ± 0.09837.614 ± 0.4590.973 ± 0.551
NGC 73218.633 ± 0.003−0.077 ± 0.005−3.016 ± 0.0140.090 ± 0.02338.660 ± 0.0430.820 ± 0.071
NGC 74898.626 ± 0.007−0.396 ± 0.012−2.878 ± 0.016−0.156 ± 0.02638.525 ± 0.0601.287 ± 0.115
NGC 76538.673 ± 0.003−0.230 ± 0.006−2.903 ± 0.0120.118 ± 0.02638.444 ± 0.0430.400 ± 0.091
NGC 77168.613 ± 0.005−0.109 ± 0.010−2.890 ± 0.0190.064 ± 0.03938.621 ± 0.0560.615 ± 0.112
NGC 77388.689 ± 0.031−0.125 ± 0.041−3.318 ± 0.1100.316 ± 0.14440.199 ± 0.524−1.097 ± 0.684
NGC 78198.650 ± 0.009−0.272 ± 0.012−2.882 ± 0.031−0.112 ± 0.04438.088 ± 0.0871.484 ± 0.123
IC 7768.217 ± 0.008−0.074 ± 0.015−3.193 ± 0.026−0.116 ± 0.04539.860 ± 0.167−0.179 ± 0.300
IC 12568.707 ± 0.012−0.316 ± 0.019−2.871 ± 0.044−0.013 ± 0.06837.536 ± 0.1571.745 ± 0.246
IC 53098.495 ± 0.030−0.044 ± 0.043−3.015 ± 0.0660.220 ± 0.09538.759 ± 0.223−0.355 ± 0.322
UGC 87338.428 ± 0.005−0.199 ± 0.009−2.974 ± 0.017−0.172 ± 0.02839.262 ± 0.0520.896 ± 0.131
UGC 122248.587 ± 0.032−0.226 ± 0.054−2.680 ± 0.103−0.256 ± 0.17237.458 ± 0.2562.164 ± 0.427
UGC 128168.478 ± 0.010−0.187 ± 0.016−2.942 ± 0.026−0.057 ± 0.04238.799 ± 0.0670.845 ± 0.123

3 RESULTS AND DISCUSSION

In Fig. 5, we present three histograms containing the oxygen abundances, logarithm of the ionization parameter and Teff values obtained for the objects in our sample by applying the methodology described above. It can be seen that the oxygen abundance values (top panel) are in the range |$\rm 8.2 \: \lesssim \: 12+\log (O/H) \: \lesssim \: 8.8$| [equivalent to 0.3 ≲ (Z/Z⊙) ≲ 1.3], with most objects presenting a value of 12 + log(O/H) around 8.6 [(Z/Z⊙) ≈ 0.8].

Histograms containing the oxygen abundances (top panel), logarithm of the ionization parameter (middle panel) and effective temperature values (bottom panel) for the sample of objects presented in Section 2.2.
Figure 5.

Histograms containing the oxygen abundances (top panel), logarithm of the ionization parameter (middle panel) and effective temperature values (bottom panel) for the sample of objects presented in Section 2.2.

Open in new tabDownload slide

The distribution of the ionization parameter (Fig. 5, middle panel) is in the range −3.4 ≲ log U ≲ − 2.5, with an average value of about −2.8. Higher values for the ionization parameter than the ones derived by us seem to be most often found in objects with low metallicity, such as the U values (≈− 1.3 dex) derived by Lagos et al. (2018) for the central parts of the star-forming dwarf galaxies UM 461 and Mrk 600.

Concerning the effective temperature, it can be seen in Fig. 5 (bottom panel) that most of the estimated Teff values are around 39 kK, with with the scatter of 1 kK, which is within the uncertainty of our method, namely 2.5 kK (see Paper I). It should be noted that this estimation for the uncertainty is an upper limit of the uncertainty for a single star-forming region, while in this work we use many data points to estimate the distribution of Teff. As described above, there is an artificial cut in Teff at 40 kK as a result of the applied method (see Paper I). Star-forming regions can, however, be ionized by stars with Teff higher than 40 kK. For example, Morisset et al. (2016) and Stasińska & Leitherer (1996) compared the results of a grid of photonization models with observational data of star-forming regions. They estimated the slopes of the spectral energy distributions (SEDs) of the ionizing sources, defined as the ratio between the number of neutral hydrogen (⁠|$\rm H^{0}$|⁠) and helium (⁠|$\rm He^{0}$|⁠) ionizing photons: |$Q_{o/1}=Q({\rm H^{0}})/Q(\rm He^{0})$| (a type of softness parameter). These estimated slopes are in the range 0.1–1.0, which translates into Teff close to or above 40 kK. It should be noted that only a few objects had estimated Teff values higher than 40 kK; in other words, most of the objects present Teff values in the range 30–40 kK. This result is in agreement with recent Teff estimations by Ramírez-Agudelo et al. (2017), who used ground-based optical spectroscopy obtained in the framework of the VLT-FLAMES Tarantula Survey (VFTS) to determine parameters of 72 single O-type stars.

Estimations of Teff and consequently the Teff gradients are dependent on the stellar atmosphere model assumed in the photoionization models (e.g. Stasińska & Schaerer 1997; Dors & Copetti 2003; Morisset et al. 2004; Morisset 2004) and on the match between the metallicity of the atmosphere models and the gas (Morisset 2004). In our case, the Teff–R relationship was derived assuming the WM- basic stellar atmosphere models (Pauldrach, Hoffmann & Lennon 2001), which are available only for two metallicities: solar and half-solar. Therefore, there is an inconsistency between the stellar and gas metallicities for photoionization models with (Z/Z⊙) = 0.03 and 0.2, which overestimate the Teff value for low-metallicity objects, reducing the effective gradient usually found in spiral galaxies (Morisset 2004; Dors et al. 2011). However, as can be seen in Fig. 5 (middle panel), most of the objects (⁠|${\approx }82{{\ \rm per\ cent}}$|⁠) present |$\rm 12+log(O/H) \: \gtrsim \:8.4$||$[\mathrm{i.e.\ } ({Z/{\rm Z}}_{\odot }) \: \gtrsim \: 0.5]$|⁠. Therefore, the mismatch between the stellar and gas metallicities in low-metallicity models has little effect on our Teff estimations.

In Fig. 6 we present histograms of the estimated values for gradients of Teff, log U, and oxygen abundance for our sample of galaxies. It can be seen that most galaxies (∼70 per cent) have positive derived values of the Teff gradient, although there are a number of flat and negative gradients. The median value of the Teff radial gradient is 0.762 kK/R25, and the minimum and the maximum values are –1.8 and 2.9, respectively. The prevalence of positive Teff gradients is compatible with what is expected under the hypothesis that stars are formed following an initial mass function (IMF) with a universal upper mass limit (Mup) and the variation of Teff with galactocentric distance is due to line blanketing effects taking place in the stellar atmosphere. Alternatively, this prevalence could be the result of an increase in the Mup of the IMF (and then in Teff) as the metallicity decreases.

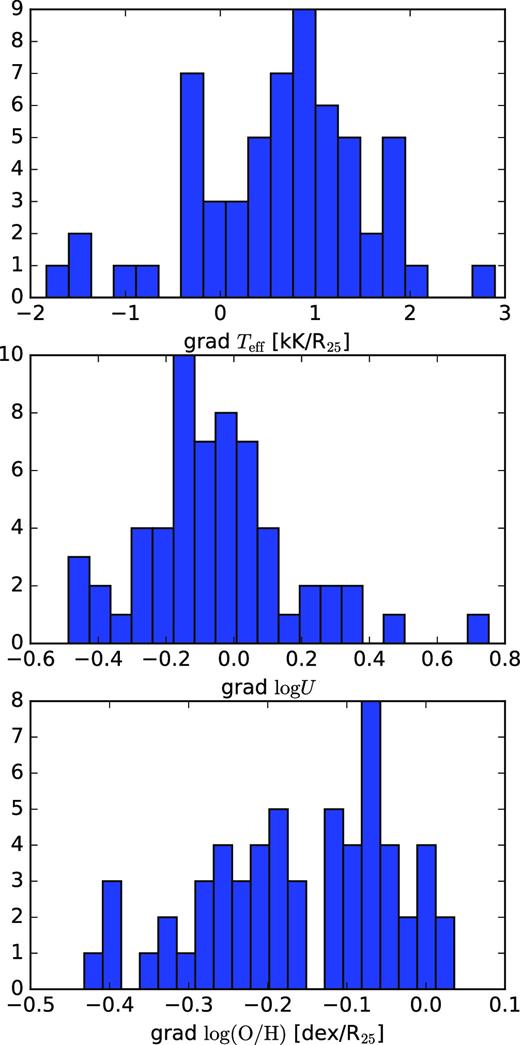
Histograms of estimated values for the gradients of: Teff (upper panel), log U (middle panel), and $\log (\rm O/H)$ (lower panel) for our sample of galaxies.
Figure 6.

Histograms of estimated values for the gradients of: Teff (upper panel), log U (middle panel), and |$\log (\rm O/H)$| (lower panel) for our sample of galaxies.

Open in new tabDownload slide

Dors et al. (2017) analysed Teff in a small sample of 14 spiral galaxies and likewise found that most galaxies (∼80 per cent) presented positive gradients, with the others showing flat (∼15 per cent) or negative (∼5 per cent) slopes. Similar results were found by Pérez-Montero & Vílchez (2009), who studied the behaviour of the η′ parameter (sensitive to Teff) along the discs of 12 galaxies. Therefore, in agreement with Dors et al. (2017) and Pérez-Montero & Vílchez (2009), we found that although most spiral galaxies display positive Teff gradients in the disc, this is not a universal property.

From the middle panel of Fig. 6 it can be seen that both negative and positive gradients of log U are derived for our sample of galaxies. They range from –0.5 to 0.8 dex/R25 and have a median value of –0.1 dex/R25, with negative gradients being more frequent. The overwhelming majority of galaxies in our sample have negative oxygen abundance gradients, with a range from –0.43 to 0.04 dex/R25 (see the lower panel of the same figure). The median value of the oxygen abundance gradient is –0.15 dex/R25.

In order to investigate the correlation between Teff and the other studied nebular parameters, log U and 12 + |$\log (\rm O/H)$|⁠, we plot in Fig. 7 these parameters as a function of Teff for the individual spaxels of our sample. The top panel of this figure shows that log U decreases as Teff increases. This result is in agreement with that derived by Morisset et al. (2016), who found that Q0/1 (which is inversely proportional to Teff) increases with log U. This result indicates that cooler stars have higher values of U, which is contrary to the assumption that H ii regions ionized by hotter stars will have higher values of U because these stars are emitting more ionizing photons. Sanders et al. (2016) showed that the ionization parameter has a weak dependence on both the rate of ionizing photon production and the gas density, and is more sensitive to the volume filling factor (ε):
(6)
Therefore, it is possibly that nebulae ionized by cooler stars present higher values of ε (and consequently higher U) than those ionized by hotter stars.
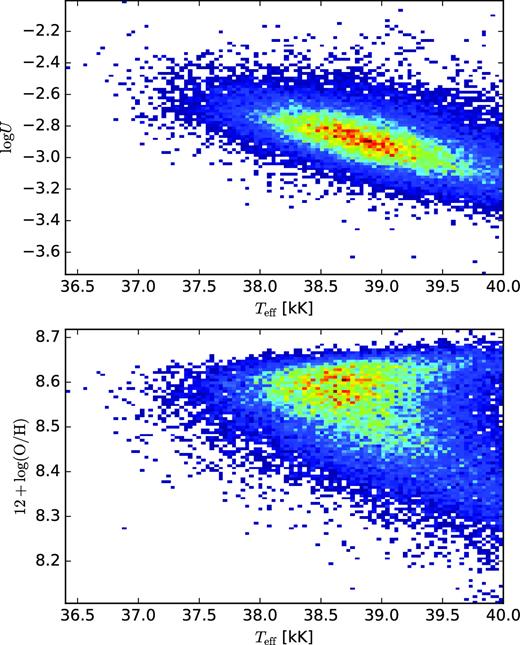
Density maps for the individual spaxels of our sample of CALIFA galaxies. (Top) log U as a function of Teff. (Bottom) Oxygen abundance as a function of Teff.
Figure 7.

Density maps for the individual spaxels of our sample of CALIFA galaxies. (Top) log U as a function of Teff. (Bottom) Oxygen abundance as a function of Teff.

Open in new tabDownload slide

Despite the conclusions of Shields & Searle (1978), Vilchez & Pagel (1988), Henry & Howard (1995) and Dors & Copetti (2003, 2005), who claimed that H ii regions with high metallicity have lower values of Teff than those with low metallicity, we do not find any clear correlation between Teff and 12 + |$\log (\rm O/H)$| for the spaxels of all galaxies in our sample (see also Morisset 2004; Dors et al. 2017). The contradiction between the previous and current results could be caused by the fact that the Teff–metallicity relationship is not unique; that is, this relationship is different for different galaxies. This suggestion will be discussed below.

Fig. 8 plots 12 + |$\log (\rm O/H)$| versus log U. There is a large scatter and no apparent correlation between the two parameters. This result is in agreement with, for example, Dors et al. (2011), who derived oxygen abundances and ionization parameters from diagnostic diagrams containing photoionization model results and observational data of H ii regions. Kaplan et al. (2016) presented a study of the excitation conditions and metallicities in eight nearby spiral galaxies from the VIRUS-P Exploration of Nearby Galaxies (VENGA) survey. These authors calculated the ionization parameter using an iterative determination proposed by Kewley & Ellison (2008), and did not find any clear trends between U and Z (see also Lara-López, López-Sánchez & Hopkins 2013). On the other hand, a trend for H ii regions showing that those with higher values of log U present lower metallicities was derived by, for example, Morisset et al. (2016), who used a large grid of photoionzation models in order to reproduce emission-line intensities also taken from the CALIFA data base (see also Pérez-Montero & Amorín 2017 and references therein). The relationship between the ionization parameter and oxygen abundance seems to be dependent on the methodology employed to calculate these parameters (e.g. Krühler et al. 2017) or on the geometry assumed in the photoionization models (see, for example, fig. 13 of Morisset et al. 2016.)

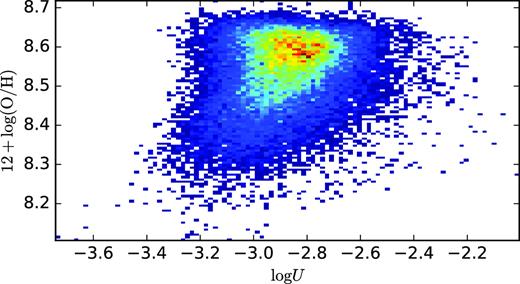
As Fig. 7, but for 12 + $\log (\rm O/H)$ as a function of log U.
Figure 8.

As Fig. 7, but for 12 + |$\log (\rm O/H)$| as a function of log U.

Open in new tabDownload slide

Fig. 9 shows the central Teff, the gradients of Teff and log U, and 12 + |$\log (\rm O/H)_0$| as a function of the stellar mass of the galaxies. The central Teff was calculated as the average values for the spaxels with R < 0.2R25. We found no correlation between the central Teff, the Teff and log U gradients, and the stellar mass of the galaxies.

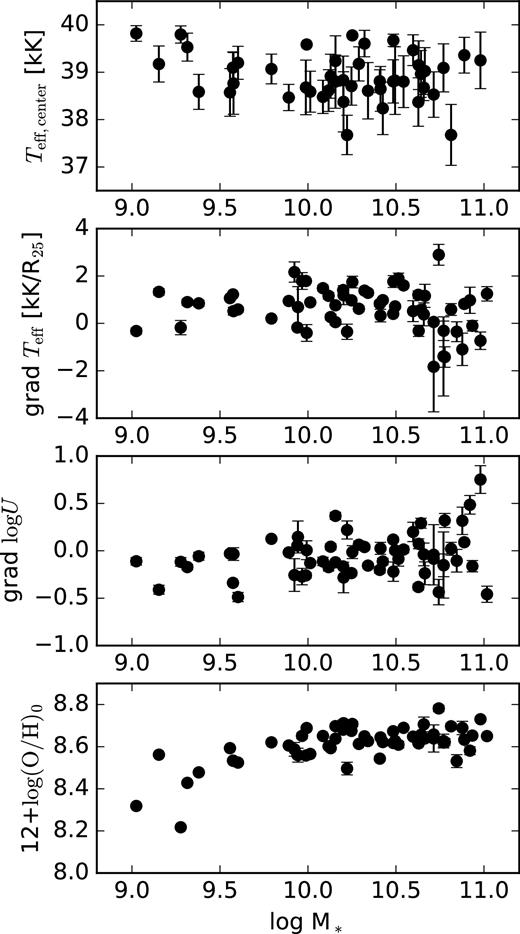
Panels from top to bottom: central Teff (average values), radial gradients of Teff, radial gradients of log U, and 12 + log (O/H)0 as a function of the stellar mass of the galaxy.
Figure 9.

Panels from top to bottom: central Teff (average values), radial gradients of Teff, radial gradients of log U, and 12 + log (O/H)0 as a function of the stellar mass of the galaxy.

Open in new tabDownload slide
The radial gradients of log U and Teff as a function of the oxygen abundance gradient are shown in Fig. 10, which reveals a correlation in both cases. The former presents a positive correlation – the gradient of log U increases as the |$\log (\rm O/H)$| gradient increases. Because the p-value is 0.0001, the null hypothesis that there is no correlation between log U and O/H should be rejected. An anti-correlation between the gradient of Teff and the oxygen abundance gradient is, however, clearly seen for our sample, with a p-value of 10−5. Moreover, galaxies with flat oxygen abundance gradients tend to have flat log U and Teff gradients too. Therefore, one can expect an anti-correlation between Teff and the oxygen abundance. Indeed, such an anti-correlation can be seen in the low-metallicity zone in the bottom panel of Fig. 7. In the high-metallicity regime, however, there is no correlation between Teff and |$\log (\rm O/H)$| for individual spaxels. Using the softness parameter defined by Vilchez & Pagel (1988), namely
\begin{eqnarray*} \eta ^{\prime }\, =\, \frac{([\rm{O\,\,\, {\small II}}]\lambda \lambda 3727,3729/[\rm{O\,\,\,{\small III}}]\lambda \lambda 4959,5007)}{([\rm{S\,\,\, {\small II}}]\lambda \lambda 6717,6731/[\rm{S\,\,\, {\small III}}]\lambda \lambda 9069,9532)}, \end{eqnarray*}
which works as a diagnostic for the nature and the effective temperature of the ionizing radiation field (see Díaz, Pagel & Wilson 1985), Díaz et al. (2007) and Hägele (2008) compared the ionization structure for star-forming regions in different environments. They found that high-metallicity circumnuclear star-forming regions (CNSFRs) segregate from high-metallicity disc H ii regions, with the former regions showing Teff values of about 40 kK and the latter ones values of about 35 kK, which is a temperature range similar to those found by us for the objects in the high-metallicity regime. On the other hand, these authors also found that the low-metallicity H ii galaxies belonging to their sample (see also the H ii galaxies studied by Hägele et al. 2006, 2008, 2011, 2012; Pérez-Montero et al. 2010) present a similar behaviour and Teff values (40 kK) to those found in CNSFRs. In all cases, the low-metallicity H ii galaxies show high Teff values, in agreement with the results derived from Fig. 7. A possible explanation of this could be that, for an individual galaxy, Teff increases as the oxygen abundance decreases but there is not a unique Teff–|$\log (\rm O/H)$| relationship for all galaxies.
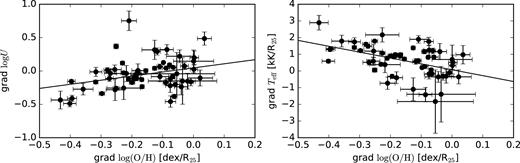
(Left) Radial gradient of log U as a function of the oxygen abundance radial gradient. (Right) Radial gradient of Teff as a function of the oxygen abundance radial gradient. Solid lines are the best-fitting linear regressions to the data.
Figure 10.

(Left) Radial gradient of log U as a function of the oxygen abundance radial gradient. (Right) Radial gradient of Teff as a function of the oxygen abundance radial gradient. Solid lines are the best-fitting linear regressions to the data.

Open in new tabDownload slide

Finally, the averaged Teff for the spaxels with R < 0.2R25 (Teff, 0) as a function of the Teff value extrapolated to R = 0.1R25 (Teff,centre) is plotted in the upper panel of Fig. 11. The plot shows that for the galaxies in our sample Teff,0 can be significantly lower than Teff,centre. This fact could be considered as an indication that the star formation processes in the central parts of galaxies, which determine Teff, are not similar to those along discs. This could be a result of metallicity effects, in the sense that metallicities at the centre could be higher than those expected by extrapolating the radial O/H gradient, which leads to a cooling of the atmospheres of massive stars. However, the behaviour of the |$\rm (O/H)_{0}$| versus |$\rm (O/H)_{centre}$| relationship for the galaxies in our sample (bottom panel of Fig. 11) does not show a significant bias between |$\rm (O/H)_{0}$| and |$\rm (O/H)_{centre}$|⁠. Thus, an effect other than metallicity seems to be responsible for producing the discrepancy between Teff,0 and Teff,centre, because it is not only the metallicity that controls Teff. Star formation processes in the nuclear regions of galaxies can be altered by, for example, supernova explosions and/or the presence of Wolf–Rayet stars (which are most common in high-metallicity environments). Moreover, the gas outflows found in nuclear starbursts and in AGNs, which extend on kiloparsec scales, could potentially suppress star formation in their host galaxies (Gallagher et al. 2018), modifying the Teff expected from the radial gradient and producing the discrepancy seen in Fig. 11. Furthermore, gas flux from the outskirts of discs (e.g. Rosa et al. 2014) could be falling into the nucleus and modifying the star formation processes.

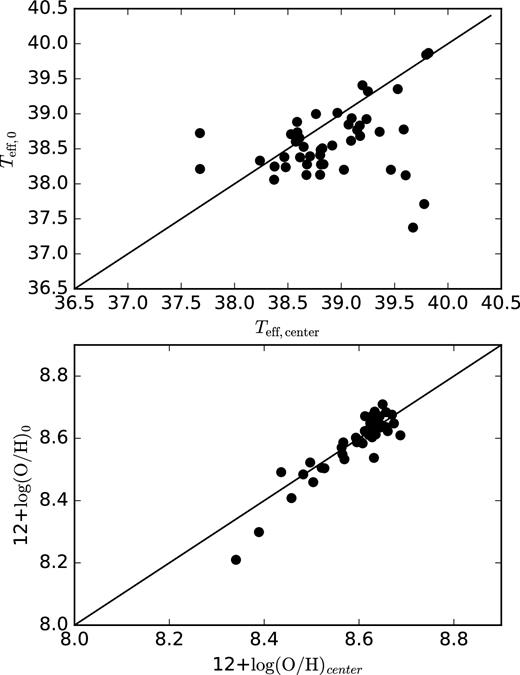
(Top) Comparison of Teff,0 and Teff,centre. (Bottom) Relationship between 12 + log(O/H)0 and 12 + log(O/H)centre. Both panels show the one-to-one relationship.
Figure 11.

(Top) Comparison of Teff,0 and Teff,centre. (Bottom) Relationship between 12 + log(O/H)0 and 12 + log(O/H)centre. Both panels show the one-to-one relationship.

Open in new tabDownload slide

4 CONCLUSION

We used homogeneous spectroscopic data of H ii regions taken from the CALIFA survey and a theoretical calibration between the effective temperature of ionizing star(s) (Teff) and the ratio R  = log ([O ii]λλ3727, 3729/[O iii]λ5007) to investigate the universality of Teff gradients in spiral galaxies as well as the correlation between Teff, the ionization parameter (U) and the oxygen abundance of H ii regions. We found that most of the galaxies in our sample (∼70 per cent) present positive Teff radial gradients, with a median value of 0.762 kK/R25, although some galaxies exhibit negative or flat Teff radial gradients. Therefore, we conclude that Teff gradients are not a universal property of spiral galaxies. We also found that the radial gradients of both log U and Teff depend on the oxygen abundance gradient, in the sense that the gradient of log U increases as the log (O/H) gradient increases while the Teff gradient decreases as the log (O/H) increases. Moreover, galaxies with a flat oxygen abundance gradient tend to have flat log U and Teff gradients.

SUPPORTING INFORMATION

CALIFA-Teff_append.pdf

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

ACKNOWLEDGEMENTS

We are grateful to the referee for his/her constructive comments. IAZ thanks FAPESP for financial support during his visit to UNIVAP (FAPESP grant number 2017/19538-1). OLD and ACK thank FAPESP and CNPq. IAZ acknowledges support from the Ukrainian National Grid Project (especially project 400Kt) of the NAS of Ukraine.

This study used data provided by the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://califa.caha.es/). It is based on observations collected at the Centro Astronomico Hispano Aleman (CAHA) at Calar Alto, operated jointly by the Max-Planck-Institut für Astronomie and the Instituto de Astrofisica de Andalucia (CSIC).

Footnotes

1

http://www.califa.caha.es/

2

We assumed a spatially flat cosmology with H0  =  71 |$\rm km\:s^{-1} Mpc^{-1}$|⁠, Ωm = 0.270, and Ωvac = 0.730 (Wright 2006).

3

http://www.nordugrid.org/

REFERENCES

Abbott
D. C.
,
Hummer
D. G.
,
1985
,
ApJ
,
294
,
286
10.1086/163297

Crossref
Search ADS
 

Allende Prieto
C.
,
Lambert
D. L.
,
Asplund
M.
,
2001
,
ApJ
,
556
,
L63
10.1086/322874

Crossref
Search ADS
 

Asari
N. V.
,
Cid Fernandes
R.
,
Stasińska
G.
,
Torres-Papaqui
J. P.
,
Mateus
A.
,
Sodré
L.
,
Schoenell
W.
,
Gomes
J. M.
,
2007
,
MNRAS
,
381
,
263
10.1111/j.1365-2966.2007.12255.x

Crossref
Search ADS
 

Baldwin
J. A.
,
Phillips
M. M.
,
Terlevich
R.
,
1981
,
PASP
,
93
,
5
10.1086/130766

Crossref
Search ADS
 

Bastian
N.
,
Covey
K. R.
,
Meyer
M. R.
,
2010
,
ARA&A
,
48
,
339
10.1146/annurev-astro-082708-101642

Crossref
Search ADS
 

Bruzual
G.
,
Charlot
S.
,
2003
,
MNRAS
,
344
,
1000
10.1046/j.1365-8711.2003.06897.x

Crossref
Search ADS
 

Cardelli
J. A.
,
Clayton
G. C.
,
Mathis
J. S.
,
1989
,
ApJ
,
345
,
245
10.1086/167900

Crossref
Search ADS
 

Cid Fernandes
R.
,
Mateus
A.
,
Sodré
L.
,
Stasińska
G.
,
Gomes
J. M.
,
2005
,
MNRAS
,
358
,
363
10.1111/j.1365-2966.2005.08752.x

Crossref
Search ADS
 

Corti
M.
,
Bosch
G.
,
Niemela
V.
,
2007
,
A&A
,
467
,
137
10.1051/0004-6361:20065041

Crossref
Search ADS
 

Crowther
P. A.
et al. ,
2016
,
MNRAS
,
458
,
624
10.1093/mnras/stw273

Crossref
Search ADS
 

Díaz
A. I.
,
Pagel
B. E. J.
,
Wilson
I. R. G.
,
1985
,
MNRAS
,
212
,
737
10.1093/mnras/212.3.737

Crossref
Search ADS
 

Díaz
A. I.
,
Terlevich
E.
,
Castellanos
M.
et al. ,
2007
,
MNRAS
,
382
,
251
10.1111/j.1365-2966.2007.12351.x

Crossref
Search ADS
 

Dors
O. L.
Jr,
Copetti
M. V. F.
,
2003
,
A&A
,
404
,
969
10.1051/0004-6361:20030636

Crossref
Search ADS
 

Dors
O. L.
Jr,
Copetti
M. V. F.
,
2005
,
A&A
,
437
,
837
10.1051/0004-6361:20040219

Crossref
Search ADS
 

Dors
O. L.
Jr,
Krabbe
A.
,
Hägele
G. F.
,
Pérez-Montero
E.
,
2011
,
MNRAS
,
415
,
3616
10.1111/j.1365-2966.2011.18978.x

Crossref
Search ADS
 

Dors
O. L.
,
Hägele
G. F.
,
Cardaci
M. V.
,
Krabbe
A. C.
,
2017
,
MNRAS
,
466
,
726
10.1093/mnras/stw3115

Crossref
Search ADS
 

Ellison
S. L.
,
Patton
D. R.
,
Simard
L.
,
McConnachie
A. W.
,
2008
,
ApJ
,
672
,
L107
10.1086/527296

Crossref
Search ADS
 

Ellison
S. L.
,
Sánchez
S. F.
,
Ibarra-Medel
H.
,
Antonio
B.
,
Mendel
J. T.
,
Barrera-Ballesteros
J.
,
2018
,
MNRAS
,
474
,
2039
10.1093/mnras/stx2882

Crossref
Search ADS
 

Evans
C. J.
et al. ,
2015
,
A&A
,
574
,
A13
10.1051/0004-6361/201424414

Crossref
Search ADS
 

Evans
I. N.
,
1986
,
ApJ
,
309
,
544
10.1086/164623

Crossref
Search ADS
 

Fierro
J.
,
Torres-Peimbert
S.
,
Peimbert
M.
,
1986
,
PASP
,
98
,
1032
10.1086/131868

Crossref
Search ADS
 

Gallagher
R.
,
Maiolino
R.
,
Belfiore
F.
,
Drory
N.
,
Riffel
R.
,
Riffel
R. A.
,
2018
, preprint (arXiv:1806.03311)

Hägele
G. F.
,
2008
,
PhD thesis
,
Univ. Autónoma de Madrid

Google Scholar

OpenURL Placeholder Text

 

Hägele
G. F.
,
Pérez-Montero
E.
,
Díaz
A. I.
,
Terlevich
E.
,
Terlevich
R.
,
2006
,
MNRAS
,
372
,
293
10.1111/j.1365-2966.2006.10856.x

Crossref
Search ADS
 

Hägele
G. F.
,
Díaz
A. I.
,
Terlevich
E.
,
Terlevich
R.
,
Pérez-Montero
E.
,
Cardaci
M. V.
,
2008
,
MNRAS
,
383
,
209
10.1111/j.1365-2966.2007.12527.x

Crossref
Search ADS
 

Hägele
G. F.
,
García-Benito
R.
,
Pérez-Montero
E.
,
Díaz
A. I.
,
Cardaci
M. V.
,
Firpo
V.
,
Terlevich
E.
,
Terlevich
R.
,
2011
,
MNRAS
,
414
,
272
10.1111/j.1365-2966.2011.18389.x

Crossref
Search ADS
 

Hägele
G. F.
et al. ,
2012
,
MNRAS
,
422
,
3475
10.1111/j.1365-2966.2012.20858.x

Crossref
Search ADS
 

Henry
R. B. C.
,
Howard
J. W.
,
1995
,
ApJ
,
438
,
170
10.1086/175062

Crossref
Search ADS
 

Holgado
G.
et al. ,
2018
,
A&A
,
613
,
A65
10.1051/0004-6361/201731543

Crossref
Search ADS
 

Husemann
B.
,
Wisotzki
L.
,
Sánchez
S. F.
,
Jahnke
K.
,
2013
,
A&A
,
549
,
A43
10.1051/0004-6361/201220076

Crossref
Search ADS
 

Izotov
Y. I.
,
Thuan
T. X.
,
Lipovetsky
V. A.
,
1994
,
ApJ
,
435
,
647
10.1086/174843

Crossref
Search ADS
 

Kaplan
K. F.
et al. ,
2016
,
MNRAS
,
462
,
1642
10.1093/mnras/stw1422

Crossref
Search ADS
 

Kennicutt
R. C.
Jr,
Bresolin
F.
,
French
H.
,
Martin
P.
,
2000
,
ApJ
,
537
,
589
10.1086/309075

Crossref
Search ADS
 

Kewley
L. J.
,
Ellison
S. L.
,
2008
,
ApJ
,
681
,
1183
10.1086/587500

Crossref
Search ADS
 

Kewley
L. J.
,
Dopita
M. A.
,
Sutherland
R. S.
,
Heisler
C. A.
,
Trevena
J.
,
2001
,
ApJ
,
556
,
121
10.1086/321545

Crossref
Search ADS
 

Kinman
T. D.
,
Davidson
K.
,
1981
,
ApJ
,
243
,
127
10.1086/158575

Crossref
Search ADS
 

Krühler
T.
,
Kuncarayakti
H.
,
Schady
P.
,
Anderson
J. P.
,
Galbany
L.
,
Gensior
J.
,
2017
,
A&A
,
602
,
A85
10.1051/0004-6361/201630268

Crossref
Search ADS
 

Lagos
P.
,
Scott
T. C.
,
Nigoche-Netro
A.
,
Demarco
R.
,
Humphrey
A.
,
Papaderos
P.
,
2018
,
MNRAS
,
477
,
392
10.1093/mnras/sty601

Crossref
Search ADS
 

Lamb
J. B.
,
Oey
M. S.
,
Segura-Cox
D. M.
,
Graus
A. S.
,
Kiminki
D. C.
,
Golden-Marx
J. B.
,
Parker
J. W.
,
2016
,
ApJ
,
817
,
113
10.3847/0004-637X/817/2/113

Crossref
Search ADS
 

Lara-López
M. A.
et al. ,
2010
,
A&A
,
521
,
L53
10.1051/0004-6361/201014803

Crossref
Search ADS
 

Lara-López
M. A.
,
López-Sánchez
Á. R.
,
Hopkins
A. M.
,
2013
,
ApJ
,
764
,
178
10.1088/0004-637X/764/2/178

Crossref
Search ADS
 

Lequeux
J.
,
Peimbert
M.
,
Rayo
J. F.
,
Serrano
A.
,
Torres-Peimbert
S.
,
1979
,
A&A
,
80
,
155

 

Mannucci
F.
,
Cresci
G.
,
Maiolino
R.
,
Marconi
A.
,
Gnerucci
A.
,
2010
,
MNRAS
,
408
,
2115
10.1111/j.1365-2966.2010.17291.x

Crossref
Search ADS
 

Markova
N.
,
Puls
J.
,
Langer
N.
,
2018
,
A&A
,
613
,
A12
10.1051/0004-6361/201731361

Crossref
Search ADS
 

Martins
F.
,
Palacios
A.
,
2017
,
A&A
,
598
,
A56
10.1051/0004-6361/201629538

Crossref
Search ADS
 

Martins
F.
,
Schaerer
D.
,
Hillier
D. J.
,
Heydari-Malayeri
M.
,
2004
,
A&A
,
420
,
1087
10.1051/0004-6361:20034509

Crossref
Search ADS
 

Martins
F.
,
Schaerer
D.
,
Hillier
D. J.
,
2005
,
A&A
,
436
,
1049
10.1051/0004-6361:20042386

Crossref
Search ADS
 

Massey
P.
,
Puls
J.
,
Pauldrach
A. W. A.
,
Bresolin
F.
,
Kudritzki
R. P.
,
Simon
T.
,
2005
,
ApJ
,
627
,
477
10.1086/430417

Crossref
Search ADS
 

Massey
P.
,
Zangari
A. M.
,
Morrell
N. I.
,
Puls
J.
,
DeGioia-Eastwood
K.
,
Bresolin
F.
,
Kudritzki
R.-P.
,
2009
,
ApJ
,
692
,
618
10.1088/0004-637X/692/1/618

Crossref
Search ADS
 

Mateus
A.
,
Sodré
L.
,
Cid Fernandes
R.
,
Stasińska
G.
,
Schoenell
W.
,
Gomes
J. M.
,
2006
,
MNRAS
,
370
,
721
10.1111/j.1365-2966.2006.10565.x

Crossref
Search ADS
 

Mohr-Smith
M.
et al. ,
2017
,
MNRAS
,
465
,
1807
10.1093/mnras/stw2751

Crossref
Search ADS
 

Mokiem
M. R.
,
Martín-Hernández
N. L.
,
Lenorzer
A.
,
de Koter
A.
,
Tielens
A. G. G. M.
,
2004
,
A&A
,
419
,
319
10.1051/0004-6361:20040074

Crossref
Search ADS
 

Morisset
C.
,
2004
,
ApJ
,
601
,
858
10.1086/380596

Crossref
Search ADS
 

Morisset
C.
,
Schaerer
D.
,
Bouret
J.-C.
,
Martins
F.
,
2004
,
A&A
,
415
,
577
10.1051/0004-6361:20034622

Crossref
Search ADS
 

Morisset
C.
et al. ,
2016
,
A&A
,
594
,
A37
10.1051/0004-6361/201628559

Crossref
Search ADS
 

Morrell
N. I.
,
Massey
P.
,
Neugent
K. F.
,
Penny
L. R.
,
Gies
D. R.
,
2014
,
ApJ
,
789
,
139
10.1088/0004-637X/789/2/139

Crossref
Search ADS
 

Pauldrach
A. W. A.
,
Hoffmann
T. L.
,
Lennon
M.
,
2001
,
A&A
,
375
,
161
10.1051/0004-6361:20010805

Crossref
Search ADS
 

Peimbert
M.
,
Serrano
A.
,
1982
,
MNRAS
,
198
,
563
10.1093/mnras/198.2.563

Crossref
Search ADS
 

Pérez-Montero
E.
,
Amorín
R.
,
2017
,
MNRAS
,
467
,
1287
10.1093/mnras/stx186

Crossref

 

Pérez-Montero
E.
,
Vílchez
J. M.
,
2009
,
MNRAS
,
400
,
1721
10.1111/j.1365-2966.2009.15590.x

Crossref
Search ADS
 

Pérez-Montero
E.
,
García-Benito
R.
,
Hägele
G. F.
,
Díaz
Á. I.
,
2010
,
MNRAS
,
404
,
2037
10.1111/j.1365-2966.2010.16421.x

Crossref

 

Pilyugin
L. S.
,
Grebel
E. K.
,
2016
,
MNRAS
,
457
,
3678
10.1093/mnras/stw238

Crossref
Search ADS
 

Pilyugin
L. S.
,
Vílchez
J. M.
,
Contini
T.
,
2004
,
A&A
,
425
,
849
10.1051/0004-6361:20034522

Crossref
Search ADS
 

Ramírez-Agudelo
O. H.
et al. ,
2017
,
A&A
,
600
,
A81
10.1051/0004-6361/201628914

Crossref
Search ADS
 

Rosa
D. A.
,
Dors
O. L.
,
Krabbe
A. C.
,
Hägele
G. F.
,
Cardaci
M. V.
,
Pastoriza
M. G.
,
Rodrigues
I.
,
Winge
C.
,
2014
,
MNRAS
,
444
,
2005
10.1093/mnras/stu1578

Crossref
Search ADS
 

Rubin
V. C.
,
Ford
W. K.
Jr,
Whitmore
B. C.
,
1984
,
ApJ
,
281
,
L21
10.1086/184276

Crossref
Search ADS
 

Sánchez
S. F.
et al. ,
2012
,
A&A
,
538
,
A8
10.1051/0004-6361/201117353

Crossref
Search ADS
 

Sánchez
S. F.
et al. ,
2013
,
A&A
,
554
,
A58
10.1051/0004-6361/201220669

Crossref
Search ADS
 

Sánchez
S. F.
et al. ,
2016
,
A&A
,
594
,
A36
10.1051/0004-6361/201628661

Crossref
Search ADS
 

Sánchez
S. F.
et al. ,
2017
,
MNRAS
,
469
,
2121
10.1093/mnras/stx808

Crossref
Search ADS
 

Sanders
R. L.
et al. ,
2016
,
ApJ
,
816
,
23
10.3847/0004-637X/816/1/23

Crossref
Search ADS
 

Schaerer
D.
,
Schmutz
W.
,
1994
,
A&A
,
288
,
231

 

Shields
G. A.
,
Searle
L.
,
1978
,
ApJ
,
222
,
821
10.1086/156201

Crossref
Search ADS
 

Simón-Díaz
S.
,
Herrero
A.
,
Sabín-Sanjulián
C.
,
Najarro
F.
,
Garcia
M.
,
Puls
J.
,
Castro
N.
,
Evans
C. J.
,
2014
,
A&A
,
570
,
L6
10.1051/0004-6361/201424742

Crossref
Search ADS
 

Skillman
E. D.
,
1992
, in
Edmunds
M. G.
,
Terlevich
R.
, eds,
Elements and the Cosmos
,
Cambridge University Press
,
New York
. p.
246

Google Scholar

OpenURL Placeholder Text

 

Sota
A.
,
Maíz Apellániz
J.
,
Walborn
N. R.
,
Alfaro
E. J.
,
Barbá
R. H.
,
Morrell
N. I.
,
Gamen
R. C.
,
Arias
J. I.
,
2011
,
ApJS
,
193
,
24
10.1088/0067-0049/193/2/24

Crossref
Search ADS
 

Stasińska
G.
,
Leitherer
C.
,
1996
,
ApJS
,
107
,
661
10.1086/192377

Crossref
Search ADS
 

Stasińska
G.
,
Schaerer
D.
,
1997
,
A&A
,
322
,
615

 

Storey
P. J.
,
Zeippen
C. J.
,
2000
,
MNRAS
,
312
,
813
10.1046/j.1365-8711.2000.03184.x

Crossref
Search ADS
 

Tramper
F.
,
Sana
H.
,
de Koter
A.
,
Kaper
L.
,
Ramírez-Agudelo
O. H.
,
2014
,
A&A
,
572
,
A36
10.1051/0004-6361/201424312

Crossref
Search ADS
 

Tremonti
C. A.
et al. ,
2004
,
ApJ
,
613
,
898
10.1086/423264

Crossref
Search ADS
 

Vilchez
J. M.
,
Pagel
B. E. J.
,
1988
,
MNRAS
,
231
,
257
10.1093/mnras/231.2.257

Crossref
Search ADS
 

Walborn
N. R.
et al. ,
2014
,
A&A
,
564
,
A40
10.1051/0004-6361/201323082

Crossref
Search ADS
 

Walcher
C. J.
et al. ,
2014
,
A&A
,
569
,
A1
10.1051/0004-6361/201424198

Crossref
Search ADS
 

Wright
N. J.
,
Drew
J. E.
,
Mohr-Smith
M.
,
2015
,
MNRAS
,
449
,
741
10.1093/mnras/stv323

Crossref
Search ADS
 

Wright
E. L.
,
2006
,
PASP
,
118
,
1711
10.1086/510102

Crossref
Search ADS
 

Zanstra
H.
,
1929
,
Pub. Dominion Astrophys. Observ. Victoria
,
4
:

 

Zinchenko
I. A.
,
Pilyugin
L. S.
,
Grebel
E. K.
,
Sánchez
S. F.
,
Vílchez
J. M.
,
2016
,
MNRAS
,
462
,
2715
10.1093/mnras/stw1857

Crossref
Search ADS
 

Zinchenko
I. A.
,
Just
A.
,
Pilyugin
L. S.
,
Lara-Lopez
M. A.
,
2018
, preprint (arXiv:1810.08006)

© 2018 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Article
Download all slides
  • Supplementary data

    • Supplementary data

    Supplemental File - pdf file