-
PDF
- Split View
-
Views
-
Cite
Cite
Kai-Xing Lu, Yinghe Zhao, Jin-Ming Bai, Xu-Liang Fan, Reddening of the BLR and NLR in AGNs from a systematic analysis of Balmer decrement, Monthly Notices of the Royal Astronomical Society, Volume 483, Issue 2, February 2019, Pages 1722–1730, https://doi.org/10.1093/mnras/sty3229
Close - Share Icon Share
ABSTRACT
We selected an active galactic nuclei (AGNs) sample (0 < |$z$| ≤ 0.35) from Sloan Digital Sky Survey Data Release 7, and measured the broad- (|$\rm H\alpha ^{b}/H\beta ^{b}$|) and narrow-line Balmer decrements (|$\rm H\alpha ^{n}/H\beta ^{n}$|) of 554 selected AGNs. We found that the distributions of Balmer decrements can be fitted by a Gaussian function and give the best estimates of |$\rm H\alpha ^{b}/H\beta ^{b}= 3.16$| with a standard deviation 0.07 dex, and |$\rm H\alpha ^{n}/H\beta ^{n}= 4.37$| with a standard deviation 0.10 dex. We inspected the distributions of |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$| in the Baldwin−Phillips−Terlevich (BPT) diagram and found that only narrow-line Balmer decrements depend on the physical conditions of the narrow-line region (NLR). We tested the relationship between |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$|, and found that |$\rm H\alpha ^{b}/H\beta ^{b}$| does not correlate with |$\rm H\alpha ^{n}/H\beta ^{n}$|. We investigated the relationship between Balmer decrements and Seyfert sub-type, and found that only broad-line Balmer decrements correlate with Seyfert sub-type, We also examined the dependency of Balmer decrements on AGN properties, and found that Balmer decrements have no correlation with optical luminosity, but show some dependence on accretion rate. These results indicate that the NLR is subject to more reddening by dust than the broad-line region.
1 INTRODUCTION
The unified model of active galactic nuclei (AGNs) proposes that the variety in AGN type is just the result of viewing from different orientations (Antonucci 1993; Urry & Padovani 1995). A dusty toroidal structure (i.e. the torus) surrounding an accreting massive black hole (BH) is believed to be a common feature of AGNs. The broad-line region (BLR) is close to the central region and is believed to be located within the inner radius of the dusty torus. The narrow-line region (NLR) is located farther from the black hole and accretion disc, at the distance of a few pc. Many hard X-ray surveys have showed that ∼70 per cent of all local AGNs are obscured, where the obscuration in X-ray regime is produced by multiple absorbers mostly associated with the torus and the BLR, the obscuring material in the infrared is a transition zone between the BLR and NLR (e.g. Burlon et al. 2011; Ramos Almeida & Ricci 2017). In the optical regime, Gaskell & Harrington (2017) suggests that outflowing dusty clumps driven by radiation pressure acting on the dust complicate the study of the geometric structure and kinematics of the BLR and the search for sub-parsec supermassive black hole binaries.
The internal reddening caused by obscuring material attenuates the activity of AGNs and blurs the nature of AGNs, such as the underestimate of luminosity and accretion rate. For example, The reverberation mapped spectra of IRAS F12397 + 333 (|$z$| = 0.0435) have a very red colour resulting from the internal reddening of AGNs (Galactic extinction corrected; Du et al. 2014). After correcting internal reddening, the luminosity at 5100 Å and dimensionless accretion rate increase 4 and 9 times, respectively (Du et al. 2014; Hu et al. 2015). In addition, the internal reddening in AGNs, which always produced by dust in the local of AGNs or the host galaxy, are useful for us to understand the accretion and feedback process of AGNs.
Using the Balmer decrement as an indicator of reddening, many works have studied the internal reddening of AGNs in detail for different AGN samples (e.g. Costero & Osterbrock 1977; Gaskell 1982, 1984; Gaskell et al. 2004; Dong et al. 2005; La Mura et al. 2007; Dong et al. 2008; Baron et al. 2016; Heard & Gaskell 2016; Gaskell 2017). For the BLR, Gaskell (2017) suggested that the intrinsic Balmer decrement in extremely blue AGNs is |$\rm H\alpha ^{b}/H\beta ^{b}\approx 2.72\pm 0.04$|,1 which is consistent with the Baker–Menzel Case B value of 2.74 (Osterbrock & Ferland 2006). For the NLR, the best overall average value of 3.1 is adopted for the intrinsic |$\rm H\alpha ^{n}/H\beta ^{n}$| ratio (Gaskell 1982, 1984; Wysota & Gaskell 1988; Heard & Gaskell 2016), which is a bit larger than the recombination value of 2.85 resulting from the effects of collisional excitation (Osterbrock & Ferland 2006).
However, there still exist some open questions including (1) many works show that the distributions of the broad-line Balmer decrement cover a wide range, but the median or average value varies from one sample to another. For example, La Mura et al. (2007) derived |$\rm H\alpha ^{b}/H\beta ^{b}= 3.45\pm 0.65$|, Dong et al. (2008) gave |$\rm H\alpha ^{b}/H\beta ^{b}= 3.06$| with standard deviation 0.03 dex, Gaskell (2017) suggested that the intrinsic |$\rm H\alpha ^{b}/H\beta ^{b}$| is 2.72, Zhou et al. (2006) found the mean |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio to be 3.028 with a dispersion of 0.36, etc. (2) de Zotti & Gaskell (1985) and Heard & Gaskell (2016) found that broad-line Balmer decrements are greater than narrow-line Balmer decrements, which is opposite to the result of Baron et al. (2016); (3) The nature and distribution of dust causing internal reddening of AGNs remain unknown (e.g. Baron et al. 2016; Heard & Gaskell 2016; Gaskell 2017), for example whether dust causing reddening in the BLR and continuum also causes in the NLR or not. To investigate these issues, in this paper, we study the properties of broad- and narrow-line Blamer decrements based on an AGN sample selected from the Sloan Digital Sky Survey Data Release 7 (SDSS DR7; York et al. 2000; Schneider et al. 2010). In Section 2, we describe the construction of sample. We fit spectra and obtain the measurements of emission-line fluxes in Section 3, and give results in Section 4. Section 5 is discussion. We draw our conclusions in Section 6.
2 SAMPLE CONSTRUCTION
Based on the H β and H α emission line, in this paper, we concentrate on studying the properties of Balmer decrements and exploring potential difference (if existences) between broad- and narrow-line Balmer decrements. However, it is hard to separate the NLR Balmer lines from the BLR Balmer lines, since narrow lines sometimes blend with broad lines (Dong et al. 2008; Hu et al. 2008; Stern & Laor 2012a,b, 2013). To this purpose, we selected a sample of broad-line AGNs from the SDSS DR7 (Schneider et al. 2010) using the following criteria:
We limited redshifts ≤0.35 at first so that the H α line has a sufficient number of good spectral pixels within the SDSS spectral wavelength coverage, which gives a total sample consisting of 3532 AGNs.
Then we selected objects with spectral signal-to-noise ratio (S/N)>15 to limit the complex model well in spectral fitting scheme (see Section 3). Therefore, 1005 AGNs are excluded from parent sample.
In order to ensure reliable measurement of narrow emission line, we further selected objects that the S/N ratio of the peak of narrow emission lines (including H βn∼λ4861, H αn∼λ6563 and [N ii] λ6584) greater than 10, and found only 616 AGNs satisfy with this criteria.
We excluded those objects with apparent absorption lines which indicates significant contamination from host galaxies. Finally, we selected 554 AGNs.
To check whether the selected sample bias from the parent sample in AGN properties, we plotted the cumulative distribution function of the primary AGN parameters (calculated from the best-fitting results, see Section 3) for selected 554 AGNs and total sample in Fig. 1. Then we employed Kolmogorov−Smirnov (KS) test to quantify the differences, the results are quoted in Fig. 1. The test shows that the distribution of selected 554 AGNs are almost same with parent sample (except for redshift).
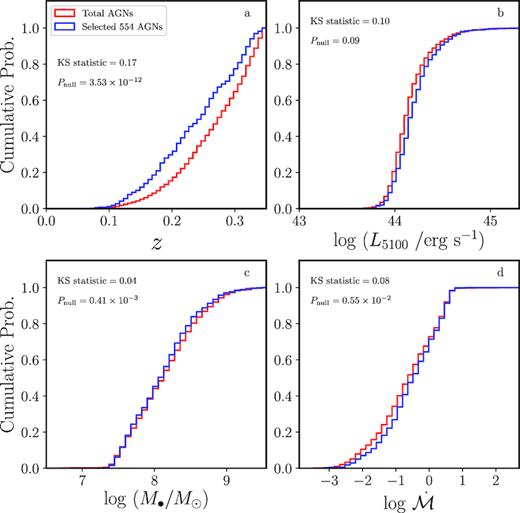
Two-sample KS test. The cumulative distribution function in red and blue correspond to the total sample and selected sample (see Section 2). KS statistics and null hypothesis are quoted in each panel.
3 SPECTRAL FITTING AND MEASUREMENTS
Spectral fitting scheme is widely used in the optical spectra study of AGNs (e.g. Dong et al. 2008, 2011; Hu et al. 2008; Wang et al. 2009; Shen et al. 2011; Stern & Laor 2013; Lu et al. 2016b). Meanwhile, the disadvantage of spectral decomposition is also emphasized in many works (Dong et al. 2008; Stern & Laor 2013). Briefly, the limitations and complexities of spectral decomposition attributes to the facts that there are essentially no emission-line free regions where the continuum can be determined well; Fe ii emission lines and narrow corona lines are blended with broad lines; AGN continuum cannot be described by a single power law from red to blue side of spectrum, which means that we have to determine the local continuum for the H α and H β regions separately (also see Dong et al. 2008). Therefore, we simultaneously fit the spectrum with multiple components, which include the continuum, the Fe ii multiplets and several emission lines, giving emphasis on proper determination of the local pseudo-continua. This fitting scheme is similar to the process adopted by Dong et al. (2008). In brief, main process of spectral fitting is described as follows.
We corrected Galactic extinction and redshift for each SDSS spectrum, then we fit spectrum in rest-frame wavelength range of 4200–7500 Å using a broken power law with a break wavelength at 5600 Å. The optical Fe ii emission lines are modelled by two separate sets of templates constructed by Dong et al. (2008, 2011) based on the measurements of I Zw 1 by Véron-Cetty, Joly & Véron (2004), one for broad Fe ii line system and the other for narrow Fe ii line system. We modelled emission lines from H γ to [S ii] λ67312 as follows. Broad hydrogen Balmer lines (H αb, H βb, H γb) are modelled with 2–4 Gaussians. The broad He ii λ4686 line is modelled with one Gaussian. [O iii] λ4363 and the λλ4959, 5007 doublet are assumed to have the same redshifts and profiles, and each is modelled with 1–2 Gaussians. Other corona lines are modelled with one Gaussian. Narrow Balmer lines (H αn, H βn, H γn), [N ii] and [S ii] doublets are assumed to have the same redshift and profile. The flux ratio of the [O iii] doublet λ5007/λ4959 and [N ii] doublet λ6583/λ6548 are fixed to the theoretical value of 2.96 (more details refer to Dong et al. 2008). In Fig. 2, we also overplotted the fitted results, as shown by the orange line in each panel.
![Representative examples of multicomponent fitting of the SDSS spectra. In each panel, we plot the the SDSS spectra corrected for Galactic extinction and redshift (blue). The sum of the best-fitting components is displayed in orange. The continuum, which is modelled as a broken power law with a break at 5600 Å, plus the broad Balmer lines, are shown in purple. Where the broad Balmer lines are fitted with 2, 3, and 4 Gaussian functions from top, middle to bottom panel, respectively. Narrow Balmer lines (H βn∼λ4861 and H αn∼λ6563) are plotted in red. The [O iii] doublet λ5007/λ4959 and [N ii] doublet λ6583/λ6548 are plotted in green.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/483/2/10.1093_mnras_sty3229/1/m_sty3229fig2.jpeg?Expires=1749876328&Signature=BGdMr1M6p7PUawQOM5ibvpdfqHhFivPLDMKbGOwYPEAebxtyQXBtbarn52Sd6FIC1aNef4oavojQ-Vsu5O6RIfx2vqG7C83fckYm7z0TkvGasQ7Nj9v1oRnppPhXr3V3uoF8gXYgjFMJ5DMgHbSnZpc6u9wQ4bcLscaQYICI9UlmKfZKa7SssGOwmWLKU3frCzmF8~rg8aBukzQ5TpH~61Y5SRa7a2u44mL659ME6SG8YQG7eVtoU1N~9xZE-OPdDIyssyVWS90w-LK4ae1XFg8rfxS5TNIDKaSc95KtdEPKFqt4sWb6mVqfclwZn0Eq6JYz9VJNs-U9HqHExfp0iQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Representative examples of multicomponent fitting of the SDSS spectra. In each panel, we plot the the SDSS spectra corrected for Galactic extinction and redshift (blue). The sum of the best-fitting components is displayed in orange. The continuum, which is modelled as a broken power law with a break at 5600 Å, plus the broad Balmer lines, are shown in purple. Where the broad Balmer lines are fitted with 2, 3, and 4 Gaussian functions from top, middle to bottom panel, respectively. Narrow Balmer lines (H βn∼λ4861 and H αn∼λ6563) are plotted in red. The [O iii] doublet λ5007/λ4959 and [N ii] doublet λ6583/λ6548 are plotted in green.
4 RESULTS
4.1 The distribution of Balmer decrements
Using the Balmer line (H β and H α) fluxes, we calculated the broad-line Balmer decrements of |$\rm H\alpha ^{b}/H\beta ^{b}$| and the narrow-line Balmer decrements of |$\rm H\alpha ^{n}/H\beta ^{n}$| for the 554 AGNs. In Figs 3(a) and (b), we plotted the distributions of |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$| ratios in logarithm form by dividing the samples into 14 bins, respectively. Both distributions can be fitted by a Gaussian function, as shown with the red dashed line in Fig. 3. The best-fitting results give the mean log(|$\rm H\alpha ^{b}/H\beta ^{b}$|) = 0.50 (i.e. |$\rm H\alpha ^{b}/H\beta ^{b}$| = 3.16) with a standard deviation of 0.07 dex, and the mean log(|$\rm H\alpha ^{n}/H\beta ^{n}$|) = 0.64 (i.e. |$\rm H\alpha ^{b}/H\beta ^{b}$| = 4.37), with a standard deviation of 0.10 dex. These average ratios are, respectively, larger than the intrinsic values of |$\rm H\alpha ^{b}/H\beta ^{b}= 2.72$| (refer to Gaskell 2017 for this value) and |$\rm H\alpha ^{n}/H\beta ^{n}= 3.1$| (Gaskell 1982, 1984; Wysota & Gaskell 1988). The average ratios of |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$| strongly show that the narrow-line Balmer decrements are much larger than broad-line systematically. This suggests that the level of reddening in the NLR is higher than the BLR if we accept that the observed Balmer decrements depend on the reddening.
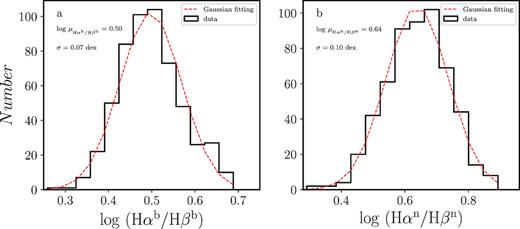
The distributions of broad- and narrow-line Balmer decrements, respectively. Panel (a) shows the histogram of |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio in base-10 logarithm form, and panel (b) is the histogram of |$\rm H\alpha ^{n}/H\beta ^{n}$| ratio. In panels (a, b), we also noted the average value (μ) and standard deviation of distributions.
4.2 Balmer decrements and BPT diagram
The 2D line-intensity ratio calculated from relatively strong lines of [O iii] λ5007, H β∼λ4861, [N ii] λ6584, and H α∼λ6563 (here Balmer emission-line refer only to the narrow component) can be used to probe the nebular conditions of a source (i.e. BPT diagram promoted by Baldwin, Phillips & Terlevich 1981 and modified by Veilleux & Osterbrock 1987). Using Balmer decrements as third parameter, we constructed 2D distributions of BPT−Balmer decrement for 554 AGNs in Figs 4(a) and (b), and investigated the relationship between Balmer decrements and physical condition of nebular. We found that only 35 (6 per cent) of 554 AGNs lie below Ke01 line (Kewley et al. 2001), which means that the ionization of the NLR is dominated by AGNs rather than host galaxy.
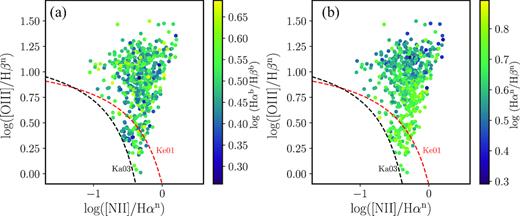
The 2D distributions of BPT−Balmer decrements. Panel (a) is BPT−|$\rm H\alpha ^{b}/H\beta ^{b}$| diagram, panel (b) is BPT−|$\rm H\alpha ^{n}/H\beta ^{n}$| diagram. The Ke01 line is the theoretical predictions of the scenarios from Kewley et al. (2001), and the Ka03 line is defined by Kauffmann et al. (2003).
In Fig. 4(a), we can see that |$\rm H\alpha ^{b}/H\beta ^{b}$| distribute in the BPT diagram randomly, which is confirmed by the correlation analysis (see Table 1). Panel (b) of Fig. 4 shows that most of the AGNs with the largest |$\rm H\alpha ^{n}/H\beta ^{n}$| ratios locate on the bottom of the BPT diagram (the direction of [O iii]/H βn axis), which in fact indicates a correlation between |$\rm H\alpha ^{n}/H\beta ^{n}$| and [O iii]/H βn. This is confirmed by the correlation analysis, with correlation coefficient rs = −0.55, and probability of no correlation Pnull = 1.80 × 10−45. These results indicate that the broad-line Balmer decrements are independent on the physical conditions of the NLR, whereas the narrow-line Balmer decrements are associated with the physical conditions of the NLR. We will further discuss this in the following analysis.
Summary of the Spearman rank correlation coefficient rs and probability of the null hypothesis Pnull.
| Parameter 1 . | Parameter 2 . | rs . | Pnull . |
|---|---|---|---|
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\alpha ^{b}/H\beta ^{b}$| | 0.02 | 0.61 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.60 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | 0.06 | 0.19 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.68 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.24 | 1.26 × 10−8 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.21 | 3.95 × 10−7 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | L5100 | -0.10 | 0.01 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | L5100 | -0.01 | 0.75 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\dot{\mathcal{M}}$| | -0.18 | 2.47 × 10−5 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | 0.24 | 6.16 × 10−9 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | -0.55 | 1.80 × 10−45 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | EW(|$\rm [O\,{\small III}]$|) | -0.59 | 2.04 × 10−52 |
| |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | -0.33 | 3.41 × 10−15 |
| EW(|$\rm [O\,{\small III}]$|) | |$\dot{\mathcal{M}}$| | -0.25 | 2.46 × 10−9 |
| Parameter 1 . | Parameter 2 . | rs . | Pnull . |
|---|---|---|---|
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\alpha ^{b}/H\beta ^{b}$| | 0.02 | 0.61 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.60 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | 0.06 | 0.19 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.68 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.24 | 1.26 × 10−8 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.21 | 3.95 × 10−7 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | L5100 | -0.10 | 0.01 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | L5100 | -0.01 | 0.75 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\dot{\mathcal{M}}$| | -0.18 | 2.47 × 10−5 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | 0.24 | 6.16 × 10−9 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | -0.55 | 1.80 × 10−45 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | EW(|$\rm [O\,{\small III}]$|) | -0.59 | 2.04 × 10−52 |
| |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | -0.33 | 3.41 × 10−15 |
| EW(|$\rm [O\,{\small III}]$|) | |$\dot{\mathcal{M}}$| | -0.25 | 2.46 × 10−9 |
Summary of the Spearman rank correlation coefficient rs and probability of the null hypothesis Pnull.
| Parameter 1 . | Parameter 2 . | rs . | Pnull . |
|---|---|---|---|
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\alpha ^{b}/H\beta ^{b}$| | 0.02 | 0.61 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.60 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | 0.06 | 0.19 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.68 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.24 | 1.26 × 10−8 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.21 | 3.95 × 10−7 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | L5100 | -0.10 | 0.01 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | L5100 | -0.01 | 0.75 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\dot{\mathcal{M}}$| | -0.18 | 2.47 × 10−5 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | 0.24 | 6.16 × 10−9 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | -0.55 | 1.80 × 10−45 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | EW(|$\rm [O\,{\small III}]$|) | -0.59 | 2.04 × 10−52 |
| |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | -0.33 | 3.41 × 10−15 |
| EW(|$\rm [O\,{\small III}]$|) | |$\dot{\mathcal{M}}$| | -0.25 | 2.46 × 10−9 |
| Parameter 1 . | Parameter 2 . | rs . | Pnull . |
|---|---|---|---|
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\alpha ^{b}/H\beta ^{b}$| | 0.02 | 0.61 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.60 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | 0.06 | 0.19 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [N\,{\small II}]~\lambda 6584\rm /H\alpha ^{n}$| | 0.02 | 0.68 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.24 | 1.26 × 10−8 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm H\beta ^{n}/\rm H\beta ^{b}$| | 0.21 | 3.95 × 10−7 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | L5100 | -0.10 | 0.01 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | L5100 | -0.01 | 0.75 |
| |$\rm H\alpha ^{b}/H\beta ^{b}$| | |$\dot{\mathcal{M}}$| | -0.18 | 2.47 × 10−5 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | 0.24 | 6.16 × 10−9 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | -0.55 | 1.80 × 10−45 |
| |$\rm H\alpha ^{n}/H\beta ^{n}$| | EW(|$\rm [O\,{\small III}]$|) | -0.59 | 2.04 × 10−52 |
| |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| | |$\dot{\mathcal{M}}$| | -0.33 | 3.41 × 10−15 |
| EW(|$\rm [O\,{\small III}]$|) | |$\dot{\mathcal{M}}$| | -0.25 | 2.46 × 10−9 |
4.3 Relationship of |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$|
In this section, we attempt to investigate the relationship between |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$| for our sample, as shown in Fig. 5. The Spearman rank correlation coefficient rs and probability of the null hypothesis Pnull (listed in Table 1) are 0.02 and 0.61, respectively, indicating that |$\rm H\alpha ^{n}/H\beta ^{n}$| does not correlate with |$\rm H\alpha ^{b}/H\beta ^{b}$|, which is consistent with the find of de Zotti & Gaskell (1985). The dust causing the common reddening of both the BLR and NLR could be associated with the dust of host galaxy (de Zotti & Gaskell 1985; Baron et al. 2016), because host galaxy is extremely extended. However, if reddening of the BLR and NLR is caused fully by the same dust in the line of sight, the broad-line Balmer decrements should be significantly correlated with the narrow-line Balmer decrements, vice versa. We found that the averaged |$\rm H\alpha ^{b}/H\beta ^{b}$| is smaller than the averaged |$\rm H\alpha ^{n}/H\beta ^{n}$| (Section 4.1), and they are independent on each other. These indicate that the NLR could be covered by more dust in the light of sight, and the dust causing the reddening of the BLR and NLR may be different. Many cases can account for this result. For example, in the frame of AGN unified model (Antonucci 1993), it is possible that the partial dusty torus of AGNs cause the reddening of the BLR, and the dust amount obscuring the BLR in the line of sight depend on the inclination angle of AGNs. But the NLR may be free from the dust torus since the NLR gas lies under the gravitational influence of host galaxy (e.g. Ho 2009). However, as suggested by Mor, Netzer & Elitzur (2009), Stern, Laor & Baskin (2014), Baron et al. (2016), and Ramos Almeida & Ricci (2017), the NLR is dusty clouds, which may cause the reddening of the NLR in observation. Certainly, it is also possible that both the BLR and NLR may be reddened by the dust in the host galaxy, and thus the total dust amount sustained by the BLR and NLR are dependent on their sizes and the observing angle.
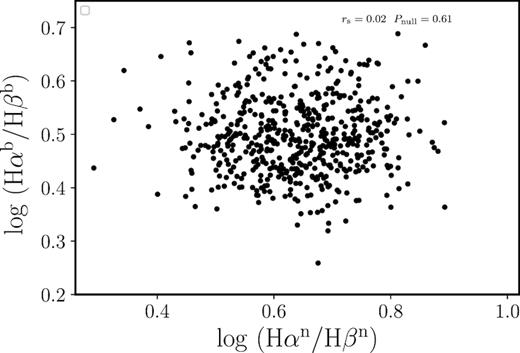
The relationship between |$\rm H\alpha ^{b}/H\beta ^{b}$| and |$\rm H\alpha ^{n}/H\beta ^{n}$|. rs and Pnull are the Spearman rank correlation coefficient and probability of the null hypothesis, respectively.
4.4 Balmer decrements and Seyfert sub-type
In order to investigate the relation between Balmer decrements and Seyfert sub-type. We chose the most physical scheme used by Osterbrock (1977), which subdivides the AGN population into Seyfert 1.0, 1.2, and 1.5 according to the prominence of the broad compared to the narrow component of H β (i.e H βn/H βb ratio). That is, in the frame of AGN unified model (Antonucci 1993), the higher H βn/H βb ratio means the AGN with larger inclination angle to the telescope. However, Stern & Laor (2012b) found that the NLR to BLR luminosity ratio (H αn/H αb) decreases with increasing H αb luminosity (|$L_{\rm H\alpha ^{b}}$|), and suggested that the drop of H αn/H αb with |$L_{\rm H\alpha ^{b}}$| is most likely due to the decrease in covering factor of the NLR with AGN luminosity (also see Ludwig et al. 2009). Therefore, in the next, we test the relationship between Balmer decrements and H βn/H βb by removing the influence of H βb luminosity (|$L_{\rm H\beta ^{\rm b}}$|) using the partial correlation analysis (Kendall & Stuart 1979; Lu et al. 2016b).
Figs 6(a) and (b) shows the broad- and narrow-line Balmer decrement as a function of H βn/H βb ratio. We employed correlation analysis to investigate the dependency of broad- and narrow-line Balmer decrement on H βn/H βb ratio. The Spearman rank correlation coefficient rs and probability of the null hypothesis Pnull are quoted in panels (a, b) and also listed in Tabel 1. The result shows that the broad-line Balmer decrements weakly correlate with H βn/H βb ratio (rs = 0.24, Pnull = 1.26 × 10−8), and the narrow-line Balmer decrements weakly correlate with H βn/Hβb ratio (rs = 0.21, Pnull = 3.95 × 10−7). Meanwhile, we found that H βn/H βb ratio decreases with increasing |$L_{\rm H\beta ^{b}}$| in our sample (rs = −0.63, Pnull = 8.68 × 10−63), which is consistent with previous result (see fig. 3 of Stern & Laor 2012b, who adopt H αn/H αb ratio and |$L_{\rm H\alpha ^{\rm b}}$|). Therefore, we further employed partial correlation analysis to investigate whether these correlations are affected by |$L_{\rm H\beta ^{\rm b}}$|. The partial correlation coefficients show that |$\rm H\alpha ^{b}/H\beta ^{b}$| still weakly correlates with H βn/H βb ratio (rxy, z = 0.22, Pnull = 4.13 × 10−8, where x ≡ H βn/H βb, |$y \equiv \rm H\alpha ^{b}/H\beta ^{b}$| and |$z \equiv L_{\rm H\beta ^{\rm b}}$|), whereas there is no correlation between |$\rm H\alpha ^{n}/H\beta ^{n}$| and H βn/H βb (rxy, z = 0.05, Pnull = 0.07, where |$y \equiv \rm H\alpha ^{n}/H\beta ^{n}$|). The former trend is supported by the fact that the |$\rm H\alpha ^{b}/H\beta ^{b}$| of Seyfert 1.8–1.9s is above 10 and might be as high as 20 (Osterbrock 1981; Crenshaw, Peterson & Wagner 1988; Osterbrock & Ferland 2006). The lack of correlation between |$\rm H\alpha ^{n}/H\beta ^{n}$| and H βn/H βb indicates that the inclination has little effect on the reddening of NLR emission lines, which might suggest that the reddening of NLR seems to be mainly caused by the dust embedded in the NLR clouds.
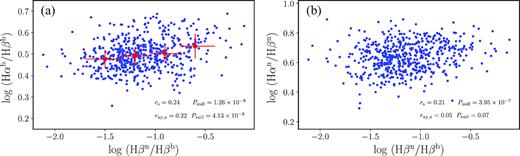
The relationship between Balmer decrement (|$\rm H\alpha ^{n}/H\beta ^{n}$| and |$\rm H\alpha ^{b}/H\beta ^{b}$|) and H βn/H βb. The results of correlation analysis are quoted in panels. Splitting H βn/H βb ratios in logarithm into four bins, and estimating the median value of |$\rm H\alpha ^{b}/H\beta ^{b}$| in each bin, we plotted the results (red dots) in panel (a). Whereas partial correlation analysis shows that there is no correlation between |$\rm H\alpha ^{n}/H\beta ^{n}$| and H βn/H βb, we did not bin them in panel (b).
4.5 Balmer decrements and optical luminosity
To check the dependency of Balmer decrements on optical luminosity, we employed the Spearman rank correlation analysis. The Spearman rank correlation coefficient of rs and probability of the null hypothesis of Pnull are also given in Table 1. The test shows that broad-line Balmer decrements do not correlate with optical luminosity, which is consistent with the result of Dong et al. (2008). This suggests that dust covering factor in the BLR remains a constant with optical luminosity increasing. This case is opposite with receding torus models suggested that obscured fraction in the line of sight decreases with optical luminosity increasing (Lawrence 1991). However, recent studies Based on sophisticated dusty torus model suggested that the dust covering factor weakly depends on AGN luminosity (Stalevski et al. 2016). Meanwhile, we found that the narrow-line Balmer decrement is also independent on optical luminosity of AGNs.
Infrared (IR) time-lag observations show that the inner dust torus radius scales with the AGN luminosity as r ∝ L1/2 (‘size–luminosity' relation; Suganuma et al. 2006), as well as from theoretical calculation (Barvainis 1987) and near-IR (NIR) interferometric observations (Kishimoto et al. 2011). However, based on mid-IR (MIR) observational study of 23 AGNs, Burtscher et al. (2013) suggest that a common ‘size–luminosity' relation does not exist for AGN torus due to the fact that the torus sizes of these fainter sources are smaller than that expected from r ∝ L1/2 relation and show a large scatter, and two torus model components are needed to explain the observed results. The polar component was detected directly in NGC 1068 using high-angular-resoluiton MIR observations (Mason et al. 2006). Recently, the studies of MIR observation for ∼20 AGNs indicate that the bulk of the MIR emission comes from a diffuse polar component (Asmus, Hönig & Gandhi 2016). These results show that the nature of the nuclear environment of accreting systems is extremely complex. Our result suggests that the dust in the line of sight causing the reddening of the BLR and NLR do not be impacted by radiation pressure (i.e. optical luminosity) of accretion disc. This may caused by the fact that the intrinsic differences in their dust structures. It is also possible that the dust near the central region is destroyed (MacAlpine 1985; Osterbrock & Ferland 2006), and the dust causing the reddening of AGNs survives at the radius far from the central region of AGNs, which attenuates the role of AGN optical luminosity on Balmer decrements.
4.6 Balmer decrements and accretion rate
Ricci et al. (2017) found that the covering factor of dusty torus drops dramatically with increasing L/LEdd. This could be a natural result that a part of dusty torus supply gas for accretion flow, and a part of dusty torus in high latitude may drop to the low latitude of accretion disc. In this case, AGN reddening (especially, for the region within the dusty torus) will be weakened with increasing accretion rate if the BLR (and accretion disk) are obscured by dusty torus. Therefore, broad-line Balmer decrement decreases as accretion rate increases. This expectation is supported by the test shown in Fig. 7(a), where we plot Balmer decrements as a function of accretion rate, to some degree. The Spearman rank correlation analysis shows that broad-line Balmer decrements weakly correlate with accretion rate (see Table 1 and Fig. 7a).
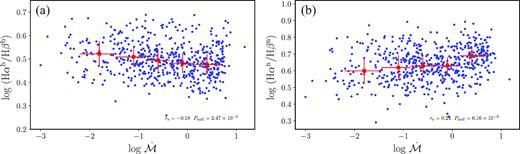
Same as Fig. 6, but for the relationship between Balmer decrement (|$\rm H\alpha ^{n}/H\beta ^{n}$| and |$\rm H\alpha ^{b}/H\beta ^{b}$|) and accretion rate |$\dot{\mathcal{M}}$|.
Meanwhile, we found an interested results that the narrow-line Balmer decrement increases with increasing accretion rate (see Fig. 7b). Recall that the narrow-line Balmer decrements correlate with physical conditions of the NLR (Section 4.2), it is possible that the physical conditions in the NLR are driven/modulated by accretion rate. We will further investigate this issue in the next section.
4.7 Narrow-line Balmer decrements and NLR physics
We have found that narrow-line Balmer decrements are independent on the inclination of AGNs (Section 4.4), but depend on the accretion rate (Section 4.6) and physical conditions of the NLR (Section 4.2). Using photoionization code CLOUDY, Baskin & Laor (2005) calculated emission-line flux ratio of |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$|, and found that |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| depends on the electron density and ionization parameter of the NLR gas. Based on Palomar–Green quasar sample, Baskin & Laor (2005) found that the strength of |$\rm [O\,{\small III}]~\lambda$|5007 is modulated by the covering factor, electron density, and ionization parameter of the NLR gas (fig. 5 of Baskin & Laor 2005). Therefore, we use |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| and EW(|$\rm [O\,{\small III}]$|) represent the physical conditions of the NLR to investigate the properties of narrow-line Balmer decrements in this section.
Fig. 8(a) displays |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}-\rm H\alpha ^{n}/H\beta ^{n}$| relationship. The result of correlation analysis (noted in panel and listed in Table 1) shows that |$\rm H\alpha ^{n}/H\beta ^{n}$| inversely correlates with |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$|. Fig. 8(b) displays |$\dot{\mathcal{M}}-\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| relationship, which shows that |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| inversely correlates with accretion rate. This result indicates that narrow-line Balmer decrement increases with decreasing |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$|, which could be attribute to the electron density increases and ionization parameter decreases of the NLR gas as accretion rate increases. In addition, we can see from Fig. 8(b) that the observed |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| ratio trends to have a maximum value ∼10. This observed ratio is consistent with the expectation of photoionization model, which give out the maximum |$\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}$| ratio ∼10 (the top panel of fig. 2 in Baskin & Laor 2005).
![Same as Fig. 6, but for $\rm H\alpha ^{n}/H\beta ^{n}-\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}-\dot{\mathcal{M}}$ relationships.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/483/2/10.1093_mnras_sty3229/1/m_sty3229fig8.jpeg?Expires=1749876328&Signature=e4hH7XY9wPx3uFBAoIYzZ6QUX3bVgrMp3Ov2F~358Cy83rXYb5xpOj5eAcqw2Sfj616x1b8CumclivN5lZBWYL78gsnSoaway1pQ0sE2NgvDpfMnisLdn9zrjMTSmdir82C60rzt7g5FmCaPW1-u6-P8Tt2OS-ZXYvPuZiSUpFMjPI03z7FiZ6blel~cQHXYCkEwxs8ylwOGNhKfq-3B5d5uaoTw7i~KCnP-Z~iZl-Tmlotk5fybYrxrJfDr417GuXBHKIt6JA~eqvKQy2C0ONnh5W7A7drPdJB6RkygZcHdMCeFW4ydJg-ODCzoJXhFMSE0-h~VA1Jpr4mpZDMphw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Same as Fig. 6, but for |$\rm H\alpha ^{n}/H\beta ^{n}-\rm [O\,{\small III}]~\lambda 5007/\rm H\beta ^{n}-\dot{\mathcal{M}}$| relationships.
Similarly, Figs 9(a) and (b) display |$\rm EW([O\,{\small III}])-\rm H\alpha ^{n}/H\beta ^{n}$| and |$\dot{\mathcal{M}}-\rm EW([O\,{\small III}])$| relationship, respectively. The results of correlation analysis show that |$\rm EW([O\,{\small III}])$| inversely correlates with |$\rm H\alpha ^{n}/H\beta ^{n}$|, and |$\dot{\mathcal{M}}$| inversely correlates with |$\rm EW([O\,{\small III}])$|. When the accretion rate increases, AGN outflows or winds might increase. However, there are no theoretical calculations or observations that support outflows or winds can reach to the NLR (Netzer 2006; Hickox & Alexander 2018). That is the covering factor of the NLR might not increase with accretion rate. Therefore, the inverse correlation between |$\rm EW([O\,{\small III}])$| and accretion rate might indicates that the electron density increases and/or ionization parameter decreases as accretion rate increases.
![Same as Fig. 6, but for $\rm H\alpha ^{n}/H\beta ^{n}-\rm EW([O\,{\small III}])-\dot{\mathcal{M}}$ relationships.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/483/2/10.1093_mnras_sty3229/1/m_sty3229fig9.jpeg?Expires=1749876328&Signature=ZR2~qxguJOrcMWSXAP~GHw9f6EmwGBNHvD7USoQf9on8LxJNnw5xwp0otEMDCHXXIW4Z3EF5QJlKZGejmw82hb9A9JasWf9kjmqrcnB92VBnaxjnc9XXCAK6o~u54w7ng6JhyMNUYOUEMEL5C58wHdaohjfe8MpnY~LeluqAflXIAYGo3PlLLb045I4C04Xyw97u9NxLNbYQaPQb6jQGlaQ9Hs8Ll5Y6hyNaocTDmNhdtUwIAqHNmUYZBF33pOV33U6njGL92tEr8K2oZLEnU2PzdIAqylZEkp3FKplKfqV6aomzIzauKBRfIsnl1vw-RC~0393Nrwahu-gD0dh31w__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Same as Fig. 6, but for |$\rm H\alpha ^{n}/H\beta ^{n}-\rm EW([O\,{\small III}])-\dot{\mathcal{M}}$| relationships.
5 DISCUSSION
5.1 Comparison with previous work
Previous results from different AGN samples give different |$\rm H\alpha ^{b}/H\beta ^{b}$|. For example, La Mura et al. (2007) derived |$\rm H\alpha ^{b}/H\beta ^{b}= 3.45\pm 0.65$| based on 90 Seyfert 1 galaxies from SDSS. Zhou et al. (2006) measured |$\rm H\alpha ^{b}/H\beta ^{b}$| ratios for 2000 narrow-line Seyfert 1 galaxies (NLS1s) and obtained the average |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio is 3.028 with a dispersion of 0.36 (refer to Fig. 6 of Zhou et al. 2006). Dong et al. (2008) selected 446 low-redshift (z ≤ 0.35) AGNs in which the spectral slopes vary in the range from 1.5 to 2.7, the |$\rm H\alpha ^{b}/H\beta ^{b}$| ratios range from 2.3 to 4.2 and the distribution of the |$\rm H\alpha ^{b}/H\beta ^{b}$| ratios can be well described by log-Gaussian (fig. 3 of Dong et al. 2008), with a mean |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio of 3.06. Gaskell (2017) selected an extremely blue AGN sample with αν > +0.2 (where |$f_{\nu }\varpropto \nu ^{\alpha _{\nu }}$|, αν is measured from λ4030 Å to λ5600 Å), these bluest AGNs have a significantly flatter Balmer decrement (see fig. 1 of Gaskell 2017), which give the geometric mean |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio is 2.86 ± 0.06. For our sample, the |$\rm H\alpha ^{b}/H\beta ^{b}$| ratios can be described by a Gaussian function with a peak value 3.16 and standard deviation 0.07 dex. Dong et al. (2008) shown that the Balmer decrement is a good indicator of internal reddening in AGNs. Gaskell (2017) gave a conclusion that the bluest 10 per cent of SDSS AGNs have significant reddening, and suggested that the un-reddening Balmer decrement of the BLR is the Case B value of |$\rm H\alpha ^{b}/H\beta ^{b}\approx 2.72$|. On the whole, the results obtained from early small samples and our sample point to the mean |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio of the BLR is larger than the Baker–Menzel Case B value, suggesting that the observed BLR is reddened by the dust in the line of sight. In addition, the recombination theory gives the narrow-line Balmer decrement of |$\rm H\alpha ^{n}/H\beta ^{n}\approx 2.85$|, the best overall average value of 3.1 is adopt for the intrinsic |$\rm H\alpha ^{n}/H\beta ^{n}$| ratio of the NLR by taking into account the collisional excitation in the partly ionized transition region (Osterbrock & Ferland 2006). For our sample, the |$\rm H\alpha ^{n}/H\beta ^{n}$| ratios of the NLR also can be described by a Gaussian function with a peak value of 4.37 and standard deviation 0.10 dex, which is significantly larger than the typical value of 3.1. Combining with the suggestion that the narrow-line Balmer decrements do give a reliable indication of reddening (Gaskell 1982), we concluse that the NLR is also reddened by the dust in the line of sight.
On the other hand, Heard & Gaskell (2016) studied a compiled sample, which is composed of Dong et al. (2008) blue AGNs, Dong et al. (2005) partially obscured AGNs, very high S/N AGNs observed by Osterbrock (1977) and Cohen (1983) in Lick observatory, and found that the average broad-line Balmer decrement is larger than the average narrow-line Balmer decrement. However, this is opposite to the result obtained from 109 nearby Seyfert galaxies by de Zotti & Gaskell (1985). For our selected AGN sample, the average |$\rm H\alpha ^{n}/H\beta ^{n}$| ratio is also larger than the |$\rm H\alpha ^{b}/H\beta ^{b}$| ratio, this is consistent with result of de Zotti & Gaskell (1985) and Baron et al. (2016).3
5.2 Spatial distribution of dust
In Section 4, we investigated the physical properties of broad- and narrow-line Balmer decrements systematically, and discovered many differences between the broad- and narrow-line Balmer decrements. If we accept that the steeper Balmer decrement primarily depends on internal reddening of AGNs, our results are an important clue to investigate the space distribution of dust causing internal reddening of AGNs.
A probable case is that the dust causing the reddening of observed AGNs survive in the radius far from the centre of AGNs resulting from the broad-line Balmer decrements are a constant with optical luminosity (equivalently radiation pressure). As suggested by Ramos Almeida & Ricci (2017), these dust may include equatorial/toroidal structure (torus) and polar component. For the BLR, it is possible that partial dust torus may cause the reddening of the BLR, and covering fractions of dusty torus in the line of sight depend on the inclination angle and accretion rate of AGNs, which is supported by the fact that the broad-line Balmer decrement correlates with H βn/H βb ratio and accretion rate (see Figs 6a and 7a) and by the unified model of AGNs. But complicated structure of the dusty torus, such as clumpy geometry and broad range of covering factors, and the existence of pole dust (Ramos Almeida & Ricci 2017), where covering factors of torus marginally depend on the accretion rate, could be attenuate the correlation between broad-line Balmer decrements and H βn/H βb ratio. For the NLR, there is no significant correlation between the broad- and narrow-line Balmer decrement, and averaged broad-line Balmer decrement is lower than the narrow line, suggesting that there are more and different dust reddening the NLR compared to the BLR. Interestingly, we found that narrow-line Balmer decrements correlate with physical conditions of the NLR and accretion rate. It is possible that many dust indwell in the NLR and redden the NLR (e.g. Mor et al. 2009; Stern et al. 2014; Baron et al. 2016; Ramos Almeida & Ricci 2017).
It should be noted, de Zotti & Gaskell (1985) argued that the reddening in the BLR arises in the plane of the galaxies. This argument is based on interpreting the Balmer decrement of the BLR slightly correlates with axial ratio, but the significant level of this correlation is very low. To interprete NaI D as interstellar absorption line in the host galaxies, and the correlation of equivalent width of NaI D with optical continuum slope (αopt), Baron et al. (2016) suggested that the dusty gas causing the AGN reddening is the interstellar medium (ISM) of the host galaxy. As Gaskell (2017) concerned, it is possible that the variation in equivalent widths of NaI D is due to varying amounts of host-galaxy starlight.
6 CONCLUSION
In this paper, we selected an AGN sample and investigated many physical properties of broad- and narrow-line Balmer decrement. Our main results are:
The distributions of the broad- and narrow-line Balmer decrements in our sample can be described by a Gaussian function, and the average broad- and narrow-line Balmer decrements are 3.16 and 4.37, respectively. The narrow-line Balmer decrements are systematically larger than the broad-line decrements, which is contrary in part to previous results. Using Balmer decrements as indicator of internal reddening of AGNs, we can conclude that the dust causing the reddening in the NLR is larger than the BLR.
The broad- and narrow-line Balmer decrements are independent and dependent on the physical conditions of the NLR, respectively. The broad-line Balmer decrements do not correlate with narrow-line Balmer decrements (e.g. de Zotti & Gaskell 1985; Heard & Gaskell 2016).
Using H βn/H βb ratio (Seyfert sub-type) as the proxy of inclination angle, We found that the broad-line Balmer decrements weakly correlate with the inclination of AGNs, while narrow-line Balmer decrements are independent on the inclination. We also found that broad- and narrow-line Balmer decrements are independent on AGN optical luminosity in our samples, which is consistent with the results of Dong et al. (2008).
The Balmer decrements of the BLR (NLR) inversely (positively) correlate with accretion rates, which probably indicates that the reddening of the BLR and NLR may be modulated by accretion rate.
ACKNOWLEDGEMENTS
We are grateful to the referee for constructive suggestions that significantly improved the manuscript. We acknowledge the support of the staff of the Lijiang 2.4m telescope. Funding for the telescope has been provided by CAS and the People’s Government of Yunnan Province. YZ is supported by the National Key Research and Development Program of China (no. 2017YFA0402704). KXL is supported by the Light of West China Program provided by CAS (no. Y7XB016001), and the National Natural Science Foundation of China (grant no. 11703077).
Footnotes
The superscript b and n in the text stand for the broad emission-line and narrow emission-line, respectively.
Some emission-line regions in the fitting window are masked out, because they have no effect on the results. They includes [Cl iii] λ5538, He i λ5876, and [Ar iii] λ7136. Some emission lines are not added to the fitting model, because either they are too weak to constrain in the fit or they have little effect on the results. They includes He i λ4471, [Fe vii] λ5158 and the λλ5721, 6086, [N i] λ5200, [Ca v] λ5310, He i λ7066, and [O ii] λ7320.



