-
PDF
- Split View
-
Views
-
Cite
Cite
L Petrov, Y Y Kovalev, A V Plavin, A quantitative analysis of systematic differences in the positions and proper motions of Gaia DR2 with respect to VLBI, Monthly Notices of the Royal Astronomical Society, Volume 482, Issue 3, January 2019, Pages 3023–3031, https://doi.org/10.1093/mnras/sty2807
Close - Share Icon Share
ABSTRACT
We have analysed the differences in positions of 9081 matched sources between the Gaia Data Release 2 (DR2) and very long baseline interferometry (VLBI) catalogues. The median position uncertainty of matched sources in the VLBI catalogue is a factor of two larger than the median position uncertainty in Gaia DR2. There are 9 per cent matched sources with statistically significant offsets between both catalogues. We found that the reported positional errors should be rescaled by a factor of 1.3 for VLBI and 1.06 for Gaia and, in addition, the Gaia errors should be multiplied by the square root of chi squared per degree of freedom in order to best fit the normalized position differences to the Rayleigh distribution. We have established that the major contributor to statistically significant position offsets is the presence of optical jets. Among the sources for which the jet direction was determined, the position offsets are parallel to the jet directions for 62 per cent of the outliers. Among the matched sources with significant proper motion, the fraction of objects with proper motion directions parallel to jets is a factor of three greater than on average. Such sources have systematically higher chi squared per degree of freedom. We explain these proper motions as a manifestation of the source position jitter caused by flares, which we predicted earlier. Therefore, the assumption that quasars are fixed points, and thus that differential proper motions determined with respect to quasar photocentres can be regarded as absolute proper motions, should be treated with great caution.
1 INTRODUCTION
Since the 1980s very long baseline interferometry (VLBI) has been the most accurate absolute astrometry technique. The accuracy of VLBI absolute positions can reach the 0.1 mas level. With few exceptions, VLBI is able to provide absolute positions of only active galactic nuclei (AGNs). In 2016, the Gaia Data Release 1 (DR1) (Lindegren et al. 2016) led to the emergence of a technique that rivals VLBI in accuracy. A quick analysis by Mignard et al. (2016) found that, in general, the differences between common AGNs in the VLBI and Gaia DR1 catalogues are close to their uncertainties, except for 6 per cent of common objects. Mignard et al. (2016) claim that ‘individual examination of a number of these cases shows that a likely explanation for the offset can often be found, for example in the form of a bright host galaxy or nearby star’. They conclude (p. 13) that ‘the overall agreement between the optical and radio positions is excellent’. We see it differently. If two independent observing campaigns produced small (negligible) differences, that also implies that the contribution of a new campaign is also small (negligible) with respect to what has been known before. Science does not emerge from agreements. It emerges from disagreements. Therefore, we focused our analysis on the differences between the VLBI and Gaia AGN positions.
Our analysis of Gaia DR1 confirmed the existence of a population of sources with statistically significant VLBI/Gaia offsets (Petrov & Kovalev 2017a). We found that such factors as failures in quality control in both VLBI and Gaia, blended nearby stars, or bright host galaxies can account for at maximum 1/3 of that population. This analysis, as well as recent work by others (Mignard et al. 2016; Makarov et al. 2017; Frouard et al. 2018; Liu, Zhu & Liu 2018a; Liu, Malkin & Zhu 2018b; Liu, Zhu & Liu 2018c), used arc lengths of VLBI/Gaia differences. Including the second dimension, the position angle of the VLBI/Gaia offsets, resulted in a breakthrough. Though the distribution of the position angles counted from the declination axis turned out to be close to uniform, the distribution of the position angles with respect to the jet direction determined from analysis of VLBI images of matched sources revealed a strong anisotropy (Kovalev, Petrov & Plavin 2017): the offsets have a preferable direction along the jet, and to a lesser extent in the direction opposite to the jet. We interpret this as a manifestation of the presence of optical jets at scales finer than the Gaia point spread function (PSF), i.e. 100–300 mas. Known optical jets in AGNs resolved with the Hubble Space Telescope are cospatial (Gabuzda et al. 2006; Perlman et al. 2010; Meyer et al. 2018). Even in that case there will be position differences. It was emphasized in Petrov & Kovalev (2017b) that the response to an extended structure of a power detector used by Gaia and an interferometer that records voltage is fundamentally different. The Gaia positions correspond to the location of the optical centroid, while the VLBI positions are associated with the most compact and bright feature at the jet base. Therefore, the physical meaning of a VLBI/Gaia offset is a displacement of the optical centroid with respect to the jet base.
In 2018 April, Gaia DR2 was published (Lindegren et al. 2018). It has 48 per cent more sources than Gaia DR1 and a significantly higher accuracy. Mignard et al. (2018) reported that, in general, the VLBI/Gaia DR2 differences are small with some exceptions. They set out five reasons for the discrepancies (p. 10): (1) real offsets between the centres of emission at optical and radio wavelengths; (2) errors in matching VLBI and Gaia objects; (3) an extended galaxy around the quasar; (4) double or lensed quasars; or (5) simply statistical outliers. The presence of optical jets was not put in the list as a likely explanation.
In Petrov & Kovalev (2017b) we examined the consequences of our interpretation of the VLBI/Gaia offsets due to the presence of optical jets. Among others, we made two predictions: (1) ‘further improvement in the position accuracy of VLBI and Gaia will not result in a reconciliation of radio and optical positions, but will result in improvement of the accuracy of determination of these position differences’; and (2) ‘we predict a jitter in the Gaia centroid position estimates for radio-loud AGNs’. Since the Gaia DR2 accuracy is noticeably better than the Gaia DR1 accuracy, this motivated us to extend our previous analysis to Gaia DR2 and check whether these predictions came true. The goal of this article is to answer the question of what the most significant contributor is to systematic position differences.
2 COMPARISON OF VLBI/|$\textit{Gaia}$| POSITIONS
We matched the Gaia DR2 catalogue of 1692 919 135 objects against the Radio Fundamental Catalogue rfc_2018b (RFC, Petrov and Kovalev in preparation)1 of 15 155 sources. The RFC catalogue is derived using all VLBI observations under astrometric programs publicly available by 2018 August 1. We used the same procedure of matching Gaia objects against the VLBI catalogue described in detail in Petrov & Kovalev (2017a) and got 9081 matches with the probability of false association below the 2 x 10−4 level. The immediate comparison of formal uncertainties among matches showed that the Gaia uncertainties are smaller (see Fig. 1). The median of the VLBI semi-major axes of error ellipses is 0.74 mas against 0.34 mas for Gaia. Although VLBI can reach accuracies of 0.1 mas in absolute positions of strong sources, the majority of the sources were observed only once for 60 s, which is insufficient to derive their positions with that level of accuracy. The Gaia uncertainties of matches are roughly twice as small as the VLBI uncertainties, though this statement cannot be generalized to the entire Gaia or VLBI catalogues.
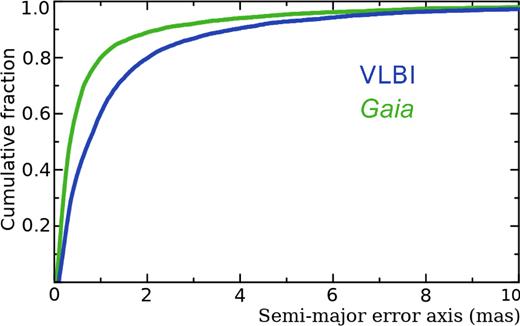
The cumulative distribution function of semi-major axes of error ellipses P(σmaj < a): green (top) curve for Gaia and blue (bottom) curve for VLBI.
Among 9081 matches, radio images at milliarcsecond resolution for 8143 sources are available. Using these, we have evaluated the jet directions for 4030 sources, i.e. for one half of the sample. We removed 48 sources that include 13 radio stars, one supernova remnant in the nearby star-forming galaxy, 10 gravitational lenses, and 24 double objects.
2.1 Analysis of VLBI/Gaia position angles with respect to the jet direction
Fig. 2 shows the distribution of the normalized arc lengths a/σa among all the matches. The last bin contains 1067 sources with normalized arcs greater than 5, or 11.4 per cent. The number of sources with normalized arcs greater than 4, which for this work we consider statistically significant, is 16.3 per cent, or 1/6. The goal of our study is to explain these outliers.
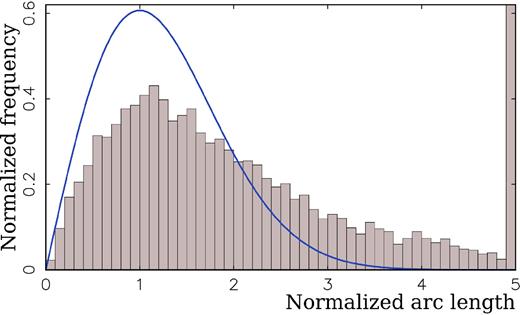
The distribution of the normalized VLBI/Gaia arc lengths over 9033 matched sources. The last bin that holds 1067 normalized arc lengths > 5 exceeds the plot bounding box. The smooth blue curve shows the Rayleigh distribution with σ = 1.
We computed the histograms of the distribution of the position angle offsets with respect to the jet directions determined from an analysis of VLBI images at milliarcsecond scales. We denote this quantity as ψ. Such a histogram is shown in Fig. 3. Comparing this figure with the upper-left figure 3 in Kovalev et al. (2017) demonstrates that the anisotropy is revealed even more clearly: the peaks became sharper and narrower. The height of the peak with respect to the background is 2.8 versus 1.7 and the full width at half maximum (FWHM) is 0.42 rad versus 0.62 rad. We confirmed that the anisotropy of the ψ angle is not an artefact of Gaia DR1, and the prediction made in Petrov & Kovalev (2017b) has come true.
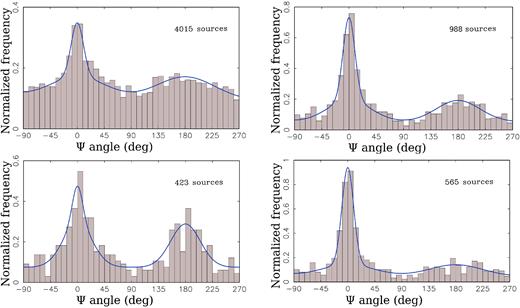
Histograms of the distribution of the position angle of Gaia offset with respect to the VLBI position counted anticlockwise with respect to the jet direction. Top left (a): all the matches with known jet directions. Top right (b): the matches with σψ < 0.3 rad. Bottom left (c): the matches with σψ < 0.3 rad and arc lengths < 2.5 mas. Bottom right (d): the matches with σψ < 0.3 rad and arc lengths > 2.5 mas. Blue curves are the best approximation of a three-component model.
We should note that the histogram of ψ angles is affected by its measurement errors that depend on a/σϕ. We assume σψ = σϕ, neglecting errors in the determination of jet direction angles because at the moment we cannot precisely characterize them. At large a/σϕ (say, more than 4), the distribution of the ψ errors for a given measurement converges to a normal distribution. At low a/σϕ (say, less than 0.25), the distribution converges to a uniform distribution. The analytic expression for the ψ errors can be found on p. 233 of Thompson, Moran & Swenson (2017). Including measurements of ψ with large errors smears the histogram. In order to mitigate smearing, we filtered out matches with σψ > 0.3 rad. We found empirically that reducing the threshold further degrades the histograms as a consequence of the scarcity of remaining points, though it does not change their shape noticeably.
Fig. 3(b) shows a histogram of ψ angles for all the matches with σψ < 0.3 rad. The peaks at 0° and 180° became much stronger. A further analysis revealed that the histograms are different for short and long arc lengths between the VLBI and Gaia positions, as shown in Figs 3(c) and (d).
| Case . | α . | fwhm1 . | β . | fwhm2 . | 1 − α − 2β . | #src . |
|---|---|---|---|---|---|---|
| . | . | rad . | . | rad . | . | . |
| a | 0.08 | 0.42 | 0.17 | 2.03 | 0.58 | 4017 |
| b | 0.23 | 0.40 | 0.22 | 1.48 | 0.33 | 985 |
| c | 0.07 | 0.35 | 0.17 | 1.01 | 0.47 | 423 |
| d | 0.24 | 0.40 | 0.17 | 1.84 | 0.28 | 565 |
| Case . | α . | fwhm1 . | β . | fwhm2 . | 1 − α − 2β . | #src . |
|---|---|---|---|---|---|---|
| . | . | rad . | . | rad . | . | . |
| a | 0.08 | 0.42 | 0.17 | 2.03 | 0.58 | 4017 |
| b | 0.23 | 0.40 | 0.22 | 1.48 | 0.33 | 985 |
| c | 0.07 | 0.35 | 0.17 | 1.01 | 0.47 | 423 |
| d | 0.24 | 0.40 | 0.17 | 1.84 | 0.28 | 565 |
| Case . | α . | fwhm1 . | β . | fwhm2 . | 1 − α − 2β . | #src . |
|---|---|---|---|---|---|---|
| . | . | rad . | . | rad . | . | . |
| a | 0.08 | 0.42 | 0.17 | 2.03 | 0.58 | 4017 |
| b | 0.23 | 0.40 | 0.22 | 1.48 | 0.33 | 985 |
| c | 0.07 | 0.35 | 0.17 | 1.01 | 0.47 | 423 |
| d | 0.24 | 0.40 | 0.17 | 1.84 | 0.28 | 565 |
| Case . | α . | fwhm1 . | β . | fwhm2 . | 1 − α − 2β . | #src . |
|---|---|---|---|---|---|---|
| . | . | rad . | . | rad . | . | . |
| a | 0.08 | 0.42 | 0.17 | 2.03 | 0.58 | 4017 |
| b | 0.23 | 0.40 | 0.22 | 1.48 | 0.33 | 985 |
| c | 0.07 | 0.35 | 0.17 | 1.01 | 0.47 | 423 |
| d | 0.24 | 0.40 | 0.17 | 1.84 | 0.28 | 565 |
We see that the main peak at ψ = 0 with an FWHM around 0.4 rad is rather insensitive to the way in which a subsample is drawn. We tentatively conclude that the fitted FWHM is the intrinsic width of the peak. The peak at ψ = 0 is contributed predominantly by the matches with large position offsets, and it is related to the presence of optical jets. Several factors contribute to the peak broadening: (a) the intrinsic jet width; (b) errors in determination of the jet direction; and (c) curvature of the jet, which makes jet direction determination problematic. Perturbations in the jet shape are magnified because of Doppler boosting. Typically, only the beginning of a jet is discernible in the VLBI images due to limited dynamic range, while the Gaia centroid is sensitive to jets at scales comparable with the PSF and smaller.
Two secondary peaks are broad, with maxima at ψ = 0 and π. They are formed by matches almost exclusively with offsets shorter than 2–2.5 mas. The fraction of these secondary peaks in the distribution weakly depends on the subsample selection, 0.17–0.22, but its FWHM varies between subsamples. We interpret this as an indication that a simplistic four-parameter model is too coarse to fully describe the empirical distribution, the shape of which depends on the VLBI/Gaia offset length.
The sixth column in Table 1 shows the fraction of the sources whose offset position angles have a uniform distribution, i.e. their offsets are not related to the core–jet morphology. This fraction is 0.58 for the histogram made using all the observations. The fraction is reduced to 0.33 for the subsample of observations with σψ < 0.3 rad and to 0.25 for the subsample with σψ < 0.2 rad. This reduction occurs partly due to mitigation of the histogram smearing and partly due to selection bias. Since σψ depends on both an uncertainty of position estimates and an arc length, selecting a subsample with the upper limit for σψ disproportionately favours matches with long VLBI/Gaia offsets that for given position uncertainties get higher chances to have low σψ.
The distribution of the VLBI/Gaia position offset angles was studied by Plavin, Kovalev & Petrov (2018) for different purposes applying a different fraction analysis approach. The outcome of their study qualitatively agrees with results presented here.
2.2 Rescaling the reported VLBI and Gaia position uncertainties
The presence of strong peaks in the histograms in Fig. 3 means that these matches are affected by systematic differences. These differences also affect the distribution of normalized arc lengths shown in Fig. 2. In order to mitigate their impact, we redrew the histogram and excluded the sources with ψ angles within 0.5 rad of peaks at 0 and π. As a result, we got a clean sample that is not affected by the presence of optical jets. We used this clean sample for characterizing the reported Gaia and VLBI position uncertainties. We wanted to answer the question of how realistic the uncertainties are.
We noticed that the number of outliers, i.e. the matches with the normalized arc > 4, grows with an increase of χ2/ndf, where ndf is the number of degrees of freedom. χ2 is provided in the variable astrometric_chi2_al of the Gaia DR2 archive. The number of degrees of freedom was computed as the difference of the variables astrometric_n_good_obs_al and astrometric_params_solved.
We sorted the dataset in increasing order over χ2/ndf and split it into 100 percentile groups of 91 objects each. Then we computed the fraction of outliers for each percentile group. The dependence of the fraction of outliers as a function of the mean χ2/ndf within a percentile is shown with a green curve in Fig. 4. It grows approximately as |$\sqrt{\chi ^2/\mbox{ndf}}$| when χ2/ndf > 1.5–2. Since the number of degrees of freedom is the mathematical expectation of χ2, in the case in which all uncertainties of Gaia observables of a given source are underestimated by a common factor, multiplying them by |$\sqrt{ \chi ^2/\mbox{ndf}}$| corrects the impact of the measurement error underestimation. The blue curve in Fig. 4 demonstrates that, after rescaling the Gaia position uncertainties, the dependence of the number of outliers as a function of χ2/ndf has disappeared. Scaling position errors by χ2/ndf inflate them, which makes the normalized arc lengths smaller. We argue that rescaling the Gaia position errors makes them more realistic by accounting for the additional noise that also increases χ2/ndf.
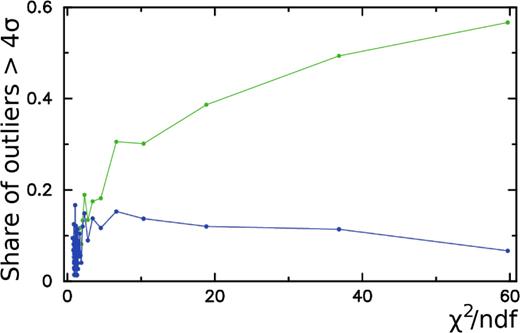
The fraction of outliers with normalized arc length of VLBI and Gaia matches > 4 for 1 per cent percentile bins of χ2/ndf. The horizontal axis is along the median value of χ2/ndf within each percentile. The upper green curve was computed using the original Gaia position uncertainties. The lower blue curve was computed using Gaia uncertainties multiplied by the|$\sqrt{ \chi ^2/\mbox{ndf}}$| factor.
In addition to source-dependent rescaling that is based on the χ2/ndf statistics of a given source, we evaluated global scaling factors for both VLBI and Gaia that affect every source. This is the simplest way to mitigate the impact of systematic errors on uncertainties and make them more realistic without rerunning a solution. Since the normalized arc lengths are affected by both uncertainties in the VLBI and Gaia positions, we estimated the scaling factors of the VLBI uncertainties by processing the subset of observations with |$\sigma _{\rm g,maj} \gt 5 \, \sigma _{\rm v,maj}$| and vice versa: we estimated scaling factors for the Gaia uncertainties (after scaling them by |$\sqrt{ \chi ^2/\mbox{ndf}}\:$|) by processing the subset of observations with |$\sigma _{\rm g,maj} \lt 1/5\, \sigma _{\rm v,maj}$|. We adjusted the scaling factors in such a way that the distribution of normalized arc lengths of the subsample is approximated by the Rayleigh distribution σ = 1 (See Fig. 8). The scaling factors are 1.06 for Gaia and 1.30 for VLBI. Applying scaling parameters to uncertainties to account for the contribution of systematic errors is a common technique. For instance, a scaling factor of 1.5 was used to inflate source position uncertainties in the ICRF1 catalogue (Ma et al. 1998).
Since, as we have established, the Gaia systematic errors in AGN positions caused by optical structure have a strong concentration towards ψ = 0 and ψ = π, we expected that the removal of the matches with ψ ∈ [−0.5, −0.5] and ψ ∈ [π − 0.5, π + 0.5] rad and keeping only ‘off-peak’ matches should affect the statistics of the number of outliers. We computed the fraction of matches with normalized residuals > 4 for for several subsamples. Since we applied error rescaling, the number of outliers has reduced with respect to our initial estimate mentioned above. The first row of Table 2 shows that excluding the sources within the peaks of the distribution of ψ angle reduces the number of outliers by a factor of 1.36. In contrast, considering only the sources within 0.5 rad of the peaks doubles the number of outliers. Since the jet directions were determined for only 45 per cent of the matches, these statistics underestimate the impact of the presence of optical jets on Gaia positions. If only the sources with known jet directions are counted, excluding the sources within the peaks reduces the number of outliers by a factor of 2.07. The second and fourth rows of Table 2 also show the statistics for the subsamples of the low 50 per cent percentile of VLBI rescaled errors. The reduction of the number of outliers is 1.77 for the 50 per cent percentile of the overall sample of matched sources and 2.65 for the subsample of the sources with known jet directions. The reduction of the number of outliers is greater for the lower 50 per cent percentile because the sources with smaller position uncertainties have smaller errors in determining the ψ angle, making discrimination of the ‘on-peak’ and ‘off-peak’ sources more reliable.
The fraction of matches with normalized residuals > 4 for a number of subsamples in pro cents (column r). The last two rows show the subsamples of matches with known jet directions. The second and fourth rows use a subsample of matches with VLBI semi-major error ellipse less than the median among all matches and the matches with known jet directions, respectively. The ‘off-peak’ column excludes the sources with ψ ∈ [−0.5, −0.5] and ψ ∈ [π − 0.5, π + 0.5] rad. The ‘on-peak’ column includes the sources with ψ in these ranges and excludes everything else.
| . | all . | off-peak . | on-peak . | |||
|---|---|---|---|---|---|---|
| . | r . | #src . | r . | #src . | r . | #src . |
| all | 9.0 | 9033 | 6.6 | 7288 | 19.4 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.963 mas | 10.0 | 4496 | 5.9 | 3169 | 19.7 | 1323 |
| all with known ψ | 11.2 | 4017 | 5.4 | 2313 | 22.1 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.455 mas | 11.4 | 1997 | 4.3 | 1109 | 20.3 | 888 |
| . | all . | off-peak . | on-peak . | |||
|---|---|---|---|---|---|---|
| . | r . | #src . | r . | #src . | r . | #src . |
| all | 9.0 | 9033 | 6.6 | 7288 | 19.4 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.963 mas | 10.0 | 4496 | 5.9 | 3169 | 19.7 | 1323 |
| all with known ψ | 11.2 | 4017 | 5.4 | 2313 | 22.1 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.455 mas | 11.4 | 1997 | 4.3 | 1109 | 20.3 | 888 |
The fraction of matches with normalized residuals > 4 for a number of subsamples in pro cents (column r). The last two rows show the subsamples of matches with known jet directions. The second and fourth rows use a subsample of matches with VLBI semi-major error ellipse less than the median among all matches and the matches with known jet directions, respectively. The ‘off-peak’ column excludes the sources with ψ ∈ [−0.5, −0.5] and ψ ∈ [π − 0.5, π + 0.5] rad. The ‘on-peak’ column includes the sources with ψ in these ranges and excludes everything else.
| . | all . | off-peak . | on-peak . | |||
|---|---|---|---|---|---|---|
| . | r . | #src . | r . | #src . | r . | #src . |
| all | 9.0 | 9033 | 6.6 | 7288 | 19.4 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.963 mas | 10.0 | 4496 | 5.9 | 3169 | 19.7 | 1323 |
| all with known ψ | 11.2 | 4017 | 5.4 | 2313 | 22.1 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.455 mas | 11.4 | 1997 | 4.3 | 1109 | 20.3 | 888 |
| . | all . | off-peak . | on-peak . | |||
|---|---|---|---|---|---|---|
| . | r . | #src . | r . | #src . | r . | #src . |
| all | 9.0 | 9033 | 6.6 | 7288 | 19.4 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.963 mas | 10.0 | 4496 | 5.9 | 3169 | 19.7 | 1323 |
| all with known ψ | 11.2 | 4017 | 5.4 | 2313 | 22.1 | 1702 |
| σ|$\mathrm{v}$| ≤ 0.455 mas | 11.4 | 1997 | 4.3 | 1109 | 20.3 | 888 |
The results in Table 2 show that the presence of optical structure parallel to the jet explains 62 per cent of VLBI/Gaia position offsets significant at the 4σ level for a subsample of 23 per cent of VLBI/Gaia matches that have known jet directions and VLBI position errors lower than the median. In order to generalize this result to the entire population of radio-loud AGNs, we need to assume that the significance of VLBI/Gaia offsets does not depend on VLBI position error and does not depend on the measurability of the radio jet directions. The VLBI position errors above the 0.2–0.3 mas level are limited by thermal noise, and thus the first assumption is valid. The validity of the second assumption is questionable. The detectability of parsec-scale radio jets depends on the jet brightness and the dynamic range of observations that in turn depends on the source flux density. Since the correlation between radio and optical fluxes is low, missing a jet just because a source was weak does not create a selection bias. However, if a jet direction for a given source was not detected because its radio jet is intrinsically weaker, missing such a source may create a selection bias, because a weak radio jet may imply a weak optical jet. A subsample of sources with determined jet direction may have a selection bias towards jets brighter in radio and optical with respect to the overall population.
2.3 The impact of systematic errors on determination of the orientation of the Gaia catalogue with respect to the VLBI catalogue
Any source catalogue can be rotated at an arbitrary angle, and the observables, e.g. group delays, remain the same. The orientation of a catalogue can be described by three angles. These three angles cannot be determined from observations in principle and are set by imposing certain conditions. The orientation of the RFC catalogue is set to require that the net rotation with respect to the 212 so-called ‘defining’ sources in the ICRF1 catalogue (Ma et al. 1998) be zero. The orientation of the Gaia DR2 catalogue was established to have zero rotation with respect to 2843 counterparts in the ICRF3-prototype catalogue using the frame rotator technique described in detail in Lindegren et al. (2012).
The systematic differences caused by the optical structure affect the procedure for establishing the catalogue orientation. To provide a quantitative measure of sensitivity of the orientation angles to systematic errors, we computed the three angles of Gaia DR2 orientation with respect to the RFC VLBI catalogue (see Table 3). We see that selecting different samples, including those most affected (on-peak) and least affected (off-peak) by systematic errors, resulted in differences in orientation angles around 0.02 mas. A large value of the orientation angle around axis 2 is somewhat unexpected, but since the ICRF3-prototype catalogue used for alignment of Gaia DR2 is not publicly available, the origin of this relatively large value cannot be established.
Estimates of rotation angles around axes 1, 2, 3 of the Gaia positions of matches with respect to VLBI positions of four subsamples. Units are milliarcseconds.
| . | #Obs . | Axis 1 . | Axis 2 . | Axis 3 . |
|---|---|---|---|---|
| all | 9033 | −0.030 ± 0.004 | 0.090 ± 0.004 | −0.030 ± 0.005 |
| with jets | 4016 | −0.010 ± 0.005 | 0.092 ± 0.005 | −0.010 ± 0.006 |
| off-peak | 2647 | −0.013 ± 0.006 | 0.095 ± 0.006 | 0.008 ± 0.007 |
| on-peak | 1369 | −0.005 ± 0.008 | 0.091 ± 0.007 | −0.037 ± 0.009 |
| . | #Obs . | Axis 1 . | Axis 2 . | Axis 3 . |
|---|---|---|---|---|
| all | 9033 | −0.030 ± 0.004 | 0.090 ± 0.004 | −0.030 ± 0.005 |
| with jets | 4016 | −0.010 ± 0.005 | 0.092 ± 0.005 | −0.010 ± 0.006 |
| off-peak | 2647 | −0.013 ± 0.006 | 0.095 ± 0.006 | 0.008 ± 0.007 |
| on-peak | 1369 | −0.005 ± 0.008 | 0.091 ± 0.007 | −0.037 ± 0.009 |
Estimates of rotation angles around axes 1, 2, 3 of the Gaia positions of matches with respect to VLBI positions of four subsamples. Units are milliarcseconds.
| . | #Obs . | Axis 1 . | Axis 2 . | Axis 3 . |
|---|---|---|---|---|
| all | 9033 | −0.030 ± 0.004 | 0.090 ± 0.004 | −0.030 ± 0.005 |
| with jets | 4016 | −0.010 ± 0.005 | 0.092 ± 0.005 | −0.010 ± 0.006 |
| off-peak | 2647 | −0.013 ± 0.006 | 0.095 ± 0.006 | 0.008 ± 0.007 |
| on-peak | 1369 | −0.005 ± 0.008 | 0.091 ± 0.007 | −0.037 ± 0.009 |
| . | #Obs . | Axis 1 . | Axis 2 . | Axis 3 . |
|---|---|---|---|---|
| all | 9033 | −0.030 ± 0.004 | 0.090 ± 0.004 | −0.030 ± 0.005 |
| with jets | 4016 | −0.010 ± 0.005 | 0.092 ± 0.005 | −0.010 ± 0.006 |
| off-peak | 2647 | −0.013 ± 0.006 | 0.095 ± 0.006 | 0.008 ± 0.007 |
| on-peak | 1369 | −0.005 ± 0.008 | 0.091 ± 0.007 | −0.037 ± 0.009 |
3 ANALYSIS OF |$\textit{Gaia}$| AND VLBI PROPER MOTIONS
Gaia DR2 provides proper motions and parallaxes for 78 per cent sources. Among 9081 matches, proper motion estimates are available for 7774 sources. Since the AGNs are located at cosmological distances, their proper motions considered as bulk tangential displacements are supposed to be well below the Gaia detection limit. A flare at the accretion disc or jet will change the position of the centroid. It will cause a shift in the position of the centroid, and therefore will result in a non-zero estimate of proper motion. Such a proper motion may be statistically significant even at the Gaia level of accuracy. To check this, we made histograms of proper motions as a function of the position angles of the proper motion with respect to the jet directions denoted as |$\bar{\psi }$|. We analysed a sample of 613 matched sources with |$\sigma (\bar{\psi }) \lt 0.4$| rad. The histograms showed weak peaks. The peaks become much sharper when we split the sample into two subsets: one with χ2/ndf less then the median 1.125 and one with χ2/ndf greater than the median (see Fig. 5).
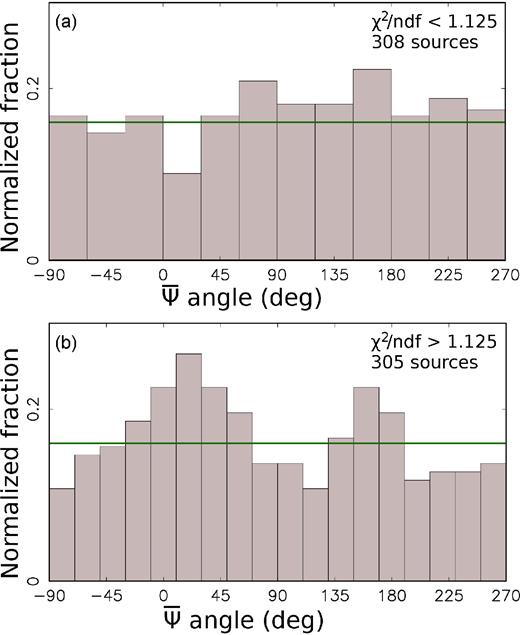
Histograms of the distribution of Gaia proper motion position angles with errors <0.4 rad among the matches with different χ2/ndf. The top panel uses matches with χ2/ndf lower than the median in this subsample, 1.125. The bottom uses matches with χ2/ndf greater than the median in this subsample, 1.125. For comparison, the green line shows the uniform distribution.
We see that the subsample of matches with large χ2/ndf shows two peaks at |$\bar{\psi }=0$| and |$\bar{\psi }=\pi$| that are significant, while the subsample with χ2/ndf below the median does not. A non-linear motion is one of the reasons why χ2/ndf deviates from 1. The histogram in Fig. 5(b) tells us that, among the sources with non-linear motion, the fraction of objects with proper motions along or opposite to the jet direction is disproportionately high. This dependence on angle |$\bar{\psi }$| implies that the proper motion is caused by the photocentre changes parallel to the jet direction at least for a fraction of the sources.
We expect that most optical flares happen close to the centre of an AGN, either in the accretion disc or in the jet base. We cannot directly see where the optical jet flares occur. However, the following arguments apply. The radio variability is associated with the apparent jet base – the core (e.g. Kovalev et al. 2005; Lister et al. 2016). Optical synchrotron emission is more transparent with an even brighter core and steeper jet spectrum (e.g. Mimica et al. 2009). As a result, the jet base is expected to be the prime source of optical flares. The correlation between the direction of linear polarization between optical flares and the radio core reported by Jorstad et al. (2007) confirms this.
Brightening a jet component shifts the centroid temporarily and irregularly. We call this behaviour jitter and we predicted it in Petrov & Kovalev (2017b). Unlike proper motions of stars, extending the observation interval does not result in a convergence of a proper motion estimate to some value with small uncertainty. Instead, it slowly converges to zero. Peaks at 0 and π in the histogram of |$\bar{\psi }$| over the subsamples with high χ2/ndf provide us with the first evidence that the predicted jitter indeed takes place. We used here estimates of AGN proper motions and χ2/ndf as a proxy for jitter detection.
We explored further the impact of a selection based on χ2/ndf on the distribution of position offset angles with respect to jet direction. We did not find a noticeable impact of χ2/ndf for VLBI/Gaia offsets longer than 2.5 mas, but we found that such a selection affects the matches with VLBI/Gaia offsets shorter than 2.5 mas. Fig. 6 shows the distributions of ψ angles for matches with σ(ψ) < 0.3 rad divided into three subsamples approximately equally distributed over χ2/ndf. The peaks at ψ = 0 and ψ = π are broad for the subsample of low χ2/ndf. They are getting sharper for the subsample of intermediate χ2/ndf. The subsample with large χ2/ndf is strikingly different to the subsample with low sample is approximated by the Rayleigh χ2/ndf: the histogram has a very strong peak at ψ = 0, i.e. along the jet direction, and a smaller fraction of matches outside the main peaks.
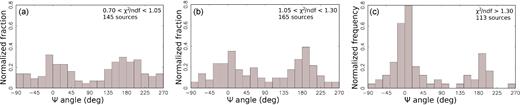
Histograms of the distribution of the position angle of Gaia offsets with respect to VLBI positions for matches with σψ < 0.3 rad, arc lengths < 2.5 mas and different ranges of χ2/ndf.
Analysis of the connection of the Gaia DR2 proper motions with χ2/ndf suggests that the matches with large χ2/ndf are more prone to exhibiting jitter. This allows us to conclude tentatively that, among the subsample of sources with VLBI/Gaia offsets shorter than 2.5 mas, flares and jitter occur predominantly in the objects that have Gaia offsets along the jet direction. This indicates that the mechanism that causes an increase of χ2/ndf may not work or at least is not dominating for sources with ψ = π. At the same time, Figs 6 and 8 suggest there is no strong preferable sign of motion direction, either along or opposite to the jet. Such a pattern is consistent with jitter caused by flares: depending on when a flare has happened, at the beginning or end of the observing interval, the direction of the proper motion may be opposite.
It is instructive to examine whether proper motions in AGN positions derived from VLBI data analysis show the same pattern. We ran a special VLBI solution using all available ionosphere-free linear combinations of group delays at 8.4 and 2.3 GHz from 1980 to 2018 August 1 and estimated the proper motions of 3039 sources using a least-squares fit. Source structure was considered as a δ-function in processing VLBI observations during both fringe fitting and computation of theoretical group delays. We selected the sources that were observed in at least two sessions over an interval of at least three years and each observing session had at least 20 usable combinations of group delays. We applied the data reduction for the acceleration of the barycentre of the Solar system towards the Galactic Centre with RA 17h45m36|${^{\rm s}_{.}}$|6, Dec. −28°56′00|${^{\prime\prime}_{.}}$|0, and magnitude 1.845 x 10−10 m s−2. We applied no-net-rotation constraints on proper motion estimates among 628 sources with a strong history of observations, namely, observed in at least eight sessions over four years or longer and with at least 128 usable linear combinations of group delays.
Fig. 7 shows the histograms of the proper motion position angles |$\bar{\psi }_{\rm g}$| and |$\bar{\psi }_{\rm v}$| with respect to jet directions among those matched sources from Gaia and VLBI that have magnitudes of the proper motions and position offsets significant at the 3σ level for Gaia and 4σ for VLBI. There are 75 such sources in the Gaia dataset and 284 in the VLBI dataset. The fraction of Gaia sources in bins at |$\bar{\psi }_\mathrm{g}=0$| and |$\bar{\psi }_\mathrm{g}=\pi$| is a factor of three greater than on average. The median proper motions in these samples is 1.15 mas in the Gaia subset and 0.022 mas in the VLBI subset, i.e. a factor of 52 less. The Gaia proper motions were evaluated over a 1.15 yr time interval. The VLBI proper motions were evaluated over a time span in the range of 7.9–38.2 yr with the median 26.5 yr, a factor of 22.8 longer. The median magnitude of proper motions parallel to jet directions does not differ from the median magnitudes over the entire populations for both VLBI and Gaia.
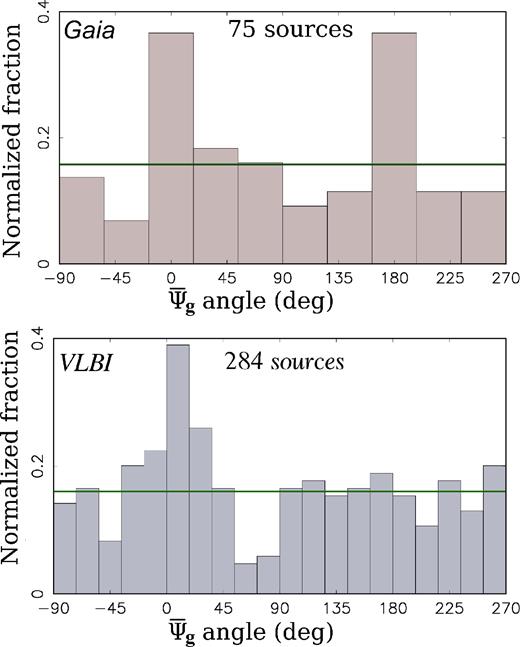
The histograms of significant AGN proper motion position angles with respect to jet directions among matched sources |$\bar{\Psi }_{\rm g}$| for Gaia and |$\bar{\Psi }_{\rm v}$| for VLBI. Top: the Gaia DR2 proper motions with magnitudes >3σ in both proper motions and position offsets. Bottom: the proper motions from the VLBI global solution. The horizontal green line shows the uniform distribution.
While the histogram of the Gaia proper motion position angles shows peaks at both |$\bar{\psi }_\mathrm{g}=0$| and |$\bar{\psi }_\mathrm{g}=\pi$|, a similar histogram of the VLBI proper motion position angles only shows a peak at |$\bar{\psi }_\mathrm{v}=0$|. Explanation of this pattern in VLBI proper motions requires further investigation. As we showed in Petrov & Kovalev (2017b), unlike a power detector, e.g. a CCD, an interferometer is not sensitive to the centroid change. Unaccounted contribution of an extended jet affects source position estimates at scales of tens of microarcseconds. The unaccounted contribution of source structure to VLBI positions may reach a level of 0.1–1 mas if the image has more than one compact component, especially if the compact component is located at a distance comparable with the resolution of the interferometer. A change in the relative brightness or the distance between components due to flares causes a change in position estimates at given epochs and, as a result, proper motion. The peak around |$\bar{\Psi _v}=0$| in the lower plot in Fig. 7 confirms that at least for some sources this mechanisms works.
4 OTHER KNOWN CAUSES OF VLBI/|$\textit{Gaia}$| POSITIONS OFFSETS
A number of authors (Mignard et al. 2016; Makarov et al. 2017; Frouard et al. 2018) have suggested alternative explanations of statistically significant offsets:
Errors in matching VLBI and Gaia objects. These are easily controlled by computing the probability of false association based on the source density in the vicinity of the candidates for association. The cut-off of the probability of false association 2 x 10−4 results in a mathematical expectation of the total number of false associations of 2. The coarseness of the source density model may increase the number of false associations, but it is very unlikely that it can increase their count by an order of magnitude.
An extended galaxy around a quasar. Position estimates of extended objects may suffer from deficiencies of the current Gaia PSF model. To examine to what extent this affects the VLBI/Gaia offsets, we investigated a subsample of galaxies from the NGC catalogue (Sinnnott & de Jager 1990). Since these are the brightest known background galaxies, if emission of background galaxies affects the VLBI/Gaia offsets, the contribution of such emission is supposed to be the highest among the NGC subsample. We used the positions of these sources from the SIMBAD database (Wenger et al. 2000), cross-matched them against the RFC catalogue, and found 167 associations. Of these, 49, or 29 per cent, have a counterpart in Gaia DR2. It is worth noting that the fraction of VLBI/Gaia matches among NGC galaxies is half the size of that in the full sample. Without rescaling the Gaia position uncertainties by the |$\sqrt{\chi ^2/\mbox{ndf}}$| factor, approximately half of these counterparts, 26 objects, have normalized arc lengths exceeding 4. However, these objects have large χ2/ndf. After rescaling the Gaia position uncertainties, all but one object had a normalized arc length below 4.
We conclude that extended galaxies may have large VLBI/Gaia offsets, but they also have large χ2/ndf. Scaling the uncertainties by the |$\sqrt{\chi ^2/\mbox{ndf}}$| makes the normalized arc lengths of galaxies indistinguishable from the rest of the sample.
Lensed quasars. There are 10 known gravitational lenses in the sample of VLBI/Gaia matches. Since gravitational lenses were extensively hunted using radio surveys (e.g. Browne et al. 2003), it is unlikely that the RFC has more than several missed gravitational lenses.
Double quasars. Makarov et al. (2017) presented a list of 28 sources with VLBI/Gaia DR1 significant offsets that have a close component on PanSTARRS images. Of them, 24 were found in Gaia DR2 and passed our test of the probability of false association less than 2 x 10−4. Of them, 11 have significant VLBI/Gaia DR2 offsets. The second component may be either a star or a merging galaxy. During galaxy mergers, the nuclei may be dislodged with respect to the centre of mass of each individual galaxy. A study of such systems may help to constrain theories of galaxy mergers. However, the number of such systems is small (11 out of 2293 identified in Makarov et al. (2017), i.e. 0.5 per cent).
5 SUMMARY AND CONCLUSIONS
Here we summarize the main results of our comparison of AGN positions and proper motions from Gaia DR2 against the most complete catalogue of VLBI positions to date, the RFC.
The Gaia DR2 AGN position uncertainties of VLBI matched sources are a factor of two smaller than the VLBI position uncertainties. Gaia position catalogues are becoming the most precise astrometry catalogues at present.
We predicted in Petrov & Kovalev (2017b) that the improvement in accuracy of VLBI and/or Gaia will not reconcile the VLBI and Gaia positions, but will make these differences more significant. This prediction has come true. The fraction of outliers grew from 6 to 9 per cent, and the distribution of the position offset directions as a function of ψ became sharper.
We demonstrated that the main reason for the statistically significant VLBI/Gaia position offset is the presence of optical structure. Among the matched sources with normalized arc lengths exceeding 4 that have measured jet directions, 52–62 per cent, i.e. the majority, have position offsets parallel to the jet direction. Therefore, we conclude that the optical jet is the cause. Although this fraction may be somewhat lower for the entire population of matched AGNs, we have obtained its firm lower limit: 27 per cent. Other reasons mentioned by Mignard et al. (2018) can explain only a small fraction of outliers.
The presence of emission from a host galaxy within the Gaia point spread function may shift the centroid with respect to the nucleus if the galaxy central region structure is asymmetric or the AGN is dislodged with respect to the galaxy centre of mass; we assume that such a shift is independent on jet direction angle in the absence of evidence of such a dependence. Table 1 provides the upper limit of the fraction of outliers whose position offsets do not depend on ψ: 33 per cent. It does not seem likely that all of these offsets are caused by the contribution of host galaxies, because the fraction of AGNs with discernible host galaxies is much smaller.
We found that scaling the Gaia position uncertainties by |$\sqrt{\chi ^2/\mbox{ndf}}$| eliminated the dependence of the fraction of outliers on χ2/ndf. Examining the subset of matches with dominating VLBI or Gaia errors allowed us to evaluate the scaling factors for the VLBI uncertainties, 1.30, and the Gaia position uncertainties: |$1.06 \, \sqrt{\chi ^2/\mbox{ndf}}$|. Eliminating the observations within 0.5 rad of ψ = 0 and ψ = π and using rescaled uncertainties made the distribution of normalized VLBI/Gaia arc lengths much closer to the Rayleigh distribution: compare Figs 2 and 8.
The contribution of VLBI and/or Gaia systematic errors on estimates of the orientation angles of the Gaia DR2 catalogue with respect to the VLBI catalogue does not exceed 0.02 mas.
We predicted in Petrov & Kovalev (2017b) that flares in AGNs would cause a jitter in their positions because an increase of flux in one of the components of an extended source will change the centroid position. The analysis of Gaia proper motions provided us with an indirect confirmation of this prediction: the sources with excessive Gaia residuals, i.e. large χ2/ndf, have proper motion directions predominately parallel to the jet directions. The median magnitude of statistically significant proper motions is larger than 1 mas yr-1 over a 1.16 yr interval, which is significantly higher than the <0.05 mas yr-1 over five years anticipated before the Gaia launch (Perryman, Spergel & Lindegren 2014). Although AGN proper motions should not be interpreted as a bulk tangential motion, at the same time, these proper motions are not always artefacts of Gaia data analysis. The photocentres of at least some quasars are not fixed points and the possibility of quasar proper motion should be taken into account in interpreting results of differential astrometry.
We found that VLBI proper motions have a preferable direction along with the jet. Median VLBI proper motions of AGNs are a factor of 50 smaller than Gaia proper motions.
![The distribution of normalized VLBI/Gaia arc lengths over 2313 matched sources. The sample includes all the sources with known jet directions and excludes the sources with ψ ∈ [−0.5, −0.5] and ψ ∈ [π − 0.5, π + 0.5] rad. Scaling factors 1.05 and $1.30 \sqrt{\chi ^2/\mbox{ndf}}$ were applied to Gaia and VLBI. The smooth blue curve shows the Rayleigh distribution with σ = 1.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/3/10.1093_mnras_sty2807/1/m_sty2807fig8.jpeg?Expires=1749870593&Signature=BBOr4pB50~BpgakGqiBbyYRcHMN9piUp0YooQFCo~ZE4dSHJmdkrVeo2wVxuJThFGLquVB2qtGKxFho6IQkrW9u~ayoqh97xe6teVSHNEbhDEZYC9GLSwmYjfE3ig3Z1exmjs4Cc-Q3~10pgrWDjyXBkHRbemnJwlc9nL~jCFTk2~JNi7ATWFHlTUmcdZ6lM2kka9gdYmqOaRMNYY2rADrgII4tIqXri9mfYgxaFJyL18wy4WSFZisRmxSCmanupU3tAR3JuGBm7skMNbrDMV-mfb7QrRDvLNvfFScWmBFqjciMBhuROOgNbeU~dMqjNxfpFYiUXHr~NP-aZarMnYA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of normalized VLBI/Gaia arc lengths over 2313 matched sources. The sample includes all the sources with known jet directions and excludes the sources with ψ ∈ [−0.5, −0.5] and ψ ∈ [π − 0.5, π + 0.5] rad. Scaling factors 1.05 and |$1.30 \sqrt{\chi ^2/\mbox{ndf}}$| were applied to Gaia and VLBI. The smooth blue curve shows the Rayleigh distribution with σ = 1.
We do not claim that we have solved the problem of establishing the nature of all outliers. The distribution in Fig. 8 still deviates from Rayleigh and we still have not uncovered the nature of the 1/3 statistically significant offsets, but we made quite substantial progress. We anticipate that a study of VLBI/Gaia position offsets will become a powerful tool for probing the properties of the accretion disc and the relativistic jet in AGNs, in line with the work of Plavin et al. (2018).
ACKNOWLEDGEMENTS
We used in our work the Astrogeo VLBI FITS image database2 that contains radio images contributed by A. Bertarini, L. Garcia, N. Corey, Y. Cui, L. Gurvits, X. He, D. Homan, S. Jorstad, S. Lee, R. Lico, M. Lister, E. Liuzzo, A. Marscher, C. Marvin, A. B. Pushkarev, E. Ros, T. Savolainen, K. Sokolovski, G. Taylor, A. de Witt, M. Xu, B. Zhang, and the authors. It is our pleasure to thank Eduardo Ros for suggestions that led to improvements in the manuscript.
This project is supported by the Russian Science Foundation grant 16-12-10481. This work has made use of data from the European Space Agency (ESA) mission Gaia, processed by the Gaia Data Processing and Analysis Consortium. Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. We used in our work VLBA data provided by the Long Baseline Observatory that is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Footnotes
Available online at http://astrogeo.org/rfc.
Available at http://astrogeo.org/vlbi_images.



