On the ISW-cluster cross-correlation in future surveys

Ballardini, Mario; Paoletti, Daniela; Finelli, Fabio; Moscardini, Lauro; Sartoris, Barbara; Valenziano, Luca

doi:10.1093/mnras/sty2795

ABSTRACT

We investigate the cosmological information contained in the cross-correlation between the integrated Sachs–Wolfe (ISW) of the cosmic microwave background (CMB) anisotropy pattern and galaxy clusters from future wide surveys. Future surveys will provide cluster catalogues with a number of objects comparable with galaxy catalogues currently used for the detection of the ISW signal by cross-correlation with the CMB anisotropy pattern. By computing the angular power spectra of clusters and the corresponding cross-correlation with CMB, we perform a signal-to-noise ratio (SNR) analysis for the ISW detection as expected from the eROSITA and the Euclid space missions. We discuss the dependence of the SNR of the ISW-cluster cross-correlation on the specifications of the catalogues and on the reference cosmology. We forecast that the SNRs for ISW-cluster cross-correlation are slightly smaller compared to those which can be obtained from future galaxy surveys but the signal is expected to be detected at high significance, i.e. more than |$\gt\! 3\, \sigma$|⁠. We also forecast the joint constraints on parameters of model extensions of the concordance Λ cold dark matter (ΛCDM) cosmology by combining CMB and the ISW-cluster cross-correlation.

galaxies: clusters: general, cosmic background radiation, cosmological parameters

1 INTRODUCTION

One of the key predictions of the recent accelerated expansion is the late integrated Sachs–Wolfe (ISW) effect (Sachs & Wolfe 1967) in the cosmic microwave background (CMB) anisotropy pattern. The ISW effect is caused by the time evolution of the gravitational potentials encountered by CMB photons during their journey from the last scattering surface to the observer. The change of the gravitational potentials on large scales is caused by the accelerated expansion of the Universe driven by dark energy (Kofman & Starobinsky 1985) and is therefore correlated with density fluctuations at low redshifts.

The late ISW effect is just a small fraction of the CMB temperature anisotropy signal for a Λ cold dark matter (ΛCDM) concordance cosmology and is maximum at largest angular scales (Kofman & Starobinsky 1985), where cosmic variance is dominant. An extraction of the ISW effect was predicted as feasible by cross-correlating CMB with large-scale structure (LSS) tracers of the matter distribution (Crittenden & Turok 1996). Several measurements of the ISW-LSS cross-correlation have been reported since the release of the WMAP first-year data (Nolta et al. 2004) by using different dark matter (DM) tracers. These measurements have been performed by using different estimators in different domains (e.g. Afshordi, Loh & Strauss 2004; Boughn & Crittenden 2004; Fosalba & Gaztanaga 2004; Vielva, Martinez-Gonzalez & Tucci 2006; McEwen et al. 2007; Giannantonio et al. 2008; Ho et al. 2008; Hernandez-Monteagudo 2010; Schiavon et al. 2012; Bianchini, Renzi & Marinucci 2016; Stölzner et al. 2017). See Dupe et al. (2011) and references therein for a review of pre-Planck ISW measurements.

A detection at 2.9|$\, \sigma$| level of the ISW effect has beeen obtained by Planck Collaboration XXI (2016) by cross-correlating the Planck temperature map with a compilation of publicly available galaxy surveys (see Planck Collaboration XIX 2014 for the results based on the nominal mission). This cross-correlation measurement of the ISW effect is compatible with the predictions of a concordance ΛCDM model with |$\Omega _\Lambda \sim 0.7$| (Planck Collaboration XXI 2016). Cross-correlation between CMB lensing and matter tracers improve the significance of the ISW detection (see Manzotti & Dodelson 2014; Ferraro, Sherwin & Spergel 2015; Planck Collaboration XXI 2016; Shajib & Wright 2016). Note also that the ISW could be targeted by using its cross-correlation with CIB (Ilic et al. 2011) or tSZ (Taburet et al. 2011).

Future LSS experiments, such as DESI¹ (Levi et al. 2013; Aghamousa et al. 2016a,b), Euclid² (Laureijs et al. 2011; Amendola et al. 2013), LSST³ (Abell et al. 2009), and SKA⁴ (Maartens et al. 2015), will provide surveys with a larger number of objects and sky fraction probing a larger volume, then allowing a better determination of the ISW signal. The next generation of LSS surveys will not only lead to an improvement in the ISW measurement with matter tracers already employed for this purpose but could also provide different catalogues of matter tracers suitable for novel detections of the ISW effect (Raccanelli et al. 2015, 2016; Pourtsidou, Bacon & Crittenden 2017).

Current cluster surveys are not optimal for the detection of the ISW effect since photometric catalogues are limited to small redshift |$z$| ≲ 0.4 (Rozo et al. 2010) and X-ray catalogues cover small patches of the sky (Mantz et al. 2015).⁵

Otherwise, the cluster catalogues from the next generation of LSS surveys are indeed expected to contain a higher number of clusters over a wider redshift range. These future catalogues will allow precision cosmology with clusters, as from the cosmological parameter forecasts from the Euclid cluster survey (Sartoris et al. 2016). It is therefore interesting to study the potential for an ISW detection by a cross-correlation with future cluster catalogues as matter tracers.

In this paper, by computing the angular power spectra of cluster counts and of their cross-correlation with CMB, we perform a signal-to-noise ratio (SNR) analysis for the ISW detection with two representative examples for future cluster catalogues, as those expected from the eROSITA (Predehl et al. 2010) and Euclid (Laureijs et al. 2011) space missions and we forecast how ISW-cluster cross-correlation could improve the constraints on cosmological parameters for different extended models. This analysis is complementary to the stacking of CMB data in correspondence of superclusters (Granett et al. 2008; Papai, Szapudi & Granett 2011; Ilic et al. 2011; Planck Collaboration XIX 2014; Planck Collaboration XXI 2016), whose theoretical interpretation is more difficult, although consistent with ΛCDM.

Our paper is organized as follows. In Section 2, we review the angular power spectrum of the cross-correlation between CMB and a generic matter tracer, such as clusters or galaxies. In Section 3, we review the calculations of the bias and the number density distribution for cluster catalogues. In Section 4, we describe the future surveys considered in our work: eROSITA and Euclid for clusters, Euclid photometric and spectroscopic surveys for galaxies. In Section 5, we compute the auto- and CMB cross-correlation angular power spectra for these surveys and perform an SNR analysis. In Section 6, we present forecasted constraints on cosmological parameters of extensions of the concordance ΛCDM model by combining CMB and the CMB-LSS cross-correlation. We draw our conclusions in Section 7.

Throughout this work, we adopt a fiducial cosmological model compatible with the most recent Planck data (Aghanim et al. 2016), corresponding to |$\omega _\textrm{b}\equiv \Omega _\textrm{b}\, h^2=0.02214$|⁠, |$\omega _\textrm{c}\equiv \Omega _\textrm{c}\, h^2=0.1206$|⁠, H₀ = 66.89, τ = 0.0581, n_s = 0.9625, and log (10¹⁰ A_s) = 3.053.

2 CROSS-CORRELATION OF ISW EFFECT WITH NUMBER COUNTS

We consider the projected density contrast of a tracer of matter X (clusters or galaxies in this paper) in the direction |$\hat{n}$| as

\begin{eqnarray*} \delta _\mathrm{X} (\hat{n}) = \int \mathrm{d}z\, b_\mathrm{X} (z) \frac{\mathrm{d}N_\mathrm{X}}{\mathrm{d}z} \delta _\mathrm{m} (\hat{n}, z) \, . \end{eqnarray*}

(1)

In equation (1), we denote by b_X(⁠|$z$|⁠) the linear bias and by dN_X/d|$z$| the redshift distribution of the tracer. The observed tracer density is correlated with the ISW contribution to temperature fluctuations in direction |$\hat{m}$|⁠:

\begin{eqnarray*} \frac{\delta T_\mathrm{ISW}}{T} (\hat{m}) = - \int \mathrm{d}z\, e^{-\tau (z)} \left(\frac{\mathrm{d}\Phi }{\mathrm{d}z} (\hat{m}\, , z) + \frac{\mathrm{d}\Psi }{\mathrm{d}z} (\hat{m}\, , z) \right) \, , \end{eqnarray*}

(2)

where Φ and Ψ are the gravitational potentials in the longitudinal gauge and e^{−τ(⁠|$z$|⁠)} is the visibility function.

With these assumptions, the angular power spectrum of the tracer |$C_{\ell }^\mathrm{XX}$| and of its cross-correlation with CMB temperature |$C_{\ell }^\mathrm{TX}$| are respectively

\begin{eqnarray*} C_{\ell }^\mathrm{XX} &=& 4 \pi \int \frac{\mathrm{d}k}{k} \Delta ^2 (k) \left[I_\ell ^\mathrm{X} (k)\right]^2 \, , \\ C_{\ell }^\mathrm{TX} &=& 4 \pi \int \frac{\mathrm{d}k}{k} \Delta ^2 (k) I_\ell ^\mathrm{ISW} (k) I_\ell ^\mathrm{X} (k)\,, \end{eqnarray*}

(3),(4)

where we denote by Δ²(k) the scale invariant matter power spectrum Δ²(k) ≡ k³P(k)/(4|$\pi$|²), and define the kernels of the counts distribution and of the cross-correlation as

\begin{eqnarray*} I_\ell ^\mathrm{X} (k) &=& \int \mathrm{d}z \, b_\mathrm{X}(z) \, \frac{\mathrm{d}N_\mathrm{X}}{\mathrm{d}z} D(z) j_\ell \left(k \chi (z) \right) \, , \\ I_\ell ^\mathrm{ISW} (k) &=& - \int \mathrm{d}z \, e^{-\tau } \, \left(\frac{\mathrm{d}\Phi }{\mathrm{d}z} + \frac{\mathrm{d}\Psi }{\mathrm{d}z} \right) j_\ell \left(k \chi (z) \right) \, , \end{eqnarray*}

(5),(6)

where D(⁠|$z$|⁠) is the growth factor and χ(⁠|$z$|⁠) is the conformal distance.

3 CLUSTER NUMBER DENSITY

We now review the computation of the number density for clusters and the corresponding bias that we will use in equation (3). The number density of expected clusters within the solid angle ΔΩ is

\begin{eqnarray*} \frac{\mathrm{d}N(z)}{\mathrm{d}z} = \int _{\Delta \Omega }\textrm{d}\Omega \, \frac{\textrm{d}V_\textrm{c}}{\textrm{d}z\, \textrm{d}\Omega } \int _0^{\infty } \textrm{d}M \, X(M,z) n_\textrm{h}(M,z) \, , \end{eqnarray*}

(7)

where V_c is the comoving volume, n_h(M, |$z$|⁠) and X(M, |$z$|⁠) are the DM halo mass function and the survey characteristic function, respectively.

3.1 Halo mass function

The distribution n_h(M_h, |$z$|⁠) of DM haloes in mass, position, and redshift describes the overall abundance and clustering properties of galaxies, and the dependence on the underlying cosmological model. As halo mass function, we use (Tinker et al. 2008)

\begin{eqnarray*} n_\textrm{h}(M,z) &=& -f(\sigma) \frac{\rho _\textrm{m}}{M} \frac{\textrm{d}\ln \sigma (M,z)}{{\textrm{d}} M} \, , \\ f(\sigma) &=& C_1(z)\left[1+\left(\frac{\sigma (M,z)}{C_3(z)}\right)^{-C_2(z)}\right] {\rm e}^{-C_0/\sigma (M,z)^2} \, , \end{eqnarray*}

(8),(9)

where ρ_m is the total physical matter density and σ(M, |$z$|⁠) is the root mean square density fluctuation within a sphere. The variance of the fractional density fluctuation,

\begin{eqnarray*} \sigma ^2(M,z) = \int _0^{\infty } \frac{k^2\textrm{d}k}{2\pi ^2} P(k,z) W^2(k,M) \, , \end{eqnarray*}

(10)

is calculated by integrating the linear matter power spectrum P(k, |$z$|⁠) smoothed by a top-hat window in real space window function W(k, M).

According to Tinker et al. (2008), we parametrize the redshift evolution of the parameters of the mass function in equation (8) as different power-law functions of (1 |$+$||$z$|⁠)

\begin{eqnarray*} C_1(z) &=& C_{1,0}(1+z)^{-0.14} \, ,\nonumber \\ C_2(z) &=& C_{2,0}(1+z)^{-0.06} \, ,\nonumber \\ C_2(z) &=& C_{3,0}(1+z)^{-\gamma } \, ,\nonumber \\ \log \left(\gamma \right) &=& -\left(\frac{0.75}{\log \left(\Delta _\textrm{c}/75\right)}\right)^{1.2} \, , \end{eqnarray*}

(11)

where the subscript 0 denotes the value of the quantity at |$z$| = 0 and Δ_c defines the mean overdensity of the spherical haloes in terms of the critical density of the universe. The quantities C₀, C_1,0, C_2,0, C_3,0 depend on Δ_c and we refer the reader to Tinker et al. (2008) for their numerical values. We use for our forecasts Δ_c = 200 and 500 for Euclid and eROSITA, respectively.

3.2 Halo bias function

We now specify the halo bias function, b_eff(⁠|$z$|⁠). The linear bias weighted by the halo mass function is

\begin{eqnarray*} b_\textrm{eff}(z) = \frac{1}{n_\textrm{h}(z)} \int _0^\infty \textrm{d}M n_\textrm{h}(M,z)b_\textrm{h}(M,z) X(M,z) \, , \end{eqnarray*}

(12)

where the integrated halo redshift distribution is

\begin{eqnarray*} n_\textrm{h}(z) = \int _0^\infty \textrm{d}M n_\textrm{h}(M,z) X(M,z) \, . \end{eqnarray*}

(13)

According to Tinker et al. (2010), the Eulerian halo bias is

\begin{eqnarray*} b_\textrm{h}(M_\textrm{h},z) = 1-c_1\frac{\nu ^{c_4}}{\nu ^{c_4}+\delta _\textrm{c}^{c_4}}+c_2\nu ^{c_5}+c_3\nu ^{c_6} \, , \end{eqnarray*}

(14)

where ν = δ_c/σ(M_h, |$z$|⁠) and δ_c is the critical density for collapse (in all calculations we use δ_c = 1.686) and the parameters of the halo bias function in equation (14) as a function of Δ_c are

\begin{eqnarray*} c_1 &=& 1+0.24x{\rm e}^{-\left(4/x\right)^4},\nonumber \\ c_2 &=& 0.183,\nonumber \\ c_3 &=& 0.019+0.107x+0.19{\rm e}^{-\left(4/x\right)^4},\nonumber \\ c_4 &=& 0.44x-0.88,\nonumber \\ c_5 &=& 1.5,\nonumber \\ c_6 &=& 2.4, \end{eqnarray*}

where x ≡ log Δ_c.

3.3 Survey characteristic function

We express the survey characteristic completeness function in equation (7) as

\begin{eqnarray*} X(M,z) = \int _{M_\textrm{lim}(z)}^\infty \mathrm{d}M^{\textrm{obs}}P(M^{\textrm{obs}}|M) \, , \end{eqnarray*}

(15)

where M_lim(⁠|$z$|⁠) represents the minimum value of the observed mass for a cluster to be included in the survey, and it is determined by the survey selection function. The function P(M^obs|M) gives the probability that a cluster of true mass M has a measured mass M^obs and takes into account the uncertainties that a scaling relation introduces in the knowledge of the cluster mass. Following Lima & Hu (2005) and Sartoris et al. (2010), the probability of assigning to a cluster of true mass M an observed mass M^obs can be well approximated with a lognormal density distribution:

\begin{eqnarray*} P(M^{\textrm{obs}}|M) &=& \frac{1}{M^\textrm{obs}\sqrt{2\pi \sigma ^2_{\log M}}}\nonumber\\ &&\times \, \text{exp}\left[-\frac{(\ln M^\textrm{obs}-B_M-\ln M)^2}{2\sigma ^2_{\log M}}\right] \, , \end{eqnarray*}

(16)

where the parameter B_M = B_{M, 0}|$+$| α log (1 + |$z$|⁠) represents the fractional value of the systematic bias in the mass estimate and |$\sigma _{\log M}^2 = \sigma _{\log M,0}^2 - 1 + (1+z)^{2\beta }$| is the intrinsic scattering. We treat B_{M, 0} = 0, α = 0, σ_{log M, 0} = 0.2, and β = 0.125 as fiducial as in Sartoris et al. (2016) and we consider them as nuisance parameters in the following analysis.

4 FUTURE SURVEYS

In this section, we describe two future cluster catalogues suitable for the ISW detection by cross-correlation with CMB, i.e. those expected from eROSITA (Predehl et al. 2010) and Euclid (Laureijs et al. 2011). For comparison, we also present the specifications for the photometric and spectroscopic galaxy surveys expected from Euclid, which are expected to improve on the current statistical significance of the ISW detection with galaxy surveys.

4.1 eROSITA cluster survey

eROSITA⁶ (Predehl et al. 2010) is the primary science instrument onboard the Spectrum Roentgen-Gamma (SRG) satellite,⁷ launched in 2017.

eROSITA is expected to perform an X-ray all-sky survey with a sensitivity ∼30 times better than ROSAT and to cover a redshift range of 0 ≤ |$z$| ≤ 1.5 with a sky coverage of 27 000 deg². We consider the eROSITA cluster selection function presented in Pillepich, Porciani & Reiprich (2012), computed for a mass at Δ_c = 500 with an exposure time of 1.6 × 10³ s and a detection threshold of 50 photons. In addition, we adopt as lower cut for the minimum mass |$5\times 10^{13}\ \mathrm{M}_\odot \, h^{-1}$|⁠.

The resulting specifications of the eROSITA cluster catalogue (hereafter referred eR_cl) are summarized in Table 1, leading to a total number of clusters ∼8.1 × 10⁴. The corresponding redshift density distribution and the linear bias for eROSITA are shown in Fig. 1.

Figure 1.

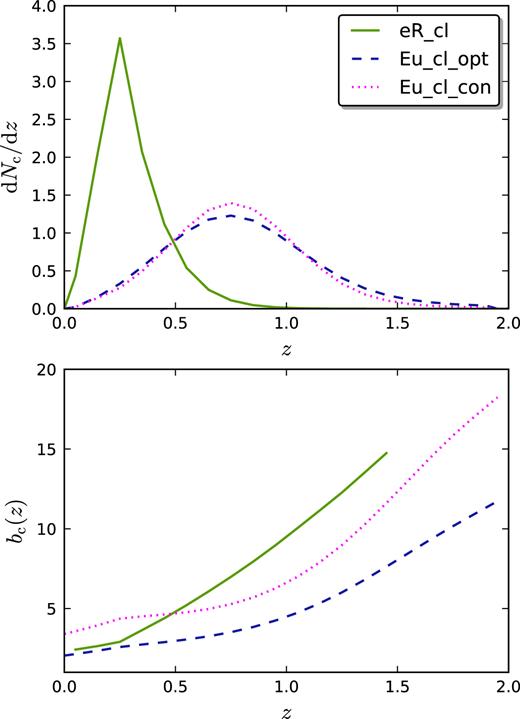
In the top panel, we plot the normalized cluster redshift distributions adopted for each survey: eROSITA (solid green), optimistic Euclid (dashed blue), and conservative Euclid (dotted magenta). In the bottom panel, we plot the corresponding linear bias.

Open in new tab Download slide

Table 1.

Open in new tab

Summary of the characteristics of the surveys studied in this paper: fraction of the sky available f_sky and surface density of tracer |$\bar{n}_\textrm{X}$|⁠.

	f_sky (deg²)	\|$\bar{n}_\textrm{X}$\| (deg⁻²)
eR_cl	27 000	2.9
Eu_cl_opt	15 000	72
Eu_cl_con	15 000	10.8
Eu_gal_sp	15 000	3960
Eu_gal_ph	15 000	108 000

Table 1.

Open in new tab

Summary of the characteristics of the surveys studied in this paper: fraction of the sky available f_sky and surface density of tracer |$\bar{n}_\textrm{X}$|⁠.

	f_sky (deg²)	\|$\bar{n}_\textrm{X}$\| (deg⁻²)
eR_cl	27 000	2.9
Eu_cl_opt	15 000	72
Eu_cl_con	15 000	10.8
Eu_gal_sp	15 000	3960
Eu_gal_ph	15 000	108 000

4.2 Euclid cluster survey

The European Space Agency (ESA) Cosmic Vision mission Euclid (Laureijs et al. 2011) is scheduled to be launched in 2021, with the goal of exploring the dark sector of the Universe.

As selection function for the expected Euclid cluster catalogue we consider the one presented in Sartoris et al. (2016) computed for a mass at Δ_c = 200 with a threshold for the significance of the clusters detection of 3 in terms of the ratio between the cluster galaxy number counts and the field rms (hereafter referred Eu_cl_opt) with a sky coverage of 15 000 deg² over a redshift range of 0.2 ≤ |$z$| ≤ 2. We also consider a detection threshold of 5 as a more conservative case (hereafter referred Eu_cl_con). This selection function was obtained following a phenomenological approach. In summary, the number of cluster galaxies is obtained by integration of observed cluster luminosity function down to the H-band magnitude limit of the Euclid survey, and the variance in the field counts takes into account both Poisson noise and cosmic variance (see Sartoris et al. (2016) for more details). Even if the galaxy cluster mass selection function used for the Euclid photometric survey is not constant (see Sartoris et al. 2016), a mass limit of |$8\times 10^{13}\ \mathrm{M}_\odot \, h^{-1}$| and |$3\times 10^{14}\ \mathrm{M}_\odot \, h^{-1}$| approximately mimics the counts of Eu_cl_opt and of Eu_cl_con, respectively.

The resulting specifications of the optimistic and conservative Euclid expected cluster catalogues are summarized in Table 1, leading to a total number of clusters 1.3 × 10⁶ and 2.0 × 10⁵, respectively. See also Fig. 1 for the corresponding redshift density distribution and the linear bias.

4.3 Euclid galaxy surveys

Euclid will measure the galaxy clustering in a spectroscopic survey of tens of millions of H α emitting galaxies and the cosmic shear in a photometric survey of billions of galaxies.

For the Euclid wide spectroscopic survey (hereafter referred Eu_gal_sp), we consider an area of 15 000 deg². According to the updated predictions obtained by Pozzetti et al. (2016), the Euclid wide single-grism survey will reach a flux limit of F_H α > 2 × 10⁻¹⁶ erg cm⁻² s⁻¹ and will cover a redshift range of 0.9 ≤ |$z$| ≤ 1.8.

As specifications for the Euclid photometric survey (hereafter referred Eu_gal_ph), we adopt dN/d|$z$| ∝ |$z$|²exp[−(⁠|$z$|/|$z$|₀)^3/2], with |$z$|₀ = |$z$|_mean/1.412 the peak of the distribution and |$z$|_mean the median (Amendola et al. 2013). We choose |$z$|_mean = 0.9, a surface density |$\bar{n}_\mathrm{g}=30$| per arcmin² and a bias |$b_\textrm{g}(z)=\sqrt{1+z}$| (Amendola et al. 2013).

The specifications for the Euclid spectroscopic and photometric galaxy surveys are summarized in Table 1. In Fig. 2, we plot the normalized redshift density distribution and the effective bias.

Figure 2.

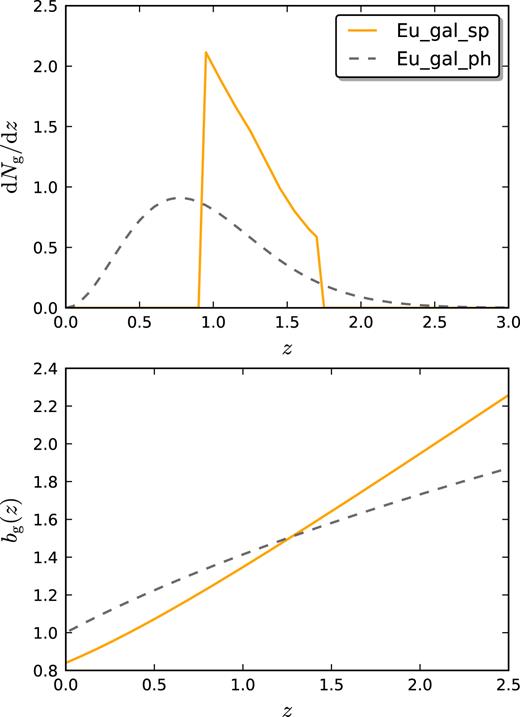
In the top panel, we plot the normalized galaxy redshift distribution adopted for each survey: spectroscopic Euclid (solid orange) and photometric Euclid (dashed grey). In the bottom panel, we plot the corresponding linear bias.

Open in new tab Download slide

5 AN SNR ANALYSIS

We now investigate the detection level of the ISW effect by computing the SNR, which we define as (Cooray 2002; Afshordi 2004)

\begin{eqnarray*} \left(\frac{S}{N}\right)^2_\textrm{X} = \sum _{\ell =2}^{\ell _\textrm{max}} \left(\frac{S}{N}\right)^2_{\textrm{X},\, \ell } \, , \end{eqnarray*}

(17)

and

\begin{eqnarray*} \left(\frac{S}{N}\right)^2_{\textrm{T},\ell } = \left(2\ell +1\right) \frac{f_\textrm{sky}^\textrm{X}\left(C_\ell ^\mathrm{TX}\right)^2}{\left(C_\ell ^\mathrm{TX}\right)^2+\bar{C}_\ell ^\mathrm{TT} \bar{C}_\ell ^\mathrm{XX}} \, , \end{eqnarray*}

(18)

where f_sky is the sky coverage of the survey and an overall bar stands for the sum of the signal and its noise. By |$\bar{C}_\ell ^\mathrm{TT}$| we denote the total CMB temperature angular power spectrum, which includes both the ISW and the Sachs–Wolfe terms, plus the effective noise:

\begin{eqnarray*} \bar{C}_\ell ^\mathrm{TT} = C_\ell ^\mathrm{TT} + {\cal N}_\ell ^\mathrm{T} \, . \end{eqnarray*}

(19)

At low and intermediate multipoles, Planck provides a measurement with a high SNR of the total anisotropy signal and the effective noise in temperature can therefore be neglected. The noise contribution for the mass tracer associated with a finite number of counts corresponds to a shot-noise as

\begin{eqnarray*} {\cal N}_\ell ^\textrm{X} = \frac{1}{\bar{n}_\mathrm{X}} \, , \end{eqnarray*}

(20)

where |$\bar{n}_\mathrm{X}$| is the surface density of tracers per steradian.

We show in Figs 3 and 4 the angular power spectra and the noises, for cluster and galaxy surveys respectively, calculated with the assumed fiducial cosmology and used in the SNR analysis.

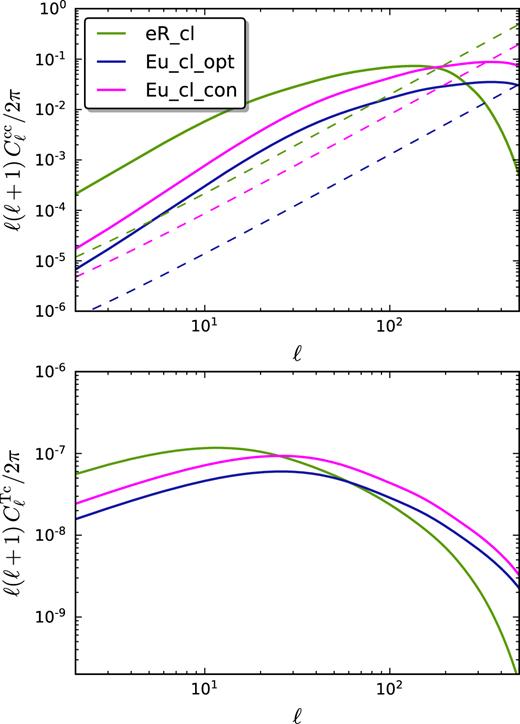
$Cluster angular power spectra $C_\ell ^\textrm{cc}$ (top panel) and cross-correlation angular power spectra $C_\ell ^\textrm{Tc}$ (bottom panel) for the three surveys of clusters: eROSITA (solid green), optimistic Euclid (solid blue), and conservative Euclid (solid magenta). In the top panel, the corresponding shot-noise (dashed lines) is also shown.$

Figure 3.

Cluster angular power spectra |$C_\ell ^\textrm{cc}$| (top panel) and cross-correlation angular power spectra |$C_\ell ^\textrm{Tc}$| (bottom panel) for the three surveys of clusters: eROSITA (solid green), optimistic Euclid (solid blue), and conservative Euclid (solid magenta). In the top panel, the corresponding shot-noise (dashed lines) is also shown.

Open in new tab Download slide

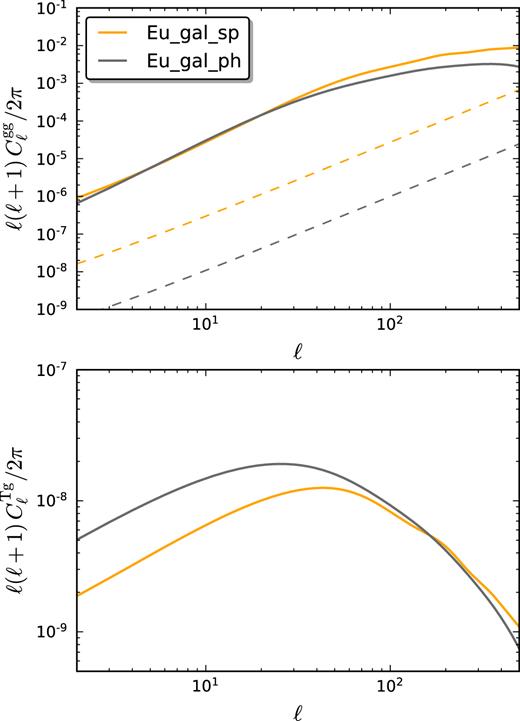
$Galaxy angular power spectra $C_\ell ^\textrm{gg}$ (top panel) and cross-correlation angular power spectra $C_\ell ^\textrm{Tg}$ (bottom panel) for two surveys of galaxies: spectroscopic Euclid (solid orange) and photometric Euclid (solid grey). In the top panel, the corresponding shot-noise (dashed lines) is also shown.$

Figure 4.

Galaxy angular power spectra |$C_\ell ^\textrm{gg}$| (top panel) and cross-correlation angular power spectra |$C_\ell ^\textrm{Tg}$| (bottom panel) for two surveys of galaxies: spectroscopic Euclid (solid orange) and photometric Euclid (solid grey). In the top panel, the corresponding shot-noise (dashed lines) is also shown.

Open in new tab Download slide

The ISW effect leaves also an imprint on the E-mode polarization that can be quantified in analogy with equation (17), by substituting T with E. We have checked that the SNR is at most 0.2 for the surveys considered here. Whereas the cross-correlation between the CMB E-mode polarization and LSS tracers is small as expected (Cooray & Melchiorri 2006), the inclusion of polarization data allows a reduction of the error bars in the overall detection of the ISW effect (Frommert & Enßlin 2009). Indeed, the E-mode polarization is correlated with primary temperature anisotropy (Zaldarriaga 1997) and therefore indirectly helps in disentangling the ISW effect. It is possible to extend the SNR analysis in equation (17) to the inclusion of polarization as in Frommert & Enßlin (2009):

\begin{eqnarray*} \left(\frac{S}{N}\right)^2_{\rm{T,\, ~E},\, \ell } =\left(2\ell +1\right) \frac{f_\textrm{sky}^\textrm{X}\left(C_\ell ^\mathrm{TX}\right)^2}{\left(C_\ell ^\mathrm{TX}\right)^2+\left(\bar{C}_\ell ^\mathrm{TT}-\frac{\left(C_\ell ^\mathrm{TE}\right)^2}{\bar{C}_\ell ^\mathrm{EE}}\right)\bar{C}_\ell ^\mathrm{XX}} \, . \end{eqnarray*}

(21)

In the denominator of the latter equation, the power spectrum of temperature anisotropies is substituted by the corresponding one of the E-mode uncorrelated temperature map:

\begin{eqnarray*} a_\mathrm{\ell m}^\mathrm{T} \rightarrow a_\mathrm{\ell m}^\mathrm{T} - \frac{C_\ell ^\mathrm{TE}}{\bar{C}_\ell ^\mathrm{EE}}a_\mathrm{\ell m}^\mathrm{E} \, . \end{eqnarray*}

(22)

The E-uncorrelated temperature map has been already introduced in the ISW-LSS cross-correlation analysis of the Planck 2015 release (Planck Collaboration XXI 2016).

We summarize in Table 2 the SNR for the cluster and galaxy catalogues introduced in Section 2 with the estimators in equations (17) and (21). Future cluster catalogues from eROSITA and Euclid could lead to a detection of the ISW effect at high significance |$\gt 3\, \sigma$| thanks to the high number of clusters detected, i.e. a small noise level. We find that the SNR for these two cluster surveys will be comparable to the one obtainable from future galaxy surveys. In particular, for a Euclid survey, the SNR from clusters is smaller than the one expected from the photometric survey, but it is still larger than the SNR forecasted for the spectroscopic survey. The reason resides in the high bias expected for clusters that compensate the larger shot-noise in the observed cluster maps. The inclusion of CMB polarization information in the analysis increases the SNR by approximately 18 per cent as compared to the temperature only, with a weak dependence of the type of survey considered; this is fully consistent with Frommert & Enßlin (2009); Giannantonio et al. (2012). We find the possibility of detecting the ISW effect at |$4\, \sigma$| both the cluster and the galaxy Euclid photometric surveys by adding the CMB polarization information. A comparison between the two SNR calculated from the two estimators is also shown in Fig. 5.

$Comparison of $(S/N)_{\textrm{X}, \ell }$ for temperature only (dashed) and including polarization (solid) according to equations (17) and (21), respectively, for the eROSITA and optimistic Euclid survey of clusters, together with the Euclid photometric survey of galaxies.$

Figure 5.

Comparison of |$(S/N)_{\textrm{X}, \ell }$| for temperature only (dashed) and including polarization (solid) according to equations (17) and (21), respectively, for the eROSITA and optimistic Euclid survey of clusters, together with the Euclid photometric survey of galaxies.

Open in new tab Download slide

Table 2.

Open in new tab

SNR for ISW detection with future cluster and galaxy catalogues. The first row refers to the SNR with CMB temperature in equation (17); the second one to the estimate taking into account both CMB temperature and E-mode polarization as in equation (21).

	eR_cl	Eu_cl_opt	Eu_cl_con	Eu_gal_sp	Eu_gal_ph
T	2.3	3.5	3.3	2.2	3.7
T,E	2.8	4.1	3.9	2.5	4.3

Table 2.

Open in new tab

SNR for ISW detection with future cluster and galaxy catalogues. The first row refers to the SNR with CMB temperature in equation (17); the second one to the estimate taking into account both CMB temperature and E-mode polarization as in equation (21).

	eR_cl	Eu_cl_opt	Eu_cl_con	Eu_gal_sp	Eu_gal_ph
T	2.3	3.5	3.3	2.2	3.7
T,E	2.8	4.1	3.9	2.5	4.3

5.1 Robustness from the specifications of the survey and cosmology

We now test the dependence of the SNR obtainable for clusters on some of the specifications of the surveys, namely the smallest multipoles ℓ_min, the covered sky fraction |$f_\textrm{sky}^\textrm{X}$|⁠, the maximum redshift |$z$|_max, and the minimum detectable mass M_min; for the sake of brevity, we present this analysis for the optimistic Euclid cluster (Eu_cl_opt) survey only and considering the inclusion of polarization in the SNR estimation.

Given the possibility to lose the first multipoles because of some mask effects and possible systematics on the largest scales, we show in Fig. 6 (top left-hand panel) the dependence of SNR on ℓ_min. The SNR remains approximately constant when removing the first few multipoles and is decreased approximately by |$0.5\, \sigma$| cutting the first 10 multipoles.

Figure 6.

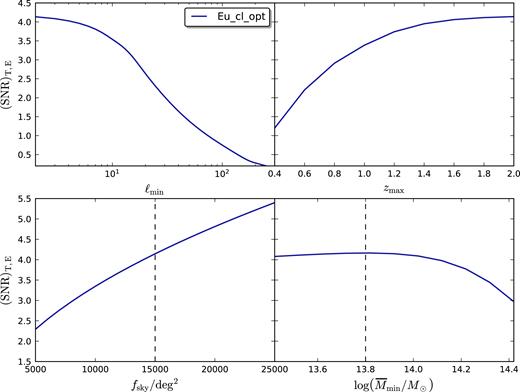
We plot the SNR for the optimistic Euclid cluster survey (Eu_cl_opt) as a function of ℓ_min (top left), the maximum redshift probed by the survey (top right), the area of the sky survey (bottom left), and the minimum observed mass as over the redshift range 0.2 ≤ |$z$| ≤ 2 (bottom right). Dashed line represents the expected SNR for the Eu_cl_opt specifications. All the SNR take into account of the contribution from CMB E-mode polarization according to equation (21).

Open in new tab Download slide

Bottom left-hand panel of Fig. 6 shows the SNR as a function of the observed sky fraction, which does not affect just equation (21) as SNR|$\ \propto \sqrt{f_\textrm{sky}^\textrm{X}}$|⁠, but it changes also the amount of total clusters observed, i.e. the shot-noise error.

We finally study the dependence of the SNR when changing M_min. We vertically shift a redshift independent selection function around 8 × 10¹³ M_⊙, as representative of the selection function from (Sartoris et al. 2016) for the photometric Euclid cluster survey. The results in Fig. 6 (bottom left-hand panel) show that the expected selection function for Euclid would be optimal in terms of SNR.

We can conclude that for the ISW detection is more important to have wide surveys, covering a large fraction of the sky, than deeper ones, since the surveys analysed are already signal dominated on the scales relevant for the ISW.

We now briefly discuss the dependence of the SNR on the underlying cosmology. The cross-correlation power spectrum is sensitive to the total matter density Ω_m and to the dark energy equation of state |$w$|₀. They both change the amplitude of |$C_\ell ^\mathrm{TX}$| (since for a flat universe an increased amount of matter density corresponds to have a smaller amount of dark energy density). Moreover, the peak of |$C_\ell ^\mathrm{TX}$| is shifted according to a different matter-dark energy equivalence. We show the dependence of the SNR on these two parameters in Fig. 7 by keeping fixed all the other cosmological parameters (note that we change σ₈ according to the variation of Ω_m and |$w$|₀). The SNR varies less than |$0.2\, \sigma$| when we change Ω_m up to |$3\, \sigma$| away from the Planck best fit (Aghanim et al. 2016). We find a stronger effect on the dark energy parameter of state |$w$|₀. Even a small shift of Δ|$w$|₀ ≃ 0.2 would lead to a difference larger than |$0.5\, \sigma$| on the SNR. In particular, by assuming a fiducial cosmology with a smaller value of |$w$|₀ leads to a higher SNR.

Figure 7.

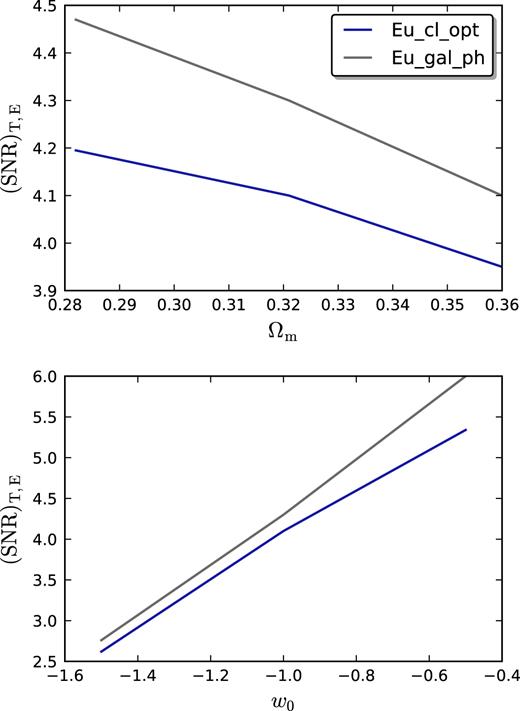
Top panel: dependence on Ω_m of the SNR for the ISW detection with clusters (optimistic Euclid cluster survey, blue line) and with galaxies (photometric Euclid galaxy survey, grey line). Bottom panel: dependence on the dark energy equation of state |$w$|₀ of the SNR for the ISW detection.

Open in new tab Download slide

5.2 Combining clusters with galaxies

Different LSS surveys can be combined to increase the significance of the ISW detection. The best improvement comes for uncorrelated LSS surveys for which the SNR squared can be simply added. In this case, we would obtain for the ISW detection an SNR of 3.2/4.1/4.0 for the combination of Eu_gal_sp and 4.3/5.1/5.0 for the combination of Eu_gal_ph with eR_cl, Eu_cl_opt, Eu_cl_con, respectively. However, this ideal case is usually reached for surveys that cover different redshifts or for distributions of tracers which peak at different redshifts.

The Euclid’s cluster catalogue will be extracted from the photometric galaxy survey. Thus, they will trace by construction the same cosmological information mostly, having a similar redshift distribution and covering the same redshift range.

In order to take into account the cross-correlation between different LSS tracers, we extend the expression for the SNR (17) to

\begin{eqnarray*} \left(\frac{S}{N}\right)^2_{\rm{T,\, ~c\times g},\, \ell } =\sum _{\rm X,Y=c,g} C_\ell ^\mathrm{TX} \left[\text{Cov}_\ell ^{-1}\right]_{\rm XY} \, , C_\ell ^\mathrm{TY} \end{eqnarray*}

(23)

where

\begin{eqnarray*} \left[\text{Cov}_\ell \right]_{\rm XY} = \frac{C_\ell ^\mathrm{TX}C_\ell ^\mathrm{TY}+\bar{C}_\ell ^\mathrm{TT}\bar{C}_\ell ^\mathrm{XY}}{\left(2\ell +1\right)\sqrt{f_\textrm{sky}^\textrm{X}f_\textrm{sky}^\textrm{Y}}} \, . \end{eqnarray*}

(24)

In this case, the SNR by adding the information from Eu_gal_ph becomes 3.7 for both Eu_cl_opt and Eu_cl_con. There is no actual improvement compared to using Eu_gal_ph alone, but nevertheless it offers the possibility of a more robust ISW detection when cosmological parameters are not kept fixed.

The combination of the two Euclid cluster surveys with Eu_gal_sp brings a little improvement of |$+$| 0.2 in the SNR.

Finally, we find that for eROSITA the combination of cluster survey with the galaxy survey from Euclid will be more promising in order to raise the SNR thanks to the low-z coverage from eROSITA. We find a SNR of 3.2/4.1 by combining and cross-correlating eR_cl with Eu_gal_sp and Eu_gal_ph.

Also in this case the addition of the CMB polarization information increases the SNR by a further 18 per cent for all the combinations.

6 COSMOLOGICAL FORECASTS WITH CMB-CLUSTER CROSS-CORRELATION

In this section, we use the Fisher matrix technique (Tegmark, Taylor & Heavens 1997) to compute the joint CMB and cross-correlation forecast constraints on few extensions of the ΛCDM cosmological concordance model.

6.1 Methodology

We use the Fisher matrix derived from the Gaussian approximation of the full likelihood |${\cal L}$|⁠. By using the Gaussian hypothesis for the data d, the likelihood function of the cosmological parameters θ reads as

\begin{eqnarray*} \mathcal {L}\left({\bf \theta }|{\bf d}\right) \propto \frac{1}{\sqrt{|{\bf C}\left({\bf \theta }\right)|}} \text{exp}\left\lbrace -\frac{1}{2}\left({\bf d}^\textrm{obs}\right)^\dagger \left[{\bf C}\left({\bf \theta }\right)\right]^{-1}{\bf d}^\textrm{obs}\right\rbrace, \end{eqnarray*}

(25)

where

\begin{eqnarray*} {\bf C} = \left({\begin{array}{@{}l@{\quad}c@{\quad}c@{\quad}c@{}}C_\ell ^\textrm{TT} & C_\ell ^\textrm{TE} & C_\ell ^\textrm{TX} \\ C_\ell ^\textrm{TE} & C_\ell ^\textrm{EE} & C_\ell ^\textrm{EX} \\ C_\ell ^\textrm{TX} & C_\ell ^\textrm{EX} & C_\ell ^\textrm{XX} \\ \end{array} } \right) \, , \end{eqnarray*}

(26)

is the theoretical covariance matrix of the modelled data |${\bf d}=\left\lbrace a_{\ell m}^\mathrm{T},a_{\ell m}^\mathrm{E},a_{\ell m}^\mathrm{X}\right\rbrace$| where X = {c, g} and |C(θ)| its determinant. From equation (25), we write the Fisher matrix in compact form as

\begin{eqnarray*} {\cal F}_{\alpha \beta } &=& \left\langle \frac{\partial ^2\log {\cal L}}{\partial \theta _\alpha \partial \theta _\beta } \right\rangle \, ,\nonumber \\ &=& \frac{1}{2} \text{tr} \left[\frac{\partial {\bf C}}{\partial \theta _\alpha }{\bf C}^{-1}\frac{\partial {\bf C}}{\partial \theta _\alpha }{\bf C}^{-1}\right]\, , \nonumber \\ &=& \sum _{\ell }\frac{\left(2\ell +1\right)f_\textrm{sky}^\textrm{X}}{2} \frac{\partial C_\ell ^\textrm{AB}}{\partial \theta _\alpha } \text{Cov}^{-1}\left(C_\ell ^\textrm{AB},C_\ell ^\textrm{CD}\right) \frac{\partial C_\ell ^\textrm{CD}}{\partial \theta _\beta } \, , \end{eqnarray*}

(27)

where |$\bar{C}_\ell ^{\rm AB} = C^{\rm AB}_\ell + \delta _\textrm{AB}N^{\rm A}_\ell$| is the sum of the signal and the noise, with |${\cal N}^{\rm\, TE}_\ell ,{\cal N}^{\rm\, TX}_\ell ,{\cal N}^{\rm \,EX}_\ell =0$|⁠. For the temperature and polarization angular power spectra, here |${\cal N}^{\rm\, T,E}_\ell =\sigma _{\rm T,E}\, b^{-2}_\ell$| is the isotropic noise deconvolved with the instrument beam, |$b_\ell ^2$| is the beam window function, assumed Gaussian, with |$b_\ell = {\rm e}^{-\ell (\ell + 1) \theta _{\rm FWHM}^2/16\ln 2}$|⁠; θ_FWHM is the full width half-maximum (FWHM) of the beam in radians; σ_TT and σ_EE are the square of the detector noise level on a steradian patch for temperature and polarization, respectively. See the Appendix for the full structure of the covariance matrix Cov in equation (27).

As representative specifications for CMB we consider the Planck 143 GHz channel full mission sensitivity and angular resolution as given in Adam et al. (2016) and used in Ballardini et al. (2016). These correspond to θ_FWHM = 7.3 arcmin, σ_T = 33 arcmin|$\, \mu$|K and σ_E = 70.2 arcmin|$\, \mu$|K. For cluster and galaxy specifications, we use those listed in Table 1.

We consider as set of cosmological parameters in our forecast analysis the six standard ΛCDM parameters ω_b, ω_c, H₀, τ, n_s, and log (10¹⁰ A_s), plus some extra parameters described in the following subsection. We also consider the bias as a nuisance parameter marginalizing over it.

In the case of clusters, in addition to the variation on all the cosmological parameters we consider the dependence on four nuisance parameters |$B_\rm{M,\, ~0},\alpha ,\sigma ^2_{\log \, M,0},\, \beta$| introduced in Section 3.3, as sources of uncertainties on the cluster selection function, as in Sartoris et al. (2016), by marginalizing over them.

6.2 Results

In this paper, we restrict ourselves to forecast the joint CMB and ISW-cluster cross-correlation constraints on few relevant cosmological models as in Douspis et al. (2008). With this setting, the impact of ISW-cluster cross-correlation can be easily evaluated, whereas it would be hardly visible if we were considering the full combination of CMB and cluster cosmological information. As for the SNR in the previous section, we compare these results with those obtained by the joint CMB and ISW-galaxy cross-correlation expected from the Euclid spectroscopic and photometric surveys.

We first forecast the constraints on the redshift-independent parameter of state of dark energy |$w$|₀. Fig. 8 shows how the CMB-cluster cross-correlation improves on the CMB results alone. Our results show that CMB-cluster cross-correlation could lead to constraints similar to the one expected from the CMB-galaxy one, improving the constraints on |$w$|₀ obtained from CMB data alone by around 20–30 per cent.

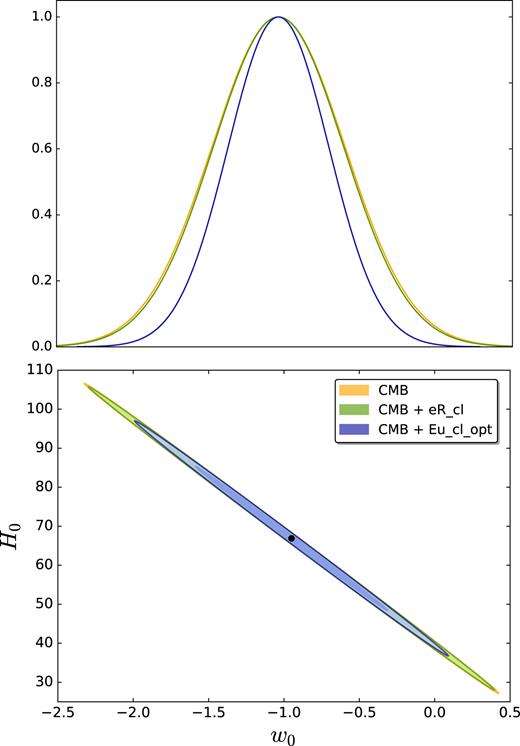
In the bottom panel, we show the joint constraints on ($w$0, H0) at the 68 per cent and 95 per cent CL. We show forecasts for the combination of the CMB and the CMB-LSS cross-correlation from eROSITA (green) and from the optimistic Euclid photometric cluster survey (blue). We show also the results for the CMB alone (yellow). In the top panel, we show the corresponding posterior distributions for $w$0.

Figure 8.

In the bottom panel, we show the joint constraints on (⁠|$w$|₀, H₀) at the 68 per cent and 95 per cent CL. We show forecasts for the combination of the CMB and the CMB-LSS cross-correlation from eROSITA (green) and from the optimistic Euclid photometric cluster survey (blue). We show also the results for the CMB alone (yellow). In the top panel, we show the corresponding posterior distributions for |$w$|₀.

Open in new tab Download slide

As second cosmological scenario, we show the constraints for a cosmology in which the parameter of state of dark energy is allowed to be redshift dependent (Chevallier & Polarski 2001; Linder 2003):

\begin{eqnarray*} w(z) = w_0 + \frac{z}{1+z} w_a \, , \end{eqnarray*}

(28)

where |$w$|₀ is the present value of the equation of state and |$w$|_a is its first derivative with respect to the scale parameter a(t). Also in this case, we see from Fig. 9 that the addition of CMB-cluster cross-correlations leads to a significant improvement for the dark energy parameters, with a similar performance between eROSITA and Euclid. The improvement with respect to CMB-only constraints for the |$w$|₀−|$w$|_a CDM cosmological model corresponds to 6 per cent on H₀, 4 per cent over n_s, 5 per cent on |$w$|₀, and 20 per cent on |$w$|_a. The figure of merit (FoM) for the dark energy parameters (Albrecht et al. 2009) improves by a factor of 1.5 when the ISW-cluster cross-correlation is included. In Fig. 9, the difference between the orientation of the con tour of eROSITA and the one of Euclid in the |$w$|₀–|$w$|_a parameters space is not only due to the different redshift range probed by the two surveys but also due to the larger sky coverage from eROSITA that helps in breaking the degeneracy between the two parameters.

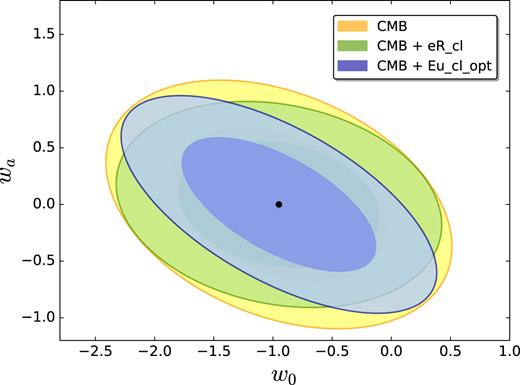
Joint constraints on ($w$0, $w$a) at the 68 per cent and 95 per cent CL. We show forecasts for the combination of the CMB and the CMB-LSS cross-correlation from eROSITA(green) and from the optimistic Euclidphotometric cluster survey (blue). We show also the results for the CMB alone (yellow).

Figure 9.

Joint constraints on (⁠|$w$|₀, |$w$|_a) at the 68 per cent and 95 per cent CL. We show forecasts for the combination of the CMB and the CMB-LSS cross-correlation from eROSITA(green) and from the optimistic Euclidphotometric cluster survey (blue). We show also the results for the CMB alone (yellow).

Open in new tab Download slide

We consider a cosmological model in which there is a suppression on large scales of the primodial curvature power spectrum (Contaldi et al. 2003):

\begin{eqnarray*} \mathcal {P}_{\cal R}(k) = \mathcal {P}_{{\cal R},\, 0}(k) \left\lbrace 1 - \exp \left[- \left(\frac{k}{k_{\rm c}} \right)^{\lambda _{\rm c}} \right] \right\rbrace \, , \end{eqnarray*}

(29)

where k_c is the relevant scale of deviation from a power-law spectrum and λ_c adjusts the stiffness of the suppression. For this model, the addition of the CMB-cluster cross-correlation leads to a hardly visible improvement in the constraints on (λ_c, k_c) with respect to the CMB constraints, since, even if on large scales, the suppression induces a change in the SW contribution rather than on the ISW one. Nevertheless, the ISW-LSS cross-correlation is useful to break degeneracies in the physical effects at play on the largest scales.

Note that in our calculations we have taken into account the dependence of both the halo mass and bias functions on the underlying cosmology through the variance of the fractional density fluctuation σ²(M, |$z$|⁠). We consider this dependence when varying the angular power spectra |$C_\ell ^\textrm{cc}$| and |$C_\ell ^\textrm{Tc}$| around the fiducial cosmology in the calculation of the Fisher matrix (27). The effect of neglecting this dependence would lead to an increase in the uncertainties on the cosmological parameters of about 10 per cent for the most significant parameters such as |$w$|₀, and |$w$|_a.

As a semi-idealized case, we also consider the constraints on the |$w$|₀–|$w$|_a plane by assuming perfect knowledge of the scaling relation between the true and the observed cluster mass, i.e. by fixing all the corresponding nuisance parameters: this semi-idealized case would cast the cluster case at the same footing of the galaxy one, in which no nuisance parameter is considered. In Fig. 10, we show the comparison of the constraints in the |$w$|₀–|$w$|_a parameters space between the CMB-cluster cross-correlation from Eu_cl_opt, with and without perfect knowledge of the scaling relation, and the CMB-galaxy cross-correlation from Eu_gal_ph. Assuming a perfect knowledge of the nuisance parameters connected to the cluster selection function leads to an improvement in the constraints obtainable with the help the CMB-cluster cross-correlation. In particular, we found an improvement of 10 per cent for |$w$|₀, of 20 per cent and 40 per cent for |$w$|₀ and |$w$|_a, of 5 per cent for k_c and λ_c.

Figure 10.

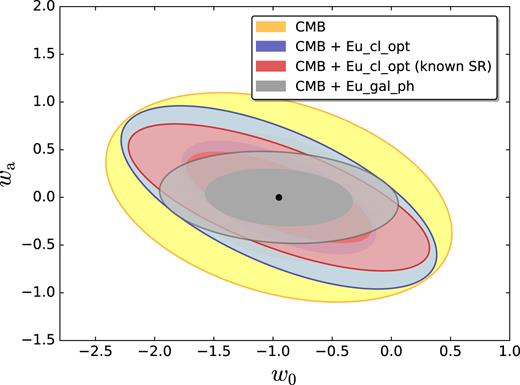
Joint constraints on (⁠|$w$|₀, |$w$|_a) at the 68 per cent and 95 per cent CL. We show forecasts for the combination of the CMB and the CMB-LSS cross-correlation from the optimistic Euclid photometric cluster survey with (red) and without (blue) assuming a perfect knowledge of the scaling relation, and from the photometric Euclid galaxy survey (grey). We also show the results for the CMB alone for comparison (yellow).

Open in new tab Download slide

7 CONCLUSIONS

Cosmology with clusters is a rapidly evolving field, thanks to improvements in observations. Current catalogues are already sufficient to obtain an accurate measurement of the baryon acoustic oscillation with galaxy clusters as from the Sloan Digital Sky Survey leading to a distance-redshift relation in full agreement with Planck observations and with uncertainties similar to the one obtained by galaxy surveys (Veropalumbo et al. 2014, 2016). In the perspective of future surveys in several wavelengths which will provide catalogues with a higher number of clusters over a wider redshift range, we have studied the capabilities to detect the ISW effect by a CMB-cluster cross-correlation. Note that this ISW-cluster cross-correlation is not internal to CMB as the previously studied ISW-tSZ cross-correlation (Taburet et al. 2011). In this perspective, it will be essential to control the SZ cluster residuals in CMB maps that could bias the cross-correlation measurements between clusters and CMB (Chen, Remazeilles & Dickinson 2018).

As two representative cases, we have considered the specifications of the cluster catalogues as expected from two coming space missions, i.e. eROSITA (Predehl et al. 2010) and Euclid (Laureijs et al. 2011). We have found that the CMB-cluster cross-correlation could be used for a statistically significant detection of the ISW effect. As two general remarks, we have found that (1) the SNR of the CMB-cluster cross-correlation benefits of the large cluster bias that balances the larger shot-noise in cluster catalogues compared to galaxy surveys; (2) the dependence of the cluster bias on cosmology needs to be taken into account to extract the full information from the cross-correlation with CMB. Whereas for eROSITA the cross-correlation with CMB would be an added value for the legacy of its cluster catalogue, for Euclid it would constitute a sort of coarse graining of the CMB galaxy cross-correlation and a key verification of the structure formation process. Nevertheless, the CMB-cluster would be another valuable cross-correlation within the Euclid probes and would add useful information on the bias for the cluster catalogue. The cross-correlation studied here would be of interest for other surveys as well, as LSST (Abell et al. 2009) and SKA (Maartens et al. 2015).

ACKNOWLEDGEMENTS

We thank Nabila Aghanim and Carlo Baccigalupi for useful comments to the paper. We acknowledge financial contribution from the agreement ASI n.I/023/12/0 ‘Attività relative alla fase B2/C per la missione Euclid’. The support by the ‘ASI/INAF Agreement 2014-024-R.0 for the Planck LFI Activity of Phase E2’ is also acknowledged. MB, DP, FF, and LM acknowledge the support from the grant MIUR PRIN 2015 ‘Cosmology and Fundamental Physics: illuminating the Dark Universe with Euclid’. MB was supported by the South African Radio Astronomy Observatory, which is a facility of the National Research Foundation, an agency of the Department of Science and Technology and the Claude Leon Foundation. BS acknowledges financial support from the University of Trieste through the program ‘Finanziamento di Ateneo per progetti di ricerca scientifica – FRA 2015’, a grant from ’Consorzio per la Fisica – Trieste’ and from the PRIN 2015W7KAWC project, funded by the Italian Minister for University and Research.

Footnotes

1

http://desi.lbl.gov/

2

http://sci.esa.int/euclid/

3

http://www.lsst.org/

4

http://www.skatelescope.org/

5

The only analysis of the late ISW using clusters has been performed by Granett, Neyrinck & Szapudi (2008) stacking WMAP data behind 50 superclusters (and 50 supervoids) to study the residual signal from the detection of the thermal SZ effect.

6

Extended ROentgen Survey with an Imaging Telescope Array, http://www.mpe.mpg.de/erosita/.

7

http://hea.iki.rssi.ru/SRG/en/index.php

REFERENCES

Adam

R.

Planck, et al. ,

Planck

,

2016

,

A&A

,

594

,

A1

10.1051/0004-6361/201527101

Crossref

Search ADS

Afshordi

N.

,

2004

,

Phys. Rev. D

,

70

,

083536

10.1103/PhysRevD.70.083536

Crossref

Search ADS

Afshordi

N.

,

Loh

Y.-S.

,

Strauss

M. A.

,

2004

,

Phys. Rev. D

,

69

,

083524

10.1103/PhysRevD.69.083524

Crossref

Search ADS

Albrecht

A.

et al. ,

2009

, preprint (arXiv:0901.0721)

Amendola

L.

et al. ,

2013

,

Living Rev. Rel.

,

16

,

6

Crossref

Search ADS

Ballardini

M.

,

Finelli

F.

,

Fedeli

C.

,

Moscardini

L.

,

2016

,

JCAP

,

1610

,

041

10.1088/1475-7516/2016/10/041

Crossref

Search ADS

Bianchini

F.

,

Renzi

A.

,

Marinucci

D.

,

2016

,

JCAP

,

1611

,

050

10.1088/1475-7516/2016/11/050

Crossref

Search ADS

Boughn

S.

,

Crittenden

R.

,

2004

,

Nature

,

427

,

45

Chen

T.

,

Remazeilles

M.

,

Dickinson

C.

,

2018

,

MNRAS

,

479

,

4239

Crossref

Search ADS

Chevallier

M.

,

Polarski

D.

,

2001

,

Int. J. Mod. Phys. D

,

10

,

213

10.1142/S0218271801000822

Crossref

Search ADS

Contaldi

C. R.

,

Peloso

M.

,

Kofman

L.

,

Linde

A. D.

,

2003

,

JCAP

,

0307

,

002

10.1088/1475-7516/2003/07/002

Crossref

Search ADS

Cooray

A.

,

2002

,

Phys. Rev. D

,

65

,

103510

10.1103/PhysRevD.65.103510

Crossref

Search ADS

Cooray

A.

,

Melchiorri

A.

,

2006

,

JCAP

,

0601

,

018

10.1088/1475-7516/2006/01/018

Crossref

Search ADS

Crittenden

R. G.

,

Turok

N.

,

1996

,

Phys. Rev. Lett.

,

76

,

575

10.1103/PhysRevLett.76.575

Crossref

Search ADS

PubMed

DESI Collaboration

, et al. ,

2013

, preprint (arXiv:1308.0847)

DESI Collaboration, et al. ,

2016a

,

preprint (

arXiv:1611.00036)

DESI Collaboration

, et al. ,

2016b

, preprint

(arXiv:1611.00037)

Douspis

M.

,

Castro

P. G.

,

Caprini

C.

,

Aghanim

N.

,

2008

,

A&A

,

485

,

395

10.1051/0004-6361:200809499

Crossref

Search ADS

Dupe

F. X.

,

Rassat

A.

,

Starck

J. L.

,

Fadili

M. J.

,

2011

,

A&A

,

534

,

A51

10.1051/0004-6361/201015893

Crossref

Search ADS

Ferraro

S.

,

Sherwin

B. D.

,

Spergel

D. N.

,

2015

,

Phys. Rev. D

,

91

,

083533

10.1103/PhysRevD.91.083533

Crossref

Search ADS

Fosalba

P.

,

Gaztanaga

E.

,

2004

,

MNRAS

,

350

,

L37

10.1111/j.1365-2966.2004.07837.x

Crossref

Search ADS

Frommert

M.

,

Enßlin

T. A.

,

2009

,

MNRAS

,

395

,

1837

10.1111/j.1365-2966.2009.14637.x

Crossref

Search ADS

Giannantonio

T.

,

Crittenden

R.

,

Nichol

R.

,

Ross

A. J.

,

2012

,

MNRAS

,

426

,

2581

10.1111/j.1365-2966.2012.21896.x

Crossref

Search ADS

Giannantonio

T.

,

Scranton

R.

,

Crittenden

R. G.

,

Nichol

R. C.

,

Boughn

S. P.

,

Myers

A. D.

,

Richards

G. T.

,

2008

,

Phys. Rev. D

,

77

,

123520

10.1103/PhysRevD.77.123520

Crossref

Search ADS

Granett

B. R.

,

Neyrinck

M. C.

,

Szapudi

I.

,

2008

,

ApJ

,

683

,

L99

10.1086/591670

Crossref

Search ADS

Hernandez-Monteagudo

C.

,

2010

,

A&A

,

520

,

A101

10.1051/0004-6361/200913344

Crossref

Search ADS

Ho

S.

,

Hirata

C.

,

Padmanabhan

N.

,

Seljak

U.

,

Bahcall

N.

,

2008

,

Phys. Rev. D

,

78

,

043519

10.1103/PhysRevD.78.043519

Crossref

Search ADS

Ilic

S.

,

Douspis

M.

,

Langer

M.

,

Penin

A.

,

Lagache

G.

,

2011

,

MNRAS

,

416

,

2688

10.1111/j.1365-2966.2011.19221.x

Crossref

Search ADS

Kofman

L.

,

Starobinsky

A. A.

,

1985

,

Sov. Astron. Lett.

,

11

,

271

Laureijs

R.

Euclid, et al. ,

Euclid

,

2011

, preprint

(arXiv:1110.3193)

Lima

M.

,

Hu

W.

,

2005

,

Phys. Rev. D

,

72

,

043006

10.1103/PhysRevD.72.043006

Crossref

Search ADS

Linder

E. V.

,

2003

,

Phys. Rev. D

,

68

,

083504

10.1103/PhysRevD.68.083504

Crossref

Search ADS

LSST Science, LSST Project

, et al. ,

2009

, preprint (arXiv:0912.0201)

Maartens

R.

,

Abdalla

F. B.

,

Jarvis

M.

,

Santos

M. G.

,

2015

,

PoS

,

AASKA14

,

016

Mantz

A. B.

,

Allen

S. W.

,

Morris

R. G.

,

Schmidt

R. W.

,

von der Linden

A.

,

Urban

O.

,

2015

,

MNRAS

,

449

,

199

10.1093/mnras/stv219

Crossref

Search ADS

Manzotti

A.

,

Dodelson

S.

,

2014

,

Phys. Rev. D

,

90

,

123009

10.1103/PhysRevD.90.123009

Crossref

Search ADS

McEwen

J. D.

,

Vielva

P.

,

Hobson

M. P.

,

Martinez-Gonzalez

E.

,

Lasenby

A. N.

,

2007

,

MNRAS

,

376

,

1211

10.1111/j.1365-2966.2007.11505.x

Crossref

Search ADS

Nolta

M. R.

et al. ,

2004

,

ApJ

,

608

,

10

10.1086/386536

Crossref

Search ADS

Papai

P.

,

Szapudi

I.

,

Granett

B. R.

,

2011

,

ApJ

,

732

,

27

10.1088/0004-637X/732/1/27

Crossref

Search ADS

Pillepich

A.

,

Porciani

C.

,

Reiprich

T. H.

,

2012

,

MNRAS

,

422

,

44

10.1111/j.1365-2966.2012.20443.x

Crossref

Search ADS

Planck Collaboration

XIX

,

2014

,

A&A

,

571

,

A19

10.1051/0004-6361/201321526

Crossref

Search ADS

Planck Collaboration XLVI, ,

2016

,

A&A

,

596

,

A107

10.1051/0004-6361/201628890

Crossref

Search ADS

Planck Collaboration

et al. ,

2016

,

A&A

,

594

,

A21

10.1051/0004-6361/201525831

Crossref

Search ADS

Pourtsidou

A.

,

Bacon

D.

,

Crittenden

R.

,

2017

,

MNRAS

,

470

,

4251

10.1093/mnras/stx1479

Crossref

Search ADS

Pozzetti

L.

et al. ,

2016

,

A&A

,

590

,

A3

10.1051/0004-6361/201527081

Crossref

Search ADS

Predehl

P.

et al. ,

2010

,

Proc. SPIE

,

7732

,

77320U

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Raccanelli

A.

,

Kovetz

E.

,

Dai

L.

,

Kamionkowski

M.

,

2016

,

Phys. Rev. D

,

93

,

083512

10.1103/PhysRevD.93.083512

Crossref

Search ADS

Raccanelli

A.

et al. ,

2015

,

JCAP

,

1501

,

042

10.1088/1475-7516/2015/01/042

Crossref

Search ADS

Rozo

E.

et al. ,

2010

,

ApJ

,

708

,

645

10.1088/0004-637X/708/1/645

Crossref

Search ADS

Sachs

R. K.

,

Wolfe

A. M.

,

1967

,

ApJ

,

147

,

73

10.1086/148982

Crossref

Search ADS

Sartoris

B.

,

Borgani

S.

,

Fedeli

C.

,

Matarrese

S.

,

Moscardini

L.

,

Rosati

P.

,

Weller

J.

,

2010

,

MNRAS

,

407

,

2339

10.1111/j.1365-2966.2010.17050.x

Crossref

Search ADS

Sartoris

B.

et al. ,

2016

,

MNRAS

,

459

,

1764

10.1093/mnras/stw630

Crossref

Search ADS

Schiavon

F.

,

Finelli

F.

,

Gruppuso

A.

,

Marcos-Caballero

A.

,

Vielva

P.

,

Crittenden

R. G.

,

Barreiro

R. B.

,

Martinez-Gonzalez

E.

,

2012

,

MNRAS

,

427

,

3044

10.1111/j.1365-2966.2012.21974.x

Crossref

Search ADS

Shajib

A. J.

,

Wright

E. L.

,

2016

,

ApJ

,

827

,

116

10.3847/0004-637X/827/2/116

Crossref

Search ADS

Stölzner

B.

,

Cuoco

A.

,

Lesgourgues

J.

,

Bilicki

M.

,

2017

;

Taburet

N.

,

Hernandez-Monteagudo

C.

,

Aghanim

N.

,

Douspis

M.

,

Sunyaev

R. A.

,

2011

,

MNRAS

,

418

,

2207

10.1111/j.1365-2966.2011.19474.x

Crossref

Search ADS

Tegmark

M.

,

Taylor

A.

,

Heavens

A.

,

1997

,

ApJ

,

480

,

22

10.1086/303939

Crossref

Search ADS

Tinker

J. L.

,

Kravtsov

A. V.

,

Klypin

A.

,

Abazajian

K.

,

Warren

M. S.

,

Yepes

G.

,

Gottlober

S.

,

Holz

D. E.

,

2008

,

ApJ

,

688

,

709

10.1086/591439

Crossref

Search ADS

Tinker

J. L.

,

Robertson

B. E.

,

Kravtsov

A. V.

,

Klypin

A.

,

Warren

M. S.

,

Yepes

G.

,

Gottlober

S.

,

2010

,

ApJ

,

724

,

878

10.1088/0004-637X/724/2/878

Crossref

Search ADS

Veropalumbo

A.

,

Marulli

F.

,

Moscardini

L.

,

Moresco

M.

,

Cimatti

A.

,

2014

,

MNRAS

,

442

,

3275

10.1093/mnras/stu1050

Crossref

Search ADS

Veropalumbo

A.

,

Marulli

F.

,

Moscardini

L.

,

Moresco

M.

,

Cimatti

A.

,

2016

,

MNRAS

,

458

,

1909

10.1093/mnras/stw306

Crossref

Search ADS

Vielva

P.

,

Martinez-Gonzalez

E.

,

Tucci

M.

,

2006

,

MNRAS

,

365

,

891

10.1111/j.1365-2966.2005.09764.x

Crossref

Search ADS

Zaldarriaga

M.

,

1997

,

Phys. Rev. D

,

55

,

1822

10.1103/PhysRevD.55.1822

Crossref

Search ADS

APPENDIX: THE COVARIANCE IN THE FISHER APPROACH

Since we are interested in the effect coming from the cross-correlation between the CMB and LSS surveys alone, we do not consider information coming from the LSS tracer angular power spectrum, i.e. we use |$C_\ell ^\textrm{XX}$| just for the covariance. The non-vanishing elements of the symmetric angular power-spectrum covariance matrix Cov_ℓ at the ℓth multipole are

\begin{eqnarray*} \text{Cov}\left(C_\ell ^\textrm{AB},C_\ell ^\textrm{CD}\right) = \bar{C}_\ell ^\textrm{AC}\bar{C}_\ell ^\textrm{BD} + \bar{C}_\ell ^\textrm{AD}\bar{C}_\ell ^\textrm{BC} \, . \end{eqnarray*}

(A1)

The exact structure of |$\text{Cov}^{-1}_\ell$| is more useful compared to its inverse, since it allows to derive all the reduced cases for its inverse when some cross-correlation terms go to zero:

\begin{eqnarray*} \text{Cov}^{-1}_\ell &=& \frac{1}{\left(|{\bf C}\left({\bf \theta }\right)|\right)^2} \nonumber \\ &&\times \,\left({\begin{array}{@{}l@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}}\Sigma _\textrm{TTTT} & \Sigma _\textrm{TTEE} & \Sigma _\textrm{TTTE} & \Sigma _\textrm{TTXX} & \Sigma _\textrm{TTTX} & \Sigma _\textrm{TTEX}\\ \Sigma _\textrm{TTEE} & \Sigma _\textrm{EEEE} & \Sigma _\textrm{EETE} & \Sigma _\textrm{EEXX} & \Sigma _\textrm{EETX} & \Sigma _\textrm{EEEX}\\ \Sigma _\textrm{TTTE} & \Sigma _\textrm{EETE} & \Sigma _\textrm{TETE} & \Sigma _\textrm{TEXX} & \Sigma _\textrm{TETX} & \Sigma _\textrm{TEEX}\\ \Sigma _\textrm{TTXX} & \Sigma _\textrm{EEXX} & \Sigma _\textrm{TEXX} & \Sigma _\textrm{XXXX} & \Sigma _\textrm{XXTX} & \Sigma _\textrm{XXEX}\\ \Sigma _\textrm{TTTX} & \Sigma _\textrm{EETX} & \Sigma _\textrm{TETX} & \Sigma _\textrm{XXTX} & \Sigma _\textrm{TXTX} & \Sigma _\textrm{TXEX}\\ \Sigma _\textrm{TTEX} & \Sigma _\textrm{EEEX} & \Sigma _\textrm{TEEX} & \Sigma _\textrm{XXEX} & \Sigma _\textrm{TXEX} & \Sigma _\textrm{EXEX}\\ \end{array} } \right) \, , \end{eqnarray*}

(A2)

where the autocorrelation are

\begin{eqnarray*} \Sigma _\textrm{TTTT} &=& \left[ \left(\bar{C}_\ell ^{\rm EX}\right)^2-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm XX}\right]^2 \, , \\ \Sigma _\textrm{EEEE} &=& \left[ \left(\bar{C}_\ell ^{\rm TX}\right)^2-\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm XX}\right]^2 \, , \end{eqnarray*}

(A3),(A4)

\begin{eqnarray*} \Sigma _\textrm{TETE} &=& 2\left\lbrace 2\left(\bar{C}_\ell ^{\rm TX}\right)^2\left(\bar{C}_\ell ^{\rm EX}\right)^2\right. \nonumber \\ && \left. +\,\left(\bar{C}_\ell ^{\rm XX}\right)^2\left[\left(\bar{C}_\ell ^{\rm TE}\right)^2- \bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\right] \right.\nonumber \\ && \left.-\,\bar{C}_\ell ^{\rm XX}\left[ 2\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm EX} +\bar{C}_\ell ^{\rm TT}\left(\bar{C}_\ell ^{\rm EX}\right)^2 \right.\right.\nonumber \\ && \left.\left.+\,\bar{C}_\ell ^{\rm EE}\left(\bar{C}_\ell ^{\rm TX}\right)^2\right]\right\rbrace \, , \end{eqnarray*}

(A5)

\begin{eqnarray*} \Sigma _\textrm{XXXX} &=& \left[ \left(\bar{C}_\ell ^{\rm TE}\right)^2-\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\right]^2 \, , \end{eqnarray*}

(A6)

\begin{eqnarray*} \Sigma _\textrm{TXTX} &=& 2\Big\lbrace -2\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm EX} \nonumber \\ && \left.+\,\left(\bar{C}_\ell ^{\rm EX}\right)^2\left[2\left(\bar{C}_\ell ^{\rm TE}\right)^2 - \bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\right] \right.\nonumber \\ && \left.+\,\bar{C}_\ell ^{\rm EE}\left[ \bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm XX} +\bar{C}_\ell ^{\rm EE}\left(\bar{C}_\ell ^{\rm TX}\right)^2 \right.\right.\nonumber \\ && \left.\left.-\,\bar{C}_\ell ^{\rm XX}\left(\bar{C}_\ell ^{\rm TE}\right)^2\right]\right\rbrace \, , \end{eqnarray*}

(A7)

\begin{eqnarray*} \Sigma _\textrm{EXEX} &=& 2\left\lbrace 2\left(\bar{C}_\ell ^{\rm TE}\right)^2\left(\bar{C}_\ell ^{\rm TX}\right)^2 -\bar{C}_\ell ^{\rm XX}\left(\bar{C}_\ell ^{\rm TE}\right)^2\right.\nonumber \\ && \left.+\,\left(\bar{C}_\ell ^{\rm TT}\right)^2\left[\left(\bar{C}_\ell ^{\rm EX}\right)^2+ \bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm XX}\right] \right.\nonumber \\ && -\,\bar{C}_\ell ^{\rm TX}\left(2\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX} +\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}\right)\Big\rbrace \, , \end{eqnarray*}

(A8)

and the cross-correlation are

\begin{eqnarray*} \Sigma _\textrm{TTEE} &=& \left[ \bar{C}_\ell ^{\rm XX}\bar{C}_\ell ^{\rm TE}-\bar{C}_\ell ^{\rm EX}\bar{C}_\ell ^{\rm TX}\right]^2 \, , \end{eqnarray*}

(A9)

\begin{eqnarray*} \Sigma _\textrm{TTTE} &=& 2\left[ \left(\bar{C}_\ell ^{\rm EX}\right)^2-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm XX}\right]\left(\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm XX}-\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm EX}\right) \, , \end{eqnarray*}

(A10)

\begin{eqnarray*} \Sigma _\textrm{TTXX} &=& \left(\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}\right)^2 \, , \end{eqnarray*}

(A11)

\begin{eqnarray*} \Sigma _\textrm{TTTX} &=& 2\left[ \left(\bar{C}_\ell ^{\rm EX}\right)^2-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm XX}\right]\left(\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX}\right) \, , \end{eqnarray*}

(A12)

\begin{eqnarray*} \Sigma _\textrm{TTEX} &=& 2\left(\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}\right) \left(\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm XX}\right) \, , \end{eqnarray*}

(A13)

\begin{eqnarray*} \Sigma _\textrm{EETE} &=& 2\left[ \left(-\bar{C}_\ell ^{\rm TX}\right)^2+\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm XX}\right]\left(\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm XX}\right) \, , \end{eqnarray*}

(A14)

\begin{eqnarray*} \Sigma _\textrm{EEXX} &=& \left(\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX}-\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EX}\right)^2 \, , \end{eqnarray*}

(A15)

\begin{eqnarray*} \Sigma _\textrm{EETX} &=& 2\left(\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm XX}-\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm EX}\right) \left(\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX}\right) \, , \end{eqnarray*}

(A16)

\begin{eqnarray*} \Sigma _\textrm{EEEX} &=& 2\left[ \left(\bar{C}_\ell ^{\rm TX}\right)^2-\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm XX}\right]\left(\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX}\right) \, , \end{eqnarray*}

(A17)

\begin{eqnarray*} \Sigma _\textrm{TEXX} &=& 2\left(\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX}\right) \left(\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX}\right) \, , \end{eqnarray*}

(A18)

\begin{eqnarray*} \Sigma _\textrm{TETX} &=& -2\left\lbrace -2\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm XX}\bar{C}_\ell ^{\rm TX} -\bar{C}_\ell ^{\rm TT}\left(\bar{C}_\ell ^{\rm EX}\right)^3 \right.\nonumber \\ &&\left.+\,\bar{C}_\ell ^{\rm EX}\left[\left(\bar{C}_\ell ^{\rm TX}\right)^2\bar{C}_\ell ^{\rm EE} \right.\right.\nonumber \\ && \left.\left. +\,\bar{C}_\ell ^{\rm XX}\left[\left(\bar{C}_\ell ^{\rm TE}\right)^2+\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\right]\right]\right\rbrace \, , \end{eqnarray*}

(A19)

\begin{eqnarray*} \Sigma _\textrm{TEEX} &=& -2\left\lbrace \left(\bar{C}_\ell ^{\rm EX}\right)^2\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm TX} -\bar{C}_\ell ^{\rm EE}\left(\bar{C}_\ell ^{\rm TX}\right)^3 \right.\nonumber \\ && \left. +\,\bar{C}_\ell ^{\rm XX}\left[\left(\bar{C}_\ell ^{\rm TE}\right)^2\bar{C}_\ell ^{\rm TX} -2\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX} \right.\right.\nonumber \\ && +\,\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}\Big]\Big\rbrace \, , \end{eqnarray*}

(A20)

\begin{eqnarray*} \Sigma _\textrm{XXTX} &=& 2\left[ \left(\bar{C}_\ell ^{\rm TE}\right)^2-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TT}\right]\left(\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}-\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm EX}\right) \, , \end{eqnarray*}

(A21)

\begin{eqnarray*} \Sigma _\textrm{XXEX} &=& 2\left[ \left(\bar{C}_\ell ^{\rm TE}\right)^2-\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TT}\right]\left(\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EX}-\bar{C}_\ell ^{\rm TX}\bar{C}_\ell ^{\rm TE}\right) \, , \end{eqnarray*}

(A22)

\begin{eqnarray*} \Sigma _\textrm{TXEX} &=& -2\left\lbrace \left(\bar{C}_\ell ^{\rm EX}\right)^2\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm TE} \right.\nonumber \\ && \left. +\,\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TX}\left(\bar{C}_\ell ^{\rm TE}\bar{C}_\ell ^{\rm TX} -2\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EX}\right) \right.\nonumber \\ && \left. +\,\bar{C}_\ell ^{\rm XX}\left[\bar{C}_\ell ^{\rm TT}\bar{C}_\ell ^{\rm EE}\bar{C}_\ell ^{\rm TE} -\left(\bar{C}_\ell ^{\rm TE}\right)^3\right]\right\rbrace \, . \end{eqnarray*}

(A23)

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
October 2018	11
November 2018	15
December 2018	2
January 2019	3
February 2019	4
March 2019	9
April 2019	1
May 2019	3
June 2019	8
July 2019	1
August 2019	2
September 2019	9
October 2019	11
December 2019	2
January 2020	3
June 2020	3
October 2020	2
December 2020	5
March 2021	2
April 2021	4
June 2021	3
July 2021	2
October 2021	7
January 2022	4
February 2022	20
March 2022	7
April 2022	18
May 2022	5
June 2022	5
July 2022	24
August 2022	18
September 2022	21
October 2022	22
November 2022	10
December 2022	19
January 2023	6
February 2023	10
March 2023	7
April 2023	16
May 2023	17
June 2023	10
July 2023	1
August 2023	7
September 2023	6
October 2023	3
November 2023	6
December 2023	14
January 2024	9
February 2024	12
March 2024	16
April 2024	11
May 2024	9
June 2024	8
July 2024	21
August 2024	4
September 2024	9
October 2024	18
November 2024	14
December 2024	10
February 2025	6
March 2025	13
April 2025	11
May 2025	5

Article Contents

On the ISW-cluster cross-correlation in future surveys

ABSTRACT

1 INTRODUCTION

2 CROSS-CORRELATION OF ISW EFFECT WITH NUMBER COUNTS

3 CLUSTER NUMBER DENSITY

3.1 Halo mass function

3.2 Halo bias function

3.3 Survey characteristic function

4 FUTURE SURVEYS

4.1 eROSITA cluster survey

4.2 Euclid cluster survey

4.3 Euclid galaxy surveys

5 AN SNR ANALYSIS

5.1 Robustness from the specifications of the survey and cosmology

5.2 Combining clusters with galaxies

6 COSMOLOGICAL FORECASTS WITH CMB-CLUSTER CROSS-CORRELATION

6.1 Methodology

6.2 Results

7 CONCLUSIONS

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

APPENDIX: THE COVARIANCE IN THE FISHER APPROACH

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

On the ISW-cluster cross-correlation in future surveys

ABSTRACT

1 INTRODUCTION

2 CROSS-CORRELATION OF ISW EFFECT WITH NUMBER COUNTS

3 CLUSTER NUMBER DENSITY

3.1 Halo mass function

3.2 Halo bias function

3.3 Survey characteristic function

4 FUTURE SURVEYS

4.1 eROSITA cluster survey

4.2 Euclid cluster survey

4.3 Euclid galaxy surveys

5 AN SNR ANALYSIS

5.1 Robustness from the specifications of the survey and cosmology

5.2 Combining clusters with galaxies

6 COSMOLOGICAL FORECASTS WITH CMB-CLUSTER CROSS-CORRELATION

6.1 Methodology

6.2 Results

7 CONCLUSIONS

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

APPENDIX: THE COVARIANCE IN THE FISHER APPROACH

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only