-
PDF
- Split View
-
Views
-
Cite
Cite
Noam Soker, The requirement for mixing-heating to utilize bubble cosmic rays to heat the intracluster medium, Monthly Notices of the Royal Astronomical Society, Volume 482, Issue 2, January 2019, Pages 1883–1888, https://doi.org/10.1093/mnras/sty2816
Close - Share Icon Share
Abstract
I conduct simple analytical estimates and conclude that mixing by vortices is a more efficient process to transfer the cosmic ray energy of jet-inflated bubbles to the intracluster medium (ICM) than streaming of cosmic rays along magnetic field lines. Jets and the bubbles they inflate transfer heat to the ambient gas in cooling flows in cluster of galaxies and in galaxies. The internal energy of the jet-inflated bubbles is dominate by very hot thermal gas and/or cosmic rays. Cosmic rays that stream along magnetic field lines that connect the bubbles with the ICM heat the ICM as their energy is dissipated there. I find that about half of the cosmic ray energy is dissipated in the bubbles themselves. I also find that the ICM volume that the cosmic ray streaming process heats is only about five times as large as the volume of the bubbles. The outcome of heating by streaming only is that the cosmic rays form a larger bubble filled with very hot thermal gas. Therefore, there is a requirement for a more efficient process to transfer the internal energy of the bubbles to the ICM. I suggest that this process is heating by mixing that operates very well for both cosmic rays and the very hot thermal gas inside the bubbles. This leaves mixing-heating to be the dominant heating process of cooling flows.
1 INTRODUCTION
Although the old ‘cooling-flow problem’ in clusters and groups of galaxies, and in galaxies, has been solved, there is still no consensus on the heating mechanism of the intracluster medium (ICM; for a recent review see Soker 2016). The ICM in many clusters of galaxies has short radiative cooling times. If no heating processes of the ICM exist large amounts of ICM should cool to low temperatures (by ICM I refer also to the interstellar medium in galactic cooling flows). The cooling-flow problem refers to the contradiction between the large mass cooling rates of the ICM that the no-heating assumption implies and the observations of much lower mass cooling rates. The solution is simply to relax the no-heating assumption and to consider the heating of the ICM in all cooling flows. The vast majority of heating models involve jets that the active galactic nucleus (AGN) at the centre of the cooling flow launches. The jets and the hot low-density bubbles they inflate heat the ICM via a negative feedback mechanism that prevents a run-away heating or cooling (e.g. Fabian 2012; Farage, McGregor & Dopita 2012; McNamara & Nulsen 2012; Gaspari, Brighenti & Ruszkowski 2013; Pfrommer 2013; Barai et al. 2016; Soker 2016; Bîrzan et al. 2017; Iqbal et al. 2017).
The two parts that compose the negative feedback cycle are the feeding of the AGN by the ICM and the heating of the ICM by the AGN. There are tens of observational and theoretical studies in recent years that support models in which the ICM feed the AGN with cold clumps (e.g. limiting the list to the last 3 years; Choudhury & Sharma 2016; Hamer et al. 2016; Loubser et al. 2016; McNamara et al. 2016; Russell et al. 2016; Tremblay et al. 2016; Yang & Reynolds 2016; David et al. 2017; Donahue et al. 2017; Gaspari, Temi & Brighenti 2017; Hogan et al. 2017; Meece, Voit & O’Shea 2017; Prasad, Sharma & Babul 2017; Russell et al. 2017a; Voit et al. 2017; Babyk et al. 2018; Gaspari et al. 2018; Ji, Oh & McCourt 2018; Prasad, Sharma & Babul 2018; Pulido et al. 2018; Vantyghem et al. 2018; Voit 2018; Yang et al. 2018). These models can be grouped under the cold feedback mechanism that Pizzolato & Soker (2005) developed to replace the then popular Bondi accretion. In the cold feedback mechanism gas flows inward to form cold clouds and to feed the central AGN. Cold clumps are observed now down to the AGN, e.g. in Perseus (Fujita & Nagai 2017). This implies that a cooling flow does take place, like the extreme cooling flow in the Phoenix cluster (e.g. Pinto et al. 2018), although in most cases the cooling flow is a moderate one. For that, in this study I use the term cooling flow (rather than other names that were invented later and caused some confusions; Soker 2010).
On the other hand, there is no agreement on the processes that contribute the most to the heating of the ICM by the jets that the AGN launches and the bubbles that they inflate. I find it useful to distinguish between heating processes where the jets and jet-inflated bubbles do work on the ICM and between heating by energy transport. In the first class of processes the jets and the jet-inflated bubbles do work on the ICM by exciting sound waves (e.g. Fabian et al. 2006, 2017; Tang & Churazov 2018), by driving shocks (e.g. Forman et al. 2007; Randall et al. 2015; Guo, Duan & Yuan 2018), by powering turbulence (e.g. De Young 2010; Gaspari et al. 2014; Zhuravleva et al. 2014, 2018), and/or by uplifting gas from inner regions (e.g. Gendron-Marsolais et al. 2017). However, there are studies that show that these processes do not heat the ICM efficiently enough, despite the fact that these processes themselves take place to some degree. Although turbulence is observed in the ICM (e.g. Zhuravleva et al. 2014, 2015; Anderson & Sunyaev 2016; Arévalo et al. 2016; Hitomi Collaboration 2016; Hofmann et al. 2016; Hitomi Collaboration 2018), there are studies that question turbulent heating (e.g. Falceta-Gonçalves et al. 2010; Reynolds, Balbus & Schekochihin 2015; Hitomi Collaboration 2016; Hillel & Soker 2017a; Bambic, Morsony & Reynolds 2018; Mohapatra & Sharma 2018). Sound waves also are unable to supply the entire heating (e.g. Fujita & Suzuki 2005). Heating by shocks has some problems as well (e.g. Soker, Hillel & Sternberg 2016). Observations show that bubbles can uplift cooler gas (e.g. Gendron-Marsolais et al. 2017; Russell et al. 2017b; Su et al. 2017), and some studies simulate the uplifting process (e.g. Churazov et al. 2001; Guo et al. 2018), but Hillel & Soker (2018) claim that this cannot be the main heating process of the ICM.
In the second class of heating processes the energy from the hot jet-inflated bubbles is carried into the ICM. One possibility, that is the main subject of the present study, is that cosmic rays that are accelerated within the jet-inflated bubbles, stream into the ICM and heat it (e.g. Fujita, Kimura & Ohira 2013; Fujita & Ohira 2013; Pfrommer 2013). The second possibility is heating by mixing that works as follows. As the jets propagate through the ICM and inflate bubbles they form many vortices inside the bubble and on the boundary between the ICM and the bubbles. These vortices mix hot bubble gas into the ICM (e.g. Brüggen & Kaiser 2002; Brüggen, Scannapieco & Heinz 2009; Gilkis & Soker 2012; Hillel & Soker 2014; Yang & Reynolds 2016).
Finally, some studies suggest that two or more processes out of the different process can work together, e.g. thermal conduction and cosmic rays (e.g. Guo & Oh 2008), mixing of cosmic rays that were accelerated inside jet-inflated bubbles with the the ICM (Pfrommer 2013), and heating by turbulence together with turbulent-mixing (e.g. Banerjee & Sharma 2014).
In a series of papers (e.g. Hillel & Soker 2017a, 2018 for most recent papers) we argued that although the inflation of bubbles also excite sound waves, shocks, and ICM turbulence, heating by mixing is much more efficient than the heating mechanisms where the jets and bubbles do work on the ICM. The heating by mixing can work for bubbles that are filled with very hot thermal gas or with cosmic rays, or a combination of the two. I consider these simulations to describe the inflation of bubbles by jets and the bubble evolution even when weak magnetic fields are present. Although magnetic fields can change the details of the interaction of the bubbles with the ICM (e.g. Dursi & Pfrommer 2008; Weinberger et al. 2017), I take the view that the main effect is that the bubbles amplify the ICM magnetic fields (e.g. Dursi & Pfrommer 2008; Soker 2017). For example, magnetic fields can suppress the Kelvin--Helmholtz instability along the field lines (e.g. Dursi & Pfrommer 2008; Weinberger et al. 2017), but not perpendicular to the field lines. Therefore, magnetic fields are expected to change the geometry of the instabilities and to some extent the geometry of vortices that mix the ICM and bubbles, but magnetic fields are not expected to change the existence and global roles of the vortices, that include mixing and the amplification of the magnetic fields.
We did not compare the heating by mixing with the heating process where cosmic rays from the bubbles stream, instead of being mixed by vortices, into the ICM and heat it. Observations show that in older bubbles the contribution from sources other than the cosmic ray electrons to the pressure tends to be larger than in younger bubbles (e.g. Dunn & Fabian 2004; Bîrzan et al. 2008; Croston et al. 2008). According to the results of the present study this additional pressure component could result from thermal hot gas heated by the mixing-heating process. The mixing-heating proceeds and increases the amount of thermal gas on the expense of the cosmic ray energy as the bubbles age.
In light of some recent interest in cosmic ray heating by streaming (e.g. Ruszkowski, Yang & Reynolds 2017; Ehlert et al. 2018; Jiang & Oh 2018; Ruszkowski, Yang & Reynolds 2018), and the possibility that in many cases cosmic ray energy is the main energy content of bubbles (e,g. Abdulla et al. 2018 for MS 0735.6 + 7421), in this study I examine some of the properties of this process. In Section 2 I consider only cosmic ray streaming, without mixing by vortices, and study the partition of cosmic ray energy between heating the bubbles themselves and heating the ICM, and in Section 3 I estimate the volume of the ICM that can be heated by streaming cosmic rays. I discuss and summarize my results in Section 4 where I consider mixing of cosmic rays by vortices to be much more efficient than streaming.
2 HEATING THE BUBBLE AND THE ICM
Consider an ideal situation where the bubble is filled with cosmic rays that are disconnected from the ICM by magnetic fields. Then in a short time magnetic field lines from the bubble reconnect to the magnetic field lines in the ICM, and the cosmic rays stream to the ICM and heat it. Namely, there is a magnetic flux tube of cross-section S that connects the bubble to the ICM.
Let as take the geometry as Ehlert et al. (2018) obtain in their simulations, where the cosmic rays leaks from the bottom of the bubbles in a pseudo-cylindrical stream. Namely, the cross-section of the cosmic ray stream stays about constant. We can treat then the flow as a one-dimensional flow. The situation before reconnection is depicted schematically in the upper panel of Fig. 1. I take the x coordinate to be along the magnetic field lines, with x = 0 at the boundary between the bubble and the ICM. The initial cosmic ray pressure inside the bubble is Pcr,0 while in the ICM it is zero. The magnetic field in the bubble, Bb, is expected to be stronger than that in the ICM, BI, and the density inside the bubble much smaller than that in the ISM. As such, the Alfven speed inside the bubble is much larger than that in the ICM |$v$|A,b ≫ |$v$|A,I.
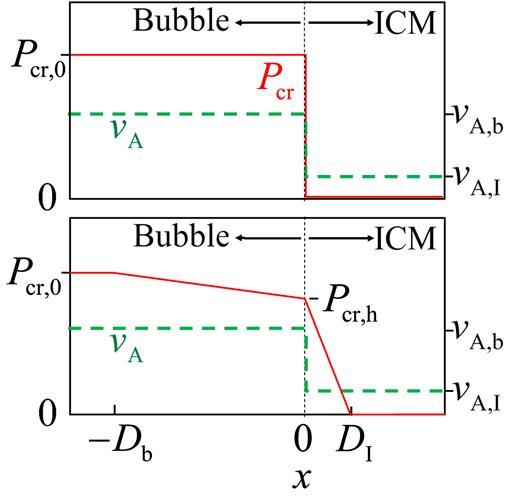
A schematic drawing of the contact between the hot bubble, on the left of the dashed vertical line, and the ICM, as marked. The x coordinate is along the magnetic flux tube that connects the bubble to the ICM. The upper panel represents the case at t = 0 when reconnection of the magnetic field lines inside the bubble and in the ICM takes place. The lower panel represents the flow at some time later. The green-dashed and red-solid lines depict the Alfven speed (scale on the right) and the cosmic ray pressure (scale on the left), respectively.
The lower panel of Fig. 1 schematically presents the flow some time after reconnection. The value of the cosmic ray pressure in the boundary between the bubble and the ICM decreases to a value of Pcr(x = 0) = Pcr,h, and it extends to distance DI into the ICM, i.e. Pcr(x = DI) = 0, while the reduction in cosmic ray pressure extends to a distance of Db into the bubble.
It is important to note that both the Alfven velocity in the bubble and in the ICM have been cancelled out from the final expression (7). In particular, even if the Alfven velocity inside the bubble is relativistic equation (7) holds. This is true also in the case that the information inside the bubble travels at a speed of |$c/\sqrt{3}$|, where c is the speed of light, as argued for by Thomas & Pfrommer (2018).
I examine some recent works on cosmic ray heating in light of equation (7). Equation (7) implies that one cannot ignore the cosmic ray energy that is transferred to heat the jet-inflated bubbles themselves. Ehlert et al. (2018), for example, turn-off the cosmic ray dissipation in regions where the matter from the bubble dominates. I find this unjustified. Jacob & Pfrommer (2017a,b) derive the cosmic ray heating from a steady-state solution to clusters. They do not include the inflation of bubbles self-consistently in their treatment, and therefore I claim that they substantially underestimate the dissipation of cosmic ray inside the bubbles and near the bubble surface. Namely, they substantially underestimate the dissipation of cosmic ray energy near the source of the cosmic rays.
Ruszkowski et al. (2017) present simulations of feedback heating by cosmic rays. Unfortunately they do not present the evolution with time of the velocity flow of the ICM, nor the magnetic field in the regions where they inject the jets. Therefore, I cannot use their results to estimate the role of mixing or cosmic ray heating inside the hot bubbles. But I do note that they assume that a fraction of fcr = 0.8 of the energy of the jets ends as cosmic rays. Equation (7) implies that in that case, at most a fraction of 0.5fcr = 0.4 of the jets’ energy will end up as cosmic ray heating of the ICM. But I argue in this paper that most of the cosmic ray energy is carried to the ICM by mixing, and not by streaming.
I neglected above the process by which turbulence inside the bubble can smooth the cosmic ray pressure, and by that reducing the dissipation of cosmic ray energy inside the bubble. However, this does not seem to be a problem to the derivation of equation (7). First, I do think that there is a strong turbulence, including large vortices, inside the bubble, as the vortices play a significant role in the heating by mixing process, which I take to be the most significant heating process. Secondly, turbulence entangles magnetic field lines that reconnect. This process prevents a smooth flow of cosmic rays into the ICM, increasing further the problem that the cosmic rays do not heat a large enough volume of the ICM. I turn to discuss this problem next.
3 THE HEATED ICM VOLUME
The approximate equation (10) together with equation (7) implies that by streaming alone the cosmic ray energy is channelled to thermal energy that heats a region of approximately only five times the initial volume of the bubbles. From then on, we have larger hot bubbles that still need to heat most of the ICM. There must be another much more efficient process to transfer the energy from the hot bubbles to the ICM.
I further clarify two issues related to the simple model that I have been using here. I studied the case of a bubble that is no longer energized by jets. A more thorough study is required for the less ideal case where the jets continuously pump energy into the bubble. I do not expect the conclusions to change much.
I also assumed above that the cosmic rays stream along magnetic filed lines. Cosmic rays can also diffuse between field lines. The diffusion between field lines is a slow process and might make the cosmic ray distribution less steep, resulting in a slower energy dissipation in the ICM. However, for the cosmic ray streaming to be significant in the heating process it must transfer the cosmic ray energy before the bubbles move outward. Let me consider an example.
In the simulation of Ehlert et al. (2018) at |$t=60\, {\rm Myr}$| the lower part of the bubble is at |$r \simeq 60\, {\rm kpc}$| and the upper boundary of the bubble is at |$r \simeq 90\, {\rm kpc}$|. This implies that the bubble leaves the centre of the cluster, |$r {\lesssim} 30\, {\rm kpc}$|, at a speed of |$v_{r,{\rm bubble}} {\lesssim} 1000\, {\rm km}\,{\rm s}^{-1}$|. The cosmic rays stream at about the Alfven speed. Since the magnetic pressure in the ICM is typically less than |$10 {{\ \rm per\ cent}}$| of the thermal pressure, the Alfven speed is at most 30 per cent the sound speed. Namely, |$v_{\rm A} {\lesssim} 0.3 c_s \approx 200\, {\rm km}\,{\rm s}^{-1} \ll v_{r,{\rm bubble}}$|. If the cosmic rays diffusion time is slower than what I assume in the present study, then the cosmic rays will not have time to diffuse out from the bubbles and heat the centre of the cluster before the bubbles move out. It is in the centre of the cluster where the heating is most needed.
In that regard, I notice that Sharma et al. (2009a) argued that the cosmic ray diffusion in the ICM takes place on a longer time-scale than the buoyancy time. They (see also Sharma et al. 2009b) also argued that turbulent mixing is more efficient than diffusion in transporting cosmic ray energy in the ICM. My results on the unitizing of the cosmic ray energy inside bubbles is compatible with their findings for the transport of cosmic ray energy in the ICM.
4 DISCUSSION AND SUMMARY
By means of simple analytical estimates I examined the efficiency by which streaming of cosmic rays along magnetic field lines can transfer energy from the jet-inflated bubbles to the ICM. In Section 2 I found that about half of the cosmic ray energy is dissipated in the bubbles themselves. Even before the dissipation of cosmic ray energy starts, some of the kinetic energy of the jets has been converted to thermal energy of very hot gas inside the bubbles. Over all, more than half of the kinetic energy of the jets ends up as very hot thermal gas inside the bubbles. In Section 3 I found that by streaming alone the cosmic rays heat a total ICM volume of about five times the volume of the bubbles, and hence this mechanism does not cover a large enough volume of the ICM for an efficient heating to work.
Taking these two conclusions together, I argue that the effect of cosmic ray heating by streaming alone turns a bubble filled with cosmic rays to a larger bubble filled with very hot thermal gas. Therefore, although heating by cosmic ray streaming does take place, I think there is a need for an additional and a more efficient process to carry the energy from the bubbles to the ICM.
I take this more efficient process to be heating by mixing (for references see Section 1). The propagation of jets through the ICM and the inflation of the bubbles form many vortices in the ICM and in the bubbles, and these mix the content of the bubbles, i.e. the very hot thermal gas, the cosmic rays, and the magnetic fields, with the ICM. When the bubble content and the ICM are well mixed we expect that magnetic fields from the bubble content and from the ICM reconnect on small scales. Then streaming of cosmic rays on small scale can make the final cosmic ray energy transfer, as much as heat conduction can locally transfer energy from the very hot thermal gas, which is now well mixed with the ICM, to the ICM.
The heating by mixing process that I refer to results from the vortices that the inflation of bubbles form (e.g. Gilkis & Soker 2012; Hillel & Soker 2016), and it is indiscriminate to the content of the bubble, and hence works for cosmic rays as well as for the thermal gas. Indeed, Pfrommer (2013) already mentioned the mixing of cosmic rays with the ICM and referred to it as an important process. Here I argue that it is more significant than heating by cosmic ray streaming, and hence I strengthen our earlier claim that heating by mixing is the main process by which jets-inflated bubbles heat the ICM (see Section 1).
I emphasize that the non-relativistic thermal gas inside bubbles must be very hot, |$T \gtrsim 10^9\, {\rm K}$|. There are strong observational limits on the mass inside the bubbles (e.g. Sanders & Fabian 2007; Abdulla et al. 2018), and pressure balance between the bubbles and the ICM requires therefore the gas inside the bubbles to be very hot. Both mixing of the ICM with cosmic rays and inflation of the bubbles with jets at velocities of |${\gtrsim } 10^4\, {\rm km}\,{\rm s}^{-1}$| can account for this very hot gas. Another observational constrain comes from observations of cold rims around some bubbles (e.g. Blanton, Sarazin & McNamara 2003). Our 3D hydrodynamical simulations show that a cold dense gas around rising bubbles exists alongside the operation of the mixing-heating process (Hillel & Soker 2018). More studies are required to better compare heating-mixing with these and other observations, e.g. radio observations. These studies require new sets of 3D magnetohydrodynamical simulations.
The simulation of the feedback process in cooling flows is a very complicated task, e.g. as Martizzi et al. (2018) show in a very recent study. There are many physical and numerical issues to consider. One of the key ingredients that simulations must include is the launching of kinetic jets. Sternberg & Soker (2008) show that injecting energy off-centre instead of launching jets might miss key processes, such as the formation of many vortices. It might be that by inserting their jets in a sphere off-centre Weinberger et al. (2017) and Ehlert et al. (2018) underestimated the role of heating by mixing (Hillel & Soker 2017b).
The heating by mixing also has some implications to the mass feeding part of the feedback cycle. Pizzolato & Soker (2005) showed that nonlinear perturbations in the ICM are required to form the cooling clumps that feed the AGN, as was also confirmed in following studies (e.g. Gaspari et al. 2018). Pizzolato & Soker (2005) also suggested that the AGN activity form these nonlinear perturbations. This is most likely a result of the vortices and the mixing process. Therefore, in an indirect way, the results of the present study that further strengthen the mixing-heating mechanism add also to the cold feedback mechanism.
ACKNOWLEDGEMENTS
I thank Karen Yang, Yutaka Fujita, Prateek Sharma, Christoph Pfrommer and an anonymous referee for useful comments. This research was supported by the Israel Science Foundation, and by the E. and J. Bishop Research Fund at the Technion.



