-
PDF
- Split View
-
Views
-
Cite
Cite
I Cortzen, J Garrett, G Magdis, D Rigopoulou, F Valentino, M Pereira-Santaella, F Combes, A Alonso-Herrero, S Toft, E Daddi, D Elbaz, C Gómez-Guijarro, M Stockmann, J Huang, C Kramer, PAHs as tracers of the molecular gas in star-forming galaxies, Monthly Notices of the Royal Astronomical Society, Volume 482, Issue 2, January 2019, Pages 1618–1633, https://doi.org/10.1093/mnras/sty2777
Close - Share Icon Share
ABSTRACT
We combine new CO(1–0) line observations of 24 intermediate redshift galaxies (0.03 < |$z$| < 0.28) along with literature data of galaxies at 0 < |$z$| < 4 to explore scaling relations between the dust and gas content using polycyclic aromatic hydrocarbon (PAH) 6.2 |$\mu$|m (L6.2), CO (|$L^{\prime }_{\rm CO}$|), and infrared (LIR) luminosities for a wide range of redshifts and physical environments. Our analysis confirms the existence of a universal L6.2–|$L^{\prime }_{\rm CO}$| correlation followed by normal star-forming galaxies (SFGs) and starbursts (SBs) at all redshifts. This relation is also followed by local ultraluminous infrared galaxies that appear as outliers in the L6.2–LIR and LIR–|$L^{\prime }_{\rm CO}$| relations defined by normal SFGs. The emerging tight (σ ≈ 0.26 dex) and linear (α = 1.03) relation between L6.2 and |$L^{\prime }_{\rm CO}$| indicates a L6.2 to molecular gas (|$M_{\rm H_{\rm 2}}$|) conversion factor of α6.2 = |$M_{\rm H_{\rm 2}}$|/L6.2 = (2.7 ± 1.3) × αCO, where αCO is the |$L^{\prime }_{\rm CO}$| to |$M_{\rm H_{\rm 2}}$| conversion factor. We also find that on galaxy integrated scales, PAH emission is better correlated with cold rather than with warm dust emission, suggesting that PAHs are associated with the diffuse cold dust, which is another proxy for |$M_{\rm H_{\rm 2}}$|. Focusing on normal SFGs among our sample, we employ the dust continuum emission to derive |$M_{\rm H_{\rm 2}}$| estimates and find a constant |$M_{\rm H_{\rm 2}}$|/L6.2 ratio of α6.2 = 12.3 |$\rm M_{\odot}$|/L⊙(σ ≈ 0.3 dex). This ratio is in excellent agreement with the |$L^{\prime }_{\rm CO}$|-based |$M_{\rm H_{\rm 2}}$|/L6.2 values for αCO = 4.5 |$\rm M_{\odot }/$|(K km s−1 pc2) which is typical of normal SFGs. We propose that the presented L6.2–|$L^{\prime }_{\rm CO}$| and L6.2–|$M_{\rm H_{\rm 2}}$| relations will serve as useful tools for the determination of the physical properties of high-|$z$| SFGs, for which PAH emission will be routinely detected by the James Webb Space Telescope.
1 INTRODUCTION
The mid-infrared (MIR; 3–25 |$\mu$|m) spectrum of star-forming galaxies (SFGs) is dominated by strong emission features generally attributed to polycyclic aromatic hydrocarbons (PAHs) (Sellgren 1984; Puget & Leger 1989; Helou et al. 2001; Pahre et al. 2004; Tielens 2008). The extensive observations of PAH emission in galaxies at both low and high redshifts from either the Infrared Space Observatory (Genzel et al. 1998; Lutz et al. 1998; Rigopoulou et al. 1999) or InfraRed Spectrograph (IRS) on the Spitzer Space Telescope (Armus et al. 2007; Houck et al. 2007; Spoon et al. 2007; Valiante et al. 2007; Yan et al. 2007; Farrah et al. 2008; Sajina et al. 2008; Murphy et al. 2009; O’Dowd et al. 2009; Veilleux et al. 2009; Fadda et al. 2010; Pereira-Santaella et al. 2010; Riechers et al. 2014) indicate that they are ubiquitous and an important tracer of the interstellar medium (ISM). PAH molecules, which are stochastically heated by optical and UV photons, dominate the photoelectric heating rates of the neutral gas and the ionization balance within molecular clouds (Bakes & Tielens 1994). The emission arising from these abundant species can contribute up to 20 per cent of the total infrared (IR) emission in galaxies depending on the physical conditions (Smith et al. 2007; Dale et al. 2009). Hard UV photon fields are thought to destroy, fragment, or ionize the PAH molecules (Boulanger et al. 1988, 1990; Helou, Ryter & Soifer 1991; Pety et al. 2005), whereas low-metallicity systems reveal suppressed PAH emission (Engelbracht et al. 2005; Hunt et al. 2010). The origin of PAHs has been widely discussed in previous studies suggesting that they can be formed in either the envelopes or outflows of carbon-rich AGB stars (Latter 1991; Cherchneff, Barker & Tielens 1992), massive red supergiants (Melbourne & Boyer 2013), or in the ISM itself (Tielens et al. 1987; Puget & Leger 1989; Herbst 1991; Sandstrom et al. 2010, 2012, 2013).
In the local Universe, PAH emission and its link to star formation has been thoroughly studied within the Milky Way and in nearby galaxies through various star formation tracers: individual observations of H ii regions revealed that the PAH emission is found in shell-like structures around the star-forming regions (Churchwell et al. 2006; Rho et al. 2006), with a notable decrease of their strength within the H ii regions (Helou et al. 2004; Calzetti et al. 2005, 2007; Lebouteiller et al. 2007; Povich et al. 2007; Thilker et al. 2007). On larger scales, previous studies have found that SFGs at both low and high redshifts follow a linear relation between the integrated luminosity of the PAH 6.2 |$\mu$|m feature (L6.2) and the total infrared luminosity (LIR), where the latter is the sum of the re-radiated emission from dust grains and a commonly used tracer for the star formation rate (SFR) (Schmidt 1959; Kennicutt 1998; Roussel et al. 2001; Förster Schreiber et al. 2004; Armus et al. 2007; Huang et al. 2009; Menéndez-Delmestre et al. 2009; Rujopakarn et al. 2013). PAH emission has also been observed in both ultraluminous infrared galaxies (ULIRGs; LIR> 1012 L⊙) (Genzel et al. 1998; Armus et al. 2007; Desai et al. 2007) and galaxies with the presence of an active galactic nucleus (AGN) (Moorwood 1986; Roche et al. 1991; Weedman et al. 2005; Smith et al. 2007; Alonso-Herrero et al. 2016; Jensen et al. 2017; Kirkpatrick et al. 2017), however with an on average smaller PAH equivalent. As such the equivalent width of the PAH features can be used to distinguish between AGN and/or strong starbursting galaxies from normal, star-formation dominated systems (Laurent et al. 2000; Brandl et al. 2006; Sajina et al. 2007; Spoon et al. 2007; Pope et al. 2008; Shipley et al. 2013; Esquej et al. 2014). For AGN-dominated galaxies, the total IR emission may also arise from dust heated by the AGN rather than star formation activity, especially in wavelengths shorter than the peak of the FIR SED (e.g. Smith et al. 2007; Wu et al. 2010; Mullaney et al. 2013; Shipley et al. 2013). Lower LPAH/LIR ratios have previously been observed in AGN-dominated sources with respect to SFGs (Armus et al. 2007; Valiante et al. 2007; Sajina et al. 2008) suggesting that PAHs at 6.2, 7.7, and 8.6 |$\mu$|m are suppressed due to the presence of an AGN (Diamond-Stanic & Rieke 2010). Interestingly though, recent works in the local Universe report strong PAH 11.3 |$\mu$|m emission from the nuclear regions of Seyfert galaxies and QSOs (Hönig et al. 2010; Alonso-Herrero et al. 2014; Esquej et al. 2014; Alonso-Herrero et al. 2016), indicating that PAH molecules could be excited, rather than destroyed, by the AGN itself (Jensen et al. 2017).
A similar trend to LPAH–LIR has been observed between the luminosity of the CO(1–0) transition line (|$L^{\prime }_{\rm CO}$|), a common tracer of molecular gas, and the LIR. The majority of SFGs follow a tight relation between the SFR (traced by LIR) and the cold molecular gas (traced by |$L^{\prime }_{\rm CO}$|) or the total gas content (Mgas), which is known as the Kennicutt–Schmidt (KS) law spanning a large dynamical range (Schmidt 1959; Kennicutt 1998). Similar to the LIR–L6.2 relation starbursting systems also appear as outliers in LIR–|$L^{\prime }_{\rm CO}$| relation, exhibiting an enhanced star formation efficiency (SFE = LIR/|$L^{\prime }_{\rm CO}$|) possibly driven by a major merger event, as supported by observations of local ULIRGs and a fraction of submillimeter galaxies (SMGs) at high redshift (Rigopoulou et al. 1999; Pope et al. 2013). The weaker PAH and CO emission (for a fixed LIR) in these star-formation dominated galaxies can be explained by compact star-forming regions and high SFEs due to a larger fraction of dense molecular gas (Tacconi et al. 2008; Daddi et al. 2010a,b; Díaz-Santos et al. 2011; Pope et al. 2013; Kirkpatrick et al. 2014). To this direction, Elbaz et al. (2011) found that the IR8 = LIR/L81 ratio can be used to separate normal SFGs with extended star-formation activity that also lay predominantly on the so-called ‘main-sequence’ (MS) of galaxies (Elbaz et al. 2007; Magdis et al. 2010; Schreiber et al. 2015) from compact starbursts (SBs). Also, for star-formation dominated galaxies, Magdis et al. (2013) reported that IR8 variations are driven mainly by the strength of the PAH features rather than continuum variations, again indicative of more compact star formation for sources with weaker PAH features.
Finally, several studies have revealed a connection between PAHs and the molecular gas (|$M_{\rm H_{\rm 2}}$|) as traced by CO emission. Analyses of the observed radial profiles of PAH and CO emission in local galaxies indicate that PAHs can be used as a proxy for the molecular ISM in galaxies (Regan et al. 2006). The link between PAHs and molecular gas is further supported not only by the observed correlations between PAHs and CO emission on galaxy integrated scales (Pope et al. 2013), but also between PAHs and cold dust emission at ≥160 |$\mu$|m (e.g. Haas, Klaas & Bianchi 2002; Bendo et al. 2008; Jones et al. 2015).
In this work, we further explore the connection between the PAHs and the molecular gas of galaxies, with new single-dish CO(1–0) line observations of 34 IR-bright PAH-emitting SFGs across the MS selected from the 5MUSES survey (Wu et al. 2010), increasing the existing sample of PAH-, IR-, and CO-detected galaxies at intermediate redshifts (0.03 < |$z$| < 0.28) by a factor of 2.4 (Section 2). We complement our sample with existing CO(1–0) and PAH observations from the literature in order to determine the scatter of the scaling relations between IR, PAH, and CO data spanning two orders of magnitude in luminosity and covering a broad range of redshifts (0 < |$z$| < 4). In Section 3.1, we present the L6.2–LIR for normal SFGs and identify local ULIRGs and high-|$z$| SBs as clear outliers characterized by lower L6.2/LIR ratios. In Section 3.2, we show that these outliers also exhibit lower |$L^{\prime }_{\rm CO}$|/LIR ratios compared to the |$L^{\prime }_{\rm CO}$|–LIR relation defined by the general population of normal galaxies. On the other hand, in Section 3.3 we present a universal L6.2–|$L^{\prime }_{\rm CO}$| relation followed by both normal SFGs and SBs at all redshifts. This, along with the strong correlation between the PAH and cold dust emission (λ ≥ 160 |$\mu$|m) presented in Section 3.4, motivates us to explore PAHs as a proxy for the molecular gas in Section 3.5.
Throughout this paper we adopt a standard cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.30, and ΩΛ = 0.70.
2 DATA SAMPLE
We have selected 34 star-forming targets from the 5 mJy Unbiased Spitzer Extragalactic Survey (5MUSES; Wu et al. 2010) in order to examine the gas and ISM properties of star-formation dominated galaxies at intermediate redshift (0.03 < |$z$| < 0.28) by detecting CO(1–0) emission and using existing observations. 5MUSES is a 24 |$\mu$|m flux-limited (f24μm > 5 mJy) spectroscopic survey with Spitzer IRS, containing 330 galaxies with LIR ∼ 1010–1012 L⊙ located in the SWIRE (Lonsdale et al. 2003) and Extragalactic First Look Survey (XFLS) fields (Fadda et al. 2006). The sample fills out the gap between local SFGs (Kennicutt et al. 2003; Smith et al. 2007; Dale et al. 2009), low-|$z$| ULIRGs (Armus et al. 2007; Desai et al. 2007; Veilleux et al. 2009), and more distant galaxies with available spectroscopy data (Houck et al. 2005; Yan et al. 2007). In addition, the full sample has Spitzer Infrared Array Camera observations (IRAC; Fazio et al. 2004) at 3.6–8 |$\mu$|m and Multiband Imaging Photometer (MIPS; Rieke et al. 2004) at 70–160 |$\mu$|m (Wu et al. 2010), where 90 per cent and 54 per cent of the galaxies are detected at 70 and 160 |$\mu$|m, respectively.
From the 5MUSES sample, 280 galaxies have spectroscopically confirmed redshifts with low-resolution (R = 64–128) MIR spectra which were collected using the short-low (SL: 5.5–14.5 |$\mu$|m) and long-low (LL: 14–35 |$\mu$|m) spectral modules of the Spitzer IRS (Houck et al. 2005) as described in Wu et al. (2010). In addition to Spitzer IRAC, MIPS, and IRS observations, a subsample of 188 galaxies (with spectroscopically confirmed redshifts) have FIR photometric coverage at 250, 350, and 500 |$\mu$|m obtained with the Herschel Space Observatory (Griffin et al. 2010) through SPIRE observations as part of the Herschel Multi-tiered Extragalactic Survey (HerMES; Oliver et al. 2010, 2012). Out of the 188 sources, a flux density limit of Sν > 15 mJy in the Herschel SPIRE bands yields a detection for 154 (82 per cent), 108 (57 per cent), and 50 (27 per cent) sources at 250 |$\mu$|m, 350 |$\mu$|m, and 500 |$\mu$|m, respectively (Magdis et al. 2013). Stellar masses of the full 5MUSES sample have been estimated by Shi et al. (2011) using the Bruzual & Charlot (2003) population synthesis model to fit optical and IR photometry assuming a Chabrier (2003) IMF.
In Fig. 1, we present the equivalent width of the PAH 6.2 |$\mu$|m (EW6.2) versus distance from the MS for the full 5MUSES sample. The offset from the MS, SFR/SFRMS(|$z$|, M*), is determined by adopting equation 9 in Schreiber et al. (2015) after converting our stellar masses from a Chabrier (2003) IMF to a Salpeter (1955) IMF using |$M_{\ast }^{\rm S} = 1.70 \times M_{\ast }^{\rm C}$| (Speagle et al. 2014). SFRs are derived using LIR estimates (Section 2.3). We use optical spectroscopy and/or the EW6.2 to identify AGN-dominated sources in the sample. In the absence of optical spectroscopy, we classify sources with EW6.2 ≤ 0.4 |$\mu$|m as AGN and composite sources (see Wu et al. 2010; Magdis et al. 2013, for a detailed AGN characterization of the 5MUSES sample). Since we aim at examining the ISM properties of normal galaxies at intermediate redshifts, we primarily selected targets with EW6.2 > 0.4 |$\mu$|m across the MS (SFR/SFRMS < 4) for follow-up CO(1–0) line observations. Moreover, all of our targets have Spitzer and Herschel observations, LIR = 109.2–1011.8 L⊙, and stellar masses of 〈M*〉 = 1010 |$\rm M_{\odot}$|.
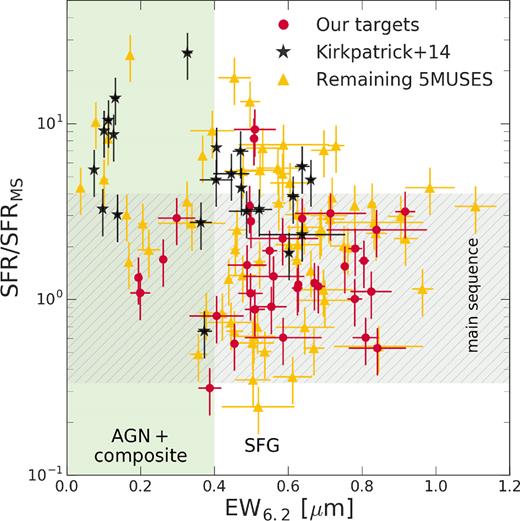
The equivalent width of the PAH 6.2 |$\mu$|m feature (EW6.2) versus offset from the MS (grey shaded region). The red points depict galaxies selected for CO(1–0) line observations presented in this study. Previously CO-detected 5MUSES galaxies from Kirkpatrick et al. (2014) are shown in black, whereas the rest of the 5MUSES sources are shown in yellow. Galaxies with EW6.2 ≤ 0.4 |$\mu$|m are classified as AGN-dominated or composite sources (green region).
2.1 New CO(1–0) line observations
Spectra were reduced using the class/gildas2 software, where each galaxy spectrum was averaged and smoothed to a velocity resolution of 70–100 km s−1. Linear baselines were assumed for all targets. The spectra of galaxies with detected CO(1–0) line emission are shown in Fig. 2. A detected CO line is considered when the integrated signal is above 3σ. We detect significant CO line emission in 24 galaxies, whereas upper limits are determined for the remaining targets assuming a CO(1–0) line width of 300 km s−1. The CO luminosities and the observed properties of each galaxy from our observing runs are listed in Table 1.
CO(1–0) spectra with antenna temperature [mK] as a function of velocity [km s−1] of CO-detected 5MUSES galaxies followed-up with IRAM/EMIR. All spectra are smoothed to a velocity resolution of ∼70 km s−1. A line is considered detected if the integrated signal is above 3σ. The black line shows the best-fitting Gaussian profile to the observed CO line.
| IDa . | RA . | Dec. . | |$z$|co . | FWHMe . | SCOΔ|$v$| . | log(|$L^{\prime }_{\rm CO}$|d) . | rmsf . |
|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | [km s−1] . | [Jy km s−1] . | . | [mK] . |
| 20 | 02:19:09.6 | −05:25:12.9 | 0.098b | – | <0.16 | <7.87 | 0.94 |
| 22 | 02:19:16.1 | −05:57:27.0 | 0.103 | 311 ± 84 | 1.79 ± 0.47 | 8.95 ± 0.11 | 0.30 |
| 28 | 02:19:53.0 | −05:18:24.2 | 0.073 | 261 ± 73 | 5.94 ± 1.40 | 9.16 ± 0.10 | 0.61 |
| 36 | 02:21:47.9 | −04:46:13.5 | 0.025b | – | <0.65 | <7.27 | 0.57 |
| 64 | 02:25:48.2 | −05:00:51.5 | 0.150c | – | <0.31 | <8.52 | 0.29 |
| 66 | 02:26:00.0 | −05:01:45.3 | 0.205 | 274 ± 59 | 2.37 ± 0.45 | 9.69 ± 0.08 | 0.16 |
| 75 | 02:27:41.6 | −04:56:50.6 | 0.055 | 173 ± 61 | 3.27 ± 0.85 | 8.66 ± 0.11 | 0.07 |
| 86 | 10:36:46.4 | +58:43:30.6 | 0.140 | 307 ± 80 | 2.58 ± 0.71 | 9.38 ± 0.12 | 0.28 |
| 106 | 10:44:38.2 | +56:22:10.8 | 0.024 | 375 ± 68 | 15.22 ± 2.38 | 8.64 ± 0.07 | 1.31 |
| 107 | 10:44:54.1 | +57:44:25.8 | 0.118 | 345 ± 74 | 3.59 ± 0.79 | 9.37 ± 0.10 | 0.21 |
| 118 | 10:49:07.2 | +56:57:15.4 | 0.071 | – | <3.55 | <8.93 | 0.80 |
| 123 | 10:50:06.0 | +56:15:00.0 | 0.118 | 215 ± 56 | 2.65 ± 0.63 | 9.25 ± 0.10 | 0.21 |
| 146 | 10:59:03.5 | +57:21:55.1 | 0.117b | – | <0.87 | <8.76 | 0.51 |
| 152 | 11:01:33.8 | +57:52:06.6 | 0.275 | 285 ± 89 | 3.71 ± 1.15 | 10.15 ± 0.13 | 0.24 |
| 185 | 16:08:58.4 | +55:30:10.3 | 0.065 | 221 ± 38 | 3.40 ± 0.66 | 8.84 ± 0.08 | 0.37 |
| 187 | 16:09:07.6 | +55:24:28.4 | 0.065 | 396 ± 300 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.39 |
| 188 | 16:09:08.3 | +55:22:41.5 | 0.085 | 313 ± 73 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.54 |
| 191 | 16:09:31.6 | +54:18:27.4 | 0.086 | 645 ± 165 | 7.58 ± 1.67 | 9.38 ± 0.10 | 0.36 |
| 192 | 16:09:37.5 | +54:12:59.3 | 0.086 | 294 ± 136 | 3.28 ± 0.64 | 9.06 ± 0.08 | 0.13 |
| 196 | 16:12:23.4 | +54:03:39.2 | 0.138 | 210 ± 65 | 1.93 ± 0.53 | 9.24 ± 0.12 | 0.18 |
| 197 | 16:12:33.4 | +54:56:30.5 | 0.084 | 279 ± 38 | 7.76 ± 1.13 | 9.40 ± 0.06 | 0.88 |
| 198 | 16:12:41.1 | +54:39:56.8 | 0.035b | – | <1.23 | <7.84 | 0.61 |
| 200 | 16:12:50.9 | +53:23:05.0 | 0.047 | – | <5.50 | <8.77 | 0.85 |
| 202 | 16:12:54.2 | +54:55:25.4 | 0.065 | – | <5.48 | <9.03 | 0.99 |
| 294 | 17:12:32.4 | +59:21:26.2 | 0.210 | 307 ± 55 | 2.00 ± 0.26 | 9.64 ± 0.06 | 0.03 |
| 297 | 17:13:16.6 | +58:32:34.9 | 0.079 | 437 ± 101 | 3.62 ± 0.97 | 9.02 ± 0.12 | 0.33 |
| 302 | 17:14:46.4 | +59:33:59.8 | 0.131 | – | <3.49 | <9.44 | 0.75 |
| 310 | 17:17:11.1 | +60:27:10.0 | 0.110 | 350 ± 99 | 3.15 ± 0.79 | 9.26 ± 0.11 | 0.17 |
| 315 | 17:19:33.3 | +59:27:42.7 | 0.139 | 423 ± 131 | 3.85 ± 1.05 | 9.55 ± 0.12 | 0.42 |
| 316 | 17:19:44.9 | +59:57:07.1 | 0.069 | – | <2.15 | <9.03 | 1.36 |
| 317 | 17:20:43.3 | +58:40:26.9 | 0.125 | 329 ± 152 | 2.81 ± 0.73 | 9.32 ± 0.11 | 0.11 |
| 319 | 17:21:59.3 | +59:50:34.2 | 0.028 | 168 ± 46 | 7.67 ± 1.96 | 8.44 ± 0.11 | 0.51 |
| 328 | 17:25:46.8 | +59:36:55.3 | 0.035 | 393 ± 137 | 13.89 ± 2.53 | 8.89 ± 0.08 | 0.24 |
| 329 | 17:25:51.3 | +60:11:38.9 | 0.029 | 171 ± 35 | 9.10 ± 1.67 | 8.54 ± 0.08 | 0.04 |
| IDa . | RA . | Dec. . | |$z$|co . | FWHMe . | SCOΔ|$v$| . | log(|$L^{\prime }_{\rm CO}$|d) . | rmsf . |
|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | [km s−1] . | [Jy km s−1] . | . | [mK] . |
| 20 | 02:19:09.6 | −05:25:12.9 | 0.098b | – | <0.16 | <7.87 | 0.94 |
| 22 | 02:19:16.1 | −05:57:27.0 | 0.103 | 311 ± 84 | 1.79 ± 0.47 | 8.95 ± 0.11 | 0.30 |
| 28 | 02:19:53.0 | −05:18:24.2 | 0.073 | 261 ± 73 | 5.94 ± 1.40 | 9.16 ± 0.10 | 0.61 |
| 36 | 02:21:47.9 | −04:46:13.5 | 0.025b | – | <0.65 | <7.27 | 0.57 |
| 64 | 02:25:48.2 | −05:00:51.5 | 0.150c | – | <0.31 | <8.52 | 0.29 |
| 66 | 02:26:00.0 | −05:01:45.3 | 0.205 | 274 ± 59 | 2.37 ± 0.45 | 9.69 ± 0.08 | 0.16 |
| 75 | 02:27:41.6 | −04:56:50.6 | 0.055 | 173 ± 61 | 3.27 ± 0.85 | 8.66 ± 0.11 | 0.07 |
| 86 | 10:36:46.4 | +58:43:30.6 | 0.140 | 307 ± 80 | 2.58 ± 0.71 | 9.38 ± 0.12 | 0.28 |
| 106 | 10:44:38.2 | +56:22:10.8 | 0.024 | 375 ± 68 | 15.22 ± 2.38 | 8.64 ± 0.07 | 1.31 |
| 107 | 10:44:54.1 | +57:44:25.8 | 0.118 | 345 ± 74 | 3.59 ± 0.79 | 9.37 ± 0.10 | 0.21 |
| 118 | 10:49:07.2 | +56:57:15.4 | 0.071 | – | <3.55 | <8.93 | 0.80 |
| 123 | 10:50:06.0 | +56:15:00.0 | 0.118 | 215 ± 56 | 2.65 ± 0.63 | 9.25 ± 0.10 | 0.21 |
| 146 | 10:59:03.5 | +57:21:55.1 | 0.117b | – | <0.87 | <8.76 | 0.51 |
| 152 | 11:01:33.8 | +57:52:06.6 | 0.275 | 285 ± 89 | 3.71 ± 1.15 | 10.15 ± 0.13 | 0.24 |
| 185 | 16:08:58.4 | +55:30:10.3 | 0.065 | 221 ± 38 | 3.40 ± 0.66 | 8.84 ± 0.08 | 0.37 |
| 187 | 16:09:07.6 | +55:24:28.4 | 0.065 | 396 ± 300 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.39 |
| 188 | 16:09:08.3 | +55:22:41.5 | 0.085 | 313 ± 73 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.54 |
| 191 | 16:09:31.6 | +54:18:27.4 | 0.086 | 645 ± 165 | 7.58 ± 1.67 | 9.38 ± 0.10 | 0.36 |
| 192 | 16:09:37.5 | +54:12:59.3 | 0.086 | 294 ± 136 | 3.28 ± 0.64 | 9.06 ± 0.08 | 0.13 |
| 196 | 16:12:23.4 | +54:03:39.2 | 0.138 | 210 ± 65 | 1.93 ± 0.53 | 9.24 ± 0.12 | 0.18 |
| 197 | 16:12:33.4 | +54:56:30.5 | 0.084 | 279 ± 38 | 7.76 ± 1.13 | 9.40 ± 0.06 | 0.88 |
| 198 | 16:12:41.1 | +54:39:56.8 | 0.035b | – | <1.23 | <7.84 | 0.61 |
| 200 | 16:12:50.9 | +53:23:05.0 | 0.047 | – | <5.50 | <8.77 | 0.85 |
| 202 | 16:12:54.2 | +54:55:25.4 | 0.065 | – | <5.48 | <9.03 | 0.99 |
| 294 | 17:12:32.4 | +59:21:26.2 | 0.210 | 307 ± 55 | 2.00 ± 0.26 | 9.64 ± 0.06 | 0.03 |
| 297 | 17:13:16.6 | +58:32:34.9 | 0.079 | 437 ± 101 | 3.62 ± 0.97 | 9.02 ± 0.12 | 0.33 |
| 302 | 17:14:46.4 | +59:33:59.8 | 0.131 | – | <3.49 | <9.44 | 0.75 |
| 310 | 17:17:11.1 | +60:27:10.0 | 0.110 | 350 ± 99 | 3.15 ± 0.79 | 9.26 ± 0.11 | 0.17 |
| 315 | 17:19:33.3 | +59:27:42.7 | 0.139 | 423 ± 131 | 3.85 ± 1.05 | 9.55 ± 0.12 | 0.42 |
| 316 | 17:19:44.9 | +59:57:07.1 | 0.069 | – | <2.15 | <9.03 | 1.36 |
| 317 | 17:20:43.3 | +58:40:26.9 | 0.125 | 329 ± 152 | 2.81 ± 0.73 | 9.32 ± 0.11 | 0.11 |
| 319 | 17:21:59.3 | +59:50:34.2 | 0.028 | 168 ± 46 | 7.67 ± 1.96 | 8.44 ± 0.11 | 0.51 |
| 328 | 17:25:46.8 | +59:36:55.3 | 0.035 | 393 ± 137 | 13.89 ± 2.53 | 8.89 ± 0.08 | 0.24 |
| 329 | 17:25:51.3 | +60:11:38.9 | 0.029 | 171 ± 35 | 9.10 ± 1.67 | 8.54 ± 0.08 | 0.04 |
Notes.a5MUSES ID name.
bThe NASA/IPAC Extragalactic Data base (NED) is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
cFor sources with CO(1–0) 3σ upper limits, the redshift is derived from the IRS spectra (b) or obtained from the NASA/IPAC Extragalactic Data base (c) as listed in Wu et al. (2010).
d|$L^{\prime }_{\rm CO}$| luminosities are in units of [K km s−1 pc2].
eThe CO line width is estimated by measuring the full width at half-maximum (FWHM) of the Gaussian profile.
f For galaxies with >3σ CO detection and upper limits, we list the RMS of the CO line and the baseline, respectively.
| IDa . | RA . | Dec. . | |$z$|co . | FWHMe . | SCOΔ|$v$| . | log(|$L^{\prime }_{\rm CO}$|d) . | rmsf . |
|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | [km s−1] . | [Jy km s−1] . | . | [mK] . |
| 20 | 02:19:09.6 | −05:25:12.9 | 0.098b | – | <0.16 | <7.87 | 0.94 |
| 22 | 02:19:16.1 | −05:57:27.0 | 0.103 | 311 ± 84 | 1.79 ± 0.47 | 8.95 ± 0.11 | 0.30 |
| 28 | 02:19:53.0 | −05:18:24.2 | 0.073 | 261 ± 73 | 5.94 ± 1.40 | 9.16 ± 0.10 | 0.61 |
| 36 | 02:21:47.9 | −04:46:13.5 | 0.025b | – | <0.65 | <7.27 | 0.57 |
| 64 | 02:25:48.2 | −05:00:51.5 | 0.150c | – | <0.31 | <8.52 | 0.29 |
| 66 | 02:26:00.0 | −05:01:45.3 | 0.205 | 274 ± 59 | 2.37 ± 0.45 | 9.69 ± 0.08 | 0.16 |
| 75 | 02:27:41.6 | −04:56:50.6 | 0.055 | 173 ± 61 | 3.27 ± 0.85 | 8.66 ± 0.11 | 0.07 |
| 86 | 10:36:46.4 | +58:43:30.6 | 0.140 | 307 ± 80 | 2.58 ± 0.71 | 9.38 ± 0.12 | 0.28 |
| 106 | 10:44:38.2 | +56:22:10.8 | 0.024 | 375 ± 68 | 15.22 ± 2.38 | 8.64 ± 0.07 | 1.31 |
| 107 | 10:44:54.1 | +57:44:25.8 | 0.118 | 345 ± 74 | 3.59 ± 0.79 | 9.37 ± 0.10 | 0.21 |
| 118 | 10:49:07.2 | +56:57:15.4 | 0.071 | – | <3.55 | <8.93 | 0.80 |
| 123 | 10:50:06.0 | +56:15:00.0 | 0.118 | 215 ± 56 | 2.65 ± 0.63 | 9.25 ± 0.10 | 0.21 |
| 146 | 10:59:03.5 | +57:21:55.1 | 0.117b | – | <0.87 | <8.76 | 0.51 |
| 152 | 11:01:33.8 | +57:52:06.6 | 0.275 | 285 ± 89 | 3.71 ± 1.15 | 10.15 ± 0.13 | 0.24 |
| 185 | 16:08:58.4 | +55:30:10.3 | 0.065 | 221 ± 38 | 3.40 ± 0.66 | 8.84 ± 0.08 | 0.37 |
| 187 | 16:09:07.6 | +55:24:28.4 | 0.065 | 396 ± 300 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.39 |
| 188 | 16:09:08.3 | +55:22:41.5 | 0.085 | 313 ± 73 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.54 |
| 191 | 16:09:31.6 | +54:18:27.4 | 0.086 | 645 ± 165 | 7.58 ± 1.67 | 9.38 ± 0.10 | 0.36 |
| 192 | 16:09:37.5 | +54:12:59.3 | 0.086 | 294 ± 136 | 3.28 ± 0.64 | 9.06 ± 0.08 | 0.13 |
| 196 | 16:12:23.4 | +54:03:39.2 | 0.138 | 210 ± 65 | 1.93 ± 0.53 | 9.24 ± 0.12 | 0.18 |
| 197 | 16:12:33.4 | +54:56:30.5 | 0.084 | 279 ± 38 | 7.76 ± 1.13 | 9.40 ± 0.06 | 0.88 |
| 198 | 16:12:41.1 | +54:39:56.8 | 0.035b | – | <1.23 | <7.84 | 0.61 |
| 200 | 16:12:50.9 | +53:23:05.0 | 0.047 | – | <5.50 | <8.77 | 0.85 |
| 202 | 16:12:54.2 | +54:55:25.4 | 0.065 | – | <5.48 | <9.03 | 0.99 |
| 294 | 17:12:32.4 | +59:21:26.2 | 0.210 | 307 ± 55 | 2.00 ± 0.26 | 9.64 ± 0.06 | 0.03 |
| 297 | 17:13:16.6 | +58:32:34.9 | 0.079 | 437 ± 101 | 3.62 ± 0.97 | 9.02 ± 0.12 | 0.33 |
| 302 | 17:14:46.4 | +59:33:59.8 | 0.131 | – | <3.49 | <9.44 | 0.75 |
| 310 | 17:17:11.1 | +60:27:10.0 | 0.110 | 350 ± 99 | 3.15 ± 0.79 | 9.26 ± 0.11 | 0.17 |
| 315 | 17:19:33.3 | +59:27:42.7 | 0.139 | 423 ± 131 | 3.85 ± 1.05 | 9.55 ± 0.12 | 0.42 |
| 316 | 17:19:44.9 | +59:57:07.1 | 0.069 | – | <2.15 | <9.03 | 1.36 |
| 317 | 17:20:43.3 | +58:40:26.9 | 0.125 | 329 ± 152 | 2.81 ± 0.73 | 9.32 ± 0.11 | 0.11 |
| 319 | 17:21:59.3 | +59:50:34.2 | 0.028 | 168 ± 46 | 7.67 ± 1.96 | 8.44 ± 0.11 | 0.51 |
| 328 | 17:25:46.8 | +59:36:55.3 | 0.035 | 393 ± 137 | 13.89 ± 2.53 | 8.89 ± 0.08 | 0.24 |
| 329 | 17:25:51.3 | +60:11:38.9 | 0.029 | 171 ± 35 | 9.10 ± 1.67 | 8.54 ± 0.08 | 0.04 |
| IDa . | RA . | Dec. . | |$z$|co . | FWHMe . | SCOΔ|$v$| . | log(|$L^{\prime }_{\rm CO}$|d) . | rmsf . |
|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | [km s−1] . | [Jy km s−1] . | . | [mK] . |
| 20 | 02:19:09.6 | −05:25:12.9 | 0.098b | – | <0.16 | <7.87 | 0.94 |
| 22 | 02:19:16.1 | −05:57:27.0 | 0.103 | 311 ± 84 | 1.79 ± 0.47 | 8.95 ± 0.11 | 0.30 |
| 28 | 02:19:53.0 | −05:18:24.2 | 0.073 | 261 ± 73 | 5.94 ± 1.40 | 9.16 ± 0.10 | 0.61 |
| 36 | 02:21:47.9 | −04:46:13.5 | 0.025b | – | <0.65 | <7.27 | 0.57 |
| 64 | 02:25:48.2 | −05:00:51.5 | 0.150c | – | <0.31 | <8.52 | 0.29 |
| 66 | 02:26:00.0 | −05:01:45.3 | 0.205 | 274 ± 59 | 2.37 ± 0.45 | 9.69 ± 0.08 | 0.16 |
| 75 | 02:27:41.6 | −04:56:50.6 | 0.055 | 173 ± 61 | 3.27 ± 0.85 | 8.66 ± 0.11 | 0.07 |
| 86 | 10:36:46.4 | +58:43:30.6 | 0.140 | 307 ± 80 | 2.58 ± 0.71 | 9.38 ± 0.12 | 0.28 |
| 106 | 10:44:38.2 | +56:22:10.8 | 0.024 | 375 ± 68 | 15.22 ± 2.38 | 8.64 ± 0.07 | 1.31 |
| 107 | 10:44:54.1 | +57:44:25.8 | 0.118 | 345 ± 74 | 3.59 ± 0.79 | 9.37 ± 0.10 | 0.21 |
| 118 | 10:49:07.2 | +56:57:15.4 | 0.071 | – | <3.55 | <8.93 | 0.80 |
| 123 | 10:50:06.0 | +56:15:00.0 | 0.118 | 215 ± 56 | 2.65 ± 0.63 | 9.25 ± 0.10 | 0.21 |
| 146 | 10:59:03.5 | +57:21:55.1 | 0.117b | – | <0.87 | <8.76 | 0.51 |
| 152 | 11:01:33.8 | +57:52:06.6 | 0.275 | 285 ± 89 | 3.71 ± 1.15 | 10.15 ± 0.13 | 0.24 |
| 185 | 16:08:58.4 | +55:30:10.3 | 0.065 | 221 ± 38 | 3.40 ± 0.66 | 8.84 ± 0.08 | 0.37 |
| 187 | 16:09:07.6 | +55:24:28.4 | 0.065 | 396 ± 300 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.39 |
| 188 | 16:09:08.3 | +55:22:41.5 | 0.085 | 313 ± 73 | 5.28 ± 1.07 | 9.01 ± 0.09 | 0.54 |
| 191 | 16:09:31.6 | +54:18:27.4 | 0.086 | 645 ± 165 | 7.58 ± 1.67 | 9.38 ± 0.10 | 0.36 |
| 192 | 16:09:37.5 | +54:12:59.3 | 0.086 | 294 ± 136 | 3.28 ± 0.64 | 9.06 ± 0.08 | 0.13 |
| 196 | 16:12:23.4 | +54:03:39.2 | 0.138 | 210 ± 65 | 1.93 ± 0.53 | 9.24 ± 0.12 | 0.18 |
| 197 | 16:12:33.4 | +54:56:30.5 | 0.084 | 279 ± 38 | 7.76 ± 1.13 | 9.40 ± 0.06 | 0.88 |
| 198 | 16:12:41.1 | +54:39:56.8 | 0.035b | – | <1.23 | <7.84 | 0.61 |
| 200 | 16:12:50.9 | +53:23:05.0 | 0.047 | – | <5.50 | <8.77 | 0.85 |
| 202 | 16:12:54.2 | +54:55:25.4 | 0.065 | – | <5.48 | <9.03 | 0.99 |
| 294 | 17:12:32.4 | +59:21:26.2 | 0.210 | 307 ± 55 | 2.00 ± 0.26 | 9.64 ± 0.06 | 0.03 |
| 297 | 17:13:16.6 | +58:32:34.9 | 0.079 | 437 ± 101 | 3.62 ± 0.97 | 9.02 ± 0.12 | 0.33 |
| 302 | 17:14:46.4 | +59:33:59.8 | 0.131 | – | <3.49 | <9.44 | 0.75 |
| 310 | 17:17:11.1 | +60:27:10.0 | 0.110 | 350 ± 99 | 3.15 ± 0.79 | 9.26 ± 0.11 | 0.17 |
| 315 | 17:19:33.3 | +59:27:42.7 | 0.139 | 423 ± 131 | 3.85 ± 1.05 | 9.55 ± 0.12 | 0.42 |
| 316 | 17:19:44.9 | +59:57:07.1 | 0.069 | – | <2.15 | <9.03 | 1.36 |
| 317 | 17:20:43.3 | +58:40:26.9 | 0.125 | 329 ± 152 | 2.81 ± 0.73 | 9.32 ± 0.11 | 0.11 |
| 319 | 17:21:59.3 | +59:50:34.2 | 0.028 | 168 ± 46 | 7.67 ± 1.96 | 8.44 ± 0.11 | 0.51 |
| 328 | 17:25:46.8 | +59:36:55.3 | 0.035 | 393 ± 137 | 13.89 ± 2.53 | 8.89 ± 0.08 | 0.24 |
| 329 | 17:25:51.3 | +60:11:38.9 | 0.029 | 171 ± 35 | 9.10 ± 1.67 | 8.54 ± 0.08 | 0.04 |
Notes.a5MUSES ID name.
bThe NASA/IPAC Extragalactic Data base (NED) is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
cFor sources with CO(1–0) 3σ upper limits, the redshift is derived from the IRS spectra (b) or obtained from the NASA/IPAC Extragalactic Data base (c) as listed in Wu et al. (2010).
d|$L^{\prime }_{\rm CO}$| luminosities are in units of [K km s−1 pc2].
eThe CO line width is estimated by measuring the full width at half-maximum (FWHM) of the Gaussian profile.
f For galaxies with >3σ CO detection and upper limits, we list the RMS of the CO line and the baseline, respectively.
2.2 Literature data
To expand our data sample, we include published observations of galaxies at all redshifts with both CO, IR, and PAH detection from the literature. General properties of the data compilation are listed in Table 2.
| Sample . | N . | |$z$| . | log(LIR/L⊙) . | PAH feature . | CO line . | References [PAH, CO] . |
|---|---|---|---|---|---|---|
| SINGS | 36 | 0.001–0.007 | 7.31–10.60 | 6.2 |$\mu$|m | (3–2) | S07, W12 |
| Local ULIRGs | 9, (9) | 0.018–0.191 | 11.99–12.42 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | P13 |
| 5MUSES | 22, (24) | 0.025–0.277 | 9.23–11.81 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, this paper |
| 5MUSES | 14, (15) | 0.053–0.360 | 10.35–12.10 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, K14 |
| high-|$z$| SFGs | 4, (3) | 1.016–1.523 | 11.86–12.66 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1) | P13 |
| SMGs | 6, (8) | 1.562–4.055 | 12.30–13.08 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1), (3–2), (4–3) | P13 |
| High-|$z$| SBs | (6) | 1.562–2.470 | 12.55–12.93 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (2–1), (3–2) | Sa07, Y07 |
| Sample . | N . | |$z$| . | log(LIR/L⊙) . | PAH feature . | CO line . | References [PAH, CO] . |
|---|---|---|---|---|---|---|
| SINGS | 36 | 0.001–0.007 | 7.31–10.60 | 6.2 |$\mu$|m | (3–2) | S07, W12 |
| Local ULIRGs | 9, (9) | 0.018–0.191 | 11.99–12.42 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | P13 |
| 5MUSES | 22, (24) | 0.025–0.277 | 9.23–11.81 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, this paper |
| 5MUSES | 14, (15) | 0.053–0.360 | 10.35–12.10 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, K14 |
| high-|$z$| SFGs | 4, (3) | 1.016–1.523 | 11.86–12.66 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1) | P13 |
| SMGs | 6, (8) | 1.562–4.055 | 12.30–13.08 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1), (3–2), (4–3) | P13 |
| High-|$z$| SBs | (6) | 1.562–2.470 | 12.55–12.93 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (2–1), (3–2) | Sa07, Y07 |
Notes. The table includes all galaxies with at 3 ≥ σ CO and PAH detections.
Column (1): Galaxy sample; column (2): Number of galaxies with PAH 6.2 |$\mu$|m (and 7.7 |$\mu$|m) detections; column (3): Redshift range; column (4): IR luminosity range; column (5): Detected PAH feature; column (6): Observed CO transition line; column (7): References: S07: Smith et al. (2007), W12: Wilson et al. (2012), P13: Pope et al. (2013) and references therein, W10: Wu et al. (2010), K14: Kirkpatrick et al. (2014), Sa07: Sajina et al. (2007), Y07: Yan et al. (2007).
| Sample . | N . | |$z$| . | log(LIR/L⊙) . | PAH feature . | CO line . | References [PAH, CO] . |
|---|---|---|---|---|---|---|
| SINGS | 36 | 0.001–0.007 | 7.31–10.60 | 6.2 |$\mu$|m | (3–2) | S07, W12 |
| Local ULIRGs | 9, (9) | 0.018–0.191 | 11.99–12.42 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | P13 |
| 5MUSES | 22, (24) | 0.025–0.277 | 9.23–11.81 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, this paper |
| 5MUSES | 14, (15) | 0.053–0.360 | 10.35–12.10 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, K14 |
| high-|$z$| SFGs | 4, (3) | 1.016–1.523 | 11.86–12.66 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1) | P13 |
| SMGs | 6, (8) | 1.562–4.055 | 12.30–13.08 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1), (3–2), (4–3) | P13 |
| High-|$z$| SBs | (6) | 1.562–2.470 | 12.55–12.93 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (2–1), (3–2) | Sa07, Y07 |
| Sample . | N . | |$z$| . | log(LIR/L⊙) . | PAH feature . | CO line . | References [PAH, CO] . |
|---|---|---|---|---|---|---|
| SINGS | 36 | 0.001–0.007 | 7.31–10.60 | 6.2 |$\mu$|m | (3–2) | S07, W12 |
| Local ULIRGs | 9, (9) | 0.018–0.191 | 11.99–12.42 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | P13 |
| 5MUSES | 22, (24) | 0.025–0.277 | 9.23–11.81 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, this paper |
| 5MUSES | 14, (15) | 0.053–0.360 | 10.35–12.10 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0) | W10, K14 |
| high-|$z$| SFGs | 4, (3) | 1.016–1.523 | 11.86–12.66 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1) | P13 |
| SMGs | 6, (8) | 1.562–4.055 | 12.30–13.08 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (1–0), (2–1), (3–2), (4–3) | P13 |
| High-|$z$| SBs | (6) | 1.562–2.470 | 12.55–12.93 | 6.2 |$\mu$|m, 7.7 |$\mu$|m | (2–1), (3–2) | Sa07, Y07 |
Notes. The table includes all galaxies with at 3 ≥ σ CO and PAH detections.
Column (1): Galaxy sample; column (2): Number of galaxies with PAH 6.2 |$\mu$|m (and 7.7 |$\mu$|m) detections; column (3): Redshift range; column (4): IR luminosity range; column (5): Detected PAH feature; column (6): Observed CO transition line; column (7): References: S07: Smith et al. (2007), W12: Wilson et al. (2012), P13: Pope et al. (2013) and references therein, W10: Wu et al. (2010), K14: Kirkpatrick et al. (2014), Sa07: Sajina et al. (2007), Y07: Yan et al. (2007).
| IDa . | RA . | Dec. . | |$z$| . | log(L6.2/L⊙)b . | EW6.2 . | log(L7.7/L⊙)b . | log(M*/|$\rm M_{\odot}$|)c . | log(LIR/L⊙) . | log(Mdust/|$\rm M_{\odot}$|) . | log(|$M_{\rm H_{\rm 2}}$|/|$\rm M_{\odot}$|) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | [|$\mu$|m] . | . | . | . | . | . |
| 2 | 02:15:03.5 | −04:24:21.7 | 0.137 | 8.58 ± 0.19 | 0.78 ± 0.01 | 9.19 ± 0.14 | 10.51 | 10.86 ± 0.04 | 8.01 ± 0.28 | 10.01 |
| 4 | 02:15:57.1 | −03:37:29.1 | 0.032 | 7.59 ± 0.08 | 0.50 ± 0.05 | 8.09 ± 0.09 | 9.97 | 9.83 ± 0.02 | 7.18 ± 0.29 | 9.18 |
| 5 | 02:16:38.2 | −04:22:50.9 | 0.304 | 9.06 ± 0.24 | <0.09 | 9.48 ± 0.11 | 10.80 | 11.54 ± 0.02d | – | – |
| 6 | 02:16:40.7 | −04:44:05.1 | 0.870 | 9.13 ± 1.62 | <0.05 | – | 11.82 | 12.70 ± 0.01d | – | – |
| 8 | 02:16:49.7 | −04:25:54.8 | 0.143 | 9.01 ± 0.09 | 1.11 ± 0.06 | 9.48 ± 0.08 | 10.06 | 10.99 ± 0.01 | 7.29 ± 0.42 | 9.29 |
| – | – | – | – | – | – | – | – | – | – | – |
| IDa . | RA . | Dec. . | |$z$| . | log(L6.2/L⊙)b . | EW6.2 . | log(L7.7/L⊙)b . | log(M*/|$\rm M_{\odot}$|)c . | log(LIR/L⊙) . | log(Mdust/|$\rm M_{\odot}$|) . | log(|$M_{\rm H_{\rm 2}}$|/|$\rm M_{\odot}$|) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | [|$\mu$|m] . | . | . | . | . | . |
| 2 | 02:15:03.5 | −04:24:21.7 | 0.137 | 8.58 ± 0.19 | 0.78 ± 0.01 | 9.19 ± 0.14 | 10.51 | 10.86 ± 0.04 | 8.01 ± 0.28 | 10.01 |
| 4 | 02:15:57.1 | −03:37:29.1 | 0.032 | 7.59 ± 0.08 | 0.50 ± 0.05 | 8.09 ± 0.09 | 9.97 | 9.83 ± 0.02 | 7.18 ± 0.29 | 9.18 |
| 5 | 02:16:38.2 | −04:22:50.9 | 0.304 | 9.06 ± 0.24 | <0.09 | 9.48 ± 0.11 | 10.80 | 11.54 ± 0.02d | – | – |
| 6 | 02:16:40.7 | −04:44:05.1 | 0.870 | 9.13 ± 1.62 | <0.05 | – | 11.82 | 12.70 ± 0.01d | – | – |
| 8 | 02:16:49.7 | −04:25:54.8 | 0.143 | 9.01 ± 0.09 | 1.11 ± 0.06 | 9.48 ± 0.08 | 10.06 | 10.99 ± 0.01 | 7.29 ± 0.42 | 9.29 |
| – | – | – | – | – | – | – | – | – | – | – |
Notes. Column (1): Source name; column (2): Right ascension in units of hours, minutes, and seconds; column (3): Declination in units of degrees, arcminutes, and arcseconds; column (4): Redshift; column (5): PAH 6.2 |$\mu$|m luminosity; column (6): Equivalent width of the PAH 6.2 |$\mu$|m feature; column (7): PAH 7.7 |$\mu$|m luminosity; column (8): Stellar mass; column (9): Infrared luminosity (integrated from 8 to 1000 |$\mu$|m); column (10): Dust mass; column (13): Molecular gas mass derived using the Mdust–|$\delta _{ \rm GDR}$| method.
a5MUSES ID name.
bPAH luminosity from Magdis et al. (2013).
cStellar masses from Shi et al. (2011).
dLIR from Shi et al. (2011).
| IDa . | RA . | Dec. . | |$z$| . | log(L6.2/L⊙)b . | EW6.2 . | log(L7.7/L⊙)b . | log(M*/|$\rm M_{\odot}$|)c . | log(LIR/L⊙) . | log(Mdust/|$\rm M_{\odot}$|) . | log(|$M_{\rm H_{\rm 2}}$|/|$\rm M_{\odot}$|) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | [|$\mu$|m] . | . | . | . | . | . |
| 2 | 02:15:03.5 | −04:24:21.7 | 0.137 | 8.58 ± 0.19 | 0.78 ± 0.01 | 9.19 ± 0.14 | 10.51 | 10.86 ± 0.04 | 8.01 ± 0.28 | 10.01 |
| 4 | 02:15:57.1 | −03:37:29.1 | 0.032 | 7.59 ± 0.08 | 0.50 ± 0.05 | 8.09 ± 0.09 | 9.97 | 9.83 ± 0.02 | 7.18 ± 0.29 | 9.18 |
| 5 | 02:16:38.2 | −04:22:50.9 | 0.304 | 9.06 ± 0.24 | <0.09 | 9.48 ± 0.11 | 10.80 | 11.54 ± 0.02d | – | – |
| 6 | 02:16:40.7 | −04:44:05.1 | 0.870 | 9.13 ± 1.62 | <0.05 | – | 11.82 | 12.70 ± 0.01d | – | – |
| 8 | 02:16:49.7 | −04:25:54.8 | 0.143 | 9.01 ± 0.09 | 1.11 ± 0.06 | 9.48 ± 0.08 | 10.06 | 10.99 ± 0.01 | 7.29 ± 0.42 | 9.29 |
| – | – | – | – | – | – | – | – | – | – | – |
| IDa . | RA . | Dec. . | |$z$| . | log(L6.2/L⊙)b . | EW6.2 . | log(L7.7/L⊙)b . | log(M*/|$\rm M_{\odot}$|)c . | log(LIR/L⊙) . | log(Mdust/|$\rm M_{\odot}$|) . | log(|$M_{\rm H_{\rm 2}}$|/|$\rm M_{\odot}$|) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | [|$\mu$|m] . | . | . | . | . | . |
| 2 | 02:15:03.5 | −04:24:21.7 | 0.137 | 8.58 ± 0.19 | 0.78 ± 0.01 | 9.19 ± 0.14 | 10.51 | 10.86 ± 0.04 | 8.01 ± 0.28 | 10.01 |
| 4 | 02:15:57.1 | −03:37:29.1 | 0.032 | 7.59 ± 0.08 | 0.50 ± 0.05 | 8.09 ± 0.09 | 9.97 | 9.83 ± 0.02 | 7.18 ± 0.29 | 9.18 |
| 5 | 02:16:38.2 | −04:22:50.9 | 0.304 | 9.06 ± 0.24 | <0.09 | 9.48 ± 0.11 | 10.80 | 11.54 ± 0.02d | – | – |
| 6 | 02:16:40.7 | −04:44:05.1 | 0.870 | 9.13 ± 1.62 | <0.05 | – | 11.82 | 12.70 ± 0.01d | – | – |
| 8 | 02:16:49.7 | −04:25:54.8 | 0.143 | 9.01 ± 0.09 | 1.11 ± 0.06 | 9.48 ± 0.08 | 10.06 | 10.99 ± 0.01 | 7.29 ± 0.42 | 9.29 |
| – | – | – | – | – | – | – | – | – | – | – |
Notes. Column (1): Source name; column (2): Right ascension in units of hours, minutes, and seconds; column (3): Declination in units of degrees, arcminutes, and arcseconds; column (4): Redshift; column (5): PAH 6.2 |$\mu$|m luminosity; column (6): Equivalent width of the PAH 6.2 |$\mu$|m feature; column (7): PAH 7.7 |$\mu$|m luminosity; column (8): Stellar mass; column (9): Infrared luminosity (integrated from 8 to 1000 |$\mu$|m); column (10): Dust mass; column (13): Molecular gas mass derived using the Mdust–|$\delta _{ \rm GDR}$| method.
a5MUSES ID name.
bPAH luminosity from Magdis et al. (2013).
cStellar masses from Shi et al. (2011).
dLIR from Shi et al. (2011).
2.2.1 5MUSES galaxies
In a recent study, Kirkpatrick et al. (2014) carried out CO(1–0) line observations of 24 intermediate redshift galaxies (|$z$| = 0.04–0.36), also selected from the 5MUSES sample, with the Redshift Search Receiver on the Large Millimetre Telescope. Their sample covers a broader range of LIR (1010.4–1012.1 L⊙) and EW6.2 (0.07–0.70 |$\mu$|m) as opposed to our targets. They detected CO(1–0) emission in 17 of the 24 sources which we combine with our sample for the analysis (14 of these have 3σ PAH 6.2 |$\mu$|m detection). For consistency, we derive CO line luminosities using the velocity-integrated line flux reported in Kirkpatrick et al. (2014). The final sample of intermediate redshift galaxies with both CO and PAH 6.2 |$\mu$|m detections in our study consists of 36 targets, all drawn from the 5MUSES compilation, of which 24 are from our new IRAM survey and 14 from Kirkpatrick et al. (2014).
2.2.2 SINGS
The Spitzer Infrared Nearby Galaxy Survey (SINGS; Kennicutt et al. 2003) is an imaging and low-resolution (R ∼ 50–100) spectroscopic survey of 75 local galaxies with 5–38 |$\mu$|m spectral mapping with Spitzer IRS. The low-resolution 5–15 |$\mu$|m spectral map (55 arcsec × 34 arcsec) is centred on the nucleus of each galaxy. From the SINGS sample, Smith et al. (2007) selected 59 galaxies with spectral coverage between 5 and 38 |$\mu$|m from both SL and LL in order to detect PAH emission within the central regions of each galaxy. PAH features were derived using pahfit (Smith et al. 2007) and fitted with Drude profiles. A subsample of 57 SINGS galaxies have both PAH emission and FIR coverage based on Herschel PACS and SPIRE observations as presented in Dale et al. (2012).
From the SINGS survey, Wilson et al. (2012) selected 47 galaxies (NGLS: Nearby Galaxies Legacy Survey) to carry out CO(3–2) line observations with the James Clerk Maxwell Telescope. To correct the CO(3–2) emission to CO(1–0) we adopt a CO(3–2)/CO(1–0) line ratio of r32/10 = 0.18 ± 0.02 based on a comparison study by Wilson et al. (2012). They estimate an average CO(3–2) and CO(1–0) line ratio using 11 nearby galaxies from the NGLS sample that overlap with CO(2–1) observations carried out by Kuno et al. (2007). We apply an aperture correction (fTIR) listed in Smith et al. (2007) to the IR and CO(1–0) luminosities and increase the uncertainties of the aperture-corrected luminosities by a factor of 2 in order to compare these with the PAH emission arising from the central part of the galaxy.
Given the different physical scales probed by the available PAH, CO, and dust emission observations of the SINGS galaxies, we choose to exclude them from our statistical analysis to avoid biases in our regression models due to possible systematics and uncertainties introduced by the aperture corrections. However, since the SINGS sample consists of representative, normal PAH emitting SFGs in the local Universe, for the sake of completeness we choose to overplot them in the various luminosity scaling relations presented in this study.
2.2.3 Local ULIRGs and high-|$z$| galaxies
Pope et al. (2013) carried out CO(2–1) observations using IRAM PdBI and Spitzer MIR spectroscopy of six 70 |$\mu$|m selected galaxies from the Spitzer Far-Infrared Deep Extragalactic Legacy survey (Dickinson & FIDEL Team 2007) of GOODS-N with optical spectroscopic redshift at |$z$| = 1–1.5. The sample has Spitzer IRS observations and photometric coverage from Spitzer MIPS (24 and 70 |$\mu$|m) and Herschel PACS (100 and 160 |$\mu$|m) and SPIRE (250, 350, and 500 |$\mu$|m) observations from the GOODS-Herschel survey (Elbaz et al. 2011). As in Pope et al. (2013), we complement our sample with galaxies from the literature containing detected CO and PAH emission at all redshifts. These include 12 high-|$z$| galaxies (SMGs, BzKs, and 70 |$\mu$|m selected galaxies) from various studies at 1.1 < |$z$| < 4.1 (Frayer et al. 2008; Pope et al. 2008; Aravena et al. 2010; Carilli et al. 2010; Casey et al. 2011; Ivison et al. 2011; Magnelli et al. 2012; Bothwell et al. 2013; Riechers et al. 2013). Stellar masses from Pope et al. (2013) are available for the 70 |$\mu$|m selected galaxies. Based on the offset from the MS, we classify the 70 |$\mu$|m as high-|$z$| SFGs galaxies whereas the remaining galaxies at |$z$| > 1 are labelled as SMGs. Similarly, we include the 24 |$\mu$|m selected sample (S24 > 0.9 mJy) of nine |$z$| ∼ 1–2 ULIRGs in the Spitzer XFLS field with CO(2–1) or CO(3–2) observations from Yan et al. (2010) that also has existing Spitzer MIR spectra published in Yan et al. (2007) and Sajina et al. (2007).
For galaxies with only high-J CO line observations, we convert the CO luminosities to |$L^{\prime }_{\rm CO}$| by adopting the conversion factors listed in Bothwell et al. (2013, r21/10 = 0.84 ± 0.13, r32/10 = 0.52 ± 0.09, r43/10 = 0.41 ± 0.07). At lower redshift, we also include 13 local ULIRGs with Spitzer IRS MIR spectra from Armus et al. (2007) and Desai et al. (2007) with existing CO observations and IR luminosities (Sanders, Scoville & Soifer 1991; Solomon et al. 1997; Kim, Veilleux & Sanders 1998; Farrah et al. 2003; Gao & Solomon 2004; Chung et al. 2009). The CO, IR, and PAH luminosities of the literature compilation are available in the online version (See Table 4).
| Name . | RA . | Dec. . | Sample . | |$z$| . | log(L6.2/L⊙) . | EW6.2 . | log(L7.7/L⊙) . | log(LIR/L⊙) . | Line . | log(|$L^{\prime }_{\rm CO}$|/L⊙) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | . | [|$\mu$|m] . | . | . | . | . |
| NGC 3049 | 09:54:49.59 | +09:16:18.1 | SINGS | 0.006 | 7.81 ± 0.02a | – | – | 9.65 ± 0.02a | CO(3–2) | 7.68 ± 0.21b |
| IRAS 10565 + 2448 | 10:59:18.12 | +24:32:34.5 | local ULIRGs | 0.043 | 9.57 ± 0.01 | – | – | 12.04 ± 0.02c | CO(1–0) | 9.72 ± 0.03c |
| GN26 | 12:36:34.51 | +62:12:40.9 | SMGs | 1.223 | 10.48 ± 0.02 | 0.38 ± 0.04 | 11.01 ± 0.10 | 12.66 ± 0.17c | CO(2–1) | 10.92 ± 0.12c |
| GN70.211 | 12:37:10.60 | +62:22:34.5 | High-|$z$| SFGs | 1.523 | 10.39 ± 0.10 | – | 10.84 ± 0.12 | 11.94 ± 0.17c | CO(1–0) | 10.20 ± 0.12c |
| MIPS506 | 17:11:38.59 | +58:38:38.6 | High-|$z$| SBs | 2.470 | – | 0.30 ± 0.14d | 11.11 ± 0.13 | 12.93 ± 0.09e | CO(3–2) | 10.52 ± 0.09e |
| – | – | – | – | – | – | – | – | – | – |
| Name . | RA . | Dec. . | Sample . | |$z$| . | log(L6.2/L⊙) . | EW6.2 . | log(L7.7/L⊙) . | log(LIR/L⊙) . | Line . | log(|$L^{\prime }_{\rm CO}$|/L⊙) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | . | [|$\mu$|m] . | . | . | . | . |
| NGC 3049 | 09:54:49.59 | +09:16:18.1 | SINGS | 0.006 | 7.81 ± 0.02a | – | – | 9.65 ± 0.02a | CO(3–2) | 7.68 ± 0.21b |
| IRAS 10565 + 2448 | 10:59:18.12 | +24:32:34.5 | local ULIRGs | 0.043 | 9.57 ± 0.01 | – | – | 12.04 ± 0.02c | CO(1–0) | 9.72 ± 0.03c |
| GN26 | 12:36:34.51 | +62:12:40.9 | SMGs | 1.223 | 10.48 ± 0.02 | 0.38 ± 0.04 | 11.01 ± 0.10 | 12.66 ± 0.17c | CO(2–1) | 10.92 ± 0.12c |
| GN70.211 | 12:37:10.60 | +62:22:34.5 | High-|$z$| SFGs | 1.523 | 10.39 ± 0.10 | – | 10.84 ± 0.12 | 11.94 ± 0.17c | CO(1–0) | 10.20 ± 0.12c |
| MIPS506 | 17:11:38.59 | +58:38:38.6 | High-|$z$| SBs | 2.470 | – | 0.30 ± 0.14d | 11.11 ± 0.13 | 12.93 ± 0.09e | CO(3–2) | 10.52 ± 0.09e |
| – | – | – | – | – | – | – | – | – | – |
Notes. Column (1): Source name; column (2): Right ascension in units of hours, minutes, and seconds; column (3): Declination in units of degrees, arcminutes, and arcseconds; column (4): Galaxy sample or selection; column (5): Redshift; column (6): PAH 6.2 |$\mu$|m luminosity; column (7): Equivalent width of the PAH 6.2 |$\mu$|m feature; column (8): Infrared luminosity (integrated from 8−1000 |$\mu$|m); column (9): Observed CO line; column (10): CO(1–0) luminosity.
aFrom Smith et al. (2007). IR luminosities are aperture corrected.
bFrom Wilson et al. (2012). Converted to CO(1-0) luminosities using r32/10 = 0.18 ± 0.02.
cFrom Pope et al. (2013). For the CO luminosities, we corrected higher J transitions using the conversion scheme listed in Bothwell et al. (2013): r21/10 = 0.84 ± 0.13, r32/10 = 0.52 ± 0.09, r43/10 = 0.41 ± 0.07.
dFrom Sajina et al. (2007).
eFrom Yan et al. (2010).
| Name . | RA . | Dec. . | Sample . | |$z$| . | log(L6.2/L⊙) . | EW6.2 . | log(L7.7/L⊙) . | log(LIR/L⊙) . | Line . | log(|$L^{\prime }_{\rm CO}$|/L⊙) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | . | [|$\mu$|m] . | . | . | . | . |
| NGC 3049 | 09:54:49.59 | +09:16:18.1 | SINGS | 0.006 | 7.81 ± 0.02a | – | – | 9.65 ± 0.02a | CO(3–2) | 7.68 ± 0.21b |
| IRAS 10565 + 2448 | 10:59:18.12 | +24:32:34.5 | local ULIRGs | 0.043 | 9.57 ± 0.01 | – | – | 12.04 ± 0.02c | CO(1–0) | 9.72 ± 0.03c |
| GN26 | 12:36:34.51 | +62:12:40.9 | SMGs | 1.223 | 10.48 ± 0.02 | 0.38 ± 0.04 | 11.01 ± 0.10 | 12.66 ± 0.17c | CO(2–1) | 10.92 ± 0.12c |
| GN70.211 | 12:37:10.60 | +62:22:34.5 | High-|$z$| SFGs | 1.523 | 10.39 ± 0.10 | – | 10.84 ± 0.12 | 11.94 ± 0.17c | CO(1–0) | 10.20 ± 0.12c |
| MIPS506 | 17:11:38.59 | +58:38:38.6 | High-|$z$| SBs | 2.470 | – | 0.30 ± 0.14d | 11.11 ± 0.13 | 12.93 ± 0.09e | CO(3–2) | 10.52 ± 0.09e |
| – | – | – | – | – | – | – | – | – | – |
| Name . | RA . | Dec. . | Sample . | |$z$| . | log(L6.2/L⊙) . | EW6.2 . | log(L7.7/L⊙) . | log(LIR/L⊙) . | Line . | log(|$L^{\prime }_{\rm CO}$|/L⊙) . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | [hh:mm:ss] . | [dd:mm:ss] . | . | . | . | [|$\mu$|m] . | . | . | . | . |
| NGC 3049 | 09:54:49.59 | +09:16:18.1 | SINGS | 0.006 | 7.81 ± 0.02a | – | – | 9.65 ± 0.02a | CO(3–2) | 7.68 ± 0.21b |
| IRAS 10565 + 2448 | 10:59:18.12 | +24:32:34.5 | local ULIRGs | 0.043 | 9.57 ± 0.01 | – | – | 12.04 ± 0.02c | CO(1–0) | 9.72 ± 0.03c |
| GN26 | 12:36:34.51 | +62:12:40.9 | SMGs | 1.223 | 10.48 ± 0.02 | 0.38 ± 0.04 | 11.01 ± 0.10 | 12.66 ± 0.17c | CO(2–1) | 10.92 ± 0.12c |
| GN70.211 | 12:37:10.60 | +62:22:34.5 | High-|$z$| SFGs | 1.523 | 10.39 ± 0.10 | – | 10.84 ± 0.12 | 11.94 ± 0.17c | CO(1–0) | 10.20 ± 0.12c |
| MIPS506 | 17:11:38.59 | +58:38:38.6 | High-|$z$| SBs | 2.470 | – | 0.30 ± 0.14d | 11.11 ± 0.13 | 12.93 ± 0.09e | CO(3–2) | 10.52 ± 0.09e |
| – | – | – | – | – | – | – | – | – | – |
Notes. Column (1): Source name; column (2): Right ascension in units of hours, minutes, and seconds; column (3): Declination in units of degrees, arcminutes, and arcseconds; column (4): Galaxy sample or selection; column (5): Redshift; column (6): PAH 6.2 |$\mu$|m luminosity; column (7): Equivalent width of the PAH 6.2 |$\mu$|m feature; column (8): Infrared luminosity (integrated from 8−1000 |$\mu$|m); column (9): Observed CO line; column (10): CO(1–0) luminosity.
aFrom Smith et al. (2007). IR luminosities are aperture corrected.
bFrom Wilson et al. (2012). Converted to CO(1-0) luminosities using r32/10 = 0.18 ± 0.02.
cFrom Pope et al. (2013). For the CO luminosities, we corrected higher J transitions using the conversion scheme listed in Bothwell et al. (2013): r21/10 = 0.84 ± 0.13, r32/10 = 0.52 ± 0.09, r43/10 = 0.41 ± 0.07.
dFrom Sajina et al. (2007).
eFrom Yan et al. (2010).
2.3 Derivation of MIR and FIR dust properties
We combine the existing multiwavelength photometry from Spitzer (MIPS: 24, 160 |$\mu$|m) and Herschel (SPIRE: 250, 350, 500 |$\mu$|m) in order to estimate IR luminosities and dust masses (Mdust) by modelling the FIR part of the spectral energy distribution (SED) for each galaxy in the 5MUSES sample. We use silicate–graphite–PAH models from Draine & Li (2007) (DL07) including diffuse ISM and photodissociation region (PDR) components. The best-fitting parameters and results are listed in the online version (see Table 3). LIR is derived by integrating the SED model between rest frame 8–1000 |$\mu$|m. The SFR for each galaxy is estimated using the LIR–SFR conversion in Kennicutt (1998) assuming a Salpeter (1955) IMF: SFR [M⊙ yr−1] = 1.72 × 10−10LIR. This technique of FIR SED modelling is applied to the 5MUSES sample including 165 galaxies. In addition, we estimate monochromatic dust luminosities using the Spitzer MIPS (24 and 160 |$\mu$|m) and Herschel SPIRE photometric bands (250, 350, and 500 |$\mu$|m). We derive PAH luminosities from the Spitzer IRS data using pahfit. For galaxies in the literature where the PAH luminosities have been estimated using the spline method, we derive the PAH luminosities using pahfit to ensure that the PAH 6.2 and 7.7 |$\mu$|m emissions have been estimated in a consistent way for both our targets and the literature compilation.
To summarize, the full sample with both detected CO, PAH 6.2 |$\mu$|m, and IR emission contains 36 5MUSES galaxies (including 5 AGNs and composite sources), 36 SINGS galaxies, nine local ULIRGs, four high-|$z$| SFGs, and six SMGs (See Table 2).
3 RESULTS
Previous works have studied scaling relations between the LIR, LPAH, and |$L^{\prime }_{\rm CO}$| of various galaxy populations across a wide range of redshifts (e.g. Calzetti et al. 2005; Smith et al. 2007; Bendo et al. 2008; Pope et al. 2013; Rujopakarn et al. 2013; Kirkpatrick et al. 2014). In this section, we will revisit these relations for our sample, attempting to identify outliers and investigate them not only as a function of lookback time but also as a function of physical conditions (AGN, SBs, normal galaxies, etc).
3.1 The relation between IR and PAH luminosity
As discussed in the Introduction, LPAH/LIR variations may not only be driven by the presence of an AGN and the geometry of the star formation but also by the metallicity and the hardness of the radiation field. To investigate the LPAH/LIR variations in different galaxy populations across a wide range of redshifts, we consider the L6.2, L7.7, and LIR measurements for the 5MUSES sample as well as for other galaxies in the literature for which such measurements are available, including local ULIRGs (Armus et al. 2007; Desai et al. 2007), high-|$z$| (1 < |$z$| < 4) SMGs, BzKs and 70 |$\mu$|m selected galaxies (Pope et al. 2008; Pope et al. 2013, and references therein), and 24 |$\mu$|m selected SBs at |$z$| ∼ 2 (Yan et al. 2010). Due to possible biases introduced from the aperture correction applied to the SINGS galaxies (Kennicutt et al. 2003), we omit them from the best-fitting regression models.
In Fig. 3, we plot the PAH 6.2 |$\mu$|m and 7.7 |$\mu$|m luminosities as a function LIR for our full sample of galaxies and model the data in the logarithmic space using the Bayesian linear regression analysis as described in Kelly (2007). This method accounts for measurement errors of both the dependent and independent variables and it returns posterior distributions of the best-fitting parameters, including the intrinsic scatter. All the best-fitting parameters of the regression model: log y = α × log x + β are listed in Table 5. Focusing only on local/intermediate redshift star-formation dominated sources and high-|$z$| SFGs that are part of the MS of star formation, we find a tight, linear correlation, with a slope of α = 0.98 ± 0.03 and intrinsic scatter of σ = 0.13 dex for the L6.2–LIR relation, while α = 1.00 ± 0.03 and σ = 0.13 dex for L7.7–LIR, in agreement with the best-fitting relations reported in Pope et al. (2008) and similar studies (e.g. Sajina et al. 2008; Rujopakarn et al. 2013; Shipley et al. 2016). The dispersion of the LPAH/LIR ratios as a function of LIR and galaxy type is shown in the top panels of Fig. 3. From these relations, local ULIRGs (and high-|$z$| SBs with available L7.7 estimates) exhibit systematically lower PAH/IR luminosity ratios. We quantify these galaxies as outliers lying 3.2σ from the best-fitting relations (2.5σ for L7.7–LIR). Fitting the full sample (excluding upper limits) yields a shallower slope but also an increased intrinsic scatter of σ = 0.21 dex and σ = 0.20 dex for the L6.2–LIR and L7.7–LIR relations, respectively. We note though, that a considerable fraction of local ULIRGs and high-|$z$| SBs are still outliers, even when attempting to fit the whole sample, in agreement with Shipley et al. (2016). It is thus evident that a universal LIR–L6.2 relation, accommodating the various physical conditions of different galaxy populations, cannot be established.
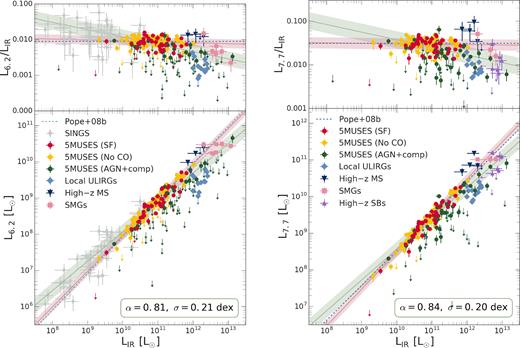
Correlation between the total infrared luminosity (LIR) versus PAH 6.2 |$\mu$|m luminosity (L6.2) (left) and PAH 7.7 |$\mu$|m luminosity (L7.7) (right). For the 5MUSES sample, we include CO-detected SFGs (red), AGNs and composite sources (green), and the remaining sample of SFGs (yellow). L6.2 and L7.7 upper limits are shown as arrows. We also include SINGS galaxies (grey, only for L6.2), local ULIRGs (light blue), high-|$z$| SFGs (dark blue), SMGs (pink), and high-|$z$| SBs (purple, only for L7.7). The green and pink lines depict the LPAH–LIR linear regression models of the SFGs (5MUSES and high-|$z$| SFGs) and the full sample, respectively, excluding the SINGS sources as described in Section 2.2.2. The same method is applied to the LPAH/LIR versus LIR relations presented in the upper panels. The shaded regions present the intrinsic scatter of the best fits. The blue dashed lines show the best-fitting relations from Pope et al. (2008) of local SBs and SMGs. For the upper panels, the dashed lines are the median value of the LPAH/LIR assuming LPAH–LIR slopes of unity.
Linear scaling relations between the emission from PAHs, IR, and CO, and various galaxy properties.
| log x . | log y . | α . | β . | σ . | Sample . |
|---|---|---|---|---|---|
| LIR [L⊙] | L6.2 [L⊙] | 0.98 ± 0.03 | −1.89 ± 0.30 | 0.13 | SFGs |
| LIR [L⊙] | L6.2 [L⊙] | 0.81 ± 0.03 | −0.04 ± 0.29 | 0.21 | All |
| LIR [L⊙] | L7.7 [L⊙] | 1.00 ± 0.03 | −1.53 ± 0.28 | 0.13 | SFGs |
| LIR [L⊙] | L7.7 [L⊙] | 0.84 ± 0.02 | −0.15 ± 0.26 | 0.20 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.02 ± 0.06 | −0.65 ± 0.31 | 0.24 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.03 ± 0.06 | −0.73 ± 0.38 | 0.26 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 0.99 ± 0.07 | −0.37 ± 0.70 | 0.24 | With CO(1–0) |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.03 ± 0.08 | −0.13 ± 0.19 | 0.21 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.04 ± 0.08 | −0.21 ± 0.20 | 0.23 | All |
| L24 [L⊙] | L6.2 [L⊙] | 0.99 ± 0.05 | 1.51 ± 0.37 | 0.20 | 5MUSES SFGs |
| L24 [L⊙] | L6.2 [L⊙] | 0.90 ± 0.05 | 2.14 ± 0.35 | 0.21 | 5MUSES |
| L160 [L⊙] | L6.2 [L⊙] | 1.02 ± 0.04 | −0.11 ± 0.37 | 0.11 | 5MUSES |
| L250 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.04 | 1.48 ± 0.31 | 0.17 | 5MUSES |
| L350 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.05 | 1.83 ± 0.38 | 0.19 | 5MUSES |
| L500 [L⊙] | L6.2 [L⊙] | 0.83 ± 0.06 | 2.34 ± 0.42 | 0.17 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L24 [L⊙] | L7.7 [L⊙] | 0.97 ± 0.05 | 2.15 ± 0.37 | 0.21 | 5MUSES SFGs |
| L24 [L⊙] | L7.7 [L⊙] | 0.79 ± 0.05 | 3.46 ± 0.40 | 0.28 | 5MUSES |
| L160 [L⊙] | L7.7 [L⊙] | 1.04 ± 0.04 | 0.23 ± 0.37 | 0.12 | 5MUSES |
| L250 [L⊙] | L7.7 [L⊙] | 0.87 ± 0.04 | 2.03 ± 0.3 | 0.19 | 5MUSES |
| L350 [L⊙] | L7.7 [L⊙] | 0.85 ± 0.05 | 2.45 ± 0.40 | 0.22 | 5MUSES |
| L500 [L⊙] | L7.7 [L⊙] | 0.82 ± 0.06 | 3.00 ± 0.48 | 0.22 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.02 ± 0.02 | 0.36 ± 0.19 | 0.06 | All |
| L6.2 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 1.10 ± 0.01 | 0.28 | 5MUSES MS SFGsb |
| L7.7 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 0.55 ± 0.02 | 0.28 | 5MUSES MS SFGsb |
| log x . | log y . | α . | β . | σ . | Sample . |
|---|---|---|---|---|---|
| LIR [L⊙] | L6.2 [L⊙] | 0.98 ± 0.03 | −1.89 ± 0.30 | 0.13 | SFGs |
| LIR [L⊙] | L6.2 [L⊙] | 0.81 ± 0.03 | −0.04 ± 0.29 | 0.21 | All |
| LIR [L⊙] | L7.7 [L⊙] | 1.00 ± 0.03 | −1.53 ± 0.28 | 0.13 | SFGs |
| LIR [L⊙] | L7.7 [L⊙] | 0.84 ± 0.02 | −0.15 ± 0.26 | 0.20 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.02 ± 0.06 | −0.65 ± 0.31 | 0.24 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.03 ± 0.06 | −0.73 ± 0.38 | 0.26 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 0.99 ± 0.07 | −0.37 ± 0.70 | 0.24 | With CO(1–0) |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.03 ± 0.08 | −0.13 ± 0.19 | 0.21 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.04 ± 0.08 | −0.21 ± 0.20 | 0.23 | All |
| L24 [L⊙] | L6.2 [L⊙] | 0.99 ± 0.05 | 1.51 ± 0.37 | 0.20 | 5MUSES SFGs |
| L24 [L⊙] | L6.2 [L⊙] | 0.90 ± 0.05 | 2.14 ± 0.35 | 0.21 | 5MUSES |
| L160 [L⊙] | L6.2 [L⊙] | 1.02 ± 0.04 | −0.11 ± 0.37 | 0.11 | 5MUSES |
| L250 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.04 | 1.48 ± 0.31 | 0.17 | 5MUSES |
| L350 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.05 | 1.83 ± 0.38 | 0.19 | 5MUSES |
| L500 [L⊙] | L6.2 [L⊙] | 0.83 ± 0.06 | 2.34 ± 0.42 | 0.17 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L24 [L⊙] | L7.7 [L⊙] | 0.97 ± 0.05 | 2.15 ± 0.37 | 0.21 | 5MUSES SFGs |
| L24 [L⊙] | L7.7 [L⊙] | 0.79 ± 0.05 | 3.46 ± 0.40 | 0.28 | 5MUSES |
| L160 [L⊙] | L7.7 [L⊙] | 1.04 ± 0.04 | 0.23 ± 0.37 | 0.12 | 5MUSES |
| L250 [L⊙] | L7.7 [L⊙] | 0.87 ± 0.04 | 2.03 ± 0.3 | 0.19 | 5MUSES |
| L350 [L⊙] | L7.7 [L⊙] | 0.85 ± 0.05 | 2.45 ± 0.40 | 0.22 | 5MUSES |
| L500 [L⊙] | L7.7 [L⊙] | 0.82 ± 0.06 | 3.00 ± 0.48 | 0.22 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.02 ± 0.02 | 0.36 ± 0.19 | 0.06 | All |
| L6.2 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 1.10 ± 0.01 | 0.28 | 5MUSES MS SFGsb |
| L7.7 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 0.55 ± 0.02 | 0.28 | 5MUSES MS SFGsb |
Notes. The linear fits are obtained in the logarithmic space : log y = α × log x + β. The best-fitting parameters and the intrinsic scatter are estimated from the Bayesian linear regression method described in Kelly (2007).
aDust-derived molecular gas masses assuming solar metallicity.
bWith log(M*/|$\rm M_{\odot}$|) > 10.
Linear scaling relations between the emission from PAHs, IR, and CO, and various galaxy properties.
| log x . | log y . | α . | β . | σ . | Sample . |
|---|---|---|---|---|---|
| LIR [L⊙] | L6.2 [L⊙] | 0.98 ± 0.03 | −1.89 ± 0.30 | 0.13 | SFGs |
| LIR [L⊙] | L6.2 [L⊙] | 0.81 ± 0.03 | −0.04 ± 0.29 | 0.21 | All |
| LIR [L⊙] | L7.7 [L⊙] | 1.00 ± 0.03 | −1.53 ± 0.28 | 0.13 | SFGs |
| LIR [L⊙] | L7.7 [L⊙] | 0.84 ± 0.02 | −0.15 ± 0.26 | 0.20 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.02 ± 0.06 | −0.65 ± 0.31 | 0.24 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.03 ± 0.06 | −0.73 ± 0.38 | 0.26 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 0.99 ± 0.07 | −0.37 ± 0.70 | 0.24 | With CO(1–0) |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.03 ± 0.08 | −0.13 ± 0.19 | 0.21 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.04 ± 0.08 | −0.21 ± 0.20 | 0.23 | All |
| L24 [L⊙] | L6.2 [L⊙] | 0.99 ± 0.05 | 1.51 ± 0.37 | 0.20 | 5MUSES SFGs |
| L24 [L⊙] | L6.2 [L⊙] | 0.90 ± 0.05 | 2.14 ± 0.35 | 0.21 | 5MUSES |
| L160 [L⊙] | L6.2 [L⊙] | 1.02 ± 0.04 | −0.11 ± 0.37 | 0.11 | 5MUSES |
| L250 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.04 | 1.48 ± 0.31 | 0.17 | 5MUSES |
| L350 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.05 | 1.83 ± 0.38 | 0.19 | 5MUSES |
| L500 [L⊙] | L6.2 [L⊙] | 0.83 ± 0.06 | 2.34 ± 0.42 | 0.17 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L24 [L⊙] | L7.7 [L⊙] | 0.97 ± 0.05 | 2.15 ± 0.37 | 0.21 | 5MUSES SFGs |
| L24 [L⊙] | L7.7 [L⊙] | 0.79 ± 0.05 | 3.46 ± 0.40 | 0.28 | 5MUSES |
| L160 [L⊙] | L7.7 [L⊙] | 1.04 ± 0.04 | 0.23 ± 0.37 | 0.12 | 5MUSES |
| L250 [L⊙] | L7.7 [L⊙] | 0.87 ± 0.04 | 2.03 ± 0.3 | 0.19 | 5MUSES |
| L350 [L⊙] | L7.7 [L⊙] | 0.85 ± 0.05 | 2.45 ± 0.40 | 0.22 | 5MUSES |
| L500 [L⊙] | L7.7 [L⊙] | 0.82 ± 0.06 | 3.00 ± 0.48 | 0.22 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.02 ± 0.02 | 0.36 ± 0.19 | 0.06 | All |
| L6.2 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 1.10 ± 0.01 | 0.28 | 5MUSES MS SFGsb |
| L7.7 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 0.55 ± 0.02 | 0.28 | 5MUSES MS SFGsb |
| log x . | log y . | α . | β . | σ . | Sample . |
|---|---|---|---|---|---|
| LIR [L⊙] | L6.2 [L⊙] | 0.98 ± 0.03 | −1.89 ± 0.30 | 0.13 | SFGs |
| LIR [L⊙] | L6.2 [L⊙] | 0.81 ± 0.03 | −0.04 ± 0.29 | 0.21 | All |
| LIR [L⊙] | L7.7 [L⊙] | 1.00 ± 0.03 | −1.53 ± 0.28 | 0.13 | SFGs |
| LIR [L⊙] | L7.7 [L⊙] | 0.84 ± 0.02 | −0.15 ± 0.26 | 0.20 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.02 ± 0.06 | −0.65 ± 0.31 | 0.24 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 1.03 ± 0.06 | −0.73 ± 0.38 | 0.26 | All |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L6.2 [L⊙] | 0.99 ± 0.07 | −0.37 ± 0.70 | 0.24 | With CO(1–0) |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.03 ± 0.08 | −0.13 ± 0.19 | 0.21 | SFGs |
| |$L^{\prime }_{\rm CO}$| [K km s−1 pc2] | L7.7 [L⊙] | 1.04 ± 0.08 | −0.21 ± 0.20 | 0.23 | All |
| L24 [L⊙] | L6.2 [L⊙] | 0.99 ± 0.05 | 1.51 ± 0.37 | 0.20 | 5MUSES SFGs |
| L24 [L⊙] | L6.2 [L⊙] | 0.90 ± 0.05 | 2.14 ± 0.35 | 0.21 | 5MUSES |
| L160 [L⊙] | L6.2 [L⊙] | 1.02 ± 0.04 | −0.11 ± 0.37 | 0.11 | 5MUSES |
| L250 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.04 | 1.48 ± 0.31 | 0.17 | 5MUSES |
| L350 [L⊙] | L6.2 [L⊙] | 0.87 ± 0.05 | 1.83 ± 0.38 | 0.19 | 5MUSES |
| L500 [L⊙] | L6.2 [L⊙] | 0.83 ± 0.06 | 2.34 ± 0.42 | 0.17 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L24 [L⊙] | L7.7 [L⊙] | 0.97 ± 0.05 | 2.15 ± 0.37 | 0.21 | 5MUSES SFGs |
| L24 [L⊙] | L7.7 [L⊙] | 0.79 ± 0.05 | 3.46 ± 0.40 | 0.28 | 5MUSES |
| L160 [L⊙] | L7.7 [L⊙] | 1.04 ± 0.04 | 0.23 ± 0.37 | 0.12 | 5MUSES |
| L250 [L⊙] | L7.7 [L⊙] | 0.87 ± 0.04 | 2.03 ± 0.3 | 0.19 | 5MUSES |
| L350 [L⊙] | L7.7 [L⊙] | 0.85 ± 0.05 | 2.45 ± 0.40 | 0.22 | 5MUSES |
| L500 [L⊙] | L7.7 [L⊙] | 0.82 ± 0.06 | 3.00 ± 0.48 | 0.22 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.00 ± 0.02 | 0.62 ± 0.13 | 0.01 | 5MUSES |
| L6.2 [L⊙] | L7.7 [L⊙] | 1.02 ± 0.02 | 0.36 ± 0.19 | 0.06 | All |
| L6.2 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 1.10 ± 0.01 | 0.28 | 5MUSES MS SFGsb |
| L7.7 [L⊙] | |$M_{\rm H_{\rm 2}}$|a [|$\rm M_{\odot}$|] | 1.00 (fixed) | 0.55 ± 0.02 | 0.28 | 5MUSES MS SFGsb |
Notes. The linear fits are obtained in the logarithmic space : log y = α × log x + β. The best-fitting parameters and the intrinsic scatter are estimated from the Bayesian linear regression method described in Kelly (2007).
aDust-derived molecular gas masses assuming solar metallicity.
bWith log(M*/|$\rm M_{\odot}$|) > 10.
3.2 The CO–IR luminosity relation
The use of LIR as an SFR tracer and the fact that CO emission is directly associated with the molecular gas reservoir of a galaxy has motivated several studies to investigate the |$L^{\prime }_{\rm CO}$|–LIR relation as a proxy for the star formation law that links the SFR to the molecular gas of galaxies (KS law). The existence of a universal |$L^{\prime }_{\rm CO}$|–LIR (and thus of a universal Mgas–SFR) relation has been challenged by recent observations of different galaxy populations at various redshifts (e.g. Bouché et al. 2007; Daddi et al. 2010b; Genzel et al. 2010; Krumholz, Dekel & McKee 2012; Silverman et al. 2015). Although the debate is still open, there are claims that MS galaxies at all redshifts tend to follow a unique |$L^{\prime }_{\rm CO}$|–LIR relation from which local ULIRGs and high-|$z$| SBs are outliers exhibiting lower |$L^{\prime }_{\rm CO}$|/LIR ratios, indicative of higher SFEs (e.g. Daddi et al. 2010b; Genzel et al. 2010, Magdis et al. 2017). Addressing the question of this possible bimodality is beyond the scope of our work. Instead, we wish to investigate how the galaxies at different redshifts and with different physical conditions populate the |$L^{\prime }_{\rm CO}$|–LIR parameter space and explore how the global |$L^{\prime }_{\rm CO}$|–LIR relation behaves with respect to the observed trends between LPAH–LIR and LPAH–|$L^{\prime }_{\rm CO}$|.
In Fig. 4, we present the LIR–|$L^{\prime }_{\rm CO}$| relation for the 5MUSES sample along with the literature compilation included in Fig. 3 (See Table 2). We also consider the LIR–|$L^{\prime }_{\rm CO}$| relation of Sargent et al. (2014) calibrated on MS galaxies with M* ≥ 1010|$\rm M_{\odot}$| at 0 < |$z$| < 3.2 with a slope of 0.81 and a dispersion of 0.21 dex. The vast majority of SFGs, including our 5MUSES sample and the high-|$z$| SFGs appear to follow the Sargent relation. On the other hand, local ULIRGs and high-|$z$| SBs are outliers, a situation that resembles the L6.2–LIR and L7.7–LIR relations (Fig. 3). In other words, sources exhibiting lower |$L^{\prime }_{\rm CO}$|/LIR ratios with respect to the general population of normal galaxies tend to also exhibit lower LPAH/LIR ratios. In the next subsection, we bring these two together by exploring the relations between PAH and CO luminosities.
![Correlation between CO(1–0) line luminosity ($L^{\prime }_{\rm CO}$) and LIR. Colour coding and symbols follow Fig. 3. Higher-J CO transitions from the literature are corrected to CO(1–0) using Wilson et al. (2012) for the SINGS galaxies and Bothwell et al. (2013) are adopted for the remaining sample. The blue lines show the $L^{\prime }_{\rm CO}$–LIR relation from Sargent et al. (2014). The top panel shows the $L^{\prime }_{\rm CO}$/LIR ratio in units of [(K km s−1 pc2)/L⊙] as a function of LIR along with the Sargent et al. (2014) relation. The blue shaded regions depict the observed dispersion of 0.21 dex.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2777/1/m_sty2777fig4.jpeg?Expires=1749847666&Signature=hB2FP836860UoHTydawxRmCpYvKftayuGJKq6Gxf303aHvYKwoWHb9~D~NIhi-AltXg9YUwFBG-Ems11yOJ9rgD8UiMpBD4mgZOwks~m8XIgkMeQmFaLM7rp~fIC1SbPz0~Iqqxi-1mIkliKvp4IBITbpUjTj1sj-9h1OfrVmTOoeCho4djWyZV8J6OehpsuWAhEpPDObYaN5m9WLiEYq9XueWxu7jby9G0sj~Vrc-b6z~T6rbAfp2aJvkRtW66llIheiUaE~NKTbky1zG8gnnATSqgcpMl6ZpGcJhcgcEQSUxDuzBmXkDddTobueQEeKCwdlmHxxm5yphcsxDeRpw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Correlation between CO(1–0) line luminosity (|$L^{\prime }_{\rm CO}$|) and LIR. Colour coding and symbols follow Fig. 3. Higher-J CO transitions from the literature are corrected to CO(1–0) using Wilson et al. (2012) for the SINGS galaxies and Bothwell et al. (2013) are adopted for the remaining sample. The blue lines show the |$L^{\prime }_{\rm CO}$|–LIR relation from Sargent et al. (2014). The top panel shows the |$L^{\prime }_{\rm CO}$|/LIR ratio in units of [(K km s−1 pc2)/L⊙] as a function of LIR along with the Sargent et al. (2014) relation. The blue shaded regions depict the observed dispersion of 0.21 dex.
3.3 The relations between CO and PAH emission
![Correlation between L6.2 versus $L^{\prime }_{\rm CO}$(left) and L7.7 versus $L^{\prime }_{\rm CO}$ (right). Colour coding and symbols follow Fig. 3. The top panels show the PAH and CO luminosity ratios in units of [L⊙/(K km s−1 pc2)] and as a function of $L^{\prime }_{\rm CO}$. SINGS galaxies (grey) are excluded from the fitting procedure due to possible systematics introduced from the applied aperture correction (See Section 2.2.2). The purple lines and shaded regions depict the best-fitting linear regression and its intrinsic scatter for all the galaxies. For the upper panels, we show the observed dispersion assuming a LPAH–$L^{\prime }_{\rm CO}$ slope of unity. The fit parameters of the CO–PAH luminosity relations are listed in Table 5.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2777/1/m_sty2777fig5.jpeg?Expires=1749847666&Signature=WJcgVRv-8mDr4LUZP01LWmjfR5p-s-fNOau2zdYo7w-6AcGypqbnlMAPNBXJHnWTny9V5fNizLfsnKY1b138WxJLEgOfgBxvI7PUmBIowItbsEAfK4h4HGEvdrZLPdLQhmb3~gxC7YPWU2j~wtd8Izn6egrYogo2rsobnlJCXAZUpHc~kLs2j~uaWko~reTGUas5G8BE0hm1Lzm1bb4DyIfFkevLed8bQ7jVxGNqRv4zWkJ9Q~2L4J50xT~SButsss69bqPduce67loQbCAoOQc3Pay1NM9FLXMpiLXvkHVL0wLLcQjOkY-IovsjYBFa95Y5wf1V6saHcF0zkvIGNw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Correlation between L6.2 versus |$L^{\prime }_{\rm CO}$|(left) and L7.7 versus |$L^{\prime }_{\rm CO}$| (right). Colour coding and symbols follow Fig. 3. The top panels show the PAH and CO luminosity ratios in units of [L⊙/(K km s−1 pc2)] and as a function of |$L^{\prime }_{\rm CO}$|. SINGS galaxies (grey) are excluded from the fitting procedure due to possible systematics introduced from the applied aperture correction (See Section 2.2.2). The purple lines and shaded regions depict the best-fitting linear regression and its intrinsic scatter for all the galaxies. For the upper panels, we show the observed dispersion assuming a LPAH–|$L^{\prime }_{\rm CO}$| slope of unity. The fit parameters of the CO–PAH luminosity relations are listed in Table 5.
3.4 The relation between PAH and dust emission
In the previous section, we showed that the emission from PAHs on global scales correlate with CO(1–0) luminosity over a wide range of redshifts and various galaxy types. This result suggests a link between the PAH emission and the Mgas of a galaxy. Since Mgas is a derived physical parameter rather than a direct observable, before exploring a possible LPAH–Mgas relation, it is informative to investigate the scaling relations and the scatter between LPAH and the warm and the cold dust emission through MIR and FIR photometric bands. The motivation behind this exercise is that Mgas is known to be directly associated with the cold dust emission of galaxies (Leroy et al. 2011; Eales et al. 2012; Magdis et al. 2012; Magdis et al. 2013; Scoville et al. 2017), whereas the warm dust emission is linked to star formation. For the sake of brevity and clarity, we only present the results for the PAH 6.2 |$\mu$|m feature which is least affected by silicate absorption and extinction (Peeters, Spoon & Tielens 2004). However, the same applies to the PAH 7.7 |$\mu$|m feature due to the linear correlation between these two in logarithmic scales (L6.2–L7.7: α = 1.02 ± 0.02, see Table 5).
Using Spitzer and Herschel photometric observations of the 5MUSES sample, we derive monochromatic luminosities at 24, 160, 250, 350, and 500 |$\mu$|m (see Section 2.3) and plot them against L6.2 in Figs 6 and 7, including galaxies with secure dust luminosities (>3σ). To minimize the effects of K-correction, we restrict our sample to a redshift range of 0.1 < |$z$| < 0.3 (〈|$z$|〉 = 0.12 ± 0.05). While L6.2 is found to correlate with both the warm dust emission as traced by L24 as well as with the colder dust emission (at L160, L250, L350, and L500), we obtain a lower scatter for the latter, even when AGNs are excluded from the fit. We note that quite naturally galaxies with the presence of an AGN appear as prominent outliers only in the L6.2−L24 relation due to the intrinsic AGN dust emission that peaks between rest frame 15 and 60 |$\mu$|m (Mullaney et al. 2011), boosting the L24 (for fixed LIR) with respect to star-formation dominated galaxies.
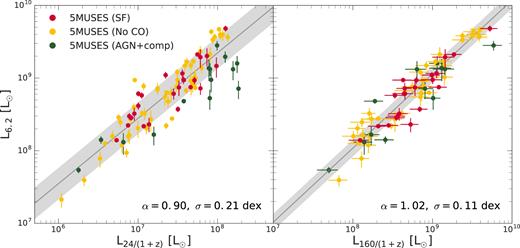
Correlation between L6.2 and the 24 |$\mu$|m (left) and 160 |$\mu$|m luminosity (right) for the 5MUSES sample. Colour coding follow Fig. 3. The dark grey line depicts the best linear regression fit to the 5MUSES sample and the 1σ dispersion of the correlation presented as the shaded region. Note the reduced intrinsic scatter of the L6.2−L160 relation as opposed to L6.2−L24 and the fact that AGN/composite sources are clear outliers in the L6.2−L24 relation. The fit parameters are listed in Table 5.

Correlation between L6.2 and the 250 |$\mu$|m (left), 350 |$\mu$|m (middle), and 500 |$\mu$|m luminosity (right) for the 5MUSES sample. The fit parameters are listed in Table 5.
The correlation between the cold dust and PAH emission has been supported by various spatially resolved observations of local galaxies. For example, using Spitzer observations of local normal galaxies, Bendo et al. (2008) find the PAH emission to be well correlated with the 160 |$\mu$|m emission on spatial scales of ∼2 kpc, and a significant scatter in the relation between PAH and 24 |$\mu$|m emission, concluding that the PAHs are associated with the diffuse, cold dust. Similar results, based on SMC observations, were reached by Sandstrom et al. (2010, 2012), who also reported a strong correlation between the PAH and CO(1–0) emission. Furthermore, Haas et al. (2002), find a good spatial coincidence between the 850 |$\mu$|m continuum emission and the strength of the PAH 7.7 |$\mu$|m line, suggesting again that the PAH carriers are preferentially related to the regions dominated by cold dust and molecular clouds, where they are excited mainly by the interstellar radiation field.
These findings are also in agreement with recent modelling studies of the various dust components within H ii regions and their surrounding envelopes (Pavlyuchenkov et al. submitted; see also Akimkin et al. 2015, 2017). They argue for a lower correlation between PAHs and graphite grains, responsible for the majority of the dust emission at 24 |$\mu$|m, due to possible destruction of PAHs within the H ii regions. By modelling the intensity distributions of the different dust components, they find similar intensity distributions between PAHs and silicates that are the dominant dust component at ∼100–500 |$\mu$|m. This could indicate that PAHs located in the molecular clouds are excited by escaping UV photons from the H ii regions (Pavlyuchenkov et al. submitted).
Put together, our analysis suggests that on global integrated scales PAH emission is linked to the cold dust and the CO emission in our sample, both of which are tracers of the molecular gas.
3.5 The L6.2–|$M_{\rm H_{\rm 2}}$| relation in MS galaxies
However, both observational and theoretical studies suggest that αCO varies with specific properties of the ISM, including metallicity and galaxy morphology (e.g. Leroy et al. 2011; Narayanan et al. 2012; Papadopoulos et al. 2012; Sandstrom et al. 2013), ranging between 〈αCO〉 ≈ 4.5 |$\rm M_{\odot }/$|(K km s−1 pc2) for normal MS galaxies and 〈αCO〉 ≈ 0.8 |$\rm M_{\odot }/$|(K km s−1 pc2) for local ULIRGs and high-|$z$| SBs (e.g. Solomon et al. 1987; Tacconi et al. 2006; Tacconi et al. 2008; Daddi et al. 2010b; Leroy et al. 2011; Magdis et al. 2011; Magdis et al. 2012; Casey, Narayanan & Cooray 2014).
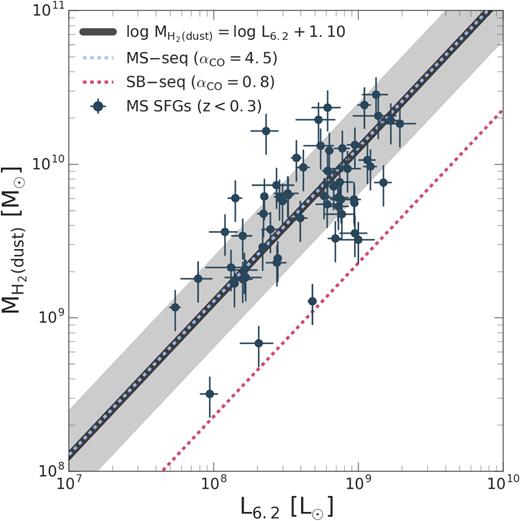
Correlation between L6.2 and dust-derived molecular gas mass (|$M_{\rm H_{\rm 2}}$|) for normal galaxies assuming solar metallicity. The sample includes 5MUSES MS galaxies at |$z$| < 0.3 with log(M*/|$\rm M_{\odot}$|) > 10. The black line corresponds to the best fit with a fixed slope of 1 with an intrinsic scatter of 0.30 dex (grey shaded region). The light blue and red dashed lines are the |$M_{\rm H_{\rm 2}}$|–|$L^{\prime }_{\rm CO}$| relation for MS and SB galaxies adopting αCO = 4.5 |$\rm M_{\odot }/$|(K km s−1 pc2) and αCO = 0.8 |$\rm M_{\odot }/$|(K km s−1 pc2), respectively.
4 DISCUSSION
In the previous sections, we have explored the global scaling laws between L6.2, |$L^{\prime }_{\rm CO}$|, and LIR for a large compilation of different galaxy populations at various redshifts. We have seen that variations in the L6.2/LIR and |$L^{\prime }_{\rm CO}$|/LIR ratios among different galaxy populations are not permeated in their L6.2/|$L^{\prime }_{\rm CO}$| ratios that instead appear to be rather constant through a universal L6.2–|$L^{\prime }_{\rm CO}$| relation with a slope of unity.
This is further demonstrated in Fig. 9. While the distribution of the log(L6.2/|$L^{\prime }_{\rm CO}$|) ratios is symmetric around the central value, we find a negatively skewed distribution of the log(L6.2/LIR) ratios. This skewness is driven by systematically lower log(L6.2/LIR) ratios of local ULIRGs. In fact, we find a 8.70σ significant difference between the mean values of log(L6.2/LIR) for the local ULIRGs (−2.68 ± 0.06) and the 5MUSES SFGs (−2.11 ± 0.03). On the other hand, we do not find any significant systematic variations in the log(L6.2/|$L^{\prime }_{\rm CO}$|) ratios (ULIRGs: 0.36 ± 0.06, 5MUSES SFGs: 0.44 ± 0.04). This suggests that L6.2 is, in fact, a better tracer of CO (and thus of |$M_{\rm H_{\rm 2}}$|) than the total IR emission.
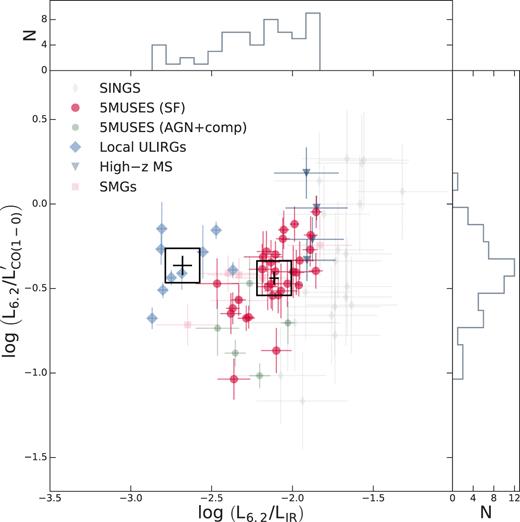
log(L6.2/|$L^{\prime }_{\rm CO}$|) versus log(L6.2/LIR) for the full sample with both PAH and CO emission. Colour coding and symbols follow Fig. 3. The black open squares correspond to the median values for the 5MUSES SFGs and the local ULIRGs. The top and right panels show the distribution of L6.2/LIR and L6.2/|$L^{\prime }_{\rm CO}$|, respectively.
While the emerging PAH–CO luminosity relation has also been reported in spatially resolved observation of local galaxies, its physical origin (if any) is still debated. Bendo et al. (2010) suggest that the correlation between PAH and CO emission observed in NGC 2403 on large scales can be explained if they share similar excitation mechanisms, or if the molecular cloud formation is triggered in regions with stellar potential wells as described in Leroy et al. (2008). For the latter, CO emission could then arise from newly formed molecular clouds, while starlight in the potential wells would heat surrounding regions enhancing the PAH emission. This scenario would also explain the variations between PAH and CO emission on sub-kpc scales and the similar radial profiles on larger spatial scales (Regan et al. 2006). Finally, recent studies have suggested that in dense PDRs, PAHs may be responsible for a significant fraction of the |$\rm {H}_{2}$| formation at a rate comparable to that of |$\rm {H}_{2}$| formation on dust grains (Castellanos et al. 2018a,b). If so, a correlation between PAHs and |$M_{\rm H_{\rm 2}}$| could thus be expected.
The CO–PAH luminosity relation is not the only piece of evidence for a potential link between L6.2 and |$M_{\rm H_{\rm 2}}$|. In Section 3.5, we used CO-independent |$M_{\rm H_{\rm 2}}$| estimates through the δGDR−Z technique and found a linear L6.2–|$M_{\rm H_{\rm 2}}$| relation for normal SFGs. The relation in equation (5) can then be used to define: |$M_{\rm H_{\rm 2}}$| = α6.2 × L6.2, where α6.2 is the parameter converting L6.2 to |$M_{\rm H_{\rm 2}}$|. The inferred α6.2 conversion factor of our sample of MS galaxies are shown in Fig. 10 (left). It appears that α6.2 is independent of redshift for MS galaxies with an average value of 〈log(α6.2)〉 = 1.09 and a standard deviation of 0.30 (Fig. 10right). An obvious caveat for the derivation of |$M_{\rm H_{\rm 2}}$| from L6.2 , similar to the δGDR and CO technique, is the dependence on metallicity which becomes challenging especially for SB systems and low-mass galaxies. For speculation, we overplot local ULIRGs in Fig. 10 (left) inferring their |$M_{\rm H_{\rm 2}}$| estimates from |$L^{\prime }_{\rm CO}$| and assuming the commonly adopted αCO = 0.8 |$\rm M_{\odot }/$|(K km s−1 pc2). Naturally, lower αCO values lead to lower α6.2 values for SB systems.
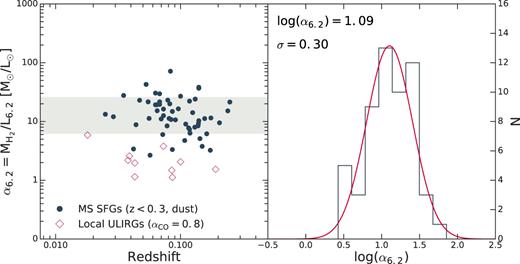
Left: Correlation between the α6.2 conversion factor versus redshift. The sample includes dust-derived Mgas estimates of 5MUSES MS galaxies at |$z$| < 0.3 (dark blue). The grey region depicts the average α6.2 value of the sample and the 1σ dispersion. We overplot local ULIRGs (red) assuming αCO = 0.8 |$\rm M_{\odot }/$|(K km s−1 pc2). Right: Distribution of log(α6.2) for the 5MUSES MS galaxies. The red line corresponds to the best-fitting Gaussian profile to the data with a mean value of 1.09 and a standard deviation σ = 0.30.
5 CONCLUSIONS
We have presented 24 new CO(1–0) observations of intermediate redshift (0.03 < |$z$| < 0.30) SFGs drawn from the 5MUSES sample that also benefits from existing Spitzer IRS spectroscopy and FIR photometry observations from Spitzer and Herschel. Complementing our study with literature CO, PAH, and dust observations, we investigate scaling relations between the various components of the ISM of galaxies covering a wide range of redshifts and physical conditions. We summarize our conclusions as follows:
We confirm the existence of a correlation between the PAH and CO emission on global integrated scales and for the first time determine its slope and scatter in a robust statistical way. The linear and tight L6.2–|$L^{\prime }_{\rm CO}$| correlation (slope of ∼1.0 and intrinsic scatter σ = 0.26 dex) is followed by the majority of galaxies at all redshifts, independent of the galaxy type.
We find evidence that on galaxy integrated scales, L6.2 traces better the cold dust (λ > 100 |$\mu$|m) rather than the warm dust emission (λ = 24 |$\mu$|m). This is in agreement with spatially resolved observations of local galaxies. The fact that both CO and cold dust emission are tracing molecular gas, motivates us to propose that PAHs may serve as a gas tracer in SFGs.
We define a α6.2 = |$M_{\rm H_{\rm 2}}$|/L6.2 conversion factor of 2.7 × αCO, where αCO is the |$L^{\prime }_{\rm CO}$| to |$M_{\rm H_{\rm 2}}$| conversion factor. For normal SFGs we find α6.2 = 12.30 |$\rm M_{\odot}$|/L⊙ (σ = 0.30 dex), which is consistent with αCO ≈ 4.5 |$\rm M_{\odot }/$|(K km s−1 pc2), typical of normal SFGs.
We conclude that L6.2 can effectively probe the molecular gas mass in galaxies within a factor of ∼2 and propose that with the launch of JWST, PAHs could serve as a useful tool to trace the ISM properties in SFGs up to |$z$| ∼ 3.5.
SUPPORTING INFORMATION
Table 3. General properties of the 5MUSES sample.
Table 4. Galaxies from the literature with PAH, IR, and/or CO emission.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
IC acknowledges support from Villum Fonden research grant (13160). GEM acknowledges support from the Carlsberg Foundation and a research grant (13160) from Villum Fonden. GEM, ST, CGC, and MS acknowledge support from the ERC Consolidator Grant funding scheme (project ConTExt, grant number No. 648179). This work includes observations carried with the IRAM 30 m telescope, which is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain). The Cosmic Dawn Center is funded by the Danish National Research Foundation. This research has made use of the NASA/IPAC Extragalactic Data base (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Footnotes
L8 is the monochromatic luminosity at rest frame 8 |$\mu$|m as traced by the IRAC 8.0 |$\mu$|m band, which covers both the PAH 6.2, 7.7, and 8.6 |$\mu$|m complex at low redshift.



![CO(1–0) spectra with antenna temperature [mK] as a function of velocity [km s−1] of CO-detected 5MUSES galaxies followed-up with IRAM/EMIR. All spectra are smoothed to a velocity resolution of ∼70 km s−1. A line is considered detected if the integrated signal is above 3σ. The black line shows the best-fitting Gaussian profile to the observed CO line.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2777/1/m_sty2777fig2a.jpeg?Expires=1749847666&Signature=aE7QhJl21--7UhibKw9Zf3XTVK0j7ZcHrhdiPy4GeIbmb3j-5~G9uQEVksNiv5ZfjqvtHfeEzWyW0M~~Oxa61tHgXsJJUzZ5UjEc~5cgIV76-BxuhXHdnvdR7ffDBJX6mg8TbEBnm87K-dnA9YRdDq689CXAYWKilRxD9AE6WyqpBpKKexbr9Ksi~VgJuYnnNn-JZOt-1fj-RvMhd~i~ut6qjhpl25DONWcuUBp6ma88r7XNux6sbi6~Qg-j2CYWX1IIbl2HjXGJHl7YN~KrAyxvcQrQip2afzLU-Z8FInOmusVWLmx0VB3~FDT--N9pZnL63PgzO9QeaCPjJewd-Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![CO(1–0) spectra with antenna temperature [mK] as a function of velocity [km s−1] of CO-detected 5MUSES galaxies followed-up with IRAM/EMIR. All spectra are smoothed to a velocity resolution of ∼70 km s−1. A line is considered detected if the integrated signal is above 3σ. The black line shows the best-fitting Gaussian profile to the observed CO line.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2777/1/m_sty2777fig2b.jpeg?Expires=1749847666&Signature=rQBaNUbRQCg9xlIxF0ha5mPX5VJRydIytM~UwuXrOYwsEuTT~JhPLFuEzMvNr9CghLCPj6Hatdu9Rv-1llMEE9Afe8As2LnTKo4dDPRJpfTr5I8JsZFaAlHyHkiKAJm~kjm3yiPEwPMKow-2LCqHs-wbw-nfYSV4dAFU28YeX4hnSFaRGDRl1nbr~ZsUUGRazXhzu2ctMT-YAtOF9oJSxkUUIGIbOoQrN8JSBc7zTUqcXVzPyP1RQnmPwH4ya4eCTGMOssv7i9h-MRoA5k5JNMSJdKDwYJMRN4iapmOfiNztWPbGndDbaauiNIRpsdD78qv-ayHgYqWbye0rWtM3FA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![CO(1–0) spectra with antenna temperature [mK] as a function of velocity [km s−1] of CO-detected 5MUSES galaxies followed-up with IRAM/EMIR. All spectra are smoothed to a velocity resolution of ∼70 km s−1. A line is considered detected if the integrated signal is above 3σ. The black line shows the best-fitting Gaussian profile to the observed CO line.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2777/1/m_sty2777fig2c.jpeg?Expires=1749847666&Signature=RG0-VHlU65c2-yryHqo6RwVXfEQqx57uBpPWWbnYTltopjoy~X1R5Yvr4nXeBN1g~AGrk0vL69-ebfS4BlOQgJ1EKayWmMC9FpzWx~p~kbamoZbfizHz1poIhzdJlfgDLP11e1VCl0jOjn3nEBaqV1FKBIgTxgjMQXeaYB3H4wvvroH6cxWclSyr788eD2bhlKtl~b6Z1vr93pltFKPwSPRw1yhWMcddgIogmUSY0Cc2pJvaPaay8CqQp~gPW4QCZRmnVuQTX8F53VkiHv5oJk~7BJoiWDgmndrYXn0MS1wGAo0vVJl4w8BbQi~2GjLE8OjyUZqU7AfDPenM9IUCug__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
