-
PDF
- Split View
-
Views
-
Cite
Cite
Andreas Christ Sølvsten Jørgensen, Achim Weiss, Addressing the acoustic tachocline anomaly and the lithium depletion problem at the same time, Monthly Notices of the Royal Astronomical Society, Volume 481, Issue 4, December 2018, Pages 4389–4396, https://doi.org/10.1093/mnras/sty2590
Close - Share Icon Share
Abstract
Current standard solar models neither account properly for the photospheric lithium abundance nor reproduce the inferred solar sound speed profile. Diffusive overshooting at the base of the solar convective envelope has previously been shown to solve either of these model inadequacies. In this paper, we present an analysis of solar models with four different parametrizations of diffusive overshooting. We find that these models are able to recover the correct lithium depletion, regardless of the parametrization, if overshooting is suppressed, during the early evolutionary stages. Further, parametrizations of diffusive overshooting have been shown to improve the inferred sound speed profile. However, none of the presented models are able to simultaneously solve both model inadequacies, showing that diffusive overshooting on its own is deficient to account for observations.
1 INTRODUCTION
Comparisons between observations and model predictions reveal several shortcomings of modern stellar structure models. Present model inadequacies include discrepancies between the predicted solar sound speed profile and the solar sound speed profile inferred from helioseismology (Christensen-Dalsgaard et al. 1985; Christensen-Dalsgaard, Gough & Thompson 1991), i.e. the study of solar oscillations (Leighton 1960; Ulrich 1970). Especially near the tachocline, the sound speed difference between the Sun and current standard solar models show a striking anomaly. Lithium depletion in stellar convective envelopes is another issue that still has to be properly accounted for: meteoritic measurements and spectroscopic measurements of the solar photosphere show that the present solar abundance of 7Li is roughly 100–200 times lower than the initial one (Greenstein & Richardson 1951; Asplund et al. 2009). Standard solar models do not reproduce this depletion. Moreover, surveys reveal that the Sun is not exceptional for a star of its age, mass, and metallicity: solar-like stars are generally lithium poor (e.g. Baumann et al. 2010).
The tachocline anomaly was immediately apparent from the first inversions of helioseismic data (Christensen-Dalsgaard et al. 1985; Christensen-Dalsgaard, Gough & Thompson 1988). This discrepancy in the sound speed profile may partly reflect errors in the opacities (Christensen-Dalsgaard & Houdek 2010) but can also be addressed, by including additional mixing beyond the convective boundaries of stellar models (Christensen-Dalsgaard, Proffitt & Thomson 1993; Richard et al. 1996; Elliott, Gough & Sekii 1998). This additional mixing affects the composition and hereby alters the sound speed, potentially getting rid of the tachocline anomaly. Other seismic properties, such as the mode amplitudes, can be employed to impose further restrictions on the mixing processes (Christensen-Dalsgaard et al. 2011).
Mixing below the solar convective envelope furthermore transports lithium to hotter layers, where it is depleted in thermonuclear reactions, solving the lithium depletion problem. This solution was originally suggested by Böhm (1963) and does indeed deplete lithium sufficiently to match the present solar photospheric values, if the parameters involved are adequately tuned. That being said, while observations (e.g. Chaboyer et al. 1998) indicate that this depletion takes place on the main sequence (MS), solar models with overshooting deplete lithium prematurely (e.g. Ahrens, Stix & Thorn1992), unless the suggested additional mixing is somehow inhibited on the pre-main sequence (pre-MS; Schlattl & Weiss 1999). We will elaborate upon this in Section 3.
Consequently, as discussed by several authors, both of the issues raised above can be addressed simultaneously, by including mixing in the radiative zone (Christensen-Dalsgaard et al. 1993; Richard et al. 1996; Schlattl & Weiss 1999; Andrássy & Spruit 2013).
Several processes have been advocated to contribute to the necessary additional mixing, including differential rotation between the radiative and the convective zones (e.g. Spiegel & Zahn 1992), internal gravity waves (e.g. García Lopez & Spruit 1991), and the penetration of convective plumes into the radiative zone, so-called overshooting. Different authors offer different pictures and models for the latter; for instance, based on Spruit (1997), Andrássy & Spruit (2013, 2015) argue for overshooting, assuming that convective settling beyond the convective boundary can be understood in terms of an entropy difference between the sinking material and its surroundings.
One way of taking overshooting into account amounts to extending the adiabatic region by a fraction of a pressure scale height into the subadiabatic region beyond the base of the convection envelope. Such quasi-adiabatic penetration can be achieved, using mixing-length theory (Zahn 1991). However, just as it is the case for models without overshooting, this approach gives rise to an abrupt transition in the temperature gradient, which is neither favoured by helioseismic measurements nor by hydrodynamical simulation of the convective plumes. Other treatments of overshooting, on the other hand, do not suffer from this deficit (e.g. Andrássy & Spruit 2013). For a detailed discussion of this topic, we refer to Christensen-Dalsgaard et al. (2011).
Yet another method to take the structural effects of overshooting into account is to adjust the temperature gradient in the overshooting region, drawing from helioseismology and the overshooting profiles of 3D simulations (Christensen-Dalsgaard et al. 2011). Finally, one may introduce additional mixing, by altering the diffusion coefficients in the overshooting layer (e.g. Baraffe et al. 2017; Christensen-Dalsgaard, Gough & Knudstrup 2018; Schlattl & Weiss 1999). Such adjustments of the diffusions coefficient may be justified by the attempt to mimic the outcome of 2D or 3D hydrodynamic simulations (Freytag, Ludwig & Steffen 1996; Pratt et al. 2016).
In this paper, we follow the last approach mentioned above, and hence restrict ourselves to diffusive overshooting. While the diffusion coefficients are altered to accommodate for additional mixing in the radiative zone, the radiative temperature gradient is used within the overshooting layer.
We investigate four different parametrizations of the diffusion coefficients in the overshooting layer, restricting ourselves to the solar case. The aim is to evaluate, whether each of these parametrizations can solve the lithium depletion problem, and whether models that succeed simultaneously solve the tachocline anomaly. To this end, we have performed solar calibrations for each overshooting parametrization, using the Garching Stellar Evolution Code, garstec (Weiss & Schlattl 2008). All solar models have a radius R⊙ of |$6.95508\times 10^{10}\, \mathrm{cm}$|, a total luminosity L⊙ of |$3.846\times 10^{33}\, \mathrm{erg \, s^{-1}}$|, and an age of t⊙ of |$4.57\, \mathrm{Gyr}$|. We employ the OPAL equation of state (EOS; Rogers, Swenson & Iglesias 1996; Rogers & Nayfonov 2002). At low temperatures, we extend the EOS with the EOS by Hummer & Mihalas (1988). We use either the composition suggested by Grevesse & Sauval (1998) (GS98) or by Asplund et al. (2009) (AGSS09) with the corresponding OPAL opacities (Iglesias & Rogers 1996; Ferguson et al. 2005) and surface abundance Zs of heavy elements relative to the surface abundance Xs of hydrogen. In all cases, we use the reaction rates suggested by Adelberger, García & Hamish Robertson (2010). We include microscopic diffusion of H, 3He, 4He, 12C, 13C, 14N, 15N, 16O, 17O, 20Ne, 24Mg, and 28Si that are considered in the nuclear reaction network (Weiss & Schlattl 2008). 7Li and 9Be are likewise diffused but are treated as tracer elements. Moreover, we have only implemented overshooting at the bottom of the convective envelope. We note that overshooting at the core must generally be modelled differently from envelope overshooting (e.g. Schlattl & Weiss 1999). In the case of solar calibration models, core overshooting is only relevant on the pre-MS.
2 OVERSHOOTING APPROACHES
In equation (1), r denotes the distance from the stellar centre, and rcz denotes the radius of the lower convective boundary, i.e. the radius below which the Schwarzschild criterion of convective instability, ∇rad > ∇ad, no longer holds true. D0 takes the value of the diffusion coefficient half a scale height above the convective boundary, as the diffusive velocity is formally zero at the boundary. Hence, based on mixing length theory, D0 is |$\frac{1}{3}\ell _\mathrm{mix}v_\mathrm{MLT}$|. Here, ℓmix and |$v$|MLT are the mixing length and the convective velocity, respectively. The units are hence |$\mathrm{cm^2 \, s^{-1}}$|. The width lov of this overshooting layer may be chosen freely to fit observations.
In equation (2), fov is a free parameter, and D0 is defined as above. Finally, Hp denotes the pressure scale height at the base of the convection zone, including a geometrical restriction: If 2Hp exceed the extent of the convection zone (Δrcz), Hp is adjusted by a factor of (Δrcz/(2Hp))2. This geometrical limitation of overshooting is especially important, when considering core overshooting but is mostly irrelevant in the present case. We refer to Higl & Weiss (2017), who have modelled detached eclipsing binaries, for a discussion of a case for which the implementation of this geometrical cut-off becomes essential. We apply this geometrical cut-off for all diffusive overshooting parametrizations presented in this paper.
The seismic implications of the overshooting parametrization by Freytag et al. (1996) and the associated lithium depletion have previously been discussed by Schlattl & Weiss (1999). While they also address cases, where core overshooting is taken into account, we only include envelope overshooting, in order to facilitate a meaningful comparison between the different approaches. We introduce a cut-off, when Dov(r) becomes smaller than 10−20D0.
Generally speaking, exponentially decaying diffusive mixing is often used to improve stellar models (e.g. Miglio, Montalbàn & Maceroni 2007; Buldgen 2017, where the scale height is determined by the density).
In accordance with Christensen-Dalsgaard et al. (2018), we adopt α = 4.25 and |$v_0 = 0.15\, \mathrm{g^{-1}cm^3}$| and introduce a cut-off at |$v$| = |$v$|0. If Dov(r) becomes smaller than 10−20Dov(rcz), we likewise introduce a cut-off. We have varied |$D_\mathrm{\mathrm{JCD}}$|, including the value employed by Christensen-Dalsgaard et al. (2018): |$D_\mathrm{\mathrm{JCD}}=150\, \mathrm{cm^2 \, s^{-1}}$|.
3 LITHIUM DEPLETION
We have adjusted the free parameters lov, fov, dov, and |$D_\mathrm{\mathrm{JCD}}$|, in order to obtain a lithium depletion by a factor of 100–200, using the four different overshooting parametrizations described in Section 2.
Properties of the models presented in Fig. 1, using GS98. Li0/Li⊙ denotes the initial model surface lithium abundance (N(Li)/N(H)) relative to the predicted present one. Δrov refers to the width of the overshooting layer. As regards the JCD parametrization described by equation (4), |$D_{\small JCD}=150 \, \mathrm{cm^2 \, s^{-1}}$| in case a, while |$D_{\small JCD}$| is two magnitudes higher in case b. The values for |$D_{\small JCD}$| and the remaining free parameters can be found in the text. |$\alpha _{\small MLT}$| denotes the mixing length parameter. The initial abundance of helium and heavy elements predicted by the calibration lie in the intervals 0.265–0.269 and 0.0178–0.0187, respectively. All models in this table take microscopic diffusion of metals into account.
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| (s) . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 3.7 | – | 0.715 | 2083 | 0.2393 | 1.80 |
| CON | 1.2 × 102 | 0.08 | 0.718 | 2074 | 0.2451 | 1.77 |
| FOV | 1.7 × 102 | 0.16 | 0.718 | 2073 | 0.2454 | 1.77 |
| PB | 1.6 × 102 | 0.08 | 0.718 | 2074 | 0.2450 | 1.77 |
| JCD, a | 4.0 | 0.36 | 0.717 | 2078 | 0.2415 | 1.79 |
| JCD, b | 1.4 × 102 | 0.36 | 0.719 | 2072 | 0.2465 | 1.77 |
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| (s) . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 3.7 | – | 0.715 | 2083 | 0.2393 | 1.80 |
| CON | 1.2 × 102 | 0.08 | 0.718 | 2074 | 0.2451 | 1.77 |
| FOV | 1.7 × 102 | 0.16 | 0.718 | 2073 | 0.2454 | 1.77 |
| PB | 1.6 × 102 | 0.08 | 0.718 | 2074 | 0.2450 | 1.77 |
| JCD, a | 4.0 | 0.36 | 0.717 | 2078 | 0.2415 | 1.79 |
| JCD, b | 1.4 × 102 | 0.36 | 0.719 | 2072 | 0.2465 | 1.77 |
Properties of the models presented in Fig. 1, using GS98. Li0/Li⊙ denotes the initial model surface lithium abundance (N(Li)/N(H)) relative to the predicted present one. Δrov refers to the width of the overshooting layer. As regards the JCD parametrization described by equation (4), |$D_{\small JCD}=150 \, \mathrm{cm^2 \, s^{-1}}$| in case a, while |$D_{\small JCD}$| is two magnitudes higher in case b. The values for |$D_{\small JCD}$| and the remaining free parameters can be found in the text. |$\alpha _{\small MLT}$| denotes the mixing length parameter. The initial abundance of helium and heavy elements predicted by the calibration lie in the intervals 0.265–0.269 and 0.0178–0.0187, respectively. All models in this table take microscopic diffusion of metals into account.
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| (s) . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 3.7 | – | 0.715 | 2083 | 0.2393 | 1.80 |
| CON | 1.2 × 102 | 0.08 | 0.718 | 2074 | 0.2451 | 1.77 |
| FOV | 1.7 × 102 | 0.16 | 0.718 | 2073 | 0.2454 | 1.77 |
| PB | 1.6 × 102 | 0.08 | 0.718 | 2074 | 0.2450 | 1.77 |
| JCD, a | 4.0 | 0.36 | 0.717 | 2078 | 0.2415 | 1.79 |
| JCD, b | 1.4 × 102 | 0.36 | 0.719 | 2072 | 0.2465 | 1.77 |
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| (s) . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 3.7 | – | 0.715 | 2083 | 0.2393 | 1.80 |
| CON | 1.2 × 102 | 0.08 | 0.718 | 2074 | 0.2451 | 1.77 |
| FOV | 1.7 × 102 | 0.16 | 0.718 | 2073 | 0.2454 | 1.77 |
| PB | 1.6 × 102 | 0.08 | 0.718 | 2074 | 0.2450 | 1.77 |
| JCD, a | 4.0 | 0.36 | 0.717 | 2078 | 0.2415 | 1.79 |
| JCD, b | 1.4 × 102 | 0.36 | 0.719 | 2072 | 0.2465 | 1.77 |
When computing Dov(r), using equation (1)–(3), lithium is sufficiently depleted. However, this depletion takes place on the pre-MS, as already discussed by Baraffe et al. (2017) and Schlattl & Weiss (1999). This is inconsistent with observations (cf. e.g. the Pleiades or the Hyades), according to which the depletion takes place on the MS at a rate that depends on the angular momentum (cf. e.g. Jones et al. 1997; Chaboyer et al. 1998; Jones, Fischer & Soderblom 1999).
Ventura et al. (1998) propose that the inhibition of the lithium depletion on the pre-MS may be explained by rotationally induced magnetic fields – the authors also address the influence of changes in other input physics, such as the composition. Based on numerical studies (cf. Ziegler & Rüdiger 2003; Brummell 2007; Brun et al. 2017), Baraffe et al. (2017) equally argue that rotation limits the convective plumes, reducing dov at high angular velocities. Hence, Baraffe et al. (2017) evaluate the rotation period, using Kawaler’s law (Kawaler 1988; Bouvier, Forestini & Allain 1997; Viallet & Baraffe 2012), and assume dov to be a step function of the angular velocity. This necessitates the introduction of additional parameters that are neither restricted by simulations nor by observations. That being said, for many choices of these parameters, their method effectively amounts to introducing one additional free parameter: the time tov, before which overshooting is negligible or, at least, relatively inefficient.
Setting tov to the first |$10^8\, \mathrm{yr}$| and changing dov from 0.10Hp to 0.99Hp at tov, we obtain models that deplete Lithium predominantly on the MS, when using GS98 and the PB parametrization. These parameter values are overall consistent with the results presented by Baraffe et al. (2017), who effectively use a higher value of tov.
Applying the same arguments regarding the suppression of overshooting during the early evolutionary stages, we have also introduced the parameter tov, when employing the CON or FOV parametrization, i.e. equation (1) or (2). In accordance with Schlattl & Weiss (1999), who likewise initialized overshooting on the ZAMS, this allows us to compute models, for which the main lithium depletion takes place on the MS.
When employing the CON or FOV parametrization, we set |$t_\mathrm{ov}=10^8\,$|yr, lov = 1.03, and fov = 0.083, respectively, and neglect overshooting completely before tov. These parameter values seem qualitatively consistent with Schlattl & Weiss (1999), according to whom a satisfactory lithium depletion can be obtained, using fov = 0.07, when starting envelope overshooting on the ZAMS and ignoring core overshooting.3
In the case of the JCD parametrization, i.e. equation (4), overshooting only depletes the surface lithium abundance by factor of four (cf. case a in Table 1), when using the parameter values suggested by Christensen-Dalsgaard et al. (2018). We therefore vary |$D_{\small JCD}$|. To obtain a lithium depletion by a factor of 100–200, we need to increase |$D_{\small JCD}$| by two orders of magnitude. Fig. 1 shows the results for4|$D_{\small JCD} = 1.1\times 10^4 \, \mathrm{cm^2 \, s^{-1}}$| (cf. case b in Table 1). Although |$D_{\small JCD}$| is several orders of magnitudes lower than D0, a high lithium depletion is achieved, as the overshooting layer is significantly deeper than for the other three parametrization schemes.
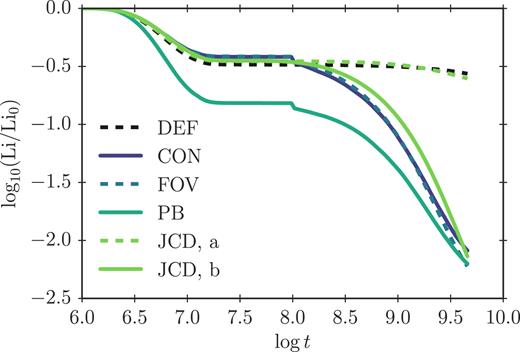
Relative change in N(Li)/N(H) at the solar surface surface as a function of time (t) for solar models, using GS98 and four different overshooting parametrizations, as well as a standard solar model, for which overshooting is neglected. Li0 denotes the initial surface lithium abundance: A(Li0) = 3.3.
In contrast to the other overshooting parametrizations presented in this paper, no additional parameter is needed to prevent a significant lithium depletion during the early evolutionary stages, in the case of the JCD parametrization. Here, we have set5tov = 0.
Fig. 1 summarizes the evolution of the surface lithium abundance for all models described above. Here, we compare the initial number density N(Li) of Lithium relative to the number density N(H) of hydrogen with the final one, since the abundance A(Li), to which the literature refers, is log10[N(Li)/N(H)] |$+$| 12.
It is worth noting that we found the lithium depletion to be rather sensitive to the input physics, the overshooting parameters and the other model parameters, by computing several additional solar calibration models. This includes the opacities, the element diffusion and the bulk composition. We attribute this sensitivity to the extreme temperature dependence of the lithium burning rate.
To illustrate this sensitivity to the input physics, we have repeated the calculations for AGSS09. We set Zs/Xs = 0.0179. The results are summarized in Table 2. Here, we likewise use |$t_\mathrm{ov} = 10^8\,$|yr but adjust the remaining overshooting parameters, in order to obtain the required lithium depletion: we set lov = 1.26, fov = 0.103 and |$D_{\small JCD}=2.5\times 10^4\, \mathrm{cm^2 \, s^{-1}}$|. In the case of the PB parametrization, dov switches from 0.1Hp to 1.23Hp at tov.
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| [s] . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 2.5 | – | 0.725 | 2051 | 0.2338 | 1.79 |
| CON | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2407 | 1.76 |
| FOV | 1.5 × 102 | 0.19 | 0.728 | 2040 | 0.2410 | 1.75 |
| PB | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2406 | 1.76 |
| JCD, a | 2.6 | 0.37 | 0.726 | 2048 | 0.2361 | 1.78 |
| JCD, b | 1.5 × 102 | 0.37 | 0.729 | 2038 | 0.2421 | 1.75 |
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| [s] . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 2.5 | – | 0.725 | 2051 | 0.2338 | 1.79 |
| CON | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2407 | 1.76 |
| FOV | 1.5 × 102 | 0.19 | 0.728 | 2040 | 0.2410 | 1.75 |
| PB | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2406 | 1.76 |
| JCD, a | 2.6 | 0.37 | 0.726 | 2048 | 0.2361 | 1.78 |
| JCD, b | 1.5 × 102 | 0.37 | 0.729 | 2038 | 0.2421 | 1.75 |
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| [s] . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 2.5 | – | 0.725 | 2051 | 0.2338 | 1.79 |
| CON | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2407 | 1.76 |
| FOV | 1.5 × 102 | 0.19 | 0.728 | 2040 | 0.2410 | 1.75 |
| PB | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2406 | 1.76 |
| JCD, a | 2.6 | 0.37 | 0.726 | 2048 | 0.2361 | 1.78 |
| JCD, b | 1.5 × 102 | 0.37 | 0.729 | 2038 | 0.2421 | 1.75 |
| Dov . | Li0/Li⊙ . | |$\frac{\Delta r_\mathrm{ov}}{R_\mathrm{\odot }}$| . | |$\frac{r_\mathrm{cz}}{R_\mathrm{\odot }}$| . | |$\mathrm{\tau _\mathrm{cz}}$| [s] . | YS . | |$\alpha _{\small MLT}$| . |
|---|---|---|---|---|---|---|
| DEF | 2.5 | – | 0.725 | 2051 | 0.2338 | 1.79 |
| CON | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2407 | 1.76 |
| FOV | 1.5 × 102 | 0.19 | 0.728 | 2040 | 0.2410 | 1.75 |
| PB | 1.3 × 102 | 0.10 | 0.728 | 2040 | 0.2406 | 1.76 |
| JCD, a | 2.6 | 0.37 | 0.726 | 2048 | 0.2361 | 1.78 |
| JCD, b | 1.5 × 102 | 0.37 | 0.729 | 2038 | 0.2421 | 1.75 |
Again, the predicted helium mass fraction at the solar surface is higher, when including overshooting. Moreover, the convective envelope is too shallow, as is well known for AGSS09 (Serenelli et al. 2009). This explains the deeper overshooting required in these models.
For both compositions, all models with and without overshooting predict an decrease in the surface abundance of 9Be by a factor of 1.1–1.3. While lithium is effectively destroyed at temperatures above |$2.5\times 10^6\, \mathrm{K}$|, the destruction of beryllium sets in at temperatures exceeding |$3.5\times 10^6\, \mathrm{K}$| and hence requires deeper mixing. Measurements of the solar beryllium depletion are notoriously difficult, but studies seem to suggest a very small difference between the photospheric and meteoritic values (Grevesse & Sauval 1998; Asplund et al. 2009). Data are even consistent with beryllium being undepleted Balachandran & Bell (1998). We hence note that none of the overshooting parametrizations strongly contradict measurements of beryllium destruction.
Moreover, according to Gloeckler & Geiss (1996) and Geiss & Gloeckler (1998), the 3He/4He ratio has not changed by more than approximately |$10\, {{\ \rm per\ cent}}$| over the last |$3\, \mathrm{Gyr}$|. Consequently, just as beryllium, 3He/4He restricts the mixing below the base of the convection zone (cf. Vauclair 2000). For all models, we find 3He/4He to increase by |$3\!-\!4\, {{\ \rm per\ cent}}$|, throughout the entire evolution from the pre-MS up to the present solar age.
4 HELIOSEISMIC PROPERTIES
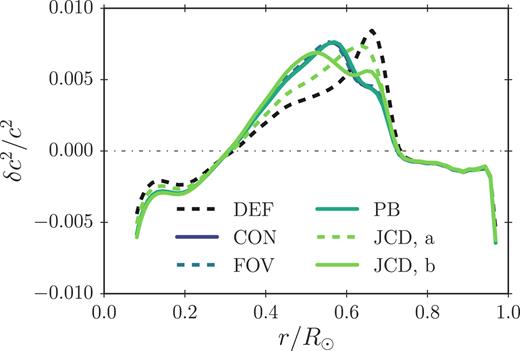
Squared sound speed difference between models with different overshooting approaches and the Sun inferred by SOLA inversion. We use GS98. The results are based on the observed `best-set’ frequencies by Basu et al. (1997). The associated confidence intervals of δc2/c2 and the centres of the averaging kernels are not included for clarity. All solar calibration models in this figure take microscopic diffusion of metals into account.
In stead of inferring δc2/c2 by inversion, many authors compare to a previously inferred solar sound speed profile based on a reference model.6 To check our inversion results, we have compared the sound speed profile of each of our solar calibration models with the solar sound speed profile inferred by Basu & Antia (2008). From these comparisons, we draw the exact same conclusions as elaborated upon below.
As can be seen from the Fig. 2, the model without overshooting shows a characteristic anomaly near the base of the convective envelope: This is the tachocline anomaly.
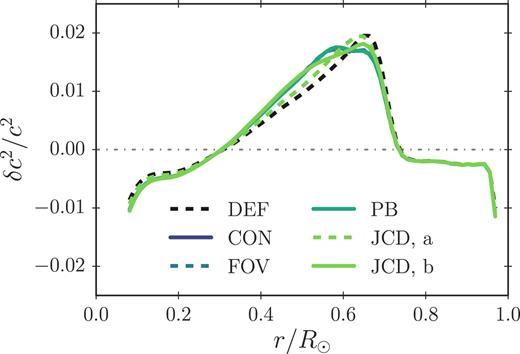
While overshooting slightly modifies the tachocline anomaly, the implementation of overshooting alone leads to a higher discrepancy in the sound speed at lower depths (cf. Fig. 2), in accordance with the work published by other authors (e.g. Schlattl & Weiss 1999; Christensen-Dalsgaard et al. 2011, 2018). We find that this feature does not appear, if microscopic diffusion of metals (i.e. diffusion of elements other than H and 4He) is ignored: including the microscopic diffusion of metals improves the sound speed of the model without overshooting, throughout the radiative region, but worsens the agreement, especially in the broader vicinity of the tachocline anomaly, in the case of models with overshooting. Fig. 3 shows the squared sound speed difference between the helioseismic Sun and solar calibration models, for which microscopic diffusion of metals other than lithium and beryllium has been neglected. We note that the inclusion of the trace elements, lithium and beryllium, has no influence on the sound speed profile. We have used the same values for the overshooting parameters as in the case of the models presented in Fig. 2. The neglect of microscopic diffusion of metals reduces the lithium depletion slightly. Comparing Figs 2 and 3, it is clear that the inclusion of overshooting creates a sensitivity on metal diffusion. The fact that the models in Fig. 3 get rid of the Tachocline anomaly without introducing new anomalies in the sound speed profile is a tantalizing result. Here, we refrain ourselves from performing a detailed investigation of the treatment of diffusion, as this is beyond the scope and not the focus of this paper.
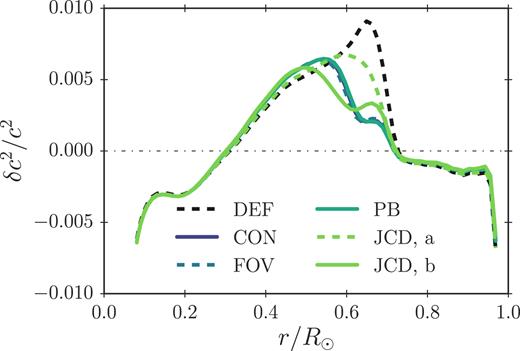
Equivalent to Fig. 2 but only including diffusion of H, 4He, 7Li, and 9Be.
Diffusive overshooting has been shown to lead to better agreement between the predicted sound speed and observations for lower values of the overshooting parameters involved – see e.g. Schlattl & Weiss (1999) and Christensen-Dalsgaard et al. (2018) for the FOV and the JCD parametrization, respectively. These models do, however, not simultaneously solve the lithium problem.
Of course dynamical processes, such as magnetic fields and rotation, may likewise alter the solar structure, partly explaining the remaining discrepancies in the obtained sound speed profile. Alternatively, corrections to the opacities may be required, as suggested by Christensen-Dalsgaard & Houdek (2010).
Fig. 4 shows the hydrogen mass fraction X as a function of radius for our solar calibration models that include microscopic diffusion of metals. The strong gradient in X near the bottom of the convective zone in the model with no overshooting gives rise to the tachocline sound speed anomaly in Fig. 2. Due to overshooting, X increases, which results in an increase of the sound speed in this layer. As can be seen from Fig. 4, the JCD parametrization b leads to a dramatically different hydrogen abundance profile than the other overshooting parametrizations, while case a lies intermediate between the default and the other cases. However, just as the simplistic CON parametrization, the JCD parametrization is a mere toy model. Indeed, since equation (4) is a polynomial with three free parameters, the other suggested functional forms of Dov(r) can be roughly mimicked by this equation.
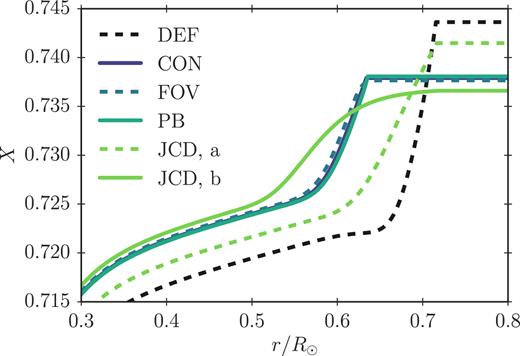
Hydrogen abundance X as a function of radius for the solar calibration models presented in Table 1 – i.e. the models include microscopic diffusion of metals.
Based on the figures discussed above, we further note that all overshooting parametrizations lead to very similar chemical and thermal structures for the present Sun, if they are to reproduce the desired lithium depletion. In this respect, the parametrization does not matter.
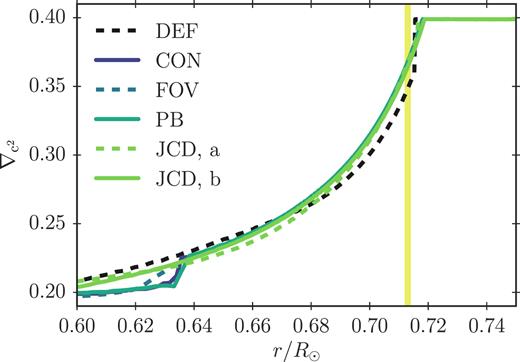
The gradient of the squared sound speed for the solar calibration models presented in Table 1 – i.e. the models include microscopic diffusion of metals. The shaded area shows the seismically inferred confidence interval for the location of the base of the convective envelope found by Basu & Antia (1997).
Furthermore, it is worth noting from Fig. 5 that the transition in |$\nabla _{c^2}$| is somewhat smoother for all models with overshooting than for the model with no overshooting – setting |$D_{\small JCD} = 150\, \mathrm{cm^2 \, s^{-1}}$|, the transition is still rather abrupt. While a lower value of |$D_{\small JCD}$| partly removes the tachocline anomaly (Christensen-Dalsgaard et al. 2018), it does not necessarily improve all seismic properties of the model. However, in order to obtain quantitative helioseismic restrictions on the model, a detailed analysis of the oscillatory signal arising from the acoustic glitch is needed (Christensen-Dalsgaard et al. 2011, and references herein), which is beyond the scope of this paper.
For comparison, we have included the squared sound speed difference (δc2/c2) for solar calibration models obtained for AGSS09 in Fig. 6 (cf. Table 2). The same conclusions are drawn: Overshooting alone does not mend the inadequacies of the sound speed profile of the presented models. As in the case of GS98, the implementation of diffusive overshooting shifts the convective boundary outwards (cf. Table 2) and leads to a somewhat smoother transitions in |$\nabla _{c^2}$|. Overall, the use of AGSS09 leads to a stronger disagreement between the model and the helioseismic Sun than the use of GS98 does. This well-known deterioration has haunted helioseismology for a decade (Serenelli et al. 2009).
5 CONCLUSION
Diffusive overshooting has been shown to either improve the predicted sound speed profile (Christensen-Dalsgaard & Di Mauro 2007; Christensen-Dalsgaard et al. 2018) or to allow for the solution of the lithium problem (Baraffe et al. 2017), when choosing suitable overshooting parameters. Discouragingly, none of the models presented in this paper solves both problems in tandem.
For all investigated combinations of input physics, overshooting itself is not enough to obtain a perfect match between the model predictions and the inferred solar structure. In order to ensure a sufficiently high lithium depletion, each diffusive overshooting scheme introduces a new anomaly in the sound speed profile, when microscopic diffusion is taken into account. Further improvements of the input physics are needed.
Hence, the ability of a particular parametrization to solve either of these problems is itself insufficient to establish, whether said parametrization leads to a physically correct description of the overshooting layer. On the other hand, combining helioseismic measurements with information of solar abundances allows for the exclusion of some scenarios and parameter choices, imposing restrictions on additional mixing processes in the radiative zone.
This being said, all four diffusive overshooting parametrizations lead to very similar sound speed profiles, when predicting comparable evolutions of the surface lithium abundance. To this extend, the parametrization is irrelevant, i.e. on their own, the suggested diagnostic tools do not lead to a clear preference. This is not to say that all models that yield the correct surface lithium abundance are indistinguishable: As shown by Schlattl & Weiss (1999), models that deplete their lithium on the pre-MS show different sound speed profiles than the models presented in this paper.
In order for the CON, FOV, and PB parametrizations given by equation (1)–(3) to recover the observed trend of lithium depletion, a suppression of overshooting is required during the early stellar evolutionary stages. In accordance with Baraffe et al. (2017), we hence assume overshooting to be far less effective during the initial evolution, when using the PB parametrization. We take this into account by limiting the width of the overshooting layers as suggested by Baraffe et al. (2017). As argued by several authors, this may be justified based on rotation (e.g. Ziegler & Rüdiger 2003; Brummell 2007; Brun et al. 2017). Since the underlying physical parameters describing rotation are insufficiently constrained, however, we have restricted ourselves to a more simplistic approach, when dealing with the CON and FOV parametrizations, in order to reduce the number of free parameters: we completely neglect overshooting for the first |$10^8\,$|yr of evolution. Additional constraints on stellar rotation would render this simplification obsolete and may potentially favour one of the diffusive overshooting schemes presented here, since there is also evidence for additional mixing in young clusters (Baraffe et al. 2017; Bouvier et al. 2017). However, this is beyond the scope of this paper.
We find that the overshooting parameters involved are rather sensitive to the input physics. It is therefore not clear, to which extend the obtained parameter values from a solar calibration can be applied in the analyses of other stars without the necessity of tuning, even if the lithium problem and the tachocline anomaly were to be solved simultaneously. Likewise, it is unclear, whether the obtained parameter values lead to an apposite description of lithium depletion at later evolutionary stages of the Sun. Simulations and observations that yield solid restrictions of and physical justifications for the employed overshooting parameters are hence much needed.
ACKNOWLEDGEMENTS
We thank J. Christensen-Dalsgaard, I. Baraffe, and our referee for their collaboration, input and insights. We thank J. Christensen-Dalsgaard for kindly providing the inversion tools that were used to infer the solar sound speed profile for each of our solar calibration models. He provided indispensable guidance as well as all necessary kernels and settings. Furthermore, we record our gratitude to IMPRS on Astrophysics at the Ludwig-Maximilians University as well as the funding we received from the Max-Planck Society.
Footnotes
In order to avoid extensive lithium depletion on the pre-MS, Baraffe et al. (2017) set dov to |$0.1\, H_\mathrm{p}$|, when the rotation rate exceeds a certain critical value. Below this critical rotation rate, dov is set to |$1\, H_\mathrm{p}$|. For further details, we refer to Section 3 and the quoted paper.
The value of the mixing length parameter depends on the boundary conditions used in the solar model calibration (e.g. Weiss & Schlattl 2008). We have here consistently used Eddington grey atmospheres.
For this choice of |$D_{\small JCD}$|, ρc in equation (4) is |$0.1756\, \mathrm{g\, cm^{-3}}$| at the age of the present Sun. When using |$D_{\small JCD} = 150 \, \mathrm{cm^2 \, s^{-1}}$|, |$\rho _\mathrm{c}=0.1789\, \mathrm{g\, cm^{-3}}$| for the solar calibration model. For comparison, |$\rho _\mathrm{c}=0.1902\, \mathrm{g\, cm^{-3}}$| for the modified Model S (Christensen-Dalsgaard et al. 1996), used by Christensen-Dalsgaard et al. (2018). We have rerun the calculations keeping ρc fixed, using the value from Christensen-Dalsgaard et al. (2018). While this affects the choice of |$D_{\small JCD}$|, we reach the same qualitative conclusions as drawn in this paper.
Christensen-Dalsgaard et al. (2018) start their simulation on the ZAMS. For the sake of consistency, one may hence choose a finite tov. We have therefore repeated the computations for the JCD parametrization, setting |$t_\mathrm{ov} = 10^7\,$|yr and |$10^8\,$|yr. The corresponding change in the depletion factor of the surface lithium abundance is |${\lesssim } 10\,$| per cent.
When comparing to a pre-inferred sound speed profile of the Sun, one may include the uncertainties evaluated by Degl’Innocenti et al. (1997) (see also Vinyoles et al. 2017). However, the fact that we repeat the inversion for each solar calibration model makes these uncertainties somewhat misleading as they are most certainly too conservative (cf. J. Christensen-Dalsgaard, private communication, based on a discussion between J. Christensen-Dalsgaard and A. Serenelli). We have hence omitted these uncertainties in the plots.
REFERENCES



