-
PDF
- Split View
-
Views
-
Cite
Cite
Nicholas Scott, Jesse van de Sande, Scott M Croom, Brent Groves, Matt S Owers, Henry Poetrodjojo, Francesco D’Eugenio, Anne M Medling, Dilyar Barat, Tania M Barone, Joss Bland-Hawthorn, Sarah Brough, Julia Bryant, Luca Cortese, Caroline Foster, Andrew W Green, Sree Oh, Matthew Colless, Michael J Drinkwater, Simon P Driver, Michael Goodwin, Madusha L P Gunawardhana, Christoph Federrath, Lloyd Harischandra, Yifei Jin, J S Lawrence, Nuria P Lorente, Elizabeth Mannering, Simon O’Toole, Samuel N Richards, Sebastian F Sanchez, Adam L Schaefer, Katrina Sealey, Rob Sharp, Sarah M Sweet, Dan S Taranu, Mathew Varidel, The SAMI Galaxy Survey: Data Release Two with absorption-line physics value-added products, Monthly Notices of the Royal Astronomical Society, Volume 481, Issue 2, December 2018, Pages 2299–2319, https://doi.org/10.1093/mnras/sty2355
Close - Share Icon Share
ABSTRACT
We present the second major release of data from the Sydney – Australian Astronomical Observatory Multi-Object Integral Field Spectrograph (SAMI) Galaxy Survey. Data Release Two includes data for 1559 galaxies, about 50 per cent of the full survey. Galaxies included have a redshift range 0.004 < |$z$| < 0.113 and a large stellar mass range 7.5 < log (M⋆/M⊙) < 11.6. The core data for each galaxy consist of two primary spectral cubes covering the blue and red optical wavelength ranges. For each primary cube, we also provide three spatially binned spectral cubes and a set of standardized aperture spectra. For each core data product, we provide a set of value-added data products. This includes all emission line value-added products from Data Release One, expanded to the larger sample. In addition, we include stellar kinematic and stellar population value-added products derived from absorption line measurements. The data are provided online through Australian Astronomical Optics’ Data Central. We illustrate the potential of this release by presenting the distribution of |${\sim } 350\, 000$| stellar velocity dispersion measurements from individual spaxels as a function of R/Re, divided in four galaxy mass bins. In the highest stellar mass bin [log (M⋆/M⊙) > 11], the velocity dispersion strongly increases towards the centre, whereas below log (M⋆/M⊙) < 10 we find no evidence for a clear increase in the central velocity dispersion. This suggests a transition mass around log (M⋆/M⊙) ∼ 10 for galaxies with or without a dispersion-dominated bulge.
1 INTRODUCTION
Galaxies are composed of multiple distinct components, such as thin and thick discs, bulge, bar(s), spiral arms, ring(s), and many others. As well as having different spatial structures, these components can also differ in terms of their kinematics and their compositions, either narrowly in terms of differing chemistry, or more broadly into stellar, gaseous, and dark matter. Determining how these distinct components interact and change over time is critical to a deeper understanding of galaxy evolution (e.g. Mo, van den Bosch & White 2010).
Spatially resolving galaxiesis essential to understand the different components. While imaging studies, particularly multiwavelength imaging, can begin to disentangle these components, access to kinematic and chemical separation is largely unavailable. Spatially resolved spectroscopy is ideally suited to this task, as the simultaneous separation of the observed light, both spectrally and spatially, provides the most detailed dissection of the internal structure of galaxies currently available (e.g. Cappellari 2016).
The challenge of spatially resolved spectroscopy is that spreading the light out both spatially and spectrally drastically reduces the signal-to-noise ratio (S/N) per resolving element. This limitation has restricted initial work in this area to relatively small samples of objects, or to specific classes of object that are more easily observed. While these kinds of studies have been very successful in addressing the role of specific physical processes that shape galaxies, a broader view is required to develop a holistic understanding of galaxy evolution.
Galaxies are very diverse, and the physical processes involved in galaxy evolution are many and varied. To fully understand the primary drivers of galaxy evolution, one requires large samples that encompass the complete diversity of the galaxy population. This can be achieved with spatially resolved spectroscopy by either investing large amounts of telescope time with a single-object instrument, e.g. surveys with N > 250, ATLAS3D (Cappellari et al. 2011), and CALIFA (Sánchez et al. 2012), or through the use of a multiplexed integral field spectrograph (IFS), such as the Sydney – Australian Astronomical Observatory Multi-Object Integral Field Spectrograph (SAMI; Croom et al. 2012), MaNGA (Bundy et al. 2015), or KMOS (Wisnioski et al. 2015; Stott et al. 2016). Since the beginning of this decade, large integral field spectroscopy surveys such as these have been assembling samples of hundreds or thousands of galaxies, allowing us to dissect, in detail, the entire population of local galaxies.
Green et al. (2018, SAMI Data Release One, hereafter DR1) discussed the broad role integral field spectroscopy has played in furthering our understanding of galaxies. In the current release, we hope to push forward the exploration of new analyses that utilize the full power of combining emission, absorption, and dynamical measurements by providing extensive value-added data products.
In this paper, we present the second public release (DR2) of SAMI Galaxy Survey observations, including both fully processed spectral data cubes and a large array of derived science products that enable an extremely broad approach for studying galaxies. In Section 2 we briefly review the survey and instrument design and progress on observing and processing the data since DR1. In Section 3 we describe the galaxies presented in this sample. In Section 4 we describe the core data of this release, spatially resolved spectral cubes and additional spectral data derived from these cubes, and the quality of the data. In Section 5 we describe the emission line products included in this release, with a focus on changes since DR1, and in Section 6 we describe the new absorption line products being released for the first time. Finally, in Section 7 we describe how these data can be accessed through the Data Central web service and provide an example science use of these data to illustrate the potential power of this data release. Throughout this release, we adopt the concordance cosmology: (|$\Omega _\Lambda , \Omega _m, h) = (0.7, 0.3, 0.7) $| (Hinshaw et al. 2009).
2 THE SAMI GALAXY SURVEY
The SAMI Galaxy Survey (Bryant et al. 2015) is a spatially resolved spectroscopic survey of a large sample of nearby (|$z$| ≲ 0.1) galaxies, conducted with the SAMI instrument (Croom et al. 2012).
The SAMI instrument is a multi-object IFS mounted at the prime focus of the 3.9 m Anglo-Australian Telescope (AAT). SAMI uses 13 fused optical fibre bundles (hexabundles; Bland-Hawthorn et al. 2011; Bryant et al. 2011, 2014) that can be deployed across a 1 deg diameter field of view. Each hexabundle consists of 61 closely packed optical fibres, where each fibre has a diameter of 1.6 arcsec, resulting in an integral field unit (IFU) with a diameter of 15 arcsec and a fill factor of 75 per cent; 26 additional fibres provide simultaneous blank sky observations.
SAMI feeds the AAOmega optical spectrograph (Sharp et al. 2006). The SAMI Galaxy Survey makes use of the 580V and 1000R gratings, with a dichroic to split the light at 5700 Å between the two spectrograph arms. The precise wavelength coverage and spectral resolution of this instrumental set-up are given in Table 1.
SAMI spectral resolution parameters in blue and red. This table gives an overview of the wavelength range (λrange), central wavelength (λcentral), median FWHM of the best-fitting Gaussian to the spectral instrumental LSF in Å, the standard deviation of this Gaussian in Å, the spectral resolution at λcentral (R|$_{\lambda -\rm {central}}$|), the velocity resolution (FWHM) in km s−1 (Δ|$v$|), and the dispersion resolution (1σ) in km s−1 (Δσ).
| Arm . | λrange (Å) . | λcentral (Å) . | FWHM (Å) . | σ (Å) . | R|$_{\lambda -\rm {central}}$| . | Δ|$v$| (km s−1) . | Δσ (km s−1) . |
|---|---|---|---|---|---|---|---|
| Blue | 3750–5750 | 4800 | |$2.66_{-0.070}^{+0.076}$| | 1.13 | 1808 | 165.9 | 70.4 |
| Red | 6300–7400 | 6850 | |$1.59_{-0.040}^{+0.049}$| | 0.68 | 4304 | 69.7 | 29.6 |
| Arm . | λrange (Å) . | λcentral (Å) . | FWHM (Å) . | σ (Å) . | R|$_{\lambda -\rm {central}}$| . | Δ|$v$| (km s−1) . | Δσ (km s−1) . |
|---|---|---|---|---|---|---|---|
| Blue | 3750–5750 | 4800 | |$2.66_{-0.070}^{+0.076}$| | 1.13 | 1808 | 165.9 | 70.4 |
| Red | 6300–7400 | 6850 | |$1.59_{-0.040}^{+0.049}$| | 0.68 | 4304 | 69.7 | 29.6 |
SAMI spectral resolution parameters in blue and red. This table gives an overview of the wavelength range (λrange), central wavelength (λcentral), median FWHM of the best-fitting Gaussian to the spectral instrumental LSF in Å, the standard deviation of this Gaussian in Å, the spectral resolution at λcentral (R|$_{\lambda -\rm {central}}$|), the velocity resolution (FWHM) in km s−1 (Δ|$v$|), and the dispersion resolution (1σ) in km s−1 (Δσ).
| Arm . | λrange (Å) . | λcentral (Å) . | FWHM (Å) . | σ (Å) . | R|$_{\lambda -\rm {central}}$| . | Δ|$v$| (km s−1) . | Δσ (km s−1) . |
|---|---|---|---|---|---|---|---|
| Blue | 3750–5750 | 4800 | |$2.66_{-0.070}^{+0.076}$| | 1.13 | 1808 | 165.9 | 70.4 |
| Red | 6300–7400 | 6850 | |$1.59_{-0.040}^{+0.049}$| | 0.68 | 4304 | 69.7 | 29.6 |
| Arm . | λrange (Å) . | λcentral (Å) . | FWHM (Å) . | σ (Å) . | R|$_{\lambda -\rm {central}}$| . | Δ|$v$| (km s−1) . | Δσ (km s−1) . |
|---|---|---|---|---|---|---|---|
| Blue | 3750–5750 | 4800 | |$2.66_{-0.070}^{+0.076}$| | 1.13 | 1808 | 165.9 | 70.4 |
| Red | 6300–7400 | 6850 | |$1.59_{-0.040}^{+0.049}$| | 0.68 | 4304 | 69.7 | 29.6 |
2.1 Survey sample and observing status
The selection of the SAMI Galaxy Survey sample is described in detail in Bryant et al. (2015), with further details in Owers et al. (2017). Here we briefly summarize the primary sample and describe the status of secondary targets.
The SAMI Galaxy Survey sample consists of two separate but complementary samples with matched selection criteria; a SAMI–GAMA sample drawn from the Galaxy And Mass Assembly (GAMA) survey (Driver et al. 2011) and an additional cluster sample. The SAMI–GAMA sample consists of a series of volume-limited samples, where the stellar mass limit for each sample increases with redshift. Stellar masses are estimated from the rest-frame i-band absolute magnitude and g − i colour by using the colour–mass relation following the method of Taylor et al. (2011), assuming a Chabrier (2003) stellar initial mass function (IMF) and exponentially declining star formation histories. The SAMI–GAMA sample is drawn from the three 4 × 12 deg fields of the initial GAMA-I survey (Driver et al. 2011). These regions include galaxies in a range of environments, from isolated up to massive groups, but do not contain any galaxy clusters within the |$z$| ≤ 0.1 SAMI limit. To complete the environmental coverage, the SAMI Galaxy Survey includes an additional cluster sample, drawn from eight |$z$| ≤ 0.1 clusters, described in Owers et al. (2017). The same stellar mass selection limits were applied to the cluster sample as for the main sample. In practice, for the clusters with |$z$| < 0.045 we target cluster galaxies with log (M⋆/M⊙) > 9.5, and for the clusters with 0.045 < |$z$| < 0.06 we target cluster galaxies with log (M⋆/M⊙) > 10.0.
In addition, a sample of secondary target galaxies is defined by galaxies with slightly lower stellar mass cuts in each redshift bin, along with high-mass [log (M⋆/M⊙) > 10.9] galaxies at slightly higher redshift (0.095 < |$z$| < 0.115). The secondary targets were observed when a hexabundle could not be allocated to a primary target. This became necessary as the completeness of the survey grew. In the final semester of observations an extra set of ancillary galaxies was needed to occupy all hexabundles. These were primarily drawn from GAMA galaxies that are in pairs or groups with SAMI galaxies but did not meet the stellar mass cuts of the original selection criteria. None of the ancillary targets are included in DR2.
Survey observations began in 2013 March and were completed in 2018 May. There were a total of 250 observing nights, spread over 34 individual observing runs. At the completion of survey observing, just over 3000 total galaxies were observed. The primary sample was observed to a completeness of 80 and 84 per cent in the GAMA and cluster regions, respectively, with 1930 and 724 unique primary targets in those regions.
2.2 Data reduction
The reduction of SAMI data and the production of data cubes are described fully in Allen et al. (2015) and Sharp et al. (2015). Here we briefly summarize the process and in the following section describe in detail the changes since the previous release.
SAMI data reduction broadly falls into two phases: the extraction of row stacked spectra (RSS) from raw observations and the construction of data cubes from the RSS frames. The creation of RSS frames is handled by the 2dfDR data reduction package.1 Cube creation is carried out using the SAMI python package (Allen et al. 2014), and the entire process is automated using the ‘SAMI Manager’, part of the SAMI python package.
Initial reduction consists of the standard steps of overscan subtraction, spectral extraction, flat-fielding, fibre throughput calibration, wavelength calibration, and sky subtraction. These steps are all accomplished with 2dfDR, and result in one RSS frame per observation. Each RSS frame contains data for 12 galaxies and a single calibration star for secondary spectrophotometric calibration and telluric correction.
Relative and absolute flux calibration and telluric correction are applied to each RSS frame using the SAMI python package. The flux-calibrated RSS frames are combined into three-dimensional data cubes by resampling on to a regular grid. This combination includes dither registration and differential atmospheric refraction correction and an additional absolute flux calibration step. The result is a three-dimensional (two spatial and one spectral) data cube. Covariance between spaxels is calculated and stored within the cubes in a compressed form (see Sharp et al. 2015 for details). Binned cubes and aperture spectra are also produced at this stage (see Sections 4.2 and 4.3 for details).
2.2.1 Changes between DR1 and DR2
For this release, we use the SAMI python package snapshot identified as mercurial changeset 17ebc0ff0a1c, and 2dfDR version 6.65. Several aspects of the data reduction have been improved between these software versions and those used for DR1, which we document in detail below. In addition, the SAMI python package has experienced some quality-of-life improvements including optimization of computationally intensive aspects of the package as compiled c code, support for python 3 compatibility, and increased terminal feedback during data reduction. Three main aspects of the data reduction have been improved for this release. They are as follows: extraction of spectra, flat-fielding, and wavelength calibration.
Spectral extraction requires an accurate trace of the fibre locations across the detector. These traces (that we call a tram-line map) are derived from a calibration frame, and are based on Gaussian profile fits to each fibre in the spatial direction. This fit is repeated for each CCD column and the resulting fibre locations are then fitted with a smoothly varying function. For DR1 and earlier releases, this tram-line map was determined from dome flat calibrations taken as part of a standard science observation sequence. However, the dome flat frames have relatively low counts below ∼4000 Å, resulting in higher uncertainties in the tram-line maps in the far blue. For DR2 we used twilight sky frames to derive tram-line maps, resulting in more accurate traces below ∼4000 Å with improved spectral extraction and reduced cross-talk between adjacent fibres. Where twilight sky observations are not available for a given field, we use twilights from different fields. To account for shifts between tram-line maps from different fields (and on occasion different nights), we measure a 1D (in the spatial direction on the CCD) cross-correlation between the image frames used to generate the tram-line map and the object frame to be extracted. This also corrects for the small shift caused by the boiling off of liquid nitrogen in the dewars attached to AAOmega’s cameras (Sharp et al. 2015). The cross-correlation is done in 16 × 16 blocks across the CCD and then averaged (with outlier rejection). This approach allows us to estimate uncertainty on the measured tram-line shift, which is typically a few thousandths of a pixel (standard error on the mean). Once small bulk shifts in the fibre positions are taken into account, we find no difference to final data quality when using a tram-line map derived from a different field. In addition, we have improved the preliminary scattered light model applied before fitting the fibre profiles, which again results in improved spectral extraction, particularly at bluer wavelengths where scattered light represents a larger fraction of the total counts.
Fibre flat-fielding in DR1 also used dome flat observations, which, as noted above, suffer from reduced counts at bluer wavelengths. In DR2 we instead used twilight sky observations (where available) that have significantly higher counts at the bluer wavelengths, compared to dome flats. In DR1, at wavelengths below ∼4000 Å, variations in the fibre flat-field with fibre number were caused by unaccounted-for scattered light (at the level of a few tens of counts). This issue resulted in large, unphysical variations in the fibre flat-field frame at blue wavelengths. The increased blue counts in the twilight sky frames largely eliminate this issue. While the twilight sky has considerable spectral structure, once this is divided by the mean spectrum, the residual structure is small (a few per cent in the strongest spectral features, e.g. the Ca ii H and K lines). This remaining structure was removed by fitting a B-spline (with 16 knots positioned uniformly along the spectrum), including sigma clipping of outlying points. This effective smoothing of the fibre flat–field is appropriate as small-scale pixel-to-pixel differences in CCD response have already been removed at an earlier stage. Therefore, the fibre flat-field is only removing any residual difference in the slowly varying wavelength response of the system. Any individual outlying fibres were identified and replaced by comparison with a median stack of at least five twilight sky observations, before applying the fibre flat-field to the science frames. Further, the colour response of the SAMI fibres is stable over an observing run, such that the RMS scatter between fibre flat-fields derived from twilight frames is 0.5 per cent or less (typically 0.2–0.3 per cent).
The resampling of the data on to a calibrated wavelength axis has been modified in two ways that do not affect the quality of the wavelength calibration but instead improve the usability of the data. First, all SAMI Galaxy Survey data are now sampled on to a single, common wavelength scale, 3650–5800 Å in the blue and 6240–7460 Å in the red (with dispersions of 1.050 and 0.596 Å pixel−1, respectively). This uniformity facilitates the combining of data observed under different central wavelength settings without the need for a second resampling of the data. Secondly, at the time of resampling, the data are automatically corrected to a heliocentric frame. Both the heliocentric velocity correction and fixed wavelength range modifications are applied within the wavelength calibration step of data reduction, so no new interpolations of the data are required. The modified wavelength range compared to DR1 results in a very small (1–2 per cent) reduction in spectral sampling.
Finally, we note the recently discovered issue of weak charge-traps in the new (installed in mid-2014) red arm CCD of AAOmega (Lidman et al. 2018). There are a small number of partial rows (typically a few tens of pixels in length) that have shallow traps (typically a few tens of counts). These are located near the top of the new AAOmega red CCD. These have not been corrected in the current DR2 data, but will be in future releases. The impact of these features in the current DR2 data is that for galaxies with data near the top of the detector (FITS header keyword IFUPROBE = 1 in the final cubes), there can be a small number of spectra that show small (few tens of counts) dips in the final cubes.
3 DATA RELEASE TWO
The SAMI Galaxy Survey Second Public Data Release (DR2) sample consists of 1559 unique galaxies. This sample represents all SAMI Galaxy Survey galaxies observed up to the 2017 July 1 that lie in the GAMA regions of the survey and for which all value-added products have been derived. In addition, we require that all galaxies satisfy a set of quality criteria. Their data must consist of at least six observations (out of the seven nominal dither positions) where each observation has (i) a measured point spread function (PSF), derived from a Moffat profile fit, with full width at half-maximum (FWHM) better than 3.1 arcsec and (ii) atmospheric transmission better than 55 per cent. These criteria result in 72 galaxies being excluded from DR2. One further observed galaxy is rejected due to being an ancillary target that was not part of the GAMA survey and so lacks important supporting photometric data. Of the 1632 galaxies eligible for DR2, we therefore reject 73, for a final sample of 1559 unique galaxies. This sample represents approximately a factor of 2 increase over DR1. The remaining galaxies will be made publicly available as part of a future data release.
The galaxies in DR2 span a broad range in stellar mass, M⋆, effective radius, Re, redshift and visual morphology. M⋆, Re, and redshift (along with a number of other general galaxy properties) are provided by the GAMA survey (Driver et al. 2011; Bryant et al. 2015). Visual morphology classification has been performed taking advantage of SDSS DR9 gri colour images, as discussed in Cortese et al. (2016). Briefly, galaxies are first divided into late and early types according to the presence/absence of spiral arms and/or signs of star formation. Pure bulges are then classified as ellipticals (E) and early-types with discs as S0s. Similarly, late-types with only a disc component are Sc or later, while disc plus bulge late types are Sa–Sb.
All votes (varying between 8 and 14 individuals) are then combined. For each galaxy, the morphological type with at least two thirds of the votes is chosen. If no agreement is found, adjacent votes are combined into intermediate classes (E/S0, S0/Sa, Sbc) and, if the two-thirds threshold is met, the galaxy is given the corresponding intermediate type. When no agreement is reached, a new round of classifications is performed. However, this time the choice is limited to the two types with the most votes during the first iteration, with the galaxy being marked as unclassified if agreement is still not reached. For galaxies in DR2, 1450 galaxies (93 per cent) have been successfully classified during the first step, 46 (3 per cent) required a second iteration and for 63 (4 per cent) no agreement was found even after the second iteration.
Fig. 1 shows that the DR2 sample is unbiased with respect to the SAMI–GAMA parent sample in stellar mass, effective radius, and redshift. We do not show the comparison for morphology because morphological classifications are not available for the full parent sample. These general galaxy properties are provided in the DR2 sample table included in this release.
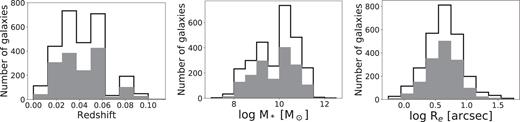
Histograms showing the distribution of DR2 galaxy properties (gray histograms) with respect to the full SAMI–GAMA sample (clear histograms). From left to right the panels show the distribution with: redshift, log stellar mass M⋆, and log effective radius Re. The DR2 sample is unbiased with respect to the complete, volume limited SAMI–GAMA parent sample.
3.1 Data quality
3.1.1 Spectral resolution
In this section we describe the spectral resolution as derived from SAMI-AAOmega data using reduced arc-line frames. We follow the method outlined in van de Sande et al. (2017b) that has been implemented in 2dfDR (Beta Version 6.65). The FWHM of the spectral instrumental line spread function (LSF) is derived using a Gaussian function, which is a good approximation for the SAMI-AAOmega LSF (van de Sande et al. 2017b). 2dfDR fits 24 unsaturated, unblended CuAr arc lines in the blue arm, and 12 lines in the red arm for all 819 fibres. The instrumental resolution over the entire wavelength region is derived from interpolating over individual arc lines. Thus for every arc-line frame, we obtain a spectral resolution map of wavelength versus fibre number. We then calculate the spectral resolution maps for all 942 arc-line frames between 2013 March 5 to 2017 September 26. All data are combined into a three-dimensional array with dimensions wavelength, fibre number, and observation date. In order to show the FWHM as a function of one dimension (e.g. wavelength, fibre number, or date), we will first collapse the three-dimensional array along the two other dimensions using a median.
In Fig. 2 we present the spectral resolution distributions, and the key resolution quantities for SAMI are given in Table 1. We show the distribution of the spectral resolution in Figs 2a and c, where we have taken the median along the fibre number dimension to reduce the number of FWHM values. We find that the distribution of the FWHM is more skewed in the red than in the blue. There are small but significant resolution changes from fibre-to-fibre and with fibre position on the detector (Figs 2b and d). In the blue, the resolution (FWHM) changes from ∼2.55 Å, at the ‘bottom’ of the detector to ∼2.7 Å two thirds up (fibre 600). In the red, the fibre-to-fibre resolution also changes with fibre position on the detector, from 1.55 Å for fibre 1 to a maximum of 1.65 Å around fibre ∼500.
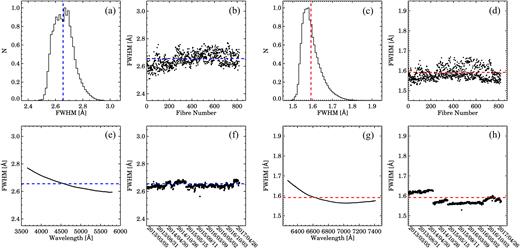
SAMI-AAOmega spectral resolution in the blue arm and the red arm derived from reduced arc-line frames. Panels a, b, e, and f show the FWHM distribution, FWHM versus fibre number, FWHM versus wavelength, and FWHM versus date in the blue data (note that dates are linearly spaced on frame number, not time), and similar for panels c, d, g, and h for the red data.
We find a decrease in FWHM (increase in resolution) as a function of wavelength as shown in Figs 2e and g. For the blue arm, the FWHM changes from 2.75 Å at 3700 Å to 2.6 Å at 5500 Å; for the red we find FWHM = 1.65 Å at 6300 Å to 1.57 Å at 7000 Å, but then stays constant. Finally, in Figs 2f and h, we present the spectral resolution as a function of observing date. We find a change in the blue FWHM at the start of 2014, when the blue CCD was replaced (with an identical CCD, but with fewer cosmetic defects). However, the change is small (∼1 per cent) and no greater than other changes at other times. In the red arm, we see a drop of ∼4 per cent in the FWHM starting from 2014 October onwards. This drop coincides with the time when the red CCD was upgraded.
In summary, in the blue arm, we find a median resolution of FWHMblue = 2.66 Å, and in the red arm of FWHMred = 1.59 Å. The fibre-to-fibre FWHM variation is 0.048 Å (RMS scatter) in the blue and 0.030 Å in the red. Over a period of 4 yr, we find FWHM variations of 0.016 Å in the blue arm and 0.024 Å in the red arm. The FWHM decreases with increasing wavelength in the blue arm by 0.051 Å and in the red arm by 0.031 Å.
3.1.2 Sky subtraction accuracy
The improvements to profile measurement and fibre flat-fielding outlined in Section 2.2.1 lead to a substantial reduction in systematic sky subtraction residuals, particularly in the blue arm of the spectrograph. In Fig. 3 we show the median fractional sky subtraction residuals across 1750 individual data frames (for exposures of at least 900s), in 20 wavelength bins for each sky fibre in each arm of the spectrograph. The sky fibres are uniformly distributed along the slit, so systematic variations with sky fibre number relate to variations along the slit. There is no change in the red arm residuals between DR1 and DR2. The DR2 residuals in the blue arm (Fig. 3, centre) are significantly reduced compared to the same measurement from DR1 (Fig. 3, left), particularly at the corners of the CCD. This reduction is because the new approach to fibre flat–fielding reduces the impact of ghost features present at these locations in the AAOmega spectrograph. Previously these features were at the level of up to ∼20 per cent, but are now reduced to ∼5 per cent or less. Other weak systematic features remain, including a gradient at the level of ∼1 per cent from top to bottom of the CCD, higher residuals for the slit end fibres (fibres 1 and 26) and an increase for all fibres at the blue end. This last feature is largely driven by reduced S/N at the blue end of the blue arm, rather than any actual systematic reduction in sky subtraction accuracy.
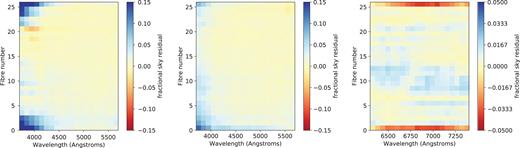
The median fractional residuals in sky subtraction for SAMI sky fibres. From left to right we show the old residuals from DR1 in the blue, the new residuals for DR2 in the blue, and the new residuals for DR2 in the red (unchanged from DR1). For each sky fibre the flux is summed within 20 uniform bins in wavelength before determining the fractional residual. The median residual within each bin is then calculated across all object frames within the survey. Various low-level systematic trends can be seen, including increased residuals for the sky fibres at the very edges of the slit.
We perform a second test of DR2 data quality that examines our improved spectral extraction and sky subtraction (see Section 2.2.1). As we saw in Fig. 3, there is a significant improvement in sky subtraction below 4000 Å at the top and bottom of the detector. This most strongly influences IFUs number 1 and 13 that are located at either end of the spectrograph slit. To demonstrate the improvement, we measure the D4000n (Balogh et al. 1999) and H δA (Worthey & Ottaviani 1997) indices for all spaxels with median S/N > 10 from galaxies that are contained within both DR1 and DR2. For SAMI DR1 the data in IFUs 1 and 13 (at the ends of the slit) show a systematic offset to lower values of D4000n (red contours and points in Fig. 4a). In contrast, the same spaxels in SAMI DR2 are completely consistent with the distribution in the other IFUs (Fig. 4b). We note that in this test we have not corrected the indices for emission lines, so a small number of spaxels lie at lower H δA values than might otherwise be expected (e.g. red points at D4000n ≃ 1 and H δA ≃ −4).
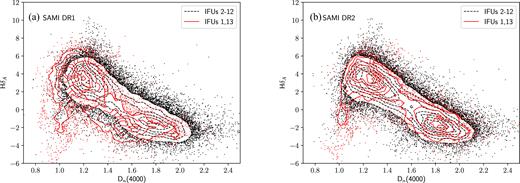
The distribution of SAMI spaxels with median blue arm S/N > 10 in the D4000n versus H δA plane for (a) data in SAMI DR1, and (b) data in SAMI DR2. Only spaxels from galaxies that are common to both DR1 and DR2 are shown. IFUs 2–12 (black dashed contours and points) and IFUs 1, 13 (red contours and points) are shown separately. The improved DR2 data reduction leads to consistent locations in the D4000n versus H δA for all IFUs. Contours are linearly spaced in point density.
3.1.3 Flux calibration
We compare the flux calibration of SAMI DR2 data to SDSS g–band images. The same procedure as described for the DR1 sample in Green et al. (2018) is also carried out on DR2. This procedure compares fluxes in SDSS g–band images and SAMI cubes within an 8 arcsec diameter aperture. The SAMI cubes are convolved with the SDSS g–band filter curve and the SDSS images are convolved to the median seeing of SAMI. Galaxies with integrated fluxes below 100 μJy were not included, to avoid extra scatter from low S/N. The median flux ratio (SAMI/SDSS) is 1.048 ± 0.003 (where the error is the uncertainty on the median, not the RMS scatter), consistent with results from DR1. As can be seen in Fig. 5, the distribution of flux ratios is slightly narrower for DR2 (solid line) than DR1 (dotted line). 95 per cent of objects have a flux ratio within ±0.15 of the median. Regarding the accuracy of relative flux calibration, this is unchanged compared to previous data releases. As noted in Allen et al. (2015), we find a colour offset, Δ(g − r), of 0.043 with a standard deviation of 0.040, with respect to the SDSS PSF magnitude derived colours of the SAMI secondary standard stars.
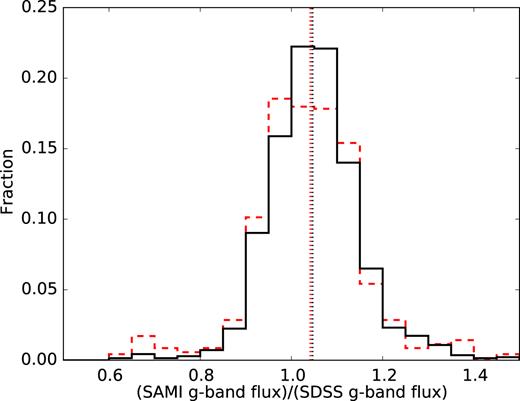
The distribution of flux ratios between SAMI cubes and SDSS images in the g–band using 8 arcsec diameter circular apertures. We compare SAMI DR1 (red dashed lines) and DR2 (solid black lines), with the vertical dotted lines showing the median flux ratio for each sample. Each histogram is normalized to the number of objects in the sample.
3.1.4 WCS accuracy
During cube construction, we register the galaxy centroid in each individual dither by fitting a two-dimensional Gaussian to the observed flux. The dithers are aligned using these centroids, and are then combined such that the galaxy centre is located at cube spaxel coordinates (25.5, 25.5). We then assign the catalogue right ascension (RA) and declination (Dec.) of the galaxy to this spaxel coordinate and define the World Coordinate System (WCS) of the cube relative to this position. While accurate for the majority of galaxies, there remains some uncertainty in the WCS due to the centroiding process, and, in a limited number of cases, the pipeline can misidentify the galaxy centre resulting in a significant offset.
We verify the accuracy of the WCS of the data by visual inspection and matching to r–band images from the Kilo Degree Survey (KiDS; de Jong et al. 2017). In Fig. 6 we show the offset in RA and Dec. between the centre of the collapsed SAMI cube and the centre of the galaxy in the KiDS image. We find the mean offset is −0.016 ± 0.020 arcsec in RA and −0.102 ± 0.017 arcsec in Dec. When we remove catastrophic failures (see below), the mean offset changes to −0.027 ± 0.009 in RA and −0.106 ± 0.008 in Dec., resulting in a decreased rms scatter, however the small statistically significant offset remains.
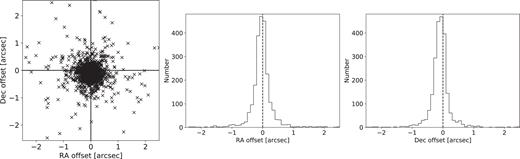
Offset between the SAMI cube WCS and KiDS r–band imaging. The left-hand panel shows the offsets for all DR2 galaxies. Note that 24 galaxies with large offsets lie outside the figure. The centre and right-hand panel show histograms of the offset in RA and Dec., respectively. Catastrophic failures have not been removed.
For cubes where multiple galaxies or a foreground star is present in the hexabundle or the galaxy is highly structured, the simple two-dimensional Gaussian fit can misidentify the galaxy centre, resulting in a large positional offset between the cube centre and the true galaxy centre. After visual inspection of the cubes, we determined that 50 galaxies suffered from significant offsets (>1 arcsec in radial offset) due to these issues. For these galaxies, we shift the cube WCS to match that determined from the KiDS imaging.
3.1.5 Seeing distribution
Each observation has an associated PSF, characterized by the FWHM. For individual observations these are measured by fitting a Moffat profile to the flux distribution of the secondary standard star. The output data cubes also have a PSF that depends on the PSFs of the input observations, as well as the accuracy of registering these inputs to a common coordinate system. In the upper panel of Fig. 7 we show the FWHM of the PSF of the cube of the secondary standard star as a function of the mean FWHM of the input observations. For mean input FWHM ≳ 1.5 arcsec, the input and output FWHM are linearly related, with the PSF of the cube being ∼0.2 arcsec broader than the mean input PSF. In good seeing, the difference between the cube PSF and the input PSF is increased. This is caused by two effects; the additional broadening in the output PSF due to uncertainties in the centroids of each input frame and the effect of the optical fibres, whose finite size effectively imposes a minimum FWHM on the PSF, even if atmospheric seeing is ignored. Atmospheric broadening is still the most significant factor in determining the FWHM of the output PSF.
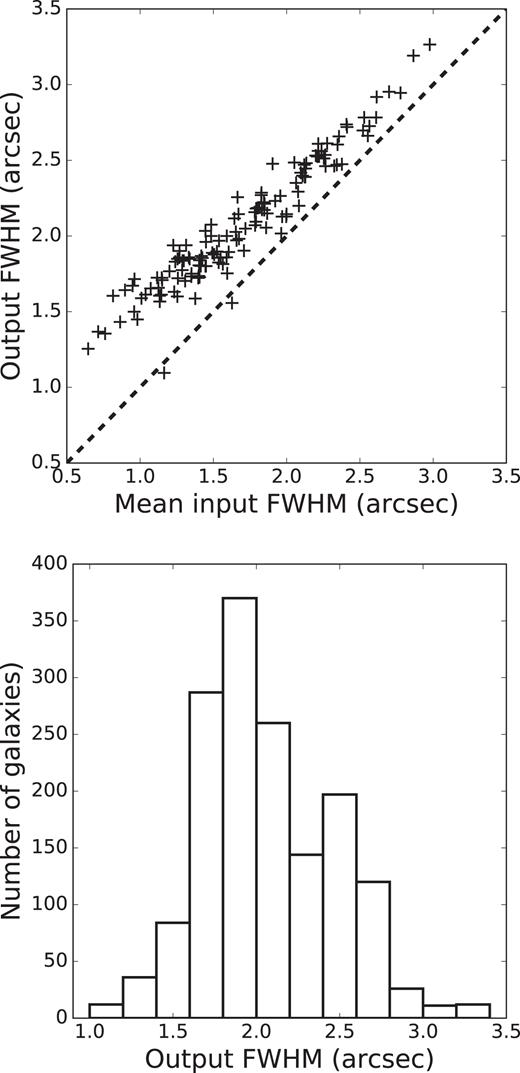
Upper panel: comparison of the mean measured FWHM of individual dithered exposures to the FWHM of the reconstructed secondary standard star cubes. FWHMs are from Moffat-profile fits. The dashed black line is the 1:1 relation. Lower panel: distribution of the FWHM in the reconstructed cube for all SAMI DR2 galaxies. The mean of the FWHM is 2.06 arcsec, and the standard deviation is 0.40 arcsec.
In the lower panel of Fig. 7 we show the distribution of FWHM for all galaxies in DR2, determined from Moffat profile fits to the secondary standard star cubes observed simultaneously with the galaxies. The mean FWHM of the output cubes is 2.06 arcsec, varying between 1.10 and 3.27 arcsec. 84 per cent of galaxies have FWHM better than 2.5 arcsec.
4 CORE DATA
The data in SAMI DR2 is broadly divided into core data, produced directly from the SAMI data reduction pipeline, and value-added data products, derived from SAMI Galaxy Survey science analysis pipelines. Here we describe the core data, with the data products being described in Sections 5 and 6.
4.1 Cubes
The primary data produced by the SAMI Galaxy Survey are pairs of spectral data cubes for each observed galaxy, covering the blue and red parts of the optical wavelength range. Each data cube consists of 2048 spectral slices, where each slice is a 50 × 50 square area of spatial pixels (spaxels). The sampling of the spatial axes is 0.5 arcsec. For the blue cube the spectral sampling is 1.050 Å pixel−1 with a spectral FWHM of 2.66 Å, covering the wavelength range 3650 to 5800 Å. For the red cube the spectral sampling is 0.596 Å pixel−1 with a spectral FWHM of 1.59 Å, covering the wavelength range 6240–7460 Å. See Table 1 for further details. In addition to the measured fluxes, each cube contains the variance, weight map, and compressed covariance; see Sharp et al. (2015) for details.
4.2 Binned cubes
To complement the default cubes, we provide a set of three pre-binned data cubes, that we refer to as ‘adaptive’, ‘annular’, and ‘sectors’.
Adaptive: Bins are adaptively generated to contain a target S/N of 10, using the Voronoi binning code of Cappellari & Copin (2003). The S/N is calculated from the flux and variance spectra of each spaxel as the median across the entire blue wavelength range. Spaxels with S/N >10 are not binned.
Annular: Bins are generated as a series of elliptical annuli, centred on the centre of the cube. The position angle, PA, and ellipticity, ε, of the galaxy are determined using the find_galaxyPython routine of Cappellari (2002) from the image generated by summing the cube along its wavelength axis. The spaxels are then allocated to five linearly spaced elliptical annuli, each with the PA and ε of the whole galaxy.
Sectors: Bins are generated as a series of elliptical annuli, with each annulus further subdivided azimuthally into eight regions of equal area. The axes of the sectors are defined in reference to the PA of the galaxy. The annuli are generated as for the annular binning scheme.
For each binned cube, we first generate a bin mask from the blue cube using the criteria described above, then sum the spectra for each spaxel contributing to a given bin to generate the binned spectrum. The bin masks generated from the blue cubes are applied to the red cubes as well to allow direct comparison. The output binned data cubes consist of 50 × 50 × 2048 arrays, maintaining consistency with the original cubes. Each spaxel in the output cube contains the binned spectrum for the bin that it belongs to – spaxels from the same bin contain identical spectra. All spaxels containing flux are allocated to a bin. This procedure is repeated for the variance cube, accounting for the covariance between spaxels in each bin. We note that the variance of large bins (≳25 spaxels) may be underestimated by up to 5 per cent due to a small component of unaccounted-for covariance between included spaxels (this will be corrected in future releases). Each binned cube consists of the flux and variance cubes and an additional bin mask image, indicating which spaxels have been combined into each bin. All binned data are generated using the binning module of the SAMI data reduction pipeline. Variations on the adaptive and annular/sectors binning schemes can easily be generated by modifying functions within this module.
4.3 Aperture spectra
To facilitate comparison to existing single aperture surveys, we also provide a set of aperture spectra derived from the SAMI cubes. These aperture spectra are generated using the binning module of the SAMI data-reduction pipeline as single-bin binned spectra, with two exceptions: spaxels lying outside the aperture are not allocated to a bin, and the flux of the aperture spectrum is re-scaled to account for the difference in area between the included spaxels and the true bin area. The data format is also different; for each aperture we generate a one-dimensional flux array, a one-dimensional variance array (accounting for spatial covariance between contributing spaxels), and a two-dimensional bin mask image, indicating which spaxels have been summed to form the aperture. As for the binned data cubes, large apertures may have their variance underestimated by up to ∼5 per cent.
We provide six apertures, four of which are circular apertures centred on the centre of the cube with diameter 1|${^{\prime\prime}_{.}}$|4, 2″, 3″, and 4″ respectively. We provide a fifth circular aperture with fixed physical diameter of 3 kpc, determined using the observed redshift of the galaxy from the GAMA survey and our adopted cosmology. The sixth aperture is an elliptical aperture of major axis radius Re, where ε, PA, and Re are taken from v09 of the GAMA Sérsic catalogue (Kelvin et al. 2012).
4.3.1 S/N
We estimate the aperture S/N by taking the median S/N value per Å between 4600 and 4800 Å in the rest frame. This range is clear of skylines and is fully contained within the SAMI blue arm. In Fig. 8 we show histograms of the median S/N for the six available apertures. We also show the median S/N map for a typical galaxy in Fig. 9, outlining the Re and 3kpc apertures for reference. The 1Re aperture spectra have a median S/N of 32; 92 per cent have an S/N above 10, and 25 per cent have a value above 50. The median S/N of the central pixel in the data cubes is 14 with a standard deviation of 13.
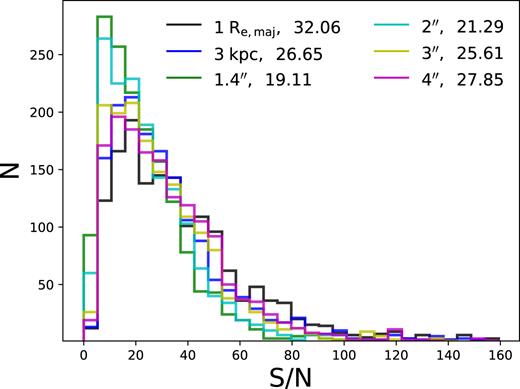
Histograms of the aperture S/N for all DR2 galaxies, in the six available apertures. The S/N is the median value in the range from 4600 to 4800 Å. The median value in each aperture is included in the line labels.

The median S/N per Å in the blue cube for GAMA ID 91926. The median is measured between 4600 and 4800 Å. The white lines show the relative sizes and shapes of two of the six available apertures; the solid line outlines the elliptical aperture with 1 Re semi-major axis, and the dashed line shows the circular aperture of 3 kpc diameter. For this galaxy, the S/N per Å in both the 3 kpc diameter and Re semi-major aperture spectra are 51.
5 VALUE-ADDED DATA PRODUCTS: EMISSION-LINE PHYSICS
For each of the core data products listed above (cubes, binned cubes, and aperture spectra), we fit strong emission lines arising from ionized gas and extract line fluxes, velocities, and velocity dispersions. From these we then create maps of value-added products such as extinction maps (derived from the Balmer decrement), star-formation rate surface densities, and excitation mechanism classifications. We summarize here the emission line analysis, but note that the methods and products are very similar to those released in DR1. We refer the reader to Green et al. (2018), Ho et al. (2016b), and Medling et al. (2018) for further details on the emission-line fitting and resulting data products.
5.1 Emission-line fitting
We fit seven strong optical emission lines within the SAMI wavelength range: [O ii]3726+3729, H β, [O iii]5007, [O i]6300, H α, [N ii]6583, [S ii]6716, and [S ii]6731. We also fit the lines [O iii]4959 and [N ii]6548, but their fluxes are fixed to their physical ratios relative to the stronger [O iii] and [N ii] lines. Using version 1.1 of the lzifu software package (Ho et al. 2016a), we stitch together the blue and red spectra accounting for the differing spectral resolution (Section 3.1.1). We then subtract the underlying stellar continuum before fitting each emission line with one to three Gaussian profiles. The Gaussian profiles are fit using the Levenberg–Marquardt least-square method implemented in (mpfit; Markwardt 2009). All selected emission lines are then fit simultaneously with each kinematic component constrained to the same velocity and velocity dispersion. From the Gaussian fits, we obtain the emission line fluxes, velocities, and velocity dispersions.
For the spectral cubes (Section 4.1), we follow DR1 in providing both a 1-component Gaussian fit capturing the bulk emission and gas motions, and a multicomponent fit. The multicomponent fit captures both the dominant gas emission and fainter velocity structures such as outflows, and represents a more accurate total gas emission. Each spaxel is fit 3 times using lzifu to obtain one-, two-, and three-component fits to each emission line. The number of components in the multicomponent fits are determined using an artificial neural network trained by astronomers (for full details on the neural network, and precision success with SAMI data, see Hampton et al. 2017).
One significant difference between the emission line fits to the spectral cubes provided in DR2 relative to DR1 is the fitting of the underlying stellar continuum. In DR1, the stellar continuum was fit on a spaxel-by-spaxel basis using the penalized pixel-fitting routine (pPXF; Cappellari & Emsellem 2004; Cappellari 2017), even when the S/N in the continuum was low. Doing so can lead to large uncertainties in the correction for the underlying absorption lines, specifically impacting the Balmer emission lines. To account for this impact, we included an additional systematic uncertainty in the Balmer lines (described in Medling et al. 2018).
In DR2, we now use the significantly improved stellar continuum fitting to better subtract the continuum prior to fitting the emission lines. Here, we give a brief description of the continuum fitting procedure and refer to Owers et al. (in preparation) for further details. We use the Voronoi-binned data, which has S/N ∼ 10 in the continuum, to constrain the number of templates that are used to fit each spaxel within the Voronoi bin of interest. This is achieved by using pPXF to fit the Voronoi-binned spectrum with a subset of the MILES simple stellar population (SSP) spectral library (Vazdekis et al. 2010) that contains four metallicities ([M/H] = −0.71, −0.40, 0.00, 0.22) and 13 logarithmically spaced ages ranging from 0.0063 to 15.85 Gyrs. Following Cid Fernandes et al. (2013), the MILES SSPs are supplemented with younger SSP templates drawn from González Delgado et al. (2005) with metallicities [M/H] = −0.71, −0.40, 0.00, and ages 0.001–0.025 Gyr. During the fitting, emission line templates are included for the Balmer lines, as well as strong forbidden lines. Importantly, this simultaneous fitting of emission and absorption components allows the regions surrounding the age-sensitive Balmer lines to be included in the continuum fits. The stellar kinematics are not fitted for during this process, and are fixed to the values determined in Section 6.1.
The subset of SSP templates that have non-zero weights assigned in the fits to the Voronoi binned spectra is then used during the fitting of each spaxel contained within the region defined by the Vorenoi bin. Again, emission lines are fitted simultaneously, and the stellar kinematics are fixed to those determined in Section 6.1, while allowing pPXF to re-determine the optimal template weights only for spaxels where the S/N > 5. For spaxels with S/N < 5, the weights determined during the Voronoi binned fitting are used to produce a single optimal template, while the stellar kinematics are fixed to those derived from the Voronoi-binned data. This helps to guard against poor fits due to low S/N. In all of the pPXF fitting described above, we include a 12th-order multiplicative polynomial. This continuum fit is then used in lzifu to subtract the continuum and measure the final line fluxes for the 1- to 3-component fits. Overall this method produces similar line fluxes to those found in DR1, but with better constraints in spaxels with low-S/N continua, and some systematic offsets in galaxies with significant Balmer absorption features.
In terms of the H α emission line flux, for most pixels with low continuum S/N the new continuum fitting procedure produces a similar line flux, especially for strong lines. Fig. 10 a shows a 2D density diagram of the relative difference in 1-component H α flux for the original DR1 and new DR2 continuum fitting methods for all spaxels with significant line emission (H α S/N >5) and weak continuum (S/Ncont < 10). The median relative difference for all spaxels is 0.003, but with a standard deviation of 0.3, with these differences clearly increasing for low line fluxes. The majority of spaxels (∼80 per cent) have H α fluxes that agree within 10 per cent, and only ∼6 per cent of the low continuum S/N spaxels disagree by more than 30 per cent.
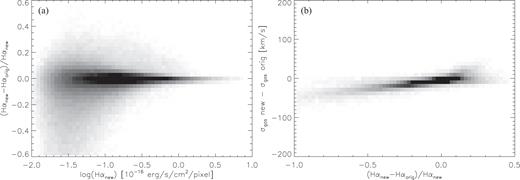
Comparison of the LZIFU determined 1-component H α flux based on the original DR1 continuum method and the new DR2 continuum method. All spaxels with weak continuum (S/Ncont < 10) and significant line detection (S/NH α > 5) in DR2 are examined here. (a) A 2D density histogram of the relative difference in H α flux as a function of the new DR2 continuum H α flux. (b) A 2D density histogram showing how the relative difference in H α flux between the two methods correlates with the difference in the determined gas velocity dispersion between the two methods. These figures demonstrate that the majority of spaxels are consistent (>80 per cent), but at weak line flux (|$\lt\! 2.10^{-17} \rm erg/s/cm^2/pixel$|), errors in the Balmer line absorption feature due to poor continuum fitting in the original DR1 method lead to weak but incorrect broad lines.
To reveal the origin of this change, we show the relative difference of H α flux against the difference in determined gas velocity dispersion in Fig. 10b. We again show this for all spaxels with significant line emission (H α S/N > 5) and weak continuum (S/Ncont < 10). All spaxels with similar H α fluxes show similar velocity dispersions, but for spaxels with a substantially different H α flux we see that the velocity dispersion of the original method is also systemically different, arising from an improperly determined Balmer absorption feature in the low continuum S/N.
With the aim of understanding the systematic effects of the different continuum fitting procedures between DR1 and DR2, we investigate whether the Balmer decrements measured using higher-order Balmer emission lines depart from the expectations of a Calzetti dust extinction law. These tests are similar to those performed by Groves, Brinchmann & Walcher (2012) for the SDSS. To do this, we select a subset of the DR2 galaxies that have more than 10 high-quality (continuum S/N > 5) spaxels that are classified as star-forming, and have well-detected H β and H α fluxes (S/N>5). For the high-quality star-forming spaxels in these galaxies, we measure emission fluxes for the Balmer lines H ε, H δ, H γ, and H β using direct summation in windows surrounding those lines. The window width is set to |$\pm 3\sigma _{\rm win}$| around the redshifted line centre, where σwin is defined by the quadrature sum of the instrumental resolution and the gas-velocity dispersion determined by the 1-component lzifu fits. The redshift used to determine the line centre includes contributions from both the galaxy redshift and the gas velocity from lzifu. For each line, we measure two sets of emission line fluxes: one after subtracting the continuum defined using the procedure outlined for DR1, and another after subtracting the continuum measured as outlined above. The emission line fluxes are corrected for Galactic extinction, and then used to measure Balmer decrements for the higher order lines.
In Fig. 11 for each galaxy we plot the median value of the higher order Balmer decrements against the median H α/H β decrements, where H α and H β are determined from the lzifu fits, and are also corrected for Galactic extinction. The decrements are normalized by the theoretical value for Case B recombination. The red line shows the expected trend due to a Calzetti et al. (2000) extinction law. In the top panels, the results derived using the new continuum fitting are shown, while the bottom panels show the results from the DR1 continuum fitting method. Neither the new continuum fitting method used for DR2, nor the method used in DR1 produces results that align with the expectations of a Calzetti et al. (2000) extinction law. However, the DR2 results show both a smaller offset and scatter when compared with the DR1 results, and this is particularly true for the H δ/H β and H ε/H β ratios shown in the middle and right-most panels, respectively.
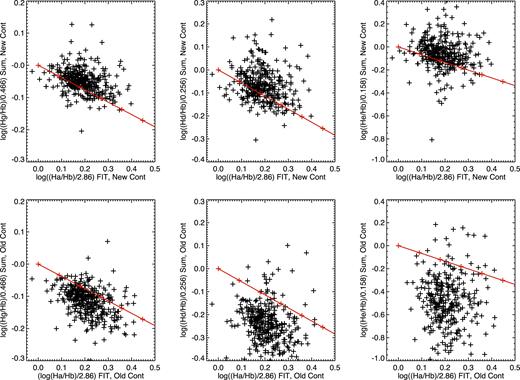
Comparison of the higher-order Balmer decrements derived from emission line fluxes measured after subtracting continua using the continuum fitting method used in DR2 (top row) and the continuum method used in DR1 (bottom row). The comparisons are made for H γ/H β, H δ/H β, and H ε/H β, determined by direct summation over a narrow window around the line centre (left-hand, middle, and right-hand panels), with the H β/H α ratio shown on the x-axis, taken from the lzifu fits. The red line shows the trend in the Balmer decrements of interest derived from a Calzetti et al. (2000) extinction law. We see an improvement in both the magnitude of the offset and the scatter in the distribution when comparing DR2 with DR1, although the offsets from the Calzetti et al. (2000) line are in the opposite sense.
Given that we have selected only relatively high S/N spaxels, the difference in the results from the two continuum fitting methods is likely driven by two changes. First, in DR2 we now modulate the SSP templates with a multiplicative polynomial rather than the additive polynomial used in DR1. Second, we now simultaneously fit for emission and absorption in the vicinity of the Balmer lines, whereas previously these regions were masked during the fit. The combined effect of using an additive polynomial alongside masking the age-sensitive Balmer lines was that younger templates were often excluded from the fit; the blue flux was modelled by the additive polynomial rather than a young stellar population, thereby underestimating the Balmer absorption at bluer wavelengths. We note that the offset observed in the new DR2 values in Fig. 11 is similar to that noted by Groves et al. (2012) for SDSS DR7 data. Investigation into the origin of the offset is ongoing. At this stage this alternative continuum fitting approach has been applied to the original spectral cubes only because they are more susceptible to inaccurate continuum subtraction due to their typically lower S/N than the other spectral data products.
In addition to the original spectral cubes, we also provide emission line fits for the binned cubes (Section 4.2) and aperture spectra (Section 4.3). For the adaptively binned and sectors-binned spectral cubes, we follow the same conventions as for the original spectral cubes, providing both 1- and multicomponent fits.
For the annular-binned spectral cubes we provide only 2-component fits, and fit the stellar continuum directly within lzifu using pPXF given the higher continuum S/N. Only 2-component fits are provided given that in many cases rotation dominates the emission structure in the outer bins leading to double-horned profiles that require two separate components to be fit.
All aperture spectra are also fit using lzifu, treating each spectrum as an individual spaxel. As with the original cubes we provide both 1-component and multicomponent fits to the aperture spectra. These are provided as tabulated line fluxes, gas velocities (relative to the input heliocentric GAMA redshifts) and velocity dispersions, and associated errors for all apertures described in Section 4.3.
5.2 Star formation rates and other products
As in DR1, we also release higher-order data products based upon the emission line fitting: Balmer decrement-based attenuation maps, classification of star-forming regions, and star formation rates. For full details on the determination of these products, we refer the reader to Medling et al. (2018), but briefly summarize these here.
For all spaxels we also classify whether the emission-line spectrum is dominated by photoionization by massive stars associated with recent star formation, or by other mechanisms (such as active galactic nucleus, shocks, etc.). This is done using cuts on emission line ratio based upon the classification scheme described in Kewley et al. (2006) and fully described in Medling et al. (2018). For both the original and binned data we present these as star formation masks, where any spaxel dominated by mechanisms other than star formation are set to 0.
6 VALUE-ADDED DATA PRODUCTS: ABSORPTION-LINE PHYSICS
6.1 Stellar kinematics
6.1.1 Method
Stellar kinematic parameters are extracted from the SAMI cubed data following the method described in detail in van de Sande et al. (2017b). We use the pPXF code to fit all spectra. Our method is summarized below.
SAMI blue and red spectra are combined by first convolving the red spectra to match the instrumental resolution in the blue. We use the code log_rebin provided with the pPXF package to rebin the combined blue and red spectra on to a logarithmic wavelength scale with constant velocity spacing (57.9 km s−1). We use annular binned spectra (Section 4.2) to derive local optimal templates from the MILES stellar library (Sánchez-Blázquez et al. 2006) that consists of 985 stars spanning a large range in stellar atmospheric parameters. A Gaussian line-of-sight velocity distribution (LOSVD) is assumed, i.e. we extract only the stellar velocity V and stellar velocity dispersion σ.
After the optimal template is constructed for each annular bin, we run pPXF three times on each galaxy spaxel. For every step, we mask the following emission lines: [O ii], H δ, H γ, H β, [O iii], [O i], H α, [N ii], and [S ii], even if no emission lines are detected. The first fit is used for determining a precise measure of the noise scaling from the residual of the fit. We use an additive Legendre polynomial to remove residuals from small errors in the flux calibration, and as in van de Sande et al. (2017b), we demonstrated that a 12th-order additive Legendre polynomial is sufficient for SAMI data. In the second fit, we clip outliers using the CLEAN parameter in pPXF. In the third and final iteration, pPXF is allowed to use the optimal templates from the annular bin in which the spaxel is located, as well as the optimal templates from neighbouring annular bins.
Uncertainties on the LOSVD parameters are estimated using a Monte Carlo approach. We estimate the uncertainties on the LOSVD parameters for each spaxel from the residuals of the best fit minus the observed spectrum. These residuals are then randomly rearranged in wavelength and added to the best-fitting template. This simulated spectrum is refitted with pPXF, and we repeat the process 150 times. The uncertainties on the LOSVD parameters are the standard deviations of the resulting simulated distributions.
We follow the same method for the binned data (Section 4.2). For the aperture spectra (Section 4.3), we construct an optimal template for each individual aperture and then use the same procedure as described above to extract the LOSVD.
We note that the varying spectral resolution from fibre to fibre (Section 3.1.1) can have a significant impact on the stellar kinematic measurements if the intrinsic stellar dispersion is close to or less than the instrumental dispersion (Federrath et al. 2017; Zhou et al. 2017). However, the stellar kinematic measurements are obtained from the cubed frames, where a dither pattern is applied. As individual spaxels are constructed from a combination of multiple fibres, the spectral resolution will be an average of all the contributing fibres. We do not consider the changing resolution as a function of wavelength to be significant enough to impact the extracted stellar kinematic measurements, as those are derived from a simultaneous fit over the entire wavelength range, and the full wavelength variation is comparable to the fibre-to-fibre variation.
6.1.2 S/N estimate from the stellar kinematic fits
Residuals from the observed spectrum minus the best-fitting template provide a good test of the accuracy of the variance spectra. Here, we compare the S/N derived from the flux and variance spectrum to the S/N derived from the stellar kinematic best-fit residual for every unbinned spaxel that meets the quality criteria in the next Section 6.1.3. The variance spectrum S/N was derived in the blue wavelength region between spectral pixel 1100 and 1600 (approximately between 4500 Å and 5000 Å), whereas the S/N from the residuals is determined for all ‘goodpixels’ in the pPXF fit (i.e. excluding emission lines and 3σ outliers). Therefore, we stress that this comparison should be considered a consistency check, not an exact derivation of the cube variance scaling.
In the left-hand panel of Fig. 12 we find that >95 per cent of the data are above the one-to-one relation, which indicates that the variances may be slightly overestimated. While there are considerably fewer data-points above S/N ≳ 50, the scatter between the two S/N estimates becomes increasingly larger and the S/N from the best-fitting residual drops below the S/N from the variance spectrum. However, we note that at this high S/N, uncertainties from the adopted stellar library, template mismatch, and other fitting related issue are starting to dominate the residual S/N estimate. Thus, above S/N ∼ 50, the S/N comparison becomes harder to interpret.
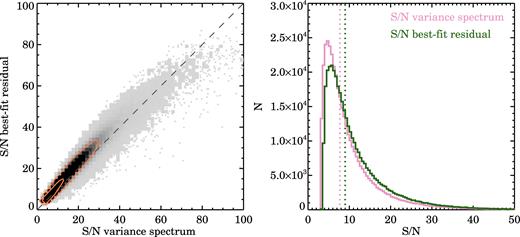
S/N per Å from the flux and variance spectrum compared to the S/N derived from the residual of the stellar kinematic best fit. The grey squares in the left-hand panel show the density of all unbinned spaxels in DR2 that pass the kinematic quality cut (Section 6.1.3); darker grey means higher density. The orange contours enclose 68 and 95 per cent of the data, and the dashed line shows the one-to-one relation. We show the distribution of the two S/N estimates in the right-hand panel. The median S/N from the variance spectrum (pink) is 16.6 per cent lower than the median S/N from the best-fitting residual (green; 7.70 versus 8.98, respectively).
We show the distribution of both S/N estimates in the right-hand panel of Fig. 12. Note that we only show data where the S/N estimated from the variance spectrum is greater than 3 Å−1, as lower S/N spaxels are not fit by the stellar kinematics pipeline. As before, we find that the median variance spectrum S/N is lower than the S/N derived from the best-fitting residual. The difference in medians is 16.6 per cent. Thus, while we find that the DR2 variances may be slightly overestimated, we conclude that this offset is relatively mild.
6.1.3 Kinematic quality cuts
For SAMI data we recommend applying the following quality criteria to the stellar kinematic data: signal-to-noise (S/N) >3 Å−1, σobs> FWHMinstr/2 ∼ 35 km s−1, Verror < 30 km s−1 (Q1 from van de Sande et al. 2017b), and σerror < σobs*0.1 + 25 km s−1 (Q2 from van de Sande et al. 2017b).
For kinematic data products such as kinemetry, the kinematic PA, V/σ, and λR, we have additional flags. We perform a visual inspection of all 1559 SAMI kinematic maps and exclude 42 galaxies with irregular kinematic maps due to nearby objects or mergers that influence the stellar kinematics of the main object. We furthermore exclude 481 galaxies where Re < 1|${^{\prime\prime}_{.}}$|5 or where either Re or the radius out to which we can accurately measure the stellar kinematics is less than the half-width at half-maximum of the PSF (HWHMPSF). This brings the final number of galaxies for which we can derive reliable 2D stellar kinematic data products to 1036. The number of galaxies with Re aperture velocity dispersion measurements is 1171.
6.1.4 Aperture velocity dispersion comparison
We compare our aperture velocity dispersion values to measurements from SDSS 3-arcsec single-fibre spectra. We refit the SDSS spectra, using the same technique and templates as described in Section 6.1.1. Our values are in good agreement with the standard SDSS pipeline velocity dispersions and the measurements by Thomas, Maraston & Johansson (2011). We show the comparison in Fig. 13, where any measurements with (S/N)SDSS < 5 Å−1, σobs< FWHMinstr/2, and σerror > σobs*0.025 + 10 km s−1are excluded. The first and last quality criteria are stricter than described in Section 6.1.3 due to the higher mean S/N of the SAMI and SDSS aperture spectra. We quantify the comparison, using the median σ offset (σSDSS − σSAMI) and the fractional dispersion difference, Δσ = (σSDSS − σSAMI)/σSAMI. There is excellent agreement between the SAMI and SDSS measurements when the velocity dispersion is higher than the SAMI instrumental resolution of ∼70 km s−1 (median σ offset = 1.4 km s−1, RMS Δσ = 0.10), or when the S/N of the SAMI aperture spectra is greater than 25 per Å (median σ offset = 1.9 km s−1, RMS Δσ = 0.12). Below 70 km s−1, we find a larger median σ offset = 14.9 km s−1 and the RMS scatter in Δσ increases to 0.47, but we note that the majority of galaxies with low-velocity dispersion also have the lowest S/N.
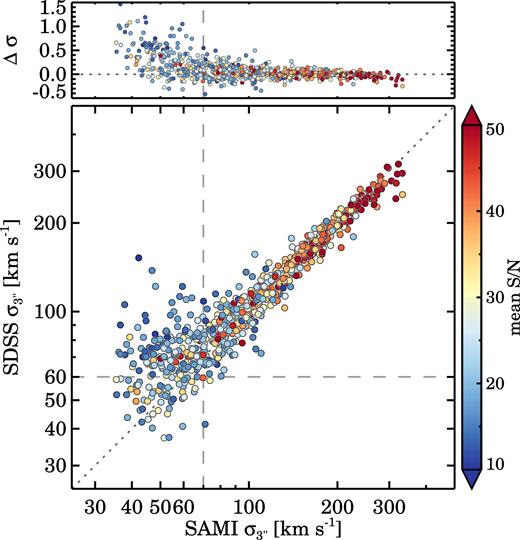
Comparison of the stellar velocity dispersions from the SAMI 3-arcsec aperture spectra versus 3-arcsec SDSS spectra (main panel). In the top panel, we show the ratio of the velocity dispersions, Δσ, which is defined as (σSDSS − σSAMI)/σSAMI. The data are colour coded by the mean continuum S/N of the SDSS single-fibre spectra. The dashed lines show the adopted instrumental resolution of the SAMI blue arm and the SDSS spectrograph, whereas the dotted line shows the one-to-one relation. Above the spectral resolution limits of both spectrographs, we find an excellent agreement. Below the instrumental resolution the scatter increases due to the lower S/N of these spectra, but there is also an increasing offset from the one-to-one relation.
Below the instrumental resolution we detect a deviation from the one-to-one relation; the SDSS velocity dispersions are increasingly higher than the SAMI measurements. This hints at a systematic bias in the SDSS velocity dispersions at low σ. Note that it is extremely difficult to reconstruct an exact SDSS single-fibre measurement using IFS data; the SDSS aperture is circular, convolved with an observed PSF, and differential atmospheric refraction cannot be corrected for. Thus, we believe the SAMI aperture spectra to be more reliable for three reasons. First, the SDSS spectrograph is mounted on the telescope near the Cassegrain focus and therefore suffers from flexure that can change the spectral resolution, whereas the SAMI-AAOmega is a bench-mounted spectrograph and is therefore more stable. Secondly, the S/N in the SAMI spectra is higher, and thirdly our simulations of the recovery of σ from synthetic SAMI spectra do not reveal a systematic offset below the instrumental resolution (Fogarty et al. 2015) in the SAMI measurements.
There are two notable outliers at the highest SAMI velocity dispersion, where the SDSS velocity dispersion is significantly lower than the SAMI value (|$\sigma _{\rm {SDSS}}\sim 250{\, \rm {km}\, \rm {s}^{-1}}$| versus |$\sigma _{\rm {SAMI}}\sim 300{\, \rm {km}\, \rm {s}^{-1}}$|, respectively). A closer investigation of these two objects revealed that one galaxy is a merger remnant with strong emission lines, where a small misplacement of the fibre centre can cause a large change in the velocity dispersion. The second object consists of two galaxies, one in the foreground and another in the background, with the peak flux of the sources separated by less than 3 arcsec. Similar to the first object, a small offset in position results in a large change in σ.
6.1.5 Kinematic asymmetry
We estimate the kinematic asymmetry of the galaxy velocity fields in DR2 following the method outlined in van de Sande et al. (2017b). We assume that the velocity field of a galaxy can be described with a simple cosine law along ellipses. Kinematic deviations from the cosine law can be modelled by using Fourier harmonics. The first-order decomposition k1 is equivalent to the rotational velocity, whereas the high-order terms (k3, k5) describe the kinematic anomalies. The kinematic asymmetry can be quantified by using the amplitudes of the Fourier harmonics. Following Krajnović et al. (2011), the kinematic asymmetry is defined using the amplitudes of the Fourier harmonics ratio k5/k1.
We determine the amplitude of the Fourier harmonics on all velocity data that pass the quality cut Q1, measured using the kinemetry routine (Krajnović et al. 2006, 2008). In the fit, the PA is a free parameter, whereas the ellipticity is restricted to vary between ±0.1 of the photometric ellipticity. For each ellipse, the kinemetry routine determines a best-fitting amplitude for k1, k3, and k5. We use the SAMI flux images to determine the luminosity-weighted average ratio k5/k1 within one effective radius. The uncertainty on k5/k1 for each measurement is estimated from Monte Carlo simulations.
6.1.6 Kinematic position angle
The PA of the stellar rotation was measured from the two-dimensional stellar velocity kinematic maps on all spaxels that pass the quality cut Q1. We use the fit_kinematic_pa code that is based on the method described in Appendix C of Krajnović et al. (2006). The kinematic PA was measured with an assumed centre of the map at (25.5,25.5). We checked whether the kinematic PA is sensitive to the centroid choice by performing the kinematic PA fit an additional four times, each with a different centre position: (25,25), (26,26), (25,26), and (26,25). We found no systematic difference between the average of these four fits and our default centre.
6.1.7 V/σ and λR
In both equations, the subscript i refers to the ith spaxel within the ellipse, Fi is the flux of the ith spaxel, Vi is the stellar velocity in km s−1, and σi is the velocity dispersion in km s−1. For λR, Ri is the semi-major axis of the ellipse on which spaxel i lies, which is different from other surveys that use the circular projected radius to the centre (e.g. ATLAS3D; Emsellem et al. 2007). The sum is taken over all spaxels Nspx that pass the quality cut Q1 and Q2 within an ellipse with semi-major axis Re and axis ratio b/a.
We require a fill factor of 95 per cent of good spaxels within the aperture for producing Re measurements. This selection results in 695 galaxies with (V/σ)e and |$\lambda _{R_{\rm {e}}}$| measurements in DR2. For the data where the largest kinematic aperture radius is smaller than the effective radius or where the effective radius is smaller than the seeing disc (238 galaxies), we apply an aperture correction as described in van de Sande et al. (2017a). Including the aperture corrections, 933 galaxies have (V/σ)e and |$\lambda _{R_{\rm {e}}}$| measurements out of the total 1559 galaxies in DR2 (59.8 per cent).
6.2 Stellar populations
Stellar population parameters are measured from the aperture spectra described in Section 4.3, using the method described in Scott et al. (2017), which we briefly summarize below. We note that the Re aperture measurements presented as part of this release are not identical to those used in Scott et al. (2017) as (i) a new internal SAMI version of the reduced data has been used and (ii) the apertures are elliptical as opposed to circular and use different measurements of Re.
We began by measuring Lick absorption line strength indices for all spectra (Faber 1973; Worthey et al. 1994). We begin by correcting for ionized gas emission and bad pixels by comparing the observed spectra to a set of MILES SSP template spectra that are unaffected by emission, identifying pixels that differ significantly between the observed spectrum and best-fitting linear combination of template spectra, and replacing affected pixels with the values of the template spectra. We then broaden each spectrum to the wavelength-dependent Lick spectral resolution. We measured absorption line strengths for a set of 20 Lick indices on the emission-corrected, broadened spectra following the index definitions of Trager et al. (1998). For spectra where the effective resolution is already broader than the Lick resolution, we correct for the effect of intrinsic broadening following Schiavon (2007). Uncertainties on all indices are determined by a Monte Carlo reallocation of the residuals and repeating the measurements on 100 realizations of the spectra.
The observed Lick index measurements are converted to Single Stellar Population (SSP) equivalent age, metallicity, [Z/H], and alpha-abundance, [α/Fe]. This conversion is done by comparing the observed absorption line strengths to the predictions of the stellar population synthesis models of Schiavon (2007) and Thomas et al. (2010). We use a χ2 minimization approach with an iterative rejection of discrepant indices to determine the best-matching SSP parameters, as first implemented by Proctor, Forbes & Beasley (2004). For the Thomas et al. (2010) models, we use all 20 measured indices. For the Schiavon (2007) models only 16 of the measured indices are predicted by the stellar population synthesis models. For the reasons outlined in Scott et al. (2017), we use SSP equivalent ages from Schiavon (2007) models and SSP equivalent [Z/H] and [α/Fe] from Thomas et al. (2010) models.
In this release we make available all 20 Lick index measurements and the three SSP equivalent stellar population measurements for all six apertures. For the Lick index measurements, we provide a flag for each aperture to indicate where the measurements may be unreliable, predominantly due to low S/N. For the SSP equivalent measurements, we provide age and [Z/H] only where the S/N of the given aperture spectrum is greater than 10 per Å. We provide [α/Fe] only where the S/N of the aperture spectrum is greater than 20 per Å.
7 ONLINE DATA
In Fig. 14 and Table 2 we provide an overview of some of the data available for each of the 1559 galaxies in DR2. Fig. 14 presents the spatially resolved measurements, while aperture measurements and other tabular data are presented in Table 2. In the following subsections we describe how these data can be accessed, searched for, and downloaded, and provide an illustration of how the combined data products can be used.
![Summary of data available for galaxy ID 22887. Along with Table 2, this figure provides an overview of data available for each galaxy in the release. The upper panel shows the flux-calibrated aperture spectra for the six apertures included in this release. For this object, the 4 arcsec and 3 kpc apertures are identical. The lower panels show, from left to right, top to bottom: log-scaled median flux from the blue cube, log-scaled median flux from the red cube, H β emission line flux, H α emission line flux, stellar velocity and stellar velocity dispersion in km s−1, gas velocity and velocity dispersion in km s−1, log-scaled flux ratio of [N ii]6583 to H α, log-scaled flux ratio of [O iii]5007 to H β, Balmer decrement and log-scaled g′r′i′ Hyper Suprime-Cam image (Aihara et al. 2018). For the upper row, lighter colours indicate higher fluxes. For the lower two rows, the range of the colour scale is indicated in the upper right of each panel, with the sense indicated by the accompanying colour bar. The dashed white circle indicates the location of the SAMI bundle footprint in the HSC image.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/481/2/10.1093_mnras_sty2355/1/m_sty2355fig14.jpeg?Expires=1750217205&Signature=TLXdScJMTX2f7mjVH2r6Xi-b~xkWSZ6VBcFY0CGPHSdwcBHuKumu0u7Ptib9b-5RAiHLX6oIFyEdOv7n7QNGK1X3hJXfX0lvQHeNIatm7AG51BfDeWL8mR6sL8laLKShQsotiYUZMMTiIvg2Y4hMsjv-GBZTG-nfa2XfNjODpNtWTo0coZIG2yrCczE~xQp7Q-S9ICOJmnyFCAqyEYSNBNAqws3Fz2LRbSWHbtJjkx1tkO-E6ZRGK8loaPFbAjs3Q-~~bBeAEwPDmkCUucClzfXvSo3f1kcS-Qa6FAEMyGk3vkJq2FchWlyp9GDqkoN3w0j8n0bBT2xwJe3~e1IG8A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Summary of data available for galaxy ID 22887. Along with Table 2, this figure provides an overview of data available for each galaxy in the release. The upper panel shows the flux-calibrated aperture spectra for the six apertures included in this release. For this object, the 4 arcsec and 3 kpc apertures are identical. The lower panels show, from left to right, top to bottom: log-scaled median flux from the blue cube, log-scaled median flux from the red cube, H β emission line flux, H α emission line flux, stellar velocity and stellar velocity dispersion in km s−1, gas velocity and velocity dispersion in km s−1, log-scaled flux ratio of [N ii]6583 to H α, log-scaled flux ratio of [O iii]5007 to H β, Balmer decrement and log-scaled g′r′i′ Hyper Suprime-Cam image (Aihara et al. 2018). For the upper row, lighter colours indicate higher fluxes. For the lower two rows, the range of the colour scale is indicated in the upper right of each panel, with the sense indicated by the accompanying colour bar. The dashed white circle indicates the location of the SAMI bundle footprint in the HSC image.
Summary of data available for galaxy ID 22887. Along with Fig. 14, this table provides an overview of data available for each galaxy in the release. Note that this table presents data for only one aperture, the Re aperture, of the six apertures for which data is available in the release. (1) SAMI/GAMA galaxy ID, (2) right ascension, (3) Declination, (4) flow-corrected redshift, (5) stellar mass, (6) GAMA r-band effective radius, (7) GAMA light-weighted r-band ellipticity, (8) mean stellar age, (9) mean stellar metallicity, (10) mean stellar α-abundance, (11) stellar velocity dispersion, (12) ratio of stellar velocity to velocity dispersion, (13) stellar spin parameter proxy, (14) photometric position angle, (15) stellar kinematic position angle, (16) gas velocity dispersion, (17) star formation rate, (18) H α flux, (19) H β flux, (20) ratio of N[II] to H α flux, (21) ratio of [O iii] to H β flux.
| CATID . | RA(J2000) . | Dec. (J2000) . | |$z$| . | log M⋆ . | Re . | ε . | Age . | [Z/H] . | [α/Fe] . | σe, stars . |
|---|---|---|---|---|---|---|---|---|---|---|
| deg | deg | M⊙ | arcsec | Gyrs | km s−1 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| 22887 | 179.403 | 1.14077 | 0.0375 | 10.47 | 6.2 | 0.54 | 2.1 ± 0.5 | −0.08 ± 0.14 | 0.04 ± 0.11 | 124 ± 1 |
| (V/σ)e, stars | λR | PAphot | PAstars | σe, gas | SFR | Hα flux | Hβ flux | log([N ii]/Hα) | log([O iii]/Hβ) | |
| deg | deg | km s−1 | M⊙ yr−1 | 10−16 ergs | 10−16 ergs | |||||
| cm−2 s−1 | cm−2 s−1 | |||||||||
| (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | |
| 0.62 ± 0.01 | 0.51 ± 0.01 | -36 | 108 | 101 | 0.72 | 116.7 ± 0.3 | 22.9 ± 0.3 | -0.34 | -0.49 |
| CATID . | RA(J2000) . | Dec. (J2000) . | |$z$| . | log M⋆ . | Re . | ε . | Age . | [Z/H] . | [α/Fe] . | σe, stars . |
|---|---|---|---|---|---|---|---|---|---|---|
| deg | deg | M⊙ | arcsec | Gyrs | km s−1 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| 22887 | 179.403 | 1.14077 | 0.0375 | 10.47 | 6.2 | 0.54 | 2.1 ± 0.5 | −0.08 ± 0.14 | 0.04 ± 0.11 | 124 ± 1 |
| (V/σ)e, stars | λR | PAphot | PAstars | σe, gas | SFR | Hα flux | Hβ flux | log([N ii]/Hα) | log([O iii]/Hβ) | |
| deg | deg | km s−1 | M⊙ yr−1 | 10−16 ergs | 10−16 ergs | |||||
| cm−2 s−1 | cm−2 s−1 | |||||||||
| (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | |
| 0.62 ± 0.01 | 0.51 ± 0.01 | -36 | 108 | 101 | 0.72 | 116.7 ± 0.3 | 22.9 ± 0.3 | -0.34 | -0.49 |
Summary of data available for galaxy ID 22887. Along with Fig. 14, this table provides an overview of data available for each galaxy in the release. Note that this table presents data for only one aperture, the Re aperture, of the six apertures for which data is available in the release. (1) SAMI/GAMA galaxy ID, (2) right ascension, (3) Declination, (4) flow-corrected redshift, (5) stellar mass, (6) GAMA r-band effective radius, (7) GAMA light-weighted r-band ellipticity, (8) mean stellar age, (9) mean stellar metallicity, (10) mean stellar α-abundance, (11) stellar velocity dispersion, (12) ratio of stellar velocity to velocity dispersion, (13) stellar spin parameter proxy, (14) photometric position angle, (15) stellar kinematic position angle, (16) gas velocity dispersion, (17) star formation rate, (18) H α flux, (19) H β flux, (20) ratio of N[II] to H α flux, (21) ratio of [O iii] to H β flux.
| CATID . | RA(J2000) . | Dec. (J2000) . | |$z$| . | log M⋆ . | Re . | ε . | Age . | [Z/H] . | [α/Fe] . | σe, stars . |
|---|---|---|---|---|---|---|---|---|---|---|
| deg | deg | M⊙ | arcsec | Gyrs | km s−1 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| 22887 | 179.403 | 1.14077 | 0.0375 | 10.47 | 6.2 | 0.54 | 2.1 ± 0.5 | −0.08 ± 0.14 | 0.04 ± 0.11 | 124 ± 1 |
| (V/σ)e, stars | λR | PAphot | PAstars | σe, gas | SFR | Hα flux | Hβ flux | log([N ii]/Hα) | log([O iii]/Hβ) | |
| deg | deg | km s−1 | M⊙ yr−1 | 10−16 ergs | 10−16 ergs | |||||
| cm−2 s−1 | cm−2 s−1 | |||||||||
| (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | |
| 0.62 ± 0.01 | 0.51 ± 0.01 | -36 | 108 | 101 | 0.72 | 116.7 ± 0.3 | 22.9 ± 0.3 | -0.34 | -0.49 |
| CATID . | RA(J2000) . | Dec. (J2000) . | |$z$| . | log M⋆ . | Re . | ε . | Age . | [Z/H] . | [α/Fe] . | σe, stars . |
|---|---|---|---|---|---|---|---|---|---|---|
| deg | deg | M⊙ | arcsec | Gyrs | km s−1 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| 22887 | 179.403 | 1.14077 | 0.0375 | 10.47 | 6.2 | 0.54 | 2.1 ± 0.5 | −0.08 ± 0.14 | 0.04 ± 0.11 | 124 ± 1 |
| (V/σ)e, stars | λR | PAphot | PAstars | σe, gas | SFR | Hα flux | Hβ flux | log([N ii]/Hα) | log([O iii]/Hβ) | |
| deg | deg | km s−1 | M⊙ yr−1 | 10−16 ergs | 10−16 ergs | |||||
| cm−2 s−1 | cm−2 s−1 | |||||||||
| (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | |
| 0.62 ± 0.01 | 0.51 ± 0.01 | -36 | 108 | 101 | 0.72 | 116.7 ± 0.3 | 22.9 ± 0.3 | -0.34 | -0.49 |
7.1 Data access
The data of this release are available through an online database provided by Australian Astronomical Optics’ Data Central2 service. Data Central delivers a variety of astronomical data sets of significance to Australian astronomical research. As well as storing and serving data, Data Central provides a flexible query tool, allowing users to search for and link data across multiple surveys. Users can search based not only on source position, but also on any measured property stored in Data Central data tables, allowing highly flexible science queries to be executed.
DR2 data products are available for download as multi-extension fits files, while table data are available in a variety of formats including fits, csv and VOTable files. The contents and structure of all SAMI data products are fully described in the Data Central schema browser. Further documentation describing how data products are derived, as well as many other details relating to the SAMI Galaxy Survey and DR2 in particular, can be found in Data Central’s accompanying documentation. The data products available in DR2 are summarized in Tables 3–6. All table data is searchable. All one-, two- and three-dimensional data products and tables can be downloaded through Data Central.
| Product . | Versions . |
|---|---|
| Default cubes | Blue/red |
| Adaptive binned cubes | Blue/red |
| Annular binned cubes | Blue/red |
| Sectors binned cubes | Blue/red |
| Product . | Versions . |
|---|---|
| Default cubes | Blue/red |
| Adaptive binned cubes | Blue/red |
| Annular binned cubes | Blue/red |
| Sectors binned cubes | Blue/red |
| Product . | Versions . |
|---|---|
| Default cubes | Blue/red |
| Adaptive binned cubes | Blue/red |
| Annular binned cubes | Blue/red |
| Sectors binned cubes | Blue/red |
| Product . | Versions . |
|---|---|
| Default cubes | Blue/red |
| Adaptive binned cubes | Blue/red |
| Annular binned cubes | Blue/red |
| Sectors binned cubes | Blue/red |
Summary of two-dimensional data products included in DR2. 1-comp, 2-comp, and recom–comp refer to the one-component, two-component, and recommended component lzifu fits; see Section 5.1 for details. For the annular binning scheme we provide only two-component data. For the other binning schemes and the unbinned data, we provide both one-component and recommended component data.
| Product . | Versions . |
|---|---|
| Stellar velocity | n/a |
| Stellar velocity dispersion | n/a |
| Gas velocity | 1-comp, 2-comp, recom-comp |
| Gas velocity dispersion | 1-comp, 2-comp, recom-comp |
| Star formation rate | 1-comp, 2-comp, recom-comp |
| Star formation rate density | 1-comp, 2-comp, recom-comp |
| Balmer decrement | 1-comp, 2-comp, recom-comp |
| H α flux | 1-comp, 2-comp, recom-comp |
| H β flux | 1-comp, 2-comp, recom-comp |
| [O ii]3726+3729 flux | 1-comp, 2-comp, recom-comp |
| [O iii]5007 flux | 1-comp, 2-comp, recom-comp |
| [O i]6300 flux | 1-comp, 2-comp, recom-comp |
| [N ii]6583 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6716 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6731 flux | 1-comp, 2-comp, recom-comp |
| Product . | Versions . |
|---|---|
| Stellar velocity | n/a |
| Stellar velocity dispersion | n/a |
| Gas velocity | 1-comp, 2-comp, recom-comp |
| Gas velocity dispersion | 1-comp, 2-comp, recom-comp |
| Star formation rate | 1-comp, 2-comp, recom-comp |
| Star formation rate density | 1-comp, 2-comp, recom-comp |
| Balmer decrement | 1-comp, 2-comp, recom-comp |
| H α flux | 1-comp, 2-comp, recom-comp |
| H β flux | 1-comp, 2-comp, recom-comp |
| [O ii]3726+3729 flux | 1-comp, 2-comp, recom-comp |
| [O iii]5007 flux | 1-comp, 2-comp, recom-comp |
| [O i]6300 flux | 1-comp, 2-comp, recom-comp |
| [N ii]6583 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6716 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6731 flux | 1-comp, 2-comp, recom-comp |
Summary of two-dimensional data products included in DR2. 1-comp, 2-comp, and recom–comp refer to the one-component, two-component, and recommended component lzifu fits; see Section 5.1 for details. For the annular binning scheme we provide only two-component data. For the other binning schemes and the unbinned data, we provide both one-component and recommended component data.
| Product . | Versions . |
|---|---|
| Stellar velocity | n/a |
| Stellar velocity dispersion | n/a |
| Gas velocity | 1-comp, 2-comp, recom-comp |
| Gas velocity dispersion | 1-comp, 2-comp, recom-comp |
| Star formation rate | 1-comp, 2-comp, recom-comp |
| Star formation rate density | 1-comp, 2-comp, recom-comp |
| Balmer decrement | 1-comp, 2-comp, recom-comp |
| H α flux | 1-comp, 2-comp, recom-comp |
| H β flux | 1-comp, 2-comp, recom-comp |
| [O ii]3726+3729 flux | 1-comp, 2-comp, recom-comp |
| [O iii]5007 flux | 1-comp, 2-comp, recom-comp |
| [O i]6300 flux | 1-comp, 2-comp, recom-comp |
| [N ii]6583 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6716 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6731 flux | 1-comp, 2-comp, recom-comp |
| Product . | Versions . |
|---|---|
| Stellar velocity | n/a |
| Stellar velocity dispersion | n/a |
| Gas velocity | 1-comp, 2-comp, recom-comp |
| Gas velocity dispersion | 1-comp, 2-comp, recom-comp |
| Star formation rate | 1-comp, 2-comp, recom-comp |
| Star formation rate density | 1-comp, 2-comp, recom-comp |
| Balmer decrement | 1-comp, 2-comp, recom-comp |
| H α flux | 1-comp, 2-comp, recom-comp |
| H β flux | 1-comp, 2-comp, recom-comp |
| [O ii]3726+3729 flux | 1-comp, 2-comp, recom-comp |
| [O iii]5007 flux | 1-comp, 2-comp, recom-comp |
| [O i]6300 flux | 1-comp, 2-comp, recom-comp |
| [N ii]6583 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6716 flux | 1-comp, 2-comp, recom-comp |
| [S ii]6731 flux | 1-comp, 2-comp, recom-comp |
| Product . | Versions . |
|---|---|
| 3 kpc circular aperture spectrum | Blue/red |
| Re elliptical aperture spectrum | Blue/red |
| 1|${^{\prime\prime}_{.}}$|4 circular aperture spectrum | Blue/red |
| 2″ circular aperture spectrum | Blue/red |
| 3″ circular aperture spectrum | Blue/red |
| 4″ circular aperture spectrum | Blue/red |
| Product . | Versions . |
|---|---|
| 3 kpc circular aperture spectrum | Blue/red |
| Re elliptical aperture spectrum | Blue/red |
| 1|${^{\prime\prime}_{.}}$|4 circular aperture spectrum | Blue/red |
| 2″ circular aperture spectrum | Blue/red |
| 3″ circular aperture spectrum | Blue/red |
| 4″ circular aperture spectrum | Blue/red |
| Product . | Versions . |
|---|---|
| 3 kpc circular aperture spectrum | Blue/red |
| Re elliptical aperture spectrum | Blue/red |
| 1|${^{\prime\prime}_{.}}$|4 circular aperture spectrum | Blue/red |
| 2″ circular aperture spectrum | Blue/red |
| 3″ circular aperture spectrum | Blue/red |
| 4″ circular aperture spectrum | Blue/red |
| Product . | Versions . |
|---|---|
| 3 kpc circular aperture spectrum | Blue/red |
| Re elliptical aperture spectrum | Blue/red |
| 1|${^{\prime\prime}_{.}}$|4 circular aperture spectrum | Blue/red |
| 2″ circular aperture spectrum | Blue/red |
| 3″ circular aperture spectrum | Blue/red |
| 4″ circular aperture spectrum | Blue/red |
Summary of data tables included in DR2. All tables are fully queryable through the Data Central interface.
| Catalogue . | Summary . |
|---|---|
| Sample | General galaxy properties including M⋆, Re, |$z$|, morphological classification etc. |
| Lick indices | Measurements and uncertainties of Lick absorption line strengths from aperture spectra. |
| SSP values | Measurements and uncertainties of SSP-equivalent age, metallicity and [α/Fe] from aperture spectra. |
| Aperture stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from aperture spectra. |
| Resolved stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from maps. |
| Aperture emission line properties | Measurements and uncertainties of emission line quantities from aperture spectra. |
| Catalogue . | Summary . |
|---|---|
| Sample | General galaxy properties including M⋆, Re, |$z$|, morphological classification etc. |
| Lick indices | Measurements and uncertainties of Lick absorption line strengths from aperture spectra. |
| SSP values | Measurements and uncertainties of SSP-equivalent age, metallicity and [α/Fe] from aperture spectra. |
| Aperture stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from aperture spectra. |
| Resolved stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from maps. |
| Aperture emission line properties | Measurements and uncertainties of emission line quantities from aperture spectra. |
Summary of data tables included in DR2. All tables are fully queryable through the Data Central interface.
| Catalogue . | Summary . |
|---|---|
| Sample | General galaxy properties including M⋆, Re, |$z$|, morphological classification etc. |
| Lick indices | Measurements and uncertainties of Lick absorption line strengths from aperture spectra. |
| SSP values | Measurements and uncertainties of SSP-equivalent age, metallicity and [α/Fe] from aperture spectra. |
| Aperture stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from aperture spectra. |
| Resolved stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from maps. |
| Aperture emission line properties | Measurements and uncertainties of emission line quantities from aperture spectra. |
| Catalogue . | Summary . |
|---|---|
| Sample | General galaxy properties including M⋆, Re, |$z$|, morphological classification etc. |
| Lick indices | Measurements and uncertainties of Lick absorption line strengths from aperture spectra. |
| SSP values | Measurements and uncertainties of SSP-equivalent age, metallicity and [α/Fe] from aperture spectra. |
| Aperture stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from aperture spectra. |
| Resolved stellar kinematics | Measurements and uncertainties of stellar kinematic quantities from maps. |
| Aperture emission line properties | Measurements and uncertainties of emission line quantities from aperture spectra. |
7.2 Data demonstration
In this section, we present a demonstration of the science that can be done with the data products within DR2. In Fig. 15, we show the distribution of the velocity V and velocity dispersion σ of all individual spaxels as a function of R/Re (normalized elliptical distance from the galaxy centre). Here, we use spaxels with the stellar kinematic quality criteria from Section 6.1.3. These criteria result in a total of 344 965 spaxels that we divide into four stellar mass bins.
![Distribution of individual spaxel velocity (top row) and velocity dispersions (2nd row) as a function of radius, divided into four stellar mass bins. The contours show 68 per cent and 95 per cent of the data, and are smoothed with a boxcar filter. The dashed line indicates the adopted velocity dispersion limit of 35 km s−1 as described in Section 6.1.3. We also show a Hyper Suprime-Cam g′r′i′ combined colour image, a SAMI gsrsis colour image reconstructed from the spectra, and the stellar and gas velocity V and velocity dispersion σ maps. We indicate the range of the kinematic maps between ‘[ ]’ brackets. For the velocity fields, blue (stellar) and green (gas) indicate negative velocities, whereas red (stellar) and purple (gas) show positive velocities. For the velocity dispersion maps, yellow-to-red and beige-to-green indicate low-to-high values. In the HSC colour image, the white circle indicates the SAMI hexabundle field-of-view. The blue dashed ellipse in the SAMI reconstructed colour image indicates one effective radius. The small circle in the stellar and gas velocity dispersion map shows the size of the PSF-FWHM. For each mass bin, we highlight one galaxy with coloured points and the image and maps; from left to right we show GAMA560883, GAMA84900, GAMA8353, and GAMA16863. We refer to the text for details on each individual galaxy.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/481/2/10.1093_mnras_sty2355/1/m_sty2355fig15.jpeg?Expires=1750217205&Signature=etyepDufV1JOhIHUIz-T8ZtYzmsg8xSbF9mZ2XHjftG3MVh8psiizSss1McV~vQd5XXWkiYDPWKsn5ADXSNfRDciPtF1ECZxVfPSjh~sNytOrJw5JsHi-e9onz0NvjA5O9PdOB0MnSDTHgapd2XMQIZ6Y1UI8qxZb8sj~e1IQyTqtolXt0LXCWpY7fTSZUo~anRINsDKUPq8~Mh5xQAS6PwSjUF6CB4olp2dm1sOE1i-B6Q1Cm1QuFcXmsgvqNUQ9G1mWz~sbgKN5u-6yq-OBMvTB2NUfUTCzheBbGsc9hu6ulXWsm4Q7MMyo~VAfx~wl33Anj4V7kIMl8ey3g8uBQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Distribution of individual spaxel velocity (top row) and velocity dispersions (2nd row) as a function of radius, divided into four stellar mass bins. The contours show 68 per cent and 95 per cent of the data, and are smoothed with a boxcar filter. The dashed line indicates the adopted velocity dispersion limit of 35 km s−1 as described in Section 6.1.3. We also show a Hyper Suprime-Cam g′r′i′ combined colour image, a SAMI gsrsis colour image reconstructed from the spectra, and the stellar and gas velocity V and velocity dispersion σ maps. We indicate the range of the kinematic maps between ‘[ ]’ brackets. For the velocity fields, blue (stellar) and green (gas) indicate negative velocities, whereas red (stellar) and purple (gas) show positive velocities. For the velocity dispersion maps, yellow-to-red and beige-to-green indicate low-to-high values. In the HSC colour image, the white circle indicates the SAMI hexabundle field-of-view. The blue dashed ellipse in the SAMI reconstructed colour image indicates one effective radius. The small circle in the stellar and gas velocity dispersion map shows the size of the PSF-FWHM. For each mass bin, we highlight one galaxy with coloured points and the image and maps; from left to right we show GAMA560883, GAMA84900, GAMA8353, and GAMA16863. We refer to the text for details on each individual galaxy.
From the lowest to highest mass bin (right-to-left), we find an increasingly high maximum velocity and velocity dispersion. These correlations are the well-known Tully & Fisher (1977) and Faber & Jackson (1976) relations. The declining average rotation as a function of radius is a selection effect, rather than a physical effect. Due to SAMI’s round hexabundles, any galaxy with an ellipticity greater than zero will have more velocity measurements extracted from spaxels along the minor axis than major axis. As the plane of rotation is usually along the major axis, measurements along the minor axis will have relatively low velocity, which causes an apparent decrease at R/Re > 1.5.
In the highest mass bin (left-hand panel, log (M⋆/M⊙) > 11), the maximum of the 1σ contour in velocity is lower than for the intermediate mass bin (10 < log (M⋆/M⊙) < 11), along with an increase in the velocity dispersion. Above log (M⋆/M⊙) ∼ 11 is also the mass regime where most galaxies appear to change from regular rotating oblate spheroids to mildly triaxial, dispersion dominated spheroids (e.g. Cappellari 2016).
For galaxies with log (M⋆/M⊙) > 10 we find an increase in the velocity dispersion towards the centre due to a dispersion-dominated central component or classical bulge. Below log (M⋆/M⊙) < 10 we find no evidence for an increase in the velocity dispersion near the centre; this was also noticed by Falcón-Barroso et al. (2017). However, the results from Falcón-Barroso et al. (2017) suggest lower velocity dispersions in the centre as compared to the galaxy outskirts. While our data also show an average radial increase in σ, this increase is mostly caused by an increase in the measurement uncertainties at large radius. The stellar mass (log (M⋆/M⊙) ∼ 10) at which galaxies transition from having classical bulges (e.g. Kormendy & Kennicutt 2004) to a pseudo-bulge was also seen in Fisher & Drory (2011), based on photometric analysis of galaxy surface brightness profiles.
We highlight the stellar velocity and velocity dispersion of four example galaxies using the coloured points. For each example galaxy we also show the Hyper Suprime-Cam (HSC; Aihara et al. 2018) Subaru Strategic Program gri combined colour image, a SAMI gri colour image reconstructed from the spectra, and the stellar and gas V and σ maps. Even though we consider any stellar velocity dispersion measurement that is lower than half the instrumental resolution (|${\sim }35 {\, \rm {km}\, \rm {s}^{-1}}$|) to be unreliable, we nonetheless show these data for individual galaxies in the top row of Fig. 15 and the velocity dispersion maps. We do this to demonstrate at what stellar mass a large fraction of the spaxels become unusable.
The example galaxy with the highest stellar mass (first column, GAMA560883, log (M⋆/M⊙) = 11.21) shows an offset between the photometric and stellar velocity PA, and between the stellar and gas kinematic PA. The gas velocity map seems to be aligned with a faint dust lane that is visible in the HSC image when zoomed in. GAMA84900 (second column) is a typical fast-rotating early-spiral with log (M⋆/M⊙) = 10.44, where the photometric, stellar velocity, and gas velocity PAs are all perfectly aligned. The central bulge clearly stands out in the stellar velocity dispersion, whereas the gas velocity dispersion shows a complex central structure. The two low-mass late-spiral-type galaxies (third and fourth columns), GAMA8353 with log (M⋆/M⊙) = 9.44, and GAMA16863 with log (M⋆/M⊙) = 8.67, show no sign of a dispersion-dominated bulge. It is evident that this is not caused by the limiting spectral resolution because the majority of data are well above the adopted spectral resolution limit.
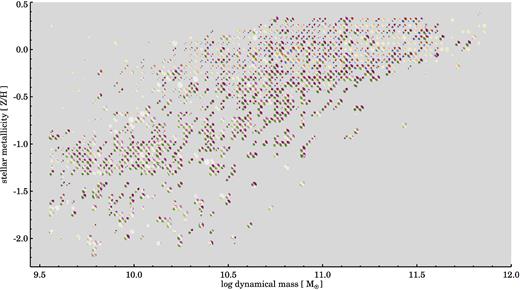
Stellar metallicity within one Re versus dynamical mass. We show stellar velocity maps for all early-type galaxies (blue-red) and gas velocity maps for the late-type galaxies (green-purple). For each galaxy we show its velocity map aligned to 45° using the stellar or gas kinematic position angle, with the velocity range set by the stellar mass Tully–Fisher relation (Dutton et al. 2011). A regularization algorithm is applied to avoid overlap of the velocity maps; dynamical masses and metallicities are indicative, not exact. The velocity maps are shown at full resolution; individual galaxies are best viewed in high-zoom in the online version.
For galaxies visually classified as early-types we show the stellar velocity map using the blue–red colour scheme, whereas for late-types we show the gas velocity maps in green–purple. From Fig. 16, we can see that most early-type galaxies are on a high stellar metallicity sequence, whereas late-type galaxies have a large range in metallicity, but typically lie below the early-type galaxies. With increasing dynamical mass, we start to find an increasing amount of galaxies with little rotation.
8 SUMMARY
In this paper, we present the SAMI Galaxy Survey’s second data release that includes data for 1559 galaxies. This release contains galaxies with redshifts between 0.004 < |$z$| < 0.113 and mass range 7.5 < log (M⋆/M⊙) < 11.6. We release both the primary spectral cubes covering the blue and red optical wavelength ranges, combined with emission and absorption line value-added products. The data are presented online through Australian Astronomical Optics’ Data Central.
Observations for the SAMI Galaxy Survey finished May 2018. The next and final data release of the SAMI Galaxy Survey is planned for mid-2020, and will include further data and value-added products.
ACKNOWLEDGEMENTS
The SAMI Galaxy Survey is based on observations made at the AAT. The Sydney-AAO SAMI was developed jointly by the University of Sydney and the Australian Astronomical Observatory. The SAMI input catalogue is based on the data taken from the Sloan Digital Sky Survey, the GAMA Survey, and the VST ATLAS Survey. The SAMI Galaxy Survey is supported by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013, the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020, and other participating institutions. The SAMI Galaxy Survey website is http://sami-survey.org/.
NS acknowledges support of a University of Sydney Postdoctoral Research Fellowship. JvdS is funded under Bland-Hawthorn’s ARC Laureate Fellowship (FL140100278). SMC acknowledges the support of an Australian Research Council Future Fellowship (FT100100457). BG is the recipient of an Australian Research Council Future Fellowship (FT140101202). MSO acknowledges the funding support from the Australian Research Council through a Future Fellowship (FT140100255). Support for AMM is provided by NASA through Hubble Fellowship grant #HST-HF2-51377 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. CFe gratefully acknowledges funding provided by the Australian Research Council’s Discovery Projects (grants DP150104329 and DP170100603). SB acknowledges the funding support from the Australian Research Council through a Future Fellowship (FT140101166). TMB is supported by an Australian Government Research Training Program Scholarship. MLPG acknowledges the funding received from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 707693.
Author contributions. NS and JvdS oversaw DR2, edited the paper and unless explicitly noted wrote the text. NS prepared the core and stellar population data products. JvdS prepared the stellar kinematics data products. BG oversaw preparation of the emission line data products, with assistance from MSO, TP, and AMM. MSO produced the continuum fits outlined in Secton 5.1, as well as Fig. 11, and wrote the parts of Section 5.1 describing those products. LC prepared the visual morphology classifications. SMC is the survey’s Principal Investigator. JB oversaw target selection and wrote parts of Section 2.1. SMC wrote Sections 3.1.2 and 3.1.3 and provided Figs 3 and 5. FDE and SO provided the data for Section 3.1.4 and Fig. 6. TMB and CFo wrote Section 4.3.1 and provided Figs 8 and 9. BG wrote Section 5.1. DB provided the data for Section 6.1.4 and Fig. 13. Remaining authors contributed to overall team operations including target catalogue and observing preparation, instrument maintenance, observing at the telescope, writing data reduction and analysis software, managing various pieces of team infrastructure such as the website and data storage systems, and innumerable other tasks critical to the preparation and presentation of a large data set such as this DR2.
Footnotes
REFERENCES
Author notes
Hubble Fellow.



