-
PDF
- Split View
-
Views
-
Cite
Cite
Fangzhou Zhu, Nikhil Padmanabhan, Ashley J Ross, Martin White, Will J Percival, Rossana Ruggeri, Gong-bo Zhao, Dandan Wang, Eva-Maria Mueller, Etienne Burtin, Héctor Gil-Marín, Julian Bautista, Florian Beutler, Jonathan Brinkmann, Joel R Brownstein, Kyle Dawson, Axel de la Macorra, Graziano Rossi, Donald P Schneider, Rita Tojeiro, Yuting Wang, The clustering of theSDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: measuring the anisotropic baryon acoustic oscillations with redshift weights, Monthly Notices of the Royal Astronomical Society, Volume 480, Issue 1, October 2018, Pages 1096–1105, https://doi.org/10.1093/mnras/sty1955
Close - Share Icon Share
ABSTRACT
We present an anisotropic analysis of baryon acoustic oscillation (BAO) signal from the Sloan Digital Sky Survey IV extended Baryon Oscillation Spectroscopic Survey Data Release 14 quasar sample. The sample consists of 147 000 quasars distributed over a redshift range of 0.8 < |$z$| < 2.2. We apply the redshift weights technique to the clustering of quasars in this sample and achieve a 4.6 per cent measurement of the angular distance measurement DM at |$z$| = 2.2 and Hubble parameter H at |$z$| = 0.8. We parametrize the distance–redshift relation, relative to a fiducial model, as a Taylor series. The coefficients of this expansion are used to reconstruct the distance–redshift relation and obtain distance and Hubble parameter measurements at all redshifts within the redshift range of the sample. Reporting the result at two characteristic redshifts, we determine DM(|$z$| = 1) = 3405 ± 305 (rd/rd, fid) Mpc, |$H(z=1) = 120.7\pm 7.3 \ (r_{\rm d,fid} / r_{\rm d}) \ {\rm km} \ {\rm s}^{-1}\, {\rm Mpc}^{-1}$| and DM(|$z$| = 2) = 5325 ± 249 (rd/rd, fid) Mpc, |$H(z=2) = 189.9\pm 32.9 \ (r_{\rm d,fid} / r_{\rm d}) \ {\rm km} \ {\rm s}^{-1}\, {\rm Mpc}^{-1}$|. These measurements are highly correlated. We assess the outlook of BAO analysis from the final quasar sample by testing the method on a set of mocks that mimic the noise level in the final sample. We demonstrate on these mocks that redshift weighting shrinks the measurement error by over 25 per cent on average. We conclude redshift weighting can bring us closer to the cosmological goal of the final quasar sample.
1 INTRODUCTION
Baryon acoustic oscillations (BAO) in the distribution of the galaxies are a powerful tool to map the expansion history of the universe via a ‘standard ruler’ in galaxy clustering (Peebles & Yu 1970; Sunyaev & Zeldovich 1970; Bond & Efstathiou 1987; Hu & Sugiyama 1996; Eisenstein & Hu 1998). Pressure waves prior to recombination imprint a characteristic scale in the matter clustering at the radius of the sound horizon rd when the photons and baryons decouple shortly after recombination. The BAO manifests itself today in the two-point matter correlation function as an ‘acoustic peak’ of roughly 150 Mpc. This feature of known length can be used as a standard ruler to constrain the distance–redshift relation and the expansion history of the universe.
Different tracers of the underlying dark matter distribution have been used successfully to measure the peak. These analyses include galaxies (Alam et al. 2017), the Ly α forest (Delubac et al. 2015; Bautista et al. 2017), voids (Kitaura et al. 2016), and quasar-Ly α forest cross correlations (Font-Ribera et al. 2014). Since the first detection of BAO (Cole et al. 2005; Eisenstein et al. 2005) in the galaxy distribution over a decade ago, galaxy surveys (Blake et al. 2007; Kazin et al. 2010; Percival et al. 2010; Beutler et al. 2011; Padmanabhan et al. 2012; Alam et al. 2017) have been driving the measurement to ever increasing precision. Notably, Baryon Oscillation Spectroscopic Survey (BOSS; Dawson et al. 2013; Alam et al. 2015) as a part of the Sloan Digital Sky Survey III (SDSS-III; Eisenstein et al. 2011) has enjoyed great success in making cosmological distance measurements at the per cent level.
The extended Baryon Oscillation Spectroscopic Survey (eBOSS; Dawson et al. 2016) is a new redshift survey within SDSS-IV (Blanton et al. 2017), the observations for which started in 2014 July. The photometry was obtained on the 2.5-m Sloan Telescope (Gunn et al. 2006) at the Apache Point Observatory in New Mexico, USA. As part of this programme, eBOSS observes quasars that are selected to enable clustering studies. The quasar sample covers a redshift range of 0.8 < |$z$| < 2.2. The final sample is forecasted to produce a 1.6 per cent spherically averaged distance measurement (Zhao et al. 2016). This paper uses the Data Release 14 (DR14) quasar sample whose targeting and observation details are described in Abolfathi et al. (2017).
Samples from current and future generations of BAO surveys such as the eBOSS span a wide redshift range. To improve the resolution of distance–redshift relation measurement, traditional BAO analyses usually split the samples into multiple redshift bins and analyse the signals in these slices. One drawback of splitting the sample into multiple redshift bins is that the signal-to-noise ratio in each bin becomes lower, making the analysis more sensitive to the tails of the likelihood distribution. Furthermore, signals from galaxy pairs across disjoint bin boundaries are lost in such an analysis. While some of these disadvantages may be overcome by properly accounting for all the covariances among the slices, they add to the complexity of the analysis. There is also no consensus on how to optimally split the sample.
To solve the problems faced with binning outlined above, Zhu, Padmanabhan & White (2015) introduced a set of redshift weights to compress the BAO information in the redshift direction on to a small number of ‘weighted correlation functions’. Applying the redshift weights to the galaxy pair counts efficiently preserves nearly all the BAO information in the sample, leading to improved constraints of the distance–redshift relation parametrized in a simple generic form over the entire redshift extent of the survey. Zhu et al. (2016) validated the redshift weighting method on BOSS DR12 galaxy mock catalogues. Applying redshift weighting provides tighter distance and Hubble estimates over a sample’s redshift range compared with the unweighted single-bin analysis. The method has also been demonstrated to produce robust and unbiased BAO measurements.
This paper applies redshift weighting to the BAO analysis of the eBOSS DR14 quasar sample. These measurements complement the analysis in Ata et al. (2017) and provide a first measurement of H(|$z$|) from this sample. The paper has the following structure: Section 2 describes the redshift weights and BAO modelling for the correlation functions. Section 3 describes the data sets and simulations used in this paper. In Section 4, we present the implemented redshift weighting algorithm and describe the fitting model. We present our DR14 data and mock results in Section 5 and show the improvement due to redshift weighting. We share an outlook of the BAO constraints from the final quasar sample in Section 6. We emphasize the efficacy of redshift weighting for such a sample. We summarize our results with a discussion in Section 7.
2 THEORY
2.1 Distance–redshift relation
Truncating the expansion to the first order is sufficient for recovering the distance–redshift relation to sub-percent levels over the redshift range of interest for an assortment of cosmologies. Even for the rather extreme ΩM = 0.2 and ΩM = 0.4 cases, the errors are less than 0.3 per cent over the redshift range of the eBOSS DR14 quasar sample 0.8 < |$z$| < 2.2. We will thus focus on α0 and α1 and drop all higher order terms in the BAO analysis presented in this paper.
2.2 Redshift-weighted correlation function
The second component |$w$|ℓ, i is a linear combination of 1 and x. The specific linear combination depends on the parameter (α0 or α1, indicated by the subscript i) and the multipoles (monopoles or quadrupoles, indicated by ℓ) in question. The redshift weights are generalizations of the FKP weights produced by up-weighting the regions where the signal is most sensitive to the model parameters, in addition to balancing the quasars by number densities.
In these models, the integrals are over the redshift range of the sample. They can be efficiently computed as summations over contributions from discrete redshift slices. We follow the same procedure as in Zhu et al. (2016) and compute the contributions from redshift slices of width Δ|$z$| = 0.1 within the redshift range [0.8, 2.2]. In each redshift slice, given α0 and α1, we compute α(|$z$|) and ε(|$z$|) according to equations (5) and 6 at different redshifts. This feature is different from traditional analyses in which α and ε values only at the ‘effective’ redshift of the sample are measured. We will describe how α and ε shift and distort the correlation function in Section 2.3.2. Our model parameters α0 and α1, which we will obtain directly from our fits to the measured ξ, provide constraints on α(|$z$|) and ε(|$z$|) given our perturbative model.
2.3 Fitting the correlation function
We fit the correlation function with the ESW template given in Eisenstein, Seo & White (2007a).1 We will outline the ESW template below and explain its ingredients and how mis-estimate of the cosmology distorts the correlation function and how to model it. The fitting model is similar as in recent BOSS BAO analyses (Anderson et al. 2014; Alam et al. 2017).
2.3.1 BAO modelling
Our template combines the supercluster infall of linear theory (Kaiser 1987) and the Finger of God (FoG) effect from non-linear growth of structure.
2.3.2 Modelling the mis-estimate of cosmology
Given α0 and α1, we can calculate α(|$z$|) and ε(|$z$|) within the redshift range of the sample. These α and ε indicate how r and μ are distorted at different redshifts, allowing us to incorporate the mis-estimate of the cosmology into model correlation functions.
3 DATA SETS
3.1 SDSS DR14 quasar sample
The observational data set is the eBOSS (Dawson et al. 2016) quasar sample released as part of the SDSS-IV (Blanton et al. 2017). The survey has an effective area of 1192 deg2 in the Northern Galactic Cap (NGC) and 857 deg2 in the Southern Galactic Cap (SGC). The quasar target selection is presented in Ross et al. (2012) and Myers et al. (2015). Quasars that do not have a known redshift are selected for spectroscopic observation. Spectroscopy is obtained through the BOSS double-armed spectrographs (Smee et al. 2013). In our DR14 sample, we applied veto masks as in Reid et al. (2016). To correct for missing targets, redshift failures, fibre collisions, depth dependency, and Galactic extinction, we utilize completion weights and systematic weights according to Laurent et al. (2017) and Ross et al. (2017).
3.2 Simulations
We validate the redshift weighting method by implementing the algorithm on 1000 mock catalogues. These catalogues simulate the clustering of eBOSS DR14 quasars based on the ‘quick particle mesh’ (QPM) method (White, Tinker & McBride 2014). Each N-body simulation utilizes 25603 particles in a box of side length |$5120 \, h^{-1}\, {\rm Mpc}$|. The simulations assume a flat Λ cold dark matter (ΛCDM) cosmology, with Ωm = 0.31, Ωbh2 = 0.0220, h = 0.676, ns = 0.97, and σ8 = 0.8. Each simulation is initialized by using the second-order Lagrangian perturbation at |$z$| = 25. The catalogues cover the redshift extent of 0.8 < |$z$| < 2.2 for both the NGC and SGC of the eBOSS footprint. The halo occupation of quasars is parametrized according to the five-parameter halo occupation distribution presented in Tinker et al. (2012).
Rotating the orientations of the 100 simulated cubic boxes, we identify four configurations with less than 1.5 per cent overlap. This enables us to produce 400 QPM mocks for both Galactic caps. Veto masks are applied in the same way as for the data. FKP weights (Feldman et al. 1994) are applied assuming |$P_0 = 6000 \, h^{-3}\, {\rm Mpc}^3$|. Redshift smearing is applied according to Dawson et al. (2016). For specifics of these eBOSS quasar mocks, we refer the readers to Ata et al. (2017).
4 ANALYSIS
4.1 Computing the weighted correlation functions
We analyse the mock catalogues in a similar manner as previous BOSS analyses (Anderson et al. 2014; Alam et al. 2017). In this section, we focus on the steps involving redshift weighting. We also point out that we do not apply density field reconstruction (Eisenstein et al. 2007b), as it is not expected to be efficient or significant for this sample because of the low density of quasars.
4.1.1 The fitting model
In our fiducial weighted fits, we use a total of 13 fitting parameters: α0, α1, β, B1, Bx, and 8 nuisance parameters to absorb the broad-band features. We use the fiducial fitting range |$48 \lt r \lt 184 {h^{-1} \, \rm Mpc}$| with 8 |${h^{-1}\, \rm Mpc}$| bins.
4.2 Parameter inference
Given α0 and α1, we minimize the χ2 via a downhill simplex algorithm (Nelder & Mead 1965) designed to handle the non-linear parameters. We fit the linear nuisance parameters by a nested least-squares. The simplex algorithm searches for the best-fitting parameters by finding the minimum χ2 within the non-linear parameter space.
We calculate the likelihood surface through computing best-fitting χ2 on a two-dimensional grid for 0.7 < α0 < 1.3 and −0.5 < α1 < 0.5 at spacings of 0.01 and 0.02, respectively. The likelihood surface enables one to calculate the distribution of α0 and α1. The low signal-to-noise BAO feature of some mocks causes the nuisance polynomial to dominate the model correlation function. To address this issue, we place a Gaussian prior on β centred at 0.4 with width 0.2. We also adopt a Gaussian prior on |$B_1^2$| and |$B_x^2$| at 1 with width 0.2. To suppress the unphysical downturns in χ2, we have applied Gaussian priors of width 0.1 centred around α0 = 1 and width 0.2 centred around α1 = 0. These priors do not dominate our calculation of the likelihood of α0 and α1. Their implications are discussed in more detail in Section 5.
5 RESULTS
The fits to the mock correlation functions assume the QPM cosmology as the fiducial cosmology using a pivot redshift |$z$|0 = 1.8. The fitting model and procedure are sketched out in Section 4.
Fig. 1 shows the DR14 quasar correlation functions and the average of these from 400 mocks. The DR14 quasar correlation functions are indicated as points with error bars. The bands in the figure correspond to the 1σ error for individual mocks. The mocks are consistent with the DR14 points. The quadrupole moments show significant noise. Despite the uncertainties, the monopole moments demonstrate a clearly visible acoustic feature in both the ‘1-weighted’ and ‘x-weightedmonopoles.
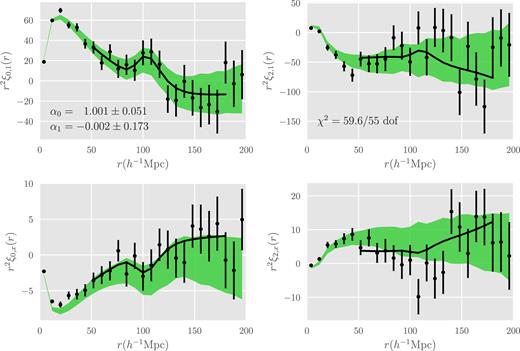
The DR14 quasar correlation function and the average QPM mock correlation functions. The black circles with error bars are the correlation function multipoles from the DR14 sample. The top panels display the ‘unweighted’ monopoles (left) and quadrupoles (right); the bottom pair displays the ‘x-weighted’ ones. The associated error bars are 1σ errors of the mocks. The solid black line passing through the black points show the best fitting to the DR14 points with relevant statistics on the top panels. The green bands in each on the figure represent the average monopoles (left) and quadrupoles (right) from the 400 mocks with 1 standard deviation errors. The bands plotted are errors of an individual mock, which are |$\sqrt{400}$| times larger than that of the average correlation function. The ‘x-weighted’ monopoles and quadrupoles show an inverted shape because of an overall negative weight.
The thick black line is the best fitting to the DR14 data points with relevant statistics labelled on the figure. In the fiducial case, we measure α0 = 1.001 ± 0.051 and α1 = −0.002 ± 0.173. The ‘unweighted’ fits without redshift weighting yield α0 = 1.003 ± 0.041 and α1 = −0.004 ± 0.136. The distribution of α0 and α1 measured from the DR14 quasar sample is shown in Fig. 2. For the DR14 sample, applying redshift weighting does not yield reduction in the size of the error bars for the measured α0 and α1.
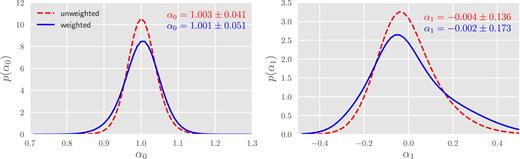
Distribution of α0 and α1 from the DR14 fits. The left- and right-hand panels show the derived p(α0) and p(α1) distributions, respectively. The red dashed lines represent the distribution from fitting the ‘unweighted’ estimator; the blue solid lines correspond to the sharpened distribution we obtained from applying redshift weighting. The mean and standard deviation of both distributions are labelled in the panels.
We test the robustness of our result by varying various aspects of the fit including the fitting range, binning, streaming parameters, and pivot redshift. The results all agree within 1σ uncertainties. Table 1 presents a summary of our fitting results. In the table, poly3 corresponds to fitting with a third degree nuisance polynomial of the form A(r) = a1/r2 + a2/r + a3. In addition, we perform an isotropic BAO fit by setting α1 = 0 and only allowing α0 to vary. This analysis produces α0 = 0.996 ± 0.031, consistent with the result 0.994 ± 0.037 in Ata et al. (2017). The small discrepancy in the error could be due to differences in the applied priors, as Ata et al. (2017) restricts to the prior range 0.8 < α < 1.2. In our calculation of the likelihood, we use a larger prior range 0.7 < α0 < 1.3 and a Gaussian prior of width 0.1 centred aroundα0 = 1.
BAO fitting results of the DR14 quasar data and QPM mocks. Our fiducial analysis assumes a pivot redshift of |$z$|0 = 1.8 and a fitting range of |$48 \lt r \lt 184h^{-1}\, {\rm Mpc}$| with |$8h^{-1}\, {\rm Mpc}$| binning. The fiducial analysis utilizes redshift weighting. The mock results shown here are the inverse variance weighted average of the 400 QPM mock fits.
| Model . | α0 . | α1 . |
|---|---|---|
| DR14 results | ||
| Fiducial | 1.001 ± 0.051 | 0.002 ± 0.173 |
| Fiducial, unweighted | 1.003 ± 0.041 | −0.004 ± 0.136 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 1.004 ± 0.052 | 0.014 ± 0.172 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 1.002 ± 0.051 | 0.007 ± 0.172 |
| Fi w/ poly3 | 1.001 ± 0.048 | −0.023 ± 0.175 |
| Fit w/o x-weighted quadrupole | 1.006 ± 0.043 | 0.013 ± 0.134 |
| α0 only | 0.996 ± 0.031 | − |
| |$48 \lt r \lt 136 \ \, h^{-1} \, {\rm Mpc}$| | 0.999 ± 0.053 | −0.015 ± 0.167 |
| |$48 \lt r \lt 160 \ \, h^{-1}\, {\rm Mpc}$| | 0.987 ± 0.061 | −0.009 ± 0.193 |
| |$\Delta r = 4 \ \, h^{-1}\, {\rm Mpc}$| | 0.997 ± 0.049 | 0.090 ± 0.165 |
| |$z$|pivot = 1.2 | 1.002 ± 0.072 | −0.002 ± 0.131 |
| |$z$|pivot = 2 | 0.999 ± 0.049 | 0.001 ± 0.179 |
| Mock results | ||
| Fiducial | 0.992 ± 0.052 | 0.001 ± 0.141 |
| Fiducial, unweighted | 0.998 ± 0.054 | 0.014 ± 0.157 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 0.993 ± 0.054 | 0.003 ± 0.144 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 0.992 ± 0.052 | 0.003 ± 0.141 |
| Fit w/ poly3 | 0.991 ± 0.053 | 0.001 ± 0.147 |
| Fit w/o x-weighted quadrupole | 0.993 ± 0.052 | 0.001 ± 0.143 |
| |$48 \lt r \lt 136 \ \, h^{-1}\, {\rm Mpc}$| | 0.988 ± 0.055 | −0.006 ± 0.143 |
| |$z$|pivot = 1.2 | 0.991 ± 0.067 | −0.014 ± 0.115 |
| |$z$|pivot = 2 | 0.993 ± 0.050 | −0.001 ± 0.146 |
| ‘4x’ Mock results | ||
| ‘4x’ mocks, fiducial | 0.995 ± 0.028 | 0.001 ± 0.077 |
| ‘4x’ mocks, unweighted | 0.996 ± 0.031 | 0.017 ± 0.105 |
| ‘4x’ mocks, |$z$|pivot = 1.2 | 0.993 ± 0.040 | −0.001 ± 0.060 |
| ‘4x’ mocks, |$z$|pivot = 2 | 0.996 ± 0.026 | −0.001 ± 0.081 |
| Model . | α0 . | α1 . |
|---|---|---|
| DR14 results | ||
| Fiducial | 1.001 ± 0.051 | 0.002 ± 0.173 |
| Fiducial, unweighted | 1.003 ± 0.041 | −0.004 ± 0.136 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 1.004 ± 0.052 | 0.014 ± 0.172 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 1.002 ± 0.051 | 0.007 ± 0.172 |
| Fi w/ poly3 | 1.001 ± 0.048 | −0.023 ± 0.175 |
| Fit w/o x-weighted quadrupole | 1.006 ± 0.043 | 0.013 ± 0.134 |
| α0 only | 0.996 ± 0.031 | − |
| |$48 \lt r \lt 136 \ \, h^{-1} \, {\rm Mpc}$| | 0.999 ± 0.053 | −0.015 ± 0.167 |
| |$48 \lt r \lt 160 \ \, h^{-1}\, {\rm Mpc}$| | 0.987 ± 0.061 | −0.009 ± 0.193 |
| |$\Delta r = 4 \ \, h^{-1}\, {\rm Mpc}$| | 0.997 ± 0.049 | 0.090 ± 0.165 |
| |$z$|pivot = 1.2 | 1.002 ± 0.072 | −0.002 ± 0.131 |
| |$z$|pivot = 2 | 0.999 ± 0.049 | 0.001 ± 0.179 |
| Mock results | ||
| Fiducial | 0.992 ± 0.052 | 0.001 ± 0.141 |
| Fiducial, unweighted | 0.998 ± 0.054 | 0.014 ± 0.157 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 0.993 ± 0.054 | 0.003 ± 0.144 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 0.992 ± 0.052 | 0.003 ± 0.141 |
| Fit w/ poly3 | 0.991 ± 0.053 | 0.001 ± 0.147 |
| Fit w/o x-weighted quadrupole | 0.993 ± 0.052 | 0.001 ± 0.143 |
| |$48 \lt r \lt 136 \ \, h^{-1}\, {\rm Mpc}$| | 0.988 ± 0.055 | −0.006 ± 0.143 |
| |$z$|pivot = 1.2 | 0.991 ± 0.067 | −0.014 ± 0.115 |
| |$z$|pivot = 2 | 0.993 ± 0.050 | −0.001 ± 0.146 |
| ‘4x’ Mock results | ||
| ‘4x’ mocks, fiducial | 0.995 ± 0.028 | 0.001 ± 0.077 |
| ‘4x’ mocks, unweighted | 0.996 ± 0.031 | 0.017 ± 0.105 |
| ‘4x’ mocks, |$z$|pivot = 1.2 | 0.993 ± 0.040 | −0.001 ± 0.060 |
| ‘4x’ mocks, |$z$|pivot = 2 | 0.996 ± 0.026 | −0.001 ± 0.081 |
BAO fitting results of the DR14 quasar data and QPM mocks. Our fiducial analysis assumes a pivot redshift of |$z$|0 = 1.8 and a fitting range of |$48 \lt r \lt 184h^{-1}\, {\rm Mpc}$| with |$8h^{-1}\, {\rm Mpc}$| binning. The fiducial analysis utilizes redshift weighting. The mock results shown here are the inverse variance weighted average of the 400 QPM mock fits.
| Model . | α0 . | α1 . |
|---|---|---|
| DR14 results | ||
| Fiducial | 1.001 ± 0.051 | 0.002 ± 0.173 |
| Fiducial, unweighted | 1.003 ± 0.041 | −0.004 ± 0.136 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 1.004 ± 0.052 | 0.014 ± 0.172 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 1.002 ± 0.051 | 0.007 ± 0.172 |
| Fi w/ poly3 | 1.001 ± 0.048 | −0.023 ± 0.175 |
| Fit w/o x-weighted quadrupole | 1.006 ± 0.043 | 0.013 ± 0.134 |
| α0 only | 0.996 ± 0.031 | − |
| |$48 \lt r \lt 136 \ \, h^{-1} \, {\rm Mpc}$| | 0.999 ± 0.053 | −0.015 ± 0.167 |
| |$48 \lt r \lt 160 \ \, h^{-1}\, {\rm Mpc}$| | 0.987 ± 0.061 | −0.009 ± 0.193 |
| |$\Delta r = 4 \ \, h^{-1}\, {\rm Mpc}$| | 0.997 ± 0.049 | 0.090 ± 0.165 |
| |$z$|pivot = 1.2 | 1.002 ± 0.072 | −0.002 ± 0.131 |
| |$z$|pivot = 2 | 0.999 ± 0.049 | 0.001 ± 0.179 |
| Mock results | ||
| Fiducial | 0.992 ± 0.052 | 0.001 ± 0.141 |
| Fiducial, unweighted | 0.998 ± 0.054 | 0.014 ± 0.157 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 0.993 ± 0.054 | 0.003 ± 0.144 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 0.992 ± 0.052 | 0.003 ± 0.141 |
| Fit w/ poly3 | 0.991 ± 0.053 | 0.001 ± 0.147 |
| Fit w/o x-weighted quadrupole | 0.993 ± 0.052 | 0.001 ± 0.143 |
| |$48 \lt r \lt 136 \ \, h^{-1}\, {\rm Mpc}$| | 0.988 ± 0.055 | −0.006 ± 0.143 |
| |$z$|pivot = 1.2 | 0.991 ± 0.067 | −0.014 ± 0.115 |
| |$z$|pivot = 2 | 0.993 ± 0.050 | −0.001 ± 0.146 |
| ‘4x’ Mock results | ||
| ‘4x’ mocks, fiducial | 0.995 ± 0.028 | 0.001 ± 0.077 |
| ‘4x’ mocks, unweighted | 0.996 ± 0.031 | 0.017 ± 0.105 |
| ‘4x’ mocks, |$z$|pivot = 1.2 | 0.993 ± 0.040 | −0.001 ± 0.060 |
| ‘4x’ mocks, |$z$|pivot = 2 | 0.996 ± 0.026 | −0.001 ± 0.081 |
| Model . | α0 . | α1 . |
|---|---|---|
| DR14 results | ||
| Fiducial | 1.001 ± 0.051 | 0.002 ± 0.173 |
| Fiducial, unweighted | 1.003 ± 0.041 | −0.004 ± 0.136 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 1.004 ± 0.052 | 0.014 ± 0.172 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 1.002 ± 0.051 | 0.007 ± 0.172 |
| Fi w/ poly3 | 1.001 ± 0.048 | −0.023 ± 0.175 |
| Fit w/o x-weighted quadrupole | 1.006 ± 0.043 | 0.013 ± 0.134 |
| α0 only | 0.996 ± 0.031 | − |
| |$48 \lt r \lt 136 \ \, h^{-1} \, {\rm Mpc}$| | 0.999 ± 0.053 | −0.015 ± 0.167 |
| |$48 \lt r \lt 160 \ \, h^{-1}\, {\rm Mpc}$| | 0.987 ± 0.061 | −0.009 ± 0.193 |
| |$\Delta r = 4 \ \, h^{-1}\, {\rm Mpc}$| | 0.997 ± 0.049 | 0.090 ± 0.165 |
| |$z$|pivot = 1.2 | 1.002 ± 0.072 | −0.002 ± 0.131 |
| |$z$|pivot = 2 | 0.999 ± 0.049 | 0.001 ± 0.179 |
| Mock results | ||
| Fiducial | 0.992 ± 0.052 | 0.001 ± 0.141 |
| Fiducial, unweighted | 0.998 ± 0.054 | 0.014 ± 0.157 |
| Fit w/ |$\Sigma _s = 2 \ \, h^{-1}\, {\rm Mpc}$| | 0.993 ± 0.054 | 0.003 ± 0.144 |
| |$(\Sigma _\perp ,\Sigma _\parallel) = (4, 8)\ \, h^{-1}\, {\rm Mpc}$| | 0.992 ± 0.052 | 0.003 ± 0.141 |
| Fit w/ poly3 | 0.991 ± 0.053 | 0.001 ± 0.147 |
| Fit w/o x-weighted quadrupole | 0.993 ± 0.052 | 0.001 ± 0.143 |
| |$48 \lt r \lt 136 \ \, h^{-1}\, {\rm Mpc}$| | 0.988 ± 0.055 | −0.006 ± 0.143 |
| |$z$|pivot = 1.2 | 0.991 ± 0.067 | −0.014 ± 0.115 |
| |$z$|pivot = 2 | 0.993 ± 0.050 | −0.001 ± 0.146 |
| ‘4x’ Mock results | ||
| ‘4x’ mocks, fiducial | 0.995 ± 0.028 | 0.001 ± 0.077 |
| ‘4x’ mocks, unweighted | 0.996 ± 0.031 | 0.017 ± 0.105 |
| ‘4x’ mocks, |$z$|pivot = 1.2 | 0.993 ± 0.040 | −0.001 ± 0.060 |
| ‘4x’ mocks, |$z$|pivot = 2 | 0.996 ± 0.026 | −0.001 ± 0.081 |
To validate our methodology, we fit 400 QPM mocks and measure α0 and α1. Since we use the simulation cosmology as our fiducial cosmology, we anticipate our measurements to agree with 〈α0〉 = 1 and 〈α1〉 = 0 within uncertainty if the measurements are unbiased. A summary of the mock results can be found in Table 1. We indeed verify our method to yield unbiased estimators of α0 and α1.
The errors of α0 and α1 measured from the 400 QPM mocks are indicated as blue points in Fig. 3. The orange points in the background show the errors from the ‘unweighted’ fits. The fitted DR14 data point is also displayed. The mock α0 and α1 errors are representative of the DR14 errors.
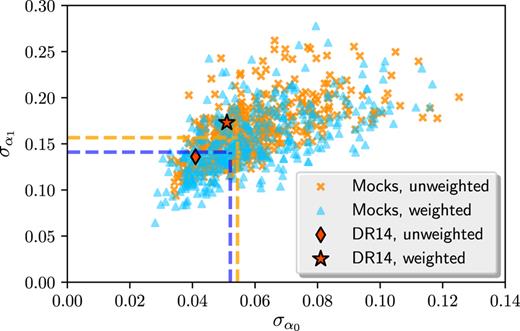
The |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| values measured from the 400 mocks and from the DR14 sample. The blue triangles correspond to the ‘weighted’ measurement errors and the orange triangles are the ‘unweighted’ values. The errors denoted by the horizontal and vertical dashed lines are the errors of the inverse variance weighted average of the mock results, multiplied by |$\sqrt{400}$| for ease of comparison with individual mock points. Our DR14 |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| are labelled as the red star (‘weighted’) and diamond (‘unweighted’). The DR14 point situates within the locus of mock points.
We compare the |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| obtained from the ‘unweighted’ and ‘weighted’ analysis mock by mock. Among the 400 mock measurements, 221 produce an improved |$\sigma _{\alpha _0}$|, and 275 show an improved |$\sigma _{\alpha _1}$| when we apply the redshift weights. These values correspond to 55 per cent and 69 per cent of the mocks. Given the magnitude of these percentages, it is not surprising that redshift weighting does not yield smaller |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| errors for the current DR14 sample.
Overall, however, redshift weighting does shrink the measured error bars. We aggregate the mock measurements of α0 and α1 through inverse variance weighting to minimize the variance of the weighted average. Each mock measurement of α0 and α1 is weighted in inverse proportion to its variance. We obtain this weighted average as |${\hat{\alpha }} = \frac{\sum \alpha _i/\sigma _{\alpha _i}^2}{\sum 1/\sigma _{\alpha _i}^2}$|. The summation is performed over the 400 mocks. The error of |${\hat{\alpha }}$| is given by |$\sigma ({\hat{\alpha }}) = 1/\sqrt{\sum \frac{1}{\sigma _{\alpha _i}^2}}$|. This error is scaled by |$\sqrt{400}$| for ease of comparison with errors from individual mock measurements. The aggregated mock statistics are presented in Table 1. We observe a decrease in |$\sigma _{\alpha _1}$| from 0.157 without redshift weights to 0.141 with redshift weights. This change corresponds to a 10 per cent decrease. We will further comment on the magnitude of this improvement in Section 6.
The joint likelihood distribution of α0 and α1 allows us an estimate to be made of the joint distribution of χ and H. To perform this calculation, we first draw random variables from the joint distribution of α0 and α1. We reconstruct the distance–redshift relation χ(|$z$|) and Hubble parameter H(|$z$|) from equations (1) and (2) with the drawn α0 and α1. This approach enables us to obtain an estimated joint distribution of χ and H. It is then straightforward to calculate statistics of χ and H. Since these χ and H measurements at different redshifts are derived from the same model of the distance–redshift relation, they are highly correlated. To use our result for cosmological comparisons, it is advisable to directly use the joint likelihood distribution of α0 and α1 we measured.
Constraints on DM(rd, fid/rd) and H(rd/rd, fid) measured from the DR14 quasar sample from our analysis with redshift weighting. Also listed are the derived spherically averaged distance measurements DV(rd, fid/rd) from our DM and H measurements. The measurements at different redshifts are correlated.
| Redshift . | DM(rd, fid/rd) . | H(rd/rd, fid) . | DV(rd, fid/rd)* . |
|---|---|---|---|
| . | (Mpc) . | (|${\rm km}\ \, {\rm s}^{-1}\, {\rm Mpc}^{-1}$|) . | (Mpc) . |
| 0.8 | 2876 ± 304 | 106.9 ± 4.9 | 2646 ± 205 |
| 1.0 | 3405 ± 305 | 120.7 ± 7.3 | 3065 ± 182 |
| 1.5 | 4491 ± 272 | 161.4 ± 30.9 | 3840 ± 182 |
| 2.0 | 5325 ± 249 | 189.9 ± 32.9 | 4356 ± 300 |
| 2.2 | 5606 ± 255 | 232.5 ± 54.6 | 4514 ± 359 |
| Redshift . | DM(rd, fid/rd) . | H(rd/rd, fid) . | DV(rd, fid/rd)* . |
|---|---|---|---|
| . | (Mpc) . | (|${\rm km}\ \, {\rm s}^{-1}\, {\rm Mpc}^{-1}$|) . | (Mpc) . |
| 0.8 | 2876 ± 304 | 106.9 ± 4.9 | 2646 ± 205 |
| 1.0 | 3405 ± 305 | 120.7 ± 7.3 | 3065 ± 182 |
| 1.5 | 4491 ± 272 | 161.4 ± 30.9 | 3840 ± 182 |
| 2.0 | 5325 ± 249 | 189.9 ± 32.9 | 4356 ± 300 |
| 2.2 | 5606 ± 255 | 232.5 ± 54.6 | 4514 ± 359 |
Constraints on DM(rd, fid/rd) and H(rd/rd, fid) measured from the DR14 quasar sample from our analysis with redshift weighting. Also listed are the derived spherically averaged distance measurements DV(rd, fid/rd) from our DM and H measurements. The measurements at different redshifts are correlated.
| Redshift . | DM(rd, fid/rd) . | H(rd/rd, fid) . | DV(rd, fid/rd)* . |
|---|---|---|---|
| . | (Mpc) . | (|${\rm km}\ \, {\rm s}^{-1}\, {\rm Mpc}^{-1}$|) . | (Mpc) . |
| 0.8 | 2876 ± 304 | 106.9 ± 4.9 | 2646 ± 205 |
| 1.0 | 3405 ± 305 | 120.7 ± 7.3 | 3065 ± 182 |
| 1.5 | 4491 ± 272 | 161.4 ± 30.9 | 3840 ± 182 |
| 2.0 | 5325 ± 249 | 189.9 ± 32.9 | 4356 ± 300 |
| 2.2 | 5606 ± 255 | 232.5 ± 54.6 | 4514 ± 359 |
| Redshift . | DM(rd, fid/rd) . | H(rd/rd, fid) . | DV(rd, fid/rd)* . |
|---|---|---|---|
| . | (Mpc) . | (|${\rm km}\ \, {\rm s}^{-1}\, {\rm Mpc}^{-1}$|) . | (Mpc) . |
| 0.8 | 2876 ± 304 | 106.9 ± 4.9 | 2646 ± 205 |
| 1.0 | 3405 ± 305 | 120.7 ± 7.3 | 3065 ± 182 |
| 1.5 | 4491 ± 272 | 161.4 ± 30.9 | 3840 ± 182 |
| 2.0 | 5325 ± 249 | 189.9 ± 32.9 | 4356 ± 300 |
| 2.2 | 5606 ± 255 | 232.5 ± 54.6 | 4514 ± 359 |
In analyzing the BAO from the BOSS DR 12 galaxy mock catalogues, Zhu et al. (2016) reported that the distance and Hubble parameter measurements are insensitive to the choice of pivot redshifts. Our mock measurements confirm this finding.
At different pivot redshifts, a large error in α0 is usually compensated by a smaller error in α1, and vice versa. Table 1 lists fitting results at three different pivot redshifts |$z$|0 = 1.2, 1.8, and 2. Selecting |$z$|0 = 2 yields the smallest |$\sigma _{\alpha _0}$| but has the largest |$\sigma _{\alpha _1}$|. Conversely, |$z$|0 = 1.2 yields the largest |$\sigma _{\alpha _0}$| but has the smallest |$\sigma _{\alpha _1}$|. When reconstructing DM and H constraints from α0 and α1, the error from the two parameters compensate one another and makes the distance and Hubble parameter constraints insensitive to the choice of the pivot redshift.
We compare our results with recent measurements of DM and H. Fig. 4 displays our DM and H measurements along with the ΛCDM prediction from Planck (Planck Collaboration 2016). Our distance and Hubble parameter measurements are in agreement with the Planck results within the 1σ uncertainty. We also show similar measurements in the literature: the BOSS DR12 results from Alam et al. (2017), the BOSS Ly α from Bautista et al. (2017), and the cross correlation of Ly α forest and quasars from Font-Ribera et al. (2014). These measurements provide both distance and Hubble parameter measurements at the effective redshift of their respective samples. Additional spherically averaged distance measurements (DV) are 6dFGS Beutler et al. (2011), SDSS MGS Ross et al. (2015), WiggleZ Kazin et al. (2014), and eBOSS DR14 isotropic BAO Ata et al. (2017). In particular, the DR14 isotropic BAO result (labelled as ‘DR14-Iso’ in Fig. 4) analyses the same sample as our work and reports a spherically averaged distance measurement of DV(|$z$| = 1.52) = 3843 ± 147 (rd,fid/rd) Mpc. As a comparison, we derive spherically averaged distance measurement from our DM and H measurements at the same redshift and obtain DV(|$z$| = 1.52) = 3871 ± 157 (rd/rd,fid) Mpc without redshift weighting and 3860 ± 204 (rd, fid/rd) Mpc with redshift weighting. These measurements are all consistent with Ata et al. (2017) measurement. In addition, we note that our Hubble parameter measurement spans a redshift range (0.8 < |$z$| < 2.2) that has not been measured in previous redshift surveys.
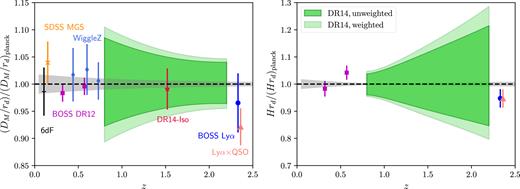
Our DR14 DM and H measurements from ‘unweighted’ and ’weighted’ analyses compared to the Planck flat-ΛCDM predictions. All error bands and error bars correspond to 1 standard deviation errors. Our DR14 measurements (green bands) are consistent with the Planck results (grey bands) within uncertainty. We emphasize that the DM and H measurements at different redshifts are highly correlated. We also show several recent measurements for comparison, some of which are spherically averaged BAO distance measurements (DV). See texts for descriptions of these additional measurements.
6 FINAL SAMPLE OUTLOOK
The DR14 quasar sample covers 1192 deg2 and 852 deg2 of NGC and SGC regions. This solid angle is approximately a quarter of the final footprint of 7500 deg2 for clustering quasars. The quadruple increase in footprint will result in reduced noise in the final sample. In this section, we assess the outlook of BAO measurements as would be obtained from the final eBOSS sample.
To mimic the noise level in the final sample clustering quasars, we average the correlation functions from every four mock catalogues. This simple averaging serves to reflect the quadruple increase in footprint. After the averaging, we obtain 100 averaged mock correlation functions (labelled ‘4x’ mocks) from the original 400 QPM mocks. We indeed observe greatly reduced noise in these ‘4x’ mock correlation functions.
We analyse the aforementioned 100 ‘4x’ mock correlation functions with the same method described in Section 4. The fitting results of these mocks are unbiased (see Table 1). Fig. 5 presents the errors |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| measured from the 100 ‘4x’ mocks. We aggregate the mock measurements of α0 and α1 by calculating the inverse variance weighted average by |${\hat{\alpha }} = \frac{\sum \alpha _i/\sigma _{\alpha _i}^2}{\sum 1/\sigma _{\alpha _i}^2}$|. The summation is over the 100 ‘4x’ mocks. The error of |${\hat{\alpha }}$| is given by |$\sigma ({\hat{\alpha }}) = 1/\sqrt{\sum \frac{1}{\sigma _{\alpha _i}^2}}$|. We scale this error by |$\sqrt{100}$| for ease of comparison with individual ‘4x’ mock errors. The vertical and horizontal dashed lines in Fig. 5 show these statistics. The error |$\sigma _{{\hat{\alpha }}_0}$| decreases from 3.1 per cent to 2.8 per cent. Similarly, the weighted analysis gives an error of |$\sigma _{{\hat{\alpha }}_1}$| of 7.7 per cent, compared to a 10.5 per cent without redshift weighting. These results correspond to a 10 per cent improvement in α0 and a 27 per cent improvement in α1.
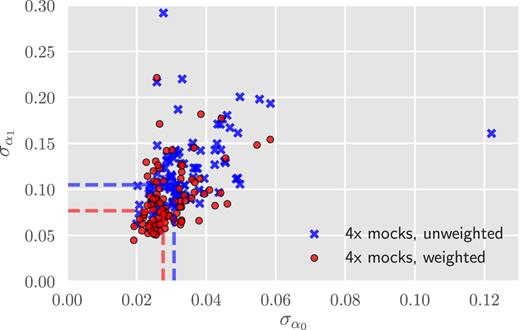
The |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| values measured from the ‘4x’ mocks. The measurements without redshift weighting are denoted by blue crosses, while the ones with redshift weighting are denoted by red circles. The vertical and horizontal dashed lines correspond to the error of inverse variance weighted mean of α0 and α1 from the mocks, multiplied by |$\sqrt{100}$| for easy comparison with individual ‘4x’ mock points.
Among the 100 ‘4x’ mock measurements, 83 have an improved |$\sigma _{\alpha _0}$| and 89 show an improved |$\sigma _{\alpha _1}$| when we apply the redshift weights. This behaviour can be clearly seen in Fig. 6. The dashed line in the figure corresponds to a straight line of unit slope. The majority of points fall below this equality line. Redshift weighting produces improved measurement errors for more than 80 per cent of the ‘4x’ mocks, demonstrating that although redshift weighting does not yield smaller |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| for the current sample, it will likely be efficient for the final quasar sample.
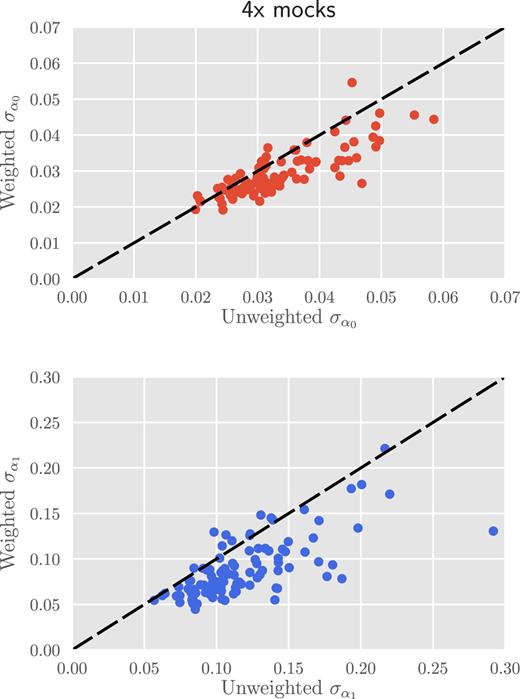
The weighted and unweighted |$\sigma _{\alpha _0}$| and |$\sigma _{\alpha _1}$| values measured from the 100 ‘4x’ mocks. The dashed line in the figure corresponds to a straight line of unit slope. The majority of points lie below the dashed line, suggesting redshift weighting is likely to be efficient for the final quasar sample.
The gains from redshift weighting in the ‘4x’ mocks are much more significant than in the original QPM mocks. This result occurs because some mocks among the 400 individual QPM mocks are quite noisy and possess a weak BAO feature. As a result, these weak BAO detections lead to non-Gaussian likelihood surface. While redshift weighting is powerful at turning a ‘mediocre’ measurement into a ‘good’ one, it cannot turn a ‘bad’ measurement (a non-detection of the BAO feature, for example) into a ‘mediocre’ or ‘good’ measurement. These noisy mocks thus render redshift weighting not as effective. After averaging, the ‘4x’ mocks have better signal-to-noise ratio and enhanced BAO features. In fitting the ‘4x’ mocks, the number of weak and non-detections is significantly reduced an redshift weighting thus becomes much more efficient in tightening the error bars. The substantial gains demonstrated in the ‘4x’ mocks suggest redshift weighting will play an important role in unlocking the full potential of the BAO constraints from the final quasar sample.
7 DISCUSSION
The DR14 quasar sample covers a wide redshift range from |$z$| = 0.8 to 2.2. To analyse the BAO information in such a large range without sacrificing signal-to-noise ratio by splitting the sample into redshift slices, redshift weighting (Zhu et al. 2016) is a natural choice. We have presented in this paper an anisotropic BAO analysis of the BOSS DR14 quasar sample using this technique.
We first model the distance–redshift relation as a Taylor expansion. Estimating the coefficients of this expansion allows us to reconstruct DM(|$z$|) and H(|$z$|) within the range of redshifts of the sample.
We establish the effectiveness of redshift weighting in producing unbiased optimized constraints from a set of mock catalogues. With the same methodology, we analyse the BOSS DR14 quasar sample and achieve improved DM and H constraints in fitting the BAO feature in the sample. Our DM error ranges from 4.6 per cent at |$z$| = 2.2 to 10.5 per cent at |$z$| = 0.8. Our H error ranges from 4.6 per cent at |$z$| = 0.8 to 23.5 per cent at |$z$| = 2.2.
To examine what will be possible when the final quasar sample becomes available, we generate a new set of mock catalogues with smaller noises by averaging every four of the original DR14 mocks to approximate the final eBOSS quasar sample. We analyse these averaged mocks with the same methodology and observe that redshift weighting offers significant improvement in the measurement errors over the single-bin analysis without redshift weighting. This demonstration suggests redshift weighting is important to unlocking the full BAO information within the sample.
The power of redshift weighting lies in its optimal use of the information without splitting the sample into redshift slices. Although one can retain sensitivity to redshift by repeating traditional analyses on multiple slices and properly accounting for covariance between slices, redshift weighting provides a more efficient and straightforward implementation.
The method is especially useful when the survey covers a wide range of redshifts. Its success on the set of mock catalogues that mimic the final quasar sample shows promise that the method will be extremely useful for upcoming surveys like the Dark Energy Spectroscopic Instrument (DESI; DESI Collaboration 2016a,b). An anisotropic BAO analysis with similar redshift weighting techniques in Fourier space will appear in Wang et al. (in preparation). They optimize the measurements by deploying redshift weights constructed for the BAO signal in the quasar power spectrum. Different from how this work utilizes the redshift weights, Wang et al. (in preparation) assign the weights to individual quasars instead of weighting quasar pairs. Apart from this difference, the methodology is similar to Zhu et al. (2016) and this work. Different from the result of this work, Wang et al. (in preparation) find applying redshift weighting on the DR14 sample produces improved measurement over the traditional single-bin analysis. This difference may be due to the difference in methodology and noise properties of the power spectrum and the correlation function. Despite this difference, the results reported in both works are fully consistent with each other within uncertainty. Besides these works, similar analysis methods inspired by the BAO redshift weights have been proposed to constrain redshift space distortions (Ruggeri et al. 2016) and primordial non-Gaussianity (Mueller, Percival & Ruggeri 2017) in upcoming surveys. Redshift Space Distortions measurements on the DR14 sample utilizing a similar methodology will appear in Ruggeri et al. (2018) and Zhao et al. (in preparation). Redshift weighting can bring us closer to realizing the full capabilities of these surveys as we aim towards an ever increasing understanding of the expansion history of the universe.
ACKNOWLEDGEMENTS
FZ would like to thank Tomomi Sunayama for useful conversations. This work was supported in part by the National Science Foundation under grant no. PHYS-1066293. NP and FZ are supported in part by a DOE Early Career grant DE-SC0008080. FB is a Royal Society University Research Fellow.
Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofsica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut fr Astrophysik Potsdam (AIP), Max-Planck-Institut fr Astronomie (MPIA Heidelberg), Max-Planck-Institut fr Astrophysik (MPA Garching), Max-Planck-Institut fr Extraterrestrische Physik (MPE), National Astronomical Observatory of China, New Mexico State University, New York University, University of Notre Dame, Observatrio Nacional/ MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autnoma de Mxico, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.



