-
PDF
- Split View
-
Views
-
Cite
Cite
H Dénes, N M McClure-Griffiths, J M Dickey, J R Dawson, C E Murray, Calibrating the HISA temperature: Measuring the temperature of the Riegel–Crutcher cloud, Monthly Notices of the Royal Astronomical Society, Volume 479, Issue 2, September 2018, Pages 1465–1490, https://doi.org/10.1093/mnras/sty1384
Close - Share Icon Share
ABSTRACT
H i self-absorption (HISA) clouds are clumps of cold neutral hydrogen (H i) visible in front of warm background gas, which makes them ideal places to study the properties of the cold atomic component of the interstellar medium. The Riegel–Crutcher (R–C) cloud is the most striking HISA feature in the Galaxy. It is one of the closest HISA clouds to us and is located in the direction of the Galactic Centre, which provides a bright background. High-resolution interferometric measurements have revealed the filamentary structure of this cloud; however, it is difficult to accurately determine the temperature and the density of the gas without optical depth measurements. In this paper, we present new H i absorption observations with the Australia Telescope Compact Array against 46 continuum sources behind the R–C cloud to directly measure the optical depth of the cloud. We decompose the complex H i absorption spectra into Gaussian components using an automated machine learning algorithm. We find 300 Gaussian components, from which 67 are associated with the R–C cloud (0 < |$v$|LSR < 10 km s−1, full width at half maximum < 10 km s−1). Combining the new H i absorption data with H i emission data from previous surveys, we calculate the spin temperature and find it to be between 20 and 80 K. Our measurements uncover a temperature gradient across the cloud with spin temperatures decreasing towards positive Galactic latitudes. We also find three new OH absorption lines associated with the cloud, which support the presence of molecular gas.
1 INTRODUCTION
Theoretical models (e.g. Field, Goldsmith, & Habing 1969; McKee & Ostriker 1977; Wolfire et al. 2003) predict that the neutral hydrogen (H i) in the interstellar medium (ISM) is in two phases – a warm and a cold phase. The warm neutral medium (WNM) has typical temperatures of ∼104 K and the cold neutral medium (CNM) has typical temperatures < 300K. These two phases are predicted to be in thermal equilibrium throughout most of the Galaxy (McKee & Ostriker 1977; Wolfire et al. 2003) and play an important role in regulating star formation. Observations support the two-phase nature of the neutral medium (e.g. Kulkarni & Heiles 1987; Garwood & Dickey 1989; Liszt, Braun, & Greisen 1993). The WNM is mostly detected in emission and the CNM in absorption. H i emission–absorption studies find that typically 20–50 per cent of the H i mass is cold and largely missed by emission studies (e.g. Dickey & Benson 1982; Heiles & Troland 2003b; Strasser & Taylor 2004; Dickey et al. 2009). Observational constraints on the physical properties are important for understanding how much of the H i is in the cold phase, when it transitions into molecular gas, and which heating and cooling processes influence it. By combining H i emission and absorption measurements we can directly measure the spin temperature (Ts) and column density of CNM and WNM structures along the line of sight. However, this method provides only very limited information on the spatial structure of the cold gas.
H i self-absorption (HISA) clouds are unique places where we can study the structure and the physical properties of the CNM at the same time. HISA arises when cold H i gas is located in front of warm H i. If the two gas components have the same velocity and the cold gas has a lower excitation temperature compared to the background H i brightness temperature, the cold gas appears in absorption against the warm background gas. Large sky surveys, such as the Canadian Galactic Plane Survey (CGPS; Taylor et al. 2003) and the Southern Galactic Plane Survey (SGPS; McClure-Griffiths et al. 2005), showed that HISA is prevalent throughout the Galaxy and probes the spatial structure of the cold H i (e.g. Gibson et al. 2000, 2005; Kavars et al. 2005). Several studies suggest that HISA clouds are transitional clouds where either the atomic H i gas is transitioning into H2 molecular gas via cooling, or the molecular H2 gas is dissociating into H i (e.g. Minter et al. 2001; Kavars et al. 2003, 2005). This theory is supported by the wide range of molecular gas associated with HISA clouds. Some HISA clouds have a significant fraction of molecular gas (e.g. Baker & Burton 1979; Liszt & Burton 1981; Jacq, Baudry, & Walmsley 1988), but others do not have any (e.g. Garwood & Dickey 1989; Gibson et al. 2005). Kavars et al. (2005) found that ∼60 per cent of the HISA clouds in the SGPS have associated CO emission. However, a challenge in interpreting HISA is that variations in the background emission make it difficult to accurately determine the temperature and optical depth of the HISA. A way to overcome this challenge is to measure the H i optical depth directly from H i absorption measurements against bright continuum background sources. By combining the H i emission and absorption measurements, we can derive spin temperatures for the cold gas.
To better understand the physical conditions inside cold H i clouds, we mapped the optical depth and spin temperature structure of one of the most prominent HISA clouds, the Riegel–Crutcher (R–C) cloud. The R–C cloud is one of the best studied HISA clouds, located 125 ± 25 pc from us (Crutcher & Lien 1984) in the direction of the Galactic Centre (GC) (Crutcher 1973). The H i emission towards the centre of the Galaxy provides an ideal bright background against which to image the CNM. The R–C cloud was discovered by Heeschen (1955) and fully mapped later by Riegel & Jennings (1969), who found that the cloud extends ∼40° of Galactic longitude and ∼10° of latitude. It has been suggested that the cloud could be part of a large extended structure at the wall of the Local Bubble, called Lindblad’s Feature A (Lindblad et al. 1973). The cloud covers a velocity range of ∼10 km s−1 centred at |$v$|LSR = 5 km s−1 (Riegel & Jennings 1969; Montgomery, Bates, & Davies 1995). Based on background stellar observations, its thickness is estimated to be 1–5pc (Crutcher & Riegel 1974). Observations with the Australia Telescope Compact Array (ATCA) revealed a highly filamentary structure aligned with the local magnetic field (McClure-Griffiths et al. 2006; Clark, Peek, & Putman 2014). Previous studies also found molecular gas associated with the cloud. Riegel & Jennings (1969) and Crutcher (1973) observed OH absorption against several lines of sight (LOS) towards the R–C cloud. Overlapping 12CO emission was detected by Dame, Hartmann, & Thaddeus (2001) at the positive latitude region of the cloud. In addition to the detected molecular gas, carbon radio recombination lines (CRRL) at 327 MHz were also observed by Roshi & Kantharia (2011) in the direction of the cloud. Roshi & Kantharia (2011) concluded that based on their models, the electron temperature of the cloud is between 40 and 60K and the C ii line cooling is the dominant process in the cloud suggesting that the R–C cloud is in the early stages of molecular formation.
Based on the HISA feature in the H i emission data, the excitation or spin temperature of the R–C cloud was estimated to be ∼40 K (Riegel & Jennings 1969; Montgomery et al. 1995; McClure-Griffiths et al. 2006), which is consistent with the results of the CRRLs. However, the spin temperatures derived from the HISA observation alone have a large uncertainty due to the degeneracy of the optical depth and the spin temperature in the radiative transfer equations. To break this degeneracy and to gain a better understanding of the temperature structure of the cloud, we observed H i and OH absorption against 46 continuum sources distributed across the whole R–C cloud. We compare the new absorption data to the H i emission data from the Galactic All Sky Survey (GASS; McClure-Griffiths et al. 2009; Kalberla et al. 2010; Kalberla & Haud 2015) and the SGPS Galactic Centre Survey (SGPS GC; McClure-Griffiths et al. 2012) to measure the spin temperature and column density distribution across the cloud.
This paper is structured in the following way: In Section 2, we describe our ATCA observations. In Section 3, we discuss the radiative transfer equations and the Gaussian decomposition of the H i absorption data. In Section 4, we discuss the derived optical depths, spin temperatures, and column densities. In Section 5, we discuss the presence of associated molecular gas and compare our results to H i absorption studies in the literature. Finally, we summarize our results in Section 6.
2 DATA
In this section, we describe our source selection, the ATCA observations, and the archival H i emission data that we use in this paper.
2.1 H i absorption measurements with ATCA
To measure the optical depth and spin temperature across the R–C cloud, we targeted the brightest compact continuum sources in the direction of the HISA cloud. Our aim was an optical depth sensitivity of στ ∼ 0.1, which depends on the flux density of the sources: στ = σS/S, where S is the background source flux density and σS is the observational sensitivity. To achieve this, we selected background continuum sources from the NRAO VLA Sky Survey Catalogue (NVSS; Condon et al. 1998) based on the following criteria: (i) integrated 1.4 GHz flux ⩾ 200 mJy and (ii) spatialy unresolved in NVSS (diameter ⩽ 20 arcsec). This selection resulted in 47 target sources.
We obtained high-resolution synthesis H i line observations for the sample with the ATCA. We used a single pointing for each source with the 1.5C antenna configuration, observing each target for 100 min. Observations were carried out in May–June 2015. Details of the observations are given in Table 1. The ATCA is a radio-interferometer consisting of six 22 m dishes, creating 15 baselines in a single configuration. While five antennas (CA01–CA05) are reconfigurable along a 3 km long east–west track (and a 214 m long north–south spur), one antenna (CA06) is fixed at a distance of 3 km from the end of the track creating the longest baselines.
Summary of ATCA observations. S1.4 are 1.4 GHz fluxes from the NVSS catalogue (Condon et al. 1998).
| NVSS name . | RA . | Decl. . | l . | b . | S1.4 . | Time . | Synthesized beam . | στ . |
|---|---|---|---|---|---|---|---|---|
| . | (hh:mm:ss) . | (dd:mm:ss) . | (°) . | (°) . | (mJy) . | (h) . | (arcsec2) . | . |
| NVSS J172829−284610 | 17:28:28 | −28:45:50 | −1.8738 | 3.2555 | 585.3 | 1.81 | 51 × 22 | 0.17 |
| NVSS J172836−271236 | 17:28:36 | −27:12:36 | −0.5563 | 4.0941 | 530.4 | 1.63 | 60 × 21 | 0.07 |
| NVSS J172908−265751 | 17:29:08 | −26:57:51 | −0.2845 | 4.1296 | 364.1 | 1.64 | 60 × 21 | 0.21 |
| NVSS J172920−234535 | 17:29:20 | −23:45:35 | 2.432 | 5.8467 | 1825 | 1.81 | 61 × 22 | 0.04 |
| NVSS J173107−245703 | 17:31:07 | −24:57:03 | 1.6506 | 4.8577 | 284.8 | 1.81 | 58 × 22 | 0.14 |
| NVSS J173133−264015 | 17:31:33 | −26:40:15 | 0.2574 | 3.8392 | 236.1 | 1.69 | 59 × 21 | 0.18 |
| NVSS J173203−285516 | 17:32:03 | −28:55:16 | −1.5699 | 2.5169 | 213.4 | 1.81 | 51 × 22 | 0.3 |
| NVSS J173205−242651 | 17:32:05 | −24:26:51 | 2.1956 | 4.945 | 597.2 | 1.64 | 66 × 21 | 0.08 |
| NVSS J173252−223511 | 17:32:52 | −22:35:21 | 3.8664 | 5.7991 | 353.2 | 1.48 | 80 × 20 | 0.11 |
| NVSS J173524−251036 | 17:35:24 | −25:10:26 | 1.9877 | 3.9175 | 258.6 | 1.64 | 64 × 21 | 0.21 |
| NVSS J173620−283552 | 17:36:20 | −28:35:42 | −0.7887 | 1.9026 | 210.8 | 1.64 | 74 × 27 | 0.58 |
| NVSS J173713−224734 | 17:37:13 | −22:47:34 | 4.2289 | 4.8441 | 209.9 | 1.65 | 70 × 21 | 0.19 |
| NVSS J173718−260426 | 17:37:18 | −26:04:26 | 1.4579 | 3.0762 | 283.1 | 1.81 | 56 × 22 | 0.14 |
| NVSS J173722−223000 | 17:37:22 | −22:30:00 | 4.498 | 4.968 | 317.7 | 1.48 | 80 × 19 | 0.14 |
| NVSS J173753−254642 | 17:37:53 | −25:46:42 | 1.7778 | 3.1242 | 217.2 | 1.81 | 56 × 22 | 0.24 |
| NVSS J173806−262443 | 17:38:06 | −26:24:43 | 1.2669 | 2.7455 | 309.7 | 1.81 | 55 × 22 | 0.14 |
| NVSS J173811−204411 | 17:38:13 | −20:42:41 | 6.1012 | 5.7415 | 342.4 | 1.64 | 77 × 21 | 0.12 |
| NVSS J173850−221918 | 17:38:50 | −22:19:18 | 4.8301 | 4.7751 | 244.9 | 1.65 | 72 × 21 | 0.19 |
| NVSS J173939−205505 | 17:39:41 | −20:53:35 | 6.1259 | 5.3569 | 544.1 | 1.64 | 77 × 21 | 0.07 |
| NVSS J174007−284203 | 17:40:07 | −28:42:03 | −0.4324 | 1.1463 | 219.1 | 1.81 | 67 × 30 | 0.74 |
| NVSS J174202−271311 | 17:42:02 | −27:13:11 | 1.0472 | 1.5731 | 204.2 | 1.64 | 77 × 27 | 0.61 |
| NVSS J174224−203729 | 17:42:26 | −20:35:59 | 6.7168 | 4.9604 | 434.5 | 1.64 | 77 × 21 | 0.1 |
| NVSS J174317−305819 | 17:43:18 | −30:58:29 | −1.9982 | −0.6363 | 357.5 | 1.81 | 48 × 22 | 0.13 |
| NVSS J174343−182838 | 17:43:45 | −18:26:58 | 8.7203 | 5.8132 | 568.3 | 1.64 | 87 × 21 | 0.06 |
| NVSS J174351−261059 | 17:43:51 | −26:10:59 | 2.1435 | 1.7718 | 229.6 | 1.64 | 80 × 27 | 0.41 |
| NVSS J174423−311636 | 17:44:24 | −31:16:46 | −2.135 | −0.9956 | 424.6 | 1.81 | 47 × 22 | 0.1 |
| NVSS J174513−315104 | 17:45:14 | −31:51:04 | −2.533 | −1.446 | 406.6 | 1.81 | 46 × 22 | 0.39 |
| NVSS J174618−193006 | 17:46:18 | −19:30:16 | 8.1553 | 4.7619 | 300.2 | 1.64 | 82 × 21 | 0.2 |
| NVSS J174637−182629 | 17:46:39 | −18:24:49 | 9.1081 | 5.2404 | 268.7 | 1.63 | 87 × 21 | 0.15 |
| NVSS J174709−295802 | 17:47:12 | −29:58:12 | −0.7073 | −0.8216 | 269.9 | 1.81 | 63 × 30 | 0.3 |
| NVSS J174713−192135 | 17:47:13 | −19:21:35 | 8.3906 | 4.6467 | 2276.5 | 1.64 | 83 × 21 | 0.02 |
| NVSS J174716−191954 | 17:47:16 | −19:19:54 | 8.4192 | 4.6536 | 1286.2 | 1.7 | 79 × 21 | 0.02 |
| NVSS J174748−312315 | 17:47:50 | −31:23:15 | −1.8502 | −1.6766 | 540.7 | 1.93 | 44 × 24 | 0.19 |
| NVSS J174831−324102 | 17:48:32 | −32:41:22 | −2.8834 | −2.4753 | 398 | 1.79 | 45 × 22 | 0.24 |
| NVSS J174832−225211 | 17:48:31 | −22:52:21 | 5.5312 | 2.5801 | 282.8 | 1.65 | 71 × 21 | 0.42 |
| NVSS J174915−200033 | 17:49:15 | −20:00:33 | 8.0755 | 3.9058 | 344.2 | 1.64 | 80 × 21 | 0.29 |
| NVSS J174931−210847 | 17:49:31 | −21:08:37 | 7.1301 | 3.2676 | 355.4 | 1.64 | 76 × 21 | 0.27 |
| NVSS J175104−235215 | 17:51:04 | −23:52:05 | 4.9686 | 1.5693 | 267.2 | 1.58 | 57 × 24 | 0.24 |
| NVSS J175114−323538 | 17:51:14 | −32:35:38 | −2.514 | −2.9188 | 646.8 | 1.83 | 45 × 23 | 0.1 |
| NVSS J175151−252359 | 17:51:51 | −25:23:59 | 3.745 | 0.6349 | 1223.6 | 1.67 | 57 × 22 | 0.04 |
| NVSS J175157−240425 | 17:51:57 | −24:04:25 | 4.8976 | 1.2915 | 220.9 | 1.64 | 54 × 25 | 0.29 |
| NVSS J175218−210508 | 17:52:18 | −21:04:56 | 7.513 | 2.7416 | 242.5 | 1.8 | 69 × 22 | 0.2 |
| NVSS J175233−223012 | 17:52:33 | −22:30:12 | 6.32 | 1.9719 | 1936.5 | 1.78 | 64 × 22 | 0.02 |
| NVSS J175427−235235 | 17:54:27 | −23:52:25 | 5.358 | 0.8988 | 267.7 | 1.48 | 58 × 23 | 0.27 |
| NVSS J175526−223211 | 17:55:26 | −22:32:11 | 6.6287 | 1.3809 | 225.6 | 1.81 | 64 × 22 | 0.1 |
| NVSS J175548−233322 | 17:55:48 | −23:33:22 | 5.7906 | 0.7936 | 439.8 | 1.53 | 60 × 23 | 0.14 |
| NVSS J175727−223901 | 17:57:26 | −22:39:01 | 6.7646 | 0.9197 | 541.5 | 1.64 | 66 × 21.65 | 0.29 |
| NVSS name . | RA . | Decl. . | l . | b . | S1.4 . | Time . | Synthesized beam . | στ . |
|---|---|---|---|---|---|---|---|---|
| . | (hh:mm:ss) . | (dd:mm:ss) . | (°) . | (°) . | (mJy) . | (h) . | (arcsec2) . | . |
| NVSS J172829−284610 | 17:28:28 | −28:45:50 | −1.8738 | 3.2555 | 585.3 | 1.81 | 51 × 22 | 0.17 |
| NVSS J172836−271236 | 17:28:36 | −27:12:36 | −0.5563 | 4.0941 | 530.4 | 1.63 | 60 × 21 | 0.07 |
| NVSS J172908−265751 | 17:29:08 | −26:57:51 | −0.2845 | 4.1296 | 364.1 | 1.64 | 60 × 21 | 0.21 |
| NVSS J172920−234535 | 17:29:20 | −23:45:35 | 2.432 | 5.8467 | 1825 | 1.81 | 61 × 22 | 0.04 |
| NVSS J173107−245703 | 17:31:07 | −24:57:03 | 1.6506 | 4.8577 | 284.8 | 1.81 | 58 × 22 | 0.14 |
| NVSS J173133−264015 | 17:31:33 | −26:40:15 | 0.2574 | 3.8392 | 236.1 | 1.69 | 59 × 21 | 0.18 |
| NVSS J173203−285516 | 17:32:03 | −28:55:16 | −1.5699 | 2.5169 | 213.4 | 1.81 | 51 × 22 | 0.3 |
| NVSS J173205−242651 | 17:32:05 | −24:26:51 | 2.1956 | 4.945 | 597.2 | 1.64 | 66 × 21 | 0.08 |
| NVSS J173252−223511 | 17:32:52 | −22:35:21 | 3.8664 | 5.7991 | 353.2 | 1.48 | 80 × 20 | 0.11 |
| NVSS J173524−251036 | 17:35:24 | −25:10:26 | 1.9877 | 3.9175 | 258.6 | 1.64 | 64 × 21 | 0.21 |
| NVSS J173620−283552 | 17:36:20 | −28:35:42 | −0.7887 | 1.9026 | 210.8 | 1.64 | 74 × 27 | 0.58 |
| NVSS J173713−224734 | 17:37:13 | −22:47:34 | 4.2289 | 4.8441 | 209.9 | 1.65 | 70 × 21 | 0.19 |
| NVSS J173718−260426 | 17:37:18 | −26:04:26 | 1.4579 | 3.0762 | 283.1 | 1.81 | 56 × 22 | 0.14 |
| NVSS J173722−223000 | 17:37:22 | −22:30:00 | 4.498 | 4.968 | 317.7 | 1.48 | 80 × 19 | 0.14 |
| NVSS J173753−254642 | 17:37:53 | −25:46:42 | 1.7778 | 3.1242 | 217.2 | 1.81 | 56 × 22 | 0.24 |
| NVSS J173806−262443 | 17:38:06 | −26:24:43 | 1.2669 | 2.7455 | 309.7 | 1.81 | 55 × 22 | 0.14 |
| NVSS J173811−204411 | 17:38:13 | −20:42:41 | 6.1012 | 5.7415 | 342.4 | 1.64 | 77 × 21 | 0.12 |
| NVSS J173850−221918 | 17:38:50 | −22:19:18 | 4.8301 | 4.7751 | 244.9 | 1.65 | 72 × 21 | 0.19 |
| NVSS J173939−205505 | 17:39:41 | −20:53:35 | 6.1259 | 5.3569 | 544.1 | 1.64 | 77 × 21 | 0.07 |
| NVSS J174007−284203 | 17:40:07 | −28:42:03 | −0.4324 | 1.1463 | 219.1 | 1.81 | 67 × 30 | 0.74 |
| NVSS J174202−271311 | 17:42:02 | −27:13:11 | 1.0472 | 1.5731 | 204.2 | 1.64 | 77 × 27 | 0.61 |
| NVSS J174224−203729 | 17:42:26 | −20:35:59 | 6.7168 | 4.9604 | 434.5 | 1.64 | 77 × 21 | 0.1 |
| NVSS J174317−305819 | 17:43:18 | −30:58:29 | −1.9982 | −0.6363 | 357.5 | 1.81 | 48 × 22 | 0.13 |
| NVSS J174343−182838 | 17:43:45 | −18:26:58 | 8.7203 | 5.8132 | 568.3 | 1.64 | 87 × 21 | 0.06 |
| NVSS J174351−261059 | 17:43:51 | −26:10:59 | 2.1435 | 1.7718 | 229.6 | 1.64 | 80 × 27 | 0.41 |
| NVSS J174423−311636 | 17:44:24 | −31:16:46 | −2.135 | −0.9956 | 424.6 | 1.81 | 47 × 22 | 0.1 |
| NVSS J174513−315104 | 17:45:14 | −31:51:04 | −2.533 | −1.446 | 406.6 | 1.81 | 46 × 22 | 0.39 |
| NVSS J174618−193006 | 17:46:18 | −19:30:16 | 8.1553 | 4.7619 | 300.2 | 1.64 | 82 × 21 | 0.2 |
| NVSS J174637−182629 | 17:46:39 | −18:24:49 | 9.1081 | 5.2404 | 268.7 | 1.63 | 87 × 21 | 0.15 |
| NVSS J174709−295802 | 17:47:12 | −29:58:12 | −0.7073 | −0.8216 | 269.9 | 1.81 | 63 × 30 | 0.3 |
| NVSS J174713−192135 | 17:47:13 | −19:21:35 | 8.3906 | 4.6467 | 2276.5 | 1.64 | 83 × 21 | 0.02 |
| NVSS J174716−191954 | 17:47:16 | −19:19:54 | 8.4192 | 4.6536 | 1286.2 | 1.7 | 79 × 21 | 0.02 |
| NVSS J174748−312315 | 17:47:50 | −31:23:15 | −1.8502 | −1.6766 | 540.7 | 1.93 | 44 × 24 | 0.19 |
| NVSS J174831−324102 | 17:48:32 | −32:41:22 | −2.8834 | −2.4753 | 398 | 1.79 | 45 × 22 | 0.24 |
| NVSS J174832−225211 | 17:48:31 | −22:52:21 | 5.5312 | 2.5801 | 282.8 | 1.65 | 71 × 21 | 0.42 |
| NVSS J174915−200033 | 17:49:15 | −20:00:33 | 8.0755 | 3.9058 | 344.2 | 1.64 | 80 × 21 | 0.29 |
| NVSS J174931−210847 | 17:49:31 | −21:08:37 | 7.1301 | 3.2676 | 355.4 | 1.64 | 76 × 21 | 0.27 |
| NVSS J175104−235215 | 17:51:04 | −23:52:05 | 4.9686 | 1.5693 | 267.2 | 1.58 | 57 × 24 | 0.24 |
| NVSS J175114−323538 | 17:51:14 | −32:35:38 | −2.514 | −2.9188 | 646.8 | 1.83 | 45 × 23 | 0.1 |
| NVSS J175151−252359 | 17:51:51 | −25:23:59 | 3.745 | 0.6349 | 1223.6 | 1.67 | 57 × 22 | 0.04 |
| NVSS J175157−240425 | 17:51:57 | −24:04:25 | 4.8976 | 1.2915 | 220.9 | 1.64 | 54 × 25 | 0.29 |
| NVSS J175218−210508 | 17:52:18 | −21:04:56 | 7.513 | 2.7416 | 242.5 | 1.8 | 69 × 22 | 0.2 |
| NVSS J175233−223012 | 17:52:33 | −22:30:12 | 6.32 | 1.9719 | 1936.5 | 1.78 | 64 × 22 | 0.02 |
| NVSS J175427−235235 | 17:54:27 | −23:52:25 | 5.358 | 0.8988 | 267.7 | 1.48 | 58 × 23 | 0.27 |
| NVSS J175526−223211 | 17:55:26 | −22:32:11 | 6.6287 | 1.3809 | 225.6 | 1.81 | 64 × 22 | 0.1 |
| NVSS J175548−233322 | 17:55:48 | −23:33:22 | 5.7906 | 0.7936 | 439.8 | 1.53 | 60 × 23 | 0.14 |
| NVSS J175727−223901 | 17:57:26 | −22:39:01 | 6.7646 | 0.9197 | 541.5 | 1.64 | 66 × 21.65 | 0.29 |
Summary of ATCA observations. S1.4 are 1.4 GHz fluxes from the NVSS catalogue (Condon et al. 1998).
| NVSS name . | RA . | Decl. . | l . | b . | S1.4 . | Time . | Synthesized beam . | στ . |
|---|---|---|---|---|---|---|---|---|
| . | (hh:mm:ss) . | (dd:mm:ss) . | (°) . | (°) . | (mJy) . | (h) . | (arcsec2) . | . |
| NVSS J172829−284610 | 17:28:28 | −28:45:50 | −1.8738 | 3.2555 | 585.3 | 1.81 | 51 × 22 | 0.17 |
| NVSS J172836−271236 | 17:28:36 | −27:12:36 | −0.5563 | 4.0941 | 530.4 | 1.63 | 60 × 21 | 0.07 |
| NVSS J172908−265751 | 17:29:08 | −26:57:51 | −0.2845 | 4.1296 | 364.1 | 1.64 | 60 × 21 | 0.21 |
| NVSS J172920−234535 | 17:29:20 | −23:45:35 | 2.432 | 5.8467 | 1825 | 1.81 | 61 × 22 | 0.04 |
| NVSS J173107−245703 | 17:31:07 | −24:57:03 | 1.6506 | 4.8577 | 284.8 | 1.81 | 58 × 22 | 0.14 |
| NVSS J173133−264015 | 17:31:33 | −26:40:15 | 0.2574 | 3.8392 | 236.1 | 1.69 | 59 × 21 | 0.18 |
| NVSS J173203−285516 | 17:32:03 | −28:55:16 | −1.5699 | 2.5169 | 213.4 | 1.81 | 51 × 22 | 0.3 |
| NVSS J173205−242651 | 17:32:05 | −24:26:51 | 2.1956 | 4.945 | 597.2 | 1.64 | 66 × 21 | 0.08 |
| NVSS J173252−223511 | 17:32:52 | −22:35:21 | 3.8664 | 5.7991 | 353.2 | 1.48 | 80 × 20 | 0.11 |
| NVSS J173524−251036 | 17:35:24 | −25:10:26 | 1.9877 | 3.9175 | 258.6 | 1.64 | 64 × 21 | 0.21 |
| NVSS J173620−283552 | 17:36:20 | −28:35:42 | −0.7887 | 1.9026 | 210.8 | 1.64 | 74 × 27 | 0.58 |
| NVSS J173713−224734 | 17:37:13 | −22:47:34 | 4.2289 | 4.8441 | 209.9 | 1.65 | 70 × 21 | 0.19 |
| NVSS J173718−260426 | 17:37:18 | −26:04:26 | 1.4579 | 3.0762 | 283.1 | 1.81 | 56 × 22 | 0.14 |
| NVSS J173722−223000 | 17:37:22 | −22:30:00 | 4.498 | 4.968 | 317.7 | 1.48 | 80 × 19 | 0.14 |
| NVSS J173753−254642 | 17:37:53 | −25:46:42 | 1.7778 | 3.1242 | 217.2 | 1.81 | 56 × 22 | 0.24 |
| NVSS J173806−262443 | 17:38:06 | −26:24:43 | 1.2669 | 2.7455 | 309.7 | 1.81 | 55 × 22 | 0.14 |
| NVSS J173811−204411 | 17:38:13 | −20:42:41 | 6.1012 | 5.7415 | 342.4 | 1.64 | 77 × 21 | 0.12 |
| NVSS J173850−221918 | 17:38:50 | −22:19:18 | 4.8301 | 4.7751 | 244.9 | 1.65 | 72 × 21 | 0.19 |
| NVSS J173939−205505 | 17:39:41 | −20:53:35 | 6.1259 | 5.3569 | 544.1 | 1.64 | 77 × 21 | 0.07 |
| NVSS J174007−284203 | 17:40:07 | −28:42:03 | −0.4324 | 1.1463 | 219.1 | 1.81 | 67 × 30 | 0.74 |
| NVSS J174202−271311 | 17:42:02 | −27:13:11 | 1.0472 | 1.5731 | 204.2 | 1.64 | 77 × 27 | 0.61 |
| NVSS J174224−203729 | 17:42:26 | −20:35:59 | 6.7168 | 4.9604 | 434.5 | 1.64 | 77 × 21 | 0.1 |
| NVSS J174317−305819 | 17:43:18 | −30:58:29 | −1.9982 | −0.6363 | 357.5 | 1.81 | 48 × 22 | 0.13 |
| NVSS J174343−182838 | 17:43:45 | −18:26:58 | 8.7203 | 5.8132 | 568.3 | 1.64 | 87 × 21 | 0.06 |
| NVSS J174351−261059 | 17:43:51 | −26:10:59 | 2.1435 | 1.7718 | 229.6 | 1.64 | 80 × 27 | 0.41 |
| NVSS J174423−311636 | 17:44:24 | −31:16:46 | −2.135 | −0.9956 | 424.6 | 1.81 | 47 × 22 | 0.1 |
| NVSS J174513−315104 | 17:45:14 | −31:51:04 | −2.533 | −1.446 | 406.6 | 1.81 | 46 × 22 | 0.39 |
| NVSS J174618−193006 | 17:46:18 | −19:30:16 | 8.1553 | 4.7619 | 300.2 | 1.64 | 82 × 21 | 0.2 |
| NVSS J174637−182629 | 17:46:39 | −18:24:49 | 9.1081 | 5.2404 | 268.7 | 1.63 | 87 × 21 | 0.15 |
| NVSS J174709−295802 | 17:47:12 | −29:58:12 | −0.7073 | −0.8216 | 269.9 | 1.81 | 63 × 30 | 0.3 |
| NVSS J174713−192135 | 17:47:13 | −19:21:35 | 8.3906 | 4.6467 | 2276.5 | 1.64 | 83 × 21 | 0.02 |
| NVSS J174716−191954 | 17:47:16 | −19:19:54 | 8.4192 | 4.6536 | 1286.2 | 1.7 | 79 × 21 | 0.02 |
| NVSS J174748−312315 | 17:47:50 | −31:23:15 | −1.8502 | −1.6766 | 540.7 | 1.93 | 44 × 24 | 0.19 |
| NVSS J174831−324102 | 17:48:32 | −32:41:22 | −2.8834 | −2.4753 | 398 | 1.79 | 45 × 22 | 0.24 |
| NVSS J174832−225211 | 17:48:31 | −22:52:21 | 5.5312 | 2.5801 | 282.8 | 1.65 | 71 × 21 | 0.42 |
| NVSS J174915−200033 | 17:49:15 | −20:00:33 | 8.0755 | 3.9058 | 344.2 | 1.64 | 80 × 21 | 0.29 |
| NVSS J174931−210847 | 17:49:31 | −21:08:37 | 7.1301 | 3.2676 | 355.4 | 1.64 | 76 × 21 | 0.27 |
| NVSS J175104−235215 | 17:51:04 | −23:52:05 | 4.9686 | 1.5693 | 267.2 | 1.58 | 57 × 24 | 0.24 |
| NVSS J175114−323538 | 17:51:14 | −32:35:38 | −2.514 | −2.9188 | 646.8 | 1.83 | 45 × 23 | 0.1 |
| NVSS J175151−252359 | 17:51:51 | −25:23:59 | 3.745 | 0.6349 | 1223.6 | 1.67 | 57 × 22 | 0.04 |
| NVSS J175157−240425 | 17:51:57 | −24:04:25 | 4.8976 | 1.2915 | 220.9 | 1.64 | 54 × 25 | 0.29 |
| NVSS J175218−210508 | 17:52:18 | −21:04:56 | 7.513 | 2.7416 | 242.5 | 1.8 | 69 × 22 | 0.2 |
| NVSS J175233−223012 | 17:52:33 | −22:30:12 | 6.32 | 1.9719 | 1936.5 | 1.78 | 64 × 22 | 0.02 |
| NVSS J175427−235235 | 17:54:27 | −23:52:25 | 5.358 | 0.8988 | 267.7 | 1.48 | 58 × 23 | 0.27 |
| NVSS J175526−223211 | 17:55:26 | −22:32:11 | 6.6287 | 1.3809 | 225.6 | 1.81 | 64 × 22 | 0.1 |
| NVSS J175548−233322 | 17:55:48 | −23:33:22 | 5.7906 | 0.7936 | 439.8 | 1.53 | 60 × 23 | 0.14 |
| NVSS J175727−223901 | 17:57:26 | −22:39:01 | 6.7646 | 0.9197 | 541.5 | 1.64 | 66 × 21.65 | 0.29 |
| NVSS name . | RA . | Decl. . | l . | b . | S1.4 . | Time . | Synthesized beam . | στ . |
|---|---|---|---|---|---|---|---|---|
| . | (hh:mm:ss) . | (dd:mm:ss) . | (°) . | (°) . | (mJy) . | (h) . | (arcsec2) . | . |
| NVSS J172829−284610 | 17:28:28 | −28:45:50 | −1.8738 | 3.2555 | 585.3 | 1.81 | 51 × 22 | 0.17 |
| NVSS J172836−271236 | 17:28:36 | −27:12:36 | −0.5563 | 4.0941 | 530.4 | 1.63 | 60 × 21 | 0.07 |
| NVSS J172908−265751 | 17:29:08 | −26:57:51 | −0.2845 | 4.1296 | 364.1 | 1.64 | 60 × 21 | 0.21 |
| NVSS J172920−234535 | 17:29:20 | −23:45:35 | 2.432 | 5.8467 | 1825 | 1.81 | 61 × 22 | 0.04 |
| NVSS J173107−245703 | 17:31:07 | −24:57:03 | 1.6506 | 4.8577 | 284.8 | 1.81 | 58 × 22 | 0.14 |
| NVSS J173133−264015 | 17:31:33 | −26:40:15 | 0.2574 | 3.8392 | 236.1 | 1.69 | 59 × 21 | 0.18 |
| NVSS J173203−285516 | 17:32:03 | −28:55:16 | −1.5699 | 2.5169 | 213.4 | 1.81 | 51 × 22 | 0.3 |
| NVSS J173205−242651 | 17:32:05 | −24:26:51 | 2.1956 | 4.945 | 597.2 | 1.64 | 66 × 21 | 0.08 |
| NVSS J173252−223511 | 17:32:52 | −22:35:21 | 3.8664 | 5.7991 | 353.2 | 1.48 | 80 × 20 | 0.11 |
| NVSS J173524−251036 | 17:35:24 | −25:10:26 | 1.9877 | 3.9175 | 258.6 | 1.64 | 64 × 21 | 0.21 |
| NVSS J173620−283552 | 17:36:20 | −28:35:42 | −0.7887 | 1.9026 | 210.8 | 1.64 | 74 × 27 | 0.58 |
| NVSS J173713−224734 | 17:37:13 | −22:47:34 | 4.2289 | 4.8441 | 209.9 | 1.65 | 70 × 21 | 0.19 |
| NVSS J173718−260426 | 17:37:18 | −26:04:26 | 1.4579 | 3.0762 | 283.1 | 1.81 | 56 × 22 | 0.14 |
| NVSS J173722−223000 | 17:37:22 | −22:30:00 | 4.498 | 4.968 | 317.7 | 1.48 | 80 × 19 | 0.14 |
| NVSS J173753−254642 | 17:37:53 | −25:46:42 | 1.7778 | 3.1242 | 217.2 | 1.81 | 56 × 22 | 0.24 |
| NVSS J173806−262443 | 17:38:06 | −26:24:43 | 1.2669 | 2.7455 | 309.7 | 1.81 | 55 × 22 | 0.14 |
| NVSS J173811−204411 | 17:38:13 | −20:42:41 | 6.1012 | 5.7415 | 342.4 | 1.64 | 77 × 21 | 0.12 |
| NVSS J173850−221918 | 17:38:50 | −22:19:18 | 4.8301 | 4.7751 | 244.9 | 1.65 | 72 × 21 | 0.19 |
| NVSS J173939−205505 | 17:39:41 | −20:53:35 | 6.1259 | 5.3569 | 544.1 | 1.64 | 77 × 21 | 0.07 |
| NVSS J174007−284203 | 17:40:07 | −28:42:03 | −0.4324 | 1.1463 | 219.1 | 1.81 | 67 × 30 | 0.74 |
| NVSS J174202−271311 | 17:42:02 | −27:13:11 | 1.0472 | 1.5731 | 204.2 | 1.64 | 77 × 27 | 0.61 |
| NVSS J174224−203729 | 17:42:26 | −20:35:59 | 6.7168 | 4.9604 | 434.5 | 1.64 | 77 × 21 | 0.1 |
| NVSS J174317−305819 | 17:43:18 | −30:58:29 | −1.9982 | −0.6363 | 357.5 | 1.81 | 48 × 22 | 0.13 |
| NVSS J174343−182838 | 17:43:45 | −18:26:58 | 8.7203 | 5.8132 | 568.3 | 1.64 | 87 × 21 | 0.06 |
| NVSS J174351−261059 | 17:43:51 | −26:10:59 | 2.1435 | 1.7718 | 229.6 | 1.64 | 80 × 27 | 0.41 |
| NVSS J174423−311636 | 17:44:24 | −31:16:46 | −2.135 | −0.9956 | 424.6 | 1.81 | 47 × 22 | 0.1 |
| NVSS J174513−315104 | 17:45:14 | −31:51:04 | −2.533 | −1.446 | 406.6 | 1.81 | 46 × 22 | 0.39 |
| NVSS J174618−193006 | 17:46:18 | −19:30:16 | 8.1553 | 4.7619 | 300.2 | 1.64 | 82 × 21 | 0.2 |
| NVSS J174637−182629 | 17:46:39 | −18:24:49 | 9.1081 | 5.2404 | 268.7 | 1.63 | 87 × 21 | 0.15 |
| NVSS J174709−295802 | 17:47:12 | −29:58:12 | −0.7073 | −0.8216 | 269.9 | 1.81 | 63 × 30 | 0.3 |
| NVSS J174713−192135 | 17:47:13 | −19:21:35 | 8.3906 | 4.6467 | 2276.5 | 1.64 | 83 × 21 | 0.02 |
| NVSS J174716−191954 | 17:47:16 | −19:19:54 | 8.4192 | 4.6536 | 1286.2 | 1.7 | 79 × 21 | 0.02 |
| NVSS J174748−312315 | 17:47:50 | −31:23:15 | −1.8502 | −1.6766 | 540.7 | 1.93 | 44 × 24 | 0.19 |
| NVSS J174831−324102 | 17:48:32 | −32:41:22 | −2.8834 | −2.4753 | 398 | 1.79 | 45 × 22 | 0.24 |
| NVSS J174832−225211 | 17:48:31 | −22:52:21 | 5.5312 | 2.5801 | 282.8 | 1.65 | 71 × 21 | 0.42 |
| NVSS J174915−200033 | 17:49:15 | −20:00:33 | 8.0755 | 3.9058 | 344.2 | 1.64 | 80 × 21 | 0.29 |
| NVSS J174931−210847 | 17:49:31 | −21:08:37 | 7.1301 | 3.2676 | 355.4 | 1.64 | 76 × 21 | 0.27 |
| NVSS J175104−235215 | 17:51:04 | −23:52:05 | 4.9686 | 1.5693 | 267.2 | 1.58 | 57 × 24 | 0.24 |
| NVSS J175114−323538 | 17:51:14 | −32:35:38 | −2.514 | −2.9188 | 646.8 | 1.83 | 45 × 23 | 0.1 |
| NVSS J175151−252359 | 17:51:51 | −25:23:59 | 3.745 | 0.6349 | 1223.6 | 1.67 | 57 × 22 | 0.04 |
| NVSS J175157−240425 | 17:51:57 | −24:04:25 | 4.8976 | 1.2915 | 220.9 | 1.64 | 54 × 25 | 0.29 |
| NVSS J175218−210508 | 17:52:18 | −21:04:56 | 7.513 | 2.7416 | 242.5 | 1.8 | 69 × 22 | 0.2 |
| NVSS J175233−223012 | 17:52:33 | −22:30:12 | 6.32 | 1.9719 | 1936.5 | 1.78 | 64 × 22 | 0.02 |
| NVSS J175427−235235 | 17:54:27 | −23:52:25 | 5.358 | 0.8988 | 267.7 | 1.48 | 58 × 23 | 0.27 |
| NVSS J175526−223211 | 17:55:26 | −22:32:11 | 6.6287 | 1.3809 | 225.6 | 1.81 | 64 × 22 | 0.1 |
| NVSS J175548−233322 | 17:55:48 | −23:33:22 | 5.7906 | 0.7936 | 439.8 | 1.53 | 60 × 23 | 0.14 |
| NVSS J175727−223901 | 17:57:26 | −22:39:01 | 6.7646 | 0.9197 | 541.5 | 1.64 | 66 × 21.65 | 0.29 |
We observed each source hourly for 10 min in a 12-h observing run, which gave sufficient uv coverage for imaging. For each 12-h observing session, we observed the ATCA flux and bandpass calibrator PKS 1934−638 for 30 min at the start and at the end of the observation. We used the 1M-0.5k correlator configuration on the Compact Array Broad-band Backend (CABB; Wilson et al. 2011) with a 3 MHz wide zoom band1 divided into 6145 channels. This gives a velocity resolution of 0.103 km s−1. We used two zoom bands for the H i observations centred at 1417 and at 1420 MHz. The 1417 MHz band was used for bandpass calibration.
Data reduction was carried out with the miriad software package (Sault, Teuben, & Wright 1995). We used the standard ATCA primary calibrator PKS 1934−638 for bandpass and amplitude calibration and the brightest continuum source observed each day for phase calibration (NVSS J172920−234535, J174713−192135, J172836−271236, J175233−223012, J175151−252359, J174713−192135, J175114−323538, J174716−191954). The bandpass calibration is not trivial because all potential bandpass calibrators, including PKS 1934−638, show strong H i absorption near |$v$|LSR = 0 km s−1 (see Fig. A1), which is close to the velocity of the R–C cloud. We tested two different methods for bandpass calibration:
Flagging the H i absorption from the calibrator’s data and interpolating across the flagged channels to derive the bandpass solution. The absorption affects ∼ 150–200 channels in the middle of the spectra. This method relies on the assumption that the bandpass is flat throughout the zoom band, which is a fair assumption for CABB data.
An alternative option is to use frequency switching to calibrate the bandpass. In this case, we used two zoom bands, one centred at 1420 MHz and the second one centred at 1417 MHz, where both bands have the same number of channels. This assumes that the bandpass is the same in the two neighbouring zoom bands.
Employing both methods, we found that the two bandpass solutions were very similar, such that the difference between the solutions is smaller than the measured RMS of the PKS 1934−638 data. However, we did find that after calibration there was a consistently net positive inflection in the bandpass derived via the first method. We therefore chose to proceed with the frequency-switched bandpass solution for all data described below.
After the calibration, we made data cubes for all sources using natural weighting with three different velocity channel samplings: 0.2 km s−1, 0.824 km s−1, and 0.826 km s−1. The 0.2 km s−1 resolution was created to have a high velocity resolution cube, while the 0.824 and 0.826 km s−1 cubes were created to match the velocity resolution of the H i emission data sets (described below). We made several different sets of data cubes (i) using all 15 baselines, (ii) excluding baselines with antenna 6 (longest baselines ranging from 3 km to 4.5 km), and (iii) excluding the shortest baseline (76.5 m, between antennas 4 and 5).
Our use of the 1.5 k array ensured that we did not resolve the targeted continuum sources, while simultaneously providing good spatial filtering of the H i emission towards most of the observed sources, because the fluctuations in H i emission at our sensitivity are on large angular scales. However, very close to the GC bright emission fluctuations are also observed on smaller scales. To accurately measure H i absorption, we need to filter out any contributions from H i emission. These contribute both positively and negatively to the interferometric spectrum, effectively increasing the measured noise. Excluding the shortest baseline from the data cubes provides additional spatial filtering of the H i emission. We found that we obtained the best signal to noise when we excluded the shortest baseline and all baselines with antenna 6 as well.
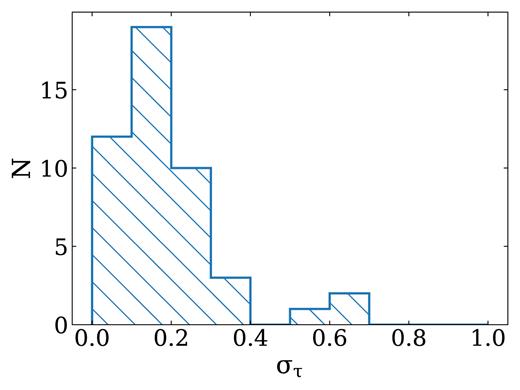
Sensitivity (στ) histogram of the H i absorption measurements. The majority of our sources (41/47) have optical depth sensitivity στ < 0.3.
2.2 H i emission data
We use H i emission data from two sources: the GASS (McClure-Griffiths et al. 2009; Kalberla et al. 2010; Kalberla & Haud 2015) and the SGPS GC (McClure-Griffiths et al. 2012). GASS maps the Galactic H i emission across the whole Southern sky (δ ⩽ 1°), including the whole area of the R–C cloud around the GC. GASS has a spatial resolution of 16 arcmin, a velocity resolution of 0.826 km s−1 and an RMS brightness temperature noise of 57 mK.
The SGPS GC data cover 100 deg2 around the GC (−5° ⩽ l ⩽ 5°, −5° ⩽ b ⩽ 5°) and encompass most of the R–C cloud. The SGPS GC H i data cubes are constructed from interferometric data observed with the ATCA in several different array configurations, combined with Parkes single dish data (for details see McClure-Griffiths et al. 2012). These data have higher spatial resolution, θ = 145 arcsec, but worse RMS brightness temperature sensitivity, ∼2 K, compared to GASS. The velocity resolution is 0.824 km s−1.
We extract spectra from the GASS cubes at the same position as from the ATCA data cubes. For the SGPS GC data cube, we average spectra from four positions 145 arcsec away from the ATCA positions. This is to avoid contamination of the emission spectra with remaining absorption towards the continuum source. When comparing the four-point average spectra and the spectra at the continuum sources position we find that there is only a small, 3–8 K (3–6 per cent of the peak flux) difference between the two.
2.3 OH data
In addition to the H i observation, we observed all continuum sources in the two main OH lines (1665 and 1667 MHz) with the ATCA. We centred the two OH zoom bands on 1665 and 1667 MHz, with a bandwidth of 2 MHz divided into 4097 channels,2 which gives a velocity resolution of 0.088 km s−1.
We reduced the OH data in the same way as the H i using PKS 1934−638 for bandpass and amplitude calibration and the brightest continuum source observed each day for phase calibration (see Section 2.1). After the calibration, we made OH data cubes for all sources using natural weighting and 0.26 km s−1 velocity channels. We extracted OH spectra for each source at the same position as the H i spectra.
3 METHODS
In this section, we describe our methodology for calculating spin temperatures, our decomposition of the H i absorption spectra into Gaussian components, and our method to reconstruct the H i emission without the HISA.
3.1 Deriving the spin temperature of the cold H i
Several methods are used to calculate spin temperatures for the cold H i gas. Each of these methods has different assumptions, advantages and disadvantages, and is generally suitable for different science goals. For a detailed summary of the various methods of deriving Ts, see Dickey et al. (2003) and Murray et al. (2015). In this work, we are investigating the spin temperature of a HISA cloud that is seen towards the GC and has a large angular extent on the sky (more than 100 square degrees). This means that the H i spectra are a complex mixture of various overlapping emission components and at least one deep self-absorption feature. The H i absorption spectra measured with the ATCA are composed of several strong, blended absorption lines. Fig. 2 shows two typical emission and absorption spectra pairs towards the R–C cloud (NVSS J174713−192135 and NVSS J175548−233322). The strong HISA feature at ∼ 5 km s−1 is evident in both emission spectra. Fig. 2 also illustrates that several of the absorption lines from the ATCA data have corresponding emission features in the GASS data, but only the absorption lines at ∼5 km s−1 appear as HISA.
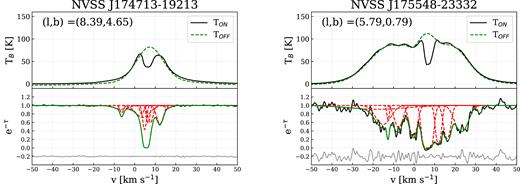
Example H i emission and absorption spectra of sources NVSS J174713−192135 (l, b = 8.39, 4.64) and NVSS J175548−233322 (l, b = 5.78, 0.79), with στ 0.02 and 0.14, respectively. Top panel: The solid black line shows the emission spectra (TON) extracted from GASS and the dashed line shows the modelled TOFF spectra. Bottom panel: The black line shows the ATCA absorption spectra, the green line is the fitted Gaussian model, and the red dashed lines are the individual components of the fit. The grey line is the residual from the absorption model shifted to −0.2.
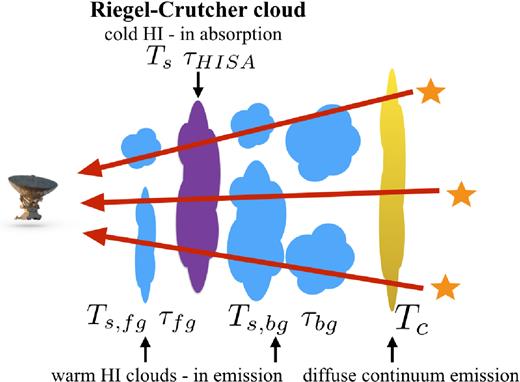
Illustration of the Riegel-Crutcher cloud observations. We are observing the cold gas from the R–C cloud in H i absorption and we are observing the background and foreground warmer H i clouds in emission.
3.2 Gaussian decomposition
The ATCA H i absorption spectrum (e−τ) is a composition of several H i clouds (τi) along the LOS from which the HISA (τHISA) is only one or two components. The τ spectra can be described as the sum of Gaussian components (e.g. Heiles & Troland 2003a; Murray et al. 2017). To decompose the absorption spectra into Gaussian components, we use the Autonomous Gaussian Decomposition algorithm (AGD; gausspy) from Lindner et al. (2015). AGD uses computer vision and machine learning algorithms to decompose complicated spectra and provide a multicomponent Gaussian model. The algorithm uses a two-step approach by first providing initial guesses for the Gaussian parameters and then performing a least-squares fit of the model to the data. The initial guesses for the number, location, and width of the components are estimated from the derivatives of the spectra with respect to velocity. The location is determined from the maxima in the second and fourth derivatives and the width is determined from the value of the second derivative at the location. AGD is a flexible algorithm that can be tuned to the properties of different data sets, e.g. the signal to noise of the data set and the number and expected width of the Gaussian components. Derivative spectroscopy is frequently used to study spectral-line properties (e.g. Krčo et al. 2008; Krčo & Goldsmith 2010).
AGD can be fine-tuned primarily through the use of the α parameters, which control the balance between smoothness and data fidelity in the solution by suppressing the noise when decomposing the spectra. Setting these parameters to an optimal value is essential to avoid classifying noise as a Gaussian component and yet also finding all the weak-signal components. The ideal α parameters vary between different data sets, depending on the noise level of the spectra, the width of the components, and how blended the components are. The best α values can be determined with machine learning, by 'training' AGD with a representative data set, where we know the underlying distribution of Gaussian components.
For the training, we created a set of artificial absorption spectra with the following parameters: 800 spectra, with 3–15 Gaussian components each, a varying RMS level (0.01–0.32), amplitude between the RMS level and 1, and FWHM randomly distributed between 4 and 50 channels (for a channel width of 0.2 km s−1 this corresponds to lines with FWHM 0.8–10 km s−1). These parameters are representative of our ATCA absorption spectra. We use these spectra to determine the best α1 and α2 values to decompose our spectra with AGD (for details see Lindner et al. 2015). We found the values α1 = 2.5 and α2 = 5.97 using a signal-to-noise threshold of 5.
The bottom panels of Fig. 2 show two examples of the decomposition with AGD. NVSS J174713−192135 is one of the brightest sources in our sample with στ = 0.02 and NVSS J175548−233322 is an average source with στ = 0.14. The black line shows the observed spectra (Gaussian-smoothed), the green line is the fitted model, and the red dashed lines are the individual e−τ(|$v$|) components. We also show the GASS H i emission spectra and the interpolated (TOFF) spectra in the upper panel of Fig. 2. All decomposed spectra are presented in Appendix D.
3.3 Interpolating the H i emission data
The strong HISA feature and the complicated structure of the H i emission towards the GC makes it difficult to determine the 'off-source' brightness temperature (TOFF). To overcome this, we fitted the GASS and the SGPS GC spectra with a combination of negative and positive Gaussian components, which we identify with AGD.
We trained the algorithm to fit the H i emission data of GASS and SGPS. For the training, we constructed spectra with the following parameters: 1000 spectra, with 5–15 Gaussian components each, a varying RMS level, amplitude between 100 and 1000 times the RMS level, and FWHM randomly distributed between 4 and 50 channels. The resulting α1 and α2 parameters are 9.01 and 5.39. We determine the position and width of the HISA feature based on the second derivative of the spectra and mask the absorption. Then we fit the emission and the HISA feature separately with gausspy and use the fitted components as the initial guess parameters for a composite model, which we fit to the GASS and SGPS GC spectra. We extract the positive emission components from the final fitted model and combine them into TOFF. Fig. 4 illustrates this method with the H i emission spectrum towards NVSS J173203−285516, where the pink line shows the composite model, the red and blue dashed lines show the individual emission and absorption components, and the green line is the reconstructed TOFF spectrum. The observed spectrum is under the pink line in black and the residuals of the fit are shown in grey.
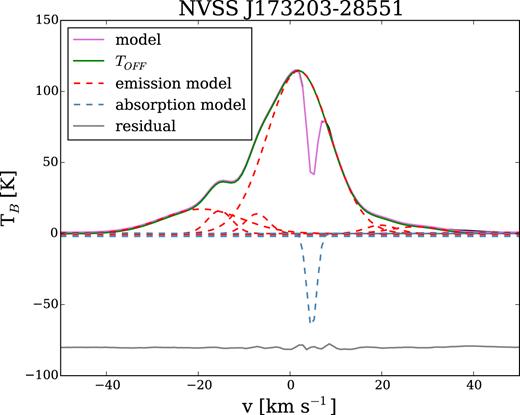
An example GASS spectra towards NVSS J173203−285516 (black). The modelled spectra are shown with a pink line. The interpolated TOFF is shown with a solid green line and the individual Gaussian components of our model are shown with dashed lines, red for emission and blue for absorption. The residual between the GASS spectra and our model is shown in grey.
This method gives a reasonable TOFF model for most LOS. We estimate the uncertainty of the fitted model by comparing the maximum of the emission spectra and the maximum of the TOFF model. This is a conservative approach that gives TOFF errors on the order of 10 K. The average TOFF uncertainty for GASS data is 8 K and for SGPS GC is 13 K.
4 RESULTS
4.1 Optical depth
Inspecting the H i absorption spectra, we find that all LOS have multiple blended absorption components (See Fig. 2 and Appendix D). To disentangle which absorption components belong to the R–C cloud, we decompose the absorption spectra using our hybrid fitting method. We find between 1 and 12 components for the individual LOS, with an average of 6 components. Altogether, we find 300 Gaussian components for 46 LOS. From these, 85 have τ > 1.
We select the components associated with the R–C cloud based on the following criteria: 2 < |$v$|LSR < 10 km s−1 and FWHM <10 km s−1, assuming that all the components of the cloud are relatively cold with narrow line widths. Based on this, 67 Gaussian components are associated with the R–C cloud. Of these, 53 have τHISA > 0.5 and 43 have τHISA > 1. In Fig. 2, we show two typical absorption spectra, with the fitted model (green) and the individual fitted components (red). For comparison, we also plot the H i emission spectra from GASS with the TOFF model (green dashed line) and the individual Gaussian components (red dashed lines). We present all of the spectra with the fitted models in Appendix D.
We present the Gaussian parameters of the decomposition in Table 2 and in Fig. 5. We note that Table 2 only contains the Gaussian parameters of components associated with the R–C cloud. Some of our low signal-to-noise spectra do not have components matching the criteria and so not all sources from Table 1 have components in Table 2. Fig. 5 shows the distribution of all Gaussian parameters – position, optical depth, FWHM – of the whole sample in grey and the line parameters associated with the R–C cloud (0 < |$v$|LSR < 10 km s−1, FWHM <10 km s−1) in black hatched.
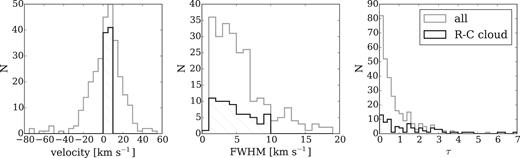
Parameters of the fitted Gaussian components of the H i absorption spectra: velocity of the components, FWHM and derived optical depth. All components of the sample are shown in the grey histogram and the R–C cloud components are highlighted in the black hatched histogram.
Line parameters from the Gaussian decomposition associated with the R–C cloud (0 < |$v$|LSR < 10 km s−1, FWHM <10 km s−1) and calculated Tk,max, Ts, and N(H i). See full version in Appendix C.
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | – ± – | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | – ± – | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
Line parameters from the Gaussian decomposition associated with the R–C cloud (0 < |$v$|LSR < 10 km s−1, FWHM <10 km s−1) and calculated Tk,max, Ts, and N(H i). See full version in Appendix C.
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | – ± – | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | – ± – | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
Fig. 6 shows the optical depth distribution across the R–C cloud overplotted on the GASS and SGPS GC H i intensity maps. The symbol sizes are colour coded and scaled with the optical depth from each Gaussian component. Some LOS have multiple Gaussian components associated with the cloud, indicating internal sub-structure. Montgomery et al. (1995) found that the R–C cloud has two main components at |$v$|LSR = 5 and |$v$|LSR = 7 km s−1. We also find that several sightlines have more than one component associated with the R–C cloud. We find most components at 5 km s−1 and do not see a peak in the distribution at 7 km s−1. This may be due to the fact that we are only sampling 46 LOS across the whole cloud.

GASS (left, |$v$| = 5.2 km s−1) and SGPS GC (right, |$v$| = 5.7 km s−1) H i intensity maps of the R–C cloud. The circles show the position of the observed continuum background sources scaled and coloured by the optical depth. Most LOS have two Gaussian components between 0 < |$v$| < 10 km s−1and FWHM < 10 km s−1.
4.2 Spin temperature and column density
We derive Ts using equation (4) in two different ways. (i) We calculate Ts,HISA for the individual Gaussian components of the absorption spectra in the range of the R–C cloud (0 < |$v$|LSR < 10 km s−1, FWHM < 10km s−1) and (ii) we calculate Ts at the minimum point of the HISA feature (Ts,HISA,peak). The difference between the two approaches is that the first method estimates the temperature for different velocity components, while the second method derives a single harmonic mean temperature at the given position. We consider the second method a better representation of Ts because it does not depend on the uncertainties of the Gaussian decomposition. Fig. 7 compares the distribution of Ts,HISA,peak for the GASS (blue) and SGPS GC (red) data. Both histograms peak at 50 K, but the SGPS GC data have a longer tail towards warmer temperatures. This is due to a systematic offset in brightness temperature between the two surveys, which we will discuss further in Section 4.3.
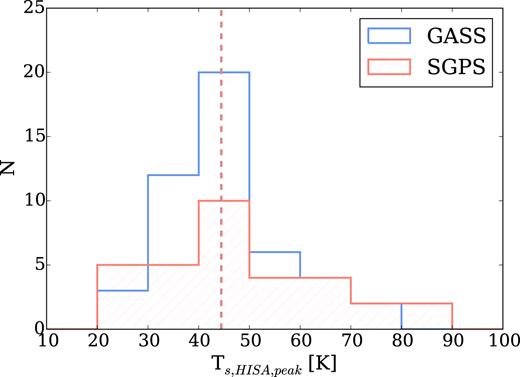
Distribution of Ts,HISA,peak. The blue histogram shows temperatures calculated with the GASS data and the red histogram shows temperatures calculated with the SGPS data. The dashed lines show the median values.
We find that Ts,HISA,peak varies across the cloud between 20 and 80K, with a median Ts,HISA,peak of 48 ± 7 K for GASS and 64 ± 9 K for SGPS GC. This is slightly higher compared to previous studies which found temperatures around ∼40 K (Crutcher & Lien 1984; Montgomery et al. 1995; McClure-Griffiths et al. 2006). The range of spin temperatures is also slightly larger compared to the ones estimated by McClure-Griffiths et al. (2006), who found temperatures between 30 and 65K. However, we directly measure the optical depth with the ATCA H i absorption spectra, which make our results better constrained compared to previous studies.
In Fig. 8, we show the distribution of Ts with Galactic latitude. We mark Ts,HISA from GASS with blue circles and Ts,HISA from SGPS GC with red triangles (see also Table 2). We find an offset between the GASS and the SGPS GC results, with systematically lower temperatures based on the GASS data. We mark Ts,HISA,peak from the GASS data with magenta squares (see also Table 3). For this method we only show the GASS data because it has better brightness-temperature sensitivity compared to SGPS GC. For comparison, we also included the brightness temperature of the GASS data at the minimum point of the HISA (black triangles), which is an upper limit on the spin temperature of the cold gas. We note that in some cases Ts,HISA,peak has a lower temperature compared to Ts,HISA. This is because several LOS have two separate Gaussian components associated with the R–C cloud and in some cases the Gaussian decomposition underestimates the optical depth. We discuss this further in Section 4.3. The coloured lines in Fig. 8 are linear fits to the data, showing the trend of decreasing Ts towards higher Galactic latitudes. This temperature gradient is steepest for Ts,HISA derived for individual Gaussian components; however, it also has the largest scatter and a Pearson’s r of −0.5 (for the GASS data). The temperature gradient is present in all the data and Ts,HISA,peak and Ts,max show a slightly stronger correlation with a Pearson’s r of −0.6.
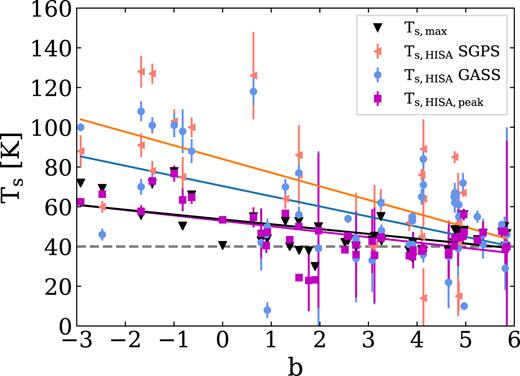
Spin temperatures as a function of Galactic latitude. Blue circles show Ts calculated with GASS data and red triangles show Ts calculated with SGPS GC data. The black triangles show TB at the tip of the HISA in the GASS data for each LOS, which are lower limits for Ts. The purple squares are Ts,HISA,peak calculated at the tip of the HISA for each LOS. The coloured lines are linear fits to the data to show the decrease of Ts towards higher Galactic latitudes.
Ts calculated at the minimum point (|$v$|min, Tmin) of the HISA feature in the H i emission spectra for both GASS and SGPS data. See full table in Appendix C.
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
Ts calculated at the minimum point (|$v$|min, Tmin) of the HISA feature in the H i emission spectra for both GASS and SGPS data. See full table in Appendix C.
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
In Fig. 9, we show the temperature distribution (Ts,HISA,peak) with colour-coded circles overplotted on the H i intensity map from GASS and SGPS GC. The temperature gradient is also evident here, with temperatures decreasing towards higher latitudes in the cloud. The coldest temperatures are between 6° < l < 9°, 1° < b < 3° (30 and 50K) and warmer temperatures are in the filamentary tip of the cloud (50–80 K).
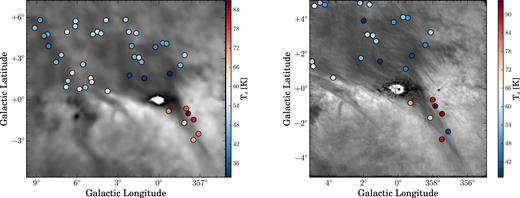
Ts,HISA,peak for each LOS overplotted on the H i intensity map of the R–C cloud (|$v$| = 5.2 and 5.7 km s−1 for the GASS and the SGPS GC, respectively). The left side shows Ts,HISA,peak calculated from GASS data, the right side Ts,HISA,peak calculated from SGPS GC data.
We find an average column density of 11.1 ± 0.2 × 1020 cm−2 for GASS and 15.3 ± 0.3 × 1020 cm−2 for SGPS GC, which is higher than the 2 ± 1.4 × 1020 cm−2 found by McClure-Griffiths et al. (2006). The reason for the difference is that we have more accurate measurements of the optical depth for this study. McClure-Griffiths et al. (2006) assumed Ts = 40 K for the whole cloud, which resulted in τ ∼ 2.5. In contrast to that approach, we use optical depths derived from the Gaussian decomposition and spin temperatures (Ts,HISA GASS) ranging between 10 and 120 K. Furthermore, McClure-Griffiths et al. (2006) found that the positive-latitude region of the cloud has higher N(H i), which we do not see in our data (Fig. 10). This is due to the fact that McClure-Griffiths et al. (2006) assumed a constant spin temperature throughout the cloud, where we find that the spin temperature decreases towards positive latitudes.
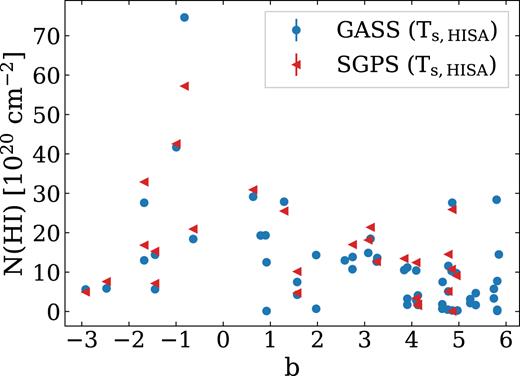
H i column density as a function of Galactic latitude. The blue circles show N(H i) calculated from Ts,HISA GASS and the red circles show N(H I) calculated from Ts,HISA SGPS GC.
4.3 Sources of uncertainty and errors
We take the following sources of uncertainties into account when calculating the spin temperature:
The RMS noise of the observations. This is the smallest source of uncertainty for Ts.
Errors in estimating TOFF. We estimate the uncertainty by comparing the maximum of the emission spectra and the maximum of the TOFF model. This is a conservative approach that gives errors on the order of 10 K.
The errors of the line parameters in Table 2 (τHISA, |$v$|LSR, FWHM) are based on the errors calculated by gausspy, the errors on Ts and N(H i) are propagated errors.
Additional sources of uncertainty are as follows:
H i emission fluctuations on a small scale can introduce errors because the spatial scale probed by the H i emission data (16 arcmin) is much larger compared to the H i absorption data (∼60 arcsec). To investigate this issue, we compared Ts for the closest absorption pair in our sample (NVSS J174713−19213 and NVSS J174716−19195), separated by 1.7 arcmin, and found that the derived spin temperatures (Ts,HISA,peak) agree well (42 ± 14 K and 43 ± 17 K). This suggests that our data are not too sensitive to arcminute scale variations.
Comparing Ts,HISA,peak derived with SGPS GC and GASS data, we find that SGPS GC gives on average 6 K higher temperatures. This is due to the 1.2 scaling factor between GASS and SGPS GC. Since SGPS GC data are a combination of interferometric and single-dish data, the single-dish TB needs to be scaled to match the interferometric data. Because of this, and the fact that the GASS data have better brightness sensitivity, we use the results from the GASS data to derive our main conclusions.
The fraction of the foreground H i emission compared to the background H i emission (p) can introduce some errors. Allowing a 10 per cent variation in p gives a 10 K uncertainty for Ts.
- If τbg is not negligible, the spin temperature is calculated the following way:τbg only appears in the term for the diffuse continuum emission. If τbg varies between 0.1 and 1, Ts can decrease by 0.5 to 10 K.(8)\begin{equation*} T_{\mathrm{ s}} = \frac{ T_{\mathrm{ ON}} - T_{\mathrm{ OFF}}}{1-e^{-\tau _{\mathrm{ HISA}}}} + T_{\mathrm{ c}}e^{-\tau _{\mathrm{ bg}}} + pT_{\mathrm{ OFF}}. \end{equation*}
Spectral baseline errors are due to difficulties in data calibration. For the H i absorption data, the problem is the strong absorption line in the bandpass calibrator between 0 and 10 km s−1(see Appendix A). This bandpass uncertainty is negligible compared to the other sources of errors. For the H i emission data, the main difficulty is the strong continuum emission around the GC. The uncertainty from this is of the order of a few K.
Decomposing the H i absorption spectra has inherent uncertainty as there is no unique solution for decomposing spectra with multiple blended components. Because of the location of the R–C cloud, in the Galactic plane and in front of the GC, these data are especially susceptible. Murray et al. (2017) investigated the recovery rate of the AGD algorithm on simulated H i spectra. They found that AGD has a very good recovery rate for simple LOS, e.g. high-latitude spectra (99 per cent for |b| > 50°), performs well for moderately complex spectra (67 per cent for 20° < |b| < 50°), and accurately recovers 53 per cent of the components of complex, Galactic plane sources (4° < |b| < 20°). All our sources fall into the last category, which means that AGD recovers approximately 50 per cent of the underlying Gaussian distribution towards the R–C cloud. Considering the complexity of the spectra in this region and the sensitivity of our observations, this is a reasonable recovery rate. We find that in some cases AGD fits one broad Gaussian to spectra, which are likely composed of two or three components based on visual inspection. This means that AGD will underestimate the number of components and their optical depths. This would then lead to higher spin temperatures and kinetic temperatures. However, the advantage of AGD over other decomposition methods is that it does not require any subjective initial guesses and the decomposition allows us to compare our results with studies such as the Millennium (Heiles & Troland 2003a) and the Perseus (Stanimirović et al. 2014) survey data in a quantitative way. To avoid systematic bias from the line decomposition, we also calculate Ts without decomposing the spectra (Ts,HISA,peak) and consider these our most accurate temperatures for this region.
4.4 OH absorption lines
We detected four OH absorption line candidates at |$v$|LSR ∼ 3−7 km s−1 towards three sources: NVSS J172920−23453, NVSS J173850−22191, and NVSS J175526−22321 (FigsE1 and E2). We detect lines towards NVSS J172920−23453 in both frequencies, 1665 and 1667 MHz. Our detection criteria are τOH,max > 3σtau,OH, where τOH,max is the maximum of the OH optical depth spectra and σtau,OH is the optical depth sensitivity. Typical τOH are much smaller than τHI (e.g. Colgan, Salpeter, & Terzian 1989; Liszt & Lucas 1996; Li et al. 2018). Liszt & Lucas (1996) found τOH between 0.006 and 0.27 for the 1667 MHz line, in regions where τH i was between 0.06 and 3.16. For our observations, στOH is between 0.01 and 0.6. We note that our OH detections are weak and would need follow up observations to better constrain the optical depth and the column density. To estimate the OH optical depth and column density, we fitted a single Gaussian to each spectrum. The fitted parameters are presented in Table 4. We found optical depths between 0.05 ± 0.01 and 0.23 ± 0.07, where the errors are based on the RMS of the spectra and the spectral resolution (0.26 km s−1).
Fitted Gaussian parameters to the OH lines. For calculating N(OH), we assume that Tex is between 3 and 20 K.
| Name . | l . | b . | Frequency . | Amplitude . | τ . | v . | FWHM . | N(OH) . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (MHz) . | . | . | (km s−1) . | (km s−1) . | (1014 cm−2) . |
| NVSS J172920−23453 | 2.43 | 5.85 | 1665 | 0.05 ± 0.01 | 0.05 ± 0.01 | 7.0 ± 0.3 | 1.5 ± 0.3 | 1.0–6.5 |
| NVSS J173850−22191 | 4.83 | 4.77 | 1665 | 0.23 ± 0.07 | 0.27 ± 0.07 | 3.9 ± 0.3 | 1.8 ± 0.3 | 6.4–42.8 |
| NVSS J172920−23453 | 2.43 | 5.85 | 1667 | 0.05 ± 0.01 | 0.05 ± 0.01 | 6.4 ± 0.3 | 2.7 ± 0.3 | 1.0–6.5 |
| NVSS J175526−22321 | 6.63 | 1.38 | 1667 | 0.11 ± 0.03 | 0.12 ± 0.03 | 7.7 ± 0.3 | 1.2 ± 0.3 | 1.1–7.1 |
| Name . | l . | b . | Frequency . | Amplitude . | τ . | v . | FWHM . | N(OH) . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (MHz) . | . | . | (km s−1) . | (km s−1) . | (1014 cm−2) . |
| NVSS J172920−23453 | 2.43 | 5.85 | 1665 | 0.05 ± 0.01 | 0.05 ± 0.01 | 7.0 ± 0.3 | 1.5 ± 0.3 | 1.0–6.5 |
| NVSS J173850−22191 | 4.83 | 4.77 | 1665 | 0.23 ± 0.07 | 0.27 ± 0.07 | 3.9 ± 0.3 | 1.8 ± 0.3 | 6.4–42.8 |
| NVSS J172920−23453 | 2.43 | 5.85 | 1667 | 0.05 ± 0.01 | 0.05 ± 0.01 | 6.4 ± 0.3 | 2.7 ± 0.3 | 1.0–6.5 |
| NVSS J175526−22321 | 6.63 | 1.38 | 1667 | 0.11 ± 0.03 | 0.12 ± 0.03 | 7.7 ± 0.3 | 1.2 ± 0.3 | 1.1–7.1 |
Fitted Gaussian parameters to the OH lines. For calculating N(OH), we assume that Tex is between 3 and 20 K.
| Name . | l . | b . | Frequency . | Amplitude . | τ . | v . | FWHM . | N(OH) . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (MHz) . | . | . | (km s−1) . | (km s−1) . | (1014 cm−2) . |
| NVSS J172920−23453 | 2.43 | 5.85 | 1665 | 0.05 ± 0.01 | 0.05 ± 0.01 | 7.0 ± 0.3 | 1.5 ± 0.3 | 1.0–6.5 |
| NVSS J173850−22191 | 4.83 | 4.77 | 1665 | 0.23 ± 0.07 | 0.27 ± 0.07 | 3.9 ± 0.3 | 1.8 ± 0.3 | 6.4–42.8 |
| NVSS J172920−23453 | 2.43 | 5.85 | 1667 | 0.05 ± 0.01 | 0.05 ± 0.01 | 6.4 ± 0.3 | 2.7 ± 0.3 | 1.0–6.5 |
| NVSS J175526−22321 | 6.63 | 1.38 | 1667 | 0.11 ± 0.03 | 0.12 ± 0.03 | 7.7 ± 0.3 | 1.2 ± 0.3 | 1.1–7.1 |
| Name . | l . | b . | Frequency . | Amplitude . | τ . | v . | FWHM . | N(OH) . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (MHz) . | . | . | (km s−1) . | (km s−1) . | (1014 cm−2) . |
| NVSS J172920−23453 | 2.43 | 5.85 | 1665 | 0.05 ± 0.01 | 0.05 ± 0.01 | 7.0 ± 0.3 | 1.5 ± 0.3 | 1.0–6.5 |
| NVSS J173850−22191 | 4.83 | 4.77 | 1665 | 0.23 ± 0.07 | 0.27 ± 0.07 | 3.9 ± 0.3 | 1.8 ± 0.3 | 6.4–42.8 |
| NVSS J172920−23453 | 2.43 | 5.85 | 1667 | 0.05 ± 0.01 | 0.05 ± 0.01 | 6.4 ± 0.3 | 2.7 ± 0.3 | 1.0–6.5 |
| NVSS J175526−22321 | 6.63 | 1.38 | 1667 | 0.11 ± 0.03 | 0.12 ± 0.03 | 7.7 ± 0.3 | 1.2 ± 0.3 | 1.1–7.1 |
In addition, we detected two un-associated OH absorption lines in two different LOS at |$v$| ∼ 50 km s−1 and |$v$| ∼ 160 km s−1. We also detected an OH maser in the field of view of NVSS J174513−31510 at 1667 MHz.
5 DISCUSSION
The R–C cloud is a cold H i structure at the edge of the Local Bubble. According to theories of its formation (e.g. Weaver 1979; Heiles 1998), a collection of massive stars and supernovae swept out the material from the Local Bubble and stretched the magnetic field along the wall of the cavity. The cold material swept up at the edge of the bubble ended up entrained in the strong magnetic field of the wall and produced the filamentary structure that was observed by McClure-Griffiths et al. (2006). Since HISA clouds are theorized to be transitional clouds between purely atomic and molecular clouds, the R–C cloud may also be a location where the ISM is transitioning from an atomic to a molecular phase. In this section, we discuss the presence of associated molecular gas and compare our results with the literature.
5.1 Associated molecular gas
Kavars et al. (2005) found that 60 per cent of HISA clouds in the SGPS have associated molecular gas. The R–C cloud is one of the largest HISA complexes in the Galaxy and as our results show, it has a substantial amount of high-optical-depth (τ > 1) cold gas. Furthermore, our results in Figs 8 and 9 reveal a temperature gradient across the cloud, varying from ∼30 K in the upper left of the cloud (base) to almost 80 K at the lower right (tip) of the cloud. This might suggest that the presence or absence of molecular gas would correlate with the temperature variations, with molecular gas more likely at the base of the cloud than at the tip. Indeed, the R–C cloud has a significant amount of associated OH and 12CO gas. Crutcher (1973) found several OH absorption lines across the cloud, indicating the presence of substantial molecular gas. This is further supported by detected 12CO emission at l ∼ 5°, b ∼ 6°, |$v$| ∼ 5 km s−1(Dame et al. 2001).
Fig. 11 shows the integrated 12CO intensity4 between 2.6 < |$v$|LSR < 7.8 km s−1 overlaid on the GASS H i intensity map. We also marked the location of the OH lines detected by Crutcher (1973) with pink diamonds, our OH line candidates with pink crosses, and the detected CRRL lines with green triangles (Roshi & Kantharia 2011). For reference, we also plot Ts,HISA,peak as red and blue circles. Fig. 11 shows significant 12CO emission in the Galactic plane, which is expected, and it also shows an elongated feature across the base of the cloud. The OH detections from Crutcher (1973) and our strongest OH line candidate (NVSS J172920−23453 at l, b = 2.43°, 5.85°) overlap with the 12CO emission.

GASS H i intensity map of the R–C cloud (|$v$|LSR = 5.2). White contours show the integrated 12CO intensity between 2.6 and 7.8 km s−1 (Dame et al. 2001). Contour levels are 2, 4, 8, 16, 32 K km s−1. The pink diamonds show OH lines detected by Crutcher (1973) and the pink crosses show our OH line detections, the green triangles show the CRRL lines from Roshi & Kantharia (2011). The red and blue circles show the measured spin temperatures (Ts,HISA,peak) for reference.
The Southern Parkes Large-Area Survey (SPLASH; Dawson et al. 2014) has detected significant OH emission and absorption throughout the R–C cloud. The SPLASH survey covers the same region of the R–C cloud that is covered by the SGPS GC cube (b ∼ 5°). Approximately 30 per cent of the LOS we observed have OH lines associated with the R–C cloud in the SPLASH data. These lines mostly overlap with the 12CO emission. One of our OH absorption line candidates (NVSS J175526−22321; l, b = 6.63°, 1.38°) overlaps with the SPLASH data, which confirms our detection. We will further discuss the SPLASH OH detections for this region in an upcoming publication.
Assuming that the R–C cloud was formed by the Local Bubble pushing out and piling up the H i in a sheet-like structure, which we observe as an H i self-absorption cloud, makes it a plausible site for triggered molecular cloud formation similar to the edges of other supershells (e.g. Fukui & Kawamura 2010; Dawson et al. 2011; Ehlerová & Palouš 2016; Dawson 2013 and references within).
5.2 Comparison to the literature
In this section, we briefly compare our results with Galactic H i absorption data sets from the Millenium survey (Heiles & Troland 2003a, b) and the Perseus (Stanimirović et al. 2014) molecular cloud. Fig. 12 compares the optical depth and the maximum kinetic temperature (Tk,max) of our sample (grey, including all Gaussian components from the decomposition) with data from the Millenium survey (red) and data from around the Perseus molecular cloud (blue). The Millennium survey consists of 79 continuum sources mostly towards high Galactic latitudes observed with the Arecibo telescope (for details see Heiles & Troland 2003a). The Perseus sample has 26 continuum sources distributed around the molecular cloud observed with Arecibo (Stanimirović et al. 2014). Both surveys have an optical depth sensitivity of 0.002 per 1 km s−1 channel. The Perseus sample is similar to our sample in the sense that it is also probing a region that is expected to have a significant amount of cold ISM, whereas the Millennium survey does not have a specific target region. This gives us the opportunity to compare the cold gas fraction of a HISA cloud, where atomic gas may be transitioning into molecular gas, to a molecular cloud, where this transition already happened, and to the general distribution of the ISM.
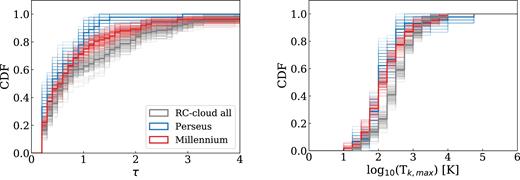
Comparison of optical depth and maximum kinetic temperature (Tk,max) with data from the Millennium survey (red) and the Perseus molecular cloud (blue). To illustrate the uncertainties of the distributions, we plot 100 bootstrap samples for each data set as lighter-shaded lines.
Considering that we had a different observing strategy compared to the Millennium and the Perseus surveys, our data have a much poorer optical depth sensitivity 0.01 < στ < 0.66 per 0.2 km s−1 channel. To fairly compare our data to the literature, we only include Gaussian components in Figs 12 and 13 which have τ > 0.2 and στ < 0.2. The optical depth cumulative density function (CDF) in Fig. 12 shows that we detect more components with high optical depths, especially compared to Perseus. The highest optical depth around Perseus is 2.9, whereas for our sample and for Millennium τmax ∼ 7.

CDF for Ts,HISA,peak (black) and Ts (green). Data from the Perseus molecular cloud and the Millennium survey are in red and blue for comparison. To illustrate the uncertainties of the distributions, we plot 100 bootstrap samples for each data set as lighter-shaded lines.
We find that overall the R–C cloud has a much narrower spin temperature range and a significantly lower median spin temperature (44 K for Ts,HISA,peak and 49 K for Ts,HISA based on GASS data), compared to the median Ts found in the Millennium survey (114 K) and in Perseus (115 K). However, if we only include components from Millenium and Perseus with τ > 0.2 (Fig. 13) in our comparison, we find that the Ts distribution of all three samples is very similar. With this cut, the median spin temperature of the Millennium survey is 42 K and the Perseus survey is 44 K.
If we compare our results to other HISA measurements, the R–C cloud seems relatively 'warm'. Gibson et al. (2000) find that Ts for HISA clouds in the CGPS is between 7 and 20 K and Kavars et al. (2005) find Ts ranging between 6 and 41 K for HISA clouds in the SGPS survey. Kavars et al. (2003) analysed a HISA cloud in detail from the SGPS survey and found Ts between 20 and 25 K and also found associated 12CO with the cloud. These values are lower than the R–C cloud Ts,HISA,peak range of 20–80K. There can be several reasons for this difference. One of the biggest uncertainties is the assumed fraction of foreground H i emission. A 10 per cent difference in the foreground can result in a ∼10 K temperature difference. Typical assumptions on the foreground are 25–50 per cent. In the case of the R–C cloud, we know that the cloud is approximately at the edge of the Local Bubble and that there should not be much gas in the foreground. For this reason, we assume a 10 per cent foreground fraction for all our calculations. Another key difference is that we have better constraints on the optical depth with 46 LOS where we directly measure τ which we use to 'calibrate' the HISA spin temperature. Kavars et al. (2003) found a likely range of τ between 0.06 and 2.3, whereas we measure τ between 0.09 and 6.8. The temperature and optical depth difference could also indicate that the two clouds are at different evolutionary stages.
It has been suggested that the R–C cloud may be the wall of the Local Bubble (e.g. Weaver 1979; Heiles 1998), which makes it a similar structure to the walls of Galactic supershells. HISA features with high optical depths (τ > 1) and low spin temperatures (10–40 K) were also observed in the walls of Galactic supershells (e.g. Knee & Brunt 2001; Moss et al. 2012), providing further support to the idea that the R–C cloud could be part of the wall of the Local Bubble.
Our Ts,HISA,peak temperatures are in agreement with the results found by Roshi & Kantharia (2011), who derived an electron temperature between 40 and 60 K for the R–C cloud from CRRLs. If we assume that the CII gas is co-located with the H i, then the electron temperature should be the same as the spin temperature. We find very similar temperatures (∼50 K) close to the region where the CRRLs were measured (see Figs 9 and 11).
6 SUMMARY AND CONCLUSIONS
HISA clouds are ideal places to study the cold neutral component of the ISM. They are common across the Galaxy, and abundantly detected in large-scale H i surveys such as GASS (McClure-Griffiths et al. 2006), CGPS (Gibson et al. 2000, 2005), and SGPS (Kavars et al. 2003, 2005). These surveys provide data to study the location and spatial structure of these clouds. However, determining the physical properties of the cold gas, such as the optical depth, spin temperature and column density, is uncertain. Here we present a method to calibrate the HISA spin temperature by directly measuring the optical depth with H i absorption measurements against continuum sources.
We present new high-resolution H i absorption observations with the ATCA towards 46 LOS across the Riegel–Crutcher cloud. We use the AGD algorithm (Lindner et al. 2015) to decompose the strongly blended H i absorption spectra towards the R–C cloud and find overall 300 Gaussian components, from which 67 are associated with the R–C cloud (0 < |$v$|LSR < 10 km s−1, FWHM <10 km s−1). We find high optical depths (τ > 1) throughout the cloud.
We calculate spin temperatures for the cloud for the individual Gaussian components (Ts,HISA) and for the peak of the HISA feature (Ts,HISA,peak) by using a four-component ISM model. For Ts,HISA,peak, we find temperatures ranging from 20 to 80 K with a median of 48 ± 7 K for GASS and 64 ± 9 K for SGPS GC. These median temperatures are higher compared to the estimated 40 K in previous studies (Crutcher & Lien 1984; Montgomery et al. 1995; McClure-Griffiths et al. 2006). However, our estimates should be more accurate given the direct measurements of the optical depth. We find a clear temperature gradient across the R–C cloud. The spin temperature is decreasing towards the high-latitude base of the R–C cloud.
We compared our spin temperature results from the Gaussian decomposition and the Ts calculations to results from the Millennium Survey (Heiles & Troland 2003a) and the Perseus molecular cloud (Stanimirović et al. 2014). The R–C cloud seems to have more high-optical-depth components, with slightly broader line widths. We also found that if we take the sensitivity limitations of our survey into account, then the spin temperature distribution of the three samples is very similar.
There is evidence for associated molecular gas with the R–C cloud. Crutcher (1973) found OH absorption in the region and Dame et al. (2001) detected 12CO emission across the high latitude part of the cloud. We add to the detected molecular gas with four new OH absorption lines.
We are planning to use the method presented in this paper in future Galactic H i absorption surveys and map the Ts distribution across a large range of H i self-absorption clouds. One such upcoming survey is the Galactic Australian SKA Pathfinder Survey (GASKAP; Dickey et al. 2013) with the Australian Square Kilometre Array Pathfinder (ASKAP). GASKAP will map the plane of the Milky Way and the Magellanic system in H i and OH lines in high-spatial and high-frequency resolution. It will provide H i absorption measurements against hundreds of continuum sources.
ACKNOWLEDGEMENTS
We would like to thank the anonymous referee for the useful comments and suggestions, which helped us to greatly improve the paper. The Australia Telescope Compact Array and the Parkes telescope are part of the Australia Telescope National Facility, which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. N.M.-G. acknowledges the support of the Australian Research Council through Future Fellowship FT150100024. We thank Patrick Jacobson for his help in the original planning for this project. This research made use of astropy, a community-developed core python package for Astronomy (Astropy Collaboration 2013, http://www.astropy.org).
Footnotes
The 3 MHz wide zoom band consists of five concatenated 1 MHz zoom bands, each with 2048 channels overlapped by 50 per cent to obtain a flat bandpass.
The 2 MHz wide zoom band consists of three concatenated 1 MHz zoom bands, each with 2048 channels overlapped by 50 per cent to obtain a flat bandpass.
REFERENCES
APPENDIX A: PKS 1934−638
PKS 1934−638 is the main source used for ATCA 16 cm bandpass calibration. However, PKS 1934−638 has a strong absorption line between 0 and 10 km s−1, which is exactly the velocity range where the R–C cloud is located. In addition to the well-known absorption line, there are also absorption features between −15 and 0 km s−1. Fig. A1 shows the optical depth spectrum of PKS 1934−638 (total integration time: 15.44 h, στ = 8 × 10−4 per 0.1 km s−1 per channel). We decomposed the optical depth spectra of PKS 1934−638 with gausspy following Lindner et al. (2015) (α1 = 1.12 and α2 = 2.73). We present the results of the decomposition in Table A1 and Fig. A1.
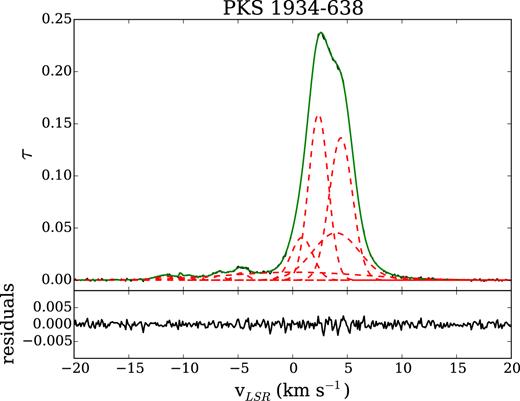
Optical depth spectrum of PKS 1934−638 (total integration time: 15.44 h, στ = 8 × 10−4 per 0.1 km s−1 per channel). Red dashed lines show the Gaussian components found by gausspy and the green line shows the fitted model to the data.
Line parameters from the Gaussian decomposition for PKS 1934−638 (l, b = 332.7461°, −29.3893°) and calculated Tk,max.
| τ . | |$v$|LSR . | FWHM . | Tk,max . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | (K) . |
| 0.16 ± 0.014 | 2.36 ± 0.07 | 2.1 ± 0.09 | 96.53 ± 0.17 |
| 0.137 ± 0.016 | 4.41 ± 0.06 | 2.49 ± 0.09 | 135.27 ± 0.19 |
| 0.044 ± 0.019 | 4.05 ± 0.75 | 4.96 ± 0.48 | 537.1 ± 4.97 |
| 0.043 ± 0.025 | 0.87 ± 0.44 | 2.36 ± 0.47 | 122.12 ± 4.89 |
| 0.008 ± 0.001 | 0.37 ± 0.39 | 14.52 ± 0.69 | 4610.19 ± 10.36 |
| 0.007 ± 0.001 | −4.73 ± 0.04 | 1.42 ± 0.14 | 44.06 ± 0.44 |
| 0.004 ± 0.001 | −6.74 ± 0.06 | 1.18 ± 0.19 | 30.38 ± 0.77 |
| 0.004 ± 0.001 | −11.64 ± 0.08 | 1.9 ± 0.23 | 79.35 ± 1.2 |
| 0.003 ± 0.001 | −10.26 ± 0.03 | 0.28 ± 0.08 | 1.7 ± 0.15 |
| 0.002 ± 0.001 | −8.2 ± 0.05 | 0.21 ± 0.13 | 1.01 ± 0.35 |
| 0.001 ± 0.001 | −5.8 ± 0.1 | 0.35 ± 0.26 | 2.72 ± 1.52 |
| τ . | |$v$|LSR . | FWHM . | Tk,max . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | (K) . |
| 0.16 ± 0.014 | 2.36 ± 0.07 | 2.1 ± 0.09 | 96.53 ± 0.17 |
| 0.137 ± 0.016 | 4.41 ± 0.06 | 2.49 ± 0.09 | 135.27 ± 0.19 |
| 0.044 ± 0.019 | 4.05 ± 0.75 | 4.96 ± 0.48 | 537.1 ± 4.97 |
| 0.043 ± 0.025 | 0.87 ± 0.44 | 2.36 ± 0.47 | 122.12 ± 4.89 |
| 0.008 ± 0.001 | 0.37 ± 0.39 | 14.52 ± 0.69 | 4610.19 ± 10.36 |
| 0.007 ± 0.001 | −4.73 ± 0.04 | 1.42 ± 0.14 | 44.06 ± 0.44 |
| 0.004 ± 0.001 | −6.74 ± 0.06 | 1.18 ± 0.19 | 30.38 ± 0.77 |
| 0.004 ± 0.001 | −11.64 ± 0.08 | 1.9 ± 0.23 | 79.35 ± 1.2 |
| 0.003 ± 0.001 | −10.26 ± 0.03 | 0.28 ± 0.08 | 1.7 ± 0.15 |
| 0.002 ± 0.001 | −8.2 ± 0.05 | 0.21 ± 0.13 | 1.01 ± 0.35 |
| 0.001 ± 0.001 | −5.8 ± 0.1 | 0.35 ± 0.26 | 2.72 ± 1.52 |
Line parameters from the Gaussian decomposition for PKS 1934−638 (l, b = 332.7461°, −29.3893°) and calculated Tk,max.
| τ . | |$v$|LSR . | FWHM . | Tk,max . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | (K) . |
| 0.16 ± 0.014 | 2.36 ± 0.07 | 2.1 ± 0.09 | 96.53 ± 0.17 |
| 0.137 ± 0.016 | 4.41 ± 0.06 | 2.49 ± 0.09 | 135.27 ± 0.19 |
| 0.044 ± 0.019 | 4.05 ± 0.75 | 4.96 ± 0.48 | 537.1 ± 4.97 |
| 0.043 ± 0.025 | 0.87 ± 0.44 | 2.36 ± 0.47 | 122.12 ± 4.89 |
| 0.008 ± 0.001 | 0.37 ± 0.39 | 14.52 ± 0.69 | 4610.19 ± 10.36 |
| 0.007 ± 0.001 | −4.73 ± 0.04 | 1.42 ± 0.14 | 44.06 ± 0.44 |
| 0.004 ± 0.001 | −6.74 ± 0.06 | 1.18 ± 0.19 | 30.38 ± 0.77 |
| 0.004 ± 0.001 | −11.64 ± 0.08 | 1.9 ± 0.23 | 79.35 ± 1.2 |
| 0.003 ± 0.001 | −10.26 ± 0.03 | 0.28 ± 0.08 | 1.7 ± 0.15 |
| 0.002 ± 0.001 | −8.2 ± 0.05 | 0.21 ± 0.13 | 1.01 ± 0.35 |
| 0.001 ± 0.001 | −5.8 ± 0.1 | 0.35 ± 0.26 | 2.72 ± 1.52 |
| τ . | |$v$|LSR . | FWHM . | Tk,max . |
|---|---|---|---|
| . | (km s−1) . | (km s−1) . | (K) . |
| 0.16 ± 0.014 | 2.36 ± 0.07 | 2.1 ± 0.09 | 96.53 ± 0.17 |
| 0.137 ± 0.016 | 4.41 ± 0.06 | 2.49 ± 0.09 | 135.27 ± 0.19 |
| 0.044 ± 0.019 | 4.05 ± 0.75 | 4.96 ± 0.48 | 537.1 ± 4.97 |
| 0.043 ± 0.025 | 0.87 ± 0.44 | 2.36 ± 0.47 | 122.12 ± 4.89 |
| 0.008 ± 0.001 | 0.37 ± 0.39 | 14.52 ± 0.69 | 4610.19 ± 10.36 |
| 0.007 ± 0.001 | −4.73 ± 0.04 | 1.42 ± 0.14 | 44.06 ± 0.44 |
| 0.004 ± 0.001 | −6.74 ± 0.06 | 1.18 ± 0.19 | 30.38 ± 0.77 |
| 0.004 ± 0.001 | −11.64 ± 0.08 | 1.9 ± 0.23 | 79.35 ± 1.2 |
| 0.003 ± 0.001 | −10.26 ± 0.03 | 0.28 ± 0.08 | 1.7 ± 0.15 |
| 0.002 ± 0.001 | −8.2 ± 0.05 | 0.21 ± 0.13 | 1.01 ± 0.35 |
| 0.001 ± 0.001 | −5.8 ± 0.1 | 0.35 ± 0.26 | 2.72 ± 1.52 |
APPENDIX B: DIFFUSE CONTINUUM EMISSION
Fig. B1 shows the distribution of the diffuse continuum emission (Tc) extracted from CHIPASS at the positions of our sources. Except for one source, all Tc values range between 5 and 15 K. Fig.B2 displays the distribution of Tc overlayed on the GASS H i intensity map. Tc smoothly decreases with distance from the Galactic plain and the highest Tc (22 K) is at the closest position to theGC.
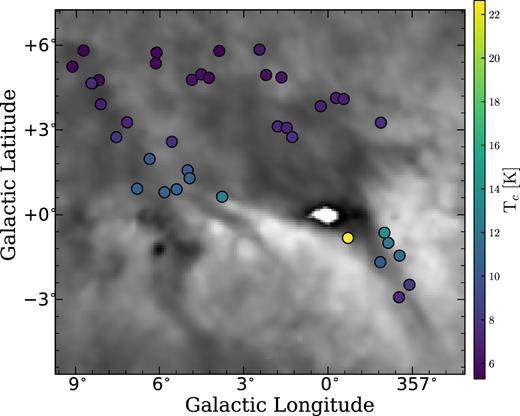
Tc distribution overlayed on the GASS H i intensity map (|$v$|LSR = 5.2) of the R–C cloud. Tc decreases with Galactic latitude and all LOS with |b| > 2° have Tc < 8K.
APPENDIX C: TABLES
Line parameters from the Gaussian decomposition in the velocity range of the R–C cloud (0 < |$v$|LSR < 10 km s−1) and calculated Tk,max, Ts, and N(H i).
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | - ± - | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
| NVSS J173107−245703 | 2.77 ± 0.26 | 2.9 ± 0.2 | 9.2 ± 0.2 | 1847 ± 1 | 55 ± 1 | 52 ± 1 | 27.62 ± 0.05 | 25.88 ± 0.05 |
| NVSS J173107−245703 | 0.12 ± 0.03 | 7.3 ± 0.2 | 1.9 ± 0.5 | 80 ± 6 | 61 ± 7 | 15 ± 7 | 0.28 ± 0.02 | 0.07 ± 0.01 |
| NVSS J173718−260426 | 2.71 ± 0.44 | 4.9 ± 0.7 | 8.5 ± 0.6 | 1564 ± 8 | 33 ± 16 | 40 ± 1 | 14.87 ± 0.17 | 18.14 ± 0.2 |
| NVSS J173252−223511 | 6.88 ± 0.75 | 4.3 ± 0.2 | 4.4 ± 0.2 | 416 ± 0 | 48 ± 7 | – ± – | 28.37 ± 0.1 | – ± – |
| NVSS J173722−223000 | 0.41 ± 0.04 | 4.4 ± 0.2 | 3.3 ± 0.3 | 245 ± 2 | 10 ± 1 | – ± – | 0.27 ± 0.1 | – ± – |
| NVSS J174618−193006 | 0.34 ± 0.12 | 1.0 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | 65 ± 1 | – ± – | 0.48 ± 0.05 | – ± – |
| NVSS J173713−224734 | 2.02 ± 0.35 | 4.9 ± 0.2 | 6.6 ± 0.3 | 966 ± 2 | 39 ± 14 | 41 ± 36 | 10.29 ± 0.08 | 10.72 ± 0.08 |
| NVSS J173850−221918 | 1.74 ± 0.33 | 2.5 ± 0.4 | 5.1 ± 0.4 | 560 ± 3 | 67 ± 4 | 85 ± 2 | 11.57 ± 0.17 | 14.52 ± 0.21 |
| NVSS J173850−221918 | 0.82 ± 0.21 | 7.7 ± 0.7 | 5.2 ± 0.6 | 581 ± 8 | 62 ± 4 | 62 ± 2 | 5.1 ± 0.16 | 5.11 ± 0.16 |
| NVSS J174713−192135 | 0.84 ± 0.69 | 4.8 ± 0.2 | 1.9 ± 0.2 | 78 ± 0 | 22 ± 13 | – ± – | 0.7 ± 0.04 | – ± – |
| NVSS J174713−192135 | 0.52 ± 0.36 | 7.6 ± 0.4 | 2.8 ± 0.6 | 168 ± 8 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174713−192135 | 0.33 ± 0.13 | 3.9 ± 2.2 | 7.8 ± 2.3 | 1328 ± 115 | 36 ± 13 | – ± – | 1.84 ± 0.22 | – ± – |
| NVSS J172829−284610 | 1.55 ± 0.01 | 6.6 ± 0.2 | 6.8 ± 0.2 | 1013 ± 0 | 62 ± 1 | 62 ± 6 | 12.67 ± 0.1 | 12.68 ± 0.01 |
| NVSS J172908−265751 | 0.57 ± 0.3 | 8.5 ± 0.2 | 2.1 ± 0.3 | 98 ± 2 | 71 ± 3 | 64 ± 15 | 1.67 ± 0.14 | 1.5 ± 0.12 |
| NVSS J172908−265751 | 0.57 ± 0.17 | 0.9 ± 0.2 | 1.9 ± 0.3 | 79 ± 2 | 84 ± 5 | 89 ± 15 | 1.78 ± 0.08 | 1.88 ± 0.09 |
| NVSS J172908−265751 | 1.34 ± 0.16 | 4.9 ± 0.3 | 4.3 ± 1.1 | 406 ± 24 | 36 ± 3 | 14 ± 15 | 4.08 ± 0.12 | 1.64 ± 0.05 |
| NVSS J173203−285516 | 0.46 ± 0.06 | 5.6 ± 0.2 | 3.3 ± 0.4 | 242 ± 4 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172836−271236 | 4.77 ± 0.26 | 3.3 ± 0.2 | 3.0 ± 0.2 | 191 ± 0 | 38 ± 4 | 45 ± 4 | 10.41 ± 0.01 | 12.43 ± 0.02 |
| NVSS J172836−271236 | 0.82 ± 0.02 | 7.9 ± 0.2 | 2.8 ± 0.2 | 169 ± 0 | 65 ± 4 | 76 ± 2 | 2.87 ± 0.01 | 3.39 ± 0.01 |
| NVSS J173133−264015 | 2.43 ± 0.4 | 6.3 ± 0.4 | 5.5 ± 0.3 | 650 ± 2 | 41 ± 1 | 52 ± 3 | 10.52 ± 0.09 | 13.44 ± 0.11 |
| NVSS J173806−262443 | 2.13 ± 0.26 | 3.5 ± 0.3 | 9.8 ± 0.4 | 2100 ± 4 | 34 ± 21 | 41 ± 26 | 13.84 ± 0.07 | 16.99 ± 0.09 |
| NVSS J174832−225211 | 1.47 ± 0.14 | 6.2 ± 0.2 | 8.4 ± 0.5 | 1525 ± 5 | 54 ± 1 | – ± – | 12.98 ± 0.07 | – ± – |
| NVSS J174931−210847 | 2.36 ± 0.01 | 7.3 ± 0.2 | 6.1 ± 0.2 | 826 ± 0 | 48 ± 2 | – ± – | 13.59 ± 0.01 | – ± – |
| NVSS J175233−223012 | 0.17 ± 0.01 | 0.1 ± 0.2 | 5.3 ± 0.2 | 606 ± 0 | 39 ± 41 | – ± – | 0.7 ± 0.01 | – ± – |
| NVSS J175233−223012 | 3.2 ± 0.01 | 5.5 ± 0.2 | 4.7 ± 0.2 | 493 ± 0 | 48 ± 39 | – ± – | 14.33 ± 0.01 | – ± – |
| NVSS J174915−200033 | 1.6 ± 0.46 | 3.5 ± 0.2 | 1.9 ± 0.2 | 77 ± 1 | 55 ± 1 | – ± – | 3.25 ± 0.12 | – ± – |
| NVSS J174915−200033 | 1.46 ± 0.24 | 0.1 ± 0.2 | 1.1 ± 0.2 | 29 ± 0 | 53 ± 1 | – ± – | 1.72 ± 0.03 | – ± – |
| NVSS J174915−200033 | 4.29 ± 1.1 | 7.4 ± 0.3 | 3.3 ± 0.4 | 232 ± 3 | 41 ± 3 | – ± – | 11.17 ± 0.32 | – ± – |
| NVSS J175218−210508 | 1.79 ± 0.11 | 6.4 ± 0.2 | 7.0 ± 0.4 | 1073 ± 3 | 44 ± 1 | – ± – | 10.74 ± 0.03 | – ± – |
| NVSS J175104−235215 | 1.45 ± 0.01 | 7.9 ± 0.2 | 4.7 ± 0.2 | 490 ± 0 | 56 ± 1 | 76 ± 14 | 7.49 ± 0.01 | 10.14 ± 0.01 |
| NVSS J175104−235215 | 1.1 ± 0.01 | 3.4 ± 0.2 | 2.6 ± 0.2 | 143 ± 0 | 77 ± 1 | 86 ± 14 | 4.25 ± 0.01 | 4.72 ± 0.01 |
| NVSS J175157−240425 | 0.27 ± 0.2 | 8.8 ± 0.2 | 1.4 ± 0.8 | 42 ± 13 | – ± – | – ± – | – ± – | – ± – |
| NVSS J175157−240425 | 3.65 ± 0.72 | 4.7 ± 0.4 | 5.6 ± 0.4 | 674 ± 4 | 70 ± 2 | 64 ± 4 | 27.87 ± 0.45 | 25.5 ± 0.41 |
| NVSS J175548−233322 | 6.28 ± 1.22 | 6.6 ± 0.2 | 3.7 ± 0.3 | 299 ± 2 | 42 ± 13 | – ± – | 19.3 ± 0.32 | – ± – |
| NVSS J175151−252359 | 1.49 ± 0.01 | 0.1 ± 0.2 | 8.5 ± 0.2 | 1562 ± 0 | 118 ± 6 | 126 ± 21 | 29.13 ± 0.01 | 30.9 ± 0.01 |
| NVSS J175427−235235 | 4.53 ± 0.73 | 7.2 ± 0.2 | 4.8 ± 0.3 | 498 ± 2 | 46 ± 5 | – ± – | 19.34 ± 0.19 | – ± – |
| NVSS J175727−223901 | 0.45 ± 0.4 | 8.3 ± 0.2 | 1.8 ± 0.5 | 67 ± 6 | 8 ± 2 | – ± – | 0.13 ± 0.04 | – ± – |
| NVSS J175727−223901 | 2.9 ± 0.5 | 5.1 ± 0.5 | 4.4 ± 0.6 | 427 ± 8 | 50 ± 2 | – ± – | 12.5 ± 0.29 | – ± – |
| NVSS J174709−295802 | 6.16 ± 2.41 | 4.7 ± 0.2 | 6.3 ± 1.0 | 877 ± 22 | 98 ± 7 | 75 ± 6 | 74.64 ± 4.67 | 57.2 ± 3.58 |
| NVSS J174317−305819 | 1.46 ± 0.01 | 5.6 ± 0.2 | 7.4 ± 0.2 | 1183 ± 0 | 88 ± 3 | 100 ± 2 | 18.4 ± 0.01 | 20.93 ± 0.01 |
| NVSS J174423−311636 | 3.93 ± 0.6 | 5.4 ± 0.4 | 5.4 ± 0.3 | 638 ± 3 | 101 ± 5 | 103 ± 3 | 41.69 ± 0.41 | 42.56 ± 0.41 |
| NVSS J174513−315104 | 1.09 ± 0.37 | 3.6 ± 0.2 | 2.6 ± 0.4 | 152 ± 3 | 101 ± 1 | 127 ± 3 | 5.66 ± 0.25 | 7.13 ± 0.32 |
| NVSS J174513−315104 | 1.1 ± 0.09 | 8.6 ± 0.7 | 9.1 ± 1.2 | 1820 ± 30 | 73 ± 1 | 78 ± 3 | 14.41 ± 0.16 | 15.29 ± 0.17 |
| NVSS J174748−312315 | 1.92 ± 0.47 | 8.0 ± 0.4 | 5.0 ± 0.3 | 536 ± 2 | 70 ± 3 | 91 ± 5 | 12.99 ± 0.2 | 16.85 ± 0.26 |
| NVSS J174748−312315 | 2.08 ± 0.38 | 0.5 ± 0.7 | 6.3 ± 0.6 | 874 ± 9 | 108 ± 4 | 128 ± 7 | 27.6 ± 0.5 | 32.88 ± 0.6 |
| NVSS J174831−324102 | 0.91 ± 2.27 | 4.5 ± 3.2 | 7.1 ± 2.6 | 1103 ± 152 | 46 ± 1 | 60 ± 1 | 5.86 ± 5.44 | 7.6 ± 7.06 |
| NVSS J175114−323538 | 0.29 ± 0.27 | 9.4 ± 0.8 | 9.9 ± 0.9 | 2152 ± 19 | 100 ± 1 | 88 ± 8 | 5.6 ± 0.5 | 4.94 ± 0.44 |
| NVSS J173811−204411 | 1.53 ± 0.18 | 5.0 ± 0.2 | 2.3 ± 0.2 | 112 ± 1 | 49 ± 1 | – ± – | 3.33 ± 0.03 | – ± – |
| NVSS J173811−204411 | 2.75 ± 0.46 | 2.2 ± 0.2 | 2.1 ± 0.2 | 97 ± 0 | 51 ± 1 | – ± – | 5.74 ± 0.04 | – ± – |
| NVSS J173939−205505 | 1.69 ± 0.14 | 3.5 ± 0.2 | 3.1 ± 0.2 | 206 ± 0 | 46 ± 7 | – ± – | 4.67 ± 0.01 | – ± – |
| NVSS J173939−205505 | 0.46 ± 0.04 | 8.1 ± 0.3 | 4.4 ± 0.5 | 415 ± 6 | 41 ± 7 | – ± – | 1.64 ± 0.02 | – ± – |
| NVSS J174343−182838 | 0.16 ± 0.03 | 0.9 ± 0.2 | 1.2 ± 0.2 | 33 ± 1 | 39 ± 10 | – ± – | 0.15 ± 0.0 | – ± – |
| NVSS J174343−182838 | 0.09 ± 0.02 | 5.9 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174343−182838 | 0.1 ± 0.02 | 0.5 ± 0.9 | 7.8 ± 1.5 | 1342 ± 52 | 29 ± 11 | – ± – | 0.44 ± 0.02 | – ± – |
| NVSS J174343−182838 | 2.91 ± 0.4 | 4.7 ± 0.2 | 3.3 ± 0.2 | 245 ± 0 | 41 ± 8 | – ± – | 7.74 ± 0.03 | – ± – |
| NVSS J174637−182629 | 0.56 ± 0.05 | 8.8 ± 0.2 | 3.6 ± 0.4 | 278 ± 4 | 55 ± 3 | – ± – | 2.14 ± 0.02 | – ± – |
| NVSS J174637−182629 | 1.2 ± 0.07 | 3.5 ± 0.2 | 3.2 ± 0.2 | 219 ± 1 | 43 ± 1 | – ± – | 3.16 ± 0.01 | – ± – |
| NVSS J174716−191954 | 3.07 ± 0.25 | 5.0 ± 0.2 | 3.6 ± 0.2 | 278 ± 0 | 35 ± 16 | – ± – | 7.51 ± 0.02 | – ± – |
| NVSS J174716−191954 | 0.33 ± 0.12 | 7.3 ± 0.2 | 1.6 ± 0.2 | 58 ± 1 | - ± - | – ± – | – ± – | – ± – |
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | - ± - | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
| NVSS J173107−245703 | 2.77 ± 0.26 | 2.9 ± 0.2 | 9.2 ± 0.2 | 1847 ± 1 | 55 ± 1 | 52 ± 1 | 27.62 ± 0.05 | 25.88 ± 0.05 |
| NVSS J173107−245703 | 0.12 ± 0.03 | 7.3 ± 0.2 | 1.9 ± 0.5 | 80 ± 6 | 61 ± 7 | 15 ± 7 | 0.28 ± 0.02 | 0.07 ± 0.01 |
| NVSS J173718−260426 | 2.71 ± 0.44 | 4.9 ± 0.7 | 8.5 ± 0.6 | 1564 ± 8 | 33 ± 16 | 40 ± 1 | 14.87 ± 0.17 | 18.14 ± 0.2 |
| NVSS J173252−223511 | 6.88 ± 0.75 | 4.3 ± 0.2 | 4.4 ± 0.2 | 416 ± 0 | 48 ± 7 | – ± – | 28.37 ± 0.1 | – ± – |
| NVSS J173722−223000 | 0.41 ± 0.04 | 4.4 ± 0.2 | 3.3 ± 0.3 | 245 ± 2 | 10 ± 1 | – ± – | 0.27 ± 0.1 | – ± – |
| NVSS J174618−193006 | 0.34 ± 0.12 | 1.0 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | 65 ± 1 | – ± – | 0.48 ± 0.05 | – ± – |
| NVSS J173713−224734 | 2.02 ± 0.35 | 4.9 ± 0.2 | 6.6 ± 0.3 | 966 ± 2 | 39 ± 14 | 41 ± 36 | 10.29 ± 0.08 | 10.72 ± 0.08 |
| NVSS J173850−221918 | 1.74 ± 0.33 | 2.5 ± 0.4 | 5.1 ± 0.4 | 560 ± 3 | 67 ± 4 | 85 ± 2 | 11.57 ± 0.17 | 14.52 ± 0.21 |
| NVSS J173850−221918 | 0.82 ± 0.21 | 7.7 ± 0.7 | 5.2 ± 0.6 | 581 ± 8 | 62 ± 4 | 62 ± 2 | 5.1 ± 0.16 | 5.11 ± 0.16 |
| NVSS J174713−192135 | 0.84 ± 0.69 | 4.8 ± 0.2 | 1.9 ± 0.2 | 78 ± 0 | 22 ± 13 | – ± – | 0.7 ± 0.04 | – ± – |
| NVSS J174713−192135 | 0.52 ± 0.36 | 7.6 ± 0.4 | 2.8 ± 0.6 | 168 ± 8 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174713−192135 | 0.33 ± 0.13 | 3.9 ± 2.2 | 7.8 ± 2.3 | 1328 ± 115 | 36 ± 13 | – ± – | 1.84 ± 0.22 | – ± – |
| NVSS J172829−284610 | 1.55 ± 0.01 | 6.6 ± 0.2 | 6.8 ± 0.2 | 1013 ± 0 | 62 ± 1 | 62 ± 6 | 12.67 ± 0.1 | 12.68 ± 0.01 |
| NVSS J172908−265751 | 0.57 ± 0.3 | 8.5 ± 0.2 | 2.1 ± 0.3 | 98 ± 2 | 71 ± 3 | 64 ± 15 | 1.67 ± 0.14 | 1.5 ± 0.12 |
| NVSS J172908−265751 | 0.57 ± 0.17 | 0.9 ± 0.2 | 1.9 ± 0.3 | 79 ± 2 | 84 ± 5 | 89 ± 15 | 1.78 ± 0.08 | 1.88 ± 0.09 |
| NVSS J172908−265751 | 1.34 ± 0.16 | 4.9 ± 0.3 | 4.3 ± 1.1 | 406 ± 24 | 36 ± 3 | 14 ± 15 | 4.08 ± 0.12 | 1.64 ± 0.05 |
| NVSS J173203−285516 | 0.46 ± 0.06 | 5.6 ± 0.2 | 3.3 ± 0.4 | 242 ± 4 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172836−271236 | 4.77 ± 0.26 | 3.3 ± 0.2 | 3.0 ± 0.2 | 191 ± 0 | 38 ± 4 | 45 ± 4 | 10.41 ± 0.01 | 12.43 ± 0.02 |
| NVSS J172836−271236 | 0.82 ± 0.02 | 7.9 ± 0.2 | 2.8 ± 0.2 | 169 ± 0 | 65 ± 4 | 76 ± 2 | 2.87 ± 0.01 | 3.39 ± 0.01 |
| NVSS J173133−264015 | 2.43 ± 0.4 | 6.3 ± 0.4 | 5.5 ± 0.3 | 650 ± 2 | 41 ± 1 | 52 ± 3 | 10.52 ± 0.09 | 13.44 ± 0.11 |
| NVSS J173806−262443 | 2.13 ± 0.26 | 3.5 ± 0.3 | 9.8 ± 0.4 | 2100 ± 4 | 34 ± 21 | 41 ± 26 | 13.84 ± 0.07 | 16.99 ± 0.09 |
| NVSS J174832−225211 | 1.47 ± 0.14 | 6.2 ± 0.2 | 8.4 ± 0.5 | 1525 ± 5 | 54 ± 1 | – ± – | 12.98 ± 0.07 | – ± – |
| NVSS J174931−210847 | 2.36 ± 0.01 | 7.3 ± 0.2 | 6.1 ± 0.2 | 826 ± 0 | 48 ± 2 | – ± – | 13.59 ± 0.01 | – ± – |
| NVSS J175233−223012 | 0.17 ± 0.01 | 0.1 ± 0.2 | 5.3 ± 0.2 | 606 ± 0 | 39 ± 41 | – ± – | 0.7 ± 0.01 | – ± – |
| NVSS J175233−223012 | 3.2 ± 0.01 | 5.5 ± 0.2 | 4.7 ± 0.2 | 493 ± 0 | 48 ± 39 | – ± – | 14.33 ± 0.01 | – ± – |
| NVSS J174915−200033 | 1.6 ± 0.46 | 3.5 ± 0.2 | 1.9 ± 0.2 | 77 ± 1 | 55 ± 1 | – ± – | 3.25 ± 0.12 | – ± – |
| NVSS J174915−200033 | 1.46 ± 0.24 | 0.1 ± 0.2 | 1.1 ± 0.2 | 29 ± 0 | 53 ± 1 | – ± – | 1.72 ± 0.03 | – ± – |
| NVSS J174915−200033 | 4.29 ± 1.1 | 7.4 ± 0.3 | 3.3 ± 0.4 | 232 ± 3 | 41 ± 3 | – ± – | 11.17 ± 0.32 | – ± – |
| NVSS J175218−210508 | 1.79 ± 0.11 | 6.4 ± 0.2 | 7.0 ± 0.4 | 1073 ± 3 | 44 ± 1 | – ± – | 10.74 ± 0.03 | – ± – |
| NVSS J175104−235215 | 1.45 ± 0.01 | 7.9 ± 0.2 | 4.7 ± 0.2 | 490 ± 0 | 56 ± 1 | 76 ± 14 | 7.49 ± 0.01 | 10.14 ± 0.01 |
| NVSS J175104−235215 | 1.1 ± 0.01 | 3.4 ± 0.2 | 2.6 ± 0.2 | 143 ± 0 | 77 ± 1 | 86 ± 14 | 4.25 ± 0.01 | 4.72 ± 0.01 |
| NVSS J175157−240425 | 0.27 ± 0.2 | 8.8 ± 0.2 | 1.4 ± 0.8 | 42 ± 13 | – ± – | – ± – | – ± – | – ± – |
| NVSS J175157−240425 | 3.65 ± 0.72 | 4.7 ± 0.4 | 5.6 ± 0.4 | 674 ± 4 | 70 ± 2 | 64 ± 4 | 27.87 ± 0.45 | 25.5 ± 0.41 |
| NVSS J175548−233322 | 6.28 ± 1.22 | 6.6 ± 0.2 | 3.7 ± 0.3 | 299 ± 2 | 42 ± 13 | – ± – | 19.3 ± 0.32 | – ± – |
| NVSS J175151−252359 | 1.49 ± 0.01 | 0.1 ± 0.2 | 8.5 ± 0.2 | 1562 ± 0 | 118 ± 6 | 126 ± 21 | 29.13 ± 0.01 | 30.9 ± 0.01 |
| NVSS J175427−235235 | 4.53 ± 0.73 | 7.2 ± 0.2 | 4.8 ± 0.3 | 498 ± 2 | 46 ± 5 | – ± – | 19.34 ± 0.19 | – ± – |
| NVSS J175727−223901 | 0.45 ± 0.4 | 8.3 ± 0.2 | 1.8 ± 0.5 | 67 ± 6 | 8 ± 2 | – ± – | 0.13 ± 0.04 | – ± – |
| NVSS J175727−223901 | 2.9 ± 0.5 | 5.1 ± 0.5 | 4.4 ± 0.6 | 427 ± 8 | 50 ± 2 | – ± – | 12.5 ± 0.29 | – ± – |
| NVSS J174709−295802 | 6.16 ± 2.41 | 4.7 ± 0.2 | 6.3 ± 1.0 | 877 ± 22 | 98 ± 7 | 75 ± 6 | 74.64 ± 4.67 | 57.2 ± 3.58 |
| NVSS J174317−305819 | 1.46 ± 0.01 | 5.6 ± 0.2 | 7.4 ± 0.2 | 1183 ± 0 | 88 ± 3 | 100 ± 2 | 18.4 ± 0.01 | 20.93 ± 0.01 |
| NVSS J174423−311636 | 3.93 ± 0.6 | 5.4 ± 0.4 | 5.4 ± 0.3 | 638 ± 3 | 101 ± 5 | 103 ± 3 | 41.69 ± 0.41 | 42.56 ± 0.41 |
| NVSS J174513−315104 | 1.09 ± 0.37 | 3.6 ± 0.2 | 2.6 ± 0.4 | 152 ± 3 | 101 ± 1 | 127 ± 3 | 5.66 ± 0.25 | 7.13 ± 0.32 |
| NVSS J174513−315104 | 1.1 ± 0.09 | 8.6 ± 0.7 | 9.1 ± 1.2 | 1820 ± 30 | 73 ± 1 | 78 ± 3 | 14.41 ± 0.16 | 15.29 ± 0.17 |
| NVSS J174748−312315 | 1.92 ± 0.47 | 8.0 ± 0.4 | 5.0 ± 0.3 | 536 ± 2 | 70 ± 3 | 91 ± 5 | 12.99 ± 0.2 | 16.85 ± 0.26 |
| NVSS J174748−312315 | 2.08 ± 0.38 | 0.5 ± 0.7 | 6.3 ± 0.6 | 874 ± 9 | 108 ± 4 | 128 ± 7 | 27.6 ± 0.5 | 32.88 ± 0.6 |
| NVSS J174831−324102 | 0.91 ± 2.27 | 4.5 ± 3.2 | 7.1 ± 2.6 | 1103 ± 152 | 46 ± 1 | 60 ± 1 | 5.86 ± 5.44 | 7.6 ± 7.06 |
| NVSS J175114−323538 | 0.29 ± 0.27 | 9.4 ± 0.8 | 9.9 ± 0.9 | 2152 ± 19 | 100 ± 1 | 88 ± 8 | 5.6 ± 0.5 | 4.94 ± 0.44 |
| NVSS J173811−204411 | 1.53 ± 0.18 | 5.0 ± 0.2 | 2.3 ± 0.2 | 112 ± 1 | 49 ± 1 | – ± – | 3.33 ± 0.03 | – ± – |
| NVSS J173811−204411 | 2.75 ± 0.46 | 2.2 ± 0.2 | 2.1 ± 0.2 | 97 ± 0 | 51 ± 1 | – ± – | 5.74 ± 0.04 | – ± – |
| NVSS J173939−205505 | 1.69 ± 0.14 | 3.5 ± 0.2 | 3.1 ± 0.2 | 206 ± 0 | 46 ± 7 | – ± – | 4.67 ± 0.01 | – ± – |
| NVSS J173939−205505 | 0.46 ± 0.04 | 8.1 ± 0.3 | 4.4 ± 0.5 | 415 ± 6 | 41 ± 7 | – ± – | 1.64 ± 0.02 | – ± – |
| NVSS J174343−182838 | 0.16 ± 0.03 | 0.9 ± 0.2 | 1.2 ± 0.2 | 33 ± 1 | 39 ± 10 | – ± – | 0.15 ± 0.0 | – ± – |
| NVSS J174343−182838 | 0.09 ± 0.02 | 5.9 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174343−182838 | 0.1 ± 0.02 | 0.5 ± 0.9 | 7.8 ± 1.5 | 1342 ± 52 | 29 ± 11 | – ± – | 0.44 ± 0.02 | – ± – |
| NVSS J174343−182838 | 2.91 ± 0.4 | 4.7 ± 0.2 | 3.3 ± 0.2 | 245 ± 0 | 41 ± 8 | – ± – | 7.74 ± 0.03 | – ± – |
| NVSS J174637−182629 | 0.56 ± 0.05 | 8.8 ± 0.2 | 3.6 ± 0.4 | 278 ± 4 | 55 ± 3 | – ± – | 2.14 ± 0.02 | – ± – |
| NVSS J174637−182629 | 1.2 ± 0.07 | 3.5 ± 0.2 | 3.2 ± 0.2 | 219 ± 1 | 43 ± 1 | – ± – | 3.16 ± 0.01 | – ± – |
| NVSS J174716−191954 | 3.07 ± 0.25 | 5.0 ± 0.2 | 3.6 ± 0.2 | 278 ± 0 | 35 ± 16 | – ± – | 7.51 ± 0.02 | – ± – |
| NVSS J174716−191954 | 0.33 ± 0.12 | 7.3 ± 0.2 | 1.6 ± 0.2 | 58 ± 1 | - ± - | – ± – | – ± – | – ± – |
Line parameters from the Gaussian decomposition in the velocity range of the R–C cloud (0 < |$v$|LSR < 10 km s−1) and calculated Tk,max, Ts, and N(H i).
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | - ± - | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
| NVSS J173107−245703 | 2.77 ± 0.26 | 2.9 ± 0.2 | 9.2 ± 0.2 | 1847 ± 1 | 55 ± 1 | 52 ± 1 | 27.62 ± 0.05 | 25.88 ± 0.05 |
| NVSS J173107−245703 | 0.12 ± 0.03 | 7.3 ± 0.2 | 1.9 ± 0.5 | 80 ± 6 | 61 ± 7 | 15 ± 7 | 0.28 ± 0.02 | 0.07 ± 0.01 |
| NVSS J173718−260426 | 2.71 ± 0.44 | 4.9 ± 0.7 | 8.5 ± 0.6 | 1564 ± 8 | 33 ± 16 | 40 ± 1 | 14.87 ± 0.17 | 18.14 ± 0.2 |
| NVSS J173252−223511 | 6.88 ± 0.75 | 4.3 ± 0.2 | 4.4 ± 0.2 | 416 ± 0 | 48 ± 7 | – ± – | 28.37 ± 0.1 | – ± – |
| NVSS J173722−223000 | 0.41 ± 0.04 | 4.4 ± 0.2 | 3.3 ± 0.3 | 245 ± 2 | 10 ± 1 | – ± – | 0.27 ± 0.1 | – ± – |
| NVSS J174618−193006 | 0.34 ± 0.12 | 1.0 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | 65 ± 1 | – ± – | 0.48 ± 0.05 | – ± – |
| NVSS J173713−224734 | 2.02 ± 0.35 | 4.9 ± 0.2 | 6.6 ± 0.3 | 966 ± 2 | 39 ± 14 | 41 ± 36 | 10.29 ± 0.08 | 10.72 ± 0.08 |
| NVSS J173850−221918 | 1.74 ± 0.33 | 2.5 ± 0.4 | 5.1 ± 0.4 | 560 ± 3 | 67 ± 4 | 85 ± 2 | 11.57 ± 0.17 | 14.52 ± 0.21 |
| NVSS J173850−221918 | 0.82 ± 0.21 | 7.7 ± 0.7 | 5.2 ± 0.6 | 581 ± 8 | 62 ± 4 | 62 ± 2 | 5.1 ± 0.16 | 5.11 ± 0.16 |
| NVSS J174713−192135 | 0.84 ± 0.69 | 4.8 ± 0.2 | 1.9 ± 0.2 | 78 ± 0 | 22 ± 13 | – ± – | 0.7 ± 0.04 | – ± – |
| NVSS J174713−192135 | 0.52 ± 0.36 | 7.6 ± 0.4 | 2.8 ± 0.6 | 168 ± 8 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174713−192135 | 0.33 ± 0.13 | 3.9 ± 2.2 | 7.8 ± 2.3 | 1328 ± 115 | 36 ± 13 | – ± – | 1.84 ± 0.22 | – ± – |
| NVSS J172829−284610 | 1.55 ± 0.01 | 6.6 ± 0.2 | 6.8 ± 0.2 | 1013 ± 0 | 62 ± 1 | 62 ± 6 | 12.67 ± 0.1 | 12.68 ± 0.01 |
| NVSS J172908−265751 | 0.57 ± 0.3 | 8.5 ± 0.2 | 2.1 ± 0.3 | 98 ± 2 | 71 ± 3 | 64 ± 15 | 1.67 ± 0.14 | 1.5 ± 0.12 |
| NVSS J172908−265751 | 0.57 ± 0.17 | 0.9 ± 0.2 | 1.9 ± 0.3 | 79 ± 2 | 84 ± 5 | 89 ± 15 | 1.78 ± 0.08 | 1.88 ± 0.09 |
| NVSS J172908−265751 | 1.34 ± 0.16 | 4.9 ± 0.3 | 4.3 ± 1.1 | 406 ± 24 | 36 ± 3 | 14 ± 15 | 4.08 ± 0.12 | 1.64 ± 0.05 |
| NVSS J173203−285516 | 0.46 ± 0.06 | 5.6 ± 0.2 | 3.3 ± 0.4 | 242 ± 4 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172836−271236 | 4.77 ± 0.26 | 3.3 ± 0.2 | 3.0 ± 0.2 | 191 ± 0 | 38 ± 4 | 45 ± 4 | 10.41 ± 0.01 | 12.43 ± 0.02 |
| NVSS J172836−271236 | 0.82 ± 0.02 | 7.9 ± 0.2 | 2.8 ± 0.2 | 169 ± 0 | 65 ± 4 | 76 ± 2 | 2.87 ± 0.01 | 3.39 ± 0.01 |
| NVSS J173133−264015 | 2.43 ± 0.4 | 6.3 ± 0.4 | 5.5 ± 0.3 | 650 ± 2 | 41 ± 1 | 52 ± 3 | 10.52 ± 0.09 | 13.44 ± 0.11 |
| NVSS J173806−262443 | 2.13 ± 0.26 | 3.5 ± 0.3 | 9.8 ± 0.4 | 2100 ± 4 | 34 ± 21 | 41 ± 26 | 13.84 ± 0.07 | 16.99 ± 0.09 |
| NVSS J174832−225211 | 1.47 ± 0.14 | 6.2 ± 0.2 | 8.4 ± 0.5 | 1525 ± 5 | 54 ± 1 | – ± – | 12.98 ± 0.07 | – ± – |
| NVSS J174931−210847 | 2.36 ± 0.01 | 7.3 ± 0.2 | 6.1 ± 0.2 | 826 ± 0 | 48 ± 2 | – ± – | 13.59 ± 0.01 | – ± – |
| NVSS J175233−223012 | 0.17 ± 0.01 | 0.1 ± 0.2 | 5.3 ± 0.2 | 606 ± 0 | 39 ± 41 | – ± – | 0.7 ± 0.01 | – ± – |
| NVSS J175233−223012 | 3.2 ± 0.01 | 5.5 ± 0.2 | 4.7 ± 0.2 | 493 ± 0 | 48 ± 39 | – ± – | 14.33 ± 0.01 | – ± – |
| NVSS J174915−200033 | 1.6 ± 0.46 | 3.5 ± 0.2 | 1.9 ± 0.2 | 77 ± 1 | 55 ± 1 | – ± – | 3.25 ± 0.12 | – ± – |
| NVSS J174915−200033 | 1.46 ± 0.24 | 0.1 ± 0.2 | 1.1 ± 0.2 | 29 ± 0 | 53 ± 1 | – ± – | 1.72 ± 0.03 | – ± – |
| NVSS J174915−200033 | 4.29 ± 1.1 | 7.4 ± 0.3 | 3.3 ± 0.4 | 232 ± 3 | 41 ± 3 | – ± – | 11.17 ± 0.32 | – ± – |
| NVSS J175218−210508 | 1.79 ± 0.11 | 6.4 ± 0.2 | 7.0 ± 0.4 | 1073 ± 3 | 44 ± 1 | – ± – | 10.74 ± 0.03 | – ± – |
| NVSS J175104−235215 | 1.45 ± 0.01 | 7.9 ± 0.2 | 4.7 ± 0.2 | 490 ± 0 | 56 ± 1 | 76 ± 14 | 7.49 ± 0.01 | 10.14 ± 0.01 |
| NVSS J175104−235215 | 1.1 ± 0.01 | 3.4 ± 0.2 | 2.6 ± 0.2 | 143 ± 0 | 77 ± 1 | 86 ± 14 | 4.25 ± 0.01 | 4.72 ± 0.01 |
| NVSS J175157−240425 | 0.27 ± 0.2 | 8.8 ± 0.2 | 1.4 ± 0.8 | 42 ± 13 | – ± – | – ± – | – ± – | – ± – |
| NVSS J175157−240425 | 3.65 ± 0.72 | 4.7 ± 0.4 | 5.6 ± 0.4 | 674 ± 4 | 70 ± 2 | 64 ± 4 | 27.87 ± 0.45 | 25.5 ± 0.41 |
| NVSS J175548−233322 | 6.28 ± 1.22 | 6.6 ± 0.2 | 3.7 ± 0.3 | 299 ± 2 | 42 ± 13 | – ± – | 19.3 ± 0.32 | – ± – |
| NVSS J175151−252359 | 1.49 ± 0.01 | 0.1 ± 0.2 | 8.5 ± 0.2 | 1562 ± 0 | 118 ± 6 | 126 ± 21 | 29.13 ± 0.01 | 30.9 ± 0.01 |
| NVSS J175427−235235 | 4.53 ± 0.73 | 7.2 ± 0.2 | 4.8 ± 0.3 | 498 ± 2 | 46 ± 5 | – ± – | 19.34 ± 0.19 | – ± – |
| NVSS J175727−223901 | 0.45 ± 0.4 | 8.3 ± 0.2 | 1.8 ± 0.5 | 67 ± 6 | 8 ± 2 | – ± – | 0.13 ± 0.04 | – ± – |
| NVSS J175727−223901 | 2.9 ± 0.5 | 5.1 ± 0.5 | 4.4 ± 0.6 | 427 ± 8 | 50 ± 2 | – ± – | 12.5 ± 0.29 | – ± – |
| NVSS J174709−295802 | 6.16 ± 2.41 | 4.7 ± 0.2 | 6.3 ± 1.0 | 877 ± 22 | 98 ± 7 | 75 ± 6 | 74.64 ± 4.67 | 57.2 ± 3.58 |
| NVSS J174317−305819 | 1.46 ± 0.01 | 5.6 ± 0.2 | 7.4 ± 0.2 | 1183 ± 0 | 88 ± 3 | 100 ± 2 | 18.4 ± 0.01 | 20.93 ± 0.01 |
| NVSS J174423−311636 | 3.93 ± 0.6 | 5.4 ± 0.4 | 5.4 ± 0.3 | 638 ± 3 | 101 ± 5 | 103 ± 3 | 41.69 ± 0.41 | 42.56 ± 0.41 |
| NVSS J174513−315104 | 1.09 ± 0.37 | 3.6 ± 0.2 | 2.6 ± 0.4 | 152 ± 3 | 101 ± 1 | 127 ± 3 | 5.66 ± 0.25 | 7.13 ± 0.32 |
| NVSS J174513−315104 | 1.1 ± 0.09 | 8.6 ± 0.7 | 9.1 ± 1.2 | 1820 ± 30 | 73 ± 1 | 78 ± 3 | 14.41 ± 0.16 | 15.29 ± 0.17 |
| NVSS J174748−312315 | 1.92 ± 0.47 | 8.0 ± 0.4 | 5.0 ± 0.3 | 536 ± 2 | 70 ± 3 | 91 ± 5 | 12.99 ± 0.2 | 16.85 ± 0.26 |
| NVSS J174748−312315 | 2.08 ± 0.38 | 0.5 ± 0.7 | 6.3 ± 0.6 | 874 ± 9 | 108 ± 4 | 128 ± 7 | 27.6 ± 0.5 | 32.88 ± 0.6 |
| NVSS J174831−324102 | 0.91 ± 2.27 | 4.5 ± 3.2 | 7.1 ± 2.6 | 1103 ± 152 | 46 ± 1 | 60 ± 1 | 5.86 ± 5.44 | 7.6 ± 7.06 |
| NVSS J175114−323538 | 0.29 ± 0.27 | 9.4 ± 0.8 | 9.9 ± 0.9 | 2152 ± 19 | 100 ± 1 | 88 ± 8 | 5.6 ± 0.5 | 4.94 ± 0.44 |
| NVSS J173811−204411 | 1.53 ± 0.18 | 5.0 ± 0.2 | 2.3 ± 0.2 | 112 ± 1 | 49 ± 1 | – ± – | 3.33 ± 0.03 | – ± – |
| NVSS J173811−204411 | 2.75 ± 0.46 | 2.2 ± 0.2 | 2.1 ± 0.2 | 97 ± 0 | 51 ± 1 | – ± – | 5.74 ± 0.04 | – ± – |
| NVSS J173939−205505 | 1.69 ± 0.14 | 3.5 ± 0.2 | 3.1 ± 0.2 | 206 ± 0 | 46 ± 7 | – ± – | 4.67 ± 0.01 | – ± – |
| NVSS J173939−205505 | 0.46 ± 0.04 | 8.1 ± 0.3 | 4.4 ± 0.5 | 415 ± 6 | 41 ± 7 | – ± – | 1.64 ± 0.02 | – ± – |
| NVSS J174343−182838 | 0.16 ± 0.03 | 0.9 ± 0.2 | 1.2 ± 0.2 | 33 ± 1 | 39 ± 10 | – ± – | 0.15 ± 0.0 | – ± – |
| NVSS J174343−182838 | 0.09 ± 0.02 | 5.9 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174343−182838 | 0.1 ± 0.02 | 0.5 ± 0.9 | 7.8 ± 1.5 | 1342 ± 52 | 29 ± 11 | – ± – | 0.44 ± 0.02 | – ± – |
| NVSS J174343−182838 | 2.91 ± 0.4 | 4.7 ± 0.2 | 3.3 ± 0.2 | 245 ± 0 | 41 ± 8 | – ± – | 7.74 ± 0.03 | – ± – |
| NVSS J174637−182629 | 0.56 ± 0.05 | 8.8 ± 0.2 | 3.6 ± 0.4 | 278 ± 4 | 55 ± 3 | – ± – | 2.14 ± 0.02 | – ± – |
| NVSS J174637−182629 | 1.2 ± 0.07 | 3.5 ± 0.2 | 3.2 ± 0.2 | 219 ± 1 | 43 ± 1 | – ± – | 3.16 ± 0.01 | – ± – |
| NVSS J174716−191954 | 3.07 ± 0.25 | 5.0 ± 0.2 | 3.6 ± 0.2 | 278 ± 0 | 35 ± 16 | – ± – | 7.51 ± 0.02 | – ± – |
| NVSS J174716−191954 | 0.33 ± 0.12 | 7.3 ± 0.2 | 1.6 ± 0.2 | 58 ± 1 | - ± - | – ± – | – ± – | – ± – |
| Name . | τHISA . | |$v$|LSR . | FWHM . | Tk,max . | Ts,HISA GASS . | Ts,HISA SGPS . | N(H i) GASS . | N(H i) SGPS . |
|---|---|---|---|---|---|---|---|---|
| . | . | (km s−1) . | (km s−1) . | (K) . | (K) . | (K) . | (1020 cm−2) . | (1020 cm−2) . |
| NVSS J172920−234535 | 0.29 ± 0.16 | 3.2 ± 0.2 | 2.4 ± 0.2 | 127 ± 1 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172920−234535 | 3.38 ± 0.31 | 6.7 ± 0.2 | 4.7 ± 0.2 | 485 ± 1 | 46 ± 54 | - ± - | 14.48 ± 0.05 | – ± – |
| NVSS J172920−234535 | 0.16 ± 0.02 | 0.4 ± 0.3 | 3.4 ± 0.6 | 254 ± 7 | – ± – | – ± – | – ± – | – ± – |
| NVSS J173205−242651 | 2.33 ± 0.43 | 2.2 ± 0.2 | 3.0 ± 0.2 | 192 ± 1 | 72 ± 4 | 67 ± 1 | 9.75 ± 0.11 | 9.08 ± 0.1 |
| NVSS J173753−254642 | 2.73 ± 0.21 | 3.4 ± 0.2 | 9.8 ± 0.3 | 2098 ± 2 | 35 ± 24 | 41 ± 30 | 18.46 ± 0.04 | 21.38 ± 0.04 |
| NVSS J173107−245703 | 2.77 ± 0.26 | 2.9 ± 0.2 | 9.2 ± 0.2 | 1847 ± 1 | 55 ± 1 | 52 ± 1 | 27.62 ± 0.05 | 25.88 ± 0.05 |
| NVSS J173107−245703 | 0.12 ± 0.03 | 7.3 ± 0.2 | 1.9 ± 0.5 | 80 ± 6 | 61 ± 7 | 15 ± 7 | 0.28 ± 0.02 | 0.07 ± 0.01 |
| NVSS J173718−260426 | 2.71 ± 0.44 | 4.9 ± 0.7 | 8.5 ± 0.6 | 1564 ± 8 | 33 ± 16 | 40 ± 1 | 14.87 ± 0.17 | 18.14 ± 0.2 |
| NVSS J173252−223511 | 6.88 ± 0.75 | 4.3 ± 0.2 | 4.4 ± 0.2 | 416 ± 0 | 48 ± 7 | – ± – | 28.37 ± 0.1 | – ± – |
| NVSS J173722−223000 | 0.41 ± 0.04 | 4.4 ± 0.2 | 3.3 ± 0.3 | 245 ± 2 | 10 ± 1 | – ± – | 0.27 ± 0.1 | – ± – |
| NVSS J174618−193006 | 0.34 ± 0.12 | 1.0 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | 65 ± 1 | – ± – | 0.48 ± 0.05 | – ± – |
| NVSS J173713−224734 | 2.02 ± 0.35 | 4.9 ± 0.2 | 6.6 ± 0.3 | 966 ± 2 | 39 ± 14 | 41 ± 36 | 10.29 ± 0.08 | 10.72 ± 0.08 |
| NVSS J173850−221918 | 1.74 ± 0.33 | 2.5 ± 0.4 | 5.1 ± 0.4 | 560 ± 3 | 67 ± 4 | 85 ± 2 | 11.57 ± 0.17 | 14.52 ± 0.21 |
| NVSS J173850−221918 | 0.82 ± 0.21 | 7.7 ± 0.7 | 5.2 ± 0.6 | 581 ± 8 | 62 ± 4 | 62 ± 2 | 5.1 ± 0.16 | 5.11 ± 0.16 |
| NVSS J174713−192135 | 0.84 ± 0.69 | 4.8 ± 0.2 | 1.9 ± 0.2 | 78 ± 0 | 22 ± 13 | – ± – | 0.7 ± 0.04 | – ± – |
| NVSS J174713−192135 | 0.52 ± 0.36 | 7.6 ± 0.4 | 2.8 ± 0.6 | 168 ± 8 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174713−192135 | 0.33 ± 0.13 | 3.9 ± 2.2 | 7.8 ± 2.3 | 1328 ± 115 | 36 ± 13 | – ± – | 1.84 ± 0.22 | – ± – |
| NVSS J172829−284610 | 1.55 ± 0.01 | 6.6 ± 0.2 | 6.8 ± 0.2 | 1013 ± 0 | 62 ± 1 | 62 ± 6 | 12.67 ± 0.1 | 12.68 ± 0.01 |
| NVSS J172908−265751 | 0.57 ± 0.3 | 8.5 ± 0.2 | 2.1 ± 0.3 | 98 ± 2 | 71 ± 3 | 64 ± 15 | 1.67 ± 0.14 | 1.5 ± 0.12 |
| NVSS J172908−265751 | 0.57 ± 0.17 | 0.9 ± 0.2 | 1.9 ± 0.3 | 79 ± 2 | 84 ± 5 | 89 ± 15 | 1.78 ± 0.08 | 1.88 ± 0.09 |
| NVSS J172908−265751 | 1.34 ± 0.16 | 4.9 ± 0.3 | 4.3 ± 1.1 | 406 ± 24 | 36 ± 3 | 14 ± 15 | 4.08 ± 0.12 | 1.64 ± 0.05 |
| NVSS J173203−285516 | 0.46 ± 0.06 | 5.6 ± 0.2 | 3.3 ± 0.4 | 242 ± 4 | – ± – | – ± – | – ± – | – ± – |
| NVSS J172836−271236 | 4.77 ± 0.26 | 3.3 ± 0.2 | 3.0 ± 0.2 | 191 ± 0 | 38 ± 4 | 45 ± 4 | 10.41 ± 0.01 | 12.43 ± 0.02 |
| NVSS J172836−271236 | 0.82 ± 0.02 | 7.9 ± 0.2 | 2.8 ± 0.2 | 169 ± 0 | 65 ± 4 | 76 ± 2 | 2.87 ± 0.01 | 3.39 ± 0.01 |
| NVSS J173133−264015 | 2.43 ± 0.4 | 6.3 ± 0.4 | 5.5 ± 0.3 | 650 ± 2 | 41 ± 1 | 52 ± 3 | 10.52 ± 0.09 | 13.44 ± 0.11 |
| NVSS J173806−262443 | 2.13 ± 0.26 | 3.5 ± 0.3 | 9.8 ± 0.4 | 2100 ± 4 | 34 ± 21 | 41 ± 26 | 13.84 ± 0.07 | 16.99 ± 0.09 |
| NVSS J174832−225211 | 1.47 ± 0.14 | 6.2 ± 0.2 | 8.4 ± 0.5 | 1525 ± 5 | 54 ± 1 | – ± – | 12.98 ± 0.07 | – ± – |
| NVSS J174931−210847 | 2.36 ± 0.01 | 7.3 ± 0.2 | 6.1 ± 0.2 | 826 ± 0 | 48 ± 2 | – ± – | 13.59 ± 0.01 | – ± – |
| NVSS J175233−223012 | 0.17 ± 0.01 | 0.1 ± 0.2 | 5.3 ± 0.2 | 606 ± 0 | 39 ± 41 | – ± – | 0.7 ± 0.01 | – ± – |
| NVSS J175233−223012 | 3.2 ± 0.01 | 5.5 ± 0.2 | 4.7 ± 0.2 | 493 ± 0 | 48 ± 39 | – ± – | 14.33 ± 0.01 | – ± – |
| NVSS J174915−200033 | 1.6 ± 0.46 | 3.5 ± 0.2 | 1.9 ± 0.2 | 77 ± 1 | 55 ± 1 | – ± – | 3.25 ± 0.12 | – ± – |
| NVSS J174915−200033 | 1.46 ± 0.24 | 0.1 ± 0.2 | 1.1 ± 0.2 | 29 ± 0 | 53 ± 1 | – ± – | 1.72 ± 0.03 | – ± – |
| NVSS J174915−200033 | 4.29 ± 1.1 | 7.4 ± 0.3 | 3.3 ± 0.4 | 232 ± 3 | 41 ± 3 | – ± – | 11.17 ± 0.32 | – ± – |
| NVSS J175218−210508 | 1.79 ± 0.11 | 6.4 ± 0.2 | 7.0 ± 0.4 | 1073 ± 3 | 44 ± 1 | – ± – | 10.74 ± 0.03 | – ± – |
| NVSS J175104−235215 | 1.45 ± 0.01 | 7.9 ± 0.2 | 4.7 ± 0.2 | 490 ± 0 | 56 ± 1 | 76 ± 14 | 7.49 ± 0.01 | 10.14 ± 0.01 |
| NVSS J175104−235215 | 1.1 ± 0.01 | 3.4 ± 0.2 | 2.6 ± 0.2 | 143 ± 0 | 77 ± 1 | 86 ± 14 | 4.25 ± 0.01 | 4.72 ± 0.01 |
| NVSS J175157−240425 | 0.27 ± 0.2 | 8.8 ± 0.2 | 1.4 ± 0.8 | 42 ± 13 | – ± – | – ± – | – ± – | – ± – |
| NVSS J175157−240425 | 3.65 ± 0.72 | 4.7 ± 0.4 | 5.6 ± 0.4 | 674 ± 4 | 70 ± 2 | 64 ± 4 | 27.87 ± 0.45 | 25.5 ± 0.41 |
| NVSS J175548−233322 | 6.28 ± 1.22 | 6.6 ± 0.2 | 3.7 ± 0.3 | 299 ± 2 | 42 ± 13 | – ± – | 19.3 ± 0.32 | – ± – |
| NVSS J175151−252359 | 1.49 ± 0.01 | 0.1 ± 0.2 | 8.5 ± 0.2 | 1562 ± 0 | 118 ± 6 | 126 ± 21 | 29.13 ± 0.01 | 30.9 ± 0.01 |
| NVSS J175427−235235 | 4.53 ± 0.73 | 7.2 ± 0.2 | 4.8 ± 0.3 | 498 ± 2 | 46 ± 5 | – ± – | 19.34 ± 0.19 | – ± – |
| NVSS J175727−223901 | 0.45 ± 0.4 | 8.3 ± 0.2 | 1.8 ± 0.5 | 67 ± 6 | 8 ± 2 | – ± – | 0.13 ± 0.04 | – ± – |
| NVSS J175727−223901 | 2.9 ± 0.5 | 5.1 ± 0.5 | 4.4 ± 0.6 | 427 ± 8 | 50 ± 2 | – ± – | 12.5 ± 0.29 | – ± – |
| NVSS J174709−295802 | 6.16 ± 2.41 | 4.7 ± 0.2 | 6.3 ± 1.0 | 877 ± 22 | 98 ± 7 | 75 ± 6 | 74.64 ± 4.67 | 57.2 ± 3.58 |
| NVSS J174317−305819 | 1.46 ± 0.01 | 5.6 ± 0.2 | 7.4 ± 0.2 | 1183 ± 0 | 88 ± 3 | 100 ± 2 | 18.4 ± 0.01 | 20.93 ± 0.01 |
| NVSS J174423−311636 | 3.93 ± 0.6 | 5.4 ± 0.4 | 5.4 ± 0.3 | 638 ± 3 | 101 ± 5 | 103 ± 3 | 41.69 ± 0.41 | 42.56 ± 0.41 |
| NVSS J174513−315104 | 1.09 ± 0.37 | 3.6 ± 0.2 | 2.6 ± 0.4 | 152 ± 3 | 101 ± 1 | 127 ± 3 | 5.66 ± 0.25 | 7.13 ± 0.32 |
| NVSS J174513−315104 | 1.1 ± 0.09 | 8.6 ± 0.7 | 9.1 ± 1.2 | 1820 ± 30 | 73 ± 1 | 78 ± 3 | 14.41 ± 0.16 | 15.29 ± 0.17 |
| NVSS J174748−312315 | 1.92 ± 0.47 | 8.0 ± 0.4 | 5.0 ± 0.3 | 536 ± 2 | 70 ± 3 | 91 ± 5 | 12.99 ± 0.2 | 16.85 ± 0.26 |
| NVSS J174748−312315 | 2.08 ± 0.38 | 0.5 ± 0.7 | 6.3 ± 0.6 | 874 ± 9 | 108 ± 4 | 128 ± 7 | 27.6 ± 0.5 | 32.88 ± 0.6 |
| NVSS J174831−324102 | 0.91 ± 2.27 | 4.5 ± 3.2 | 7.1 ± 2.6 | 1103 ± 152 | 46 ± 1 | 60 ± 1 | 5.86 ± 5.44 | 7.6 ± 7.06 |
| NVSS J175114−323538 | 0.29 ± 0.27 | 9.4 ± 0.8 | 9.9 ± 0.9 | 2152 ± 19 | 100 ± 1 | 88 ± 8 | 5.6 ± 0.5 | 4.94 ± 0.44 |
| NVSS J173811−204411 | 1.53 ± 0.18 | 5.0 ± 0.2 | 2.3 ± 0.2 | 112 ± 1 | 49 ± 1 | – ± – | 3.33 ± 0.03 | – ± – |
| NVSS J173811−204411 | 2.75 ± 0.46 | 2.2 ± 0.2 | 2.1 ± 0.2 | 97 ± 0 | 51 ± 1 | – ± – | 5.74 ± 0.04 | – ± – |
| NVSS J173939−205505 | 1.69 ± 0.14 | 3.5 ± 0.2 | 3.1 ± 0.2 | 206 ± 0 | 46 ± 7 | – ± – | 4.67 ± 0.01 | – ± – |
| NVSS J173939−205505 | 0.46 ± 0.04 | 8.1 ± 0.3 | 4.4 ± 0.5 | 415 ± 6 | 41 ± 7 | – ± – | 1.64 ± 0.02 | – ± – |
| NVSS J174343−182838 | 0.16 ± 0.03 | 0.9 ± 0.2 | 1.2 ± 0.2 | 33 ± 1 | 39 ± 10 | – ± – | 0.15 ± 0.0 | – ± – |
| NVSS J174343−182838 | 0.09 ± 0.02 | 5.9 ± 0.2 | 1.1 ± 0.3 | 27 ± 2 | - ± - | – ± – | – ± – | – ± – |
| NVSS J174343−182838 | 0.1 ± 0.02 | 0.5 ± 0.9 | 7.8 ± 1.5 | 1342 ± 52 | 29 ± 11 | – ± – | 0.44 ± 0.02 | – ± – |
| NVSS J174343−182838 | 2.91 ± 0.4 | 4.7 ± 0.2 | 3.3 ± 0.2 | 245 ± 0 | 41 ± 8 | – ± – | 7.74 ± 0.03 | – ± – |
| NVSS J174637−182629 | 0.56 ± 0.05 | 8.8 ± 0.2 | 3.6 ± 0.4 | 278 ± 4 | 55 ± 3 | – ± – | 2.14 ± 0.02 | – ± – |
| NVSS J174637−182629 | 1.2 ± 0.07 | 3.5 ± 0.2 | 3.2 ± 0.2 | 219 ± 1 | 43 ± 1 | – ± – | 3.16 ± 0.01 | – ± – |
| NVSS J174716−191954 | 3.07 ± 0.25 | 5.0 ± 0.2 | 3.6 ± 0.2 | 278 ± 0 | 35 ± 16 | – ± – | 7.51 ± 0.02 | – ± – |
| NVSS J174716−191954 | 0.33 ± 0.12 | 7.3 ± 0.2 | 1.6 ± 0.2 | 58 ± 1 | - ± - | – ± – | – ± – | – ± – |
Ts calculated at the minimum point (|$v$|min, Tmin) of the HISA feature in the H i emission spectra for both GASS and SGPS data.
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
| NVSS J173133−264015 | 0.2574 | 3.8392 | 5.3 | 37.96 | 41 ± 1 | 4.9 | 44.72 | 48 ± 2 |
| NVSS J173203−285516 | −1.5699 | 2.5169 | 5.3 | 42.06 | 46 ± 1 | 4.9 | 43.25 | 46 ± 3 |
| NVSS J173205−242651 | 2.1956 | 4.945 | 4.4 | 46.14 | 50 ± 4 | 4.1 | 52.35 | 56 ± 1 |
| NVSS J173252−223511 | 3.8664 | 5.7991 | 5.3 | 50.1 | 53 ± 4 | – | – | – ± – |
| NVSS J173524−251036 | 1.9877 | 3.9175 | 4.4 | 42.17 | 45 ± 10 | 4.1 | 49.03 | 37 ± 39 |
| NVSS J173620−283552 | −0.7887 | 1.9026 | 5.3 | 29.96 | 31 ± 1 | 4.9 | 34.21 | 39 ± 1 |
| NVSS J173713−224734 | 4.2289 | 4.8441 | 5.3 | 47.75 | 51 ± 15 | 5.8 | 47.34 | 48 ± 38 |
| NVSS J173718−260426 | 1.4579 | 3.0762 | 5.3 | 43.22 | 51 ± 17 | 4.9 | 50.54 | 57 ± 1 |
| NVSS J173722−223000 | 4.498 | 4.968 | 5.3 | 48.19 | 52 ± 1 | 5.8 | 52.47 | 54 ± 32 |
| NVSS J173753−254642 | 1.7778 | 3.1242 | 5.3 | 45.22 | 46 ± 25 | 4.9 | 52.52 | 57 ± 32 |
| NVSS J173806−262443 | 1.2669 | 2.7455 | 5.3 | 39.83 | 45 ± 23 | 4.9 | 45.53 | 55 ± 28 |
| NVSS J173811−204411 | 6.1012 | 5.7415 | 3.6 | 47.13 | 51 ± 1 | – | – | – ± – |
| NVSS J173850−221918 | 4.8301 | 4.7751 | 5.3 | 48.56 | 50 ± 4 | 5.8 | 57.25 | 59 ± 2 |
| NVSS J173939−205505 | 6.1259 | 5.3569 | 3.6 | 46.58 | 51 ± 5 | – | – | – ± – |
| NVSS J174202−271311 | 1.0472 | 1.5731 | 5.3 | 38.11 | 33 ± 1 | 5.8 | 41.72 | 36 ± 15 |
| NVSS J174224−203729 | 6.7168 | 4.9604 | 4.4 | 56.06 | 60 ± 2 | – | – | – ± – |
| NVSS J174317−305819 | −1.9982 | −0.6363 | 6.9 | 66.0 | 76 ± 3 | 7.4 | 82.63 | 88 ± 2 |
| NVSS J174343−182838 | 8.7203 | 5.8132 | 6.1 | 40.23 | 44 ± 8 | – | – | – ± – |
| NVSS J174351−261059 | 2.1435 | 1.7718 | 5.3 | 37.92 | 33 ± 16 | 5.8 | 45.71 | 51 ± 13 |
| NVSS J174423−311636 | −2.135 | −0.9956 | 6.9 | 77.73 | 86 ± 4 | 7.4 | 86.47 | 94 ± 2 |
| NVSS J174513−315104 | −2.533 | −1.446 | 7.7 | 71.66 | 80 ± 1 | 7.4 | 84.13 | 92 ± 3 |
| NVSS J174618−193006 | 8.1553 | 4.7619 | 5.3 | 41.91 | 45 ± 1 | – | – | – ± – |
| NVSS J174637−182629 | 9.1081 | 5.2404 | 5.3 | 43.51 | 47 ± 1 | – | – | – ± – |
| NVSS J174709−295802 | −0.7073 | −0.8216 | 5.3 | 50.32 | 73 ± 6 | 5.8 | 58.65 | 77 ± 4 |
| NVSS J174713−192135 | 8.3906 | 4.6467 | 6.9 | 37.53 | 42 ± 14 | – | – | – ± – |
| NVSS J174716−191954 | 8.4192 | 4.6536 | 6.1 | 38.29 | 43 ± 17 | – | – | – ± – |
| NVSS J174748−312315 | −1.8502 | −1.6766 | 6.1 | 55.64 | 66 ± 3 | 5.8 | 65.1 | 73 ± 5 |
| NVSS J174831−324102 | −2.8834 | −2.4753 | 4.4 | 69.29 | 74 ± 1 | 4.9 | 82.54 | 39 ± 1 |
| NVSS J174832−225211 | 5.5312 | 2.5801 | 3.6 | 43.06 | 50 ± 1 | – | – | – ± – |
| NVSS J174915−200033 | 8.0755 | 3.9058 | 5.3 | 34.23 | 40 ± 1 | – | – | – ± – |
| NVSS J174931−210847 | 7.1301 | 3.2676 | 8.6 | 42.84 | 50 ± 1 | – | – | – ± – |
| NVSS J175104−235215 | 4.9686 | 1.5693 | 5.3 | 52.62 | 56 ± 1 | 6.6 | 65.66 | 72 ± 15 |
| NVSS J175114−323538 | −2.514 | −2.9188 | 5.3 | 71.94 | 69 ± 1 | 4.9 | 88.18 | 89 ± 8 |
| NVSS J175151−252359 | 3.745 | 0.6349 | 6.1 | 54.98 | 64 ± 5 | 5.8 | 60.73 | 69 ± 23 |
| NVSS J175157−240425 | 4.8976 | 1.2915 | 5.3 | 52.75 | 64 ± 1 | 5.8 | 60.05 | 67 ± 3 |
| NVSS J175218−210508 | 7.513 | 2.7416 | 5.3 | 40.48 | 46 ± 1 | – | – | – ± – |
| NVSS J175233−223012 | 6.32 | 1.9719 | 6.9 | 49.97 | 56 ± 42 | – | – | – ± – |
| NVSS J175427−235235 | 5.358 | 0.8988 | 6.9 | 45.45 | 48 ± 4 | – | – | – ± – |
| NVSS J175526−223211 | 6.6287 | 1.3809 | 6.9 | 39.96 | 49 ± 1 | – | – | – ± – |
| NVSS J175548−233322 | 5.7906 | 0.7936 | 6.1 | 42.94 | 55 ± 13 | – | – | – ± – |
| NVSS J175727−223901 | 6.7646 | 0.9197 | 6.1 | 43.97 | 54 ± 1 | – | – | – ± – |
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
| NVSS J173133−264015 | 0.2574 | 3.8392 | 5.3 | 37.96 | 41 ± 1 | 4.9 | 44.72 | 48 ± 2 |
| NVSS J173203−285516 | −1.5699 | 2.5169 | 5.3 | 42.06 | 46 ± 1 | 4.9 | 43.25 | 46 ± 3 |
| NVSS J173205−242651 | 2.1956 | 4.945 | 4.4 | 46.14 | 50 ± 4 | 4.1 | 52.35 | 56 ± 1 |
| NVSS J173252−223511 | 3.8664 | 5.7991 | 5.3 | 50.1 | 53 ± 4 | – | – | – ± – |
| NVSS J173524−251036 | 1.9877 | 3.9175 | 4.4 | 42.17 | 45 ± 10 | 4.1 | 49.03 | 37 ± 39 |
| NVSS J173620−283552 | −0.7887 | 1.9026 | 5.3 | 29.96 | 31 ± 1 | 4.9 | 34.21 | 39 ± 1 |
| NVSS J173713−224734 | 4.2289 | 4.8441 | 5.3 | 47.75 | 51 ± 15 | 5.8 | 47.34 | 48 ± 38 |
| NVSS J173718−260426 | 1.4579 | 3.0762 | 5.3 | 43.22 | 51 ± 17 | 4.9 | 50.54 | 57 ± 1 |
| NVSS J173722−223000 | 4.498 | 4.968 | 5.3 | 48.19 | 52 ± 1 | 5.8 | 52.47 | 54 ± 32 |
| NVSS J173753−254642 | 1.7778 | 3.1242 | 5.3 | 45.22 | 46 ± 25 | 4.9 | 52.52 | 57 ± 32 |
| NVSS J173806−262443 | 1.2669 | 2.7455 | 5.3 | 39.83 | 45 ± 23 | 4.9 | 45.53 | 55 ± 28 |
| NVSS J173811−204411 | 6.1012 | 5.7415 | 3.6 | 47.13 | 51 ± 1 | – | – | – ± – |
| NVSS J173850−221918 | 4.8301 | 4.7751 | 5.3 | 48.56 | 50 ± 4 | 5.8 | 57.25 | 59 ± 2 |
| NVSS J173939−205505 | 6.1259 | 5.3569 | 3.6 | 46.58 | 51 ± 5 | – | – | – ± – |
| NVSS J174202−271311 | 1.0472 | 1.5731 | 5.3 | 38.11 | 33 ± 1 | 5.8 | 41.72 | 36 ± 15 |
| NVSS J174224−203729 | 6.7168 | 4.9604 | 4.4 | 56.06 | 60 ± 2 | – | – | – ± – |
| NVSS J174317−305819 | −1.9982 | −0.6363 | 6.9 | 66.0 | 76 ± 3 | 7.4 | 82.63 | 88 ± 2 |
| NVSS J174343−182838 | 8.7203 | 5.8132 | 6.1 | 40.23 | 44 ± 8 | – | – | – ± – |
| NVSS J174351−261059 | 2.1435 | 1.7718 | 5.3 | 37.92 | 33 ± 16 | 5.8 | 45.71 | 51 ± 13 |
| NVSS J174423−311636 | −2.135 | −0.9956 | 6.9 | 77.73 | 86 ± 4 | 7.4 | 86.47 | 94 ± 2 |
| NVSS J174513−315104 | −2.533 | −1.446 | 7.7 | 71.66 | 80 ± 1 | 7.4 | 84.13 | 92 ± 3 |
| NVSS J174618−193006 | 8.1553 | 4.7619 | 5.3 | 41.91 | 45 ± 1 | – | – | – ± – |
| NVSS J174637−182629 | 9.1081 | 5.2404 | 5.3 | 43.51 | 47 ± 1 | – | – | – ± – |
| NVSS J174709−295802 | −0.7073 | −0.8216 | 5.3 | 50.32 | 73 ± 6 | 5.8 | 58.65 | 77 ± 4 |
| NVSS J174713−192135 | 8.3906 | 4.6467 | 6.9 | 37.53 | 42 ± 14 | – | – | – ± – |
| NVSS J174716−191954 | 8.4192 | 4.6536 | 6.1 | 38.29 | 43 ± 17 | – | – | – ± – |
| NVSS J174748−312315 | −1.8502 | −1.6766 | 6.1 | 55.64 | 66 ± 3 | 5.8 | 65.1 | 73 ± 5 |
| NVSS J174831−324102 | −2.8834 | −2.4753 | 4.4 | 69.29 | 74 ± 1 | 4.9 | 82.54 | 39 ± 1 |
| NVSS J174832−225211 | 5.5312 | 2.5801 | 3.6 | 43.06 | 50 ± 1 | – | – | – ± – |
| NVSS J174915−200033 | 8.0755 | 3.9058 | 5.3 | 34.23 | 40 ± 1 | – | – | – ± – |
| NVSS J174931−210847 | 7.1301 | 3.2676 | 8.6 | 42.84 | 50 ± 1 | – | – | – ± – |
| NVSS J175104−235215 | 4.9686 | 1.5693 | 5.3 | 52.62 | 56 ± 1 | 6.6 | 65.66 | 72 ± 15 |
| NVSS J175114−323538 | −2.514 | −2.9188 | 5.3 | 71.94 | 69 ± 1 | 4.9 | 88.18 | 89 ± 8 |
| NVSS J175151−252359 | 3.745 | 0.6349 | 6.1 | 54.98 | 64 ± 5 | 5.8 | 60.73 | 69 ± 23 |
| NVSS J175157−240425 | 4.8976 | 1.2915 | 5.3 | 52.75 | 64 ± 1 | 5.8 | 60.05 | 67 ± 3 |
| NVSS J175218−210508 | 7.513 | 2.7416 | 5.3 | 40.48 | 46 ± 1 | – | – | – ± – |
| NVSS J175233−223012 | 6.32 | 1.9719 | 6.9 | 49.97 | 56 ± 42 | – | – | – ± – |
| NVSS J175427−235235 | 5.358 | 0.8988 | 6.9 | 45.45 | 48 ± 4 | – | – | – ± – |
| NVSS J175526−223211 | 6.6287 | 1.3809 | 6.9 | 39.96 | 49 ± 1 | – | – | – ± – |
| NVSS J175548−233322 | 5.7906 | 0.7936 | 6.1 | 42.94 | 55 ± 13 | – | – | – ± – |
| NVSS J175727−223901 | 6.7646 | 0.9197 | 6.1 | 43.97 | 54 ± 1 | – | – | – ± – |
Ts calculated at the minimum point (|$v$|min, Tmin) of the HISA feature in the H i emission spectra for both GASS and SGPS data.
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
| NVSS J173133−264015 | 0.2574 | 3.8392 | 5.3 | 37.96 | 41 ± 1 | 4.9 | 44.72 | 48 ± 2 |
| NVSS J173203−285516 | −1.5699 | 2.5169 | 5.3 | 42.06 | 46 ± 1 | 4.9 | 43.25 | 46 ± 3 |
| NVSS J173205−242651 | 2.1956 | 4.945 | 4.4 | 46.14 | 50 ± 4 | 4.1 | 52.35 | 56 ± 1 |
| NVSS J173252−223511 | 3.8664 | 5.7991 | 5.3 | 50.1 | 53 ± 4 | – | – | – ± – |
| NVSS J173524−251036 | 1.9877 | 3.9175 | 4.4 | 42.17 | 45 ± 10 | 4.1 | 49.03 | 37 ± 39 |
| NVSS J173620−283552 | −0.7887 | 1.9026 | 5.3 | 29.96 | 31 ± 1 | 4.9 | 34.21 | 39 ± 1 |
| NVSS J173713−224734 | 4.2289 | 4.8441 | 5.3 | 47.75 | 51 ± 15 | 5.8 | 47.34 | 48 ± 38 |
| NVSS J173718−260426 | 1.4579 | 3.0762 | 5.3 | 43.22 | 51 ± 17 | 4.9 | 50.54 | 57 ± 1 |
| NVSS J173722−223000 | 4.498 | 4.968 | 5.3 | 48.19 | 52 ± 1 | 5.8 | 52.47 | 54 ± 32 |
| NVSS J173753−254642 | 1.7778 | 3.1242 | 5.3 | 45.22 | 46 ± 25 | 4.9 | 52.52 | 57 ± 32 |
| NVSS J173806−262443 | 1.2669 | 2.7455 | 5.3 | 39.83 | 45 ± 23 | 4.9 | 45.53 | 55 ± 28 |
| NVSS J173811−204411 | 6.1012 | 5.7415 | 3.6 | 47.13 | 51 ± 1 | – | – | – ± – |
| NVSS J173850−221918 | 4.8301 | 4.7751 | 5.3 | 48.56 | 50 ± 4 | 5.8 | 57.25 | 59 ± 2 |
| NVSS J173939−205505 | 6.1259 | 5.3569 | 3.6 | 46.58 | 51 ± 5 | – | – | – ± – |
| NVSS J174202−271311 | 1.0472 | 1.5731 | 5.3 | 38.11 | 33 ± 1 | 5.8 | 41.72 | 36 ± 15 |
| NVSS J174224−203729 | 6.7168 | 4.9604 | 4.4 | 56.06 | 60 ± 2 | – | – | – ± – |
| NVSS J174317−305819 | −1.9982 | −0.6363 | 6.9 | 66.0 | 76 ± 3 | 7.4 | 82.63 | 88 ± 2 |
| NVSS J174343−182838 | 8.7203 | 5.8132 | 6.1 | 40.23 | 44 ± 8 | – | – | – ± – |
| NVSS J174351−261059 | 2.1435 | 1.7718 | 5.3 | 37.92 | 33 ± 16 | 5.8 | 45.71 | 51 ± 13 |
| NVSS J174423−311636 | −2.135 | −0.9956 | 6.9 | 77.73 | 86 ± 4 | 7.4 | 86.47 | 94 ± 2 |
| NVSS J174513−315104 | −2.533 | −1.446 | 7.7 | 71.66 | 80 ± 1 | 7.4 | 84.13 | 92 ± 3 |
| NVSS J174618−193006 | 8.1553 | 4.7619 | 5.3 | 41.91 | 45 ± 1 | – | – | – ± – |
| NVSS J174637−182629 | 9.1081 | 5.2404 | 5.3 | 43.51 | 47 ± 1 | – | – | – ± – |
| NVSS J174709−295802 | −0.7073 | −0.8216 | 5.3 | 50.32 | 73 ± 6 | 5.8 | 58.65 | 77 ± 4 |
| NVSS J174713−192135 | 8.3906 | 4.6467 | 6.9 | 37.53 | 42 ± 14 | – | – | – ± – |
| NVSS J174716−191954 | 8.4192 | 4.6536 | 6.1 | 38.29 | 43 ± 17 | – | – | – ± – |
| NVSS J174748−312315 | −1.8502 | −1.6766 | 6.1 | 55.64 | 66 ± 3 | 5.8 | 65.1 | 73 ± 5 |
| NVSS J174831−324102 | −2.8834 | −2.4753 | 4.4 | 69.29 | 74 ± 1 | 4.9 | 82.54 | 39 ± 1 |
| NVSS J174832−225211 | 5.5312 | 2.5801 | 3.6 | 43.06 | 50 ± 1 | – | – | – ± – |
| NVSS J174915−200033 | 8.0755 | 3.9058 | 5.3 | 34.23 | 40 ± 1 | – | – | – ± – |
| NVSS J174931−210847 | 7.1301 | 3.2676 | 8.6 | 42.84 | 50 ± 1 | – | – | – ± – |
| NVSS J175104−235215 | 4.9686 | 1.5693 | 5.3 | 52.62 | 56 ± 1 | 6.6 | 65.66 | 72 ± 15 |
| NVSS J175114−323538 | −2.514 | −2.9188 | 5.3 | 71.94 | 69 ± 1 | 4.9 | 88.18 | 89 ± 8 |
| NVSS J175151−252359 | 3.745 | 0.6349 | 6.1 | 54.98 | 64 ± 5 | 5.8 | 60.73 | 69 ± 23 |
| NVSS J175157−240425 | 4.8976 | 1.2915 | 5.3 | 52.75 | 64 ± 1 | 5.8 | 60.05 | 67 ± 3 |
| NVSS J175218−210508 | 7.513 | 2.7416 | 5.3 | 40.48 | 46 ± 1 | – | – | – ± – |
| NVSS J175233−223012 | 6.32 | 1.9719 | 6.9 | 49.97 | 56 ± 42 | – | – | – ± – |
| NVSS J175427−235235 | 5.358 | 0.8988 | 6.9 | 45.45 | 48 ± 4 | – | – | – ± – |
| NVSS J175526−223211 | 6.6287 | 1.3809 | 6.9 | 39.96 | 49 ± 1 | – | – | – ± – |
| NVSS J175548−233322 | 5.7906 | 0.7936 | 6.1 | 42.94 | 55 ± 13 | – | – | – ± – |
| NVSS J175727−223901 | 6.7646 | 0.9197 | 6.1 | 43.97 | 54 ± 1 | – | – | – ± – |
| Name . | l . | b . | |$v$|min (GASS) . | Ts,max . | Ts,HISA,peak . | |$v$|min (SGPS) . | Ts,max . | Ts,HISA,peak . |
|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | (km s−1) . | (GASS) (K) . | (GASS) (K) . | (km s−1) . | (SGPS) (K) . | (SGPS) (K) . |
| NVSS J172829−284610 | −1.8738 | 3.2555 | 4.4 | 55.11 | 51 ± 1 | 4.9 | 66.06 | 57 ± 7 |
| NVSS J172836−271236 | −0.5563 | 4.0941 | 4.4 | 38.65 | 44 ± 1 | 4.1 | 44.05 | 49 ± 2 |
| NVSS J172908−265751 | −0.2845 | 4.1296 | 4.4 | 37.75 | 44 ± 3 | 4.1 | 44.66 | 53 ± 16 |
| NVSS J172920−234535 | 2.432 | 5.8467 | 5.3 | 46.58 | 50 ± 58 | – | – | – ± – |
| NVSS J173107−245703 | 1.6506 | 4.8577 | 3.6 | 46.52 | 51 ± 1 | 4.1 | 56.83 | 59 ± 1 |
| NVSS J173133−264015 | 0.2574 | 3.8392 | 5.3 | 37.96 | 41 ± 1 | 4.9 | 44.72 | 48 ± 2 |
| NVSS J173203−285516 | −1.5699 | 2.5169 | 5.3 | 42.06 | 46 ± 1 | 4.9 | 43.25 | 46 ± 3 |
| NVSS J173205−242651 | 2.1956 | 4.945 | 4.4 | 46.14 | 50 ± 4 | 4.1 | 52.35 | 56 ± 1 |
| NVSS J173252−223511 | 3.8664 | 5.7991 | 5.3 | 50.1 | 53 ± 4 | – | – | – ± – |
| NVSS J173524−251036 | 1.9877 | 3.9175 | 4.4 | 42.17 | 45 ± 10 | 4.1 | 49.03 | 37 ± 39 |
| NVSS J173620−283552 | −0.7887 | 1.9026 | 5.3 | 29.96 | 31 ± 1 | 4.9 | 34.21 | 39 ± 1 |
| NVSS J173713−224734 | 4.2289 | 4.8441 | 5.3 | 47.75 | 51 ± 15 | 5.8 | 47.34 | 48 ± 38 |
| NVSS J173718−260426 | 1.4579 | 3.0762 | 5.3 | 43.22 | 51 ± 17 | 4.9 | 50.54 | 57 ± 1 |
| NVSS J173722−223000 | 4.498 | 4.968 | 5.3 | 48.19 | 52 ± 1 | 5.8 | 52.47 | 54 ± 32 |
| NVSS J173753−254642 | 1.7778 | 3.1242 | 5.3 | 45.22 | 46 ± 25 | 4.9 | 52.52 | 57 ± 32 |
| NVSS J173806−262443 | 1.2669 | 2.7455 | 5.3 | 39.83 | 45 ± 23 | 4.9 | 45.53 | 55 ± 28 |
| NVSS J173811−204411 | 6.1012 | 5.7415 | 3.6 | 47.13 | 51 ± 1 | – | – | – ± – |
| NVSS J173850−221918 | 4.8301 | 4.7751 | 5.3 | 48.56 | 50 ± 4 | 5.8 | 57.25 | 59 ± 2 |
| NVSS J173939−205505 | 6.1259 | 5.3569 | 3.6 | 46.58 | 51 ± 5 | – | – | – ± – |
| NVSS J174202−271311 | 1.0472 | 1.5731 | 5.3 | 38.11 | 33 ± 1 | 5.8 | 41.72 | 36 ± 15 |
| NVSS J174224−203729 | 6.7168 | 4.9604 | 4.4 | 56.06 | 60 ± 2 | – | – | – ± – |
| NVSS J174317−305819 | −1.9982 | −0.6363 | 6.9 | 66.0 | 76 ± 3 | 7.4 | 82.63 | 88 ± 2 |
| NVSS J174343−182838 | 8.7203 | 5.8132 | 6.1 | 40.23 | 44 ± 8 | – | – | – ± – |
| NVSS J174351−261059 | 2.1435 | 1.7718 | 5.3 | 37.92 | 33 ± 16 | 5.8 | 45.71 | 51 ± 13 |
| NVSS J174423−311636 | −2.135 | −0.9956 | 6.9 | 77.73 | 86 ± 4 | 7.4 | 86.47 | 94 ± 2 |
| NVSS J174513−315104 | −2.533 | −1.446 | 7.7 | 71.66 | 80 ± 1 | 7.4 | 84.13 | 92 ± 3 |
| NVSS J174618−193006 | 8.1553 | 4.7619 | 5.3 | 41.91 | 45 ± 1 | – | – | – ± – |
| NVSS J174637−182629 | 9.1081 | 5.2404 | 5.3 | 43.51 | 47 ± 1 | – | – | – ± – |
| NVSS J174709−295802 | −0.7073 | −0.8216 | 5.3 | 50.32 | 73 ± 6 | 5.8 | 58.65 | 77 ± 4 |
| NVSS J174713−192135 | 8.3906 | 4.6467 | 6.9 | 37.53 | 42 ± 14 | – | – | – ± – |
| NVSS J174716−191954 | 8.4192 | 4.6536 | 6.1 | 38.29 | 43 ± 17 | – | – | – ± – |
| NVSS J174748−312315 | −1.8502 | −1.6766 | 6.1 | 55.64 | 66 ± 3 | 5.8 | 65.1 | 73 ± 5 |
| NVSS J174831−324102 | −2.8834 | −2.4753 | 4.4 | 69.29 | 74 ± 1 | 4.9 | 82.54 | 39 ± 1 |
| NVSS J174832−225211 | 5.5312 | 2.5801 | 3.6 | 43.06 | 50 ± 1 | – | – | – ± – |
| NVSS J174915−200033 | 8.0755 | 3.9058 | 5.3 | 34.23 | 40 ± 1 | – | – | – ± – |
| NVSS J174931−210847 | 7.1301 | 3.2676 | 8.6 | 42.84 | 50 ± 1 | – | – | – ± – |
| NVSS J175104−235215 | 4.9686 | 1.5693 | 5.3 | 52.62 | 56 ± 1 | 6.6 | 65.66 | 72 ± 15 |
| NVSS J175114−323538 | −2.514 | −2.9188 | 5.3 | 71.94 | 69 ± 1 | 4.9 | 88.18 | 89 ± 8 |
| NVSS J175151−252359 | 3.745 | 0.6349 | 6.1 | 54.98 | 64 ± 5 | 5.8 | 60.73 | 69 ± 23 |
| NVSS J175157−240425 | 4.8976 | 1.2915 | 5.3 | 52.75 | 64 ± 1 | 5.8 | 60.05 | 67 ± 3 |
| NVSS J175218−210508 | 7.513 | 2.7416 | 5.3 | 40.48 | 46 ± 1 | – | – | – ± – |
| NVSS J175233−223012 | 6.32 | 1.9719 | 6.9 | 49.97 | 56 ± 42 | – | – | – ± – |
| NVSS J175427−235235 | 5.358 | 0.8988 | 6.9 | 45.45 | 48 ± 4 | – | – | – ± – |
| NVSS J175526−223211 | 6.6287 | 1.3809 | 6.9 | 39.96 | 49 ± 1 | – | – | – ± – |
| NVSS J175548−233322 | 5.7906 | 0.7936 | 6.1 | 42.94 | 55 ± 13 | – | – | – ± – |
| NVSS J175727−223901 | 6.7646 | 0.9197 | 6.1 | 43.97 | 54 ± 1 | – | – | – ± – |
APPENDIX D: H i ABSORPTION AND EMISSION SPECTRA FOR ALL OBSERVED SOURCES

Top panel: The solid black line shows the emission spectra (TON) extracted from GASS and the dashed line shows the modelled TOFF spectra. Bottom panel: The black line shows the ATCA absorption spectra, the green line is the fitted Gaussian model, and the red dashed lines are the individual Gaussian components of the fit. The grey line is the residual from the absorption model shifted to −0.2.
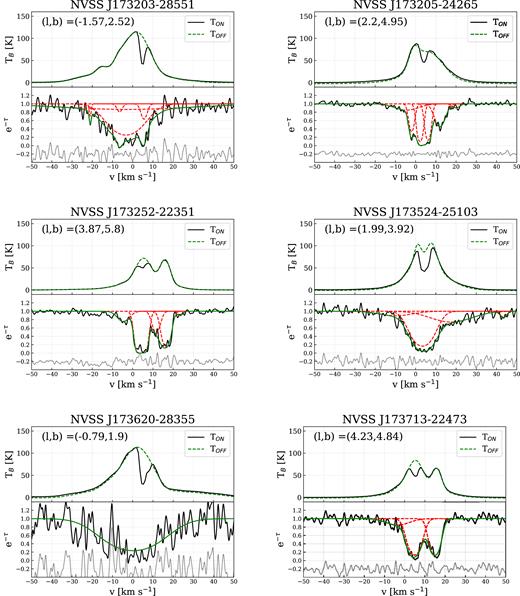
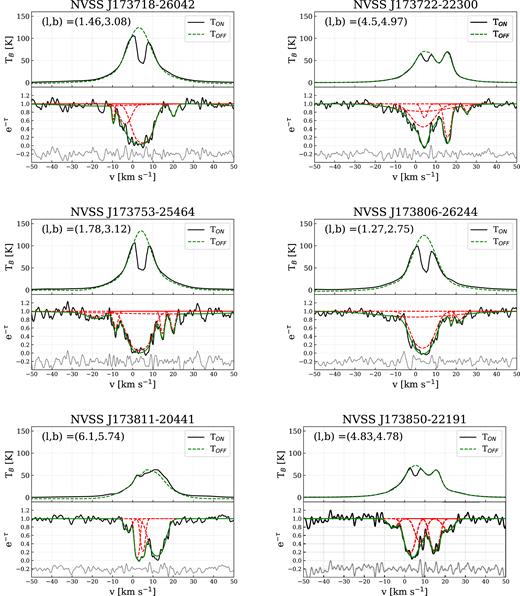
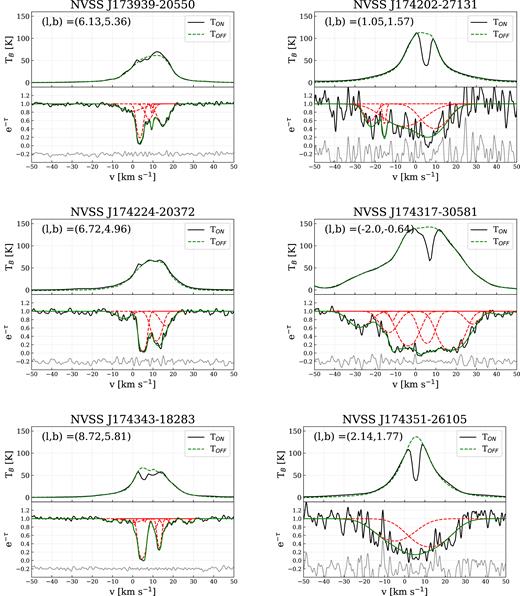
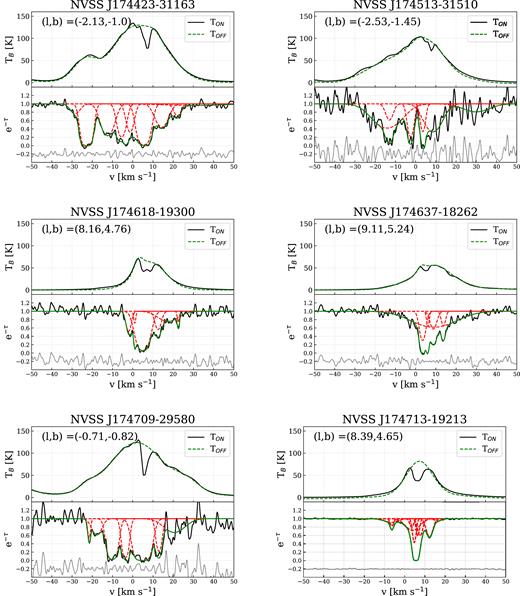
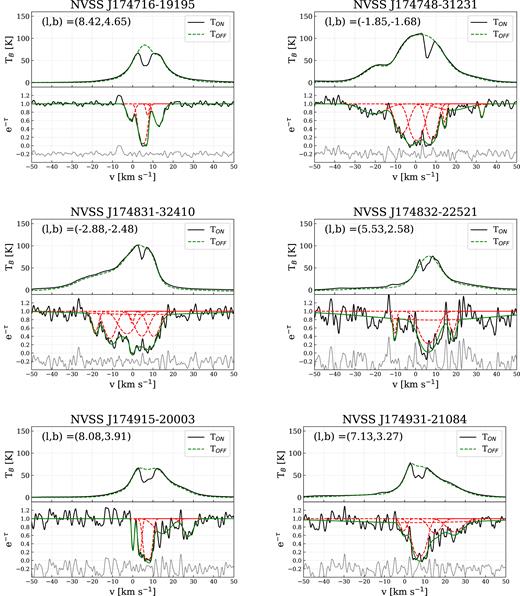
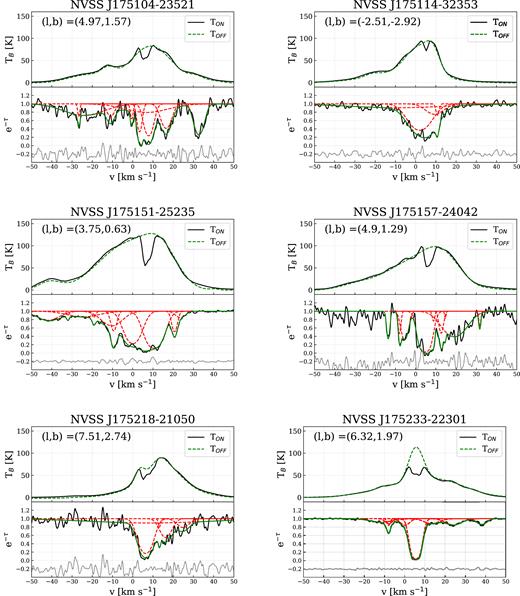
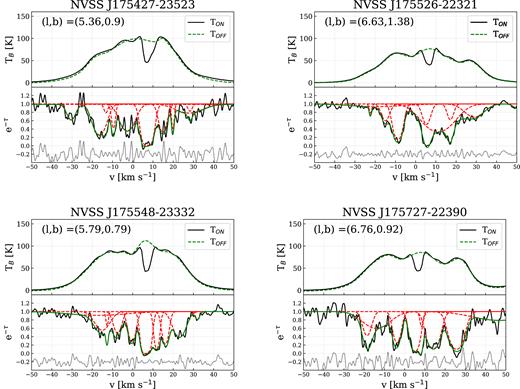
APPENDIX E: FITTED OH SPECTRA
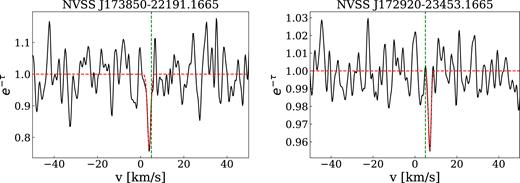
1665 MHz OH absorption spectra. The red dashed line shows the fitted Gaussian profile to the line. The green dashed line is |$v$|LSR = 5 km s−1.
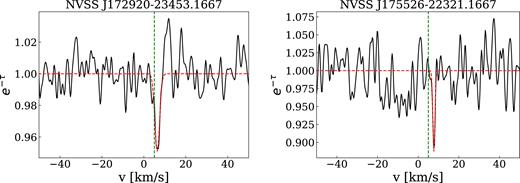
1667 MHz OH absorption spectra. The red dashed line shows the fitted Gaussian profile to the line. The green dashed line is |$v$|LSR = 5 km s−1.



