-
PDF
- Split View
-
Views
-
Cite
Cite
Benjamin Desrousseaux, François Lique, The rotational excitation of HF by H, Monthly Notices of the Royal Astronomical Society, Volume 476, Issue 4, June 2018, Pages 4719–4724, https://doi.org/10.1093/mnras/sty605
Close - Share Icon Share
Abstract
The HF molecule is a key tracer of molecular hydrogen in diffuse interstellar medium (ISM). Accurate modelling of the HF abundance in such media requires one to model its excitation by both radiation and collisions. In diffuse ISM, the dominant collisional partners are atomic and molecular hydrogen. We report quantum time-independent calculations of collisional cross-sections and rate coefficients for the rotational excitation of HF by H. The reactive hydrogen exchange channels are taken into account in the scattering calculations. For the first time, HF–H rate coefficients are provided for temperature ranging from 10 to 500 K. The strongest collision-induced rotational HF transitions are those with Δj = 1, and the order of magnitude of the new HF–H rate coefficients is similar to that of the HF–H2 ones previously computed. As a first application, we simulate the excitation of HF by both H and H2 in typical diffuse ISM. We show that, depending on the rotational transition, hydrogen atoms increase or decrease the simulated excitation temperatures compared to collisional excitation only due to H2 molecules. Such results suggest that the new HF–H collisional data have to be used for properly modelling the abundance of HF in diffuse ISM.
1 INTRODUCTION
The chemistry of interstellar fluorine is qualitatively different from that of any other element since fluorine is the most reactive species observed in the diffuse interstellar medium (ISM) (Neufeld, Wolfire & Schilke 2005; Neufeld & Wolfire 2009). Atomic fluorine undergoes an exothermic reaction with molecular hydrogen (Tizniti et al. 2014) so that the diatomic molecule HF is predicted to be abundant (Neufeld et al. 2005). The abundance of HF should compete with, or even dominate over, the abundance of atomic F in interstellar clouds (Snow, Destree & Jensen 2007). Hence, hydrogen fluoride (HF) is predicted to be the dominant gas-phase reservoir of interstellar fluorine nuclei over a wide range of physical conditions.
The HF molecule was first detected in space by Neufeld et al. (1997) towards Sgr B2, using the Infrared Space Observatory. Recently, HF was detected in many interstellar clouds with the Heterodyne Instrument for the Far-Infrared onboard the Herschel Space Observatory (Neufeld et al. 2010; Phillips et al. 2010; Sonnentrucker et al. 2010, 2015; Monje et al. 2011). HF was also detected in nearby galaxies (Monje et al. 2014) and in the circumstellar gas (Agúndez et al. 2011). These observations are powerful tools to study the fluorine chemistry in space.
It is then crucial to accurately derive the HF abundance in the diffuse atomic and molecular clouds from the observational spectra. The analysis of the HF rotational spectra, especially those in emission, requires one to know the HF collisional rate coefficients with the most abundant interstellar species. Without these data, only approximate estimates of the molecular column density are possible assuming local thermodynamic equilibrium (LTE), which is generally not a good approximation (Roueff & Lique 2013).
The main collider in the interstellar molecular clouds is generally molecular hydrogen, H2. Collisional rate coefficients for the excitation of HF by He (as a template for H2) and H2 have been computed by Stoecklin and co-workers (Reese et al. 2005; Guillon & Stoecklin 2012). The He-rate coefficients have been revised recently by Yang et al. (2015).
In interstellar diffuse atomic clouds, the dominant collisional partner is the atomic hydrogen. Bott & Heidner (1977) measured rate coefficients for the vibrational deactivation of HF by H at room temperature using laser-induced fluorescence in a discharge flow tube in which H atoms were produced by a microwave discharge. Later, Tao & Alexander (2007) have studied the vibrational relaxation of HF by H, including the reactive channel, namely |${\rm HF} + {\rm H} \leftrightarrow {\rm F}+\rm {H}_2$|. They were focused on the appearance of resonances in the integral cross-sections due to the existence of bound and quasi-bound states supported by the van der Waals well of the HF–H complex. However, no collisional rate coefficients were provided in their study. Hence, to the best of our knowledge, there are no collisional data available for the (rotational) excitation of HF by H that can be relevant for astrophysical modelling. In this paper, we focus on the calculation of the first state-to-state rate coefficients for the HF–H collisional system.
The |${\rm HF} + {\rm H} \leftrightarrow {\rm F}+\rm {H}_2$| reaction is a prototype for the theoretical study of bimolecular reactions (Manolopoulos 1997; Alexander, Manolopoulos & Werner 2000; Chao & Skodje 2000; Althorpe & Clary 2003; Aquilanti et al. 2003; Che et al. 2007; Lique et al. 2008b, 2011; Tizniti et al. 2014). Accurate theoretical studies were enabled by the availability of high-quality potential energy surfaces (PES; Stark & Werner 1996; Li et al. 2007), and it is now established that theory and experiments have converged for this system. During collisions between HF and H, the reactive and the exchange processes are expected to proceed slowly because of a large endothermicity and activation barrier, respectively (Tao & Alexander 2007). Hence, the collisional energy transfer during HF + H collisions is by far the most probable process at low temperatures. However, accurate determination of pure rotational excitation cross-sections have to be obtained from approaches that include the reactive and exchange channels as recently discussed by Lique (2015) in the case of HCl–H collisions.
In this paper, we study the rotational excitation of HF by H using an exact quantum three-dimensional (3D) approach including the reactive and exchange channels. The paper is organized as follows: Section 2 provides a brief description of the scattering calculations. In Section 3, we present the results. Concluding remarks are drawn in Section 4.
2 THEORETICAL APPROACH
In our investigation of the scattering dynamics, we used the lowest adiabatic FH2 LWA-78 PES (Li et al. 2007). The ab initio LWA-78 PES has been calculated at the internally contracted multireference configuration interaction (Werner & Knowles 1988) level using a large atomic basis set. The non-adiabatic couplings were neglected because they have negligible effect on the rotational excitation of HF by H.
Fig. 1 shows the HF–H LWA-78 PES as a function of the Jacobi coordinates R and θ for a fixed internuclear rHF distance of 1.75 bohr, corresponding to the equilibrium distance of the ground vibrational state. In the Jacobi coordinate system, the centre of coordinates is placed in the HF centre of mass, and the vector |${\boldsymbol R}$| connects the HF centre of mass with the H atom. The rotation of HF molecule is defined by the θ angle (θ = 0° corresponds to the H··F–H configuration).
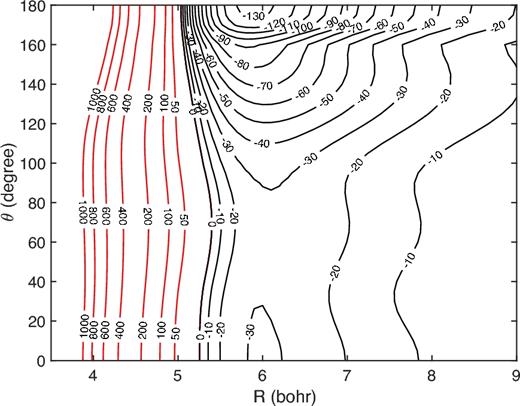
Contour plot of the HF–H LWA-78 PES (in cm−1) as a function of the Jacobi coordinates for a fixed internuclear rHF distance of 1.75 bohr.
As can be seen, the HF–H PES is highly anisotropic with respect to H rotation. The minimum configuration corresponds to linear H··H–F configuration with a well depth of ∼135 cm−1. Such a well depth is much deeper than the ∼40 cm−1 obtained for the HF–He PES (Yang et al. 2015) and half of that computed by Guillon & Stoecklin (2012) for the HF–H2 PES.
We used the abc reactive scattering code (Skouteris, Castillo & Manolopoulos 2000) to perform quantum time-independent calculations. It is computationally efficient to choose basis functions that are eigenfunctions of the operator corresponding to interchange of the two hydrogens. Hence, since the Hamiltonian is symmetric with respect to interchange of the two hydrogens, there will be no coupling between odd (ortho) and even (para) rotational states of H2, so that the number of coupled channels is reduced. Inelastic and exchange integral cross-sections were then obtained following the approach described in Tao & Alexander (2007) and recently used to study the rotational excitation of HCl by H (Lique 2015). We calculated the cross-sections involving the nine first rotational levels of HF (0 ≤ j ≤ 8). While excited vibrational states are included in the calculation to ensure convergence, cross-sections are reported only for rotational excitations of HF in its ground vibrational state. The reactive channels were energetically closed considering the collision energy range considered in this work (up to 3000 cm−1). However, the reactive channels were explicitly included in the calculations.
3 RESULTS
Fig. 2 displays the collision energy variation of the integral cross-sections obtained for the inelastic and exchange processes for collisions of HF(j = 0) and HF(j = 1) with H. The cross-sections are summed over all the possible final rotational states.
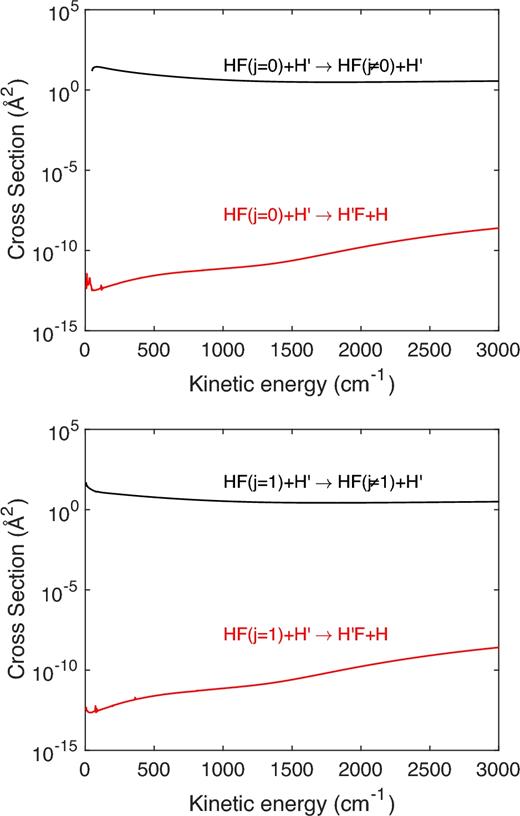
Inelastic and exchange rotational excitation cross-sections of HF(j = 0) and HF(j = 1) by H.
As one can see, the exchange processes are completely negligible over all the collision energy range explored in this work. Such effect can be attributed to the activation barrier of 20 000 K that implies the exchange process to proceed only through tunnelling at low temperatures. From the astrophysical point of view, rotational excitation through inelastic or exchange process cannot be distinguished so that, in the following, the inelastic and exchange cross-sections were summed even if the final result will be almost that of the pure inelastic collisions.
Fig. 3 displays the collision energy variation of the integral cross-sections for the rotational de-excitation of HF(j) to HF(j = 0) and HF(j = 1) induced by collisions with H.
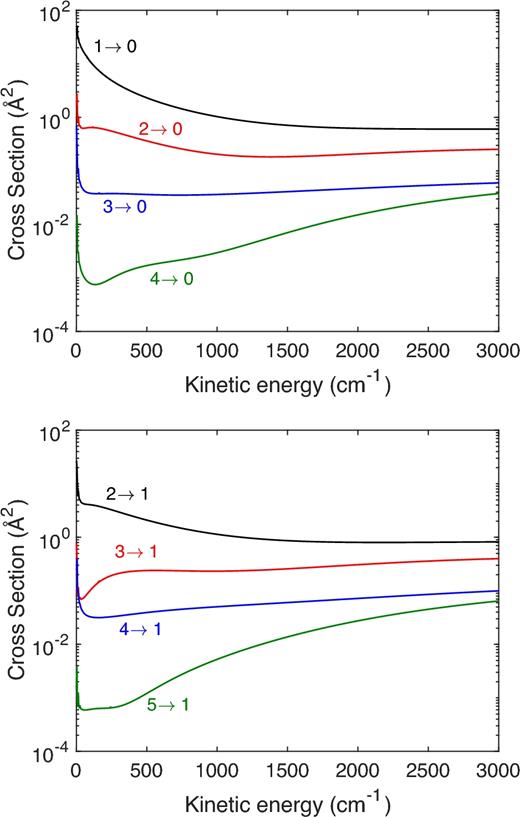
Collision energy variation of the cross-sections for the rotational de-excitation of HF(j) to HF(j = 0) and HF(j = 1) induced by collisions with H.
As expected, the cross-sections decrease with increasing Δj. The strongest collision-induced rotational HF transitions are the transitions with Δj = 1 as one can see in Fig. 3 where the rate coefficients for the j = 1 → j΄ = 0 and j = 2 → j΄ = 1 are the largest in magnitude. Such finding can be attributed to the strong odd anisotropy of the HF–H PES with respect to the H approach. The same propensity rules were obtained for the HCl–H collisional system (Lique 2015).
The corresponding rate coefficients are shown in Fig. 4. Obviously, they display the same feature as the collisional cross-sections and confirm the propensity rules in favour of transitions with Δj = 1.
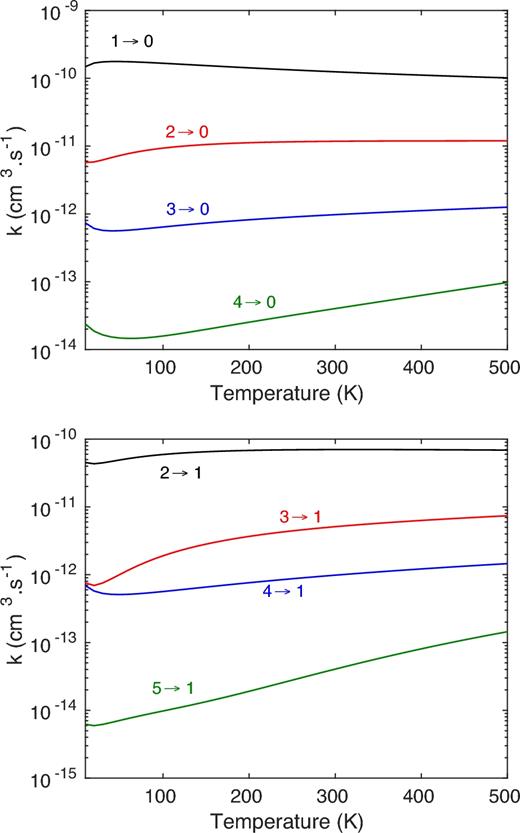
Temperature variation of the rate coefficients for the rotational de-excitation of HF(j) to HF(j = 0) and HF(j = 1) induced by collisions with H.
Then, we compare the new HF–H rate coefficients with those reported recently for the rotational excitation of HF by He (Yang et al. 2015)1 and H2 (Guillon & Stoecklin 2012). The three sets of rate coefficients were computed at a similar level of accuracy using highly correlated ab initio PES and quantum time-independent scattering approaches. Hence, in this comparison, we should be able to evaluate the impact of the different collisional partners. In Fig. 5, we compare the HF–H, HF–He, and HF–H2 (both para- and ortho-H2) rate coefficients for a selected number of transitions.
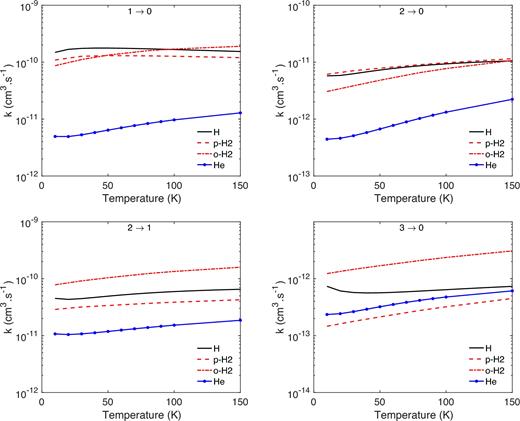
Comparison between HF–H, HF–He, and HF–H2 (both para- and ortho-H2) rate coefficients for a selected number of rotational (j → j΄) transitions.
As expected, the rate coefficients with the He collisional partner are lower than those with H and H2 collisional partner. However, differences larger than an order of magnitude are found, especially at low temperatures whereas they are predicted to be within a factor of 2 by the scaling relationships. Such low rate coefficients can be attributed to the weak potential well and anisotropy of the HF–He PES that do not favour fast collisional energy transfer and show that H or H2 rate coefficients cannot be obtained from the He ones in the case of the HF molecule.
Then, one can see that the rate coefficients for collisions with H do not always have the highest magnitude as expected from the scaling relationships. We also note that the differences between H and H2 rate coefficients depend on the transitions and on the temperature leading to the impossibility of extrapolating accurate H collisional data from H2 collisional data, or reverse. Hence, it confirms that, for hydrides, it is unrealistic to estimate unknown collisional rate coefficients by simply applying a scaling factor to existing rate coefficients. This result was previously observed for water (Daniel et al. 2015) and ammonia (Bouhafs et al. 2017). Nevertheless, in the present case, both the H and H2 sets of collisional data have similar magnitude and we anticipate that the excitation of HF due to H or H2 collisional partner will be similar.
The complete set of collisional rate coefficients is also available online from the LAMDA (Schöier et al. 2005) and BASECOL (Dubernet et al. 2013) websites.
4 DISCUSSION AND CONCLUSION
To summarize, we have presented quantum mechanical calculations of rate coefficients for the collisional excitation of HF by H. The results show that HF can be easily excited through collisions with H. The new HF–H rate coefficients are much larger in magnitude than that of HF–He and similar in magnitude as that of HF–H2.
As a first application and in order to test the impact of the new collisional excitation rate coefficients, we have performed radiative transfer calculations to simulate the excitation of HF in diffuse atomic and molecular clouds.
Non-local thermodynamic equilibrium (non-LTE) radiative transfer calculations were performed with the radex code (van der Tak et al. 2007) using the escape probability formalism approximation. Here, we computed the excitation temperatures of the j = 1 → j΄ = 0 and j = 2 → j΄ = 1 lines using different molecular fraction of the gas (i.e. different abundance for the atomic and molecular hydrogen). The only radiation field is the cosmic microwave background at 2.73 K.
We consider an HF column density of 1013 cm−2 and a kinetic temperature of 50 K. The gas density was fixed at 103 cm−3. The molecular fraction of the gas varies from 0.1 to 0.9 corresponding to an almost pure atomic and molecular gas. Finally, H2 was assumed to lie in the ground para and ortho rotational states |$j_{\rm H_2}=0$| and |$j_{\rm H_2}=1$|, respectively, with the ortho-to-para ratio corresponding to the LTE conditions. Fig. 6 shows the results of our radiative transfer calculations.
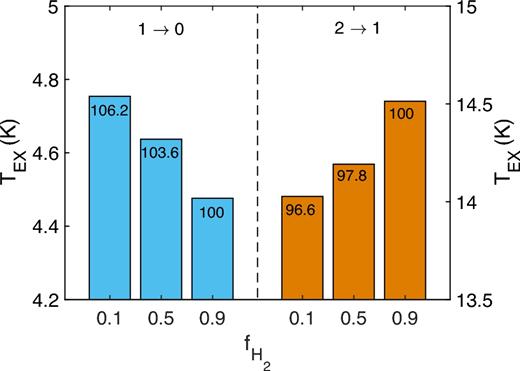
Excitation temperatures for the j = 1 → j΄ = 0 and j = 2 → j΄ = 1 lines of HF as a function of the molecular fraction (the numbers on the histograms are percentages relative to the intensity with the 0.9 molecular fraction).
First of all, we can observe, whatever the molecular fractions are, that the excitation temperatures are higher than the background radiation temperature of 2.73 K, especially for the j = 2 → j΄ = 1 line and much lower than the kinetic temperature of 50 K. Such finding clearly confirms the need of non-LTE radiative transfer calculations to analyse the HF absorption of emission spectra.
Then, one can see that the molecular fraction has a moderate impact on the excitation temperatures. The variation between considering mostly atomic or molecular gas is only of the order of 5–10 per cent. It shows that the excitation of HF cannot be used as a probe of the molecular fraction of the diffuse gas. Such finding can be explained by the similar magnitude of the HF–H and HF–H2 collisional data.
However, one can see that the variation of the excitation temperatures with increasing molecular fraction of the gas depends on the rotational line. Indeed, the excitation temperature of the j = 1 → j΄ = 0 line decreases with increasing molecular fraction while the reverse is observed for the j = 2 → j΄ = 1 line. Hence, it can be important to properly simulate the excitation of HF in diffuse molecular clouds using both sets of collisional data. Then, we recommend the use of the new HF–H collisional rate coefficients to accurately derive the HF abundance in the ISM and to enable a better understanding of the interstellar fluorine chemistry as well as a promotion of HF as key tracer of H2 in diffuse interstellar clouds.
Acknowledgements
This research was supported by the Agence Nationale de la Recherche (ANR-HYDRIDES), contract ANR-12-BS05-0011-01. Support by the Programme National ‘Physique et Chimie du Milieu Interstellaire’ (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES is also acknowledged. FL and BD acknowledge financial support from the Institut Universitaire de France.



