-
PDF
- Split View
-
Views
-
Cite
Cite
H ESS Collaboration, H Abdalla, A Abramowski, F Aharonian, F Ait Benkhali, A G Akhperjanian, T Andersson, E O Angüner, M Arrieta, P Aubert, M Backes, A Balzer, M Barnard, Y Becherini, J Becker Tjus, D Berge, S Bernhard, K Bernlöhr, R Blackwell, M Böttcher, C Boisson, J Bolmont, P Bordas, J Bregeon, F Brun, P Brun, M Bryan, T Bulik, M Capasso, J Carr, S Casanova, M Cerruti, N Chakraborty, R Chalme-Calvet, R C G Chaves, A Chen, J Chevalier, M Chrétien, S Colafrancesco, G Cologna, B Condon, J Conrad, Y Cui, I D Davids, J Decock, B Degrange, C Deil, J Devin, P deWilt, L Dirson, A Djannati-Ataï, W Domainko, A Donath, L O'C Drury, G Dubus, K Dutson, J Dyks, M Dyrda, T Edwards, K Egberts, P Eger, J-P Ernenwein, S Eschbach, C Farnier, S Fegan, M V Fernandes, A Fiasson, G Fontaine, A Förster, S Funk, M Füßling, S Gabici, M Gajdus, Y A Gallant, T Garrigoux, G Giavitto, B Giebels, J F Glicenstein, D Gottschall, A Goyal, M-H Grondin, D Hadasch, J Hahn, M Haupt, J Hawkes, G Heinzelmann, G Henri, G Hermann, O Hervet, J A Hinton, W Hofmann, C Hoischen, M Holler, D Horns, A Ivascenko, A Jacholkowska, M Jamrozy, M Janiak, D Jankowsky, F Jankowsky, M Jingo, T Jogler, L Jouvin, I Jung-Richardt, M A Kastendieck, K Katarzyński, U Katz, D Kerszberg, B Khélifi, M Kieffer, J King, S Klepser, D Klochkov, W Kluźniak, D Kolitzus, Nu Komin, K Kosack, S Krakau, M Kraus, F Krayzel, P P Krüger, H Laffon, G Lamanna, J Lau, J-P Lees, J Lefaucheur, V Lefranc, A Lemière, M Lemoine-Goumard, J-P Lenain, E Leser, T Lohse, M Lorentz, R Liu, R López-Coto, I Lypova, V Marandon, A Marcowith, C Mariaud, R Marx, G Maurin, N Maxted, M Mayer, P J Meintjes, M Meyer, A M W Mitchell, R Moderski, M Mohamed, L Mohrmann, K Morå, E Moulin, T Murach, M de Naurois, F Niederwanger, J Niemiec, L Oakes, P O'Brien, H Odaka, S Öttl, S Ohm, M Ostrowski, I Oya, M Padovani, M Panter, R D Parsons, N W Pekeur, G Pelletier, C Perennes, P-O Petrucci, B Peyaud, Q Piel, S Pita, H Poon, D Prokhorov, H Prokoph, G Pühlhofer, M Punch, A Quirrenbach, S Raab, A Reimer, O Reimer, M Renaud, R de los Reyes, F Rieger, C Romoli, S Rosier-Lees, G Rowell, B Rudak, C B Rulten, V Sahakian, D Salek, D A Sanchez, A Santangelo, M Sasaki, R Schlickeiser, F Schüssler, A Schulz, U Schwanke, S Schwemmer, M Settimo, A S Seyffert, N Shafi, I Shilon, R Simoni, H Sol, F Spanier, G Spengler, F Spies, Ł Stawarz, R Steenkamp, C Stegmann, F Stinzing, K Stycz, I Sushch, J-P Tavernet, T Tavernier, A M Taylor, R Terrier, L Tibaldo, D Tiziani, M Tluczykont, C Trichard, R Tuffs, Y Uchiyama, D J van der Walt, C van Eldik, C van Rensburg, B van Soelen, G Vasileiadis, J Veh, C Venter, A Viana, P Vincent, J Vink, F Voisin, H J Völk, T Vuillaume, Z Wadiasingh, S J Wagner, P Wagner, R M Wagner, R White, A Wierzcholska, P Willmann, A Wörnlein, D Wouters, R Yang, V Zabalza, D Zaborov, M Zacharias, R Zanin, A A Zdziarski, A Zech, F Zefi, A Ziegler, N Żywucka, H.E.S.S. discovery of very high energy γ-ray emission from PKS 0625−354, Monthly Notices of the Royal Astronomical Society, Volume 476, Issue 3, May 2018, Pages 4187–4198, https://doi.org/10.1093/mnras/sty439
Close - Share Icon Share
Abstract
PKS 0625−354 (z = 0.055) was observed with the four High Energy Stereoscopic System (H.E.S.S.) telescopes in 2012 during 5.5 h. The source was detected above an energy threshold of 200 GeV at a significance level of 6.1σ. No significant variability is found in these observations. The source is well described with a power-law spectrum with photon index Γ = 2.84 ± 0.50stat ± 0.10syst and normalization (at E0 = 1.0 TeV) N0(E0) = (0.58 ± 0.22stat ± 0.12syst) × 10−12 TeV−1 cm−2 s−1. Multiwavelength data collected with Fermi-LAT, Swift-XRT, Swift-UVOT, ATOM and WISE are also analysed. Significant variability is observed only in the Fermi-LAT γ-ray and Swift-XRT X-ray energy bands. Having a good multiwavelength coverage from radio to very high energy, we performed a broad-band modelling from two types of emission scenarios. The results from a one zone lepto-hadronic and a multizone leptonic models are compared and discussed. On the grounds of energetics, our analysis favours a leptonic multizone model. Models associated to the X-ray variability constraint support previous results, suggesting a BL Lac nature of PKS 0625−354 with, however, a large-scale jet structure typical of a radio galaxy.
1 INTRODUCTION
PKS 0625−354 (OH 342) (RA = 06h27m06.7s, Dec. = −35°29΄15΄, J2000) is a source located in the Cluster Abell 3392, observed at a redshift of z = 0.055 (Jones et al. 2009). The galaxy hosts a supermassive black hole with a mass of 109.19 ± 0.37 Msun, deduced by Bettoni et al. (2003) from bulge luminosity and stellar velocity dispersion relations. The nature of PKS 0625−354 is still a matter of debate, since it reveals features that appear both radio galaxy and blazar-like in nature.
Ekers et al. (1989) reported the discovery of one-sided jet with a position angle of +160° and radio halo observed at 5 GHz with VLA (Very Large Array) extending up to 4 arcmin. Radio observations with VLBA (Very Long Baseline Array) performed at 5 GHz revealed a strong central core and a quite faint radio component located at the southern-east side of the core, consistent with the direction of the large-scale jet orientation (Fomalont et al. 2000). A bright core emission and a one-sided jet, with orientation of +150°, have been found by Venturi et al. (2000) in VLBI (Very Long Baseline Interferometry) observations at 2.3 GHz. More recent radio monitoring performed as part of the TANAMI (Tracking Active Galactic Nuclei with Austral Milliarcsecond Interferometry) program has shown a radio-jet structure on intermediate scales out to 95 mas from the core, corresponding to a distance of 143 pc (Ojha et al. 2010).
Using radio observations of PKS 0625−354, an estimation of the maximal possible viewing angle of θ ≤ 61° is obtained from jet to counter-jet ratio, and θ ≤ 43° from the square root of the ratio of jet power to the jet power for a source at 60°, as defined in Giovannini et al. (1994).
Spectroscopic optical observations of PKS 0625−354 have revealed that the source could be a BL Lac object due to the results of the 4000 Å break and the fit to the optical continuum (Wills et al. 2004).
X-ray BeppoSAX observations in the energy range of 0.2–10 keV of PKS 0625−354 have shown a non-thermal hard X-ray component (Γ = 1.7) with a luminosity of 1.8 × 1043 erg s−1, likely originated in the central object (Trussoni et al. 1999). More recent studies focusing on Suzaku and Fermi-LAT observations have revealed to possess a soft spectrum in the X-ray regime and a hard spectrum in the γ-ray range (Fukazawa et al. 2015). The authors present broad-band spectral modelling with a low Lorentz factor, typical to that usually found for FR I radio galaxies.
In the high-energy (HE) band, the source has been detected with the Fermi-LAT from 11 months of observations, and was announced in the first Fermi-LAT source catalogue (1FGL; Abdo et al. 2010a). The published third Fermi-LAT source catalogue (3FGL) reports a flux from PKS 0625−354 of F1 GeV − 100 GeV = (1.43 ± 0.11) × 10−9 ph cm−2 s−1 and the hard spectrum characterized by the power-law distribution with the photon index Γ3FGL = 1.88 ± 0.06 (Acero et al. 2015).
This paper reports the discovery of very high energy (VHE) γ-ray emission from the region of PKS 0625−354. The layout is as follows: Section 2 introduces the High Energy Stereoscopic System (H.E.S.S.) experiment and presents VHE observations of PKS 0625−354, Section 3 reports multifrequency observations of the source, and Section 4 compares leptonic and lepto-hadronic multiwavelength (MWL) models, and discusses the physical properties and the source classification. Hereafter, we adopt a cosmology with H0 = 71 km s−1 Mpc−1, ΩΛ = 0.73, and ΩM = 0.27.
2 H.E.S.S. OBSERVATIONS OF PKS 0625−354
The H.E.S.S. is an array of five Imaging Atmospheric Cherenkov Telescopes, located in the Khomas Highland in Namibia, dedicated to observations of VHE γ rays (E > 100 GeV), described in detail in Aharonian et al. (2006a). Until 2012, H.E.S.S. I observations were carried out with four 12-m telescopes, each with a mirror area of 108 m2, whereas in 2012, the array was upgraded with a fifth telescope with a mirror area of 614 m2.
PKS 0625−354 was observed with H.E.S.S. I four telescope array during eight nights in 2012 November and December, resulting in a total exposure of 5.5 h of good quality data. All data were taken in wobble mode with the offset of 0|${^{\circ}_{.}}$|5. For all the data taken, the observations were between zenith angles of 11°–19°.
The data were analysed using the Model Analysis chain (de Naurois & Rolland 2009) with the Loose Cuts configuration (Aharonian et al. 2006b). The measured excess of 60.7 events corresponds to 6.1σ significance (following Li & Ma 1983). The emission observed is centred on RA = 06h26m58.2s|$\pm 2.6^\mathrm{s}_{\rm stat}$| and Dec. = −35°29΄50΄ ± 50΄ ± 33΄stat, J2000. All the results presented in this paper were cross-checked with independently generated calibration files, and an independent analysis chain called ImPACT (Parsons & Hinton 2014). Fig. 1 shows the significance map for PKS 0625−354. Within the statistical uncertainties, the source exhibits a point-like morphology. The differential energy spectrum of the VHE γ-ray emission has been derived using a forward folding method (Piron et al. 2001, see Fig. 2). The data are fitted with a power-law model defined as dN/dE = N0(E/E0)−Γ with a normalization N0(1 TeV) = (0.58 ± 0.22stat ± 0.12syst) × 10−12 TeV−1 cm−2 s−1, with a photon index Γ = 2.84 ± 0.50stat ± 0.20syst. The goodness of the fit is χ2/ndof = 24.4/21.
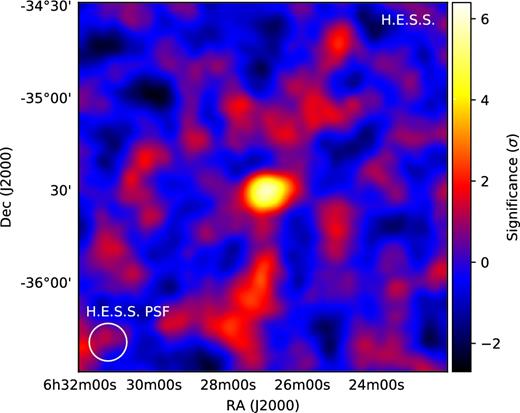
H.E.S.S. significance map centred on the position of PKS 0625−354. The white circle in the bottom left corner shows the H.E.S.S. PSF as the 68|$\rm{\,\,per\,\,cent}$| containment radius.
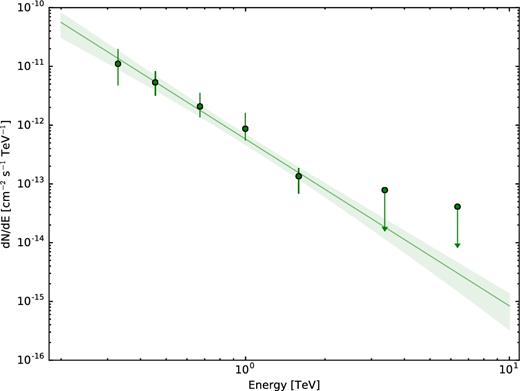
H.E.S.S. spectrum of PKS 0625−354 above 200 GeV. The panel presents best power-law fit to the data as a function of the true energy. Upper limits are given at 99|$\rm{\,\,per\,\,cent}$| confidential level with Feldman & Cousins (1998) confidence intervals. The green bow tie area gives the uncertainty of the fit at the 1σ confidence level.
The observed integrated flux of PKS 0625−354 is |$I(>{}575\,\rm GeV) = (8.8\pm 3.2_{\rm stat}\pm 1.6_{\rm syst})\times 10^{-13}$| cm−2 s−1.
The VHE light curve of the nightly integrated flux (E > 200 GeV) is presented in the upper panel of Fig. 3. A fit with a constant to the data set yields χ2/ndof = 5.95/7 (p = 0.55), indicating no evidence for variability in VHE γ-ray emission during the observation period.
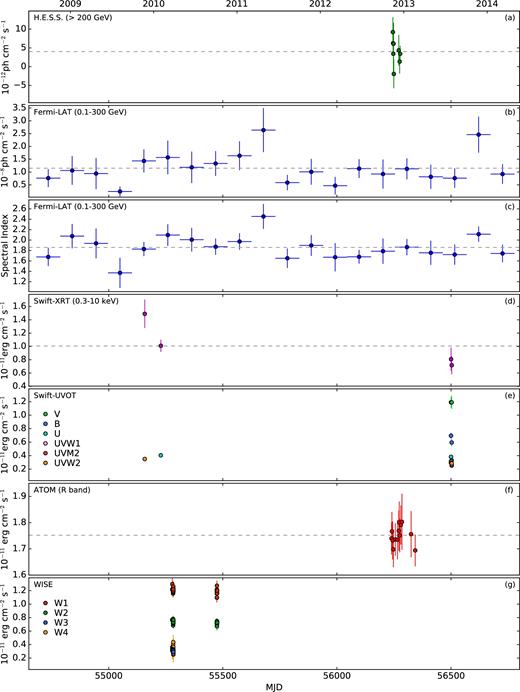
MWL light curve of PKS 0625−354. Panels from the top to bottom present: H.E.S.S. flux points above 200 GeV given in night-wise bins; the Fermi-LAT flux and photon index points in the energy range of 0.1–300 GeV, each point represents about 120 d of monitoring; Swift-XRT flux points for the energy range of 0.3–10 keV binned in one-day intervals; Swift-UVOT flux points for V, B, U, UVW1, UVM2, and UVW2 filters, each point represents one day of observations; ATOM optical flux points given in R band; WISE observations in W1–W4 filters. Swift-UVOT, ATOM, and WISE observations are corrected for the influence of the extinction. The horizontal dashed lines in most of the panels represent the average flux for all observations presented in a given band.
3 MULTIWAVELENGTH DATA
3.1 Fermi-LAT observations
High energy (HE, E > 100 GeV) γ-ray emission from the direction of PKS 0625−354 was first reported in the 1FGL. The source has also been included in the 2FGL and 3FGL (Nolan et al. 2012; Acero et al. 2015).
In this paper, the Fermi-LAT data collected between 2008 August 4 and 2015 May 30 have been analysed using standard Fermi Science Tools (version v10r0p5) with P8R2_SOURCE_V6 instrument response functions (IRFs), which is the latest LAT data release (i.e. Pass 8; Atwood et al. 2013). For these studies, all photons in the energy range from 100 MeV to 300 GeV are selected. The maximum zenith angle of 90° has been applied. The region of interest (ROI) is defined to have 10° size and it is centred on the source.
The binned maximum-likelihood method (Mattox et al. 1996) was applied, with the Galactic diffuse background modelled using the gll_iem_v06 map cube, and the extragalactic diffuse and residual instrument backgrounds modelled jointly using the iso_P8R2_SOURCE_V6_v06 template.
All the sources from the 3FGL inside the ROI of PKS 0625−354 were included in the model. The residual maps showed an excess in four regions, with a significance higher than 5σ. The model was refined by adding four point-like sources, whose emission was described by a power-law spectrum. After fitting the spectral parameters of the additional sources, the residual maps have been improved and no additional regions with significant excess have been found. The spectral parameters of PKS 0625−354 were fitted simultaneously with those of the Galactic and isotropic emission, and those of the closest sources.
In order to find the best description of the HE spectrum of PKS 0625−354, two models were tested:
a power-law in the form of dN/dE = Np(E/E0, p)−Γ, where Np is the normalization, Γ the photon index, and E0, p the scale energy parameter; and
a logarithmic parabola in the form of |${\rm d}N/{\rm d}E = N_l (E/E_{0,l})^{-(\alpha + \beta \log (E/E_{0,l})) }$|, where Nl is the normalization, α the spectral index, β the curvature parameter, and E0, l the scale energy parameter.
The fit parameters are collected in Table 1. The Test Statistic (TS) value between the log-parabola and power-law model is 2.2, meaning that the fit was not significantly improved. For further studies, we limit the analysis to the simpler, power-law model.
Results of spectral fits to Fermi-LAT data using single power-law and log-parabola models. The columns present: (1) the data model; (2) the normalization (given in 10−13 cm−2 s−1 MeV−1); (3) the photon index for the power-law or log-parabola; (4) the curvature parameter; and (5) the scale energy in MeV.
| Model . | Normalization . | Γ/α . | β . | E0, p/E0, l . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| power-law | 3.54 ± 0.22stat ± 0.30syst | 1.87 ± 0.04stat ± 0.01syst | – | 2000 |
| log-parabola | 3.74 ± 0.27stat ± 0.30syst | 1.83 ± 0.05stat ± 0.01syst | 0.034 ± 0.025stat ± 0.002syst | 2000 |
| Model . | Normalization . | Γ/α . | β . | E0, p/E0, l . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| power-law | 3.54 ± 0.22stat ± 0.30syst | 1.87 ± 0.04stat ± 0.01syst | – | 2000 |
| log-parabola | 3.74 ± 0.27stat ± 0.30syst | 1.83 ± 0.05stat ± 0.01syst | 0.034 ± 0.025stat ± 0.002syst | 2000 |
Results of spectral fits to Fermi-LAT data using single power-law and log-parabola models. The columns present: (1) the data model; (2) the normalization (given in 10−13 cm−2 s−1 MeV−1); (3) the photon index for the power-law or log-parabola; (4) the curvature parameter; and (5) the scale energy in MeV.
| Model . | Normalization . | Γ/α . | β . | E0, p/E0, l . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| power-law | 3.54 ± 0.22stat ± 0.30syst | 1.87 ± 0.04stat ± 0.01syst | – | 2000 |
| log-parabola | 3.74 ± 0.27stat ± 0.30syst | 1.83 ± 0.05stat ± 0.01syst | 0.034 ± 0.025stat ± 0.002syst | 2000 |
| Model . | Normalization . | Γ/α . | β . | E0, p/E0, l . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| power-law | 3.54 ± 0.22stat ± 0.30syst | 1.87 ± 0.04stat ± 0.01syst | – | 2000 |
| log-parabola | 3.74 ± 0.27stat ± 0.30syst | 1.83 ± 0.05stat ± 0.01syst | 0.034 ± 0.025stat ± 0.002syst | 2000 |
In order to calculate spectral points, the data have been divided into six logarithmically equally spaced energy bins and for each bin a separate likelihood analysis has been run. The normalization of the three nearest point sources (one from the 3FGL and two additionnal sources of the four mentioned above) has been let free during the fit, as the spectral parameters of the Galactic and isotropic diffuse emissions. We fix the spectral index of PKS 0625−354 to 2 to avoid any dependence on the spectral model found for the whole energy range. A threshold of TS > 9 (corresponding to a significance of 3σ) is imposed in each energy bin for a flux calculation, otherwise an upper limit is calculated. A 1σ confidence contour has been calculated using the covariance matrix obtained with the gtlike procedure (see Fig. 4). For the light curves, the same spectral parameters have been let free as for the spectral energy distribution (SED) computation, with free spectral index for PKS 0625−354. The long-term HE flux and spectral index light curves for PKS 0625−354 are presented in the second and third panels (b and c) of Fig. 3. Each bin corresponds to about 120 d of monitoring. A fit to a constant for the flux points, not considering systematic errors, yieldsχ2/ndof = 41.4/19 (p < 0.01), showing indication for variability in the HE γ-ray regime. This is also confirmed in the fractional variability amplitude value, calculated following Vaughan et al. (2003), equal Fvar = 75 per cent. Also, significant variability has been found in the case of the spectral index time evolution. A fit with a constant results in χ2/ndof = 34.0/19 (p = 0.02).
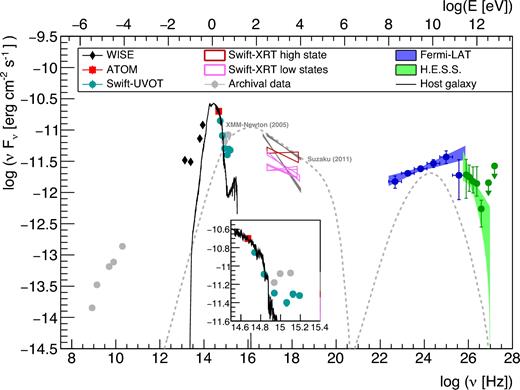
MWL SED. The black line is the simulated emission of the host galaxy seen in the UVOT aperture of 5 arcsec. The dotted grey lines are synchrotron- and inverse-Compton emission from a leptonic SSC model, with a variability time-scale of 105 s performed in Fukazawa et al. (2015). An optical-UV zoom of the SED is presented in the inset.
3.2 Swift-XRT and Swift-UVOT observations
X-ray observations of PKS 0625−354 were performed with the XRT detector onboard the Swift spacecraft (Burrows et al. 2005). The source was observed in photon counting (PC) mode in the energy range of 0.3–10 keV in four pointing observations with a total exposure of 16.5 ks. All the observations were analysed with the heasoft version 6.15 package1 following the standard xrtpipeline procedure. The spectral analysis was performed with the xspec package (version 12.8.2). A circular region with a radius of 5 arcsec around the position of the source was used. The same size off region was used in order to determine the background. The logarithmic energy bin sizes were adopted so as to ensure a minimum count of 20 events per bin. The spectra were fitted with a single power-law function with a Galactic absorption value of NH = 6.5 × 1020 cm−2 taken from Kalberla et al. (2005), which was set as a frozen parameter. All measured Swift-XRT fluxes are collected in Table 2.
Parameters of the spectral analysis of the Swift-XRT data. The columns present: (1) the observation ID number; (2) the observation date; (3) the time exposure given in seconds; (4) the flux observed in the energy range of 0.3–10 keV in units of 10−11 erg cm−2 s−1; (5) the spectral index for the power-law fit to data; and (6) χ2 statistics value and the number of degrees of freedom.
| Observation ID . | Observation date . | Exposure . | F0.3 − 10 keV . | Γ . | χ2/dof . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| 00039136001 | 22/11/2009 | 1384.1 | 1.49|$^{+0.21}_{-0.19}$| | 2.079 ± 0.093 | 8.64/10 |
| 00039136002 | 01/02/2010 | 4550.2 | 1.01|$^{+0.10}_{-0.11}$| | 2.271 ± 0.051 | 38.24/30 |
| 00049667001 | 26/07/2013 | 8110.6 | 0.81|$^{+0.19}_{-0.17}$| | 2.125 ± 0.041 | 49.68/43 |
| 00049667002 | 29/07/2013 | 2462.1 | 0.72|$^{+0.14}_{-0.14}$| | 2.069 ± 0.084 | 12.54/10 |
| All observations | 16506.0 | 0.81|$^{+0.20}_{-0.19}$| | 2.149 ± 0.027 | 88.82/87 |
| Observation ID . | Observation date . | Exposure . | F0.3 − 10 keV . | Γ . | χ2/dof . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| 00039136001 | 22/11/2009 | 1384.1 | 1.49|$^{+0.21}_{-0.19}$| | 2.079 ± 0.093 | 8.64/10 |
| 00039136002 | 01/02/2010 | 4550.2 | 1.01|$^{+0.10}_{-0.11}$| | 2.271 ± 0.051 | 38.24/30 |
| 00049667001 | 26/07/2013 | 8110.6 | 0.81|$^{+0.19}_{-0.17}$| | 2.125 ± 0.041 | 49.68/43 |
| 00049667002 | 29/07/2013 | 2462.1 | 0.72|$^{+0.14}_{-0.14}$| | 2.069 ± 0.084 | 12.54/10 |
| All observations | 16506.0 | 0.81|$^{+0.20}_{-0.19}$| | 2.149 ± 0.027 | 88.82/87 |
Parameters of the spectral analysis of the Swift-XRT data. The columns present: (1) the observation ID number; (2) the observation date; (3) the time exposure given in seconds; (4) the flux observed in the energy range of 0.3–10 keV in units of 10−11 erg cm−2 s−1; (5) the spectral index for the power-law fit to data; and (6) χ2 statistics value and the number of degrees of freedom.
| Observation ID . | Observation date . | Exposure . | F0.3 − 10 keV . | Γ . | χ2/dof . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| 00039136001 | 22/11/2009 | 1384.1 | 1.49|$^{+0.21}_{-0.19}$| | 2.079 ± 0.093 | 8.64/10 |
| 00039136002 | 01/02/2010 | 4550.2 | 1.01|$^{+0.10}_{-0.11}$| | 2.271 ± 0.051 | 38.24/30 |
| 00049667001 | 26/07/2013 | 8110.6 | 0.81|$^{+0.19}_{-0.17}$| | 2.125 ± 0.041 | 49.68/43 |
| 00049667002 | 29/07/2013 | 2462.1 | 0.72|$^{+0.14}_{-0.14}$| | 2.069 ± 0.084 | 12.54/10 |
| All observations | 16506.0 | 0.81|$^{+0.20}_{-0.19}$| | 2.149 ± 0.027 | 88.82/87 |
| Observation ID . | Observation date . | Exposure . | F0.3 − 10 keV . | Γ . | χ2/dof . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| 00039136001 | 22/11/2009 | 1384.1 | 1.49|$^{+0.21}_{-0.19}$| | 2.079 ± 0.093 | 8.64/10 |
| 00039136002 | 01/02/2010 | 4550.2 | 1.01|$^{+0.10}_{-0.11}$| | 2.271 ± 0.051 | 38.24/30 |
| 00049667001 | 26/07/2013 | 8110.6 | 0.81|$^{+0.19}_{-0.17}$| | 2.125 ± 0.041 | 49.68/43 |
| 00049667002 | 29/07/2013 | 2462.1 | 0.72|$^{+0.14}_{-0.14}$| | 2.069 ± 0.084 | 12.54/10 |
| All observations | 16506.0 | 0.81|$^{+0.20}_{-0.19}$| | 2.149 ± 0.027 | 88.82/87 |
Simultaneously with XRT, PKS 0625−354 was observed with the UVOT instrument (Roming et al. 2005) onboard the Swift spacecraft in six optical and ultraviolet (UV) filters, namely: U (345 nm), B (439 nm), V (544 nm), UVW1 (251 nm), UVM2 (217 nm), and UVW2 (188 nm). The magnitudes and corresponding fluxes were calculated using the uvotmaghist tool and the conversion factors provided by Poole et al. (2008). The optical and ultraviolet observations were corrected for dust absorption using the reddening coefficient E(B − V) = 0.0562 mag (Schlafly & Finkbeiner 2011) and the ratios of the extinction to reddening, Aλ/E(B − V), for each filter from Giommi et al. (2006). The magnitudes are collected in Table 3.
Magnitudes for different epochs from the Swift-UVOT data. The columns present: (1) the observation ID number and (2)–(7) the observed magnitudes in V, B, U, UVW1, UVM2, and UVW2 bands, respectively. The magnitudes are not corrected for the Galactic extinction. The hyphen (–) indicates that there were no observation taken in a given filter for a specific observation ID.
| Observation ID . | V . | B . | U . | UVW1 . | UVW2 . | UVM2 . |
|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 00039136001 | – | – | – | – | 16.29 ± 0.06 | – |
| 00039136002 | – | – | 16.21 ± 0.05 | – | – | – |
| 00049667001 | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.27 ± 0.08 | 16.37 ± 0.06 | 16.48 ± 0.07 | 16.29 ± 0.06 |
| 00049667002 | 15.57 ± 0.09 | 16.69 ± 0.10 | 16.43 ± 0.12 | 16.54 ± 0.12 | 16.51 ± 0.08 | 16.51 ± 0.12 |
| Average magnitude | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.34 ± 0.05 | 16.38 ± 0.06 | 16.47 ± 0.07 | 16.29 ± 0.06 |
| Observation ID . | V . | B . | U . | UVW1 . | UVW2 . | UVM2 . |
|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 00039136001 | – | – | – | – | 16.29 ± 0.06 | – |
| 00039136002 | – | – | 16.21 ± 0.05 | – | – | – |
| 00049667001 | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.27 ± 0.08 | 16.37 ± 0.06 | 16.48 ± 0.07 | 16.29 ± 0.06 |
| 00049667002 | 15.57 ± 0.09 | 16.69 ± 0.10 | 16.43 ± 0.12 | 16.54 ± 0.12 | 16.51 ± 0.08 | 16.51 ± 0.12 |
| Average magnitude | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.34 ± 0.05 | 16.38 ± 0.06 | 16.47 ± 0.07 | 16.29 ± 0.06 |
Magnitudes for different epochs from the Swift-UVOT data. The columns present: (1) the observation ID number and (2)–(7) the observed magnitudes in V, B, U, UVW1, UVM2, and UVW2 bands, respectively. The magnitudes are not corrected for the Galactic extinction. The hyphen (–) indicates that there were no observation taken in a given filter for a specific observation ID.
| Observation ID . | V . | B . | U . | UVW1 . | UVW2 . | UVM2 . |
|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 00039136001 | – | – | – | – | 16.29 ± 0.06 | – |
| 00039136002 | – | – | 16.21 ± 0.05 | – | – | – |
| 00049667001 | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.27 ± 0.08 | 16.37 ± 0.06 | 16.48 ± 0.07 | 16.29 ± 0.06 |
| 00049667002 | 15.57 ± 0.09 | 16.69 ± 0.10 | 16.43 ± 0.12 | 16.54 ± 0.12 | 16.51 ± 0.08 | 16.51 ± 0.12 |
| Average magnitude | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.34 ± 0.05 | 16.38 ± 0.06 | 16.47 ± 0.07 | 16.29 ± 0.06 |
| Observation ID . | V . | B . | U . | UVW1 . | UVW2 . | UVM2 . |
|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 00039136001 | – | – | – | – | 16.29 ± 0.06 | – |
| 00039136002 | – | – | 16.21 ± 0.05 | – | – | – |
| 00049667001 | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.27 ± 0.08 | 16.37 ± 0.06 | 16.48 ± 0.07 | 16.29 ± 0.06 |
| 00049667002 | 15.57 ± 0.09 | 16.69 ± 0.10 | 16.43 ± 0.12 | 16.54 ± 0.12 | 16.51 ± 0.08 | 16.51 ± 0.12 |
| Average magnitude | 15.57 ± 0.07 | 16.52 ± 0.07 | 16.34 ± 0.05 | 16.38 ± 0.06 | 16.47 ± 0.07 | 16.29 ± 0.06 |
The optical XRT and UVOT light curves are presented in Fig. 3 (d)–(e). In the X-ray regime, the first observation represents a significantly higher state of the source than in the case of the three latter data points. The limited number of UVOT observations does not allow either claiming or excluding source variability in the optical and ultraviolet bands. However, in the optical and ultraviolet UV bands, there is no indication for an elevated flux level corresponding with the one found in the X-ray observations in 2009 November. The X-ray bright state is not associated with a simultaneous brightening at lower energies, even though the X-ray spectral index of about 2 (consistent with the average value) would suggest an achromatic variability of the synchrotron component. This may indicate that the UV and X-ray photons do not share a common origin.
3.3 ATOM observations
ATOM (Automatic Telescope for Optical Monitoring) is a 75-cm optical telescope located in Namibia near the H.E.S.S. site (Hauser et al. 2004). PKS 0625−354 was observed with ATOM only in the R band in 13 observations. The data collected have been analysed using an aperture of 4 arcsecc radius and differential photometry. The observations have been corrected for dust absorption using the absorption magnitude AR = 0.144 mag from Schlafly & Finkbeiner (2011). The optical ATOM light curve is presented in Fig. 3(f). The long-term ATOM observations do not indicate variability during the period presented in the paper. A fit with a constant to the data results in χ2/ndof = 2.75/12 (p = 0.997).
3.4 WISE observations
Wide-field Infrared Survey Explorer (WISE) is a space telescope that performs observations in the infrared energy band at four wavelengths: 3.4 |$\mu$|m (W1), 4.6 |$\mu$|m (W2), 12 |$\mu$|m (W3) and 22 |$\mu$|m (W4). The spectral data are taken from the AllWISE Source Catalogue and the light curve from the AllWISE Multiepoch Photometry Table.2 The magnitudes are converted to flux by applying the standard procedure (Wright et al. 2010), and for W1 and W2 we apply the colour correction to a power law with a photon index of 0, as suggested for Galactic emission. Since W3 and W4 are widely dominated by the non-thermal radiation and show similar flux densities, we use the colour correction to a power law with a photon index of −2. The infrared light curves do not show variability within uncertainties of the measurements. For each of the two observational sessions, the reduced χ2 of a fit with a constant value is lower than 0.5 for a given filter.
4 MODELLING
4.1 MWL spectral energy distribution
The data from H.E.S.S., Fermi-LAT, Swift-XRT, Swift-UVOT, ATOM, and WISE have been used together to build the global MWL SED of the source in addition to archival radio data from the Australia Telescope 20-GHz Survey (Murphy et al. 2010), NRAO VLA Sky Survey (Condon et al. 1998), and Sydney University Molonglo Sky Survey (Mauch et al. 2003) catalogues. In order to have a deeper look at the source variability, UV and X-ray data from XMM–Newton in 2005 (Gliozzi et al. 2008), and an X-ray spectrum from Suzaku in 2011 (Fukazawa et al. 2015), are also represented in the SED (see Fig. 4). Two states of the multiple Swift-XRT observations are differentiated, one high state observed on 2009 November 22 and low states from 2010 February 1 to 2013 July 29. The lack of frequent X-ray monitoring leaves room for the possibility of a fast X-ray flare on 2009 November 22, which in such a case could have been missed by Fermi-LAT and thus would be inconsistent with the HE spectra used for the modelling. In the absence of evidence for such a fast event, we assume for the following MWL models that the measured X-ray variability does not significantly impact the Fermi-LAT and H.E.S.S. spectra.
The prominent IR-optical bump of the SED is due to the host galaxy emission. In order to avoid a misidentification of the non-thermal flux density at these energies, a separate host galaxy contribution is included in the model fit. Following Inskip et al. (2010), the host galaxy presents an effective radius of 18.77 ± 0.98 arcsec for a flux density of 6.00 × 10−11 erg cm−2 s−1 in the Ks band. By simulating the emission from a giant elliptical galaxy, as suggested in Wills et al. (2004), with pegase 2 templates (Fioc & Rocca-Volmerange 1999), we deduce an associated galaxy mass of Mhost = 9.15 × 1011 M⊙.
The associated host mass is then |$\log ({M_{\mathrm{host}} / \mathrm{M}_{{\odot }}}) = 12.66^{+0.67}_{- 0.55}$|. The lower limit of this result is slightly bigger than our value with a factor 1.4. We can however note that relation 1 is derived from sources with significantly lower black hole masses than the one of PKS 0625−354(log (M•/M⊙) < 8.2), leading to a possible bias of this estimation.
We report the galaxy emission in the SED as seen in the UVOT filters with an aperture of 5 arcsec, this emission is hence underestimated in WISE filters (W1, W2) having much wider apertures. As seen in Fig. 4, this model of the host galaxy is in good agreement with the UVOT and ATOM data, where the optical points are dominated by the host.
The difference in luminosity between Swift-UVOT and XMM–Newton observations is indicative of significant variability in the UV range. The UV data from XMM–Newton are also suggestive of a hard spectrum. Considering the strong excess due to the host galaxy at low frequencies, the intrinsic spectrum should be much harder than that observed. This indicates a sharp spectral variation in the UV band. The X-ray data indicate strong variability in both flux and photon index. Both high and low states reveal various photon indexes throughout the observation period, making difficult the deduction of a variability pattern.
One-zone modelling of the source emission was recently discussed by Fukazawa et al. (2015), presented in Fig. 4. They found parameters compatible with the source being radio galaxy in nature, such as a low Doppler factor. We note however that the only weak observational constraints were available for such conclusions. Indeed, their model takes into account XMM–Newton UV data from 2005 and Suzaku X-ray data from 2011. Considering the complex UV and X-ray variabilities, these data from different periods cannot be safely used for a general broad-band emission model. With the new data set presented in this paper, we are able to provide stronger constraints for MWL emission scenarios.
4.2 Leptonic scenario
With the WISE data showing no variability for observing periods, we made the strong assumption of a constant IR flux for the source. As seen in Fig. 4, luminosities measured in WISE W4 and W3 bands cannot be associated to thermal emission from the host galaxy or a dusty torus, due to their low frequencies. These bands are therefore considered to be dominated by synchrotron emission. No hints of MWL variation associated with the two Swift-XRT X-ray states can be deduced from the observations (see Fig. 3). The steady state of the UVM2 band simultaneously with two X-ray states can lead to at least two possible interpretations:
Two non-correlated non-thermal components are radiating from far-IR (WISE W4 and W3 bands) to X-rays bands.
There is only one component from far-IR to X-rays and the UVM2 band is precisely at the tipping point of a spectral change of the synchrotron emission between the two states.
The second interpretation is not appropriate for a one-zone leptonic synchrotron-self-Compton (SSC) scenario. It would induce a very wide gap between a synchrotron peak in the IR-optical range and the inverse-Compton peak at the energy of about 100 GeV, leading to unconventional parameters such as an unusually low magnetic field and a wide emitting region resulting in emission being far from equipartition between magnetic field and non-thermal particles. Moreover, the synchrotron bump would be much wider than the inverse-Compton one with similar peak luminosities. Such asymmetry is not describable by a pure one-zone SSC scenario (similar case of SED as AP Librae; H.E.S.S. Collaboration et al. 2015).
Hence, in this first approach, we consider the presence of two SSC components, following the ‘blob-in-jet’ description given in Katarzyński, Sol & Kus (2001), and completed by Hervet, Boisson & Sol (2015). The main radiating component is a Doppler boosted spherical compact blob, composed of a turbulent magnetic field and e+e− non-thermal population following a broken power-law energy spectrum. The second component is the leptonic conical stratified base of the extended jet surrounding (or in front of) the blob, with its particle energy spectrum defined by a simple power law. A similar stratified conical jet model was also described by Potter & Cotter (2012). We consider its synchrotron emission dominating the radio-to-IR luminosity of the source. The high radio flux and the bright kpc jet structure of PKS 0625−354 does support such a scenario. The resulting MWL model is presented in Fig. 5, with the associated parameters adopted being provided in Table 4. The modelling provides a good MWL representation for both states, with the radio-to-IR emission described by the synchrotron radiation of the jet and a blob synchrotron peak in the UV–X-ray range. Hence, the two XRT states can be modelled by changing only the second slope index of the electron energy spectrum, from n2 = 3.15 to n2 = 3.35, which has only a minor effect on the spectrum in the HE bump. However, a natural explanation of index variation remains unclear.

Leptonic multizone SSC modelling of the SED. The blob synchrotron and SSC emissions are represented in blue for the low state and dotted red for the high state. The magenta dot–dashed lines are the jet synchrotron and SSC emissions. The EBL absorption is taken into account following the description of Finke, Razzaque & Dermer (2010).
Values of parameters used for the leptonic multizone SSC model shown in Fig. 5. θ is the angle of the jet direction with the line of sight, Γ expresses the Lorentz factor, K is the normalization factor of the particle density, n1 and n2 are the first and second slope of the blob electron spectrum, R is the radius of the blob, B1 and R1 are the magnetic field and the radius of the first the stratified jet slice, respectively. L is the total length of the jet, α/2 is the semi-aperture angle of the jet. Parameters marked with asterisk (*) are considered in the host galaxy frame (see Katarzyński et al. 2001; Hervet et al. 2015 for a detailed description of the model).
| Parameter . | Value . | Unit . |
|---|---|---|
| θ . | 1.0 . | ° . |
| Blob | ||
| Γ | 10.4 | – |
| K | 2.3 × 103 | cm−3 |
| n1 | 2.0 | – |
| n2 (low state) | 3.35 | – |
| n2 (high state) | 3.15 | – |
| γmin | 1.0 | – |
| γmax | 6.0 × 106 | – |
| γb | 4.0 × 104 | – |
| B | 4.0 × 10−2 | G |
| R | 9.0 × 1015 | cm |
| Jet | ||
| Γ | 4.1 | – |
| K | 8.5 × 102 | cm−3 |
| n | 2.1 | – |
| γmin | 1.0 | – |
| γmax | 3.2 × 103 | – |
| B1 | 3.1 × 10−1 | G |
| R1 | 1.5 × 1016 | cm |
| L* | 3.0 × 102 | pc |
| α/2* | 1.0 | deg |
| Parameter . | Value . | Unit . |
|---|---|---|
| θ . | 1.0 . | ° . |
| Blob | ||
| Γ | 10.4 | – |
| K | 2.3 × 103 | cm−3 |
| n1 | 2.0 | – |
| n2 (low state) | 3.35 | – |
| n2 (high state) | 3.15 | – |
| γmin | 1.0 | – |
| γmax | 6.0 × 106 | – |
| γb | 4.0 × 104 | – |
| B | 4.0 × 10−2 | G |
| R | 9.0 × 1015 | cm |
| Jet | ||
| Γ | 4.1 | – |
| K | 8.5 × 102 | cm−3 |
| n | 2.1 | – |
| γmin | 1.0 | – |
| γmax | 3.2 × 103 | – |
| B1 | 3.1 × 10−1 | G |
| R1 | 1.5 × 1016 | cm |
| L* | 3.0 × 102 | pc |
| α/2* | 1.0 | deg |
Values of parameters used for the leptonic multizone SSC model shown in Fig. 5. θ is the angle of the jet direction with the line of sight, Γ expresses the Lorentz factor, K is the normalization factor of the particle density, n1 and n2 are the first and second slope of the blob electron spectrum, R is the radius of the blob, B1 and R1 are the magnetic field and the radius of the first the stratified jet slice, respectively. L is the total length of the jet, α/2 is the semi-aperture angle of the jet. Parameters marked with asterisk (*) are considered in the host galaxy frame (see Katarzyński et al. 2001; Hervet et al. 2015 for a detailed description of the model).
| Parameter . | Value . | Unit . |
|---|---|---|
| θ . | 1.0 . | ° . |
| Blob | ||
| Γ | 10.4 | – |
| K | 2.3 × 103 | cm−3 |
| n1 | 2.0 | – |
| n2 (low state) | 3.35 | – |
| n2 (high state) | 3.15 | – |
| γmin | 1.0 | – |
| γmax | 6.0 × 106 | – |
| γb | 4.0 × 104 | – |
| B | 4.0 × 10−2 | G |
| R | 9.0 × 1015 | cm |
| Jet | ||
| Γ | 4.1 | – |
| K | 8.5 × 102 | cm−3 |
| n | 2.1 | – |
| γmin | 1.0 | – |
| γmax | 3.2 × 103 | – |
| B1 | 3.1 × 10−1 | G |
| R1 | 1.5 × 1016 | cm |
| L* | 3.0 × 102 | pc |
| α/2* | 1.0 | deg |
| Parameter . | Value . | Unit . |
|---|---|---|
| θ . | 1.0 . | ° . |
| Blob | ||
| Γ | 10.4 | – |
| K | 2.3 × 103 | cm−3 |
| n1 | 2.0 | – |
| n2 (low state) | 3.35 | – |
| n2 (high state) | 3.15 | – |
| γmin | 1.0 | – |
| γmax | 6.0 × 106 | – |
| γb | 4.0 × 104 | – |
| B | 4.0 × 10−2 | G |
| R | 9.0 × 1015 | cm |
| Jet | ||
| Γ | 4.1 | – |
| K | 8.5 × 102 | cm−3 |
| n | 2.1 | – |
| γmin | 1.0 | – |
| γmax | 3.2 × 103 | – |
| B1 | 3.1 × 10−1 | G |
| R1 | 1.5 × 1016 | cm |
| L* | 3.0 × 102 | pc |
| α/2* | 1.0 | deg |
The parameters used provide a minimal variability of 4.4 h for the blob and 18.3 h for the jet. The equipartition parameter deduced from the energetics (see Table 5) indicates a matter-dominated blob with PB/Pe = 2.97 × 10−3 in the low state and PB/Pe = 2.95 × 10−3 in the high state. The jet emission is considered stationary and close to equipartition, with an output value PB/Pe = 0.99. In this blob-in-jet structure, the blob is carrying |${\simeq } 83 \,\,\rm{per\,\,cent}$| of the total power (Ptot ≃ 2.1 × 1043 erg s−1).
Source energetics deduced from the leptonic model of jet and blob for the low and high activity states. PB, Pe and PR are, respectively, magnetic, non-thermal kinetic, and radiating powers. All powers are expressed in (erg s−1).
| Powers . | Jet . | Blob low . | Blob high . |
|---|---|---|---|
| PB | 1.35 × 1042 | 5.20 × 1040 | 5.20 × 1040 |
| Pe | 1.36 × 1042 | 1.75 × 1043 | 1.76 × 1043 |
| PR | 4.21 × 1041 | 2.19 × 1041 | 2.81 × 1041 |
| Powers . | Jet . | Blob low . | Blob high . |
|---|---|---|---|
| PB | 1.35 × 1042 | 5.20 × 1040 | 5.20 × 1040 |
| Pe | 1.36 × 1042 | 1.75 × 1043 | 1.76 × 1043 |
| PR | 4.21 × 1041 | 2.19 × 1041 | 2.81 × 1041 |
Source energetics deduced from the leptonic model of jet and blob for the low and high activity states. PB, Pe and PR are, respectively, magnetic, non-thermal kinetic, and radiating powers. All powers are expressed in (erg s−1).
| Powers . | Jet . | Blob low . | Blob high . |
|---|---|---|---|
| PB | 1.35 × 1042 | 5.20 × 1040 | 5.20 × 1040 |
| Pe | 1.36 × 1042 | 1.75 × 1043 | 1.76 × 1043 |
| PR | 4.21 × 1041 | 2.19 × 1041 | 2.81 × 1041 |
| Powers . | Jet . | Blob low . | Blob high . |
|---|---|---|---|
| PB | 1.35 × 1042 | 5.20 × 1040 | 5.20 × 1040 |
| Pe | 1.36 × 1042 | 1.75 × 1043 | 1.76 × 1043 |
| PR | 4.21 × 1041 | 2.19 × 1041 | 2.81 × 1041 |
The SED shape naturally favours a rather high Doppler factor associated to a small angle with the line of sight. However, even by having a less convincing fit and higher energetics, the known parameter degeneracy of SSC models allows a significant increase of the angle, associated to low Doppler factor and wide emission zone. A limit of θ ≲ 15° is, however, placed by when the maximum variability time constraint of 41 d between the two Swift-XRT states cannot be sustained anymore with a good MWL representation.
4.3 Lepto-hadronic scenario
As discussed in the previous section, a wide one-zone synchrotron bump from IR to X-rays is not well suited for a leptonic scenario. However, this interpretation can be explained if we consider a lepto-hadronic scenario.
In this case, we interpret the low-energy SED bump as synchrotron radiation from primary relativistic electrons and an HE bump strongly dominated by synchrotron radiation from relativistic protons (Aharonian 2000; Mücke & Protheroe 2000; Böttcher et al. 2013; Mastichiadis, Petropoulou & Dimitrakoudis 2013; Cerruti et al. 2015). The following results are based on the model developed by Böttcher et al. (2013).
Contrary to a leptonic SSC scenario, the lepto-hadronic model can naturally produce asymmetric low-energy and HE emission bumps. Indeed, the energy spectra may be different, which strongly reduces the constraints given by the SED shape. The main parameter differentiating the two states is the index of the electron energy spectrum, which is harder for the high state. The ways that a change of the electron spectrum can affect the protons are complex and not included in this model. Without the observation of X-ray flux variability, the parameters of the proton population are assumed as constant. The resulting MWL model is presented in Fig. 6, with the associated parameters adopted being provided in Table 6.
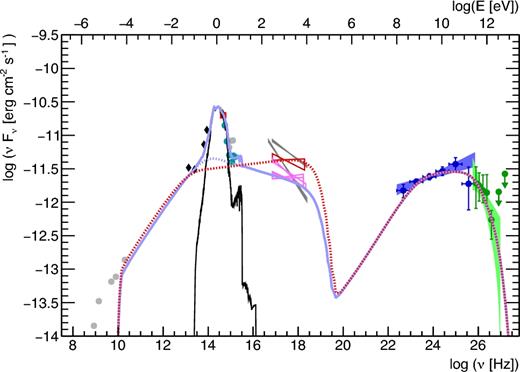
Lepto-hadronic one-zone SSC modelling of the SED. The low state is represented by the blue line and the high state is represented by the red dotted line. The EBL absorption is taken into account following the description by Finke et al. (2010).
Values of parameters used for the lepto-hadronic one-zone SSC model shown in Fig. 6. Γ is the blob Lorentz factor, θ is the angle of the blob direction with the line of sight, ne and np are the slope of the electron and proton spectra, R is the radius of the emitting region, ηesc is the escape-time parameter, defining a break in the particle spectra (more details on Böttcher et al. 2013).
| Parameter . | Value . | Unit . |
|---|---|---|
| General | ||
| Γ | 10.0 | – |
| θ | 5.74 | deg |
| B | 1.0 × 102 | G |
| R | 1.0 × 1016 | cm |
| ηesc | 3.0 | – |
| Electrons | ||
| Pe (low state) | 4.28 × 1039 | erg s−1 |
| Pe (high state) | 4.72 × 1039 | erg s−1 |
| ne (low state) | 2.20 | – |
| ne (high state) | 1.92 | – |
| γmin, e(low state) | 1.40 × 102 | – |
| γmin, e(high state) | 6.50 × 102 | – |
| γmax, e | 4.50 × 104 | – |
| Protons | ||
| Pp | 8.75 × 1042 | erg s−1 |
| np | 1.90 | – |
| γmin, p | 1.07 | – |
| γmax, p | 2.13 × 1010 | – |
| Parameter . | Value . | Unit . |
|---|---|---|
| General | ||
| Γ | 10.0 | – |
| θ | 5.74 | deg |
| B | 1.0 × 102 | G |
| R | 1.0 × 1016 | cm |
| ηesc | 3.0 | – |
| Electrons | ||
| Pe (low state) | 4.28 × 1039 | erg s−1 |
| Pe (high state) | 4.72 × 1039 | erg s−1 |
| ne (low state) | 2.20 | – |
| ne (high state) | 1.92 | – |
| γmin, e(low state) | 1.40 × 102 | – |
| γmin, e(high state) | 6.50 × 102 | – |
| γmax, e | 4.50 × 104 | – |
| Protons | ||
| Pp | 8.75 × 1042 | erg s−1 |
| np | 1.90 | – |
| γmin, p | 1.07 | – |
| γmax, p | 2.13 × 1010 | – |
Values of parameters used for the lepto-hadronic one-zone SSC model shown in Fig. 6. Γ is the blob Lorentz factor, θ is the angle of the blob direction with the line of sight, ne and np are the slope of the electron and proton spectra, R is the radius of the emitting region, ηesc is the escape-time parameter, defining a break in the particle spectra (more details on Böttcher et al. 2013).
| Parameter . | Value . | Unit . |
|---|---|---|
| General | ||
| Γ | 10.0 | – |
| θ | 5.74 | deg |
| B | 1.0 × 102 | G |
| R | 1.0 × 1016 | cm |
| ηesc | 3.0 | – |
| Electrons | ||
| Pe (low state) | 4.28 × 1039 | erg s−1 |
| Pe (high state) | 4.72 × 1039 | erg s−1 |
| ne (low state) | 2.20 | – |
| ne (high state) | 1.92 | – |
| γmin, e(low state) | 1.40 × 102 | – |
| γmin, e(high state) | 6.50 × 102 | – |
| γmax, e | 4.50 × 104 | – |
| Protons | ||
| Pp | 8.75 × 1042 | erg s−1 |
| np | 1.90 | – |
| γmin, p | 1.07 | – |
| γmax, p | 2.13 × 1010 | – |
| Parameter . | Value . | Unit . |
|---|---|---|
| General | ||
| Γ | 10.0 | – |
| θ | 5.74 | deg |
| B | 1.0 × 102 | G |
| R | 1.0 × 1016 | cm |
| ηesc | 3.0 | – |
| Electrons | ||
| Pe (low state) | 4.28 × 1039 | erg s−1 |
| Pe (high state) | 4.72 × 1039 | erg s−1 |
| ne (low state) | 2.20 | – |
| ne (high state) | 1.92 | – |
| γmin, e(low state) | 1.40 × 102 | – |
| γmin, e(high state) | 6.50 × 102 | – |
| γmax, e | 4.50 × 104 | – |
| Protons | ||
| Pp | 8.75 × 1042 | erg s−1 |
| np | 1.90 | – |
| γmin, p | 1.07 | – |
| γmax, p | 2.13 × 1010 | – |
In order to accelerate protons to these high energies, an extremely large magnetic field of 100 G is needed for this model. This implies that the system is extremely far from equipartition, with PB/Pe = (7.9–8.8) × 107 (respectively, high and low states), and PB/Pp = 4.29 × 104. This leads to the requirement of unrealistic large jet power of Pjet ≃ PB = 3.8 × 1047 erg s−1, significantly larger than the one required by the leptonic scenario. We note that this power is within the common range of what is required by hadronic scenario for multiple sources (Protheroe & Mücke 2001; Böttcher et al. 2013)
Also, for this model, the maximum particle Lorentz factor of protons is about 6 magnitudes greater than that one of electrons. A more efficient acceleration for protons does make sense as they are subject to much smaller radiative losses. However, despite this, reaching such a difference between the two populations raises difficulties in interpreting the particle acceleration process.
5 DISCUSSION
By working with multiple non-simultaneous data, we modelled the source within the framework of the assumptions we made of its MWL variability. Both the one-zone lepto-hadronic and multizone leptonic models provide a good MWL representation to the observed SED. Although the SED alone cannot exclude one of these scenarios, the multizone leptonic scenario is favoured by the energy budget calculations. Significantly less power by a factor of ∼2.5 × 104 and ratio of non-thermal electron to B-field power closer to equipartition is required. Moreover, the very steep X-ray spectrum observed in 2005 by XMM–Newton favours a synchrotron peak within the UV–X-ray range.
Since the host galaxy is widely dominating the optical spectrum, the slight excess in the UVW2 and UVM2 filter of Swift-UVOT (see Fig. 4) is naturally explained in our models by the galactic UV emission. However, the stronger UV excess observed with XMM–Newton in 2005 is not expected in the two scenarios presented here. The most probable explanation is a past high luminosity of the nucleus big blue bump emission, also supported by the detection of [OII] and [OIII] lines (Wills et al. 2004). Due to the lack of observational constraints, a nuclear emission component (accretion emission reprocessed by the broad line region) is not considered in the models.
The radio-galaxy nature of PKS 0625−354 has previously been often discussed (Trussoni et al. 1999; Wills et al. 2004; Nesci et al. 2013; Fukazawa et al. 2015). Although the large-scale radio structure of the source is typical of an FR I radio galaxy (Ekers et al. 1989), there is now an accumulated body of evidence for the BL Lac nature of the nucleus and the pc-scale jet. We present now a summary of the arguments favouring a blazar, or moderately misaligned blazar nature of the source. PKS 0625−354 was defined as a radio galaxy emitting in HE γ rays by Abdo et al. (2010b), based on directional associations between the 15 month Fermi catalogue and the radio catalogues 3CR, 3CRR, and MS4. The main criterion used here to define a radio galaxy was the spectral slope with an index α = (Γ − 1) ≥ −0.5 (Sν ∝ να), which relates to a photon index Γ, at low frequencies (178–408 MHz). However, the VLBI map from the TANAMI collaboration (Ojha et al. 2010) shows a clearly one-sided pc jet with superluminal apparent velocities (Müller et al. 2013) of βa = 3 ± 0.5 c, requiring a maximum jet misalignment |$\theta \le $| 37|$^{+7}_{-5}$°|.
The VHE detection of the source that we report highlights also a significant peculiarity compared to the other VHE radio galaxies. The flux and frequency of the synchrotron peak, most likely between UV and X-rays, is also pushing for a BL Lac nature. According to the blazar-envelope unification scheme (Meyer et al. 2011), this synchrotron peak position is actually the most extreme one among all known VHE radio galaxies, as presented in fig. 8 in Fukazawa et al. (2015).
The redshift of the source (z = 0.055) is very high compared to the other VHE radio galaxies. As on date, the farthest VHE radio galaxies observed are NGC 1275 (Aleksić et al. 2012), with a redshift of z = 0.017, and IC 310 (Aleksić et al. 2010), with z = 0.0189, when considering misaligned blazars. If strongly misaligned, this would imply an extremely powerful jet. Also, Wills et al. (2004) have shown that the nuclei of BL Lac type objects and FR I radio galaxies can be used to discriminate the nature following the intensity of their [O iii] emission line, with log10|$L_{\rm [O\,\,{\small III}], \ BL\ Lac} = 40.840 \pm 0.156$| erg s−1 and log |$L_{\rm [O\,\,{\small III}],\,\,FRI} = 39.509 \pm 0.213$| erg s−1. The measured [O iii] line of PKS 0625−354 falls within the BL Lac category with a luminosity of log10|$L_{\rm [O\,\,{\small III}]} = 40.64$| erg s−1.
Finally, in order to reproduce the observed MWL SED, and especially the VHE spectrum, the leptonic and lepto-hadronic models presented here naturally need significant Doppler boosting of the emission associate to small angles with the line of sight. The X-ray variability gives a constrains on the maximal possible misalignment of θmax ≃ 15°. Throughout this paper, we did not explore the effects of external inverse-Compton emission between different non-thermal zones that may lose the viewing angle constraint. This scenario has been successfully applied to describe wide inverse-Compton emissions from X rays to VHE for radio galaxies, as M 87 or NGC 1275 (Tavecchio & Ghisellini 2008, 2014). Even if the HE bump observed in the SED does not reveal an extra wideness expected by such a scenario, such a possibility could be tested by future MWL observations.
Hence, PKS 0625−354 is an additional VHE emitting AGN in the blurry zone between being blazar and radio-galaxy-like in nature. According to MWL observations and different aspects of the source presented in this paper, both interpretations of PKS 0625−354 should be borne in mind. Results of modelling could evolve by having further more simultaneous observations.
6 SUMMARY
In this paper, the discovery of the VHE γ-ray emission from PKS 0625−354 is reported. The significance of the detection is 6.1σ, following the exposure of 5. 5 h. The VHE source is well characterized by a power-law function with a photon index Γ = 2.84 ± 0.50 and normalization N0(1TeV) = (2.78 ± 0.70) × 10−12 TeV−1 cm−2s−1. H.E.S.S. monitoring of the object is augmented with multifrequency observations collected with Fermi-LAT, Swift-XRT, Swift-UVOT, ATOM, and WISE. Pronounced variability is observed at HE and X-ray regimes, whereas in VHE, optical, and IR bands no significant variability has been found. However, the past observations of high UV emission with a hard spectrum point towards a variability of the nuclear emission.
None of the leptonic or lepto-hadronic models can be rejected by our current MWL data, even if the energetics favour a leptonic scenario. Only a further MWL campaign during a high level of source activity allows further probe of the nature of the non-thermal emission.
The current classification of PKS 0625−354 as a regular radio galaxy is problematic due to its unusual properties. Therefore, we argue that a classification as a blazar, or moderately misaligned blazar, is strongly favoured. However, only more simultaneous further MWL observation campaigns would provide the final word of this peculiar source classification.
ACKNOWLEDGEMENTS
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the Alexander von Humboldt Foundation, the Deutsche Forschungsgemeinschaft, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the U.K. Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish National Science Centre, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the National Commission on Research, Science and Technology of Namibia (NCRST), the Innsbruck University, the Austrian Science Fund (FWF), and the Austrian Federal Ministry for Science, Research and Economy, the University of Adelaide and the Australian Research Council, the Japan Society for the Promotion of Science, and the University of Amsterdam. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. This work was benefitted from services provided by the H.E.S.S. Virtual Organization, supported by the national resource providers of the EGI Federation. AW is supported by the Foundation for Polish Science (FNP). OH thanks the U.S. National Science Foundation for support under grant PHY-1307311 and the Observatoire de Paris for financial support with ATER position. RCGC is funded by EU FP7 Marie Curie under grant agreement No. PIEF-GA-2012-332350.
Footnotes
REFERENCES
Author notes
Deceased.
Wallenberg Academy Fellow.
Present address: Santa Cruz Institute for Particle Physics and Department of Physics, University of California at Santa Cruz, Santa Cruz, CA 95064, USA.



